-
PDF
- Split View
-
Views
-
Cite
Cite
L R Rímulo, A C Carciofi, R G Vieira, Th Rivinius, D M Faes, A L Figueiredo, J E Bjorkman, C Georgy, M R Ghoreyshi, I Soszyński, The life cycles of Be viscous decretion discs: fundamental disc parameters of 54 SMC Be stars, Monthly Notices of the Royal Astronomical Society, Volume 476, Issue 3, May 2018, Pages 3555–3579, https://doi.org/10.1093/mnras/sty431
Close - Share Icon Share
Abstract
Be stars are main-sequence massive stars with emission features in their spectrum, which originates in circumstellar gaseous discs. Even though the viscous decretion disc model can satisfactorily explain most observations, two important physical ingredients, namely the magnitude of the viscosity (α) and the disc mass injection rate, remain poorly constrained. The light curves of Be stars that undergo events of disc formation and dissipation offer an opportunity to constrain these quantities. A pipeline was developed to model these events that use a grid of synthetic light curves, computed from coupled hydrodynamic and radiative transfer calculations. A sample of 54 Be stars from the OGLE survey of the Small Magellanic Cloud (SMC) was selected for this study. Because of the way our sample was selected (bright stars with clear disc events), it likely represents the densest discs in the SMC. Like their siblings in the Galaxy, the mass of the disc in the SMC increases with the stellar mass. The typical mass and angular momentum loss rates associated with the disc events are of the order of ∼10−10 M⊙ yr−1 and ∼5 × 1036 g cm2 s−2, respectively. The values of α found in this work are typically of a few tenths, consistent with recent results in the literature and with the ones found in dwarf novae, but larger than current theory predicts. Considering the sample as a whole, the viscosity parameter is roughly two times larger at build-up (〈αbu〉 = 0.63) than at dissipation (〈αd〉 = 0.26). Further work is necessary to verify whether this trend is real or a result of some of the model assumptions.
1 INTRODUCTION
In a classical, observational, and quite broad definition, a Be star is a hot, massive star, with a B spectral type (mass ranging roughly from 3 to 17 M⊙), non-supergiant, whose spectrum has, or had at some time, one or more Balmer lines in emission (Jaschek, Slettebak & Jaschek 1981; Collins 1987). In a more modern and theoretically oriented definition, a Be star is a very rapidly rotating and non-radially pulsating B star that forms a geometrically thin viscous decretion disc (VDD) composed of an outwardly diffusing, viscosity-driven gaseous Keplerian disc that is fed by mass ejected from the central star (Rivinius, Carciofi & Martayan 2013), and a possibly non-negligible line-driven wind (Kee, Owocki & Sundqvist 2016). There is no evidence of large-scale magnetic fields in Be stars (Wade, Grunhut & MiMeS Collaboration 2012; Wade et al. 2016). Fast stellar rotation lowers the effective gravity near the stellar equator and a second mechanism, likely to be stellar pulsation (Rivinius et al. 1998; Baade et al. 2016; Rivinius, Baade & Carciofi 2016), is responsible for pushing this near equatorial matter into orbit in the inner disc. Once in orbit, a viscous mechanism takes place, diffusing matter and angular momentum outwards, thus making the disc grow.
Be stars are usually quite variable in all observables and in several time-scales (days, weeks, months, or even years). The variability observed in Be stars indicates that the injection of matter and angular momentum into the disc is frequently quite erratic, with sudden outbursts of mass injection and periods of no or negligible mass injection. Rivinius et al. (2016) propose a terminology, which will be used here, in which a star that possesses a disc is said to be active and, conversely, when there is no detectable disc, the star is inactive. Two additional terms are used to distinguish the phases of active disc formation (outbursting Be star) and dissipation (dissipating Be star).
It has been demonstrated (e.g. Haubois et al. 2012) that a Be disc fed roughly at a constant rate, and for a sufficiently long time (a few to several years, depending on the value of the viscosity), reaches a quasi-steady state in which the density is nearly constant in time. If the gas temperature is properly taken into consideration, the radial density profile is typically a complicated function of the distance from the star (e.g. Carciofi & Bjorkman 2008). However, a usual approximation is to consider the gas to be isothermal, in which case the density profile assumes a power-law form. This simple steady-state VDD has been successful in describing the main observed features of individual Be discs (Carciofi et al. 2006, 2007; Jones et al. 2008b; Carciofi et al. 2009; Klement et al. 2015, 2017) and samples of Be stars (Silaj et al. 2010; Touhami, Gies & Schaefer 2011; Vieira et al. 2017). However, despite its great success, there are several open and intriguing theoretical questions about the VDD model. Besides the fact that a good description of the mechanism responsible for putting stellar material into orbit is still needed, a complete physical understanding of the forces that drive these discs is also lacking. It has been commonly assumed that the forces operating on the discs are the gravity from the central star and the forces that come from the gradient of pressure and from viscosity, the latter being the one capable of producing torque. Recently, Kee et al. (2016) showed that radiative line forces may also generate a non-negligible torque, at least for gaseous discs with Solar metallicity. In this work, we will proceed with the assumption that line-driven forces are negligible. We mitigate this potential issue by choosing to study Be stars in the SMC, whose low metallicity will greatly decrease the strength of the line forces.
In the alpha-disc formalism, the kinematic viscosity is scaled with the α parameter, defined such that the Rϕ component of the stress tensor is proportional to the gas pressure: WRϕ = −αP. The most reliable and direct way of estimating α is to study the time-dependent disc behaviour, where the diffusive effect of viscosity will have clear observational counterparts. Therefore, light curves of long temporal coverage, such as the ones given by microlensing or planetary transit surveys, are excellent instruments to study the dynamical processes in action on the disc, as it builds up and dissipates.
Dynamical studies of Be star viscous discs are still quite scarce. Jones, Sigut & Porter (2008a), using a 1D time-dependent treatment of the alpha-disc and a non-LTE radiative transfer code, studied the temperature and density profiles of a dynamical disc and their respective H α line profiles. Haubois et al. (2012) studied the theoretical photometric effects of time variable mass injection rates on the structure of the disc also using a 1D time-dependent treatment of the alpha-disc, associated with the Monte Carlo radiative transfer code hdust (Carciofi & Bjorkman 2006, 2008). Carciofi et al. (2012), by fitting these dynamical models to a dissipating portion in the light curve of the Be star 28 CMa (which passed from an outbursting phase, that lasted from 2001 to 2003, to a dissipating phase at the end of 2003), estimated the value of the α parameter for the Be disc of 28 CMa to be α = 1.0 ± 0.2. Later, however, it was realized that a proper consideration of the previous history of the disc must be taken into consideration even when fitting the dissipating portion of the light curve, and this quite high value has been revisited to be closer to α = 0.2 (Ghoreyshi & Carciofi 2017).
Another intriguing issue regarding Be stars is how they acquired such high rotation rates (typically 80 per cent of breakup, Rivinius et al. 2013). As the rotating B star evolves, core contraction and internal angular momentum redistribution generally tends to enhance surface angular rotation (Ekström et al. 2008; Granada et al. 2013). Another scenario (e.g. Pols et al. 1991) would involve a past mass-transfer phase in a binary system, during which the primary donates mass and angular momentum to the secondary. The left-over of such a system would be a fast-spinning Be star (the former mass gainer) and a subdwarf O or B star (sdO/sdB, the former mass donor). Regardless of how they were spun-up, it has been proposed (Krtička, Owocki & Meynet 2011) that the discs of Be stars may provide natural mechanisms for removing large quantities of angular momentum from the fast rotating stars, preventing them to reach the rotation critical limit. The evolutionary models of Granada et al. (2013) assumed the appearance of completely formed viscous discs every time their models reached a near-critical rotation. The mass density and the rate of angular momentum loss of their discs were roughly similar to the ones estimated by Vieira et al. (2017), who modelled the spectral energy distribution (SED) of 80 Be stars using the VDD model, provided that values of α of at least a few tenths were assumed in both approaches.
The main objective of this paper is to build upon the previous dynamical studies of Be discs and provide, for the first time, a detailed study of the temporal evolution of a large sample of Be stars from the Small Magellanic Cloud (SMC). By studying a large sample of stars, we may begin to answer several open questions related to Be stars and their discs, namely: (i) What is the typical value of the viscosity in these discs? (ii) Is there any significant evidence for a dependence of α with parameters such as the density of the disc, the spectral type of the star, etc.? (iii) What are the typical rates of mass and angular momentum loss in these stars? To reach these goals we developed a new method for modelling the light curves of Be stars, described in Sections 2 and 3. The sample of studied light curves is described in Section 4, and the model results are discussed in Section 5, followed by the conclusions.
2 VISCOUS DECRETION DISCS AROUND BE STARS
The optical light curves of early-type Be stars (with spectral type ranging roughly from B0 to B4) are usually quite variable in time-scales of days to years, with amplitudes of up to tenths of a magnitude (Rivinius et al. 2013). The majority of them show very irregular variability. Most present clear single bump-like features, characterized by a fast rise in brightness followed by a slower fading. Frequently, between the brightening and the fading phases some sort of plateau of nearly constant brightness is seen. Sometimes these bumps are reversed, so that an initial fast fading is followed by a slow recovering of the stellar brightness. Two examples of light curves showing these dips are presented in Fig. 1, taken from OGLE-II (Udalski, Kubiak & Szymanski 1997) and OGLE-III (Udalski et al. 2008) data, for two Be star candidates from the SMC, based on the selection made by Mennickent et al. (2002). Object SMC_SC1 75701 shows two bumps, while SMC_SC6 128831 shows a dip.
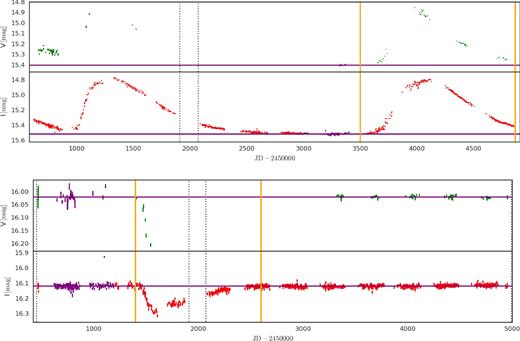
Two light curves, in photometric bands V (green) and I (red), selected from the OGLE-II and OGLE-III photometric surveys. Above: Light curve of SMC_SC1 75701, showing two bumps. Below: Light curve of SMC_SC6 128831, showing a dip. The pair of vertical dotted straight lines near JD-2450000 = 2000 separates OGLE-II from OGLE-III data. The measurements shown in purple are assumed to represent the inactive (discless) brightness level of the Be star. Their mean is given by the horizontal purple straight lines. The pairs of vertical orange straight lines bracket our visually selected bumps. These bumps are modelled in Figs 8 and 9.
These bumps and dips resemble the photometric features shown in Haubois et al. (2012, e.g. their fig. 14), where a circumstellar viscous disc builds up as a result of a mass injection into the disc at a constant rate, and then dissipates after the mass injection ceases. Haubois et al. (2012) studied several disc feeding scenarios (constant, cyclic, and outburst) and their photometric counterparts, and demonstrated that the bumps are disc formation/dissipation events of active Be stars seen at near pole-on inclination angles (|$i\lesssim 70\deg$|), while the dips are associated with near edge-on Be stars (often called shell stars, |$i\gtrsim 70\deg$|). The inclination angle plays an important role on how the stellar brightness is modified by the presence of disc because, in the second case (edge-on), the disc is seen projected against the stellar disc, thus causing an attenuation of the stellar radiation. This attenuation does not happen for the pole-on case, where the net effect of the disc is to increase the optical brightness as a result of free–bound and free–free radiation from the gas (Gehrz, Hackwell & Jones 1974; Vieira, Carciofi & Bjorkman 2015).
The orbital velocity of the disc, |$v$|ϕ, is assumed to be Keplerian (|$v_\phi = v_K = v_\mathrm{orb}\tilde{R}^{-{1}/{2}}$|, with |$v$|orb = (GM/Req)1/2 and |$\tilde{R}=R/R_\mathrm{eq}$|, where Req is the stellar equatorial radius). This assumption holds as long as the gravitational force is much larger than the force due to the pressure gradient, which is generally true for distances from the star of dozens to a few hundreds of stellar radii (Okazaki 2001), as long as (cs/|$v$|K)2 ≪ 1.
In addition, mass can flow away from the disc through its boundaries. Mass can fall back into the star through the inner boundary at Req, or it can leave the system at an outer boundary, Rout. The outer boundary can be interpreted as the limiting radius of the disc due to a binary companion (e.g. Okazaki et al. 2002) or due to the photoevaporation of the disc (e.g. Okazaki 2001). We consider that all mass that eventually reaches the stellar equator Req is totally absorbed. The same is assumed for the mass that eventually reaches an outer radius Rout (see below for the definition of Rout). Therefore, the boundaries consist of Σ(Req, t) = Σ(Rout, t) = 0.
The solution of equation (5) is scaled in time by the time-scale parameter, which controls how fast matter is distributed throughout the disc and, consequently, its observational counterparts. It follows that by fitting observed light curves of Be stars, this parameter can be estimated, and once other parameters are known (Req, M, Tdisc), the α value can be determined (e.g. Carciofi et al. 2012).
Before moving on to the modelling of bump-like events such as the ones of Fig. 1, we introduce in the next section some important parameters of the dynamical discs implied in the equations shown above.
2.1 Dynamical disc parameters
We may extend equation (11) to the general case of a time-dependent |$\dot{M}_\mathrm{inj}(\tilde{\tau })$|, which would define, by the same equation, a time-dependent asymptotic surface density, |$\Sigma _0(\tilde{\tau })$|. The function |$\Sigma _0(\tilde{\tau })$| therefore is just another way of specifying the history of mass injection from the star into the disc. It has, however, the advantage of being a surface density, which is a quantity that may be determined from, e.g. SED analyses, in contrast to the mass injection rate and the radius of mass injection, which are parameters that cannot be observationally determined.
The steady-state solution (equation 10) shows that, in the wider domain |$\tilde{R}_\mathrm{inj} \le \tilde{R}\le \tilde{R}_\mathrm{out}$|, the density profile of the disc is not altered if |$\tilde{R}_\mathrm{inj}$| is changed, provided that |$\dot{M}_\mathrm{inj}$| is also changed in order to maintain Σ0 fixed, according to equation (11). In fact, we verified that the time-dependent solutions of equation (5) in the domain |$\tilde{R}_\mathrm{inj} \le \tilde{R}\le \tilde{R}_\mathrm{out}$| are negligibly affected by the particular choice of |$\tilde{R}_\mathrm{inj}$| or |$\dot{M}_\mathrm{inj}(\tilde{\tau })$|, as long as the quantity |$\Sigma _0(\tilde{\tau })$| is kept fixed. This is a consequence of the fact that the dynamical solutions reach a near steady state very quickly in the vicinity of the injection radius (Haubois et al. 2012). Furthermore, provided that mass is injected not too far from the stellar photosphere (i.e. assuming |$\tilde{R}_\mathrm{inj} \gtrapprox 1$|), the domain |$1\le \tilde{R}\le \tilde{R}_\mathrm{inj}$| is much narrower than the region where the continuum visual flux of Be stars is generated (Carciofi 2011), which means that the emission from this region can be ignored. Consequently, we conclude that |$\Sigma _0(\tilde{\tau })$| (with the assumption that |$\tilde{R}_\mathrm{inj}\gtrapprox 1$|) is a much better parameter for describing the mass injection history of the disc than the pair of parameters |$\dot{M}_\mathrm{inj}(\tilde{\tau })$| and |$\tilde{R}_\mathrm{inj}$|.
The time-dependent solutions of equation (5) generally show that, for Be stars dynamically feeding the disc but still far from steady state, the mass flux close to |$\tilde{R}_\mathrm{inj}$| has absolute values of the order of |$\left(-\mathrm{\partial} M/\mathrm{\partial} t\right)_\mathrm{typ}$|, defined by equation (11). Therefore, we refer to this quantity as the typical decretion rate, which depends on parameters relatively easy to estimate from SEDs of Be stars.
In our simulations, since the values of |$\dot{M}_\mathrm{inj}$| and |$\tilde{R}_\mathrm{inj}$| are of no interest, and the value of |$\tilde{R}_\mathrm{out}$| is quite uncertain, we arbitrarily chose |$\tilde{R}_\mathrm{inj}=1.017$| and |$\tilde{R}_\mathrm{out}=1000$| (we discuss below how this choice of |$\tilde{R}_\mathrm{out}$| might affect our results). Equation (11) therefore shows that the typical decretion rate is much smaller than the mass injection rate |$\dot{M}_\mathrm{inj}(\tilde{\tau })$|. In our case, the typical decretion rate is only |$8.46\times 10^{-3} \dot{M}_\mathrm{inj}$|. This means that the majority of the injected mass flows inwards and is absorbed by the inner boundary at the stellar equator, and only a small remaining fraction of the injected mass is responsible for the growth of the disc. These results were first obtained from SPH simulations of Be discs by Okazaki et al. (2002), who found that only about 0.1 per cent of the injected material flows outward, as a direct result of their choice for Rinj.
2.2 The mass reservoir effect
It is important to stress that the solution |$\Sigma (\tilde{R}, \tilde{\tau })$| is shaped not just by the mass injection rate |$\Sigma _0(\tilde{\tau })$| at the specific instant |$\tilde{\tau }$|, but by the whole mass injection history before the instant |$\tilde{\tau }$|. Therefore, the advantage of studying the relatively isolated bumps like the ones exemplified in Fig. 1, which started after a clear inactive phase, is that there is no disc present when the bump starts developing; thus, no previous history of mass injection has to be taken into account in the beginning of the modelling.
The light curves of several Be stars show that the duration of the build-up phase, which we refer to as the build-up time, is variable between Be stars and even between different bumps from the same star, ranging from a few days to years. The following phase of disc dissipation, however, contrary to the build-up phase, depends of the previous history of mass injection. For this reason, the modelling of the dissipation phase must not be disconnected from the modelling of the build-up phase that happened before it.
One of the main consequences of this fact is the mass reservoir effect (see also Ghoreyshi & Carciofi 2017). Basically, discs that had a longer build-up phase necessarily transported more matter and angular momentum outwards and created a larger external reservoir of mass and angular momentum in its outer regions, which usually extend far beyond the first few stellar radii where the visible photometric observables are formed. It is common, for instance, that some bumps reach plateaus during the build-up phase. The plateau indicates that the density in the inner disc has reached near-steady-state values and, consequently, there is little photometric variation in the visible wavelengths. The outer disc, however, will likely be far from steady state and thus will continue to increase in density and mass. When mass injection ceases, the dissipation phase begins. Re-accretion occurs and, due to the more massive outer disc, the inner disc remains relatively denser for a longer time. This makes the dissipation of the disc appear slower in the observed light curves. Conversely, a disc that had a small build-up time would dissipate much faster.
The importance of the mass reservoir effect can be assessed by the reevaluation of the α parameter in 28 CMa by Ghoreyshi & Carciofi (2017). Carciofi et al. (2012) modelled the 2003 dissipation phase of 28 CMa by considering a very long previous build-up time, and found that a high value of α was necessary (1.0 ± 0.2) to match the observed dissipation rate. Ghoreyshi & Carciofi have shown that when the previous build-up phase is properly accounted for in the modelling, the value of α required to match the dissipation rate is much smaller (0.21 ± 0.05).
3 A MODEL GRID OF DISC FORMATION AND DISSIPATION EVENTS
In this section, we describe the method we developed for fitting the light curves associated with events of disc formation and dissipation. The method consists of pre-computing a large grid of dynamical models of the time-dependent disc structure, covering the entire range of observed scenarios (Section 3.1) and performing the radiative transfer in these models to produce synthetic light curves (Section 3.2). The observed light curves are then fitted by the synthetic one using the procedure described in Sections 3.3 and 3.4.
3.1 Dynamical model grid
For building a comprehensive grid of dynamical models that are solutions of equation (5), we used the definitions of Section 2 that allow us to write the solution |$\Sigma (\tilde{R}, \tilde{\tau })$| in terms of |$\Sigma _0(\tilde{\tau })$| and the dimensionless parameter |$\tilde{\tau }$|.
As discussed in Section 2.2, the advantage of studying relatively isolated bumps like the ones exemplified in Fig. 1, which started after a clear inactive phase, is that there is no previous history of mass injection to be taken into account for the modelling, so that during build-up the shape of the curve is controlled solely by |$\Sigma _0(\tilde{\tau })$| and |$\tilde{\tau }$|, while for dissipation the previous disc build-up time should also be considered (Section 2.2). By using the time parameter (equation 7) instead of the physical time, our dynamical models are independent of the specific physical parameters M, Teff, Req, and α(t) of the Be star under consideration (equation 6). Also, from the linearity of equation (5), it follows that multiplying |$\Sigma _0(\tilde{\tau })$| by some constant results in the solution |$\Sigma (\tilde{R}, \tilde{\tau })$| multiplied by the same constant. Consequently, only one value of Σ0 during the build-up phase is necessary.
For our grid of dynamical models, we therefore assume that our Be stars start discless. At instant |$\tilde{\tau }=0$|, mass injection into the disc begins at an arbitrary constant rate (Σ0 > 0) that lasts until |$\tilde{\tau }=\tilde{\tau }_\mathrm{bu}$|, which we refer to as the scaled build-up time, since it is related to the above-mentioned build-up time, but scaled by the time-scale parameter. After that (|$\tilde{\tau }>\tilde{\tau }_\mathrm{bu}$|), mass injection no longer occurs (Σ0 = 0) and the disc dissipates. In Appendix A, we further discuss the properties of these dynamical models.
We chose 11 values of |$\tilde{\tau }_\mathrm{bu}$|, listed in Table 1. Since the time-scale parameter (equation 6) is roughly given by ∼(100–200)/α d for early Be stars in the main sequence with α ≲ 1, these values correspond to real build-up times of at least 15 d, which brackets the observed build-up times of the sample described below (Section 4, Table 5). In this study, we decided not to model the bumps with observed build-up times lower than about 15 d, usually referred to as flickers (Keller et al. 2002).
| Star . | i (deg) . | Σ0 (g cm−2) . | |$\tilde{\tau }_\mathrm{bu}$| . |
|---|---|---|---|
| Star 1 | 00.0 | 0.30 | 00.15 |
| Star 2 | 21.8 | 0.41 | 00.45 |
| Star 3 | 31.0 | 0.56 | 00.75 |
| 38.2 | 0.75 | 01.50 | |
| 44.4 | 1.01 | 02.25 | |
| 50.0 | 1.37 | 03.00 | |
| 55.2 | 1.85 | 04.50 | |
| 60.0 | 2.50 | 06.00 | |
| 64.6 | 09.00 | ||
| 69.1 | 15.00 | ||
| 73.4 | 30.00 | ||
| 77.6 | |||
| 81.8 | |||
| 85.9 | |||
| 90.0 |
| Star . | i (deg) . | Σ0 (g cm−2) . | |$\tilde{\tau }_\mathrm{bu}$| . |
|---|---|---|---|
| Star 1 | 00.0 | 0.30 | 00.15 |
| Star 2 | 21.8 | 0.41 | 00.45 |
| Star 3 | 31.0 | 0.56 | 00.75 |
| 38.2 | 0.75 | 01.50 | |
| 44.4 | 1.01 | 02.25 | |
| 50.0 | 1.37 | 03.00 | |
| 55.2 | 1.85 | 04.50 | |
| 60.0 | 2.50 | 06.00 | |
| 64.6 | 09.00 | ||
| 69.1 | 15.00 | ||
| 73.4 | 30.00 | ||
| 77.6 | |||
| 81.8 | |||
| 85.9 | |||
| 90.0 |
| Star . | i (deg) . | Σ0 (g cm−2) . | |$\tilde{\tau }_\mathrm{bu}$| . |
|---|---|---|---|
| Star 1 | 00.0 | 0.30 | 00.15 |
| Star 2 | 21.8 | 0.41 | 00.45 |
| Star 3 | 31.0 | 0.56 | 00.75 |
| 38.2 | 0.75 | 01.50 | |
| 44.4 | 1.01 | 02.25 | |
| 50.0 | 1.37 | 03.00 | |
| 55.2 | 1.85 | 04.50 | |
| 60.0 | 2.50 | 06.00 | |
| 64.6 | 09.00 | ||
| 69.1 | 15.00 | ||
| 73.4 | 30.00 | ||
| 77.6 | |||
| 81.8 | |||
| 85.9 | |||
| 90.0 |
| Star . | i (deg) . | Σ0 (g cm−2) . | |$\tilde{\tau }_\mathrm{bu}$| . |
|---|---|---|---|
| Star 1 | 00.0 | 0.30 | 00.15 |
| Star 2 | 21.8 | 0.41 | 00.45 |
| Star 3 | 31.0 | 0.56 | 00.75 |
| 38.2 | 0.75 | 01.50 | |
| 44.4 | 1.01 | 02.25 | |
| 50.0 | 1.37 | 03.00 | |
| 55.2 | 1.85 | 04.50 | |
| 60.0 | 2.50 | 06.00 | |
| 64.6 | 09.00 | ||
| 69.1 | 15.00 | ||
| 73.4 | 30.00 | ||
| 77.6 | |||
| 81.8 | |||
| 85.9 | |||
| 90.0 |
3.2 Radiative transfer models
Having selected a set of suitable hydrodynamic bump models, the next step is to produce photometric light curves of these models. The radiative transfer part of the problem requires a stellar model, which will be the primary source of radiation. The stellar model depends on the physical parameters M, Req, and Teff, which were left unspecified in the dynamical model grid. In addition, three other parameters must be specified: the viewing angle, i (i = 0 means pole-on orientation), the distance to the star, d, and the interstellar reddening.
One important feature of the central stars of Be stars is that they are fast rotators. Fast rotation causes the star to be oblate, with hotter poles and colder equatorial regions. Rotation is specified by the ratio of the rotation velocity at the equator to the Keplerian velocity at the equator, W = |$v$|eq/|$v$|orb. The ratio between the equatorial radius to the polar radius is given by Req/Rpole = 1 + W2/2 for a Roche-shaped star. All these parameters evolve in time as a consequence of stellar evolution, and Be stars can be found in luminosity classes from V to III (Rivinius et al. 2013). We adopt the Geneva evolutionary tracks (Georgy et al. 2013) to determine Req and Teff given M and the age in the main sequence, tMS.
The current version of hdust allows for a spheroidal rotationally oblate star, with the latitude-dependent surface temperature being given by |$T_\mathrm{surf}\propto g_\mathrm{eff}^\beta$| (Carciofi et al. 2008). Here, the coefficient β(W) is calculated by fitting a straight line to the gradient |$\mathrm{\partial} \ln T_\mathrm{surf}/\mathrm{\partial} \ln g_\mathrm{eff}$| given by the flux theory of Espinosa Lara & Rieutord (2011). For the disc scale height (equation 9), we assume an isothermal disc with Tdisc = 0.6Teff, where Teff is the effective temperature of the star, defined by Teff = (L*)1/4(σS*)−1/4, with S* being the surface area of the star.
In order to generate synthetic absolute magnitudes from the computed SEDs, we used the standard BVRI Johnson–Cousins passbands from Bessell (1990) and the Vega flux from Castelli & Kurucz (1994) as standard of calibration.
A grid of model light curves was computed using the 11 dynamical models described in Section 3.1, with 8 different values of Σ0 (third column of Table 1). For each of these disc models, radiative transfer models were calculated with hdust at 17 different time parameters (not shown in the table) and 15 equally spaced values of cos i (second column). This whole process was done for three different stellar models (‘Star 1’, ‘Star 2’, and ‘Star 3’, first column of Table 1, according to the stellar models of Georgy et al. 2013). Details on the stellar models are given in Table 2. They were chosen to represent early B-type stars from the SMC (Z = 0.002), in the middle of their life in the main sequence, with the rotation parameter given by the mean value obtained for Be stars (W = 0.81, Rivinius, Štefl & Baade 2006). In the sixth column of Table 2, we present the values of ατ (equation 6) for the discs of these stars (with the assumption that Tdisc = 0.6Teff). In short, a single light curve is specified by taking one element of each column of Table 1. The end result was a grid of 3 × 15 × 8 × 11 = 3960 light curves, for each of the BVRI bands.
| Star . | Z . | M (M⊙) . | W . | t/tMS . | ατ (d) . |
|---|---|---|---|---|---|
| Star 1 | 0.002 | 7 | 0.81 | 0.5 | 90.4 |
| Star 2 | 0.002 | 11 | 0.81 | 0.5 | 103.3 |
| Star 3 | 0.002 | 15 | 0.81 | 0.5 | 118.9 |
| Star . | Z . | M (M⊙) . | W . | t/tMS . | ατ (d) . |
|---|---|---|---|---|---|
| Star 1 | 0.002 | 7 | 0.81 | 0.5 | 90.4 |
| Star 2 | 0.002 | 11 | 0.81 | 0.5 | 103.3 |
| Star 3 | 0.002 | 15 | 0.81 | 0.5 | 118.9 |
| Star . | Z . | M (M⊙) . | W . | t/tMS . | ατ (d) . |
|---|---|---|---|---|---|
| Star 1 | 0.002 | 7 | 0.81 | 0.5 | 90.4 |
| Star 2 | 0.002 | 11 | 0.81 | 0.5 | 103.3 |
| Star 3 | 0.002 | 15 | 0.81 | 0.5 | 118.9 |
| Star . | Z . | M (M⊙) . | W . | t/tMS . | ατ (d) . |
|---|---|---|---|---|---|
| Star 1 | 0.002 | 7 | 0.81 | 0.5 | 90.4 |
| Star 2 | 0.002 | 11 | 0.81 | 0.5 | 103.3 |
| Star 3 | 0.002 | 15 | 0.81 | 0.5 | 118.9 |
A grid of inactive (discless) stellar models was also calculated. Because these models can be computed much faster than the bump models, we were able to cover a much finer grid of stellar parameters (Table 3), aiming at a better determination of the stellar parameters. The grid is composed by models for 13 different masses (second column), 5 different rotation rates (third column), 6 equally spaced values for the age in the main sequence (forth column), and 10 equally spaced values of cos i (fifth column), resulting in a total of 13 × 5 × 6 × 10 = 3900 photometric models for each of the BVRI bands.
| Z . | M (M⊙) . | W . | t/tMS . | i (deg) . |
|---|---|---|---|---|
| 0.002 | 2.50 | 0.447 | 0.00 | 00.0 |
| 3.68 | 0.633 | 0.20 | 27.3 | |
| 4.85 | 0.775 | 0.40 | 38.9 | |
| 6.00 | 0.894 | 0.60 | 48.2 | |
| 7.15 | 0.949 | 0.80 | 56.3 | |
| 8.29 | 1.00 | 63.6 | ||
| 9.42 | 70.5 | |||
| 10.54 | 77.2 | |||
| 11.66 | 83.6 | |||
| 12.78 | 90.0 | |||
| 13.89 | ||||
| 15.00 | ||||
| 20.00 |
| Z . | M (M⊙) . | W . | t/tMS . | i (deg) . |
|---|---|---|---|---|
| 0.002 | 2.50 | 0.447 | 0.00 | 00.0 |
| 3.68 | 0.633 | 0.20 | 27.3 | |
| 4.85 | 0.775 | 0.40 | 38.9 | |
| 6.00 | 0.894 | 0.60 | 48.2 | |
| 7.15 | 0.949 | 0.80 | 56.3 | |
| 8.29 | 1.00 | 63.6 | ||
| 9.42 | 70.5 | |||
| 10.54 | 77.2 | |||
| 11.66 | 83.6 | |||
| 12.78 | 90.0 | |||
| 13.89 | ||||
| 15.00 | ||||
| 20.00 |
| Z . | M (M⊙) . | W . | t/tMS . | i (deg) . |
|---|---|---|---|---|
| 0.002 | 2.50 | 0.447 | 0.00 | 00.0 |
| 3.68 | 0.633 | 0.20 | 27.3 | |
| 4.85 | 0.775 | 0.40 | 38.9 | |
| 6.00 | 0.894 | 0.60 | 48.2 | |
| 7.15 | 0.949 | 0.80 | 56.3 | |
| 8.29 | 1.00 | 63.6 | ||
| 9.42 | 70.5 | |||
| 10.54 | 77.2 | |||
| 11.66 | 83.6 | |||
| 12.78 | 90.0 | |||
| 13.89 | ||||
| 15.00 | ||||
| 20.00 |
| Z . | M (M⊙) . | W . | t/tMS . | i (deg) . |
|---|---|---|---|---|
| 0.002 | 2.50 | 0.447 | 0.00 | 00.0 |
| 3.68 | 0.633 | 0.20 | 27.3 | |
| 4.85 | 0.775 | 0.40 | 38.9 | |
| 6.00 | 0.894 | 0.60 | 48.2 | |
| 7.15 | 0.949 | 0.80 | 56.3 | |
| 8.29 | 1.00 | 63.6 | ||
| 9.42 | 70.5 | |||
| 10.54 | 77.2 | |||
| 11.66 | 83.6 | |||
| 12.78 | 90.0 | |||
| 13.89 | ||||
| 15.00 | ||||
| 20.00 |
3.3 Empirical law
In order to facilitate the comparison of the synthetic light curves (Section 3.2) with the observed ones (Section 4), we developed two empirical laws that match quite closely the synthetic light curves for build-up and dissipation. The usefulness of these formulae will become clear in the next section.
In our discussion of the features of the light curves, it is useful to separate them in three groups: (i) pole-on light curves, of stars seen at small inclination angles (|$0\le i \lesssim 70\deg$|), which should statistically correspond to the majority of the observed light curves; (ii) edge-on light curves, of shell stars (|$i \approx 90\deg$|); and (iii) intermediate light curves, of stars seen at intermediate angles (|$70 \lesssim i \lesssim 85\deg$| – the extension of this intermediate region varies depending the photometric band under consideration and will be defined below). Pole-on light curves show an increase in apparent brightness, due to the additional flux coming from the disc. Conversely, edge-on light curves show a decrease in apparent brightness, due to obscuration of the star by the disc. The intermediate case shows the smallest variations in apparent brightness, and frequently the light curve has a more complicated shape, as it is influenced by variable amounts of disc emission/absorption.
|$\Delta X_\mathrm{d}(\tilde{\tau })/\Delta X_\mathrm{d}^0$| is a function that goes from 1 to 0 as |$\tilde{\tau }-\tilde{\tau }_\mathrm{bu}$| goes from 0 to ∞. In Appendix B, we show examples of light curves that accompany the conclusions drawn on this section.
The values of |$\Delta I_\mathrm{bu}^\infty$| for our grid are shown in Fig. 2, plotted against cos i. The values for the BVR bands show qualitatively similar patterns to the ones presented in this figure. Each panel shows the results for a different star, and all 11 values of Σ0 (Table 1) are represented in the figure by different colours and symbols. The curves monotonically increase with cos i, starting with negative values at edge-on orientation and reaching a maximum for pole-on viewing. The angle for which |$\Delta X_\mathrm{bu}^\infty = 0$|, where the disc excess emission is exactly matched by the absorption of photospheric light by the disc, depends both on the density scale (as shown in the figure) and (most importantly) on the band pass.
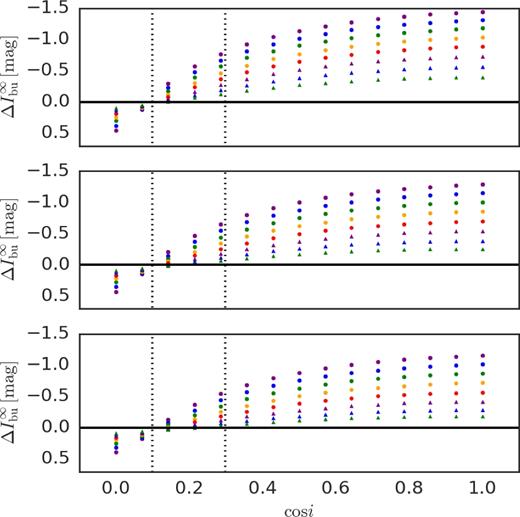
The values of |$\Delta I_\mathrm{bu}^\infty$| versus cos i for our grid. From top to bottom, the results are for Star 1, Star 2, and Star 3, respectively. Purple, blue, green, orange, and red circles correspond to Σ0 = 2.50, 1.85, 1.37, 1.01, 0.75 g cm−2. Purple, blue, and green triangles correspond to Σ0 = 0.56, 0.41, 0.30 g cm−2. Vertical dotted lines define the region of intermediate angles for the I band (|$73 \lesssim i \lesssim 84\deg$|).
An analysis of our model grid allowed us to determine the ranges in inclination angle for which the light curve displays the intermediate behaviour described above. They were determined by visual inspection of our model grid, as the angles for which the light curves present more complex shapes (see e.g. the I-band light curves seen at |$i=81.8\deg$| and |$i=77.6\deg$| in Fig. B1 of Appendix B). Their adopted values are 53–|$78\deg$|, 60–|$78\deg$|, 66–|$84\deg$|, and 73–|$84\deg$| for the BVRI bands, respectively.
Fig. 2 also shows that the excesses increase a little when moving from a low- to a high-mass star, for discs with the same other features. This is a consequence of the fact that the stellar flux relative to the disc flux increases with the luminosity of the star.
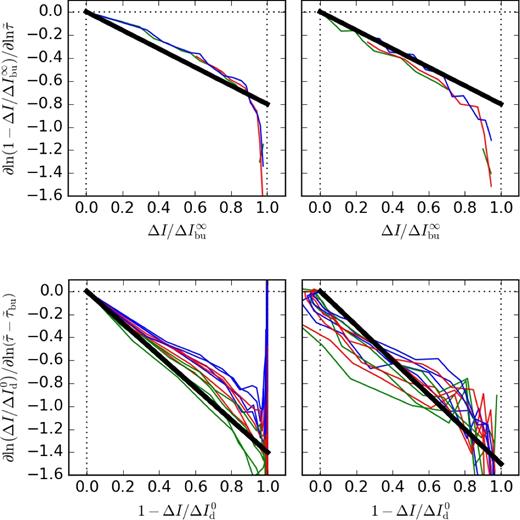
Comparison of the empirical law (black straight lines) with the computed light curves for build-up and dissipation. Top panels: log –log derivative of |$1-\Delta I_\mathrm{bu}(\tilde{\tau })/\Delta I_\mathrm{bu}^\infty$| versus |$\Delta I_\mathrm{bu}(\tilde{\tau })/\Delta I_\mathrm{bu}^\infty$|. Bottom panels: log –log derivative of |$\Delta {I}_\mathrm{d}/\Delta {I}_\mathrm{d}^0$| versus |$1-\Delta {I}_\mathrm{d}/\Delta {I}_\mathrm{d}^0$|, for values of |$\tilde{\tau }_\mathrm{bu}$| equal to 0.45, 1.5, 6, and 30. The results are shown for Star 2 at two inclination angles: |$i=0\,\deg$| (left), and |$i=90\,\deg$| (right). The green, red, and blue curves correspond to Σ0 equal to 1.37, 0.75, and 0.41 g cm−2.
| . | . | B . | V . | R . | I . |
|---|---|---|---|---|---|
| ηbu | (edge-on) | 0.8 | 0.8 | 0.8 | 0.8 |
| (pole-on) | 0.8 | 0.8 | 0.8 | 0.8 | |
| ηd | (edge-on) | 1.5 | 1.5 | 1.5 | 1.5 |
| (pole-on) | 1.1 | 1.2 | 1.3 | 1.4 |
| . | . | B . | V . | R . | I . |
|---|---|---|---|---|---|
| ηbu | (edge-on) | 0.8 | 0.8 | 0.8 | 0.8 |
| (pole-on) | 0.8 | 0.8 | 0.8 | 0.8 | |
| ηd | (edge-on) | 1.5 | 1.5 | 1.5 | 1.5 |
| (pole-on) | 1.1 | 1.2 | 1.3 | 1.4 |
| . | . | B . | V . | R . | I . |
|---|---|---|---|---|---|
| ηbu | (edge-on) | 0.8 | 0.8 | 0.8 | 0.8 |
| (pole-on) | 0.8 | 0.8 | 0.8 | 0.8 | |
| ηd | (edge-on) | 1.5 | 1.5 | 1.5 | 1.5 |
| (pole-on) | 1.1 | 1.2 | 1.3 | 1.4 |
| . | . | B . | V . | R . | I . |
|---|---|---|---|---|---|
| ηbu | (edge-on) | 0.8 | 0.8 | 0.8 | 0.8 |
| (pole-on) | 0.8 | 0.8 | 0.8 | 0.8 | |
| ηd | (edge-on) | 1.5 | 1.5 | 1.5 | 1.5 |
| (pole-on) | 1.1 | 1.2 | 1.3 | 1.4 |
Representative I-band values of ξbu and ξd for our grid are shown in Figs 4–6 (the values of ξbu and ξd for the BVR bands show qualitatively similar patterns to the ones presented in these figures). Each row shows the results for a different star. The left (right) panels are for edge-on (pole-on) models. The values of ξ are directly related to the rate of photometric variations: the smaller the ξ, the slower the variation (see equations 17 and 18).
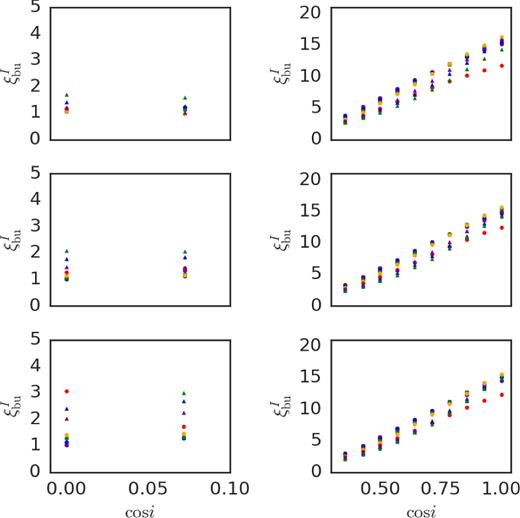
The I-band values of ξbu for our grid versus cos i. Left: Edge-on models. Right: Pole-on models. From top to bottom, the results for Star 1, 2, and 3, respectively. The markers are the same as in Fig. 2.
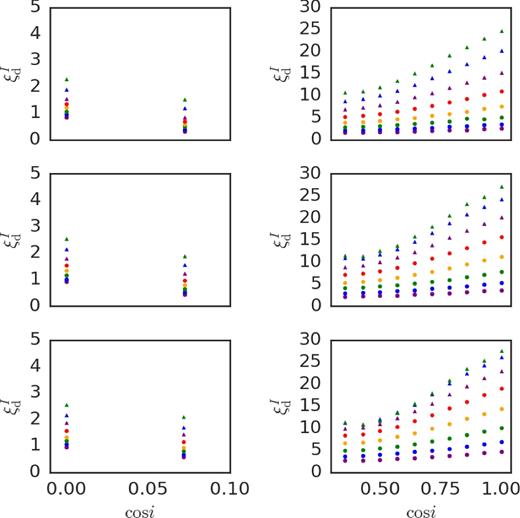
Selected I-band values of ξd for our grid versus cos i. The scaled build-up time was fixed to |$\tilde{\tau }_\mathrm{bu}=2.25$|. Left: Edge-on models. Right: Pole-on models. From top to bottom, the results for Star 1, 2, and 3, respectively. The markers are the same as in Fig. 2.
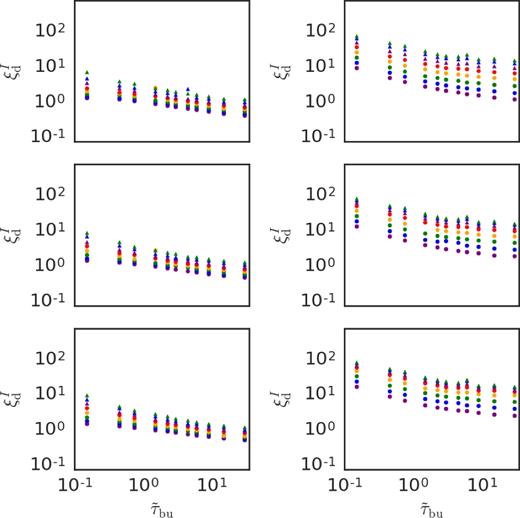
Selected I-band values of ξd for our grid versus |$\tilde{\tau }_\mathrm{bu}$|. Left: Edge-on models with |$i=90\,\deg$|. Right: Pole-on models with |$i=0\,\deg$|. From top to bottom, the results for Star 1, 2, and 3, respectively. The markers are the same as in Fig. 2.
Fig. 4 exemplifies the strong variation of ξbu with i, for the pole-on case. This is probably due to the fact that, in the build-up process, the density grows from the inside out (see Appendix A), which means that the optically thick part of the disc (an expanding pseudo-photosphere) forms first, and the optically thin part takes longer to be built. Since the optical excess of the disc is given by ΔX ∝ Fthickcos i + Fthin, it follows that, as we move from pole-on to edge-on angles, only the optically thick contribution (proportional to cos i) varies. As a consequence, the observed rate of increase in flux moves from being more to less optically thick dominated.
In the dissipation process, the density rapidly adjusts to a self-similar dissipation pattern in the inner disc (Appendix A). Therefore, the flux from the disc is the result of the decrease and disappearance of the optically thick region – transformed into an optically thin region – and the diminishing of the whole optically thin region. The pole-on values of ξd (right panels of Fig. 5) are affected by cos i to a less extent, when compared to the values of ξbu. In the dissipation process, by the same reasoning applied to the build-up process, since the optically thick emission is attenuated by the effect of cos i, its disappearance has a reduced effect for more inclined discs and therefore the disc should apparently disappear at a slower rate.
The values of ξd also show great variation with the asymptotic surface density (Figs 5 and 6). More specifically, increasing Σ0 results in a light curve with a slower decay rate. This is probably due to different levels of saturation in the optically thick region. The denser the optically thick region, the bigger its optical depth and the greater the amount of time for it to turn into an optically thin region.
In addition, Fig. 6 shows that ξd strongly depends on the scaled build-up time. As expected from the mass reservoir effect (Section 2.2), increasing |$\tilde{\tau }_\mathrm{bu}$| results in smaller values of ξd, which implies slower decay rates.
From the above an important conclusion can be drawn: viscosity is not the only parameter affecting the rate of photometric variations in a Be light curve. The stellar parameters, the asymptotic surface density, as well as the inclination angle, all affect the observed shape of the light curve. Thus, extracting α from light curves, one of the main goals of this paper, cannot be done without some knowledge about these parameters.
3.4 Fitting pipeline
So far, our model light curves were given in terms of the adimensional time parameter, |$\tilde{\tau }$|. Thus, an equation is necessary to transform from the physical time t to |$\tilde{\tau }$|, in order to connect the real light curves to our simulated ones.
Our goal is to fit an observed light curve with equation (21), in order to obtain, in a self-consistent way, all the stellar and disc parameters of interest. For that, the following chain of procedures is adopted:
Find a light curve of a Be star that contains at least one clear inactive phase and one complete photometric bump.
Obtain the magnitudes X* at the inactive phase. Subtract these magnitudes from the light curve and obtain the excesses ΔX(t).
Without a clear inactive phase, it is not possible to obtain the pure photospheric level (e.g. the horizontal purple straight lines in Fig. 1) and, consequently, it is not possible to know how much of the observed bumps represent the disc contribution to the total flux. In addition, the photometric bump must contain a completely identified build-up phase, from which the instants t1 and t2 can be extracted, and a considerable extension of the dissipation phase.
Fit equation (21) to the selected bumps, obtaining the coefficients |$\Delta X_\mathrm{bu}^\infty$|, Cbu and Cd, as well as the times t1 and t2 for the onsets of build-up and dissipation.
Transform the magnitudes at the inactive phase, X*, to absolute magnitudes, MX*, by correcting for the distance to the star and reddening at each observed band.
Given the theoretical dependence of the coefficients in equation (21) on the stellar parameters, the absolute magnitudes are required to estimate the stellar parameters (M, W, and t/tMS). From them, the parameter ατ (see equation 6) can be estimated. Clearly, if the stellar parameters are known from some other way (e.g. by spectroscopic analysis), this requirement is no longer necessary. Unfortunately, this is not the case for our sample.
Estimate the stellar parameters, the geometric parameter (cos i) and the bump parameters (Σ0, αbu, and αd, for each bump) that best reproduce the fitted stellar (MX*) and bump (|$\Delta X_\mathrm{bu}^\infty$|, Cbu, and Cd) parameters [see equations (22) and (23) and the parameters |$\Delta X_\mathrm{bu}^\infty$|, ξbu, and ξd from Section 3.3].
In practice, the above process involves several complications (e.g. estimating the goodness of the fit) that are described in the next section.
3.5 Fitting using a MCMC sampling
The task of fitting the measured stellar absolute magnitude (MX*) and bump parameters (|$\Delta X_\mathrm{bu}^\infty$|, Cbu, and Cd) for estimating the model parameters – step 5, above – was done using the Markov Chain Monte Carlo (MCMC) sampling technique. We used the python MCMC sampler emcee (Foreman-Mackey et al. 2013). The code samples a large collection of models by varying all model parameters within a pre-specified range. The sampler provides a distribution of model parameters according to a posterior distribution p(model∣data) ∝ L(data∣model)π(model), where L and π are the likelihood and the prior distributions, respectively.
In our fitting procedure, there are 4 + 5Nbumps model parameters for each light curve containing Nbumps identified bumps. There are three stellar parameters (M, t/tMS, W) and one geometric parameter (cos i), and, for each bump in the light curve, there are five parameters: the initial times of the build-up and dissipation phases (t1 and t2), the asymptotic surface density (Σ0), and the viscosity parameters during the build-up and dissipation phases (αbu and αd).
For the parameter sampling, we have chosen hundreds of ‘walkers’,1 proportional to the number of 4 + 5Nbumps model parameters. For a randomly chosen set of parameters sampled by emcee in the course of the simulation, the corresponding stellar and bump observables are calculated by a multidimensional linear interpolation of the model grid. During the raffle of parameters the prior probability was set to zero if one of the values were sampled outside of the allowed range of a given parameter (Tables 1 and 3). The simulation consists of two steps, the so-called burn-in phase and the sampling phase. We verified that 1000 iterations in the burn-in phase were sufficient for the convergence of all our models. For each parameter, the best-fitting values were chosen to be the median of distribution of the posterior probabilities, with upper (lower) uncertainties estimated from the differences between |$84\,\,\rm{per\,\,cent}$|(|$16\,\,\rm{per\,\,cent}$|) of the sample and the median
In order to test our fitting routine, we applied it to synthetic light curves with levels of astrophysical noise and uncertainties similar to the observed light curves used in this work. In general, the parameters used to generate the synthetic light curves were fairly recovered, with the exception of cos i and αbu, for which a strong correlation is expected on theoretical grounds (Fig. 4). As expected, when multiband data was used the errors in the derived parameters were smaller. This test indicates that Σ0 and αd can be reliably estimated from the light curves, while cos i and αbu less so.
In Section 4, we present a selection of light curves of Be stars from the SMC, and measure their stellar and bump quantities (steps 1 to 4 of the pipeline). Later, in Section 5, we apply step 5 of the pipeline, as described in this section, in order to estimate the relevant parameters of the selected Be stars.
4 OGLE LIGHT CURVES OF BE STAR CANDIDATES
Mennickent et al. (2002) selected roughly one thousand Be star candidates from the SMC, by studying light-curve variations using the OGLE-II data base (Udalski et al. 1997). They classified the morphologies found in the light curves into four categories. The majority of the light curves (|${\sim } 65\,\,\rm{per\,\,cent}$|) belonged to their type-4 category, composed by the light curves showing irregular and non-periodic variations. These light curves should correspond to Be stars showing episodes of mass injection more complicated than the simple build-up followed by dissipation scenario described in Section 3.
Most interesting for us is the type-1 group (|${\sim }13\,\,\rm{per\,\,cent}$| of the sample), composed by light curves that show single sharp or hump-like bumps, like the bumps of the light curve of SMC_SC1 75701 (Fig. 1). These bumps should be the result of single nearly continuous episodes of mass injection followed by dissipation of the disc, like the theoretical scenario explored in Section 3.
The type-2 group (|${\sim }14\,\,\rm{per\,\,cent}$| of the sample), containing light curves showing high and low plateaus, also has some interesting cases for our purposes. High plateaus are usually the photometric result of a longer build-up process in which a near steady state has been reached in the inner disc. The low plateaus are frequently the portions of the light curve during inactive phases.
Sabogal et al. (2005) selected roughly two thousand Be star candidates from the LMC and classified their light curves into the same four categories described by Mennickent et al. (2002). Previously, Keller et al. (2002) also studied light curves from the LMC using the MACHO survey. They spectroscopically analysed a subsample of their Be star candidates and found that |$90\,\,\rm{per\,\,cent}$| of them were Be stars. They also classified morphologically their light curves in a slightly different manner. Their so called bumper events and ‘flicker events’ more or less correspond to the bumps of type-1 light curves, but also to features of the more irregular type-4 light curves. The bumpers have duration of a few hundred days, while the flicker events are faster, with durations of a few dozens of days. Dips like the one exemplified by the light curve of SMC_SC6 128831 (Fig. 1) were called ‘fading events’. The frequency of these events was quite smaller than the bumpers, in accordance to the picture that fading events are associated with the less numerous shell stars.
Paul et al. (2012) studied the spectral properties of stars from the catalogues of Mennickent et al. (2002) and Sabogal et al. (2005). For the candidates from the SMC, they found that the majority of type-1 and type-2 light curves belong to early B-type stars with emission features characteristic of circumstellar material (Paul et al. 2012). Therefore, these light curves are very likely to be from Be stars.
In this work, we selected light curves from the catalogue of Be star candidates from the SMC of Mennickent et al. (2002). In order to have light curves of a longer time baseline, we combined OGLE-II data with OGLE-III (Udalski et al. 2008). Due to a calibration issue between OGLE-II and OGLE-III, namely a shift in the zero-points present in some of the light curves, it was necessary to find inactivity intervals in both the OGLE-II and OGLE-III portions of these light curves to measure and correct the problem.
The light curves were visually inspected according to the criteria of item 1, Section 3.4, i.e. light curves with at least one clear inactive phase and one bump. In this initial work we focused on well-behaved light curves with clear bumps. We also avoided the short events (flickers, with build-up times ≲15 d), due to the fact that most of them are poorly sampled. The end result was a sample of 54 stars, containing 81 selected bumps, shown in Table 5. In the table, horizontal lines separate the data for each of the 54 stars. Each row in the table contain the data for each of the 81 selected bumps. The fifth and sixth columns in the table contain the beginning and ending of the selected inactive interval for the light curve. The seventh, eighth, and ninth columns contain the B*V*I* magnitudes obtained at the inactive phase for the light curve. Due to the nature of the OGLE survey, the B*V* are not available for all sources. The 11th column contains the bands that were considered in the fitting process of the specific bumps, depending on the availability of measurements in each band. The last two columns are initial visual estimates of t1 and t2, which were used as input for emcee.
| OGLE-II . | OGLE-III . | Discless interval . | B* . | V* . | I* . | Bump . | Bands . | Bump interval . | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Field . | ID . | Field . | ID . | (JD-2450000) . | . | . | . | ID . | . | (JD-2450000) . | ||
| SMC_SC1 | 7612 | SMC133.4 | 8877 | 600 | 1300 | 15.926 ± 0.01 | 16.164 ± 0.009 | 16.443 ± 0.009 | 01 | I | 1420 | 2000 |
| 02 | I | 3250 | 3800 | |||||||||
| SMC_SC1 | 60553 | SMC128.6 | 57 | 3000 | 3500 | – | 15.418 ± 0.003 | 15.601 ± 0.007 | 01 | V I | 3500 | 5000 |
| SMC_SC1 | 75701 | SMC125.7 | 20383 | 3000 | 3500 | – | 15.397 ± 0.003 | 15.51 ± 0.006 | 01 | V I | 3650 | 5000 |
| SMC_SC1 | 92262 | SMC128.6 | 147 | 3500 | 3800 | – | 15.623 ± 0.003 | 15.811 ± 0.007 | 01 | I | 2600 | 3100 |
| 02 | V I | 3900 | 5000 | |||||||||
| SMC_SC2 | 94939 | SMC125.3 | 52 | 1000 | 1100 | 15.832 ± 0.008 | 15.991 ± 0.013 | 16.126 ± 0.007 | 01 | I | 1100 | 2000 |
| SMC_SC3 | 5719 | SMC125.1 | 20231 | 2980 | 3020 | – | – | 16.233 ± 0.01 | 01 | I | 1200 | 4500 |
| SMC_SC3 | 15970 | SMC125.2 | 28056 | 700 | 750 | 15.282 ± 0.01 | 15.412 ± 0.006 | 15.541 ± 0.006 | 01 | B V I | 750 | 2000 |
| 02 | I | 2200 | 3500 | |||||||||
| 03 | V I | 4000 | 5000 | |||||||||
| SMC_SC3 | 71445 | SMC125.2 | 34818 | 700 | 800 | 16.227 ± 0.01 | 16.425 ± 0.009 | 16.608 ± 0.012 | 01 | I | 1450 | 2400 |
| 02 | I | 4400 | 4700 | |||||||||
| SMC_SC3 | 125899 | SMC125.2 | 6200 | 3500 | 3750 | – | 15.837 ± 0.004 | 15.956 ± 0.008 | 01 | I | 2320 | 3400 |
| SMC_SC3 | 197941 | SMC125.3 | 25034 | 4000 | 4060 | – | 15.671 ± 0.003 | 15.724 ± 0.006 | 01 | V I | 2350 | 4000 |
| SMC_SC4 | 22859 | SMC125.4 | 22723 | 700 | 1200 | 17.068 ± 0.013 | 17.133 ± 0.012 | 17.129 ± 0.015 | 01 | V I | 1200 | 3500 |
| SMC_SC4 | 71499 | SMC100.7 | 34896 | 1000 | 1450 | 15.414 ± 0.011 | 15.553 ± 0.007 | 15.597 ± 0.006 | 01 | V I | 1430 | 2400 |
| 02 | V I | 2900 | 4400 | |||||||||
| SMC_SC4 | 120783 | SMC100.6 | 7129 | 4250 | 4500 | – | 14.401 ± 0.003 | 14.442 ± 0.005 | 01 | V I | 2750 | 4500 |
| SMC_SC4 | 127840 | SMC100.6 | 38372 | 3500 | 4500 | – | 14.853 ± 0.003 | 15.026 ± 0.006 | 01 | I | 2800 | 3500 |
| SMC_SC4 | 156248 | SMC100.8 | 14683 | 1000 | 1200 | 15.91 ± 0.01 | 15.964 ± 0.007 | 15.852 ± 0.006 | 01 | I | 1320 | 2300 |
| SMC_SC4 | 156251 | SMC100.8 | 14642 | 600 | 680 | 14.881 ± 0.005 | 15.13 ± 0.007 | 15.338 ± 0.005 | 01 | B V I | 650 | 1200 |
| 02 | V I | 3170 | 3600 | |||||||||
| 03 | V I | 3770 | 4600 | |||||||||
| SMC_SC4 | 159829 | SMC100.8 | 37214 | 4450 | 4500 | – | 15.895 ± 0.005 | 15.959 ± 0.009 | 01 | I | 2600 | 3000 |
| 02 | V I | 3430 | 4500 | |||||||||
| SMC_SC4 | 159857 | SMC100.8 | 45127 | 3000 | 3500 | – | 15.626 ± 0.004 | 15.8 ± 0.008 | 01 | I | 780 | 1400 |
| 02 | V I | 3600 | 4300 | |||||||||
| SMC_SC4 | 163828 | SMC100.7 | 8813 | 600 | 700 | 17.171 ± 0.009 | 17.164 ± 0.009 | 16.953 ± 0.013 | 01 | B V I | 700 | 2400 |
| SMC_SC4 | 167554 | SMC100.7 | 51098 | 3000 | 4500 | – | 17.258 ± 0.009 | 17.2 ± 0.016 | 01 | I | 1620 | 1900 |
| 02 | V I | 4700 | 5000 | |||||||||
| SMC_SC4 | 171253 | SMC100.7 | 42620 | 700 | 1200 | 15.674 ± 0.01 | 15.714 ± 0.009 | 15.691 ± 0.006 | 01 | I | 1410 | 1900 |
| 02 | V I | 3245 | 4000 | |||||||||
| SMC_SC4 | 175272 | SMC100.6 | 7362 | 3950 | 4000 | – | 16.579 ± 0.005 | 16.431 ± 0.009 | 01 | I | 2600 | 3800 |
| SMC_SC4 | 179053 | SMC100.6 | 38443 | 0 | 1000 | 16.304 ± 0.009 | 16.339 ± 0.009 | 16.148 ± 0.008 | 01 | I | 1300 | 2400 |
| SMC_SC5 | 11453 | SMC100.8 | 14734 | 3300 | 3400 | – | 15.871 ± 0.004 | 15.779 ± 0.008 | 01 | I | 3400 | 5000 |
| SMC_SC5 | 21117 | SMC100.8 | 52883 | 3650 | 3750 | – | 16.051 ± 0.004 | 16.143 ± 0.009 | 01 | V I | 970 | 2000 |
| 02 | I | 2200 | 2800 | |||||||||
| 03 | I | 2900 | 3400 | |||||||||
| 04 | V I | 3850 | 5000 | |||||||||
| SMC_SC5 | 21134 | SMC100.8 | 45175 | 1000 | 1500 | 15.994 ± 0.013 | 16.023 ± 0.006 | 16.091 ± 0.007 | 01 | I | 1600 | 2000 |
| SMC_SC5 | 32377 | SMC100.7 | 50838 | 4050 | 4100 | – | 15.844 ± 0.003 | 15.941 ± 0.008 | 01 | I | 3030 | 3400 |
| 02 | I | 4350 | 5000 | |||||||||
| SMC_SC5 | 43650 | SMC100.6 | 15248 | 1400 | 2000 | 17.177 ± 0.013 | 17.214 ± 0.01 | 17.305 ± 0.017 | 01 | V I | 750 | 2000 |
| 02 | V I | 2550 | 5000 | |||||||||
| SMC_SC5 | 54851 | SMC100.5 | 14725 | 600 | 850 | 16.264 ± 0.01 | 16.311 ± 0.009 | 16.366 ± 0.008 | 01 | B V I | 850 | 2000 |
| 02 | I | 2120 | 3600 | |||||||||
| 03 | V I | 3650 | 5000 | |||||||||
| SMC_SC5 | 65500 | SMC101.8 | 21127 | 1000 | 1500 | 16.034 ± 0.011 | 15.981 ± 0.007 | 15.959 ± 0.006 | 01 | B V I | 600 | 1000 |
| SMC_SC5 | 129535 | SMC100.6 | 53957 | 4700 | 4800 | – | 16.923 ± 0.008 | 16.953 ± 0.013 | 01 | V I | 3300 | 5000 |
| SMC_SC5 | 145724 | SMC101.8 | 21370 | 3000 | 3200 | – | – | 17.116 ± 0.019 | 01 | I | 3230 | 5000 |
| SMC_SC5 | 180034 | SMC100.1 | 27826 | 3900 | 4100 | – | 16.436 ± 0.005 | 16.431 ± 0.009 | 01 | V I | 4120 | 5000 |
| SMC_SC5 | 260841 | SMC100.1 | 36050 | 800 | 900 | 15.858 ± 0.011 | 16.013 ± 0.008 | 16.182 ± 0.008 | 01 | I | 1500 | 2200 |
| 02 | V I | 3800 | 4800 | |||||||||
| SMC_SC5 | 260957 | SMC100.1 | 36101 | 1200 | 1700 | 16.747 ± 0.009 | 16.917 ± 0.009 | 17.043 ± 0.015 | 01 | V I | 3620 | 5000 |
| SMC_SC5 | 266088 | SMC100.2 | 9240 | 700 | 750 | 17.227 ± 0.012 | 17.315 ± 0.01 | 17.408 ± 0.016 | 01 | B V I | 750 | 2000 |
| SMC_SC5 | 276982 | SMC100.3 | 9403 | 4400 | 4500 | – | 15.993 ± 0.005 | 15.757 ± 0.008 | 01 | V I | 3030 | 4500 |
| SMC_SC5 | 282963 | SMC100.3 | 9408 | 1000 | 1500 | 15.431 ± 0.009 | 15.591 ± 0.006 | 15.665 ± 0.005 | 01 | I | 1600 | 4300 |
| SMC_SC6 | 11085 | SMC100.1 | 36096 | 700 | 1100 | 15.52 ± 0.01 | 15.667 ± 0.007 | 15.863 ± 0.006 | 01 | V I | 1400 | 2000 |
| 02 | V I | 3900 | 5000 | |||||||||
| SMC_SC6 | 17538 | SMC100.2 | 9240 | 0 | 750 | 17.213 ± 0.012 | 17.315 ± 0.013 | 17.424 ± 0.015 | 01 | V I | 800 | 3000 |
| SMC_SC6 | 42440 | SMC100.3 | 56046 | 700 | 1100 | 16.867 ± 0.012 | 17.01 ± 0.011 | 17.19 ± 0.017 | 01 | I | 1400 | 3500 |
| SMC_SC6 | 99991 | SMC100.1 | 43700 | 1300 | 1800 | 15.755 ± 0.007 | 15.923 ± 0.007 | 16.126 ± 0.009 | 01 | I | 650 | 1400 |
| 02 | I | 1800 | 2500 | |||||||||
| 03 | I | 3150 | 4000 | |||||||||
| 04 | I | 4200 | 5000 | |||||||||
| SMC_SC6 | 105368 | SMC100.2 | 17645 | 600 | 1200 | 16.462 ± 0.011 | 16.592 ± 0.008 | 16.681 ± 0.011 | 01 | V I | 1150 | 2000 |
| 02 | I | 2700 | 4000 | |||||||||
| SMC_SC6 | 116294 | SMC100.2 | 49901 | 0 | 900 | 16.775 ± 0.012 | 16.958 ± 0.01 | 17.085 ± 0.013 | 01 | I | 985 | 2000 |
| SMC_SC6 | 128831 | SMC100.3 | 55954 | 600 | 1200 | 15.849 ± 0.009 | 16.018 ± 0.007 | 16.116 ± 0.007 | 01 | I | 1445 | 2600 |
| SMC_SC6 | 199611 | SMC100.3 | 29080 | 600 | 1300 | 15.265 ± 0.011 | 15.447 ± 0.008 | 15.594 ± 0.006 | 01 | I | 1500 | 2000 |
| SMC_SC6 | 272665 | SMC106.6 | 26640 | 1000 | 1500 | 17.784 ± 0.016 | 17.962 ± 0.016 | 18.04 ± 0.029 | 01 | I | 1620 | 4500 |
| SMC_SC7 | 57131 | SMC105.6 | 33029 | 1200 | 2000 | 16.037 ± 0.015 | 16.127 ± 0.008 | 16.269 ± 0.008 | 01 | I | 2780 | 3500 |
| SMC_SC8 | 183240 | SMC105.2 | 32029 | 3000 | 4000 | – | 14.783 ± 0.003 | 14.946 ± 0.005 | 01 | V I | 4150 | 4800 |
| SMC_SC9 | 105383 | SMC110.6 | 114 | 1000 | 1300 | 16.115 ± 0.01 | 16.264 ± 0.007 | 16.4 ± 0.009 | 01 | V I | 1240 | 3500 |
| 02 | V I | 3780 | 4800 | |||||||||
| SMC_SC9 | 168422 | SMC113.7 | 6330 | 4700 | 4850 | – | 17.002 ± 0.009 | 17.057 ± 0.014 | 01 | V I | 2700 | 4850 |
| SMC_SC10 | 8906 | SMC110.6 | 22338 | 4500 | 5000 | – | 15.253 ± 0.003 | 15.382 ± 0.006 | 01 | I | 2935 | 3300 |
| 02 | V I | 3650 | 3710 | |||||||||
| SMC_SC11 | 28090 | SMC113.2 | 4458 | 4500 | 5000 | – | 15.248 ± 0.004 | 15.433 ± 0.006 | 01 | V I | 2300 | 4500 |
| SMC_SC11 | 46587 | SMC110.3 | 16096 | 600 | 1000 | 17.087 ± 0.013 | 17.248 ± 0.01 | 17.343 ± 0.021 | 01 | I | 1110 | 4500 |
| OGLE-II . | OGLE-III . | Discless interval . | B* . | V* . | I* . | Bump . | Bands . | Bump interval . | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Field . | ID . | Field . | ID . | (JD-2450000) . | . | . | . | ID . | . | (JD-2450000) . | ||
| SMC_SC1 | 7612 | SMC133.4 | 8877 | 600 | 1300 | 15.926 ± 0.01 | 16.164 ± 0.009 | 16.443 ± 0.009 | 01 | I | 1420 | 2000 |
| 02 | I | 3250 | 3800 | |||||||||
| SMC_SC1 | 60553 | SMC128.6 | 57 | 3000 | 3500 | – | 15.418 ± 0.003 | 15.601 ± 0.007 | 01 | V I | 3500 | 5000 |
| SMC_SC1 | 75701 | SMC125.7 | 20383 | 3000 | 3500 | – | 15.397 ± 0.003 | 15.51 ± 0.006 | 01 | V I | 3650 | 5000 |
| SMC_SC1 | 92262 | SMC128.6 | 147 | 3500 | 3800 | – | 15.623 ± 0.003 | 15.811 ± 0.007 | 01 | I | 2600 | 3100 |
| 02 | V I | 3900 | 5000 | |||||||||
| SMC_SC2 | 94939 | SMC125.3 | 52 | 1000 | 1100 | 15.832 ± 0.008 | 15.991 ± 0.013 | 16.126 ± 0.007 | 01 | I | 1100 | 2000 |
| SMC_SC3 | 5719 | SMC125.1 | 20231 | 2980 | 3020 | – | – | 16.233 ± 0.01 | 01 | I | 1200 | 4500 |
| SMC_SC3 | 15970 | SMC125.2 | 28056 | 700 | 750 | 15.282 ± 0.01 | 15.412 ± 0.006 | 15.541 ± 0.006 | 01 | B V I | 750 | 2000 |
| 02 | I | 2200 | 3500 | |||||||||
| 03 | V I | 4000 | 5000 | |||||||||
| SMC_SC3 | 71445 | SMC125.2 | 34818 | 700 | 800 | 16.227 ± 0.01 | 16.425 ± 0.009 | 16.608 ± 0.012 | 01 | I | 1450 | 2400 |
| 02 | I | 4400 | 4700 | |||||||||
| SMC_SC3 | 125899 | SMC125.2 | 6200 | 3500 | 3750 | – | 15.837 ± 0.004 | 15.956 ± 0.008 | 01 | I | 2320 | 3400 |
| SMC_SC3 | 197941 | SMC125.3 | 25034 | 4000 | 4060 | – | 15.671 ± 0.003 | 15.724 ± 0.006 | 01 | V I | 2350 | 4000 |
| SMC_SC4 | 22859 | SMC125.4 | 22723 | 700 | 1200 | 17.068 ± 0.013 | 17.133 ± 0.012 | 17.129 ± 0.015 | 01 | V I | 1200 | 3500 |
| SMC_SC4 | 71499 | SMC100.7 | 34896 | 1000 | 1450 | 15.414 ± 0.011 | 15.553 ± 0.007 | 15.597 ± 0.006 | 01 | V I | 1430 | 2400 |
| 02 | V I | 2900 | 4400 | |||||||||
| SMC_SC4 | 120783 | SMC100.6 | 7129 | 4250 | 4500 | – | 14.401 ± 0.003 | 14.442 ± 0.005 | 01 | V I | 2750 | 4500 |
| SMC_SC4 | 127840 | SMC100.6 | 38372 | 3500 | 4500 | – | 14.853 ± 0.003 | 15.026 ± 0.006 | 01 | I | 2800 | 3500 |
| SMC_SC4 | 156248 | SMC100.8 | 14683 | 1000 | 1200 | 15.91 ± 0.01 | 15.964 ± 0.007 | 15.852 ± 0.006 | 01 | I | 1320 | 2300 |
| SMC_SC4 | 156251 | SMC100.8 | 14642 | 600 | 680 | 14.881 ± 0.005 | 15.13 ± 0.007 | 15.338 ± 0.005 | 01 | B V I | 650 | 1200 |
| 02 | V I | 3170 | 3600 | |||||||||
| 03 | V I | 3770 | 4600 | |||||||||
| SMC_SC4 | 159829 | SMC100.8 | 37214 | 4450 | 4500 | – | 15.895 ± 0.005 | 15.959 ± 0.009 | 01 | I | 2600 | 3000 |
| 02 | V I | 3430 | 4500 | |||||||||
| SMC_SC4 | 159857 | SMC100.8 | 45127 | 3000 | 3500 | – | 15.626 ± 0.004 | 15.8 ± 0.008 | 01 | I | 780 | 1400 |
| 02 | V I | 3600 | 4300 | |||||||||
| SMC_SC4 | 163828 | SMC100.7 | 8813 | 600 | 700 | 17.171 ± 0.009 | 17.164 ± 0.009 | 16.953 ± 0.013 | 01 | B V I | 700 | 2400 |
| SMC_SC4 | 167554 | SMC100.7 | 51098 | 3000 | 4500 | – | 17.258 ± 0.009 | 17.2 ± 0.016 | 01 | I | 1620 | 1900 |
| 02 | V I | 4700 | 5000 | |||||||||
| SMC_SC4 | 171253 | SMC100.7 | 42620 | 700 | 1200 | 15.674 ± 0.01 | 15.714 ± 0.009 | 15.691 ± 0.006 | 01 | I | 1410 | 1900 |
| 02 | V I | 3245 | 4000 | |||||||||
| SMC_SC4 | 175272 | SMC100.6 | 7362 | 3950 | 4000 | – | 16.579 ± 0.005 | 16.431 ± 0.009 | 01 | I | 2600 | 3800 |
| SMC_SC4 | 179053 | SMC100.6 | 38443 | 0 | 1000 | 16.304 ± 0.009 | 16.339 ± 0.009 | 16.148 ± 0.008 | 01 | I | 1300 | 2400 |
| SMC_SC5 | 11453 | SMC100.8 | 14734 | 3300 | 3400 | – | 15.871 ± 0.004 | 15.779 ± 0.008 | 01 | I | 3400 | 5000 |
| SMC_SC5 | 21117 | SMC100.8 | 52883 | 3650 | 3750 | – | 16.051 ± 0.004 | 16.143 ± 0.009 | 01 | V I | 970 | 2000 |
| 02 | I | 2200 | 2800 | |||||||||
| 03 | I | 2900 | 3400 | |||||||||
| 04 | V I | 3850 | 5000 | |||||||||
| SMC_SC5 | 21134 | SMC100.8 | 45175 | 1000 | 1500 | 15.994 ± 0.013 | 16.023 ± 0.006 | 16.091 ± 0.007 | 01 | I | 1600 | 2000 |
| SMC_SC5 | 32377 | SMC100.7 | 50838 | 4050 | 4100 | – | 15.844 ± 0.003 | 15.941 ± 0.008 | 01 | I | 3030 | 3400 |
| 02 | I | 4350 | 5000 | |||||||||
| SMC_SC5 | 43650 | SMC100.6 | 15248 | 1400 | 2000 | 17.177 ± 0.013 | 17.214 ± 0.01 | 17.305 ± 0.017 | 01 | V I | 750 | 2000 |
| 02 | V I | 2550 | 5000 | |||||||||
| SMC_SC5 | 54851 | SMC100.5 | 14725 | 600 | 850 | 16.264 ± 0.01 | 16.311 ± 0.009 | 16.366 ± 0.008 | 01 | B V I | 850 | 2000 |
| 02 | I | 2120 | 3600 | |||||||||
| 03 | V I | 3650 | 5000 | |||||||||
| SMC_SC5 | 65500 | SMC101.8 | 21127 | 1000 | 1500 | 16.034 ± 0.011 | 15.981 ± 0.007 | 15.959 ± 0.006 | 01 | B V I | 600 | 1000 |
| SMC_SC5 | 129535 | SMC100.6 | 53957 | 4700 | 4800 | – | 16.923 ± 0.008 | 16.953 ± 0.013 | 01 | V I | 3300 | 5000 |
| SMC_SC5 | 145724 | SMC101.8 | 21370 | 3000 | 3200 | – | – | 17.116 ± 0.019 | 01 | I | 3230 | 5000 |
| SMC_SC5 | 180034 | SMC100.1 | 27826 | 3900 | 4100 | – | 16.436 ± 0.005 | 16.431 ± 0.009 | 01 | V I | 4120 | 5000 |
| SMC_SC5 | 260841 | SMC100.1 | 36050 | 800 | 900 | 15.858 ± 0.011 | 16.013 ± 0.008 | 16.182 ± 0.008 | 01 | I | 1500 | 2200 |
| 02 | V I | 3800 | 4800 | |||||||||
| SMC_SC5 | 260957 | SMC100.1 | 36101 | 1200 | 1700 | 16.747 ± 0.009 | 16.917 ± 0.009 | 17.043 ± 0.015 | 01 | V I | 3620 | 5000 |
| SMC_SC5 | 266088 | SMC100.2 | 9240 | 700 | 750 | 17.227 ± 0.012 | 17.315 ± 0.01 | 17.408 ± 0.016 | 01 | B V I | 750 | 2000 |
| SMC_SC5 | 276982 | SMC100.3 | 9403 | 4400 | 4500 | – | 15.993 ± 0.005 | 15.757 ± 0.008 | 01 | V I | 3030 | 4500 |
| SMC_SC5 | 282963 | SMC100.3 | 9408 | 1000 | 1500 | 15.431 ± 0.009 | 15.591 ± 0.006 | 15.665 ± 0.005 | 01 | I | 1600 | 4300 |
| SMC_SC6 | 11085 | SMC100.1 | 36096 | 700 | 1100 | 15.52 ± 0.01 | 15.667 ± 0.007 | 15.863 ± 0.006 | 01 | V I | 1400 | 2000 |
| 02 | V I | 3900 | 5000 | |||||||||
| SMC_SC6 | 17538 | SMC100.2 | 9240 | 0 | 750 | 17.213 ± 0.012 | 17.315 ± 0.013 | 17.424 ± 0.015 | 01 | V I | 800 | 3000 |
| SMC_SC6 | 42440 | SMC100.3 | 56046 | 700 | 1100 | 16.867 ± 0.012 | 17.01 ± 0.011 | 17.19 ± 0.017 | 01 | I | 1400 | 3500 |
| SMC_SC6 | 99991 | SMC100.1 | 43700 | 1300 | 1800 | 15.755 ± 0.007 | 15.923 ± 0.007 | 16.126 ± 0.009 | 01 | I | 650 | 1400 |
| 02 | I | 1800 | 2500 | |||||||||
| 03 | I | 3150 | 4000 | |||||||||
| 04 | I | 4200 | 5000 | |||||||||
| SMC_SC6 | 105368 | SMC100.2 | 17645 | 600 | 1200 | 16.462 ± 0.011 | 16.592 ± 0.008 | 16.681 ± 0.011 | 01 | V I | 1150 | 2000 |
| 02 | I | 2700 | 4000 | |||||||||
| SMC_SC6 | 116294 | SMC100.2 | 49901 | 0 | 900 | 16.775 ± 0.012 | 16.958 ± 0.01 | 17.085 ± 0.013 | 01 | I | 985 | 2000 |
| SMC_SC6 | 128831 | SMC100.3 | 55954 | 600 | 1200 | 15.849 ± 0.009 | 16.018 ± 0.007 | 16.116 ± 0.007 | 01 | I | 1445 | 2600 |
| SMC_SC6 | 199611 | SMC100.3 | 29080 | 600 | 1300 | 15.265 ± 0.011 | 15.447 ± 0.008 | 15.594 ± 0.006 | 01 | I | 1500 | 2000 |
| SMC_SC6 | 272665 | SMC106.6 | 26640 | 1000 | 1500 | 17.784 ± 0.016 | 17.962 ± 0.016 | 18.04 ± 0.029 | 01 | I | 1620 | 4500 |
| SMC_SC7 | 57131 | SMC105.6 | 33029 | 1200 | 2000 | 16.037 ± 0.015 | 16.127 ± 0.008 | 16.269 ± 0.008 | 01 | I | 2780 | 3500 |
| SMC_SC8 | 183240 | SMC105.2 | 32029 | 3000 | 4000 | – | 14.783 ± 0.003 | 14.946 ± 0.005 | 01 | V I | 4150 | 4800 |
| SMC_SC9 | 105383 | SMC110.6 | 114 | 1000 | 1300 | 16.115 ± 0.01 | 16.264 ± 0.007 | 16.4 ± 0.009 | 01 | V I | 1240 | 3500 |
| 02 | V I | 3780 | 4800 | |||||||||
| SMC_SC9 | 168422 | SMC113.7 | 6330 | 4700 | 4850 | – | 17.002 ± 0.009 | 17.057 ± 0.014 | 01 | V I | 2700 | 4850 |
| SMC_SC10 | 8906 | SMC110.6 | 22338 | 4500 | 5000 | – | 15.253 ± 0.003 | 15.382 ± 0.006 | 01 | I | 2935 | 3300 |
| 02 | V I | 3650 | 3710 | |||||||||
| SMC_SC11 | 28090 | SMC113.2 | 4458 | 4500 | 5000 | – | 15.248 ± 0.004 | 15.433 ± 0.006 | 01 | V I | 2300 | 4500 |
| SMC_SC11 | 46587 | SMC110.3 | 16096 | 600 | 1000 | 17.087 ± 0.013 | 17.248 ± 0.01 | 17.343 ± 0.021 | 01 | I | 1110 | 4500 |
| OGLE-II . | OGLE-III . | Discless interval . | B* . | V* . | I* . | Bump . | Bands . | Bump interval . | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Field . | ID . | Field . | ID . | (JD-2450000) . | . | . | . | ID . | . | (JD-2450000) . | ||
| SMC_SC1 | 7612 | SMC133.4 | 8877 | 600 | 1300 | 15.926 ± 0.01 | 16.164 ± 0.009 | 16.443 ± 0.009 | 01 | I | 1420 | 2000 |
| 02 | I | 3250 | 3800 | |||||||||
| SMC_SC1 | 60553 | SMC128.6 | 57 | 3000 | 3500 | – | 15.418 ± 0.003 | 15.601 ± 0.007 | 01 | V I | 3500 | 5000 |
| SMC_SC1 | 75701 | SMC125.7 | 20383 | 3000 | 3500 | – | 15.397 ± 0.003 | 15.51 ± 0.006 | 01 | V I | 3650 | 5000 |
| SMC_SC1 | 92262 | SMC128.6 | 147 | 3500 | 3800 | – | 15.623 ± 0.003 | 15.811 ± 0.007 | 01 | I | 2600 | 3100 |
| 02 | V I | 3900 | 5000 | |||||||||
| SMC_SC2 | 94939 | SMC125.3 | 52 | 1000 | 1100 | 15.832 ± 0.008 | 15.991 ± 0.013 | 16.126 ± 0.007 | 01 | I | 1100 | 2000 |
| SMC_SC3 | 5719 | SMC125.1 | 20231 | 2980 | 3020 | – | – | 16.233 ± 0.01 | 01 | I | 1200 | 4500 |
| SMC_SC3 | 15970 | SMC125.2 | 28056 | 700 | 750 | 15.282 ± 0.01 | 15.412 ± 0.006 | 15.541 ± 0.006 | 01 | B V I | 750 | 2000 |
| 02 | I | 2200 | 3500 | |||||||||
| 03 | V I | 4000 | 5000 | |||||||||
| SMC_SC3 | 71445 | SMC125.2 | 34818 | 700 | 800 | 16.227 ± 0.01 | 16.425 ± 0.009 | 16.608 ± 0.012 | 01 | I | 1450 | 2400 |
| 02 | I | 4400 | 4700 | |||||||||
| SMC_SC3 | 125899 | SMC125.2 | 6200 | 3500 | 3750 | – | 15.837 ± 0.004 | 15.956 ± 0.008 | 01 | I | 2320 | 3400 |
| SMC_SC3 | 197941 | SMC125.3 | 25034 | 4000 | 4060 | – | 15.671 ± 0.003 | 15.724 ± 0.006 | 01 | V I | 2350 | 4000 |
| SMC_SC4 | 22859 | SMC125.4 | 22723 | 700 | 1200 | 17.068 ± 0.013 | 17.133 ± 0.012 | 17.129 ± 0.015 | 01 | V I | 1200 | 3500 |
| SMC_SC4 | 71499 | SMC100.7 | 34896 | 1000 | 1450 | 15.414 ± 0.011 | 15.553 ± 0.007 | 15.597 ± 0.006 | 01 | V I | 1430 | 2400 |
| 02 | V I | 2900 | 4400 | |||||||||
| SMC_SC4 | 120783 | SMC100.6 | 7129 | 4250 | 4500 | – | 14.401 ± 0.003 | 14.442 ± 0.005 | 01 | V I | 2750 | 4500 |
| SMC_SC4 | 127840 | SMC100.6 | 38372 | 3500 | 4500 | – | 14.853 ± 0.003 | 15.026 ± 0.006 | 01 | I | 2800 | 3500 |
| SMC_SC4 | 156248 | SMC100.8 | 14683 | 1000 | 1200 | 15.91 ± 0.01 | 15.964 ± 0.007 | 15.852 ± 0.006 | 01 | I | 1320 | 2300 |
| SMC_SC4 | 156251 | SMC100.8 | 14642 | 600 | 680 | 14.881 ± 0.005 | 15.13 ± 0.007 | 15.338 ± 0.005 | 01 | B V I | 650 | 1200 |
| 02 | V I | 3170 | 3600 | |||||||||
| 03 | V I | 3770 | 4600 | |||||||||
| SMC_SC4 | 159829 | SMC100.8 | 37214 | 4450 | 4500 | – | 15.895 ± 0.005 | 15.959 ± 0.009 | 01 | I | 2600 | 3000 |
| 02 | V I | 3430 | 4500 | |||||||||
| SMC_SC4 | 159857 | SMC100.8 | 45127 | 3000 | 3500 | – | 15.626 ± 0.004 | 15.8 ± 0.008 | 01 | I | 780 | 1400 |
| 02 | V I | 3600 | 4300 | |||||||||
| SMC_SC4 | 163828 | SMC100.7 | 8813 | 600 | 700 | 17.171 ± 0.009 | 17.164 ± 0.009 | 16.953 ± 0.013 | 01 | B V I | 700 | 2400 |
| SMC_SC4 | 167554 | SMC100.7 | 51098 | 3000 | 4500 | – | 17.258 ± 0.009 | 17.2 ± 0.016 | 01 | I | 1620 | 1900 |
| 02 | V I | 4700 | 5000 | |||||||||
| SMC_SC4 | 171253 | SMC100.7 | 42620 | 700 | 1200 | 15.674 ± 0.01 | 15.714 ± 0.009 | 15.691 ± 0.006 | 01 | I | 1410 | 1900 |
| 02 | V I | 3245 | 4000 | |||||||||
| SMC_SC4 | 175272 | SMC100.6 | 7362 | 3950 | 4000 | – | 16.579 ± 0.005 | 16.431 ± 0.009 | 01 | I | 2600 | 3800 |
| SMC_SC4 | 179053 | SMC100.6 | 38443 | 0 | 1000 | 16.304 ± 0.009 | 16.339 ± 0.009 | 16.148 ± 0.008 | 01 | I | 1300 | 2400 |
| SMC_SC5 | 11453 | SMC100.8 | 14734 | 3300 | 3400 | – | 15.871 ± 0.004 | 15.779 ± 0.008 | 01 | I | 3400 | 5000 |
| SMC_SC5 | 21117 | SMC100.8 | 52883 | 3650 | 3750 | – | 16.051 ± 0.004 | 16.143 ± 0.009 | 01 | V I | 970 | 2000 |
| 02 | I | 2200 | 2800 | |||||||||
| 03 | I | 2900 | 3400 | |||||||||
| 04 | V I | 3850 | 5000 | |||||||||
| SMC_SC5 | 21134 | SMC100.8 | 45175 | 1000 | 1500 | 15.994 ± 0.013 | 16.023 ± 0.006 | 16.091 ± 0.007 | 01 | I | 1600 | 2000 |
| SMC_SC5 | 32377 | SMC100.7 | 50838 | 4050 | 4100 | – | 15.844 ± 0.003 | 15.941 ± 0.008 | 01 | I | 3030 | 3400 |
| 02 | I | 4350 | 5000 | |||||||||
| SMC_SC5 | 43650 | SMC100.6 | 15248 | 1400 | 2000 | 17.177 ± 0.013 | 17.214 ± 0.01 | 17.305 ± 0.017 | 01 | V I | 750 | 2000 |
| 02 | V I | 2550 | 5000 | |||||||||
| SMC_SC5 | 54851 | SMC100.5 | 14725 | 600 | 850 | 16.264 ± 0.01 | 16.311 ± 0.009 | 16.366 ± 0.008 | 01 | B V I | 850 | 2000 |
| 02 | I | 2120 | 3600 | |||||||||
| 03 | V I | 3650 | 5000 | |||||||||
| SMC_SC5 | 65500 | SMC101.8 | 21127 | 1000 | 1500 | 16.034 ± 0.011 | 15.981 ± 0.007 | 15.959 ± 0.006 | 01 | B V I | 600 | 1000 |
| SMC_SC5 | 129535 | SMC100.6 | 53957 | 4700 | 4800 | – | 16.923 ± 0.008 | 16.953 ± 0.013 | 01 | V I | 3300 | 5000 |
| SMC_SC5 | 145724 | SMC101.8 | 21370 | 3000 | 3200 | – | – | 17.116 ± 0.019 | 01 | I | 3230 | 5000 |
| SMC_SC5 | 180034 | SMC100.1 | 27826 | 3900 | 4100 | – | 16.436 ± 0.005 | 16.431 ± 0.009 | 01 | V I | 4120 | 5000 |
| SMC_SC5 | 260841 | SMC100.1 | 36050 | 800 | 900 | 15.858 ± 0.011 | 16.013 ± 0.008 | 16.182 ± 0.008 | 01 | I | 1500 | 2200 |
| 02 | V I | 3800 | 4800 | |||||||||
| SMC_SC5 | 260957 | SMC100.1 | 36101 | 1200 | 1700 | 16.747 ± 0.009 | 16.917 ± 0.009 | 17.043 ± 0.015 | 01 | V I | 3620 | 5000 |
| SMC_SC5 | 266088 | SMC100.2 | 9240 | 700 | 750 | 17.227 ± 0.012 | 17.315 ± 0.01 | 17.408 ± 0.016 | 01 | B V I | 750 | 2000 |
| SMC_SC5 | 276982 | SMC100.3 | 9403 | 4400 | 4500 | – | 15.993 ± 0.005 | 15.757 ± 0.008 | 01 | V I | 3030 | 4500 |
| SMC_SC5 | 282963 | SMC100.3 | 9408 | 1000 | 1500 | 15.431 ± 0.009 | 15.591 ± 0.006 | 15.665 ± 0.005 | 01 | I | 1600 | 4300 |
| SMC_SC6 | 11085 | SMC100.1 | 36096 | 700 | 1100 | 15.52 ± 0.01 | 15.667 ± 0.007 | 15.863 ± 0.006 | 01 | V I | 1400 | 2000 |
| 02 | V I | 3900 | 5000 | |||||||||
| SMC_SC6 | 17538 | SMC100.2 | 9240 | 0 | 750 | 17.213 ± 0.012 | 17.315 ± 0.013 | 17.424 ± 0.015 | 01 | V I | 800 | 3000 |
| SMC_SC6 | 42440 | SMC100.3 | 56046 | 700 | 1100 | 16.867 ± 0.012 | 17.01 ± 0.011 | 17.19 ± 0.017 | 01 | I | 1400 | 3500 |
| SMC_SC6 | 99991 | SMC100.1 | 43700 | 1300 | 1800 | 15.755 ± 0.007 | 15.923 ± 0.007 | 16.126 ± 0.009 | 01 | I | 650 | 1400 |
| 02 | I | 1800 | 2500 | |||||||||
| 03 | I | 3150 | 4000 | |||||||||
| 04 | I | 4200 | 5000 | |||||||||
| SMC_SC6 | 105368 | SMC100.2 | 17645 | 600 | 1200 | 16.462 ± 0.011 | 16.592 ± 0.008 | 16.681 ± 0.011 | 01 | V I | 1150 | 2000 |
| 02 | I | 2700 | 4000 | |||||||||
| SMC_SC6 | 116294 | SMC100.2 | 49901 | 0 | 900 | 16.775 ± 0.012 | 16.958 ± 0.01 | 17.085 ± 0.013 | 01 | I | 985 | 2000 |
| SMC_SC6 | 128831 | SMC100.3 | 55954 | 600 | 1200 | 15.849 ± 0.009 | 16.018 ± 0.007 | 16.116 ± 0.007 | 01 | I | 1445 | 2600 |
| SMC_SC6 | 199611 | SMC100.3 | 29080 | 600 | 1300 | 15.265 ± 0.011 | 15.447 ± 0.008 | 15.594 ± 0.006 | 01 | I | 1500 | 2000 |
| SMC_SC6 | 272665 | SMC106.6 | 26640 | 1000 | 1500 | 17.784 ± 0.016 | 17.962 ± 0.016 | 18.04 ± 0.029 | 01 | I | 1620 | 4500 |
| SMC_SC7 | 57131 | SMC105.6 | 33029 | 1200 | 2000 | 16.037 ± 0.015 | 16.127 ± 0.008 | 16.269 ± 0.008 | 01 | I | 2780 | 3500 |
| SMC_SC8 | 183240 | SMC105.2 | 32029 | 3000 | 4000 | – | 14.783 ± 0.003 | 14.946 ± 0.005 | 01 | V I | 4150 | 4800 |
| SMC_SC9 | 105383 | SMC110.6 | 114 | 1000 | 1300 | 16.115 ± 0.01 | 16.264 ± 0.007 | 16.4 ± 0.009 | 01 | V I | 1240 | 3500 |
| 02 | V I | 3780 | 4800 | |||||||||
| SMC_SC9 | 168422 | SMC113.7 | 6330 | 4700 | 4850 | – | 17.002 ± 0.009 | 17.057 ± 0.014 | 01 | V I | 2700 | 4850 |
| SMC_SC10 | 8906 | SMC110.6 | 22338 | 4500 | 5000 | – | 15.253 ± 0.003 | 15.382 ± 0.006 | 01 | I | 2935 | 3300 |
| 02 | V I | 3650 | 3710 | |||||||||
| SMC_SC11 | 28090 | SMC113.2 | 4458 | 4500 | 5000 | – | 15.248 ± 0.004 | 15.433 ± 0.006 | 01 | V I | 2300 | 4500 |
| SMC_SC11 | 46587 | SMC110.3 | 16096 | 600 | 1000 | 17.087 ± 0.013 | 17.248 ± 0.01 | 17.343 ± 0.021 | 01 | I | 1110 | 4500 |
| OGLE-II . | OGLE-III . | Discless interval . | B* . | V* . | I* . | Bump . | Bands . | Bump interval . | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Field . | ID . | Field . | ID . | (JD-2450000) . | . | . | . | ID . | . | (JD-2450000) . | ||
| SMC_SC1 | 7612 | SMC133.4 | 8877 | 600 | 1300 | 15.926 ± 0.01 | 16.164 ± 0.009 | 16.443 ± 0.009 | 01 | I | 1420 | 2000 |
| 02 | I | 3250 | 3800 | |||||||||
| SMC_SC1 | 60553 | SMC128.6 | 57 | 3000 | 3500 | – | 15.418 ± 0.003 | 15.601 ± 0.007 | 01 | V I | 3500 | 5000 |
| SMC_SC1 | 75701 | SMC125.7 | 20383 | 3000 | 3500 | – | 15.397 ± 0.003 | 15.51 ± 0.006 | 01 | V I | 3650 | 5000 |
| SMC_SC1 | 92262 | SMC128.6 | 147 | 3500 | 3800 | – | 15.623 ± 0.003 | 15.811 ± 0.007 | 01 | I | 2600 | 3100 |
| 02 | V I | 3900 | 5000 | |||||||||
| SMC_SC2 | 94939 | SMC125.3 | 52 | 1000 | 1100 | 15.832 ± 0.008 | 15.991 ± 0.013 | 16.126 ± 0.007 | 01 | I | 1100 | 2000 |
| SMC_SC3 | 5719 | SMC125.1 | 20231 | 2980 | 3020 | – | – | 16.233 ± 0.01 | 01 | I | 1200 | 4500 |
| SMC_SC3 | 15970 | SMC125.2 | 28056 | 700 | 750 | 15.282 ± 0.01 | 15.412 ± 0.006 | 15.541 ± 0.006 | 01 | B V I | 750 | 2000 |
| 02 | I | 2200 | 3500 | |||||||||
| 03 | V I | 4000 | 5000 | |||||||||
| SMC_SC3 | 71445 | SMC125.2 | 34818 | 700 | 800 | 16.227 ± 0.01 | 16.425 ± 0.009 | 16.608 ± 0.012 | 01 | I | 1450 | 2400 |
| 02 | I | 4400 | 4700 | |||||||||
| SMC_SC3 | 125899 | SMC125.2 | 6200 | 3500 | 3750 | – | 15.837 ± 0.004 | 15.956 ± 0.008 | 01 | I | 2320 | 3400 |
| SMC_SC3 | 197941 | SMC125.3 | 25034 | 4000 | 4060 | – | 15.671 ± 0.003 | 15.724 ± 0.006 | 01 | V I | 2350 | 4000 |
| SMC_SC4 | 22859 | SMC125.4 | 22723 | 700 | 1200 | 17.068 ± 0.013 | 17.133 ± 0.012 | 17.129 ± 0.015 | 01 | V I | 1200 | 3500 |
| SMC_SC4 | 71499 | SMC100.7 | 34896 | 1000 | 1450 | 15.414 ± 0.011 | 15.553 ± 0.007 | 15.597 ± 0.006 | 01 | V I | 1430 | 2400 |
| 02 | V I | 2900 | 4400 | |||||||||
| SMC_SC4 | 120783 | SMC100.6 | 7129 | 4250 | 4500 | – | 14.401 ± 0.003 | 14.442 ± 0.005 | 01 | V I | 2750 | 4500 |
| SMC_SC4 | 127840 | SMC100.6 | 38372 | 3500 | 4500 | – | 14.853 ± 0.003 | 15.026 ± 0.006 | 01 | I | 2800 | 3500 |
| SMC_SC4 | 156248 | SMC100.8 | 14683 | 1000 | 1200 | 15.91 ± 0.01 | 15.964 ± 0.007 | 15.852 ± 0.006 | 01 | I | 1320 | 2300 |
| SMC_SC4 | 156251 | SMC100.8 | 14642 | 600 | 680 | 14.881 ± 0.005 | 15.13 ± 0.007 | 15.338 ± 0.005 | 01 | B V I | 650 | 1200 |
| 02 | V I | 3170 | 3600 | |||||||||
| 03 | V I | 3770 | 4600 | |||||||||
| SMC_SC4 | 159829 | SMC100.8 | 37214 | 4450 | 4500 | – | 15.895 ± 0.005 | 15.959 ± 0.009 | 01 | I | 2600 | 3000 |
| 02 | V I | 3430 | 4500 | |||||||||
| SMC_SC4 | 159857 | SMC100.8 | 45127 | 3000 | 3500 | – | 15.626 ± 0.004 | 15.8 ± 0.008 | 01 | I | 780 | 1400 |
| 02 | V I | 3600 | 4300 | |||||||||
| SMC_SC4 | 163828 | SMC100.7 | 8813 | 600 | 700 | 17.171 ± 0.009 | 17.164 ± 0.009 | 16.953 ± 0.013 | 01 | B V I | 700 | 2400 |
| SMC_SC4 | 167554 | SMC100.7 | 51098 | 3000 | 4500 | – | 17.258 ± 0.009 | 17.2 ± 0.016 | 01 | I | 1620 | 1900 |
| 02 | V I | 4700 | 5000 | |||||||||
| SMC_SC4 | 171253 | SMC100.7 | 42620 | 700 | 1200 | 15.674 ± 0.01 | 15.714 ± 0.009 | 15.691 ± 0.006 | 01 | I | 1410 | 1900 |
| 02 | V I | 3245 | 4000 | |||||||||
| SMC_SC4 | 175272 | SMC100.6 | 7362 | 3950 | 4000 | – | 16.579 ± 0.005 | 16.431 ± 0.009 | 01 | I | 2600 | 3800 |
| SMC_SC4 | 179053 | SMC100.6 | 38443 | 0 | 1000 | 16.304 ± 0.009 | 16.339 ± 0.009 | 16.148 ± 0.008 | 01 | I | 1300 | 2400 |
| SMC_SC5 | 11453 | SMC100.8 | 14734 | 3300 | 3400 | – | 15.871 ± 0.004 | 15.779 ± 0.008 | 01 | I | 3400 | 5000 |
| SMC_SC5 | 21117 | SMC100.8 | 52883 | 3650 | 3750 | – | 16.051 ± 0.004 | 16.143 ± 0.009 | 01 | V I | 970 | 2000 |
| 02 | I | 2200 | 2800 | |||||||||
| 03 | I | 2900 | 3400 | |||||||||
| 04 | V I | 3850 | 5000 | |||||||||
| SMC_SC5 | 21134 | SMC100.8 | 45175 | 1000 | 1500 | 15.994 ± 0.013 | 16.023 ± 0.006 | 16.091 ± 0.007 | 01 | I | 1600 | 2000 |
| SMC_SC5 | 32377 | SMC100.7 | 50838 | 4050 | 4100 | – | 15.844 ± 0.003 | 15.941 ± 0.008 | 01 | I | 3030 | 3400 |
| 02 | I | 4350 | 5000 | |||||||||
| SMC_SC5 | 43650 | SMC100.6 | 15248 | 1400 | 2000 | 17.177 ± 0.013 | 17.214 ± 0.01 | 17.305 ± 0.017 | 01 | V I | 750 | 2000 |
| 02 | V I | 2550 | 5000 | |||||||||
| SMC_SC5 | 54851 | SMC100.5 | 14725 | 600 | 850 | 16.264 ± 0.01 | 16.311 ± 0.009 | 16.366 ± 0.008 | 01 | B V I | 850 | 2000 |
| 02 | I | 2120 | 3600 | |||||||||
| 03 | V I | 3650 | 5000 | |||||||||
| SMC_SC5 | 65500 | SMC101.8 | 21127 | 1000 | 1500 | 16.034 ± 0.011 | 15.981 ± 0.007 | 15.959 ± 0.006 | 01 | B V I | 600 | 1000 |
| SMC_SC5 | 129535 | SMC100.6 | 53957 | 4700 | 4800 | – | 16.923 ± 0.008 | 16.953 ± 0.013 | 01 | V I | 3300 | 5000 |
| SMC_SC5 | 145724 | SMC101.8 | 21370 | 3000 | 3200 | – | – | 17.116 ± 0.019 | 01 | I | 3230 | 5000 |
| SMC_SC5 | 180034 | SMC100.1 | 27826 | 3900 | 4100 | – | 16.436 ± 0.005 | 16.431 ± 0.009 | 01 | V I | 4120 | 5000 |
| SMC_SC5 | 260841 | SMC100.1 | 36050 | 800 | 900 | 15.858 ± 0.011 | 16.013 ± 0.008 | 16.182 ± 0.008 | 01 | I | 1500 | 2200 |
| 02 | V I | 3800 | 4800 | |||||||||
| SMC_SC5 | 260957 | SMC100.1 | 36101 | 1200 | 1700 | 16.747 ± 0.009 | 16.917 ± 0.009 | 17.043 ± 0.015 | 01 | V I | 3620 | 5000 |
| SMC_SC5 | 266088 | SMC100.2 | 9240 | 700 | 750 | 17.227 ± 0.012 | 17.315 ± 0.01 | 17.408 ± 0.016 | 01 | B V I | 750 | 2000 |
| SMC_SC5 | 276982 | SMC100.3 | 9403 | 4400 | 4500 | – | 15.993 ± 0.005 | 15.757 ± 0.008 | 01 | V I | 3030 | 4500 |
| SMC_SC5 | 282963 | SMC100.3 | 9408 | 1000 | 1500 | 15.431 ± 0.009 | 15.591 ± 0.006 | 15.665 ± 0.005 | 01 | I | 1600 | 4300 |
| SMC_SC6 | 11085 | SMC100.1 | 36096 | 700 | 1100 | 15.52 ± 0.01 | 15.667 ± 0.007 | 15.863 ± 0.006 | 01 | V I | 1400 | 2000 |
| 02 | V I | 3900 | 5000 | |||||||||
| SMC_SC6 | 17538 | SMC100.2 | 9240 | 0 | 750 | 17.213 ± 0.012 | 17.315 ± 0.013 | 17.424 ± 0.015 | 01 | V I | 800 | 3000 |
| SMC_SC6 | 42440 | SMC100.3 | 56046 | 700 | 1100 | 16.867 ± 0.012 | 17.01 ± 0.011 | 17.19 ± 0.017 | 01 | I | 1400 | 3500 |
| SMC_SC6 | 99991 | SMC100.1 | 43700 | 1300 | 1800 | 15.755 ± 0.007 | 15.923 ± 0.007 | 16.126 ± 0.009 | 01 | I | 650 | 1400 |
| 02 | I | 1800 | 2500 | |||||||||
| 03 | I | 3150 | 4000 | |||||||||
| 04 | I | 4200 | 5000 | |||||||||
| SMC_SC6 | 105368 | SMC100.2 | 17645 | 600 | 1200 | 16.462 ± 0.011 | 16.592 ± 0.008 | 16.681 ± 0.011 | 01 | V I | 1150 | 2000 |
| 02 | I | 2700 | 4000 | |||||||||
| SMC_SC6 | 116294 | SMC100.2 | 49901 | 0 | 900 | 16.775 ± 0.012 | 16.958 ± 0.01 | 17.085 ± 0.013 | 01 | I | 985 | 2000 |
| SMC_SC6 | 128831 | SMC100.3 | 55954 | 600 | 1200 | 15.849 ± 0.009 | 16.018 ± 0.007 | 16.116 ± 0.007 | 01 | I | 1445 | 2600 |
| SMC_SC6 | 199611 | SMC100.3 | 29080 | 600 | 1300 | 15.265 ± 0.011 | 15.447 ± 0.008 | 15.594 ± 0.006 | 01 | I | 1500 | 2000 |
| SMC_SC6 | 272665 | SMC106.6 | 26640 | 1000 | 1500 | 17.784 ± 0.016 | 17.962 ± 0.016 | 18.04 ± 0.029 | 01 | I | 1620 | 4500 |
| SMC_SC7 | 57131 | SMC105.6 | 33029 | 1200 | 2000 | 16.037 ± 0.015 | 16.127 ± 0.008 | 16.269 ± 0.008 | 01 | I | 2780 | 3500 |
| SMC_SC8 | 183240 | SMC105.2 | 32029 | 3000 | 4000 | – | 14.783 ± 0.003 | 14.946 ± 0.005 | 01 | V I | 4150 | 4800 |
| SMC_SC9 | 105383 | SMC110.6 | 114 | 1000 | 1300 | 16.115 ± 0.01 | 16.264 ± 0.007 | 16.4 ± 0.009 | 01 | V I | 1240 | 3500 |
| 02 | V I | 3780 | 4800 | |||||||||
| SMC_SC9 | 168422 | SMC113.7 | 6330 | 4700 | 4850 | – | 17.002 ± 0.009 | 17.057 ± 0.014 | 01 | V I | 2700 | 4850 |
| SMC_SC10 | 8906 | SMC110.6 | 22338 | 4500 | 5000 | – | 15.253 ± 0.003 | 15.382 ± 0.006 | 01 | I | 2935 | 3300 |
| 02 | V I | 3650 | 3710 | |||||||||
| SMC_SC11 | 28090 | SMC113.2 | 4458 | 4500 | 5000 | – | 15.248 ± 0.004 | 15.433 ± 0.006 | 01 | V I | 2300 | 4500 |
| SMC_SC11 | 46587 | SMC110.3 | 16096 | 600 | 1000 | 17.087 ± 0.013 | 17.248 ± 0.01 | 17.343 ± 0.021 | 01 | I | 1110 | 4500 |
As explained in Section 3.4, the magnitudes at the inactive phase are necessary to set the baseline level of the light curves and to provide an estimate of stellar parameters. In order to do the latter, these apparent magnitudes must be colour-corrected and converted to absolute magnitudes by the standard formula MX* = X* − (5 log d − 5) − AX. We adopted as the distance to the SMC d = 60.3 ± 3.8 kpc from Hilditch, Howarth & Harries (2005). The mean E(V − I) of the RR Lyrae stars over the whole SMC is E(V − I) = 0.07 ± 0.06 mag (Haschke, Grebel & Duffau 2011). The reddening in the B, V, and I bands were obtained by the relations AX/AV given by Gordon et al. (2003).
The colour–magnitude diagram (CMD) of Fig. 7 compares the grid of discless models (Table 3) to our sample of Be stars. The majority of our sample is comprised of early-type Be stars, as further discussed in Section 5.2.1.
Colour–magnitude diagram of simulated discless stars (Table 3). Circles, triangles, squares, and diamonds correspond to stellar models with M = 6.0, 8.3, 11.7, 20.0 M⊙, respectively. The colours red, orange, yellow, green, and blue correspond, respectively, to the five values of W in increasing order. The six different stellar ages are seen as the groups of points move in the upper-right direction. For each star, the effect of going from |$90\,\deg$| to |$0\,\deg$| is to move in the upper-left direction. Also shown, as error bars, is the position of our selected stars (see eighth and ninth columns of Table 5). The blue and red error bars mark the positions of SMC_SC1 75701 and SMC_SC6 128831, respectively.
Our sample is also distributed in a broader range of MV − MI than our grid of main-sequence discless models, which is in accordance with the distribution Be star candidates of Mennickent et al. (2002) (see their fig. 7). It must be reminded also that our sample consists of type-1 and type-2 light curves from the SMC, meaning that they very likely belong to Be stars (Paul et al. 2012). There are two non-exclusive possibilities to explain these Be stars on the right of the main-sequence discless models: (1) The usage of an average E(V − I) for the entire SMS obviously does not take into consideration local variations of the reddening; therefore, the stars with large MV − MI in our sample may be the ones for which the reddening is larger than the average value. (2) These stars are post-main-sequence Be stars.
5 RESULTS
In this section, the results obtained by applying the pipeline to the stars and bumps of our sample are described. Initially, the results for the two objects of Fig. 1 are examined in detail (Section 5.1), followed by an analysis of the results obtained for the entire sample (Section 5.2).
5.1 SMC_SC1 75701 and SMC_SC6 128831
The results for SMC_SC1 75701 and SMC_SC6 128831 are shown in Figs 8 and 9, respectively. For SMC_SC1 75701 there was enough data for both the I and V bands to allow these two light curves to be fitted simultaneously. For SMC_SC6 128831, however, only I-band data was available. The times for the beginning of the build-up (t1) and dissipation (t2) are fitted quantities in the pipeline, but an initial estimate for them is provided to emcee by graphically analysing each light curve. These estimates are shown as the purple and orange segments in the horizontal straight lines in the figure. In the MCMC sampling, after a sufficient number of iterations, a stationary sample is obtained, for which the model parameters are more concentrated in the regions of higher posterior probability. In the plots we show 100 sets of randomly selected model curves obtained after the stationary sample was reached. The dispersion of the curves gives a visual measure of the goodness of the fits.
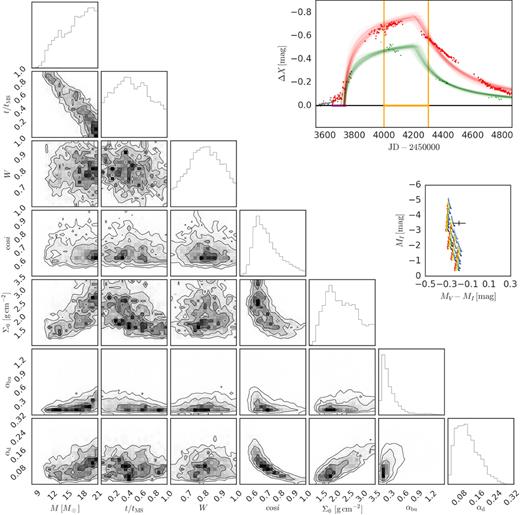
Upper-right: Light curve of SMC_SC1 75701. Thin lines: 100 model curves randomly selected from the stationary sample of the emcee code. The red (green) colour indicates the I (V) band. The purple and orange time intervals marked in the horizontal straight lines are the allowed intervals for the model parameters t1 and t2, respectively. Middle-right: CMD displaying the model grid of inactive Be stars and the position of SMC_SC1 75701 (see Fig. 7 for details). Below: Results of the emcee run for SMC_SC1 75701. Histogram distributions of the posterior probabilities (top panels) and two-by-two correlations of the stellar (M, t/tMS, and W), geometrical (cos i), and bump (Σ0, αbu, and αd) parameters (off-diagonal panels). The parameters t1 and t2 were not shown for convenience. The normalized density levels shown in the off-diagonal panels are |$12\,\,\rm{per\,\,cent}$|, |$39\,\,\rm{per\,\,cent}$|, |$68\,\,\rm{per\,\,cent}$|, |$87\,\,\rm{per\,\,cent}$| of the peak probability.
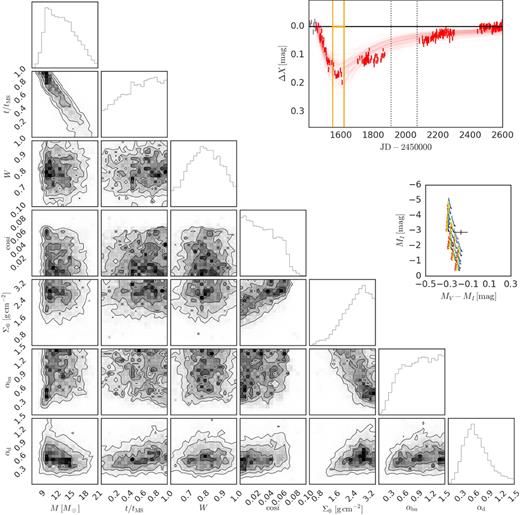
The goodness of the fit can be quantitatively assessed from the distribution of the posterior probabilities of each fitted parameter shown in Figs 8 and 9. The main diagonal of the triangular diagram plots the distributions of the stellar (M, t/tMS, and W), geometrical (cos i), and bump (Σ0, αbu, and αd) parameters, and they can be used to assess how well constrained each parameter is. The images below the diagonal show how the parameters correlate with each other.
The stellar parameters (M, t/tMS, and W) are mainly constrained by the magnitudes at the inactive phase. In Fig. 8, the three leftmost histograms along the diagonal have broad distributions, which means that these parameters are not well constrained. The first histogram shows that SMC_SC1 75701 is an early Be star, perhaps even more massive than the available stellar models (Table 3). The mass is anticorrelated with the main-sequence age (see t/tMS × M plane), as expected from the fact that a less massive but more evolved star can have a similar absolute magnitude of a younger, more massive star.
The bump parameters (Σ0, αbu, and αd) are mainly constrained by the shape of the observed bump. Roughly, the amplitude of the bump depends mostly on Σ0 (and cos i, see Fig. 2), while the value of viscosity parameter in each phase controls the rate of brightness variation. For SMC_SC1 75701, Σ0 has a broad distribution peaking around ∼1.5 g cm−2, indicating a quite dense disc, close to the densest cases in the sample of Vieira et al. (2017) for the same spectral type. This fact can also be inferred from Fig. 2, given the large observed |$\Delta I_\mathrm{bu}^\infty$|. The best-fitting viscosity parameters are |$\alpha _\mathrm{bu} = 0.25^{+0.21}_{-0.09}$| and |$\alpha _\mathrm{d} = 0.11^{+0.06}_{-0.04}$|.
Of the three bump parameters derived for SMC_SC1 75701, Σ0 and αd clearly anticorrelate with cos i, while αbu shows a weaker correlation. In fact, an anticorrelation of these three parameters with cos i is expected, as a consequence of the dependence of |$\Delta X_\mathrm{bu}^\infty$|, ξbu, and ξd, defined in Section 3.3, on cos i. Fig. 2 shows that, if the star is seen more pole-on (higher values of cos i), smaller values of Σ0 are required in order to obtain the fitted |$\Delta X_\mathrm{bu}^\infty$|, hence the strong anticorrelation seen in the Σ0 × cos i plane. Equation (22) shows that the fitted coefficient Cbu is proportional to the product of αbu and ξbu, and it was shown (Fig. 4) that discs seen more pole-on (higher values of cos i) appear to build-up faster (having higher values of ξbu). Therefore, for higher values of cos i, smaller values of αbu are required to obtain the fitted Cbu, which explains the anticorrelation in the αbu × cos i plane. Finally, equation (23) shows that the Cd is proportional to the product of αd and ξd, and it was shown in Fig. 5 that the more pole-on and the less dense the disc, the faster the rate of brightness variation in the dissipation, thus the anticorrelation expected in the αd × cos i plane.
The results for SMC_SC6 128831 (Fig. 9) point to a less massive star (|$M=12.9^{+3.6}_{-2.9}\, \mathrm{M}_{\odot }$|) surrounded by a much more massive disc (|$\Sigma _0=2.7^{+0.5}_{-0.8}\, \rm g\,cm^{-2}$|). SMC_SC6 128831 is an example of a dip, which means that this Be star is seen at a near edge-on angles. The very steep build-up phase of SMC_SC6 128831 hints to large mass injection rate and viscosity during build-up, as confirmed by the fifth and sixth histograms along the diagonal of Fig. 9. The viscosity parameter during dissipation was found to be |$\alpha _\mathrm{d} = 0.62^{+0.33}_{-0.23}$|. The plane αd × Σ0 shows a correlation, just as for the case of SMC_SC1 75701, which is a consequence of the decrescent relationship between ξd with Σ0, also expected for near-edge-on inclinations (see Fig. 5).
For SMC_SC6 128831 a positive correlation between Σ0, αbu, and αd with cos i was observed. Fig. 2 shows that, if the star moves away from the edge-on case (cos i = 0), bigger values of Σ0 are required in order to obtain the fitted |$\Delta X_\mathrm{bu}^\infty$|, hence the correlation seen in the Σ0 × cos i plane. Fig. 4 shows that, for the edge-on case there is no strong variation of ξbu with cos i. However, there is the trend that a more tenuous discs appear to build-up faster, specially for a hotter star. Therefore, since equation (22) shows that Cbu ∝ αbuξbu, it follows that, with the increase of Σ0 with cos i, the function ξbu decreases and, hence, αbu increases. Finally, equation (23) shows that Cd ∝ αdξd and Fig. 6 shows that ξd decreases with cos i and Σ0. Therefore, as Σ0 increases with cos i, it follows that ξd decreases and, hence, αd must increase. Similar trends were found for the other two edge-on stars in our samples SMC_SC1 92262 (Figs C4 and C5) and SMC_SC4 179053 (Fig. C34).
In general, the histograms of Fig. 9 are broader than the ones in Fig. 8, indicating that parameters are worse constrained than for SMC_SC1 75701. There are two main reasons for this. First, only I-band data was available for this star, which has a negative impact on the pipeline's ability to constrain the stellar parameters. The MCMC method ensures that the uncertainties in the stellar parameters are properly propagated into the other model parameters. Secondly, the fact that the dips have smaller amplitudes than the bumps of pole-on stars, even for higher values of Σ0, is a great disadvantage, because the bump amplitude is much closer to the noise level of the measurements.
The results of the pipeline for all stars in Table 5 are shown in Figs C1–C79, available electronically only. The best-fitting model parameters for all stars and bumps are listed in Table 6.
| OGLE-II ID . | Bump . | M (M⊙) . | t/tMS . | W . | cos i . | Σ0 . | αbu . | αd . | |$\tilde{\tau }_\mathrm{bu}$| . | |$\left(-\frac{\mathrm{\partial} M}{\mathrm{\partial} t}\right)_\mathrm{typ}$| . | |$\left(-\frac{\mathrm{\partial} J}{\mathrm{\partial} t}\right)_\mathrm{std}$| . | −ΔJ* . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | ID . | . | . | . | . | (g cm−2) . | . | . | . | (10−9 × . | (1036 × . | (1044 × . |
| . | . | . | . | . | . | . | . | . | . | M⊙ yr−1) . | g cm2 s−2) . | g cm2 s−1) . |
| SMC_SC1 7612 | 01 | |$13.7^{+3.0}_{-3.0}$| | |$0.4^{+0.3}_{-0.2}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.37^{+0.16}_{-0.05}$| | |$0.9^{+1.4}_{-0.5}$| | |$0.44^{+0.68}_{-0.34}$| | |$0.62^{+0.52}_{-0.4}$| | |$0.23^{+0.35}_{-0.18}$| | |$0.55^{+0.66}_{-0.34}$| | |$0.94^{+1.31}_{-0.6}$| | |$0.06^{+0.08}_{-0.04}$| |
| 02 | |$1.1^{+1.5}_{-0.6}$| | |$0.47^{+0.64}_{-0.34}$| | |$0.56^{+0.62}_{-0.38}$| | |$0.2^{+0.3}_{-0.14}$| | |$0.7^{+0.76}_{-0.44}$| | |$1.18^{+1.51}_{-0.76}$| | |$0.06^{+0.08}_{-0.04}$| | |||||
| SMC_SC1 60553 | 01 | |$13.8^{+3.5}_{-2.7}$| | |$0.7^{+0.2}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.62^{+0.1}_{-0.05}$| | |$1.9^{+1.0}_{-0.5}$| | |$1.26^{+0.17}_{-0.28}$| | |$0.1^{+0.04}_{-0.03}$| | |$3.07^{+0.57}_{-0.72}$| | |$4.72^{+1.94}_{-1.59}$| | |$9.12^{+4.64}_{-3.45}$| | |$2.93^{+1.45}_{-1.11}$| |
| SMC_SC1 75701 | 01 | |$17.0^{+2.8}_{-3.9}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.7^{+0.13}_{-0.07}$| | |$2.2^{+0.7}_{-0.5}$| | |$0.25^{+0.21}_{-0.09}$| | |$0.11^{+0.06}_{-0.04}$| | |$0.81^{+0.65}_{-0.3}$| | |$1.11^{+1.24}_{-0.51}$| | |$2.33^{+2.92}_{-1.17}$| | |$0.97^{+1.22}_{-0.49}$| |
| SMC_SC1 92262 | 01 | |$14.7^{+3.3}_{-2.9}$| | |$0.6^{+0.2}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.04^{+0.02}_{-0.02}$| | |$1.3^{+1.1}_{-0.7}$| | |$0.49^{+0.53}_{-0.3}$| | |$0.89^{+0.41}_{-0.47}$| | |$0.53^{+0.58}_{-0.31}$| | |$1.11^{+1.2}_{-0.6}$| | |$2.2^{+2.42}_{-1.21}$| | |$0.32^{+0.33}_{-0.17}$| |
| 02 | |$2.6^{+0.5}_{-0.5}$| | |$0.99^{+0.33}_{-0.36}$| | |$0.94^{+0.34}_{-0.32}$| | |$1.14^{+0.64}_{-0.44}$| | |$4.86^{+1.81}_{-1.35}$| | |$9.61^{+4.13}_{-2.88}$| | |$1.52^{+0.72}_{-0.48}$| | |||||
| SMC_SC2 94939 | 01 | |$12.0^{+3.0}_{-2.4}$| | |$0.6^{+0.3}_{-0.4}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.46^{+0.14}_{-0.07}$| | |$2.4^{+0.8}_{-0.8}$| | |$0.9^{+0.42}_{-0.43}$| | |$0.63^{+0.34}_{-0.32}$| | |$1.31^{+0.59}_{-0.61}$| | |$3.26^{+2.5}_{-1.74}$| | |$5.47^{+4.52}_{-2.98}$| | |$0.96^{+0.77}_{-0.53}$| |
| SMC_SC3 5719 | 01 | |$12.1^{+2.9}_{-2.6}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.41^{+0.1}_{-0.06}$| | |$2.6^{+0.6}_{-0.8}$| | |$0.68^{+0.46}_{-0.33}$| | |$0.38^{+0.21}_{-0.18}$| | |$4.15^{+2.74}_{-1.98}$| | |$2.74^{+2.49}_{-1.6}$| | |$4.59^{+4.31}_{-2.72}$| | |$3.28^{+3.06}_{-1.95}$| |
| SMC_SC3 15970 | 01 | |$15.0^{+2.7}_{-2.4}$| | |$0.7^{+0.2}_{-0.2}$| | |$0.82^{+0.09}_{-0.1}$| | |$0.62^{+0.03}_{-0.02}$| | |$1.3^{+0.4}_{-0.2}$| | |$0.72^{+0.3}_{-0.29}$| | |$0.12^{+0.05}_{-0.03}$| | |$1.52^{+0.69}_{-0.67}$| | |$2.08^{+1.17}_{-0.76}$| | |$4.3^{+3.07}_{-1.71}$| | |$1.26^{+0.81}_{-0.5}$| |
| 02 | |$1.5^{+0.4}_{-0.3}$| | |$0.78^{+0.37}_{-0.3}$| | |$0.17^{+0.05}_{-0.03}$| | |$2.05^{+1.01}_{-0.81}$| | |$2.68^{+1.64}_{-1.01}$| | |$5.53^{+4.21}_{-2.24}$| | |$2.02^{+1.58}_{-0.82}$| | |||||
| 03 | |$1.3^{+0.3}_{-0.2}$| | |$1.08^{+0.26}_{-0.27}$| | |$0.13^{+0.05}_{-0.05}$| | |$3.17^{+0.93}_{-0.96}$| | |$3.13^{+1.26}_{-0.99}$| | |$6.5^{+3.54}_{-2.39}$| | |$2.62^{+1.39}_{-0.96}$| | |||||
| SMC_SC3 71445 | 01 | |$10.5^{+2.4}_{-2.1}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.43^{+0.09}_{-0.06}$| | |$2.5^{+0.6}_{-0.7}$| | |$0.58^{+0.45}_{-0.28}$| | |$0.67^{+0.38}_{-0.29}$| | |$1.3^{+1.02}_{-0.6}$| | |$1.96^{+1.67}_{-1.05}$| | |$2.88^{+2.58}_{-1.6}$| | |$0.7^{+0.64}_{-0.39}$| |
| 02 | |$1.2^{+0.6}_{-0.4}$| | |$0.67^{+0.52}_{-0.35}$| | |$1.0^{+0.34}_{-0.37}$| | |$0.59^{+0.5}_{-0.31}$| | |$1.12^{+0.71}_{-0.49}$| | |$1.64^{+1.12}_{-0.74}$| | |$0.16^{+0.12}_{-0.07}$| | |||||
| SMC_SC3 125899 | 01 | |$13.9^{+3.3}_{-3.2}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.39^{+0.2}_{-0.07}$| | |$1.6^{+1.2}_{-0.8}$| | |$0.73^{+0.48}_{-0.4}$| | |$0.35^{+0.29}_{-0.19}$| | |$1.09^{+0.73}_{-0.61}$| | |$1.88^{+1.82}_{-1.13}$| | |$3.49^{+3.65}_{-2.16}$| | |$0.64^{+0.68}_{-0.39}$| |
| SMC_SC3 197941 | 01 | |$12.1^{+4.5}_{-2.0}$| | |$0.7^{+0.2}_{-0.4}$| | |$0.83^{+0.09}_{-0.11}$| | |$0.56^{+0.14}_{-0.04}$| | |$0.8^{+0.4}_{-0.2}$| | |$0.36^{+0.57}_{-0.21}$| | |$0.1^{+0.04}_{-0.03}$| | |$1.38^{+2.24}_{-0.82}$| | |$0.62^{+0.77}_{-0.34}$| | |$1.14^{+1.5}_{-0.66}$| | |$0.58^{+0.76}_{-0.33}$| |
| SMC_SC4 22859 | 01 | |$8.2^{+1.7}_{-1.6}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.8^{+0.11}_{-0.1}$| | |$0.64^{+0.19}_{-0.11}$| | |$0.3^{+0.2}_{-0.1}$| | |$0.68^{+0.56}_{-0.55}$| | |$0.03^{+0.66}_{-0.02}$| | |$4.16^{+4.08}_{-3.37}$| | |$0.2^{+0.18}_{-0.15}$| | |$0.23^{+0.23}_{-0.17}$| | |$0.13^{+0.15}_{-0.1}$| |
| SMC_SC4 71499 | 01 | |$17.3^{+2.4}_{-3.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.53^{+0.05}_{-0.03}$| | |$1.5^{+0.6}_{-0.4}$| | |$0.7^{+0.46}_{-0.32}$| | |$0.25^{+0.1}_{-0.07}$| | |$1.1^{+0.7}_{-0.51}$| | |$2.09^{+1.16}_{-0.86}$| | |$4.41^{+2.86}_{-2.0}$| | |$0.9^{+0.59}_{-0.4}$| |
| 02 | |$1.8^{+0.7}_{-0.5}$| | |$0.68^{+0.44}_{-0.31}$| | |$0.19^{+0.07}_{-0.06}$| | |$1.37^{+0.93}_{-0.62}$| | |$2.32^{+1.49}_{-1.0}$| | |$4.9^{+3.62}_{-2.28}$| | |$1.34^{+0.97}_{-0.62}$| | |||||
| SMC_SC4 120783 | 01 | |$18.2^{+1.9}_{-2.4}$| | |$0.9^{+0.1}_{-0.1}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.6^{+0.18}_{-0.08}$| | |$0.9^{+0.3}_{-0.2}$| | |$0.73^{+0.5}_{-0.47}$| | |$0.13^{+0.07}_{-0.05}$| | |$1.72^{+1.11}_{-1.1}$| | |$2.01^{+1.61}_{-1.05}$| | |$5.47^{+4.82}_{-2.84}$| | |$2.25^{+1.97}_{-1.16}$| |
| SMC_SC4 127840 | 01 | |$15.2^{+3.0}_{-2.3}$| | |$0.8^{+0.1}_{-0.2}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.65^{+0.12}_{-0.09}$| | |$2.8^{+0.5}_{-0.6}$| | |$0.39^{+0.21}_{-0.13}$| | |$0.76^{+0.4}_{-0.32}$| | |$0.57^{+0.28}_{-0.18}$| | |$2.95^{+2.15}_{-1.19}$| | |$6.77^{+5.27}_{-2.88}$| | |$1.52^{+1.16}_{-0.66}$| |
| SMC_SC4 156248 | 01 | |$12.9^{+3.2}_{-2.4}$| | |$0.7^{+0.2}_{-0.4}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.07^{+0.02}_{-0.04}$| | |$1.2^{+1.3}_{-0.8}$| | |$0.46^{+0.63}_{-0.32}$| | |$0.89^{+0.42}_{-0.48}$| | |$1.5^{+2.08}_{-1.05}$| | |$0.69^{+1.94}_{-0.45}$| | |$1.28^{+3.51}_{-0.83}$| | |$0.53^{+1.51}_{-0.35}$| |
| SMC_SC4 156251 | 01 | |$17.3^{+2.0}_{-2.4}$| | |$0.6^{+0.2}_{-0.2}$| | |$0.83^{+0.09}_{-0.1}$| | |$0.78^{+0.06}_{-0.05}$| | |$2.3^{+0.3}_{-0.4}$| | |$0.41^{+0.16}_{-0.09}$| | |$0.67^{+0.36}_{-0.27}$| | |$0.43^{+0.17}_{-0.1}$| | |$2.14^{+0.95}_{-0.63}$| | |$4.84^{+2.55}_{-1.58}$| | |$0.73^{+0.38}_{-0.25}$| |
| 02 | |$1.6^{+0.2}_{-0.2}$| | |$0.6^{+0.31}_{-0.2}$| | |$0.49^{+0.36}_{-0.16}$| | |$0.64^{+0.29}_{-0.2}$| | |$2.24^{+1.19}_{-0.7}$| | |$5.08^{+3.01}_{-1.77}$| | |$0.76^{+0.43}_{-0.26}$| | |||||
| 03 | |$2.8^{+0.4}_{-0.4}$| | |$0.93^{+0.36}_{-0.34}$| | |$0.49^{+0.16}_{-0.11}$| | |$1.25^{+0.48}_{-0.42}$| | |$5.88^{+2.75}_{-2.18}$| | |$13.27^{+7.36}_{-5.32}$| | |$2.52^{+1.42}_{-0.96}$| | |||||
| SMC_SC4 159829 | 01 | |$14.5^{+2.8}_{-3.0}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.59^{+0.07}_{-0.05}$| | |$2.5^{+0.7}_{-0.6}$| | |$1.05^{+0.29}_{-0.31}$| | |$0.26^{+0.09}_{-0.07}$| | |$1.64^{+0.5}_{-0.48}$| | |$4.16^{+1.75}_{-1.48}$| | |$7.59^{+3.8}_{-2.93}$| | |$1.44^{+0.68}_{-0.55}$| |
| 02 | |$2.5^{+0.6}_{-0.6}$| | |$0.96^{+0.34}_{-0.37}$| | |$0.72^{+0.28}_{-0.23}$| | |$2.6^{+0.91}_{-0.95}$| | |$3.82^{+1.64}_{-1.47}$| | |$6.92^{+3.45}_{-2.79}$| | |$2.25^{+1.11}_{-0.91}$| | |||||
| SMC_SC4 159857 | 01 | |$15.2^{+3.4}_{-3.3}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.54^{+0.08}_{-0.03}$| | |$0.7^{+1.2}_{-0.3}$| | |$0.45^{+0.63}_{-0.35}$| | |$0.67^{+0.49}_{-0.37}$| | |$0.33^{+0.5}_{-0.26}$| | |$0.59^{+0.48}_{-0.3}$| | |$1.15^{+1.08}_{-0.61}$| | |$0.11^{+0.11}_{-0.06}$| |
| 02 | |$1.1^{+0.7}_{-0.3}$| | |$0.62^{+0.48}_{-0.37}$| | |$0.32^{+0.62}_{-0.15}$| | |$0.43^{+0.3}_{-0.27}$| | |$1.33^{+0.77}_{-0.61}$| | |$2.63^{+1.79}_{-1.29}$| | |$0.22^{+0.15}_{-0.11}$| | |||||
| SMC_SC4 163828 | 01 | |$8.7^{+1.8}_{-1.8}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.72^{+0.14}_{-0.08}$| | |$0.6^{+0.2}_{-0.1}$| | |$0.48^{+0.58}_{-0.31}$| | |$0.04^{+0.04}_{-0.02}$| | |$3.76^{+4.54}_{-2.4}$| | |$0.29^{+0.33}_{-0.18}$| | |$0.34^{+0.42}_{-0.21}$| | |$0.25^{+0.31}_{-0.15}$| |
| SMC_SC4 167554 | 01 | |$9.2^{+1.9}_{-2.1}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.59^{+0.08}_{-0.05}$| | |$0.8^{+0.5}_{-0.2}$| | |$0.56^{+0.46}_{-0.34}$| | |$0.54^{+0.45}_{-0.24}$| | |$0.54^{+0.44}_{-0.34}$| | |$0.47^{+0.32}_{-0.2}$| | |$0.57^{+0.44}_{-0.25}$| | |$0.05^{+0.04}_{-0.02}$| |
| 02 | |$1.5^{+0.6}_{-0.4}$| | |$0.42^{+0.36}_{-0.18}$| | |$0.84^{+0.42}_{-0.34}$| | |$0.51^{+0.47}_{-0.21}$| | |$0.7^{+0.5}_{-0.29}$| | |$0.86^{+0.71}_{-0.39}$| | |$0.1^{+0.08}_{-0.05}$| | |||||
| SMC_SC4 171253 | 01 | |$16.5^{+2.5}_{-3.4}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.1}$| | |$0.59^{+0.14}_{-0.07}$| | |$0.3^{+1.2}_{-0.1}$| | |$0.41^{+0.73}_{-0.39}$| | |$0.78^{+0.5}_{-0.47}$| | |$0.38^{+0.65}_{-0.36}$| | |$0.2^{+0.28}_{-0.15}$| | |$0.41^{+0.58}_{-0.31}$| | |$0.05^{+0.07}_{-0.03}$| |
| 02 | |$0.4^{+0.5}_{-0.1}$| | |$0.54^{+0.6}_{-0.47}$| | |$0.67^{+0.5}_{-0.46}$| | |$0.4^{+0.44}_{-0.36}$| | |$0.3^{+0.32}_{-0.2}$| | |$0.59^{+0.69}_{-0.4}$| | |$0.05^{+0.07}_{-0.04}$| | |||||
| SMC_SC4 175272 | 01 | |$12.1^{+2.6}_{-2.8}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.12}$| | |$0.37^{+0.15}_{-0.05}$| | |$1.8^{+1.1}_{-0.7}$| | |$0.72^{+0.46}_{-0.39}$| | |$0.46^{+0.34}_{-0.23}$| | |$2.54^{+1.6}_{-1.38}$| | |$1.87^{+1.68}_{-1.13}$| | |$2.96^{+2.97}_{-1.82}$| | |$1.19^{+1.17}_{-0.74}$| |
| SMC_SC4 179053 | 01 | |$12.5^{+3.0}_{-2.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.03^{+0.03}_{-0.02}$| | |$2.1^{+0.9}_{-0.7}$| | |$0.78^{+0.46}_{-0.43}$| | |$1.08^{+0.3}_{-0.35}$| | |$2.12^{+1.4}_{-1.18}$| | |$2.28^{+1.67}_{-1.02}$| | |$3.81^{+3.09}_{-1.77}$| | |$1.2^{+0.98}_{-0.54}$| |
| SMC_SC5 11453 | 01 | |$14.6^{+3.3}_{-3.4}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.39^{+0.14}_{-0.06}$| | |$1.9^{+1.0}_{-0.8}$| | |$0.89^{+0.38}_{-0.39}$| | |$0.24^{+0.15}_{-0.11}$| | |$4.72^{+2.18}_{-2.0}$| | |$2.96^{+2.47}_{-1.71}$| | |$5.66^{+5.16}_{-3.43}$| | |$3.85^{+3.47}_{-2.35}$| |
| SMC_SC5 21117 | 01 | |$16.0^{+2.3}_{-2.6}$| | |$0.5^{+0.2}_{-0.2}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.52^{+0.03}_{-0.01}$| | |$1.4^{+0.4}_{-0.3}$| | |$0.55^{+0.37}_{-0.21}$| | |$0.55^{+0.42}_{-0.25}$| | |$0.83^{+0.57}_{-0.31}$| | |$1.48^{+0.84}_{-0.55}$| | |$3.0^{+2.0}_{-1.25}$| | |$0.58^{+0.39}_{-0.24}$| |
| 02 | |$2.1^{+0.8}_{-0.4}$| | |$0.75^{+0.38}_{-0.29}$| | |$0.15^{+0.08}_{-0.04}$| | |$1.15^{+0.55}_{-0.41}$| | |$2.89^{+2.02}_{-1.16}$| | |$5.77^{+4.94}_{-2.51}$| | |$1.16^{+0.94}_{-0.5}$| | |||||
| 03 | |$2.1^{+0.6}_{-0.5}$| | |$0.62^{+0.28}_{-0.21}$| | |$0.33^{+0.21}_{-0.11}$| | |$0.74^{+0.37}_{-0.25}$| | |$2.42^{+1.36}_{-0.86}$| | |$4.86^{+3.4}_{-1.97}$| | |$0.75^{+0.51}_{-0.3}$| | |||||
| 04 | |$1.6^{+0.3}_{-0.3}$| | |$0.72^{+0.31}_{-0.23}$| | |$0.13^{+0.07}_{-0.04}$| | |$2.96^{+1.15}_{-1.03}$| | |$2.23^{+1.11}_{-0.78}$| | |$4.5^{+2.69}_{-1.75}$| | |$2.28^{+1.48}_{-0.92}$| | |||||
| SMC_SC5 21134 | 01 | |$12.9^{+3.7}_{-2.8}$| | |$0.5^{+0.3}_{-0.4}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.41^{+0.22}_{-0.08}$| | |$0.7^{+1.6}_{-0.4}$| | |$0.43^{+0.66}_{-0.37}$| | |$0.15^{+0.3}_{-0.09}$| | |$0.44^{+0.74}_{-0.38}$| | |$0.42^{+0.56}_{-0.3}$| | |$0.72^{+1.06}_{-0.53}$| | |$0.09^{+0.13}_{-0.06}$| |
| SMC_SC5 32377 | 01 | |$14.3^{+3.1}_{-3.1}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.35^{+0.08}_{-0.04}$| | |$1.8^{+1.0}_{-0.7}$| | |$0.75^{+0.48}_{-0.41}$| | |$0.57^{+0.4}_{-0.26}$| | |$0.37^{+0.33}_{-0.2}$| | |$2.25^{+1.85}_{-1.11}$| | |$4.31^{+3.82}_{-2.24}$| | |$0.28^{+0.26}_{-0.15}$| |
| 02 | |$2.1^{+0.8}_{-0.7}$| | |$0.6^{+0.37}_{-0.27}$| | |$0.27^{+0.12}_{-0.11}$| | |$1.13^{+0.73}_{-0.49}$| | |$2.26^{+1.73}_{-1.11}$| | |$4.23^{+3.75}_{-2.13}$| | |$1.02^{+0.89}_{-0.52}$| | |||||
| SMC_SC5 43650 | 01 | |$8.9^{+2.0}_{-1.9}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.79^{+0.11}_{-0.1}$| | |$0.55^{+0.1}_{-0.04}$| | |$0.4^{+0.7}_{-0.1}$| | |$0.5^{+0.64}_{-0.45}$| | |$0.34^{+0.73}_{-0.26}$| | |$1.07^{+1.36}_{-0.95}$| | |$0.18^{+0.18}_{-0.12}$| | |$0.21^{+0.23}_{-0.14}$| | |$0.04^{+0.05}_{-0.03}$| |
| 02 | |$0.5^{+0.2}_{-0.1}$| | |$0.58^{+0.59}_{-0.43}$| | |$0.62^{+0.59}_{-0.51}$| | |$6.62^{+6.56}_{-4.92}$| | |$0.29^{+0.27}_{-0.19}$| | |$0.34^{+0.35}_{-0.23}$| | |$0.36^{+0.41}_{-0.24}$| | |||||
| SMC_SC5 54851 | 01 | |$12.5^{+2.4}_{-2.0}$| | |$0.6^{+0.2}_{-0.2}$| | |$0.82^{+0.09}_{-0.09}$| | |$0.62^{+0.03}_{-0.01}$| | |$1.1^{+0.3}_{-0.2}$| | |$0.74^{+0.35}_{-0.33}$| | |$0.1^{+0.04}_{-0.03}$| | |$1.85^{+0.85}_{-0.85}$| | |$1.41^{+0.74}_{-0.56}$| | |$2.44^{+1.54}_{-1.04}$| | |$0.73^{+0.48}_{-0.32}$| |
| 02 | |$1.2^{+0.3}_{-0.2}$| | |$0.76^{+0.35}_{-0.34}$| | |$0.11^{+0.03}_{-0.03}$| | |$2.08^{+0.89}_{-0.95}$| | |$1.55^{+0.8}_{-0.61}$| | |$2.67^{+1.67}_{-1.13}$| | |$0.88^{+0.52}_{-0.37}$| | |||||
| 03 | |$1.1^{+0.2}_{-0.1}$| | |$0.5^{+0.31}_{-0.18}$| | |$0.05^{+0.01}_{-0.01}$| | |$2.42^{+1.6}_{-0.86}$| | |$0.97^{+0.63}_{-0.39}$| | |$1.69^{+1.3}_{-0.76}$| | |$0.99^{+0.81}_{-0.45}$| | |||||
| SMC_SC5 65500 | 01 | |$12.8^{+3.3}_{-2.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.66^{+0.11}_{-0.05}$| | |$2.0^{+1.0}_{-0.6}$| | |$0.61^{+0.38}_{-0.27}$| | |$0.29^{+0.13}_{-0.11}$| | |$0.46^{+0.27}_{-0.19}$| | |$1.91^{+1.23}_{-0.88}$| | |$3.21^{+2.57}_{-1.62}$| | |$0.28^{+0.22}_{-0.14}$| |
| SMC_SC5 129535 | 01 | |$9.1^{+2.1}_{-2.0}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.57^{+0.13}_{-0.05}$| | |$0.7^{+0.2}_{-0.2}$| | |$0.63^{+0.53}_{-0.36}$| | |$0.22^{+0.27}_{-0.11}$| | |$4.4^{+3.69}_{-2.6}$| | |$0.49^{+0.39}_{-0.27}$| | |$0.61^{+0.52}_{-0.34}$| | |$0.42^{+0.37}_{-0.23}$| |
| SMC_SC5 145724 | 01 | |$8.6^{+2.1}_{-1.8}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.42^{+0.1}_{-0.05}$| | |$2.4^{+0.7}_{-0.8}$| | |$0.81^{+0.44}_{-0.41}$| | |$0.13^{+0.07}_{-0.06}$| | |$4.2^{+2.39}_{-2.09}$| | |$2.05^{+1.73}_{-1.15}$| | |$2.51^{+2.24}_{-1.4}$| | |$1.31^{+1.21}_{-0.75}$| |
| SMC_SC5 180034 | 01 | |$12.0^{+2.5}_{-2.5}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.63^{+0.15}_{-0.1}$| | |$1.0^{+0.5}_{-0.3}$| | |$0.32^{+0.55}_{-0.19}$| | |$0.19^{+0.15}_{-0.08}$| | |$0.91^{+1.56}_{-0.54}$| | |$0.45^{+0.57}_{-0.25}$| | |$0.71^{+0.95}_{-0.42}$| | |$0.22^{+0.27}_{-0.13}$| |
| SMC_SC5 260841 | 01 | |$13.4^{+4.0}_{-3.2}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.53^{+0.06}_{-0.02}$| | |$0.6^{+0.5}_{-0.1}$| | |$0.78^{+0.45}_{-0.52}$| | |$0.06^{+0.26}_{-0.02}$| | |$1.53^{+0.95}_{-1.05}$| | |$0.77^{+0.52}_{-0.4}$| | |$1.34^{+1.17}_{-0.69}$| | |$0.33^{+0.29}_{-0.17}$| |
| 02 | |$0.6^{+0.3}_{-0.1}$| | |$0.75^{+0.44}_{-0.44}$| | |$0.06^{+0.77}_{-0.03}$| | |$2.74^{+1.74}_{-1.78}$| | |$0.72^{+0.44}_{-0.35}$| | |$1.27^{+0.92}_{-0.62}$| | |$0.54^{+0.43}_{-0.28}$| | |||||
| SMC_SC5 260957 | 01 | |$8.9^{+2.1}_{-2.0}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.82^{+0.09}_{-0.11}$| | |$0.58^{+0.14}_{-0.06}$| | |$1.2^{+0.4}_{-0.3}$| | |$0.55^{+0.5}_{-0.24}$| | |$0.04^{+0.02}_{-0.02}$| | |$2.45^{+2.21}_{-1.1}$| | |$0.78^{+0.63}_{-0.4}$| | |$0.98^{+0.86}_{-0.54}$| | |$0.43^{+0.4}_{-0.23}$| |
| SMC_SC5 266088 | 01 | |$7.8^{+1.5}_{-1.6}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.7^{+0.14}_{-0.08}$| | |$0.7^{+0.4}_{-0.1}$| | |$0.3^{+0.69}_{-0.24}$| | |$0.06^{+0.05}_{-0.02}$| | |$1.92^{+4.42}_{-1.56}$| | |$0.17^{+0.3}_{-0.11}$| | |$0.18^{+0.34}_{-0.12}$| | |$0.11^{+0.19}_{-0.07}$| |
| SMC_SC5 276982 | 01 | |$17.1^{+2.2}_{-2.6}$| | |$0.2^{+0.2}_{-0.2}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.75^{+0.11}_{-0.1}$| | |$1.2^{+0.4}_{-0.3}$| | |$0.06^{+0.19}_{-0.03}$| | |$0.05^{+0.04}_{-0.02}$| | |$0.31^{+1.0}_{-0.16}$| | |$0.12^{+0.26}_{-0.06}$| | |$0.23^{+0.54}_{-0.13}$| | |$0.15^{+0.33}_{-0.08}$| |
| SMC_SC5 282963 | 01 | |$15.6^{+3.1}_{-3.6}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.38^{+0.19}_{-0.06}$| | |$1.7^{+1.0}_{-0.8}$| | |$0.62^{+0.51}_{-0.33}$| | |$0.39^{+0.32}_{-0.21}$| | |$5.62^{+4.36}_{-2.92}$| | |$2.07^{+2.43}_{-1.35}$| | |$4.14^{+5.39}_{-2.78}$| | |$4.96^{+6.18}_{-3.36}$| |
| SMC_SC6 11085 | 01 | |$17.8^{+1.9}_{-2.9}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.74^{+0.06}_{-0.05}$| | |$2.4^{+0.6}_{-0.5}$| | |$0.59^{+0.26}_{-0.18}$| | |$0.13^{+0.05}_{-0.04}$| | |$0.99^{+0.45}_{-0.3}$| | |$2.53^{+1.13}_{-0.87}$| | |$5.19^{+2.71}_{-1.99}$| | |$1.06^{+0.57}_{-0.4}$| |
| 02 | |$2.6^{+0.5}_{-0.4}$| | |$0.78^{+0.34}_{-0.27}$| | |$0.27^{+0.09}_{-0.07}$| | |$1.49^{+0.63}_{-0.5}$| | |$3.41^{+1.75}_{-1.29}$| | |$7.07^{+4.11}_{-3.0}$| | |$1.64^{+0.95}_{-0.68}$| | |||||
| SMC_SC6 17538 | 01 | |$7.8^{+1.6}_{-1.4}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.61^{+0.15}_{-0.08}$| | |$0.7^{+0.3}_{-0.2}$| | |$0.59^{+0.58}_{-0.41}$| | |$0.08^{+0.09}_{-0.04}$| | |$3.55^{+3.44}_{-2.47}$| | |$0.37^{+0.34}_{-0.22}$| | |$0.4^{+0.39}_{-0.24}$| | |$0.22^{+0.21}_{-0.13}$| |
| SMC_SC6 42440 | 01 | |$8.9^{+2.0}_{-2.0}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.36^{+0.15}_{-0.05}$| | |$1.8^{+1.2}_{-0.8}$| | |$0.78^{+0.45}_{-0.42}$| | |$0.19^{+0.17}_{-0.1}$| | |$2.82^{+1.81}_{-1.46}$| | |$1.36^{+1.32}_{-0.79}$| | |$1.66^{+1.84}_{-0.99}$| | |$0.61^{+0.72}_{-0.37}$| |
| SMC_SC6 99991 | 01 | |$14.8^{+2.6}_{-2.8}$| | |$0.5^{+0.2}_{-0.2}$| | |$0.83^{+0.09}_{-0.09}$| | |$0.34^{+0.04}_{-0.02}$| | |$1.7^{+0.6}_{-0.5}$| | |$0.62^{+0.43}_{-0.25}$| | |$0.98^{+0.31}_{-0.29}$| | |$0.88^{+0.64}_{-0.36}$| | |$1.85^{+1.11}_{-0.75}$| | |$3.54^{+2.45}_{-1.55}$| | |$0.64^{+0.44}_{-0.27}$| |
| 02 | |$2.2^{+0.7}_{-0.6}$| | |$0.62^{+0.33}_{-0.25}$| | |$0.74^{+0.33}_{-0.26}$| | |$1.13^{+0.62}_{-0.44}$| | |$2.37^{+1.58}_{-0.97}$| | |$4.47^{+3.48}_{-1.93}$| | |$1.02^{+0.8}_{-0.43}$| | |||||
| 03 | |$1.9^{+0.6}_{-0.5}$| | |$0.55^{+0.45}_{-0.22}$| | |$0.76^{+0.3}_{-0.24}$| | |$1.03^{+0.83}_{-0.43}$| | |$1.94^{+1.17}_{-0.77}$| | |$3.72^{+2.63}_{-1.65}$| | |$0.85^{+0.62}_{-0.37}$| | |||||
| 04 | |$1.7^{+0.5}_{-0.4}$| | |$0.53^{+0.36}_{-0.22}$| | |$0.92^{+0.3}_{-0.26}$| | |$1.12^{+0.77}_{-0.47}$| | |$1.56^{+0.97}_{-0.59}$| | |$2.96^{+2.18}_{-1.24}$| | |$0.79^{+0.59}_{-0.33}$| | |||||
| SMC_SC6 105368 | 01 | |$11.2^{+2.7}_{-2.9}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.53^{+0.04}_{-0.02}$| | |$0.9^{+0.4}_{-0.2}$| | |$0.51^{+0.57}_{-0.31}$| | |$0.17^{+0.1}_{-0.06}$| | |$1.12^{+1.23}_{-0.68}$| | |$0.61^{+0.56}_{-0.3}$| | |$0.92^{+0.91}_{-0.47}$| | |$0.22^{+0.22}_{-0.11}$| |
| 02 | |$1.2^{+0.5}_{-0.4}$| | |$0.28^{+0.48}_{-0.13}$| | |$0.19^{+0.13}_{-0.07}$| | |$0.78^{+1.38}_{-0.37}$| | |$0.5^{+0.48}_{-0.21}$| | |$0.76^{+0.77}_{-0.34}$| | |$0.23^{+0.25}_{-0.1}$| | |||||
| SMC_SC6 116294 | 01 | |$8.6^{+2.1}_{-1.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.41^{+0.1}_{-0.05}$| | |$2.6^{+0.7}_{-1.0}$| | |$0.87^{+0.4}_{-0.39}$| | |$0.16^{+0.09}_{-0.07}$| | |$2.71^{+1.35}_{-1.23}$| | |$2.42^{+1.65}_{-1.34}$| | |$2.99^{+2.11}_{-1.69}$| | |$0.93^{+0.71}_{-0.53}$| |
| SMC_SC6 128831 | 01 | |$12.9^{+3.6}_{-2.9}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.03^{+0.03}_{-0.02}$| | |$2.7^{+0.5}_{-0.8}$| | |$0.96^{+0.37}_{-0.42}$| | |$0.62^{+0.33}_{-0.23}$| | |$0.85^{+0.38}_{-0.37}$| | |$3.93^{+2.09}_{-1.61}$| | |$6.95^{+4.2}_{-2.98}$| | |$0.79^{+0.45}_{-0.35}$| |
| SMC_SC6 199611 | 01 | |$15.5^{+3.6}_{-3.3}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.39^{+0.17}_{-0.07}$| | |$1.5^{+1.3}_{-0.8}$| | |$0.51^{+0.58}_{-0.36}$| | |$0.29^{+0.26}_{-0.16}$| | |$0.44^{+0.52}_{-0.31}$| | |$1.33^{+1.47}_{-0.84}$| | |$2.75^{+3.38}_{-1.76}$| | |$0.33^{+0.39}_{-0.21}$| |
| SMC_SC6 272665 | 01 | |$6.3^{+1.2}_{-0.9}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.81^{+0.12}_{-0.11}$| | |$0.39^{+0.19}_{-0.07}$| | |$0.6^{+0.3}_{-0.2}$| | |$0.7^{+0.51}_{-0.47}$| | |$0.07^{+0.41}_{-0.05}$| | |$7.81^{+6.55}_{-5.28}$| | |$0.26^{+0.25}_{-0.15}$| | |$0.23^{+0.24}_{-0.14}$| | |$0.22^{+0.23}_{-0.14}$| |
| SMC_SC7 57131 | 01 | |$12.0^{+2.8}_{-2.4}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.39^{+0.14}_{-0.06}$| | |$2.0^{+0.8}_{-0.7}$| | |$0.73^{+0.43}_{-0.4}$| | |$0.65^{+0.41}_{-0.36}$| | |$1.81^{+1.04}_{-0.98}$| | |$2.11^{+1.81}_{-1.3}$| | |$3.4^{+3.27}_{-2.12}$| | |$0.99^{+0.93}_{-0.62}$| |
| SMC_SC8 183240 | 01 | |$17.6^{+2.3}_{-2.9}$| | |$0.7^{+0.2}_{-0.2}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.61^{+0.15}_{-0.08}$| | |$0.9^{+0.4}_{-0.2}$| | |$0.64^{+0.51}_{-0.44}$| | |$0.28^{+0.23}_{-0.13}$| | |$1.18^{+0.87}_{-0.77}$| | |$1.45^{+1.3}_{-0.79}$| | |$3.46^{+3.52}_{-1.93}$| | |$0.98^{+1.0}_{-0.54}$| |
| SMC_SC9 105383 | 01 | |$13.0^{+3.0}_{-2.6}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.56^{+0.06}_{-0.04}$| | |$1.9^{+0.7}_{-0.5}$| | |$0.53^{+0.44}_{-0.26}$| | |$0.09^{+0.04}_{-0.02}$| | |$1.43^{+1.21}_{-0.69}$| | |$1.47^{+1.17}_{-0.68}$| | |$2.42^{+2.29}_{-1.19}$| | |$0.74^{+0.7}_{-0.37}$| |
| 02 | |$1.7^{+0.6}_{-0.4}$| | |$0.77^{+0.41}_{-0.32}$| | |$0.09^{+0.03}_{-0.03}$| | |$1.9^{+0.91}_{-0.78}$| | |$1.94^{+1.22}_{-0.81}$| | |$3.2^{+2.55}_{-1.44}$| | |$0.87^{+0.71}_{-0.38}$| | |||||
| SMC_SC9 168422 | 01 | |$8.8^{+1.8}_{-1.8}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.61^{+0.18}_{-0.08}$| | |$0.5^{+0.3}_{-0.1}$| | |$0.56^{+0.6}_{-0.43}$| | |$0.07^{+0.11}_{-0.03}$| | |$2.55^{+2.96}_{-2.01}$| | |$0.27^{+0.27}_{-0.18}$| | |$0.33^{+0.34}_{-0.21}$| | |$0.15^{+0.16}_{-0.1}$| |
| SMC_SC10 8906 | 01 | |$16.1^{+3.3}_{-3.4}$| | |$0.6^{+0.2}_{-0.3}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.56^{+0.09}_{-0.04}$| | |$2.2^{+0.9}_{-0.7}$| | |$0.89^{+0.38}_{-0.31}$| | |$0.44^{+0.23}_{-0.16}$| | |$0.2^{+0.1}_{-0.07}$| | |$4.23^{+2.33}_{-1.6}$| | |$9.05^{+5.83}_{-3.69}$| | |$0.3^{+0.19}_{-0.12}$| |
| 02 | |$2.0^{+0.8}_{-0.7}$| | |$0.82^{+0.36}_{-0.31}$| | |$0.9^{+0.35}_{-0.31}$| | |$0.07^{+0.03}_{-0.02}$| | |$3.5^{+1.98}_{-1.35}$| | |$7.5^{+4.86}_{-3.08}$| | |$0.09^{+0.05}_{-0.04}$| | |||||
| SMC_SC11 28090 | 01 | |$14.5^{+3.8}_{-2.8}$| | |$0.7^{+0.2}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.57^{+0.13}_{-0.05}$| | |$1.8^{+0.8}_{-0.7}$| | |$0.1^{+0.09}_{-0.05}$| | |$0.12^{+0.05}_{-0.05}$| | |$0.46^{+0.41}_{-0.2}$| | |$0.45^{+0.38}_{-0.22}$| | |$0.94^{+0.96}_{-0.5}$| | |$0.59^{+0.59}_{-0.32}$| |
| SMC_SC11 46587 | 01 | |$8.2^{+1.8}_{-1.6}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.38^{+0.21}_{-0.06}$| | |$0.8^{+0.6}_{-0.3}$| | |$0.61^{+0.57}_{-0.46}$| | |$0.3^{+0.47}_{-0.18}$| | |$4.93^{+4.65}_{-3.7}$| | |$0.39^{+0.47}_{-0.25}$| | |$0.44^{+0.57}_{-0.29}$| | |$0.34^{+0.43}_{-0.22}$| |
| OGLE-II ID . | Bump . | M (M⊙) . | t/tMS . | W . | cos i . | Σ0 . | αbu . | αd . | |$\tilde{\tau }_\mathrm{bu}$| . | |$\left(-\frac{\mathrm{\partial} M}{\mathrm{\partial} t}\right)_\mathrm{typ}$| . | |$\left(-\frac{\mathrm{\partial} J}{\mathrm{\partial} t}\right)_\mathrm{std}$| . | −ΔJ* . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | ID . | . | . | . | . | (g cm−2) . | . | . | . | (10−9 × . | (1036 × . | (1044 × . |
| . | . | . | . | . | . | . | . | . | . | M⊙ yr−1) . | g cm2 s−2) . | g cm2 s−1) . |
| SMC_SC1 7612 | 01 | |$13.7^{+3.0}_{-3.0}$| | |$0.4^{+0.3}_{-0.2}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.37^{+0.16}_{-0.05}$| | |$0.9^{+1.4}_{-0.5}$| | |$0.44^{+0.68}_{-0.34}$| | |$0.62^{+0.52}_{-0.4}$| | |$0.23^{+0.35}_{-0.18}$| | |$0.55^{+0.66}_{-0.34}$| | |$0.94^{+1.31}_{-0.6}$| | |$0.06^{+0.08}_{-0.04}$| |
| 02 | |$1.1^{+1.5}_{-0.6}$| | |$0.47^{+0.64}_{-0.34}$| | |$0.56^{+0.62}_{-0.38}$| | |$0.2^{+0.3}_{-0.14}$| | |$0.7^{+0.76}_{-0.44}$| | |$1.18^{+1.51}_{-0.76}$| | |$0.06^{+0.08}_{-0.04}$| | |||||
| SMC_SC1 60553 | 01 | |$13.8^{+3.5}_{-2.7}$| | |$0.7^{+0.2}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.62^{+0.1}_{-0.05}$| | |$1.9^{+1.0}_{-0.5}$| | |$1.26^{+0.17}_{-0.28}$| | |$0.1^{+0.04}_{-0.03}$| | |$3.07^{+0.57}_{-0.72}$| | |$4.72^{+1.94}_{-1.59}$| | |$9.12^{+4.64}_{-3.45}$| | |$2.93^{+1.45}_{-1.11}$| |
| SMC_SC1 75701 | 01 | |$17.0^{+2.8}_{-3.9}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.7^{+0.13}_{-0.07}$| | |$2.2^{+0.7}_{-0.5}$| | |$0.25^{+0.21}_{-0.09}$| | |$0.11^{+0.06}_{-0.04}$| | |$0.81^{+0.65}_{-0.3}$| | |$1.11^{+1.24}_{-0.51}$| | |$2.33^{+2.92}_{-1.17}$| | |$0.97^{+1.22}_{-0.49}$| |
| SMC_SC1 92262 | 01 | |$14.7^{+3.3}_{-2.9}$| | |$0.6^{+0.2}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.04^{+0.02}_{-0.02}$| | |$1.3^{+1.1}_{-0.7}$| | |$0.49^{+0.53}_{-0.3}$| | |$0.89^{+0.41}_{-0.47}$| | |$0.53^{+0.58}_{-0.31}$| | |$1.11^{+1.2}_{-0.6}$| | |$2.2^{+2.42}_{-1.21}$| | |$0.32^{+0.33}_{-0.17}$| |
| 02 | |$2.6^{+0.5}_{-0.5}$| | |$0.99^{+0.33}_{-0.36}$| | |$0.94^{+0.34}_{-0.32}$| | |$1.14^{+0.64}_{-0.44}$| | |$4.86^{+1.81}_{-1.35}$| | |$9.61^{+4.13}_{-2.88}$| | |$1.52^{+0.72}_{-0.48}$| | |||||
| SMC_SC2 94939 | 01 | |$12.0^{+3.0}_{-2.4}$| | |$0.6^{+0.3}_{-0.4}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.46^{+0.14}_{-0.07}$| | |$2.4^{+0.8}_{-0.8}$| | |$0.9^{+0.42}_{-0.43}$| | |$0.63^{+0.34}_{-0.32}$| | |$1.31^{+0.59}_{-0.61}$| | |$3.26^{+2.5}_{-1.74}$| | |$5.47^{+4.52}_{-2.98}$| | |$0.96^{+0.77}_{-0.53}$| |
| SMC_SC3 5719 | 01 | |$12.1^{+2.9}_{-2.6}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.41^{+0.1}_{-0.06}$| | |$2.6^{+0.6}_{-0.8}$| | |$0.68^{+0.46}_{-0.33}$| | |$0.38^{+0.21}_{-0.18}$| | |$4.15^{+2.74}_{-1.98}$| | |$2.74^{+2.49}_{-1.6}$| | |$4.59^{+4.31}_{-2.72}$| | |$3.28^{+3.06}_{-1.95}$| |
| SMC_SC3 15970 | 01 | |$15.0^{+2.7}_{-2.4}$| | |$0.7^{+0.2}_{-0.2}$| | |$0.82^{+0.09}_{-0.1}$| | |$0.62^{+0.03}_{-0.02}$| | |$1.3^{+0.4}_{-0.2}$| | |$0.72^{+0.3}_{-0.29}$| | |$0.12^{+0.05}_{-0.03}$| | |$1.52^{+0.69}_{-0.67}$| | |$2.08^{+1.17}_{-0.76}$| | |$4.3^{+3.07}_{-1.71}$| | |$1.26^{+0.81}_{-0.5}$| |
| 02 | |$1.5^{+0.4}_{-0.3}$| | |$0.78^{+0.37}_{-0.3}$| | |$0.17^{+0.05}_{-0.03}$| | |$2.05^{+1.01}_{-0.81}$| | |$2.68^{+1.64}_{-1.01}$| | |$5.53^{+4.21}_{-2.24}$| | |$2.02^{+1.58}_{-0.82}$| | |||||
| 03 | |$1.3^{+0.3}_{-0.2}$| | |$1.08^{+0.26}_{-0.27}$| | |$0.13^{+0.05}_{-0.05}$| | |$3.17^{+0.93}_{-0.96}$| | |$3.13^{+1.26}_{-0.99}$| | |$6.5^{+3.54}_{-2.39}$| | |$2.62^{+1.39}_{-0.96}$| | |||||
| SMC_SC3 71445 | 01 | |$10.5^{+2.4}_{-2.1}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.43^{+0.09}_{-0.06}$| | |$2.5^{+0.6}_{-0.7}$| | |$0.58^{+0.45}_{-0.28}$| | |$0.67^{+0.38}_{-0.29}$| | |$1.3^{+1.02}_{-0.6}$| | |$1.96^{+1.67}_{-1.05}$| | |$2.88^{+2.58}_{-1.6}$| | |$0.7^{+0.64}_{-0.39}$| |
| 02 | |$1.2^{+0.6}_{-0.4}$| | |$0.67^{+0.52}_{-0.35}$| | |$1.0^{+0.34}_{-0.37}$| | |$0.59^{+0.5}_{-0.31}$| | |$1.12^{+0.71}_{-0.49}$| | |$1.64^{+1.12}_{-0.74}$| | |$0.16^{+0.12}_{-0.07}$| | |||||
| SMC_SC3 125899 | 01 | |$13.9^{+3.3}_{-3.2}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.39^{+0.2}_{-0.07}$| | |$1.6^{+1.2}_{-0.8}$| | |$0.73^{+0.48}_{-0.4}$| | |$0.35^{+0.29}_{-0.19}$| | |$1.09^{+0.73}_{-0.61}$| | |$1.88^{+1.82}_{-1.13}$| | |$3.49^{+3.65}_{-2.16}$| | |$0.64^{+0.68}_{-0.39}$| |
| SMC_SC3 197941 | 01 | |$12.1^{+4.5}_{-2.0}$| | |$0.7^{+0.2}_{-0.4}$| | |$0.83^{+0.09}_{-0.11}$| | |$0.56^{+0.14}_{-0.04}$| | |$0.8^{+0.4}_{-0.2}$| | |$0.36^{+0.57}_{-0.21}$| | |$0.1^{+0.04}_{-0.03}$| | |$1.38^{+2.24}_{-0.82}$| | |$0.62^{+0.77}_{-0.34}$| | |$1.14^{+1.5}_{-0.66}$| | |$0.58^{+0.76}_{-0.33}$| |
| SMC_SC4 22859 | 01 | |$8.2^{+1.7}_{-1.6}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.8^{+0.11}_{-0.1}$| | |$0.64^{+0.19}_{-0.11}$| | |$0.3^{+0.2}_{-0.1}$| | |$0.68^{+0.56}_{-0.55}$| | |$0.03^{+0.66}_{-0.02}$| | |$4.16^{+4.08}_{-3.37}$| | |$0.2^{+0.18}_{-0.15}$| | |$0.23^{+0.23}_{-0.17}$| | |$0.13^{+0.15}_{-0.1}$| |
| SMC_SC4 71499 | 01 | |$17.3^{+2.4}_{-3.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.53^{+0.05}_{-0.03}$| | |$1.5^{+0.6}_{-0.4}$| | |$0.7^{+0.46}_{-0.32}$| | |$0.25^{+0.1}_{-0.07}$| | |$1.1^{+0.7}_{-0.51}$| | |$2.09^{+1.16}_{-0.86}$| | |$4.41^{+2.86}_{-2.0}$| | |$0.9^{+0.59}_{-0.4}$| |
| 02 | |$1.8^{+0.7}_{-0.5}$| | |$0.68^{+0.44}_{-0.31}$| | |$0.19^{+0.07}_{-0.06}$| | |$1.37^{+0.93}_{-0.62}$| | |$2.32^{+1.49}_{-1.0}$| | |$4.9^{+3.62}_{-2.28}$| | |$1.34^{+0.97}_{-0.62}$| | |||||
| SMC_SC4 120783 | 01 | |$18.2^{+1.9}_{-2.4}$| | |$0.9^{+0.1}_{-0.1}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.6^{+0.18}_{-0.08}$| | |$0.9^{+0.3}_{-0.2}$| | |$0.73^{+0.5}_{-0.47}$| | |$0.13^{+0.07}_{-0.05}$| | |$1.72^{+1.11}_{-1.1}$| | |$2.01^{+1.61}_{-1.05}$| | |$5.47^{+4.82}_{-2.84}$| | |$2.25^{+1.97}_{-1.16}$| |
| SMC_SC4 127840 | 01 | |$15.2^{+3.0}_{-2.3}$| | |$0.8^{+0.1}_{-0.2}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.65^{+0.12}_{-0.09}$| | |$2.8^{+0.5}_{-0.6}$| | |$0.39^{+0.21}_{-0.13}$| | |$0.76^{+0.4}_{-0.32}$| | |$0.57^{+0.28}_{-0.18}$| | |$2.95^{+2.15}_{-1.19}$| | |$6.77^{+5.27}_{-2.88}$| | |$1.52^{+1.16}_{-0.66}$| |
| SMC_SC4 156248 | 01 | |$12.9^{+3.2}_{-2.4}$| | |$0.7^{+0.2}_{-0.4}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.07^{+0.02}_{-0.04}$| | |$1.2^{+1.3}_{-0.8}$| | |$0.46^{+0.63}_{-0.32}$| | |$0.89^{+0.42}_{-0.48}$| | |$1.5^{+2.08}_{-1.05}$| | |$0.69^{+1.94}_{-0.45}$| | |$1.28^{+3.51}_{-0.83}$| | |$0.53^{+1.51}_{-0.35}$| |
| SMC_SC4 156251 | 01 | |$17.3^{+2.0}_{-2.4}$| | |$0.6^{+0.2}_{-0.2}$| | |$0.83^{+0.09}_{-0.1}$| | |$0.78^{+0.06}_{-0.05}$| | |$2.3^{+0.3}_{-0.4}$| | |$0.41^{+0.16}_{-0.09}$| | |$0.67^{+0.36}_{-0.27}$| | |$0.43^{+0.17}_{-0.1}$| | |$2.14^{+0.95}_{-0.63}$| | |$4.84^{+2.55}_{-1.58}$| | |$0.73^{+0.38}_{-0.25}$| |
| 02 | |$1.6^{+0.2}_{-0.2}$| | |$0.6^{+0.31}_{-0.2}$| | |$0.49^{+0.36}_{-0.16}$| | |$0.64^{+0.29}_{-0.2}$| | |$2.24^{+1.19}_{-0.7}$| | |$5.08^{+3.01}_{-1.77}$| | |$0.76^{+0.43}_{-0.26}$| | |||||
| 03 | |$2.8^{+0.4}_{-0.4}$| | |$0.93^{+0.36}_{-0.34}$| | |$0.49^{+0.16}_{-0.11}$| | |$1.25^{+0.48}_{-0.42}$| | |$5.88^{+2.75}_{-2.18}$| | |$13.27^{+7.36}_{-5.32}$| | |$2.52^{+1.42}_{-0.96}$| | |||||
| SMC_SC4 159829 | 01 | |$14.5^{+2.8}_{-3.0}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.59^{+0.07}_{-0.05}$| | |$2.5^{+0.7}_{-0.6}$| | |$1.05^{+0.29}_{-0.31}$| | |$0.26^{+0.09}_{-0.07}$| | |$1.64^{+0.5}_{-0.48}$| | |$4.16^{+1.75}_{-1.48}$| | |$7.59^{+3.8}_{-2.93}$| | |$1.44^{+0.68}_{-0.55}$| |
| 02 | |$2.5^{+0.6}_{-0.6}$| | |$0.96^{+0.34}_{-0.37}$| | |$0.72^{+0.28}_{-0.23}$| | |$2.6^{+0.91}_{-0.95}$| | |$3.82^{+1.64}_{-1.47}$| | |$6.92^{+3.45}_{-2.79}$| | |$2.25^{+1.11}_{-0.91}$| | |||||
| SMC_SC4 159857 | 01 | |$15.2^{+3.4}_{-3.3}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.54^{+0.08}_{-0.03}$| | |$0.7^{+1.2}_{-0.3}$| | |$0.45^{+0.63}_{-0.35}$| | |$0.67^{+0.49}_{-0.37}$| | |$0.33^{+0.5}_{-0.26}$| | |$0.59^{+0.48}_{-0.3}$| | |$1.15^{+1.08}_{-0.61}$| | |$0.11^{+0.11}_{-0.06}$| |
| 02 | |$1.1^{+0.7}_{-0.3}$| | |$0.62^{+0.48}_{-0.37}$| | |$0.32^{+0.62}_{-0.15}$| | |$0.43^{+0.3}_{-0.27}$| | |$1.33^{+0.77}_{-0.61}$| | |$2.63^{+1.79}_{-1.29}$| | |$0.22^{+0.15}_{-0.11}$| | |||||
| SMC_SC4 163828 | 01 | |$8.7^{+1.8}_{-1.8}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.72^{+0.14}_{-0.08}$| | |$0.6^{+0.2}_{-0.1}$| | |$0.48^{+0.58}_{-0.31}$| | |$0.04^{+0.04}_{-0.02}$| | |$3.76^{+4.54}_{-2.4}$| | |$0.29^{+0.33}_{-0.18}$| | |$0.34^{+0.42}_{-0.21}$| | |$0.25^{+0.31}_{-0.15}$| |
| SMC_SC4 167554 | 01 | |$9.2^{+1.9}_{-2.1}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.59^{+0.08}_{-0.05}$| | |$0.8^{+0.5}_{-0.2}$| | |$0.56^{+0.46}_{-0.34}$| | |$0.54^{+0.45}_{-0.24}$| | |$0.54^{+0.44}_{-0.34}$| | |$0.47^{+0.32}_{-0.2}$| | |$0.57^{+0.44}_{-0.25}$| | |$0.05^{+0.04}_{-0.02}$| |
| 02 | |$1.5^{+0.6}_{-0.4}$| | |$0.42^{+0.36}_{-0.18}$| | |$0.84^{+0.42}_{-0.34}$| | |$0.51^{+0.47}_{-0.21}$| | |$0.7^{+0.5}_{-0.29}$| | |$0.86^{+0.71}_{-0.39}$| | |$0.1^{+0.08}_{-0.05}$| | |||||
| SMC_SC4 171253 | 01 | |$16.5^{+2.5}_{-3.4}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.1}$| | |$0.59^{+0.14}_{-0.07}$| | |$0.3^{+1.2}_{-0.1}$| | |$0.41^{+0.73}_{-0.39}$| | |$0.78^{+0.5}_{-0.47}$| | |$0.38^{+0.65}_{-0.36}$| | |$0.2^{+0.28}_{-0.15}$| | |$0.41^{+0.58}_{-0.31}$| | |$0.05^{+0.07}_{-0.03}$| |
| 02 | |$0.4^{+0.5}_{-0.1}$| | |$0.54^{+0.6}_{-0.47}$| | |$0.67^{+0.5}_{-0.46}$| | |$0.4^{+0.44}_{-0.36}$| | |$0.3^{+0.32}_{-0.2}$| | |$0.59^{+0.69}_{-0.4}$| | |$0.05^{+0.07}_{-0.04}$| | |||||
| SMC_SC4 175272 | 01 | |$12.1^{+2.6}_{-2.8}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.12}$| | |$0.37^{+0.15}_{-0.05}$| | |$1.8^{+1.1}_{-0.7}$| | |$0.72^{+0.46}_{-0.39}$| | |$0.46^{+0.34}_{-0.23}$| | |$2.54^{+1.6}_{-1.38}$| | |$1.87^{+1.68}_{-1.13}$| | |$2.96^{+2.97}_{-1.82}$| | |$1.19^{+1.17}_{-0.74}$| |
| SMC_SC4 179053 | 01 | |$12.5^{+3.0}_{-2.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.03^{+0.03}_{-0.02}$| | |$2.1^{+0.9}_{-0.7}$| | |$0.78^{+0.46}_{-0.43}$| | |$1.08^{+0.3}_{-0.35}$| | |$2.12^{+1.4}_{-1.18}$| | |$2.28^{+1.67}_{-1.02}$| | |$3.81^{+3.09}_{-1.77}$| | |$1.2^{+0.98}_{-0.54}$| |
| SMC_SC5 11453 | 01 | |$14.6^{+3.3}_{-3.4}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.39^{+0.14}_{-0.06}$| | |$1.9^{+1.0}_{-0.8}$| | |$0.89^{+0.38}_{-0.39}$| | |$0.24^{+0.15}_{-0.11}$| | |$4.72^{+2.18}_{-2.0}$| | |$2.96^{+2.47}_{-1.71}$| | |$5.66^{+5.16}_{-3.43}$| | |$3.85^{+3.47}_{-2.35}$| |
| SMC_SC5 21117 | 01 | |$16.0^{+2.3}_{-2.6}$| | |$0.5^{+0.2}_{-0.2}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.52^{+0.03}_{-0.01}$| | |$1.4^{+0.4}_{-0.3}$| | |$0.55^{+0.37}_{-0.21}$| | |$0.55^{+0.42}_{-0.25}$| | |$0.83^{+0.57}_{-0.31}$| | |$1.48^{+0.84}_{-0.55}$| | |$3.0^{+2.0}_{-1.25}$| | |$0.58^{+0.39}_{-0.24}$| |
| 02 | |$2.1^{+0.8}_{-0.4}$| | |$0.75^{+0.38}_{-0.29}$| | |$0.15^{+0.08}_{-0.04}$| | |$1.15^{+0.55}_{-0.41}$| | |$2.89^{+2.02}_{-1.16}$| | |$5.77^{+4.94}_{-2.51}$| | |$1.16^{+0.94}_{-0.5}$| | |||||
| 03 | |$2.1^{+0.6}_{-0.5}$| | |$0.62^{+0.28}_{-0.21}$| | |$0.33^{+0.21}_{-0.11}$| | |$0.74^{+0.37}_{-0.25}$| | |$2.42^{+1.36}_{-0.86}$| | |$4.86^{+3.4}_{-1.97}$| | |$0.75^{+0.51}_{-0.3}$| | |||||
| 04 | |$1.6^{+0.3}_{-0.3}$| | |$0.72^{+0.31}_{-0.23}$| | |$0.13^{+0.07}_{-0.04}$| | |$2.96^{+1.15}_{-1.03}$| | |$2.23^{+1.11}_{-0.78}$| | |$4.5^{+2.69}_{-1.75}$| | |$2.28^{+1.48}_{-0.92}$| | |||||
| SMC_SC5 21134 | 01 | |$12.9^{+3.7}_{-2.8}$| | |$0.5^{+0.3}_{-0.4}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.41^{+0.22}_{-0.08}$| | |$0.7^{+1.6}_{-0.4}$| | |$0.43^{+0.66}_{-0.37}$| | |$0.15^{+0.3}_{-0.09}$| | |$0.44^{+0.74}_{-0.38}$| | |$0.42^{+0.56}_{-0.3}$| | |$0.72^{+1.06}_{-0.53}$| | |$0.09^{+0.13}_{-0.06}$| |
| SMC_SC5 32377 | 01 | |$14.3^{+3.1}_{-3.1}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.35^{+0.08}_{-0.04}$| | |$1.8^{+1.0}_{-0.7}$| | |$0.75^{+0.48}_{-0.41}$| | |$0.57^{+0.4}_{-0.26}$| | |$0.37^{+0.33}_{-0.2}$| | |$2.25^{+1.85}_{-1.11}$| | |$4.31^{+3.82}_{-2.24}$| | |$0.28^{+0.26}_{-0.15}$| |
| 02 | |$2.1^{+0.8}_{-0.7}$| | |$0.6^{+0.37}_{-0.27}$| | |$0.27^{+0.12}_{-0.11}$| | |$1.13^{+0.73}_{-0.49}$| | |$2.26^{+1.73}_{-1.11}$| | |$4.23^{+3.75}_{-2.13}$| | |$1.02^{+0.89}_{-0.52}$| | |||||
| SMC_SC5 43650 | 01 | |$8.9^{+2.0}_{-1.9}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.79^{+0.11}_{-0.1}$| | |$0.55^{+0.1}_{-0.04}$| | |$0.4^{+0.7}_{-0.1}$| | |$0.5^{+0.64}_{-0.45}$| | |$0.34^{+0.73}_{-0.26}$| | |$1.07^{+1.36}_{-0.95}$| | |$0.18^{+0.18}_{-0.12}$| | |$0.21^{+0.23}_{-0.14}$| | |$0.04^{+0.05}_{-0.03}$| |
| 02 | |$0.5^{+0.2}_{-0.1}$| | |$0.58^{+0.59}_{-0.43}$| | |$0.62^{+0.59}_{-0.51}$| | |$6.62^{+6.56}_{-4.92}$| | |$0.29^{+0.27}_{-0.19}$| | |$0.34^{+0.35}_{-0.23}$| | |$0.36^{+0.41}_{-0.24}$| | |||||
| SMC_SC5 54851 | 01 | |$12.5^{+2.4}_{-2.0}$| | |$0.6^{+0.2}_{-0.2}$| | |$0.82^{+0.09}_{-0.09}$| | |$0.62^{+0.03}_{-0.01}$| | |$1.1^{+0.3}_{-0.2}$| | |$0.74^{+0.35}_{-0.33}$| | |$0.1^{+0.04}_{-0.03}$| | |$1.85^{+0.85}_{-0.85}$| | |$1.41^{+0.74}_{-0.56}$| | |$2.44^{+1.54}_{-1.04}$| | |$0.73^{+0.48}_{-0.32}$| |
| 02 | |$1.2^{+0.3}_{-0.2}$| | |$0.76^{+0.35}_{-0.34}$| | |$0.11^{+0.03}_{-0.03}$| | |$2.08^{+0.89}_{-0.95}$| | |$1.55^{+0.8}_{-0.61}$| | |$2.67^{+1.67}_{-1.13}$| | |$0.88^{+0.52}_{-0.37}$| | |||||
| 03 | |$1.1^{+0.2}_{-0.1}$| | |$0.5^{+0.31}_{-0.18}$| | |$0.05^{+0.01}_{-0.01}$| | |$2.42^{+1.6}_{-0.86}$| | |$0.97^{+0.63}_{-0.39}$| | |$1.69^{+1.3}_{-0.76}$| | |$0.99^{+0.81}_{-0.45}$| | |||||
| SMC_SC5 65500 | 01 | |$12.8^{+3.3}_{-2.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.66^{+0.11}_{-0.05}$| | |$2.0^{+1.0}_{-0.6}$| | |$0.61^{+0.38}_{-0.27}$| | |$0.29^{+0.13}_{-0.11}$| | |$0.46^{+0.27}_{-0.19}$| | |$1.91^{+1.23}_{-0.88}$| | |$3.21^{+2.57}_{-1.62}$| | |$0.28^{+0.22}_{-0.14}$| |
| SMC_SC5 129535 | 01 | |$9.1^{+2.1}_{-2.0}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.57^{+0.13}_{-0.05}$| | |$0.7^{+0.2}_{-0.2}$| | |$0.63^{+0.53}_{-0.36}$| | |$0.22^{+0.27}_{-0.11}$| | |$4.4^{+3.69}_{-2.6}$| | |$0.49^{+0.39}_{-0.27}$| | |$0.61^{+0.52}_{-0.34}$| | |$0.42^{+0.37}_{-0.23}$| |
| SMC_SC5 145724 | 01 | |$8.6^{+2.1}_{-1.8}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.42^{+0.1}_{-0.05}$| | |$2.4^{+0.7}_{-0.8}$| | |$0.81^{+0.44}_{-0.41}$| | |$0.13^{+0.07}_{-0.06}$| | |$4.2^{+2.39}_{-2.09}$| | |$2.05^{+1.73}_{-1.15}$| | |$2.51^{+2.24}_{-1.4}$| | |$1.31^{+1.21}_{-0.75}$| |
| SMC_SC5 180034 | 01 | |$12.0^{+2.5}_{-2.5}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.63^{+0.15}_{-0.1}$| | |$1.0^{+0.5}_{-0.3}$| | |$0.32^{+0.55}_{-0.19}$| | |$0.19^{+0.15}_{-0.08}$| | |$0.91^{+1.56}_{-0.54}$| | |$0.45^{+0.57}_{-0.25}$| | |$0.71^{+0.95}_{-0.42}$| | |$0.22^{+0.27}_{-0.13}$| |
| SMC_SC5 260841 | 01 | |$13.4^{+4.0}_{-3.2}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.53^{+0.06}_{-0.02}$| | |$0.6^{+0.5}_{-0.1}$| | |$0.78^{+0.45}_{-0.52}$| | |$0.06^{+0.26}_{-0.02}$| | |$1.53^{+0.95}_{-1.05}$| | |$0.77^{+0.52}_{-0.4}$| | |$1.34^{+1.17}_{-0.69}$| | |$0.33^{+0.29}_{-0.17}$| |
| 02 | |$0.6^{+0.3}_{-0.1}$| | |$0.75^{+0.44}_{-0.44}$| | |$0.06^{+0.77}_{-0.03}$| | |$2.74^{+1.74}_{-1.78}$| | |$0.72^{+0.44}_{-0.35}$| | |$1.27^{+0.92}_{-0.62}$| | |$0.54^{+0.43}_{-0.28}$| | |||||
| SMC_SC5 260957 | 01 | |$8.9^{+2.1}_{-2.0}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.82^{+0.09}_{-0.11}$| | |$0.58^{+0.14}_{-0.06}$| | |$1.2^{+0.4}_{-0.3}$| | |$0.55^{+0.5}_{-0.24}$| | |$0.04^{+0.02}_{-0.02}$| | |$2.45^{+2.21}_{-1.1}$| | |$0.78^{+0.63}_{-0.4}$| | |$0.98^{+0.86}_{-0.54}$| | |$0.43^{+0.4}_{-0.23}$| |
| SMC_SC5 266088 | 01 | |$7.8^{+1.5}_{-1.6}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.7^{+0.14}_{-0.08}$| | |$0.7^{+0.4}_{-0.1}$| | |$0.3^{+0.69}_{-0.24}$| | |$0.06^{+0.05}_{-0.02}$| | |$1.92^{+4.42}_{-1.56}$| | |$0.17^{+0.3}_{-0.11}$| | |$0.18^{+0.34}_{-0.12}$| | |$0.11^{+0.19}_{-0.07}$| |
| SMC_SC5 276982 | 01 | |$17.1^{+2.2}_{-2.6}$| | |$0.2^{+0.2}_{-0.2}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.75^{+0.11}_{-0.1}$| | |$1.2^{+0.4}_{-0.3}$| | |$0.06^{+0.19}_{-0.03}$| | |$0.05^{+0.04}_{-0.02}$| | |$0.31^{+1.0}_{-0.16}$| | |$0.12^{+0.26}_{-0.06}$| | |$0.23^{+0.54}_{-0.13}$| | |$0.15^{+0.33}_{-0.08}$| |
| SMC_SC5 282963 | 01 | |$15.6^{+3.1}_{-3.6}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.38^{+0.19}_{-0.06}$| | |$1.7^{+1.0}_{-0.8}$| | |$0.62^{+0.51}_{-0.33}$| | |$0.39^{+0.32}_{-0.21}$| | |$5.62^{+4.36}_{-2.92}$| | |$2.07^{+2.43}_{-1.35}$| | |$4.14^{+5.39}_{-2.78}$| | |$4.96^{+6.18}_{-3.36}$| |
| SMC_SC6 11085 | 01 | |$17.8^{+1.9}_{-2.9}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.74^{+0.06}_{-0.05}$| | |$2.4^{+0.6}_{-0.5}$| | |$0.59^{+0.26}_{-0.18}$| | |$0.13^{+0.05}_{-0.04}$| | |$0.99^{+0.45}_{-0.3}$| | |$2.53^{+1.13}_{-0.87}$| | |$5.19^{+2.71}_{-1.99}$| | |$1.06^{+0.57}_{-0.4}$| |
| 02 | |$2.6^{+0.5}_{-0.4}$| | |$0.78^{+0.34}_{-0.27}$| | |$0.27^{+0.09}_{-0.07}$| | |$1.49^{+0.63}_{-0.5}$| | |$3.41^{+1.75}_{-1.29}$| | |$7.07^{+4.11}_{-3.0}$| | |$1.64^{+0.95}_{-0.68}$| | |||||
| SMC_SC6 17538 | 01 | |$7.8^{+1.6}_{-1.4}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.61^{+0.15}_{-0.08}$| | |$0.7^{+0.3}_{-0.2}$| | |$0.59^{+0.58}_{-0.41}$| | |$0.08^{+0.09}_{-0.04}$| | |$3.55^{+3.44}_{-2.47}$| | |$0.37^{+0.34}_{-0.22}$| | |$0.4^{+0.39}_{-0.24}$| | |$0.22^{+0.21}_{-0.13}$| |
| SMC_SC6 42440 | 01 | |$8.9^{+2.0}_{-2.0}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.36^{+0.15}_{-0.05}$| | |$1.8^{+1.2}_{-0.8}$| | |$0.78^{+0.45}_{-0.42}$| | |$0.19^{+0.17}_{-0.1}$| | |$2.82^{+1.81}_{-1.46}$| | |$1.36^{+1.32}_{-0.79}$| | |$1.66^{+1.84}_{-0.99}$| | |$0.61^{+0.72}_{-0.37}$| |
| SMC_SC6 99991 | 01 | |$14.8^{+2.6}_{-2.8}$| | |$0.5^{+0.2}_{-0.2}$| | |$0.83^{+0.09}_{-0.09}$| | |$0.34^{+0.04}_{-0.02}$| | |$1.7^{+0.6}_{-0.5}$| | |$0.62^{+0.43}_{-0.25}$| | |$0.98^{+0.31}_{-0.29}$| | |$0.88^{+0.64}_{-0.36}$| | |$1.85^{+1.11}_{-0.75}$| | |$3.54^{+2.45}_{-1.55}$| | |$0.64^{+0.44}_{-0.27}$| |
| 02 | |$2.2^{+0.7}_{-0.6}$| | |$0.62^{+0.33}_{-0.25}$| | |$0.74^{+0.33}_{-0.26}$| | |$1.13^{+0.62}_{-0.44}$| | |$2.37^{+1.58}_{-0.97}$| | |$4.47^{+3.48}_{-1.93}$| | |$1.02^{+0.8}_{-0.43}$| | |||||
| 03 | |$1.9^{+0.6}_{-0.5}$| | |$0.55^{+0.45}_{-0.22}$| | |$0.76^{+0.3}_{-0.24}$| | |$1.03^{+0.83}_{-0.43}$| | |$1.94^{+1.17}_{-0.77}$| | |$3.72^{+2.63}_{-1.65}$| | |$0.85^{+0.62}_{-0.37}$| | |||||
| 04 | |$1.7^{+0.5}_{-0.4}$| | |$0.53^{+0.36}_{-0.22}$| | |$0.92^{+0.3}_{-0.26}$| | |$1.12^{+0.77}_{-0.47}$| | |$1.56^{+0.97}_{-0.59}$| | |$2.96^{+2.18}_{-1.24}$| | |$0.79^{+0.59}_{-0.33}$| | |||||
| SMC_SC6 105368 | 01 | |$11.2^{+2.7}_{-2.9}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.53^{+0.04}_{-0.02}$| | |$0.9^{+0.4}_{-0.2}$| | |$0.51^{+0.57}_{-0.31}$| | |$0.17^{+0.1}_{-0.06}$| | |$1.12^{+1.23}_{-0.68}$| | |$0.61^{+0.56}_{-0.3}$| | |$0.92^{+0.91}_{-0.47}$| | |$0.22^{+0.22}_{-0.11}$| |
| 02 | |$1.2^{+0.5}_{-0.4}$| | |$0.28^{+0.48}_{-0.13}$| | |$0.19^{+0.13}_{-0.07}$| | |$0.78^{+1.38}_{-0.37}$| | |$0.5^{+0.48}_{-0.21}$| | |$0.76^{+0.77}_{-0.34}$| | |$0.23^{+0.25}_{-0.1}$| | |||||
| SMC_SC6 116294 | 01 | |$8.6^{+2.1}_{-1.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.41^{+0.1}_{-0.05}$| | |$2.6^{+0.7}_{-1.0}$| | |$0.87^{+0.4}_{-0.39}$| | |$0.16^{+0.09}_{-0.07}$| | |$2.71^{+1.35}_{-1.23}$| | |$2.42^{+1.65}_{-1.34}$| | |$2.99^{+2.11}_{-1.69}$| | |$0.93^{+0.71}_{-0.53}$| |
| SMC_SC6 128831 | 01 | |$12.9^{+3.6}_{-2.9}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.03^{+0.03}_{-0.02}$| | |$2.7^{+0.5}_{-0.8}$| | |$0.96^{+0.37}_{-0.42}$| | |$0.62^{+0.33}_{-0.23}$| | |$0.85^{+0.38}_{-0.37}$| | |$3.93^{+2.09}_{-1.61}$| | |$6.95^{+4.2}_{-2.98}$| | |$0.79^{+0.45}_{-0.35}$| |
| SMC_SC6 199611 | 01 | |$15.5^{+3.6}_{-3.3}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.39^{+0.17}_{-0.07}$| | |$1.5^{+1.3}_{-0.8}$| | |$0.51^{+0.58}_{-0.36}$| | |$0.29^{+0.26}_{-0.16}$| | |$0.44^{+0.52}_{-0.31}$| | |$1.33^{+1.47}_{-0.84}$| | |$2.75^{+3.38}_{-1.76}$| | |$0.33^{+0.39}_{-0.21}$| |
| SMC_SC6 272665 | 01 | |$6.3^{+1.2}_{-0.9}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.81^{+0.12}_{-0.11}$| | |$0.39^{+0.19}_{-0.07}$| | |$0.6^{+0.3}_{-0.2}$| | |$0.7^{+0.51}_{-0.47}$| | |$0.07^{+0.41}_{-0.05}$| | |$7.81^{+6.55}_{-5.28}$| | |$0.26^{+0.25}_{-0.15}$| | |$0.23^{+0.24}_{-0.14}$| | |$0.22^{+0.23}_{-0.14}$| |
| SMC_SC7 57131 | 01 | |$12.0^{+2.8}_{-2.4}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.39^{+0.14}_{-0.06}$| | |$2.0^{+0.8}_{-0.7}$| | |$0.73^{+0.43}_{-0.4}$| | |$0.65^{+0.41}_{-0.36}$| | |$1.81^{+1.04}_{-0.98}$| | |$2.11^{+1.81}_{-1.3}$| | |$3.4^{+3.27}_{-2.12}$| | |$0.99^{+0.93}_{-0.62}$| |
| SMC_SC8 183240 | 01 | |$17.6^{+2.3}_{-2.9}$| | |$0.7^{+0.2}_{-0.2}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.61^{+0.15}_{-0.08}$| | |$0.9^{+0.4}_{-0.2}$| | |$0.64^{+0.51}_{-0.44}$| | |$0.28^{+0.23}_{-0.13}$| | |$1.18^{+0.87}_{-0.77}$| | |$1.45^{+1.3}_{-0.79}$| | |$3.46^{+3.52}_{-1.93}$| | |$0.98^{+1.0}_{-0.54}$| |
| SMC_SC9 105383 | 01 | |$13.0^{+3.0}_{-2.6}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.56^{+0.06}_{-0.04}$| | |$1.9^{+0.7}_{-0.5}$| | |$0.53^{+0.44}_{-0.26}$| | |$0.09^{+0.04}_{-0.02}$| | |$1.43^{+1.21}_{-0.69}$| | |$1.47^{+1.17}_{-0.68}$| | |$2.42^{+2.29}_{-1.19}$| | |$0.74^{+0.7}_{-0.37}$| |
| 02 | |$1.7^{+0.6}_{-0.4}$| | |$0.77^{+0.41}_{-0.32}$| | |$0.09^{+0.03}_{-0.03}$| | |$1.9^{+0.91}_{-0.78}$| | |$1.94^{+1.22}_{-0.81}$| | |$3.2^{+2.55}_{-1.44}$| | |$0.87^{+0.71}_{-0.38}$| | |||||
| SMC_SC9 168422 | 01 | |$8.8^{+1.8}_{-1.8}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.61^{+0.18}_{-0.08}$| | |$0.5^{+0.3}_{-0.1}$| | |$0.56^{+0.6}_{-0.43}$| | |$0.07^{+0.11}_{-0.03}$| | |$2.55^{+2.96}_{-2.01}$| | |$0.27^{+0.27}_{-0.18}$| | |$0.33^{+0.34}_{-0.21}$| | |$0.15^{+0.16}_{-0.1}$| |
| SMC_SC10 8906 | 01 | |$16.1^{+3.3}_{-3.4}$| | |$0.6^{+0.2}_{-0.3}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.56^{+0.09}_{-0.04}$| | |$2.2^{+0.9}_{-0.7}$| | |$0.89^{+0.38}_{-0.31}$| | |$0.44^{+0.23}_{-0.16}$| | |$0.2^{+0.1}_{-0.07}$| | |$4.23^{+2.33}_{-1.6}$| | |$9.05^{+5.83}_{-3.69}$| | |$0.3^{+0.19}_{-0.12}$| |
| 02 | |$2.0^{+0.8}_{-0.7}$| | |$0.82^{+0.36}_{-0.31}$| | |$0.9^{+0.35}_{-0.31}$| | |$0.07^{+0.03}_{-0.02}$| | |$3.5^{+1.98}_{-1.35}$| | |$7.5^{+4.86}_{-3.08}$| | |$0.09^{+0.05}_{-0.04}$| | |||||
| SMC_SC11 28090 | 01 | |$14.5^{+3.8}_{-2.8}$| | |$0.7^{+0.2}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.57^{+0.13}_{-0.05}$| | |$1.8^{+0.8}_{-0.7}$| | |$0.1^{+0.09}_{-0.05}$| | |$0.12^{+0.05}_{-0.05}$| | |$0.46^{+0.41}_{-0.2}$| | |$0.45^{+0.38}_{-0.22}$| | |$0.94^{+0.96}_{-0.5}$| | |$0.59^{+0.59}_{-0.32}$| |
| SMC_SC11 46587 | 01 | |$8.2^{+1.8}_{-1.6}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.38^{+0.21}_{-0.06}$| | |$0.8^{+0.6}_{-0.3}$| | |$0.61^{+0.57}_{-0.46}$| | |$0.3^{+0.47}_{-0.18}$| | |$4.93^{+4.65}_{-3.7}$| | |$0.39^{+0.47}_{-0.25}$| | |$0.44^{+0.57}_{-0.29}$| | |$0.34^{+0.43}_{-0.22}$| |
| OGLE-II ID . | Bump . | M (M⊙) . | t/tMS . | W . | cos i . | Σ0 . | αbu . | αd . | |$\tilde{\tau }_\mathrm{bu}$| . | |$\left(-\frac{\mathrm{\partial} M}{\mathrm{\partial} t}\right)_\mathrm{typ}$| . | |$\left(-\frac{\mathrm{\partial} J}{\mathrm{\partial} t}\right)_\mathrm{std}$| . | −ΔJ* . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | ID . | . | . | . | . | (g cm−2) . | . | . | . | (10−9 × . | (1036 × . | (1044 × . |
| . | . | . | . | . | . | . | . | . | . | M⊙ yr−1) . | g cm2 s−2) . | g cm2 s−1) . |
| SMC_SC1 7612 | 01 | |$13.7^{+3.0}_{-3.0}$| | |$0.4^{+0.3}_{-0.2}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.37^{+0.16}_{-0.05}$| | |$0.9^{+1.4}_{-0.5}$| | |$0.44^{+0.68}_{-0.34}$| | |$0.62^{+0.52}_{-0.4}$| | |$0.23^{+0.35}_{-0.18}$| | |$0.55^{+0.66}_{-0.34}$| | |$0.94^{+1.31}_{-0.6}$| | |$0.06^{+0.08}_{-0.04}$| |
| 02 | |$1.1^{+1.5}_{-0.6}$| | |$0.47^{+0.64}_{-0.34}$| | |$0.56^{+0.62}_{-0.38}$| | |$0.2^{+0.3}_{-0.14}$| | |$0.7^{+0.76}_{-0.44}$| | |$1.18^{+1.51}_{-0.76}$| | |$0.06^{+0.08}_{-0.04}$| | |||||
| SMC_SC1 60553 | 01 | |$13.8^{+3.5}_{-2.7}$| | |$0.7^{+0.2}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.62^{+0.1}_{-0.05}$| | |$1.9^{+1.0}_{-0.5}$| | |$1.26^{+0.17}_{-0.28}$| | |$0.1^{+0.04}_{-0.03}$| | |$3.07^{+0.57}_{-0.72}$| | |$4.72^{+1.94}_{-1.59}$| | |$9.12^{+4.64}_{-3.45}$| | |$2.93^{+1.45}_{-1.11}$| |
| SMC_SC1 75701 | 01 | |$17.0^{+2.8}_{-3.9}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.7^{+0.13}_{-0.07}$| | |$2.2^{+0.7}_{-0.5}$| | |$0.25^{+0.21}_{-0.09}$| | |$0.11^{+0.06}_{-0.04}$| | |$0.81^{+0.65}_{-0.3}$| | |$1.11^{+1.24}_{-0.51}$| | |$2.33^{+2.92}_{-1.17}$| | |$0.97^{+1.22}_{-0.49}$| |
| SMC_SC1 92262 | 01 | |$14.7^{+3.3}_{-2.9}$| | |$0.6^{+0.2}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.04^{+0.02}_{-0.02}$| | |$1.3^{+1.1}_{-0.7}$| | |$0.49^{+0.53}_{-0.3}$| | |$0.89^{+0.41}_{-0.47}$| | |$0.53^{+0.58}_{-0.31}$| | |$1.11^{+1.2}_{-0.6}$| | |$2.2^{+2.42}_{-1.21}$| | |$0.32^{+0.33}_{-0.17}$| |
| 02 | |$2.6^{+0.5}_{-0.5}$| | |$0.99^{+0.33}_{-0.36}$| | |$0.94^{+0.34}_{-0.32}$| | |$1.14^{+0.64}_{-0.44}$| | |$4.86^{+1.81}_{-1.35}$| | |$9.61^{+4.13}_{-2.88}$| | |$1.52^{+0.72}_{-0.48}$| | |||||
| SMC_SC2 94939 | 01 | |$12.0^{+3.0}_{-2.4}$| | |$0.6^{+0.3}_{-0.4}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.46^{+0.14}_{-0.07}$| | |$2.4^{+0.8}_{-0.8}$| | |$0.9^{+0.42}_{-0.43}$| | |$0.63^{+0.34}_{-0.32}$| | |$1.31^{+0.59}_{-0.61}$| | |$3.26^{+2.5}_{-1.74}$| | |$5.47^{+4.52}_{-2.98}$| | |$0.96^{+0.77}_{-0.53}$| |
| SMC_SC3 5719 | 01 | |$12.1^{+2.9}_{-2.6}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.41^{+0.1}_{-0.06}$| | |$2.6^{+0.6}_{-0.8}$| | |$0.68^{+0.46}_{-0.33}$| | |$0.38^{+0.21}_{-0.18}$| | |$4.15^{+2.74}_{-1.98}$| | |$2.74^{+2.49}_{-1.6}$| | |$4.59^{+4.31}_{-2.72}$| | |$3.28^{+3.06}_{-1.95}$| |
| SMC_SC3 15970 | 01 | |$15.0^{+2.7}_{-2.4}$| | |$0.7^{+0.2}_{-0.2}$| | |$0.82^{+0.09}_{-0.1}$| | |$0.62^{+0.03}_{-0.02}$| | |$1.3^{+0.4}_{-0.2}$| | |$0.72^{+0.3}_{-0.29}$| | |$0.12^{+0.05}_{-0.03}$| | |$1.52^{+0.69}_{-0.67}$| | |$2.08^{+1.17}_{-0.76}$| | |$4.3^{+3.07}_{-1.71}$| | |$1.26^{+0.81}_{-0.5}$| |
| 02 | |$1.5^{+0.4}_{-0.3}$| | |$0.78^{+0.37}_{-0.3}$| | |$0.17^{+0.05}_{-0.03}$| | |$2.05^{+1.01}_{-0.81}$| | |$2.68^{+1.64}_{-1.01}$| | |$5.53^{+4.21}_{-2.24}$| | |$2.02^{+1.58}_{-0.82}$| | |||||
| 03 | |$1.3^{+0.3}_{-0.2}$| | |$1.08^{+0.26}_{-0.27}$| | |$0.13^{+0.05}_{-0.05}$| | |$3.17^{+0.93}_{-0.96}$| | |$3.13^{+1.26}_{-0.99}$| | |$6.5^{+3.54}_{-2.39}$| | |$2.62^{+1.39}_{-0.96}$| | |||||
| SMC_SC3 71445 | 01 | |$10.5^{+2.4}_{-2.1}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.43^{+0.09}_{-0.06}$| | |$2.5^{+0.6}_{-0.7}$| | |$0.58^{+0.45}_{-0.28}$| | |$0.67^{+0.38}_{-0.29}$| | |$1.3^{+1.02}_{-0.6}$| | |$1.96^{+1.67}_{-1.05}$| | |$2.88^{+2.58}_{-1.6}$| | |$0.7^{+0.64}_{-0.39}$| |
| 02 | |$1.2^{+0.6}_{-0.4}$| | |$0.67^{+0.52}_{-0.35}$| | |$1.0^{+0.34}_{-0.37}$| | |$0.59^{+0.5}_{-0.31}$| | |$1.12^{+0.71}_{-0.49}$| | |$1.64^{+1.12}_{-0.74}$| | |$0.16^{+0.12}_{-0.07}$| | |||||
| SMC_SC3 125899 | 01 | |$13.9^{+3.3}_{-3.2}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.39^{+0.2}_{-0.07}$| | |$1.6^{+1.2}_{-0.8}$| | |$0.73^{+0.48}_{-0.4}$| | |$0.35^{+0.29}_{-0.19}$| | |$1.09^{+0.73}_{-0.61}$| | |$1.88^{+1.82}_{-1.13}$| | |$3.49^{+3.65}_{-2.16}$| | |$0.64^{+0.68}_{-0.39}$| |
| SMC_SC3 197941 | 01 | |$12.1^{+4.5}_{-2.0}$| | |$0.7^{+0.2}_{-0.4}$| | |$0.83^{+0.09}_{-0.11}$| | |$0.56^{+0.14}_{-0.04}$| | |$0.8^{+0.4}_{-0.2}$| | |$0.36^{+0.57}_{-0.21}$| | |$0.1^{+0.04}_{-0.03}$| | |$1.38^{+2.24}_{-0.82}$| | |$0.62^{+0.77}_{-0.34}$| | |$1.14^{+1.5}_{-0.66}$| | |$0.58^{+0.76}_{-0.33}$| |
| SMC_SC4 22859 | 01 | |$8.2^{+1.7}_{-1.6}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.8^{+0.11}_{-0.1}$| | |$0.64^{+0.19}_{-0.11}$| | |$0.3^{+0.2}_{-0.1}$| | |$0.68^{+0.56}_{-0.55}$| | |$0.03^{+0.66}_{-0.02}$| | |$4.16^{+4.08}_{-3.37}$| | |$0.2^{+0.18}_{-0.15}$| | |$0.23^{+0.23}_{-0.17}$| | |$0.13^{+0.15}_{-0.1}$| |
| SMC_SC4 71499 | 01 | |$17.3^{+2.4}_{-3.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.53^{+0.05}_{-0.03}$| | |$1.5^{+0.6}_{-0.4}$| | |$0.7^{+0.46}_{-0.32}$| | |$0.25^{+0.1}_{-0.07}$| | |$1.1^{+0.7}_{-0.51}$| | |$2.09^{+1.16}_{-0.86}$| | |$4.41^{+2.86}_{-2.0}$| | |$0.9^{+0.59}_{-0.4}$| |
| 02 | |$1.8^{+0.7}_{-0.5}$| | |$0.68^{+0.44}_{-0.31}$| | |$0.19^{+0.07}_{-0.06}$| | |$1.37^{+0.93}_{-0.62}$| | |$2.32^{+1.49}_{-1.0}$| | |$4.9^{+3.62}_{-2.28}$| | |$1.34^{+0.97}_{-0.62}$| | |||||
| SMC_SC4 120783 | 01 | |$18.2^{+1.9}_{-2.4}$| | |$0.9^{+0.1}_{-0.1}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.6^{+0.18}_{-0.08}$| | |$0.9^{+0.3}_{-0.2}$| | |$0.73^{+0.5}_{-0.47}$| | |$0.13^{+0.07}_{-0.05}$| | |$1.72^{+1.11}_{-1.1}$| | |$2.01^{+1.61}_{-1.05}$| | |$5.47^{+4.82}_{-2.84}$| | |$2.25^{+1.97}_{-1.16}$| |
| SMC_SC4 127840 | 01 | |$15.2^{+3.0}_{-2.3}$| | |$0.8^{+0.1}_{-0.2}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.65^{+0.12}_{-0.09}$| | |$2.8^{+0.5}_{-0.6}$| | |$0.39^{+0.21}_{-0.13}$| | |$0.76^{+0.4}_{-0.32}$| | |$0.57^{+0.28}_{-0.18}$| | |$2.95^{+2.15}_{-1.19}$| | |$6.77^{+5.27}_{-2.88}$| | |$1.52^{+1.16}_{-0.66}$| |
| SMC_SC4 156248 | 01 | |$12.9^{+3.2}_{-2.4}$| | |$0.7^{+0.2}_{-0.4}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.07^{+0.02}_{-0.04}$| | |$1.2^{+1.3}_{-0.8}$| | |$0.46^{+0.63}_{-0.32}$| | |$0.89^{+0.42}_{-0.48}$| | |$1.5^{+2.08}_{-1.05}$| | |$0.69^{+1.94}_{-0.45}$| | |$1.28^{+3.51}_{-0.83}$| | |$0.53^{+1.51}_{-0.35}$| |
| SMC_SC4 156251 | 01 | |$17.3^{+2.0}_{-2.4}$| | |$0.6^{+0.2}_{-0.2}$| | |$0.83^{+0.09}_{-0.1}$| | |$0.78^{+0.06}_{-0.05}$| | |$2.3^{+0.3}_{-0.4}$| | |$0.41^{+0.16}_{-0.09}$| | |$0.67^{+0.36}_{-0.27}$| | |$0.43^{+0.17}_{-0.1}$| | |$2.14^{+0.95}_{-0.63}$| | |$4.84^{+2.55}_{-1.58}$| | |$0.73^{+0.38}_{-0.25}$| |
| 02 | |$1.6^{+0.2}_{-0.2}$| | |$0.6^{+0.31}_{-0.2}$| | |$0.49^{+0.36}_{-0.16}$| | |$0.64^{+0.29}_{-0.2}$| | |$2.24^{+1.19}_{-0.7}$| | |$5.08^{+3.01}_{-1.77}$| | |$0.76^{+0.43}_{-0.26}$| | |||||
| 03 | |$2.8^{+0.4}_{-0.4}$| | |$0.93^{+0.36}_{-0.34}$| | |$0.49^{+0.16}_{-0.11}$| | |$1.25^{+0.48}_{-0.42}$| | |$5.88^{+2.75}_{-2.18}$| | |$13.27^{+7.36}_{-5.32}$| | |$2.52^{+1.42}_{-0.96}$| | |||||
| SMC_SC4 159829 | 01 | |$14.5^{+2.8}_{-3.0}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.59^{+0.07}_{-0.05}$| | |$2.5^{+0.7}_{-0.6}$| | |$1.05^{+0.29}_{-0.31}$| | |$0.26^{+0.09}_{-0.07}$| | |$1.64^{+0.5}_{-0.48}$| | |$4.16^{+1.75}_{-1.48}$| | |$7.59^{+3.8}_{-2.93}$| | |$1.44^{+0.68}_{-0.55}$| |
| 02 | |$2.5^{+0.6}_{-0.6}$| | |$0.96^{+0.34}_{-0.37}$| | |$0.72^{+0.28}_{-0.23}$| | |$2.6^{+0.91}_{-0.95}$| | |$3.82^{+1.64}_{-1.47}$| | |$6.92^{+3.45}_{-2.79}$| | |$2.25^{+1.11}_{-0.91}$| | |||||
| SMC_SC4 159857 | 01 | |$15.2^{+3.4}_{-3.3}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.54^{+0.08}_{-0.03}$| | |$0.7^{+1.2}_{-0.3}$| | |$0.45^{+0.63}_{-0.35}$| | |$0.67^{+0.49}_{-0.37}$| | |$0.33^{+0.5}_{-0.26}$| | |$0.59^{+0.48}_{-0.3}$| | |$1.15^{+1.08}_{-0.61}$| | |$0.11^{+0.11}_{-0.06}$| |
| 02 | |$1.1^{+0.7}_{-0.3}$| | |$0.62^{+0.48}_{-0.37}$| | |$0.32^{+0.62}_{-0.15}$| | |$0.43^{+0.3}_{-0.27}$| | |$1.33^{+0.77}_{-0.61}$| | |$2.63^{+1.79}_{-1.29}$| | |$0.22^{+0.15}_{-0.11}$| | |||||
| SMC_SC4 163828 | 01 | |$8.7^{+1.8}_{-1.8}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.72^{+0.14}_{-0.08}$| | |$0.6^{+0.2}_{-0.1}$| | |$0.48^{+0.58}_{-0.31}$| | |$0.04^{+0.04}_{-0.02}$| | |$3.76^{+4.54}_{-2.4}$| | |$0.29^{+0.33}_{-0.18}$| | |$0.34^{+0.42}_{-0.21}$| | |$0.25^{+0.31}_{-0.15}$| |
| SMC_SC4 167554 | 01 | |$9.2^{+1.9}_{-2.1}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.59^{+0.08}_{-0.05}$| | |$0.8^{+0.5}_{-0.2}$| | |$0.56^{+0.46}_{-0.34}$| | |$0.54^{+0.45}_{-0.24}$| | |$0.54^{+0.44}_{-0.34}$| | |$0.47^{+0.32}_{-0.2}$| | |$0.57^{+0.44}_{-0.25}$| | |$0.05^{+0.04}_{-0.02}$| |
| 02 | |$1.5^{+0.6}_{-0.4}$| | |$0.42^{+0.36}_{-0.18}$| | |$0.84^{+0.42}_{-0.34}$| | |$0.51^{+0.47}_{-0.21}$| | |$0.7^{+0.5}_{-0.29}$| | |$0.86^{+0.71}_{-0.39}$| | |$0.1^{+0.08}_{-0.05}$| | |||||
| SMC_SC4 171253 | 01 | |$16.5^{+2.5}_{-3.4}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.1}$| | |$0.59^{+0.14}_{-0.07}$| | |$0.3^{+1.2}_{-0.1}$| | |$0.41^{+0.73}_{-0.39}$| | |$0.78^{+0.5}_{-0.47}$| | |$0.38^{+0.65}_{-0.36}$| | |$0.2^{+0.28}_{-0.15}$| | |$0.41^{+0.58}_{-0.31}$| | |$0.05^{+0.07}_{-0.03}$| |
| 02 | |$0.4^{+0.5}_{-0.1}$| | |$0.54^{+0.6}_{-0.47}$| | |$0.67^{+0.5}_{-0.46}$| | |$0.4^{+0.44}_{-0.36}$| | |$0.3^{+0.32}_{-0.2}$| | |$0.59^{+0.69}_{-0.4}$| | |$0.05^{+0.07}_{-0.04}$| | |||||
| SMC_SC4 175272 | 01 | |$12.1^{+2.6}_{-2.8}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.12}$| | |$0.37^{+0.15}_{-0.05}$| | |$1.8^{+1.1}_{-0.7}$| | |$0.72^{+0.46}_{-0.39}$| | |$0.46^{+0.34}_{-0.23}$| | |$2.54^{+1.6}_{-1.38}$| | |$1.87^{+1.68}_{-1.13}$| | |$2.96^{+2.97}_{-1.82}$| | |$1.19^{+1.17}_{-0.74}$| |
| SMC_SC4 179053 | 01 | |$12.5^{+3.0}_{-2.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.03^{+0.03}_{-0.02}$| | |$2.1^{+0.9}_{-0.7}$| | |$0.78^{+0.46}_{-0.43}$| | |$1.08^{+0.3}_{-0.35}$| | |$2.12^{+1.4}_{-1.18}$| | |$2.28^{+1.67}_{-1.02}$| | |$3.81^{+3.09}_{-1.77}$| | |$1.2^{+0.98}_{-0.54}$| |
| SMC_SC5 11453 | 01 | |$14.6^{+3.3}_{-3.4}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.39^{+0.14}_{-0.06}$| | |$1.9^{+1.0}_{-0.8}$| | |$0.89^{+0.38}_{-0.39}$| | |$0.24^{+0.15}_{-0.11}$| | |$4.72^{+2.18}_{-2.0}$| | |$2.96^{+2.47}_{-1.71}$| | |$5.66^{+5.16}_{-3.43}$| | |$3.85^{+3.47}_{-2.35}$| |
| SMC_SC5 21117 | 01 | |$16.0^{+2.3}_{-2.6}$| | |$0.5^{+0.2}_{-0.2}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.52^{+0.03}_{-0.01}$| | |$1.4^{+0.4}_{-0.3}$| | |$0.55^{+0.37}_{-0.21}$| | |$0.55^{+0.42}_{-0.25}$| | |$0.83^{+0.57}_{-0.31}$| | |$1.48^{+0.84}_{-0.55}$| | |$3.0^{+2.0}_{-1.25}$| | |$0.58^{+0.39}_{-0.24}$| |
| 02 | |$2.1^{+0.8}_{-0.4}$| | |$0.75^{+0.38}_{-0.29}$| | |$0.15^{+0.08}_{-0.04}$| | |$1.15^{+0.55}_{-0.41}$| | |$2.89^{+2.02}_{-1.16}$| | |$5.77^{+4.94}_{-2.51}$| | |$1.16^{+0.94}_{-0.5}$| | |||||
| 03 | |$2.1^{+0.6}_{-0.5}$| | |$0.62^{+0.28}_{-0.21}$| | |$0.33^{+0.21}_{-0.11}$| | |$0.74^{+0.37}_{-0.25}$| | |$2.42^{+1.36}_{-0.86}$| | |$4.86^{+3.4}_{-1.97}$| | |$0.75^{+0.51}_{-0.3}$| | |||||
| 04 | |$1.6^{+0.3}_{-0.3}$| | |$0.72^{+0.31}_{-0.23}$| | |$0.13^{+0.07}_{-0.04}$| | |$2.96^{+1.15}_{-1.03}$| | |$2.23^{+1.11}_{-0.78}$| | |$4.5^{+2.69}_{-1.75}$| | |$2.28^{+1.48}_{-0.92}$| | |||||
| SMC_SC5 21134 | 01 | |$12.9^{+3.7}_{-2.8}$| | |$0.5^{+0.3}_{-0.4}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.41^{+0.22}_{-0.08}$| | |$0.7^{+1.6}_{-0.4}$| | |$0.43^{+0.66}_{-0.37}$| | |$0.15^{+0.3}_{-0.09}$| | |$0.44^{+0.74}_{-0.38}$| | |$0.42^{+0.56}_{-0.3}$| | |$0.72^{+1.06}_{-0.53}$| | |$0.09^{+0.13}_{-0.06}$| |
| SMC_SC5 32377 | 01 | |$14.3^{+3.1}_{-3.1}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.35^{+0.08}_{-0.04}$| | |$1.8^{+1.0}_{-0.7}$| | |$0.75^{+0.48}_{-0.41}$| | |$0.57^{+0.4}_{-0.26}$| | |$0.37^{+0.33}_{-0.2}$| | |$2.25^{+1.85}_{-1.11}$| | |$4.31^{+3.82}_{-2.24}$| | |$0.28^{+0.26}_{-0.15}$| |
| 02 | |$2.1^{+0.8}_{-0.7}$| | |$0.6^{+0.37}_{-0.27}$| | |$0.27^{+0.12}_{-0.11}$| | |$1.13^{+0.73}_{-0.49}$| | |$2.26^{+1.73}_{-1.11}$| | |$4.23^{+3.75}_{-2.13}$| | |$1.02^{+0.89}_{-0.52}$| | |||||
| SMC_SC5 43650 | 01 | |$8.9^{+2.0}_{-1.9}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.79^{+0.11}_{-0.1}$| | |$0.55^{+0.1}_{-0.04}$| | |$0.4^{+0.7}_{-0.1}$| | |$0.5^{+0.64}_{-0.45}$| | |$0.34^{+0.73}_{-0.26}$| | |$1.07^{+1.36}_{-0.95}$| | |$0.18^{+0.18}_{-0.12}$| | |$0.21^{+0.23}_{-0.14}$| | |$0.04^{+0.05}_{-0.03}$| |
| 02 | |$0.5^{+0.2}_{-0.1}$| | |$0.58^{+0.59}_{-0.43}$| | |$0.62^{+0.59}_{-0.51}$| | |$6.62^{+6.56}_{-4.92}$| | |$0.29^{+0.27}_{-0.19}$| | |$0.34^{+0.35}_{-0.23}$| | |$0.36^{+0.41}_{-0.24}$| | |||||
| SMC_SC5 54851 | 01 | |$12.5^{+2.4}_{-2.0}$| | |$0.6^{+0.2}_{-0.2}$| | |$0.82^{+0.09}_{-0.09}$| | |$0.62^{+0.03}_{-0.01}$| | |$1.1^{+0.3}_{-0.2}$| | |$0.74^{+0.35}_{-0.33}$| | |$0.1^{+0.04}_{-0.03}$| | |$1.85^{+0.85}_{-0.85}$| | |$1.41^{+0.74}_{-0.56}$| | |$2.44^{+1.54}_{-1.04}$| | |$0.73^{+0.48}_{-0.32}$| |
| 02 | |$1.2^{+0.3}_{-0.2}$| | |$0.76^{+0.35}_{-0.34}$| | |$0.11^{+0.03}_{-0.03}$| | |$2.08^{+0.89}_{-0.95}$| | |$1.55^{+0.8}_{-0.61}$| | |$2.67^{+1.67}_{-1.13}$| | |$0.88^{+0.52}_{-0.37}$| | |||||
| 03 | |$1.1^{+0.2}_{-0.1}$| | |$0.5^{+0.31}_{-0.18}$| | |$0.05^{+0.01}_{-0.01}$| | |$2.42^{+1.6}_{-0.86}$| | |$0.97^{+0.63}_{-0.39}$| | |$1.69^{+1.3}_{-0.76}$| | |$0.99^{+0.81}_{-0.45}$| | |||||
| SMC_SC5 65500 | 01 | |$12.8^{+3.3}_{-2.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.66^{+0.11}_{-0.05}$| | |$2.0^{+1.0}_{-0.6}$| | |$0.61^{+0.38}_{-0.27}$| | |$0.29^{+0.13}_{-0.11}$| | |$0.46^{+0.27}_{-0.19}$| | |$1.91^{+1.23}_{-0.88}$| | |$3.21^{+2.57}_{-1.62}$| | |$0.28^{+0.22}_{-0.14}$| |
| SMC_SC5 129535 | 01 | |$9.1^{+2.1}_{-2.0}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.57^{+0.13}_{-0.05}$| | |$0.7^{+0.2}_{-0.2}$| | |$0.63^{+0.53}_{-0.36}$| | |$0.22^{+0.27}_{-0.11}$| | |$4.4^{+3.69}_{-2.6}$| | |$0.49^{+0.39}_{-0.27}$| | |$0.61^{+0.52}_{-0.34}$| | |$0.42^{+0.37}_{-0.23}$| |
| SMC_SC5 145724 | 01 | |$8.6^{+2.1}_{-1.8}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.42^{+0.1}_{-0.05}$| | |$2.4^{+0.7}_{-0.8}$| | |$0.81^{+0.44}_{-0.41}$| | |$0.13^{+0.07}_{-0.06}$| | |$4.2^{+2.39}_{-2.09}$| | |$2.05^{+1.73}_{-1.15}$| | |$2.51^{+2.24}_{-1.4}$| | |$1.31^{+1.21}_{-0.75}$| |
| SMC_SC5 180034 | 01 | |$12.0^{+2.5}_{-2.5}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.63^{+0.15}_{-0.1}$| | |$1.0^{+0.5}_{-0.3}$| | |$0.32^{+0.55}_{-0.19}$| | |$0.19^{+0.15}_{-0.08}$| | |$0.91^{+1.56}_{-0.54}$| | |$0.45^{+0.57}_{-0.25}$| | |$0.71^{+0.95}_{-0.42}$| | |$0.22^{+0.27}_{-0.13}$| |
| SMC_SC5 260841 | 01 | |$13.4^{+4.0}_{-3.2}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.53^{+0.06}_{-0.02}$| | |$0.6^{+0.5}_{-0.1}$| | |$0.78^{+0.45}_{-0.52}$| | |$0.06^{+0.26}_{-0.02}$| | |$1.53^{+0.95}_{-1.05}$| | |$0.77^{+0.52}_{-0.4}$| | |$1.34^{+1.17}_{-0.69}$| | |$0.33^{+0.29}_{-0.17}$| |
| 02 | |$0.6^{+0.3}_{-0.1}$| | |$0.75^{+0.44}_{-0.44}$| | |$0.06^{+0.77}_{-0.03}$| | |$2.74^{+1.74}_{-1.78}$| | |$0.72^{+0.44}_{-0.35}$| | |$1.27^{+0.92}_{-0.62}$| | |$0.54^{+0.43}_{-0.28}$| | |||||
| SMC_SC5 260957 | 01 | |$8.9^{+2.1}_{-2.0}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.82^{+0.09}_{-0.11}$| | |$0.58^{+0.14}_{-0.06}$| | |$1.2^{+0.4}_{-0.3}$| | |$0.55^{+0.5}_{-0.24}$| | |$0.04^{+0.02}_{-0.02}$| | |$2.45^{+2.21}_{-1.1}$| | |$0.78^{+0.63}_{-0.4}$| | |$0.98^{+0.86}_{-0.54}$| | |$0.43^{+0.4}_{-0.23}$| |
| SMC_SC5 266088 | 01 | |$7.8^{+1.5}_{-1.6}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.7^{+0.14}_{-0.08}$| | |$0.7^{+0.4}_{-0.1}$| | |$0.3^{+0.69}_{-0.24}$| | |$0.06^{+0.05}_{-0.02}$| | |$1.92^{+4.42}_{-1.56}$| | |$0.17^{+0.3}_{-0.11}$| | |$0.18^{+0.34}_{-0.12}$| | |$0.11^{+0.19}_{-0.07}$| |
| SMC_SC5 276982 | 01 | |$17.1^{+2.2}_{-2.6}$| | |$0.2^{+0.2}_{-0.2}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.75^{+0.11}_{-0.1}$| | |$1.2^{+0.4}_{-0.3}$| | |$0.06^{+0.19}_{-0.03}$| | |$0.05^{+0.04}_{-0.02}$| | |$0.31^{+1.0}_{-0.16}$| | |$0.12^{+0.26}_{-0.06}$| | |$0.23^{+0.54}_{-0.13}$| | |$0.15^{+0.33}_{-0.08}$| |
| SMC_SC5 282963 | 01 | |$15.6^{+3.1}_{-3.6}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.38^{+0.19}_{-0.06}$| | |$1.7^{+1.0}_{-0.8}$| | |$0.62^{+0.51}_{-0.33}$| | |$0.39^{+0.32}_{-0.21}$| | |$5.62^{+4.36}_{-2.92}$| | |$2.07^{+2.43}_{-1.35}$| | |$4.14^{+5.39}_{-2.78}$| | |$4.96^{+6.18}_{-3.36}$| |
| SMC_SC6 11085 | 01 | |$17.8^{+1.9}_{-2.9}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.74^{+0.06}_{-0.05}$| | |$2.4^{+0.6}_{-0.5}$| | |$0.59^{+0.26}_{-0.18}$| | |$0.13^{+0.05}_{-0.04}$| | |$0.99^{+0.45}_{-0.3}$| | |$2.53^{+1.13}_{-0.87}$| | |$5.19^{+2.71}_{-1.99}$| | |$1.06^{+0.57}_{-0.4}$| |
| 02 | |$2.6^{+0.5}_{-0.4}$| | |$0.78^{+0.34}_{-0.27}$| | |$0.27^{+0.09}_{-0.07}$| | |$1.49^{+0.63}_{-0.5}$| | |$3.41^{+1.75}_{-1.29}$| | |$7.07^{+4.11}_{-3.0}$| | |$1.64^{+0.95}_{-0.68}$| | |||||
| SMC_SC6 17538 | 01 | |$7.8^{+1.6}_{-1.4}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.61^{+0.15}_{-0.08}$| | |$0.7^{+0.3}_{-0.2}$| | |$0.59^{+0.58}_{-0.41}$| | |$0.08^{+0.09}_{-0.04}$| | |$3.55^{+3.44}_{-2.47}$| | |$0.37^{+0.34}_{-0.22}$| | |$0.4^{+0.39}_{-0.24}$| | |$0.22^{+0.21}_{-0.13}$| |
| SMC_SC6 42440 | 01 | |$8.9^{+2.0}_{-2.0}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.36^{+0.15}_{-0.05}$| | |$1.8^{+1.2}_{-0.8}$| | |$0.78^{+0.45}_{-0.42}$| | |$0.19^{+0.17}_{-0.1}$| | |$2.82^{+1.81}_{-1.46}$| | |$1.36^{+1.32}_{-0.79}$| | |$1.66^{+1.84}_{-0.99}$| | |$0.61^{+0.72}_{-0.37}$| |
| SMC_SC6 99991 | 01 | |$14.8^{+2.6}_{-2.8}$| | |$0.5^{+0.2}_{-0.2}$| | |$0.83^{+0.09}_{-0.09}$| | |$0.34^{+0.04}_{-0.02}$| | |$1.7^{+0.6}_{-0.5}$| | |$0.62^{+0.43}_{-0.25}$| | |$0.98^{+0.31}_{-0.29}$| | |$0.88^{+0.64}_{-0.36}$| | |$1.85^{+1.11}_{-0.75}$| | |$3.54^{+2.45}_{-1.55}$| | |$0.64^{+0.44}_{-0.27}$| |
| 02 | |$2.2^{+0.7}_{-0.6}$| | |$0.62^{+0.33}_{-0.25}$| | |$0.74^{+0.33}_{-0.26}$| | |$1.13^{+0.62}_{-0.44}$| | |$2.37^{+1.58}_{-0.97}$| | |$4.47^{+3.48}_{-1.93}$| | |$1.02^{+0.8}_{-0.43}$| | |||||
| 03 | |$1.9^{+0.6}_{-0.5}$| | |$0.55^{+0.45}_{-0.22}$| | |$0.76^{+0.3}_{-0.24}$| | |$1.03^{+0.83}_{-0.43}$| | |$1.94^{+1.17}_{-0.77}$| | |$3.72^{+2.63}_{-1.65}$| | |$0.85^{+0.62}_{-0.37}$| | |||||
| 04 | |$1.7^{+0.5}_{-0.4}$| | |$0.53^{+0.36}_{-0.22}$| | |$0.92^{+0.3}_{-0.26}$| | |$1.12^{+0.77}_{-0.47}$| | |$1.56^{+0.97}_{-0.59}$| | |$2.96^{+2.18}_{-1.24}$| | |$0.79^{+0.59}_{-0.33}$| | |||||
| SMC_SC6 105368 | 01 | |$11.2^{+2.7}_{-2.9}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.53^{+0.04}_{-0.02}$| | |$0.9^{+0.4}_{-0.2}$| | |$0.51^{+0.57}_{-0.31}$| | |$0.17^{+0.1}_{-0.06}$| | |$1.12^{+1.23}_{-0.68}$| | |$0.61^{+0.56}_{-0.3}$| | |$0.92^{+0.91}_{-0.47}$| | |$0.22^{+0.22}_{-0.11}$| |
| 02 | |$1.2^{+0.5}_{-0.4}$| | |$0.28^{+0.48}_{-0.13}$| | |$0.19^{+0.13}_{-0.07}$| | |$0.78^{+1.38}_{-0.37}$| | |$0.5^{+0.48}_{-0.21}$| | |$0.76^{+0.77}_{-0.34}$| | |$0.23^{+0.25}_{-0.1}$| | |||||
| SMC_SC6 116294 | 01 | |$8.6^{+2.1}_{-1.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.41^{+0.1}_{-0.05}$| | |$2.6^{+0.7}_{-1.0}$| | |$0.87^{+0.4}_{-0.39}$| | |$0.16^{+0.09}_{-0.07}$| | |$2.71^{+1.35}_{-1.23}$| | |$2.42^{+1.65}_{-1.34}$| | |$2.99^{+2.11}_{-1.69}$| | |$0.93^{+0.71}_{-0.53}$| |
| SMC_SC6 128831 | 01 | |$12.9^{+3.6}_{-2.9}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.03^{+0.03}_{-0.02}$| | |$2.7^{+0.5}_{-0.8}$| | |$0.96^{+0.37}_{-0.42}$| | |$0.62^{+0.33}_{-0.23}$| | |$0.85^{+0.38}_{-0.37}$| | |$3.93^{+2.09}_{-1.61}$| | |$6.95^{+4.2}_{-2.98}$| | |$0.79^{+0.45}_{-0.35}$| |
| SMC_SC6 199611 | 01 | |$15.5^{+3.6}_{-3.3}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.39^{+0.17}_{-0.07}$| | |$1.5^{+1.3}_{-0.8}$| | |$0.51^{+0.58}_{-0.36}$| | |$0.29^{+0.26}_{-0.16}$| | |$0.44^{+0.52}_{-0.31}$| | |$1.33^{+1.47}_{-0.84}$| | |$2.75^{+3.38}_{-1.76}$| | |$0.33^{+0.39}_{-0.21}$| |
| SMC_SC6 272665 | 01 | |$6.3^{+1.2}_{-0.9}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.81^{+0.12}_{-0.11}$| | |$0.39^{+0.19}_{-0.07}$| | |$0.6^{+0.3}_{-0.2}$| | |$0.7^{+0.51}_{-0.47}$| | |$0.07^{+0.41}_{-0.05}$| | |$7.81^{+6.55}_{-5.28}$| | |$0.26^{+0.25}_{-0.15}$| | |$0.23^{+0.24}_{-0.14}$| | |$0.22^{+0.23}_{-0.14}$| |
| SMC_SC7 57131 | 01 | |$12.0^{+2.8}_{-2.4}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.39^{+0.14}_{-0.06}$| | |$2.0^{+0.8}_{-0.7}$| | |$0.73^{+0.43}_{-0.4}$| | |$0.65^{+0.41}_{-0.36}$| | |$1.81^{+1.04}_{-0.98}$| | |$2.11^{+1.81}_{-1.3}$| | |$3.4^{+3.27}_{-2.12}$| | |$0.99^{+0.93}_{-0.62}$| |
| SMC_SC8 183240 | 01 | |$17.6^{+2.3}_{-2.9}$| | |$0.7^{+0.2}_{-0.2}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.61^{+0.15}_{-0.08}$| | |$0.9^{+0.4}_{-0.2}$| | |$0.64^{+0.51}_{-0.44}$| | |$0.28^{+0.23}_{-0.13}$| | |$1.18^{+0.87}_{-0.77}$| | |$1.45^{+1.3}_{-0.79}$| | |$3.46^{+3.52}_{-1.93}$| | |$0.98^{+1.0}_{-0.54}$| |
| SMC_SC9 105383 | 01 | |$13.0^{+3.0}_{-2.6}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.56^{+0.06}_{-0.04}$| | |$1.9^{+0.7}_{-0.5}$| | |$0.53^{+0.44}_{-0.26}$| | |$0.09^{+0.04}_{-0.02}$| | |$1.43^{+1.21}_{-0.69}$| | |$1.47^{+1.17}_{-0.68}$| | |$2.42^{+2.29}_{-1.19}$| | |$0.74^{+0.7}_{-0.37}$| |
| 02 | |$1.7^{+0.6}_{-0.4}$| | |$0.77^{+0.41}_{-0.32}$| | |$0.09^{+0.03}_{-0.03}$| | |$1.9^{+0.91}_{-0.78}$| | |$1.94^{+1.22}_{-0.81}$| | |$3.2^{+2.55}_{-1.44}$| | |$0.87^{+0.71}_{-0.38}$| | |||||
| SMC_SC9 168422 | 01 | |$8.8^{+1.8}_{-1.8}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.61^{+0.18}_{-0.08}$| | |$0.5^{+0.3}_{-0.1}$| | |$0.56^{+0.6}_{-0.43}$| | |$0.07^{+0.11}_{-0.03}$| | |$2.55^{+2.96}_{-2.01}$| | |$0.27^{+0.27}_{-0.18}$| | |$0.33^{+0.34}_{-0.21}$| | |$0.15^{+0.16}_{-0.1}$| |
| SMC_SC10 8906 | 01 | |$16.1^{+3.3}_{-3.4}$| | |$0.6^{+0.2}_{-0.3}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.56^{+0.09}_{-0.04}$| | |$2.2^{+0.9}_{-0.7}$| | |$0.89^{+0.38}_{-0.31}$| | |$0.44^{+0.23}_{-0.16}$| | |$0.2^{+0.1}_{-0.07}$| | |$4.23^{+2.33}_{-1.6}$| | |$9.05^{+5.83}_{-3.69}$| | |$0.3^{+0.19}_{-0.12}$| |
| 02 | |$2.0^{+0.8}_{-0.7}$| | |$0.82^{+0.36}_{-0.31}$| | |$0.9^{+0.35}_{-0.31}$| | |$0.07^{+0.03}_{-0.02}$| | |$3.5^{+1.98}_{-1.35}$| | |$7.5^{+4.86}_{-3.08}$| | |$0.09^{+0.05}_{-0.04}$| | |||||
| SMC_SC11 28090 | 01 | |$14.5^{+3.8}_{-2.8}$| | |$0.7^{+0.2}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.57^{+0.13}_{-0.05}$| | |$1.8^{+0.8}_{-0.7}$| | |$0.1^{+0.09}_{-0.05}$| | |$0.12^{+0.05}_{-0.05}$| | |$0.46^{+0.41}_{-0.2}$| | |$0.45^{+0.38}_{-0.22}$| | |$0.94^{+0.96}_{-0.5}$| | |$0.59^{+0.59}_{-0.32}$| |
| SMC_SC11 46587 | 01 | |$8.2^{+1.8}_{-1.6}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.38^{+0.21}_{-0.06}$| | |$0.8^{+0.6}_{-0.3}$| | |$0.61^{+0.57}_{-0.46}$| | |$0.3^{+0.47}_{-0.18}$| | |$4.93^{+4.65}_{-3.7}$| | |$0.39^{+0.47}_{-0.25}$| | |$0.44^{+0.57}_{-0.29}$| | |$0.34^{+0.43}_{-0.22}$| |
| OGLE-II ID . | Bump . | M (M⊙) . | t/tMS . | W . | cos i . | Σ0 . | αbu . | αd . | |$\tilde{\tau }_\mathrm{bu}$| . | |$\left(-\frac{\mathrm{\partial} M}{\mathrm{\partial} t}\right)_\mathrm{typ}$| . | |$\left(-\frac{\mathrm{\partial} J}{\mathrm{\partial} t}\right)_\mathrm{std}$| . | −ΔJ* . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| . | ID . | . | . | . | . | (g cm−2) . | . | . | . | (10−9 × . | (1036 × . | (1044 × . |
| . | . | . | . | . | . | . | . | . | . | M⊙ yr−1) . | g cm2 s−2) . | g cm2 s−1) . |
| SMC_SC1 7612 | 01 | |$13.7^{+3.0}_{-3.0}$| | |$0.4^{+0.3}_{-0.2}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.37^{+0.16}_{-0.05}$| | |$0.9^{+1.4}_{-0.5}$| | |$0.44^{+0.68}_{-0.34}$| | |$0.62^{+0.52}_{-0.4}$| | |$0.23^{+0.35}_{-0.18}$| | |$0.55^{+0.66}_{-0.34}$| | |$0.94^{+1.31}_{-0.6}$| | |$0.06^{+0.08}_{-0.04}$| |
| 02 | |$1.1^{+1.5}_{-0.6}$| | |$0.47^{+0.64}_{-0.34}$| | |$0.56^{+0.62}_{-0.38}$| | |$0.2^{+0.3}_{-0.14}$| | |$0.7^{+0.76}_{-0.44}$| | |$1.18^{+1.51}_{-0.76}$| | |$0.06^{+0.08}_{-0.04}$| | |||||
| SMC_SC1 60553 | 01 | |$13.8^{+3.5}_{-2.7}$| | |$0.7^{+0.2}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.62^{+0.1}_{-0.05}$| | |$1.9^{+1.0}_{-0.5}$| | |$1.26^{+0.17}_{-0.28}$| | |$0.1^{+0.04}_{-0.03}$| | |$3.07^{+0.57}_{-0.72}$| | |$4.72^{+1.94}_{-1.59}$| | |$9.12^{+4.64}_{-3.45}$| | |$2.93^{+1.45}_{-1.11}$| |
| SMC_SC1 75701 | 01 | |$17.0^{+2.8}_{-3.9}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.7^{+0.13}_{-0.07}$| | |$2.2^{+0.7}_{-0.5}$| | |$0.25^{+0.21}_{-0.09}$| | |$0.11^{+0.06}_{-0.04}$| | |$0.81^{+0.65}_{-0.3}$| | |$1.11^{+1.24}_{-0.51}$| | |$2.33^{+2.92}_{-1.17}$| | |$0.97^{+1.22}_{-0.49}$| |
| SMC_SC1 92262 | 01 | |$14.7^{+3.3}_{-2.9}$| | |$0.6^{+0.2}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.04^{+0.02}_{-0.02}$| | |$1.3^{+1.1}_{-0.7}$| | |$0.49^{+0.53}_{-0.3}$| | |$0.89^{+0.41}_{-0.47}$| | |$0.53^{+0.58}_{-0.31}$| | |$1.11^{+1.2}_{-0.6}$| | |$2.2^{+2.42}_{-1.21}$| | |$0.32^{+0.33}_{-0.17}$| |
| 02 | |$2.6^{+0.5}_{-0.5}$| | |$0.99^{+0.33}_{-0.36}$| | |$0.94^{+0.34}_{-0.32}$| | |$1.14^{+0.64}_{-0.44}$| | |$4.86^{+1.81}_{-1.35}$| | |$9.61^{+4.13}_{-2.88}$| | |$1.52^{+0.72}_{-0.48}$| | |||||
| SMC_SC2 94939 | 01 | |$12.0^{+3.0}_{-2.4}$| | |$0.6^{+0.3}_{-0.4}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.46^{+0.14}_{-0.07}$| | |$2.4^{+0.8}_{-0.8}$| | |$0.9^{+0.42}_{-0.43}$| | |$0.63^{+0.34}_{-0.32}$| | |$1.31^{+0.59}_{-0.61}$| | |$3.26^{+2.5}_{-1.74}$| | |$5.47^{+4.52}_{-2.98}$| | |$0.96^{+0.77}_{-0.53}$| |
| SMC_SC3 5719 | 01 | |$12.1^{+2.9}_{-2.6}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.41^{+0.1}_{-0.06}$| | |$2.6^{+0.6}_{-0.8}$| | |$0.68^{+0.46}_{-0.33}$| | |$0.38^{+0.21}_{-0.18}$| | |$4.15^{+2.74}_{-1.98}$| | |$2.74^{+2.49}_{-1.6}$| | |$4.59^{+4.31}_{-2.72}$| | |$3.28^{+3.06}_{-1.95}$| |
| SMC_SC3 15970 | 01 | |$15.0^{+2.7}_{-2.4}$| | |$0.7^{+0.2}_{-0.2}$| | |$0.82^{+0.09}_{-0.1}$| | |$0.62^{+0.03}_{-0.02}$| | |$1.3^{+0.4}_{-0.2}$| | |$0.72^{+0.3}_{-0.29}$| | |$0.12^{+0.05}_{-0.03}$| | |$1.52^{+0.69}_{-0.67}$| | |$2.08^{+1.17}_{-0.76}$| | |$4.3^{+3.07}_{-1.71}$| | |$1.26^{+0.81}_{-0.5}$| |
| 02 | |$1.5^{+0.4}_{-0.3}$| | |$0.78^{+0.37}_{-0.3}$| | |$0.17^{+0.05}_{-0.03}$| | |$2.05^{+1.01}_{-0.81}$| | |$2.68^{+1.64}_{-1.01}$| | |$5.53^{+4.21}_{-2.24}$| | |$2.02^{+1.58}_{-0.82}$| | |||||
| 03 | |$1.3^{+0.3}_{-0.2}$| | |$1.08^{+0.26}_{-0.27}$| | |$0.13^{+0.05}_{-0.05}$| | |$3.17^{+0.93}_{-0.96}$| | |$3.13^{+1.26}_{-0.99}$| | |$6.5^{+3.54}_{-2.39}$| | |$2.62^{+1.39}_{-0.96}$| | |||||
| SMC_SC3 71445 | 01 | |$10.5^{+2.4}_{-2.1}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.43^{+0.09}_{-0.06}$| | |$2.5^{+0.6}_{-0.7}$| | |$0.58^{+0.45}_{-0.28}$| | |$0.67^{+0.38}_{-0.29}$| | |$1.3^{+1.02}_{-0.6}$| | |$1.96^{+1.67}_{-1.05}$| | |$2.88^{+2.58}_{-1.6}$| | |$0.7^{+0.64}_{-0.39}$| |
| 02 | |$1.2^{+0.6}_{-0.4}$| | |$0.67^{+0.52}_{-0.35}$| | |$1.0^{+0.34}_{-0.37}$| | |$0.59^{+0.5}_{-0.31}$| | |$1.12^{+0.71}_{-0.49}$| | |$1.64^{+1.12}_{-0.74}$| | |$0.16^{+0.12}_{-0.07}$| | |||||
| SMC_SC3 125899 | 01 | |$13.9^{+3.3}_{-3.2}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.39^{+0.2}_{-0.07}$| | |$1.6^{+1.2}_{-0.8}$| | |$0.73^{+0.48}_{-0.4}$| | |$0.35^{+0.29}_{-0.19}$| | |$1.09^{+0.73}_{-0.61}$| | |$1.88^{+1.82}_{-1.13}$| | |$3.49^{+3.65}_{-2.16}$| | |$0.64^{+0.68}_{-0.39}$| |
| SMC_SC3 197941 | 01 | |$12.1^{+4.5}_{-2.0}$| | |$0.7^{+0.2}_{-0.4}$| | |$0.83^{+0.09}_{-0.11}$| | |$0.56^{+0.14}_{-0.04}$| | |$0.8^{+0.4}_{-0.2}$| | |$0.36^{+0.57}_{-0.21}$| | |$0.1^{+0.04}_{-0.03}$| | |$1.38^{+2.24}_{-0.82}$| | |$0.62^{+0.77}_{-0.34}$| | |$1.14^{+1.5}_{-0.66}$| | |$0.58^{+0.76}_{-0.33}$| |
| SMC_SC4 22859 | 01 | |$8.2^{+1.7}_{-1.6}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.8^{+0.11}_{-0.1}$| | |$0.64^{+0.19}_{-0.11}$| | |$0.3^{+0.2}_{-0.1}$| | |$0.68^{+0.56}_{-0.55}$| | |$0.03^{+0.66}_{-0.02}$| | |$4.16^{+4.08}_{-3.37}$| | |$0.2^{+0.18}_{-0.15}$| | |$0.23^{+0.23}_{-0.17}$| | |$0.13^{+0.15}_{-0.1}$| |
| SMC_SC4 71499 | 01 | |$17.3^{+2.4}_{-3.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.53^{+0.05}_{-0.03}$| | |$1.5^{+0.6}_{-0.4}$| | |$0.7^{+0.46}_{-0.32}$| | |$0.25^{+0.1}_{-0.07}$| | |$1.1^{+0.7}_{-0.51}$| | |$2.09^{+1.16}_{-0.86}$| | |$4.41^{+2.86}_{-2.0}$| | |$0.9^{+0.59}_{-0.4}$| |
| 02 | |$1.8^{+0.7}_{-0.5}$| | |$0.68^{+0.44}_{-0.31}$| | |$0.19^{+0.07}_{-0.06}$| | |$1.37^{+0.93}_{-0.62}$| | |$2.32^{+1.49}_{-1.0}$| | |$4.9^{+3.62}_{-2.28}$| | |$1.34^{+0.97}_{-0.62}$| | |||||
| SMC_SC4 120783 | 01 | |$18.2^{+1.9}_{-2.4}$| | |$0.9^{+0.1}_{-0.1}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.6^{+0.18}_{-0.08}$| | |$0.9^{+0.3}_{-0.2}$| | |$0.73^{+0.5}_{-0.47}$| | |$0.13^{+0.07}_{-0.05}$| | |$1.72^{+1.11}_{-1.1}$| | |$2.01^{+1.61}_{-1.05}$| | |$5.47^{+4.82}_{-2.84}$| | |$2.25^{+1.97}_{-1.16}$| |
| SMC_SC4 127840 | 01 | |$15.2^{+3.0}_{-2.3}$| | |$0.8^{+0.1}_{-0.2}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.65^{+0.12}_{-0.09}$| | |$2.8^{+0.5}_{-0.6}$| | |$0.39^{+0.21}_{-0.13}$| | |$0.76^{+0.4}_{-0.32}$| | |$0.57^{+0.28}_{-0.18}$| | |$2.95^{+2.15}_{-1.19}$| | |$6.77^{+5.27}_{-2.88}$| | |$1.52^{+1.16}_{-0.66}$| |
| SMC_SC4 156248 | 01 | |$12.9^{+3.2}_{-2.4}$| | |$0.7^{+0.2}_{-0.4}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.07^{+0.02}_{-0.04}$| | |$1.2^{+1.3}_{-0.8}$| | |$0.46^{+0.63}_{-0.32}$| | |$0.89^{+0.42}_{-0.48}$| | |$1.5^{+2.08}_{-1.05}$| | |$0.69^{+1.94}_{-0.45}$| | |$1.28^{+3.51}_{-0.83}$| | |$0.53^{+1.51}_{-0.35}$| |
| SMC_SC4 156251 | 01 | |$17.3^{+2.0}_{-2.4}$| | |$0.6^{+0.2}_{-0.2}$| | |$0.83^{+0.09}_{-0.1}$| | |$0.78^{+0.06}_{-0.05}$| | |$2.3^{+0.3}_{-0.4}$| | |$0.41^{+0.16}_{-0.09}$| | |$0.67^{+0.36}_{-0.27}$| | |$0.43^{+0.17}_{-0.1}$| | |$2.14^{+0.95}_{-0.63}$| | |$4.84^{+2.55}_{-1.58}$| | |$0.73^{+0.38}_{-0.25}$| |
| 02 | |$1.6^{+0.2}_{-0.2}$| | |$0.6^{+0.31}_{-0.2}$| | |$0.49^{+0.36}_{-0.16}$| | |$0.64^{+0.29}_{-0.2}$| | |$2.24^{+1.19}_{-0.7}$| | |$5.08^{+3.01}_{-1.77}$| | |$0.76^{+0.43}_{-0.26}$| | |||||
| 03 | |$2.8^{+0.4}_{-0.4}$| | |$0.93^{+0.36}_{-0.34}$| | |$0.49^{+0.16}_{-0.11}$| | |$1.25^{+0.48}_{-0.42}$| | |$5.88^{+2.75}_{-2.18}$| | |$13.27^{+7.36}_{-5.32}$| | |$2.52^{+1.42}_{-0.96}$| | |||||
| SMC_SC4 159829 | 01 | |$14.5^{+2.8}_{-3.0}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.59^{+0.07}_{-0.05}$| | |$2.5^{+0.7}_{-0.6}$| | |$1.05^{+0.29}_{-0.31}$| | |$0.26^{+0.09}_{-0.07}$| | |$1.64^{+0.5}_{-0.48}$| | |$4.16^{+1.75}_{-1.48}$| | |$7.59^{+3.8}_{-2.93}$| | |$1.44^{+0.68}_{-0.55}$| |
| 02 | |$2.5^{+0.6}_{-0.6}$| | |$0.96^{+0.34}_{-0.37}$| | |$0.72^{+0.28}_{-0.23}$| | |$2.6^{+0.91}_{-0.95}$| | |$3.82^{+1.64}_{-1.47}$| | |$6.92^{+3.45}_{-2.79}$| | |$2.25^{+1.11}_{-0.91}$| | |||||
| SMC_SC4 159857 | 01 | |$15.2^{+3.4}_{-3.3}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.54^{+0.08}_{-0.03}$| | |$0.7^{+1.2}_{-0.3}$| | |$0.45^{+0.63}_{-0.35}$| | |$0.67^{+0.49}_{-0.37}$| | |$0.33^{+0.5}_{-0.26}$| | |$0.59^{+0.48}_{-0.3}$| | |$1.15^{+1.08}_{-0.61}$| | |$0.11^{+0.11}_{-0.06}$| |
| 02 | |$1.1^{+0.7}_{-0.3}$| | |$0.62^{+0.48}_{-0.37}$| | |$0.32^{+0.62}_{-0.15}$| | |$0.43^{+0.3}_{-0.27}$| | |$1.33^{+0.77}_{-0.61}$| | |$2.63^{+1.79}_{-1.29}$| | |$0.22^{+0.15}_{-0.11}$| | |||||
| SMC_SC4 163828 | 01 | |$8.7^{+1.8}_{-1.8}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.72^{+0.14}_{-0.08}$| | |$0.6^{+0.2}_{-0.1}$| | |$0.48^{+0.58}_{-0.31}$| | |$0.04^{+0.04}_{-0.02}$| | |$3.76^{+4.54}_{-2.4}$| | |$0.29^{+0.33}_{-0.18}$| | |$0.34^{+0.42}_{-0.21}$| | |$0.25^{+0.31}_{-0.15}$| |
| SMC_SC4 167554 | 01 | |$9.2^{+1.9}_{-2.1}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.59^{+0.08}_{-0.05}$| | |$0.8^{+0.5}_{-0.2}$| | |$0.56^{+0.46}_{-0.34}$| | |$0.54^{+0.45}_{-0.24}$| | |$0.54^{+0.44}_{-0.34}$| | |$0.47^{+0.32}_{-0.2}$| | |$0.57^{+0.44}_{-0.25}$| | |$0.05^{+0.04}_{-0.02}$| |
| 02 | |$1.5^{+0.6}_{-0.4}$| | |$0.42^{+0.36}_{-0.18}$| | |$0.84^{+0.42}_{-0.34}$| | |$0.51^{+0.47}_{-0.21}$| | |$0.7^{+0.5}_{-0.29}$| | |$0.86^{+0.71}_{-0.39}$| | |$0.1^{+0.08}_{-0.05}$| | |||||
| SMC_SC4 171253 | 01 | |$16.5^{+2.5}_{-3.4}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.1}$| | |$0.59^{+0.14}_{-0.07}$| | |$0.3^{+1.2}_{-0.1}$| | |$0.41^{+0.73}_{-0.39}$| | |$0.78^{+0.5}_{-0.47}$| | |$0.38^{+0.65}_{-0.36}$| | |$0.2^{+0.28}_{-0.15}$| | |$0.41^{+0.58}_{-0.31}$| | |$0.05^{+0.07}_{-0.03}$| |
| 02 | |$0.4^{+0.5}_{-0.1}$| | |$0.54^{+0.6}_{-0.47}$| | |$0.67^{+0.5}_{-0.46}$| | |$0.4^{+0.44}_{-0.36}$| | |$0.3^{+0.32}_{-0.2}$| | |$0.59^{+0.69}_{-0.4}$| | |$0.05^{+0.07}_{-0.04}$| | |||||
| SMC_SC4 175272 | 01 | |$12.1^{+2.6}_{-2.8}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.12}$| | |$0.37^{+0.15}_{-0.05}$| | |$1.8^{+1.1}_{-0.7}$| | |$0.72^{+0.46}_{-0.39}$| | |$0.46^{+0.34}_{-0.23}$| | |$2.54^{+1.6}_{-1.38}$| | |$1.87^{+1.68}_{-1.13}$| | |$2.96^{+2.97}_{-1.82}$| | |$1.19^{+1.17}_{-0.74}$| |
| SMC_SC4 179053 | 01 | |$12.5^{+3.0}_{-2.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.03^{+0.03}_{-0.02}$| | |$2.1^{+0.9}_{-0.7}$| | |$0.78^{+0.46}_{-0.43}$| | |$1.08^{+0.3}_{-0.35}$| | |$2.12^{+1.4}_{-1.18}$| | |$2.28^{+1.67}_{-1.02}$| | |$3.81^{+3.09}_{-1.77}$| | |$1.2^{+0.98}_{-0.54}$| |
| SMC_SC5 11453 | 01 | |$14.6^{+3.3}_{-3.4}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.39^{+0.14}_{-0.06}$| | |$1.9^{+1.0}_{-0.8}$| | |$0.89^{+0.38}_{-0.39}$| | |$0.24^{+0.15}_{-0.11}$| | |$4.72^{+2.18}_{-2.0}$| | |$2.96^{+2.47}_{-1.71}$| | |$5.66^{+5.16}_{-3.43}$| | |$3.85^{+3.47}_{-2.35}$| |
| SMC_SC5 21117 | 01 | |$16.0^{+2.3}_{-2.6}$| | |$0.5^{+0.2}_{-0.2}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.52^{+0.03}_{-0.01}$| | |$1.4^{+0.4}_{-0.3}$| | |$0.55^{+0.37}_{-0.21}$| | |$0.55^{+0.42}_{-0.25}$| | |$0.83^{+0.57}_{-0.31}$| | |$1.48^{+0.84}_{-0.55}$| | |$3.0^{+2.0}_{-1.25}$| | |$0.58^{+0.39}_{-0.24}$| |
| 02 | |$2.1^{+0.8}_{-0.4}$| | |$0.75^{+0.38}_{-0.29}$| | |$0.15^{+0.08}_{-0.04}$| | |$1.15^{+0.55}_{-0.41}$| | |$2.89^{+2.02}_{-1.16}$| | |$5.77^{+4.94}_{-2.51}$| | |$1.16^{+0.94}_{-0.5}$| | |||||
| 03 | |$2.1^{+0.6}_{-0.5}$| | |$0.62^{+0.28}_{-0.21}$| | |$0.33^{+0.21}_{-0.11}$| | |$0.74^{+0.37}_{-0.25}$| | |$2.42^{+1.36}_{-0.86}$| | |$4.86^{+3.4}_{-1.97}$| | |$0.75^{+0.51}_{-0.3}$| | |||||
| 04 | |$1.6^{+0.3}_{-0.3}$| | |$0.72^{+0.31}_{-0.23}$| | |$0.13^{+0.07}_{-0.04}$| | |$2.96^{+1.15}_{-1.03}$| | |$2.23^{+1.11}_{-0.78}$| | |$4.5^{+2.69}_{-1.75}$| | |$2.28^{+1.48}_{-0.92}$| | |||||
| SMC_SC5 21134 | 01 | |$12.9^{+3.7}_{-2.8}$| | |$0.5^{+0.3}_{-0.4}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.41^{+0.22}_{-0.08}$| | |$0.7^{+1.6}_{-0.4}$| | |$0.43^{+0.66}_{-0.37}$| | |$0.15^{+0.3}_{-0.09}$| | |$0.44^{+0.74}_{-0.38}$| | |$0.42^{+0.56}_{-0.3}$| | |$0.72^{+1.06}_{-0.53}$| | |$0.09^{+0.13}_{-0.06}$| |
| SMC_SC5 32377 | 01 | |$14.3^{+3.1}_{-3.1}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.35^{+0.08}_{-0.04}$| | |$1.8^{+1.0}_{-0.7}$| | |$0.75^{+0.48}_{-0.41}$| | |$0.57^{+0.4}_{-0.26}$| | |$0.37^{+0.33}_{-0.2}$| | |$2.25^{+1.85}_{-1.11}$| | |$4.31^{+3.82}_{-2.24}$| | |$0.28^{+0.26}_{-0.15}$| |
| 02 | |$2.1^{+0.8}_{-0.7}$| | |$0.6^{+0.37}_{-0.27}$| | |$0.27^{+0.12}_{-0.11}$| | |$1.13^{+0.73}_{-0.49}$| | |$2.26^{+1.73}_{-1.11}$| | |$4.23^{+3.75}_{-2.13}$| | |$1.02^{+0.89}_{-0.52}$| | |||||
| SMC_SC5 43650 | 01 | |$8.9^{+2.0}_{-1.9}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.79^{+0.11}_{-0.1}$| | |$0.55^{+0.1}_{-0.04}$| | |$0.4^{+0.7}_{-0.1}$| | |$0.5^{+0.64}_{-0.45}$| | |$0.34^{+0.73}_{-0.26}$| | |$1.07^{+1.36}_{-0.95}$| | |$0.18^{+0.18}_{-0.12}$| | |$0.21^{+0.23}_{-0.14}$| | |$0.04^{+0.05}_{-0.03}$| |
| 02 | |$0.5^{+0.2}_{-0.1}$| | |$0.58^{+0.59}_{-0.43}$| | |$0.62^{+0.59}_{-0.51}$| | |$6.62^{+6.56}_{-4.92}$| | |$0.29^{+0.27}_{-0.19}$| | |$0.34^{+0.35}_{-0.23}$| | |$0.36^{+0.41}_{-0.24}$| | |||||
| SMC_SC5 54851 | 01 | |$12.5^{+2.4}_{-2.0}$| | |$0.6^{+0.2}_{-0.2}$| | |$0.82^{+0.09}_{-0.09}$| | |$0.62^{+0.03}_{-0.01}$| | |$1.1^{+0.3}_{-0.2}$| | |$0.74^{+0.35}_{-0.33}$| | |$0.1^{+0.04}_{-0.03}$| | |$1.85^{+0.85}_{-0.85}$| | |$1.41^{+0.74}_{-0.56}$| | |$2.44^{+1.54}_{-1.04}$| | |$0.73^{+0.48}_{-0.32}$| |
| 02 | |$1.2^{+0.3}_{-0.2}$| | |$0.76^{+0.35}_{-0.34}$| | |$0.11^{+0.03}_{-0.03}$| | |$2.08^{+0.89}_{-0.95}$| | |$1.55^{+0.8}_{-0.61}$| | |$2.67^{+1.67}_{-1.13}$| | |$0.88^{+0.52}_{-0.37}$| | |||||
| 03 | |$1.1^{+0.2}_{-0.1}$| | |$0.5^{+0.31}_{-0.18}$| | |$0.05^{+0.01}_{-0.01}$| | |$2.42^{+1.6}_{-0.86}$| | |$0.97^{+0.63}_{-0.39}$| | |$1.69^{+1.3}_{-0.76}$| | |$0.99^{+0.81}_{-0.45}$| | |||||
| SMC_SC5 65500 | 01 | |$12.8^{+3.3}_{-2.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.66^{+0.11}_{-0.05}$| | |$2.0^{+1.0}_{-0.6}$| | |$0.61^{+0.38}_{-0.27}$| | |$0.29^{+0.13}_{-0.11}$| | |$0.46^{+0.27}_{-0.19}$| | |$1.91^{+1.23}_{-0.88}$| | |$3.21^{+2.57}_{-1.62}$| | |$0.28^{+0.22}_{-0.14}$| |
| SMC_SC5 129535 | 01 | |$9.1^{+2.1}_{-2.0}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.57^{+0.13}_{-0.05}$| | |$0.7^{+0.2}_{-0.2}$| | |$0.63^{+0.53}_{-0.36}$| | |$0.22^{+0.27}_{-0.11}$| | |$4.4^{+3.69}_{-2.6}$| | |$0.49^{+0.39}_{-0.27}$| | |$0.61^{+0.52}_{-0.34}$| | |$0.42^{+0.37}_{-0.23}$| |
| SMC_SC5 145724 | 01 | |$8.6^{+2.1}_{-1.8}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.42^{+0.1}_{-0.05}$| | |$2.4^{+0.7}_{-0.8}$| | |$0.81^{+0.44}_{-0.41}$| | |$0.13^{+0.07}_{-0.06}$| | |$4.2^{+2.39}_{-2.09}$| | |$2.05^{+1.73}_{-1.15}$| | |$2.51^{+2.24}_{-1.4}$| | |$1.31^{+1.21}_{-0.75}$| |
| SMC_SC5 180034 | 01 | |$12.0^{+2.5}_{-2.5}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.63^{+0.15}_{-0.1}$| | |$1.0^{+0.5}_{-0.3}$| | |$0.32^{+0.55}_{-0.19}$| | |$0.19^{+0.15}_{-0.08}$| | |$0.91^{+1.56}_{-0.54}$| | |$0.45^{+0.57}_{-0.25}$| | |$0.71^{+0.95}_{-0.42}$| | |$0.22^{+0.27}_{-0.13}$| |
| SMC_SC5 260841 | 01 | |$13.4^{+4.0}_{-3.2}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.53^{+0.06}_{-0.02}$| | |$0.6^{+0.5}_{-0.1}$| | |$0.78^{+0.45}_{-0.52}$| | |$0.06^{+0.26}_{-0.02}$| | |$1.53^{+0.95}_{-1.05}$| | |$0.77^{+0.52}_{-0.4}$| | |$1.34^{+1.17}_{-0.69}$| | |$0.33^{+0.29}_{-0.17}$| |
| 02 | |$0.6^{+0.3}_{-0.1}$| | |$0.75^{+0.44}_{-0.44}$| | |$0.06^{+0.77}_{-0.03}$| | |$2.74^{+1.74}_{-1.78}$| | |$0.72^{+0.44}_{-0.35}$| | |$1.27^{+0.92}_{-0.62}$| | |$0.54^{+0.43}_{-0.28}$| | |||||
| SMC_SC5 260957 | 01 | |$8.9^{+2.1}_{-2.0}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.82^{+0.09}_{-0.11}$| | |$0.58^{+0.14}_{-0.06}$| | |$1.2^{+0.4}_{-0.3}$| | |$0.55^{+0.5}_{-0.24}$| | |$0.04^{+0.02}_{-0.02}$| | |$2.45^{+2.21}_{-1.1}$| | |$0.78^{+0.63}_{-0.4}$| | |$0.98^{+0.86}_{-0.54}$| | |$0.43^{+0.4}_{-0.23}$| |
| SMC_SC5 266088 | 01 | |$7.8^{+1.5}_{-1.6}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.7^{+0.14}_{-0.08}$| | |$0.7^{+0.4}_{-0.1}$| | |$0.3^{+0.69}_{-0.24}$| | |$0.06^{+0.05}_{-0.02}$| | |$1.92^{+4.42}_{-1.56}$| | |$0.17^{+0.3}_{-0.11}$| | |$0.18^{+0.34}_{-0.12}$| | |$0.11^{+0.19}_{-0.07}$| |
| SMC_SC5 276982 | 01 | |$17.1^{+2.2}_{-2.6}$| | |$0.2^{+0.2}_{-0.2}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.75^{+0.11}_{-0.1}$| | |$1.2^{+0.4}_{-0.3}$| | |$0.06^{+0.19}_{-0.03}$| | |$0.05^{+0.04}_{-0.02}$| | |$0.31^{+1.0}_{-0.16}$| | |$0.12^{+0.26}_{-0.06}$| | |$0.23^{+0.54}_{-0.13}$| | |$0.15^{+0.33}_{-0.08}$| |
| SMC_SC5 282963 | 01 | |$15.6^{+3.1}_{-3.6}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.38^{+0.19}_{-0.06}$| | |$1.7^{+1.0}_{-0.8}$| | |$0.62^{+0.51}_{-0.33}$| | |$0.39^{+0.32}_{-0.21}$| | |$5.62^{+4.36}_{-2.92}$| | |$2.07^{+2.43}_{-1.35}$| | |$4.14^{+5.39}_{-2.78}$| | |$4.96^{+6.18}_{-3.36}$| |
| SMC_SC6 11085 | 01 | |$17.8^{+1.9}_{-2.9}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.74^{+0.06}_{-0.05}$| | |$2.4^{+0.6}_{-0.5}$| | |$0.59^{+0.26}_{-0.18}$| | |$0.13^{+0.05}_{-0.04}$| | |$0.99^{+0.45}_{-0.3}$| | |$2.53^{+1.13}_{-0.87}$| | |$5.19^{+2.71}_{-1.99}$| | |$1.06^{+0.57}_{-0.4}$| |
| 02 | |$2.6^{+0.5}_{-0.4}$| | |$0.78^{+0.34}_{-0.27}$| | |$0.27^{+0.09}_{-0.07}$| | |$1.49^{+0.63}_{-0.5}$| | |$3.41^{+1.75}_{-1.29}$| | |$7.07^{+4.11}_{-3.0}$| | |$1.64^{+0.95}_{-0.68}$| | |||||
| SMC_SC6 17538 | 01 | |$7.8^{+1.6}_{-1.4}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.61^{+0.15}_{-0.08}$| | |$0.7^{+0.3}_{-0.2}$| | |$0.59^{+0.58}_{-0.41}$| | |$0.08^{+0.09}_{-0.04}$| | |$3.55^{+3.44}_{-2.47}$| | |$0.37^{+0.34}_{-0.22}$| | |$0.4^{+0.39}_{-0.24}$| | |$0.22^{+0.21}_{-0.13}$| |
| SMC_SC6 42440 | 01 | |$8.9^{+2.0}_{-2.0}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.36^{+0.15}_{-0.05}$| | |$1.8^{+1.2}_{-0.8}$| | |$0.78^{+0.45}_{-0.42}$| | |$0.19^{+0.17}_{-0.1}$| | |$2.82^{+1.81}_{-1.46}$| | |$1.36^{+1.32}_{-0.79}$| | |$1.66^{+1.84}_{-0.99}$| | |$0.61^{+0.72}_{-0.37}$| |
| SMC_SC6 99991 | 01 | |$14.8^{+2.6}_{-2.8}$| | |$0.5^{+0.2}_{-0.2}$| | |$0.83^{+0.09}_{-0.09}$| | |$0.34^{+0.04}_{-0.02}$| | |$1.7^{+0.6}_{-0.5}$| | |$0.62^{+0.43}_{-0.25}$| | |$0.98^{+0.31}_{-0.29}$| | |$0.88^{+0.64}_{-0.36}$| | |$1.85^{+1.11}_{-0.75}$| | |$3.54^{+2.45}_{-1.55}$| | |$0.64^{+0.44}_{-0.27}$| |
| 02 | |$2.2^{+0.7}_{-0.6}$| | |$0.62^{+0.33}_{-0.25}$| | |$0.74^{+0.33}_{-0.26}$| | |$1.13^{+0.62}_{-0.44}$| | |$2.37^{+1.58}_{-0.97}$| | |$4.47^{+3.48}_{-1.93}$| | |$1.02^{+0.8}_{-0.43}$| | |||||
| 03 | |$1.9^{+0.6}_{-0.5}$| | |$0.55^{+0.45}_{-0.22}$| | |$0.76^{+0.3}_{-0.24}$| | |$1.03^{+0.83}_{-0.43}$| | |$1.94^{+1.17}_{-0.77}$| | |$3.72^{+2.63}_{-1.65}$| | |$0.85^{+0.62}_{-0.37}$| | |||||
| 04 | |$1.7^{+0.5}_{-0.4}$| | |$0.53^{+0.36}_{-0.22}$| | |$0.92^{+0.3}_{-0.26}$| | |$1.12^{+0.77}_{-0.47}$| | |$1.56^{+0.97}_{-0.59}$| | |$2.96^{+2.18}_{-1.24}$| | |$0.79^{+0.59}_{-0.33}$| | |||||
| SMC_SC6 105368 | 01 | |$11.2^{+2.7}_{-2.9}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.53^{+0.04}_{-0.02}$| | |$0.9^{+0.4}_{-0.2}$| | |$0.51^{+0.57}_{-0.31}$| | |$0.17^{+0.1}_{-0.06}$| | |$1.12^{+1.23}_{-0.68}$| | |$0.61^{+0.56}_{-0.3}$| | |$0.92^{+0.91}_{-0.47}$| | |$0.22^{+0.22}_{-0.11}$| |
| 02 | |$1.2^{+0.5}_{-0.4}$| | |$0.28^{+0.48}_{-0.13}$| | |$0.19^{+0.13}_{-0.07}$| | |$0.78^{+1.38}_{-0.37}$| | |$0.5^{+0.48}_{-0.21}$| | |$0.76^{+0.77}_{-0.34}$| | |$0.23^{+0.25}_{-0.1}$| | |||||
| SMC_SC6 116294 | 01 | |$8.6^{+2.1}_{-1.7}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.41^{+0.1}_{-0.05}$| | |$2.6^{+0.7}_{-1.0}$| | |$0.87^{+0.4}_{-0.39}$| | |$0.16^{+0.09}_{-0.07}$| | |$2.71^{+1.35}_{-1.23}$| | |$2.42^{+1.65}_{-1.34}$| | |$2.99^{+2.11}_{-1.69}$| | |$0.93^{+0.71}_{-0.53}$| |
| SMC_SC6 128831 | 01 | |$12.9^{+3.6}_{-2.9}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.1}$| | |$0.03^{+0.03}_{-0.02}$| | |$2.7^{+0.5}_{-0.8}$| | |$0.96^{+0.37}_{-0.42}$| | |$0.62^{+0.33}_{-0.23}$| | |$0.85^{+0.38}_{-0.37}$| | |$3.93^{+2.09}_{-1.61}$| | |$6.95^{+4.2}_{-2.98}$| | |$0.79^{+0.45}_{-0.35}$| |
| SMC_SC6 199611 | 01 | |$15.5^{+3.6}_{-3.3}$| | |$0.6^{+0.3}_{-0.3}$| | |$0.81^{+0.11}_{-0.11}$| | |$0.39^{+0.17}_{-0.07}$| | |$1.5^{+1.3}_{-0.8}$| | |$0.51^{+0.58}_{-0.36}$| | |$0.29^{+0.26}_{-0.16}$| | |$0.44^{+0.52}_{-0.31}$| | |$1.33^{+1.47}_{-0.84}$| | |$2.75^{+3.38}_{-1.76}$| | |$0.33^{+0.39}_{-0.21}$| |
| SMC_SC6 272665 | 01 | |$6.3^{+1.2}_{-0.9}$| | |$0.3^{+0.3}_{-0.2}$| | |$0.81^{+0.12}_{-0.11}$| | |$0.39^{+0.19}_{-0.07}$| | |$0.6^{+0.3}_{-0.2}$| | |$0.7^{+0.51}_{-0.47}$| | |$0.07^{+0.41}_{-0.05}$| | |$7.81^{+6.55}_{-5.28}$| | |$0.26^{+0.25}_{-0.15}$| | |$0.23^{+0.24}_{-0.14}$| | |$0.22^{+0.23}_{-0.14}$| |
| SMC_SC7 57131 | 01 | |$12.0^{+2.8}_{-2.4}$| | |$0.5^{+0.3}_{-0.3}$| | |$0.81^{+0.1}_{-0.11}$| | |$0.39^{+0.14}_{-0.06}$| | |$2.0^{+0.8}_{-0.7}$| | |$0.73^{+0.43}_{-0.4}$| | |$0.65^{+0.41}_{-0.36}$| | |$1.81^{+1.04}_{-0.98}$| | |$2.11^{+1.81}_{-1.3}$| | |$3.4^{+3.27}_{-2.12}$| | |$0.99^{+0.93}_{-0.62}$| |
| SMC_SC8 183240 | 01 | |$17.6^{+2.3}_{-2.9}$| | |$0.7^{+0.2}_{-0.2}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.61^{+0.15}_{-0.08}$| | |$0.9^{+0.4}_{-0.2}$| | |$0.64^{+0.51}_{-0.44}$| | |$0.28^{+0.23}_{-0.13}$| | |$1.18^{+0.87}_{-0.77}$| | |$1.45^{+1.3}_{-0.79}$| | |$3.46^{+3.52}_{-1.93}$| | |$0.98^{+1.0}_{-0.54}$| |
| SMC_SC9 105383 | 01 | |$13.0^{+3.0}_{-2.6}$| | |$0.4^{+0.3}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.56^{+0.06}_{-0.04}$| | |$1.9^{+0.7}_{-0.5}$| | |$0.53^{+0.44}_{-0.26}$| | |$0.09^{+0.04}_{-0.02}$| | |$1.43^{+1.21}_{-0.69}$| | |$1.47^{+1.17}_{-0.68}$| | |$2.42^{+2.29}_{-1.19}$| | |$0.74^{+0.7}_{-0.37}$| |
| 02 | |$1.7^{+0.6}_{-0.4}$| | |$0.77^{+0.41}_{-0.32}$| | |$0.09^{+0.03}_{-0.03}$| | |$1.9^{+0.91}_{-0.78}$| | |$1.94^{+1.22}_{-0.81}$| | |$3.2^{+2.55}_{-1.44}$| | |$0.87^{+0.71}_{-0.38}$| | |||||
| SMC_SC9 168422 | 01 | |$8.8^{+1.8}_{-1.8}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.8^{+0.1}_{-0.1}$| | |$0.61^{+0.18}_{-0.08}$| | |$0.5^{+0.3}_{-0.1}$| | |$0.56^{+0.6}_{-0.43}$| | |$0.07^{+0.11}_{-0.03}$| | |$2.55^{+2.96}_{-2.01}$| | |$0.27^{+0.27}_{-0.18}$| | |$0.33^{+0.34}_{-0.21}$| | |$0.15^{+0.16}_{-0.1}$| |
| SMC_SC10 8906 | 01 | |$16.1^{+3.3}_{-3.4}$| | |$0.6^{+0.2}_{-0.3}$| | |$0.82^{+0.1}_{-0.1}$| | |$0.56^{+0.09}_{-0.04}$| | |$2.2^{+0.9}_{-0.7}$| | |$0.89^{+0.38}_{-0.31}$| | |$0.44^{+0.23}_{-0.16}$| | |$0.2^{+0.1}_{-0.07}$| | |$4.23^{+2.33}_{-1.6}$| | |$9.05^{+5.83}_{-3.69}$| | |$0.3^{+0.19}_{-0.12}$| |
| 02 | |$2.0^{+0.8}_{-0.7}$| | |$0.82^{+0.36}_{-0.31}$| | |$0.9^{+0.35}_{-0.31}$| | |$0.07^{+0.03}_{-0.02}$| | |$3.5^{+1.98}_{-1.35}$| | |$7.5^{+4.86}_{-3.08}$| | |$0.09^{+0.05}_{-0.04}$| | |||||
| SMC_SC11 28090 | 01 | |$14.5^{+3.8}_{-2.8}$| | |$0.7^{+0.2}_{-0.3}$| | |$0.82^{+0.1}_{-0.11}$| | |$0.57^{+0.13}_{-0.05}$| | |$1.8^{+0.8}_{-0.7}$| | |$0.1^{+0.09}_{-0.05}$| | |$0.12^{+0.05}_{-0.05}$| | |$0.46^{+0.41}_{-0.2}$| | |$0.45^{+0.38}_{-0.22}$| | |$0.94^{+0.96}_{-0.5}$| | |$0.59^{+0.59}_{-0.32}$| |
| SMC_SC11 46587 | 01 | |$8.2^{+1.8}_{-1.6}$| | |$0.4^{+0.4}_{-0.3}$| | |$0.8^{+0.1}_{-0.11}$| | |$0.38^{+0.21}_{-0.06}$| | |$0.8^{+0.6}_{-0.3}$| | |$0.61^{+0.57}_{-0.46}$| | |$0.3^{+0.47}_{-0.18}$| | |$4.93^{+4.65}_{-3.7}$| | |$0.39^{+0.47}_{-0.25}$| | |$0.44^{+0.57}_{-0.29}$| | |$0.34^{+0.43}_{-0.22}$| |
5.2 Results for the whole sample
As seen previously, the scarcity of information about the central star (one, two, or at most three photometric bands only) causes a poor determination of its fundamental stellar parameters, which, owing to the nature of the MCMC method, propagates on to the disc parameters. The main result of this work therefore does not lie on the individual determination of the bump parameters, but on the statistical properties of the sample as a whole.
5.2.1 Mass distribution
Let us initially discuss the properties of our sample, in order to determine whether it represents a typical population of Be stars in SMC, or whether one or more selection biases where introduced.
Our selection of stars and bumps comes from the catalogue of visual photometric Be star candidates of Mennickent et al. (2002), where the candidate stars were selected according to the expected location of Be stars in colour–magnitude diagrams and according to the observed variability in the light curves. In Fig. 10, we show the sum of the posterior probabilities of parameter M for all our sample of stars (solid line). Clearly, most of our stars are early-type Be stars, in agreement to the position of our sample in the CMD (Fig. 7). We also show the factor ∝ M−2.3fBe(M) of equation (28) (dashed line). We recall that this factor was assumed as a prior in the MCMC fitting, and it represents our current knowledge about the populations of Be stars in the SMC. The green curve shows that, although the fraction of Be stars over B stars [fBe(M), estimated by Martayan et al. (2007a) from a cluster of the SMC] generally increases with M, the higher probability of the formation of less massive stars expressed in the IMF of Kroupa (2001) results in a bigger incidence of late-type over early-type Be stars. Our sample therefore is biased towards more massive stars.
This bias likely has several reasons:
The typical apparent I-band magnitudes of a B0 and B9 star in the SMC are ∼15.5 and ∼19.5, with rms uncertainties given by ≳0.005 and ≳0.15, respectively (Wyrzykowski et al. 2009). Therefore, the threshold of detectability of a good bump increases for late-type Be stars.
Late-type Be stars tend to have more tenuous discs than early-type ones (Vieira et al. 2017, see also next subsections), and therefore should develop bumps with much smaller amplitudes.
Late-type Be stars tend to show less variability (Rivinius et al. 2013; Labadie-Bartz et al. 2017, see also next subsections), which would make it less probable to identify bumps in their light curves.
5.2.2 Asymptotic surface density
In the upper panel of Fig. 11, we show how Σ0 varies with stellar mass in our sample, demonstrating a clear tendency of denser discs around the more massive stars. Vieira et al. (2017) have shown that, for the Be stars in the Galaxy, the incidence of denser discs increases with the mass of the stars. Comparison of our results with the ones of Vieira et al. is done in Fig. 12. While our sample is biased towards large masses, their sample is more evenly distributed in mass. Another difference is that our results are all concentrated in a region of high disc density, while theirs cover a much wider range of densities for all spectral types. The reason for this lies in fact that for this initial study we selected light curves with large and well-defined bumps, disregarding low-amplitude and short-duration ones. In fact, the detection of tenuous discs by Vieira et al. was only possible because they studied the SED in the IR (typically between 9 and 60 |$\mu \rm m$|), where the disc emission is much stronger than in the visible range. Therefore, all but the most dense of their discs would be too tenuous to generate appreciable photometric excesses in visual photometric bands, suitable for our fitting procedure.
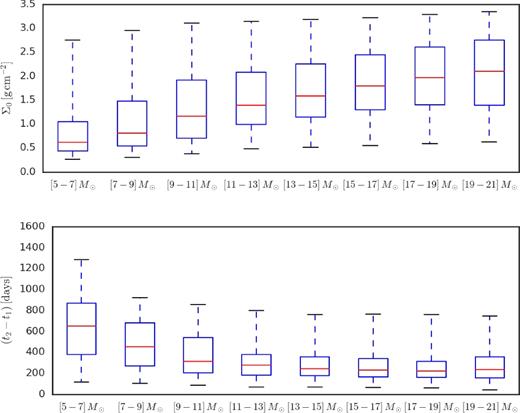
Boxplots of Σ0 (above) and t2 − t1 (below) for the summed posterior probabilities of our sample of bumps, separated in eight equal intervals of mass, ranging from 5 to 21 solar masses. The middle line of the boxes mark the median (|$50\,\,\rm{per\,\,cent}$|) of the samples. The lower and upper ends of the boxes mark |$25\,\,\rm{per\,\,cent}$| and |$75\,\,\rm{per\,\,cent}$| of the samples. The lower and upper whiskers mark |$5\,\,\rm{per\,\,cent}$| and |$95\,\,\rm{per\,\,cent}$| of the samples.
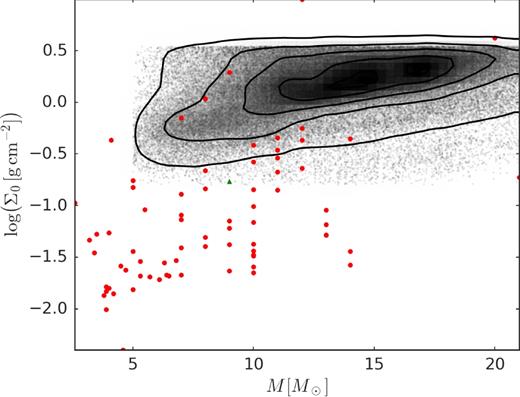
Distribution of the parameters M and Σ0 for our sample. The contour levels are the same as in Fig. 8. The red dots correspond to the surface densities at the base of the disc of Galactic Be stars, measured by Vieira et al. (2017). The green triangle corresponds to the initial state of the ablating disc model of Kee et al. (2016) for a B2e star.
We conclude that our sample of visual bumps should represent the upper limit for the densities found in the discs of SMC Be stars. In the Galaxy, these large densities are only found in early-type Be stars. The median of the Σ0 for our sample is |$\left\langle \Sigma _0\right\rangle = 1.50^{+1.12}_{-0.83}\, \mathrm{g\, cm^{-2}}$|. Furthermore, there may be some indication that the Be stars in the SMC may have more massive discs, on average, than their galactic counterparts, in line with results from the literature that report higher H α equivalent widths in the SMC Be stars than in the Galaxy (Martayan et al. 2007b). This last point, however, should be viewed with some caution given the large biases present in our sample.
5.2.3 Disc life cycles
In the lower panel of Fig. 11, we plot the distribution of the build-up time, t2 − t1, versus the stellar mass. We see that the duration of the bump is much shorter for massive stars, which indicates that these stars are much more variable than their late-type siblings. Similar findings were reported in the Galaxy (e.g. Rivinius et al. 2013; Labadie-Bartz et al. 2017). For a complete characterization the disc life cycles a census of the number of bumps present during the timespan of OGLE-II and OGLE-III observations (roughly 12 yr) would be required. Unfortunately, this cannot be done for our sample because in this study we focused only on the well-defined bumps. The median of the build-up time for our sample is |$\left\langle t_2-t_1\right\rangle =304^{+351}_{-168}$| d.
5.2.4 Viscosity parameter
The majority of our determinations of the viscosity parameter had broad uncertainty distributions, and it was found that the errors in the determinations of αbu were generally greater than those of αd. This has to do with the fact that the inclination angle is a poorly constrained quantity in our analysis, and the rate of photometric variations during build-up depends much more on cos i (Fig. 4) than the rate of photometric variations during dissipation (Fig. 5). Considering the sample as a whole, we find that there is no variation of αbu with the stellar mass (Fig. 13, top), but there is a slight hint that αd may grow with the stellar mass (Fig. 13, bottom). Furthermore, we find that on average the viscosity parameter is roughly two times larger at build-up than at dissipation (|$\left\langle \alpha _\mathrm{bu}\right\rangle = 0.64^{+0.50}_{-0.38}$| versus |$\left\langle \alpha _\mathrm{d}\right\rangle = 0.26^{+0.60}_{-0.18}$|).
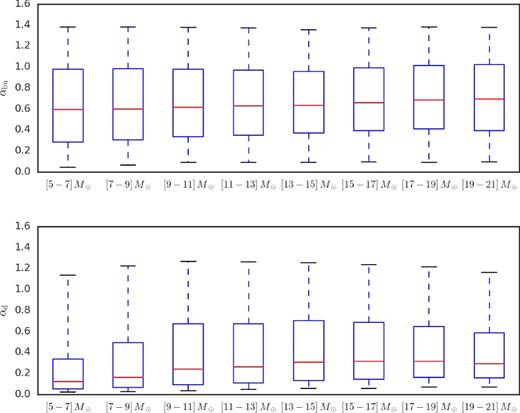
The estimated values of α in the range of a few tenths to one is in agreement with the usual values obtained for the hot and variable discs of dwarf novae (King, Pringle & Livio 2007; Kotko & Lasota 2012), as well as with the values obtained for the Be star 28 CMa by Ghoreyshi & Carciofi (2017). They are, however, an order of magnitude or more above the usual values obtained in magnetohydrodynamic simulations, where the magnetorotational instability ( Balbus & Hawley 1991) is the main theoretical assumption for the mechanism that generates the necessary viscosity (King et al. 2007).
In Fig. 14, we show the distributions of αbu (right) and αd (above) and the distribution in the αbu × αd plane. We found that, for most of the bumps, there was a correlation between αbu and αd, with values of αbu greater than values of αd being more likely. This trend can be seen in the darker areas of the αbu × αd plane. Ghoreyshi & Carciofi (2017) found the same trend for 28 CMa.
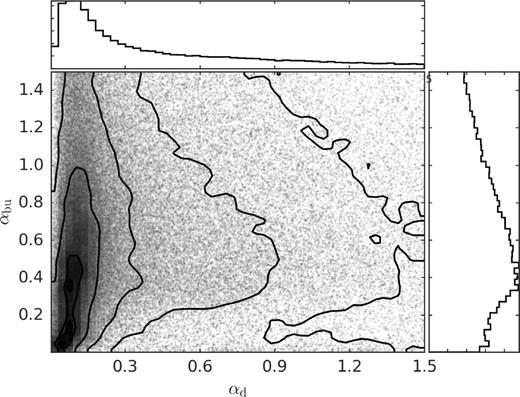
Distribution of the two viscosity parameters αbu and αd. The histograms above and on the right are the projections for αd and αbu, respectively. The contour levels are the same as in Fig. 8.
It is unclear whether the higher likelihood of αbu > αd is real a phenomenon or a result of the approximations employed in this work. One key approximation made in our model is that the hydrodynamical equations are solved assuming that the entire disc is isothermal. Earlier studies (e.g. Jones, Sigut & Marlborough 2004; Carciofi & Bjorkman 2006) have shown the disc to be highly non-isothermal, which means that cs in equation (3) is a complicated function both of R and time. Another approximation is that the possible effects of line forces were neglected. Recently, Kee et al. (2016) simulated the effects of a line-driven wind from early B-type stars over a non-viscous gaseous disc of solar metallicity and typical density. They showed that the line-driven wind was able to destroy the disc in time-scales compatible with the observed large-amplitude photometric variations of Be stars. They argued that the presence of the line-driven wind might be the cause of the apparent abnormal value estimated for α by Carciofi et al. (2012), Ghoreyshi & Carciofi (2017), and this work. Future work must explore if the viscous force and the line force working together can produce the variability of Be stars with smaller values of α.
The line force of an outwardly diffusing near-Keplerian optically thin disc under irradiation by the hot star will have a negative component in the azimuthal direction, removing angular momentum from the gas (Gayley & Owocki 2000; Gayley, Ignace & Owocki 2001). It is possible that this sink of angular momentum, during the build-up phase, may induce a clumping of material closer to the stellar equator, where the visual observables are generated, making the disc photometrically appear to build-up faster. In the dissipation phase, re-accretion occurs (|$v$|R becomes negative) and the line force would probably now point in the positive azimuthal direction, being a source of angular momentum to the disc and making the inner disc clear at a slower rate. If that is true, it would contribute to the observed trend of αbu > αd. We expect, however, that for our low-metallicity SMC Be stars, the possible effect of the line force will be greatly diminished. It is also worth reminding that Owocki, Cranmer & Gayley (1996) showed that winds from rapidly rotating, oblate stars are weakest near the equatorial plane. Consequently, a wind alone is incapable of building the disc and, even at Solar metallicity, can only act to help viscosity in disc building, but not replace it. Furthermore, so far all studies of the effects of line forces in gaseous Keplerian discs assumed that the gas is optically thin, which is not the case for our inner discs near the disc plane. The green triangle in Fig. 12 marks the mass and density at the stellar equator of the initial state of the ablating disc model of Kee et al. (2016) for a B2e star. Our calculations show that their initial state would generate only a modest excess ΔI = −0.1 mag, if seen pole-on.
On the other hand, it is possible that an opposite scenario might happen. The line force might operate ablating the tenuous material above the disc plane. These regions would receive radiation from the stellar surface and radiation reprocessed by the optically thick disc, behaving as a sink of mass and angular momentum of the disc (e.g. Krtička et al. 2011). In that case, the line-driven wind would actually slow down the build-up phase, because it would take a longer time for the disc to reach a near steady state, and would speed up the dissipation phase. If the above were true, that would result in αbu < αd, contrary to the results of Ghoreyshi & Carciofi (2017) and in this work.
We end this section by speculating about another possible cause for the observed trend αbu > αd. The disc formation is probably a mechanically violent process, with outbursts of matter injecting mechanical energy into the disc that is likely to disrupt its hydrostatic equilibrium and induce further turbulent motion. The dissipation, on the other hand, is expected to be a more gentle process, much less perturbed by stellar activity. The mechanically driven turbulence during outburst might account for the larger values of α at these phases.
5.2.5 Mass and angular momentum loss
Although the discs of Be stars in our sample are generally not in steady state, their steady-state mass and angular momentum loss rates (equations 12 and 13) are useful estimates of the actual quantities that are lost by the star after the bump event ends (see Appendix A). The panels of Fig. 15 show our distributions of the steady-state mass (above) and angular momentum (below) loss rates. For the calculation of |$(-\mathrm{\partial} M/\mathrm{\partial} t)_\mathrm{steady}$|, we considered the radius of the outer boundary to be given by the radius at which the disc outflow becomes angular momentum conserving (which can be seen as an outer radius of the viscous disc), estimated as |$\tilde{R}_\mathrm{out}=0.3(v_\mathrm{orb}/c_s)^2$| by Krtička et al. (2011). The red dots (upper panel) are the estimates of |$(-\mathrm{\partial} M/\mathrm{\partial} t)_\mathrm{steady}$| made from the results of Vieira et al. (2017) for Galactic Be stars, assuming that α = 1.
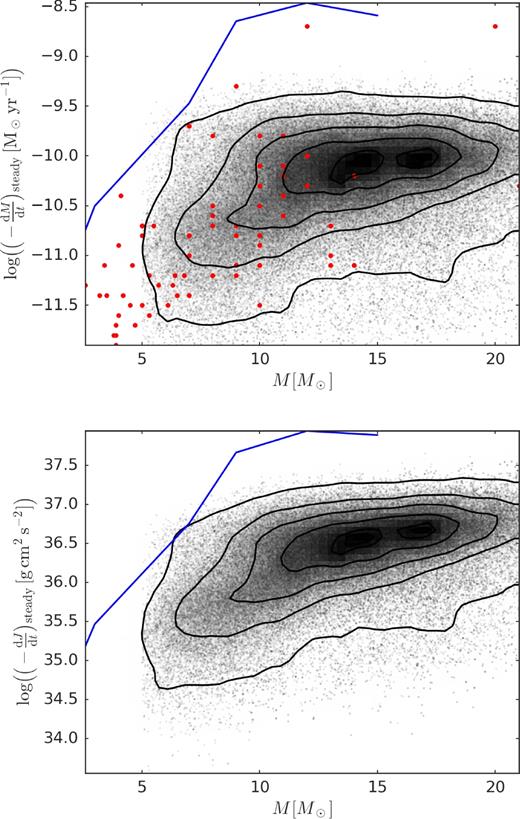
Distributions of the steady-state mass (above) and angular momentum (below) loss rates for our sample. The contour levels are the same as in Fig. 8. The red dots (upper panel) are the values of |$(-\mathrm{\partial} M/\mathrm{\partial} t)_\mathrm{steady}$|, calculated from the results of Vieira et al. (2017) for galactic Be stars. The blue curves are the estimations made by Granada et al. (2013) of the steady-state mass and angular momentum loss of their Z = 0.002 stars during their episodes of disc formation.
The steady-state mass and angular momentum loss rates for our densest bumps are of the order of ∼10−10 M⊙ yr−1 and ∼5 × 1036 g cm2 s−2, respectively. The typical decretion rate, which estimates the flux of mass in the disc near the stellar equator, is an order of magnitude higher than |$(-\mathrm{\partial} M/\mathrm{\partial} t)_\mathrm{steady}$|, being of the order of ∼10−9 M⊙ yr−1 , which also corresponds to the upper limit of the observed wind mass-loss rate of B stars (Snow 1981; Puls, Vink & Najarro 2008). Values of the typical decretion rate and steady-state angular momentum loss rate are given in the 11th and 12th columns of Table 6, respectively. The total angular momentum lost by the star as a consequence of the bump, −ΔJ*, is given by |$(-\mathrm{\partial} J/\mathrm{\partial} t)_\mathrm{steady}$| times the build-up time (equation A4), and the total mass lost is simply −ΔM* = −ΔJ*/(GMRout)1/2, if we still approximate the VDD as a Keplerian disc at Rout. If we consider that a typical bump has a build-up time of roughly one year, then the mass and angular momentum lost by the star as a consequence of one dense complete bump are of the order of ∼10−10 M⊙ and ∼1044 g cm2 s−1 (or ∼0.01 Moon masses and ∼10−3 times Earth's orbital angular momentum around the Sun, respectively). The VDD is, thus, a physical mechanism capable of extracting a large quantity of angular momentum from the outer layers of the star, without requiring the loss of too much mass. It is therefore a breaking mechanism of the outer layers. The angular momentum lost by the star for each individual bump is given in the 13th column of Table 6.
It was proposed (e.g. Krtička et al. 2011) that, with the evolution of the star, the formation of the VDD might be a natural mechanism to extract angular momentum from the outer layers of the star, preventing it to exceed the breakup velocity. Granada et al. (2013) assumed the appearance of a steady-state VDD in the Geneva stellar evolution code every time the outer layers of the star reached W > 0.88 (or ω > 0.99, in their notation, where |$\omega =\Omega /(8GM/27R_\mathrm{pole}^3)^{1/2}$|). The blue curves in Fig. 15 are the estimates made by Granada et al. (2013) of the steady-state mass and angular momentum loss of their Z = 0.002 stars during their episodes of disc formation. The fact that the curves of Granada et al. (2013) lie up to one order of magnitude above our results and the ones of Vieira et al. suggest that their assumed discs were made much too dense to be able to remove the needed angular momentum.
Although the Be phenomenon is probably a powerful velocity breaking mechanism for the outer layers of the star, its effect on the star as a whole is expected to be modest. Our determinations of angular momentum loss show that, even if the Be phenomenon happened during |${\sim }30\,\,\rm{per\,\,cent}$| of the stellar main-sequence lifetime, and the integrated time of all the build-up phases was |${\sim }30\,\,\rm{per\,\,cent}$| of that time, that would lead to the removal of |${\sim }1\,\,\rm{per\,\,cent}$| of the initial angular momentum of the star, which, for fast rotating stars of masses from 7 to 15 M⊙ is (8–30) × 1051 g cm2 s−1 (Granada et al. 2013).
In conclusion, light-curve modelling offers a reliable way to measure directly the amount of angular momentum lost by disc formation events in Be stars. Coupling this information with future studies about the fraction of the main-sequence lifetime a Be star spends in outburst will allow us to estimate the total amount of angular momentum that is lost by the disc during the main sequence. To obtain the total angular momentum lost we must sum the amount lost by the stellar wind. This quantity, hitherto unknown, will provide an essential constraint on stellar evolution models, in effect allowing for calibration of the core-surface angular momentum coupling of a star.
6 CONCLUSIONS
We present a new method to model the light curves of Be stars with the goal of extracting quantitative information about the fundamental parameters of their discs, such as the viscosity parameter, α, and the asymptotic surface density (Σ0, which is related to the disc mass injection rate). The method uses a large pre-computed grid of synthetic Be light curves, calculated using detailed hydrodynamic calculations coupled with three-dimensional NLTE radiative transfer calculations. The comparison between the model grid and the observed light curves was made possible by the identification of two empirical laws, which consists of simple formulas that closely match the photometric behaviour during disc build-up and dissipation.
An initial analysis of our model grid allowed us to draw important conclusions about the properties of VDD around Be stars, and their effect on the stellar SED as they evolve in time:
The viscosity parameter α is the most important parameter controlling the observed rate of photometric variations in Be light curves, but it is not the only one. Stellar parameters (mass, radius and effective temperature), as well as the disc viewing angle and density level, all concur to change the rate of brightness variations in complicated ways, which means that if meaningful information about α is to be extracted from the data, these parameters must be somehow estimated.
We identified a previously unknown effect, dubbed mass-reservoir effect, which also controls the rate of photometric variations during phases of disc dissipation. This effect is a consequence of the fact that VDDs build a mass reservoir at their outer regions, which is undetectable at short wavelengths (e.g. visible). The longer the build-up phase of a disc, the bigger its mass reservoir. When mass injection from the star stops and re-accretion occurs, the reservoir feeds the inner disc with mass. Clearly, the larger the reservoir, the longer it will be able to supply mass to the inner disc, and the slower the photometric dissipation will appear.
We applied our fitting pipeline to a sample of light curves of 54 Be star candidates from the SMC (Mennickent et al. 2002) containing 81 clearly identified events of disc formation/dissipation (here referred to as bumps). The light curves come from OGLE-II and OGLE-III data, covering roughly 12 yr. A MCMC technique was used to properly estimate the posterior probabilities of each fitted parameter.
It was found that our sample is biased towards early-type Be stars, likely because these stars are more variable and their discs are denser, resulting in clearer bumps. Also, photometric uncertainties increase for late-type Be stars. Since our sample was selected based on the appearance of their bumps, we conclude that our Be discs must be among the densest found for Be stars in the SMC. We verified an increase of Σ0 with the stellar mass and the median for our whole sample is |$\left\langle \Sigma _0\right\rangle = 1.50^{+1.12}_{-0.83}\, \mathrm{g\, cm^{-2}}$|. Our results may suggest that Be discs in the SMC are denser than their siblings in the Galaxy, in line with H α surveys that found stronger line emission in the SMC than in our Galaxy.
The durations of the build-up phases become shorter for more massive stars, which indicates that, as it was already observed in the Galaxy, late-type Be stars are less variable than early-type ones. The median of the build-up time for our sample is |$\left\langle t_2-t_1\right\rangle = 304^{+351}_{-168}$| d.
We obtained, for the first time, estimates of α for a statistically significant sample of Be stars. In our work, we explored the possibility that the viscosity parameter might be different at build-up (αbu) and dissipation (αd). We found no significant variation of αbu with the stellar mass (Fig. 13, top), but some evidence points to a correlation between αd with M (Fig. 13, bottom). Furthermore, we find that on average the viscosity parameter is sensibly larger at build-up than at dissipation. Our medians of the two viscosity parameters are |$\left\langle \alpha _\mathrm{bu}\right\rangle = 0.63^{+0.50}_{-0.38}$| and |$\left\langle \alpha _\mathrm{d}\right\rangle = 0.26^{+0.59}_{-0.18}$|. These values are in agreement in magnitude with the determinations of Carciofi et al. (2012) and Ghoreyshi & Carciofi (2017) for the Galactic Be star 28 CMa. They are also similar to the values of α usually found in cataclysmic variables (King et al. 2007; Kotko & Lasota 2012).
The trend that αbu > αd was also seen by Ghoreyshi & Carciofi (2017) in the different cycles of activity of the Be star 28 CMa. Further work is necessary to establish whether this trend is real or simply a result of our model assumptions. In particular, two important physical effects were ignored in this work, namely the fact that Be discs are non-isothermal and the line forces known to act on the disc material. This last point, however, may be of little importance for Be stars in the SMC, given their low metallicity.
It must be further emphasized that in this work what is really measured are the time-scales for disc build-up and dissipation. Under the assumption that viscosity is the only driving mechanism operating on the disc, these time-scales can in turn be converted to estimates of the viscosity parameter. The presence of other driving mechanisms (such as the aforementioned ablation) might affect the determination of α in unpredictable ways.
The steady-state mass and angular momentum loss rates for the studied bumps are of the order of ∼10−10 M⊙ yr−1 and ∼5 × 1036 g cm2 s−2, respectively. The typical decretion rate is of the order of ∼10−9 M⊙ yr−1. These values are in agreement with the upper limit of the observed wind mass-loss rate of B stars (Snow 1981; Puls et al. 2008). In addition, these values roughly agree in magnitude with the work of Vieira et al. (2017), who studied a sample of 80 Galactic Be stars.
Future perspectives for this work are threefold. First, an effort must be made to remove the biases of our current sample, by including late-type Be stars and smaller amplitude bumps. Secondly, the availability of a great number of past and current automated surveys (e.g. MACHO – Alcock et al. 1997; EROS – Aubourg et al. 1993; ASAS – Pojmanski 1997; VISTA-VVV – Minniti et al. 2010; KELT – Pepper et al. 2007) will allow us not only to greatly increase the number of Be stars studied, but also to explore the Be phenomenon and associated disc properties for other metallicities (Galaxy, LMC, etc.). Finally, also important is to obtain a better estimate of the central star properties, e.g. via spectroscopic modelling or using stars belonging to clusters with known age. Our current analysis was bound by the limited amount of information available on the central stars.
The α determinations made in this work should help in investigating the physical mechanisms originating the anomalous viscosity in circumstellar discs environments. In addition, the estimates of the net mass and angular momentum loss rates are important for understanding the conditions in which the Be phenomenon appears, and its consequences for the evolution of B-type stars.
ACKNOWLEDGEMENTS
This work made use of the computing facilities of the Laboratory of Astroinformatics (IAG/USP, NAT/Unicsul), whose purchase was made possible by the Brazilian agency FAPESP (grant 2009/54006-4) and the INCT-A. LRR acknowledges the support from FAPESP (grant 2012/21518-5) and from CNPq (grant 142411/2011-6). ACC acknowledges the support from CNPq (grant 307594/2015-7) and FAPESP (grant 2015/17967-7). DMF acknowledges the support from FAPESP (grant 2016/16844-1). RGV acknowledges the support from FAPESP (grant 2012/20364-4). MRG acknowledges the support from CAPES PROEX Programa Astronomia. JEB was supported by NSF grant AST-1412135. The OGLE project has received funding from the National Science Centre, Poland, grant MAESTRO 2014/14/A/ST9/00121. We also thank Nathaniel Dylan Kee for the very fruitful discussions on the results of this work.
Footnotes
Each walker can be viewed as a separated Markov Chain in the sample, although the walkers influence each another (Foreman-Mackey et al. 2013).
REFERENCES
SUPPORTING INFORMATION
Supplementary data are available at MNRAS online.
Appendix C: Figure C1–C79
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
APPENDIX A: PROPERTIES OF THE HYDRODYNAMICAL SOLUTIONS OF THE VDD MODEL
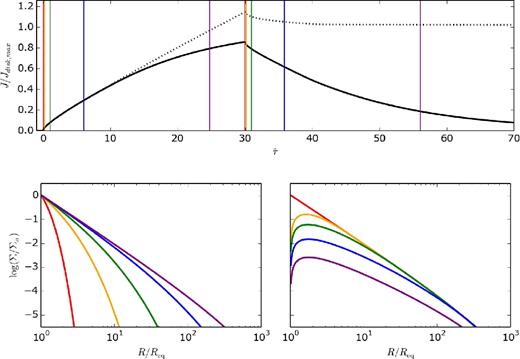
Dynamical bump model with |$\tilde{\tau }_\mathrm{bu}=30$|. Top: the amount of angular momentum in the disc (solid black curve) and the amount of angular momentum that is lost by the star (dotted black curve). Coloured vertical straight lines mark the five instants |$\tilde{\tau }=0,0.2,1,6,25$| (during the build-up phase), and the five instants |$\tilde{\tau }=30,30.2,31,36,55$| (during the dissipation phase). Surface density profiles are shown at the first five instants (bottom left) and at the last five instants (bottom right).
The bottom panels of Fig. A1 show surface density radial profiles at the specify instants marked in the top panel. During build-up, the disc grows in an inside out pattern, with the inner regions reaching a near stationary regime earlier than the outer parts. During dissipation, however, the disc becomes less and less dense as a whole, more or less self-similar way, because the entire disc is coupled by viscous forces.
APPENDIX B: EXAMPLES OF MODEL LIGHT CURVES
Fig. B1 shows examples of I-band light curves from our grid (see Table 1 and Sections 3.2 and 3.3). The dashed black curves correspond to |$\Delta I_\mathrm{bu}/\Delta I_\mathrm{bu}^\infty$| versus |$\tilde{\tau }$|. The solid curves correspond to |$\Delta I_\mathrm{d}/\Delta I_\mathrm{d}^0$| versus |$\tilde{\tau }-\tilde{\tau }_\mathrm{bu}$| for four dissipating light curves with increasing scaled build-up times. Since |$\Delta I_\mathrm{bu}^\infty$| is the limiting magnitude of the build-up light curves and |$\Delta I_\mathrm{d}^0$| is the magnitude at the instant of the beginning of dissipation, it follows that all |$\Delta I_\mathrm{bu}/\Delta I_\mathrm{bu}^\infty$| curves go from 0 to 1 and all |$\Delta I_\mathrm{d}/\Delta I_\mathrm{d}^0$| curves go from 1 to 0.
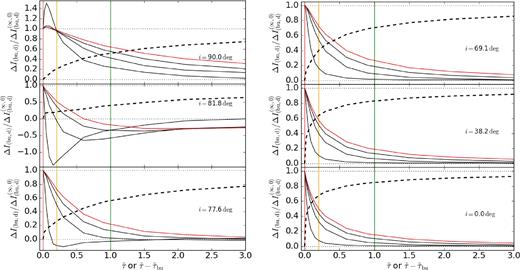
Examples of model I-band light curves. Each panel shows the results for different inclination angles, as indicated. The dashed black curves correspond to |$\Delta I_\mathrm{bu}/\Delta I_\mathrm{bu}^\infty$| versus |$\tilde{\tau }$|, and the solid curves correspond to |$\Delta I_\mathrm{d}/\Delta I_\mathrm{d}^0$| versus |$\tilde{\tau }-\tilde{\tau }_\mathrm{bu}$|, for four dissipating light curves with scaled build-up times given by |$\tilde{\tau }_\mathrm{bu}=0.15,1.5,6$| (in black), and |$\tilde{\tau }_\mathrm{bu}=30$| (in red). Vertical coloured straight lines mark the instants |$\tilde{\tau }$| or |$\tilde{\tau }-\tilde{\tau }_\mathrm{bu}=0,0.2,1$| (same colour-code as in Fig. A1). All light curves are from Star 2 and Σ0 = 1.37 g cm−2.
The build-up and dissipation light curves of the edge-on (upper-left panel) and nearly pole-on cases (right panels) can be approximated by the mathematical formulae given by equations (17) and (18), respectively. The light curves at intermediate angles like the ones of the middle-left and lower-left panels show more complex forms that cannot be described by equations (17) and (18). The light curves show that, at |$\tilde{\tau }\approx 1$|, the simulated bump has reached a significant fraction of its limiting value, and, at |$\tilde{\tau }-\tilde{\tau }_\mathrm{bu}\approx 1$|, the bump has already fallen considerably from its previous magnitude before the beginning of the dissipation.
Furthermore, dissipating curves with larger scaled build-up times dissipate at slower rates, as a result of the mass reservoir effect (Section 2.2). Also, as discussed in Section 3.3, both the dissipation and growth rates depend on the viewing angle.
APPENDIX C: ONLINE FIGURES
Figures C1– C79 are given in supporting information.




