Axisymmetric magnetic modes of neutron stars having mixed poloidal and toroidal magnetic fields

Lee, Umin

doi:10.1093/mnras/sty406

Abstract

We calculate axisymmetric magnetic modes of a neutron star possessing a mixed poloidal and toroidal magnetic field, where the toroidal field is assumed to be proportional to a dimensionless parameter ζ₀. Here, we assume an isentropic structure for the neutron star and consider no effects of rotation. Ignoring the equilibrium deformation due to the magnetic field, we employ a polytrope of the index n = 1 as the background model for our modal analyses. For the mixed poloidal and toroidal magnetic field with |$\zeta _0\not=0$|⁠, axisymmetric spheroidal and toroidal modes are coupled. We compute axisymmetric spheroidal and toroidal magnetic modes as a function of the parameter ζ₀ from 0 to ∼1 for the surface field strengths B_S = 10¹⁴ G and 10¹⁵ G. We find that the frequency ω of the magnetic modes decreases with increasing ζ₀. We also find that the frequency of the spheroidal magnetic modes is almost exactly proportional to B_S for ζ₀ ≲ 1 but that this proportionality holds only when ζ₀ ≪ 1 for the toroidal magnetic modes. The wave patterns of the spheroidal magnetic modes and toroidal magnetic modes are not strongly affected by the coupling so long as ζ₀ ≲ 1. We find no unstable modes having ω² < 0.

stars: magnetars, stars: magnetic field, stars: neutron, stars: oscillations

1 INTRODUCTION

Quasi-periodic-oscillations (QPOs) found in the tail of the giant X/γ-ray flares of SGR 1806-204 (Israel et al. 2005) and SGR 1900+14 (e.g. Strohmayer & Watts 2005, 2006; Watts & Strohmayer 2006) have brought about an intense interest in the oscillations of magnetars, i.e. strongly magnetized neutron stars (e.g. Woods & Thompson 2006; Mereghetti 2008). Because of the suggestion made by Duncan (1998) before the detection of the magnetar QPOs, the crustal torsional oscillations of magnetized neutron stars were first investigated as a candidate for the QPOs (e.g. Glampedakis, Samuelsson & Andersson 2006). However, motivated by the suggestion that the torsional modes in the solid crust will be quickly damped by frequency resonance with Alfvén continuum in the fluid core (Levin 2006, 2007), many researches carried out MHD simulations that follow time evolution of small amplitude and global toroidal perturbations to investigate modal properties of magnetars (e.g. Sotani, Colaiuda & Kokkotas 2008; Cerdá-Durán, Stergioulas & Font 2009; Colaiuda & Kokkotas 2011; Gabler et al. 2011, 2012). For example, Gabler et al. (2011, 2012) showed that because of resonant damping associated with Alfvén continuum in the fluid core the crustal modes cannot survive long enough to explain the observed QPOs. They also suggested that Alfvén modes, instead of crustal modes, could be responsible for the QPOs if the field strength is higher than ∼10¹⁵ G since the damping time-scales of Alfvén modes are much longer than those of the crustal torsional modes suffering resonant damping with Alfvén continuum.

These early studies of the oscillations of magnetars are mainly concerned with axisymmetric toroidal modes of the stars, expecting that toroidal modes are probably easily excited to observable amplitudes since they produce no density perturbations. For axisymmetric oscillations of magnetized stars, spheroidal and toroidal components of the perturbed velocity fields are decoupled and can be treated separately for a purely poloidal or toroidal magnetic field configuration for non-rotating stars. This property remains true even for general relativistic treatment. For non-axisymmetric oscillations of magnetized stars, however, the toroidal velocity component is coupled with the spheroidal one which accompanies the density and pressure perturbations, even if we assume a pure poloidal or toroidal magnetic field for non-rotating stars.

Lander, Jones & Passamonti (2010) and Passamonti & Lander (2013) discussed, using MHD simulations, such non-axisymmetric oscillation modes of magnetized stars assuming a purely toroidal magnetic field. For rotating magnetized stars, the modal property will be more complicated because the spheroidal (polar) and toroidal (axial) components of the perturbed velocity fields are coupled and rotational modes such as inertial modes and r-modes come in as additional classes of oscillation modes. Lander & Jones (2011) calculated non-axisymmetric oscillations of magnetized rotating stars for a purely poloidal magnetic field. They obtained polar-led Alfvén modes which reduce to inertial modes in the limit of |${\cal M}/{\cal T}\rightarrow 0$|⁠, where |$\cal M$| and |$\cal T$| are magnetic and rotation energies of the star. Lander & Jones (2011) also suggested that the axial-led Alfvén modes could be unstable.

For mixed poloidal and toroidal magnetic fields, coupled spheroidal and toroidal velocity fields have to be considered to describe global oscillations of the magnetized stars, even for axisymmetric oscillations. Note that assuming mixed poloidal and toroidal fields for the modal analyses is favorable from a magnetic stability point of view since pure poloidal and pure toroidal magnetic field configurations are known to be unstable (e.g. Tayler 1973; Markey & Tayler 1973, 1974; Yoshida & Eriguchi 2006; Yoshida, Yoshida & Eriguchi 2006; Akgün et al. 2013; Herbrik & Kokkotas 2017). Colaiuda & Kokkotas (2012) calculated axisymmetric toroidal oscillations of neutron stars for such a mixed field configuration. They found that the oscillation spectra of the toroidal modes in the core are significantly modified, losing their continuum character, by introducing a toroidal field component and that the crustal torsional modes now become long-living oscillations. This finding may be similar to the finding by van Hoven & Levin (2011, 2012), who suggested the existence of discrete modes in the gaps between frequency continua, using a spectral method. Using MHD simulations, Gabler et al. (2013) discussed axisymmetric toroidal modes of magnetized stars assuming various magnetic field configurations, but they did not find any long-lived discrete crustal modes in the gap between Alfvén continua in the core.

In this paper, instead of MHD simulations of small amplitude oscillations, we carry out normal mode analyses of a magnetized neutron star which possesses a mixed poloidal and toroidal magnetic field for axisymmetric oscillations. In normal mode analysis, the time dependence of the oscillations is given by the factor e^iωt and we look for the oscillation frequency ω as an eigenvalue to the set of linear differential equations that govern the oscillations. This paper will belong to a series of studies of normal modes of magnetized neutron stars (Lee 2007, 2008, 2010, 2018; Asai & Lee 2014; Asai, Lee & Yoshida 2015, 2016). The frequency ranges of magnetic modes obtained by normal mode calculations are similar to those by MHD simulations. However, the results obtained by normal mode analyses and MHD simulations are not necessarily fully consistent with each other. For example, although Lee (2008) and Asai & Lee (2014) obtained discrete toroidal magnetic normal modes of neutron stars for a poloidal magnetic field, MHD simulations for axisymmetric toroidal oscillations do not necessarily support the existence of such discrete magnetic normal modes. In this paper, employing a polytrope of the index n = 1 as the background model, we compute axisymmetric normal modes of a neutron star possessing a mixed poloidal and toroidal magnetic field. Note that we ignore the existence of a solid crust in neutron stars for simplicity. Section 2 describes the method of solution we employ in this paper. Section 3 gives numerical results and Section 4 is for conclusions. In Appendices A and B, we give the derivations of the equilibrium magnetic fields and of the outer boundary conditions. In Appendix C, we also briefly revisit the problem of pure toroidal magnetic modes of a neutron star with a pure poloidal field, applying two different outer boundary conditions.

2 METHOD OF SOLUTION

2.1 Equilibrium state

The magneto-hydrostatic equilibrium may be given by

\begin{eqnarray} {1\over \rho }\nabla p+\nabla \Phi -{1\over 4\pi \rho }\left(\nabla \times {\boldsymbol B}\right)\times {\boldsymbol B}=0, \end{eqnarray}

(1)

where ρ is the mass density, p is the pressure, Φ is the gravitational potential, and |${\boldsymbol B}$| denotes the magnetic field. As discussed in the Appendix, assuming the ϕ component of the Lorentz force |$\left(\nabla \times {\boldsymbol B}\right)\times {\boldsymbol B}/4\pi$| vanishes identically, we may derive an axisymmetric equilibrium magnetic field |${\boldsymbol B}$| in the star given by (e.g. Colaiuda et al. 2008; see also Appendix A)

\begin{eqnarray} B_r=2f(r)\cos \theta , \quad B_\theta =-{1\over r}{\text{d}r^2f(r)\over \text{d}r}\sin \theta , \quad B_\phi =-\zeta rf(r)\sin \theta , \end{eqnarray}

(2)

where ζ is a constant and the function f is a solution to the differential equation given by

\begin{eqnarray} {\text{d}^2f\over \text{d}r^2}+{4\over r}{\text{d}f\over \text{d}r}+\zeta ^2 f=-4\pi c_0\rho , \end{eqnarray}

(3)

and f(r) = α₀ + O(r²) is assumed at the stellar centre, where c₀ and α₀ are constants. With the magnetic fields given by equations (2), the magneto-hydrostatic equation may reduce to

\begin{eqnarray} {1\over \rho }\nabla p+\nabla \left(\Phi -c_0fr^2\sin ^2\theta \right)=0, \end{eqnarray}

(4)

where the term c₀fr²sin ²θ is responsible for the deviation of the equilibrium from spherical symmetry. In this paper, we ignore the term c₀fr²sin ²θ so that p, ρ, and Φ depend only on the radial distance r from the centre. This approximation makes it possible to integrate equation (3), given a spherical symmetric model, which is provided by a polytrope. See Asai et al. (2016), who took account of the equilibrium deformation caused by toroidal magnetic fields to calculate various oscillation modes.

Assuming that ρ = 0 and ζ = 0 for r > R with R being the radius of the star, we have the exterior solution f^ex given by f^ex = μ_b/r³, where μ_b is the magnetic dipole moment of the star. The constants c₀ and α₀ are determined so that the interior solution f and df/dr are matched with the exterior solution f^ex and df^ex/dr at the surface r = R. Although B_r and B_θ are continuous at the stellar surface, B_ϕ is discontinuous at r = R, which results in the existence of a surface current J_θ (see Appendix A).

We note that for the magnetic field given by equation (2), the poloidal component |${\boldsymbol B}_{\rm pl}=B_r{\boldsymbol e}_r+B_\theta {\boldsymbol e}_\theta$| is antisymmetric with respect to the equator and the toroidal component |${\boldsymbol B}_{\rm tr}=B_\phi {\boldsymbol e}_\phi$| is symmetric, and hence that the field |${\boldsymbol B}={\boldsymbol B}_{\rm pl}+{\boldsymbol B}_{\rm tr}$| has no definite parity with respect to the equator.

2.2 Oscillation Equations

Assuming the spherical symmetric structure of the star, neglecting the equilibrium deformation due to the magnetic field, we linearize the ideal MHD equations to obtain

\begin{eqnarray} \rho ^{\prime }+\nabla \cdot \left(\rho {\boldsymbol \xi} \right)=0, \end{eqnarray}

(5)

\begin{eqnarray} -\omega ^2{\boldsymbol \xi} +{1\over \rho }\nabla p^{\prime }-{\rho ^{\prime }\over \rho ^2}{\text{d}p\over \text{d}r}{\boldsymbol e}_r -{1\over 4\pi \rho }\left[\left(\nabla \times {\boldsymbol B}^{\prime }\right)\times {\boldsymbol B}+\left(\nabla \times {\boldsymbol B}\right)\times {\boldsymbol B}^{\prime }\right]=0, \end{eqnarray}

(6)

\begin{eqnarray} {\boldsymbol B}^{\prime }=\nabla \times \left({\boldsymbol \xi} \times {\boldsymbol B}\right)\!, \end{eqnarray}

(7)

\begin{eqnarray} {\rho ^{\prime }\over \rho }={1\over \Gamma _1}{p^{\prime }\over p}-rA{\xi _r\over r}, \end{eqnarray}

(8)

where |${\boldsymbol \xi}$| is the displacement vector and the prime (΄) indicates Euler perturbations, and we have assumed that the time dependence of the perturbations is given by the factor e^iωt with ω being the oscillation frequency, and

\begin{eqnarray} \Gamma _1=\left({\mathrm{\partial} \ln p\over \mathrm{\partial} \ln \rho }\right)_{\rm ad}, \quad rA={\text{d}\ln \rho \over \text{d}\ln r}-{1\over \Gamma _1}{\text{d}\ln p\over \text{d}\ln r}, \end{eqnarray}

(9)

and A is called the Schwarzschild discriminant. Note that we have applied the Cowling approximation neglecting Φ΄, the Eulerian perturbation of the gravitational potential.

We may write the ϕ component of the perturbed induction equation (7) as

\begin{eqnarray} B^\prime _\phi ={1\over r}\left[{\mathrm{\partial} \over \mathrm{\partial} r}r\left(\xi _\phi B_r-\xi _r B_\phi \right)-{\mathrm{\partial} \over \mathrm{\partial} \theta }\left(\xi _\theta B_\phi -\xi _\phi B_\theta \right)\right]. \end{eqnarray}

(10)

Since B_r is an odd function of cos θ and B_θ and B_ϕ are even functions, for |$B^\prime _\phi$| to have a definite parity, ξ_θ and ξ_ϕ must be antisymmetric about the equator for symmetric ξ_r or symmetric for antisymmetric ξ_r. Similarly, using the ϕ component of the equation of motion (6) given by

\begin{eqnarray} \omega ^2\xi _\phi =-{1\over 4\pi \rho }\left[{1\over r}{\mathrm{\partial} \over \mathrm{\partial} \theta }B_\theta B^\prime _\phi +{B_r\over r}{\mathrm{\partial} \over \mathrm{\partial} r}rB^\prime _\phi +\zeta \left(-B_rB^\prime _\theta +B_\theta B^\prime _r\right)\right], \end{eqnarray}

(11)

Because of the Lorentz terms in equation (6), separation of variables using a single spherical harmonic function |$Y_l^m(\theta ,\phi )$| is not possible to represent the perturbations of magnetized stars. We therefore employ the series expansion in terms of spherical harmonic functions |$Y_l^m$| for the perturbations. For the displacement vector |${\boldsymbol \xi}$| of axisymmetric modes of m = 0, we write

\begin{eqnarray} {{\boldsymbol \xi} \over r}=\sum _j^{j_{\rm max}}\left[{\boldsymbol e}_r S_{l_j}(r)+{\boldsymbol e}_\theta H_{l_j}(r){\mathrm{\partial} \over \mathrm{\partial} \theta } -{\boldsymbol e}_\phi T_{l_j}(r){\mathrm{\partial} \over \mathrm{\partial} \theta }\right]Y_{l_j}^0(\theta ,\phi ){\rm e}^{{\rm i}\omega t}, \end{eqnarray}

(12)

and for the perturbed magnetic fields |${\boldsymbol B}^{\prime }$|

\begin{eqnarray} {{\boldsymbol B}^\prime \over f}=\sum _j^{j_{\rm max}}\left[{\boldsymbol e}_r b^S_{l^{\prime }_j}(r)+{\boldsymbol e}_\theta b^H_{l^{\prime }_j}(r){\mathrm{\partial} \over \mathrm{\partial} \theta } -{\boldsymbol e}_\phi b^T_{l^{\prime }_j}(r){\mathrm{\partial} \over \mathrm{\partial} \theta }\right]Y_{l^{\prime }_j}^0(\theta ,\phi ){\rm e}^{{\rm i}\omega t}, \end{eqnarray}

(13)

where |${\boldsymbol e}_r$|⁠, |${\boldsymbol e}_\theta$|⁠, and |${\boldsymbol e}_\phi$| are the orthonormal vectors in the r, θ, and ϕ directions, respectively, and for the pressure perturbation, p΄, we write

\begin{eqnarray} p^{\prime }=\sum _j^{j_{\rm max}}p^{\prime }_{l_j}(r)Y_{l_j}^0(\theta ,\phi ){\rm e}^{{\rm i}\omega t}. \end{eqnarray}

(14)

Note that the modes represented by the series expansions are separated into two groups according to |$(l_j,l^{\prime }_j)$|⁠, that is, |$(l_j,l^{\prime }_j)=(2j-2,2j-1)$| for one group and |$(l_j,l^{\prime }_j)=(2j-1,2j-2)$| for the other where j = 1, 2, 3, …. In this paper we call the former even modes and the latter odd modes since the pressure perturbation p΄ is symmetric with respect to the equator for the former and antisymmetric for the latter.

If we define the spheroidal |${\boldsymbol\xi} _{\rm SH}$| and toroidal |${\boldsymbol\xi} _{\rm T}$| components of |${\boldsymbol\xi}$| as

\begin{eqnarray} {{\boldsymbol\xi} _{\rm SH}\over r}=\sum _j^{j_{\rm max}}\left({\boldsymbol e}_r S_{l_j}+{\boldsymbol e}_\theta H_{l_j}{\mathrm{\partial} \over \mathrm{\partial} \theta } \right)Y_{l_j}^0{\rm e}^{{\rm i}\omega t}, \quad {{\boldsymbol\xi} _{\rm T}\over r}=-{\boldsymbol e}_\phi \sum _j^{j_{\rm max}} T_{l_j}{\mathrm{\partial} \over \mathrm{\partial} \theta }Y_{l_j}^0{\rm e}^{{\rm i}\omega t}, \end{eqnarray}

(15)

and the spheroidal |${\boldsymbol B}^\prime _{\rm SH}$| and toroidal |${\boldsymbol B}^\prime _{\rm T}$| components of |${\boldsymbol B}^\prime$| as

\begin{eqnarray} {{\boldsymbol B}^\prime _{\rm SH}\over f}=\sum _j^{j_{\rm max}}\left({\boldsymbol e}_r b^S_{l^{\prime }_j}+{\boldsymbol e}_\theta b^H_{l^{\prime }_j}{\mathrm{\partial} \over \mathrm{\partial} \theta } \right)Y_{l_j}^0{\rm e}^{{\rm i}\omega t}, \quad {{\boldsymbol B}^\prime _{\rm T}\over f}=-{\boldsymbol e}_\phi \sum _j^{j_{\rm max}} b^T_{l^{\prime }_j}{\mathrm{\partial} \over \mathrm{\partial} \theta }Y_{l^{\prime }_j}^0{\rm e}^{{\rm i}\omega t}, \end{eqnarray}

(16)

|${\boldsymbol\xi} _{\rm SH}$| and |${\boldsymbol B}^\prime _{\rm T}$| are symmetric about the equator and |${\boldsymbol\xi} _{\rm T}$| and |${\boldsymbol B}^\prime _{\rm SH}$| are antisymmetric for |$(l_j,l^{\prime }_j)=(2j-2,2j-1)$| and vice versa for |$(l_j,l^{\prime }_j)=(2j-1,2j-2)$|⁠. When ζ = 0, the spheroidal components |$({\boldsymbol\xi} _{\rm SH},{\boldsymbol B}^\prime _{\rm SH})$| are decoupled from the toroidal ones |$({\boldsymbol\xi} _{\rm T},{\boldsymbol B}^\prime _{\rm T})$|⁠, and we call |$({\boldsymbol\xi} _{\rm SH},{\boldsymbol B}^\prime _{\rm SH})$| even spheroidal modes for |$(l_j,l^{\prime }_j)=(2j-2,2j-1)$| and odd spheroidal modes for |$(l_j,l^{\prime }_j)=(2j-1,2j-2)$| according to the parity of |${\boldsymbol\xi} _{\rm SH}$|⁠, while we call |$({\boldsymbol\xi} _{\rm T},{\boldsymbol B}^\prime _{\rm T})$| odd toroidal modes for |$(l_j,l^{\prime }_j)=(2j-2,2j-1)$| and even toroidal modes for |$(l_j,l^{\prime }_j)=(2j-1,2j-2)$|⁠, according to the parity of |${\boldsymbol\xi} _{\rm T}$|⁠. In this paper, we use this terminology even for |$\zeta \not=0$|⁠. It is important to note that for the perturbations as defined by equations (12), (13), and (14), we consider that even spheroidal modes |$({\boldsymbol\xi} _{\rm SH},{\boldsymbol B}^\prime _{\rm SH})$| are coupled with odd toroidal modes |$({\boldsymbol\xi} _{\rm T},{\boldsymbol B}^\prime _{\rm T})$| and vice versa when |$\zeta \not=0$|⁠. We thus note that the vectors |${\boldsymbol\xi}$| and |${\boldsymbol B}^{\prime }$| as defined by the expansions (12) and (13) do not have a definite parity about the equator.

Substituting the series expansions into the perturbed basic equations (5)–(8), we obtain a set of linear ordinary differential equations for the expansion coefficients. For the dependent variables defined as

\begin{eqnarray} {\boldsymbol y}_1=\left({S_{l_j}}\right)\!, \quad {\boldsymbol y}_2=\left({p^{\prime }_{l_j}\over \rho g r}\right)\!, \quad {\boldsymbol y}_3=\left(H_{l_j}\right)\!, \quad {\boldsymbol y}_4=\left(b^H_{l^{\prime }_j}\right)\!, \quad {\boldsymbol y}_5=\left(T_{l_j}\right)\!, \quad {\boldsymbol y}_6=\left(b^T_{l^{\prime }_j}\right)\!,\quad {\boldsymbol b}^S=\left(b^S_{l^{\prime }_j}\right)\!, \end{eqnarray}

(17)

we obtain

\begin{eqnarray} r{{\rm d}{\boldsymbol y}_1\over {\rm d}r}=\left({V\over \Gamma _1}-3\right){\boldsymbol y}_1-{V\over \Gamma _1}{\boldsymbol y}_2+{\boldsymbol {\Lambda}}_0{\boldsymbol y}_3, \end{eqnarray}

(18)

\begin{eqnarray} r{{\rm d}{\boldsymbol y}_2\over {\rm d}r} &=&\left[\left(c_1\bar{\omega }^2+rA\right){\boldsymbol{\sf 1}}-{1\over 2}\left({{\cal Q}\over f}\right)^2 {\cal S}{\boldsymbol{\sf C}}_0{\boldsymbol{\sf B}}_1^{-1}{\boldsymbol{\sf W}}_0{\boldsymbol{\sf W}}_1 \right]{\boldsymbol y}_1 -\left[\left(rA+U-1\right){\boldsymbol{\sf 1}}+{1\over 2}{{\cal Q}\over f}{\boldsymbol{\sf C}}_0{\boldsymbol{\sf B}}_1^{-1}{\boldsymbol {\Lambda}}_0\right]{\boldsymbol y}_2\nonumber \\ &&+\,{{\cal Q}\over f}\left[{1\over 2}c_1\bar{\omega }^2{\boldsymbol{\sf C}}_0{\boldsymbol{\sf B}}_1^{-1}{\sf \boldsymbol \Lambda}_0 -{\cal S}{\boldsymbol{\sf C}}_0{\boldsymbol{\sf B}}_1^{-1}{\boldsymbol{\sf W}}_0{\boldsymbol{\sf B}}_0 \right]{\boldsymbol y}_3 -{\cal S}{{\boldsymbol{\sf C}}_0{\boldsymbol y}_4 +{1\over 2}\zeta _{0}} xc_1\bar{\omega }^2{\boldsymbol{\sf C}}_0{\boldsymbol{\sf B}}_1^{-1}{\boldsymbol {\Lambda}}_0{\boldsymbol y}_5, \end{eqnarray}

(19)

\begin{eqnarray} r{{\rm d}{\boldsymbol y}_3\over {\rm d}r}={1\over 2}{{\cal Q}\over f}\left(3-{V\over \Gamma _1}+{{\cal Q}\over f}-{d\ln {\cal Q}/f\over d\ln r}\right) {\boldsymbol{\sf B}}_0^{-1}{\boldsymbol{\sf W}}_1{\boldsymbol y}_1 + {1\over 2}{V\over \Gamma _{1}}{{\cal Q}\over f}{\boldsymbol{\sf B}}_{0}^{-1}{\boldsymbol{\sf W}}_1{\boldsymbol y}_{2} +{{\cal Q}\over f}\left({\boldsymbol{\sf 1}}-{1\over 2}{\boldsymbol{\sf B}}_0^{-1}{\boldsymbol{\sf W}}_1{\boldsymbol {\Lambda}} _0\right){\boldsymbol y}_3 +{1\over 2}{\boldsymbol{\sf B}}_0^{-1}{\boldsymbol {\Lambda}}_1{\boldsymbol y}_4, \end{eqnarray}

(20)

\begin{eqnarray} r{{\rm d}{\boldsymbol y}_4\over {\rm d}r} &=&{{\cal Q}\over f}\left({\boldsymbol{\sf 1}}+{1\over 2}{{\cal R}\over f}{\boldsymbol{\sf B}}_1^{-1}{\boldsymbol{\sf W}}_0\right){\boldsymbol{\sf W}}_1{\boldsymbol y}_1 +{1\over 2\beta }{\boldsymbol{\sf B}}_1^{-1}{\boldsymbol {\Lambda}}_0{\boldsymbol y}_2 +\left[2\left({\boldsymbol{\sf 1}}+{1\over 2}{{\cal R}\over f}{\boldsymbol{\sf B}}_1^{-1}{\boldsymbol{\sf W}}_0\right){\boldsymbol{\sf B}}_0-{1\over 2\beta }{c}_1\bar{\omega}^2{\boldsymbol{\sf B}}_1^{-1}{\boldsymbol {\Lambda}}_0\right]{\boldsymbol y}_3-{d\, \ln\, rf\over d\, \ln\, r}{\boldsymbol y}_{4}\nonumber \\ &&+\,{1\over 2}\zeta _0x\left({\boldsymbol{\sf B}}_1^{-1}{\boldsymbol{\sf W}}_0{\boldsymbol {\Lambda}}_1+2\sf 1\right){\boldsymbol y}_6, \end{eqnarray}

(21)

\begin{eqnarray} r{{\rm d}{\boldsymbol y}_5\over {\rm d}r} =-{{\cal Q}\over f}\left({1\over 2}{\boldsymbol{\sf B}}_0^{-1}{\boldsymbol{\sf W}}_1{\boldsymbol {\Lambda}} _0-{\boldsymbol{\sf 1}}\right){\boldsymbol y}_5 +{1\over 2}{\boldsymbol{\sf B}}_{0}^{-1}{\boldsymbol {\Lambda}}_1{\boldsymbol y}_6-{1\over 2}\zeta _0x{\boldsymbol{\sf B}}_0^{-1}{\boldsymbol{\sf W}}_1\left[\left({V\over \Gamma _1}-2-{{Q\over f}}\right){\boldsymbol y}_1- {V\over {\sf {\boldsymbol \Gamma _1}}}{\boldsymbol y}_2\right], \end{eqnarray}

(22)

\begin{eqnarray} r{{\rm d} {\boldsymbol y}_6\over {\rm d}r} =-{1\over 2\beta }c_1\bar{\omega }^2{\boldsymbol{\sf B}}_1^{-1}{\boldsymbol {\Lambda}}_0{\boldsymbol y}_5 -\left({ {1\over 2}{{\cal Q}\over f}}{\boldsymbol{\sf B}}_1^{-1}{\boldsymbol{\sf W}}_0{\boldsymbol {\Lambda}}_1+{d\,\ln fr\over d\, \ln r}{\boldsymbol{\sf 1}}\right){{\boldsymbol y}_6 -{\zeta _0\over 2}}x\left[\left({{Q\over f}}\right)^{\boldsymbol{\sf 2}}{\boldsymbol{\sf B}}_1^{-1}{\boldsymbol{\sf W}}_0{\boldsymbol{\sf W}}_1{{\boldsymbol y}_1}+{\boldsymbol 2}{Q\over f}{\boldsymbol{\sf B}}_1^{-1}{\boldsymbol{\sf W}}_0{\boldsymbol{\sf B}}_0{\boldsymbol y}_3+{\boldsymbol 2}{\boldsymbol y}_4\right], \end{eqnarray}

(23)

where

\begin{eqnarray} \bar{\omega }={\omega \over \sigma _0}, \quad \sigma _0=\sqrt{GM\over R^3}, \quad U={\text{d}\ln M_r\over \text{d}\ln r}, \quad V=-{\text{d}\ln p\over \text{d}\ln r}, \end{eqnarray}

(24)

\begin{eqnarray} c_1={(r/R)^3\over M_r/M}, \quad g={GM_r\over r^2}, \quad M_r=\int _0^r4\pi r^2\rho \text{d}r, \end{eqnarray}

(25)

\begin{eqnarray} {\cal Q}=-{1\over r}{\text{d}(r^2f)\over \text{d}r}, \quad {\cal R} =-r^2\left({\text{d}^2f\over \text{d}r^2}+{4\over r}{\text{d}f\over \text{d}r}\right), \quad {\cal S}=\beta \left({{\cal R}\over f}-\zeta _0^2x^2\right), \end{eqnarray}

(26)

\begin{eqnarray} \beta ={f^2\over 4\pi pV}, \quad \zeta _0=\zeta R, \quad x={r\over R}, \end{eqnarray}

(27)

and |$\sf 1$| denotes the identity matrix, and the matrices |${\boldsymbol{\sf B}}_0$|⁠, |${\boldsymbol{\sf B}}_1$|⁠, |${\boldsymbol{\sf W}}_0$|⁠, and |${\boldsymbol{\sf W}}_1$| are defined as

\begin{eqnarray} {\boldsymbol{\sf B}}_0={\boldsymbol{\sf Q}}_1{\boldsymbol {\Lambda}}_0+{\boldsymbol{\sf C}}_1, \quad {\boldsymbol{\sf B}}_1={\boldsymbol{\sf Q}}_0{\boldsymbol {\Lambda}}_1+{\boldsymbol{\sf C}}_0, \quad {\boldsymbol{\sf W}}_0=2{\boldsymbol{\sf Q}}_0+{\boldsymbol{\sf C}}_0, \quad {\boldsymbol{\sf W}}_1=2{\boldsymbol{\sf Q}}_1+{\boldsymbol{\sf C}}_1, \end{eqnarray}

(28)

and the definition of the matrices |${\boldsymbol{\sf Q}}_0$|⁠, |${\boldsymbol{\sf Q}}_1$|⁠, |${\boldsymbol{\sf C}}_0$|⁠, |${\boldsymbol{\sf C}}_1$|⁠, |${\boldsymbol \Lambda} _0$|⁠, and |${\boldsymbol {\Lambda}}_1$| is given in Yoshida & Lee (2000). We note that

\begin{eqnarray} {\boldsymbol{\sf W}}_1{\boldsymbol {\Lambda}}_0={\sf {\boldsymbol\Lambda}}_1{\boldsymbol{\sf C}}_1, \quad {\boldsymbol{\sf W}}_0{\sf {\boldsymbol\Lambda}}_1={\boldsymbol \Lambda}_0{\boldsymbol{\sf C}}_0, \quad {\boldsymbol{\sf W}}_0=-{\boldsymbol{\sf C}}_1\!\!^T, \quad {\boldsymbol{\sf W}}_1=-{\boldsymbol{\sf C}}_0\!\!^T, \end{eqnarray}

(29)

and that although the quantity β diverges both at the centre and at the surface, the quantity |$\cal S$| remains finite in the interior. It is important to note that since the expansion coefficient |$H_{l_1}=H_0$|⁠, for example, vanishes identically for even modes, we take |$H_{l_2}$| to |$H_{l_{j_{{\rm max}}+1}}$| as dependent variables and hence we have to redefine the matrices given above accordingly (see e.g. Lee 2008). To simplify the set of differential equations, we have used

\begin{eqnarray} {\boldsymbol b}^S={Q\over f}{\boldsymbol{\sf W}}_1{\boldsymbol y}_1+{\boldsymbol 2}{\boldsymbol{\sf B}}_0{\boldsymbol y}_3, \end{eqnarray}

(30)

which comes from the radial component of the induction equation (7), and

\begin{eqnarray} r{{\rm d}{\boldsymbol b}^S\over {\rm d}r}={Q\over f}{\boldsymbol b}^S+{\boldsymbol {\Lambda}}_1{\boldsymbol y}_4, \end{eqnarray}

(31)

which comes from |$\nabla \cdot {\boldsymbol B}^{\prime }=0$|⁠. Note that the parameter ζ₀ represents the ratio of the toroidal component of the magnetic field to the poloidal one and that the parameter |$\zeta _0\not=0$| couples the spheroidal modes and toroidal modes, that is, when ζ₀ = 0 the set of differential equations from (18) to (23) are decoupled into those for spheroidal modes described by the variables |$({\boldsymbol y}_1, {\boldsymbol y}_2, {\boldsymbol y}_3, {\boldsymbol y}_4)$| and for toroidal modes by |$({\boldsymbol y}_5, {\boldsymbol y}_6)$| (see e.g. Lee 2007).

Imposing appropriate boundary conditions at the centre and at the surface of the star, we solve equations (18)–(23) as an eigenvalue problem for the oscillation frequency ω. The inner boundary conditions are regularity conditions for the variables |${\boldsymbol\xi}$|⁠, p΄, and |${\boldsymbol B}^{\prime }$| at the stellar centre. The surface boundary conditions are given by

\begin{eqnarray} -{\boldsymbol y}_1+{\boldsymbol y}_2+\zeta _0\beta \left({{\cal Q}\over f}+2\right){\boldsymbol{\sf Q}}_0{\boldsymbol{\sf C}}_1{\boldsymbol y}_5=0, \end{eqnarray}

(32)

\begin{eqnarray} \left[{{\cal Q}\over f}{\boldsymbol{\sf W}}_1+\zeta _0^2{\boldsymbol{\sf L}}^+{\boldsymbol{\sf C}}_0^{-1}\left({\boldsymbol{\sf 1}}-{\boldsymbol{\sf Q}}_0{\boldsymbol{\sf Q}}_1\right)\right]{\boldsymbol y}_1+2{\boldsymbol{\sf B}}_0{\boldsymbol y}_3+{\boldsymbol{\sf L}}^+{\boldsymbol y}_4 +{\sf \zeta} _0\left({\boldsymbol{\sf C}}_1-{\boldsymbol{\sf L}}^+{\boldsymbol{\sf C}}_0^{-1}{\boldsymbol{\sf Q}}_0 {\boldsymbol{\sf C}}_1\right){\boldsymbol y}_5=0, \end{eqnarray}

(33)

and

\begin{eqnarray} -\zeta _0{\boldsymbol{\sf C}}_0^{-1}\left[\left({{{\sf \cal Q}\over {f}}+{1}}\right)\left({\boldsymbol{\sf 1}}-{\boldsymbol{\sf Q}}_0{\boldsymbol{\sf Q}}_1\right){\boldsymbol{\sf y}}_1-{\boldsymbol{\sf Q}}_0{\boldsymbol{\sf C}}_1{\boldsymbol y}_3\right]+{\boldsymbol y}_6=0, \end{eqnarray}

(34)

where |$({\boldsymbol{\sf L}}^+)_{ij}=(l^{\prime }_i+{\boldsymbol{\sf 1}})\delta _{ij}$| and the derivation of the surface boundary conditions are given in Appendix B.

2.3 Energy equation

It is useful to derive an energy equation for the perturbations associated with adiabatic flows. We start with introducing the force operator |${\boldsymbol F}({\boldsymbol\xi} )$| defin ed by

\begin{eqnarray} {\boldsymbol F}({\boldsymbol\xi} )=-\rho \nabla \Phi ^{\prime }-\nabla p^{\prime }+{\rho ^{\prime }\over \rho }\nabla p+{1\over 4\pi }\left[\left(\nabla \times {\boldsymbol B}^\prime \right)\times {\boldsymbol B}+\left(\nabla \times {\boldsymbol B}\right)\times {\boldsymbol B}^\prime \right]\!, \end{eqnarray}

(35)

which satisfies the perturbed equation of motion

\begin{eqnarray} \rho \mathrm{\partial} ^2{\boldsymbol\xi} /\mathrm{\partial} t^2={\boldsymbol F}({\boldsymbol\xi} ). \end{eqnarray}

(36)

The energy equation may be given by multiplying the perturbed equation of motion (36) by |${\boldsymbol\xi} ^*$|⁠, the complex conjugate of the displacement vector |${\boldsymbol\xi}$|⁠. Assuming the time dependency of the perturbations is given by e^iωt, we obtain

\begin{eqnarray} \omega ^2{\boldsymbol\xi} ^*\cdot {\boldsymbol\xi} &=& {1\over \Gamma _1}{p^{\prime }\over \rho }{p^{\prime *}\over p}+{p\over \rho }\left({\boldsymbol\xi} ^*\cdot \nabla \ln p\right)\left({\boldsymbol\xi} \cdot {\boldsymbol A}\right)-{\nabla \Phi ^{\prime }\cdot \nabla \Phi ^{\prime *}\over 4\pi G\rho } -{1\over 4\pi \rho }{\boldsymbol\xi} ^*\cdot \left[\left(\nabla \times {\boldsymbol B}^{\prime }\right)\times {\boldsymbol B}+\left(\nabla \times {\boldsymbol B}\right)\times {\boldsymbol B}^{\prime }\right] \nonumber \\ && +\,{1\over \rho }\nabla \cdot \left[{\boldsymbol\xi} ^*\left(p^{\prime }+\rho \Phi ^{\prime }\right) +{\Phi ^{\prime }\nabla \Phi ^{\prime *}\over 4\pi G}\right], \end{eqnarray}

(37)

where

\begin{eqnarray} {\boldsymbol A}=\nabla \ln \rho -{1\over \Gamma _1}\nabla \ln p. \end{eqnarray}

(38)

When we assume spherical symmetry of the equilibrium configuration, neglecting |${\boldsymbol J}\times {\boldsymbol B}$| term in the magneto-hydrostatic equilibrium, we may obtain, using the relation |${\boldsymbol B}^{\prime }=\nabla \times \left({\boldsymbol\xi} \times {\boldsymbol B}\right)$|⁠,

\begin{eqnarray} \omega ^2{\boldsymbol\xi} ^*\cdot {\boldsymbol\xi} ={1\over \rho }\nabla \cdot \left({\boldsymbol\xi} ^* p^{\prime }\right)+{V\over \Gamma _1}{p^{\prime *} \over \rho gr}{p\over \rho }-grA{\xi _r^*\xi _r\over r}+{1\over 4\pi \rho }\left[\left|{\boldsymbol B}^{\prime }\right|^2 +\left(\nabla \times {\boldsymbol B}\right)\cdot \left({\boldsymbol\xi} ^*\times {\boldsymbol B}^{\prime }\right)\right] -{1\over 4\pi \rho }\nabla \cdot \left[\left({\boldsymbol\xi} ^*\times {\boldsymbol B}\right)\times {\boldsymbol B}^{\prime }\right]\!, \end{eqnarray}

(39)

where A is the radial component of |${\boldsymbol A}$| and we have applied the Cowling approximation, neglecting Φ΄. Integrating over the stellar mass, we obtain

\begin{eqnarray} \omega ^2\int \text{d}V\rho {\boldsymbol\xi} ^*\cdot {\boldsymbol\xi} &=&\int \text{d}V\rho \left\lbrace {V\over \Gamma _1}{p^{\prime }\over \rho }{p^{\prime *}\over \rho gr} -grA{\xi _r^*\xi _r\over r}+{1\over 4\pi \rho }\left[\left|{\boldsymbol B}^{\prime }\right|^2+\left(\nabla \times {\boldsymbol B}\right)\cdot \left({\boldsymbol\xi} ^*\times {\boldsymbol B}^{\prime }\right)\right]\right\rbrace \nonumber \\ &&+\int \text{d}S{\boldsymbol n}\cdot \left[{\boldsymbol\xi} ^*p^{\prime }-{1\over 4\pi }\left({\boldsymbol\xi} ^*\times {\boldsymbol B}\right)\times {\boldsymbol B}^{\prime }\right], \end{eqnarray}

(40)

where |${\boldsymbol n}$| is the unit normal vector at the surface. Note that the surface term may be rewritten as

\begin{eqnarray} \int \text{d}S{\boldsymbol n}\cdot \left[{\boldsymbol\xi} ^*p^{\prime }-{1\over 4\pi }\left({\boldsymbol\xi} ^*\times {\boldsymbol B}\right)\times {\boldsymbol B}^{\prime }\right] =\int \text{d}S\left\lbrace \xi _r^*\left[p^{\prime }+{1\over 4\pi }\left({\boldsymbol B}\cdot {\boldsymbol B}^{\prime }\right)\right]-{1\over 4\pi }\left({\boldsymbol\xi} ^*\cdot {\boldsymbol B}^{\prime }\right){\boldsymbol B}_r\right\rbrace . \end{eqnarray}

(41)

The square of the oscillation frequency is now given by using the eigenfunctions as

\begin{eqnarray} \omega ^2={\displaystyle \int \text{d}V\rho \left\lbrace {V\over \Gamma _1}{p^{\prime }\over \rho }{p^{\prime *}\over \rho gr} -grA{\xi _r^*\xi _r\over r}+{1\over 4\pi \rho }\left[\left|{\boldsymbol B}^{\prime }\right|^2+\left(\nabla \times {\boldsymbol B}\right)\cdot \left({\boldsymbol\xi} ^*\times {\boldsymbol B}^{\prime }\right)\right]\right\rbrace +\int \text{d}S{\boldsymbol n}\cdot \left[{\boldsymbol\xi} ^*p^{\prime }-{1\over 4\pi }\left({\boldsymbol\xi} ^*\times {\boldsymbol B}\right)\times {\boldsymbol B}^{\prime }\right]\over \displaystyle \int \text{d}V\rho {\boldsymbol\xi} ^*\cdot {\boldsymbol\xi} }, \end{eqnarray}

(42)

which we may use to check numerical consistency of our eigen-mode computations. We let |$\omega ^2_{\rm int}$| denote the right-hand side of equation (42) and define δ_cs, using an eigenfrequency ω and ω_int computed with the corresponding eigenfunctions, as

\begin{eqnarray} \delta _{\rm cs}\equiv 2\left|{\omega -\omega _{\rm int}\over \omega +\omega _{\rm int}}\right|. \end{eqnarray}

(43)

We may consider that δ_cs ≪ 1 suggests a good consistency in the computation.

3 NUMERICAL RESULTS

Ignoring the |${\boldsymbol J}\times {\boldsymbol B}$| term in the magneto-hydrostatic equilibrium, we use a polytrope of the index n = 1, which is spherical symmetric, as the background model for our modal analyses. Here, we assume the mass M = 1.4 M_⊙ and radius R = 10⁶ cm for the polytrope. We also assume that the polytrope is isentropic, that is, A = 0 in the entire interior of the star.

For given ζ₀ ≡ ζR, B_S ≡ μ_b/R³, and j_max, we integrate equation (3) to compute the function f using ρ(r) from the polytrope, and solve the set of differential equations from (18) to (23) together with the boundary conditions to obtain an eigen-solution, that is, an eigenfrequency ω and the corresponding eigenfunctions |${\boldsymbol y}_j$|⁠. We usually find numerous eigen-solutions to the set of differential equations for a given j_max and we pick up only eigen-solutions whose eigenfrequency ω well converges as j_max increases. Good convergence is usually expected for solutions that have only a few nodes of the eigenfunctions of dominating amplitudes. In Fig. 1, we plot the functions f and df/dr for ζ₀ = 0.01 and ζ₀ = 1. Although the magnitudes of the parameter ζ₀ are different by a factor of 100, the difference of the functions f and df/dr between the two cases is not necessarily significant. This may be because the constant ζ² ∼ 0.1 in equation (3) for ζ₀ = 1 and because the function f is well determined by the outer boundary conditions that do not depend on the parameter ζ₀. Note that at ζ₀ = 0, a magnetic field line |${\boldsymbol B}$| given by equation (2) stays in a plane perpendicular to the equatorial plane, and the field lines in such a plane look like those given in Lee (2018), for example. For |$\zeta _0\not=0$|⁠, however, no field lines can stay in a plane because of |$B_\phi \not=0$|⁠. The open field lines at ζ₀ = 0 will be twisted for |$\zeta _0\not=0$| and the closed field lines are not closed in a plane any more.

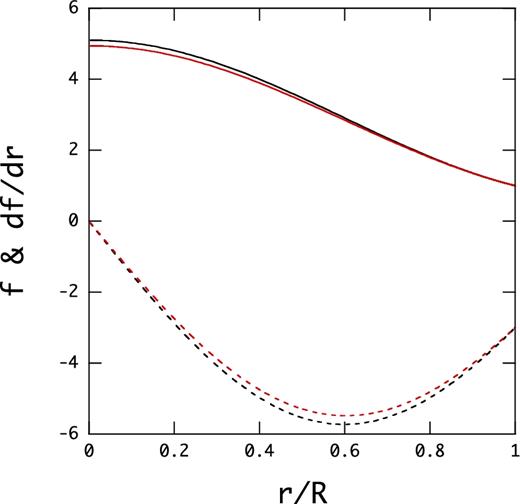
Functions f (solid lines) and df/dr (dotted lines) versus x = r/R for a polytrope of the index n = 1 for ζ0 = 0.01 (black lines) and ζ0 = 1 (red lines), where f and df/dr are normalized by BS ≡ μb/R3 and BS/R, respectively.

Figure 1.

Functions f (solid lines) and df/dr (dotted lines) versus x = r/R for a polytrope of the index n = 1 for ζ₀ = 0.01 (black lines) and ζ₀ = 1 (red lines), where f and df/dr are normalized by B_S ≡ μ_b/R³ and B_S/R, respectively.

Open in new tab Download slide

3.1 Spheroidal modes

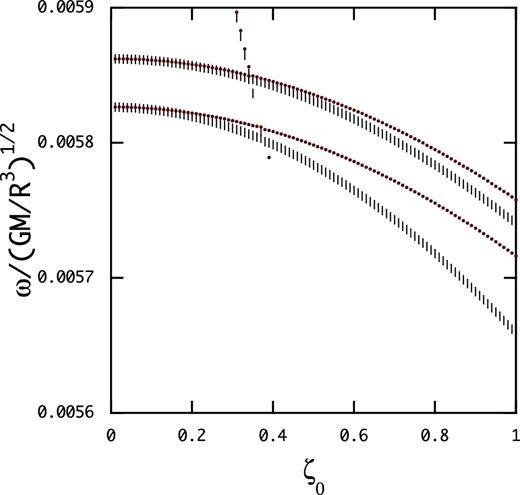
In Fig. 2 we plot |$\bar{\omega }$| of the first two spheroidal magnetic modes of even parity (left-hand panel) and of odd parity (right-hand panel) as a function of ζ₀ for B_S = 10¹⁴ G (red dots) and B_S = 10¹⁵ G (short vertical lines), where we have used j_max = 14 and |$10\times \bar{\omega }$| is plotted for B_S = 10¹⁴ G. The figure suggests that the frequency of the spheroidal magnetic modes is almost exactly proportional to the field strength B_S for ζ₀ ≲ 1. We find δ_cs ∼ 10⁻³ for even parity modes and δ_cs ∼ 10⁻² for odd parity modes, that is, odd parity modes show rather poor consistency compared to even parity modes. The figure also shows that as the parameter ζ₀ increases the frequency |$\bar{\omega }$| decreases and that the magnetic modes sometimes suffer avoided crossings with other magnetic modes. We find that the consistency δ_cs becomes poor at such avoided crossings.

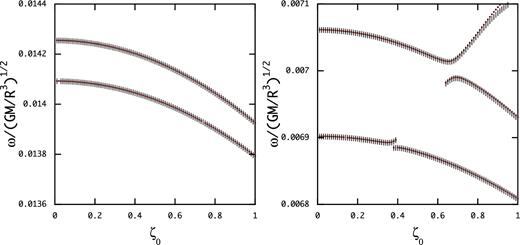
$Eigenfrequency $\bar{\omega }$ of the first two magnetic modes of even parity (left-hand panel) and odd parity (right-hand panel) versus ζ0 for BS = 1015 G (short vertical lines) and BS = 1014 G (red dots), where the frequency $10\times \bar{\omega }$ is plotted for BS = 1014 G.$

Figure 2.

Eigenfrequency |$\bar{\omega }$| of the first two magnetic modes of even parity (left-hand panel) and odd parity (right-hand panel) versus ζ₀ for B_S = 10¹⁵ G (short vertical lines) and B_S = 10¹⁴ G (red dots), where the frequency |$10\times \bar{\omega }$| is plotted for B_S = 10¹⁴ G.

Open in new tab Download slide

Defining the function |$\hat{\xi }_j$| for j = r, θ, ϕ as

\begin{eqnarray} \hat{\xi }_j(r,\theta )=\xi _j(r,\theta ,t){\rm e}^{-{\rm i}\omega t}, \end{eqnarray}

(44)

we plot the patterns of |$\hat{\xi }_j(r,\theta )$| for the magnetic modes on the x–z plane where x = rsin θ and z = rcos θ. Fig. 3 shows the patterns |$\hat{\xi }_j$| of the spheroidal magnetic mode of even parity for B_S = 10¹⁵ G at ζ₀ = 0.01, where the frequency is |$\bar{\omega }=1.426\times 10^{-2}$|⁠. For even modes, the pattern |$\hat{\xi }_r$| is symmetric and those of |$\hat{\xi }_\theta$| and |$\hat{\xi }_\phi$| are antisymmetric about the equator, that is, with respect to the z = 0 plane. Note also that |$\hat{\xi }_r$| has finite amplitudes on the magnetic (z-) axis but |$\hat{\xi }_\theta$| and |$\hat{\xi }_\phi$| have vanishing amplitudes. The patterns |$\hat{\xi }_r$| and |$\hat{\xi }_\theta$| look quite similar to those computed by assuming ζ₀ = 0 (see Lee 2018), and the amplitudes are mostly confined to the region along the magnetic axis. |$\hat{\xi }_\theta$| also shows wavy patterns in the region of closed magnetic fields. The amplitude of ξ_ϕ (and |$B^{\prime }_\phi$|⁠) is proportional to ζ₀ and is much smaller than ξ_r and ξ_θ for ζ₀ = 0.01, and the patterns |$\hat{\xi }_\phi$| show short wavy features both in the region of closed magnetic fields and in the region along the magnetic axis. These short wavy features may suggest that the eigenfunction ξ_ϕ is not necessarily well converged for j_max = 14.

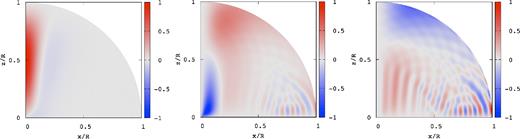
$Wave patterns $\hat{\xi }_r$ (left-hand panel), $\hat{\xi }_\theta$ (middle panel), and $\hat{\xi }_\phi$ (right-hand panel) for the spheroidal magnetic mode of even parity for BS = 1015 G at ζ0 = 0.01, where $\bar{\omega }=1.426\times 10^{-2}$.$

Figure 3.

Wave patterns |$\hat{\xi }_r$| (left-hand panel), |$\hat{\xi }_\theta$| (middle panel), and |$\hat{\xi }_\phi$| (right-hand panel) for the spheroidal magnetic mode of even parity for B_S = 10¹⁵ G at ζ₀ = 0.01, where |$\bar{\omega }=1.426\times 10^{-2}$|⁠.

Open in new tab Download slide

Fig. 4 shows the patterns |$\hat{\xi }_j$| for the same mode as in Fig. 3 but for ζ₀ = 1, where the frequency is |$\bar{\omega }=1.392\times 10^{-2}$|⁠. The patterns of |$\hat{\xi }_r$| and |$\hat{\xi }_\theta$| at ζ₀ = 1 are almost the same as those at ζ₀ = 0.01. The pattern |$\hat{\xi }_\phi$| at ζ₀ = 1, however, is significantly different from that at ζ = 0.01, and the short wavy patterns found for ζ₀ = 0.01 disappear for ζ₀ = 1. Note that the amplitude of ξ_ϕ at ζ₀ = 1 is comparable to those of ξ_r and ξ_θ.

$Same as Fig. 3 but for ζ0 = 1, where $\bar{\omega }=1.392\times 10^{-2}$.$

Figure 4.

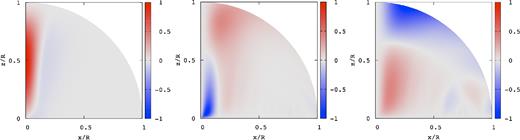
Same as Fig. 3 but for ζ₀ = 1, where |$\bar{\omega }=1.392\times 10^{-2}$|⁠.

Open in new tab Download slide

Figs 5 and 6 show the patterns of |$\hat{\xi }_j$| for the odd magnetic mode at ζ₀ = 0.01 and ζ₀ = 1, where the frequency is |$\bar{\omega }=5.846\times 10^{-3}$| for the former and |$\bar{\omega }=5.704\times 10^{-3}$| for the latter. The pattern |$\hat{\xi }_r$| is antisymmetric and those of |$\hat{\xi }_\theta$| and |$\hat{\xi }_\phi$| are symmetric about the equator for odd modes. Interestingly, no significant differences in the wave patterns |$\hat{\xi }_j$| are found between the cases of ζ₀ = 0.01 and ζ₀ = 1 although the amplitudes of ξ_ϕ at ζ₀ = 1 are by about a factor 100 larger than those at ζ₀ = 0.01. The amplitudes of |$\hat{\xi }_r$| and |$\hat{\xi }_\theta$| are confined to the region along the magnetic axis, but |$\hat{\xi }_\phi$| has amplitudes in the whole interior except on the magnetic axis.

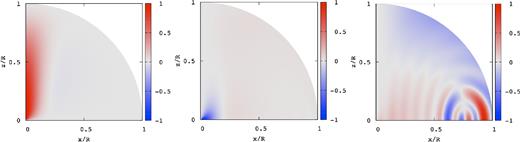
$Wave patterns $\hat{\xi }_r$ (left), $\hat{\xi }_\theta$ (middle), and $\hat{\xi }_\phi$ (right) for the spheroidal magnetic mode of odd parity at ζ0 = 0.01, where $\bar{\omega }=5.846\times 10^{-3}$.$

Figure 5.

Wave patterns |$\hat{\xi }_r$| (left), |$\hat{\xi }_\theta$| (middle), and |$\hat{\xi }_\phi$| (right) for the spheroidal magnetic mode of odd parity at ζ₀ = 0.01, where |$\bar{\omega }=5.846\times 10^{-3}$|⁠.

Open in new tab Download slide

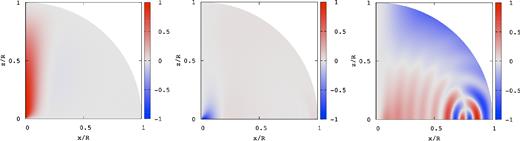
$Same as Fig. 5 but for ζ0 = 1, where $\bar{\omega }=5.704\times 10^{-3}$.$

Figure 6.

Same as Fig. 5 but for ζ₀ = 1, where |$\bar{\omega }=5.704\times 10^{-3}$|⁠.

Open in new tab Download slide

3.2 Toroidal modes

In Fig. 7, |$\bar{\omega }$| of the toroidal magnetic modes is plotted as a function of ζ₀, where the red dots and short vertical lines are for the cases of B_S = 10¹⁴ G and 10¹⁵ G, respectively, and |$10\times \bar{\omega }$| is plotted for the former.¹ The frequencies decrease with increasing ζ₀, which behaviour is similar to that found for spheroidal magnetic modes, and we find δ_cs ∼ 10⁻³ for the toroidal modes except at and near the avoided crossings. The frequencies |$10\times \bar{\omega }$| for B_S = 10¹⁴ G and |$\bar{\omega }$| for B_S = 10¹⁵ G agree with each other only when ζ₀ ≪ 1, and the agreement is lost as ζ₀ increases, that is, except when ζ₀ ∼ 0 the frequency of the toroidal magnetic modes does not linearly scale with B_S, which is different from what we find for spheroidal magnetic modes. The toroidal magnetic modes are governed by the differential equations (22) and (23) and are described by the variables |${\boldsymbol y}_5$| and |${\boldsymbol y}_6$| when ζ₀ = 0. As ζ₀ increases from ζ₀ = 0, however, the variables |${\boldsymbol y}_1$| and |${\boldsymbol y}_2$| come in and play a non-negligible role to determine the frequency in equations (22) and (23). Since the variables |${\boldsymbol y}_1$| and |${\boldsymbol y}_2$| are also affected by compressibility, which may be independent of the field strength B, the proportionality of the frequency of the toroidal modes with the field strength B_S may be lost.

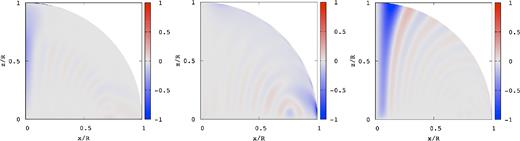
$Eigenfrequency $\bar{\omega }$ of the first two toroidal magnetic modes of odd parity versus ζ0 for BS = 1014 G (red dots) and BS = 1015 G (vertical short lines), where $10\times \bar{\omega }$ is plotted for BS = 1014 G.$

Figure 7.

Eigenfrequency |$\bar{\omega }$| of the first two toroidal magnetic modes of odd parity versus ζ₀ for B_S = 10¹⁴ G (red dots) and B_S = 10¹⁵ G (vertical short lines), where |$10\times \bar{\omega }$| is plotted for B_S = 10¹⁴ G.

Open in new tab Download slide

Figs 8 and 9 show the wave patterns |$\hat{\xi }_j$| for the toroidal modes at ζ₀ = 0.01 and ζ₀ = 1, respectively. We find no significant differences in the wave patterns between the two cases, and the amplitudes of ξ_ϕ always dominate those of ξ_r and ξ_θ for ζ₀ ≲ 1. These wave patterns may suggest that the eigenfunctions are not necessarily well converged for j_max = 14.

$Wave patterns $\hat{\xi }_r$ (left-hand panel), $\hat{\xi }_\theta$ (middle panel), and $\hat{\xi }_\phi$ (right-hand panel) for the toroidal magnetic mode of odd parity at ζ0 = 0.01 for BS = 1015 G, where $\bar{\omega }=5.862\times 10^{-3}$. The mode tends to the pure toroidal magnetic mode of odd parity as ζ0 → 0.$

Figure 8.

Wave patterns |$\hat{\xi }_r$| (left-hand panel), |$\hat{\xi }_\theta$| (middle panel), and |$\hat{\xi }_\phi$| (right-hand panel) for the toroidal magnetic mode of odd parity at ζ₀ = 0.01 for B_S = 10¹⁵ G, where |$\bar{\omega }=5.862\times 10^{-3}$|⁠. The mode tends to the pure toroidal magnetic mode of odd parity as ζ₀ → 0.

Open in new tab Download slide

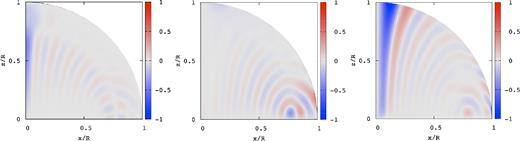
$Same as Fig. 8 but for ζ0 = 1 where $\bar{\omega }=5.741\times 10^{-3}$.$

Figure 9.

Same as Fig. 8 but for ζ₀ = 1 where |$\bar{\omega }=5.741\times 10^{-3}$|⁠.

Open in new tab Download slide

4 CONCLUSION

We have computed axisymmetric magnetic modes of neutron stars magnetized by a mixed poloidal and toroidal field. For the mixed magnetic field (⁠|$\zeta _0\not=0$|⁠), axisymmetric spheroidal and toroidal modes are coupled. Calculating magnetic modes as a function of ζ₀ from 0 to ∼1, we find that the frequency decreases with increasing ζ₀ and that they suffer avoided crossings with other magnetic modes as ζ₀ changes. We also find that the frequency of the spheroidal magnetic modes is almost exactly proportional to B_S for ζ₀ ≲ 1. The amplitude of ξ_ϕ of the spheroidal magnetic modes is roughly proportional to ζ₀ and become comparable to those of ξ_r and ξ_θ when ζ₀ ∼ 1. For toroidal magnetic modes, on the other hand, the proportionality of the frequency to B_S holds only when ζ₀ ≪ 1 and is lost with increasing ζ₀, and ξ_ϕ is always dominating the other components for ζ₀ ≲ 1. We find no unstable modes of ω² < 0 for axisymmetric magnetic modes.

We recognize several inconsistencies in our treatment of the oscillations of magnetized stars employed in this paper. First, we have ignored the equilibrium deformation due to magnetic fields. The magnitudes of magnetic deformation may be of order of B², which is much smaller than the gas pressure in most of the interior region of the star, except for the case of extremely strong magnetic fields as strong as B ∼ 10¹⁸ G. Secondly, the discontinuity in B_ϕ at the surface induces a surface current and hence the tangential force at the surface when |$B_r\not=0$|⁠, which effects are not taken account of in our modal analyses.

As discussed in Appendix C, the surface boundary conditions can be very important to determine the modal property of pure toroidal modes of a neutron star possessing a pure poloidal magnetic field. For the surface boundary condition |$B^{\prime }_\phi =0$|⁠, we obtain only eigenmodes having real ω and eigenfunctions. For the surface boundary condition |${\mathrm{\partial} (\xi _\phi /r)/\mathrm{\partial} r}=0$|⁠, however, we find an eigenmode having complex ω and eigenfunctions as well as real eigenmodes which have converging wave patterns with increasing j_max. For this boundary condition, the force operator |${\boldsymbol F}({\boldsymbol\xi} )$| is not self-adjoint and may permit complex modes. The boundary condition |${\mathrm{\partial} (\xi _\phi /r)/\mathrm{\partial} r}=0$| may be used to satisfy the condition that the traction vanishes at the surface of a solid crust. This may suggest that if we consider a neutron star with a solid crust the property of the toroidal magnetic modes in the fluid core could be significantly different from what we have found in this paper. Besides, if a neutron star has a solid crust, there exist spheroidal and toroidal sound waves travelling in the solid crust. It is interesting for us to examine how the sound waves in the solid crust will be affected by introducing the toroidal magnetic field since the toroidal sound waves are possibly coupled with Alfvén modes in the core and could be quickly damped (e.g. Levin 2006, 2007). Whether or not this strong damping of the crustal modes is still relevant for mixed poloidal and toroidal field configurations is a question to be answered in terms of normal mode analyses (e.g. Colaiuda & Kokkotas 2012 in terms of MHD simulations).

Introducing the toroidal magnetic field, the spheroidal component of the displacement vector of even parity is coupled with the toroidal component of odd parity and vice versa. In the case of rotating stars, however, the Coriolis force couples the even (odd) spheroidal component with even (odd) toroidal component of the displacement vector. This means that if we consider rotating stars magnetized by mixed poloidal and toroidal fields, the perturbations are not separated into two different mode groups according to the parity, which probably makes it difficult to analyse the modal properties of magnetized stars.

For mixed poloidal and toroidal magnetic field configurations, which are more favorable for magnetized stars from the stability point of view, toroidal (axial) and spheroidal (polar) components of the velocity fields of the perturbations are coupled even for axisymmetric modes of non-rotating stars. In this paper, we show that spheroidal and toroidal magnetic modes are separately obtained as discrete normal modes even with the coupling between them. Because of the coupling, toroidal magnetic modes are accompanied by density perturbations, which could affect the stability and hence the lifetime of the toroidal modes. We have to take account of the effects of a solid crust on the magnetic modes to closely compare our results to those by Colaiuda & Kokkotas (2012). It is also interesting to examine whether or not the coherent magnetic modes discussed by Gabler et al. (2016) and Passamonti & Pons (2016) can be regarded as normal modes. These will be among our future projects.

Footnotes

1

At ζ₀ = 0, axisymmetric toroidal modes and spheroidal modes are decoupled. We have computed axisymmetric toroidal modes for ζ₀ = 0 using the surface boundary conditions |${\boldsymbol y}_6=0$| and |${\rm d}{\boldsymbol y}_5/{\rm d}r=0$|⁠, and the frequency |$\bar{\omega }$| of the magnetic toroidal modes for B_S = 10¹⁵ G is tabulated for the two boundary conditions in Table C1 in Appendix C.

REFERENCES

Akgün

T.

,

Reisenegger

A.

,

Mastrano

A.

,

Marchant

P.

,

2013

,

MNRAS

,

433

,

2445

Crossref

Search ADS

Asai

H.

,

Lee

U.

,

2014

,

ApJ

,

790

,

66

Crossref

Search ADS

Asai

H.

,

Lee

U.

,

Yoshida

S.

,

2015

,

MNRAS

,

449

,

3620

Crossref

Search ADS

Asai

H.

,

Lee

U.

,

Yoshida

S.

,

2016

,

MNRAS

,

455

,

2228

Crossref

Search ADS

Cerdá-Durán

P.

,

Stergioulas

N.

,

Font

J. A.

,

2009

,

MNRAS

,

397

,

1607

Crossref

Search ADS

Colaiuda

A.

,

Kokkotas

K. D.

,

2011

,

MNRAS

,

414

,

3014

Crossref

Search ADS

Colaiuda

A.

,

Kokkotas

K. D.

,

2012

,

MNRAS

,

423

,

818

Crossref

Search ADS

Colaiuda

A.

,

Ferrari

V.

,

Gualtieri

L.

,

Pons

J. A.

,

2008

,

MNRAS

,

385

,

2080

Crossref

Search ADS

Duncan

R. C.

,

1998

,

ApJ

,

498

,

L45

Crossref

Search ADS

Gabler

M.

,

Cerdá-Durán

P.

,

Font

J. A.

,

Müller

E.

,

Stergioulas

N.

,

2011

,

MNRAS

,

410

,

L37

Crossref

Search ADS

Gabler

M.

,

Cerdá-Durán

P.

,

Stergioulas

N.

,

Font

J. A.

,

Müller

E.

,

2012

,

MNRAS

,

421

,

2054

Crossref

Search ADS

Gabler

M.

,

Cerdá-Durán

P.

,

Font

J. A.

,

Müller

E.

,

Stergioulas

N.

,

2013

,

MNRAS

,

430

,

1811

Crossref

Search ADS

Gabler

M.

,

Cerdá-Durán

P.

,

Stergioulas

N.

,

Font

J. A.

,

Múller

E.

,

2016

,

MNRAS

,

460

,

4242

Crossref

Search ADS

Glampedakis

K.

,

Samuelsson

L.

,

Andersson

N.

,

2006

,

MNRAS

,

371

,

L74

Crossref

Search ADS

Herbrik

M.

,

Kokkotas

K. D.

,

2017

,

MNRAS

,

466

,

1330

Crossref

Search ADS

Israel

G.

et al. ,

2005

,

ApJ

,

628

,

L53

Crossref

Search ADS

Lander

S. K.

,

Jones

D. I.

,

2011

,

MNRAS

,

412

,

1730

Crossref

Search ADS

Lander

S. K.

,

Jones

D. I.

,

Passamonti

A.

,

2010

,

MNRAS

,

405

,

318

Lee

U.

,

2007

,

MNRAS

,

374

,

1015

Crossref

Search ADS

Lee

U.

,

2008

,

MNRAS

,

385

,

2069

Crossref

Search ADS

Lee

U.

,

2010

,

MNRAS

,

405

,

1444

Crossref

Search ADS

Lee

U.

,

2018

,

MNRAS

,

473

,

3661

Crossref

Search ADS

Levin

Y.

,

2006

,

MNRAS

,

368

,

L35

Crossref

Search ADS

Levin

Y.

,

2007

,

MNRAS

,

377

,

159

Crossref

Search ADS

Markey

P.

,

Tayler

R. J.

,

1973

,

MNRAS

,

163

,

77

Crossref

Search ADS

Markey

P.

,

Tayler

R. J.

,

1974

,

MNRAS

,

168

,

505

Crossref

Search ADS

Melrose

D. B.

,

1986

,

Instabilities in Space and Laboratory Plasma

.

Cambridge Univ. Press

,

Cambridge, UK

Mereghetti

S.

,

2008

,

A&AR

,

15

,

225

Crossref

Search ADS

Passamonti

A.

,

Lander

S. K.

,

2013

,

MNRAS

,

429

,

767

Crossref

Search ADS

Passamonti

A.

,

Pons

J. A.

,

2016

,

MNRAS

,

463

,

1173

Crossref

Search ADS

Sotani

H.

,

Colaiuda

A.

,

Kokkotas

K. D.

,

2008

,

MNRAS

,

385

,

2161

Crossref

Search ADS

Strohmayer

T. E.

,

Watts

A. L.

,

2005

,

ApJ

,

632

,

L111

Crossref

Search ADS

Strohmayer

T. E.

,

Watts

A. L.

,

2006

,

ApJ

,

653

,

593

Crossref

Search ADS

Tayler

R. J.

,

1973

,

MNRAS

,

161

,

365

Crossref

Search ADS

van Hoven

M. B.

,

Levin

Y.

,

2011

,

MNRAS

,

410

,

1036

Crossref

Search ADS

van Hoven

M. B.

,

Levin

Y.

,

2012

,

MNRAS

,

420

,

3035

Crossref

Search ADS

Watts

A. L.

,

Strohmayer

T. E.

,

2006

,

ApJ

,

637

,

L117

Crossref

Search ADS

Woods

P. M.

,

Thompson

C.

,

2006

, in

Lewin

W. H. G.

,

van der Klis

M.

, eds,

Compact Stellar X-Ray Sources

.

Cambridge Univ. Press

,

Cambridge, UK

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Yoshida

S.

,

Eriguchi

Y.

,

2006

,

ApJS

,

120

,

353

Yoshida

S.

,

Lee

U.

,

2000

,

ApJ

,

529

,

997

Crossref

Search ADS

Yoshida

S.

,

Yoshida

S.

,

Eriguchi

Y.

,

2006

,

ApJ

,

651

,

462

Crossref

Search ADS

APPENDIX A: EQUILIBRIUM MAGNETIC FIELDS

We consider neutron stars magnetized with a mixed poloidal and toroidal field. We closely follow Colaiuda et al. (2008) to derive the static mixed magnetic field in Newtonian gravity. We start with a vector potential |$\tilde{{\boldsymbol A}}=(\tilde{A}_r, \tilde{A}_\theta ,\tilde{A}_\phi )$| given in spherical polar coordinates (r, θ, ϕ). Applying a gauge transformation such that |$A_\theta =\tilde{A}_\theta -\mathrm{\partial} \chi /r\mathrm{\partial} \theta =0$|⁠, we will work with the gauged potential

\begin{eqnarray} {\boldsymbol A}=(A_r,0,A_\phi ), \end{eqnarray}

(A1)

which is assumed axisymmetric so that |$\mathrm{\partial} {\boldsymbol A}/\mathrm{\partial} \phi =0$|⁠. With this vector potential, magnetic fields may be given by

\begin{eqnarray} {\boldsymbol B}=\nabla \times {\boldsymbol A}={\boldsymbol e}_r{1\over r\sin \theta }{\mathrm{\partial} \over \mathrm{\partial} \theta }\sin \theta A_\phi +{\boldsymbol e}_\theta \left(-{1\over r}{\mathrm{\partial} rA_\phi \over \mathrm{\partial} r}\right) +{\boldsymbol e}_\phi \left(-{1\over r}{\mathrm{\partial} A_r\over \mathrm{\partial} \theta }\right), \end{eqnarray}

(A2)

and the Ampére law |$\nabla \times {\boldsymbol B}=4\pi {\boldsymbol J}/c$| reduces to

\begin{eqnarray} {4\pi \over c}{\boldsymbol J} =-\left({1\over r^2\sin \theta }{\mathrm{\partial} \over \mathrm{\partial} \theta }\sin \theta {\mathrm{\partial} \over \mathrm{\partial} \theta }A_r\right){\boldsymbol e}_r +\left({1\over r}{\mathrm{\partial} ^2\over \mathrm{\partial} r\mathrm{\partial} \theta }A_r\right){\boldsymbol e}_\theta -\left(\nabla ^2A_\phi -{1\over r^2\sin ^2\theta }A_\phi \right){\boldsymbol e}_\phi , \end{eqnarray}

(A3)

where |${\boldsymbol J}$| is the current density and c denotes the velocity of light. For the Lorentz force we may write

\begin{eqnarray} \left(\nabla \times {\boldsymbol B}\right)\times {\boldsymbol B} &=&-{\boldsymbol e}_r\left[{1\over r}{\mathrm{\partial} rA_\phi \over \mathrm{\partial} r}\left(\nabla ^2A_\phi -{1\over r^2\sin ^2\theta }A_\phi \right)+{1\over r}{\mathrm{\partial} A_r\over \mathrm{\partial} \theta }{1\over r}{\mathrm{\partial} ^2A_r\over \mathrm{\partial} r\mathrm{\partial} \theta }\right]\nonumber \\ &&-{\boldsymbol e}_\theta \left[{1\over r}{\mathrm{\partial} A_r\over \mathrm{\partial} \theta }{1\over r^2\sin \theta }{\mathrm{\partial} \over \mathrm{\partial} \theta }\sin \theta {\mathrm{\partial} \over \mathrm{\partial} \theta }A_r+\left({1\over r\sin \theta }{\mathrm{\partial} \over \mathrm{\partial} \theta }\sin \theta A_\phi \right)\left(\nabla ^2A_\phi -{1\over r^2\sin ^2\theta }A_\phi \right)\right]\nonumber \\ &&+{\boldsymbol e}_\phi \left[{1\over r}{\mathrm{\partial} rA_\phi \over \mathrm{\partial} r}{1\over r^2\sin \theta }{\mathrm{\partial} \over \mathrm{\partial} \theta } \sin \theta {\mathrm{\partial} \over \mathrm{\partial} \theta }A_r-\left({1\over r\sin \theta }{\mathrm{\partial} \over \mathrm{\partial} \theta }\sin \theta A_\phi \right)\left({1\over r}{\mathrm{\partial} ^2A_r\over \mathrm{\partial} r\mathrm{\partial} \theta }\right)\right]. \end{eqnarray}

(A4)

Assuming that the ϕ component of the Lorenz force vanishes identically, we obtain

\begin{eqnarray} {1\over r^3\sin ^2\theta }\left[\left({\mathrm{\partial} \over \mathrm{\partial} r}r\sin \theta A_\phi \right)\left({\mathrm{\partial} \over \mathrm{\partial} \theta } \sin \theta {\mathrm{\partial} \over \mathrm{\partial} \theta }A_r\right)-\left({\mathrm{\partial} \over \mathrm{\partial} \theta }r\sin \theta A_\phi \right)\left({\mathrm{\partial} \over \mathrm{\partial} r}\sin \theta {\mathrm{\partial} \over \mathrm{\partial} \theta }A_r\right)\right]=0, \end{eqnarray}

(A5)

which is equivalent to, when |$\mathrm{\partial} A_j/\mathrm{\partial} \phi =0$|⁠,

\begin{eqnarray} \nabla \left(r\sin \theta A_\phi \right)\times \nabla \left(\sin \theta {\mathrm{\partial} \over \mathrm{\partial} \theta }A_r\right)=0. \end{eqnarray}

(A6)

We therefore assume, using an arbitrary function H(x),

\begin{eqnarray} \sin \theta {\mathrm{\partial} A_r\over \mathrm{\partial} \theta }=H(r\sin \theta A_\phi ). \end{eqnarray}

(A7)

For the function H(x), we employ H(x) = ζx so that

\begin{eqnarray} {\mathrm{\partial} \over \mathrm{\partial} \theta }A_r=\zeta r A_\phi , \end{eqnarray}

(A8)

where ζ is a constant. Introducing a function a(r, θ), which satisfies

\begin{eqnarray} A_\phi ={1\over r}{\mathrm{\partial} a\over \mathrm{\partial} \theta }, \quad A_r=\zeta a, \end{eqnarray}

(A9)

we obtain

\begin{eqnarray} {\boldsymbol B}={1\over r^2\sin \theta }{\mathrm{\partial} \over \mathrm{\partial} \theta }\sin \theta {\mathrm{\partial} a\over \mathrm{\partial} \theta }{\boldsymbol e}_r -{1\over r}{\mathrm{\partial} ^2a\over \mathrm{\partial} r\mathrm{\partial} \theta }{\boldsymbol e}_\theta -\zeta {1\over r}{\mathrm{\partial} a\over \mathrm{\partial} \theta }{\boldsymbol e}_\phi , \end{eqnarray}

(A10)

\begin{eqnarray} {4\pi \over c}{\boldsymbol J} =-\zeta B_r{\boldsymbol e}_r-\zeta B_\theta {\boldsymbol e}_\theta -\left[\nabla ^2\left({1\over r}{\mathrm{\partial} a\over \mathrm{\partial} \theta }\right)-{1\over r^2\sin ^2\theta } {1\over r}{\mathrm{\partial} a\over \mathrm{\partial} \theta }\right]{\boldsymbol e}_\phi , \end{eqnarray}

(A11)

and

\begin{eqnarray} \left(\nabla \times {\boldsymbol B}\right)\times {\boldsymbol B} ={4\pi \over c}\hat{J}_\phi {1\over r\sin \theta }\nabla \left(\sin \theta {\mathrm{\partial} a\over \mathrm{\partial} \theta }\right), \end{eqnarray}

(A12)

where

\begin{eqnarray} {4\pi \over c}\hat{J}_\phi ={4\pi \over c}J_\phi +\zeta B_\phi . \end{eqnarray}

(A13)

The equilibrium state of a magnetized star is given by

\begin{eqnarray} {1\over \rho }\nabla p+\nabla \Phi -{1\over 4\pi \rho }\left(\nabla \times {\boldsymbol B}\right)\times {\boldsymbol B}=0, \end{eqnarray}

(A14)

which may reduce to

\begin{eqnarray} \nabla \left(u+{p\over \rho }+\Phi \right)={1\over \rho c}{\hat{J}_\phi \over r\sin \theta }\nabla \left(\sin \theta {\mathrm{\partial} a\over \mathrm{\partial} \theta }\right), \end{eqnarray}

(A15)

where we have used the first law of thermodynamics for adiabatic flows given by

\begin{eqnarray} \text{d}u=-pd\left({1\over \rho }\right), \end{eqnarray}

(A16)

and u denotes the internal energy per unit mass. Since

\begin{eqnarray} 0=\nabla \times \nabla \left(u+{p\over \rho }+\Phi \right)=\nabla \left({1\over \rho c}{\hat{J}_\phi \over r\sin \theta }\right)\times \nabla \left(\sin \theta {\mathrm{\partial} a\over \mathrm{\partial} \theta }\right)\!, \end{eqnarray}

(A17)

we may write, using an arbitrary function F(x),

\begin{eqnarray} {1\over \rho c}{\hat{J}_\phi \over r\sin \theta }=F\left(\sin \theta {\mathrm{\partial} a\over \mathrm{\partial} \theta }\right). \end{eqnarray}

(A18)

Since |$a\propto B\equiv |{\boldsymbol B}|$|⁠, the function F(x) may be expanded in terms of the field strength B as

\begin{eqnarray} F\left(\sin \theta {\mathrm{\partial} a\over \mathrm{\partial} \theta }\right)=c_0+c_1\sin \theta {\mathrm{\partial} a\over \mathrm{\partial} \theta }+O\left(B^2\right)\!, \end{eqnarray}

(A19)

where c₀ and c₁ are expansion constants. Keeping only the first term c₀, we obtain

\begin{eqnarray} 4\pi c_0\rho r\sin \theta ={4\pi \over c}\hat{J}_\phi =-\left[\nabla ^2\left({1\over r}{\mathrm{\partial} a\over \mathrm{\partial} \theta }\right)-{1\over r^2\sin ^2\theta } {1\over r}{\mathrm{\partial} a\over \mathrm{\partial} \theta }\right]-\zeta ^2{1\over r}{\mathrm{\partial} a\over \mathrm{\partial} \theta }. \end{eqnarray}

(A20)

When we ignore the equilibrium deformation due to magnetic fields so that ρ depends only on the radial distance r from the centre, substituting into (A20) for simplicity

\begin{eqnarray} a(r,\theta )=a_1(r)P_1(\cos \theta ) \end{eqnarray}

(A21)

with P₁(cos θ) = cos θ being a Legendre polynomial, we obtain

\begin{eqnarray} {\text{d}^2a_1\over \text{d}r^2}+\left(\zeta ^2-{2\over r}\right)a_1=4\pi c_0\rho r^2, \end{eqnarray}

(A22)

which may be rewritten as

\begin{eqnarray} {\text{d}^2f\over \text{d}r^2}+{4\over r}{\text{d}f\over \text{d}r}+\zeta ^2 f=-4\pi c_0\rho , \end{eqnarray}

(A23)

where

\begin{eqnarray} f=-{a_1\over r^2}, \end{eqnarray}

(A24)

and f(r) = α₀ + O(r²) is assumed at the stellar centre with a constant α₀. Numerically integrating equation (A23) from the stellar centre to the surface, we may determine the two constants c₀ and α₀ so that the two boundary conditions are satisfied at the stellar surface. Using the function f thus computed, we write

\begin{eqnarray} B_r=2f(r)\cos \theta , \quad B_\theta =-{1\over r}{\text{d}r^2f(r)\over \text{d}r}\sin \theta \equiv {\cal Q}\sin \theta , \quad B_\phi =-\zeta rf(r)\sin \theta , \end{eqnarray}

(A25)

and ζ may be treated as a free parameter.

APPENDIX B: SURFACE BOUNDARY CONDITIONS

The surface boundary conditions we apply at r = R are

\begin{eqnarray} \left[\delta {\boldsymbol B}\right]^+_-=0, \quad \left[\delta \left(p+{1\over 8\pi }{\boldsymbol B}^2\right)\right]^+_-=0, \end{eqnarray}

(B1)

where

\begin{eqnarray} \left[f(r)\right]^+_-=\lim _{\epsilon \rightarrow 0}\left[f(r+\epsilon )-f(r-\epsilon )\right]. \end{eqnarray}

(B2)

Since we have assumed the continuity of the functions f and df/dr to the functions f^ex = μ_b/r³ and df^ex/dr at the surface, we have at the surface

\begin{eqnarray} \left[B_r\right]^+_-=0, \quad \left[B_\theta \right]^+_-=0. \end{eqnarray}

(B3)

But, since we assume the parameter |$\zeta \not=0$| for r < R and ζ = 0 for r > R, we have at r = R

\begin{eqnarray} \left[B_\phi (R)\right]^+_-=\zeta Rf\sin \theta \not=0, \end{eqnarray}

(B4)

which suggests the existence of the surface current given by

\begin{eqnarray} J_\theta =\zeta {c\over 4\pi }{a\over r}\sin \theta \delta (r-R), \end{eqnarray}

(B5)

where δ(r − R) is the delta function. The existence of the surface current, however, induces a tangential force given by |$J_\theta {\boldsymbol e}_\theta \times {\boldsymbol B}$| unless |${\boldsymbol n}\cdot {\boldsymbol B}=0$| at the surface, where |${\boldsymbol n}$| denotes the unit normal vector to the surface (e.g. Melrose 1986). Since |${\boldsymbol n}\cdot {\boldsymbol B}\not=0$| is assumed in this paper, we have |$J_\theta {\boldsymbol e}_\theta \times {\boldsymbol B}\not=0$|⁠, which may suggest that the inconsistency will be serious for large values of ζ.

Neglecting the displacement current in the perturbed Ampere law, we get |$\nabla \times {\boldsymbol B}^{\prime (+)}=0$| outside the star, where we have assumed p = ρ = 0 and |${\boldsymbol J}=0$|⁠. For this |${\boldsymbol B}^{\prime (+)}$| we may write |${\boldsymbol B}^{\prime (+)}=\nabla \psi$|⁠, where we have used the superscript ^( + ) to indicate quantities for r > R and we shall use a superscript ^( − ) for r < R. Since |$\nabla \cdot {\boldsymbol B}^{\prime }=0$|⁠, the scalar potential ψ satisfies the Laplace equation ∇²ψ = 0, the solution of which may be given as

\begin{eqnarray} \psi =\sum _{l=0}^\infty c_lr^{-l-1}Y_l^0(\theta ,\phi )e^{{\rm i}\omega t}, \end{eqnarray}

(B6)

where c_l is the expansion coefficients and we have assumed that the potential ψ is axisymmetric (m = 0) and vanishes at infinity. We then obtain

\begin{eqnarray} B^{\prime (+)}_r=-\sum _l(l+1)c_lr^{-l-2}Y_l^0(\theta ,\phi )e^{{\rm i}\omega t}, \quad B^{\prime (+)}_\theta =\sum _lc_lr^{-l-2}{\mathrm{\partial} \over \mathrm{\partial} \theta }Y_l^0(\theta ,\phi )e^{{\rm i}\omega t}, \quad B^{\prime (+)}_\phi =0. \end{eqnarray}

(B7)

The surface condition |$\left[\delta {\boldsymbol B}\right]^+_-=0$| may lead to

\begin{eqnarray} \left[B^{\prime }_r-{B_\phi \over r}\xi _\phi \right]^+_-=B^{\prime (+)}_r -\left(B^{\prime (-)}_r+{\zeta f\sin \theta }\xi _\phi ^{(-)}\right)=0, \end{eqnarray}

(B8)

\begin{eqnarray} \left[B^{\prime }_\theta +\xi _r{\mathrm{\partial} B_\theta \over \mathrm{\partial} r}-\xi _\phi {B_\phi \over r}{\cos \theta \over \sin \theta }\right]^+_-=B^{\prime (+)}_\theta -\left(B^{\prime (-)}_\theta +\left[{\text{d}{\cal Q}\over \text{d} r}\right]^+_-\sin \theta \xi _r^{(-)} + \zeta f {\cos \theta }\xi _\phi ^{(-)}\right)=0, \end{eqnarray}

(B9)

\begin{eqnarray} \left[B^{\prime }_\phi +\xi _r{\mathrm{\partial} B_\phi \over \mathrm{\partial} r}+\xi _\theta {\mathrm{\partial} \over \mathrm{\partial} \theta }{B_\phi \over r}\right]^+_-=B^{\prime (+)}_\phi -\left(B^{\prime (-)}_\phi -\zeta {\text{d}rf \over \text{d} r}\sin \theta \xi _r^{(-)} -\zeta f\cos \theta \xi _\theta ^{(-)}\right)=0, \end{eqnarray}

(B10)

and the mechanical force balance condition at the surface to

\begin{eqnarray} 0=\left[\delta \left(p+{1\over 8\pi }{\boldsymbol B}^2\right)\right]^+_-&=&\left[\delta p\right]^+_-+{1\over 4\pi }\left[{\boldsymbol B}\cdot \delta {\boldsymbol B}\right]^+_-\nonumber \\ &=&-\delta p^{(-)}+{1\over 4\pi }\zeta Rf\sin \theta \left(B^{\prime (-)}_\phi -\zeta {\text{d} rf \over \text{d} r}\sin \theta \xi _r^{(-)} -\zeta f\cos \theta \xi _\theta ^{(-)}+\left({\cal Q} +2f\right)\cos \theta {\xi _\phi ^{(-)}\over r}\right). \end{eqnarray}

(B11)

If we write

\begin{eqnarray} {B_r^{\prime (+)}\over f}=\sum _jc_{l^{\prime }_j}^SY_{l^{\prime }_j}^0(\theta ,\phi )e^{{\rm i}\omega t}, \quad {B_\theta ^{\prime (+)}\over f}=\sum _jc_{l^{\prime }_j}^H{\mathrm{\partial} \over \mathrm{\partial} \theta }Y_{l^{\prime }_j}^0(\theta ,\phi )e^{{\rm i}\omega t}, \quad {B_\phi ^{\prime (+)}\over f}=-\sum _jc_{l^{\prime }_j}^T{\mathrm{\partial} \over \mathrm{\partial} \theta }Y_{l^{\prime }_j}^0(\theta ,\phi )e^{{\rm i}\omega t}, \end{eqnarray}

(B12)

equations (B7) at the surface reduce to

\begin{eqnarray} {\boldsymbol c}^S+{\boldsymbol{\sf L}}^+{\boldsymbol c}^H=0, \quad {\boldsymbol c}^T={0}, \end{eqnarray}

(B13)

where

\begin{eqnarray} {\boldsymbol c}^S=\left(c^S_{l^{\prime }_j}\right), \quad {\boldsymbol c}^H=\left(c^H_{l^{\prime }_j}\right), \quad {\boldsymbol c}^T=\left(c^T_{l^{\prime }_j}\right), \end{eqnarray}

(B14)

and

\begin{eqnarray} \left(\sf L^+\right)_{ij}=\left(l^{\prime }_j+1\right)\delta _{ij}. \end{eqnarray}

(B15)

The boundary conditions (B8), (B9), and (B10) can be rewritten as

\begin{eqnarray} {\boldsymbol c}^S={\boldsymbol b}^S+\zeta _0{\boldsymbol{\sf C}}_1{\boldsymbol y}_5, \end{eqnarray}

(B16)

\begin{eqnarray} {\boldsymbol{\sf C}}_0{c}^H= {\boldsymbol{\sf C}}_0{\boldsymbol b}^H + \zeta _{ 0}^{2}\left({1}-{\boldsymbol{\sf Q}}_0{\boldsymbol{\sf Q}}_1\right){\boldsymbol y}_1 -\zeta _0{\boldsymbol{\sf Q}}_0{\boldsymbol{\sf C}}_1{\boldsymbol y}_5, \end{eqnarray}

(B17)

\begin{eqnarray} {\boldsymbol{\sf C}}_0{c}^T= {\boldsymbol{\sf C}}_0{\boldsymbol b}^T-\zeta _{0}\left({{\cal Q}\over {f}}+{1}\right)\left({\boldsymbol{\sf 1}}-{\boldsymbol{\sf Q}}_0{\boldsymbol{\sf Q}}_1\right){\boldsymbol y}_1+\zeta _{0}{\boldsymbol{\sf Q}}_0{\boldsymbol{\sf C}}_1{\boldsymbol y}_3 = 0, \end{eqnarray}

(B18)

and the condition (B11) as

\begin{eqnarray} {\boldsymbol y}_2-{\boldsymbol y}_1 =-\zeta _0\beta \left({{\cal Q}\over f}+2\right){\boldsymbol{\sf Q}}_0{\boldsymbol{\sf C}}_1{\boldsymbol y}_5, \end{eqnarray}

(B19)

where ζ₀ ≡ ζR and we have used at the surface

\begin{eqnarray} \left[{\text{d}\ln {\cal Q}\over \text{d}\ln r}\right]^+_-=\zeta _0^2{f\over {\cal Q}}. \end{eqnarray}

(B20)

Eliminating the vectors |${\boldsymbol c}^S$| and |${\boldsymbol c}^H$| using equation (B13), we obtain

\begin{eqnarray} {\boldsymbol b}^S+\zeta _0{\boldsymbol{\sf C}}_1{\boldsymbol y}_5+{\boldsymbol{\sf L}}^+\left[{\boldsymbol b}^H+\zeta _0^2{\boldsymbol{\sf C}}_0^{-{1}}\left({\boldsymbol{\sf 1}}-{\boldsymbol{\sf Q}}_0{\boldsymbol{\sf Q}}_1\right){\boldsymbol y}_1-\zeta _0{\boldsymbol{\sf C}}_0^{-{1}}{\boldsymbol{\sf Q}}_0{\boldsymbol{\sf C}}_1{\boldsymbol y}_5\right]=0, \end{eqnarray}

(B21)

and

\begin{eqnarray} {\boldsymbol b}^T=\zeta _0{\boldsymbol{\sf C}}_0^{-{1}}\left[\left({{\cal Q}\over f}+{1}\right)\left({\boldsymbol{\sf 1}}-{\boldsymbol{\sf Q}}_0{\boldsymbol{\sf Q}}_1\right){\boldsymbol y}_1-{\boldsymbol{\sf Q}}_0{\boldsymbol{\sf C}}_1{\boldsymbol y}_3\right]. \end{eqnarray}

(B22)

APPENDIX C: TOROIDAL MODES FOR POLOIDAL MAGNETIC FIELDS

Here, we revisit the problem of pure toroidal magnetic modes of a neutron star magnetized with a pure poloidal field, corresponding to the case of ζ₀ = 0. The perturbed equations may be given as

\begin{eqnarray} \omega ^2\xi _\phi =-{1\over 4\pi \rho }\left({\boldsymbol B}\cdot \nabla B^{\prime }_\phi +{B_\theta \cot \theta +B_r\over r}B^{\prime }_\phi \right), \end{eqnarray}

(C1)

\begin{eqnarray} B^{\prime }_\phi ={\boldsymbol B}\cdot \nabla \xi _\phi +\left({\mathrm{\partial} B_r\over \mathrm{\partial} r} +{B_\theta \cot \theta +B_r\over r}\right)\xi _\phi , \end{eqnarray}

(C2)

where |${\boldsymbol B}=B_r{\boldsymbol e}_r+B_\theta {\boldsymbol e}_\theta$|⁠, and substituting the series expansions in terms of |$Y_l^m$|⁠, we obtain for the expansion coefficients the oscillation equations for a fluid star, which are given by

\begin{eqnarray} r{{\rm d}{\boldsymbol y}_5\over {\rm d}r} =-{{\cal Q}\over f}\left({1\over 2}{\boldsymbol{\sf B}}_0^{-{1}}{\boldsymbol{\sf W}}_1{\boldsymbol {\Lambda}}_0-{\boldsymbol{\sf 1}}\right){\boldsymbol y}_5 +{1\over 2}{\boldsymbol{\sf B}}_0^{-{1}}{\boldsymbol {\Lambda}}_1{\boldsymbol y}_6, \end{eqnarray}

(C3)

\begin{eqnarray} r{{\rm d} {\boldsymbol y}_6\over {\rm d}r} =-{1\over 2\beta }c_1\bar{\omega }^2{\boldsymbol{\sf B}}_1^{-{1}}{\boldsymbol {\Lambda}}_0{\boldsymbol y}_5 -\left({1\over 2}{{\cal Q}\over f}{\boldsymbol{\sf B}}_1^{-{1}}{\boldsymbol{\sf W}}_0{\boldsymbol {\Lambda}}_1+{{\rm d}\ln fr\over {\rm d}\ln r}{\boldsymbol{\sf 1}}\right){\boldsymbol y}_6, \end{eqnarray}

(C4)

and are solved for the frequency ω with appropriate boundary conditions at the centre and the surface of the star. The inner boundary conditions are the regularity condition for the functions |${\boldsymbol y}_5$| and |${\boldsymbol y}_6$| at the centre. For the surface boundary condition, we may use |$B^{\prime }_\phi =0$|⁠, which is equivalent to the condition employed in this paper, or |$\mathrm{\partial} (\xi _\phi /r)/\mathrm{\partial} r=0$|⁠, which could be applied at the surface of the solid crust of a neutron star so that the traction vanishes. These two surface boundary conditions are represented by |${\boldsymbol y}_6=0$| and |${{\rm d}{\boldsymbol y}_5/{\rm d}r}=0$|⁠, respectively. In Table C1, we tabulate |$\bar{\omega }$| of pure toroidal magnetic modes for the two different surface boundary conditions. For the condition |$B^{\prime }_\phi =0$|⁠, we find pure toroidal magnetic modes only for odd parity. On the other hand, pure toroidal magnetic modes of even and odd parity are found for the surface boundary condition |$\mathrm{\partial} (\xi _\phi /r)/\mathrm{\partial} r=0$|⁠. For this boundary condition, we find a complex eigen-mode having no radial nodes of the eigenfunctions of dominant amplitudes, which is the only complex mode we find. The complex frequency, however, does not necessarily well converge with increasing j_max, although the frequency of the real modes shows good convergence. Wave patterns |$\hat{\xi }_\phi$| of the pure toroidal modes calculated for the condition |$B^{\prime }_\phi$| are quite the same as those shown in Fig. 8. Wave patterns obtained for the condition |$\mathrm{\partial} (\xi _\phi /r)/\mathrm{\partial} r=0$|⁠, however, are quite different as shown by Fig. C1, in which the wave patterns |$\hat{\xi }_\phi$| and |$\hat{B}^{\prime }_\phi$| of the pure toroidal magnetic mode of odd parity are depicted for B_S = 10¹⁵ G, where |$\bar{\omega }=1.923\times 10^{-2}$|⁠. The patterns we obtain for |$\mathrm{\partial} (\xi _\phi /r)/\mathrm{\partial} r=0$| are well converged for j_max = 14 and look similar to one of the patterns obtained by Cerdá-Durán et al. (2009).

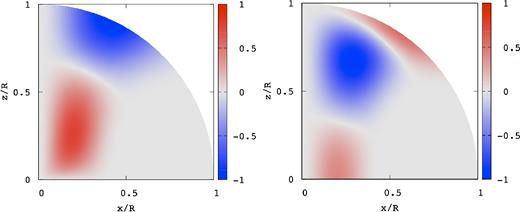
$Wave patterns $\hat{\xi }_\phi$ (left) and $\hat{B}^{\prime }_\phi$ (right) of the pure toroidal magnetic mode of odd parity for BS = 1015 G, where $\bar{\omega }=1.923\times 10^{-2}$.$

Figure C1.

Wave patterns |$\hat{\xi }_\phi$| (left) and |$\hat{B}^{\prime }_\phi$| (right) of the pure toroidal magnetic mode of odd parity for B_S = 10¹⁵ G, where |$\bar{\omega }=1.923\times 10^{-2}$|⁠.

Open in new tab Download slide

Table C1.

Open in new tab

Eigenfrequency |$\bar{\omega }$| of pure toroidal magnetic modes for B_S = 10¹⁵ G for two different surface boundary conditions, where the largest eigenfrequency for a given number of radial nodes is tabulated.

Parity	Number of radial nodes
	0	1	2
\|$B^{\prime }_\phi =0$\|
Odd	5.862 × 10⁻³	1.918 × 10⁻²	3.176 × 10⁻²
Even	⋅⋅⋅	⋅⋅⋅	⋅⋅⋅
\|${\mathrm{\partial} (\xi _\phi /r)/\mathrm{\partial} r}=0$\|
Odd	⋅⋅⋅ ^a	1.923 × 10⁻²	3.186 × 10⁻²
Even	⋅⋅⋅	⋅⋅⋅	2.556 × 10⁻²

Parity	Number of radial nodes
	0	1	2
\|$B^{\prime }_\phi =0$\|
Odd	5.862 × 10⁻³	1.918 × 10⁻²	3.176 × 10⁻²
Even	⋅⋅⋅	⋅⋅⋅	⋅⋅⋅
\|${\mathrm{\partial} (\xi _\phi /r)/\mathrm{\partial} r}=0$\|
Odd	⋅⋅⋅ ^a	1.923 × 10⁻²	3.186 × 10⁻²
Even	⋅⋅⋅	⋅⋅⋅	2.556 × 10⁻²

Note. ^aWe obtain |$\bar{\omega }=7.188\times 10^{-3}\pm 2.73\times 10^{-4}{\rm i}$| for j_max = 14.

Table C1.

Open in new tab

Eigenfrequency |$\bar{\omega }$| of pure toroidal magnetic modes for B_S = 10¹⁵ G for two different surface boundary conditions, where the largest eigenfrequency for a given number of radial nodes is tabulated.

Parity	Number of radial nodes
	0	1	2
\|$B^{\prime }_\phi =0$\|
Odd	5.862 × 10⁻³	1.918 × 10⁻²	3.176 × 10⁻²
Even	⋅⋅⋅	⋅⋅⋅	⋅⋅⋅
\|${\mathrm{\partial} (\xi _\phi /r)/\mathrm{\partial} r}=0$\|
Odd	⋅⋅⋅ ^a	1.923 × 10⁻²	3.186 × 10⁻²
Even	⋅⋅⋅	⋅⋅⋅	2.556 × 10⁻²

Parity	Number of radial nodes
	0	1	2
\|$B^{\prime }_\phi =0$\|
Odd	5.862 × 10⁻³	1.918 × 10⁻²	3.176 × 10⁻²
Even	⋅⋅⋅	⋅⋅⋅	⋅⋅⋅
\|${\mathrm{\partial} (\xi _\phi /r)/\mathrm{\partial} r}=0$\|
Odd	⋅⋅⋅ ^a	1.923 × 10⁻²	3.186 × 10⁻²
Even	⋅⋅⋅	⋅⋅⋅	2.556 × 10⁻²

Note. ^aWe obtain |$\bar{\omega }=7.188\times 10^{-3}\pm 2.73\times 10^{-4}{\rm i}$| for j_max = 14.

We may understand a reason for the existence of complex eigenfrequencies using the energy equation derived in Section 2.3. For pure toroidal modes, we have

\begin{eqnarray} \omega ^2={1\over 4\pi }{\displaystyle \int {\rm d}V \left|B^{\prime }_\phi \right|^2-\int {\rm d}S\xi _\phi ^*B^{\prime }_\phi B_r\over \displaystyle \int {\rm d}V\rho \left|\xi _\phi \right|^2}. \end{eqnarray}

(C5)

Note that |${\boldsymbol n}\cdot {\boldsymbol B}\not=0$| at the surface of the star. Equation (C5) suggests that ω² is always a real number for the surface boundary condition |$B^{\prime }_\phi =0$|⁠. For |$\mathrm{\partial} (\xi _\phi /r)/\mathrm{\partial} r=0$|⁠, on the other hand, the surface term becomes

\begin{eqnarray} \int {\rm d}S B_r\xi _\phi ^*B^{\prime }_\phi =\int {\rm d}S B_r\left[B_\theta {1\over r}\xi _\phi ^*{\mathrm{\partial} \xi _\phi \over \mathrm{\partial} \theta } +\left|\xi _\phi \right|^2\left({1\over r}{\mathrm{\partial} rB_r\over \mathrm{\partial} r}+{B_\theta \over r}\cot \theta \right)\right], \end{eqnarray}

(C6)

which can be a complex number, leading to complex ω². Note that both ω and its complex conjugate ω* can be a solution. For the boundary condition |$\mathrm{\partial} (\xi _\phi /r)/\mathrm{\partial} r=0$|⁠, the force operator |${\boldsymbol F}({\boldsymbol\xi})$| cannot be self-adjoint, and hence complex solutions are permitted.

It is interesting to note that, using equations (C3) and (C4), we may derive

\begin{eqnarray} {{\rm d}^2\xi _\phi \over {\rm d}\tau ^2}+{{\rm d}\ln \sqrt{4\pi \rho }\over {\rm d}\tau }{{\rm d}\xi _\phi \over {\rm d}\tau }+\left(\omega ^2-\Psi \right)\xi _\phi =0, \end{eqnarray}

(C7)

where

\begin{eqnarray} {{\rm d}\over {\rm d}\tau }={{\boldsymbol B}\over \sqrt{4\pi \rho }}\cdot \nabla , \quad \Psi =\omega _A^2+{1\over \sqrt{4\pi \rho }}{{\rm d}\over {\rm d}\tau }\sqrt{4\pi \rho }\omega _A, \quad \omega _A=-{1\over \sqrt{4\pi \rho }}{{\rm d}f\over {\rm d}r}\cos \theta . \end{eqnarray}

(C8)

Equation (C7) may describe wave propagation along a magnetic field line, and the propagation region along a field line may be given by ω² ≥ Ψ. Wave propagation along a magnetic field line is not independent of that along different field lines since the functions ρ and Ψ cannot be regarded as a function which depends only on τ. Ignoring the terms dξ_ϕ/dτ and Ψ, we obtain the wave equation similar to that used, for example, by Cerdá-Durán et al. (2009).

Download all slides

Month:	Total Views:
February 2018	10
March 2018	1
April 2018	9
May 2018	8
June 2018	4
July 2018	2
August 2018	7
September 2018	1
October 2018	4
November 2018	6
December 2018	10
March 2019	1
May 2019	3
June 2019	1
September 2019	2
October 2019	4
December 2019	4
February 2020	2
April 2020	1
June 2020	5
July 2020	14
August 2020	1
December 2020	2
March 2021	1
June 2021	5
July 2021	2
September 2021	2
November 2021	4
December 2021	2
January 2022	2
February 2022	2
March 2022	1
April 2022	1
May 2022	8
June 2022	3
July 2022	5
August 2022	4
September 2022	6
October 2022	6
November 2022	2
December 2022	4
January 2023	3
February 2023	3
March 2023	7
April 2023	3
June 2023	1
August 2023	3
September 2023	3
October 2023	2
November 2023	4
December 2023	8
January 2024	3
February 2024	7
March 2024	2
April 2024	4
May 2024	8
June 2024	2
July 2024	19
August 2024	2
September 2024	10
October 2024	4
November 2024	5
December 2024	12
January 2025	4
February 2025	4
March 2025	7
April 2025	3
May 2025	6

Article Contents

Axisymmetric magnetic modes of neutron stars having mixed poloidal and toroidal magnetic fields

Abstract

1 INTRODUCTION

2 METHOD OF SOLUTION

2.1 Equilibrium state

2.2 Oscillation Equations

2.3 Energy equation

3 NUMERICAL RESULTS

3.1 Spheroidal modes

3.2 Toroidal modes

4 CONCLUSION

Footnotes

REFERENCES

APPENDIX A: EQUILIBRIUM MAGNETIC FIELDS

APPENDIX B: SURFACE BOUNDARY CONDITIONS

APPENDIX C: TOROIDAL MODES FOR POLOIDAL MAGNETIC FIELDS

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Axisymmetric magnetic modes of neutron stars having mixed poloidal and toroidal magnetic fields

Abstract

1 INTRODUCTION

2 METHOD OF SOLUTION

2.1 Equilibrium state

2.2 Oscillation Equations

2.3 Energy equation

3 NUMERICAL RESULTS

3.1 Spheroidal modes

3.2 Toroidal modes

4 CONCLUSION

Footnotes

REFERENCES

APPENDIX A: EQUILIBRIUM MAGNETIC FIELDS

APPENDIX B: SURFACE BOUNDARY CONDITIONS

APPENDIX C: TOROIDAL MODES FOR POLOIDAL MAGNETIC FIELDS

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only