Magnetized SASI: its mechanism and possible connection to some QPOs in XRBs

Dhang, Prasun; Sharma, Prateek; Mukhopadhyay, Banibrata

doi:10.1093/mnras/sty488

Abstract

The presence of a surface at the inner boundary, such as in a neutron star or a white dwarf, allows the existence of a standing shock in steady spherical accretion. The standing shock can become unstable in 2D or 3D; this is called the standing accretion shock instability (SASI). Two mechanisms – advective-acoustic and purely acoustic – have been proposed to explain SASI. Using axisymmetric hydrodynamic and magnetohydrodynamic simulations, we find that the advective-acoustic mechanism better matches the observed oscillation time-scales in our simulations. The global shock oscillations present in the accretion flow can explain many observed high frequency (≳100 Hz) quasi-periodic oscillations (QPOs) in X-ray binaries. The presence of a moderately strong magnetic field adds more features to the shock oscillation pattern, giving rise to low frequency modulation in the computed light curve. This low frequency modulation can be responsible for ∼100 Hz QPOs (known as hHz QPOs). We propose that the appearance of hHz QPO determines the separation of twin peak QPOs of higher frequencies.

accretion, accretion discs, hydrodynamics, instabilities, magnetic fields, MHD, shock waves

1 INTRODUCTION

Spherically symmetric steady-state accretion of adiabatic gas on to a point mass that can accrete the supersonically infalling gas (e.g. a black hole) is characterized by the classical transonic solution given by Bondi (Bondi 1952). On the other hand, if the central accretor has a surface that accretes very slowly, a standing shock may form within the sonic radius (McCrea 1956). For a detailed discussion, see section 5.1 of Dhang, Sharma & Mukhopadhyay (2016, hereafter Paper I).

The standing shock is stable in 1D under radial perturbations, but is unstable in 2D. The shock structure oscillates with l = 1 and higher order modes (axisymmetric sloshing modes). In the context of supernovae, Herant et al. (1994) advocated convective instability as the possible mechanism behind the oscillations of the stalled shock front. But, Foglizzo, Scheck & Janka (2006) showed that in presence of advection in the post-shock region, negative entropy gradient is no longer a sufficient condition for convective instability; advection acts as a stabilizing factor. The shock instability exists even in the absence of an entropy gradient (Blondin, Mezzacappa & DeMarino 2003; Dhang et al. 2016). Blondin et al. (2003) named this instability as standing accretion shock instability (SASI) and identified advective-acoustic feedback (Foglizzo 2002) as its possible mechanism. Later, Blondin & Mezzacappa (2006) attributed SASI to a purely acoustic cycle, and thus triggering the debate on the physical origin of SASI. Some other studies reached divergent conclusions. While studies of Ohnishi, Kotake & Yamada (2006) and Scheck et al. (2008) identified advective-acoustic cycle as the possible mechanism, Laming (2007) in his analytical studies claimed that both advective-acoustic and purely acoustic cycles can be possible depending on the ratio of the shock radius to the inner radius.

In 3D, in addition to these axisymmetric modes, SASI also shows a non-axisymmetric spiral mode (m = 1) (Blondin & Mezzacappa 2007). Fernández (2010) interpreted spiral modes as the combination of two sloshing modes, whereas Blondin & Shaw (2007) showed that sloshing modes can be constructed by combining two equal and opposite non-axisymmetric spiral modes. According to Kazeroni, Guilet & Foglizzo (2016), spiral modes dominate the dynamics of SASI only if the ratio of the initial shock radius to the neutron star radius exceeds a critical value. Otherwise, dynamics is dominated by the sloshing mode. The actual mechanism behind the shock instability is still not fully understood.

SASI has been studied extensively in the context of stellar collapse simulations over the years including different aspects of physics (e.g. neutrino transport, cooling, rotation, magnetic fields). There are state of the art realistic simulations (Burrows et al. 2006; Bruenn et al. 2006; Marek & Janka 2009) in which neutrino transport, self-gravity of stellar gas, and nuclear equation of state are considered. Also, there are simplified planar toy models of SASI without any extra physics (Foglizzo 2009; Sato, Foglizzo & Fromang 2009). Models of SASI considering the angular momentum of the infalling gas are markedly different from models without angular momentum (Blondin & Mezzacappa 2007). Spiral modes become more prominent relative to sloshing modes in presence of rotation both in linear (Yamasaki & Foglizzo 2008) and in non-linear regime (Iwakami et al. 2009). Endeve et al. (2010) and Endeve et al. (2012) explored the effects of a weak magnetic field in the absence and presence of rotation both in axisymmetric and non-axisymmetric simulations. While axisymmetric models give magnetic field amplification of the order of 2, non-axisymmetric models provide an amplification of the order of 4. They also observe that magnetic field beyond a certain strength stabilizes SASI.

As discussed earlier, different studies reached divergent conclusions by inspecting the linear properties of eigen modes, including the fundamental mode and its harmonics. In this paper, we study the physics of SASI in the non-linear regime using numerical simulations and try to shed some light on its mechanism by two different approaches: (i) by changing the ratio of the shock radius to the inner radius in hydrodynamic (HD) simulations; and (ii) by changing the magnetic field strength in magnetohydrodynamic (MHD) simulations. If SASI is an outcome of a meridional acoustic cycle, the weak magnetic field in the downstream region close to the shock should not affect the oscillation time-scales. On the other hand, a somewhat stronger magnetic field close to the centre can affect the radial advective-acoustic cycle (Guilet & Foglizzo 2010).

In Paper I, using our HD axisymmetric simulations, we proposed that SASI in accretion flows may give rise to some of the quasi-periodic oscillations (QPOs) observed in the light curves of X-ray binaries (XRBs). Most of the proposed QPO mechanisms are based on the physics of test particle motion (e.g. Strohmayer et al. 1996; Miller, Lamb & Psaltis 1998; Stella & Vietri 1999; Kluzniak & Abramowicz 2002; Kluźniak et al. 2004; Mukhopadhyay 2009), which is not affected by pressure and magnetic fields. However, for a particular model, the QPO frequencies obtained considering bulk motion significantly differ from the ones corresponding to free particles (Blaes et al. 2007). Along with our model, there are few models (e.g. Kato & Fukue 1980; Kato 1990; Ipser & Lindblom 1991; Ryu et al. 1995; Yang & Kafatos 1995; Molteni, Sponholz & Chakrabarti 1996; Chakrabarti & Manickam 2000; Wagoner, Silbergleit & Ortega-Rodríguez 2001; Mukhopadhyay et al. 2003) where bulk motion of the flow is considered to explain the origin of QPOs.

In reality, accreting matter around a compact object has angular momentum and is magnetized. As a first step, here we incorporate magnetic field and explore the origin of QPOs appearing in the light curve due to SASI in a magnetized accreting medium. This will help to understand the sole effect of magnetic field on SASI and QPOs. Our particular emphasis is QPO frequencies ≳100 Hz in XRBs, the origin of which is still not understood. We show that the presence of magnetic fields, hence magnetized SASI, appears to uncover some of the important characteristics of QPOs. In other words, the inclusion of magnetic fields introduces important physics in the SASI model to predict certain QPOs, which is absent in an unmagnetized case.

The paper is organized as follows. In Section 2, we briefly discuss the two different mechanisms proposed to explain SASI. In Section 3, we describe the physical set-up and the solution method. In Section 4, we qualitatively discuss the effects of a split-monopolar magnetic field on steady Bondi accretion. In Section 5, we describe the results obtained from our numerical simulations. In Section 6, we discuss the possible mechanism behind SASI and its astrophysical implications (in particular, QPOs), and summarize in Section 7.

2 WHAT IS SASI AND WHY?

Two different mechanisms, namely advective-acoustic and acoustic mechanisms, have been proposed to explain SASI. Most recent studies (e.g. Foglizzo et al. 2007; Foglizzo 2009) favour the former. For a comparative and detailed discussion of the two mechanisms, see Guilet & Foglizzo (2012).

2.1 Advective-acoustic cycle

Advective-acoustic cycle was first proposed by Foglizzo & Tagger (2000) in the context of Bondi–Hoyle–Lyttleton accretion. Two different waves – an outward propagating acoustic wave and an inward propagating entropy-vorticity wave – contribute to this mechanism and complete a single cycle (Foglizzo 2002, Foglizzo et al. 2007). Due to the compression of gas in the post-shock region (specially near the surface of neutron star), an acoustic wave is produced. The acoustic wave (propagation direction need not be purely radial) reaching the shock surface distorts it. The distortion of the shock surface, in turn, creates entropy-vorticity wave that advects down to the central neutron star and decelerates near the surface. Deceleration creates a positive acoustic feedback that completes the cycle. Over many cycles, the instability attains an exponential growth. With appropriate boundary conditions (like ours in this paper), the system reaches a quasi-steady state with stable non-linear oscillations.

2.2 Acoustic cycle

Acoustic cycle is thought to be driven by a trapped acoustic wave in the post-shock cavity. Blondin & Mezzacappa (2006) proposed that any density inhomogeneity produces sound waves near the shock surface. Due to refraction, these sound waves propagate around the circumference of the shock until they meet on the other side. There their excess pressure produces a shock deformation that sends another pair of sound waves back again. The growth of the mode depends on how pressure perturbation in the post shock region interacts with the shock front.

A comparison of sonic and advection time-scales should help us to distinguish these two mechanisms.

3 METHOD

To study SASI, we set up an initial value problem, in which a central accretor (e.g. a neutron star) is embedded in a stationary, spherically symmetric uniform medium. We solve the MHD equations to study the problem.

3.1 Equations solved

We use the pluto code (Mignone et al. 2007) to solve the Newtonian MHD equations in spherical coordinates (r, θ, ϕ). The equations are

\begin{equation} \frac{\mathrm{\partial} \rho }{\mathrm{\partial} t} + \nabla .(\rho {\boldsymbol v})= 0, \end{equation}

(1)

\begin{equation} \frac{\mathrm{\partial} }{\mathrm{\partial} t}\left(\rho {\boldsymbol v}\right)+ \nabla . \left( \rho {\boldsymbol v}{\boldsymbol v} - {\boldsymbol B}{\boldsymbol B} \right)= -\rho \nabla \Phi - \nabla P^*, \end{equation}

(2)

\begin{equation} \frac{\mathrm{\partial} E}{\mathrm{\partial} t} + \nabla . \left((E + P^*){\boldsymbol v} - {\boldsymbol B}({\boldsymbol B}{\boldsymbol v}) \right)= -\rho \nabla \Phi .{\boldsymbol v}, \end{equation}

(3)

\begin{equation} \frac{\mathrm{\partial} {\boldsymbol B}}{\mathrm{\partial} t} + \nabla . \left({\boldsymbol v} {\boldsymbol B} - {\boldsymbol B}{\boldsymbol v} \right) = 0, \end{equation}

(4)

where ρ is the gas density, |${\boldsymbol v}$| is the velocity, |${\boldsymbol B}$| is the magnetic field (a factor of |$1/\sqrt{4 \pi }$| is absorbed in the definition of |${\boldsymbol B}$|⁠), P* = P + B²/2 is the total pressure (P is gas pressure), and E is the total energy density related to the internal energy density ε as E = ε + ρv²/2 + B²/2. The adiabatic index γ relating pressure and internal energy density (P = [γ − 1]ε) is chosen to be 1.4. Gravitational potential due to the central accretor is given by the Newtonian potential due to a point mass at the origin, Φ = −GM/r.

pluto uses a Godunov-type scheme, which solves the equations in conservative form. We use the HLLD solver with second-order slope limited reconstruction. For time-integration, second-order Runge–Kutta (RK2) is used with a CFL number of 0.4. Divergence free constraint on magnetic field is enforced by solving a modified system of conservation laws, in which the induction equation is coupled to a generalized Lagrange multiplier (Dedner et al. 2002; Mignone & Tzeferacos 2010). In this scheme, magnetic fields retain a cell centred representation.

We solve equations (1)–(4) in dimensionless form, we express our results in both code units (e.g. time-scales are expressed in units of r_g/c, r_g = GM/c²) and in CGS units. In the latter case, we use the central compact object mass to be 1 M_⊙. It is straightforward to convert from one system of units to another.

3.2 Grid and boundary conditions

Our spherical computational domain (r, θ, ϕ) extends from an inner boundary r_in = 6r_g to an outer boundary r_out = 10⁴r_g in the radial direction and from 0 to |$\pi$| in the meridional (θ) direction. Here, r_g = GM/c² is the gravitational radius, where G is gravitational constant and M is mass of the central accretor. We use two logarithmic grids along radial direction, one from r_in to 50r_g with 512 grid points and another from 50r_g to r_out with 256 grid points. In the meridional direction, we use a uniform grid with 256 grid points.

We fix the values of velocity components at the inner boundary; radial component v_r is set to v_in, whereas meridional component v_θ = 0 (we obtain similar results even if v_θ is copied in the inner radial ghost zones). The fiducial value of v_in is 0.05c, but we change it to control the equilibrium shock radius. Density, pressure, and magnetic field components in the ghost zones are copied from the last computational zone near the inner boundary. At the outer boundary, the values of pressure, density, and velocity field components are set to their initial values. The values of magnetic field components in the outer ghost zones are copied from the last computational zone. Axisymmetric boundary conditions (scalars and tangential components of vector fields are copied and normal components of vector fields are reflected) are used at both the θ boundaries (⁠|$\theta =0, \pi$|⁠).

3.3 Initial conditions

We carry out 2D, axisymmetric MHD simulations in spherical (r, θ, ϕ) co-ordinates in an initially static (v_r = v_θ = 0) uniform ambient medium of density ρ_ini. Initial pressure of the medium is also uniform and is given by |$p_{\rm ini} = \rho _{\rm ini} c^2_{s \infty }$|⁠. We choose the value of |$c^2_{s \infty }$| to be 0.002γc² to mimic the typical proton temperature (≳10¹¹K) of the sub-Keplerian hot flow in XRBs (Narayan & Yi 1995; Rajesh & Mukhopadhyay 2010). Moreover, this choice of temperature gives rise to a sonic radius r_c ≈ 71.43r_g and the Bondi radius r_B ≈ 714r_g, which are well inside the computational domain. We initialize a split monopolar magnetic field given by

\begin{eqnarray} B_{r} = \frac{C}{r^2} {\rm sign} (\cos \theta ). \end{eqnarray}

(5)

The advantage of using this magnetic field configuration is that the flow structure is expected to change only close to the central accretor (i.e. at small r where the field is strong), whereas at larger radii the solution remains unaffected (see Section 4). The strength of magnetic field is determined by the value of the constant C.

4 BONDI ACCRETION WITH SPLIT-MONOPOLAR FIELD

Before discussing the simulation results, we want to investigate the effects of magnetic field configuration given in equation (5) on the standard Bondi accretion. Taking the spherically symmetric form of equations (1) and (2) and using a polytropic equation of state, P = Kρ^γ (K is a constant related to entropy), and rearranging, we get the following set of equations

\begin{equation} \frac{{\rm d}v}{{\rm d}r} = \frac{ \frac{2c^2_{\rm s}}{r} - \frac{GM}{r^2} }{v - \frac{c^2_{\rm s}}{v}}, \end{equation}

(6)

\begin{equation} \frac{{\rm d}c_{\rm s}}{{\rm d}r} = -\frac{c_{\rm s}}{2n} \left[\frac{1}{v}\frac{{\rm d}v}{{\rm d}r} +\frac{2}{r} \right], \end{equation}

(7)

where n = 1/(γ − 1) and c_s(r) is the adiabatic sound speed given by |$c_{\rm s} = \sqrt{\gamma P/\rho }$|⁠.

Equation (6) has a critical point (sonic point) where c_s = v. The location of the sonic point r_c can be obtained if we set the numerator of equation (6) to zero to avoid divergence, namely

\begin{eqnarray} r_c = \frac{G M}{2c^2_{sc}}, \end{eqnarray}

(8)

where c_sc is sound speed at the critical point. Note that the expression for r_c is identical to the HD Bondi solution. So the presence of a split-monopolar magnetic field does not affect the steady spherically symmetric accretion solution. Physically, the current is concentrated in the equator where the field vanishes and therefore |${\boldsymbol J} \times {\boldsymbol B}$| force vanishes everywhere. But if spherical symmetry is broken, as it happens due to SASI, magnetic fields will have an effect especially at smaller radii where the field strength is large.

5 RESULTS

In this section, we present results from our simulations with and without magnetic fields. We begin with results in the HD limit.

5.1 HD

To study SASI in the HD regime, we choose C in equation (5) to be very small such that the terms involving magnetic field in equations (2) and (3) vanish. We run simulations to study unmagnetized SASI with five different radial velocities imposed at the inner radial ghost zones (v_in; see Table 1). We change v_in to control the mean shock radius r_sh, a larger value of v_in gives rise to smaller r_sh (for details see section 5.1 of Paper I). This way we can study SASI for different values of r_sh/r_in.

Table 1.

Open in new tab

The radial velocity at the inner boundary, v_in, mainly determines the mean shock radius r_sh; r_sh is calculated by taking the time average of a₀ (see equation 12) in quasi-steady state. The inner boundary is fixed at r_in = 6 r_g; C determines the magnetic field strength; very small value of C implies that we are in the HD limit; SASI time period is measured by two different methods (see Section 5.1.3). Time-scales related to the advective-acoustic mechanism are: t_aac, t_{aacA +}, t_aacA- (equations 14, 18, 19) and that related to the purely acoustic mechanism are: t_rcs, t_mcs (equations 15 and 16).

Simulation details
v_in	C	Label	r_sh/r_in	T_a1	\|$T_{v_{\theta }}$\|	t_aac	t_{aacA +}	t_aacA-	t_rcs	t_mcs
(c)				(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)
0.045	1	HD	4.65	808.17	808.90	732.55	–	–	472.73	718.07
0.048	1	HD	4.17	656.19	658.56	621.11	–	–	400.62	619.26
0.05^a	1	HD	3.91	580.24	581.62	567.42	–	–	368.08	567.81
0.06	1	HD	2.96	351.65	351.79	359.07	–	–	234.01	386.90
0.07	1	HD	2.35	240.48	240.46	242.84	–	–	159.39	280.29
0.05	10⁶	MHD	3.90	579.64	580.35	567.83	567.17	568.50	368.70	566.65
0.05	1.25 × 10⁷	MHD	3.90	581.97	581.89	563.08	555.20	572.57	364.20	566.28
0.05	1.67 × 10⁷	MHD	3.91	593.26	592.93	569.09	555.99	593.25	369.25	565.96
0.05	2 × 10⁷	MHD	3.91	595.24	595.73	554.65	539.57	582.20	354.55	566.33
0.05	2.5 × 10⁷	MHD	3.90	600.91	600.66	561.84	543.36	595.85	362.34	562.42
0.05	3.33 × 10⁷	MHD	3.92	598.06	599.36	555.85	534.58	597.72	356.19	567.68
0.05	4 × 10⁷	MHD	3.93	601.56	601.03	555.91	531.55	604.24	355.72	570.24
0.05^b	5 × 10⁷	MHD	3.94	617.01	615.07	565.36	534.40	630.84	363.61	571.29
0.05	5.55 × 10⁷	MHD	3.95	630.83	629.70	575.86	541.71	642.61	372.54	572.71
0.05	6.68 × 10⁷	MHD	3.96	651.40	652.32	580.70	539.97	659.55	375.80	573.30
0.05	7.69 × 10⁷	MHD	3.98	667.81	666.94	583.06	536.02	680.49	376.37	576.00
0.05	7.94 × 10⁷	MHD	3.98	672.25	671.98	584.13	536.94	694.75	376.87	576.96

Simulation details
v_in	C	Label	r_sh/r_in	T_a1	\|$T_{v_{\theta }}$\|	t_aac	t_{aacA +}	t_aacA-	t_rcs	t_mcs
(c)				(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)
0.045	1	HD	4.65	808.17	808.90	732.55	–	–	472.73	718.07
0.048	1	HD	4.17	656.19	658.56	621.11	–	–	400.62	619.26
0.05^a	1	HD	3.91	580.24	581.62	567.42	–	–	368.08	567.81
0.06	1	HD	2.96	351.65	351.79	359.07	–	–	234.01	386.90
0.07	1	HD	2.35	240.48	240.46	242.84	–	–	159.39	280.29
0.05	10⁶	MHD	3.90	579.64	580.35	567.83	567.17	568.50	368.70	566.65
0.05	1.25 × 10⁷	MHD	3.90	581.97	581.89	563.08	555.20	572.57	364.20	566.28
0.05	1.67 × 10⁷	MHD	3.91	593.26	592.93	569.09	555.99	593.25	369.25	565.96
0.05	2 × 10⁷	MHD	3.91	595.24	595.73	554.65	539.57	582.20	354.55	566.33
0.05	2.5 × 10⁷	MHD	3.90	600.91	600.66	561.84	543.36	595.85	362.34	562.42
0.05	3.33 × 10⁷	MHD	3.92	598.06	599.36	555.85	534.58	597.72	356.19	567.68
0.05	4 × 10⁷	MHD	3.93	601.56	601.03	555.91	531.55	604.24	355.72	570.24
0.05^b	5 × 10⁷	MHD	3.94	617.01	615.07	565.36	534.40	630.84	363.61	571.29
0.05	5.55 × 10⁷	MHD	3.95	630.83	629.70	575.86	541.71	642.61	372.54	572.71
0.05	6.68 × 10⁷	MHD	3.96	651.40	652.32	580.70	539.97	659.55	375.80	573.30
0.05	7.69 × 10⁷	MHD	3.98	667.81	666.94	583.06	536.02	680.49	376.37	576.00
0.05	7.94 × 10⁷	MHD	3.98	672.25	671.98	584.13	536.94	694.75	376.87	576.96

^aThe fiducial hydro run.

^bThe fiducial MHD run (Case I in Section 5.2.1).

^cTwo MHD runs used only for QPO analysis with v_in = 0.06c and v_in = 0.048c, respectively, are not listed in the table.

Table 1.

Open in new tab

The radial velocity at the inner boundary, v_in, mainly determines the mean shock radius r_sh; r_sh is calculated by taking the time average of a₀ (see equation 12) in quasi-steady state. The inner boundary is fixed at r_in = 6 r_g; C determines the magnetic field strength; very small value of C implies that we are in the HD limit; SASI time period is measured by two different methods (see Section 5.1.3). Time-scales related to the advective-acoustic mechanism are: t_aac, t_{aacA +}, t_aacA- (equations 14, 18, 19) and that related to the purely acoustic mechanism are: t_rcs, t_mcs (equations 15 and 16).

Simulation details
v_in	C	Label	r_sh/r_in	T_a1	\|$T_{v_{\theta }}$\|	t_aac	t_{aacA +}	t_aacA-	t_rcs	t_mcs
(c)				(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)
0.045	1	HD	4.65	808.17	808.90	732.55	–	–	472.73	718.07
0.048	1	HD	4.17	656.19	658.56	621.11	–	–	400.62	619.26
0.05^a	1	HD	3.91	580.24	581.62	567.42	–	–	368.08	567.81
0.06	1	HD	2.96	351.65	351.79	359.07	–	–	234.01	386.90
0.07	1	HD	2.35	240.48	240.46	242.84	–	–	159.39	280.29
0.05	10⁶	MHD	3.90	579.64	580.35	567.83	567.17	568.50	368.70	566.65
0.05	1.25 × 10⁷	MHD	3.90	581.97	581.89	563.08	555.20	572.57	364.20	566.28
0.05	1.67 × 10⁷	MHD	3.91	593.26	592.93	569.09	555.99	593.25	369.25	565.96
0.05	2 × 10⁷	MHD	3.91	595.24	595.73	554.65	539.57	582.20	354.55	566.33
0.05	2.5 × 10⁷	MHD	3.90	600.91	600.66	561.84	543.36	595.85	362.34	562.42
0.05	3.33 × 10⁷	MHD	3.92	598.06	599.36	555.85	534.58	597.72	356.19	567.68
0.05	4 × 10⁷	MHD	3.93	601.56	601.03	555.91	531.55	604.24	355.72	570.24
0.05^b	5 × 10⁷	MHD	3.94	617.01	615.07	565.36	534.40	630.84	363.61	571.29
0.05	5.55 × 10⁷	MHD	3.95	630.83	629.70	575.86	541.71	642.61	372.54	572.71
0.05	6.68 × 10⁷	MHD	3.96	651.40	652.32	580.70	539.97	659.55	375.80	573.30
0.05	7.69 × 10⁷	MHD	3.98	667.81	666.94	583.06	536.02	680.49	376.37	576.00
0.05	7.94 × 10⁷	MHD	3.98	672.25	671.98	584.13	536.94	694.75	376.87	576.96

Simulation details
v_in	C	Label	r_sh/r_in	T_a1	\|$T_{v_{\theta }}$\|	t_aac	t_{aacA +}	t_aacA-	t_rcs	t_mcs
(c)				(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)	(r_g/c)
0.045	1	HD	4.65	808.17	808.90	732.55	–	–	472.73	718.07
0.048	1	HD	4.17	656.19	658.56	621.11	–	–	400.62	619.26
0.05^a	1	HD	3.91	580.24	581.62	567.42	–	–	368.08	567.81
0.06	1	HD	2.96	351.65	351.79	359.07	–	–	234.01	386.90
0.07	1	HD	2.35	240.48	240.46	242.84	–	–	159.39	280.29
0.05	10⁶	MHD	3.90	579.64	580.35	567.83	567.17	568.50	368.70	566.65
0.05	1.25 × 10⁷	MHD	3.90	581.97	581.89	563.08	555.20	572.57	364.20	566.28
0.05	1.67 × 10⁷	MHD	3.91	593.26	592.93	569.09	555.99	593.25	369.25	565.96
0.05	2 × 10⁷	MHD	3.91	595.24	595.73	554.65	539.57	582.20	354.55	566.33
0.05	2.5 × 10⁷	MHD	3.90	600.91	600.66	561.84	543.36	595.85	362.34	562.42
0.05	3.33 × 10⁷	MHD	3.92	598.06	599.36	555.85	534.58	597.72	356.19	567.68
0.05	4 × 10⁷	MHD	3.93	601.56	601.03	555.91	531.55	604.24	355.72	570.24
0.05^b	5 × 10⁷	MHD	3.94	617.01	615.07	565.36	534.40	630.84	363.61	571.29
0.05	5.55 × 10⁷	MHD	3.95	630.83	629.70	575.86	541.71	642.61	372.54	572.71
0.05	6.68 × 10⁷	MHD	3.96	651.40	652.32	580.70	539.97	659.55	375.80	573.30
0.05	7.69 × 10⁷	MHD	3.98	667.81	666.94	583.06	536.02	680.49	376.37	576.00
0.05	7.94 × 10⁷	MHD	3.98	672.25	671.98	584.13	536.94	694.75	376.87	576.96

^aThe fiducial hydro run.

^bThe fiducial MHD run (Case I in Section 5.2.1).

^cTwo MHD runs used only for QPO analysis with v_in = 0.06c and v_in = 0.048c, respectively, are not listed in the table.

5.1.1 Flow evolution

Fig. 1 shows the density snapshots at different times for our fiducial run of unmagnetized SASI. The details of flow evolution in an unmagnetized medium are described in Paper I; here, we only give a brief description. We can divide the time evolution into three phases: the early non-equilibrium phase, the intermediate transition phase, and the final quasi-stationary oscillating non-linear phase. At t = 0, the ambient medium is uniform and static. As the central gravitating object starts accreting, matter attains supersonic velocity. Both density and pressure build up near the accretor. Unlike classical Bondi accretion, here the supersonic matter falling under gravity feels an obstruction at the inner boundary as the radial velocity there is fixed at v_in.

Figure 1.

Density snapshots of the unmagnetized fiducial run at different time. Arrows represent the direction of velocity. Top left-hand panel shows the initial uniform density distribution. Due to accretion of matter from the surrounding medium, both density and pressure increase, which is shown in the second panel. Unlike the moderately magnetized case (cf. Fig. 7), the shock appears at a later time. The snapshot at t = 2685.49 (t is in units of r_g/c) shows the first development of the shock surface. The next four panels (from t = 3266.13 to t = 4173.39) show radial expansion of the shock surface as well as the initial build up of the vertical oscillation modes. Then, the post-shock cavity goes through a vigorously oscillating phase (snapshots at t = 5733.88, 5879.04, and 6024.20). Finally, the system enters a quasi-stationary non-linear phase in which the post-shock cavity oscillates with a definite time period. The last five panels show a full period of coherent oscillations of global modes.

Open in new tab Download slide

The accretion shock can be easily seen at t = 2685.49 r_g/c. With time, thermal pressure builds up behind the shock due to the conversion of kinetic energy to thermal energy and shock surface starts expanding. The initial expansion is purely radial, but with time the radial expansion is accompanied by non-spherical global oscillations with l = 1 and higher order modes. This can be seen in the snapshots at t = 3919.36 r_g/c, 3991.94 r_g/c, and 4173.39 r_g/c. As the shock becomes aspherical, it becomes oblique, resulting in the generation of meridional component of velocity (v_θ) in the post-shock region (see the change in direction of velocity arrows in the post-shock region for the snapshots at and after t = 3919.36 r_g/c), as the mass flux (ρv_⊥) and the tangential component of velocity (v_||) have to be conserved across the shock. Due to the build up of thermal pressure, the shock overcomes the inward gravitational pull and the post-shock cavity expands out (see snapshots at t = 5733.88 r_g/c, 5879.04 r_g/c, 6024.20 r_g/c.). With the advection of mass and thermal energy across the inner boundary, after a few adjustments the systems attains a quasi-stationary state, in which the inward gravitational pull is balanced by outward thermal pressure. In this state, the post-shock cavity incessantly oscillates about the equatorial plane (the last five panels in Fig. 1 show one full oscillation period).

The equilibrium standing shock is linearly unstable to aspherical SASI modes but non-linearly the systems settle into stable, long-lived, large-amplitude oscillations. The effective potential for such oscillations can be thought of as a local maximum within a stable potential well experienced at large amplitudes.

5.1.2 Mode analysis

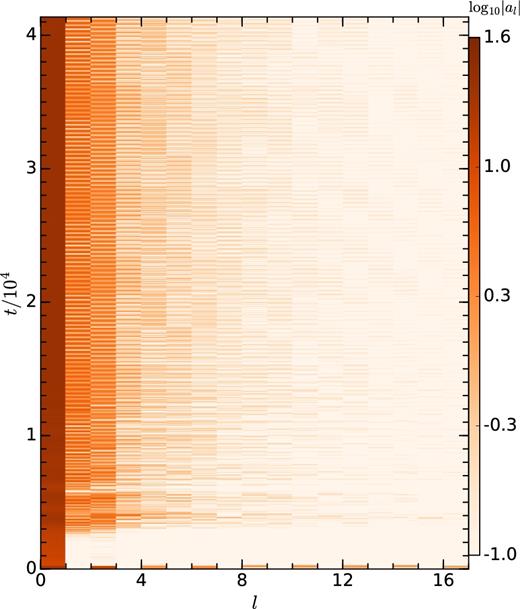
Shock surface can be easily identified just by looking at the density jumps in different snapshots of Fig. 1. We see that in the non-linear quasi-stationary state, shock surface can be considered as a sphere with sub-structure on top of it. To quantify the sub-structures, we perform mode analysis using the method of spherical harmonics decomposition (SHD).

Any spherical function f(θ, ϕ) can be expanded as a linear combination of spherical harmonics as

\begin{eqnarray} f(\theta , \phi ) = \sum _{l=0}^{\infty } \sum _{m=-l}^{l} a_{lm}Y_{lm}(\theta , \phi ), \end{eqnarray}

(9)

where the spherical harmonics Y_lm(θ, ϕ) are given by

\begin{eqnarray} Y_{lm}(\theta , \phi ) = \sqrt{\frac{(2l+1)(l-|m|)!}{4\pi (l+|m|)!}} P_{lm}({\rm cos}\theta ) \text{e}^{\text{i}m\phi }, \end{eqnarray}

(10)

where P_lm(cosθ) are the associated Legendre polynomials. For an axisymmetric system, m = 0 and Y_lm reduces to Legendre polynomial P_l(cosθ) with a normalization factor. Then, the deformed (from spherical shape) shock surface R_s(θ) can be decomposed as

\begin{eqnarray} R_s(\theta ) = \sum _{l=0}^{\infty }a_{l}P_{l}({\rm cos}\theta ), \end{eqnarray}

(11)

where the coefficients can be calculated as

\begin{eqnarray} a_{l} = \frac{2l+1}{2} \int _{\theta =0}^{\pi }R_s(\theta ) P_{l}({\rm cos}\theta ) {\rm sin}\theta \text{ d}\theta. \end{eqnarray}

(12)

Fig. 2 shows the time evolution of mode amplitudes a_l for the fiducial unmagnetized SASI run. R_s(θ) is computed using the pressure jump across the shock. Initially, the vanishing mode amplitudes reflect the absence of a shock. The first emergence of shock is reflected in the non-vanishing value of a₀, while other mode amplitudes are still zero, as the shock is spherical. As the shock starts oscillating vertically about the equatorial plane, it becomes aspherical in nature and l = 1 and 2 modes become prominent. In the fully non-linear regime, we see that apart from l = 0 mode, l = 1, 2, and 3 are the most prominent modes present. The higher order modes (specially l ≤ 8) are also present but with a smaller amplitude.

Figure 2.

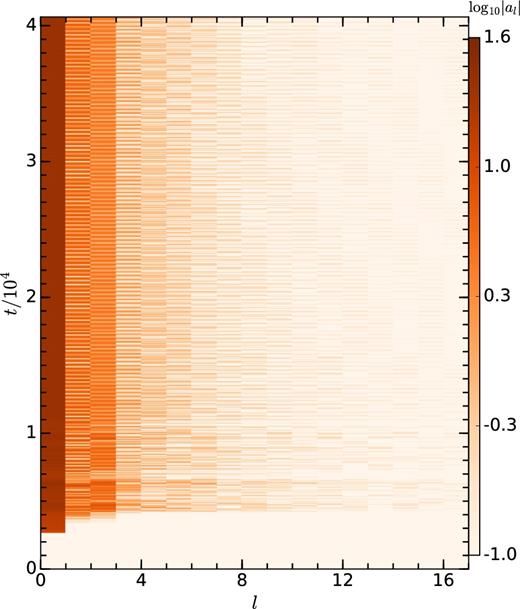
Result of mode analysis of the shock radius for our fiducial unmagnetized SASI run. Colour represents the absolute value of mode amplitude. In the quasi-stationary state, apart from the dominant l = 0 mode, l = 1, 2, and 3 modes are prominent.

Open in new tab Download slide

5.1.3 Methods to measure SASI time period

It is clear from Fig. 1 that there are global non-linear oscillation modes associated with the post-shock cavity. We want to determine the time period of oscillations. We use two different methods to find the precise oscillation period:

Following Ohnishi et al. (2006), we fit the mode amplitude (in quasi-steady state) associated with l = 1 with a sin e curve given by ψ₁ = A₁ sin(ω₁t + ϕ₁). Time period is obtained from the value of ω₁ as |$T_{a1}=2 \pi /\omega _1$|⁠. Top panel of Fig. 3 shows the temporal variation of a₁ for our fiducial unmagnetized SASI run (v_in = 0.05c, C = 1). After the initial growing phase, a₁ attains a quasi-steady state and oscillates about a mean value close to 0. In the bottom panel of Fig. 3, the simultaneous plots of a₁ and the fitting function ψ₁ are shown. The original data and the fitting function match well and the measured time period of SASI is T_a1 = 580.24 r_g/c.
The second method to obtain the time period of oscillations is based on calculating the temporal variation of a local quantity at a single point in space. We choose v_θ to be the local quantity because v_θ changes sign as the post-shock cavity goes from the upper hemisphere to the lower hemisphere. We compute v_θ(t) in the equatorial plane (⁠|$\theta = \pi /2$|⁠) at r = 8r_g as a function of time, which is shown in the top panel of Fig. 4 for the fiducial HD run. Note that v_θ(t) is not a purely sinusoidal function (see the inset in top panel of Fig. 4). To find the time period associated with it, we take the fast Fourier transform (FFT) and identify the most prominent peak in the power spectrum (defined here as simply the absolute value of the Fourier transform). To find the centroid frequency (⁠|$f_{v_{\theta }}$|⁠), we fit the prominent peak with a Lorentzian given by

\begin{eqnarray} P(f) = \frac{A_L \Gamma }{(f-f_{v_{\theta }})^2 + \Gamma ^2/4}, \end{eqnarray}

(13)

where A_L is the normalization and Γ is the full width at half-maximum. Inverse of |$f_{v_{\theta }}$| gives the oscillation period (⁠|$T_{v_{\theta }}$|⁠) measured by this method. Bottom panel of Fig. 4 shows the power spectrum of v_θ(t); the fitting function P(f) is plotted on top of it to compare the actual and fitted values of the power spectrum. The time period of the oscillations obtained by this method is |$T_{v_{\theta }}=581.62$|r_g/c. We note that both methods (i) and (ii) give almost identical results.

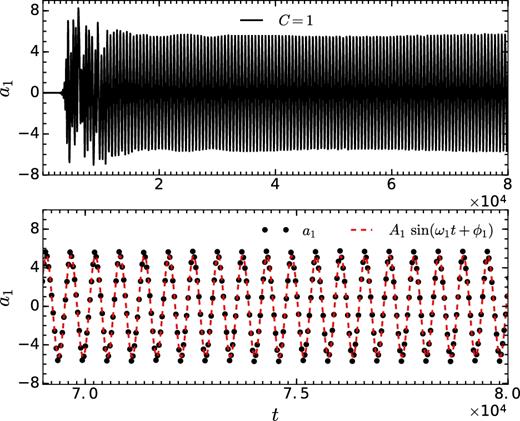
$Top panel shows the temporal evolution of the l = 1 component of the shock radius (a1) for the fiducial unmagnetized SASI run. To find the time period of oscillations of global modes, a1(t) is fit with a function ψ1 = A1sin(ω1t + ϕ1). The best-fitting time period is $T_{a1}= 2 \pi /\omega _1 = 580.24$rg/c. Plots of a1(t) and the best-fitting function are shown in the bottom panel.$

Figure 3.

Top panel shows the temporal evolution of the l = 1 component of the shock radius (a₁) for the fiducial unmagnetized SASI run. To find the time period of oscillations of global modes, a₁(t) is fit with a function ψ₁ = A₁sin(ω₁t + ϕ₁). The best-fitting time period is |$T_{a1}= 2 \pi /\omega _1 = 580.24$|r_g/c. Plots of a₁(t) and the best-fitting function are shown in the bottom panel.

Open in new tab Download slide

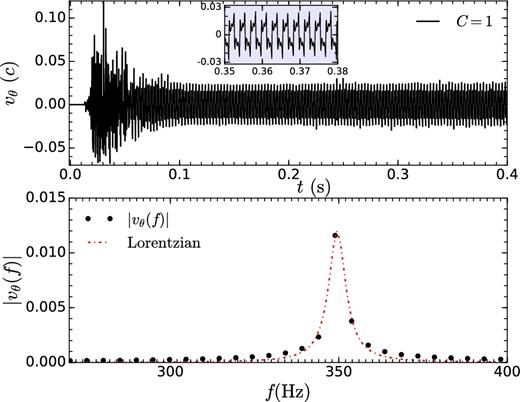
$Top panel shows the temporal evolution of vθ at a fixed location ($r=8 r_{\rm g}/c, \ \theta =\pi /2$) for the fiducial HD run. FFT of vθ(t) (bottom panel) fitted with a Lorentzian (equation 13) gives the time period of vθ(t). Time period of the oscillations is $T_{v_{\theta }}= 1/f_{v_{\theta }} = 581.62$rg/c.$

Figure 4.

Top panel shows the temporal evolution of v_θ at a fixed location (⁠|$r=8 r_{\rm g}/c, \ \theta =\pi /2$|⁠) for the fiducial HD run. FFT of v_θ(t) (bottom panel) fitted with a Lorentzian (equation 13) gives the time period of v_θ(t). Time period of the oscillations is |$T_{v_{\theta }}= 1/f_{v_{\theta }} = 581.62$|r_g/c.

Open in new tab Download slide

5.1.4 Timescales from linear theory

We measure the time period of oscillations in the quasi-steady, non-linear phase with large amplitude. Linear theories of SASI predict important time-scales related to the propagation of various perturbations. While not strictly valid, the various signal propagation time-scales are expected to provide an appropriate scaling even for the non-linear oscillations. The following arguments based on simple signal propagation time-scales stem from the fact that the disturbances have to reflect and travel back to the origin of waves to interfere and create a standing wave. In some mechanisms, mode conversion (e.g. from acoustic to vorticity/entropy modes and vice versa) is invoked at the boundaries.

First, we define an advective-acoustic time-scale (Foglizzo et al. 2007) as the sum of the radial advection time from shock surface to the inner boundary and the acoustic time to return back to the shock surface in radial approximation

\begin{eqnarray} t_{\rm aac} = \int _{r_{\rm in}}^{r_{\rm sh,O}} \frac{{\rm d}r}{|\bar{v}_r(r)|} + \int _{r_{\rm in}}^{r_{\rm sh,I}} \frac{{\rm d}r}{(\bar{c}_s(r) - |\bar{v}_r(r)|)}, \end{eqnarray}

(14)

where |$\bar{v}_r(r)$| is the θ-averaged (throughout the paper we use an overline to represent angle average) radial velocity within the shock and the integrals are performed within the shock, in the sense that (the following also applies to the other radial time-scales that follow; cf. equation 15)

\begin{equation*} \bar{v}_r(r) = \frac{\int _{0}^{\pi } H v_{\rm r}(r, \theta ) {\rm sin} \theta \text{ d}\theta }{\int _{0}^{\pi } H {\rm sin} \theta \text{d}\theta }, \end{equation*}

where, H = H[r_sh(θ) − r] is the Heaviside step function whose value is zero for negative argument and one for positive argument. Here, we want to emphasize that there are two shock surfaces at certain times (e.g. see snapshot at t = 23 915.35 r_g/c in Fig. 1), and for calculating the advection time (or any time associated with signals propagating inward), we compute the time taken by the fluid element to reach inner boundary r_in from the maximum outer shock radius r_{sh, O}. But for calculating the acoustic time (or any time associated with outward-propagating signals), we compute the time taken by the outward-propagating sound wave to reach the maximum inner shock radius r_{sh, I} from the inner boundary r_in, as acoustic signals cannot propagate outside the shock at r_{sh, I}. The time-scales vary with time because of the finite amplitude of the shock oscillations, but average time-scales should be indicative of the fundamental mode.

Secondly, we compute the radial acoustic time-scale, sum of the times taken by the sound waves to reach the shock surface from the inner boundary and back,

\begin{eqnarray} t_{\rm rcs} = \int _{r_{\rm in}}^{r_{\rm sh,O}} \frac{{\rm d}r}{(\bar{c}_s(r) + |\bar{v}_r(r)|)} + \int _{r_{\rm in}}^{r_{\rm sh,I}} \frac{{\rm d}r}{(\bar{c}_s(r) - |\bar{v}_r(r)|)}. \end{eqnarray}

(15)

Thirdly, we compute the meridional acoustic time (Blondin & Mezzacappa 2006), considering the propagation of sound wave along the circumference of the shock,

\begin{eqnarray} t_{\rm mcs} = \int _{0}^{\pi } \frac{r_{\rm sh}(\theta )}{c_{\rm s}(r_{\rm sh}, \theta )} \text{d}\theta . \end{eqnarray}

(16)

Fig. 5 shows the plots of the observed time period T_a1 (since T_a1 and |$T_{v_{\theta }}$| are almost identical, we plot only T_a1) with the above time-scales obtained from linear theory for the fiducial unmagnetized SASI simulation. In the quasi-steady state, the theoretical time-scales oscillate in time with a large amplitude ( 80–300 r_g/c). While both the advective-acoustic time t_aac and meridional acoustic time t_mcs contain T_a1 within their range of variations, radial acoustic time t_rcs is shorter.

Figure 5.

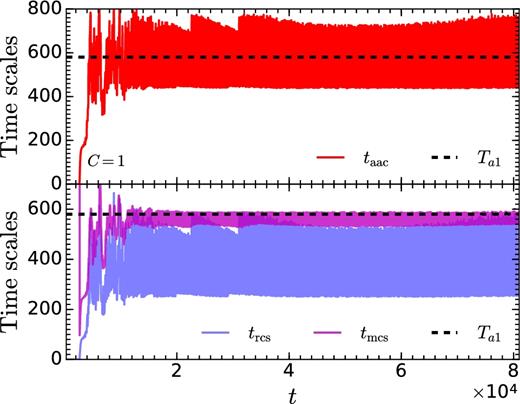
Comparison of different time-scales obtained from linear theory (namely, advective-acoustic cycle, t_aac; radial acoustic cycle, t_rcs; meridional acoustic cycle, t_mcs) and SASI time period T_a1 = 580.24 for the fiducial model of unmagnetized SASI (C = 1 and v_in = 0.05c). The time averaged (in the quasi-steady state) values of the time-scales are 〈t_aac〉 = 567.41, 〈t_mcs〉 = 567.81, 〈t_rcs〉 = 368.03; time is in units of r_g/c.

Open in new tab Download slide

As the variations in time-scales are large, we take the time average between t = 50 000 r_g/c and 82 000 r_g/c. The time averaged values of advective-acoustic scales (〈t_aac〉 = 567.41 r_g/c) and meridional acoustic time-scales (〈t_mcs〉 = 567.81 r_g/c) are close to the observed time period T_a1 = 580.24 r_g/c. It is a coincidence that 〈t_aac〉 and 〈t_mcs〉 are so close. Note that according to Blondin & Mezzacappa (2006), the time period of SASI oscillations is expected to be 2t_mcs (so that the two waves originated at one point near the shock surface can interfere on the other side and return back to the origin), whereas we find a close match of t_mcs to the measured SASI time period. On the contrary, the time averaged value of radial acoustic time is 〈t_rcs〉 = 368.03 r_g/c, much less than the SASI time period. So there appears to be a degeneracy between the two time-scales t_aac and t_mcs derived from two different physical mechanisms, namely advective-acoustic and purely acoustic cycles.

To break this degeneracy (between t_aac and t_mcs) because of our choice of parameters, we change the shock location by tuning the value of v_in and measure the oscillation period as well as the relevant time-scales. Top panel of Fig. 6 shows the time averaged values of velocity oscillation time period (⁠|$T_{v_{\theta }}$|⁠; described in (ii) in Section 5.1.3), the advective-acoustic time (t_aac), and the meridional acoustic time (t_mcs) as a function r_sh/r_in. The bottom panel of Fig. 6 shows the absolute value of the difference between different relevant time-scales – (⁠|$\Delta _{v_{\theta }, {\rm aac}} = |T_{v_{\theta }} - t_{\rm aac}|$|⁠; |$\Delta _{v_{\theta }, {\rm mcs}} = |T_{v_{\theta }} - t_{\rm mcs}|$|⁠; Δ_{aac, mcs} = |t_aac − t_mcs|) – as a function of r_sh/r_in. For smaller r_sh/r_in, the advective-acoustic time (t_aac) matches the SASI time period measured by |$T_{v_{\theta }}$|⁠. For larger r_sh/r_in, the radial advective-acoustic time-scale is shorter perhaps because of non-radial propagation of sound waves. Also note the closeness between t_aac and t_mcs for r_sh/r_in ≳ 3.9, which makes it harder to choose between the two cycles in this regime.

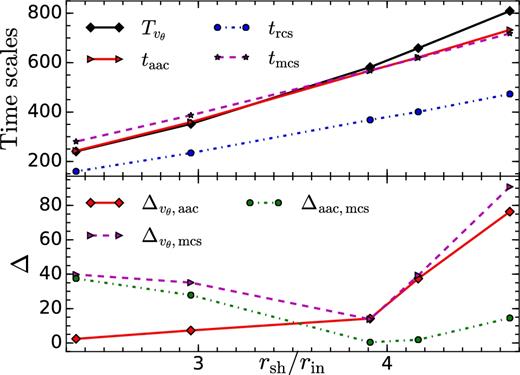
$Top panel: Variation of different average time-scales (namely, advective-acoustic cycle, taac; radial acoustic cycle, trcs; meridional acoustic cycle, tmcs; and SASI time period $T_{v_{\theta }}$; in units of rg/c) with change in the ratio of the mean shock radius and the inner radius, rsh/rin for unmagnetized SASI. Bottom panel: Change in the absolute value of difference (Δ) between two time-scales with rsh/rin: $\Delta _{v_{\theta }, {\rm aac}} = |T_{v_{\theta }} - t_{\rm aac}|$; $\Delta _{v_{\theta }, {\rm mcs}} = |T_{v_{\theta }} - t_{\rm mcs}|$; Δaac, mcs = |taac − tmcs|. Note that of the various time-scales, the advective-acoustic time-scale most closely matches the observed SASI time period.$

Figure 6.

Top panel: Variation of different average time-scales (namely, advective-acoustic cycle, t_aac; radial acoustic cycle, t_rcs; meridional acoustic cycle, t_mcs; and SASI time period |$T_{v_{\theta }}$|⁠; in units of r_g/c) with change in the ratio of the mean shock radius and the inner radius, r_sh/r_in for unmagnetized SASI. Bottom panel: Change in the absolute value of difference (Δ) between two time-scales with r_sh/r_in: |$\Delta _{v_{\theta }, {\rm aac}} = |T_{v_{\theta }} - t_{\rm aac}|$|⁠; |$\Delta _{v_{\theta }, {\rm mcs}} = |T_{v_{\theta }} - t_{\rm mcs}|$|⁠; Δ_{aac, mcs} = |t_aac − t_mcs|. Note that of the various time-scales, the advective-acoustic time-scale most closely matches the observed SASI time period.

Open in new tab Download slide

5.2 MHD

In this section, we present results from our simulations of initially split-monopolar magnetic fields with varying field strengths.

5.2.1 Evolution of the flow

In this section, we discuss the time evolution of the magnetized flow with the radial inward velocity at the inner boundary set to v_in = 0.05c, as in the fiducial HD run. We focus on two different cases with moderate and high field strengths.

Case I: in which the magnetic field strength is moderate and SASI (identified by coherent shock oscillations) exists; this is the fiducial MHD run with C = 5 × 10⁷ (see equation 5) marked in Table 1.

Case II: in which a strong magnetic field prevents a shock from existing at late times, with C = 8 × 10⁷.

Fig. 7 shows the density snapshots for Case I. Streamlines show magnetic field lines. At t = 0, the ambient density is uniform and the magnetic pressure is comparable to the thermal pressure close to the accretor. Like the unmagnetized simulations, the magnetized runs with moderate field strengths go through three phases: an early phase in which a shock develops (top panels in Fig. 7), the intermediate transition period (middle panels in Fig. 7), and a final quasi-stationary phase (bottom panels in Fig. 7). The flow undergoes a very early transient phase (see snapshot at t = 115.77 r_g/c), during which thermal pressure builds up due to the conversion of gravitational (via kinetic energy) to thermal energy, and the shock surface starts expanding radially outwards (see snapshots at t = 385.90 r_g/c and at t = 2006.67 r_g/c). Finally, the shock executes coherent oscillations.

Figure 7.

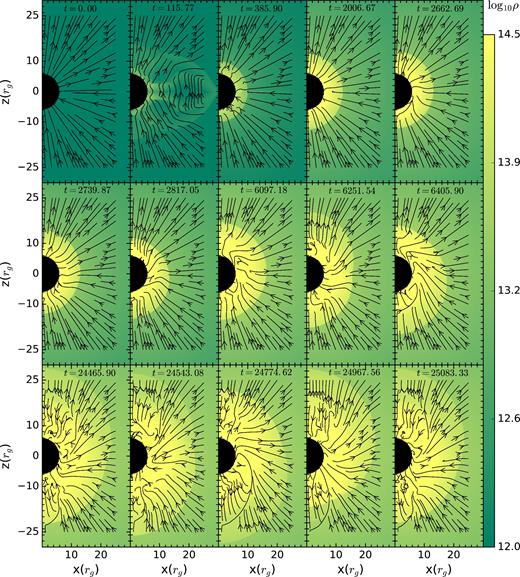
Case I: Evolution of the flow with time for the fiducial MHD run. Colour represents the density and streamlines show the magnetic field lines. First panel shows the initial uniform density distribution. A transient phase is shown in second panel. The next two panels (from t = 385.90 to 2006.67) describe growing phase of post-shock cavity. A transition period from an growing phase to an quasi-steady phase of SASI is shown in next six panels (from t = 2662.69 to 6405.90). The last five panels shows a full period of coherent oscillations of global modes. t is in units of r_g/c.

Open in new tab Download slide

Even with a slightly higher magnetic field strength (1.6 times Case I), the temporal evolution of Case II is qualitatively different because the shock is absent at late times. Fig. 8 shows the density snapshots for Case II, overplotted with arrows showing the velocity unit vectors. Like in Case I, after undergoing a transient phase (see snapshot at t = 126 r_g/c), a spherical shock is formed that expands in time (see snapshots at t = 588 r_g/c and 1134 r_g/c). However, the shock does not stall but keeps on expanding and becoming weaker, as gravitational pull is unable to balance the outward (thermal + magnetic) pressure. When shock reaches the sonic point (r_c ∼ 71 r_g/c), the flow becomes subsonic and the shock disappears. Eventually, a hydrostatic atmosphere is formed. Snapshots at t = 1848 r_g/c and at 2478 r_g/c show the outward propagation of shock, while snapshots at t = 7182 r_g/c and at 10920 r_g/c show the flow structure when shock disappears.

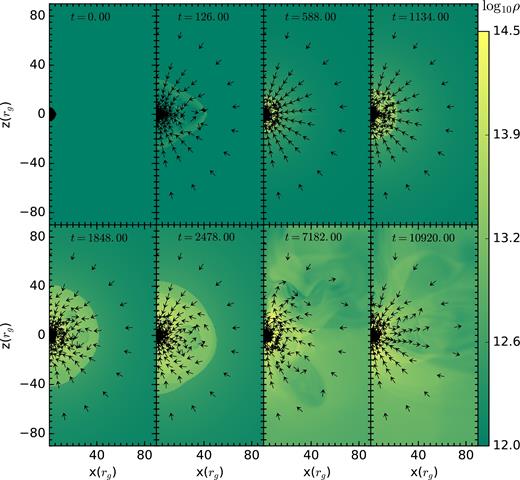
Case II: Evolution of the flow with time for C = 8 × 107 and vin = 0.05c. Colour represents the density and arrows are for velocity directions. Starting with an initial uniform density distribution (left most top panel), system undergoes a transient phase (second panel on top). Then, like in Case I a spherical shock appears which grows in time (t = 588). But unlike Case I, the shock does not stall, but keeps on propagating out(t = 1134 and 1848) and loses its strength and vanishes ultimately (t = 7182.00 and 10 920). t is in units of rg/c.

Figure 8.

Case II: Evolution of the flow with time for C = 8 × 10⁷ and v_in = 0.05c. Colour represents the density and arrows are for velocity directions. Starting with an initial uniform density distribution (left most top panel), system undergoes a transient phase (second panel on top). Then, like in Case I a spherical shock appears which grows in time (t = 588). But unlike Case I, the shock does not stall, but keeps on propagating out(t = 1134 and 1848) and loses its strength and vanishes ultimately (t = 7182.00 and 10 920). t is in units of r_g/c.

Open in new tab Download slide

Fig. 9 shows the snapshots of plasma β (the ratio of thermal and magnetic pressures) in quasi-steady state for Case I. Plasma β close to the shock surface is ≳ 10³, and therefore magnetic fields are not expected to noticeably change the shock oscillation period if the underlying mechanism for SASI involves meridional propagation of fast MHD waves (generalization of sound waves in the MHD regime), characterized by the meridional acoustic time-scale t_mcs (equation 16). Later, we shall see that the SASI oscillation frequency in presence of magnetic field changes noticeably (cf. black solid line with square symbols in Fig. 15), ruling out the meridional acoustic mechanism for SASI.

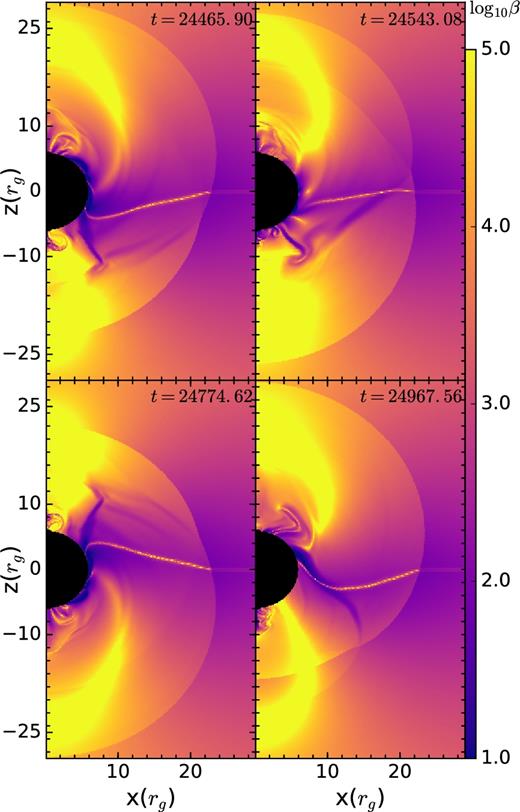
Snapshots of plasma β (≡2P/B2) at late times for Case I; t is in units of rg/c. The colour scale has been cut off at the minimum and maximum value shown in the colour bar. The inner and equatorial regions have a higher field strength. Close to the mid-plane, one can clearly see an oscillating current sheet.

Figure 9.

Snapshots of plasma β (≡2P/B²) at late times for Case I; t is in units of r_g/c. The colour scale has been cut off at the minimum and maximum value shown in the colour bar. The inner and equatorial regions have a higher field strength. Close to the mid-plane, one can clearly see an oscillating current sheet.

Open in new tab Download slide

To quantify the magnetic field strength within the shock, we define a volume averaged quantity

\begin{eqnarray} \beta _V = \frac{\int _V P\text{d}V}{\int _V (B^2/2)\text{d}V} = \frac{ (\gamma -1) E_{{\rm th},V}}{E_{{B_r,V}}+E_{B_{\theta },V}}, \end{eqnarray}

(17)

where the volume V over which the integral is done extends from inner boundary to r = 30r_g; this radius is well inside the sonic radius r_c (=71r_g for our parameters; equation 8), and the shock radius r_sh is always within it. Similarly, E_{th, V} is the volume averaged thermal energy, and |$E_{B_r,V}$| and |$E_{B_{\theta },V}$| are the volume averaged magnetic energies of the radial and meridional components of the magnetic field.

The top panel of Fig. 10 shows the evolution of volume averaged magnetic and thermal energies within 30r_g (top panel) with time for Cases Iand II; bottom panel shows the evolution of β_V (equation 17). In the top panel of Fig. 10 for Case I, during purely radial expansion of post-shock cavity, thermal energy (yellow line) increases rapidly with time due to shock heating, but magnetic energy remains roughly constant because radial flows cannot amplify a radial field. As a result, β_V increases during this phase of evolution. Later, the radial expansion of the shock is accompanied by global oscillations with l = 1 and higher order modes (see snapshots at t = 2662.69 r_g/c, 2739.87 r_g/c, and 2817.05 r_g/c in Fig. 7). The turbulent (in transition phase) and oscillatory meridional velocities associated with non-spherical modes amplify magnetic fields at later times. Simultaneous increase of thermal and magnetic pressure causes further expansion of the post-shock cavity (in Fig. 7, see snapshots at t = 6097.18 r_g/c, 6251.54 r_g/c, and 6405.90 r_g/c). Though, both thermal and magnetic energies increase simultaneously, the build up of magnetic energy is more erratic. Eventually, Case I attains a quasi-stationary state, in which both thermal and magnetic energies start oscillating about a mean value.

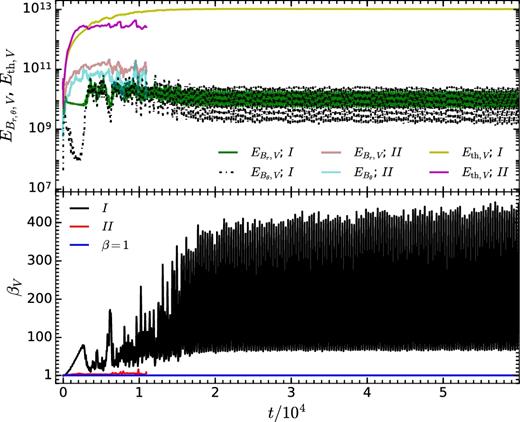
$Top panel: Temporal evolution of average (over the volume V enclosed within r = 30rg) thermal energy Eth, V and magnetic energies associated with radial ($E_{B_{r},V}$) and meridional ($E_{B_{\theta },V}$) components of magnetic field for Case I and Case II. Bottom panel: Temporal evolution of the βV, the ratio of volume averaged gas pressure (P) to magnetic pressure (B2/2) for the same runs. While time averaged βV in quasi-stationary state is ∼300 and shock persists, in Case II due to presence of stronger initial magnetic field, the flow gets choked and the final βV ∼ 5 and shock disappears at late times.$

Figure 10.

Top panel: Temporal evolution of average (over the volume V enclosed within r = 30r_g) thermal energy E_{th, V} and magnetic energies associated with radial (⁠|$E_{B_{r},V}$|⁠) and meridional (⁠|$E_{B_{\theta },V}$|⁠) components of magnetic field for Case I and Case II. Bottom panel: Temporal evolution of the β_V, the ratio of volume averaged gas pressure (P) to magnetic pressure (B²/2) for the same runs. While time averaged β_V in quasi-stationary state is ∼300 and shock persists, in Case II due to presence of stronger initial magnetic field, the flow gets choked and the final β_V ∼ 5 and shock disappears at late times.

Open in new tab Download slide

For Case II, magnetic field amplification happens earlier compared to Case I due to presence of aspherical shock from the very beginning of the flow evolution (see snapshots at t = 126 r_g/c, 588 r_g/c, and 1134 r_g/c in Fig. 8). Once shock disappears, magnetic energies (both |$E_{B_r, V}$| and |$E_{B_{\theta },V}$|⁠) saturate. This early amplification of magnetic field results in a low β_V (close to ∼5) during the flow evolution which, in turn, chokes the flow. The temporal evolution of the flow in Case II is equivalent to a hydro set-up with reflective inner radial boundary condition, or more precisely, if v_in is smaller than the lower limit of velocity (at the inner boundary) for which a stationary shock solution is possible (see fig. 15 and section 5.1 in Paper I).

5.2.2 Mode analysis

Fig. 11 shows the evolution of mode amplitudes a_l (measured by decomposing the shock radius into spherical harmonics; see Section 5.2.2) with time for the Case I MHD run. As in HD evolution, l = 0 is always the dominant mode. But unlike HD, during the very early evolution of the flow (t < 400r_g/c), all the even order modes (l = 2, 4, 6 etc.) are more dominant compared to the odd modes (l = 1, 3, 5 etc.). This can be attributed to the anisotropic nature of the initial transient phase of evolution, which is symmetric about |$\theta =\pi /2$| (see snapshot at t = 115.77r_g/c in Fig. 7). When the post-shock cavity attains an almost spherical shape and starts expanding radially, contribution from even order modes with l ≥ 2 becomes negligible. As the shock starts oscillating vertically about the equatorial plane, l = 1 mode starts to dominate the higher order modes. In the fully non-linear quasi-steady regime, apart from the l = 0 mode, l = 1, 2 and 3 are the most prominent modes.

Figure 11.

Results of mode analysis for the fiducial MHD run. Colour represents the absolute value of mode amplitude. l = 0 is the most dominant mode at all time. During the very early transient phase, only even modes (l = 0, 2, 4,6 etc) dominate. After the transient phase, during pure radial expansion of shock, only l = 0 mode dominates. As soon as shock-structure starts oscillating in the vertical direction, apart from l = 0 mode, l = 1, 2 and 3 modes dominate over the higher order modes.

Open in new tab Download slide

Comparing Fig. 11 and Fig. 2, it is very difficult to quantitatively study the differences in modal contribution of the HD and MHD runs. Fig. 12 shows the temporal evolution of a₀ (see equation 12), a measure of spherical radius of the aspherical shock, for different magnetic field strengths. At the very early stage of evolution, a large value of a₀ reflects the transient phase at t = 115r_g/c (see Fig. 7). After the transient phase, a spherical shock emerges, and the value of a₀ drops. After showing large fluctuations in a₀ in the transition phase, the shock attains a quasi-stationary state with a₀ oscillating about a mean value. The inset at top right-hand side shows the zoomed-in view of a₀(t) in steady state. As expected, the average shock radius increases with an increase in the magnetic field strength. Even in the quasi-steady state, a₀ does not show sinusoidal variation at a single frequency.

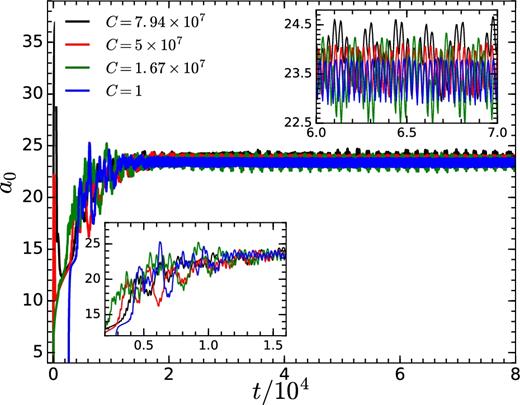
Temporal evolution of the amplitude a0 (mean shock radius) of l = 0 mode for different initial strength of magnetic fields and vin = 0.05c. Zoomed-in view of the initial phase is shown in inset figure on bottom left-hand side. The inset figure on the top right-hand side shows the zoomed-in view of the quasi-steady phase. Shock radius increases with time and eventually settles into an oscillating value. The mean shock radius is larger for a stronger field (see inset in the top right-hand side)

Figure 12.

Temporal evolution of the amplitude a₀ (mean shock radius) of l = 0 mode for different initial strength of magnetic fields and v_in = 0.05c. Zoomed-in view of the initial phase is shown in inset figure on bottom left-hand side. The inset figure on the top right-hand side shows the zoomed-in view of the quasi-steady phase. Shock radius increases with time and eventually settles into an oscillating value. The mean shock radius is larger for a stronger field (see inset in the top right-hand side)

Open in new tab Download slide

Fig. 13 shows the variation of time-averaged mode amplitude for l = 0, 1, 2, and 3 with the initial magnetic field strength. For a₀ and a₂, we take time average in the quasi-steady state. For l = 1 and 3, as a₁ and a₃ oscillate about a vanishing mean value, we fit the quasi-steady a₁(t) and a₃(t) with a sinusoidal curve, and plot the variation of the amplitudes A₁ and A₃ with the magnetic field strength. As expected, Fig. 13 shows that a stronger magnetic field suppresses the higher order modes due to higher magnetic tension.

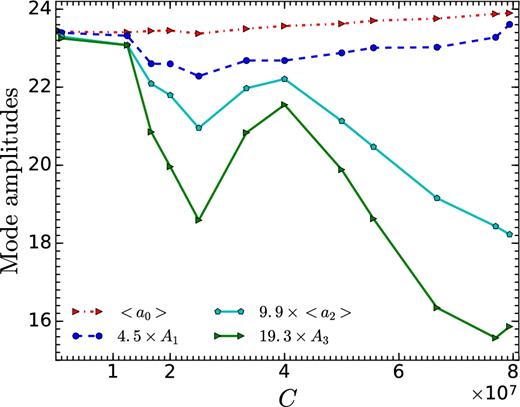
Variation of mode amplitudes al with initial magnetic field strength (quantified by C) for vin = 0.05c. For l = 0 and 2 modes, amplitudes (a0 and a2, respectively) are time averaged in the quasi-steady state. For l = 1 and 3, the amplitudes A1 and A3 are obtained by fitting a1 and a3 with fitting functions, ψ1 = A1sin(ω1t + ϕ1) and ψ3 = A3sin(ω3t + ϕ3), respectively.

Figure 13.

Variation of mode amplitudes a_l with initial magnetic field strength (quantified by C) for v_in = 0.05c. For l = 0 and 2 modes, amplitudes (a₀ and a₂, respectively) are time averaged in the quasi-steady state. For l = 1 and 3, the amplitudes A₁ and A₃ are obtained by fitting a₁ and a₃ with fitting functions, ψ₁ = A₁sin(ω₁t + ϕ₁) and ψ₃ = A₃sin(ω₃t + ϕ₃), respectively.

Open in new tab Download slide

5.2.3 Timescales from linear theory

Any disturbance in HD is carried by either sound waves propagating at ±c_s relative to the inflow or by entropy/vorticity waves travelling at the local flow velocity. In MHD, the sound wave generalizes to the fast mode and the entropy mode still consists of perturbations in total (thermal+magnetic) pressure balance. However, there are two new modes in MHD: the shear Alfvén wave and the slow magnetosonic waves. Therefore, the advective part of the advective-acoustic cycle is expected to split into five different cycles: an entropy wave, two Alfvén waves, and two slow magnetosonic waves (Guilet & Foglizzo 2010).

To interpret the SASI oscillation time-scales in presence of magnetic fields, we compute two more time-scales in addition to the three time-scales introduced in Section 5.1.4. For computing time-scales in the MHD set-up, we assume that for radial propagation (wave-vector |${\boldsymbol k} || {\boldsymbol B_0}$|⁠; fields are roughly radial even in the quasi-steady state as seen in Fig. 7), v_slow ≈ v_A and v_fast ≈ c_s (valid for c_s > v_A; see equation 19 in chapter 5 of Kulsrud 2005; Fig. 9 indeed shows that β ≫ 1 throughout), and for meridional propagation (⁠|${\boldsymbol k} \perp {\boldsymbol B_0}$|⁠), |$v_{\rm fast} \approx \sqrt{c^2_{\rm s} + v^2_A}$|⁠.

We compute two Alfvén/slow-magnetosonic time-scales: one in which the inward propagating disturbances are propagating at the sum of local Alfvén and flow speeds

\begin{eqnarray} t_{\rm aacA+} = \int _{r_{\rm in}}^{r_{\rm sh,I}} \frac{{\rm d}r}{(\bar{c}_s(r) - |\bar{v}_r(r)|)} + \int _{r_{\rm in}}^{r_{\rm sh,O}} \frac{{\rm d}r}{(|\bar{v}_{r}(r)| + \bar{v}_A(r))}, \end{eqnarray}

(18)

and t_aacA- in which Alfvénic disturbances travel outward with respect to the inflow

\begin{eqnarray} t_{{\rm aacA-}} = \int _{r_{\rm in}}^{r_{\rm sh,I}} \frac{{\rm d}r}{(\bar{c}_s(r) - |\bar{v}_r(r)|)} + \int _{r_{\rm in}}^{r_{\rm sh,O}} \frac{{\rm d}r}{(|\bar{v}_{r}(r)| - \bar{v}_A(r))}. \end{eqnarray}

(19)

In both these cases, the outward signal propagation happens at the fast speed relative to the inflow.

Fig. 14 shows the temporal variation of all the relevant time-scales for the fiducial MHD run (Case I). While T_a1 = 617.01 r_g/c (SASI time-scale measured by the period of l = 1 perturbation in the shock location) still lies in the range of variations of t_aac, t_{aacA +}, and t_aacA- (equations 14, 19 and 18) related to the advective-acoustic cycle, it is longer than the meridional and radial sonic time-scales, t_mcs and t_rcs (equations 16 and 15).

Figure 14.

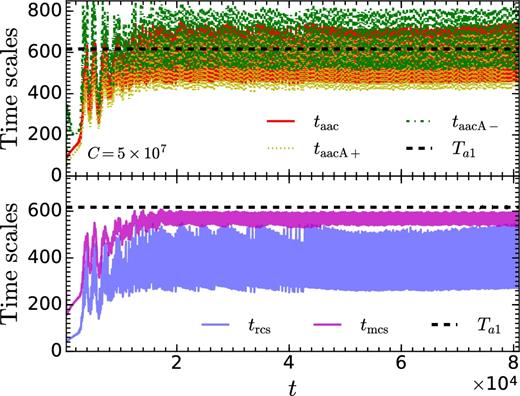
Various time-scales as a function of time for fiducial MHD run. The observed time period of oscillation T_a1 = 617.01. Time averaged value of time-scales are 〈t_aac〉 = 565.36, 〈t_rcs〉 = 363.61 〈t_mcs〉 = 571.29, 〈t_{aacA +}〉 = 534.40, 〈t_rcs〉 = 630.84. Time-scales are expressed in units of r_g/c.

Open in new tab Download slide

Fig. 15 shows the variation of SASI time period (measured by both methods, T_a1 and |$T_{v_{\theta }}$|⁠; see Section 5.1.3) and the time-averaged time-scales (obtained from various signal propagation time-scales) as a function of the initial magnetic field strength (quantified by C; see equation 5). While the maximum relative change (compared to HD) in SASI time period is |${\approx } 15.84 \,\,\rm{per\,\,cent}$|⁠, that in t_mcs is only |${\approx } 1.75 \,\,\rm{per\,\,cent}$|⁠. In presence of a weak magnetic field (β ≫ 1), SASI time period is not expected to be affected if the mechanism is purely acoustic. Even the variation in the HD advective-acoustic time-scale is small. However, the t_aacA- time-scale in which the inward-propagating signal travels at |$|\bar{v}_r|-\bar{v}_A$| (i.e. Alfvén wave travels outwards relative to the flow) matches the variation of the observed SASI time-scale fairly well. In principle, the inward propagating signal should consist of five waves (Guilet & Foglizzo 2010), but a cycle consisting of outward propagating fast waves and inward-propagating Alfvén disturbances (travelling inward at |$|\bar{v}_r|-\bar{v}_A$|⁠) seems to quantitatively describe the shock oscillations observed in our simulations.

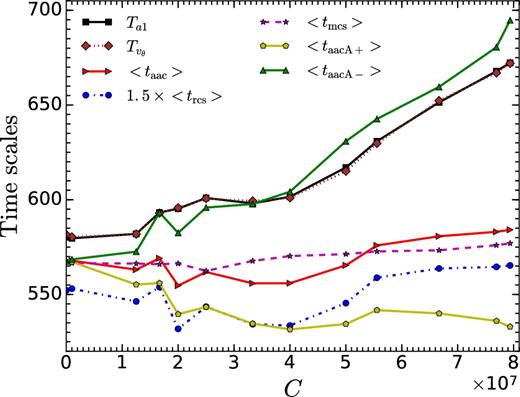
$Variation of the observed time period of oscillation (Ta1 and $T_{v_{\theta }}$) and average (over time in quasi-steady state) signal propagation time-scales (taac, trcs, tmcs, taacA +, taacA-; equations 14, 15, 16, 18 and 19) as a function of the initial magnetic field strength (C) for vin = 0.05c. Time-scales are expressed in units of rg/c.$

Figure 15.

Variation of the observed time period of oscillation (T_a1 and |$T_{v_{\theta }}$|⁠) and average (over time in quasi-steady state) signal propagation time-scales (t_aac, t_rcs, t_mcs, t_{aacA +}, t_aacA-; equations 14, 15, 16, 18 and 19) as a function of the initial magnetic field strength (C) for v_in = 0.05c. Time-scales are expressed in units of r_g/c.

Open in new tab Download slide

6 DISCUSSIONS AND CONCLUSIONS

In this paper, we describe the effects of an initial split-monopolar magnetic field on the SASI. Now, we discuss the key results of our work and draw conclusions.

6.1 Flow structure

In Section 4, we showed that a radial magnetic field does not modify the Bondi accretion solution. In this section, we discuss how the flow structure changes in the saturated state for v_in = 0.05c and different magnetic field strengths. Beyond a certain magnetic field strength (for v_in = 0.05c, the critical value is C = 7.94 × 10⁷), SASI does not occur. We choose four different strength of magnetic field: C = 1, unmagnetized; C = 5 × 10⁷, moderately magnetized; C = 7.94 × 10⁷, the strongest magnetic field for which SASI occurs and C = 8 × 10⁷, the strength of magnetic field at which SASI cannot occur.

Fig. 16 shows the average flow profiles for four different initial magnetic field strengths. We take the time and angle average of the quantity q as

\begin{eqnarray} \langle \bar{q}\rangle = \frac{1}{T} \frac{ \int _{T_0}^{T_0+T} \text{d}t \int _{0}^{\pi }q (r, \theta , t) {\rm sin} \theta \text{ d}\theta }{\int _{0}^{\pi } {\rm sin} \theta \text{d}\theta }, \end{eqnarray}

(20)

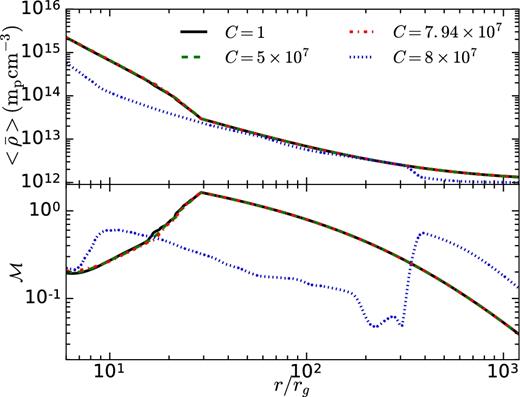
$Top panel: θ− and time averaged density profile for different initial magnetic field strengths – C = 1 (almost unmagnetized), C = 5 × 107 (moderately magnetized), C = 7.94 × 107 (the strongest magnetic field for which SASI can occur), and C = 8 × 107 (magnetic field strength at which SASI cannot occur). Bottom panel: Mach number $\mathcal {M}= -\langle \bar{v}_r\rangle /\langle \bar{c}_s\rangle$ as a function of r for different value of C.$

Figure 16.

Top panel: θ− and time averaged density profile for different initial magnetic field strengths – C = 1 (almost unmagnetized), C = 5 × 10⁷ (moderately magnetized), C = 7.94 × 10⁷ (the strongest magnetic field for which SASI can occur), and C = 8 × 10⁷ (magnetic field strength at which SASI cannot occur). Bottom panel: Mach number |$\mathcal {M}= -\langle \bar{v}_r\rangle /\langle \bar{c}_s\rangle$| as a function of r for different value of C.

Open in new tab Download slide

where T is the averaging period. We represent time average by ‘〈〉’ and θ− average by ‘−’. Top panel shows the average density as a function of r. For magnetic field strengths that allow SASI, radial density profiles fall on top of each other, irrespective of the magnetic field strength. This implies that the local flow structure may be different for different field strengths, but on average the flow structures are identical. Bottom panel shows the radial profile of local Mach number |$\mathcal {M}= -\langle \bar{v}_r\rangle /\langle \bar{c}_s\rangle$|⁠. Here, also for all three magnetic field strengths for which SASI occurs, profiles are identical. But for C = 8 × 10⁷, for which an oscillating shock does not occur, the density and Mach number profiles are different from the other three cases. The roughly hydrostatic flow is unsteady but eventually expected to asymptote to the settling flow described by lower branch in Bondi solution (see the first panel of fig. 14 in Paper I).

Thus, strong magnetic field beyond a critical strength chokes the flow, reducing the effective v_in. In our idealized model, for the same sonic radius r_c, the critical magnetic field strength depends on the advection velocity at the inner boundary v_in, which determines the shock radius. Larger the v_in, higher the advection of thermal and magnetic energies through the inner boundary. As a result, gravity can counter stronger magnetic pressure (within post-shock cavity) which acts outward along with the thermal pressure.

6.2 SASI mechanism

Unlike most of the previous simulations, our set-up leads to a quasi-steady state in which the non-linear oscillations essentially last forever. We compare the SASI time period with time-scales obtained from two different mechanisms (namely advective-acoustic and purely acoustic) in HD and MHD.

In HD regime, we change the ratio of mean shock radius (r_sh) to inner radius (r_in) keeping r_in fixed, and study the variation of different time-scales with this ratio. For small values of r_sh/r_in, the match between the advective-acoustic time-scale t_aac and the SASI time period (⁠|$T_{v_{\theta }}$| or T_a1) is excellent. With an increase in r_sh/r_in, the deviation of the time-scale becomes larger (see Fig. 6). Purely acoustic mechanism gives rise to two different time-scales: the radial acoustic time t_rcs (considering purely radial propagation) and the meridional acoustic time t_mcs (considering meridional propagation). In all cases, t_rcs is always much less than the SASI time period, so we can discard purely radial acoustic mechanism as the possible cause for SASI. The match between the t_mcs and SASI time period becomes best around r_sh/r_in ∼ 3.9. But it is to be noted that according to Blondin & Mezzacappa (2006), SASI time period is expected to be equal to the round trip time of two sound waves advancing along the shock surface i.e. 2t_mcs. Instead, we observe the closeness between t_mcs and SASI time period.

In MHD regime, we study the variation of SASI time-scales with the change in initial magnetic field strength. In presence of a weak magnetic field, the advective-acoustic cycle is expected to split into five different cycles that constitute the actual cycle (see Section 5.2.3). We compute three time-scales to quantify five cycles, t_aac – outgoing fast magnetosonic wave + ingoing entropy wave, t_{aacA +} – outgoing fast magnetosonic wave + ingoing (with respect to local inflow) Alfvén/slow wave, t_aacA- – outgoing fast magnetosonic wave + outgoing (with respect to local inflow) Alfvén/slow wave. While the maximum relative change (to HD) in time-scales obtained from the advective-acoustic mechanism is |$\approx 18 \,\,\rm{per\,\,cent}$| (for t_aacA-), in the meridional acoustic mechanism it is only |${\approx } 1.75 \,\,\rm{per\,\,cent}$| (for t_mcs), compared to the change in SASI time period of |${\approx } 15.84 \,\,\rm{per\,\,cent}$|⁠. In purely acoustic mechanism, weak magnetic fields do not affect the SASI time period, but in advective-acoustic mechanism weak magnetic fields affect the SASI time period. The effects depend on the ratio v_A/v_r, the ratio of Alfvén, and radial advection speeds.

Both in HD and MHD regimes, advective-acoustic mechanism is favoured as the possible mechanism for SASI. Further, if SASI is a purely acoustic mechanism, the dispersion relation in the local limit is given by ω = kc_s, which means that the frequency of different modes should be proportional to the wavenumber. To find the frequency associated with different modes, we take the temporal FFT of shock deformation modes (a_l(t)) and best fit the lowest frequency peak with a Lorentzian (equation 13); centroid frequency gives the frequency of the corresponding mode. Fig. 17 shows the representative examples of FFT of a_l for l = 0, 1, 15, and 16 for our fiducial hydro run. Bar plot in Fig. 18 shows the variation of mode frequency with mode number. All the even modes (l = 0, 2, 4 etc.) have frequency ≈700 Hz, and odd modes (l = 1, 3, 5 etc.) have frequency ≈350 Hz, which is against the expectation f ∝ l for acoustic signals.

Figure 17.

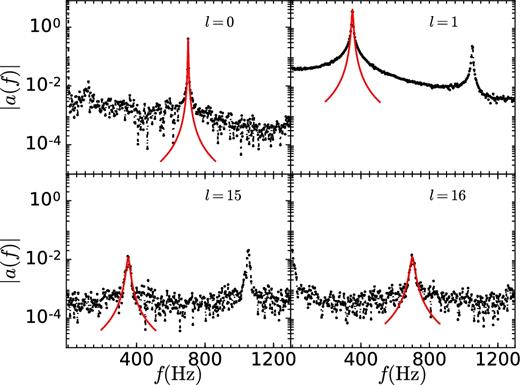
FFT of the mode amplitudes a_l for l = 0, 1, 15, 16 for the fiducial hydro run. The lowest frequency peaks are fitted individually by a Lorentzian using the least squares fit method. Centroid of the Lorentzian gives the frequency associated with the corresponding mode.

Open in new tab Download slide

Figure 18.

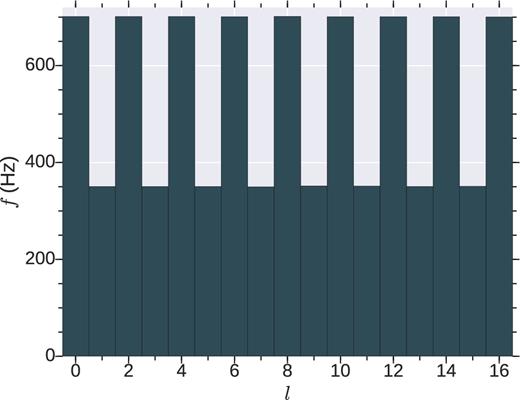
Lowest frequency associated with different modes (l) of oscillation for the fiducial HD run.

Open in new tab Download slide

Guilet & Foglizzo (2010), in their toy model, showed that the effects of magnetic field on the advective-acoustic cycle depend on the ratio of Alfvén speed to advection speed (v_A/v_r) instead of the ratio of gas pressure to magnetic pressure (β). Even a weak magnetic field is able to significantly affect the advective-acoustic cycle provided v_A/v_r is of the order of

\begin{eqnarray} \frac{v_{\rm A}}{v_{\rm r}} \sim \frac{r_{\rm sh}}{2h\sqrt{l(l+1)}}, \end{eqnarray}

(21)

where r_sh is the shock radius, h is the distance over which flow is decelerated, and l is mode number (see their equation 18). If we take r_sh ≈ h, we get the ratio 0.353 and 0.204 for l = 1 and 2 modes, respectively. Fig. 19 shows the change in the ratio of Alfvén speed to advection speed considering the average over the whole post-shock volume (v_A/v_r) and over the volume within the half shock radius (v_{A, h}/v_{r, h}) with the change in initial magnetic field strength (C). To quantify the magnetization of the accreting medium in the quasi-steady state, the ratio of average gas pressure to average magnetic pressure in the post-shock volume (β) is plotted as a function of C in Fig. 19. SASI time period (T_a1, |$T_{v_{\theta }}$|⁠) and time-scales corresponding to the advective-acoustic mechanism (t_aac, t_{aacA +}, and t_aacA-) encounter a significant change from the time-scales in HD case for C = 1.67 × 10⁷ (as seen in Fig. 15), for which v_A/v_r = 0.053 and v_{A, h}/v_{r, h} = 0.11 and β ≈ 3200. So it appears that in our set-up, SASI is affected at a smaller value of v_A/v_r compared to the estimates of Guilet & Foglizzo (2010). This is not surprising, because we use an initial split-monopolar magnetic field configuration that leaves its imprint even in the quasi-steady state. Therefore, magnetic field is stronger at small r in contrast to the uniform field distribution used by Guilet & Foglizzo (2010). This argument is supported by the larger value of v_{A, h}/v_{r, h} (when average is done over the volume within half the shock radius) compared to v_A/v_r (when average is done over whole post-shock volume) for the same value of C (see Fig. 19). Moreover, the shape of v_A/v_r versus C curve (in Fig. 19) and T_a1 or |$T_{v_{\theta }}$| versus C (in Fig. 15) are very similar; whenever ratio increases or decreases, the observed time periods follow them. This is expected because

\begin{equation*} \int \frac{{\rm d}r}{(|v_{\rm r}| - v_{\rm A})} \approx \int \frac{{\rm d}r}{|v_{\rm r}|}\left(1+\frac{v_{\rm A}}{|v_{\rm r}|}\right), \end{equation*}

if v_A < v_r.

Figure 19.

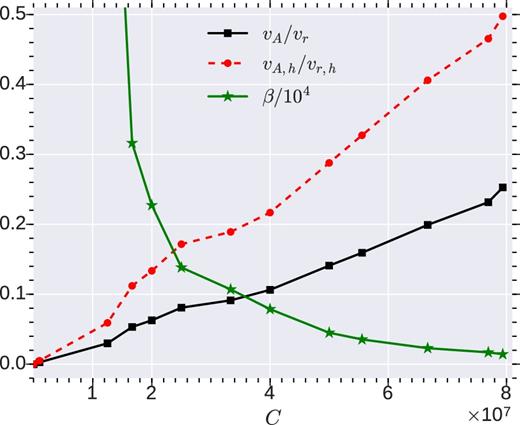
The ratio of average Alfvén speed (v_A) to average advection speed (v_r) and ratio of gas pressure to magnetic pressure (β) with initial magnetic field strength (C). For v_A/v_r and β, average is done over whole post-shock volume, whereas for v_{A, h}/v_{r, h}, average is done within the half shock radius.

Open in new tab Download slide

Equation (21) tells that for the same strength of magnetic field, the higher order modes are more affected compared to lower order modes, which is clear from Fig. 13. We also see that the SASI period is not a monotonically increasing functions of magnetic field strength; there are irregularities that are expected in the framework of advective-acoustic mechanism due to interference of different cycles (see fig. 6 of Guilet & Foglizzo 2010).

So, we conclude that the physical mechanism behind SASI (at least in the parameter regime that we explored) is more likely to be the advective-acoustic mechanism instead of a purely acoustic mechanism (either meridional or radial).

6.3 QPOs and SASI

SASI in an accretion flow gives rise to an intrinsic time variability in the flow, which may explain some of the QPOs observed in XRBs. In this section, we try to connect different time-scales associated with magnetized SASI with different high frequency (HF ≳ 100 Hz) QPOs observed in XRBs (both in black hole and neutron star binaries).

Kilohertz (kHz) QPOs are the fastest variability components in neutron star XRBs (van der Klis 2004), seen in most Z and atoll sources. Sometimes kHz QPOs appear in pairs; the peak with the higher frequency is called the upper kHz QPO at frequency f_u and the other is called lower kHz QPO with frequency f_l. Many models associate orbital motion in the disc with one of the kHz QPOs (Strohmayer et al. 1996; Miller et al. 1998; Mukhopadhyay et al. 2003). While Mukhopadhyay et al. 2003 attributes global shock oscillations as the origin of upper kHz QPOs for the first time, some other models argue that both QPOs arise via non-linear resonance between fundamental frequencies, e.g. between radial and vertical epicyclic oscillation frequencies along with the spin frequency of neutron star (Kluźniak et al. 2004; Pétri 2005; Blaes et al. 2007; Mukhopadhyay 2009). Parametric resonance models are particularly attractive if f_u − f_l is linked with the spin frequency ν_s of the neutron star, when f_u − f_l ∼ ν_s/2 (if ν_s ≳ 400 Hz; e.g. KS 1731−260, 4U 1636−53) or f_u − f_l ∼ ν_s (if ν_s ≲ 400 Hz; e.g. 4U 1728−34, 4U 1702−429) (Strohmayer et al. 1996; van der Klis et al. 1996; Ford et al. 2000; Wijnands et al. 2003). However, later on this interpretation was questioned (Méndez & Belloni 2007).

For black hole sources, on the other hand, the observed twin HF QPOs are often argued to be seen in 2 : 3 ratio [e.g GRO J1655−40 (300, 450 Hz; Remillard et al. 1999; Strohmayer 2001), XTE J1550−564 (184, 276 Hz; Homan et al. 2001), and GRS 1915+105 (113, 168 Hz; Remillard 2004)], which again was explained based on non-linear resonance by the groups mentioned above. Some recent observations question the 2 : 3 appearance of HF QPOs in black hole XRBs [e.g IGR J17091−3624 (66, 164 Hz; Altamirano & Belloni 2012)].

Another ≳100 Hz variability phenomenon is the hectohertz (hHz) QPO (Ford & van der Klis 1998) with a frequency f_hHz in the range 100–270 Hz (e.g see Altamirano et al. 2008) in atoll sources in most states. Fragile, Mathews & Wilson (2001) proposed that accreting material passing through the transition region formed due to Bardeen–Petterson effect may generate hHz frequencies. Kato (2007) proposed that a warp in accretion disc gives rise to the hectohertz QPOs in atoll sources. The black hole sources also exhibit QPO frequency of order hHz or slightly less, e.g. GRS 1915+105, XTE J1550−564, simultaneously with HF ones (e.g. Remillard et al. 2002). Earlier non-linear resonance models can be modified to explain it (Mukhopadhyay, Bhattacharya & Sreekumar 2012).

Fig. 20 shows the power spectrum of the light curve L(t) obtained in the quasi-steady state for different initial magnetic field strengths (quantified by C; see equation 5) and v_in = 0.05c. Luminosity L(t) is assumed to be due to free–free emission (a similar time variability is expected for other mechanisms such as synchrotron and inverse-Compton) from the volume V, and computed as

\begin{eqnarray} L = \int _{V} 1.4 \times 10^{-27} \left(\frac{\rho }{m_{\rm p}} \right)^2 T^{\frac{1}{2}} \text{d}V \ {\rm erg \ s}^{-1}, \end{eqnarray}

(22)

Figure 20.

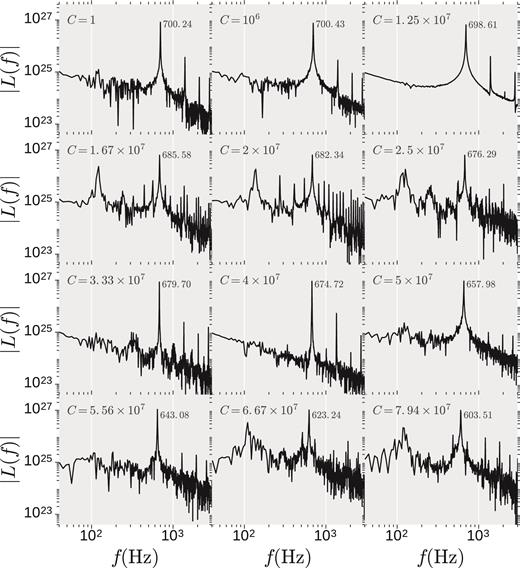
Power spectrum of the light curves assuming free–free emission for different magnetic field strength (C) and v_in = 0.05c. With the increment in magnetic field strength, low frequency features appear and disappear non-monotonically. The most prominent peak whose frequency is the frequency of l = 0 mode and half the frequency of l = 1 mode can be related to upper kHz QPO. For some strengths of magnetic field, alongside the main peak, there are some comparatively low frequency peaks that can be related to some other types of HF QPOs such as lower kHz QPO and hHz QPO.

Open in new tab Download slide

where V is the spherical volume of radius r = 30r_g, dominated by post-shock region. The post-shock temperature in simulations is very high (T ∼ 10¹¹K). The electrons in hot accretion flows are at lower temperature compared to that of the ions and other emission process may be important (e.g. Sharma et al. 2007; Rajesh & Mukhopadhyay 2010; Yuan & Narayan 2014). Therefore, light curves from simulations (which assume a single temperature fluid) should be only taken as trends.

First panel of Fig. 20 shows the power spectrum for the unmagnetized (C = 1) SASI run and the power spectrum has the most prominent peak at f₀ = 700.24 Hz along with its harmonics (the peak frequency is obtained by fitting with a Lorentzian). This is the frequency associated with the l = 0 mode and double the frequency of l = 1 mode. There is some low frequency noise present in the power spectrum. With the increase in magnetic field strength, the prominent peak frequency shifts to lower value and the low frequency noise becomes less prominent (for C = 10⁶) and vanishes for C = 1.25 × 10⁷. As the magnetic field strength is increased more, some extra peaks arise at low and intermediate frequencies along with the main peak (e.g. C = 1.67 × 10⁷ and 2 × 10⁷). The lowest frequency is associated with the modulation frequency on top of a regular frequency of mode amplitude a₀(t) (e.g. see the variation of a₀(t) for C = 7.94 × 10⁷ in Fig. 12). With the increase in magnetic field strength, low frequency features appear and disappear non-monotonically.

In this analysis, the origin of QPOs (whether kHz, HF or hHz) is different from past proposals. Fig. 21 shows the power spectrum for C = 2 × 10⁷ and v_in = 0.05c. The most prominent peak appears at 681.78 Hz, which can be related to the upper kHz QPOs at f_u. The lowest frequency peak is at 135.96 Hz, which can be identified as the hHz QPO at f_hHz. In between these two peaks, there are three more peaks. One of them is the harmonic of the hHz QPO (f_hHz2 = 273.44 Hz ≈2f_hHz), other two peaks are the beat frequencies, f_l1 = 545.40 Hz ≈f_u − f_hHz and f_l2 = 408.21 Hz ≈f_u − f_hHz2, one of which can be related to the lower kHz QPO. Whereas, f_u is equal to the frequency associated with l = 0 mode, f_hHz is the frequency of modulation in the mode amplitude a₀ due to magnetic field, as seen in inset at upper right-hand side of Fig. 12. With magnetic field strength (C), the upper kHz QPO frequency f_u tracks 2/T_a1, the frequency of l = 0 mode (which is double the l = 1 mode frequency). For all field strengths, the hHz QPO frequency remains constrained in the range (110–135) Hz.

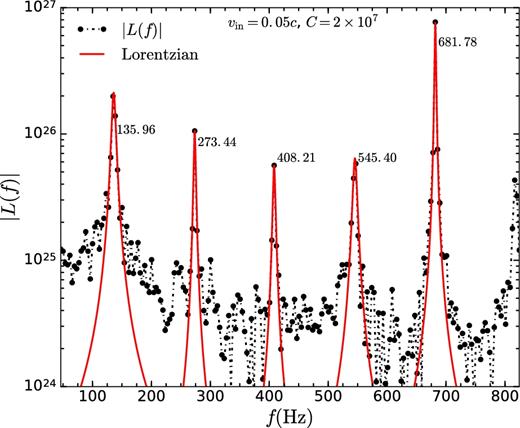
Power spectrum of light curve for vin = 0.05c and C = 2 × 107. The prominent peaks appears at fu = 681.78 Hz, fhHz = 135.96 Hz, and at its harmonics, fhHz2 = 273.44 Hz, and at the beat frequencies, fl1 = 545.40 Hz∼ fu − fhHz, fl2 = 408.21 Hz∼ fu − fhHz2. The peaks are fitted individually by Lorentzians using least squares fit method.

Figure 21.

Power spectrum of light curve for v_in = 0.05c and C = 2 × 10⁷. The prominent peaks appears at f_u = 681.78 Hz, f_hHz = 135.96 Hz, and at its harmonics, f_hHz2 = 273.44 Hz, and at the beat frequencies, f_l1 = 545.40 Hz∼ f_u − f_hHz, f_l2 = 408.21 Hz∼ f_u − f_hHz2. The peaks are fitted individually by Lorentzians using least squares fit method.

Open in new tab Download slide

If the shock location is changed by tuning the value of v_in, SASI time period changes (as shown in Fig. 6), so does f_u, as f_u ≈ 2/T_a1. On the other hand, the hHz QPO arises due to magnetic effects. To see the variation in f_hHz with the change in shock location, we decrease and increase the shock radius by changing v_in to 0.06c and 0.048c, respectively. For v_in = 0.048c, power spectrum of the light curve for C = 2 × 10⁷ is shown in Fig. 22; three peaks are present in the power spectrum. Upper kHz QPO frequency f_u = 599.90 Hz is shifted to a lower value compared to the fiducial case (v_in = 0.05c), so does the hHz QPO frequency (f_hHz = 105.22 Hz). The frequency of lower kHz QPO is f_l = 495.82 Hz ≈f_u − f_hHz. Fig. 23 shows the power spectrum of light curve for v_in = 0.06c and C = 5 × 10⁷, with a smaller shock radius. As expected, the upper kHz QPO frequency (f_u = 1081.10 Hz) related to SASI time period increases. Also, the hHz QPO frequency (f_hHz = 225 Hz) moves to a higher value. The lower kHz QPO (f_l = 869.54 Hz) structure becomes fainter (this might be immersed in noise in real observations).

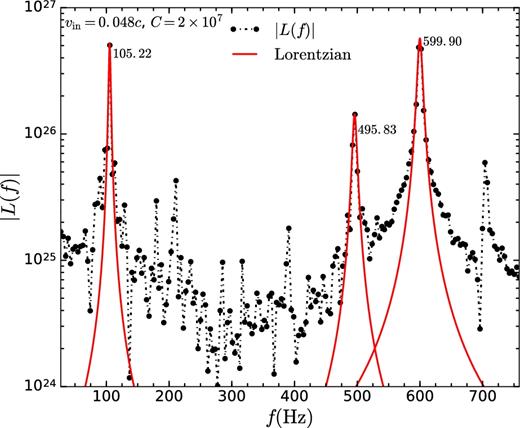
Power spectrum of light curve for vin = 0.048c and C = 2 × 107. The prominent peaks appear at fu = 599.90 Hz, fhHz = 105.22 Hz, and at the beat frequency of the former two, fl = 405.82 Hz∼ fu − fhHz. The peaks are fitted individually by Lorentzians using least squares fit method.

Figure 22.

Power spectrum of light curve for v_in = 0.048c and C = 2 × 10⁷. The prominent peaks appear at f_u = 599.90 Hz, f_hHz = 105.22 Hz, and at the beat frequency of the former two, f_l = 405.82 Hz∼ f_u − f_hHz. The peaks are fitted individually by Lorentzians using least squares fit method.

Open in new tab Download slide

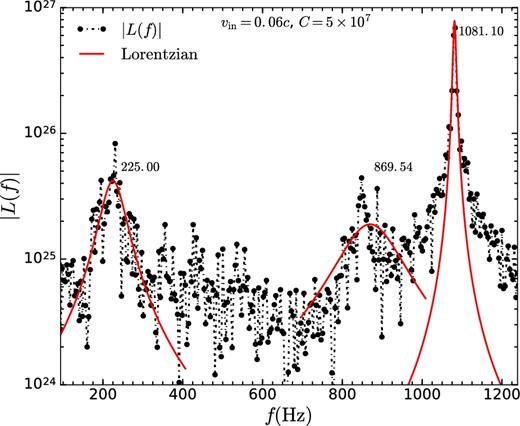
Power spectrum of light curve for vin = 0.06c and C = 5 × 107. The most prominent peaks appear at fu = 1081.10 Hz, and at fh = 225 Hz, which can be considered as upper kHz QPO and hHz QPO, respectively. A fainter peak is seen at fl = 869.54 Hz, which can be considered as lower kHz QPO. The peaks are fitted individually by Lorentzians using least squares fit method.

Figure 23.

Power spectrum of light curve for v_in = 0.06c and C = 5 × 10⁷. The most prominent peaks appear at f_u = 1081.10 Hz, and at f_h = 225 Hz, which can be considered as upper kHz QPO and hHz QPO, respectively. A fainter peak is seen at f_l = 869.54 Hz, which can be considered as lower kHz QPO. The peaks are fitted individually by Lorentzians using least squares fit method.

Open in new tab Download slide

Our idealized simulations suggest shock oscillations as the origin of QPOs. in particular kHz/HF/hHz ones. We identify the l = 0 SASI mode frequency (which is double the frequency of l = 1 mode) as the frequency of upper kHz QPO. It is the appearance of the hHz QPO that determines the separation of twin QPO peaks. We do not observe the hHZ QPOs in our simulations without magnetic fields, indicating that they originate only in the presence of a magnetic field. Hence, one does not necessarily need to introduce the spin of the compact objects to explain QPOs.

6.4 Caveats of the model

The present model is very simplistic. In reality, accretion flows have complicated magnetic field geometry, angular momentum, cooling (depending on the spectral state of the XRBs), which might change the above results. A brief discussion of the above-mentioned factors is given below.

We initialize the simplest magnetic field configuration, a split-monopole. Because of the absence of magnetic force in the pre-shock flow, the equilibrium is not affected by the magnetic field (see Section 4), but the mode frequencies are. The mode frequencies are expected to behave differently for different field geometries (Guilet &Foglizzo 2010).

Accreting matter in XRBs is expected to have angular momentum. QPOs are observed in the hard state, in which the inner flow is expected to be hot, quasi-spherical, and sub-Keplerian (e.g see Chakrabarti 1989). To approximate that we study the spherical, adiabatic, non-rotating accretion flow on to a compact object. However, even small angular momentum can affect the global shock oscillations (Blondin & Mezzacappa 2006; Yamasaki & Foglizzo 2008; Kazeroni, Guilet & Foglizzo 2017). Shock instabilities in rotating accretion flows were invoked to explain time variability (mostly low frequency phenomena) in accreting systems (Molteni et al. 1996; Nagakura & Yamada 2009).

We also assume axisymmetry, breakdown of which may significantly alter the oscillation frequencies. While in the non-rotating flow, non-axisymmetric modes of SASI redistribute angular momentum (Blondin & Mezzacappa 2007; Fernández 2010; Guilet & Fernández 2014; Kazeroni et al. 2016), in a rotating flow the spiral modes become more prominent over the sloshing modes (Iwakami et al. 2009; Kazeroni et al. 2017) and dominate the dynamics of the flow. The occurrence of non-axisymmetric Papaloizou-Pringle instability (Papaloizou & Pringle 1984), its interplay with the advective-acoustic cycle (Gu & Foglizzo 2003), and the magneto-rotational instability (Balbus & Hawley 1991) are additional complications in a rotating accretion flow.

We also neglect radiative cooling because in the hard state the inner accretion flow is expected to be hot and non-radiative with the cooling time much longer than the infall time of the flow. Some earlier studies showed that the shock is unstable even in 1D in presence of cooling (Langer, Chanmugam & Shaviv 1981; Chevalier & Imamura 1982; Saxton 2002), but our non-radiative simulations require 2D or 3D to be unstable (see Paper I).

We expect shock oscillations in inner, hot, transonic accretion flows (rotating or non-rotating). But for comparing with the observations, one needs to study them in more realistic 3D simulations with rotation, magnetic fields.

7 SUMMARY

In this work, we study SASI in unmagnetized and magnetized spherical accretion flow around a central gravitating accretor, in particular the ones with a hard surface. The key findings of the work are listed below.

A standing shock does not occur above a critical strength of magnetic field as the sum of outward magnetic and thermal pressure becomes high enough to overcome the inward gravitational attraction and the shock moves into the subsonic region and vanishes.
A comparison of various signal propagation time-scales and the observed shock oscillation frequency agrees with the advective acoustic mechanism, and not a purely acoustic one (at least for our parameters).
The global shock oscillations in the accretion flow give rise to a prominent peak in the power spectrum of the light curve, which can be related to the upper kHz QPOs. In presence of magnetic field, there are a few low frequency peaks that can be related to lower kHz and hHz QPOs.

ACKNOWLEDGEMENTS

We thank Srikara S (IISER Pune) for taking part in discussions during initial part of the work. PD thanks Nagendra Kumar for helpful discussions on QPOs. We thank the anonymous reviewer for thoughtful suggestions. This work is partly supported by an India–Israel joint research grant (6-10/2014[IC]) and by the ISRO project with research Grant No. ISTC/PPH/BMP/0362. PS and PD thank KITP for their participation in the program ‘Confronting MHD Theories of Accretion Disks with Observations’. This research was supported in part by the National Science Foundation under Grant No. NSF PHY-1125915. Some of the simulations were carried out on Cray XC40-SahasraT cluster at Supercomputing Education and Research Centre (SERC), IISc.

REFERENCES

Altamirano

D.

,

Belloni

T.

,

2012

,

ApJ

,

747

,

L4

10.1088/2041-8205/747/1/L4

Crossref

Search ADS

Altamirano

D.

,

van der Klis

M.

,

Méndez

M.

,

Jonker

P. G.

,

Klein-Wolt

M.

,

Lewin

W. H. G.

,

2008

,

ApJ

,

685

,

436

10.1086/590897

Crossref

Search ADS

Balbus

S. A.

,

Hawley

J. F.

,

1991

,

ApJ

,

376

,

214

10.1086/170270

Crossref

Search ADS

Blaes

O. M.

,

Šrámková

E.

,

Abramowicz

M. A.

,

Kluźniak

W.

,

Torkelsson

U.

,

2007

,

ApJ

,

665

,

642

10.1086/519782

Crossref

Search ADS

Blondin

J. M.

,

Mezzacappa

A.

,

2006

,

ApJ

,

642

,

401

10.1086/500817

Crossref

Search ADS

Blondin

J. M.

,

Mezzacappa

A.

,

2007

,

Nature

,

445

,

58

Blondin

J. M.

,

Shaw

S.

,

2007

,

ApJ

,

656

,

366

10.1086/510614

Crossref

Search ADS

Blondin

J. M.

,

Mezzacappa

A.

,

DeMarino

C.

,

2003

,

ApJ

,

584

,

971

10.1086/345812

Crossref

Search ADS

Bondi

H.

,

1952

,

MNRAS

,

112

,

195

10.1093/mnras/112.2.195

Crossref

Search ADS

Bruenn

S. W.

,

Dirk

C. J.

,

Mezzacappa

A.

,

Hayes

J. C.

,

Blondin

J. M.

,

Hix

W. R.

,

Messer

O. E. B.

,

2006

,

J. Phys.

,

46

,

393

preprint

(arXiv:0709.0537)

,

Burrows

A.

,

Livne

E.

,

Dessart

L.

,

Ott

C. D.

,

Murphy

J.

,

2006

,

ApJ

,

640

,

878

10.1086/500174

Crossref

Search ADS

Chakrabarti

S. K.

,

1989

,

ApJ

,

347

,

365

10.1086/168125

Crossref

Search ADS

Chakrabarti

S. K.

,

Manickam

S. G.

,

2000

,

ApJ

,

531

,

L41

10.1086/312512

Crossref

Search ADS

Chevalier

R. A.

,

Imamura

J. N.

,

1982

,

ApJ

,

261

,

543

10.1086/160364

Crossref

Search ADS

Dedner

A.

,

Kemm

F.

,

Kröner

D.

,

Munz

C.-D.

,

Schnitzer

T.

,

Wesenberg

M.

,

2002

,

J. Comput. Phys.

,

175

,

645

10.1006/jcph.2001.6961

Crossref

Search ADS

Dhang

P.

,

Sharma

P.

,

Mukhopadhyay

B.

,

2016

,

MNRAS

,

461

,

2426

(Paper I)

10.1093/mnras/stw1480

Crossref

Search ADS

Endeve

E.

,

Cardall

C. Y.

,

Budiardja

R. D.

,

Mezzacappa

A.

,

2010

,

ApJ

,

713

,

1219

10.1088/0004-637X/713/2/1219

Crossref

Search ADS

Endeve

E.

,

Cardall

C. Y.

,

Budiardja

R. D.

,

Beck

S. W.

,

Bejnood

A.

,

Toedte

R. J.

,

Mezzacappa

A.

,

Blondin

J. M.

,

2012

,

ApJ

,

751

,

26

10.1088/0004-637X/751/1/26

Crossref

Search ADS

Fernández

R.

,

2010

,

ApJ

,

725

,

1563

10.1088/0004-637X/725/2/1563

Crossref

Search ADS

Foglizzo

T.

,

2002

,

A&A

,

392

,

353

10.1051/0004-6361:20020912

Crossref

Search ADS

Foglizzo

T.

,

2009

,

ApJ

,

694

,

820

10.1088/0004-637X/694/2/820

Crossref

Search ADS

Foglizzo

T.

,

Tagger

M.

,

2000

,

A&A

,

363

,

174

Foglizzo

T.

,

Scheck

L.

,

Janka

H.-T.

,

2006

,

ApJ

,

652

,

1436

10.1086/508443

Crossref

Search ADS

Foglizzo

T.

,

Galletti

P.

,

Scheck

L.

,

Janka

H.-T.

,

2007

,

ApJ

,

654

,

1006

10.1086/509612

Crossref

Search ADS

Ford

E. C.

,

van der Klis

M.

,

1998

,

ApJ

,

506

,

L39

10.1086/311638

Crossref

Search ADS

Ford

E. C.

,

van der Klis

M.

,

Méndez

M.

,

Wijnands

R.

,

Homan

J.

,

Jonker

P. G.

,

van Paradijs

J.

,

2000

,

ApJ

,

537

,

368

10.1086/309032

Crossref

Search ADS

Fragile

P. C.

,

Mathews

G. J.

,

Wilson

J. R.

,

2001

,

ApJ

,

553

,

955

10.1086/320990

Crossref

Search ADS

Guilet

J.

,

Fernández

R.

,

2014

,

MNRAS

,

441

,

2782

10.1093/mnras/stu718

Crossref

Search ADS

Guilet

J.

,

Foglizzo

T.

,

2010

,

ApJ

,

711

,

99

10.1088/0004-637X/711/1/99

Crossref

Search ADS

Guilet

J.

,

Foglizzo

T.

,

2012

,

MNRAS

,

421

,

546

Gu

W.-M.

,

Foglizzo

T.

,

2003

,

A&A

,

409

,

1

10.1051/0004-6361:20031080

Crossref

Search ADS

Herant

M.

,

Benz

W.

,

Hix

W. R.

,

Fryer

C. L.

,

Colgate

S. A.

,

1994

,

ApJ

,

435

,

339

10.1086/174817

Crossref

Search ADS

Homan

J.

,

Wijnands

R.

,

van der Klis

M.

,

Belloni

T.

,

van Paradijs

J.

,

Klein-Wolt

M.

,

Fender

R.

,

Méndez

M.

,

2001

,

ApJS

,

132

,

377

10.1086/318954

Crossref

Search ADS

Ipser

J. R.

,

Lindblom

L.

,

1991

,

ApJ

,

379

,

285

10.1086/170503

Crossref

Search ADS

Iwakami

W.

,

Kotake

K.

,

Ohnishi

N.

,

Yamada

S.

,

Sawada

K.

,

2009

,

ApJ

,

700

,

232

10.1088/0004-637X/700/1/232

Crossref

Search ADS

Kato

S.

,

1990

,

PASJ

,

42

,

99

Kato

S.

,

2007

,

PASJ

,

59

,

451

10.1093/pasj/59.2.451

Crossref

Search ADS

Kato

S.

,

Fukue

J.

,

1980

,

PASJ

,

32

,

377

Kazeroni

R.

,

Guilet

J.

,

Foglizzo

T.

,

2016

,

MNRAS

,

456

,

126

10.1093/mnras/stv2666

Crossref

Search ADS

Kazeroni

R.

,

Guilet

J.

,

Foglizzo

T.

,

2017

,

MNRAS

,

471

,

914

10.1093/mnras/stx1566

Crossref

Search ADS

Kluzniak

W.

,

Abramowicz

M. A.

,

2002

,

preprint (arXiv:astro-ph/0203314)

Kluźniak

W.

,

Abramowicz

M. A.

,

Kato

S.

,

Lee

W. H.

,

Stergioulas

N.

,

2004

,

ApJ

,

603

,

L89

.

Princeton Univ. Press

.

10.1086/383143

Crossref

Search ADS

Kulsrud

R. M.

,

2005

,

Plasma Physics for Astrophysics

.

Princeton Univ. Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Laming

J. M.

,

2007

,

ApJ

,

659

,

1449

10.1086/512534

Crossref

Search ADS

Langer

S. H.

,

Chanmugam

G.

,

Shaviv

G.

,

1981

,

ApJ

,

245

,

L23

10.1086/183514

Crossref

Search ADS

McCrea

W. H.

,

1956

,

ApJ

,

124

,

461

10.1086/146242

Crossref

Search ADS

Marek

A.

,

Janka

H.-T.

,

2009

,

ApJ

,

694

,

664

10.1088/0004-637X/694/1/664

Crossref

Search ADS

Méndez

M.

,

Belloni

T.

,

2007

,

MNRAS

,

381

,

790

10.1111/j.1365-2966.2007.12306.x

Crossref

Search ADS

Mignone

A.

,

Tzeferacos

P.

,

2010

,

J. Comput. Phys.

,

229

,

2117

10.1016/j.jcp.2009.11.026

Crossref

Search ADS

Mignone

A.

,

Bodo

G.

,

Massaglia

S.

,

Matsakos

T.

,

Tesileanu

O.

,

Zanni

C.

,

Ferrari

A.

,

2007

,

ApJS

,

170

,

228

10.1086/513316

Crossref

Search ADS

Miller

M. C.

,

Lamb

F. K.

,

Psaltis

D.

,

1998

,

ApJ

,

508

,

791

10.1086/306408

Crossref

Search ADS

Molteni

D.

,

Sponholz

H.

,

Chakrabarti

S. K.

,

1996

,

ApJ

,

457

,

805

10.1086/176775

Crossref

Search ADS

Mukhopadhyay

B.

,

2009

,

ApJ

,

694

,

387

10.1088/0004-637X/694/1/387

Crossref

Search ADS

Mukhopadhyay

B.

,

Ray

S.

,

Dey

J.

,

Dey

M.

,

2003

,

ApJ

,

584

,

L83

10.1086/373890

Crossref

Search ADS

Mukhopadhyay

B.

,

Bhattacharya

D.

,

Sreekumar

P.

,

2012

,

Int. J. Mod. Phys. D

,

21

,

1250086

10.1142/S0218271812500861

Crossref

Search ADS

Nagakura

H.

,

Yamada

S.

,

2009

,

ApJ

,

696

,

2026

10.1088/0004-637X/696/2/2026

Crossref

Search ADS

Narayan

R.

,

Yi

I.

,

1995

,

ApJ

,

452

,

710

10.1086/176343

Crossref

Search ADS

Ohnishi

N.

,

Kotake

K.

,

Yamada

S.

,

2006

,

ApJ

,

641

,

1018

10.1086/500554

Crossref

Search ADS

Papaloizou

J. C. B.

,

Pringle

J. E.

,

1984

,

MNRAS

,

208

,

721

10.1093/mnras/208.4.721

Crossref

Search ADS

Pétri

J.

,

2005

,

A&A

,

439

,

L27

10.1051/0004-6361:200500151

Crossref

Search ADS

Rajesh

S. R.

,

Mukhopadhyay

B.

,

2010

,

MNRAS

,

402

,

961

10.1111/j.1365-2966.2009.15925.x

Crossref

Search ADS

Remillard

R. A.

,

2004

, in

Kaaret

P.

,

Lamb

F. K.

,

Swank

J. H.

, eds,

AIP Conf. Proc. Vol. 714, X-ray Timing 2003: Rossi and Beyond

.

Am. Inst. Phys.

,

New York

, p.

13

,

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Remillard

R. A.

,

Morgan

E. H.

,

McClintock

J. E.

,

Bailyn

C. D.

,

Orosz

J. A.

,

1999

,

ApJ

,

522

,

397

10.1086/307606

Crossref

Search ADS

Remillard

R. A.

,

Muno

M. P.

,

McClintock

J. E.

,

Orosz

J. A.

,

2002

,

ApJ

,

580

,

1030

10.1086/343791

Crossref

Search ADS

Ryu

D.

,

Brown

G. L.

,

Ostriker

J. P.

,

Loeb

A.

,

1995

,

ApJ

,

452

,

364

10.1086/176308

Crossref

Search ADS

Sato

J.

,

Foglizzo

T.

,

Fromang

S.

,

2009

,

ApJ

,

694

,

833

10.1088/0004-637X/694/2/833

Crossref

Search ADS

Saxton

C. J.

,

2002

,

PASA

,

19

,

282

10.1071/AS02004

Crossref

Search ADS

Scheck

L.

,

Janka

H.-T.

,

Foglizzo

T.

,

Kifonidis

K.

,

2008

,

A&A

,

477

,

931

10.1051/0004-6361:20077701

Crossref

Search ADS

Sharma

P.

,

Quataert

E.

,

Hammett

G. W.

,

Stone

J. M.

,

2007

,

ApJ

,

667

,

714

10.1086/520800

Crossref

Search ADS

Stella

L.

,

Vietri

M.

,

1999

,

Phys. Rev. Lett.

,

82

,

17

10.1103/PhysRevLett.82.17

Crossref

Search ADS

Strohmayer

T. E.

,

2001

,

ApJ

,

552

,

L49

10.1086/320258

Crossref

Search ADS

Strohmayer

T. E.

,

Zhang

W.

,

Swank

J. H.

,

Smale

A.

,

Titarchuk

L.

,

Day

C.

,

Lee

U.

,

1996

,

ApJ

,

469

,

L9

10.1086/310261

Crossref

Search ADS

van der Klis

M.

,

2004

,

preprint (arXiv:e-prints)

van der Klis

M.

,

van Paradijs

J.

,

Lewin

W. H. G.

,

Lamb

F. K.

,

Vaughan

B.

,

Kuulkers

E.

,

Augusteijn

T.

,

1996

,

IAU Circ.

,

6428

Wagoner

R. V.

,

Silbergleit

A. S.

,

Ortega-Rodríguez

M.

,

2001

,

ApJ

,

559

,

L25

10.1086/323655

Crossref

Search ADS

Wijnands

R.

,

van der Klis

M.

,

Homan

J.

,

Chakrabarty

D.

,

Markwardt

C. B.

,

Morgan

E. H.

,

2003

,

Nature

,

424

,

44

Yamasaki

T.

,

Foglizzo

T.

,

2008

,

ApJ

,

679

,

607

10.1086/587732

Crossref

Search ADS

Yang

R.

,

Kafatos

M.

,

1995

,

A&A

,

295

,

238

Yuan

F.

,

Narayan

R.

,

2014

,

ARA&A

,

52

,

529

10.1146/annurev-astro-082812-141003

Crossref

Search ADS

Download all slides

Month:	Total Views:
February 2018	4
March 2018	4
April 2018	10
May 2018	5
June 2018	7
July 2018	5
August 2018	5
September 2018	9
October 2018	6
November 2018	5
December 2018	12
February 2019	5
March 2019	17
April 2019	11
May 2019	11
June 2019	14
July 2019	18
August 2019	14
September 2019	9
October 2019	27
November 2019	12
December 2019	8
January 2020	10
February 2020	9
March 2020	8
April 2020	12
May 2020	6
June 2020	11
July 2020	19
August 2020	4
September 2020	3
October 2020	8
November 2020	2
December 2020	4
January 2021	2
February 2021	3
March 2021	12
April 2021	5
June 2021	9
July 2021	14
August 2021	4
September 2021	10
October 2021	8
November 2021	4
December 2021	2
January 2022	14
February 2022	4
March 2022	5
April 2022	5
May 2022	1
June 2022	7
July 2022	7
August 2022	13
September 2022	28
October 2022	12
November 2022	2
December 2022	6
January 2023	13
February 2023	4
March 2023	16
April 2023	4
May 2023	6
June 2023	2
July 2023	4
August 2023	5
September 2023	6
October 2023	5
November 2023	3
December 2023	9
January 2024	8
February 2024	8
March 2024	6
April 2024	4
May 2024	28
June 2024	7
July 2024	16
August 2024	2
September 2024	11
October 2024	4
November 2024	4
December 2024	3
January 2025	2
February 2025	1
March 2025	12
April 2025	4
May 2025	4

Article Contents

Magnetized SASI: its mechanism and possible connection to some QPOs in XRBs

Abstract

1 INTRODUCTION

2 WHAT IS SASI AND WHY?

2.1 Advective-acoustic cycle

2.2 Acoustic cycle

3 METHOD

3.1 Equations solved

3.2 Grid and boundary conditions

3.3 Initial conditions

4 BONDI ACCRETION WITH SPLIT-MONOPOLAR FIELD

5 RESULTS

5.1 HD

5.1.1 Flow evolution

5.1.2 Mode analysis

5.1.3 Methods to measure SASI time period

5.1.4 Timescales from linear theory

5.2 MHD

5.2.1 Evolution of the flow

5.2.2 Mode analysis

5.2.3 Timescales from linear theory

6 DISCUSSIONS AND CONCLUSIONS

6.1 Flow structure

6.2 SASI mechanism

6.3 QPOs and SASI

6.4 Caveats of the model

7 SUMMARY

ACKNOWLEDGEMENTS

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Magnetized SASI: its mechanism and possible connection to some QPOs in XRBs

Abstract

1 INTRODUCTION

2 WHAT IS SASI AND WHY?

2.1 Advective-acoustic cycle

2.2 Acoustic cycle

3 METHOD

3.1 Equations solved

3.2 Grid and boundary conditions

3.3 Initial conditions

4 BONDI ACCRETION WITH SPLIT-MONOPOLAR FIELD

5 RESULTS

5.1 HD

5.1.1 Flow evolution

5.1.2 Mode analysis

5.1.3 Methods to measure SASI time period

5.1.4 Timescales from linear theory

5.2 MHD

5.2.1 Evolution of the flow

5.2.2 Mode analysis

5.2.3 Timescales from linear theory

6 DISCUSSIONS AND CONCLUSIONS

6.1 Flow structure

6.2 SASI mechanism

6.3 QPOs and SASI

6.4 Caveats of the model

7 SUMMARY

ACKNOWLEDGEMENTS

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only