-
PDF
- Split View
-
Views
-
Cite
Cite
Yan Xu, Xiu Lin Huang, Xiao Jun Zhang, Zi Yu, Cun Bo Fan, Wen Bo Ding, Cheng Zhi Liu, The influence of antikaon condensations on nucleon 1S0 superfluidity in neutron star matter, Monthly Notices of the Royal Astronomical Society, Volume 474, Issue 3, March 2018, Pages 3576–3581, https://doi.org/10.1093/mnras/stx2999
Close - Share Icon Share
Abstract
The properties of neutron and proton 1S0 superfluidity are studied within the relativistic mean field and the Bardeen–Cooper–Schrieffer theories by taking the effects of K− and |$\bar{K}^{0}$| condensations into account in neutron star matter without the hyperon degrees of freedom. It is found that antikaon condensations change the Fermi momenta, the effective masses and the single particle energies of nucleons in neutron star matter. These changes lead to a strong suppression of the neutron 1S0 superfluidity and an obvious enhancement of the proton 1S0 superfluidity in neutron star matter, respectively. In particular, the neutron and proton 1S0 pairing gaps are gradually shrinking with the optical potential of antikaons from −80 to −130 MeV. And antikaon condensations have little influence on the neutron 1S0 superfluid range, however, they have been markedly downsized the proton 1S0 superfluid range as the deepening of the optical potential of antikaons in neutron star matter. We also found that the nucleon 1S0 superfluidity and K− condensations within the scope of above optical potential of antikaons can occur in the core of PSR J1614-2230 and PSR J0348+0432 at the same time. Whereas |$\bar{K}^{0}$| condensations only occur in the two pulsars when the range of optical potential of antikaons is from −100 to −130 MeV.
1 INTRODUCTION
It is well known that a neutron star (NS) is one of the most interesting stellar objects for nuclear physics and astrophysics in the Universe. Its structure depends in a straightforward way on the equation of state (EOS) of dense matter. However, the inner structure of NS remains unknown mainly due to the theoretical uncertainties in the extrapolation of dense matter physics to high densities (Lattimer & Prakash 2016). But it is certain that the exotic matter, such as hyperons, antikaon condensation, strange quark matter, and the mixed phase of hadron and quark, can come into NS matter as growing the baryon density. Neutrons, protons and hyperons in NS interiors can transition into the superfluid states because of the attractive interactions between two baryons. Migdal first proposed that neutron superfuidity may appear in NS matter at a fairly low temperature, through the generation of nn Cooper pairs (Migdal 1959). When an NS is reduced to the neutron superfluid critical temperature within a few years after its birth, neutrons are supposed to form 1S0 pairings in NS inner crust and 3P2 pairings in NS core, respectively (Takatsuka 1995; Yakovlev, Levenfish & Shibanov 1999; Gnedin, Yakovlev & Potekhin 2001; Dean & Hjorth-Jensen 2003; Chen et al. 2006; Shternin & Yakovlev 2011; Huang et al. 2016). Protons (and possible hyperons) are also likely to form superfluidity in NS core with supranuclear density. It is generally believed that the presence of neutron and proton superfluids is closely related to the cooling processes via neutrino emission which dominates about 105–106 years of NS thermal evolution (Kaminker, Yakovlev & Gnedin 2002; Zuo et al. 2004; Tanigawa, Matsuzaki & Chiba 2004; Zuo & Lombardo 2010; Gao et al. 2011; Xu et al. 2012, 2013, 2014, 2015, 2016; Huang et al. 2015; Luo & Yin 2015). The properties of neutron and proton superfluidity might heavily affect how to explain the pulsar observational data. The precise theoretical calculations of nucleon pairing gaps have been considered using different model potentials of the nucleon–nucleon (NN) interaction based on microscopic many-body approaches and give similar density ranges for the presence of the nucleon 1S0 pairings. Nevertheless, because of many uncertain factors about the NN interaction such as indirect observational data in extreme conditions leading to approximations used in above calculations, these processes cannot obtain accurate results for the nucleon pairing gaps and estimate the quantitative effects of the nucleon superfluids on NS matter.
In 1986, Kaplan and Nelson have, for the first time, shown that K− mesons could undergo Bose–Einstein condensation in dense matter (Kaplan & Nelson 1986; Nelson & Kaplan 1987). In recent years, studies also demonstrated that antikaon condensations, including both K− and |$\bar{K}^{0}$| condensations, could occur in NS matter and can soften the EOS, change the distributions of particles, the effective masses and the single particle energy of baryons, and reduce the maximum masses of NSs. Consequently the properties of neutron and proton superfluidity in NS matter should be affected. However, the intensity of antikaon condensations is very sensitive to the optical potential of antikaons |$U_{\bar{K}}$| at saturation density of nuclear matter (Lee et al. 1995; Glendenning & Schaffner-Bielich 1999; Banik & Bandyopadhyay 2002; Kolomeistev & Voskresensky 2003; Gu et al. 2005; Ding et al. 2008, 2009), which is restricted from −80 to −150 MeV by the experiments, we choose |$U_{\bar{K}}$| = −80, −90, −100, −110, −120 and −130 MeV for the calculation below. Up to now, we do not know how the nucleon 1S0 pairing gaps change if antikaon condensates appear in NS matter, so the research mainly focuses on the effects of antikaon condensations on the nucleon 1S0 pairing gaps in NS matter.
The content of the paper is arranged in the following way. The properties of NSs including antikaon condensations and nucleon 1S0 pairings are described using the relativistic mean field (RMF) and the Bardeen–Cooper–Schrieffer (BCS) theories in Section 2. We employ the simplest NS model, assuming that an NS core consists of n, p, e and possibly μ (npeμ matter). The numerical results about how K− and |$\bar{K}^{0}$| affect the properties of neutron and proton 1S0 superfluidity in npeμ matter are discussed in Section 3. The summary and conclusion are presented in Section 4.
2 THEORETICAL FRAMEWORK
2.1 RMF theory
2.2 Superfluidity theory
3 RESULTS AND DISCUSSION
3.1 Properties of NSs
When K− and |$\bar{K}^{0}$| condensations appear in NS matter, the main contribution of them is to change that EOS. The change of EOS must lead to the change of the bulk properties of NSs. According to equation (21), the important physical quantities for the neutron and proton 1S0 superfluidity are the NN potential, the Fermi momentum, the effective mass and the single-particle energy of nucleons. Because the uncertainty of the NN potential remains, in this work, we use the Reid soft core (RSC) potential for the NN potential (Sprung & Banerjee 1971; Amundsen & Østgaard 1985; Nishizaki et al. 1991; Wambach, Ainsworth & Pines 1993), as an example to demonstrate the influence of antikaon condensations on the nucleon 1S0 pairing gaps in npeμ matter. The possibility that the presence of a pairing force induced by the exchange of a soft neutral pionic mode influences the neutron and proton 1S0 superfluidity (Yu, Huang & Yin 2009; Pankratov, Baldo & Saperstein 2015; Ding D et al. 2016) in NS matter cannot be excluded but is beyond the scope of this work. Next, we will present the results of numerical calculation for the nucleon 1S0 pairing gaps in npeμ and npe|$\mu K^{-} \bar{K}^{0}$| matter, respectively. The properties of NSs are derived using the successful RMF parameter set GM1 (Banik & Bandyopadhyay 2001; Miyatsu, Cheoun & Saito 2013).
Fig. 1 shows the EOSs and NS masses as a functions of nucleon density nN in the various optical potential depth of antikaons |$U_{\bar{K}}$|, respectively. In the paper, the black, red, blue, dark cyan, magenta, dark yellow and green lines represent the seven cases of |$U_{\bar{K}}$| = −80, −90, −100, −110, −120, −130 and 0 MeV, respectively. It is shown in Fig. 1(a) that the onset of K− and |$\bar{K}^{0}$| condensations leads to the softened EOSs of NSs. And the deeper optical potential of antikaons |$U_{\bar{K}}$|, the softer EOSs, which will inevitably cause obvious changes of bulk properties for NSs. The maximum masses of NSs, and the corresponding radii, the centre densities as well as the threshold densities of K− and |$\bar{K}^{0}$| condensations are listed in Table 1. As described in Fig. 1(b) and Table 1, the maximum masses of NSs are consistent with the observed values of PSR J1614-2230 (1.97 ± 0.04 M⊙) and J0348+0432 (2.01 ± 0.04 M⊙) (Demorest et al. 2010; Antoniadis et al. 2013), when K− and |$\bar{K}^{0}$| condensations appear with the various values of the optical potential of antikaons |$U_{\bar{K}}$|, from −80 to −130 MeV. Fig. 2 gives the particle fraction Yi as a function of nucleon density nN with and without K− and |$\bar{K}^{0}$| condensations in NS matter. In Fig. 2(a), one can see that the deeper optical potential of antikaons |$U_{\bar{K}}$|, the earlier onset of K− and |$\bar{K}^{0}$| condensations in NS matter. Moreover, |$\bar{K}^{0}$| condensation in comparison with K− condensation always occurs at a higher density. It can be seen from equation (10) that the threshold condition for |$\bar{K}^{0}$| condensations is more difficult to fulfill compared with the threshold condition for K− condensation in NSs. In our model, |$\bar{K}^{0}$| condensations only appear in stable NSs when the optical potential of antikaons |$U_{\bar{K}}$| = −100, −110, −120 and −130 MeV, and the presence of them suppresses the increase of the fraction of K− mesons as indicated in Fig. 2(a) and Table 1. Besides, it can be also seen from Figs 2(b) and (c) that the increase of K− mesons makes the dramatical decrease of e and μ fractions in NSs. It is because that K− meson is boson in the lowest energy state, replacing negatively charged particles, makes the system energy lower. In order to keep the conditions of the electrical neutrality, the proton fraction grows faster and then the growth is suppressed when |$\bar{K}^{0}$| mesons appears in NSs. Eventually, the proton fraction turns out to be almost identical neutron fraction in NS matter. Therefore, according to equation (15), the Fermi momenta of neutrons decrease and the corresponding values of protons increase including K− and |$\bar{K}^{0}$| condensations in NS matter, which are displayed in Fig. 3(a).
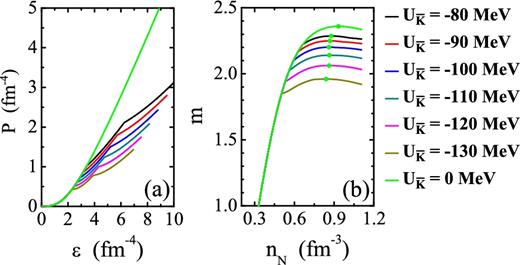
EOSs and NSs masses as a function of nucleon density nN. In the paper, the black, red, blue, dark cyan, magenta, dark yellow and green lines represent the seven cases of |$U_{\bar{K}}$| = −80, −90, −100, −110, −120, −130 and 0 MeV, respectively. The dots stand for the maximum masses of NSs for the seven cases.

Composition of NSs as a function of nucleon density nN with and without antikaon condensations. We take the optical potential of antikaons |$U_{\bar{K}}$| = −80, −90, −100, −110, −120, −130 and 0 MeV.
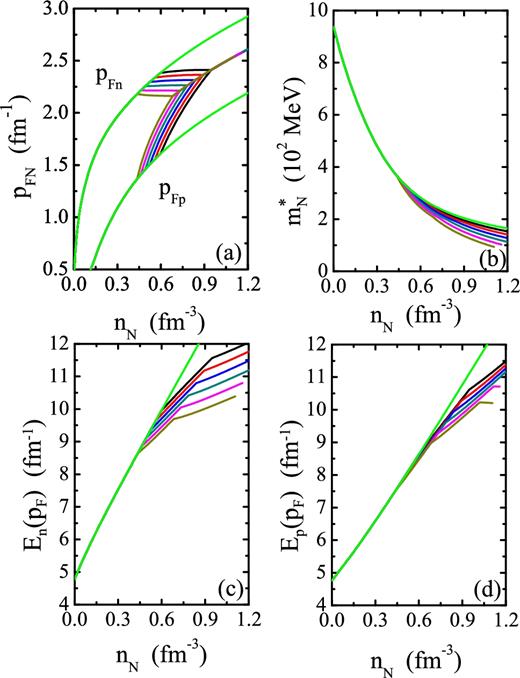
The nucleon Fermi momentum, the effective mass and the single particle energy EN(pF) at the Fermi surface versus nucleon density nN in npeμ and npe|$\mu K^{-} \bar{K}^{0}$| matter. We take the optical potential of antikaons |$U_{\bar{K}}$| = −80, −90, −100, −110, −120, −130 and 0 MeV.
Maximum masses mmax = Mmax/M⊙, and the corresponding radii R and the centre densities nC as well as the threshold densities |$n_{K^{-}C}$| and |$n_{\bar{K}^{0}C}$| of K− and |$\bar{K}^{0}$| condensations for the optical potential of antikaons |$U_{\bar{K}}$| = −80, −90, −100, −110, −120, −130 and 0 MeV, respectively.
| |$U_{\bar{K}}$|(MeV) . | mmax . | R (km) . | nC(fm−3) . | |$n_{K^{-}C}$| (fm−3) . | |$n_{{\bar{K}}^{0}C}$| (fm−3) . |
|---|---|---|---|---|---|
| −80 | 2.286 | 12.450 | 0.878 | 0.599 | 0.950 |
| −90 | 2.250 | 12.533 | 0.868 | 0.562 | 0.895 |
| −100 | 2.202 | 12.597 | 0.860 | 0.527 | 0.841 |
| −110 | 2.141 | 12.624 | 0.864 | 0.494 | 0.788 |
| −120 | 2.062 | 12.752 | 0.862 | 0.465 | 0.735 |
| −130 | 1.960 | 12.912 | 0.839 | 0.437 | 0.685 |
| |$\hphantom{0}$|0 | 2.359 | 11.913 | 0.932 | – | – |
| |$U_{\bar{K}}$|(MeV) . | mmax . | R (km) . | nC(fm−3) . | |$n_{K^{-}C}$| (fm−3) . | |$n_{{\bar{K}}^{0}C}$| (fm−3) . |
|---|---|---|---|---|---|
| −80 | 2.286 | 12.450 | 0.878 | 0.599 | 0.950 |
| −90 | 2.250 | 12.533 | 0.868 | 0.562 | 0.895 |
| −100 | 2.202 | 12.597 | 0.860 | 0.527 | 0.841 |
| −110 | 2.141 | 12.624 | 0.864 | 0.494 | 0.788 |
| −120 | 2.062 | 12.752 | 0.862 | 0.465 | 0.735 |
| −130 | 1.960 | 12.912 | 0.839 | 0.437 | 0.685 |
| |$\hphantom{0}$|0 | 2.359 | 11.913 | 0.932 | – | – |
Maximum masses mmax = Mmax/M⊙, and the corresponding radii R and the centre densities nC as well as the threshold densities |$n_{K^{-}C}$| and |$n_{\bar{K}^{0}C}$| of K− and |$\bar{K}^{0}$| condensations for the optical potential of antikaons |$U_{\bar{K}}$| = −80, −90, −100, −110, −120, −130 and 0 MeV, respectively.
| |$U_{\bar{K}}$|(MeV) . | mmax . | R (km) . | nC(fm−3) . | |$n_{K^{-}C}$| (fm−3) . | |$n_{{\bar{K}}^{0}C}$| (fm−3) . |
|---|---|---|---|---|---|
| −80 | 2.286 | 12.450 | 0.878 | 0.599 | 0.950 |
| −90 | 2.250 | 12.533 | 0.868 | 0.562 | 0.895 |
| −100 | 2.202 | 12.597 | 0.860 | 0.527 | 0.841 |
| −110 | 2.141 | 12.624 | 0.864 | 0.494 | 0.788 |
| −120 | 2.062 | 12.752 | 0.862 | 0.465 | 0.735 |
| −130 | 1.960 | 12.912 | 0.839 | 0.437 | 0.685 |
| |$\hphantom{0}$|0 | 2.359 | 11.913 | 0.932 | – | – |
| |$U_{\bar{K}}$|(MeV) . | mmax . | R (km) . | nC(fm−3) . | |$n_{K^{-}C}$| (fm−3) . | |$n_{{\bar{K}}^{0}C}$| (fm−3) . |
|---|---|---|---|---|---|
| −80 | 2.286 | 12.450 | 0.878 | 0.599 | 0.950 |
| −90 | 2.250 | 12.533 | 0.868 | 0.562 | 0.895 |
| −100 | 2.202 | 12.597 | 0.860 | 0.527 | 0.841 |
| −110 | 2.141 | 12.624 | 0.864 | 0.494 | 0.788 |
| −120 | 2.062 | 12.752 | 0.862 | 0.465 | 0.735 |
| −130 | 1.960 | 12.912 | 0.839 | 0.437 | 0.685 |
| |$\hphantom{0}$|0 | 2.359 | 11.913 | 0.932 | – | – |
Fig. 3 gives the nucleon Fermi momentum pFN, the effective mass |$m_{N}^{*}$| and the single particle energy EN(pF) at the Fermi surface as a function of nucleon density nN including and not including K− and |$\bar{K}^{0}$| condensations in npeμ matter. We could see that the nucleon effective mass |$m_{N}^{*}$| with K− and |$\bar{K}^{0}$| condensations is smaller than the corresponding values without K− and |$\bar{K}^{0}$| condensations, and it gradually declines along with the optical potential of antikaons |$U_{\bar{K}}$| growth in npe|$\mu K^{-} \bar{K}^{0}$| matter in Fig. 3(b). The individual single particle energies of neutrons and protons in npe|$\mu K^{-} \bar{K}^{0}$| matter are all much less than their values in npeμ matter, as depicted in Figs 3(c) and (d). Moreover, according to equation (22), the decrease of the Fermi momentum pFn, the effective mass |$m_{{\rm n}}^{*}$| and |$m_{{\rm p}}^{*}$| with the deepening of the optical potential of antikaons |$U_{\bar{K}}$| results in gradually reduced the single particle energies of nucleons in npe|$\mu K^{-} \bar{K}^{0}$| matter. Whereas the single particle energy of proton decreases slowly, which is due to the increasing of Fermi momentum of proton pFp with increasing the optical potential of antikaons |$U_{\bar{K}}$| in npe|$\mu K^{-} \bar{K}^{0}$| matter (see Fig. 3a for details). Fig. 4 presents the nucleon 1S0 pairing gaps ΔN(pF) at the Fermi surface as a function of nucleon density nN with and without K− and |$\bar{K}^{0}$| condensations in NS matter. In Fig. 4, one can see that the neutron 1S0 pairing gap always exists in the region with lower densities whether K− and |$\bar{K}^{0}$| condensations appear. Thus, the region with the neutron 1S0 superfluids only affects the surface cooling of NSs. The proton 1S0 superfluids can reach relatively high densities which are closely associated with the cooling processes via neutrino emission governing most of the time NS cooling. To clearly see the influence of K− and |$\bar{K}^{0}$| condensations on the nucleon 1S0 pairing gaps in NS matter more intuitively, the maximums of the nucleon 1S0 pairing gaps at the Fermi surface and the corresponding critical temperatures as well as the density ranges of the nucleon 1S0 superfluids with and without K− and |$\bar{K}^{0}$| condensations are listed in Table 2. As seen in Fig. 4 and Table 2, in relation to npeμ matter, the appearance of K− and |$\bar{K}^{0}$| condensations causes the decay of the neutron 1S0 pairing gap Δn(pF) and the growth of the proton 1S0 pairing gap Δp(pF) in NS matter, respectively. According to equation (23), it necessarily leads to the growth of the critical temperatures of the proton 1S0 superfluids in npe|$\mu K^{-} \bar{K}^{0}$| matter, which will result in a more pronounced inhibition of the neutrino emissivities for the neutrino emission processes involving protons, the system thermal capacity and can further affect the rate of NS thermal evolution. Furthermore, the neutron and proton 1S0 pairing gaps ΔN(pF) decrease along with the increase of the optical potential of antikaons |$U_{\bar{K}}$| in npe|$\mu K^{-} \bar{K}^{0}$| matter. In addition, as shown in Table 2, the appearance of K− and |$\bar{K}^{0}$| condensations has little or no effect on the scope of nucleon density for the neutron 1S0 superfluidity, while obviously shrinks the scope of nucleon density for the proton 1S0 superfluidity as the deepening of the optical potential of antikaons |$U_{\bar{K}}$| in NS matter. This is mainly due to the fact that the neutron fraction Yn has not changed within the scope of nucleon density involving the neutron 1S0 superfluidity, whereas the proton fraction Yp is improved evidently within the scope of nucleon density involving the proton 1S0 superfluidity as the deepening of the optical potential of antikaons |$U_{\bar{K}}$| in NS matter (see Fig. 2 for details), respectively. In future, we will further study and work in-depth study about the influence of K− and |$\bar{K}^{0}$| condensations on the rate of NS cooling.
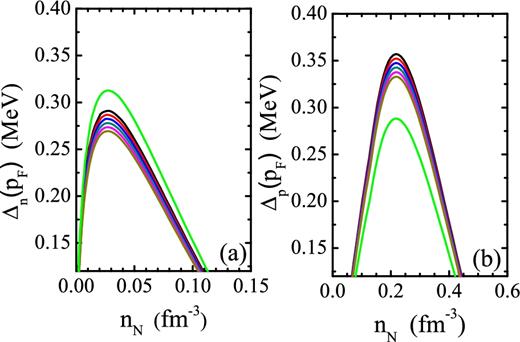
The nucleon 1S0 pairing gaps ΔN(pF) at the Fermi surface as a function of nucleon density nN in npeμ and npe|$\mu K^{-} \bar{K}^{0}$| matter. We take the optical potential of antikaons |$U_{\bar{K}}$| = −80, −90, −100, −110, −120, −130 and 0 MeV.
Maximums of the nucleon 1S0 pairing gaps at the Fermi surface and the corresponding critical temperatures as well as density ranges of the nucleon 1S0 superfluidity in npeμ and npe|$\mu K^{-} \bar{K}^{0}$| matter. We choose the optical potential of antikaons |$U_{\bar{K}}$| = −80, −90, −100, −110, −120, −130 and 0 MeV.
| |$U_{\bar{K}}$| (MeV) . | |$\Delta _{n}^{{\rm max}}$| . | |$\Delta _{p}^{{\rm max}}$| . | TCn (109K) . | TCp (109K) . | Neutron 1S0 SF . | Proton 1S0 SF . |
|---|---|---|---|---|---|---|
| −80 | 0.291 | 0.357 | 1.92 | 2.35 | 0.0 ≤ nN ≤ 0.235 | 0.0 ≤ nN ≤ 0.618 |
| −90 | 0.287 | 0.352 | 1.89 | 2.32 | 0.0 ≤ nN ≤ 0.235 | 0.0 ≤ nN ≤ 0.603 |
| −100 | 0.282 | 0.348 | 1.86 | 2.29 | 0.0 ≤ nN ≤ 0.225 | 0.0 ≤ nN ≤ 0.580 |
| −110 | 0.278 | 0.343 | 1.83 | 2.26 | 0.0 ≤ nN ≤ 0.234 | 0.0 ≤ nN ≤ 0.558 |
| −120 | 0.274 | 0.338 | 1.81 | 2.23 | 0.0 ≤ nN ≤ 0.233 | 0.0 ≤ nN ≤ 0.514 |
| −130 | 0.269 | 0.333 | 1.78 | 2.20 | 0.0 ≤ nN ≤ 0.232 | 0.0 ≤ nN ≤ 0.513 |
| |$\hphantom{0}$|0 | 0.313 | 0.288 | 2.06 | 1.90 | 0.0 ≤ nN ≤ 0.232 | 0.0 ≤ nN ≤ 0.647 |
| |$U_{\bar{K}}$| (MeV) . | |$\Delta _{n}^{{\rm max}}$| . | |$\Delta _{p}^{{\rm max}}$| . | TCn (109K) . | TCp (109K) . | Neutron 1S0 SF . | Proton 1S0 SF . |
|---|---|---|---|---|---|---|
| −80 | 0.291 | 0.357 | 1.92 | 2.35 | 0.0 ≤ nN ≤ 0.235 | 0.0 ≤ nN ≤ 0.618 |
| −90 | 0.287 | 0.352 | 1.89 | 2.32 | 0.0 ≤ nN ≤ 0.235 | 0.0 ≤ nN ≤ 0.603 |
| −100 | 0.282 | 0.348 | 1.86 | 2.29 | 0.0 ≤ nN ≤ 0.225 | 0.0 ≤ nN ≤ 0.580 |
| −110 | 0.278 | 0.343 | 1.83 | 2.26 | 0.0 ≤ nN ≤ 0.234 | 0.0 ≤ nN ≤ 0.558 |
| −120 | 0.274 | 0.338 | 1.81 | 2.23 | 0.0 ≤ nN ≤ 0.233 | 0.0 ≤ nN ≤ 0.514 |
| −130 | 0.269 | 0.333 | 1.78 | 2.20 | 0.0 ≤ nN ≤ 0.232 | 0.0 ≤ nN ≤ 0.513 |
| |$\hphantom{0}$|0 | 0.313 | 0.288 | 2.06 | 1.90 | 0.0 ≤ nN ≤ 0.232 | 0.0 ≤ nN ≤ 0.647 |
Maximums of the nucleon 1S0 pairing gaps at the Fermi surface and the corresponding critical temperatures as well as density ranges of the nucleon 1S0 superfluidity in npeμ and npe|$\mu K^{-} \bar{K}^{0}$| matter. We choose the optical potential of antikaons |$U_{\bar{K}}$| = −80, −90, −100, −110, −120, −130 and 0 MeV.
| |$U_{\bar{K}}$| (MeV) . | |$\Delta _{n}^{{\rm max}}$| . | |$\Delta _{p}^{{\rm max}}$| . | TCn (109K) . | TCp (109K) . | Neutron 1S0 SF . | Proton 1S0 SF . |
|---|---|---|---|---|---|---|
| −80 | 0.291 | 0.357 | 1.92 | 2.35 | 0.0 ≤ nN ≤ 0.235 | 0.0 ≤ nN ≤ 0.618 |
| −90 | 0.287 | 0.352 | 1.89 | 2.32 | 0.0 ≤ nN ≤ 0.235 | 0.0 ≤ nN ≤ 0.603 |
| −100 | 0.282 | 0.348 | 1.86 | 2.29 | 0.0 ≤ nN ≤ 0.225 | 0.0 ≤ nN ≤ 0.580 |
| −110 | 0.278 | 0.343 | 1.83 | 2.26 | 0.0 ≤ nN ≤ 0.234 | 0.0 ≤ nN ≤ 0.558 |
| −120 | 0.274 | 0.338 | 1.81 | 2.23 | 0.0 ≤ nN ≤ 0.233 | 0.0 ≤ nN ≤ 0.514 |
| −130 | 0.269 | 0.333 | 1.78 | 2.20 | 0.0 ≤ nN ≤ 0.232 | 0.0 ≤ nN ≤ 0.513 |
| |$\hphantom{0}$|0 | 0.313 | 0.288 | 2.06 | 1.90 | 0.0 ≤ nN ≤ 0.232 | 0.0 ≤ nN ≤ 0.647 |
| |$U_{\bar{K}}$| (MeV) . | |$\Delta _{n}^{{\rm max}}$| . | |$\Delta _{p}^{{\rm max}}$| . | TCn (109K) . | TCp (109K) . | Neutron 1S0 SF . | Proton 1S0 SF . |
|---|---|---|---|---|---|---|
| −80 | 0.291 | 0.357 | 1.92 | 2.35 | 0.0 ≤ nN ≤ 0.235 | 0.0 ≤ nN ≤ 0.618 |
| −90 | 0.287 | 0.352 | 1.89 | 2.32 | 0.0 ≤ nN ≤ 0.235 | 0.0 ≤ nN ≤ 0.603 |
| −100 | 0.282 | 0.348 | 1.86 | 2.29 | 0.0 ≤ nN ≤ 0.225 | 0.0 ≤ nN ≤ 0.580 |
| −110 | 0.278 | 0.343 | 1.83 | 2.26 | 0.0 ≤ nN ≤ 0.234 | 0.0 ≤ nN ≤ 0.558 |
| −120 | 0.274 | 0.338 | 1.81 | 2.23 | 0.0 ≤ nN ≤ 0.233 | 0.0 ≤ nN ≤ 0.514 |
| −130 | 0.269 | 0.333 | 1.78 | 2.20 | 0.0 ≤ nN ≤ 0.232 | 0.0 ≤ nN ≤ 0.513 |
| |$\hphantom{0}$|0 | 0.313 | 0.288 | 2.06 | 1.90 | 0.0 ≤ nN ≤ 0.232 | 0.0 ≤ nN ≤ 0.647 |
4 CONCLUSIONS
We have studied the effects of antikaon condensations on the nucleon 1S0 superfluidity in NS matter using the RMF and the BCS theories. The results indicate that the presence of antikaon condensations has almost no influence on the scope of nucleon density for the neutron 1S0 superfluidity and significantly reduces the scope of nucleon density for the proton 1S0 superfluidity in NS matter, respectively. The neutron 1S0 pairing gaps with antikaon condensations are clearly below the corresponding values without antikaon condensations, while the proton 1S0 pairing gaps with antikaon condensations are obviously higher than the corresponding values without antikaon condensations in NS matter. In addition, the neutron and proton 1S0 pairing gaps both decrease with the deepening of the optical potential of antikaons in npe|$\mu K^{-} \bar{K}^{0}$| matter. The above change is bound to change the cooling rate of NSs.
Our model may be a simplification because it adopts the lowest level of approximation in the BCS equation as well as neglecting the possible influence of inhomogeneity in NS crust and hyperon superfluidity in NS core on the nucleon 1S0 superfluidity. While it can still clearly describe the effects of antikaon condensations on the nucleon 1S0 pairing gaps in npeμ matter. We will analyse more complicated models in future studies.
Acknowledgements
We acknowledge fruitful discussions with Prof. Lan Yin in School of Physics, Peking University. This work is funded by the National Natural Science Foundation of China (grant nos. 11447165, 11373047, 11404336 and U1731240) and Youth Innovation Promotion Association, CAS (grant nos. 2016056).



