Testing the isotropy of the Universe with Type Ia supernovae in a model-independent way

Wang, Yu-Yang; Wang, F Y

doi:10.1093/mnras/stx2982

Abstract

In this paper, we study an anisotropic universe model with Bianchi-I metric using Joint light-curve analysis (JLA) sample of Type Ia supernovae (SNe Ia). Because light-curve parameters of SNe Ia vary with different cosmological models and SNe Ia samples, we fit the SNe Ia light-curve parameters and cosmological parameters simultaneously employing Markov chain Monte Carlo method. Therefore, the results on the amount of deviation from isotropy of the dark energy equation of state (δ), and the level of anisotropy of the large-scale geometry (Σ₀) at present, are totally model-independent. The constraints on the skewness and cosmic shear are −0.101 < δ < 0.071 and −0.007 < Σ₀ < 0.008. This result is consistent with a standard isotropic universe (δ = Σ₀ = 0). However, a moderate level of anisotropy in the geometry of the Universe and the equation of state of dark energy, is allowed. Besides, there is no obvious evidence for a preferred direction of anisotropic axis in this model.

cosmological parameters

1 INTRODUCTION

Astronomical observations revealed that our Universe is undergoing an accelerating expansion (Riess et al. 1998;Perlmutter et al. 1999), which is one of the most surprising astronomical discoveries in recent years. Accelerating expansion implies that the universe is dominated by an unknown form of energy called ‘dark energy’ with negative pressure, or that Einstein’s theory of gravity fails on cosmological scales and requires some modifications.

The standard Lambda cold dark matter (ΛCDM) model is established based on the cosmological principle and parametrization of the big bang cosmological model. It depicts a homogeneous and isotropic universe on large scales with approximately 30 per cent matter (including baryonic matter and dark matter) and 70 per cent dark energy at present time, which is consistent with vast majority of several precise astronomical observations, including cosmic microwave background (CMB) power spectrum (WMAP Collaboration 2011; Planck Collaboration XIII 2016) and baryon acoustic oscillations (Eisenstein et al. 2005).

However, the standard cosmological model is challenged by a few puzzling cosmological observations (Perivolaropoulos 2014), which may require modifications. Evidence for cosmology anisotropy has been obtained by the power asymmetry of CMB perturbation maps (Eriksen et al. 2007; Hoftuft et al. 2009; Paci et al. 2010; Mariano & Perivolaropoulos 2013; Zhao & Santos 2015), the large-scale velocity flows (Kashlinsky et al. 2008; Watkins, Feldman & Hudson 2009; Feldman, Watkins & Hudson 2010; Kashkinsky et al. 2010; Lavaux et al. 2010), anisotropy in accelerating expansion rate (Antoniou & Perivolaropoulos 2010; Mariano & Perivolaropoulos 2012; Wang & Wang 2014; Yang, Wang & Chu 2014), spatial dependence of the value of the fine structure constant α (Moss et al. 2011; Webb et al. 2011; King et al. 2012; Mariano & Perivolaropoulos 2012; Pinho et al. 2016) and so on. These puzzles are in favour of preferred cosmological directions, which seem to violate the cosmological principle. The so-called ‘cosmic anomalies’ (Perivolaropoulos 2014) may either be simply large statistical fluctuations or have some physical origins, which could be either geometric or energy-related (Perivolaropoulos 2014).

Here, we focus on an anisotropic universe model that has a plane-symmetric Bianchi – I metric (Taub 1951; Aluri et al. 2013; Schücker, Tilquin & Valent 2014), namely ellipsoidal universe (Campanelli, Cea & Tedesco 2006). The ellipsoidal universe model was first proposed in Campanelli et al. (2006) to solve the CMB quadrupole problem by assuming a plane-symmetric universe with an eccentricity of the order of 10⁻² at decoupling. Campanelli, Cea & Tedesco (2007) discussed that the anisotropic expansion can be generated by cosmological magnetic fields, cosmic domain walls or cosmic strings. The cosmic shear Σ₀ and skewness δ are introduced (Campanelli et al. 2011a) to describe the anisotropy level of cosmic geometry and dark energy fluids, respectively. Campanelli et al. (2011c) analysed Union and Union2 compilation and concluded that an isotropic universe is consistent with Type Ia supernovae (SNe Ia) data. However, their analysis directly used μ_obs and σ obtained in ΛCDM model (Amanullah 2010). The results are model-dependent, because light-curve parameters change with different universe models and SNe Ia sample. Schücker et al. (2014) fitted the Bianchi – I metric to the Hubble diagram of SNe Ia.

Therefore, we improve the previous research by fitting the SNe Ia light-curve parameters and cosmological parameters simultaneously. This paper is organized as follows. In the next section, we introduce the ellipsoidal universe model and derive the magnitude–redshift relation. In Section 3, we use SNe Ia data of Joint light-curve analysis (JLA) sample to constrain all the free parameters simultaneously, including light-curve and cosmological parameters. The fitting results are shown in Section 4. Conclusion and discussions are given in Section 5.

2 ELLIPSOIDAL UNIVERSE MODEL

The Bianchi type I cosmological model is extensively discussed in Campanelli et al. (2006) and Campanelli et al. (2011a). In this section, we briefly introduce this model. The Bianchi-I metric (Taub 1951; Schücker et al. 2014) with planar symmetry (Campanelli et al. 2006, 2007; Campanelli et al. 2011a,b, 2011c) is described by Taub line element (Campanelli et al. 2011a,b) as

$$ \begin{equation} {\rm d}\tau ^2 = {\rm d}t^2 - a(t)^2({\rm d}x^2 + {\rm d}y^2) - b(t)^2{\rm d}z^2, \quad a(t), b(t) > 0, \end{equation} $$

(1)

where a(t) and b(t) are the scale factors, which can be normalized as a(t₀) = b(t₀) = 1 at the present time t₀.

According to the plane-symmetric metric, the ‘mean Hubble parameter’ H can be defined as (Campanelli et al. 2011b, 2011c)

$$ \begin{equation} H \equiv \frac{\dot{A}}{A}\, , \end{equation} $$

(2)

where |$A\equiv (a^2b)^{\frac{1}{3}}$| is the ‘mean expansion parameter’ (Campanelli et al. 2011b).

In order to measure the level of anisotropy, we define cosmic shear Σ and skewness δ (Campanelli et al. 2011a,b,c) as

$$ \begin{equation} \Sigma \equiv \frac{H_{\rm a} - H}{H}\, , \qquad {\rm and} \qquad \delta \equiv w_{\parallel } - w_{\perp }\, , \end{equation} $$

(3)

respectively. In the above equation, |$H_{\rm a} = \frac{\dot{a}}{a}$| represents the Hubble parameter in the symmetry plane. w_∥ and w_⊥ are parameters of state equation parallel and perpendicular to the symmetry plane, respectively. Besides, the mean parameter of state equation is defined as

$$ \begin{equation} w \equiv \frac{2w_\parallel + w_\perp }{3}\, . \end{equation} $$

(4)

2.1 Anisotropy axis

In the Galactic coordinate reference, the direction cosine of the symmetry axis is

$$ \begin{equation} \hat{n}_{\rm A} = (\cos b_{\rm A}\cos l_{\rm A}, \cos b_{\rm A}\sin l_{\rm A}, \sin b_{\rm A})\, . \end{equation} $$

(5)

For an arbitrary direction

$$ \begin{equation} \hat{n} = (\cos b\cos l, \cos b\sin l, \sin b), \end{equation} $$

(6)

the angle θ between |$\hat{n}$| and |$\hat{n}_{\rm A}$| is

$$ \begin{equation} \cos \theta \equiv \hat{n}\cdot \hat{n}_{\rm A}\, . \end{equation} $$

(7)

2.2 Redshift–distance relation

We introduce the ‘eccentricity’ e as

$$ \begin{equation} {e}^2 \equiv 1- \frac{b^2}{a^2}\, . \end{equation} $$

(8)

In galactic coordinates system, the luminosity distance is given by (Campanelli et al. 2011c)

$$ \begin{equation} d_{\rm L}(z,\theta ) = \frac{c(1+z)}{H_0}\int _{A(z)}^{1}\frac{(1-e^2)^\frac{1}{6}}{(1-e^2\cos ^2\theta )^{\frac{1}{2}}}\frac{{\rm d}A}{A^2\bar{H}}\, , \end{equation} $$

(9)

where |$\bar{H}$| is the Hubble constant normalized to its actual at t₀. Both |$\bar{H}$| and e are functions of A.

3 JLA SAMPLE AND MCMC FITTING

The JLA sample (Betoule et al. 2014) is based on Conley et al. (2011) compilation. It includes three-season data from SDSS-II (0.05 < z < 0.4), three-year data from SNLS (0.2 < z < 1), HST data (0.8 < z < 1.4), and several low-redshift samples (z < 0.1) such as Calán/Tololo Survey and Carnegie Supernova Project. The JLA sample totals 740 spectroscopically confirmed SNe Ia with high-quality light curves.

3.1 Angular position

In order to determine the anisotropy axis in the galactic coordinate system, we need galactic latitude and longitude (l, b) for each supernova. For transformations from equatorial to Galactic coordinates, we have

$$ \begin{equation} \sin b = \sin \delta _{{\rm NGP}}\sin \delta + \cos \delta _{{\rm NGP}}\cos \delta \cos (\alpha -\alpha _{{\rm NGP}})\, , \end{equation} $$

(10)

$$ \begin{equation} \cos b\sin (l_{{\rm NCP}}-l) = \cos \delta \sin (\alpha - \alpha _{{\rm NGP}})\, , \end{equation} $$

(11)

$$ \begin{eqnarray} \cos b\cos (l_{{\rm NCP}}-l)\! = \!\cos \delta _{{\rm NGP}}\sin \delta - \sin \delta _{{\rm NGP}}\cos \delta \cos (\alpha - \alpha _{{\rm NGP}}) . \nonumber \\ \end{eqnarray} $$

(12)

The angular position of SNe Ia are shown in Fig. 1.

Figure 1.

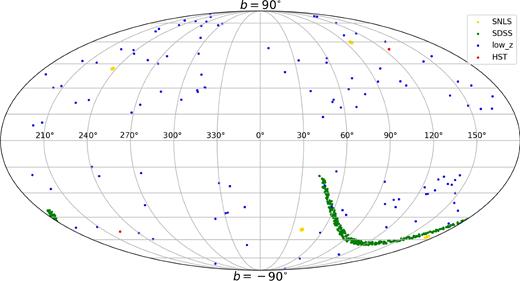
Angular positions of SNe Ia in the JLA sample. b (−90° ≤ b ≤ 90°) is the galactic latitude and l (0° ≤ l < 360°) is the galactic longitude. SNe from four subsets are marked with different colours.

Open in new tab Download slide

3.2 Distance modulus

The analysis of SNe light curves (Betoule et al. 2014) gives the distance estimation μ_obs as

$$ \begin{equation} \mu _{{\rm obs}} = m_B^{*} - M_B +\alpha x_1 - \beta c\, , \end{equation} $$

(13)

where |$m_B^{*}$| corresponds to the observed peak magnitude in rest-frame B band and M_B is the absolute B band magnitude. x₁ and c are SALT2 shape parameter and colour correction, respectively. α and β are nuisance parameters in the distance estimate to be determined.

We correct the effects of host galaxy properties assuming that the absolute magnitude is related to the host stellar mass (M_stellar) by a simple step function (Betoule et al. 2014)

$$ \begin{equation*} M_B = \left\lbrace \begin{array}{ll}M_B^1 & \textrm{if}\,M_{{\rm stellar}}<10^{10}\, {\rm M}_{{\odot }}{\rm .}\\\\ M_B^1 + \Delta _M & \textrm{otherwise.} \end{array} \right. \end{equation*} $$

Here, we introduce the theoretical distance modulus μ as

$$ \begin{equation} \mu _{{\rm th}} = 5\lg \left(\frac{d_{\rm L}}{{\rm Mpc}}\right) + 25\, . \end{equation} $$

(14)

3.3 The hubble diagram covariance matrix

Betoule et al. (2014) assemble a 3N_SN × 3N_SN = 2220 × 2220 covariance matrix for the light-curve parameters, which includes statistical and systematic uncertainties.

$$ \begin{eqnarray} {\bf C}_{\eta } &=& {\bf C}_{{\rm stat}} + ({\bf C}_{{\rm pecvel}} + {\bf C}_{{\rm nonIa}})_{{\bf C} 11} \nonumber \\ &&+ ({\bf C}_{{\rm cal}} + {\bf C}_{{\rm model}} + {\bf C}_{{\rm bias}} + {\bf C}_{{\rm host}} + {\bf C}_{{\rm dust}})_{{\rm re-evaluated}}\, . \end{eqnarray} $$

(15)

C_stat is obtained from error propagation of light-curve fit uncertainties. The systematic uncertainties include seven components, namely the calibration uncertainty |${\bf C}$|_cal, the light-curve model uncertainty |${\bf C}$|_model, the bias correction uncertainty |${\bf C}$|_bias, the mass step uncertainty |${\bf C}$|_host, the peculiar velocity uncertainty |${\bf C}$|_pecvel, and the non-Ia events uncertainty |${\bf C}$|_nonIa.

The covariance matrix (Betoule et al. 2014) of the vector of distance modulus estimate μ_obs is

$$ \begin{eqnarray} {}{\bf C} = {\bf {AC}}_{\eta }{\bf A}^{\dagger } + {\rm diag}\bigg (\frac{5\sigma _z}{z\ln 10}\bigg )^2 + {\rm diag}\left(\sigma _{{\rm lens}}^2\right) + {\rm diag}\left(\sigma _{{\rm coh}}^2\right),\nonumber\\ \end{eqnarray} $$

(16)

where |${\bf A}$| = |${\bf A}$|₀ + α|${\bf A}$|₁ − β|${\bf A}$|₂ is a 2220 × 740 matrix with (⁠|${\bf A}$|_k)_{i, j} = δ_{i, 3j + k} such that |$\boldsymbol{\mu } = {\bf A}\boldsymbol{\eta } - M_{B}$|⁠. Here, |$\boldsymbol{\eta } = ((m_B^*, x_1, c)_1,\ldots ,(m_B^*, x_1, c)_{740})$|⁠. The σ_z, σ_lens, and σ_coh account for the uncertainty in cosmological redshift due to peculiar velocities, the variation of magnitudes caused by gravitational lensing, and the intrinsic variation in SN magnitude not described by the other terms, respectively. Betoule et al. (2014) suggest cσ_z = 150 km s⁻¹ and σ_lens = 0.055 × z, while values of σ_coh are listed in Table 1.

Table 1.

Open in new tab

Values of σ_coh used in the cosmological fits for different samples.

Sample	Low-z	SDSS-II	SNLS	HST
\|$\boldsymbol{\sigma _{{\rm coh}}}$\|	0.134	0.108	0.080	0.100

Table 1.

Open in new tab

Values of σ_coh used in the cosmological fits for different samples.

Sample	Low-z	SDSS-II	SNLS	HST
\|$\boldsymbol{\sigma _{{\rm coh}}}$\|	0.134	0.108	0.080	0.100

3.4 Markov chain Monte Carlo fitting

We employ the emcee to carry out parameters fitting (Goodman & Weare 2010; Foreman-Mackey et al. 2013). The emcee is a python module that employs the affine-invariant ensemble sampler for Markov chain Monte Carlo (MCMC) algorithm. In this package, many samplers (called walkers) run in parallel and periodically exchange states to more efficiently sample the parameter space. The maximum likelihood estimation (MLE) is applied to MCMC algorithm. The likelihood L is sum of many normal distributions:

$$ \begin{equation} L = \prod _{i=1}^{740}\frac{1}{\sqrt{2\pi }\sigma _i}\exp \bigg [\frac{-(\mu _{{{\rm obs},i}}-\mu _{{{\rm th},i}})^2}{2\sigma _i^2}\bigg ], \end{equation} $$

(17)

where

$$ \begin{equation} \sigma _i = {\bf C}_{ii}. \end{equation} $$

(18)

Then the log-likelihood is

$$ \begin{equation} \ln L = -\frac{1}{2}\sum _{i=1}^{740}\bigg [\frac{(\mu _{{\rm obs,i}}-\mu _{{\rm th,i}})^2}{\sigma _i^2}+\ln \left(\sigma _i^2\right) + \ln (2\pi )\bigg ]\, . \end{equation} $$

(19)

The observational distance modulus μ_obs depends on light-curve parameters {|$\alpha , \beta , M_B^1, \Delta _M$|} , while the theoretical distance modulus μ_th depends on cosmological parameters {H₀, Ω_m, Σ₀, w, δ, l_A, b_A} in ellipsoidal universe model. The priors of parameters are listed in Table 2.

Table 2.

Open in new tab

The priors of free parameters in MCMC fitting.

Parameter	Prior	Parameter	Prior
α	[0.1, 0.2]	Σ₀	[−0.5, 0.5]
β	[2.0, 4.0]	w	[−2.0, 0.0]
\|$M_B^1$\|	[−19.3, -18.6]	δ	[−0.5, 0.5]
Δ_M	[−0.1, 0.0]	l_A	[0, π]
H₀	[60, 80]	b_A	[\|$-\frac{\pi }{2}$\|⁠, \|$\frac{\pi }{2}$\|]
Ω_m	[0.0, 0.5]

Parameter	Prior	Parameter	Prior
α	[0.1, 0.2]	Σ₀	[−0.5, 0.5]
β	[2.0, 4.0]	w	[−2.0, 0.0]
\|$M_B^1$\|	[−19.3, -18.6]	δ	[−0.5, 0.5]
Δ_M	[−0.1, 0.0]	l_A	[0, π]
H₀	[60, 80]	b_A	[\|$-\frac{\pi }{2}$\|⁠, \|$\frac{\pi }{2}$\|]
Ω_m	[0.0, 0.5]

Table 2.

Open in new tab

The priors of free parameters in MCMC fitting.

Parameter	Prior	Parameter	Prior
α	[0.1, 0.2]	Σ₀	[−0.5, 0.5]
β	[2.0, 4.0]	w	[−2.0, 0.0]
\|$M_B^1$\|	[−19.3, -18.6]	δ	[−0.5, 0.5]
Δ_M	[−0.1, 0.0]	l_A	[0, π]
H₀	[60, 80]	b_A	[\|$-\frac{\pi }{2}$\|⁠, \|$\frac{\pi }{2}$\|]
Ω_m	[0.0, 0.5]

Parameter	Prior	Parameter	Prior
α	[0.1, 0.2]	Σ₀	[−0.5, 0.5]
β	[2.0, 4.0]	w	[−2.0, 0.0]
\|$M_B^1$\|	[−19.3, -18.6]	δ	[−0.5, 0.5]
Δ_M	[−0.1, 0.0]	l_A	[0, π]
H₀	[60, 80]	b_A	[\|$-\frac{\pi }{2}$\|⁠, \|$\frac{\pi }{2}$\|]
Ω_m	[0.0, 0.5]

Campanelli et al. (2011c) studied an anisotropic Bianchi type I cosmological model using Union2 compilation, in which μ_obs and σ are derived in the ΛCDM model (Amanullah 2010). Therefore, the light-curve parameters {|$\alpha , \beta , M_B^1, \Delta _M$|} are fixed. However, the light-curve parameters vary with different cosmological model. It’s unreasonable to fit just cosmological parameters. Different from Campanelli et al. (2011c), we fit four light-curve parameters and seven cosmological parameters {H₀, Ω_m, Σ₀, w, δ, l_A, b_A} simultaneously. So the likelihood function depends on eleven free parameters. The derived results are model-independent.

As a comparison, we carried out another MCMC fitting, which constrained parameters {|$\alpha , \beta , M_B^1, \Delta _M, H_0, \Omega _{\rm m}, w$|} in a flat wCDM cosmology with an arbitrary equation of state w.

4 RESULTS

The confidence contours (1σ, 2σ and 3σ) and marginalized likelihood distribution functions for the parameters (⁠|$\alpha , \beta , M_B^1, \Delta _M, H_0, \Omega _{\rm m}, \Sigma _0, w, \delta$|⁠) from MCMC fittings are shown in Fig. 2. Table 3 lists the best-fitting value and the 1σ, 2σ, and 3σ confidence level intervals. Since |$M_B^1$| entirely degenerates with H₀, their values cannot be constrained well simultaneously. If we take Hubble constant H₀ = 73.24km s⁻¹ Mpc⁻¹ (Riess et al. 2016), the corresponding |$M_B^1$| is −18.95.

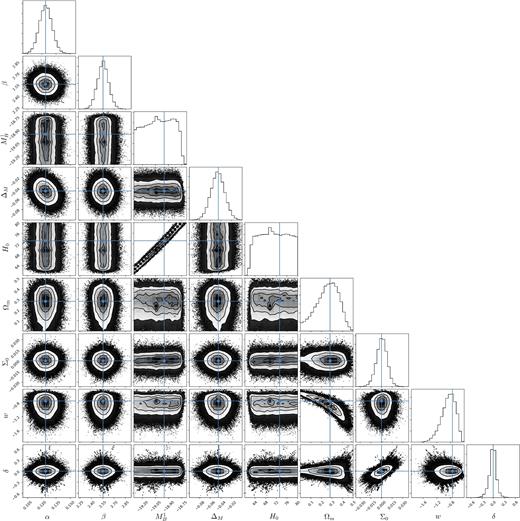
$Confidence contours (1σ, 2σ and 3σ) and marginalized likelihood distributions for the parameters ($\alpha , \beta , M_B^1, \Delta _M, H_0, \Omega _{\rm m}, \Sigma _0, w, \delta$) in ellipsoidal universe model. True values (shown as dots) of {$\alpha , \beta , M_B^1, \Delta _M, \Omega _{\rm m}, w$} are taken from wCDM fitting results as comparison.$

Figure 2.

Confidence contours (1σ, 2σ and 3σ) and marginalized likelihood distributions for the parameters (⁠|$\alpha , \beta , M_B^1, \Delta _M, H_0, \Omega _{\rm m}, \Sigma _0, w, \delta$|⁠) in ellipsoidal universe model. True values (shown as dots) of {|$\alpha , \beta , M_B^1, \Delta _M, \Omega _{\rm m}, w$|} are taken from wCDM fitting results as comparison.

Open in new tab Download slide

Table 3.

Open in new tab

Best-fitting values, and the 1σ, 2σ, and 3σ confidence level intervals derived from the JLA sample.

	α	β	Δ_M	Ω_m	Σ₀	w	δ
BF	0.124	2.554	−0.045	0.314	0.001	−0.774	−0.008
1σ	[0.118, 0.131]	[2.475, 2.622]	[−0.059, −0.032]	[0.173, 0.383]	[−0.007, 0.008]	[−1.028, −0.633]	[−0.101, 0.071]
2σ	[0.111, 0.137]	[2.406, 2.701]	[−0.072, −0.020]	[0.046, 0.443]	[−0.015, 0.015]	[−1.296, −0.535]	[−0.236, 0.185]
3σ	[0.105, 0.144]	[2.335, 2.777]	[−0.086, −0.007]	[0.003, 0.488]	[−0.024, 0.023]	[−1.527, −0.468]	[−0.451, 0.388]

	α	β	Δ_M	Ω_m	Σ₀	w	δ
BF	0.124	2.554	−0.045	0.314	0.001	−0.774	−0.008
1σ	[0.118, 0.131]	[2.475, 2.622]	[−0.059, −0.032]	[0.173, 0.383]	[−0.007, 0.008]	[−1.028, −0.633]	[−0.101, 0.071]
2σ	[0.111, 0.137]	[2.406, 2.701]	[−0.072, −0.020]	[0.046, 0.443]	[−0.015, 0.015]	[−1.296, −0.535]	[−0.236, 0.185]
3σ	[0.105, 0.144]	[2.335, 2.777]	[−0.086, −0.007]	[0.003, 0.488]	[−0.024, 0.023]	[−1.527, −0.468]	[−0.451, 0.388]

Table 3.

Open in new tab

Best-fitting values, and the 1σ, 2σ, and 3σ confidence level intervals derived from the JLA sample.

	α	β	Δ_M	Ω_m	Σ₀	w	δ
BF	0.124	2.554	−0.045	0.314	0.001	−0.774	−0.008
1σ	[0.118, 0.131]	[2.475, 2.622]	[−0.059, −0.032]	[0.173, 0.383]	[−0.007, 0.008]	[−1.028, −0.633]	[−0.101, 0.071]
2σ	[0.111, 0.137]	[2.406, 2.701]	[−0.072, −0.020]	[0.046, 0.443]	[−0.015, 0.015]	[−1.296, −0.535]	[−0.236, 0.185]
3σ	[0.105, 0.144]	[2.335, 2.777]	[−0.086, −0.007]	[0.003, 0.488]	[−0.024, 0.023]	[−1.527, −0.468]	[−0.451, 0.388]

	α	β	Δ_M	Ω_m	Σ₀	w	δ
BF	0.124	2.554	−0.045	0.314	0.001	−0.774	−0.008
1σ	[0.118, 0.131]	[2.475, 2.622]	[−0.059, −0.032]	[0.173, 0.383]	[−0.007, 0.008]	[−1.028, −0.633]	[−0.101, 0.071]
2σ	[0.111, 0.137]	[2.406, 2.701]	[−0.072, −0.020]	[0.046, 0.443]	[−0.015, 0.015]	[−1.296, −0.535]	[−0.236, 0.185]
3σ	[0.105, 0.144]	[2.335, 2.777]	[−0.086, −0.007]	[0.003, 0.488]	[−0.024, 0.023]	[−1.527, −0.468]	[−0.451, 0.388]

Table 4.

Open in new tab

Comparisons between best-fitting values in wCDM model and ellipsoidal universe model.

	α	β	\|$M_{B}^1$\|	Δ_M	Ω_m	w
wCDM	0.124	2.554	−18.95	−0.045	0.281	−0.750
Ellipsoidal	0.124	2.554	−18.95	−0.045	0.314	−0.774

	α	β	\|$M_{B}^1$\|	Δ_M	Ω_m	w
wCDM	0.124	2.554	−18.95	−0.045	0.281	−0.750
Ellipsoidal	0.124	2.554	−18.95	−0.045	0.314	−0.774

Table 4.

Open in new tab

Comparisons between best-fitting values in wCDM model and ellipsoidal universe model.

	α	β	\|$M_{B}^1$\|	Δ_M	Ω_m	w
wCDM	0.124	2.554	−18.95	−0.045	0.281	−0.750
Ellipsoidal	0.124	2.554	−18.95	−0.045	0.314	−0.774

	α	β	\|$M_{B}^1$\|	Δ_M	Ω_m	w
wCDM	0.124	2.554	−18.95	−0.045	0.281	−0.750
Ellipsoidal	0.124	2.554	−18.95	−0.045	0.314	−0.774

The constraints on the anisotropy parameters δ and Σ₀ from JLA sample are

$$ \begin{equation} -0.101<\delta <0.071 \quad (1\sigma )\, , \end{equation} $$

(20)

and

$$ \begin{equation} -0.007<\Sigma _0<0.008 \quad (1\sigma )\, . \end{equation} $$

(21)

Compared with −0.16 < δ < 0.12 and −0.012 < Σ₀ < 0.012 (1σ) from Union2 sample (Campanelli et al. 2011c), we can see that our result is more tight. The result implies that there is no evidence in favour of either geometric anisotropy (Σ₀ ≠ 0) or dark energy anisotropy (δ ≠ 0).

The direction cosine of anisotropy axis is

$$ \begin{equation} \hat{n}_{\rm A} = (\cos b_{\rm A}\cos l_{\rm A}, \cos b_{\rm A}\sin l_{\rm A}, \sin b_{\rm A})\, . \end{equation} $$

(22)

The opposite direction cosine |$\hat{n}_{\rm A}^{\prime }$| is then

$$ \begin{equation} \hat{n}_{\rm A}^{\prime } = (-\cos b_{\rm A}\cos l_{\rm A}, -\cos b_{\rm A}\sin l_{\rm A}, -\sin b_{\rm A})\, , \end{equation} $$

(23)

corresponding to an opposite direction (l_A ± π, −b_A) of the same axis. Therefore, we just use the parameter space [0, π] for l_A. Fig. 3 gives confidence contours of preferred direction in the galactic coordinate system. Since the distance modulus depends weakly on both the angular position of SNe Ia, |$\hat{n}$|⁠, and the direction of the symmetry axis |$\hat{n}_{\rm A}$| for small values of the shear Σ₀, the SNe Ia data are not able to constrain the anisotropy parameters (Σ₀ and δ) and the preferred direction defined by the anisotropy itself at the same time.

The anticorrelation between w and Ω_m comes from the dependence of luminosity distance on w and Ω_m:

$$ \begin{equation} \bar{H} = \sqrt{\Omega _{{\rm m}}A^{-3} + \Omega _{{\rm DE}}A^{-3(1+w)}}\, . \end{equation} $$

(24)

Meanwhile, the correlation between δ and Σ₀ (Campanelli et al. 2011c) is given by

$$ \begin{equation} \Sigma (A) = \frac{\Sigma _0 + (E-E_0)\delta }{A^3\bar{H}}\, , \end{equation} $$

(25)

which shows effects of energy distribution on the spatial curvature of the universe. Meanwhile, we find the best-fitting value for matter density parameter |$\Omega _{{\rm m}} = 0.314_{-0.131}^{+0.069}\quad (1\sigma )\, ,$| and dark energy equation of state |$w = -0.774_{-0.254}^{+0.141}\quad (1\sigma )\, .$|

The best-fitting results of the flat wCDM model are displayed in Fig. 4 for comparison. We find that best-fitting values of parameters in ellipsoidal model are quite similar to those in the wCDM model (see Table 4). Considering that the best-fitting values of Σ₀ and δ are nearly zero, and wCDM is the limiting case of ellipsoidal universe model, this result can be expected. Fig. 5 shows the Hubble diagram for JLA sample in two different cosmological models. One is the best-fitting model with (Ω_m, Σ₀, w, δ) = (0.314, 0.001, −0.774, −0.008) (blue dashed line). The other is the flat wCDM model with Ω_m = 0.281, w = −0.750 (black line). In the lower panel, we show the corresponding distance modulus fitting residuals (distance modulus minus the best-fitting wCDM distance modulus) as a function of redshift. The comparison between the best-fitting values of cosmological parameters from Union2 (Campanelli et al. 2011c) and JLA sample is shown in Table 5. The constraints are more tight than those of Campanelli et al. (2011c).

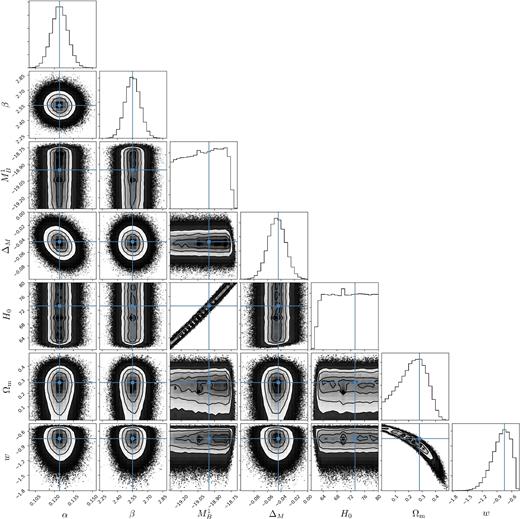
$Confidence contours (1σ, 2σ and 3σ) and marginalized likelihood distribution functions for the parameters ($\alpha , \beta , M_B^1, \Delta _M$, H0, Ωm, w) in the wCDM model.$

Figure 4.

Confidence contours (1σ, 2σ and 3σ) and marginalized likelihood distribution functions for the parameters (⁠|$\alpha , \beta , M_B^1, \Delta _M$|⁠, H₀, Ω_m, w) in the wCDM model.

Open in new tab Download slide

Figure 3.

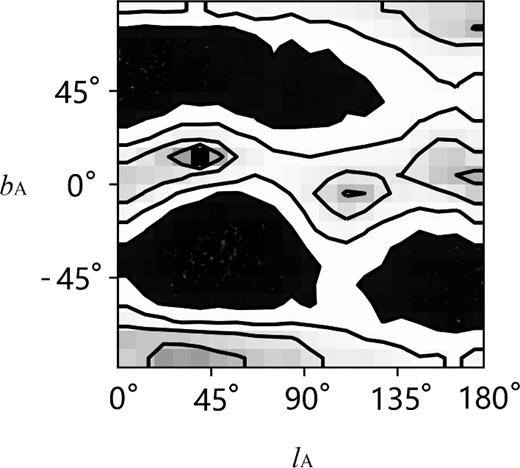
Confidence level contours of preferred direction in the galactic coordinate system.

Open in new tab Download slide

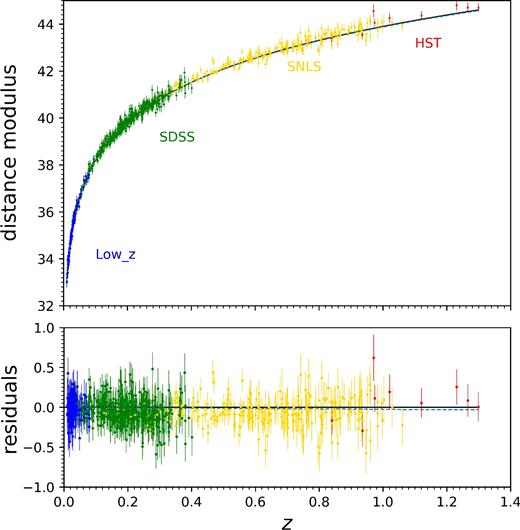
Upper panel: Hubble diagram for the 740 SNe Ia in the JLA compilation for different cosmological models: best-fitting ellipsoidal model (Ωm, Σ0, w, δ) ≃ (0.314, 0.001, −0.774, −0.008) (blue dashed line), and wCDM model (Ωm, w) ≃ (0.281, −0.750) (black line). Lower panel: residuals (distance modulus minus distance modulus for the wCDM model) for the same models in the upper panel.

Figure 5.

Upper panel: Hubble diagram for the 740 SNe Ia in the JLA compilation for different cosmological models: best-fitting ellipsoidal model (Ω_m, Σ₀, w, δ) ≃ (0.314, 0.001, −0.774, −0.008) (blue dashed line), and wCDM model (Ω_m, w) ≃ (0.281, −0.750) (black line). Lower panel: residuals (distance modulus minus distance modulus for the wCDM model) for the same models in the upper panel.

Open in new tab Download slide

Table 5.

Open in new tab

Comparisons between best-fitting values of cosmological parameters from Union2 and JLA sample for ellipsoidal universe model.

	Σ₀	δ	Ω_m	w
Union2	−0.004	−0.050	0.37	−1.32
JLA	0.001	−0.008	0.314	−0.774

Table 5.

Open in new tab

Comparisons between best-fitting values of cosmological parameters from Union2 and JLA sample for ellipsoidal universe model.

	Σ₀	δ	Ω_m	w
Union2	−0.004	−0.050	0.37	−1.32
JLA	0.001	−0.008	0.314	−0.774

5 CONCLUSIONS

In this paper, we study the ellipsoidal universe model with plane-symmetric metric and constrain the anisotropy level of cosmic geometry and dark energy fluids. By analysing the magnitude-redshift data of 740 SNe Ia in the JLA sample, we find a more tight constraint on cosmic shear Σ₀ and skewness δ. The best constraints are

$$ \begin{equation*} -0.007<\Sigma _0<0.008 \quad (1\sigma )\, , \nonumber \end{equation*} $$

and

$$ \begin{equation*} -0.101<\delta <0.071 \quad (1\sigma )\, . \nonumber \end{equation*} $$

In conclusion, the fitting results favour an isotropic universe without a preferred direction at present time. With the progress of astronomical observations such SNe Ia and CMB, we will have better constraints on universe anisotropy in the near future. The question that whether the cosmic anomalies such as dark energy dipole, fine structure constant dipole or dark flow have same physical origin remains to be answered. Cosmological principle is so vital to modern cosmology that much more effort should be made to verify the fundamental postulation.

Acknowledgements

We thank the anonymous referee for constructive comments. This work is supported by the National Basic Research Program of China (973 Program, grant No. 2014CB845800) and the National Natural Science Foundation of China (grants 11422325 and 11373022), and the Excellent Youth Foundation of Jiangsu Province (BK20140016).

REFERENCES

Aluri

P. K.

,

Panda

S.

,

Sharma

M.

,

Thakur

S.

,

2013

,

JCAP

,

12

,

003

Crossref

Search ADS

Amanullah

R.

et al. . ,

2010

,

ApJ

,

716

,

712

Crossref

Search ADS

Antoniou

I.

,

Perivolaropoulos

L.

,

2010

,

J. Cosmol. Astropart. Phys.

,

12

,

012

Crossref

Search ADS

Betoule

M.

et al. . ,

2014

,

A&A

,

568

,

A22

Crossref

Search ADS

Campanelli

L.

,

Cea

P.

,

Tedesco

L.

,

2006

,

Phys. Rev. Lett.

,

97

,

131302

Crossref

Search ADS

PubMed

Campanelli

L.

,

Cea

P.

,

Tedesco

L.

,

2007

,

Phys. Rev. D

,

76

,

063007

Crossref

Search ADS

Campanelli

L.

,

Cea

P.

,

Fogli

G. L.

,

Tedesco

L.

,

2011a

,

Int. J. Mod. Phys. D, 20

,

6

,

1153

Crossref

Search ADS

Campanelli

L.

,

Cea

P.

,

Fogli

G. L.

,

Tedesco

L.

,

2011b

,

Mod. Phys. Lett. A

,

26

,

1169

Crossref

Search ADS

Campanelli

L.

,

Cea

P.

,

Fogli

G. L.

,

Marrone

A.

,

2011c

,

Phys. Rev. D

,

83

,

103503

Crossref

Search ADS

Conley

A.

et al. . ,

2011

,

ApJS

,

192

,

1

Crossref

Search ADS

Eisenstein

D. J.

et al. . ,

2005

,

ApJ

,

633

,

560

Crossref

Search ADS

Eriksen

H. K.

,

Banday

A. J.

,

Górski

K. M.

,

Hansen

F. K.

,

Lilje

P. B.

,

2007

,

ApJ

,

660

,

L81

Crossref

Search ADS

Feldman

H. A.

,

Watkins

R.

,

Hudson

M. J.

,

2010

,

MNRAS

,

407

,

2328

Crossref

Search ADS

Foreman-Mackey

D.

,

Hogg

D. W.

,

Lang

D.

,

Goodman

J.

,

2013

,

PASP

,

125

,

306

Crossref

Search ADS

Goodman

J.

,

Weare

J.

,

2010

,

Commun. Appl. Math. Comput. Sci.

,

5

,

65

Crossref

Search ADS

Hoftuft

J.

,

Eriksen

H. K.

,

Banday

A. J.

,

Górski

K. M.

,

Hansen

F. K.

,

Lilje

P. B.

,

2009

,

ApJ

,

699

,

985

Crossref

Search ADS

Kashlinsky

A.

,

Atrio-Barandela

F.

,

Kocevski

D.

,

Ebeling

H.

,

2008

,

ApJ

,

686

,

L49

Crossref

Search ADS

Kashlinsky

A.

,

Atrio-Barandela

F.

,

Ebeling

H.

,

Edge

A.

,

Kocevski

D.

,

2010

,

ApJ

,

712

,

L81

Crossref

Search ADS

King

J. A.

,

Webb

J. K.

,

Murphy Michael

T.

,

Flambaum

V. V.

,

Carswell

R. F.

,

Bainbridge

M. B.

,

Wilczynska

M. R.

,

Koch

F. E.

,

2012

,

MNRAS

,

422

,

3370

Crossref

Search ADS

Komatsu

E.

et al. . ,

2011

,

ApJS

,

192

,

18

Crossref

Search ADS

Lavaux

G.

,

Tully

R. B.

,

Mohayaee

R.

,

Colombi

S.

,

2010

,

ApJ

,

709

,

483

Crossref

Search ADS

Li

X.

,

Lin

H.-N.

,

Wang

S.

,

Chang

Z.

,

2013

,

Eur. Phys. J. C.

,

73

,

2653

Crossref

Search ADS

Mariano

A.

,

Perivolaropoulos

L.

,

2012

,

Phys. Rev. D

,

86

,

083517

Crossref

Search ADS

Mariano

A.

,

Perivolaropoulos

L.

,

2013

,

Phys. Rev. D

,

87

,

043511

Crossref

Search ADS

Moss

A.

,

Scott

D.

,

Zibin

J. P.

,

Battye

R.

,

2011

,

Phys. Rev. D

,

84

,

023014

Crossref

Search ADS

Paci

F.

,

Gruppuso

A.

,

Finelli

F.

,

Cabella

P.

,

de Rosa

A.

,

Mandolesi

N.

,

Natoli

P.

,

2010

,

MNRAS

,

407

,

399

Crossref

Search ADS

Perivolaropoulos

L.

,

2014

,

Galaxies

,

2

,

22

Crossref

Search ADS

Perlmutter

S.

et al. . ,

1999

,

ApJ

,

517

,

565

Crossref

Search ADS

Pinho

A. M. M.

,

Martins

C. J. A. P.

,

2016

,

Phys. Lett. B.

,

756

,

121

Crossref

Search ADS

Planck Collaboration XIII

,

2016

,

A&A

,

594

,

A13

Crossref

Search ADS

Riess

A. G.

et al. . ,

1998

,

AJ

,

116

,

1009

Crossref

Search ADS

Riess

A. G.

et al. . ,

2016

,

ApJ

,

826

,

56

Crossref

Search ADS

Schücker

T.

,

Tilquin

A.

,

Valent

G.

,

2014

,

MNRAS

,

444

,

2820

Crossref

Search ADS

Taub

A. H.

,

1951

,

Ann. Math.

53

,

472

Crossref

Search ADS

Wang

J. S.

,

Wang

F. Y.

,

2014

,

MNRAS

,

443

,

1680

Crossref

Search ADS

Watkins

R.

,

Feldman

H. A.

,

Hudson

M. J.

,

2009

,

MNRAS

,

392

,

743

Crossref

Search ADS

Webb

J. K.

,

King

J. A.

,

Murphy

M. T.

,

Flambaum

V. V.

,

Carswell

R. F.

,

Bainbridge

M. B.

,

2011

,

Phys. Rev. Lett.

,

107

,

191101

Crossref

Search ADS

PubMed

Yang

X. F.

,

Wang

F. Y.

,

Chu

Z.

,

2014

,

MNRAS

,

437

,

1840

Crossref

Search ADS

Zhao

W.

,

Santos

L.

,

2015

,

The Universe

,

3

,

9

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model ( https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
November 2017	18
December 2017	4
January 2018	14
February 2018	1
March 2018	7
April 2018	1
May 2018	10
June 2018	4
July 2018	1
August 2018	2
September 2018	1
October 2018	2
November 2018	6
December 2018	5
February 2019	1
April 2019	4
May 2019	2
September 2019	3
October 2019	1
February 2020	1
March 2020	1
April 2020	2
May 2020	1
June 2020	6
July 2020	18
August 2020	1
November 2020	2
July 2021	1
October 2021	2
November 2021	3
December 2021	7
January 2022	1
February 2022	4
March 2022	13
April 2022	4
May 2022	4
June 2022	7
July 2022	7
August 2022	8
September 2022	5
October 2022	6
November 2022	5
December 2022	2
January 2023	1
February 2023	2
March 2023	6
April 2023	7
May 2023	5
June 2023	7
July 2023	3
August 2023	12
September 2023	1
October 2023	5
November 2023	1
December 2023	12
January 2024	21
February 2024	10
March 2024	7
April 2024	11
May 2024	10
June 2024	6
July 2024	11
August 2024	5
September 2024	8
October 2024	10
November 2024	16
December 2024	1
February 2025	2
March 2025	22
April 2025	4
May 2025	4

Article Contents

Testing the isotropy of the Universe with Type Ia supernovae in a model-independent way

Abstract

1 INTRODUCTION

2 ELLIPSOIDAL UNIVERSE MODEL

2.1 Anisotropy axis

2.2 Redshift–distance relation

3 JLA SAMPLE AND MCMC FITTING

3.1 Angular position

3.2 Distance modulus

3.3 The hubble diagram covariance matrix

3.4 Markov chain Monte Carlo fitting

4 RESULTS

5 CONCLUSIONS

Acknowledgements

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Testing the isotropy of the Universe with Type Ia supernovae in a model-independent way

Abstract

1 INTRODUCTION

2 ELLIPSOIDAL UNIVERSE MODEL

2.1 Anisotropy axis

2.2 Redshift–distance relation

3 JLA SAMPLE AND MCMC FITTING

3.1 Angular position

3.2 Distance modulus

3.3 The hubble diagram covariance matrix

3.4 Markov chain Monte Carlo fitting

4 RESULTS

5 CONCLUSIONS

Acknowledgements

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only