-
PDF
- Split View
-
Views
-
Cite
Cite
Frank C van den Bosch, Go Ogiya, Oliver Hahn, Andreas Burkert, Disruption of dark matter substructure: fact or fiction?, Monthly Notices of the Royal Astronomical Society, Volume 474, Issue 3, March 2018, Pages 3043–3066, https://doi.org/10.1093/mnras/stx2956
Close - Share Icon Share
Abstract
Accurately predicting the demographics of dark matter (DM) substructure is of paramount importance for many fields of astrophysics, including gravitational lensing, galaxy evolution, halo occupation modelling, and constraining the nature of DM. Because of its strongly non-linear nature, DM substructure is typically modelled using N-body simulations, which reveal that large fractions of DM subhaloes undergo complete disruption. In this paper, we use both analytical estimates and idealized numerical simulations to investigate whether this disruption is mainly physical, due to tidal heating and stripping, or numerical (i.e. artificial). We show that, contrary to naive expectation, subhaloes that experience a tidal shock ΔE that exceeds the subhalo's binding energy, |Eb|, do not undergo disruption, even when ΔE/|Eb| is as large as 100. Along the same line, and contrary to existing claims in the literature, instantaneously stripping matter from the outskirts of a DM subhalo also does not result in its complete disruption, even when the instantaneous remnant has positive binding energy. In addition, we show that tidal heating due to high-speed (impulsive) encounters with other subhaloes (‘harassment’) is negligible compared to the tidal effects due to the host halo. Hence, we conclude that, in the absence of baryonic processes, the complete physical disruption of CDM substructure is extremely rare and that most disruption in numerical simulations therefore must be artificial. We discuss various processes that have been associated with numerical overmerging and conclude that inadequate force softening is the most likely culprit.
1 INTRODUCTION
In the Λ cold dark matter (ΛCDM) concordance cosmology, structure develops as primordial density fluctuations grow to form virialized structures. Because of the negligible thermal velocity of CDM, fluctuations survive the early universe on all scales, and structure develops from the bottom up as small, dense CDM clumps merge together to build-up large dark matter (DM) haloes. During this hierarchical assembly, the inner regions of early virialized haloes often survive accretion on to a larger system, thus giving rise to a population of subhaloes. These are subjected to forces that try to dissolve them: dynamical friction, tides from the host halo, and impulsive encounters with other substructure.
Being able to accurately predict the abundance and demographics of DM substructure is of crucial importance for a wide range of astrophysics. First of all, it is one of the prime discriminators between different DM models; if DM is warm (WDM), rather than cold, free-streaming and enhanced tidal disruption will cause a significantly reduced abundance of low -mass subhaloes (e.g. Knebe et al. 2008; Lovell et al. 2014; Colín et al. 2015; Bose et al. 2016). If DM has a significant cross-section for self-interaction (SIDM), subhaloes are predicted to have constant-density cores, with significantly lower central densities than their CDM counterparts (e.g. Burkert 2000; Vogelsberger, Zavala & Loeb 2012; Rocha et al. 2013). The main methods that are used to test these different DM models are gravitational lensing, either by using time-delays (e.g. Keeton & Moustakas 2009), flux-ratio anomalies (e.g. Metcalf & Madau 2001; Bradač et al. 2002; Dalal & Kochanek 2002), or perturbations of the surface brightness distribution of lensed arcs and Einstein rings (e.g. Vegetti & Koopmans 2009; Vegetti et al. 2014). Alternatively, low-mass substructure can reveal its presence by creating gaps in tidal (stellar) streams (e.g. Carlberg 2009; Erkal et al. 2016; Sanders, Bovy & Erkal 2016). The detailed structure of subhaloes can be tested using kinematic data of dwarf galaxies (e.g. Mateo et al. 1993; Łokas 2009; Walker et al. 2009). The latter has given rise to a potential problem for the ΛCDM paradigm in the form of the ‘too-big-to-fail’ problem (Boylan-Kolchin et al. 2010; Boylan-Kolchin, Bullock & Kaplinghat 2011; Garrison-Kimmel et al. 2014; Ogiya & Burkert 2015), which has sparked renewed interest in alternatives such as WDM or SIDM, although baryonic solutions have also been proposed (e.g. Zolotov et al. 2012; Ogiya & Mori 2014; Arraki et al. 2014; Dutton et al. 2016). Finally, DM substructure boosts the expected DM annihilation signal (Bergström et al. 1999), an effect that is typically quantified in terms of a ‘boost-factor’ (e.g. Strigari et al. 2007; Giocoli, Pieri & Tormen 2008b; Kuhlen, Diemand & Madau 2008; Pieri, Bertone & Branchini 2008; Moliné et al. 2017).
In addition to carrying a wealth of information regarding the dark sector, DM substructure is also important for our quest to understand galaxy formation and large-scale structure. DM subhaloes are believed to host satellite galaxies and the demographics of DM substructure is therefore directly related to the (small scale) clustering of galaxies. This idea underlies the popular technique of subhalo abundance matching (e.g. Vale & Ostriker 2004; Conroy, Wechsler & Kravtsov 2006; Guo et al. 2010; Behroozi, Wechsler & Conroy 2013b; Hearin et al. 2013; Moster, Naab & White 2013), in which galaxies are assigned to DM host and sub-haloes in simulations to create mock galaxy samples. This has become a prime tool for interpreting galaxy clustering, galaxy–galaxy lensing, and group multiplicity functions, and is even used to constrain cosmological parameters (Trujillo-Gomez et al. 2011; Reddick et al. 2014; Zentner, Hearin & van den Bosch 2014; Hearin, Watson & van den Bosch 2015; Hearin et al. 2016; Zentner et al. 2016; Lehmann et al. 2017).
The formation and evolution of DM substructure is best studied using numerical N-body simulations. Nowadays, large cosmological simulations routinely resolve an entire hierarchy of substructure, with haloes hosting subhaloes, which themselves host sub-subhaloes, etc. (e.g. Ghigna et al. 1998; Tormen, Diaferio & Syer 1998; Diemand et al. 2004a; Gao et al. 2004; Kravtsov et al. 2004; Giocoli, Tormen & van den Bosch 2008a; Giocoli et al. 2010). Since simulations are CPU-expensive and suffer from limiting mass and force resolution, various authors have attempted to construct semi-analytical models for the evolution of DM substructure (e.g. Taylor & Babul 2001; Peñarrubia & Benson 2005; van den Bosch, Tormen & Giocoli 2005; Zentner et al. 2005; Kampakoglou & Benson 2007; Pullen, Benson & Moustakas 2014; Jiang & van den Bosch 2016). However, since we lack accurate, analytical descriptions, based on first principles, for how the mass, structure and orbits of subhaloes evolve with time, these models typically have several free parameters that are tuned to reproduce results from numerical simulations.
Prior to 1997, numerical N-body simulations suffered from a serious ‘overmerging’ problem, in that the DM haloes revealed little to no substructure. This was in clear contrast with the wealth of ‘substructure’ (i.e. satellite galaxies) observed in galaxy groups and clusters. While some speculated that baryonic physics would resolve this problem (e.g. Frenk et al. 1988), others argued that overmerging might actually be a numerical artefact arising from insufficient mass and/or force resolution. In particular, Carlberg (1994) and van Kampen (1995, 2000a) identified particle-subhalo two-body heating as the main cause for overmerging, while others blamed inadequate force softening (e.g. Moore, Katz & Lake 1996b; Klypin et al. 1999a). At the close of the last millennium, when simulations started to resolve surviving populations of subhaloes (e.g. Tormen, Bouchet & White 1997; Brainerd, Goldberg & Verner Villumsen 1998; Moore et al. 1998), the discussion as to what might cause numerical overmerging was quickly eclipsed by a new issue, namely that CDM simulations seem to predict too much substructure (Klypin et al. 1999b; Moore et al. 1999). Over the years, though, it has become clear that this ‘missing satellite problem’ is mainly a manifestation of poorly understood baryonic physics related to galaxy formation (see Bullock & Boylan-Kolchin 2017, for a review).
As for overmerging, it has become clear that modern, state-of-the-art numerical simulations still suffer from numerical overmerging, with important ramifications for small-scale clustering (e.g. Conroy, Wechsler & Kravtsov 2006; Guo & White 2014; Campbell et al. 2017; Moster, Naab & White 2017), semi-analytical models for galaxy formation (e.g. Springel et al. 2001; Kang et al. 2005; Kitzbichler & White 2008), and other studies that rely on the phase-space distribution of subhaloes (e.g. Faltenbacher & Diemand 2006; Wu et al. 2013; Tollet et al. 2017). However, the general consensus seems to be that this numerical overmerging only affects subhaloes below a mass resolution limit of 50–100 particles. This notion is based on the fact that simulations seem to yield consistent, converged results for the mass function of subhaloes above this mass resolution limit (e.g. Springel et al. 2008; Onions et al. 2012; Knebe et al. 2013; Cautun et al. 2014; Griffen et al. 2016; van den Bosch & Jiang 2016).
In a recent study, van den Bosch (2017) showed that subhalo disruption is extremely prevalent in modern simulations, with inferred fractional disruption rates (at z = 0) of ∼13 per cent per Gyr (see also Diemand, Moore & Stadel 2004b). This implies that ∼65 (90) per cent of all subhaloes accreted around z = 1 (z = 2) are disrupted by z = 0 (Han et al. 2016; Jiang & van den Bosch 2017). In the simulation studied by van den Bosch (2017), roughly 20 per cent of this disruption occurs above the mass resolution limit of 50 particles, with a mass function of disrupting subhaloes that is indistinguishable from that of the surviving population! What is the dominant cause of this prevalent disruption of subhaloes in numerical simulations? In particular, is it artificial (numerical) or real (physical)? Based on the fact that subhalo mass functions are deemed converged above a mass resolution limit of 50–100 particles, it is tempting to conclude that disruption above this ‘resolution limit’ be physical, rather than numerical. However, convergence is a necessary, but not a sufficient condition, to guarantee that the simulation results are physically correct. Furthermore, there is no consensus as to what physical mechanism dominates, with most studies arguing either for tidal heating or tidal stripping. We therefore initiated a comprehensive study aimed at answering these questions. While researching the existing literature on this topic, we came across a variety of conflicting results and claims, and this paper is largely intended to clarify this confusion, correct a number of misconceptions, and present a comprehensive overview. As such, this paper serves as a compendium to two follow-up papers. In van den Bosch & Ogiya (2018, hereafter Paper II), we use a large suite of idealized numerical simulations and experiments to show that state-of-the-art numerical N-body simulations still suffer from an enormous amount of overmerging, mainly driven by inadequate force softening and an amplification of discreteness noise due to the tidal field. In Ogiya et al. (in preparation; hereafter Paper III), we use a large suite of similar idealized simulations, which are properly converged, to probe large parts of parameter space. The results of these simulations can be used to calibrate semi-analytical models of subhalo evolution and to gauge the reliability and accuracy of cosmological simulations. In this paper, we
show that impulsive, tidal heating during peri-centric passage of the host halo can inject as much as 100 times the binding energy. Yet, even under those extreme conditions, a remnant containing ∼20 per cent of the mass remains.
demonstrate that harassment has a negligible impact on the evolution of DM substructure.
underscore the problems and uncertainties associated with analytical treatments of tidal stripping.
demonstrate that simply removing matter from the outskirts of a DM subhalo will never result in its complete disruption, even if the remnant has positive binding energy.
correct and elucidate a number of errors and misconceptions regarding the numerical, artificial disruption of substructure.
We start in Section 2 with a discussion of the concept of ‘tidal radius’, including an overview of the various definitions that are used in the literature. Section 3 describes the idealized, numerical simulations that we use in this paper for comparison with simple analytical estimates of various physical disruption mechanisms (Section 4), and for assessing the impact of instantaneously stripping matter off of DM haloes (Section 5). Section 6 discusses a variety of numerical processes that might potentially give rise to artificial disruption of substructure in N-body simulations, including two-body relaxation, impulsive heating due to interactions with overly massive host halo particles, and inadequate force softening. Finally, Section 7 summarizes our findings and briefly discusses some implications for various areas of astrophysics.
2 TIDAL RADIUS
We start our discussion of the tidal evolution of DM substructure by addressing an important concept, namely the tidal radius. There are a number of different definitions that are used in the literature, with varying degrees of approximation. For the sake of completeness, we briefly overview and compare the most commonly used definitions.
Following the suggestion by Klypin et al. (1999a), several studies have taken the tidal radius to be the minimum of rt,1 and rt,3 (e.g. Oguri & Lee 2004; Arraki et al. 2014; Klypin et al. 2015).
Although the tidal radius is a common concept used to discuss tidal stripping, it is important to realize that all the various definitions discussed above are only approximate (see e.g. Binney & Tremaine 2008; Mo, van den Bosch & White 2010). First of all, the two-dimensional surface along which the radial acceleration of a test particle vanishes is not spherical, even if m and M are point masses, and can therefore not be characterized by a single radius (see Tollet et al. 2017, for a detailed discussion). Secondly, variance in the orbital motion of the particles within the subhalo gives rise to scatter in the coriolis forces on these particles, which in turn introduces some ‘thickness’ to the shell of particles for which |$\ddot{r}=0$| (see Read et al. 2006, for a detailed discussion). Thirdly, the various expressions for rt are all derived under the distant-tide approximation, which implies that the distance R between m and M is large compared to the size of m. This condition is not necessarily valid in the case of subhaloes, since the orbit's peri-centre can be comparable to, or even smaller than, the size of the subhalo. Finally, the optimal definition of tidal radius is likely to depend on the orbit in question. For instance, whereas rt,2 (equation 4) is expected to be most applicable to circular orbits, rt,1 (equation 3) is likely to be more relevant for more radial orbits. In what follows, we will consider both in order to assess how the ‘choice’ for the definition of tidal radius impacts simple models for tidal stripping. As for rt,3 (equation 6), since this definition of tidal radius is basically bracketed by the other two, i.e. one typically has rt,2 < rt,3 < rt,1, we will no longer consider this definition of the tidal radius in what follows.
2.1 Properties of newly accreted subhaloes
As a subhalo moves towards the central region of its host halo, its tidal radius typically shrinks,1 reaching a minimum value during peri-centric passage. Hence, it is commonly assumed that the amount of material stripped off a subhalo during a radial orbital period depends on its tidal radius at peri-centre. In what follows, we refer to this as the ‘peri-tidal radius’, for which we use the symbol rt|p.
What are realistic values for rt|p for DM subhaloes during their first radial orbit? In order to address this question, we consider DM subhaloes in the cosmological Bolshoi simulation (Klypin, Trujillo-Gomez & Primack 2011), which follows the evolution of 20483 DM particles using the Adaptive Refinement Tree (art) code (Kravtsov, Klypin & Khokhlov 1997) in a flat ΛCDM model with parameters Ωm,0 = 1 − ΩΛ, 0 = 0.27, Ωb,0 = 0.0469, h = H0/(100 km s−1 Mpc−1) = 0.7, σ8 = 0.82 and ns = 0.95 (hereafter ‘Bolshoi cosmology’). The box size of the Bolshoi simulation is Lbox = 250h−1 Mpc, resulting in a particle mass of mp = 1.35 × 108 h− 1 M⊙.
We use the publicly available halo catalogues2 obtained using the phase-space halo finder ROCKSTAR (Behroozi, Wechsler & Wu 2013a), which uses adaptive, hierarchical refinement of friends-of-friends groups in six phase-space dimensions and one time dimension. ROCKSTAR haloes are defined as spheres with an average density equal to Δvir(z)ρcrit(z). Here, ρcrit(z) = 3H2(z)/8πG is the critical density for closure at redshift z, and Δvir(z) is given by the fitting function of Bryan & Norman (1998).
Following van den Bosch (2017, hereafter ‘vdB17’), we use the 19 simulation outputs at z ≤ 0.0605, from which we select a random subset of 5000 newly accreted subhaloes (labelled ‘A’ subhaloes in vdB17) by identifying those subhaloes in the halo catalogues that in the previous output were still considered host haloes and which had never before been subhaloes. In order to focus on well-resolved systems, each subhalo is requested to have at least 250 particles and to be accreted in a host halo with mass Mh ≥ 3 × 1013 h− 1 M⊙. For each of the subhaloes thus selected, we register
xc ≡ Rc(E)/Rh, the radius of the circular orbit corresponding to the orbital energy, E, expressed in terms of the virial radius of the host halo, Rh.
η ≡ L/Lc(E), the orbital circularity, defined as the ratio of the orbital angular momentum, L, and the angular momentum Lc(E) corresponding to a circular orbit of energy E. Radial and circular orbits have η = 0 and 1, respectively.
Ms/Mh, the ratio of subhalo mass to host halo mass.
cs the concentration parameter of the subhalo.
ch the concentration parameter of the host halo.
The concentration parameters are defined as the ratios of the virial radius and the scale parameter of the NFW profile (see below) that best fits the density distribution of the (sub)halo (see Behroozi et al. 2013a, for details on how these quantities are computed in ROCKSTAR ).
The upper left and middle panels of Fig. 1 show the distributions of xc and η, characterizing the orbits of newly accreted subhaloes. The median xc is 1.26, and the distribution is skewed towards higher values, indicating that at accretion the orbits of subhaloes are only weakly bound (cf. vdB17). The η distribution is fairly symmetric around η ∼ 0.5, indicating that purely radial and circular orbits are rare (cf. Tormen 1997; Zentner et al. 2005; Wetzel 2011; Jiang et al. 2015). The mass ratio, Ms/Mh, is peaked around 10−3 (upper right-hand panel),3 while the concentration ratio follows a roughly lognormal distribution centred around cs/ch ≃ 2. Hence, subhaloes are, on average, more concentrated than their host haloes, which is a natural outcome of the concentration–mass relation of CDM haloes. The lower, middle panel depicts the ratio of the subhalo's peri-centre Rp to the host halo's virial ratio, Rh. The median Rp/Rh = 0.37, while 7.3 per cent (0.9 per cent) of subhaloes have a first peri-centric passage Rp < 0.1Rh (0.03 Rh). These numbers are in good agreement with (Wetzel 2011, see his appendix A). Finally, the lower-right-hand panel plots the distributions of the peri-tidal radius, rt|p, in units of the subhalo's original (at accretion) virial radius, rs. Red and blue histograms correspond to the two different definitions of the tidal radius, rt, 1 and rt, 2, respectively. Note that rt, 1, which ignores the centrifugal force, is significantly larger than rt, 2; the median rt, 1 is 0.43rs, with only 0.7 per cent of subhaloes having rt, 1/rs < 0.1. In comparison, the median rt, 2 is 0.21rs, with 21.5 per cent (2.0 per cent) of subhaloes having rt, 2/rs < 0.1 (<0.01). Thus, we see that the definition of tidal radius can have a big impact on the expected stripping rate (see Section 4.3).

Properties of subhaloes in the Bolshoi simulation at the moment they are accreted by their host halo. From left to right and top to bottom, the different panels show distributions of the orbital energy, characterized by xc = Rc(E)/Rh, orbital circularity, η = L/Lc(E), the mass ratio of subhalo to host halo, Ms/Mh, the ratio of concentration parameters of subhalo and host halo, cs/ch, the orbit's peri-centre in units of the virial radius of the host halo, Rp/Rh, and finally the peri-tidal radius, rt|p (defined as the tidal radius at peri-centre), normalized by the size of the subhalo. For the latter, we have used the two different definitions of the tidal radius, as indicated. See the text for a detailed discussion.
3 NUMERICAL SIMULATIONS
Although this paper mainly focuses on simple (semi)-analytical treatments of subhalo evolution, we also present some simulation results for comparison. This section briefly describes these numerical simulations, and we refer the interested reader to Papers II and III for more details (and many more simulation results). Our (idealized) simulations follow the evolution of a single N-body subhalo orbiting in the fixed, analytical potential of a host halo. Our goal is to investigate how much mass is stripped from the subhalo during its first radial orbital period and to compare the results to expectations based on the various processes discussed in Section 4.
Throughout we assume that, prior to stripping, the halo has an isotropic velocity distribution, such that its distribution function (DF) depends only on energy, i.e. f = f(E). We use the method of Widrow (2000) to sample particles from the DF using the standard acceptance-rejection technique (Press et al. 1992; Kuijken & Dubinski 1994; Drakos, Taylor & Benson 2017) and truncate the halo at its virial radius. Since the DF that we use to generate the initial conditions (ICs) is computed using the Eddington (1916) inversion equation, which assumes that the halo extends to infinity, our initial system is not going to be in perfect equilibrium. However, as we demonstrate and discuss in Paper II, this has no significant impact on our results.
Throughout we adopt model units in which the gravitational constant, G, the scale radius, r0, and the initial (virial) mass of the subhalo, Ms, are all unity. We restrict ourselves to subhaloes with a concentration parameter cs = 10, for which |$t_{\rm cross} = c_{\rm s}^{3/2} = 31.6$|. Based on equation (12), we thus have that a time interval of Δt = 1 (model units) corresponds to 63.4 Myr.
The simulations are carried out using a treecode designed for graphic processing unit clusters. This code, which is optimized for speed, uses a second-order Runge–Kutta integrator and is described in Ogiya et al. (2013). We have compared the results of this simulation code with those of the treecode described in Section 5.1, with uses a second-order leap-frog integrator, and find the results to be in excellent agreement.
We integrate the subhalo in the external tidal field of an NFW host halo whose virial mass (radius) is 1000 (10) times larger than that of the subhalo. For such a large mass ratio, dynamical friction, which is not accounted for in our idealized simulations, can be safely ignored. In the ΛCDM cosmology, to good approximation, concentration scales with halo mass as c ∝ M−0.1 (e.g. Dutton & Macciò 2014). Hence, for a mass ratio of 1000, the ratio in concentration parameters is roughly 2, in agreement with the results shown in Fig. 1, and we therefore adopt a concentration for the host halo of ch = 5. Each subhalo is modelled using N = 107 particles and a softening length of ε = 0.003. All simulations adopt a tree opening angle of θ = 0.7, and a fixed time step of Δt = 0.02 (corresponding to ∼1.3 Myr). The latter implies that we resolve the minimal orbital time of the system, defined as |$\tau _{\rm min} \simeq [3 \pi / G \bar{\rho }(<\varepsilon )]^{1/2}$|, with |$\bar{\rho }(<\!\varepsilon )$| the average density enclosed by the softening length, with 30 time steps. As discussed in great detail in Paper II, for these parameters we obtain results that are both converged (i.e. stable to an increase in N) and reproducible (i.e. different random realizations yield indistinguishable results). We initially position the subhalo at the apo-centre of an orbit with xc = 1 and η = 0.0, 0.1, ..., 1.0 and integrate the system for a total of 10 Gyr (corresponding to ∼7890 time steps). This is slightly longer than a radial orbital period, which varies from Tr = 9.18 Gyr for η = 0.0 to Tr = 9.53 Gyr for η = 1.0. We use an extremely robust, iterative approach to determine the bound fraction, fbound, as function of time, which is described in detail in Appendix A (see also Paper II).
3.1 Results
Fig. 2 shows some of the simulation results. The left-hand panel shows the logarithm of the bound fraction as a function of time, normalized by the radial period, Tr, while the middle and right-hand panels show the radius and velocity of the subhalo with respect to the host halo, again as functions of t/Tr. Different colours correspond to different values of the orbital circularity, η, as indicated, and for clarity, we only show the results for a subset of six simulations. Table 1 lists the bound fractions at five different epochs for the full set of 11 simulations. Note how, for fixed orbital energy, subhaloes on more radial orbits are stripped of a larger fraction of their mass per orbital period. For the purely radial orbit (η = 0), as much as 89 per cent of the original subhalo mass is stripped away during its first radial orbit.
![Results for a subset of the idealized numerical simulations described in Section 3 and listed in Table 1. From left to right, the panels show the time-evolution (where t/Tr is the time normalized by the radial period) of the logarithm of the bound mass fraction, log [fbound], the orbital radius in units of the virial radius of the host, r/rvir, h, and the orbital speed, in units of the virial velocity of the host, v/Vvir, h. Different colours corresponds to different orbital circularities, as indicated. Note how the subhalo loses between ∼40 (η = 1) and ∼90 (η = 0) per cent of its mass during its first radial period.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/474/3/10.1093_mnras_stx2956/2/m_stx2956fig2.jpeg?Expires=1749988357&Signature=ckmhSURbYwHSRabe53-h5ht-~8FY-EB94rXlnd7aR7TVfDxlghfCQ~Ldx4EVwFlhr5VQtmQBtYMos1JCHk~sEoJkh3yNcG9YdEUl4CvQPGppyohLDZjgLxDFs9oIyj11vuXDaIGb2Cxl42Ha0sAmbNE8oUT0ZfP0bx6StWbbjKcwYEaz-Zafnwqzimja47SopxHANcE5jr5RPyOCQA27GMhAUNfzGSkx1XNm0w16Cl05OJkKbmvr~o6bro4TenZVJ4eE0juyTjJdN2L~cFhgW1uvPQtC~L-cdLzIdINbI5RK1BBV3PSX7bNLQL376fejBW8YW51bNTWMJjkenSIsAA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Results for a subset of the idealized numerical simulations described in Section 3 and listed in Table 1. From left to right, the panels show the time-evolution (where t/Tr is the time normalized by the radial period) of the logarithm of the bound mass fraction, log [fbound], the orbital radius in units of the virial radius of the host, r/rvir, h, and the orbital speed, in units of the virial velocity of the host, v/Vvir, h. Different colours corresponds to different orbital circularities, as indicated. Note how the subhalo loses between ∼40 (η = 1) and ∼90 (η = 0) per cent of its mass during its first radial period.
| ID . | η . | fbound . | fbound . | fbound . | fbound . | fbound . |
|---|---|---|---|---|---|---|
| . | . | 0.2Tr . | 0.4Tr . | 0.6Tr . | 0.8Tr . | Tr . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| S0 | 0.0 | 0.982 | 0.909 | 0.120 | 0.111 | 0.110 |
| S1 | 0.1 | 0.982 | 0.908 | 0.262 | 0.244 | 0.230 |
| S2 | 0.2 | 0.982 | 0.905 | 0.367 | 0.347 | 0.323 |
| S3 | 0.3 | 0.981 | 0.901 | 0.429 | 0.409 | 0.378 |
| S4 | 0.4 | 0.981 | 0.894 | 0.479 | 0.454 | 0.419 |
| S5 | 0.5 | 0.980 | 0.887 | 0.522 | 0.489 | 0.453 |
| S6 | 0.6 | 0.979 | 0.877 | 0.559 | 0.520 | 0.484 |
| S7 | 0.7 | 0.977 | 0.867 | 0.594 | 0.550 | 0.514 |
| S8 | 0.8 | 0.975 | 0.858 | 0.631 | 0.580 | 0.543 |
| S9 | 0.9 | 0.969 | 0.849 | 0.672 | 0.612 | 0.573 |
| S10 | 1.0 | 0.942 | 0.837 | 0.732 | 0.664 | 0.613 |
| ID . | η . | fbound . | fbound . | fbound . | fbound . | fbound . |
|---|---|---|---|---|---|---|
| . | . | 0.2Tr . | 0.4Tr . | 0.6Tr . | 0.8Tr . | Tr . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| S0 | 0.0 | 0.982 | 0.909 | 0.120 | 0.111 | 0.110 |
| S1 | 0.1 | 0.982 | 0.908 | 0.262 | 0.244 | 0.230 |
| S2 | 0.2 | 0.982 | 0.905 | 0.367 | 0.347 | 0.323 |
| S3 | 0.3 | 0.981 | 0.901 | 0.429 | 0.409 | 0.378 |
| S4 | 0.4 | 0.981 | 0.894 | 0.479 | 0.454 | 0.419 |
| S5 | 0.5 | 0.980 | 0.887 | 0.522 | 0.489 | 0.453 |
| S6 | 0.6 | 0.979 | 0.877 | 0.559 | 0.520 | 0.484 |
| S7 | 0.7 | 0.977 | 0.867 | 0.594 | 0.550 | 0.514 |
| S8 | 0.8 | 0.975 | 0.858 | 0.631 | 0.580 | 0.543 |
| S9 | 0.9 | 0.969 | 0.849 | 0.672 | 0.612 | 0.573 |
| S10 | 1.0 | 0.942 | 0.837 | 0.732 | 0.664 | 0.613 |
Note. The bound fractions at five different epochs, t/Tr = 0.2, 0.4, ..., 1.0 (Columns 3–7), inferred from our idealized simulations of subhaloes orbiting in the fixed potential of an NFW host. Each simulation has Mh/Ms = 1000, ch = 5, cs = 10 and xc = 1.0, and only differ in their value for the orbital circularity, η (Column 2). In each simulation, the subhalo, which is simulated with N = 107 particles, starts out at its own apo-centre (cf. Fig. 2).
| ID . | η . | fbound . | fbound . | fbound . | fbound . | fbound . |
|---|---|---|---|---|---|---|
| . | . | 0.2Tr . | 0.4Tr . | 0.6Tr . | 0.8Tr . | Tr . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| S0 | 0.0 | 0.982 | 0.909 | 0.120 | 0.111 | 0.110 |
| S1 | 0.1 | 0.982 | 0.908 | 0.262 | 0.244 | 0.230 |
| S2 | 0.2 | 0.982 | 0.905 | 0.367 | 0.347 | 0.323 |
| S3 | 0.3 | 0.981 | 0.901 | 0.429 | 0.409 | 0.378 |
| S4 | 0.4 | 0.981 | 0.894 | 0.479 | 0.454 | 0.419 |
| S5 | 0.5 | 0.980 | 0.887 | 0.522 | 0.489 | 0.453 |
| S6 | 0.6 | 0.979 | 0.877 | 0.559 | 0.520 | 0.484 |
| S7 | 0.7 | 0.977 | 0.867 | 0.594 | 0.550 | 0.514 |
| S8 | 0.8 | 0.975 | 0.858 | 0.631 | 0.580 | 0.543 |
| S9 | 0.9 | 0.969 | 0.849 | 0.672 | 0.612 | 0.573 |
| S10 | 1.0 | 0.942 | 0.837 | 0.732 | 0.664 | 0.613 |
| ID . | η . | fbound . | fbound . | fbound . | fbound . | fbound . |
|---|---|---|---|---|---|---|
| . | . | 0.2Tr . | 0.4Tr . | 0.6Tr . | 0.8Tr . | Tr . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| S0 | 0.0 | 0.982 | 0.909 | 0.120 | 0.111 | 0.110 |
| S1 | 0.1 | 0.982 | 0.908 | 0.262 | 0.244 | 0.230 |
| S2 | 0.2 | 0.982 | 0.905 | 0.367 | 0.347 | 0.323 |
| S3 | 0.3 | 0.981 | 0.901 | 0.429 | 0.409 | 0.378 |
| S4 | 0.4 | 0.981 | 0.894 | 0.479 | 0.454 | 0.419 |
| S5 | 0.5 | 0.980 | 0.887 | 0.522 | 0.489 | 0.453 |
| S6 | 0.6 | 0.979 | 0.877 | 0.559 | 0.520 | 0.484 |
| S7 | 0.7 | 0.977 | 0.867 | 0.594 | 0.550 | 0.514 |
| S8 | 0.8 | 0.975 | 0.858 | 0.631 | 0.580 | 0.543 |
| S9 | 0.9 | 0.969 | 0.849 | 0.672 | 0.612 | 0.573 |
| S10 | 1.0 | 0.942 | 0.837 | 0.732 | 0.664 | 0.613 |
Note. The bound fractions at five different epochs, t/Tr = 0.2, 0.4, ..., 1.0 (Columns 3–7), inferred from our idealized simulations of subhaloes orbiting in the fixed potential of an NFW host. Each simulation has Mh/Ms = 1000, ch = 5, cs = 10 and xc = 1.0, and only differ in their value for the orbital circularity, η (Column 2). In each simulation, the subhalo, which is simulated with N = 107 particles, starts out at its own apo-centre (cf. Fig. 2).
During peri-centric passage, the bound mass fraction can fluctuate rapidly, especially for the more radial orbits (see also Diemand, Kuhlen & Madau 2007; Han et al. 2012). This is a manifestation of the re-binding of some particles as a consequence of the subhalo undergoing re-virialization. The tidal shock causes a stretching of the subhalo in the direction towards the centre of the host halo and a compression in the direction perpendicular to the orbital plane. Hence, immediately following the tidal shock the subhalo finds itself out of virial equilibrium. While some matter has received a large enough boost in kinetic energy that it leaves the subhalo indefinitely, some of the particles that are unbound immediately following the tidal shock get rebound as the subhalo's potential re-adjusts as part of the re-virialization process.
What is most relevant for the discussion in this paper is that none of the simulated subhaloes undergo complete disruption. All orbits simulated have xc = 1, which is at the low end of the distribution (cf. the upper-left-hand panel of Fig. 1). Hence, these are among the most bound orbits among newly accreted subhaloes. And the simulations suggest that at most about 90 per cent of the subhalo mass will be stripped during the first radial period (which lasts between 9 and 9.5 Gyr). It is intriguing to contrast this with results from the cosmological Bolshoi simulation, in which a significant fraction of subhaloes are disrupted during, or shortly after, their first peri-centric passage (vdB17). This suggests that much of this disruption is likely to be a numerical artefact. We will elaborate on this in the following sections, as well as in Papers II and III.
4 PHYSICAL DISRUPTION PROCESSES
As discussed in Section 1, DM subhaloes are subjected to tidal forces that strip the subhaloes of their mass and which may ultimately result in their complete disruption. Depending on the rate with which the tidal forces change, the subhalo will respond differently. In the limit where the external tidal field changes slowly (i.e. along close-to-circular orbits), the subhalo will lose mass from beyond some limiting tidal radius. We refer to this as ‘tidal stripping’. If the tidal field changes rapidly, particles in the subhalo experience an impulsive kick, resulting in a net heating of the subhalo. We refer to this as tidal heating or tidal shocking. Throughout we distinguish between tidal heating due to the host halo (associated with the fast peri-centric passage along highly eccentric orbits), and due to high-speed encounters with other subhaloes, to which we refer as ‘harassment’. In this section, we describe each of these processes, in turn, and use simple analytical estimates together with the simulation results presented in the previous section to compare their relative importance.
Another process that is relevant for the evolution of DM substructure is dynamical friction, which transfers orbital energy and angular momentum of the subhalo to the particles of the host halo, thereby causing the subhalo to ‘sink’ towards the centre of the host, where the tidal forces are stronger. Dynamical friction is only expected to be significant for the most massive subhaloes, with a mass that exceeds a few per cent of that of the host halo (e.g. Binney & Tremaine 2008; Mo et al. 2010), and various studies have pointed out that indeed dynamical friction makes a negligible contribution to the evolution of the ensemble of subhaloes (e.g. Zhao 2004; Peñarrubia & Benson 2005; Ogiya & Burkert 2016). In this paper, we mainly focus on less massive subhaloes, which vastly outnumber their more massive counter-parts, and therefore ignore dynamical friction in what follows.
4.1 Impulsive heating due to the host halo
During the high-speed peri-centric passage, the rapid, impulsive change in the external potential causes a transfer of orbital energy to subhalo internal energy. The resulting increase in subhalo internal energy, ΔE, can be computed using the impulse approximation (Spitzer 1958), and in what follows we closely follow the treatment of Gnedin, Hernquist & Ostriker (1999, hereafter GHO99).
4.1.1 Application to Bolshoi subhaloes
![Left-hand panel: the distribution of log [ΔE/|Eb|] for the same set of newly accreted subhaloes as in Fig. 1. Here, ΔE is the energy injected into the subhalo during its first radial period, due to the impulsive shock associated with peri-centric passage (equation 22), while Eb is the subhalo's binding energy (equation 24). Ochre and green histograms indicate the results obtained with and without the adiabatic correction (equation 21), respectively, which has little impact. The grey-shaded region indicates where ΔE > |Eb|, and thus where the energy injected due to the impulsive shock exceeds the subhalo's original binding energy. The fractions of subhaloes that meet this criterion are indicated. Right-hand panel: the corresponding fraction of mass lost by the subhalo as a consequence of the tidal shock, calculated under the instantaneous mass-loss approximation as described in the text.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/474/3/10.1093_mnras_stx2956/2/m_stx2956fig3.jpeg?Expires=1749988357&Signature=AzwDbGiIakW1uPpeIEasGJP6KASU2Iu83cK0n7MOXqy-8dt9K9FD0j5f-i96RbzL1hhZjXzQJ5hyo0UwmHSVBznZlUOuvrnnsVplEFzoW6TmXnBgG0wlvpeu2wHCnJ0a4VDS38q4KPONMjQHZ22Y1qpNtyOH0QYAyWzZNfCOxsv-WAUV02mo6k0T7EXlvdLomCmurtxOBgMZ9kk9wqsKxzEWbEPZ8302ZHuvdY9m50BPuNnbnpmAK-l3~Zv76sB-pric1Nr8R3z59gfJ0mbrHyVjjB6KFpf-ttWWYoLYFAGFG2SJh~Hqq5AaFbjMHi3lsh9p2hJ-Sp9fJYiW2G7iZA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Left-hand panel: the distribution of log [ΔE/|Eb|] for the same set of newly accreted subhaloes as in Fig. 1. Here, ΔE is the energy injected into the subhalo during its first radial period, due to the impulsive shock associated with peri-centric passage (equation 22), while Eb is the subhalo's binding energy (equation 24). Ochre and green histograms indicate the results obtained with and without the adiabatic correction (equation 21), respectively, which has little impact. The grey-shaded region indicates where ΔE > |Eb|, and thus where the energy injected due to the impulsive shock exceeds the subhalo's original binding energy. The fractions of subhaloes that meet this criterion are indicated. Right-hand panel: the corresponding fraction of mass lost by the subhalo as a consequence of the tidal shock, calculated under the instantaneous mass-loss approximation as described in the text.
There are two important points to be made here. First of all, the overall impact of adiabatic shielding is fairly modest, and one does not make a large error if one simply ignores the adiabatic correction. Secondly, if indeed subhaloes for which ΔE > |Eb| were to experience complete disruption, the inference would be that the vast majority of subhaloes do not survive first peri-centric passage. However, this interpretation of ΔE/|Eb| is extremely naive and dramatically overestimates the efficiency of subhalo disruption. The reason is that ΔE does not specify how that energy is distributed over the particles. The following reduction ad absurdum makes it clear why this distribution is important; if all the energy were given to only a single particle, the system clearly would not disrupt, even if ΔE ≫ |Eb|. Rather, only that single particle would escape and leave the remainder of the halo virtually intact. As is evident from equation (20), the average change in kinetic energy due to an impulsive tidal shock scales with r2. Hence, particles at the outskirts of the subhalo, which need less energy to escape, receive far more energy than the more bound particles in the central regions.
In order to properly assess the impact of ΔE on the system as a whole, one needs to compare, for each individual particle i, the particle's individual (ΔE)i to its individual binding energy, |Ei|. One can then express the impact of the tidal shock in terms of the fraction of particles with (ΔE)i > |Ei|. We will refer to this fraction as fstrip. Note that this ‘instantaneous mass-loss approximation’ (cf. Aguilar & White 1985) ignores potential re-binding and unbinding of particles during the re-virialization process immediately following the tidal shock. However, these processes are neither calculable nor do they appear to have a significant impact, as demonstrated in Section 4.1.2.
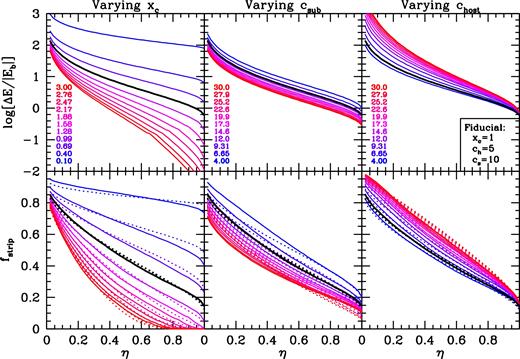
The logarithm of the ratio ΔE/|Eb| (upper panels) and the corresponding stripped mass fraction, fstrip (lower panels) as functions of the orbital circularity, η. All results assume a host halo to sub-halo mass ratio of 1000. The solid curves indicate the results obtained using the Monte Carlo method described in the text. Results are shown for different values of the orbital energy, as parametrized via xc (left-hand column), the concentration of the subhalo, cs (middle column), and the concentration of the host halo, ch (right-hand column); corresponding values are indicated. The black line corresponds to the fiducial model, which has xc = 1, cs = 10, and ch = 5. Note that ΔE/|Eb| = 1 corresponds to fstrip ∼ 0.2; hence even if the energy injected impulsively exceeds the original subhalo binding energy, only a modest fraction of subhalo mass will be stripped. The dotted curves in the lower panels indicate the predictions from equation (27).
The right-hand panel of Fig. 3 shows the distribution of fstrip, computed using the Monte Carlo method described above, for the newly accreted subhaloes in the Bolshoi simulation. Ochre and green histograms correspond to the bound fractions obtained with and without the adiabatic correction, respectively, which has little impact. Under the instantaneous mass-loss, approximation tidal heating due to the first peri-centric passage is expected to strip on average about 20–30 per cent of the mass of a subhalo. Note that there are no subhaloes for which fstrip > 0.9.
4.1.2 Comparison with idealized simulations
We now compare our semi-analytical predictions to the results of our idealized numerical simulations described in Section 3. We thus consider subhaloes with mass Ms and concentration parameter cs = 10 orbiting in a host halo of mass Mh = 1000Ms and concentration parameter ch = 5. We adopt an orbital energy characterized by xc = 1 and vary the orbital circularity η. The solid ochre curve in Fig. 5 shows the mass fraction that is stripped due to tidal heating during the subhalo's first radial orbital period, computed under the instantaneous mass-loss approximation as the fraction of particles with (ΔE)i > |Ei|. For comparison, the solid dots show the stripped mass fraction in the simulations after one radial period.
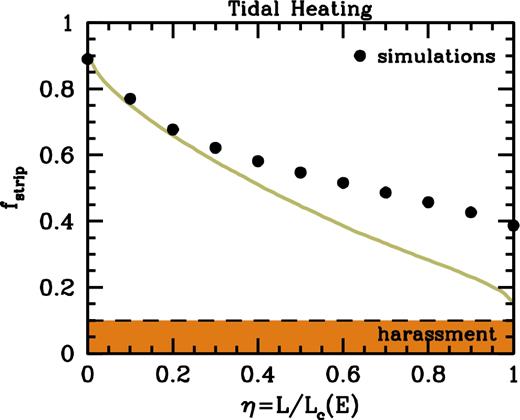
The subhalo mass fraction that is stripped off during the first radial period, fstrip, as function of the orbital circularity, η. The subhalo is modelled as a spherical NFW halo with concentration parameter cs = 10, orbiting in a host halo of mass Mh = 1000Ms and concentration parameter ch = 5, on an orbit with xc = 1. Solid dots indicate the results from our numerical simulations (see Section 3 and Table 1). The solid, ochre curve indicates the fraction of subhalo particles that receive an impulsive, tidal shock, ΔE, that is larger than its binding energy, computed using the method described in Section 4.1.1. Note the good agreement with the simulation results for the more radial orbits with η ≲ 0.2. The orange-shaded region indicates the mass fractions stripped during one radial period due to harassment, calculated using the method described in Section 4.2.
For η ≲ 0.2, the semi-analytical predictions are in excellent agreement with the simulation results, indicating that the evolution of the bound fraction for subhaloes on relatively radial orbits is governed by tidal shocking and that the impulse approximation combined with the instantaneous mass-loss approximation accurately describes the resulting mass evolution of subhaloes. For less radial orbits, tidal heating by itself underpredicts the stripped mass fraction. This is expected, since the changes in the tidal field become less ‘impulsive’ and the impact of tidal stripping is expected to become more important.
In Paper III in this series (Ogiya et al. in preparation), we compare our analytical estimates presented here to a large suite of (properly converged) simulations, covering a much larger range in orbital energies, orbital angular momentum, and halo concentrations.
4.2 Impulsive heating due to subhalo–subhalo encounters
In addition to experiencing tidal shocks during peri-centric passages, subhaloes also undergo tidal heating due to high-speed (impulsive) encounters with other subhaloes. The cumulative impact of many such high-speed impulsive encounters is sometimes called ‘harassment’ (Moore et al. 1996a).
In this section, we estimate how the tidal heating due to harassment compares to that due to a peri-centric passage. Consider a target subhalo (hereafter the subject) of mass Ms and size rs on a radial orbit (η = 0) in a host halo of mass Mh and size Rh. Assume for simplicity that the host halo has a uniform distribution of subhaloes with mass function dn/dm, which are orbiting the host with an orbital velocity dispersion σh ≃ (GMh/2Rh)1/2 (a good approximation for the global 1D velocity dispersion of an isotropic NFW halo).
The left-hand panel of Fig. 6 shows (ΔE)cross/|Eb| as function of the mass ratio Mh/Ms, computed with equation (40) using the universal fitting function for the (evolved) subhalo mass function of Jiang & van den Bosch (2016), and adopting a typical subhalo mass fraction of 10 per cent. For simplicity, we assume that all subhaloes (subject as well as perturbers) have the same NFW concentration parameter, c. Results are shown for three values of c, as indicated. Note that the expected amount of tidal heating due to harassment experienced by a subhalo is typically between 10 and 50 per cent of its binding energy, per crossing time. Typically, as one might expect, more massive subhaloes experience less harassment, but the mass dependence is fairly weak.
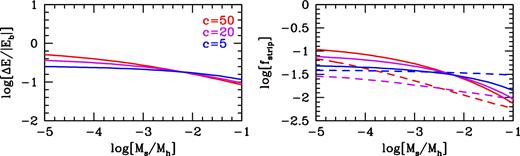
Left-hand panel: the tidal heating per crossing time due to impulsive subhalo–subhalo encounters (harassment). Different curves plot the logarithm of (ΔE)cross/|Eb| (equation 40) as function of the logarithm of the ratio of the mass of the target subhalo, Ms, to the mass of the host halo, Mh, for three different values of the assumed concentration of DM subhaloes, as indicated. Right-hand panel: the logarithm of the corresponding stripped mass fraction, fstrip, computed under two extreme conditions, where ΔE is dominated by a single encounter (solid lines) and by many independent encounters (dashed lines). Note how tidal harassment due to subhalo–subhalo encounters is expected to only strip between 1 and 10 per cent of the subhalo's mass per crossing time. This is significantly less than the mass fraction stripped due to the first peri-centric passage of the host halo (cf. Figs 3 and 4).
As discussed in Section 4.1.1, it is difficult to gauge the impact of ΔE on a subhalo without addressing how this energy is distributed over the N constituent particles. In the case of harassment, this is difficult to address with accuracy. The reason is that particles in the subject mass move in between separate collisions with individual perturbing subhaloes. However, we may get some insight using two limiting cases. If ΔE is dominated by the impulsive shock from a single encounter (with a massive subhalo and/or a small impact parameter), then we are in the limit where the energy gain for particle i scales as |$(\Delta E)_i \propto r_i^2$| and we can use equation (27) to estimate the stripped mass fraction. The results are indicated as solid lines in the right-hand panel of Fig. 6. If, on the other hand, ΔE is dominated by the cumulative effect of many encounters (with small subhaloes, covering the entire range of impact parameters), then we are in the regime where (ΔE)i = (ΔE)cross/N; i.e. the energy gain is independent of location within the subhalo (see Section 6.3). In this limit, we can compute the stripped mass fraction using a similar Monte Carlo approach as in Section 4.1.1 and simply counting the fraction of particles for which (ΔE)i > Ei. This results in the stripped mass fractions indicated by dashed lines in the right-hand panel. Interestingly, the two extreme cases yield stripped mass fractions that are relatively similar, spanning the range 0.01 ≲ fstrip ≲ 0.1. This range is indicated as an orange-shaded region in Fig. 5.
Although the above estimate for the tidal heating due to harassment is fairly crude, it is clear that the impact of harassment is subdominant to that due to the subhalo's first peri-centric passage. We therefore conclude that the tidal heating due to subhalo–subhalo encounters can safely be neglected when trying to assess the survivability of DM substructure.
This conclusion is at odds with a study by Knebe et al. (2006), who claim that harassment may contribute as much as 40 per cent to the total mass-loss rate of a subhalo. However, their estimate is based on comparing the force on the subhalo due to the host halo to that due to all other subhaloes, without taking account of the actual tides (relevant for tidal stripping) or the relative velocities (relevant for tidal heating). Although we believe our estimate to be more accurate, a more detailed study is required to settle this disagreement, which is beyond the scope of this paper.
4.3 Tidal stripping
In the previous two subsections, we focused on tidal shocking, which manifests itself whenever the tidal field changes rapidly. We now turn to the impact of a slowly varying tidal field. This is the situation one encounters for subhaloes on close to circular orbits. In this limit, one expects the material outside of the tidal radius to be stripped off. Modelling this tidal stripping, however, is far from trivial. First of all, as discussed in Section 2, the tidal radius is a poorly defined concept, with significantly different definitions in use. Secondly, it is unclear a priori at what rate the material that is located outside of the (instantaneous) tidal radius is going to be stripped off.
Using this method, and the properties and orbits of the 5000 subhaloes at accretion from the Bolshoi simulation depicted in Fig. 1, we obtain the stripped mass fractions shown in Fig. 7. The three panels differ in the value of the parameter α, as indicated, while the red and blue histograms correspond to the results obtained using rt, 1 (equation 3) and rt, 2 (equation 4), respectively. Note that α = ∞ (right-hand panel) corresponds to instantaneous stripping, in which case the stripped mass fraction is simply given by fstrip = Ms(>rt|p)/Ms.
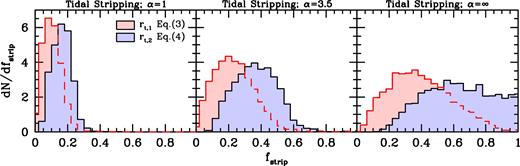
Distributions of the mass fraction fstrip that is stripped off during a subhalo's first radial orbital period due to tidal (non-impulsive) stripping for the same set of newly accreted subhaloes as in Fig. 1. Red and blue histograms are based on the different definitions of the tidal radius, as indicated, while different panels correspond to different stripping rates, as parametrized by α (cf. equation 41). The case where α = ∞ (right-hand panel) corresponds to instantaneous stripping, for which fstrip = Ms(>rt|p)/Ms.
In general, since rt, 2 < rt, 1, accounting for the centrifugal force in the definition of the tidal radius results in predictions for the stripped mass fraction that are significantly larger. Also, fstrip depends strongly on the value of α: for α = 1, the median fstrip for subhaloes during their first radial orbit is only 0.10 (0.16) for rt = rt, 1 (rt, 2). For α = ∞, this increases to 0.38 (0.63). Note that the assumption of instantaneous stripping combined with rt = rt, 2 results in an appreciable fraction of subhaloes with extremely large stripped mass fractions; among our sample of 5000 newly accreted subhaloes 3.4 (1.2) per cent have fstrip > 0.99 (>0.999). Clearly, depending on how one defines the tidal radius and what one assumes regarding the rate at which material beyond the tidal radius is stripped, the predicted impact of tidal stripping varies dramatically. This is also evident from Fig. 8, which compares our semi-analytical predictions for fstrip (for the first radial orbital period), to the results from our idealized numerical simulations. The two panels differ in the definition of the tidal radius, as indicated, while different curves in each panel correspond to different values of α.
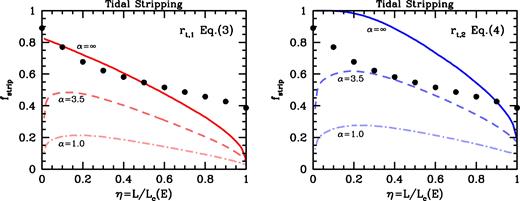
Same as Fig. 5, except that this time the curves reflect the predicted mass fractions that are stripped off subhaloes during their first radial orbit due to (non-impulsive) tidal stripping. The two panels differ in the adopted definition for the tidal radius, as indicated, while solid, dashed, and dot–dashed curves correspond to assumed stripping rates with α = ∞, 3.5, and 1.0, respectively. As in Fig. 5, the solid dots indicate the results from the idealized numerical simulations (see Section 3 and Table 1). See the text for a detailed discussion.
Clearly, no single combination of tidal radius definition and value for α results in predictions for fstrip that are in good agreement with the simulation results over the entire range in η. It is not surprising that tidal stripping is unable to capture the tidal evolution of subhaloes on highly radial (i.e. low η) orbits, as their evolution is clearly governed by impulsive, tidal heating (cf. Fig. 5). However, it may seem surprising that the tidal stripping model also fails to describe the results along close-to-circular orbits. After all, this is the regime where the tidal field varies slowly, and thus where the tidal stripping model is expected to be most accurate. However, there are several problems with the tidal stripping model that are ultimately responsible for its failure.
First of all, the notion that only the matter that is initially located outside of rt will be stripped off is clearly incorrect. After all, some of the particles inside of the tidal radius will be on orbits whose apo-centre rapo > rt; Hence, if the tidal radius does not evolve much with time (i.e. if the orbit is close to circular), one expects those particles to be stripped as well. And since the dynamical time of particles in the subhalo is comparable to the orbital time of the subhalo within its host, the time-scale over which this stripping occurs should be comparable to the radial orbital period Tr. Using the same Monte Carlo realization used to compute the stripped mass fraction due to tidal heating (see Section 4.1.1), we compute the apo-centre for each of the 50 000 subhalo particles. For η = 1 (i.e. circular orbit), we find that 41 per cent of all subhalo particles have an apo-centre ra > rt, 2. This is in excellent agreement with the stripped mass fraction in the simulation, which has fstrip = 0.394 (after one radial period) for η = 1 (cf. Table 1), and suggests that along orbits that are close to circular, one may estimate fstrip as the fraction of particles with ra > rt, 2. Note, though, that this approximation rapidly deteriorates for decreasing η.7 Furthermore, there is an additional problem with the stripping model that is even more difficult to overcome. After the outer layers of a subhalo are (instantaneously) removed, the remaining remnant is no longer in virial equilibrium. As we show in Appendix B, the remnant has a virial ratio K/|W| > 0.5. Hence, the only way the system can re-virialize is by converting kinetic to potential energy. In doing so, the system ‘puffs up’; i.e. its characteristic radius increases while its overall density decreases. This, in turn, results in a decrease of the tidal radius, and hence in additional mass-loss (Kampakoglou & Benson 2007). As a result, the mass-loss is a continuous process, even in the static field experienced along a circular orbit. This is evident from the left-hand panel of Fig. 2 (red curve), which shows the evolution of the bound fraction for the duration of one radial period, Tr = 9.53 Gyr. In Paper II, we show that the mass-loss continuous well beyond that, and that subhaloes on circular orbits continue to loose mass even after 60 Gyr of evolution.
5 CAN INSTANTANEOUS STRIPPING RESULT IN DISRUPTION?
In an influential paper, Hayashi et al. (2003) pointed out that instantaneously removing all material from a halo down to some truncation radius, rtr, may leave a remnant with positive binding energy, as long as rtr < rcrit. For a spherical, isotropic NFW halo, rcrit is 0.77 times the NFW scale radius. This is demonstrated in Appendix B, where it is also shown how the critical radius, rcrit, depends on the halo's anisotropy. Typically, rcrit becomes larger for haloes that are more radially anisotropic, and in general rcrit > 0, unless haloes are strongly tangentially anisotropic.
This seems to suggest, as was advocated by Hayashi et al., that a subhalo whose tidal radius is smaller than rcrit would ‘spontaneously’ disrupt, even without the need to invoke tidal shock heating. And since a typical NFW halo has roughly between 5 and 10 per cent of its mass enclosed within this critical radius, this suggests that a typical subhalo should physically disrupt once it has lost between 90 and 95 per cent of its original (i.e. at accretion) mass. Interestingly, this is not inconsistent with the results from numerical simulations, which indeed reveal very few subhaloes whose mass is less than 5 per cent of that at accretion (e.g. Han et al. 2016; Jiang & van den Bosch 2016; van den Bosch 2017), and various authors have implemented a treatment of subhalo disruption based on this notion (e.g. Zentner & Bullock 2003; Taylor & Babul 2004; Klypin et al. 2015).
However, as we now demonstrate, this notion is seriously flawed, and, if simulated with sufficient resolution, the instantaneous removal of outer layers always leaves a bound remnant, even when these outer layers contain more than 99.9 per cent of the total virial mass. The reason is once again that the total binding energy is not sufficiently informative. What matters is the distribution of binding energies of the constituent particles, not its sum. Note that we already encountered an example of subhaloes with positive binding energy, namely subhaloes immediately following an impulsive shock with ΔE/|Eb| > 1. As we saw in Section 4.1 neither of these disrupted, even when ΔE > 100|Eb|. In order to test how subhaloes respond to instantaneous mass stripping down to radii below rcrit, we now use numerical N-body simulations to evolve instantaneously stripped, isotropic NFW haloes and track their bound mass fraction over time.
5.1 Numerical simulations
We simulate the evolution of isolated, spherical NFW host haloes that are instantaneously truncated. We use the same method as in Section 3 to draw the initial positions and velocities of the particles: we assume that, prior to truncation, the halo has an isotropic velocity distribution, and we truncate the halo at a radius rtr, which is a free parameter, while initializing the velocities as if the halo extends out to infinity (this is the expected result if the stripping is instantaneous). All our simulations have N = 105 particles inside the truncation radius, and are carried out using a modified version of the hierarchical N-body code treecode, written by Joshua Barnes with some modifications due to John Dubinski. treecode uses a Barnes & Hut (1986) octree to compute accelerations based on a multipole expansion up to quadrupole order, and uses a straightforward second-order leap-frog integration scheme to solve the equations of motion. Since we use fixed time steps, our integration scheme is fully symplectic. Forces between particles are softened using a simple Plummer softening.
As in Section 3, we adopt model units in which the gravitational constant, G, the scale radius, r0, and the virial mass of the halo, Mvir, are all unity. Using numerical simulations of NFW haloes in isolation (see Paper II), we infer an optimal softening length of ε = 0.05 (in model units) for simulations with N = 105 particles inside the virial radius. In order to gauge the sensitivity to the specific choice of the softening length, we run two different sets of simulations: in set TruncA we adopt a softening length of ε = 0.05, independent of rtr, while in set TruncB, we scale the softening length linearly with the size of the simulated system according to ε = 0.05 (rtr/rvir); such a scaling is consistent with simple expectations for the optimal softening length (e.g. van Kampen 2000a; Power et al. 2003). We run each truncated halo in isolation for 40 000 time steps of Δt = 0.02, corresponding to a total integration time of ∼50 Gyr. Finally, we adopt a tree opening angle of θ = 0.7, and we have verified that our results are extremely stable to changes in Δt and/or θ. The parameters of the simulations in TruncA and TruncB are listed in Table 2.
| ID . | rtr/r0 . | f(rtr) . | ε/r0 . | fb, rem . | fb, rem . |
|---|---|---|---|---|---|
| . | . | . | . | (t = 0) . | (50 Gyr) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| A01 | 7.11 | 0.817 | 0.05 | 0.98 | 0.98 |
| A02 | 6.46 | 0.768 | 0.05 | 0.98 | 0.98 |
| A03 | 5.81 | 0.715 | 0.05 | 0.98 | 0.97 |
| A04 | 5.16 | 0.659 | 0.05 | 0.98 | 0.97 |
| A05 | 4.51 | 0.596 | 0.05 | 0.97 | 0.97 |
| A06 | 3.85 | 0.528 | 0.05 | 0.97 | 0.96 |
| A07 | 3.19 | 0.451 | 0.05 | 0.96 | 0.95 |
| A08 | 2.52 | 0.365 | 0.05 | 0.94 | 0.93 |
| A09 | 1.83 | 0.265 | 0.05 | 0.91 | 0.90 |
| A10 | 1.48 | 0.209 | 0.05 | 0.89 | 0.88 |
| A11 | 1.10 | 0.147 | 0.05 | 0.83 | 0.82 |
| A12 | 0.68 | 0.076 | 0.05 | 0.71 | 0.71 |
| A13 | 0.48 | 0.046 | 0.05 | 0.61 | 0.62 |
| A14 | 0.35 | 0.027 | 0.05 | 0.46 | 0.49 |
| A15 | 0.20 | 0.011 | 0.05 | 0.23 | 0.31 |
| A16 | 0.10 | 0.003 | 0.05 | 0.15 | 0.18 |
| A17 | 0.08 | 0.001 | 0.05 | 0.00 | Disrupt |
| B01 | 2.52 | 0.365 | 0.0125 | 0.94 | 0.93 |
| B02 | 1.83 | 0.265 | 0.0092 | 0.91 | 0.90 |
| B03 | 1.48 | 0.209 | 0.0074 | 0.89 | 0.88 |
| B04 | 1.10 | 0.147 | 0.0051 | 0.83 | 0.82 |
| B05 | 0.68 | 0.076 | 0.0034 | 0.73 | 0.72 |
| B06 | 0.35 | 0.027 | 0.0017 | 0.55 | 0.57 |
| B07 | 0.20 | 0.011 | 0.0010 | 0.43 | 0.46 |
| B08 | 0.10 | 0.003 | 0.0005 | 0.34 | 0.37 |
| B09 | 0.08 | 0.001 | 0.0004 | 0.31 | 0.35 |
| ID . | rtr/r0 . | f(rtr) . | ε/r0 . | fb, rem . | fb, rem . |
|---|---|---|---|---|---|
| . | . | . | . | (t = 0) . | (50 Gyr) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| A01 | 7.11 | 0.817 | 0.05 | 0.98 | 0.98 |
| A02 | 6.46 | 0.768 | 0.05 | 0.98 | 0.98 |
| A03 | 5.81 | 0.715 | 0.05 | 0.98 | 0.97 |
| A04 | 5.16 | 0.659 | 0.05 | 0.98 | 0.97 |
| A05 | 4.51 | 0.596 | 0.05 | 0.97 | 0.97 |
| A06 | 3.85 | 0.528 | 0.05 | 0.97 | 0.96 |
| A07 | 3.19 | 0.451 | 0.05 | 0.96 | 0.95 |
| A08 | 2.52 | 0.365 | 0.05 | 0.94 | 0.93 |
| A09 | 1.83 | 0.265 | 0.05 | 0.91 | 0.90 |
| A10 | 1.48 | 0.209 | 0.05 | 0.89 | 0.88 |
| A11 | 1.10 | 0.147 | 0.05 | 0.83 | 0.82 |
| A12 | 0.68 | 0.076 | 0.05 | 0.71 | 0.71 |
| A13 | 0.48 | 0.046 | 0.05 | 0.61 | 0.62 |
| A14 | 0.35 | 0.027 | 0.05 | 0.46 | 0.49 |
| A15 | 0.20 | 0.011 | 0.05 | 0.23 | 0.31 |
| A16 | 0.10 | 0.003 | 0.05 | 0.15 | 0.18 |
| A17 | 0.08 | 0.001 | 0.05 | 0.00 | Disrupt |
| B01 | 2.52 | 0.365 | 0.0125 | 0.94 | 0.93 |
| B02 | 1.83 | 0.265 | 0.0092 | 0.91 | 0.90 |
| B03 | 1.48 | 0.209 | 0.0074 | 0.89 | 0.88 |
| B04 | 1.10 | 0.147 | 0.0051 | 0.83 | 0.82 |
| B05 | 0.68 | 0.076 | 0.0034 | 0.73 | 0.72 |
| B06 | 0.35 | 0.027 | 0.0017 | 0.55 | 0.57 |
| B07 | 0.20 | 0.011 | 0.0010 | 0.43 | 0.46 |
| B08 | 0.10 | 0.003 | 0.0005 | 0.34 | 0.37 |
| B09 | 0.08 | 0.001 | 0.0004 | 0.31 | 0.35 |
Note. Simulations of instantaneously truncated NFW haloes. Listed are the simulation ID (column 1), the ratio of the truncation radius, rtr, to the scale radius r0 (column 2), the fraction f(rtr) ≡ M(rtr)/Mvir of the virial mass located inside the truncation radius (column 3), the softening length in units of the scale radius (column 4), and the bound fractions of the remnants, fb, rem, at t = 0 (column 5) and t = 50 Gyr (column 6). Simulations A01–A17 belong to TruncA, and all adopt a softening length of ε = 0.05, while the TruncB simulations B01–B09 adopt a softening length that scales linearly with the truncation radius according to ε = 0.05(rtr/rvir).
| ID . | rtr/r0 . | f(rtr) . | ε/r0 . | fb, rem . | fb, rem . |
|---|---|---|---|---|---|
| . | . | . | . | (t = 0) . | (50 Gyr) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| A01 | 7.11 | 0.817 | 0.05 | 0.98 | 0.98 |
| A02 | 6.46 | 0.768 | 0.05 | 0.98 | 0.98 |
| A03 | 5.81 | 0.715 | 0.05 | 0.98 | 0.97 |
| A04 | 5.16 | 0.659 | 0.05 | 0.98 | 0.97 |
| A05 | 4.51 | 0.596 | 0.05 | 0.97 | 0.97 |
| A06 | 3.85 | 0.528 | 0.05 | 0.97 | 0.96 |
| A07 | 3.19 | 0.451 | 0.05 | 0.96 | 0.95 |
| A08 | 2.52 | 0.365 | 0.05 | 0.94 | 0.93 |
| A09 | 1.83 | 0.265 | 0.05 | 0.91 | 0.90 |
| A10 | 1.48 | 0.209 | 0.05 | 0.89 | 0.88 |
| A11 | 1.10 | 0.147 | 0.05 | 0.83 | 0.82 |
| A12 | 0.68 | 0.076 | 0.05 | 0.71 | 0.71 |
| A13 | 0.48 | 0.046 | 0.05 | 0.61 | 0.62 |
| A14 | 0.35 | 0.027 | 0.05 | 0.46 | 0.49 |
| A15 | 0.20 | 0.011 | 0.05 | 0.23 | 0.31 |
| A16 | 0.10 | 0.003 | 0.05 | 0.15 | 0.18 |
| A17 | 0.08 | 0.001 | 0.05 | 0.00 | Disrupt |
| B01 | 2.52 | 0.365 | 0.0125 | 0.94 | 0.93 |
| B02 | 1.83 | 0.265 | 0.0092 | 0.91 | 0.90 |
| B03 | 1.48 | 0.209 | 0.0074 | 0.89 | 0.88 |
| B04 | 1.10 | 0.147 | 0.0051 | 0.83 | 0.82 |
| B05 | 0.68 | 0.076 | 0.0034 | 0.73 | 0.72 |
| B06 | 0.35 | 0.027 | 0.0017 | 0.55 | 0.57 |
| B07 | 0.20 | 0.011 | 0.0010 | 0.43 | 0.46 |
| B08 | 0.10 | 0.003 | 0.0005 | 0.34 | 0.37 |
| B09 | 0.08 | 0.001 | 0.0004 | 0.31 | 0.35 |
| ID . | rtr/r0 . | f(rtr) . | ε/r0 . | fb, rem . | fb, rem . |
|---|---|---|---|---|---|
| . | . | . | . | (t = 0) . | (50 Gyr) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| A01 | 7.11 | 0.817 | 0.05 | 0.98 | 0.98 |
| A02 | 6.46 | 0.768 | 0.05 | 0.98 | 0.98 |
| A03 | 5.81 | 0.715 | 0.05 | 0.98 | 0.97 |
| A04 | 5.16 | 0.659 | 0.05 | 0.98 | 0.97 |
| A05 | 4.51 | 0.596 | 0.05 | 0.97 | 0.97 |
| A06 | 3.85 | 0.528 | 0.05 | 0.97 | 0.96 |
| A07 | 3.19 | 0.451 | 0.05 | 0.96 | 0.95 |
| A08 | 2.52 | 0.365 | 0.05 | 0.94 | 0.93 |
| A09 | 1.83 | 0.265 | 0.05 | 0.91 | 0.90 |
| A10 | 1.48 | 0.209 | 0.05 | 0.89 | 0.88 |
| A11 | 1.10 | 0.147 | 0.05 | 0.83 | 0.82 |
| A12 | 0.68 | 0.076 | 0.05 | 0.71 | 0.71 |
| A13 | 0.48 | 0.046 | 0.05 | 0.61 | 0.62 |
| A14 | 0.35 | 0.027 | 0.05 | 0.46 | 0.49 |
| A15 | 0.20 | 0.011 | 0.05 | 0.23 | 0.31 |
| A16 | 0.10 | 0.003 | 0.05 | 0.15 | 0.18 |
| A17 | 0.08 | 0.001 | 0.05 | 0.00 | Disrupt |
| B01 | 2.52 | 0.365 | 0.0125 | 0.94 | 0.93 |
| B02 | 1.83 | 0.265 | 0.0092 | 0.91 | 0.90 |
| B03 | 1.48 | 0.209 | 0.0074 | 0.89 | 0.88 |
| B04 | 1.10 | 0.147 | 0.0051 | 0.83 | 0.82 |
| B05 | 0.68 | 0.076 | 0.0034 | 0.73 | 0.72 |
| B06 | 0.35 | 0.027 | 0.0017 | 0.55 | 0.57 |
| B07 | 0.20 | 0.011 | 0.0010 | 0.43 | 0.46 |
| B08 | 0.10 | 0.003 | 0.0005 | 0.34 | 0.37 |
| B09 | 0.08 | 0.001 | 0.0004 | 0.31 | 0.35 |
Note. Simulations of instantaneously truncated NFW haloes. Listed are the simulation ID (column 1), the ratio of the truncation radius, rtr, to the scale radius r0 (column 2), the fraction f(rtr) ≡ M(rtr)/Mvir of the virial mass located inside the truncation radius (column 3), the softening length in units of the scale radius (column 4), and the bound fractions of the remnants, fb, rem, at t = 0 (column 5) and t = 50 Gyr (column 6). Simulations A01–A17 belong to TruncA, and all adopt a softening length of ε = 0.05, while the TruncB simulations B01–B09 adopt a softening length that scales linearly with the truncation radius according to ε = 0.05(rtr/rvir).
5.2 Results
Fig. 9 summarizes the simulation results (see also Table 2). The open circles indicate fb,tot at the end of each simulation (i.e. after 50 Gyr of evolution). Blue and red circles correspond to simulations from TruncA and TruncB, respectively, and the results are shown as a function of the truncation radius, rtr, in units of the halo's (original) scale radius, r0. The green, solid line indicates M(rtr)/Mvir, and reflects the initial mass fraction enclosed by rtr. The dashed, vertical line marks rtr = 0.77r0, which is the critical value for the truncation radius, to the left of which the remnants (immediately after the instantaneous truncation) have positive binding energy. Clearly, there is no indication of anything special happening around this scale. In fact, in all simulations we find that part of the remnant remains bound, and quickly resettles into a new, virialized halo. As an example, Fig. 10 shows the evolution in the density profile (upper panel), enclosed mass profile (middle panel), and radial velocity dispersion profile (lower panel) for an NFW halo that is instantaneously truncated at rtr = 0.68r0. The inner region quickly (within ∼2 Gyr) re-virializes, while it takes more than a Hubble time for the weakly bound particles to build a virialized structure that extends to >10r0 (i.e. beyond the original virial radius of the subhalo).
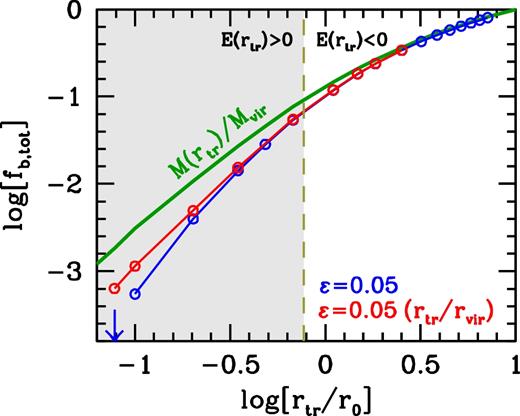
The bound fraction, fb,tot, for NFW haloes with concentration parameter c = 10 as a function of their truncation radius, rtr, expressed in units of the scale radius r0. The green solid line indicates M(rtr)/Mvir and reflects the initial mass fraction enclosed by rtr. The open circles are the mass fractions that are found to be bound in numerical simulations with N = 105 particles after 50 Gyr of evolution. Blue and red circles correspond to simulations from TruncA and TruncB, respectively, that only differ in their choice of softening length, as indicated. The dashed, vertical line corresponds to rtr = 0.77r0, where the binding energy of the remnant transits from being negative to being positive. The blue, downward arrow indicates that the TruncA simulation with rtr = 0.078r0 disrupts (i.e. has fbound → 0).
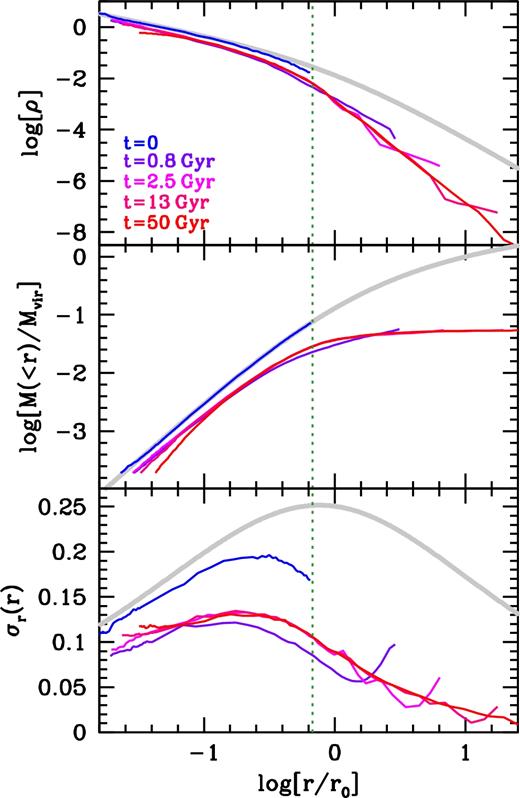
The density profiles (upper panel), enclosed mass profiles (middle panel), and radial velocity dispersion profiles (lower panel) at five different evolutionary stages for an NFW halo that is instantaneously truncated (at t = 0) at rtr = 0.68r0 (simulation B05 in Table 2). Note that the profiles are for the bound particles only.
In general, a smaller truncation radius implies a larger fraction of particles inside this truncation radius that are unbound (and escape), but in each case a bound subset remains. The only exception is simulation A17 from TruncA, which has rtr = 0.078r0 and which experiences complete disruption immediately after the onset of the simulation (indicated by a blue, downward pointing arrow in Fig. 9). We point out, though, that in this case rtr is only ∼1.5 times the softening length; clearly, the potential is ‘over-softened’ and has little to no resemblance to the central region of an NFW profile. The same simulation in TruncB (simulation B09), which uses a much smaller softening length (see Table 2), results in ∼35 per cent of the initial particles of the remnant surviving as a self-bound entity.
In all simulations, we find that the bound fraction does not evolve significantly with time: the fraction of particles that remain bound together is basically the same after more than 50 Gyr of evolution, as it is at t = 0 (cf. columns (5) and (6) of Table 2). Only when rtr ≲ r0/2 do we find that the bound fraction evolves somewhat (typically fb, remincreases by a few per cent), during the first ∼0.2 Gyr after the onset of the simulation. This is a manifestation of (violent) relaxation in response to the instantaneous removal of the halo's outer layers; as shown in Appendix B, the remnant can be far from virial equilibrium.
To summarize, unless DM haloes are strongly tangentially anisotropic, instantaneously stripping matter from the outskirts may leave a remnant with total, positive binding energy. However, contrary to naive expectations (e.g. Hayashi et al. 2003; Taylor & Babul 2004; Klypin et al. 2015), a system with positive binding energy does not necessarily disrupt entirely. After all, the system will typically have a broad distribution of binding energies, and a significant fraction of the particles can still be bound, even if the total binding energy is positive. In the N-body experiments described above, we only find that a truncated, isotropic NFW halo disrupts if the truncation radius is less than, or comparable to, the softening length used. Although we have only tested this for isotropic NFW haloes, we emphasize that (the central parts) of NFW haloes in cosmological simulations are indeed close to isotropic (e.g. Navarro et al. 2010). We therefore conclude that instantaneous truncation of an NFW halo does not lead to halo disruption. Artificial disruption in simulations may occur, however, if the system is simulated with insufficient force resolution (see Section 6.4 and Paper II).
6 NUMERICAL DISRUPTION PROCESSES
As discussed in Section 1, it was not until 1997 that numerical N-body simulations started to resolve surviving populations of DM substructure. Prior to this, the simulations suffered from a serious overmerging problem, mainly due to inadequate force softening (Moore et al. 1996b). However, numerical overmerging (i.e. the artificial disruption of substructure in numerical simulations) is still present in modern state-of-the-art simulations. This is the reason why methods to populate DM-only simulations with galaxies, such as semi-analytical models for galaxy formation (e.g. Springel et al. 2001; Kang et al. 2005; Kitzbichler & White 2008), subhalo abundance matching models (e.g. Conroy et al. 2006; Guo & White 2014; Campbell et al. 2017), and empirical models (e.g. Moster et al. 2010, 2017; Tollet et al. 2017), often include ‘orphan’ galaxies, i.e. mock galaxies without an associated subhalo in the simulation. Although it is therefore recognized that simulations continue to experience artificial disruption, it is generally assumed that this happens only for subhaloes below a mass resolution of 50–100 particles. This notion is based on the fact that subhalo mass functions are typically converged down to this mass resolution limit (e.g. Springel et al. 2008; Onions et al. 2012; Knebe et al. 2013; van den Bosch & Jiang 2016). The general consensus therefore is that any disruption of subhaloes above this ‘resolution limit’ must be physical in origin (see Diemand et al. 2004b, for a detailed discussion).
However, as we demonstrate in Paper II, state-of-the-art numerical simulations of CDM structure formation still suffer from abundant artificial disruption well above this mass resolution limit, and it is therefore imperative that we revisit the issue of numerical overmerging. There are a number of processes that may (potentially) give rise to numerical, artificial disruption of DM substructure in numerical N-body simulations. These are (i) evaporation resulting from two-body relaxation of the subhalo, (ii) evaporation due to two-body encounters with particles from the host halo, (iii) tidal heating due to impulsive encounters with particles from the host halo, and (iv) disruption due to issues with force softening.
Each of these processes have been discussed in more or less detail in various previous studies, including Carlberg (1994), van Kampen (1995, 2000a,b), Moore et al. (1996b), and Klypin et al. (1999a). For the sake of completeness, and in order to correct and elucidate inconsistencies and errors in some of these previous studies, we discuss each of these processes in detail in what follows.
6.1 Evaporation due to two-body self-relaxation

Time-scales, in units of the crossing time, for the disruption of subhaloes due to numerical effects as a function of the number of particles, N, used in simulating the subhalo (which is assumed to have a concentration parameter c = 10). In particular, green, blue, and red lines correspond to the times scales for evaporation due to two-body relaxation, evaporation due to collisional encounters with host halo particles, and disruption due to impulsive heating by host halo particles. For the latter, the red dashed line shows the proper, corrected time-scale. See the text for details. The grey-shaded region corresponds to t/tcross ≤ 30, which roughly corresponds to time-scales shorter than a Hubble time. Left- and right-hand panels correspond to different assumptions regarding the softening length, as indicated.
There is one important caveat, though: the above estimate for trelax is based on the classical two-body treatment of Chandrasekhar (1943), in which all collisions are assumed to be independent. This ignores resonant effects and self-gravity (‘collective relaxation’), both of which can significantly boost relaxation with respect to the two-body rate (Weinberg 1993). In particular, as Weinberg demonstrates, the dominant contribution to relaxation of a gravitational system comes from large-scale modes, with wavelengths comparable to the size of the system. As a consequence, the treatment of force softening has little to no effect on the actual relaxation rate. This explains, among others, why relaxation rates in expansion-type codes, such as the self-consistent field code, reveal relaxation at a level that is similar to that of tree-based codes (Hernquist & Ostriker 1992), and why the amount of spurious (artificial) fragmentation apparent in warm DM simulations is virtually independent of the softening length (Power et al. 2016). In Paper II, we demonstrate that these same large-scale fluctuations, in the presence of a tidal field, cause a run-away instability in the mass evolution of DM subhaloes in N-body simulations.
To summarize, we caution that although the two-body relaxation rate (equation 46) may exceed the Hubble time, the actual relaxation time in numerical simulations may be significantly shorter, and the overall impact of relaxation in N-body simulations remains a contentious topic (see e.g. Melott 2007; Hahn & Angulo 2016; Power et al. 2016, and references therein).
6.2 Evaporation due to two-body collisions with host particles
In an attempt to explain the origin of numerical ‘overmerging’, Carlberg (1994) suggested that subhaloes in numerical simulations may artificially disrupt due to two-body encounters between particles in the subhalo, and those in the host halo. He argued that, since the host halo particles are so much hotter (i.e. have higher velocities) than the subhalo particles, the former will transfer kinetic energy to the latter, thereby ‘boiling’ the subhalo into dissolution. This idea was further promoted by van Kampen (1995, 2000a,b) who suggested that it is the dominant numerical process to explain the overmerging of substructure in cosmological N-body simulations. Unfortunately, Carlberg (1994) does not give a derivation of his expression for the heating time-scale, which in addition contains a typo, in that the indices ‘c’ and ‘h’ in his equation (11) are swapped. van Kampen (1995) does present a correct derivation for the relaxation time, but then incorrectly assumes that this is comparable to the disruption time, thereby underestimating the latter by two orders of magnitude. In order to set the record straight, we give a detailed derivation in what follows.
We thus see that the relaxation time due to encounters with the hot particles is significantly longer than that due to encounters with its own particles. This has its origin in the fact that encounters with host halo particles have, on average, a larger impact parameter and a higher relative velocity (cf. equation 49). This is partially compensated by the fact that there are more host halo particles than subhalo particles, but the combined effect is such that self-interactions are more important than those between host and subhalo particles.
The relaxation time derived here is identical to that in van Kampen (1995). However, van Kampen then argued that the evaporation time due to these particle–subhalo interactions is identical to the relaxation time (i.e. no multiplication with a factor 140 is required). Van Kampen incorrectly assumes that relaxation heats the cold system to the ‘temperature’ (velocity dispersion) of the hot system. If this were true, then after a single relaxation time a very large fraction of subhalo particles would evaporate, such that the evaporation time-scale is only slightly longer than the relaxation time-scale. But this is incorrect. After all, the relaxation time is defined as the time required to heat the velocity distribution of the cold system to a Maxwellian with a velocity dispersion σc, rather than σh (see equation 51). Hence, one still requires of the order of 140 relaxation times for the cold system to evaporate, which implies that the collisional heating due to interactions with host halo particles is less important than that due to self-interactions.
This is illustrated in Fig. 11, where the blue lines correspond to |$t^{\rm ch}_{\rm evap}$| for a subhalo embedded in a host halo with a mass 30 times larger than that of the subhalo. Since |$t^{\rm ch}_{\rm evap}$| is roughly proportional to (Mh/Mc)1/3 and most subhaloes have Mh/Mc ≫ 30, this estimate for |$t^{\rm ch}_{\rm heat}$| may be considered a conservative lower limit. Note that indeed |$t^{\rm ch}_{\rm evap} > t^{\rm cc}_{\rm evap}$|, except when the softening length becomes comparable to the size of the subhalo in question (which is not a meaningful situation to consider).
To summarize, contrary to claims by Carlberg (1994) and van Kampen (1995, 2000a), evaporation due to particle–subhalo interactions is always subdominant to that due to self-interactions among the subhalo particles. And since the latter is always longer than the Hubble time, evaporation due to collisional encounters with host halo particles cannot be an important numerical effect.
6.3 Impulsive heating due to encounters with host halo particles
A subtly different numerical disruption mechanism is impulsive heating of the subhalo due to encounters with the artificially massive particles of the host halo. This is different from the two-body particle–subhalo heating picture outlined above, which is a collisional process. The heating mechanism considered here, and first discussed in Moore et al. (1996b), considers the subhalo as a collisionless system being tidally heated due to the high-speed, impulsive encounters with the particles of the host halo.
Consider a particle from the hot host halo, which is modelled as a Plummer sphere of mass m and size ε (the softening length), that has an impulsive encounter with a (cold) subhalo of mass Mc = Nc m and size rc. Let b and |${\boldsymbol V} = V \, \hat{e}_z$| be the impact parameter and relative velocity (taken to be along the z-direction) of the encounter.
The function h(y) transits from |${\cal O}(1)$| for y ≪ 1 to zero for y ≫ 1. Hence, as long as the softening length used is small compared to the scale radius of the subhalo, one can simply set hc(ε/rs) = 1 in the above expression for (ΔE)cross. This is immediately evident from equation (56), which shows that every subhalo particle, independent of its cylindrical radius R, experiences roughly the same increase in kinetic energy per unit time. The only exception are the particles with R < ε, for which (Δv2)cross(R) ∝ R2. As long as ε ≪ r0, one therefore does not make a large error by simply writing the total increase in kinetic energy of the subhalo, per crossing time, as |$(\Delta E)_{\rm cross} = {1 \over 2} N_{\rm c}\, m \, (\Delta v^2)_{\rm cross}(R)$|. This yields equation (57) with hc(ε/rs) = 1.
This is illustrated in the left-hand panel of Fig. 11, where the red, solid line indicates |$t^{\rm ch}_{\rm heat}$|, computed using equation (59), once again assuming that Mh/Mc = 30. Note that this time-scale falls in the grey zone (i.e. becomes less than the Hubble time) for Nc ≲ 100 particles. When using the softening length advocated by Power et al. (2003), |$t^{\rm ch}_{\rm heat}$| is somewhat larger for small Nc, but still of order the Hubble time for Nc ≲ 100. As face-value, this seems to suggest that particle–subhalo heating might actually be an important mechanism causing artificial disruption of subhaloes in numerical simulations. However, this inference is based on the assumption that |$t^{\rm ch}_{\rm heat}$| corresponds to the actual disruption time, which, as we now argue, is incorrect.
As discussed in Sections 4.1.1 and 4.2, the problem is that the ratio between the total energy gain, ΔE, and the total binding energy, |Ec|, is of little use to gauge whether or not the system will disrupt. It is important to account for how the energy ΔE is distributed over the particles. Contrary to the case of tidal heating by a single encounter, where the energy gain of particle i is proportional to the square of the particle's distance from the centre of the subhalo, |$(\Delta E)_i \propto r^2_i$|, in the case considered here, every subhalo particle roughly receives the same amount of energy (see equation 60); the only exception are the particles with R < ε, for which |$(\Delta E)_i \propto R_i^2$|.
For each particle, we interpret |Ei|/(ΔE)i as the number of crossing times required to unbind the particle. This ignores the fact that the system will continuously re-virialize in order to adjust to the newly acquired (impulsively added) energy and the resulting mass-loss, and what follows is therefore only a rough estimate. We define the ‘corrected’ time-scale for disruption due to particle–subhalo tidal heating as the number of crossing times required for 95 per cent of all subhalo particles to become unbound; that is, we find the 95 percentile of the distribution of |Ei|/(ΔE)i and interpret that as |$t^{\rm ch}_{\rm heat,corr} / t_{\rm cross}$|. The |$t^{\rm ch}_{\rm heat,corr}$| thus obtained is shown as dashed, red lines in Fig. 11. As long as ε ≪ r0, this correction boosts |$t^{\rm ch}_{\rm heat}$| by roughly an order of magnitude, making it very similar to the two-body evaporation time, |$t^{\rm cc}_{\rm evap}$|. When the softening length becomes comparable to the size of the subhalo, |$t^{\rm ch}_{\rm heat,corr}$| becomes independent of Nc, and many orders of magnitude larger than the Hubble time.
We conclude that similar to two-body relaxation, artificial tidal heating due to impulsive encounters with the overly massive particles of the host halo cannot be responsible for artificial disruption of subhaloes in numerical simulations.
6.4 Force softening
Despite many decades of simulation work, and numerous previous studies, there is still no consensus as to the optimal choice for the softening parameter in N-body simulations. Numerous studies have argued that minimizing the scatter in certain statistical descriptions of the matter field (i.e. power spectrum or two-point correlation function) among an ensemble of N-body realizations requires a softening length ε that is at least as large as the mean inter-particle separation l = Lbox/N1/3 (e.g. Melott et al. 1997; Splinter et al. 1998; Romeo et al. 2008; Joyce, Marcos & Baertschiger 2009). Here, Lbox is the (periodic) box size of the cosmological simulation and N is the total number of particles used. Most cosmological simulations, though, are run with much smaller softening lengths, typically of the order of ε/l ∼ 0.01–0.02. For example, the Millennium simulation (Springel et al. 2005) has ε/l ∼ 0.022, while the MDPL and SMDPL simulations of Klypin et al. (2016) adopt ε/l ∼ 0.019 and ε/l ∼ 0.014, respectively. Whether such simulations produce reliable results on scales below the (comoving) mean inter-particle separation is still a matter of fierce, ongoing debate (see e.g. Knebe et al. 2000; Melott 2007; Joyce et al. 2009; Power et al. 2016; Benhaiem, Joyce & Sylos Labini 2017, and references therein).
Several studies have focused on the optimal softening length for simulating individual objects (i.e. individual DM haloes or galaxies). For example, Dehnen (2001), extending studies by Merritt (1996) and Athanassoula et al. (2000), suggests that one should aim to minimize force errors. This can be achieved by optimizing the softening length such that it simultaneously minimizes the force bias (which increases with increasing ε) and the force noise (which decreases with increasing ε). Based on such considerations, Dehnen (2001) advocates that a collisionless system with a Hernquist (1990) density profile (which has the same r−1-cusp as a NFW profile) should be simulated with a Plummer softening |$\varepsilon /r_0 = 0.017 N_5^{-0.23}$|, where r0 is the scale radius of the Hernquist (or NFW) profile and N5 = N/105 with N the number of particles used to model the system in question. Power et al. (2003) use a different criterion to optimize the softening length: by minimizing the impact of two-body effects on the (central) density profiles of virialized DM haloes in cosmological simulations, they advocate a much larger softening length of |$\varepsilon /r_0 = 0.126 \, (c/10) \, N_5^{-0.5}$|, where c is the NFW halo concentration parameter. Note that both of these criteria have the optimal softening length depend on the size of the system as well as the number of particles that is used to represent the system. If we adopt a concentration–mass relation of the form c ∝ M−0.1 (e.g. Dutton & Macciò 2014) and use that the virial radii of DM haloes scale according to rvir ∝ M1/3 ∝ N1/3, we find that the optimal softening length depends on halo mass according to εopt ∝ Mα, with α = +0.2 and −0.17 for the criteria of Dehnen and Power et al., respectively. This scaling is sufficiently weak so that the softening is close to optimal for haloes spanning a relatively large range in halo masses, as required for cosmological simulations.
Of relevance for the discussion in this paper is how softening impacts the dynamical evolution of DM substructure. To our knowledge, there has been no concerted effort to investigate this. We fill this gap in Paper II, with a detailed study of how softening impacts the evolution and survivability of subhaloes. We demonstrate that whenever the tidal field is strong (i.e. close to the centre of the host halo), the survivability of substructure is extremely sensitive to the softening used. Furthermore, as a subhalo experiences mass-loss, both its size and its number of particles change with time, which in turn causes an evolution in the optimal softening length. As we demonstrate in Paper II, typically εopt drops by an order of magnitude after the first peri-centric passage, after which it remains fairly unchanged. Since simulations do not account for this drastic drop in the optimal softening length, substructure is typically evolved with a softening length that is too large, which results in significant artificial subhalo disruption.9 Based on the discussion in this section, and the results presented in Paper II, we therefore conclude that inadequate softening is the dominant driver of subhalo disruption in numerical simulations.
7 SUMMARY AND DISCUSSION
Being able to accurately predict the abundance and demographics of DM substructure is of paramount importance for many fields of astrophysics: gravitational lensing, galaxy evolution, halo occupation modelling, and even constraining the nature of the DM. DM substructure is subject to tidal stripping and heating, which are highly non-linear processes and therefore best studied using numerical N-body simulations. These reveal prevalent subhalo disruption, with only ∼35 per cent of subhaloes accreted at z = 1 surviving until z = 0 (Jiang & van den Bosch 2016). Based on a hand-full of convergence studies, it is generally assumed that most of the disruption of subhaloes with more than 50–100 particles is physical, rather than numerical. However, there is no consensus in the literature as to what causes subhaloes to disrupt. In addition, convergence is only a necessary, but not a sufficient condition, to guarantee that the simulation results are physically correct.
All this warrants a detailed, comprehensive investigation into the disruption of substructure in numerical simulations. This is the first paper in a series in which we use both idealized numerical simulations and (semi)-analytical treatments to study under what conditions DM substructure undergoes physical and/or numerical disruption. In this paper, we have focused mainly on analytical treatments of tidal heating and tidal stripping. We also presented a crude analytical treatment of potential numerical disruption mechanisms. Our main conclusions are as follows:
During their first orbit after accretion, subhaloes pass the centre of their host halo at a median peri-centric distance of ∼0.37Rvir,h, while ∼7 per cent come within 0.1Rvir,h.
Contrary to naive expectation, subhaloes that experience a tidal shock ΔE that exceeds the subhalo's binding energy, |Eb|, do not necessarily undergo disruption. Rather, they experience mass-loss. We have presented a fitting function (equation 27) that relates the amount of mass stripped to the ratio ΔE/|Eb|, which is valid for subhaloes with NFW density distributions. An NFW subhalo for which ΔE/|Eb| = 1 (100) is stripped of only ∼20 (80) per cent of its mass.
During first peri-centric passage, tidal heating increases the internal energy of the subhalo by a median ΔE ∼ 2|Eb|. This results in the subhalo losing ∼30 per cent of its mass. In the rare case of a purely radial orbit, the subhalo experiences a tidal shock that may strip as much as 90 per cent of its mass.
The impulse approximation, combined with the instantaneous mass-loss approximation of Aguilar & White (1985), accurately predicts the amount of mass-loss experienced by subhaloes on fairly radial orbits (η ≲ 0.2).
Tidal heating due to high-speed (impulsive) encounters with other subhaloes, sometimes called ‘harassment’, is negligible compared to the tidal heating associated with the peri-centric passage of the host halo.
Modelling tidal stripping in the non-impulsive regime is extremely difficult, mainly because the concept of tidal radius is ill defined and because we lack a theory to describe how a gravitational N-body system re-virializes as it undergoes stripping. Depending on which definition one adopts for the tidal radius, and what one assumes regarding the rate at which material outside of the (instantaneous) tidal radius is stripped, one can obtain dramatically different results, none of which adequately reproduce simulation results.
Instantaneously, stripping matter from the outskirts of an NFW halo can leave a remnant with positive binding energy (cf. Hayashi et al. 2003). The remnant's binding energy depends strongly on the orbital anisotropy of the subhalo, with more radially anisotropic subhaloes having larger (i.e. more positive or less negative) binding energies for a given amount of stripping.
Instantaneously stripping matter from an NFW halo never leads to subhalo disruption, even if the remnant has positive binding energy.
Contrary to claims in the literature, two-body relaxation of subhaloes due to collisions between subhalo particles and (the more abundant) particles from the host halo is less efficient than that due to collisions among subhalo particles themselves. Neither is efficient enough, however, to cause significant evaporation of subhaloes in numerical simulations.
Tidal heating of subhaloes due to high-speed, impulsive encounters with host halo particles that are artificially massive (due to the limiting mass resolution of the simulation) cannot cause artificial disruption of substructure.
Based on these results, we conclude that it is extremely difficult to physically disrupt CDM subhaloes (in the absence of baryonic effects; see below). Tidal stripping alone never leads to complete disruption, and tidal heating is not effective in the central regions of subhaloes, which are adiabatically ‘shielded’ (Spitzer 1987; Weinberg 1994a,b). In principle, multiple tidal shocks, associated with multiple peri-centric passages, could ultimately cause the subhalo to disrupt. We did not explore such a scenario in this paper, since we lack a reliable analytical treatment for how subhaloes re-virialize after tidally induced mass-loss. However, we do investigate the impact of multiple peri-centric passages in Papers II and III, in which we use hundreds of idealized numerical simulations. As we demonstrate in those papers, physical disruption in CDM-based DM-only simulations is extremely rare (see also Diemand et al. 2007; Peñarrubia et al. 2010). On the other hand, we do find that the simulation results are extremely sensitive to the choice of softening length. In particular, we demonstrate that state-of-the-art cosmological simulations still suffer from serious overmerging, largely as a consequence of inappropriate force softening. In addition, we demonstrate that N-body simulations suffer from a discreteness-driven run-away instability, which makes it impossible to reliably trace the evolution of subhaloes in a strong tidal field unless the subhalo has at least 1000 particles.
Numerical overmerging is a serious road-block for the many astrophysical applications that require accurate characterization of halo substructure. In the coming decade, a number of large galaxy surveys, such as the Dark Energy Spectroscopic Instrument (DESI), the Large Synoptic Survey Telescope (LSST), Euclid, and the Wide Field InfraRed Space Telescope (WFIRST), will provide astrophysicists with an unprecedented wealth of data regarding galaxy evolution and cosmology. In order to optimize the scientific impact of these huge investments, it is prudent that galaxy clustering in these surveys be interpreted in an unbiased, maximally informative manner. A popular method to do so is to compare the observations to mock data, obtained by populating DM (sub)haloes in DM-only simulations with ‘mock’ galaxies, using methods such as subhalo abundance matching (see Section 1 for references). This entire programme faces a severe challenge if those simulations underpredict the abundance of subhaloes due to artificial disruption. In principle, one can correct for this by including ‘orphans’, i.e. mock galaxies without an associated subhalo in the simulation (e.g. Kitzbichler & White 2008; Moster et al. 2013, 2017; Guo & White 2014); however, unless it is known how many orphans to add, and where, this seriously diminishes the information content of small-scale clustering (see Campbell et al. 2017, for a detailed discussion). DM substructure is also an important discriminator between different DM models (cold versus warm versus self-interacting), and is important for translating a potential, observed DM annihilation signal into a mass and annihilation cross-section of the DM particle. Unless we can make accurate, and above all reliable, predictions regarding the abundance and structure of DM subhaloes, we will forfeit one of the main handles we have on learning about the nature of DM.
We end by emphasizing that this work has entirely focused on DM only, without taking account of potential baryonic effects. There is a rapidly expanding literature on how baryons may impact the abundance and demographics of DM substructure (e.g. Macciò et al. 2006; Weinberg et al. 2008; Dolag et al. 2009; Arraki et al. 2014; Brooks & Zolotov 2014; Fiacconi et al. 2016; Wetzel et al. 2016; Despali & Vegetti 2017; Garrison-Kimmel et al. 2017). Our work, in no way, aims to undermine the importance of baryons. However, before we can make reliable predictions for how baryonic processes modify substructure in the dark sector, we first need to establish a better understanding of how tides impact substructure, and develop tools and criteria to assess the reliability of simulations (be it hydro or N-body). Hence, this work is to be considered a necessary first step towards a more reliable treatment of DM substructure (including satellite galaxies), and not the final answer.
Acknowledgements
We are grateful to the referee, Chris Power, for an insightful referee report, and to Andrew Hearin, Fangzhou Jiang, and Fred Rasio for useful discussion. FvdB is supported by the Klaus Tschira Foundation and by the US National Science Foundation through grant AST 1516962 and is grateful to the Munich Excellence Cluster for its hospitality. Part of this work was performed at the Aspen Center for Physics, which is supported by the National Science Foundation under grant PHY-1066293, and at the Kavli Institute for Theoretical Physics, which is supported by the National Science Foundation under grant PHY-1125915. OH and GO were supported by funding form the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No. 679145, project ‘COSMO-SIMS’).
Footnotes
Since the tidal radius depends on the density profile of the host halo, this is not always the case though.
The drop-off at Ms/Mh < 10−3 is an artefact of our selection criteria and the limiting mass resolution of the simulation (see van den Bosch et al. 2016).
Note that the integrals for Bk (k = 1, 2, 3) defined here differ from those in GHO99 by a factor ch.
We acknowledge that this is not a particularly accurate assumption (e.g. Hayashi et al. 2003), but the detailed density profile of subhaloes has little impact on what is anyways a fairly crude estimate.
For η = 0.9, it already overpredicts fstrip by more than 30 per cent.
The simulations used in this paper adopted a softening that was carefully calibrated using the detailed convergence studies described in Paper II, and therefore do not suffer from this effect.
Except when Nbound < 10, in which case we adopt N = Nbound.
REFERENCES
APPENDIX A: Computing Bound Fractions of N-body Haloes
We begin by making an initial guess for the boundness, |${\cal Q}_i$|, of each particle. At t = 0 (ICs), we assume that each particle is bound (|${\cal Q}_i = 1 \ \, \forall i=1,...,N$|), while at later times we assume that |${\cal Q}_i$| is the same as in the previous simulation output.
For each particle, we compute Ei using equation (A1). We update |${\cal Q}_i$| accordingly and compute the new, bound fraction |$f_{\rm bound}= {1 \over N_{\rm tot}} \sum _i {\cal Q}_i$|.
Compute the centre-of-mass position and velocity of the halo, |${\boldsymbol r}_{\rm com}$| and |${\boldsymbol v}_{\rm com}$|, as the average position and velocity of the N = MAX(Nmin, fcom Nbound) particles that are most bound. Here, Nbound = fbound Ntot, while Nmin and fcom are free parameters.
Update |${\boldsymbol v}_i$| for each particle using the new centre-of-mass velocity.
Go back to (ii) and iterate until the changes in |${\boldsymbol r}_{\rm com}$| and |${\boldsymbol v}_{\rm com}$| are smaller than 10−4rvir and 10−4Vvir, respectively. This typically requires 3–10 iterations.
![Energy structure of spherical, instantaneously truncated NFW haloes. The left-hand panel plots the total binding energy, E(r), as a function of the truncation radius, r, in units of the NFW scale radius, r0. The middle panel shows the corresponding virial ratio, K(r)/|W(r)|. Different colours correspond to different values of the anisotropy parameter; from blue to red β = 1.0, 0.8, ..., −3.0. The panel on the right shows log [rcrit/r0] as function of β, where rcrit is defined as the truncation radius below which the remnant has positive binding energy. rcrit ≃ 0.77r0 for an isotropic NFW halo (β = 0), becomes ∼2.84r0 for an NFW halo with purely radial orbits (β = 1), and is absent (i.e. the remnant always has negative binding energy) whenever β ≲ −1.5.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/474/3/10.1093_mnras_stx2956/2/m_stx2956figa1.jpeg?Expires=1749988357&Signature=NtS0IEGq5fhQmG0BtjsxJojvCBARzNL28nA1-ix3uQoyMa5XvrrwP3qWKZ4ZKaLIaWGlmMawdllX36QFN6hKCRzuqn3Ezfx9dAUHFbM-jUiBntBYyCmozh8BfA9n1AKnmzShLVPT2DYR0CRT1gWBOYEChfPhZRqrI1KjBvBkYmuCvYB~79LeuDfZnWBBooPR~9w4h26673XJiELTMbCXtwcIl-z8jl5RURJDeY7FwkK3h-8UjtF9BugAD7p-zHBNzACVK7HATruCA9XyeU2mzVQ07TvpAnYrtVUmmJr0H15ZdTrcp7NFDvhYPAjS9WcPRWSXUCpOq0NGmfZKx6hmCQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Energy structure of spherical, instantaneously truncated NFW haloes. The left-hand panel plots the total binding energy, E(r), as a function of the truncation radius, r, in units of the NFW scale radius, r0. The middle panel shows the corresponding virial ratio, K(r)/|W(r)|. Different colours correspond to different values of the anisotropy parameter; from blue to red β = 1.0, 0.8, ..., −3.0. The panel on the right shows log [rcrit/r0] as function of β, where rcrit is defined as the truncation radius below which the remnant has positive binding energy. rcrit ≃ 0.77r0 for an isotropic NFW halo (β = 0), becomes ∼2.84r0 for an NFW halo with purely radial orbits (β = 1), and is absent (i.e. the remnant always has negative binding energy) whenever β ≲ −1.5.
When computing the gravitational potential term of equation (A1), we use a Barnes & Hut octree with the same opening angle, θ, as in the simulation. We also adopt the same softening. Generally, smaller values of fcom results in a more noisy time evolution of |${\boldsymbol r}_{\rm com}$| and |${\boldsymbol v}_{\rm com}$|, while for larger values of fcom it is more difficult to trace fbound(t) when it becomes small. We obtain stable results for Nmin = 10 (we never use fewer than 10 particles to determine the centre-of-mass properties10) and fcom = 0.05 (centre-of-mass properties are determined using the 5 per cent most bound particles), which are the parameters we use throughout.



