-
PDF
- Split View
-
Views
-
Cite
Cite
M. Salvato, J. Buchner, T. Budavári, T. Dwelly, A. Merloni, M. Brusa, A. Rau, S. Fotopoulou, K. Nandra, Finding counterparts for all-sky X-ray surveys with Nway: a Bayesian algorithm for cross-matching multiple catalogues, Monthly Notices of the Royal Astronomical Society, Volume 473, Issue 4, February 2018, Pages 4937–4955, https://doi.org/10.1093/mnras/stx2651
Close - Share Icon Share
Abstract
We release the AllWISE counterparts and Gaia matches to 106 573 and 17 665 X-ray sources detected in the ROSAT 2RXS and XMMSL2 surveys with |b| > 15°. These are the brightest X-ray sources in the sky, but their position uncertainties and the sparse multi-wavelength coverage until now rendered the identification of their counterparts a demanding task with uncertain results. New all-sky multi-wavelength surveys of sufficient depth, like AllWISE and Gaia, and a new Bayesian statistics based algorithm, Nway, allow us, for the first time, to provide reliable counterpart associations. Nway extends previous distance and sky density based association methods and, using one or more priors (e.g. colours, magnitudes), weights the probability that sources from two or more catalogues are simultaneously associated on the basis of their observable characteristics. Here, counterparts have been determined using a Wide-field Infrared Survey Explorer (WISE) colour-magnitude prior. A reference sample of 4524 XMM/Chandra and Swift X-ray sources demonstrates a reliability of ∼94.7 per cent (2RXS) and 97.4 per cent (XMMSL2). Combining our results with Chandra-COSMOS data, we propose a new separation between stars and AGN in the X-ray/WISE flux-magnitude plane, valid over six orders of magnitude. We also release the Nway code and its user manual. Nway was extensively tested with XMM-COSMOS data. Using two different sets of priors, we find an agreement of 96 per cent and 99 per cent with published Likelihood Ratio methods. Our results were achieved faster and without any follow-up visual inspection. With the advent of deep and wide area surveys in X-rays (e.g. SRG/eROSITA, Athena/WFI) and radio (ASKAP/EMU, LOFAR, APERTIF, etc.) Nway will provide a powerful and reliable counterpart identification tool.
1 INTRODUCTION
Active galactic nuclei (AGN) play an important role in the evolution of galaxies in the Universe. It is now established that most massive galaxies host a supermassive black hole in their centre, and that the black hole accretion activity and history might have a profound influence on their growth. A comprehensive picture of this link can only be obtained from a complete census of AGN covering the full luminosity function at any redshift. This is possible solely by merging AGN samples selected at different wavelengths and through complementary criteria (Padovani et al. 2017), and by combining shallow wide-area with deep pencil beam surveys. The broad wavelength coverage is required to identify AGN at all redshifts at the wavelengths where they dominate the Spectral Energy Distribution (SED) of their host galaxy (e.g. Gamma-ray: Armstrong et al. 2015; X-ray: Georgakakis & Nandra 2011; optical: Bovy et al. 2011; Palanque-Delabrouille et al. 2016; Mid-Infrared: Assef et al. 2013; Radio: De Breuck et al. 2002). Pencil beam surveys (e.g. Luo et al. 2017) allow the study of the high-redshift population and the faint end of the luminosity distribution, while shallower wide-area surveys (e.g. LaMassa et al. 2016; Georgakakis et al. 2017) trace the brightest sources and at the same time provide access to rare objects.
The selection of AGN at X-ray energies provides an excellent compromise between completeness and purity of the sample. X-rays are sensitive to all, but the most obscured AGN even when hosted in luminous galaxies and have very low contamination from other source populations. Limited by the available data sets, and by the small field of view of the most sensitive imaging telescopes, X-ray selected AGN samples were until now predominantly obtained from deep pencil beam surveys (e.g. COSMOS: Hasinger et al. 2007; Brusa et al. 2010; Civano et al. 2012; Marchesi et al. 2016; CDFS: Luo et al. 2010; Hsu et al. 2014; Luo et al. 2017; AEGIS-X: Nandra et al. 2015; Lockman Hole: Fotopoulou et al. 2012) or limited to the brightest and most extreme sources (e.g. BAT: Baumgartner et al. 2013). Only very recently Stripe82X (LaMassa et al. 2016; Tasnim Ananna et al. 2017) and XMM-XXL (e.g. Fotopoulou et al. 2016; Georgakakis et al. 2017; Pierre et al. 2017) opened access to two shallow, wide areas of ≈30 deg2 and ≈50 deg2. Still, the total population of X-ray selected and spectroscopically confirmed AGN counts only ≈20 000 objects and continues to be dwarfed by the ≈300 000 optically selected quasars (e.g. DR12Q: Pâris et al. 2017). The new revisions of the ROSAT All-sky Survey (2RXS; Boller et al. 2016) and the second release of the XMM–Newton Slew Survey (XMMSL21) with a total of ≈130 000 X-ray sources may finally provide AGN counts comparable to those found in the SDSS.
So far, the most challenging aspect of the exploitation of these samples was the identification of the multi-wavelength counterparts needed for the source characterization and redshift estimates. This was related to at least two shortcomings. First, the positional uncertainties of all but the brightest sources in these X-ray catalogues are in general too large to assign a single, unambiguous optical counterpart based solely on a simple coordinate match. Second, the multi-wavelength catalogues used for identifying the counterparts lacked depth and homogeneous, contiguous coverage. At least the latter problem can now be addressed with the publicly available AllWISE survey (i.e. the combination of WISE and NEOWISE: Wright et al. 2010; Mainzer et al. 2011, 2014). This survey maps the entire sky at mid-infrared wavelengths from 3.4 to 22 μm to a depth at which the majority of the point-source populations of 2RXS and XMMSL2 (AGN, stars, star-forming galaxies) is expected to be detected2 (see Section 4.1).
Even with a suitable catalogue at hand, the large X-ray positional uncertainties still require us to recognize the correct counterpart amongst the many that are possible, avoiding the bias towards the optically brightest sources (e.g. Naylor, Broos & Feigelson 2013). The most frequently used technique is based on the Likelihood Ratio (LR) method (Sutherland & Saunders 1992). Using a primary catalogue (here X-rays) and a secondary catalogue (here mid-infrared) the ratio of the likelihoods of each infrared (IR) source being the true counterpart to a X-ray or background source is calculated taking into account the coordinates (i.e. their separations), the associated uncertainties, the density of the sources in the two catalogues and the source magnitudes and distribution. For X-ray sources with large positional uncertainties, this limited set of information is often insufficient to reliably identify the counterpart.
For this reason we developed a new code, Nway, that goes beyond the LR approach by simultaneously considering in addition to astrometric information (i.e. position, associated uncertainties and sky density of sources as a function of magnitude), various known source properties (e.g. magnitudes, colours) using Bayesian statistics for each step.
The paper focusses on two main topics: first, we increase the sample of bright X-ray selected AGN by identifying and releasing the coordinates of the AllWISE counterparts to the point-like X-ray sources in 2RXS and XMMSL2 all-sky surveys. This will facilitate spectroscopic follow-up and further source characterization (e.g. Dwelly et al. 2017). Secondly, we present the Nway code and release it to the public, together with a detailed user manual. In order to keep the two aspects separated, in the main body of the paper we only provide a short description of Nway (Section 3). Instead we focus on the X-ray catalogues (Section 2), the construction of the prior based on AllWISE photometry (Section 4), the assessment of the reliability of our associations by comparison with the literature (Section 5) and the AllWISE properties of the counterparts (Section 6), in comparison with the results from X-ray pencil-beam surveys. The release of the catalogues is presented in Section 7. The detailed description of the Nway algorithm and the verification results are made available in the Appendixes A and B. Test performances of Nway are presented in Appendix C, where we also show the strength of the method and the improvement of simultaneously using two priors instead of one.
Along the paper we assume Vega magnitudes unless differently stated. In order to allow direct comparison with existing works from the literature of X-ray surveys, we adopt a flat Λ cold dark matter (CDM) cosmology with h = H0/[100 km s−1 Mpc−1] = 0.7; ΩM = 0.3; and ΩM = 0.7.
2 THE DATA SETS
In the following we describe the properties of the 2RXS, XMMSL2 and AllWISE catalogues and their preparation for this work.
2.1 ROSAT All-Sky Survey
The first all-sky imaging X-ray survey in the 0.1–2.4 keV band was performed by ROSAT (Truemper 1982) between 1990 and 1991. Besides a catalogue of extended sources, two catalogues of point-like sources were published: the Bright Source Catalogue (BSC) containing the 18 816 brightest sources (Voges et al. 1999) and the Faint Source Catalogue (FSC) encompassing the 105 924 fainter objects down to a detection likelihood limit of 6.5 (Voges et al. 2000). In view of the launch of SRG/eROSITA (Merloni et al. 2012) and taking advantage of the advancement in technology, data reduction, analysis and detection algorithms of the last 25 years, the original data have recently been reprocessed by Boller et al. (2016). The newly generated catalogue (2RXS) for point-like X-ray sources has been released to the community3 and includes ≈13 5000 sources.
When comparing with the 1RXS catalogue, which combines BSC and FSC, the number of reliable sources in the 2RXS has increased (both bright and faint) while the number of spurious detections has decreased (see Boller et al. 2016, for more details). We select all 2RXS detections which lie within the ‘extragalactic’ part of the sky, i.e. with |b| > 15° and at least 6 and 3 deg away from the optical centres of the Large and Small Magellanic Clouds, respectively. After this geometric filter, we are left with 106695 2RXS X-ray detections with an estimated coverage of 30 575.9 deg2. Observed in projection outside the crowded Galactic Plane, these sources are predominantly extragalactic. The catalogue is further cleaned by removing 122 sources without estimated positional uncertainty and without listed counts. The well-known correlation between X-ray flux4 intensity, positional uncertainty and detection likelihood is shown for the final 106 573 sources in the primary catalogue in the left-hand panel of Fig. 1, with the flux distribution (converted into the 0.5–2 keV band) shown in Fig. 2. 95 per cent of the sources have a 1σ positional error smaller than 29 arcsec compared with the 34 arcsec found in the extragalactic area of 1RXS.

Positional uncertainties for the 2RXS (left) and XMMSL2 (right) samples as a function of X-ray flux, with the sources colour coded on the basis of their respective detection likelihood. The flux of the XMMSL2 sources in the 0.2–12 keV band has been converted into the 0.5–2 keV band assuming Galactic NH = 3e20 cm−2 and a power law of 1.7. For the 802 XMMSL2 sources without catalogued 0.2–12 keV flux we converted either the flux from the 0.2–2 keV band (775 sources) or the flux from the 2–12 keV band (27 sources).
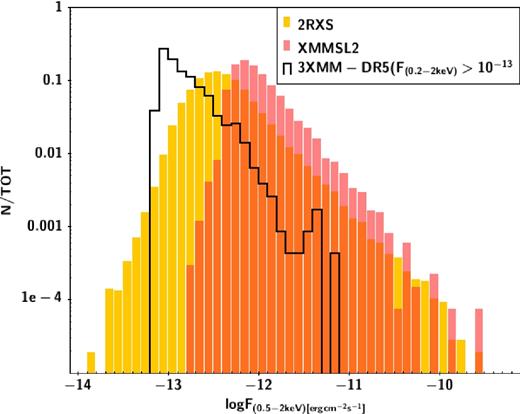
Flux distribution for the 2RXS (yellow), XMMSL2 (brown) and 3XMM-DR5 catalogues. The flux from the original bands has been transformed to the flux at (0.5–2 keV), assuming a Galactic NH = 3(2.29)e20 cm−2 and a power law of 1.7(2.4) for XMM SL2(2RXS) data, respectively.
2.2 XMM–Newton Slew 2 survey
The XMM–Newton European Photon Imaging Camera pn (EPIC-pn) accumulates data during slews between pointed observations. The most recent catalogue derived from this data set covers 84 per cent of the sky (release 2.0, 2017 March 14). We extracted all detections from the ‘Clean’ version of the catalogue (which we will henceforth refer to as the XMMSL2 catalogue), which lie in the same area as defined for 2RXS. After this geometric filter, we are left with 22 306 X-ray detections with at least 0.1 s of effective XMMSL2 exposure with an estimated coverage of ≈25 500 deg2.
The final catalogue was filtered to remove candidate duplicate detections of identical X-ray sources using the original column UNIQUE_SRCNAME, retaining a total of 17 672 sources with 2704 sources detected only at 0.2–12 keV, 553 detected only at 0.2–2 keV, and 168 sources detected only at 2–12 keV.
52.8 per cent (9333) of the XMMSL2 sources have at least one 2RXS source within a radius of 60 arcsec, with 236/21/3/1/1 XMMSL2 sources being associated with 2/3/4/5/6 2RXS sources, respectively. The distribution of the positional uncertainties as a function of the flux in the detection band, colour coded by the likelihood of the detection, is presented in the right-hand panel of Fig. 1. Note, that figure shows the original positional uncertainty augmented by 5 arcsec in quadrature to account for the systematic uncertainty on attitude reconstruction. The flux distribution (converted into the 0.5–2 keV band) shown in Fig. 2.
2.3 AllWISE catalogue
The Wide-field Infrared Survey Explorer (WISE5; Wright et al. 2010), was launched in 2009 and over the course of one year scanned the entire sky at least twice in the 3.4 and 4.6 μm bands (hereafter W1, W2, respectively) and at least once in the 12 and 22 μm bands (W3, W4). In the AllWISE data release6 (2013 November 13, Cutri et al. 2013) all the available data are combined, reaching a 5σ limiting W1, W2, W3 and W4 magnitudes of better than 17.6, 16.1, 11.5 and 7.9 (all in the Vega system) over 95 per cent of the extragalactic sky (|b| > 15°). The coverage is inhomogeneous, being deepest at the Ecliptic Poles.
We generated two independent catalogues that include all AllWISE sources located within a radius of 120 arcsec from an X-ray position listed in the 2RXS and XMMSL2 catalogues, respectively. From each catalogues duplicated sources were removed. No additional filtering was performed. This procedure results in two independent catalogues of 6252 516 unique entries for 2RXS and 1288 533 for XMMSL2, covering total unique areas of 368.81 deg2 and 60.79 deg2, respectively.
3 NWAY IN A NUTSHELL
Nway has been developed for identifying the multi-wavelength counterparts to X-ray sources to multiple catalogues in a multi-dimensional parameter space (e.g. position and positional uncertainty, density of sources, magnitudes, colours, variability, morphology, etc.) in a Bayesian framework. The code builds on the original work of Budavári & Szalay (2008), who developed the algorithm for simultaneously matching multiple catalogues and enhances it by allowing sources to be present only in a subset of the catalogues (e.g. Pineau et al. 2017). Additionally, Nway can either generate an internal prior for each source parameter following the implementation of the Maximum LR as presented in e.g. Brusa et al. (2007), or use an external, pre-constructed prior.
Nway has already been successfully applied in a number of studies, e.g. the identification of counterparts to ROSAT (1RXS; Voges et al. 1999, 2000) sources in the pilot SDSS-III/SEQUELS program (Dwelly et al. 2017) using two optical bands, simultaneously; the search for counterparts to Chandra and XMM detections in the Extended Chandra Deep Field South (Hsu et al. 2014) using three independent catalogues (optical, near-infrared and 3.6 μm) simultaneously and with internally constructed priors (see for all the options the Nway manual at https://github.com/JohannesBuchner/nway/raw/master/doc/nway-manual.pdf). It has also been applied to 1RXS and earlier XMM-Slew Survey (release 1.6, 2014 February 26) data on the BOSS imaging footprint (Dwelly et al. 2017), adopting an external, mid-infrared based colour-magnitude prior, similar to the one chosen in this work.
A comprehensive description of Nway is given in Appendix B together with a verification using internally generated priors for XMM-COSMOS (see Appendix C). In the following we focus on the application of the code to the scientific aim of the paper, the AllWISE counterparts to 2RXS and XMMSL2.
The Nway code answers the question: considering the astrometric information (i.e. distance from the X-ray source, positional uncertainties and number densities) and priors (e.g. magnitude and colour distribution), what is the posterior probability for each AllWISE source within a given radius from a 2RXS or XMMSL2 detection to be the correct counterpart to the X-ray source? For the analytical details the reader is referred to Appendix B5. In short, Nway first computes for each source in the AllWISE catalogue the Bayes factor considering only distance from the X-ray source, positional uncertainties and number densities. Next, the Bayes factor is weighted by the mid-infrared magnitude-colour information (see Section 4). Then, each AllWISE source is associated with the probability p_i of being the right counterpart to a specific X-ray detection. In addition, for each X-ray detection, Nway provides the probability, p_any, that any of the AllWISE sources is the right counterpart. The higher the value of p_any the lower is the probability of a chance association. In the output catalogue of Nway , for a given X-ray source, all the AllWISE within the search area are listed, ranked in decreasing order by their p_i. For comfort Nway flags the first AllWISE source of each group as match_flag=1, this being the best counterpart amongst those available. A match_flag=2 indicates the AllWISE sources with a |${{\tt {p}}\_i}/{{\tt {p}}\_i} _{\text{best}}<\alpha$| from the first, α being defined by the user (in this paper it is fixed to 0.5); these are considered secondary possible counterparts. Everything else is flagged as match_flag=0.
4 APPLICATION OF NWAY TO 2RXS AND XMMSL2
In this section we motivate the AllWISE colour-magnitude prior; subsequently present the results of the application of Nway to the 2RXS and XMMSL2 catalogues defined in Section 2; and finish with the comparison of the associations for sources that are in common to both X-ray catalogues.
4.1 AllWISE colour-magnitude prior
The prior is defined as the probability, given observable information alone, i.e. before considering any positional information, that a counterpart is related to an X-ray source. Given that the X-ray point-source population is an ensemble made of stars, nearby galaxies, and galaxies at unknown redshift hosting an AGN of unknown power, a prior based on a single magnitude distribution is insufficient. This is especially true for X-ray detections with large positional uncertainties. Ideally, the prior would use the entire SED as discriminator (e.g. Roseboom et al. 2009). In practice, the lack of sufficiently deep multi-wavelength coverage of the entire sky requires a compromise.
The AllWISE catalogue provides photometric coverage of the entire sky in the mid-infrared, a regime where the number density of sources is low compared with e.g. the optical bands. At the same time, virtually all point-like X-ray sources found in 2RXS and XMMSL2 are expected to be detected at the depth of the AllWISE survey, as we show later in this section.
To generate the prior we need to start with an X-ray sample that matches the sources expected at the depths of 2RXS and XMMSL2, but with secure counterpart association. Beyond a comparable flux limit this sample also needs to cover a sufficiently large area to include rare and bright objects. Both characteristics are fulfilled by the 3XMM-DR5 (Rosen et al. 2016) with a sky coverage of 877 deg2 and with a flux limit significantly deeper than 2RXS and XMMSL2. Following the same screening procedure outlined in Dwelly et al. (2017), but on the entire footprint of the survey we retained 2349 sources distributed as in Fig. 2. All the sources selected in this way have a unique AllWISE counterpart within 5 arcsec, 98 per cent within 3 arcsec. Given the PSF of WISE, this provides a high confidence that the counterpart association is reliable.
The colour-magnitude distribution of the AllWISE counterparts to the 3XMM-DR5 sources is shown in Fig. 3 together with the properties of the AllWISE field population. The 3XMM-DR5 counterparts are well separated from the bulk of the AllWISE population, suggesting this colour-magnitude distribution to be an efficient prior. As in Dwelly et al. (2017), we generated a grid on the [W2], [W1 − W2] plane with steps of 0.25 mag in [W2] and 0.1 mag in [W1 − W2] (see Fig. 4) and for each bin computed the ratio of the densities of 3XMM-DR5 counterparts and field sources. This two-dimensional distribution of density ratios encodes the prior which we apply to the Bayes factor. The Bayes factor was computed taking into account astrometry (i.e. separation between the sources and respective positional uncertainty) and number density of the sources.
![AllWISE colour-magnitude ([W2] versus [W1 − W2]) distribution of counterparts to the 3XMM-DR5 catalogue cut at the depth of 2RXS (grey) compared with the AllWISE distribution (contours and density map) of all sources within 2 arcmin of the 3XMM-DR5 sources.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/473/4/10.1093_mnras_stx2651/1/m_stx2651fig3.jpeg?Expires=1750215333&Signature=GPxrUFa4fj4lHahCu01flYwyb98ZXxNw5Wphxn5j2hcY8HozJx7YLgPeeeMxjSZg27B5g5pTw5iChamd803gHRc8iPQAINDRvb88vQCK~1L3IEZpHFnyGyBbnlqytNKC80xNlfo93Ghi9gzDttly6iDFIPIy81IHo6zyq~2piPhvwO6-ewGb35-3ZqD7YYdb18RATIDBSw8HJbsyfF-C~ymE90qgE2~yhu-cWQ3xBax1sCfENc8tw1ahKBZzQGQg3rS2MeC2S3EgvAVy8f9~boOaqFsFIicOCxKkrsGburaQfTdyrhsfKPWPRuhHrEl824ErIMzfwOItW6OmlbYcYg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
AllWISE colour-magnitude ([W2] versus [W1 − W2]) distribution of counterparts to the 3XMM-DR5 catalogue cut at the depth of 2RXS (grey) compared with the AllWISE distribution (contours and density map) of all sources within 2 arcmin of the 3XMM-DR5 sources.
4.2 2RXS and AllWISE association
We applied Nway and the prior discussed in Section 4.1 to ≈6 Million AllWISE (see Section 2.3) sources within 2 arcmin from the 106 573 2RXS sources (see Section 2.1). At least one AllWISE candidate counterpart is found for all but 93 (0.01 per cent) of the 2RXS sources. A histogram of the distribution of p_any is shown as the yellow solid line in the top panel of Fig. 5.

Histogram distribution of the probability p_any that the right counterpart is amongst the AllWISE sources for the 2RXS (top panel, gold) and XMMSL2 (middle panel, black) sources. The histogram is shown for the X-ray sources at the actual X-ray position (solid line) and after the systematic offset of the X-ray position (dashed line). The dotted lines show the distribution considering only the X-ray sources at the right position, with detection likelihood higher or equal 10. The similarity of the distribution in the case of XMMSL2 is justified by the high threshold of detection likelihood adopted in the original catalogue. The bottom panel shows at any given p_any the fraction of interlopers, measured as the fraction of sources with p_any|$_{\text{random}} > {{\tt {p}} \_any}_{\text{real}}$|, for the complete samples and for the samples limited at the respective detection likelihood ≥10.
The 93 sources without any AllWISE counterpart (green points in Fig. 6) include (a) extended X-ray sources (e.g. 2RXS_J152238.4+083422, a spectroscopically confirmed cluster at z ≈0.035); (b) X-ray sources with candidate counterparts present in the AllWISE images but not contained in the AllWISE catalogue; and (c) X-ray sources with very bright optical candidate counterparts not present in the AllWISE catalogue.

X-ray Extension versus detection likelihood for the 2RXS sources, colour coded as a function of p_any. Whilst sources with high p_any are widely distributed, the sources with low p_any are confined at low detection likelihood or significant extension. Green dots represent the sources for which an AllWISE counterpart was not found (see Section 4.2 for more details).
63 305 2RXS sources (≈59 per cent of the sample) have a p_any > 0.5 while for 35 571 sources (≈33 per cent of the sample) p_any is lower than 0.3. Interestingly, 60 per cent of the latter are fainter than 14.5 mag in W2. In this region the magnitude distribution of the prior overlaps with the bulk of the field population, indicating that the limit of the disentangling power of the prior has been reached and that the selected AllWISE counterpart could be the result of a chance association. This is partly due to astrometric scatter.
Next we investigate the typical p_any for unreliable associations. We run Nway in the same configuration after (a) shifting the coordinates of the 2RXS catalogue by 6 arcmin in Declination; (b) extracting the AllWISE sources within 2 arcmin from the new 2RXS positions; and (c) removing the 2059 sources (2 per cent of the sample) that after the shift entered in the 2 arcmin radius circles from actual 2RXS sources. As expected, the distribution of p_any (Fig. 5 top; yellow long-dashed line) peaks towards low values of p_any, with 78 per cent of the sample having p_any < ∼0.15. This coincides with the idea that in any random sky position very few sources have properties matching the prior. E.g. only 5 per cent in the randomized 2RXS sample have p_any > 0.5 and p_i > 0.8. We can easily imagine that some of these sources are counterparts to actual X-ray sources below the 2RXS flux sensitivity. This hypothesis will be validated with future deeper X-ray data, e.g. from SRG/eROSITA.
A very conservative p_any > 0.5 for a reliable association (thus with <2 per cent probability of chance association; see Fig. 5) results in a sample of 62 944 AllWISE counterparts to 2RXS sources. However, we release here the entire catalogue of 2RXS counterparts, leaving to the user to decide the acceptable level of completeness and purity for their application. Fig. 5 (bottom) shows the fraction of expected interlopers for any given value of p_any.
If we consider only sources with X-ray detection likelihood (EXI_ML; as defined in Boller et al. 2016) larger than 10, the fraction of sources with p_any > 0.5 increases to 80 per cent (40 207/50 544). This means that many of the sources with low p_any are amongst those with low detection likelihood, indicating that they could be just spurious detections. Alternatively, they could be real sources with poorer positional determination. The distribution of p_any for the sources with EXI_ML > 10 is shown with the dotted line in Fig. 5.
4.2.1 Multiple associations
There are 17 734 (16.6 per cent) 2RXS sources with more than one candidate AllWISE counterpart,7 with the possible counterparts located in areas well populated by the prior. Given the poor angular resolution of ROSAT, it would not be a surprise if the candidate counterparts belong to distinct X-ray sources, detected as one in 2RXS. This is demonstrated in Fig. 7 (top), which shows the colour-magnitude distribution of the AllWISE sources for the 47 per cent (7 per cent) of the 12 321 2RXS sources with two candidate counterparts having p_any < 0.1 (>0.9).

Primary (gold) and secondary (green) possible AllWISE counterparts to the 5844 and 899 2RXS sources having two possible counterparts and p_any < 0.1 (left-hand panel) and p_any > 0.9 (right-hand panel), respectively. The grey open circles represent the 3XMM-Bright sources used to build the prior. Two examples with p_any < 0.1 (2RXS_J054219.4-080745) and p_any > 0.9 (2RXS_J175642.5+512108) are highlighted in the left-hand and right-hand panel, respectively. A very similar result was obtained for XMMSL2 (see the text), but is not shown here for simplicity.
4.3 XMMSL2 and ALLWISE association
The analysis done in the previous section was repeated for the XMMSL2-AllWISE association, with the summarizing plot being in the middle and bottom panels of Fig. 5. First of all, the smaller X-ray positional error of XMM translates into a distribution of p_any towards higher values (compare the solid and dashed cumulative curves in the right-hand panel of the figure), with about 76 per cent of the sources having p_any > 0.5 and p_i > 0.8. Only 21 per cent of the sources have p_any < 0.3 with only 8 XMMSL2 sources without any AllWISE candidate counterpart within 2 arcmin.
As for 2RXS, we systematically offset the positions of the XMMSL2 catalogue and run Nway with the same setting. Now we find that for only 3 per cent of the cases (571/17665), p_any > 0.5 and p_i > 0.8. The smaller positional uncertainty also reduces the fraction of sources with more than one possible counterpart. In total 1210 XMMSL2 sources (6.8 per cent) have more than one possible counterpart.8 As for 2RXS, also for XMMSL2 the majority of the sources with multiple associations have low p_any, low magnitude distribution for the possible counterpart and, above all, low X-ray detection likelihood EXI_ML_B8 < 10. Like for 2RXS, we will provide all the associations in the catalogue leaving the user to decide on the threshold for the reliability.
4.4 2RXS versus XMMSL2 associations
It is interesting to compare the association found for the sources that are in common to the 2RXS and XMMSL2 catalogues as the smaller positional uncertainties of latter can give insight on the reliability of the associations for the former.
Table 1 summarizes our results for the AllWISE counterparts that are in common for X-ray sources with matching coordinates within 5/10/30/60 arcsec. Overall, the agreement between the associations is very good, with the highest fraction of identical counterparts found for the subset of X-ray sources with the smaller separation between 2RXS and XMMSL2.
| XMMSL2-2RXS . | Sources in . | Identical best . | |
|---|---|---|---|
| Sep. . | Mean sep. . | common . | AllWISE ctp. . |
| arcsec . | arcsec . | N . | per cent . |
| ≤5 | 3.2 | 1145 | 98.5 |
| ≤10 | 6.1 | 3559 | 98.5 |
| ≤30 | 12.4 | 8202 | 95.7 |
| ≤60 | 15.9 | 9330 | 91.6 |
| XMMSL2-2RXS . | Sources in . | Identical best . | |
|---|---|---|---|
| Sep. . | Mean sep. . | common . | AllWISE ctp. . |
| arcsec . | arcsec . | N . | per cent . |
| ≤5 | 3.2 | 1145 | 98.5 |
| ≤10 | 6.1 | 3559 | 98.5 |
| ≤30 | 12.4 | 8202 | 95.7 |
| ≤60 | 15.9 | 9330 | 91.6 |
| XMMSL2-2RXS . | Sources in . | Identical best . | |
|---|---|---|---|
| Sep. . | Mean sep. . | common . | AllWISE ctp. . |
| arcsec . | arcsec . | N . | per cent . |
| ≤5 | 3.2 | 1145 | 98.5 |
| ≤10 | 6.1 | 3559 | 98.5 |
| ≤30 | 12.4 | 8202 | 95.7 |
| ≤60 | 15.9 | 9330 | 91.6 |
| XMMSL2-2RXS . | Sources in . | Identical best . | |
|---|---|---|---|
| Sep. . | Mean sep. . | common . | AllWISE ctp. . |
| arcsec . | arcsec . | N . | per cent . |
| ≤5 | 3.2 | 1145 | 98.5 |
| ≤10 | 6.1 | 3559 | 98.5 |
| ≤30 | 12.4 | 8202 | 95.7 |
| ≤60 | 15.9 | 9330 | 91.6 |
5 COMPARISON WITH LITERATURE
Since the release of the first ROSAT all-sky catalogues (Voges et al. 1999, 2000) there have been many attempts to determine the multi-wavelength counterparts. Most of the follow-up of ROSAT point-like sources concentrated on the bright sources (Rutledge et al. 2000; Schwope et al. 2000; Mahony et al. 2010), even if, the adopted methodologies (e.g. association technique, secondary catalogues for the follow-up) changed over time. A direct comparison between those earlier works and the results presented here would only allow comparing the associations without assessing their correctness. In addition, the X-ray positions have changed from 1RXS to 2RXS (see Boller et al. 2016) for more details.
It is for this reason that we decided to test our associations against an astrometric reference sample of 4524 X-ray sources from XMM, Chandra and Swift in the BOSS footprint, that have reliable counterparts (see Dwelly et al. 2017, for details on the sample). A match on the X-ray positions within 60 arcsec provides 1496 unique identifications in 2RXS, while additional 14 2RXS sources have a second possible match. Of these, 1418 have identical AllWISE counterparts corresponding to an accuracy of 94.8 per cent, with ≈94 per cent of the identical associations having p_any > 0.5.
The exercise repeated for XMMSL2, results in identical AllWISE counterparts for 533 of the 547 sources that have a match within 30 arcsec in the reference catalogue, corresponding to 97.4 per cent agreement. 514/533 (96.4 per cent) have p_any > 0.5. This attests both the appropriateness of the prior and the reliability of Nway.
6 SOURCE CHARACTERIZATION
For the counterparts of the 2RXS and XMMSL2 all-sky surveys no single survey provides both photometry and spectroscopy over the full sky. However, we can make an educated guess of the type of population by (a) matching with Gaia9 (Arenou et al. 2017); (b) studying the AllWISE colour distribution of the counterparts and comparing them with literature (e.g. Wright et al. 2010; Nikutta et al. 2014); and, finally (c) comparing Infrared and X-ray properties of the counterparts with those well studied in the COSMOS field (XMM-COSMOS, Chandra-COSMOS, Legacy Chandra-COSMOS; Brusa et al. 2010; Civano et al. 2012; Marchesi et al. 2016, respectively).
6.1 2RXS and XMMSL2 counterparts in Gaia
The release of the first Gaia DR1 catalogue enables us to further characterize the AllWISE counterparts of 2RXS and XMMSL2. In particular, it allows the identification of the sources with proper motion, indicating their Galactic nature. For this purpose we used the Hot Stuff for One Year catalogue (Altmann et al. 2017). HSOY includes 583 001 653 objects with precise astrometry based on the cross-match between the catalogue of Positions and Proper Motions (PPMXL; Roeser, Demleitner & Schilbach 2010) and Gaia DR1 (Arenou et al. 2017). We find a HSOY match within 3 arcsec for 91427/132216 (70 per cent) and 14558/19120 (76 per cent) of all the AllWISE candidate counterparts (i.e. match_flag=1 and match_flag=2) to 2RXS and XMMSL2, respectively. Limiting the search only to the best AllWISE counterparts (i.e. match_flag=1), we obtained a match with Gaia for 80078/106573 (75 per cent) and 14008/17665 (80 per cent). Of these, 10472/80078 (13 per cent) and 2054/14008 (15 per cent) have a measured proper motion (above 5σ) in the HSOY catalogue, identifying them as Galactic objects.
6.2 IR/X-ray properties comparison with COSMOS
Originally, Maccacaro et al. (1988) noted that AGN found in the Einstein Observatory Extended Medium Sensitivity Survey (EMSS; Gioia et al. 1987) were characterized by log(fx/fV) = ±1, with M stars and galaxies only marginally overlapping in this region. Since then, this locus was adapted by practically all X-ray surveys, extending the relation to other wavelengths (r, i, K, IRAC/[3.6 μm]) and X-ray energy bands. The validity of the locus was confirmed with recent works (e.g. Brusa et al. 2007, 2010; Civano et al. 2012) pointing out that the near-infrared (e.g. K) or MIR (e.g. 3.6μm) bands provide a tighter correlation with X-rays than the optical bands. Here, however, the faintest of the X-ray AGN would fall below the locus (e.g. dashed line in Fig. 8) and thus would overlap more with galaxies and stars.
![Top:W1 magnitude plotted against the 0.5–2 keV flux for the counterparts to Chandra Legacy-COSMOS survey (magenta = AGN, green = galaxies, black = stars) and for the AllWISE counterparts to 2RXS (yellow) and XMMSL2 (grey) sources with detection likelihood larger than 10 and p_any > 0.5. The dashed lines define the AGN locus historically defined by Maccacaro et al. (1988) and revised by Civano et al. (2012) as described in Section 6.2. The solid line has the slope as defined in equation (2) and best separated the star/non-star bimodal distribution of the sources in the three surveys. The cuts at [W1] ≈11 and [W1] = 8 correspond to the saturation limits for IRAC/[3.6] μm in COSMOS and [W1] in AllWISE. Bottom: histogram distribution of [W1] with respect to the solid line. Most of the sources below the line (left in this plot) are stars with a measured proper motion. Most of the sources above the line are supposed to be AGN as the distribution of the AGN in COSMOS would suggest.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/473/4/10.1093_mnras_stx2651/1/m_stx2651fig8.jpeg?Expires=1750215333&Signature=MhUGgP3xeLlehCql5RCLvEn4jZTKDjc-rBniOzcijY1qy-z9VrRWV04Q5HD9ouf76ZMxDAleJU-HU2NSX1xSv7wAdtyWnuLEz~3LRdcMXe7G0omcWktoBilZceqoFJocrxrYsoUFL9VJ4w-jLnmeCkmGIUZR35GGNNDC3Gey2iNVOTZ5TLuooUcQOt~ywn9CfxUuIW0Ky0BCy~-K9FG9XYuilOT-XJwyg7ik0AoTzrD1zdzo4xPFWZypL1Y~PzIcw6sLPuormszeB2KOrjYmzqENl2brzknjTEndzKiwjnY1MXXrMz1mdcycYMniqEkH6oNPUvxKkLvuQItKAkbAeg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Top:W1 magnitude plotted against the 0.5–2 keV flux for the counterparts to Chandra Legacy-COSMOS survey (magenta = AGN, green = galaxies, black = stars) and for the AllWISE counterparts to 2RXS (yellow) and XMMSL2 (grey) sources with detection likelihood larger than 10 and p_any > 0.5. The dashed lines define the AGN locus historically defined by Maccacaro et al. (1988) and revised by Civano et al. (2012) as described in Section 6.2. The solid line has the slope as defined in equation (2) and best separated the star/non-star bimodal distribution of the sources in the three surveys. The cuts at [W1] ≈11 and [W1] = 8 correspond to the saturation limits for IRAC/[3.6] μm in COSMOS and [W1] in AllWISE. Bottom: histogram distribution of [W1] with respect to the solid line. Most of the sources below the line (left in this plot) are stars with a measured proper motion. Most of the sources above the line are supposed to be AGN as the distribution of the AGN in COSMOS would suggest.
In this paper we extend the earlier studies by combining the Chandra Legacy-COSMOS survey with 2RXS and XMMSL2. The Chandra Legacy-COSMOS survey (Civano et al. 2016; Marchesi et al. 2016) is preferred as it has a homogenous depth and covers sufficient area to host also some bright and rare sources. In addition, the counterparts are secure and well understood, thanks to the depth and amount of the available ancillary data. Furthermore, the spectroscopic follow-up and the reliable photometric redshifts via SED fitting (Salvato et al. 2011; Marchesi et al. 2016) allow the classification of the sources as Type1 (unobscured) and Type2 (obscured) AGN, Galaxies (sources with LX < 1042erg s−1), and stars. Fig. 8 (top) compares the properties of the counterparts in COSMOS, 2RXS and XMMSL2 in the W1 versus X-ray flux plane. The AllWISE/W1 total magnitude for the Chandra Legacy-COSMOS sources has been derived from the flux in IRAC/[3.6 μm] within 1.9 arcsec aperture as listed in Laigle et al. (2016) using the conversion factor 0.765 and transforming AB to Vega magnitudes as prescribed by the S-COSMOS documentation available through the Infrared Science Archive (IRAS;10 see also Sanders et al. 2007). The additional correction of W1 − [3.6] = 0.01 mag, following Stern et al. (2012) was applied.
6.3 IR properties of 2RXS and XMMSL2 counterparts
The AllWISE colours [W1 − W2] and [W2 − W3]11 of the candidate counterparts can be used for their qualitative characterization, as suggested by e.g. Wright et al. (2010); Nikutta et al. (2014). Fig. 9 shows the AllWISE colours of the 2RXS (top) and XMMSL2 (bottom) counterparts, using in background fig. 12 of Wright et al. (2010). To the well-known loci we added the location of the Fermi/Blazars identified by e.g. D'Abrusco et al. (2013). That is also the location of most of the X-ray sources that are associated with radio emitters (e.g. NVSS: Condon et al. 1998); 4308 sources in 2RXS and 1307 in XMMSL2, respectively. As suggested by Tsai et al. (2013), the sources in this locus are nearby, jetted objects (z < 0.5), suggesting indeed the presence of an AGN in their cores (Emonts private communication, Emonts et al., in preparation). As expected, the bulk of the X-ray population in 2RXS and XMMSL2 is characterized by QSO, AGN and stars. In particular, the sources below the relation 2 are concentrated in the stellar locus, while the bulk of the sources with W1 above the relation are in the AGN/QSO loci.

Density distribution of the AllWISE of counterparts to 2RXS and XMMSL2 plotted over the colour–colour diagram originally created by Chao-Wei Tsai, (used here with permission) in Wright et al. (2010), but modified by adding the approximative locus of the counterparts to Fermi sources (e.g. D'Abrusco et al. 2013). Top: the AllWISE counterparts are plotted for all the 2RXS. The sources with higher detection likelihood, with more reliable and non-saturated counterparts are plotted in the middle and right-hand panels. The sources are further split with respect to the relation defined in equation 2: the 25 000 green sources are above the relation (i.e. expected to be dominated by AGN); of these, ≈3450 have a counterpart in the NVSS catalogue. In bluish colour we plot the ≈9500 sources that are below the relation and are expected to be mostly stars. Bottom: same as in the top, but for XMMSL2 sources. There are 7259 sources dominated by AGN, 2168 stars and 891 with a NVSS counterpart, respectively. The properties of the sources correspond to the expected one based on their location in the AllWISE colour–colour plot.
7 CATALOGUES RELEASE
We release the AllWISE associations to the sources in the 2RXS and XMMSL2 catalogues outside the Galactic plane. The list and the description of columns are provided for each catalogue in the two following sections. In short, we provide few columns that are keys to the identification of the X-ray sources, simply extracted, without any modification, from their original catalogues. We complement each source with the list of possible AllWISE counterparts and the output columns of Nway that are essential for those users interested in defining more pure and complete subsamples. We provide columns that inform the user on whether or not there is more than one possible counterpart. Finally, the data are complemented with a match to the Gaia DR1 catalogue. A simple match with the unique identifier from 2RXS, XMMSL2, AllWISE, 2MASS and Gaia will allow the user to retrieve additional columns from the original catalogues, not listed in our release. The catalogues accompany this paper, but will be available also via Vizier and at the dedicated web page http://www.mpe.mpg.de/XraySurveys/2RXS_XMMSL2/.
7.1 2RXS–AllWISE catalogue
Column 1.2RXS_ID: IAU Identifier from Boller et al. (2016).
Columns 2-3.2RXS_RA, 2RXS_DEC: 2RXS J2000 Right Ascension and Declination, in degrees.
Column 4.2RXS_e_RADEC: 2RXS positional error, in arcsec.
Column 5.2RXS_ExiML: 2RXS source Detection Likelihood. User should refer to Boller et al. (2016) for discussion on the fraction of false detections as function of this parameter.
Column 6.2RXS_Ext: 2RXS source extent in units of image pixels.
Column 7.2RXS_ExtML: Probability of the 2RXS source extend.
Column 8.2RXS_SRC_FLUX: 2RXS flux in unit of |${\rm erg \, cm^{-2} \, s^{-1}}$| (see Dwelly et al. 2017, for details).
Column 9.2RXS_SRC_FLUX_ERR: 2RXS flux error (see Dwelly et al. 2017, for details).
Column 10.ALLW_ID: WISE All-Sky Release Catalogue name (Cutri et al. 2013).
Columns 11-12.ALLW_RA, ALLW_DEC: J2000 AllWISE Right Ascension and Declination, in degrees.
Column 13.ALLW_e_RADEC: AllWISE positional error, in arcsec.
Columns 14-17.ALLW_w[1234]mpro: AllWISE Vega magnitude in the W1, W2, W3, W4 bands.
Columns 18-21.ALLW_w[1234]sigmpro: AllWISE magnitude error in the W1, W2, W3, W4 bands.
Columns 22-25.ALLW_w[1234]snr: AllWISE signal to noise ratio in the W1, W2, W3, W4 bands.
Column 26.ALLW_cc_flags: AllWISE reliability flag from Cutri et al. (2013).
Column 27.Separation_ALLW_2RXS: Separation between members of this association, in arcsec.
Column 28.dist_bayesfactor: Logarithm of ratio between prior and posterior from distance matching.
Column 29.dist_post: Distance posterior probability comparing this association versus no association, as in Budavári & Szalay (2008).
Column 30.bias_ALLWOURMAG_PIX: Probability weighting introduced by AllWISE prior. 1 indicates no change.
Column 31.p_single: Same as dist_post, but weighted by the AllWISE colour-magnitude prior.
Column 32.p_any: For each entry in the X-ray catalogue, the probability that any of the associations is the correct one. The lower p_any, the lower is confidence that a reliable counterpart was found. See Section 4.2.
Column 33.p_i: Relative probability of the match, if one exists. The p_i add up to unity for each X-ray source.
Column 34.match_flag: 1 for the most probable match, if existing; 2: almost as good solutions p_i/p_ibest > 0.5).
Column 35-36.GroupID, GroupSize: if the 2RXS source has only one possible AllWISE counterpart, the two columns are blank. Otherwise, the GroupSize value indicates the number of possible counterparts while the GroupID value is the same integer for the group. A sort on the GroupID value, will rank the first non-unique match group together, followed by all the rows in the second non-unique group, etc. All the unique matches are listed last.
Column 37.1RXS_ID: Source name in the 1RXS catalogues (Voges et al. 1999, 2000).
Column 38.ALLW_2MASS_ID: 2MASS Identifier as listed in the AllWISE catalogue.
Columns 39-41.ALLW_[jhk]_m_2mass: 2MASS magnitude in the j, h, k bands, as from AllWISE catalogue.
Columns 42-44.ALLW_[jhk]_msig_2mass: 2MASS magnitude errors in the j, h, k bands, as from AllWISE catalogue.
Columns 45.Gaia_DR1_ID: Solution ID from the original Gaia DR1 catalogue (see Fabricius et al. 2016, for more details).
Columns 46-47.Gaia_DR1_RA, Gaia_DR1_DEC: Gaia J2000 Right Ascension and Declination as computed by Vizier.
Columns 48-49.pmra, pmdec: Proper motion in Right Ascension and Declination as measured by Gaia.
Columns 50-51.pmra_error, pmdec_error: Proper motion errors in Right Ascension and Declination as measured by Gaia.
Columns 52.phot_g_mean_flux: Gaia mean flux in units of e-s−1.
Columns 53.phot_g_mean_flux_error: Gaia mean flux error in units of e-s−1.
Columns 54.phot_g_mean_mag: Gaia mean magnitude.
7.2 XMMSL2–AllWISE catalogue
Column 1.XMMSL2_ID: Unique identifier from Boller et al. (2016).
Columns 2-3.XMMSL2_RA, XMMSL2_DEC: 2RXS J2000 Right Ascension and Declination, in degrees.
Column 4.XMMSL2_e_RADEC: XMMSL2 original positional uncertainty augmented by 5 arcsec in quadrature.
Columns 5-7.XMMSL2_DET_ML_B[876]: XMMSL2 source Detection Likelihood in the respective energy bands.
Column 8-10.XMMSL2_Ext_B[876]: XMMSL2 source extent in units of image pixels, in the respective energy bands.
Column 11-13.XMMSL2_Ext_ML_B[876]: Probability of the XMMSL2 source extend in the respective energy bands.
Column 14-16.XMMSL2_FLUXB[876]: XMMSL2 flux in the respective energy bands, in |${\rm erg \, cm^{-2} \, s^{-1}}$| units.
Column 17-19.2RXS_FLUX_B[876]_ERR: XMMSL2 flux errors in the respective energy bands, in |${\rm erg \, cm^{-2} \, s^{-1}}$| units.
Column 20.ALLW_ID: WISE All-Sky Release catalogue name (Cutri et al. 2013).
Columns 21-22.ALLW_RA, ALLW_DEC: J2000 AllWISE Right Ascension and Declination, in degrees.
Column 23.ALLW_e_RADEC: AllWISE positional error, in arcsec.
Columns 24-27.ALLW_w[1234]mpro: AllWISE Vega magnitude in the W1, W2, W3, W4 bands.
Columns 28-31.ALLW_w[1234]sigmpro: AllWISE magnitude error in the W1, W2, W3, W4 bands.
Columns 32-35.ALLW_w[1234]snr: AllWISE signal to noise ratio in the W1, W2, W3, W4 bands.
Column 36.ALLW_cc_flags: AllWISE reliability flag from Cutri et al. (2013).
Column 37.Separation_ALLW_XMMSL2: Separation between members of this association, in arcsec.
Column 38.dist_bayesfactor: Logarithm of ratio between prior and posterior from distance matching.
Column 39.dist_post: Distance posterior probability comparing this association versus no association, as in Budavári & Szalay (2008).
Column 40.bias_ALLWOURMAG_PIX: Probability weighting introduced by AllWISE prior. 1 indicates no change.
Column 41.p_single: Same as dist_post, but weighted by AllWISE prior.
Column 42.p_any: For each entry in the X-ray catalogue, the probability that any of the associations is the correct one. The lower p_any, lower is confidence that a reliable counterpart was found. See Section 4.2.
Column 43.p_i: Relative probability of the match, if one exists. The p_i add up to unity for each X-ray source.
Column 44.match_flag: 1 for the most probable match, if existing; 2: almost as good solutions (p_i/ p_ibest > 0.5).
Column 45-46.GroupID, GroupSize: if the 2RXS source has only one possible AllWISE counterpart, the two columns are blank. Otherwise, the GroupSize value indicate the number of possible counterparts while the GroupID value is the same integer for the group. A sort on the GroupID value, will rank the first non-unique match group together, followed by all the rows in the second non-unique group, etc. All the unique matches are listed last.
Column 47.1RXS_ID: Source name in the 1RXS catalogues (Voges et al. 1999, 2000).
Column 48.ALLW_2MASS_ID: 2MASS Identifier as listed in the AllWISE catalogue.
Columns 49-51.ALLW_[jhk]_m_2mass: 2MASS magnitude in the j, h, k bands, as from AllWISE catalogue.
Columns 52-54.ALLW_[jhk]_msig_2mass: 2MASS magnitude errors in the j, h, k bands, as from AllWISE catalogue.
Columns 55.Gaia_DR1_ID: Solution ID from the original Gaia DR1 catalogue (see Fabricius et al. 2016, for more details).
Columns 56-57.Gaia_DR1_RA, Gaia_DR1_DEC: Gaia J2000 Right Ascension and Declination as computed by Vizier.
Columns 58-59.pmra, pmdec: Proper motion in Right Ascension and Declination as measured by Gaia.
Columns 60-61.pmra_error, pmdec_error: Proper motion errors in Right Ascension and Declination as measured by Gaia.
Columns 62.phot_g_mean_flux: Gaia mean flux in units of e-s−1.
Columns 63.phot_g_mean_flux_error: Gaia mean flux error in units of e-s−1.
Columns 64.phot_g_mean_mag: Gaia mean magnitude.
8 NWAY RELEASE
Together with the AllWISE counterparts to the 2RXS and XMMSL2 catalogues, we also release Nway. The Nway software and manual are available at https://github.com/JohannesBuchner/nway. In order to make the user familiar with the code, the release is completed with the catalogues used in the testing phase discussed in Appendix C. We would like to stress that the use of Nway is not limited to finding the counterparts to X-ray sources. With the advent of deep and wide area surveys in X-rays (e.g. eROSITA, Athena) and radio (e.g. ASKAP/ EMU: Norris et al. 2011; LOFAR: van Haarlem et al. 2013; APERTIF: Oosterloo, Verheijen & van Cappellen 2010), Nway will provide a powerful and reliable counterpart identification tool.
9 DISCUSSION AND CONCLUSIONS
We presented the catalogues of secure AllWISE counterparts to the ROSAT/2RXS and XMMSL2 X-ray extragalactic all-sky surveys. Only a small fraction (less than 5 per cent) of the X-ray/AllWISE associations is expected to be due to chance associations. Associations were obtained using a new algorithm, Nway, capable of handling complicated priors. In particular, we have used here a prior based on the WISE colour-magnitude properties of about 2500 X-ray sources from the 3XMM-DR5 catalogue with flux distribution similar to 2RXS and XMMSL2.
Nway can be used for finding the right counterparts to other (not only X-ray) surveys. However, the prior which we apply Nway in this work is tuned to the properties of the input catalogues and thus is not universal. E.g. adopting for 2RXS a similar prior to that used in Dwelly et al. (2017), which was constructed with half of the sources adopted here, the AllWISE counterpart changes for 3 per cent of the sources (3431/106573). The prior is appropriate only as long as it well represents the population. For this reason, the prior adopted for the extragalactic region covered by 2RXS and XMMSL2 cannot be used with the same reliability for finding the correct counterparts of X-ray sources in the Galactic plane, where the X-ray catalogues are dominated by stars. Similarly, it will not be possible to use the same prior with the same reliability for finding the counterparts to X-ray surveys that are significantly shallower or deeper than the two discussed in this work.
9.1 Finding counterparts to eROSITA point-like sources
The design of Nway was dictated by the need of developing a flexible algorithm that could be used with the patchwork of multi-wavelength coverage of the entire sky available for finding the counterparts of eROSITA (Merloni et al. 2012).
eROSITA combines a wide field of view, large collecting area, long survey duration, broad energy bandpass and good point source location accuracy, making it by far the most powerful X-ray survey instrument ever built. In the soft energy band (0.5–2 keV), the planned four-year eROSITA all-sky survey, will have a median point source flux limit of 10−14 |${\rm erg \, cm^{-2} \, s^{-1}}$| (Merloni et al. 2012), approximately 30× deeper than the ROSAT all-sky survey (for AGN-like X-ray spectra).
In the hard X-ray band (2–10 keV), the predicted flux limit of 2 × 10−13 erg cm−2 s−1 is around 100× deeper than the only existing all-sky survey conducted at these energies (i.e. the High Energy Astronomy Observatory, HEAO-I: Wood et al. 1984). On completion, the eROSITA survey is expected to detect about four million X-ray sources, with 3/4 of them being AGN. Thankfully, the location accuracy for point-like eROSITA sources is expected to be better than 10 arcsec radius (combination of statistical and systematic uncertainties), substantially better than for typical ROSAT sources. This will also be enabled by the availability of Gaia that will allow accurate positional accuracy on eROSITA single frame by tying the two astrometric reference frames. The eROSITA data will also enable better separation between point-like (mostly AGN and stars) and extended (galaxy cluster) sources on the basis of their X-ray properties alone (Merloni et al. 2012). However, due to the fainter X-ray flux limit expected, the optical-IR counterparts to point-like eROSITA sources will typically be several magnitudes fainter than those presented here. Fig. 10 illustrates this by showing the colour-magnitude distribution of the counterparts to the X-ray sources in STRIPE82X (LaMassa et al. 2016; Tasnim Ananna et al. 2017) cut at the depth of eROSITA, colour coded as a function of X-ray flux. Given the increasing depth of eROSITA, the counterparts of the sources get progressively fainter, finally overlapping with the bulk of the AllWISE population within 30 arcsec of the X-ray position, here in grey (see for comparison the distribution in Fig. 3).
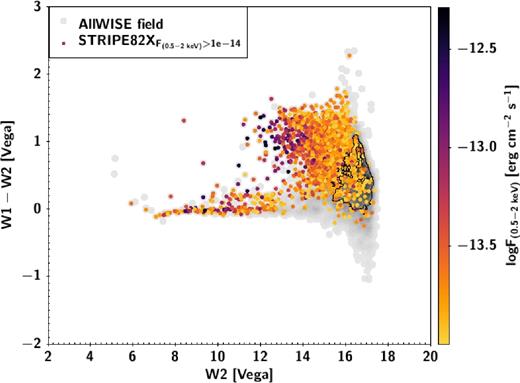
WISE colour-magnitude plane for the AllWISE counterparts to the sources in STRIPE82X (Tasnim Ananna et al. 2017), cut at the expected depth of eROSITA at the end of the survey (eRASS:8). Sources are colour coded as a function of their X-ray flux. In grey and with black contours, the AllWISE population within 30 arcsec from the STRIPE82X sources are shown. Given its shallowness AllWISE can provide a counterpart only to 80 per cent of the eROSITA sources. For the faint eROSITA sources, the AllWISE counterparts will increasingly overlap with the bulk of the AllWISE population, thus reducing the disentangling power of the prior, even though the search for the correct counterpart is limited to 30 arcsec.
Hence, in order to select the correct counterparts for several million eROSITA sources, we will need to take into account additional information to separate field populations from the true counterparts to X-ray sources. Deeper WISE catalogues, enabled by the co-addition of the ongoing multi-year NEOWISE survey data (Mainzer et al. 2011, 2014; Meisner, Lang & Schlegel 2017a) with the existing AllWISE data set, should not only probe to fainter [W1] and [W2] limits, but should also have a smaller photometric scatter at the magnitudes currently probed by the AllWISE survey. Such a reduced scatter will allow better separation of the red (in [W1–W2]) AGN population from the bluer field stars and galaxies. Note however that at the depth of ROSAT, only 0.01 per cent of the AllWISE counterparts had an upper limit in W2, while the number will increase to fainter X-ray flux, even considering the reactivation of NEOWISE (Mainzer et al. 2014; Meisner, Lang & Schlegel 2017b) post-cryogenic phase expected to reach a depth in W2 of 19.9, when combined with WISE.
In addition, we expect that one of the main drawbacks of relying on any catalogue derived from WISE data will be the relatively broad PSF (∼6 arcsec full width at half-maximum in WISE bands 1 and 2), which results in blending problems for close pairs of sources. This problem will inevitably get worse as the co-added WISE data reach to fainter magnitudes, approaching the confusion limit. In addition, once an AllWISE counterpart has been selected for each X-ray source, the final step of optical counterpart selection must still be carried out. This step becomes particularly difficult when WISE detections are blends of multiple astrophysical sources.
The forced photometry techniques and tools described by Lang, Hogg & Schlegel (2016) avoid many of the problems associated with combining data across multiple wavebands, and have already been exploited successfully, e.g. in the selection of QSO targets for eBOSS (Myers et al. 2015). By cross-matching eROSITA sources with previously compiled forced photometry catalogues (e.g. derived from Gaia in the Galactic plane, SDSS and DECaLS, DES, VHS photometry), we expect to greatly reduce both the impact of source confusion in the IR, and the general problems related to compiling data across multiple optical-IR wavebands.
The high cross-matching success rate for 2RXS and XMMSL2 has demonstrated that our cross-matching routine and priors are relatively robust. However, the dynamic range of the eROSITA catalogue will be much larger than that considered here.
Therefore, it is likely that a single, X-ray flux-independent prior (as adopted in this work) will be a sub-optimal choice for finding counterparts to all eROSITA sources. We also expect a strong dependence in the mixture of object classes which make up the eROSITA sample as a function of Galactic latitude. Thankfully, the XMM, Chandra and Swift/XRT archives already contain large samples of well-measured X-ray reference sources which populate the entire eROSITA flux range, and which can be used to define new X-ray-flux-dependent and/or Galactic-latitude-dependent optical-IR priors.
However, great care will be needed to understand the very complex inhomogeneities/biases/incompletenesses that will be imprinted by such an optimized cross-matching scheme. It is possible that a single cross-matching procedure is not suitable for all eROSITA science projects, and that a number of individually tailored cross-matching schemes will be required, depending on the patch on the sky.
The bulk of the X-ray sources in our study are stars and AGN, which are intrinsically variable objects. However, we have made the simplifying assumption throughout this work that variability (in luminosity and/or in spectral energy distribution) of X-ray sources is not important for the purposes of counterpart selection. This means that we do not take account of extremely interesting, but difficult to handle scenarios such as where an AGN that was bright at the epoch of its X-ray detection (e.g. in ROSAT) has faded substantially (in all wavebands) several years later when the measurement of its longer wavelength counterpart (e.g. WISE or SDSS) was made (e.g. ‘changing-look’ QSOs; LaMassa et al. 2015; Merloni et al. 2015; Runnoe et al. 2016). However, in the future we will use AGN and stellar variability to our advantage when selecting counterparts to eROSITA X-ray sources. With the present (PTF/iPTF/ZTF12 Rau et al. 2009; Catalina,13 Pan-STARRS:14 Chambers et al. 2016; etc.) and forthcoming generation of optical time domain surveys, (e.g. as performed by the Large Synoptic Survey Telescope; Gressler et al. 2014), every potential optical counterpart to an X-ray source will also come with robust measurements of optical variability. Such variability metrics, which naturally separate AGN and stars from field galaxies, and can be simply applied as an additional prior in Nway (see for example, Budavári, Szalay & Loredo 2017).
ACKNOWLEDGEMENTS
The authors are grateful to the referee for the valuable input on the earlier version of this paper. The authors are grateful to M. J. Freyberg, T. Boller and F. Haberl for their help in understanding the old and new ROSAT catalogues. MS and JB are grateful to G. Hasinger and T. Simm for testing and providing feedback on the various versions of Nway. MS thanks F. Guglielmetti, A. Georgakakis and D. Coffey for various discussions over the years that helped in shaping the final work. JB acknowledges support from FONDECYT Post-doctorados grant 3160439 and the Ministry of Economy, Development and Tourism's Millennium Science Initiative through grant IC120009, awarded to The Millennium Institute of Astrophysics, MAS. MB acknowledges support from the FP7 Career Integration Grant ‘eEASy?’ (CIG 321913). This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. This research has made use of data obtained from the 3XMM XMM–Newton serendipitous source catalogue compiled by the 10 institutes of the XMM–Newton Survey Science Centre selected by ESA. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This research has made use of data obtained from XMMSL2, the Second XMM–Newton Slew Survey Catalogue, produced by members of the XMM SOC, the EPIC consortium, and using work carried out in the context of the EXTraS project (‘Exploring the X-ray Transient and variable Sky’, funded from EU's Seventh Framework Programme under grant agreement no. 607452). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made use of the Vizier catalogue access tool, CDS, Strasbourg, France. The original description of the VizieR service was published in A&AS 143, 23. This publication makes use of TOPCAT (Taylor 2005) and STILTS (Taylor 2006) available at http://www.starlink.ac.uk/topcat/ and http://www.starlink.ac.uk/stilts/, respectively.
Note, that the detection of an AGN in the mid-infrared requires the availability of reprocessing dust, i.e. dust free AGN will be missed. Many Compton-Thick AGN will be missed as well.
We computed Galactic foreground absorption corrected fluxes following the procedure presented in appendix A of Dwelly et al. (2017).
see also http://irsa.ipac.caltech.edu/ Missions/wise.html for a summary and details and on the reactivated mission.
Available at http://wise2.ipac.caltech.edu/docs/release/allwise/.
12321/3681/1177/386/121/34/11/2/1 cases with 2/3/4/5/6/7/8/9/10 AllWISE counterparts within the search area, respectively. Not only do most of these sources have a low p_any, but the candidate counterparts are also faint in W2 and on average at larger distance from the X-ray position. This suggests that the X-ray sources themselves could be spurious. In fact, >75 per cent of this subsample have EXI_ML < 10. Only 7 per cent of them have p_any > 0.9.
1015/163/25/17/1/1 sources having 2/3/4/5/6/7 possible counterparts. As for 2RXS, we analyse the properties of the XMMSL2 sample with two possible counterparts. Of the 1015 sources belonging to this group, 108 (10 per cent) have p_any > 0.9 and 739 (73 per cent) have p_any < 0.1.
0.02 per cent (0.08 per cent), 0.07 per cent (0.3 per cent) and 20 per cent (20 per cent) are only upper limits in W1, W2, W3 in 2RXS (XMMSL2), respectively.
While there can be only one source from the secondary catalogues with match_flag=1 per each source of the primary catalogue, there can be many that are flagged match_flag=2.
We make the examples using magnitudes, but everything will work the same using any other parameter like colours, morphology, variability etc.
The user should refer to Marchesi et al. (2016) for details about the comparison between XMM-/Chandra- COSMOS detections.
i.e. 25 sources correspond to two or more ıChandra detections.
For this test we consider as counterpart the source with the highest p_anyp_i within each circle.
Note that we cannot exclude that these 0.09 per cent sources are the counterpart to real X-ray sources that are fainter than the depth of our survey.
REFERENCES
SUPPORTING INFORMATION
Supplementary data are available at MNRAS online.
XMMSL2_paper_2017JUN09.fits.gz
2RXS_paper_2017MAY26.fits
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
APPENDIX A: A BRIEF HISTORY OF THE MATCHING PROBLEM
In astrophysics a source can be characterized by its accurate position on the sky, its redshift and its SED. If the positional accuracy is not known at a sub-arc second precision, the source cannot be the target of a spectroscopy study, and/or multi-wavelength data cannot be correctly assembled. While sources that are identified in the Optical and Near-Infrared regime usually have the required precision, this is not the case for sources selected at shorter and longer wavelengths. For example in the Far-infrared bands, Herschel reaches 6–7 arcsec PSF at 70 μm, increasing up to ∼13 arcsec at longer wavelength. Similarly, in X-ray the positional measurement error depends on the counts and spatially varying PSF and therefore is not constant between sources. Typical positional uncertainties go from up to ≈ 3 arcsec (Chandra) to 7 arcsec (XMM) but reach up to about 29 arcsec for 95 per cent of the ROSAT sources in 2RXS, with the values increasing towards the periphery of the field of view, up to more than 1 arcmin in the extreme cases. This low positional accuracy, together with the fact that sources with different SEDs and different redshift emit the bulk of their energy in different photometric bands, make it difficult to identifying with certainty the same source in different surveys. Additionally, the entire pairing process is done by means of catalogues, which can differ in depth, technique for ‘source detection’ (and definition thereof). In the past, the data were so shallow that a simple cross match in coordinates between catalogues was enough for pairing correctly the sources. Now, we reach sources that are so faint that we must adopt a probabilistic approach.
The most used technique is based on the LR method (Sutherland & Saunders 1992). Taking into account source number densities, coordinates (with relative errors) and magnitude distribution of the sources, the method estimates the ratio between the likelihood that a given source from catalogue B is the correct counterpart to a source detected in catalogue A, and the likelihood of being a source in the background. Different factors are then considered when computing the threshold above which the likelihood ratio assures a reliable association. The procedure is repeated anew for the pairing between the catalogues A–C, A–D, etc. If catalogues are (i) from images at similar wavelength and (ii) of sufficient depth, for most of the sources in A, the counterpart in catalogues B, C, D etc. will be the same, while for a fraction of the sources further considerations based on the shape of the SED need to be taken into account for the counterpart association.
Moving from a generic description to a specific application, let us focus from now on to the case of finding the correct counterpart to X-ray sources. The LR method has been successfully applied on surveys like XMM-COSMOS (Brusa et al. 2007, 2010), CDFS (Luo et al. 2008; Xue et al. 2011; Luo et al. 2017), Chandra-COSMOS (Civano et al. 2012; Marchesi et al. 2016), XXL (Georgakakis et al. 2017), STRIPE-82X (LaMassa et al. 2016; Tasnim Ananna et al. 2017), AEGIS-X (Georgakakis & Nandra 2011; Nandra et al. 2015) just to mention a few. For each of these surveys, the authors performed the steps described above, pairing X-ray to optical, to near-infrared and to mid-infrared data, independently. Then, ranked the ancillary data available in order of reliability (i.e. deep and higher resolution data first) for selecting the correct counterpart in those cases where the LR method does not provide unique solutions.
The Bayesian approach is increasingly favoured by the entire community. Contrary to the LR method that is data-driven, the Bayesian approach uses a model for reference (prior) and thus can be applied also to small samples and areas. This is a strength of the method but a frequent criticism is that the assumption of a model distribution might not represent the reality. These criticisms are legitimate in general but in the specific case of finding the counterpart to X-ray detected sources they are somewhat outdated. In fact, deep Chandra and XMM surveys are so advanced/extended that reliable models of magnitude distribution of the counterparts to sources detected up to a desired depth, can now be constructed empirically. Another virtue of the Bayesian approach is that many priors can be adopted, each independent of the next. So we can adopt a Bayesian form for the probability of a source to be the right counterpart based on its position, its magnitude, colour etc.
At the basis of many Bayesian cross-matching algorithms is the formalism introduced by Budavári & Szalay (2008).15 This enables simultaneous cross-matching of multiple catalogues and provides the Bayes factor from the astrometric measures. This Bayes factor from the astrometry is then combined with one (or more) related to physical properties. E.g., Roseboom et al. (2009) search the right counterparts to sub-millimeter sources by computing the photometric redshift and SED fitting of each source within a certain radius circle.
Independently from the adopted method, an additional difficulty arises when the goal is to find the counterparts to X-ray surveys that cover over hundreds of square degrees (e.g. eROSITA: Merloni et al. 2012). In this case, the multi-wavelength catalogues from where to draw the correct identification will not be homogeneously covering the field, but rather a patchwork of different surveys/depths, thus effecting the actual magnitude distribution of the field sources and thus the determination of the real counterpart.
In view of these new challenges, we designed Nway, an algorithm based on two-steps Bayesian approach. In the following we provide the complete description of the code and its application to test cases in COSMOS. The code is released, together with a detailed manual and a set of test data for training purposes.
APPENDIX B: MATCHING METHODOLOGY
This section lays out in detail the computation Nway performs. Further details and clear explanations on the use of the Nway are presented in the manual and tutorial of the code, distributed via Github at https://github.com/JohannesBuchner/nway.
The features of Nway include
Matching of N catalogues simultaneously.
Computation of all combinatorially possible matches.
Consideration of partial matches across catalogues, i.e. the absence of counterparts in some catalogues.
Taking into account the positional uncertainties and the source number densities, computation of the probability of each possible match.
Computation of the probability that there is no match.
Incorporating magnitude, colour or other information about the sources of interest, refining the match probabilities.
This is done in several steps that are given below.
Finding combinatorially all possible matches. See Section B1.
Computing each match probability from number densities, separation distances and positional errors alone, taking into account the chance of a random alignment. See Section B2.
For each source of the primary catalogue (in the application from this paper: for each the X-ray source), compute (a) the probability that this source does not have a counterpart and (b), assuming this source has a counterpart, compute the relative probability for each possible match. See Section B3.
Refining the probabilities by additional prior information. See Section B4.
In Nway, only the first catalogue (primary catalogue) has a special role. For every entry in this catalogue, matches are sought in the other catalogues. The entries in the primary catalogue must come with an ID. All catalogues must contain RA, DEC, positional error information, the size of the area of sky covered by the catalogue. The latter information is used to compute the probability of a chance alignment.
B1 Computing all possible matches
First, possible associations are found. Fig. B1 shows that all possible associations between the input catalogues are considered when building the output catalogue. For this, a hashing procedure puts each object into HEALPix bins (Górski et al. 2005). The bin width w is chosen so that an association of distance w is improbable, i.e. much larger than the largest positional error. An object with coordinates ϕ, θ is placed in the bin corresponding to its coordinate, but also into its neighbouring bins to avoid boundary effects. This is done for each catalogue separately. Then, in each bin, the Cartesian product across catalogues (every possible combination of sources) is computed. All associations are collected across the bins and filtered to be unique. The hashing procedure adds very low effort |$O(\sum _{i = 1}^{k}N_{i})$|, while the Cartesian product is reduced drastically to |$O(N_{\text{bins}}\cdot \prod _{i = 1}^{k}\frac{N_{i}}{N_{\text{bins}}})$|, from a naive approach complexity of |$O(\prod _{i = 1}^{k}N_{i}).$| All primary objects that have no associations past this step have |$P({\rm `any \, real \, association'}|D) = 0$|.

All possible combinations of matches from the input catalogues are combined into the output catalogue. Each such match has a computed probability, either based on positions and number densities or additionally refined after the adoption of one or more priors. The matches are grouped by the primary catalogue entries (here: x1, x2).
A problem arises when the secondary catalogues have depths or resolution such that some of the sources appear only in some of the catalogues. So we need to consider also pairing that do not include a source from the primary catalogue. The computation becomes infeasible very quickly as the number of catalogues reaches four or more, as demonstrated in Pineau et al. (2017).
Nway first considers as an initial list all possibilities that have the primary catalogue source in an association. As shown above, this includes associations where some catalogues do not participate. The remaining sources are considered independent. Secondly, associations across the unused catalogues are considered for each case. To do this with low computational complexity, the additional associations considered are those in the initial list, but with the primary catalogue source removed. For instance, for the case of primary source x1 with the other sources independent, x1-(none)-(none), the additional associations to consider are x1-b1-c1, x1-b1-c2, x1-b2-c1, x1-b2-c2, i.e. with the primary source removed, b1-c1, b1-c2, b2-c1, b2-c2. The highest distance-based posterior of these additional associations is factored into the distance-based posterior of the association with the primary source. In practice, this solves the problem of tight unrelated associations (e.g. b2-c1), which, if not considered otherwise, would unduly favour an association which includes them (e.g. x1-b1-c1). If five or more catalogues are matched, not only one but two additional simultaneous association might need to be considered. The impact of our approximation then depends on the application. Our choice of using the highest posterior over all unrelated associations is expected to handle such many-catalogue applications well. If however several groups of similar nature (e.g. an X-ray catalogue, two radio catalogues and three optical catalogues) are to be matched, proceeding hierarchically may give better results (e.g. first match the optical catalogues together). However, more testing is needed in this area.
B2 Distance-based matching
The second step is the computation of association probabilities using the angular distances between counterparts. In the last step (Section B3), for each source in the primary catalogue these probabilities from the various possible matches are combined. In the end this gives the probability that this source does not have a counterpart and, assuming this source has a counterpart, compute the relative probability for each possible match. At this step however we first compute the probability for a particular association (e.g. x1-b1-c1, or x1-(none)-c2) to be actually the same object versus a chance alignment of unrelated objects.
The probability of a given association is computed by comparing the probability of a random chance alignment of unrelated objects (prior) to the likelihood that the sources from the various catalogues are in fact the same object. The prior is evaluated from the density of each catalogue and their effective coverage. Varying depths between the catalogues and different coverage can further reduce the fraction of expected matches, which can be adjusted for with a user-supplied incompleteness factor. The posterior for each association based on the distances only is calculated (output column dist_post). The mathematical details of this computation be found in Section B5. This probability can be modified by additional information (see Section B4).
B3 Grouping, flagging and filtering
In the final step, associations are grouped by the source from the primary catalogue (in our example, the X-ray catalogue). The posterior probabilities that this source has any real association and the relative probability for each match are computed (output columns p_any and p_i, respectively). Section B5 details this computation. To remove low-probability associations from the output catalogue, the user parameter --min-prob can be used to specify a threshold. The best match is indicated with match_flag=1 for each primary catalogue entry. Secondly, almost as good solutions are marked with match_flag=2.16 By default associations are flagged with match_flag=2 as soon as p_i|$_{{\tt {match\_flag=1}}}$|/p_i|$_{{\tt {match\_flag=2}}}>0.5$|, but the use can change the threshold with the parameter --acceptable-prob. All other associations are marked with match_flag=0.
In the output catalogue the last three columns (p_any, p_i, match_flag) allow the user to identify sources with one solution, possible secondary solutions and to build final catalogues.
B4 Matching with additional prior information
For many classes of sources, the SED provides additional hints which associations are likely real. For instance, the WISE colour distribution is different for X-ray sources than for other objects (demonstration in Section 4.1). A powerful feature of Nway is to take advantage of this additional information to improve the matching. In particular Nway allows
Multiple priors to be used from any of the input catalogues.
Arbitrary quantities can be used. Providing priors is not limited to magnitude distributions, one can use any other discriminating information (e.g. colours, morphology, variability, etc.).
It is possible to input pre-constructed information or compute the distributions from the catalogues themselves based on secure distance-only matches (see Section B6.1).
Section B6 has the mathematical details and a comparison to the Likelihood Ratio method (Sutherland & Saunders 1992).
B5 Probability for an individual association
Let us consider the problem of finding counterparts to a primary catalogue (i = 1), in our example for the X-ray source position catalogue. Let each Ni denote the number of entries for the catalogues used, and νi = Ni/Ωi denote their respective source surface density on the sky.
If a counterpart is required to exist in each of the k catalogues, there are |$\prod _{i = 1}^{k}N_{i}$| possible associations. If we assume that a counterpart might be missing in each of the matching catalogues, there are |$N_{1}\cdot \prod _{i = 2}^{k}(N_{i}+1)$| possible associations. This minor modification, negligible for Ni ≫ 1, is ignored in the following for simplicity, but handled in the code.
The output column dist_bayesfactor stores log B, while the output column dist_post is the result of equation (B7). The output column p_single is the same as dist_post, but modified if any additional information is specified (see Section B6). As mentioned several times in the literature, the Budavári & Szalay (2008) approach does not include sources absent in some of the catalogues, while the formulae we develop below incorporate absent sources. This is similar in spirit to Pineau et al. (2017), although the statistical approach is different. We now go further and develop counterpart probabilities.
A ‘very secure’ counterpart could be defined by the requirement p_any > 95 per cent and p_i > 95 per cent, for example. However, it is useful to run simulations to understand the rate of false positives. Typically, much lower thresholds are acceptable, with the threshold (dictated by the scientific applications) being a compromise between purity and completeness of the sample.
B6 Magnitudes, colours and other additional information
Nway stores the modifying factor, P(Dm|H), in bias_* output columns, one for each column giving a magnitude, colour or other distribution. This modifying factor is however renormalized so that |$P(D_{m}|H) = \frac{\bar{q}(m)}{\bar{n}(m)}/\int \frac{\bar{q}(m^{\prime })}{\bar{n} (m^{\prime })}\bar{n}(m^{\prime })\text{d}m^{\prime }$|, which makes P(D|H) = P(Dϕ|H) when m is unknown. In that case, m is marginalized over its distribution in the general population, i.e. |$\int P(D_{m}|H)\, \bar{n}(m^{\prime })\, \text{d}m$|. This has the benefit that when m is unknown, the modifying factor is unity and the probabilities remain unmodified.
B6.1 Autocalibration
The probability distributions |$\bar{n}(m)$| and |$\bar{q}(m)$| can be taken from other observations by computing the normalized magnitude17 histograms of the overall population and the target sub-population (e.g. X-ray sources). In Nway, the distributions |$\bar{q}(m)$| and |$\bar{n}(m)$| can be provided as an ASCII table, with the columns describing the bin edges, the frequency of the target population (in our example, X-ray sources) and the frequency of the field population (sources that are not X-ray sources at the depth of the catalogue).
Under certain approximations and assumptions, these histograms can also be computed during the catalogue matching procedure used for the weighting on the fly and saved for future further use. For example, one could perform the distance-based matching procedure laid out above and compute a magnitude histogram of the secure counterparts as an approximation for |$\bar{q}(m)$| and a histogram of ruled out counterparts for |$\bar{n}(m)$|. While the weights |$\bar{q}(m)/\bar{n}(m)$| may strongly influence the probabilities of the associations for a single object, the bulk of the associations will be dominated by distance-weighting. One may thus assume that the |$\bar{q}(m)$| and |$\bar{n}(m)$| are computed with and without applying the magnitude weighting are the same, which is true in practice. When differences are noticed, they will only strengthen |$\bar{q}(m)$|, and the procedure may be iterated.
In Nway auto mode, the histogram |$\bar{q}(m)$| is constructed using sources with dist_post>0.9 (safe matches) and |$\bar{n}(m)$| with dist_post < 0.01 (safe non-matches). When these ‘self-constructed priors’ are used, the breaks of the histogram bins are computed adaptively based on the empirical cumulative distribution found. Because the histogram bins are usually larger than the magnitude measurement uncertainty, the latter is currently not considered. The adaptive binning creates bin edges based on the number of objects, and is thus independent of the chosen scale (magnitudes, flux). Thus the method is not limited to magnitudes, but can be used for virtually any other known object property (colours, morphology, variability, etc.), as demonstrated in the main body of this paper.
APPENDIX C: TESTING NWAY ON COSMOS
The COSMOS field (Scoville et al. 2007) offers the ideal test bench, covering a relatively large area with homogeneous and deep observations in many bands. In particular, the field has been observed with XMM–Newton (Cappelluti et al. 2007; Hasinger et al. 2007), and its reliable association to the I-band CFHT/Megacam catalogue McCracken et al. (2007) via LR is presented in Brusa et al. (2007). Successively, Brusa et al. (2010) improved on the first associations using also the near-infrared (McCracken et al. 2010) and the mid-infrared (Sanders et al. 2007; Ilbert et al. 2010) catalogues. Each catalogue was used independently and the counterparts were chosen via LR and visually inspected.
More recently, for the same area, deeper and homogeneous observations from Chandra became available (Elvis et al. 2009; Civano et al. 2012, 2016; Marchesi et al. 2016) so that the XMM-COSMOS associations have been successively validated/changed on the basis of the smaller positional uncertainties of the Chandra X-ray data18 ( ∼ 0.5 arcsec versus ∼ 2 arcsec for XMM, averaging over the entire Field of View).
In the following two sections we describe the successful application of Nway to the XMM-COSMOS field, first using only one optical catalogue. We then repeat the association using simultaneously the optical and IRAC catalogues. We show how the associations and the key Nway parameters p_i and p_any change in the two applications. The optical and IRAC catalogues are the original ones used by Brusa et al. (2010). They are released with Nway and described in the manual so that a curious reader can practice with the code.
C1 Nway Success rate
The XMM-COSMOS catalogue of multi-wavelength counterparts presented in Brusa et al. (2010) included 1822 sources, 1797 of which are isolated.19 We focus here on the 1281(128) isolated XMM-COSMOS sources with the original confirmed (changed) association after using Chandra data.
We extracted from the catalogue the identification number, the X-ray coordinates and corresponding positional errors of the 1409 (1281+128) isolated sources. The mean positional error of the sample is 1.8 arcsec with a minimum value of 0.1 arcsec to a max of 7.33 arcsec. Similarly, we extracted from the optical (McCracken et al. 2007) and IRAC (Sanders et al. 2007; Ilbert et al. 2010) catalogues the identification numbers, the coordinates and the magnitude in the optical and 3.6 μm bands. We assumed, as in Brusa et al. (2007), a constant positional error of 0.1 arcsec and 0.5 arcsec for the two catalogues, respectively.
First, we ran Nway with the XMM and optical catalogues in mode ‘auto’ (see B6.1). Although we know that for this sample the actual counterparts are within 8 arcsec from the X-ray positions, we searched for a counterpart within a radius of 20 arcsec in order to avoid any bias in the result. In the 96 per cent (1231/1281) of the cases Nway assigned the same counterpart20 as in Brusa et al. (2007). In addition, of the 128 sources for which the counterpart has changed thanks to the higher resolution of Chandra, Nway recovered correctly (and independently) 55 of them (i.e. 43 per cent).
In the second test, we run Nway again in mode ‘auto’, but this time pairing simultaneously the XMM catalogue to the optical and IRAC catalogues. Intuitively, increasing the number of priors the number of correct associations should increase. At the same time, the number of matches due to chance association should decrease. In particular, a second prior will reinforce the probability that a source is the correct counterpart or provide an alternative, better counterpart. In fact in this second application we recovered correctly 1250/1281 (97.6 per cent) sources. Of the 128 sources that change counterpart after Chandra observations, we recovered correctly 65 (50.8 per cent) of them, without any additional information. The new sources were either very faint or completely missed in the optical catalogue.
C2 Nway parameters behaviours
As discussed when describing the code, Nway provides the quantities p_any and p_i that can help in assessing the reliability of an association. The first parameter indicates what is the probability that an X-ray source has at least a reliable counterpart amongst the possible associations, behaving as the prior. Low p_any indicates that either the prior is not able to disentangle between possible counterparts or that none of the possible counterparts behave as the prior. The second parameter, p_i indicates what is the probability for a given source to be the correct counterpart amongst the possible associations to an X-ray source.
In Fig. C1 we show p_i versus p_any for the optical prior (OPT, top-left panel) and for the optical+IRAC prior (OPT+MIR, bottom-left panel.). In Addition we show the respective cumulative distribution of p_any (right-hand panels). Additionally, we plot in grey the same parameters as before computed for random associations. This was obtained by applying Nway to the same catalogues, but after randomizing the position of the X-ray sources by shifting by 1 arcsec their Declination.

Top left: p_i versus p_any distribution for the correct counterparts to the XMM-COSMOS sources (yellow) and for the candidate counterpart to the same sources after randomizing their position (grey), using only the optical catalogue. Top right: cumulative distribution of p_any for the actual sample of correct counterparts (solid yellow) and for the counterparts to the randomized X-ray sources (solid grey). The dashed yellow line represents the distribution, including also the 26 sources for which Nway fails in identifying the correct counterparts. These sources have all p_any below 0.5 (after that value the two yellow curves coincide). Bottom left: and Bottom right: as above, but this time using simultaneously a prior in Optical and one in mid-infrared.
From the top plots we can see that the distribution of p_any for the random position, concentrate at low values while the p_any for the real sources peak at high values. For example p_anyreal > 0.6 for 80 per cent of the counterpart to real X-ray sources while only 0.09 per cent of the counterparts to randomized X-ray sources have such high p_any.21
The term p_i is the combination of two terms, one related to the pure positional match and density of the sources and one related to the prior. If the number density of sources in the optical catalogue is high, there can always be a possible counterpart due to chance association, for the randomized X-ray sources. For this reason, more than 40 per cent of the possible counterparts to the randomized X-ray source have p_i > 0.8. Only coupling p_i with p_any we can find out the actual nature of the counterpart.
The situation changes noticeably in the bottom panels of Fig. C1, where not one but two priors (one in Optical and one in mid-infrared) are simultaneously considered. Here, the distribution of p_i and p_any is similar to the previous case, while for the counterpart to actual X-ray sources, both parameters peak at high values. Again, it is noteworthy that 99.9 per cent of the counterparts were correctly identified already with only one prior. The additional prior just increased p_i indicating how the real counterparts clearly stand up from the field distribution. Intuitively, adding a third prior would reduce even strongly the possibility that a counterpart is selected due to chance association.
Finally, an important point to stress is that while the original work on the XMM and Chandra associations took months and an additional visual inspection was necessary, the reliable results presented here for Nway were obtained in less than 5 min with a single 2700 MHz CPU without any filtering or inspection.



![Map of the weighting function, π, constructed from Fig. 3 following the description in the text. Contours are drawn at log10(π([W2], [W1 − W2]) = 3, 2, 1, 0,−1, −2, −3. More description in Section 4.1.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/473/4/10.1093_mnras_stx2651/1/m_stx2651fig4.jpeg?Expires=1750215333&Signature=2OHOjrvGGpLANEzZfz5uRHQQhwbN2yqj5nURNCbMBLoowNm4FVdMWlEqdPLSFXPbY09EeCUMvokotnch11zLcDvuBXyYio~89eJTASQnnsNZyb1tZKOLyUXye9-WfyxOPgxANDN5LclN5sRICmXm1y39jzCFSXp1EhTeDZTLu4Mt7fRYxDFjLsYEq5TgOIoIFZhRCVKYdoGCxATxsMMbSLGH-IvjhbeVI~QdwhEVBrOT2PO8jR113xACMpuWluFi18zQ0P8xrzROpgzEXTdj6cuEbe9qa8RNQv8owlvNV2xv8w8d1He8ky8KXndEqNDxD9KEMqrH6u3DlQ8bWPhIbg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
