-
PDF
- Split View
-
Views
-
Cite
Cite
F. Vito, W. N. Brandt, G. Yang, R. Gilli, B. Luo, C. Vignali, Y. Q. Xue, A. Comastri, A. M. Koekemoer, B. D. Lehmer, T. Liu, M. Paolillo, P. Ranalli, D. P. Schneider, O. Shemmer, M. Volonteri, J. Wang, High-redshift AGN in the Chandra Deep Fields: the obscured fraction and space density of the sub-L* population, Monthly Notices of the Royal Astronomical Society, Volume 473, Issue 2, January 2018, Pages 2378–2406, https://doi.org/10.1093/mnras/stx2486
Close - Share Icon Share
Abstract
We investigate the population of high-redshift (3 ≤ z < 6) active galactic nuclei (AGN) selected in the two deepest X-ray surveys, the 7 Ms Chandra Deep Field-South and 2 Ms Chandra Deep Field-North. Their outstanding sensitivity and spectral characterization of faint sources allow us to focus on the sub-L* regime (logLX ≲ 44), poorly sampled by previous works using shallower data, and the obscured population. Taking fully into account the individual photometric-redshift probability distribution functions, the final sample consists of ≈102 X-ray-selected AGN at 3 ≤ z < 6. The fraction of AGN obscured by column densities logNH > 23 is ∼0.6–0.8, once incompleteness effects are taken into account, with no strong dependence on redshift or luminosity. We derived the high-redshift AGN number counts down to F0.5–2 keV = 7 × 10−18 erg cm−2 s−1, extending previous results to fainter fluxes, especially at z > 4. We put the tightest constraints to date on the low-luminosity end of AGN luminosity function at high redshift. The space density, in particular, declines at z > 3 at all luminosities, with only a marginally steeper slope for low-luminosity AGN. By comparing the evolution of the AGN and galaxy densities, we suggest that such a decline at high luminosities is mainly driven by the underlying galaxy population, while at low luminosities there are hints of an intrinsic evolution of the parameters driving nuclear activity. Also, the black hole accretion rate density and star formation rate density, which are usually found to evolve similarly at z ≲ 3, appear to diverge at higher redshifts.
1 INTRODUCTION
Supermassive black holes (SMBHs) and their hosting galaxies are broadly recognized to influence the evolution of each other over cosmic time. This ‘co-evolution’ is reflected by the tight relations between the masses of SMBH and the properties of host galaxies in the nearby Universe, such as masses and velocity dispersions of the bulges (e.g. Magorrian et al. 1998; Ferrarese & Merritt 2000; Marconi & Hunt 2003) and the broadly similar evolution of the star formation and black hole accretion densities in the last ∼10 Gyr (e.g. Aird et al. 2015), although the details of this interplay are still not well known (see e.g. Kormendy & Ho 2013, and references therein). Studying galaxies and SMBH in the early Universe, where these relations could be set in place, would boost our knowledge of how SMBH and galaxies formed and evolved. However, while galaxy properties have been traced as far back in time as z ∼ 8–10 (e.g. Bouwens et al. 2015), our knowledge of SMBH is limited to later times.
Only ∼90 accreting SMBHs, shining as active galactic nuclei (AGN), have been identified at z > 6 (e.g. Bañados et al. 2016; Wang et al. 2017) and are usually found to have masses of the order of 1–10 billion solar masses (e.g. Mortlock et al. 2011; Wu et al. 2015). The presence of such massive black holes a few 108 yr after the big bang challenges our understanding of SMBH formation and growth in the early Universe, one of the major issues in modern astrophysics (e.g. Reines & Comastri 2016, and references therein). Different classes of theories have been proposed to explain the formation of the BH seeds that eventually became SMBH, the two most promising ones involving ‘light seeds’ (M ∼ 102 M⊙), as remnants of the first Pop III stars, and ‘heavy seeds’ (M ∼ 104−6 M⊙), perhaps formed during the direct collapse of giant pristine gas clouds (e.g. Haiman 2013; Johnson & Haardt 2016; Volonteri et al. 2016b, and references therein). To match the masses of SMBH discovered at z > 6, all such models require continuous nearly Eddington-limited or even super-Eddington accretion phases during which the growing SMBH is plausibly buried in material with large column densities, even exceeding the Compton-thick level (e.g. Pacucci et al. 2015). However, these objects represent the extreme tail of the underlying distribution (in terms of both mass and luminosity) and are not representative of the overall population.
X-ray surveys are the most suitable tools for investigating the evolution of the bulk of the AGN population up to high redshift: being less affected by absorption and galaxy dilution, they provide cleaner and more complete AGN identification with respect to optical/IR surveys (Brandt & Alexander 2015, and references therein). Over the last two decades, several works have focused on the properties and evolution of X-ray selected, z > 3 AGN in wide (e.g. Brusa et al. 2009; Civano et al. 2011; Hiroi et al. 2012; Marchesi et al. 2016) and deep (e.g. Vignali et al. 2002; Fiore et al. 2012; Vito et al. 2013; Giallongo et al. 2015; Weigel et al. 2015; Cappelluti et al. 2016) surveys performed with Chandra and XMM–Newton, or using combinations of different surveys (e.g. Kalfountzou et al. 2014; Vito et al. 2014; Georgakakis et al. 2015). Common findings amongst such works are (1) a decline of the space density of luminous (logLX ≳ 44) AGN proportional to (1 + z)d with d ∼ −6 (similar to the exponential decline of the space density of optically selected quasars, e.g. McGreer et al. 2013), and (2) a larger fraction of obscured AGN than that usually derived at lower redshifts, particularly at moderate-to-high luminosities (e.g. Aird et al. 2015; Buchner et al. 2015).
However, most of the low-luminosity (logLX ≲ 43) and z ≳ 4 AGN are missed even by the deepest surveys, leading to discrepant results amongst different studies. For instance, the evolution of the space density of low-luminosity, X-ray-detected AGN is largely unconstrained, while Georgakakis et al. (2015) reported an apparent strong flattening of the faint end of the AGN X-ray luminosity function (XLF) at z > 3, Vito et al. (2014) found that the decline of the space density of low-luminosity AGN is consistent with that of AGN with higher luminosities. Moreover, Giallongo et al. (2015), using detection techniques that search for clustering of photons in energy, space and time, reported the detection of several faint AGN, resulting in a very steep XLF faint end (see also Fiore et al. 2012). These results also have strong impact on the determination of the AGN contribution to cosmic reionization (e.g. Madau & Haardt 2015). Moreover, the typical obscuration levels in these faint sources remain unknown, although hints of a decrease of the obscured AGN fraction with decreasing luminosity (for logLX ≲ 44) at high-redshift have been found (e.g. Aird et al. 2015; Buchner et al. 2015; Georgakakis et al. 2015). This relation is the opposite trend to that found at low redshift (e.g. Aird et al. 2015; Buchner et al. 2015), where the obscured AGN fraction shows a clear anticorrelation with AGN luminosity. Finally, the very detection of faint z > 5 AGN in deep X-ray surveys is debated (e.g. Vignali et al. 2002; Giallongo et al. 2015; Weigel et al. 2015; Cappelluti et al. 2016; Parsa et al. 2017).
The recently completed 7 Ms Chandra Deep Field-South (CDF-S; Luo et al. 2017) observations provide the deepest X-ray view of the early Universe, reaching a flux limit of F0.5−2 keV = 6.4 × 10−18 erg cm−2 s−1. Moreover, the catalogue of X-ray sources in the second deepest X-ray survey to date (limiting flux F0.5−2 keV = 1.2 × 10−17 erg cm−2 s−1), the 2 Ms Chandra Deep Field-North (CDF-N; Alexander et al. 2003), was recently re-analysed by Xue et al. (2016) with the same detection procedure applied to the CDF-S, which provides detections for more real sources. Therefore, the two deepest Chandra fields allow us now to study high-redshift, faint AGN using homogeneous data sets. In Vito et al. (2016), we applied a stacking technique to CANDELS (Grogin et al. 2011; Koekemoer et al. 2011) selected galaxies to study the X-ray emission from individually undetected sources in the 7 Ms CDF-S, finding that the emission is probably mostly due to X-ray binaries (XRBs) rather than nuclear accretion, and concluding that most of the SMBH growth at 3.5 < z < 6.5 occurred during bright AGN phases. In this paper, we combine the 7 Ms CDF-S and 2 Ms CDF-N data to study the X-ray properties of X-ray-detected AGN at z > 3, with a particular focus on low-luminosity sources (logLX ≲ 44), which are best sampled by deep, pencil-beam surveys. Taking fully into account the probability distribution functions (PDFs) of the photometric redshifts for sources lacking spectroscopic identifications (see e.g. Marchesi et al. 2016 for a similar use of the photometric redshifts), the final sample consists of ≈102 X-ray-detected AGN at 3 ≤ z < 6. The number of sources contributing to this sample with their PDF(z) is 118. We performed a spectral analysis on our sample assuming the X-ray spectra are well represented by power-law emission subjected to Galactic and intrinsic absorption. The spectral analysis allowed us to take into account the full probability distribution of the intrinsic column densities. We also considered the probability distribution of the count rates of X-ray-detected sources and applied a correction to mitigate the Eddington bias. The flux (and hence luminosity) probability distributions were derived by applying for each source the proper response matrices and the conversion factors between count rate and flux, which depend on the observed spectral shape. We present the trends of the obscured AGN fraction with redshift and luminosity, the number counts, and the space-density evolution of 3 < z < 6 AGN. Throughout this paper, we will use a H0 = 70 km s−1 Mpc−1, Ωm = 0.3 and |$\Omega _\Lambda =0.7$| cosmology and we will assume Galactic column densities of logNH = 0.9 × 1020 and 1.6 × 1020 cm−2 along the line of sight of CDF-S and CDF-N, respectively. Errors and upper limits are quoted at the 68 per cent confidence level, unless otherwise noted.
2 THE SAMPLE
2.1 AGN parent sample and redshifts in the 7 Ms CDF-S
We selected a sample of X-ray detected, z > 3 AGN in the 7 Ms CDF-S,1 the deepest X-ray survey to date, from the Luo et al. (2017, hereafter L17) catalogue, which also provides multiwavelength identifications and spectroscopic and photometric redshifts for the X-ray sources. In particular, photometric redshifts were collected from Luo et al. (2010), Rafferty et al. (2011), Hsu et al. (2014, hereafter H14), Skelton et al. (2014, hereafter S14), Santini et al. (2015) and Straatman et al. (2016, hereafter S16). Each X-ray source can therefore be associated with up to six different photometric redshifts. We considered only sources located in the area (∼330 arcmin2, red region in the left-hand panel of Fig. 1) of the survey where the effective exposure is ≥1 Ms, in order to exclude the outskirts of the field, where the point spread function (PSF) distortions and the effects of the vignetting affect the quality of the X-ray data and the optical identification rate and accuracy. Moreover, the inner region of the CDF-S is covered by the deepest optical/IR observations (green region), which are essential to derive highly reliable spectroscopic and photometric redshifts. With this selection, our parent sample in the CDF-S consists of 952 out of the 1008 X-ray sources in L17.
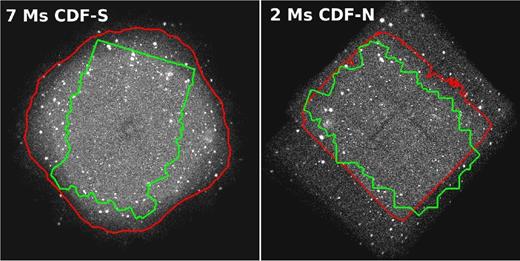
0.45° × 0.45° images of the 7 Ms CDF-S (left-hand panel) and 2 Ms CDF-N (right-hand panel) in the 0.5–2 keV band. Red regions encompass the areas with effective exposure >1 Ms that are used in this work. Green polygons denote the CANDELS surveys in these fields.
We adopted the L17 definitions for the spectroscopic redshift quality. Following L17, we associated with each X-ray source a spectroscopic redshift if it is defined as ‘secure’ or ‘insecure’ but in agreement within |$\frac{|z_{\mathrm{phot}}-z_{\mathrm{spec}}|}{1+z_{\mathrm{spec}}}<15{\rm per \, cent}$| with at least one photometric redshift. Using more conservative criteria, such as requiring that the spectroscopic redshift agrees with at least 2 or > 50 per cent of the available photometric redshifts, would have no effect on the final sample of z > 3 AGN. The photometric redshifts used to validate the ‘insecure’ spectroscopic redshifts at z > 3 are of good quality, with a 68 per cent confidence level Δz = 0.03–0.2.
We also estimated the accuracy of the confidence intervals provided by the PDFs by computing the fraction of sources whose spectroscopic redshift is included in the 68 per cent confidence interval provided by its PDF (defined as the narrowest redshift interval where the integrated redshift probability is 0.68). If the PDFs provided accurate confidence intervals, that fraction would be 0.68, while we found 0.49, 0.50 and 0.63 for H14, S14 and S16, respectively, reflecting a general mild underestimate of the confidence intervals, hence of the photometric-redshift errors. This effect could be due to underestimating the errors of the fitted photometric data (e.g. see section 5.3 in Yang et al. 2014). We found indeed that the most accurate confidence intervals are provided by S16, who addressed in detail this issue by employing an empirical technique to derive more accurate photometric errors than those usually provided by detection software such as SExtractor. The reported fractions refer to the particular comparative spectroscopic sample, i.e. X-ray-selected galaxies, and are expected to be different considering the entire galaxy samples in those works. The PDFs are usually derived by fitting the observed spectral energy distribution (SED) with models M of galactic emission varying the redshift as |$\mathrm{PDF}(z)\propto \mathrm{\mathrm{exp}}(-0.5\chi ^2(z))$|, where |$\chi ^2(z)=\sum _i\frac{(M_i(z)-\text{SED}_i)^2}{\sigma _i^2}$| is the test statistic of the fit, and the index i represents the different photometric bands. If the photometric errors σi are underestimated, the resulting PDFs will be too sharp and their confidence intervals will be underestimated as well. In this case, more accurate confidence intervals can be obtained by multiplying the photometric errors by a factor of α, which represents the average underestimating factor of the photometric errors amongst the used bands, or, equivalently, by using the ‘corrected’ distribution |$\mathrm{PDF^{corr}}(z)=\mathrm{PDF^{input}}(z)^{\frac{1}{\alpha ^2}}$|, where α2 is computed empirically such that the 68 per cent considered interval provided by their PDFs encompasses the associated spectroscopic redshift in 68 per cent of the sample. This procedure is equivalent to empirically ‘correcting’ (i.e. increasing) the photometric errors following σcorr = α × σinput. We obtained α2 = 5.2, 4.4 and 1.5 for H14, S14 and S16, respectively, and use the ‘corrected’ PDFs hereafter.
All of these tests led us to adopt the photometric redshift from S16 as first choice. The photometric redshifts from H14 and S14 have similar accuracy, but H14 provide the redshifts for the entire Extended CDF-S (E-CDF-S), while S14 (as well as S16) is limited to the GOODS-S/CANDELS region. We therefore used the photometric redshifts from H14 and S14 as second and third choices, respectively.2 Amongst the 21 remaining sources with no entries in the above-considered photometric-redshift catalogues, two sources have a photometric redshift from Rafferty et al. (2011). We approximated their PDF(z), not provided by that work, as normalized Gaussian functions centred on the nominal redshift and with σ equal to the 1σ error, separately for the positive and negative sides. Given the very low number of sources for which we adopted the Rafferty et al. (2011) redshifts (two, and only one will be included in the final sample), the approximation we used to describe their PDF(z) does not have any effect on the final results.
Nineteen sources out of the 952 X-ray sources in the parent sample (1.9 per cent) remain with no redshift information. Most of them (14/19) are not associated with any counterpart from catalogues at different wavelengths. The five sources with an optical counterpart but no redshift information have been assigned a flat PDF. We preferred not to use redshift priors based on optical magnitudes, as these sources are part of a very peculiar class of objects (i.e. extremely X-ray faint sources), whose redshift distribution is not well represented by any magnitude-based distribution derived for different classes of galaxies. We did not include the 14 X-ray sources with no optical counterparts in this work, as a significant number of them are expected to be spurious detections. In fact, L17 estimated the number of spurious detections in the entire 7 Ms CDF-S main catalogue to be ∼19 and argued that, given the superb multiwavelength coverage of the CDF-S and sharp Chandra PSF, resulting in high-confidence multiwavelength identifications, X-ray sources with multiwavelength counterparts are extremely likely to be real detections. Therefore, most of the spurious detections are expected to be accounted for by X-ray sources with no optical counterpart. This conclusion is especially true considering that most of the unmatched sources lie in the CANDELS/GOODS-S field, where the extremely deep multiwavelength observations would likely have detected their optical counterpart if they were true sources. We also checked their binomial no-source probability (PB, i.e. the probability that the detected counts of a source are due to a background fluctuation), provided by L17 for all the sources in their catalogue. Thirteen out of the 14 sources with no counterparts have PB ≳ 10−4, close to the detection threshold of PB = 0.007 (L17). For comparison, ∼ 80 per cent of the sources with optical counterparts have PB < 10−4. The notable exception is XID 912, which has no optical counterpart, but PB ∼ 10−13 and ≈77 net counts. L17 suggested that XID 912 is a off-nuclear X-ray source associated with a nearby low-redshift galaxy, detected in optical/IR observations.
(1) Redshift. (2) Number of X-ray sources that were assigned a spectroscopic redshift or (3) a photometric redshift from the different catalogues. At 3 ≤ z < 6, we considered only the fraction of PDF(z) in that redshift interval. (4) Median accuracy of the photometric redshifts and (5) σNMAD, both computed for X-ray sources with secure spectroscopic redshifts. (6) Number of sources with a multiwavelength counterpart and no redshift information, which are assigned a flat PDF(z). (7) Number of sources with no multiwavelength counterpart, which are not included in the high-redshift sample, as most of them are expected to be spurious detections. (8) Total number of sources.
| Sample . | zspec . | zphot . | |$\mathrm{Med}(\frac{|\Delta z|}{1+z_{\mathrm{s}}})$| . | σNMAD . | no z . | no cp. . | Ntot . |
|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| CDF-S | |||||||
| All | 616 | 317 | 0.008 | 0.009 | 5 | 14 | 952 |
| 3 ≤ z < 6 | 18 | 51.5 | 0.015 | 0.014 | 1.5 | – | 71.0 |
| CDF-N | |||||||
| All | 309 | 166 | 0.026 | 0.031 | 2 | 8 | 485 |
| 3 ≤ z < 6 | 10 | 20.0 | 0.074 | 0.040 | 0.6 | – | 30.6 |
| CDF-S + CDF-N | |||||||
| All | 925 | 483 | 0.013 | 0.017 | 7 | 22 | 1437 |
| 3 ≤ z < 6 | 28 | 71.5 | 0.032 | 0.039 | 2.1 | – | 101.6 |
| Sample . | zspec . | zphot . | |$\mathrm{Med}(\frac{|\Delta z|}{1+z_{\mathrm{s}}})$| . | σNMAD . | no z . | no cp. . | Ntot . |
|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| CDF-S | |||||||
| All | 616 | 317 | 0.008 | 0.009 | 5 | 14 | 952 |
| 3 ≤ z < 6 | 18 | 51.5 | 0.015 | 0.014 | 1.5 | – | 71.0 |
| CDF-N | |||||||
| All | 309 | 166 | 0.026 | 0.031 | 2 | 8 | 485 |
| 3 ≤ z < 6 | 10 | 20.0 | 0.074 | 0.040 | 0.6 | – | 30.6 |
| CDF-S + CDF-N | |||||||
| All | 925 | 483 | 0.013 | 0.017 | 7 | 22 | 1437 |
| 3 ≤ z < 6 | 28 | 71.5 | 0.032 | 0.039 | 2.1 | – | 101.6 |
(1) Redshift. (2) Number of X-ray sources that were assigned a spectroscopic redshift or (3) a photometric redshift from the different catalogues. At 3 ≤ z < 6, we considered only the fraction of PDF(z) in that redshift interval. (4) Median accuracy of the photometric redshifts and (5) σNMAD, both computed for X-ray sources with secure spectroscopic redshifts. (6) Number of sources with a multiwavelength counterpart and no redshift information, which are assigned a flat PDF(z). (7) Number of sources with no multiwavelength counterpart, which are not included in the high-redshift sample, as most of them are expected to be spurious detections. (8) Total number of sources.
| Sample . | zspec . | zphot . | |$\mathrm{Med}(\frac{|\Delta z|}{1+z_{\mathrm{s}}})$| . | σNMAD . | no z . | no cp. . | Ntot . |
|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| CDF-S | |||||||
| All | 616 | 317 | 0.008 | 0.009 | 5 | 14 | 952 |
| 3 ≤ z < 6 | 18 | 51.5 | 0.015 | 0.014 | 1.5 | – | 71.0 |
| CDF-N | |||||||
| All | 309 | 166 | 0.026 | 0.031 | 2 | 8 | 485 |
| 3 ≤ z < 6 | 10 | 20.0 | 0.074 | 0.040 | 0.6 | – | 30.6 |
| CDF-S + CDF-N | |||||||
| All | 925 | 483 | 0.013 | 0.017 | 7 | 22 | 1437 |
| 3 ≤ z < 6 | 28 | 71.5 | 0.032 | 0.039 | 2.1 | – | 101.6 |
| Sample . | zspec . | zphot . | |$\mathrm{Med}(\frac{|\Delta z|}{1+z_{\mathrm{s}}})$| . | σNMAD . | no z . | no cp. . | Ntot . |
|---|---|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . |
| CDF-S | |||||||
| All | 616 | 317 | 0.008 | 0.009 | 5 | 14 | 952 |
| 3 ≤ z < 6 | 18 | 51.5 | 0.015 | 0.014 | 1.5 | – | 71.0 |
| CDF-N | |||||||
| All | 309 | 166 | 0.026 | 0.031 | 2 | 8 | 485 |
| 3 ≤ z < 6 | 10 | 20.0 | 0.074 | 0.040 | 0.6 | – | 30.6 |
| CDF-S + CDF-N | |||||||
| All | 925 | 483 | 0.013 | 0.017 | 7 | 22 | 1437 |
| 3 ≤ z < 6 | 28 | 71.5 | 0.032 | 0.039 | 2.1 | – | 101.6 |
2.2 AGN parent sample and redshifts in the 2 Ms CDF-N
Xue et al. (2016, hereafter X16) presented an updated version (683 sources in total) of the original 2 Ms CDF-N catalogue (Alexander et al. 2003), applying the same detection procedure used in the CDF-S (Xue et al. 2011, L17) and providing multiwavelength identifications and spectroscopic and photometric redshifts from the literature. In particular, photometric redshifts were collected from S14 and Yang et al. (2014, hereafter Y14). Both of these works provide the PDF of the photometric redshifts. We adopted the spectroscopic redshifts collected from X16, as they considered only those marked as ‘secure’ in the original works.
For X-ray sources lacking spectroscopic redshift, we followed the procedure described in Section 2.1 to define a priority order amongst the two used photometric catalogues. In particular, we derived median values of |Δz|/(1 + zspec) = 0.026 both for S14 and Y14, σNMAD = 0.025 and 0.035 and α2 = 9.2 and 3.0 for S14 and Y14, respectively. The α2 values mean that the photometric redshift PDFs from Y14 account for the redshift uncertainties more realistically than the S14 ones: this behaviour can be explained again by considering that Y14 applied an empirical method to estimate the photometric errors more reliably than those provided by standard detection software. We therefore adopted the photometric redshifts from Y14 and S14 as first and second choice, respectively.
As in Section 2.1, we considered only the sources in the area covered by ≥1 Ms effective exposure (∼215 arcmin2; red contour in the right-hand panel of Fig. 1, almost coincident with the CANDELS survey in that field) as the parent sample (485 sources). Amongst them, 35 sources ( ∼ 7 per cent) have no redshift information. This non-identification rate is mostly due to the method used in X16 to match the X-ray sources with the entries in the photometric-redshift catalogues. First, for each X-ray source they identified a primary multiwavelength counterpart using a likelihood-ratio procedure (Luo et al. 2010). They then matched the coordinates of the primary counterparts with the photometric-redshift catalogues using a 0.5 arcsec radius. However, the positional uncertainties and offsets amongst the different photometric catalogues can be comparable to the utilized matching radius. We therefore visually inspected the positions of all the X-ray sources on the CANDELS/GOODS-N images3 (Grogin et al. 2011; Koekemoer et al. 2011) and could match most of the X-ray sources with no redshift information in X16 with an entry in one of the considered photometric-redshift catalogues. The visual multiwavelength matching allowed us also to associate a spectroscopic redshift from Y14 (which included only high-quality spectroscopic redshifts) with several sources with only photometric or no redshifts in X16.
The resulting number of X-ray sources with no redshift information is 12 ( ∼ 2.5 per cent). As in Section 2, we excluded sources with no multiwavelength counterpart (8 sources) from this analysis, as most of them are expected to be spurious. Two out of the remaining four sources with counterparts but no redshifts in the considered catalogues have photometric-redshift entries in the CANDELS/GOODS-N catalogue (Kodra et al. in preparation). Their PDF(z) lies entirely at z < 3, thus we excluded these sources from the high-redshift sample. Finally, we assigned flat PDF(z) over the range of z = 0–10 to the only two remaining sources with multiwavelength counterparts but no redshifts. Table 1 summarizes the number of X-ray sources in the CDF-N that are associated with spectroscopic, photometric or no redshifts.
2.3 The sample of high-redshift AGN in the Chandra Deep Fields
We checked the photometric redshift accuracy by plotting in Fig. 2 the Δz/(1 + zspec) and the σNMAD for sources with secure spectroscopic redshifts (see also Table 1). The σNMAD is computed in a shifting interval of redshift with variable width such to include 10 sources (separately for the positive and negative sides). The photometric redshift for each AGN is chosen following the priority order described in Sections 2.1 and 2.2. We considered only sources within the area covered by ≥1 Ms exposure. The scatter increases slightly at z ∼ 2.5 (by a factor of ∼2–3), but the photometric redshift accuracy does not appear to deteriorate dramatically at high redshift.
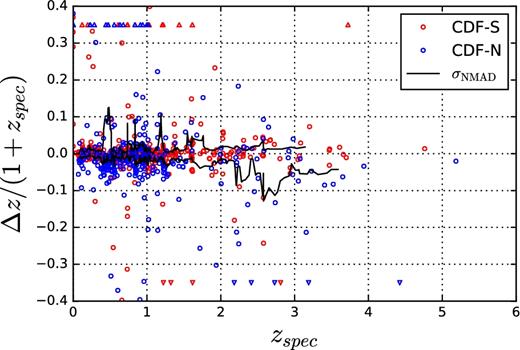
Photometric redshift accuracy for sources with secure spectroscopic redshift. The lines are the normalized median absolute deviations (σNMAD) computed in a shifting redshift interval with variable width such to include 10 sources separately for the positive and negative sides. Points at Δz/(1 + zspec) > 0.4 (<−0.4) are plotted as upward-pointing (downward-pointing) triangles at Δz/(1 + zspec) = 0.35 (−0.35).
Fig. 3 presents the redshift distributions of the sources at z > 3 in the two deep fields, considering their PDF(z). At z > 6, the source statistics are poor, and sources with no redshift information (red line), which carry little information, constitute a significant fraction of the total number of sources. We therefore chose to limit our investigation to the redshift range of 3 ≤ z < 6. To prevent the inclusion of several sources whose PDFs show long tails of extremely low probability at high redshift, we also required that the probability of a source to be in the considered redshift range (computed as in equation 4) is P(3 ≤ z < 6) > 0.2. The number of sources satisfying this criterion is Nhz = 118. Integrating their PDFs in the redshift range of 3 ≤ z < 6, the number of ‘effective’ sources included in the sample is Neffhz ≃ 101.6. The cut P(3 ≤ z < 6) > 0.2 results in the rejection of ∼2 effective sources. Table 1 reports the breakdown of the redshift type for sources at 3 ≤ z < 6. Table 2 provides the redshift along with the 68 per cent confidence interval, its origin and the probability of the source to be at 3 ≤ z < 6 according to its PDF for each source in the high-redshift sample.
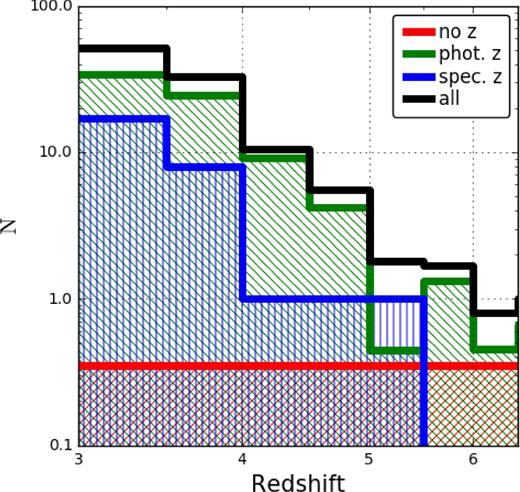
Redshift distribution of the X-ray sources in the CDF-S and CDF-N at z > 3. Different classes of sources are represented by lines of different colours.
| ID . | z . | Ref . | P . | Band . | NH . | |$\mathrm{log}F^{\mathrm{obs}}_{0.5-2\, \mathrm{keV}}$| . | |$\mathrm{log}F^{\mathrm{intr}}_{0.5-2\, \mathrm{keV}}$| . | |$\mathrm{log}L^{\mathrm{obs}}_{2-10\, \mathrm{keV}}$| . | |$\mathrm{log}L^{\mathrm{intr}}_{2-10\, \mathrm{keV}}$| . | Net counts . | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | (3 ≤ z < 6) . | . | (1022 cm−2) . | (erg cm−2 s−1) . | (erg cm−2 s−1) . | (erg s−1) . | (erg s−1) . | (0.5–2 keV) . | (2–7 keV) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| CDF-S | |||||||||||
| 8 | |$3.13_{-0.48}^{+3.28}$| | P3 | 0.55 | S | |$59_{-18}^{+24}$| | |$-15.56_{-0.08}^{+0.07}$| | |$-15.59_{-0.08}^{+0.08}$| | |$44.43_{-0.23}^{+0.20}$| | |$44.41_{-0.27}^{+0.17}$| | 99.2 | 119.4 |
| 9 | |$1.93_{-0.20}^{+1.39}$| | P3 | 0.44 | S | |$11_{-5}^{+8}$| | |$-15.31_{-0.08}^{+0.05}$| | |$-15.32_{-0.07}^{+0.06}$| | |$44.04_{-0.13}^{+0.16}$| | |$44.03_{-0.14}^{+0.15}$| | 140.7 | 95.4 |
| 10 | |$2.93_{-0.40}^{+0.85}$| | P3 | 0.32 | S | |$3_{-2}^{+2}$| | |$-15.40_{-0.11}^{+0.06}$| | |$-15.43_{-0.09}^{+0.08}$| | |$43.76_{-0.13}^{+0.09}$| | |$43.73_{-0.14}^{+0.09}$| | 70.1 | 38.9 |
| 12 | 3.153 | S2 | 1.00 | H | |$135_{-46}^{+69}$| | |$-16.59_{-0.75}^{+0.21}$| | <− 17.28 | |$44.06_{-0.18}^{+0.12}$| | |$42.21_{-0.22}^{+1.32}$| | 12.4 | 89.0 |
| 25 | −1 | N | 0.30 | S | <74 | |$-15.65_{-0.13}^{+0.08}$| | |$-15.69_{-0.15}^{+0.08}$| | |$43.63_{-0.20}^{+0.44}$| | |$43.60_{-0.18}^{+0.46}$| | 75.0 | 88.3 |
| 29 | |$3.33_{-0.29}^{+0.32}$| | P4 | 0.99 | S | <1 | |$-15.63_{-0.10}^{+0.05}$| | |$-15.65_{-0.11}^{+0.05}$| | |$43.47_{-0.13}^{+0.12}$| | |$43.45_{-0.12}^{+0.13}$| | 119.0 | 44.4 |
| 35 | −1 | N | 0.30 | S | |$25_{-17}^{+29}$| | |$-15.61_{-0.09}^{+0.09}$| | |$-15.63_{-0.11}^{+0.08}$| | |$43.97_{-0.20}^{+0.21}$| | |$43.94_{-0.22}^{+0.20}$| | 98.9 | 67.8 |
| 53 | 3.202 | S1 | 1.00 | S | <22 | |$-16.41_{-0.36}^{+0.18}$| | <−16.97 | |$42.74_{-0.40}^{+0.20}$| | <42.30 | 29.8 | 40.7 |
| 84 | |$3.12_{-0.59}^{+0.35}$| | P1 | 0.70 | S | |$49_{-13}^{+14}$| | |$-16.07_{-0.11}^{+0.06}$| | |$-16.10_{-0.12}^{+0.06}$| | |$43.75_{-0.19}^{+0.14}$| | |$43.71_{-0.19}^{+0.15}$| | 80.4 | 98.5 |
| 88 | −1 | N | 0.30 | S | |$83_{-26}^{+19}$| | |$-15.98_{-0.08}^{+0.06}$| | |$-16.01_{-0.09}^{+0.06}$| | |$44.19_{-0.27}^{+0.12}$| | |$44.16_{-0.25}^{+0.14}$| | 99.3 | 195.6 |
| 99 | |$4.24_{-0.36}^{+0.05}$| | P1 | 0.99 | S | |$30_{-28}^{+34}$| | |$-15.91_{-0.19}^{+0.14}$| | <−16.19 | |$43.55_{-0.26}^{+0.22}$| | <43.32 | 41.3 | 47.8 |
| 101 | |$4.34_{-0.61}^{+0.02}$| | P1 | 1.00 | S | |$68_{-22}^{+12}$| | |$-16.11_{-0.16}^{+0.09}$| | |$-16.20_{-0.27}^{+0.18}$| | |$43.87_{-0.24}^{+0.24}$| | |$43.78_{-0.37}^{+0.22}$| | 51.2 | 110.8 |
| 109 | |$3.58_{-0.04}^{+0.03}$| | P1 | 1.0 | S | |$28_{-6}^{+5}$| | |$-16.48_{-0.23}^{+0.15}$| | <−16.68 | |$43.14_{-0.25}^{+0.16}$| | <42.96 | 144.9 | 150.9 |
| 110 | |$3.08_{-0.08}^{+0.38}$| | P1 | 0.87 | S | <1 | |$-16.54_{-0.24}^{+0.15}$| | <−16.74 | |$42.55_{-0.24}^{+0.19}$| | <42.40 | 22.8 | 4.4 |
| 121 | |$3.42_{-0.05}^{+0.03}$| | P1 | 1.00 | S | |$68_{-21}^{+14}$| | |$-16.27_{-0.13}^{+0.09}$| | |$-16.33_{-0.16}^{+0.11}$| | |$43.69_{-0.22}^{+0.16}$| | |$43.62_{-0.27}^{+0.16}$| | 50.4 | 65.9 |
| 126 | |$3.13_{-0.03}^{+0.07}$| | P1 | 0.95 | S | <28 | |$-15.84_{-0.23}^{+0.13}$| | <−16.55 | |$43.32_{-0.22}^{+0.20}$| | <42.67 | 39.9 | 53.1 |
| 133 | 3.474 | S1 | 1.00 | H | |$141_{-50}^{+73}$| | <−16.96 | <−17.39 | |$43.61_{-0.22}^{+0.13}$| | |$42.23_{-0.15}^{+0.93}$| | 4.0 | 56.3 |
| 165 | |$3.55_{-0.02}^{+0.02}$| | P1 | 1.00 | S | |$16_{-6}^{+6}$| | |$-15.94_{-0.09}^{+0.07}$| | |$-15.96_{-0.11}^{+0.06}$| | |$43.52_{-0.13}^{+0.09}$| | |$43.5_{-0.15}^{+0.08}$| | 71.9 | 34.2 |
| 185 | |$3.09_{-0.03}^{+0.04}$| | P1 | 0.87 | S | |$39_{-24}^{+24}$| | |$-16.70_{-0.19}^{+0.11}$| | |$-16.82_{-0.29}^{+0.16}$| | |$42.86_{-0.37}^{+0.22}$| | |$42.71_{-0.45}^{+0.25}$| | 18.7 | 22.6 |
| 189 | |$3.65_{-0.04}^{+0.07}$| | P1 | 1.00 | H | |$107_{-33}^{+25}$| | <−16.97 | <−17.31 | |$43.38_{-0.16}^{+0.09}$| | |$43.30_{-0.19}^{+0.12}$| | 7.1 | 34.5 |
| 214 | 3.74 | S2 | 1.00 | S | |$26_{-2}^{+1}$| | |$-14.81_{-0.03}^{+0.00}$| | |$-14.82_{-0.03}^{+0.01}$| | |$44.81_{-0.03}^{+0.02}$| | |$44.81_{-0.03}^{+0.02}$| | 1377.4 | 1213.8 |
| 223 | |$3.76_{-0.17}^{+0.06}$| | P1 | 1.00 | S | <14 | |$-16.46_{-0.15}^{+0.11}$| | |$-16.55_{-0.22}^{+0.13}$| | |$42.80_{-0.19}^{+0.11}$| | |$42.71_{-0.23}^{+0.15}$| | 27.9 | 0.0 |
| 238 | |$5.96_{-0.04}^{+0.01}$| | P2 | 1.00 | S | <66 | |$-16.29_{-0.17}^{+0.09}$| | |$-16.37_{-0.21}^{+0.14}$| | |$43.42_{-0.17}^{+0.15}$| | |$43.35_{-0.24}^{+0.18}$| | 40.5 | 7.1 |
| 248 | |$3.44_{-0.13}^{+0.22}$| | P1 | 1.00 | S | |$39_{-7}^{+5}$| | |$-15.55_{-0.06}^{+0.04}$| | |$-15.56_{-0.06}^{+0.04}$| | |$44.18_{-0.10}^{+0.07}$| | |$44.17_{-0.10}^{+0.07}$| | 186.9 | 192.9 |
| 276 | |$3.12_{-0.01}^{+0.02}$| | P1 | 1.00 | S | |$15_{-3}^{+3}$| | |$-15.90_{-0.06}^{+0.04}$| | |$-15.91_{-0.06}^{+0.04}$| | |$43.51_{-0.08}^{+0.05}$| | |$43.50_{-0.08}^{+0.05}$| | 122.9 | 9.2 |
| 299 | |$3.79_{-0.05}^{+0.05}$| | P1 | 1.00 | S | |$10_{-9}^{+15}$| | |$-16.63_{-0.16}^{+0.10}$| | |$-16.71_{-0.19}^{+0.12}$| | |$42.67_{-0.18}^{+0.13}$| | |$42.59_{-0.21}^{+0.15}$| | 19.4 | 21.0 |
| 329 | |$3.47_{-0.10}^{+0.10}$| | P1 | 1.00 | S | |$32_{-29}^{+33}$| | |$-16.69_{-0.20}^{+0.14}$| | <−16.74 | |$42.61_{-0.25}^{+0.31}$| | <42.77 | 17.2 | 17.1 |
| 337 | 3.660 | S1 | 1.00 | S | |$98_{-9}^{+7}$| | |$-16.08_{-0.09}^{+0.04}$| | |$-16.10_{-0.08}^{+0.05}$| | |$44.16_{-0.10}^{+0.07}$| | |$44.14_{-0.09}^{+0.08}$| | 78.3 | 221.4 |
| 351 | |$3.86_{-0.54}^{+0.14}$| | P1 | 0.97 | S | |$74_{-23}^{+9}$| | |$-16.28_{-0.14}^{+0.08}$| | |$-16.34_{-0.17}^{+0.10}$| | |$43.71_{-0.19}^{+0.17}$| | |$43.65_{-0.26}^{+0.15}$| | 50.8 | 73.2 |
| 356 | |$3.38_{-0.19}^{+0.01}$| | P1 | 0.99 | S | <8 | |$-16.38_{-0.14}^{+0.07}$| | |$-16.43_{-0.15}^{+0.08}$| | |$42.76_{-0.13}^{+0.10}$| | |$42.71_{-0.15}^{+0.10}$| | 31.9 | 31.4 |
| 366 | |$3.67_{-0.18}^{+0.53}$| | P1 | 1.00 | S | |$81_{-15}^{+14}$| | |$-16.15_{-0.10}^{+0.06}$| | |$-16.18_{-0.10}^{+0.07}$| | |$43.96_{-0.14}^{+0.14}$| | |$43.93_{-0.16}^{+0.13}$| | 66.8 | 131.2 |
| 368 | |$3.21_{-0.08}^{+0.09}$| | P1 | 1.00 | S | <1 | |$-16.57_{-0.15}^{+0.10}$| | |$-16.65_{-0.19}^{+0.11}$| | |$42.52_{-0.19}^{+0.10}$| | |$42.44_{-0.20}^{+0.11}$| | 20.9 | 0.0 |
| 414 | |$3.58_{-0.10}^{+0.11}$| | P1 | 1.00 | H | −1** | <−17.28 | <−17.41 | |$42.71_{-0.36}^{+0.20}$| | <42.61 | 0.3 | 9.7 |
| 416 | 3.470 | S1 | 1.00 | S | <1 | |$-16.63_{-0.19}^{+0.10}$| | |$-16.75_{-0.27}^{+0.19}$| | |$42.52_{-0.19}^{+0.10}$| | |$42.40_{-0.26}^{+0.15}$| | 18.0 | 0.4 |
| 433 | |$4.11_{-0.12}^{+0.15}$| | P1 | 1.00 | S | <1 | |$-16.80_{-0.23}^{+0.13}$| | <−16.86 | |$42.55_{-0.24}^{+0.14}$| | <42.51 | 12.9 | 0.3 |
| 459 | |$3.91_{-0.04}^{+0.05}$| | P1 | 1.00 | H | |$166_{-64}^{+80}$| | <17.20 | <−17.43 | |$43.34_{-0.25}^{+0.17}$| | <43.11 | 0.3 | 24.4 |
| 462 | |$3.88_{-0.78}^{+0.41}$| | P1 | 0.95 | H | |$51_{-21}^{+21}$| | |$-16.24_{-0.44}^{+0.19}$| | <−17.12 | |$43.92_{-0.25}^{+0.16}$| | <42.69 | 25.6 | 63.5 |
| 464 | |$4.76_{-0.10}^{+0.02}$| | P2 | 1.00 | S | <16 | |$-15.67_{-0.07}^{+0.04}$| | |$-15.68_{-0.06}^{+0.05}$| | |$43.81_{-0.08}^{+0.06}$| | |$43.80_{-0.08}^{+0.06}$| | 160.5 | 10.1 |
| 472 | |$4.16_{-0.17}^{+0.02}$| | P1 | 1.00 | H | |$110_{-94}^{+317}$| | <−16.97 | <−17.28 | |$43.14_{-0.24}^{+0.17}$| | <43.00 | 7.0 | 19.2 |
| 490 | |$4.73_{-0.08}^{+0.06}$| | P1 | 1.00 | S | |$71_{-8}^{+9}$| | |$-16.05_{-0.07}^{+0.04}$| | |$-16.06_{-0.07}^{+0.04}$| | |$44.03_{-0.08}^{+0.07}$| | |$44.01_{-0.10}^{+0.06}$| | 86.8 | 123.3 |
| 500 | |$3.15_{-0.02}^{+0.04}$| | P1 | 1.00 | S | |$40_{-38}^{+89}$| | <−16.79 | <−17.19 | <42.83 | <42.46 | 10.4 | 16.6 |
| 503 | |$3.14_{-0.07}^{+0.03}$| | P1 | 0.99 | S | <5 | <−16.93 | <−17.19 | <42.20 | <41.95 | 7.0 | 7.6 |
| 517 | 3.256 | S2 | 1.00 | S | <1 | |$-16.24 _{-0.11}^{+0.06}$| | |$-16.27_{-0.12}^{+0.06}$| | |$42.85_{-0.10}^{+0.07}$| | |$42.82_{-0.11}^{+0.07}$| | 44.1 | 24.0 |
| 521 | |$2.96_{-0.07}^{+0.07}$| | P1 | 0.41 | S | |$21_{-19}^{+60}$| | |$-16.89 _{-0.33}^{+0.18}$| | <−17.11 | |$42.34_{-0.36}^{+0.39}$| | |$42.60_{-0.19}^{+0.15}$| | 13.0 | 27.7 |
| 527 | |$3.76_{-0.29}^{+0.05}$| | P1 | 1.00 | S | <1 | |$-16.55 _{-0.15}^{+0.10}$| | |$-16.63_{-0.19}^{+0.12}$| | |$42.68_{-0.17}^{+0.12}$| | |$42.60_{-0.19}^{+0.15}$| | 22.5 | 0.0 |
| 539 | 4.762 | S1 | 1.00 | H | |$102_{-47}^{+49}$| | |$-16.48 _{-0.42}^{+0.18}$| | <−17.09 | |$43.83_{-0.27}^{+0.13}$| | <42.83 | 27.0 | 61.2 |
| 551 | 3.700 | S1 | 1.00 | S | |$76_{-5}^{+4}$| | |$-15.71 _{-0.05}^{+0.03}$| | |$-15.72_{-0.05}^{+0.03}$| | |$44.37_{-0.05}^{+0.05}$| | |$44.37_{-0.06}^{+0.04}$| | 209.8 | 441.4 |
| 580 | |$3.17_{-0.12}^{+0.19}$| | P1 | 0.97 | S | |$42_{-8}^{+10}$| | |$-16.34 _{-0.08}^{+0.06}$| | |$-16.36_{-0.10}^{+0.05}$| | |$43.40_{-0.13}^{+0.11}$| | |$43.38_{-0.12}^{+0.12}$| | 45.1 | 66.6 |
| 617 | |$3.58_{-0.13}^{+0.20}$| | P1 | 1.00 | S | <1 | |$-15.77 _{-0.07}^{+0.03}$| | |$-15.78_{-0.07}^{+0.03}$| | |$43.41_{-0.08}^{+0.05}$| | |$43.40_{-0.07}^{+0.06}$| | 136.0 | 69.1 |
| 619 | |$3.67_{-0.09}^{+0.04}$| | P1 | 1.00 | S | |$68_{-23}^{+18}$| | |$-16.85 _{-0.20}^{+0.10}$| | |$-16.97_{-0.22}^{+0.15}$| | |$43.12_{-0.27}^{+0.19}$| | |$42.99_{-0.32}^{+0.20}$| | 12.3 | 23.2 |
| 622 | |$3.33_{-0.17}^{+0.09}$| | P1 | 1.00 | S | <1 | |$- 16.50_{-0.19}^{+0.11}$| | |$-16.62_{-0.41}^{+0.18}$| | |$42.62_{-0.20}^{+0.14}$| | |$42.49_{-0.44}^{+0.20}$| | 24.5 | 0.0 |
| 623 | |$3.58_{-0.03}^{+0.02}$| | P1 | 1.00 | S | |$27_{-10}^{+10}$| | |$- 16.43_{-0.12}^{+0.07}$| | |$-16.47_{-0.12}^{+0.08}$| | |$43.17_{-0.14}^{+0.13}$| | |$43.13_{-0.18}^{+0.11}$| | 36.7 | 34.5 |
| 640 | |$3.77_{-0.03}^{+0.02}$| | P1 | 1.00 | S | |$16_{-15}^{+18}$| | |$-16.68 _{-0.16}^{+0.10}$| | |$-16.75_{-0.19}^{+0.10}$| | |$42.65_{-0.18}^{+0.16}$| | |$42.58_{-0.18}^{+0.18}$| | 17.7 | 3.5 |
| 657 | |$3.58_{-0.10}^{+0.17}$| | P1 | 1.00 | S | |$115_{-19}^{+11}$| | |$- 16.59_{-0.14}^{+0.09}$| | |$-16.66_{-0.17}^{+0.10}$| | |$43.76_{-0.19}^{+0.13}$| | |$43.69_{-0.20}^{+0.15}$| | 26.2 | 79.6 |
| 662 | |$4.84_{-0.12}^{+0.05}$| | P1 | 1.00 | S | <54 | |$-16.82 _{-0.24}^{+0.14}$| | <−16.90 | |$42.71_{-0.27}^{+0.18}$| | <42.68 | 13.3 | 2.6 |
| 692 | |$3.42_{-0.08}^{+0.13}$| | P1 | 1.00 | H | |$117_{-51}^{+56}$| | <−17.14 | <−17.37 | |$42.84_{-0.31}^{+0.18}$| | <43.22 | 3.6 | 9.7 |
| 714 | |$3.48_{-0.09}^{+0.03}$| | P1 | 1.00 | S | <1 | |$- 16.25_{-0.10}^{+0.08}$| | |$-16.29_{-0.13}^{+0.07}$| | |$42.91_{-0.13}^{+0.07}$| | |$42.87_{-0.13}^{+0.08}$| | 44.4 | 0.0 |
| 723 | 3.045 | S1 | 1.00 | S | |$59_{-6}^{+4}$| | |$-16.02 _{-0.05}^{+0.05}$| | |$-16.03_{-0.05}^{+0.05}$| | |$43.88_{-0.10}^{+0.05}$| | |$43.87_{-0.10}^{+0.05}$| | 93.0 | 188.1 |
| 746 | 3.064 | S1 | 1.00 | S | |$52_{-2}^{+1}$| | |$- 15.14_{-0.05}^{+0.02}$| | |$-15.15_{-0.04}^{+0.03}$| | |$44.69_{-0.05}^{+0.03}$| | |$44.68_{-0.05}^{+0.03}$| | 689.2 | 1281.4 |
| 758 | |$3.08_{-0.03}^{+0.01}$| | P1 | 1.00 | S | <36 | <−17.12 | <−17.37 | <42.13 | <41.92 | 8.7 | 13.5 |
| 760 | 3.35 | S2 | 1.00 | S | |$74_{-5}^{+2}$| | |$- 15.111_{-0.03}^{+0.03}$| | |$-15.11_{-0.04}^{+0.02}$| | |$44.94_{-0.05}^{+0.03}$| | |$44.94_{-0.05}^{+0.03}$| | 763.5 | 999.8 |
| 774 | 3.61 | S1 | 1.00 | S | |$7_{-1}^{+1}$| | |$-14.71 _{-0.04}^{+0.03}$| | |$-14.71_{-0.05}^{+0.02}$| | |$44.63_{-0.03}^{+0.04}$| | |$44.63_{-0.04}^{+0.03}$| | 1162.8 | 691.5 |
| 788 | 3.193 | S2 | 1.00 | S | |$2_{-1}^{+1}$| | |$- 15.11_{-0.03}^{+0.03}$| | |$-15.11_{-0.04}^{+0.02}$| | |$44.01_{-0.05}^{+0.02}$| | |$44.01_{-0.05}^{+0.02}$| | 646.8 | 381.8 |
| 811 | 3.471 | S1 | 1.00 | S | <1 | |$- 15.37_{-0.05}^{+0.02}$| | |$-15.37_{-0.05}^{+0.02}$| | |$43.77_{-0.04}^{+0.03}$| | |$43.77_{-0.05}^{+0.02}$| | 312.9 | 194.9 |
| 853 | |$3.72_{-0.14}^ {+0.13}$| | P1 | 1.00 | S | <2 | |$- 16.21_{-0.29}^{+0.16}$| | <−16.81 | |$43.05_{-0.35}^{+0.18}$| | <42.60 | 37.0 | 69.7 |
| 859 | |$2.88_{-0.09}^{+0.13}$| | P1 | 0.22 | S | <3 | |$-16.71 _{-0.30}^{+0.17}$| | <−16.93 | |$42.38_{-0.37}^{+0.21}$| | <42.34 | 16.4 | 1.6 |
| 873 | |$3.76_{-0.06}^{+0.04}$| | P1 | 1.00 | S | <1 | |$- 16.25_{-0.12}^{+0.10}$| | |$-16.31_{-0.16}^{+0.11}$| | |$42.98_{-0.13}^{+0.10}$| | |$42.92_{-0.17}^{+0.11}$| | 41.4 | 0.0 |
| 876 | 3.470 | S2 | 1.00 | S | |$11_{-1}^{+1}$| | |$-14.57 _{-0.01}^{+0.01}$| | |$-14.57_{-0.01}^{+0.01}$| | |$44.82_{-0.02}^{+0.01}$| | |$44.82_{-0.02}^{+0.01}$| | 2211.9 | 1482.2 |
| 885 | |$3.08_{-0.10}^{+0.02}$| | P1 | 0.78 | S | |$95_{-10}^{+10}$| | |$-16.18 _{-0.10}^{+0.07}$| | |$-16.21_{-0.13}^{+0.06}$| | |$44.02_{-0.14}^{+0.10}$| | |$43.98_{-0.13}^{+0.12}$| | 64.4 | 201.9 |
| 901 | |$3.51_{-0.12}^{+0.25}$| | P1 | 1.00 | S | <43 | |$- 16.63_{-0.32}^{+0.17}$| | <−16.94 | |$42.65_{-0.34}^{+0.25}$| | <42.43 | 19.8 | 14.7 |
| 908 | |$3.60_{-0.20}^{+0.05}$| | P1 | 1.00 | H | >23 | |$-16.94 _{-0.55}^{+0.61}$| | <−17.20 | |$43.64_{-0.26}^{+0.27}$| | <43.01 | 7.5 | 52.5 |
| 921 | 3.082 | S1 | 1.00 | S | <4 | |$- 15.33_{-0.07}^{+0.02}$| | |$-15.34_{-0.06}^{+0.03}$| | |$43.73_{-0.04}^{+0.05}$| | |$43.73_{-0.07}^{+0.03}$| | 347.6 | 204.8 |
| 926 | |$4.27_{-1.5}^{+0.06}$| | P1 | 0.53 | S | <7 | |$-15.61 _{-0.05}^{+0.05}$| | |$-15.62_{-0.07}^{+0.04}$| | |$43.76_{-0.06}^{+0.06}$| | |$43.75_{-0.08}^{+0.05}$| | 182.2 | 116.4 |
| 939 | −1 | N | 0.30 | S | <1 | |$- 16.00_{-0.11}^{+0.10}$| | |$-16.05_{-0.16}^{+0.10}$| | |$43.47_{-0.36}^{+0.12}$| | |$43.38_{-0.36}^{+0.15}$| | 62.8 | 15.0 |
| 940 | |$3.00_{-0.19}^{+0.26}$| | P1 | 0.63 | S | |$35_{-10}^{+7}$| | |$-16.00 _{-0.09}^{+0.06}$| | |$-16.03_{-0.09}^{+0.07}$| | |$43.64_{-0.16}^{+0.11}$| | |$43.61_{-0.14}^{+0.13}$| | 91.7 | 97.4 |
| 962 | |$4.68_{-2.25}^{+2.25}$| | P3 | 0.45 | S | |$141_{-48}^{+49}$| | |$- 16.40_{-0.31}^{+0.15}$| | <−16.95 | |$44.01_{-0.43}^{+0.26}$| | <43.54 | 35.2 | 130.2 |
| 965 | |$3.64_{-0.80}^{+0.11}$| | P3 | 0.65 | S | <1 | |$- 15.79_{-0.10}^{+0.06}$| | |$-15.81_{-0.11}^{+0.06}$| | |$43.36_{-0.13}^{+0.10}$| | |$43.33_{-0.14}^{+0.10}$| | 104.0 | 40.2 |
| 971 | |$2.17_{-0.59}^{+1.24}$| | P3 | 0.35 | S | |$36_{-13}^{+8}$| | |$- 15.61_{-0.05}^{+0.02}$| | |$-15.16_{-0.05}^{+0.02}$| | |$44.73_{-0.28}^{+0.11}$| | |$44.73_{-0.29}^{+0.10}$| | 536.7 | 513.2 |
| 974 | |$3.23_{-0.13}^{+0.18}$| | P3 | 0.92 | S | |$9_{-8}^{+10}$| | |$-15.76 _{-0.10}^{+0.08}$| | |$-15.79_{-0.13}^{+0.07}$| | |$43.44_{-0.13}^{+0.11}$| | |$43.41_{-0.14}^{+0.11}$| | 105.6 | 71.5 |
| 977a | −1 | N | 0.3 | S | |$89_{-29}^{+34}$| | |$-16.13 _{-0.18}^{+0.10}$| | <−16.20 | |$44.04_{-0.29}^{+0.23}$| | <44.03 | 48.6 | 128.0 |
| 990 | 3.724 | S1 | 1.00 | S | |$62_{-54}^{+64}$| | |$- 16.06_{-0.28}^{+0.17}$| | <−16.99 | |$43.35_{-0.24}^{+0.58}$| | <42.86 | 41.0 | 61.3 |
| CDF-N | |||||||||||
| 31 | |$3.45_{-0.36}^{+0.21}$| | P5 | 0.95 | S | <1 | |$-15.66 _{-0.12}^{+0.08}$| | |$-15.71_{-0.15}^{+0.08}$| | |$43.48_{-0.13}^{+0.12}$| | |$43.43_{-0.17}^{+0.11}$| | 44.4 | 16.6 |
| 81 | 3.19 | S3 | 1.00 | S | <1 | |$- 15.34_{-0.10}^{+0.07}$| | |$-15.37_{-0.10}^{+0.07}$| | |$43.72_{-0.10}^{+0.07}$| | |$43.69_{-0.10}^{+0.07}$| | 74.3 | 25.9 |
| 112 | |$3.15_{-0.18}^{+0.18}$| | P5 | 0.85 | S | <14 | |$-16.15 _{-0.14}^{+0.13}$| | |$-16.24_{-0.22}^{+0.13}$| | |$43.00_{-0.19}^{+0.15}$| | |$42.90_{-0.23}^{+0.18}$| | 20.7 | 8.1 |
| 129 | 3.938 | S3 | 1.00 | S | <1 | |$-15.43 _{-0.09}^{+0.07}$| | |$-15.46_{-0.10}^{+0.07}$| | |$43.84_{-0.09}^{+0.07}$| | |$43.81_{-0.11}^{+0.06}$| | 63.7 | 24.3 |
| 133 | |$3.06_{-0.36}^{+0.46}$| | P5 | 0.63 | S | |$93_{-19}^{+16}$| | |$-16.34 _{-0.23}^{+0.15}$| | <−16.57 | |$43.84_{-0.28}^{+0.21}$| | <43.62 | 15.0 | 41.0 |
| 142 | |$2.95_{-0.13}^{+0.08}$| | P5 | 0.23 | S | |$135_{-25}^{+24}$| | |$- 16.28_{-0.18}^{+0.13}$| | |$-16.41_{-0.23}^{+0.14}$| | |$44.24_{-0.25}^{+0.23}$| | |$44.11_{-0.31}^{+0.22}$| | 14.6 | 55.0 |
| 158 | |$3.19_{-0.02}^{+0.01}$| | P2 | 1.00 | S | |$54_{-10}^{+8}$| | |$-15.74 _{-0.11}^{+0.08}$| | |$-15.68_{-0.12}^{+0.08}$| | |$44.10_{-0.14}^{+0.12}$| | |$44.06_{-0.16}^{+0.11}$| | 46.4 | 72.2 |
| 177 | |$3.44_{-0.34}^{+0.14}$| | P5 | 0.98 | S | |$33_{-12}^{+14}$| | |$- 16.09_{-0.15}^{+0.09}$| | |$-16.16_{-0.14}^{+0.11}$| | |$43.55_{-0.21}^{+0.17}$| | |$43.48_{-0.21}^{+0.18}$| | 27.5 | 29.3 |
| 195 | −1 | N | 0.30 | S | <2 | |$- 16.02_{-0.13}^{+0.11}$| | |$-16.09_{-0.14}^{+0.11}$| | |$43.46_{-0.35}^{+0.13}$| | |$43.38_{-0.33}^{+0.15}$| | 28.3 | 12.9 |
| 196 | |$3.24_{-0.02}^{+0.02}$| | P2 | 1.00 | S | |$85_{-9}^{+10}$| | |$- 16.06_{-0.13}^{+0.12}$| | |$-16.13_{-0.16}^{+0.10}$| | |$44.08_{-0.19}^{+0.12}$| | |$44.00_{-0.18}^{+0.13}$| | 29.9 | 96.9 |
| 201 | |$4.43_{-1.33}^{+0.23}$| | P5 | 0.73 | S | −1b | <−16.78 | <−17.33 | <42.98 | |$44.06_{-0.19}^{+0.12}$| | 3.4 | 15.5 |
| 207 | 3.652 | S3 | 1.00 | S | <1 | |$- 15.09_{-0.08}^{+0.05}$| | |$-15.11_{-0.08}^{+0.05}$| | |$44.10_{-0.08}^{+0.05}$| | |$42.21_{-0.15}^{+0.30}$| | 242.6 | 80.7 |
| 227 | |$4.26_{-0.07}^{+0.03}$| | P2 | 1.00 | S | −1b | |$-16.70 _{-0.31}^{+0.24}$| | <−17.00 | |$42.71_{-0.55}^{+0.40}$| | <43.18 | 6.5 | 3.9 |
| 229 | 3.413 | S4 | 1.00 | S | <1 | |$- 15.43_{-0.09}^{+0.06}$| | |$-15.46_{-0.09}^{+0.06}$| | |$43.70_{-0.09}^{+0.06}$| | |$43.67_{-0.09}^{+0.06}$| | 111.8 | 48.8 |
| 257 | |$2.95_{-0.44}^{+0.29}$| | P5 | 0.35 | S | |$60_{-32}^{+37}$| | |$-16.56 _{-0.22}^{+0.14}$| | |$-16.74_{-0.30}^{+0.19}$| | |$43.24_{-0.43}^{+0.32}$| | |$43.04_{-0.47}^{+0.37}$| | 9.6 | 16.7 |
| 290 | 4.424 | S3 | 1.00 | S | <1 | |$-16.24 _{-0.17}^{+0.10}$| | |$-16.33_{-0.18}^{+0.11}$| | |$43.14_{-0.16}^{+0.11}$| | |$43.05_{-0.17}^{+0.12}$| | 17.7 | 9.1 |
| 293 | |$3.96_{-0.30}^{+0.17}$| | P5 | 1.00 | S | <8 | |$-15.32 _{-0.07}^{+0.06}$| | |$-15.33_{-0.07}^{+0.06}$| | |$43.98_{-0.12}^{+0.07}$| | |$43.96_{-0.11}^{+0.08}$| | 115.0 | 66.9 |
| 297 | 3.23 | S3 | 1.00 | S | <1 | |$-16.09 _{-0.12}^{+0.12}$| | |$-16.16_{-0.16}^{+0.10}$| | |$42.99_{-0.15}^{+0.10}$| | |$42.02_{-0.15}^{+0.11}$| | 22.3 | 10.8 |
| 310 | |$3.06_{-0.23}^{+0.36}$| | P5 | 0.70 | S | <41 | |$16.67 _{-0.32}^{+0.19}$| | <−16.93 | |$42.52_{-0.40}^{+0.30}$| | <42.47 | 6.6 | 6.5 |
| 315 | −1 | N | 0.30 | S | <1 | |$- 16.61_{-0.25}^{+0.16}$| | |$- 16.86_{-0.51}^{+0.21}$| | |$42.78_{-0.36}^{+0.23}$| | |$42.46_{-0.51}^{+0.31}$| | 7.5 | 2.8 |
| 320 | |$3.06_{-0.20}^{+0.26}$| | P5 | 0.69 | S | <1 | |$- 16.73_{-0.28}^{+0.19}$| | <−16.91 | |$42.37_{-0.31}^{+0.21}$| | <42.23 | 5.8 | 5.5 |
| 330 | 5.186 | S3 | 1.00 | S | <1 | |$-15.53 _{-0.12}^{+0.07}$| | |$-15.57_{-0.12}^{+0.07}$| | |$44.00_{-0.12}^{+0.07}$| | |$43.96_{-0.12}^{+0.07}$| | 84.4 | 31.4 |
| 363 | |$3.28_{-0.05}^{+0.05}$| | P2 | 1.00 | S | <1 | |$-16.19 _{-0.17}^{+0.14}$| | |$-16.31_{-0.21}^{+0.14}$| | |$42.92_{-0.17}^{+0.15}$| | |$42.80_{-0.21}^{+0.15}$| | 15.8 | 3.9 |
| 373 | |$3.36_{-0.29}^{+0.34}$| | P5 | 0.84 | S | |$52_{-31}^{+31}$| | |$-16.76 _{-0.27}^{+0.19}$| | <−16.92 | |$42.98_{-0.51}^{+0.25}$| | <42.85 | 5.9 | 6.5 |
| 388 | |$2.94_{-0.12}^{+0.08}$| | P5 | 0.31 | S | <1 | |$- 15.49_{-0.12}^{+0.07}$| | |$-15.53_{-0.13}^{+0.08}$| | |$43.56_{-0.13}^{+0.08}$| | |$43.52_{-0.14}^{+0.09}$| | 56.5 | 0.0 |
| 390 | |$3.19_{-0.29}^{+0.28}$| | P5 | 0.85 | H | |$204_{-46}^{+53}$| | <−16.89 | <−17.39 | |$43.38_{-0.13}^{+0.07}$| | |$43.30_{-0.16}^{+0.09}$| | 3.1 | 31.5 |
| 404 | |$3.15_{-0.13}^{+0.04}$| | P5 | 0.91 | S | <1 | |$- 14.67_{-0.06}^{+0.03}$| | |$-14.67_{-0.06}^{+0.03}$| | |$44.37_{-0.06}^{+0.04}$| | |$44.36_{-0.06}^{+0.04}$| | 555.4 | 220.8 |
| 424 | |$4.43_{-0.26}^{+0.13}$| | P5 | 1.00 | H | |$166_{-40}^{+38}$| | |$-16.37 _{-0.36}^{+0.18}$| | <−17.17 | |$43.34_{-0.25}^{+0.17}$| | |$42.32_{-0.11}^{+0.58}$| | 13.1 | 62.2 |
| 428 | |$3.03_{-0.11}^{+0.09}$| | P5 | 0.55 | S | |$18_{-3}^{+2}$| | |$-15.07 _{0.06-}^{+0.04}$| | |$-15.08_{-0.06}^{+0.04}$| | |$44.36_{-0.08}^{+0.05}$| | |$44.35_{-0.08}^{+0.05}$| | 258.7 | 188.1 |
| 439 | 3.406 | S3 | 1.00 | S | |$27_{-26}^{+73}$| | |$-16.54 _{-0.28}^{+0.17}$| | |$-16.81_{-0.46}^{+0.27}$| | |$42.76_{-0.35}^{+0.41}$| | |$42.49_{-0.51}^{+0.46}$| | 8.5 | 15.8 |
| 498 | |$4.42_{-0.24}^{+0.31}$| | P5 | 0.99 | S | |$23_{-6}^{+6}$| | |$-15.33 _{-0.09}^{+0.06}$| | |$-15.35_{-0.10}^{+0.05}$| | |$44.36_{-0.12}^{+0.09}$| | |$44.34_{-0.12}^{+0.09}$| | 149.2 | 86.2 |
| 502 | 3.157 | S3 | 1.00 | S | <1 | |$- 15.56_{-0.13}^{+0.08}$| | |$-15.61_{-0.10}^{+0.10}$| | |$43.50_{-0.13}^{+0.08}$| | |$43.45_{-0.13}^{+0.08}$| | 73.5 | 29.8 |
| 504 | |$3.36_{-0.09}^{+0.10}$| | P5 | 1.00 | H | |$831_{-537}^{+123}$| | <−16.31 | <−17.57 | |$43.14_{-0.24}^{+0.17}$| | |$42.26_{-0.13}^{+0.59}$| | 9.8 | 30.8 |
| 509 | |$3.15_{-0.57}^{+0.12}$| | P5 | 0.47 | S | <15 | |$-16.26 _{-0.26}^{+0.18}$| | <−16.93 | |$42.88_{-0.32}^{+0.21}$| | <42.30 | 15.1 | 3.2 |
| 526 | |$4.17_{-0.13}^{+0.10}$| | P5 | 1.00 | S | |$15_{-6}^{+7}$| | |$- 15.84_{-0.10}^{+0.07}$| | |$-15.88_{-0.10}^{+0.08}$| | |$43.71_{-0.14}^{+0.09}$| | |$43.67_{-0.15}^{+0.09}$| | 89.0 | 48.0 |
| 545 | 3.524 | S3 | 1.00 | S | <11 | |$- 15.27_{-0.07}^{+0.05}$| | |$-15.28_{-0.07}^{+0.05}$| | |$43.95_{-0.09}^{+0.07}$| | |$43.93_{-0.08}^{+0.08}$| | 132.4 | 46.8 |
| 572 | |$3.77_{-0.01}^{+0.03}$| | P2 | 1.00 | S | |$10_{-2}^{+2}$| | |$-15.49 _{-0.13}^{+0.08}$| | |$-15.54_{-0.17}^{+0.10}$| | |$43.94_{-0.14}^{+0.08}$| | |$43.89_{-0.17}^{+0.11}$| | 288.9 | 156.2 |
| ID . | z . | Ref . | P . | Band . | NH . | |$\mathrm{log}F^{\mathrm{obs}}_{0.5-2\, \mathrm{keV}}$| . | |$\mathrm{log}F^{\mathrm{intr}}_{0.5-2\, \mathrm{keV}}$| . | |$\mathrm{log}L^{\mathrm{obs}}_{2-10\, \mathrm{keV}}$| . | |$\mathrm{log}L^{\mathrm{intr}}_{2-10\, \mathrm{keV}}$| . | Net counts . | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | (3 ≤ z < 6) . | . | (1022 cm−2) . | (erg cm−2 s−1) . | (erg cm−2 s−1) . | (erg s−1) . | (erg s−1) . | (0.5–2 keV) . | (2–7 keV) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| CDF-S | |||||||||||
| 8 | |$3.13_{-0.48}^{+3.28}$| | P3 | 0.55 | S | |$59_{-18}^{+24}$| | |$-15.56_{-0.08}^{+0.07}$| | |$-15.59_{-0.08}^{+0.08}$| | |$44.43_{-0.23}^{+0.20}$| | |$44.41_{-0.27}^{+0.17}$| | 99.2 | 119.4 |
| 9 | |$1.93_{-0.20}^{+1.39}$| | P3 | 0.44 | S | |$11_{-5}^{+8}$| | |$-15.31_{-0.08}^{+0.05}$| | |$-15.32_{-0.07}^{+0.06}$| | |$44.04_{-0.13}^{+0.16}$| | |$44.03_{-0.14}^{+0.15}$| | 140.7 | 95.4 |
| 10 | |$2.93_{-0.40}^{+0.85}$| | P3 | 0.32 | S | |$3_{-2}^{+2}$| | |$-15.40_{-0.11}^{+0.06}$| | |$-15.43_{-0.09}^{+0.08}$| | |$43.76_{-0.13}^{+0.09}$| | |$43.73_{-0.14}^{+0.09}$| | 70.1 | 38.9 |
| 12 | 3.153 | S2 | 1.00 | H | |$135_{-46}^{+69}$| | |$-16.59_{-0.75}^{+0.21}$| | <− 17.28 | |$44.06_{-0.18}^{+0.12}$| | |$42.21_{-0.22}^{+1.32}$| | 12.4 | 89.0 |
| 25 | −1 | N | 0.30 | S | <74 | |$-15.65_{-0.13}^{+0.08}$| | |$-15.69_{-0.15}^{+0.08}$| | |$43.63_{-0.20}^{+0.44}$| | |$43.60_{-0.18}^{+0.46}$| | 75.0 | 88.3 |
| 29 | |$3.33_{-0.29}^{+0.32}$| | P4 | 0.99 | S | <1 | |$-15.63_{-0.10}^{+0.05}$| | |$-15.65_{-0.11}^{+0.05}$| | |$43.47_{-0.13}^{+0.12}$| | |$43.45_{-0.12}^{+0.13}$| | 119.0 | 44.4 |
| 35 | −1 | N | 0.30 | S | |$25_{-17}^{+29}$| | |$-15.61_{-0.09}^{+0.09}$| | |$-15.63_{-0.11}^{+0.08}$| | |$43.97_{-0.20}^{+0.21}$| | |$43.94_{-0.22}^{+0.20}$| | 98.9 | 67.8 |
| 53 | 3.202 | S1 | 1.00 | S | <22 | |$-16.41_{-0.36}^{+0.18}$| | <−16.97 | |$42.74_{-0.40}^{+0.20}$| | <42.30 | 29.8 | 40.7 |
| 84 | |$3.12_{-0.59}^{+0.35}$| | P1 | 0.70 | S | |$49_{-13}^{+14}$| | |$-16.07_{-0.11}^{+0.06}$| | |$-16.10_{-0.12}^{+0.06}$| | |$43.75_{-0.19}^{+0.14}$| | |$43.71_{-0.19}^{+0.15}$| | 80.4 | 98.5 |
| 88 | −1 | N | 0.30 | S | |$83_{-26}^{+19}$| | |$-15.98_{-0.08}^{+0.06}$| | |$-16.01_{-0.09}^{+0.06}$| | |$44.19_{-0.27}^{+0.12}$| | |$44.16_{-0.25}^{+0.14}$| | 99.3 | 195.6 |
| 99 | |$4.24_{-0.36}^{+0.05}$| | P1 | 0.99 | S | |$30_{-28}^{+34}$| | |$-15.91_{-0.19}^{+0.14}$| | <−16.19 | |$43.55_{-0.26}^{+0.22}$| | <43.32 | 41.3 | 47.8 |
| 101 | |$4.34_{-0.61}^{+0.02}$| | P1 | 1.00 | S | |$68_{-22}^{+12}$| | |$-16.11_{-0.16}^{+0.09}$| | |$-16.20_{-0.27}^{+0.18}$| | |$43.87_{-0.24}^{+0.24}$| | |$43.78_{-0.37}^{+0.22}$| | 51.2 | 110.8 |
| 109 | |$3.58_{-0.04}^{+0.03}$| | P1 | 1.0 | S | |$28_{-6}^{+5}$| | |$-16.48_{-0.23}^{+0.15}$| | <−16.68 | |$43.14_{-0.25}^{+0.16}$| | <42.96 | 144.9 | 150.9 |
| 110 | |$3.08_{-0.08}^{+0.38}$| | P1 | 0.87 | S | <1 | |$-16.54_{-0.24}^{+0.15}$| | <−16.74 | |$42.55_{-0.24}^{+0.19}$| | <42.40 | 22.8 | 4.4 |
| 121 | |$3.42_{-0.05}^{+0.03}$| | P1 | 1.00 | S | |$68_{-21}^{+14}$| | |$-16.27_{-0.13}^{+0.09}$| | |$-16.33_{-0.16}^{+0.11}$| | |$43.69_{-0.22}^{+0.16}$| | |$43.62_{-0.27}^{+0.16}$| | 50.4 | 65.9 |
| 126 | |$3.13_{-0.03}^{+0.07}$| | P1 | 0.95 | S | <28 | |$-15.84_{-0.23}^{+0.13}$| | <−16.55 | |$43.32_{-0.22}^{+0.20}$| | <42.67 | 39.9 | 53.1 |
| 133 | 3.474 | S1 | 1.00 | H | |$141_{-50}^{+73}$| | <−16.96 | <−17.39 | |$43.61_{-0.22}^{+0.13}$| | |$42.23_{-0.15}^{+0.93}$| | 4.0 | 56.3 |
| 165 | |$3.55_{-0.02}^{+0.02}$| | P1 | 1.00 | S | |$16_{-6}^{+6}$| | |$-15.94_{-0.09}^{+0.07}$| | |$-15.96_{-0.11}^{+0.06}$| | |$43.52_{-0.13}^{+0.09}$| | |$43.5_{-0.15}^{+0.08}$| | 71.9 | 34.2 |
| 185 | |$3.09_{-0.03}^{+0.04}$| | P1 | 0.87 | S | |$39_{-24}^{+24}$| | |$-16.70_{-0.19}^{+0.11}$| | |$-16.82_{-0.29}^{+0.16}$| | |$42.86_{-0.37}^{+0.22}$| | |$42.71_{-0.45}^{+0.25}$| | 18.7 | 22.6 |
| 189 | |$3.65_{-0.04}^{+0.07}$| | P1 | 1.00 | H | |$107_{-33}^{+25}$| | <−16.97 | <−17.31 | |$43.38_{-0.16}^{+0.09}$| | |$43.30_{-0.19}^{+0.12}$| | 7.1 | 34.5 |
| 214 | 3.74 | S2 | 1.00 | S | |$26_{-2}^{+1}$| | |$-14.81_{-0.03}^{+0.00}$| | |$-14.82_{-0.03}^{+0.01}$| | |$44.81_{-0.03}^{+0.02}$| | |$44.81_{-0.03}^{+0.02}$| | 1377.4 | 1213.8 |
| 223 | |$3.76_{-0.17}^{+0.06}$| | P1 | 1.00 | S | <14 | |$-16.46_{-0.15}^{+0.11}$| | |$-16.55_{-0.22}^{+0.13}$| | |$42.80_{-0.19}^{+0.11}$| | |$42.71_{-0.23}^{+0.15}$| | 27.9 | 0.0 |
| 238 | |$5.96_{-0.04}^{+0.01}$| | P2 | 1.00 | S | <66 | |$-16.29_{-0.17}^{+0.09}$| | |$-16.37_{-0.21}^{+0.14}$| | |$43.42_{-0.17}^{+0.15}$| | |$43.35_{-0.24}^{+0.18}$| | 40.5 | 7.1 |
| 248 | |$3.44_{-0.13}^{+0.22}$| | P1 | 1.00 | S | |$39_{-7}^{+5}$| | |$-15.55_{-0.06}^{+0.04}$| | |$-15.56_{-0.06}^{+0.04}$| | |$44.18_{-0.10}^{+0.07}$| | |$44.17_{-0.10}^{+0.07}$| | 186.9 | 192.9 |
| 276 | |$3.12_{-0.01}^{+0.02}$| | P1 | 1.00 | S | |$15_{-3}^{+3}$| | |$-15.90_{-0.06}^{+0.04}$| | |$-15.91_{-0.06}^{+0.04}$| | |$43.51_{-0.08}^{+0.05}$| | |$43.50_{-0.08}^{+0.05}$| | 122.9 | 9.2 |
| 299 | |$3.79_{-0.05}^{+0.05}$| | P1 | 1.00 | S | |$10_{-9}^{+15}$| | |$-16.63_{-0.16}^{+0.10}$| | |$-16.71_{-0.19}^{+0.12}$| | |$42.67_{-0.18}^{+0.13}$| | |$42.59_{-0.21}^{+0.15}$| | 19.4 | 21.0 |
| 329 | |$3.47_{-0.10}^{+0.10}$| | P1 | 1.00 | S | |$32_{-29}^{+33}$| | |$-16.69_{-0.20}^{+0.14}$| | <−16.74 | |$42.61_{-0.25}^{+0.31}$| | <42.77 | 17.2 | 17.1 |
| 337 | 3.660 | S1 | 1.00 | S | |$98_{-9}^{+7}$| | |$-16.08_{-0.09}^{+0.04}$| | |$-16.10_{-0.08}^{+0.05}$| | |$44.16_{-0.10}^{+0.07}$| | |$44.14_{-0.09}^{+0.08}$| | 78.3 | 221.4 |
| 351 | |$3.86_{-0.54}^{+0.14}$| | P1 | 0.97 | S | |$74_{-23}^{+9}$| | |$-16.28_{-0.14}^{+0.08}$| | |$-16.34_{-0.17}^{+0.10}$| | |$43.71_{-0.19}^{+0.17}$| | |$43.65_{-0.26}^{+0.15}$| | 50.8 | 73.2 |
| 356 | |$3.38_{-0.19}^{+0.01}$| | P1 | 0.99 | S | <8 | |$-16.38_{-0.14}^{+0.07}$| | |$-16.43_{-0.15}^{+0.08}$| | |$42.76_{-0.13}^{+0.10}$| | |$42.71_{-0.15}^{+0.10}$| | 31.9 | 31.4 |
| 366 | |$3.67_{-0.18}^{+0.53}$| | P1 | 1.00 | S | |$81_{-15}^{+14}$| | |$-16.15_{-0.10}^{+0.06}$| | |$-16.18_{-0.10}^{+0.07}$| | |$43.96_{-0.14}^{+0.14}$| | |$43.93_{-0.16}^{+0.13}$| | 66.8 | 131.2 |
| 368 | |$3.21_{-0.08}^{+0.09}$| | P1 | 1.00 | S | <1 | |$-16.57_{-0.15}^{+0.10}$| | |$-16.65_{-0.19}^{+0.11}$| | |$42.52_{-0.19}^{+0.10}$| | |$42.44_{-0.20}^{+0.11}$| | 20.9 | 0.0 |
| 414 | |$3.58_{-0.10}^{+0.11}$| | P1 | 1.00 | H | −1** | <−17.28 | <−17.41 | |$42.71_{-0.36}^{+0.20}$| | <42.61 | 0.3 | 9.7 |
| 416 | 3.470 | S1 | 1.00 | S | <1 | |$-16.63_{-0.19}^{+0.10}$| | |$-16.75_{-0.27}^{+0.19}$| | |$42.52_{-0.19}^{+0.10}$| | |$42.40_{-0.26}^{+0.15}$| | 18.0 | 0.4 |
| 433 | |$4.11_{-0.12}^{+0.15}$| | P1 | 1.00 | S | <1 | |$-16.80_{-0.23}^{+0.13}$| | <−16.86 | |$42.55_{-0.24}^{+0.14}$| | <42.51 | 12.9 | 0.3 |
| 459 | |$3.91_{-0.04}^{+0.05}$| | P1 | 1.00 | H | |$166_{-64}^{+80}$| | <17.20 | <−17.43 | |$43.34_{-0.25}^{+0.17}$| | <43.11 | 0.3 | 24.4 |
| 462 | |$3.88_{-0.78}^{+0.41}$| | P1 | 0.95 | H | |$51_{-21}^{+21}$| | |$-16.24_{-0.44}^{+0.19}$| | <−17.12 | |$43.92_{-0.25}^{+0.16}$| | <42.69 | 25.6 | 63.5 |
| 464 | |$4.76_{-0.10}^{+0.02}$| | P2 | 1.00 | S | <16 | |$-15.67_{-0.07}^{+0.04}$| | |$-15.68_{-0.06}^{+0.05}$| | |$43.81_{-0.08}^{+0.06}$| | |$43.80_{-0.08}^{+0.06}$| | 160.5 | 10.1 |
| 472 | |$4.16_{-0.17}^{+0.02}$| | P1 | 1.00 | H | |$110_{-94}^{+317}$| | <−16.97 | <−17.28 | |$43.14_{-0.24}^{+0.17}$| | <43.00 | 7.0 | 19.2 |
| 490 | |$4.73_{-0.08}^{+0.06}$| | P1 | 1.00 | S | |$71_{-8}^{+9}$| | |$-16.05_{-0.07}^{+0.04}$| | |$-16.06_{-0.07}^{+0.04}$| | |$44.03_{-0.08}^{+0.07}$| | |$44.01_{-0.10}^{+0.06}$| | 86.8 | 123.3 |
| 500 | |$3.15_{-0.02}^{+0.04}$| | P1 | 1.00 | S | |$40_{-38}^{+89}$| | <−16.79 | <−17.19 | <42.83 | <42.46 | 10.4 | 16.6 |
| 503 | |$3.14_{-0.07}^{+0.03}$| | P1 | 0.99 | S | <5 | <−16.93 | <−17.19 | <42.20 | <41.95 | 7.0 | 7.6 |
| 517 | 3.256 | S2 | 1.00 | S | <1 | |$-16.24 _{-0.11}^{+0.06}$| | |$-16.27_{-0.12}^{+0.06}$| | |$42.85_{-0.10}^{+0.07}$| | |$42.82_{-0.11}^{+0.07}$| | 44.1 | 24.0 |
| 521 | |$2.96_{-0.07}^{+0.07}$| | P1 | 0.41 | S | |$21_{-19}^{+60}$| | |$-16.89 _{-0.33}^{+0.18}$| | <−17.11 | |$42.34_{-0.36}^{+0.39}$| | |$42.60_{-0.19}^{+0.15}$| | 13.0 | 27.7 |
| 527 | |$3.76_{-0.29}^{+0.05}$| | P1 | 1.00 | S | <1 | |$-16.55 _{-0.15}^{+0.10}$| | |$-16.63_{-0.19}^{+0.12}$| | |$42.68_{-0.17}^{+0.12}$| | |$42.60_{-0.19}^{+0.15}$| | 22.5 | 0.0 |
| 539 | 4.762 | S1 | 1.00 | H | |$102_{-47}^{+49}$| | |$-16.48 _{-0.42}^{+0.18}$| | <−17.09 | |$43.83_{-0.27}^{+0.13}$| | <42.83 | 27.0 | 61.2 |
| 551 | 3.700 | S1 | 1.00 | S | |$76_{-5}^{+4}$| | |$-15.71 _{-0.05}^{+0.03}$| | |$-15.72_{-0.05}^{+0.03}$| | |$44.37_{-0.05}^{+0.05}$| | |$44.37_{-0.06}^{+0.04}$| | 209.8 | 441.4 |
| 580 | |$3.17_{-0.12}^{+0.19}$| | P1 | 0.97 | S | |$42_{-8}^{+10}$| | |$-16.34 _{-0.08}^{+0.06}$| | |$-16.36_{-0.10}^{+0.05}$| | |$43.40_{-0.13}^{+0.11}$| | |$43.38_{-0.12}^{+0.12}$| | 45.1 | 66.6 |
| 617 | |$3.58_{-0.13}^{+0.20}$| | P1 | 1.00 | S | <1 | |$-15.77 _{-0.07}^{+0.03}$| | |$-15.78_{-0.07}^{+0.03}$| | |$43.41_{-0.08}^{+0.05}$| | |$43.40_{-0.07}^{+0.06}$| | 136.0 | 69.1 |
| 619 | |$3.67_{-0.09}^{+0.04}$| | P1 | 1.00 | S | |$68_{-23}^{+18}$| | |$-16.85 _{-0.20}^{+0.10}$| | |$-16.97_{-0.22}^{+0.15}$| | |$43.12_{-0.27}^{+0.19}$| | |$42.99_{-0.32}^{+0.20}$| | 12.3 | 23.2 |
| 622 | |$3.33_{-0.17}^{+0.09}$| | P1 | 1.00 | S | <1 | |$- 16.50_{-0.19}^{+0.11}$| | |$-16.62_{-0.41}^{+0.18}$| | |$42.62_{-0.20}^{+0.14}$| | |$42.49_{-0.44}^{+0.20}$| | 24.5 | 0.0 |
| 623 | |$3.58_{-0.03}^{+0.02}$| | P1 | 1.00 | S | |$27_{-10}^{+10}$| | |$- 16.43_{-0.12}^{+0.07}$| | |$-16.47_{-0.12}^{+0.08}$| | |$43.17_{-0.14}^{+0.13}$| | |$43.13_{-0.18}^{+0.11}$| | 36.7 | 34.5 |
| 640 | |$3.77_{-0.03}^{+0.02}$| | P1 | 1.00 | S | |$16_{-15}^{+18}$| | |$-16.68 _{-0.16}^{+0.10}$| | |$-16.75_{-0.19}^{+0.10}$| | |$42.65_{-0.18}^{+0.16}$| | |$42.58_{-0.18}^{+0.18}$| | 17.7 | 3.5 |
| 657 | |$3.58_{-0.10}^{+0.17}$| | P1 | 1.00 | S | |$115_{-19}^{+11}$| | |$- 16.59_{-0.14}^{+0.09}$| | |$-16.66_{-0.17}^{+0.10}$| | |$43.76_{-0.19}^{+0.13}$| | |$43.69_{-0.20}^{+0.15}$| | 26.2 | 79.6 |
| 662 | |$4.84_{-0.12}^{+0.05}$| | P1 | 1.00 | S | <54 | |$-16.82 _{-0.24}^{+0.14}$| | <−16.90 | |$42.71_{-0.27}^{+0.18}$| | <42.68 | 13.3 | 2.6 |
| 692 | |$3.42_{-0.08}^{+0.13}$| | P1 | 1.00 | H | |$117_{-51}^{+56}$| | <−17.14 | <−17.37 | |$42.84_{-0.31}^{+0.18}$| | <43.22 | 3.6 | 9.7 |
| 714 | |$3.48_{-0.09}^{+0.03}$| | P1 | 1.00 | S | <1 | |$- 16.25_{-0.10}^{+0.08}$| | |$-16.29_{-0.13}^{+0.07}$| | |$42.91_{-0.13}^{+0.07}$| | |$42.87_{-0.13}^{+0.08}$| | 44.4 | 0.0 |
| 723 | 3.045 | S1 | 1.00 | S | |$59_{-6}^{+4}$| | |$-16.02 _{-0.05}^{+0.05}$| | |$-16.03_{-0.05}^{+0.05}$| | |$43.88_{-0.10}^{+0.05}$| | |$43.87_{-0.10}^{+0.05}$| | 93.0 | 188.1 |
| 746 | 3.064 | S1 | 1.00 | S | |$52_{-2}^{+1}$| | |$- 15.14_{-0.05}^{+0.02}$| | |$-15.15_{-0.04}^{+0.03}$| | |$44.69_{-0.05}^{+0.03}$| | |$44.68_{-0.05}^{+0.03}$| | 689.2 | 1281.4 |
| 758 | |$3.08_{-0.03}^{+0.01}$| | P1 | 1.00 | S | <36 | <−17.12 | <−17.37 | <42.13 | <41.92 | 8.7 | 13.5 |
| 760 | 3.35 | S2 | 1.00 | S | |$74_{-5}^{+2}$| | |$- 15.111_{-0.03}^{+0.03}$| | |$-15.11_{-0.04}^{+0.02}$| | |$44.94_{-0.05}^{+0.03}$| | |$44.94_{-0.05}^{+0.03}$| | 763.5 | 999.8 |
| 774 | 3.61 | S1 | 1.00 | S | |$7_{-1}^{+1}$| | |$-14.71 _{-0.04}^{+0.03}$| | |$-14.71_{-0.05}^{+0.02}$| | |$44.63_{-0.03}^{+0.04}$| | |$44.63_{-0.04}^{+0.03}$| | 1162.8 | 691.5 |
| 788 | 3.193 | S2 | 1.00 | S | |$2_{-1}^{+1}$| | |$- 15.11_{-0.03}^{+0.03}$| | |$-15.11_{-0.04}^{+0.02}$| | |$44.01_{-0.05}^{+0.02}$| | |$44.01_{-0.05}^{+0.02}$| | 646.8 | 381.8 |
| 811 | 3.471 | S1 | 1.00 | S | <1 | |$- 15.37_{-0.05}^{+0.02}$| | |$-15.37_{-0.05}^{+0.02}$| | |$43.77_{-0.04}^{+0.03}$| | |$43.77_{-0.05}^{+0.02}$| | 312.9 | 194.9 |
| 853 | |$3.72_{-0.14}^ {+0.13}$| | P1 | 1.00 | S | <2 | |$- 16.21_{-0.29}^{+0.16}$| | <−16.81 | |$43.05_{-0.35}^{+0.18}$| | <42.60 | 37.0 | 69.7 |
| 859 | |$2.88_{-0.09}^{+0.13}$| | P1 | 0.22 | S | <3 | |$-16.71 _{-0.30}^{+0.17}$| | <−16.93 | |$42.38_{-0.37}^{+0.21}$| | <42.34 | 16.4 | 1.6 |
| 873 | |$3.76_{-0.06}^{+0.04}$| | P1 | 1.00 | S | <1 | |$- 16.25_{-0.12}^{+0.10}$| | |$-16.31_{-0.16}^{+0.11}$| | |$42.98_{-0.13}^{+0.10}$| | |$42.92_{-0.17}^{+0.11}$| | 41.4 | 0.0 |
| 876 | 3.470 | S2 | 1.00 | S | |$11_{-1}^{+1}$| | |$-14.57 _{-0.01}^{+0.01}$| | |$-14.57_{-0.01}^{+0.01}$| | |$44.82_{-0.02}^{+0.01}$| | |$44.82_{-0.02}^{+0.01}$| | 2211.9 | 1482.2 |
| 885 | |$3.08_{-0.10}^{+0.02}$| | P1 | 0.78 | S | |$95_{-10}^{+10}$| | |$-16.18 _{-0.10}^{+0.07}$| | |$-16.21_{-0.13}^{+0.06}$| | |$44.02_{-0.14}^{+0.10}$| | |$43.98_{-0.13}^{+0.12}$| | 64.4 | 201.9 |
| 901 | |$3.51_{-0.12}^{+0.25}$| | P1 | 1.00 | S | <43 | |$- 16.63_{-0.32}^{+0.17}$| | <−16.94 | |$42.65_{-0.34}^{+0.25}$| | <42.43 | 19.8 | 14.7 |
| 908 | |$3.60_{-0.20}^{+0.05}$| | P1 | 1.00 | H | >23 | |$-16.94 _{-0.55}^{+0.61}$| | <−17.20 | |$43.64_{-0.26}^{+0.27}$| | <43.01 | 7.5 | 52.5 |
| 921 | 3.082 | S1 | 1.00 | S | <4 | |$- 15.33_{-0.07}^{+0.02}$| | |$-15.34_{-0.06}^{+0.03}$| | |$43.73_{-0.04}^{+0.05}$| | |$43.73_{-0.07}^{+0.03}$| | 347.6 | 204.8 |
| 926 | |$4.27_{-1.5}^{+0.06}$| | P1 | 0.53 | S | <7 | |$-15.61 _{-0.05}^{+0.05}$| | |$-15.62_{-0.07}^{+0.04}$| | |$43.76_{-0.06}^{+0.06}$| | |$43.75_{-0.08}^{+0.05}$| | 182.2 | 116.4 |
| 939 | −1 | N | 0.30 | S | <1 | |$- 16.00_{-0.11}^{+0.10}$| | |$-16.05_{-0.16}^{+0.10}$| | |$43.47_{-0.36}^{+0.12}$| | |$43.38_{-0.36}^{+0.15}$| | 62.8 | 15.0 |
| 940 | |$3.00_{-0.19}^{+0.26}$| | P1 | 0.63 | S | |$35_{-10}^{+7}$| | |$-16.00 _{-0.09}^{+0.06}$| | |$-16.03_{-0.09}^{+0.07}$| | |$43.64_{-0.16}^{+0.11}$| | |$43.61_{-0.14}^{+0.13}$| | 91.7 | 97.4 |
| 962 | |$4.68_{-2.25}^{+2.25}$| | P3 | 0.45 | S | |$141_{-48}^{+49}$| | |$- 16.40_{-0.31}^{+0.15}$| | <−16.95 | |$44.01_{-0.43}^{+0.26}$| | <43.54 | 35.2 | 130.2 |
| 965 | |$3.64_{-0.80}^{+0.11}$| | P3 | 0.65 | S | <1 | |$- 15.79_{-0.10}^{+0.06}$| | |$-15.81_{-0.11}^{+0.06}$| | |$43.36_{-0.13}^{+0.10}$| | |$43.33_{-0.14}^{+0.10}$| | 104.0 | 40.2 |
| 971 | |$2.17_{-0.59}^{+1.24}$| | P3 | 0.35 | S | |$36_{-13}^{+8}$| | |$- 15.61_{-0.05}^{+0.02}$| | |$-15.16_{-0.05}^{+0.02}$| | |$44.73_{-0.28}^{+0.11}$| | |$44.73_{-0.29}^{+0.10}$| | 536.7 | 513.2 |
| 974 | |$3.23_{-0.13}^{+0.18}$| | P3 | 0.92 | S | |$9_{-8}^{+10}$| | |$-15.76 _{-0.10}^{+0.08}$| | |$-15.79_{-0.13}^{+0.07}$| | |$43.44_{-0.13}^{+0.11}$| | |$43.41_{-0.14}^{+0.11}$| | 105.6 | 71.5 |
| 977a | −1 | N | 0.3 | S | |$89_{-29}^{+34}$| | |$-16.13 _{-0.18}^{+0.10}$| | <−16.20 | |$44.04_{-0.29}^{+0.23}$| | <44.03 | 48.6 | 128.0 |
| 990 | 3.724 | S1 | 1.00 | S | |$62_{-54}^{+64}$| | |$- 16.06_{-0.28}^{+0.17}$| | <−16.99 | |$43.35_{-0.24}^{+0.58}$| | <42.86 | 41.0 | 61.3 |
| CDF-N | |||||||||||
| 31 | |$3.45_{-0.36}^{+0.21}$| | P5 | 0.95 | S | <1 | |$-15.66 _{-0.12}^{+0.08}$| | |$-15.71_{-0.15}^{+0.08}$| | |$43.48_{-0.13}^{+0.12}$| | |$43.43_{-0.17}^{+0.11}$| | 44.4 | 16.6 |
| 81 | 3.19 | S3 | 1.00 | S | <1 | |$- 15.34_{-0.10}^{+0.07}$| | |$-15.37_{-0.10}^{+0.07}$| | |$43.72_{-0.10}^{+0.07}$| | |$43.69_{-0.10}^{+0.07}$| | 74.3 | 25.9 |
| 112 | |$3.15_{-0.18}^{+0.18}$| | P5 | 0.85 | S | <14 | |$-16.15 _{-0.14}^{+0.13}$| | |$-16.24_{-0.22}^{+0.13}$| | |$43.00_{-0.19}^{+0.15}$| | |$42.90_{-0.23}^{+0.18}$| | 20.7 | 8.1 |
| 129 | 3.938 | S3 | 1.00 | S | <1 | |$-15.43 _{-0.09}^{+0.07}$| | |$-15.46_{-0.10}^{+0.07}$| | |$43.84_{-0.09}^{+0.07}$| | |$43.81_{-0.11}^{+0.06}$| | 63.7 | 24.3 |
| 133 | |$3.06_{-0.36}^{+0.46}$| | P5 | 0.63 | S | |$93_{-19}^{+16}$| | |$-16.34 _{-0.23}^{+0.15}$| | <−16.57 | |$43.84_{-0.28}^{+0.21}$| | <43.62 | 15.0 | 41.0 |
| 142 | |$2.95_{-0.13}^{+0.08}$| | P5 | 0.23 | S | |$135_{-25}^{+24}$| | |$- 16.28_{-0.18}^{+0.13}$| | |$-16.41_{-0.23}^{+0.14}$| | |$44.24_{-0.25}^{+0.23}$| | |$44.11_{-0.31}^{+0.22}$| | 14.6 | 55.0 |
| 158 | |$3.19_{-0.02}^{+0.01}$| | P2 | 1.00 | S | |$54_{-10}^{+8}$| | |$-15.74 _{-0.11}^{+0.08}$| | |$-15.68_{-0.12}^{+0.08}$| | |$44.10_{-0.14}^{+0.12}$| | |$44.06_{-0.16}^{+0.11}$| | 46.4 | 72.2 |
| 177 | |$3.44_{-0.34}^{+0.14}$| | P5 | 0.98 | S | |$33_{-12}^{+14}$| | |$- 16.09_{-0.15}^{+0.09}$| | |$-16.16_{-0.14}^{+0.11}$| | |$43.55_{-0.21}^{+0.17}$| | |$43.48_{-0.21}^{+0.18}$| | 27.5 | 29.3 |
| 195 | −1 | N | 0.30 | S | <2 | |$- 16.02_{-0.13}^{+0.11}$| | |$-16.09_{-0.14}^{+0.11}$| | |$43.46_{-0.35}^{+0.13}$| | |$43.38_{-0.33}^{+0.15}$| | 28.3 | 12.9 |
| 196 | |$3.24_{-0.02}^{+0.02}$| | P2 | 1.00 | S | |$85_{-9}^{+10}$| | |$- 16.06_{-0.13}^{+0.12}$| | |$-16.13_{-0.16}^{+0.10}$| | |$44.08_{-0.19}^{+0.12}$| | |$44.00_{-0.18}^{+0.13}$| | 29.9 | 96.9 |
| 201 | |$4.43_{-1.33}^{+0.23}$| | P5 | 0.73 | S | −1b | <−16.78 | <−17.33 | <42.98 | |$44.06_{-0.19}^{+0.12}$| | 3.4 | 15.5 |
| 207 | 3.652 | S3 | 1.00 | S | <1 | |$- 15.09_{-0.08}^{+0.05}$| | |$-15.11_{-0.08}^{+0.05}$| | |$44.10_{-0.08}^{+0.05}$| | |$42.21_{-0.15}^{+0.30}$| | 242.6 | 80.7 |
| 227 | |$4.26_{-0.07}^{+0.03}$| | P2 | 1.00 | S | −1b | |$-16.70 _{-0.31}^{+0.24}$| | <−17.00 | |$42.71_{-0.55}^{+0.40}$| | <43.18 | 6.5 | 3.9 |
| 229 | 3.413 | S4 | 1.00 | S | <1 | |$- 15.43_{-0.09}^{+0.06}$| | |$-15.46_{-0.09}^{+0.06}$| | |$43.70_{-0.09}^{+0.06}$| | |$43.67_{-0.09}^{+0.06}$| | 111.8 | 48.8 |
| 257 | |$2.95_{-0.44}^{+0.29}$| | P5 | 0.35 | S | |$60_{-32}^{+37}$| | |$-16.56 _{-0.22}^{+0.14}$| | |$-16.74_{-0.30}^{+0.19}$| | |$43.24_{-0.43}^{+0.32}$| | |$43.04_{-0.47}^{+0.37}$| | 9.6 | 16.7 |
| 290 | 4.424 | S3 | 1.00 | S | <1 | |$-16.24 _{-0.17}^{+0.10}$| | |$-16.33_{-0.18}^{+0.11}$| | |$43.14_{-0.16}^{+0.11}$| | |$43.05_{-0.17}^{+0.12}$| | 17.7 | 9.1 |
| 293 | |$3.96_{-0.30}^{+0.17}$| | P5 | 1.00 | S | <8 | |$-15.32 _{-0.07}^{+0.06}$| | |$-15.33_{-0.07}^{+0.06}$| | |$43.98_{-0.12}^{+0.07}$| | |$43.96_{-0.11}^{+0.08}$| | 115.0 | 66.9 |
| 297 | 3.23 | S3 | 1.00 | S | <1 | |$-16.09 _{-0.12}^{+0.12}$| | |$-16.16_{-0.16}^{+0.10}$| | |$42.99_{-0.15}^{+0.10}$| | |$42.02_{-0.15}^{+0.11}$| | 22.3 | 10.8 |
| 310 | |$3.06_{-0.23}^{+0.36}$| | P5 | 0.70 | S | <41 | |$16.67 _{-0.32}^{+0.19}$| | <−16.93 | |$42.52_{-0.40}^{+0.30}$| | <42.47 | 6.6 | 6.5 |
| 315 | −1 | N | 0.30 | S | <1 | |$- 16.61_{-0.25}^{+0.16}$| | |$- 16.86_{-0.51}^{+0.21}$| | |$42.78_{-0.36}^{+0.23}$| | |$42.46_{-0.51}^{+0.31}$| | 7.5 | 2.8 |
| 320 | |$3.06_{-0.20}^{+0.26}$| | P5 | 0.69 | S | <1 | |$- 16.73_{-0.28}^{+0.19}$| | <−16.91 | |$42.37_{-0.31}^{+0.21}$| | <42.23 | 5.8 | 5.5 |
| 330 | 5.186 | S3 | 1.00 | S | <1 | |$-15.53 _{-0.12}^{+0.07}$| | |$-15.57_{-0.12}^{+0.07}$| | |$44.00_{-0.12}^{+0.07}$| | |$43.96_{-0.12}^{+0.07}$| | 84.4 | 31.4 |
| 363 | |$3.28_{-0.05}^{+0.05}$| | P2 | 1.00 | S | <1 | |$-16.19 _{-0.17}^{+0.14}$| | |$-16.31_{-0.21}^{+0.14}$| | |$42.92_{-0.17}^{+0.15}$| | |$42.80_{-0.21}^{+0.15}$| | 15.8 | 3.9 |
| 373 | |$3.36_{-0.29}^{+0.34}$| | P5 | 0.84 | S | |$52_{-31}^{+31}$| | |$-16.76 _{-0.27}^{+0.19}$| | <−16.92 | |$42.98_{-0.51}^{+0.25}$| | <42.85 | 5.9 | 6.5 |
| 388 | |$2.94_{-0.12}^{+0.08}$| | P5 | 0.31 | S | <1 | |$- 15.49_{-0.12}^{+0.07}$| | |$-15.53_{-0.13}^{+0.08}$| | |$43.56_{-0.13}^{+0.08}$| | |$43.52_{-0.14}^{+0.09}$| | 56.5 | 0.0 |
| 390 | |$3.19_{-0.29}^{+0.28}$| | P5 | 0.85 | H | |$204_{-46}^{+53}$| | <−16.89 | <−17.39 | |$43.38_{-0.13}^{+0.07}$| | |$43.30_{-0.16}^{+0.09}$| | 3.1 | 31.5 |
| 404 | |$3.15_{-0.13}^{+0.04}$| | P5 | 0.91 | S | <1 | |$- 14.67_{-0.06}^{+0.03}$| | |$-14.67_{-0.06}^{+0.03}$| | |$44.37_{-0.06}^{+0.04}$| | |$44.36_{-0.06}^{+0.04}$| | 555.4 | 220.8 |
| 424 | |$4.43_{-0.26}^{+0.13}$| | P5 | 1.00 | H | |$166_{-40}^{+38}$| | |$-16.37 _{-0.36}^{+0.18}$| | <−17.17 | |$43.34_{-0.25}^{+0.17}$| | |$42.32_{-0.11}^{+0.58}$| | 13.1 | 62.2 |
| 428 | |$3.03_{-0.11}^{+0.09}$| | P5 | 0.55 | S | |$18_{-3}^{+2}$| | |$-15.07 _{0.06-}^{+0.04}$| | |$-15.08_{-0.06}^{+0.04}$| | |$44.36_{-0.08}^{+0.05}$| | |$44.35_{-0.08}^{+0.05}$| | 258.7 | 188.1 |
| 439 | 3.406 | S3 | 1.00 | S | |$27_{-26}^{+73}$| | |$-16.54 _{-0.28}^{+0.17}$| | |$-16.81_{-0.46}^{+0.27}$| | |$42.76_{-0.35}^{+0.41}$| | |$42.49_{-0.51}^{+0.46}$| | 8.5 | 15.8 |
| 498 | |$4.42_{-0.24}^{+0.31}$| | P5 | 0.99 | S | |$23_{-6}^{+6}$| | |$-15.33 _{-0.09}^{+0.06}$| | |$-15.35_{-0.10}^{+0.05}$| | |$44.36_{-0.12}^{+0.09}$| | |$44.34_{-0.12}^{+0.09}$| | 149.2 | 86.2 |
| 502 | 3.157 | S3 | 1.00 | S | <1 | |$- 15.56_{-0.13}^{+0.08}$| | |$-15.61_{-0.10}^{+0.10}$| | |$43.50_{-0.13}^{+0.08}$| | |$43.45_{-0.13}^{+0.08}$| | 73.5 | 29.8 |
| 504 | |$3.36_{-0.09}^{+0.10}$| | P5 | 1.00 | H | |$831_{-537}^{+123}$| | <−16.31 | <−17.57 | |$43.14_{-0.24}^{+0.17}$| | |$42.26_{-0.13}^{+0.59}$| | 9.8 | 30.8 |
| 509 | |$3.15_{-0.57}^{+0.12}$| | P5 | 0.47 | S | <15 | |$-16.26 _{-0.26}^{+0.18}$| | <−16.93 | |$42.88_{-0.32}^{+0.21}$| | <42.30 | 15.1 | 3.2 |
| 526 | |$4.17_{-0.13}^{+0.10}$| | P5 | 1.00 | S | |$15_{-6}^{+7}$| | |$- 15.84_{-0.10}^{+0.07}$| | |$-15.88_{-0.10}^{+0.08}$| | |$43.71_{-0.14}^{+0.09}$| | |$43.67_{-0.15}^{+0.09}$| | 89.0 | 48.0 |
| 545 | 3.524 | S3 | 1.00 | S | <11 | |$- 15.27_{-0.07}^{+0.05}$| | |$-15.28_{-0.07}^{+0.05}$| | |$43.95_{-0.09}^{+0.07}$| | |$43.93_{-0.08}^{+0.08}$| | 132.4 | 46.8 |
| 572 | |$3.77_{-0.01}^{+0.03}$| | P2 | 1.00 | S | |$10_{-2}^{+2}$| | |$-15.49 _{-0.13}^{+0.08}$| | |$-15.54_{-0.17}^{+0.10}$| | |$43.94_{-0.14}^{+0.08}$| | |$43.89_{-0.17}^{+0.11}$| | 288.9 | 156.2 |
(1) ID from L17 or X16; (2) nominal redshifts (corresponding to the peaks of the PDFs) and uncertainties corresponding to the narrowest redshift intervals in which the integral of the PDFs is 0.68; (3) reference for the redshifts and PDFs: P1, P2, P3, P4 and P5 refer to photometric redshifts from S16, S14, H14, Rafferty et al. (2011) and Y14, respectively. S1 and S2 stand for spectroscopic redshift from the collection presented in L17, flagged as ‘secure’ and ‘insecure’ (but upgraded as described in Section 2.1), respectively. S3 and S4 refer to spectroscopic redshift from X16 and Y14 (for sources for which the multiwavelength matching has been improved via the visual inspection of X-ray and optical images, see Section 2.2), respectively. N refers to no redshift and, in such a case, column 2 is assigned a value of −1 and a flat PDF(z) is assumed. (4) Fraction of the PDFs at 3 ≤ z < 6 (see equation 4); (5) primary detection band (S: soft band, H: hard band; see Section 3.1); (6), (7), (8), (9) and (10): best estimates of the intrinsic column density, soft-band flux, 2–10 keV intrinsic luminosity and 68 per cent confidence-level uncertainties, respectively. For fluxes and luminosities, both the observed (i.e. not applying the Eddington bias correction in equation 5; columns 7 and 9) and the intrinsic (i.e. for which the Eddington bias correction has been applied; columns 8 and 10) values are reported.
Notes.aXID 977 has an insecure spectroscopic redshift in L17, but no photometric redshifts. Here, we conservatively discard that spectroscopic redshift and treat this source as spectroscopically unidentified.
bFor these sources, we assumed a flat distribution in column density, as their spectral quality was too poor to perform a spectral analysis. (11) and (12): net counts in the soft and hard bands, respectively.
| ID . | z . | Ref . | P . | Band . | NH . | |$\mathrm{log}F^{\mathrm{obs}}_{0.5-2\, \mathrm{keV}}$| . | |$\mathrm{log}F^{\mathrm{intr}}_{0.5-2\, \mathrm{keV}}$| . | |$\mathrm{log}L^{\mathrm{obs}}_{2-10\, \mathrm{keV}}$| . | |$\mathrm{log}L^{\mathrm{intr}}_{2-10\, \mathrm{keV}}$| . | Net counts . | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | (3 ≤ z < 6) . | . | (1022 cm−2) . | (erg cm−2 s−1) . | (erg cm−2 s−1) . | (erg s−1) . | (erg s−1) . | (0.5–2 keV) . | (2–7 keV) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| CDF-S | |||||||||||
| 8 | |$3.13_{-0.48}^{+3.28}$| | P3 | 0.55 | S | |$59_{-18}^{+24}$| | |$-15.56_{-0.08}^{+0.07}$| | |$-15.59_{-0.08}^{+0.08}$| | |$44.43_{-0.23}^{+0.20}$| | |$44.41_{-0.27}^{+0.17}$| | 99.2 | 119.4 |
| 9 | |$1.93_{-0.20}^{+1.39}$| | P3 | 0.44 | S | |$11_{-5}^{+8}$| | |$-15.31_{-0.08}^{+0.05}$| | |$-15.32_{-0.07}^{+0.06}$| | |$44.04_{-0.13}^{+0.16}$| | |$44.03_{-0.14}^{+0.15}$| | 140.7 | 95.4 |
| 10 | |$2.93_{-0.40}^{+0.85}$| | P3 | 0.32 | S | |$3_{-2}^{+2}$| | |$-15.40_{-0.11}^{+0.06}$| | |$-15.43_{-0.09}^{+0.08}$| | |$43.76_{-0.13}^{+0.09}$| | |$43.73_{-0.14}^{+0.09}$| | 70.1 | 38.9 |
| 12 | 3.153 | S2 | 1.00 | H | |$135_{-46}^{+69}$| | |$-16.59_{-0.75}^{+0.21}$| | <− 17.28 | |$44.06_{-0.18}^{+0.12}$| | |$42.21_{-0.22}^{+1.32}$| | 12.4 | 89.0 |
| 25 | −1 | N | 0.30 | S | <74 | |$-15.65_{-0.13}^{+0.08}$| | |$-15.69_{-0.15}^{+0.08}$| | |$43.63_{-0.20}^{+0.44}$| | |$43.60_{-0.18}^{+0.46}$| | 75.0 | 88.3 |
| 29 | |$3.33_{-0.29}^{+0.32}$| | P4 | 0.99 | S | <1 | |$-15.63_{-0.10}^{+0.05}$| | |$-15.65_{-0.11}^{+0.05}$| | |$43.47_{-0.13}^{+0.12}$| | |$43.45_{-0.12}^{+0.13}$| | 119.0 | 44.4 |
| 35 | −1 | N | 0.30 | S | |$25_{-17}^{+29}$| | |$-15.61_{-0.09}^{+0.09}$| | |$-15.63_{-0.11}^{+0.08}$| | |$43.97_{-0.20}^{+0.21}$| | |$43.94_{-0.22}^{+0.20}$| | 98.9 | 67.8 |
| 53 | 3.202 | S1 | 1.00 | S | <22 | |$-16.41_{-0.36}^{+0.18}$| | <−16.97 | |$42.74_{-0.40}^{+0.20}$| | <42.30 | 29.8 | 40.7 |
| 84 | |$3.12_{-0.59}^{+0.35}$| | P1 | 0.70 | S | |$49_{-13}^{+14}$| | |$-16.07_{-0.11}^{+0.06}$| | |$-16.10_{-0.12}^{+0.06}$| | |$43.75_{-0.19}^{+0.14}$| | |$43.71_{-0.19}^{+0.15}$| | 80.4 | 98.5 |
| 88 | −1 | N | 0.30 | S | |$83_{-26}^{+19}$| | |$-15.98_{-0.08}^{+0.06}$| | |$-16.01_{-0.09}^{+0.06}$| | |$44.19_{-0.27}^{+0.12}$| | |$44.16_{-0.25}^{+0.14}$| | 99.3 | 195.6 |
| 99 | |$4.24_{-0.36}^{+0.05}$| | P1 | 0.99 | S | |$30_{-28}^{+34}$| | |$-15.91_{-0.19}^{+0.14}$| | <−16.19 | |$43.55_{-0.26}^{+0.22}$| | <43.32 | 41.3 | 47.8 |
| 101 | |$4.34_{-0.61}^{+0.02}$| | P1 | 1.00 | S | |$68_{-22}^{+12}$| | |$-16.11_{-0.16}^{+0.09}$| | |$-16.20_{-0.27}^{+0.18}$| | |$43.87_{-0.24}^{+0.24}$| | |$43.78_{-0.37}^{+0.22}$| | 51.2 | 110.8 |
| 109 | |$3.58_{-0.04}^{+0.03}$| | P1 | 1.0 | S | |$28_{-6}^{+5}$| | |$-16.48_{-0.23}^{+0.15}$| | <−16.68 | |$43.14_{-0.25}^{+0.16}$| | <42.96 | 144.9 | 150.9 |
| 110 | |$3.08_{-0.08}^{+0.38}$| | P1 | 0.87 | S | <1 | |$-16.54_{-0.24}^{+0.15}$| | <−16.74 | |$42.55_{-0.24}^{+0.19}$| | <42.40 | 22.8 | 4.4 |
| 121 | |$3.42_{-0.05}^{+0.03}$| | P1 | 1.00 | S | |$68_{-21}^{+14}$| | |$-16.27_{-0.13}^{+0.09}$| | |$-16.33_{-0.16}^{+0.11}$| | |$43.69_{-0.22}^{+0.16}$| | |$43.62_{-0.27}^{+0.16}$| | 50.4 | 65.9 |
| 126 | |$3.13_{-0.03}^{+0.07}$| | P1 | 0.95 | S | <28 | |$-15.84_{-0.23}^{+0.13}$| | <−16.55 | |$43.32_{-0.22}^{+0.20}$| | <42.67 | 39.9 | 53.1 |
| 133 | 3.474 | S1 | 1.00 | H | |$141_{-50}^{+73}$| | <−16.96 | <−17.39 | |$43.61_{-0.22}^{+0.13}$| | |$42.23_{-0.15}^{+0.93}$| | 4.0 | 56.3 |
| 165 | |$3.55_{-0.02}^{+0.02}$| | P1 | 1.00 | S | |$16_{-6}^{+6}$| | |$-15.94_{-0.09}^{+0.07}$| | |$-15.96_{-0.11}^{+0.06}$| | |$43.52_{-0.13}^{+0.09}$| | |$43.5_{-0.15}^{+0.08}$| | 71.9 | 34.2 |
| 185 | |$3.09_{-0.03}^{+0.04}$| | P1 | 0.87 | S | |$39_{-24}^{+24}$| | |$-16.70_{-0.19}^{+0.11}$| | |$-16.82_{-0.29}^{+0.16}$| | |$42.86_{-0.37}^{+0.22}$| | |$42.71_{-0.45}^{+0.25}$| | 18.7 | 22.6 |
| 189 | |$3.65_{-0.04}^{+0.07}$| | P1 | 1.00 | H | |$107_{-33}^{+25}$| | <−16.97 | <−17.31 | |$43.38_{-0.16}^{+0.09}$| | |$43.30_{-0.19}^{+0.12}$| | 7.1 | 34.5 |
| 214 | 3.74 | S2 | 1.00 | S | |$26_{-2}^{+1}$| | |$-14.81_{-0.03}^{+0.00}$| | |$-14.82_{-0.03}^{+0.01}$| | |$44.81_{-0.03}^{+0.02}$| | |$44.81_{-0.03}^{+0.02}$| | 1377.4 | 1213.8 |
| 223 | |$3.76_{-0.17}^{+0.06}$| | P1 | 1.00 | S | <14 | |$-16.46_{-0.15}^{+0.11}$| | |$-16.55_{-0.22}^{+0.13}$| | |$42.80_{-0.19}^{+0.11}$| | |$42.71_{-0.23}^{+0.15}$| | 27.9 | 0.0 |
| 238 | |$5.96_{-0.04}^{+0.01}$| | P2 | 1.00 | S | <66 | |$-16.29_{-0.17}^{+0.09}$| | |$-16.37_{-0.21}^{+0.14}$| | |$43.42_{-0.17}^{+0.15}$| | |$43.35_{-0.24}^{+0.18}$| | 40.5 | 7.1 |
| 248 | |$3.44_{-0.13}^{+0.22}$| | P1 | 1.00 | S | |$39_{-7}^{+5}$| | |$-15.55_{-0.06}^{+0.04}$| | |$-15.56_{-0.06}^{+0.04}$| | |$44.18_{-0.10}^{+0.07}$| | |$44.17_{-0.10}^{+0.07}$| | 186.9 | 192.9 |
| 276 | |$3.12_{-0.01}^{+0.02}$| | P1 | 1.00 | S | |$15_{-3}^{+3}$| | |$-15.90_{-0.06}^{+0.04}$| | |$-15.91_{-0.06}^{+0.04}$| | |$43.51_{-0.08}^{+0.05}$| | |$43.50_{-0.08}^{+0.05}$| | 122.9 | 9.2 |
| 299 | |$3.79_{-0.05}^{+0.05}$| | P1 | 1.00 | S | |$10_{-9}^{+15}$| | |$-16.63_{-0.16}^{+0.10}$| | |$-16.71_{-0.19}^{+0.12}$| | |$42.67_{-0.18}^{+0.13}$| | |$42.59_{-0.21}^{+0.15}$| | 19.4 | 21.0 |
| 329 | |$3.47_{-0.10}^{+0.10}$| | P1 | 1.00 | S | |$32_{-29}^{+33}$| | |$-16.69_{-0.20}^{+0.14}$| | <−16.74 | |$42.61_{-0.25}^{+0.31}$| | <42.77 | 17.2 | 17.1 |
| 337 | 3.660 | S1 | 1.00 | S | |$98_{-9}^{+7}$| | |$-16.08_{-0.09}^{+0.04}$| | |$-16.10_{-0.08}^{+0.05}$| | |$44.16_{-0.10}^{+0.07}$| | |$44.14_{-0.09}^{+0.08}$| | 78.3 | 221.4 |
| 351 | |$3.86_{-0.54}^{+0.14}$| | P1 | 0.97 | S | |$74_{-23}^{+9}$| | |$-16.28_{-0.14}^{+0.08}$| | |$-16.34_{-0.17}^{+0.10}$| | |$43.71_{-0.19}^{+0.17}$| | |$43.65_{-0.26}^{+0.15}$| | 50.8 | 73.2 |
| 356 | |$3.38_{-0.19}^{+0.01}$| | P1 | 0.99 | S | <8 | |$-16.38_{-0.14}^{+0.07}$| | |$-16.43_{-0.15}^{+0.08}$| | |$42.76_{-0.13}^{+0.10}$| | |$42.71_{-0.15}^{+0.10}$| | 31.9 | 31.4 |
| 366 | |$3.67_{-0.18}^{+0.53}$| | P1 | 1.00 | S | |$81_{-15}^{+14}$| | |$-16.15_{-0.10}^{+0.06}$| | |$-16.18_{-0.10}^{+0.07}$| | |$43.96_{-0.14}^{+0.14}$| | |$43.93_{-0.16}^{+0.13}$| | 66.8 | 131.2 |
| 368 | |$3.21_{-0.08}^{+0.09}$| | P1 | 1.00 | S | <1 | |$-16.57_{-0.15}^{+0.10}$| | |$-16.65_{-0.19}^{+0.11}$| | |$42.52_{-0.19}^{+0.10}$| | |$42.44_{-0.20}^{+0.11}$| | 20.9 | 0.0 |
| 414 | |$3.58_{-0.10}^{+0.11}$| | P1 | 1.00 | H | −1** | <−17.28 | <−17.41 | |$42.71_{-0.36}^{+0.20}$| | <42.61 | 0.3 | 9.7 |
| 416 | 3.470 | S1 | 1.00 | S | <1 | |$-16.63_{-0.19}^{+0.10}$| | |$-16.75_{-0.27}^{+0.19}$| | |$42.52_{-0.19}^{+0.10}$| | |$42.40_{-0.26}^{+0.15}$| | 18.0 | 0.4 |
| 433 | |$4.11_{-0.12}^{+0.15}$| | P1 | 1.00 | S | <1 | |$-16.80_{-0.23}^{+0.13}$| | <−16.86 | |$42.55_{-0.24}^{+0.14}$| | <42.51 | 12.9 | 0.3 |
| 459 | |$3.91_{-0.04}^{+0.05}$| | P1 | 1.00 | H | |$166_{-64}^{+80}$| | <17.20 | <−17.43 | |$43.34_{-0.25}^{+0.17}$| | <43.11 | 0.3 | 24.4 |
| 462 | |$3.88_{-0.78}^{+0.41}$| | P1 | 0.95 | H | |$51_{-21}^{+21}$| | |$-16.24_{-0.44}^{+0.19}$| | <−17.12 | |$43.92_{-0.25}^{+0.16}$| | <42.69 | 25.6 | 63.5 |
| 464 | |$4.76_{-0.10}^{+0.02}$| | P2 | 1.00 | S | <16 | |$-15.67_{-0.07}^{+0.04}$| | |$-15.68_{-0.06}^{+0.05}$| | |$43.81_{-0.08}^{+0.06}$| | |$43.80_{-0.08}^{+0.06}$| | 160.5 | 10.1 |
| 472 | |$4.16_{-0.17}^{+0.02}$| | P1 | 1.00 | H | |$110_{-94}^{+317}$| | <−16.97 | <−17.28 | |$43.14_{-0.24}^{+0.17}$| | <43.00 | 7.0 | 19.2 |
| 490 | |$4.73_{-0.08}^{+0.06}$| | P1 | 1.00 | S | |$71_{-8}^{+9}$| | |$-16.05_{-0.07}^{+0.04}$| | |$-16.06_{-0.07}^{+0.04}$| | |$44.03_{-0.08}^{+0.07}$| | |$44.01_{-0.10}^{+0.06}$| | 86.8 | 123.3 |
| 500 | |$3.15_{-0.02}^{+0.04}$| | P1 | 1.00 | S | |$40_{-38}^{+89}$| | <−16.79 | <−17.19 | <42.83 | <42.46 | 10.4 | 16.6 |
| 503 | |$3.14_{-0.07}^{+0.03}$| | P1 | 0.99 | S | <5 | <−16.93 | <−17.19 | <42.20 | <41.95 | 7.0 | 7.6 |
| 517 | 3.256 | S2 | 1.00 | S | <1 | |$-16.24 _{-0.11}^{+0.06}$| | |$-16.27_{-0.12}^{+0.06}$| | |$42.85_{-0.10}^{+0.07}$| | |$42.82_{-0.11}^{+0.07}$| | 44.1 | 24.0 |
| 521 | |$2.96_{-0.07}^{+0.07}$| | P1 | 0.41 | S | |$21_{-19}^{+60}$| | |$-16.89 _{-0.33}^{+0.18}$| | <−17.11 | |$42.34_{-0.36}^{+0.39}$| | |$42.60_{-0.19}^{+0.15}$| | 13.0 | 27.7 |
| 527 | |$3.76_{-0.29}^{+0.05}$| | P1 | 1.00 | S | <1 | |$-16.55 _{-0.15}^{+0.10}$| | |$-16.63_{-0.19}^{+0.12}$| | |$42.68_{-0.17}^{+0.12}$| | |$42.60_{-0.19}^{+0.15}$| | 22.5 | 0.0 |
| 539 | 4.762 | S1 | 1.00 | H | |$102_{-47}^{+49}$| | |$-16.48 _{-0.42}^{+0.18}$| | <−17.09 | |$43.83_{-0.27}^{+0.13}$| | <42.83 | 27.0 | 61.2 |
| 551 | 3.700 | S1 | 1.00 | S | |$76_{-5}^{+4}$| | |$-15.71 _{-0.05}^{+0.03}$| | |$-15.72_{-0.05}^{+0.03}$| | |$44.37_{-0.05}^{+0.05}$| | |$44.37_{-0.06}^{+0.04}$| | 209.8 | 441.4 |
| 580 | |$3.17_{-0.12}^{+0.19}$| | P1 | 0.97 | S | |$42_{-8}^{+10}$| | |$-16.34 _{-0.08}^{+0.06}$| | |$-16.36_{-0.10}^{+0.05}$| | |$43.40_{-0.13}^{+0.11}$| | |$43.38_{-0.12}^{+0.12}$| | 45.1 | 66.6 |
| 617 | |$3.58_{-0.13}^{+0.20}$| | P1 | 1.00 | S | <1 | |$-15.77 _{-0.07}^{+0.03}$| | |$-15.78_{-0.07}^{+0.03}$| | |$43.41_{-0.08}^{+0.05}$| | |$43.40_{-0.07}^{+0.06}$| | 136.0 | 69.1 |
| 619 | |$3.67_{-0.09}^{+0.04}$| | P1 | 1.00 | S | |$68_{-23}^{+18}$| | |$-16.85 _{-0.20}^{+0.10}$| | |$-16.97_{-0.22}^{+0.15}$| | |$43.12_{-0.27}^{+0.19}$| | |$42.99_{-0.32}^{+0.20}$| | 12.3 | 23.2 |
| 622 | |$3.33_{-0.17}^{+0.09}$| | P1 | 1.00 | S | <1 | |$- 16.50_{-0.19}^{+0.11}$| | |$-16.62_{-0.41}^{+0.18}$| | |$42.62_{-0.20}^{+0.14}$| | |$42.49_{-0.44}^{+0.20}$| | 24.5 | 0.0 |
| 623 | |$3.58_{-0.03}^{+0.02}$| | P1 | 1.00 | S | |$27_{-10}^{+10}$| | |$- 16.43_{-0.12}^{+0.07}$| | |$-16.47_{-0.12}^{+0.08}$| | |$43.17_{-0.14}^{+0.13}$| | |$43.13_{-0.18}^{+0.11}$| | 36.7 | 34.5 |
| 640 | |$3.77_{-0.03}^{+0.02}$| | P1 | 1.00 | S | |$16_{-15}^{+18}$| | |$-16.68 _{-0.16}^{+0.10}$| | |$-16.75_{-0.19}^{+0.10}$| | |$42.65_{-0.18}^{+0.16}$| | |$42.58_{-0.18}^{+0.18}$| | 17.7 | 3.5 |
| 657 | |$3.58_{-0.10}^{+0.17}$| | P1 | 1.00 | S | |$115_{-19}^{+11}$| | |$- 16.59_{-0.14}^{+0.09}$| | |$-16.66_{-0.17}^{+0.10}$| | |$43.76_{-0.19}^{+0.13}$| | |$43.69_{-0.20}^{+0.15}$| | 26.2 | 79.6 |
| 662 | |$4.84_{-0.12}^{+0.05}$| | P1 | 1.00 | S | <54 | |$-16.82 _{-0.24}^{+0.14}$| | <−16.90 | |$42.71_{-0.27}^{+0.18}$| | <42.68 | 13.3 | 2.6 |
| 692 | |$3.42_{-0.08}^{+0.13}$| | P1 | 1.00 | H | |$117_{-51}^{+56}$| | <−17.14 | <−17.37 | |$42.84_{-0.31}^{+0.18}$| | <43.22 | 3.6 | 9.7 |
| 714 | |$3.48_{-0.09}^{+0.03}$| | P1 | 1.00 | S | <1 | |$- 16.25_{-0.10}^{+0.08}$| | |$-16.29_{-0.13}^{+0.07}$| | |$42.91_{-0.13}^{+0.07}$| | |$42.87_{-0.13}^{+0.08}$| | 44.4 | 0.0 |
| 723 | 3.045 | S1 | 1.00 | S | |$59_{-6}^{+4}$| | |$-16.02 _{-0.05}^{+0.05}$| | |$-16.03_{-0.05}^{+0.05}$| | |$43.88_{-0.10}^{+0.05}$| | |$43.87_{-0.10}^{+0.05}$| | 93.0 | 188.1 |
| 746 | 3.064 | S1 | 1.00 | S | |$52_{-2}^{+1}$| | |$- 15.14_{-0.05}^{+0.02}$| | |$-15.15_{-0.04}^{+0.03}$| | |$44.69_{-0.05}^{+0.03}$| | |$44.68_{-0.05}^{+0.03}$| | 689.2 | 1281.4 |
| 758 | |$3.08_{-0.03}^{+0.01}$| | P1 | 1.00 | S | <36 | <−17.12 | <−17.37 | <42.13 | <41.92 | 8.7 | 13.5 |
| 760 | 3.35 | S2 | 1.00 | S | |$74_{-5}^{+2}$| | |$- 15.111_{-0.03}^{+0.03}$| | |$-15.11_{-0.04}^{+0.02}$| | |$44.94_{-0.05}^{+0.03}$| | |$44.94_{-0.05}^{+0.03}$| | 763.5 | 999.8 |
| 774 | 3.61 | S1 | 1.00 | S | |$7_{-1}^{+1}$| | |$-14.71 _{-0.04}^{+0.03}$| | |$-14.71_{-0.05}^{+0.02}$| | |$44.63_{-0.03}^{+0.04}$| | |$44.63_{-0.04}^{+0.03}$| | 1162.8 | 691.5 |
| 788 | 3.193 | S2 | 1.00 | S | |$2_{-1}^{+1}$| | |$- 15.11_{-0.03}^{+0.03}$| | |$-15.11_{-0.04}^{+0.02}$| | |$44.01_{-0.05}^{+0.02}$| | |$44.01_{-0.05}^{+0.02}$| | 646.8 | 381.8 |
| 811 | 3.471 | S1 | 1.00 | S | <1 | |$- 15.37_{-0.05}^{+0.02}$| | |$-15.37_{-0.05}^{+0.02}$| | |$43.77_{-0.04}^{+0.03}$| | |$43.77_{-0.05}^{+0.02}$| | 312.9 | 194.9 |
| 853 | |$3.72_{-0.14}^ {+0.13}$| | P1 | 1.00 | S | <2 | |$- 16.21_{-0.29}^{+0.16}$| | <−16.81 | |$43.05_{-0.35}^{+0.18}$| | <42.60 | 37.0 | 69.7 |
| 859 | |$2.88_{-0.09}^{+0.13}$| | P1 | 0.22 | S | <3 | |$-16.71 _{-0.30}^{+0.17}$| | <−16.93 | |$42.38_{-0.37}^{+0.21}$| | <42.34 | 16.4 | 1.6 |
| 873 | |$3.76_{-0.06}^{+0.04}$| | P1 | 1.00 | S | <1 | |$- 16.25_{-0.12}^{+0.10}$| | |$-16.31_{-0.16}^{+0.11}$| | |$42.98_{-0.13}^{+0.10}$| | |$42.92_{-0.17}^{+0.11}$| | 41.4 | 0.0 |
| 876 | 3.470 | S2 | 1.00 | S | |$11_{-1}^{+1}$| | |$-14.57 _{-0.01}^{+0.01}$| | |$-14.57_{-0.01}^{+0.01}$| | |$44.82_{-0.02}^{+0.01}$| | |$44.82_{-0.02}^{+0.01}$| | 2211.9 | 1482.2 |
| 885 | |$3.08_{-0.10}^{+0.02}$| | P1 | 0.78 | S | |$95_{-10}^{+10}$| | |$-16.18 _{-0.10}^{+0.07}$| | |$-16.21_{-0.13}^{+0.06}$| | |$44.02_{-0.14}^{+0.10}$| | |$43.98_{-0.13}^{+0.12}$| | 64.4 | 201.9 |
| 901 | |$3.51_{-0.12}^{+0.25}$| | P1 | 1.00 | S | <43 | |$- 16.63_{-0.32}^{+0.17}$| | <−16.94 | |$42.65_{-0.34}^{+0.25}$| | <42.43 | 19.8 | 14.7 |
| 908 | |$3.60_{-0.20}^{+0.05}$| | P1 | 1.00 | H | >23 | |$-16.94 _{-0.55}^{+0.61}$| | <−17.20 | |$43.64_{-0.26}^{+0.27}$| | <43.01 | 7.5 | 52.5 |
| 921 | 3.082 | S1 | 1.00 | S | <4 | |$- 15.33_{-0.07}^{+0.02}$| | |$-15.34_{-0.06}^{+0.03}$| | |$43.73_{-0.04}^{+0.05}$| | |$43.73_{-0.07}^{+0.03}$| | 347.6 | 204.8 |
| 926 | |$4.27_{-1.5}^{+0.06}$| | P1 | 0.53 | S | <7 | |$-15.61 _{-0.05}^{+0.05}$| | |$-15.62_{-0.07}^{+0.04}$| | |$43.76_{-0.06}^{+0.06}$| | |$43.75_{-0.08}^{+0.05}$| | 182.2 | 116.4 |
| 939 | −1 | N | 0.30 | S | <1 | |$- 16.00_{-0.11}^{+0.10}$| | |$-16.05_{-0.16}^{+0.10}$| | |$43.47_{-0.36}^{+0.12}$| | |$43.38_{-0.36}^{+0.15}$| | 62.8 | 15.0 |
| 940 | |$3.00_{-0.19}^{+0.26}$| | P1 | 0.63 | S | |$35_{-10}^{+7}$| | |$-16.00 _{-0.09}^{+0.06}$| | |$-16.03_{-0.09}^{+0.07}$| | |$43.64_{-0.16}^{+0.11}$| | |$43.61_{-0.14}^{+0.13}$| | 91.7 | 97.4 |
| 962 | |$4.68_{-2.25}^{+2.25}$| | P3 | 0.45 | S | |$141_{-48}^{+49}$| | |$- 16.40_{-0.31}^{+0.15}$| | <−16.95 | |$44.01_{-0.43}^{+0.26}$| | <43.54 | 35.2 | 130.2 |
| 965 | |$3.64_{-0.80}^{+0.11}$| | P3 | 0.65 | S | <1 | |$- 15.79_{-0.10}^{+0.06}$| | |$-15.81_{-0.11}^{+0.06}$| | |$43.36_{-0.13}^{+0.10}$| | |$43.33_{-0.14}^{+0.10}$| | 104.0 | 40.2 |
| 971 | |$2.17_{-0.59}^{+1.24}$| | P3 | 0.35 | S | |$36_{-13}^{+8}$| | |$- 15.61_{-0.05}^{+0.02}$| | |$-15.16_{-0.05}^{+0.02}$| | |$44.73_{-0.28}^{+0.11}$| | |$44.73_{-0.29}^{+0.10}$| | 536.7 | 513.2 |
| 974 | |$3.23_{-0.13}^{+0.18}$| | P3 | 0.92 | S | |$9_{-8}^{+10}$| | |$-15.76 _{-0.10}^{+0.08}$| | |$-15.79_{-0.13}^{+0.07}$| | |$43.44_{-0.13}^{+0.11}$| | |$43.41_{-0.14}^{+0.11}$| | 105.6 | 71.5 |
| 977a | −1 | N | 0.3 | S | |$89_{-29}^{+34}$| | |$-16.13 _{-0.18}^{+0.10}$| | <−16.20 | |$44.04_{-0.29}^{+0.23}$| | <44.03 | 48.6 | 128.0 |
| 990 | 3.724 | S1 | 1.00 | S | |$62_{-54}^{+64}$| | |$- 16.06_{-0.28}^{+0.17}$| | <−16.99 | |$43.35_{-0.24}^{+0.58}$| | <42.86 | 41.0 | 61.3 |
| CDF-N | |||||||||||
| 31 | |$3.45_{-0.36}^{+0.21}$| | P5 | 0.95 | S | <1 | |$-15.66 _{-0.12}^{+0.08}$| | |$-15.71_{-0.15}^{+0.08}$| | |$43.48_{-0.13}^{+0.12}$| | |$43.43_{-0.17}^{+0.11}$| | 44.4 | 16.6 |
| 81 | 3.19 | S3 | 1.00 | S | <1 | |$- 15.34_{-0.10}^{+0.07}$| | |$-15.37_{-0.10}^{+0.07}$| | |$43.72_{-0.10}^{+0.07}$| | |$43.69_{-0.10}^{+0.07}$| | 74.3 | 25.9 |
| 112 | |$3.15_{-0.18}^{+0.18}$| | P5 | 0.85 | S | <14 | |$-16.15 _{-0.14}^{+0.13}$| | |$-16.24_{-0.22}^{+0.13}$| | |$43.00_{-0.19}^{+0.15}$| | |$42.90_{-0.23}^{+0.18}$| | 20.7 | 8.1 |
| 129 | 3.938 | S3 | 1.00 | S | <1 | |$-15.43 _{-0.09}^{+0.07}$| | |$-15.46_{-0.10}^{+0.07}$| | |$43.84_{-0.09}^{+0.07}$| | |$43.81_{-0.11}^{+0.06}$| | 63.7 | 24.3 |
| 133 | |$3.06_{-0.36}^{+0.46}$| | P5 | 0.63 | S | |$93_{-19}^{+16}$| | |$-16.34 _{-0.23}^{+0.15}$| | <−16.57 | |$43.84_{-0.28}^{+0.21}$| | <43.62 | 15.0 | 41.0 |
| 142 | |$2.95_{-0.13}^{+0.08}$| | P5 | 0.23 | S | |$135_{-25}^{+24}$| | |$- 16.28_{-0.18}^{+0.13}$| | |$-16.41_{-0.23}^{+0.14}$| | |$44.24_{-0.25}^{+0.23}$| | |$44.11_{-0.31}^{+0.22}$| | 14.6 | 55.0 |
| 158 | |$3.19_{-0.02}^{+0.01}$| | P2 | 1.00 | S | |$54_{-10}^{+8}$| | |$-15.74 _{-0.11}^{+0.08}$| | |$-15.68_{-0.12}^{+0.08}$| | |$44.10_{-0.14}^{+0.12}$| | |$44.06_{-0.16}^{+0.11}$| | 46.4 | 72.2 |
| 177 | |$3.44_{-0.34}^{+0.14}$| | P5 | 0.98 | S | |$33_{-12}^{+14}$| | |$- 16.09_{-0.15}^{+0.09}$| | |$-16.16_{-0.14}^{+0.11}$| | |$43.55_{-0.21}^{+0.17}$| | |$43.48_{-0.21}^{+0.18}$| | 27.5 | 29.3 |
| 195 | −1 | N | 0.30 | S | <2 | |$- 16.02_{-0.13}^{+0.11}$| | |$-16.09_{-0.14}^{+0.11}$| | |$43.46_{-0.35}^{+0.13}$| | |$43.38_{-0.33}^{+0.15}$| | 28.3 | 12.9 |
| 196 | |$3.24_{-0.02}^{+0.02}$| | P2 | 1.00 | S | |$85_{-9}^{+10}$| | |$- 16.06_{-0.13}^{+0.12}$| | |$-16.13_{-0.16}^{+0.10}$| | |$44.08_{-0.19}^{+0.12}$| | |$44.00_{-0.18}^{+0.13}$| | 29.9 | 96.9 |
| 201 | |$4.43_{-1.33}^{+0.23}$| | P5 | 0.73 | S | −1b | <−16.78 | <−17.33 | <42.98 | |$44.06_{-0.19}^{+0.12}$| | 3.4 | 15.5 |
| 207 | 3.652 | S3 | 1.00 | S | <1 | |$- 15.09_{-0.08}^{+0.05}$| | |$-15.11_{-0.08}^{+0.05}$| | |$44.10_{-0.08}^{+0.05}$| | |$42.21_{-0.15}^{+0.30}$| | 242.6 | 80.7 |
| 227 | |$4.26_{-0.07}^{+0.03}$| | P2 | 1.00 | S | −1b | |$-16.70 _{-0.31}^{+0.24}$| | <−17.00 | |$42.71_{-0.55}^{+0.40}$| | <43.18 | 6.5 | 3.9 |
| 229 | 3.413 | S4 | 1.00 | S | <1 | |$- 15.43_{-0.09}^{+0.06}$| | |$-15.46_{-0.09}^{+0.06}$| | |$43.70_{-0.09}^{+0.06}$| | |$43.67_{-0.09}^{+0.06}$| | 111.8 | 48.8 |
| 257 | |$2.95_{-0.44}^{+0.29}$| | P5 | 0.35 | S | |$60_{-32}^{+37}$| | |$-16.56 _{-0.22}^{+0.14}$| | |$-16.74_{-0.30}^{+0.19}$| | |$43.24_{-0.43}^{+0.32}$| | |$43.04_{-0.47}^{+0.37}$| | 9.6 | 16.7 |
| 290 | 4.424 | S3 | 1.00 | S | <1 | |$-16.24 _{-0.17}^{+0.10}$| | |$-16.33_{-0.18}^{+0.11}$| | |$43.14_{-0.16}^{+0.11}$| | |$43.05_{-0.17}^{+0.12}$| | 17.7 | 9.1 |
| 293 | |$3.96_{-0.30}^{+0.17}$| | P5 | 1.00 | S | <8 | |$-15.32 _{-0.07}^{+0.06}$| | |$-15.33_{-0.07}^{+0.06}$| | |$43.98_{-0.12}^{+0.07}$| | |$43.96_{-0.11}^{+0.08}$| | 115.0 | 66.9 |
| 297 | 3.23 | S3 | 1.00 | S | <1 | |$-16.09 _{-0.12}^{+0.12}$| | |$-16.16_{-0.16}^{+0.10}$| | |$42.99_{-0.15}^{+0.10}$| | |$42.02_{-0.15}^{+0.11}$| | 22.3 | 10.8 |
| 310 | |$3.06_{-0.23}^{+0.36}$| | P5 | 0.70 | S | <41 | |$16.67 _{-0.32}^{+0.19}$| | <−16.93 | |$42.52_{-0.40}^{+0.30}$| | <42.47 | 6.6 | 6.5 |
| 315 | −1 | N | 0.30 | S | <1 | |$- 16.61_{-0.25}^{+0.16}$| | |$- 16.86_{-0.51}^{+0.21}$| | |$42.78_{-0.36}^{+0.23}$| | |$42.46_{-0.51}^{+0.31}$| | 7.5 | 2.8 |
| 320 | |$3.06_{-0.20}^{+0.26}$| | P5 | 0.69 | S | <1 | |$- 16.73_{-0.28}^{+0.19}$| | <−16.91 | |$42.37_{-0.31}^{+0.21}$| | <42.23 | 5.8 | 5.5 |
| 330 | 5.186 | S3 | 1.00 | S | <1 | |$-15.53 _{-0.12}^{+0.07}$| | |$-15.57_{-0.12}^{+0.07}$| | |$44.00_{-0.12}^{+0.07}$| | |$43.96_{-0.12}^{+0.07}$| | 84.4 | 31.4 |
| 363 | |$3.28_{-0.05}^{+0.05}$| | P2 | 1.00 | S | <1 | |$-16.19 _{-0.17}^{+0.14}$| | |$-16.31_{-0.21}^{+0.14}$| | |$42.92_{-0.17}^{+0.15}$| | |$42.80_{-0.21}^{+0.15}$| | 15.8 | 3.9 |
| 373 | |$3.36_{-0.29}^{+0.34}$| | P5 | 0.84 | S | |$52_{-31}^{+31}$| | |$-16.76 _{-0.27}^{+0.19}$| | <−16.92 | |$42.98_{-0.51}^{+0.25}$| | <42.85 | 5.9 | 6.5 |
| 388 | |$2.94_{-0.12}^{+0.08}$| | P5 | 0.31 | S | <1 | |$- 15.49_{-0.12}^{+0.07}$| | |$-15.53_{-0.13}^{+0.08}$| | |$43.56_{-0.13}^{+0.08}$| | |$43.52_{-0.14}^{+0.09}$| | 56.5 | 0.0 |
| 390 | |$3.19_{-0.29}^{+0.28}$| | P5 | 0.85 | H | |$204_{-46}^{+53}$| | <−16.89 | <−17.39 | |$43.38_{-0.13}^{+0.07}$| | |$43.30_{-0.16}^{+0.09}$| | 3.1 | 31.5 |
| 404 | |$3.15_{-0.13}^{+0.04}$| | P5 | 0.91 | S | <1 | |$- 14.67_{-0.06}^{+0.03}$| | |$-14.67_{-0.06}^{+0.03}$| | |$44.37_{-0.06}^{+0.04}$| | |$44.36_{-0.06}^{+0.04}$| | 555.4 | 220.8 |
| 424 | |$4.43_{-0.26}^{+0.13}$| | P5 | 1.00 | H | |$166_{-40}^{+38}$| | |$-16.37 _{-0.36}^{+0.18}$| | <−17.17 | |$43.34_{-0.25}^{+0.17}$| | |$42.32_{-0.11}^{+0.58}$| | 13.1 | 62.2 |
| 428 | |$3.03_{-0.11}^{+0.09}$| | P5 | 0.55 | S | |$18_{-3}^{+2}$| | |$-15.07 _{0.06-}^{+0.04}$| | |$-15.08_{-0.06}^{+0.04}$| | |$44.36_{-0.08}^{+0.05}$| | |$44.35_{-0.08}^{+0.05}$| | 258.7 | 188.1 |
| 439 | 3.406 | S3 | 1.00 | S | |$27_{-26}^{+73}$| | |$-16.54 _{-0.28}^{+0.17}$| | |$-16.81_{-0.46}^{+0.27}$| | |$42.76_{-0.35}^{+0.41}$| | |$42.49_{-0.51}^{+0.46}$| | 8.5 | 15.8 |
| 498 | |$4.42_{-0.24}^{+0.31}$| | P5 | 0.99 | S | |$23_{-6}^{+6}$| | |$-15.33 _{-0.09}^{+0.06}$| | |$-15.35_{-0.10}^{+0.05}$| | |$44.36_{-0.12}^{+0.09}$| | |$44.34_{-0.12}^{+0.09}$| | 149.2 | 86.2 |
| 502 | 3.157 | S3 | 1.00 | S | <1 | |$- 15.56_{-0.13}^{+0.08}$| | |$-15.61_{-0.10}^{+0.10}$| | |$43.50_{-0.13}^{+0.08}$| | |$43.45_{-0.13}^{+0.08}$| | 73.5 | 29.8 |
| 504 | |$3.36_{-0.09}^{+0.10}$| | P5 | 1.00 | H | |$831_{-537}^{+123}$| | <−16.31 | <−17.57 | |$43.14_{-0.24}^{+0.17}$| | |$42.26_{-0.13}^{+0.59}$| | 9.8 | 30.8 |
| 509 | |$3.15_{-0.57}^{+0.12}$| | P5 | 0.47 | S | <15 | |$-16.26 _{-0.26}^{+0.18}$| | <−16.93 | |$42.88_{-0.32}^{+0.21}$| | <42.30 | 15.1 | 3.2 |
| 526 | |$4.17_{-0.13}^{+0.10}$| | P5 | 1.00 | S | |$15_{-6}^{+7}$| | |$- 15.84_{-0.10}^{+0.07}$| | |$-15.88_{-0.10}^{+0.08}$| | |$43.71_{-0.14}^{+0.09}$| | |$43.67_{-0.15}^{+0.09}$| | 89.0 | 48.0 |
| 545 | 3.524 | S3 | 1.00 | S | <11 | |$- 15.27_{-0.07}^{+0.05}$| | |$-15.28_{-0.07}^{+0.05}$| | |$43.95_{-0.09}^{+0.07}$| | |$43.93_{-0.08}^{+0.08}$| | 132.4 | 46.8 |
| 572 | |$3.77_{-0.01}^{+0.03}$| | P2 | 1.00 | S | |$10_{-2}^{+2}$| | |$-15.49 _{-0.13}^{+0.08}$| | |$-15.54_{-0.17}^{+0.10}$| | |$43.94_{-0.14}^{+0.08}$| | |$43.89_{-0.17}^{+0.11}$| | 288.9 | 156.2 |
| ID . | z . | Ref . | P . | Band . | NH . | |$\mathrm{log}F^{\mathrm{obs}}_{0.5-2\, \mathrm{keV}}$| . | |$\mathrm{log}F^{\mathrm{intr}}_{0.5-2\, \mathrm{keV}}$| . | |$\mathrm{log}L^{\mathrm{obs}}_{2-10\, \mathrm{keV}}$| . | |$\mathrm{log}L^{\mathrm{intr}}_{2-10\, \mathrm{keV}}$| . | Net counts . | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | (3 ≤ z < 6) . | . | (1022 cm−2) . | (erg cm−2 s−1) . | (erg cm−2 s−1) . | (erg s−1) . | (erg s−1) . | (0.5–2 keV) . | (2–7 keV) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| CDF-S | |||||||||||
| 8 | |$3.13_{-0.48}^{+3.28}$| | P3 | 0.55 | S | |$59_{-18}^{+24}$| | |$-15.56_{-0.08}^{+0.07}$| | |$-15.59_{-0.08}^{+0.08}$| | |$44.43_{-0.23}^{+0.20}$| | |$44.41_{-0.27}^{+0.17}$| | 99.2 | 119.4 |
| 9 | |$1.93_{-0.20}^{+1.39}$| | P3 | 0.44 | S | |$11_{-5}^{+8}$| | |$-15.31_{-0.08}^{+0.05}$| | |$-15.32_{-0.07}^{+0.06}$| | |$44.04_{-0.13}^{+0.16}$| | |$44.03_{-0.14}^{+0.15}$| | 140.7 | 95.4 |
| 10 | |$2.93_{-0.40}^{+0.85}$| | P3 | 0.32 | S | |$3_{-2}^{+2}$| | |$-15.40_{-0.11}^{+0.06}$| | |$-15.43_{-0.09}^{+0.08}$| | |$43.76_{-0.13}^{+0.09}$| | |$43.73_{-0.14}^{+0.09}$| | 70.1 | 38.9 |
| 12 | 3.153 | S2 | 1.00 | H | |$135_{-46}^{+69}$| | |$-16.59_{-0.75}^{+0.21}$| | <− 17.28 | |$44.06_{-0.18}^{+0.12}$| | |$42.21_{-0.22}^{+1.32}$| | 12.4 | 89.0 |
| 25 | −1 | N | 0.30 | S | <74 | |$-15.65_{-0.13}^{+0.08}$| | |$-15.69_{-0.15}^{+0.08}$| | |$43.63_{-0.20}^{+0.44}$| | |$43.60_{-0.18}^{+0.46}$| | 75.0 | 88.3 |
| 29 | |$3.33_{-0.29}^{+0.32}$| | P4 | 0.99 | S | <1 | |$-15.63_{-0.10}^{+0.05}$| | |$-15.65_{-0.11}^{+0.05}$| | |$43.47_{-0.13}^{+0.12}$| | |$43.45_{-0.12}^{+0.13}$| | 119.0 | 44.4 |
| 35 | −1 | N | 0.30 | S | |$25_{-17}^{+29}$| | |$-15.61_{-0.09}^{+0.09}$| | |$-15.63_{-0.11}^{+0.08}$| | |$43.97_{-0.20}^{+0.21}$| | |$43.94_{-0.22}^{+0.20}$| | 98.9 | 67.8 |
| 53 | 3.202 | S1 | 1.00 | S | <22 | |$-16.41_{-0.36}^{+0.18}$| | <−16.97 | |$42.74_{-0.40}^{+0.20}$| | <42.30 | 29.8 | 40.7 |
| 84 | |$3.12_{-0.59}^{+0.35}$| | P1 | 0.70 | S | |$49_{-13}^{+14}$| | |$-16.07_{-0.11}^{+0.06}$| | |$-16.10_{-0.12}^{+0.06}$| | |$43.75_{-0.19}^{+0.14}$| | |$43.71_{-0.19}^{+0.15}$| | 80.4 | 98.5 |
| 88 | −1 | N | 0.30 | S | |$83_{-26}^{+19}$| | |$-15.98_{-0.08}^{+0.06}$| | |$-16.01_{-0.09}^{+0.06}$| | |$44.19_{-0.27}^{+0.12}$| | |$44.16_{-0.25}^{+0.14}$| | 99.3 | 195.6 |
| 99 | |$4.24_{-0.36}^{+0.05}$| | P1 | 0.99 | S | |$30_{-28}^{+34}$| | |$-15.91_{-0.19}^{+0.14}$| | <−16.19 | |$43.55_{-0.26}^{+0.22}$| | <43.32 | 41.3 | 47.8 |
| 101 | |$4.34_{-0.61}^{+0.02}$| | P1 | 1.00 | S | |$68_{-22}^{+12}$| | |$-16.11_{-0.16}^{+0.09}$| | |$-16.20_{-0.27}^{+0.18}$| | |$43.87_{-0.24}^{+0.24}$| | |$43.78_{-0.37}^{+0.22}$| | 51.2 | 110.8 |
| 109 | |$3.58_{-0.04}^{+0.03}$| | P1 | 1.0 | S | |$28_{-6}^{+5}$| | |$-16.48_{-0.23}^{+0.15}$| | <−16.68 | |$43.14_{-0.25}^{+0.16}$| | <42.96 | 144.9 | 150.9 |
| 110 | |$3.08_{-0.08}^{+0.38}$| | P1 | 0.87 | S | <1 | |$-16.54_{-0.24}^{+0.15}$| | <−16.74 | |$42.55_{-0.24}^{+0.19}$| | <42.40 | 22.8 | 4.4 |
| 121 | |$3.42_{-0.05}^{+0.03}$| | P1 | 1.00 | S | |$68_{-21}^{+14}$| | |$-16.27_{-0.13}^{+0.09}$| | |$-16.33_{-0.16}^{+0.11}$| | |$43.69_{-0.22}^{+0.16}$| | |$43.62_{-0.27}^{+0.16}$| | 50.4 | 65.9 |
| 126 | |$3.13_{-0.03}^{+0.07}$| | P1 | 0.95 | S | <28 | |$-15.84_{-0.23}^{+0.13}$| | <−16.55 | |$43.32_{-0.22}^{+0.20}$| | <42.67 | 39.9 | 53.1 |
| 133 | 3.474 | S1 | 1.00 | H | |$141_{-50}^{+73}$| | <−16.96 | <−17.39 | |$43.61_{-0.22}^{+0.13}$| | |$42.23_{-0.15}^{+0.93}$| | 4.0 | 56.3 |
| 165 | |$3.55_{-0.02}^{+0.02}$| | P1 | 1.00 | S | |$16_{-6}^{+6}$| | |$-15.94_{-0.09}^{+0.07}$| | |$-15.96_{-0.11}^{+0.06}$| | |$43.52_{-0.13}^{+0.09}$| | |$43.5_{-0.15}^{+0.08}$| | 71.9 | 34.2 |
| 185 | |$3.09_{-0.03}^{+0.04}$| | P1 | 0.87 | S | |$39_{-24}^{+24}$| | |$-16.70_{-0.19}^{+0.11}$| | |$-16.82_{-0.29}^{+0.16}$| | |$42.86_{-0.37}^{+0.22}$| | |$42.71_{-0.45}^{+0.25}$| | 18.7 | 22.6 |
| 189 | |$3.65_{-0.04}^{+0.07}$| | P1 | 1.00 | H | |$107_{-33}^{+25}$| | <−16.97 | <−17.31 | |$43.38_{-0.16}^{+0.09}$| | |$43.30_{-0.19}^{+0.12}$| | 7.1 | 34.5 |
| 214 | 3.74 | S2 | 1.00 | S | |$26_{-2}^{+1}$| | |$-14.81_{-0.03}^{+0.00}$| | |$-14.82_{-0.03}^{+0.01}$| | |$44.81_{-0.03}^{+0.02}$| | |$44.81_{-0.03}^{+0.02}$| | 1377.4 | 1213.8 |
| 223 | |$3.76_{-0.17}^{+0.06}$| | P1 | 1.00 | S | <14 | |$-16.46_{-0.15}^{+0.11}$| | |$-16.55_{-0.22}^{+0.13}$| | |$42.80_{-0.19}^{+0.11}$| | |$42.71_{-0.23}^{+0.15}$| | 27.9 | 0.0 |
| 238 | |$5.96_{-0.04}^{+0.01}$| | P2 | 1.00 | S | <66 | |$-16.29_{-0.17}^{+0.09}$| | |$-16.37_{-0.21}^{+0.14}$| | |$43.42_{-0.17}^{+0.15}$| | |$43.35_{-0.24}^{+0.18}$| | 40.5 | 7.1 |
| 248 | |$3.44_{-0.13}^{+0.22}$| | P1 | 1.00 | S | |$39_{-7}^{+5}$| | |$-15.55_{-0.06}^{+0.04}$| | |$-15.56_{-0.06}^{+0.04}$| | |$44.18_{-0.10}^{+0.07}$| | |$44.17_{-0.10}^{+0.07}$| | 186.9 | 192.9 |
| 276 | |$3.12_{-0.01}^{+0.02}$| | P1 | 1.00 | S | |$15_{-3}^{+3}$| | |$-15.90_{-0.06}^{+0.04}$| | |$-15.91_{-0.06}^{+0.04}$| | |$43.51_{-0.08}^{+0.05}$| | |$43.50_{-0.08}^{+0.05}$| | 122.9 | 9.2 |
| 299 | |$3.79_{-0.05}^{+0.05}$| | P1 | 1.00 | S | |$10_{-9}^{+15}$| | |$-16.63_{-0.16}^{+0.10}$| | |$-16.71_{-0.19}^{+0.12}$| | |$42.67_{-0.18}^{+0.13}$| | |$42.59_{-0.21}^{+0.15}$| | 19.4 | 21.0 |
| 329 | |$3.47_{-0.10}^{+0.10}$| | P1 | 1.00 | S | |$32_{-29}^{+33}$| | |$-16.69_{-0.20}^{+0.14}$| | <−16.74 | |$42.61_{-0.25}^{+0.31}$| | <42.77 | 17.2 | 17.1 |
| 337 | 3.660 | S1 | 1.00 | S | |$98_{-9}^{+7}$| | |$-16.08_{-0.09}^{+0.04}$| | |$-16.10_{-0.08}^{+0.05}$| | |$44.16_{-0.10}^{+0.07}$| | |$44.14_{-0.09}^{+0.08}$| | 78.3 | 221.4 |
| 351 | |$3.86_{-0.54}^{+0.14}$| | P1 | 0.97 | S | |$74_{-23}^{+9}$| | |$-16.28_{-0.14}^{+0.08}$| | |$-16.34_{-0.17}^{+0.10}$| | |$43.71_{-0.19}^{+0.17}$| | |$43.65_{-0.26}^{+0.15}$| | 50.8 | 73.2 |
| 356 | |$3.38_{-0.19}^{+0.01}$| | P1 | 0.99 | S | <8 | |$-16.38_{-0.14}^{+0.07}$| | |$-16.43_{-0.15}^{+0.08}$| | |$42.76_{-0.13}^{+0.10}$| | |$42.71_{-0.15}^{+0.10}$| | 31.9 | 31.4 |
| 366 | |$3.67_{-0.18}^{+0.53}$| | P1 | 1.00 | S | |$81_{-15}^{+14}$| | |$-16.15_{-0.10}^{+0.06}$| | |$-16.18_{-0.10}^{+0.07}$| | |$43.96_{-0.14}^{+0.14}$| | |$43.93_{-0.16}^{+0.13}$| | 66.8 | 131.2 |
| 368 | |$3.21_{-0.08}^{+0.09}$| | P1 | 1.00 | S | <1 | |$-16.57_{-0.15}^{+0.10}$| | |$-16.65_{-0.19}^{+0.11}$| | |$42.52_{-0.19}^{+0.10}$| | |$42.44_{-0.20}^{+0.11}$| | 20.9 | 0.0 |
| 414 | |$3.58_{-0.10}^{+0.11}$| | P1 | 1.00 | H | −1** | <−17.28 | <−17.41 | |$42.71_{-0.36}^{+0.20}$| | <42.61 | 0.3 | 9.7 |
| 416 | 3.470 | S1 | 1.00 | S | <1 | |$-16.63_{-0.19}^{+0.10}$| | |$-16.75_{-0.27}^{+0.19}$| | |$42.52_{-0.19}^{+0.10}$| | |$42.40_{-0.26}^{+0.15}$| | 18.0 | 0.4 |
| 433 | |$4.11_{-0.12}^{+0.15}$| | P1 | 1.00 | S | <1 | |$-16.80_{-0.23}^{+0.13}$| | <−16.86 | |$42.55_{-0.24}^{+0.14}$| | <42.51 | 12.9 | 0.3 |
| 459 | |$3.91_{-0.04}^{+0.05}$| | P1 | 1.00 | H | |$166_{-64}^{+80}$| | <17.20 | <−17.43 | |$43.34_{-0.25}^{+0.17}$| | <43.11 | 0.3 | 24.4 |
| 462 | |$3.88_{-0.78}^{+0.41}$| | P1 | 0.95 | H | |$51_{-21}^{+21}$| | |$-16.24_{-0.44}^{+0.19}$| | <−17.12 | |$43.92_{-0.25}^{+0.16}$| | <42.69 | 25.6 | 63.5 |
| 464 | |$4.76_{-0.10}^{+0.02}$| | P2 | 1.00 | S | <16 | |$-15.67_{-0.07}^{+0.04}$| | |$-15.68_{-0.06}^{+0.05}$| | |$43.81_{-0.08}^{+0.06}$| | |$43.80_{-0.08}^{+0.06}$| | 160.5 | 10.1 |
| 472 | |$4.16_{-0.17}^{+0.02}$| | P1 | 1.00 | H | |$110_{-94}^{+317}$| | <−16.97 | <−17.28 | |$43.14_{-0.24}^{+0.17}$| | <43.00 | 7.0 | 19.2 |
| 490 | |$4.73_{-0.08}^{+0.06}$| | P1 | 1.00 | S | |$71_{-8}^{+9}$| | |$-16.05_{-0.07}^{+0.04}$| | |$-16.06_{-0.07}^{+0.04}$| | |$44.03_{-0.08}^{+0.07}$| | |$44.01_{-0.10}^{+0.06}$| | 86.8 | 123.3 |
| 500 | |$3.15_{-0.02}^{+0.04}$| | P1 | 1.00 | S | |$40_{-38}^{+89}$| | <−16.79 | <−17.19 | <42.83 | <42.46 | 10.4 | 16.6 |
| 503 | |$3.14_{-0.07}^{+0.03}$| | P1 | 0.99 | S | <5 | <−16.93 | <−17.19 | <42.20 | <41.95 | 7.0 | 7.6 |
| 517 | 3.256 | S2 | 1.00 | S | <1 | |$-16.24 _{-0.11}^{+0.06}$| | |$-16.27_{-0.12}^{+0.06}$| | |$42.85_{-0.10}^{+0.07}$| | |$42.82_{-0.11}^{+0.07}$| | 44.1 | 24.0 |
| 521 | |$2.96_{-0.07}^{+0.07}$| | P1 | 0.41 | S | |$21_{-19}^{+60}$| | |$-16.89 _{-0.33}^{+0.18}$| | <−17.11 | |$42.34_{-0.36}^{+0.39}$| | |$42.60_{-0.19}^{+0.15}$| | 13.0 | 27.7 |
| 527 | |$3.76_{-0.29}^{+0.05}$| | P1 | 1.00 | S | <1 | |$-16.55 _{-0.15}^{+0.10}$| | |$-16.63_{-0.19}^{+0.12}$| | |$42.68_{-0.17}^{+0.12}$| | |$42.60_{-0.19}^{+0.15}$| | 22.5 | 0.0 |
| 539 | 4.762 | S1 | 1.00 | H | |$102_{-47}^{+49}$| | |$-16.48 _{-0.42}^{+0.18}$| | <−17.09 | |$43.83_{-0.27}^{+0.13}$| | <42.83 | 27.0 | 61.2 |
| 551 | 3.700 | S1 | 1.00 | S | |$76_{-5}^{+4}$| | |$-15.71 _{-0.05}^{+0.03}$| | |$-15.72_{-0.05}^{+0.03}$| | |$44.37_{-0.05}^{+0.05}$| | |$44.37_{-0.06}^{+0.04}$| | 209.8 | 441.4 |
| 580 | |$3.17_{-0.12}^{+0.19}$| | P1 | 0.97 | S | |$42_{-8}^{+10}$| | |$-16.34 _{-0.08}^{+0.06}$| | |$-16.36_{-0.10}^{+0.05}$| | |$43.40_{-0.13}^{+0.11}$| | |$43.38_{-0.12}^{+0.12}$| | 45.1 | 66.6 |
| 617 | |$3.58_{-0.13}^{+0.20}$| | P1 | 1.00 | S | <1 | |$-15.77 _{-0.07}^{+0.03}$| | |$-15.78_{-0.07}^{+0.03}$| | |$43.41_{-0.08}^{+0.05}$| | |$43.40_{-0.07}^{+0.06}$| | 136.0 | 69.1 |
| 619 | |$3.67_{-0.09}^{+0.04}$| | P1 | 1.00 | S | |$68_{-23}^{+18}$| | |$-16.85 _{-0.20}^{+0.10}$| | |$-16.97_{-0.22}^{+0.15}$| | |$43.12_{-0.27}^{+0.19}$| | |$42.99_{-0.32}^{+0.20}$| | 12.3 | 23.2 |
| 622 | |$3.33_{-0.17}^{+0.09}$| | P1 | 1.00 | S | <1 | |$- 16.50_{-0.19}^{+0.11}$| | |$-16.62_{-0.41}^{+0.18}$| | |$42.62_{-0.20}^{+0.14}$| | |$42.49_{-0.44}^{+0.20}$| | 24.5 | 0.0 |
| 623 | |$3.58_{-0.03}^{+0.02}$| | P1 | 1.00 | S | |$27_{-10}^{+10}$| | |$- 16.43_{-0.12}^{+0.07}$| | |$-16.47_{-0.12}^{+0.08}$| | |$43.17_{-0.14}^{+0.13}$| | |$43.13_{-0.18}^{+0.11}$| | 36.7 | 34.5 |
| 640 | |$3.77_{-0.03}^{+0.02}$| | P1 | 1.00 | S | |$16_{-15}^{+18}$| | |$-16.68 _{-0.16}^{+0.10}$| | |$-16.75_{-0.19}^{+0.10}$| | |$42.65_{-0.18}^{+0.16}$| | |$42.58_{-0.18}^{+0.18}$| | 17.7 | 3.5 |
| 657 | |$3.58_{-0.10}^{+0.17}$| | P1 | 1.00 | S | |$115_{-19}^{+11}$| | |$- 16.59_{-0.14}^{+0.09}$| | |$-16.66_{-0.17}^{+0.10}$| | |$43.76_{-0.19}^{+0.13}$| | |$43.69_{-0.20}^{+0.15}$| | 26.2 | 79.6 |
| 662 | |$4.84_{-0.12}^{+0.05}$| | P1 | 1.00 | S | <54 | |$-16.82 _{-0.24}^{+0.14}$| | <−16.90 | |$42.71_{-0.27}^{+0.18}$| | <42.68 | 13.3 | 2.6 |
| 692 | |$3.42_{-0.08}^{+0.13}$| | P1 | 1.00 | H | |$117_{-51}^{+56}$| | <−17.14 | <−17.37 | |$42.84_{-0.31}^{+0.18}$| | <43.22 | 3.6 | 9.7 |
| 714 | |$3.48_{-0.09}^{+0.03}$| | P1 | 1.00 | S | <1 | |$- 16.25_{-0.10}^{+0.08}$| | |$-16.29_{-0.13}^{+0.07}$| | |$42.91_{-0.13}^{+0.07}$| | |$42.87_{-0.13}^{+0.08}$| | 44.4 | 0.0 |
| 723 | 3.045 | S1 | 1.00 | S | |$59_{-6}^{+4}$| | |$-16.02 _{-0.05}^{+0.05}$| | |$-16.03_{-0.05}^{+0.05}$| | |$43.88_{-0.10}^{+0.05}$| | |$43.87_{-0.10}^{+0.05}$| | 93.0 | 188.1 |
| 746 | 3.064 | S1 | 1.00 | S | |$52_{-2}^{+1}$| | |$- 15.14_{-0.05}^{+0.02}$| | |$-15.15_{-0.04}^{+0.03}$| | |$44.69_{-0.05}^{+0.03}$| | |$44.68_{-0.05}^{+0.03}$| | 689.2 | 1281.4 |
| 758 | |$3.08_{-0.03}^{+0.01}$| | P1 | 1.00 | S | <36 | <−17.12 | <−17.37 | <42.13 | <41.92 | 8.7 | 13.5 |
| 760 | 3.35 | S2 | 1.00 | S | |$74_{-5}^{+2}$| | |$- 15.111_{-0.03}^{+0.03}$| | |$-15.11_{-0.04}^{+0.02}$| | |$44.94_{-0.05}^{+0.03}$| | |$44.94_{-0.05}^{+0.03}$| | 763.5 | 999.8 |
| 774 | 3.61 | S1 | 1.00 | S | |$7_{-1}^{+1}$| | |$-14.71 _{-0.04}^{+0.03}$| | |$-14.71_{-0.05}^{+0.02}$| | |$44.63_{-0.03}^{+0.04}$| | |$44.63_{-0.04}^{+0.03}$| | 1162.8 | 691.5 |
| 788 | 3.193 | S2 | 1.00 | S | |$2_{-1}^{+1}$| | |$- 15.11_{-0.03}^{+0.03}$| | |$-15.11_{-0.04}^{+0.02}$| | |$44.01_{-0.05}^{+0.02}$| | |$44.01_{-0.05}^{+0.02}$| | 646.8 | 381.8 |
| 811 | 3.471 | S1 | 1.00 | S | <1 | |$- 15.37_{-0.05}^{+0.02}$| | |$-15.37_{-0.05}^{+0.02}$| | |$43.77_{-0.04}^{+0.03}$| | |$43.77_{-0.05}^{+0.02}$| | 312.9 | 194.9 |
| 853 | |$3.72_{-0.14}^ {+0.13}$| | P1 | 1.00 | S | <2 | |$- 16.21_{-0.29}^{+0.16}$| | <−16.81 | |$43.05_{-0.35}^{+0.18}$| | <42.60 | 37.0 | 69.7 |
| 859 | |$2.88_{-0.09}^{+0.13}$| | P1 | 0.22 | S | <3 | |$-16.71 _{-0.30}^{+0.17}$| | <−16.93 | |$42.38_{-0.37}^{+0.21}$| | <42.34 | 16.4 | 1.6 |
| 873 | |$3.76_{-0.06}^{+0.04}$| | P1 | 1.00 | S | <1 | |$- 16.25_{-0.12}^{+0.10}$| | |$-16.31_{-0.16}^{+0.11}$| | |$42.98_{-0.13}^{+0.10}$| | |$42.92_{-0.17}^{+0.11}$| | 41.4 | 0.0 |
| 876 | 3.470 | S2 | 1.00 | S | |$11_{-1}^{+1}$| | |$-14.57 _{-0.01}^{+0.01}$| | |$-14.57_{-0.01}^{+0.01}$| | |$44.82_{-0.02}^{+0.01}$| | |$44.82_{-0.02}^{+0.01}$| | 2211.9 | 1482.2 |
| 885 | |$3.08_{-0.10}^{+0.02}$| | P1 | 0.78 | S | |$95_{-10}^{+10}$| | |$-16.18 _{-0.10}^{+0.07}$| | |$-16.21_{-0.13}^{+0.06}$| | |$44.02_{-0.14}^{+0.10}$| | |$43.98_{-0.13}^{+0.12}$| | 64.4 | 201.9 |
| 901 | |$3.51_{-0.12}^{+0.25}$| | P1 | 1.00 | S | <43 | |$- 16.63_{-0.32}^{+0.17}$| | <−16.94 | |$42.65_{-0.34}^{+0.25}$| | <42.43 | 19.8 | 14.7 |
| 908 | |$3.60_{-0.20}^{+0.05}$| | P1 | 1.00 | H | >23 | |$-16.94 _{-0.55}^{+0.61}$| | <−17.20 | |$43.64_{-0.26}^{+0.27}$| | <43.01 | 7.5 | 52.5 |
| 921 | 3.082 | S1 | 1.00 | S | <4 | |$- 15.33_{-0.07}^{+0.02}$| | |$-15.34_{-0.06}^{+0.03}$| | |$43.73_{-0.04}^{+0.05}$| | |$43.73_{-0.07}^{+0.03}$| | 347.6 | 204.8 |
| 926 | |$4.27_{-1.5}^{+0.06}$| | P1 | 0.53 | S | <7 | |$-15.61 _{-0.05}^{+0.05}$| | |$-15.62_{-0.07}^{+0.04}$| | |$43.76_{-0.06}^{+0.06}$| | |$43.75_{-0.08}^{+0.05}$| | 182.2 | 116.4 |
| 939 | −1 | N | 0.30 | S | <1 | |$- 16.00_{-0.11}^{+0.10}$| | |$-16.05_{-0.16}^{+0.10}$| | |$43.47_{-0.36}^{+0.12}$| | |$43.38_{-0.36}^{+0.15}$| | 62.8 | 15.0 |
| 940 | |$3.00_{-0.19}^{+0.26}$| | P1 | 0.63 | S | |$35_{-10}^{+7}$| | |$-16.00 _{-0.09}^{+0.06}$| | |$-16.03_{-0.09}^{+0.07}$| | |$43.64_{-0.16}^{+0.11}$| | |$43.61_{-0.14}^{+0.13}$| | 91.7 | 97.4 |
| 962 | |$4.68_{-2.25}^{+2.25}$| | P3 | 0.45 | S | |$141_{-48}^{+49}$| | |$- 16.40_{-0.31}^{+0.15}$| | <−16.95 | |$44.01_{-0.43}^{+0.26}$| | <43.54 | 35.2 | 130.2 |
| 965 | |$3.64_{-0.80}^{+0.11}$| | P3 | 0.65 | S | <1 | |$- 15.79_{-0.10}^{+0.06}$| | |$-15.81_{-0.11}^{+0.06}$| | |$43.36_{-0.13}^{+0.10}$| | |$43.33_{-0.14}^{+0.10}$| | 104.0 | 40.2 |
| 971 | |$2.17_{-0.59}^{+1.24}$| | P3 | 0.35 | S | |$36_{-13}^{+8}$| | |$- 15.61_{-0.05}^{+0.02}$| | |$-15.16_{-0.05}^{+0.02}$| | |$44.73_{-0.28}^{+0.11}$| | |$44.73_{-0.29}^{+0.10}$| | 536.7 | 513.2 |
| 974 | |$3.23_{-0.13}^{+0.18}$| | P3 | 0.92 | S | |$9_{-8}^{+10}$| | |$-15.76 _{-0.10}^{+0.08}$| | |$-15.79_{-0.13}^{+0.07}$| | |$43.44_{-0.13}^{+0.11}$| | |$43.41_{-0.14}^{+0.11}$| | 105.6 | 71.5 |
| 977a | −1 | N | 0.3 | S | |$89_{-29}^{+34}$| | |$-16.13 _{-0.18}^{+0.10}$| | <−16.20 | |$44.04_{-0.29}^{+0.23}$| | <44.03 | 48.6 | 128.0 |
| 990 | 3.724 | S1 | 1.00 | S | |$62_{-54}^{+64}$| | |$- 16.06_{-0.28}^{+0.17}$| | <−16.99 | |$43.35_{-0.24}^{+0.58}$| | <42.86 | 41.0 | 61.3 |
| CDF-N | |||||||||||
| 31 | |$3.45_{-0.36}^{+0.21}$| | P5 | 0.95 | S | <1 | |$-15.66 _{-0.12}^{+0.08}$| | |$-15.71_{-0.15}^{+0.08}$| | |$43.48_{-0.13}^{+0.12}$| | |$43.43_{-0.17}^{+0.11}$| | 44.4 | 16.6 |
| 81 | 3.19 | S3 | 1.00 | S | <1 | |$- 15.34_{-0.10}^{+0.07}$| | |$-15.37_{-0.10}^{+0.07}$| | |$43.72_{-0.10}^{+0.07}$| | |$43.69_{-0.10}^{+0.07}$| | 74.3 | 25.9 |
| 112 | |$3.15_{-0.18}^{+0.18}$| | P5 | 0.85 | S | <14 | |$-16.15 _{-0.14}^{+0.13}$| | |$-16.24_{-0.22}^{+0.13}$| | |$43.00_{-0.19}^{+0.15}$| | |$42.90_{-0.23}^{+0.18}$| | 20.7 | 8.1 |
| 129 | 3.938 | S3 | 1.00 | S | <1 | |$-15.43 _{-0.09}^{+0.07}$| | |$-15.46_{-0.10}^{+0.07}$| | |$43.84_{-0.09}^{+0.07}$| | |$43.81_{-0.11}^{+0.06}$| | 63.7 | 24.3 |
| 133 | |$3.06_{-0.36}^{+0.46}$| | P5 | 0.63 | S | |$93_{-19}^{+16}$| | |$-16.34 _{-0.23}^{+0.15}$| | <−16.57 | |$43.84_{-0.28}^{+0.21}$| | <43.62 | 15.0 | 41.0 |
| 142 | |$2.95_{-0.13}^{+0.08}$| | P5 | 0.23 | S | |$135_{-25}^{+24}$| | |$- 16.28_{-0.18}^{+0.13}$| | |$-16.41_{-0.23}^{+0.14}$| | |$44.24_{-0.25}^{+0.23}$| | |$44.11_{-0.31}^{+0.22}$| | 14.6 | 55.0 |
| 158 | |$3.19_{-0.02}^{+0.01}$| | P2 | 1.00 | S | |$54_{-10}^{+8}$| | |$-15.74 _{-0.11}^{+0.08}$| | |$-15.68_{-0.12}^{+0.08}$| | |$44.10_{-0.14}^{+0.12}$| | |$44.06_{-0.16}^{+0.11}$| | 46.4 | 72.2 |
| 177 | |$3.44_{-0.34}^{+0.14}$| | P5 | 0.98 | S | |$33_{-12}^{+14}$| | |$- 16.09_{-0.15}^{+0.09}$| | |$-16.16_{-0.14}^{+0.11}$| | |$43.55_{-0.21}^{+0.17}$| | |$43.48_{-0.21}^{+0.18}$| | 27.5 | 29.3 |
| 195 | −1 | N | 0.30 | S | <2 | |$- 16.02_{-0.13}^{+0.11}$| | |$-16.09_{-0.14}^{+0.11}$| | |$43.46_{-0.35}^{+0.13}$| | |$43.38_{-0.33}^{+0.15}$| | 28.3 | 12.9 |
| 196 | |$3.24_{-0.02}^{+0.02}$| | P2 | 1.00 | S | |$85_{-9}^{+10}$| | |$- 16.06_{-0.13}^{+0.12}$| | |$-16.13_{-0.16}^{+0.10}$| | |$44.08_{-0.19}^{+0.12}$| | |$44.00_{-0.18}^{+0.13}$| | 29.9 | 96.9 |
| 201 | |$4.43_{-1.33}^{+0.23}$| | P5 | 0.73 | S | −1b | <−16.78 | <−17.33 | <42.98 | |$44.06_{-0.19}^{+0.12}$| | 3.4 | 15.5 |
| 207 | 3.652 | S3 | 1.00 | S | <1 | |$- 15.09_{-0.08}^{+0.05}$| | |$-15.11_{-0.08}^{+0.05}$| | |$44.10_{-0.08}^{+0.05}$| | |$42.21_{-0.15}^{+0.30}$| | 242.6 | 80.7 |
| 227 | |$4.26_{-0.07}^{+0.03}$| | P2 | 1.00 | S | −1b | |$-16.70 _{-0.31}^{+0.24}$| | <−17.00 | |$42.71_{-0.55}^{+0.40}$| | <43.18 | 6.5 | 3.9 |
| 229 | 3.413 | S4 | 1.00 | S | <1 | |$- 15.43_{-0.09}^{+0.06}$| | |$-15.46_{-0.09}^{+0.06}$| | |$43.70_{-0.09}^{+0.06}$| | |$43.67_{-0.09}^{+0.06}$| | 111.8 | 48.8 |
| 257 | |$2.95_{-0.44}^{+0.29}$| | P5 | 0.35 | S | |$60_{-32}^{+37}$| | |$-16.56 _{-0.22}^{+0.14}$| | |$-16.74_{-0.30}^{+0.19}$| | |$43.24_{-0.43}^{+0.32}$| | |$43.04_{-0.47}^{+0.37}$| | 9.6 | 16.7 |
| 290 | 4.424 | S3 | 1.00 | S | <1 | |$-16.24 _{-0.17}^{+0.10}$| | |$-16.33_{-0.18}^{+0.11}$| | |$43.14_{-0.16}^{+0.11}$| | |$43.05_{-0.17}^{+0.12}$| | 17.7 | 9.1 |
| 293 | |$3.96_{-0.30}^{+0.17}$| | P5 | 1.00 | S | <8 | |$-15.32 _{-0.07}^{+0.06}$| | |$-15.33_{-0.07}^{+0.06}$| | |$43.98_{-0.12}^{+0.07}$| | |$43.96_{-0.11}^{+0.08}$| | 115.0 | 66.9 |
| 297 | 3.23 | S3 | 1.00 | S | <1 | |$-16.09 _{-0.12}^{+0.12}$| | |$-16.16_{-0.16}^{+0.10}$| | |$42.99_{-0.15}^{+0.10}$| | |$42.02_{-0.15}^{+0.11}$| | 22.3 | 10.8 |
| 310 | |$3.06_{-0.23}^{+0.36}$| | P5 | 0.70 | S | <41 | |$16.67 _{-0.32}^{+0.19}$| | <−16.93 | |$42.52_{-0.40}^{+0.30}$| | <42.47 | 6.6 | 6.5 |
| 315 | −1 | N | 0.30 | S | <1 | |$- 16.61_{-0.25}^{+0.16}$| | |$- 16.86_{-0.51}^{+0.21}$| | |$42.78_{-0.36}^{+0.23}$| | |$42.46_{-0.51}^{+0.31}$| | 7.5 | 2.8 |
| 320 | |$3.06_{-0.20}^{+0.26}$| | P5 | 0.69 | S | <1 | |$- 16.73_{-0.28}^{+0.19}$| | <−16.91 | |$42.37_{-0.31}^{+0.21}$| | <42.23 | 5.8 | 5.5 |
| 330 | 5.186 | S3 | 1.00 | S | <1 | |$-15.53 _{-0.12}^{+0.07}$| | |$-15.57_{-0.12}^{+0.07}$| | |$44.00_{-0.12}^{+0.07}$| | |$43.96_{-0.12}^{+0.07}$| | 84.4 | 31.4 |
| 363 | |$3.28_{-0.05}^{+0.05}$| | P2 | 1.00 | S | <1 | |$-16.19 _{-0.17}^{+0.14}$| | |$-16.31_{-0.21}^{+0.14}$| | |$42.92_{-0.17}^{+0.15}$| | |$42.80_{-0.21}^{+0.15}$| | 15.8 | 3.9 |
| 373 | |$3.36_{-0.29}^{+0.34}$| | P5 | 0.84 | S | |$52_{-31}^{+31}$| | |$-16.76 _{-0.27}^{+0.19}$| | <−16.92 | |$42.98_{-0.51}^{+0.25}$| | <42.85 | 5.9 | 6.5 |
| 388 | |$2.94_{-0.12}^{+0.08}$| | P5 | 0.31 | S | <1 | |$- 15.49_{-0.12}^{+0.07}$| | |$-15.53_{-0.13}^{+0.08}$| | |$43.56_{-0.13}^{+0.08}$| | |$43.52_{-0.14}^{+0.09}$| | 56.5 | 0.0 |
| 390 | |$3.19_{-0.29}^{+0.28}$| | P5 | 0.85 | H | |$204_{-46}^{+53}$| | <−16.89 | <−17.39 | |$43.38_{-0.13}^{+0.07}$| | |$43.30_{-0.16}^{+0.09}$| | 3.1 | 31.5 |
| 404 | |$3.15_{-0.13}^{+0.04}$| | P5 | 0.91 | S | <1 | |$- 14.67_{-0.06}^{+0.03}$| | |$-14.67_{-0.06}^{+0.03}$| | |$44.37_{-0.06}^{+0.04}$| | |$44.36_{-0.06}^{+0.04}$| | 555.4 | 220.8 |
| 424 | |$4.43_{-0.26}^{+0.13}$| | P5 | 1.00 | H | |$166_{-40}^{+38}$| | |$-16.37 _{-0.36}^{+0.18}$| | <−17.17 | |$43.34_{-0.25}^{+0.17}$| | |$42.32_{-0.11}^{+0.58}$| | 13.1 | 62.2 |
| 428 | |$3.03_{-0.11}^{+0.09}$| | P5 | 0.55 | S | |$18_{-3}^{+2}$| | |$-15.07 _{0.06-}^{+0.04}$| | |$-15.08_{-0.06}^{+0.04}$| | |$44.36_{-0.08}^{+0.05}$| | |$44.35_{-0.08}^{+0.05}$| | 258.7 | 188.1 |
| 439 | 3.406 | S3 | 1.00 | S | |$27_{-26}^{+73}$| | |$-16.54 _{-0.28}^{+0.17}$| | |$-16.81_{-0.46}^{+0.27}$| | |$42.76_{-0.35}^{+0.41}$| | |$42.49_{-0.51}^{+0.46}$| | 8.5 | 15.8 |
| 498 | |$4.42_{-0.24}^{+0.31}$| | P5 | 0.99 | S | |$23_{-6}^{+6}$| | |$-15.33 _{-0.09}^{+0.06}$| | |$-15.35_{-0.10}^{+0.05}$| | |$44.36_{-0.12}^{+0.09}$| | |$44.34_{-0.12}^{+0.09}$| | 149.2 | 86.2 |
| 502 | 3.157 | S3 | 1.00 | S | <1 | |$- 15.56_{-0.13}^{+0.08}$| | |$-15.61_{-0.10}^{+0.10}$| | |$43.50_{-0.13}^{+0.08}$| | |$43.45_{-0.13}^{+0.08}$| | 73.5 | 29.8 |
| 504 | |$3.36_{-0.09}^{+0.10}$| | P5 | 1.00 | H | |$831_{-537}^{+123}$| | <−16.31 | <−17.57 | |$43.14_{-0.24}^{+0.17}$| | |$42.26_{-0.13}^{+0.59}$| | 9.8 | 30.8 |
| 509 | |$3.15_{-0.57}^{+0.12}$| | P5 | 0.47 | S | <15 | |$-16.26 _{-0.26}^{+0.18}$| | <−16.93 | |$42.88_{-0.32}^{+0.21}$| | <42.30 | 15.1 | 3.2 |
| 526 | |$4.17_{-0.13}^{+0.10}$| | P5 | 1.00 | S | |$15_{-6}^{+7}$| | |$- 15.84_{-0.10}^{+0.07}$| | |$-15.88_{-0.10}^{+0.08}$| | |$43.71_{-0.14}^{+0.09}$| | |$43.67_{-0.15}^{+0.09}$| | 89.0 | 48.0 |
| 545 | 3.524 | S3 | 1.00 | S | <11 | |$- 15.27_{-0.07}^{+0.05}$| | |$-15.28_{-0.07}^{+0.05}$| | |$43.95_{-0.09}^{+0.07}$| | |$43.93_{-0.08}^{+0.08}$| | 132.4 | 46.8 |
| 572 | |$3.77_{-0.01}^{+0.03}$| | P2 | 1.00 | S | |$10_{-2}^{+2}$| | |$-15.49 _{-0.13}^{+0.08}$| | |$-15.54_{-0.17}^{+0.10}$| | |$43.94_{-0.14}^{+0.08}$| | |$43.89_{-0.17}^{+0.11}$| | 288.9 | 156.2 |
(1) ID from L17 or X16; (2) nominal redshifts (corresponding to the peaks of the PDFs) and uncertainties corresponding to the narrowest redshift intervals in which the integral of the PDFs is 0.68; (3) reference for the redshifts and PDFs: P1, P2, P3, P4 and P5 refer to photometric redshifts from S16, S14, H14, Rafferty et al. (2011) and Y14, respectively. S1 and S2 stand for spectroscopic redshift from the collection presented in L17, flagged as ‘secure’ and ‘insecure’ (but upgraded as described in Section 2.1), respectively. S3 and S4 refer to spectroscopic redshift from X16 and Y14 (for sources for which the multiwavelength matching has been improved via the visual inspection of X-ray and optical images, see Section 2.2), respectively. N refers to no redshift and, in such a case, column 2 is assigned a value of −1 and a flat PDF(z) is assumed. (4) Fraction of the PDFs at 3 ≤ z < 6 (see equation 4); (5) primary detection band (S: soft band, H: hard band; see Section 3.1); (6), (7), (8), (9) and (10): best estimates of the intrinsic column density, soft-band flux, 2–10 keV intrinsic luminosity and 68 per cent confidence-level uncertainties, respectively. For fluxes and luminosities, both the observed (i.e. not applying the Eddington bias correction in equation 5; columns 7 and 9) and the intrinsic (i.e. for which the Eddington bias correction has been applied; columns 8 and 10) values are reported.
Notes.aXID 977 has an insecure spectroscopic redshift in L17, but no photometric redshifts. Here, we conservatively discard that spectroscopic redshift and treat this source as spectroscopically unidentified.
bFor these sources, we assumed a flat distribution in column density, as their spectral quality was too poor to perform a spectral analysis. (11) and (12): net counts in the soft and hard bands, respectively.
In principle, equation (4) measures only the uncertainty of the photometric redshift. The probability for a source to be at z1 ≤ z < z2 can be computed by weighting equation (4) with the XLF, in order to take into account the intrinsic variation of the AGN space density with redshift, that can introduce systematic errors (e.g. Georgakakis et al. 2015). However, the general high quality of the photometric redshifts we used (see Sections 2.1 and 2.2, and Table 1), due to the availability of deep multiband data in the fields we considered, is reflected in narrow PDF(z). In fact, the PDF(z) of the spectroscopically unidentified sources included in our sample have a median 1σ uncertainty of 0.23. Such narrow PDF(z) would be at most sensitive to the ‘local’ XLF. For continuity reasons, the XLF cannot vary dramatically in a narrow redshift range and the applied weights are therefore expected to be negligible. This statement may not be true in cases of broader PDF(z), which would be therefore sensitive to the space-density variations over larger redshift intervals.
To quantify this effect in our case, we repeated the procedure followed to derive the redshift distribution of the sample, after weighting the PDF(z) with the Ueda et al. (2014) XLF. We also considered additional cases in which the Ueda et al. (2014) XLF is modified at high redshift to match the results of Vito et al. (2014) and Georgakakis et al. (2015). The new redshift distributions are barely distinguishable from Fig. 3, with |$1.7\text{--}5.9{\rm per \, cent}$| (depending on the particular XLF used) of the sample shifting below z = 3. Including in this computation sources with no redshift information (i.e. for which a flat PDF(z) is assumed), we found that |$2.5\text{--}7.7{\rm per \, cent}$| of the samples shift to low redshift. Moreover, the weighting is sensitive in particular to the assumed shape and evolution of the XLF faint end at high redshift, which is currently highly uncertain. For instance, using models with a steeper XLF faint end (e.g. Giallongo et al. 2015) would move a fractional number (<1) of sources from z ≲ 3 to z > 3, slightly increasing our sample size. Given the small effect obtained applying the XLF weighting and the source of additional uncertainty represented by the particular XLF assumed at high redshift, we will use equation (4) to measure the intrinsic redshift probability distribution.
We also made a basic assessment of the effects of the expected presence of redshift outliers in our high-redshift sample (i.e. intrinsically low-redshift sources scattered to high redshift because of the catastrophic failure of their photometric redshifts, and hence PDF(z)). We considered only X-ray sources with a high-quality spectroscopic redshift zspec < 3, assigned to them a photometric redshift following the priority order described in Sections 2.1 and 2.2, and computed the fraction of redshift outliers, defined as sources for which |zspec − zphot|/(1 + zspec) > 0.15 (see e.g. Luo et al. 2010), that would be counted in the high-redshift sample according to their photometric redshift (i.e. PDF(z)). Considering this fraction and the number of X-ray-selected, spectroscopically unidentified sources with photometric redshift zphot < 3, we estimated that ≈4 sources in our high-redshift sample ( ≈ 4 per cent) are such low-redshift interlopers. The outlier fraction may be higher for spectroscopically unidentified sources, since these are typically fainter than the control sample we used, but our results are not qualitatively affected even considering an outlier fraction of ≈ 10 per cent.
Our sample includes a few sources studied in detail in previous, dedicated works, like the two Compton-thick candidate AGN in the CDF-S at z = 4.762 (Gilli et al. 2014, ID 539 in Table 2) and z = 3.70 (Comastri et al. 2011, ID 551). We also include the three spectroscopically-identified z > 4 AGN in the CDF-N analysed by Vignali et al. (2002): ID 290 at z = 4.424, ID 330 at z = 5.186, which is also the X-ray source with the highest spectroscopic redshift in the Chandra deep fields, and ID 526 at z = 4.137.4
3 SPECTRAL ANALYSIS AND PARAMETER DISTRIBUTIONS
X-ray spectra of the sources in the z > 3 sample were extracted with acis extract (Broos et al. 2010), as described in L17 and X16. Following Vito et al. (2013), we analysed the individual X-ray spectra with xspec5 v12.9.0 (Arnaud 1996) assuming an absorbed power-law model with fixed Γ = 1.8 (a typical value for X-ray selected AGN, e.g. Liu et al. 2017), Galactic absorption (Kalberla et al. 2005) and intrinsic absorption (xspec model wabs × zwabs × powerlaw), for a total of two free parameters (the intrinsic column density, NH, which assumes solar metallicity, and the power-law normalization), in the energy range of 0.5–7 keV. More complex parametrizations are precluded by the general paucity of net counts characterizing the sources in the sample, which, being at high redshift, are typically faint. Appendix A describes our check through spectral simulations that the simplicity of the assumed spectral model does not affect the best-fitting column densities at logNH ≳ 23 (see Section 5 for discussion). In Appendix B, we study the photon index of a subsample of unobscured sources. The W statistic,6 based on the Cash statistic (Cash 1979) and suitable for Poisson data with Poisson background, was used to fit the model to the unbinned spectra. If a spectroscopic redshift is assigned to a source, the fit was performed at that redshift, otherwise we used a grid of redshifts (with step Δz = 0.01), obtaining for each source a set of best-fitting models as a function of redshift. In Section 3.1, we derive the probability distribution of net count rate for each source, including a correction for Eddington bias. In Section 3.2, we convolve the set of best-fitting models with the redshift PDF for each source to derive the probability distribution of best-fitting column density. The fluxes of the sources are derived from the observed count rates in Section 3.3, where we also present the logN-logS of the sample. In Section 3.4, we combine the fluxes and column densities to derive the intrinsic X-ray luminosities. Results from spectral analysis are reported in Table 2.
3.1 Count rates, sky-coverage and Eddington bias
The fundamental quantity measured by an X-ray detector is the count rate of a source, which can then be converted into energy flux assuming a spectral shape and using the detector response matrices. Absorption affects strongly the spectral shape, in particular in the observed soft band (0.5–2 keV). Therefore, different levels of absorption affecting sources with the same count rate result in different measured fluxes. Usually, when performing statistical studies of populations of astrophysical objects detected in X-ray surveys, weights are assigned to each source to take into account the different sensitive areas of the survey at different fluxes. The curves of the area sensitive to a given flux (namely, the sky-coverage) for the 7 Ms CDF-S and 2 Ms CDF-N are shown in Fig. 4 (where we considered only the area covered by ≥1 Ms effective exposure, as per Section 2.1) for our two detection bands (see below). Since the source-detection algorithm used by L17 and X16 operates in the count rate space, sources with the same fluxes in the detection energy band can be detected over different areas, if their spectral shapes are different (i.e. the same count rate can correspond to different fluxes). This is usually not taken into account, and an average spectral shape (usually a power-law with Γ = 1.4) is assumed for all the sources, which can introduce errors up to a factor of several in the weights associated with each source (Vito et al. 2014).
Area covered by ≥1 Ms effective exposure sensitive to a given minimum count rate (lower x-axis) or flux (upper x-axis, assuming a power-law spectral shape with Γ = 1.4) for the CDF-S (red curve), CDF-N (blue curve) and for the combination of the two surveys (black curve), in the soft band (left-hand panel) and hard band (right-hand panel). Different spectral assumptions would change only the flux axis. The dotted vertical line marks the minimum intrinsic count rate we assumed for the sources in our sample (equation 7). The vertical dashed lines indicate the minimum count rate corresponding to a 10 arcmin2 sensitive area, which we consider the observed count rate limit for a source to be detected (see equation 8) to avoid large correction factors due to the small area sensitive at lower count rates.
3.2 Intrinsic column-density distribution
For each source, we report in Table 2 the logNH that maximizes equation (10) (i.e. our best estimate of the intrinsic column density) and the 68 per cent confidence level uncertainties, corresponding to the narrowest logNH interval in which the integrated P(logNH) is 68 per cent. Fig. 5 presents the PDF(z) and P(logNH) for a source as an example. The PDF of redshift, column density, flux (see Section 3.3) and luminosity (see Section 3.4) for every source in the sample are made available with the online version of this paper. Fig. 6 presents the best-fitting column density plotted against the nominal redshift of each source (i.e. the spectroscopic redshift or the redshift corresponding to the peak of PDF(z)).
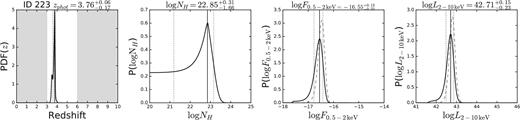
From left to right: PDFs of redshift, column density (equation 10), flux (equation 16) and luminosity (equation 20) for ID 223. The area not shadowed in the first panel shows the redshift range of this work and the part of the PDF(z) used to compute the probability distributions of the other parameters. In each panel, the solid and dotted vertical lines mark the position of the nominal value and the 68 per cent confidence interval of the relative parameter. Dashed grey curves in the last two panels are the probability distribution of flux and luminosity if the correction for Eddington bias is not applied in equation (5). Probability distributions for all sources will be made available online. Most of the distributions are well behaved like those shown here, while a few have more complex (i.e. broad or with double peaks) shapes. The complex functions are produced by the combined effects of the measured PDF(z), and, especially for faint sources, the uncertainties on NH and flux, and the area-correction (i.e. the Ω) factors.
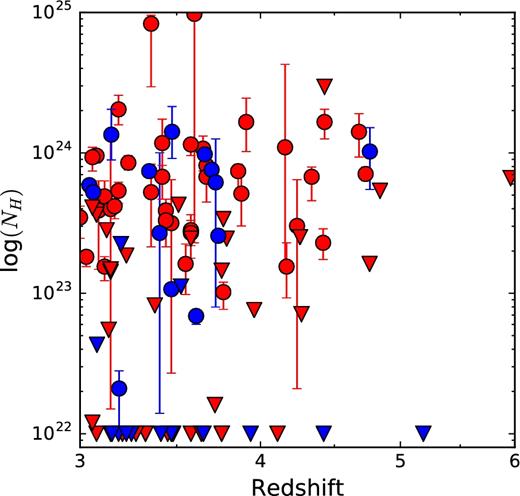
Best-fitting column density versus redshift for sources with spectroscopic (blue symbols) and photometric (red symbols) redshift. Upper limits are displayed as downward-pointing triangles.
Fig. 7 shows the binned Ntot(logNH). Errors have been computed through a bootstrap procedure: we created a list of Nhz sources randomly chosen amongst the Nhz sources in our sample, allowing for repetition (i.e. one source can appear in the new list 0, 1 or multiple times). We then recomputed Ntot(logNH). Repeating this procedure 1000 times, we derived 1000 distributions of Ntot(logNH) or, equivalently, at each logNH we derived 1000 values of probability. The 68 per cent confidence interval at each logNH has been computed by sorting the corresponding 1000 probabilities and selecting the 16th and 84th quantile values. Liu et al. (2017) presented an X-ray spectral analysis of the 7 Ms CDF-S sources with >80 net counts. Fig. 7 is consistent with the column-density distribution presented in that work in an overlapping redshift bin (z = 2.4–5), in spite of the different assumed spectral models and performed analysis. Also, the priority we assigned to the different photometric-redshift catalogues is different than that used by Liu et al. (2017), resulting in some sources having different redshifts.
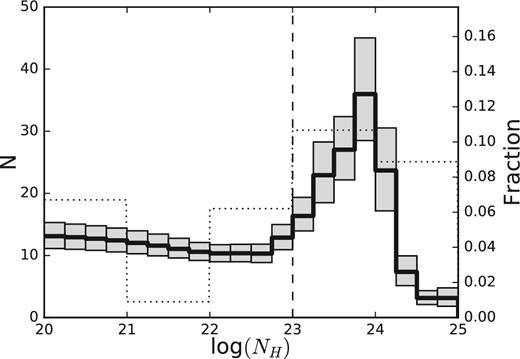
Binned intrinsic (i.e. weighted by the redshift probability distribution functions and sky-coverages associated with the individual sources) distribution of column density of our sample (equation 11). Uncertainties (at 68 per cent confidence level; grey regions) have been computed through a bootstrap procedure. The vertical dashed line represents the threshold used in this work to separate obscured and unobscured AGN at high redshift. The flatness of the distribution below logNH ≈ 23 is due to the lack of information in X-ray spectra at high redshift useful to constrain such low levels of obscuration, as discussed in Section 3.2. The dotted histogram is the column-density distribution assumed by Gilli et al. (2007), which will be used in Section 4.
The flattening at logNH ≲ 23 is due to the photoelectric cut-off detection limit. Indeed, the determination of the best-fitting NH for an X-ray spectrum is largely driven by the detection of the photoelectric cut-off, which is a function of both redshift and column density. In particular, the photoelectric cut-off shifts to higher energies for increasing NH and to lower energies for increasing redshift. Thus, at high redshift, unless a source is heavily obscured, the photoelectric cut-off is shifted outside the Chandra bandpass and, for small-to-moderate numbers of net counts, it is virtually impossible to determine the intrinsic column density. In Vito et al. (2013), we estimated the minimum column density that could be constrained for a typical (∼100 net counts) AGN in the 4 Ms CDF-S at z ∼ 3.5 to be logNH ≈ 23.
We stress that the flattening at logNH ≲ 23, due to the lack of information in X-ray spectra useful to constrain such low values of obscuration at high redshift, should not be considered real. We can derive the probability of a source having logNH ≲ 23, but not the exact probability distribution in column density bins below this threshold, resulting in a flat behaviour. According to these considerations, we will adopt logNH = 23 as the threshold between obscured and unobscured sources. This choice is further reinforced by the spectral simulations we performed in Appendix A.
3.3 Flux distribution and number counts
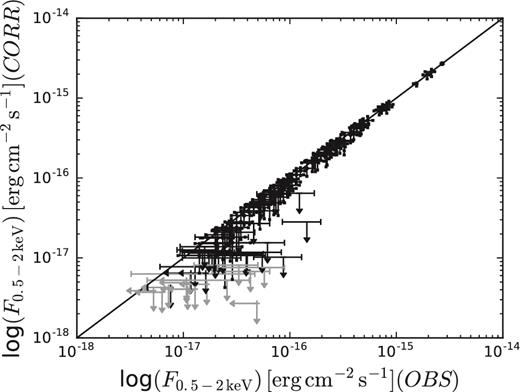
Best estimates of the soft-band flux obtained by integrating equation 16, with relative 68 per cent confidence level uncertainties, corrected for Eddington bias (see equation 5), compared to the uncorrected (i.e. observed) values. Grey symbols represent soft-band undetected sources, which are shown for completeness, for which the count rate (and therefore flux) in the hard band has been used everywhere else in this work.
Fig. 9 shows the binned Ntot(F0.5–2 keV) with 68 per cent confidence intervals derived with a bootstrapping procedure, similarly to what was done in Section 3.2 and Fig. 7. We note that, as we remained in the count rate space, the distributions extend slightly below the nominal flux-limit, since the assumed count rate limit corresponds to slightly different fluxes for different observed spectral shapes and response matrices (see Section 3.1).
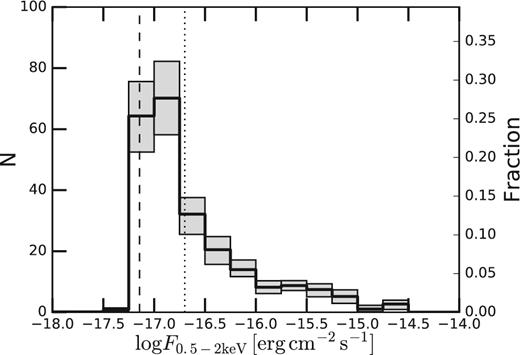
Binned intrinsic (i.e. weighted by the redshift probability distribution functions and sky-coverages associated with the individual sources) distribution of flux for our subsample of soft-band detected AGN (equation 17) and relative uncertainties (at 68 per cent confidence level; grey bars). The dashed and dotted vertical lines represent the flux limits (assuming Γ = 1.4) of the CDF-S (corresponding to a sensitive area A = 10 arcmin2, i.e. dashed line in Fig. 4) and the CDF-N, respectively.
3.3.1 AGN logN-logS at 3 ≤ z < 6
The cumulative version of equation (17), divided by the total area in deg2, is the logN-logS relation of our sample. The 68 per cent confidence region derived through the bootstrap procedure is compared with results from previous works at z > 3 and z > 4 in Fig. 10. We derived the z > 4 logN-logS by repeating the procedures described in this section, using z = 4 as the lower limit for the considered redshift range. Bright and rare sources are not sampled properly by the pencil-beam, deep surveys such as those used in this work. Therefore, Fig. 10 displays the curves up to the flux at which the median expected number of sources from the bootstrap analysis is 1 in the area considered in this work (∼550 arcmin2, see Fig. 4, corresponding to ∼6.5 deg−2 sources).
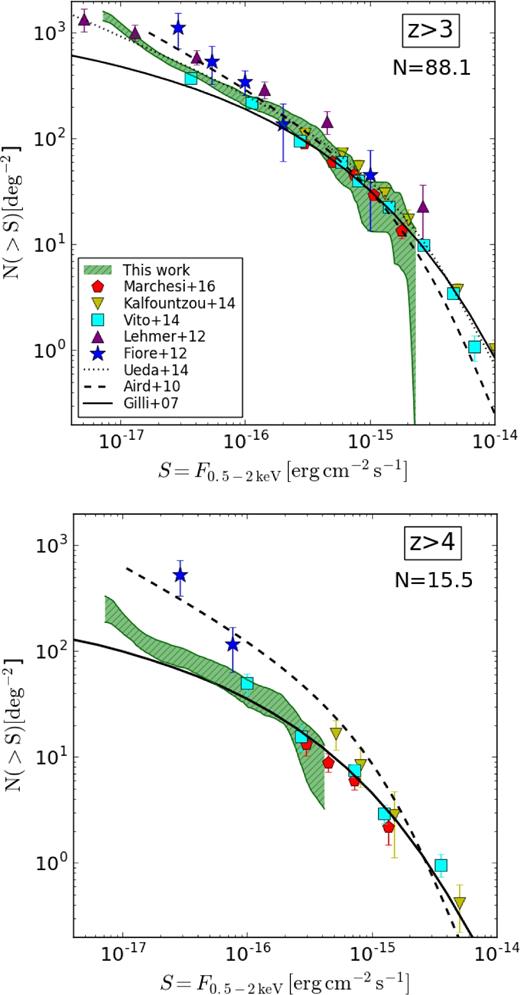
Confidence region (at the 68 per cent level) of the logN-logS of our subsample of soft-band detected, z > 3 (top panel) and z > 4 (bottom panel) AGN, compared with results from previous works. The numbers of soft-band-detected sources, weighted by the PDF(z), included in these figures are also reported.
Our results are in good agreement with previous measurements at logF0.5–2 keV ≳ −16, which is the flux regime better sampled by wide surveys. At fainter fluxes, where we can exploit the excellent sensitivity of the Chandra deep fields, our results are consistent with previous results that used data from the 4 Ms CDF-S (Lehmer et al. 2012; Vito et al. 2014) and with the Ueda et al. (2014) curve. Lehmer et al. (2012) presented the number counts derived in the 4 Ms CDF-S down to slightly fainter fluxes than those reached in this work. This is due to the less-conservative approach they used to compute the sensitivity of the 4 Ms CDF-S compared to that used by L17 for the 7 Ms CDF-S, which we adopted here.
At z > 4, we can push the AGN number counts down to logF0.5−2 keV ≈ −17. While our curve agrees with previous results at bright fluxes and with the Gilli, Comastri & Hasinger (2007) logN-logS reasonably well, it excludes very steep number counts such as those reported by Fiore et al. (2012) at faint fluxes. The selection in Fiore et al. (2012) made use of pre-determined optical positions of galaxies and adaptive X-ray detection bands, and it is therefore less conservative than a blind X-ray detection. However, about half of the 4 Ms CDF-S sources reported in that work at z > 4 were not detected even in the deeper 7 Ms exposures, leaving doubts about their detection significance (especially considering that the Fiore et al. (2012) analysis is plausibly affected by Eddington bias). This issue, together with the different, more recent photometric redshifts we used, which shift some of the Fiore et al. (2012) to lower redshifts, accounts completely for the discrepancies in Fig. 10.
By changing the limits of the integral of column density in equation (17), we derived separately the logN-logS for obscured (23 ≤ logNH < 25) and unobscured (20 ≤ logNH < 23) AGN (Fig. 11). The Gilli et al. (2007) X-ray background synthesis model underestimates the number of obscured AGN at high redshift and the steepening of our number counts of unobscured sources at logF0.5–2 keV < −16.5 (see Fig. 11). Such steepening could be due to the population of star-forming galaxies, which begin providing a significant contribution to the number counts at the faintest fluxes probed by this work (e.g. Lehmer et al. 2012).
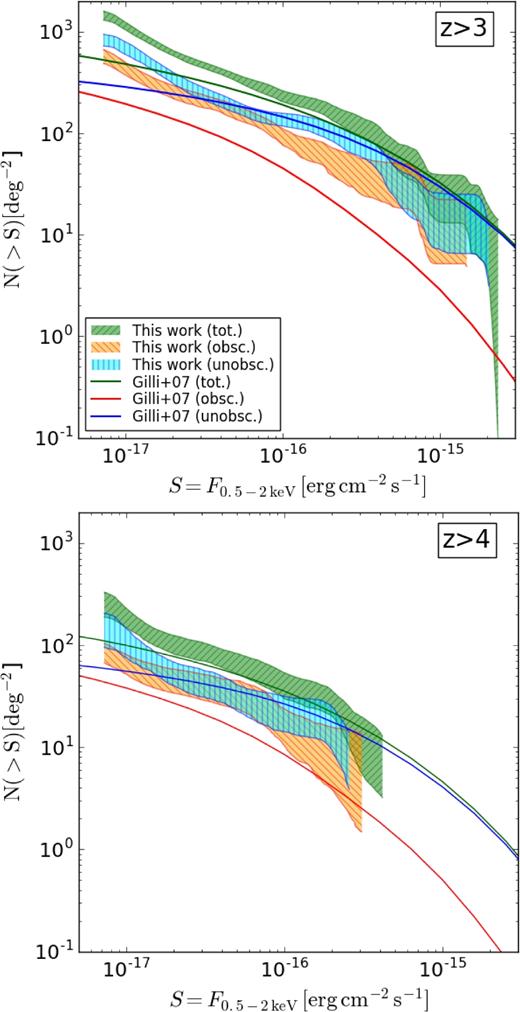
Confidence region (at the 68 per cent level) of the logN-logS of our subsample of soft-band detected, z > 3 (top panel) and z > 4 (bottom panel) AGN, for the total sample (green stripes), obscured (orange stripes) and unobscured (cyan stripes) AGN. The results are compared to the expectations of the Gilli et al. (2007) X-ray background synthesis model, using the same NH threshold to define the obscuration-based subsamples.
3.4 Luminosity distribution
P(LX, logNH, z) is normalized to unity. Equation (20) includes the correction for Eddington-bias applied in equation (5). However, we checked that neglecting this correction results in a similar luminosity distribution, with a slight decrease in the number of logLX < 42.5 sources, balanced by an increase at higher luminosities, as expected. The luminosity probability distribution (P(LX)) of each source is derived by integrating equation (20) over the considered redshift and column-density ranges. Fig. 5 presents P(LX) for a source as an example. Table 2 reports for each source the luminosity value that maximizes P(LX) (i.e. our best estimate of the luminosity of each source) and the 68 per cent confidence level uncertainties, corresponding to the narrowest interval containing 68 per cent of the total probability. If less than 68 per cent of P(CR) of a source lies above the count rate limit, we report the upper limit of P(LX).
Fig. 12 shows the binned Ntot(LX) with 68 per cent confidence intervals derived from a bootstrapping procedure, similar to what was done in Section 3.2 and Fig. 7.
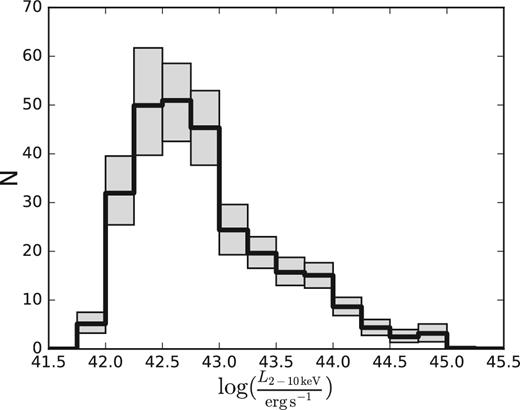
Binned intrinsic (i.e. weighted by the redshift probability distribution functions and sky-coverages associated with the individual sources) distribution of hard-band luminosity of our sample (equation 22) and relative uncertainties (at 68 per cent confidence level, grey bars).
4 OBSCURATION-DEPENDENT INCOMPLETENESS
The flux (or count rate) limit of a survey is effectively a limit in luminosity, redshift, and column density, as these are the physical parameters defining the flux (assuming our simple spectral model). Therefore, a low-luminosity AGN at a given redshift can be detected only if its column density is below a certain level, causing an obscuration-dependent incompleteness that affects the low-luminosity regime by favouring the detection of unobscured AGN (see also section 5.1.2 of Liu et al. 2017). Such incompleteness usually appears in X-ray studies of flux-limited AGN samples as a lack of detected sources in the low-luminosity and heavy-obscuration region of the LX − NH parameter space.
It is worth noting that this effect is not corrected by the Ω(CR) factor, which compensates for the different areas sensitive to different observed fluxes for detected sources, irrespective of their intrinsic properties (e.g. obscuration). In fact, while representing a potentially significant fraction of the population, low-luminosity and heavily obscured AGN are not detected at all, and are therefore not accounted for when deriving intrinsic properties (e.g. space density) of the low-luminosity population. This effect is particularly important when two obscuration-based subsamples are defined to compute the obscured AGN fraction, Fobsc, which would be biased towards lower values, and its trends with redshift and luminosity (e.g. Gilli et al. 2010). Therefore, before deriving Fobsc as a function of redshift and luminosity in Section 5, in this section we assess the effect of the obscuration-dependent incompleteness and derive suitable corrections.
The completeness level in the z–LX plane is shown in Fig. 13 by computing the mean over the NH axis separately for logNH = 23–25 and logNH = 20–23, weighted over an assumed intrinsic column-density distribution P(logNH), which we here considered to be represented by Fig. 7. At logLX ≲ 43, the two classes of objects are characterized by very different completeness levels: in the upper panel of Fig. 13, the detection of unobscured sources is complete up to z ∼ 6 for logLX ≳ 42.5, while lower-luminosity AGN can be detected only at lower redshifts. Since the photoelectric cut-off for logNH ≲ 23 shifts close to or below the lower-limit of the Chandra bandpass, for unobscured sources the completeness is almost independent of the column-density distribution. For this reason, the transition between 0 per cent and 100 per cent completeness is sharp, as it depends only on redshift and luminosity.8 The lower panel shows that for logNH = 23–25 at a given redshift the transition is smoother and occurs at larger luminosities. In fact, contrary to the case of unobscured sources, the flux of an obscured source depends strongly on the particular NH value: more heavily obscured sources can be detected only at higher luminosities than sources affected by milder obscuration. The darker stripe at logLX ∼ 43–43.5 and z ∼ 3.5–4.5 is due to the inclusion of the hard band; heavily-obscured sources in those redshift and luminosity intervals are more easily detected in the hard band than in the soft band.
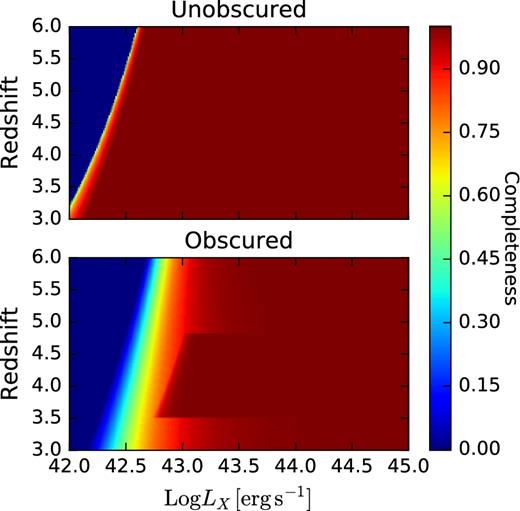
Detection completeness at the 7 Ms CDF-S depth as a function of redshift and luminosity for obscured (lower panel) and unobscured (upper panel) sources. An intrinsic column density distribution similar to Fig. 7 is assumed, as described in Section 4, where the dark thick stripe at logLX ∼ 43–43.5 and z ∼ 3.5–4.5 is also discussed.
By projecting Fig. 13 over the luminosity axis (i.e. averaging over the redshift range), we derived the completeness curve as a function of luminosity (solid lines in Fig. 14). The averaging is weighted assuming an intrinsic redshift distribution characterized by a decline in the space density of high-redshift AGN proportional to (1 + z)−6 (e.g. Hiroi et al. 2012; Vito et al. 2014, solid lines). The unweighted projection corresponds to a flat distribution in redshift and is shown for completeness as dashed lines in Fig. 14. The specific redshift distribution has a small effect on the displayed curves: this behaviour is due to the negative curvature of absorbed X-ray spectra, which causes inverted K-corrections at increasing redshift.
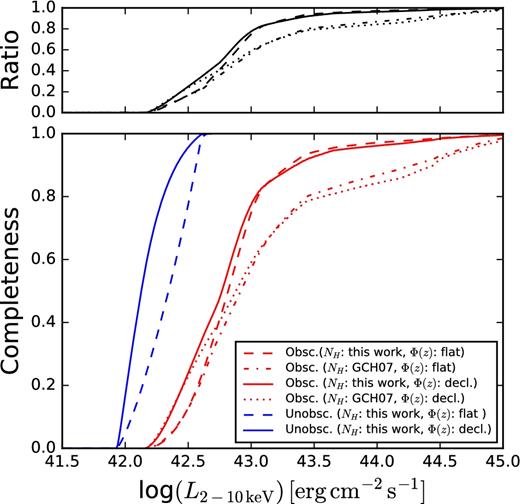
Detection completeness at the 7 Ms CDF-S depth as a function of luminosity for obscured (red lines) and unobscured (blue lines) sources, assuming different intrinsic distributions of column density (the one presented in this work in Fig. 7 and the one used in Gilli et al. 2007) and redshift (flat or more realistically declining with redshift as ∝10−6(1 + z); e.g. Hiroi et al. 2012; Vito et al. 2013), as described in Section 4. For the unobscured case, the curves corresponding to the two column-density distributions are almost indistinguishable and therefore are not plotted for clarity. The solid lines have been used to derive the correction factors applied to Figs 16 and 18. The upper panel presents the ratio of the completeness of obscured and unobscured sources.
To assess the dependence on the particular choice of column-density distribution, we also assumed the one from Gilli et al. (2007), in which, in particular, Compton-thick AGN are more numerous (see Fig. 7). While the completeness curve for unobscured sources is not sensitive to the particular choice of P(logNH) (we do not show the curve corresponding to the Gilli et al. 2007 case for clarity), the completeness curve for obscured AGN is more severely affected by the Gilli et al. (2007) P(logNH).
The bias affecting the obscured AGN fraction is linked to the relative completeness levels of the obscured and unobscured subsamples as a function of redshift and luminosity. To visualize this effect, the upper panel in Fig. 14 shows the ratio of the completeness characterizing obscured and unobscured subsamples as a function of luminosity. The ratio varies rapidly from logLX = 42–43, rising from zero to ≈0.8. This is the regime in which the incompleteness effects are strongest: at low intrinsic luminosities, the presence or absence of even moderate obscuration is crucial for observing a flux above or below the survey sensitivity limit. At higher luminosities, only the most-obscured systems cannot be detected, and incompleteness is less severe.
Similarly, we derived the completeness as a function of redshift (Fig. 15) by projecting Fig. 13 over the redshift axis and assuming an intrinsic luminosity distribution (i.e. luminosity function). We used the pure density evolution model of Vito et al. (2014). The upper panel of Fig. 15 shows that the relative strength of incompleteness for obscured and unobscured sources does not significantly vary with redshift, but the evolution is slightly stronger for unobscured sources: this behaviour is due to the inverse K-correction characterizing obscured X-ray sources, which helps the detection of these systems at higher redshifts.
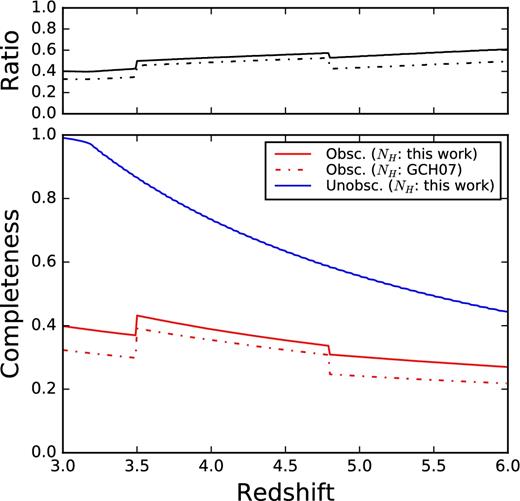
Detection completeness at the 7 Ms CDF-S depth as a function of redshift for obscured (red lines) and unobscured (blue line) sources, assuming different intrinsic distributions of column density and the luminosity function of Vito et al. (2014). The solid line has been used to derive the correction factors applied to Figs 16 and 21. The upper panel shows the ratio of the completeness of obscured and unobscured sources.
5 OBSCURED AGN FRACTION
As discussed in Section 3.2 and following Vito et al. (2013, 2014), throughout this work we used logNH = 23 as the column-density threshold dividing obscured and unobscured AGN at z > 3. This value is higher than the commonly adopted threshold of logNH = 22 in X-ray studies of the AGN population (e.g. Ueda et al. 2014; Aird et al. 2015; Buchner et al. 2015), which is also more in agreement with optical classification (e.g. Merloni et al. 2014). However, such low levels of obscuration are extremely difficult to detect at high redshift, where the photoelectric cut-off in X-ray spectra shifts below the energy band probed by X-ray observatories. The redshifted cut-off, together with the typical limited spectral quality of high-redshift sources, leads to a general overestimate of obscuration for low values of NH, as can be seen in Appendix A. This effect is especially important when considering the obscured AGN fraction and its trends with other quantities, such as redshift and luminosity. We therefore prefer to define logNH = 23, as the minimum column density of (heavily) obscured AGN at high redshift and discuss the dependence of (heavily) obscured AGN on redshift and luminosity. Unfortunately, this choice complicates the comparison with previous works utilizing more standard definitions. In Appendix C, we show that neglecting the full probability distributions of redshift and spectral parameters would lead to different results than those presented in the following subsections.
5.1 Obscured AGN fraction versus redshift
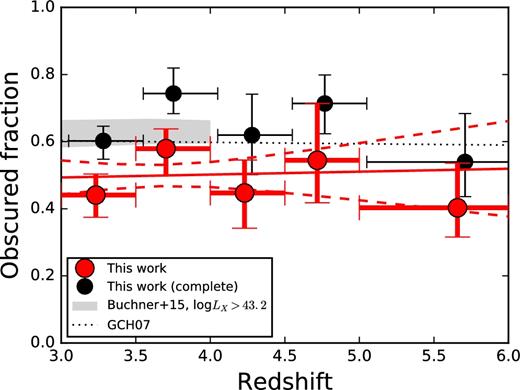
Binned estimates of the obscured AGN fraction as a function of redshift (Fobsc(z); red circles). The red solid and dashed lines show the best-fitting linear model and 68 per cent confidence level region, respectively. The continuous line is not the fit to the points: line and points are different estimates of the obscured AGN fraction as a function of redshift derived using different (parametric and non-parametric) methods. Grey regions encompass the Fobsc(z) from Buchner et al. (2015) for luminous AGN. Black circles, slightly shifted for visual purposes, indicate the non-parametric estimate of Fobsc(z), where a correction for the obscuration-dependent incompleteness has been applied (see Section 4). The dotted line is the predictions from the X-ray background synthesis model of Gilli et al. (2007).
To derive an independent and parametric estimate of the dependency of Fobsc on redshift, we performed a Bayesian analysis9 of Fobsc(z), assuming a linear model of the form Fmobsc = qz + mz(z − 3). We applied a flat prior to qz and a minimally informative prior to mz, such that |$P(m_{z})\propto (1+m_{z}^2)^{3/2}$| (e.g. VanderPlas 2014 and references therein). The latter is preferred over a flat prior on β, which would weight steep slopes more.10 We also associated a null probability to parameter pairs resulting in unphysical Fobsc values (i.e. negative or larger than unity) in the redshift interval probed by the data.
The resulting best-fitting values are |$q_{z}=0.50_{-0.05}^{+0.05}$| and |$m_{z}=0.00_{-0.06}^{+0.06}$|. The red dashed lines in Fig. 16 enclose the 68 per cent confidence interval of 106 MCMC realizations derived using this parametric approach, and the solid line is the median value. The parametric and non-parametric representations, derived independently, agree well, showing the robustness of our approach. The observed obscured AGN fraction is found in Fig. 16 to be flat at z = 3–5 at Fobsc ≈ 0.5. Fobsc is usually found to increase with redshift up to z ≈ 2–2.5, and then saturates at higher redshifts (e.g. Treister & Urry 2006; Hasinger 2008; Iwasawa et al. 2012; Buchner et al. 2015; Liu et al. 2017). We probe such behaviour up to z ∼ 6. Black circles in Fig. 16 are derived by correcting the red points using the solid lines in Fig. 15, causing Fobsc(z) generally to increase slightly, with no strong dependence on redshift, to values ≈0.65, consistent with the results by Buchner et al. (2015) at high luminosities (logLX > 43.2) up to z ∼ 4. We could push the investigation of Fobsc(z) down to lower luminosities.
5.2 Obscured AGN fraction versus soft-band flux
Considering only the soft-band detected sources, we defined Nunobs(FX) and Nobsc(FX) from equation (17) by limiting the integral over column density to the ranges logNH = 20–23 and 23–25, respectively, and summing only the soft-band-detected sources.
Similar to the process described in Section 5.1, we derived the parametric (assuming a linear model |$F_{\mathrm{obsc}}=q_{F_{\mathrm{X}}} + m_{F_{\mathrm{X}}}(\mathrm{log}F_{\mathrm{X}}-(-17))$| and non-parametric obscured AGN fraction as a function of flux. The results are shown in Fig. 17 and compared with the predictions of the Gilli et al. (2007) X-ray background synthesis model. The resulting best-fitting values are |$q_{F_{\mathrm{X}}}=0.43_{-0.04}^{+0.04}$| and |$m_{F_{\mathrm{X}}}=-0.04_{-0.06}^{+0.06}$|.
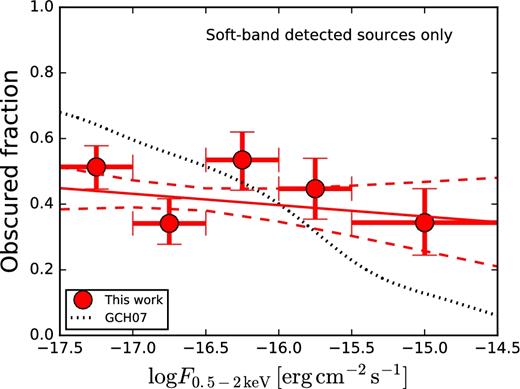
Binned estimates of the obscured, soft-band detected AGN fraction as function of flux (red circles). Red continuous and dashed lines are the best-fitting linear model and 68 per cent confidence level region, respectively. The prediction of the Gilli et al. (2007) X-ray background synthesis model are indicated by the dotted black line.
5.3 Obscured AGN fraction versus luminosity
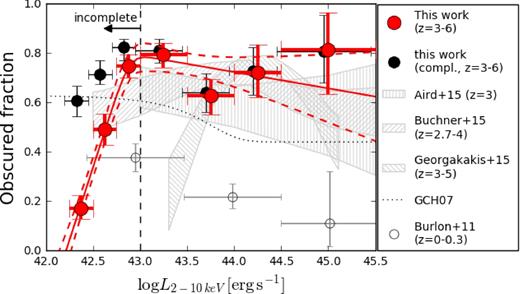
Binned estimates of the obscured AGN fraction as a function of intrinsic hard-band luminosity (Fobsc(LX), red circles). Solid and dashed lines represent the best-fitting model (as defined in equation 28) and 68 per cent confidence level region, respectively, as derived through a Bayesian analysis. Grey-dashed regions encompass the Fobsc(LX) derived by Aird et al. (2015), Buchner et al. (2015) and Georgakakis et al. (2015), as labelled in the figure. The curves are plotted for slightly different redshift ranges, as reported in the legend. Obscured AGN are defined as those with logNH = 22–24 in Aird et al. (2015) and Buchner et al. (2015), while we require logNH > 23. Georgakakis et al. (2015) derived their obscured AGN fraction by comparing X-ray and UV luminosity functions. The dotted black line indicates the prediction of the X-ray background synthesis model of Gilli et al. (2007). We also plot the results derived by Burlon et al. (2011) in the local Universe, as grey empty circles to show the strong evolution of Fobsc from low to high redshift. The Burlon et al. (2011) points use the same column-density threshold, as we assumed to define obscured and unobscured sources, and are therefore directly comparable with our points. Black circles (slightly shifted for visual purposes) show the non-parametric estimate of Fobsc(LX), where a correction for the obscuration-dependent incompleteness has been applied (see Section 4).
We compare the high fraction of heavily obscured AGN (Fobsc ≈ 0.7–0.8) we derived at high luminosities (logLX > 43) with previous findings by Aird et al. (2015) and Buchner et al. (2015), where obscured AGN are defined in a more ‘standard’ way as those characterized by logNH = 22–24. The column-density threshold used to separate obscured and unobscured AGN in their works, logNH = 22, while useful for comparison purposes with results at lower redshift, is not suitable at high redshift, where the photoelectric cut-off shifts at low energies, close to or even below the lower energy boundary of the Chandra bandpass and is therefore poorly constrained, as discussed in Section 7 and Appendix A. For completeness, we also show the results of Georgakakis et al. (2015), where the obscured AGN fraction is derived by comparing X-ray and UV luminosity functions, and therefore is not directly comparable to the other purely X-ray defined curves.
While at logLX > 43 incompleteness effects are negligible, they dominate the observed trend of Fobsc at lower luminosities in Fig. 18. Applying the corrections discussed in Section 4 results in values, represented by the black circles in Fig. 18, consistent with those at logLX > 43 (i.e. Fobsc ≈ 0.7–0.8), although at logLX < 43 a slightly decreasing trend of Fobsc, down to ≈0.6, with decreasing luminosity remains visible. However, we caution that the applied corrections depend quite strongly on the particular intrinsic column density and luminosity distributions. Also, the possible detection of star-forming galaxies, which have typically steep spectra, at the lowest luminosities probed by this work (logLX ≈ 42–42.5) may decrease Fobsc in such regime. We therefore do not consider such trend to be significant.
The curve of Buchner et al. (2015) appears to suffer less from similar issues at low luminosities, although they reported a decrease of Fobsc(LX) at low luminosities. The difference with our observed result is probably due to the different procedure used; Buchner et al. (2015) applied a Bayesian procedure that disfavours strong variations of Fobsc over close redshift and luminosity bins. At high redshift, the faint regime is not well sampled, probably causing the obscured AGN fraction at low luminosities to be dominated by the priors, i.e. to be similar to the value at lower redshift and/or higher luminosity, where incompleteness issues are less severe, alleviating this issue. The slight decrease of Fobsc towards low luminosity, which they ascribed to different possible physical mechanisms, may be at least partly due to incompleteness effects.
A strong anti-correlation between Fobsc and luminosity is usually found at low redshifts. For instance, grey empty symbols in Fig. 18 represent the fraction of AGN with logNH > 23 derived by Burlon et al. 2011 at z < 0.3. This behaviour appears not to hold at high redshift, or at least to be much less evident. Comparing our points with the Burlon et al. (2011), we note the positive evolution of Fobsc from the local Universe to high redshift, which is stronger at high luminosities. In Vito et al. (2014), where we derived similar results from a combination of different X-ray surveys, we ascribed the larger fraction of luminous obscured AGN at high redshift than at low redshift to the larger gas fractions of galaxies at earlier cosmic epochs (e.g. Carilli & Walter 2013), which can cause larger covering factors and/or longer obscuration phases. This description is especially true if luminous AGN are preferentially triggered by wet-merger episodes (e.g. Di Matteo, Springel & Hernquist 2005; Menci et al. 2008; Treister et al. 2012), whose rate is expected to be higher in the early Universe. In this case, chaotic accretion of gas on to the SMBH can produce large covering factors.
Figs 16 and 18 do not account for the covariance between the Fobsc − z and Fobsc − LX trends, due to our data set being flux limited. This could in principle bias the results when investigating Fobsc separately as a function of one of the two parameters. To check for this possible effect, we derived the trend of Fobsc with redshift separately for two luminosity bins, logLX = 43–43.5 and 43.5–45, chosen not to suffer significantly from incompleteness and to include approximately the same number of sources. For both subsamples, Fobsc is consistent with being flat at similar values, reassuring us that this result does not strongly depend on the intrinsic trend with redshift. We also repeated the procedure dividing the sample in two redshift bins and deriving the trend of Fobsc with luminosity in each of them. The results are consistent with those reported above in this section within the (larger) uncertainties.
6 EVOLUTION OF THE HIGH-REDSHIFT AGN POPULATION
6.1 The AGN XLF at high redshift
The AGN XLF can be derived from equation (22) by integrating over narrower redshift intervals and dividing the results by the volume sampled by the surveys in each redshift bin. Fig. 19 presents the XLFs in two redshift bins, chosen to include approximately the same numbers of sources. As stated in Section 3.4, ignoring the correction for Eddington bias does not change significantly the luminosity distribution of our sample, and, as a consequence, the derived XLFs. In particular, the slope of the faint end does not significantly vary when applying or neglecting such a correction. Our XLFs are fairly consistent with previous observational results from Aird et al. (2010), Ueda et al. (2014) and Vito et al. (2014, 2016). They are also in agreement with Buchner et al. (2015) at z < 3.6, which do not provide an analytical expression for the XLF, but rather confidence regions in redshift intervals. At higher redshifts, the Buchner et al. (2015) region exceeds our results. Similarly, the simulated XLFs by Habouzit, Volonteri & Dubois (2017) appear to overpredict the density of low-luminosity AGN.
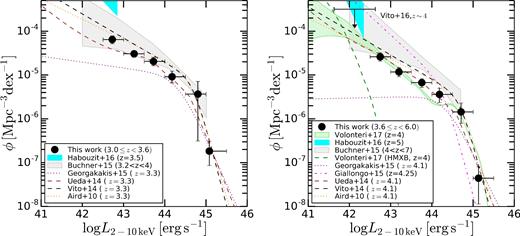
XLFs of AGN at z = 3–3.6 (left-hand panel) and z = 3.6–6 (right-hand panel), compared with results from previous observational (Aird et al. 2010; Ueda et al. 2014; Vito et al. 2014; Buchner et al. 2015; Georgakakis et al. 2015; Giallongo et al. 2015; extrapolated to lower luminosities than those probed by the original works) and theoretical (Habouzit et al. 2017; Volonteri et al. 2017) works at similar redshifts. In the right-hand panel, the downward-pointing arrow is the upper limit derived by Vito et al. (2016) through a stacking analysis of the 7 Ms CDF-S data set, and the dashed green line is the expected XLF of HMXBs at z = 4 (from Volonteri et al. 2017). Our results exclude extremely steep or flat slopes of the faint end of the AGN XLF.
Giallongo et al. (2015) applied a detection procedure based on searching for clustering of photons in energy, space and time, at the pre-determined optical positions of CANDELS-detected galaxies (see also Fiore et al. 2012), which allowed the authors to push the Chandra sensitivity beyond the limit reachable by blind detection methods (i.e. with no previous knowledge of the positions of galaxies). The large number of low-luminosity AGN at high redshift detected by Giallongo et al. (2015) suggests that AGN could have an important role in cosmic reionization (e.g. Madau & Haardt 2015; but see also Ricci et al. 2017).
Giallongo et al. (2015) derived the UV LF of their sample of X-ray detected, high-redshift AGN candidates by deriving the absolute UV magnitude from the apparent optical magnitude in the filter closest to rest-frame |$1450\, {{^{\circ}_{\rm A}} }$| at the redshift of each source. We transformed their UV LF into an X-ray LF (see Fig. 19) by assuming a SED shape Fν ∝ ν−0.5 between 1450 and |$2500\, {{^{\circ}_{\rm A}} }$| (as in Georgakakis et al. 2015), the Lusso et al. (2010) αox and Γ = 1.8 for the X-ray spectrum (see also Vito et al. 2016). Our results do not support the very steep LFs derived by Giallongo et al. (2015). Parsa et al. (2017) recently disputed the very detection of the faint z > 4 AGN in Giallongo et al. (2015). Moreover, Cappelluti et al. (2016), applying a similar procedure which makes use of pre-determined optical positions, did not find such a large number of z > 4 sources. Other issues plausibly affect the assessment of the population of faint, high-redshift AGN, such as the uncertainties in the photometric redshifts, the expected presence of Eddington bias (which leads to overestimating the number of detected faint sources), and the XRBs contribution to X-ray emission at faint fluxes (e.g. Lehmer et al. 2012). Moreover, the uncertainties related to the assumed UV/X-ray spectral slope (discussed by Giallongo et al. 2015) may affect the conversion between UV magnitude and X-ray luminosity, although reasonable values for that conversion cannot produce the tension between their slope of the AGN XLF faint end and our results.
At the low luminosities probed by the 7 Ms CDF-S (logLX = 42 − 43), X-ray emission from XRB may provide a non-negligible contribution (e.g. Bauer et al. 2002; Ranalli, Comastri & Setti 2003, 2005; Lehmer et al. 2010; Mineo, Gilfanov & Sunyaev 2012). The green dashed line in Fig. 19 (right-hand panel) is the XLF of star-forming galaxies at z = 4, where the emission is mostly due to high-mass XRB, from the model by Volonteri et al. (2017, see in particular their section 2.2 for assumptions and caveats). Briefly, they mapped the stellar-mass functions of Song et al. (2016) into an XLF through the main sequence of star-forming galaxies (Salmon et al. 2015) and the SFR-LX scaling relation by Fragos et al. (2013, model 269), which Lehmer et al. (2016) demonstrated to be the best representation at z = 0–2.5. At logLX ≳ 42.5, the luminosity limit we applied to our luminosity functions, as the 42 ≲ logLX ≲ 42.5 regime, was strongly affected by incompleteness; the density of star-forming galaxies is a factor of ≳10 lower than the AGN density. We conclude that at such luminosities, our sample is not significantly contaminated by star-forming galaxies. At lower luminosities, the XLF of star-forming galaxies is comparable to, or even exceeds, the AGN XLF, in agreement with Vito et al. (2016), who found that the X-ray emission in galaxies individually undetected in the 7 Ms CDF-S is mostly due to XRB. Similar conclusions are reached by scaling the star-formation rate functions (SFRF; i.e. the comoving space densities of galaxies per unit star-formation rate) from Smit et al. (2012) and Gruppioni et al. (2015), at z ≈ 3.5 and 4, respectively, into XLF using the best-fitting, redshift-dependent Fragos et al. (2013) and Lehmer et al. (2016) relations.
6.2 The evolution of the AGN space density and comparison with the galaxy population
Integrating the XLF over luminosity, we derived the comoving space density of AGN in three luminosity bins (Fig. 20). The decline of the space density in Fig. 20 appears to be steeper for low-luminosity AGN than for luminous sources. However, incompleteness significantly affects the detection of low-luminosity AGN, as can be seen in Fig. 13. In fact, applying the incompleteness correction discussed in Section 4 to the density of low-luminosity AGN (empty circles in Fig. 20), a slightly flatter behaviour is derived. To quantify the decline of the space density, we fitted a model Φ(z) = A((1 + z)/(1 + z0))p, where z0 = 3, to the points through a simple χ2 minimization procedure, before (dashed lines in Fig. 20) and after the correction for incompleteness was applied. Fig. 20 displays the best-fitting model corrected for incompleteness only for the low-luminosity bin (dotted line), as at higher luminosities incompleteness is negligible. Table 3 summarizes the best-fitting values for the total sample and the three luminosity-based subsamples.
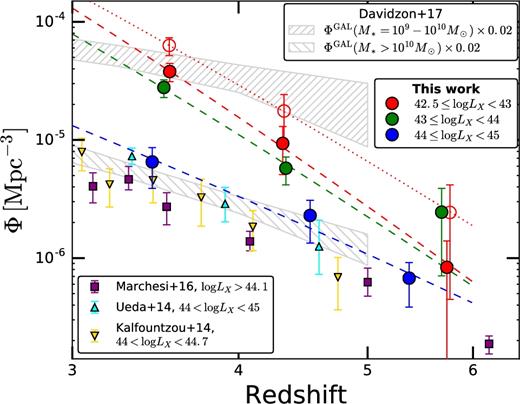
Comoving space density of three luminosity classes of AGN, divided in three redshift bins (z = 3–4, 4–5, 5–6). The points are located at the weighted average redshift of each subsample. For the low-luminosity bin, the empty circles indicate the results derived applying the correction factors described in Section 4. At higher luminosities, the corrections have negligible effects, and are not shown for clarity. Since high-luminosity sources are not well sampled by the deep, pencil-beam fields used in this work, we report previous results in similar luminosity bins derived analysing data from wider fields. The dashed curves are the best-fitting models described in Section 6. The dotted curve is the best-fitting model for the low-luminosity bin, after the correction for incompleteness. The space density of galaxies in two different mass regimes from Davidzon et al. (2017), rescaled by an arbitrary factor of 0.02, is shown as a grey stripe.
Best-fitting parameters describing the space-density evolution with redshift for the luminosity-based and obscuration-based subsamples (see Section 6).
| Subample . | A (Mpc−3) . | p . |
|---|---|---|
| All | (2.47 ± 0.57) × 10−4 | −7.59 ± 0.69 |
| 42.5 ≤ logLX < 43 | (1.31 ± 0.08) × 10−4 | −9.57 ± 0.32 |
| 43 ≤ logLX < 44 | (7.96 ± 2.70) × 10−5 | −8.85 ± 1.71 |
| 44 ≤ logLX < 45 | (1.33 ± 0.38) × 10−5 | −6.17 ± 0.87 |
| Obscured | (1.17 ± 0.43) × 10−4 | −8.12 ± 1.11 |
| Unobscured | (1.44 ± 0.34) × 10−4 | −8.25 ± 0.77 |
| After correction for incompleteness | ||
| All | (4.22 ± 1.19) × 10−4 | −7.08 ± 0.77 |
| 42.5 ≤ logLX < 43 | (1.80 ± 0.02) × 10−4 | −8.15 ± 0.36 |
| 43 ≤ logLX < 44 | (8.28 ± 2.94) × 10−5 | −8.93 ± 1.82 |
| 44 ≤ logLX < 45 | (1.35 ± 0.37) × 10−5 | −6.16 ± 0.84 |
| Obscured | (2.87 ± 1.05) × 10−4 | −7.66 ± 1.14 |
| Unobscured | (1.37 ± 0.26) × 10−4 | −6.58 ± 0.62 |
| Subample . | A (Mpc−3) . | p . |
|---|---|---|
| All | (2.47 ± 0.57) × 10−4 | −7.59 ± 0.69 |
| 42.5 ≤ logLX < 43 | (1.31 ± 0.08) × 10−4 | −9.57 ± 0.32 |
| 43 ≤ logLX < 44 | (7.96 ± 2.70) × 10−5 | −8.85 ± 1.71 |
| 44 ≤ logLX < 45 | (1.33 ± 0.38) × 10−5 | −6.17 ± 0.87 |
| Obscured | (1.17 ± 0.43) × 10−4 | −8.12 ± 1.11 |
| Unobscured | (1.44 ± 0.34) × 10−4 | −8.25 ± 0.77 |
| After correction for incompleteness | ||
| All | (4.22 ± 1.19) × 10−4 | −7.08 ± 0.77 |
| 42.5 ≤ logLX < 43 | (1.80 ± 0.02) × 10−4 | −8.15 ± 0.36 |
| 43 ≤ logLX < 44 | (8.28 ± 2.94) × 10−5 | −8.93 ± 1.82 |
| 44 ≤ logLX < 45 | (1.35 ± 0.37) × 10−5 | −6.16 ± 0.84 |
| Obscured | (2.87 ± 1.05) × 10−4 | −7.66 ± 1.14 |
| Unobscured | (1.37 ± 0.26) × 10−4 | −6.58 ± 0.62 |
Best-fitting parameters describing the space-density evolution with redshift for the luminosity-based and obscuration-based subsamples (see Section 6).
| Subample . | A (Mpc−3) . | p . |
|---|---|---|
| All | (2.47 ± 0.57) × 10−4 | −7.59 ± 0.69 |
| 42.5 ≤ logLX < 43 | (1.31 ± 0.08) × 10−4 | −9.57 ± 0.32 |
| 43 ≤ logLX < 44 | (7.96 ± 2.70) × 10−5 | −8.85 ± 1.71 |
| 44 ≤ logLX < 45 | (1.33 ± 0.38) × 10−5 | −6.17 ± 0.87 |
| Obscured | (1.17 ± 0.43) × 10−4 | −8.12 ± 1.11 |
| Unobscured | (1.44 ± 0.34) × 10−4 | −8.25 ± 0.77 |
| After correction for incompleteness | ||
| All | (4.22 ± 1.19) × 10−4 | −7.08 ± 0.77 |
| 42.5 ≤ logLX < 43 | (1.80 ± 0.02) × 10−4 | −8.15 ± 0.36 |
| 43 ≤ logLX < 44 | (8.28 ± 2.94) × 10−5 | −8.93 ± 1.82 |
| 44 ≤ logLX < 45 | (1.35 ± 0.37) × 10−5 | −6.16 ± 0.84 |
| Obscured | (2.87 ± 1.05) × 10−4 | −7.66 ± 1.14 |
| Unobscured | (1.37 ± 0.26) × 10−4 | −6.58 ± 0.62 |
| Subample . | A (Mpc−3) . | p . |
|---|---|---|
| All | (2.47 ± 0.57) × 10−4 | −7.59 ± 0.69 |
| 42.5 ≤ logLX < 43 | (1.31 ± 0.08) × 10−4 | −9.57 ± 0.32 |
| 43 ≤ logLX < 44 | (7.96 ± 2.70) × 10−5 | −8.85 ± 1.71 |
| 44 ≤ logLX < 45 | (1.33 ± 0.38) × 10−5 | −6.17 ± 0.87 |
| Obscured | (1.17 ± 0.43) × 10−4 | −8.12 ± 1.11 |
| Unobscured | (1.44 ± 0.34) × 10−4 | −8.25 ± 0.77 |
| After correction for incompleteness | ||
| All | (4.22 ± 1.19) × 10−4 | −7.08 ± 0.77 |
| 42.5 ≤ logLX < 43 | (1.80 ± 0.02) × 10−4 | −8.15 ± 0.36 |
| 43 ≤ logLX < 44 | (8.28 ± 2.94) × 10−5 | −8.93 ± 1.82 |
| 44 ≤ logLX < 45 | (1.35 ± 0.37) × 10−5 | −6.16 ± 0.84 |
| Obscured | (2.87 ± 1.05) × 10−4 | −7.66 ± 1.14 |
| Unobscured | (1.37 ± 0.26) × 10−4 | −6.58 ± 0.62 |
The evolution of the space density of luminous (logLX ≳ 44) AGN in Fig. 20 is consistent with previous results by, e.g., Hiroi et al. (2012), Kalfountzou et al. (2014), Vito et al. (2014) and Marchesi et al. (2016) (i.e. Φ ∝ (1 + z)p with p ∼ −6, see Table 3). Luminous (logLX > 44) AGN are usually hosted by massive (M* ≳ 1010M⊙) galaxies (e.g. Xue et al. 2010; Yang et al. 2017). Fig. 20 shows that the space densities of luminous AGN and massive galaxies (from Davidzon et al. 2017) evolve with similar slopes, suggesting that the decline of the space density of logLX > 44 AGN is merely driven by the evolution of the galaxy number density. This interpretation is further supported by the recent findings of Yang et al. (submitted), who derive a positive evolution of the average black hole accretion rate in massive galaxies from low redshift up to z ≈ 3, followed by a steady behaviour up to z ≈ 4. This trend would be in contrast with the well-established decline of the space density of luminous AGN if the number of massive galaxies itself did not decrease.
Thanks to the unmatched sensitivity of the Chandra deep fields, in particular the 7 Ms CDF-S, coupled with the deep multiwavelength coverage, which allows a nearly complete multiwavelength identification of the X-ray sources, we could push the investigation of the evolution of the AGN space density down to logLX = 42.5 and up to z = 6. We found a slightly steeper decline for low-luminosity sources than for high-luminosity AGN, even after applying our fiducial corrections for incompleteness (Fig. 20 and Table 3). However, such corrections depend on the assumed intrinsic distribution in redshift, column density and luminosity (see Section 4). Moreover, the fit we performed is an approximation (although widely used in literature), as the error bars of the points in Fig. 20, are derived through a bootstrap procedure, which formally returns a measurement of the dispersion of the bootstraped distribution. For these reasons, we do not consider the best-fitting values reported in Table 3 as definitive evidence, but rather a suggestion, for a differential evolution of the AGN space density in different luminosity regimes. However, the strong flattening of the XLF faint-end found by Georgakakis et al. (2015) is ruled out by Fig. 19. Future X-ray missions, discussed in Section 7.2, will shed light on the evolution of the population of low-luminosity AGN at higher redshifts than those probed in this work.
Intriguingly, the evolution of the space density of low-luminosity AGN is also steeper than the density evolution of both low-mass and high-mass galaxies (see Fig. 20), as derived by Davidzon et al. (2017). This discrepancy requires an evolution of one or more of the physical parameters driving black hole accretion for low-luminosity AGN, other than the mere evolution of the number of galaxies. For instance, a steeper evolution of the AGN density than galaxy density can be expected if the duty cycle and/or occupation fraction decrease at increasing redshift, especially for low-mass galaxies.
6.3 XLF and space density of obscured and unobscured AGN
Fig. 21 (left-hand panel) shows the luminosity functions separately for obscured and unobscured sources, obtained by performing the integral over column density in equation (22) over the ranges logNH = 23–25 and 20–23, respectively, compared with the XLFs of Hasinger, Miyaji & Schmidt (2005, used by Gilli et al. 2007 for their X-ray background synthesis model) in the same NH bins. We also report the results from Aird et al. (2015), where obscured and unobscured AGN are defined as those obscured by column densities logNH = 22–24 and 20–22, respectively. Points in the first luminosity bin (empty circles) are heavily affected by the obscuration-dependent incompleteness discussed in Section 4, as is evident by the drop of the density of obscured AGN with respect to the unobscured subsample. Fig. 21 (right-hand panel) displays the evolution of the space density of obscured and unobscured AGN. Table 3 summarizes the best-fitting values for the obscured and unobscured subsamples. We found no significant difference in the evolution of the space density of obscured and unobscured AGN. This conclusion is consistent with Fig. 16, where the obscured AGN fraction is flat with redshift. After correcting for incompleteness, a slightly shallower decline of the space density of unobscured AGN is derived, because of the faster decrease of detection completeness with increasing redshift for unobscured sources than for obscured sources (see Fig. 15). However, the uncertainties due to the procedure of correcting for incompleteness and the relatively small size of the sample prevent us from drawing strong conclusions.
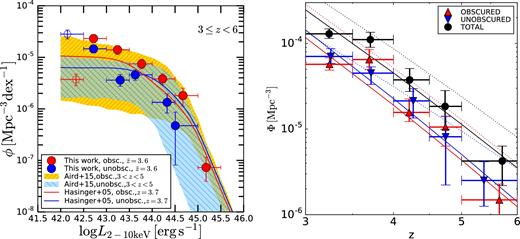
Left-hand panel: XLFs of obscured (red circles) and unobscured (blue circles) AGN at z = 3–6. The open circles are the binned points in the faintest luminosity bin, and show how incompleteness affects differentially the two subsamples at those luminosities (see Section 4). Symbols are centred at the weighted average luminosity of each bin. Red and blue lines are the XLFs of obscured (logNH > 23) and unobscured (logNH < 23) AGN, respectively, by Hasinger et al. (2005). Orange and cyan regions represent the areas covered by luminosity functions of logNH > 22 and <22 AGN, respectively, at 3 ≤ z ≤ 5 from Aird et al. (2015). The different column density thresholds assumed to define the obscuration-based subsamples are discussed in the text. Right-hand panel: evolution of the comoving space density with redshift for obscured (red symbols) and unobscured (blue symbols) subsamples. Those symbols are slightly offset for visualization purposes. Black circles represent the total sample. Solid lines are the best-fitting linear models obtained by simple χ2 minimization. To demonstrate the effects of the obscuration-dependent incompleteness (Section 4), we present the best-fitting linear models corrected for such incompleteness as dotted lines.
6.4 Black hole accretion rate density
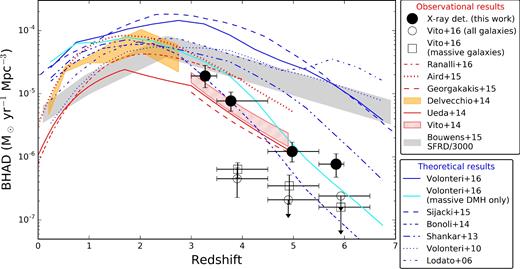
BHAD derived from our sample of X-ray-detected AGN (filled black symbols), compared with previous observational and theoretical results from literature. We also show the BHAD resulting from the stacking analysis of a sample of individually undetected galaxies (Vito et al. 2016), under the most optimistic assumption that all the stacked X-ray signal is due to accretion on to SMBH. Empty circles and squares correspond to the entire sample and the half containing the most massive galaxies, respectively. The grey stripe is the star formation rate density of Bouwens et al. (2015), rescaled by a factor of 3000.
Fig. 22 displays the BHAD corresponding to the XLFs of Ranalli et al. (2016), Aird et al. (2015), Georgakakis et al. (2015), Ueda et al. (2014) and Vito et al. (2014), converted into BHAD as described above,12 and that derived by Delvecchio et al. (2014) exploiting Herschel data. We also add the BHAD predicted by simulations (Lodato & Natarajan 2006; Volonteri 2010; Shankar, Weinberg & Miralda-Escudé 2013; Bonoli, Mayer & Callegari 2014; Sijacki et al. 2015; Volonteri et al. 2016a) under different assumptions of BH seed mass and growth mechanisms. Except for Sijacki et al. (2015), who directly reported the BHAD, we derived the curves by differentiating the BH mass densities presented in those works.
Simulations tend to derive BHAD exceeding by about one order of magnitude the observed values at z > 3 (see Fig. 22). This discrepancy is usually ascribed to the contribution of continuous, low-rate accretion, difficult to detect even in deep surveys. In Vito et al. (2016), we used a stacking procedure to demonstrate that such contribution is negligible compared to the BHAD due to X-ray-detected AGN (see also e.g. Pezzulli et al. 2017). With the refined sample of high-redshift AGN of this work, we confirmed this result up to z ∼ 6 and suggest that simulations tend to overestimate the BHAD at high redshift.
A similar issue is known to affect the faint end of the AGN LF at high redshift, with simulations finding steeper slopes than the observed ones. Volonteri et al. (2016a) suggested that this discrepancy could be due to supernovae feedback (i.e. the removal of gas in the galaxy responsible of both nuclear accretion and star formation as a consequence of supernovae activity) being underestimated in low-mass haloes in simulations. Considering only massive (M > 5 × 1011M⊙) dark-matter haloes, where supernovae feedback has little effect due to the deeper galactic gravitational potential well, improves the agreement with observations. This statement is also true for the BHAD, as can be seen in Fig. 22, where the results of Volonteri et al. (2016a) are presented without any mass cut (continuous blue curve) and for massive haloes only (cyan curve).
The common evolution of star formation rate density (SFRD) and the BHAD at z ≲ 2.5 is generally considered to be a manifestation of the BH–galaxy co-evolution. However, these two quantities are found to evolve with different slopes at higher redshifts (e.g. Silverman et al. 2008; Aird et al. 2015, see e.g. Haiman, Ciotti & Ostriker 2004 for a theoretical interpretation), mainly through extrapolations of the AGN XLF. In this work, we can probe this behaviour, whose physical causes are difficult to identify, down to the faint flux limits of the Chandra deep fields. Most of the BHAD we derived at high redshift is due to luminous (logLX > 44) AGN, which contribute 70-90 per cent to the black circles in Fig. 22; therefore, the uncertainties on the density of low-luminosity AGN have no strong impacts in this respect. In particular, the contribution of accretion in individually undetected galaxies is negligible (empty black symbols from Vito et al. 2016 in Fig. 22). Indeed, the evolution the BHAD is similar to that of the space density of luminous AGN, both declining by a factor of ≳10 from z = 3 to z = 6. In contrast, the evolution of the SFRD is more similar to that of low-mass galaxies than massive systems, both declining by a factor of ∼3 in the same redshift range (cf. Figs 22 and 20). This discrepancy may mark a breakdown of the BH–galaxy co-evolution at high redshift.
7 FUTURE PROSPECTS
7.1 Spectroscopic follow-up of high-redshift AGN candidates
One of the main sources of uncertainty affecting our knowledge of the demography of high-redshift AGN is the persistently low spectroscopic identification rates of the candidates. The deep Chandra surveys allow sampling of the bulk of the population at high redshift, which is constituted of low luminosity and/or obscured sources. However, these objects are typically faint in the optical/NIR bands (e.g. ≈ 80 per cent of our sources located in the CANDELS/GOODS-S area have H > 24), and are therefore difficult to follow up spectroscopically with current facilities in order to confirm their high-redshift nature. While photometric redshifts of good quality are available in the fields we considered, and despite the careful treatment of their PDF, they may introduce non-negligible uncertainties in the final results (e.g. see section 4.3 of Georgakakis et al. 2015). This issue is less problematic for shallower X-ray surveys, which sample AGN with brighter optical/NIR counterparts, but miss the sub-population of low-luminosity AGN.
Current facilities that could be used effectively to increase the spectroscopic completeness of our sample include ALMA13 (e.g. Walter et al. 2016), the Keck observatory14 and VLT/MUSE.15 The last, in particular, with 27 h of integration time in the Hubble Ultra Deep Field, has already been able to obtain spectroscopic redshifts for sources below the Hubble detection limit (Bacon et al. 2015). In the near future, facilities like James Webb Space Telescope (JWST),16 and, in the somewhat longer term, the Extremely Large Telescopes (with ≳30 m diameter mirrors) will provide the required spectroscopic sensitivity to perform ultradeep spectroscopic follow-up campaigns aimed at identifying high-redshift AGN candidates with extremely high efficiency (see e.g. the discussion in Brandt & Alexander 2015).
7.2 The case for Athena and Lynx
The understanding of the SMBH formation and growth mechanisms in the early Universe requires the collection of much larger samples of X-ray-selected AGN and galaxies at higher redshifts and lower luminosities than those probed by current X-ray surveys. Moreover, while Chandra and XMM–Newton, jointly with large-area optical/IR surveys, are successfully improving our knowledge of the bright quasar population up to z ≈ 7 (e.g. Brandt & Vito 2017), the bulk of the AGN population, constituted by low luminosity and possibly obscured systems, are currently completely missed beyond z ≈ 5–6 even by the deepest X-ray surveys available, and Chandra observations substantially deeper than the 7 Ms CDF-S are not foreseeable. The Athena X-ray Observatory (Nandra et al. 2013)17, which will be launched in ∼2028, is expected to detect hundreds of ≲L* AGN at z > 6 (Aird et al. 2013), thanks to its survey power a factor of ∼100 faster than Chandra or XMM–Newton, boosting our knowledge of the high-rate accretion phases, which likely dominate SMBH growth at high redshift (Vito et al. 2016).
Simulations suggest that different combinations of the physical parameters governing SMBH formation and early growth (e.g. seed-mass and Eddington ratio distributions, occupation fraction, feedback mode, and their dependence on the host-galaxy and environment properties) produce different shapes of the faint-end (logLX ≲ 42) of the AGN LF. The green-striped region in Fig. 19 (right-hand panel) is the locus of the XLF models of Volonteri et al. (2017) at z = 4, under different assumptions. In particular, the upper bound is derived using a minimum initial BH mass of 102 M⊙ and occupation fraction equal to unity, while for the lower bound a minimum initial mass of 105M⊙ and a modified occupation fraction from Habouzit et al. (2017), flagged as ‘H17low1’ in Volonteri et al. (2017). Different combinations of parameters are mostly encompassed by these boundaries. The models are normalized to the observed points, which explain the small spread at logLX ≳ 43. However, at lower luminosities, which even the currently deepest surveys cannot sample, different combinations of parameters produce significantly different XLF shapes. The spread of the XLF shapes in this faint regime is expected to increase at higher redshifts (see fig. 12 of Volonteri et al. 2017). A tremendous step forward towards understanding the early growth of SMBH will be provided by Lynx (also known as X-ray Surveyor; Weisskopf et al. 2015), which, with its Chandra-like angular resolution and ≈25 times higher sensitivity, will reach an expected flux limit of logF ≈ −18.5 in a blind 4 Ms survey, sufficient to probe the faint end of the XLF down to logLX ≈ 40–42 at z ≲ 10, providing unprecedented constraints on the combinations of parameters driving SMBH formation and early growth.
The constraints derived by X-ray telescopes will be complemented by deep optical/IR observations provided by future facilities such as JWST and WFIRST18, necessary to identify the X-ray sources. Recently, several works have focused on the multiwavelength properties of emission from BHs during the early accretion phases. For instance, Volonteri et al. (2017) proposed a colour-colour selection based on JWST bands to separate AGN from normal galaxies at high redshift. In particular, the characteristic shape of the SED of accreting direct-collapse BH (with initial MBH = 104–105 M⊙) has been used by Natarajan et al. (2017) to propose a JWST colour-colour method to select such objects. In contrast, optical/IR emission from accreting light-seeds BH (MBH = 102–103 M⊙) probably will be outshined by stellar emission in the young host galaxies. The joint effort of the next generation X-ray observatories and optical/IR telescopes therefore will open a completely new window on the cosmic epoch where SMBH formed.
8 CONCLUSIONS
We have investigated the population of 3 ≤ z < 6 AGN detected in the two deepest X-ray fields, the 7 Ms CDF-S and the 2 Ms CDF-N, selected on the basis of a careful assessment of the photometric-redshift uncertainties for sources lacking spectroscopic identification. For each source, uncertainties on redshift, column density, flux and luminosity were accounted for by using the full probability distributions of such parameters, and a statistical correction for Eddington bias was applied. Our main results are the following:
We derived the best-constrained column-density distribution of moderate-luminosity obscured AGN at high redshift, finding it to peak at logNH ∼ 23.5–24 (see Section 3.2).
Comparing the mean photon index of X-ray spectra of high-redshift, LX < L* AGN with results derived for luminous quasars, we found no significant variation with redshift and luminosity (see Appendix Section B).
The obscured AGN fraction (Fobsc), where the column-density threshold to define obscured versus unobscured AGN is set to logNH = 23, is consistent with being flat with redshift at observed values of ≈0.5–0.6. Once corrected for incompleteness, we derive Fobsc ≈ 0.6–0.7. This result agrees with previous works finding a saturation of this quantity at z ≳ 2, after a positive evolution at z ≈ 0–2 (see Section 5.1).
Thanks to the sensitivity of the Chandra deep fields, we could probe the number counts of high-redshift AGN down to fainter fluxes, especially at z > 4, than those reached by wider and shallower surveys. Comparing the logN-logS of our sample with the predictions from the Gilli et al. (2007) X-ray background synthesis model, which was constrained at lower redshifts, separately for obscured and unobscured AGN, we found an excess of obscured sources, likely caused by the positive evolution of Fobsc from the local Universe to high redshift (see Section 3.3.1).
We found Fobsc ≈ 0.7–0.8 at logLX ≳ 43, somewhat larger, but still in agreement with other works performed at similar redshifts. In contrast with previous results, derived especially at low redshift, there is no significant anticorrelation between Fobsc and luminosity at logLX ≳ 43, suggesting a stronger positive evolution of Fobsc towards earlier cosmic times for luminous AGN than for moderate-luminosity sources (see Section 5.3).
At low luminosities (logLX ≲ 43), the observed behaviour of Fobsc is strongly affected by sample incompleteness: low luminosity, obscured sources are more difficult to detect than unobscured sources, biasing the observed result towards low values of Fobsc. We suggest that recent claims of a turn-down of Fobsc towards low luminosities at high redshift may be at least partly due to similar incompleteness issues. By assuming intrinsic distributions of sources in NH and LX space, we applied tentative corrections that led Fobsc to be fairly consistent with the values at higher luminosities, although a possible slight decrease down to values of ≈0.6 is still visible (see Sections 5.3 and 4).
The space density of luminous (logLX ≳ 44) AGN declines from z = 3 to z = 6, as (1 + z)d, with d ≈ −6, in agreement with previous results. The XLF in the redshift range probed by this work does not show significant steepening of the faint end, which has been recently linked with a possible significant contribution of low-luminosity AGN to cosmic reionization. Our results tend to exclude this hypothesis. By contrast, the space density of AGN with low-to-moderate luminosity appears to decline slightly faster than for high-luminosity AGN. However, uncertainties due to incompleteness might affect this result. The evolution of the AGN XLF faint end at high redshift is particularly important for placing constraints on the combination of the physical parameters driving the formation and early growth of SMBHs, one of the goals of future X-ray observatories (see Sections 6 and 7.2).
The space densities of luminous AGN and massive galaxies show a similar trend with redshift, suggesting that the evolution of luminous AGN is driven by the underlying galaxy population. By contrast, the space density of low-luminosity AGN declines with increasing redshift faster than the space density of both high-mass and low-mass galaxies. This difference suggests an evolution in the physical parameters regulating nuclear activity, such as duty cycle and occupation fraction. We also derived the BHAD at z = 3–6, and noted that, while the BHAD and SFRD track each other at z ≈ 0–2.5, at higher redshifts the BHAD decreases with a faster rate than the SFRD (see Section 6).
Acknowledgements
We are grateful to the referee, A. Georgakakis, for useful comments that helped in clarifying several aspects of this work. FV, WNB and GY acknowledge support from Chandra X-ray Center grant GO4-15130A, the Penn State ACIS Instrument Team Contract SV4-74018 (issued by the Chandra X-ray Center, which is operated by the Smithsonian Astrophysical Observatory for and on behalf of NASA under contract NAS8-03060), and the V.M. Willaman Endowment. BL acknowledge support from the National Natural Science Foundation of China grant 11673010 and the Ministry of Science and Technology of China grant 2016YFA0400702. YQX acknowledges support from the 973 Program (2015CB857004), NSFC-11473026, NSFC-11421303, the CAS Frontier Science Key Research Program (QYZDJ-SSW-SLH006), and the Fundamental Research Funds for the Central Universities. We warmly thank Harry Ferguson and Dritan Kodra for providing PDFs of CANDELS photometric-redshifts, and Iary Davidzon, Carlotta Gruppioni, and Melanie Habouzit for providing useful data. The Guaranteed Time Observations for the CDF-N included here were selected by the ACIS Instrument Principal Investigator, Gordon P. Garmire, currently of the Huntingdon Institute for X-ray Astronomy, LLC, which is under contract to the Smithsonian Astrophysical Observatory; Contract SV2-82024.
The integrated X-ray emission from high-mass and low-mass XRB in a galaxy can reach luminosities of logLX ≈ 42 (i.e. Lehmer et al. 2016). At z > 3, the flux limit of the 7 Ms CDF-S corresponds to logLX ≳ 42. Therefore, we will consider all of the X-ray sources at z > 3 to be AGN and discuss the possible level of contamination from XRB in Section 6.
With two exceptions, relevant to the purpose of this work: (1) XID 638 has no spectroscopic redshift, a photometric redshift from S16,z ∼ 3.10 and a photometric redshift from H14,z ∼ 2.64. A significant iron line is detected in the X-ray spectrum (see also Liu et al. 2017). If it is produced by neutral iron at 6.4 keV, which is usually the strongest line, the observed line energy is consistent with the H14 redshift. Even in the case of completely ionized iron, the line is consistent with a redshift z < 3 at 90 per cent confidence level. (2) XID 341 has a photometric redshift z = 5.05 in S16, which is inconsistent with the visible emission in the GOODS-S B and V bands. Therefore, for these two sources, we adopted the H14 redshifts instead of the S16 solutions.
However, the quality of the optical spectrum of the latter source, presented in Barger et al. (2002), is low, and Y14 and X16 discarded that spectroscopic redshift in favour of a photometric redshift |$z=4.17^{+0.10}_{-0.13}$| from Y14, which we adopted too, following the procedure described in Section 2.2.
Two sources in our sample, XID 500 and 503, in the 7 Ms CDF-S catalogue are reported as full-band detections only. Given the small number of such objects, for the purposes of this work we consider them as soft-band detections.
This result again confirms that at z > 3 column densities of logNH ≲ 23 do not sensibly affect X-ray spectra, and therefore cannot be correctly identified. As a consequence, a column density threshold larger than the usual logNH = 22 value must be used to define obscured AGN.
We used the EMCEE python package (http://dan.iel.fm/emcee/current/), which implements the Affine Invariant Markov chain Monte Carlo (MCMC) Ensemble sampler by Goodman & Weare (2010).
This effect can be visualized considering that, while β can be any real number, half of the plane is covered by −1 < β < 1. Giving equal weight to values in and out of this range would in principle preferentially select |β| > 1, hence steep slopes. However, we checked that using a flat prior on mz does not affect significantly the results.
An assessment of the covariance between z and LX is discussed in Section 5.3.
Aird et al. (2015) provided directly their estimate of BHAD, but used the bolometric corrections from Hopkins, Richards & Hernquist (2007) instead of the Lusso et al. (2012) values we assumed. The slightly higher normalization of the Aird et al. (2015) curve with respect to the other observational results reflects this difference and can be therefore considered a measure of the uncertainty due to bolometric corrections.
REFERENCES
SUPPORTING INFORMATION
Supplementary data are available at MNRAS online.
online_figures
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
APPENDIX A: CHECKING THE ACCURACY OF THE X-RAY SPECTRAL ANALYSIS
In Section 3, we assumed a simple spectral model, an absorbed power law with photon index fixed to Γ = 1.8, as a representation of the X-ray spectra of the sources in our high-redshift sample, and performed a spectral analysis to derive the probability distribution of the intrinsic column density. Although the use of more complex spectral models is generally precluded by the limited number of counts in the X-ray spectra of the typically faint AGN in our sample, we check in this appendix for potential biases arising from this assumption using X-ray spectral simulations.
We assumed that the intrinsic X-ray spectra in cases of column densities logNH > 22 are well represented by the MYTorus spectral model19 (Murphy & Yaqoob 2009), which fully accounts for the transmission and scattered components, as well as the production of the iron K edge and Kα and Kβ emission lines. We fixed the Galactic absorption to logNH = 20 (the characteristic value towards the CDF-S; Kalberla et al. 2005), Γ = 1.8, the inclination angle Θ = 90° (i.e. edge-on configuration), and the normalization of the scattered and line components to unity with respect to the transmitted component. The MYTorus model does not allow lower values of column densities, and therefore for logNH < 22 we used the xspecplcabs model, which also takes into account Compton scattering. We assumed three values of observed soft-band flux, logF = −17, −16 and −15, corresponding to sources close to the flux limit of the 7 Ms CDF-S, faint sources and bright sources (in deep X-ray surveys), respectively. We also considered three different redshifts (z = 3, 4 and 5) and eight different values of column density (from logNH = 21 to 24.5 in steps of 0.5 dex). For each of the resulting 72 combinations of these parameters, we simulated 10 X-ray source and background spectra with a 6 Ms effective exposure (typical of the CDF-S), allowing for Poissonian fluctuations, using the fakeit command in xspec. The background spectrum is sampled from the real CDF-S background. We then fitted the simulated spectra with our simple model and derived the best-fitting column density and its errors at the 90 per cent confidence level.
Fig. A1 shows the best-fitting column densities against the simulated ones for the different redshift-flux combinations. The output values in cases of large simulated column densities are consistent with the input ones. When decreasing the simulated flux and increasing the redshift, low values of column density (logNH ≲ 22.5 and, less severely, logNH ∼ 23) become increasingly difficult to constrain. In particular, the output column densities of sources simulated with logNH ≤ 22 are never constrained to be lower than that value, which is the widely used threshold separating obscured and unobscured AGN at low redshift. This result is due to the photoelectric cut-off shifting close to, and even below, the low-energy spectral limit of the Chandra bandpass. Small differences in the intrinsic photon index (within the expected range of Γ = 1.7–2.0) do not affect significantly the output column densities. We therefore conclude that the spectral model we assumed, despite its simplicity, is a useful and appropriate approximation, at least for the redshift and flux ranges probed by this work.
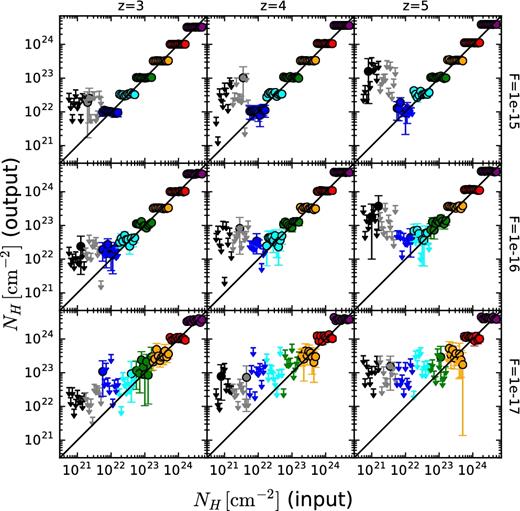
Best-fitting column density and 90 per cent CL errors derived by fitting a simple absorbed power-law model plotted against the simulated value, for different redshifts (columns) and fluxes (rows), as marked in the figure. Spectra are simulated using the MYTorus model and 8 different values of column density (in the range logNH = 20–24.5, in steps of 0.5 dex, colour coded in the figure) as described in Appendix A. The logNH positions are slightly shifted for presentation purposes. Black lines mark the 1:1 relations.
APPENDIX B: The X-ray power-law photon index of high-redshift, sub-L* AGN
The photon index (Γ) of the primary power-law emission in AGN X-ray spectra can be used to estimate the Eddington ratio (λEdd = L/LEdd) of a source through the Γ–λEdd relation (e.g. Shemmer et al. 2006, 2008; Risaliti, Young & Elvis 2009; Brightman et al. 2013, 2016; Fanali et al. 2013, but see the caveats discussed in Trakhtenbrot et al. 2017), according to which higher λEdd would produce steeper Γ. This relation is likely produced by the coupling between the accretion disc and the hot corona, and can therefore be used to investigate whether the accretion mode depends on the Eddington ratio at different redshifts.
The spectral analysis presented by Liu et al. (2017) on bright (>80 net counts) X-ray-selected AGN in the 7 Ms CDF-S reveals a median value of Γ = 1.82 ± 0.15, typical of Seyfert galaxies. Evidence for steep photon indexes in a few luminous Type-I QSOs at z > 6 have been found by Farrah et al. (2004), Page et al. (2014) (whose results are disputed by Moretti et al. 2014) and Ai et al. (2016). However, studies of samples of z = 4–7 Type-I QSOs did not find a significant evolution of the average Γ in luminous QSOs with redshift (e.g. Shemmer et al. 2005; Vignali et al. 2005; Nanni et al. 2017). Flatter photon indexes (Γ ≈ 1.1–2.0) have been derived by Vignali et al. (2002) for three spectroscopically confirmed z > 4, moderate-luminosity AGN in the CDF-N, probably due to the presence of intrinsic absorption.
Here, we compare the photon indexes of L ≲ L* AGN with results derived for much more luminous objects. We selected a subsample of bona fide unobscured sources at z = 3–6 from Table 2, requiring that the best-fitting column density is logNH < 23 at the 68 per cent confidence level and a signal-to-noise ratio (SNR) > 3 in the 0.5–7 keV band. We performed a more detailed spectral analysis than that reported in Section 3, by allowing both the intrinsic column density and the photon index to vary. Fig. B1 (blue squares) shows the resulting best-fitting values of Γ as a function of intrinsic luminosity for sources with >110 net counts in the 0.5–7 keV band. This threshold was chosen in order to obtain reasonable uncertainties on the best-fitting Γ for individual AGN.
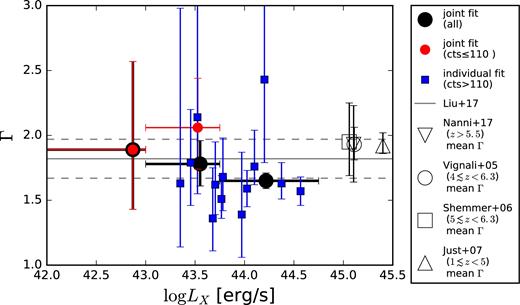
Best-fitting photon indexes for individual, bright sources with >110 net counts in the 0.5–7 keV band (blue squares), and the average values derived from a joint spectral analysis including all sources (black points) and only those with <110 net counts (red points), in three luminosity bins. No bright source lies in the first luminosity bin, where therefore the black and red points are coincident. Grey solid and dashed lines mark the median Γ derived by Liu et al. (2017) in the 7 Ms CDF-S and its standard deviation, respectively. We also show the average Γ of samples of luminous, optically selected Type-I QSOs in different redshift intervals.
For the fainter sources, we derived the average photon indexes by performing a joint spectral analysis in luminosity bins chosen to include approximately the same number of sources. During the fitting, the column density was left free to vary for each spectrum, while the photon index parameters were linked amongst all sources, in order to derive an average value. Red circles in Fig. B1 present the results of this joint analysis for sources with <110 net counts. Finally, we performed the joint spectral analysis in three luminosity bins, including both bright and faint objects (black points). Fit results are reported in Table B1 for the individual fit of bright sources and for the joint fit of faint and all (bright and faint) sources.
| ID . | Sample . | Γ . | NH . | logLX . |
|---|---|---|---|---|
| . | size . | . | (1022 cm−2) . | (erg s−1) . |
| Individual fit to bright sources | ||||
| 29 | 1 | |$2.14_{-0.59}^{+0.95}$| | <7 | 43.52 |
| 207 | 1 | |$1.76_{-0.14}^{+0.28}$| | <3 | 44.10 |
| 229 | 1 | |$1.62_{-0.23}^{+0.33}$| | <4 | 43.70 |
| 293 | 1 | |$1.39_{-0.33}^{+0.48}$| | <13 | 43.97 |
| 330 | 1 | |$2.43_{-0.64}^{+0.83}$| | <19 | 44.20 |
| 404 | 1 | |$1.63_{-0.12}^{+0.16}$| | <1 | 44.37 |
| 617 | 1 | |$1.79_{-0.33}^{+0.41}$| | <9 | 43.45 |
| 774 | 1 | |$1.57_{-0.11}^{+0.11}$| | |$3_{-2}^{+2}$| | 44.57 |
| 788 | 1 | |$1.59_{-0.14}^{+0.14}$| | <5 | 44.03 |
| 811 | 1 | |$1.51_{-0.15}^{+0.18}$| | <2 | 43.77 |
| 921 | 1 | |$1.68_{-0.26}^{+0.30}$| | <8 | 43.78 |
| 926 | 1 | |$1.36_{-0.25}^{+0.39}$| | <11 | 43.68 |
| 965 | 1 | |$1.63_{-0.49}^{+1.35}$| | <44 | 43.35 |
| Joint fit of faint sources | ||||
| – | 3 | |$1.89_{-0.46}^{+0.68}$| | – | 42–43 |
| – | 6 | |$2.06_{-0.32}^{+0.38}$| | – | 43–43.75 |
| Joint fit of all sources | ||||
| – | 3 | |$1.89_{-0.46}^{+0.68}$| | – | 42–43 |
| – | 11 | |$1.78_{-0.17}^{+0.18}$| | – | 43–43.75 |
| – | 9 | |$1.65_{-0.06}^{+0.06}$| | – | 43.75–44.75 |
| ID . | Sample . | Γ . | NH . | logLX . |
|---|---|---|---|---|
| . | size . | . | (1022 cm−2) . | (erg s−1) . |
| Individual fit to bright sources | ||||
| 29 | 1 | |$2.14_{-0.59}^{+0.95}$| | <7 | 43.52 |
| 207 | 1 | |$1.76_{-0.14}^{+0.28}$| | <3 | 44.10 |
| 229 | 1 | |$1.62_{-0.23}^{+0.33}$| | <4 | 43.70 |
| 293 | 1 | |$1.39_{-0.33}^{+0.48}$| | <13 | 43.97 |
| 330 | 1 | |$2.43_{-0.64}^{+0.83}$| | <19 | 44.20 |
| 404 | 1 | |$1.63_{-0.12}^{+0.16}$| | <1 | 44.37 |
| 617 | 1 | |$1.79_{-0.33}^{+0.41}$| | <9 | 43.45 |
| 774 | 1 | |$1.57_{-0.11}^{+0.11}$| | |$3_{-2}^{+2}$| | 44.57 |
| 788 | 1 | |$1.59_{-0.14}^{+0.14}$| | <5 | 44.03 |
| 811 | 1 | |$1.51_{-0.15}^{+0.18}$| | <2 | 43.77 |
| 921 | 1 | |$1.68_{-0.26}^{+0.30}$| | <8 | 43.78 |
| 926 | 1 | |$1.36_{-0.25}^{+0.39}$| | <11 | 43.68 |
| 965 | 1 | |$1.63_{-0.49}^{+1.35}$| | <44 | 43.35 |
| Joint fit of faint sources | ||||
| – | 3 | |$1.89_{-0.46}^{+0.68}$| | – | 42–43 |
| – | 6 | |$2.06_{-0.32}^{+0.38}$| | – | 43–43.75 |
| Joint fit of all sources | ||||
| – | 3 | |$1.89_{-0.46}^{+0.68}$| | – | 42–43 |
| – | 11 | |$1.78_{-0.17}^{+0.18}$| | – | 43–43.75 |
| – | 9 | |$1.65_{-0.06}^{+0.06}$| | – | 43.75–44.75 |
| ID . | Sample . | Γ . | NH . | logLX . |
|---|---|---|---|---|
| . | size . | . | (1022 cm−2) . | (erg s−1) . |
| Individual fit to bright sources | ||||
| 29 | 1 | |$2.14_{-0.59}^{+0.95}$| | <7 | 43.52 |
| 207 | 1 | |$1.76_{-0.14}^{+0.28}$| | <3 | 44.10 |
| 229 | 1 | |$1.62_{-0.23}^{+0.33}$| | <4 | 43.70 |
| 293 | 1 | |$1.39_{-0.33}^{+0.48}$| | <13 | 43.97 |
| 330 | 1 | |$2.43_{-0.64}^{+0.83}$| | <19 | 44.20 |
| 404 | 1 | |$1.63_{-0.12}^{+0.16}$| | <1 | 44.37 |
| 617 | 1 | |$1.79_{-0.33}^{+0.41}$| | <9 | 43.45 |
| 774 | 1 | |$1.57_{-0.11}^{+0.11}$| | |$3_{-2}^{+2}$| | 44.57 |
| 788 | 1 | |$1.59_{-0.14}^{+0.14}$| | <5 | 44.03 |
| 811 | 1 | |$1.51_{-0.15}^{+0.18}$| | <2 | 43.77 |
| 921 | 1 | |$1.68_{-0.26}^{+0.30}$| | <8 | 43.78 |
| 926 | 1 | |$1.36_{-0.25}^{+0.39}$| | <11 | 43.68 |
| 965 | 1 | |$1.63_{-0.49}^{+1.35}$| | <44 | 43.35 |
| Joint fit of faint sources | ||||
| – | 3 | |$1.89_{-0.46}^{+0.68}$| | – | 42–43 |
| – | 6 | |$2.06_{-0.32}^{+0.38}$| | – | 43–43.75 |
| Joint fit of all sources | ||||
| – | 3 | |$1.89_{-0.46}^{+0.68}$| | – | 42–43 |
| – | 11 | |$1.78_{-0.17}^{+0.18}$| | – | 43–43.75 |
| – | 9 | |$1.65_{-0.06}^{+0.06}$| | – | 43.75–44.75 |
| ID . | Sample . | Γ . | NH . | logLX . |
|---|---|---|---|---|
| . | size . | . | (1022 cm−2) . | (erg s−1) . |
| Individual fit to bright sources | ||||
| 29 | 1 | |$2.14_{-0.59}^{+0.95}$| | <7 | 43.52 |
| 207 | 1 | |$1.76_{-0.14}^{+0.28}$| | <3 | 44.10 |
| 229 | 1 | |$1.62_{-0.23}^{+0.33}$| | <4 | 43.70 |
| 293 | 1 | |$1.39_{-0.33}^{+0.48}$| | <13 | 43.97 |
| 330 | 1 | |$2.43_{-0.64}^{+0.83}$| | <19 | 44.20 |
| 404 | 1 | |$1.63_{-0.12}^{+0.16}$| | <1 | 44.37 |
| 617 | 1 | |$1.79_{-0.33}^{+0.41}$| | <9 | 43.45 |
| 774 | 1 | |$1.57_{-0.11}^{+0.11}$| | |$3_{-2}^{+2}$| | 44.57 |
| 788 | 1 | |$1.59_{-0.14}^{+0.14}$| | <5 | 44.03 |
| 811 | 1 | |$1.51_{-0.15}^{+0.18}$| | <2 | 43.77 |
| 921 | 1 | |$1.68_{-0.26}^{+0.30}$| | <8 | 43.78 |
| 926 | 1 | |$1.36_{-0.25}^{+0.39}$| | <11 | 43.68 |
| 965 | 1 | |$1.63_{-0.49}^{+1.35}$| | <44 | 43.35 |
| Joint fit of faint sources | ||||
| – | 3 | |$1.89_{-0.46}^{+0.68}$| | – | 42–43 |
| – | 6 | |$2.06_{-0.32}^{+0.38}$| | – | 43–43.75 |
| Joint fit of all sources | ||||
| – | 3 | |$1.89_{-0.46}^{+0.68}$| | – | 42–43 |
| – | 11 | |$1.78_{-0.17}^{+0.18}$| | – | 43–43.75 |
| – | 9 | |$1.65_{-0.06}^{+0.06}$| | – | 43.75–44.75 |
Fig. B1 presents as continuous and dashed grey lines the median Γ and the standard deviation of the Γ distribution (Γ = 1.82 ± 0.15), respectively, derived by Liu et al. (2017) for sources with >80 net counts in the 7 Ms CDF-S. Our sources are on average broadly consistent with such values, justifying the use of Γ = 1.8 for all sources in Section 3. The photon indexes of the luminous sources in our sample appear to be on average slightly flatter. This result is probably driven by the small number of luminous AGN considered here, which is due to the limited area covered by the deep surveys we used. Moreover, the best-fitting average Γ in the highest luminosity bin is quite strongly driven by the 1–2 brightest sources, which have Γ ≈ 1.6 and alone provide the 38–59 per cent of the net counts for the joint fitting in this luminosity bin. Neither of these two sources are detected in radio bands, and, in general, discarding the minority of sources (2 out of 23) detected in radio surveys does not change the results.
Our findings at 42 < logLX ≲ 44 are compared in Fig. B1 with the average Γ of optically selected, luminous (logLX > 45) Type-I QSOs at low-to-intermediate redshift (z = 1–5, Just et al. 2007) and z = 4–7 (Vignali et al. 2005; Shemmer et al. 2006; Nanni et al. 2017). Our results are consistent with both the median value of Γ derived by Liu et al. (2017) for similar luminosities at all redshifts and the average values of luminous QSOs up to z ≈ 7.
APPENDIX C: THE EFFECT OF NEGLECTING THE FULL PROBABILITY DISTRIBUTION OF SPECTRAL PARAMETERS
In Section 3, we derived the full probability distribution of flux, and luminosity by convolving the probability distribution of count rate and redshift, and using the proper count-rate-to-flux conversion for each source. Such information has been used in Section 5 to derive the dependence of the obscured AGN fraction on redshift, flux and luminosity.
To check the importance of applying this careful but computationally expensive procedure, we repeat the analysis in Section 5 by considering only the nominal value of parameters for each source, according to the following steps. (1) A single redshift (zpeak), corresponding to the spectroscopic redshift or the peak of PDF(z), was assigned to each source. We did not include objects with no redshift information. (2) We adopted the values corresponding to the peak of the count rate (CRpeak) and column-density (NHpeak) distributions. (3) Applying the proper conversion factor for zpeak and CRpeak, we derived single values of flux (Fpeak) and luminosity (Lpeak). Finally, following the procedures described in Section 5, we derive Fobsc as a function of redshift, flux and luminosity for our sample (Fig. C1). Larger fractions of obscured AGN are in general derived by this procedure, affecting in particular the trends with redshift and flux. This may be at least in part due to an overestimation of the best-fitting column density affecting intrinsically unobscured sources, due to statistical fluctuations in low-quality X-ray spectra discussed in section 3.3 of Vito et al. (2013). When considering the full probability distribution of column density, this issue is greatly alleviated. We also checked that, considering the Fpeak and Lpeak values, the number counts resulted not to be strongly different, while the XLF tends to be flatter at low luminosities. We again ascribe this behaviour to the tendency of overestimating the column densities, which has the effect of shifting the obscuration-corrected luminosities to larger values.
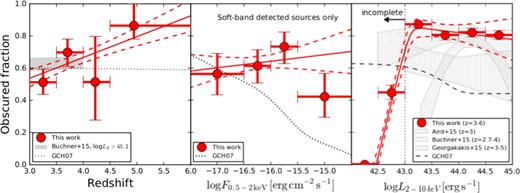
From left to right, obscured AGN fraction as a function or redshift, flux and luminosity, derived applying the procedure described in Appendix C. These figures, derived considering only the nominal values of redshift, count rate and column density for each X-ray source, are to be compared with the results in Section 5.



