Thermal winds in stellar mass black hole and neutron star binary systems Free

Abstract

1 INTRODUCTION

Absorption lines from ionized material are seen in many high-inclination low mass X-ray binary systems, both neutron star binaries (NSs) and black hole binaries (BHBs). These are most evident in the deep absorption dips that occur at specific orbital phases due to clumps formed where the accretion stream hits the disc. However, some absorption lines remain even outside of the dip events. These are seen mainly as hydrogen and helium-like iron Kα, indicating very highly ionized material, which is distributed fairly uniformly around all azimuths. These lines can be blue shifted by up to a few thousand km s⁻¹, showing clearly that there is an equatorial disc wind in these systems, where the material is strongly photoionized by the X-ray illumination from the central source (see e.g. the reviews by Diaz Trigo & Boirin 2013; 2016 and Ponti et al 2012).

The most important questions about these winds concern how they are launched, and their connection to the accretion flow and its jet. Both BHBs and NSs show a dramatic spectral transition, from a disc-dominated spectrum at high luminosity to a much harder Comptonized spectrum at lower luminosities. This can be explained as the transition between a disc and hot accretion flow (see e.g. the review by Done, Gierliński & Kubota 2007). Data from GRS1915+105 were first used to study the change in wind properties with spectral state, with Neilson & Lee (2009) showing that the wind disappeared as the source made a transition to the harder spectral state. They noted that this spectral transition also marks the onset of the compact radio jet, so speculated on the existence of a causal link, with the change in accretion flow properties also changing the magnetic field configuration so that the same magnetically driven outflow is either a wind in the soft, disc-dominated state or a jet in the low/hard state. Miller et al (2012) similarly find that the wind is not present in a hard state of H1743−322, while it is clearly evident in a soft state from the same source. The systematic survey of existing data by Ponti et al (2012) showed that none of the sources with winds in the high/soft state had significant absorption features in the low/hard state, though there are not many sources, and the most constraining data are from GRS1915+105 and H1743−322 discussed above.

An alternative explanation for the lack of wind features in the low/hard state is that the changing spectral shape at the transition changes the ionization of the wind (e.g. Diaz Trigo et al. 2014). However, other photoionization calculations show that the difference in wind properties between hard and soft spectral state cannot be completely explained by the same wind being present at different ionization level (Chakravorty, Lee & Neilsen 2013; Higginbottom & Proga 2015). This motivated studies of magnetic winds (Chakravorty et al 2016), though it is now clear that both winds and jets can co-exist at high luminosities (Kalemci et al 2016, Homan et al 2016).

However, winds in binary systems need not be magnetically driven. X-ray irradiation of the outer disc can produce a thermally driven wind/corona. The X-ray flux from the innermost regions illuminates the upper layers of the outer disc, heating it up to the Compton temperature, T_IC, which depends only on the spectral shape. The heated upper layer expands on the sound speed c_IC = (kT_IC/μ)^1/2, where μ is the mean particle mass (ions and electrons), fixed at 0.61m_p for solar abundances. The material is then unbound at radii where this sound speed is larger than the escape speed, i.e. |$R>R_{\rm IC}= GM/c_{\rm IC}^2$|⁠. This gives R_IC = 6.4 × 10⁴/T_{IC, 8}R_g (where R_g = GM/c² and T_{IC, 8} = T_IC/10⁸ K) so the material escapes as a wind (Begelman, McKee & Shields 1983, hereafter B83). A more careful treatment shows that the wind can be launched from R > 0.2R_IC as long as the luminosity is high enough to sustain rapid heating (B83; Woods et al 1996, hereafter W96). Conversely, at smaller radii/lower luminosity, the majority of the material remains bound but forms an extended atmosphere above the disc (B83; W96; Jimenez-Garate, Raymond & Liedahl 2002).

Current data from the high inclination NS systems show a good qualitative match to the thermal wind predictions, with small disc systems (short period binaries) having absorbing material which is static, while outflows are only seen at radii larger than 0.2R_IC (Diaz Trigo & Boirin 2013; 2016). Many winds in the BH systems also have a fairly large launch radius, consistent with thermal driving (e.g. Kubota et al 2007; Diaz Trigo & Boirin 2016), and the most powerful winds are seen in the systems with the biggest discs (Diaz Trigo & Boirin 2016). This is consistent with the predictions of thermal winds (see below), but not a natural consequence of magnetic wind models.

However, there is a single observation of dramatic absorption from GRO J1655−40 at low luminosities. The material has high column, and lower ionization state than is normally seen, so has multiple lines from lower atomic number elements as well as the standard H- and He-like iron absorption. These require that the wind is launched from ≪0.1R_IC if the observed luminosity is a good estimate of the intrinsic luminosity, so this cannot be a thermal wind (Miller et al 2006; Kallman et al 2009; Luketic et al 2010; Neilsen & Homan 2012; Higginbottom & Proga 2015). However, the unusual properties of the broad-band continuum seen during this observation indicate that the intrinsic source luminosity may be substantially underestimated (Done, Gierliński & Kubota 2007; Neilsen et al 2016 ; Shidatsu, Done & Ueda 2016 ). If the intrinsic source luminosity is actually close to Eddington then strong winds can be launched from much smaller radii than predicted by the thermal wind models. Electron scattering in a completely ionized, optically thick inner wind could suppress the observed luminosity to below Eddington, with the observed absorption lines tracing only lower ionization material in the outer photosphere. Whatever is the origin of the wind in this single observation, it does not represent the majority of winds seen in binaries, nor is it seen in observations at a similar luminosity of the same source (Nielsen & Homan 2012). Yet this single data set, coupled with the observed anti-correlation between wind and jet discussed above, has led to a focus on magnetic winds in the current literature.

Even if there are magnetic winds, thermal winds should also be present (e.g. Neilsen & Homan 2012), as we know that the outer disc is illuminated – the observed optical emission is dominated by reprocessed X-ray flux (van Paradijs & McClintock 1994). In marked contrast with magnetic winds, thermal winds are rather well understood theoretically in terms of overall mass-loss rates. However, models for thermal winds were developed long before the advent of detectors that could observe them, and they have been mostly sidelined due to the focus on magnetic winds, with only a few recent papers on their properties (Luketic et al 2010; Higginbottom & Proga 2015).

Here, we combine analytic and numerical thermal wind models to make quantitative predictions for the mass-loss rates for thermal winds, and their most basic observables (i.e. column density and ionization state). We couple this to a simple model of how the spectrum changes with luminosity during outbursts to quantitatively explore the effect of the spectral transition. The thermal wind models roughly predict that the column density of the wind is proportional to the mass accretion rate. Thus, the amount of material in the wind should not change much as the source switches from high/soft to low/hard at roughly constant luminosity during the spectral transition, though its visibility will be affected by the change in photoionizing spectrum (Chakravorty, Lee & Neilsen 2013; Diaz Trigo et al 2014; Higginbottom & Proga 2015). We compare this to the current observational constraints from H1743−322 on the wind in a high/soft state being supressed in a low/hard state (Miller et al 2012). We find that the thermal wind models are consistent with their data as this high/soft state is probably an order of magnitude higher mass accretion rate than the comparison low/hard state, so should have an order of magnitude stronger wind. A more stringent test would be to follow the wind evolution during a single transition, rather than to compare the wind seen in low/hard and high/soft spectra at different mass accretion rates separated by years.

We incorporate a simple correction for radiation pressure as the source approaches the Eddington limit. This allows the wind to be launched from smaller radii than R < 0.2R_IC as it reduces the effective gravity. We show that these thermal-radiative winds do indeed become optically thick as L → L_Edd, so they could potentially explain the anomalous wind in GROJ1655−40. GRS1915+105 is similarly close to Eddington, but its more complex and fast variable spectra require a specialized analysis, which is beyond the scope of this paper (e.g. Ueda et al 2010; Zoghbi et al 2016). These are the three main systems claimed to rule out the thermal wind models and hence require magnetic driving. We conclude that this is premature, and that thermal (and thermal-radiative) wind models already explain the vast majority (and perhaps all) of winds currently seen in binary systems.

2 THERMAL WIND MODELS

B83 discuss the different physical regimes in which Compton heated, thermal winds can form. We repeat here their analysis for completeness, pulling out only the required terms from their much longer, more detailed analysis.

The central source spectrum contains photons over a broad range of energies, and illuminates the disc at distance R with differential photon number rate N(ν) corresponding to energy flux F(ν) = hνN(ν) = L(ν)/(4πR²) in ergs cm⁻² s⁻¹ Hz⁻¹ or L(E)/(4πR²) in ergs cm⁻² s⁻¹ erg⁻¹. Electrons in the disc photosphere at this radius have initial temperature T_e. Photons with energies E = hν ≫ T_e will be Compton downscattered, losing some energy to the disc, typically ΔE/E = −E/(m_ec²). Conversely, those at low energies will be Compton upscattered by the hot electrons in the disc, with typical ΔE/E = 4kT_e/(m_ec²), so they cool the photosphere. Combing these gives an approximation for the energy change from both processes as ΔE = 4kT_eE/(m_ec²) − E²/(m_ec²). This reaches a steady state when heating balances cooling, so ∫ΔEN(E)dE = 0, defining the Compton temperature |$kT_{\rm IC}=\frac{1}{4}\int EL(E){\rm d}E/L$|⁠, where L = ∫L(E)dE (see e.g. Done 2010).

Compton cooling is the dominant cooling process only at high temperatures, where the material is completely ionized. Deeper down in the photosphere the heating from irradiation will be lower as the upper layers have already absorbed some of the energy, so the gas temperature, T_e, goes down. The disc is in hydrostatic equilibrium so the gas pressure, P_gas = nkT_e, must be higher to support the weight of the upper layers. Thus, the density, n, must increase downwards by more than the decrease in temperature from the lower irradiation. Higher density means that Bremsstrahlung cooling becomes important, which lowers the temperature still further, requiring an even larger increase in density to give the required pressure support for the weight of the upper layers. Eventually, the temperature is so low that electrons can start to be bound to ions, making line cooling possible. This triggers an ionization instability, as the line cooling lowers the temperature, but this allows more electrons to be bound, making more line transitions and hence more cooling (Krolik, McKee & Tarter 1981). Thus, the disc photosphere splits into a hot, high ionization skin overlying a cool, dense photosphere (Nayakshin, Kazanas & Kallman 2000). The typical temperature of the skin is the Compton temperature kT_IC, and its typical pressure can be calculated from the pressure ionization parameter Ξ = P_rad/P_gas = L/(4πR²cP_gas). The instability is triggered at Ξ ∼ 40, giving the gas density n = L/(160πR²ckT_IC) (B83; W96).

Figure 1.

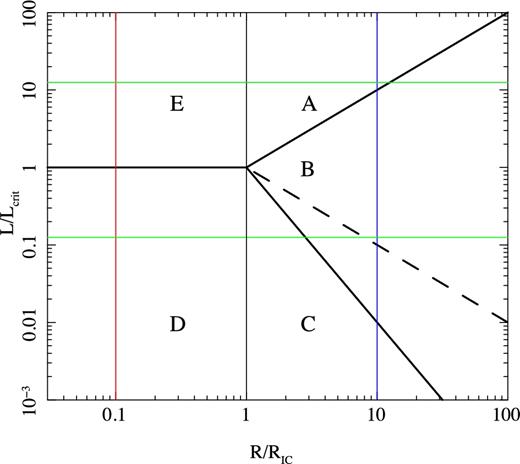
The different wind regions of B83, with boundaries shown as the thick black lines. For L > L_crit, the wind is impulsively heated to T_IC at R/R_IC < L/L_crit (e.g. upper green solid line). The mean particle velocity is smaller than the escape speed for small radii (R/R_IC < 1) so the heated skin forms an isothermal atmosphere (region E) with only small wind losses, whereas it escapes as an isothermal wind for 1 < R/R_IC < L/L_crit (region A). For R/R_IC > L/L_crit, the wind is steadily heated, only reaching temperature T_ch(R), but this can still escape as a wind (region B) for L/L_crit > 1. Instead, for L/L_crit < 1 (e.g. the lower green line), the illumination only heats the disc to T_ch rather than T_IC, so there is even less wind escape from the inner region with R/R_IC < 1 (region D). The material still cannot escape at R = R_IC as T_ch < T_IC (region C, gravity inhibited wind), and only becomes unbound for R/R_IC ≥ (L/L_crit)⁻¹ (region B again), though this inner boundary depends somewhat on the Compton temperature, with the dashed (solid) thick black line being appropriate for a low (high) Compton temperatures (W96). The red vertical line shows that at small radii, R_out = 0.1R_IC, the disc will go from region E and D as the luminosity increases, whereas the blue line shows that at large radii, R_out = 10R_IC, the disc material goes from being inhibited by gravity (region C), to being steadily heated (region B), to impulsively heated (region A) as the luminosity increases.

Open in new tabDownload slide

Similarly, for L < L_crit, the wind is only heated to a temperature of T_ch < T_IC at R_IC, so cannot escape (Region C in B83, the gravity inhibited wind). This escape condition, kT_ch > GMμ/R, defines an effective inner launch radius for the wind of R_in/R_IC ∼ (L/L_crit)⁻². This is appropriate at high Compton temperatures, T_{IC, 8} ∼ 1, where only Compton processes are important as assumed in B83, but at lower Compton temperatures then atomic cooling become important, giving R_in/R_IC ∼ (L/L_crit)⁻¹ (W96, Higginbottom & Proga 2015). Either way, this is again the steady heating region (Region B). The lower horizontal thin (green) line on Fig. 1 shows an example for L/L_crit = 0.125, where the wind is launched only for radii R/R_IC > 12.5 (low Compton temperature), or >2.82 (high Compton temperature).

For R ≪ R_IC and L > L_crit, the upper layers of the disc are heated to T_IC but this is less than the escape velocity at this point. Thus, the material forms an isothermal, exponential atmosphere above the disc with only a very small fraction of the material being able to escape (region E). At lower luminosities (L < L_crit), this atmosphere is steadily heated to characteristic temperature T_ch < T_IC, so there is even less wind (region D). Fig. 1 shows these regions schematically (B83, W96).

Regions A and B (impulsive Compton heating and steady Compton heating) are the two main regimes that contribute to the thermal wind, though other radii/luminosities ranges can power smaller mass-loss rates. W96 give fitting formula for the specific mass-loss rate in all regimes of luminosity and Compton temperature of the radiation in their equation (4.8). These were derived from smoothly matching to results from full hydrodynamical simulations of thermal winds. We integrate these over all radii, rather than using the different equations (1) and (5) with upper and lower radial limits. We show the results for the specific mass-loss rate per unit area, |$\dot{m}$| as a function of radius in Fig. 2a, reproducing the results in fig 6 of W96 for a 10⁸ M_⊙ BH with log L/L_Edd = −3, −2, −1, 0, 1, which is equivalent to L/L_crit = 1.25 × 10⁻²–1.25 × 10² for the assumed T_{IC, 8} = 0.13. Obviously, radiation pressure should also enhance the wind as the luminosity approaches and exceeds L_Edd, which was not considered in W96 or B83. We return to this point in Section 4. There is a clear peak in the specific mass-loss rate at R ∼ 0.2R_IC.

Figure 2.

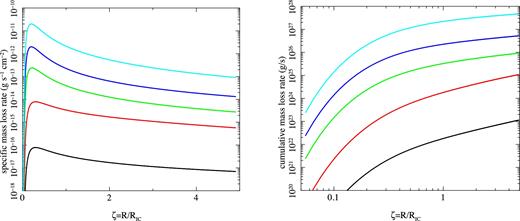
(a) The mass-loss rate from a 10⁸ M_⊙ BH per unit area of disc at a scaled radius ζ = R/R_IC for log L/L_Edd = −3 (black) −2 (red), −1 (green), 0 (blue) and 1 (cyan), as in W96. These correspond to L/L_crit = 0.0125–125 for the assumed constant T_{IC, 8} = 0.13. (b) The corresponding cumulative mass-loss rate from the disc at R < R_out = 5R_IC.

Open in new tabDownload slide

Fig. 2b shows the corresponding cumulative mass-loss in the wind, |$\dot{M}$| as a function of R/R_IC. This shows that the total mass-loss rate in the wind rises quickly at R ∼ 0.2R_IC, and then increases more slowly with increasing R. This can be understood from the previous plot of specific mass-loss rate, as this declines as R⁻² in the wind regions A and B. Hence, the increasing area at larger distances means that the total mass-loss rate from the disc increases with increasing size scale of the disc, as |$\dot{M}\propto \log R_{\rm out}/R_{\rm IC}$| for R > 3R_IC. For L < L_crit, there is a steeper dependence as a larger fraction of the wind is launched from further out in the disc.

Fig. 3 shows the efficiency of wind production, defined as the ratio of mass-loss rate in the wind to the mass accretion rate required to produce the wind (which is ∝ L). We show this efficiency as a function of L/L_crit for different disc sizes, with R_out = 0.1R_IC (black), 0.3R_IC (red) 1R_IC (green), 3R_IC (blue) and 10R_IC (cyan). For large discs, there is a clear change in behaviour from constant efficiency (wind mass-loss rate scaling with L, region A) at high L/L_crit to increasing efficiency at lower L/L_crit (wind mass-loss rate scaling with L^2/3 in region B) for L_min < L < L_crit before the steep decline in efficiency for L < L_min (region C, see (blue) vertical line in Fig. 1 for R_out = 10R_IC). Thus, the minimum luminosity to produce an efficient wind is L_min = L_crit(R_IC/R_out) (low Compton temperature) rather than L > L_crit. Most of the wind is launched from the outer disc (see Fig. 2b) so the minimum requirement for a wind is that the outer radii of the disc are in region B, rather than that the wind extends down to R_IC.

Figure 3.

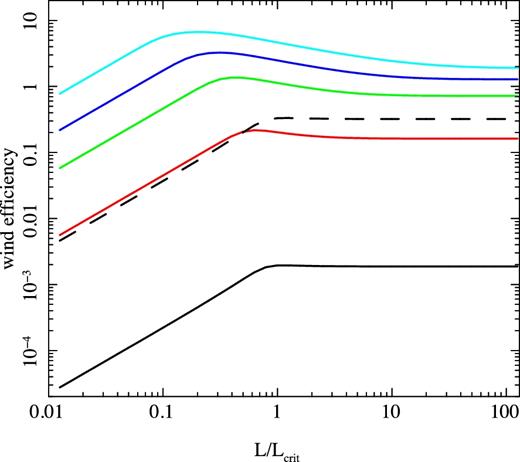
The effect of disc size on the efficiency of wind production per unit mass accretion rate. The range of irradiating luminosity is the same as in Fig. 1i.e. L/L_Edd = 10⁻³ → 10, which corresponds to L/L_crit = 1.25 × 10⁻² → 1.25 × 10² for the assumed T_{IC, 8} = 0.13. The disc size is R_out = 0.1R_IC (black), 0.3R_IC (red), R_IC (green), 3R_IC (blue) and 10R_IC (cyan). All disc sizes show that the disc is increasingly efficient at producing a wind with increasing mass accretion rate for L/L_crit → 1, but then the efficiency stabilizes to a constant for L/L_crit ≫ 1. This constant value is larger than the mass input rate for all disc sizes, where R_out ≥ R_IC, so the wind losses should have a major impact on the observed luminosity. B83 suggest that the mass-loss rates from the smallest disc sizes, with R_out ≪ R_IC, are underestimated. The dashed black line shows the impact of their suggested correction factor for small discs (R_out = 0.1R_IC), where there is no confining pressure from an outer wind.

Open in new tabDownload slide

Thus, thermal winds are predicted to be strongest in the systems with largest discs. This reflects the observed distribution. Winds are preferentially seen from systems with the longest orbital periods i.e. the systems with the largest discs (Diaz-Trigo & Boirin 2016). It is highly unlikely that a magnetic wind would depend on the outer disc size, so this alone favours a thermal wind origin to explain the observed data.

Instead, for a small disc with R_out ≪ R_IC, the wind changes from constant but a low efficiency (exponential scale height atmosphere with isothermal temperature, region E) to being strongly suppressed by inefficient heating in region D (red vertical line in Fig. 1 for a disc with R_out = 0.1R_IC).

The wind efficiency is larger than unity for all discs with R_out > R_IC and L > L_min, showing how powerful these winds can be. This is a feature of thermal winds that was stressed in the early papers, that they can remove more mass than is required to keep the source bright enough to power the wind (B83). Shields et al (1986) showed that these strong wind losses could cause oscillations in an otherwise steady state disc. However, most BHBs, especially those with large discs, are unstable to the hydrogen ionization disc instability (see e.g. Lasota 2001). Thus, the strongest wind losses are not likely to be in stable disc systems. Instead, the wind mass-loss should impact on the length of the outburst in transient BHB sources, as noted by Dubus, Hameury & Lasota (2001).

B83 comment that the mass-loss rates are probably underestimated for the smallest disc sizes (R_out < R_IC) due to the changing streamline pattern that results from not having an outer disc wind to collimate the flow from the inner regions. They suggest that this leads to an increase in the wind mass-loss rate by a factor of 1/ζ². We show the effect of this for the lowest R_out = 0.1R_IC (i.e. ζ ≤ 0.1) as the dashed black line in Fig. 3. Plainly, this correction has a very large impact on the mass-loss rate predictions from small discs, but it is highly uncertain as there are no hydrodynamical simulations in this regime. Hence, we do not consider this further here.

2.1 Predicting the absorption structures

Fig. 3 shows that the thermal wind drops dramatically when the luminosity drops below the minimum required to heat the material on the outer disc to the escape velocity. This minimum luminosity is a few percent of the Eddington limit for T_{IC, 8} = 1.0 for a disc with R_out ∼ R_IC. Co-incidentally, this is also the point at which the accretion flow makes its dramatic transition from a soft (disc-dominated) to a hard (Compton-dominated) spectrum. Thus, it is possible that the loss of the wind in the hard state is simply a consequence of the lower luminosity in this state, leading to a heating rate that is not sufficient for the wind to reach its Compton temperature. However, the large spectral change also means that there is a large change in Compton temperature, with the hard spectrum having larger T_IC, so L_crit and R_IC both go down. This illustrates the difficulty with understanding how the wind responds when the equations are written in terms of variable parameters R_IC and L_crit, which depend implicitly on T_IC rather than absolute L and R.

The key observables are the column density in the wind, and its ionization state. The velocity is also another potential observable but this requires excellent spectral resolution to accurately determine the low velocities expected from an outflow from the outer disc. These are currently only accessible using the Chandra HETGS (especially the 3rd order grating data: Miller et al 2015), but should become much better determined in the future with a calorimeter resolution. To derive these observables from the models really requires the full information on the wind density and velocity as a function of height at all radii. This is beyond the scope of the analytic equations discussed above. However, these are included in the hydrodynamic simulations of W96, and they show column as a function of angle for three of their simulations for L/L_Edd = 0.3, 0.08 and 0.01 for fixed illuminating spectrum with T_{IC, 8} = 0.13 and disc R_out = 5R_IC (except for L/L_Edd = 0.01, where R_out = 12R_IC: Woods, private communication). W96 give the total column (their tables 2-4), but this includes the column density from the static corona region as well as the wind, whereas our mass-loss rates are (by definition) for the wind alone. Hence, we use their estimate for the fraction of the column that arises in the static corona (below the softening radius) to derive the column from the wind material in order to compare with the analytic equations. The resulting wind column depends on the inclination angle, i, which can be approximately described as N_H(i) ∝ (1 − cos (i)) for all angles that do not intersect the disc photosphere itself.

Figure 4.

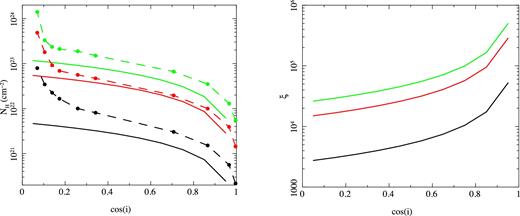
(a) The dashed line/open circles show the column density in the wind (excluding the static corona) as a function of cosine of the inclination angle from the hydrodynamic simulations of W96 for T_{IC, 8} = 0.13 for pairs of L/L_Edd, R_out of 0.01, 12 (black) 0.08, 5, (red) and 0.3, 5 (green). The solid lines show the columns resulting for each of these from the analytic approximations assuming that the density is ∝ (1 − cos (i)) and that the typical velocity of the wind is the average (mass-loss weighted) sound speed. This is ∼140, 350 and 420 km s⁻¹ for each of the simulations, respectively. The very simple analytic approximations agree with the results of the hydrodynamic simulations to within a factor ∼1.5–2 over a broad range of angles. (b) The ionization parameter of the wind. This decreases at higher inclination (lower cos (i)) as the density in the wind is higher.

Open in new tabDownload slide

Thus, the thermal wind models can predict not only the overall mass-loss rate from the disc, but also the zeroth order observables of column density, and mean ionization state and velocity along any sightline for any disc size, luminosity and for any radiation spectrum. However, current data (e.g. Miller et al 2015) already give better resolution on the structure of these winds than our simplistic, single zone model, and we stress that full hydrodynamic simulations of thermal winds are required for a detailed comparison.

3 EVOLUTION OF THE WIND WITH L/L_Edd

We use this correlated change in kT_IC with L/L_Edd to explore the predicted wind behaviour over the range 10⁻³L_Edd < L < L_Edd, with the total mass-loss rate in the wind |$\dot{M}$| calculated from the fitting formulae of W96 and the column/ionization state observables approximated as in Section 2 above. We assume a generic BH of mass M = 10 M_⊙ and set the disc outer radius to 3.7 × 10¹² cm (2.5 × 10⁶R_g, which corresponds to 5R_IC for T_{IC, 8} = 0.13 as used in most of the simulations in W96). We note that most BHBs have much smaller discs, but the most dramatic winds are indeed seen in systems that are known to be in long period orbits (GRS1915+105, GRO J1655−40), or where the orbital periods are unknown but consistent with being long (H1743−322, 4U1630−522) e.g. Diaz Trigo & Boirin (2016).

The upper panel of Fig. 5 shows the Compton temperature as a function of L/L_Edd, illustrating the dramatic change in behaviour at the hard/soft spectral transition at L ∼ 0.02L_Edd. This has a similarly dramatic impact on the radius at which Compton temperature allows material to escape, R_IC, shown as the solid line in the second panel of Fig. 5. However, the effective launch radius, R_in, depends on luminosity relative to the critical luminosity that is required to launch the wind efficiently, which itself depends on T_IC. The third panel in Fig. 5 shows L/L_crit. This only reaches unity for L > 0.1L_Edd, so only above this luminosity is R_in = 0.2R_IC (fourth panel, Fig. 5). Below this, R_in = 0.2R_IC/(L/L_crit), so it decreases with increasing luminosity in the low/hard state, as well as showing more complex behaviour at the transition due to the jump in Compton temperature. However, all of these are within the disc outer radius, so the outer parts of the disc are in the strong wind region B even for L/L_crit < 1. The final panel shows the wind efficiency i.e. the ratio of mass-loss rate in the wind with the mass accretion rate required to produce the assumed luminosity. This is fairly constant as the outer disc is always in one of the strong wind regions, and high at ∼5 × the input mass accretion rate. This is a little larger than in the simulations in W96 and Fig. 3 as we are assuming a BH with spin 0.5 rather than spin 0, so the same luminosity is produced with a lower mass accretion rate.

Figure 5.

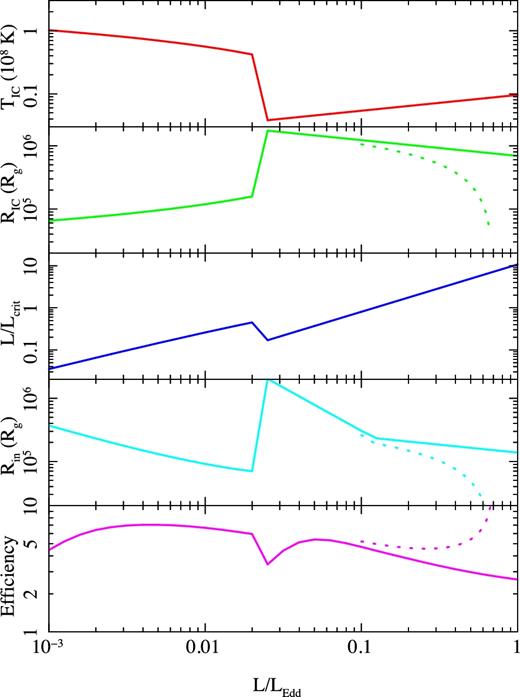
The upper panel shows the assumed change in T_IC with L/L_Edd (red). The power-law spectral index softens with increasing luminosity in the low/hard state, so the inverse Compton temperature drops. The abrupt drop at L/L_Edd = 0.02 marks the transition to the disc-dominated state, where the Compton temperature increases with luminosity. The second panel shows the effect of this on R_IC (green). A higher Compton temperature means that the wind can escape from smaller radii. The third panel shows how L/L_crit changes (blue). An increase in Compton temperature means that the radiation heats the gas faster, so it can drive the temperature up to T_IC at R_IC at a lower luminosity. The assumed L/L_Edd–T_IC behaviour means that the luminosity is only above the critical luminosity for L > 0.1L_Edd. Thus, the wind is launched from R_in = 0.2R_IC only for L > 0.1L_Edd. Below this, the wind instead is launched from R_in = 0.2R_IC/(L/L_crit), so the wind launch radius (cyan) decreases with increasing L/L_Edd in the low/hard state, as the increase in L/L_crit more than offsets the increase in R_IC. The lower panel (magenta) shows the wind efficiency (mass outflow rate in terms of the mass accretion rate). This is fairly constant at ∼5 times the mass accretion rate required to produce the luminosity, except for more complex behaviour around the transition. The dotted lines on all panels show the effect of including a simple radiation pressure term to reduce the effective gravity. The wind can be launched from progressively smaller radii, and the mass-loss rates increase.

Open in new tabDownload slide

4 RADIATION PRESSURE CORRECTION

We first assume that this correction to the inverse Compton radius, |$\overline{R}_{IC}$|⁠, is the only change in wind properties, and rerun the BHB simulation. The new results are shown as the dotted lines on Fig. 5. The lower effective gravity as the luminosity increases towards Eddington means that R_IC and hence R_in both decrease dramatically, formally going to zero at 0.71L_Edd (dashed green and cyan lines in the second and fourth panels). The wind can then be launched from everywhere on the disc, so the mass-loss rates also increase. We note that this is likely to be an underestimate of the increase in mass-loss rate as we still assume that the wind velocity is given by the sound speed, but it should be higher due to the contribution of radiation pressure to the acceleration.

5 PREDICTED ABSORPTION FEATURES

5.1 Behaviour at the transition

We calculate the observable features of the simple model for the BHB spectral evolution as a function of L/L_Edd introduced in the previous sections. Fig. 6 shows the observables of N_H (upper panel, red) and ξ (middle panel, green), extracted for an inclination of 75° (cos (i) = 0.25). The solid lines show the standard thermal wind model results. The column density is roughly proportional to mass accretion rate, but with a drop at the spectral transition due to the large change in spectral shape changing the Compton radius and critical luminosity. This predicts that there should be an abrupt increase in column by around a factor of 10 as the source declines and makes the transition to the low/hard state. This is exactly opposite to the claimed behaviour of the wind shutting off in the low/hard state.

Figure 6.

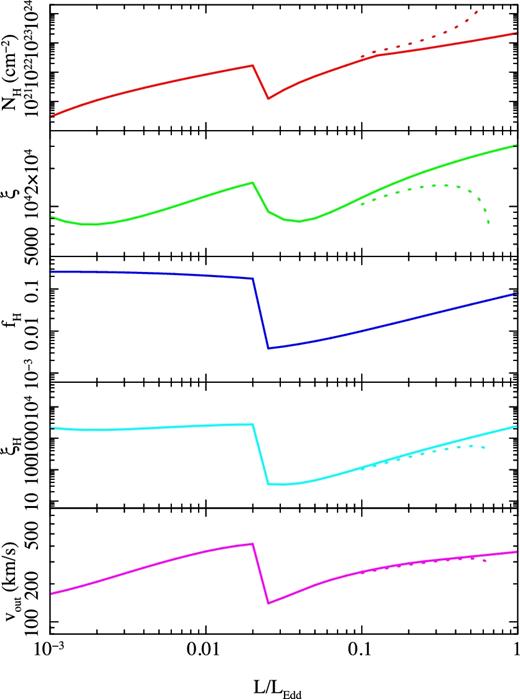
The upper panel (red) shows the column density at cos (i) = 0.25 i.e. an inclination angle of ∼75°. This is roughly proportional to the mass accretion rate, but with a dip at the spectral transition due to the lower Compton temperature of the dimmest high/soft states. The second panel (green) shows the ionization state calculated from the total bolometric flux, ξ = L_bol/nR². This is fairly constant, as the increase in luminosity is mostly balanced by an increase in density of the wind. The third panel shows the fraction of bolometric flux, which is emitted in the 8.8–30 keV high energy bandpass (blue). These are the photons that are most effective in photoionizing He- and H-like iron, and this shows a dramatic dip around the spectral transition, even including a power law to higher energies that carries 5 per cent of the total disc luminosity. The fourth panel shows the high energy ionization parameter, ξ_H = f_HL_bol/nR² (cyan). This is almost completely constant in the low/hard state, but dips dramatically in the high/soft state due to the much softer spectra, and only recovers to the same value as seen in the low/hard state at the highest luminosities. The bottom panel shows the outflow velocity. This mirrors the behaviour of the launch radius of the wind shown in Fig. 5d. The dashed lines show the effect of including a simple radiation pressure correction. The wind becomes optically thick (N_H > 2 × 10²⁴ cm⁻²), and has much lower ionization parameter around L ∼ 0.7L_Edd, as required to explain the dramatic wind in GRO J1655−40 (Miller et al 2006, Shidatsu, Done & Ueda 2016).

Open in new tabDownload slide

However, the visibility of the wind is also controlled by its ionization state. The ionization parameter calculated from the full luminosity, ξ = L/(nR²), is almost constant, changing only by a factor of 5 as the luminosity varies by a factor of a thousand. This is because the ionization is roughly proportional to ratio of luminosity and wind mass-loss rate (equation 7) so these cancel in the regime where the wind efficiency is roughly constant. However, the photoionization of iron depends on the high-energy 8.8–30 keV flux, which changes dramatically at the transition. This high energy flux would be very small for the lowest luminosity high/soft states as these have low temperature discs with very few photons emitted above 8.8 keV. However, such pure disc spectra are rare. Most high/soft states have a small, soft power-law tail giving some higher energy flux. Hence, we also include an additional power law in the high/soft state, with index fixed at Γ = 2.2, which carries 5 per cent of the total power. This has little impact on the Compton temperature, but will determine the photoionization of iron ions. The third panel in Fig. 6 (blue) shows the fraction of the bolometric flux, which is emitted in the high energy 8.8–30 keV bandpass, f_H, while the fourth panel (cyan) shows the corresponding high energy photoionization parameter, ξ_H = f_HL/(nR²) = f_Hξ. This drops by a factor of more than 50 at the transition, so the photoionization of the wind changes dramatically.

However, the baseline ion population of iron is set by collisional ionization rather than photoionization – the wind is heated to a temperature T_ch, so the ion populations cannot drop below those that characterize material at this temperature. We will explore this in detail in a subsequent paper, but here we just note that neither the Compton temperature nor the high-energy photoionization parameter is high enough to completely strip iron in the wind in the low/hard state. Thus, while there is a large change in ion populations in the wind across the transition, it is not likely that this is the origin of the lack of iron absorption features in the wind in the low/hard state (Neilsen & Lee 2009; Miller et al 2012).

5.1.1 Comparison to observations across the transition

We analyse the constraints from the data across the transition in more detail. The observations of Neilsen & Lee (2009) are of GRS1915+105, a source which is close to its Eddington limit, even in its hardest spectral states, which is a hard intermediate state rather than a true low/hard state (Done, Wardziński & Gierliński 2004). Hence, this requires more detailed modelling, which will be the subject of a later paper (Shidatsu, Done & Ueda in preparation). However, the observations of H1743−322 of Miller et al. (2012) are in standard low/hard and high/soft states, which are directly comparable to those simulated in the previous section. Hence, we can use our models to directly compare to the observed thermal wind features across the spectral transition.

We extract the simultaneous RXTE/Chandra data for these observations in order to constrain the continuum shape and luminosity as well as the wind features (Huenemoerder et al. 2011). The standard pipeline RXTE continuum spectra are shown in Fig. 7 (ObsIDs P95368-01-01-00 and P80135-02-01-11 for the low/hard and high/soft states, respectively), with the inset showing the TGCAT co-added HEG ± 1 Chandra high resolution spectra (ObsIDs 3803 and 11048, respectively) around the iron line bandpass. It is obvious that there is a large change in bolometric luminosity as well as the state change and the change in wind absorption features. The wind should clearly have higher column in this particular high/soft state than the comparison low/hard state simply because the source has higher bolometric luminosity (see Fig. 5 e and 6a).

Figure 7.

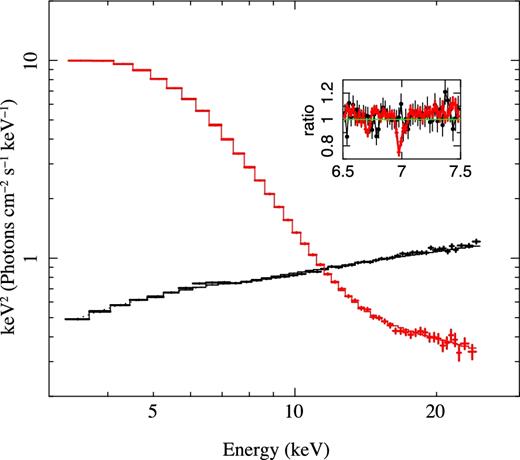
The low/hard (black) and high/soft (red) spectra from RXTE data on H1743−322, with the inset showing the simultaneous Chandra data, with a clear difference in wind absorption features. The high energy 8.8–30 keV photoionizing flux is quite similar between the two data sets, but the overall luminosity is quite different. If the wind stayed constant, responding only to the high energy photoionizing flux, then the difference in wind properties would require a change in the wind structure, potentially linked to the appearance of the jet. However, thermal winds respond to the overall flux, as well as to the high energy part, and this predicts that the column should be smaller by a factor of ∼5 in the low/hard state, consistent with the observations.

Open in new tabDownload slide

Integrating the model to get an unabsorbed bolometric flux gives 9.7 × 10⁻⁹ ergs s⁻¹ cm⁻² for the low/hard state using the nthcomp model with an assumed electron temperature of 100 keV, while the diskbb model for the high/soft state gives 4.3 × 10⁻⁸ ergs s⁻¹ cm⁻². However, the intrinsic luminosity of the high/soft state is probably higher due to projection effects as the disc is seen at a high inclination – as evidenced by the fact that it has a disc wind (Ponti et al 2012) and a strong low-frequency QPO (Ingram et al 2016) as well as a high-temperature disc (Munoz Darias et al 2013). The system parameters are not well known, but Dunn et al (2010) show the hardness–intensity diagram for the outbursts look similar to those of other BHBs for a canonical 10 M_⊙ mass and 5 kpc distance. This then gives L/L_Edd = 0.02 (low/hard) and 0.1 (high/soft) without any projected area correction, or L/L_Edd ∼ 0.4 with a cosine dependence assuming i ∼ 75° (Steiner, McClintock & Reid 2012). This fits rather well with the observed spectrum, as the diskbb temperature is 1.2 keV, i.e. 2 times higher than that assumed at the transition at L/L_Edd = 0.02, so the luminosity should be 2⁴ = 16 × higher, at L/L_Edd ∼ 0.3. The tail in the high/soft state carries roughly 5 per cent of the total bolometric power, so these two spectra are very comparable to those assumed in the simulations shown in Figs 5 and 6.

The thermal wind model then predicts that there should be a wind column of ∼8 × 10²² cm⁻² in the high/soft state, a factor of 5 larger than the predicted column of 1.6 × 10²² cm⁻² in the low/hard state. This is despite the fact that the high energy luminosities are similar in the low/hard and high/soft states. Thermal winds respond to changes in total luminosity and spectral shape and are not just dependent on the high energy photoionizing flux. The models predict that the high energy photoionization parameter is lower by a factor of 5 in the high/soft state, as there is a stronger wind, but with similar high energy flux. However, this photoionization is not sufficient to fully strip the wind in the low/hard state, so the clear prediction of the thermal wind model is that the absorption features should be ∼5 times bigger in the high/soft state at L/L_Edd = 0.3–0.4 compared to the brightest low/hard state at L/L_Edd = 0.02, despite them having similar high energy fluxes. This is easily compatible with the Miller et al (2012) results.

5.2 High luminosities and the wind in GRO J1655−40

The dotted lines on Fig. 6 show the effect of the simple radiation pressure correction (see Section 4). The column increases dramatically as L → 0.7L_Edd, becoming optically thick to electron scattering, with a corresponding drop in ionization state. The dotted lines on Fig. 5 show that this much stronger wind is launched from progressively smaller radii.

Our assumed disc-dominated spectra at high luminosity are too simple to describe those seen from GRS1915+105, so here we concentrate only on the comparison to GRO J1655−40, which had a very soft spectrum at the time when it produced the most extreme wind seen from this or any other BHB. This anomalous wind has large column, log N_H ∼ 23.8 and (compared to other binary winds) low ionization state, log ξ = 4 (Miller et al 2006; Miller et al 2008; Kallman et al 2009). This ionization state is comparable to those predicted here for the simple radiation pressure correction at L → 0.7L_Edd, but the observed column is not optically thick, and the observed luminosity is only ∼0.05L_Edd (Miller et al 2006; Miller et al 2008; Kallman et al 2009).

None the less, it seems possible that this could still be at least partly (there are multiple velocity components: Kallman et al 2009; Miller et al 2015; 2016) due to a thermal-radiative wind. The true source luminosity will be underestimated if the wind become optically thick and this optically thick material could be hidden by being completely ionized, with the observed absorption lines arising from an outer thin skin of partially ionized material. In this picture, an optically thick wind is launched by thermal-radiative driving from the inner disc, and expands outwards. Electron scattering in the completely ionized, optically thick material reduces the observed X-ray flux along the line of sight, with the observed absorption lines arising in an outer, optically thin, photosphere of the wind. The detection of the metastable Fe xxii shows that this photosphere must have n ∼ 10¹⁵ cm⁻³ (Miller et al 2008; Kallman et al 2009) and it is illuminated by the same (suppressed) continuum that we see as it is along the line of sight. Hence, the observed log ξ = 4 implies a position for this photosphere at R ∼ 8 × 10⁸ cm (≡ 800R_g), as in the magnetic wind models. The difference in this thermal-radiative picture is that the wind is actually launched from even closer to the BH, and we see only the outer shell of the expanding optically thick material.

This may seem to be an unnecessarily complex picture, given the success of the magnetic wind models in fitting the data quantitatively (e.g. Fukumura et al 2017). However, while the magnetic models can quantitatively fit to the observed optically thin wind with the observed low luminosity, they do not explain why this wind is only seen in this one observation of GRO J1655−40. There are other similarly low luminosity Chandra data sets from this source, which show much higher ionization winds, consistent with a thermal driving (Nielsen & Homan 2012), and similarly low luminosity Chandra data from other sources, which show only the expected thermal wind signatures of H- and He-like iron (e.g. Ponti et al 2012). The magnetic wind model also does not explain the other unusual features of GRO J1655−40 in this data set, namely the unusual lack of variability seen in the corona of this state (Uttley & Klein-Wolt 2015), or its unusually steep spectrum (Neilsen & Homan 2012), or give a geometry where the absorption lines only partially cover the source (Kallman et al 2009). By contrast, all these other features can be explained fairly naturally in an optically thick wind model. Downscattering in the wind steepens the spectrum, suppresses variability and makes an extended source geometry for partial covering, and it is rare for BHBs to reach (or exceed) Eddington, which explains why this wind has such different properties.

None the less, a thermal-radiative wind from a source with L → L_Edd remains a speculative explanation for this observation of GRO J1655−40. To test whether this scenario can work quantitatively requires a hydrodynamic code to calculate the two dimensional wind structure, including radiative continuum driving (e.g. Proga & Kallman 2004) with full Monte Carlo radiation transport to handle the scattered flux (e.g. Higgingbottom et al 2014). However, the limitations of the magnetic wind models in explaining why the wind in this observation of GRO J1655−40 is so different from other observations of this and other BHBs motivate a consideration of the possibility.

6 CONCLUSIONS

We use the analytic models for thermal winds of B83 and W96, combined with a very simple geometric/kinematic model for the structure of the wind to predict the column density, ionization and velocity along any line of sight at any luminosity for any spectrum. We combine this with a very simple model of the spectral evolution with luminosity in BHBs, including the major change in Compton temperature at the hard–soft spectral transition, as well as the smaller but systematic change in Compton temperature with luminosity within each state.

We show that the column density of the wind seen at any luminosity generally increases with increasing mass accretion rate except for a dip just after the transition to the high/soft state, where the much lower Compton temperature suppresses the wind. This predicts that there is more wind material just after the source makes a transition to the low/hard state, in direct contrast to claims that the wind is suppressed in the low/hard state and seen only in the high/soft state. While photoionization also plays a role in the visibility of the wind, we show that this is probably not enough to suppress a wind just after the transition to the low/hard state if it was visible in the high/soft state just beforehand.

We critically examine the data on which the claims of wind suppression are based. GRS1915+105 (Neilsen & Lee 2009) is close to Eddington, and has complex spectra so the very simple models used here are probably not applicable. Instead, H1743−322 (Miller et al 2012) shows canonical low/hard and high/soft states, with Chandra data clearly showing that the wind in the high/soft state is absent in low/hard data with similar high energy luminosity. However, these two spectra are very different in total luminosity, and this difference is enhanced by the cosine dependence of the disc flux in the high/soft state, while the low/hard state emission is more isotropic. We estimate that these two spectra differ by an order of magnitude in intrinsic luminosity, so the much stronger wind in the high/soft state is entirely in line with the thermal wind predictions.

This removes any need for suppression of the wind at the transition via magnetic fields switching from powering the wind in the high/soft state, to powering the jet in the low/hard state (Neilsen & Lee 2009). Indeed, such a switch would be very surprising, as the jet is almost certainly launched from the inner disc, while the low outflow velocities seen in the wind shows that it is most likely launched from the outer disc.

Radiation pressure should become important as the source approaches the Eddington limit, increasing the mass-loss rate as material above the disc is unbound at progressively smaller radii. We include a simple correction for this which predicts stronger winds launched from smaller radii as L → L_Edd. This may be able to explain the anomalous wind seen in GRO J1655−40 (Miller et al 2006), if the wind becomes optically thick, suppressing the observed luminosity (Shidatsu, Done & Ueda 2016). However, a quantitative comparison requires hydrodynamic simulations in the Eddington regime, which are beyond the scope of this paper. Alternatively, Fukumura et al (2017) have shown quantitatively that magnetic driving can be consistent with the broad properties of this anomalous wind, though their model does not explain why similar winds are not seen in this or other BHB at similar luminosities, nor does it address the likelihood of the required magnetic field configuration.

We conclude that there is at present no strong requirement for magnetic winds in the majority of BHB, and it is possible that they are not required in the supermassive BHs either (e.g Hagino et al 2015; 2016). Known wind launching mechanisms (thermal, UV line driven and Eddington continuum) should be explored in detail before ruling them out in favour of magnetic winds.

Acknowledgements

We acknowledge funding under Kakenhi 24105007, and CD acknowledges STFC funding under grant ST/L00075X/1 and a JSPS long term fellowship L16581. This research has made use of data and/or software provided by the High Energy Astrophysics Science Archive Research Center (HEASARC), which is a service of the Astrophysics Science Division at NASA/GSFC and the High Energy Astrophysics Division of the Smithsonian Astrophysical Observatory. We thank Daniel Proga and Norm Murray for very useful conversations, and especially thank Tod Woods for going above and beyond the call of duty in answering detailed questions on the results of his paper.

REFERENCES