-
PDF
- Split View
-
Views
-
Cite
Cite
S. E. Motta, A. Franchini, G. Lodato, G. Mastroserio, On the different flavours of Lense–Thirring precession around accreting stellar mass black holes, Monthly Notices of the Royal Astronomical Society, Volume 473, Issue 1, January 2018, Pages 431–439, https://doi.org/10.1093/mnras/stx2358
Close - Share Icon Share
Abstract
Type-C quasi-periodic oscillations (QPOs) in X-ray binaries have been often interpreted as a consequence of relativistic Lense–Thirring precession around a spinning black hole and they potentially offer a way to measure black hole spins and masses. The connection between relativistic precession and the resulting QPOs has been made either in terms of a simplified model involving a single test particle producing the QPO, or in terms of a global model where a geometrically thick accretion flow precesses coherently as a rigid body. In this paper, we analyse similarities and differences between these two models, sometimes considered as in opposition to each other. We demonstrate that the former is the limiting case of the latter when the radial extent of the precessing flow is very small, and that solid lower limits to the black hole spin can be obtained by considering the test particle model alone. We also show that the global precession model naturally accounts for the range of frequencies observed for type-C QPOs without the need to invoke a truncation of the inner accretion flow before it reaches the innermost stable circular orbit. Finally, we show that, in order to maintain rigid precession, the thick accretion flow should be radially narrow, and that if it extends beyond 10–102 gravitational radii, it aligns with the black hole spin too fast to produce a coherent QPO.
1 INTRODUCTION
Low-mass black hole X-ray binaries are typically transient systems that alternate between relatively short outbursts and long periods of (X-ray) quiescence. During outbursts, most black hole binaries show significant luminosity changes (from L ∼ 1030–31 erg s−1 in quiescence to L ∼ 1038–39 erg s−1), and display a ‘hysteresis’ behaviour that becomes apparent as q-shaped loops in the so-called hardness–intensity diagram (HID; see e.g. Homan et al. 2001). Most active black hole low-mass X-ray binaries (LMXBs) show four main different states: the low hard state (LHS), dominated by non-thermal emission; the high soft state (HSS), where the thermal emission from an accretion disc dominates the energy spectrum; the hard intermediate state (HIMS) and the soft intermediate state (SIMS), where the energy spectrum shows the contributions from both the accretion disc and the non-thermal emission, but where the most dramatic changes in the timing properties are observed. A few sources have also shown an anomalous or ultraluminous state (ULS; Motta et al. 2012), which is similar to a SIMS, but characterized by much higher luminosities. The different states are defined based on the spectral properties of the source and on the inspection of their Fourier power density spectra (PDS), where changes in the fast time variability are most clear. Among the most remarkable features detected in the PDS there are narrow peaks known as quasi-periodic oscillations (QPOs).
Discovered in the 1980s in the X-ray signal from accreting stellar mass black hole and weakly magnetized neutron stars, QPOs have been regularly observed in all accreting systems, including Ultraluminous X-ray sources (Strohmayer et al. 2003) and a few active galactic nuclei (Gierliński et al. 2008). The centroid frequencies of QPOs can be measured with high accuracy and are typically associated with the motion of matter in the accretion flow or accretion-related time-scales.QPOs yield relatively short (subsecond) time-scales and simple light crossing arguments indicate that these features must originate in the innermost regions of the accretion flow.
In black hole X-ray binaries, low-frequency QPOs (LFQPOs) are very strong and commonly observed features, and have been divided into three subclasses: type-A, B and C (see e.g. Wijnands, Homan & van der Klis 1999; Casella, Belloni & Stella 2005; Motta et al. 2015). Type-C QPOs are the most commonly observed, with frequencies spanning the ∼0.1–30 Hz range, tightly correlated with the spectral evolution of the host source (see e.g. Belloni & Motta 2016). In the LHS, type-C QPOs appear at frequencies from ≲0.1 Hz to ∼1 Hz (with frequency increasing with luminosity). As a source evolves through an outburst, moving to softer states, type-C QPOs show increasing frequencies, reaching their maximum (∼10–30 Hz, depending on the source) in the HSS. As a source crosses the SIMS, type-C QPOs are substituted by type-B QPOs. During the ULS, type-C QPOs are often observed again, occasionally simultaneously with type-B QPOs. After reaching a maximum frequency, type-C QPOs typically disappear (this is what determines the start of the SIMS), to reappear again when the source eventually makes its way back towards the LHS, after crossing again the SIMS and then the HIMS. During this phase, type-C QPOs decrease in frequency down to less than a few Hz and eventually become non-detectable.
The physical origin of QPOs is still debated, despite the fact that they have been studied extensively since their discovery. In particular, several models have been proposed to explain the common type-C QPOs, which are often interpreted as an effect of relativistic (i.e. frame dragging-related) precession within the accretion flow. The relativistic precession model is the first model based on relativistic precession and was originally proposed in the late 1990s by Stella & Vietri (1998) and Stella, Vietri & Morsink (1999) to explain QPOs in both neutron stars and black hole binaries. This model considers test particle orbits and the associated frequencies calculated in the Kerr metric. In particular, the type-C QPOs are explained as the effect of the Lense–Thirring precession of a test particle orbiting a spinning black hole.
Ingram, Done & Fragile (2009) proposed a model for type-C QPOs based on similar premises. This model requires a cool optically thick, geometrically thin accretion disc (the thin disc; Shakura & Sunyaev 1973) truncated at a certain radius (Esin, McClintock & Narayan 1997; Poutanen, Krolik & Ryde 1997), filled by a hot, geometrically thick accretion flow (the thick disc) that precesses as a consequence of frame dragging. This geometry is known as the truncated disc model. Variations in the truncation radius of the thin disc determine changes in the geometry of the thick disc (i.e. the thin disc inner truncation radius coincides with the thick disc outer radius). Since the Lense–Thirring frequency increases sharply with decreasing radius, in this model the type-C QPOs will have increasing frequency for decreasing thin disc truncation radii and vice versa. In particular, in the LHS the type-C QPOs will be produced by a thick disc with a large outer radius, which will decrease as the source moves through the LHS, HIMS and SIMS, reaching a minimum in the HSS, thus making the QPO frequency increase in the process.
In this framework, the spectral evolution of black hole binaries in outburst, the variations in frequency of type-C QPOs and the clear correlation between these two observational facts are easily explained. The QPO is produced through the modulation of the X-ray flux coming from self-occultation, projected area and relativistic effects (Ingram & Done 2012; Veledina, Poutanen & Ingram 2013; Ingram et al. 2016) that become stronger with inclination (see Motta et al. 2015). This model also naturally explains why a coherent LFQPO can be observed even when the inner flow is thought to be rather extended (tens of Rg).
In this paper, we present a study of the test particle precession and the global rigid precession. We describe the conditions under which each of these two processes can be used to explain the type-C QPOs, and to infer the properties of the accretion flow from which they arise.
2 TEST PARTICLE VERSUS RIGID PRECESSION
In the relativistic precession model by Stella & Vietri (1998), three observed QPO frequencies are associated with the Keplerian frequency, the periastron precession frequency and the nodal precession frequency related to the Lense–Thirring effect at a given radius in the disc. Motta et al. (2014) showed that the equations describing these three frequencies, predicted by the theory of General Relativity, form a system of three equations for the three unknowns: M (the black hole mass), a (the dimensionless black hole spin parameter) and R (the radial location at which the QPOs are produced around the black hole). Such a system of equations can be solved analytically if three QPOs of the correct type are observed simultaneously, or numerically when an independent measurement of the black hole mass is available (e.g. from dynamical spectrophotometric observations), together with two of the three QPOs relevant for the RPM (see Ingram & Motta 2014; Motta et al. 2014).
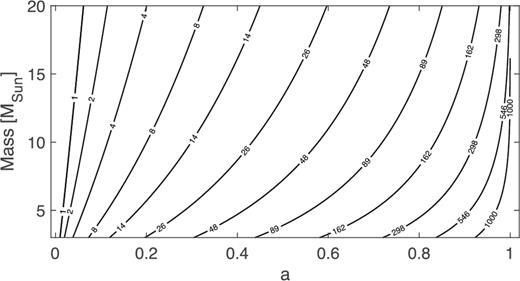
Mass–spin relation for different test particle Lense–Thirring frequencies. Each line has been obtained assuming that the frequency is produced at the ISCO. The number on each line corresponds to the frequency considered in Hz.
In Fig. 2, we show a comparison between the test particle precession frequency given by equation (1) and the rigid precession frequencies obtained through equation (2) for a 10 M⊙ black hole with spin a = 0.5. The rigid precession frequency depends on the inner radius Rin (which we fix at RISCO) and on the outer radius Rout of the thick disc. The test particle frequency depends only on the radius of the orbit that the test particle is following. For comparison, in the figure this radius is the same Rout used to compute the global frequency. The rigid precession frequency depends on the choice of p (indicated with different colours in the plot) through the surface density profile, which is displayed in the figure inset. At large radii, values of p close to zero give a steeper relation between frequency and outer radius than values of p close to one. Note, however, that the dependence on p is generally weak, especially at large radii. The spread in frequency caused by p is spin dependent and reaches its maximum at radii smaller than ≈10 Rg (note that the plot in Fig. 2 is in log-scale). This effect is better displayed in Fig. 3, where we plot the difference Δν between the rigid precession frequencies calculated assuming p = 0 and 1, as a function of Rout for a 10 M⊙ black hole. For spins lower than ≈0.7, the frequency difference remains smaller than ≈5 Hz, while it increases quickly for higher spins.
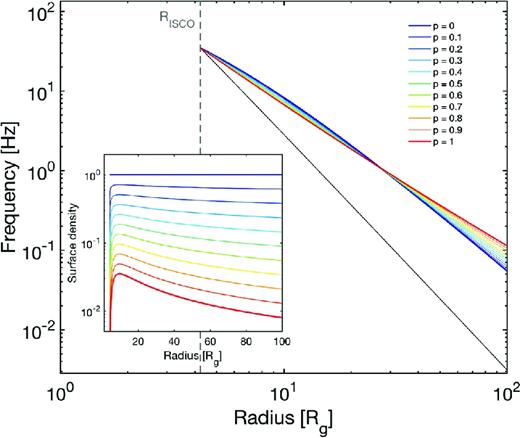
Lense–Thirring frequency for a test particle (black solid line) and rigid precession frequency (coloured lines) as a function of radius calculated using a surface density profile in the form: Σ ∝ r−p (1 − (Rin/r)1/2)p, with Rin = RISCO (displayed in the inset). In both panels, different colours correspond to different values of p (see legend). The frequencies have been calculated for a 10 M⊙ black hole with dimensionless spin parameter a = 0.5.
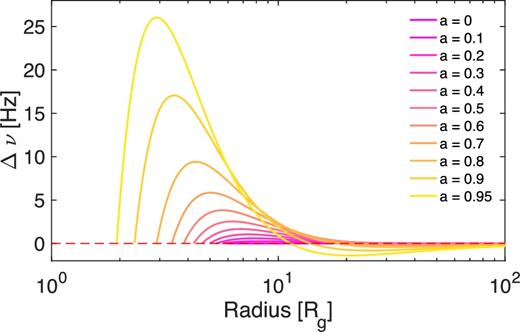
Maximum spread as a function of radius for rigid precession frequencies computed for variable spin (see legend) and a 10 M⊙ black hole. The maximum frequency spread is calculated as the difference between the rigid precession frequencies computed for p = 0 and 1.
Fig. 4 shows a comparison between the rigid precession frequencies obtained for a 10 M⊙ black hole with spin a = 0.5, calculated assuming the surface density profile given in equation (3), and the rigid precession frequencies obtained taking a surface density profile with the form |$\Sigma (R)\propto R^{-p}(1-\sqrt{\frac{R_{\rm in}}{R}})$|. In both cases, we assumed p = 3/5. The maximum difference in frequency using the two different profiles is smaller than 1 Hz at any radius. As mentioned above, p = 3/5 is the most appropriate value for a radiation-pressure-dominated Shakura–Sunyaev disc, and thus for the thick discs that we consider here, with viscosity proportional to the gas pressure and opacity dominated by electron scattering. Unless otherwise specified, from now on we will therefore assume p = 3/5.
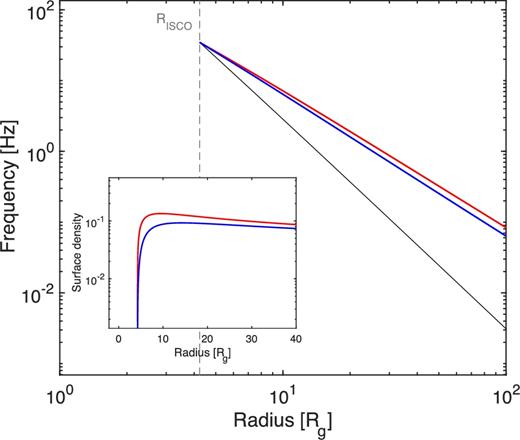
Rigid precession frequencies obtained for a 10 M⊙ black hole, with spin a = 0.5, calculated assuming the surface density profile given in equation (3) (red line) and those obtained taking a surface density profile with the form |$\Sigma (R)\propto R^{-p}(1-\sqrt{\frac{R_{\rm in}}{R}})$| (blue line). The inset shows the surface density profiles of the two cases.
3 SPIN MEASUREMENTS FROM RELATIVISTIC PRECESSION
As it is clear from Fig. 2, when the outer radius of the thick disc Rout approaches the ISCO (i.e. as the thick disc becomes more and more narrow), the rigid precession frequency asymptotically tends to the test particle frequency. Based on this property, in Franchini, Motta & Lodato (2017), we obtained lower limits (and a few upper limits) for the black hole spin in a number of systems by using the highest frequency type-C QPO detected in the soft state in a given source. We assumed that in this state the precessing thick disc is squeezed to a very narrow radial extent, such that we could substitute the (simpler) test particle frequency (equation 1) to the rigid precession frequency (equation 2) for R ≈ RISCO.
We noted, however, that the lower limits to the spins that we obtained were all significantly below the maximally spinning value a ∼ 1 (the highest spin we obtained is a = 0.47 for the case of 4U 1543–47), despite the fact that the soft-state type-C QPOs that we detected in the HSS spanned a fairly large frequency range (∼5–30 Hz). The origin of this trend can be deduced from Fig. 1, which shows that for black hole masses below 10 M⊙, a spin estimate of a ≳ 0.8 would correspond to a QPO frequency above 500 Hz, much above the maximum frequency type-C QPOs observed so far (≈30 Hz; see e.g. Motta et al. 2015). Similarly, Fig. 2 shows that for any given radius, the rigid precession frequency is higher than the test particle precession frequency by a factor that we empirically estimate to be ∼R/RISCO. This implies that for a given mass, frequencies explained via simple test particle precession at ISCO will always require spins systematically lower than those explained in terms of global rigid precession.
The spin distribution of stellar mass black holes is still largely unknown. Fragos & McClintock 2015 showed that a constant distribution of black hole spins (obtained through the fitting of the spectral continuum in outbursting black hole LMXBs; see e.g. McClintock et al. 2011) can be obtained by assuming that the natal spin of the black hole in these systems is likely to be initially low, and then increases during the accretion phase. This would result in a roughly constant spin distribution, but requires a strong coupling between the core and the envelope of the progenitor star of the back hole (which has been observed only for red giant stars with mass up to 2 M⊙). While Podsiadlowski, Rappaport & Han (2003) showed that a significant spin-up during the accretion phase is possible, King & Kolb (1999) ruled out this possibility by showing that the amount of mass accreted by the black hole would be too small to significantly change the spin.
Spin measurements obtained via fitting of the reflection features in the energy spectra from accreting black holes seem to indicate that the black hole spin distribution for black hole X-ray binaries might be skewed to high values (see e.g. Reynolds 2013). It must be noted, however, that the spin measurements obtained through this method are typically affected by large uncertainties and, in a few cases, are also in contrast with the measurements obtained through other methods (see e.g. Shafee et al. 2006; Reis, Fabian & Miller 2010 in the case of GRO J1655-40). This makes it difficult to establish what is the spin distribution underlying the measurements obtained thus far.
Given the above, there is still no obvious reason why certain spin values should be preferred, therefore the simplest assumption we can make is that the spin distribution is somewhat constant. In this work, we also consider only prograde black hole spins. Even though a few claims of retrograde spin in black hole X-ray binaries can be found in the literature (e.g. Reis et al. 2013, Morningstar et al. 2014), only a very limited region of the parameter space in a supernova explosion would lead to such a configuration, making a retrograde black hole spin scenario very rare (see e.g. Brandt & Podsiadlowski 1995). We therefore assumed that the dimensionless spin parameter of a stellar mass black hole can in principle take any value between 0 and 1. Following this argument, it seems clear that the spin measurements/lower limits based on the test particle precession are likely too conservative, especially if obtained from QPOs that are produced far from the ISCO (Franchini et al. 2017).
An obvious way to limit the maximum global precession frequency is to allow the thick disc to always maintain a finite radial extent. In other words, Rout must be always strictly larger than RISCO. Fig. 5 shows contour plots of the rigid precession frequency computed as a function of black hole mass and spin for a number of choices of the outer radius of the thick disc: from top to bottom ΔR = Rout − Rin = 0.1, 3, 5 and 10 Rg. While for ΔR = 0.1 Rg, the plot is very similar to the test particle case (see Fig. 1), for larger thick disc radial extents the resulting frequencies rapidly decrease for a given mass–spin couple. We thus see that by allowing a modest radial extent of the thick disc, we obtain Lense–Thirring frequencies that are consistent with the type-C QPOs frequencies typically observed around black hole X-ray binaries, with their maximum reaching up to ≈30 Hz when the thick disc is a few Rg wide (i.e. what we expect in the HSS). Allowing the thick disc to maintain a radial extent implies the entire spin range (0–1) must be spanned in order to obtain frequencies typical of type-C QPOs in the HSS for a reasonable range of black hole masses (∼3–20 M⊙). This essentially removes one of the limitations of the test particle model described above.
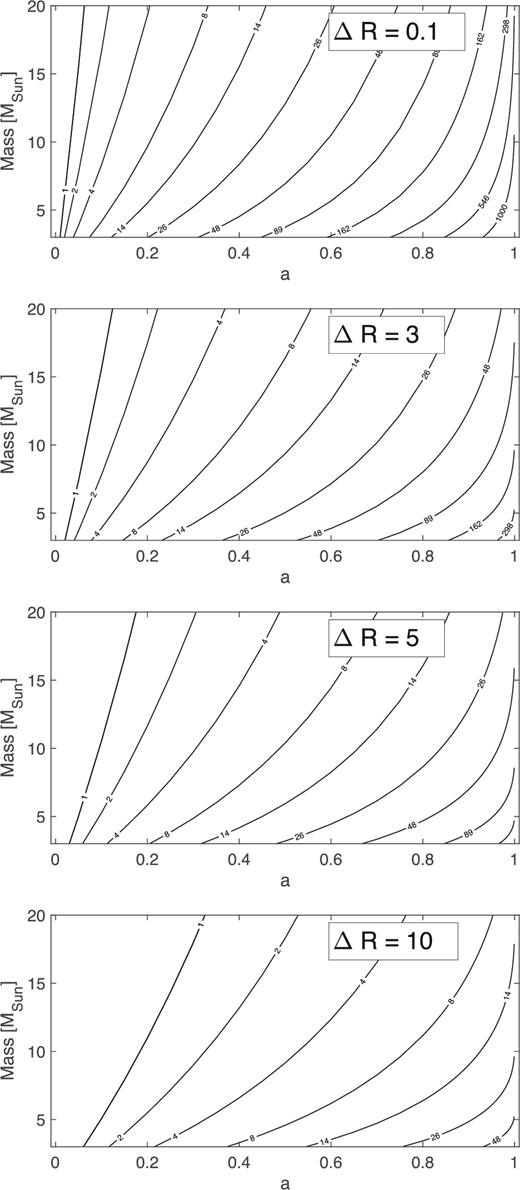
Mass–spin relation for different Lense–Thirring frequencies in the rigid precession model. Each line has been obtained assuming that the frequency is produced by a torus extending between Risco and Rout, with Rout − Risco = ΔR (indicated in each plot). These relations have been obtained assuming the same density profile as in Fig. 3, with p = 3/5.
Of course, the spin measurement that can be obtained allowing the thick disc to be radially extended depends strongly on its actual radial size. In Fig. 6, we plot the value of the black hole spin a obtained from the rigid precession model as a function of the radial extent of the thick disc, assuming a given observed type-C QPO frequency. ΔR = 0 obviously corresponds to the test particle case. The plots show that the test particle precession provides a solid lower limit to the black hole spin, while a stricter lower limit to the spin (or its actual value) could only be inferred knowing the radial extent of the thick disc reached around a given black hole. We note that for wider thick discs, the inferred spin quickly ‘saturates’ at 1 even assuming relatively low QPO frequencies, i.e. ∼5–15 Hz depending on the mass of the black hole (the higher the mass, the lower the frequency at which the spin saturates at 1). Such regions where the spin is equal to 1 for a variable ΔR correspond to areas of the parameter space for which there is no solution given a particular frequency and ΔR. Again under the assumption that the spin distribution of stellar mass black holes is close to a constant in the 0–1 range, the above suggests that it is unlikely that the thick disc will have a radial extent ΔR larger than ∼5–10 Rg in the HSS.
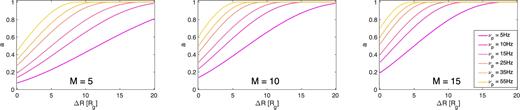
Spin inferred for a 5, 10 and 15 M⊙ black hole obtained assuming that a given frequency is produced by a thick disc with increasing Rout − Risco = ΔR. In each case, ΔR = 0 corresponds to the test particle precession. The rigid precession frequencies have been computed assuming p = 3/5.
4 REQUIREMENTS FOR THE GLOBAL RIGID PRECESSION OF THE THICK DISC
The outer radius Rout of the thick disc only depends on the physical properties of the accretion flow, and changes depending on the accretion state of a source. Since, in general, the thick disc angular momentum is not aligned with the black hole spin, the disc undergoes precession due to the Lense–Thirring effect, which induces a precession rate proportional to R−3. Thus, the innermost thick disc orbits are subject to a stronger torque and tend to align with the black hole spin while the outer parts maintain the misalignment. This leads to the formation of a warp in the thick disc. In a thick disc, the warping disturbances propagate as waves with half the sound speed (Nelson & Papaloizou 1999).1 Eventually, the thick disc becomes too wide in the radial direction for the warp to be communicated efficiently across it, and at this point rigid precession can no longer occur. Additionally, a very extended disc has the tendency to align with the black hole spin, again inhibiting precession. Hence, there exists a maximum radius Rmax beyond which the thick disc cannot precess in a rigid manner.
4.1 Rigid precession condition
Fig. 7 shows the precession time-scale and the sound crossing time-scale in the case of a black hole with M = 10 M⊙ and a = 0.5. The coloured solid lines show the rigid precession time-scale tp = 1/νp for different values of p, the same used in Fig. 2. The maximum outer radius that allows rigid precession, rrigid, can be read off as the intersection of these lines with the black dashed line, which marks twave as defined above (equation 6), where we have assumed q = 3/2 and (H/R)ISCO = 0.1. The value of q = 3/2 is appropriate for radiation-pressure-dominated discs (Frank, King & Raine 1992, equation 5.54), such as our thick disc. The aspect ratio at ISCO, (H/R)ISCO, is proportional to |$\dot{M}/\dot{M}_{\rm Edd}$| (Frank et al. 1992). Since the rigid precession condition is expected to be most relevant where the thick disc is radially very wide – e.g. in the LHS – we initially chose the value of (H/R)ISCO by considering that in this state, the accretion rate is thought to be low, i.e. ≈1–10 per cent LEdd (Dunn et al. 2010; Fender & Gallo 2014), which implies (H/R)ISCO ∼ 0.1. If the outer radius rout of the thick disc is larger than rrigid, only the section of the thick disc with r < rrigid will be able to precess rigidly. The section of the thick disc with radii larger than rrigid would not be able to precess coherently with the inner section of the disc, and could arguably either undergo differential precession (van den Eijnden et al. 2016), or break free from the (still precessing) inner flow (see e.g. Nealon, Price & Nixon 2015).

Precession time-scales (coloured solid lines) compared with the sound-crossing time-scale (black dashed line) and the viscosity-related alignment time-scale (dotted coloured lines). The solid coloured lines correspond to the precession time-scales obtained from the precession frequency shown in Fig. 2. All the time-scales have been calculated for a 10 M⊙ black hole with dimensionless spin parameter a = 0.5, by assuming (H/R)ISCO = 0.1 and q = 3/2. Each colour corresponds to a different p as in Fig. 2.
The rigid precession condition depends on spin of the black hole (while it is independent on the black hole mass M, since both twave and tp are linear functions of M), as it directly depends on the precession time-scale, as well as on the disc aspect ratio. Since higher spins mean faster precession, higher spins will also correspond to smaller maximum precession radii rrigid. In Fig. 8, we show the behaviour of rrigid (solid lines) as a function of the spin for different values of (H/R)ISCO, as obtained through equation (5) for a spin = 0.5 and mass equal to 10 M⊙ (for the bottom panel only). We see that while for low spins the precession time-scale is such that even very wide thick discs will be able to precess2 (rout ≳ 105Rg), for very high spins the thick disc will be able to precess globally only as long as its outer radius is lower than ∼10 Rg, especially for low aspect ratios. We must note, however, that in principle |$\dot{M}/\dot{M}_{\rm Edd}$| and, consequently the aspect ratio (H/R), depend on the spin, and both increase with increasing spin. For simplicity, we have not considered this effect; however, given the above, the actual maximum precession radii given by equation (5) for the thick discs around a highly spinning black hole are likely larger than those shown in Fig. 8 (solid lines).
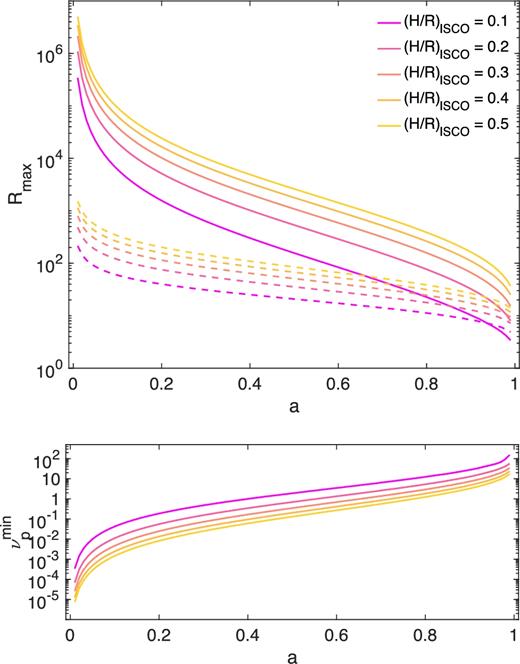
Top panel:maximum precession radius rmax due to the rigid precession condition (i.e. rrigid, solid lines) or the alignment condition (i.e. ralign, dashed lines) as a function of the spin for variable (H/R)ISCO (p = 3/5, q = 3/2, α = 0.01). The relations displayed have been obtained through equations (5) and (7), respectively. The figure shows that the maximum radius at which global rigid precession is allowed is always determined by the tendency of the disc to align with the black hole spin. Bottom panel: corresponding minimum global precession frequency as a function of the spins. The colour coding is the same used in the top panel. Frequencies have been estimated assuming a black hole mass of 10 M⊙.
4.2 Condition for disc alignment
Similar to the case of the rigid precession condition (Section 4), equation (7) implies that there is a maximum radius ralign after which the alignment time-scale is faster than the precession time-scale. When this happens, the disc aligns to the black hole spin before a complete precession cycle is over, effectively inhibiting continuous precession. Therefore, in order to maintain precession, we also require that the thick disc extends no further than ralign. In Fig. 7, we show the viscosity-related alignment time-scales (coloured dotted lines) together with the precession time-scales and the sound crossing time-scale. Since the alignment time-scale talign depends on the index p through the surface density profile Σ, each colour corresponds to a different choice of p (see legend in Fig. 2). We note that the alignment time-scale is shorter for higher black hole spins, which implies that ralign becomes smaller for increasing spin. As noted above in the case of the rigid precession condition, we are not considering the effects of the spin on H/R, which would likely make ralign larger than what obtained simply by solving equation (7), especially at high spins.
It is important to note that in the case of a black hole in a binary system, the binary partner is feeding the compact object, providing a constant stream of misaligned material. This implies that even though the flow undergoes alignment due to frame dragging within one precession cycle, there is always more matter accreting inclined with respect to the black hole equatorial plane, at least until the system eventually achieves global alignment, which may or may not take longer than the time it takes for the binary partner to evolve.
In a scenario where the alignment time-scale is fairly short, precession would still occur, but only intermittently. In other words, precession will only last for the alignment time-scale, then will break when the accretion flow reaches alignment, to start again shortly afterwards. In this context, the quality factor Q (defined as Q = νQPO/FWHMQPO, where νQPO is the QPO centroid frequency and FWHMQPO is the QPO full width at half-maximum) of the resulting QPO would then be approximately the number of precession cycles in an alignment time-scale. Since by definition QPOs have Q > 2, this means that we can impose a stricter constraint on ralign, which is then obtained by requiring talign > 2 tp.
In Fig. 8, together with the maximum radius at which rigid precession is allowed by the global criterion (equation 4), we show the maximum radius at which rigid precession is permitted before alignment (ralign, indicated with dashed lines) as a function of the spin. We calculated such radii for variable aspect ratio (H/R)ISCO, assuming α = 0.01 and p = 3/5. Interestingly, we see that the disc alignment condition given by equation (7) almost always dominates over the wave propagation condition given by equation (5), and therefore the maximum radius rmax = min(rrigid, ralign) at which continuous rigid precession can occur is basically always determined by the tendency of the disc to align with the black hole spin.
5 DISCUSSION AND CONCLUSIONS
We compared the test particle Lense–Thirring precession and the global rigid precession as likely mechanisms responsible for the presence of type-C QPOs in the light curve of accreting stellar mass black holes in binary systems. We showed that the global rigid precession of a radially extended thick disc (as opposed to the test particle precession) can produce QPO frequencies that match those of type-C QPOs typically observed in black hole binaries. This geometry is the same already proposed by other authors, in particular Ingram et al. (2009), who made the first explicit connection between the idea of rigid precession already observed in numerical simulations (e.g. Fragile et al. 2007, Liska et al. 2017) and the observed properties of type-C QPOs.
The geometry that we considered in this work consists of a thick disc whose inner radius is set by the ISCO. In agreement with the truncated disc model, the outer radius of the thick disc, instead, is set by the inner truncation radius of the thin disc concentric and surrounding it, and is always significantly larger than RISCO (i.e. the radial extent of the thick disc must never be negligible). The surface density profile we assumed is a power law with index p, with a correction at small radii, to satisfy the no-torque condition Σ = 0 at R = Rin (Shakura & Sunyaev 1973). The index p can be determined based on disc energetics arguments. In the case considered here, we assume that the disc is radiation-pressure-dominated with viscosity proportional to gas pressure, in which case p = 3/5.
We showed that in order to match the observed type-C QPOs frequencies, it is not necessary to assume that the thick accretion disc is truncated on the inside at a radius larger than the ISCO, contrary to what has been proposed by other authors (e.g. Ingram et al. 2009). Instead, we assumed that while in the HSS the thick accretion disc is significantly radially narrower than in the other states, its radial dimension should never become negligible. We showed that in order to both match the observed type-C QPOs frequencies and span the entire spin and mass range suitable for accreting stellar mass black holes, the thick accretion disc must always maintain a non-negligible, though moderate, radial extent, i.e. between a few and ≈10 Rg. Additionally, we confirmed that the test particle Lense–Thirring precession applied to the type-C QPOs observed in the HSS allows us to infer a solid lower limit to the black hole spin (see also Franchini et al. 2017).
The prediction that the thick disc should maintain a significant radial width is consistent with a well-known property of the PDS of accreting black hole binaries. PDS showing type-C QPOs can be modelled by multiple Lorentzians (see e.g. Belloni, Psaltis & van der Klis 2002). The lowest frequency Lorentzian is generally zero-centred and shows a break at a certain frequency νb, corresponding to the so-called low-frequency break in the flat-top noise typically associated with type-C QPOs. The break frequency νb is thought to be associated with the viscous time-scale tvisc = (H/R)−2(αΩ)−1 at the outer radius of the thick disc (see e.g. Done, Gierlinski & Kubota 2007, Ingram & Done 2011,). This frequency is approximately ∼0.01 Hz in the hard state and ∼1 Hz in the soft state (see e.g. Done et al. 2007) and roughly correspond to a few tens of Rg and a few Rg, respectively, for a 10 M⊙ black hole with spin a = 0.5 (assuming α = 0.01 in the disc), in agreement with our predictions on the disc radial extent in the soft state.
We then studied the conditions under which the thick disc can undergo global rigid precession around a spinning black hole. The two requirements that need to be satisfied in order for the thick disc to rigidly precess – and thus produce detectable QPOs – are that the disc warp propagates and reflects efficiently, and that the disc alignment time-scale is longer than the precession time-scale. The first requirement depends on the sound crossing time-scale within the disc and guarantees that the warp is maintained. The second requirement depends on the presence of viscosity and ensures that each precession cycle is over before the disc aligns with the black hole spin. Both conditions depend on the spin of the black hole and on the disc aspect ratio. The condition based on the alignment time-scale depends also on the viscosity parameter α. We have hence calculated the maximum outer radius that a thick disc can have in order to both maintain global rigid precession and to keep the misalignment with respect to the black hole spin. Interestingly, comparing the maximum precession radii coming from the above conditions, we found that continuous global rigid precession is always inhibited by the disc tendency to align with the spin rather than by the loss of connection between the different regions of the thick disc. In other words, beyond a certain radius rmax the disc aligns faster than it precesses, which effectively inhibits precession. Since the global precession frequency decreases with increasing outer radius, this implies that, if type-C QPOs are indeed due to global precession, for any given black hole mass there is a minimum allowed QPO frequency, which for a 10 M⊙ black hole is in the range of 0–102Hz (see Fig. 8, bottom panel). Since the vast majority of the known black holes LMXBs show QPOs below 1 Hz, this result essentially implies that none of such black holes can have a spin larger than a ≈ 0.6.
We remind the reader that both the maximum precession radii given by the rigid precession condition and the maximum precession radii given by the presence of alignment are likely higher than the values obtained from equation (5) and equation (7) for high spin values. As a consequence, the minimum allowed precession frequency is lower than those shown in Fig. 8 (bottom panel), especially for high spins. Furthermore, we note that very recently Liska et al. (2017) have found evidence in a General Relativistic 3D MHD simulation that the jet can play a role in aligning the accretion flow. In particular, the presence of a jet might cause both the precession time-scale and the alignment time-scale to slow down. Studying further the effects of high spins on the disc dynamics is beyond the scope of this work, and further investigations are left to a future work.
The existence of a maximum radius at which global rigid precession can occur has consequences for the production of type-C QPOs in different accretion states. While in the HSS (and in the ULS), the radial extent to the thick disc is thought to be small, in the LHS the thick disc could be in principle several tens of Rg wide. As a consequence, the rigid precession conditions described above could significantly influence the properties of QPOs observed in this state. For instance, a QPO could show a loss in coherence if produced in a thick disc with rout ∼ rmax with respect to those QPOs produced when rout < rmax. This might explain why type-C QPOs detected in active sources caught shortly after they left the quiescence and/or close to their return to it at the end of an outburst. Such QPOs typically appear at frequencies lower than ∼0.1 Hz and are in general broader and less coherent (Q ≈ 2) than those observed at higher frequencies (typically Q ≫ 2).
Acknowledgements
We would like to thank the anonymous referee, whose comments and suggestions helped improving this paper. We also thank Chris Fragile and the members of the ‘There it spins: the hunt for black hole spins’ ISSI team (call 2014), for useful discussion. We acknowledge ISSI Bern for hospitality and financial support. SEM acknowledges the Violette and Samuel Glasstone Research Fellowship programme and the STFC for financial support.
In a thin disc the propagation is, instead, diffusive (see for example, Lodato & Pringle 2007).
Note that the entire accretion disc filling the Roche lobe around a stellar mass black hole in a binary system can be as large as 106Rg, but it is typically smaller than this.
REFERENCES



