-
PDF
- Split View
-
Views
-
Cite
Cite
B. Lo Faro, V. Buat, Y. Roehlly, J. Alvarez-Marquez, D. Burgarella, L. Silva, A. Efstathiou, Characterizing the UV-to-NIR shape of the dust attenuation curve of IR luminous galaxies up to z ∼ 2, Monthly Notices of the Royal Astronomical Society, Volume 472, Issue 2, December 2017, Pages 1372–1391, https://doi.org/10.1093/mnras/stx1901
Close - Share Icon Share
Abstract
In this work, we investigate the far-ultraviolet (UV) to near-infrared (NIR) shape of the dust attenuation curve of a sample of IR-selected dust obscured (ultra)luminous IR galaxies at z ∼ 2. The spectral energy distributions (SEDs) are fitted with Code Investigating GALaxy Emission, a physically motivated spectral-synthesis model based on energy balance. Its flexibility allows us to test a wide range of different analytical prescriptions for the dust attenuation curve, including the well-known Calzetti and Charlot & Fall curves, and modified versions of them. The attenuation curves computed under the assumption of our reference double power-law model are in very good agreement with those derived, in previous works, with radiative transfer (RT) SED fitting. We investigate the position of our galaxies in the IRX–β diagram and find this to be consistent with greyer slopes, on average, in the UV. We also find evidence for a flattening of the attenuation curve in the NIR with respect to more classical Calzetti-like recipes. This larger NIR attenuation yields larger derived stellar masses from SED fitting, by a median factor of ∼1.4 and up to a factor ∼10 for the most extreme cases. The star formation rate appears instead to be more dependent on the total amount of attenuation in the galaxy. Our analysis highlights the need for a flexible attenuation curve when reproducing the physical properties of a large variety of objects.
1 INTRODUCTION
Dust plays a crucial role in many aspects of galaxy formation and evolution, in particular by strongly affecting the spectral energy distribution (SED): it absorbs and scatters photons, mostly at wavelengths < 1 μm, and thermally emits the absorbed energy in the infrared (IR) (λ ∼ 1–1000 μ m−1). The ratio of the IR to ultraviolet (UV) luminosity, usually referred as IRX, (IRX=log(LIR/LUV)), is tightly related to the amount of dust attenuation in a galaxy. Since the original work of Meurer, Heckman & Calzetti (1999) on local UV-bright starburst galaxies, the relation between the IRX and the UV-continuum slope, β, has been intensively used at all redshift (particularly at high-z) to estimate the total amount of attenuation in the UV. However, important deviations from this relation have been observed both for galaxies forming stars at a lower rate, as commonly found in the nearby universe (see Buat 2002; Buat et al. 2005; Gordon et al. 2004; Kong et al. 2004; Calzetti et al. 2005; Seibert et al. 2005; Boissier et al. 2007; Dale et al. 2009; Boquien et al. 2009, 2012), and for IR bright galaxies at all redshifts (Howell et al. 2010; Reddy et al. 2012; Casey et al. 2014). The interpretation of the IRX–β relation and of its deviations appears to require either different attenuation laws or star formation histories (SFHs, or both) (see e.g. Kong et al. 2004; Panuzzo et al. 2007; Conroy 2010; Forrest et al. 2016; Salmon et al. 2016).
The dust attenuation curve of a galaxy is the result of the complex blending of both the optical and physical properties of dust and the relative geometrical distribution of stars and dust within a galaxy.1 All these complex aspects are usually accounted for in radiative transfer (RT) models with varying levels of sophistication, with a general indication that shallower attenuation curves can be ascribed to larger optical depths and mixed star-dust geometries possibly masking variations of the intrinsic dust properties (e.g. Charlot & Fall 2000; Granato et al. 2000; Witt & Gordon 2000; Calzetti 2001; Pierini et al. 2004; Tuffs et al. 2004; Panuzzo et al. 2007; Chevallard et al. 2013). On the observational side most of the works dealing with dust attenuation estimates in galaxies are usually tied to UV wavelengths where dust effects are dominant and where most of the young massive stars dominating the current star formation rate (SFR) emit their photons. In their seminal work, Calzetti, Kinney & Storchi-Bergmann (1994) estimated a mean attenuation curve from a sample of 39 local UV-bright starburst using UV–optical spectra. Under the assumption of the same underlying stellar population for their galaxies, they were able to build average attenuation curves by comparing galaxies with high and low Balmer line ratios, i.e. by comparing dusty to dust-free galaxies (Calzetti 2001; Conroy 2013). Their measured attenuation curve is characterized by a greyer slope than both Milky Way (MW) and Large Magellanic Cloud (LMC) extinction curves and by the lack of the 2175 Å absorption feature.
Recently Battisti, Calzetti & Chary (2016, 2017) combined UV photometric data from GALEX with SDSS spectroscopy and near-IR (NIR) data from the UKIRT and 2MASS surveys for several thousands of local galaxies and implemented a method close to the one used by Calzetti et al. (1994). They derived an attenuation curve similar to the one of Calzetti et al. (2000) although slightly lower in the UV. Reddy et al. (2015) used a similar method at high redshift to estimate the attenuation curve of z ∼ 2 galaxies selected from the MOSDEF survey and found the shape to be similar to the Calzetti one in the UV and steeper at longer wavelength. More recently Reddy et al. (2016) presented the first measurements of the shape of the far-ultraviolet (FUV, 950 Å < λ < 1500 Å) dust attenuation curve at z ∼ 3 characterized by a lower attenuation in the FUV for a given E(B − V) than standard recipes (Calzetti et al. 2000; Reddy et al. 2015).
Important insights into the characterization of the dust attenuation curve in different galaxy samples have been also provided by SED-fitting models (Ilbert et al. 2009; Conroy 2010; Buat et al. 2010, 2011, 2012; Wild et al. 2011b; Kriek & Conroy 2013; Salmon et al. 2016). These codes optimized either to measure photometric redshifts or to derive physical parameters like SFR or stellar mass (M*) assume an attenuation law and most of them explore different scenarios and put constrains on them. The main advantage of these studies is that they allow us to consider very large samples of galaxies and/or to search for variations of the attenuation law as a function of different quantities. Variations of the UV ‘steepness’ of the dust attenuation curve have been observed for strong UV emitting galaxies (see e.g. Conroy 2010; Buat et al. 2011, 2012; Kriek & Conroy 2013), as a function of the position in the IRX–β plane and/or colour excess (e.g. Salmon et al. 2016). Variations of the shape of the dust attenuation curve in the UV–NIR range, for nearby galaxies, have been also measured as a function of either physical and structural parameter of the galaxies as the specific SFR (sSFR) and axis ratio or galaxy inclination and effective optical depth (see e.g. Wild et al. 2011b; Chevallard et al. 2013; Kriek & Conroy 2013, with more active galaxies having shallower dust curves for increasing optical depths). All these works go in the direction of confirming the non-universality of the dust attenuation law.
In this paper, we want to investigate the UV-to-NIR shape of the dust attenuation curve of IR selected and luminous sources at high redshift. We focus our attention on the sample of z ∼ 2 (ultra)luminous IR galaxies ((U)LIRGs) studied in Lo Faro et al. (2013) for which a wealth of photometric and spectroscopic data and full RT analyses are available. In order to characterize the shape of the dust attenuation curve, we implement several prescriptions for dust attenuation, both well known and new, within the context of state-of-the-art physically motivated spectral-synthesis techniques and compare the results with those derived from theoretical modelling. We take advantage here of the high flexibility offered by the cigale code (Code Investigating GALaxy Emission, Noll et al. 2009; Ciesla et al. 2014; Buat et al. 2014, 2015) which allows the user to implement his own prescriptions very easily. This work is performed within the context of the Herschel Extragalactic Legacy project (European Union FP7-SPACE HELP2) whose main goal is to assemble a new rich set of data and value-added parameters [e.g. stellar and dust mass, SFR, active galactic nucleus (AGN) contribution etc.], characterizing the physical properties of millions of galaxies in the distant Universe covering 1000 sq. deg. or 1/40th of the entire sky. It is conceived to bring together observations from many astronomical observatories to provide an integrated data set covering a wide range of wavelength from the radio to the X-ray.
The sample used in this work is part of the ‘pilot’ sample used within HELP to test and compare the different methods available to retrieve the physical properties of galaxies.
The paper is organized as follows. In Section 2, we present the reference sample of z ∼ 2 (U)LIRGs used for this analysis. In Section 3, we present the methods used in this work to investigate the shape of the dust attenuation curve of high-z IR bright sources. A detailed description of the physically motivated SED-fitting approach is given with particular attention to the assumed parametrization for the dust attenuation curve. In Section 4, we first present the general results from SED fitting related to the statistical analysis and parameter determination. We then present and discuss the attenuation curves estimated with cigale including the comparison with RT model results. In Section 5, we check the validity of our results for IR bright sources selected at lower redshifts. In Section 6, we explore the effects of the assumed parametrization for the dust attenuation curve on the derived SFR and M* of galaxies. Our summary and conclusions are then presented in Section 7.
2 SAMPLE SELECTION
As we are interested here in investigating the detailed shape of the attenuation curve of high-z (U)LIRGs, we focus on a small but well-defined set of Herschel sources selected to meet the following criteria: (1) full multiwavelength coverage from UV to sub-millimetres [sub-mm, including deep Herschel observations from both PACS (Poglitsch et al. 2010) and SPIRE (Griffin et al. 2010) instruments for the highest redshift bins]; (2) available spectroscopic redshifts; (3) galaxies powered by star formation (no AGN); and (4) available well-constrained RT-based solutions for these objects.
Our reference sample consists of 20 z ∼ 2 (U)LIRGs selected from the original sample described in Lo Faro et al. (2013). It includes the faintest 24 μm (S24 ∼ 0.15–0.45 mJy) sources observed, in GOODS-S, with the Spitzer Infrared Spectrograph (IRS) by Fadda et al. (2010) with redshift in the interval 1.75–2.4. This specific redshift range allows us to sample the major contributors to the cosmic infrared background at the most active epochs. The selected galaxies are massive systems forming stars actively although not in a starburst regime. We refer to Lo Faro et al. (2013) for a more detailed description of the sources. For the purpose of this work, the main characteristic of the sample is that it is crudely luminosity selected and that no other selection criterion has been applied.
All these galaxies benefit for high-quality spectroscopic redshift measured from their observed IRS spectra by Fadda et al. (2010). In addition to the ultradeep mid-IR spectra, these galaxies also benefit for a very rich suite of photometric data spanning a wide range in wavelengths from FUV to radio. These include FUV to mid-IR broad-band fluxes from the MUSIC catalogue by Santini et al. (2009), full deep Herschel imaging data from both SPIRE and PACS, covering the wavelength range between 70 and 500 μm and taken, respectively, from the Herschel Multitiered Extragalactic Survey (HerMES; Oliver et al. 2012) and the PACS Evolutionary Probe (PEP; Lutz et al. 2011) programs and radio Very Large Array data at 1.4 GHz. Typical noise levels in Herschel bands are ∼1 mJy for PACS 70–160 μ m and ∼6 mJy for SPIRE 250–500 μ m−1, including confusion. The collected photometry, from UV to sub-mm, spans a maximum of 19 wavebands for all the sources. All the objects classified as AGN-dominated, on the basis of several indicators such as broad and high ionization lines in optical spectra, lack of a 1.6 μ m−1 stellar bump in the SED, X-ray bright sources, low mid-IR 6.2 μ m−1 equivalent width and optical morphology, have been carefully removed from the sample by Lo Faro et al. (2013).
3 SED MODELLING WITH ENERGY BALANCE: GENERAL FEATURES AND ASSUMED CONFIGURATIONS
The analysis performed in this work makes use of state-of-the-art spectral-synthesis techniques which allow us to extract and interpret all the information contained in the observed integrated SEDs of galaxies in terms of their main physical properties and galaxy evolution in general (Walcher 2010). Particular attention is paid to a proper treatment of dust effects. We make use, here, of SED-fitting techniques based on energy balance (e.g. da Cunha, Charlot & Elbaz 2008; Noll et al. 2009) to study the shape of the dust attenuation curve of our high-z (U)LIRGs and then we compare their results to full RT computations.
The analysis is performed taking advantage of the high flexibility offered by the code cigale3 (developed in its first version with energy balance by Noll et al. 2009), to fit the SEDs of our high-z (U)LIRGs. The code allows one to derive the main physical properties of galaxies from the observed shape of the UV-to-sub-mm SED by modelling their dust-reprocessed IR emission consistently with the UV–optical stellar SED making use of physically motivated IR templates. Here, we are using an improved python version of the code (Boquien et al., in preparation). The modular structure of this new version of the code makes it very versatile for the use in different contexts and allows for higher flexibility in the SED modelling with the possibility for the user to implement his own prescriptions very easily. A description of this latest version of the code is given in Buat et al. (2015) and Ciesla et al. (2015). Here, we provide just a brief description of the code aimed at highlighting those features which have been particularly important to this analysis.
The cigale SED-fitting code is designed to provide, based on a Bayesian analysis, estimates of the mean values and uncertainties of the main physical parameters of the fitted galaxies as well as the details on the assumed dust attenuation, stellar population(s) and AGN fraction (when required), evaluated from the dispersion of the probability distribution function (PDF) computed for each parameter. The reliability of the estimated parameters is also checked by creating mock galaxy catalogues where flux densities are built from the best model obtained for each source (plus an instrumental noise added to each flux) and analysed using exactly the same method and modules used for the observed data. A description of this method will be given in Section 4.1.
In the following subsections, we briefly review the main ingredients of the code, including our own assumed configurations for each of its modules, with particular emphasis on the dust attenuation recipes considered in this work.
3.1 Stellar component
To build a galaxy SED, we first need to define the properties of the underlying stellar population in terms of assumed stellar population library, initial mass function (IMF) and SFH.
We adopt here the stellar population models of Bruzual & Charlot (2003) and a Salpeter (1955) IMF (which is the same IMF adopted in the RT model used here for comparison). Delay-τ SFHs, with varying e-folding time, are assumed to model the SFHs of our z ∼ 2 star-forming (SF) galaxies. These are consistent with our galaxies being selected from the main sequence (MS) by Fadda et al. (2010) and are nowadays the most currently used to explain the SEDs of high-redshift SF galaxies (e.g. Lee et al. 2010; Maraston et al. 2010; Wuyts et al. 2011; Pforr, Maraston & Tonini 2012). Their functional form closely resembles that one derived from galaxy chemical evolution models and the RT model used here for comparison (see Section 4.3).
The adopted parameters used, for the stellar component, in our fitting procedure are presented in Table 1.
| Parameter . | Symbol . | Range . |
|---|---|---|
| SFH (common to all the assumed dust configurations) | ||
| Age | age | 0.1, 0.5, 1., 1.2, 1.4, 1.8, 2., 2.2, 2.4, 2.8, 3., 3.2, 3.4, 3.8 Gyr |
| e-folding time-scale of delay-τ SFH | τ | 0.1, 0.5, 1., 1.5, 2., 2.5, 3., 7. Gyr |
| Dust emission | ||
| Mass fraction of PAH | qPAH | 1.12, 2.50, 3.19 |
| Minimum radiation field | Umin | 5., 10., 25.0 |
| Power-law slope dU/dM ∝ Uα | α | 2.0 |
| Dust fraction in PDRs | γ | 0.02 |
| Dust attenuation | ||
| Calzetti (2000): | ||
| Colour excess of stellar continuum light for young stars | E(B − V)young | 0.12, 0.25, 0.37, 0.5, 0.62, 0.74, 0.86, 0.98, 1.10, 1.43, 1.6, 1.98 |
| Reduction factor for the E(B-V) of the old stars compared to the young ones | fatt | 0.3, 0.5, 0.8, 1.0 |
| Modified Calzetti (Buat et al. 2011): | ||
| Colour excess of stellar continuum light for young stars | E(B − V)young | 0.12, 0.25, 0.37, 0.5, 0.62, 0.74, 0.86, 0.98, 1.10, 1.43, 1.6, 1.98 |
| Reduction factor for the E(B − V) of the old stars compared to the young ones | fatt | 0.3, 0.5, 0.8, 1.0 |
| Central wavelength of the UV bump in nm | λ0 | 217.5 |
| FWHM of the bump profile in nm | γ | 35.6 |
| Amplitude of the UV bump | Eb | 1.26 |
| Slope of the power law modifying the attenuation curve | δ | −0.13 |
| CF00 recipe (power-law attenuation curve): | ||
| V-band attenuation in the birth clouds (BCs) | |$A_{\rm V}^{\rm BC}$| | 0.5, 1., 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.8, 6.5, 8.0 |
| Power-law slope of dust attenuation in the BCs | δBC | −0.7 |
| |$A_{\rm V}^{\rm ISM}/ A_{\rm V}^{\rm BC}$| | fatt | 0.3, 0.5, 0.8, 1.0 |
| Power-law slope of dust attenuation in the ISM | δISM | −0.7 |
| magphys recipe (DBPL): | ||
| V-band attenuation in the birth clouds (BCs) | |$A_{\rm V}^{\rm BC}$| | 0.5, 1., 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.8, 6.5, 8.0 |
| Power-law slope of dust attenuation in the BCs | δBC | −1.3 |
| |$A_{\rm V}^{\rm ISM}/ A_{\rm V}^{\rm BC}$| | fatt | 0.3, 0.5, 0.8, 1.0 |
| Power-law slope of dust attenuation in the ISM | δISM | −0.7 |
| Double Power-law free (DBPL-free): | ||
| V-band attenuation in the birth clouds (BCs) | |$A_{\rm V}^{\rm BC}$| | 0.5, 1., 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.8, 6.5, 8.0 |
| Power-law slope of dust attenuation in the BCs | δBC | −1.3, −0.7, −0.5 |
| |$A_{\rm V}^{\rm ISM}/ A_{\rm V}^{\rm BC}$| | fatt | 0.3, 0.5, 0.8, 1.0 |
| Power-law slope of dust attenuation in the ISM | δISM | −0.7, −0.5, −0.3, −0.1 |
| Parameter . | Symbol . | Range . |
|---|---|---|
| SFH (common to all the assumed dust configurations) | ||
| Age | age | 0.1, 0.5, 1., 1.2, 1.4, 1.8, 2., 2.2, 2.4, 2.8, 3., 3.2, 3.4, 3.8 Gyr |
| e-folding time-scale of delay-τ SFH | τ | 0.1, 0.5, 1., 1.5, 2., 2.5, 3., 7. Gyr |
| Dust emission | ||
| Mass fraction of PAH | qPAH | 1.12, 2.50, 3.19 |
| Minimum radiation field | Umin | 5., 10., 25.0 |
| Power-law slope dU/dM ∝ Uα | α | 2.0 |
| Dust fraction in PDRs | γ | 0.02 |
| Dust attenuation | ||
| Calzetti (2000): | ||
| Colour excess of stellar continuum light for young stars | E(B − V)young | 0.12, 0.25, 0.37, 0.5, 0.62, 0.74, 0.86, 0.98, 1.10, 1.43, 1.6, 1.98 |
| Reduction factor for the E(B-V) of the old stars compared to the young ones | fatt | 0.3, 0.5, 0.8, 1.0 |
| Modified Calzetti (Buat et al. 2011): | ||
| Colour excess of stellar continuum light for young stars | E(B − V)young | 0.12, 0.25, 0.37, 0.5, 0.62, 0.74, 0.86, 0.98, 1.10, 1.43, 1.6, 1.98 |
| Reduction factor for the E(B − V) of the old stars compared to the young ones | fatt | 0.3, 0.5, 0.8, 1.0 |
| Central wavelength of the UV bump in nm | λ0 | 217.5 |
| FWHM of the bump profile in nm | γ | 35.6 |
| Amplitude of the UV bump | Eb | 1.26 |
| Slope of the power law modifying the attenuation curve | δ | −0.13 |
| CF00 recipe (power-law attenuation curve): | ||
| V-band attenuation in the birth clouds (BCs) | |$A_{\rm V}^{\rm BC}$| | 0.5, 1., 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.8, 6.5, 8.0 |
| Power-law slope of dust attenuation in the BCs | δBC | −0.7 |
| |$A_{\rm V}^{\rm ISM}/ A_{\rm V}^{\rm BC}$| | fatt | 0.3, 0.5, 0.8, 1.0 |
| Power-law slope of dust attenuation in the ISM | δISM | −0.7 |
| magphys recipe (DBPL): | ||
| V-band attenuation in the birth clouds (BCs) | |$A_{\rm V}^{\rm BC}$| | 0.5, 1., 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.8, 6.5, 8.0 |
| Power-law slope of dust attenuation in the BCs | δBC | −1.3 |
| |$A_{\rm V}^{\rm ISM}/ A_{\rm V}^{\rm BC}$| | fatt | 0.3, 0.5, 0.8, 1.0 |
| Power-law slope of dust attenuation in the ISM | δISM | −0.7 |
| Double Power-law free (DBPL-free): | ||
| V-band attenuation in the birth clouds (BCs) | |$A_{\rm V}^{\rm BC}$| | 0.5, 1., 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.8, 6.5, 8.0 |
| Power-law slope of dust attenuation in the BCs | δBC | −1.3, −0.7, −0.5 |
| |$A_{\rm V}^{\rm ISM}/ A_{\rm V}^{\rm BC}$| | fatt | 0.3, 0.5, 0.8, 1.0 |
| Power-law slope of dust attenuation in the ISM | δISM | −0.7, −0.5, −0.3, −0.1 |
| Parameter . | Symbol . | Range . |
|---|---|---|
| SFH (common to all the assumed dust configurations) | ||
| Age | age | 0.1, 0.5, 1., 1.2, 1.4, 1.8, 2., 2.2, 2.4, 2.8, 3., 3.2, 3.4, 3.8 Gyr |
| e-folding time-scale of delay-τ SFH | τ | 0.1, 0.5, 1., 1.5, 2., 2.5, 3., 7. Gyr |
| Dust emission | ||
| Mass fraction of PAH | qPAH | 1.12, 2.50, 3.19 |
| Minimum radiation field | Umin | 5., 10., 25.0 |
| Power-law slope dU/dM ∝ Uα | α | 2.0 |
| Dust fraction in PDRs | γ | 0.02 |
| Dust attenuation | ||
| Calzetti (2000): | ||
| Colour excess of stellar continuum light for young stars | E(B − V)young | 0.12, 0.25, 0.37, 0.5, 0.62, 0.74, 0.86, 0.98, 1.10, 1.43, 1.6, 1.98 |
| Reduction factor for the E(B-V) of the old stars compared to the young ones | fatt | 0.3, 0.5, 0.8, 1.0 |
| Modified Calzetti (Buat et al. 2011): | ||
| Colour excess of stellar continuum light for young stars | E(B − V)young | 0.12, 0.25, 0.37, 0.5, 0.62, 0.74, 0.86, 0.98, 1.10, 1.43, 1.6, 1.98 |
| Reduction factor for the E(B − V) of the old stars compared to the young ones | fatt | 0.3, 0.5, 0.8, 1.0 |
| Central wavelength of the UV bump in nm | λ0 | 217.5 |
| FWHM of the bump profile in nm | γ | 35.6 |
| Amplitude of the UV bump | Eb | 1.26 |
| Slope of the power law modifying the attenuation curve | δ | −0.13 |
| CF00 recipe (power-law attenuation curve): | ||
| V-band attenuation in the birth clouds (BCs) | |$A_{\rm V}^{\rm BC}$| | 0.5, 1., 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.8, 6.5, 8.0 |
| Power-law slope of dust attenuation in the BCs | δBC | −0.7 |
| |$A_{\rm V}^{\rm ISM}/ A_{\rm V}^{\rm BC}$| | fatt | 0.3, 0.5, 0.8, 1.0 |
| Power-law slope of dust attenuation in the ISM | δISM | −0.7 |
| magphys recipe (DBPL): | ||
| V-band attenuation in the birth clouds (BCs) | |$A_{\rm V}^{\rm BC}$| | 0.5, 1., 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.8, 6.5, 8.0 |
| Power-law slope of dust attenuation in the BCs | δBC | −1.3 |
| |$A_{\rm V}^{\rm ISM}/ A_{\rm V}^{\rm BC}$| | fatt | 0.3, 0.5, 0.8, 1.0 |
| Power-law slope of dust attenuation in the ISM | δISM | −0.7 |
| Double Power-law free (DBPL-free): | ||
| V-band attenuation in the birth clouds (BCs) | |$A_{\rm V}^{\rm BC}$| | 0.5, 1., 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.8, 6.5, 8.0 |
| Power-law slope of dust attenuation in the BCs | δBC | −1.3, −0.7, −0.5 |
| |$A_{\rm V}^{\rm ISM}/ A_{\rm V}^{\rm BC}$| | fatt | 0.3, 0.5, 0.8, 1.0 |
| Power-law slope of dust attenuation in the ISM | δISM | −0.7, −0.5, −0.3, −0.1 |
| Parameter . | Symbol . | Range . |
|---|---|---|
| SFH (common to all the assumed dust configurations) | ||
| Age | age | 0.1, 0.5, 1., 1.2, 1.4, 1.8, 2., 2.2, 2.4, 2.8, 3., 3.2, 3.4, 3.8 Gyr |
| e-folding time-scale of delay-τ SFH | τ | 0.1, 0.5, 1., 1.5, 2., 2.5, 3., 7. Gyr |
| Dust emission | ||
| Mass fraction of PAH | qPAH | 1.12, 2.50, 3.19 |
| Minimum radiation field | Umin | 5., 10., 25.0 |
| Power-law slope dU/dM ∝ Uα | α | 2.0 |
| Dust fraction in PDRs | γ | 0.02 |
| Dust attenuation | ||
| Calzetti (2000): | ||
| Colour excess of stellar continuum light for young stars | E(B − V)young | 0.12, 0.25, 0.37, 0.5, 0.62, 0.74, 0.86, 0.98, 1.10, 1.43, 1.6, 1.98 |
| Reduction factor for the E(B-V) of the old stars compared to the young ones | fatt | 0.3, 0.5, 0.8, 1.0 |
| Modified Calzetti (Buat et al. 2011): | ||
| Colour excess of stellar continuum light for young stars | E(B − V)young | 0.12, 0.25, 0.37, 0.5, 0.62, 0.74, 0.86, 0.98, 1.10, 1.43, 1.6, 1.98 |
| Reduction factor for the E(B − V) of the old stars compared to the young ones | fatt | 0.3, 0.5, 0.8, 1.0 |
| Central wavelength of the UV bump in nm | λ0 | 217.5 |
| FWHM of the bump profile in nm | γ | 35.6 |
| Amplitude of the UV bump | Eb | 1.26 |
| Slope of the power law modifying the attenuation curve | δ | −0.13 |
| CF00 recipe (power-law attenuation curve): | ||
| V-band attenuation in the birth clouds (BCs) | |$A_{\rm V}^{\rm BC}$| | 0.5, 1., 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.8, 6.5, 8.0 |
| Power-law slope of dust attenuation in the BCs | δBC | −0.7 |
| |$A_{\rm V}^{\rm ISM}/ A_{\rm V}^{\rm BC}$| | fatt | 0.3, 0.5, 0.8, 1.0 |
| Power-law slope of dust attenuation in the ISM | δISM | −0.7 |
| magphys recipe (DBPL): | ||
| V-band attenuation in the birth clouds (BCs) | |$A_{\rm V}^{\rm BC}$| | 0.5, 1., 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.8, 6.5, 8.0 |
| Power-law slope of dust attenuation in the BCs | δBC | −1.3 |
| |$A_{\rm V}^{\rm ISM}/ A_{\rm V}^{\rm BC}$| | fatt | 0.3, 0.5, 0.8, 1.0 |
| Power-law slope of dust attenuation in the ISM | δISM | −0.7 |
| Double Power-law free (DBPL-free): | ||
| V-band attenuation in the birth clouds (BCs) | |$A_{\rm V}^{\rm BC}$| | 0.5, 1., 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.8, 6.5, 8.0 |
| Power-law slope of dust attenuation in the BCs | δBC | −1.3, −0.7, −0.5 |
| |$A_{\rm V}^{\rm ISM}/ A_{\rm V}^{\rm BC}$| | fatt | 0.3, 0.5, 0.8, 1.0 |
| Power-law slope of dust attenuation in the ISM | δISM | −0.7, −0.5, −0.3, −0.1 |
3.2 Dust component: emission
The energy absorbed by dust in the UV–optical is re-emitted at longer wavelengths in the mid-IR to sub-mm range.
In cigale, the IR emission of SF galaxies can be estimated by fitting their mid-IR- to sub-mm SEDs with either multiparameter IR templates (e.g. Draine & Li 2007) or with one-parameter templates (e.g. Dale & Helou 2002) particularly suited when a good sampling of the IR SED is not available.
In this work, the IR emission of our galaxies is modelled by fitting the dust models of Draine & Li (2007), whose validity in reproducing the far-IR properties of Herschel detected high-z MS galaxies has been confirmed by the study of Magdis et al. (2012). In these models, the interstellar dust is described as a mixture of carbonaceous and amorphous silicate grains, whose size distributions are chosen to reproduce the observed extinction law in the MW, the LMC and the Small Magellanic Cloud (SMC) bar region. The properties of these grains are parametrized by the polycyclic aromatic hydrocarbon (PAH) index, qPAH, defined as the fraction of the dust mass in the form of PAH grains. Draine & Li (2007) assume that the majority of the dust is located in the diffuse interstellar medium (ISM), which is heated by a radiation field with a constant intensity Umin. A smaller fraction γ of the dust, representing the dust enshrouded in photodissociation regions (PDRs), is exposed to starlight with intensities ranging from Umin to Umax characterized by power-law distribution of the form, dM/dU ∝ U−α. Draine et al. (2007) showed that the overall fit of the SEDs of local galaxies is insensitive to the adopted dust model (MW, LMC and SMC) and the precise values of α and Umax. Fixed values of α = 2 and Umax = 106 can successfully reproduce the SEDs of the SINGS galaxy sample. The same values have been used by Magdis et al. (2012) to reproduce the IR properties of a sample of high-z MS galaxies. Following Magdis et al. (2012) we have considered, in this work, MW dust models with qPAH ranging from 1.12 per cent to 3.19 per cent, which are the typical values for high-z normal SF galaxies, and Umin varying in the interval 5–25. The value of the fraction γ of dust enclosed in the PDRs has been fixed to the mean value obtained by Magdis et al. (2012) for the observed average SEDs of MS galaxies at redshift 1 and 2 derived by stacking analysis (i.e. γ = 0.02).
The final adopted configuration for the Draine & Li (2007) models is shown in Table 1.
3.3 Prescriptions for dust attenuation
When modelling the SEDs of galaxies we have seen that the effect of dust depends on the combination of both the optical and physical properties of dust and the relative geometrical distribution of stars and dust. In cigale, all these complex effects can be accounted for by assuming flexible attenuation curves with varying shape according to the specific case under analysis. In order to account for the large variety of objects and possible geometrical configurations, we have implemented in cigale a new recipe for dust attenuation, called hereafter DouBle-Power law model (DBPL-free), where the UV-to-NIR shape of the curve is treated as a free parameter, and we have compared this recipe with several well-known standard prescriptions for dust attenuation. All the different recipes for the dust attenuation considered in this work are here below described, starting from the standard ones already included in cigale and ending with the newly implemented DBPL-free model.
3.3.1 Calzetti-like recipes
The Calzetti et al. (2000) attenuation law, initially calibrated on a sample of 39 nearby UV-bright starburst galaxies (Calzetti et al. 1994), is nowadays the most currently used also at high redshift. It is characterized by a greyer slope than the MW and LMC extinction laws accounting for the effects of geometry and mixing compared to simple extinction.
In complement to the exact Calzetti recipe, we implement in cigale the specific recipe described in Buat et al. (2011, 2012). The authors, by analysing a well-defined UV selected and Herschel detected sample of strong UV emitting galaxies at z >1, found evidence for a steeper UV slope than Calzetti and for a 2175 Å bump. Following Buat et al. (2011), we fix the slope of the power-law modifying the Calzetti law, δ, to −0.13. The parameters of the bump, namely the peak amplitude above the continuum, full width at half-maximum (FWHM) and central wavelength of the bump, (Eb, γ and λ0), are fixed to 1.26, 35.6 nm and 2175 Å, respectively. Note that we do not study the presence or not of a bump in this work and that we introduce the Buat et al. (2011) recipe to check the impact of a law steeper than the Calzetti one but based on the same parametrization.
In cigale, the same attenuation law is assumed for both young4 and old stars but a reduction factor of the visual attenuation (expressed in magnitude), |$f_{\rm att}=A_{{\rm V}}^{\rm ISM}/A_{{\rm V}}^{\rm BC}$|, is applied to the old stellar population in order to account for the age-dependent attenuation of stars within a galaxy (Calzetti et al. 1994, 2000; Charlot & Fall 2000; Panuzzo et al. 2007; Buat et al. 2011, 2012).
Current studies on the dust properties of high-redshift galaxies have led to contrasting results concerning the fatt parameter. Some authors have confirmed the validity of local Universe, Calzetti et al. (2000) prescription for a higher colour excess to be applied to the gas recombination lines than to the stellar continuum, even at high-z (e.g. Förster Schreiber et al. 2009; Whitaker et al. 2014; Yoshikawa et al. 2010). On the other hand, a comparable attenuation for the young (emission lines) and old (stellar continuum) component has been estimated in UV-selected z ∼ 2 galaxies by other authors (e.g. Erb et al. 2006; Reddy et al. 2010). Similar results have been recently found by Puglisi et al. (2016) for a sample of IR selected and luminous sources at z ∼ 1 by comparing the dust attenuation of continuum stellar emission and nebular emission from Herschel and H α fluxes. A decrease of the amount of extra attenuation towards SF regions with respect to diffuse dust as a function of increasing sSFR has been observed by Wild et al. (2011b) and successively by Price et al. (2014) for both local and higher redshift galaxies. This has been interpreted by the authors as a direct evidence of the two-component dust model (e.g. Calzetti et al. 1994; Charlot & Fall 2000; Granato et al. 2000). In fact, in galaxies with higher sSFRs, the continuum light is mostly contributed by young massive stars in the birth clouds, so both the continuum and emission lines may be attenuated by both dust components, thus bringing to higher fatt on average.
To account for the different observational evidences in our analysis, this attenuation factor is treated as a free parameter and five different values between 0.3 and 1.0 are considered. These are listed in Table 1.
3.3.2 Double power-law attenuation recipes
Starting from the formalism of CF00, we have developed in cigale, a new module called ‘dustatt_2powerlaws’ which allows us to combine different slopes for the attenuation curve relative to the ISM and BC components. In this way, we are able to properly account for an age-dependent attenuation where not only the total amount of dust attenuation changes as a function of the stellar age but also the way the stellar light is extinguished, as originally introduced by CF00. To be consistent with the formalism adopted in cigale for the Calzetti-like recipes, we use the parameter fatt (|$A_{\rm V}^{\rm ISM}/A_{\rm V}^{\rm BC}$|) instead of μ (|$\tau _{\rm V}^{\rm ISM}$|/(|$\tau _{\rm V}^{\rm BC} + \tau _{\rm V}^{\rm ISM}$|)). The values of fatt reported in Table 1 are equivalent to values of the μ parameter in the interval 0.2–0.5 (being μ = fatt/(1 + fatt)). We also use the total V-band attenuation experienced by young stars within the MCs, |$A_{\rm V}^{\rm BC}=1.086 \tau _{\rm V}$| in place of τV. The latter comes from the fact that, in CF00 formalism, |$L_{\lambda }/L_{\lambda }^{0} \equiv \exp (-\tau _{\lambda })$| and |$A_{\lambda } \equiv -2.5 \log (L_{\lambda }/L_{\lambda }^{0})$|.
We implement through our dustatt_2powerlaws module three different configurations here below itemized:
Standard CF00: here the slope of the attenuation curve is assumed, for simplicity, to be the same for the BC and ISM component and it is fixed to the canonical value of δISM = δBC = −0.7. This value allows the authors to successfully reproduce the observed mean relation between IRX and UV-spectral slope of nearby starburst galaxies (see e.g. Calzetti et al. 1994, 2000; Charlot & Fall 2000; Johnson et al. 2007).
magphys-like: we consider here the recipe used in the semi-empirical SED-fitting code, magphys (Multi-wavelength Analysis of Galaxy Physical Properties), of da Cunha et al. (2008), hereafter referred as ‘magphys-like’ configuration.
In this case, the same slope as in CF00 is adopted for the ISM component (δISM = −0.7) while a steeper slope, δBC = −1.3, is assumed for the dense birth clouds following the original recipe first proposed by Charlot & Fall.
DBPL-free: this represents our reference recipe in this work. Its novelty is the possibility to treat both the slopes of the ISM and BC dust attenuation curves as free parameters. Our configuration includes both steeper and greyer slopes (compared to CF00 classic recipe) for δBC and greyer values for δISM. More specifically, the BC and ISM slopes can assumed the values (−1.3, −0.7, −0.5) and (−0.7, −0.5, −0.3, −0.1), respectively.
For what concerns the BC component, despite the wide use of −1.3 as reference slope for the extinction curve of the single BCs (e.g. Charlot & Fall 2000; da Cunha et al. 2008; Wild et al. 2011a,b; Chevallard et al. 2013), evidences in favour of a greyer slope are also shown. For example, by studying the extinction and reddening of LMC H ii regions, Caplan & Deharveng (1986) found clear evidence for a total-to-selective dust extinction ratio |$R_{\lambda _{\rm H_{\beta }}} = 5.1$| corresponding to a slope for the extinction curve of LMC H ii regions of ∼−0.74 which is very close to the value adopted by CF00. A clumpy dust geometry was in this case invoked to explain the observed slope. Liu et al. (2013) have also shown that at the scale of local H ii regions (M83), greyer extinction curves coupled with more complex geometries are expected, while when averaged over large scales (>100–200 pc), the extinction becomes consistent with a ‘dust screen’ geometry. Hidden emission from young stars embedded in dense MCs can also be responsible for greyer attenuation curves, on average, in particular when dealing with ULIRGs characterized by SFR higher than ∼200 M⊙ yr (Flores et al. 2004).
The shallowness of the attenuation curve at large optical depths for the ISM component is a clear signature of mixed distributions of stars and dust (e.g. Charlot & Fall 2000; Gordon et al. 2000; Calzetti 2001; Pierini et al. 2004; Chevallard et al. 2013). The classical value of δISM = −0.7 adopted in CF00 model was specifically constrained to reproduce Calzetti et al. (2000) recipe. We have already seen in previous sections that deviations from the Calzetti relation are expected for both nearby and high-z IR luminous galaxies which lead us to explore a wider range of slopes including greyer values than −0.7.
All the different recipes for dust attenuation considered here and discussed in previous sections are shown in Fig. 1. To highlight the main differences between the two complementary formalisms presented here for the dust attenuation curve, namely the modified Calzetti and the DBPL-free one, we also plot in the figure the curves corresponding to the modified-Calzetti recipes (as black dashed lines) used in Salmon et al. (2016) to study the UV shape of the attenuation curve of CANDELS galaxies at redshift 1.5–3. Although both formalisms appear to be able to cover the same range of slopes in the UV they significantly differ at longer wavelengths where the DBPL-free recipes (colour-coded lines) provide greyer slopes than modified-Calzetti ones..

All the assumed wavelength-dependent shapes for the dust attenuation curves considered in our analysis are shown in this figure. As red long-dashed line, the Calzetti et al. (2000) attenuation law, as salmon solid line, the modified Calzetti curve based on the formalism defined in Buat et al. (2011), then colour coded from blue to violet and from top to bottom the power-law slopes assumed for the CF00-based recipe are also shown. Note that here we are showing the single power-law dependence assumed for the two, BC and ISM, components and not the combined curve obtained from their combination. The latter, in fact, depends on the physical properties of the galaxy and the relative proportion of old and young stars. Three different slopes have been assumed for the BC component (−1.3, −0.7, −0.5) and four for the ISM (−0.7, −0.5, −0.3, −0.1). The large set of different shapes for the attenuation curve considered here includes both steeper and greyer slope than the original Calzetti recipe both at short and long (NIR) wavelengths. All the recipes included in this analysis and described by the formalism specified in Section 3.3 are then compared with the modified-Calzetti recipes (black dashed lines) used in Salmon et al. (2016) to study the UV shape of the attenuation curve of CANDELS galaxies at redshift 1.5–3 and their dependence on the colour excess E(B − V). The comparison shows that we cover the same range of dust attenuation slopes in the UV, while the major differences are in the NIR, whose investigation is the main objective of this work.
Our DBPL-free recipe allows us to explore a large set of different shapes for the attenuation law including both steeper and greyer slopes than Calzetti et al. (2000) in the UV–optical and, more interestingly, greyer slopes in the NIR too.
Table 1 finally summarizes all the assumed input parameter configurations, for both the stellar and dust components, used in the phenomenological modelling to investigate the physical properties of our IR-selected and luminous galaxies at high-z. The choice of a delay-τ SFH, characterized by only two free parameters, together with an assumed configuration for the dust emission where most of the parameters have been fixed and with dust attenuation recipes where maximum three parameters (as in the DBPL-free) are treated as free, bring to a total number of free parameters ranging between 5 and 7. The number of photometric data points is always larger than 18.
4 FITTING THE SPECTRAL ENERGY DISTRIBUTIONS: DUST ATTENUATION LAWS
We discuss in this section the results obtained by fitting the observed SEDs of our high-z (U)LIRGs with cigale. The code is primarily run under our reference configuration (DBPL-free) and then for each of the parameter configurations listed in Table 1 for comparison. The fit is performed by comparing the model SED integrated over a specific set of filters with the observed flux densities provided by the input catalogue. The best model is obtained by minimizing the reduced χ2(hereafter |$\chi ^{2}_{\nu }$|) associated with each model and set of parameters. The input parameters as well as additional output parameters are estimated by building the PDF and by taking the mean and standard deviation of the PDF (see Noll et al. 2009, for a more detailed discussion about the methods used in cigale). The typical output of cigale includes, in addition to the parameters related to the dust attenuation curves, few other parameters such as SFR, M*, galaxy age and total dust attenuation.
Before discussing the attenuation curves presented in Section 4.2, we check the validity and accuracy of our estimates, also in terms of parameter degeneracy, through the mock analysis described below.
4.1 Mock analysis and parameter determination
The mock analysis is performed by generating with cigale catalogues of artificial sources for which the physical parameters are known by definition (details can be found in Buat et al. 2012, 2014; Ciesla et al. 2015). To build the mock catalogue, we use the best-fitting model of each of the studied objects previously obtained through our SED-fitting procedure. The flux densities of the mock SEDs are computed by randomly picking a flux value from the normal distribution generated using as mean value the best model flux and as standard deviation the photometric error. cigale is then run on this artificial catalogue in order to compare the exact values of the physical parameters corresponding to the artificial SEDs to the parameters estimated by the code with the PDF of each parameter.
The results are summarized in Fig. 2. The true value of the output parameter (artificial SED) on the x-axis is compared to the same parameter estimated by the code on the y-axis. The 1–1 correlation line is shown as black long dashed–dotted line in each panel. From top left to bottom right, the results for the SFR, stellar mass, total IR luminosity, age, e-folding time-scale of delay-τ SFH, BC-to-ISM attenuation factor fatt and the slope of BC and ISM attenuation curves, are shown. The latter three quantities concern only our reference recipe, the DBPL-free. In each panel, the results from the mock analysis performed under the DBPL-free configuration (solid green line) are compared to those obtained with the standard recipes listed in Table 1. While the extensive physical quantities such as recent SFR, M★, LIR seem to be quite well constrained by our analysis, as long as the information provided by the full FUV to sub-mm SED is available (see e.g. Buat et al. 2014; Boquien, Buat & Perret 2014), the characteristic time-scale of the assumed SFH appears unconstrained. Constraining the detailed SFH of a galaxy from the observed SED is, indeed, a well-known critical issue of spectral-synthesis models (see e.g. Papovich, Dickinson & Ferguson 2001; Daddi et al. 2004; Maraston et al. 2006; Santini et al. 2009; Wuyts et al. 2011; Pforr, Maraston & Tonini 2012; Michałowski et al. 2012; Boquien et al. 2015; Ciesla et al. 2015).

Comparison between the true value of the output parameters provided by our best-fitting model (artificial SEDs), on the x-axis, and the same parameter estimated by the code on the y-axis. The 1–1 correlation line is shown as black long dashed-dotted line in each panel. From top left to bottom right, the results for the SFR, stellar mass, total IR luminosity, age, e-folding time-scale of delay-τ SFH, total FUV-attenuation, BC-to-ISM attenuation factor fatt (definition in Section 3.3) and the slope of BC and ISM attenuation curves, are shown colour coded according to the five different dust attenuation recipes listed in Table 1. The regression lines for each assumed configuration are also plotted as coloured solid lines.
As will be discussed in detail in Section 4.2, one interesting aspect emerging from this mock analysis is that, although we seem to be able to constrain quite well the total amount of attenuation (AFUV – central right panel, FUV corresponding to the FUV GALEX filter in the rest frame of the galaxy) suffered by these galaxies, the exact shape of the attenuation curve appears to be more complex to constrain. This is related to the fact that the energy budget between the radiation absorbed in the UV and that one re-emitted in the IR does not depend significantly on the exact shape of the attenuation curve but rather on the total amount of attenuation extinguishing the UV–optical starlight.
For what concerns the shape of the dust attenuation curve under the DBPL-free configuration it is clear, from our mock analysis, that the slope of the power law relative to the birth-cloud component cannot be constrained, at least with the information available on these objects. Conversely, the slope of the attenuation curve relative to the diffuse component (Fig. 2, bottom right) appears to be well constrained with a Pearson's correlation coefficient for linear regression, between the true and estimated values, ∼0.80.
Another dust attenuation parameter which seems difficult to constrain from our analysis is the reduction factor for the attenuation of the old stellar population with respect to the younger one. We have performed several tests with cigale by considering this parameter both free and fixed but no relevant differences or dependencies in the results have been observed. This specific parameter is known to be usually unconstrained by broad-band photometry SED-fitting procedures (see e.g. Noll et al. 2009; Buat et al. 2011, 2012). Following Buat et al. (2012), a fixed value of 0.5 is adopted.
In the mock analysis described above the catalogue of artificial sources is created and analysed, for each configuration, under the same assumptions for the input parameters. It does not consider cross-checks among different assumed parameter configurations. It can be interesting at this point to check the robustness of our parameter estimation also against variations of the assumed attenuation curve. An interesting comparison in this sense is the one involving the two ‘extreme’ end recipes for the dust attenuation, namely our DBPL-free on the one side, and the Calzetti et al. (2000), on the other.
In addition, we thus consider the mock catalogue generated with the Calzetti (2000) recipe and fit its artificial fluxes with the DBPL-free configuration. The results relative to SFR, M★, LIR and galaxy age are shown, from top to bottom, in Fig. 3. The total IR luminosity appears, again, well constrained. The SFRs predicted by assuming a power-law-free slope attenuation curve are systematically lower than the true values of Calzetti et al. (2000) by a factor ∼ 0.2 dex. These are consistent with the higher galaxy ages obtained, on average, with the DBPL prescription. Discrepancies in the predicted stellar masses are also observed with the DBPL-free configuration providing, on average, larger stellar masses than Calzetti. The impact of the different assumed dust attenuation prescriptions on the derived SFR and M★ of IR-selected galaxies and their consequences in a cosmological context will be discuss in detail in Section 6.

Comparison between the predictions of the code under the DBPL-free configuration (y-axis) and the true values obtained by assuming the Calzetti et al. (2000) recipe (x-axis). From top to bottom, the results relative to the SFR, M★, LIR and age are shown. The 1–1 correlation line is shown as black long dashed-dotted line in each panel.
We discuss now the results of the mock analysis concerning the amount of dust attenuation in the UV and NIR bands which are contributed by different stellar populations.
We have already seen that as long as the energy budget in the galaxy is preserved, the total amount of attenuation suffered by the galaxy is always well constrained. This is shown by Fig. 4 where the results from our mock analysis concerning the estimates of the total dust attenuation in the FUV and NIR band are plotted colour coded as a function of the different prescriptions considered. The case where the catalogue of artificial sources is created and analysed under the same assumptions for the input parameters is shown in the top panels of the figure.

The results from our mock analysis concerning the estimates of the total dust attenuation in the FUV and NIR band are plotted colour coded as a function of the different prescriptions considered. In the bottom panel, we compare the true values corresponding to the assumption of a Calzetti dust attenuation curve to the mock analysis performed by assuming a DBPL-free model.
In the bottom panels we compare, instead, the true values relative to the assumption of a Calzetti dust attenuation curve with the mock analysis performed by assuming a DBPL-free model. In this case, we observe that while the total amount of attenuation in the FUV remains well constrained, independently from the specific dust attenuation law assumed, the amount of attenuation predicted by the DBPL-free model at longer wavelengths appears to be larger, on average, than the true value given by Calzetti. This is directly linked to the intrinsic shape of the dust attenuation curve adopted, particularly at longer wavelengths. In fact, as previously shown in Fig. 1, whenever the free power-law slope equals the slope of CF00 model, (δISM = −0.7), the UV–optical shape of Calzetti is well retrieved and so the AFUV. However, the same prescription tends to provide greyer slopes than Calzetti at longer wavelengths thus bringing to a larger attenuation in the NIR.
4.2 The dust attenuation curve of z ∼ 2 (U)LIRGs estimated with cigale
Fig. 5 shows, for each of the z ∼ 2 (U)LIRGs in our sample, the normalized attenuation curve estimated with cigale under the assumption of our DBPL-free configuration (solid green line). The slope of the ISM component, as derived from the PDF analysis performed with cigale, is also highlighted in each panel. The value of the slope of the BC component is omitted here because, as we have seen in Fig. 2, it is not constrained by our broad-band analysis. The DBPL-free attenuation curves are then compared, in the same figure, to those derived with standard recipes, namely, magphys-like in blue, Calzetti et al. (2000) in red and Buat et al. (2011) in grey.6
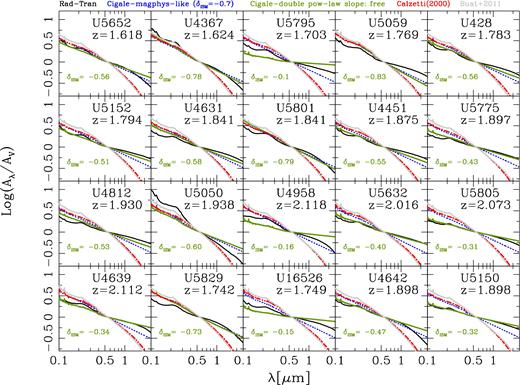
Attenuation Curves of z ∼ 2 (U)LIRGs. The attenuation curves are colour coded as a function of the different adopted prescriptions for the dust attenuation, as reported on the top of the figure. See the text for details.
4.3 Comparison with RT-derived attenuation curves
We present in this section, the attenuation curves based on RT and used for the purpose of comparison with the results found in this work.
In previous works (Lo Faro et al. 2013, 2015), we analysed the stellar masses and SFRs of diverse galaxy samples, among which the same z ∼ 2 (U)LIRGs considered in this work. The analysis was performed by fitting the observed UV to sub-mm and radio SEDs of galaxies with the spectral synthesis and RT code grasil (Silva et al. 1998, 2011; Vega et al. 2008). It is therefore interesting to compare and discuss the attenuation curves obtained with independent and very different modelling for the same data. In RT models, in fact, the attenuation curve is not an input parameter as in physically motivated SED-fitting procedures, but it results from the complex interplay among SFH, dust properties and star-dust geometry, as detailed below.
We provide here a short summary of the main features and techniques used in these previous works, and defer to the original papers for details on grasil, and in particular to the Lo Faro et al. papers for the specific approach and details on the model parameters used for the fits.
grasil is a spectral-synthesis code for the SED of galaxies which computes the RT of the stellar radiation through a two-phase dusty medium. A dense phase, representing MCs associated with newly born stars, is distributed within a diffuse medium, the cirrus, associated with more evolved stars. The clumping of both young stars and dust within the diffuse medium gives rise to an age-dependent dust attenuation where younger stars are more extinguished than older stars. A widespread in the shapes of the output attenuation curves can be obtained, including the Calzetti (2000) curve, depending on the input SFHs and age-dependent star-dust distribution (e.g. Granato et al. 2000; Panuzzo et al. 2007; Fontanot et al. 2009).
The input SFHs used in Lo Faro et al., were computed with a standard chemical evolution code and Salpeter IMF and have shapes consistent with the delay-τ models. The best fits are characterized by very short τ for half of the sample, and by more steadily evolving SFHs for the other half. No burst was required for these high-z (U)LIRGs (consistently with their MS nature). The best fit was searched within a large model library including ∼106 models, each one corresponding to a different combination of parameters among which the geometrical scalelengths, the fraction of gas in MCs with respect to the diffuse component, the typical disruption time-scale of giant MCs and galaxy age. A description of these model parameters and their range of values can be found in table 1 of Lo Faro et al. (2013). We stress that we rely here on the assumptions and specific parameter configurations adopted in Lo Faro et al. (2013, 2015). We do not discuss here the effects of different geometries or dust parameters on the RT-derived dust attenuation curves. A discussion about the implications of a disc versus spheroidal geometry on the observed SED of our sources is already partly dealt with in Lo Faro et al. (2015) and will be treated in more detail in a future work.
Fig. 6 shows the attenuation curves (solid black lines) obtained with grasil for the sample of z ∼ 2 (U)LIRGs. The curve obtained by averaging over the entire sample is also shown as solid green thick line. Compared to the Calzetti et al. (2000) attenuation law (red long-dashed line), they appear on average greyer over the entire wavelength range. The same RT-based attenuation curves are compared to those estimated with cigale in Fig. 5.

Effective attenuation curves (solid black lines) obtained with grasil for the reference sample of (U)LIRGs at z ∼ 2 (Lo Faro, 2012). The curve obtained averaging over the entire sample is also shown as solid green thick line. Compared to the classical Calzetti et al. (2000) attenuation curve (red long-dashed line), they appear on average greyer over the entire wavelength range, particularly in the NIR.
The DBPL-free recipes provide attenuation curves in most cases consistent with those derived from RT modelling. For four objects, U5795, U5050, U4958 and U16526, the curves obtained with the DBPL-free fit are much greyer than those yielded by the RT fit. Two of them (U5795 and U16526) have the largest |$\chi ^{2}_{\nu }$| (5.7 and 4.7, respectively, with the mean |$\chi ^{2}_{\nu }$| over the entire sample being ∼2.2). The SEDs of U5050 and U4958 are well fitted (|$\chi ^{2}_{\nu }\,{\simeq }$| 1.5), the curve found for U5050 is only slightly flatter than the original CF00 recipe (−0.6 against −0.7). In one case, U5059, the DBPL fit leads to an attenuation curve steeper than the RT fit but not very different from the CF00 recipe (δISM = −0.83, with |$\chi ^{2}_{\nu }$| = 1.7).
An interesting aspect emerging from this comparison is the wide range of attenuation curve shapes allowed by the RT modelling and DBPL-free recipe with respect to assuming a fixed slope for the attenuation curve. This is shown in Fig. 7 (left-hand panel), where the V-band normalized attenuation curves derived with cigale (magphys-like in blue in the top right-hand panel, the two Calzetti-like recipes in the bottom left panel and DBPL-free in green in the bottom right panel), are compared to those derived with the RT code (top left in black).

Left: the variability of the normalized effective attenuation curves derived from RT modelling (top left in black) is compared to that one of the curves computed with cigale under the different assumptions for the dust attenuation. From top left to bottom right are shown, magphys in blue, Calzetti et al. (2000) in red and Buat et al. (2011) in grey and our DBPL-free recipe in green. Right: mean attenuation curves, averaged over the entire sample, of z ∼ 2 (U)LIRGs colour coded as a function of the different empirical recipe adopted and compared to the mean attenuation curve derived from RT computations (black dotted-dashed line). Calzetti et al. (2000) is shown as red dot-long dashed line, Buat et al. (2011) as magenta dashed line, magphys as blue dotted line and our DBPL-free as solid green line. The slope of the ISM component of the free power-law recipe, as derived from the PDF analysis performed with cigale, is also highlighted in each panel. The flattening at longer wavelengths of the free-slope power-law recipe appears to be quite consistent with what predicted from RT modelling.
As anticipated above, the larger spread characterizing the attenuation curves derived from RT models can be explained as arising from a complex combination of SFHs and age-dependent relative distribution of stars and dust, including the clumping of both components (see e.g. Granato et al. 2000; Panuzzo et al. 2007; Fontanot et al. 2009). The relative importance of these ingredients is a function of the characteristics and evolutionary status of the galaxy. In very active systems, a large fraction of the rest-frame UV–optical starlight is produced by stars embedded in MCs while older stars, mainly emitting in the optical and NIR, suffer a smaller effect from the diffuse medium. These arguments were used by Granato et al. (2000) and Panuzzo et al. (2007) to explain the differences between the shallow attenuation in the UV of starburst galaxies (i.e. the Calzetti law) and the MW average extinction law, even by adopting a fixed, MW-type dust model. Similar conclusions have been reached by Charlot & Fall (2000); Pierini et al. (2004); Tuffs et al. (2004); Inoue (2005); Inoue et al. (2006) and more recently by Chevallard et al. (2013). In particular, Chevallard et al. (2013) compared the results from different RT models including grasil, Pierini et al. (2004), Tuffs et al. (2004) and Jonsson, Groves & Cox (2010) and found all of them to accordingly predict a quasi-universal relation between the slope of the attenuation curve at any wavelength and the V-band attenuation optical depth in the diffuse ISM at all galaxy inclinations. All the models yield a flattening of the dust attenuation curve at increasing optical depths.
The shape and variation of the attenuation curve can be quantified also in terms of the total-to-selective extinction ratio in the V band, RV = AV/E(B − V). In star-dust configurations with clumping of both components and connection between stars of different ages with different dusty environments, we do expect the path length through the dust to the observer to be different for each star.
Therefore the light from each star will experience a different amount of attenuation, yielding an attenuation curve for the entire galaxy which can be significantly different from the input extinction curve of the dust grains, with a value for RV that can significantly depart from the value of 3.1 characteristic of the average MW extinction curve (see e.g. Pierini et al. 2004; Gonzalez-Perez et al. 2013; Mitchell et al. 2013; Scicluna & Siebenmorgen 2015). Variations of RV as a function of V-band optical depths were indeed found by Pierini et al. (2004) for both homogeneous and clumpy media with RV increasing at larger optical depths. The non-linear dependence of RV on the total amount of dust was identified as the main cause of the flattening observed at large optical depths. More recently Scicluna & Siebenmorgen (2015) using a Monte Carlo RT code also found clumping dust distributions to be able to reproduce attenuation curves with arbitrary RV.
In the Calzetti et al. (2000) recipe, the local UV-bright starburst galaxies used for the calibration, provide a relation where the ratio RV = AV/E(B − V) is fixed to 4.05. For the magphys-like recipe the fixed input slopes for the ISM and BC components of the magphys-like recipe, (δISM = −0.7 and δBC = −1.3) lead to a total-to-selective extinction ratio equal ∼5.8. This larger value illustrates the flatter shape of magphys attenuation curve compared to Calzetti et al. (2000). As a consequence the magphys-like recipe is in better agreement with the results of RT modelling than Calzetti et al. (2000). In this work, we implement attenuation curve recipes where the shape is left free to vary, mimicking, implicitly, the effect of different geometrical configurations and situations. This is one of the main advantages of working with physically motivated SED-fitting codes and it also explains why our flexible DBPL-free recipe is able to reproduce the large variations observed in the RT models.
The right-hand panel of Fig. 7 finally shows the mean attenuation curves of our z ∼ 2 (U)LIRGs averaged over the entire sample, colour coded according to the specific recipe considered. An overall flattening from FUV to NIR, compared to the Calzetti-like recipes, is accordingly yielded by both the DBPL-free (solid green line) and RT fits (black dot–dashed line).
4.4 IRX-β as ‘a posteriori’ diagnostic to constrain the UV shape of the assumed attenuation law
Given its ascertained sensitivity to the assumed attenuation curve, we use here the IRX–β diagram (Meurer et al. 1999) as a ‘posteriori’’ diagnostic to constrain the UV shape of the dust attenuation curve of our high-z IR luminous sources.
Since the work by Meurer et al. (1999), on local UV-bright starburst galaxies, the IRX–β relation has been widely used at all redshifts to estimate the total amount of attenuation of distant galaxies in the FUV. Deviations from this relation have been interpreted as due to either different attenuation laws or SFHs, or both (see e.g. Kong et al. 2004; Panuzzo et al. 2007; Conroy 2010; Forrest et al. 2016; Salmon et al. 2016). Local LIRGs and ULIRGs, for example are found to fall above the locus defined by Meurer relation (e.g. Goldader et al. 2002; Howell et al. 2010). These galaxies are usually characterized by larger IRX for their UV slopes and clumping geometries responsible for greyer attenuation curves than Calzetti et al. (2000). Steeper curves like SMC, are instead used to fit more normal SF sources lying below that relation and characterized by low IRXs for their UV colours. In such systems, the UV colour, seems to be very sensitive to influences from both stellar populations and dust geometry variations (e.g. Kong et al. 2004; Calzetti et al. 2005; Boquien et al. 2009; Hao et al. 2011).
In a recent work, Salmon et al. (2016) analysed the UV shape of the dust attenuation curve of a sample of IR luminous sources at redshift 1.5–3 by considering several different recipes for the dust attenuation curve including Calzetti and modified Calzetti (Noll et al. 2009) laws and a steeper SMC curve. They found galaxies with high colour excess to have shallower, starburst-like attenuation, while those characterized by low colour excess to have steeper, SMC-like attenuation. Before discussing the position of our galaxies in the IRX–β diagram and its interpretation in terms of the UV shape of the measured attenuation curve, we provide in the next subsections few details about how the IRX ratio and UV-spectral slope have been computed in this work.
4.4.1 Computation of the UV-spectral slope β and rest-frame FUV luminosity
As discussed above the UV-spectral slope can be an important observational tool, particularly at high redshift, for its relatively ease of measurement. Originally β was determined from UV-continuum spectroscopy (Calzetti et al. 1994), however nowadays it is mostly computed from the UV colours provided by broad-band photometry. The classical method implemented consists in a power-law fit to the observed photometric bands. This method has been shown to provide redder β compared to the true values derived from stellar population models using the spectral windows defined by Calzetti et al. (1994), with a systematic offset at all redshifts ranging between 0.1 up to 0.5 (Salmon et al. 2016).
Independent tests using simulations and stacked samples of high-z LBGs have been also performed (Alvarez-Marquez et al. in preparation) providing similar systematic offsets when comparing β values derived from SED fitting and simple power-law fitting.
Here, we use the method described in Finkelstein et al. (2012), directly included in cigale, where β is estimated from the best fit to the UV-to-optical observed SED using the UV-spectral windows defined by Calzetti et al. (1994).7 This method has been shown to better recover the true values of β with no clear systematics and a scatter around ±0.1 up to z ∼ 4 (Salmon et al. 2016), as it is used here is reference for local starburst galaxies.
Given the redshifts (varying between 1.618 and 2.118) of our sources we have selected a subsample of about 13 sources with at least three photometric bands in the rest-frame UV–optical in order to check any possible effect in the estimated β due to the presence of a possible UV bump. We compared the results obtained by including the rest-frame band (for galaxies at this redshift being the observed V-band filter) where the absorption feature can possibly fall with those obtained removing this band. We also compared colours for the two runs and did not find any significant effect concluding that for these sources the UV-bump does not seem to affect our estimates of β.
We also found, in agreement with Salmon et al. (2016), our estimates of β to be quite independent of the specific attenuation law assumed. This is due to the fact that the best-fitting UV–optical SED always provides a close match to the UV colours as long as the assumed dust law does not have extreme features. Here we use as a reference the β values obtained through our own DBPL-free recipe.
Finally, the rest-frame FUV luminosity used to compute IRX is obtained from the best-fitting SED by fitting only the UV–optical bands in order to retrieve the best observed estimate of this quantity for our sources.
4.4.2 The observed IRX–β plot for our z ∼ 2 (U)LIRGs
Fig. 8 (left) shows the observed estimates for the IRX–β of our z ∼ 2 (U)LIRGs (filled black circles) compared to the predicted relations obtained through simulations colour coded from blue to red as a function of increasing ISM slopes from −0.8 (steeper slope than Calzetti) to −0.1 (much greyer slope than Calzetti). The thickness of the different coloured stripes reflects the effect due to the assumed SFH, stellar population properties and different E(B − V) or AV considered (see Table 1 for reference). These are also compared to the reference Meurer relation shown as solid black line and the modified Calzetti recipes, used in Salmon et al. (2016), with slopes ranging, from top to bottom, from +0.4 to −0.4. The red dot-long dashed line being that one corresponding to the assumption of a Calzetti et al. (2000) attenuation law (δ = 0 in the modified Calzetti recipe). The latter are used here as reference to show that in terms of UV shapes we cover the same range of values and they have been computed by assuming our reference SFH, namely, delay-τ model with input parameters as defined in Table 1.

Left: observed estimates for the IRX–β of our z ∼ 2 (U)LIRGs (filled black circles) compared to the predicted relations obtained through simulations colour coded from blue to red as a function of increasing ISM slopes from −0.8 to −0.1. The thickness of the different coloured stripes reflects the effect due to the assumed SFH, stellar population properties and different E(B − V)/AV considered (see Table 1 for reference). These are also compared to the reference Meurer relation shown as solid black line and the modified Calzetti recipes, used in Salmon et al. (2016), with slopes ranging, from top to bottom, from +0.4 to −0.4. The red dot-long dashed line being that one corresponding to the assumption of a Calzetti et al. (2000) attenuation law (δ = 0 in the modified Calzetti recipe). The latter are used here as reference to show that in terms of UV slope we cover the same range of values and they have been computed by assuming our reference SFH, namely, delay-τ model with input parameters as defined in Table 1. The magenta pentagons correspond to the estimates obtained through full SED fitting under the assumption of DBPL-free model. Right: the IRX–β relation (red solid line) obtained by fitting the observed estimates from our z ∼ 2 (U)LIRGs, is compared to that one obtained from simulations by assuming the CF00 model (blue solid line) and several reference relations from literature. Our relations appears to be in very good agreement with that one recently derived by Forrest et al. (2016).
The observed β obtained through the method specified above and represented by the filled black circles are then compared also with the results from full-SED fitting (magenta filled pentagons). We find good agreement between the observed estimates and those derived with SED fitting using the DBPL-free attenuation recipe. This reflects on the fact that the positions of our sources in the IRX–β plot are fully consistent with the value of the ISM slope derived from Bayesian analysis. Moreover, the figure clearly shows that greyer slopes than Calzetti et al. (2000) are needed in order to reproduce the observed IRX–β of the objects in our sample characterized by bluer β values (i.e. those falling roughly in the dark green-to-red area). We consider this as an indication of flattening of the attenuation curve in the UV as observed in Fig. 7. Fig. 8 (right) shows the mean IRX–β relation derived for our z ∼ 2 (U)LIRGs (as red thick solid line) compared to some reference relations including Meurer et al. (1999, black solid line), Overzier et al. (2011, black dashed line), Forrest et al. (2016, dot-long dashed line), Álvarez-Márquez et al. (2016, dotted line) and the same relation obtained under Charlot & Fall (2000) prescriptions. The observed flattening of our attenuation curves at all wavelengths is reflected in an IRX–β relation which is systematically above the local relations. It also appears to be in a very good agreement with the relation derived by Forrest et al. (2016) for dusty SF composite SEDs selected from a sample of ∼4000 K-band-selected sources in the ZFOURGE survey.
Of course, the IRX–β plot does not provide any information about the specific shape of the dust attenuation curve at longer wavelengths and our conclusions in this case restrict only to the UV shape. This means that in the UV, either a power-law attenuation curve with slopes ranging between −0.7 and −0.1 (or a modified Calzetti recipe with greyer slope) would be good in reproducing the observed IRX–β values of our galaxies.
4.5 Constraining the NIR shape of the dust attenuation curve
We want to understand whether we need or not, for a given range of UV slopes, a flattening in the NIR. At this aim, we compare the ability of the modified Calzetti recipe and the DBPL-free model, whose shapes strongly differ in the NIR, to reproduce our data. In order to isolate the effect of the assumed attenuation curve when comparing the two different set of models, we adopt exactly the same configuration for all the other parameters, namely the SFH and IR emission templates and we require to cover exactly the same range of UV slopes for the attenuation curve (i.e. greyer to steeper than Calzetti, see Fig. 1 for details). The four reference values for the ISM slope used in DBPL-free recipe (−0.7, −0.5, −0.3 and −0.1) are compared to the corresponding four values in the modified Calzetti recipe (0., 0.2, 0.4, 0.6 with the 0 corresponding to the reference Calzetti et al. 2000 value). In order to have the same number of parameters the slope of the BC component has also been fixed to the value of −0.7 (Charlot & Fall 2000). Within this configuration, the only difference between the two attenuation models pertains to the long wavelength range of the attenuation curve with the DBPL-free providing systematically greyer curves than modified Calzetti. We then run cigale under the two configurations and compared the resulting |$\chi ^2_{\nu }$| in Fig. 9. Only one object, U4642, appears to be best fitted by the modified Calzetti recipe. Interestingly, the RT modelling also gives a steeper attenuation curve than our DBPL-free result in the NIR for this galaxy (Fig. 1).

Comparison of |$\chi ^2_{\rm \nu }$| values for z ∼ 2 (U)LIRGs obtained with the DBPL-free recipe (x-axis) and the modified Calzetti recipe (y-axis). See the text for further details.
5 DUST ATTENUATION CONFIGURATION FOR LIRGS AND (U)LIRGS AT LOWER REDSHIFT
By fitting the UV-to-sub-mm SEDs of a sample of IR luminous sources at redshift 2, with an approach based on Bayesian analysis, we have derived a recipe for dust attenuation where the shape of the curve is characterized by a greyer slope than the one of Calzetti (2000) at all wavelengths. The universality of such a law must be questioned since some variability is expected, as seen in the Introduction, as a function of physical and structural parameters of galaxies, galaxy inclination and effective optical depth (e.g. Wild et al. 2011b; Chevallard et al. 2013; Kriek & Conroy 2013).
For this reason, we have selected objects with IR luminosities in the range of LIRGs and ULIRGs, thus similar to those of our z ∼ 2 galaxies, but at lower redshift and we have applied our analysis to these samples. This choice is also motivated by the fact that one of the aims of HELP is to analyse IR-selected sources at any redshift. We focus, in particular, on a sample of (U)LIRGs at z ∼ 0 for which we have a very good data coverage from FUV to sub-mm and a sample of LIRGs at z ∼1 for which we do not have a very good coverage in the rest-frame UV at the given redshift. The first sample, at z ∼ 0, is particularly interesting as it provides us with a class of objects characterized by IR luminosities in the range of our z ∼ 2 (U)LIRGs, but whose nature is likely to be governed by a different physical mechanism (merger-induced starbursts versus cold gas accretion). They have also been shown to lie above the Meurer et al. (1999) relation in the IRX–β diagram (see e.g. Howell et al. 2010) which suggests that they can be characterized by greyer attenuation curves than the Calzetti law. z ∼ 1 LIRGs could also be an interesting case as they dominate the SFR density at z > 0.8.
The two samples and relative results are presented in the next two sections.
5.1 Nearby (U)LIRGs
The sample of nearby (z < 0.083) (U)LIRGs presented here includes 53 LIRGs and 11 ULIRGs spanning log(LIR/L⊙) = 11.14–12.57 selected by U et al. (2012) from the flux-limited (f60 μm > 5.24 Jy) Great Observatories All-sky LIRG Survey (GOALS, Armus et al. 2009). These account for about 30 per cent of all LIRGs and 50 per cent of all ULIRGs in GOALS with a median infrared luminosity of log(LIR/L⊙) = 11.60 and redshift in the range z = 0.012–0.083 (with median z = 0.028 (DL = 119.0 Mpc). Multiwavelength AGN indicators have been used by the authors to select possible AGNs. As here we are focusing on galaxies powered by star formation in order to avoid further degeneracies in the model parameters related to the possible addition of an AGN component we have restricted our analysis only to the AGN-free (U)LIRGs.
We first fit the observed SEDs of these galaxies by assuming the mean power-law attenuation curve derived from our previous analysis and therefore characterized by δISM = −0.48. We have fixed the value of δBC to the slope of CF00 model, i.e. −0.7 (a different value would not change the results). The quality of the data allows us to obtain good fits to the observed SEDs of nearby GOALS galaxies, with about 78 per cent of the objects being fitted with a |$\chi ^{2}_{\nu } \leqslant 3$|.
As a further check, we also run our code on the observed SEDs of these local (U)LIRGs by assuming a DBPL-free attenuation curve and thus leaving the slope of the ISM component as free parameter. Interestingly, we find an attenuation curve averaged over the entire sample very similar in shape to the one estimated for our z ∼ 2 (U)LIRGs and thus greyer than Calzetti (2000) one. We interpret this result as an evidence of the ability of our dust attenuation recipe to reproduce the properties of nearby merger-induced starburst galaxies too. Indeed, despite the different nature, both local and z ∼ 2 (U)LIRGs are characterized by relatively high optical depths and dust enshrouded SF environments whose geometrical features can be responsible for similar shapes in the dust attenuation curves.
5.2 z ∼ 1 LIRGs
The sample at z ∼ 1 considered here includes ∼130 LIRGs selected from the PEP sample of Gruppioni et al. (2013) in the GOODS-S field with a spectroscopically confirmed redshift in the interval 0.5–1.5 (44 objects in the range 0.76–1.05). Following Lo Faro et al. (2013), we selected only sources with 24 μ m−1 flux in the range 0.14–0.45 mJy (same interval as for our z ∼ 2 (U)LIRGs). All the sources benefit from full PACS photometry from 70 to 160 μ m−1 and additional SPIRE data (250, 350 and 500 μ m−1) retrieved from the HerMES program. The complementary photometry at shorter wavelengths is provided by the MUSIC multiwavelength catalogue by Santini et al. (2009) bringing to a total number of photometric bands of about 19. However, at the redshifts probed by the PEP sample the wavelength coverage does not allow a good sampling of their FUV colours preventing us from performing a detailed analysis of the UV shape of the dust attenuation curve of these sources.
AGN-dominated objects have been excluded by running the spectrophotometric code cigale in combination with a reduced Fritz, Franceschini & Hatziminaoglou (2006) library of AGN models (see e.g. Ciesla et al. 2015) and computing the AGN fraction contributing to the total IR luminosity of the galaxy.
We follow a similar strategy used above for the nearby LIRGs and ULIRGs. We fit the observed SEDs by assuming the mean power-law attenuation curve derived for the z ∼ 2 (U)LIRGs. About 91 per cent of z ∼ 1 LIRGs are fitted with a χ2 ≤ 3. We did not try to run the code assuming a DBPL-free attenuation curve since the wavelength coverage do not allow a fine sampling of the rest-frame UV side of the attenuation curve.
We conclude that a realistic combination of the two main recipes considered in this work should be included in the SED-modelling, especially when dealing with a big data base including a large variety of IR bright sources. Within the context of HELP or big legacy projects including multiple surveys, it becomes inefficient to perform SED fitting including all the possible attenuation laws we do expect. In order to make the process more efficient we are now working to implement in cigale a new recipe for dust attenuation formalized by a broken power law with two different slopes for the UV and NIR range, using the V-band wavelength as reference. In this way, with one single recipe, we can reproduce both the flattening and steepening of the dust attenuation curve from UV to NIR, including the possibility to have curves which are greyer in the UV but as steep as the Calzetti law in the NIR.
6 EFFECT OF THE ASSUMED DUST ATTENUATION CURVE ON THE PREDICTED STELLAR MASS AND STAR FORMATION RATE
Despite the large efforts devoted to explore the effects that the assumed SFH (e.g. rising, declining or bursty) or wavelength coverage (e.g. availability of IR data) can have on the main physical parameters of galaxies (see e.g. Bell & de Jong 2001; Pforr et al. 2012; Michałowski et al. 2012; Conroy 2013; Buat et al. 2014), there is still a lack of specific discussion in the literature about the effect of the assumed dust attenuation recipes on the derived stellar mass and SFR of galaxies.
Lo Faro et al. (2013, 2015), by applying RT models to the sample of dust obscured z ∼ 2 (U)LIRGs analysed here, observed that the assumed parametrization for the dust attenuation together with the availability of full-multiwavelength SED, can also affect the estimates of the stellar mass of galaxies. They found stellar masses systematically higher than those computed with more classical approaches (as e.g. Hyperz by Bolzonella, Miralles & Pelló 2000), up to a factor of ∼6 for the most dramatic cases.
Here, we want to explicitly investigate the effect of the assumed shape of the dust attenuation curve on the derived stellar mass and SFR of our z ∼ 2 (U)LIRGs.
6.1 Stellar mass
To illustrate the effect of a greyer attenuation curve at longer wavelengths on the stellar mass estimate, we show, in Fig. 10, the best-fitting SEDs of one of our z ∼ 2 (U)LIRGs.

Example of a best-fitting SED obtained with cigale for a representative object, U4451, under the two ‘extreme’ assumptions for the dust attenuation law given by Calzetti et al. (2000) (left) and DBPL-free recipe (right). The figure clearly shows the effect on the un-extinguished SED of a greyer attenuation at longer wavelengths (right-hand panel) responsible for an extra attenuation in the NIR.
The two fits refer to the object U4451, whose properties are representative of the entire galaxy sample and whose attenuation curve is shown in Fig. 5. The best-fitting SED obtained under the assumption of a Calzetti (2000) attenuation law (left-hand side) is compared to that one computed adopting the DBPL-free recipe with δISM = −0.55 (right-hand side). Both fit are satisfactory in terms of |$\chi ^{2}_{\nu }$|, with |$\chi ^{2}_{\nu }\, ({\rm Calzetti 2000})=3.28$| and |$\chi ^{2}_{\nu} \,({\rm DBPL\hbox{-}free})=1.65$|. The main difference between the two pertains to the rest-frame UV–opt–NIR where the unextinguished stellar SEDs appear quite different. In particular, an extra attenuation at rest-frame NIR wavelengths is visible in the best fit performed with the DBPL-free law. Differences in the rest-frame UV are also present but they are not as significant as those at longer wavelengths.
For this specific object, the logarithm of the stellar mass computed with Calzetti is 10.46, while that one computed assuming the DBPL-free law is 11.13 about 0.6 dex difference.
Fig. 11 shows the global effect of the assumed attenuation curve on the estimated stellar mass of all the (U)LIRGs in our sample for all the recipes considered. The magphys (DBPL with δISM = −0.7 and δBC = −1.3) based stellar masses on the x-axis are compared to the stellar masses computed with all the other recipes on the y-axis. The power-law recipes adopted in the DBPL-free and magphys-like models provide, on average, larger stellar masses compared to Calzetti-like recipes because they consider flatter attenuation curves in the NIR. The difference between the stellar mass estimates is higher for the DBPL-free configuration which allows even greyer slopes for the δISM than the value of magphys (δISM = −0.7) and it can reach up to a factor of ∼10 for the most dust obscured and IR luminous objects (red filled circles in Fig. 11). The observed trend is in agreement with the results from Lo Faro et al. (2013) and Mitchell et al. (2013). A similar comparison for the two samples of IR luminous objects at z ∼ 0 and 1 is given in Appendix.

Comparison of stellar masses estimated using different assumptions for the dust attenuation curve. magphys based M* on the x-axis are compared to the stellar masses computed with all the other recipes on the y-axis. The solid black line represents the 1–1 correlation line, while the dashed lines highlight the region within a factor of 2 from the 1–1 correlation line. The results from the DBPL-free recipes are shown as filled red circles, those from Calzetti et al. (2000) as filled green rhombus, while Buat et al. (2011) modified Calzetti recipe as open black squares.
6.2 Star formation rate
The differences observed in the UV range among the different recipes considered translate into different stellar population ages and total FUV attenuation which can affect the derived SFR of our high-z (U)LIRGs. In Fig. 12, we compare the well known and widely used in literature Kennicutt (1998) calibration (x-axis) to the SFRs derived from SED fitting and averaged over the last 10 Myr. The latter are colour coded as a function of the assumed dust attenuation law.

Comparison of the SFRs derived, for our galaxies, from SED fitting and averaged over the last 10 Myr with the classical Kennicutt (1998) calibration. The SFRs derived from SED modelling are colour coded as function of the different assumed dust attenuation curves, magphys-like as filled blue squares, the DBPL-free model as filled red circles, the Calzetti et al. (2000) recipe as filled green rhombus and the modified Calzetti recipe by Buat et al. (2011) as open black squares. The black solid line highlights the 1–1 correlation line, while the two dashed lines define the region within a factor of 2 from the 1–1 correlation line.
The situation appears less dramatic than that one observed for the stellar mass. There is an overall good agreement among the different SFR estimates well within a factor of two, which is the typical uncertainty expected when comparing different recipes in the context of SED modelling (see e.g. Longhetti & Saracco 2009). Despite the global agreement, there is a tendency for the DBPL-free estimates (red circles) to be lower on average than both those derived assuming Calzetti-like recipes and those computed using the Kennicutt (1998) calibration due to the progressive flattening of the dust attenuation curve in the UV. We find the difference between the SFRs estimated with Calzetti and power-law recipes to be larger for larger differences of the measured FUV total attenuation.
For three objects, the discrepancy between the SFR estimated with our DBPL-free model (red circles in Fig. 12) and that one derived from the Kennicutt calibration is larger than a factor of two. U5795 at the bottom right of Fig. 12 is the object showing the flattest attenuation curve (δISM = −0.1) and identified as very badly fitted (Section 4.3). It is probably indicative of our inability to constrain its dust properties with the available data. For the other two sources falling below the bottom dashed line in Fig. 12, namely U4367 and U5050 our DBPL-free fit is very good (|$\chi ^{2}_{\nu }\simeq 1.3$|), both the DBPL-free (red circles) and magphys (blue squares) recipe provide SFRs which differ from those derived from the Kennicutt calibration by a factor larger than two (the consistency between the results found with both recipes is expected given the similarity of the slope of the attenuation curve for the ISM component). For these two objects even the SFRs estimated by assuming a Calzetti-like dust law (green rhombus/black open squares), lie at the limits of the dashed line delimiting the region within a factor of 2 from the 1–1 correlation line, when compared to the Kennicutt calibration. Looking at the observed SEDs, we noticed that they present the most prominent bump in the rest-frame optical–NIR among all the galaxies in the sample and also older ages than the others. Their IR SEDs do not present any deviant property compared to the other galaxy IR SEDs. We thus focus the exploration of the possible reasons at the origin of the observed discrepancy in the SFR estimates on the SFH of these galaxies.
Fig. 13 (left-hand panel) shows, for the DBPL recipe, the best-fitting delayed-τ SFHs obtained through our SED-fitting procedure for each of the z ∼ 2 (U)LIRGs in our sample. The SFHs are dropped in correspondence of the age of the galaxy as derived from our analysis. The thick green and black lines represent, respectively, the delay-τ SFH of U4367 and U5050. Differently from the other galaxies, these are the only two objects observed not at the peak of their SF activity. We can use the ‘evolutionary parameter’, defined as the ratio age/τSFH, to quantify how far from the peak a galaxy is observed. A clear anti-correlation is measured between the difference in the SFRs estimated from SED fitting and Kennicutt calibration, ΔSFR = log(SFR10Myr) − log(SFRKenn), and the evolutionary parameter (Fig. 13, right-hand panel). The plot shows that the largest discrepancies in SFR, above a factor of ∼2–2.5 (as for U4367 and U5050), are reached for values of the ‘evolutionary parameter’ above 2.5. The plot also shows that for the Calzetti-like recipes the SFHs are mostly consistent with the galaxies being observed close to the peak. We interpret the fact to be observed well after the peak of star formation as the most likely cause of the deviant behaviour in terms of SFR. This is consistent with the prominent bump in the NIR characterizing the observed SED of the two objects mentioned above. In these cases, we may expect the Kennicutt calibration to overestimate the SFR due to a non-negligible contribution of relatively evolved stellar populations to the infrared luminosity (see e.g. fig. 4 in Lo Faro et al. 2013)

Left: best-fitting SFHs of our z ∼ 2 (U)LIRGs as derived from our SED-fitting procedure under the assumption of DBPL attenuation curve, corresponding to the filled blue squares of Fig. 12. The two thick green and black lines represent the two objects showing deviant behaviour in terms of SFR in Fig. 12. Their SFHs are consistent with them being observed well after the peak of SF. Right: difference ΔSFR = log(SFR10) − log(SFRKenn) of the SFRs derived from SED fitting and Kennicutt calibration plotted as a function of the ‘evolutionary parameter’ age/τSFH indicating how far from the peak we are observing the galaxy (Fig. 13 – right-hand panel). The largest discrepancies in SFR, above a factor of ∼2–2.5, are observed in correspondence of values of the ‘evolutionary parameter’ above 2.5.
A similar comparison between the SFRs derived from SED fitting and those based on the Kennicutt (1998) calibration is performed for the two samples of IR luminous galaxies at lower redshift discussed in Section 5 and is presented in Appendix.
7 SUMMARY AND CONCLUSIONS
We have investigated the shape of the dust attenuation curve of a sample of dust-obscured IR luminous galaxies at z ∼ 2 by fitting their UV-to-sub-mm SEDs by means of the physically motivated code cigale including energy balance. The high flexibility offered by cigale allowed us to implement several different recipes for the dust attenuation, both well known and new. These include the classical Calzetti et al. (2000) law, a modified version of this curve which includes a UV-bump and steeper slope in the UV (Buat et al. 2011), and our newly implemented two component (birth clouds and diffuse ISM) power-law recipe (DBPL-free) based on the formalism of Charlot & Fall (2000). In our DBPL-free model, used here as reference, the UV-to-NIR shape of the dust attenuation curve is treated as a free parameter and implicitly includes both the Charlot & Fall (2000) and magphys-like prescriptions.
To focus our analysis on the characterization of the dust attenuation properties of these galaxies we assumed the same configuration for the input SFH, stellar library and IR emission, for all the different dust attenuation recipes considered. We explored the different recipes for dust attenuation and compared the results to those derived in previous works for the same galaxy sample with RT computations.
The comparison revealed to be successful for our DBPL-free reference model whose attenuation curves appear to be in very good agreement with those based on RT models for ∼75 per cent of the objects and greyer at all wavelengths than the Calzetti law. A greyer attenuation law also explains the position of our galaxies in the IRX–β diagram, above the Meurer et al. (1999) relation for local, UV-selected starbursts.
Our analysis thus shows that for IR selected and luminous galaxies we do expect a global flattening of the dust attenuation curve at all wavelengths from UV-to-NIR. In agreement with RT models we observe greyer slopes for the ISM component of the medium at increasing optical depths. This flattening can be explained by mixed star-dust geometries including clumping of both components.
We have checked our recipe for the dust attenuation by applying our analysis to two samples of IR bright sources with IR luminosities similar to those of our z ∼ 2 galaxies. These include a sample of ∼64 nearby (U)LIRGs for which a wealth of UV-to-sub-mm data is available and ∼130 LIRGs at z ∼ 1 with a good spectral coverage except for the rest-frame UV.
We propose a flexible recipe for the dust attenuation curve formalized by a broken power law with two different slopes for the UV and NIR range. This recipe would allow us to reproduce both the flattening and steepening of the dust attenuation curve from UV to NIR, including the possibility to have curves which are greyer in the UV but as steep as Calzetti in the NIR, mimicking, implicitly, the effect of different geometrical configurations.
We finally investigated the effect of these greyer attenuation curves on the derived main physical properties of galaxies and found, in agreement with Lo Faro et al. (2013) and Mitchell et al. (2013), that they can strongly affect the estimate of the stellar mass of galaxies up to a factor ≲ 10 for the most extreme cases (with the median factor being ∼1.4). Larger attenuations at longer wavelengths translate into larger stellar masses compared to classical Calzetti-like recipes. The SFR appears to be less affected by these variations on the specific shape of the dust attenuation curve. In two cases, the SFH is suggested to play a role in the SFR determination with a lower SFR obtained from SED fitting with respect to that one based on the Kennicutt (1998) calibration, for those galaxies observed far from the peak of SF.
Acknowledgements
The project has received funding from the European Union Seventh Framework Programme FP7/2007-2013/ under grant agreement no. 60725. BLF and YR acknowledge support from this programme. This publication reflects only the authors’ view and the European Union is not responsible for any use that may be made of the information contained therein.
Having to deal with geometrical effects, estimating dust attenuation is different than estimating dust extinction. With the term extinction, we refer to the wavelength dependence of the optical properties (absorption plus scattering) of the dust mixture. These are measured in the simple geometrical configuration of a homogeneous slab of dust placed between the observer and a point source as in case when directly measuring the extinction from observations of background stars. In this configuration, a direct relation between the ratio of the observed to intrinsic luminosity and the dust optical depth can be easily defined (see Conroy 2013, and references therein for more details).
We fix the separation age between young and old stellar populations to 10 Myr, as in Charlot & Fall (2000).
CF00 introduce a transmission function at a given wavelength by Tλ = exp (−τλ), τλ being the effective absorption optical depth.
Due to the differential attenuations, the curves plotted are not exactly the Calzetti et al. (2000) or Buat et al. (2011) curves. The figure clearly shows a global flattening up to longer wavelengths of the effective attenuation curves computed using DBPL-free recipes compared to those derived using Calzetti-like prescriptions. It is therefore clear that a larger amount of attenuation in the NIR is implied, for our IR luminous galaxies, when using either magphys-like or DBPL-free recipes. An example of a best-fitting SED obtained with cigale for a representative objects, U4451, is given in Fig. 10 which will be discussed in Section 6.1.
We use the spectral windows defined by Meurer et al. (1999) from 1268 to 1950 Å
REFERENCES
APPENDIX: Effect of the assumed attenuation curve on the estimated M* and SFR of nearby and z ∼ 1 (U)LIRGs
We present here the results concerning the global effect of our agreed prescription for the dust attenuation on the derived stellar mass and SFR also for the two samples at lower redshift presented in Section 5. As we already discussed the differential effect among all the different recipes for our reference sample of z ∼ 2 (U)LIRGs, we restrict here the analysis to the two main formalisms considered under the Calzetti et al. (2000) and DBPL-free configuration. The latter implicitly includes the standard CF00 model, the magphys-like recipe and our ‘mean’ attenuation curve derived from the analysis of the z ∼ 2 (U)LIRGs. The results are shown in Fig. A1 with the nearby GOALS galaxies represented as red circles and the z ∼ 1 LIRGs as blue squares. As for the z ∼ 2 (U)LIRGs also in this case we find the stellar masses estimated under the Calzetti recipe to be systematically lower compared to those derived with DBPL attenuation law due to the flattening at longer wavelengths. Interestingly, the effect is stronger for the local LIRGs showing the larger NIR attenuations (ANIR). The lower attenuations at longer wavelengths obtained for the z ∼ 1 LIRGs under the DBPL recipe, together with a slope of the attenuation curve being consistent in the UV with the Calzetti recipe, provide stellar masses which are systematically lower than those computed with Calzetti but mostly within a factor of 2 from the 1–1 correlation line (black solid line in the figure).
A better agreement is found when comparing the SFRs derived from SED fitting with those based on the Kennicutt (1998) calibration and it is shown in Fig. A1 (right-hand panel). In this case both nearby (red circles) and z ∼ 1 (blue squares) LIRGs present similar behaviour. On average there is a very good agreement between the SFRs computed under the Calzetti recipe and those derived from the Kennicutt calibration, while those based on the DBPL configuration appear to be lower on average but mostly within a factor of 2 from the 1–1 correlation line (black solid line in the figure). The fraction of objects falling below the above-mentioned area are those showing the most prominent flattening in the UV.

Top: the stellar masses derived under the DBPL configuration (x-axis) are compared to those derived by assuming Calzetti et al. (2000) attenuation law (y-axis). Red filled circles are for the nearby GOALS galaxies, while filled blue squares are for the z ∼ 1 LIRGs, both presented in Section 5. The black solid line represents the 1–1 correlation line, while the two dashed line define the area within a factor of 2 from the 1–1 correlation line. Bottom: the SFRs estimated by using the Kennicutt (1998) calibration (x-axis) are compared to those derived from SED fitting (y-axis) under the two main assumptions for the dust attenuation of DBPL-like (open symbols) and Calzetti-like (filled symbols).



