Gravitational wave astronomy with radio galaxy surveys

Raccanelli, Alvise

doi:10.1093/mnras/stx835

Abstract

In the next decade, new astrophysical instruments will deliver the first large-scale maps of gravitational waves (GWs) and radio sources. Therefore, it is timely to investigate the possibility to combine them to provide new and complementary ways to study the Universe. Using simulated catalogues appropriate to the planned surveys, it is possible to predict measurements of the cross-correlation between radio sources and GW maps and the effects of a stochastic GW background on galaxy maps. Effects of GWs on the large-scale structure (LSS) of the Universe can be used to investigate the nature of the progenitors of merging black holes, the validity of Einstein's general relativity, models for dark energy and detect a stochastic background of GW. The results obtained show that the galaxy–GW cross-correlation can provide useful information in the near future, while the detection of tensor perturbation effects on the LSS will require instruments with capabilities beyond the currently planned next generation of radio arrays. Nevertheless, any information from the combination of galaxy surveys with the GW maps will help provide additional information for the newly born GW astronomy.

gravitational waves, cosmological parameters, large-scale structure of Universe, radio continuum: galaxies

1 INTRODUCTION

The detection by the Laser Interferometer Gravitational-Wave Observatory (LIGO) instrument of gravitational waves (GWs; GW150914, Abbott et al. 2016a and GW151226, Abbott et al. 2016d) from the merger of binary black holes (BBHs) opened up a new window to study our Universe. In the first few months following the first detection, GWs have been used to test general relativity in a new way (Abbott et al. 2016c), the speed of GWs (Bettoni et al. 2017; Blas et al. 2016; Collett & Bacon 2017; Kahya & Desai 2016) and alternative cosmological models such as the one where the dark matter is made of primordial black holes (e.g. Bird et al. 2016).

Currently and for the foreseeable future, the main way to detect GWs is by the use of laser interferometers, on Earth and in space. Several alternatives have been proposed, and they involve detecting the effect of GWs on other observables, such as Pulsar timing arrays (Lorimer & Kramer 2005), the effect of GWs from inflation on the cosmic microwave background (CMB; Kamionkowski & Kovetz 2016), and the effect of GWs on the large-scale structure (LSS) of the Universe (Guzzetti et al. 2016).

The presence of tensor modes during the early epochs of the Universe modifies the power spectrum of primordial scalar perturbations (Jeong & Kamionkowski 2012), while at late times the presence of a GW background leads to several effects, including projection effects due to the perturbation of space–time by GWs on the galaxy distribution (Jeong & Schmidt 2012; Schmidt & Jeong 2012a), the CMB (Dodelson, Rozo & Stebbins 2003; Cooray, Kamionkowski & Caldwell 2005; Book, Kamionkowski & Souradeep 2012a) and the 21-cm background (Pen 2004; Book, Kamionkowski & Schmidt 2012b).

At the same time, radio surveys for cosmology are entering a new phase of exponential expansion on both quantity and quality of data available (Norris et al. 2013), with the construction of several instruments, including the Australian Square Kilometre Array Pathfinder (ASKAP; Johnston et al. 2008) and the design definition of the Square Kilometre Array (SKA¹). Radio galaxy surveys with such instruments will be able to detect galaxies over a large redshift range, a wide area of the sky, and down to a very low flux limit.

Radio surveys such as NVSS have been used in the past to perform cosmological analyses (see e.g. Nolta et al. 2004; Raccanelli et al. 2008; Xia et al. 2010; Bertacca et al. 2011); future surveys will have a wider redshift range and orders of magnitude and more objects observed, so it is expected they will improve the precision of cosmological measurements (Raccanelli et al. 2012). All this, combined with the fact that effects of GWs on LSS are largest at very large scales, makes it very timely to start an investigation of the combination of GW with radio galaxy maps.

This paper investigates the possibility to use future radio galaxy surveys to contribute to GW astronomy. By measuring the position and correlation of galaxies, or cross-correlating their number counts with GW maps, it will be possible to detect direct or indirect effects of GWs coming from the merger of massive compact objects or the early stages of the Universe.

GW astronomy is still in its infancy but it is predicted to grow quickly, and the coincidental exponential increase in radio survey capabilities makes it very interesting to analyse how to best combine the two fields. Therefore, it is timely to try to understand if the combination of observations of radio sources and GWs can give useful additional information about cosmological models and parameters currently investigated.

We will present forecasts of the constraints on cosmological models and parameters that will be possible to obtain both by cross-correlating future GW maps with galaxy catalogues from a variety of planned radio surveys, and by analysing the effect of GWs on position, distribution and correlation of such galaxy catalogues. Recently, ideas about cross-correlation of LSS with GW maps have been explored in e.g. Camera & Nishizawa (2013), Oguri (2016), Namikawa, Nishizawa & Taruya (2016a), Raccanelli et al. (2016c).

The structure of the paper is as follows. In Section 2, we introduce the radio galaxy surveys we consider. In Section 3, we present the studies that will be enabled by cross-correlating GW with galaxy maps, in particular angular correlations to determine the progenitor of BBH mergers in Section 3.1 and constraints on cosmic acceleration models by using lensing effects on radial correlations in Section 3.2. In Section 4, we investigate the effects of GWs on the LSS; we predict measurements that will be possible to obtain by using cosmometry in Section 4.1 and the cosmic rulers methodology in Section 4.2. We then summarize our findings and conclude in Section 5.

2 FORTHCOMING RADIO GALAXY SURVEYS

In this paper, we focus on forthcoming radio galaxy surveys; we consider the Square Kilometre Array (SKA; Maartens et al. 2015) and its pathfinders (Norris et al. 2013), in particular the cosmology survey Evolutionary Map of the Universe (EMU; Norris et al. 2011) with the ASKAP instrument. We will consider both radio continuum and H i spectroscopic cases.

We model radio surveys by using the prescription of Wilman et al. (2008); catalogues are generated from the S-cubed simulation,² using the SEX and SAX for continuum and H i surveys, respectively. We then apply a cut to the simulated data to reflect the assumed flux limit for different cases. More details on the underlying modelling and planned surveys can be found in Wilman et al. (2008); Jarvis et al. (2015); Abdalla et al. (2015). Finally, for all surveys we assume f_sky = 0.75. We expect that for some measurements, in particular the detection of GW effects using only radio surveys, the area, redshift range and number density required will often be surpassing the specifications of planned instruments. Therefore, we include in our predictions instruments with futuristic capabilities, which will be used to understand if those measurements will be possible even in principle.

Although radio continuum surveys do not have in principle redshift information, there are a variety of techniques that could enable the possibility to divide the galaxy catalogue into redshift bins. A detailed comparison of methodologies is beyond the scope of this paper, where we assume the clustering-based redshift (CBR) information proposed in Ménard et al. (2013). We will assume the possibility to divide the catalogue into bins using the CBR technique following Kovetz, Raccanelli & Rahman (2017).

2.1 EMU

At its completion, ASKAP will consist of 36 12-m antennas spread over a region 6 km in diameter. EMU is an all-sky radio continuum survey that will cover the whole southern sky, extending as far north as +30°, with a sensitivity of 10 μJy beam⁻¹ rms, over a frequency range of 1130–1430 MHz. It will be a particularly fast survey, thanks to the phased-array feed (PAF) at the focus of each antenna, which gives ASKAP a 30 deg² of instantaneous field of view. It is expected to detect ∼70 million galaxies, which will make it the largest radio galaxy survey so far.

2.2 SKA

The SKA is an international multipurpose next-generation radio interferometer that will be built in phases (SKA1 and SKA2) in the Southern hemisphere in South Africa and Australia; it will cover a frequency range of 350 MHz–15 GHz, have a central core of ∼200 km diameter, with three spiral arms spreading over 3000 km and a total collecting area of about 1 km². SKA is a facility that is planned to last for around 50 yr, and it will continuously scan the sky, producing a vast amount of data. Among many types of observations delivered by such instruments, we focus here on surveys that will detect individual galaxies, neglecting e.g. intensity mapping surveys. On longer time-scales, one can envisage significant improvements with respect to the instruments planned at the moment.

2.2.1 Radio continuum

Being unaffected by dust, radio continuum emissions can be used to detect SFGs and AGN up to very high redshift. Radio continuum surveys with the SKA will observe 30 000 deg² out to extremely high redshift, detecting ∼10⁸ galaxies in SKA1 and ∼10⁹ in SKA2.

In the top panel of Fig. 1, we show the predicted redshift distributions for continuum surveys. We show three different flux limits S_lim: (i) 50 μJy, corresponding to a 5σ detection for sources with the planned full EMU survey; (ii) an SKA-like 1μJy limit, and (iii) a futuristic distribution including all sources down to 1 nJy. In the legend, we also include the total number of objects per square degree, that corresponds to ≈8500, 135 000, 550 000, respectively.

Number of sources per deg2, as a function of redshift, for different flux limits. Top panel: radio continuum surveys; bottom panel: H i galaxy surveys. In the legend is the total number of objects. Distributions taken from the S3 simulation.

Figure 1.

Number of sources per deg², as a function of redshift, for different flux limits. Top panel: radio continuum surveys; bottom panel: H i galaxy surveys. In the legend is the total number of objects. Distributions taken from the S³ simulation.

Open in new tab Download slide

2.2.2 H i

While current H i galaxy surveys are not competitive with wide optical ones, technological advancements that will be implemented in the SKA will allow for dramatically faster survey speeds, making it possible to map the galaxy distribution out to high redshifts over large areas, therefore enabling measurements of ultra-large scales. Once the full SKA2 will be in place, it will provide what has been called the ‘billion galaxy survey’, that will be the biggest spectroscopic galaxy survey to date, detecting ∼10⁹ galaxies over 30 000 deg² out to z ∼ 2.

In the lower panel of Fig. 1, we plot the predicted redshift distributions for H i surveys. Again, we show three different cuts in sensitivity: (i) 5 μJy, corresponding roughly to the planned sensitivity of the SKA2 galaxy survey, (ii) a more optimistic 1 μJy, and once again (iii) a futuristic distribution including sources down to 1 nJy.

In order to keep our results as general as possible, we define surveys in terms of full sky surveys with the above flux limits. The two cases of S_lim = 1 nJy are shown as a proof of principle of what very futuristic surveys could in principle achieve. In addition, in order to investigate what can be done in the future (and possibly helping the planning of future instruments), we will in some cases study what instrument specifications would allow specific measurements.

2.2.3 Bias

It is necessary to model how biased the observed sources are in relation to the underlying structures. On large scales, we assume that the two-point correlation function can be written as (Matarrese et al. 1997):

\begin{equation} \xi (r,z)=b^{2}(M_{\rm eff},z)\xi _{\rm DM}(r,z) \,, \end{equation}

(1)

where ξ is the observed galaxy correlation, b is the bias, M_eff represents the effective mass of dark matter haloes in which sources reside and ξ_DM is the correlation function of dark matter. For the purposes of this paper, we use the bias in the S³ simulation for each galaxy population, which is computed assigning each population a dark matter halo mass. This dark matter halo mass is chosen to reflect the large-scale clustering found by observations.

The S³ simulation provides us with a source catalogue where sources are identified by type; each of these has a different prescription for the bias, as described in Wilman et al. (2008). We use the models of Raccanelli et al. 2012 (for continuum surveys) and of Santos et al. 2015 (for H i surveys) to assign the bias to sources at different flux limits. In Fig. 2, we show an example of the bias used for continuum and H i galaxy surveys with a flux limit of 10 μJy.

Figure 2.

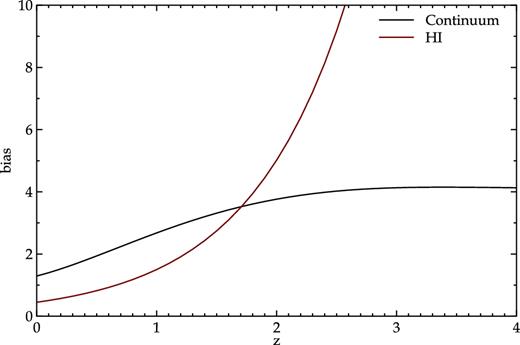
Bias for the radio continuum (black) and H i (red) galaxy surveys for an example flux limit of 10 μJy.

Open in new tab Download slide

3 GALAXY–GW CROSS-CORRELATIONS

One of the most used observables in the analysis of galaxy surveys is the galaxy power spectrum (or correlation functions). It is possible to extract a trove of information from radial and angular correlations (see e.g. Raccanelli et al. 2013, 2015b, 2016d), both by auto-correlating galaxies and by cross-correlating galaxies from different galaxy surveys (see e.g. Bacon et al. 2015) or with other observables, such as CMB temperature maps (see e.g. Bertacca et al. 2011; Raccanelli et al. 2015a). A summary of cosmological measurements from auto- and cross-correlations using radio continuum surveys can be found in Raccanelli et al. (2012).

In this section, we focus on cross-correlations of radio galaxy with GW maps, both by correlating samples in the same redshift range to investigate properties of BBH mergers, and by looking at radial cross-correlations in different redshift bins, in order to detect the lensing of GWs by foreground galaxies, and use this measurement to constrain models that explain the cosmic acceleration.

In Section 3.1, we briefly summarize the methodology for determining the nature of BBH progenitors, presented in Raccanelli et al. (2016c), and present updated forecasts.

Radial cross-correlations can be used to test models of dark energy and modified gravity, as first suggested by Cutler & Holz (2009) and then further studied in Camera & Nishizawa (2013); in Section 3.2, we will analyse this technique in the context of radio surveys correlated with BBH mergers.

3.1 Angular cross-correlations

The angular cross-correlation of galaxy catalogues with the GW maps is a natural way to investigate properties of the progenitors of compact objects whose mergers give rise to the GWs detected by laser interferometers, such as the hypothesis that BBH trace matter inhomogeneities (Namikawa et al. 2016a), or to constrain the distance–redshift relation (Oguri 2016).

In a similar way, Raccanelli et al. (2016c) recently suggested that the cross-correlation of star-forming galaxies (SFG) with GW maps can constrain the cosmological scenario in which the dark matter is comprised of primordial black holes (PBHs).

PBHs were first studied in Zel'dovich & Novikov (1967); Hawking (1971); Carr & Hawking (1974), and a vast literature on the topic was then produced. The possibility that they could make up the dark matter was first investigated in Garcia-Bellido, Linde & Wands (1996); Nakamura et al. (1997). However, these models were predicting PBHs of relatively small masses (∼1 M_⊙), that were subsequently ruled out by microlensing experiments (Wyrzykowski et al. 2011).

Recently, the LIGO detection of the merger of BBHs of larger masses (∼20–30 M_⊙) suggested that these objects might be quite common. Interestingly enough, the combination of observational constraints from microlensing and disruption of wide binaries (Wyrzykowski et al. 2011; Monroy-Rodríguez & Allen 2014) rule out the possibility of PBHs as DM for BHs with masses below ∼10 M_⊙ and above ∼80 M_⊙, but leave open the window in between.³

Therefore, Bird et al. (2016) suggested that PBHs of 30 M_⊙ comprise the dark matter; other suggestions including models with a wider mass distribution have been then studied in Clesse & García-Bellido (2017); Sasaki et al. (2016); for a recent more general review on PBHs as DM, see Carr, Kuhnel & Sandstad (2016). In addition, calculations of the formation of binary systems of such objects and their merger rate overlaps with estimates based on the first aLIGO observations. Given the ongoing difficulty in detecting weakly interacting massive particles, this model recently attracted a lot of attention and it is therefore important to develop methods to test it, and more generally determine the nature of BBH progenitors.

In this work, we follow the same formalism of Raccanelli et al. (2016c), but using an updated (including the most recent LIGO data) merger rate of 1–10 Gpc⁻³ yr⁻¹, and a wider redshift range, with |$z_{\rm max}^{\rm H\,{\small i}}=3$| and |$z_{\rm max}^{\rm cont}=5$|⁠, for H i and continuum radio surveys, respectively.

We use number count measurements in order to measure the correlation between the host haloes of BBH mergers and galaxies. We consider angular power spectra C_ℓ, that can be calculated from the underlying 3D matter power spectrum by using (see e.g. Raccanelli et al. 2008; Pullen et al. 2013):

\begin{eqnarray} C_{\ell }^{XY}(z,z^{\prime }) &=& \left\langle a^X_{\ell m}(z) a^{Y\,^*}_{\ell m}(z^{\prime }) \right\rangle \nonumber \\ &=& r \int \frac{4\pi \mathrm{d}k}{k} \Delta ^2(k) W_{\ell }^X(k, z) W_{\ell }^Y(k, z^{\prime }) \,, \end{eqnarray}

(2)

where |$W_{\ell }^{\lbrace X,Y\rbrace }$| are the source distribution window functions for the different observables (here X and Y stand for galaxies and GWs), Δ²(k) is the dimensionless matter power spectrum today and r is a cross-correlation coefficient.

The window function for the number count distributions can be written as (see e.g. Cabre et al. 2007; Raccanelli et al. 2008):

\begin{equation} W_{\ell }^X(k) = \int \frac{{\rm d} N_X(z)}{{\rm d}z} b_X(z) j_{\ell }[k\chi (z)] \mathrm{d}z \,, \end{equation}

(3)

where dN_X(z)/dz is the redshift distribution of the species X; b_X(z) is the bias that relates the observed correlation function to the underlying matter distribution; j_ℓ(x) is the spherical Bessel function of order ℓ, and χ(z) is the comoving distance.

For our galaxy catalogue, we assume the redshift distributions of Section 2; as for GW events, their number can be estimated by

\begin{equation} \frac{{\rm d} N_{GW}(z)}{{\rm d}z} \approx \mathcal {R}(z) \tau _{\rm obs} \frac{4\pi \chi ^2(z)}{(1+z)H(z)} \,, \end{equation}

(4)

where |$\mathcal {R}(z)$| is the redshift-dependent merger rate, τ_obs is the observation time and H(z) is the Hubble parameter. The errors in the auto- and cross-correlations are given by (see e.g. Cabre et al. 2007):

\begin{equation} \sigma _{C_{\ell }^{\rm X\,X}} = \sqrt {\frac{2\left(C_{\ell }^{\rm X\,X}+ \frac{1}{\bar{n}_X}\right)^2}{(2\ell +1)f_{\rm sky}}} \,, \end{equation}

(5)

and:

\begin{equation} \sigma _{C_{\ell }^{\rm X\,Y}} = \sqrt {\frac{\left(C_{\ell }^{\rm X\,Y}\right)^2 + \left[ \left( C_{\ell }^{XX} + \frac{1}{\bar{n}_X} \right) \left(C_{\ell }^{\rm Y \, Y}+ \frac{1}{\bar{n}_{\rm Y}} \right)\right]}{(2\ell +1)f_{\rm sky}}} , \end{equation}

(6)

where f_sky is the fraction of the sky observed and |$\bar{n}_{\rm X}$| is the average number of sources per steradian, in the bin considered, of the species X.

A key element to determine the nature of the progenitors of BH–BH mergers is represented by the value of the halo bias of the mergers’ hosts. While we expect that mergers of objects at the endpoint of stellar evolution will be hosted by galaxies that contain the majority of stars, and therefore be hosted in haloes of ∼10^11 − 12 M_⊙, almost all mergers of PBH binaries would happen in haloes of <10⁶ M_⊙, as shown in Bird et al. (2016). Crucially, these two types of haloes will have very different values of the bias. In particular, we assume that galaxies that host stellar GW binaries have similar properties of the SFG galaxy sample. Hence, we assume that |$b^{\rm Stellar}_{GW} = b_{\rm SFG}$|⁠, taking its redshift dependence as in Ferramacho et al. (2014). On the other hand, the bias of the small haloes that host most of the PBH mergers is expected to be ≲0.5, roughly constant with redshift, within our considered range (Mo & White 1996). Hence, considering that the bias of SFGs is predicted to be b(z) > 1.4, we set, for the threshold granting a detection, Δ_b = b_SFG − b_GW ≳ 1; this value should in reality increase with redshift, making our choice conservative.

It is worth noting that this scenario can be also tested by using the eccentricity of the binaries’ orbits before merging (Cholis et al. 2016); other ways to constrain properties of BBH mergers can be found in e.g. Kushnir et al. (2016), Stone, Metzger & Haiman (2017).

To predict the precision with which one can test models for the nature of the BBH progenitors, we consider the effective correlation amplitude, A_c ≡ r × b_GW, where r is the cross-correlation coefficient of equation (2). The cross-correlation coefficient r parametrizes the extent to which two biased tracers of the matter field are correlated (Tegmark & Peebles 1998). This factor accounts for the fact that the two sources are not necessarily correlated, and its value ranges from 0 (totally uncorrelated) to 1 (perfectly correlated). In this context, an example could be the following: if sources of GW are astrophysical, for example coming from globular clusters, they would be originated in SFGs. However, if for any dynamical process they are ejected out of their host galaxy, then the correlation coefficient would be equal to the fraction of remaining merging binaries. This effect is not important unless very high angular resolution is achievable. However, given that this number is also completely degenerate with the other amplitudes, we will constrain the combined quantity A_c defined above.

Given the specifications of the proposed future surveys, we forecast the precision in our measurements using the Fisher matrix formalism (Fisher 1935; Tegmark et al. 1998):

\begin{equation} F_{\alpha \beta } = \sum _{\ell } \frac{\mathrm{\partial} C_\ell }{\mathrm{\partial} \vartheta _\alpha } \frac{\mathrm{\partial} C_\ell }{\mathrm{\partial} \vartheta _\beta } {\sigma _{C_\ell }^{-2}} \,, \end{equation}

(7)

where ϑ_{α, β} are the parameters one wants to measure, the derivatives of the power spectra C_ℓ are evaluated at fiducial values |$\bar{\vartheta }_{\alpha }$| and |$\sigma _{C_\ell }$| are measurement errors in the power spectra.

Given that an important source of uncertainty is given by the galaxy bias, we compute a 2 × 2 Fisher matrix for the parameters {A_c, b_g}, using a prior on the galaxy bias corresponding to a precision of 1 per cent in its measurement; measurements of the bias can be obtained either by fitting the amplitude of the auto-correlation of galaxy bias, or by other probes such as measurements of the bispectrum (Gil-Marín et al. 2015) or the cross-correlation with CMB-lensing (see e.g. Vallinotto 2012). Moreover, we assume the bias to be scale-independent and limit our analysis to linear scales.

We consider four different configurations of GW detectors, all assumed to observe the full sky. Raccanelli et al. (2016c) showed that the minimum angular scale to which the GW events can be localized plays an important role in improving the constraints on the galaxy–GW cross-correlation, as does the maximum redshift observable. An accurate determination of the value of ℓ_max(=180°/θ) for all experiments and events is beyond the scope of this paper. Therefore, based on e.g. Finn (2010), Namikawa, Nishizawa & Taruya (2016b), we choose the specifications as shown in Table 1.

Table 1.

Open in new tab

Specifications of GW detectors used in this paper. For cross-correlations with the Einstein Telescope, we use z_max = 2 for H i and z_max = 5 for continuum radio surveys.

Experiment	ℓ_max	z_max
aLIGO + VIRGO	20	0.75
LIGO-net	50	1.0
Einstein Telescope	100	5 (2)
Einstein Telescope binned	100	5 (2)

Table 1.

Open in new tab

Specifications of GW detectors used in this paper. For cross-correlations with the Einstein Telescope, we use z_max = 2 for H i and z_max = 5 for continuum radio surveys.

Experiment	ℓ_max	z_max
aLIGO + VIRGO	20	0.75
LIGO-net	50	1.0
Einstein Telescope	100	5 (2)
Einstein Telescope binned	100	5 (2)

When correlating GW maps from the Einstein Telescope (ET), we use z_max = 2 for H i surveys and z_max = 5 for continuum surveys; for the continuum case, we assume we can bin sources into bins of width Δ_z = 1, at the price of discarding 90 per cent of the sources (see Kovetz et al. 2016 for details). Considering the difficulty in determining a very precise redshift of GW events at high redshift, we take the safe assumption of having bins of Δ_z = 1 also for the H i case.

In Fig. 3, we show our predicted constraints. We show forecasts for the different GW interferometers setups, after 5 yr of collecting data, correlated with radio surveys. Vertical bars show the constraints when varying the merger rate |$\mathcal {R}\in [1,10]$|⁠. Horizontal lines show the required precision in measurements of A_c to test the cases where the fraction of DM made of PBHs, f_PBH, is <1. In the cases of aLIGO and the expanded LIGO-net, correlating with continuum or H i surveys will not make a difference. When using ET data, on the other hand, the maximum redshift used for galaxy surveys will make a difference, thus we show separate results for the correlations GW-radio galaxy for H i and continuum.

Figure 3.

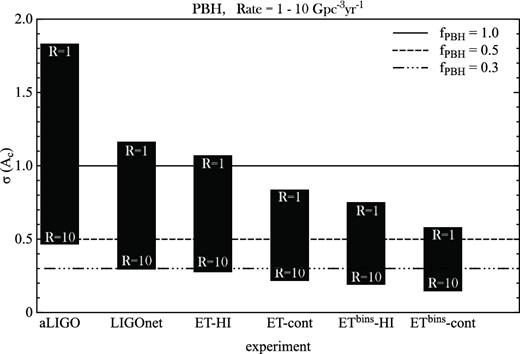
Forecast errors on the cross-correlation amplitude, A_c, for different fiducial experiment sets and varying merger rates. Each column corresponds to a GW detector experiment, for merger rates from 1 to 10 Gpc⁻³yr⁻¹. The horizontal lines show the expected difference in the cross-correlation between primordial and stellar binary progenitors, for three different values of the percentage of DM made of PBHs.

Open in new tab Download slide

As one can see, already in the case of aLIGO, if the merger rate will be towards the largest limits currently allowed by observations, one should be able to detect the signature of PBHs as DM within a few years. In the more futuristic cases of correlations of ET maps with binned continuum radio surveys, we can expect to have a few σ detection in the case of f_PBH = 1, or detect the effects of a small fraction of DM consisting of PBHs.

3.2 Cosmic magnification

Gravitational lensing causes light rays to be deflected by large-scale structures along the line of sight, introducing distortions in the observed images of distant sources (Turner, Ostriker & Gott 1984). Even though surface brightness is conserved, the sources behind a lens are magnified in size, hence inducing an increase in the total observed luminosity of a source. Therefore, sources that are just below the flux threshold of a given survey will be magnified and become detectable, and so the observed number density of sources is increased. On the other hand, lensing causes the stretching of the observed field of view, leading to a dilution of the number density. The net result of these two competing effects depends on the slope of the source number count as a function of the sources luminosity, and the effect is called magnification bias. Observationally, we can detect the effects of magnification by cross-correlating two galaxy surveys with disjoint redshift distributions, as the observed number counts can be modified as explained above, and the intrinsic galaxy clustering is negligible for long radial correlations. The implications of this effect for the observed galaxy angular correlation function were investigated in e.g. Villumsen, Freudling & da Costa (1997), Kaiser (1998). Cosmic magnification has been suggested as a probe for cosmology by Matsubara (2000) and has been subsequently studied in a variety of works (see e.g. Hui, Gaztañaga & Loverde 2007; Loverde, Hui & Gaztañaga 2008). Cosmic magnification was first detected by Scranton et al. (2005), who cross-correlated foreground SDSS LRGs with a background of SDSS quasars, and then e.g. in the Canada–France–Hawaii-Telescope Legacy Survey (Hildebrandt, van Waerbeke & Erben 2009), and Herschel (Wang et al. 2011).

The effect of cosmic magnification has been recently investigated in even more detail in the context of large-scale contributions to the observed galaxy correlation (see e.g. Montanari & Durrer 2015; Cardona et al. 2016; Raccanelli et al. 2016b,d). Lensing of GWs, in the case of NS–NS mergers, where the source has optical counterparts, has been considered as a probe to constrain models for cosmic acceleration (Cutler & Holz 2009; Camera & Nishizawa 2013), showing very promising results for future GW detectors. Gravitational lensing also affects the astrophysical parameter estimation of the binary mergers (see e.g. Laguna et al. 2010; Bertacca et al. 2017; Dai & Venumadhav 2017; Dai, Venumadhav & Sigurdson 2017), but this will not affect our study, at least at a first order.

Here, we investigate the possibility to cross-correlate foreground galaxies that act as lenses with a background of GWs. By taking redshift bins sufficiently wide and separated, there will be no need to have a precise estimation of the redshift of BH–BH mergers. Such measurement will allow additional and independent tests of general relativity and dark energy models, in a way that is independent from current tests using galaxy surveys alone or in combination with the CMB, hence providing a very interesting measurement.

Magnification bias introduces a correction to the observed galaxy overdensity, which now becomes the sum of the intrinsic galaxy overdensity and the magnification bias correction, δ_obs = δ_g + δ_μ. The magnification bias correction is given by

\begin{eqnarray} \delta _\mu = (5s - 2) \kappa \,, \end{eqnarray}

(8)

where κ is the lensing convergence:

\begin{eqnarray} \kappa (\chi ,{\bf \theta}) = \int _0^\chi \mathrm{d}\chi ^{\prime } {\chi ^{\prime }(\chi -\chi ^{\prime }) \over \chi } \nabla ^2_\perp (\Phi +\Psi ) \, ; \end{eqnarray}

(9)

here Φ, Ψ are the gravitational potentials and |$\nabla ^2_\perp$| is the 2D Laplacian in the transverse direction. The magnification bias s is defined as

\begin{eqnarray} s = {{\rm d} {\,\rm log} N_{|_{< M}} \over {\rm d} M}\bigg |_{M_{\rm lim}} \,, \end{eqnarray}

(10)

where M_lim is the magnitude (or flux) limit of the survey and |$N_{|_{< M}}$| is the number count for galaxies brighter than a magnitude (or flux) M.

Thus, cosmic magnification changes the number count of sources detected at a given redshift and fixed magnitude limit as

\begin{equation} n^{\rm obs}(z) = n_g(z) [1 + (5s-2) \kappa ] \,, \end{equation}

(11)

where n^obs, n_g are the observed and intrinsic number of sources, respectively, s is the magnification bias and κ is the convergence.

We will make use again of the same formalism of equation (2), but we will correlate bins at different redshifts, and compute the uncertainty using equation (6). We use the predicted values of magnification bias as in Wilman et al. (2008), Camera, Maartens & Santos (2015), for continuum and H i, respectively.

3.2.1 Cosmological model constraints

While in principle cosmic magnification and galaxy clustering depend (and so can be used to test on) several cosmological parameters, here we focus on tests of models that explain cosmic acceleration. To explain the accelerated expansion of the universe, it is useful to look at two possibilities, which can be easily described by looking at possible modifications of Einstein's field equations. One can introduce a dark energy component and so modify the right-hand side of the Einstein's equations, or the geometric (left) side of them:

\begin{eqnarray} G_{\mu \nu }=& \, T_{\mu \nu }+T_{\mu \nu }^{\rm de}\,, \,\,\,\,\,\,\, \end{eqnarray}

(12)

\begin{eqnarray} G_{\mu \nu }+G_{\mu \nu }^{\rm MG}=& \, T_{\mu \nu }\,. \end{eqnarray}

(13)

This corresponds, in the first case, to the introduction of some contribution to the energy-momentum tensor, usually in the form of a scalar field, and such a component is called dark energy. The second alternative is based on modifications to general relativity that lead to a modification of gravity on the largest scales and thus to acceleration, a scenario often called dark gravity or modified gravity. Differentiating between the dark energy and the modified gravity scenarios is one of the main challenges cosmologists are facing today.

Dynamical dark energy. Assuming the validity of general relativity at all scales, in order to explain cosmic acceleration it is necessary to implement the modifications of equation (12); the simplest of such modifications is the introduction of a cosmological constant, as first suggested by Zel'dovich (1968), that can be interpreted as vacuum energy. A more general model, sometimes called dynamical dark energy, generalizes the cosmological constant ones by considering the time evolution of its equation of state, w = p/ϱ, where p and ϱ are the pressure and energy density of the dark energy fluid; for a cosmological constant, w = −1. In this work, we adopt the widely used parametrization (Linder 2003):

\begin{eqnarray} w(a) = w_0 + w_a (1-a) \,. \end{eqnarray}

(14)

In this section, we predict the precision in measurements of the pair {w₀, w_a} from the radial correlation of (foreground) radio source number counts with background maps of GWs.

Modified gravity. An intriguing alternative to dark energy for the explanation of the accelerated expansion of the universe is the ‘modified gravity’ approach (see e.g. Durrer & Maartens 2008), which investigates possible modifications, on large scales, of gravity. In these models, cosmic acceleration can be obtained by modifying the Einstein–Hilbert action, hence evading the need of a dark energy component in the Universe. Referring now to equation (13), in this case we add a term to the geometric side of Einstein's equations. Modified gravity models can mimic the ΛCDM model at the level of background expansion, but in general they predict different dynamics for the growth of cosmic structures. Here, we consider scalar metric perturbations around an FRW background for which the line element in the conformal Newtonian gauge is

\begin{equation} {\rm d}s^2=-a^2(\tau )\left[\left(1+2\Psi \right){\rm d}\tau ^2-\left(1-2\Phi \right) {\rm d}\boldsymbol {x}^2\right] , \end{equation}

(15)

where the gravitational potentials Φ and Ψ are functions of time and space. We use the following parametrization to describe the relations specifying how the metric perturbations relate to each other, and how they are sourced by the perturbations of the energy-momentum tensor:

\begin{eqnarray} \frac{\Phi }{\Psi }=\eta ({\bf \bar{X}}), \end{eqnarray}

(16)

\begin{eqnarray} \Psi =\frac{-4\pi G a^2 \mu ({\bf \bar{X}}) \varrho \, \delta }{k^2} \,, \end{eqnarray}

(17)

where η and μ are two functions encoding the modifications of gravity, depending in principle on time and scale, |${\bf \bar{X}}=\lbrace z, k\rbrace$|⁠. We will consider a simple approximation where we assume μ = η = 1 at early times, with a transition to some other values at late times. This is natural in the existing models of modified gravity that aim to explain the late-time acceleration, where departures from GR occur at around the present-day horizon scales. Also, the success in explaining CMB physics relies on GR being valid at high redshifts. To model the time evolution of μ and η, we use the following functional forms to describe the transition from unity to the constants μ₀ and η₀:

\begin{eqnarray} \eta (z)=\frac{1-\eta _0}{2}\left[1+{\rm tanh}\left(\frac{z-z_s}{\Delta z}\right)\right]+\eta _0 \,, \end{eqnarray}

(18)

\begin{eqnarray} \mu (z)=\frac{1-\mu _0}{2}\left[1+{\rm tanh}\left(\frac{z-z_s}{\Delta z}\right)\right]+\mu _0 \,. \end{eqnarray}

(19)

where z_s denotes the threshold redshift where gravity starts to deviate from GR, that we fix at z = 6, and μ₀, η₀ are free parameters; following Zhao & Zhang (2010), we fix the transition width Δz to be 0.05. Other more complicated models including scale-dependent MG have been proposed and investigated, but forecasts for a variety of models is beyond the scope of this paper.

When predicting constraints on cosmic acceleration models, we parametrize our cosmology using a vector of parameters:

\begin{equation} \Theta {\equiv} {\aleph, \beth}, \end{equation}

(20)

where ℵ ∈ {w₀, η₀}, ℶ ∈ {w_a, μ₀} are the parameters we want to measure. We use a modified version of the class⁴ (Lesgourgues 2011) code to calculate our observables, and equation (7) to calculate the Fisher matrices using the ΛCDM+GR as a fiducial model in each case.

In Fig. 4, we show forecasts of the constraints on parameters for the dynamical dark energy model. We plot constraints as a function of the minimum scale used ℓ_max and for two different values of the BBH merger rate R = 50, 150.

Figure 4.

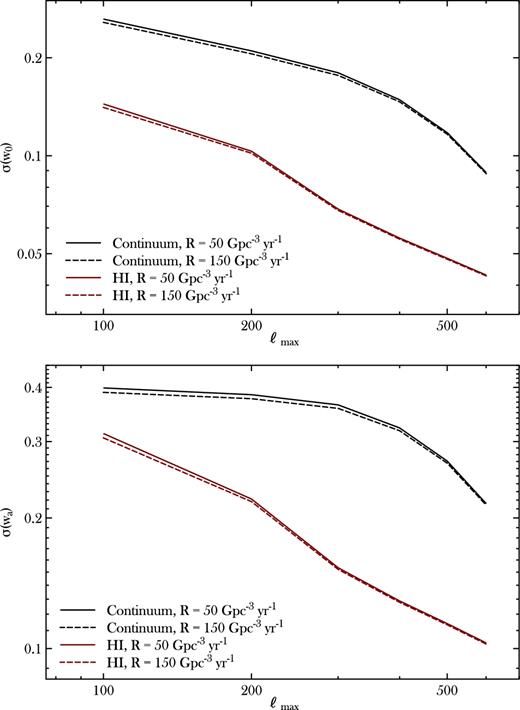
Predicted constraints on dynamical dark energy parameters, as a function of the minimum scale used ℓ_max and for two different values of the BBH merger rate R. Black lines show forecasts for continuum surveys, red lines for H i spectroscopic ones.

Open in new tab Download slide

We use the cross-correlation of foreground galaxies that act as lenses for background GWs. The main shot noise contribution comes from the GW number counts, therefore we select a larger bin for them than the one(s) for galaxies. In the continuum case, given that redshift information will allow only wide bins in z, we correlate a 0 < z < 1 bin of galaxies with a 1 < z < 3 bin of GWs. We show the predicted errors on dark energy parameters for this case with black lines. In the case of the H i surveys, high-precision redshifts will be available, therefore we cross-correlate galaxies from four z-bins with Δz = 0.25 in the range 0 < z < 1, with a background of GWs at 1 < z < 3. Results for this case are shown with red lines.

Results are virtually independent on the flux limits, as results are shot noise limited from the GW bin but will not change once n_g in equation (6) is reasonably large.

As expected, the constraining power increases in the case of more bins (and so more correlations); moreover, increasing the maximum multipole used considerably improves the constraining power of this observable, as lensing is more powerful on small scales.

In Fig. 5, we show the same predictions but for the modified gravity parameters of equation (18)–(19); results and considerations about what part of the experiment parameter space increases the constraining power are similar.

Figure 5.

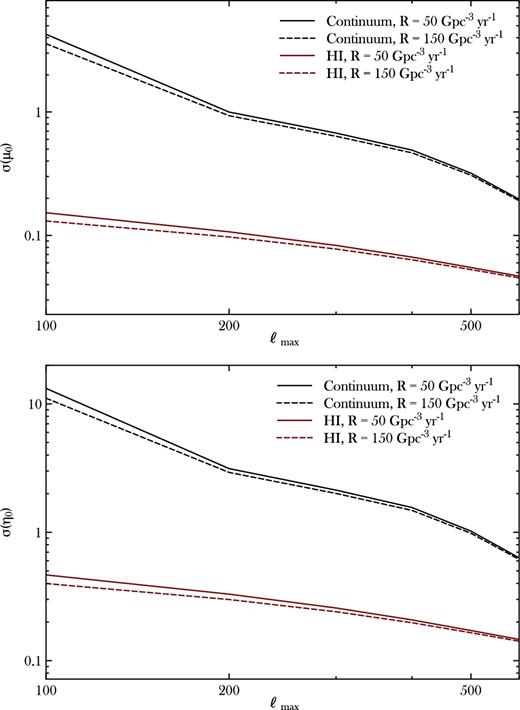
Same as Fig. 4 but for modified gravity parameters.

Open in new tab Download slide

For dark energy parameters, when using H i surveys, in the case of a conservative ℓ_max ≈ 100, constraints will be somewhat comparable to current ones, while in the optimistic case of ℓ_max = 600 they will be competitive with current best constraints (Samushia, Percival & Raccanelli 2012; Samushia et al. 2013, 2014; Alam et al. 2016) and even future ones from the combination of CMB and redshift-space distortions (Raccanelli et al. 2015b).

The situation is similar but even more positive for the modified gravity constraints. Our results show that, again, H i surveys will provide better constraints than continuum ones, given the larger number of correlations measured (and small shot noise even when bins are smaller, due to the very large number density of future radio surveys). Even when using ℓ_max = 100, measurements of lensing of GWs from radio galaxies could provide constraints stronger than current Planck (Planck Collaboration XIV 2016) and competitive with future (Zhao et al. 2015) limits. However, in this case, increasing ℓ_max would allow an improvement in the constraining power that is significative but not dramatic (mostly because in these models, deviations from GR are largest at large scales). Nevertheless, these results show that radial cross-correlations galaxy–GWs can be a very powerful instrument for testing deviations from Einstein's GR.

In any case, any measurements resulting from the cross-correlation galaxy–GW and lensing of GWs will represent a very important, independent and complementary check to results obtained with e.g. galaxy surveys or CMB.

It is important to note that the constraints presented here are purely indicative, and it is likely that a careful optimization could improve them. Possible ways to increase the constraining power can come from a targeted choice of number, width and redshift centre of the bins, the choice of specific galaxy populations with an optimal redshift distribution and bias; additionally, the multitracer technique would improve the constraints by a factor of a few. A detailed investigation of that is however beyond the scope of this paper.

4 GW BACKGROUND

A stochastic gravitational wave background (SGWB) is a key prediction of inflationary cosmology (see e.g. Maggiore 2000), so that its detection is one of the main goals of astrophysics. This can be sought either via direct or indirect measurements, as the presence of the SGWB would have left imprints on different observables.

We can divide the effects of an SGWB on cosmological observables into early- and late-time effects. Early Universe effects include modifications to the BBN process, in particular Deuterium abundance (Pagano, Salvati & Melchiorri 2016) and imprints on the CMB: both temperature and polarization of CMB photons are affected by the SGWB, in particular the formation of a B-mode pattern in the polarization (Kamionkowski, Kosowsky & Stebbins 1997; Seljak & Zaldarriaga 1997; Polnarev, Miller & Keating 2008).

Regarding late-time effects, the presence of a GW background modifies the statistics of primordial curvature perturbations and creates tidal effects that affect clustering of structures (Masui & Pen 2010; Schmidt & Jeong 2012a; Dai, Jeong & Kamionkowski 2013; Schmidt, Pajer & Zaldarriaga 2014). Moreover, the presence of tensor perturbations causes projection effects that change the observed matter density field (Jeong & Schmidt 2012) and causes a distortion of galaxy shapes (Dodelson et al. 2003; Dodelson 2010; Schmidt & Jeong 2012a).

Furthermore, GWs have an effect on local light signals propagating from closer objects; this effect could be captured by pulsar timing array observations (see e.g. Joshi 2013).

A measurement and characterization of the SGWB power spectrum will allow tests of early universe models (even though it has been seen as a possible experimental confirmation for inflation, primordial GWs can also be generated in alternative models such as ekpyrotic models (Ben-Dayan 2016; Ito & Soda 2016)), and constrain fundamental parameters such as the tensor-to-scalar ratio r (Smith, Kamionkowski & Cooray 2006a, 2008). In principle, however, the GW background could be sourced by a variety of events, including not only GWs produced during inflation, but also high-z mergers of compact objects (Regimbau & Mandic 2008; Regimbau 2011; Zhu et al. 2011; Cholis 2016; Dvorkin et al. 2016a,b; Mandic, Bird & Cholis 2016), the non-linear gravitational collapse of DM haloes (Carbone, Baccigalupi & Matarrese 2006), and possibly other phenomena, depending on details of the cosmological model (for a recent review, see Guzzetti et al. 2016).

Therefore, several theoretical and experimental efforts are underway for the direct and indirect measurement of the SGWB. The main observables that are used to try to detect the SGWB are (i) direct detection of GWs; (ii) B-modes of polarization in the CMB; (iii) pulsar timing array experiments; (iv) the anisotropy in the galaxy correlation function; (v) correlations of weak gravitational lensing; (vi) intensity mapping experiments probing the dark ages.

The direct detection of the SGWB will be attempted by a number of ground-based experiments that have been proposed, starting with a planned expansion of the LIGO network, with new LIGO nodes in India (IndIGO; Unnikrishnan 2013) and Japan (KAGRA; Aso et al. 2013). Future GW detectors include the ET (Punturo et al. 2010) and the space instrument eLISA (Klein et al. 2016). However, these instruments could detect the SGWB only in the case of non-single-field slow-roll inflation models, that predict a blue inflationary power spectrum (Guzzetti et al. 2016). In order to detect a scale-invariant inflationary power spectrum, more futuristic instruments (Crowder & Cornish 2005), such as the planned DECI-Hertz Interferometer Gravitational wave Observatory (DECIGO; Kawamura et al. 2011) and BBO (Corbin & Cornish 2006), designed primarily to detect the primordial SGWB, are required (Moore, Cole & Berry 2015).

As for the indirect detection, several ground-, balloon- and space-based CMB polarization experiments are under construction or have been proposed (Crill et al. 2008; Bouchet et al. 2011; Kogut et al. 2011; Eimer et al. 2012; Matsumura et al. 2013; Ade et al. 2014; André et al. 2014; Calabrese et al. 2014), and pulsar timing array experiments are underway (McLaughlin 2013; Manchester et al. 2013; Janssen et al. 2015; Lentati et al. 2015).

The strength of the SGWB is parametrized by their energy density per unit logarithmic frequency, Ω_GW(f):

\begin{equation} \Omega _{\rm GW} = \frac{1}{\rho _{\rm c}}\frac{\mathrm{d}\rho _{\rm GW}}{\mathrm{d\,ln} f}, \end{equation}

(21)

where ρ_GW is the gravitational energy density and ρ_c = 3H²/8πG is the critical energy density of the Universe. Current data provide bounds on its amplitude and spectral tilt.

Current observational upper limits on Ω_GW include (i) the constraint Ω_GW ≲ 10⁻¹³ for 10⁻¹⁷Hz ≲ f ≲ 10⁻¹⁶ Hz from large angular scale fluctuations in the cosmic microwave background temperature (Buonanno 2007); (ii) the combination of cosmological nucleosynthesis and cosmic microwave background constraint gives Ω_GW(f) ≲ 10⁻⁵ for f ≳ 10⁻¹⁵ Hz (Smith, Pierpaoli & Kamionkowski 2006b; Pagano, Salvati & Melchiorri 2016); (iii) the pulsar timing limit provided by EPTA, Ω_GW < 1.2 × 10⁻⁹ for f = 2.8 × 10⁻⁹ Hz (Lentati et al. 2015); (iv) joint analysis of LIGO and Virgo provides an upper limit of Ω_GW < 5.6 × 10⁻⁶ for f ∼ 100 Hz (Aasi et al. 2014), and the most recent aLIGO analysis gave |$\Omega _{\rm GW} = 1.1_{-0.9}^{+2.7} \times 10^{-9}$| for f = 25 Hz (Abbott et al. 2016b) and Ω_GW < 1.7 × 10⁻⁷ for f = 20–85 Hz (Abbott et al. 2017); (v) limits from very long baseline interferometry radio astrometry of quasars of Ω_GW ≲ 10⁻¹ for 10⁻¹⁷ Hz ≲ f ≲ 10⁻⁹ Hz (Gwinn et al. 1997) and Ω_GW ≲ 4 × 10⁻³ for f ≲ 10⁻⁹ Hz (Titov, Lambert & Gontier 2011); (vi) Ω_GW ≲ 10⁻³ for 10⁻¹⁶ Hz ≲ f ≲ 10⁻¹⁰ Hz from the observed galaxy correlation function (Linder 1988). In Fig. 6, we show these constraints in a plot as an illustration.

Figure 6.

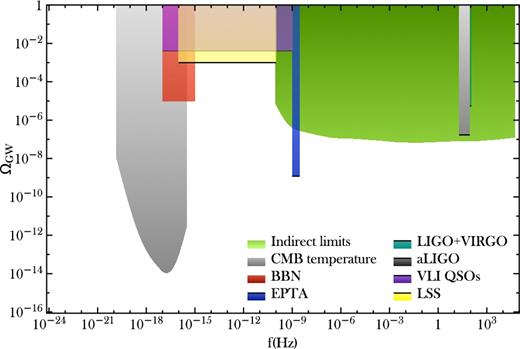
Current constraints on the stochastic GW background.

Open in new tab Download slide

From CMB data, the joint analysis of Planck, BICEP2 and Keck Array data provides an upper bound of r_0.05 < 0.09 at 95 per cent C.L. at frequencies f ∼ 10⁻¹⁷ Hz (Ade et al. 2016).

For more details on the SGWB, see the review articles Allen (1997); Maggiore (2000); Buonanno (2007), and more recently Guzzetti et al. (2016); for a recent review on the search of GWs from inflation using the CMB, see Kamionkowski & Kovetz (2016).

In the weak-field limit, where GWs can be described as space–time ripples propagating on a fixed background, one can write the Einstein equations in vacuum as (Guzzetti et al. 2016):

\begin{equation} \bar{G}_{\mu \nu }=\bar{R}_{\mu \nu }-\frac{1}{2}\bar{R}\bar{g}_{\mu \nu }=\left\langle R_{\mu \nu }^{\left(2\right)}\right\rangle -\frac{1}{2}\bar{g}_{\mu \nu }\langle R^{\left(2\right)}\rangle, \end{equation}

(22)

where the bar |$\bar{\,}$| indicates quantities evaluated at the background, and 〈...〉 indicates an average over several wavelengths.

This describes how the presence of GWs affects the background metric; following Misner, Thorne & Wheeler (1973), the stress-energy tensor of GWs is

\begin{equation} t_{\mu \nu }=\frac{1}{32\pi G}\langle \mathrm{\partial} _{\mu }h_{ij}\mathrm{\partial} _{\nu }h^{ij}\rangle , \end{equation}

(23)

and so the GW energy-density can be written as

\begin{equation} \rho _{\rm GW}=\frac{1}{32\pi G a^{2}}\langle h^{\prime }_{ij}\left({\bf x},\tau \right)h^{\prime ij}\left({\bf x},\tau \right)\rangle . \end{equation}

(24)

In this paper, we focus on effects of the SGWB on the LSS; a background of GWs will leave an imprint in the angular correlation of galaxies on large scales, and introduce correlations of galaxy shapes. However, LSS measurements will provide weaker constraints than the CMB. Realistically, CMB experiments will measure r, and if its value is not negligible (around the upper limit of current constraints), LSS could confirm or at least support those measurements.

4.1 Cosmometry

As suggested by Linder (1986); Braginsky et al. (1990); Kaiser & Jaffe (1997), a stochastic GW background causes the apparent positions of distant sources to fluctuate, with angular deflections of order the characteristic strain amplitude of the GWs, and these fluctuations may be detectable with high-precision astrometry. Estimates of the upper limits obtainable on the GW spectrum Ω_GW(f), at frequencies of order f ∼ 1 yr⁻¹ are available in literature, and they generally predict constraints comparable with the ones from pulsar timing (see e.g. Jaffe 2004; Book & Flanagan 2011).

In this paper, we extend those predictions to future radio surveys and try to understand what are the instrument requirements needed to make cosmological radio galaxy high-z astrometry, which we call ‘cosmometry’, competitive with other methods and possibly have a detection of the effects of an SGWB.

4.1.1 Effect of an SGWB on galaxy positions

The SGWB produces an apparent angular deflection |$\delta {\boldsymbol {n}}({\boldsymbol {n}},\tau )$| on the position of a source in the direction |${\boldsymbol {n}}$|⁠, given by (Pyne et al. 1996):

\begin{equation} \delta n^{i}(\tau ,{\boldsymbol {n}}) = \frac{n^i + p^i}{2 (1 + \boldsymbol {p}\cdot \boldsymbol {p})} h_{jk}(\tau ,{\bf 0}) n_j n_k - \frac{1}{2} h_{ij}(\tau ,{\bf 0}) n_j \,, \end{equation}

(25)

where |$\boldsymbol {p}$| is the direction of propagation of the GW.

The apparent angular deflection caused by such a GW background is a stationary, zero-mean, Gaussian random process. In this section, we follow the methodology suggested in Jaffe (2004) and Book & Flanagan (2011). The total power in angular fluctuations is then

\begin{equation} \left\langle \delta {\boldsymbol {n}}({\boldsymbol {n}},t)^2 \right\rangle = \frac{1}{4 \pi ^2} \int \mathrm{d}\ln f \left( \frac{H_0}{f} \right)^2 \Omega _{\rm GW}(f) \,. \end{equation}

(26)

Specifically, an SGWB will cause apparent angular deflections that are correlated over the sky and that vary randomly with time, with a rms deflection δ_rms(f) per unit logarithmic frequency interval of

\begin{equation} \delta _{\rm rms}(f) \approx h_{\rm rms}(f) \approx \frac{H_0}{f} \sqrt {\Omega _{\rm GW}(f)} \,. \end{equation}

(27)

By monitoring the position of sources in the sky with an angular accuracy of Δθ, over a time T, one could detect a proper motion of order ∼Δθ/T. For N sources, the correlated angular velocity detectable would scale as |$\sqrt {N}$|⁠. Therefore, assuming a flat GW spectrum, one should obtain an upper limit on Ω_GW of order (Pyne et al. 1996; Book & Flanagan 2011):

\begin{equation} \sigma _{\Omega _{\rm GW}} \approx \int _{f <T^{-1}} \mathrm{d} \ln f \frac{\Delta \theta ^2}{N T^2 H_0^2} \,\,\,. \end{equation}

(28)

In radio, using VLBI radio interferometry, the SKA could be able to localize sources to within ∼ 10μas (Fomalont & Reid 2004). With that precision, and using:

\begin{equation} \sigma _{\Omega _{\rm GW}} \approx \frac{4 \pi f_{\rm sky}\Delta \theta ^{2}}{N} \,, \end{equation}

(29)

it has been estimated that observing 10⁶ QSOs over a year, the SKA could set a limit of the order Ω_GW ≲ 10⁻⁶, for f ∼ 10⁻⁸Hz (Jaffe 2004).

Here, we investigate limits on Ω_GW that will be possible to set by using cosmometry from future radio surveys. In Figs 7 and 8, we show predicted upper limits on Ω_GW as a function of angular resolution, observing time and number of objects observed. We focus on GWs with a period of 1 year. We also indicate the SKA VLBI configuration in two different configurations, where we call SKAVLBI-1 a survey detecting 10⁷ objects and SKAVLBI-2 a survey detecting 10⁹ objects, in both cases with an angular resolution of 10 μarcsec and over 10 yr of observations. Different models of inflation predict different amplitude and scale dependence of the SGWB (see e.g. Guzzetti et al. 2016). As can be seen from Fig. 6, cosmometry constraints could be competitive with current ones, but it would be difficult to reach the single field slow-roll inflation prediction of ∼10⁻¹⁵. However, the background due to primordial or supermassive black hole binaries could be detected (see e.g. Abbott et al. 2017; Clesse & García-Bellido 2016).

Figure 7.

Predicted precision in the measurements of Ω_GW from cosmometry analyses, as a function of the number of objects and years of observation, assuming an angular resolution of 10 μarcsec. See text for the details about the assumed experiment.

Open in new tab Download slide

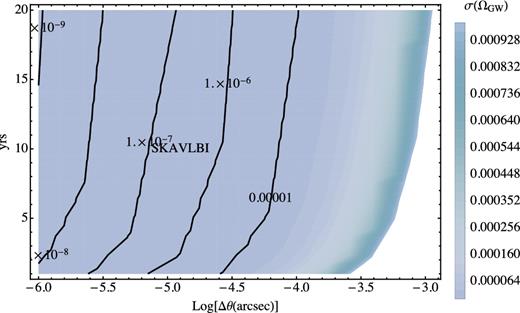
As in Fig. 7 but as a function of the angular resolution and years of observation, assuming 107 objects. See text for the details about the assumed experiment.

Figure 8.

As in Fig. 7 but as a function of the angular resolution and years of observation, assuming 10⁷ objects. See text for the details about the assumed experiment.

Open in new tab Download slide

We can see that, in order to detect the SGWB from changes in galaxy positions, extremely precise measurements will be needed. Even with a very optimistic SKA in VLBI configuration, a detection of GWs from inflation is virtually out of reach. However, configurations with baseline lengths up to 10 000 km in length are being considered (Paragi et al. 2015), therefore very precise measurements might be possible in a (relatively) near future. In any case, limits set with this methodology are complementary to the ones set by e.g. direct detection of GWs, making results from forthcoming instruments useful and interesting.

4.2 Cosmic rulers

In this section, we investigate the possibility of using LSS standard rulers to detect the effects of a background of GWs; we make use of the ‘cosmic rulers’ formalism (Schmidt & Jeong 2012b), and investigate if future radio surveys will be able to detect the SGWB by using either the anisotropy of the two-point galaxy correlation or galaxy ellipticities, as first suggested by Jeong & Schmidt (2012); Schmidt & Jeong (2012a). We will briefly review the methodology introduced in the above series of paper, that we will use to obtain our results, and then show forecasts for measurements that will be possible to obtain with future radio surveys. Note that, apart from a slightly different notation and some rearrangements, all the results here coincide with the ones in the cited ‘cosmic rulers’ series. For a direct translation between the two notations, one can compare Bertacca et al. (2012) with Jeong, Schmidt & Hirata (2012).

4.2.1 Galaxy clustering

In the context of a general relativistic description of the observed galaxy clustering (see e.g. Yoo, Fitzpatrick & Zaldarriaga 2009; Bertacca et al. 2012; Jeong, Schmidt & Hirata 2012), a series of effects need to be considered as corrections to the standard, Newtonian, formalism, which includes only scalar perturbations to the matter density field and redshift-space distortions (RSD). In a similar way, GWs (tensor perturbations) affect, on the largest scales, the clustering statistics via volume and magnification effects.

Differences in the effect of tensor perturbations from scalar ones were first noted in Kaiser & Jaffe (1997): in particular, tensor modes redshift away, so that their contribution to the clustering of LSS tracers is dominated by contributions close to the time of emission; instead, scalar perturbations grow, and the deflection is amplified by transverse modes (Jeong & Schmidt 2012).

GWs are waves in the transverse (∂ⁱh_ij) and traceless (⁠|$h^i_{\,i}$|⁠) components of the metric perturbation, defined in the FRW Universe in terms of the spatial components of the metric by g_ij = a²(δ_ij + 2h_ij).

We now compute the contribution of tensor perturbations to the observed galaxy clustering on large scales. We start by considering a spatially flat FRW background, consider only tensor modes, and we write the (perturbed) conformal metric as

\begin{equation} {\rm d}\bar{s}^2 = -{\rm d}\eta ^2 + \left(\delta _{ij}+h_{ij} \right) {\rm d}x^i{\rm d}x^j , \end{equation}

(30)

where η is the conformal time and h_ij is a metric perturbation that is transverse and traceless:

\begin{equation} h^i_{\, i} = 0 = (h_{ik})^{,i}. \end{equation}

(31)

This can be decomposed into Fourier modes of two polarization states:

\begin{eqnarray} h_{ij}(\boldsymbol {k}, \eta ) = e^+_{ij}(\hat{\boldsymbol {k}}) h^+(\boldsymbol {k},\eta ) + e^\times _{ij}(\hat{\boldsymbol {k}}) h^\times (\boldsymbol {k}, \eta ), \end{eqnarray}

(32)

where |$e^s_{ij}(\hat{\boldsymbol {k}})$|⁠, s = +, ×, are transverse (with respect to |$\hat{\boldsymbol {k}}$|⁠) and traceless polarization tensors. We assume both polarizations to be independent and to have equal power spectra:

\begin{eqnarray} \langle h_{s}(\boldsymbol {k},\eta ) h_{s^{\prime }}(\boldsymbol {k}^{\prime },\eta ^{\prime }) \rangle = (2\pi )^3 \delta _D(\boldsymbol {k}-\boldsymbol {k}^{\prime }) \delta _{ss^{\prime }} \frac{1}{4} P_T(k,\eta ,\eta ^{\prime }), \end{eqnarray}

(33)

where

\begin{eqnarray} P_{T}(k,\eta ,\eta ^{\prime }) = T_T(k,\eta ) T_T(k,\eta ^{\prime }) P_{T0}(k); \end{eqnarray}

(34)

we can write the tensor transfer function T_T(k, η) as (Guzzetti et al. 2016):

\begin{equation} T_T(k,\eta ) = \frac{3 j_1(k \eta )}{k\eta } , \end{equation}

(35)

because tensor modes propagate as free waves after recombination. Here, P_T0(k) is the primordial tensor power spectrum, which is defined as

\begin{eqnarray} P_{T0}(k) = 2\pi ^2 \Delta _T^2 k^{-3} \left(\frac{k}{k_*}\right)^{n_T} , \end{eqnarray}

(36)

where k_* = 0.002, and the tensor index satisfies the inflationary consistency relation, n_T = −r/8.

Throughout, we will assume a tensor-to-scalar ratio of r = 0.09 at k_* (consistent with current upper limits), which together with our fiducial cosmology determines the amplitude |$\Delta _T^2$|⁠.

The observed comoving number density of galaxies |$n_g^{\rm obs}$| is related to the true comoving number density n_g through (neglecting here the so-called general relativistic corrections mentioned above):

\begin{equation} n_g^{\rm obs}(\hat{\boldsymbol {x}},\tilde{z}) = n_g(\boldsymbol {x},\bar{z}) \left( 1+\frac{\mathrm{\partial} \Delta x^i}{\mathrm{\partial} \hat{x}^i} \right). \end{equation}

(37)

The factor |$n_g(\boldsymbol {x},\bar{z})$| is the true comoving number density at the point of emission, which we expand as

\begin{equation} n_g(\boldsymbol {x}, \bar{z}) = \bar{n}_g(\bar{z})\:[1 + \delta _g(\boldsymbol {x}, \bar{z})] \,, \end{equation}

(38)

where δ_g is the intrinsic perturbation to the comoving number density, |$\bar{z}$| is the redshift that would be measured for the source in an unperturbed universe, and is related to z^obs through

\begin{equation} 1 + z^{\rm obs} = (1+\bar{z})(1+\delta z). \end{equation}

(39)

Finally, 1 + ∂_iΔxⁱ is the volume distortion due to GWs, which becomes (Jeong et al. 2012)

\begin{equation} \frac{\mathrm{\partial} \Delta x^i}{\mathrm{\partial} \tilde{x}^i} = \mathrm{\partial} _{\tilde{\chi }} \Delta x_\parallel + \frac{2\Delta x_\parallel }{\tilde{\chi }} - 2 \kappa \,, \end{equation}

(40)

where from now on the tilde indicates observed quantities; here κ is the lensing convergence, defined as

\begin{eqnarray} \kappa = -\frac{1}{2}\mathrm{\partial} _{\perp i}\Delta x_\perp ^i \,. \end{eqnarray}

(41)

In the same way as the magnification bias of Section 3.2, lensing affects the observed galaxy density including tensor perturbations as

\begin{equation} \Delta _{g}^{\mathfrak {t}} = \delta _{g}^{\mathfrak {t}} + \delta _{g}^{\kappa } = \delta _{g}^{\mathfrak {t}} - \left(\delta z +\frac{1}{4}h_\parallel - \frac{\Delta x_\parallel }{\tilde{\chi }} + \kappa \right) 5s \,, \end{equation}

(42)

where with |$\Delta _{g}^{\mathfrak {t}}$| we indicate the galaxy density including tensor and lensing effects, while |$\delta _{g}^{\mathfrak {t}}$| includes tensor effects only.

Thus, GWs affect the observed density of galaxies through a volume distortion effect, and by perturbing their redshifts so that the observed galaxy density |$n_g^{\rm obs}$| is modified by the so-called evolution bias:

\begin{equation} b_e = \frac{{\rm d}\ln (a^3\bar{n}_g)}{{\rm d}\ln a} \, ; \end{equation}

(43)

for more details on this term and its effects on the observed galaxy correlation function (sometimes in literature indicated as α Szalay, Matsubara & Landy 1998), see e.g. Raccanelli, Samushia & Percival (2010), Jeong et al. (2012), Raccanelli et al. (2016a).

Therefore, the expression of the galaxy density including the linear-order tensor contributions can be written as (Jeong & Schmidt 2012):

\begin{eqnarray} \Delta _{g}^{\mathfrak {t}} &=& (b_e - 5\,s)\delta z -(2 - 5\,s)\hat{\kappa }-\frac{2 - 5 s}{4} h_\parallel - \frac{1+\tilde{z}}{2H(\tilde{z})} h_\parallel ^{\prime } \nonumber \\ &&-\, \frac{2 - 5 s}{2\tilde{\chi }} \left[ \int _0^{\tilde{\chi }} \mathrm{d}\chi h_\parallel + \frac{1+\tilde{z}}{H(\tilde{z})} \int _0^{\tilde{\chi }} \mathrm{d}\chi h_\parallel ^{\prime } \right] \nonumber \\ &&-\, \frac{H(\tilde{z})}{2} \frac{\mathrm{\partial} }{\mathrm{\partial} \tilde{z}} \left[ \frac{1+\tilde{z}}{H(\tilde{z})} \right] \int _0^{\tilde{\chi }} \mathrm{d}\chi h_\parallel ^{\prime } \,. \end{eqnarray}

(44)

In a similar fashion as for the angular correlations we used in Section 3.1, we can write the correlations between two maps {X, Y} as (Jeong & Schmidt 2012):

\begin{eqnarray} C^{X\,Y}_\ell &=& \frac{\ell }{2\ell +1} \sum _m \mbox{Re} \left\langle a^{X*}_{\ell m} a^Y_{\ell m} \right\rangle \nonumber \\ &=& \frac{1}{2\pi } \frac{(\ell +2)!}{(\ell -2)!} \int k^2 \mathrm{d}k\: P_{T0}(k) F_\ell ^X(k) F_\ell ^Y(k) \,, \end{eqnarray}

(45)

where the kernel is given by

\begin{eqnarray} F_\ell ^X(k) = \int \mathrm{d}\chi \:\mathcal {W}^X(\chi ) T_T(k,\eta _0-\chi ) \frac{j_\ell (k\chi )}{(k\chi )^2} \, ; \end{eqnarray}

(46)

|$\mathcal {W}^X(\chi )$| is the window function |$\mathcal {W}^X(\chi ) = \int _{z(\chi )}^\infty \frac{{\rm d}N}{{\rm d} z} W^X(\chi ,z) \mathrm{d} z$|⁠, in the same fashion of equation (3). To evaluate the total tensor contribution to the angular power spectrum of galaxies, one can set {X, Y} ={g(z_i),g(z_j)} to indicate the window function for samples of galaxies at redshifts z_{{i, j}}, and:

\begin{eqnarray} W_g^{\mathfrak {t}}(\chi ) &=&- \frac{1+\tilde{z}}{2H} \delta _D(\chi -\tilde{\chi }) + \frac{{\rm d}\ln T_T}{{\rm d}\eta } \bigg [ - \frac{1+\tilde{z}}{2H} \delta _D(\chi -\tilde{\chi })\nonumber\\ && + \,\frac{1}{2} \left(b_e -1 -5s + (1+\tilde{z})\frac{{\rm d}H/{\rm d}\tilde{z}}{H}\right)\nonumber\\ && - \,\frac{5s-2}{2} \left(1+\frac{1+\tilde{z}}{H\tilde{\chi }}\right)\bigg ] \nonumber \\ &&-\, \frac{15s-6}{2\chi } + \frac{5s-2}{2\tilde{\chi }} + \frac{5s-2}{4} \:\ell (\ell +1) \frac{\tilde{\chi }-\chi }{\chi \,\tilde{\chi }} \,. \end{eqnarray}

(47)

We omitted the redshift dependence of magnification and evolution bias for convenience of notation.

Now, in order to detect the effects of tensor perturbations and so of a GW background on galaxy correlations, we need to have a measurement with errors smaller than the effect we want to detect. Total contributions to the observed galaxy correlations from tensor perturbations are negligibly small compared to scalar ones. The full observed galaxy two-point angular correlation function, including all effects, can be written as (Raccanelli et al. 2016d):

\begin{equation} C_{\ell }^{ij} = 4\pi \int \frac{\mathrm{d}k}{k} \Delta ^{X}(k,z_i) \Delta ^{Y}(k,z_j) \mathcal {P}(k) \,, \end{equation}

(48)

where the Δ^X are summed over all contributions:

\begin{equation} \Delta _g^{\rm obs} = \Delta _g^{\delta } + \Delta _g^{\rm v} + \Delta _g^{\rm \kappa } + \Delta _g^{\Phi } + \Delta _g^{\mathfrak {t}} \,. \end{equation}

(49)

The different terms account for the effects of peculiar velocity (RSD and Doppler terms, |$\Delta _g^{\rm v}$|⁠), lensing (⁠|$\Delta _g^{\rm \kappa }$|⁠), gravitational potential (⁠|$\Delta _g^{\Phi }$|⁠) and tensor perturbations (⁠|$\Delta _g^{\mathfrak {t}}$|⁠). We can write them as follows:

\begin{eqnarray} \Delta _g^{\delta } &=& b \,\delta \, , \end{eqnarray}

(50)

\begin{eqnarray} \Delta _g^{\rm v} &=& \frac{1}{{\cal H}}\mathrm{\partial} _\mathfrak {r}({\boldsymbol {v}}\cdot {\boldsymbol {n}}) + \left[\frac{{\cal H}^{\prime }}{{\cal H}^2}+\frac{2-5s}{\mathfrak {r}{\cal H}} + 5s- b_e\right]({\boldsymbol {v}}\cdot {\boldsymbol {n}}) \nonumber \\ &&+\, \left[3{\cal H}-b_e\right]\Delta ^{-1} (\nabla \cdot {\boldsymbol {v}}) \, , \end{eqnarray}

(51)

\begin{eqnarray} \Delta _g^{\rm \kappa } &=& -\frac{2-5s}{2}\int _0^{\mathfrak {r}}\mathrm{d}\mathfrak {r}\frac{\mathfrak {r}-\tilde{\mathfrak {r}}}{\mathfrak {r}\tilde{\mathfrak {r}}}\Delta _2(\Phi +\Psi ) \, , \end{eqnarray}

(52)

\begin{eqnarray} \Delta _g^{\Phi } &=& [5s-2]\Phi +\Psi +\frac{\Phi ^{\prime }}{{\cal H}} + \left[\frac{{\cal H}^{\prime }}{{\cal H}^2}+\frac{2-5s}{\mathfrak {r}{\cal H}}+ 5s- b_e\right] \nonumber \\ &&\times \, \left[\Psi +\int _0^{\mathfrak {r}}\mathrm{d}\mathfrak {r} (\Phi ^{\prime }+\Psi ^{\prime })\right] + \frac{2-5s}{\mathfrak {r}}\int \mathrm{d}\mathfrak {r} (\Phi +\Psi ) \,, \end{eqnarray}

(53)

where a prime indicates a derivative w.r.t. conformal time. Here, |${\boldsymbol {v}}$| is the peculiar velocity, Φ and Ψ are the gravitational potentials, δ is the density contrast in comoving gauge, |${\cal H} = aH$| is the conformal Hubble parameter; |$\mathfrak {r}$| is the conformal distance on the light cone, |$\mathfrak {r}(z)=\tau _0-\tau (z)$|⁠, with τ(z) being the conformal time.

Errors in the angular correlations are computed as in equation (6), and they are proportional to the amplitude of the correlations, cosmic variance and the number density of objects. Hence, given a galaxy survey, the best chance to detect the effect of tensor perturbations would be, as pointed out in Jeong & Schmidt (2012), by looking at the effects on radial cross-bin correlations. In the context of the full observed galaxy correlations, radial correlations are dominated by cosmic magnification terms (Raccanelli et al. 2016b), that can be orders of magnitude larger than the Newtonian prediction (Raccanelli et al. 2016d). However, magnification terms depend on the magnification bias s; therefore, if one selects a sample of galaxies with s = 0.4, it is clear from equation (11) that the magnification contribution is cancelled. Moreover, as mentioned above, tensor perturbation effects on LSS are larger closer to the time of emission, so that high-redshift bins are the most useful. Therefore, radio continuum surveys with the CBR technique provides the ideal scenario.

Unfortunately, even in the most optimistic cases with high-z sources and small shot noise, tensor perturbations remain undetectable. In Fig. 9, we show the signal-to-noise ratio, defined as |$(C_\ell ^{\rm tot}-C_\ell ^{\mathfrak {t}})/\sigma _{C_\ell }$|⁠, for the case of the S_lim = 1 nJy continuum survey. As pointed out above, radial cross-bin correlations at high-z are the most promising ways to detect this signal, so we computed forecasts by using radio continuum surveys with five bins centred at z = {2, 3, 4, 5, 6}. The plot shows the SNR for the first 20 multipoles ℓ, for different cross-bin radial correlations.

Figure 9.

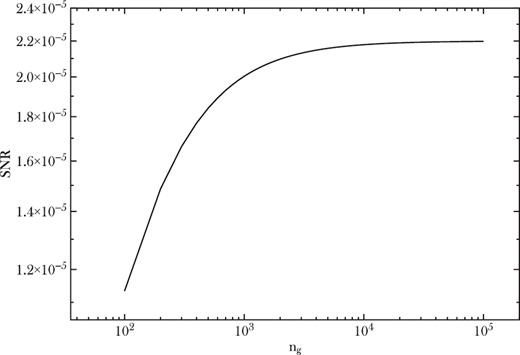
Signal-to-noise ratio for tensor perturbation contributions (assuming r = 0.09) to the observed galaxy two-point correlation function.

Open in new tab Download slide

Our results show that even in the case of negligible shot noise and high-z correlations, the total SNR achievable will not reach 0.0001. While in principle the multi-tracer technique and optimization on the number of bins, galaxy populations, bias and other parameters can significantly increase the SNR, it appears clear that it is very unlikely any survey built in the foreseeable future could allow a robust measurement using this observable.

4.2.2 Clustering fossils

In principle, another way of measuring effects from primordial GWs has been developed in Jeong & Kamionkowski (2012); Dai et al. (2016), where it is shown how to search a galaxy survey for the imprint of primordial scalar, vector, and tensor fields. However, such effects require an extremely futuristic galaxy survey and measurements in the highly non-linear regime or higher order correlations; in this paper, we do not focus on detailed modelling of non-linearities nor higher order correlations, hence we leave a careful investigation of this formalism to a future work.

4.2.3 Weak lensing

Now we turn our focus on effects of tensor perturbations on the correlation of galaxy ellipticities, referring again to the ‘cosmic rulers’ formalism, and in particular we follow Schmidt & Jeong (2012a); Schmidt et al. (2014). In the unperturbed case, one would expect galaxy ellipticities to be uncorrelated, but unlike in the case of the galaxy correlation function, shear is a tensorial quantity, and thus there is a possible intrinsic contribution correlated with the GW background; this can be thought as analogous to the intrinsic alignment effect present for scalar perturbations. Scalar perturbations contribute only to the E-mode component (at linear order), while tensor perturbations also contribute to the B-mode. Hence, the curl-mode of the correlation of galaxy ellipticities can be used to detect a stochastic GW background. In the rest of this section, we summarize what is the effect of a background of GWs to the correlation of ellipticities, and study what are the minimum experiment configurations required to detect the effect of such background, assuming r = 0.09.

Once again, we consider angular correlations, and compute them with equation (45); in the case of lensing from GWs, we obtain the angular power spectra of E- and B-modes of the shear induced by tensor modes by using

\begin{eqnarray} C_\gamma ^{\mathfrak {X}\mathfrak {X}}(\ell ) = \frac{1}{2\pi } \int k^2 \mathrm{d}k\: P_{T0}(k) |F_l^{\gamma \mathfrak {X}}(k)|^2, \,\,\,\quad {\bf \bar{\mathfrak {X}}} = \lbrace E,\,B\rbrace \,, \end{eqnarray}

(54)

where |${F_l^{\gamma \bf \bar{\mathfrak {X}}}}$| is the kernel that accounts for the effect of the gradient and curl components, |${\bf \bar{\mathfrak {X}}} = \lbrace E,\,B\rbrace$|⁠, that can be written as

\begin{eqnarray} F_l^{\gamma E}(k) &=& - \frac{1}{4} \bigg \lbrace T_T(k,\eta _0) \nonumber\\ &&\times \,\left( -\frac{1}{\mathfrak {q}_0^2} \left[ \left(2\mathfrak {q}_0^2 - \ell ^2 - 3\ell -2\right) j_\ell (\mathfrak {q}_0) + 2\mathfrak {q}_0 j_{\ell +1}(\mathfrak {q})\right] \right) \nonumber\\ && + \, \left(1 - \frac{2}{3} \frac{C_1\rho _{c_0}}{H_0^{2}\tilde{a}^{2}} \left\lbrace \mathrm{\partial} _{\tilde{\eta }}^2 + \tilde{a} \tilde{H} \mathrm{\partial} _{\tilde{\eta }}\right\rbrace \right) T_T(k,\tilde{\eta }) \nonumber \\ &&- \,\frac{1}{\tilde{\mathfrak {q}}^2} \left[ (2\tilde{\mathfrak {q}}^2 - \ell ^2 - 3\ell -2) j_\ell (\tilde{\mathfrak {q}}) + 2\tilde{\mathfrak {q}} j_{\ell +1}(\tilde{\mathfrak {q}})\right] \bigg \rbrace \nonumber\\ && + \,\int _0^{\tilde{\chi }} \frac{\mathrm{d}\chi }{\chi } \bigg [ -\frac{1}{4} (\ell +2)(\ell -1) \nonumber\\ &&\times \, \left[(\ell +1)(\ell -2) \frac{j_\ell (\mathfrak {q})}{\mathfrak {q}^2} + 2 \frac{j_{\ell +1}(\mathfrak {q})}{\mathfrak {q}}\right] \nonumber \\ &&+\, \frac{\chi }{\tilde{\chi }} \frac{1}{4} \frac{(\ell +2)!}{(\ell -2)!} \frac{j_\ell (\mathfrak {q})}{\mathfrak {q}^2} \bigg ] T_T(k, \eta _0-\chi ) \nonumber\\ &&\times \left[2(\ell -1) \frac{j_\ell (\mathfrak {q})}{\mathfrak {q}} - 2j_{\ell -1}(\mathfrak {q}) \right] \, , \nonumber \\ F_l^{\gamma B}(k) &=& - \frac{1}{4} \bigg \lbrace T_T(k,\eta _0) \left[2(\ell -1) \frac{j_\ell (\mathfrak {q}_0)}{\mathfrak {q}_0} - 2j_{\ell -1}(\mathfrak {q}_0) \right] \nonumber\\ && + \,\left(1 - \frac{2}{3} \frac{C_1\rho _{c_0}}{H_0^{2}\tilde{a}^{2}} \left\lbrace \mathrm{\partial} _{\tilde{\eta }}^2 + \tilde{a} \tilde{H} \mathrm{\partial} _{\tilde{\eta }}\right\rbrace \right) \nonumber \\ &&\times \, T_T(k,\tilde{\eta }) 2 \left[(\ell -1) \frac{j_\ell (\tilde{\mathfrak {q}})}{\tilde{\mathfrak {q}}} - j_{\ell -1}(\tilde{\mathfrak {q}}) \right] \bigg \rbrace \nonumber\\ && - \, \int _0^{\tilde{\chi }} \frac{\mathrm{d}\chi }{\chi }\frac{(\ell -1)(\ell +2)}{2} \frac{j_\ell (\mathfrak {q})}{\mathfrak {q}} T_T(k, \eta _0-\chi ), \end{eqnarray}

(55)

where |$\mathfrak {q}=k\chi$|⁠, and the constant of proportionality C₁ determines the magnitude of alignment and is usually of the order of ∼0.1.

We compute the errors on the angular correlations by using (Schmidt & Jeong 2012a):

\begin{equation} \sigma _{C_{\ell }^{\mathfrak {X}\mathfrak {X}}} = \frac{\sigma _e^2}{2 \bar{n}_g \sqrt {(2\ell +1)f_{\rm sky}}} \,, \end{equation}

(56)

where f_sky is the fraction of sky surveyed, σ_e is the rms intrinsic ellipticity of galaxies and |$\bar{n}_g$| is the number of detected galaxies per steradian.

The results are obtained by calculating the combined SNR of correlations of |$C_\gamma ^{BB}(\ell )$| at redshift bins centred at z = {2, 3, 4, 5, 6, 7, 8}, assuming an almost flat N(z) as in the continuum 1 nJy case of Fig. 1. In Fig. 10, we show the combination of σ_e and |$\bar{n}_g$| required to have a 1σ detection of the GW background with r = 0.09.

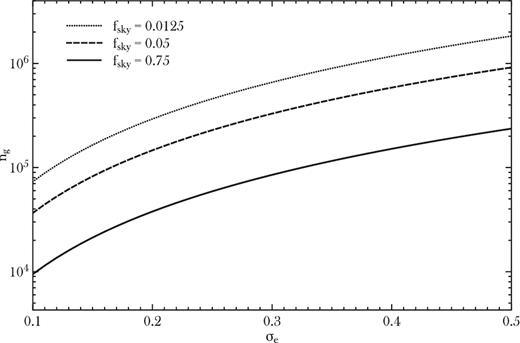
Minimum number of galaxies per deg2 per bin needed to detect GWs from inflation with r = 0.09, using the correlation of galaxy ellipticities, as a function of intrinsic ellipticity error σe, for three different sky coverage values. See text for details.

Figure 10.

Minimum number of galaxies per deg² per bin needed to detect GWs from inflation with r = 0.09, using the correlation of galaxy ellipticities, as a function of intrinsic ellipticity error σ_e, for three different sky coverage values. See text for details.

Open in new tab Download slide

We compute our results for three different survey areas, f_sky = {0.0125, 0.05, 0.75}. Of course, a smaller area surveyed would require a larger minimum number density, but very large number densities could be more easily achievable with dedicated deep surveys focusing on a smaller part of the sky.

In any case, for futuristic surveys as in Fig. 1, the most optimistic case used in this paper predicts around 10⁴ sources per deg², meaning that in order to have such detection, a survey should observe a total of ∼10⁵ objects above z = 2, with σ_e ≈ 0.1 over 75 per cent of the sky, making it a very difficult target but somewhat more doable than the galaxy clustering case.

5 CONCLUSIONS

This work analysed a few possible ways to achieve this goal: by cross-correlating radio galaxy catalogues with GW maps, it is possible to determine properties of the progenitors of merging black hole binaries and forecast how the magnification of GWs by foreground radio sources allows us to test models that explain cosmic acceleration. Furthermore, it is in principle possible to detect the effects of a background of GWs, by measuring angular motion and large-scale correlations of galaxy distribution and lensing.

By using simulated catalogues resembling planned instruments, it was possible to show that the angular galaxy–GW cross-correlation can set stringent limits on properties of the progenitors of BBHs, testing formation models and the possibility that primordial black holes are in fact the dark matter.

Radial cross-correlations can be used to detect the magnification bias of GWs that are lensed by low-redshift galaxies, and future laser interferometers, paired with forthcoming radio galaxies, can provide constraints on dynamical dark energy and modified gravity parameters that are competitive with the ones obtained with galaxy surveys alone and in combination with the CMB.

On the other hand, the detection of a stochastic GW background on galaxy position and distribution presents a much greater challenge. Tensor perturbation effects on galaxy clustering remain orders of magnitude below errors in measurements of galaxy power spectra, even in the case of very futuristic galaxy surveys. The situation is slightly more optimistic for the correlation of lensing effects: in the case of a deep, full-sky survey with very precise shape measurements, it will be possible to measure the SGWB (provided that the tensor-to-scalar ratio r is not negligibly small). In any case, any measurements of GW effects coming from radio galaxy surveys or their correlation with GW detectors, would represent a valuable cross-check of other measurements and potentially provide new insights about cosmological models of current interest.

In summary, radio galaxy surveys can be used to provide information useful for GW astronomy and contribute studying the Universe in a new and complementary way.

Acknowledgments

I am indebted to Ely Kovetz for encouraging the development of this project and carefully reading the manuscript. I would like to thank Yacine Ali-Haïmoud, Ilias Cholis, Julian Munoz, Gianfranco de Zotti, Maria Chiara Guzzetti, Raul Jimenez and Licia Verde for commenting on the manuscript; Daniele Bertacca, Stefano Camera, Marc Kamionkowski, Sabino Matarrese, Prina Patel for useful discussions. I am supported by the John Templeton foundation.

1

https://www.skatelescope.org

2

http://s-cubed.physics.ox.ac.uk

3

CMB measurements have tentatively closed this window (Ricotti, Ostriker & Mack 2008), but the result is based on several untested assumptions and until a more detailed modelling is used, one should associate a large uncertainty with this limit. Hence, we defer this issue to further studies.

4

http://class-code.net/

REFERENCES

Aasi

J.

et al. ,

2014

,

Phys. Rev. Lett.

,

113

,

231101

Crossref

Search ADS

PubMed

Abbott

B. P.

et al. ,

2016a

,

Phys. Rev. Lett.

,

116

,

061102

Crossref

Search ADS

Abbott

B. P.

et al. ,

2016b

,

Phys. Rev. Lett.

,

116

,

131102

Crossref

Search ADS

Abbott

B. P.

et al. ,

2016c

,

Phys. Rev. Lett.

,

116

,

221101

Crossref

Search ADS

Abbott

B. P.

et al. ,

2016d

,

Phys. Rev. Lett.

,

116

,

241103

Crossref

Search ADS

Abbott

B. P.

et al. ,

2017

,

Phys. Rev. Lett.

,

118

,

121101

Crossref

Search ADS

PubMed

Abdalla

F. B.

et al. ,

2015

,

PoS

,

AASKA14

,

017

Ade

P. A. R.

et al. ,

2014

,

ApJ

,

794

,

171

Crossref

Search ADS

Ade

P. A. R.

et al. ,

2016

,

Phys. Rev. Lett.

,

116

,

031302

Crossref

Search ADS

PubMed

Alam

S.

et al. ,

2016

,

preprint (arXiv:1607.03155)

Allen

B.

,

1997

,

Marck

J.-A.

Lasota

J.-P.

, ,

Relativistic Gravitation and Gravitational Radiation

.

Cambridge Contemporary Astrophysics

, .

373

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

André

P.

et al. ,

2014

,

J. Cosmol. Astropart. Phys.

,

1402

,

006

Crossref

Search ADS

Aso

Y.

,

Michimura

Y.

,

Somiya

K.

,

Ando

M.

,

Miyakawa

O.

,

Sekiguchi

T.

,

Tatsumi

D.

,

Yamamoto

H.

,

2013

,

Phys. Rev. D

,

88

,

043007

Crossref

Search ADS

Bacon

D.

et al. ,

2015

,

PoS

,

AASKA14

,

145

Ben-Dayan

I.

,

2016

,

J. Cosmol. Astropart. Phys.

,

1609

,

017

Crossref

Search ADS

Bertacca

D.

,

Raccanelli

A.

,

Piattella

O. F.

,

Pietrobon

D.

,

Bartolo

N.

,

Matarrese

S.

,

Giannantonio

T.

,

2011

,

J. Cosmol. Astropart. Phys.

,

1103

,

039

Crossref

Search ADS

Bertacca

D.

,

Maartens

R.

,

Raccanelli

A.

,

Clarkson

C.

,

2012

,

J. Cosmol. Astropart. Phys.

,

1210

,

025

Crossref

Search ADS

Bertacca

D.

Raccanelli

A.

Bartolo

N.

Matarrese

S.

,

2017

,

preprint (arXiv:1702.01750)

Bettoni

D.

Ezquiaga

J. M.

Hinterbichler

K.

Zumalacárregui

M.

,

2017

,

Phys. Rev. D

,

95

,

4029

Crossref

Search ADS

Bird

S.

,

Cholis

I.

,

Muñoz

J. B.

,

Ali-Haïmoud

Y.

,

Kamionkowski

M.

,

Kovetz

E. D.

,

Raccanelli

A.

,

Riess

A. G.

,

2016

,

Phys. Rev. Lett.

,

116

,

201301

Crossref

Search ADS

PubMed

Blas

D.

,

Ivanov

M. M.

,

Sawicki

I.

,

Sibiryakov

S.

,

2016

,

Pisma Zh. Eksp. Teor. Fiz.

,

103

,

708

Book

L. G.

,

Flanagan

É. É.

,

2011

,

Phys. Rev. D

,

83

,

024024

Crossref

Search ADS

Book

L. G.

,

Kamionkowski

M.

,

Souradeep

T.

,

2012a

,

Phys. Rev. D

,

85

,

023010

Crossref

Search ADS

Book

L.

,

Kamionkowski

M.

,

Schmidt

F.

,

2012b

,

Phys. Rev. Lett.

,

108

,

211301

Crossref

Search ADS

Bouchet

F. R.

et al. ,

2011

,

preprint (arXiv:1102.2181)

Braginsky

V. B.

,

Kardashev

N. S.

,

Polnarev

A. G.

,

Novikov

I. D.

,

1990

,

Nuovo Cimento B

,

105

,

1141

Buonanno

A.

,

2007

,

preprint (arXiv:0709.4682)

Cabre

A.

,

Fosalba

P.

,

Gaztanaga

E.

,

Manera

M.

,

2007

,

MNRAS

,

381

,

1347

Crossref

Search ADS

Calabrese

E.

et al. ,

2014

,

J. Cosmol. Astropart. Phys.

,

8

,

010

Crossref

Search ADS

Camera

S.

,

Nishizawa

A.

,

2013

,

Phys. Rev. Lett.

,

110

,

151103

Crossref

Search ADS

PubMed

Camera

S.

,

Maartens

R.

,

Santos

M. G.

,

2015

,

MNRAS

,

451

,

L80

Crossref

Search ADS

Carbone

C.

,

Baccigalupi

C.

,

Matarrese

S.

,

2006

,

Phys. Rev. D

,

73

,

063503

Crossref

Search ADS

Cardona

W.

,

Durrer

R.

,

Kunz

M.

,

Montanari

F.

,

2016

,

Phys. Rev. D

,

94

,

043007

Crossref

Search ADS

Carr

B. J.

,

Hawking

S. W.

,

1974

,

MNRAS

,

168

,

399

Crossref

Search ADS

Carr

B.

Kuhnel

F.

Sandstad

M.

,

2016

,

Phys. Rev. D

,

94

,

083504

Cholis

I.

,

2016

,

preprint (arXiv:1609.03565)

Cholis

I.

Kovetz

E. D.

Ali-Haïmoud

Y.

Bird

S.

Kamionkowski

M.

Muñoz

J. B.

Raccanelli

A.

,

2016

,

Phys. Rev. D

,

94

,

084013

Clesse

S.

García-Bellido

J.

,

2017

,

Phys. Dark Univ.

,

15

,

142

Clesse

S.

García-Bellido

J.

,

2016

,

preprint (arXiv:1610.08479)

Collett

T. E.

Bacon

D.

,

2017

,

Phys. Rev. Lett.

,

118

,

091101

Cooray

A.

,

Kamionkowski

M.

,

Caldwell

R. R.

,

2005

,

Phys. Rev. D

,

71

,

123527

Crossref

Search ADS

Corbin

V.

,

Cornish

N. J.

,

2006

,

Class. Quantum Gravity

,

23

,

2435

Crossref

Search ADS

Crill

B. P.

et al. ,

2008

,

Proc. SPIE

,

7010

,

2P

Crowder

J.

,

Cornish

N. J.

,

2005

,

Phys. Rev. D

,

72

,

083005

Crossref

Search ADS

Cutler

C.

,

Holz

D. E.

,

2009

,

Phys. Rev. D

,

80

,

104009

Crossref

Search ADS

Dai

L.

Venumadhav

T.

,

2017

,

preprint (arXiv:1702.04724)

Dai

L.

,

Jeong

D.

,

Kamionkowski

M.

,

2013

,

Phys. Rev. D

,

88

,

043507

Crossref

Search ADS

Dai

L.

,

Kamionkowski

M.

,

Kovetz

E. D.

,

Raccanelli

A.

,

Shiraishi

M.

,

2016

,

Phys. Rev. D

,

93

,

023507

Crossref

Search ADS

Dai

L.

,

Venumadhav

T.

,

Sigurdson

K.

,

2017

,

Phys. Rev. D

,

95

,

044011

Crossref

Search ADS

Dodelson

S.

,

2010

,

Phys. Rev. D

,

82

,

023522

Crossref

Search ADS

Dodelson

S.

,

Rozo

E.

,

Stebbins

A.

,

2003

,

Phys. Rev. Lett.

,

91

,

021301

Crossref

Search ADS

PubMed

Durrer

R.

,

Maartens

R.

,

2008

,

Gen. Rel. Grav.

,

40

,

301

Crossref

Search ADS

Dvorkin

I.

Uzan

J.-P.

Vangioni

E.

Silk

J.

,

2016a

,

Phys. Rev. D

,

94

,

103011

Dvorkin

I.

Vangioni

E.

Silk

J.

Uzan

J.-P.

Olive

K. A.

,

2016b

,

MNRAS

,

461

,

3877

Eimer

J. R.

Bennett

C. L.

Chuss

D. T.

Marriage

T.

Wollack

E. J.

Zeng

L.

,

2012

,

Proc. SPIE Vol. 8452, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VI

.

SPIE

,

Bellingham

, .

845220

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Ferramacho

L. D.

,

Santos

M. G.

,

Jarvis

M. J.

,

Camera

S.

,

2014

,

MNRAS

,

442

,

2511

Crossref

Search ADS

Finn

S.

,

2010

,

Report of the Committee to Compare the Scientific Cases for Two Gravitational-wave Detector Networks

,

available at https://dcc.ligo.org/public/0011/T1000251/001/committee_report_final.pdf

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Fisher

R. A.

,

1935

,

Ann. Eugen.

,

6

,

391

Crossref

Search ADS

Fomalont

E.

,

Reid

M.

,

2004

,

New Astron. Rev.

,

48

,

1473

Crossref

Search ADS

Garcia-Bellido

J.

,

Linde

A. D.

,

Wands

D.

,

1996

,

Phys. Rev. D

,

54

,

6040

Crossref

Search ADS

Gil-Marín

H.

,

Noreña

J.

,

Verde

L.

,

Percival

W. J.

,

Wagner

C.

,

Manera

M.

,

Schneider

D. P.

,

2015

,

MNRAS

,

451

,

539

Crossref

Search ADS

Guzzetti

M. C.

,

Bartolo

N.

,

Liguori

M.

,

Matarrese

S.

,

2016

,

Riv. Nuovo Cim.

,

39

,

399

Gwinn

C. R.

,

Eubanks

T. M.

,

Pyne

T.

,

Birkinshaw

M.

,

Matsakis

D. N.

,

1997

,

ApJ

,

485

,

87

Crossref

Search ADS

Hawking

S.

,

1971

,

MNRAS

,

152

,

75

Crossref

Search ADS

Hildebrandt

H.

,

van Waerbeke

L.

,

Erben

T.

,

2009

,

A&A

,

507

,

683

Crossref

Search ADS

Hui

L.

,

Gaztañaga

E.

,

Loverde

M.

,

2007

,

Phys. Rev. D

,

76

,

103502

Crossref

Search ADS

Ito

A.

Soda

J.

,

2016

,

preprint (arXiv:1607.07062)

Jaffe

A. H.

,

2004

,

New Astron. Rev.

,

48

,

1483

Crossref

Search ADS

Janssen

G.

et al. ,

2015

,

PoS

,

AASKA14

,

037

Jarvis

M.

,

Bacon

D.

,

Blake

C.

,

Brown

M.

,

Lindsay

S.

,

Raccanelli

A.

,

Santos

M.

,

Schwarz

D. J.

,

2015

,

PoS

,

AASKA14

,

018

Jeong

D.

,

Kamionkowski

M.

,

2012

,

Phys. Rev. Lett.

,

108

,

251301

Crossref

Search ADS

PubMed

Jeong

D.

,

Schmidt

F.

,

2012

,

Phys. Rev. D

,

86

,

083512

Crossref

Search ADS

Jeong

D.

,

Schmidt

F.

,

Hirata

C. M.

,

2012

,

Phys. Rev. D

,

85

,

023504

Crossref

Search ADS

Johnston

S.

et al. ,

2008

,

Exp. Astron.

,

22

,

151

Crossref

Search ADS

Joshi

B. C.

,

2013

,

Int. J. Mod. Phys. D

,

22

,

1341008

Crossref

Search ADS

Kahya

E. O.

,

Desai

S.

,

2016

,

Phys. Lett. B

,

756

,

265

Crossref

Search ADS

Kaiser

N.

,

1998

,

ApJ

,

498

,

26

Crossref

Search ADS

Kaiser

N.

,

Jaffe

A.

,

1997

,

ApJ

,

484

,

545

Crossref

Search ADS

Kamionkowski

M.

Kovetz

E. D.

,

2016

,

ARA&A

,

54

,

227

Kamionkowski

M.

,

Kosowsky

A.

,

Stebbins

A.

,

1997

,

Phys. Rev. Lett.

,

78

,

2058

Crossref

Search ADS

Kawamura

S.

et al. ,

2011

,

Class. Quantum Gravity

,

28

,

094011

Crossref

Search ADS

Klein

A.

et al. ,

2016

,

Phys. Rev. D

,

93

,

024003

Crossref

Search ADS

Kogut

A.

et al. ,

2011

,

J. Cosmol. Astropart. Phys.

,

1107

,

025

Crossref

Search ADS

Kovetz

E. D.

Raccanelli

A.

Rahman

M.

,

2017

,

MNRAS

,

468

,

3650

Kushnir

D.

Zaldarriaga

M.

Kollmeier

J. A.

Waldman

R.

,

2016

,

MNRAS

,

462

,

844

Laguna

P.

,

Larson

S. L.

,

Spergel

D.

,

Yunes

N.

,

2010

,

ApJ

,

715

,

L12

Crossref

Search ADS

Lentati

L.

et al. ,

2015

,

MNRAS

,

453

,

2576

Crossref

Search ADS

Lesgourgues

J.

,

2011

,

preprint (arXiv:1104.2932)

Linder

E. V.

,

1986

,

Phys. Rev. D

,

34

,

1759

Crossref

Search ADS

Linder

E. V.

,

1988

,

ApJ

,

328

,

77

Crossref

Search ADS

Linder

E. V.

,

2003

,

Phys. Rev. Lett.

,

90

,

091301

Crossref

Search ADS

PubMed

Lorimer

D. R.

Kramer

M.

,

2005

,

Handbook of Pulsar Astronomy

.

Cambridge Univ. Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Loverde

M.

,

Hui

L.

,

Gaztañaga

E.

,

2008

,

Phys. Rev. D

,

77

,

023512

Crossref

Search ADS

Maartens

R.

,

Abdalla

F. B.

,

Jarvis

M.

,

Santos

M. G.

,

2015

,

PoS

,

AASKA14

,

016

McLaughlin

M. A.

,

2013

,

Class. Quantum Gravity

,

30

,

224008

Crossref

Search ADS

Maggiore

M.

,

2000

,

Phys. Rep.

,

331

,

283

Crossref

Search ADS

Manchester

R. N.

et al. ,

2013

,

PASA

,

30

,

e017

Crossref

Search ADS

Mandic

V.

Bird

S.

Cholis

I.

,

2016

,

Phys. Rev. Lett.

,

117

,

201102

Masui

K. W.

,

Pen

U.-L.

,

2010

,

Phys. Rev. Lett.

,

105

,

161302

Crossref

Search ADS

PubMed

Matarrese

S.

,

Coles

P.

,

Lucchin

F.

,

Moscardini

L.

,

1997

,

MNRAS

,

286

,

115

Crossref

Search ADS

Matsubara

T.

,

2000

,

ApJ

,

537

,

L77

Crossref

Search ADS

Matsumura

T.

et al. ,

2013

,

J. Low. Temp. Phys.

,

176

,

733

Crossref

Search ADS

Ménard

B.

Scranton

R.

Schmidt

S.

Morrison

C.

Jeong

D.

Budavari

T.

Rahman

M.

,

2013

,

preprint (arXiv:1303.4722)

Misner

C. W.

Thorne

K. S.

Wheeler

J. A.

,

1973

,

Gravitation

.

W. H. Freeman and Company

,

San Francisco

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Mo

H. J.

,

White

S. D. M.

,

1996

,

MNRAS

,

282

,

347

Crossref

Search ADS

Monroy-Rodríguez

M. A.

,

Allen

C.

,

2014

,

ApJ

,

790

,

159

Crossref

Search ADS

Montanari

F.

,

Durrer

R.

,

2015

,

J. Cosmol. Astropart. Phys.

,

1510

,

070

Crossref

Search ADS

Moore

C. J.

,

Cole

R. H.

,

Berry

C. P. L.

,

2015

,

Class. Quantum Gravity

,

32

,

015014

Crossref

Search ADS

Nakamura

T.

,

Sasaki

M.

,

Tanaka

T.

,

Thorne

K. S.

,

1997

,

ApJ

,

487

,

L139

Crossref

Search ADS

Namikawa

T.

Nishizawa

A.

Taruya

A.

,

2016a

,

Phys. Rev. D

,

94

,

024013

Namikawa

T.

,

Nishizawa

A.

,

Taruya

A.

,

2016b

,

Phys. Rev. Lett.

,

116

,

121302

Crossref

Search ADS

Nolta

M. R.

et al. ,

2004

,

ApJ

,

608

,

10

Crossref

Search ADS

Norris

R. P.

et al. ,

2011

,

PASA

,

28

,

215

Crossref

Search ADS

Norris

R. P.

et al. ,

2013

,

PASA

,

30

,

20

Crossref

Search ADS

Oguri

M.

,

2016

,

Phys. Rev. D

,

93

,

083511

Pagano

L.

,

Salvati

L.

,

Melchiorri

A.

,

2016

,

Phys. Lett. B

,

760

,

823

Crossref

Search ADS

Paragi

Z.

et al. ,

2015

,

Proc. Sci., Very Long Baseline Interferometry with the SKA

.

SISSA

,

Trieste

,

PoS(AASKA14)143

Pen

U.-L.

,

2004

,

New Astron.

,

9

,

417

Crossref

Search ADS

Planck Collaboration XIV

,

2016

,

A&A

,

594

,

A14

Crossref

Search ADS

Polnarev

A. G.

,

Miller

N. J.

,

Keating

B. G.

,

2008

,

MNRAS

,

386

,

1053

Crossref

Search ADS

Pullen

A. R.

,

Chang

T.-C.

,

Doré

O.

,

Lidz

A.

,

2013

,

ApJ

,

768

,

15

Crossref

Search ADS

Punturo

M.

et al. ,

2010

,

Class. Quantum Gravity

,

27

,

084007

Crossref

Search ADS

Pyne

T.

,

Gwinn

C. R.

,

Birkinshaw

M.

,

Eubanks

T. M.

,

Matsakis

D. N.

,

1996

,

ApJ

,

465

,

566

Crossref

Search ADS

Raccanelli

A.

,

Bonaldi

A.

,

Negrello

M.

,

Matarrese

S.

,

Tormen

G.

,

De Zotti

G.

,

2008

,

MNRAS

,

386

,

2161

Crossref

Search ADS

Raccanelli

A.

,

Samushia

L.

,

Percival

W. J.

,

2010

,

MNRAS

,

409

,

1525

Crossref

Search ADS

Raccanelli

A.

et al. ,

2012

,

MNRAS

,

424

,

801

Crossref

Search ADS

Raccanelli

A.

et al. ,

2013

,

MNRAS

,

436

,

89

Crossref

Search ADS

Raccanelli

A.

et al. ,

2015a

,

J. Cosmol. Astropart. Phys.

,

1501

,

042

Crossref

Search ADS

Raccanelli

A.

et al. ,

2015b

,

PoS

,

AASKA14

,

031

Raccanelli

A.

Bertacca

D.

Jeong

D.

Neyrinck

M. C.

Szalay

A. S.

,

2016a

,

preprint (arXiv:1602.03186)

Raccanelli

A.

,

Bertacca

D.

,

Maartens

R.

,

Clarkson

C.

,

Doré

O.

,

2016b

,

Gen. Rel. Grav.

,

48

,

84

Crossref

Search ADS

Raccanelli

A.

,

Kovetz

E. D.

,

Bird

S.

,

Cholis

I.

,

Munoz

J. B.

,

2016c

,

Phys. Rev. D

,

94

,

023516

Crossref

Search ADS

Raccanelli

A.

,

Montanari

F.

,

Bertacca

D.

,

Doré

O.

,

Durrer

R.

,

2016d

,

J. Cosmol. Astropart. Phys.

,

1605

,

009

Crossref

Search ADS

Regimbau

T.

,

2011

,

Res. Astron. Astrophys.

,

11

,

369

Crossref

Search ADS

Regimbau

T.

,

Mandic

V.

,

2008

,

Class. Quantum Gravity

,

25

,

184018

Crossref

Search ADS

Ricotti

M.

,

Ostriker

J. P.

,

Mack

K. J.

,

2008

,

ApJ

,

680

,

829

Crossref

Search ADS

Samushia

L.

,

Percival

W. J.

,

Raccanelli

A.

,

2012

,

MNRAS

,

420

,

2102

Crossref

Search ADS

Samushia

L.

et al. ,

2013

,

MNRAS

,

429

,

1514

Crossref

Search ADS

Samushia

L.

et al. ,

2014

,

MNRAS

,

439

,

3504

Crossref

Search ADS

Santos

M. G.

Alonso

D.

Bull

P.

Silva

M.

Yahya

S.

,

2015

,

Proc. Sci., HI galaxy simulations for the SKA: number counts and bias

,

SISSA

,

Trieste

,

PoS(AASKA14)021

Sasaki

M.

Suyama

T.

Tanaka

T.

Yokoyama

S.

,

2016

,

Phys. Rev. Lett.

,

117

,

061101

Schmidt

F.

,

Jeong

D.

,

2012a

,

Phys. Rev. D

,

86

,

083513

Crossref

Search ADS

Schmidt

F.

,

Jeong

D.

,

2012b

,

Phys. Rev. D

,

86

,

083527

Crossref

Search ADS

Schmidt

F.

,

Pajer

E.

,

Zaldarriaga

M.

,

2014

,

Phys. Rev. D

,

89

,

083507

Crossref

Search ADS

Scranton

R.

et al. ,

2005

,

ApJ

,

633

,

589

Crossref

Search ADS

Seljak

U.

,

Zaldarriaga

M.

,

1997

,

Phys. Rev. Lett.

,

78

,

2054

Crossref

Search ADS

Smith

T. L.

,

Kamionkowski

M.

,

Cooray

A.

,

2006a

,

Phys. Rev. D

,

73

,

023504

Crossref

Search ADS

Smith

T. L.

,

Pierpaoli

E.

,

Kamionkowski

M.

,

2006b

,

Phys. Rev. Lett.

,

97

,

021301

Crossref

Search ADS

Smith

T. L.

,

Kamionkowski

M.

,

Cooray

A.

,

2008

,

Phys. Rev. D

,

78

,

083525

Crossref

Search ADS

Stone

N. C.

Metzger

B. D.

Haiman

Z.

,

2017

,

MNRAS

,

464

,

946

Szalay

A. S.

,

Matsubara

T.

,

Landy

S. D.

,

1998

,

ApJ

,

498

,

L1

Crossref

Search ADS

Tegmark

M.

,

Peebles

P. J. E.

,

1998

,

ApJ

,

500

,

L79

Crossref

Search ADS

Tegmark

M.

,

Hamilton

A. J. S.

,

Strauss

M. A.

,

Vogeley

M. S.

,

Szalay

A. S.

,

1998

,

ApJ

,

499

,

555

Crossref

Search ADS

Titov

O.

,

Lambert

S. B.

,

Gontier

A.-M.

,

2011

,

A&A

,

529

,

A91

Crossref

Search ADS

Turner

E. L.

,

Ostriker

J. P.

,

Gott

J. R.

,

III

,

1984

,

ApJ

,

284

,

1

Crossref

Search ADS

Unnikrishnan

C. S.

,

2013

,

Int. J. Mod. Phys. D

,

22

,

1341010

Crossref

Search ADS

Vallinotto

A.

,

2012

,

ApJ

,

759

,

32

Crossref

Search ADS

Villumsen

J. V.

,

Freudling

W.

,

da Costa

L. N.

,

1997

,

ApJ

,

481

,

578

Crossref

Search ADS

Wang

L.

et al. ,

2011

,

MNRAS

,

414

,

596

Crossref

Search ADS

Wilman

R. J.

et al. ,

2008

,

MNRAS

,

388

,

1335

Wyrzykowski

L.

et al. ,

2011

,

MNRAS

,

416

,

2949

Crossref

Search ADS

Xia

J.-Q.

,

Viel

M.

,

Baccigalupi

C.

,

De Zotti

G.

,

Matarrese

S.

,

Verde

L.

,

2010

,

ApJ

,

717

,

L17

Crossref

Search ADS

Yoo

J.

,

Fitzpatrick

A. L.

,

Zaldarriaga

M.

,

2009

,

Phys. Rev. D

,

80

,

083514

Crossref

Search ADS

Zel'dovich

Y. B.

,

1968

,

Sov. Phys. Usp.

,

11

,

381

Crossref

Search ADS

Zel'dovich

Y. B.

,

Novikov

I. D.

,

1967

,

SvA

,

10

,

602

Zhao

G.

,

Bacon

D.

,

Maartens

R.

,

Santos

M.

,

Raccanelli

A.

,

2015

,

PoS

,

AASKA14

,

165

Zhao

G.-B.

,

Zhang

X.

,

2010

,

Phys. Rev. D

,

81

,

043518

Crossref

Search ADS

Zhu

X.-J.

,

Howell

E.

,

Regimbau

T.

,

Blair

D.

,

Zhu

Z.-H.

,

2011

,

ApJ

,

739

,

86

Crossref

Search ADS

Download all slides

Month:	Total Views:
April 2017	1
May 2017	6
June 2017	5
July 2017	12
August 2017	6
September 2017	8
October 2017	6
November 2017	7
December 2017	3
January 2018	3
February 2018	1
March 2018	5
May 2018	1
June 2018	1
July 2018	5
August 2018	4
September 2018	1
October 2018	3
December 2018	5
January 2019	2
February 2019	6
March 2019	5
May 2019	11
June 2019	1
August 2019	1
October 2019	7
November 2019	1
December 2019	3
February 2020	2
April 2020	2
May 2020	2
June 2020	6
July 2020	4
August 2020	2
September 2020	3
October 2020	4
November 2020	2
December 2020	6
January 2021	3
February 2021	4
March 2021	6
April 2021	9
May 2021	7
June 2021	5
July 2021	11
August 2021	2
September 2021	26
October 2021	17
November 2021	9
December 2021	7
January 2022	8
February 2022	1
March 2022	7
April 2022	11
May 2022	12
June 2022	3
July 2022	17
August 2022	15
September 2022	14
October 2022	19
November 2022	5
December 2022	7
January 2023	10
February 2023	2
March 2023	4
April 2023	6
May 2023	13
June 2023	1
July 2023	5
August 2023	6
September 2023	4
October 2023	5
November 2023	2
December 2023	11
January 2024	7
February 2024	5
March 2024	10
April 2024	4
May 2024	8
June 2024	7
July 2024	10
August 2024	7
September 2024	10
October 2024	12
November 2024	10
December 2024	9
January 2025	6
February 2025	2
March 2025	7
April 2025	9
May 2025	7

Article Contents

Gravitational wave astronomy with radio galaxy surveys

Abstract

1 INTRODUCTION

2 FORTHCOMING RADIO GALAXY SURVEYS

2.1 EMU

2.2 SKA

2.2.1 Radio continuum

2.2.2 H i

2.2.3 Bias

3 GALAXY–GW CROSS-CORRELATIONS

3.1 Angular cross-correlations

3.2 Cosmic magnification

3.2.1 Cosmological model constraints

4 GW BACKGROUND

4.1 Cosmometry

4.1.1 Effect of an SGWB on galaxy positions

4.2 Cosmic rulers

4.2.1 Galaxy clustering

4.2.2 Clustering fossils

4.2.3 Weak lensing

5 CONCLUSIONS

Acknowledgments

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Gravitational wave astronomy with radio galaxy surveys Free

Abstract

1 INTRODUCTION

2 FORTHCOMING RADIO GALAXY SURVEYS

2.1 EMU

2.2 SKA

2.2.1 Radio continuum

2.2.2 H i

2.2.3 Bias

3 GALAXY–GW CROSS-CORRELATIONS

3.1 Angular cross-correlations

3.2 Cosmic magnification

3.2.1 Cosmological model constraints

4 GW BACKGROUND

4.1 Cosmometry

4.1.1 Effect of an SGWB on galaxy positions

4.2 Cosmic rulers

4.2.1 Galaxy clustering

4.2.2 Clustering fossils

4.2.3 Weak lensing

5 CONCLUSIONS

Acknowledgments

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Gravitational wave astronomy with radio galaxy surveys