Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

Standard big bang cosmology predicts a cosmic neutrino background at Tν ≃ 1.95 K. Given the current neutrino oscillation measurements, we know most neutrinos move at large, but non-relativistic, velocities. Therefore, dark matter haloes moving in the sea of primordial neutrinos form a neutrino wake behind them, which would slow them down, due to the effect of dynamical friction. In this paper, we quantify this effect for realistic haloes, in the context of the halo model of structure formation, and show that it scales as |$m_\nu ^4$|× relative velocity and monotonically grows with the halo mass. Galaxy redshift surveys can be sensitive to this effect (at >3σ confidence level, depending on survey properties, neutrino mass and hierarchy) through redshift space distortions of distinct galaxy populations.

galaxies: haloes, cosmology: theory, dark matter

1 INTRODUCTION

Neutrinos are an interesting component of the standard model of particles that play a number of unique roles in particle physics, astroparticle physics and cosmology. In the standard model of particle physics, they are depicted as massless and not clearly associated as Majorana or Dirac particles. Observations of flavour oscillations in solar and atmospheric neutrinos point to the existence of the neutrino mass. In cosmology, the presence of massive active neutrinos potentially resolves some of the tension between the observed galaxy counts and those predicted by the Planck cosmological parameters as suggested by Mark et al. (2014), Battye & Moss (2014) and Beutler et al. (2014).

Constraints on the mass-squared difference of neutrinos via oscillation experiments give best-fitting values of |$\Delta m_{12}^2 \equiv m_2^2 - m_1^2 = 7.54 \times 10^{-5}\,\, {\rm eV}^2$| and |$\Delta m_{13}^2 \equiv m_3^2 - (m_1^2 + m_2^2)/2 = 2.43(2) \times 10^{-3}\,\, {\rm eV}^2$| for the normal (inverted) hierarchy (Maltoni et al. 2003; Fogli et al. 2012). These constraints lead to a lower limit on the sum of the masses of these neutrinos, Mν ≡ ∑imi > 0.058 eV for the normal hierarchy and Mν > 0.11 eV for the inverted hierarchy (see Lesgourgues & Pastor 2006, 2012, for a more comprehensive review of the role of massive neutrinos in cosmology). Thus, any limit on Mν < 0.1 eV rules out the inverted neutrino hierarchy. Alternative limits on the sum of the neutrino mass Mν may also be placed by cosmological observations and measurements. Although some degeneracy exists between the Hubble constant and the neutrino mass on the background cosmology, the cosmic microwave background (CMB) temperature perturbations are affected by the neutrino mass through the early-time integrated Sachs–Wolfe effect and the lensing effect on the power spectrum. The baryon acoustic oscillations (BAO) and measurements of the CMB temperature anisotropy have placed limits on the sum of the mass of the neutrinos as Mν < 0.23 eV (Planck Collaboration XIII 2016), albeit, slightly dependent on the assumed cosmological model parameters. First described by Bond, Efstathiou & Silk (1980), galaxy surveys present yet another method to constrain the mass of neutrinos as presented in Riemer-Sørensen et al. (2012). Suppression of structure below the free-streaming scale of the neutrinos, when they first become non-relativistic, leads to a decline in the matter power spectrum (usually at the per cent level). However, in practice, galaxy power spectra are measured and so precise knowledge of the galaxy bias as a function of scale is required since the galaxies do not cluster as matter. Notwithstanding, Riemer-Sørensen et al. (2012) explored this technique in the WiggleZ Dark Energy Survey and placed an upper limit on the sum of the neutrino masses, Mν < 0.18 eV, for three degenerate neutrino species with no prior placed on the minimum sum of neutrino masses. More recent estimates by Cuesta et al. (2016) using the WiggleZ Dark Energy Survey and SDSS-DR7 LRG, together with the BAO and CMB temperature and polarization anisotropies measurements by Planck, have yielded even tighter constraints of Mν < 0.13 eV at the 95 per cent C.L. on the sum of the neutrino masses.

2 THE NEUTRINO–CDM RELATIVE VELOCITY

A complementary technique to measure the neutrino masses using their peculiar velocities relative to dark matter has been suggested by Zhu et al. (2014). The relative velocity between the neutrinos and dark matter leads to an observable dipole distortion in the cross-correlation of different tracers. This effect is similar to the relative velocity between baryons and cold dark matter, first suggested by Tseliakhovich & Hirata (2010) and explored in a number of other works, including Yoo & Seljak (2013). The neutrino particles stream coherently across the cold dark matter (CDM) haloes over a coherence/Jeans scale of 20–50 h−1 Mpc.

In this work, we provide a semi-analytic derivation of this effect in the non-linear regime, which is equivalent to the dynamical friction for CDM haloes moving in the primordial neutrino sea. The outline is as follows. Section 2 introduces the relations between velocities and density perturbations for both neutrinos and CDM in the linear regime. Section 3 examines the effect of dynamical friction on the dark matter structures due to the streaming neutrinos. We then present the methodology and expected signal to noise for detecting this effect in current and future surveys in Section 4. Finally, Section 5 summarizes our results and concludes the paper, while the appendices provide details of signal-to-noise calculations and comparison to non-linear effects in ΛCDM simulations without neutrinos.

For the calculations below, we use a ΛCDM camb(Lewis et al. 2000) power spectrum with Planck1 parameters (Ωm0, ΩΛ0, Ω0b) = (0.32, 0.68, 0.049), Hubble parameter h = 0.67, rms (root-mean-square) density fluctuation in 8 h−1 Mpc spheres σ8 = 0.8344 and scalar spectral index ns = 0.963. We also utilize the analytic power spectrum of Eisenstein & Hu (1998) where necessary. The dark energy density and the total matter density Ωm0 = Ωc0 + Ωb0 + Ων0 are kept fixed while the CDM density Ωc0 and the neutrino density Ων0 are adjusted as needed. The relation between the neutrino density and neutrino mass is given by
(1)
with the sum being over the three neutrino species. We assume an effective number of relativistic species Neff = 3.046 (Planck Collaboration XIII 2016). The notation |$M_{\nu } \equiv \sum _{i=1}^3 m_{i}$| will be mostly used to replace the sum over neutrino mass in the rest of this article.
We proceed to calculate the CDM–neutrino relative velocity power spectrum following Tseliakhovich & Hirata (2010) and Zhu et al. (2014). The relative velocity, as we will see in the next section, is relevant for estimating the dynamical friction on a halo due to neutrinos. Assuming the linearized continuity equation holds for both neutrinos and CDM (on scales k ≲ 1 h Mpc−1), in Fourier space it is given by
(2)
where a = 1/(1 + z) is the cosmic scale factor and we have assumed that there is no vorticity (curl of the vector perturbation is zero). This is tested in Inman et al. (2015), where the velocity was seen to be curl-free on scales k ≲ 1 h Mpc−1.
The variance in the relative velocity |${\boldsymbol {v}_{\nu c} \equiv \boldsymbol {v}_\nu - \boldsymbol {v}_c}$| between neutrinos (ν) and CDM (c) can be calculated to be
(3)
where |$\widetilde{W}(kR)$| is the Fourier transform of the window function and |$\Delta ^2_{v \nu c}(k,z)$| is the neutrino–CDM relative velocity power spectrum. The essence of the window function is to filter the velocity perturbation field to get a smooth field. We will adopt one of the most commonly used window functions – the spherical top-hat2 – defined as
(4)
In Fourier space, it is given by
(5)
where j1 is the first-order spherical Bessel function. The relative velocity power spectrum can be written in terms of the transfer functions of neutrinos and CDM as
(6)
where |$\mathcal {P}_\chi \propto k^{n_s +3}/(2\pi ^2)$| is the primordial power spectrum of density perturbations and |$\dot{T}(k,z)$| is the time derivative of the transfer function at redshift z.

We show the derivative of the transfer function, |$\dot{T}$|⁠, at z = 0 for CDM and neutrinos of different masses, in Fig. 1, which demonstrates the impact of free steaming on their density perturbations. As expected, more free streaming leads to more suppression of growth on small scales for lighter neutrinos. The relative velocity power spectrum for different sum of neutrino masses (unless otherwise stated, all sum of neutrino masses assume the normal hierarchy) is shown in Fig. 2.

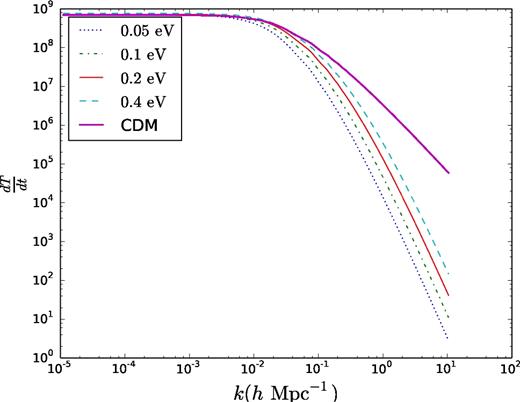
Derivative of the transfer function, $\dot{T}(k) = {\rm d}T(k)/{\rm d}t$, at z = 0 for CDM and neutrinos of different masses.
Figure 1.

Derivative of the transfer function, |$\dot{T}(k) = {\rm d}T(k)/{\rm d}t$|⁠, at z = 0 for CDM and neutrinos of different masses.

Open in new tabDownload slide
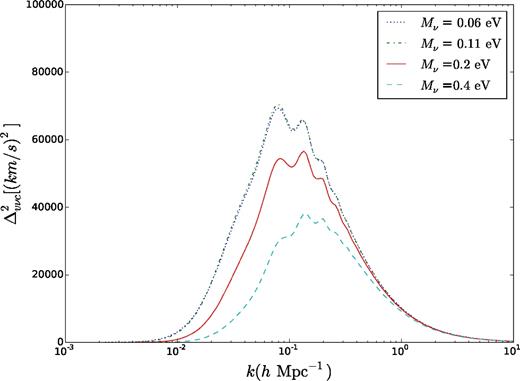
The power spectrum of the relative velocity between the neutrinos and CDM. The different curves represent different values of Mν = ∑mν (assuming normal hierarchy). The two lowest Mν’s are close due to the fact that the most massive of the three neutrinos in each sum have similar masses and dominate in the sum.
Figure 2.

The power spectrum of the relative velocity between the neutrinos and CDM. The different curves represent different values of Mν = ∑mν (assuming normal hierarchy). The two lowest Mν’s are close due to the fact that the most massive of the three neutrinos in each sum have similar masses and dominate in the sum.

Open in new tabDownload slide

Obviously, in Fig. 2 the power lies in the range k ∼ [0.01, 1]. The rms relative velocity vνc within a sphere as a function of the radius of the window function used is shown in Fig. 3 for different sum of neutrino masses. The relative velocity between the neutrino and dark matter decreases as the mass in the neutrinos increases.

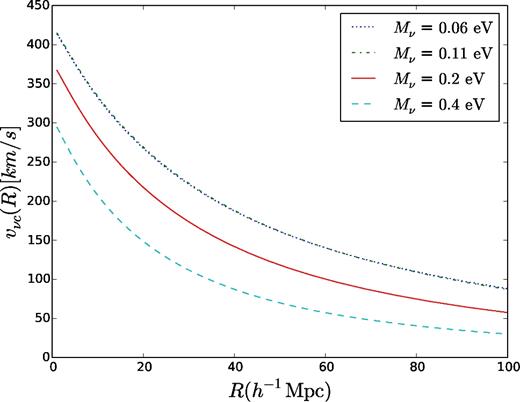
Relative CDM–neutrino velocity vνc as a function of the top-hat window function radius R for four different neutrino masses.
Figure 3.

Relative CDM–neutrino velocity vνc as a function of the top-hat window function radius R for four different neutrino masses.

Open in new tabDownload slide

3 DYNAMICAL FRICTION DUE TO MASSIVE NEUTRINOS

Dark matter haloes sitting in a streaming background of neutrinos will experience a deceleration due to dynamical friction. Larger haloes experience a larger dynamical friction force than smaller mass haloes, and so larger and smaller mass haloes will have different displacements relative to the neutrino streaming direction.

In this section, we calculate the general structure of massive neutrino wakes and their dynamical friction force on dark matter haloes with a Navarro–Frenk–White (NFW) profile (Navarro et al. 1996). This drag on the halo should lead to a displacement, which is non-existent in the absence of neutrinos. This displacement Δx, in the halo's position, will be first estimated by approximating dark matter haloes as single spheres in Section 3.1. We then develop the general formalism for computing the neutrino wake in Fourier space in Section 3.2 and use it to derive dynamical friction assuming the full halo model in Section 3.3. The halo model consists of contributions from the one-halo and two-halo terms. We shall see that, while the one-halo term is equivalent to the solid sphere approximation, the two-halo term dominates the drag on small haloes.

3.1 Solid sphere approximation

The phase space distribution of neutrinos is given by the Fermi-Dirac distribution:
(7)
where
(8)
TCMB is the temperature of the CMB today and Nν is the number of massive neutrino species. In the rest frame of a dark matter halo that moves with velocity |$\boldsymbol {v}_{\nu c}$| relative to the neutrinos, the phase space density takes the form
(9)
with the factor of 2 accounting for antineutrinos along with neutrinos. The dynamical friction force is then given by integrating over all range of impact parameter, b, and over a dark matter halo of mass, say Mh:
(10)
Notice that the terms in the integral are similar to the well-known Chandrasekhar dynamical friction formula (Binney & Tremaine 2008). The first term in the first integral accounts for the range of impact parameters of interaction between the neutrino and the halo. The second term in the first integral is the drag force due to an interaction between a neutrino and a halo. The second integral incorporates the density distribution of the neutrinos. Using Newton's second law, |$\boldsymbol {F} = M \dot{\boldsymbol v}$|⁠, we can find the change in relative velocity due to dynamical friction over a Hubble time t ≃ H−1:
(11)
where H = H(z) is the Hubble constant, h is the Hubble parameter and ln Λ = ∫db/b is the Coulomb logarithm. |$\ln \Lambda \equiv \ln \frac{b_{{\rm max}}}{b_{{\rm min}}}$|⁠, where bmax and bmin are the maximum and minimum impact parameters, respectively. Here, we use bmax ∼ 30 Mpc as the typical neutrino free steaming length and bmin ∼ 1 Mpc as the typical size of CDM haloes. This leads to an average displacement over a Hubble time of
(12)
If there exist different neutrino mass eigenstates, these will have different velocities and different displacements, which can be calculated independently. The total displacement is equal to the sum of displacements due to each neutrino species i, so that Δxtot = ∑iΔxi.

3.2 Dynamical friction: general formalism

Now, let us consider a more realistic dark matter distribution. For large thermal velocity of neutrinos |$\frac{T_\nu }{m_\nu c} \gg v_{\rm halo}$|⁠, we can assume a steady-state neutrino distribution, i.e. it satisfies the time-independent Boltzmann equation:
(13)
where |$\Phi ({\boldsymbol x})$| is the gravitational potential of CDM structure. This approximation is also valid in comoving phase space on large scales, as long as the neutrino thermal velocity exceeds the Hubble flow, i.e. Δx ≲ 25 Mpc(mν/0.1 eV)−1.
To linear order in Φ (in line with the assumption of linear regime), we can consider linear perturbations |$\delta f({\boldsymbol x, p}) = f({\boldsymbol x, p}) - \skew5\bar{f}({\boldsymbol p})$| in Fourier space:
(14)
The density of the neutrinos in Fourier space is
(15)
where we have changed the integration variable |${\boldsymbol p} \rightarrow {\boldsymbol p}- m_\nu \boldsymbol {v}_{\nu c}$| in the last step and used the shifted Fermi–Dirac distribution. We can write the integral in spherical coordinates (using |${\boldsymbol p\cdot k} = p |{\boldsymbol k}| \cos \theta$|⁠):
(16)
The integral over cos θ has a singularity and therefore requires regularization. To this end, we need to set the initial conditions upstream in the neutrino flow. Assuming that the gravitational potential of haloes is turned on gradually as |$\exp (- \epsilon {\boldsymbol {v}_{\nu c} \cdot {\boldsymbol x} })$|⁠, which is equivalent to taking |${\boldsymbol k} \rightarrow {\boldsymbol k} +i \epsilon \boldsymbol {v}_{\nu c}$| in the |$\exp (i {\boldsymbol k\cdot x})$| Fourier phase factor, we can use the Sokhatsky–Weierstrass identity:
(17)
This regularization ensures that neutrino wakes form behind the haloes and is similar to the one used in the derivation of Landau damping in plasmas (e.g. Padmanabhan 2000).
Substituting into the angular integral in equation (16) yields
(18)
The real part of this integral is symmetric under |$\boldsymbol {v}_{\nu c} \rightarrow -\boldsymbol {v}_{\nu c}$|⁠, and thus only the imaginary part contributes to the dynamical ‘friction’ of interest. Substituting into equation (16), the p2’s cancel, making the integrand a total derivative. Therefore, only the boundary term at |$p=m_\nu |\boldsymbol {v}_{\nu c}\cdot {\boldsymbol k}|/|{\boldsymbol k}|$| contributes to the integral:
(19)
which using Gauss's law |${\nabla \cdot {\boldsymbol g}}= -4\pi G\rho$| leads to the gravitational field due to dynamical friction:
(20)
where 0.7 ≲ μ < 1 captures the velocity dependence of the exponential term in the denominator of the first equation. We will assume μ = 1 where necessary in our numerical evaluations.

Let us briefly discuss the physical picture of a neutrino wake for a plane wave. For a finite object such as a halo (or solid sphere discussed above), a neutrino wake would form downstream, due to gravitational focusing, which is responsible for slowing down the halo (hence the term dynamical friction). The picture is qualitatively different for a CDM plane wave, as planar symmetry appears to prevent any focusing. The key here though is that, in nature, we always deal with finite wave packets, which do break exact planar symmetry. As the wave packet moves through the neutrino sea, the neutrinos with velocities nearly parallel to the wavefront (in the packet rest frame, corresponding to the singularity in equation 16) can get trapped in between the potential peaks of the travelling wave. While the neutrinos that are trapped are preferentially travelling downstream, their velocity randomizes by the time they get out, implying that they impart a net momentum on the wave packet, in the direction of the wind (see Fig. 4). Despite this qualitative difference, we shall see below that if we construct a spherical halo from the superposition of Fourier modes in equation (20), we shall recover the standard dynamical friction for an isolated sphere (equation 10).

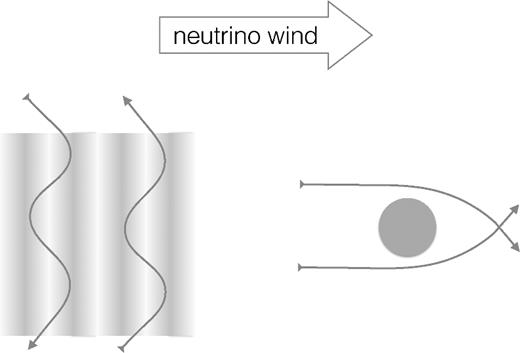
A depiction of dynamical friction experienced by a plane wave packet (left) and a compact halo (right), caused by neutrino wind (see the text for details).
Figure 4.

A depiction of dynamical friction experienced by a plane wave packet (left) and a compact halo (right), caused by neutrino wind (see the text for details).

Open in new tabDownload slide

3.3 Halo model

The halo model provides a realistic description of the non-linear CDM distribution, which includes modelling the profiles of individual haloes, as well as their clustering (see Cooray & Sheth 2002, for a general review of the halo model formalism). As a result, clustered haloes will contribute to each other's wakes. The dynamical friction force on a halo |${\boldsymbol F} |_{\rm dyn. fric.}$| is given by
(21)
where in the last two steps, we used spherical symmetry and Poisson's equation. Using the halo model, this can be written as
(22)
where PCDM(k) is the CDM linear power spectrum. The formula for the acceleration due to dynamical friction is then given as
(23)
For the halo model, we use the convention of Cooray & Sheth (2002) for the normalized Fourier transform of the halo profile (their equation 107):
(24)
where b(M) and dn/dM are the linear bias and mass function, respectively, estimated using the fitting formula of Tinker et al. (2008, 2010) and the concentration–mass relation of Okoli & Afshordi (2016). Our final predictions are not sensitive to the specifics of the structure formation parameters such as the form of the density profile, the concentration–mass relation, the linear bias model, the mass function, etc. We will also assume the NFW halo mass profile proposed by Navarro et al. (1996) that has the form
(25)
where rs is a characteristic scale radius (the radius at which the logarithmic slope of the density is −2) and ρs is an inner density parameter.
Incorporating the details of the halo model, the change in relative velocity for a dark matter halo in terms of the sum of the neutrino mass is given by
(26)
The first term in square brackets (the one-halo term) illustrates the contribution to dynamical friction by the main halo (identical to what we found for a solid sphere, equation 11, for μ = 1) while the second term (the two-halo term) describes that due to nearby haloes clustered with the main halo. We show the behaviour of the first and second parts of the term in square brackets in Fig. 5.
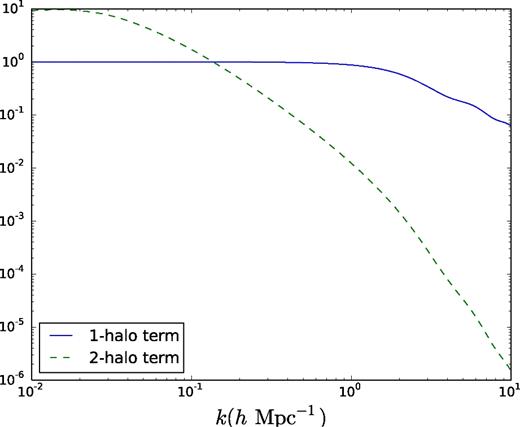
The one-halo and two-halo terms in square brackets in eq-uation (26), as a function of k, for Mhalo = 1015 h−1 M⊙ and a concentration of 4.
Figure 5.

The one-halo and two-halo terms in square brackets in eq-uation (26), as a function of k, for Mhalo = 1015 h−1 M⊙ and a concentration of 4.

Open in new tabDownload slide
The integral over k in equation (26) is logarithmically divergent since both the one- and two-halo terms formally extend to infinity; suitable limits in k must therefore be chosen. In order to set limits that are physically meaningful, we can multiply both sides of equation (26) by |$v_{\nu c}^2$| and incorporate this relative velocity inside the integral (as shown in Fig. 6). At a given wavenumber k, the contribution to the neutrino–CDM relative velocity is only from larger length-scales outside the scale of the halo. We also introduce the sum of the different neutrino species. This form integrates the hierarchy of the neutrinos into our calculations and relaxes the assumption of the degenerate neutrino species. Thus, the equation for Δvνc becomes
(27)
where
(28)
and i is for the different neutrino species and vνc is the relative velocity from all scales and from all neutrino species.
The one-halo and two-halo terms of the term in square brackets including $[v^{\prime }_{\nu c}(<\!k)]^2$ as in equation (27), for Mhalo = 1015 h−1 M⊙ and a 0.2 eV neutrino.
Figure 6.

The one-halo and two-halo terms of the term in square brackets including |$[v^{\prime }_{\nu c}(<\!k)]^2$| as in equation (27), for Mhalo = 1015 h−1 M⊙ and a 0.2 eV neutrino.

Open in new tabDownload slide

Recall that the relative velocity between the neutrino and dark matter decreases with scale and goes to zero on very large scales (Fig. 3). On the other hand, the effects of non-linearities are expected to be more significant on smaller scales. Therefore, for concreteness, we choose a mid-point of 16 h−1 Mpc to filter relative neutrino–CDM velocity field vνc.

A good fit (for a single neutrino) for the drift velocity Δvνc and displacement |$\Delta x \, (\simeq\!\frac{1}{2} \Delta v_{\nu c} \times t)$| over a Hubble time in terms of the neutrino mass mν and the halo mass Mh is given by
(29)
(30)
(31)
where vνc, 16 is the relative velocity of neutrinos and CDM, averaged over a sphere of radius 16 h−1 Mpc, centred around the halo. The explicit dependence of the displacement, Δx, on the one-halo and two-halo terms as a function of mass is shown in Fig. 7. Fig. 8 shows a comparison between Δx and the best fit in equation (31).
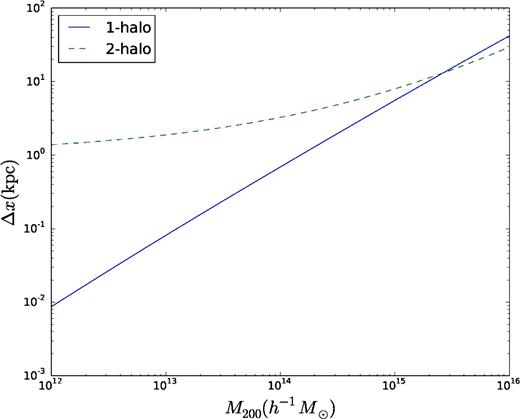
The one-halo and two-halo contribution to the displacement due to dynamical friction for a 0.1 eV neutrino. It is evident that the two-halo term dominates for all masses less than ∼1015 h−1 M⊙ where the one-halo term starts dominating.
Figure 7.

The one-halo and two-halo contribution to the displacement due to dynamical friction for a 0.1 eV neutrino. It is evident that the two-halo term dominates for all masses less than ∼1015 h−1 M⊙ where the one-halo term starts dominating.

Open in new tabDownload slide
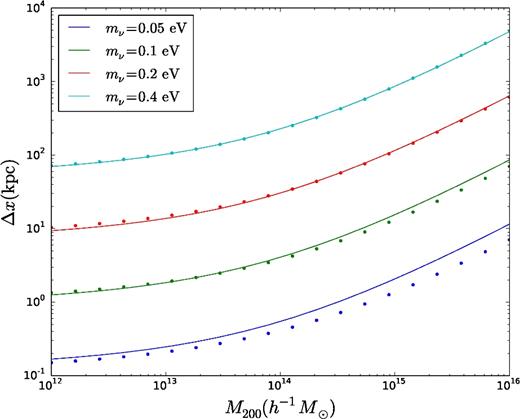
A plot comparing the fitting function in equation (31) with the calculated values for different neutrino masses. The dots are the calculated values while the line is the fitting function.
Figure 8.

A plot comparing the fitting function in equation (31) with the calculated values for different neutrino masses. The dots are the calculated values while the line is the fitting function.

Open in new tabDownload slide

4 PREDICTED SIGNAL TO NOISE FOR NOMINAL SURVEYS

In this section, we predict the observational prospects for the detection of neutrino dynamical friction in galaxy surveys. One may be tempted to interpret equation (31) as a relative displacement/velocity of haloes of different mass due the drag by the neutrino wind. However, this is only correct given the assumption that the haloes are not in the same neighbourhood and thus have their individual wakes. To make the theoretical predictions in equation (31), we have averaged over all the haloes distributed around a given halo. In practice, this would lead to an insignificant signal in cross-correlating two haloes in the same neighbourhood. The reason for this infinitesimal signal is that they share the same large-scale neutrino wake (as depicted in Fig. 9) and thus only experience a small fraction of Δvνc. To achieve an acceptable signal-to-noise estimate, we shall focus on the effect on the large-scale distribution of haloes due to the gravity of the neutrino wake.

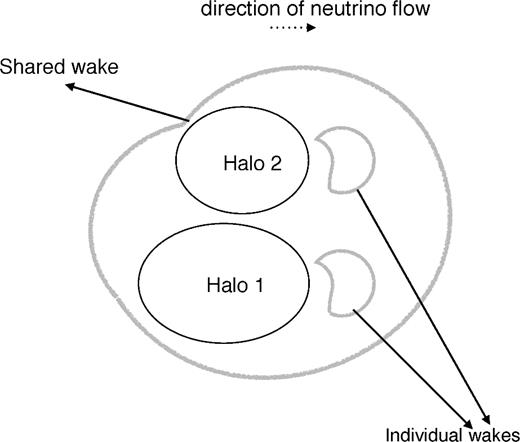
A sketch of the effect of shared wakes on the displacement of two haloes.
Figure 9.

A sketch of the effect of shared wakes on the displacement of two haloes.

Open in new tabDownload slide
Recall that the effect of dynamical friction on the gravitational field of the halo is given by equation (20), which is repeated here for convenience,
\begin{equation*} {\boldsymbol g}_{\nu , \boldsymbol k} |_{\rm dyn. fric.} \simeq \frac{ 2\,G m^4_\nu \mu (|\boldsymbol {v}_{\nu c}|) \Phi _{\boldsymbol k} (\boldsymbol {v}_{\nu c}\cdot {\boldsymbol k}) {\boldsymbol k}}{ \hbar ^3 |{\boldsymbol k}|^3}. \end{equation*}
This extra effect modifies the total density of gravitating matter in Fourier space, including the neutrino hierarchy, as
(32)
where
(33)

Thus, the density is modified by an extra time-dependent phase that manifests through the time dependence of the ν–CDM relative velocity. We aim to measure this consequence of dynamical friction due to neutrinos. To this end, we cross-correlate the densities of two tracers (possibly galaxies with different biases) in redshift space. The signal appears as an imaginary term in the redshift–space cross-correlation spectrum (see Appendix A for more details). The signal to noise for such a measurement is proportional to the difference in bias for the two populations, (bl − bf), the effective volume of the survey Veff and the time derivative of the phase term in equation (33).

Let us make some simple theoretical predictions for signal to noise for a generic redshift survey. For a given survey with two tracers that have differing bias such as ‘luminous galaxies’ (l) and ‘faint galaxies’ (f), the signal to noise for the imaginary part of the galaxy–cluster redshift–space power spectrum due to the neutrino dynamical friction of the haloes can be calculated to be (see Appendix A for further details):
(34)
where Δb is the relative linear bias between the two tracers (we include only the linear bias and consider the non-linear bias a part of the non-linearities in structure formation in Section 5), Pk is the power spectrum of matter fluctuations and Veff is the effective survey volume.3 We see that the S/N increases with the square root of the survey volume and is larger for tracers with considerable relative bias.
Fig. 10 shows our projection for (S/N)2 per galaxy for the detection of the imaginary part in the redshift–space cross-power spectrum of two tracers (in a nominal survey) with a relative bias Δb ∼ 1 (a typical relative bias between luminous and faint galaxies, e.g. Skibba et al. 2014), as a function of redshift. These estimates are made over a filtering comoving radius of 16 h−1 Mpc. The (S/N)2 per galaxy decreases as the redshift increases due to the steep drop in |$\dot{\phi }_{\rm k}$|⁠. For a single neutrino of mass 0.07 eV, a survey with about 2 million galaxies at z ≲ 0.5 can achieve a 2σ–3σ detection. This may be already achievable by the SDSS main sample (Abazajian et al. 2009) or BOSS redshift surveys (Ahn et al. 2014), and will be improved by a factor of 3, in the upcoming DESI survey (Levi et al. 2013). Signals from higher neutrino masses due to dynamical friction effects from the neutrino distribution are significantly easier to extract, with |$(S/N)^2 \propto m_\nu ^6$|⁠. For a generic redshift survey, we project that
(35)
galaxies can lead to >3σ detection of the neutrino drag.
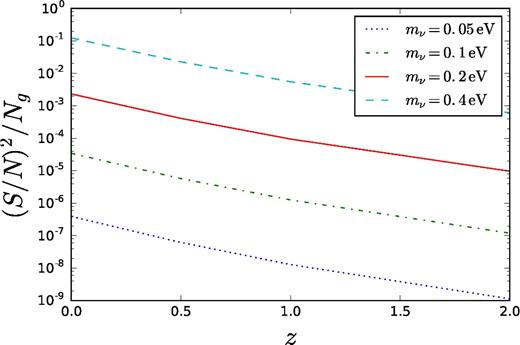
The signal-to-noise squared per galaxy as a function of redshift for various neutrino masses. This signal is estimated with a number density nl ∼ nf = 0.02 h3 Mpc− 3.
Figure 10.

The signal-to-noise squared per galaxy as a function of redshift for various neutrino masses. This signal is estimated with a number density nl ∼ nf = 0.02 h3 Mpc− 3.

Open in new tabDownload slide

For constraints on the sum of neutrino masses, Mν, one will have to sum over the signal from the various contributing species. Fig. 11 shows these estimates as a function of the minimum neutrino mass (which can easily be related to the sum of neutrino masses, Mν) for the normal and inverted neutrino hierarchies. Even though we have assumed the number density of the luminous and faint galaxies to be ∼ 0.02 h3 Mpc− 3, Fig. 12 confirms that the signal-to-noise squared per galaxy is insensitive of the number density of galaxies. Thus, the total signal-to-noise squared is proportional to the number of galaxies Ng, Δb2 and |$m_{\nu }^6$|⁠.

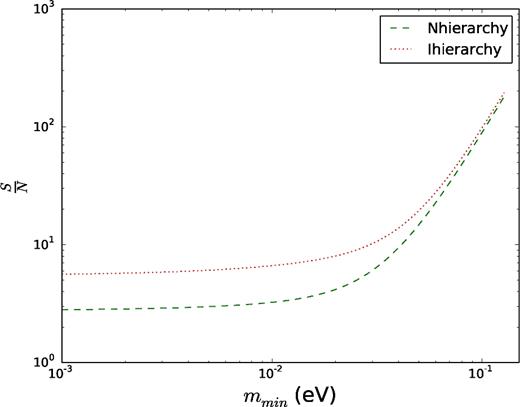
S/N for the detection of the imaginary part of the redshift–space cross-power spectrum of two tracers due to the dynamical friction effect of massive neutrinos. The dashed line and dotted line represent the S/N for the sum of the neutrino masses assuming the normal and inverted hierarchies, respectively. Both plots are for a theoretical survey assuming a volume of Veff = 1 h−3 Gpc3, Δb = 1 and nl ∼ nf = 0.02 h3 Mpc− 3.
Figure 11.

S/N for the detection of the imaginary part of the redshift–space cross-power spectrum of two tracers due to the dynamical friction effect of massive neutrinos. The dashed line and dotted line represent the S/N for the sum of the neutrino masses assuming the normal and inverted hierarchies, respectively. Both plots are for a theoretical survey assuming a volume of Veff = 1 h−3 Gpc3, Δb = 1 and nl ∼ nf = 0.02 h3 Mpc− 3.

Open in new tabDownload slide
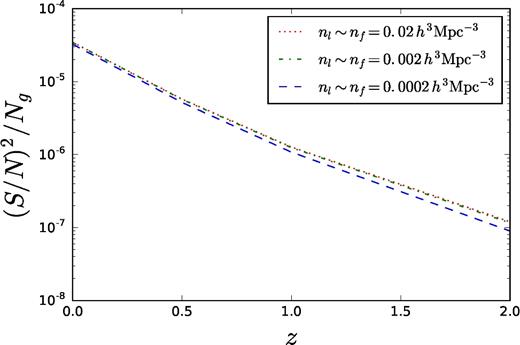
The signal-to-noise squared per galaxy as a function of redshift for various number densities, nl and nf, expected from the SPHEREX all sky survey (Doré et al. 2014). This signal is estimated for a 0.1 eV neutrino.
Figure 12.

The signal-to-noise squared per galaxy as a function of redshift for various number densities, nl and nf, expected from the SPHEREX all sky survey (Doré et al. 2014). This signal is estimated for a 0.1 eV neutrino.

Open in new tabDownload slide
An alternative measurement of the dynamical friction effect from neutrinos comes from a direct measurement of the velocities of galaxies, e.g. using the kinematic Sunyaev–Zel'dovich (kSZ) effect (e.g. Lavaux, Afshordi & Hudson 2013; De Bernardis et al. 2017; Schaan et al. 2016). In this case, the (S/N)2 is given as
(36)
with Δvνc given by equation (31) and σv ∼ 1500 km s− 1 is the velocity error per galaxy, expected from the future CMB S4 kSZ measurements (e.g. Sugiyama, Okumura & Spergel 2017). For a 0.1 eV neutrino and a halo of mass Mh ∼ 1013 h−1 M⊙, in future spectroscopic surveys such as DESI, EUCLID and SPHEREX (spectro), with ≲108 galaxies, we only get S/N ≲ 1. Therefore, the next generation of kSZ surveys will not be an efficient probe of neutrino dynamical friction.

In Appendix B, we look at the contamination of the relative velocity signal by non-linear structure formation using ΛCDM N-body simulations, which can become comparable to kSZ measurement errors. We find that the detection of the dynamical friction effects from neutrino require about 0.1 per cent precision in the measurement of the bulk velocity. Although current experiments do not have this precision, the required precision may be met with future experiments.

5 DISCUSSION AND CONCLUSION

We have investigated the prospects for detecting a novel signal from the cross-correlation of different galaxy populations in redshift space expected in the presence of neutrinos. This is due to the dynamical friction drag experienced by dark matter haloes that move in the primordial neutrino sea. Even though the neutrinos and dark matter cannot be observed, these effects make imprints on the galaxies and should be detectable in future surveys. With current surveys, a high ( ≳10) S/N is predicted for Mν ∼ 0.2 eV, which are marginally allowed by a combination of galaxy surveys and CMB. Given the current limits on the neutrino mass, future generations of high-density redshift surveys such as DESI will be able to detect smaller mass neutrinos or sum of masses Mν < 0.1 eV.

We should note that gravitational redshift can also introduce an imaginary part to the redshift space cross-power spectrum (McDonald 2009). However, the signal from this effect is smaller than that from the effect of dynamical friction by neutrinos (for a 0.1 eV neutrino) and has a different scale dependence (∝k−1 versus the scale-dependent neutrino signal that peaks at k ∼ 0.01 Mpc h−1).

Other effects of neutrinos on large-scale structure have been discussed by Garay, Verde & Jimenez (2017). Their study serves as a method for distinguishing the mass splitting of the neutrinos given a measured constraint on the sum of neutrino masses Mν. The authors consider the effect of different neutrino masses on the power spectrum on different scales – power suppression on small scales and the change of the matter-radiation equality scale on large scales. They also claim that this method may be used to distinguish the mass splitting of neutrinos given a precise measurement of the matter power spectrum that constrains the sum of the neutrino mass. These effects become measurable on large linear scales and do not suffer from non-linearities and systematic effects. Thus, given a measured constraint on the sum of neutrino masses, this method gives another independent confirmation/test of the mass splitting seen in neutrino oscillation experiments. Yet another impact of neutrinos on large-scale structure was studied by LoVerde (2016), who proposes a method in which the neutrino mass may be constrained by the measurement of the scale-dependent bias and the linear growth parameter in upcoming large surveys. Notably, similar to our proposal, this measurement is not limited by cosmic variance.

We next discuss some of the major systematics that may affect our predictions for the signal.

5.1 Galaxy and bias

Our estimates for the S/N are based on the number density of galaxies in a survey. Using galaxies requires a good estimate of the galaxy bias. Details and precision in defining the galaxy bias (with respect to the total matter in the presence of neutrinos or to the CDM alone; Castorina et al. 2014) are required in constraining the mass of neutrinos through the suppression of power on small scales. However, we expect the exact definition of bias to be less important in extracting the dynamical friction effect, given the large-scale coherence of neutrino wind.

The extra scale dependence of the halo bias which may be due to non-linearities and the free-streaming scale of the neutrino is an extra observable proposed by LoVerde (2016). However, these affect the magnitude, not the phase, of the Fourier amplitudes at per cent level and thus should not bias our projections for neutrino drag.

5.2 Non-linearities in structure formation

The impact of non-linearities on the CDM–neutrino relative velocity was investigated by Inman et al. (2015) in a number of νΛCDM simulations. The authors were interested in the effectiveness of the simple linear theory approximation given the non-linear complexities of structure formation. Their measurements show that the relative velocity power spectra predicted from linear theory are higher than that in simulations, but are still within 30 per cent of each other for the empirically allowed neutrino masses. Reconstructing the relative velocity power spectra using the halo density field and the dark matter density field, the authors show that they are correlated with the simulations for scales k ≲ 1 h Mpc− 1 and also have the right direction of the relative velocity with a mass-dependent correlation coefficient. The magnitude of the reconstruction may be corrected for non-linearities by the ratio of the non-linear to linear CDM power spectra. This reconstruction procedure may be implemented in practice to estimate the full neutrino–CDM relative velocity power spectrum.

A more serious issue is whether non-linear effects in standard non-linear structure formation can mimic the effect of dynamical friction by neutrinos. After all, the modulation of galaxy (cross-)power spectrum, or relative velocity, by reconstructed vνc can be interpreted as a particular contribution to the galaxy bispectrum, which might be partially degenerate with the (much larger) non-linear halo bispectrum. While Appendix B provides a first look at the magnitude of this degeneracy, a more complete study of this degeneracy in νΛCDM simulations (Inman et al. 2015) is currently underway. Indeed, our preliminary analysis suggests that non linear effects are not degenerate with the expected signal from dynamical friction of neutrinos, and only have marginal impact on our predictions.

5.3 Prospects for detection

In practice, measuring the mass of neutrinos from the dynamical friction effect will be quite challenging, and requires a good knowledge and control of standard non-linear structure formation, neutrino effects and halo bias. Our S/N estimates have only included the statistical error, and control of systematic uncertainties will only come from a careful study of simulated haloes. Nevertheless, our statistical projection of S/N ≳ 3 for future surveys (see equation 35 or Fig. 10) provides an incentive for further theoretical study and improvement. The dynamical friction effect, described here, may be a powerful complement to the various ways in which neutrinos will be probed over the next decade.

Acknowledgments

We thank Derek Inman, Dustin Lang, Marilena LoVerde, Ue-Li Pen and Rafael Sorkin for valuable discussions. We also thank the anonymous referee for comments that improved the presentation of this work. This work is supported by the University of Waterloo and the Perimeter Institute for Theoretical Physics. MJH acknowledges support from NSERC. Research at the Perimeter Institute is supported by in part by the Government of Canada through Innovation, Science and Economic Development Canada and by the Province of Ontario through the Ministry of Research, Innovation and Science.

1

Planck collaboration XVI (2014). We use the Planck-only best-fitting values.

2

The advantage of using the top-hat window function is that it is localized in real space, and thus can be applied to finite real-space data. However, we do not expect our conclusions to be sensitive to this choice.

3

For the integral, we have assumed kmax = 1 h−1 Mpc.

REFERENCES

Abazajian
K. N.
et al. ,
2009
,
ApJS
,
182
,
543

Crossref
Search ADS
 

Ahn
C. P.
et al. ,
2014
,
ApJS
,
211
,
17

Crossref
Search ADS
 

Battye
R. A.
Moss
A.
,
2014
,
Phys. Rev. Lett.
,
112
,
051303

Crossref
Search ADS
PubMed
 

Beutler
et al.
,
2014
,
MNRAS
,
444
,
3501

Crossref
Search ADS
 

Binney
J.
Tremaine
S.
,
2008
,
Galactic Dynamics
.
Princeton Univ. Press
,
Princeton, NJ

Google Scholar

OpenURL Placeholder Text

 

Bond
J. R.
Efstathiou
G.
Silk
J.
,
1980
,
Phys. Rev. Lett.
,
45
,
1980

Crossref
Search ADS
 

Castorina
Sefusatti
E.
Sheth
R. K.
Villaescusa-Navarro
F.
Viel
M.
,
2014
,
J. Cosmol. Astropart. Phys.
,
02
,
049

Crossref
Search ADS
 

Cooray
A.
Sheth
R.
,
2002
,
Phys. Rep.
,
372
,
1

Crossref
Search ADS
 

Cuesta
et al. ,
2016
,
Phys. Dark Universe
,
13
,
77

Crossref
Search ADS
 

De Bernardis
F.
et al. ,
2017
,
J. Cosmol. Astropart. Phys.
,
03
,
008

Doré
O.
et al. ,
2014
,
preprint (arXiv:1412.4872)

Eisenstein
D. J.
Hu
W.
,
1998
,
ApJ
,
496
,
605

Crossref
Search ADS
 

Garay
P. C.
Verde
L.
Jimenez
R.
,
2017
,
Phys. Dark Universe
,
15
,
31

Crossref
Search ADS
 

Fogli
G. L.
Lisi
E.
Marrone
A.
Montanino
D.
Palazzo
A.
Rotunno
A. M.
,
2012
,
Phys. Rev. D
,
86
,
013012

Crossref
Search ADS
 

Inman
D.
Emberson
J. D.
Pen
U.-L.
Farchi
A.
Yu
H.-R.
Harnois-Déraps
J.
,
2015
,
Phys. Rev. D
,
92
,
023502

Crossref
Search ADS
 

Lavaux
G.
Afshordi
N.
Hudson
M. J.
,
2013
,
MNRAS
,
430
,
1617

Crossref
Search ADS
 

Lesgourgues
J.
Pastor
S.
,
2006
,
Phys. Rep.
,
429
,
307

Crossref
Search ADS
 

Lesgourgues
J.
Pastor
S.
,
2012
,
Adv. High Energy Phys.
,
2012
,
608515

Crossref
Search ADS
 

Levi
M.
et al. ,
2013
,
preprint (arXiv:1308.0847)

Lewis
A.
Challinor
A.
Lasenby
A.
,
2000
,
ApJ
,
538
,
473

Crossref
Search ADS
 

LoVerde
M.
,
2016
,
Phys. Rev. D
,
93
,
103526

Crossref
Search ADS
 

McDonald
P.
,
2009
,
J. Cosmol. Astropart. Phys.
,
11
,
026

Crossref
Search ADS
 

McDonald
P.
Seljak
U.
,
2009
,
J. Cosmol. Astropart. Phys.
,
10
,
007

Crossref
Search ADS
 

Maltoni
M.
Schwetz
T.
Tórtola
M. A.
Valle
J. W.
,
2003
,
Phys. Rev. D
,
68
,
113010

Crossref
Search ADS
 

Mark
W.
Rudd
D. H.
Vanderveld
R. A.
Hu
W.
,
2014
,
Phys. Rev. Lett.
,
112
,
051302

Crossref
Search ADS
PubMed
 

Navarro
J. F.
Frenk
C. S.
White
S. D. M.
,
1996
,
ApJ
,
462
,
563

Crossref
Search ADS
 

Okoli
C.
Afshordi
N.
,
2016
,
MNRAS
,
456
,
3068

Crossref
Search ADS
 

Padmanabhan
T.
,
2000
,
Theoretical Astrophysics - Volume 1, Astrophysical Processes
.
Cambridge Univ. Press
,
Cambridge

Google Scholar

OpenURL Placeholder Text

 

Planck Collaboration XVI
,
2014
,
A&A
,
571
,
A16

Crossref
Search ADS
 

Planck Collaboration XIII
,
2016
,
A&A
,
594
,
A13

Crossref
Search ADS
 

Poole
G. B.
et al. ,
2015
,
MNRAS
,
449
,
1454

Crossref
Search ADS
 

Riemer-Sørensen
S.
,
2012
,
Phys. Rev. D
,
85
,
081101

Crossref
Search ADS
 

Schaan
E.
et al. ,
2016
,
Phys. Rev. D
,
93
,
082002

Crossref
Search ADS
 

Skibba
R. A.
et al. ,
2014
,
ApJ
,
784
,
128

Crossref
Search ADS
 

Springel
V.
Yoshida
N.
White
S. D. M.
,
2001
,
New Astron.
,
6
,
79

Crossref
Search ADS
 

Sugiyama
N. S.
Okumura
T.
Spergel
D. N.
,
2017
,
J. Cosmol. Astropart. Phys.
,
1
,
057

Crossref
Search ADS
 

Tinker
J.
Kravtsov
A. V.
Klypin
A.
Abazajian
K.
Warren
M.
Yepes
G.
Gottlöber
S.
Holz
D. E.
,
2008
,
ApJ
,
688
,
709

Crossref
Search ADS
 

Tinker
J. L.
Robertson
B. E.
Kravtsov
A. V.
Klypin
A.
Warren
M. S.
Yepes
G.
Gottlöber
S.
,
2010
,
ApJ
,
724
,
878

Crossref
Search ADS
 

Tseliakhovich
D.
Hirata
C.
,
2010
,
Phys. Rev. D
,
82
,
083520

Crossref
Search ADS
 

Yoo
J.
Seljak
U.
,
2013
,
Phys. Rev. D
,
88
,
103520

Crossref
Search ADS
 

Zhu
H. M.
Pen
U.-L.
Chen
X.
Inman
D.
Yu
Y.
,
2014
,
Phys. Rev. Lett.
,
113
,
131301

Crossref
Search ADS
PubMed
 

APPENDIX A: SIGNAL TO NOISE FROM THE GRAVITATIONAL FIELD DUE TO DYNAMICAL FRICTION

Following the correction to the gravitational field due the dynamical friction effect from neutrinos, |${\boldsymbol g_k} \rightarrow {\boldsymbol g_k} + {\boldsymbol g}_{\nu , {\boldsymbol k}}$|⁠, we can express this as a measurable effect to the power spectrum of galaxies in a redshift survey. Using divergence form of Gauss's equation for gravity, |$\nabla \cdot {\boldsymbol g} = - 4\pi a G \rho$|⁠, the Fourier space version is given as
(A1)
while that of the Poisson equation is
(A2)
Thus,
(A3)
where we have used equation (20) in comoving coordinates to substitute for |${\boldsymbol g}_{\nu , {\boldsymbol k}}$|⁠.
We shall see that this signal can be extracted by looking at the redshift space distortion (RSD) of galaxy surveys. Recall that the redshift–space distance rs is related to the real-space distance rd through
(A4)
where vx is the velocity along the line of sight and H is the Hubble constant. Using continuity equation for matter, we can find the redshift space overdensity for galaxies |$\delta ^{\rm s}_{\rm g}$| in terms of its real space overdensity |$\delta ^{\rm d}_{\rm g}$| and matter overdensity δm:
(A5)
Due to the dynamical friction of the neutrinos (assuming a uniform |${\boldsymbol v}_{\nu c}$|⁠), the matter overdensity has a redshift-dependent phase (A3):
(A6)
where DL(k, z) is the (scale-dependent) linear growth factor for νΛCDM cosmology. For a single tracer in redshift space, the density perturbation is given as
(A7)
The first two terms in the above equation are the standard RSD terms while the last term is new, as a result of the effect of dynamical friction due to neutrinos. Measuring this signal from a single tracer requires a very good knowledge of the linear bias term and is also susceptible to sample variance. One may eliminate the sample variance limitation by considering multiple tracers, as first suggested in McDonald & Seljak (2009). This is because, in the absence of shot noise, the ratio of Fourier amplitudes for two tracers can be measured perfectly, even for a single mode. While this ratio is real in standard multitracer RSD (McDonald & Seljak 2009), it finds an imaginary part (leading to a dipole) in the presence of a neutrino wind. There could also be a comparable imaginary term for different tracer biases, bf and bl, which we shall ignore for our simple S/N estimate here.
We will consider cross-correlating two distinct populations of galaxies with similar comoving densities nl and nf, and biases bl and bf. This is given as
(A8)
As can be seen from the last equation, the dynamical friction due to neutrinos has introduced an imaginary term to the redshift-space cross-power spectrum. This imaginary term is the signal per mode we hope to capture. Recall that
(A9)
Ignoring the effect of neutrinos, the noise variance for every mode is given by (e.g. McDonald 2009)
(A10)
Consider these as the elements of a matrix C given by
\begin{equation*} {\left[\begin{array}{cc}C_{\rm ll} & C_{\rm fl} \\ C_{\rm fl} & C_{\rm ff} \end{array}\right]}, \end{equation*}
the noise variance is thus one half of the determinant of C, |$\det C$|⁠.

The amplitude of our signal,  Im Cfl, its error Δ Im Cfl and the autopower spectrum of faint galaxies are shown in Fig. A1. This figure shows that the signal is dominated by large-scale modes. The decline of the signal at small scales suggests that the measurement is not improved by summing lots of modes. It is therefore not sample variance limited.

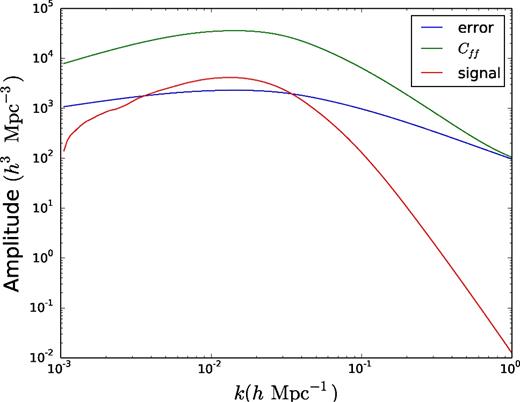
The amplitude of the signal from the imaginary part of the cross-power spectrum, the error on the signal and the autopower spectrum of faint galaxies, Cff, are shown for a 0.1 eV neutrino, nf = nl = 0.02 h3 Mpc−3 and bl = 2bf = 2.
Figure A1.

The amplitude of the signal from the imaginary part of the cross-power spectrum, the error on the signal and the autopower spectrum of faint galaxies, Cff, are shown for a 0.1 eV neutrino, nf = nl = 0.02 h3 Mpc−3 and bl = 2bf = 2.

Open in new tabDownload slide
To evaluate the signal to noise, we should also note that the neutrino–CDM relative velocity is not uniform and vanishes on large scales (see Fig. 3). To this end, we evaluate |$\langle \dot{\phi }_{\boldsymbol k}^2 \rangle$|⁠, we note that only the coherent part of |${\boldsymbol v}_{\nu c}$| contributes to the phase shift, equation (A6):
(A11)
where |$\beta \equiv \frac{2G m^4_i \mu H}{\hbar ^3}.$| This yields
(A12)
where Δvic is defined in equation (6).
The total signal-to-noise squared for a single neutrino, i, for all modes is given by
(A13)
where Δb = bl − bf. For our estimates, we have set μ = 1 in |$\dot{\phi }_{i \boldsymbol k}$| (recall that μ ranges between 0.7 and 1 and the signal to noise is directly proportional to μ). Given that the velocities of different neutrino species are highly correlated, the total signal to noise can be well approximated by the sum of individual signal to noises, i.e.
(A14)

APPENDIX B: Testing non-linear effects using N-body simulations

We shall next examine to what extent the non-linear structure formation in the standard ΛCDM model could mimic the effects of neutrino dynamical friction on cosmological haloes. We therefore use an N-body simulation without neutrinos in order to systematically account for the non-linear effects.

The signal we study is the difference in relative displacement due to neutrinos, Δx, for two different tracers, given by |$(\Delta x_1 - \Delta x_2) = \frac{1}{2} (\Delta v_{\nu c, 1}-\Delta v_{\nu c,2}) t = \frac{1}{2} v_{\rm rel} t$|⁠, where we denote the relative velocity between tracers 1 and 2 by vrel. We want to know whether non-linear velocities due to the growth of structure on small scales could produce a signal that could interfere with the signal from massive neutrinos.

To this end, we use an N-body simulation without massive neutrinos to investigate the possibility of any existing contaminating signal from non-linear effects. Assuming the neutrino streaming direction in any given volume is the same direction as the CDM bulk flow |$\boldsymbol {v}_{\rm c}$| (which it should be to first order), then we would expect the relative velocity |$\boldsymbol {v}_{\rm rel}$| between halo populations 1 and 2 to be in that direction also. So, we want to know whether there is any non-zero correlation between the direction of |$\boldsymbol {v}_{\rm rel}$| and |$\boldsymbol {v}_{\rm c}$| in the absence of massive neutrinos. That is, we want
(B1)
where the averaging is over independent volumes, which we take to be spheres of radius R, and the hat denotes the unit vector.
This effect is tested using the Gigaparsec WiggleZ (GiggleZ) N-body simulation (Poole et al. 2015). The GiggleZ main simulation contains 21603 dark matter particles in a periodic box of side 1 h−1 Gpc. The particle mass is 7.5 × 109 h−1 M⊙, which allows bound systems with masses ≳1.5 × 1011 h−1 M⊙ to be resolved. The clustering bias b of the haloes range from ∼1 to greater than 2. Halo finding for GiggleZ was performed using subfind (Springel et al. 2001), which utilizes a friends-of-friends (FoF) algorithm to identify coherent overdensities of particles and a substructure analysis to determine bound overdensities within each FoF halo. The resulting subfind substructure catalogues are rank-ordered by their maximum circular velocity (Vmax,sub) as a proxy for halo size,
(B2)
In the absence of neutrinos, the equivalence principle implies that α ≡ 1, so we expect |$\langle \boldsymbol {v}_{\rm rel} \rangle = 0$|⁠, i.e. α1 = α2 = 1, and |$\langle \boldsymbol {v}_{\rm rel} \cdot \boldsymbol {v}_{\rm c} \rangle = 0$|⁠.
In the presence of massive neutrinos, we expect that for haloes of mass M within a volume of radius R,
(B3)

Fig. A2 a shows the measured value of α from the relative velocity of our halo samples, which is consistent with zero at <per cent level, with no evident systematic bias. A larger sample and/or simulation box will lead to lower stochastic noise in α, and can potentially reveal a systematic bias, albeit at a lower level.

Left: fitted value of α over 100 spheres of radius r, for the (x, y, z) components (solid, dashed and dot–dashed lines) of the bulk flow of our two halo samples. Right: ΛCDM prediction for α from equation (B3) [for a 1015(h−1 M⊙ halo)] as a function of top-hat window function radius R and different sum of neutrino mass.
Figure A2.

Left: fitted value of α over 100 spheres of radius r, for the (x, y, z) components (solid, dashed and dot–dashed lines) of the bulk flow of our two halo samples. Right: ΛCDM prediction for α from equation (B3) [for a 1015(h−1 M⊙ halo)] as a function of top-hat window function radius R and different sum of neutrino mass.

Open in new tabDownload slide
The expected value of α can be calculated from our equation for Δvνc and the ΛCDM prediction for |$\boldsymbol {v}_{\rm c}$|⁠. The 1D rms velocity dispersion of CDM is
(B4)
For the halo model estimation, Δvνc is given by equation (26) and thus
(B5)
and
(B6)

The k integral is over the Fourier modes of the halo distribution while the k΄ integral is due to the modes from the neutrino distribution. We plot α as a function of the top-hat window function radius R and different sum of neutrino mass in Fig. A2b for a halo of mass Mh = 1015 h−1 M⊙. Clearly, the predicted value of α − 1 is quite small. For example, for Mν = 0.11  eV, the value of α − 1 is below 10−3 for all radii requiring 0.1 per cent level precision of the bulk flow to detect the neutrino effects.

© 2017 The Authors Published by Oxford University Press on behalf of the Royal Astronomical Society
Issue Section:
Article
Download all slides