-
PDF
- Split View
-
Views
-
Cite
Cite
Xuefei Chen, P. F. L. Maxted, Jiao Li, Zhanwen Han, The formation of EL CVn-type binaries, Monthly Notices of the Royal Astronomical Society, Volume 467, Issue 2, May 2017, Pages 1874–1889, https://doi.org/10.1093/mnras/stx115
Close - Share Icon Share
Abstract
EL CVn-type binaries are eclipsing binaries that contain an A- or F-type dwarf star and a very low mass (∼0.2 M⊙) helium white dwarf precursor (proto-He WD). A number of such objects have been discovered in the Wide Angle Search for Planets and Kepler photometric surveys. Here, we have studied the formation of EL CVn-type binaries and give the properties and the space density of this population of stars in the Galaxy. We show that EL CVn binaries cannot be produced by common envelope evolution as previously believed because this process leads to merging of the components when giants have such low-mass cores. Stable mass transfer in low-mass binaries, from more than 65 000 runs of Population I binary evolution, may well reproduce the properties of EL CVn stars such as the evolutionary phase, mass ratios and the WD mass–period (MWD–P) relation. The study shows that the most common donor mass range for producing the observed EL CVn-type stars is 1.15–1.20 M⊙ and that the lifetime of such objects increases dramatically with decreasing proto-He WD mass. This leads to an intrinsic peak mass around the minimum mass of proto-He WDs of ∼0.16 M⊙. The most probable proto-He WD mass is 0.17–0.21 M⊙ after selection effects included. We estimated the number of EL CVn stars with P ≤ 2.2 d to be 2–5 × 106 in the Galaxy, indicating a local density of 4–10 × 10−6 pc−3. We conclude that many more EL CVn-type binaries remain to be discovered and that these binaries will be predominantly low-mass systems in old stellar populations.
1 INTRODUCTION
Using the Wide Angle Search for Planets (WASP; Pollacco et al. 2006) photometric data base, Maxted et al. (2014a) recently discovered 17 bright eclipsing binaries that contain an A- or F-type dwarf (main-sequence, MS) star and a helium white-dwarf precursor (proto-He WD hereinafter), i.e. being in a rarely observed state evolving to higher effective temperatures at a nearly constant luminosity prior to being a very low mass WD. Among these stars, EL CVn is the brightest and is the only one previously identified as a variable star, so has been adopted as the prototype of this class of eclipsing binary star. In this paper, we define a binary as an EL CVn-type binary if it has an A- or F-type dwarf star (with mass of 1.05–2.9 M⊙) and a proto-He WD being in the constant-L phase. Multiperiodic pulsations were first discovered in the proto-He WD companion of 1SWASP J024743.37-251549.2 (J0247-25 hereinafter) where the proto-He WD has a mass of ∼0.2 M⊙ (Maxted et al. 2011, 2013), then in 1SWASP J162842.31+101416.7 (WASP 1628+10) where the mass of the proto-He WD companion is only about 0.135 ± 0.02 M⊙(Maxted et al. 2014b). This provides an opportunity to study the structure and formation of such low-mass WDs in details through the application of asteroseismology to this new class of pulsating variable stars.
Objects similar to the proto-He WD companions of EL CVn-type binaries, i.e. low-mass, thermally bloated hot WDs have been discovered in the Kepler field. They are KOI 74, KOI 81(van Kerkwijk et al. 2010), KHWD3 (KOI 1375, Carter, Rappaport & Fabrycky 2011), KOI 1224 (Breton et al. 2012), KIC 9164561 and KIC 10727668 (Rappaport et al. 2015). Some of them are obviously the descendants of EL CVn- type stars – they have just departed from the constant-L phase and some may be in the stage of surface H flash. Moreover, the RR Lyr star OGLE-BLG-RRLYR-02792 was found to be an eclipsing binary system where the pulsator is a proto-He WD with a mass of 0.26 M⊙ (Pietrzyński et al. 2012). EL CVn-type stars are then probably common in Universe and it is necessary to study their formation in details and estimate their number in the Galaxy.
Extremely low-mass WD (ELM, with masses below 0.2–0.3 M⊙, descendants of proto-He WDs) has also been found in some millisecond pulsars (MSPs; see a summary in table 1 of Istrate et al. 2014a) and in double degenerate systems (DDs; see the latest paper of the ELM survey of Brown et al. 2016). In general, low-mass He WDs (MWD ≲ 0.4 M⊙) can be produced by binary evolution through stable mass transfer or rapid common-envelope evolution (CEE). The CEE is unlikely to produce the low-mass He WDs in MSPs since the neutron star should be spun up through stable mass accretion. Our simple analysis for the 17 EL CVn samples (see the Appendix) shows that EL CVn-type stars are also unlikely to be produced from the CEE, in which the donor (the progenitor of the proto-He WD) should be at or very close to the base of red giant branch (RGB) (due to the very low mass of the proto-He WDs, ∼0.2 M⊙), where the envelope is tightly bound and the ejection of the CE results in a system with a much shorter orbital period, e.g. some DDs in the ELM survey, than those of EL CVn stars. We are therefore only concerned here with the stable mass transfer channel for the formation of EL CVn-type stars.
Before we go into the details of stable mass transfer channel, we first introduce the bifurcation period, Pb, in low-mass binary evolution, which is crucial for the formation of EL CVn-type stars. Fig. 1 presents a group of evolutionary tracks of the donors for binaries with component masses of 1.0 and 0.9 M⊙ but various initial orbital periods, P0. We can see two evolutionary regimes based on the value of P0. The donor evolves to ever-decreasing luminosity for short P0 while it passes through a nearly constant-L phase and leaves a degenerate remnant eventually when P0 is longer than the critical value Pb. This is known as the bifurcation period (see also Nelson, Dubeau & Mac Cannell 2004). Binaries below the bifurcation period (P0 < Pb) typically evolve to a minimum orbital period (on the order of 1 h) and then back to slightly increasing orbital periods. For binaries with P0 > Pb, there is a fairly tight MWD–P relation, where MWD and P are the remnant masses of the donor and the final orbital period, respectively. The MWD–P relation has been observed in several types of close binary stars such as binary radio pulsars (Rappaport et al. 1995; Lin et al. 2011; Smedley et al. 2014; Tauris & van den Heuvel 2014), hot subdwarfs (Chen et al. 2013) and a number of Kepler binaries containing low-mass hot WDs (Rappaport et al. 2015). The predicted value of Pb depends on the initial parameters of each binary and the assumptions in the modelling of the binary evolution process.
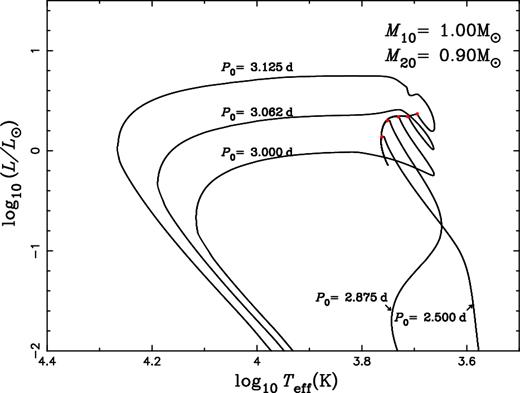
Evolutionary tracks on the Hertzsprung–Russel diagram for binaries with the same initial component masses (M10, M20) but various initial orbital periods (P0), as denoted in the figure. It clearly shows the bifurcation period in binary evolution: for initial orbital period P0 less than the bifurcation period Pb (Pb ≃ 3 d in this case) the mass donor evolves directly to very low luminosity, and for P0 slightly greater than Pb the evolution can produce a long-lived phase of evolution at nearly constant luminosity (proto-He WD phase).
The very low mass of the proto-He WDs and the short orbital periods mean that only binaries with initial orbital periods slightly longer than Pb can produce EL CVn-type stars. For example, the reconstructions of the evolutionary history for WASP J0247-25 and WASP 1628+10 (Maxted et al. 2013, 2014b) showed that both the objects are probably from stable mass transfer where the mass donor starts to lose mass before it leaves the MS, i.e. the central H abundance is larger than zero. The parameter space for producing EL CVn-type stars in this way is then expected to be small since both MWD and P increase significantly with P0. The expectation is against the fact that many such objects have been discovered. The time-scale for the nearly constant-L phase, t, may play a role here. Some particular examples (e.g. Nelson et al. 2004) show that the value of t can be up to nearly 109 yr when the proto-He WD mass is lower than about 0.21 M⊙. The majority of the products in Nelson et al. (2004) have He WDs larger than 0.2 M⊙, more massive than those in EL CVn-type stars. Istrate et al. (2014a,b) studied the formation of the low-mass He WD in MSPs through stable mass transfer near the bifurcation period and obtained a very strong dependence of the proto-He WD lifetime on its mass, approximately as the reciprocal of WD mass to the seventh power. And very recently, they (Istrate et al. 2016) give the detailed models of the low-mass He WD produced in low-mass X-ray binaries, including some microphysics such as gravitational settling, thermal and chemical diffusion and rotational mixing. In principle, the proto-He WDs in EL CVn-type binaries have properties similar to those in MSPs. However, a complete binary evolution study and a binary population synthesis are still necessary for our comprehensive understanding of the formation and characteristics of EL CVn-type stars, e.g. which binary systems can produce EL CVn-type stars, whether the number of such binaries from the stable mass transfer channel is sufficient to explain the observations, whether the binary properties are consistent with observations, what are the minimum mass and the peak mass, etc.
We carried out more than 65 000 runs of binary evolution for Population I (Pop I) low-mass binaries for this comprehensive study. The details for the computation are introduced in Section 2, and the evolutionary consequences are summarized in Section 3. In Section 4, we show the number and parameter distributions of EL CVn-type stars from our binary population synthesis. In Section 5, we give some discussions, and the conclusions are shown in Section 6.
2 THE COMPUTATIONS
We carried out binary evolution calculations with a newly developed Henyey code called mesa (Modules for Experiments in Stellar Astrophysics; Paxton et al. 2011, 2013, 2015). The advantages of mesa for our calculations are the inclusion of equations of state that are able to handle the low mass and high degree of degeneracy that the donors achieve, and the powerful capabilities of handling the huge fluctuations during the evolution such as H or He flashes.
The mass transfer is assumed to be non-conservative, with 50 per cent of the material lost from the donor being accreted by the companion while the other 50 per cent leaves the system with the same specific angular momentum as pertains to the donor. The treatment of non-conservative mass transfer, in particular the amount of specific angular momentum that is lost from the system, is a major uncertainty in modelling binary evolution and different reasonable prescriptions can give very different evolutionary paths (Podsiadlowski 2008; Eggleton 2010; Lin et al. 2011; Istrate et al. 2014a). Varying the assumptions on the amount of mass and angular momentum loss will affect the value of the bifurcation period, resulting in a change in the parameter space available for the production of EL CVn-type stars, but has little effect on the properties such as the lifetime of the proto-He WDs and the proto-HeWD mass-orbital period relation etc. We will give a discussion on this in Sections 3 and 4.
The behaviour of the accreting companion is complicated, e.g. it will lose thermal equilibrium when the mass accreting rate is larger than a certain value (depending on the mass of the accretor) and expand (Kippenhahn & Meyer-Hofmeister 1977), and may overfill its Roche lobe, leading to the formation of a contact binary and the subsequent termination of the formation process of EL CVn stars (Nelson & Eggleton 2001). We stop the calculations when the accretor overfills its Roche lobe even being in thermal equilibrium (i.e. the radius is obtained from equation 2) or the luminosity of the donor drops below log(L/L⊙) ≤ −2.5 (the system evolves below the bifurcation period and the donor cannot contract to be an He WD) and discard the models if the mass transfer rate |$\dot{M}$| is larger than 10−4 M⊙ yr−1 since (1) |$\dot{M}$| will be up to 1 M⊙ yr−1 soon after 10−4 M⊙ yr−1 in most binaries that we checked (see Section 3.1), leading to dynamically unstable mass transfer,2 and (2) the accretor will expand rapidly within such a high accretion rate and overfill its Roche lobe very likely (the binary cannot evolve to an EL CVn binary in both cases).
The main-sequence lifetime of the companion (from the zero-age main sequence to the termination of main sequence), tMS, is obtained from the fitting formula in Hurley's paper (Hurley, Tout & Pols 2002). Since the companion has evolved for a while before mass accretion, the companion star is not exactly at the zero-age main sequence and the tMS here is in fact an upper limit. But we checked that it has little effect on the final result. We reduced the main-sequence lifetime of the companion to be 0.5tMS and obtained a very similar result as shown in Section 3.
Our study is focused on Pop I low-mass binaries (with a metallicity Z = 0.02) and the initial parameters of our models are summarized as follows:
The donor mass (M10 in M⊙): 0.90, 0.95, 1.0, 1.05, 1.10,..., 2.0 (with ΔM = 0.05 M⊙)
Initial mass ratio (q0 = M10/M20, where M20 is the initial mass of the secondary): 1.1, 1.2, 1.3,..., 4.0 (with Δq0 = 0.1)
Initial orbital period (P0 in days, by step of ΔP0 = 0.02): from 2.5 to 4.5 for M10 = 0.9–1.05 M⊙ and 0.5–2.5 for M10 ≥ 1.10 M⊙.
Various values of P0 for different donor masses and such a small interval in P0 are chosen so that we obtain a relatively accurate value of Pb and a dense grid around Pb for each set of (M10, q0). This is important since the parameter space for EL CVn-type stars is expected to be just beyondPb, as mentioned in Section 1.
3 BINARY EVOLUTION RESULTS
3.1 Parameter space leading to the formation of EL CVn binaries
Two typical evolutionary tracks for EL CVn-type stars in our calculation are presented in Fig. 2, where the two binaries have the same component masses, (M10, q0) = (1.00, 1.1), but different initial periods, that is, P0 = 2.92 d for the upper panel and P0 = 3.02 d for the lower one. For the binary in the upper panel, P0 > Pb but very close to Pb, the donor does not ascend the RGB during mass transfer and the core has not been degenerate yet at the termination of mass transfer (defined as |${\dot{M}}_{\rm RLOF}\le 10^{-12}\,\mathrm{M}_{\odot } \,{\rm yr}^{-1}$|). The remnant has a final mass of MWD = 0.17 M⊙ and cools directly to become a WD after the nearly constant-L phase. For the binary in the lower panel, however, P0 is a little bit larger than Pb, the donor ascends the RGB during mass transfer and the core is degenerate at the end of mass transfer. As a consequence, the remnant has a larger final mass (MWD = 0.22 M⊙) and suffers several H shell flashes after the nearly constant-L phase but before the cooling. The H shell flashes cause the luminosity of the remnant to increase by several orders of magnitude on a dynamical time-scale. The remnant is then highly bloated during the flashes and has characteristics very different from that in the constant-L phase. In this paper, we only focus on the nearly constant-L phase before H flashes, and define the end of the nearly constant-L phase to be the point of maximum Teff before H flashes or the He WD cooling if no flash occurs.
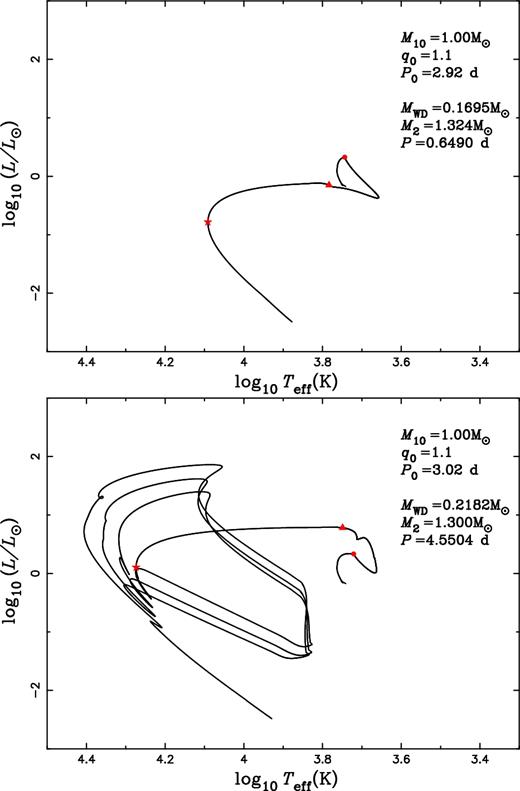
Two typical evolutionary tracks in our study on the Hertzsprung–Russel diagram. The binaries have the same component masses, that is, M10 = 1.00 M⊙ and q0 = 1.1. The initial period and final parameters for each binary are indicated in the figure. The circles, triangles and stars indicate the onset of mass transfer, the end of mass transfer and the end of the nearly constant luminosity phase, respectively. For the binary in the upper panel, P0 > Pb but very close to Pb, the donor does not ascend the RGB during mass transfer and cools directly to become a white dwarf after the nearly constant-L phase. For the one in the lower panel, P0 is a little bit larger than Pb, and the donor ascends the RGB during mass transfer. The remnant suffers several H shell flashes after the nearly constant-L phase before it cools down.
The evolution paths predicted by our calculations are summarized in Figs 3–5. According to observations, EL CVn-type binaries are defined as the binaries consisting of a proto-He WD and an A- or F- type dwarf companions, i.e. an MS star with its mass in the range of 1.05–2.9 M⊙. In each panel of the figures, the lower boundary is determined by the bifurcation period, while the upper and right boundaries are determined by the limit of maximum mass transfer rate (10-4 M⊙ yr−1). From the figures, we see that when M10 < 1.30 M⊙ only binaries in which the donor starts mass transfer after the end of MS can leave degenerate remnants and so contribute to the production of EL CVn-type stars. For more massive donors, EL CVn-type stars can be produced when the donor starts mass transfer on the MS if q0 is not very large. The most likely mass for producing short orbital period EL CVn-type stars (i.e. P ≤ 2.2 d) is in the range of 1.15–1.20 M⊙. For M10 > 1.2 M⊙, the parameter space decreases with the mass increasing and few models can produce EL CVn-type binaries with P < 2.2 d when M10 ≥ 1.60 M⊙. We see also small parameter spaces for M10 ≤ 1.10 M⊙. We explain this as follows.
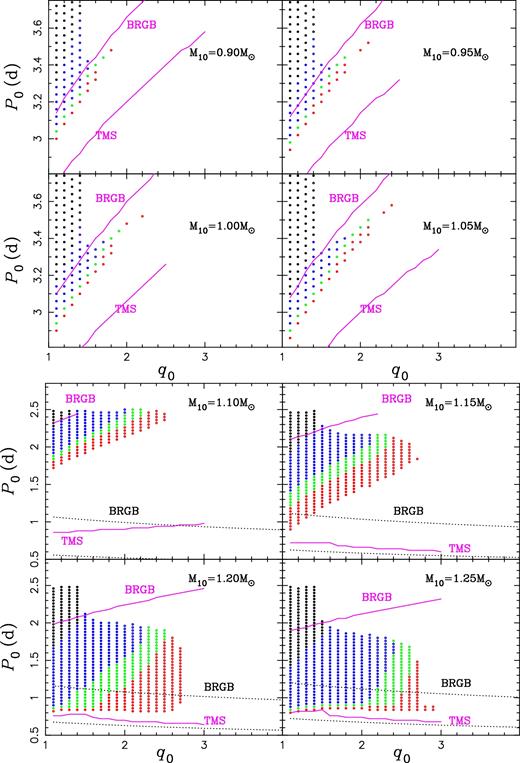
Summary of our calculations in the (P0, q0) plane. Symbols of open circles indicate the binaries that can produce He WDs and the filled circles overlapped on the open circles are those that can produce EL CVn-type stars. The initial donor mass is indicated in each panel. Various orbital periods at the end of mass transfer are denoted with different colours, i.e. the red, green, blue and black are for P in the range of 0.5–1.0, 1.0–2.2, 2.2–10 and >10 d, respectively. Models not presented are those binaries that evolve into contact, below the bifurcation point, and |${\dot{M}}_{\rm RLOF}> 10^{\rm -4}\,\mathrm{M}_{\odot } \,{\rm yr}^{-1}$|. The purple solid lines show the boundaries for models that start mass transfer at the termination of MS (TMS) and at the base of RGB (BRGB), while the black dotted ones are for the same boundaries for models where MB is not included (The dotted lines are below the minimum value of the respective y-axis variables in the upper four panels and are not presented). For clarity, one model was removed between every two points.
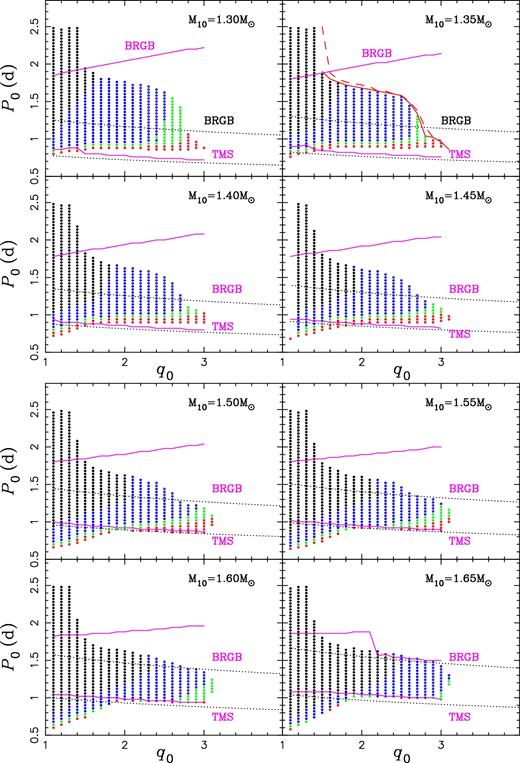
Similar to Fig. 3 but for M10 = 1.30–1.65 M⊙. The thick solid and dashed lines in the upper right panel (M10 = 1.35 M⊙) show the boundaries for mass transfer rate of 10-4 M⊙ yr−1 and 1 M⊙ yr−1, respectively.
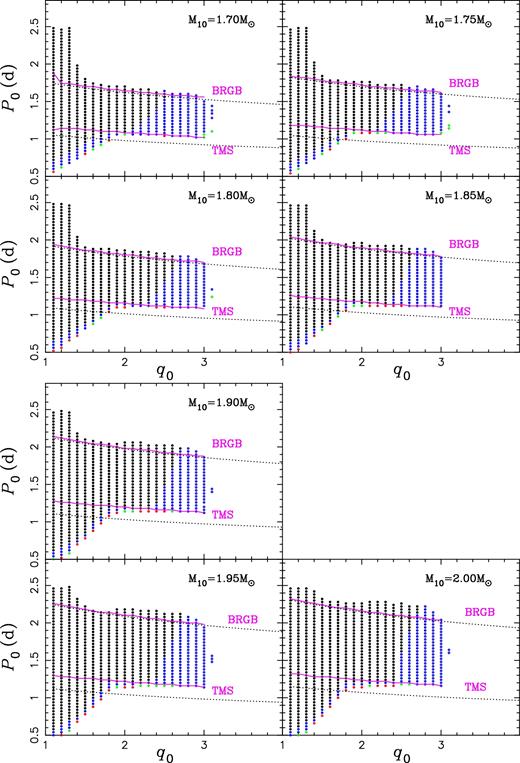
It is the MB that determines the parameter space for producing EL CVn stars. The discontinuous change between 1.10 M⊙ and 1.15 M⊙ is due to the fact that MB works when the donor is on the MS for M10 ≤ 1.10 M⊙ but does not for M10 ≥ 1.15 M⊙. When M10 ≤ 1.10 M⊙, many binaries that would evolve beyond the bifurcation period (then producing proto-He WDs) now evolve below the bifurcation period since the MB leads the mass transfer starting in advance. These binaries then cannot produce EL CVn stars any more, resulting in the small parameter space in low-mass range. For binaries with M10 ≥ 1.15 M⊙, the convection envelope develops in the late phase of Hertzsprung gap (HG) and the MB plays a crucial role in that phase, i.e. many of the progenitors of the proto-He WDs, which would start mass transfer on RGB if MB were not included, start mass transfer in advance, resulting in stable mass transfer and low-mass He WDs are more likely. With the increasing of the donor mass, the mass transfer rate becomes larger and larger in HG and may be up to 10-4 M⊙ yr−1 before the donor develops the surface convection region, and the MB does not affect the result any more. This occurs when M10 > 1.65 M⊙. To trace the effect of MB on parameter space, we show the boundaries at which the donor overfills its Roche lobe at the termination of the MS (TMS) and at the base of RGB (BRGB) when the MB has been included (the thin solid lines) and when the MB has not been included (the dotted lines) in Figs 3–5. We see that the TMS lines in the two cases are similar when M10 ≥ 1.15 M⊙ and the BRGB lines are similar when M10 > 1.65 M⊙, clearly showing the parameter space affected by the MB, as we described above. Note that, even when the MB does not play a role with mass increasing gradually, the TMS (BRGB) lines in our models are not exactly overlapped with that of no MB effect included since we adopted equation (1) to calculate the mass transfer rate; that is, the mass transfer starts before the donor overfills its Roche lobe.
As mentioned before, we have not included the models with mass transfer rates exceeding 10-4 M⊙ yr−1 in Figs 3–5. However, it is very valuable for binary evolution to trace the following behaviours of the donor when the mass transfer rate is larger than 10-4 M⊙ yr−1. We then set the maximum allowed mass transfer rate to be 1 M⊙ yr−1 in our calculation and recalculate the models of M10 = 1.35 M⊙. In our original parameter space, the mass transfer rates for binaries with this donor mass are always smaller than 10-4 M⊙ yr−1 when the initial mass ratio q0 ≤ 1.4. We therefore only examined the models with q0 ≥ 1.5. We found that, in a few models, the mass transfer rate may exceed 10-4 M⊙ yr−1 but does not increase up to 1 M⊙ yr−1. However, in most binaries we studied, the mass transfer rate will increase up to 1 M⊙ yr−1 soon after 10-4 M⊙ yr−1 is reached. The time-scale of this process (from 10-4 M⊙ yr−1 to 1 M⊙ yr−1) is a few years to ∼300 yr, and the amount of mass transferred during this process is less than 0.1 M⊙. For example, if q0 = 1.7, the mass transfer rate is always less than 10-4 M⊙ yr−1 when P0 ≤ 1.76 d, and it exceeds 10-4 M⊙ yr−1 for a while but never reaches 1 M⊙ yr−1 when P0 = 1.78 and 1.80 d. When P0 ≥ 1.82 d, the mass transfer rate increases up to 1 M⊙ yr−1 soon after 10-4 M⊙ yr−1 is reached, with a time-scale less than 300 yr and the amount of mass transferred less than 0.1 M⊙. The dashed line in the upper right panel of Fig. 4 shows the boundary for 1 M⊙ yr−1, very close to that for 10-4 M⊙ yr−1. This indicates that the mass transfer rate of 10-4 M⊙ yr−1 might be a good (though not very strict) criterion for dynamical instability. Please note that the models with initial orbital periods in the gap between the boundary for 10-4 M⊙ yr−1 and that for 1 M⊙ yr−1 have no contribution to the formation of EL CVn stars, though the mass transfer process is probably dynamically stable, since the companions will lose thermal equilibrium in such high mass accretion rates and expand to overfill their Roche lobes. The systems then become contact and the formation process of EL CVn stars is terminated (see Section 2).
3.2 Lifetime during the proto-He WD phase
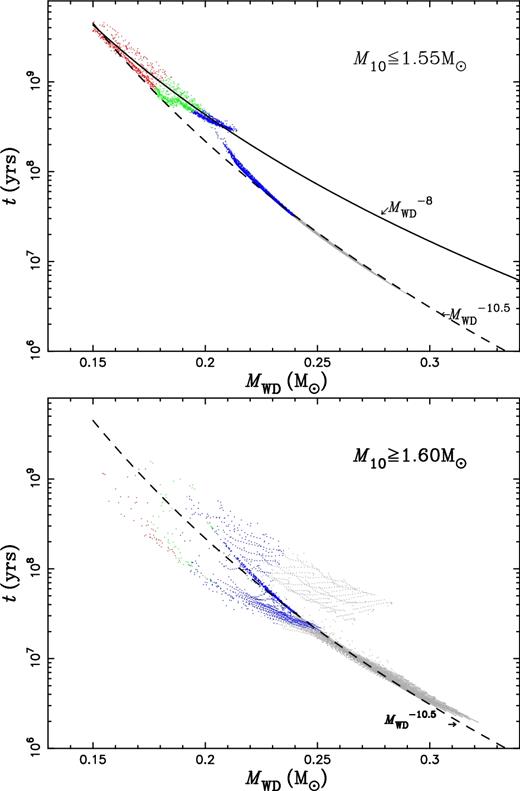
Timescale for the nearly constant luminosity phase versus the final mass of the donor, MWD, for EL CVn-type stars. The colours of red, green, blue and grey are for the final orbital period in the range of 0.5–1.0 d, 1.0–2.2 d, 2.2–10 d and >10 d, respectively. The upper panel is for M10 ≤ 1.55 M⊙ and the lower panel for M10 ≥ 1.60 M⊙. The solid and dashed lines show two exponential relationships between t and MWD (equations 6 and 7 in the text) as indicated in the figure.

Evolutionary tracks of the donors from the zero-age main sequence to a WD and the time elapsed during the proto-He WD phase. Initial parameters of each binary are indicated in the figure. The circles, triangles and stars are for the onset of mass transfer, the end of mass transfer, and the end of constant luminosity phase, respectively. The age differences between adjacent crosses, Δt, are equal and have been indicated in the figure for each track.
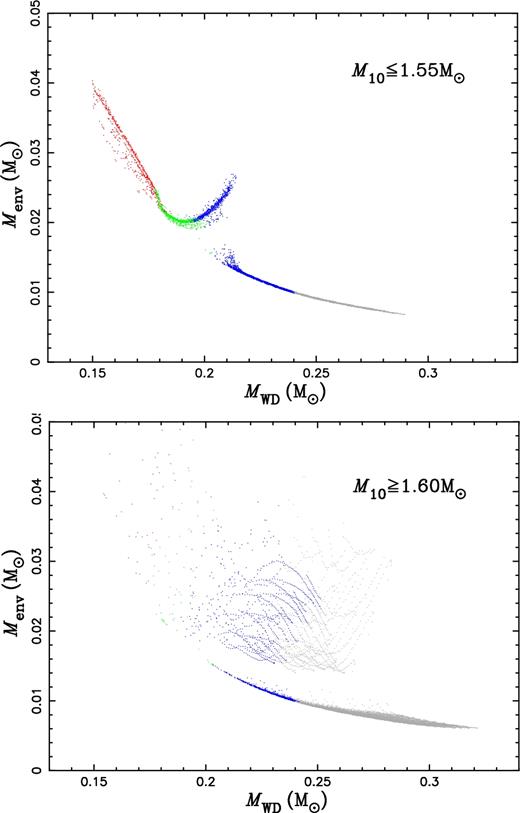
The dependance of envelope mass on the proto-He WD mass, MWD, at the end of mass transfer. The colours of red, green, blue and grey are for the final orbital period in the range of 0.5–1.0, 1.0–2.2, 2.2–10 and >10 d, respectively. The upper panel is for M10 = 0.90–1.55 M⊙ and the lower panel for M10 = 1.60–2.00 M⊙.
The anti-correlation between Menv and MWD for remnants from donors with degenerate cores comes from the competition between radiation pressure, Pr, and gravity pressure, Pgrav, near the end of mass transfer process. A large MWD indicates a larger core mass Mc, then a larger Pgrav and a higher Tb as mentioned above. So, more shell-burning energy is produced and needs to be transferred outwards, resulting in a higher Pr as well. When Menv is small enough, i.e. the shell-burning energy can be effectively transferred to the surface and radiate away, Pr reduces dramatically and the giant suffers a sudden collapse and terminates the mass transfer process. The radiation pressure dominates the process and leads to the fact that a massive remnant has a smaller envelope mass. However, the products appear as two groups as shown in Fig. 8, and there is a small tail in the upper group, i.e. Menv increases with MWD as MWD ≳ 0.19 M⊙. This is related to the discontinuous composition gradient produced by the first dredge up in stars evolving on the RGB. The donor's H-burning shell does not cross the composition jump during the mass transfer process for the products on the upper group, but does for those in the lower group. The tail of the upper group is due to the fact that the contraction of the donor now is induced by the H-burning shell crossing the composition jump, rather than Menv being less than a certain value.
For binaries with donors having non-degenerate cores (the lower panel of Fig. 8), the termination of mass transfer is a gradual process, i.e. the donor gradually draws back into its Roche lobe. The envelope mass of the remnant therefore depends on the details of mass transfer process as well as the initial parameters of each binary, and results in a big scatter seen in the lower panel of Fig. 8. In general, for a given MWD, a large initial mass ratio q0 indicates a relatively larger Roche lobe radius of the donor, then a larger radius and Menv for the remnant at the end of mass transfer. However, we still see a clear lower Menv limit in the figure, which is very similar to the Menv–MWD relation for degenerate donors. The donors located on the lower limit are generally more evolved than those beyond the limit, and their cores are degenerate.
3.3 Comparison with observations
To examine the reliability of our calculations for the stable mass transfer channel for the formation of EL CVn-type stars, we have compared the results to the observed properties of the current sample of EL CVn binaries.
3.3.1 Evolutionary stage
Fig. 9 shows the radius of the donor in comparison to its Roche lobe radius at the end of mass transfer, i.e. the onset of the nearly constant-L phase. Both of the radii are divided by the orbital separation a for easy comparison with observations, which are denoted with filled circles. The observations are from Maxted et al. (2014a) and the values of RL1/a and the corresponding error bars are derived from the mass ratios and their error bars. We see that all of the donor's radii are located in the range of 0.75–1.0RL1 at the end of mass transfer, and that the donor is closer to RL1 for a short orbital period (see the red points). The ratio of R1/RL1 at the termination of mass transfer indicates a relative density of the envelope at that time and, for a shorter P, the higher value of R1/RL1 is consistent with a lower MWD and a larger Menv as described in Section 3.2. During the subsequent evolution the value of RL1/a is constant for each binary, since the separation and the component masses hardly change during the whole constant-L phase. The models will then move horizontally to the left in this figure and cross the observed region for EL CVn-type stars due to the contraction of R1.
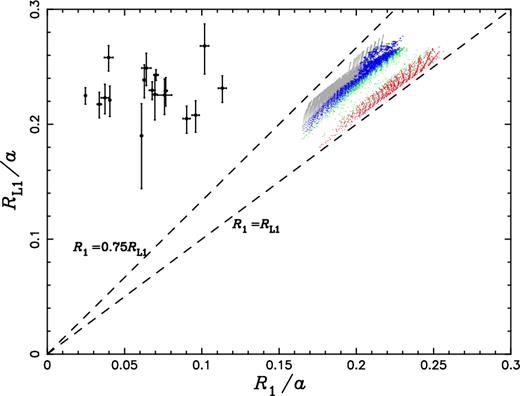
The donor's radius (R1) versus its Roche lobe radius (RL1) at the end of mass transfer. Both of the radii are divided by the orbital separation a for easily comparing with observations. The colours of red, green, blue and grey are for the final orbital period in the range of 0.5–1.0, 1.0–2.2, 2.2–10 and >10 d, respectively. The dashed lines are for R1 = RL1 and R1 = 0.75RL1 as indicated in the figure. The filled circles are observed EL CVn-type stars from Maxted et al. (2014a), where the values of RL1/a and the corresponding error bars are derived from the mass ratios and their error bars. In following evolution, the models will move straightforwardly to the left and cross the observed region for EL CVn-type stars due to the contraction of R1.
The onset and end positions of the products for the nearly constant-L phase on the (R1/a, Teff) plane are presented in Fig. 10, where several typical evolutionary tracks are also shown. The theoretical tracks are in general agreement with the observations. When M10 ≥ 1.60 M⊙, the theoretical evolutionary tracks may well match the location of the EL CVn samples, but the parameter space for short orbital-period EL CVn stars (P ≤ 2.2 d) is very small (see Section 3.1). It is unlikely that most of the observed EL CVn stars are produced from the systems with M10 ≥ 1.60 M⊙. For the models of M10 ≤ 1.55 M⊙, the observed systems tend to be 1000 K hotter than the predicted Teff values. For most of these systems, the Teff estimates are based only on photometric data and the proto-He WD contributes only 5–10 per cent of the light from the binary at most wavelengths, so it may be that this offset is due to a bias in the method used to estimate Teff of these stars. The sample of EL CVn-type stars were identified by looking for short-period light curves with a characteristic ‘boxy’ shape (sharp ingress and egress) that is deeper than the more rounded secondary eclipse. This indicates that the smaller star in the binary is hotter and so must be a highly evolved star. Near the onset of the constant-L phase, the proto-He WD has a similar radius and effective temperature to its companion. The light curve of such a binary shows strong ellipsoidal effect and smoother eclipse, quite similar to the light curve of W UMa-type contact binaries. Indeed, AW UMa is an example of a binary system with a W UMa type light curve that has subsequently been found to be a binary containing a proto-He WD (Pribulla & Rucinski 2008, but see Eaton 2016, for an alternative interpretation of this system). The Kepler object KIC 8262223 is a good candidate being in the onset of the constant-L phase according to its orbital parameters. We see obviously the ellipsoidal effect in its light curve but without the ‘boxy’ shape (Guo et al. 2016). Near the end of the constant-L phase the eclipses become shallow and difficult to spot in ground-based light curves, but several systems have been identified using photometry from the Kepler spacecraft (Carter et al. 2011; Breton et al. 2012; Faigler et al. 2015; Rappaport et al. 2015).
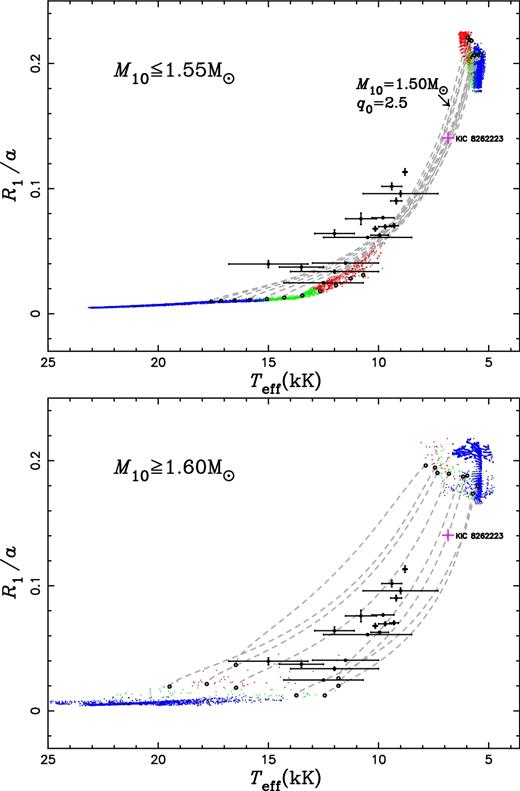
Evolutionary tracks of the proto-He WDs in the (R1/a, Teff) plane, where a is the orbital separation, R1 and Teff are the radius and the effective temperature of the proto-He WDs, respectively. For clarity, we only present the onset (dots, the upper right group) and end points (dots, the lower left group) for the nearly constant-L phase and several typical evolutionary tracks during this phase (the starting and ending places are indicated with open circles). Various colours are for different orbital period ranges, i.e. the red, green, blue and grey are for the final orbital period in the range of 0.5–1.0, 1.0–2.2, 2.2–10 and >10 d, respectively. The filled circles are the observed EL CVn-type stars from Maxted et al. (2014a). The pink plus indicates the location of KIC 8262223 from Guo et al. (2016).
3.3.2 The mass–period relation
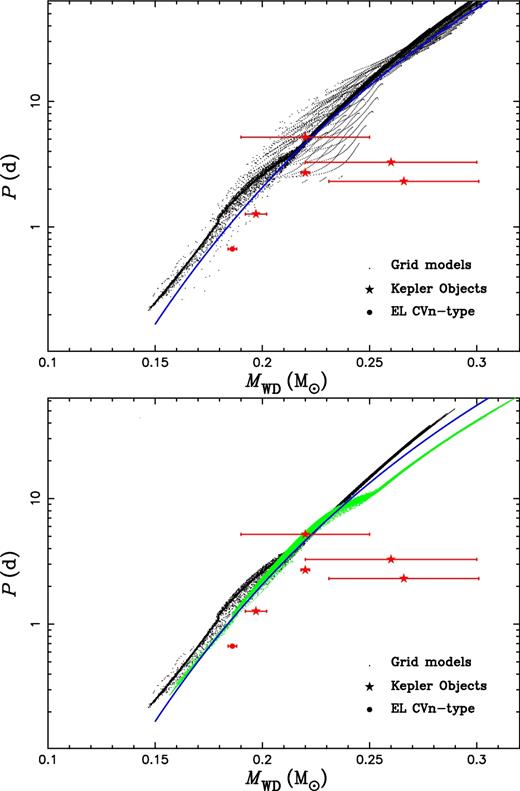
The orbital period–WD mass relation obtained from stable mass transfer. The upper panel shows all the products (black dots) in our calculations. The filled circles and stars are for EL CVn-type stars (Maxted et al. 2013, 2014b) and Kepler objects (van Kerkwijk et al. 2010; Carter et al. 2011; Breton et al. 2012; Rappaport et al. 2015), respectively. The fitting formula from Lin et al. (2011) is also presented for comparison. The lower panel is only for M10 ≤ 1.55 M⊙. The black dots are for Z = 0.02 and the green ones are for Z = 0.004 for comparison.
We notice a small bulge for MWD ≲ 0.22 M⊙ on the MWD–P band, which results from relatively large stellar radii due to the fact that the cores (Mc ≲ 0.19 M⊙) in such low-mass stars are non-degenerate at the termination of mass transfer. For Z = 0.004 (see the lower panel of Fig. 11), the bulge appears when MWD ≲ 0.25 M⊙ (or Mc ≲ 0.22 M⊙) due to the higher He abundance in the core at a low Z. We see a similar bulge (appeared at the proto-He WD mass of 0.21 M⊙) in fig. 13 of Istrate et al. (2014a). Accompanying the bulges, the MWD–P relation has a certain degree of dispersion, consistent with non-degenerate cores of the donors in this mass range. We also notice that the appearance of the bulges reduces the difference of the relation induced by the metallicity: products with low-mass He cores from various metallities likely mix together and become undistinguishable, different from those with more massive He cores.
As mentioned in Section 1 and studied by many authors in literature, the MWD–P relation is determined by the core mass–luminosity relation of stars with degenerate cores, and it is hardly affected by the assumptions in the modelling of binary evolution. In the low mass end, however, the cores are not degenerate yet at the termination of mass transfer. We then checked the influence of assumptions adopted in binary evolution on the MWD–P relation. The results are shown in Fig. 12, in which we include the products in the following cases: (1) models from our model grid with M10 ≤ 1.55 M⊙ (the black dots), (2) mass transfer is completely conservative (no mass and angular momentum loss, the red dots), (3) mass transfer is completely non-conservative and the lost mass takes away the specific angular momentum of the donor (the grey crosses), (4) 50 per cent of the lost mass from the primary leaves the system but does not take away any angular momentum (the filled green circles) and (5) similar to case (4) but all the mass lost from the primary leaves the system (the filled red circles).3
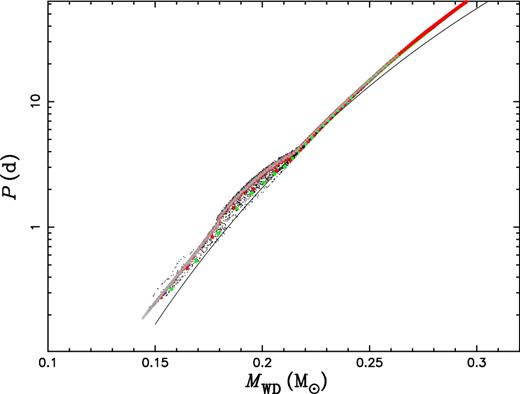
The orbital period-He WD mass relation from various assumptions in the modelling binary evolution. The black dots are for the models of our grids with M10 ≤ 1.55 M⊙, the red dots and grey crosses, overlapped on the black dots, are for those from completely conservation and completely non-conservation cases, respectively, and the green and red filled circles are for those from the assumptions that 50 per cent and 100 per cent of the lost mass from the primary leaves the system but does not take away any angular momentum, respectively.
From Fig. 12, we see that the products from the former three cases are well overlapped, and those from the last two are very close to them, indicating that the assumptions in the modelling of binary evolution (even in some extreme assumptions) have very little influence on the MWD–P relation. In fact, if we assume no angular momentum being taken away by the lost mass, as for the last two cases here, the change of the orbital separation becomes small and the termination of mass transfer is more dependent on the structure of the donor than before, and the resulting binary may agree with the MWD–P relation better.
Moreover, when we plot all the products on Figs 6 and 8, we find that they are undistinguishable with those of our model grid calculations, indicating that they have similar lifetimes and envelope masses at a certain proto-He WD mass. It is easily understood by the fact that, from the theory of stellar structure and evolution, whether a star contracts (mass transfer terminates) or not is only determined by its intrinsic structure (e.g. chemical composition), independent of detailed mass loss process. From this point of view, we may expect a similar minimum proto-He WD mass from various assumptions in binary evolution at a given chemical composition.
Based on the MWD–P relation, we estimate that the first two ‘bloated hot WDs’ discovered using Kepler photometry have masses in the range 0.26–0.27 M⊙ for KOI 81b and 0.205–0.25 M⊙ for KOI 74b. The relatively large span of the mass range for KOI 74b is due to the fact that the donors with non-degenerate cores also leave remnants with such an orbital period (P = 5.188 75 d) but various masses at the termination of mass transfer (see the discussion in Section 3.2). It is around 0.22 M⊙ if we only consider the contribution from donors with degenerate cores. Both of the masses for the two objects match the result of van Kerkwijk et al. (2010), where the mass of KOI 74b is derived from Doppler boosting and the MWD–P relation of Rappaport et al. (1995). With the constraint on orbital period in Maxted et al. (2014a), i.e. P ≤ 2.2 d, all the discovered EL CVn stars have masses ≤∼0.2 M⊙, so remain discoverable for much longer lifetimes than more massive proto-He WDs.
4 BINARY POPULATION SYNTHESIS
We perform a Monte Carlo simulation to obtain a stellar population and then interpolate in the grid above to obtain binary proto-HeWDs produced from stable mass transfer. In the Monte Carlo simulation, all stars are assumed to be members of binaries and have circular orbits. The primaries follow the initial mass function of Miller & Scalo (1979) and are generated according to the formula of Eggleton, Fitchett & Tout (1989), in the mass range 0.08–100 M⊙. The secondary mass, also with a lower limit of 0.08 M⊙, is obtained from a constant mass-ratio distribution n(q) = 1. Two other mass ratio distributions, n(q) = 2q, and uncorrelated component masses (i.e. the component mass is given in a way the same as that of the primary), are examined for estimating the uncertainty induced by the mass-ratio distribution. The distribution of orbital separations a is taken to be constant in log a for wide binaries. This separation distribution has been used in many Monte Carlo simulations and implies an equal number of wide binary systems per logarithmic interval and approximately 50 per cent of stellar systems with orbital periods less than 100 yr (Chen & Han 2009). Long-orbital-period binaries are effectively single stars. To mimic the case of the Galaxy, we assume a constant star formation rate of 5 M⊙ yr−1 (Yungelson & Livio 1998; Wang, Justham & Han 2013). Table 1 gives a brief summary of the parameters.
Initial parameters for binary population synthesis. IMF – initial mass function, q – mass ratio (the primary/the secondary), a – separation.
| IMF for the primary | Miller & Scalo (1979) |
| n(q) = 1 (standard) | |
| Mass-ratio distribution | n(q) = 2q |
| uncorrelated | |
| Separation distribution | n(loga)=const |
| Star formation rate | 5 M⊙ yr−1 |
| IMF for the primary | Miller & Scalo (1979) |
| n(q) = 1 (standard) | |
| Mass-ratio distribution | n(q) = 2q |
| uncorrelated | |
| Separation distribution | n(loga)=const |
| Star formation rate | 5 M⊙ yr−1 |
Initial parameters for binary population synthesis. IMF – initial mass function, q – mass ratio (the primary/the secondary), a – separation.
| IMF for the primary | Miller & Scalo (1979) |
| n(q) = 1 (standard) | |
| Mass-ratio distribution | n(q) = 2q |
| uncorrelated | |
| Separation distribution | n(loga)=const |
| Star formation rate | 5 M⊙ yr−1 |
| IMF for the primary | Miller & Scalo (1979) |
| n(q) = 1 (standard) | |
| Mass-ratio distribution | n(q) = 2q |
| uncorrelated | |
| Separation distribution | n(loga)=const |
| Star formation rate | 5 M⊙ yr−1 |
4.1 Distributions of binary parameters
Figs 13–15 show the distributions of orbital period P, the WD mass MWD and the companion mass M2, respectively, for EL CVn-type stars at 13.8 Gyr from the simulation of n(q) = 1 (the standard model). Different initial mass ratio distributions give similar results on the three binary parameters. In each of the figures, the black solid line is intrinsic while some selection effects are included for the dashed and dotted lines. For the dashed lines, we simply multiply a factor of |$L_{\rm A}^{3/2}$| to include the volume limit induced by the luminosity. Here, LA is the luminosity of the A- or F-type dwarf companion and is given by the classical mass–luminosity relation of MS stars (equation 3). The most typical feature for EL CVn-type stars is the boxy eclipse of the light curve, so the most important selection effect probably comes from the factor that prevents us to discover this feature, e.g. the luminosity ratio of both components in the WASP band (400–700 nm). The boxy eclipse becomes very shallow and difficult to find if the luminosity of proto-He WD in this band is far below its companion's. However, it is a little bit difficult to obtain the luminosity of the proto-He WD components in this band since they pass through a very large effective temperature range. We therefore artificially choose the luminosity of the proto-He WDs at Teff = 10 000 K, LHe, compare it with LA, and assume that the objects with LHe/LA < 0.2 (we referred the case of WASP J0247-25) cannot be discovered since the depth of the eclipse is shallow and the boxy property is not obvious on the light curves. This effect is superimposed to the luminosity limit of the companion and the result is shown as dotted lines in the figures. Though the considerations of the selection effects here are very simple, but they still give us some useful information.4
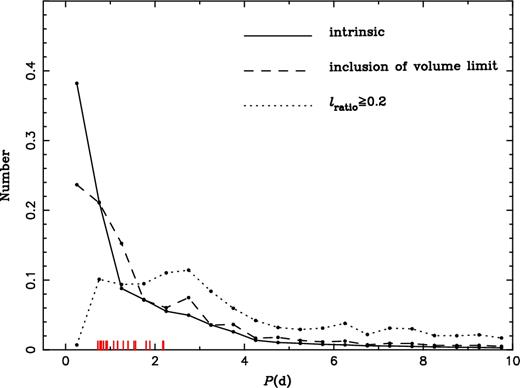
Orbital period distributions of EL CVn-type stars from the simulation of n(q) = 1 (the standard case, normalized). The solid line is intrinsic while selection effects are simply included for the dashed and dotted lines, i.e. the dashed line is for the inclusion of volume limit simply based on the luminosity of A- or F-type component, and the dotted line is for the constraint on the luminosity ratio of both components superimposed on the volume limit (see the text for the details). Short ticks along the x-axis indicate the positions of EL CVn stars in table 2 of Maxted et al. (2014a).
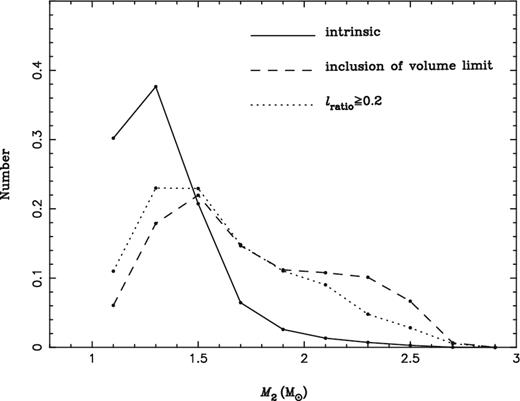
For the intrinsic distributions, since low-mass proto-He WDs have much longer lifetimes and shorter P as discussed in Section 3, most EL CVn-type binaries have proto-He WDs with mass around the minimum mass allowed for such objects, i.e. the proto-He WDs have a mass peak around 0.16 M⊙ (Fig. 14) and the corresponding orbital period peak is 0.2 d (Fig. 13). These distributions are unlikely to be affected by the treatment of mass transfer process since whether a star evolves across the constant-L phase or ever decreasing mass is only related to its intrinsic structure, which is determined by initial chemical composition and descriptions of the basic theory of stellar structure and evolution. The consideration of volume limit shifts the WD mass peak to ∼0.18 M⊙, and the constraint on the luminosity of both components further shifts the peak to 0.21 M⊙. The orbital period distribution changes accordingly. We see that, with the inclusion of both of the selection effects, the WD mass distribution becomes more flat, indicating similar possibilities in a relatively wide WD mass range. Fig. 13 shows that the observed EL CVn-type binaries are well located in the orbital period range given by the two selection effects (the dotted line). The companion mass peak also changes with selection effects; however, this distribution is more likely to be affected by the assumption of mass loss during mass transfer (see discussion in Section 5).
We can see more details from 2D distributions of the binary parameters, i.e. the (P, q) plane and the (MWD, M2) plane, as shown in Figs 16–17. There are four panels in both figures, where panel (a) is for the case at birth and panel (b) for the inclusion of weight of lifetime. In panel (c), we simply multiply a factor of |$L_{\rm A}^{3/2}$| and in panel (d) we further assume the objects with LHe/LA < 0.2 cannot be discovered based on panel (c). We first see the (P, q) plane, which can be directly compared with observations. Note that most of the mass ratio estimates in this figure are based on the amplitude of the ellipsoidal effect in the light curve. These will be biased towards higher values of q if this amplitude is underestimated, e.g. due to contamination of the light curve by light from a third star in the system or systematic errors in the photometry. The theoretical EL CVn-type stars are distributed over a wide range of period at birth (panel a), but gather at the short-P end due to long lifetimes of low-mass proto-He WDs (panel b), similar to the solid line in Fig. 13. The consideration of volume limit from the companion's luminosity has not improved the situation significantly (panel c). However, if we further include the constraint on the luminosity ratio of both components, the observation may be well reproduced (panel d) except for those with very shorter P, i.e. less than 1 d. Such short-P EL CVn-type stars are likely from the less-conservative mass transfer process than that assumed in this paper. The grey-scale image of (MWD, M2) shows that the most common component masses of EL CVn-type stars are MWD = 0.17–0.21 M⊙ and M2 = 1.3–1.5 M⊙, and that the object WASP J0247-25 is well located in the most common region. This is also consistent with the observations that the brighter component in most EL CVn-type binaries is typically an A-type dwarf.
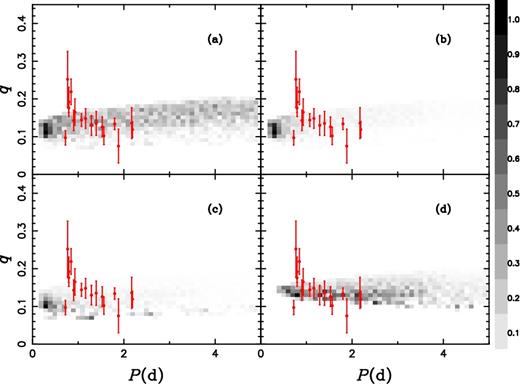
Distribution of EL CVn-type stars in the (P, q) plane, where q is mass ratio and P is orbital period. Panel (a) is for the case at birth and panel (b) for the inclusion of weight of lifetime in the nearly constant-L phase. Selection effects are simply included in panels (c) and (d), i.e. panel (c) is for the volume limit based on the luminosity of A- or F-type component, and panel (d) further includes the constraint on luminosity ratio of both components in addition to the volume limit (see the text for the details).
4.2 Birthrates and numbers
The birthrates for EL CVn-type stars are shown in the upper panel of Fig. 18, where the upper three red thin lines are for P ≤ 10 d (referred as f10) and the bottom black thick ones for P ≤ 2.2 d (referred as f2.2). Both f2.2 and f10 increase with age and are nearly constant for ages >∼9 × 109 yr, where f2.2 ≃ 0.0015, f10 ≃ 0.005 for the uncorrelated mass ratio distribution and f2.2 ≃ 0.004, f10 ≃ 0.015 for the other two mass ratio distributions. The corresponding numbers of EL CVn-type stars are shown in the lower panel of the figure. Since the most common donor mass for producing EL CVn-type stars with P ≤ 2.2 d are in the range 1.15–1.2 M⊙ (Figs 3–5) and those with short P have much longer lifetimes, short orbital-period EL CVn-type stars become more and more important in all of such binaries, e.g. the number of EL CVn-type stars with P ≤ 2.2 d is 2 × 106 from a total population of 2.5 × 106 such binaries with P ≤ 10 d for the uncorrelated mass ratio distribution, or 5 × 106 in a total of 6 × 106 for the other two. The local density is then 4–10 × 10−6 pc−3 for EL CVn-type stars with P ≤ 2.2 d (the volume of the Galaxy is adopted as 5 × 1011 pc3). For populations younger than 2.5 Gyr, f2.2 ≤ 10−5 yr−1, which results in less than 1000 EL CVn-type stars with P ≤ 2.2 d and a local density less than 2 × 10−9 pc−3 under various mass ratio distributions. Therefore, many more low-mass EL CVn-type stars remain to be discovered, and these stars will mostly belong to old stellar populations. Only eight of the known EL CVn-type binaries currently have measurements of their Galactic kinematics (Maxted et al. 2014a), but two of them are members of old stellar populations (halo or thick disc). The velocity dispersion of the other six stars is σv ≈ 45 km s−1, suggesting a mean kinematic age for this sub-sample ≈4 Gyr (Cox, Becker & Pesnell 2000). This is consistent with our prediction that the Galactic population of EL CVn-type stars is dominated by old stars.
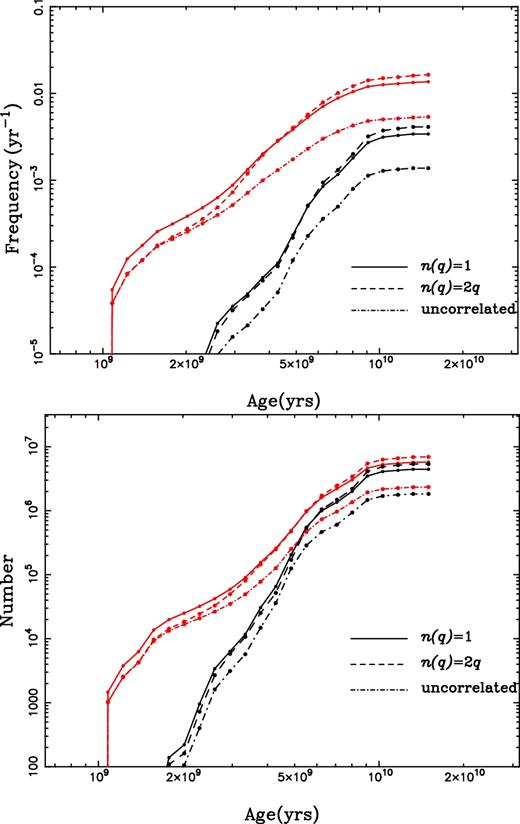
Birthrates (the upper panel) and numbers (the lower panel) of EL CVn-type stars for a constant star formation rate of 5 M⊙ yr−1. The upper three red thin lines are for all the products with orbital period P ≤ 10 d, and the bottom three black thick lines are just for those with P ≤ 2.2 d. Different line styles are for different mass ratio distributions as indicated in the figure (see the text for details).
5 DISCUSSIONS
5.1 The assumption of non-conservative mass transfer
As mentioned in Section 2, non-conservative mass transfer is among the major uncertainties in binary evolution. We have discussed that some of the intrinsic properties of the proto-He WDs in EL CVn stars, such as the minimum mass, the envelope mass, lifetime, evolutionary track and the MWD–P relation, will not change with the assumptions in binary evolution in Section 3.3.2. However, the parameter space for producing EL CVn-type stars, their predicted birthrate and the number of such objects do change with what we assume for the binary evolution. Here, we examined two other assumptions in the modelling binary evolution; that is, the mass transfer process is completely conservative (all the mass lost from the donor is accreted by the companion) or completely non-conservative (no mass to be accreted by the companion). We checked the models with M10 = 1.20 M⊙, and found that the assumption of completely conservative mass transfer may significantly increase the parameter space for producing EL CVn stars (see Fig. 19) while that of completely non-conservation dramatically reduces the parameter space since the companion cannot increase in mass to become an A- or F-type dwarf star under this assumption. In our study, we adopted general assumptions as has been done in previous studies (Chen & Han 2002, 2009) and the produced EL CVn-type stars have mass ratios consistent with observations except for those with P < 1 d, indicating that the assumption on the amount of mass loss is in general reasonable. Some more evolved donors at the onset of mass transfer may have less conservative evolution, and this may explain the observed relatively high mass ratios for P < 1 d.
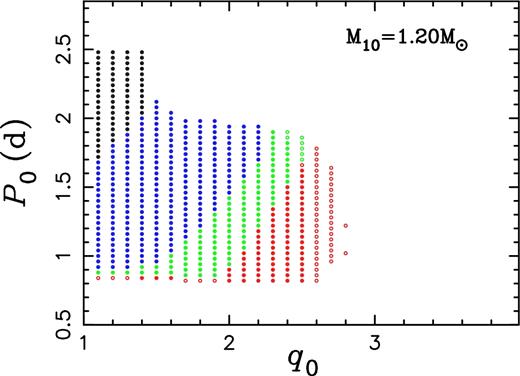
The influence of variable angular momentum loss can be estimated in the following way. In each (q0, P0) plane, the upper boundary is determined by the maximum mass transfer rate while the lower boundary is related to Pb. Although Pb changes with assumptions in binary evolution, the lowest mass (or core mass) for a given star to evolve through the constant-L phase does not change with any assumptions on binary evolution since whether a star contracts (mass transfer terminates) or not is only determined by its intrinsic structure, independent of detailed mass loss process. So, more angular momentum loss in comparison to that adopted in the calculations means a rapid shrinkage of the Roche lobe and a faster mass transfer process. The star must then be more evolved at the onset of mass transfer (a longer Pb) to evolve beyond the bifurcation period. As a consequence, the lower boundary moves upwards. Meanwhile, the rapid shrinkage of Roche lobe makes dynamically unstable mass transfer more likely so the upper boundary moves downwards. This effect might be small since most potential progenitors of EL CVn-type stars obtained in this paper have orbital periods just above the bifurcation period and start mass transfer on the MS or in Hertzsprung Gap (HG), where the mass transfer is generally stable unless we artificially adopt an unreasonable large angular momentum loss. In general, a large angular momentum loss leads to a smaller parameter space for producing EL CVn-type stars, resulting in a lower birth rate and fewer such objects.
5.2 Effects of metallicity
In this study, we have only considered Pop I stars. Here, we discuss the expected influence of metallicity on the formation of EL CVn binaries. Since the He cores in low-mass stars are very similar, we may get several general impressions from the structure of the envelope. (1) The envelope mass Menv. For a given core mass Mc, a high Z means a larger opacity in the envelope, then a lower Menv when the star contracts to be sure that the radiation pressure Pr is less than the gravity pressure Pgrav at that time. As a consequence, the minimum mass (and the mass peak) increases with the decreasing of Z. (2) The lifetime of EL CVn-type stars, t. As discussion in Section 3.2, |$t \propto M_{\rm env}/\dot{M}_{\rm nuc}$|, where |$\dot{M}_{\rm nuc}$| is very sensitive to the temperature in the burning shell Tb. Since Tb ∼ Mc/Rc (Refsdal & Weigert 1970) and Rc decreases with Z for a given Mc, the temperature Tb, then |$\dot{M}_{\rm nuc}$|, increase with decreasing Z. So, the value of t may not significantly deviate from that shown in this paper since Menv also increases with the decreasing Z as discussed above. (3) The parameter space for EL CVn stars. For a given (M10, q0, P0), a low Z indicates a lower opacity, then a smaller stellar radius, which means that, in comparison to a binary with the same parameters but a high Z, the donor fills its Roche lobe at a later evolutionary stage (or more evolved, since RL is determined and not affected by Z) and so is more likely to evolve through the constant-L phase. So, the bifurcation period, Pb, becomes smaller with decreasing Z, and the whole parameter spaces move downwards.
6 CONCLUSIONS
In this paper, we systematically studied the properties of EL CVn stars from the stable mass transfer channel, such as the evolutionary tracks, the envelope masses, the lifetimes in the nearly constant-L phase, the component masses and the MWD–Porb relation. The results are summarized as follows.
In general, the evolutionary tracks, mass ratios and the MWD–P relation are in good agreement with observations. There is a small bulge at the low-mass end on the MWD–P relation due to non-degenerate cores of such low-mass donors at the termination of mass transfer. It starts from ∼0.22 M⊙ for Z = 0.02 and ∼0.25 M⊙ for Z = 0.004. The bulges may reduce the differences of the MWD–P relation induced by metallicity and makes the products from various metallicities indistinguishable. Based on the MWD–P relation, the derived masses for the first two Kepler hot WDs are consistent with that in previous studies, and all the discovered EL CVn-type stars in Maxted et al. (2014a) have low-mass (≤∼0.2 M⊙) proto-He WDs.
The lifetimes in the nearly constant-L phase t are strongly dependent on the masses of proto-He WDs MWD, i.e. |$t \propto M_{\rm WD}^{-8}$| for MWD ≤ 0.21 M⊙ and |$t\propto M_{\rm WD}^{-10.5}$| for the lower lifetime limit. The study gives t ∼ 2 × 107 yr for MWD = 0.25 M⊙, ∼4 × 108 yr for MWD = 0.2 M⊙ and up to ∼4 × 109 yr when MWD = 0.15 M⊙. This leads to an intrinsic peak mass around the minimum mass of proto-He WDs (∼0.16 M⊙), which is only determined by initial composition and does not depend on details of the mass transfer processes. The most common component masses of EL CVn-type stars are MWD = 0.17–0.21 M⊙ and MWD = 1.3–1.5 M⊙ if selection effects are included, consistent with the observations.
The most likely progenitor mass for producing the observed EL CVn-type stars (with orbital period less than 2.2 d) is in the range 1.15–1.20 M⊙. Assuming an appropriate star formation rate for the Galaxy (5 M⊙ yr−1), we find that the birth rate of EL CVn-type stars with shorter P is very small and the local density is less than 2 × 10−9 pc−3 for P ≤ 2.2 d in populations younger than 2.5 Gyr. However, the role of EL CVn-type stars with short P becomes more and more important with age due to the very long lifetime, and the number is 2–5 × 106 for those with P ≤ 2.2 d in the Galaxy, with a local density of 4–10 × 10−6 pc−3. Though the number or local density may change significantly with the assumptions in modelling binary evolution, many more low-mass EL CVn-type stars are still expected and they are in old populations more likely, as can be confirmed observationally in future.
Acknowledgments
We thank the anonymous referee for his/her very helpful suggestions on the manuscript. This work is supported by the Natural Science Foundation of China (Nos 11422324, 11521303, 11390374), by Yunnan province (Nos 2012HB037, 2013HA005) and by the Chinese Academy of Sciences (No. KJZD-EW-M06-01).
In our calculation, we used the default option for the atmosphere boundary condition, that is, ‘simple-photosphere’, an Eddington approximation estimated for optical depth equal to 2/3. The choice of this boundary condition almost has no effect on our results in this paper since we are only concerned on the temperature but not the spectral energy distribution.
Extensive effort has been put into developing reliable criteria to distinguish between dynamically stable and unstable mass transfer (Hjellming & Webbink 1987; Webbink 1988; Soberman, Phinney & van den Heuvel 1997; Han et al. 2002; Chen & Han 2008; Woods et al. 2012; Ge et al. 2015; Pavlovskii & Ivanova 2015), but there are still many problems and no consensus on this issue.
The former three cases are usually adopted in the modelling of binary evolution for different objects, e.g. Nelson & Eggleton (2001); Han et al. (2002), while the last two are not common in the study of binary evolution. We include the last two cases here to see the maximum effect in some extreme assumptions.
In Fig. 14, we have included the Kepler systems though they suffer from different selection effects than those analysed in the figure since we have only one EL CVn star that has the exact proto-He WD mass presently.
REFERENCES
APPENDIX: THE COMMON ENVELOPE EJECTION CHANNEL
For convenience, we denote the left part of equation (A5) as y. The criterion for CE ejection is then written as y ≥ 0. Note that there is an additional constraint on the initial mass ratio, i.e. qi > 1, since the donor is the initially more massive component from binary evolution.
the value of Pi can be approximately given by M1i and Mc. So we can obtain the value of y from equations (A6– A8) and the observed qf and Pf, for given values of Mc, αλ and qi. It is considered to be reasonable to suppose the value of αλ to be in the range of 0.5–1 (Rappaport et al. 2015). By setting αλ = 1.0, which is an extreme case and gives the maximum value of y, we examined a series values of Mc and qi for all the 17 EL CVn-type stars in table 2 of Maxted et al. (2014a). For each EL CVn-type sample, the constraints of y ≥ 0 and qi > 1 require Mc > 0.3 M⊙ (see Fig. A1 for an example), far beyond the mass of proto-He WDs in EL CVn-type binaries. This means that the CEE cannot produce the observed EL CVn-type stars.
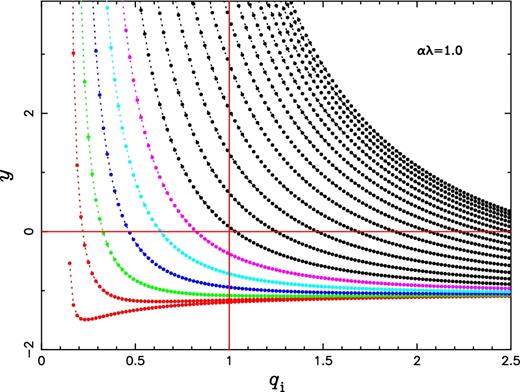
The (y, qi) plane for WASP 2328-39, with orbital period of 1.29 d and mass ratio of 0.13. The parameter y indicates the left part of equation (A5) and qi is initial mass ratio. The core mass Mc changes from 0.15 to 1.1 M⊙ in steps of 0.05 M⊙ from left to right. The common envelope can only be ejected when y ≥ 0 (the horizontal line) and the initial mass ratio should be greater than 1 (the vertical line) from binary evolution. So, only the upper right part in the figure is appropriate for the object produced from the CEE. To satisfy both constraints, we have Mc ≥ ∼0.45 M⊙ for this object when αλ = 1.0, which is an extreme case and gives the maximum value of y.





