-
PDF
- Split View
-
Views
-
Cite
Cite
M. J. Burke, M. Gilfanov, R. Sunyaev, A dichotomy between the hard state spectral properties of black hole and neutron star X-ray binaries, Monthly Notices of the Royal Astronomical Society, Volume 466, Issue 1, April 2017, Pages 194–212, https://doi.org/10.1093/mnras/stw2514
Close - Share Icon Share
Abstract
We analyse the spectra of black hole (BH) and neutron star (NS) X-ray binaries (XBs) in the hard state using archival RXTE observations. We find that there is a clear dichotomy in the strength of Comptonization between NS and BH sources, as measured by both the Compton y-parameter and the amplification factor A, with distinct groups of BH and NS XBs separated at y ∼ 0.9 and A ∼ 3. The electron temperature kTe can occupy a broad range in BH systems, from kTe ∼ 30 to 200 keV, whereas for NSs kTe is peaked at ∼15–25 keV, but can extend to higher values. The difference between BHs and NSs in y implies that kTe is higher at a given optical depth for BH XBs. Our results also imply that for NS systems the accreting material loses ∼1/2–2/3 of its energy through Comptonization in the corona. The remaining energy is released on the surface of the NS, making it a powerful source of soft radiation, which alters the properties of the Comptonizing corona. Finally, we find evidence at the ∼2.4σ confidence level that Comptonization parameters may be correlated with the NS spin, whereas no correlation with the BH spin is found. Our results highlight a further observational distinction between BH and NS XBs, which is a consequence of NSs possessing a physical surface.
1 INTRODUCTION
X-ray binaries (XBs) are observed in a rich variety of states and phenomenologies (e.g. Remillard & McClintock 2006; Belloni 2010; Gilfanov 2010). However, from a broad perspective, their behaviour can be reduced to a discussion of two spectral states. These are comprised of a soft state, where the spectra peak below 10 keV and are well described as optically thick emission from a geometrically thin disc (Shakura & Sunyaev 1973), and a hard state where the spectra follow a roughly power-law shape to tens or hundreds of kiloelectronvolts (e.g. Syunyaev et al. 1991; Tanaka & Shibazaki 1996; Ibragimov et al. 2005; Gilfanov 2010).
Comptonization is a cooling process, where hot electrons impart energy through scattering with lower energy photons, which means that the supply and temperature of the seed photons will affect the properties of the Comptonizing media. Sunyaev & Titarchuk (1989) showed that if the seed photons originate in the accretion disc and close to the Comptonizing cloud then it is necessary to account for photon feedback, where Comptonized photons are subsequently absorbed by the disc, increasing the temperature and numerosity of seed photons going into the cloud, causing more Comptonization and a greater cooling of the Comptonizing media. In the case of a uniform thermal electron cloud blanketing the disc, this will result in softer (and more rapidly softening) spectra than is typically observed from black hole (BH) XBs (Haardt & Maraschi 1993), thus strongly disfavouring such a scenario (Gilfanov et al. 1995; Churazov, Gilfanov & Revnivtsev 2001). The hard state geometry is therefore subjected to two important constraints; the absence of the soft state emission consistent with an optically thick accretion disc (with kTi ∼ 1 keV) and the positioning of the two emission regions (seed photon source and Comptonizing electron cloud) such that the effect of photon feedback is reduced.
Some fraction of the Comptonized photons will be intercepted by the disc and ‘reflected’ into the line of sight by further Compton scattering and florescence. These processes give rise to a complex spectral component that typically peaks at energies of ≈30–50 keV (the so-called ‘Compton hump’, see Sunyaev & Titarchuk 1980, figs 10a and c) and adds further fluorescent emission to the spectrum. The reflection component is present in both BH XBs (due to interaction of X-rays with the accretion disc and the surface of the normal star; Basko, Sunyaev & Titarchuk 1974) and active galactic nuclei (AGNs; Nandra & Pounds 1994), and complicates attempts to understand the dominant Comptonized emission owing to proximity of the Compton hump to the plausible location of the high-energy turn-off (corresponding to ≈3kTe). Typical attempts to take reflection into account involve adding sophisticated reflection components (such as the xspec models pexrav (Magdziarz & Zdziarski 1995) or reflionx (Ross & Fabian 2005)) to unsophisticated models of Comptonization, such as a cut-off power law. This inaccurate representation of the Comptonization means that interesting properties such as the electron temperature or Compton y-parameter are then inferred from the best fit of a cut-off power law to the data, rather than a direct treatment of these quantities. In addition to this, Ibragimov et al. (2005) showed that the strength of the reflected component R (defined in terms of the solid angle Ω subtended by the portion of the disc in line of sight to the corona) is systematically overestimated by such treatment. It has been known for some time that R correlates strongly with photon index Γ (Gilfanov, Churazov & Revnivtsev 1999; Revnivtsev, Gilfanov & Churazov 2001; Ibragimov et al. 2005), increasing as spectra become softer (implying a decreasing y-parameter). Similar behaviour has been observed for AGN spectra (Zdziarski, Lubiński & Smith 1999; Gilfanov, Churazov & Revnivtsev 2000; Zdziarski et al. 2003). This relationship clearly favours the accretion disc as the source of the seed photons for Comptonization, as the radiation being intercepted by the disc is increasing in tandem with the seed photon flux incident on the electron cloud. However, there is increasing evidence that at lower luminosities synchrotron photons from the magnetized corona may contribute a significant, perhaps dominant, population of seed photons, motivating the creation of so-called hybrid models. Such models typically comprise both a low-energy thermal population and an additional high-energy non-thermal population of electrons (see, e.g. Coppi 1999; Merloni & Fabian 2001; Del Santo et al. 2013).
Typically, attempts to understand the geometry of the hard state either consider a truncated disc with an electron cloud close to the compact object (e.g. Poutanen, Krolik & Ryde 1997), where the innermost portions of the disc have either evaporated to form an optically thin, hot flow (Meyer & Meyer-Hofmeister 1994) or are absent altogether, with the hard X-ray emission stemming from the base of the jet (Markoff, Falcke & Fender 2001; Markoff, Nowak & Wilms 2005), which is always concurrent with the hard state (Fender, Belloni & Gallo 2004). Other plausible geometries invoke the presence of non-uniform or dynamic coronae (Beloborodov 1999). Possible hard state geometries are discussed in detail by Done, Gierliński & Kubota (2007) and Gilfanov (2010).
A majority of neutron star (NS) XBs also exhibit soft and hard states (Hasinger & van der Klis 1989), but differ observationally from BH XBs (e.g. Barret 2001; Gilfanov 2010); in that the hard state is always at a relatively low luminosity in the range of 1036–1037 erg cm−2 s−1 (0.01–0.1LEdd), what is often referred to as the ‘island state’. The majority of observational differences arise due to the presence of a physical surface. The difference in angular momentum between the innermost portions of the disc and the surface leads to the formation of a boundary layer, an ever-present (Shakura & Sunyaev 1988) portion of the flow where the kinetic energy of the accreting material is surrendered (Sibgatullin & Sunyaev 2000). In addition, material will accumulate on the NS surface until the critical density for thermonuclear ignition is reached, which leads to powerful explosions that are observed as type-I X-ray bursts (see Strohmayer & Bildsten 2006, for a review).
Gilfanov, Revnivtsev & Molkov (2003) used Fourier-resolved spectroscopy to show that the boundary layer has a similar spectrum across a handful of sources, and can be approximated by a Wien spectrum of characteristic temperature kT ∼ 2.4 keV. The emission from the boundary layer, or even the NS surface itself, should provide additional seed photons for Comptonization in the hard state, affecting the properties of the Comptonizing media (Sunyaev & Titarchuk 1989). Indeed, it is observed that the hard state of NSs is generally softer than that of BHs (Syunyaev et al. 1991; Gilfanov et al. 1993; Churazov et al. 1995; Barret, McClintock & Grindlay 1996; Done & Gierliński 2003), which could be attributed to the Comptonizing corona being cooler in such systems. We emphasize that when discussing the hard state in this paper we refer specifically to the traditional ‘low/hard’ state, where the source is at comparatively low luminosity (≲1037 erg s−1, 0.1LEdd in the case of NSs) and not the states that can occur at higher luminosities when a strongly Comptonized component is also present in the spectrum.
Distinguishing BH from NS in an XB requires dynamical mass measurements obtained by optical or IR spectroscopy of transient sources during quiescence, when the optical emission is dominated by the companion (see Charles & Coe 2006, for a review). However, our ability to firmly identify BHs is limited by the necessity for a source to be transient and for the secondary to be observable with optical instrumentation. Such limitations mean that formally discerning BH from NS in extragalactic studies is practically impossible. Therefore, there is an increasing list of behaviours that can be used to identify an XB as a black hole ‘candidate’ (BHC), or definitively as an NS. Most strikingly, NS low mass X-ray binaries (LMXBs) display temporal behaviour that is not observed from BH LMXBs, such as type-I X-ray bursts and, when in the hard state, a significant amount of noise in their X-ray variability for frequencies greater than ∼500 Hz (Sunyaev & Revnivtsev 2000). While BHs and NSs exhibit similar X-ray states, there are some important state-dependent spectral differences, as BH sources should be softer during the so-called soft or thermal dominant state when the strongest source of emission is from the disc (Titarchuk & Shaposhnikov 2005). This emission is characterized by the temperature of innermost portion of the disc; its position being determined by the innermost stable circular orbit (ISCO) of the compact object, which will be larger for BHs than for NSs (for which the minimum inner disc radius can also be set by the radius of the NS). In this paper, we propose another spectral technique for distinguishing the nature of the compact object in XBs based on the Comptonization properties of their coronae in the hard state.
The paper is organized as follows. In Section 2, we assemble a sample of BH and NS XBs for which RXTE observations of the hard states are available and outline the subsequent reduction process. We also outline the reduction of a handful of archival, simultaneous XMM–Newton observations (Section 2.2). In Section 3, we analyse RXTE spectra over a broad energy range (3–200 keV) with the sophisticated Comptonization model of Poutanen & Svensson (1996), allowing us to separate out the properties of the seed photon population, reprocessing materials and the Comptonizing region, then present our results in Section 3.2. Discussion in Section 5.1 demonstrates that NSs have a systemically lower Compton y-parameter and we posit that this is a consequence of the physical surface providing additional seed photons for Comptonization, producing different physical properties of the Comptonizing media. The diagnostic potential of the observed differences in hard state spectra is considered, both in the context of Galactic and Extragalactic XB studies. We then investigate surprisingly high-seed photon temperatures (Section 5.5), and use simultaneous XMM observations to show that these are systematically overestimated by fitting to the RXTE bandpass and establish that this does not alter significantly the principal conclusions of this work. We summarize our conclusions in Section 6.
2 DATA REDUCTION
2.1 RXTE data
We first identified a selection of known BH and NS XBs (Ritter & Kolb 2003) where repeated RXTE observations exist in the HEASARC archive.1 In the case of NSs, our requirement that the source exhibits the classic hard (aka ‘island’) state means that no Z-track sources were considered. As a preliminary step, we constructed light curves for each source, covering the whole RXTE mission, in order to identify periods when each source was in the hard state. For each subobservation, we retrieved the PCA standard2 data products, housekeeping data and filter file. These files allow us to produce deadtime corrected, background uncorrected light curves and hardness–intensity diagrams (HIDs) without having to download the entire RXTE archive of observations for each source. For this exercise, we use data exclusively from PCU2, which was always turned on during observations. Using heasoft 6.15, we extract 16 s binned light curves from three energy ranges; 4.00–6.00, 6.00–7.50 and 7.50–18.50 keV. In order to compensate for long-term variation in the gain of the detector we converted to absolute channels, which depend on the mission epoch.2 Using the intensities I for each band we calculate a hardness ratio H = I7.50–18.50/I6.00–7.50 for each point in the light curve. This hardness ratio is similar to that used by Lin, Remillard & Homan (2007), who showed that for typical NS XBs the hard and soft states are fully distinguishable by comparing the intensity in the PCA above and below ≈8 keV. Based on inspection of the HIDs, we chose subobservations for analysis where H ≥ 2.0 for the majority of time bins. We apply an additional constraint by considering data only where I4.0–18.0 > 50 counts s−1 PCU−1, in the interest of achieving good statistics for spectral fitting as well as consistent handling of the background for all sources. Where possible we include data from multiple outbursts of a given source. A list of the sources studied in this work is presented in Table 1 together with the assumed distance, BH mass and equivalent hydrogen column density used in our analyses.
Source properties. We make use of equivalent hydrogen column densities inferred from 21 cm emission (Kalberla et al. 2005), plus the best measurements of distance and compact object mass for each source. References correspond as A: Casares et al. (2009), B: Hjellming & Rupen (1995), C: Hynes et al. (2004),D: Orosz et al. (2002), E: Gelino et al. (2006), F: Reid et al. (2011), G: Galloway et al. (2006), H: Casares & Jonker (2014), I: Galloway et al. (2003), J: Jonker & Nelemans (2004), K: Orosz et al. (1998), L: Muñoz-Darias, Casares & Martínez-Pais (2008), M: Shahbaz (2003), N: Orosz et al. (2011b), O: Khargharia et al. (2013) and P: Orosz et al. (2011a). For further discussion on BH mass estimates see Casares & Jonker (2014) .
| Source . | NH . | Distance . | Mass . | Ref. . |
|---|---|---|---|---|
| . | (1022 cm− 2) . | (kpc) . | (M⊙) . | . |
| GS 1354−64 | 0.73 | 26 ± 1.0 | >7.6 | A |
| GRO J1654−40 | 0.53 | 3.2 ± 0.2 | 6.6 ± 0.5 | B,M |
| GX 339−4 | 0.37 | 10 ± 4 | >6.0 | C,L |
| XTE J1550−564 | 1.01 | 5.3 ± 2.3 | 7.8 − 15.6 | D,N |
| XTE J1118+480 | 0.013 | 1.72 ± 0.1 | 6.9 − 8.2 | E,O |
| Cyg X−1 | 0.721 | |$1.86^{+0.11}_{-0.12}$| | 14.8 ± 1.0 | F,P |
| 4U 1543−47 | 0.35 | 7.5 ± 0.5 | 2.7 − 7.5 | K |
| 4U 1636−536 | 0.27 | 6.0 ± 0.5 | G | |
| 4U 1705−44 | 0.67 | 8.4±1.2 | J | |
| 4U 1728−33 | 1.24 | 4.6 ± 0.2 | I | |
| Aql X−1 | 0.28 | 5.2 ± 0.8 | J | |
| 4U 1608−52 | 1.81 | 3.3 ± 0.5 | J |
| Source . | NH . | Distance . | Mass . | Ref. . |
|---|---|---|---|---|
| . | (1022 cm− 2) . | (kpc) . | (M⊙) . | . |
| GS 1354−64 | 0.73 | 26 ± 1.0 | >7.6 | A |
| GRO J1654−40 | 0.53 | 3.2 ± 0.2 | 6.6 ± 0.5 | B,M |
| GX 339−4 | 0.37 | 10 ± 4 | >6.0 | C,L |
| XTE J1550−564 | 1.01 | 5.3 ± 2.3 | 7.8 − 15.6 | D,N |
| XTE J1118+480 | 0.013 | 1.72 ± 0.1 | 6.9 − 8.2 | E,O |
| Cyg X−1 | 0.721 | |$1.86^{+0.11}_{-0.12}$| | 14.8 ± 1.0 | F,P |
| 4U 1543−47 | 0.35 | 7.5 ± 0.5 | 2.7 − 7.5 | K |
| 4U 1636−536 | 0.27 | 6.0 ± 0.5 | G | |
| 4U 1705−44 | 0.67 | 8.4±1.2 | J | |
| 4U 1728−33 | 1.24 | 4.6 ± 0.2 | I | |
| Aql X−1 | 0.28 | 5.2 ± 0.8 | J | |
| 4U 1608−52 | 1.81 | 3.3 ± 0.5 | J |
Source properties. We make use of equivalent hydrogen column densities inferred from 21 cm emission (Kalberla et al. 2005), plus the best measurements of distance and compact object mass for each source. References correspond as A: Casares et al. (2009), B: Hjellming & Rupen (1995), C: Hynes et al. (2004),D: Orosz et al. (2002), E: Gelino et al. (2006), F: Reid et al. (2011), G: Galloway et al. (2006), H: Casares & Jonker (2014), I: Galloway et al. (2003), J: Jonker & Nelemans (2004), K: Orosz et al. (1998), L: Muñoz-Darias, Casares & Martínez-Pais (2008), M: Shahbaz (2003), N: Orosz et al. (2011b), O: Khargharia et al. (2013) and P: Orosz et al. (2011a). For further discussion on BH mass estimates see Casares & Jonker (2014) .
| Source . | NH . | Distance . | Mass . | Ref. . |
|---|---|---|---|---|
| . | (1022 cm− 2) . | (kpc) . | (M⊙) . | . |
| GS 1354−64 | 0.73 | 26 ± 1.0 | >7.6 | A |
| GRO J1654−40 | 0.53 | 3.2 ± 0.2 | 6.6 ± 0.5 | B,M |
| GX 339−4 | 0.37 | 10 ± 4 | >6.0 | C,L |
| XTE J1550−564 | 1.01 | 5.3 ± 2.3 | 7.8 − 15.6 | D,N |
| XTE J1118+480 | 0.013 | 1.72 ± 0.1 | 6.9 − 8.2 | E,O |
| Cyg X−1 | 0.721 | |$1.86^{+0.11}_{-0.12}$| | 14.8 ± 1.0 | F,P |
| 4U 1543−47 | 0.35 | 7.5 ± 0.5 | 2.7 − 7.5 | K |
| 4U 1636−536 | 0.27 | 6.0 ± 0.5 | G | |
| 4U 1705−44 | 0.67 | 8.4±1.2 | J | |
| 4U 1728−33 | 1.24 | 4.6 ± 0.2 | I | |
| Aql X−1 | 0.28 | 5.2 ± 0.8 | J | |
| 4U 1608−52 | 1.81 | 3.3 ± 0.5 | J |
| Source . | NH . | Distance . | Mass . | Ref. . |
|---|---|---|---|---|
| . | (1022 cm− 2) . | (kpc) . | (M⊙) . | . |
| GS 1354−64 | 0.73 | 26 ± 1.0 | >7.6 | A |
| GRO J1654−40 | 0.53 | 3.2 ± 0.2 | 6.6 ± 0.5 | B,M |
| GX 339−4 | 0.37 | 10 ± 4 | >6.0 | C,L |
| XTE J1550−564 | 1.01 | 5.3 ± 2.3 | 7.8 − 15.6 | D,N |
| XTE J1118+480 | 0.013 | 1.72 ± 0.1 | 6.9 − 8.2 | E,O |
| Cyg X−1 | 0.721 | |$1.86^{+0.11}_{-0.12}$| | 14.8 ± 1.0 | F,P |
| 4U 1543−47 | 0.35 | 7.5 ± 0.5 | 2.7 − 7.5 | K |
| 4U 1636−536 | 0.27 | 6.0 ± 0.5 | G | |
| 4U 1705−44 | 0.67 | 8.4±1.2 | J | |
| 4U 1728−33 | 1.24 | 4.6 ± 0.2 | I | |
| Aql X−1 | 0.28 | 5.2 ± 0.8 | J | |
| 4U 1608−52 | 1.81 | 3.3 ± 0.5 | J |
The hard state data sets used in this work are presented in Table 2. After downloading the full data set for each subobservation, we produced full 64 s binned light curves using both the left- and right-anode chains from the first xenon layer PCU2 data that were both deadtime and background corrected (using the bright background model). In the interests of good calibration, we chose not to include PCU0 or PCU1 data obtained after the failure of their respective propane layers in 2000 and 2006. Furthermore, we filtered these data to exclude periods when the pointing was greater than 0|$_{.}^{\circ}$|02 off-target, when the elevation was less than 10°, in the period immediately preceding the passage of the satellite through the South Atlantic Anomaly, and periods of 600 s after PCA breakdown events. We determined the optimal PCA configuration for each observation, so as to maximize the number of counts in the eventual spectra, and produced light curves and hardness ratios using these configurations. Good time interval (GTI) files were produced based on these light curves, covering continuous portions of the observation and also ignoring any short-term events such as X-ray bursts. These GTIs have typical durations of ∼1–3 ks.
Sources and observations, with the PCA configuration and the exposure of each spectrum by detector.
| Source name . | Observations . | PCUs . | Exposure (ks) . | . | . |
|---|---|---|---|---|---|
| Black holes | PCA | HEXTE-B | HEXTE-A | ||
| GS 1354−64 | 20431-01-03-00 | 0,1,2,3,4 | 26.787 | 1.666 | 1.67 |
| GS 1354−64 | 20431-01-04-00 | 0,1,2,3,4 | 13.58 | 0.774 | 0.792 |
| GS 1354−64 | 20431-01-05-00 | 0,1,2,3,4 | 12.493 | 0.776 | 0.776 |
| GS 1354−64 | 20431-01-05-00 | 0,1,2,3,4 | 15.6 | 0.969 | 0.999 |
| 4U 1543−47 | 70124-02-06-00 | 2,3 | 1.692 | 0.293 | 0.293 |
| 4U 1550−564 | 30188-06-01-00 | 0,1,2,3,4 | 2.014 | 0.129 | 0.126 |
| 4U 1550−564 | 30188-06-01-01 | 0,1,2,3,4 | 3.249 | 0.237 | 0.259 |
| 4U 1550−564 | 30188-06-01-02 | 0,1,2,3,4 | 5.905 | 0.362 | 0.368 |
| 4U 1550−564 | 50134-02-01-00 | 0,1,2,3,4 | 3.872 | 0.255 | 0.255 |
| 4U 1550−564 | 50135-01-03-00 | 2,3,4 | 6.781 | 0.674 | 0.662 |
| 4U 1550−564 | 50135-01-05-00 | 2,3,4 | 3.594 | 0.403 | 0.391 |
| 4U 1550−564 | 50135-01-06-00 | 2,3 | 2.743 | 0.475 | 0.476 |
| 4U 1550−564 | 50137-02-07-00 | 2,3,4 | 1.404 | 0.18 | 0.158 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 9.639 | 0.621 | 0.604 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 14.492 | 0.922 | 0.909 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 16.237 | 1.025 | 1.003 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 16.936 | 1.029 | 1.022 |
| Cyg X-1 | 20173-01-02-00 | 0,1,2,3,4 | 12.704 | 0.789 | 0.786 |
| Cyg X-1 | 20173-01-02-00 | 0,1,2,3,4 | 15.66 | 0.969 | 0.945 |
| Cyg X-1 | 20173-01-02-00 | 0,1,2,3,4 | 16.044 | 0.969 | 0.974 |
| Cyg X-1 | 80110-01-43-00 | 2,3 | 6.348 | 0.989 | |
| Cyg X-1 | 80110-01-44-00 | 2,3 | 3.318 | 0.584 | |
| Cyg X-1 | 80110-01-45-00 | 2,3 | 3.38 | 0.621 | |
| Cyg X-1 | 94108-01-01-00 | 2 | 2.982 | 1.028 | |
| GX 339−4 | 92035-01-01-01 | 2 | 3.049 | 1.139 | |
| GX 339−4 | 92035-01-01-02 | 2 | 3.581 | 1.243 | |
| GX 339−4 | 92035-01-02-04 | 2 | 3.071 | 0.962 | |
| GX 339−4 | 92035-01-02-04 | 2 | 2.99 | 0.999 | |
| GX 339−4 | 90118-01-06-00 | 2 | 1.520 | 0.523 | 0.522 |
| XTE J1118+480 | 50133-01-01-00 | 2,3,4 | 6.757 | 0.703 | 0.733 |
| XTE J1118+480 | 50133-01-02-00 | 2,3,4 | 7.98 | 0.859 | 0.868 |
| XTE J1118+480 | 50133-01-02-01 | 2,3,4 | 6.636 | 0.757 | 0.767 |
| XTE J1118+480 | 50133-01-02-01 | 2,3,4 | 7.439 | 0.869 | 0.864 |
| XTE J1118+480 | 50133-01-02-01 | 2,3,4 | 6.741 | 0.79 | 0.788 |
| XTE J1118+480 | 50133-01-03-00 | 2,3,4 | 9.478 | 1 | 1.026 |
| XTE J1118+480 | 50133-01-03-00 | 2,3,4 | 9.608 | 0.985 | 1.03 |
| GRO J1654−40 | 50133-01-03-00 | 2,3 | 3.477 | 0.317 | |
| GRO J1654−40 | 91702-01-01-03 | 2,3 | 3.273 | 0.53 | |
| GRO J1654−40 | 91702-01-01-04 | 2,3 | 5.697 | 0.92 | |
| GRO J1654−40 | 91702-01-01-05 | 2,3 | 1.908 | 0.359 | |
| Neutron stars | |||||
| 4U 1608-52 | 60052-03-01-06 | 2,3,4 | 10.451 | 1.265 | 1.274 |
| 4U 1608−52 | 60052-03-02-02 | 2,3,4 | 13.786 | 1.487 | 1.501 |
| 4U 1608−52 | 60052-03-02-02 | 2,3,4 | 13.119 | 1.384 | 1.41 |
| 4U 1608−52 | 60052-03-02-04 | 2,3,4 | 9.422 | 1.13 | 1.136 |
| 4U 1608−52 | 60052-03-02-06 | 2,3,4 | 9.378 | 1.136 | 1.136 |
| 4U 1636−536 | 92023-02-08-00 | 2 | 1.949 | 0.666 | |
| 4U 1636−536 | 92023-02-09-00 | 2 | 1.469 | 0.464 | |
| 4U 1636−536 | 92023-02-10-00 | 2 | 1.4 | 0.411 | |
| 4U 1636−536 | 92023-02-11-00 | 2 | 2.023 | 0.696 | |
| 4U 1636−536 | 92023-02-12-00 | 2 | 0.801 | 0.294 | |
| 4U 1636−536 | 94310-01-04-00 | 2 | 2.322 | 0.708 | |
| 4U 1705−44 | 20073-04-01-00 | 0,1,2,3,4 | 12.255 | 0.677 | 0.678 |
| 4U 1705−44 | 20073-04-01-00 | 0,1,2,3,4 | 13.974 | 0.804 | 0.804 |
| 4U 1728−34 | 92023-03-47-00 | 2 | 1.958 | 0.614 | |
| 4U 1728−34 | 92023-03-49-00 | 2 | 2.11 | 0.733 | |
| Aql X-1 | 50049-01-04-01 | 1,2,3 | 6.049 | 0.749 | 0.763 |
| Aql X-1 | 91414-01-07-03 | 2,3,4 | 5.934 | 0.722 | |
| Aql X-1 | 91414-01-08-05 | 2,3,4 | 3.703 | 0.433 | |
| Aql X-1 | 91414-01-08-07 | 2,3,4 | 5.834 | 0.623 |
| Source name . | Observations . | PCUs . | Exposure (ks) . | . | . |
|---|---|---|---|---|---|
| Black holes | PCA | HEXTE-B | HEXTE-A | ||
| GS 1354−64 | 20431-01-03-00 | 0,1,2,3,4 | 26.787 | 1.666 | 1.67 |
| GS 1354−64 | 20431-01-04-00 | 0,1,2,3,4 | 13.58 | 0.774 | 0.792 |
| GS 1354−64 | 20431-01-05-00 | 0,1,2,3,4 | 12.493 | 0.776 | 0.776 |
| GS 1354−64 | 20431-01-05-00 | 0,1,2,3,4 | 15.6 | 0.969 | 0.999 |
| 4U 1543−47 | 70124-02-06-00 | 2,3 | 1.692 | 0.293 | 0.293 |
| 4U 1550−564 | 30188-06-01-00 | 0,1,2,3,4 | 2.014 | 0.129 | 0.126 |
| 4U 1550−564 | 30188-06-01-01 | 0,1,2,3,4 | 3.249 | 0.237 | 0.259 |
| 4U 1550−564 | 30188-06-01-02 | 0,1,2,3,4 | 5.905 | 0.362 | 0.368 |
| 4U 1550−564 | 50134-02-01-00 | 0,1,2,3,4 | 3.872 | 0.255 | 0.255 |
| 4U 1550−564 | 50135-01-03-00 | 2,3,4 | 6.781 | 0.674 | 0.662 |
| 4U 1550−564 | 50135-01-05-00 | 2,3,4 | 3.594 | 0.403 | 0.391 |
| 4U 1550−564 | 50135-01-06-00 | 2,3 | 2.743 | 0.475 | 0.476 |
| 4U 1550−564 | 50137-02-07-00 | 2,3,4 | 1.404 | 0.18 | 0.158 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 9.639 | 0.621 | 0.604 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 14.492 | 0.922 | 0.909 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 16.237 | 1.025 | 1.003 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 16.936 | 1.029 | 1.022 |
| Cyg X-1 | 20173-01-02-00 | 0,1,2,3,4 | 12.704 | 0.789 | 0.786 |
| Cyg X-1 | 20173-01-02-00 | 0,1,2,3,4 | 15.66 | 0.969 | 0.945 |
| Cyg X-1 | 20173-01-02-00 | 0,1,2,3,4 | 16.044 | 0.969 | 0.974 |
| Cyg X-1 | 80110-01-43-00 | 2,3 | 6.348 | 0.989 | |
| Cyg X-1 | 80110-01-44-00 | 2,3 | 3.318 | 0.584 | |
| Cyg X-1 | 80110-01-45-00 | 2,3 | 3.38 | 0.621 | |
| Cyg X-1 | 94108-01-01-00 | 2 | 2.982 | 1.028 | |
| GX 339−4 | 92035-01-01-01 | 2 | 3.049 | 1.139 | |
| GX 339−4 | 92035-01-01-02 | 2 | 3.581 | 1.243 | |
| GX 339−4 | 92035-01-02-04 | 2 | 3.071 | 0.962 | |
| GX 339−4 | 92035-01-02-04 | 2 | 2.99 | 0.999 | |
| GX 339−4 | 90118-01-06-00 | 2 | 1.520 | 0.523 | 0.522 |
| XTE J1118+480 | 50133-01-01-00 | 2,3,4 | 6.757 | 0.703 | 0.733 |
| XTE J1118+480 | 50133-01-02-00 | 2,3,4 | 7.98 | 0.859 | 0.868 |
| XTE J1118+480 | 50133-01-02-01 | 2,3,4 | 6.636 | 0.757 | 0.767 |
| XTE J1118+480 | 50133-01-02-01 | 2,3,4 | 7.439 | 0.869 | 0.864 |
| XTE J1118+480 | 50133-01-02-01 | 2,3,4 | 6.741 | 0.79 | 0.788 |
| XTE J1118+480 | 50133-01-03-00 | 2,3,4 | 9.478 | 1 | 1.026 |
| XTE J1118+480 | 50133-01-03-00 | 2,3,4 | 9.608 | 0.985 | 1.03 |
| GRO J1654−40 | 50133-01-03-00 | 2,3 | 3.477 | 0.317 | |
| GRO J1654−40 | 91702-01-01-03 | 2,3 | 3.273 | 0.53 | |
| GRO J1654−40 | 91702-01-01-04 | 2,3 | 5.697 | 0.92 | |
| GRO J1654−40 | 91702-01-01-05 | 2,3 | 1.908 | 0.359 | |
| Neutron stars | |||||
| 4U 1608-52 | 60052-03-01-06 | 2,3,4 | 10.451 | 1.265 | 1.274 |
| 4U 1608−52 | 60052-03-02-02 | 2,3,4 | 13.786 | 1.487 | 1.501 |
| 4U 1608−52 | 60052-03-02-02 | 2,3,4 | 13.119 | 1.384 | 1.41 |
| 4U 1608−52 | 60052-03-02-04 | 2,3,4 | 9.422 | 1.13 | 1.136 |
| 4U 1608−52 | 60052-03-02-06 | 2,3,4 | 9.378 | 1.136 | 1.136 |
| 4U 1636−536 | 92023-02-08-00 | 2 | 1.949 | 0.666 | |
| 4U 1636−536 | 92023-02-09-00 | 2 | 1.469 | 0.464 | |
| 4U 1636−536 | 92023-02-10-00 | 2 | 1.4 | 0.411 | |
| 4U 1636−536 | 92023-02-11-00 | 2 | 2.023 | 0.696 | |
| 4U 1636−536 | 92023-02-12-00 | 2 | 0.801 | 0.294 | |
| 4U 1636−536 | 94310-01-04-00 | 2 | 2.322 | 0.708 | |
| 4U 1705−44 | 20073-04-01-00 | 0,1,2,3,4 | 12.255 | 0.677 | 0.678 |
| 4U 1705−44 | 20073-04-01-00 | 0,1,2,3,4 | 13.974 | 0.804 | 0.804 |
| 4U 1728−34 | 92023-03-47-00 | 2 | 1.958 | 0.614 | |
| 4U 1728−34 | 92023-03-49-00 | 2 | 2.11 | 0.733 | |
| Aql X-1 | 50049-01-04-01 | 1,2,3 | 6.049 | 0.749 | 0.763 |
| Aql X-1 | 91414-01-07-03 | 2,3,4 | 5.934 | 0.722 | |
| Aql X-1 | 91414-01-08-05 | 2,3,4 | 3.703 | 0.433 | |
| Aql X-1 | 91414-01-08-07 | 2,3,4 | 5.834 | 0.623 |
Sources and observations, with the PCA configuration and the exposure of each spectrum by detector.
| Source name . | Observations . | PCUs . | Exposure (ks) . | . | . |
|---|---|---|---|---|---|
| Black holes | PCA | HEXTE-B | HEXTE-A | ||
| GS 1354−64 | 20431-01-03-00 | 0,1,2,3,4 | 26.787 | 1.666 | 1.67 |
| GS 1354−64 | 20431-01-04-00 | 0,1,2,3,4 | 13.58 | 0.774 | 0.792 |
| GS 1354−64 | 20431-01-05-00 | 0,1,2,3,4 | 12.493 | 0.776 | 0.776 |
| GS 1354−64 | 20431-01-05-00 | 0,1,2,3,4 | 15.6 | 0.969 | 0.999 |
| 4U 1543−47 | 70124-02-06-00 | 2,3 | 1.692 | 0.293 | 0.293 |
| 4U 1550−564 | 30188-06-01-00 | 0,1,2,3,4 | 2.014 | 0.129 | 0.126 |
| 4U 1550−564 | 30188-06-01-01 | 0,1,2,3,4 | 3.249 | 0.237 | 0.259 |
| 4U 1550−564 | 30188-06-01-02 | 0,1,2,3,4 | 5.905 | 0.362 | 0.368 |
| 4U 1550−564 | 50134-02-01-00 | 0,1,2,3,4 | 3.872 | 0.255 | 0.255 |
| 4U 1550−564 | 50135-01-03-00 | 2,3,4 | 6.781 | 0.674 | 0.662 |
| 4U 1550−564 | 50135-01-05-00 | 2,3,4 | 3.594 | 0.403 | 0.391 |
| 4U 1550−564 | 50135-01-06-00 | 2,3 | 2.743 | 0.475 | 0.476 |
| 4U 1550−564 | 50137-02-07-00 | 2,3,4 | 1.404 | 0.18 | 0.158 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 9.639 | 0.621 | 0.604 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 14.492 | 0.922 | 0.909 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 16.237 | 1.025 | 1.003 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 16.936 | 1.029 | 1.022 |
| Cyg X-1 | 20173-01-02-00 | 0,1,2,3,4 | 12.704 | 0.789 | 0.786 |
| Cyg X-1 | 20173-01-02-00 | 0,1,2,3,4 | 15.66 | 0.969 | 0.945 |
| Cyg X-1 | 20173-01-02-00 | 0,1,2,3,4 | 16.044 | 0.969 | 0.974 |
| Cyg X-1 | 80110-01-43-00 | 2,3 | 6.348 | 0.989 | |
| Cyg X-1 | 80110-01-44-00 | 2,3 | 3.318 | 0.584 | |
| Cyg X-1 | 80110-01-45-00 | 2,3 | 3.38 | 0.621 | |
| Cyg X-1 | 94108-01-01-00 | 2 | 2.982 | 1.028 | |
| GX 339−4 | 92035-01-01-01 | 2 | 3.049 | 1.139 | |
| GX 339−4 | 92035-01-01-02 | 2 | 3.581 | 1.243 | |
| GX 339−4 | 92035-01-02-04 | 2 | 3.071 | 0.962 | |
| GX 339−4 | 92035-01-02-04 | 2 | 2.99 | 0.999 | |
| GX 339−4 | 90118-01-06-00 | 2 | 1.520 | 0.523 | 0.522 |
| XTE J1118+480 | 50133-01-01-00 | 2,3,4 | 6.757 | 0.703 | 0.733 |
| XTE J1118+480 | 50133-01-02-00 | 2,3,4 | 7.98 | 0.859 | 0.868 |
| XTE J1118+480 | 50133-01-02-01 | 2,3,4 | 6.636 | 0.757 | 0.767 |
| XTE J1118+480 | 50133-01-02-01 | 2,3,4 | 7.439 | 0.869 | 0.864 |
| XTE J1118+480 | 50133-01-02-01 | 2,3,4 | 6.741 | 0.79 | 0.788 |
| XTE J1118+480 | 50133-01-03-00 | 2,3,4 | 9.478 | 1 | 1.026 |
| XTE J1118+480 | 50133-01-03-00 | 2,3,4 | 9.608 | 0.985 | 1.03 |
| GRO J1654−40 | 50133-01-03-00 | 2,3 | 3.477 | 0.317 | |
| GRO J1654−40 | 91702-01-01-03 | 2,3 | 3.273 | 0.53 | |
| GRO J1654−40 | 91702-01-01-04 | 2,3 | 5.697 | 0.92 | |
| GRO J1654−40 | 91702-01-01-05 | 2,3 | 1.908 | 0.359 | |
| Neutron stars | |||||
| 4U 1608-52 | 60052-03-01-06 | 2,3,4 | 10.451 | 1.265 | 1.274 |
| 4U 1608−52 | 60052-03-02-02 | 2,3,4 | 13.786 | 1.487 | 1.501 |
| 4U 1608−52 | 60052-03-02-02 | 2,3,4 | 13.119 | 1.384 | 1.41 |
| 4U 1608−52 | 60052-03-02-04 | 2,3,4 | 9.422 | 1.13 | 1.136 |
| 4U 1608−52 | 60052-03-02-06 | 2,3,4 | 9.378 | 1.136 | 1.136 |
| 4U 1636−536 | 92023-02-08-00 | 2 | 1.949 | 0.666 | |
| 4U 1636−536 | 92023-02-09-00 | 2 | 1.469 | 0.464 | |
| 4U 1636−536 | 92023-02-10-00 | 2 | 1.4 | 0.411 | |
| 4U 1636−536 | 92023-02-11-00 | 2 | 2.023 | 0.696 | |
| 4U 1636−536 | 92023-02-12-00 | 2 | 0.801 | 0.294 | |
| 4U 1636−536 | 94310-01-04-00 | 2 | 2.322 | 0.708 | |
| 4U 1705−44 | 20073-04-01-00 | 0,1,2,3,4 | 12.255 | 0.677 | 0.678 |
| 4U 1705−44 | 20073-04-01-00 | 0,1,2,3,4 | 13.974 | 0.804 | 0.804 |
| 4U 1728−34 | 92023-03-47-00 | 2 | 1.958 | 0.614 | |
| 4U 1728−34 | 92023-03-49-00 | 2 | 2.11 | 0.733 | |
| Aql X-1 | 50049-01-04-01 | 1,2,3 | 6.049 | 0.749 | 0.763 |
| Aql X-1 | 91414-01-07-03 | 2,3,4 | 5.934 | 0.722 | |
| Aql X-1 | 91414-01-08-05 | 2,3,4 | 3.703 | 0.433 | |
| Aql X-1 | 91414-01-08-07 | 2,3,4 | 5.834 | 0.623 |
| Source name . | Observations . | PCUs . | Exposure (ks) . | . | . |
|---|---|---|---|---|---|
| Black holes | PCA | HEXTE-B | HEXTE-A | ||
| GS 1354−64 | 20431-01-03-00 | 0,1,2,3,4 | 26.787 | 1.666 | 1.67 |
| GS 1354−64 | 20431-01-04-00 | 0,1,2,3,4 | 13.58 | 0.774 | 0.792 |
| GS 1354−64 | 20431-01-05-00 | 0,1,2,3,4 | 12.493 | 0.776 | 0.776 |
| GS 1354−64 | 20431-01-05-00 | 0,1,2,3,4 | 15.6 | 0.969 | 0.999 |
| 4U 1543−47 | 70124-02-06-00 | 2,3 | 1.692 | 0.293 | 0.293 |
| 4U 1550−564 | 30188-06-01-00 | 0,1,2,3,4 | 2.014 | 0.129 | 0.126 |
| 4U 1550−564 | 30188-06-01-01 | 0,1,2,3,4 | 3.249 | 0.237 | 0.259 |
| 4U 1550−564 | 30188-06-01-02 | 0,1,2,3,4 | 5.905 | 0.362 | 0.368 |
| 4U 1550−564 | 50134-02-01-00 | 0,1,2,3,4 | 3.872 | 0.255 | 0.255 |
| 4U 1550−564 | 50135-01-03-00 | 2,3,4 | 6.781 | 0.674 | 0.662 |
| 4U 1550−564 | 50135-01-05-00 | 2,3,4 | 3.594 | 0.403 | 0.391 |
| 4U 1550−564 | 50135-01-06-00 | 2,3 | 2.743 | 0.475 | 0.476 |
| 4U 1550−564 | 50137-02-07-00 | 2,3,4 | 1.404 | 0.18 | 0.158 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 9.639 | 0.621 | 0.604 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 14.492 | 0.922 | 0.909 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 16.237 | 1.025 | 1.003 |
| Cyg X-1 | 20173-01-01-00 | 0,1,2,3,4 | 16.936 | 1.029 | 1.022 |
| Cyg X-1 | 20173-01-02-00 | 0,1,2,3,4 | 12.704 | 0.789 | 0.786 |
| Cyg X-1 | 20173-01-02-00 | 0,1,2,3,4 | 15.66 | 0.969 | 0.945 |
| Cyg X-1 | 20173-01-02-00 | 0,1,2,3,4 | 16.044 | 0.969 | 0.974 |
| Cyg X-1 | 80110-01-43-00 | 2,3 | 6.348 | 0.989 | |
| Cyg X-1 | 80110-01-44-00 | 2,3 | 3.318 | 0.584 | |
| Cyg X-1 | 80110-01-45-00 | 2,3 | 3.38 | 0.621 | |
| Cyg X-1 | 94108-01-01-00 | 2 | 2.982 | 1.028 | |
| GX 339−4 | 92035-01-01-01 | 2 | 3.049 | 1.139 | |
| GX 339−4 | 92035-01-01-02 | 2 | 3.581 | 1.243 | |
| GX 339−4 | 92035-01-02-04 | 2 | 3.071 | 0.962 | |
| GX 339−4 | 92035-01-02-04 | 2 | 2.99 | 0.999 | |
| GX 339−4 | 90118-01-06-00 | 2 | 1.520 | 0.523 | 0.522 |
| XTE J1118+480 | 50133-01-01-00 | 2,3,4 | 6.757 | 0.703 | 0.733 |
| XTE J1118+480 | 50133-01-02-00 | 2,3,4 | 7.98 | 0.859 | 0.868 |
| XTE J1118+480 | 50133-01-02-01 | 2,3,4 | 6.636 | 0.757 | 0.767 |
| XTE J1118+480 | 50133-01-02-01 | 2,3,4 | 7.439 | 0.869 | 0.864 |
| XTE J1118+480 | 50133-01-02-01 | 2,3,4 | 6.741 | 0.79 | 0.788 |
| XTE J1118+480 | 50133-01-03-00 | 2,3,4 | 9.478 | 1 | 1.026 |
| XTE J1118+480 | 50133-01-03-00 | 2,3,4 | 9.608 | 0.985 | 1.03 |
| GRO J1654−40 | 50133-01-03-00 | 2,3 | 3.477 | 0.317 | |
| GRO J1654−40 | 91702-01-01-03 | 2,3 | 3.273 | 0.53 | |
| GRO J1654−40 | 91702-01-01-04 | 2,3 | 5.697 | 0.92 | |
| GRO J1654−40 | 91702-01-01-05 | 2,3 | 1.908 | 0.359 | |
| Neutron stars | |||||
| 4U 1608-52 | 60052-03-01-06 | 2,3,4 | 10.451 | 1.265 | 1.274 |
| 4U 1608−52 | 60052-03-02-02 | 2,3,4 | 13.786 | 1.487 | 1.501 |
| 4U 1608−52 | 60052-03-02-02 | 2,3,4 | 13.119 | 1.384 | 1.41 |
| 4U 1608−52 | 60052-03-02-04 | 2,3,4 | 9.422 | 1.13 | 1.136 |
| 4U 1608−52 | 60052-03-02-06 | 2,3,4 | 9.378 | 1.136 | 1.136 |
| 4U 1636−536 | 92023-02-08-00 | 2 | 1.949 | 0.666 | |
| 4U 1636−536 | 92023-02-09-00 | 2 | 1.469 | 0.464 | |
| 4U 1636−536 | 92023-02-10-00 | 2 | 1.4 | 0.411 | |
| 4U 1636−536 | 92023-02-11-00 | 2 | 2.023 | 0.696 | |
| 4U 1636−536 | 92023-02-12-00 | 2 | 0.801 | 0.294 | |
| 4U 1636−536 | 94310-01-04-00 | 2 | 2.322 | 0.708 | |
| 4U 1705−44 | 20073-04-01-00 | 0,1,2,3,4 | 12.255 | 0.677 | 0.678 |
| 4U 1705−44 | 20073-04-01-00 | 0,1,2,3,4 | 13.974 | 0.804 | 0.804 |
| 4U 1728−34 | 92023-03-47-00 | 2 | 1.958 | 0.614 | |
| 4U 1728−34 | 92023-03-49-00 | 2 | 2.11 | 0.733 | |
| Aql X-1 | 50049-01-04-01 | 1,2,3 | 6.049 | 0.749 | 0.763 |
| Aql X-1 | 91414-01-07-03 | 2,3,4 | 5.934 | 0.722 | |
| Aql X-1 | 91414-01-08-05 | 2,3,4 | 3.703 | 0.433 | |
| Aql X-1 | 91414-01-08-07 | 2,3,4 | 5.834 | 0.623 |
We extract source and background PCA spectra for each GTI, again using both left and right anodes. Both source and background are subsequently deadtime corrected and response files generated. The PCA spectra are then rebinned such that there are a minimum of 40 counts per bin, which enable the use of the χ2 statistic in spectral fitting. As is standard practice, we add a 0.5 per cent systematic uncertainty to each bin.
HEXTE source and background spectra were extracted over the same GTI files using the ftoolHXTLCURV, and the correct response files generated. We use both clusters A and B data prior to 2004, when cluster A ceased to move between on- and off-target pointings, and use only cluster B data for the period between 2004 and December 2010. This process also produced 64 s binned background-subtracted light curves, which were used in the creation of GTIs.
2.2 XMM data
To explore the effects of bandpass on our spectral fitting results, we identified three simultaneous XMM observations where three of our sources were in the hard state. We chose to reduce only EPIC-pn data obtained in timing mode to avoid the controversial arguments surrounding the data reduction of bright point sources observed in imaging mode (Done & Diaz Trigo 2010; Miller et al. 2010); see Table 3 for a list of XMM observations used, the exposure of the resulting spectrum and the corresponding simultaneous RXTE observation ID.
Each data set was reduced using SAS release 14.0.0 (SAS Development Team 2014). Based on inspection of the ≥12 keV light curve, background flares were identified and filtered out into a new event file. The spectra were extracted from all RAWY and from five RAWX, from either side of the three central columns, which were excluded in the interests of reducing the effect of pileup. Pileup was found to be negligible in the resultant spectra using the tool epatplot. The high number of counts present in the wings of the point-spread function means that any attempt to extract a background spectrum from a supposed ‘source-free’ region will be impossible, and most likely result in the oversubtraction of background during spectral fitting, skewing the spectral shape (see the discussion in Done & Diaz Trigo 2010). As is now standard practice, we chose to assume that the contribution from the background spectrum will be negligible in comparison with the source spectra. We applied a grouping of a minimum of 50 counts per spectral bin, and added a 1 per cent systematic uncertainty. These spectra are analysed and discussed in Section 5.5.
3 ANALYSIS
Spectral fitting was carried out for each source using an absorbed Comptonization model with an additional Gaussian component to model the fluorescent Fe emission. Using the combined PCA and HEXTE spectra, we were able to fit over the 3.0–20.0 and 20.0–200.0 keV ranges, respectively, for all spectra with the exception of those from P20431 (GS 1354-64), when we used HEXTE spectra above 30 keV owing to calibration uncertainties beneath this energy. We chose to employ the xspec model compps (Poutanen & Svensson 1996), which models the Comptonized emission and its reflection by material in the accretion disc. For compps we leave as free parameters the electron temperature Te, seed photon temperature of a multicolour disc Tbb, Compton y-parameter, relative reflection factor R( = Ω/2π) and the normalization. We fix the relevant parameters such that the electron distribution is Maxwellian, and assume a spherical geometry (geom = 0) for the treatment of radiative transfer and photon escape probability and a binary inclination of 45°. All other parameters remain at their default values. We model the absorption column using phabs, with NH being fixed at the Galactic value (Table 1) as reported from the 21 cm survey carried out by Kalberla et al. (2005). A multiplicative constant is included in the model so as to account for the difference in calibration between PCA and HEXTE. Ultimately the spectral model used in xspec can be described as const(phabs(compps+gauss)).
Before fitting the spectra, we attempted to constrain the calibration constant C by reducing contemporaneous Crab observations for each data set when the right combination of PCUs was active. We found while subsequently fitting XBs that the calibration constant recovered from fitting was consistent with that found from fitting the Crab spectra with an absorbed power law, with C being in the range (0.7-0.9)pcu− 1.
We chose to limit the available parameter space to explore, based on reasonable physical criteria. We restricted the peak energy of the Gaussian to a range of 5.5–7.1 keV, allowing for the moderate resolution of RXTE in the vicinity of the relativistically broadened Fe Kα line, where crudely modelling the excess emission with a Gaussian could conceivably lead to a recovered Epeak in the range described. We also restrict the Gaussian width σ < 2.0 keV. We restrict the electron temperature of the plasma kTe to values above 10 keV, the minimum value for which the numerical method used by the model can be expected to produce reasonable results. Finally, we constrain the seed photon temperature kTbb to negative values, which forces xspec to model the seed photon spectra as emission from a conventional disc blackbody (i.e. Shakura & Sunyaev 1973).
3.1 Mitigating contamination from Galactic ridge emission
The majority of sources within our sample lie within 10° of the Galactic plane. The low spatial resolution of RXTE ( ≈ 1°) means that the spectra of sources in our sample are susceptible to contamination from the Galactic ridge (GR). The 3.0–20.0 keV GR flux can be as high as 6 × 10−11 erg cm−2 s−1 (Revnivtsev 2003), or ≈5 counts s−1 PCU−1 in RXTE PCA terms. For many sources in our sample, their Galactic longitudes are large enough and/or their count rates are so high (>500 counts s−1 PCU−1) as to render any effect on the spectral shape negligible, and we do not take GR emission into account for modelling their spectra. However, some spectra were observed at count rates of the order of 50–300 counts s−1 PCU−1, and for sources close to the Galactic plane we take further consideration.
For the majority of sources, the GR emission was found to be <1 × 10−11 erg cm−2 s−1; however, of particular note is the NS source 4U 1728–33, for which we estimate the GR flux to be ∼6 × 10−11 erg cm−2 s−1 due to its position close to the Galactic Centre.
3.2 Parameter estimation
Performing traditional spectral fitting using models containing a compps component with R as a free parameter is computationally expensive; a single spectral fit can take a typical desktop computer many minutes to complete. A fortiori the calculation of 1D uncertainty intervals using the error command, or even a 2D examination of the parameter space using a steppar grid will be even slower. Therefore, we choose to employ Monte Carlo (MC) algorithms to robustly explore the parameter space favoured by our spectra. Facility for Markov Chain MC has been integrated into xspec for some time, and has proved successful in the past for the calculation of confidence intervals (e.g. Burke et al. 2013); however, it is non-trivial to assess how well the chain has converged around the posterior distribution in a consistent way. To bypass this problem, we make use of analysis software BXA (Buchner et al. 2014), which connects the nested sampling algorithm multinest (Feroz, Hobson & Bridges 2009) with xspec. Our methodology followed a two-step approach, primarily fitting the spectra in the nominal way with xspec, to guarantee that the model can describe the data in a manner acceptable by the χ2 test, and then using BXA to explore the parameter space. To find 2D confidence regions, we bin over a given 2D plane, rank each bin by a number of MCMC samples it contains and then iteratively sum successive bins of decreasing rank until we have defined an area containing 90 per cent of samples. In Fig. 1, we display examples of the best-fitting model and unfolded spectra.
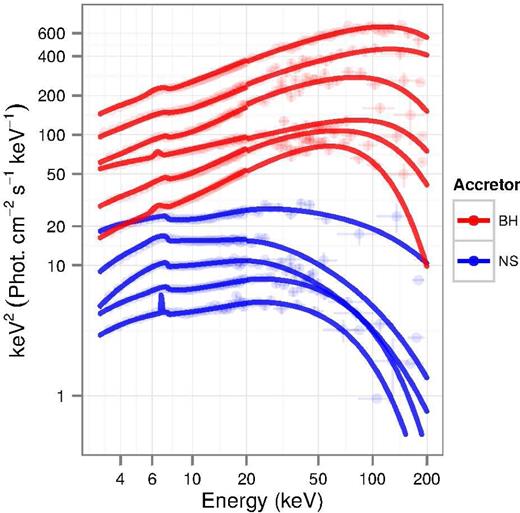
Example hard state unfolded RXTE spectra of BH and NS XBs. The data points were obtained with the xspecplot eeufs command with the model fixed to a Γ = 2.0 power law, the lines indicate the best-fitting const(phabs(compps+gauss)) model. Spectra are artificially offset in y-axis.
We present the 1D confidence intervals of compps parameters in Table 4, which we quote at the 90 per cent level throughout this work unless stated otherwise. In the top two rows of Fig. 2, we present the R–y and kTe–y planes for individual BHs and NSs. In the lower row, we present the two samples together.
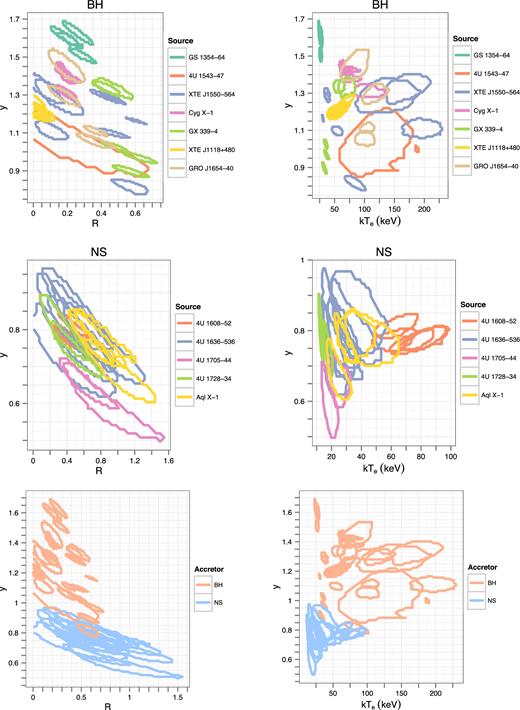
The confidence regions of individual spectra in the R–y (left) and kTe–y (right) planes for NSs and BHs, where each source is identified by colour, and each contour represents an individual RXTE spectrum (two top rows). The lower panels show the superposition of both results with colour denoting compact object class.
4 DISCUSSION
5 THE R–Y PLANE
There is a strong degeneracy between y and R, which is similar to the well-known degeneracy between R and photon index Γ (Zdziarski et al. 1999; Gilfanov et al. 1999). This degeneracy coupled with the relatively large confidence intervals means that no obvious trend can be seen for NS systems on the y–R plane. Most spectra for a particular NS occupy a similar position in the parameter space, showing no clear evolution. This is to be expected because these sources spend most of their time in the soft (banana) state, which transitions to a low/hard state where the data are of lower quality, leading to larger uncertainties in spectral fitting. The transition to the high-intensity soft state occurs on such short time-scales that it is unlikely to observe an Atoll source over a range of intensities while the spectra are hard. In contrast, there is some notable evolution in the R–y plane for several BH sources, most notably 4U 1550 − 56, GX 339 − 4, and XTE J1654 − 40. When the spectra are taken from the same outburst where the source rises in intensity through the hard state, near to the point where the source transitions, this leads to an increased R and a reduction in y. This behaviour is of the same nature as the R–Γ correlations in XBs and AGN observed previously (Zdziarski et al. 1999; Gilfanov et al. 1999, 2000; Zdziarski et al. 2003), albeit with larger scatter.
In our spectral model, there are two independent measures of the strength of reprocessed emission; the reflection strength R (=Ω/2π) in the Comptonizing component and the EW of the Gaussian line used to model the Fe Kα emission. While it is likely that a Gaussian is a poor description of the line profile, the moderate spectral resolution of the PCA instrument means that it is adequate for the purpose of characterizing the emission strength. Using similar spectral models, it has been shown that R and the EW of the line correctly rank the spectra in terms of the relative amount of reprocessed emission contributing to the spectrum (e.g. Gilfanov et al. 1999). In Fig. 3 (full results in Table 5), we show that there is a reasonable correlation between the EW and R when the two parameters are well constrained (which includes a majority of BH sources but not NS sources). This demonstrates that the spectral modelling returns a consistent measure of the relative amount of reprocessed emission present in a spectrum, even if the exact value of R is systematically under- or overestimated as a result of not accounting for certain physical variables, such as the ionization state of the reprocessing material. We also find a clear anticorrelation between y and EW. Interestingly, it has much smaller scatter than the relation between y and R, and in this respect, it is more similar to the previously observed R–Γ correlations.
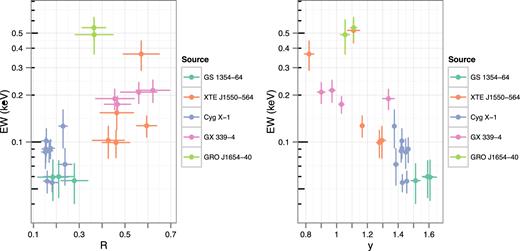
The variation of Gaussian EW with reflection strength (left) and Compton y-parameter (right) for BH sources. We exclude points where σEW/EW > 0.3, and also points where σR/R > 0.3 or σy/y > 0.3, respectively.
In Fig. 4, we plot R against luminosity, indicating a trend of increasing R with accretion rate. The highest luminosities are consistent with ≈(0.1–0.3)LEdd for both BH and NS samples (we note that the large uncertainties in L for some sources originate from the large uncertainties in the distances to some sources). For NSs, the connection between luminosity and reflection is less clear, though this is more difficult to ascertain because of the lack of luminosity variation in the NS hard state compared to that of BH XBs. The trend between R with L/LEdd is not mirrored by the Compton y-parameter, for which a much larger scatter is observed.
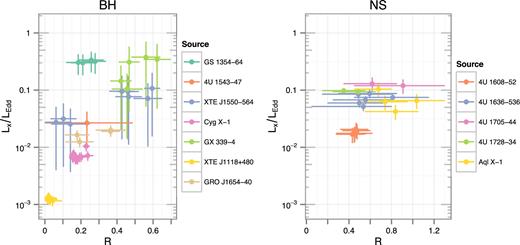
The variation of reflection strength with luminosity for BHs (left) and NSs (right). In the calculation of Lx/LEdd, we have assumed the distances and BH masses given in Table 1, and a mass of 1.4 M⊙ for NSs. We use 15 M⊙ as a reasonable upper limit on BH mass when only a lower limit is available.
5.1 Comptonization properties of LMXBs
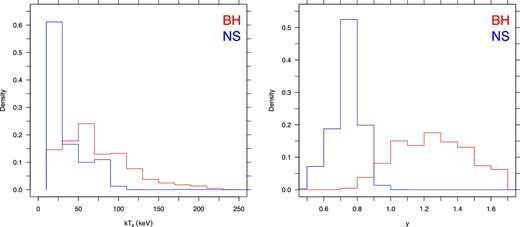
The 1D posterior distribution of kTe (left) and Compton y-parameter (right) for BHs and NSs, as defined by equation (3).
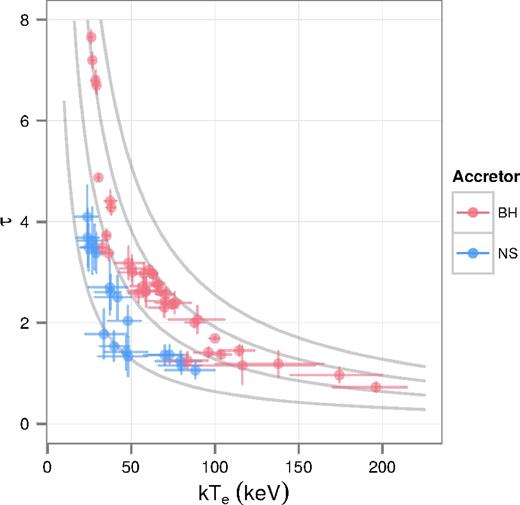
Calculated optical depth against electron temperature for all NS and BH spectra, overlaid on lines of constant Compton y-parameter, where y = 0.5, 1.0, 1.5 and 2.0 (ascends with τ).
Several assumptions were made during spectral analysis, including freezing some parameters at a fixed value for all sources. However, it is unlikely that this greatly affects our conclusions. The inclination i is not well constrained for a given source unless in extremis, for which dips or eclipses would be observed, but this is also when the inclination would have the greatest effect on our results (some studies suggest a dependence on y with inclination; Makishima et al. 2008; Zhang et al. 2014). Therefore, the lack of extreme inclinations in our sample means that it is unlikely that the observed difference in y is the result of some systematic difference in inclination between the BH and NS groups. To see if any dependence exists in our results, it is instructive to compare the analyses of Cyg X−1 and GRO J1654−40, which are known to have i ≈ 45° and 70°, respectively. We find no firm evidence of a dependence between y and i in the current work. Two of the GRO J1654-40 spectra are consistent with those of Cyg X-1 in terms of y (Fig. 2), while two have significantly smaller y, and larger R. The two GRO J1654-40 spectra that are consistent with those of Cyg X-1 in terms of y and R are at a higher L/LEdd (Table 4), and this fits with simple geometric reasoning that the higher the y (lower R) observed for a given luminosity the greater the inclination of the source.
5.2 Compton amplification
In Fig. 7, we plot the Compton y-parameter against A, following a positive trend, which is expected as both quantities are a direct proxy for the Comptonizing ability of the corona. We find that no NSs have A > 3, while BHs occupy a range of A ∼ 2.8–7, as it is further illustrated in Fig. 8, where we plot the distribution of sources over the amplification factor, separately for NS and BH systems.
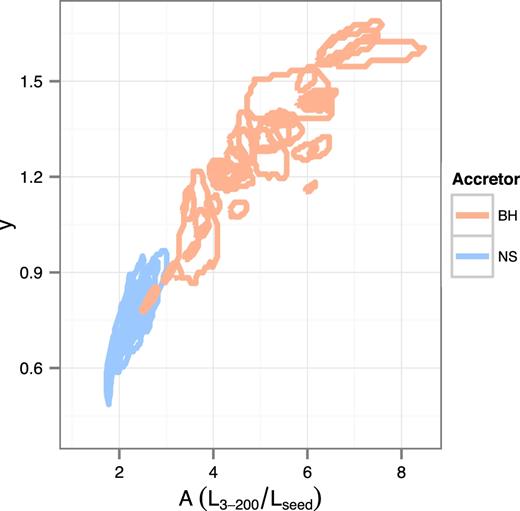
Compton y-parameter against Compton amplification for all sources.
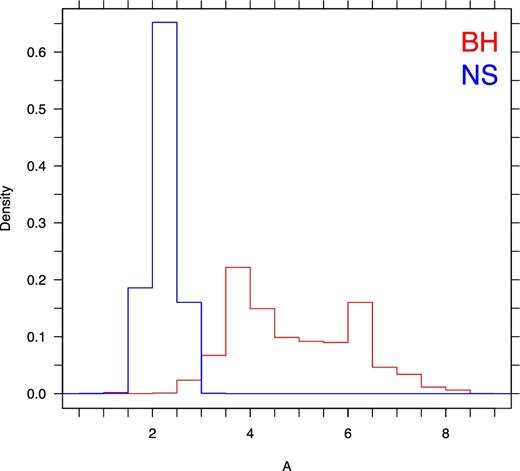
The cumulative 1D posterior distribution of A, as with Fig. 5.
5.3 Effects of rotation on Comptonization properties
It is anticipated that the rotation of a compact object is an important parameter in the context of the spectral formation, and to test this we take the step of plotting the Comptonization parameters against rotation frequency (for sources for which the rotation is known). For NS rotation, we use measurements of the burst oscillation frequency (see, e.g. Strohmayer et al. 1996) or in one instance the difference in frequency between kilohertz QPOs (4U 1705–44, for which burst oscillations have never been observed; Ford, van der Klis & Kaaret 1998), while for BHs we use the dimensionless spin parameter, a, as found from either studies of the fluorescent iron line profile (see Fabian et al. 1989; Laor 1991; Reynolds & Nowak 2003), in the case of GX339 − 4, or the thermal continuum of the accretion disc (Zhang, Cui & Chen 1997; McClintock, Narayan & Steiner 2014) for all other sources. In Fig. 9, we present the key Comptonization parameters against compact object rotation. For each source we defined the mean value for each spectral parameter to be used as a characteristic value. BH spins were obtained from García et al. (2015) (GX 339 − 4), Narayan, McClintock & Tchekhovskoy (2014) (GRO J1655 − 40, 4U 1543 − 47), Gou et al. (2014) (Cyg X − 1) and Steiner et al. (2011) (XTE J1550 − 564). NS rotation frequencies were obtained from Muno et al. (2001) and Ford et al. (1998) (4U 1705 − 44).

Average of Comptonization parameters against BH spin (left) and NS rotation frequency (right); error bars represent standard deviation (or 90 per cent confidence in the case of only one spectrum).
In the case of NSs, there seems to be some correlation between the spin frequency and the Compton amplification A, which may also be present with y and kTe. The Spearman rank correlation test (Spearman 1904) gives an estimate of the probability of appearance of the observed correlations of points by chance of 0.017, 0.08 and 0.13 for A, y and kTe, respectively. Therefore, the correlation of A with spin frequency is detected at the confidence level equivalent to ≈2.4σ for a Gaussian distribution. Although this is not enough to claim a confident detection, the probability of such a correlation to be real is quite high.
For BHs, there is no such obvious trend between the Comptonization properties and spin; however, these spins are much less well constrained than NS rotation frequencies and may be subjected to systematic uncertainties arising from the choice of the spectral model.
5.4 Classifying compact objects from Comptonization parameters
The observed dichotomy between BH and NS LMXBs in the properties of the Comptonizing media has an intriguing potential as a diagnostic. Conclusive classification of a compact object as a BH requires dynamical mass measurements obtained by optical or IR spectroscopy of transient sources during quiescence, when the optical emission is dominated by the companion (see Charles & Coe 2006, for a review). The necessity for a source to be transient, and for the secondary to be bright enough to study with optical instrumentation, limits our ability to firmly identify BHs. However, there is an increasing list of behaviours that can be used to identify a system as containing a BHC. Examples of temporal behaviour displayed by NS LMXBs, but not by BH LMXBs, include type-I X-ray bursts and a significant amount of noise in their X-ray variability at frequencies greater than ∼500 Hz while in the hard state (Sunyaev & Revnivtsev 2000). We can also look into the spectral properties, as BH sources should be softer during the so-called high state, where the emission from the disc dominates. Such emission is characterized by the temperature of innermost portion of the disc, the position of which is determined by the ISCO of the compact object, which we naturally expect to be larger for BHs than for NSs (for which the inner disc radius may be determined by the NS radius). The temperature of the inner accretion disc has been used for the classification of BHs in extragalactic studies (e.g. Brassington et al. 2010; Burke et al. 2013; Lin et al. 2015), where dynamical determination of the mass is nearly impossible and photon-starved X-ray light curves limit our ability to identify X-ray bursts but longer observation times yield an adequate spectral quality for analysis.
From the observed distribution of the Compton y-parameter and amplification factor during the hard state we propose a further characteristic property for distinguishing BHs from NSs. The population is clearly bimodal about y ≈ 0.9 and A ≈ 3 (as measured over the 3–200 keV energy band; see further discussion in Section 5.5), with some slight overlap (Fig. 5). Determination of the Compton y-parameter can be immediately incorporated into the analysis of newly discovered Galactic XBs and may prove effective for studying populations of Extragalactic XBs using future X-ray telescopes.
5.4.1 Comparison with other Comptonization models
It is prudent to examine whether the observed parameter degeneracy is apparent when using different or more sophisticated Comptonization models. For this task, we choose eqpair (an extension of the code presented in Coppi 1992, 1999), which considers a hot plasma within which a hybrid of thermal and non-thermal emission processes take place, while the reflection component is considered by the same routines as compps. The model is parametrized in terms of the ratio of the hard to soft compactnesses lh/ls, the soft photon compactness ls, seed photon blackbody temperature kTbb, Thomson scattering depth τp, the fraction of power supplied to energetic particles that goes into accelerating non-thermal particles lnt/lh and the reflection fraction R. An aspect of this particular model is that the electron temperature kTe is not a parameter, but it is calculated self-consistently and can be extracted through setting the xspec chatter level to 15.
Taking sources whose spectra were typical of those possessing either a BH or NS – 4U 1636 − 536 from the NSs and Cyg X-1 from the BHs – and we analysed several spectra for each source (those from P92023 for 4U 1636 − 536, and from P20173 for Cyg X-1), but with eqpair taking the place of compps, achieving acceptable fits. The range of reported kTe for each source was 15–22 keV for the NS, and 55–67 keV for the BH, consistent with our compps results (Table 4). Most strikingly, we observe a clear difference in the range of best-fitting lh/ls and τp values for the two objects. For the BH we find lh/ls ≈ 12.1–12.8, while the NS varies between 3.1 and 3.7. As the total luminosity of escaping photons must be equal to the luminosity of the input photons for this model, which is to say lh + ls = ltotal, one can consider lh/ls, a proxy for the amplification factor, the dichotomy in which it appears to be preserved. For the NS we find τp in the range of 3.1–4.0, and a range of 1.7–2.0 for the BH. Just as the dichotomy in spectral parameters found using compps can be expressed as a different optical depth for a given kTe (Fig. 6) and the two sources have quite different kTe, the significance of the difference in τp is not immediately apparent. However, τp and kTe seem to obey a separation between NSs and BHs in the same sense as the separation seen in Fig. 6. For this experiment, xspec returned a range of lnt/lh ≈ 0.55–0.80, with no clear separation between BH and NS sources. Finally, we find R ≈ 0.18–0.23 for the BH, fully consistent with the value returned from compps; however, for the NS we find R ≈ 0.0–0.13, significantly less than that found previously. As the treatment of the reflection is the same for both compps and eqpair (using the ireflct model), this suggests there is some difference in spectral shape between the two Comptonization models.
We emphasize that any attempt to use Comptonization properties as a diagnostic of the nature of the compact object should first establish how the dichotomy is manifested in the specific spectral model being used. We caution against the practice of taking any favoured Comptonization model that might happen to feature y as a free parameter, performing spectral fitting and declaring evidence in favour of a BH or NS based on the results of this paper. Such experiments should always be prefaced by work establishing the dichotomy for that particular model using either known sources (as in this work) or by studying the effects of fitting such models to simulated compps spectra based on the ‘typical’ BH and NS spectral shapes (Table 4).
5.5 Systematic inaccuracies in seed photon spectral parameters
On inspection, the seed photon temperatures (kTbb) and compps normalizations for some of the sources appear incompatible with the interpretation of the hard state in terms of a truncated disc. In this scenario, an optically thick accretion disc provides the seed photons for Comptonization in a hot corona close to the compact object. Truncation of the disc in the hard state is motivated by the absence of the thermal component that dominates the spectra during the high/soft state that is well described in terms of the thermal spectrum expected from the optically thick, geometrically thin disc of Shakura & Sunyaev (1973). The peak temperature of this disc in the soft state is ≈1 keV for BHs, and the inferred radius is consistent with the range of conceivable radii for the ISCO (see the review by Done et al. 2007). In the absence of such emission, it follows that the disc must either be truncated at some radius during the hard state (Esin, McClintock & Narayan 1997; Gilfanov, Churazov & Sunyaev 1997; Churazov et al. 2001), or have significant portions obscured by the Comptonizing media. However, a non-truncated disc would cool the corona too quickly; increased Comptonization leads to a reduction in the coronal temperature but increasing the incident flux of upscattered photons back into the disc, in turn, increases the supply of seed photons.
Truncation models are disputed despite a strong theoretical justification and an ability to offer prosaic qualitative explanations for various hard state phenomena, such as the launching of jets (e.g. Fender et al. 2004). Detractors primarily argue that the broadening of emission lines by smearing due to special and general relativistic effects shows that the line-emitting region, assumed to be in the disc, must be close to the compact object (Miller et al. 2006; Reis, Fabian & Miller 2010; Reis et al. 2012). These results are, in turn, disputed on grounds of unreliable data reduction (see discussions in Done & Diaz Trigo 2010; Miller et al. 2010, regarding pileup effects on line profiles), the nature of the continuum modelling (Kolehmainen, Done & Díaz Trigo 2014) and the constituents of the line profile itself [Plant et al. (2015) argue that there are many ionized species present in the vicinity of the Fe Kα] that result in an apparently broader line profile than any one individual line possesses.
For our BH sample, 3–200 keV luminosities are typically in the ∼1036 − 1.5 × 1038 ergs−1 range, corresponding to the mass accretion rate of |$\dot{M}\sim 2\times \ 10^{-10}-3\times 10^{-8}\ {\rm M_{\odot }\ yr^{-1}}$|. From these mass accretion rates and the lower limit to BH masses taken from Table 1, the theory of the standard accretion disc (Shakura & Sunyaev 1973) predicts a maximal disc temperature for a non-rotating BH in the kTmax ∼ 0.13–0.57 keV range. Correcting for spectral hardening (f ∼ 1.6; Suleimanov et al. 2011), the observed temperatures should be in the range of kTmax ∼ 0.2–0.9 keV. These values of kTmax should be considered an upper limit since they are calculated based on the lower mass estimate of the BHs, and we do not expect the disc to extend to the vicinity of the ISCO while in the hard state. For example, a disc truncated at 15–100rg will have innermost temperatures reduced to ≈0.8–0.2 of the theoretical maximum because |$T(R)\propto R^{-0.75} (1-\sqrt{R_{{\ast }} /R})^{0.25}$|.
Across our sample of NS LMXBs, the theoretical maximum disc temperature that we estimate from the luminosities is kTmax ∼ 0.37–0.63 keV, which becomes kTmax ∼ 0.6–1.0 keV after correcting for spectral hardening. As for BHs, the temperature will be, by a factor of a few, smaller for a disc truncated at a ∼50–100Rg. However, in the case of NS, a significant fraction of the seed photons may originate on the surface of the NS itself. Taking into account that the typical luminosity enhancement factor for NS sources is A ∼ 2 (Fig. 8), this implies an average seed photon luminosity ∼0.5 × 1037 erg s−1 (0.05LEdd). Therefore, the maximum temperature of the seed photon spectra, corrected for spectral hardening (assuming a correction factor of f ∼ 1.6, Suleimanov et al. 2011) should produce a typical kTNS ∼ 1 keV, assuming the NS radius of ≈15 km. These figures are in good agreement with an ongoing Suzaku study by Zhang et al. (in preparation).
From fitting RXTE spectra we obtain values of kTbb ≈ 0.5–1.0 keV for BHs, and of kTbb ≈ 1.0–1.5 keV for NSs (Table 4). For the majority of BHs, the best-fitting values are a factor of ∼1.5–5 times larger than the expected kTmax for the truncated disc. The difference between measured and predicted temperatures may be much smaller in the case of NS systems, especially if the seed photon flux is dominated by the NS emission.
An important limitation of PCA data is that the spectral fitting can only be performed at energies ≳3 keV, greater than the plausible values of kTbb, especially for BH XBs. We utilized data from simultaneous XMM–Newton observations for three sources (Table 3) to scrutinize the effect of the RXTE bandpass on kTbb, and other parameters. For each source, we perform a joint analysis of the EPIC-pn spectrum between 0.7 and 9.0 keV, the PCA data from 9.0 to 20.0 keV and HEXTE data over 20.0–200.0 keV. Prior inspection of the XMM data revealed a couple of narrow lines at ∼1.7 and ∼2.2 keV, which are thought to be the result of incorrect compensation for the charge transfer inefficiency of the CCD (Done & Diaz Trigo 2010). We chose to ignore the data between 1.5 and 2.4 keV rather than further complicate the spectral model with additional lines. We fixed the PCA–HEXTE calibration to the values found from our principal RXTE analysis. A clear excess can be seen at energies ≤1 keV, which is a well-documented feature often modelled as disc emission characterized by kTin ∼ 0.1–0.4 keV (e.g. Miller et al. 2006; Gierliński, Done & Page 2008; Reis et al. 2010; Kolehmainen et al. 2014), or as an additional Comptonizing component (Ibragimov et al. 2005) or as additional reflection (Clavel et al. 2016). We chose to describe this broad excess emission as the standard geometrically thin, optically thick accretion disc of Shakura & Sunyaev (1973) using the xspec model diskbb(Mitsuda et al. 1984). NH was allowed to vary during the fitting process because of the greater spectral resolution of XMM at energies that are especially influential to the behaviour of this parameter. Acceptable fits were obtained for all three sources and the recovered parameters of interest are presented in Table 6.
Archival XMM data sets of XBs in the hard state observed simultaneously by RXTE. We list the observation index, simultaneous RXTE observation and the effective exposure of the final spectra used in spectral fitting (see Section 5.5).
| Source . | ObsID . | Sim. RXTE . | Exp. (ks) . |
|---|---|---|---|
| 4U 1636−536 | 0606070401 | 94310-01-04-00 | 25.553 |
| Cyg X-1 | 0605610401 | 94108-01-01-00 | 19.754 |
| GX 339−4 | 0204730201 | 90118-01-06-00 | 80.022 |
| Source . | ObsID . | Sim. RXTE . | Exp. (ks) . |
|---|---|---|---|
| 4U 1636−536 | 0606070401 | 94310-01-04-00 | 25.553 |
| Cyg X-1 | 0605610401 | 94108-01-01-00 | 19.754 |
| GX 339−4 | 0204730201 | 90118-01-06-00 | 80.022 |
Archival XMM data sets of XBs in the hard state observed simultaneously by RXTE. We list the observation index, simultaneous RXTE observation and the effective exposure of the final spectra used in spectral fitting (see Section 5.5).
| Source . | ObsID . | Sim. RXTE . | Exp. (ks) . |
|---|---|---|---|
| 4U 1636−536 | 0606070401 | 94310-01-04-00 | 25.553 |
| Cyg X-1 | 0605610401 | 94108-01-01-00 | 19.754 |
| GX 339−4 | 0204730201 | 90118-01-06-00 | 80.022 |
| Source . | ObsID . | Sim. RXTE . | Exp. (ks) . |
|---|---|---|---|
| 4U 1636−536 | 0606070401 | 94310-01-04-00 | 25.553 |
| Cyg X-1 | 0605610401 | 94108-01-01-00 | 19.754 |
| GX 339−4 | 0204730201 | 90118-01-06-00 | 80.022 |
The excess below 1 keV was adequately described by the diskbb component, and is characterized by an inner-disc temperature of 0.1–0.4 keV, consistent with previous results (Miller et al. 2006; Shidatsu et al. 2013; Kolehmainen et al. 2014). It should be noted that exact spectral composition of the lower energy spectral shape is the subject of continued debate (e.g. there are good arguments for the addition of a second Comptonized component or additional reflection, Ibragimov et al. 2005; Sakurai et al. 2012; Clavel et al. 2016), and it is beyond the scope of the current work to reach a complete understanding of the disc geometry. Crucially, the disc seed photon temperatures are in line with expectations and other results in the literature.
As expected, there is reduction in the recovered seed photon temperature of compps when one considers a wider bandpass. For Cyg X-1 with the 0.7–200 keV luminosity of 1.46 × 1037 erg s−1 (|$\dot{M}\approx 2.6 \times \ 10^{-9}$| M⊙ yr−1), the maximal disc colour temperature after correcting for spectral hardening (f = 1.6) is kTmax ≈ 0.28 keV. The measured value of kT = 0.21 keV is consistent with the disc truncated at r ∼ 17rg for a non-rotating BH. In the case of GX 339 − 4, which is probably a less massive BH than Cyg X-1, the expected maximal colour temperature of the disc spans a plausible range of ≈0.3–0.8 keV (corrected for spectral hardening). The measured value of 0.63 keV implies a truncation could be as large as ∼16 Rg. Interestingly, for 4U 1636-536 we obtain from the broad-band fit the temperature of kT ≈ 0.17 keV, much smaller than the maximum expected for this NS luminosity,4kTNS ∼ 0.80 keV, and comparable to the value expected in the accretion disc at r ∼ 102Rg.
The shift in kTbb between the different analyses is accompanied by some changes in other parameters of interest, in particular in the Comptonization parameter y. On the other hand, the electron temperature kTe remains almost unaffected (Tables 4 and 6).
Results from spectral analysis of BH (top) and NS (bottom) XBs for the compps parameters; best-fitting location together with 1D 90 per cent confidence. The F2 − 200 is the unabsorbed 2–200 keV flux in the units of 10−9 erg cm−2 s−1; temperatures are given in keV.
| Source . | ObsID . | F2 − 200 . | kTbb . | kTe . | R . | y . | Norm. . |
|---|---|---|---|---|---|---|---|
| GS 1354−64 | P20431 | 5.31 | |$0.94_{-0.14}^{+0.14}$| | |$24.1_{-1.5}^{+1.5}$| | |$0.24_{-0.08}^{+0.08}$| | |$1.64_{-0.05}^{+0.05}$| | |$47_{-19}^{+31}$| |
| GS 1354−64 | P20431 | 5.03 | |$0.96_{-0.02}^{+0.09}$| | |$26.3_{-2.0}^{+2.0}$| | |$0.270_{-0.07}^{+0.07}$| | |$1.53_{-0.04}^{+0.04}$| | |$45.5_{-12.0}^{+3.9}$| |
| GS 1354−64 | P20431 | 4.73 | |$0.56_{-0.19}^{+0.30}$| | |$25.4_{-3.0}^{+3.3}$| | |$0.18_{-0.09}^{+0.09}$| | |$1.60_{-0.04}^{+0.04}$| | |$258_{-203}^{+934}$| |
| GS 1354−64 | P20431 | 4.80 | |$0.83_{-0.10}^{+0.19}$| | |$26.2_{-2.6}^{+2.7}$| | |$0.18_{-0.07}^{+0.07}$| | |$1.62_{-0.05}^{+0.05}$| | |$67_{-34}^{+39}$| |
| 4U 1543−47 | P70124 | 1.92 | |$0.90_{-0.22}^{+0.22}$| | |$110_{-50}^{+50}$| | |$0.19_{-0.19}^{+0.32}$| | |$1.06_{-0.15}^{+0.15}$| | |$36_{-24}^{+71}$| |
| XTE J1550−564 | P30188 | 26.0 | |$0.71_{-0.02}^{+0.08}$| | |$36.8_{-4.2}^{+4.2}$| | |$0.40_{-0.08}^{+0.09}$| | |$1.30_{-0.03}^{+0.03}$| | |$753_{-246}^{+77}$| |
| XTE J1550−564 | P30188 | 25.7 | |$0.62_{-0.01}^{+0.13}$| | |$38.9_{-3.4}^{+3.4}$| | |$0.450_{-0.07}^{+0.07}$| | |$1.28_{-0.02}^{+0.02}$| | |$1340_{-690}^{+9}$| |
| XTE J1550−564 | P30188 | 29.3 | |$0.42_{-0.02}^{+0.02}$| | |$30.4_{-1.2}^{+1.2}$| | |$0.580_{-0.06}^{+0.06}$| | |$1.17_{-0.02}^{+0.02}$| | |$7240_{-1100}^{+1150}$| |
| XTE J1550−564 | P50134 | 19.4 | |$0.71_{-0.08}^{+0.08}$| | |$77_{-16}^{+18}$| | |$0.56_{-0.09}^{+0.09}$| | |$0.83_{-0.04}^{+0.04}$| | |$1320_{-526}^{+917}$| |
| XTE J1550−564 | P50135 | 8.58 | |$0.83_{-0.03}^{+0.09}$| | |$221_{-45}^{+26}$| | |$0.08_{-0.08}^{+0.08}$| | |$1.10_{-0.05}^{+0.05}$| | |$253_{-93}^{+51}$| |
| XTE J1550−564 | P50135 | 7.45 | |$0.88_{-0.08}^{+0.10}$| | |$201_{-54}^{+26}$| | |$0.02_{-0.02}^{+0.13}$| | |$1.37_{-0.09}^{+0.08}$| | |$127_{-45}^{+59}$| |
| XTE J1550−564 | P50135 | 6.93 | |$0.84_{-0.11}^{+0.11}$| | |$158_{-54}^{+53}$| | |$0.15_{-0.11}^{+0.11}$| | |$1.29_{-0.08}^{+0.08}$| | |$129_{-53}^{+88}$| |
| XTE J1550−564 | P50137 | 20.9 | |$0.66_{-0.02}^{+0.15}$| | |$56.4_{-8.0}^{+7.8}$| | |$0.49_{-0.09}^{+0.09}$| | |$1.09_{-0.03}^{+0.03}$| | |$1080_{-592}^{+158}$| |
| Cyg X-1 | P20173 | 30.0 | |$0.89_{-0.10}^{+0.10}$| | |$63.0_{-5.9}^{+6.9}$| | |$0.15_{-0.03}^{+0.03}$| | |$1.42_{-0.01}^{+0.01}$| | |$353_{-121}^{+184}$| |
| Cyg X-1 | P20173 | 33.8 | |$0.92_{-0.03}^{+0.14}$| | |$62.2_{-3.9}^{+4.0}$| | |$0.16_{-0.02}^{+0.02}$| | |$1.46_{-0.01}^{+0.01}$| | |$331_{-136}^{+39}$| |
| Cyg X-1 | P20173 | 35.6 | |$1.03_{-0.03}^{+0.07}$| | |$63.1_{-2.8}^{+2.8}$| | |$0.160_{-0.02}^{+0.02}$| | |$1.46_{-0.01}^{+0.01}$| | |$235_{-48}^{+23}$| |
| Cyg X-1 | P20173 | 31.7 | |$0.94_{-0.04}^{+0.18}$| | |$60.8_{-3.3}^{+3.3}$| | |$0.16_{-0.02}^{+0.02}$| | |$1.45_{-0.01}^{+0.01}$| | |$295_{-136}^{+46}$| |
| Cyg X-1 | P20173 | 28.5 | |$0.820_{-0.10}^{+0.10}$| | |$70.9_{-12}^{+16}$| | |$0.170_{-0.04}^{+0.04}$| | |$1.43_{-0.02}^{+0.02}$| | |$472_{-188}^{+310}$| |
| Cyg X-1 | P20173 | 29.2 | |$0.79_{-0.01}^{+0.10}$| | |$75.1_{-9.5}^{+9.2}$| | |$0.18_{-0.03}^{+0.02}$| | |$1.42_{-0.01}^{+0.01}$| | |$539_{-199}^{+5}$| |
| Cyg X-1 | P20173 | 28.4 | |$0.880_{-0.01}^{+0.10}$| | |$67.3_{-5.0}^{+5.0}$| | |$0.16_{-0.02}^{+0.02}$| | |$1.42_{-0.01}^{+0.01}$| | |$362_{-123}^{+18}$| |
| Cyg X-1 | P80110 | 48.2 | |$1.01_{-0.10}^{+0.11}$| | |$87.0_{-6.1}^{+6.1}$| | |$0.240_{-0.02}^{+0.02}$| | |$1.37_{-0.01}^{+0.01}$| | |$394_{-125}^{+182}$| |
| Cyg X-1 | P80110 | 31.5 | |$1.08_{-0.11}^{+0.13}$| | |$75.1_{-5.9}^{+5.9}$| | |$0.20_{-0.03}^{+0.03}$| | |$1.39_{-0.02}^{+0.02}$| | |$191_{-64}^{+92}$| |
| Cyg X-1 | P80110 | 32.9 | |$1.27_{-0.09}^{+0.09}$| | |$69.3_{-5.9}^{+5.5}$| | |$0.24_{-0.03}^{+0.03}$| | |$1.39_{-0.02}^{+0.02}$| | |$110_{-24}^{+31}$| |
| Cyg X-1 | P94108 | 31.1 | |$0.94_{-0.13}^{+0.14}$| | |$102_{-22}^{+22}$| | |$0.18_{-0.05}^{+0.05}$| | |$1.32_{-0.03}^{+0.03}$| | |$362_{-160}^{+286}$| |
| GX 339−4 | P92035 | 19.2 | |$0.99_{-0.03}^{+0.13}$| | |$33.9_{-2.7}^{+3.5}$| | |$0.45_{-0.07}^{+0.07}$| | |$1.04_{-0.03}^{+0.02}$| | |$242_{-88}^{+31}$| |
| GX 339−4 | P92035 | 21.4 | |$1.09_{-0.08}^{+0.12}$| | |$35.4_{-3.4}^{+4.2}$| | |$0.60_{-0.09}^{+0.09}$| | |$0.98_{-0.03}^{+0.03}$| | |$196_{-61}^{+58}$| |
| GX 339−4 | P92035 | 23.4 | |$1.13_{-0.10}^{+0.10}$| | |$33.0_{-3.0}^{+3.0}$| | |$0.56_{-0.09}^{+0.09}$| | |$0.90_{-0.03}^{+0.03}$| | |$219_{-59}^{+80}$| |
| GX 339−4 | P92052 | 8.95 | |$1.12_{-0.02}^{+0.21}$| | |$53.9_{-7.0}^{+10}$| | |$0.420_{-0.07}^{+0.07}$| | |$1.35_{-0.04}^{+0.03}$| | |$44.7_{-20.0}^{+1.8}$| |
| GX 339−4 | P90118 | 6.47 | |$1.33_{-0.07}^{+0.19}$| | |$65.6_{-13}^{+14}$| | |$0.45_{-0.09}^{+0.09}$| | |$1.34_{-0.04}^{+0.04}$| | |$17.8_{-6.6}^{+3.7}$| |
| XTE J1118+480 | P50133 | 3.14 | |$1.01_{-0.15}^{+0.15}$| | |$67.4_{-18}^{+13}$| | |$0.00_{-0.00}^{+0.10}$| | |$1.24_{-0.06}^{+0.04}$| | |$34_{-14}^{+26}$| |
| XTE J1118+480 | P50133 | 3.66 | |$1.02_{-0.10}^{+0.10}$| | |$71.5_{-11}^{+11}$| | |$0.01_{-0.01}^{+0.04}$| | |$1.27_{-0.03}^{+0.03}$| | |$34.8_{-10}^{+15}$| |
| XTE J1118+480 | P50133 | 3.33 | |$0.840_{-0.08}^{+0.16}$| | |$46_{-10}^{+10}$| | |$0.02_{-0.02}^{+0.06}$| | |$1.21_{-0.03}^{+0.03}$| | |$70_{-33}^{+32}$| |
| XTE J1118+480 | P50133 | 3.43 | |$0.910_{-0.15}^{+0.15}$| | |$53.1_{-9.1}^{+9.1}$| | |$0.00_{-0.00}^{+0.04}$| | |$1.22_{-0.03}^{+0.03}$| | |$53_{-23}^{+52}$| |
| XTE J1118+480 | P50133 | 3.33 | |$0.96_{-0.22}^{+0.16}$| | |$50.2_{-9.7}^{+9.7}$| | |$0.01_{-0.01}^{+0.06}$| | |$1.20_{-0.03}^{+0.03}$| | |$41_{-17}^{+70}$| |
| XTE J1118+480 | P50133 | 3.51 | |$1.02_{-0.09}^{+0.09}$| | |$56.3_{-9.9}^{+9.9}$| | |$0.01_{-0.01}^{+0.06}$| | |$1.22_{-0.03}^{+0.03}$| | |$34.7_{-9.8}^{+14.0}$| |
| XTE J1118+480 | P50133 | 3.48 | |$1.02_{-0.11}^{+0.11}$| | |$57.0_{-9.0}^{+9.0}$| | |$0.01_{-0.01}^{+0.05}$| | |$1.23_{-0.03}^{+0.03}$| | |$35_{-12}^{+18}$| |
| GRO J1654−40 | P91702 | 8.55 | |$0.90_{-0.05}^{+0.54}$| | |$83.8_{-19}^{+19}$| | |$0.17_{-0.09}^{+0.09}$| | |$1.48_{-0.08}^{+0.08}$| | |$97_{-78}^{+21}$| |
| GRO J1654−40 | P91702 | 11.3 | |$0.93_{-0.10}^{+0.24}$| | |$122_{-18}^{+18}$| | |$0.19_{-0.08}^{+0.08}$| | |$1.29_{-0.04}^{+0.04}$| | |$146_{-84}^{+84}$| |
| GRO J1654−40 | P91702 | 13.0 | |$0.94_{-0.09}^{+0.12}$| | |$103_{-10}^{+10}$| | |$0.38_{-0.06}^{+0.06}$| | |$1.11_{-0.02}^{+0.02}$| | |$188_{-69}^{+97}$| |
| GRO J1654−40 | P91702 | 13.7 | |$0.87_{-0.12}^{+0.15}$| | |$103_{-15}^{+15}$| | |$0.38_{-0.09}^{+0.09}$| | |$1.05_{-0.03}^{+0.03}$| | |$298_{-138}^{+236}$| |
| 4U 1608−52 | P60052 | 2.63 | |$0.93_{-0.09}^{+0.09}$| | |$61.6_{-12}^{+12}$| | |$0.51_{-0.16}^{+0.16}$| | |$0.77_{-0.03}^{+0.03}$| | |$68_{-20}^{+29}$| |
| 4U 1608−52 | P60052 | 2.27 | |$0.84_{-0.07}^{+0.07}$| | |$77.2_{-9.4}^{+9.4}$| | |$0.37_{-0.17}^{+0.17}$| | |$0.78_{-0.03}^{+0.03}$| | |$91_{-27}^{+38}$| |
| 4U 1608−52 | P60052 | 2.31 | |$0.93_{-0.06}^{+0.06}$| | |$82.4_{-12}^{+12}$| | |$0.47_{-0.15}^{+0.15}$| | |$0.77_{-0.03}^{+0.03}$| | |$61_{-14}^{+18}$| |
| 4U 1608−52 | P60052 | 2.36 | |$0.87_{-0.07}^{+0.07}$| | |$80.2_{-15}^{+15}$| | |$0.47_{-0.18}^{+0.18}$| | |$0.76_{-0.03}^{+0.03}$| | |$87_{-23}^{+32}$| |
| 4U 1608−52 | P60052 | 2.78 | |$0.87_{-0.12}^{+0.13}$| | |$57.6_{-14}^{+16}$| | |$0.45_{-0.15}^{+0.15}$| | |$0.81_{-0.03}^{+0.03}$| | |$85_{-34}^{+57}$| |
| 4U 1636−536 | P92023 | 2.49 | |$0.97_{-0.01}^{+0.53}$| | |$22.8_{-3.4}^{+26}$| | |$0.18_{-0.14}^{+0.57}$| | |$0.96_{-0.19}^{+0.03}$| | |$44.0_{-34.0}^{+1.0}$| |
| 4U 1636−536 | P92023 | 2.83 | |$1.40_{-0.20}^{+0.20}$| | |$23.4_{-9.1}^{+11}$| | |$0.45_{-0.37}^{+0.37}$| | |$0.81_{-0.09}^{+0.09}$| | |$13.7_{-5.1}^{+8.2}$| |
| 4U 1636−536 | P92023 | 3.13 | |$1.50_{-0.19}^{+0.19}$| | |$25_{-10}^{+10}$| | |$0.80_{-0.39}^{+0.39}$| | |$0.76_{-0.09}^{+0.09}$| | |$11.6_{-4.1}^{+6.3}$| |
| 4U 1636−536 | P92023 | 3.65 | |$1.59_{-0.25}^{+0.25}$| | |$32_{-14}^{+14}$| | |$0.57_{-0.31}^{+0.31}$| | |$0.80_{-0.09}^{+0.09}$| | |$10.7_{-4.5}^{+7.6}$| |
| 4U 1636-536 | P92023 | 3.56 | |$1.32_{-0.11}^{+0.51}$| | |$15.1_{-2.4}^{+14.0}$| | |$0.18_{-0.18}^{+0.61}$| | |$0.94_{-0.24}^{+0.06}$| | |$21.1_{-14.0}^{+8.1}$| |
| 4U 1636-536 | P94310 | 2.17 | |$1.23_{-0.25}^{+0.25}$| | |$18.1_{-6.7}^{+9.2}$| | |$0.38_{-0.37}^{+0.41}$| | |$0.75_{-0.11}^{+0.11}$| | |$20.5_{-10}^{+20}$| |
| 4U 1705-44 | P20073 | 2.73 | |$1.98_{-0.10}^{+0.02}$| | |$26.6_{-5.5}^{+5.5}$| | |$0.75_{-0.35}^{+0.35}$| | |$0.62_{-0.07}^{+0.08}$| | |$4.23_{-0.27}^{+0.76}$| |
| 4U 1705-44 | P20073 | 2.52 | |$1.97_{-0.14}^{+0.03}$| | |$20.9_{-5.9}^{+5.7}$| | |$1.01_{-0.50}^{+0.49}$| | |$0.56_{-0.10}^{+0.10}$| | |$4.40_{-0.33}^{+1.2}$| |
| 4U 1728-33 | P92023 | 6.69 | |$2.00_{-0.07}^{+0.00}$| | |$18.9_{-2.9}^{+2.9}$| | |$0.52_{-0.25}^{+0.25}$| | |$0.72_{-0.07}^{+0.07}$| | |$9.03_{-0.53}^{+0.98}$| |
| 4U 1728-33 | P92023 | 6.97 | |$1.99_{-0.05}^{+0.01}$| | |$12.8_{-1.2}^{+1.2}$| | |$0.29_{-0.25}^{+0.25}$| | |$0.81_{-0.08}^{+0.08}$| | |$9.48_{-0.39}^{+0.81}$| |
| Aql X-1 | P50049 | 5.85 | |$1.56_{-0.14}^{+0.16}$| | |$26.2_{-6.8}^{+7.7}$| | |$0.57_{-0.26}^{+0.27}$| | |$0.80_{-0.07}^{+0.07}$| | |$18.4_{-5.1}^{+7.0}$| |
| Aql X-1 | P91414 | 2.37 | |$1.09_{-0.15}^{+0.24}$| | |$30.4_{-11}^{+15}$| | |$0.69_{-0.34}^{+0.38}$| | |$0.82_{-0.08}^{+0.08}$| | |$28_{-14}^{+20}$| |
| Aql X-1 | P91414 | 3.68 | |$1.46_{-0.16}^{+0.16}$| | |$25.4_{-6.8}^{+6.8}$| | |$1.11_{-0.36}^{+0.36}$| | |$0.66_{-0.07}^{+0.07}$| | |$17.6_{-5.6}^{+8.3}$| |
| Aql X-1 | P91414 | 3.51 | |$1.40_{-0.21}^{+0.21}$| | |$46.5_{-14.0}^{+14.0}$| | |$0.77_{-0.27}^{+0.27}$| | |$0.76_{-0.06}^{+0.06}$| | |$17.7_{-7.2}^{+12.0}$| |
| Source . | ObsID . | F2 − 200 . | kTbb . | kTe . | R . | y . | Norm. . |
|---|---|---|---|---|---|---|---|
| GS 1354−64 | P20431 | 5.31 | |$0.94_{-0.14}^{+0.14}$| | |$24.1_{-1.5}^{+1.5}$| | |$0.24_{-0.08}^{+0.08}$| | |$1.64_{-0.05}^{+0.05}$| | |$47_{-19}^{+31}$| |
| GS 1354−64 | P20431 | 5.03 | |$0.96_{-0.02}^{+0.09}$| | |$26.3_{-2.0}^{+2.0}$| | |$0.270_{-0.07}^{+0.07}$| | |$1.53_{-0.04}^{+0.04}$| | |$45.5_{-12.0}^{+3.9}$| |
| GS 1354−64 | P20431 | 4.73 | |$0.56_{-0.19}^{+0.30}$| | |$25.4_{-3.0}^{+3.3}$| | |$0.18_{-0.09}^{+0.09}$| | |$1.60_{-0.04}^{+0.04}$| | |$258_{-203}^{+934}$| |
| GS 1354−64 | P20431 | 4.80 | |$0.83_{-0.10}^{+0.19}$| | |$26.2_{-2.6}^{+2.7}$| | |$0.18_{-0.07}^{+0.07}$| | |$1.62_{-0.05}^{+0.05}$| | |$67_{-34}^{+39}$| |
| 4U 1543−47 | P70124 | 1.92 | |$0.90_{-0.22}^{+0.22}$| | |$110_{-50}^{+50}$| | |$0.19_{-0.19}^{+0.32}$| | |$1.06_{-0.15}^{+0.15}$| | |$36_{-24}^{+71}$| |
| XTE J1550−564 | P30188 | 26.0 | |$0.71_{-0.02}^{+0.08}$| | |$36.8_{-4.2}^{+4.2}$| | |$0.40_{-0.08}^{+0.09}$| | |$1.30_{-0.03}^{+0.03}$| | |$753_{-246}^{+77}$| |
| XTE J1550−564 | P30188 | 25.7 | |$0.62_{-0.01}^{+0.13}$| | |$38.9_{-3.4}^{+3.4}$| | |$0.450_{-0.07}^{+0.07}$| | |$1.28_{-0.02}^{+0.02}$| | |$1340_{-690}^{+9}$| |
| XTE J1550−564 | P30188 | 29.3 | |$0.42_{-0.02}^{+0.02}$| | |$30.4_{-1.2}^{+1.2}$| | |$0.580_{-0.06}^{+0.06}$| | |$1.17_{-0.02}^{+0.02}$| | |$7240_{-1100}^{+1150}$| |
| XTE J1550−564 | P50134 | 19.4 | |$0.71_{-0.08}^{+0.08}$| | |$77_{-16}^{+18}$| | |$0.56_{-0.09}^{+0.09}$| | |$0.83_{-0.04}^{+0.04}$| | |$1320_{-526}^{+917}$| |
| XTE J1550−564 | P50135 | 8.58 | |$0.83_{-0.03}^{+0.09}$| | |$221_{-45}^{+26}$| | |$0.08_{-0.08}^{+0.08}$| | |$1.10_{-0.05}^{+0.05}$| | |$253_{-93}^{+51}$| |
| XTE J1550−564 | P50135 | 7.45 | |$0.88_{-0.08}^{+0.10}$| | |$201_{-54}^{+26}$| | |$0.02_{-0.02}^{+0.13}$| | |$1.37_{-0.09}^{+0.08}$| | |$127_{-45}^{+59}$| |
| XTE J1550−564 | P50135 | 6.93 | |$0.84_{-0.11}^{+0.11}$| | |$158_{-54}^{+53}$| | |$0.15_{-0.11}^{+0.11}$| | |$1.29_{-0.08}^{+0.08}$| | |$129_{-53}^{+88}$| |
| XTE J1550−564 | P50137 | 20.9 | |$0.66_{-0.02}^{+0.15}$| | |$56.4_{-8.0}^{+7.8}$| | |$0.49_{-0.09}^{+0.09}$| | |$1.09_{-0.03}^{+0.03}$| | |$1080_{-592}^{+158}$| |
| Cyg X-1 | P20173 | 30.0 | |$0.89_{-0.10}^{+0.10}$| | |$63.0_{-5.9}^{+6.9}$| | |$0.15_{-0.03}^{+0.03}$| | |$1.42_{-0.01}^{+0.01}$| | |$353_{-121}^{+184}$| |
| Cyg X-1 | P20173 | 33.8 | |$0.92_{-0.03}^{+0.14}$| | |$62.2_{-3.9}^{+4.0}$| | |$0.16_{-0.02}^{+0.02}$| | |$1.46_{-0.01}^{+0.01}$| | |$331_{-136}^{+39}$| |
| Cyg X-1 | P20173 | 35.6 | |$1.03_{-0.03}^{+0.07}$| | |$63.1_{-2.8}^{+2.8}$| | |$0.160_{-0.02}^{+0.02}$| | |$1.46_{-0.01}^{+0.01}$| | |$235_{-48}^{+23}$| |
| Cyg X-1 | P20173 | 31.7 | |$0.94_{-0.04}^{+0.18}$| | |$60.8_{-3.3}^{+3.3}$| | |$0.16_{-0.02}^{+0.02}$| | |$1.45_{-0.01}^{+0.01}$| | |$295_{-136}^{+46}$| |
| Cyg X-1 | P20173 | 28.5 | |$0.820_{-0.10}^{+0.10}$| | |$70.9_{-12}^{+16}$| | |$0.170_{-0.04}^{+0.04}$| | |$1.43_{-0.02}^{+0.02}$| | |$472_{-188}^{+310}$| |
| Cyg X-1 | P20173 | 29.2 | |$0.79_{-0.01}^{+0.10}$| | |$75.1_{-9.5}^{+9.2}$| | |$0.18_{-0.03}^{+0.02}$| | |$1.42_{-0.01}^{+0.01}$| | |$539_{-199}^{+5}$| |
| Cyg X-1 | P20173 | 28.4 | |$0.880_{-0.01}^{+0.10}$| | |$67.3_{-5.0}^{+5.0}$| | |$0.16_{-0.02}^{+0.02}$| | |$1.42_{-0.01}^{+0.01}$| | |$362_{-123}^{+18}$| |
| Cyg X-1 | P80110 | 48.2 | |$1.01_{-0.10}^{+0.11}$| | |$87.0_{-6.1}^{+6.1}$| | |$0.240_{-0.02}^{+0.02}$| | |$1.37_{-0.01}^{+0.01}$| | |$394_{-125}^{+182}$| |
| Cyg X-1 | P80110 | 31.5 | |$1.08_{-0.11}^{+0.13}$| | |$75.1_{-5.9}^{+5.9}$| | |$0.20_{-0.03}^{+0.03}$| | |$1.39_{-0.02}^{+0.02}$| | |$191_{-64}^{+92}$| |
| Cyg X-1 | P80110 | 32.9 | |$1.27_{-0.09}^{+0.09}$| | |$69.3_{-5.9}^{+5.5}$| | |$0.24_{-0.03}^{+0.03}$| | |$1.39_{-0.02}^{+0.02}$| | |$110_{-24}^{+31}$| |
| Cyg X-1 | P94108 | 31.1 | |$0.94_{-0.13}^{+0.14}$| | |$102_{-22}^{+22}$| | |$0.18_{-0.05}^{+0.05}$| | |$1.32_{-0.03}^{+0.03}$| | |$362_{-160}^{+286}$| |
| GX 339−4 | P92035 | 19.2 | |$0.99_{-0.03}^{+0.13}$| | |$33.9_{-2.7}^{+3.5}$| | |$0.45_{-0.07}^{+0.07}$| | |$1.04_{-0.03}^{+0.02}$| | |$242_{-88}^{+31}$| |
| GX 339−4 | P92035 | 21.4 | |$1.09_{-0.08}^{+0.12}$| | |$35.4_{-3.4}^{+4.2}$| | |$0.60_{-0.09}^{+0.09}$| | |$0.98_{-0.03}^{+0.03}$| | |$196_{-61}^{+58}$| |
| GX 339−4 | P92035 | 23.4 | |$1.13_{-0.10}^{+0.10}$| | |$33.0_{-3.0}^{+3.0}$| | |$0.56_{-0.09}^{+0.09}$| | |$0.90_{-0.03}^{+0.03}$| | |$219_{-59}^{+80}$| |
| GX 339−4 | P92052 | 8.95 | |$1.12_{-0.02}^{+0.21}$| | |$53.9_{-7.0}^{+10}$| | |$0.420_{-0.07}^{+0.07}$| | |$1.35_{-0.04}^{+0.03}$| | |$44.7_{-20.0}^{+1.8}$| |
| GX 339−4 | P90118 | 6.47 | |$1.33_{-0.07}^{+0.19}$| | |$65.6_{-13}^{+14}$| | |$0.45_{-0.09}^{+0.09}$| | |$1.34_{-0.04}^{+0.04}$| | |$17.8_{-6.6}^{+3.7}$| |
| XTE J1118+480 | P50133 | 3.14 | |$1.01_{-0.15}^{+0.15}$| | |$67.4_{-18}^{+13}$| | |$0.00_{-0.00}^{+0.10}$| | |$1.24_{-0.06}^{+0.04}$| | |$34_{-14}^{+26}$| |
| XTE J1118+480 | P50133 | 3.66 | |$1.02_{-0.10}^{+0.10}$| | |$71.5_{-11}^{+11}$| | |$0.01_{-0.01}^{+0.04}$| | |$1.27_{-0.03}^{+0.03}$| | |$34.8_{-10}^{+15}$| |
| XTE J1118+480 | P50133 | 3.33 | |$0.840_{-0.08}^{+0.16}$| | |$46_{-10}^{+10}$| | |$0.02_{-0.02}^{+0.06}$| | |$1.21_{-0.03}^{+0.03}$| | |$70_{-33}^{+32}$| |
| XTE J1118+480 | P50133 | 3.43 | |$0.910_{-0.15}^{+0.15}$| | |$53.1_{-9.1}^{+9.1}$| | |$0.00_{-0.00}^{+0.04}$| | |$1.22_{-0.03}^{+0.03}$| | |$53_{-23}^{+52}$| |
| XTE J1118+480 | P50133 | 3.33 | |$0.96_{-0.22}^{+0.16}$| | |$50.2_{-9.7}^{+9.7}$| | |$0.01_{-0.01}^{+0.06}$| | |$1.20_{-0.03}^{+0.03}$| | |$41_{-17}^{+70}$| |
| XTE J1118+480 | P50133 | 3.51 | |$1.02_{-0.09}^{+0.09}$| | |$56.3_{-9.9}^{+9.9}$| | |$0.01_{-0.01}^{+0.06}$| | |$1.22_{-0.03}^{+0.03}$| | |$34.7_{-9.8}^{+14.0}$| |
| XTE J1118+480 | P50133 | 3.48 | |$1.02_{-0.11}^{+0.11}$| | |$57.0_{-9.0}^{+9.0}$| | |$0.01_{-0.01}^{+0.05}$| | |$1.23_{-0.03}^{+0.03}$| | |$35_{-12}^{+18}$| |
| GRO J1654−40 | P91702 | 8.55 | |$0.90_{-0.05}^{+0.54}$| | |$83.8_{-19}^{+19}$| | |$0.17_{-0.09}^{+0.09}$| | |$1.48_{-0.08}^{+0.08}$| | |$97_{-78}^{+21}$| |
| GRO J1654−40 | P91702 | 11.3 | |$0.93_{-0.10}^{+0.24}$| | |$122_{-18}^{+18}$| | |$0.19_{-0.08}^{+0.08}$| | |$1.29_{-0.04}^{+0.04}$| | |$146_{-84}^{+84}$| |
| GRO J1654−40 | P91702 | 13.0 | |$0.94_{-0.09}^{+0.12}$| | |$103_{-10}^{+10}$| | |$0.38_{-0.06}^{+0.06}$| | |$1.11_{-0.02}^{+0.02}$| | |$188_{-69}^{+97}$| |
| GRO J1654−40 | P91702 | 13.7 | |$0.87_{-0.12}^{+0.15}$| | |$103_{-15}^{+15}$| | |$0.38_{-0.09}^{+0.09}$| | |$1.05_{-0.03}^{+0.03}$| | |$298_{-138}^{+236}$| |
| 4U 1608−52 | P60052 | 2.63 | |$0.93_{-0.09}^{+0.09}$| | |$61.6_{-12}^{+12}$| | |$0.51_{-0.16}^{+0.16}$| | |$0.77_{-0.03}^{+0.03}$| | |$68_{-20}^{+29}$| |
| 4U 1608−52 | P60052 | 2.27 | |$0.84_{-0.07}^{+0.07}$| | |$77.2_{-9.4}^{+9.4}$| | |$0.37_{-0.17}^{+0.17}$| | |$0.78_{-0.03}^{+0.03}$| | |$91_{-27}^{+38}$| |
| 4U 1608−52 | P60052 | 2.31 | |$0.93_{-0.06}^{+0.06}$| | |$82.4_{-12}^{+12}$| | |$0.47_{-0.15}^{+0.15}$| | |$0.77_{-0.03}^{+0.03}$| | |$61_{-14}^{+18}$| |
| 4U 1608−52 | P60052 | 2.36 | |$0.87_{-0.07}^{+0.07}$| | |$80.2_{-15}^{+15}$| | |$0.47_{-0.18}^{+0.18}$| | |$0.76_{-0.03}^{+0.03}$| | |$87_{-23}^{+32}$| |
| 4U 1608−52 | P60052 | 2.78 | |$0.87_{-0.12}^{+0.13}$| | |$57.6_{-14}^{+16}$| | |$0.45_{-0.15}^{+0.15}$| | |$0.81_{-0.03}^{+0.03}$| | |$85_{-34}^{+57}$| |
| 4U 1636−536 | P92023 | 2.49 | |$0.97_{-0.01}^{+0.53}$| | |$22.8_{-3.4}^{+26}$| | |$0.18_{-0.14}^{+0.57}$| | |$0.96_{-0.19}^{+0.03}$| | |$44.0_{-34.0}^{+1.0}$| |
| 4U 1636−536 | P92023 | 2.83 | |$1.40_{-0.20}^{+0.20}$| | |$23.4_{-9.1}^{+11}$| | |$0.45_{-0.37}^{+0.37}$| | |$0.81_{-0.09}^{+0.09}$| | |$13.7_{-5.1}^{+8.2}$| |
| 4U 1636−536 | P92023 | 3.13 | |$1.50_{-0.19}^{+0.19}$| | |$25_{-10}^{+10}$| | |$0.80_{-0.39}^{+0.39}$| | |$0.76_{-0.09}^{+0.09}$| | |$11.6_{-4.1}^{+6.3}$| |
| 4U 1636−536 | P92023 | 3.65 | |$1.59_{-0.25}^{+0.25}$| | |$32_{-14}^{+14}$| | |$0.57_{-0.31}^{+0.31}$| | |$0.80_{-0.09}^{+0.09}$| | |$10.7_{-4.5}^{+7.6}$| |
| 4U 1636-536 | P92023 | 3.56 | |$1.32_{-0.11}^{+0.51}$| | |$15.1_{-2.4}^{+14.0}$| | |$0.18_{-0.18}^{+0.61}$| | |$0.94_{-0.24}^{+0.06}$| | |$21.1_{-14.0}^{+8.1}$| |
| 4U 1636-536 | P94310 | 2.17 | |$1.23_{-0.25}^{+0.25}$| | |$18.1_{-6.7}^{+9.2}$| | |$0.38_{-0.37}^{+0.41}$| | |$0.75_{-0.11}^{+0.11}$| | |$20.5_{-10}^{+20}$| |
| 4U 1705-44 | P20073 | 2.73 | |$1.98_{-0.10}^{+0.02}$| | |$26.6_{-5.5}^{+5.5}$| | |$0.75_{-0.35}^{+0.35}$| | |$0.62_{-0.07}^{+0.08}$| | |$4.23_{-0.27}^{+0.76}$| |
| 4U 1705-44 | P20073 | 2.52 | |$1.97_{-0.14}^{+0.03}$| | |$20.9_{-5.9}^{+5.7}$| | |$1.01_{-0.50}^{+0.49}$| | |$0.56_{-0.10}^{+0.10}$| | |$4.40_{-0.33}^{+1.2}$| |
| 4U 1728-33 | P92023 | 6.69 | |$2.00_{-0.07}^{+0.00}$| | |$18.9_{-2.9}^{+2.9}$| | |$0.52_{-0.25}^{+0.25}$| | |$0.72_{-0.07}^{+0.07}$| | |$9.03_{-0.53}^{+0.98}$| |
| 4U 1728-33 | P92023 | 6.97 | |$1.99_{-0.05}^{+0.01}$| | |$12.8_{-1.2}^{+1.2}$| | |$0.29_{-0.25}^{+0.25}$| | |$0.81_{-0.08}^{+0.08}$| | |$9.48_{-0.39}^{+0.81}$| |
| Aql X-1 | P50049 | 5.85 | |$1.56_{-0.14}^{+0.16}$| | |$26.2_{-6.8}^{+7.7}$| | |$0.57_{-0.26}^{+0.27}$| | |$0.80_{-0.07}^{+0.07}$| | |$18.4_{-5.1}^{+7.0}$| |
| Aql X-1 | P91414 | 2.37 | |$1.09_{-0.15}^{+0.24}$| | |$30.4_{-11}^{+15}$| | |$0.69_{-0.34}^{+0.38}$| | |$0.82_{-0.08}^{+0.08}$| | |$28_{-14}^{+20}$| |
| Aql X-1 | P91414 | 3.68 | |$1.46_{-0.16}^{+0.16}$| | |$25.4_{-6.8}^{+6.8}$| | |$1.11_{-0.36}^{+0.36}$| | |$0.66_{-0.07}^{+0.07}$| | |$17.6_{-5.6}^{+8.3}$| |
| Aql X-1 | P91414 | 3.51 | |$1.40_{-0.21}^{+0.21}$| | |$46.5_{-14.0}^{+14.0}$| | |$0.77_{-0.27}^{+0.27}$| | |$0.76_{-0.06}^{+0.06}$| | |$17.7_{-7.2}^{+12.0}$| |
Results from spectral analysis of BH (top) and NS (bottom) XBs for the compps parameters; best-fitting location together with 1D 90 per cent confidence. The F2 − 200 is the unabsorbed 2–200 keV flux in the units of 10−9 erg cm−2 s−1; temperatures are given in keV.
| Source . | ObsID . | F2 − 200 . | kTbb . | kTe . | R . | y . | Norm. . |
|---|---|---|---|---|---|---|---|
| GS 1354−64 | P20431 | 5.31 | |$0.94_{-0.14}^{+0.14}$| | |$24.1_{-1.5}^{+1.5}$| | |$0.24_{-0.08}^{+0.08}$| | |$1.64_{-0.05}^{+0.05}$| | |$47_{-19}^{+31}$| |
| GS 1354−64 | P20431 | 5.03 | |$0.96_{-0.02}^{+0.09}$| | |$26.3_{-2.0}^{+2.0}$| | |$0.270_{-0.07}^{+0.07}$| | |$1.53_{-0.04}^{+0.04}$| | |$45.5_{-12.0}^{+3.9}$| |
| GS 1354−64 | P20431 | 4.73 | |$0.56_{-0.19}^{+0.30}$| | |$25.4_{-3.0}^{+3.3}$| | |$0.18_{-0.09}^{+0.09}$| | |$1.60_{-0.04}^{+0.04}$| | |$258_{-203}^{+934}$| |
| GS 1354−64 | P20431 | 4.80 | |$0.83_{-0.10}^{+0.19}$| | |$26.2_{-2.6}^{+2.7}$| | |$0.18_{-0.07}^{+0.07}$| | |$1.62_{-0.05}^{+0.05}$| | |$67_{-34}^{+39}$| |
| 4U 1543−47 | P70124 | 1.92 | |$0.90_{-0.22}^{+0.22}$| | |$110_{-50}^{+50}$| | |$0.19_{-0.19}^{+0.32}$| | |$1.06_{-0.15}^{+0.15}$| | |$36_{-24}^{+71}$| |
| XTE J1550−564 | P30188 | 26.0 | |$0.71_{-0.02}^{+0.08}$| | |$36.8_{-4.2}^{+4.2}$| | |$0.40_{-0.08}^{+0.09}$| | |$1.30_{-0.03}^{+0.03}$| | |$753_{-246}^{+77}$| |
| XTE J1550−564 | P30188 | 25.7 | |$0.62_{-0.01}^{+0.13}$| | |$38.9_{-3.4}^{+3.4}$| | |$0.450_{-0.07}^{+0.07}$| | |$1.28_{-0.02}^{+0.02}$| | |$1340_{-690}^{+9}$| |
| XTE J1550−564 | P30188 | 29.3 | |$0.42_{-0.02}^{+0.02}$| | |$30.4_{-1.2}^{+1.2}$| | |$0.580_{-0.06}^{+0.06}$| | |$1.17_{-0.02}^{+0.02}$| | |$7240_{-1100}^{+1150}$| |
| XTE J1550−564 | P50134 | 19.4 | |$0.71_{-0.08}^{+0.08}$| | |$77_{-16}^{+18}$| | |$0.56_{-0.09}^{+0.09}$| | |$0.83_{-0.04}^{+0.04}$| | |$1320_{-526}^{+917}$| |
| XTE J1550−564 | P50135 | 8.58 | |$0.83_{-0.03}^{+0.09}$| | |$221_{-45}^{+26}$| | |$0.08_{-0.08}^{+0.08}$| | |$1.10_{-0.05}^{+0.05}$| | |$253_{-93}^{+51}$| |
| XTE J1550−564 | P50135 | 7.45 | |$0.88_{-0.08}^{+0.10}$| | |$201_{-54}^{+26}$| | |$0.02_{-0.02}^{+0.13}$| | |$1.37_{-0.09}^{+0.08}$| | |$127_{-45}^{+59}$| |
| XTE J1550−564 | P50135 | 6.93 | |$0.84_{-0.11}^{+0.11}$| | |$158_{-54}^{+53}$| | |$0.15_{-0.11}^{+0.11}$| | |$1.29_{-0.08}^{+0.08}$| | |$129_{-53}^{+88}$| |
| XTE J1550−564 | P50137 | 20.9 | |$0.66_{-0.02}^{+0.15}$| | |$56.4_{-8.0}^{+7.8}$| | |$0.49_{-0.09}^{+0.09}$| | |$1.09_{-0.03}^{+0.03}$| | |$1080_{-592}^{+158}$| |
| Cyg X-1 | P20173 | 30.0 | |$0.89_{-0.10}^{+0.10}$| | |$63.0_{-5.9}^{+6.9}$| | |$0.15_{-0.03}^{+0.03}$| | |$1.42_{-0.01}^{+0.01}$| | |$353_{-121}^{+184}$| |
| Cyg X-1 | P20173 | 33.8 | |$0.92_{-0.03}^{+0.14}$| | |$62.2_{-3.9}^{+4.0}$| | |$0.16_{-0.02}^{+0.02}$| | |$1.46_{-0.01}^{+0.01}$| | |$331_{-136}^{+39}$| |
| Cyg X-1 | P20173 | 35.6 | |$1.03_{-0.03}^{+0.07}$| | |$63.1_{-2.8}^{+2.8}$| | |$0.160_{-0.02}^{+0.02}$| | |$1.46_{-0.01}^{+0.01}$| | |$235_{-48}^{+23}$| |
| Cyg X-1 | P20173 | 31.7 | |$0.94_{-0.04}^{+0.18}$| | |$60.8_{-3.3}^{+3.3}$| | |$0.16_{-0.02}^{+0.02}$| | |$1.45_{-0.01}^{+0.01}$| | |$295_{-136}^{+46}$| |
| Cyg X-1 | P20173 | 28.5 | |$0.820_{-0.10}^{+0.10}$| | |$70.9_{-12}^{+16}$| | |$0.170_{-0.04}^{+0.04}$| | |$1.43_{-0.02}^{+0.02}$| | |$472_{-188}^{+310}$| |
| Cyg X-1 | P20173 | 29.2 | |$0.79_{-0.01}^{+0.10}$| | |$75.1_{-9.5}^{+9.2}$| | |$0.18_{-0.03}^{+0.02}$| | |$1.42_{-0.01}^{+0.01}$| | |$539_{-199}^{+5}$| |
| Cyg X-1 | P20173 | 28.4 | |$0.880_{-0.01}^{+0.10}$| | |$67.3_{-5.0}^{+5.0}$| | |$0.16_{-0.02}^{+0.02}$| | |$1.42_{-0.01}^{+0.01}$| | |$362_{-123}^{+18}$| |
| Cyg X-1 | P80110 | 48.2 | |$1.01_{-0.10}^{+0.11}$| | |$87.0_{-6.1}^{+6.1}$| | |$0.240_{-0.02}^{+0.02}$| | |$1.37_{-0.01}^{+0.01}$| | |$394_{-125}^{+182}$| |
| Cyg X-1 | P80110 | 31.5 | |$1.08_{-0.11}^{+0.13}$| | |$75.1_{-5.9}^{+5.9}$| | |$0.20_{-0.03}^{+0.03}$| | |$1.39_{-0.02}^{+0.02}$| | |$191_{-64}^{+92}$| |
| Cyg X-1 | P80110 | 32.9 | |$1.27_{-0.09}^{+0.09}$| | |$69.3_{-5.9}^{+5.5}$| | |$0.24_{-0.03}^{+0.03}$| | |$1.39_{-0.02}^{+0.02}$| | |$110_{-24}^{+31}$| |
| Cyg X-1 | P94108 | 31.1 | |$0.94_{-0.13}^{+0.14}$| | |$102_{-22}^{+22}$| | |$0.18_{-0.05}^{+0.05}$| | |$1.32_{-0.03}^{+0.03}$| | |$362_{-160}^{+286}$| |
| GX 339−4 | P92035 | 19.2 | |$0.99_{-0.03}^{+0.13}$| | |$33.9_{-2.7}^{+3.5}$| | |$0.45_{-0.07}^{+0.07}$| | |$1.04_{-0.03}^{+0.02}$| | |$242_{-88}^{+31}$| |
| GX 339−4 | P92035 | 21.4 | |$1.09_{-0.08}^{+0.12}$| | |$35.4_{-3.4}^{+4.2}$| | |$0.60_{-0.09}^{+0.09}$| | |$0.98_{-0.03}^{+0.03}$| | |$196_{-61}^{+58}$| |
| GX 339−4 | P92035 | 23.4 | |$1.13_{-0.10}^{+0.10}$| | |$33.0_{-3.0}^{+3.0}$| | |$0.56_{-0.09}^{+0.09}$| | |$0.90_{-0.03}^{+0.03}$| | |$219_{-59}^{+80}$| |
| GX 339−4 | P92052 | 8.95 | |$1.12_{-0.02}^{+0.21}$| | |$53.9_{-7.0}^{+10}$| | |$0.420_{-0.07}^{+0.07}$| | |$1.35_{-0.04}^{+0.03}$| | |$44.7_{-20.0}^{+1.8}$| |
| GX 339−4 | P90118 | 6.47 | |$1.33_{-0.07}^{+0.19}$| | |$65.6_{-13}^{+14}$| | |$0.45_{-0.09}^{+0.09}$| | |$1.34_{-0.04}^{+0.04}$| | |$17.8_{-6.6}^{+3.7}$| |
| XTE J1118+480 | P50133 | 3.14 | |$1.01_{-0.15}^{+0.15}$| | |$67.4_{-18}^{+13}$| | |$0.00_{-0.00}^{+0.10}$| | |$1.24_{-0.06}^{+0.04}$| | |$34_{-14}^{+26}$| |
| XTE J1118+480 | P50133 | 3.66 | |$1.02_{-0.10}^{+0.10}$| | |$71.5_{-11}^{+11}$| | |$0.01_{-0.01}^{+0.04}$| | |$1.27_{-0.03}^{+0.03}$| | |$34.8_{-10}^{+15}$| |
| XTE J1118+480 | P50133 | 3.33 | |$0.840_{-0.08}^{+0.16}$| | |$46_{-10}^{+10}$| | |$0.02_{-0.02}^{+0.06}$| | |$1.21_{-0.03}^{+0.03}$| | |$70_{-33}^{+32}$| |
| XTE J1118+480 | P50133 | 3.43 | |$0.910_{-0.15}^{+0.15}$| | |$53.1_{-9.1}^{+9.1}$| | |$0.00_{-0.00}^{+0.04}$| | |$1.22_{-0.03}^{+0.03}$| | |$53_{-23}^{+52}$| |
| XTE J1118+480 | P50133 | 3.33 | |$0.96_{-0.22}^{+0.16}$| | |$50.2_{-9.7}^{+9.7}$| | |$0.01_{-0.01}^{+0.06}$| | |$1.20_{-0.03}^{+0.03}$| | |$41_{-17}^{+70}$| |
| XTE J1118+480 | P50133 | 3.51 | |$1.02_{-0.09}^{+0.09}$| | |$56.3_{-9.9}^{+9.9}$| | |$0.01_{-0.01}^{+0.06}$| | |$1.22_{-0.03}^{+0.03}$| | |$34.7_{-9.8}^{+14.0}$| |
| XTE J1118+480 | P50133 | 3.48 | |$1.02_{-0.11}^{+0.11}$| | |$57.0_{-9.0}^{+9.0}$| | |$0.01_{-0.01}^{+0.05}$| | |$1.23_{-0.03}^{+0.03}$| | |$35_{-12}^{+18}$| |
| GRO J1654−40 | P91702 | 8.55 | |$0.90_{-0.05}^{+0.54}$| | |$83.8_{-19}^{+19}$| | |$0.17_{-0.09}^{+0.09}$| | |$1.48_{-0.08}^{+0.08}$| | |$97_{-78}^{+21}$| |
| GRO J1654−40 | P91702 | 11.3 | |$0.93_{-0.10}^{+0.24}$| | |$122_{-18}^{+18}$| | |$0.19_{-0.08}^{+0.08}$| | |$1.29_{-0.04}^{+0.04}$| | |$146_{-84}^{+84}$| |
| GRO J1654−40 | P91702 | 13.0 | |$0.94_{-0.09}^{+0.12}$| | |$103_{-10}^{+10}$| | |$0.38_{-0.06}^{+0.06}$| | |$1.11_{-0.02}^{+0.02}$| | |$188_{-69}^{+97}$| |
| GRO J1654−40 | P91702 | 13.7 | |$0.87_{-0.12}^{+0.15}$| | |$103_{-15}^{+15}$| | |$0.38_{-0.09}^{+0.09}$| | |$1.05_{-0.03}^{+0.03}$| | |$298_{-138}^{+236}$| |
| 4U 1608−52 | P60052 | 2.63 | |$0.93_{-0.09}^{+0.09}$| | |$61.6_{-12}^{+12}$| | |$0.51_{-0.16}^{+0.16}$| | |$0.77_{-0.03}^{+0.03}$| | |$68_{-20}^{+29}$| |
| 4U 1608−52 | P60052 | 2.27 | |$0.84_{-0.07}^{+0.07}$| | |$77.2_{-9.4}^{+9.4}$| | |$0.37_{-0.17}^{+0.17}$| | |$0.78_{-0.03}^{+0.03}$| | |$91_{-27}^{+38}$| |
| 4U 1608−52 | P60052 | 2.31 | |$0.93_{-0.06}^{+0.06}$| | |$82.4_{-12}^{+12}$| | |$0.47_{-0.15}^{+0.15}$| | |$0.77_{-0.03}^{+0.03}$| | |$61_{-14}^{+18}$| |
| 4U 1608−52 | P60052 | 2.36 | |$0.87_{-0.07}^{+0.07}$| | |$80.2_{-15}^{+15}$| | |$0.47_{-0.18}^{+0.18}$| | |$0.76_{-0.03}^{+0.03}$| | |$87_{-23}^{+32}$| |
| 4U 1608−52 | P60052 | 2.78 | |$0.87_{-0.12}^{+0.13}$| | |$57.6_{-14}^{+16}$| | |$0.45_{-0.15}^{+0.15}$| | |$0.81_{-0.03}^{+0.03}$| | |$85_{-34}^{+57}$| |
| 4U 1636−536 | P92023 | 2.49 | |$0.97_{-0.01}^{+0.53}$| | |$22.8_{-3.4}^{+26}$| | |$0.18_{-0.14}^{+0.57}$| | |$0.96_{-0.19}^{+0.03}$| | |$44.0_{-34.0}^{+1.0}$| |
| 4U 1636−536 | P92023 | 2.83 | |$1.40_{-0.20}^{+0.20}$| | |$23.4_{-9.1}^{+11}$| | |$0.45_{-0.37}^{+0.37}$| | |$0.81_{-0.09}^{+0.09}$| | |$13.7_{-5.1}^{+8.2}$| |
| 4U 1636−536 | P92023 | 3.13 | |$1.50_{-0.19}^{+0.19}$| | |$25_{-10}^{+10}$| | |$0.80_{-0.39}^{+0.39}$| | |$0.76_{-0.09}^{+0.09}$| | |$11.6_{-4.1}^{+6.3}$| |
| 4U 1636−536 | P92023 | 3.65 | |$1.59_{-0.25}^{+0.25}$| | |$32_{-14}^{+14}$| | |$0.57_{-0.31}^{+0.31}$| | |$0.80_{-0.09}^{+0.09}$| | |$10.7_{-4.5}^{+7.6}$| |
| 4U 1636-536 | P92023 | 3.56 | |$1.32_{-0.11}^{+0.51}$| | |$15.1_{-2.4}^{+14.0}$| | |$0.18_{-0.18}^{+0.61}$| | |$0.94_{-0.24}^{+0.06}$| | |$21.1_{-14.0}^{+8.1}$| |
| 4U 1636-536 | P94310 | 2.17 | |$1.23_{-0.25}^{+0.25}$| | |$18.1_{-6.7}^{+9.2}$| | |$0.38_{-0.37}^{+0.41}$| | |$0.75_{-0.11}^{+0.11}$| | |$20.5_{-10}^{+20}$| |
| 4U 1705-44 | P20073 | 2.73 | |$1.98_{-0.10}^{+0.02}$| | |$26.6_{-5.5}^{+5.5}$| | |$0.75_{-0.35}^{+0.35}$| | |$0.62_{-0.07}^{+0.08}$| | |$4.23_{-0.27}^{+0.76}$| |
| 4U 1705-44 | P20073 | 2.52 | |$1.97_{-0.14}^{+0.03}$| | |$20.9_{-5.9}^{+5.7}$| | |$1.01_{-0.50}^{+0.49}$| | |$0.56_{-0.10}^{+0.10}$| | |$4.40_{-0.33}^{+1.2}$| |
| 4U 1728-33 | P92023 | 6.69 | |$2.00_{-0.07}^{+0.00}$| | |$18.9_{-2.9}^{+2.9}$| | |$0.52_{-0.25}^{+0.25}$| | |$0.72_{-0.07}^{+0.07}$| | |$9.03_{-0.53}^{+0.98}$| |
| 4U 1728-33 | P92023 | 6.97 | |$1.99_{-0.05}^{+0.01}$| | |$12.8_{-1.2}^{+1.2}$| | |$0.29_{-0.25}^{+0.25}$| | |$0.81_{-0.08}^{+0.08}$| | |$9.48_{-0.39}^{+0.81}$| |
| Aql X-1 | P50049 | 5.85 | |$1.56_{-0.14}^{+0.16}$| | |$26.2_{-6.8}^{+7.7}$| | |$0.57_{-0.26}^{+0.27}$| | |$0.80_{-0.07}^{+0.07}$| | |$18.4_{-5.1}^{+7.0}$| |
| Aql X-1 | P91414 | 2.37 | |$1.09_{-0.15}^{+0.24}$| | |$30.4_{-11}^{+15}$| | |$0.69_{-0.34}^{+0.38}$| | |$0.82_{-0.08}^{+0.08}$| | |$28_{-14}^{+20}$| |
| Aql X-1 | P91414 | 3.68 | |$1.46_{-0.16}^{+0.16}$| | |$25.4_{-6.8}^{+6.8}$| | |$1.11_{-0.36}^{+0.36}$| | |$0.66_{-0.07}^{+0.07}$| | |$17.6_{-5.6}^{+8.3}$| |
| Aql X-1 | P91414 | 3.51 | |$1.40_{-0.21}^{+0.21}$| | |$46.5_{-14.0}^{+14.0}$| | |$0.77_{-0.27}^{+0.27}$| | |$0.76_{-0.06}^{+0.06}$| | |$17.7_{-7.2}^{+12.0}$| |
| Source . | ObsID . | F2 − 200 . | kTbb . | kTe . | R . | y . | Norm. . |
|---|---|---|---|---|---|---|---|
| GS 1354−64 | P20431 | 5.31 | |$0.94_{-0.14}^{+0.14}$| | |$24.1_{-1.5}^{+1.5}$| | |$0.24_{-0.08}^{+0.08}$| | |$1.64_{-0.05}^{+0.05}$| | |$47_{-19}^{+31}$| |
| GS 1354−64 | P20431 | 5.03 | |$0.96_{-0.02}^{+0.09}$| | |$26.3_{-2.0}^{+2.0}$| | |$0.270_{-0.07}^{+0.07}$| | |$1.53_{-0.04}^{+0.04}$| | |$45.5_{-12.0}^{+3.9}$| |
| GS 1354−64 | P20431 | 4.73 | |$0.56_{-0.19}^{+0.30}$| | |$25.4_{-3.0}^{+3.3}$| | |$0.18_{-0.09}^{+0.09}$| | |$1.60_{-0.04}^{+0.04}$| | |$258_{-203}^{+934}$| |
| GS 1354−64 | P20431 | 4.80 | |$0.83_{-0.10}^{+0.19}$| | |$26.2_{-2.6}^{+2.7}$| | |$0.18_{-0.07}^{+0.07}$| | |$1.62_{-0.05}^{+0.05}$| | |$67_{-34}^{+39}$| |
| 4U 1543−47 | P70124 | 1.92 | |$0.90_{-0.22}^{+0.22}$| | |$110_{-50}^{+50}$| | |$0.19_{-0.19}^{+0.32}$| | |$1.06_{-0.15}^{+0.15}$| | |$36_{-24}^{+71}$| |
| XTE J1550−564 | P30188 | 26.0 | |$0.71_{-0.02}^{+0.08}$| | |$36.8_{-4.2}^{+4.2}$| | |$0.40_{-0.08}^{+0.09}$| | |$1.30_{-0.03}^{+0.03}$| | |$753_{-246}^{+77}$| |
| XTE J1550−564 | P30188 | 25.7 | |$0.62_{-0.01}^{+0.13}$| | |$38.9_{-3.4}^{+3.4}$| | |$0.450_{-0.07}^{+0.07}$| | |$1.28_{-0.02}^{+0.02}$| | |$1340_{-690}^{+9}$| |
| XTE J1550−564 | P30188 | 29.3 | |$0.42_{-0.02}^{+0.02}$| | |$30.4_{-1.2}^{+1.2}$| | |$0.580_{-0.06}^{+0.06}$| | |$1.17_{-0.02}^{+0.02}$| | |$7240_{-1100}^{+1150}$| |
| XTE J1550−564 | P50134 | 19.4 | |$0.71_{-0.08}^{+0.08}$| | |$77_{-16}^{+18}$| | |$0.56_{-0.09}^{+0.09}$| | |$0.83_{-0.04}^{+0.04}$| | |$1320_{-526}^{+917}$| |
| XTE J1550−564 | P50135 | 8.58 | |$0.83_{-0.03}^{+0.09}$| | |$221_{-45}^{+26}$| | |$0.08_{-0.08}^{+0.08}$| | |$1.10_{-0.05}^{+0.05}$| | |$253_{-93}^{+51}$| |
| XTE J1550−564 | P50135 | 7.45 | |$0.88_{-0.08}^{+0.10}$| | |$201_{-54}^{+26}$| | |$0.02_{-0.02}^{+0.13}$| | |$1.37_{-0.09}^{+0.08}$| | |$127_{-45}^{+59}$| |
| XTE J1550−564 | P50135 | 6.93 | |$0.84_{-0.11}^{+0.11}$| | |$158_{-54}^{+53}$| | |$0.15_{-0.11}^{+0.11}$| | |$1.29_{-0.08}^{+0.08}$| | |$129_{-53}^{+88}$| |
| XTE J1550−564 | P50137 | 20.9 | |$0.66_{-0.02}^{+0.15}$| | |$56.4_{-8.0}^{+7.8}$| | |$0.49_{-0.09}^{+0.09}$| | |$1.09_{-0.03}^{+0.03}$| | |$1080_{-592}^{+158}$| |
| Cyg X-1 | P20173 | 30.0 | |$0.89_{-0.10}^{+0.10}$| | |$63.0_{-5.9}^{+6.9}$| | |$0.15_{-0.03}^{+0.03}$| | |$1.42_{-0.01}^{+0.01}$| | |$353_{-121}^{+184}$| |
| Cyg X-1 | P20173 | 33.8 | |$0.92_{-0.03}^{+0.14}$| | |$62.2_{-3.9}^{+4.0}$| | |$0.16_{-0.02}^{+0.02}$| | |$1.46_{-0.01}^{+0.01}$| | |$331_{-136}^{+39}$| |
| Cyg X-1 | P20173 | 35.6 | |$1.03_{-0.03}^{+0.07}$| | |$63.1_{-2.8}^{+2.8}$| | |$0.160_{-0.02}^{+0.02}$| | |$1.46_{-0.01}^{+0.01}$| | |$235_{-48}^{+23}$| |
| Cyg X-1 | P20173 | 31.7 | |$0.94_{-0.04}^{+0.18}$| | |$60.8_{-3.3}^{+3.3}$| | |$0.16_{-0.02}^{+0.02}$| | |$1.45_{-0.01}^{+0.01}$| | |$295_{-136}^{+46}$| |
| Cyg X-1 | P20173 | 28.5 | |$0.820_{-0.10}^{+0.10}$| | |$70.9_{-12}^{+16}$| | |$0.170_{-0.04}^{+0.04}$| | |$1.43_{-0.02}^{+0.02}$| | |$472_{-188}^{+310}$| |
| Cyg X-1 | P20173 | 29.2 | |$0.79_{-0.01}^{+0.10}$| | |$75.1_{-9.5}^{+9.2}$| | |$0.18_{-0.03}^{+0.02}$| | |$1.42_{-0.01}^{+0.01}$| | |$539_{-199}^{+5}$| |
| Cyg X-1 | P20173 | 28.4 | |$0.880_{-0.01}^{+0.10}$| | |$67.3_{-5.0}^{+5.0}$| | |$0.16_{-0.02}^{+0.02}$| | |$1.42_{-0.01}^{+0.01}$| | |$362_{-123}^{+18}$| |
| Cyg X-1 | P80110 | 48.2 | |$1.01_{-0.10}^{+0.11}$| | |$87.0_{-6.1}^{+6.1}$| | |$0.240_{-0.02}^{+0.02}$| | |$1.37_{-0.01}^{+0.01}$| | |$394_{-125}^{+182}$| |
| Cyg X-1 | P80110 | 31.5 | |$1.08_{-0.11}^{+0.13}$| | |$75.1_{-5.9}^{+5.9}$| | |$0.20_{-0.03}^{+0.03}$| | |$1.39_{-0.02}^{+0.02}$| | |$191_{-64}^{+92}$| |
| Cyg X-1 | P80110 | 32.9 | |$1.27_{-0.09}^{+0.09}$| | |$69.3_{-5.9}^{+5.5}$| | |$0.24_{-0.03}^{+0.03}$| | |$1.39_{-0.02}^{+0.02}$| | |$110_{-24}^{+31}$| |
| Cyg X-1 | P94108 | 31.1 | |$0.94_{-0.13}^{+0.14}$| | |$102_{-22}^{+22}$| | |$0.18_{-0.05}^{+0.05}$| | |$1.32_{-0.03}^{+0.03}$| | |$362_{-160}^{+286}$| |
| GX 339−4 | P92035 | 19.2 | |$0.99_{-0.03}^{+0.13}$| | |$33.9_{-2.7}^{+3.5}$| | |$0.45_{-0.07}^{+0.07}$| | |$1.04_{-0.03}^{+0.02}$| | |$242_{-88}^{+31}$| |
| GX 339−4 | P92035 | 21.4 | |$1.09_{-0.08}^{+0.12}$| | |$35.4_{-3.4}^{+4.2}$| | |$0.60_{-0.09}^{+0.09}$| | |$0.98_{-0.03}^{+0.03}$| | |$196_{-61}^{+58}$| |
| GX 339−4 | P92035 | 23.4 | |$1.13_{-0.10}^{+0.10}$| | |$33.0_{-3.0}^{+3.0}$| | |$0.56_{-0.09}^{+0.09}$| | |$0.90_{-0.03}^{+0.03}$| | |$219_{-59}^{+80}$| |
| GX 339−4 | P92052 | 8.95 | |$1.12_{-0.02}^{+0.21}$| | |$53.9_{-7.0}^{+10}$| | |$0.420_{-0.07}^{+0.07}$| | |$1.35_{-0.04}^{+0.03}$| | |$44.7_{-20.0}^{+1.8}$| |
| GX 339−4 | P90118 | 6.47 | |$1.33_{-0.07}^{+0.19}$| | |$65.6_{-13}^{+14}$| | |$0.45_{-0.09}^{+0.09}$| | |$1.34_{-0.04}^{+0.04}$| | |$17.8_{-6.6}^{+3.7}$| |
| XTE J1118+480 | P50133 | 3.14 | |$1.01_{-0.15}^{+0.15}$| | |$67.4_{-18}^{+13}$| | |$0.00_{-0.00}^{+0.10}$| | |$1.24_{-0.06}^{+0.04}$| | |$34_{-14}^{+26}$| |
| XTE J1118+480 | P50133 | 3.66 | |$1.02_{-0.10}^{+0.10}$| | |$71.5_{-11}^{+11}$| | |$0.01_{-0.01}^{+0.04}$| | |$1.27_{-0.03}^{+0.03}$| | |$34.8_{-10}^{+15}$| |
| XTE J1118+480 | P50133 | 3.33 | |$0.840_{-0.08}^{+0.16}$| | |$46_{-10}^{+10}$| | |$0.02_{-0.02}^{+0.06}$| | |$1.21_{-0.03}^{+0.03}$| | |$70_{-33}^{+32}$| |
| XTE J1118+480 | P50133 | 3.43 | |$0.910_{-0.15}^{+0.15}$| | |$53.1_{-9.1}^{+9.1}$| | |$0.00_{-0.00}^{+0.04}$| | |$1.22_{-0.03}^{+0.03}$| | |$53_{-23}^{+52}$| |
| XTE J1118+480 | P50133 | 3.33 | |$0.96_{-0.22}^{+0.16}$| | |$50.2_{-9.7}^{+9.7}$| | |$0.01_{-0.01}^{+0.06}$| | |$1.20_{-0.03}^{+0.03}$| | |$41_{-17}^{+70}$| |
| XTE J1118+480 | P50133 | 3.51 | |$1.02_{-0.09}^{+0.09}$| | |$56.3_{-9.9}^{+9.9}$| | |$0.01_{-0.01}^{+0.06}$| | |$1.22_{-0.03}^{+0.03}$| | |$34.7_{-9.8}^{+14.0}$| |
| XTE J1118+480 | P50133 | 3.48 | |$1.02_{-0.11}^{+0.11}$| | |$57.0_{-9.0}^{+9.0}$| | |$0.01_{-0.01}^{+0.05}$| | |$1.23_{-0.03}^{+0.03}$| | |$35_{-12}^{+18}$| |
| GRO J1654−40 | P91702 | 8.55 | |$0.90_{-0.05}^{+0.54}$| | |$83.8_{-19}^{+19}$| | |$0.17_{-0.09}^{+0.09}$| | |$1.48_{-0.08}^{+0.08}$| | |$97_{-78}^{+21}$| |
| GRO J1654−40 | P91702 | 11.3 | |$0.93_{-0.10}^{+0.24}$| | |$122_{-18}^{+18}$| | |$0.19_{-0.08}^{+0.08}$| | |$1.29_{-0.04}^{+0.04}$| | |$146_{-84}^{+84}$| |
| GRO J1654−40 | P91702 | 13.0 | |$0.94_{-0.09}^{+0.12}$| | |$103_{-10}^{+10}$| | |$0.38_{-0.06}^{+0.06}$| | |$1.11_{-0.02}^{+0.02}$| | |$188_{-69}^{+97}$| |
| GRO J1654−40 | P91702 | 13.7 | |$0.87_{-0.12}^{+0.15}$| | |$103_{-15}^{+15}$| | |$0.38_{-0.09}^{+0.09}$| | |$1.05_{-0.03}^{+0.03}$| | |$298_{-138}^{+236}$| |
| 4U 1608−52 | P60052 | 2.63 | |$0.93_{-0.09}^{+0.09}$| | |$61.6_{-12}^{+12}$| | |$0.51_{-0.16}^{+0.16}$| | |$0.77_{-0.03}^{+0.03}$| | |$68_{-20}^{+29}$| |
| 4U 1608−52 | P60052 | 2.27 | |$0.84_{-0.07}^{+0.07}$| | |$77.2_{-9.4}^{+9.4}$| | |$0.37_{-0.17}^{+0.17}$| | |$0.78_{-0.03}^{+0.03}$| | |$91_{-27}^{+38}$| |
| 4U 1608−52 | P60052 | 2.31 | |$0.93_{-0.06}^{+0.06}$| | |$82.4_{-12}^{+12}$| | |$0.47_{-0.15}^{+0.15}$| | |$0.77_{-0.03}^{+0.03}$| | |$61_{-14}^{+18}$| |
| 4U 1608−52 | P60052 | 2.36 | |$0.87_{-0.07}^{+0.07}$| | |$80.2_{-15}^{+15}$| | |$0.47_{-0.18}^{+0.18}$| | |$0.76_{-0.03}^{+0.03}$| | |$87_{-23}^{+32}$| |
| 4U 1608−52 | P60052 | 2.78 | |$0.87_{-0.12}^{+0.13}$| | |$57.6_{-14}^{+16}$| | |$0.45_{-0.15}^{+0.15}$| | |$0.81_{-0.03}^{+0.03}$| | |$85_{-34}^{+57}$| |
| 4U 1636−536 | P92023 | 2.49 | |$0.97_{-0.01}^{+0.53}$| | |$22.8_{-3.4}^{+26}$| | |$0.18_{-0.14}^{+0.57}$| | |$0.96_{-0.19}^{+0.03}$| | |$44.0_{-34.0}^{+1.0}$| |
| 4U 1636−536 | P92023 | 2.83 | |$1.40_{-0.20}^{+0.20}$| | |$23.4_{-9.1}^{+11}$| | |$0.45_{-0.37}^{+0.37}$| | |$0.81_{-0.09}^{+0.09}$| | |$13.7_{-5.1}^{+8.2}$| |
| 4U 1636−536 | P92023 | 3.13 | |$1.50_{-0.19}^{+0.19}$| | |$25_{-10}^{+10}$| | |$0.80_{-0.39}^{+0.39}$| | |$0.76_{-0.09}^{+0.09}$| | |$11.6_{-4.1}^{+6.3}$| |
| 4U 1636−536 | P92023 | 3.65 | |$1.59_{-0.25}^{+0.25}$| | |$32_{-14}^{+14}$| | |$0.57_{-0.31}^{+0.31}$| | |$0.80_{-0.09}^{+0.09}$| | |$10.7_{-4.5}^{+7.6}$| |
| 4U 1636-536 | P92023 | 3.56 | |$1.32_{-0.11}^{+0.51}$| | |$15.1_{-2.4}^{+14.0}$| | |$0.18_{-0.18}^{+0.61}$| | |$0.94_{-0.24}^{+0.06}$| | |$21.1_{-14.0}^{+8.1}$| |
| 4U 1636-536 | P94310 | 2.17 | |$1.23_{-0.25}^{+0.25}$| | |$18.1_{-6.7}^{+9.2}$| | |$0.38_{-0.37}^{+0.41}$| | |$0.75_{-0.11}^{+0.11}$| | |$20.5_{-10}^{+20}$| |
| 4U 1705-44 | P20073 | 2.73 | |$1.98_{-0.10}^{+0.02}$| | |$26.6_{-5.5}^{+5.5}$| | |$0.75_{-0.35}^{+0.35}$| | |$0.62_{-0.07}^{+0.08}$| | |$4.23_{-0.27}^{+0.76}$| |
| 4U 1705-44 | P20073 | 2.52 | |$1.97_{-0.14}^{+0.03}$| | |$20.9_{-5.9}^{+5.7}$| | |$1.01_{-0.50}^{+0.49}$| | |$0.56_{-0.10}^{+0.10}$| | |$4.40_{-0.33}^{+1.2}$| |
| 4U 1728-33 | P92023 | 6.69 | |$2.00_{-0.07}^{+0.00}$| | |$18.9_{-2.9}^{+2.9}$| | |$0.52_{-0.25}^{+0.25}$| | |$0.72_{-0.07}^{+0.07}$| | |$9.03_{-0.53}^{+0.98}$| |
| 4U 1728-33 | P92023 | 6.97 | |$1.99_{-0.05}^{+0.01}$| | |$12.8_{-1.2}^{+1.2}$| | |$0.29_{-0.25}^{+0.25}$| | |$0.81_{-0.08}^{+0.08}$| | |$9.48_{-0.39}^{+0.81}$| |
| Aql X-1 | P50049 | 5.85 | |$1.56_{-0.14}^{+0.16}$| | |$26.2_{-6.8}^{+7.7}$| | |$0.57_{-0.26}^{+0.27}$| | |$0.80_{-0.07}^{+0.07}$| | |$18.4_{-5.1}^{+7.0}$| |
| Aql X-1 | P91414 | 2.37 | |$1.09_{-0.15}^{+0.24}$| | |$30.4_{-11}^{+15}$| | |$0.69_{-0.34}^{+0.38}$| | |$0.82_{-0.08}^{+0.08}$| | |$28_{-14}^{+20}$| |
| Aql X-1 | P91414 | 3.68 | |$1.46_{-0.16}^{+0.16}$| | |$25.4_{-6.8}^{+6.8}$| | |$1.11_{-0.36}^{+0.36}$| | |$0.66_{-0.07}^{+0.07}$| | |$17.6_{-5.6}^{+8.3}$| |
| Aql X-1 | P91414 | 3.51 | |$1.40_{-0.21}^{+0.21}$| | |$46.5_{-14.0}^{+14.0}$| | |$0.77_{-0.27}^{+0.27}$| | |$0.76_{-0.06}^{+0.06}$| | |$17.7_{-7.2}^{+12.0}$| |
Results from spectral analysis of BH (top) and NS (bottom) XBs for the Gaussian component; best-fitting location together with 1D 90 per cent confidence. The Epeak, σ and EW are in keV, and the normalization (line flux) in |$10^{-3}\ {\rm phot{\rm ons}\ cm^{-2}\ s^{-1}}$|.
| Source . | ObsID . | Epeak . | σ . | EW . | Norm. . |
|---|---|---|---|---|---|
| GS 1354−64 | P20431 | |$6.3_{-0.2}^{+0.2}$| | |$0.36_{-0.29}^{+0.29}$| | |$0.06_{-0.04}^{+0.08}$| | |$0.70_{-0.19}^{+0.25}$| |
| GS 1354−64 | P20431 | |$6.4_{-0.5}^{+0.5}$| | |$0.40_{-0.39}^{+0.77}$| | |$0.06_{-0.04}^{+0.07}$| | |$0.60_{-0.10}^{+0.31}$| |
| GS 1354−64 | P20431 | |$6.2_{-0.3}^{+0.3}$| | |$0.51_{-0.50}^{+0.50}$| | |$0.06_{-0.04}^{+0.08}$| | |$0.60_{-0.10}^{+0.25}$| |
| GS 1354−64 | P20431 | |$6.1_{-0.2}^{+0.2}$| | |$0.64_{-0.42}^{+0.42}$| | |$0.06_{-0.04}^{+0.08}$| | |$0.80_{-0.28}^{+0.42}$| |
| 4U 1543−47 | P70124 | |$6.2_{-0.3}^{+0.3}$| | |$0.62_{-0.40}^{+0.40}$| | |$0.30_{-0.15}^{+0.46}$| | |$1.40_{-0.64}^{+1.10}$| |
| XTE J1550−564 | P30188 | |$6.6_{-0.2}^{+0.2}$| | |$0.81_{-0.22}^{+0.22}$| | |$0.10_{-0.08}^{+0.13}$| | |$6.4_{-1.3}^{+1.6}$| |
| XTE J1550−564 | P30188 | |$6.6_{-0.2}^{+0.2}$| | |$0.85_{-0.20}^{+0.20}$| | |$0.10_{-0.08}^{+0.12}$| | |$7.5_{-1.3}^{+1.6}$| |
| XTE J1550−564 | P30188 | |$6.7_{-0.1}^{+0.1}$| | |$1.1_{-0.07}^{+0.17}$| | |$0.13_{-0.11}^{+0.15}$| | |$13._{-1.4}^{+1.7}$| |
| XTE J1550−564 | P50134 | |$6.2_{-0.4}^{+0.4}$| | |$1.5_{-0.31}^{+0.31}$| | |$0.37_{-0.29}^{+0.45}$| | |$26._{-7.3}^{+10.}$| |
| XTE J1550−564 | P50135 | |$5.5_{-0.01}^{+0.7}$| | |$2.0_{-0.33}^{+0.02}$| | |$0.52_{-0.43}^{+0.61}$| | |$22_{-9.1}^{+2.5}$| |
| XTE J1550−564 | P50135 | |$5.5_{-0.01}^{+0.8}$| | |$1.9_{-0.6}^{+0.2}$| | |$0.36_{-0.22}^{+0.51}$| | |$11_{-6.4}^{+1.8}$| |
| XTE J1550−564 | P50135 | |$5.7_{-0.2}^{+0.8}$| | |$1.9_{-0.7}^{+0.09}$| | |$0.30_{-0.15}^{+0.46}$| | |$7.7_{-4.9}^{+3.9}$| |
| XTE J1550−564 | P50137 | |$6.5_{-0.2}^{+0.2}$| | |$1.1_{-0.3}^{+0.3}$| | |$0.15_{-0.12}^{+0.19}$| | |$11_{-2.9}^{+3.9}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.1}$| | |$0.60_{-0.20}^{+0.20}$| | |$0.10_{-0.08}^{+0.12}$| | |$7.3_{-1.6}^{+1.9}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.2}$| | |$0.61_{-0.23}^{+0.19}$| | |$0.09_{-0.07}^{+0.11}$| | |$8.1_{-2.0}^{+1.6}$| |
| Cyg X-1 | P20173 | |$6.4_{-0.1}^{+0.1}$| | |$0.51_{-0.18}^{+0.18}$| | |$0.06_{-0.05}^{+0.07}$| | |$7.2_{-1.6}^{+1.3}$| |
| Cyg X-1 | P20173 | |$6.4_{-0.1}^{+0.1}$| | |$0.56_{-0.23}^{+0.23}$| | |$0.09_{-0.07}^{+0.11}$| | |$7.6_{-2.4}^{+1.6}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.1}$| | |$0.56_{-0.17}^{+0.18}$| | |$0.05_{-0.05}^{+0.06}$| | |$8.4_{-1.4}^{+1.7}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.1}$| | |$0.57_{-0.16}^{+0.15}$| | |$0.09_{-0.08}^{+0.10}$| | |$8.1_{-1.4}^{+1.4}$| |
| Cyg X-1 | P20173 | |$6.4_{-0.1}^{+0.1}$| | |$0.53_{-0.15}^{+0.15}$| | |$0.09_{-0.07}^{+0.10}$| | |$7.0_{-1.4}^{+1.4}$| |
| Cyg X-1 | P80110 | |$6.3_{-0.2}^{+0.2}$| | |$0.70_{-0.22}^{+0.23}$| | |$0.13_{-0.09}^{+0.16}$| | |$15._{-4.6}^{+6.5}$| |
| Cyg X-1 | P80110 | |$6.3_{-0.2}^{+0.2}$| | |$0.57_{-0.28}^{+0.28}$| | |$0.08_{-0.05}^{+0.11}$| | |$7.0_{-2.5}^{+3.8}$| |
| Cyg X-1 | P80110 | |$6.3_{-0.1}^{+0.1}$| | |$0.32_{-0.26}^{+0.26}$| | |$0.07_{-0.05}^{+0.09}$| | |$5.3_{-1.5}^{+2.1}$| |
| Cyg X-1 | P94108 | |$6.3_{-0.3}^{+0.3}$| | |$0.76_{-0.33}^{+0.33}$| | |$0.19_{-0.12}^{+0.26}$| | |$13._{-5.3}^{+8.8}$| |
| GX 339−4 | P92035 | |$6.5_{-0.1}^{+0.1}$| | |$0.87_{-0.15}^{+0.15}$| | |$0.17_{-0.15}^{+0.20}$| | |$14._{-2.4}^{+2.7}$| |
| GX 339−4 | P92035 | |$6.5_{-0.2}^{+0.2}$| | |$1.1_{-0.2}^{+0.2}$| | |$0.21_{-0.18}^{+0.25}$| | |$18._{-3.9}^{+4.9}$| |
| GX 339−4 | P92035 | |$6.6_{-0.1}^{+0.1}$| | |$0.96_{-0.16}^{+0.16}$| | |$0.21_{-0.18}^{+0.24}$| | |$21._{-3.9}^{+4.7}$| |
| GX 339−4 | P92052 | |$6.4_{-0.2}^{+0.2}$| | |$0.68_{-0.38}^{+0.37}$| | |$0.09_{-0.07}^{+0.12}$| | |$2.7_{-1.3}^{+0.88}$| |
| GX 339−4 | P90118 | |$6.5_{-0.3}^{+0.3}$| | |$0.050_{-0.040}^{+0.73}$| | |$0.19_{-0.16}^{+0.22}$| | |$0.97_{-0.41}^{+0.73}$| |
| XTE J1118+480 | P50133 | |$6.4_{-0.4}^{+0.4}$| | |$0.75_{-0.51}^{+0.50}$| | |$0.08_{-0.05}^{+0.11}$| | |$0.98_{-0.46}^{+0.86}$| |
| XTE J1118+480 | P50133 | |$6.3_{-0.3}^{+0.3}$| | |$0.75_{-0.41}^{+0.41}$| | |$0.11_{-0.06}^{+0.16}$| | |$1.1_{-0.42}^{+0.71}$| |
| XTE J1118+480 | P50133 | |$6.3_{-0.3}^{+0.3}$| | |$0.65_{-0.49}^{+0.49}$| | |$0.07_{-0.04}^{+0.10}$| | |$0.74_{-0.31}^{+0.54}$| |
| XTE J1118+480 | P50133 | |$6.2_{-0.3}^{+0.3}$| | |$0.30_{-0.29}^{+0.55}$| | |$0.05_{-0.03}^{+0.07}$| | |$0.56_{-0.24}^{+0.41}$| |
| XTE J1118+480 | P50133 | |$6.4_{-0.6}^{+0.6}$| | |$0.24_{-0.23}^{+1.10}$| | |$0.07_{-0.03}^{+0.11}$| | |$0.39_{-0.090}^{+0.84}$| |
| XTE J1118+480 | P50133 | |$6.5_{-0.4}^{+0.4}$| | |$0.55_{-0.53}^{+0.63}$| | |$0.08_{-0.04}^{+0.12}$| | |$0.53_{-0.23}^{+0.46}$| |
| XTE J1118+480 | P50133 | |$6.3_{-0.4}^{+0.4}$| | |$0.61_{-0.59}^{+0.59}$| | |$0.07_{-0.03}^{+0.10}$| | |$0.61_{-0.29}^{+0.55}$| |
| GRO J1654−40 | P91702 | |$5.6_{-0.1}^{+0.9}$| | |$1.5_{-0.7}^{+0.5}$| | |$0.21_{-0.06}^{+0.36}$| | |$7.9_{-6.2}^{+3.7}$| |
| GRO J1654−40 | P91702 | |$5.7_{-0.2}^{+0.9}$| | |$1.7_{-0.}^{+0.3}$| | |$0.35_{-0.18}^{+0.52}$| | |$15_{-8.9}^{+6.9}$| |
| GRO J1654−40 | P91702 | |$5.7_{-0.2}^{+0.5}$| | |$2.0_{-0.2}^{+0.0}$| | |$0.54_{-0.45}^{+0.64}$| | |$26_{-7.1}^{+4.9}$| |
| GRO J1654−40 | P91702 | |$5.6_{-0.1}^{+0.6}$| | |$1.9_{-0.3}^{+0.1}$| | |$0.49_{-0.36}^{+0.61}$| | |$27_{-10}^{+7.7}$| |
| 4U 1608−52 | P60052 | |$6.5_{-0.7}^{+0.5}$| | |$1.8_{-0.5}^{+0.3}$| | |$0.12_{-0.05}^{+0.18}$| | |$1.3_{-0.70}^{+1.5}$| |
| 4U 1608−52 | P60052 | |$5.5_{-0.01}^{+1.10}$| | |$0.0_{-0.0}^{+1.9}$| | |$0.05_{-0.03}^{+0.07}$| | |$0.34_{-0.04}^{+0.22}$| |
| 4U 1608−52 | P60052 | |$7.0_{-1.3}^{+0.09}$| | |$1.6_{-0.4}^{+0.4}$| | |$0.07_{-0.03}^{+0.11}$| | |$0.42_{-0.12}^{+0.46}$| |
| 4U 1608−52 | P60052 | |$6.4_{-0.4}^{+0.4}$| | |$0.85_{-0.42}^{+0.42}$| | |$0.12_{-0.06}^{+0.17}$| | |$1.1_{-0.5}^{+0.9}$| |
| 4U 1608−52 | P60052 | |$5.6_{-0.1}^{+1.2}$| | |$0.07_{-0.07}^{+1.8}$| | |$0.06_{-0.02}^{+0.10}$| | |$0.34_{-0.04}^{+0.72}$| |
| 4U 1636−536 | P92023 | |$5.8_{-0.3}^{+1.1}$| | |$1.6_{-0.58}^{+0.38}$| | |$0.23_{-0.08}^{+0.39}$| | |$4.5_{-3.5}^{+2.4}$| |
| 4U 1636−536 | P92023 | |$6.8_{-0.5}^{+0.3}$| | |$0.29_{-0.29}^{+1.3}$| | |$0.09_{-0.01}^{+0.16}$| | |$0.74_{-0.52}^{+1.8}$| |
| 4U 1636−536 | P92023 | |$6.8_{-0.3}^{+0.3}$| | |$0.16_{-0.16}^{+0.80}$| | |$0.08_{-0.03}^{+0.13}$| | |$0.83_{-0.46}^{+1.00}$| |
| 4U 1636−536 | P92023 | |$6.8_{-0.4}^{+0.3}$| | |$0.57_{-0.57}^{+1.1}$| | |$0.15_{-0.03}^{+0.27}$| | |$1.3_{-0.86}^{+2.7}$| |
| 4U 1636−536 | P92023 | |$6.5_{-0.7}^{+0.6}$| | |$1.5_{-1.1}^{+0.5}$| | |$0.08_{-0.01}^{+0.15}$| | |$3.5_{-3.4}^{+2.8}$| |
| 4U 1636−536 | P94310 | |$6.7_{-0.5}^{+0.4}$| | |$1.1_{-0.6}^{+0.6}$| | |$0.13_{-0.06}^{+0.21}$| | |$2.2_{-1.4}^{+3.6}$| |
| 4U 1705-44 | P20073 | |$6.1_{-0.20}^{+0.20}$| | |$1.0_{-0.2}^{+0.2}$| | |$0.23_{-0.18}^{+0.29}$| | |$3.2_{-0.9}^{+1.2}$| |
| 4U 1705-44 | P20073 | |$6.1_{-0.25}^{+0.25}$| | |$1.1_{-0.3}^{+0.3}$| | |$0.23_{-0.17}^{+0.28}$| | |$3.4_{-0.9}^{+1.3}$| |
| 4U 1728-33 | P92023 | |$5.9_{-0.4}^{+0.4}$| | |$1.2_{-0.3}^{+0.3}$| | |$0.31_{-0.22}^{+0.40}$| | |$10._{-3.4}^{+5.1}$| |
| 4U 1728-33 | P92023 | |$5.5_{-0.3}^{+0.3}$| | |$1.4_{-0.2}^{+0.2}$| | |$0.40_{-0.29}^{+0.52}$| | |$19._{-5.5}^{+7.7}$| |
| Aql X-1 | P50049 | |$6.7_{-0.2}^{+0.2}$| | |$0.66_{-0.25}^{+0.25}$| | |$0.09_{-0.05}^{+0.12}$| | |$2.5_{-1.0}^{+1.5}$| |
| Aql X-1 | P91414 | |$6.1_{-0.6}^{+0.7}$| | |$1.2_{-0.7}^{+0.7}$| | |$0.08_{-0.03}^{+0.12}$| | |$1.3_{-0.9}^{+1.8}$| |
| Aql X-1 | P91414 | |$7.0_{-0.5}^{+0.1}$| | |$0.79_{-0.52}^{+0.53}$| | |$0.10_{-0.05}^{+0.15}$| | |$1.4_{-0.8}^{+1.6}$| |
| Aql X-1 | P91414 | |$6.8_{-0.9}^{+0.3}$| | |$1.4_{-0.6}^{+0.6}$| | |$0.15_{-0.04}^{+0.25}$| | |$2.0_{-1.3}^{+4.0}$| |
| Source . | ObsID . | Epeak . | σ . | EW . | Norm. . |
|---|---|---|---|---|---|
| GS 1354−64 | P20431 | |$6.3_{-0.2}^{+0.2}$| | |$0.36_{-0.29}^{+0.29}$| | |$0.06_{-0.04}^{+0.08}$| | |$0.70_{-0.19}^{+0.25}$| |
| GS 1354−64 | P20431 | |$6.4_{-0.5}^{+0.5}$| | |$0.40_{-0.39}^{+0.77}$| | |$0.06_{-0.04}^{+0.07}$| | |$0.60_{-0.10}^{+0.31}$| |
| GS 1354−64 | P20431 | |$6.2_{-0.3}^{+0.3}$| | |$0.51_{-0.50}^{+0.50}$| | |$0.06_{-0.04}^{+0.08}$| | |$0.60_{-0.10}^{+0.25}$| |
| GS 1354−64 | P20431 | |$6.1_{-0.2}^{+0.2}$| | |$0.64_{-0.42}^{+0.42}$| | |$0.06_{-0.04}^{+0.08}$| | |$0.80_{-0.28}^{+0.42}$| |
| 4U 1543−47 | P70124 | |$6.2_{-0.3}^{+0.3}$| | |$0.62_{-0.40}^{+0.40}$| | |$0.30_{-0.15}^{+0.46}$| | |$1.40_{-0.64}^{+1.10}$| |
| XTE J1550−564 | P30188 | |$6.6_{-0.2}^{+0.2}$| | |$0.81_{-0.22}^{+0.22}$| | |$0.10_{-0.08}^{+0.13}$| | |$6.4_{-1.3}^{+1.6}$| |
| XTE J1550−564 | P30188 | |$6.6_{-0.2}^{+0.2}$| | |$0.85_{-0.20}^{+0.20}$| | |$0.10_{-0.08}^{+0.12}$| | |$7.5_{-1.3}^{+1.6}$| |
| XTE J1550−564 | P30188 | |$6.7_{-0.1}^{+0.1}$| | |$1.1_{-0.07}^{+0.17}$| | |$0.13_{-0.11}^{+0.15}$| | |$13._{-1.4}^{+1.7}$| |
| XTE J1550−564 | P50134 | |$6.2_{-0.4}^{+0.4}$| | |$1.5_{-0.31}^{+0.31}$| | |$0.37_{-0.29}^{+0.45}$| | |$26._{-7.3}^{+10.}$| |
| XTE J1550−564 | P50135 | |$5.5_{-0.01}^{+0.7}$| | |$2.0_{-0.33}^{+0.02}$| | |$0.52_{-0.43}^{+0.61}$| | |$22_{-9.1}^{+2.5}$| |
| XTE J1550−564 | P50135 | |$5.5_{-0.01}^{+0.8}$| | |$1.9_{-0.6}^{+0.2}$| | |$0.36_{-0.22}^{+0.51}$| | |$11_{-6.4}^{+1.8}$| |
| XTE J1550−564 | P50135 | |$5.7_{-0.2}^{+0.8}$| | |$1.9_{-0.7}^{+0.09}$| | |$0.30_{-0.15}^{+0.46}$| | |$7.7_{-4.9}^{+3.9}$| |
| XTE J1550−564 | P50137 | |$6.5_{-0.2}^{+0.2}$| | |$1.1_{-0.3}^{+0.3}$| | |$0.15_{-0.12}^{+0.19}$| | |$11_{-2.9}^{+3.9}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.1}$| | |$0.60_{-0.20}^{+0.20}$| | |$0.10_{-0.08}^{+0.12}$| | |$7.3_{-1.6}^{+1.9}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.2}$| | |$0.61_{-0.23}^{+0.19}$| | |$0.09_{-0.07}^{+0.11}$| | |$8.1_{-2.0}^{+1.6}$| |
| Cyg X-1 | P20173 | |$6.4_{-0.1}^{+0.1}$| | |$0.51_{-0.18}^{+0.18}$| | |$0.06_{-0.05}^{+0.07}$| | |$7.2_{-1.6}^{+1.3}$| |
| Cyg X-1 | P20173 | |$6.4_{-0.1}^{+0.1}$| | |$0.56_{-0.23}^{+0.23}$| | |$0.09_{-0.07}^{+0.11}$| | |$7.6_{-2.4}^{+1.6}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.1}$| | |$0.56_{-0.17}^{+0.18}$| | |$0.05_{-0.05}^{+0.06}$| | |$8.4_{-1.4}^{+1.7}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.1}$| | |$0.57_{-0.16}^{+0.15}$| | |$0.09_{-0.08}^{+0.10}$| | |$8.1_{-1.4}^{+1.4}$| |
| Cyg X-1 | P20173 | |$6.4_{-0.1}^{+0.1}$| | |$0.53_{-0.15}^{+0.15}$| | |$0.09_{-0.07}^{+0.10}$| | |$7.0_{-1.4}^{+1.4}$| |
| Cyg X-1 | P80110 | |$6.3_{-0.2}^{+0.2}$| | |$0.70_{-0.22}^{+0.23}$| | |$0.13_{-0.09}^{+0.16}$| | |$15._{-4.6}^{+6.5}$| |
| Cyg X-1 | P80110 | |$6.3_{-0.2}^{+0.2}$| | |$0.57_{-0.28}^{+0.28}$| | |$0.08_{-0.05}^{+0.11}$| | |$7.0_{-2.5}^{+3.8}$| |
| Cyg X-1 | P80110 | |$6.3_{-0.1}^{+0.1}$| | |$0.32_{-0.26}^{+0.26}$| | |$0.07_{-0.05}^{+0.09}$| | |$5.3_{-1.5}^{+2.1}$| |
| Cyg X-1 | P94108 | |$6.3_{-0.3}^{+0.3}$| | |$0.76_{-0.33}^{+0.33}$| | |$0.19_{-0.12}^{+0.26}$| | |$13._{-5.3}^{+8.8}$| |
| GX 339−4 | P92035 | |$6.5_{-0.1}^{+0.1}$| | |$0.87_{-0.15}^{+0.15}$| | |$0.17_{-0.15}^{+0.20}$| | |$14._{-2.4}^{+2.7}$| |
| GX 339−4 | P92035 | |$6.5_{-0.2}^{+0.2}$| | |$1.1_{-0.2}^{+0.2}$| | |$0.21_{-0.18}^{+0.25}$| | |$18._{-3.9}^{+4.9}$| |
| GX 339−4 | P92035 | |$6.6_{-0.1}^{+0.1}$| | |$0.96_{-0.16}^{+0.16}$| | |$0.21_{-0.18}^{+0.24}$| | |$21._{-3.9}^{+4.7}$| |
| GX 339−4 | P92052 | |$6.4_{-0.2}^{+0.2}$| | |$0.68_{-0.38}^{+0.37}$| | |$0.09_{-0.07}^{+0.12}$| | |$2.7_{-1.3}^{+0.88}$| |
| GX 339−4 | P90118 | |$6.5_{-0.3}^{+0.3}$| | |$0.050_{-0.040}^{+0.73}$| | |$0.19_{-0.16}^{+0.22}$| | |$0.97_{-0.41}^{+0.73}$| |
| XTE J1118+480 | P50133 | |$6.4_{-0.4}^{+0.4}$| | |$0.75_{-0.51}^{+0.50}$| | |$0.08_{-0.05}^{+0.11}$| | |$0.98_{-0.46}^{+0.86}$| |
| XTE J1118+480 | P50133 | |$6.3_{-0.3}^{+0.3}$| | |$0.75_{-0.41}^{+0.41}$| | |$0.11_{-0.06}^{+0.16}$| | |$1.1_{-0.42}^{+0.71}$| |
| XTE J1118+480 | P50133 | |$6.3_{-0.3}^{+0.3}$| | |$0.65_{-0.49}^{+0.49}$| | |$0.07_{-0.04}^{+0.10}$| | |$0.74_{-0.31}^{+0.54}$| |
| XTE J1118+480 | P50133 | |$6.2_{-0.3}^{+0.3}$| | |$0.30_{-0.29}^{+0.55}$| | |$0.05_{-0.03}^{+0.07}$| | |$0.56_{-0.24}^{+0.41}$| |
| XTE J1118+480 | P50133 | |$6.4_{-0.6}^{+0.6}$| | |$0.24_{-0.23}^{+1.10}$| | |$0.07_{-0.03}^{+0.11}$| | |$0.39_{-0.090}^{+0.84}$| |
| XTE J1118+480 | P50133 | |$6.5_{-0.4}^{+0.4}$| | |$0.55_{-0.53}^{+0.63}$| | |$0.08_{-0.04}^{+0.12}$| | |$0.53_{-0.23}^{+0.46}$| |
| XTE J1118+480 | P50133 | |$6.3_{-0.4}^{+0.4}$| | |$0.61_{-0.59}^{+0.59}$| | |$0.07_{-0.03}^{+0.10}$| | |$0.61_{-0.29}^{+0.55}$| |
| GRO J1654−40 | P91702 | |$5.6_{-0.1}^{+0.9}$| | |$1.5_{-0.7}^{+0.5}$| | |$0.21_{-0.06}^{+0.36}$| | |$7.9_{-6.2}^{+3.7}$| |
| GRO J1654−40 | P91702 | |$5.7_{-0.2}^{+0.9}$| | |$1.7_{-0.}^{+0.3}$| | |$0.35_{-0.18}^{+0.52}$| | |$15_{-8.9}^{+6.9}$| |
| GRO J1654−40 | P91702 | |$5.7_{-0.2}^{+0.5}$| | |$2.0_{-0.2}^{+0.0}$| | |$0.54_{-0.45}^{+0.64}$| | |$26_{-7.1}^{+4.9}$| |
| GRO J1654−40 | P91702 | |$5.6_{-0.1}^{+0.6}$| | |$1.9_{-0.3}^{+0.1}$| | |$0.49_{-0.36}^{+0.61}$| | |$27_{-10}^{+7.7}$| |
| 4U 1608−52 | P60052 | |$6.5_{-0.7}^{+0.5}$| | |$1.8_{-0.5}^{+0.3}$| | |$0.12_{-0.05}^{+0.18}$| | |$1.3_{-0.70}^{+1.5}$| |
| 4U 1608−52 | P60052 | |$5.5_{-0.01}^{+1.10}$| | |$0.0_{-0.0}^{+1.9}$| | |$0.05_{-0.03}^{+0.07}$| | |$0.34_{-0.04}^{+0.22}$| |
| 4U 1608−52 | P60052 | |$7.0_{-1.3}^{+0.09}$| | |$1.6_{-0.4}^{+0.4}$| | |$0.07_{-0.03}^{+0.11}$| | |$0.42_{-0.12}^{+0.46}$| |
| 4U 1608−52 | P60052 | |$6.4_{-0.4}^{+0.4}$| | |$0.85_{-0.42}^{+0.42}$| | |$0.12_{-0.06}^{+0.17}$| | |$1.1_{-0.5}^{+0.9}$| |
| 4U 1608−52 | P60052 | |$5.6_{-0.1}^{+1.2}$| | |$0.07_{-0.07}^{+1.8}$| | |$0.06_{-0.02}^{+0.10}$| | |$0.34_{-0.04}^{+0.72}$| |
| 4U 1636−536 | P92023 | |$5.8_{-0.3}^{+1.1}$| | |$1.6_{-0.58}^{+0.38}$| | |$0.23_{-0.08}^{+0.39}$| | |$4.5_{-3.5}^{+2.4}$| |
| 4U 1636−536 | P92023 | |$6.8_{-0.5}^{+0.3}$| | |$0.29_{-0.29}^{+1.3}$| | |$0.09_{-0.01}^{+0.16}$| | |$0.74_{-0.52}^{+1.8}$| |
| 4U 1636−536 | P92023 | |$6.8_{-0.3}^{+0.3}$| | |$0.16_{-0.16}^{+0.80}$| | |$0.08_{-0.03}^{+0.13}$| | |$0.83_{-0.46}^{+1.00}$| |
| 4U 1636−536 | P92023 | |$6.8_{-0.4}^{+0.3}$| | |$0.57_{-0.57}^{+1.1}$| | |$0.15_{-0.03}^{+0.27}$| | |$1.3_{-0.86}^{+2.7}$| |
| 4U 1636−536 | P92023 | |$6.5_{-0.7}^{+0.6}$| | |$1.5_{-1.1}^{+0.5}$| | |$0.08_{-0.01}^{+0.15}$| | |$3.5_{-3.4}^{+2.8}$| |
| 4U 1636−536 | P94310 | |$6.7_{-0.5}^{+0.4}$| | |$1.1_{-0.6}^{+0.6}$| | |$0.13_{-0.06}^{+0.21}$| | |$2.2_{-1.4}^{+3.6}$| |
| 4U 1705-44 | P20073 | |$6.1_{-0.20}^{+0.20}$| | |$1.0_{-0.2}^{+0.2}$| | |$0.23_{-0.18}^{+0.29}$| | |$3.2_{-0.9}^{+1.2}$| |
| 4U 1705-44 | P20073 | |$6.1_{-0.25}^{+0.25}$| | |$1.1_{-0.3}^{+0.3}$| | |$0.23_{-0.17}^{+0.28}$| | |$3.4_{-0.9}^{+1.3}$| |
| 4U 1728-33 | P92023 | |$5.9_{-0.4}^{+0.4}$| | |$1.2_{-0.3}^{+0.3}$| | |$0.31_{-0.22}^{+0.40}$| | |$10._{-3.4}^{+5.1}$| |
| 4U 1728-33 | P92023 | |$5.5_{-0.3}^{+0.3}$| | |$1.4_{-0.2}^{+0.2}$| | |$0.40_{-0.29}^{+0.52}$| | |$19._{-5.5}^{+7.7}$| |
| Aql X-1 | P50049 | |$6.7_{-0.2}^{+0.2}$| | |$0.66_{-0.25}^{+0.25}$| | |$0.09_{-0.05}^{+0.12}$| | |$2.5_{-1.0}^{+1.5}$| |
| Aql X-1 | P91414 | |$6.1_{-0.6}^{+0.7}$| | |$1.2_{-0.7}^{+0.7}$| | |$0.08_{-0.03}^{+0.12}$| | |$1.3_{-0.9}^{+1.8}$| |
| Aql X-1 | P91414 | |$7.0_{-0.5}^{+0.1}$| | |$0.79_{-0.52}^{+0.53}$| | |$0.10_{-0.05}^{+0.15}$| | |$1.4_{-0.8}^{+1.6}$| |
| Aql X-1 | P91414 | |$6.8_{-0.9}^{+0.3}$| | |$1.4_{-0.6}^{+0.6}$| | |$0.15_{-0.04}^{+0.25}$| | |$2.0_{-1.3}^{+4.0}$| |
Results from spectral analysis of BH (top) and NS (bottom) XBs for the Gaussian component; best-fitting location together with 1D 90 per cent confidence. The Epeak, σ and EW are in keV, and the normalization (line flux) in |$10^{-3}\ {\rm phot{\rm ons}\ cm^{-2}\ s^{-1}}$|.
| Source . | ObsID . | Epeak . | σ . | EW . | Norm. . |
|---|---|---|---|---|---|
| GS 1354−64 | P20431 | |$6.3_{-0.2}^{+0.2}$| | |$0.36_{-0.29}^{+0.29}$| | |$0.06_{-0.04}^{+0.08}$| | |$0.70_{-0.19}^{+0.25}$| |
| GS 1354−64 | P20431 | |$6.4_{-0.5}^{+0.5}$| | |$0.40_{-0.39}^{+0.77}$| | |$0.06_{-0.04}^{+0.07}$| | |$0.60_{-0.10}^{+0.31}$| |
| GS 1354−64 | P20431 | |$6.2_{-0.3}^{+0.3}$| | |$0.51_{-0.50}^{+0.50}$| | |$0.06_{-0.04}^{+0.08}$| | |$0.60_{-0.10}^{+0.25}$| |
| GS 1354−64 | P20431 | |$6.1_{-0.2}^{+0.2}$| | |$0.64_{-0.42}^{+0.42}$| | |$0.06_{-0.04}^{+0.08}$| | |$0.80_{-0.28}^{+0.42}$| |
| 4U 1543−47 | P70124 | |$6.2_{-0.3}^{+0.3}$| | |$0.62_{-0.40}^{+0.40}$| | |$0.30_{-0.15}^{+0.46}$| | |$1.40_{-0.64}^{+1.10}$| |
| XTE J1550−564 | P30188 | |$6.6_{-0.2}^{+0.2}$| | |$0.81_{-0.22}^{+0.22}$| | |$0.10_{-0.08}^{+0.13}$| | |$6.4_{-1.3}^{+1.6}$| |
| XTE J1550−564 | P30188 | |$6.6_{-0.2}^{+0.2}$| | |$0.85_{-0.20}^{+0.20}$| | |$0.10_{-0.08}^{+0.12}$| | |$7.5_{-1.3}^{+1.6}$| |
| XTE J1550−564 | P30188 | |$6.7_{-0.1}^{+0.1}$| | |$1.1_{-0.07}^{+0.17}$| | |$0.13_{-0.11}^{+0.15}$| | |$13._{-1.4}^{+1.7}$| |
| XTE J1550−564 | P50134 | |$6.2_{-0.4}^{+0.4}$| | |$1.5_{-0.31}^{+0.31}$| | |$0.37_{-0.29}^{+0.45}$| | |$26._{-7.3}^{+10.}$| |
| XTE J1550−564 | P50135 | |$5.5_{-0.01}^{+0.7}$| | |$2.0_{-0.33}^{+0.02}$| | |$0.52_{-0.43}^{+0.61}$| | |$22_{-9.1}^{+2.5}$| |
| XTE J1550−564 | P50135 | |$5.5_{-0.01}^{+0.8}$| | |$1.9_{-0.6}^{+0.2}$| | |$0.36_{-0.22}^{+0.51}$| | |$11_{-6.4}^{+1.8}$| |
| XTE J1550−564 | P50135 | |$5.7_{-0.2}^{+0.8}$| | |$1.9_{-0.7}^{+0.09}$| | |$0.30_{-0.15}^{+0.46}$| | |$7.7_{-4.9}^{+3.9}$| |
| XTE J1550−564 | P50137 | |$6.5_{-0.2}^{+0.2}$| | |$1.1_{-0.3}^{+0.3}$| | |$0.15_{-0.12}^{+0.19}$| | |$11_{-2.9}^{+3.9}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.1}$| | |$0.60_{-0.20}^{+0.20}$| | |$0.10_{-0.08}^{+0.12}$| | |$7.3_{-1.6}^{+1.9}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.2}$| | |$0.61_{-0.23}^{+0.19}$| | |$0.09_{-0.07}^{+0.11}$| | |$8.1_{-2.0}^{+1.6}$| |
| Cyg X-1 | P20173 | |$6.4_{-0.1}^{+0.1}$| | |$0.51_{-0.18}^{+0.18}$| | |$0.06_{-0.05}^{+0.07}$| | |$7.2_{-1.6}^{+1.3}$| |
| Cyg X-1 | P20173 | |$6.4_{-0.1}^{+0.1}$| | |$0.56_{-0.23}^{+0.23}$| | |$0.09_{-0.07}^{+0.11}$| | |$7.6_{-2.4}^{+1.6}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.1}$| | |$0.56_{-0.17}^{+0.18}$| | |$0.05_{-0.05}^{+0.06}$| | |$8.4_{-1.4}^{+1.7}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.1}$| | |$0.57_{-0.16}^{+0.15}$| | |$0.09_{-0.08}^{+0.10}$| | |$8.1_{-1.4}^{+1.4}$| |
| Cyg X-1 | P20173 | |$6.4_{-0.1}^{+0.1}$| | |$0.53_{-0.15}^{+0.15}$| | |$0.09_{-0.07}^{+0.10}$| | |$7.0_{-1.4}^{+1.4}$| |
| Cyg X-1 | P80110 | |$6.3_{-0.2}^{+0.2}$| | |$0.70_{-0.22}^{+0.23}$| | |$0.13_{-0.09}^{+0.16}$| | |$15._{-4.6}^{+6.5}$| |
| Cyg X-1 | P80110 | |$6.3_{-0.2}^{+0.2}$| | |$0.57_{-0.28}^{+0.28}$| | |$0.08_{-0.05}^{+0.11}$| | |$7.0_{-2.5}^{+3.8}$| |
| Cyg X-1 | P80110 | |$6.3_{-0.1}^{+0.1}$| | |$0.32_{-0.26}^{+0.26}$| | |$0.07_{-0.05}^{+0.09}$| | |$5.3_{-1.5}^{+2.1}$| |
| Cyg X-1 | P94108 | |$6.3_{-0.3}^{+0.3}$| | |$0.76_{-0.33}^{+0.33}$| | |$0.19_{-0.12}^{+0.26}$| | |$13._{-5.3}^{+8.8}$| |
| GX 339−4 | P92035 | |$6.5_{-0.1}^{+0.1}$| | |$0.87_{-0.15}^{+0.15}$| | |$0.17_{-0.15}^{+0.20}$| | |$14._{-2.4}^{+2.7}$| |
| GX 339−4 | P92035 | |$6.5_{-0.2}^{+0.2}$| | |$1.1_{-0.2}^{+0.2}$| | |$0.21_{-0.18}^{+0.25}$| | |$18._{-3.9}^{+4.9}$| |
| GX 339−4 | P92035 | |$6.6_{-0.1}^{+0.1}$| | |$0.96_{-0.16}^{+0.16}$| | |$0.21_{-0.18}^{+0.24}$| | |$21._{-3.9}^{+4.7}$| |
| GX 339−4 | P92052 | |$6.4_{-0.2}^{+0.2}$| | |$0.68_{-0.38}^{+0.37}$| | |$0.09_{-0.07}^{+0.12}$| | |$2.7_{-1.3}^{+0.88}$| |
| GX 339−4 | P90118 | |$6.5_{-0.3}^{+0.3}$| | |$0.050_{-0.040}^{+0.73}$| | |$0.19_{-0.16}^{+0.22}$| | |$0.97_{-0.41}^{+0.73}$| |
| XTE J1118+480 | P50133 | |$6.4_{-0.4}^{+0.4}$| | |$0.75_{-0.51}^{+0.50}$| | |$0.08_{-0.05}^{+0.11}$| | |$0.98_{-0.46}^{+0.86}$| |
| XTE J1118+480 | P50133 | |$6.3_{-0.3}^{+0.3}$| | |$0.75_{-0.41}^{+0.41}$| | |$0.11_{-0.06}^{+0.16}$| | |$1.1_{-0.42}^{+0.71}$| |
| XTE J1118+480 | P50133 | |$6.3_{-0.3}^{+0.3}$| | |$0.65_{-0.49}^{+0.49}$| | |$0.07_{-0.04}^{+0.10}$| | |$0.74_{-0.31}^{+0.54}$| |
| XTE J1118+480 | P50133 | |$6.2_{-0.3}^{+0.3}$| | |$0.30_{-0.29}^{+0.55}$| | |$0.05_{-0.03}^{+0.07}$| | |$0.56_{-0.24}^{+0.41}$| |
| XTE J1118+480 | P50133 | |$6.4_{-0.6}^{+0.6}$| | |$0.24_{-0.23}^{+1.10}$| | |$0.07_{-0.03}^{+0.11}$| | |$0.39_{-0.090}^{+0.84}$| |
| XTE J1118+480 | P50133 | |$6.5_{-0.4}^{+0.4}$| | |$0.55_{-0.53}^{+0.63}$| | |$0.08_{-0.04}^{+0.12}$| | |$0.53_{-0.23}^{+0.46}$| |
| XTE J1118+480 | P50133 | |$6.3_{-0.4}^{+0.4}$| | |$0.61_{-0.59}^{+0.59}$| | |$0.07_{-0.03}^{+0.10}$| | |$0.61_{-0.29}^{+0.55}$| |
| GRO J1654−40 | P91702 | |$5.6_{-0.1}^{+0.9}$| | |$1.5_{-0.7}^{+0.5}$| | |$0.21_{-0.06}^{+0.36}$| | |$7.9_{-6.2}^{+3.7}$| |
| GRO J1654−40 | P91702 | |$5.7_{-0.2}^{+0.9}$| | |$1.7_{-0.}^{+0.3}$| | |$0.35_{-0.18}^{+0.52}$| | |$15_{-8.9}^{+6.9}$| |
| GRO J1654−40 | P91702 | |$5.7_{-0.2}^{+0.5}$| | |$2.0_{-0.2}^{+0.0}$| | |$0.54_{-0.45}^{+0.64}$| | |$26_{-7.1}^{+4.9}$| |
| GRO J1654−40 | P91702 | |$5.6_{-0.1}^{+0.6}$| | |$1.9_{-0.3}^{+0.1}$| | |$0.49_{-0.36}^{+0.61}$| | |$27_{-10}^{+7.7}$| |
| 4U 1608−52 | P60052 | |$6.5_{-0.7}^{+0.5}$| | |$1.8_{-0.5}^{+0.3}$| | |$0.12_{-0.05}^{+0.18}$| | |$1.3_{-0.70}^{+1.5}$| |
| 4U 1608−52 | P60052 | |$5.5_{-0.01}^{+1.10}$| | |$0.0_{-0.0}^{+1.9}$| | |$0.05_{-0.03}^{+0.07}$| | |$0.34_{-0.04}^{+0.22}$| |
| 4U 1608−52 | P60052 | |$7.0_{-1.3}^{+0.09}$| | |$1.6_{-0.4}^{+0.4}$| | |$0.07_{-0.03}^{+0.11}$| | |$0.42_{-0.12}^{+0.46}$| |
| 4U 1608−52 | P60052 | |$6.4_{-0.4}^{+0.4}$| | |$0.85_{-0.42}^{+0.42}$| | |$0.12_{-0.06}^{+0.17}$| | |$1.1_{-0.5}^{+0.9}$| |
| 4U 1608−52 | P60052 | |$5.6_{-0.1}^{+1.2}$| | |$0.07_{-0.07}^{+1.8}$| | |$0.06_{-0.02}^{+0.10}$| | |$0.34_{-0.04}^{+0.72}$| |
| 4U 1636−536 | P92023 | |$5.8_{-0.3}^{+1.1}$| | |$1.6_{-0.58}^{+0.38}$| | |$0.23_{-0.08}^{+0.39}$| | |$4.5_{-3.5}^{+2.4}$| |
| 4U 1636−536 | P92023 | |$6.8_{-0.5}^{+0.3}$| | |$0.29_{-0.29}^{+1.3}$| | |$0.09_{-0.01}^{+0.16}$| | |$0.74_{-0.52}^{+1.8}$| |
| 4U 1636−536 | P92023 | |$6.8_{-0.3}^{+0.3}$| | |$0.16_{-0.16}^{+0.80}$| | |$0.08_{-0.03}^{+0.13}$| | |$0.83_{-0.46}^{+1.00}$| |
| 4U 1636−536 | P92023 | |$6.8_{-0.4}^{+0.3}$| | |$0.57_{-0.57}^{+1.1}$| | |$0.15_{-0.03}^{+0.27}$| | |$1.3_{-0.86}^{+2.7}$| |
| 4U 1636−536 | P92023 | |$6.5_{-0.7}^{+0.6}$| | |$1.5_{-1.1}^{+0.5}$| | |$0.08_{-0.01}^{+0.15}$| | |$3.5_{-3.4}^{+2.8}$| |
| 4U 1636−536 | P94310 | |$6.7_{-0.5}^{+0.4}$| | |$1.1_{-0.6}^{+0.6}$| | |$0.13_{-0.06}^{+0.21}$| | |$2.2_{-1.4}^{+3.6}$| |
| 4U 1705-44 | P20073 | |$6.1_{-0.20}^{+0.20}$| | |$1.0_{-0.2}^{+0.2}$| | |$0.23_{-0.18}^{+0.29}$| | |$3.2_{-0.9}^{+1.2}$| |
| 4U 1705-44 | P20073 | |$6.1_{-0.25}^{+0.25}$| | |$1.1_{-0.3}^{+0.3}$| | |$0.23_{-0.17}^{+0.28}$| | |$3.4_{-0.9}^{+1.3}$| |
| 4U 1728-33 | P92023 | |$5.9_{-0.4}^{+0.4}$| | |$1.2_{-0.3}^{+0.3}$| | |$0.31_{-0.22}^{+0.40}$| | |$10._{-3.4}^{+5.1}$| |
| 4U 1728-33 | P92023 | |$5.5_{-0.3}^{+0.3}$| | |$1.4_{-0.2}^{+0.2}$| | |$0.40_{-0.29}^{+0.52}$| | |$19._{-5.5}^{+7.7}$| |
| Aql X-1 | P50049 | |$6.7_{-0.2}^{+0.2}$| | |$0.66_{-0.25}^{+0.25}$| | |$0.09_{-0.05}^{+0.12}$| | |$2.5_{-1.0}^{+1.5}$| |
| Aql X-1 | P91414 | |$6.1_{-0.6}^{+0.7}$| | |$1.2_{-0.7}^{+0.7}$| | |$0.08_{-0.03}^{+0.12}$| | |$1.3_{-0.9}^{+1.8}$| |
| Aql X-1 | P91414 | |$7.0_{-0.5}^{+0.1}$| | |$0.79_{-0.52}^{+0.53}$| | |$0.10_{-0.05}^{+0.15}$| | |$1.4_{-0.8}^{+1.6}$| |
| Aql X-1 | P91414 | |$6.8_{-0.9}^{+0.3}$| | |$1.4_{-0.6}^{+0.6}$| | |$0.15_{-0.04}^{+0.25}$| | |$2.0_{-1.3}^{+4.0}$| |
| Source . | ObsID . | Epeak . | σ . | EW . | Norm. . |
|---|---|---|---|---|---|
| GS 1354−64 | P20431 | |$6.3_{-0.2}^{+0.2}$| | |$0.36_{-0.29}^{+0.29}$| | |$0.06_{-0.04}^{+0.08}$| | |$0.70_{-0.19}^{+0.25}$| |
| GS 1354−64 | P20431 | |$6.4_{-0.5}^{+0.5}$| | |$0.40_{-0.39}^{+0.77}$| | |$0.06_{-0.04}^{+0.07}$| | |$0.60_{-0.10}^{+0.31}$| |
| GS 1354−64 | P20431 | |$6.2_{-0.3}^{+0.3}$| | |$0.51_{-0.50}^{+0.50}$| | |$0.06_{-0.04}^{+0.08}$| | |$0.60_{-0.10}^{+0.25}$| |
| GS 1354−64 | P20431 | |$6.1_{-0.2}^{+0.2}$| | |$0.64_{-0.42}^{+0.42}$| | |$0.06_{-0.04}^{+0.08}$| | |$0.80_{-0.28}^{+0.42}$| |
| 4U 1543−47 | P70124 | |$6.2_{-0.3}^{+0.3}$| | |$0.62_{-0.40}^{+0.40}$| | |$0.30_{-0.15}^{+0.46}$| | |$1.40_{-0.64}^{+1.10}$| |
| XTE J1550−564 | P30188 | |$6.6_{-0.2}^{+0.2}$| | |$0.81_{-0.22}^{+0.22}$| | |$0.10_{-0.08}^{+0.13}$| | |$6.4_{-1.3}^{+1.6}$| |
| XTE J1550−564 | P30188 | |$6.6_{-0.2}^{+0.2}$| | |$0.85_{-0.20}^{+0.20}$| | |$0.10_{-0.08}^{+0.12}$| | |$7.5_{-1.3}^{+1.6}$| |
| XTE J1550−564 | P30188 | |$6.7_{-0.1}^{+0.1}$| | |$1.1_{-0.07}^{+0.17}$| | |$0.13_{-0.11}^{+0.15}$| | |$13._{-1.4}^{+1.7}$| |
| XTE J1550−564 | P50134 | |$6.2_{-0.4}^{+0.4}$| | |$1.5_{-0.31}^{+0.31}$| | |$0.37_{-0.29}^{+0.45}$| | |$26._{-7.3}^{+10.}$| |
| XTE J1550−564 | P50135 | |$5.5_{-0.01}^{+0.7}$| | |$2.0_{-0.33}^{+0.02}$| | |$0.52_{-0.43}^{+0.61}$| | |$22_{-9.1}^{+2.5}$| |
| XTE J1550−564 | P50135 | |$5.5_{-0.01}^{+0.8}$| | |$1.9_{-0.6}^{+0.2}$| | |$0.36_{-0.22}^{+0.51}$| | |$11_{-6.4}^{+1.8}$| |
| XTE J1550−564 | P50135 | |$5.7_{-0.2}^{+0.8}$| | |$1.9_{-0.7}^{+0.09}$| | |$0.30_{-0.15}^{+0.46}$| | |$7.7_{-4.9}^{+3.9}$| |
| XTE J1550−564 | P50137 | |$6.5_{-0.2}^{+0.2}$| | |$1.1_{-0.3}^{+0.3}$| | |$0.15_{-0.12}^{+0.19}$| | |$11_{-2.9}^{+3.9}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.1}$| | |$0.60_{-0.20}^{+0.20}$| | |$0.10_{-0.08}^{+0.12}$| | |$7.3_{-1.6}^{+1.9}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.2}$| | |$0.61_{-0.23}^{+0.19}$| | |$0.09_{-0.07}^{+0.11}$| | |$8.1_{-2.0}^{+1.6}$| |
| Cyg X-1 | P20173 | |$6.4_{-0.1}^{+0.1}$| | |$0.51_{-0.18}^{+0.18}$| | |$0.06_{-0.05}^{+0.07}$| | |$7.2_{-1.6}^{+1.3}$| |
| Cyg X-1 | P20173 | |$6.4_{-0.1}^{+0.1}$| | |$0.56_{-0.23}^{+0.23}$| | |$0.09_{-0.07}^{+0.11}$| | |$7.6_{-2.4}^{+1.6}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.1}$| | |$0.56_{-0.17}^{+0.18}$| | |$0.05_{-0.05}^{+0.06}$| | |$8.4_{-1.4}^{+1.7}$| |
| Cyg X-1 | P20173 | |$6.3_{-0.1}^{+0.1}$| | |$0.57_{-0.16}^{+0.15}$| | |$0.09_{-0.08}^{+0.10}$| | |$8.1_{-1.4}^{+1.4}$| |
| Cyg X-1 | P20173 | |$6.4_{-0.1}^{+0.1}$| | |$0.53_{-0.15}^{+0.15}$| | |$0.09_{-0.07}^{+0.10}$| | |$7.0_{-1.4}^{+1.4}$| |
| Cyg X-1 | P80110 | |$6.3_{-0.2}^{+0.2}$| | |$0.70_{-0.22}^{+0.23}$| | |$0.13_{-0.09}^{+0.16}$| | |$15._{-4.6}^{+6.5}$| |
| Cyg X-1 | P80110 | |$6.3_{-0.2}^{+0.2}$| | |$0.57_{-0.28}^{+0.28}$| | |$0.08_{-0.05}^{+0.11}$| | |$7.0_{-2.5}^{+3.8}$| |
| Cyg X-1 | P80110 | |$6.3_{-0.1}^{+0.1}$| | |$0.32_{-0.26}^{+0.26}$| | |$0.07_{-0.05}^{+0.09}$| | |$5.3_{-1.5}^{+2.1}$| |
| Cyg X-1 | P94108 | |$6.3_{-0.3}^{+0.3}$| | |$0.76_{-0.33}^{+0.33}$| | |$0.19_{-0.12}^{+0.26}$| | |$13._{-5.3}^{+8.8}$| |
| GX 339−4 | P92035 | |$6.5_{-0.1}^{+0.1}$| | |$0.87_{-0.15}^{+0.15}$| | |$0.17_{-0.15}^{+0.20}$| | |$14._{-2.4}^{+2.7}$| |
| GX 339−4 | P92035 | |$6.5_{-0.2}^{+0.2}$| | |$1.1_{-0.2}^{+0.2}$| | |$0.21_{-0.18}^{+0.25}$| | |$18._{-3.9}^{+4.9}$| |
| GX 339−4 | P92035 | |$6.6_{-0.1}^{+0.1}$| | |$0.96_{-0.16}^{+0.16}$| | |$0.21_{-0.18}^{+0.24}$| | |$21._{-3.9}^{+4.7}$| |
| GX 339−4 | P92052 | |$6.4_{-0.2}^{+0.2}$| | |$0.68_{-0.38}^{+0.37}$| | |$0.09_{-0.07}^{+0.12}$| | |$2.7_{-1.3}^{+0.88}$| |
| GX 339−4 | P90118 | |$6.5_{-0.3}^{+0.3}$| | |$0.050_{-0.040}^{+0.73}$| | |$0.19_{-0.16}^{+0.22}$| | |$0.97_{-0.41}^{+0.73}$| |
| XTE J1118+480 | P50133 | |$6.4_{-0.4}^{+0.4}$| | |$0.75_{-0.51}^{+0.50}$| | |$0.08_{-0.05}^{+0.11}$| | |$0.98_{-0.46}^{+0.86}$| |
| XTE J1118+480 | P50133 | |$6.3_{-0.3}^{+0.3}$| | |$0.75_{-0.41}^{+0.41}$| | |$0.11_{-0.06}^{+0.16}$| | |$1.1_{-0.42}^{+0.71}$| |
| XTE J1118+480 | P50133 | |$6.3_{-0.3}^{+0.3}$| | |$0.65_{-0.49}^{+0.49}$| | |$0.07_{-0.04}^{+0.10}$| | |$0.74_{-0.31}^{+0.54}$| |
| XTE J1118+480 | P50133 | |$6.2_{-0.3}^{+0.3}$| | |$0.30_{-0.29}^{+0.55}$| | |$0.05_{-0.03}^{+0.07}$| | |$0.56_{-0.24}^{+0.41}$| |
| XTE J1118+480 | P50133 | |$6.4_{-0.6}^{+0.6}$| | |$0.24_{-0.23}^{+1.10}$| | |$0.07_{-0.03}^{+0.11}$| | |$0.39_{-0.090}^{+0.84}$| |
| XTE J1118+480 | P50133 | |$6.5_{-0.4}^{+0.4}$| | |$0.55_{-0.53}^{+0.63}$| | |$0.08_{-0.04}^{+0.12}$| | |$0.53_{-0.23}^{+0.46}$| |
| XTE J1118+480 | P50133 | |$6.3_{-0.4}^{+0.4}$| | |$0.61_{-0.59}^{+0.59}$| | |$0.07_{-0.03}^{+0.10}$| | |$0.61_{-0.29}^{+0.55}$| |
| GRO J1654−40 | P91702 | |$5.6_{-0.1}^{+0.9}$| | |$1.5_{-0.7}^{+0.5}$| | |$0.21_{-0.06}^{+0.36}$| | |$7.9_{-6.2}^{+3.7}$| |
| GRO J1654−40 | P91702 | |$5.7_{-0.2}^{+0.9}$| | |$1.7_{-0.}^{+0.3}$| | |$0.35_{-0.18}^{+0.52}$| | |$15_{-8.9}^{+6.9}$| |
| GRO J1654−40 | P91702 | |$5.7_{-0.2}^{+0.5}$| | |$2.0_{-0.2}^{+0.0}$| | |$0.54_{-0.45}^{+0.64}$| | |$26_{-7.1}^{+4.9}$| |
| GRO J1654−40 | P91702 | |$5.6_{-0.1}^{+0.6}$| | |$1.9_{-0.3}^{+0.1}$| | |$0.49_{-0.36}^{+0.61}$| | |$27_{-10}^{+7.7}$| |
| 4U 1608−52 | P60052 | |$6.5_{-0.7}^{+0.5}$| | |$1.8_{-0.5}^{+0.3}$| | |$0.12_{-0.05}^{+0.18}$| | |$1.3_{-0.70}^{+1.5}$| |
| 4U 1608−52 | P60052 | |$5.5_{-0.01}^{+1.10}$| | |$0.0_{-0.0}^{+1.9}$| | |$0.05_{-0.03}^{+0.07}$| | |$0.34_{-0.04}^{+0.22}$| |
| 4U 1608−52 | P60052 | |$7.0_{-1.3}^{+0.09}$| | |$1.6_{-0.4}^{+0.4}$| | |$0.07_{-0.03}^{+0.11}$| | |$0.42_{-0.12}^{+0.46}$| |
| 4U 1608−52 | P60052 | |$6.4_{-0.4}^{+0.4}$| | |$0.85_{-0.42}^{+0.42}$| | |$0.12_{-0.06}^{+0.17}$| | |$1.1_{-0.5}^{+0.9}$| |
| 4U 1608−52 | P60052 | |$5.6_{-0.1}^{+1.2}$| | |$0.07_{-0.07}^{+1.8}$| | |$0.06_{-0.02}^{+0.10}$| | |$0.34_{-0.04}^{+0.72}$| |
| 4U 1636−536 | P92023 | |$5.8_{-0.3}^{+1.1}$| | |$1.6_{-0.58}^{+0.38}$| | |$0.23_{-0.08}^{+0.39}$| | |$4.5_{-3.5}^{+2.4}$| |
| 4U 1636−536 | P92023 | |$6.8_{-0.5}^{+0.3}$| | |$0.29_{-0.29}^{+1.3}$| | |$0.09_{-0.01}^{+0.16}$| | |$0.74_{-0.52}^{+1.8}$| |
| 4U 1636−536 | P92023 | |$6.8_{-0.3}^{+0.3}$| | |$0.16_{-0.16}^{+0.80}$| | |$0.08_{-0.03}^{+0.13}$| | |$0.83_{-0.46}^{+1.00}$| |
| 4U 1636−536 | P92023 | |$6.8_{-0.4}^{+0.3}$| | |$0.57_{-0.57}^{+1.1}$| | |$0.15_{-0.03}^{+0.27}$| | |$1.3_{-0.86}^{+2.7}$| |
| 4U 1636−536 | P92023 | |$6.5_{-0.7}^{+0.6}$| | |$1.5_{-1.1}^{+0.5}$| | |$0.08_{-0.01}^{+0.15}$| | |$3.5_{-3.4}^{+2.8}$| |
| 4U 1636−536 | P94310 | |$6.7_{-0.5}^{+0.4}$| | |$1.1_{-0.6}^{+0.6}$| | |$0.13_{-0.06}^{+0.21}$| | |$2.2_{-1.4}^{+3.6}$| |
| 4U 1705-44 | P20073 | |$6.1_{-0.20}^{+0.20}$| | |$1.0_{-0.2}^{+0.2}$| | |$0.23_{-0.18}^{+0.29}$| | |$3.2_{-0.9}^{+1.2}$| |
| 4U 1705-44 | P20073 | |$6.1_{-0.25}^{+0.25}$| | |$1.1_{-0.3}^{+0.3}$| | |$0.23_{-0.17}^{+0.28}$| | |$3.4_{-0.9}^{+1.3}$| |
| 4U 1728-33 | P92023 | |$5.9_{-0.4}^{+0.4}$| | |$1.2_{-0.3}^{+0.3}$| | |$0.31_{-0.22}^{+0.40}$| | |$10._{-3.4}^{+5.1}$| |
| 4U 1728-33 | P92023 | |$5.5_{-0.3}^{+0.3}$| | |$1.4_{-0.2}^{+0.2}$| | |$0.40_{-0.29}^{+0.52}$| | |$19._{-5.5}^{+7.7}$| |
| Aql X-1 | P50049 | |$6.7_{-0.2}^{+0.2}$| | |$0.66_{-0.25}^{+0.25}$| | |$0.09_{-0.05}^{+0.12}$| | |$2.5_{-1.0}^{+1.5}$| |
| Aql X-1 | P91414 | |$6.1_{-0.6}^{+0.7}$| | |$1.2_{-0.7}^{+0.7}$| | |$0.08_{-0.03}^{+0.12}$| | |$1.3_{-0.9}^{+1.8}$| |
| Aql X-1 | P91414 | |$7.0_{-0.5}^{+0.1}$| | |$0.79_{-0.52}^{+0.53}$| | |$0.10_{-0.05}^{+0.15}$| | |$1.4_{-0.8}^{+1.6}$| |
| Aql X-1 | P91414 | |$6.8_{-0.9}^{+0.3}$| | |$1.4_{-0.6}^{+0.6}$| | |$0.15_{-0.04}^{+0.25}$| | |$2.0_{-1.3}^{+4.0}$| |
As in Table 4, analysis of XMM+RXTE data, using EPIC-pn data over 0.7–9.0 keV and RXTE data over 9.0–200 keV. We also include the calculated value of amplification factor A.
| Source . | kTbb . | kTe . | R . | y . | Norm. . | kTin . | |${\rm Norm.}_{{{\rm \small diskbb}}}$| . | A . |
|---|---|---|---|---|---|---|---|---|
| . | (keV) . | (keV) . | . | . | . | (keV) . | . | . |
| 4U 1636−536 | |$0.167_{-0.008}^{+0.009}$| | |$16.7_{-2.}^{+2.}$| | |$0.22_{-0.2}^{+0.2}$| | |$0.91_{-0.03}^{+0.02}$| | |$42900._{-8500.}^{+10000.}$| | |$0.24_{-0.01}^{+0.01}$| | |$2200_{-470}^{+600}$| | 3.0 |
| Cyg X-1 | |$0.21_{-0.006}^{+0.01}$| | |$118._{-8.}^{+8.}$| | |$0.44_{-0.03}^{+0.03}$| | |$1.15_{-0.02}^{+0.01}$| | |${ 99800}._{-16800.}^{+10000.}$| | |$0.235_{-0.004}^{+0.004}$| | |$46200_{-4500}^{+4100}$| | 7.7 |
| GX 339−4 | |$0.63_{-0.4}^{+0.09}$| | |$57.4_{-9.}^{+10}$| | |$0.46_{-0.08}^{+0.09}$| | |$1.32_{-0.03}^{+0.03}$| | |$284._{-134.}^{+816.}$| | |${0.196}_{-0.005}^{+0.005}$| | |$69700_{-6400}^{+7000}$| | 6.7 |
| Source . | kTbb . | kTe . | R . | y . | Norm. . | kTin . | |${\rm Norm.}_{{{\rm \small diskbb}}}$| . | A . |
|---|---|---|---|---|---|---|---|---|
| . | (keV) . | (keV) . | . | . | . | (keV) . | . | . |
| 4U 1636−536 | |$0.167_{-0.008}^{+0.009}$| | |$16.7_{-2.}^{+2.}$| | |$0.22_{-0.2}^{+0.2}$| | |$0.91_{-0.03}^{+0.02}$| | |$42900._{-8500.}^{+10000.}$| | |$0.24_{-0.01}^{+0.01}$| | |$2200_{-470}^{+600}$| | 3.0 |
| Cyg X-1 | |$0.21_{-0.006}^{+0.01}$| | |$118._{-8.}^{+8.}$| | |$0.44_{-0.03}^{+0.03}$| | |$1.15_{-0.02}^{+0.01}$| | |${ 99800}._{-16800.}^{+10000.}$| | |$0.235_{-0.004}^{+0.004}$| | |$46200_{-4500}^{+4100}$| | 7.7 |
| GX 339−4 | |$0.63_{-0.4}^{+0.09}$| | |$57.4_{-9.}^{+10}$| | |$0.46_{-0.08}^{+0.09}$| | |$1.32_{-0.03}^{+0.03}$| | |$284._{-134.}^{+816.}$| | |${0.196}_{-0.005}^{+0.005}$| | |$69700_{-6400}^{+7000}$| | 6.7 |
As in Table 4, analysis of XMM+RXTE data, using EPIC-pn data over 0.7–9.0 keV and RXTE data over 9.0–200 keV. We also include the calculated value of amplification factor A.
| Source . | kTbb . | kTe . | R . | y . | Norm. . | kTin . | |${\rm Norm.}_{{{\rm \small diskbb}}}$| . | A . |
|---|---|---|---|---|---|---|---|---|
| . | (keV) . | (keV) . | . | . | . | (keV) . | . | . |
| 4U 1636−536 | |$0.167_{-0.008}^{+0.009}$| | |$16.7_{-2.}^{+2.}$| | |$0.22_{-0.2}^{+0.2}$| | |$0.91_{-0.03}^{+0.02}$| | |$42900._{-8500.}^{+10000.}$| | |$0.24_{-0.01}^{+0.01}$| | |$2200_{-470}^{+600}$| | 3.0 |
| Cyg X-1 | |$0.21_{-0.006}^{+0.01}$| | |$118._{-8.}^{+8.}$| | |$0.44_{-0.03}^{+0.03}$| | |$1.15_{-0.02}^{+0.01}$| | |${ 99800}._{-16800.}^{+10000.}$| | |$0.235_{-0.004}^{+0.004}$| | |$46200_{-4500}^{+4100}$| | 7.7 |
| GX 339−4 | |$0.63_{-0.4}^{+0.09}$| | |$57.4_{-9.}^{+10}$| | |$0.46_{-0.08}^{+0.09}$| | |$1.32_{-0.03}^{+0.03}$| | |$284._{-134.}^{+816.}$| | |${0.196}_{-0.005}^{+0.005}$| | |$69700_{-6400}^{+7000}$| | 6.7 |
| Source . | kTbb . | kTe . | R . | y . | Norm. . | kTin . | |${\rm Norm.}_{{{\rm \small diskbb}}}$| . | A . |
|---|---|---|---|---|---|---|---|---|
| . | (keV) . | (keV) . | . | . | . | (keV) . | . | . |
| 4U 1636−536 | |$0.167_{-0.008}^{+0.009}$| | |$16.7_{-2.}^{+2.}$| | |$0.22_{-0.2}^{+0.2}$| | |$0.91_{-0.03}^{+0.02}$| | |$42900._{-8500.}^{+10000.}$| | |$0.24_{-0.01}^{+0.01}$| | |$2200_{-470}^{+600}$| | 3.0 |
| Cyg X-1 | |$0.21_{-0.006}^{+0.01}$| | |$118._{-8.}^{+8.}$| | |$0.44_{-0.03}^{+0.03}$| | |$1.15_{-0.02}^{+0.01}$| | |${ 99800}._{-16800.}^{+10000.}$| | |$0.235_{-0.004}^{+0.004}$| | |$46200_{-4500}^{+4100}$| | 7.7 |
| GX 339−4 | |$0.63_{-0.4}^{+0.09}$| | |$57.4_{-9.}^{+10}$| | |$0.46_{-0.08}^{+0.09}$| | |$1.32_{-0.03}^{+0.03}$| | |$284._{-134.}^{+816.}$| | |${0.196}_{-0.005}^{+0.005}$| | |$69700_{-6400}^{+7000}$| | 6.7 |
In order to investigate, how significantly the Comptonization parameter may be affected by the bias in the seed photon temperature caused by the limited bandpass of RXTE, we conduct the following experiment. For a subsample of spectra (one spectrum for each source except for 4U1636-536 for which we analysed two spectra, see below), we perform simple fitting with our default spectral model, fixing kTbb across a grid of values. For each kTbb, we note the χ2, and compare it with a limit corresponding to the theoretical null hypothesis of 1 per cent for a χ2-distribution described by the number of degrees of freedom in that fit, and points with χ2 in excess of this are rejected. This gives an indication of the space covered by potential fits that we define as being ‘formally acceptable’. We present the results of this exercise in Fig. 10, which shows the behaviour of y-parameter with kTbb, with the quality of the fit denoted by point size.
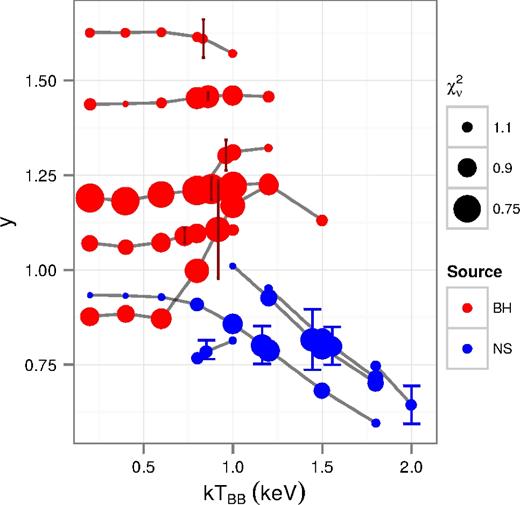
Behaviour of y with fixed values of kTbb. Compact object type denoted by colour and goodness of fit indicated by point size. Points where the theoretical null hypothesis is less than 1 per cent (large chi-squared) are omitted. Therefore, the lines connecting blue (red) points show the parameter region accessible to each NS (BH), with decreasing point size corresponding to decreasing goodness of fit.
From this experiment, we find that BH spectra are generally compatible with a broad range of kTbb, including low values kTbb ∼ 0.2 keV predicted by the standard accretion disc model. While best fits generally prefer kTbb ∼ 1 keV, low values of kTbb ∼ 0.2 keV result in sufficiently small χ2, which are formally acceptable (although often outside formal ∼1–2σ confidence intervals). NS systems, on the other hand, tend to favour higher values of kTbb ∼ 1–1.5 keV. For majority of NS spectra low values of kTbb ≲ 1 keV result in unacceptable fit quality. This behaviour is consistent with our expectations that the source of seed photons in BH systems is the (truncated) accretion disc, while in NS systems it is the NS surface, having significantly higher temperature. BH systems are subjected to a notable upward bias in the seed photon temperatures determined from fitting the 3–200 keV band data, which appears to be the result of the limited bandpass combined with the spectral model which is simplified and not fully adequate. However, there is virtually no degeneracy (with the exception of 4U 1543 − 47) between the seed photon temperature and the y-parameter and electron temperature. The NS systems are subjected to the bias in the kTbb to a much lesser extent, if at all, because of the typically higher seed photon temperatures. Although they do show some kTbb − y degeneracy, their seed photon temperatures are measured sufficiently well with the RXTE data. Therefore, the dichotomy between the BH coronal properties and those of NSs is secure irrespective of the inaccuracies in determination of the seed spectral properties.
The observation of 4U1636-536, for which simultaneous RXTE and XMM–Newton data were analysed above, seems to differ from other NS spectra.5 The 0.5–200 keV band fitting gave low kTbb ≈ 0.17 keV. Consistent with this, in the 3–200 keV fit, low values of kTbb ∼ 0.2 keV result in formally acceptable χ2 values. On the other hand, the broad-band data are consistent with high kTbb ∼ 1 keV, producing formally acceptable χ2 values. In either case, the y-parameter is staying well below the y ∼ 1 boundary. While interpreting these results one should bear in mind that the 0.5–200 and 3–200 keV data were fitted with different spectral model, which in the former case included the diskbb component. Such behaviour is demonstrated by only this particular observation of the source. For comparison, we plot in Fig. 10 results for another spectrum of 4U1636-536, which in RXTE data shows a pattern similar to other NS systems.
Any systematic bias in estimating the seed spectral properties, when considering energies >3 keV, will propagate to a bias in our calculation of the amplification factor A (Section 5.2). However, the effect of the reduced seed photon temperature on the calculated seed luminosity is countered by a concurrent increase in model normalization, obtained in the 0.7–200 keV band fits. Using only RXTE data Cyg X-1 was found to have Lseed = 2.41 × 1036erg s− 1 (≈0.001LEdd), while fitting XMM+RXTE data indicates Lseed = 1.63 × 1036erg s− 1 (see Table 6). Comparing the joint XMM–RXTE fitting results with those found from studying the RXTE data only, the Lseed of 4U 1636-536 and GX 339-4 goes from 4.64 × 1036 to 3.10 × 1036erg s− 1 (≈0.025–0.017LEdd) and from 14.5 × 1036 to 11.5 × 1036erg s− 1 (≈0.07–0.06LEdd), respectively. Therefore, for these three sources, the Lseed found from fitting the 0.7–200 keV data is ≈0.7Lseed found from fitting the 3–200 keV data. This further demonstrates that the inaccuracy in the seed photon parameters does not affect our conclusion that the coronae in BH systems are more strongly Comptonizing than those found in NS XBs. For completeness, estimating the total unabsorbed flux in the upscattered component over the full bandwidth, 0.7–200.0 keV, leads to a marginal increase in A by 0.7, 0.05, and 0.4 for 4U 1636-536, Cyg X-1 and GX 339-4, respectively. The resulting values of A are shown in Table 6.
6 SUMMARY
We have analysed hard state spectra from a sample of Galactic XBs observed by the RXTE satellite. The spectra were well described by thermal Comptonization of seed photons from an accretion disc, which we modelled using the compps component in xspec with an additional Gaussian component to account for fluorescent emission in the vicinity of the Fe Kα complex. Our most striking result is the clear dichotomy in the Compton y-parameter and the Compton enhancement factor A between NSs and BHs (Fig. 7). The boundary is located at y ≈ 0.9 and A ≈ 3 with BH systems having systematically higher values of y and A. Distribution of y and A for NSs is rather narrow and strongly peaked at y ≈ 0.7–0.8 and A ≈ 2 (A ∼ 3 after correction for absorption and RXTE bandpass). Electron temperature in BH systems can occupy rather a broad range of values from ∼30 to 200 keV, while in NS their distribution is strongly peaked at kTe ∼ 15–25 keV with very few spectra exceeding kTe ∼ 50–70 keV. For a given optical depth, the electron temperature of the Comptonizing media is systematically larger in BHs than in the NSs (Fig. 6). The values of the Compton amplification factor typical for NS systems suggest that in the hard state, accreting material is losing due to Comptonization in the corona about ∼1/2–2/3 of the total energy it possessed upon entering the Comptonization region. Remaining energy is released on the surface of the NS in the form of kinetic energy of the infalling material, making it a powerful source of soft radiation. The smaller Compton y-parameter for NS LMXBs can be explained in terms of this additional supply of seed photons by the NS surface that is of course absent in the case of BHs. The observed dichotomy as a diagnostic tool has excellent potential for distinguishing BH from NS XBs both in our galaxy and beyond.
Acknowledgments
We acknowledge the use of the Legacy Archive for Microwave Background Data Analysis (LAMBDA), part of the High Energy Astrophysics Science Archive Center (HEASARC). HEASARC/LAMBDA is a service of the Astrophysics Science Division at the NASA Goddard Space Flight Center. MG acknowledges a partial support by the RFBR grant no. 15-42-02573. MG also acknowledges hospitality of the Kazan Federal University (KFU) and support by the Russian Government Program of Competitive Growth of KFU. We thank the referee for their careful reading of the manuscript and insightful suggestions that improved the quality of the paper.
Note that in all cases where the NS spin is measured, vNS < vK.
Note that replacing the multicolour disc seed photon spectrum with a blackbody spectrum further decreases the best-fitting value of the seed photon temperature by 0.06 keV.
Unfortunately, this was the only NS spectrum from our sample, for which simultaneous RXTE and XMM–Newton hard state data were available.



