Multifrequency polarimetry of a complete sample of PACO radio sources Free

Summary of some of the surveys in polarization available at high radio frequencies. The tabulated detection rates and polarization fractions (see the columns labelled as ‘Det. rate’ and ‘Pol. fraction’, respectively) refer in each case to the frequency closest to 20 GHz, when available.

References	Freq. (GHz)	No. of sources	Det. rate	Pol. fraction	Notes
Ricci et al. (2004)	18.5	250	68 %	2.7 %^a	Complete sample with S_5 GHz > 1 Jy
Sadler et al. (2006)	20	173	75 %	2.3 %	Complete sample with S_20 GHz > 0.1 Jy
Massardi et al. (2008) AT20G-BSS	4.8, 8.6, 20	320	67 %	2.5 %	AT20G bright (S_20 GHz > 0.5 Jy) sample
Murphy et al. (2010); Massardi et al. (2011)
AT20G	4.8, 8.6, 20	5890	72.5 %^b	2.7 %	Survey 93 % complete with S_20 GHz > 40 mJy
Sajina et al. (2011)	4.86, 8.46, 22.46, 43.34	159	56 %	3.82 %	Complete sample of AT20G objects with S_20 GHz > 40 mJy in an equatorial field
Battye et al. (2011)	8.4, 22, 43	203	83 %	2.0 %	WMAP sources follow-up
Massardi et al. (2013)	4.8, 8.6, 18	193	91.4 %^c	2 %	Complete sample with S_20 GHz > 500 mJy
Agudo et al. (2014)	15, 86, 229	211	88 %^d	3.2 %; 4.6 %^e	Complete sample with S_86 GHz > 0.9 Jy

References	Freq. (GHz)	No. of sources	Det. rate	Pol. fraction	Notes
Ricci et al. (2004)	18.5	250	68 %	2.7 %^a	Complete sample with S_5 GHz > 1 Jy
Sadler et al. (2006)	20	173	75 %	2.3 %	Complete sample with S_20 GHz > 0.1 Jy
Massardi et al. (2008) AT20G-BSS	4.8, 8.6, 20	320	67 %	2.5 %	AT20G bright (S_20 GHz > 0.5 Jy) sample
Murphy et al. (2010); Massardi et al. (2011)
AT20G	4.8, 8.6, 20	5890	72.5 %^b	2.7 %	Survey 93 % complete with S_20 GHz > 40 mJy
Sajina et al. (2011)	4.86, 8.46, 22.46, 43.34	159	56 %	3.82 %	Complete sample of AT20G objects with S_20 GHz > 40 mJy in an equatorial field
Battye et al. (2011)	8.4, 22, 43	203	83 %	2.0 %	WMAP sources follow-up
Massardi et al. (2013)	4.8, 8.6, 18	193	91.4 %^c	2 %	Complete sample with S_20 GHz > 500 mJy
Agudo et al. (2014)	15, 86, 229	211	88 %^d	3.2 %; 4.6 %^e	Complete sample with S_86 GHz > 0.9 Jy

Notes.^aThis median value is found considering the flat-spectrum sub-sample only.

^bThe analysis is limited to objects with S_20 GHz > 250 mJy.

^cThe detection rate is ≃94 per cent considering the sub-sample of point-like objects.

^dThe detection rate is reported for the 86 GHz observations.

^eThese values refer to quasars and BL Lacs, respectively.

Table 1.

Summary of some of the surveys in polarization available at high radio frequencies. The tabulated detection rates and polarization fractions (see the columns labelled as ‘Det. rate’ and ‘Pol. fraction’, respectively) refer in each case to the frequency closest to 20 GHz, when available.

References	Freq. (GHz)	No. of sources	Det. rate	Pol. fraction	Notes
Ricci et al. (2004)	18.5	250	68 %	2.7 %^a	Complete sample with S_5 GHz > 1 Jy
Sadler et al. (2006)	20	173	75 %	2.3 %	Complete sample with S_20 GHz > 0.1 Jy
Massardi et al. (2008) AT20G-BSS	4.8, 8.6, 20	320	67 %	2.5 %	AT20G bright (S_20 GHz > 0.5 Jy) sample
Murphy et al. (2010); Massardi et al. (2011)
AT20G	4.8, 8.6, 20	5890	72.5 %^b	2.7 %	Survey 93 % complete with S_20 GHz > 40 mJy
Sajina et al. (2011)	4.86, 8.46, 22.46, 43.34	159	56 %	3.82 %	Complete sample of AT20G objects with S_20 GHz > 40 mJy in an equatorial field
Battye et al. (2011)	8.4, 22, 43	203	83 %	2.0 %	WMAP sources follow-up
Massardi et al. (2013)	4.8, 8.6, 18	193	91.4 %^c	2 %	Complete sample with S_20 GHz > 500 mJy
Agudo et al. (2014)	15, 86, 229	211	88 %^d	3.2 %; 4.6 %^e	Complete sample with S_86 GHz > 0.9 Jy

References	Freq. (GHz)	No. of sources	Det. rate	Pol. fraction	Notes
Ricci et al. (2004)	18.5	250	68 %	2.7 %^a	Complete sample with S_5 GHz > 1 Jy
Sadler et al. (2006)	20	173	75 %	2.3 %	Complete sample with S_20 GHz > 0.1 Jy
Massardi et al. (2008) AT20G-BSS	4.8, 8.6, 20	320	67 %	2.5 %	AT20G bright (S_20 GHz > 0.5 Jy) sample
Murphy et al. (2010); Massardi et al. (2011)
AT20G	4.8, 8.6, 20	5890	72.5 %^b	2.7 %	Survey 93 % complete with S_20 GHz > 40 mJy
Sajina et al. (2011)	4.86, 8.46, 22.46, 43.34	159	56 %	3.82 %	Complete sample of AT20G objects with S_20 GHz > 40 mJy in an equatorial field
Battye et al. (2011)	8.4, 22, 43	203	83 %	2.0 %	WMAP sources follow-up
Massardi et al. (2013)	4.8, 8.6, 18	193	91.4 %^c	2 %	Complete sample with S_20 GHz > 500 mJy
Agudo et al. (2014)	15, 86, 229	211	88 %^d	3.2 %; 4.6 %^e	Complete sample with S_86 GHz > 0.9 Jy

Notes.^aThis median value is found considering the flat-spectrum sub-sample only.

^bThe analysis is limited to objects with S_20 GHz > 250 mJy.

^cThe detection rate is ≃94 per cent considering the sub-sample of point-like objects.

^dThe detection rate is reported for the 86 GHz observations.

^eThese values refer to quasars and BL Lacs, respectively.

On the whole, our understanding of the high-radio-frequency polarization properties of extragalactic sources is still limited. This has motivated the new high-sensitivity (σ_P ≃0.6 mJy, a factor ≃2 better than the sensitivity of “The Australia Telescope 20 GHz Survey”, hereafter AT20G) and nearly simultaneous, multifrequency polarimetric observations over a wide spectral range (5.5–38 GHz) whose results are reported here. We observed with the Australia Telescope Compact Array (ATCA), the Planck–ATCA Coeval Observations (PACO) ‘faint sample’ (Massardi et al. 2016b), a complete sample of AT20G sources with S_20 GHz ≥ 200 mJy. The instrumental capabilities were exploited to reconstruct the polarimetric spectral profile to unprecedented detail.

High-frequency observations are easily affected by spectral, detection and variability-related biases. This work, owing to the completeness of the sample, the high sensitivity and the close-in-time multifrequency characterization, allows us to minimize all these effects. Thus, we provide a new statistical assessment of the polarimetric properties of high-frequency extragalactic radio sources, analysing and describing their spectral and polarization behaviour with frequency. Moreover, exploiting also the AT20G and PACO observations in total intensity, we investigate the source variability for 4–5 and 8 yr time lags at several frequencies up to 38 GHz.

Multifrequency and multi-epoch polarimetric observations of radio sources are useful cosmological tools for several reasons. Radio sources are the most relevant foreground contaminants of the cosmic microwave background (CMB) polarization maps (on scales of up to ∼30 arcmin) in the relatively clean 70–100 GHz frequency range (Massardi et al. 2016a). A proper characterization of the radio-source contribution to the power spectrum in polarization is essential for a precise assessment of the lensing B-mode signal (Hanson et al. 2013; POLARBEAR: Ade et al. 2014). This, in turn, is essential for the detection and the characterization of the power spectrum of the primordial B modes associated with the stochastic background of gravitational waves, the most ambitious goal of current and future CMB projects (André et al. 2014). Because of the broad variety of polarized emission spectra, extrapolations from low frequencies (<20 GHz) are inadequate to model the radio-source contribution in CMB polarization maps (Huffenberger et al. 2015).

At the same time, radio sources are the privileged calibrators both of the polarized intensity and of the polarization angle for CMB experiments. The systematic errors due to inaccuracies in the calibration of the polarization angle are becoming the limiting factor for CMB polarization experiments (e.g. Kaufman et al. 2014). Unfortunately, the number of compact, bright, highly polarized and stable-enough extragalactic sources, suitable for accurately calibrating CMB polarization maps are rare. One of the purposes of our polarization survey was to identify good candidates.

The paper is organized as follows. In Section 2, we briefly present the PACO project, its main results and the polarimetric observations of the selected sub-sample held in 2014 September with ATCA. In Section 3, we describe the data reduction. In Section 4, we discuss the data analysis and the spectral behaviours in total intensity and polarization. In Section 5, we address the variability properties for our sample. Finally, in Section 6 we draw our conclusions.

2 OBSERVATIONS

The PACO project yielded observations of 464 AT20G sources in 65 epochs between 2009 July and 2010 August in the 5.5–39 GHz frequency range with ATCA, nearly simultaneously (within 10 d) with the Planck observations (Massardi et al. 2016b). The main goal of the project was to characterize, in combination with Planck data, the total intensity spectra and their variability over a wide frequency range (at least from 5 to 217 GHz, but up to 857 GHz for some sources).

A multifrequency observing run was dedicated to polarimetry in 2014 September with ATCA. The sample was extracted from the ‘faint’ PACO sample (S_20GHz > 200 mJy) selecting sources in the Southern Ecliptic Pole region (ecliptic latitude |$<-75\,\deg$|⁠), where the satellite scanning strategy implies a better sensitivity.

The five extended sources in the sample (i.e. sources larger than the PACO resolution of ≃1 arcsec) were left out as the techniques to extract flux densities used in the PACO project underestimate their flux densities. The final complete sample comprises 53 compact sources with S_20GHz > 200 mJy in the AT20G catalogue.

The spectral setup consisted in three sets of 2 × 2 GHz CABB (Compact Array Broadband Backend) bands centred at 5.5–9, 18–24 and 33–38 GHz, similar to those for the PACO programme. A total of ≃12 h were allocated in three slots of ≃4 h each (including overheads and calibration) dedicated to each of the three bands over a period of least three days. Each object was observed for ≃3 min in two 1.5 min scans at different hour angles for each frequency. Weather conditions were very good during all the campaign.

The array configuration was H214, a hybrid (antenna are displayed also along the N–S direction) compact array with a nominal spatial resolution ranging from 36 to 5 arcsec in the 5.5–38 GHz interval if we consider only the five most-packed antennas. The resolution goes down to 0.5–4 arcsec considering also the longest baselines with the sixth antenna, but with a lower sensitivity. Adopting a hybrid configuration results in a more homogeneous uv-plane coverage of the largest spatial scales in less time. This results in a better imaging with respect to a non-hybrid solution, at least for our sample of mostly point-like objects.

3 DATA REDUCTION

The data reduction was done using the miriad software package (Sault, Teuben & Wright 1995) treating each frequency separately, as indicated in the ATCA User's Guide.¹ While loading the data, we corrected for the time-dependent instrumental xy-phase variation, exploiting the known signal injected from a noise diode mounted in one of the feeds of each antenna.

The reference flux-density calibrator (at all frequencies) was the source PKS1934−638, a bright (point-like) gigahertz peaked-spectrum radio galaxy, stable, unpolarized (at least below 30–40 GHz), whose model (see Reynolds 1994; Sault 2003; Partridge et al. 2016) is encoded into miriad itself. It is the only known source with all these characteristics in the Southern sky.

Once the calibration tables were derived, all solutions were ingested in the code for flux-density extraction. To better characterize the source spectra, we decided to split each 2 GHz-wide frequency band in sub-bands. Each of them was calibrated separately. For total intensity, we split each band into 512 MHz-wide sub-bands, as done in the past analyses for the PACO project. For polarized flux densities, we split bands in only two sub-bands to limit the Δν^−1/2 degradation in sensitivity.

Flux densities were estimated via the miriad task UVFLUX. Our sources are known to exhibit linear polarization (up to ∼10 per cent; Massardi et al. 2008, 2013), defined by the Q and U Stokes parameters. Observations of the circular polarization of extragalactic radio sources have demonstrated that it is very low, generally below 0.1–0.2 per cent, at least one order of magnitude lower than the linear polarization (Rayner, Norris & Sault 2000), hence generally undetectable for our sources, given the 0.6 mJy sensitivity. Hence, the rms σ_V (of the retrieved V Stokes parameter) is used as a noise estimator of the total intensity flux density I. The polarized emission, P, is given by the simple relation

\begin{equation} P=\sqrt{Q^2+U^2-\sigma ^2}, \end{equation}

(1)

where the σ² term removes the noise bias on P under the assumption of equal noise values, σ, for the Q and U parameters (e.g. Wardle & Kronberg 1974).²

The polarization angle ϕ and fraction m (usually in terms of a percentage) are

\begin{eqnarray} \phi =\frac{1}{2}\arctan {\left(\frac{U}{Q}\right)}, \end{eqnarray}

(2)

\begin{eqnarray} m=100\times P/I. \end{eqnarray}

(3)

3.1 Error budget

Assuming Gaussian noise, the error scales as |$1/\sqrt{N}$|⁠, N being the number of correlations at a given ν. A suitable estimate of the total intensity error is the sum in quadrature of σ_V with a systematic term, mainly accounting for the calibration uncertainty. Based on the past experience with PACO observations and on a comparison between flux densities obtained from different calibrators, the calibration error amounts to ∼2.5 per cent of the I flux density, giving for σ_I, the global error on I,

\begin{equation} \sigma ^2_I=\sigma ^2_V+(0.025\,I)^2. \end{equation}

(4)

The error, σ_P, on the polarized flux density, P, can be derived from the equation (1). A conservative ∼10 per cent error in the polarization calibration is adopted in this case. Then, we have

\begin{equation} \sigma ^2_P=\frac{Q^2\sigma ^2_Q+U^2\sigma ^2_U}{Q^2+U^2}+(0.1\,P)^2 , \end{equation}

(5)

σ_{Q, U} being the rms errors on the Stokes parameters Q and U, respectively. This estimate of the calibration error is consistent with the differences between flux densities obtained using two different calibrators for reducing our data.

From error propagation, the global error on the polarization fraction is

\begin{equation} \sigma ^2_m=\left(\frac{\sigma _I}{I}\right)^2+\left(\frac{\sigma _P}{P}\right)^2, \end{equation}

(6)

and that on ϕ is

\begin{equation} \sigma ^2_\phi =\frac{Q^2\sigma ^2_U+U^2\sigma ^2_Q}{4(Q^2+U^2)^2}+\sigma ^2_{\phi \,{\rm CAL}} , \end{equation}

(7)

where, again, the calibration error on the polarization angle, σ_{ϕ, CAL}, is added in quadrature. Under the hypothesis that the calibration error affects equally the Q and U parameters (σ_{Q, CAL} ≃σ_{U, CAL} = σ_CAL), σ_{P, CAL} ≃0.1P gives |$\sigma _{\rm CAL}= 0.1 P/\sqrt{2}$|⁠. Finally,

\begin{equation} \sigma ^2_{\phi ,{\rm CAL}}\simeq \frac{1}{4(Q^2+U^2)}2\sigma ^2_{\rm CAL}\simeq (0.05\,\mbox{rad})^2 , \end{equation}

(8)

implying |$\sigma _{\phi \,{\rm CAL}}\simeq 3\deg$|⁠. This estimation turns out to be consistent with differences in the polarization angle obtained by using different calibrators.

3.2 Imaging and flux-density measurements

To check our assumption of target compactness at all frequencies and the flux-density extraction, we created maps for each Stokes parameter by means of the standard miriad procedure. We adopted the natural weighting, the standard for point sources, to ensure the lowest noise level. We used multifrequency synthesis imaging and a standard Högbom algorithm.

The detection threshold was set at 5σ in both I and P. The |$\sigma _{I_{\rm map}}$| was derived from the I image region with no emission.

We use the task UVFLUX for flux-density measurements (except for a few cases described below). This task is designed for point-like sources and works directly on visibilities, minimizing artefacts and phase-instabilities which may affect more image-based measurements. Since our sample excludes extended sources (at least up to 20 GHz), we expect that flux densities provided by UVFLUX and by IMSTAT (the miriad task for flux-density estimation from imaging) show differences no greater than ≃10 per cent in total intensity (due to residual phase instabilities in the images). Moreover, we assumed a source pointing accurate enough to keep objects in the phase centre of the uv-plane. The latter hypothesis is supported by the fact that the PACO catalogue is drawn from the AT20G one, for which all positions are known with an accuracy ≲1 arcsec (Murphy et al. 2010).

Afterwards, we compared the IMSTAT image peak (in mJy beam⁻¹) and the UVFLUX flux-density estimation (for all the objects for which the uv-coverage allows imaging, i.e. ≃90 per cent of the cases) to reveal, in both I and P, whether an extended or displaced (from the phase centre) component is present. The median discrepancies, ΔI/I and ΔP/P, are ≃2.7 per cent and ≃4.3 per cent, respectively. In total intensity the relative discrepancy is >10 per cent for ≃4 per cent of the images. These large discrepancies are registered for frequencies >24 GHz; they reach maximum values between 20 and 25 per cent for two objects (AT20GJ080633−711217 and AT20GJ080649−610131, respectively) at 38 GHz. In all the cases, the image peak values are higher than the UVFLUX estimation. A visual inspection of the images confirms that the sources are barely resolved.

In polarization, the fractional discrepancy is >15 per cent in ≃11 per cent of the available images and >20 per cent in ≃8 per cent of the cases. In particular, there is one object, AT20GJ040848−750720, for which the excess of flux density (with respect to UVFLUX) measured in correspondence of the peak in the image reaches ≃361 per cent at 33 GHz and ≃352 per cent at 38 GHz. We show images for this source (see Fig. 1) at all the five frequencies at which they could be obtained in total intensity. Polarized emissions are instead displayed by contour levels. It can be seen that the object is marginally resolved at the lower frequencies. At the higher frequencies, a second component appears and the polarized emission mainly comes from it. According to Morganti et al. (1999), AT20GJ0408−7507 is a bright FR II radio galaxy at z ≃0.7, dominated by two bright lobes. Both lobes have high depolarization, slightly higher in the eastern one.

Figure 1.

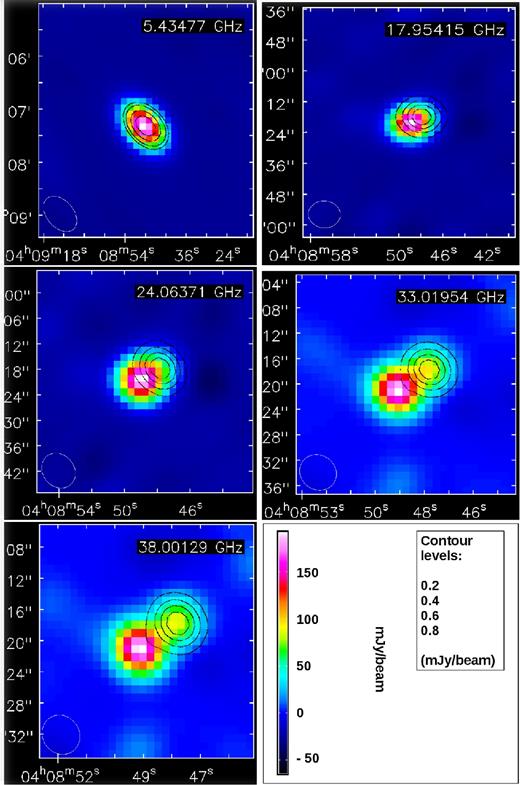
Maps in total intensity (colours) and polarization (contours) for AT20GJ0408−7507 at 5.5, 18, 24, 33 and 38 GHz. The two-lobe structure is resolved at the higher frequencies. The eastern lobe appears to be strongly depolarized.

Given the good matching between flux densities from imaging and from visibilities for point-like objects (both in total intensity and in polarization), we decided to integrate over a suitable region on I images to recover the total intensity flux densities in the case of slightly resolved objects. In the case of the flux discrepancies in polarization, as images reveal an emerging point-like component displaced from the phase centre, we estimated the flux density by considering the peak of the P image.

The complete catalogue (flux densities and fitting parameters, polarization fractions and angles) for the observations discussed in this paper is available online, as Supporting Information.

4 DATA ANALYSIS

We obtained 5 σ detections in polarization, with a median error of ≃0.6 mJy, for ≃91 per cent of our sources. The detection rate is nearly uniform across the observed frequencies (48 sources detected at 5.5 GHz and 49 detected at 38 GHz). To check whether our data are affected by intraband depolarization at any frequency, we have sub-divided each 2 GHz-wide band into two 1 GHz-wide sub-bands and compared the polarization degrees measured in the sub-bands. As illustrated by the examples shown in Fig. 2, no systematic difference was found.

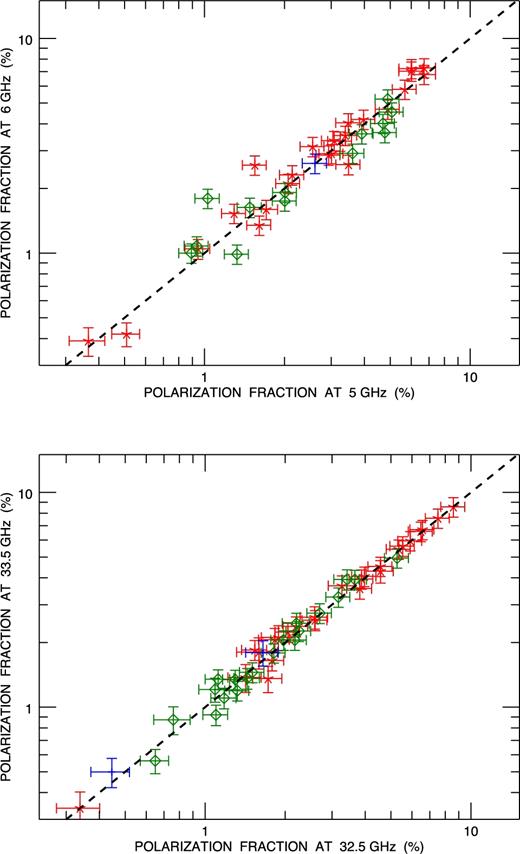
$Comparison of the fractional polarization measured in the two 1 GHz-wide sub-bands of the 2 GHz-wide bands at 5.5 GHz (upper panel) and at 33 GHz (lower panel). Red asterisks, blue ‘+’ signs and green diamonds refer to steep-spectrum, flat-spectrum and peaked-spectrum sources, respectively (the spectral classification is described in Section 4.2). The bisector is shown as a dashed line.$

Figure 2.

Comparison of the fractional polarization measured in the two 1 GHz-wide sub-bands of the 2 GHz-wide bands at 5.5 GHz (upper panel) and at 33 GHz (lower panel). Red asterisks, blue ‘+’ signs and green diamonds refer to steep-spectrum, flat-spectrum and peaked-spectrum sources, respectively (the spectral classification is described in Section 4.2). The bisector is shown as a dashed line.

4.1 Fitting procedures

To properly fit source spectra, we start considering a double power law represented by the expression

\begin{equation} S(\nu )=\frac{S_0}{\left(\frac{\nu }{\nu _0}\right)^{-a}+\left(\frac{\nu }{\nu _0}\right)^{-b}}, \end{equation}

(9)

or by a concave version of it (needed in two cases):

\begin{equation} S(\nu )=S_0\left(1-\frac{1}{\left(\frac{\nu }{\nu _0}\right)^{-a}+\left(\frac{\nu }{\nu _0}\right)^{-b}}\right), \end{equation}

(10)

where S₀, ν₀, a and b are free parameters. This function properly fits the total intensity data in ≃96 per cent of the cases, confirming what was found in previous works (e.g. Massardi et al. 2016b). In two cases (sources AT20GJ0546−6415 and AT20GJ0719−6218), the double power law provided a poor fit and we resorted to a triple-power-law model which requires three additional parameters, i.e. S₁, ν₁ and c:

\begin{eqnarray} S(\nu )=\frac{S_0}{\left(\frac{\nu }{\nu _0}\right)^{-a}+\left(\frac{\nu }{\nu _0}\right)^{-b}}+ \frac{S_1}{\left(\frac{\nu }{\nu _1}\right)^{-b}+\left(\frac{\nu }{\nu _1}\right)^{-c}}. \end{eqnarray}

(11)

As for fitting procedures in polarization, we need detections at no less than six frequencies (over a maximum of 12) in the case of a double power law and at no less than nine frequencies for a triple power law. If a point source was not detected in one (or both) of the split frequency ranges of a band, we used the corresponding non-split detection, when available. Given the small fraction (≃9 per cent) of non-detections, we did not consider the upper limits in doing the spectral fits. In only three cases (AT20GJ054641−641522, AT20GJ062524−602030 and AT20GJ075714−735308), we do not have detections at enough frequencies to get a proper fit.

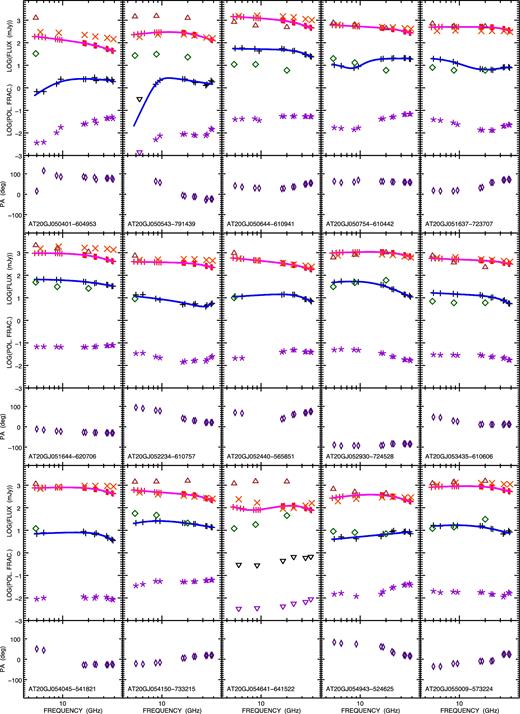
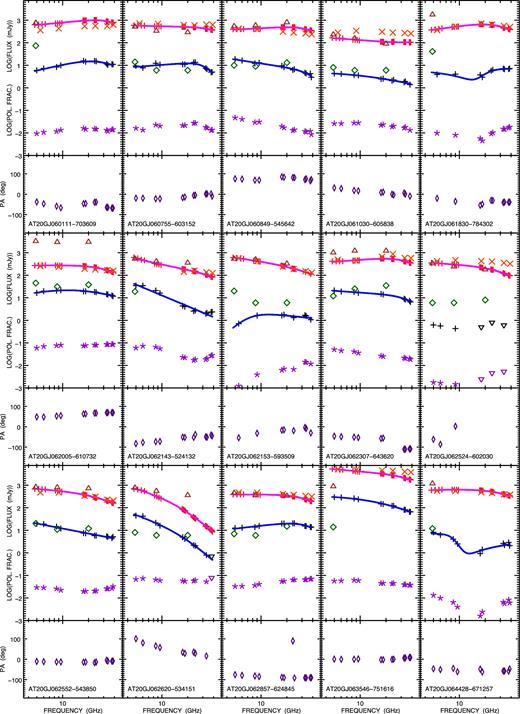
About 90 per cent of our source spectra could be fitted with either a double power law or by a concave version of it (needed in six cases). The median-reduced χ² are 0.31 and 0.82 for I and P, respectively. This seems to confirm that our approach in error estimates is indeed conservative. Fig. 3 shows the data, the fitting curves and, when available, the previous PACO best epoch (2009–2010) observations in total intensity and the AT20G best epoch (2004–2008) observations in total intensity and in polarization.

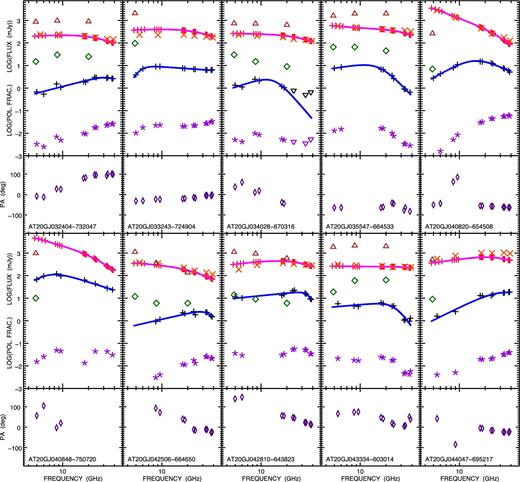
$Spectra in total intensity and polarization, polarization fraction and angle for the 53 objects of the faint PACO sample, observed in 2014 September. The error bars are not displayed since they are smaller than the symbols. Total intensity: red pluses indicate ATCA 2014 September observations (each point represents a 512 MHz-wide sub-band) and the solid magenta lines show the fitting curves. The orange crosses show the median PACO flux densities (2009 July–2010 August) while the brown triangles show the AT20G observations (best epoch in 2004–2008). Polarization (flux density): black pluses refer to 2014 September observations and correspond to 1 GHz sub-bands or to the full 2 GHz band. Upper limits are shown as black downward triangles. The solid blue lines show the fitting curves. The AT20G observations (best epoch in 2004–2008) are represented by green diamonds. Polarization fraction: violet asterisks refer to 2014 September observations. Upper limits are shown as downward violet triangles. Polarization angle: this is displayed below each panel with flux densities and polarization fraction. Indigo diamonds refer to the 2014 September campaign.$

Figure 3.

Spectra in total intensity and polarization, polarization fraction and angle for the 53 objects of the faint PACO sample, observed in 2014 September. The error bars are not displayed since they are smaller than the symbols. Total intensity: red pluses indicate ATCA 2014 September observations (each point represents a 512 MHz-wide sub-band) and the solid magenta lines show the fitting curves. The orange crosses show the median PACO flux densities (2009 July–2010 August) while the brown triangles show the AT20G observations (best epoch in 2004–2008). Polarization (flux density): black pluses refer to 2014 September observations and correspond to 1 GHz sub-bands or to the full 2 GHz band. Upper limits are shown as black downward triangles. The solid blue lines show the fitting curves. The AT20G observations (best epoch in 2004–2008) are represented by green diamonds. Polarization fraction: violet asterisks refer to 2014 September observations. Upper limits are shown as downward violet triangles. Polarization angle: this is displayed below each panel with flux densities and polarization fraction. Indigo diamonds refer to the 2014 September campaign.

Figure 3

– continued

Figure 3

– continued

Figure 3

– continued

4.2 Spectral properties of the sample

We define the spectral index |$\alpha _{\nu _1}^{\nu _2}$| between the frequencies ν₁ and ν₂ as

\begin{equation} \alpha _{\nu _1}^{\nu _2}=\frac{\log {\left(S(\nu _2)/S(\nu _1)\right)}}{\log {\left(\nu _2/\nu _1\right)}} , \end{equation}

(12)

where S(ν₁) and S(ν₂) are the flux densities at the two frequencies. To minimize fluctuations due to noise, spectral indices were calculated using the spectral fits in total intensity and in polarization. We selected five frequencies (almost) equally spaced in a logarithmic scale, namely 5.5, 10, 18, 28 and 38 GHz.

We classified the sources according to their |$\alpha _{5.5}^{10}$| and |$\alpha _{28}^{38}$| spectral indices. The choice of these frequency intervals follows from the fact that the majority of spectral peaks occur around 10–20 GHz.

We defined as flat-spectrum (F) sources those with |$-0.5<\alpha _{5.5}^{10}<0.5$| and |$-0.5<\alpha _{28}^{38}<0.5$|⁠. Sources outside these spectral index ranges were sub-divided as follows:

steep-spectrum (S), if |$\alpha _{5.5}^{10}<0$| and |$\alpha _{28}^{38}<0$|⁠;
inverted-spectrum (I), if |$\alpha _{5.5}^{10}>0$| and |$\alpha _{28}^{38}>0$|⁠;
peaked-spectrum (P), if |$\alpha _{5.5}^{10}>0$| and |$\alpha _{28}^{38}<0$|⁠;
upturning-spectrum (U), if |$\alpha _{5.5}^{10}<0$| and |$\alpha _{28}^{38}>0$|⁠.

Table 2 reports the distribution among these spectral types for the complete sample. In both cases, the most populated spectral types are P and S. However, there is only a weak correspondence between spectral types in total intensity and in polarization: less than half P- or S-type sources in total intensity have the same classification in polarization. On the other hand, the statistics is quite low so that any firm conclusion is premature.

Table 2.

Distribution of sources per spectral type in total intensity and in polarization. The row ‘NA’ refers to the three objects classified in total intensity but missing a spectral fit in polarization. The last row reports the total for a given spectral class in total intensity, while the last column does the same in polarization.

Tot. Int. →	(I)	(P)	(F)	(S)	(U)
Pol. Int. ↓
(I)	0	1	0	0	0	1
(P)	0	10	1	13	0	24
(F)	0	3	0	2	0	5
(S)	0	2	1	11	0	14
(U)	0	4	0	2	0	6
(NA)	0	1	0	2	0	3
	0	21	2	30	0

Tot. Int. →	(I)	(P)	(F)	(S)	(U)
Pol. Int. ↓
(I)	0	1	0	0	0	1
(P)	0	10	1	13	0	24
(F)	0	3	0	2	0	5
(S)	0	2	1	11	0	14
(U)	0	4	0	2	0	6
(NA)	0	1	0	2	0	3
	0	21	2	30	0

Table 2.

Distribution of sources per spectral type in total intensity and in polarization. The row ‘NA’ refers to the three objects classified in total intensity but missing a spectral fit in polarization. The last row reports the total for a given spectral class in total intensity, while the last column does the same in polarization.

Tot. Int. →	(I)	(P)	(F)	(S)	(U)
Pol. Int. ↓
(I)	0	1	0	0	0	1
(P)	0	10	1	13	0	24
(F)	0	3	0	2	0	5
(S)	0	2	1	11	0	14
(U)	0	4	0	2	0	6
(NA)	0	1	0	2	0	3
	0	21	2	30	0

Tot. Int. →	(I)	(P)	(F)	(S)	(U)
Pol. Int. ↓
(I)	0	1	0	0	0	1
(P)	0	10	1	13	0	24
(F)	0	3	0	2	0	5
(S)	0	2	1	11	0	14
(U)	0	4	0	2	0	6
(NA)	0	1	0	2	0	3
	0	21	2	30	0

In Table 3, we list the quartiles of spectral indices, both in total intensity and in polarization, for the full sample and for the two most populated spectral classes: steep- and peaked-spectrum sources. Also in the polarization case, we kept the spectral classification done in total intensity.

Table 3.

First, second (median) and third quartiles of spectral indices in total intensity and in polarization for different frequency ranges. We give values for the full sample and for the two main spectral classes, as classified in total intensity.

Tot. Int.	5.5–10			10–18			18–28			28–38 GHz
Quart.	1	2	3	1	2	3	1	2	3	1	2	3
All (50)	−0.29	−0.09	0.07	−0.44	−0.19	−0.06	−0.77	−0.53	−0.35	−1.22	−1.07	−0.88
Steep (30)	−0.44	−0.27	−0.15	−0.60	−0.39	−0.25	−0.93	−0.66	−0.53	−1.31	−1.19	−1.03
Peaked (21)	0.05	0.12	0.37	−0.10	−0.02	0.25	−0.52	−0.39	−0.23	−1.10	−0.95	−0.80
Pol. Int.	5.5–10			10–18			18–28			28–38 GHz
Quart.	1	2	3	1	2	3	1	2	3	1	2	3
All (50)	−0.32	0.12	0.48	−0.60	−0.26	0.29	−0.81	−0.50	0.00	−1.63	−0.94	−0.32
Steep (28)	−0.29	0.03	0.41	−0.72	−0.29	0.17	−1.07	−0.55	−0.34	−1.74	−1.21	−0.61
Peaked (20)	−0.45	0.25	0.87	−0.35	−0.03	0.53	−0.58	0.01	0.62	−1.24	−0.47	0.29

Tot. Int.	5.5–10			10–18			18–28			28–38 GHz
Quart.	1	2	3	1	2	3	1	2	3	1	2	3
All (50)	−0.29	−0.09	0.07	−0.44	−0.19	−0.06	−0.77	−0.53	−0.35	−1.22	−1.07	−0.88
Steep (30)	−0.44	−0.27	−0.15	−0.60	−0.39	−0.25	−0.93	−0.66	−0.53	−1.31	−1.19	−1.03
Peaked (21)	0.05	0.12	0.37	−0.10	−0.02	0.25	−0.52	−0.39	−0.23	−1.10	−0.95	−0.80
Pol. Int.	5.5–10			10–18			18–28			28–38 GHz
Quart.	1	2	3	1	2	3	1	2	3	1	2	3
All (50)	−0.32	0.12	0.48	−0.60	−0.26	0.29	−0.81	−0.50	0.00	−1.63	−0.94	−0.32
Steep (28)	−0.29	0.03	0.41	−0.72	−0.29	0.17	−1.07	−0.55	−0.34	−1.74	−1.21	−0.61
Peaked (20)	−0.45	0.25	0.87	−0.35	−0.03	0.53	−0.58	0.01	0.62	−1.24	−0.47	0.29

Table 3.

First, second (median) and third quartiles of spectral indices in total intensity and in polarization for different frequency ranges. We give values for the full sample and for the two main spectral classes, as classified in total intensity.

Tot. Int.	5.5–10			10–18			18–28			28–38 GHz
Quart.	1	2	3	1	2	3	1	2	3	1	2	3
All (50)	−0.29	−0.09	0.07	−0.44	−0.19	−0.06	−0.77	−0.53	−0.35	−1.22	−1.07	−0.88
Steep (30)	−0.44	−0.27	−0.15	−0.60	−0.39	−0.25	−0.93	−0.66	−0.53	−1.31	−1.19	−1.03
Peaked (21)	0.05	0.12	0.37	−0.10	−0.02	0.25	−0.52	−0.39	−0.23	−1.10	−0.95	−0.80
Pol. Int.	5.5–10			10–18			18–28			28–38 GHz
Quart.	1	2	3	1	2	3	1	2	3	1	2	3
All (50)	−0.32	0.12	0.48	−0.60	−0.26	0.29	−0.81	−0.50	0.00	−1.63	−0.94	−0.32
Steep (28)	−0.29	0.03	0.41	−0.72	−0.29	0.17	−1.07	−0.55	−0.34	−1.74	−1.21	−0.61
Peaked (20)	−0.45	0.25	0.87	−0.35	−0.03	0.53	−0.58	0.01	0.62	−1.24	−0.47	0.29

Tot. Int.	5.5–10			10–18			18–28			28–38 GHz
Quart.	1	2	3	1	2	3	1	2	3	1	2	3
All (50)	−0.29	−0.09	0.07	−0.44	−0.19	−0.06	−0.77	−0.53	−0.35	−1.22	−1.07	−0.88
Steep (30)	−0.44	−0.27	−0.15	−0.60	−0.39	−0.25	−0.93	−0.66	−0.53	−1.31	−1.19	−1.03
Peaked (21)	0.05	0.12	0.37	−0.10	−0.02	0.25	−0.52	−0.39	−0.23	−1.10	−0.95	−0.80
Pol. Int.	5.5–10			10–18			18–28			28–38 GHz
Quart.	1	2	3	1	2	3	1	2	3	1	2	3
All (50)	−0.32	0.12	0.48	−0.60	−0.26	0.29	−0.81	−0.50	0.00	−1.63	−0.94	−0.32
Steep (28)	−0.29	0.03	0.41	−0.72	−0.29	0.17	−1.07	−0.55	−0.34	−1.74	−1.21	−0.61
Peaked (20)	−0.45	0.25	0.87	−0.35	−0.03	0.53	−0.58	0.01	0.62	−1.24	−0.47	0.29

The median spectral indices become steeper and steeper with increasing frequency. In total intensity they become, at ν ≳ 28 GHz, steeper than the typical spectral index of classical low-frequency steep-spectrum sources (α ≃−0.75), even though almost all these sources are classified as ‘flat-spectrum’ at low frequencies. A similar trend is found in the polarized flux density, although the high-frequency steepening is somewhat less pronounced.

A less steep median high-frequency spectral index in total intensity (⁠|$\alpha _{30}^{40}\simeq -0.69$|⁠) was reported by Bonavera et al. (2011) for the full PACO ‘faint’ sample of 159 sources. We have checked that the difference can be accounted for by the revision of the model for the reference flux-density calibrator, PKS1934−638. Using the previous model, adopted by Bonavera et al. (2011) but less accurate for frequencies >11 GHz, we get, for our sample, a median spectral index of −0.68 ± 0.05, consistent with the results by Bonavera et al. (2011). Somewhat flatter spectral indices in polarization, compared to total intensity, were also found by Massardi et al. (2013) for the ‘bright’ AT20G sample (S_20 GHz > 500 mJy); for these objects, however, the data were limited to ν ≤ 18 GHz.

Fig. 4 shows total intensity and polarization colour–colour (28–38 GHz versus 5.5–10 GHz) plots. As explained in the caption, the symbols correspond to the spectral classification in total intensity mentioned above while the colours correspond to the spectral shape in the 5.5–18 GHz range. The left-hand panel shows a clear segregation of sources of each colour. The median spectral steepening |$\Delta \alpha =\alpha _{28}^{38}-\alpha _{5}^{10}$| varies from −0.86, the value obtained both for the red (steep-spectrum) and blue (flat-spectrum), to −1.41 for the green (peaked-spectrum) ones. No analogous segregation is seen when considering the spectral indices of the polarized emission (right-hand panel). Fig. 5 shows that there is no significant correlation between the 5.5–10 GHz (left-hand panel) or the 28–38 GHz (right-hand panel) spectral indices in total intensity and in polarization. This implies that the polarization degree of individual sources varies with frequency, as pointed out by previous analyses. Here, we reiterate this result with higher accuracy and extend it to higher frequencies and fainter flux densities. On the other hand, as discussed in the following sub-section, we do not find any significant frequency dependence of the mean polarization degree.

Figure 4.

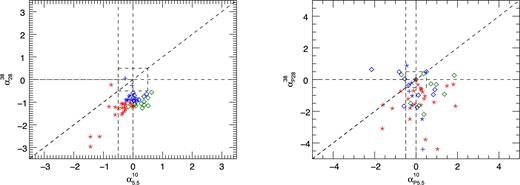
Radio colour–colour diagrams for (from left to right) total intensity and polarized flux density. Symbols identify the spectral type in total intensity: pluses for flat-spectrum, asterisks for steep-spectrum, diamonds for peaked-spectrum. Colours refer to the spectral shape between 5.5 and 18 GHz: red for steep-spectrum, blue for flat-spectrum and green for peaked-spectrum sources.

Figure 5.

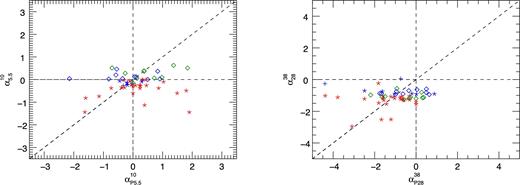
Comparison between the spectral index in total intensity and in polarization in the ranges 5.5–10 GHz (left) and 28–38 GHz (right). The meaning of symbols and colours is the same as in Fig. 4.

4.3 Polarization fraction

Polarization data, provided by the National Radio Astronomy Observatory Very Large Array Sky Survey (NVSS) at 1.4 GHz, brought Tucci et al. (2004) to argue that Faraday depolarization can be significant up to ≃10 GHz. Furthermore, especially for compact objects, magnetic fields may be expected to be increasingly ordered for regions closer and closer to the central AGN, which are likely to dominate at the highest radio frequencies.

Both elements would lead to an increase of the polarization degree with rest-frame frequency. According to Tucci et al. (2004), the mild anticorrelation between polarization degree and 1.4 GHz flux density, detected for steep-spectrum sources in the NVSS, could be due to an increase of the mean redshift of sources (hence of the rest-frame frequency) with decreasing flux density. However, no trend of the polarization degree with 1.4 GHz flux density was detected for NVSS flat-spectrum sources and the reality of the anticorrelation for steep-spectrum sources was questioned by Hales et al. (2014).

No significant variations of the polarization degree with either flux density or with frequency were found by Massardi et al. (2013) and Battye et al. (2011). Higher polarization degrees at mm wavelengths were reported by Agudo et al. (2010, 2014) and by Sajina et al. (2011). However, the former studies a higher frequency selected sample (S_86GHz > 0.9 Jy), while the latter focuses on a fainter population (S_20GHz > 40 mJy) and their high-frequency results are likely biased by not having taken into account non-detections (Tucci & Toffolatti 2012).

We addressed this issue with a slightly better combination of flux density and frequency ranges than the previous studies of samples selected at high frequency. The high detection rate in polarization of our complete sample and the use of survival analysis techniques to take into account upper limits ensure that the selection bias must be negligible. The significance of the rejection of the null hypothesis (no correlation of the polarization degree with frequency) was tested computing the distributions of polarization degrees at each frequency by means of the Kaplan–Meier estimator included in the asurv package (Lavalley, Isobe & Feigelson 1992). Then, the distributions (cf. Table 4) were compared using the Kolmogorov–Smirnov test included in the same package. The distributions at 5.5 and 38 GHz are consistent with being drawn from the same parent distribution (see also Fig. 6) in all the cases (all the sample, steep sources only and peaked sources only) with a rejection level <1σ. However, we are aware that a hypothetical trend may be easily washed out given the dispersions of polarization fractions and the limited size of the sample. To justify this, we point out the variety of behaviours in polarized spectra (cf. Table 2), which results in higher dispersions shown by spectral indices in polarization with respect to total intensity ones (cf. Table 3), hence in higher scatters of polarization degrees. Again, we warn the reader that the flux-density range spanned by our sample is quite limited.

$Median polarization fraction behaviour with frequency (at 5.5, 9, 18, 24, 33 and 38 GHz) for all the sources (black), for steep sources (red) and for peaked ones (green). The errors on median values are given by $1.253\, {\rm rms}/\sqrt{N}$, where rms is the standard deviation around the mean and N is the number of the data (at a given frequency) for a given class of objects (cf. Arkin & Colton 1970).$

Figure 6.

Median polarization fraction behaviour with frequency (at 5.5, 9, 18, 24, 33 and 38 GHz) for all the sources (black), for steep sources (red) and for peaked ones (green). The errors on median values are given by |$1.253\, {\rm rms}/\sqrt{N}$|⁠, where rms is the standard deviation around the mean and N is the number of the data (at a given frequency) for a given class of objects (cf. Arkin & Colton 1970).

Table 4.

First, second (median) and third quartiles of the polarization fraction at each observed frequency given by the Kaplan–Meier estimator, taking into account the upper limits, for the full sample and for the steep- and peaked-spectrum sources. The last row reports probabilities for the null hypothesis (i.e. the two samples are drawn from the same parent distribution) given by the Kolmogorov–Smirnov test performed on the steep and peaked groups, considering together 5.5 and 9 GHz, the 18–38 GHz frequency interval and all the frequencies, respectively.

Class.	Frequencies (GHz)
	5.5			9			18			24			33			38
	1	2	3	1	2	3	1	2	3	1	2	3	1	2	3	1	2	3
All	0.92	1.92	3.52	0.89	2.00	3.49	1.10	2.02	2.99	1.28	2.01	3.33	1.26	2.01	3.79	1.37	2.27	3.88
Steep	0.98	2.82	3.74	1.03	2.27	4.13	1.55	2.35	4.27	1.59	2.42	4.67	1.69	2.58	5.09	1.53	2.80	4.68
Peaked	0.47	1.09	2.91	0.61	1.24	2.32	0.90	1.45	1.92	1.04	1.48	2.14	1.14	1.44	2.30	1.34	1.69	2.53
Prob.	(5.5–9 GHz)			0.035 5238			(18–38 GHz)			8.756 41 × 10⁻⁷			(All freqs.)			5.393 17 × 10⁻⁸

Class.	Frequencies (GHz)
	5.5			9			18			24			33			38
	1	2	3	1	2	3	1	2	3	1	2	3	1	2	3	1	2	3
All	0.92	1.92	3.52	0.89	2.00	3.49	1.10	2.02	2.99	1.28	2.01	3.33	1.26	2.01	3.79	1.37	2.27	3.88
Steep	0.98	2.82	3.74	1.03	2.27	4.13	1.55	2.35	4.27	1.59	2.42	4.67	1.69	2.58	5.09	1.53	2.80	4.68
Peaked	0.47	1.09	2.91	0.61	1.24	2.32	0.90	1.45	1.92	1.04	1.48	2.14	1.14	1.44	2.30	1.34	1.69	2.53
Prob.	(5.5–9 GHz)			0.035 5238			(18–38 GHz)			8.756 41 × 10⁻⁷			(All freqs.)			5.393 17 × 10⁻⁸

Table 4.

First, second (median) and third quartiles of the polarization fraction at each observed frequency given by the Kaplan–Meier estimator, taking into account the upper limits, for the full sample and for the steep- and peaked-spectrum sources. The last row reports probabilities for the null hypothesis (i.e. the two samples are drawn from the same parent distribution) given by the Kolmogorov–Smirnov test performed on the steep and peaked groups, considering together 5.5 and 9 GHz, the 18–38 GHz frequency interval and all the frequencies, respectively.

Class.	Frequencies (GHz)
	5.5			9			18			24			33			38
	1	2	3	1	2	3	1	2	3	1	2	3	1	2	3	1	2	3
All	0.92	1.92	3.52	0.89	2.00	3.49	1.10	2.02	2.99	1.28	2.01	3.33	1.26	2.01	3.79	1.37	2.27	3.88
Steep	0.98	2.82	3.74	1.03	2.27	4.13	1.55	2.35	4.27	1.59	2.42	4.67	1.69	2.58	5.09	1.53	2.80	4.68
Peaked	0.47	1.09	2.91	0.61	1.24	2.32	0.90	1.45	1.92	1.04	1.48	2.14	1.14	1.44	2.30	1.34	1.69	2.53
Prob.	(5.5–9 GHz)			0.035 5238			(18–38 GHz)			8.756 41 × 10⁻⁷			(All freqs.)			5.393 17 × 10⁻⁸

Class.	Frequencies (GHz)
	5.5			9			18			24			33			38
	1	2	3	1	2	3	1	2	3	1	2	3	1	2	3	1	2	3
All	0.92	1.92	3.52	0.89	2.00	3.49	1.10	2.02	2.99	1.28	2.01	3.33	1.26	2.01	3.79	1.37	2.27	3.88
Steep	0.98	2.82	3.74	1.03	2.27	4.13	1.55	2.35	4.27	1.59	2.42	4.67	1.69	2.58	5.09	1.53	2.80	4.68
Peaked	0.47	1.09	2.91	0.61	1.24	2.32	0.90	1.45	1.92	1.04	1.48	2.14	1.14	1.44	2.30	1.34	1.69	2.53
Prob.	(5.5–9 GHz)			0.035 5238			(18–38 GHz)			8.756 41 × 10⁻⁷			(All freqs.)			5.393 17 × 10⁻⁸

As shown by the Table 4 and by Fig. 6, the median polarization fraction is generally slightly higher for steep-spectrum sources than for the peaked-spectrum ones. The last line of Table 4 shows, for each frequency, the probability that the two source types are drawn from the same parent population (null hypothesis), obtained from the Kolmogorov–Smirnov test. At 5.5 and 9.0 GHz, this hypothesis can be rejected at a level between 2 σ and 3 σ, while at higher frequencies the rejection level is between 4 σ and 5 σ. Combining the data at all frequencies, the probability of the null hypothesis is ∼5 × 10⁻⁸ so that the hypothesis can be rejected at a >5 σ significance.

4.4 Rotation measures

The polarization angle was calibrated setting the parameter ‘xycorr’ in the miriad task ATLOD, which applies phase corrections provided by a noise diode mounted on one antenna feed. Partridge et al. (2016) found that the polarization angles measured by ATCA in this way agree with those measured by Planck to within |$\pm 2\,\deg$|⁠.

Our multifrequency data have allowed us to perform a search for Faraday rotation. To this end, we divided each 2 GHz band in 1 GHz sub-bands. We first checked the compatibility of the position angles measured for each sub-band with those measured for the full band. In almost all cases, we found good agreement within the errors. Considering the sub-bands we have position angle measurements for each source at up to 12 wavelengths. In the presence of Faraday rotation, the polarization angle, ϕ, has a simple dependence on the wavelength, λ, namely

\begin{equation} \phi =\phi _0+\text{RM} \lambda ^2, \end{equation}

(13)

where ϕ₀ is the intrinsic polarization angle and RM is the rotation measure. We adopt the idl³ procedure ‘linfit’ for estimating the fitting parameters. We assume a fit is considered acceptable if the reduced χ² < 3 and the associated probability level p > 0.1 (as suggested by the algorithm), which means that the computed parameters are believable. According to these criteria, our polarization measurements show evidence of non-zero Faraday rotation only for two sources considering the whole spectral range 5.5–38 GHz (AT20GJ051644−620706 and AT20GJ070031−661045). The derived values of the rotation measure are (96 ± 13) rad m⁻² and (30 ± 13) rad m⁻², respectively. The rest of the sample shows various and more complex behaviours: we notice a marked difference typically occurring between the lower frequencies (5.5 and 9 GHz) and the higher frequencies (18 and 24 GHz). This suggests different plasma conditions and/or magnetic field structures in the regions dominating the emission in the two frequency ranges. We defer a detailed analysis of this issue to a future paper that will take advantage of a larger sample and of a wider spectral coverage obtained, in our most recent ATCA polarimetric observations.

5 VARIABILITY

Taking into account also the PACO and the AT20G measurements, the 53 sources analysed in this work have at least three epochs of observations in total intensity and two epochs in polarization (no polarization data from PACO). The AT20G data were taken between 2004 and 2008, the PACO data between 2009 July and 2010 August and our observations were done in 2014 September. The typical global time span is of about eight years.

In combining the PACO measurements with the two other data sets, we neglected the small difference in the central frequencies (39 versus 38 GHz) of the highest frequency channels. For each but three sources in our sample, there is at least one PACO epoch for which all the six frequencies were observed. In several cases, all the frequencies were observed two or three times. In many more cases, we have repeated observations for only a sub-set of frequencies. Since the variability on time-scales from a few months to 2–4 yr were discussed in previous works of our group (e.g. Massardi et al. 2016b), we focus here on longer time-scales (5–8 yr).

We have considered only PACO observations of at least four frequencies, all carried out within several months. Multiple PACO observations of sources at a given frequency were averaged. Indeed, similarly to what was done here with total intensity flux densities, the PACO catalogue reports for each 2 GHz frequency band four flux densities, one for each 512 MHz sub-band. Before performing any temporal average, we consider the median value over the four chunks to provide a value for each frequency. Then, the error associated with the averaged PACO flux densities σ_PACO, is given by

\begin{equation} \sigma _{\rm PACO} = \sqrt{\sigma ^2_{\rm max}+\sigma ^2_{\langle S \rangle _{\rm PACO}}} , \end{equation}

(14)

were σ_max is the maximum error over the four 512 MHz sub-bands and |$\sigma _{\langle S \rangle _{\rm PACO}}$| the error associated with the average of the PACO fluxes over the selected epochs, 〈S〉_PACO.

The AT20G data were collected at 4.86, 8.64 and 20 GHz with the old ATCA correlator set with a 2 × 128 MHz contiguous bands for each frequency. We can straightforwardly compare these observations with ours at 5.5, 9 and 18 GHz, neglecting the small differences in the central frequencies.

Following Sadler et al. (2006), the variability index (VI) of a population is defined as

\begin{equation} \hbox{VI} = \frac{100}{\langle S \rangle } \sqrt{\frac{\displaystyle \sum _{i=1}^{n}\left( S_i-\langle S \rangle \right)^2 - \displaystyle \sum _{i=1}^{n} \sigma _i^2}{n}}, \end{equation}

(15)

〈S〉 being the average of the n flux-density measurements at a given frequency, S_i, having error σ_i.

In Table 5, we report the mean VIs in total intensity at each frequency for two time lags, 4–5 and 8 yr, corresponding to the intervals between the present observations and the PACO or the AT20G ones, respectively. Variability indices were computed both for the full sample and for the steep- and peaked-spectrum populations. The errors provided in the table are the rms of the VIs rescaled by the |$\sqrt{N}$|⁠, where N is the number of objects in the considered class.

Table 5.

Mean variability indices in total intensity and in polarization (last row).

Sel.	Time (yr)	5.5	9	18	24	33	38
All	4–5	14 ± 2	14 ± 2	15 ± 2	16 ± 2	21 ± 2	22 ± 2
	8	36 ± 3	32 ± 3	36 ± 3
Steep	4–5	10 ± 2	10 ± 2	12 ± 2	14 ± 2	21 ± 3	24 ± 3
	8	35 ± 5	32 ± 5	38 ± 5
Peaked	4–5	20 ± 3	20 ± 3	18 ± 3	19 ± 3	20 ± 4	19 ± 3
	8	38 ± 5	32 ± 5	31 ± 5
All (pol.)	8	50 ± 7	57 ± 6	53 ± 6

Sel.	Time (yr)	5.5	9	18	24	33	38
All	4–5	14 ± 2	14 ± 2	15 ± 2	16 ± 2	21 ± 2	22 ± 2
	8	36 ± 3	32 ± 3	36 ± 3
Steep	4–5	10 ± 2	10 ± 2	12 ± 2	14 ± 2	21 ± 3	24 ± 3
	8	35 ± 5	32 ± 5	38 ± 5
Peaked	4–5	20 ± 3	20 ± 3	18 ± 3	19 ± 3	20 ± 4	19 ± 3
	8	38 ± 5	32 ± 5	31 ± 5
All (pol.)	8	50 ± 7	57 ± 6	53 ± 6

Table 5.

Mean variability indices in total intensity and in polarization (last row).

Sel.	Time (yr)	5.5	9	18	24	33	38
All	4–5	14 ± 2	14 ± 2	15 ± 2	16 ± 2	21 ± 2	22 ± 2
	8	36 ± 3	32 ± 3	36 ± 3
Steep	4–5	10 ± 2	10 ± 2	12 ± 2	14 ± 2	21 ± 3	24 ± 3
	8	35 ± 5	32 ± 5	38 ± 5
Peaked	4–5	20 ± 3	20 ± 3	18 ± 3	19 ± 3	20 ± 4	19 ± 3
	8	38 ± 5	32 ± 5	31 ± 5
All (pol.)	8	50 ± 7	57 ± 6	53 ± 6

Sel.	Time (yr)	5.5	9	18	24	33	38
All	4–5	14 ± 2	14 ± 2	15 ± 2	16 ± 2	21 ± 2	22 ± 2
	8	36 ± 3	32 ± 3	36 ± 3
Steep	4–5	10 ± 2	10 ± 2	12 ± 2	14 ± 2	21 ± 3	24 ± 3
	8	35 ± 5	32 ± 5	38 ± 5
Peaked	4–5	20 ± 3	20 ± 3	18 ± 3	19 ± 3	20 ± 4	19 ± 3
	8	38 ± 5	32 ± 5	31 ± 5
All (pol.)	8	50 ± 7	57 ± 6	53 ± 6

For a time lag of 4–5 yr, the mean VI of steep-spectrum sources increases with frequency, consistent with earlier results (Impey & Neugebauer 1988; Ciaramella et al. 2004; Bonavera et al. 2011). The increase is slightly milder for the full sample because it is not seen in the case of peaked-spectrum sources. No trend with frequency is found for the 8 yr lag.

Fig. 7 reports for each frequency (different colours) the variability index against the time lag. Our time lag coverage is complemented by variability measurements provided by Massardi et al. (2016a) for the faint PACO sample: on average, there appears an increase of the variability index with the time lag at all the frequencies. Moreover, for those time lags for which there are also measurements at the highest frequencies, namely 33 and 38 GHz, the variability indices are typically higher than those associated with lower frequencies.

Figure 7.

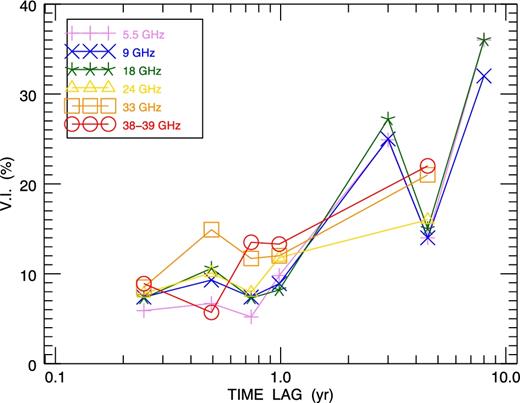
Mean variability indices in total intensity versus time lag at the observed frequencies (different colours). Variability measurements for the faint PACO sample are also displayed (Massardi et al. 2016a).

www.narrabri.atnf.csiro.au/observing/users_guide

Due to the lack of PACO polarization data, we could estimate the VI only for the 8 yr lag (last line of Table 5). Also, due to the larger fractional uncertainties, we could make the analysis only for the full sample. The VI turned out to be substantially larger than in total intensity, with no significant frequency dependence.

6 CONCLUSIONS

We have presented high-sensitivity (σ_P ≃0.6 mJy) polarimetric observations of a complete sample of 53 compact extragalactic radio sources drawn from the ‘faint’ PACO sample. Thanks to the high sensitivity, we achieved a high (∼91 per cent) 5 σ detection rate in polarization.

The continuum spectra of over 95 per cent of sources are well fitted by double power laws, both in total intensity and in polarization. However, substantial variations of the polarization degree with frequency were found, implying different spectral shapes in polarization compared to total intensity.

Within the spectral range covered by our observations (5.5–38 GHz), most sources can be classified either as steep-spectrum or as peaked-spectrum, both in total intensity and in polarization, although less than half of sources have the same classification in the two cases.

Between 28 and 38 GHz, all spectral indices are steep, so that the dichotomy between flat and steep spectra, associated with compact and extended sources, well established at low frequencies, no longer holds at these frequencies.

No significant trend of the fractional polarization with either flux density or frequency was found, although we caution that the limited ranges covered by our sample and the variety of spectral behaviours may hamper the detection of weak trends. However, steep-spectrum sources show higher polarization fractions than peaked-spectrum ones at all the observed frequencies.

We found evidence of Faraday rotation for two sources. The derived values of the rotation measures are (96 ± 13) rad m⁻² and (30 ± 13) rad m⁻², respectively.

The mean variability index in total intensity of steep-spectrum sources increases with frequency for a 4–5 yr lag, while no significant trend shows up for peaked-spectrum sources and for the 8 yr lag. In polarization, the variability index, which could be computed only for the 8 yr lag, is substantially higher than in total intensity and has no significant frequency dependence.

Acknowledgments

We thank the anonymous referee for useful comments. We acknowledge financial support by the Italian Ministero dell'Istruzione, Università e Ricerca through the grant Progetti Premiali 2012-iALMA (CUP C52I13000140001). Partial support by ASI/INAF Agreement 2014-024-R.1 for the Planck LFI Activity of Phase E2 and by ASI through the contract I-022-11-0 LSPE is acknowledged. We thank the staff at the Australia Telescope Compact Array site, Narrabri (NSW), for the valuable support they provide in running the telescope and in data reduction. The Australia Telescope Compact Array is part of the Australia Telescope which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO. AB acknowledges support from the European Research Council under the EC FP7 grant number 280127. VC acknowledges DustPedia, a collaborative focused research project supported by the European Union under the Seventh Framework Programme (2007–2013) call (proposal no. 606824). The participating institutions are as follows: Cardiff University, UK; National Observatory of Athens, Greece; Ghent University, Belgium; Université Paris Sud, France; National Institute for Astrophysics, Italy and CEA (Paris), France. LT and LB acknowledges partial financial support from the Spanish Ministry of Economy and Competitiveness (MINECO), under project AYA-2015-65887-P.

1

2

The error associated with the bias correction is negligible and will be omitted in next sub-sections.

3

The ‘Interactive Data Language’ (idl) is a scientific programming language released by Harris Geospatial Solutions (http://www.harrisgeospatial.com).

REFERENCES

Ade

P. A. R.

et al. ,

2014

,

Phys. Rev. Lett.

,

113

,

021301

PubMed

Agudo

I.

,

Thum

C.

,

Wiesemeyer

H.

,

Krichbaum

T. P.

,

2010

,

ApJS

,

189

,

1

Agudo

I.

,

Thum

C.

,

Gómez

J. L.

,

Wiesemeyer

H.

,

2014

,

A&A

,

566

,

A59

André

P.

et al. ,

2014

,

J. Cosmol. Astropart. Phys.

,

2

,

006

Arkin

H.

,

Colton

R. R.

,

1970

,

Statistical Methods

, 5th edn.

Barnes & Noble

,

New York

Battye

R. A.

,

Browne

I. W. A.

,

Peel

M. W.

,

Jackson

N. J.

,

Dickinson

C.

,

2011

,

MNRAS

,

413

,

132

Blandford

R. D.

,

Königl

A.

,

1979

,

ApJ

,

232

,

34

Bonavera

L.

,

Massardi

M.

,

Bonaldi

A.

,

González-Nuevo

J.

,

de Zotti

G.

,

Ekers

R. D.

,

2011

,

MNRAS

,

416

,

559

Ciaramella

A.

et al. ,

2004

,

A&A

,

419

,

485

Galluzzi

V.

,

Massardi

M.

,

2016

,

Int. J. Mod. Phys. D

,

25

,

1640005

Grant

J. K.

,

Taylor

A. R.

,

Stil

J. M.

,

Landecker

T. L.

,

Kothes

R.

,

Ransom

R. R.

,

Scott

D.

,

2010

,

ApJ

,

714

,

1689

Hales

C. A.

,

Norris

R. P.

,

Gaensler

B. M.

,

Middelberg

E.

,

2014

,

MNRAS

,

440

,

3113

Hanson

D.

et al. ,

2013

,

Phys. Rev. Lett.

,

111

,

141301

PubMed

Huffenberger

K. M.

et al. ,

2015

,

ApJ

,

806

,

112

Impey

C. D.

,

Neugebauer

G.

,

1988

,

AJ

,

95

,

307

Kaufman

J. P.

et al. ,

2014

,

Phys. Rev. D

,

89

,

062006

Lavalley

M.

,

Isobe

T.

,

Feigelson

E.

,

1992

, in

Worrall

D. M.

,

Biemesderfer

C.

,

Barnes

J.

, eds,

ASP Conf. Ser. Vol. 25, Astronomical Data Analysis Software and Systems I

.

Astron. Soc. Pac.

,

San Francisco

, p.

245

Massardi

M.

et al. ,

2008

,

MNRAS

,

384

,

775

Massardi

M.

et al. ,

2011

,

MNRAS

,

412

,

318

Massardi

M.

et al. ,

2013

,

MNRAS

,

436

,

2915

Massardi

M.

,

Bonaldi

A.

,

Bonavera

L.

,

De Zotti

G.

,

López-Caniego

M.

,

Galluzzi

V.

,

2016a

,

MNRAS

,

455

,

3249

Massardi

M.

,

Galluzzi

V.

,

Paladino

R.

,

Burigana

C.

,

2016b

,

Int. J. Mod. Phys. D

,

25

,

1640009

Mesa

D.

,

Baccigalupi

C.

,

De Zotti

G.

,

Gregorini

L.

,

Mack

K.-H.

,

Vigotti

M.

,

Klein

U.

,

2002

,

A&A

,

396

,

463

Morganti

R.

,

Oosterloo

T.

,

Tadhunter

C. N.

,

Aiudi

R.

,

Jones

P.

,

Villar-Martin

M.

,

1999

,

A&AS

,

140

,

355

Murphy

T.

et al. ,

2010

,

MNRAS

,

402

,

2403

Partridge

B.

,

López-Caniego

M.

,

Perley

R. A.

,

Stevens

J.

,

Butler

B. J.

,

Rocha

G.

,

Walter

B.

,

Zacchei

A.

,

2016

,

ApJ

,

821

,

61

Rayner

D. P.

,

Norris

R. P.

,

Sault

R. J.

,

2000

,

MNRAS

,

319

,

484

Reynolds

J. E.

,

1994

,

ATNF Memo AT/39.3/040, A Revised Flux Scale for the AT Compact Array

.

Australia Telescope National Facility

,

Epping, NSW, Australia

Ricci

R.

,

Prandoni

I.

,

Gruppioni

C.

,

Sault

R. J.

,

De Zotti

G.

,

2004

,

A&A

,

415

,

549

Sadler

E. M.

et al. ,

2006

,

MNRAS

,

371

,

898

Sajina

A.

,

Partridge

B.

,

Evans

T.

,

Stefl

S.

,

Vechik

N.

,

Myers

S.

,

Dicker

S.

,

Korngut

P.

,

2011

,

ApJ

,

732

,

45

Sault

R. J.

,

2003

,

ATNF Memo AT/39.3/124, ATCA Flux Density Scale at 12mm

.

Australia Telescope National Facility

,

Epping, NSW, Australia

Sault

R. J.

,

Teuben

P. J.

,

Wright

M. C. H.

,

1995

, in

Shaw

R. A.

,

Payne

H. E.

,

Hayes

J. J. E.

, eds,

ASP Conf. Ser. Vol. 77, Astronomical Data Analysis Software and Systems IV

.

Astron. Soc. Pac.

,

San Francisco

, p.

433

Subrahmanyan

R.

,

Ekers

R. D.

,

Saripalli

L.

,

Sadler

E. M.

,

2010

,

MNRAS

,

402

,

2792

Taylor

A. R.

et al. ,

2007

,

ApJ

,

666

,

201

Tucci

M.

,

Toffolatti

L.

,

2012

,

Adv. Astron.

,

2012

,

624987

Tucci

M.

,

Martínez-González

E.

,

Toffolatti

L.

,

González-Nuevo

J.

,

De Zotti

G.

,

2004

,

MNRAS

,

349

,

1267

Wardle

J. F. C.

,

Kronberg

P. P.

,

1974

,

ApJ

,

194

,

249