-
PDF
- Split View
-
Views
-
Cite
Cite
Ethan Lake, Zheng Zheng, Subo Dong, Detecting extrasolar asteroid belts through their microlensing signatures, Monthly Notices of the Royal Astronomical Society, Volume 465, Issue 2, February 2017, Pages 2010–2017, https://doi.org/10.1093/mnras/stw2645
Close - Share Icon Share
Abstract
We propose that extrasolar asteroid belts can be detected through their gravitational microlensing signatures. Asteroid belt + star lens systems create so-called ‘pseudo-caustics’, regions in the source plane where the magnification exhibits a finite but discontinuous jump. These features allow such systems to generate distinctive signatures in the microlensing light curves for a wide range of belt configurations, with source trajectories as far as tenths of the Einstein ring radius from the centre of the lens. Sample light curves for a range of asteroid belt parameters are presented. In the near future, space-based microlensing surveys like WFIRST, which will have the power of detecting per cent-level changes in microlensing light curves even with subminute exposure times, may be able to discover extrasolar asteroid belts with masses of the order of an earth mass.
1 INTRODUCTION
Gravitational microlensing has established itself as a valuable tool for detecting objects covering a wide range of mass (e.g. Paczynski 1986). Successful microlensing surveys began over two decades ago with target star fields in both the Galactic bulge (Udalski et al. 1993) and the Small Magellanic Cloud and Large Magellanic Cloud (LMC; Alcock et al. 1993; Aubourg et al. 1993). As pointed out by Mao & Paczynski (1991), microlensing can be used to probe extrasolar planetary systems. Following the discovery of exoplanets through the microlensing technique (e.g. Bond et al. 2004; Udalski et al. 2005; Beaulieu et al. 2006), the number of detections has been steadily increasing into the several dozen (e.g. Kains et al. 2013; Batista et al. 2014; Gould et al. 2014; Suzuki et al. 2014). Owing to its sensitivity to low-mass planets and planets beyond the snow line, microlensing has emerged as an important method to detect and study exoplanets (e.g. Seager 2011). In addition, microlensing can also be applied to detect and characterize free-floating planets (Gaudi 2002; Sumi et al. 2011).
It has also been suggested that microlensing can lend itself to the observational study of various parts of the planet-formation process, like circumstellar discs around source stars (Zheng & Menard 2005) and lens stars (Hundertmark, Hessman & Dreizler 2009). In this paper, we propose to use microlensing to detect extrasolar asteroid belts around lens stars.
The observational study of extrasolar asteroid belts and debris discs has recently become an active field of study. Asteroid-belt-like and Kuiper-belt-like analogues have been inferred around several extrasolar systems from the observed infrared excess of their host stars (e.g. Chen & Jura 2001; Beichman et al. 2005; Moerchen et al. 2007b; Backman et al. 2009; Chen et al. 2009; Moerchen, Telesco & Packham 2010), resulting from dust generated by collisions of asteroids. Multiple asteroid-sized objects have also been found to transit a white dwarf (e.g. Croll et al. 2015; Vanderburg et al. 2015). Residual timing variations in millisecond pulsars are proposed as originating from asteroid belts (e.g. Shannon et al. 2013). Determining the prevalence of extrasolar asteroid belts could shed insight into the planet-formation process and even help estimate the frequency of extraterrestrial life (Martin & Livio 2013). Therefore, it would be valuable if we have complementary and effective methods to probe extrasolar asteroid belts around main sequence stars.
In this paper, we show that microlensing by the lens system composed of a star and an asteroid belt can be a promising detection method. Microlensing is useful in this regard because of its sensitivity to low-mass objects located near the Einstein ring radius, which is typically on the order of a few au. We find that asteroid belt + star lenses produce a wide variety of so-called ‘pseudo-caustics’, loci in the source plane across which the magnification of a source has a finite jump (e.g. Evans & Wilkinson 1998; Rhie 2010; Lee & Kim 2014; Lake & Zheng 2016). A detailed investigation on the magnification properties for the general ring/belt+point lens has been presented in Lake & Zheng (2016). In this paper, we show that sources passing over the pseudo-caustics can leave unique signatures in the resulting microlensing light curves, which should be easily identifiable in upcoming observational surveys. Furthermore, the pseudo-caustics have a comparatively large radial extent in the source plane, meaning that the probability for source trajectories to cross pseudo-caustics can be significantly higher than to cross the formal caustics associated with planetary microlensing events.
The structure of this paper is as follows. In Section 2, we recall key gravitational lensing equations and describe the pseudo-caustics that are formed by the lenses we consider. Section 3 is devoted to the presentation of model light curves for a few illustrative cases. Finally, Section 4 consists of a summary and a discussion of our results.
2 MAGNIFICATION PROPERTIES OF BELT+STAR LENSES
2.1 Lensing equations
The lens systems we consider are composed of a star and an asteroid belt. In each model, the circularly symmetric belt is centred at the star. We denote the distance between the observer and the lens (source) as DL (DS) and the distance between the lens and source as DLS (DS = DL + DLS). The belt is described by an inner radius ai and an outer radius ao, the inclination angle i (i.e. the angle between the normal of the belt plane and the line of sight direction), and the mass ratio q = Mbelt/Mstar of the belt to the central lens star. We assume the asteroid belt has a constant mass density. This is obviously an idealization. For example, the mass distribution of asteroids and the discreteness effect (e.g. Heng & Keeton 2009) are not accounted for. However, it allows us to gain a clear understanding for how asteroid belts as a whole can be expected to behave as lenses.
Lake & Zheng (2016) perform a study on the gravitational lensing properties with a system made of a point mass surrounded by a ring/belt and focus their discussions on examples with large q. We refer the readers to the above paper for details. In this paper, we present cases with low mass ratios that are more suitable for the study of extrasolar asteroid belts.
2.2 Pseudo-caustics
Key to understanding the behaviour of gravitational lenses is the study of the so-called ‘caustic curves’. The caustic set contains the points in the source plane where the magnification μ for a point source is formally divergent and represents points where the determinant of the lens mapping Jacobian vanishes.
Normally, the magnification is a smooth function for sources located away from the caustics. However, the belt+star lens models considered here possess regions in the source plane dubbed ‘pseudo-caustics’, where the magnification is finite but changes discontinuously. Pseudo-caustics have been studied before in lensing systems with singular isothermal density distributions (e.g. Kovner 1987; Wang & Turner 1997; Shin & Evans 2008; Rhie 2010; Lee & Kim 2014), and they were associated with regions where the image multiplicity changes by one. In the systems considered here, the pseudo-caustics can be associated either with regions where the image multiplicity changes or where an image of a source suddenly changes in size, depending on the width of the belt. They are found to possess a broad variety of morphologies across the parameter space of the models we consider. A more detailed analysis of the pseudo-caustics is presented in Lake & Zheng (2016).
Since the boundaries of the pseudo-caustics represent areas where the magnification map is non-differentiable (at least for the idealized constant-density belts considered here), they can in principle be found by finding points in the source plane where |∇μ| → ∞. In practice, we perform an inverse ray-shooting calculation (e.g. Schneider & Weiss 1986) by shooting rays from a uniform grid in the lens plane and collecting them on a grid in the source plane. The magnification of a cell in the source plane is then computed by dividing the number of rays it collects by the number it would collect in the absence of the lens.
Fig. 1 shows magnification maps in the source plane for a belt with semimajor axes ai = 1.2, ao = 1.4 and mass ratio q = 10−3 across a range of inclinations. The pseudo-caustics show up as the X-shaped features for the cases with high inclinations (e.g. i ≳ 50°), which are fairly generic for the types of lenses we consider. The mass ratio q = 10−3 may be rather unrealistic for asteroid belts, but the morphologies of the pseudo-caustics do not change significantly when q is lowered (the primary change being in the width of the pseudo-caustics), and so this case allows us to gain a qualitative understanding of the general behaviour of belt+star lenses. When the inclination of the belt is low, the pseudo-caustics are subdued. As shown in Lake & Zheng (2016), the deflection by a face-on belt is zero for rays passing interior to the inner edge of the belt, while for those passing outside the belt it is identical to the deflection produced by a point lens of dimensionless mass q/(1 + q) located at the origin. Therefore, for the case of a low mass ratio, the magnification map of the belt+star system is close to that of the central star, meaning that such low-inclination belts do not cause significant perturbations to the star-only magnification pattern.
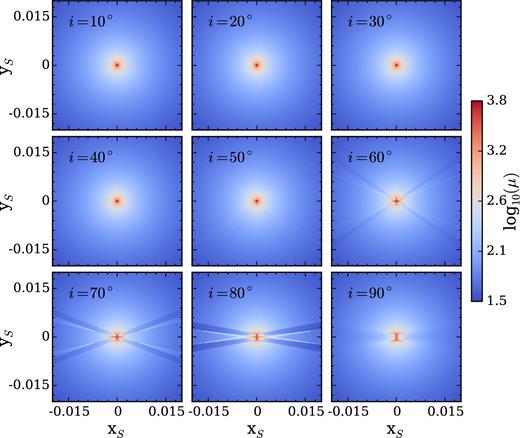
Magnification maps near the centre region in the source plane for a lens composed of a central star and a belt with inner and outer semimajor axes ai = 1.2 and ao = 1.4, a belt-to-stellar mass ratio of q = 10−3 and plotted across various inclinations. For low inclinations, the belt acts as a point mass, and the perturbations it induces to the star's magnification map are insignificant. As the inclination passes ∼50°, an X-shaped pseudo-caustic feature appears. As the inclination increases, the limbs of the X fold down and become wider, eventually merging when the ring is seen edge-on. A source moving across these features generates a very distinctive light curve (see text for more details). The features seen in this plot remain qualitatively unchanged for smaller q.
As the inclination of the belt increases, the limbs of the X-shaped pseudo-caustic feature fold down towards the xS-axis and eventually merge when the belt is seen edge-on. For the edge-on case, the system exhibits some features degenerate with that of an equal-separation triple point-mass lens (e.g. Daněk & Heyrovský 2015), although it remains qualitatively different from the behaviour of the magnification caused by edge-on circumstellar discs [see e.g. fig. 3 of Hundertmark et al. (2009), which considers spatially extended discs at a much larger distance from the central star than the asteroid belts considered here].
We find that the pseudo-caustics are most pronounced for belts whose central semimajor axis ac = (ai + ao)/2 is at or slightly beyond the Einstein ring radii (1 ≲ ac ≲ 2), as is the case of caustics for planetary microlensing (Gould & Loeb 1992).
When the width of the belt is increased, the pseudo-caustics become smoother and ‘smeared out’, although the effect is not too dramatic for moderate belt widths Δa ≲ 0.75. For comparison, our own asteroid belt extends from ∼2.2 to ∼3.2 au (Petit, Morbidelli & Chambers 2001), which if considered as a lens around a Sun-like star halfway between the Sun and the Galactic Centre gives a belt width of Δa ∼ 0.25.
Finally, we note that while Fig. 1 only shows a close-up of the magnification map near the centre of the source plane, the X-shaped pseudo-caustics seen at large i extend radially outward to cover a large region of the source plane. This means that source trajectories with comparatively large impact parameters (b0 ≲ 0.5) have a high likelihood of crossing a region of the pseudo-caustic with significant perturbation to the source plane magnification, implying a high asteroid belt lensing probability. The pseudo-caustic crossing leads to distinct features in the microlensing light curves as shown in Section 3.
3 MODEL LIGHT CURVES
In this section, we present simulated light curves across a range of parameter combinations to demonstrate the expected behaviour of belt+star microlensing events. Throughout this section, we assume the source star to be a Sun-like star with mass of 1 M⊙ and radius of 1 R⊙ located near the Galactic Centre with the belt+star lens located halfway to the Galactic Centre, i.e. we set DL = 4 kpc and DS = 8 kpc. We take the lens star to be a Sun-like star of mass Mstar = 1 M⊙, which gives θEDL ≈ 4 au and a dimensionless radius (radius in units of Einstein ring radius) for the source star of ρ ∼ 5.8 × 10−4.
We first consider cases with belt-to-star mass ratio of q = 10−3. While this is a rather high-mass (probably unrealistic) asteroid belt, compared to the one in our Solar system, it provides a clear illustration for the main microlensing features. The cases with lower mass ratios share similar features and will be presented afterward. Fig. 2 shows three model light curves for a belt+star system with ai = 1.2, ao = 1.4, q = 10−3, and i = 80°. We focus on trajectories relatively close to the centre of the source plane, which lead to high-magnification microlensing events. The top-left panel shows the magnification map of the central region in the source plane, superimposed with the corresponding source trajectories for three light curves in the other three panels. The yellow circle at the top-left corner of the magnification map corresponds to the size of the source star, and we account for the finite source effect in calculating the light curves. In each light curve, the black dashed line shows the light curve for the star-only lens, with the bottom subpanel showing the fractional deviation between the belt+star and star-only light curves. The time is given in units of tE, the Einstein radius crossing time. For a typical lens-source relative velocity of v⊥ = 110 km s−1, tE is ∼65 d.
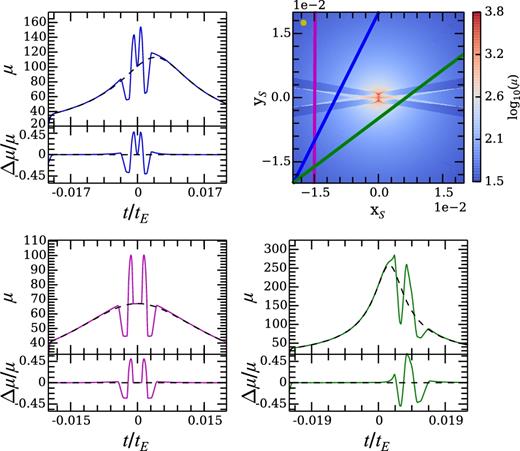
Sample microlensing light curves for a lens with a central star and a belt with semimajor axes ai = 1.2, ao = 1.4, mass ratio q = 10−3, and inclination i = 80°. The top-right panel shows the magnification near the centre of the source plane. The circle at the top-left corner represents the dimensionless size of the source star. The other three panels show light curves corresponding to the given trajectories in the source plane, with the black dashed lines showing the light curve for the star-only case. The bottom subpanels show the relative deviation between the star+belt and star-only light curves. The source is assumed to move along each trajectory in the top-left panel from bottom-left to top-right, with t = 0 set to be at the halfway point of the trajectory.
The distinct X-shaped pseudo-caustic feature in the magnification map shows up in each of the three light curves. Given the shape of the pseudo-caustics, the source has a high likelihood of crossing the pseudo-caustics twice, resulting in a light curve that exhibits a rapid decrease and increase in magnification, followed by a corresponding increase and decrease some time later. The maximum fractional change in magnification, Δμ/μ, can be as high as ∼50 per cent. An observed light curve exhibiting these features would provide strong evidence for the presence of a belt+star lens.
Fig. 3 is the same as Fig. 2 but with the inclination reduced to i = 60°. Reducing the inclination has the effect of ‘folding up’ the X-shaped pseudo-caustics about the yS-axis, and increasing the separation between the high- and low-magnification areas of the pseudo-caustics. Additionally, the width of the pseudo-caustics becomes smaller and the perturbations to the star-only light-curve decrease.
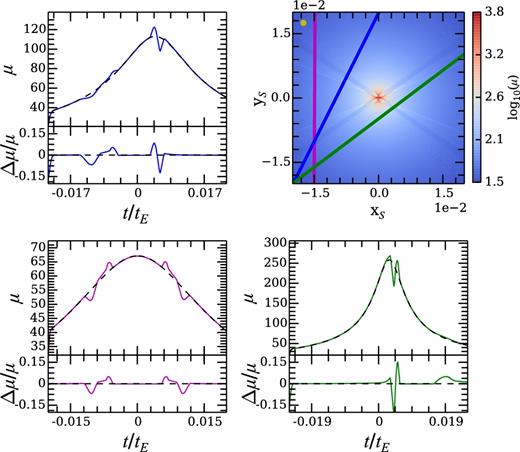
Same as in Fig. 2, but with the inclination of the belt changed to i = 60°.
Fig. 4 shows a case where both the inner and outer semimajor axes of the belt lie within the Einstein radius, with ai = 0.7 and ao = 0.9. Lowering the semimajor axes of the belt folds the X-shaped feature down on to the x-axis and smoothens the pseudo-caustics. The maximum relative magnification Δμ/μ between the belt+star case and the star-only case decreases to 5–15 per cent. In general, decreasing the semimajor axes even further results in a smaller perturbation to the star-only light curve.
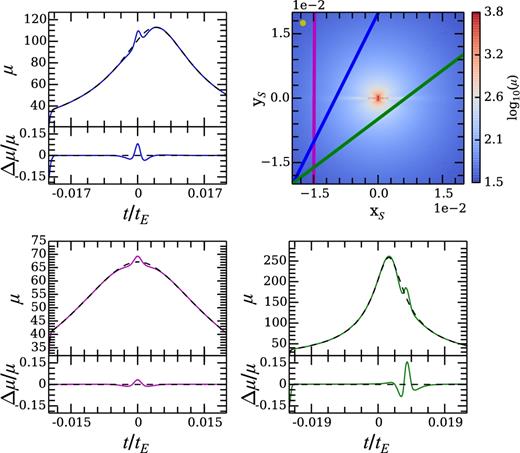
Same as in Fig. 2, but with semimajor axes ai = 0.7 and ao = 0.9.
Fig. 5 is again the same as Fig. 2, but with the thickness of the belt increased to Δa = 0.6, by setting ai = 1, ao = 1.6. If a belt of this width were placed around a Sun-like lens star, a width of Δa = 0.6 would correspond to a physical width of ∼2.5 au. Thickening the ring smooths out the pseudo-caustics, with the light curves retaining their overall shape but possessing slightly more subdued peaks and flatter troughs.
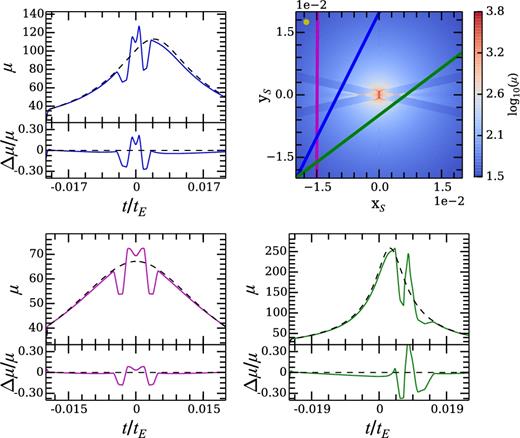
Same as in Fig. 2, but with semimajor axes ai = 1 and ao = 1.6.
The above q = 10−3 examples illustrate the expected features in the microlensing light curves for belt+star systems. More realistic systems are likely to have much lower belt-to-star mass ratios. We show below that the main features remain but with lower amplitudes. In Fig. 6, we present three sample light curves for different trajectories for a system with a lower belt-to-star mass ratio, q = 10−5, which corresponds to a belt mass of ∼3 M⊕ for a Sun-like lens star. The inclination of the belt is fixed at i = 80°. From the left-hand to right-hand panel, the belts are centred at a = 1, 1.2, and 2, respectively, with width Δa = 0.3, and the source trajectories have impact parameters of b0 = 0.05, 0.004, and 0.002, respectively. The trajectories are chosen to make an angle of θ ∼ 80° with respect to the xS axis, ensuring that the sources cross the X-shaped pseudo-caustics (similar to those seen in the top-right panel of Fig. 2) within short time intervals. Trajectories of small impact parameters with smaller θ angles would correspond to longer time intervals between pseudo-caustic crossings, while trajectories of large impact parameters with smaller θ angles are unlikely to experience strong pseudo-caustic crossings. While the characteristic shape of the perturbations caused by the belt remains similar to the previous cases, the fractional change in magnification drops to the level of a per cent. Approximately, the fractional perturbations with respect to the star-only light curve are proportional to the mass ratio q, of the order of 0.5(q/10−3).
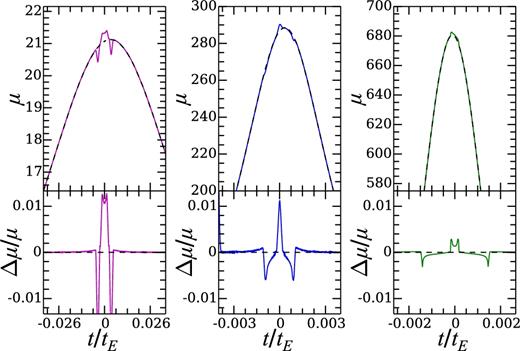
Three sample microlensing light curves for a lens composed of a star and a belt with q = 10−5, i = 80°, and Δa = 0.3 for different semimajor axes and source trajectories. We assume a typical Sun-like source star located in the Galactic Centre. From left-hand to right-hand, the belts are centred at a = 1, 1.2, and 2, respectively, and the trajectories of the source star have impact parameters b0 = 0.05, 0.004, and 0.002, respectively. All trajectories make an angle of θ ∼ 80° with respect to the xS axis.
The above light curves all possess small impact parameters, corresponding to high-magnification microlensing events. However, the pseudo-caustic features of the belt+star lens can extend to large impact parameters, which will show up even in low-magnification events. Fig. 7 shows a magnification map in the source plane for a region farther away from the centre. The belt has q = 10−5 and is centred at a = 1.3 with Δa = 0.3 and inclination i = 80°. The horizontal stripe features are the limbs of the X-shaped pseudo-caustic seen earlier (e.g. in Fig. 1). At large rS, the high-μ and low-μ sections of the X-shaped pseudo-caustic separate from one another, which would make the peaks and troughs in the resulting light curves further apart. The fact that the pseudo-caustics extend out to large rS (e.g. beyond rS = 0.35 from the figure) implies a comparatively high probability for source trajectories to cross pseudo-caustics. As a rather conservative estimate, by approximating the pseudo-caustics as a linear feature along the xS axis, we find that among all trajectories with impact parameter b0 < 0.35, about 50 per cent of them cross the pseudo-caustics at xS < 0.35.
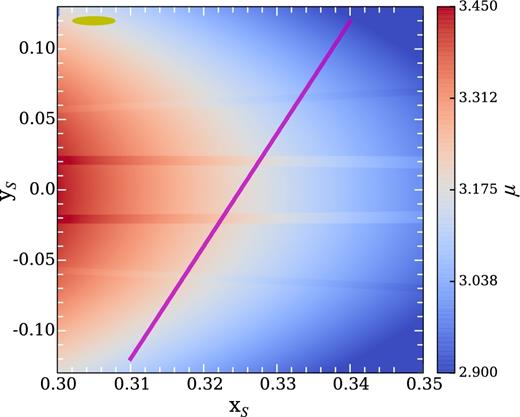
Magnification map in the source plane for a region farther away from the centre for a star+belt lens with q = 10−5, i = 80°, ai = 1.15, and ao = 1.45. The horizontal stripe features are limbs of the X-shaped pseudo-caustic seen in Fig. 1 at high inclination. The pseudo-caustic features, showing up at large distances from the centre, imply a comparatively large probability of belt lensing events. The purple line shows a trajectory with impact parameter b0 ∼0.3, proceeding from bottom left to top right, which corresponds to the microlensing light curve shown in the left-hand panel of Fig. 8. Note that in this plot the ranges along the xS and yS axes are different (about 1: 5). A circular source (corresponding to an R = 5 R⊙ source star) is illustrated by the yellow ellipse in the upper-right corner.
Finally, the light curve corresponding to the purple line (with impact parameter b0 ∼0.3) in Fig. 7 is shown in the left-hand panel of Fig. 8. The middle and right-hand panels show two additional light curves for relatively low-magnification events, by changing the belt to have a = 1.3 and 1.6 with Δa = 0.3 and impact parameter b0 ∼ 0.08 and 0.1, respectively. As before, all the light curves are chosen to cross the xS axis, so that they intersect the pseudo-caustics. In all the three panels, the characteristic pseudo-caustic crossing features caused by the belt clearly show up, with the relative magnification dropping to subpercent levels. The figure shows that the typical time-scale for crossing a single pseudo-caustic feature for the presented light curves is about tenths of per cent of the Einstein ring crossing time, i.e. on the order of hours for microlensing events with Galactic Centre sources and disc lenses, well within reach of future microlensing surveys like WFIRST (see more details in Section 4).
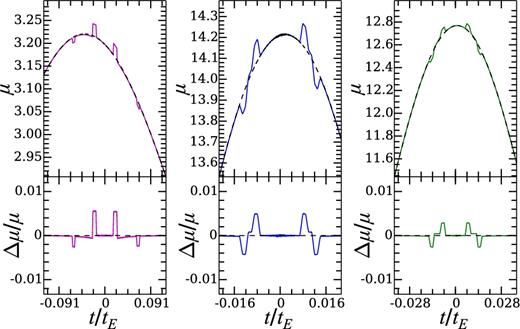
Three more sample microlensing light curves for a lens composed of a central star and a belt with q = 10−5 and i = 80°. In the left-hand, middle, and right-hand panel, the belt is centred at a = 1.3, 1.3, and 1.6, respectively, with the belt width set to Δa = 0.3. From left-hand to right-hand, the trajectories of the source star have impact parameters of b0 ∼ 0.3, 0.08, and 0.1, with all trajectories making an angle of θ ∼ 85° with respect to the xS axis. These examples demonstrate that the large extent of the pseudo-caustics allows them to leave signatures even in comparatively low-magnification events.
Overall, microlensing events from belt+star lenses can be generically characterized by a rapid decrease and increase in magnification followed by a reversed increase and decrease in magnification, caused by the perturbation from the asteroid belt. Such a semisymmetric feature is seen across a wide range of belt semimajor axes, belt widths, belt inclinations, belt-to-star mass ratios, and source trajectories, making it a robust observational signal. Such a feature is not usually seen in the light curves generated by other types of lensing systems, except a moderate degeneracy with an equal-separation triple point-mass lens when the belt is seen nearly edge-on.
The feature is distinct from that produced by planet microlensing. Observationally, it would be unlikely for a belt+star microlensing event to be misidentified as a planet+star one. To establish this quantitatively, we perform tests by fitting belt+star microlensing curves with a planet+star lens model. We produce theoretical belt+star microlensing light-curve data and add photometric errors of 5 mmag (reasonable for the best ground-based microlensing surveys for high-magnification events). We then employ the method in Dong et al. (2009) to explore the parameter space of a planet+star lens system to model the data. Fig. 9 shows an example, taken from a lens model with a belt of width Δa = 0.2 centred at a = 1.25 and with i = 80° and q = 10−5. In the top panel, the points are the densely sampled light curve of the belt+star lens system, and the black curve is the best-fit from a single lens model. The bottom panel shows the residuals to the best-fitting single lens model as well as the difference between the best-fitting planet+star model and the best-fitting single lens model (in blue). The planet+star model tends to fit the broad deviations from the single-lens model but fails to account for the small structures caused by the belt+star lens. The χ2 difference between the planet+star and belt+star models is 215.7 for 902 degrees of freedom (i.e. 5.1σ). For future applications, a systematic investigation on the differences in planet+star, belt+star, and planet+belt+star lens systems will be helpful.
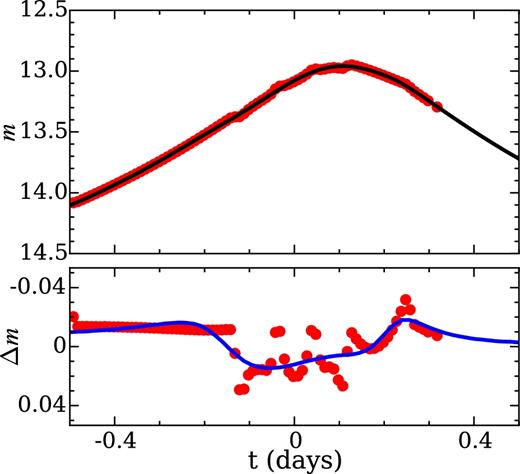
An example of fitting a sample belt+star light curve with a planet+star lens model. The top panel shows the belt+star light curve (red dots) plotted against the best-fitting single lens model (black curve), shown in magnitudes. The bottom panel shows the difference between the belt+star light curve and the best-fitting single lens model (red dots) compared to the difference between the best-fitting planet+star lens model and the best-fitting single lens model (blue curve).
The width of the pseudo-caustic for systems with mass ratio q = 10−3 is roughly 10−3 times the Einstein ring radius for source trajectories near the centre of the source plane, and it does not seem to vary substantially with the mass ratio. The pseudo-caustics typically become broader at a larger distance from the centre of the source plane. In addition, the width also depends on the inclination of the belts, with less inclined belts generically possessing thinner pseudo-caustics. For comparison, a Sun-like source star near the Galactic Centre has a dimensionless radius of ρ ∼ 5.8 × 10−4. This means that the magnification jump caused by a pseudo-caustic crossing is smeared out by the finite source effect, which ultimately limits the sensitivity to detect extrasolar asteroid belt systems.
Fig. 10 illustrates the effects of changing the size of the source star on the light curve plotted in the middle panel of Fig. 8. As before, we assume a source star located in the galactic centre, with DL = 4 kpc and DS = 8 kpc. For a typical 0.3 M⊙ M-dwarf source star with dimensionless radius ρ ≈ 1.7 × 10−4 (red curve), the perturbations caused by the belt are sharp, and are essentially the same as the curve created by an idealized point source. Changing the source to a Sun-like star with ρ ≈ 5.8 × 10−4 (blue curve) results in a slight damping of the light curve, although the perturbations become significantly more damped when the source has a radius of ρ ≈ 2.9 × 10−3, corresponding to either a massive or subgiant star with radius 5 R⊙ (green curve). Note that the typical width of the pseudo-caustics here is about 1.5 × 10−3. The diameter of the M-dwarf source is much smaller than the pseudo-caustic width, and the finite source has almost no effect (red curve). The Sun-like star source has a diameter comparable to (but still smaller than) the pseudo-caustic width, and the finite source effect tends to slightly smooth the pseudo-caustic features (blue curve). For the source with radius of 5 R⊙, the finite source effect causes the pseudo-caustic features in the light curve to be smeared significantly (green curve). Compared to the crossing of a formal caustic, where the magnification sharply increases to infinity, the finite source effect for the crossing of a pseudo-caustic with finite magnification jump is less dramatic. For smaller mass ratios (q ∼ 10−6), events of pseudo-caustic crossing involving larger sources (R ∼ 5 R⊙) are unlikely to be observable except in the most extreme circumstances.
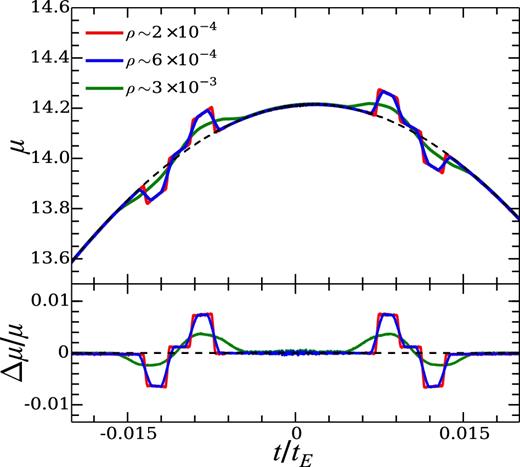
The effects of changing the size of the source star for a sample light curve involving a belt with semimajor axes ai = 1.15, ao = 1.45, mass ratio q = 10−5, and i = 80°. We assume a lensing geometry with DL = 4 kpc, DS = 8 kpc. The dimensionless source radii ρ correspond to an M-dwarf star with radius 0.3 R⊙ (red curve), a Sun-like star with radius 1 R⊙ (blue curve), and a subgiant star with radius 5 R⊙ (green curve). The dashed lines show the star-only case for comparison.
4 SUMMARY AND DISCUSSION
We investigate detecting extrasolar asteroid belts around stars through microlensing. Existence of asteroid belts leaves distinct signatures in microlensing light curves. Belt+star lenses generically create so-called ‘pseudo-caustics’, regions in the source plane where the magnification of a source is finite but changes discontinuously. The probability of pseudo-caustic crossing events is large for a wide range of belt configurations. In the light curves for most source trajectories, the X-shaped pseudo-caustics lead to a rapid fall and rise, followed by a subsequent reversed rise and fall. Such a characteristic, semisymmetric feature can be used to identify belt+star microlensing events.
The finite source effect means that sources at large distances (large values of DS) are ideal, and that surveys should ideally target main sequence source stars rather than giants, as has been pointed out by Bennett & Rhie (1996). Detecting asteroid belts with q ≲ 5 × 10−6 for Sun-like sources near the Galactic Centre is an approximate lower bound for the masses of belts that are likely to be observed. The same type of sources appear to be ∼8 times smaller (ρ ∼ 7 × 10−5) if located in the LMC. Therefore, targeting stars in the LMC would enable us to detect lower mass asteroid belts, although most upcoming surveys (i.e. WFIRST; Spergel et al. 2015) are being designed to target the Galactic bulge.
The small width of the pseudo-caustics in the source plane also means that pseudo-caustic crossing events only last for a short period of time (e.g. minutes to hours for Galactic Centre sources). The required high cadence rates for detection are similar to those in current surveys like MOA and OGLE (Sumi 2010; Udalski, Szymański & Szymański 2015). As a concrete example for future surveys, we consider the photometric survey towards the Galactic bulge by the WFIRST satellite. With a 52 s exposure, the photometric precision in a broad H band is about σ(H) ∼ 10(2/15)(H − 15) mmag (Gould et al. 2015), where H is the apparent magnitude of the source. A 0.3 M⊙ M-dwarf source star (with absolute magnitude MH ∼ 7.05 mag; Henry & McCarthy 1993) in the Galactic Centre has an apparent magnitude H ∼ 21.57 mag, and the corresponding photometric precision is ∼7.5 mmag. So even for microlensing events with moderate magnifications, per cent-level features caused by extrasolar asteroid belts in the light curves can be detected with high significance.
While microlensing features by extrasolar asteroid belts can be detected at high precision, one may wonder whether or not asteroid belts similar to the idealized ones considered here actually exist. Clearly the key parameter here is the mass ratio q of the asteroid belt to its parent star. The present mass of our own asteroid belt is only ∼5 × 10−4M⊕ (Petit et al. 2001), giving q ∼ 5 × 10−9 even for a 0.3 M⊙ M-dwarf parent star. Observing such a low-mass belt would be very unlikely, even for a survey targeting the LMC to reduce the finite source effect. However, our asteroid belt is thought to have been several orders of magnitude more massive in the early years of our Solar system, with a primordial mass of ∼1 M⊕ before it lost most of its mass to ejection by interactions with other planets (Weidenschilling 1977; Petit et al. 2001) over a time-scale of a few million years. For systems that lack massive planets orbiting near the belt, the lifetime of early, massive asteroid belts may be significantly longer. Furthermore, the Kepler mission has found evidence that extrasolar super Earths are likely common (e.g. Howard et al. 2012; Dong & Zhu 2013), and that the extrasolar minimum mass solar nebular (MMSN) can have surface densities many times higher than the solar MMSN (Chiang & Laughlin 2013; Raymond & Cossou 2014). Like extrasolar planets, extrasolar asteroid belts may be very diverse, and there may exist extrasolar asteroid belts that are orders of magnitude more massive than the Solar system's asteroid belt.
Cold planetesimal discs / asteroid belts of masses on the order of a few M⊕ at a distance a few au from a solar mass star can be dynamically stable over Gyr time-scales (Heng & Tremaine 2010). There are hints from observations that massive asteroid belts or ring-like structures exist. For example, the inferred parent mass of the asteroid belt around the A-type star ζ Leporis from the observation of dust emission a few au from the star is about 0.1 M⊕ (Chen & Jura 2001; Moerchen et al. 2007a), substantially more massive than our own. Another example comes from the eclipse light curve of J1407 (Kenworthy & Mamajek 2015), which can be interpreted as caused by a companion star, J1407b, with a giant ring system (∼1 M⊕, extending to a radius of ∼0.6 au).
Overall, it is not unlikely that belt structures with masses of |$\mathcal {O}(10)$| times the mass of the moon (corresponding q ≳ 2 × 10−6 for a typical M-dwarf host star) exist, which in principle can produce detectable microlensing features. The favourable configurations include a reasonably high inclination (i ≳ 70°), a central semimajor axis of 1 ≲ ac ≲ 2, and a belt width of Δa ≲ 0.75.
It is natural to assume that most asteroid belts will have semimajor axes close to the snow line, beyond which the temperature from their parent stars is low enough to allow ices to form. This is encouraging, given that the snow line rsnow ≈ 2.7(M/M⊙)1/3 au (Martin & Livio 2013) is fairly close to θEDL (around which the perturbations caused by the belt are most significant; see equation 2) for a typical Galactic microlensing event. Other disc-like objects like Kuiper belt analogues will be more difficult to detect observationally, since they will typically be located many Einstein radii away from their host stars. Therefore, we focus on asteroid belts in this study.
In our calculation of the microlensing signal, we assume a smooth asteroid belt with constant mass density, as this idealization allows us to gain a simple understanding of how asteroid belts behave as gravitational lenses. In reality, asteroid belts are made of discrete bodies, with a smooth belt corresponding to the limit of small bodies. Depending on the mass distribution of the belt, effects arising from the discrete nature of the true mass distribution need to be investigated and need to be accounted for in modelling the microlensing light curve in observations. We note that a study of microlensing caused by planetesimal discs modelled as an ensemble of point masses was considered in Heng & Keeton (2009).
All in all, it does not seem unreasonable to consider the existence of long-lived massive asteroid belts. If they exist, microlensing is an ideal method for observing them. Observational techniques are continuing to improve, with microlensing surveys reaching increasingly high levels of sensitivity. New space-based surveys like WFIRST will be able to detect Mercury-mass planets (Spergel et al. 2013) and will be well poised to make the first detections of extrasolar asteroid belts, which will provide useful information on the formation of planets and dynamical evolution of asteroid belts.
Acknowledgments
We thank the anonymous referee for helpful comments. The support and resources from the centre for High Performance Computing at the University of Utah are gratefully acknowledged. SD is supported by the Strategic Priority Research Program ‘The Emergence of Cosmological Structures of the Chinese Academy of Sciences’ (Grant No. XDB09000000) and Project 11573003 supported by NSFC.



