-
PDF
- Split View
-
Views
-
Cite
Cite
H. Ghasemi, E. Moravveji, C. Aerts, H. Safari, M. Vučković, The effects of near-core convective shells on the gravity modes of the subdwarf B pulsator KIC 10553698A, Monthly Notices of the Royal Astronomical Society, Volume 465, Issue 2, February 2017, Pages 1518–1531, https://doi.org/10.1093/mnras/stw2839
Close - Share Icon Share
Abstract
KIC 10553698A is a hot pulsating subdwarf B (sdB) star observed by the Kepler satellite. It exhibits dipole (l = 1) and quadrupole (l = 2) gravity modes with a clear period spacing structure. The seismic properties of the KIC 10553698A provide a test of stellar evolution models, and offer a unique opportunity to determine mixing processes. We consider mixing due to convective overshooting beyond the boundary of the helium burning core. Very small overshooting (f = 10−6) results in a progressive increase in the size of convective core. However, moderate (f = 10−2) and small (f = 10−5) overshooting both lead to the occurrence of inert outer convective shells in the near-core region. We illustrate that the chemical stratifications induced by convective shells are able to change the g-mode period spacing pattern of an sdB star appreciably. The mean period spacing and trapping of the gravity modes in the model with moderate and small core overshooting are fully consistent with the period-spacing trends observed in KIC 10553698A. Atomic diffusion driven by gravitational settling as well as thermal and chemical gradients is applied to reach a better match with the observed period spacings. Models that include small or very small overshooting with atomic diffusion have a decreased lifetime of the extreme horizontal branch phase and produce chemical stratification induced by convective shells during helium burning phase. In addition of being consistent with asteroseismology, their calculated values of the R2 parameter are more compatible with the observed R2 values.
1 INTRODUCTION
Subdwarf B (sdB) stars are low-mass core helium burning objects situated at the extreme horizontal branch (EHB). Close binary interaction and Roche lobe overflow (RLOF) on the red giant branch are two essential ingredients of the formation scenarios that strip off the outer envelope and produce an sdB star (e.g. Heber 2009). Short-period binary systems form as a consequence of common envelope interaction while stable RLOF produces wider binary systems. The sdB stars lose almost their entire outer hydrogen-rich envelope and occur on the EHB.
In core He burning models, the mixing between CO-rich and He-rich layers changes the chemical discontinuity between the fully mixed core and the stable radiative envelope. This increases the opacity beyond the convective boundary. Therefore, during the horizontal branch (HB) phase, the helium core size can increase or stay unchanged depending on the details of the adopted mixing. In fact, the detailed prescription for near-core mixing phenomena has been debated in the literature over the past decades. As an example, semiconvection was proposed as a plausible mixing mechanism in the radiative interior of core He burning stars by Castellani et al. (1985), while Sweigart (1990) excluded it. Alternatively, mixing due to core overshooting by the penetration of convective eddies from the fully convective core into the radiatively stable regions was also proposed for core He burning models (see Bossini et al. 2015; Constantino et al. 2015, and references therein). As a result, the properties of He burning cores remain largely unknown.
The shape and efficiency of near-core mixing is connected with the ratio R2, which stands for the number of stars observed on the early asymptotic giant branch (AGB) versus the number of stars in the HB phase (e.g. Renzini & Fusi Pecci 1988, for a review). The traditional canonical evolutionary theory for the HB, relying on semiconvection and suppressing the so-called breathing pulses near the end of the HB phase, was found to be compatible with the measured values of R2 = 0.15 ± 0.01 in globular clusters (e.g. Buonanno, Corsi & Fusi Pecci 1985; Cassisi et al. 2001). Constantino et al. (2016) recently obtained R2 = 0.117 ± 0.005 from observations based on different criteria to restrict the counts of AGB stars.
We argue that asteroseismology of pulsating compact stars offers a new window on the discrimination between different mixing mechanisms, thanks to the high sensitivity of the pulsation frequencies to the details of the input physics of evolutionary models (e.g. Kawaler & Bradley 1994). So far, three classes of pulsating sdB stars were recognized:
EC 14026 pulsators exhibit short-period pulsations first discovered by Kilkenny et al. (1997) and corresponding to theoretical low-degree pressure (p) modes driven by the κ mechanism due to the iron opacity bump boosted by radiative levitation (Charpinet et al. 1996). The dominant restoring force for these rapid p modes is connected with the pressure gradient.
PG 1716 pulsators exhibit long-period pulsations discovered by Green et al. (2003). These slow pulsations are interpreted as gravity (g) modes (Fontaine et al. 2003). The dominant restoring force for these long-period instabilities is the buoyancy force, which depends on the detailed internal structure of the sdB. The theoretical instability strip for g modes excited by the κ mechanism operating in the iron opacity bump around log T ∼ 5.2 is consistent with observations (Bloemen et al. 2014, and references therein).
Hybrid sdB stars demonstrate both p modes and g modes simultaneously (Schuh et al. 2006).
The detection and identification of long-period low-amplitude g modes from the ground-based data are challenging. However, the high-precision space observations of sdB pulsators with the CoRoT and Kepler satellites has facilitated in-depth seismic modelling of these class of pulsating stars. A breakthrough in linking the pulsations with the size of convective cores in sdB stars has occurred by the studies of Charpinet et al. (2010, 2011) and Van Grootel et al. (2010a,b).
In sdB stars, g modes propagate from the surface all the way down to the boundary of the convective core because the envelopes of these stars are predominantly radiative. Therefore, asteroseismology of sdB stars based on high-precision space photometry is one of the best tools to test various mixing scenarios on top of convective core. This is the method we adopt in this work.
In this paper, we use measured period spacings of the selected g-mode sdB pulsator KIC 10553698A as a laboratory to test the efficiency of mixing due to convective overshooting at the edge of the convective core. Our evolutionary and asteroseismic models are computed with the publicly available code mesa (modules for experiment in stellar astrophysics Paxton et al. 2011, 2013, 2015, version 7385), in combination with the GYRE linear adiabatic pulsation code (Townsend & Teitler 2013, version 4.0).
We compare the evolutionary and asteroseismic properties of models with inefficient and moderately efficient overshooting with the observations. We find that models with moderate and small core overshooting lead to inert convective shells adjacent to the convective core. These shells can effectively contribute to the trapping of g modes. The period spacing pattern of KIC 10553698A provides evidence in support of the presence of such a convective shells.
Equipped with the measured period spacing pattern of its g modes, we investigate the effect of atomic diffusion as an extra mixing process beyond the convective core, which leads to different behaviour of the convective core (e.g. Schindler, Green & Arnett 2015) and better match with observed period spacing. Different kinds of mixing due to core overshooting or atomic diffusion in HB stars lead to various shapes of the growing convective core, with similar EHB evolution scenarios. We consider the R2 parameter as a second test of the nature of the overshooting beyond the growing inner core for the core helium burning stars.
2 THE CASE OF THE sdB PULSATOR KIC 10553698A
The evenly spaced long-cadence high-quality Kepler data provide an excellent opportunity to study low-frequency g-mode pulsations, for which ground-based surveys have hardly provided seismic solutions. As examples, the uninterrupted nature of these data opened the discovery of g-mode period spacings of pulsators in the core hydrogen burning phase whose seismic modelling was impossible from the ground (Pápics et al. 2014, 2015; Schmid et al. 2015; Van Reeth et al. 2015) and illustrated the requirement of chemical mixing in the near-core regions of such stars (Moravveji et al. 2015, 2016; Schmid & Aerts 2016; Van Reeth, Tkachenko & Aerts 2016). The high-order g-mode frequencies in sdB stars required short-cadence Kepler data with 58.5 s integration times. Observational investigations of Kepler sdB stars have been published in a series of papers, e.g. Kawaler et al. (2010a,b), Østensen et al. (2010, 2011, 2012, 2014a), Reed et al. (2010, 2011, 2012, 2014), Baran et al. (2011, 2012, 2016), Telting et al. (2012, 2014), and Foster et al. (2015). Here, we focus on the target with the highest potential for near-core structure probing by trapped g modes.
KIC 10553698A was observed with the short-cadence mode of Kepler for most of the duration of the mission and turned out to be a rich g-mode pulsator orbiting the white dwarf KIC 10553698B in a 3.38 d orbit. This binary was extensively studied by Østensen et al. (2014b), who analysed the light curve and detected 156 significant frequencies identified as dipole (l = 1) and quadrupole (l = 2) modes. The observed period spacing for dipole and quadrupole modes provide a clear indication of mode trapping, revealed by its unambiguous large deviations from the uniform spacing (fig. 10 in Østensen et al. 2014b). This structure of g-mode period spacings is sensitive to the density and chemical stratifications between the convective core and the radiative envelope (Charpinet et al. 2000, 2002a,b).
3 COMPUTATION OF STELLAR MODELS
We used the mesa code to evolve a model with 1.5 M⊙ initial mass from the pre-main-sequence phase until the core He depletion, with the following input physics. The chemical composition was taken from the Asplund et al. (2009) solar mixture (abbreviated as A09). The initial mass fractions of H, He, and heavy elements were set to Xini = 0.738, Yini = 0.248, and Zini = 0.014, respectively. The Schwarzschild criterion for convective instability was used, with the mixing length parameter fixed to the value αMLT = 1.8. The default equation of state for Helmholtz free energy was used, with the density and temperature as independent variables. Due to the critical role of local carbon and oxygen abundance on the behaviour of the core boundary, we employ the opal Type II opacity tables (Iglesias & Rogers 1996), which consider the fractional abundance of carbon and oxygen. The adopted nuclear burning networks cover the hot CNO reactions, the triple alpha reaction and carbon/oxygen burning, in addition to successive alpha captures and the weak nuclear interactions.
mesa calculates the neutrino energy loss rates produced by nuclear neutrinos due to weak interactions and thermal neutrinos generated by a range of processes including plasmon decay, pair annihilation, Bremsstrahlung, recombination, and photo-neutrinos (Compton scattering). This consistent treatment of the input physics allows mesa to model off-centre helium flashes in the electron-degenerate cores of low-mass stars (Paxton et al. 2011; Bildsten et al. 2012). Rotation was neglected during the entire evolution. Mass-loss was ignored during the core hydrogen and core helium burning phases while a Reimers’ wind with η = 0.1 (Paxton et al. 2011; Bildsten et al. 2012, for a definition) was used during the red giant branch phase.
4 TIME STEPS
mesa offers a time step selection algorithm based on absolute or relative changes in the physical quantities throughout the evolution of a star. mesa uses mixing-length theory to treat the convective mixing (Paxton et al. 2011). The mixing length theory determines the convective boundary before solving the coupled structure, nuclear burning, and chemical mixing equations. An exponential diffusive core overshoot pattern leads to a high mixing coefficient in the first layers beyond the convective core that is almost equal to the one in the convective core itself. Consequently, these layers become convective even with a small time step during the helium burning phase. In the next time step, the equations should solve for a larger convective core and a different temperature distribution. After several consecutive small time steps, the convective core evolution is distinct from the case where one adopts a single large time step equal to the total of the smaller time steps. The behaviour of the convective core is clearly sensitive to the number of time steps taken during the HB. In general terms, smaller time steps are required when adopting large core overshooting values when studying the evolution of the convective core. In this paper, all evolutionary scenarios are done by adopting max_years_for_timestep = 5000 yr as an upper limit for the time steps while using varcontrol_target = 10−6 to control relative variations in the interior structure from one stellar model to the next.
5 EVOLUTIONARY ASPECTS
mesa is able to evolve a model of a single (sdB) star from the pre-main-sequence phase to the tip of the red giant branch (TRGB). While a star ascends the red giant branch, the core contracts, and the mean separation between the particles decreases. Eventually, the mean separation between electrons becomes of the order of the de Broglie wavelength, and the helium core becomes electron degenerate, while the gravitational energy released from the core expands the envelope. Fig. 1 illustrates the evolutionary track of our 1.5 M⊙ model.

The evolutionary track of a 1.5 M⊙ star. The evolution from the pre-main-sequence to the tip of the RGB is plotted by a black dash–dotted line. The helium flash phase is plotted by the blue dashed line, while the red solid line illustrates the EHB phase.
To mimic the effect of binary interaction and envelope mass stripping to form an sdB star, we use the relax_mass option in mesa, starting at the TRGB. This is achieved by including a huge mass-loss rate in such a way that the degenerate core is surrounded by a very thin inert hydrogen envelope of mass 0.0008 M⊙ after the envelope mass stripping. In the next step, the model was evolved to the onset of the successive core helium flashes. The weak interaction of neutrinos with matter leads to effective cooling of the central regions of the degenerate helium core. During the helium flashes almost 5 per cent of helium gets burnt into carbon and oxygen. The energy released by the nuclear processes increases the core temperature and consequently the de Broglie wavelength of the electrons, removing the electron degeneracy from the helium core. Fig. 2 shows the Kippenhahn diagram illustrating the inward progression of the helium flashes in ∼2 Myr (see also Bildsten et al. 2012). Finally, stable helium burning through the triple alpha reaction produces carbon during the EHB phase.
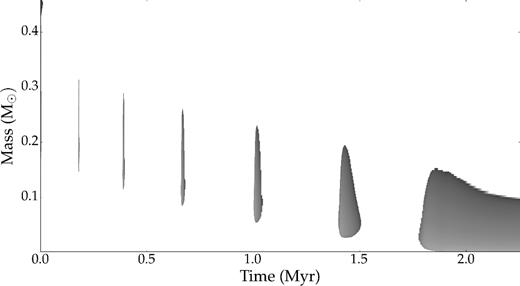
Illustration of the helium flash of the 1.5 M⊙ star. Dark regions show convective mixing created by the successive helium subflashes. White regions show the inert radiative regions.
The convective core evolution during the EHB is not homogeneous, but rather a progression through various states with almost unique characteristics. In total, there are three stages that can be distinguished from each other. The first stage is the period between the zero age extreme horizontal branch (ZAEHB) and the time when almost half of the helium is burnt. During this stage, the convective core grows uniformly. The second stage continues until about 10 per cent of helium in core remain, while the third stage covers the final EHB evolution. During this third stage, so-called breathing pulses (see, e.g. Castellani et al. 1985, for a definition) occur due to the efficiency of nuclear conversion of carbon to oxygen, which leads to a higher opacity. Hence, the convective core grows rapidly and mixes large amounts of helium into the burning region. The number of pulses is very sensitive to the amount of overshooting. If the convective core boundary reaches the outer layers with low enough temperature, the pulses will occur prior to the nuclear fuel exhaustion in the core.
During the EHB, models based on three overshooting scenarios were considered:
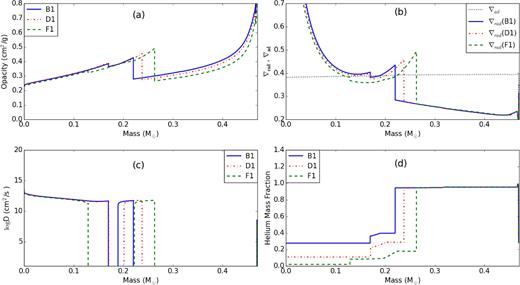
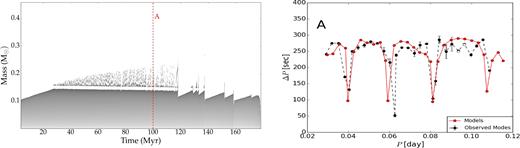
Moderate overshooting with f = 0.01, which is shown in Fig. 3. The transfer of carbon and oxygen into the radiative part increases the opacities and hence the convective core grows progressively at first (see, e.g. point A1 in Fig. 3). After first stage, in addition to the inner convective core, outer convective shells occur (see, e.g. points B1, C1, D1, E1, F1 in Fig. 3). At the inner part of the convective core, the burning power generated by the triple alpha nuclear fusion is very temperature dependent. As a consequence, in this region convection is the dominant source of energy transport.
At the outer region of the convective core, on one hand, the transfer of carbon and oxygen into the radiative part increases the opacities. On the other hand, follows Kramers’ law, i.e. κ ∝ ρT−3.5, the temperature decreases towards the outer part of core (see Fig. 4a) and hence the opacity decreases. Hence, the regions with lower ∇rad near the core become radiative and a convective shells occurs simultaneously at the outer regions (see Fig. 4b). Because of mixing due to the overshooting between the convective shells and the outer He-rich radiative zone (see Fig. 4c), fresh helium can enter the shells, lowering the opacity in the shells locally; consequently, the inner base of the convective shells become radiative, while on the other hand, carbon and oxygen can enter the outer He-rich radiative zones, increase the opacity locally; hence, the radiative zones near the outer base of convective shells become convective. Convective shells move along the outer regions and finally disappear.
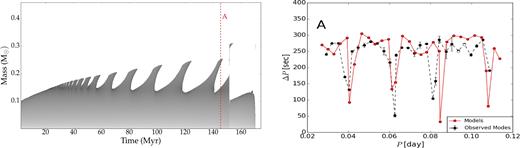
Small overshooting with f = 10−5, which is shown in Fig. 5. The convective core grows uniformly at first, and then the convective region splits into an inner convective core and an outer convective shell (see, e.g. points A2, B2 in Fig. 5). Due to the transport of less opaque matter into the convective region, the regions inside the convective core become radiative and a convective shell remains at the outer regions (see Fig. 6a and b). Because of the mixing due to the overshooting at the external border of the convective shell, the entire convective shell stabilizes, and becomes radiative. Several abrupt breathing pulses occur at the third stage of the core He burning (see, e.g. point C2 in Fig. 5). Similar He burning models have already been calculated for the convective core by, e.g. Sweigart (1990).
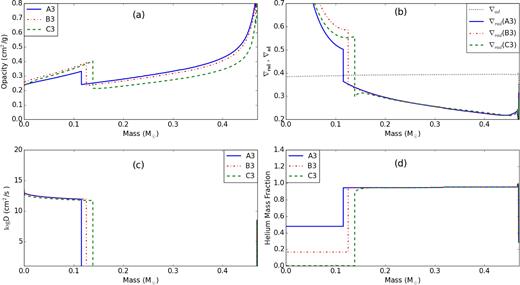
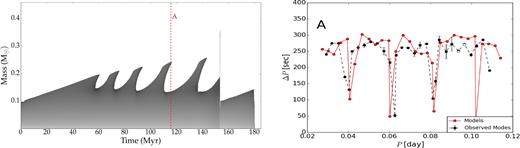
Very small overshooting with f = 10−6, which is shown in Fig. 7. The convective core grows monotonically (see, e.g. points A3, B3, C3 in Fig. 7) and reaches its maximum size towards the end of core helium burning. Carbon and oxygen are more opaque than helium. Thus, an excess in the local abundance of carbon and oxygen increases the local Rosseland mean opacity κR (see Fig. 8a), and consequently increases the radiative temperature gradient ∇rad ∝ κR (see Fig. 8b). As a result, the convective core size grows steadily for all stages of the helium burning.
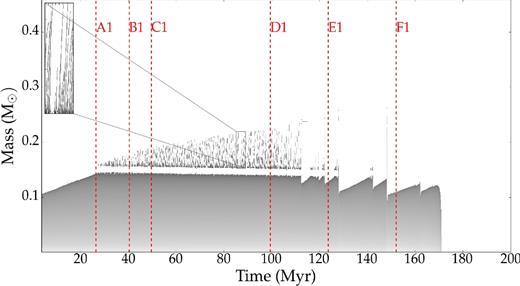
Evolution of the He burning core (dark regions) during the EHB phase, for the model with moderate overshooting described by the value f = 0.01. Temporal appearances and disappearances of convective shells on top of the core occur, with narrow inert radiative regions (white) in between.
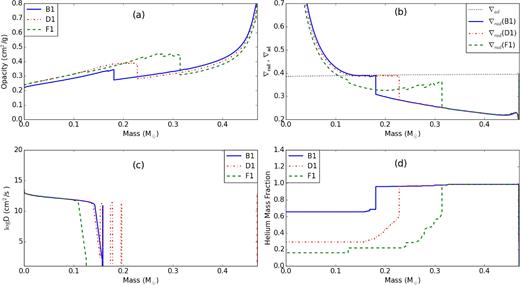
Physical quantities profiles of the model with moderate overshooting for points B1, D1, and F1 on Fig. 3. (a) Opacity. (b) ∇rad, and ∇ad. (c) Diffusion coefficient. (d) Helium mass fraction.
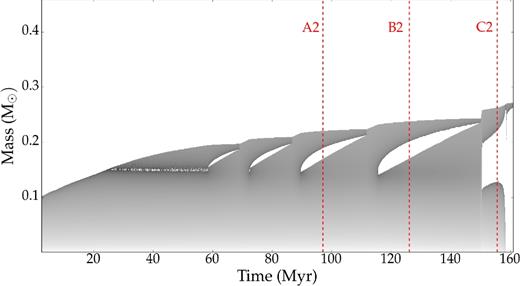
Evolution of the He burning core (dark regions) during the EHB phase, for the model with small overshooting (f = 10−5). The core grows monotonically until ∼25 Myr, where it suddenly splits into two convective regions.
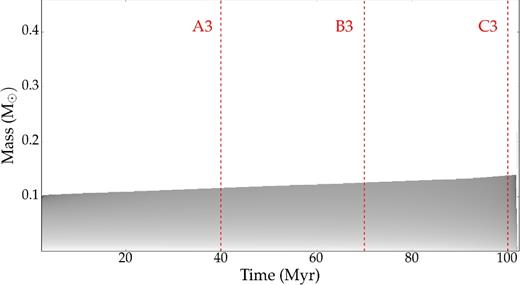
Evolution of the He burning core (dark regions) during the EHB phase, for the model with very small overshooting (f = 10−6). The core grows monotonically during EHB phase.
6 ASTEROSEISMIC ASPECTS
Asteroseismology is an astrophysical tool to unravel the internal structure of stars, due to the strong dependence of oscillation frequencies on the properties of the stellar interior (Unno et al. 1989; Aerts, Christensen-Dalsgaard & Kurtz 2010). Since p modes are most sensitive to the structure of the outer layers while g modes to the deep interior, density and chemical stratification near the edge of a convective core have large effects on the g-mode behaviour.
6.1 Period spacings
Asymptotic analysis predicts equally spaced periods for high-order g modes. On the other hand, the measured period spacings of g modes are known to deviate from uniformity. Here, we exploit such deviations in terms of the properties of the stellar interior, more particularly the character of the mixing.
Brassard et al. (1992a,b) extended the asymptotic theory to incorporate the effect of a discontinuity in chemical composition and/or the presence of an outer convection zone in the white dwarfs. Charpinet et al. (2000) developed further the asymptotic theory to the specific case of sdB stars with a convective core and a radiative envelope.
Different mixing processes (overshooting, atomic diffusion, rotation, etc.) lead to different shapes of the chemical gradient outside the convective core and hence the period spacing pattern depends on the detailed properties of the buoyancy frequency in the vicinity of convective core (Miglio et al. 2008). Observed period spacing patterns can therefore be used to understand and pinpoint what kind of mixing is acting near the convective core and how efficient the mixing processes are.
For the moderate and small overshooting scenarios, the CO/He transition layer has the most important influence on the period spacing pattern. Deep mode trapping patterns can be created by the convective shells. Alongside the evolutionary path, the distance between the sharp composition gradients remaining between the convective shells and the lower convective core are larger and the number of trapped modes increases (Figs 9 and 10).
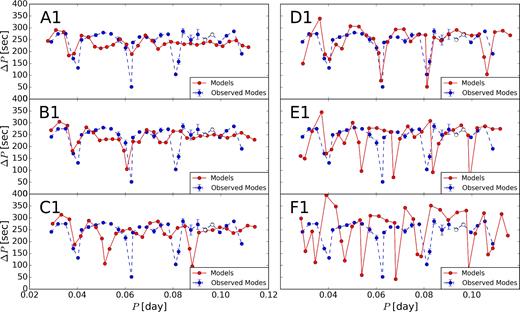
Period spacing of the model with moderate overshooting for six points indicated in Fig. 3.
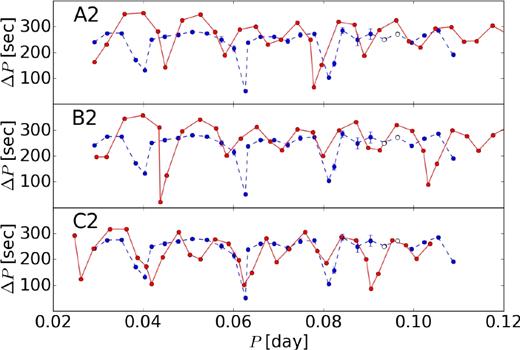
Period spacing of the model with small overshooting for three points indicated in Fig. 5.
In the very small overshooting scenario, the He/H transition layer has the largest influence on the period spacing pattern. At the EHB, this He/H transition interface remains constant. The gradual decrease in the period spacing arises due to the growing convective core and along with it the shrinking of the propagation cavity. Therefore, the period spacing pattern depends on the detailed properties of the buoyancy frequency in the vicinity of He/H transition layer (cf. Fig. 11). Charpinet et al. (2000, 2002a,b) have already demonstrated that the period spacing pattern for such a convective core structure is not very sensitive to the presence of the CO/He transition layer.
6.2 Trapped modes
The radiative gradient and/or chemical gradients change the density profile and consequently the Brunt–Väisälä frequency. In sdB models, the H to He transition layer in the outer envelope, and the He to CO transition layer near the convective boundary implies sharp features in the Brunt–Väisälä frequency. Such sharp features leave observable fingerprints in the period spacing patterns of g modes (Miglio et al. 2008; Cunha et al. 2015). The displacement eigenfunctions of trapped modes have two nodes close to the local peak associated with the inner transition layer near the core. Fig. 12 shows that the horizontal component of the eigendisplacement ξh is trapped in the vicinity of the Brunt–Väisälä frequency peak (blue solid line).
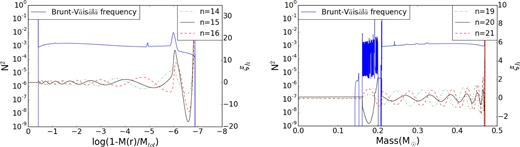
The Brunt–Väisälä frequency (left y-axis) and the horizontal eigendisplacement ξh (right y-axis) of three dipole g modes with different radial order (n). Right-hand and left-hand panels illustrate the behaviour of the trapped modes (black solid lines) near the He/H transition layer for models with monotonically growing core based on very small overshooting and near the CO/He convective boundary for fluctuating growth stages of models with a moderate overshooting.
The results derived from our models illustrate that the nature of the He/H and CO/He chemical transition layers determines the effect they have on the mode trapping. In the case of mixing due to very small overshooting and the first stage of moderate and small overshooting, the CO/He transition layer has negligible impact on the trapping, and the He/H transition layer controls the trapping of the modes. The results for this scenario are in good agreement with those of Charpinet et al. (2000, 2002a,b). On the other hand, the mixing caused by moderate and small overshooting in fluctuating stages reveals that both transition layers play a considerable role on the mode trapping. The He/H transition layer and the convective shells produce deeply trapped modes. A sharp density stratification at the outer edge of the convective shells change the buoyancy restoring force and gives rise to a sinusoidal variation of the amplitude of the eigenfunction. Some of the displacement eigenfunctions having nodes very close to the convective shells obtain a large amplitude at the radiative regions between the convective core and shells (see Fig. 12).
6.3 Mode inertia
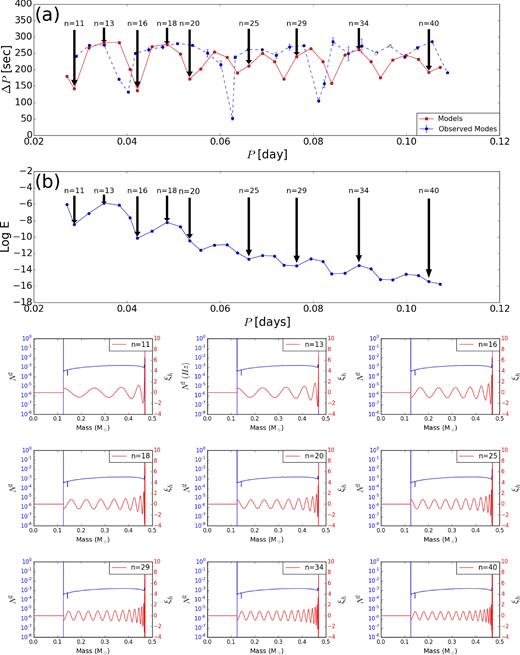
In the fluctuating stages of the scenario with moderate and small overshooting, the few trapped modes have large amplitude inside the radiative layer between the convective core and the convective shells. Therefore, such deeply trapped modes have large mode inertia as can be seen in panel (b) of Fig. 13). Such centrally enhanced mode energies connected with high local amplitudes of trapped modes in the deep stellar interior near the He/CO core boundary have been reported before (e.g. Brassard et al. 1992a,b, in the case of white dwarfs). For the very small overshooting scenario and uniformly growing stages of other scenarios, the trapped modes have lower amplitude at the inner layers of the sdB star in comparison with the outer edge of the He/H transition zone. Therefore, such trapped modes have small mode inertia. They are shown in the panels (b) of Fig. 14. Charpinet et al. (2000, 2002a,b) have found out that for such a very small overshooting scenario, all g modes are reflected in the vicinity of the convective core boundary. Therefore, the mode inertia is not sensitive to the CO/He transition layer.
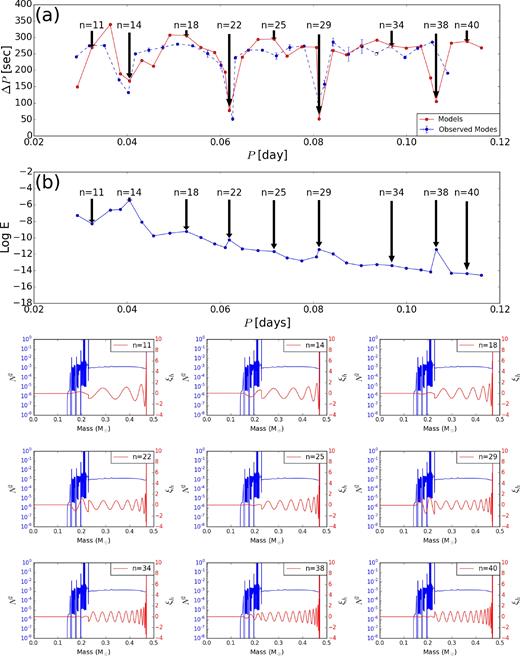
Panel (a): period spacing pattern of g modes with the same degree (l = 1) and consecutive radial order (n) for a model with moderate overshooting for the point D1 on Fig. 3. Panel (b): the normalized mode inertia as a function of the periods of the dipole g modes. Lower panels: red solid lines show the horizontal displacement eigenfunction of the dipole g modes for different radial order as indicated. The blue solid lines illustrate the Brunt–Väisälä frequency in the stellar interior.
7 DIFFUSION
Atomic diffusion in mesa includes gravitational settling, thermal and concentration diffusion. Gravitational settling leads heavy elements to settle in the inner regions and concentration diffusion implies charged particles to be subjected to an electric field. Thermal diffusion causes heavy particles to move more slowly than light ones at any temperature or kinetic energy. mesa solves the Burgers flow equations (Burgers 1969) based on a routine provided by Thoul et al. (1994), with modifications by Hu et al. (2011) for non-Coulomb interactions and radiative levitation.
Considering atomic diffusion as the only mixing process between the convective core and the radiative regions, increases the convective core mass (Schindler et al. 2015). When moderate or small overshoot is added to the atomic diffusion, we see the same behaviour of the convective core discussed above for the moderate or small overshoot models without atomic diffusion. In these cases, overshooting is the dominant mechanism for the matter transfer between the convective core and the radiative regions. The maximum convective core size and the lifetime are both almost the same (see Figs 15 and 16).
Evolution of the He burning core (dark regions) during the EHB phase, for the model with moderate overshooting described by the value f = 0.01 in presence of the diffusion. Temporal appearances and disappearances of convective shells on top of the core occur, with narrow inert radiative regions (white) in between.
Evolution of the He burning core (dark regions) during the EHB phase, for the model with small overshooting described by the value f = 10−5 in presence of the diffusion. The convective region splits into an inner convective core and an outer convective shell.
For the very small overshooting models, diffusion leads to a split of the convective core. Also, diffusion increases the lifetime of the EHB phase (see Fig. 17). Atomic diffusion is also able to change the profile of the Brunt–Väisälä frequency in the outer layers. Diffusion broadens the steep composition gradients leading to less efficient mode trapping in the H/He transition layer. In phases with a monotonically growing core, the region above the He/H transition layer has the largest influence on the period spacing pattern because the He/H transition interface is smoothed by atomic diffusion. On the other hand, at the late phases of models with a convective shell, the C–O/He transition layer has the most important influence on the period spacing pattern, due to deep mode trapping patterns created by the convective shell.
Evolution of the He burning core (dark regions) during the EHB phase, for the model with very small overshooting by the value f = 10−6 in presence of the diffusion.
8 DISCUSSION
We investigated the influence of three overshooting scenarios on the evolution of convective cores of sdB stars. In all mixing cases due to small and moderate overshooting, the accompanying mixing leads to fluctuations in the size of the convective core accompanied by the occurrence of convective shells during various stages of evolution.
The deviations from a constant g-mode period spacing are sensitive to the detailed properties of the buoyancy frequency inside pulsating sdB stars. These deviations can be interpreted by means of comparison with theoretical calculations of the displacement eigenfrequencies and eigenfunctions. Our results illustrate that a small amount of core overshooting, accompanied by outer Brunt–Väisälä peaks due to convective shells are able to produce the period spacing patterns observed in KIC 10553698A at late stages. The Brunt–Väisälä peak of the transition layer between the He-rich envelope and the carbon core influences the trapping of modes and hence the period spacing patterns.
In mesa, a bare use of mixing length theory without additional mixing beyond the convective core prohibits the core growth during EHB phase (see Paxton et al. 2011, their fig. 15). Other stellar evolution codes rely on an implementation of the mixing-length theory that allows for core growth even for the cases without convective overshoot (Gabriel et al. 2014; Constantino et al. 2015, 2016). Here, we have only considered mesa models including convective overshoot as a phenomenon of convection carrying material beyond the boundary of convective core; hence, the convective velocity is non-zero at the core boundary and it declines exponentially with distance in the overshooting layers. Constantino et al. (2015) argued that the mode trapping in KIC 10553698A is a consequence of the sharp composition gradient at the outer region of the convective boundary in their standard-overshoot mode adopted, which has f = 0.001. In their work, which is based on independent evolution and pulsation codes, this amount of overshooting tends to grow the core. At the outer edge of the convective core, the region becomes radiative. The process continuously repeats, leaving behind a characteristic stepped abundance profile. It is not clear to us how their treatment of smoothing, atomic diffusion, and the chosen time steps along the evolutionary track compare to ours. In their adopted moderate overshooting scenario, the convective core growth explicitly prevented the splitting of the core and the authors were able to produce the observed period spacing pattern of KIC 10553698A. In both our moderate and small overshooting models, the appearance of convective shells occurs and it also leads to the correct number of non-trapped modes between trapped modes compared with the observations. In addition, atomic diffusion smooths the other Brunt–Väisälä peaks and leads to a better match with the observations.
HB stars burn helium in their core and hydrogen in a convective shell. According to Fig. 18, HB convective core growing scenarios due to different amount of core overshooting are almost similar to the EHB evolutionary scenarios. The R2 parameter is the fraction of AGB stars to HB stars in globular clusters (Buonanno et al. 1985; Cassisi et al. 2001). Theoretical models allow to predict R2 from the duration of the various evolutionary phases and to consider this as test that is very sensitive to the extension of the convective core, which is independent of the seismic modelling of the period spacings. The R2 parameter is less sensitive to other stellar quantities such as initial mass and metallicity (Caputo et al. 1989). We computed the R2 value for our models with convective core overshoot mixing due to moderate, small, and very small overshooting, with and without diffusion (see Fig. 19). Our results are listed in Table 1: for small overshooting and for very small overshooting in presence diffusion, R2 = 0.11, which is compatible with recent observed values (Constantino et al. 2016). Moreover, based on theoretical grounds, Castellani, Giannone & Renzini (1971) proposed a very small overshooting layer because the high gravity in the core helium burning phase acts as a braking force for convective motions inside the overshooting layers. This is entirely compatible with our results.

Convective core growing of HB stars as a function of star age for models with moderate (a), moderate plus diffusion (b), small (c), small plus diffusion (d), very small (e), and very small plus diffusion (f).
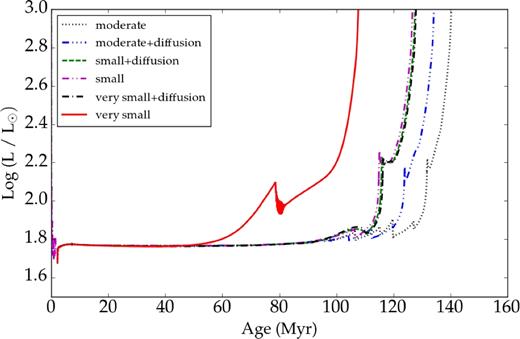
Luminosity of a HB star as a function of age, from the start of the helium flashes to the first thermal pulse on the asymptotic giant branch (TP-AGB).
| . | HeCB phase lifetime (Myr) . | R2 parameter . |
|---|---|---|
| Moderate | 131.7 | 0.07 |
| Small | 114.8 | 0.11 |
| Very small | 79.1 | 0.38 |
| Moderate + diffusion | 123.8 | 0.09 |
| Small + diffusion | 115.7 | 0.11 |
| Very small + diffusion | 116.2 | 0.11 |
| . | HeCB phase lifetime (Myr) . | R2 parameter . |
|---|---|---|
| Moderate | 131.7 | 0.07 |
| Small | 114.8 | 0.11 |
| Very small | 79.1 | 0.38 |
| Moderate + diffusion | 123.8 | 0.09 |
| Small + diffusion | 115.7 | 0.11 |
| Very small + diffusion | 116.2 | 0.11 |
| . | HeCB phase lifetime (Myr) . | R2 parameter . |
|---|---|---|
| Moderate | 131.7 | 0.07 |
| Small | 114.8 | 0.11 |
| Very small | 79.1 | 0.38 |
| Moderate + diffusion | 123.8 | 0.09 |
| Small + diffusion | 115.7 | 0.11 |
| Very small + diffusion | 116.2 | 0.11 |
| . | HeCB phase lifetime (Myr) . | R2 parameter . |
|---|---|---|
| Moderate | 131.7 | 0.07 |
| Small | 114.8 | 0.11 |
| Very small | 79.1 | 0.38 |
| Moderate + diffusion | 123.8 | 0.09 |
| Small + diffusion | 115.7 | 0.11 |
| Very small + diffusion | 116.2 | 0.11 |
An increased number of observed pulsating sdB stars with uninterrupted high-precision space photometry will hopefully lead to an increased fraction of sdB stars with trapped modes in the near future. This would allow to investigate the effects of time-dependent core overshooting on the size of the convective core and g-mode behaviour of sdB pulsators. The overshooting distance is inversely proportional to the differences of the mean atomic weight in the interior and exterior of the convective core and depends on the gravitational acceleration in the overshooting layers. Matter exterior to the core is highly buoyant relative to matter inside the core and only a fraction of additional matter will be carried by the convective flows, as discussed in Sweigart (1990) and Spruit (2015). Different cooling process of overshooting layers, such as neutrino cooling, can be studied as a time-dependent overshooting undoubtedly influencing the breathing pulses for the late carbon burning phases (Arnett et al. 2015; Viallet et al. 2015). Generally, asteroseismic studies of g-mode pulsating stars provide an excellent opportunity to improve models of convection and overshooting in different stages of stellar evolution, as indicated in the recent 321D algorithm development by Arnett et al. (2015).
Acknowledgments
The first author wishes to especially thank Roy Østensen for interesting discussions which helped to improve several parts of this study. The work was initiated during a 9 months research stay at Leuven University. Part of the research stay of HG at Leuven University was funded by the Francqui Prize offered to CA in 2012 by the Francqui Foundation, Belgium. This research was also partly funded from the European Community's Seventh Framework Programme FP7-SPACE-2011-1, project number 312844 (SPACEINN). The research leading to these results has received funding from the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme FP7/2007–2013/ under REA grant agreement No. 623303 (ASAMBA).




