-
PDF
- Split View
-
Views
-
Cite
Cite
Marco Baldi, Fergus Simpson, Structure formation simulations with momentum exchange: alleviating tensions between high-redshift and low-redshift cosmological probes, Monthly Notices of the Royal Astronomical Society, Volume 465, Issue 1, 11 February 2017, Pages 653–666, https://doi.org/10.1093/mnras/stw2702
Close - Share Icon Share
Abstract
Persisting tensions between the cosmological constraints derived from low-redshift probes and the ones obtained from temperature and polarization anisotropies of the cosmic microwave background (CMB) – although not yet providing compelling evidence against the Λcold dark matter model – seem to consistently indicate a slower growth of density perturbations as compared to the predictions of the standard cosmological scenario. Such behaviour is not easily accommodated by the simplest extensions of General Relativity, such as f(R) models, which generically predict an enhanced growth rate. In this work, we present the outcomes of a suite of large N-body simulations carried out in the context of a cosmological model featuring a non-vanishing scattering cross-section between the dark matter and the dark energy fields, for two different parametrizations of the dark energy equation of state. Our results indicate that these dark scattering models have very mild effects on many observables related to large-scale structures formation and evolution, while providing a significant suppression of the amplitude of linear density perturbations and the abundance of massive clusters. Our simulations therefore confirm that these models offer a promising route to alleviate existing tensions between low-redshift measurements and those of the CMB.
1 INTRODUCTION
The physical characteristics of dark matter and dark energy (DE) remain poorly constrained. Proposed candidates for dark matter include axions, weakly interacting massive particles (WIMPs), and black holes, while DE has been linked to a cosmological constant and scalar fields. And of course, there remains ample scope for either dark matter or DE to be described by a fundamentally new form of physics. One fairly well-determined feature is their current energy density and, in that respect, these two phenomena appear comparable. This has fuelled speculation that their relationship is not purely gravitational.
A further hint of a connection between the universe's two dominant constituents stems from small but consistent deviations between low-redshift measurements of the amplitude of density perturbations and the extrapolated value based on the amplitude of primary anisotropies in the cosmic microwave background (CMB; Ade et al. 2015). These low-redshift measurements include weak gravitational lensing from CFHTLenS (Heymans et al. 2013), redshift space distortions induced by the motions of galaxies (Blake et al. 2011; Reid et al. 2012; Macaulay, Wehus & Eriksen 2013; Beutler et al. 2014; Gil-Marín et al. 2016; Simpson et al. 2016), and galaxy clusters (Vikhlinin et al. 2009; Planck Collaboration XXIV 2016), all indicating a slightly lower amplitude of clustering than has been inferred from the CMB. Additionally, even lensing of the CMB itself prefers lower values of the amplitude of linear perturbations (Ade et al. 2015).
Such tension may be just the result of some unaccounted systematic effect. However, if the growth of cosmological structure is confirmed to deviate from the theoretical predictions of the Λcold dark matter (CDM) model, one interpretation of this result would be the discovery of a new regime of gravitational physics. However, many of the most popular modified gravity theories, such as f(R), Symmetron, and nDGP models, generically lead to a strengthening of the gravitational force. This naturally implies an enhanced growth of perturbations, in contrast with the observations which favour a suppressed growth rate (Hu & Raveri 2015). In this respect, it appears more plausible that a non-gravitational interaction is responsible for the anomalous behaviour. Furthermore, in light of the stringent constraints on General Relativity derived from Solar system measurements (Bertotti, Iess & Tortora 2003; Will 2005) and further restrictions derived from the propagation of gravitational waves (Lombriser & Lima 2016), the latter options would also appear to offer a more natural solution.
Many models of coupled DE have been proposed in the literature (see e.g. Amendola 2000; Barrow & Clifton 2006; Baldi 2011). However, the overwhelming majority focus on a specific form of energy–momentum exchange between the two fluids, in which the coupling current is time-like. In other words, the theoretical models predominantly take the form of energy exchange rather than momentum exchange. This choice was originally motivated by the fact that an energy exchange might have an impact on the background expansion history of the universe and could then provide solutions to the fine-tuning and coincidence problems of the cosmological constant.
More recently, motivated by the tendency for low-energy interactions between standard model particles to result in elastic scattering, Simpson (2010) proposed a model which invokes pure momentum exchange between the two fluids. Subsequently, Pourtsidou, Skordis & Copeland (2013) presented a comprehensive classification of interacting DE models where they identified a class of models (termed ‘Type 3’) which invoke pure momentum exchange between dark matter and a scalar field. The properties of these models were explored in greater detail in Skordis, Pourtsidou & Copeland (2015). In this work, we will aim to develop our understanding of the relationship between the Type 3 models and the elastic scattering model and explore their phenomenological effects.
In Baldi & Simpson (2015), it was shown that if the dark matter particles experience a drag force as they pass through a canonical (i.e. non-phantom) DE fluid, they leave two key observational signatures. First of all, the matter power spectrum is suppressed in a scale-independent fashion on linear scales and secondly, it is scale-dependently enhanced on non-linear scales. Here we present results from a suite of N-body simulations in which the DE fluid has an evolving equation of state, as is to be expected from dynamical models, and compare the resulting large-scale structure with those found in Baldi & Simpson (2015). Our aim is then to test whether such a class of cosmologies might provide a way to reconcile cosmological constraints arising from CMB data analysis and low-redshift measurements of the growth of structures
In Section 2, we explore the relationship between the phenomenological dark scattering model and those which invoke a velocity coupling to the derivative of a scalar field. Then, in Section 3, we review the particular models chosen for further investigation using a suite of numerical simulations. Specifications of the simulations are given in Section 4 and their outputs are analysed in Section 5. Our concluding remarks are presented in Section 6.
2 MOMENTUM EXCHANGE WITH SCALAR FIELDS
Note that in defining a continuous velocity field, as is required to form Z, we necessarily introduce a smoothing length over which the particle velocities are averaged. The smoothing length is assumed to be smaller than the cosmological perturbations under consideration.
3 DARK SCATTERING MODELS BEYOND A CONSTANT EQUATION OF STATE: TWO DE PARAMETRIzATIONS
Motivated by the above outlined relation between models of elastic scattering in the dark sector and the particular sub-class of ‘Type 3’ coupled quintessence models proposed in Skordis et al. (2015), we briefly review in this section the main features of dark scattering cosmologies. We also present the specific models under investigation in this work, providing an overview of their background evolution and of their main features related to linear and non-linear structure formation.
3.1 Background evolution
We will consider cosmological models characterized by an exchange of momentum between CDM particles and a DE field, modelled as a nearly homogeneous fluid with a time-dependent equation-of-state parameter w(a). In this work, we will consider two possible parametrizations of a freezing DE equation-of-state parameter w(a). We focus on freezing models as they are expected to produce substantial effects on structure formation in the linear regime, while the impact of the momentum exchange should be suppressed at low redshifts by a factor (1 + w), as we will show below.
The evolution of the equation-of-state parameter as a function of redshift for these two parametrizations is shown in Fig. 1 for the parameters summarized in Table 1. In Fig. 1, like in all the figures of this work, we also display for comparison the behaviour of the two constant-w models with w = −0.9 and −1.1 that were studied in our previous paper Baldi & Simpson (2015) (as dashed and triple-dot–dashed lines, respectively).
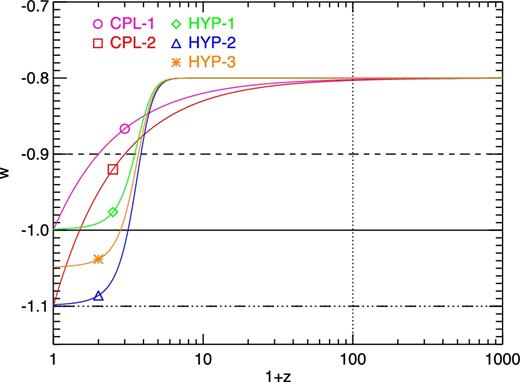
The equation-of-state evolution for the various parametrizations considered in this work. The black dashed and triple-dot–dashed lines represent the constant values w = −0.9 and −1.1, respectively, which have been discussed in Baldi & Simpson (2015).
The various DE parametrizations considered in this work with their main parameters and the resulting value of σ8 at z = 0.
| Parametrization . | w0 . | wa . | zt . | ξ . | σ8 . |
|---|---|---|---|---|---|
| ΛCDM | −1 | – | – | – | 0.83 |
| w09 | −0.9 | – | – | 10, 50 | 0.79, 0.75 |
| w11 | −1.1 | – | – | 10, 50 | 0.85, 0.87 |
| CPL-1 | −1 | 0.2 | – | 50 | 0.75 |
| CPL-2 | −1.1 | 0.3 | – | 50 | 0.79 |
| HYP-1 | −1 | 0.2 | 1.5 | 50 | 0.78 |
| HYP-2 | −1.1 | 0.3 | 1.5 | 50 | 0.83 |
| HYP-3 | −1.05 | 0.25 | 1.5 | 50 | 0.81 |
| Parametrization . | w0 . | wa . | zt . | ξ . | σ8 . |
|---|---|---|---|---|---|
| ΛCDM | −1 | – | – | – | 0.83 |
| w09 | −0.9 | – | – | 10, 50 | 0.79, 0.75 |
| w11 | −1.1 | – | – | 10, 50 | 0.85, 0.87 |
| CPL-1 | −1 | 0.2 | – | 50 | 0.75 |
| CPL-2 | −1.1 | 0.3 | – | 50 | 0.79 |
| HYP-1 | −1 | 0.2 | 1.5 | 50 | 0.78 |
| HYP-2 | −1.1 | 0.3 | 1.5 | 50 | 0.83 |
| HYP-3 | −1.05 | 0.25 | 1.5 | 50 | 0.81 |
The various DE parametrizations considered in this work with their main parameters and the resulting value of σ8 at z = 0.
| Parametrization . | w0 . | wa . | zt . | ξ . | σ8 . |
|---|---|---|---|---|---|
| ΛCDM | −1 | – | – | – | 0.83 |
| w09 | −0.9 | – | – | 10, 50 | 0.79, 0.75 |
| w11 | −1.1 | – | – | 10, 50 | 0.85, 0.87 |
| CPL-1 | −1 | 0.2 | – | 50 | 0.75 |
| CPL-2 | −1.1 | 0.3 | – | 50 | 0.79 |
| HYP-1 | −1 | 0.2 | 1.5 | 50 | 0.78 |
| HYP-2 | −1.1 | 0.3 | 1.5 | 50 | 0.83 |
| HYP-3 | −1.05 | 0.25 | 1.5 | 50 | 0.81 |
| Parametrization . | w0 . | wa . | zt . | ξ . | σ8 . |
|---|---|---|---|---|---|
| ΛCDM | −1 | – | – | – | 0.83 |
| w09 | −0.9 | – | – | 10, 50 | 0.79, 0.75 |
| w11 | −1.1 | – | – | 10, 50 | 0.85, 0.87 |
| CPL-1 | −1 | 0.2 | – | 50 | 0.75 |
| CPL-2 | −1.1 | 0.3 | – | 50 | 0.79 |
| HYP-1 | −1 | 0.2 | 1.5 | 50 | 0.78 |
| HYP-2 | −1.1 | 0.3 | 1.5 | 50 | 0.83 |
| HYP-3 | −1.05 | 0.25 | 1.5 | 50 | 0.81 |
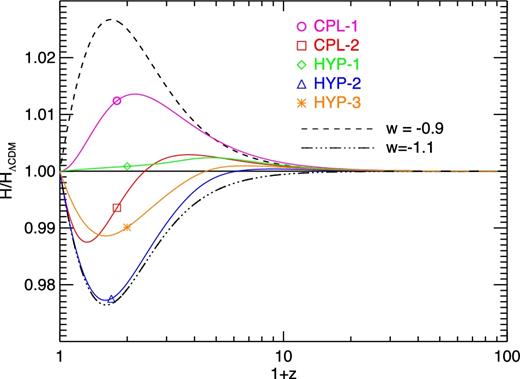
The Hubble function ratio to the standard ΛCDM case for the various parametrizations considered in this work. The black solid and dashed lines represent the constant values w = −0.9 and −1.1, respectively, that have been discussed in Baldi & Simpson (2015).
3.2 Linear and non-linear structure formation in dark scattering cosmologies
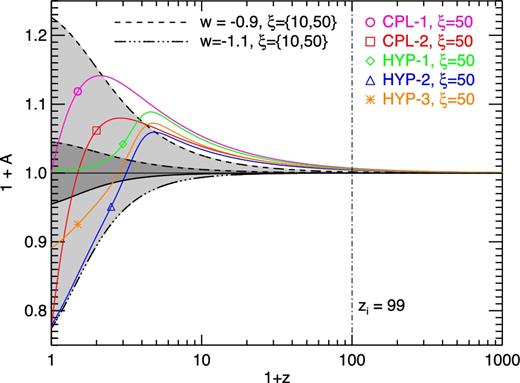
The modified friction term (1 + A) for the various parametrizations considered in this work. As one can see in the figure, the variable-w models determine a stronger modification at high redshifts and a weaker modification at low redshifts compared with the constant-w case. Colours and linestyles are the same as in Fig. 2.
4 THE SIMULATIONS
For all the models summarized in Table 1 and for a reference ΛCDM cosmology, we have performed a set of intermediate-size simulations with the modified version of GADGET (Springel 2005) described in Baldi & Simpson (2015), which self-consistently implements the drag force associated with the DE-CDM momentum exchange. These simulations have a box size of 250 Mpc h−1 a side and follow the evolution of 5123 CDM particles in a periodic cosmological volume from zi = 99 down to z = 0. The mass resolution is m = 1 × 1010 M⊙ h−1 and the gravitational softening employed to avoid two-body scattering processes is ε ≈ 12 kpc h−1, corresponding to 1/40th of the mean inter-particle separation. All the simulations share the same initial conditions (since the effect of the momentum exchange is negligible at z ≳ 100, see Fig. 3) and cosmological parameters (consistent with the results of the Planck satellite mission; Ade et al. 2015, see Table 2). We decided to fix the values of all standard cosmological parameters (with the exception of σ8) to the same best-fitting values summarized in Table 2 in order to isolate as much as possible the effects of the momentum exchange from possible degenerate effects arising from shifting one or more standard parameters to slightly different values. Nonetheless, an investigation of the possible impact of e.g. a different value of the Hubble parameter H0, as suggested by low-redshift observations, may be required in the future to quantitatively estimate the best-fitting value of the interaction strength ξ.
A summary of the cosmological parameters adopted for all the simulations discussed in this work.
| Parameter . | Value . |
|---|---|
| H0 | 67.8 km s−1 Mpc−1 |
| ΩM(z = 0) | 0.308 |
| ΩDE(z = 0) | 0.692 |
| Ωb(z = 0) | 0.0482 |
| |${\cal A}_{{\rm s}}$| | 2.215 × 10−9 |
| ns | 0.966 |
| Parameter . | Value . |
|---|---|
| H0 | 67.8 km s−1 Mpc−1 |
| ΩM(z = 0) | 0.308 |
| ΩDE(z = 0) | 0.692 |
| Ωb(z = 0) | 0.0482 |
| |${\cal A}_{{\rm s}}$| | 2.215 × 10−9 |
| ns | 0.966 |
A summary of the cosmological parameters adopted for all the simulations discussed in this work.
| Parameter . | Value . |
|---|---|
| H0 | 67.8 km s−1 Mpc−1 |
| ΩM(z = 0) | 0.308 |
| ΩDE(z = 0) | 0.692 |
| Ωb(z = 0) | 0.0482 |
| |${\cal A}_{{\rm s}}$| | 2.215 × 10−9 |
| ns | 0.966 |
| Parameter . | Value . |
|---|---|
| H0 | 67.8 km s−1 Mpc−1 |
| ΩM(z = 0) | 0.308 |
| ΩDE(z = 0) | 0.692 |
| Ωb(z = 0) | 0.0482 |
| |${\cal A}_{{\rm s}}$| | 2.215 × 10−9 |
| ns | 0.966 |
This suite of simulations has been employed to test the effects of the variable-w models on two basic cosmological observables: the non-linear matter power spectrum and the halo mass function (see Section 5.1). These preliminary results allowed us to identify the most relevant sets of parameters for both the CPL and the HYP parametrizations to be investigated more extensively with a set of larger simulations. The latter are cosmological boxes of 1 Gpc h−1 a side, filled with 10243 CDM particles and have therefore a poorer mass (m = 8 × 1010 M⊙ h−1) and space (ε ≈ 24 kpc h−1) resolution compared to the smaller runs, but significantly improve the statistics of massive clusters and of cosmic voids (see Section 5.2), thereby allowing a more significant assessment of the impact of the momentum exchange on the statistical and structural properties of these classes of objects.
For all the simulations, initial conditions have been generated by displacing particle positions from a ‘glass’ homogeneous distribution (Davis et al. 1985) according to the Zeldovich approximation (Zel'dovich 1970) to set up a random-phase realization of the power spectrum predicted by CAMB3 (Lewis, Challinor & Lasenby 2000) for a ΛCDM cosmology with the chosen cosmological parameters. Therefore, all the differences that will be identified among the simulations outputs at low redshifts can be unambiguously ascribed to the effects of the different cosmological models. Furthermore, as the initial conditions are identical, the comparison of the various models will not be affected by sample variance and statistical uncertainties will be only due to Poisson noise.
5 RESULTS
In this section, we will discuss the main outcomes of our simulations, starting with the results of the intermediate-scale runs and then moving to the large-scale realizations for the selected subset of models.
5.1 Intermediate-size simulations: selecting target models through the non-linear matter power spectrum and the halo mass function
For all our intermediate-size simulations, we extract the non-linear matter power spectrum through a Cloud-in-Cell (CIC) mass assignment to a cubic Cartesian grid having the same spacing of the mesh used for the large-scale N-body integration, i.e. 5123 grid nodes. This allows us to measure the power spectrum from the fundamental mode k0 ≈ 0.01 h Mpc−1 up to the Nyquist frequency of the grid kNy ≈ 6.43 h Mpc−1. In order to extend this range to smaller scales, we employ the folding method of Jenkins et al. (1998) and Colombi et al. (2009) and we smoothly interpolate the two estimations around kNy. Then, the combined power spectrum obtained in this way is truncated at the scale where the shot noise reaches 20 per cent of the measured power. We apply this procedure to the simulation snapshots corresponding to three different redshifts z = {0 , 0.5 , 1}. The results are displayed in Fig. 4 where we show the ratio of the measured power of each simulation to the corresponding ΛCDM result. All the variable-w cosmologies (solid coloured lines with symbols) are characterized by a value of ξ = 50 [bn/GeV], while, for the two constant-w models used as a reference (dashed and dot–dashed black lines), we consider both ξ = 10 (thin lines) and 50 [bn/GeV] (thick lines).
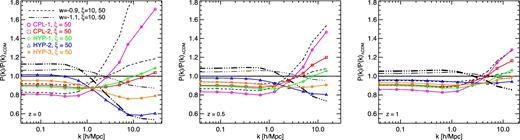
The non-linear matter power spectrum ratio to the reference ΛCDM model at three different redshifts z = 0 ( left), 0.5 (middle), and 1 ( right) for the various models investigated with our intermediate-size simulations. The colours and linestyles are the same as in Fig. 1.
As one can see in the plots and most evidently in the z = 0 panel, the variability of the DE equation of state introduces non-trivial features in the behaviour of the matter power as a function of scale. For constant-w (as already discussed in Baldi & Simpson 2015), the effect of the DE-CDM momentum exchange on the power spectrum shows a scale-independent suppression (enhancement) of power at large scales and a transition to a scale-dependent enhancement (suppression) at small scales for w > −1 (w < −1). The transition corresponds to the scale where non-linear effects come into play and expectedly shifts towards smaller k for decreasing redshift. Also, there is a direct correspondence between the magnitude of the linear and non-linear effects, with a larger effect at linear scales being always associated with a larger effect also at non-linear scales.
For the variable-w case, the effects appear more diverse, with a wide range of behaviours and of possible linear-non-linear transitions, as well as a less direct correspondence between the magnitude of the effect at linear scales and its non-linear counterpart. In this respect, it is interesting to consider the relation between the power spectrum ratio at large scales and that at smaller scales as the former will have mostly an impact on the statistical properties of large-scale structures while the latter will have direct consequences on the structural properties of collapsed objects. This comparison is shown in Fig. 5, where we display the relative difference of the observed power enhancement at k = 0.1 and 10 h Mpc−1 defined as Δ ≡ [P(k)/P(k)ΛCDM]k = 10/[P(k)/P(k)ΛCDM]k = 0.1 − 1, as a function of redshift. As one can see in the plot, all the variable-w models have a weaker impact at non-linear scales compared to the constant-w models with the same value of the ξ parameter (ξ = 50 [bn/GeV], thick lines) and two of them (the CPL-2 and the HYP-1 models) even show a smaller non-linear impact at z = 0 compared to the constant-w models with the lower value of ξ = 10 [bn/GeV] (thin lines). This provides us with a useful guideline to select relevant combinations of parameters, since we are interested in identifying models that produce a sizeable suppression of the large-scale structures growth without changing too dramatically the structural properties of collapsed haloes.
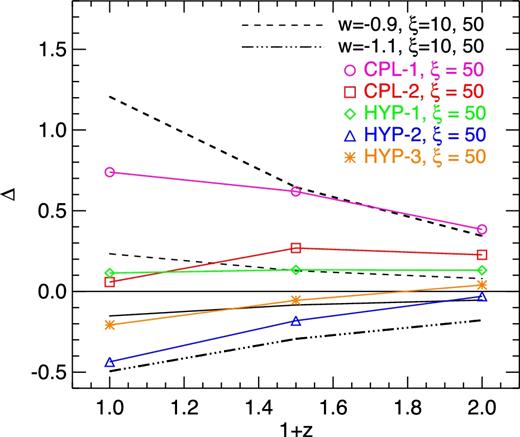
The relative difference between the non-linear (i.e. measured at k = 10 h Mpc−1) and the linear (i.e. measured at k = 0.1 h Mpc−1) effects on the matter power spectrum for the various models of momentum exchange.
A similar analysis can be performed using the abundance of haloes as a test observable. To this end, we have identified particle groups in our simulations by means of a Friends-of-Friends (FOF) algorithm with linking length 0.2 times the mean inter-particle separation and subsequently performed a particle unbinding on all the identified groups by means of the SUBFIND algorithm (Springel et al. 2001) in order to select gravitationally bound substructures. With these catalogues at hand, we have computed the cumulative halo mass function for all the models by binning the haloes in mass bins according to their M200 mass defined as the mass contained in a sphere centred on the most bound particle of each main substructure with a radius R200 enclosing a mean density 200 times larger than the critical density of the universe. We have then compared these mass functions to the outcome of the ΛCDM simulation and the results are displayed in Fig. 6.
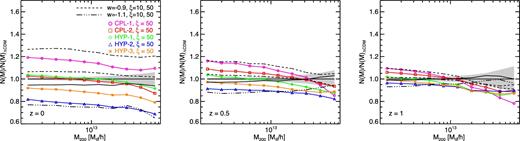
The mass function ratio to the ΛCDM case for all the models under investigation in this work. The three panels refer to the same redshifts considered above (z = 0 , 0.5, and 1), and colours, symbols, and line styles are the same as displayed in Fig. 4.
As one can see in the figure, also in this case, we find that the variable-w models predict a milder impact on the abundance of haloes at all masses compared to their constant-w counterparts with the same value of ξ = 50 [bn/GeV], especially at z = 0. Furthermore, consistently with the previous findings shown in Figs 5 and 4, the two models CPL-2 and HYP-1 appear to be the closest match to the ΛCDM result at low masses, while showing some significant suppression of the abundance of haloes at the high-mass end of the available catalogues, differently from all the other models that are found to determine large deviations in the abundance also for galaxy-sized haloes. This is a consequence of the suppression of large-scale linear clustering, since the halo mass function is exponentially sensitive to the value of σ8 and to the relatively weak impact of the interaction at highly non-linear scales. Therefore, these models represent promising candidates to ease the persisting tensions between both the observed weak lensing amplitude (Heymans et al. 2013) and abundance of Planck SZ clusters (Planck Collaboration XXIV 2016) on one side and their predicted values based on the maximum likelihood Planck 2015 cosmological parameters estimation (Ade et al. 2015).
Based on these preliminary checks, we have then selected the two models CPL-2 and HYP-1 to be investigated in more detail through larger simulations, along with two constant-w models with ξ = 10 [bn/GeV] and a reference ΛCDM cosmology. Interestingly, these two models show very similar effects on the matter power spectrum and the halo mass function, despite having a quite different evolution of w(z). This is due to a compensation of effects between the w > −1 and the w < −1 regimes of the CPL-2 model, since the A parameter changes sign at the phantom crossing (see equation 9), as we have verified through some preliminary numerical checks. The outcomes of our larger simulations, which represent the core results of this work, are discussed in the following section.
5.2 The large simulations
We present here the results of our suite of large simulations focusing on the effects that the momentum exchange between DE and CDM particles has on a series of standard cosmological observables. As our analysis will show, the two selected models CPL-2 and HYP-1 will result in a cosmological evolution of structures that closely resembles that of ΛCDM for most of the observables, with the noticeable exception of the abundance of very massive objects and the overall normalization of the linear matter power spectrum, possibly easing tensions between CMB constraints and local measurements of large-scale structures.
5.2.1 Large-scale matter distribution
As a first diagnostic of the effects of the momentum exchange in the two selected variable-w models, we compute the projected density field of a slice of thickness 30 Mpc h−1 through the simulation box. We assign the mass of particles in the slice to a 40962 Cartesian grid trough a CIC mass assignment scheme based on their projected positions in the x–y plane and we compute the logarithm of the density contrast in the grid. In Fig. 7, we show the density field at z = 0 in a region of side 500 Mpc h−1 centred on the most massive halo identified in the simulation. In the inset displayed in the bottom-right part of the maps, we show a zoom on the central halo with side 50 Mpc h−1.
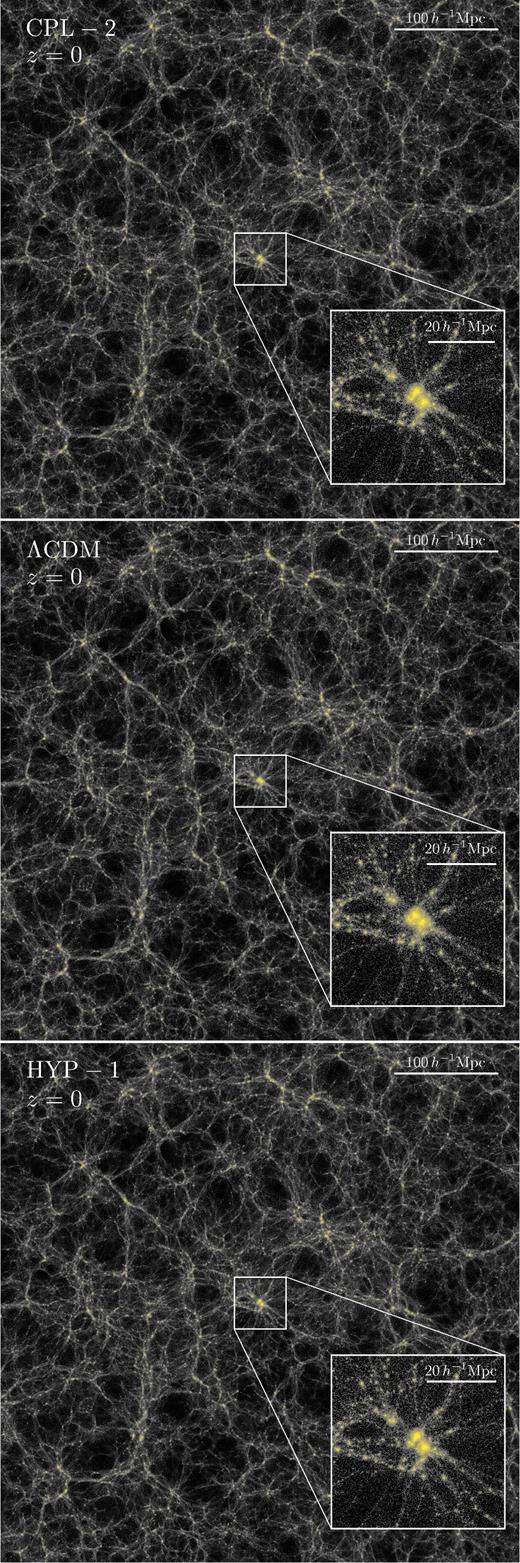
The density field at z = 0 in a slice of size 500 Mpc h−1 and thickness 30 Mpc h−1 for the reference ΛCDM simulation (central panel) and for the selected CPL and HYP parametrizations (top and bottom panels, respectively). The slices have been centred on the most massive structure identified in the simulations which is displayed in the zoomed inset.
This preliminary visual inspection shows a very similar shape of the large-scale matter distribution, with no significant difference in the location, shape, and size of overdense regions and voids. The closer look at the region around a massive halo displayed in the zoomed inset highlights an almost identical geometry of the cosmic web of filaments converging on to the central structure, even though some differences appear in the relative position of the most prominent substructures in the vicinity of the central halo.
Therefore, the overall density field seems very mildly affected by the momentum exchange with some appreciable effect showing up only in the vicinity of the most overdense regions of the simulated volume. By comparing these images to the corresponding ones discussed in Baldi & Simpson (2015) – where significant differences among the models were already visible by eye in the location of some of the most prominent substructures – it is already possible to see how the time-dependence of the equation of state determines a weaker impact of the momentum exchange on the formation and evolution of large-scale structures.
5.2.2 The non-linear matter power spectrum
In Fig. 8, we show the non-linear mater power spectrum ratio to the ΛCDM reference simulation for all the models simulated in the large box. The plots are the same as in Fig. 4, although covering a different range of scales due to the larger size of the simulated box. As the plots clearly show, the effect of the momentum exchange at large linear scales in the CPL-2 and HYP-1 models is twice as large as for the constant-w model with w = −0.9 and ξ = 10 [bn/GeV] at high redshift, while it becomes comparable to the latter at z = 0. This is consistent with the variable-w models having a more efficient momentum transfer at high z due to the larger value of w (see Fig. 3). At the same time, it is interesting to notice that also the scale-dependence of the effect at small non-linear scales is much more pronounced in the variable-w models than in the constant-w case at high redshift, while the opposite occurs at z = 0. This suggests that at high redshift, our selected models of dark scattering might be characterized by significantly overconcentrated collapsed structures embedded in a less evolved large-scale matter distribution, as will be explicitly verified below (see Section 5.2.5). Such prediction could be verified by combining weak and strong lensing observations at high z.
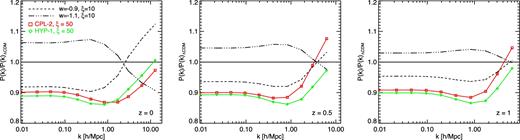
The non-linear matter power spectrum ratio to the reference ΛCDM model at three different redshifts z = 0 ( left), 0.5 (middle), and 1 (right) for the selected models of parametrized w(z) and for the two constant-w cosmologies already investigated in Baldi & Simpson (2015). The colour coding and linestyles are the same as in all previous figures.
5.2.3 Cosmic voids
For all our large box simulations, we have identified cosmic voids using the VIDE public toolkit4 (Sutter et al. 2015) based on the zobov algorithm (Neyrinck 2008) in both a random subsampling of the CDM particle distribution with a tracer density of 0.02 particles per cubic Mpc h−1 and in the distribution of haloes of our FoF sample, with a minimum halo mass MFoF, min(z = 0) ≈ 2.5 × 1012 M⊙ h−1, for the same three redshifts investigated above z = {0 , 0.5 , 1}. The voids are identified using a Voronoi tessellation procedure and a watershed algorithm to join underdense Voronoi cells until a border to a neighbouring underdense region is reached. Then, an effective radius Reff ≡ [3Vvoid/(4π)]1/3 is associated with the void volume Vvoid assuming sphericity (see Sutter et al. 2015, for a detailed description of the algorithm implemented in the vide code).
Starting from the void catalogue produced by VIDE, we identify the main voids (i.e. those voids that are not embedded within larger voids) and remove pathological voids following the procedure described in Pollina et al. (2016). In this way, we ensure that the final void catalogue contains only disjoint voids with a central overdensity δmin < 0.2 and a density contrast between the density minimum and the void boundary δc > 1.57. With such catalogue of selected voids, we compute the differential void size distribution, i.e. the number density of voids as a function of their effective radius Reff. The comparison of the void size distribution functions of the different models is displayed in Fig. 9 where the upper plot refers to the voids in the subsampled CDM field while the lower plot to the voids in the FoF haloes catalogues. In each plot, the top panel shows the void size distribution function while the bottom panel presents the relative difference with respect to the ΛCDM reference in units of the statistical significance σ computed by propagating the Poisson noise in each bin of effective radius to the relative difference.
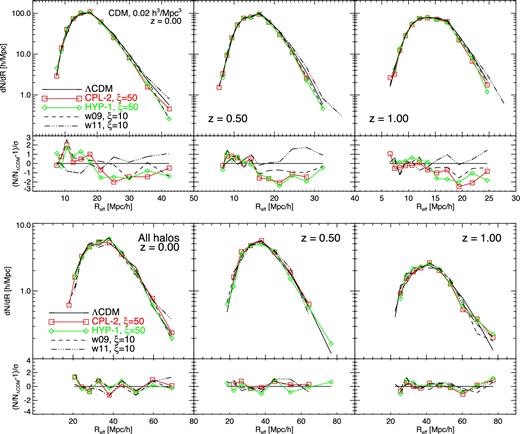
The differential void size distribution in the CDM field (top) and in the haloes distribution (bottom) as computed using the VIDE void finding toolkit. As one can see in the figures, the slight reduction in the abundance of large voids found for the CDM field is mostly erased in the distribution of haloes.
As one can see from the plots, the variable-w models CPL-2 and HYP-1 show a slight suppression of the abundance of large voids in the CDM density field compared to the reference ΛCDM simulation. The effect is not too dramatic, with a significance level of ≈1–2σ, and is consistent with the suppression of large-scale perturbations already shown by the power spectrum comparison. Interestingly, also for this class of models – as it has already been shown to occur for modified gravity (Cai et al. 2014; Achitouv et al. 2016), massive neutrinos (Massara et al. 2015), and interacting DE (Pollina et al. 2016) cosmologies – this effect is strongly suppressed when looking at the distribution of voids in the halo catalogues, where no significant deviation can be observed besides statistical oscillations around the reference model, at all redshifts.
We also compared the structural properties of voids in the different models by computing the stacked radial density profiles around the voids macrocenters identified in the ΛCDM simulation for 100 randomly selected voids within two bins of void effective radius, namely Reff ∈ {10–20 , 30–40} Mpc h−1. The results are shown in Fig. 10 and clearly show how the variable-w models of momentum exchange result in shallower profiles for voids of both bins. Therefore, voids appear to be less empty in dark scattering cosmologies, which might result in a lower weak lensing signal at low multipoles.
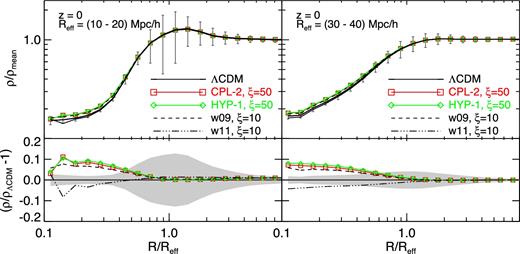
The stacked density profiles for voids identified in the CDM distribution of the various large simulations. The stacking has been performed using 100 randomly selected voids with effective radius in the range of 10–20 (left-hand plot) and 30–40 Mpc h−1 (right-hand plot). The bottom panels display the ratio of the density profiles to the reference ΛCDM model and the grey-shaded region represents the 1σ statistical significance according to a bootstrap estimation. As one can see in the figure, the momentum exchange determines slightly but significantly shallower void profiles.
5.2.4 The halo mass function
As already done in Fig. 6 for the intermediate-scale simulations, in Fig. 11, we display the ratio of the differential halo mass function to the ΛCDM case for the models that were simulated in the larger boxes. This allows us to increase the statistics of massive haloes and extend the range of the computed mass function to larger masses, thereby investigating the impact of the momentum exchange on the abundance of massive clusters of galaxies as a function of redshift.
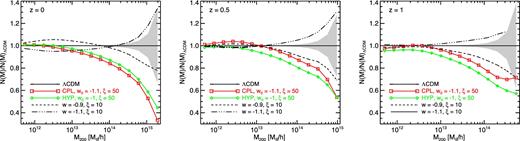
The mass function ratio to the ΛCDM case for the models included in our suite of large-scale simulations. The three redshifts displayed in the different panels, as well as colours, symbols, and line styles are the same as displayed in Fig. 8. As one can see in the figures, the variable-w models – differently from the constant-w cases – determine a very significant suppression of the abundance of cluster-sized haloes, thereby alleviating current persisting tensions between low-z observational data and best-fitting cosmological parameters derived from primary CMB anisotropies.
This more extended mass range allows us to see that both the variable-w cosmologies have a very significant impact on the abundance of very massive objects, suppressing the number density of clusters with mass around 1015h−1 M⊙ by ≈40–50 per cent at z = 0. The effect is milder at higher redshifts, but still significant with a suppression of the abundance of 1014h−1 M⊙ haloes by ≈20–30 per cent at z = 1.
This represents one of the most prominent features of the cosmological models under investigation and might provide a way to reconcile the low abundance of SZ clusters detected by Planck (Planck Collaboration XXIV 2016) with their expected number based on the cosmological constraints arising from the angular power spectrum of temperature and polarization anisotropies (Ade et al. 2015). It is also remarkable that the impact on the abundance of smaller objects – down to Milky Way-sized haloes of ∼1012 M⊙ h−1 – is very mild, thereby leaving the expected number of galaxies unaffected.
5.2.5 Halos concentrations
In Fig. 12, we show the ratio of these average concentrations at the usual three different redshifts z = {0, 0.5, 1} as a function of the halo mass M200 for a set of logarithmically equispaced mass bins. The grey shaded area shows the Poissonian error based on the number of haloes in each bin for the reference ΛCDM run. As the figures show, at z = 0, the variable-w models have a significantly weaker impact on the halo concentrations than the constant-w ones even for a higher value of the interaction parameter ξ. Both models determine an increase of concentrations below 7 per cent over the whole mass range covered by our halo catalogues. This implies that no dramatic effect in low-redshift strong lensing observations is expected for the models under investigation. On the other hand, as anticipated in Section 5.2.2, the situation changes at higher redshifts where the models with a variable equation of state show a more significant increase of halo concentrations. They are comparable to (at z = 0.5) or even larger than (at z = 1) the constant-w case (even though the latter has a weaker interaction parameter ξ). Therefore, these models predict a somewhat enhanced strong lensing efficiency at high redshift despite the overall reduction of large-scale power which is expected to result in a lower weak lensing signal.
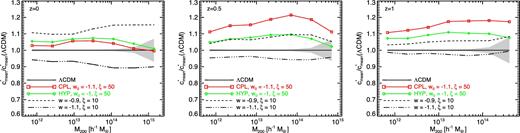
The ratio of the binned average concentration to the ΛCDM reference at the same three different redshifts considered in the previous figures. As one can see in the plots, the variable-w models do not show a strong impact on the concentrations of haloes at very low redshifts, while, at higher redshifts, the effect appears to be somewhat enhanced.
The latter feature may allow us to distinguish momentum exchange models from other alternative cosmological scenarios that imply some modification of the concentration–mass relation. As it was shown by several studies over the past decade, the c–M relation is sensitive to changes in standard cosmological parameters (see e.g. Macciò, Dutton & van den Bosch 2008; Prada et al. 2012; Klypin et al. 2016) as well as to changes of the underlying cosmological scenario (see e.g. Grossi & Springel 2009; Baldi et al. 2010; Baldi 2011; De Boni et al. 2013; Baldi 2014; Ludlow et al. 2016), with deviations pointing towards higher or lower values of the overall normalization as well as giving rise to a modification of the slope. None the less, such effects are normally monotonically increasing with decreasing redshift, while, as we have shown above, the exchange of momentum in the dark sector may give rise to a non-trivial redshift dependence of the c–M relation.
5.2.6 Halo substructures
As a final probe of the momentum exchange between DE and dark matter particles, we investigate the abundance and spatial distribution of substructures within massive collapsed haloes.
First, we compute the subhalo mass function, defined as the number of substructures with a given fractional mass with respect to the virial mass of their host main halo (Msub/M200) as a function of the fractional mass itself. We compute this quantity by binning in logarithmic fractional mass bins the whole sample of substructures belonging to host haloes with virial mass above a minimum threshold of Mmin = 1014 M⊙ h−1, thereby restricting this analysis to massive galaxy cluster haloes (due to the limited resolution of the simulations). In the left-hand panel of Fig. 13, we show the subhalo mass function at z = 0 for the various models and, in the bottom plot, we display their ratio to the fiducial ΛCDM cosmology.
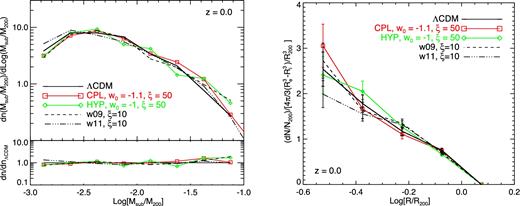
The sub halo mass function (left) and the sub halo radial distribution (right) for the various models considered in our suite of large-scale simulations at z = 0. As one can see in the plots, the momentum exchange does not significantly alter the abundance and the radial distribution of substructures identified in the mass range allowed by the resolution of our simulations.
Then, we also compute the subhalo radial distribution (shown in the right-hand panel of Fig. 13), defined as the fractional number density of substructures in a series of logarithmically equispaced radial bins (of inner radius Ri and outer radius Re) in units of the virial radius R200 of the host halo.
Both these observables show very little deviations among all the models and the reference ΛCDM cosmology, thereby showing that the momentum exchange does not significantly alter the distribution of substructures at small scales.
5.2.7 Halo velocity dispersions
For all the haloes of each simulation sample, we compute the 1D velocity dispersion σ2 and compare it to the corresponding behaviour of the ΛCDM run. The results are shown in Fig. 14 for the present epoch (z = 0), across 10 logarithmically equispaced mass bins for the different models. In the upper panel, we display as coloured dots a random subsample of all the haloes in the catalogues, while the lines trace the mean value of σ2. In the bottom panels, we plot the ratio of the binned average 1D velocity dispersion to the ΛCDM case and the grey shaded region indicates the Poissonian error associated with number counts of haloes in each bin of the reference simulation.
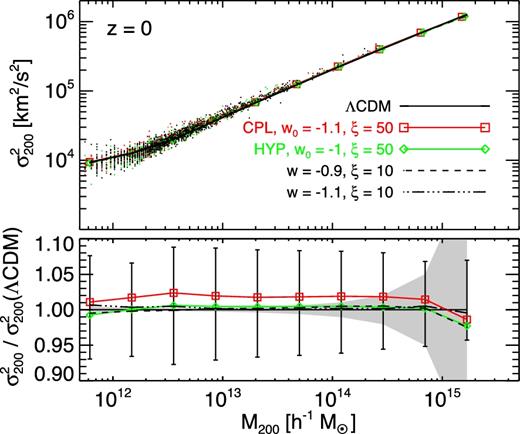
The velocity dispersion of haloes at z = 0 as a function of halo mass for the various models under investigation. The overall deviation from the reference ΛCDM cosmology does not exceed a few per cent over the whole mass range accessible to our simulations.
As one can see from the plots, the dark scattering models generate a very mild enhancement (only ≈1–2 per cent) of the 1D velocity dispersion with respect to the ΛCDM reference over the whole mass range covered by our simulations, with a roughly mass-independent behaviour.
5.2.8 Halo bias
As a final test of our models, we compute the halo bias b(k) by taking the ratio of the halo–matter cross-power spectrum Phm(k) to the matter–matter power spectrum Pmm(k) for haloes with mass above 5 × 1011 M⊙ h−1. In Fig. 15, we display the ratio of the halo bias of the various models to the ΛCDM case in the range of scales 0.04 ≤ k · h Mpc−1 ≤ 1. As already shown in Baldi & Simpson (2015), the constant-w models determine an ≈5–7 per cent increase (reduction) of the halo bias with a slight scale-dependence for the interaction parameter ξ = 10 adopted in our simulations for w = −0.9 (w = −1.1).
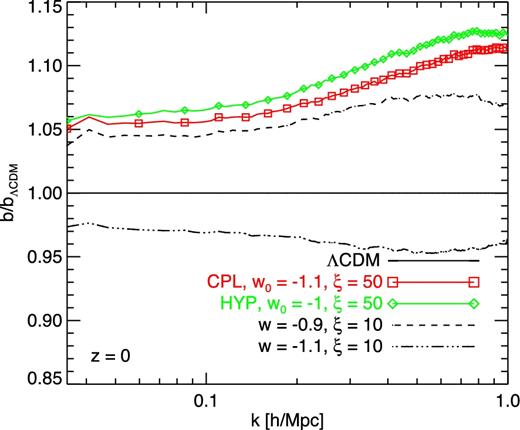
The halo bias as a function of scale at z = 0 for the models considered in the large-scale simulations. As one can see in the figure, the momentum exchange determines a slight increase of the bias with a characteristic scale-dependence of the enhancement.
Interestingly, the variable-w models under investigation, despite the higher interaction parameter ξ = 50, are found to yield only a marginal increase of the large-scale bias. The effect at the smallest scales under consideration is moderately stronger than before, reaching an ≈10–12 per cent deviation from ΛCDM. Furthermore, these models show a more pronounced scale-dependence, which might represent a further testable prediction of the dark scattering scenario.
6 CONCLUSIONS
The physical nature of dark matter and DE remains a highly active topic of theoretical and experimental investigation. In this work, we began by highlighting a connection between the phenomenologically motivated elastic scattering model and a subclass of coupled scalar field models. Furthermore, we showed that quite generically, the prediction of models which invoke momentum exchange between DE and dark matter is one where the linear growth rate is modulated in a scale-independent manner. In order to investigate further consequences of this interaction, we performed a series of N-body simulations, building on the work of Baldi & Simpson (2015), but now incorporating a more realistic trajectory for the DE equation of state. In this context, the key consequence of an evolving equation of state – specifically freezing models which tend to mimic a cosmological constant at late times – is that the coupling is naturally weakened in the late universe, when the bulk of the non-linear structure formation takes place. As a result, the amplification of the non-linear matter power spectrum which had been found in the earlier simulations of Baldi & Simpson (2015) is significantly suppressed.
We began by considering two different realisations of a freezing DE equation-of-state w(z) with either negative or positive convexity near the present epoch, namely the widely used CPL parametrization and a novel step-like parametrization based on hyperbolic functions, respectively. We then explored the relevant parameter space of these two forms of freezing DE models with a suite of intermediate-size simulations, assuming a relatively large value of the interaction parameter (ξ = 50 bn GeV−1). With these simulations at hand, we identified those specific models that appear to affect some basic statistics of the large-scale matter distribution (such as the non-linear matter power spectrum and the halo mass function) in the direction of a suppressed growth of perturbations, without impacting too dramatically on the highly non-linear regime at very small scales. For such models, we performed simulations on larger scales to improve the statistics of our results.
Finally, by means of these larger simulations, we have been able to verify that a number of observable quantities are not significantly perturbed by the interaction. More specifically:
The density field of the dark scattering models shows the same shape of the large-scale cosmic web as compared to the standard ΛCDM realization, with tiny differences in the position of prominent substructures around very massive systems appearing only at very small scales;
The abundance of galaxy-sized and group-sized haloes (up to 1013 M⊙ h−1) is mildly affected by the interaction in the redshift range 0 ≤ z ≤ 1;
The abundance of cosmic voids identified in the distribution of collapsed haloes does not show any significant deviation compared to ΛCDM;
The relative abundance of substructures encoded by the subhalo mass function as well as the radial distribution of substructures around their host halo is basically unchanged, with differences appearing consistent with statistical uncertainties.
The 1D velocity dispersion of haloes is only very slightly enhanced in dark scattering models as compared to ΛCDM, with an effect not exceeding ≈1–2 per cent at z = 0;
The halo bias is weakly increased (in a scale-dependent fashion), with a deviation from the ΛCDM reference ranging between ≈5 per cent at large scales (k ≈ 10−2 h Mpc−1) and ≈12 per cent at small scales (k ≈ 1 h Mpc−1); more specifically, the bias at k ∼ 0.05–0.1 h Mpc−1 is enhanced from the value b ≈ 1.08 in ΛCDM to b ≈ 1.15 for both the CPL and HYP parametrizations.
On the other hand, we identified a set of characteristic observational footprints of the model that might alleviate the persisting tensions between high-redshift and low-redshift cosmological constraints. In particular:
The matter power spectrum is suppressed at linear scales by up to ∼10 per cent at z = 0 for the specific parameters considered in our analysis, thereby providing a weaker contribution to the overall weak lensing signal and a lower determination of σ8 from low-redshift probes;
The abundance of cluster-sized haloes is very significantly reduced, with a suppression reaching ∼60 per cent for haloes of ∼1015 M⊙ h−1 at z = 0;
The concentration–mass relation, which appears very mildly affected at the present epoch (with a mass-independent increase of the normalization below 7 per cent), shows a somewhat larger deviation from ΛCDM at higher redshifts, with an enhancement up to ∼20 per cent at 0.5 ≤ z ≤ 1, which might result in a higher efficiency for strong lensing at these redshifts;
The abundance of cosmic voids in the CDM distribution shows a statistically significant suppression (at the level of about 1–2σ) for voids with radius ≳20 Mpc h−1, while the spherically-averaged stacked density profiles of voids are found to be shallower, with an ≈10 per cent higher central overdensity compared to ΛCDM, which is also consistent with a lower expected weak lensing efficiency.
To summarize, the cosmological models featuring elastic scattering between CDM particles and a DE field with variable equation-of-state w(z) defined as in equations (2) and (3) are challenging to distinguish from the standard ΛCDM cosmology at the level of the background expansion history, while providing a growth of structures that results in a lower amplitude of linear density perturbations (i.e. lower weak lensing signal, lower σ8) and a strongly suppressed abundance of very massive clusters at redshifts below 1. A similar conclusion has been recently reached – based on linear structure formation only – for some specific realisations of Type 3 interacting DE models by Pourtsidou & Tram (2016), while some completely different mechanisms giving rise to a suppression of structure formation have been recently discussed by Lesgourgues, Marques-Tavares & Schmaltz (2016) and D'Amico et al. (2016a). In this respect, these different classes of models might alleviate current observational tensions and deserve further investigations.
As a final note, let us briefly consider the relative merits of interpreting abnormal structure formation as either signs of coupled DE or as an indication of modified gravity. A priori, before any experiments are conducted, we might consider both scenarios equally likely. But over the past few decades, a huge swathe of the modified gravity landscape has been erased. Following high-precision measurements of local gravitational potentials within the Solar system and cosmological potentials in the CMB, only a small fraction of (the very large) parameter space remains viable. A further null result was recently derived from the velocity of gravitational waves in the Laser Interferometer Gravitational-wave Observatory (LIGO) detection of merging black holes (Abbott et al. 2016). So there have been numerous opportunities for modified gravity to show its face elsewhere, but it has failed to. In contrast, coupled models do not directly alter the motions of planets, the gravitational potentials, nor the speed of gravitational waves. Crucially, then, from the perspective of Bayesian model selection, coupling models are favoured because they are more predictive. Then, even though most of the standard coupled DE models have been tightly bound by observations and their formulation at the level of quantum field theory has been recently shown to strongly constrain the nature of the dark matter particle (D'Amico, Hamill & Kaloper 2016b), it is still remarkable that coupled models can induce a pure change in cosmological structure formation, while naturally satisfying the above-mentioned complementary tests. Furthermore, a broad spectrum of modified gravity models generically predict an enhancement of structure formation, which would aggravate rather than alleviate the aforementioned tensions in observational data, while, as we have shown in this work, some specific forms of coupled DE may result in a substantial suppression of structure formation as compared to the standard ΛCDM scenario.
Ultimately, these two distinct explanations are observationally distinguishable, due to the coupled model producing a small segregation of the baryonic and dark matter motions. This would represent a highly challenging but not insurmountable task for future cosmological surveys.
Acknowledgments
We are deeply thankful to Alkistis Pourtsidou for useful discussions on the connection between the dark scattering models and the Type 3 class of coupled DE. FS would like to thank Baojiu Li for helpful comments. MB acknowledges support from the Italian Ministry for Education, University and Research (MIUR) through the SIR individual grant SIMCODE, project number RBSI14P4IH. FS acknowledges support by the European Research Council under the European Community's Seventh Framework Programme FP7-IDEAS-Phys.LSS 240117 and by the Spanish Mineco grant AYA2014-58747-P and MDM-2014-0369 of ICCUB (Unidad de Excelencia ‘Mara de Maeztu’). The numerical simulations presented in this work have been performed and analysed on the Hydra cluster at the RZG supercomputing centre in Garching.
A similar shape of the equation-of-state w(z) has been recently proposed also by Jaber & de la Macorra (2016) using a different functional parametrization.
In this paper – if not stated otherwise – we will always assume units in which the speed of light is unity, c = 1.



