-
PDF
- Split View
-
Views
-
Cite
Cite
Diego N. Mikhaloff, Hagai B. Perets, Short- and long-term evolution of a stellar disc around a massive black hole: the role of the cusp, stellar evolution and binaries, Monthly Notices of the Royal Astronomical Society, Volume 465, Issue 1, 11 February 2017, Pages 281–292, https://doi.org/10.1093/mnras/stw2813
Close - Share Icon Share
Abstract
We study the dynamical evolution of a stellar disc orbiting a massive black hole. We explore the role of two-body relaxation, mass segregation, stellar evolution and binary-heating in affecting the disc evolution and consider the impact of the nuclear cluster properties and the stellar-disc mass-function. We use analytic arguments and apply them to study the evolution of a the velocity dispersion of stars in a Galatic Centre (GC) – like stellar disc on both short (few million years) and longer (100 Myr) evolutionary time-scales. The dominant processes affecting the disc evolution are two-body relaxation and mass-stratification, where the massive stars play a key role in kinematically heating lower mass stars; binary-heating has only a little contribution. In particular, models with realistic mass-functions show the disc structure to be mass-stratified. The number of massive stars in the disc decrease due to stellar evolution, consequently leading to slower relaxation. At these later evolutionary stages, dynamical heating by the nuclear cluster plays a progressively more important role. Given these findings, it is likely that two-body relaxation alone could not produce the observed configuration of the stellar disc in the GC and other collective processes might have played an important role. Such processes are less likely to produce mass-stratification in the disc and therefore a detailed study of the mass-stratification of the GC disc may provide a handle on the processes that dominate its evolution. Finally, two-body relaxation would leave a stellar disc in a relatively thin configuration even after 100 Myr and therefore earlier discs, now containing only older, lower mass stars, might still be observed in the GC, unless destroyed/smeared by other processes.
1 INTRODUCTION
Stellar discs are known to exist around massive black holes (MBHs) in galactic nuclei and are typically composed of relatively young stellar populations (Seth et al. 2006). Observations of the central parsec of the Milky Way Galaxy show more than 100 young WR-, O- and B-stars (Paumard et al. 2006), likely formed ∼4–7 Myr ago. These stars are found between ∼0.04 and 0.5 pc from the MBH, with ∼20 per cent of which reside in a disc-like structure, and are observed to have mean high eccentricity of 〈e〉 ∼ 0.2–0.4 (Yelda et al. 2014). Such discs, existing in the Galactic Centre (GC) and elsewhere, are thought to form following the infall of gaseous material and the formation of a gaseous disc. Such a disc can later fragment to form a stellar disc (Hobbs & Nayakshin 2009, and references therein). Here we explore the dynamical evolution of such stellar discs and focus on discs similar to that observed in the GC.
Alexander, Begelman & Armitage (2007) have been the first to describe the behaviour of a stellar disc around an MBH. They used an analytic approach and then verified and calibrated them through the use of N-body simulations. The analytic model they devised includes the effects of two-body relaxation and included simple multimass models (two or three populations). Their N-body simulations also included a simplified stellar evolution.
Later studies (Cuadra, Armitage & Alexander 2008; Perets et al. 2008; Löckmann, Baumgardt & Kroupa 2009; Šubr & Haas 2014) performed additional N-body simulations and considered additional components and/or more realistic aspects. Cuadra et al. (2008) included stellar binaries in the disc, the role of a putative intermediate mass black holes and initially eccentric discs. Kocsis & Tremaine (2011) discussed the evolution of the stellar disc, mainly focusing on the effects of resonant relaxation (Rauch & Tremaine 1996), not considered here. The influence of the stellar cusp was studied numerically by Perets et al. (2008) and Löckmann et al. (2009), who performed N-body simulation for different models (including models with cusp and models with two stellar discs); they concluded that the cusp could provide an additional heating of the stellar disc, leading to faster eccentricity/inclination growth.
Here we follow up on the initial analytic work by Alexander et al. (2007) and extend it to include the role of a realistic detailed mass-function, the effects of stellar evolution, the impact of binary-heating and additional relaxation effects by a stellar cusp. This approach allows us to better understand and identify the role played by each of these processes and components, as well as to study the long-term evolution of realistic discs, in terms of the velocity dispersion of their stellar populations, which is more difficult (and computationally expensive) to study using full N-body simulations.
We begin by describing the dynamical processes that contribute to the stellar disc evolution, including stellar scattering, mass-stratification and binary-heating (Section 2). We then briefly review the structural components of the nuclear stellar cluster (NSC) in which the disc is embedded and consider various models for the mass function of the stellar disc and the possible core-like or cusp-like structure of the NSC. The physical processes we consider as well as the NSC structural components are used to devise a multitude of possible models for the stellar disc evolution under diverse conditions, including considerations of stellar evolution (Section 3.2). We present the results of the short- and long-term evolution of the discs considered in these models in Section 4 and then discuss the results and their implications (Section 5). We also briefly mention other possible physical processes not included in our current modelling. Finally, we conclude and summarize our results in Section 6.
2 THE DYNAMICS AND PHYSICAL PROCESSES IN A STELLAR DISC
In the following, we briefly review several dynamical processes that contribute to the disc evolution. We first follow Alexander et al. (2007) in describing the two-body relaxation and mass-stratification (dynamical friction) of multiple stellar populations (extended to an arbitrary number of stellar populations) and then consider the analytic description of the effects of binary-heating on stellar discs, not discussed before in this context.
2.1 Relaxation and single-star scattering
Let us follow Alexander et al. (2007) and consider a supermassive black hole (SMBH) with mass M• and N single stars with mass M orbiting the MBH in an initially thin stellar disc, with an external radius R0 + ΔR/2 and an internal radius R0 − ΔR/2.
2.2 Multimass components and mass-stratification
From analysing these set of equations, we note that for two species, k and j, for which Ek > Ej, the population of k-species particles dynamically heat the population of the j-species ones (leading to increased velocity dispersion) and vice versa (a less energetic population dynamically cools a more energetic one, dumping its velocity dispersion). Note that the cooling/heating depends on the energies ratio and not only the mass ratio of the stars.
2.3 Interaction between the stellar disc and the nuclear cluster
The two-body relaxation of disc stars due to interaction with the background stars of the nuclear cluster can be modelled in a similar method to the two-body relaxation by different stellar populations discussed above. In this case, the cluster stellar population is considered as a distinct population with different properties. The disc stars interact with those cluster stars which go through the disc, i.e. if the volume of the disc is V = 4πR0HΔR, the number of clusters stars considered is the local nuclear cluster stellar density at the relevant region of the disc times this volume. The velocity dispersion of this isotropic cluster population is |$\sigma _{{\rm cluster}}=V_{{\rm K}}/\sqrt{3}$| (Binney & Tremaine 2008) with VK the Keplerian velocity around the MBH. We now use the same type of two-population interaction term in equation (8) to account for the effects of the cluster stars on this stellar population. Note that the cluster stellar population is much greater than the disc population and can be assumed as a constant ‘heat’ bath.
2.4 Binary-heating
Any stellar population is likely to contain some fraction of binary stars. An encounter between single stars and binaries could lead to an energy exchange between the binary orbital energy and the kinetic energy of the stars, i.e. energy can be exchanged between the inner degree of freedom of the binary and the outer external kinetic energy of the stars; thereby, binaries can assist in dynamically heating the stellar disc.
Binary–single encounters had been explored extensively, with the pioneering studies by Heggie (1975) and Hills (1975). Binaries can be divided into two dynamical categories; ‘Hard Binaries’ and ‘Soft Binaries’: when the kinetic energy of the intruding mass, Ek, is such that Ek/mbV2 ≪ 1 (where mb = m1 + m2 is the binary total mass), a binary is considered to be hard (where, the lower the ratio, the harder the binary). A binary is termed ‘soft’ when Ek/mbV2 ≫ 1. Heggie (1975) and Hills (1975) found that following a binary–single encounter, soft binaries become softer and hard binaries become harder (on average), a behaviour typically termed ‘Heggie's law’.
We can now use equation (13) as the binary-heating term to be added to the dynamical evolution equation for the stellar disc populations (equation 4), allowing us to model the binary-heating contribution.
We can now compare the relative contribution by single-star scattering and binary-heating through the comparison of the two terms in equation (15). If we consider some typical initial conditions in the GC, taking ln (Λ) ≃ 7.5 (as the disc heats up the scaleheight grows but with only a small corresponding change in ln (Λ) due to the logarithmic dependence), C1 ≃ 3 and a binary fraction of fb = 0.4 (where fb = nb/(nb + N) with nb = (2/3)N), we find that the relative contribution of binary-heating is only 1/10th of the contribution due to single star scattering. This can be seen explicitly in the evolution of the velocity dispersion shown in Fig. 1. We find that the exclusion of the binary-heating contribution (for a disc in which Msingle = Mbinary = 20 M⊙) makes only a very small difference. Although the effect of binary-heating by itself is not negligible, the contribution is dominated by the two-body regular scattering and their combined effects (not shown in the figure) are effectively almost similar to that of only the two-body relaxation seen in the figure. We can therefore conclude that although the binaries binding energy could be larger than the kinetic energy of the disc, the rate of extraction of this energy and its exchange into the disc kinetic energy is negligible, at least for the relatively thin discs considered here.
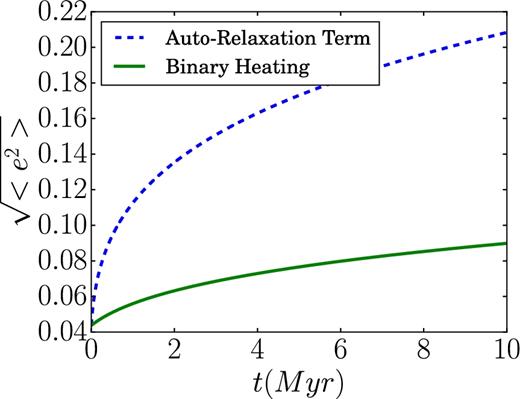
Evolution of the rms eccentricity for model X (see Section 3.2 and Table 2 for more information about the models). The evolution due only self-relaxation by single disc stars corresponds to the dashed line and that due to or binary-heating corresponds to the solid line. The evolution due to the combined effects (not shown) is almost the same at that due only to the disc single stars relaxation.
2.5 Full model
|$\Lambda _{j-{\rm cusp},l}=\overline{\sigma }_{j-{\rm cusp},l}\Delta R/2GM_{{\odot }}$|,
|$\overline{\sigma }_{j-{\rm cusp},l}=(\sigma _{cusp}+\sigma _{j})/2$|, the same velocity dispersion for all stars in the NSC,
|$\sigma _{{\rm cusp}}=\frac{1}{3}\sqrt{GM_{T}\left(R\right)/R}$|,
MT(R) = MSMBH + ∑lMcusp, l(R),
|$M_{{\rm cusp},l}\left(R\right)=\int _{R_{{\rm min}}}^{R_{{\rm max}}}4\pi r^{2}\rho _{{\rm cusp},l}\left(r\right){\rm d}r$| , where we consider the effective region to affect the stars to be between Rmin = 0.5R and Rmax = 1.5R and
where ρcusp, l(r) is discussed in Section 3.3,
|$M^{{\ast }}_{{\rm cusp},l}=M_{{\rm cusp},l}/N_{{\rm cusp},l}$|,
|$E_{{\rm cusp},l}=3M^{{\ast }}_{{\rm cusp},l}\sigma ^{2}_{{\rm cusp}}/2$|,
|$N_{{\rm cusp},l}^{{\ast }}=N_{{\rm cusp},l}*(V/V_{{\rm cusp},l})$|, where Ncusp, l is the number of stars of type l in the NSC, V is the volume of the stellar disc (see Section 2.3) and Vcusp, l is the volume between radius Rmin and Rmax (|$V_{{\rm cusp},l}=\int _{R_{{\rm min}}}^{R_{{\rm max}}}4\pi r^{2}{\rm d}r$|),
Λj − binary − i = (σj + Vi − orbital/2)2ΔR/(2GMbinary − i), where |$V_{i-{\rm orbital}}^{2}=Gm_{{\rm binary}-i}/a_{i}$| and ai is semimajor axis of the binary.
|$\Lambda _{jk}=\left(\overline{\sigma }_{jk}\right)^{2}\Delta R/\left(2GM_{k}\right)$|
and l runs for different NSC population (i.e. if all the stars in the NSC have the same mass and velocity dispersion l = 1).
2.6 Other physical processes (and caveats)
Our analytic approach considered the role of two-body relaxation and binary-heating and included realistic disc and NSC components. However, throughout the study, we assume the radial evolution of the disc and the NSCs are negligible. This assumption should be well satisfied for the NSC, given the long relaxation times. However, as shown by Šubr & Haas (2014), the relaxation times in the disc where velocity dispersions are initially low are much shorter and some radial evolution can occur. Nevertheless, in the models most comparable to those considered here, the radial evolution shown by Šubr & Haas (2014) is modest and affects only a relatively small number of stars in the disc and therefore the analytic models, though inaccurate in that respect, should reasonably capture the main dynamical aspects of the disc two-body relaxation processes. We also note that the models presented here consider a ring of stars rather than a full disc. We take the scale of the ring to be comparable to its distance from the MBH. The dependence on the exact outer/inner radius chosen is relatively small given its logarithmic dependence through the Coulomb logarithm. Moreover, stars significantly far from the ring centre would have high relative velocities and contribute little to the relaxation. Nevertheless, the model used is simplified in that respect and the results we discuss are most relevant to the main region of the disc and do not accurately capture regions farther out. Nevertheless, we have compared the results of our models with the results of N-body simulations by Alexander et al. (2007) and found excellent agreement in those simple cases.
Secular processes and possible collective effects are beyond the scope of such a model; we briefly review studies of these processes. Resonant relaxation processes (Rauch & Tremaine 1996) could potentially lead to fast evolution of disc stars inclinations through the vector resonant relaxation (and slower evolution of the eccentricities), especially in the inner parts of the disc (Hopman & Alexander 2006b). Kocsis & Tremaine (2011) suggested that resonant relaxation can produce significant effects, however, they assumed an unrealistic effective mass of NSC stars, which is 5–10 times larger than expected in the GC (even when including stellar black holes, SBH). Further study of this effect under realistic conditions could shed more light on this issue.
Fast two-body relaxation as well as secular evolution of disc stars could also be induced by massive coherent components, massive perturbers (Perets, Hopman & Alexander 2007) such as molecular clouds, stellar clusters, intermediate black hole or a second stellar disc (Yu et al. 2007; Löckmann et al. 2009; Šubr, Schovancová & Kroupa 2009; Haas, Šubr & Kroupa 2011a; Haas, Šubr & Vokrouhlický 2011b; Mapelli, Gualandris & Hayfield 2013). Whether such objects exist/had existed in such configurations as to influence the evolution of the stellar disc is still actively studied.
Madigan, Levin & Hopman (2009) considered the collective eccentric disc instability effect. Such effect could lead to rapid change in the distribution of eccentricities in the disc, but it requires initially highly eccentric disc (see also Gualandris, Mapelli & Perets 2012). Such a process may give rise to a significant population of highly eccentric stars in the disc, which is not seen in most recent studies (Yelda et al. 2014).
It is important to note that by their nature, most of the collective and secular effects mentioned above affect both low-mass and high-mass stars in a similar manner, leading to similar eccentricity distribution. Discerning the kinematic properties of low-mass versus high-mass stars is therefore highly important in order to understand the roles of such processes compared with stellar two-body relaxation processes that lead to mass-stratification, as shown here in details. In particular, non-dependence of the stellar kinematics on the stellar masses would strongly suggest collective effects dominate the stellar disc evolution.
3 DISC AND NSC MODELS
In the following, we describe the observed properties of the cluster and the embedded stellar disc, as well as theoretical models for the NSC. We use these to motivate the detailed models we use in our analysis. The detailed models are described below and summarized in Table 2. In addition, we present the stellar evolutionary aspects used in the relevant models.
3.1 Observed disc structure
Beginning with the analysis of Levin & Beloborodov (2003), observations have shown the existence of a young stellar disc near the MBH in the GC. Paumard et al. (2006) showed that many of the observed young O/WR/B-stars reside in a disc-like structure between ∼0.05and0.5 pc from the MBH.
Early measurements suggested the disc stars revolve around the MBH in somewhat eccentric orbits. Bartko et al. (2009) found an rms eccentricity of 〈e〉 = 0.37 ± 0.07 for the disc stars, but the most recent studies suggest a smaller value of 〈e〉 = 0.27 ± 0.07 (Yelda et al. 2014). The disc stars appear to be young, forming only 4–7 Myr ago (Paumard et al. 2006). The radial surface density profile of the disc can be described by a power-law distribution, Σ(R) ∼ R−β, with β in the range [1.5, 2.3] (Paumard et al. 2006; Bartko et al. 2009, 2010; Lu et al. 2009). Initially, it was thought that ∼40–50 per cent of the young stars belong in the disc structure; however, more recent studies suggest that only ∼20 per cent of these reside in the disc, while most of the stars have more spherical distribution outside the disc (Lu et al. 2009). Here we consider only the evolution of disc stars and do not discuss the origin and evolution of the more spherical component of the young stars in the GC.
3.2 Disc models
In the following we describe the specific evolutionary models we study. We consider a disc of stars orbiting an MBH with mass M• = 4 × 106 M⊙. The inner disc radius is Rin = 0.05pc and the external radius Rout = 0.15 pc (so ΔR = 0.1 pc). We begin with an initially thin cool disc (H ≪ ΔR) and low initial eccentricities for the stars, i.e. the initial velocity dispersion is assumed to be low, compared with the Keplerian speed (where Ω = VK/R0 is the angular speed and VK the Keplerian velocity). We therefore assume the initial velocity dispersion σj0 ≪ VK for any disc population j (σj0 = 0.03VK). We take a disc surface density of Σ(R) ∝ R−1 (following similar assumptions as Cuadra et al. 2008; Prodan, Antonini & Perets 2015).
We studied three different types of discs: a single-mass disc, a multimass disc with given specific initial mass functions (IMFs) and a disc with binaries. In the following, we describe in more detail the detailed properties characterizing these models.
3.2.1 The mass function of stars in the disc
In most galactic environments, the IMF describes the distribution of stellar masses at birth. Analysis of observations (Salpeter 1955; Chabrier 2001; Kroupa 2002) shows an almost universal power-law behaviour, with dN(m) ∝ m−Γ(m)dm, with a typical exponent of Γ ∼ 2.3, for stars above one Solar mass and up to ∼120 M⊙. The analysis done by Bartko et al. (2010) based on spectroscopic survey made with SINgle Faint Object Near-IR Investigation conclude that the present-day mass function and the IMF for the disc of young stars in the GC obey a power law, but the slope is flatter than the ‘regular’ IMF. In particular, they conclude that Γ = 0.45 ± 0.3. In such a ‘top heavy’ IMF, massive stars are much more frequent compared with the Salpeter IMF.
We consider various mass functions for the stars in the stellar disc and the cusp. These different models are summarized in the following.
Single-mass model: in the simplest, unrealistic model studied here, we consider a stellar disc composed of single-mass stars, similar to the basic models considered by Alexander et al. (2007), as a test case for comparison.
Top-heavy IMF model: in this model, we assume the IMF of the disc stars is a top-heavy mass function with masses in the range of 0.6–120 M⊙ and a power-law Γ = 0.45, as suggested by Bartko et al. (2010).
Salpeter mass function: in this case, we assume the IMF of the stars in the stellar disc is a Salpeter mass function (Γ = 2.35) with masses in the range of 0.6–120 M⊙.
3.2.2 Binarity
Our knowledge about binaries in the GC is currently limited, but observation by Ott et al. (1999) and Martins et al. (2006) show the existence of at least some young binaries in the GC. In particular, they found that one of the brightest O/WR star in the GC is a massive binary star (mb ∼ 100 M⊙). More recent works (Rafelski et al. 2007) found a few additional binary O-star candidates, though no binaries had been found among the young B-stars. These studies either rely on detection of eclipsing binaries or through radial velocity detection of short-period binaries and are therefore mostly sensitive to close binaries. It is therefore difficult to estimate the underlying binary fraction among the young stars in the GC using these limited statistics. Taking them at face value would suggest a very high binary fraction, comparable or even larger than the high binary fraction observed in the field for similarly young massive stars (Sana et al. 2012).
On the theoretical side, most binaries in the GC are expected to be ‘soft’ binaries and therefore have relatively short lifetime due to perturbations by other stars (Bahcall & Wolf 1977; Ozernoi & Dokuchaev 1982; Hopman 2009; Perets 2009a; Alexander & Pfuhl 2014) or merge due to secular perturbations by the MBH (Perets 2009b; Antonini & Perets 2012; Prodan et al. 2015). The binary fraction among the old stellar population in the nuclear cluster is therefore likely to be negligible and we do not include it in any of our calculations.
Binaries in the disc could, however, be ‘hard’ in respect to the other disc stars, given the low-velocity dispersion in the disc. The young age of the disc also suggests that most of the initially formed binaries should still survive. Overall, it is therefore likely that the binary fraction of the massive stars in the GC stellar disc is high as in the field (>50 per cent) and that the binary fraction does not evolve much since its formation.
As we discussed above, binaries are generally not very important for the disc evolution, but we do consider them in some of our models for completeness. In these cases, we assume a binary fraction of 40 per cent.
3.3 Nuclear stellar clusters
We consider both discs which evolve in isolation, as well as discs embedded in an NSC. In the following, we briefly discuss the motivation and details of the latter case of NSC-embedded discs.
A stellar cluster around an MBH is expected to evolve into a stellar cusp structure over a relaxation time (Bahcall & Wolf 1976, 1977). For a spherically symmetric distribution of equal-mass stars, analytic considerations and N-body simulations show that in equilibrium, the density profile of the cluster has a power-law distribution, ρ ∝ r−γ, with γ = 7/4 (Bahcall & Wolf 1976). Mass-stratification in multimass clusters produce mass-dependent density profiles for the different mass stellar populations, with ρ(m) ∝ r−γ(m), where γ(m) = 1.5 + m/(4mmax ), with mmax the mass of the heaviest stellar element (Bahcall & Wolf 1977).
Hopman & Alexander (2006a) used Fokker–planck calculations to show that γ should be 1.4 for solar-mass main sequence (MS) stars and up to 2 for SBH. Similar results from Monte Carlo calculations were found by Freitag, Amaro-Seoane & Kalogera (2006) However, observations of red giants in the GC suggest a core-like structure in the inner regions of the GC (γ in the range of 0–0.5; Do et al. 2009; Bartko et al. 2010; Genzel, Eisenhauer & Gillessen 2010). Nevertheless, it is not yet clear whether the distribution of red giants reflect the overall distribution of stars in the GC and various models had been suggested to explain both a ‘real’ core distribution (Merritt 2010) or an apparent one (i.e. only reflecting the distribution of red giants; Dale et al. 2009; Amaro-Seoane & Chen 2014; Aharon & Perets 2015). We therefore consider several models for the nuclear cluster, motivated by the above theoretical models and the observations of the GC NSC. We consider both a cusp and a core models (the former based on theoretical models of relaxed NSCs and the latter based on the possible observations of a core-like distribution in the GC). We study two different cusp models.
3.3.1 NSC models
NSC models. For CUSP II in the total mass column, the total mass of each component of the NSC is shown.
| Model . | Star . | M(M⊙) . | γ . | ρ0(M⊙pc−3) . | Total mass ( M⊙) . |
|---|---|---|---|---|---|
| CUSP I | MS | 1 | 2.0 | 5.2 × 105 | 1.64 × 105 |
| CUSP II | MS | 1 | 1.4 | 1.9 × 106 | 4.71 × 104 |
| SBH | 10 | 2.0 | 1.8 × 105 | 1.83 × 104 | |
| CORE | MS | 1 | 0.5 | 5.2 × 105 | 1.46 × 104 |
| Model . | Star . | M(M⊙) . | γ . | ρ0(M⊙pc−3) . | Total mass ( M⊙) . |
|---|---|---|---|---|---|
| CUSP I | MS | 1 | 2.0 | 5.2 × 105 | 1.64 × 105 |
| CUSP II | MS | 1 | 1.4 | 1.9 × 106 | 4.71 × 104 |
| SBH | 10 | 2.0 | 1.8 × 105 | 1.83 × 104 | |
| CORE | MS | 1 | 0.5 | 5.2 × 105 | 1.46 × 104 |
NSC models. For CUSP II in the total mass column, the total mass of each component of the NSC is shown.
| Model . | Star . | M(M⊙) . | γ . | ρ0(M⊙pc−3) . | Total mass ( M⊙) . |
|---|---|---|---|---|---|
| CUSP I | MS | 1 | 2.0 | 5.2 × 105 | 1.64 × 105 |
| CUSP II | MS | 1 | 1.4 | 1.9 × 106 | 4.71 × 104 |
| SBH | 10 | 2.0 | 1.8 × 105 | 1.83 × 104 | |
| CORE | MS | 1 | 0.5 | 5.2 × 105 | 1.46 × 104 |
| Model . | Star . | M(M⊙) . | γ . | ρ0(M⊙pc−3) . | Total mass ( M⊙) . |
|---|---|---|---|---|---|
| CUSP I | MS | 1 | 2.0 | 5.2 × 105 | 1.64 × 105 |
| CUSP II | MS | 1 | 1.4 | 1.9 × 106 | 4.71 × 104 |
| SBH | 10 | 2.0 | 1.8 × 105 | 1.83 × 104 | |
| CORE | MS | 1 | 0.5 | 5.2 × 105 | 1.46 × 104 |
For each of these generic models as well as the models of stellar discs evolved in isolation, we studied several possibilities for disc and cluster combinations. A brief summary of the properties of the models is given in Table 2, including the disc mass function and its binary fraction.
Summary of the properties of the disc and nuclear cluster models, including their mass functions and density profiles.
| |$\#$| . | Disc . | Cusp/core . | Masses in the cusp . | γ . | Mmin . | Mmax . | Γ . | Binary fraction . |
|---|---|---|---|---|---|---|---|---|
| I | O-stars with M⋆ = 20 M⊙ | – | – | – | – | – | – | – |
| II | O-stars with M⋆ = 20 M⊙ | CUSP I | 1 M⊙ MS stars | 2 | – | – | – | – |
| III | O-stars with M⋆ = 20 M⊙ | CORE | 1 M⊙ MS stars | 0.5 | – | – | – | – |
| IV | Salpeter IMF | – | – | – | 0.6 M⊙ | 120 M⊙ | 2.35 | – |
| V | Salpeter IMF | CUSP I | 1 M⊙ MS stars | 2 | 0.6 M⊙ | 120 M⊙ | 2.35 | – |
| VI | Salpeter IMF | CORE | 1 M⊙ MS stars | 0.5 | 0.6 M⊙ | 120 M⊙ | 2.35 | – |
| VII | Top-heavy IMF | – | – | – | 0.6 M⊙ | 120 M⊙ | 0.45 | – |
| VIII | Top-heavy IMF | CUSP I | 1 M⊙ MS stars | 2 | 0.6 M⊙ | 120 M⊙ | 0.45 | – |
| IX | Top-heavy IMF | CORE | 1 M⊙ MS stars | 0.5 | 0.6 M⊙ | 120 M⊙ | 0.45 | – |
| X | O-stars with M⋆ = 20 M⊙ | – | – | – | – | – | – | 0.4 |
| XI | O-stars with M⋆ = 20 M⊙ | CUSP II | 1 M⊙ MS /10 M⊙ SBH | 1.4/ 2.0 | – | – | – | - |
| XII | O-stars with M⋆ = 20 M⊙ | CUSP II | 1 M⊙ MS (same NSC mass as model XI) | 1.4 | – | – | – | - |
| |$\#$| . | Disc . | Cusp/core . | Masses in the cusp . | γ . | Mmin . | Mmax . | Γ . | Binary fraction . |
|---|---|---|---|---|---|---|---|---|
| I | O-stars with M⋆ = 20 M⊙ | – | – | – | – | – | – | – |
| II | O-stars with M⋆ = 20 M⊙ | CUSP I | 1 M⊙ MS stars | 2 | – | – | – | – |
| III | O-stars with M⋆ = 20 M⊙ | CORE | 1 M⊙ MS stars | 0.5 | – | – | – | – |
| IV | Salpeter IMF | – | – | – | 0.6 M⊙ | 120 M⊙ | 2.35 | – |
| V | Salpeter IMF | CUSP I | 1 M⊙ MS stars | 2 | 0.6 M⊙ | 120 M⊙ | 2.35 | – |
| VI | Salpeter IMF | CORE | 1 M⊙ MS stars | 0.5 | 0.6 M⊙ | 120 M⊙ | 2.35 | – |
| VII | Top-heavy IMF | – | – | – | 0.6 M⊙ | 120 M⊙ | 0.45 | – |
| VIII | Top-heavy IMF | CUSP I | 1 M⊙ MS stars | 2 | 0.6 M⊙ | 120 M⊙ | 0.45 | – |
| IX | Top-heavy IMF | CORE | 1 M⊙ MS stars | 0.5 | 0.6 M⊙ | 120 M⊙ | 0.45 | – |
| X | O-stars with M⋆ = 20 M⊙ | – | – | – | – | – | – | 0.4 |
| XI | O-stars with M⋆ = 20 M⊙ | CUSP II | 1 M⊙ MS /10 M⊙ SBH | 1.4/ 2.0 | – | – | – | - |
| XII | O-stars with M⋆ = 20 M⊙ | CUSP II | 1 M⊙ MS (same NSC mass as model XI) | 1.4 | – | – | – | - |
Summary of the properties of the disc and nuclear cluster models, including their mass functions and density profiles.
| |$\#$| . | Disc . | Cusp/core . | Masses in the cusp . | γ . | Mmin . | Mmax . | Γ . | Binary fraction . |
|---|---|---|---|---|---|---|---|---|
| I | O-stars with M⋆ = 20 M⊙ | – | – | – | – | – | – | – |
| II | O-stars with M⋆ = 20 M⊙ | CUSP I | 1 M⊙ MS stars | 2 | – | – | – | – |
| III | O-stars with M⋆ = 20 M⊙ | CORE | 1 M⊙ MS stars | 0.5 | – | – | – | – |
| IV | Salpeter IMF | – | – | – | 0.6 M⊙ | 120 M⊙ | 2.35 | – |
| V | Salpeter IMF | CUSP I | 1 M⊙ MS stars | 2 | 0.6 M⊙ | 120 M⊙ | 2.35 | – |
| VI | Salpeter IMF | CORE | 1 M⊙ MS stars | 0.5 | 0.6 M⊙ | 120 M⊙ | 2.35 | – |
| VII | Top-heavy IMF | – | – | – | 0.6 M⊙ | 120 M⊙ | 0.45 | – |
| VIII | Top-heavy IMF | CUSP I | 1 M⊙ MS stars | 2 | 0.6 M⊙ | 120 M⊙ | 0.45 | – |
| IX | Top-heavy IMF | CORE | 1 M⊙ MS stars | 0.5 | 0.6 M⊙ | 120 M⊙ | 0.45 | – |
| X | O-stars with M⋆ = 20 M⊙ | – | – | – | – | – | – | 0.4 |
| XI | O-stars with M⋆ = 20 M⊙ | CUSP II | 1 M⊙ MS /10 M⊙ SBH | 1.4/ 2.0 | – | – | – | - |
| XII | O-stars with M⋆ = 20 M⊙ | CUSP II | 1 M⊙ MS (same NSC mass as model XI) | 1.4 | – | – | – | - |
| |$\#$| . | Disc . | Cusp/core . | Masses in the cusp . | γ . | Mmin . | Mmax . | Γ . | Binary fraction . |
|---|---|---|---|---|---|---|---|---|
| I | O-stars with M⋆ = 20 M⊙ | – | – | – | – | – | – | – |
| II | O-stars with M⋆ = 20 M⊙ | CUSP I | 1 M⊙ MS stars | 2 | – | – | – | – |
| III | O-stars with M⋆ = 20 M⊙ | CORE | 1 M⊙ MS stars | 0.5 | – | – | – | – |
| IV | Salpeter IMF | – | – | – | 0.6 M⊙ | 120 M⊙ | 2.35 | – |
| V | Salpeter IMF | CUSP I | 1 M⊙ MS stars | 2 | 0.6 M⊙ | 120 M⊙ | 2.35 | – |
| VI | Salpeter IMF | CORE | 1 M⊙ MS stars | 0.5 | 0.6 M⊙ | 120 M⊙ | 2.35 | – |
| VII | Top-heavy IMF | – | – | – | 0.6 M⊙ | 120 M⊙ | 0.45 | – |
| VIII | Top-heavy IMF | CUSP I | 1 M⊙ MS stars | 2 | 0.6 M⊙ | 120 M⊙ | 0.45 | – |
| IX | Top-heavy IMF | CORE | 1 M⊙ MS stars | 0.5 | 0.6 M⊙ | 120 M⊙ | 0.45 | – |
| X | O-stars with M⋆ = 20 M⊙ | – | – | – | – | – | – | 0.4 |
| XI | O-stars with M⋆ = 20 M⊙ | CUSP II | 1 M⊙ MS /10 M⊙ SBH | 1.4/ 2.0 | – | – | – | - |
| XII | O-stars with M⋆ = 20 M⊙ | CUSP II | 1 M⊙ MS (same NSC mass as model XI) | 1.4 | – | – | – | - |
3.4 Stellar evolution and the long-term evolution of discs
In addition to our study of the role of the different NSC and disc components, we also considered the effects of stellar evolution, which becomes especially important once the long-term evolution of a stellar disc is explored. We consider the evolution of discs with various properties (see below) both at times comparable to the observed stellar disc in the GC (up to 10 Myr), as well as a longer term (100 Myr) evolution.
We first considered simple models in which we did not introduce any stellar evolution and assumed stars do not change over time. We then considered the effects of stellar evolution in a simplified manner, For each stellar population in a given mass bin, we consider the appropriate MS lifetime for a star of such mass, TMS, according to stellar evolutionary models Schaller et al. (1992). After that period, we replace the star in the model with the stellar remnant it produces, assuming a simplified prescription as described in Table 3 (where SBH, NS, WD and MS stand for stellar black hole, neutron star, white dwarf and MS star, respectively); in particular, the continuous mass-loss process is simplified and the mass-loss is assumed to be immediate. We also consider NS kick such that the NS remnant gets a random kick of the order of |$200/\sqrt{3}$|km s−1 (Hobbs et al. 2005). We only considered evolution of up to 100 Myr and hence we do not consider the stellar evolution of stars with masses smaller than 6 M⊙.
The final mass and final type after TMS (of each star) for different intervals of mass. However, star with initial mass less than 6.5 M⊙ has TMS greater than 100 Myr.
| Initial mass (M⊙) . | Final remnant mass (M⊙) . | Type of remnant . |
|---|---|---|
| 30 < M ≤ 120 | 10 | SBH |
| 15 < M ≤ 30 | 7 | SBH |
| 8 ≤ M ≤ 15 | 1.4 | NS |
| 6 ≤ M ≤ 8 | 1 | WD |
| Initial mass (M⊙) . | Final remnant mass (M⊙) . | Type of remnant . |
|---|---|---|
| 30 < M ≤ 120 | 10 | SBH |
| 15 < M ≤ 30 | 7 | SBH |
| 8 ≤ M ≤ 15 | 1.4 | NS |
| 6 ≤ M ≤ 8 | 1 | WD |
The final mass and final type after TMS (of each star) for different intervals of mass. However, star with initial mass less than 6.5 M⊙ has TMS greater than 100 Myr.
| Initial mass (M⊙) . | Final remnant mass (M⊙) . | Type of remnant . |
|---|---|---|
| 30 < M ≤ 120 | 10 | SBH |
| 15 < M ≤ 30 | 7 | SBH |
| 8 ≤ M ≤ 15 | 1.4 | NS |
| 6 ≤ M ≤ 8 | 1 | WD |
| Initial mass (M⊙) . | Final remnant mass (M⊙) . | Type of remnant . |
|---|---|---|
| 30 < M ≤ 120 | 10 | SBH |
| 15 < M ≤ 30 | 7 | SBH |
| 8 ≤ M ≤ 15 | 1.4 | NS |
| 6 ≤ M ≤ 8 | 1 | WD |
4 RESULTS
In the following, we present the evolution of stellar discs for the different models considered. We first study simpler cases with single-mass discs and then progressively consider more and more realistic cases. These include discs composed of stars with a range of masses and different mass-functions and the effects of different models of the NSCs in which they are embedded that determine the local density of stars affecting the disc relaxation. In this case, we also explore the differential evolution of stars of different masses in the same disc and their stratification. We then consider the effects of stellar evolution on the disc and the long-term (100 Myr) evolution of stellar discs.
4.1 Evolution of single-mass discs
Fig. 2 shows the evolution of the rms eccentricity of the disc stars for discs with single-mass stars (models I, II, III and XI), for different choices of mass (10 and 20 M⊙ stars). In model III (core), the evolution is dominated by the self-heating of the disc stars and therefore the model results resemble that of an isolated disc irrespective of the mass of the disc stars. The effects of the SBHs dominate the evolution of model XI (multimass cusp) and their mass is comparable to that of the disc stars, such that they always dominate the heating and the mass of the disc stars has a negligible effect. In the case of model II (a cusp with only solar mass stars), the ratio between the energies per star (equation 8) are such that the cusp stars hardly contribute to the heating, beyond the effects of the disc stars themselves (for the case of disc stars of 20 M⊙). However, when the masses of the disc stars are decreased, the contribution of the disc-stars relaxation decreases and the energies ratio becomes larger, such that the contribution of the NSC stars becomes comparable to that of the disc stars and they heat the disc more than the disc-stars self-relaxation, leading to a hotter disc compared with the isolated disc and core models (I, III).
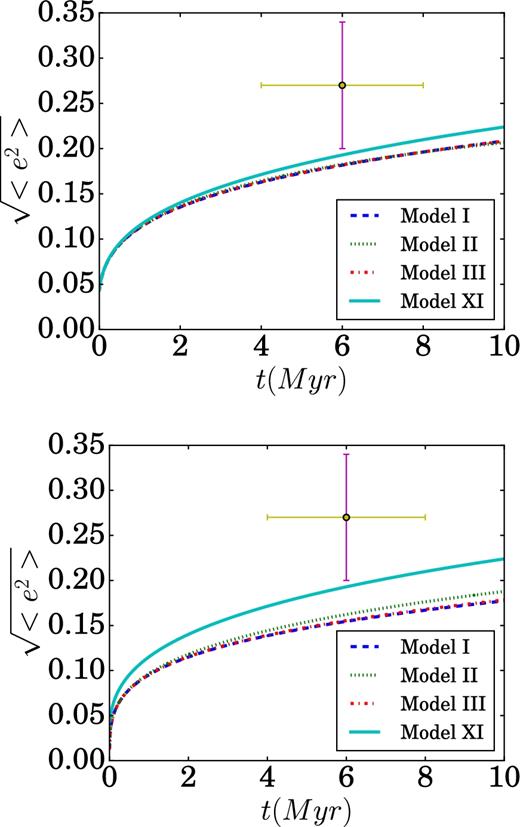
Evolution of the rms eccentricity of single-mass disc stars. Upper panel shows the results for models I, II, III and XI. Bottom panel shows the evolution of similar models but with disc stars of 10 M⊙ instead of 20 M⊙. Also shown is the measured rms eccentricity of the O-stars in the GC disc (Yelda et al. 2014).
Dependence on the mass of single stars and the local density of the NSC: Fig. 3 shows the role of the cusp on the evolution of disc stars and the role of the masses of single stars in the disc. The final rms eccentricity (after 10 Myr) is shown for a range of single-mass discs (models I–III). Each point in the lines corresponds to a disc with the same total mass, but the mass of the stars composing the disc indicated on the x-axis (same for all stars in the disc) differs. Discs composed of lighter stars can be seen to be more sensitive to the heating by NSC stars, with the cusp model being more effective than the core one. In contrast, discs composed of heavy stars are cooled down by the NSC (compared with the model with no existing NSC).
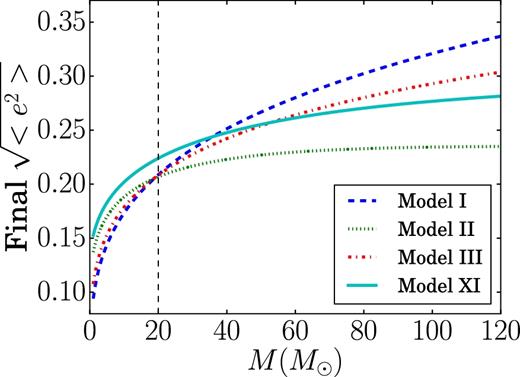
The rms eccentricity of disc stars after 10 Myr of evolution. The double dotted line corresponds to model II, dot–dashed is for core (model III), the solid line corresponds to multicomponent NSC (model XI) and the dashed line corresponds to the case where no NSC exists (model I).
We have also studied the effect of changing the masses of stars in the cusp, while keeping the overall mass density of the cluster constant (Fig. 4). In the CORE models the NSC structure has a small effect in the evolution of the rms eccentricity compared to the effect of the auto-relaxation of the disk. However, the strong dependence on the NSC can be clearly seen in the CUSP I case. This can be seen in equation (16), where the kinetic energy growth rate is linearly dependent on the mass of the stellar component of the NSC (|$M^{\star }_{{\rm cusp},l}$|).
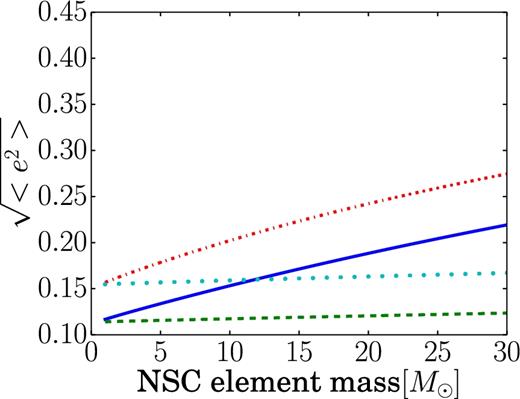
The rms eccentricity of disc stars after 6 Myr of evolution (the inferred age of the disc in the range of 5–7 Myr (Yelda et al. 2014), as a function of the mass of single stars in the cusp (keeping a constant mass density of the NSC for all models). The dash–dotted and solid lines refer to models of a cusp-like (CUSP I) NSC and top-heavy disc IMF (model VIII), showing the effects on 3–40 M⊙ stars (dash–dotted) and on all disc stars (solid) stars in the disc. The dotted and dashed lines similar show the results for a core-like NSC (model IX). We chose to show lines corresponding to the observed stars in the disc, all of which are OB and WR stars (Bartko et al. 2010), which therefore typically correspond to stellar masses in the range of 3–40 M⊙.
Multicomponent NSCs: in the previous section, we principally studied the evolution of stellar discs and their interaction with single-mass NSC stellar population. In the following, we consider a more complex and potentially more realistic model for the NSC. In our multicomponent NSC, we follow model XI (model XI itself and variations for different parameters), where the NSC includes both SBHs and MS solar-mass stars. Fig. 5 shows the disc evolution in such model (where |$\tilde{e}=e_{{\rm RMS}}-e_{{\rm rms},I}$| is the difference in the rms eccentricity compared with the results from model I). Though the number of SBHs in the cusp is relatively small, they can play an important role in heating a disc of massive 20 M⊙stars, where more massive SBHs lead to stronger heating of the disc.
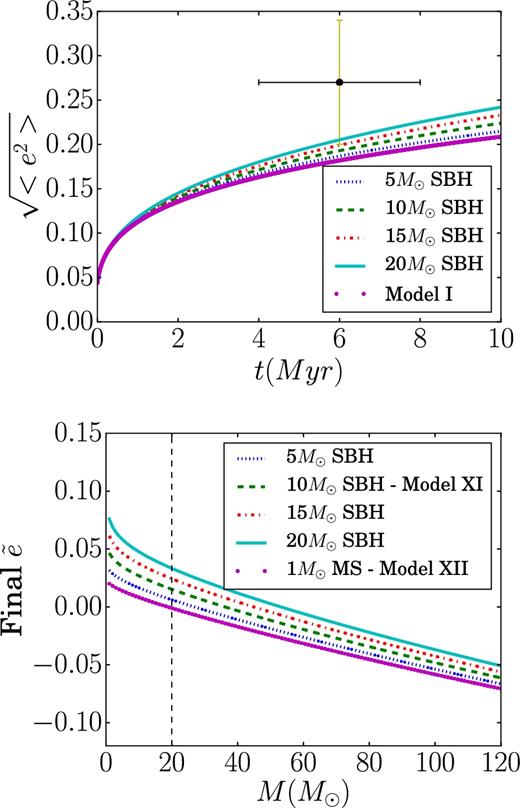
Evolution of rms eccentricity for a disc of O-stars with multicomponent cusp (model XI), each colour is for different SBH mass. On the upper panel is plotted the evolution through the time of a disc embedded in cusp-like NSCs (CUSP I for the dotted line and CUSP II for the other lines), where different masses for the NSC SBH population are considered. The dotted line (the bottom line) is compared to model I. Also shown are the measured rms eccentricity of the GC O-stars (Yelda et al. 2014). The bottom panel is the difference between the final eccentricity for each model compared to model I. The dotted line (the bottom line) is for model XII.
Fig. 3 shows that the inclusion of SBHs in addition to solar-mass stars in the cusp (model XI) leads to a more prominent disc heating due to the additional contribution from the SBHs.
Due to the two-body relaxation processes, the rate of the evolution of the disc depends on both the local density of stars as well as their mass and, in particular, on their combination through |$<N_{{\rm cusp},l}\times (M^{{\ast }}_{{\rm cusp},l})^2>$| (where one should add the contribution of stars of each mass and their relative numbers), which appears in terms arising from the relaxation processes. In Fig. 6, we show the dependence of the mean eccentricity of the disc stars after 6 Myr as a function of the rms mass of the NSC stars. Vertical lines correspond to models III, II and XI (from left to right, respectively).
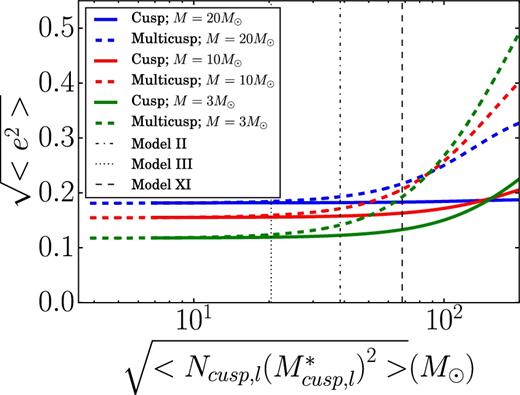
The rms eccentricity of low, intermediate and massive stars in the disc, as a function of the combined number and mass of the NSC stellar components |$<N_{{\rm cusp},l}\times (M^{{\ast }}_{{\rm cusp},l})^2>$|. Vertical lines correspond to the position of models III, II and XI in this representation.
4.2 Evolution of multimass discs
In models IV–IX, we studied the evolution of multimass stellar populations in a disc, where we considered both discs with Salpeter IMFs as well as discs with top-heavy IMFs. For each model, we divided the masses into 20 logarithmic mass bins for the Salpeter IMF cases; for better mass resolution, we considered linear mass bins for the top-heavy IMF. For each mass bin, we add a coupled equation (8), where we took the mass-weighted average to represent the mass bin, with the appropriate number of stars in that mass bin.
Fig. 7 shows that the disc evolution leads to a mass-stratified structure of the disc, with lighter stellar populations being excited to higher velocity dispersion (and should therefore correspond to higher eccentricities/inclinations and larger scaleheight for their disc component) compared with populations of more massive stars, which are segregated to more circular orbits in the central part of the disc (lower scaleheight). Such stratification is also observed for models including the effect of the NSC, where only small differences exist as a function of the stellar masses; lower mass stars are more sensitive to the NSC heating (not shown).
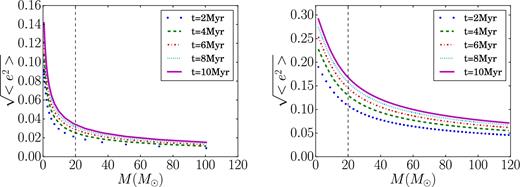
Evolution of the rms eccentricity of stars with different masses in the same disc. The left-hand panel corresponds to a disc with a Canonical IMF (Salpeter, Γ = 2.35, model IV) and the right-hand one corresponds to a disc with a top-heavy IMF (Γ = 0.45, model VII). The different lines, ordered from bottom to top, correspond to the evolutionary times: 2, 4, 6, 8 and 10 Myr, respectively.
The top-heavy IMF models include a significantly larger number of more massive stars, leading to a much faster heating of the stellar disc, as also observed in the simple models considered by Alexander et al. (2007). The NSC can further contribute to the disc heating, leading to ∼10 per cent higher rms eccentricity, but its contribution becomes negligible in the top-heavy IMF cases, where the heating is dominated by the massive stars in the disc (not shown). Note that the direction of cooling versus heating (equation 8) depends on the relation between the energy of the stars, not just their masses, i.e. the NSC stars have lower masses but they have higher velocities, so only the most massive disc stars are cooled by the NSC stars while the majority of the disc stars are heated.
In order to compare these results with the measured rms eccentricity of the O-stars in the GC, we now consider only the rms eccentricity of 3–40 M⊙ stars, more comparable to the O/B-stars observed in the disc today. For an age of 5–7 Myr for the GC stellar disc, we expect an rms eccentricity of the order of 0.17 lower than the measured 〈e〉 = 0.27 ± 0.07 (Yelda et al. 2014).
4.3 Stellar evolution and the long-term evolution of stellar discs
Fig. 8 shows the long-term (100 Myr) evolution of the stellar populations in discs with continuous (Salpeter or top-heavy) IMFs, where simplified stellar evolutionary mass-loss is considered (see Section 3.4).
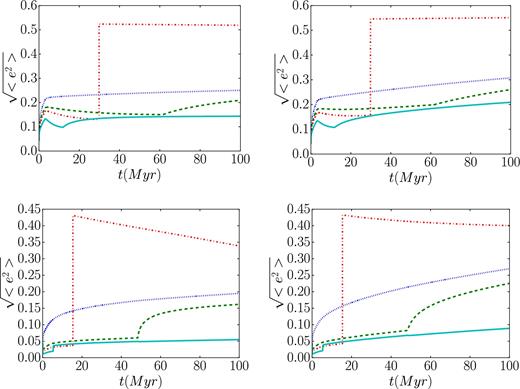
The long-term evolution of the rms eccentricity of disc stars over 100 Myr. Simplified stellar evolution prescriptions are included (see the main text). Top panels show the evolution of a disc with a top-heavy IMF (Γ = 0.45, left-hand panel: model VII, right-hand panel: model VIII). Bottom panels show the evolution of a disc with a Salpeter IMF (Γ = 2.35, left-hand panel: model IV, right-hand panel: model V). The left-hand and right-hand panels correspond to models without an NSC and with an NSC (CUSP I), respectively. The lines from bottom to top (initially) correspond to increasingly less massive stars. The solid, dash–dotted, dashed and double dotted lines correspond to stars that evolve to become SBHs, NSs, WDs or stay on the MS, respectively.
As each of the modelled discs evolve progressively, more massive stars end their life and become lower mass stellar remnants. These (now) lower mass remnants can then be heated much more effectively through mass-stratification processes. Once the more massive stars evolve, the role of the cusp heating becomes more significant, as can be seen from the comparison between the no-NSC and cusp-like NSC (CUSP I) models. Moreover, with the absence of high-mass stars, intermediate-mass populations begin to cool, when no cusp exists; but these same populations continue to heat up when a cusp population do exist. The typical natal kicks to neutron are sufficiently high as to effectively making them part of the spherical NSC; these NSs would not typically reside in the disc and will contribute negligibly to its further evolution.
4.4 Radial dependence of the disc aspect ratio
Throughout this study, we considered the evolution of the velocity dispersion of the disc stars, centred around 0.1 pc from the MBH. However, we also considered the evolution of stars in other regions of the disc, thereby obtaining an insight on the radial dependence and structure of the disc. Fig. 9 shows the dependence of the disc aspect ratio |$H/R=\langle {\sqrt{e^{2}}}\rangle /\sqrt{2}$| on the radius. We find that the rms eccentricity decreases farther from the MBH in both models with an NSC (CUSP I) and without, but the Salpeter IMF cases quantitatively differ, while in the top-heavy IMF models, the disc evolution is dominated by the disc stars rather than the NSC and negligible difference is seen between models with and without an NSC. Overall, this behaviour can be well understood. The Keplerian velocity of stars decreases with the distance from the MBH (Vk ∝ R−1/2), but the velocity dispersion decreases even more steeply with the radius (equation 4) and therefore the overall aspect ratio of the disc decreases with radius.
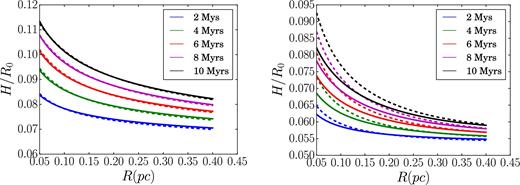
The rms aspect ratio of the disc stars in over 10 Myr. Left-hand panel show the evolution of a disc with a top-heavy IMF (Γ = 0.45). Right-hand panel show the evolution of a disc with a Salpeter IMF (Γ = 2.35). The solid lines correspond to models without an NSC (models IV and VII), the dashed ones correspond to models with an NSC (models V and VIII).
5 DISCUSSION
Disc heating and mass-stratification: similar to the results of Alexander et al. (2007), we confirm that for isolated stellar discs, the disc heating is dominated by dynamical friction/mass-stratification processes in which the more massive stars heat the low-mass stars. Correspondingly, the more massive stars are cooled by the interaction with the low-mass stars, but two-body relaxation of the massive stars by themselves still keeps heating them. Models with top-heavy mass function include a larger fraction of massive stars and therefore allow for more rapid heating of the disc, producing larger rms eccentricities.
Our models considered detailed mass-functions for the stars in the disc, allowing us to estimate the evolution of different stellar populations. As seen in Fig. 7, the discs develop mass-stratification where higher mass stellar populations are expected to have significantly lower disc height-scale and more circular orbits compared with the low-mass stars in the disc. The existence or lack of such mass-stratification in the GC stellar disc could therefore be an important tool in assessing the processes involved in the evolution of the GC disc and its initial conditions.
The role of the cusp: the effect of the NSC on the evolution of the stellar disc was not considers before in analytic models. The NSC stellar population has a high velocity dispersion, i.e. it is an effectively ‘hotter’ population than the ‘cool’ stellar disc population. The NSC can therefore potentially heat the stellar disc, even when it is composed of low-mass stars.
Our results suggest that a dense NSC can play a non-negligible, though limited role in heating the stellar disc. When the disc contains a large population of massive stars, these dominate the disc heating and evolution and the NSC plays a relatively minor role. Nevertheless, even young discs in which massive stars still exist are affected by the NSC, with top-heavy IMF discs being relatively little affects, but Salpeter-IMF discs showing non-negligible heating up to ∼10 per cent higher rms eccentricities.
The NSC effects are more prominent in cases where the disc is dominated by low-mass stars. These include unrealistic cases of discs composed of low single-mass stars, but they also relevant for the long-term evolution of stellar discs with realistic IMFs. In the latter case, stellar evolution leads to the transformation of massive stars into low-mass stellar remnants over time. The effective mass-function of such evolving stellar discs therefore becomes progressively centred around lower mass stars and stellar remnants which replace the previously existing massive stars. Correspondingly, the NSC heating of the cusp plays a progressively more dominant role in the disc evolution as can be seen in Fig. 8.
The role of binary-heating: in this study, we extended the analytic study of stellar disc evolution to include binary-heating processes. In principle, the binding energy stored in binaries is significant; however, the rate of energy exchange between the binaries and the single stars in the disc is slow. Therefore, binary-heating is inefficient in heating the stellar disc, compared with two-body relaxation and mass-stratification processes. These results are consistent with N-body simulation results which included binaries done by Cuadra et al. (2008).
Note that we consider the overall averaged evolution of the stellar disc population; atypical single–binary encounters with short-period massive binaries can lead to strong kicks ejecting stars at high velocities, even beyond the escape velocity from the NSC (Perets & Šubr 2012). Such encounters may produce a small number of outlying stars at highly eccentric/inclined orbits, but are not likely to significantly affect the overall evolution of the disc and its averaged properties (see also Perets, Kupi & Alexander 2008).
The long-term evolution of stellar discs and their signature: we find that the disc evolution over times as long as 100 Myr is slow. Two-body relaxation is too inefficient for the disc to assimilate into the nuclear cluster on such time-scales. The disc structure is expected to keep its coherency and be observed as a relatively thin disc even at 100 Myr (besides the NS remnant). This suggests that the existence of older discs formed before the one currently observed in the GC might still be inferred from the stellar kinematics of older, lower mass stars, which may still show a disc-like structure, unless destroyed/smeared by other non-two-body relaxation processes.
Radial disc aspect-ratio dependence: we find that the aspect ratio of the disc decreases with separation from the MBH.
Comparison with observations of the GC: the observed eccentricity of O-stars in the stellar disc in the GC, 〈e〉 = 0.27 ± 0.07 (Yelda et al. 2014), is higher than that obtained in the realistic models considered here. This suggest either initial conditions with significantly higher eccentricities for the disc stars or that other processes besides two-body relaxation play an important role in the disc evolution.
Detailed studies of the eccentricity/inclination distribution of disc stars as a function of mass are not currently available (but see Madigan et al. 2014 for important global statistical trends). Moreover, lower mass B-stars in these regions may have a different origin than the disc and may have been captured following a binary disruption (Perets et al. 2007); such stars would have high eccentricities (Perets & Gualandris 2010) and may mask the real distribution of the disc stars eccentricities. Nevertheless, a focused study on stars most likely related to the disc and their eccentricity–mass relation is highly desirable to assess the existence of possible mass-stratification in the stellar disc.
Finally, two-body relaxation processes suggest a factor of 2 ratio between the eccentricities and inclination of stars in the disc, while different relation might be expected from other processes (e.g. secular Kozai-like evolution induced by an inclined massive structure). A good handle on the eccentricity versus inclination from observation could give additional clues on the dynamical processes involved.
6 SUMMARY
In this study, we analysed the evolution of a stellar disc around a MBH due to two-body relaxation processes and binary-heating. We explored realistic mass functions for the disc stars and included the effects of two-body relaxation by the nuclear cluster stellar population in which the disc is embedded. We also considered the effects of stellar evolution and studied the long-term evolution of such discs. Our main finding can be summarized as follows.
The evolution of the disc is dominated by dynamical friction (mass segregation) and heating by massive stars, consistent with previous results by Alexander et al. (2007). The use of detailed mass functions does not qualitatively change the results, but differences in the IMF can quantitatively affect the overall evolution and, in particular, the level of mass-stratification.
Evolution of stellar discs due to two-body relaxation should produce significant mass-stratification in the disc and could be used as a probe for the dominant physical processes dominating the disc evolution; in particular, differentiating between collective processes and two-body relaxation processes.
Binary-heating is ineffective changing the disc evolution since the binary – single-star coupling are inefficient in transferring binary potential energy into effective disc heating.
The NSC can significantly affect the evolution of the stellar disc, depending on its overall mass (the effective density in the disc region), the typical mass of the NSC stars and its relation to the masses of stars in the disc (mass function). Discs with more top-heavy IMF are less affected by the NSC.
Two-body relaxation processes are too slow to completely disperse a stellar disc even on a time-scale of 100 Myr. Kinematic signature of past discs could therefore potentially be observed in the form of mass-stratification and non-sphericity of the stellar population of <100 Myr-old discs.
The observed rms eccentricity of the O-stars in the stellar disc in the GC (∼0.27) is larger than obtained in any of our models with realistic conditions, suggesting either an initially hot and/or eccentric disc or that other secular/collective effects play an important role in the disc evolution.
Acknowledgments
We acknowledge support from the I-CORE Program of the Planning and Budgeting Committee and ISF grant 1829/12.



