-
PDF
- Split View
-
Views
-
Cite
Cite
Han-Seek Kim, J. Stuart. B. Wyithe, C. M. Baugh, C. d. P. Lagos, C. Power, Jaehong Park, The spatial distribution of neutral hydrogen as traced by low H i mass galaxies, Monthly Notices of the Royal Astronomical Society, Volume 465, Issue 1, 11 February 2017, Pages 111–122, https://doi.org/10.1093/mnras/stw2779
Close - Share Icon Share
Abstract
The formation and evolution of galaxies with low neutral atomic hydrogen (H i) masses, |$M_{\rm H\,\small {I}}$| < 108 h−2 M⊙, are affected by host dark matter halo mass and photoionization feedback from the UV background after the end of reionization. We study how the physical processes governing the formation of galaxies with low H i mass are imprinted on the distribution of neutral hydrogen in the Universe using the hierarchical galaxy formation model, galform. We calculate the effect on the correlation function of changing the H i mass detection threshold at redshifts 0 ≤ z ≤ 0.5. We parametrize the clustering as ξ(r) = (r/r0)−γ and we find that including galaxies with |$M_{\rm H\,\small {I}}$| < 108 h−2 M⊙ increases the clustering amplitude r0 and slope γ compared to samples of higher H i masses. This is due to these galaxies with low H i masses typically being hosted by haloes with masses greater than 1012 h−1 M⊙, and is in contrast to optically selected surveys for which the inclusion of faint, blue galaxies lowers the clustering amplitude. We show the H i mass function for different host dark matter halo masses and galaxy types (central or satellite) to interpret the values of r0 and γ of the clustering of H i-selected galaxies. We also predict the contribution of low H i mass galaxies to the 21 cm intensity mapping signal. We calculate that a dark matter halo mass resolution better than ∼1010 h−1 M⊙ at redshifts higher than 0.5 is required in order to predict converged 21 cm brightness temperature fluctuations.
1 INTRODUCTION
In hierarchical structure formation theory, the distribution of galaxies is related to the distribution of dark matter in the Universe. Studies of the spatial distribution of galaxies as a function of colour, luminosity, type and stellar mass therefore give important information about where galaxies form and which haloes host them Brown, Webster & Boyle (2000; Norberg et al. 2002; Madgwick et al. 2003; Loh et al. 2010; Zehavi et al. 2011; Campbell et al. 2015).
Neutral hydrogen is a key ingredient of galaxy formation as it traces the processes of gas accretion, outflow from galaxies and star formation. It is therefore important to understand the relation between neutral hydrogen and dark matter haloes. However, understanding galaxy formation and evolution using neutral hydrogen observations is hampered by the weakness of the signal compared to optical observations. The last decade has seen improvements in both the volume and flux limit of surveys which probe the H i content of galaxies from the H i Parkes All Sky Survey (HIPASS; Zwaan et al. 2005), the Arecibo Legacy Fast ALFA (ALFALFA; Martin et al. 2010) and the Arecibo Ultra-Deep Survey (Hoppmann et al. 2015). Studies of the distribution of H i-selected galaxies in the local Universe have shown that these galaxies are an unbiased (weakly clustered) galaxy population Meyer et al. (2007); Martin et al. (2012); Papastergis et al. (2013).
There have been previous studies of the large-scale structure of galaxies based on their neutral hydrogen using the halo occupation distribution formalism Wyithe et al. (2009) and hierarchical galaxy formation models Kim et al. (2011, 2013b). These works have focused on high H i mass galaxies (|$M_{\rm H\,\small {I}}$| > 109.25 h−2 M⊙), which are mainly central galaxies located in dark matter haloes of masses ∼1012 h−1 M⊙. In contrast, red massive galaxies have either consumed most of their gas (neutral hydrogen) in forming stars or have expelled it by feedback processes Power, Baugh & Lacey (2010); Kim et al. (2011); Lagos et al. (2011a), as shown by their very low neutral gas content Young et al. (2011); Serra et al. (2012); Boselli et al. (2014b). H i-deficient galaxies also result from ram pressure stripping by hot gaseous atmospheres around satellite galaxies in groups and clusters, and tidal interactions between galaxies in high-density environments Font et al. (2008); McCarthy et al. (2008); Cortese et al. (2012); Boselli et al. (2014a); Bahé & McCarthy (2015). These processes, all affect the distribution of satellite galaxies in groups and clusters.
Kim et al. (2015) demonstrated the importance of photoionization feedback for galaxy formation and evolution in low-mass dark matter haloes, and the low-mass end of the H i mass function in the local Universe (see also Lagos et al. 2011a; Kim et al. 2013b). Kim et al. (2015) showed that the contribution of low-mass dark matter haloes to the low-mass end of the H i mass function changes dramatically when different photoionization feedback modelling schemes are applied. Therefore, it is natural to expect these models to affect the predicted clustering of low H i mass galaxies.
The number of individual galaxies detected in H i will greatly increase through ongoing and upcoming large volume H i-selected galaxy surveys using the SKA (Square Kilometre Array; e.g. Baugh et al. 2004; Power et al. 2010; Kim et al. 2011) and its pathfinders, such as ASKAP (Australian Square Kilometre Array Pathfinder; cf. Johnston et al. 2008) and MeerKAT (Meer Karoo Array Telescope; cf. Jonas 2007) in the Southern hemisphere, FAST (Five-hundred-meter Aperture Spherical Telescope)1 and APERTIF (APERture Tile In Focus)2 in the Northern hemisphere. In addition, the BINGO (the BAO in Neutral Gas Observations; Battye et al. 2012), CHIME (the Canadian Hydrogen Intensity Mapping Experiment; Bandura et al. 2014) and SKA are expected to detect the distribution of neutral hydrogen at 0.5 < z < 3 in the Universe using the 21 cm intensity mapping technique which does not require individual H i-selected galaxies to be resolved Wyithe & Loeb (2007); Wolz et al. (2014); Santos et al. (2015). There have been several theoretical models predicting the H i intensity during the post-reionization era. Each model includes a prescription for the relation between H i and dark matter halo masses. This results in the implicit assumption that the H i traces the underlying matter distribution with a linear bias (Bagla, Khandai & Datta 2010; Guha Sarkar et al. 2012; Padmanabhan, Choudhury & Refregier 2015; Villaescusa-Navarro et al. 2016). For example, Bagla et al. (2010) propose phenomenological functions for this relation based on the observation that haloes much more massive than a few times 1011 M⊙ do not host significant amounts of H i (Catinella et al. 2013; Dénes, Kilborn & Koribalski 2014). This simple model successfully explains both observations of the abundance of damped Lyman α absorbers at redshifts between 2.4 and 4, and the bias of H i-selected galaxies in the local Universe (Villaescusa-Navarro et al. 2014; Padmanabhan, Choudhury & Refregier 2015; Sarkar, Bharadwaj & Anathpindika 2016). On the other hand, using zoom hydrodynamic simulations, Villaescusa-Navarro et al. (2016) found that the mass in neutral hydrogen of dark matter haloes increases monotonically with halo mass, and can be well described by a power law. Here, we show the importance of the contribution of galaxies with low H i masses to the large-scale distribution of neutral hydrogen in the Universe, and why they cannot be neglected if an accurate measurement the H i intensity mapping power spectrum is desired.
The structure of the paper is as follows. In Section 2, we provide a brief overview of the hierarchical galaxy formation models used. In Section 3, we show the clustering of H i-selected galaxies from the models and the comparison between the models and observations. In Section 4, we extend predictions of H i galaxy clustering to higher redshifts and show predictions for 21 cm brightness fluctuations at different redshifts in Section 5. We finish with a summary of our results in Section 6.
2 THE GALAXY FORMATION MODEL
We use the semi-analytical galaxy formation model galform (cf. Cole et al. 2000; Baugh 2006; Lacey et al. 2016) described in Lagos et al. (2012) and Kim et al. (2015) to predict the properties of galaxies which form and evolve in the ΛCDM cosmology. galform models the key physical processes involved in galaxy formation, including the gravitationally driven assembly of dark matter haloes, radiative cooling of gas and its collapse to form centrifugally supported discs, star formation, feedback from supernovae and active galactic nuclei (AGN), and photoionization. We implement galform in halo merger trees extracted from the Millennium-II cosmological N-body simulation3 which has a 100 h−1 Mpc box size (Boylan-Kolchin et al. 2009).
We use the Dhalo merger trees (D-Trees; Jiang et al. 2014). These were designed for galaxy formation modelling and form the basis of the Durham semi-analytic galaxy formation model, galform. The D-Trees algorithm is based on the friends-of-friends algorithm, FOF (Davis et al. 1985). The FOF haloes are decomposed into subhaloes by subfind (Springel 2005). In the D-Trees, subhaloes have consistent membership over time in the sense that once a subhalo is accreted by a Dhalo it never demerges. In contrast to the FOF haloes, in this process we also split some FOF haloes into two or more Dhaloes when subfind substructures are well separated and only linked into a single FOF halo by bridges of low-density material. The central is associated with the main subhalo. Satellite galaxies were originally centrals until their FOF halo merged with a larger one, and are associated with the corresponding subhalo, or the most bound particle from this subhalo if the subhalo itself can no longer be identified. Full details of the Dhaloes can be found in Merson et al. (2013) and Jiang et al. (2014).
The particle mass of the simulation is 6.89 × 106 h−1 M⊙ and we retain haloes down to 20 particles. In the extreme case where all available baryons are in H i, the H i mass of a galaxy in such a halo would be ∼1.8 × 106h−2 M⊙. Thus, the resolution limit of the Millennium-II simulation is sufficient to model the H i mass function over the range of current observations (i.e. down to |$M_{\rm H\,\small {I}}$| ∼ 106 M⊙).
Lagos et al. (2011a) extended galform by modelling the splitting of cold gas in the interstellar medium (ISM) into its H i and H2 components and by explicitly linking star formation to the amount of H2 present in a galaxy. Lagos et al. (2011a) compared empirically and theoretically derived star formation laws (cf. Blitz & Rosolowsky 2006; Krumholz, McKee & Tumlinson 2009) with a variety of observations and found that the empirical law of Blitz & Rosolowsky (2006, see also Leroy et al. 2008) is favoured by these data.
Another important physical process affecting H i masses in galaxies is reionization. The standard reionization model in galform suppresses cooling in galaxies with host halo circular velocity Vcirc below a threshold Vcut below redshift zcut (see Benson et al. 2002). Lagos et al. (2011b) adopted Vcut = 30 km s−1 and zcut = 10. Lagos et al. (2012) changed two parameters corresponding to the star formation time-scale during starbursts, τmin = 100 Myr and fdyn = 50 when the star formation time-scale is calculated as τSF = min(fdyn × τdyn, bulge, τmin), to better match the observed rest-frame UV luminosity function over the redshift range z = 3–6 (hereafter Lagos2012). Here, τdyn, bulge is the dynamical time-scale of the bulge.
3 LARGE-SCALE DISTRIBUTION OF NEUTRAL HYDROGEN IN THE LOCAL UNIVERSE
We show clustering predictions for galaxies selected using different H i mass thresholds in Section 3.1. To compare the spatial distributions of galaxies selected by different H i mass criteria, we investigate the contributions of different host dark matter halo masses and types of galaxies to the H i mass function in Section 3.2.
3.1 H i mass-dependent clustering
The ALFALFA survey measures the H i mass function down to H i masses of ∼106 h−2 M⊙. This low-mass limit provides an important test for galaxy formation models. The Kim15 model is able to reproduce the observed H i mass function from ALFALFA by adopting a redshift-dependent photoionization feedback model (see Section 2 and also Fig. 2).
In Fig. 1, we show clustering predictions for galaxies selected using different H i mass thresholds. The clustering predictions for the two highest H i mass thresholds (|$M_{\rm H\,\small {I}}$| > 108 h−2 M⊙ and |$M_{\rm H\,\small {I}}$| > 109 h−2 M⊙) are very similar, both in shape (γ) and the correlation length (r0). However, the two lowest H i mass thresholds (|$M_{\rm H\,\small {I}}$|> 106 h−2 M⊙ and |$M_{\rm H\,\small {I}}$| > 107 h−2 M⊙) show larger correlation lengths (larger r0) and also steeper correlation functions (larger γ) than the two high H i mass samples (see values of r0 and γ in Table 1 and Fig. 7 at z = 0). Overall, the trend of clustering as a function of H i mass threshold shows that galaxies become more clustered as the H i mass threshold decreases.
The best-fitting parameters (r0[h−1Mpc] and γ) in equation (4) for predicted correlation functions of different H i mass thresholds at z = 0, 0.2 and 0.5 in the Kim15 model. In the square bracket at z = 0, we show the r0 and γ values following Meyer et al. (2007) using the projected correlation function.
| H i mass threshold . | r0[r0, pow] (z = 0) . | γ [γ,pow] (z = 0) . | r0 (z = 0.2) . | γ (z = 0.2) . | r0 (z = 0.5) . | γ (z = 0.5) . |
|---|---|---|---|---|---|---|
| >106 h−2 M⊙ | 5.12 [4.91] | 1.87 [1.99] | 4.61 | 1.81 | 3.84 | 1.62 |
| >107 h−2 M⊙ | 4.72 [4.42] | 1.74 [1.91] | 4.06 | 1.65 | 3.19 | 1.49 |
| >108 h−2 M⊙ | 3.99 [3.71] | 1.54 [1.80] | 3.34 | 1.48 | 2.77 | 1.39 |
| >109 h−2 M⊙ | 3.77 [3.52] | 1.50 [1.76] | 3.29 | 1.45 | 2.95 | 1.38 |
| H i mass threshold . | r0[r0, pow] (z = 0) . | γ [γ,pow] (z = 0) . | r0 (z = 0.2) . | γ (z = 0.2) . | r0 (z = 0.5) . | γ (z = 0.5) . |
|---|---|---|---|---|---|---|
| >106 h−2 M⊙ | 5.12 [4.91] | 1.87 [1.99] | 4.61 | 1.81 | 3.84 | 1.62 |
| >107 h−2 M⊙ | 4.72 [4.42] | 1.74 [1.91] | 4.06 | 1.65 | 3.19 | 1.49 |
| >108 h−2 M⊙ | 3.99 [3.71] | 1.54 [1.80] | 3.34 | 1.48 | 2.77 | 1.39 |
| >109 h−2 M⊙ | 3.77 [3.52] | 1.50 [1.76] | 3.29 | 1.45 | 2.95 | 1.38 |
The best-fitting parameters (r0[h−1Mpc] and γ) in equation (4) for predicted correlation functions of different H i mass thresholds at z = 0, 0.2 and 0.5 in the Kim15 model. In the square bracket at z = 0, we show the r0 and γ values following Meyer et al. (2007) using the projected correlation function.
| H i mass threshold . | r0[r0, pow] (z = 0) . | γ [γ,pow] (z = 0) . | r0 (z = 0.2) . | γ (z = 0.2) . | r0 (z = 0.5) . | γ (z = 0.5) . |
|---|---|---|---|---|---|---|
| >106 h−2 M⊙ | 5.12 [4.91] | 1.87 [1.99] | 4.61 | 1.81 | 3.84 | 1.62 |
| >107 h−2 M⊙ | 4.72 [4.42] | 1.74 [1.91] | 4.06 | 1.65 | 3.19 | 1.49 |
| >108 h−2 M⊙ | 3.99 [3.71] | 1.54 [1.80] | 3.34 | 1.48 | 2.77 | 1.39 |
| >109 h−2 M⊙ | 3.77 [3.52] | 1.50 [1.76] | 3.29 | 1.45 | 2.95 | 1.38 |
| H i mass threshold . | r0[r0, pow] (z = 0) . | γ [γ,pow] (z = 0) . | r0 (z = 0.2) . | γ (z = 0.2) . | r0 (z = 0.5) . | γ (z = 0.5) . |
|---|---|---|---|---|---|---|
| >106 h−2 M⊙ | 5.12 [4.91] | 1.87 [1.99] | 4.61 | 1.81 | 3.84 | 1.62 |
| >107 h−2 M⊙ | 4.72 [4.42] | 1.74 [1.91] | 4.06 | 1.65 | 3.19 | 1.49 |
| >108 h−2 M⊙ | 3.99 [3.71] | 1.54 [1.80] | 3.34 | 1.48 | 2.77 | 1.39 |
| >109 h−2 M⊙ | 3.77 [3.52] | 1.50 [1.76] | 3.29 | 1.45 | 2.95 | 1.38 |
3.2 Understanding the H i mass-dependent clustering in the Kim15 model
The clustering of galaxy samples can be broken down into the contribution of the host dark matter haloes Berlind & Weinberg (2002); Kravtsov et al. (2004); Kim et al. (2011, 2012). We therefore investigate the contributions to the H i mass function from different galaxies and different mass host dark matter haloes.
The top-left panel of Fig. 2 shows the contribution of different types of H i-selected galaxies (black solid line for all galaxies, blue dotted line for central galaxies and red dashed line for satellite galaxies) to the H i mass function. Central galaxies are the dominant (over 90 per cent) type of galaxy when we focus on galaxies with H i masses |$M_{\rm H\,\small {I}}$| > 108.5 h−2 M⊙. However, the contributions of central galaxies and satellite galaxies to the H i mass function are similar for |$M_{\rm H\,\small {I}}$| < 108 h−2 M⊙. This is consistent with the findings from hydrodynamic simulations (Davé et al. 2013).
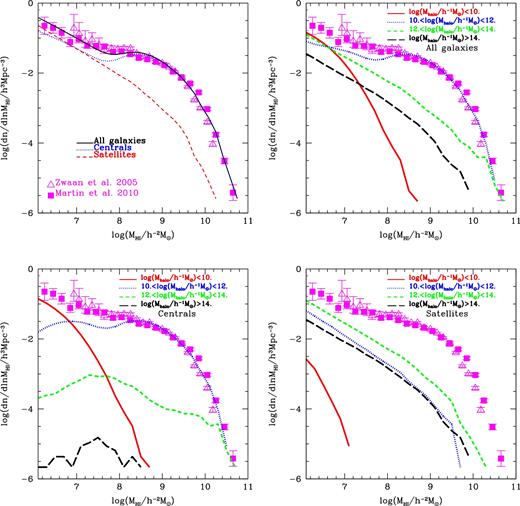
The predicted H i mass function in the Kim15 model. The top-left panel shows the contribution of central and satellite galaxies to the HIMF (originally plotted in Kim et al. 2015). The top-right panel shows the contribution of different masses of host dark matter haloes. The bottom panels show the contribution of different masses of host dark matter haloes for central galaxies (left-hand panel) and satellite galaxies (right-hand panel). The symbols correspond to observational estimations from the local Universe from HIPASS (open triangles; cf. Zwaan et al. 2005) and ALFALFA (filled squares; cf. Martin et al. 2010). Mhalo is the mass of the associated Dhalo.
The top-right panel of Fig. 2 shows the H i mass functions for galaxies in different bins of host dark matter halo mass. Note that the host dark matter halo mass, Mhalo, is the mass of the associated host Dhalo. Most galaxies with H i masses >107.5 h−2 M⊙ reside in host dark matter haloes with masses between 1010 and 1012 h−1 M⊙. Host dark matter haloes with mass <1010 h−1 M⊙ mainly contribute to the low-mass end of the H i mass function, |$M_{\rm H\,\small {I}}$| < 107 h−2 M⊙, while making a negligible contribution to the H i mass function at H i masses higher than 108 h−2 M⊙. The most massive host dark matter haloes (>1014 h−1 M⊙) contribute less than 10 per cent to the abundance of galaxies at all H i masses.
We show host dark matter halo contributions divided into central (bottom-left panel of Fig. 2) and satellite galaxies (bottom-right panel of Fig. 2). For central galaxies, the dominant contribution to the H i mass function at |$M_{\rm H\,\small {I}}$| > 107.5 h−2 M⊙ is from host dark matter haloes with masses 1010 h−1 M⊙ < Mhalo < 1012 h−1 M⊙. Central galaxies which reside in higher mass host dark matter haloes (1012 h−1 M⊙ < Mhalo < 1014 h−1 M⊙ and >1014 h−1 M⊙) represent a very small fraction of H i-selected galaxies. Host dark matter haloes with masses less than 1010 h−1 M⊙ mainly host central galaxies with |$M_{\rm H\,\small {I}}$| < 107 h−2 M⊙.
Photoionization feedback in the model suppresses the cooling of gas in central galaxies which have circular velocities less than Vcut. Therefore, the suppressed cooling of gas in central galaxies introduces the departure from a Schechter-like function. On the other hand, the abundance of satellite galaxies in massive dark matter haloes increases monotonically towards low H i mass. The reason why the H i mass function (HIMF) of satellite galaxies does not show a dip at low H i masses is that the satellites were mainly formed before reionization.
We find that the number of H i-selected galaxies that are satellites increases with decreasing H i mass for all host dark matter halo masses. Furthermore, at |$M_{\rm H\,\small {I}}$| < 107 h−2 M⊙, H i satellite galaxies dominate the number density. These satellite galaxies tend to lie in host dark matter haloes of mass Mhalo > 1012 h−1 M⊙.
In Fig. 1, we found that the correlation length r0 becomes larger as the H i mass threshold decreases for the selected galaxy samples. This is due to the larger contributions of high-mass host dark matter haloes (Mhalo > 1012 h−1 M⊙) to the H i mass function (see top-right panel of Fig. 2) at |$M_{\rm H\,\small {I}}$| < 108 h−2 M⊙. In addition, the contribution of satellite galaxies residing in the highest mass host dark matter haloes (Mhalo > 1014 h−1 M⊙) at |$M_{\rm H\,\small {I}}$| < 108 h−2 M⊙ leads to a boost in the clustering amplitude at small separations (see Fig. 1). We also find that the slope of the correlation function decreases with increasing H i mass due to the reduced contribution of satellite galaxies.
We show the distribution of host dark matter halo mass as a function of H i mass in galaxies in the top-left panel of Fig. 3. The symbols show the median host dark matter halo mass as a function of H i mass for central galaxies (blue squares), satellite galaxies (red triangles) and all galaxies (black circles). The bars show the 10th–90th percentile range of the distribution of host dark matter halo masses. The host dark matter halo mass of central galaxies increases as the H i mass increases. In contrast, the median host dark matter halo mass for satellite H i-selected galaxies is constant over the entire range of H i masses (median value ∼1013 h−1 M⊙).
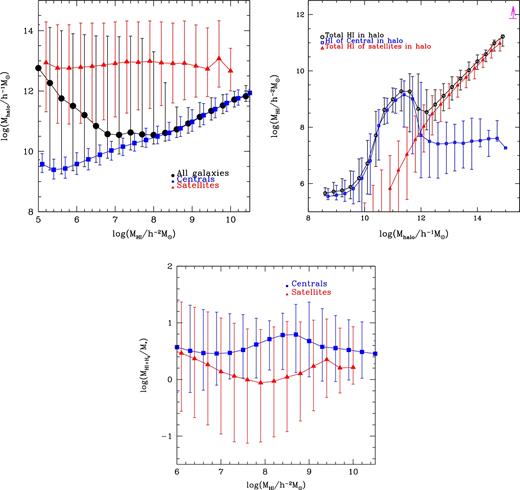
The top-left panel shows the host halo mass plotted in bins of H i mass at z = 0. The symbols show the median dark matter mass as a function of the H i mass of galaxies, for central galaxies (blue squares), satellite galaxies (red triangles) and all galaxies (black circles). The bars show the 10th–90th percentile ranges of the distributions of host dark matter halo masses. The top-right panel shows the total H i mass contained in a halo at z = 0. The symbols show the median total H i mass as a function of host dark matter halo mass, for central galaxies (open blue squares), all satellite galaxies (open red triangles) and all galaxies (open black circles) in a halo. The bars show the 10th–90th percentile ranges of the distributions of total H i masses. In this figure, we include all galaxies which have H i mass larger than 104 h−1 M⊙. The magenta arrow represents the lower limit of the overall H i mass of the Coma cluster by summing H i masses of 223 H i-detected late-type galaxies in Gavazzi et al. (2006). The total mass of the Coma cluster from Kubo et al. (2007) is shown for comparison. Mhalo is the mass of the associated Dhalo. The bottom panel shows the neutral hydrogen gas fraction in bins of H i mass. The symbols show the median neutral hydrogen gas (|$M_{\rm H\,\small {I}+H_{2}}$|) fraction as a function of the H i mass of galaxies, for central galaxies (blue squares) and satellite galaxies (red triangles). |$M_{\rm H_{2}}$| is the molecular hydrogen mass and M⋆ is the stellar mass. The bars show the 10th–90th percentile ranges of the distributions of neutral hydrogen gas fractions.
We also show in the top-right panel of Fig. 3 the total H i mass contained in all galaxies within a halo. The symbols show the median total H i mass as a function of host dark matter halo mass, for central galaxies (open blue squares), all satellite galaxies (open red triangles) and all galaxies (open black circles) in a halo. The bars show the 10th–90th percentile range of the distribution of total H i masses. The total H i mass in a halo is contributed mainly by the central galaxy for host dark matter haloes less massive than 1012 h−1 M⊙ and satellite galaxies for host dark matter haloes more massive than 1012 h−1 M⊙. Note that these measurements have not been made observations yet and thus these are model predictions that need to be verified by future observations. In this model, there is very little H i gas in the central galaxy haloes more massive than this due to the shutdown of the cooling flow by AGN heating (Kim et al. 2011). The total H i mass of satellites (adding all H i masses of satellites together in a halo) increases as the halo mass increases. This predicted relation between total H i mass in a host dark matter halo and dark matter halo mass would be the physically motivated input to make H i intensity mapping mock observations based on dark haloes using large volume dark matter only simulations. The bottom panel of Fig. 3 shows the neutral hydrogen gas fraction, |$M_{\rm H\,\small {I}+H_2}/M_{\star }$|, in bins of H i mass. |$M_{\rm H_{2}}$| is the molecular hydrogen mass and M⋆ is the stellar mass. The symbols show the median neutral hydrogen gas fraction as a function of the H i mass of galaxies, for central galaxies (blue squares) and satellite galaxies (red triangles). The bars show the 10th–90th percentile ranges of the distributions of neutral hydrogen gas fractions. The overall neutral hydrogen gas fraction for satellites is lower than centrals. Because the hot gas in the subhaloes around satellites is removed instantaneously and is transferred to the hot gas reservoir of the main halo once a galaxy becomes a satellite in the model. This removal of the hot gas prevents the satellite galaxy to accrete newly cooled gas, condemning it to have ever lower gas fractions as star formation continues (see discussion in Lagos et al. 2011a for the competing environment and star formation processes). The feedback effects are also imprinted on the low H i mass end from the suppression of cooling of gas by the photoionization and the high H i mass end from the shutting down of the cooling flow by the AGN feedback for centrals.
3.3 Imprinted photoionization feedback on H i clustering
In the previous subsection, we presented predictions for H i galaxy clustering and the mass function. By comparing these predictions with the observed H i mass function and clustering of H i-selected galaxies from HIPASS Meyer et al. (2007) and ALFALFA (Martin et al. 2012, see Kim et al. 2011, 2013a, 2015), we can test the galaxy formation model. Martin et al. (2012) showed that H i-selected galaxies display an anisotropic clustering pattern, and are less clustered than dark matter on scales <5 Mpc. Furthermore, Papastergis et al. (2013) found no evidence for H i mass-dependent clustering over the H i mass range between 108.5 and 1010.5 M⊙. Meyer et al. (2007) used 4315 sources from the HIPASS survey to measure the clustering of H i-selected galaxies. Martin et al. (2012) used a sample of ∼10 150 galaxies (|$M_{\rm H\,\small {I}}$| > 106.2 h−2 M⊙) and Papastergis et al. (2013) used a sample of ∼6000 galaxies detected by the ALFALFA 21 cm survey (|$M_{\rm H\,\small {I}}$| > 107.5 h−2 M⊙), to measure the clustering properties of H i-selected galaxies. Whilst these surveys represent a tremendous step forwards in terms of blind surveys of the H i content of galaxies, it is important to bear in mind when considering clustering measurements made from them that they contain orders of magnitude fewer galaxies and sample smaller volumes than local optical surveys, such as the two-degree-Field Galaxy Redshift Survey (Colless et al. 2001), or Sloan Digital Sky Survey (York et al. 2000).
The left-hand panel of Fig. 4 shows the H i mass functions predicted by the Lagos2012 (red dotted line) and the Kim15 (black solid line) models. The Kim15 model applied a new scheme for photoionization feedback in order to improve the agreement of the predicted low-mass end of the H i mass function with the estimation from the ALFALFA survey at z = 0. This work is based on the model in Kim et al. (2015) which improves the modelling of the lower mass end of H i mass function. Here, we also show the ALFALFA observations for comparison to the model, which extend to low masses than the HIPASS data.
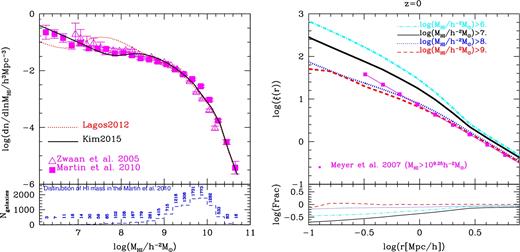
The left-hand panel shows the H i mass function at z = 0 predicted by the Lagos2012 (red dotted line) and the Kim15 (black solid line) models compared with local Universe observations from HIPASS (open triangles; cf. Zwaan et al. 2005) and ALFALFA (filled squares; cf. Martin et al. 2010). The bottom-left sub-panel shows the distribution of H i mass in the sample of Martin et al. (2010) to estimate the H i mass function. The right-hand panel shows the correlation function of different H i mass threshold samples at z = 0 for the Kim15 model. The bottom-right sub-panel shows the ratio between the predictions of the Lagos2012 and the Kim15 models for the same H i mass threshold samples labelled in the top-right sub-panel. The magenta filled squares connected by the solid line in the top-right sub-panel show the measurement of Meyer et al. (2007) using their best-fitting r0 and γ values for galaxies with H i masses >109.25 h −2 M⊙ from the local Universe.
Surveys of H i-selected galaxies are not volume-limited and low H i mass galaxies are visible over a smaller volume than high H i mass galaxies. The blue dashed line in the bottom-left sub-panel shows the distribution of H i mass in the sample of Martin et al. (2010) used to estimate the H i mass function.
The sample used in Martin et al. (2010) from the ALFALFA survey has complete source extraction for 40 per cent of its total sky area. Martin et al. (2010) measure the H i mass function from a sample of ∼10 150 galaxies and apply both the 1/Vmax (Schmidt 1968) and the Two-Dimensional Step-Wise Maximum Likelihood methods Zwaan et al. (2005). In this work, we use the H i mass function estimated using the 1/Vmax method when comparing with our model predictions.4
The right-hand panel of Fig. 4 shows the correlation functions for different H i mass thresholds in the Kim15 model, compared with observations from Meyer et al. (2007) using the best-fitting r0 and γ values for galaxies with H i masses >109.25 h−2 M⊙. The bottom-right sub-panel shows the ratio between the predictions of the Lagos2012 and the Kim15 models, for the same H i mass thresholds used in the second top sub-panel. These models differ in their treatment of photoionization feedback as described in Section 2. The right-hand panel of Fig. 4 shows that H i-selected galaxies down to |$M_{\rm H\,\small {I}}$| > 107 h−2 M⊙ could constrain the properties of photoionization feedback (which is also imprinted on the H i mass function, Kim et al. 2015), and the contribution of satellite galaxies to the distribution of H i-selected galaxies from H i clustering measurements through the γ value of the correlation function.
Fig. 4 illustrates that observational H i clustering measurements which contain H i galaxies with |$M_{\rm H\,\small {I}}$| < 108 h−2 M⊙ are necessary to constrain the modelling of galaxy formation, particularly how photoionization affects small galaxies Kim et al. (2015), and the contribution of satellite galaxies to the distribution of H i galaxies.
4 DISTRIBUTION OF NEUTRAL HYDROGEN AT HIGH REDSHIFTS
We now investigate the predicted clustering of H i-selected galaxies at high redshift in ongoing and future H i galaxy surveys.
Power et al. (2010) showed that the H i mass function undergoes little evolution from z = 1 to 0 (see also, Kim et al. 2011; Lagos et al. 2011a). This is due to a competition between gas cooling, the transition from H i to H2 and star formation, together with mass ejection by winds. This is a generic feature predicted by galaxy formation models for high H i mass galaxies (see Power et al. 2010). However, this picture could break down for H i-poor galaxies, which reside in low-mass host dark matter haloes. These haloes are more sensitive to photoionization feedback, which hampers gas cooling. Here, we investigate the evolution of the H i mass function. The left-hand panel of Fig. 5 shows the predicted H i mass functions at z = 0, 0.2 and 0.5 (corresponding to maximum redshifts expected to be observed by the WALLABY5 (z ∼ 0.2), DINGO6 (z ∼ 0.5) and LADUMA7 (z ∼ 0.5)), together with the H i mass function from the ALFALFA survey at z = 0 for reference. The largest difference between the H i mass functions at z = 0.2 (or 0.5) and z = 0 is predicted to be for galaxies with masses in the range 107 h−2 M⊙ < |$M_{\rm H\,\small {I}}<10^{8.5}\,h^{-2}$| M⊙. The circular velocities of the host dark matter haloes of these galaxies are between ∼ 30 km s−1 and ∼ 50 km s−1 in the Kim15 model. These velocities correspond to galaxies which become affected by photoionization feedback between z = 0.5 and 0.
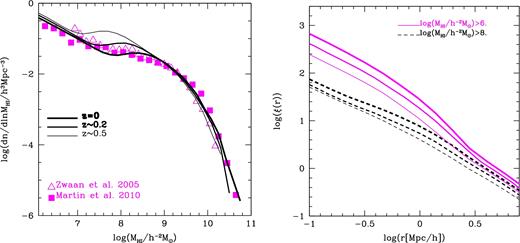
Left-hand panel: the H i mass function predicted by the Kim15 model at z = 0, 0.2 and 0.5 as labelled, compared with local Universe observations from HIPASS (open triangles; cf. Zwaan et al. 2005) and ALFALFA (filled squares; cf. Martin et al. 2010). Right-hand panel: the real-space correlation function predicted for two different H i mass thresholds samples at redshifts z = 0, 0.2 and 0.5, as labelled in the left-hand panel.
The right-hand panel of Fig. 5 shows the predicted correlation functions at z = 0, 0.2 and 0.5 for two different H i mass thresholds (|$M_{\rm H\,\small {I}}>10^{6}\,h^{-2}$| M⊙ and |$M_{\rm H\,\small {I}}>10^{8}\,h^{-2}$| M⊙). The correlation functions at higher redshift have lower correlation length (r0) and slope (γ) than at lower redshift for the same H i mass thresholds (see Table 1). The parameters r0 and γ were derived by minimizing χ2 of predicted correlation functions of the form shown in e quation (4) over separations between 1 and 10 h−1 Mpc and considering γ values between 0 and 5. The separation range was chosen based on the approach in Meyer et al. (2007) and Martin et al. (2012), who used projected separations <10 h−1 Mpc and Papastergis et al. (2013) used projected separation between 0.5 and 10 h−1 Mpc.
Fig. 6 shows the projected correlation functions in the model by projecting galaxy samples on to the 2D x-y plane within the z range ∼40 h−1 Mpc by applying the distant-observer approximation. The points with error bars show an observational estimate made from the ALFALFA catalogue by Martin et al. (2010) at local Universe. The projected correlation functions from the model do not show a power-law shape. To see the effect of the power-law assumption, we estimate the r0 and γ values following Meyer et al. (2007) using the projected correlation function from the model. We have also included the r0 and γ values from these results in Table. 1 (in the square bracket) and Fig. 7 for z = 0 (connected open triangles by the dotted line) for comparison between the values from the real-space correlation function and extracted values from the projected correlation function in the model.
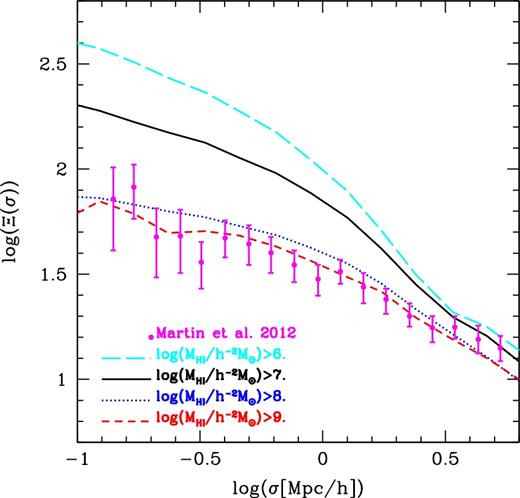
The projected galaxy correlation function at z = 0 for different H i mass threshold samples from the model. σ indicates the projected separations. The points with error bars show an observational estimate made from the ALFALFA catalogue by Martin et al. (2010) at local Universe.
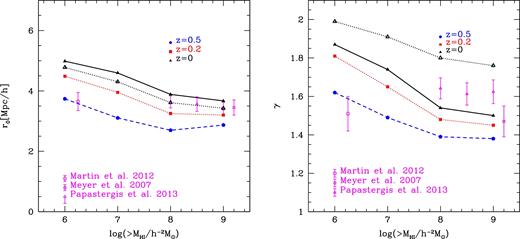
Left-hand panel: the correlation length (r0) of the correlation function for different H i mass thresholds at z = 0, 0.2 and 0.5, as labelled. Right-hand panel: the slope (γ) of the correlation function for different H i mass thresholds at z = 0, 0.2 and 0.5, as labelled. For reference, the symbols with error bars (the standard deviation) show the best-fitting r0 and γ values from observations of H i-selected galaxies measured by Meyer et al. (2007), Martin et al. (2012) and Papastergis et al. (2013) in the local Universe. The open triangles show the r0, power (left-hand panel) and γpow (right-hand panel) from the projected correlation function of the model following Meyer et al. (2007).
In the left-hand panel of Fig. 7, we show variations on the predicted correlation length (r0) at different redshifts and H i mass thresholds. In agreement with the z = 0 predictions, we find that lower H i mass threshold samples show a larger correlation length than higher H i mass threshold samples at all redshifts in contrast to optically selected galaxy samples (cf. red galaxy samples show an increasing r0 at faint luminosities). This is because the contribution of galaxies hosted by high mass host dark matter haloes increases with decreasing H i mass threshold (see Fig. 2).
In the right-hand panel of Fig. 7, we show the predicted correlation function slope (γ) for different redshifts and H i mass thresholds. γ displays similar trends with redshift and H i mass threshold to r0 (left-hand panel of Fig. 7). Samples selected using lower H i mass thresholds show steeper correlation functions compared to samples using higher H i mass thresholds due to the contribution of satellite galaxies hosted by host dark matter haloes of Mhalo > 1014 h−1 M⊙. In addition, the correlation length (r0) and slope (γ) increase as redshift decreases from z = 0.5 to 0. This implies that galaxies at low redshift are more clustered than higher redshift galaxies selected above the same H i mass threshold, which is consistent with the hierarchical growth of structures. For comparison, the symbols with error bars show the best-fitting values of r0 (the left-hand panel of Fig. 7) and γ (the right-hand panel of Fig. 7) estimated from observations in the local Universe of H i-selected for galaxies with |$M_{\rm H\,\small {I}}$| > 109.25 h−2 M⊙ (Meyer et al. 2007), |$M_{\rm H\,\small {I}}$| > 106.2 h−2 M⊙ (Martin et al. 2012) and |$M_{\rm H\,\small {I}}$| > 108, 108.5 and 109 h−2 M⊙ (Papastergis et al. 2013).
Note that the predictions are in reasonable agreement with the observations for |$M_{\rm H\,\small {I}}>10^{8}\,h^{-2}$| M⊙. However, the model does not reproduce the clustering estimated by Martin et al. (2012) for samples with |$M_{\rm H\,\small {I}}>10^{6.2}\,h^{-2}$| M⊙. The values of r0 do not change significantly if the value of γ is held fixed at the value found in the observational study. On the other hand, we remind the reader that the observational clustering measurements come from small volumes, which can be affected by cosmic variance. Although Martin et al. (2012) attempted to correct for the selection function of the sample, to account for the fact that low H i mass galaxies are seen over a much smaller volume than high H i mass galaxies, the cleanest approach for measuring galaxy clustering is to use volume-limited samples. However, this is not yet feasible with current H i surveys as this requires many galaxies to be omitted from the analysis (see for example, the volume-limited samples used in an optical galaxy survey by Norberg et al. 2001). The assumption of a power law in the observed estimate of r0 may also introduce a bias increasing the value of γ and/or decreasing r0 value.
5 EFFECT OF GALAXIES WITH LOW H i MASSES ON THE SIGNAL FOR 21CM INTENSITY MAPPING
As noted above, clustering studies of low H i mass-selected galaxies will be restricted to z ∼ 0.5, even within the deepest H i surveys planned (e.g. DINGO). An alternative way to study the clustering of galaxies down to low H i masses and at high redshifts (0.5 < z < 3) is through 21 cm intensity mapping, which measures the fluctuation in the 21 cm signal from unresolved H i-selected galaxies (Wyithe & Loeb 2007). This is a new strategy to economically map much larger volumes of the Universe, by measuring the collective 21 cm emission from all galaxies within some volume set by the angular resolution of the telescope and the frequency interval samples.
We predict the 21 cm intensity mapping signal using the Kim15 model. First, we divide the volume of the simulation into 2563 cells (0.39 Mpc h−1 cell size corresponds to ∼ 1 arcmin at z = 1, but the value is arbitrary). We then sum the mass of all H i in galaxies in each cell, and measure the resulting fluctuations of 21 cm intensity.
Fig. 8 shows the predicted 21 cm brightness temperature power spectrum predicted by the Kim15 model for four different H i mass thresholds. The amplitude of the 21 cm brightness temperature power spectrum decreases as the H i mass threshold increases, while the slope of the 21 cm power spectrum increases with increasing H i mass threshold. We find that the 21 cm intensity mapping power spectrum converges for |$M_{\rm H\,\small {I}}$| > 107 h−2 M⊙. We also show the ratio ΔP / P21cm, G6 in the sub-panel, where ΔP is the difference between a 21 cm power spectrum using the galaxies above a given H i mass threshold and the 21 cm power spectrum using all galaxies with |$M_{\rm H\,\small {I}}$| ≥ 106 h−2 M⊙ (P21cm, G6). Note that we choose the P21cm, G6 to compare with other H i mass thresholds because |$M_{\rm H\,\small {I}}$| ∼ 106 h−2 M⊙ is the minimum H i mass which can be trusted in the Kim15 model based on the Millennium-II simulation (which has a minimum halo mass of few times 108 h−1 M⊙).
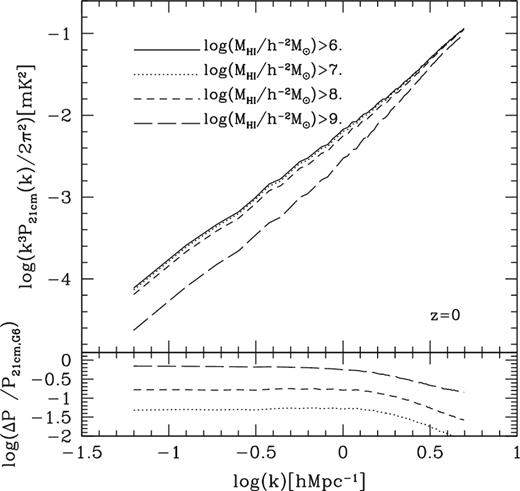
The predicted 21 cm brightness temperature power spectrum as a function of H i mass threshold, as labelled, at z = 0. We show the ΔP/P21cm, G6 ratio in the bottom panel. P21cm, G6 is the 21 cm power spectrum using all galaxies with |$M_{\rm H\,\small {I}}$| ≥ 106 h−2 M⊙, and ΔP is the difference between power spectra of larger mass threshold and P21cm, G6.
We extend the prediction of the 21 cm brightness temperature fluctuation to higher redshifts in Fig. 9. There are three main factors driving the evolution of the 21 cm brightness temperature power spectrum. The first is |$\Omega _{\rm H\,\small {I}}$|(z), which is the neutral hydrogen density. The second is the bias governed by the mass of host dark matter haloes hosting the H i-selected galaxies (r0 and γ). The third is H i mass contributions from each galaxy (i.e. H i masses) to H i mass intensity fluctuations. The predicted value of |$\Omega _{\rm H\,\small {I}}$|(z) at z = 1 is larger than at z = 0.5 and 0 (see fig. 9 in Kim et al. 2015). However, the clustering of host dark matter haloes hosting the H i-selected galaxies at z = 0 is stronger, particularly at small separations (compare Fig. 1 to Fig. 5 and see Fig. 7). Thus, these three main competing drivers lead to different amplitudes and slopes for the predicted 21 cm brightness temperature power spectra at different redshifts. The third driver results in the largest difference between the H i galaxy correlation function results and 21 cm intensity mapping power spectrum results.
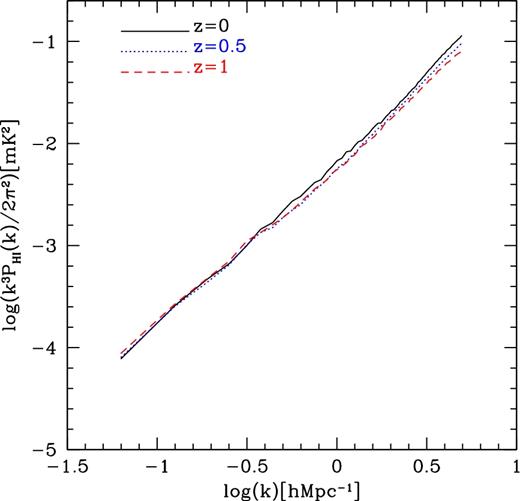
The predicted 21 cm brightness temperature power spectrum (P21cm, G6) for the Kim15 model at z = 0 (black solid line), 0.5 (blue dotted line) and 1 (red dashed line).
We now focus on the contribution of unresolved galaxies. Power et al. (2010) showed that in the Millennium simulation, galaxies with |$M_{\rm H\,\small {I}}$| < 108 h−2 M⊙ cannot be properly resolved (and so the completeness of the simulation drops below this H i mass). We explore the effect of unresolved galaxies on the 21 cm signals from intensity mapping (Fig. 10; see also Table 2). We first ignore H i masses in galaxies that reside in the dark matter haloes (both host and subhaloes) less massive than 1.72 × 1010 h−1 M⊙ in the Millennium-II simulation (corresponding to the dark matter halo mass resolution of the larger Millennium simulation). The difference in 21 cm brightness temperature fluctuations increases at higher redshifts (see long dashed lines in sub-panels of Fig. 10). This shows that low H i mass galaxies cannot be ignored if we aim to provide accurate predictions of the 21 cm brightness temperature fluctuations at higher redshifts.
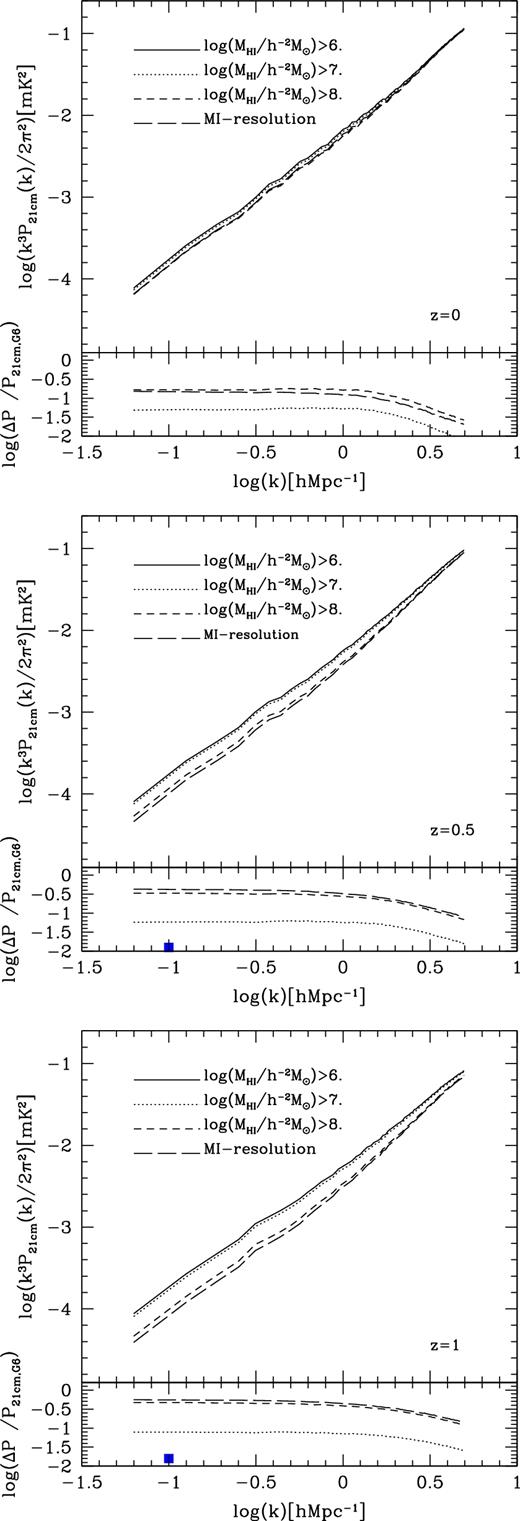
The predicted 21 cm brightness temperature power spectrum for the Kim15 model as a function of H i mass threshold at high redshifts, z = 0 (top panel), 0.5 (middle panel) and z = 1 (bottom panel). The long dashed line shows the measurement using the H i-selected galaxies in the host dark matter haloes which have the Millennium dark matter halo resolution imposed (labelled as MI-resolution). We show ΔP / P21cm, G6, the fluctuation between thresholds and P21cm, G6, in the sub-panels. The filled squares in the middle and bottom panels show the predicted constraint (noise over signal) at k ∼ 0.1 h Mpc−1 expected for the SKA1-MID (Santos et al. 2015).
The predicted dimensionless 21 cm brightness temperature Δ2(k,z)[mk2] = k3P21cm(k,z)/2/π2 at kp ∼ 0.126 h Mpc−1 of different H i mass thresholds and the Millennium simulation dark matter resolution case at z = 0, 0.5 and 1 in the model.
| H i mass threshold . | Δ2(kp,0) . | Δ2(kp,0.5) . | Δ2(kp,1) . |
|---|---|---|---|
| (or Millennium resolution) . | . | . | . |
| >106 h−2 M⊙ | 2.375e-4 | 2.5398e-4 | 2.674e-4 |
| >107 h−2 M⊙ | 2.283e-4 | 2.389e-4 | 2.463e-4 |
| >108 h−2 M⊙ | 2.056e-4 | 1.698e-4 | 1.422e-4 |
| Millennium resolution | 2.049e-4 | 1.479e-4 | 1.197e-4 |
| H i mass threshold . | Δ2(kp,0) . | Δ2(kp,0.5) . | Δ2(kp,1) . |
|---|---|---|---|
| (or Millennium resolution) . | . | . | . |
| >106 h−2 M⊙ | 2.375e-4 | 2.5398e-4 | 2.674e-4 |
| >107 h−2 M⊙ | 2.283e-4 | 2.389e-4 | 2.463e-4 |
| >108 h−2 M⊙ | 2.056e-4 | 1.698e-4 | 1.422e-4 |
| Millennium resolution | 2.049e-4 | 1.479e-4 | 1.197e-4 |
The predicted dimensionless 21 cm brightness temperature Δ2(k,z)[mk2] = k3P21cm(k,z)/2/π2 at kp ∼ 0.126 h Mpc−1 of different H i mass thresholds and the Millennium simulation dark matter resolution case at z = 0, 0.5 and 1 in the model.
| H i mass threshold . | Δ2(kp,0) . | Δ2(kp,0.5) . | Δ2(kp,1) . |
|---|---|---|---|
| (or Millennium resolution) . | . | . | . |
| >106 h−2 M⊙ | 2.375e-4 | 2.5398e-4 | 2.674e-4 |
| >107 h−2 M⊙ | 2.283e-4 | 2.389e-4 | 2.463e-4 |
| >108 h−2 M⊙ | 2.056e-4 | 1.698e-4 | 1.422e-4 |
| Millennium resolution | 2.049e-4 | 1.479e-4 | 1.197e-4 |
| H i mass threshold . | Δ2(kp,0) . | Δ2(kp,0.5) . | Δ2(kp,1) . |
|---|---|---|---|
| (or Millennium resolution) . | . | . | . |
| >106 h−2 M⊙ | 2.375e-4 | 2.5398e-4 | 2.674e-4 |
| >107 h−2 M⊙ | 2.283e-4 | 2.389e-4 | 2.463e-4 |
| >108 h−2 M⊙ | 2.056e-4 | 1.698e-4 | 1.422e-4 |
| Millennium resolution | 2.049e-4 | 1.479e-4 | 1.197e-4 |
The Green Bank Telescope has pioneered the detection of the large-scale structure using the technique of 21 cm intensity mapping Chang et al. (2010); Masui et al. (2013); Switzer et al. (2013). In the near future, more sensitive experiments will improve upon this work, including BINGO, CHIME and the SKA which will carry out 21 cm intensity mapping measurements at different redshifts. We show the predicted sensitivity of SKA in the second and third panels of Fig. 10 at k ∼ 0.1 h Mpc−1 based on calculations of Santos et al. (2015). This predicted sensitivity of the SKA is one of main drivers of the effort behind the modelling of the H i content of galaxies down to low H i mass galaxies (|$M_{\rm H\,\small {I}}$| < 107 h−2 M⊙) using a high enough resolution simulation with a physically motivated galaxy formation model to properly include these low H i mass galaxies.
6 SUMMARY
We have predicted the clustering of H i galaxy samples as a function of H i mass threshold. The clustering of H i-selected galaxies is very similar for H i-selected galaxies with masses greater than 108 h−2 M⊙. This similarity can be explained in terms of the contribution of host dark matter haloes to the H i mass function. We estimate power-law fits for the predicted correlation functions and derive the correlation length r0 and slope γ, as a function of redshift. We find that r0 and γ increase as the H i mass threshold decreases, which is the contrary to the expectations for optically selected galaxy samples. In addition, the predictions of clustering for different redshifts show that the correlation length and slope increase as redshift decreases from z = 0.5 to 0. We calculate the contribution of low H i mass galaxies to 21 cm intensity mapping (z = 0, ∼0.5 and ∼1). We find that it is important to model the H i mass function down to low H i masses of ∼107 h−2 M⊙ in order to correctly predict shape and amplitude of forthcoming observations of power spectra of 21 cm intensity fluctuations. We also show that the importance of low H i mass galaxies to the 21 cm brightness fluctuations increases at higher redshifts. Dark matter halo mass resolution in simulations must be sufficient (at least better than ∼1010 h−1 M⊙) in order to properly predict the 21 cm brightness temperature signal. With correct modelling of the distribution of H i-selected galaxies, 21 cm intensity mapping surveys will provide a window to understanding of the small mass galaxy formation physics.
Acknowledgments
We thank an anonymous referee for helpful comments on the manuscript. H-SK is supported by Discovery Early Career Researcher Awards from the Australian Research Council (DE140100940). CP thanks Simon Driver and Aaron Robotham for helpful discussions. CP is supported by DP130100117, DP140100198, and FT130100041. This work was supported by an STFC rolling grant at Durham. CL is funded by the ARC project DE150100618. CMB acknowledges receipt of a Research Fellowship from the Leverhulme Trust. The calculations for this paper were performed on the ICC Cosmology Machine, which is part of the DiRAC Facility jointly funded by the STFC, the Large Facilities Capital Fund of BIS, and Durham University. Part of the research presented in this paper was undertaken as part of the Survey Simulation Pipeline (SSimPL; http://www.astronomy.swin.edu.au/SSimPL/). The Centre for All-Sky Astrophysics is an Australian Research Council Centre of Excellence, funded by grant CE110001020.
Details at http://fast.bao.ac.cn/en/.
Details at http://www.astron.nl/jozsa/wnshs.
The cosmological parameters adopted for the Millennium simulations are total matter density ΩM = 0.25, baryon density Ωb = 0.045, dark energy density ΩΛ = 0.75, Hubble parameter H0 = 73 kms−1 Mpc−1, the primordial scalar spectral index ns = 1 and the fluctuation amplitude σ8 = 0.9.
The 1/Vmax method treats each individual galaxy by weighting the galaxy counts by the maximum volume Vmax, i. This strategy allows the inclusion of low-mass galaxies (only detected in the nearby Universe) in the same sample as rare high-mass galaxies (only found in larger volumes). In addition, the weights may be adjusted in order to correct for a variety of selection effects, large-scale structure effects and missing volume within the data set.
http://askap.org/wallaby; the Widefield ASKAP L−band Legacy All-sky Blind surveY.
http://internal.physics.uwa.edu.au/∼mmeyer/dingo/welcome.html; Deep Investigations of Neutral Gas Origins.
http://www.ast.uct.ac.za/laduma/node/6; Looking at the Distant Universe with the MeerKAT Array.




