-
PDF
- Split View
-
Views
-
Cite
Cite
S. Recchia, P. Blasi, G. Morlino, Cosmic ray driven Galactic winds, Monthly Notices of the Royal Astronomical Society, Volume 462, Issue 4, 11 November 2016, Pages 4227–4239, https://doi.org/10.1093/mnras/stw1966
Close - Share Icon Share
Abstract
The escape of cosmic rays from the Galaxy leads to a gradient in the cosmic ray pressure that acts as a force on the background plasma, in the direction opposite to the gravitational pull. If this force is large enough to win against gravity, a wind can be launched that removes gas from the Galaxy, thereby regulating several physical processes, including star formation. The dynamics of these cosmic ray driven winds is intrinsically non-linear in that the spectrum of cosmic rays determines the characteristics of the wind (velocity, pressure, magnetic field) and in turn the wind dynamics affects the cosmic ray spectrum. Moreover, the gradient of the cosmic ray distribution function causes excitation of Alfvén waves, that in turn determines the scattering properties of cosmic rays, namely their diffusive transport. These effects all feed into each other so that what we see at the Earth is the result of these non-linear effects. Here, we investigate the launch and evolution of such winds, and we determine the implications for the spectrum of cosmic rays by solving together the hydrodynamical equations for the wind and the transport equation for cosmic rays under the action of self-generated diffusion and advection with the wind and the self-excited Alfvén waves.
INTRODUCTION
The possibility of a galaxy to launch winds has attracted attention for many different reasons. For instance, star formation is regulated by the amount of gas available, and winds affect the availability of such gas. In fact, galactic models that do not include feedback processes suffer from overpredicting the amount of baryons and star formation rates (Crain et al. 2007; Stinson et al. 2013). Winds also pollute Galactic haloes with hot dilute plasma that may provide an important contribution to the number of baryons in the Universe (Kalberla et al. 1998; Kalberla & Dedes 2008; Miller & Bregman 2013). Such gas might in fact have already been detected (Snowden et al. 1995) in the form of an X-ray emitting plasma with temperature of several million degrees, and possibly associated with a Galactic wind by Breitschwerdt & Schmutzler (1994, 1999) (see also Everett et al. 2008). Finally winds can affect the transport of cosmic rays (CRs) in a galaxy, by advecting them away from their sources.
Galactic winds may be thermally driven, namely powered by core-collapse SNe (see e.g. Chevalier & Clegg 1985) or momentum-driven, powered by starburst radiation (Scoville 2003; Murray, Quataert & Thompson 2005). These two mechanisms of wind launching are thought to be at work in starburst galaxies and galaxies with active nuclei (see e.g. Veilleux, Cecil & Bland-Hawthorn 2005, for a comprehensive review). On the other hand in a galaxy like the Milky Way, winds are unlikely to be due to such processes because thermal and radiation pressure gradients are expected to be too small. A possible exception is the innermost part of the Galactic Centre region where the recently discovered Fermi Bubbles may have their origin through direct bursts from Sgr A* (Cheng et al. 2011; Zubovas, King & Nayakshin 2011) or because of past starburst activities (Lacki 2014). On the other hand, CRs can play an important role in launching winds because of the gradient that their pressure develops as a consequence of the gradual escape of CRs from the Galaxy. The force −∇PCR associated with such gradient is directed opposite to the gravitational force, and in certain conditions the plasma above and below the disc can be lifted off to form a CR-driven wind. Notice that the gravitational force may be dominated by the dark matter component or the baryonic (gas and stars) components depending on the location. The force exerted by CRs depends in a complicated manner not only on the density of sources of CRs but also on non-linear processes of excitation of Alfvén waves through streaming instability. Both the force induced by CRs on the background plasma and the streaming instability induced by CRs depend on the gradient in CR density. In turn the distribution function of CRs is affected by their transport: diffusion is self-regulated through the production of Alfvén waves, and advection is determined by the velocity of the wind, if any is launched, and by the Alfvén waves’ velocity, directed away from the sources of CRs. This complex interplay makes the problem non-linear and in fact the full problem of calculating at the same time the properties of the wind and the spectrum of CRs as a function of the location in the Galaxy has never been solved before. The first pioneering attempt to describe the hydrodynamics of a CR-driven wind was described in a paper by Ipavich (1975), where the author used a spherically symmetric model of the Galaxy and considered only baryons and stars for the calculation of the gravitational potential. Later Breitschwerdt, McKenzie & Voelk (1991) presented an extensive discussion of the hydrodynamics of CR-driven winds: dark matter was included and a realistic geometry of the wind was considered, in which the launch takes place at some distance from the Galactic disc and proceeds in a roughly cylindrical symmetry out to a distance of about ∼15 kpc, where the flow opens up into a spherical shape. Such a geometry became a milestone for future calculations of CR-driven winds and is adopted also in our paper, as discussed below. The calculations of Breitschwerdt et al. (1991) treated CRs as a fluid, hence no information on the spectrum of CRs was retained. The important role of wave damping in the wind region was also discussed by Breitschwerdt et al. (1991), although only in the simplified case of a spherical outflow. As mentioned above, Breitschwerdt et al. (1991) assumed that the wind is launched some distance away from the disc of the Galaxy and this assumption raises the issue of what happens in the region between the disc and the base of the wind, a problem of both mathematical and physical importance discussed by Breitschwerdt, McKenzie & Voelk (1993) and that will be central to our paper as well.
The paper by Breitschwerdt et al. (1991) represented a milestone in the investigation of CR-driven winds and their calculation was adopted in much of the future literature in the field, including the recent work by Everett et al. (2008) that used the model of a CR-driven wind (including damping) to explain the observed Galactic soft X-ray emission.
The dynamical role of CRs in launching the winds was also studied via purely hydrodynamical simulations (Uhlig et al. 2012; Booth et al. 2013; Salem & Bryan 2014) and through MHD simulations (Peters et al. 2015; Girichidis et al. 2016; Ruszkowski, Yang & Zweibel 2016). These simulations, with their progressive level of sophistication, demonstrated that CRs play an important role in wind launching. Nevertheless, all this bulk of work treated CRs as a fluid, thereby not providing any information on the CR spectrum.
The first calculation of the spectrum of CRs in a Galaxy with a CR-driven wind was made by Ptuskin et al. (1997), where the rotation of the Galaxy over cosmological time-scales was also taken into account Zirakashvili et al. (1996). The authors used a simplified approach to the characteristics of the wind (for instance the assumption that the advection velocity for small heights above the disc scales linearly with distance from the disc) to infer some general implications for the spectrum of CRs. To our knowledge, the paper by Ptuskin et al. (1997) represents the only attempt to account for both a CR-driven wind and its effects of the transport of CRs. Much work has been done in later years on treating the wind in a more realistic way, including the recent time-dependent approach to the wind evolution (Dorfi & Breitschwerdt 2012) and numerical simulations of the wind dynamics (Uhlig et al. 2012) and chemical evolution (Girichidis et al. 2016), but none of these efforts included the kinetic description of CRs.
In this paper we present the first semi-analytical calculation of the hydrodynamics of a CR-driven wind, including the self-generation of Alfvén waves through streaming instability and their damping through non-linear Landau damping (NLLD), and the calculation of the diffusive-convective transport of CRs in such wind. Throughout the paper, we assume that the general topology of the magnetic field lines is such that the transport of the wind and of CRs occurs along the field lines (parallel geometry).
At present, for the sake of simplicity, we decided to leave rotation out of this calculation, but its introduction is straightforward from the technical point of view. The spectrum of CRs at the position of the Earth is calculated for several cases of interest, so as to emphasize that several of the cases that are considered feasible from the point of view of hydrodynamics actually lead to spectra that are not consistent with observations. Special attention is devoted to the discussion of the role of the near disc region, where waves cannot be produced because of ion-neutral damping, and CR scattering, if any is present, is most likely guaranteed by some sort of turbulence directly injected by the same sources of CRs, for instance supernova explosions.
We find that the spectrum of CRs observed at the Earth in the low-energy regime (E ≲ 1 TeV) is mainly affected by the wind launching and evolution, because of the interplay between advection with the wind (and Alfvén waves) and self-generated diffusion. In general, at E ≲ 10 GeV advection is dominant, while a relatively steep spectrum is found at higher energies. For E ≳ 1 TeV the CR transport is dominated by what happens in the near-disc region. In general, this situation may lead to a spectral change in the TeV range, which under some conditions may resemble the hardening observed by PAMELA (Adriani et al. 2011) and AMS-02 (Aguilar et al. 2015), at least qualitatively.
The paper is organized as follows: in Section 2 we describe the basic formalism and the mathematical methods used to compute the structure of the wind in the presence of self-generated waves. The details of how to solve the hydrodynamical equations and the CR transport equation are provided in Sections 3 and 4, respectively. Our results are discussed in Section 5 for our reference model (Section 5.1) and for an alternative scenario devised to illustrate the importance of the near-disc region (Section 5.2). We draw our conclusions in Section 6.
A SEMI-ANALYTICAL APPROACH TO CR-DRIVEN WINDS
We introduced the Alfvén velocity |${\boldsymbol v}_{\rm A}(z)$|, while Φ(R0, z) is the gravitational potential of the Galaxy (see Section 2.1). The fact that the wave pressure does not appear in the equations reflects the assumption of fast damping, which results in small wave pressure compared to the gas and CR pressures.
In Sections 3 and 4 we will describe the method adopted to solve the hydrodynamical equations and the transport equation, respectively. Here we describe the way the two pieces are linked together in an iterative procedure. We initiate our computational procedure by solving the equation for the wind structure, by assuming that all quantities are known at the base of the wind, and by requiring that |$\overline{D}=0$|. This first step allows us to derive a guess for the launching velocity of the wind u0 and the wind properties (velocity, pressure of the gas, CRs and waves). At this point this guess is used as an input for the quantities entering the transport equation (17): most important, the wind velocity u(z) and the Alfvén speed |$v_{\rm A}(z)=B(z)/\sqrt{4\pi \rho (z)}$| are calculated from the output of the hydrodynamical part of the calculation. The solution of equation (17) leads to the spectrum of CRs as a function of location z and momentum p, f(z, p), and to knowing the diffusion coefficient D(z, p) as due to self-generated Alfvén waves. Notice that in general the CR pressure obtained by integrating the distribution function f(z, p) (and especially the CR pressure at the base of the wind) is different from the one assumed in order to determine the wind structure. This leads to the second iteration: the updated CR pressure at the base is used to compute the structure of the wind and the whole calculation is repeated. Moreover, the diffusion coefficient and the distribution function are used to compute γ(z) and |$\overline{D}$|. Notice that the latter quantity is no longer bound to vanish, as assumed in previous calculations by Breitschwerdt et al. (1991). This iterative scheme continues until the spectrum of CRs reaches convergence at all distances and at all momenta. As a consequence the CR pressure at the base converges to the actual solution, so it does the whole structure of the CR induced wind. Clearly, if the goal is to apply this calculation to the case of our own Galaxy at the location of the Sun, R⊙, then the CR injection is modified so as to reach a solution where the CR pressure is the same as observed. It is very important to stress that this condition alone is not sufficient to guarantee that the CR spectrum observed at the Earth is also consistent with observations: in fact, a generic wind solution leads to spectra of CRs at the Earth location that are quite different from the observed ones, mainly as a result of the strong advection with the wind, which corresponds to exceedingly hard spectra at low energy. We will discuss the qualitative comparison between the wind solutions and the observed CR spectra in Section 5.
Since the properties of the wind depend in a rather sensible way upon the properties of the gravitational potential, in Section 2.1 we describe in detail our assumptions on the contribution of disc and bulge content and dark matter to the gravitational potential.
Galactic gravitational potential
IDENTIFICATION OF THE WIND SOLUTION
Here we discuss the procedure adopted for the determination of the wind solution for a given set of conditions at the base of the wind. We recall that, as discussed above, this calculation is embedded in an iterative computation that is repeated until convergence of the overall structure of the wind and of the CR spectrum is achieved.
We look for a wind solution of equations (10)–(16), namely a solution for the flow velocity u(z) that shows a transition from subsonic (u < c*) to supersonic (u > c*) motion, where c*(z) is the compound sound speed as a function of z.
The topology of the solutions (see also Breitschwerdt et al. 1991) of equation (10)–(16) depends on the nature of the critical points of the wind equation (12), namely the points in which the velocity derivative has zero numerator |$(c_{{\ast }}^2= \frac{{\rm d}\Phi }{{\rm d}z}/\frac{1}{A} \frac{{\rm d}A}{{\rm d}z})$| and/or zero denominator (|$u^2=c_{{\ast }}^2$|), and is schematically represented in Fig. 3. The point for which both numerator and denominator are zero is the critical (sonic) point and it corresponds to the location where the flow velocity equals the compound sound speed, u = c*. As shown in Fig. 3, there are two curves passing through the critical point. The one corresponding to a subsonic flow at z0 is the one relevant for our problem. The other one corresponds to an accretion (infall) solution. The curves in the lower branch of solutions shown in Fig. 3 correspond to flows that remain subsonic, the so-called ‘breezes’. The upper branch corresponds to supersonic flow and is physically irrelevant. For both families of curves, there is a point where the numerator of equation (12) vanishes. The other two branches are unphysical and for both there is a point where the denominator of equation (12) vanishes.
For given values of the magnetic field B0, gas density ρ0, gas pressure Pg0 and CR pressure Pc0 at z = z0, we compute the velocity at the base of the wind u0 that corresponds to the wind solution, namely the value of u0 for which the flow starts as subsonic and then smoothly becomes supersonic at the critical point zc (see Fig. 3). Both the location of the sonic point and the launching velocity u0 are outputs of the calculation. For each iteration, Pc0 and |$\mathcal {D}(z)$| in equation (16) are computed based on the solution of the transport equation in the previous iteration.
From the technical point of view, we start the search for the wind solution by bracketing the range of values of u0 that may potentially correspond to a wind solution. In order to do so, we impose three conditions: (1) the flow starts as subsonic (c*0 > u0); (2) u(z) is a growing function of z at z0, namely |$\frac{{\rm d}u}{{\rm d}z}\vert _{z_0} >0$|; (3) the solution leads to a final wind velocity at infinity that is physical, namely |$u_{f}^{2}>0$|.
This last point corresponds to imposing energy conservation between z = z0 and infinity and requiring that at z = ∞ all fluxes vanish with the exception of the kinetic flux associated with the wind bulk motion. This condition selects the solutions that correspond to |$u_{f}^{2}>0$|.
Once a closed interval for u0, say |$[u_{0,\rm min}, u_{0,\rm max}]$|, has been determined, we numerically integrate the hydrodynamic equations starting at z0 and for values of u0 in this range, stepped by Δu0. In this way we sample the topology of the solutions and can identify the transition between the last breeze and the first unphysical solution by gradually increasing the value of u0. This procedure can be repeated to narrow down the region where the actual wind solution is located (see Fig. 4).
KINETIC CALCULATION
This rewriting of the transport equations hides the non-linearity of the problem in the function G(z, p), which depends on f(z, p) and on the CR diffusion coefficient D(z, p) (see equation 18). The solution of equation (40) is computed with an iterative procedure.
The procedure reaches convergence when, for a given iteration j, f j(z, p) and f j − 1(z, p) are close to each other within a desired precision. Note that the advection velocity U(z) is computed from the hydrodynamic equations and is fixed while iterating upon the distribution function f j.
RESULTS
In this section we illustrate some selected cases of CR induced winds, aimed at addressing different issues that arise in this type of problem. The first case is what we will refer to as our reference case, namely a case that illustrates the most basic characteristics of a CR-induced wind, with a minimal number of physical parameters introduced. The wind is launched very close to the disc of the Galaxy, and we consider the specific situation expected at the solar radius, namely at the Galactocentric distance R = R⊙ = 8.5 kpc, where the Sun is located. This information is crucial in that it determines the gravitational potential that the wind has to fight against. The second model considered below is that in which a wind is launched at some distance from the Galactic disc, while particle transport in the near-disc region is assigned. This latter situation is physically motivated by the fact that ion-neutral damping is expected to damp self-generated Alfvénic turbulence within ∼ 0.5–1 kpc from the disc, because of the presence of a substantial amount of neutral hydrogen. We will show that the consequences of this setup for the spectrum of CRs observed at the Earth are very prominent.
Reference case

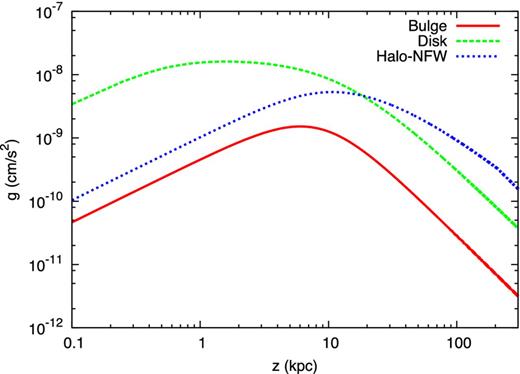
Gravitational acceleration as due to the three components: the bulge, the disc and the dark matter halo. All curves are computed at the Sun's position (R⊙ = 8.5 kpc).
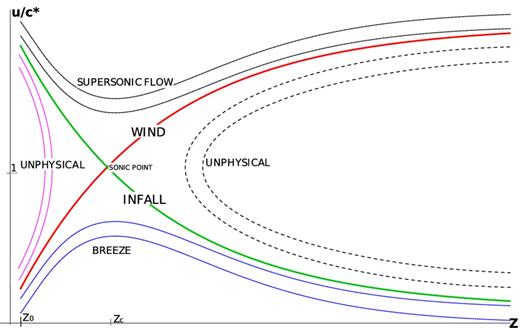
Topology of the solutions of the hydrodynamics equations: z0 indicates the base of the wind, while zc is the critical point, where u(zc) = c*(zc). The (red) solid line represents a wind solution that starts as subsonic and becomes supersonic at the critical point. The branches of the solutions that are unphysical are labelled as such.
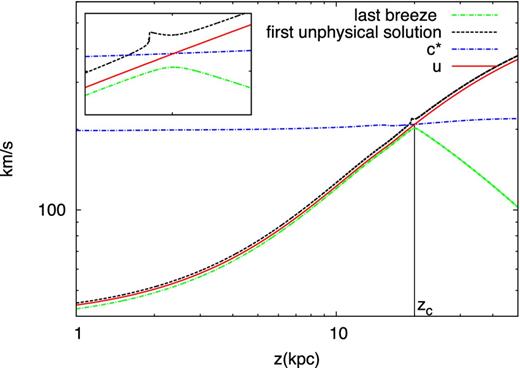
Schematic picture of the solution method for the hydrodynamic equations: the wind curve lies between a breeze, obtained by integrating with u0 = u0B, and an unphysical solution, obtained by integrating with u0 = u0U, where u0B < u0U. The location of the sonic point zc can be estimated as the location of the maximum of the breeze. The small box shows a zoomed region around the sonic point.
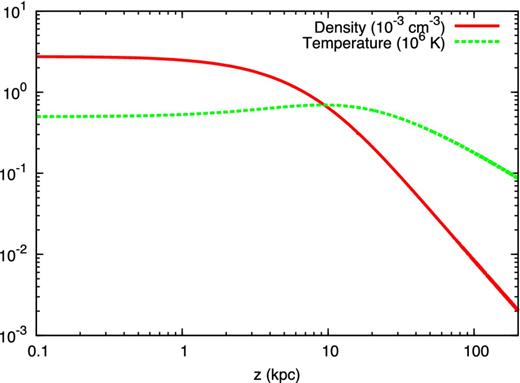
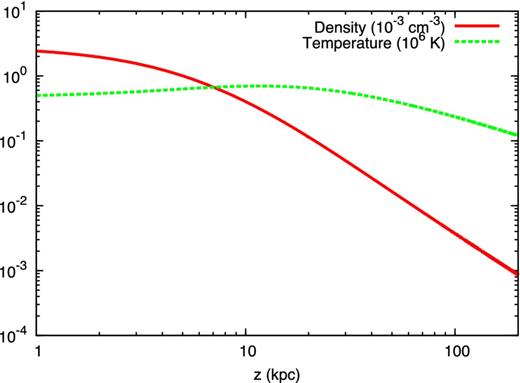
Density (red solid line) in units of 10− 3 cm− 3 and temperature (greed dashed line) in units of 106 K for the wind solution in the reference case.
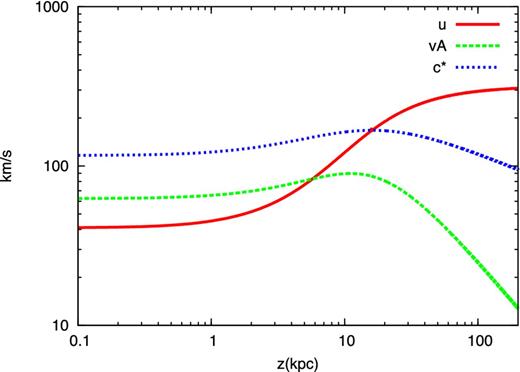
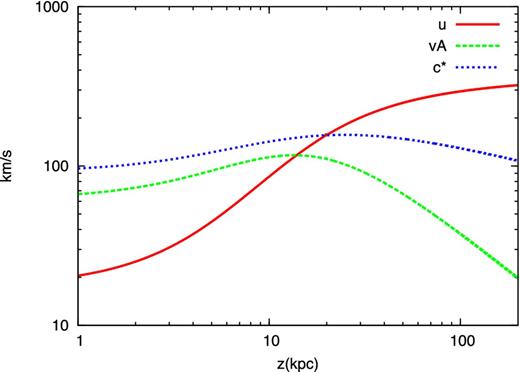
Wind velocity (red solid line), Alfvén velocity (green dashed line) and sound speed (blue dotted line) as a function of the height z above the disc, for the reference case.
For the sake of future discussion it is important to notice here that the CR advection velocity at the base of the wind is dominated by the Alfvén speed and that the latter is non-zero at the base of the wind (because of a finite density and magnetic field).
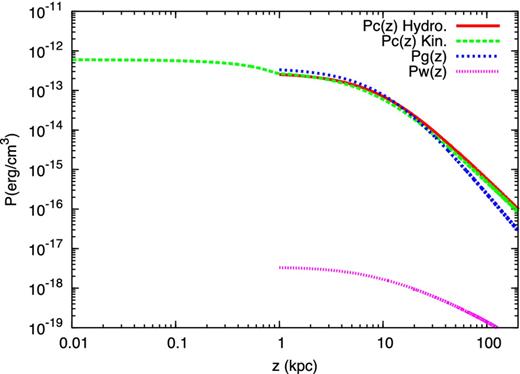
The pressure of CRs as a function of the distance z from the disc is shown in Fig. 7, together with the gas pressure and the CR pressure as derived from the kinetic calculation: the fact that the latter is basically overlapped to Pc(z) as derived from hydrodynamics shows that the system of equations (hydro plus kinetic) reached convergence (with accuracy of ∼0.1 per cent at heights z close to the base of the wind and ∼10–20 per cent at z close to the outer edge of the box used for numerical computation; here all quantities, with the exception of the wind velocity, are bound to vanish).
The gas temperature obtained for z ≲ 10 kpc (see Fig. 5) suggests that cooling may be important. At such temperature the gas is cooled by the emission of forbidden lines and soft X-rays (Dalgarno & McCray 1972) but, on the other hand, it is also heated by SN explosions through the injection of hot gas and magnetic turbulence that will eventually decay into thermal energy. Recently, it was suggested that also Coulomb losses of CRs themselves might be a substantial source of heating (Walker 2016). The relevance of cooling was already recognized by Breitschwerdt et al. (1991) which, nevertheless, assumed that energy balance exists between heating and cooling processes. Which process dominates the heating is at the moment unclear but observations reveal that the temperature in the halo reaches ∼105–106 K (see e.g. Miller & Bregman 2013), hence supporting the idea that either the cooling is negligible or it is balanced by heating processes. In this paper we decided to neglect the role of cooling, deferring a more complete study to a future work.

CR pressure (red solid line) and gas pressure (blue dotted line) in the reference case. The green dashed line shows the CR pressure as obtained from the solution of the transport equation. The same calculation also returns the wave pressure Pw(z) (pink dotted line) that is assumed to vanish in the hydrodynamical equation.
The spectrum of CRs as a function of particle momentum is reported in Fig. 8 for several distances from the Galactic plane. The most striking feature of the spectrum at the disc is the pronounced spectral hardness: the spectrum that should be measured at the Earth location at momenta below ∼1 TeV/c is roughly ∝ p−4.4, only slightly steeper than the injection spectrum (Q(p) ∝ p−4.3). This finding reflects the fact that the Alfvén speed at the base of the wind is very large and dominates CR advection up to high energies. One could argue that a larger value of the density at the base of the wind would make the Alfvén speed smaller, but in that case two problems appear: (1) it may become harder if not impossible to launch the wind because of excessive baryonic load. In other words, for a given CR pressure at the base, there may be cases in which the wind is not launched. (2) When the wind is in fact launched, its initial velocity may easily be super-Alfvénic, so that again advection dominates up to relatively high energies.
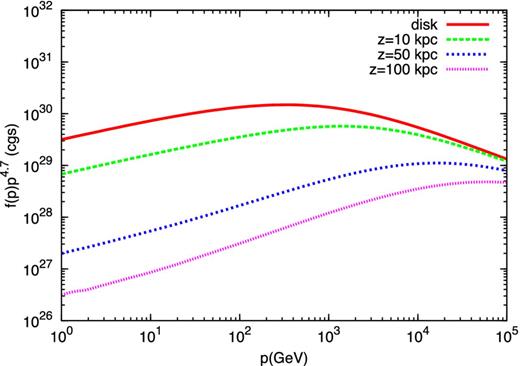
CR spectrum, f(p) × p4.7, in the reference case, at different locations in the wind: base of the wind (red solid line), z = 10 kpc (green dashed line), z = 50 kpc (blue short-dashed line) and z = 100 kpc (pink dotted line).
The problem with this argument, put forward by Ptuskin et al. (1997), is that it is strictly valid only when the advection velocity vanishes while approaching the base of the wind. One can see from equation (35) that the assumption that diffusion is the dominant process at z → 0 holds true only if U0 = 0. The solution of the combined hydrodynamical equations and transport equation of CRs as presented above clearly shows that this is not the case. At low energies the slope of the CR spectrum at the base of the disc, as shown in Fig. 8, is ∼4.3 (see also Fig. 14, lower panel), basically the same as the injection spectrum. The same point can be also made by plotting s*(p) (Fig. 9) and the diffusion coefficient D(p) (Fig. 10): the simple scaling s*(p)∝D(p)1/2 can be easily seen to be not satisfied by the actual solution of the problem. Notice that s*(p) becomes larger than Zs, the location where there is a transition to a spherical-like flow, at p ∼ 1 TeV/c. At energies much larger than this one can assume that the advection velocity tends to a constant, uf. The equilibrium spectrum observed at the Earth can then be written as |$f_{0}(p)\sim Q_{0}(p)\pi R_{\rm d}^{2}/(u_{f} s_{{\ast }}^{2})$|, while s*∝D(p), so that the equilibrium spectrum has a slope −3γ + 7. This effect corresponds to a steepening of the equilibrium spectrum at the transition energy, which for the values of the parameters used in Fig. 8 corresponds to about ∼1 TeV.
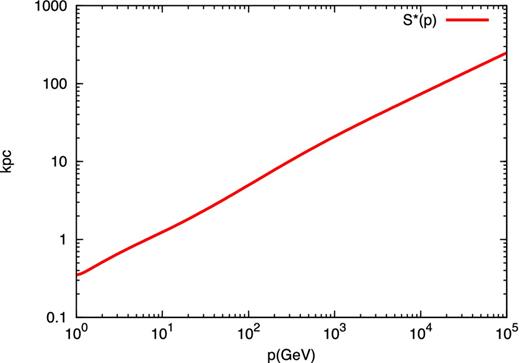
Effective boundary, s*(p), between the diffusion-dominated and the advection-dominated region of the wind in the reference case.
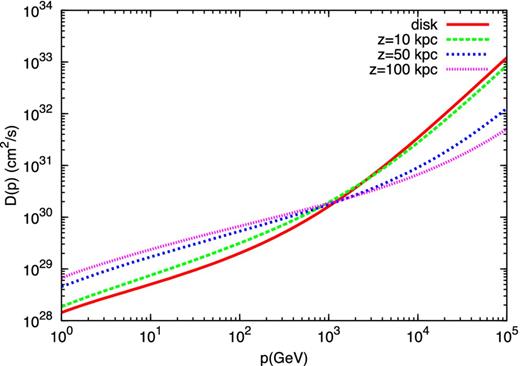
Self-generated diffusion coefficient, D(p), in the reference case at different locations in the wind: base of the wind (red solid line), z = 10 kpc (green dashed line), z = 50 kpc (blue short-dashed line) and z = 100 kpc (pink dotted line). The transition from the cylindrical to the spherical geometry of the wind flow is clearly visible in the momentum dependence of D(p).
Even qualitatively one can see that the CR spectrum in Fig. 8 is quite different from the one actually observed at the Earth: it is harder than observed at low energies, and it is softer than observed at high energies, even though the pressure carried by these CRs is as observed.
This example clearly shows that it is possible to construct solutions of the hydrodynamical equations that correspond to CR-driven winds, with pressures at the base of the wind that are compatible with observations and yet leading to CR spectra that are not compatible with the CR spectra observed at the Earth. In particular, the basic wind model discussed in this section does not lead to any hardening of the spectrum at high energy, hence it is not possible to fit spectral hardening such as the ones observed by PAMELA (Adriani et al. 2011) and AMS-02 (Aguilar et al. 2015). In Section 5.2, we discuss a situation in which this conclusion may not apply.
The importance of the near-disc region
As already pointed out in the original work on CR-driven winds Breitschwerdt et al. (1991) the region close to the disc may be plagued by severe ion-neutral damping which suppresses the generation of Alfvén waves Kulsrud & Cesarsky (1971). Since waves provide the coupling between CRs and the ionized plasma, their severe damping leads to quenching of the wind. In fact, ion-neutral damping was recognized as a hindering factor for diffusion even in the absence of winds Skilling (1971); Holmes (1975): in these pioneering papers, the near disc region was assumed to be wave-free and the propagation of CRs in that region was taken to be ballistic. Diffusion in the outer halo, where the density of neutral hydrogen is expected to drop and the role of ion-neutral damping to become negligible, was considered as the actual diffusion region. One could, however, speculate that some type of turbulence may be maintained in the near-disc region, perhaps due to SN explosions themselves, though the waves may be considered to be isotropic, so that the effective Alfvén speed vanishes.
The density and temperature of the wind, limited to the region z ≥ z0 = 1 kpc where the wind can be launched, are plotted in Fig. 11. The corresponding wind velocity, Alfvén speed and sound speed in the wind region are plotted in Fig. 12: the advection velocity is again dominated by the Alfvén velocity at the base of the wind. The wind becomes supersonic at zc ∼ 20 kpc, and eventually reaches uf ∼ 400 km/s at large distances from the disc. The pressures of the gas and CRs are shown in Fig. 13, where the gas pressure is limited to the wind region while the CR pressure extends to the whole diffusion region. We also plotted there the CR pressure that is returned by the kinetic calculation to show that with good accuracy it coincides with the one derived from the hydrodynamical calculation. The wave pressure as derived from the kinetic calculation is also shown: the plateau at z < z0 has been estimated from the assigned diffusion coefficient. The fact that Pw(z) is always much smaller than all other terms justifies the assumption of instantaneous damping (Pw = 0) in the hydrodynamical computation.
Density (red solid line) in units of 10− 3 cm− 3 and temperature (greed dashed line) in units of 106 K limited to the region where the wind is launched, z ≥ z0 = 1 kpc.
Wind velocity (red solid line), Alfvén velocity (green dashed line) and sound speed (blue dotted line) as a function of the height z above the disc, limited to the region where the wind is launched, z ≥ z0 = 1 kpc.
CR pressure and gas pressure in the case of Kolmogorov turbulence in the near-disc region. The green dashed line shows the CR pressure as obtained from the solution of the transport equation. The same calculation also returns the wave pressure Pw(z) that is assumed to vanish in the hydrodynamical equation.
Using the approach described in Sections 2, 3 and 4, we also calculated the spectrum of Galactic CRs: in the upper panel of Fig. 14 we show the CR distribution in the Galactic disc for the reference case compared to the case where the wind is launched at a finite distance z0 from the disc. One can immediately see the dramatic difference that the near-disc region makes in terms of CR spectrum observed at the Earth (or, for that matter, anywhere). In the second case there are at least two spectral breaks that can be identified and explained in a reasonably easy way: the low-energy part of the spectrum is affected by advection (below ∼10 GeV) as well as from self-generation of waves at z ≥ z0 (at 10 GeV ≲ E ≲ 1000 GeV). At energies higher than ∼1 TeV the spectrum hardens. All these changes of slope are illustrated more clearly in the lower panel of Fig. 14, where we show the slope of the CR distribution in the disc for the reference case (red solid line) and for the case with a wind launched at a finite distance z0 from the disc (green dashed line).
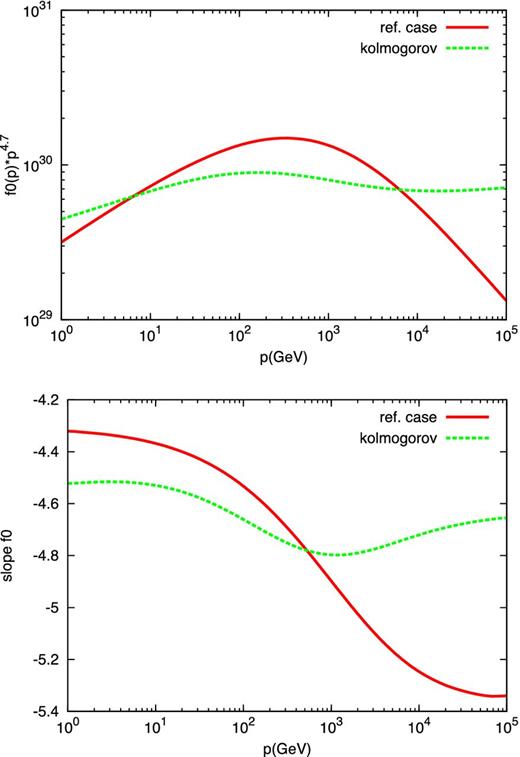
Upper panel: spectrum of CRs in the disc of the Galaxy at the position of the Sun for the reference case (red solid line) and for the case in which the wind is launched at z0 = 1 kpc from the disc and there is a near-disc region where the diffusion coefficient is assigned and advection is absent (green dashed line). The lower panel shows the corresponding slopes.
The hard spectrum (slope ∼4.5 below ∼10 GeV reflects advection and is similar to the effect already seen in non-linear models of galactic CR propagation (Aloisio, Blasi & Serpico 2015, see for instance). On the other hand, the spectrum has a continuous steepening at higher energies up to ≲1 TeV: this effects is also similar to the one claimed by Aloisio et al. (2015) and reflects the very rapid energy dependence of the self-generated diffusion coefficient. Finally, the slope of the spectrum becomes ∼4.63 at E ≳ 1 TeV, because of the assumption of Kolmogorov turbulence in the near disc region (z ≤ z0). This hardening is qualitatively similar to the one found by Tomassetti (2012) in a simple two-zone model of the Galactic halo: the low-energy part is sensitive to the far zone, while the high-energy part is sensitive to the near zone, where the assumption of Kolmogorov turbulence leads to an expected slope 4.3(injection) + 1/3(Kolmogorov) ≃ 4.63. The important point we wish to make here is that the diffusion coefficient that determines the low-energy behaviour of the bulk of CRs is not assumed here, but rather derived from the condition of self-generation of waves and advection with the CR-induced Galactic wind, as calculated above.
Although here we did not make any attempt to fit our curves to real data, it is interesting to notice that qualitatively the scenario presented in this section (contrary to the reference model in Section 5.1) has the same feature as the spectrum of CR protons as recently measured by PAMELA (Adriani et al. 2011) and AMS-02 (Aguilar et al. 2015).
CONCLUSIONS
We presented a semi-analytical calculation of the structure of a CR-driven Galactic wind that returns the hydrodynamical structure of the wind (velocity and pressure of the plasma), and at the same time the spectrum of CRs at any location in the disc or in the wind region. The transport of CRs is described as advective and diffusive: advection occurs at a local speed that is the sum of the Alfvén speed and the wind speed at that point. Diffusion is due to scattering off self-generated turbulence, as generated by the same CRs due to streaming instability. The non-linear nature of the problem is manifold: the wind is driven by the CR gradient in the z direction, perpendicular to the Galactic disc, which results from the gradual escape of CRs from the Galaxy. The force −∇PCR acts in the direction opposite to gravity, so that, under certain conditions, it can lift ionized gas and launch a wind. On the other hand, the amount of waves generated by CRs depends on their transport, which in turn depends on the wind speed. The diffusion coefficient is calculated in a self-consistent manner from the local spectrum of waves excited by streaming instability and damped through NLLD.
Qualitatively, we confirm earlier findings that CRs can drive winds with asymptotic velocities of the order of several hundred km s−1. Contrary to previous calculations, we also derived the spectrum of CRs as observed at the Earth (or any other location): for most of the parameter space for which a CR-driven wind is launched, the spectrum is in disagreement with observations: the main reason for such a finding is that the CR advection with the wind is very strong and leads to hard spectra that are unlike the one observed at the Earth. However, this conclusion is found to depend in a critical way on the conditions in the near-disc region (z ≲ 1 kpc). The conditions in such region affect the high-energy behaviour of the spectrum, and change the launching speed of the wind at z ∼ z0 ∼ 1 kpc, so that the low-energy region of the spectrum is also changed. For certain assumptions on the diffusion coefficient in the near-disc region, the predicted CR spectrum may resemble the observed one: as an instance we showed one case in which the spectrum is relatively hard at E ≲ 10 GeV (as previously found by Aloisio et al. 2015), steeper for 10 ≲ E ≲ 1000 GeV, and show a hardening at higher energies as recently claimed by Adriani et al. (2011) and Aguilar et al. (2015). From the physical point of view, we expect that the region at z ≲ 1 kpc is rich in neutral gas, which may damp Alfvén waves through ion-neutral damping. This implies that the coupling between CRs and gas may be exceedingly weak in this region so as to inhibit the launch of the wind. In the near-disc region, diffusion, if any is present, should be guaranteed by some source other than CR self-generation.
The calculation presented here is very general and can be applied to a variety of conditions. This will allow us to explore the conditions in which a CR-driven wind could develop with a CR spectrum at the Earth resembling the observed one. This type of calculations is also useful to develop possible diagnostics of the existence of CR-driven winds in our own Galaxy as well as in others.
The authors are glad to acknowledge a continuous ongoing collaboration with the rest of the Arcetri high-energy Group. This work was partially funded through Grant PRIN-INAF 2012.
REFERENCES
APPENDIX A: DERIVATION OF THE HYDRODYNAMIC EQUATIONS
In this section we derive the hydrodynamic equations used throughout this paper. They describe the macroscopic behaviour of the thermal plasma and CRs and their mutual interactions. As we already pointed out in Section 2, the wave component is not present in these equations because we are assuming that all Alfvén waves (generated through CR streaming instability) are locally dumped on short time-scales, so that the energy fed by CRs into waves just results in the heating of the gas. Here, we are also neglecting any external loss of mass, momentum and energy. A general form of those equations, with and without damping of waves, is reported in Breitschwerdt et al. (1991).



