-
PDF
- Split View
-
Views
-
Cite
Cite
Tilman Hartwig, Muhammad A. Latif, Mattis Magg, Volker Bromm, Ralf S. Klessen, Simon C. O. Glover, Daniel J. Whalen, Eric W. Pellegrini, Marta Volonteri, Exploring the nature of the Lyman-α emitter CR7, Monthly Notices of the Royal Astronomical Society, Volume 462, Issue 2, 21 October 2016, Pages 2184–2202, https://doi.org/10.1093/mnras/stw1775
Close - Share Icon Share
Abstract
CR7 is the brightest Lyman-α emitter observed at z > 6, which shows very strong Lyman-α and He ii 1640 Å line luminosities, but no metal-line emission. Previous studies suggest that CR7 hosts either young primordial stars with a total stellar mass of ∼107 M⊙ or a black hole of ≳106 M⊙. Here, we explore different formation scenarios for CR7 with a semi-analytical model, based on the random sampling of dark matter merger trees. We are unable to reproduce the observational constraints with a primordial stellar source, given our model assumptions, due to the short stellar lifetimes and the early metal enrichment. Black holes that are the remnants of the first stars are either not massive enough, or reside in metal-polluted haloes, ruling out this possible explanation of CR7. Our models instead suggest that direct collapse black holes, which form in metal-free haloes exposed to large Lyman–Werner fluxes, are more likely the origin of CR7. However, this result is derived under optimistic assumptions and future observations are necessary to further constrain the nature of CR7.
1 INTRODUCTION
The first sources of light ushered the Universe out of the cosmic dark ages, thus initiating the long history of star and galaxy formation. In the Lambda cold dark matter (ΛCDM) paradigm of hierarchical structure formation, the first generation of stars, or Population III (Pop III) stars, were assembled in dark matter minihaloes of a few times 105 M⊙. They later merged to form more massive haloes of ≳107 M⊙, which could be the birthplaces of the first galaxies (Bromm & Yoshida 2011). Understanding the formation of the first galaxies is of paramount importance because they constitute the basic building blocks of present-day galaxies.
The first stars influenced subsequent structure formation by chemical, radiative and mechanical feedback. They enriched the Universe with metals, led to the formation of second-generation Population II (Pop II) stars, and produced energetic photons that contributed to the reionization of the Universe. Various theoretical studies suggest that Pop III stars were more massive than Pop II stars because of the absence of efficient coolants in the pristine gas [see the recent reviews by (Bromm 2013), (Glover 2013) and (Greif 2015)]. Strong nebular emission lines, such as Lyman-α (Ly α) and those of He ii, are expected to be present in the gas ionized by Pop III stars (Tumlinson & Shull 2000; Bromm, Kudritzki & Loeb 2001b; Oh, Haiman & Rees 2001; Schaerer 2002, 2003). The prime targets to detect these nebular emission lines are the first galaxies, which are expected to host both Pop III and Pop II stars.
Large ground based telescopes and the Hubble Space Telescope (HST) have opened a new window on high redshifts. Ly α has emerged as a powerful probe to detect distant galaxies at z > 5. The search for high-redshift galaxies has intensified over the past few years and candidate galaxies have now been detected between z = 8 and 11 (Bouwens et al. 2011; Ellis et al. 2013; McLeod et al. 2015; McLeod, McLure & Dunlop 2016). Numerous galaxies have been detected at z > 6 using both the strong Ly α emission and the Lyman break techniques (Ouchi et al. 2008, 2009, 2010; Vanzella et al. 2011; Ono et al. 2012; Finkelstein et al. 2013; Pentericci et al. 2014; Matthee et al. 2015; Oesch et al. 2015). Recently, Oesch et al. (2016) even claim the observation of a galaxy at z = 11.1. Although such galaxies have been detected at these redshifts, the presence of Pop III stars has not been observationally confirmed in any system. On the other hand, detections of high-redshift quasars reveal the existence of supermassive black holes (SMBHs) of a few billion solar masses at z > 6 (Fan et al. 2006; Mortlock et al. 2011; Venemans 2015; Wu et al. 2015). Various models have been proposed to explain the formation of SMBHs which include the growth of stellar-mass black holes (BHs) as well as so-called ‘direct collapse’ black holes (DCBHs) (Loeb & Rasio 1994; Bromm & Loeb 2003; Alvarez, Wise & Abel 2009; Volonteri 2010; Haiman 2013; Latif et al. 2013a, 2015). Direct observational constraints on both seed BH masses and the Pop III initial mass function (IMF) are necessary to understand the formation of the first galaxies and high-redshift quasars.
The recent discovery of strong He ii line emission from the Ly α emitter CR7 (COSMOS redshift 7) at z = 6.6 by Sobral et al. (2015) may constitute the first detection of either a Pop III star cluster or an accreting seed BH. It is the most luminous Ly αemitter at z > 6 and has very strong Ly α and He ii 1640 Å emission lines but no metal lines in the rest-frame UV. Sobral et al. (2015) suggest that CR7 can be explained by the composite spectra of normal metal-enriched stars and primordial stars. Deep HST imaging shows that CR7 is composed of three clumps, A, B, and C. The spectral energy distributions (SEDs) of clumps B and C are best fitted by an evolved stellar population while clump A has strong Ly α and He ii 1640 Å lines and can be explained either by a young primordial stellar population or an accreting BH. Sobral et al. (2015) find that Pop III stars with an age of a few Myr and a total stellar mass of ∼107 M⊙ with a top-heavy IMF are required to explain such strong emission lines and Visbal, Haiman & Bryan (2016) demonstrate how photoionization feedback can promote the formation of metal-free galaxies at lower redshift. The required stellar mass in Pop III stars is degenerate with the uncertain IMF and the required stellar mass might even be higher. The possibility that CR7 hosts a BH has also been discussed in Sobral et al. (2015).
Pallottini et al. (2015) have proposed that the strong Ly α and He ii 1640 Å line emission in CR7 can be explained by either a <2 Myr old Pop III stellar cluster of ∼107 M⊙ with a top-heavy IMF or an ∼105 M⊙ BH formed at z = 7.3. Agarwal et al. (2016a), Dijkstra, Gronke & Sobral (2016), and Smidt, Wiggins & Johnson (2016) have also shown that the observations can be explained by an ∼106–107 M⊙ BH in the progenitor haloes of CR7. But neither of their studies have shown how such a large reservoir of metal-free gas can exist at z = 6.6 in clump A, which is required both for the formation of a young metal-free Pop III stellar cluster or a DCBH (although see Fumagalli, O'Meara & Prochaska 2011). More observations are required to find how common are sources like CR7 at such redshifts and under what conditions can they form. In addition to these further observations, a self-consistent model, which takes into account both in situ star formation and metal enrichment, is required to better understand the assembly history and nature of CR7.
In this paper, we use a semi-analytical model to examine the nature of CR7 and its assembly history. The model includes recipes for Pop III and Pop II star formation as well as a self-consistent treatment of metal enrichment. We consider a range of halo masses, star formation efficiencies and IMFs with a sufficient number of realizations to obtain statistically sound results. We investigate the possibility of a massive BH forming from either a Pop III remnant or a DCBH. The results suggest that our model of Pop III star formation, with Pop III stars being less massive than 300 M⊙, cannot reproduce the observed Ly α and He ii line luminosities and that a DCBH likely powers CR7. In Section 2, we review the observational constraints on CR7. We present our model in Section 3 and our results in Section 4. We discuss the caveats of our approach in Section 5 and conclude in Section 6.
2 OBSERVATIONAL CONSTRAINTS
CR7, the brightest Ly α emitter at z > 6, was first classified as an unreliable high-redshift candidate (Bowler et al. 2012) and as a brown dwarf candidate in the Milky Way (Ilbert et al. 2013). It was then found as a Ly α emitter candidate at z = 6.6 by Matthee et al. (2015) and spectroscopically confirmed by Sobral et al. (2015). This spectroscopic follow-up revealed strong Ly α and He ii 1640 Å lines with luminosities of LLy α = (8.5 ± 1.0) × 1043 erg s−1 and LHeII = (2.0 ± 0.8) × 1043erg s−1. These observed luminosities imply a line ratio of He ii/Ly α ≈ 0.23 or a ratio of Q(He+)/Q(H) ≈ 0.42 for ionizing photon emission rates. This line ratio corresponds to a very hard spectrum with an effective temperature of Teff > 105 K, and even Pop III stars with a mass of 1000 M⊙ only have Q(He+)/Q(H) ≈ 0.1 (Schaerer 2002).
One possible explanation for this extreme ratio is that a fraction of the Ly α photons was not observed due to trapping in the intergalactic medium (IGM) or dust absorption (Dijkstra, Haiman & Spaans 2006; Dijkstra, Lidz & Wyithe 2007; Dijkstra & Wyithe 2010; Zheng et al. 2010; Latif et al. 2011b; Latif, Zaroubi & Spaans 2011a; Smith et al. 2015a; Matthee et al. 2016; Smith, Bromm & Loeb 2016). By post-processing cosmological hydrodynamic simulations with a multiwavelength radiative transfer scheme, Laursen, Sommer-Larsen & Andersen (2009) and Yajima et al. (2014) find that the escape fraction of Ly α photons can be as low as ∼10 per cent, with the exact value depending on specific properties such as mass, star formation, dust content, or metallicity. They also show that Ly α photons do not escape isotropically, but the flux generally depends on the direction (Dijkstra et al. 2006). Consequently, the observed Ly α luminosity is only a lower limit to the actual luminosity and the line ratio of He ii/Ly α should hence be treated with caution.
Line luminosities for single, non-rotating Pop III stars, averaged over their lifetimes with no mass loss (Schaerer 2002). We extrapolate and interpolate linearly between the originally tabulated values. The model assumes an electron temperature, Te, and density, ne, of 30 000 K and 100 cm−3, which are typical values for gas around the first stars. Decreasing the electron temperature to Te = 10 000 K would increase the He ii line luminosity by at most ∼10 per cent. The luminosities are a very steep function of mass, and the line ratio of He ii/ Ly α is ≲0.02 for the considered primordial stellar populations.
| M*( M⊙) . | LLy α(erg s−1) . | LHe ii(erg s−1) . | LHe ii/LLy α . |
|---|---|---|---|
| 1 | 2.1 × 1028 | 4.8 × 1013 | 2.4 × 10−15 |
| 10 | 4.3 × 1036 | 4.4 × 1030 | 1.0 × 10−6 |
| 100 | 1.1 × 1039 | 1.8 × 1037 | 1.6 × 10−2 |
| 1000 | 1.6 × 1040 | 3.7 × 1038 | 2.3 × 10−2 |
| M*( M⊙) . | LLy α(erg s−1) . | LHe ii(erg s−1) . | LHe ii/LLy α . |
|---|---|---|---|
| 1 | 2.1 × 1028 | 4.8 × 1013 | 2.4 × 10−15 |
| 10 | 4.3 × 1036 | 4.4 × 1030 | 1.0 × 10−6 |
| 100 | 1.1 × 1039 | 1.8 × 1037 | 1.6 × 10−2 |
| 1000 | 1.6 × 1040 | 3.7 × 1038 | 2.3 × 10−2 |
Line luminosities for single, non-rotating Pop III stars, averaged over their lifetimes with no mass loss (Schaerer 2002). We extrapolate and interpolate linearly between the originally tabulated values. The model assumes an electron temperature, Te, and density, ne, of 30 000 K and 100 cm−3, which are typical values for gas around the first stars. Decreasing the electron temperature to Te = 10 000 K would increase the He ii line luminosity by at most ∼10 per cent. The luminosities are a very steep function of mass, and the line ratio of He ii/ Ly α is ≲0.02 for the considered primordial stellar populations.
| M*( M⊙) . | LLy α(erg s−1) . | LHe ii(erg s−1) . | LHe ii/LLy α . |
|---|---|---|---|
| 1 | 2.1 × 1028 | 4.8 × 1013 | 2.4 × 10−15 |
| 10 | 4.3 × 1036 | 4.4 × 1030 | 1.0 × 10−6 |
| 100 | 1.1 × 1039 | 1.8 × 1037 | 1.6 × 10−2 |
| 1000 | 1.6 × 1040 | 3.7 × 1038 | 2.3 × 10−2 |
| M*( M⊙) . | LLy α(erg s−1) . | LHe ii(erg s−1) . | LHe ii/LLy α . |
|---|---|---|---|
| 1 | 2.1 × 1028 | 4.8 × 1013 | 2.4 × 10−15 |
| 10 | 4.3 × 1036 | 4.4 × 1030 | 1.0 × 10−6 |
| 100 | 1.1 × 1039 | 1.8 × 1037 | 1.6 × 10−2 |
| 1000 | 1.6 × 1040 | 3.7 × 1038 | 2.3 × 10−2 |
In Table 1, we list line luminosities and He ii/Ly α ratios for 1 − 1000 M⊙ Pop III stars. The line ratios of a primordial stellar population in this mass range are much smaller than the one observed for CR7. The Ly α luminosity can be reduced by trapping or absorption, but we still have to account for the very high He ii luminosity. Put differently, we have to explain a system with LLy α > 8.32 × 1043 erg s−1 and LHe ii = |$1.95 \times 10^{43} \mathrm{erg}\,\mathrm{s}^{-1}$|. We will focus on the He ii luminosity, which is more difficult to explain in the context of early structure formation, because if a primordial stellar population fulfils the He ii constraint, it automatically satisfies the Ly α constraint.
The rate of ionizing photons per stellar baryon for metal-free stars in the mass range 300 − 1000 M⊙ is almost constant (Bromm et al. 2001b). In this mass range, models suggest that Pop III stars have an effective temperature of ∼100 kK (Bromm et al. 2001b; Schaerer 2002) and we also see from Table 1 that the hardness of the spectrum, quantified by He ii/Ly α, does not change significantly in the mass range 100 − 1000 M⊙. Since the binary properties and the initial rotational velocities of Pop III stars are not well known (Stacy, Greif & Bromm 2012; Stacy, Bromm & Lee 2016), we use stellar models of single, non-rotating stars. Rotation and binary evolution might however have an influence on the evolution of massive, metal-free stars and can change their stellar lifetime, spectrum, final fate, or the remnant masses (Ekström et al. 2008; de Mink et al. 2013). In Hartwig et al. (2015b), we have investigated the effect of rapidly rotating Pop III stars in our semi-analytical model and did not find a significant influence on the star formation or metal enrichment.
The Full width at half maximum (FWHM) line widths of these lines are (266 ± 15) km s−1 for Ly α and (130 ± 30) km s−1 for He ii. Other strong radiative sources such as Wolf–Rayet stars or active galactic nuclei (AGN) generally produce broader lines with FWHM ≳103 km s−1 (Brinchmann, Pettini & Charlot 2008). Recently, Smidt et al. (2016) demonstrate by post-processing cosmological simulations with a radiative transfer code that a massive BH of ∼107 M⊙ accreting at 25 per cent of the Eddington limit yields a line width for Ly α that is in good agreement with the observation and a line width of ∼210 km s−1 for He ii, which is slightly above the observed value. Smith et al. (2016) show with a one-dimensional radiation-hydrodynamics simulation that the observed 160km s−1 velocity offset between the Ly α and He ii line peaks is more likely to be produced by an accreting BH than by a stellar population with an effective temperature of 105 K. Such a stellar population might ionize its environment too efficiently and can account neither for the velocity offset, nor for the spatial extension of ∼16 kpc of the Ly α emitting region. The UV slope of β = −2.3 ± 0.08 cannot be used to distinguish between different models, since both a young metal-free stellar population and an accreting BH yield a blue UV slope in this frequency range (Dijkstra et al. 2016).
Another striking feature of CR7 is the absence of metal lines with upper limits of, e.g. He ii/O iii] 1663 Å > 3 and He ii/C iii] 1908 Å > 2.5. This does not mean that there are no metals at all, just that the He ii line dominates and hence normal stellar populations are excluded as the only explanation, since they would produce He ii/O iii] 1663 Å ≲0.3, He ii/C iii] 1908 Å ≲0.3 (Gutkin, Charlot & Bruzual 2016). These upper limits for the metal recombination lines also set the absolute metallicity of the gas (see Section 3.5). Due to the above constraints, the main source of ionizing photons in CR7 has to be embedded in gas with a low metallicity.
The observed equivalent widths are EWLy α > 230 Å and EW|$_{\mathrm{He\,\small {II}}} = (80 \pm 20)$| Å. The EW of Ly α is only a lower limit (since no UV continuum is detected) and has consequently no strong constraining power, because both a young stellar population and an accreting BH can yield an Ly α EW of >230 Å (Shields & Ferland 1993; Malhotra & Rhoads 2002; Schaerer 2003). Also Dijkstra et al. (2016) do not use this observational constraint in their spectral fit since it does not yield any additional information. However, the large EW of He ii can be used to confine the age and ambient metallicity of a potential Pop III stellar population. A comparison to the very detailed stellar evolutionary synthesis models of Schaerer (2003) and Raiter, Schaerer & Fosbury (2010) yields a metallicity of <10−7 and a very recent starburst of <1 Myr in order for the models to be consistent with the EW of He ii. Unfortunately, there is not such a sophisticated model with the required parameter dependences for the EWs of an AGN spectrum. Moreover, the determination of the He ii EW for an AGN spectrum would require the modelling of the underlying continuum. This is problematic because the AGN and stellar continuum overlap at these wavelengths and they degenerate without knowing the respective luminosities (Stark et al. 2015). The detailed modelling of this problem is beyond the scope of the paper.
HST observations show that CR7 is composed of three clumps with a projected separation of ∼5 kpc, with one clump hosting a young, blue stellar population and the other clumps hosting older, red populations. This might be evidence for an ongoing merger, which makes it even more important to take the merger history of this system into account. Sobral et al. (2015) find that the best-fitting SED model is a combination of an older 1.6 × 1010 M⊙, 0.2 Z⊙ population with an age of 360 Myr and a metal-free population with a top-heavy IMF, a total stellar mass of ∼107 M⊙ and an age of a few Myr. However, a radiation source with a lifetime of at least 10 − 100 Myr is required to account for the spatial extent of the Ly α emitting region (Smith et al. 2016), which favours an accreting BH over a young, metal-free stellar population.
3 METHODOLOGY
We use a semi-analytical model that is based on the work of Hartwig et al. (2015b) and enables us to efficiently test a large parameter space with high mass resolution. In this section, we present the code and introduce the techniques we use to explore the nature of CR7.
3.1 Our basic model
3.1.1 Cosmological context
According to the hierarchical scenario of structure formation, haloes merge over time to form larger structures. The distribution of halo masses as a function of redshift can be described analytically by the model of Press & Schechter (1974). Based on this idea, Bond et al. (1991) and Lacey & Cole (1993) developed methods to construct assembly histories of individual haloes that allow the construction of dark matter merger trees. Our code is based on the merger tree algorithm by Parkinson, Cole & Helly (2008), which generates dark matter merger trees with arbitrary mass resolution. We use a resolution mass of Mres = 2.5 × 105 M⊙ for the merger tree, which is sufficient to resolve all haloes for the redshifts of interest. We assume a flat ΛCDM Universe and use the Planck Collaboration XIII (2015) cosmological parameters, most importantly the new optical depth to Thompson scattering τe = 0.066 ± 0.016, which is significantly lower than τe = 0.0907 ± 0.0102 from their previous release (Planck Collaboration XVI 2014).
3.1.2 Halo mass
As a starting point to constructing the merger tree backwards in cosmic time, we need an approximation for the halo mass of CR7 at z = 6.6. We use the value of 1.6 × 1010 M⊙ proposed by Sobral et al. (2015) as a fiducial total stellar mass for our model. This mass has been derived with SED fitting under the assumption that CR7 hosts a normal stellar population, although this might not be the case. This simplifying assumption might lead to errors of a factor of a few in the estimation of the total stellar mass. Moreover, estimates of stellar mass based on SED fitting are subject to uncertainties related to degeneracies between several stellar population parameters [star formation rate (SFR), metallicity, IMF, rotation, binarity].
3.1.3 Star formation
We use spectra tabulated by Schaerer (2002, 2003) to determine the number of ionizing and LW photons and the Ly α and He ii line luminosities for each Pop III star individually as a function of its mass. Lifetimes for the stars are also taken from Schaerer (2002, 2003). The associated line luminosities for Pop III stars are listed in Table 1. We adopt luminosities averaged over the stellar lifetime, which are smaller than the zero-age main-sequence luminosities by a factor of a few. This might be relevant for a recent burst in Pop III stars but does not change our final conclusions.
We model the formation of subsequent generations of stars (Pop II) from the observed cosmic star formation history at high redshift and account for their chemical and radiative feedback (ionizing and LW photons). We take cosmic SFRs from Behroozi & Silk (2015), extrapolate them to z > 15 and set them to zero for z > 30.
3.1.4 Escape fractions
For the escape fraction of ionizing radiation we use fesc, III = 0.5 for Pop III star-forming haloes and fesc = 0.1 for later generations of stars in more massive haloes. Generally, the escape fraction depends on the halo mass, redshift and the stellar physics (Paardekooper, Khochfar & Dalla Vecchia 2013; Trebitsch, Blaizot & Rosdahl 2015), but we use these average values for our simplified model, which are in good agreement with previous studies (Johnson et al. 2009; Finkelstein et al. 2012; Wise et al. 2014; Xu et al. 2016a). A higher escape fraction of ionizing radiation would lead to a lower SFE, which only weakly affects the final results as we show in Section 4.2.
Escape fractions for LW photons are taken from Schauer et al. (2015), who find that they are a function of both halo and Pop III star mass. The escape fraction is dominated by the most massive star in each halo, which first ionizes the surrounding gas. Hence, we use the escape fraction values in the far field approximation for the most massive star in each halo.
3.1.5 Metal enrichment and critical metallicity
After its lifetime and depending on its mass, a Pop III star explodes in a SN and pollutes its environment with metals. We use metal yields from Heger & Woosley (2010) and assume a Sedov–Taylor expansion of the enriched volume. By summing the volumes of these SN remnants in all haloes, we calculate the time-dependent fraction of the total volume that is already polluted. Once a new halo forms, we check statistically whether it is already metal-enriched or still pristine. A key assumption of this model is that the SN remnant is still in the Sedov–Taylor phase when it breaks out of its host halo. This is valid for minihaloes, as the H ii region expansion has already cleared most of the gas from the halo (Kitayama et al. 2004; Whalen, Abel & Norman 2004; Alvarez, Bromm & Shapiro 2006; Abel, Wise & Bryan 2007). For later generations of stars in more massive haloes, we assume that they do not contribute to the pollution of the IGM by metals (although see Mac Low & Ferrara 1999).
In principle, a halo can host several Pop III SNe and their metal-enriched remnants can overlap. Since the expansion of the enriched gas is mainly dominated by the most massive (and consequently first) SN to go off (Ritter et al. 2015), we only account for the expansion of the SN of the most massive progenitor per halo. This approximation is valid, as long as there are not too many highly energetic SNe in one halo, which is generally not the case in our models.
3.1.6 SFEs based on merger history
3.1.7 Sampling the halo mass function and calibrating SFEs
To determine the star formation efficiencies η and ϵ1 : 1 we calibrate them against τe, which is a measure of the integrated ionization history of the Universe. The optical depth is very sensitive to the number of ionizing photons in the early Universe and can therefore be used to calibrate the SFE. To do so, we sample the halo mass function at z = 6.6 from 108–1013 M⊙ and weight the number of ionizing photons from a given halo by the number density of haloes of this mass at that redshift. This yields a cosmologically representative sample, since haloes with masses below 108 M⊙ at z = 6.6 hardly produce any ionizing photons and haloes above 1013 M⊙ are very rare at this redshift. For more details and a thorough comparison to analytical models of the halo mass function see Magg et al. (2016).
For 11 equally distributed halo masses in this range we generate 100 merger trees, which yield a statistically representative number of realizations. We then calculate τe from the ionization history of these haloes. We chose the SFE accordingly, to match the observed value of τe = 0.066. Reionization is mainly driven by Pop II stars, but we also need the contribution by primordial stars. We do not account for other sources in the total ionizing budget in the early Universe, such as quasars (e.g. Volonteri & Gnedin 2009; Madau & Haardt 2015) or high-mass X-ray binaries, and the uncertainty in τe might yield different SFEs. However, we demonstrate in Section 4.2 that a different SFE has no influence on metal enrichment or our final conclusions.
For this implementation of the halo mass function and 100 randomly generated merger trees we probe a cosmologically representative volume of ∼106 Mpc−3. This is statistically sufficient for most of our purposes, but might be too small to probe certain rare scenarios of SMBH seed formation (see Section 3.4).
3.2 Models of Pop III star formation
We model the star formation history of CR7, focusing on the primordial stellar component, with our semi-analytical code. To investigate the possibility of having 107 M⊙ of Pop III stars at z = 6.6 and the corresponding high He ii line luminosity and EW we test several models of primordial star formation, which are summarized in Table 2. For the ‘fiducial’ model we assume a logarithmically flat IMF from Mmin = 3 M⊙ to Mmax = 300 M⊙ and an SFE η = 0.14, which yields an optical depth τe = 0.067. The mass range of the IMF is consistent with recent simulations (Greif et al. 2011; Susa et al. 2014; Hirano et al. 2014; Hosokawa et al. 2016) and it covers all possible stellar remnants relevant to our model. In a second model, which we label ‘1→100’, we assume a lower mass IMF from Mmin = 1 M⊙ to Mmax = 100 M⊙, motivated by recent simulations of primordial star formation (Clark et al. 2011; Stacy et al. 2012; Dopcke et al. 2013; Hartwig et al. 2015a; Stacy et al. 2016), which manifest disc fragmentation and hence lower mass Pop III stars. This model should illustrate the effects of a different mass range of primordial stars, since the actual values are not well constrained. In this second model, we adopt η = 0.20 which results in τe = 0.066.
Overview of the four models we use for primordial star formation. The fiducial model assumes an IMF from 3 to 300 M⊙ and only pristine gas can form Pop III stars. In the second model, we change the IMF to slightly lower masses from 1 to 100 M⊙. The third model allows Pop III star formation up to a metallicity of Zcrit = 10−3.5. In the last model, we determine the stellar mass per halo based on the merger history. In all the models, we calibrate the SFE to reproduce the optical depth to Thomson scattering.
Overview of the four models we use for primordial star formation. The fiducial model assumes an IMF from 3 to 300 M⊙ and only pristine gas can form Pop III stars. In the second model, we change the IMF to slightly lower masses from 1 to 100 M⊙. The third model allows Pop III star formation up to a metallicity of Zcrit = 10−3.5. In the last model, we determine the stellar mass per halo based on the merger history. In all the models, we calibrate the SFE to reproduce the optical depth to Thomson scattering.
The main difference between primordial and later generations of star formation is the ability of the gas to cool efficiently. Metal lines can cool the gas to lower temperatures than cooling by molecular hydrogen, which is the most efficient coolant in primordial gas. Hence, the Jeans mass in metal-enriched gas is smaller than in primordial gas and the cloud consequently fragments into more and smaller clumps, which then collapse to form protostars. So far we assumed that Pop III stars form from pristine gas with a top-heavy IMF, but several studies show that even with trace amount of metals a top-heavy IMF is possible (Bromm et al. 2001a; Schneider et al. 2002, 2012; Frebel, Johnson & Bromm 2007; Dopcke et al. 2013; Safranek-Shrader, Milosavljević & Bromm 2014).
Consequently, in the third scenario, named Zcrit, we assume that Pop III stars form with a top-heavy IMF out of metal-enriched gas with a metallicity of Z < Zcrit with Zcrit = 10−3.5. Although dust cooling can yield a lower Zcrit (Schneider et al. 2012; Dopcke et al. 2013), we adopt this value as a conservative upper limit. We use a flat IMF from Mmin = 3 M⊙ to Mmin = 300 M⊙. The effective temperature is lower for a metal-enriched star than for a primordial star of the same mass so its spectrum is softer (Bromm et al. 2001b). The LW and Ly α luminosities are only weakly affected but the He ii line luminosity is generally smaller for 0 < Z ≲ Zcrit compared to the metal-free case (Cojazzi et al. 2000; Schaerer 2003). On average, it is smaller by a factor of ∼10, but the exact value depends on the treatment of stellar winds and metallicity. Due to this uncertainty, we will still use the line luminosities for the metal-free case but keep in mind that this yields a strict upper limit for the He ii line. We also verified that the final results are insensitive to the choice of Zcrit. This is in agreement with Latif et al. (2016), who show that the fraction of haloes that are enriched up to a certain metallicity is only a weak function of the actual metallicity for 10−6 < Z < 10−4. An SFE η = 0.12 yields an optical depth τe = 0.068.
In the fourth model, which we label ‘merger’, we couple the star formation to the merger history based on equation (8) with ϵ1 : 1 = 4 × 10−3. For mergers with a mass ratio below 0.2, we set ϵ1 : 1 = 10−5, which allows about one star to form per halo. The IMF extends from Mmin = 3 M⊙ to Mmin = 300 M⊙ and only pristine gas can form Pop III stars. We use radiative feedback in this model only to check if a minihalo can collapse in a given LW background, but we do not use this value to determine the final mass in Pop III stars as we do in the other models. We obtain an optical depth of τe = 0.067 with this model.
One should keep in mind that our understanding of primordial star formation is still quite incomplete and uncertain due to the lack of any direct observations. We try to overcome this uncertainty by implementing different scenarios of Pop III star formation that cover the most likely theories about the formation of the first stars. We have also tested other parameters, such as a primordial IMF extending to masses above 300 M⊙ (see section 4.1), but since these results deviate even further from the observational constraints of CR7, we do not explicitly discuss them here.
3.3 Pop III remnant BH
We also investigate the possibility that CR7 hosts a massive BH. Pallottini et al. (2015) show that a BH with an initial mass of ∼105 M⊙ embedded in a halo of total gas mass 107 M⊙ can account for the observed line luminosities about 100 Myr after formation. This result was derived by coupling a 1D radiation-hydrodynamic code (Pacucci & Ferrara 2015) to the spectral synthesis code cloudy (Ferland et al. 2013) as described in detail in Pacucci et al. (2015). After ∼100 Myr the gas in the halo is depleted and the He ii luminosity decreases. Generally it is possible to obtain the necessary fluxes at later times if the reservoir of metal-poor gas is large enough. First, we explore the formation scenario in which massive BHs grow from Pop III stellar remnants (Haiman & Loeb 2001; Madau & Rees 2001; Volonteri, Haardt & Madau 2003; Whalen & Fryer 2012).
The final fate of a star depends mainly on its mass. Pop III stars with masses of |$25 \,\mathrm{M}_{\odot }\le M_{\ast } \le 140 \,\mathrm{M}_{\odot }$| or with M* > 260 M⊙ collapse to BHs, although the exact ranges depend on rotation and magnetic field strengths (Karlsson, Bromm & Bland-Hawthorn 2013). 140 − 260 M⊙ Pop III stars are completely disrupted in pair-instability SNe (PI SNe) that leave no remnant behind. Primordial stars that directly collapse to a BH do not pollute their host halo with metals. This is an important characteristic of primordial stars, which facilitates having an accreting BH in a metal-free environment.
We trace the formation of Pop III remnant BHs in the assembly history of CR7 and merge the BHs if the mass ratio of a merger of two galaxies is >0.1 (Taffoni et al. 2003; Volonteri et al. 2003; Van Wassenhove et al. 2014). For smaller mass ratios, we only follow the growth of the more massive BH. The rate at which Pop III remnant BHs grow by accretion is a subject of ongoing debate and depends on the gas supply, the depth of the gravitational potential well of the halo, the merger history, and the radiative feedback (Milosavljević, Couch & Bromm 2009a; Milosavljević et al. 2009b; Park & Ricotti 2011, 2012; Whalen & Fryer 2012; Park & Ricotti 2013; Pacucci et al. 2015). Existing simulations have indicated that accretion on to stellar-mass Pop III remnants may be substantially suppressed, due to radiation-hydrodynamical feedback (Johnson, Greif & Bromm 2007; Milosavljević et al. 2009a; Milosavljević et al. 2009b; Jeon et al. 2012, 2014). Hence, we do not take gas accretion into account and note that the derived values of the BH masses are a strict lower limit. We discuss the issue of gas accretion on to Pop III remnant BHs in more detail in Section 5.
3.4 Direct collapse black hole
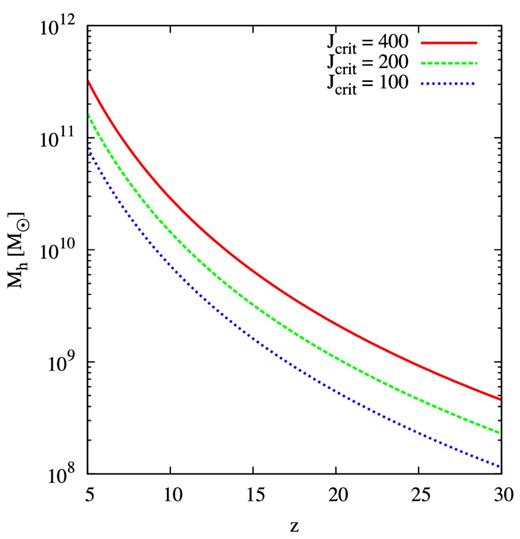
Minimum halo mass required to produce Jcrit without polluting its neighbour halo with metals, plotted as a function of redshift. Depending on the redshift and the required LW flux, a halo of ∼109–1011 M⊙ is needed to suppress H2 formation in its neighbour and produce a DCBH.
To identify formation sites of DCBHs we first find a metal-free halo with a mass ≥Matom and its most massive neighbour in the merger tree. These are two haloes at the present time step that merge in the next time step. This condition of an incipient merger guarantees a small spatial distance between the two haloes. If, for a given Jcrit, the mass of the nearby halo fulfils equation (13), we assume that it provides a sufficient LW flux without polluting the atomic cooling halo and that a DCBH forms.
![Line ratio as a function of the gas metallicity for a 100 kK blackbody (top) and an AGN SED (bottom). The dashed line indicates the upper observational limit of C iii] 1908 Å/He ii < 0.4 and the three different lines represent different ionization parameters of the gas. For metallicities below ∼10−2, all models are in agreement with the observation.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/462/2/10.1093_mnras_stw1775/2/m_stw1775fig2.jpeg?Expires=1750550224&Signature=a0twYP-n-y6s0KtARTLa0Cv2bKGf2iywBSJxqLR9XfJlfmYX9W3zG27Xtqoh6r~oC5ccvQdfVcN1X8DOCyFfzfOiT~RBWe0J6vxNd4y7CL4y23PYRKbG-WoPdEQMBKDm1UwSPl0kcDo1PBqaFiEv~E5UAJRGuvYRN~tB2mp7~u6PLeog-4dfacDtwOS676TpXU8RHp7QZZgLDEt9A8tKg-UbPAHRbR0GTD1aoCZK3IV-QowWb1ULD3ozvGbuZOoiN9a9mt3bCovzvexvnjr0DiKwuRnH19JS~bmq7~qNkS7QAHLcB8IECdNhmnlLsO4nXzLwRcht6Tp98GNOdJrz5w__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Line ratio as a function of the gas metallicity for a 100 kK blackbody (top) and an AGN SED (bottom). The dashed line indicates the upper observational limit of C iii] 1908 Å/He ii < 0.4 and the three different lines represent different ionization parameters of the gas. For metallicities below ∼10−2, all models are in agreement with the observation.
Agarwal et al. (2016a) propose that CR7 hosts a DCBH. In ∼20 per cent of their merger tree realizations, which represent the mass assembly histories of CR7, a DCBH may form. The formation redshift of the DCBH is z ∼ 20, which is limited by two factors: at higher redshift, the LW flux, which they calculate from Agarwal et al. (2016b), is not high enough. At lower redshift the formation site of the DCBH is polluted by metals, where they assume that metals are ejected at a constant wind speed of 100 km s−1. For a seed mass of 2 × 104 M⊙, accretion at 40 per cent of the Eddington rate, and an escape fraction of fesc = 0.16 for Ly α photons, they show that a DCBH is able to reproduce the observed line luminosities of Ly α and He ii. Hence, if the BH is able to accrete metal-free gas for long enough, formation at higher redshifts is also possible. Following Pallottini et al. (2015) and Agarwal et al. (2016a), we assume that a DCBH formed before z = 7.3 can account for the observed line luminosities if it accretes low-metallicity gas at z = 6.6. Motivated by Latif et al. (2013b) and Ferrara et al. (2014), we assume that DCBHs form with an initial seed mass of 104–105 M⊙ in our model. These masses, however, are plausibly upper limits, as the strength of the LW flux we assumed is lower than assumed in those papers. Latif & Volonteri (2015), for instance, find that lower LW fluxes result in lower mass concentrations in the precursors of DCBHs when J21 < 1000.
3.5 Determination of the metal tax
A different approach is to further investigate the non-detection of the C iii] doublet at ∼1908 Å. For the spectral resolution of 0.4 Å (Sobral et al. 2015), we expect the EW of C iii] to be below ≲1 Å, since it should otherwise be detected as an emission line in the spectrum. This yields an additional constraint on the gas metallicity as can be seen in Fig. 3. From the cloudy model at different ionization parameters we can constrain that only gas metallicities of ≲10−3 are consistent with the non-detection of the C iii] doublet. Although this is even more constraining than our previous approach based on the line ratios, we use the conservative value of Zlimit = 10−2, due to the difficulties in modelling the EW with our simple model. We check the influence of a possibly lower metal tax in the final discussion.
4 RESULTS
In this section, we present the main results of our analysis and investigate whether CR7 can be explained with our models of Pop III star formation or by an accreting BH. For each set of parameters, we create 100 independent merger tree realizations and average the derived quantities over the different realizations (if not stated otherwise). This yields a cosmologically and statistically representative sample with statistical scatter of <10 per cent.
4.1 Cosmologically representative models of primordial star formation
We sample the halo mass function from 108 to 1013 M⊙ and weight the contribution to the number of ionizing photons by the number density of those haloes at z = 6.6. This enables us to reproduce the observed value of the optical depth.
![Modelled EW of C iii] as a function of the gas metallicity for a stellar population (top) or a AGN spectrum (bottom). Given the spectral resolution, the EW should be below ≲1 Å, which sets an upper limit to the gas metallicity of ∼10−3.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/462/2/10.1093_mnras_stw1775/2/m_stw1775fig3.jpeg?Expires=1750550224&Signature=ZwRA1K0W5aEMVkFrBV2ipiBH02-BLVighOXCB9PNvZEdzTNmStmlUqiWc2ykORe-lysSYzL-~BQ91AqSSY9Dlj07gik02zzZLpkDsiHc8sCn3IiIyzOYLfmTKzKiDO6aA-EuhrCPw2qMa6VJHbGaMao1VhfPaOq4ipXE7mddywLy0ahtmHXYjFNbgFqhI7AUUrZ7EOzS52mYfhixZ~yF2jIBnOQ9BkmLCfbHaM-y09MMypvdH0d1yD2ZpZlv49aiXW2QSXwQ3HM6H8lAEn~9tWTiIhkf3~JKTCeoLnuFqxOpAM0LSXqMPS2G52xKHT-13NI9sjyQ1xT9nWHpjh9O3g__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Modelled EW of C iii] as a function of the gas metallicity for a stellar population (top) or a AGN spectrum (bottom). Given the spectral resolution, the EW should be below ≲1 Å, which sets an upper limit to the gas metallicity of ∼10−3.
The total mass of Pop III stars per halo depends on either the LW background (equation 5) or on the merger history (equation 8). To compare these recipes for star formation, we define the effective SFE as |$\eta _\mathrm{eff}=M_{\ast }/M_{\rm h}$|, which is shown in Fig. 4 as a function of cosmic time. Typical values for ηeff are ∼10−4 for all the models. Minihaloes have masses on the order of ∼106 M⊙, and for ηeff ∼ 10−4 we form a total stellar mass of ∼100 M⊙ on average per Pop III star-forming minihalo. The random sampling of the IMF leads to statistical variance from halo to halo and there are haloes with multiple Pop III stars and masses >100 M⊙. Indeed, the majority of primordial stars in our model form in multiples of two to six stars, as predicted by simulations of early star formation (Clark et al. 2011; Greif et al. 2011; Stacy et al. 2012; Dopcke et al. 2013; Hartwig et al. 2015a; Stacy et al. 2016).
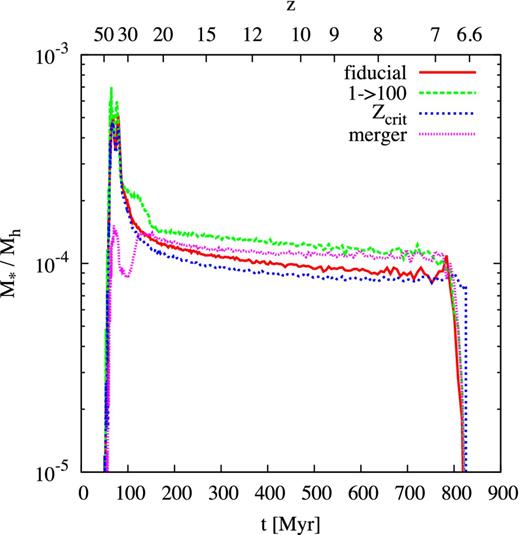
Effective SFE for Pop III stars as a function of cosmic time for the four models. After a small early peak, the SFE is approximately constant around 10−4.
The cosmic mean Pop III star formation density as a function of time for all four models is shown in Fig. 5. It is roughly the same for all the models because they are constructed to satisfy the latest constraints on τe. The Zcrit model's values are slightly higher just shortly above z = 6.6 because Pop III stars also form in low-metallicity gas and hence also at later times. Consequently, this model is less affected by metal pollution at lower redshifts. The derived cosmic star formation densities are in agreement with those of Visbal, Haiman & Bryan (2015). They show that the recent constraints on τe by the Planck Collaboration XIII (2015) limit the mean cosmic star formation density of primordial stars to ≲10−4 M⊙ yr−1 Mpc−3. The SFR density at z ∼ 6.6 might not be cosmologically representative due to ongoing Pop III star formation at z ≲6.6, which is not captured by our method.
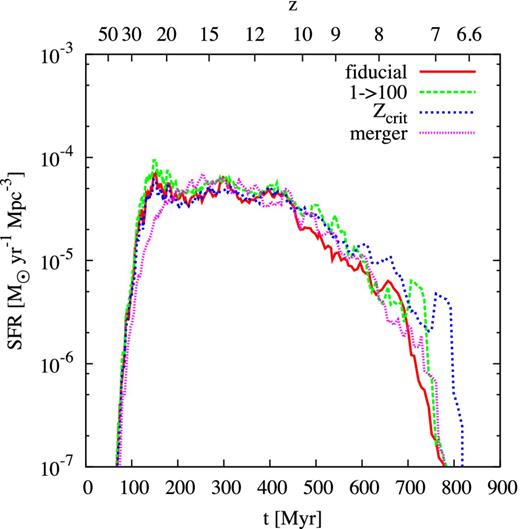
Mean cosmic Pop III SFR for all four models per comoving volume. The primordial SFR peaks around redshift 20, and decreases at z < 12.
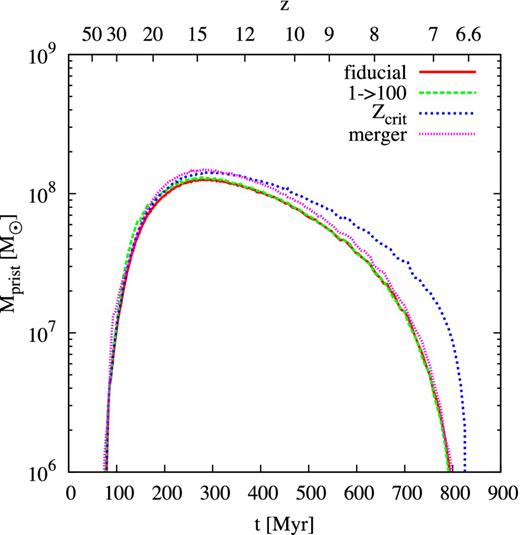
Mass of metal-free or metal-poor gas as a function of time for all four models. Here, we assume that the final halo has a mass Mh = 1.2 × 1012 M⊙ at z = 6.6 and we only account for gas in its resolved progenitor haloes, which explains the rise at early times. This plot illustrates the maximum available amount of gas to form Pop III stars, but even in the most promising Zcrit model the mass of gas available for Pop III star formation is limited to ≲108 M⊙.
The fact that we have more gas available to form primordial stars in the Zcrit model can be seen in the plots of metal-poor gas mass as a function of time in Fig. 6. At a given redshift, this is the sum of the metal-free gas in all resolved haloes in the merger tree. Hence, it is a measure of the maximum available mass to form Pop III stars, assuming an SFE of 100 per cent. For all the models this mass remains below ∼108 M⊙. In the model in which we allow primordial stars to also form in metal-enriched gas at Z < Zcrit, we have more gas to form Pop III stars at lower redshifts and still 107 M⊙ of low-metallicity gas just above z = 6.6. These values are derived for Mh = 1.2 × 1012 M⊙.
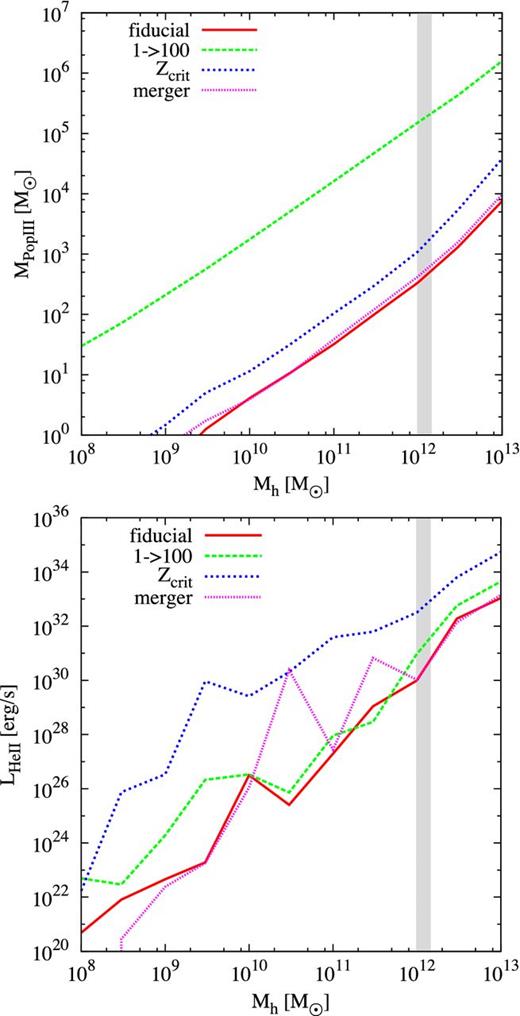
Stellar masses in Pop III stars (top) and corresponding He ii luminosities (bottom) at z = 6.6 for a variety of halo masses. Here, we illustrate the entire range of simulated halo masses, and the most likely mass range for CR7 is shaded in grey. The model with a lower mass IMF produces a significantly higher stellar mass in Pop III stars, mainly because of the longer lifetimes of these stars. In the expected mass range of CR7, the stellar primordial mass is limited to 102–105 M⊙, depending on the model. The Zcrit model produces the highest He ii luminosity, because this model is less affected by metal enrichment at lower redshifts and can hence form Pop III stars out to later times. The He ii luminosity is significantly lower than the observed value of 1.95 × 1043erg s−1.
The stellar mass in Pop III stars and He ii line luminosities are shown in Fig. 7. For the lower mass IMF there are 105 M⊙ of Pop III stars in CR7, whereas the other models yield values of 102–103 M⊙. This is in agreement with the results of Xu et al. (2016b), who find in their cosmological simulation ≲103 M⊙ of Pop III stars in haloes at z = 7.6. The mass of pristine gas drops steeply before this redshift and only less massive stars with longer lifetimes can survive to be present in CR7. The He ii luminosity is a steep function of the stellar mass, and massive stars are favoured to reproduce the observations. The Zcrit model yields larger masses of low-metallicity gas down to smaller redshifts and consequently allows primordial star formation at later times. Hence, more massive stars can also survive to contribute to the He ii luminosity at z = 6.6. The Zcrit model produces the highest He ii luminosities, which are still more than 10 orders of magnitude below the observed value of 1.95 × 1043erg s−1. Even for a higher halo mass, which might be possible within the uncertainties of the determination of the stellar and halo mass of CR7 (see Section 3.1.2), the final luminosities are too small. We note that the corresponding Ly α luminosity for Pop III stars in a ∼1012 M⊙ halo is of the order of 1036–1037 erg s−1, which is about 7 orders of magnitude below the observed value.
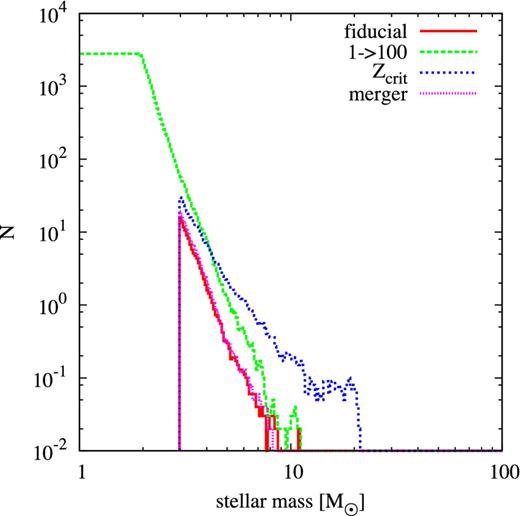
Number of stars per logarithmic mass bin that are present in the final 1.2 × 1012 M⊙ halo at z = 6.6, summed over 100 realizations. The more massive the stars, the shorter their lifetimes and the lower the probability that they survive from their time of formation until the final redshift. The model with the less massive IMF produces many low-mass stars, which survive down to z = 6.6 if they are less than ∼2 M⊙. In the Zcrit model primordial stars form up to just above z = 6.6, so more massive survivors are present in the final halo.
What mostly limits the He ii luminosity is the mass of Pop III stars that survive until z = 6.6. To show this effect, we plot the stellar mass distribution of primordial stars in Fig. 8. The more massive the stars, the shorter the lifetimes and the smaller the probability that they survive long enough to be present down to z = 6.6. For M < 2 M⊙ this plot represents the IMF, since the lifetimes of these stars are long enough for them to survive until z = 6.6. For higher masses we see that the Zcrit model is the most likely one to also contain stars that are ∼10 M⊙ since it has the largest amount of gas available for star formation down to lower redshifts. But even these stars are not massive enough to contribute significantly to the He ii luminosity, due to the steep dependence of the He ii luminosity on the stellar mass (see also Table 1). We also test more extreme models for the Pop III IMF with a mass range from Mmin = 10 M⊙ to Mmax = 1000 M⊙ and find significantly fewer primordial stars at z = 6.6 and also a smaller He ii line luminosity than in the fiducial model. For Mmin ≳50 M⊙ there are no Pop III stars at all that might contribute to the He ii luminosity at z = 6.6, because such massive stars explode within a few Myr as SNe.
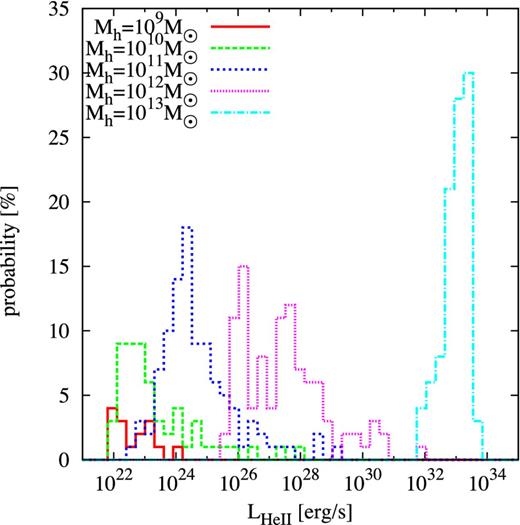
Probability distribution function for the expected He ii line luminosities in the merger model for a variety of final halo masses. Due to the random sampling of merger histories, the scatter in the final He ii luminosity in this model is broader compared to the other models. However, even the scatter and the associated probabilities for large values of LHe ii cannot account for the missing 10 orders of magnitude between model and observation.
Coupling star formation to the merger history of the haloes induces a higher scatter in the stellar mass per halo. Hence, the merger model leads to a broader distribution of He ii luminosities at z = 6.6. We show the probability distribution function of the luminosities at this redshift in Fig. 9. The expected He ii luminosities for a halo mass of Mh = 1012 M⊙ span more than 6 orders of magnitude with a maximum value of ∼1032 erg s−1. The recipe for star formation in mergers (equation 8) is only an extrapolation to lower-mass haloes and higher redshifts. But even in the most optimistic case, in which all the pristine gas turns into Pop III stars during a major merger of two ∼106 M⊙ minihaloes, ∼100 such mergers are required just above z = 6.6 to account for 107 M⊙ of Pop III stars at that redshift. It is therefore difficult to explain the He ii emission in CR7 with our models for primordial star formation.
4.2 Alternative scenarios of primordial star formation
The host halo of CR7 corresponds to a rare ∼3σ peak in the cosmological density field at z = 6.6. Such rare haloes have a comoving number density of only ∼10−7 Mpc−3 at this redshift, and it is possible that star formation within these rare objects might proceed differently than in the average galaxy at this redshift. So far, we have assumed that CR7 is cosmologically ‘representative’ and our star formation recipes reproduce the reionization history of the Universe. Since CR7 cannot be explained in this way, we now drop the constraint of the optical depth, which enables us to vary the SFE of primordial star formation. In other words, we no longer require the mean Pop III SFE in the progenitors of CR7 to be the same as the global mean required to produce the right Thomson scattering optical depth, but instead treat it as a free parameter. We show the effect of changing the SFE in Fig. 10. Even if we change the SFE by 4 orders of magnitude, the mass of zero-metallicity gas is only weakly affected. In none of the models is this mass sufficient to explain the observational signatures of CR7, and the He ii line luminosity is limited to ≲3 × 1032 erg s−1. To understand this rather weak dependence of pristine gas mass and final luminosity on the SFE, we investigate the two limiting cases for the metal enrichment model. As described in Section 3.1.5, we only account for the SN expansion of the most massive star per halo, which could either be a core-collapse SN with an explosion energy of E0 = 1.2 × 1051 erg, or an PI SN with E0 = 1052–1053 erg, depending on the mass of the star. For a very low value of η, we form only one star per halo and the probability that this star explodes is ∼45 per cent for a logarithmically flat IMF from 3 − 300 M⊙. For a very high value of η, we form many Pop III stars per halo and have a correspondingly high probability to obtain a star that explodes as a highly energetic PI SN. The radius of the metal-enriched volume is approximately proportional to |$E_0^{1/5}$| so it is only weakly affected by SNe with different explosion energies. This explains the small variations in the mass of pristine gas between the models with different SFEs. Having several SNe going off in one halo might break the conservative assumption of our metal enrichment model that the pollution of metals is dominated by the most massive SN. Considering multiple SNe per minihalo would lead to even less pristine gas at lower redshifts.
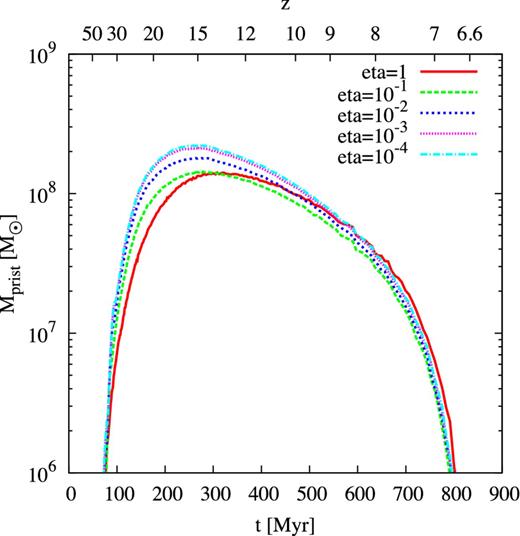
Mass of pristine gas in a 1.2 × 1012 M⊙ halo as a function of time for a range of SFE parameters. The probability that a halo pollutes its environment with metals is not a strong function of the SFE, but only depends on the probability that there is at least one highly energetic SN in the halo.
We have assumed that CR7 is one halo at z = 6.6, although we clearly see three distinct clumps. By construction, the final halo is polluted by metals because its progenitors were enriched by SNe or external metal enrichment. Consequently, there is no Pop III star formation at z = 6.6. In an alternative scenario, we now assume that CR7 is an ongoing merger and that the three clumps will merge to one halo in 100 Myr (z0 = 6.0) or 200 Myr (z0 = 5.6). Based on Behroozi et al. (2013), we estimate the halo masses of halo A and C to be MA = (3 ± 0.6) × 1010 M⊙ and MC = (6 ± 1.2) × 1011 M⊙. The merger time of these haloes with the more massive halo B are ≳50 Myr at this redshift (Boylan-Kolchin, Ma & Quataert 2008). For z0 ≲5.6, the masses of the third and fourth most massive halo tend to be approximately equal, which does not match the constellation of CR7, where we only observe three clumps (see also Section 4.6). This limits the possible range to 5.6 ≲ z0 ≲6.0.
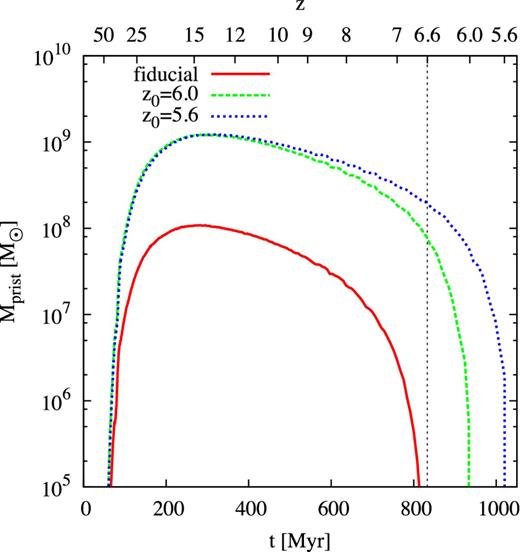
Mass of pristine gas as a function of cosmic time for models that assume a final mass of 1.2 × 1012 M⊙ but several final redshifts, for which the merger trees are created backwards in time. The gas mass available at this redshift is much higher for those models, but we would still need an SFE of 10 per cent and to overcome other problems (see the text).
These redshifts are the starting points for constructing merger trees backwards in time so that we can determine the primordial stellar mass and corresponding He ii luminosity at z = 6.6. The primordial gas mass is shown as a function of time in Fig. 11. The primordial gas mass at z = 6.6 is much higher for the haloes whose merger tree extends down to redshifts z0 < 6.6. The two additional models yield ∼108 M⊙ of pristine gas at z = 6.6. The corresponding total masses of Pop III stars are 2 × 104and 1 × 105 M⊙, which are 2 to 3 orders of magnitude higher than in the fiducial model but still not sufficient to account for the observational constraints. The He ii luminosities are 7 × 1039 erg s−1 and 3 × 1040 erg s−1 for the z0 = 6.0 and 5.6 models, respectively. If Pop III stars form instantaneously out of the pristine gas with 10 per cent efficiency just above z = 6.6, the mass of pristine gas in these models would be sufficient to explain observations of CR7. However, there is no plausible mechanism that could trigger an instantaneous starburst of this intensity, which is required to explain both the luminosity and the EW of the He ii emission.
Although the models with z0 < 6.6 could in principle explain CR7, there are two shortcomings. First, the primordial stars are distributed over all the CR7 progenitors. In our model, we just add up all the Pop III stars at z = 6.6 although they should be confined to clump A. This additional constraint would limit the Pop III stars (and their total mass) to just this one clump (see Section 4.6). Another effect becomes important at lower redshifts that we have not considered. After the reionization of the Universe, photoionization heating counteracts the cooling in minihaloes and might prevent their collapse (Abel & Haehnelt 1999; Pawlik, Schaye & van Scherpenzeel 2009), which further limits the number of Pop III stars that can form at lower redshifts.
4.3 Pop III remnant BHs
While an accreting BH can also explain the line luminosities from CR7, these observations cannot yet differentiate between seed BH formation mechanisms. We first study BH formation in the progenitor haloes of CR7 by mergers of Pop III stellar remnants. We follow the mass assembly history of these BHs in merger tree realisations and illustrate 30 randomly selected histories for three host halo masses in Fig. 12. The Pop III remnant BHs grow to 104–105 M⊙ by z = 6.6, depending on the mass of the halo. Since we only account for mass growth due to mergers of BHs, these values should be treated as an lower limit. We discuss the effect of additional mass accretion in Section 5. For the 1012 M⊙ halo, we expect a BH with a mass of ∼105 M⊙ at z ≈ 7, which could explain CR7 (Pallottini et al. 2015; Pacucci et al. 2016). Note that this quantifies the most massive BH in all progenitors of CR7. In section 4.6 we investigate explicitly those BHs that reside in clump A. Previous studies assume that the BH can accrete low metallicity gas down to z = 6.6. This is a strong assumption, and we show in Section 4.5 that the host haloes of stellar remnant BHs of this mass are generally polluted before z = 6.6.
4.4 Direct collapse black hole
We also consider under which conditions a DCBH can form in the progenitor haloes of CR7. The DCBH formation rate density is shown in Fig. 13. DCBHs form in the five models at redshifts z ≥ 7.3. Generally, a higher halo mass and a lower value of Jcrit facilitates the formation of DCBHs. This is because a higher halo mass yields more progenitors and hence more possible formation sites for a DCBH, whereas for a lower value of Jcrit haloes with lower masses can provide sufficient flux to enable isothermal collapse. The peak formation rate of DCBHs is around z = 15 and the rate decreases steeply at z < 10. In our models no DCBH can form at Jcrit > 600 in the progenitors of CR7, whereas this is also limited by the finite number of merger tree realisations. Our implementation yields results similar to those by Dijkstra et al. (2014) and Habouzit et al. (2016). The difference emerges from our implementation of Pop III star formation and the fixed time of 10 Myr that we require for an atomic cooling halo to collapse, whereas they assume a redshift-dependent collapse time, which is generally longer. Hence, our assumptions are more optimistic, and similar to Agarwal et al. (2012, 2014).
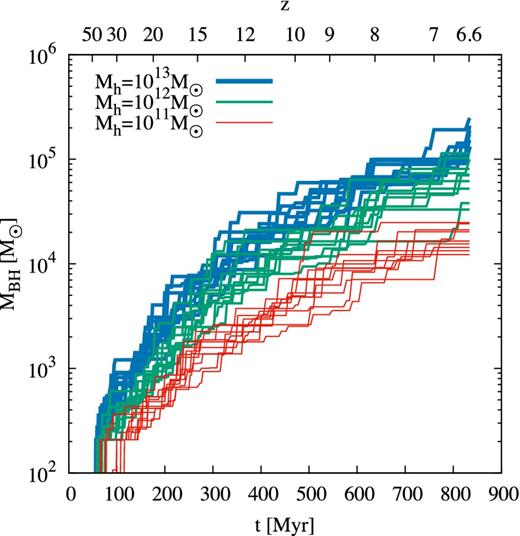
Growth history for Pop III stellar remnant BHs that gain mass via galaxy mergers. Here we show 10 random realizations for each halo mass of 1011 M⊙ (red), 1012 M⊙ (green), and 1013 M⊙ (blue). The BHs can reach final masses of 104–105 M⊙ by z = 6.6.
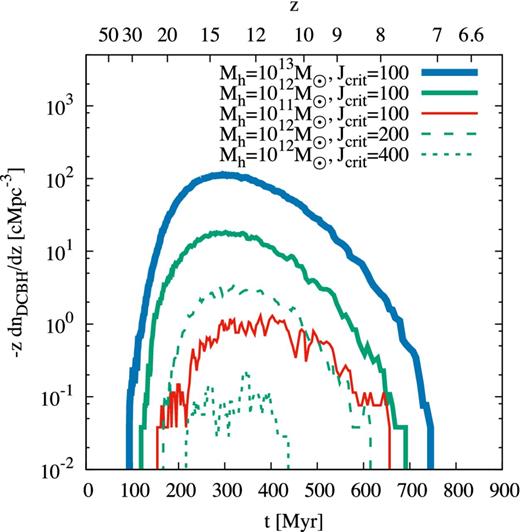
DCBH formation rate as a function of redshift for several halo masses and values of Jcrit. The formation rate is normalized to the comoving volume of the main halo, where the red, green, and blue lines are for halo masses of 1011 M⊙, 1012 M⊙, and 1013 M⊙, respectively. The solid, dashed, and dotted green lines show the numbers of DCBHs per redshift for Jcrit = 100, 200, 400, respectively. The comoving volume is calculated as the mass of the main halo Mh divided by the average cosmic density. In all these cases, we can form DCBHs during the assembly of the halo. A larger halo mass and a lower value of Jcrit facilitates the formation of a DCBH down to lower redshifts. In none of the cases can we form a DCBH at redshifts z < 7.3.
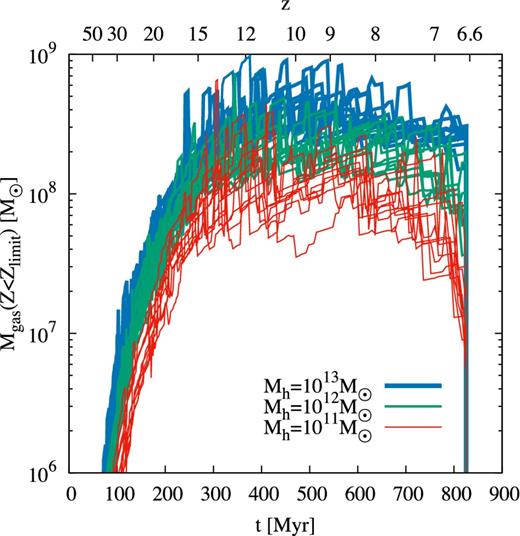
Maximum gas mass in the given halo with Z < Zlimit. We plot 10 random realizations for final halo masses of 1011 M⊙ (red), 1012 M⊙ (green), and 1013 M⊙ (blue). Even at low redshifts, it is possible for haloes to have a low metallicity and a gas mass of ∼108 M⊙.
The difference between our results and those of Agarwal et al. (2016a) arise mainly from the treatment of metal enrichment. They assume a constant velocity for the enriched winds that yields a window of 50 Myr in which DCBH formation is possible before the line-cooled halo is polluted with metals. In our model, we follow the pollution of individual haloes self-consistently. However, the important question is not only if DCBHs form in the progenitor haloes of CR7, but also if those haloes can remain below Zlimit for long enough. Otherwise, we should see the imprint of those metals in the spectrum.
4.5 Mass of metal-poor gas
We have shown in the previous sections that DCBHs and Pop III remnant BHs can reach the masses needed to explain the Ly α and the He ii luminosities of CR7. However, another important constraint are the upper limits on the O iii] 1663 Å and C iii] 1908 Å lines. The absence of these recombination lines requires the photon source to be embedded in metal-poor gas at z = 6.6. In this section, we quantify the amount of low-metallicity gas that is present in the progenitors of CR7. We use the fiducial model and account for gas in haloes with a metallicity Z < Zlimit. In previous sections we analysed the total mass of low-metallicity gas at a given redshift in all progenitors, but now we examine the maximum mass of metal-poor gas in a single halo at a given time. Its evolution over time is shown in Fig. 14. This plot shows that metal-poor haloes with a gas mass of ∼108 M⊙ are present down to redshift z = 6.6. The more important question is if these metal-poor haloes can also host a sufficiently massive BH to explain the observed line luminosities. To answer this question we show the mass of low-metallicity gas in haloes that host either a DCBH or a Pop III BH remnant in Fig. 15. Here, we plot the mass of low-metallicity gas surrounding BHs at the moment before the halo is polluted to Z > Zlimit. This enables us to quantify the lowest redshift at which a BH can reside in a pocket of low-metallicity gas. For the Pop III remnant scenario, we expect BHs in haloes with a gas mass of ≲107 M⊙ down to z = 6.6 but these BHs have masses of ≲800 M⊙, much smaller than the required mass of ≥105 M⊙. This is mainly due to the fact that either the BH progenitor itself pollutes its host halo with metals at the end of its lifetime or that another Pop III star in the same halo enriches it with metals. The only possibility to remain below Zlimit is to have Pop III stars that collapse directly to a BH. In our model, Pop III BH remnants only grow by mergers with other BHs and might be polluted during the merger. Only a few BHs merge and remain in a low-metallicity environment. We find few Pop III remnant BHs that can grow to ∼800 M⊙ before their host halo is polluted to Z > Zlimit.
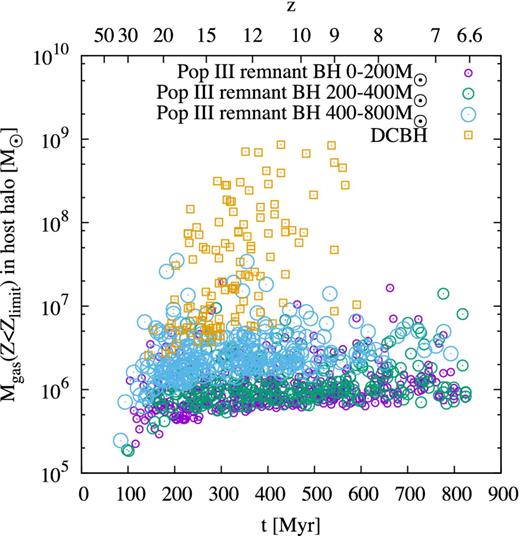
Mass of metal-poor gas (Z < Zlimit) surrounding BHs of different origin. The squares denote DCBHs, the circles are Pop III stellar remnant BHs and the colours and sizes of the circles indicates the mass of the BH. The data is taken one time step before the haloes are polluted with metals to Z > Zlimit, so the symbols mark out to which time a given type of BH can be surrounded by the indicated mass of metal-poor gas. For the red and green circles we plot only every 50th data point. By construction, the host halo of a DCBH is metal-free at the moment of formation, but shortly afterwards it generally merges with the enriched halo that previously provided the required LW flux.
In contrast, the DCBHs reside by construction in low-metallicity haloes with a much higher gas mass of up to ∼109 M⊙. These higher masses can be reached because we quench Pop III star formation in the host halo with a strong LW flux from a nearby star-forming halo. We find that DCBHs reside in a metal-free environment for only several tens of Myr before they are polluted by merging with the neighbour halo. DCBHs therefore reside in low-metallicity haloes only down to z ≈ 8.5, which is ∼240 Myr before z = 6.6. When interpreting this result, one should keep in mind that the rapidly changing metallicity of the host halo due to the merger is an artefact of our recipe for DCBH formation. For this analysis, we use an optimistic value of Jcrit = 100. The actual value can be up to an order of magnitude higher (Section 5) so the derived values should be treated with caution, since a higher Jcrit might inhibit the formation of DCBHs.
4.6 Comparison of scenarios
In this section, we compare the three models and estimate, which have the highest probability to reproduce the observations of CR7. To do so, we assume that CR7 is an ongoing merger of the three clumps A, B, and C, which merge at z0 = 6.0. This is the most plausible scenario to obtain the right constellation of masses in CR7 as shown in Fig. 16. The most massive halo B always fulfils the requirement of MB ≈ 1012 M⊙, whereas only <10 per cent of the merger tree realizations yield masses in the right range for halo A and C. As an additional constraint, we require a significant gap between the masses of the third and the fourth most massive halo at z = 6.6, because we only see three clumps in CR7 and there is no evidence of a fourth equally massive clump. Hence, we assume that the fourth most massive halo D in the merger tree should be at least an order of magnitude less massive than halo A (MD/MA ≲0.1). This mass distribution is the anticipated constellation of CR7. We analyse the metallicity, and estimate the masses of both Pop III stars (with the fiducial model) and BHs resulting from the two different seeding scenarios in halo A at z = 6.6. The results are shown in Fig. 17. For a given scenario, this plot illustrates the possible mass-metallicity combinations of the three scenarios. For Pop III stars, the stellar mass in clump A at z = 6.6 remains always below 103 M⊙ and the halo has a metallicity of ∼10−3. Pop III remnant BHs might reside in metal-poor haloes at z = 6.6, but are not massive enough (≲103 M⊙) to explain CR7. Only the DCBH scenario can explain the observed line luminosities. For the given mass constellation of the haloes A, B, C, and D, the probability that clump A hosts Pop III stars is 37 per cent, that it hosts a Pop III remnant BH is 98 per cent and that it hosts a DCBH is 10 per cent. These probabilities add up to over 100 per cent, because due to merging of the progenitor haloes, clump A can contain Pop III stars and BHs at the same time. Comparing these results to, e.g. Fig. 12 shows that it is crucial to treat CR7 as three individual clumps, since the BH mass in clump A is generally lower than the most massive BH in all CR7 progenitor haloes. The third most massive halo A is less affected by metal enrichment, but the Pop III remnant BHs do not merge to masses above 103 M⊙. Under these conditions and with the optimistic assumption of Jcrit = 100 we find that ∼90 per cent of the DCBHs reside in sufficiently metal-poor gas at z = 6.6.
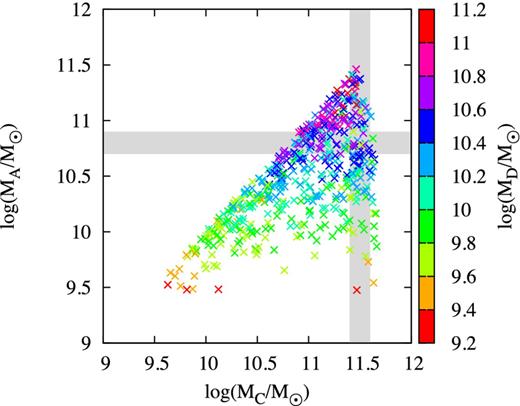
Masses of the second, third, and forth most massive haloes at z = 6.6, assuming that they merge to one halo within 100 Myr. The grey region indicates the required mass range for clump A and C of CR7 and we show 512 different merger tree realizations. Since we do not see a fourth clump within a projected distance of ∼10 kpc to CR7, we require that the fourth most massive clump in the merger tree is significantly less massive than clump A. In this sample, we find constellations in the right mass range and with MD/MA ≲0.1. The most massive clump B has always a mass of ∼1012 M⊙.
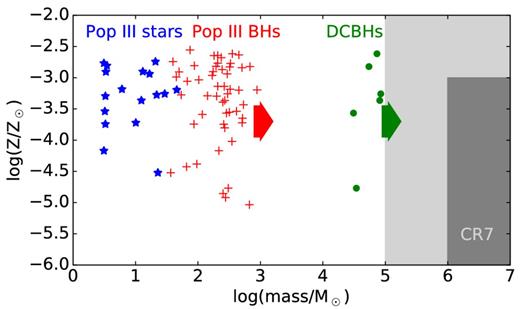
Comparison of the three different models, regarding the metallicity of clump A at z = 6.6 and the mass of the stellar population or of the BH, respectively. The grey shaded area indicates the region in which we expect the system to have the same observational signature as CR7. A Pop III stellar population has to have a mass of ∼107 M⊙ and a black hole should be in the mass range 105–107 M⊙ to yield the observed line luminosities. The upper limit of the metallicity is set by Zlimit, in order not to violate the observed metal tax, but lower values are favourable. BHs of different origin can reside in sufficiently metal-poor haloes, but, without including growth by accretion neither Pop III remnants nor DCBH are sufficiently massive to account for the observations. The arrows for the BH populations symbolize possible mass growth by gas accretion; DCBHs require less mass growth by accretion to account for the spectral properties of CR7.
Only ∼0.5 per cent of all the merger tree realizations, yield the right mass constellation and out of these, only 9 per cent produce results that are consistent with the observations of CR7. According to the Press–Schechter formalism, the number density of the host halo (Mh = 1.2 × 1012 M⊙ at z = 6.0) is n ≲10−5 Mpc−3. This yields an expected abundance of n ≲5 × 10−9 Mpc−3 for objects with the same constellation and observational signature as CR7. These estimates might even be lower with a smaller value of Zlimit, suggested by the non-detection of C iii]. The survey of Matthee et al. (2015) covers 5 deg2 in the redshift range z = 6.5 − 6.6, which corresponds to an observed volume of ∼4.3 × 106 Mpc3. The volume in the COSMOS fields, where CR7 was found, is ∼1.5 × 105 Mpc3 and the expected number density of CR7-like sources is of the order 10−6–10−7 Mpc−3 (Pallottini et al. 2015; Visbal et al. 2016). CR7, therefore, appears to have been a fortunate discovery, for the design of that survey. Larger surveys can confirm whether the mechanisms suggested in this paper occur with the expected probability or if we might have to adopt the model and assumptions to account for such rare sources.
There are other galaxies near the epoch of reionization that have comparable observational signatures. Matthee et al. (2015) find more than 10 Ly α emitter candidates potentially similar to CR7, which are worth being further investigated. Also the ‘Himiko’ galaxy is very bright and extended in Ly α, consists of three clumps of which one is very blue, and shows no sign of metals emission lines in the rest-frame UV (Ouchi et al. 2009, 2013; Zabl et al. 2015). However, no He ii emission has be confirmed for this galaxy, which disfavours Himiko as a potential host of Pop III stars.
5 CAVEATS
The main shortcoming of our semi-analytical approach is the lack of spatial information in the merger tree and hence the simplified treatment of metal enrichment. We check statistically if a halo is polluted, which yields reasonable results on average over many merger tree realizations. Once a halo is polluted we assume that the metals mix homogeneously with the gas and assign a single metallicity to the halo. However, metal-enriched winds may not mix effectively with the dense gas in minihaloes and a large fraction of this gas might remain at low metallicity (Cen & Riquelme 2008; Pallottini et al. 2014; Ritter et al. 2015; Smith et al. 2015b). Three-dimensional hydrodynamical simulations are required to obtain a more reliable metal enrichment history and identify pockets of metal-free gas.
We do not explicitly account for accretion on to BHs. In our model, the DCBHs have a seed mass of 104–105 M⊙ and the Pop III remnant BHs only gain mass by mergers. The accretion of large masses of gas is necessary to account for the observed BH mass density at z = 6 (Tanaka & Haiman 2009). Pop III remnant BHs form in minihaloes with shallow potential wells, which are unable to retain the photoionized heated gas (Johnson et al. 2007; Alvarez et al. 2009). Also the energy of a single SN from a massive star is sufficient to clear the halo of accretable gas. The average time that Pop III remnant BHs can accrete mass in our model is ∼400 Myr. To grow from a seed mass of ∼200 M⊙ to a final mass of 106 M⊙ at z = 6.6 they would have to accrete constantly at 80 per cent the Eddington rate. Using cosmological zoom-in simulations, Jeon et al. (2012) study the assembly of the first galaxies under feedback from a central BH. They find that the accretion rate on to Pop III remnant BHs remains always below 10−6 M⊙ yr−1 for a radiative efficiency of ϵ = 0.1. This is below the required accretion rate to account for the BH in CR7 at z = 6.6. Hence, the mass of the Pop III remnant BHs in our model might generally be higher, but they cannot grow sufficiently massive to account for the observations (but see Lupi et al. 2016).
In our analysis, we investigate Jcrit = 100 − 400 as the LW flux required to enable isothermal direct collapse of an atomic cooling halo. The probability for forming a DCBH is a steep function of this value (Inayoshi & Tanaka 2015) and we do not find any DCBHs in our model at Jcrit > 600. The required flux varies from halo to halo (Shang, Bryan & Haiman 2010; Latif et al. 2014) and also depends on the stellar spectrum. Pop III stars with effective temperatures of ∼105 K require Jcrit ≈ 105, whereas subsequent stellar populations have lower effective temperatures and require a smaller Jcrit (Bromm & Loeb 2003; Shang et al. 2010; Sugimura et al. 2014; Agarwal & Khochfar 2015; Latif et al. 2015). In our model, a young population of Pop II stars provides the required flux for isothermal direct collapse. We therefore expect Jcrit < 1000 (Shang et al. 2010; Agarwal et al. 2016b), but the exact value remains an open question.
A third way to form SMBHs in the early Universe is the fragmentation of gas in a low-metallicity halo into a dense nuclear cluster of low-mass stars and the subsequent build-up of a ∼103 M⊙ star via runaway mergers in the cluster (Portegies Zwart et al. 2004; Devecchi & Volonteri 2009; Lupi et al. 2014). This scenario results in the creation of a 103 M⊙ BH and requires enough low-metallicity gas to form the cluster. Although this channel can generally produce as many BHs as Pop III BH remnants, it faces the same problem as the other scenarios: how can such a BH grow to sufficient masses without the host halo being polluted by metals? Given the formation criteria for a dense cluster we expect that it might yield results comparable to those of the Pop III remnant scenario and hence not be able to explain the properties of CR7.
To create the merger trees, we use a code based on Parkinson et al. (2008). This method is tuned to reproduce the halo mass function of the Millennium simulation (Springel et al. 2005) of intermediate and high-mass haloes at redshifts z ≲4. For higher redshifts (z ≈ 30), this method tends to yield slightly more minihaloes, which are possible formation sites of Pop III stars. Using the original method by Cole et al. (2000), which is not calibrated to match the halo mass function of the Millennium simulation, we form fewer primordial stars at z > 15. This leads to a metal enrichment at later times and a higher SFR for Pop III stars at z ∼ 10. For z < 8, the mass of pristine gas is roughly the same in both models so there is no difference in the probability of finding a massive primordial halo at z = 6.6. The method of Parkinson et al. (2008) yields total stellar masses of Pop III stars at z = 6.6 that are about a factor of two lower compared to the original method by Cole et al. (2000), but this is not sufficient to account for the lack of luminosity. The mass function of minihaloes at high redshift still remains an open question and better constraints might help to improve our model of Pop III star formation.
6 CONCLUSION
We have explored the nature of CR7, a Ly α emitter at z = 6.6 (Matthee et al. 2015; Sobral et al. 2015), which has very strong Ly α and He ii signatures without any detection of metal lines in the spectrum. Using a semi-analytical merger tree model, we have investigated a variety of formation histories for CR7 and tested different scenarios for its origin.
Sobral et al. (2015) originally proposed that a recent Pop III starburst with a total stellar mass of ∼107 M⊙ or an accreting BH can account for the observational constraints. Based on our current understanding of Pop III star formation, we show that such a starburst seems not to be possible for several reasons. The mass of metal-free gas decreases with time since more and more haloes are polluted by SNe. Hence, after peaking around z ∼ 15, the cosmic SFR for Pop III stars declines sharply at lower redshifts. Moreover, very hot massive stars are required for the He ii line emission and the short lifetimes of these stars consequently requires a very recent burst, ≲1 Myr to be in agreement with the observed EW of He ii. Our model fails to reproduce the observed He ii line luminosity by about 10 orders of magnitude. Besides this fiducial model of primordial star formation, we also tested various models in which Pop III stars form in gas with a metallicity Z < Zcrit, in which star formation is based on the merger history of the halo, and in which we adopt a different IMF. None of these models can explain CR7 as a primordial star cluster.
If CR7 hosts Pop III stars, the metal pollution by these first stars must be significantly less efficient than previously assumed and we need a mechanism to form 107 M⊙ of metal-free stars synchronized in one halo within ∼1 Myr. Recently, Visbal et al. (2016) propose that photoionization feedback could prevent early star formation and hence enable the collapse of a ∼109 M⊙ halo at z ≈ 7.
We also investigate the possibility that CR7 hosts an accreting BH. This scenario seems more appealing than Pop III stars because DCBHs form down to z ∼ 7.3 and Pop III BH remnants can form down to z = 6.6. Several groups have shown that such BHs can reproduce the observational constraints (Pallottini et al. 2015; Agarwal et al. 2016a; Dijkstra et al. 2016; Pacucci et al. 2016; Smidt et al. 2016; Smith et al. 2016). However, they assume that the BH is embedded in metal-poor gas at z = 6.6, which is difficult to obtain with our model because when a Pop III star BH forms, it is very likely that a SN also enriches the halo with metals. Furthermore, we assume that Pop III star BHs mainly grow via mergers and consequently the already low possibility of finding a BH in a metal-poor halo shrinks with every merger with another halo, which could be enriched with metals. Finally, we only find Pop III BH remnants with masses <103 M⊙ in low-metallicity haloes with gas masses of ∼106 M⊙ at z = 6.6.
The most promising explanation for CR7 is an accreting DCBH. By construction, they form in a metal-free haloes and may remain in metal-poor gas until z = 6.6. Under the optimistic condition of Jcrit = 100, we find that a small fraction of systems can host DCBHs that are able to reproduce the line luminosities of CR7 without violating the upper limit of the metal-line luminosities. Our findings are supported by other observational constraints. Only an accreting BH can account for the spatial extension of the Ly α emitting region and for the velocity offset between the Ly α and He ii line peaks, because this velocity offset requires a source lifetime of >10 Myr (Smith et al. 2016). A stellar source in CR7 would however require a recent burst of ≲1 Myr, and a very low metallicity of <10−7 to account for the large EW of He ii (Schaerer 2003; Raiter et al. 2010). We note that we are not able to confirm, if an accreting BH is able to produce the EW of He ii, which is an important question to address in the future.
There are other observations that might help to better understand the nature of CR7 and distinguish between the different formation scenarios. The dwarf galaxy I ZW 18 at a distance of 18 Mpc also shows strong He ii emission and has a very low metallicity (Kehrig et al. 2015, 2016). It might host either metal-free or Wolf–Rayet stars, which could account for these observational features. Smaller haloes, such as I ZW 18, might remain unpolluted by their progenitors down to lower redshift and e.g. photoionization heating might prevent star formation for a long time (Visbal et al. 2016). The study of the assembly history of such systems might reveal interesting new insights that can help to understand more massive low-metallicity counterparts at higher redshift.
Another observational signature of whether CR7 hosts a BH or a Pop III stellar population is the X-ray flux. The expected luminosity from X-ray binaries is Lx ≈ 1040 erg s−1 for a SFR of 1 M⊙ yr−1 (Glover & Brand 2003; Grimm, Gilfanov & Sunyaev 2003; Mineo, Gilfanov & Sunyaev 2012), which is at least 2 orders of magnitude lower than the emission from a BH of ∼106 M⊙. CR7 was not detected as a point source in the Chandra COSMOS Survey. Therefore its X-ray luminosity in the energy range 0.2 − 10 keV is less than 1044 erg s−1 (Elvis et al. 2009). For a BH with a mass of 106 M⊙, accreting at 40 per cent of the Eddington rate, and a bolometric correction based on Marconi et al. (2004) we find Lx ≲2 × 1042 erg s−1 in the observer rest frame 0.2 − 10 keV band. This translates into a flux of Fx ≲8.2 × 10−18 erg cm−2 s−1 or ∼1.4 × 10−7 counts per second with Chandra in the 0.2 − 10 keV band. Hence, integration times of several years might be required, which seems infeasible until the next generation of X-ray telescopes, such as Athena (Nandra et al. 2013), could approach this problem with a significantly higher effective collecting area. Alternatively, if many more DCBH candidates similar to CR7 are found, one could stack deep X-ray observations of these objects and attempt to detect their X-ray emission using the stacked image. In this case, a successful detection would imply that some significant fraction of the candidates are indeed DCBHs, although it would not allow us to say with certainty that any particular candidate is a DCBH. With this method, however, there is no X-ray detected in the stack of Ly α emitters in the Chandra COSMOS Legacy survey (Civano et al. 2016), down to a total depth of 1.38 Ms corresponding to a luminosity of 1043 erg s−1 (at the redshift of the sources) in the 0.5 − 2 keV band (Civano, private communication). Another method to identify DCBHs was recently proposed by Pacucci et al. (2016). They identify two objects with a robust X-ray detection found in the CANDELS/GOODS-S survey with a steep spectral slope in the infrared and an extremely red spectra. They argue, based on their assumptions, that this can be explained by either a DCBH or an atypically high SFR of >1000 M⊙ yr−1. Another explanation of this spectra could be a dusty AGN without the constraint of being a DCBH.
More crucially, validation of the general scenario of a low metallicity in CR7 requires further deep spectroscopy to estimate the level of metallicity and the source of the hard spectrum in CR7. The focus should hence be to obtain deeper spectra from UV to near-IR to improve the limits on the metal-line emission and to further constrain the different formation histories. Beyond current instruments, such as MOSFIRE and X-SHOOTER, NIRSpec on JWST will be the ideal instrument to probe sources such as CR7, which provide a tantalizing preview into the initial episodes of star and BH formation, which will fully be elucidated in the near future with an array of next-generation observational facilities.
The authors would like to thank Julia Gutkin, Aida Wofford, Anna Feltre, Dan Stark, Jorryt Matthee, Mélanie Habouzit, Andrea Negri, Carolina Kehrig, and Francesca Civano for valuable discussions and helpful contributions. The authors acknowledge funding from the European Research Council under the European Community's Seventh Framework Programme (FP7/2007-2013) via the ERC Grant ‘BLACK’ under the project number 614199 (TH, MV) and via the ERC Advanced Grant ‘STARLIGHT: Formation of the First Stars’ under the project number 339177 (MM, DJW, RSK, SCOG, EWP). SCOG, RSK, and EWP acknowledge support from the DFG via SFB 881, ‘The Milky Way System’ (sub-projects B1, B2 and B8) and from SPP 1573 ‘Physics of the Interstellar Medium’. MAL has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 656428. VB was supported by NSF grant AST-1413501.
REFERENCES



