-
PDF
- Split View
-
Views
-
Cite
Cite
D. Emmanoulopoulos, I. E. Papadakis, A. Epitropakis, T. Pecháček, M. Dovčiak, I. M. McHardy, A search for X-ray reprocessing echoes in the power spectral density functions of AGN, Monthly Notices of the Royal Astronomical Society, Volume 461, Issue 2, 11 September 2016, Pages 1642–1655, https://doi.org/10.1093/mnras/stw1359
Close - Share Icon Share
Abstract
We present the results of a detailed study of the X-ray power spectral density (PSD) functions of 12 X-ray bright AGN, using almost all the archival XMM–Newton data. The total net exposure of the EPIC-pn light curves is larger than 350 ks in all cases (and exceeds 1 Ms in the case of 1H 0707−497). In a physical scenario in which X-ray reflection occurs in the inner part of the accretion disc of AGN, the X-ray reflection component should be a filtered echo of the X-ray continuum signal and should be equal to the convolution of the primary emission with the response function of the disc. Our primary objective is to search for these reflection features in the 5–7 keV (iron line) and 0.5–1 keV (soft) bands, where the X-ray reflection fraction is expected to be dominant. We fit to the observed periodograms two models: a simple bending power-law model (BPL) and a BPL model convolved with the transfer function of the accretion disc assuming the lamp-post geometry and X-ray reflection from a homogeneous disc. We do not find any significant features in the best-fitting BPL model residuals either in individual PSDs in the iron band, soft and full band (0.3–10 keV) or in the average PSD residuals of the brightest and more variable sources (with similar black hole mass estimates). The typical amplitude of the soft and full-band residuals is around 3–5 per cent. It is possible that the expected general relativistic effects are not detected because they are intrinsically lower than the uncertainty of the current PSDs, even in the strong relativistic case in which X-ray reflection occurs on a disc around a fast rotating black hole having an X-ray source very close above it. However, we could place strong constrains to the X-ray reflection geometry with the current data sets if we knew in advance the intrinsic shape of the X-ray PSDs, particularly its high-frequency slope.
1 INTRODUCTION
It has been over 20 years since the first detection of iron emission lines in the X-ray spectra of active galactic nuclei (AGN), and the first observational evidence of their asymmetrical shape (e.g. Nandra & Pounds 1994; Tanaka et al. 1995). Since then, the general and special relativity effects to the line's shape have been studied extensively (e.g. Fabian et al. 1989; Laor 1991; Dovčiak, Karas & Matt 2004; Brenneman & Reynolds 2006; Dauser et al. 2010). The modelling of the iron-line profiles, and of other X-ray reflection spectral features (like e.g. the ‘soft-excess’ and the ‘Compton-hump’), has been an important tool for the investigation of the X-ray source/accretion disc geometry in X-ray bright AGN. Recently, the discovery of the so-called ‘X-ray reverberation time-lags’ in many AGN, e.g. Fabian et al. (2009), Emmanoulopoulos, McHardy & Papadakis (2011), De Marco et al. (2013), Zoghbi et al. (2013), Kara et al. (2015) (also see for a recent review Uttley et al. 2014), has provided an extra support for the case of the X-ray illumination of the innermost regions of the accretion disc. The observed time delays suggest a small-sized X-ray source located atop a disc, extending down to the innermost stable orbital radius (ISCO) around a supermassive black hole (BH), which is in many cases fast rotating (e.g. Wilkins & Fabian 2013; Cackett et al. 2014; Emmanoulopoulos et al. 2014; Chainakun & Young 2015).
Recently, Papadakis et al. (2016) (hereafter P16) proposed a new method to investigate the X-ray reprocessing scenario, based on the study of the X-ray power spectral density (PSD) functions. If the innermost parts of AGN are illuminated by the X-ray source, the observed X-rays should be the sum of the X-ray photons emitted by the source and those which are reprocessed by the disc. The latter component is a filtered echo of the X-ray continuum signal, and should be equal to the convolution of the primary emission with the response function of the disc. As a result, the observed power spectra should display features of this echo.
P16 assumed the so-called lamp-post geometry, a neutral disc with solar iron abundance, and considered various X-ray source heights, inclinations, and spin values of the central BH. They found that the ratio between the observed PSDs over the intrinsic ones should show a prominent dip, followed by oscillations around a constant power level, with decreasing amplitude at higher frequencies. The frequency of the main dip is determined by both the BH mass and the X-ray source height, and it is energy independent. The amplitude of the dip increases with increasing BH spin and inclination angle, as long as the height of the lamp is smaller than 10 gravitational radii, rg.
We present the results from a detailed X-ray PSD study of 12 AGN, observed by XMM–Newton. Our primary aim is to search for X-ray reverberation signals in the observed PSDs by fitting them with the theoretical models developed by P16. The reflection fraction is expected to be quite strong in the 5–7 keV band, which includes most of the iron-line emission at around 6.4 keV (the iron-line band hereafter), and the P16 results are directly applicable to the PSDs in this band. However, the signal-to-noise ratio of the light curves in the iron-line band is significantly smaller than the signal-to-noise ratio of light curves at lower energies of 0.5–1.5 keV. Many AGN show emission in excess of the extrapolation of the power-law spectral component at such low energies, which can be more than twice the power-law continuum flux. This so-called ‘soft-excess’ component is consistent with X-ray reflection from the inner parts of a mildly ionized accretion disc (e.g. Crummy et al. 2006). We therefore decided to study PSD in both the iron-line and the 0.5–1 keV band (the soft band hereafter) in order to search for relativistically induced echo features.
In Section 2 we present our sample, the observations and the data reduction procedure for the construction of the light curves. Following that, in Section 3 we outline the power spectrum estimation method together with our objective. In Section 4 we present in detail our model fitting approach to the observed PSDs, giving also the best-fitting results. In Section 5 we compare the best-fitting results from the different models. Finally, in Section 6 we summarize our results and discuss possible implications.
2 OBSERVATIONS AND DATA REDUCTION
Table 1 lists the objects that we study, together with the details about the corresponding XMM–Newton observations. The first, second and third columns list the source name together with the BH mass estimate (MBH), the observation identifier (obs ID), and the net exposure of each observation, respectively. Note that the objects are listed in order of increasing MBH. The number in the parenthesis, next to the source name, indicates the number of 10 ks segments that we use to estimate the PSDs (see Section 3).
The sample and the XMM–Newton observations. Columns 1 list the source name and BH mass estimate (together with the corresponding reference). The number in square brackets, next to the AGN name, indicates the number of the 10 ks light-curve segments that we used for the PSD estimation. Columns 2 list the XMM–Newton observation IDs, and Columns 3 list the net exposure of the observations that we used (i.e. the total light-curve duration after background subtraction and screening).
| (1) . | (2) . | (3) . |
|---|---|---|
| AGN name . | Obs ID . | Net exp. . |
| BH mass (× 106 M⊙) . | . | (ks) . |
| NGC 7314 [36] | ||
| 0.87 ± 0.45 | 0111790101 | 43.3 |
| McHardy (2013) | 0311190101 | 77.5 |
| 0725200101 | 124.7 | |
| 0725200301 | 130.6 | |
| NGC 4051 [51] | ||
| |$1.73^{+0.55}_{-0.52}$| | 0109141401 | 103.0 |
| Denney et al. (2010) | 0157560101 | 50.0 |
| 0606320101 | 45.3 | |
| 0606320201 | 42.0 | |
| 0606320301 | 21.1 | |
| 0606320401 | 18.9 | |
| 0606321301 | 30.2 | |
| 0606321501 | 34.0 | |
| 0606321601 | 41.5 | |
| 0606321701 | 38.4 | |
| 0606321801 | 18.8 | |
| 0606322001 | 22.1 | |
| 0606322101 | 29.2 | |
| 0606322201 | 30.8 | |
| 0606322301 | 42.3 | |
| Mrk 766 [55] | ||
| |$1.76^{+1.56}_{-1.40}$| | 0109141301 | 116.9 |
| Bentz et al. (2009) | 0304030101 | 95.1 |
| 0304030301 | 98.5 | |
| 0304030401 | 93.0 | |
| 0304030501 | 74.7 | |
| 0304030601 | 85.2 | |
| 0304030701 | 29.1 | |
| Ark 564 [50] | ||
| 2.32 ± 0.41a | 0206400101 | 98.7 |
| 0670130201 | 59.1 | |
| 0670130301 | 55.5 | |
| 0670130401 | 56.7 | |
| 0670130501 | 66.9 | |
| 0670130601 | 57.0 | |
| 0670130701 | 43.5 | |
| 0670130801 | 57.8 | |
| 0670130901 | 55.5 | |
| 0006810101 | 10.6 | |
| 1H 0707−495 [121] | ||
| 2.34 ± 0.71 | 0110890201 | 40.7 |
| Zhou & Wang (2005) | 0148010301 | 78.1 |
| 0506200201 | 38.7 | |
| 0506200301 | 38.7 | |
| 0506200401 | 40.6 | |
| 0506200501 | 40.9 | |
| 0511580101 | 121.6 | |
| 0511580201 | 102.1 | |
| 0511580301 | 104.1 | |
| 0511580401 | 101.8 | |
| 0554710801 | 96.1 | |
| 0653510301 | 113.8 | |
| 0653510401 | 125.7 | |
| 0653510501 | 116.9 | |
| 0653510601 | 119.5 | |
| MCG–6-30-15 [68] | ||
| |$4.5^{+1.5}_{-1.0}$| | 0693781201 | 127.2 |
| McHardy (2013) | 0693781301 | 129.7 |
| 0693781401 | 48.5 | |
| 0111570101 | 33.1 | |
| 0111570201 | 53.0 | |
| 0029740101 | 80.6 | |
| 0029740701 | 122.5 | |
| 0029740801 | 124.1 | |
| IRAS 13224−3809 [34] | ||
| 5.75 ± 0.82 | 0110890101 | 37.4 |
| Zhou & Wang (2005) | 0673580101 | 50.3 |
| 0673580201 | 84.1 | |
| 0673580301 | 73.9 | |
| 0673580401 | 113.5 | |
| SWIFT J2127+5654 [43] | ||
| 15 | 0655450101 | 117.1 |
| Malizia et al. (2008) | 0693781701 | 134.6 |
| 0693781801 | 129.7 | |
| 0693781901 | 71.4 | |
| Mrk 335 [35] | ||
| 26 ± 8 | 0101040101 | 31.6 |
| Grier et al. (2012) | 0306870101 | 122.5 |
| 0510010701 | 16.8 | |
| 0600540501 | 80.7 | |
| 0600540601 | 112.3 | |
| NGC 3516 [40] | ||
| |$31.7^{+2.8}_{-4.2}$| | 0107460601 | 89.4 |
| Denney et al. (2010) | 0107460701 | 122.2 |
| 0401210401 | 51.8 | |
| 0401210501 | 60.8 | |
| 0401210601 | 61.7 | |
| 0401211001 | 36.2 | |
| PG 1211+143b [62] | ||
| 146 ± 44 | 0112610101 | 53.1 |
| Peterson et al. (2004) | 0502050101 | 46.3 |
| 0745110101 | 77.4 | |
| 0745110201 | 98.2 | |
| 0745110301 | 51.8 | |
| 0745110401 | 92.0 | |
| 0745110501 | 54.6 | |
| 0745110601 | 91.9 | |
| 0745110701 | 95.6 | |
| PKS 0558−504 [56] | ||
| |$250^{+50}_{-190}$| | 0555170201 | 102.7 |
| Gliozzi et al. (2010) | 0555170301 | 111.3 |
| 0555170401 | 123.3 | |
| 0555170501 | 123.1 | |
| 0555170601 | 111.0 |
| (1) . | (2) . | (3) . |
|---|---|---|
| AGN name . | Obs ID . | Net exp. . |
| BH mass (× 106 M⊙) . | . | (ks) . |
| NGC 7314 [36] | ||
| 0.87 ± 0.45 | 0111790101 | 43.3 |
| McHardy (2013) | 0311190101 | 77.5 |
| 0725200101 | 124.7 | |
| 0725200301 | 130.6 | |
| NGC 4051 [51] | ||
| |$1.73^{+0.55}_{-0.52}$| | 0109141401 | 103.0 |
| Denney et al. (2010) | 0157560101 | 50.0 |
| 0606320101 | 45.3 | |
| 0606320201 | 42.0 | |
| 0606320301 | 21.1 | |
| 0606320401 | 18.9 | |
| 0606321301 | 30.2 | |
| 0606321501 | 34.0 | |
| 0606321601 | 41.5 | |
| 0606321701 | 38.4 | |
| 0606321801 | 18.8 | |
| 0606322001 | 22.1 | |
| 0606322101 | 29.2 | |
| 0606322201 | 30.8 | |
| 0606322301 | 42.3 | |
| Mrk 766 [55] | ||
| |$1.76^{+1.56}_{-1.40}$| | 0109141301 | 116.9 |
| Bentz et al. (2009) | 0304030101 | 95.1 |
| 0304030301 | 98.5 | |
| 0304030401 | 93.0 | |
| 0304030501 | 74.7 | |
| 0304030601 | 85.2 | |
| 0304030701 | 29.1 | |
| Ark 564 [50] | ||
| 2.32 ± 0.41a | 0206400101 | 98.7 |
| 0670130201 | 59.1 | |
| 0670130301 | 55.5 | |
| 0670130401 | 56.7 | |
| 0670130501 | 66.9 | |
| 0670130601 | 57.0 | |
| 0670130701 | 43.5 | |
| 0670130801 | 57.8 | |
| 0670130901 | 55.5 | |
| 0006810101 | 10.6 | |
| 1H 0707−495 [121] | ||
| 2.34 ± 0.71 | 0110890201 | 40.7 |
| Zhou & Wang (2005) | 0148010301 | 78.1 |
| 0506200201 | 38.7 | |
| 0506200301 | 38.7 | |
| 0506200401 | 40.6 | |
| 0506200501 | 40.9 | |
| 0511580101 | 121.6 | |
| 0511580201 | 102.1 | |
| 0511580301 | 104.1 | |
| 0511580401 | 101.8 | |
| 0554710801 | 96.1 | |
| 0653510301 | 113.8 | |
| 0653510401 | 125.7 | |
| 0653510501 | 116.9 | |
| 0653510601 | 119.5 | |
| MCG–6-30-15 [68] | ||
| |$4.5^{+1.5}_{-1.0}$| | 0693781201 | 127.2 |
| McHardy (2013) | 0693781301 | 129.7 |
| 0693781401 | 48.5 | |
| 0111570101 | 33.1 | |
| 0111570201 | 53.0 | |
| 0029740101 | 80.6 | |
| 0029740701 | 122.5 | |
| 0029740801 | 124.1 | |
| IRAS 13224−3809 [34] | ||
| 5.75 ± 0.82 | 0110890101 | 37.4 |
| Zhou & Wang (2005) | 0673580101 | 50.3 |
| 0673580201 | 84.1 | |
| 0673580301 | 73.9 | |
| 0673580401 | 113.5 | |
| SWIFT J2127+5654 [43] | ||
| 15 | 0655450101 | 117.1 |
| Malizia et al. (2008) | 0693781701 | 134.6 |
| 0693781801 | 129.7 | |
| 0693781901 | 71.4 | |
| Mrk 335 [35] | ||
| 26 ± 8 | 0101040101 | 31.6 |
| Grier et al. (2012) | 0306870101 | 122.5 |
| 0510010701 | 16.8 | |
| 0600540501 | 80.7 | |
| 0600540601 | 112.3 | |
| NGC 3516 [40] | ||
| |$31.7^{+2.8}_{-4.2}$| | 0107460601 | 89.4 |
| Denney et al. (2010) | 0107460701 | 122.2 |
| 0401210401 | 51.8 | |
| 0401210501 | 60.8 | |
| 0401210601 | 61.7 | |
| 0401211001 | 36.2 | |
| PG 1211+143b [62] | ||
| 146 ± 44 | 0112610101 | 53.1 |
| Peterson et al. (2004) | 0502050101 | 46.3 |
| 0745110101 | 77.4 | |
| 0745110201 | 98.2 | |
| 0745110301 | 51.8 | |
| 0745110401 | 92.0 | |
| 0745110501 | 54.6 | |
| 0745110601 | 91.9 | |
| 0745110701 | 95.6 | |
| PKS 0558−504 [56] | ||
| |$250^{+50}_{-190}$| | 0555170201 | 102.7 |
| Gliozzi et al. (2010) | 0555170301 | 111.3 |
| 0555170401 | 123.3 | |
| 0555170501 | 123.1 | |
| 0555170601 | 111.0 |
The sample and the XMM–Newton observations. Columns 1 list the source name and BH mass estimate (together with the corresponding reference). The number in square brackets, next to the AGN name, indicates the number of the 10 ks light-curve segments that we used for the PSD estimation. Columns 2 list the XMM–Newton observation IDs, and Columns 3 list the net exposure of the observations that we used (i.e. the total light-curve duration after background subtraction and screening).
| (1) . | (2) . | (3) . |
|---|---|---|
| AGN name . | Obs ID . | Net exp. . |
| BH mass (× 106 M⊙) . | . | (ks) . |
| NGC 7314 [36] | ||
| 0.87 ± 0.45 | 0111790101 | 43.3 |
| McHardy (2013) | 0311190101 | 77.5 |
| 0725200101 | 124.7 | |
| 0725200301 | 130.6 | |
| NGC 4051 [51] | ||
| |$1.73^{+0.55}_{-0.52}$| | 0109141401 | 103.0 |
| Denney et al. (2010) | 0157560101 | 50.0 |
| 0606320101 | 45.3 | |
| 0606320201 | 42.0 | |
| 0606320301 | 21.1 | |
| 0606320401 | 18.9 | |
| 0606321301 | 30.2 | |
| 0606321501 | 34.0 | |
| 0606321601 | 41.5 | |
| 0606321701 | 38.4 | |
| 0606321801 | 18.8 | |
| 0606322001 | 22.1 | |
| 0606322101 | 29.2 | |
| 0606322201 | 30.8 | |
| 0606322301 | 42.3 | |
| Mrk 766 [55] | ||
| |$1.76^{+1.56}_{-1.40}$| | 0109141301 | 116.9 |
| Bentz et al. (2009) | 0304030101 | 95.1 |
| 0304030301 | 98.5 | |
| 0304030401 | 93.0 | |
| 0304030501 | 74.7 | |
| 0304030601 | 85.2 | |
| 0304030701 | 29.1 | |
| Ark 564 [50] | ||
| 2.32 ± 0.41a | 0206400101 | 98.7 |
| 0670130201 | 59.1 | |
| 0670130301 | 55.5 | |
| 0670130401 | 56.7 | |
| 0670130501 | 66.9 | |
| 0670130601 | 57.0 | |
| 0670130701 | 43.5 | |
| 0670130801 | 57.8 | |
| 0670130901 | 55.5 | |
| 0006810101 | 10.6 | |
| 1H 0707−495 [121] | ||
| 2.34 ± 0.71 | 0110890201 | 40.7 |
| Zhou & Wang (2005) | 0148010301 | 78.1 |
| 0506200201 | 38.7 | |
| 0506200301 | 38.7 | |
| 0506200401 | 40.6 | |
| 0506200501 | 40.9 | |
| 0511580101 | 121.6 | |
| 0511580201 | 102.1 | |
| 0511580301 | 104.1 | |
| 0511580401 | 101.8 | |
| 0554710801 | 96.1 | |
| 0653510301 | 113.8 | |
| 0653510401 | 125.7 | |
| 0653510501 | 116.9 | |
| 0653510601 | 119.5 | |
| MCG–6-30-15 [68] | ||
| |$4.5^{+1.5}_{-1.0}$| | 0693781201 | 127.2 |
| McHardy (2013) | 0693781301 | 129.7 |
| 0693781401 | 48.5 | |
| 0111570101 | 33.1 | |
| 0111570201 | 53.0 | |
| 0029740101 | 80.6 | |
| 0029740701 | 122.5 | |
| 0029740801 | 124.1 | |
| IRAS 13224−3809 [34] | ||
| 5.75 ± 0.82 | 0110890101 | 37.4 |
| Zhou & Wang (2005) | 0673580101 | 50.3 |
| 0673580201 | 84.1 | |
| 0673580301 | 73.9 | |
| 0673580401 | 113.5 | |
| SWIFT J2127+5654 [43] | ||
| 15 | 0655450101 | 117.1 |
| Malizia et al. (2008) | 0693781701 | 134.6 |
| 0693781801 | 129.7 | |
| 0693781901 | 71.4 | |
| Mrk 335 [35] | ||
| 26 ± 8 | 0101040101 | 31.6 |
| Grier et al. (2012) | 0306870101 | 122.5 |
| 0510010701 | 16.8 | |
| 0600540501 | 80.7 | |
| 0600540601 | 112.3 | |
| NGC 3516 [40] | ||
| |$31.7^{+2.8}_{-4.2}$| | 0107460601 | 89.4 |
| Denney et al. (2010) | 0107460701 | 122.2 |
| 0401210401 | 51.8 | |
| 0401210501 | 60.8 | |
| 0401210601 | 61.7 | |
| 0401211001 | 36.2 | |
| PG 1211+143b [62] | ||
| 146 ± 44 | 0112610101 | 53.1 |
| Peterson et al. (2004) | 0502050101 | 46.3 |
| 0745110101 | 77.4 | |
| 0745110201 | 98.2 | |
| 0745110301 | 51.8 | |
| 0745110401 | 92.0 | |
| 0745110501 | 54.6 | |
| 0745110601 | 91.9 | |
| 0745110701 | 95.6 | |
| PKS 0558−504 [56] | ||
| |$250^{+50}_{-190}$| | 0555170201 | 102.7 |
| Gliozzi et al. (2010) | 0555170301 | 111.3 |
| 0555170401 | 123.3 | |
| 0555170501 | 123.1 | |
| 0555170601 | 111.0 |
| (1) . | (2) . | (3) . |
|---|---|---|
| AGN name . | Obs ID . | Net exp. . |
| BH mass (× 106 M⊙) . | . | (ks) . |
| NGC 7314 [36] | ||
| 0.87 ± 0.45 | 0111790101 | 43.3 |
| McHardy (2013) | 0311190101 | 77.5 |
| 0725200101 | 124.7 | |
| 0725200301 | 130.6 | |
| NGC 4051 [51] | ||
| |$1.73^{+0.55}_{-0.52}$| | 0109141401 | 103.0 |
| Denney et al. (2010) | 0157560101 | 50.0 |
| 0606320101 | 45.3 | |
| 0606320201 | 42.0 | |
| 0606320301 | 21.1 | |
| 0606320401 | 18.9 | |
| 0606321301 | 30.2 | |
| 0606321501 | 34.0 | |
| 0606321601 | 41.5 | |
| 0606321701 | 38.4 | |
| 0606321801 | 18.8 | |
| 0606322001 | 22.1 | |
| 0606322101 | 29.2 | |
| 0606322201 | 30.8 | |
| 0606322301 | 42.3 | |
| Mrk 766 [55] | ||
| |$1.76^{+1.56}_{-1.40}$| | 0109141301 | 116.9 |
| Bentz et al. (2009) | 0304030101 | 95.1 |
| 0304030301 | 98.5 | |
| 0304030401 | 93.0 | |
| 0304030501 | 74.7 | |
| 0304030601 | 85.2 | |
| 0304030701 | 29.1 | |
| Ark 564 [50] | ||
| 2.32 ± 0.41a | 0206400101 | 98.7 |
| 0670130201 | 59.1 | |
| 0670130301 | 55.5 | |
| 0670130401 | 56.7 | |
| 0670130501 | 66.9 | |
| 0670130601 | 57.0 | |
| 0670130701 | 43.5 | |
| 0670130801 | 57.8 | |
| 0670130901 | 55.5 | |
| 0006810101 | 10.6 | |
| 1H 0707−495 [121] | ||
| 2.34 ± 0.71 | 0110890201 | 40.7 |
| Zhou & Wang (2005) | 0148010301 | 78.1 |
| 0506200201 | 38.7 | |
| 0506200301 | 38.7 | |
| 0506200401 | 40.6 | |
| 0506200501 | 40.9 | |
| 0511580101 | 121.6 | |
| 0511580201 | 102.1 | |
| 0511580301 | 104.1 | |
| 0511580401 | 101.8 | |
| 0554710801 | 96.1 | |
| 0653510301 | 113.8 | |
| 0653510401 | 125.7 | |
| 0653510501 | 116.9 | |
| 0653510601 | 119.5 | |
| MCG–6-30-15 [68] | ||
| |$4.5^{+1.5}_{-1.0}$| | 0693781201 | 127.2 |
| McHardy (2013) | 0693781301 | 129.7 |
| 0693781401 | 48.5 | |
| 0111570101 | 33.1 | |
| 0111570201 | 53.0 | |
| 0029740101 | 80.6 | |
| 0029740701 | 122.5 | |
| 0029740801 | 124.1 | |
| IRAS 13224−3809 [34] | ||
| 5.75 ± 0.82 | 0110890101 | 37.4 |
| Zhou & Wang (2005) | 0673580101 | 50.3 |
| 0673580201 | 84.1 | |
| 0673580301 | 73.9 | |
| 0673580401 | 113.5 | |
| SWIFT J2127+5654 [43] | ||
| 15 | 0655450101 | 117.1 |
| Malizia et al. (2008) | 0693781701 | 134.6 |
| 0693781801 | 129.7 | |
| 0693781901 | 71.4 | |
| Mrk 335 [35] | ||
| 26 ± 8 | 0101040101 | 31.6 |
| Grier et al. (2012) | 0306870101 | 122.5 |
| 0510010701 | 16.8 | |
| 0600540501 | 80.7 | |
| 0600540601 | 112.3 | |
| NGC 3516 [40] | ||
| |$31.7^{+2.8}_{-4.2}$| | 0107460601 | 89.4 |
| Denney et al. (2010) | 0107460701 | 122.2 |
| 0401210401 | 51.8 | |
| 0401210501 | 60.8 | |
| 0401210601 | 61.7 | |
| 0401211001 | 36.2 | |
| PG 1211+143b [62] | ||
| 146 ± 44 | 0112610101 | 53.1 |
| Peterson et al. (2004) | 0502050101 | 46.3 |
| 0745110101 | 77.4 | |
| 0745110201 | 98.2 | |
| 0745110301 | 51.8 | |
| 0745110401 | 92.0 | |
| 0745110501 | 54.6 | |
| 0745110601 | 91.9 | |
| 0745110701 | 95.6 | |
| PKS 0558−504 [56] | ||
| |$250^{+50}_{-190}$| | 0555170201 | 102.7 |
| Gliozzi et al. (2010) | 0555170301 | 111.3 |
| 0555170401 | 123.3 | |
| 0555170501 | 123.1 | |
| 0555170601 | 111.0 |
The objects in our sample are X-ray bright AGN and have been extensively studied in X-rays and they were selected based on the large number of XMM–Newton observations obtained for each one of them. We have used almost all observations in the XMM–Newton archive for each object, except from few observations having a net exposure time less than 10 ks, as this is the minimum duration for the periodogram estimation (see Section 3). The total net exposure of the light curves is larger than 350 ks for all objects in the sample.
We processed the data from the XMM–Newton satellite using the scientific analysis system (sas v. 14.0.0; Gabriel et al. 2004). We considered only EPIC-pn data (Strüder et al. 2001). Source and background light curves were extracted from circular regions on the CCD, with the former having a fixed radius of 800 pixels (40 arcsec) centred at the source coordinates listed on the NASA/IPAC Extragalactic Database. The positions and radii of the background regions were determined by placing them sufficiently far from the location of the source, while remaining within the boundaries of the same CCD chip.
The source and background light curves were extracted in the 0.5–1 and 5–7 keV energy bands, with a bin size of Δt = 100 s, using the sas command evselect. We included the criteria PATTERN = 0 − 4 and FLAG = 0 in the extraction process, which select only single and double pixel events, rejecting at the same time bad pixels from the edges of the detector's CCD chips. Periods of high background flaring activity were determined by inspecting the 10–12 keV light curves (which should include a negligible number of source photons) and they were extracted from the whole surface of the detector. These periods were then excluded during the source and background light curve extraction process.
We checked all source light curves for pile-up using the sas task epatplot, and found that only observations 670130201, 670130501 and 670130901 of Ark 564 are affected. For those observations we used annular instead of circular source regions with inner radii of 280, 200 and 250 pixels (the outer radii were held at 800 pixels), respectively, which we found to adequately reduce the effects of ‘pile-up’.
The background light curves were then subtracted from the corresponding source light curves using the sas tool epiclccorr. Most of the resulting light curves were continuously sampled, except for a few cases which contained a small number of missing observations. These were either randomly distributed throughout the duration of an observation, or appeared in groups of less than 10 points. We replaced the missing observations by linear interpolation, with the addition of the appropriate Poisson noise.
3 POWER SPECTRAL DENSITY ESTIMATION
This PSD estimation method is meaningful in the case when the intrinsic PSD does not vary with time, i.e. the X-ray variability process is stationary. The well-known rms–flux relation in AGN (Uttley & McHardy 2001) suggests that AGN PSDs should vary in amplitude with flux and, at least in the case of NGC 4051, this has been observed (Vaughan et al. 2011). Even if that is the case in all AGN, the PSDs we estimate should be representative of the mean PSDs in AGN. We discuss this issue further in Appendices A and B.
Fig. 1 shows the observed power spectra of MCG–6-30-15 and IRAS 13224−3809 (upper and lower panels, respectively). The left and right panels show the soft and iron-line band PSDs, respectively, and the open circles, at high frequencies, indicate the absolute value of the negative PSD points, i.e. when the Poisson noise level, at a given Fourier frequency, is greater than the actual observed PSD value. The iron-line band PSDs at high frequencies are more ‘noisy’ than the soft-band PSDs. In fact, the iron-line band PSD in the case of IRAS 13224−3809 is heavily dominated by the experimental noise variations even up to the lowest frequencies probed by the 10 ks segments. As a result, the error of the averaged periodograms at almost all frequencies is very large. This is mainly due to the fact that this source is not as bright as MCG–6-30-15 in the 5–7 keV band.
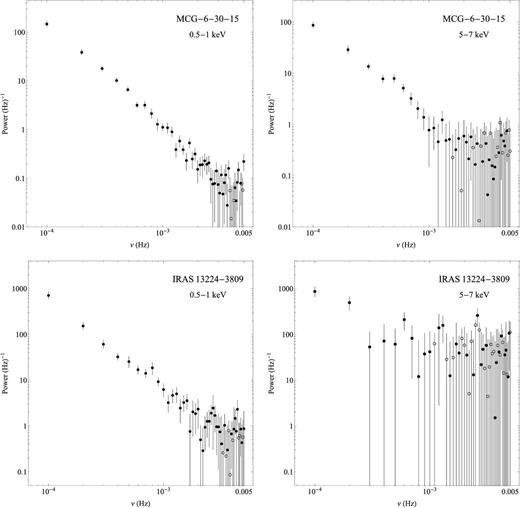
The observed PSDs for MCG–6-30-15 and IRAS 13224−3809 with the Poison noise level (equation 2) subtracted, in the top and bottom panels, respectively. The filled circles correspond to the positive estimates and the open circles correspond to the absolute values of the negative estimates, i.e. when the Poisson noise level, at a given Fourier frequency, is greater than the actual observed PSD value. Left-hand panels: the observed PSDs in the soft band. Right-hand panels: the observed PSDs in the iron-line band.
The 5–7 keV PSD of IRAS 13224−3809 is characteristic of most sources in the sample. The Poisson noise dominates the observed variations at frequencies higher than 10−3 Hz, except from four sources, namely MCG–6-30-15, NGC 4051, Ark 564, and NGC 7314. The iron-line band PSD in these sources is well defined over the lowest sampled frequency decade, i.e. between 10−4 and 10−3 Hz. This is not surprising, as these sources are among the X-ray brightest in our sample (hence the Poisson noise level is low) and they probably host a low-mass BH as well, implying large amplitude variations at high frequencies.
3.1 Our objective
After fitting the simple BPL model (equation 3) to the observed PSDs, we will also fit to them the BPLGRE model (equation 4). The main objective of this study is to compare the goodness of fit between the BPL and BPLGRE models and investigate whether the BPLGRE is favoured over the BPL model. In such a scenario reprocessing GRE signatures should be imprinted in the X-ray PSDs of AGN, despite the fact that such detections are not trivial, as we discuss below.
3.2 Detecting the GRE signatures in the currently observed PSDs
In this section we check how ‘easy it will be to detect the GRE features in practice. The continuous lines in the upper two panels of Fig. 2 show the BPL model with A = 0.03, νb = 2.3 × 10−4 Hz, and sh = 2.2 (these parameters are similar to the best-fitting BPL model parameters in the 0.5–1 keV band periodogram of NGC 4051; Emmanoulopoulos, McHardy & Papadakis 2013). The continuous lines in the lower panels of the same figure show the BPL model in the case of the PSD bend frequency being 10 times lower. The BPL normalization is defined in such a way so that the power at the bend frequency (i.e. PSD(νb) × νb) will be the same in both PSDs. In all panels, the data are plotted in the frequency range that our PSD samples are estimated (i.e. between 10−4 and 5 × 10−3 Hz).
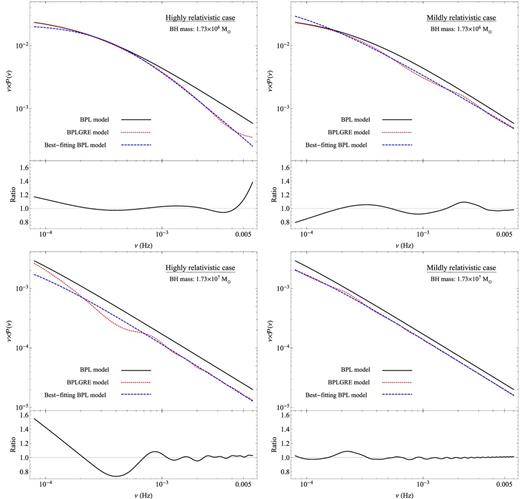
The expected GRE features for a BH mass of 1.73 × 106 M⊙ (as the one in NGC 4051) and 1.73 × 107 M⊙, in the top and bottom panels, respectively. Left-hand panels: the ‘highly relativistic’ case (α = 1, and a point-like X-ray source located at a height of h = 3.6rg). The black solid lines indicate the BPL model PSD, the red dotted lines indicate the respective BPLGRE model PSDs and the blue dashed lines indicate the best-fitting BPL model to the BPLGRE model PSDs. The attached plots, at the bottom of each panel, show the ratio of the BPLGRE model PSDs (red dotted lines in the upper panels) over the respective best-fitting BPL model (blue dashed lines in the upper panels). Right-hand panels: the same as before for a ‘mildly relativistic’ case (α = 0 and h = 21.3rg) (see Section 3.2 for further details).
The red dotted lines indicate the same BPL models multiplied by |$|\Gamma (\nu ;3.6\,r_{\rm g},1,40{^\circ } )|^{2}$| and |$|\Gamma (\nu ;21.3\,r_{\rm g},0,40{^\circ } )|^{2}$| (left and right panels, respectively). The former is the square of the transfer function in a ‘highly relativistic’ case: a Kerr BH where the lamp is located at a distance of 3.6 rg above the disc (this is similar to the mean height of the X-ray source in AGN, according to the results of Emmanoulopoulos et al. 2014). The latter corresponds to a ‘mildly relativistic’ case: a non-rotating BH and the X-ray source located further away from the disc at 21.3rg. In the upper panel plots, we assume MBH = 1.73 × 106 M⊙, i.e. the BH mass estimate of NGC 4051. In the lower panels we assume a 10 times larger BH mass (since the bend frequency is 10 times lower). If the intrinsic PSDs have a BPL shape, and the X-ray/disc geometry in AGN is similar to the lamp-post configuration, the observed PSDs should be similar to the red dotted lines, i.e. the expected BPLGRE PSDs, in Fig. 2.
To check in practice the detectability of the GRE features, we fit a simple BPL model (black solid lines) to the predicted BPLGRE PSDs (red dotted lines). The resulting best-fitting models are indicated by the blue dashed lines. The bottom plots in each panel indicate the ratio of the BPLGRE PSDs over the best-fitting BPL models to them. Interestingly, a simple BPL model fits well the BPLGRE model PSDs over the frequency range we sample. The GRE features have a smaller amplitude in the ‘mildly relativistic’ case but, even in the ‘highly relativistic’ case, the best-fitting ratios are less than 20 per cent, at all frequencies, except from the lowest frequency point in the large BH mass case (see the bottom plot in the lower left-hand panel of Fig. 2).
The results above show that it will be difficult to detect the GRE effects in objects with small BHs (like NGC 4051). The observed PSDs should be well fitted by a BPL model, with a slope steeper than the intrinsic one (which is unknown a priori). The amplitude of the expected best-fitting residuals for a BPL model fit will be less than 20 per cent, even in the ‘highly relativistic’ case. The amplitude of the residuals may increase at the highest frequency sampled by the data, but the PSD uncertainties due to the Poisson noise will be much larger there, even for the brightest and most variable sources in our sample. Similarly, the detection will not be much easier for larger BH mass objects. The largest amplitude residual is expected at the lowest frequency points in the observed PSDs in the ‘highly relativistic’ case. At all the other frequencies the residuals’ amplitude will be smaller than 20 per cent, and significantly smaller in the ‘mildly relativistic’ case.
The main objective of the discussion above is not to provide an extensive investigation of the detectability of the GRE features in the observed PSDs, taking into account the full range of the BH masses in the objects of the sample and the count rate of the available light curves. It mainly aims to highlight the difficulties associated with the detection of the GRE effects in the individual PSDs: for most objects in the sample, and for most of the observed frequency range, the error of the observed PSDs is larger than 20 per cent. With this in mind, we present below the best-fitting results of the BPL and BPLGRE models to the observed PSDs.
4 PSD MODEL FITTING
The model fitting is performed using the traditional χ2 as the fit statistic. For the minimization of the χ2 merit function, we use the classical Levenberg–Marquardt method (Bevington & Robinson 1992). The number of light curve segments is larger than 50 for eight out of 12 sources in our sample. In this case, the distribution of the averaged periodogram estimates approximates reasonably well a Gaussian distribution (Papadakis & Lawrence 1993). We therefore assume Gaussian statistics, and we quote the 68.3 per cent confidence intervals for the each best-fitting parameter, estimated by increasing Δχ2 by one. We fit models to the iron-line PSDs of the four sources that we discussed above (i.e. the ones with well-defined, low-frequency shapes), and to the soft-band PSDs of all the sources in our sample.
4.1 Bending power-law model fits
Tables 2 and 3 list our best-fitting BPL model results for the 5–7 and 0.5–1 keV observed PSDs, respectively. Our best-fitting parameter values are similar to those usually determined by the BPL model fits to AGN power spectra. For example, our soft-band, best-fitting parameters of νb and α are entirely consistent (within the errors and for the same sources) with the best-fitting results of González-Martín & Vaughan (2012) in the 0.2–2 keV using a bending power-law plus constant model (their Model B).
Bending power law model best-fitting results, 5–7 keV band PSDs (for 47 d.o.f.).
| . | Bending power law (5–7 keV) . | . | ||
|---|---|---|---|---|
| AGN name | A | νb | sh | χ2 |
| (10−3 Hz−1) | (10−4 Hz) | |||
| NGC 7314 | |$12.7^{+4.1}_{-3.8}$| | |$3.82^{+1.59}_{-1.88}$| | |$2.84^{+0.43}_{-0.61}$| | 70.1 |
| NGC 4051 | |$39.2^{+15.2}_{-17.3}$| | |$1.87^{+1.13}_{-0.94}$| | |$2.29^{+0.20}_{-0.29}$| | 49.5 |
| Ark 564 | |$12.8^{+2.3}_{-2.4}$| | |$6.64^{+1.95}_{-1.83}$| | |$3.59^{+1.12}_{-1.32}$| | 75.6 |
| MCG–6-30-15 | |$9.4^{+3.2}_{-2.5}$| | |$2.91^{+1.46}_{-1.08}$| | |$2.59^{+0.29}_{-0.32}$| | 53.1 |
| . | Bending power law (5–7 keV) . | . | ||
|---|---|---|---|---|
| AGN name | A | νb | sh | χ2 |
| (10−3 Hz−1) | (10−4 Hz) | |||
| NGC 7314 | |$12.7^{+4.1}_{-3.8}$| | |$3.82^{+1.59}_{-1.88}$| | |$2.84^{+0.43}_{-0.61}$| | 70.1 |
| NGC 4051 | |$39.2^{+15.2}_{-17.3}$| | |$1.87^{+1.13}_{-0.94}$| | |$2.29^{+0.20}_{-0.29}$| | 49.5 |
| Ark 564 | |$12.8^{+2.3}_{-2.4}$| | |$6.64^{+1.95}_{-1.83}$| | |$3.59^{+1.12}_{-1.32}$| | 75.6 |
| MCG–6-30-15 | |$9.4^{+3.2}_{-2.5}$| | |$2.91^{+1.46}_{-1.08}$| | |$2.59^{+0.29}_{-0.32}$| | 53.1 |
Bending power law model best-fitting results, 5–7 keV band PSDs (for 47 d.o.f.).
| . | Bending power law (5–7 keV) . | . | ||
|---|---|---|---|---|
| AGN name | A | νb | sh | χ2 |
| (10−3 Hz−1) | (10−4 Hz) | |||
| NGC 7314 | |$12.7^{+4.1}_{-3.8}$| | |$3.82^{+1.59}_{-1.88}$| | |$2.84^{+0.43}_{-0.61}$| | 70.1 |
| NGC 4051 | |$39.2^{+15.2}_{-17.3}$| | |$1.87^{+1.13}_{-0.94}$| | |$2.29^{+0.20}_{-0.29}$| | 49.5 |
| Ark 564 | |$12.8^{+2.3}_{-2.4}$| | |$6.64^{+1.95}_{-1.83}$| | |$3.59^{+1.12}_{-1.32}$| | 75.6 |
| MCG–6-30-15 | |$9.4^{+3.2}_{-2.5}$| | |$2.91^{+1.46}_{-1.08}$| | |$2.59^{+0.29}_{-0.32}$| | 53.1 |
| . | Bending power law (5–7 keV) . | . | ||
|---|---|---|---|---|
| AGN name | A | νb | sh | χ2 |
| (10−3 Hz−1) | (10−4 Hz) | |||
| NGC 7314 | |$12.7^{+4.1}_{-3.8}$| | |$3.82^{+1.59}_{-1.88}$| | |$2.84^{+0.43}_{-0.61}$| | 70.1 |
| NGC 4051 | |$39.2^{+15.2}_{-17.3}$| | |$1.87^{+1.13}_{-0.94}$| | |$2.29^{+0.20}_{-0.29}$| | 49.5 |
| Ark 564 | |$12.8^{+2.3}_{-2.4}$| | |$6.64^{+1.95}_{-1.83}$| | |$3.59^{+1.12}_{-1.32}$| | 75.6 |
| MCG–6-30-15 | |$9.4^{+3.2}_{-2.5}$| | |$2.91^{+1.46}_{-1.08}$| | |$2.59^{+0.29}_{-0.32}$| | 53.1 |
Bending power law model best-fitting results, 0.5–1 keV band PSDs (for 47 d.o.f.).
| . | Bending power law (0.5–1 keV) . | . | ||
|---|---|---|---|---|
| AGN name | A | νb | sh | χ2 |
| (10−3 Hz−1) | (10−4 Hz) | |||
| NGC 7314 | |$15.9^{+6.5}_{-7.2}$| | |$2.89^{+0.18}_{-0.19}$| | |$2.47^{+0.52}_{-0.54}$| | 51.8 |
| NGC 4051 | |$111^{+37}_{-30}$| | |$1.39^{+0.59}_{-0.62}$| | |$2.24^{+0.08}_{-0.11}$| | 58.4 |
| Mrk 766 | |$11.9^{+2.3}_{-2.2}$| | |$2.68^{+0.66}_{-0.57}$| | |$2.93^{+0.23}_{-0.20}$| | 48.9 |
| Ark 564 | |$5.9^{+0.7}_{-0.7}$| | |$6.79^{+0.10}_{-0.13}$| | |$2.89^{+0.17}_{-0.14}$| | 54.8 |
| 1H 0707−495 | |$51.4^{+8.3}_{-7.9}$| | |$2.41^{+0.48}_{-0.42}$| | |$2.69^{+0.15}_{-0.16}$| | 68.5 |
| MCG–6-30-15 | |$23.4^{+8.7}_{-6.3}$| | |$1.36^{+0.52}_{-0.42}$| | |$2.49^{+0.21}_{-0.12}$| | 54.2 |
| IRAS 13224−3809 | |$531^{+424}_{-295}$| | |$0.16^{+0.60}_{-}$| | |$2.10^{+0.13}_{-0.11}$| | 42.6 |
| SWIFT J2127+5654 | |$10.3^{+5.4}_{-6.3}$| | |$1.83^{+1.25}_{-1.32}$| | 3.2 ± 1.3 | 68.4 |
| Mrk 335 | 4.3 ± 1.9 | |$2.97^{+1.23}_{-1.09}$| | |$3.42^{+0.62}_{-0.76}$| | 48.2 |
| NGC 3516 | |$7.1^{+6.1}_{-7.2}$| | |$0.48^{+0.49}_{-0.46}$| | |$2.51^{+0.62}_{-0.56}$| | 78.2 |
| PG 1211+143 | |$8.6^{+2.3}_{-4.9}$| | |$0.61^{+0.45}_{-0.56}$| | |$2.94^{+0.34}_{-0.73}$| | 61.7 |
| PKS 0558-504 | |$11.7^{+8.9}_{-7.9}$| | |$0.58^{+0.44}_{-0.39}$| | |$2.38^{+0.31}_{-0.36}$| | 21.8 |
| . | Bending power law (0.5–1 keV) . | . | ||
|---|---|---|---|---|
| AGN name | A | νb | sh | χ2 |
| (10−3 Hz−1) | (10−4 Hz) | |||
| NGC 7314 | |$15.9^{+6.5}_{-7.2}$| | |$2.89^{+0.18}_{-0.19}$| | |$2.47^{+0.52}_{-0.54}$| | 51.8 |
| NGC 4051 | |$111^{+37}_{-30}$| | |$1.39^{+0.59}_{-0.62}$| | |$2.24^{+0.08}_{-0.11}$| | 58.4 |
| Mrk 766 | |$11.9^{+2.3}_{-2.2}$| | |$2.68^{+0.66}_{-0.57}$| | |$2.93^{+0.23}_{-0.20}$| | 48.9 |
| Ark 564 | |$5.9^{+0.7}_{-0.7}$| | |$6.79^{+0.10}_{-0.13}$| | |$2.89^{+0.17}_{-0.14}$| | 54.8 |
| 1H 0707−495 | |$51.4^{+8.3}_{-7.9}$| | |$2.41^{+0.48}_{-0.42}$| | |$2.69^{+0.15}_{-0.16}$| | 68.5 |
| MCG–6-30-15 | |$23.4^{+8.7}_{-6.3}$| | |$1.36^{+0.52}_{-0.42}$| | |$2.49^{+0.21}_{-0.12}$| | 54.2 |
| IRAS 13224−3809 | |$531^{+424}_{-295}$| | |$0.16^{+0.60}_{-}$| | |$2.10^{+0.13}_{-0.11}$| | 42.6 |
| SWIFT J2127+5654 | |$10.3^{+5.4}_{-6.3}$| | |$1.83^{+1.25}_{-1.32}$| | 3.2 ± 1.3 | 68.4 |
| Mrk 335 | 4.3 ± 1.9 | |$2.97^{+1.23}_{-1.09}$| | |$3.42^{+0.62}_{-0.76}$| | 48.2 |
| NGC 3516 | |$7.1^{+6.1}_{-7.2}$| | |$0.48^{+0.49}_{-0.46}$| | |$2.51^{+0.62}_{-0.56}$| | 78.2 |
| PG 1211+143 | |$8.6^{+2.3}_{-4.9}$| | |$0.61^{+0.45}_{-0.56}$| | |$2.94^{+0.34}_{-0.73}$| | 61.7 |
| PKS 0558-504 | |$11.7^{+8.9}_{-7.9}$| | |$0.58^{+0.44}_{-0.39}$| | |$2.38^{+0.31}_{-0.36}$| | 21.8 |
Bending power law model best-fitting results, 0.5–1 keV band PSDs (for 47 d.o.f.).
| . | Bending power law (0.5–1 keV) . | . | ||
|---|---|---|---|---|
| AGN name | A | νb | sh | χ2 |
| (10−3 Hz−1) | (10−4 Hz) | |||
| NGC 7314 | |$15.9^{+6.5}_{-7.2}$| | |$2.89^{+0.18}_{-0.19}$| | |$2.47^{+0.52}_{-0.54}$| | 51.8 |
| NGC 4051 | |$111^{+37}_{-30}$| | |$1.39^{+0.59}_{-0.62}$| | |$2.24^{+0.08}_{-0.11}$| | 58.4 |
| Mrk 766 | |$11.9^{+2.3}_{-2.2}$| | |$2.68^{+0.66}_{-0.57}$| | |$2.93^{+0.23}_{-0.20}$| | 48.9 |
| Ark 564 | |$5.9^{+0.7}_{-0.7}$| | |$6.79^{+0.10}_{-0.13}$| | |$2.89^{+0.17}_{-0.14}$| | 54.8 |
| 1H 0707−495 | |$51.4^{+8.3}_{-7.9}$| | |$2.41^{+0.48}_{-0.42}$| | |$2.69^{+0.15}_{-0.16}$| | 68.5 |
| MCG–6-30-15 | |$23.4^{+8.7}_{-6.3}$| | |$1.36^{+0.52}_{-0.42}$| | |$2.49^{+0.21}_{-0.12}$| | 54.2 |
| IRAS 13224−3809 | |$531^{+424}_{-295}$| | |$0.16^{+0.60}_{-}$| | |$2.10^{+0.13}_{-0.11}$| | 42.6 |
| SWIFT J2127+5654 | |$10.3^{+5.4}_{-6.3}$| | |$1.83^{+1.25}_{-1.32}$| | 3.2 ± 1.3 | 68.4 |
| Mrk 335 | 4.3 ± 1.9 | |$2.97^{+1.23}_{-1.09}$| | |$3.42^{+0.62}_{-0.76}$| | 48.2 |
| NGC 3516 | |$7.1^{+6.1}_{-7.2}$| | |$0.48^{+0.49}_{-0.46}$| | |$2.51^{+0.62}_{-0.56}$| | 78.2 |
| PG 1211+143 | |$8.6^{+2.3}_{-4.9}$| | |$0.61^{+0.45}_{-0.56}$| | |$2.94^{+0.34}_{-0.73}$| | 61.7 |
| PKS 0558-504 | |$11.7^{+8.9}_{-7.9}$| | |$0.58^{+0.44}_{-0.39}$| | |$2.38^{+0.31}_{-0.36}$| | 21.8 |
| . | Bending power law (0.5–1 keV) . | . | ||
|---|---|---|---|---|
| AGN name | A | νb | sh | χ2 |
| (10−3 Hz−1) | (10−4 Hz) | |||
| NGC 7314 | |$15.9^{+6.5}_{-7.2}$| | |$2.89^{+0.18}_{-0.19}$| | |$2.47^{+0.52}_{-0.54}$| | 51.8 |
| NGC 4051 | |$111^{+37}_{-30}$| | |$1.39^{+0.59}_{-0.62}$| | |$2.24^{+0.08}_{-0.11}$| | 58.4 |
| Mrk 766 | |$11.9^{+2.3}_{-2.2}$| | |$2.68^{+0.66}_{-0.57}$| | |$2.93^{+0.23}_{-0.20}$| | 48.9 |
| Ark 564 | |$5.9^{+0.7}_{-0.7}$| | |$6.79^{+0.10}_{-0.13}$| | |$2.89^{+0.17}_{-0.14}$| | 54.8 |
| 1H 0707−495 | |$51.4^{+8.3}_{-7.9}$| | |$2.41^{+0.48}_{-0.42}$| | |$2.69^{+0.15}_{-0.16}$| | 68.5 |
| MCG–6-30-15 | |$23.4^{+8.7}_{-6.3}$| | |$1.36^{+0.52}_{-0.42}$| | |$2.49^{+0.21}_{-0.12}$| | 54.2 |
| IRAS 13224−3809 | |$531^{+424}_{-295}$| | |$0.16^{+0.60}_{-}$| | |$2.10^{+0.13}_{-0.11}$| | 42.6 |
| SWIFT J2127+5654 | |$10.3^{+5.4}_{-6.3}$| | |$1.83^{+1.25}_{-1.32}$| | 3.2 ± 1.3 | 68.4 |
| Mrk 335 | 4.3 ± 1.9 | |$2.97^{+1.23}_{-1.09}$| | |$3.42^{+0.62}_{-0.76}$| | 48.2 |
| NGC 3516 | |$7.1^{+6.1}_{-7.2}$| | |$0.48^{+0.49}_{-0.46}$| | |$2.51^{+0.62}_{-0.56}$| | 78.2 |
| PG 1211+143 | |$8.6^{+2.3}_{-4.9}$| | |$0.61^{+0.45}_{-0.56}$| | |$2.94^{+0.34}_{-0.73}$| | 61.7 |
| PKS 0558-504 | |$11.7^{+8.9}_{-7.9}$| | |$0.58^{+0.44}_{-0.39}$| | |$2.38^{+0.31}_{-0.36}$| | 21.8 |
The left-hand panels in Fig. 3 show the best-fitting BPL models to the soft-band PSDs of 1H 0707−495 and Mrk 766 (top and bottom panels, respectively). The lower plots, attached to each panel, show the best-fitting residual at each Fourier frequency, νj, i.e. |$[\scr {P}_{\rm {best\hbox{-}fit}}(\nu _j;\mathbf {\mathit {\gamma }})-P_{\rm obs}(\nu _j)]/{\rm {std}}[P_{\rm obs}(\nu _j)]$| in which std[Pobs(νj)] is the standard deviation of the average periodograms. According to the resulting χ2 values, the BPL model fits well the observed power spectrum of Mrk 766, but less so the 1H 0707−495 PSD (the null hypothesis probability, pnull, is less than 2.2 per cent in this source.). In fact, the null hypothesis probability for the best-fitting BPL model fit to the iron-line PSDs of NGC 7314 and Ark 564 is rather low (pnull = 1.6 and 0.6 per cent, respectively). pnull is also low in the case of the BPL best fits to the soft-band PSDs of SWIFT J2127+5654 and NGC 3516 (pnull = 2.1 and 0.3 per cent, respectively). If the BPL model would represent correctly the underlying PSD of all sources, we would expect just one or two pnull values smaller than 5 per cent among the 16 fitted PSDs, as opposed to the five cases among our sample. We discuss in Appendix B the case of the ‘bad’ BPL model fits in more detail.

The best-fitting PSD models in the soft band (solid lines) for 1H 0707−495 and Mrk 766 (top and bottom panels, respectively) together with the corresponding best-fitting residual plots attached at the bottom of each panel. The filled circles correspond to the positive PSD estimates and the open circles correspond to the absolute values of the negative PSD estimates, i.e. when the Poisson noise level, at a given Fourier frequency, is greater than the actual observed PSD value. Left-hand panels: the best-fitting BPL model. Right-hand panels: the best-fitting BPLGRE model.
4.2 Bending power law with general relativistic echo model fits
In order to define the BPLGRE models that we fit to the observed PSDs, we compute the transfer function as explained by P16, assuming three values for the BH spin: α = 0 (Schwarzschild BH, rin = 6 rg), 0.676 (intermediate spin BH, rin = 3 rg), and 1 (Kerr BH, rin = 1 rg). Regarding the height of the X-ray source, we consider a variety of values, depending on the BH spin, 18 values in the case of the Schwarzschild BHs (2.3, 2.9, 3.6, 4.5, 5.7, 7, 8.8, 11, 13.7, 17.1, 21.3, 26.5, 33.1, 41.3, 51.5, 64.3, 80.2, and 100 rg), we add the value of 1.9 rg in the case of BHs with α = 0.676, and the value of 1.5 rg in the case of Kerr BHs. As for the inclination angle, we consider systems that are observed by a distant observer at a viewing angle of θ = 20°, 40° and 60° (θ = 0° or 90° correspond to a disc seen face on and edge on, respectively). In total, the model parameter space, regarding the physical quantities α, h, and θ, yields a total of (20 + 19 + 18) × 3 = 171 different geometrical layouts of the lamp-post model.
In principle, MBH should also be left as a free parameter during the model fitting process. However, given the complex nature of the fitting procedure, and the need to determine as accurately as possible the model parameters, we compute the 171 model transfer functions assuming the MBH estimates listed in Table 1. Note that we actually repeated the fits by letting MBH be a free model parameter; we comment on these results at the end of this section. Then, using the 171 model transfer functions, we create a linearly interpolated function of |Γ(ν; h, α, θ)|2, describing the entire parameter space among the 171 transfer function models. This interpolated transfer function is used in equation (4) to fit the observed PSDs.
Tables 4 and 5 list our best-fitting BPLGRE model results for the 5–7 keV and 0.5–1 keV PSDs, respectively. Overall, we do not detect significant differences between the best-fitting GRE parameter values in the soft and iron-line bands. The best-fitting heights are smaller in the iron-line band PSDs, although they are still consistent, within the errors, with the soft-band best-fitting values. The best-fitting parameter values of the BPL component listed in Tables 4 and 5 are also consistent, within the errors, with the values that we get from the BPL model fit to the observed PSDs (Tables 2 and 3).
Bending power law with GRE model best-fitting results, 5–7 keV band PSDs (for 44 d.o.f.).
| . | Bending power-law model . | GR echo model . | . | ||||
|---|---|---|---|---|---|---|---|
| AGN name | A | νb | sh | h | θ | α | χ2 |
| (10−3 Hz−1) | (10−4 Hz) | (rg) | |$({^\circ } )$| | ||||
| NGC 7314 | |$12.6^{+3.0}_{-2.6}$| | |$5.36^{+1.91}_{-1.42}$| | |$3.37^{+0.83}_{-0.69}$| | |$64.91^{+10.12}_{-11.43}$| | |$37.81^{+11.31}_{-12.78}$| | |$0.82^{+0.15}_{-0.29}$| | 68.9 |
| NGC 4051 | |$32.3^{+8.4}_{-6.3}$| | |$3.62^{+1.10}_{-1.18}$| | |$2.60^{+0.32}_{-0.21}$| | |$52.34^{+15.27}_{-12.46}$| | |$27.74^{+11.46}_{-{\rm ---}}$| | |$0.89^{+{\rm ---}}_{-0.42}$| | 45.8 |
| Ark 564 | |$15.9^{+4.6}_{-2.5}$| | |$6.93^{+2.03}_{-1.54}$| | |$3.23^{+1.25}_{-1.24}$| | |$5.5^{+6.52}_{-{\rm ---}}$| | |$35.35^{+16.87}_{-13.39}$| | |$0.51^{+0.42}_{-0.38}$| | 73.7 |
| MCG–6-30-15 | |$10.0^{+10.4}_{-9.4}$| | |$4.06^{+0.86}_{-0.75}$| | |$2.99^{+0.37}_{-0.42}$| | |$27.43^{+21.31}_{-19.23}$| | |$46.06^{+13.12}_{-12.54}$| | |$0.92^{+{\rm ---}}_{-0.28}$| | 47.7 |
| . | Bending power-law model . | GR echo model . | . | ||||
|---|---|---|---|---|---|---|---|
| AGN name | A | νb | sh | h | θ | α | χ2 |
| (10−3 Hz−1) | (10−4 Hz) | (rg) | |$({^\circ } )$| | ||||
| NGC 7314 | |$12.6^{+3.0}_{-2.6}$| | |$5.36^{+1.91}_{-1.42}$| | |$3.37^{+0.83}_{-0.69}$| | |$64.91^{+10.12}_{-11.43}$| | |$37.81^{+11.31}_{-12.78}$| | |$0.82^{+0.15}_{-0.29}$| | 68.9 |
| NGC 4051 | |$32.3^{+8.4}_{-6.3}$| | |$3.62^{+1.10}_{-1.18}$| | |$2.60^{+0.32}_{-0.21}$| | |$52.34^{+15.27}_{-12.46}$| | |$27.74^{+11.46}_{-{\rm ---}}$| | |$0.89^{+{\rm ---}}_{-0.42}$| | 45.8 |
| Ark 564 | |$15.9^{+4.6}_{-2.5}$| | |$6.93^{+2.03}_{-1.54}$| | |$3.23^{+1.25}_{-1.24}$| | |$5.5^{+6.52}_{-{\rm ---}}$| | |$35.35^{+16.87}_{-13.39}$| | |$0.51^{+0.42}_{-0.38}$| | 73.7 |
| MCG–6-30-15 | |$10.0^{+10.4}_{-9.4}$| | |$4.06^{+0.86}_{-0.75}$| | |$2.99^{+0.37}_{-0.42}$| | |$27.43^{+21.31}_{-19.23}$| | |$46.06^{+13.12}_{-12.54}$| | |$0.92^{+{\rm ---}}_{-0.28}$| | 47.7 |
Bending power law with GRE model best-fitting results, 5–7 keV band PSDs (for 44 d.o.f.).
| . | Bending power-law model . | GR echo model . | . | ||||
|---|---|---|---|---|---|---|---|
| AGN name | A | νb | sh | h | θ | α | χ2 |
| (10−3 Hz−1) | (10−4 Hz) | (rg) | |$({^\circ } )$| | ||||
| NGC 7314 | |$12.6^{+3.0}_{-2.6}$| | |$5.36^{+1.91}_{-1.42}$| | |$3.37^{+0.83}_{-0.69}$| | |$64.91^{+10.12}_{-11.43}$| | |$37.81^{+11.31}_{-12.78}$| | |$0.82^{+0.15}_{-0.29}$| | 68.9 |
| NGC 4051 | |$32.3^{+8.4}_{-6.3}$| | |$3.62^{+1.10}_{-1.18}$| | |$2.60^{+0.32}_{-0.21}$| | |$52.34^{+15.27}_{-12.46}$| | |$27.74^{+11.46}_{-{\rm ---}}$| | |$0.89^{+{\rm ---}}_{-0.42}$| | 45.8 |
| Ark 564 | |$15.9^{+4.6}_{-2.5}$| | |$6.93^{+2.03}_{-1.54}$| | |$3.23^{+1.25}_{-1.24}$| | |$5.5^{+6.52}_{-{\rm ---}}$| | |$35.35^{+16.87}_{-13.39}$| | |$0.51^{+0.42}_{-0.38}$| | 73.7 |
| MCG–6-30-15 | |$10.0^{+10.4}_{-9.4}$| | |$4.06^{+0.86}_{-0.75}$| | |$2.99^{+0.37}_{-0.42}$| | |$27.43^{+21.31}_{-19.23}$| | |$46.06^{+13.12}_{-12.54}$| | |$0.92^{+{\rm ---}}_{-0.28}$| | 47.7 |
| . | Bending power-law model . | GR echo model . | . | ||||
|---|---|---|---|---|---|---|---|
| AGN name | A | νb | sh | h | θ | α | χ2 |
| (10−3 Hz−1) | (10−4 Hz) | (rg) | |$({^\circ } )$| | ||||
| NGC 7314 | |$12.6^{+3.0}_{-2.6}$| | |$5.36^{+1.91}_{-1.42}$| | |$3.37^{+0.83}_{-0.69}$| | |$64.91^{+10.12}_{-11.43}$| | |$37.81^{+11.31}_{-12.78}$| | |$0.82^{+0.15}_{-0.29}$| | 68.9 |
| NGC 4051 | |$32.3^{+8.4}_{-6.3}$| | |$3.62^{+1.10}_{-1.18}$| | |$2.60^{+0.32}_{-0.21}$| | |$52.34^{+15.27}_{-12.46}$| | |$27.74^{+11.46}_{-{\rm ---}}$| | |$0.89^{+{\rm ---}}_{-0.42}$| | 45.8 |
| Ark 564 | |$15.9^{+4.6}_{-2.5}$| | |$6.93^{+2.03}_{-1.54}$| | |$3.23^{+1.25}_{-1.24}$| | |$5.5^{+6.52}_{-{\rm ---}}$| | |$35.35^{+16.87}_{-13.39}$| | |$0.51^{+0.42}_{-0.38}$| | 73.7 |
| MCG–6-30-15 | |$10.0^{+10.4}_{-9.4}$| | |$4.06^{+0.86}_{-0.75}$| | |$2.99^{+0.37}_{-0.42}$| | |$27.43^{+21.31}_{-19.23}$| | |$46.06^{+13.12}_{-12.54}$| | |$0.92^{+{\rm ---}}_{-0.28}$| | 47.7 |
Bending power law with GRE model best-fitting results, 0.5–1 keV band PSDs (for 44 d.o.f.).
| . | Bending power-law model . | GR echo model . | . | |||||
|---|---|---|---|---|---|---|---|---|
| AGN name | A | νb | sh | h | θ | α | χ2 | |
| (10−3 Hz−1) | (10−4 Hz) | (rg) | |$({^\circ } )$| | |||||
| NGC 7314 | |$14.5^{+4.7}_{-3.8}$| | |$4.10^{+2.12}_{-1.98}$| | |$2.44^{+0.52}_{-0.49}$| | |$43.21^{+12.23}_{-11.02}$| | |$28.43^{13.31}_{-{\rm ---}}$| | |$0.93^{+{\rm ---}}_{-0.38}$| | 50.1 | |
| NGC 4051 | |$88.6^{+21.4}_{-19.3}$| | |$2.13^{+0.70}_{-0.73}$| | |$2.27^{+0.09}_{-0.11}$| | |$16.12^{+14.32}_{-10.31}$| | |$38.61^{+9.21}_{-8.69}$| | |$0.36^{+0.35}_{-0.22}$| | 55.3 | |
| Mrk 766 | |$12.9^{+2.3}_{-2.2}$| | |$2.69^{+0.15}_{-0.14}$| | |$2.98^{+0.16}_{-0.17}$| | |$30.22^{+20.11}_{-18.51}$| | |$24.12^{+9.43}_{-{\rm ---}}$| | |$0.67^{+0.22}_{-0.28}$| | 42.2 | |
| Ark 564 | |$17.6^{+14.6}_{-11.3}$| | |$0.78^{+1.81}_{-{\rm ---}}$| | |$1.71^{+0.18}_{-0.19}$| | |$1.92^{+2.52}_{-{\rm ---}}$| | |$53.49^{+{\rm ---}}_{-23.39}$| | |$0.49^{+0.36}_{-0.28}$| | 49.3 | |
| 1H 0707−495 | |$46.4^{+5.1}_{-7.2}$| | |$3.71^{+0.48}_{-0.38}$| | |$2.69^{+0.89}_{-0.95}$| | |$19.32^{+4.46}_{-6.45}$| | |$32.45^{+8.54}_{-9.21}$| | |$0.16^{+0.42}_{-{\rm ---}}$| | 64.5 | |
| MCG–6-30-15 | |$33.1^{+9.0}_{-7.8}$| | |$1.20^{+0.49}_{-0.38}$| | |$2.48^{+0.19}_{-0.26}$| | |$25.06^{+14.28}_{-16.96}$| | |$40.37^{+11.23}_{-10.31}$| | |$0.98^{+{\rm ---}}_{-0.38}$| | 53.3 | |
| IRAS 13224−3809 | |$199^{+164}_{-121}$| | |$0.69^{+0.84}_{-0.67}$| | 2.26 ± 0.14 | |$16.94^{+7.54}_{-9.44}$| | |$25.56^{12.26}_{-{\rm ---}}$| | |$0.54^{+0.34}_{-0.28}$| | 38.6 | |
| SWIFT J2127.4+5645 | |$11.9^{+9.1}_{-10.4}$| | |$2.00^{+1.30}_{-1.26}$| | |$3.40^{+1.04}_{-0.78}$| | |$4.23^{+3.21}_{-2.36}$| | |$59.81^{+{\rm ---}}_{-18.23}$| | |$0.09^{+3.25}_{-{\rm ---}}$| | 66.1 | |
| Mrk 335 | |$9.1^{+3.2}_{-2.6}$| | |$2.64^{+0.98}_{-1.06}$| | |$3.47^{+0.62}_{-0.58}$| | |$3.64^{+5.43}_{-2.21}$| | |$47.66^{+9.32}_{-8.24}$| | |$0.91^{+{\rm ---}}_{-0.27}$| | 46.0 | |
| NGC 3516 | |$2.6^{+2.4}_{-2.2}$| | |$2.37^{+2.81}_{-1.99}$| | |$2.83^{+1.28}_{-1.45}$| | |$1.52^{+3.25}_{-{\rm ---}}$| | |$23.49^{+12.56}_{-{\rm ---}}$| | |$0.86^{+{\rm ---}}_{-0.33}$| | 77.1 | |
| PG 1211+143 | |$12.5^{+6.5}_{-7.2}$| | |$1.01^{+0.41}_{-0.52}$| | |$3.18^{+0.46}_{-0.52}$| | |$1.93^{+3.45}_{-{\rm ---}}$| | |$50.91^{+{\rm ---}}_{-18.91}$| | |$0.95^{+{\rm ---}}_{-0.21}$| | 59.1 | |
| PKS 0558−504 | |$29.2^{+10.3}_{-8.4}$| | |$0.44^{+0.45}_{-{\rm ---}}$| | |$2.37^{+0.22}_{-0.17}$| | |$4.22^{+3.13}_{-2.09}$| | |$24.86^{+9.94}_{-{\rm ---}}$| | |$0.94^{+{\rm ---}}_{-0.41}$| | 20.2 | |
| . | Bending power-law model . | GR echo model . | . | |||||
|---|---|---|---|---|---|---|---|---|
| AGN name | A | νb | sh | h | θ | α | χ2 | |
| (10−3 Hz−1) | (10−4 Hz) | (rg) | |$({^\circ } )$| | |||||
| NGC 7314 | |$14.5^{+4.7}_{-3.8}$| | |$4.10^{+2.12}_{-1.98}$| | |$2.44^{+0.52}_{-0.49}$| | |$43.21^{+12.23}_{-11.02}$| | |$28.43^{13.31}_{-{\rm ---}}$| | |$0.93^{+{\rm ---}}_{-0.38}$| | 50.1 | |
| NGC 4051 | |$88.6^{+21.4}_{-19.3}$| | |$2.13^{+0.70}_{-0.73}$| | |$2.27^{+0.09}_{-0.11}$| | |$16.12^{+14.32}_{-10.31}$| | |$38.61^{+9.21}_{-8.69}$| | |$0.36^{+0.35}_{-0.22}$| | 55.3 | |
| Mrk 766 | |$12.9^{+2.3}_{-2.2}$| | |$2.69^{+0.15}_{-0.14}$| | |$2.98^{+0.16}_{-0.17}$| | |$30.22^{+20.11}_{-18.51}$| | |$24.12^{+9.43}_{-{\rm ---}}$| | |$0.67^{+0.22}_{-0.28}$| | 42.2 | |
| Ark 564 | |$17.6^{+14.6}_{-11.3}$| | |$0.78^{+1.81}_{-{\rm ---}}$| | |$1.71^{+0.18}_{-0.19}$| | |$1.92^{+2.52}_{-{\rm ---}}$| | |$53.49^{+{\rm ---}}_{-23.39}$| | |$0.49^{+0.36}_{-0.28}$| | 49.3 | |
| 1H 0707−495 | |$46.4^{+5.1}_{-7.2}$| | |$3.71^{+0.48}_{-0.38}$| | |$2.69^{+0.89}_{-0.95}$| | |$19.32^{+4.46}_{-6.45}$| | |$32.45^{+8.54}_{-9.21}$| | |$0.16^{+0.42}_{-{\rm ---}}$| | 64.5 | |
| MCG–6-30-15 | |$33.1^{+9.0}_{-7.8}$| | |$1.20^{+0.49}_{-0.38}$| | |$2.48^{+0.19}_{-0.26}$| | |$25.06^{+14.28}_{-16.96}$| | |$40.37^{+11.23}_{-10.31}$| | |$0.98^{+{\rm ---}}_{-0.38}$| | 53.3 | |
| IRAS 13224−3809 | |$199^{+164}_{-121}$| | |$0.69^{+0.84}_{-0.67}$| | 2.26 ± 0.14 | |$16.94^{+7.54}_{-9.44}$| | |$25.56^{12.26}_{-{\rm ---}}$| | |$0.54^{+0.34}_{-0.28}$| | 38.6 | |
| SWIFT J2127.4+5645 | |$11.9^{+9.1}_{-10.4}$| | |$2.00^{+1.30}_{-1.26}$| | |$3.40^{+1.04}_{-0.78}$| | |$4.23^{+3.21}_{-2.36}$| | |$59.81^{+{\rm ---}}_{-18.23}$| | |$0.09^{+3.25}_{-{\rm ---}}$| | 66.1 | |
| Mrk 335 | |$9.1^{+3.2}_{-2.6}$| | |$2.64^{+0.98}_{-1.06}$| | |$3.47^{+0.62}_{-0.58}$| | |$3.64^{+5.43}_{-2.21}$| | |$47.66^{+9.32}_{-8.24}$| | |$0.91^{+{\rm ---}}_{-0.27}$| | 46.0 | |
| NGC 3516 | |$2.6^{+2.4}_{-2.2}$| | |$2.37^{+2.81}_{-1.99}$| | |$2.83^{+1.28}_{-1.45}$| | |$1.52^{+3.25}_{-{\rm ---}}$| | |$23.49^{+12.56}_{-{\rm ---}}$| | |$0.86^{+{\rm ---}}_{-0.33}$| | 77.1 | |
| PG 1211+143 | |$12.5^{+6.5}_{-7.2}$| | |$1.01^{+0.41}_{-0.52}$| | |$3.18^{+0.46}_{-0.52}$| | |$1.93^{+3.45}_{-{\rm ---}}$| | |$50.91^{+{\rm ---}}_{-18.91}$| | |$0.95^{+{\rm ---}}_{-0.21}$| | 59.1 | |
| PKS 0558−504 | |$29.2^{+10.3}_{-8.4}$| | |$0.44^{+0.45}_{-{\rm ---}}$| | |$2.37^{+0.22}_{-0.17}$| | |$4.22^{+3.13}_{-2.09}$| | |$24.86^{+9.94}_{-{\rm ---}}$| | |$0.94^{+{\rm ---}}_{-0.41}$| | 20.2 | |
Bending power law with GRE model best-fitting results, 0.5–1 keV band PSDs (for 44 d.o.f.).
| . | Bending power-law model . | GR echo model . | . | |||||
|---|---|---|---|---|---|---|---|---|
| AGN name | A | νb | sh | h | θ | α | χ2 | |
| (10−3 Hz−1) | (10−4 Hz) | (rg) | |$({^\circ } )$| | |||||
| NGC 7314 | |$14.5^{+4.7}_{-3.8}$| | |$4.10^{+2.12}_{-1.98}$| | |$2.44^{+0.52}_{-0.49}$| | |$43.21^{+12.23}_{-11.02}$| | |$28.43^{13.31}_{-{\rm ---}}$| | |$0.93^{+{\rm ---}}_{-0.38}$| | 50.1 | |
| NGC 4051 | |$88.6^{+21.4}_{-19.3}$| | |$2.13^{+0.70}_{-0.73}$| | |$2.27^{+0.09}_{-0.11}$| | |$16.12^{+14.32}_{-10.31}$| | |$38.61^{+9.21}_{-8.69}$| | |$0.36^{+0.35}_{-0.22}$| | 55.3 | |
| Mrk 766 | |$12.9^{+2.3}_{-2.2}$| | |$2.69^{+0.15}_{-0.14}$| | |$2.98^{+0.16}_{-0.17}$| | |$30.22^{+20.11}_{-18.51}$| | |$24.12^{+9.43}_{-{\rm ---}}$| | |$0.67^{+0.22}_{-0.28}$| | 42.2 | |
| Ark 564 | |$17.6^{+14.6}_{-11.3}$| | |$0.78^{+1.81}_{-{\rm ---}}$| | |$1.71^{+0.18}_{-0.19}$| | |$1.92^{+2.52}_{-{\rm ---}}$| | |$53.49^{+{\rm ---}}_{-23.39}$| | |$0.49^{+0.36}_{-0.28}$| | 49.3 | |
| 1H 0707−495 | |$46.4^{+5.1}_{-7.2}$| | |$3.71^{+0.48}_{-0.38}$| | |$2.69^{+0.89}_{-0.95}$| | |$19.32^{+4.46}_{-6.45}$| | |$32.45^{+8.54}_{-9.21}$| | |$0.16^{+0.42}_{-{\rm ---}}$| | 64.5 | |
| MCG–6-30-15 | |$33.1^{+9.0}_{-7.8}$| | |$1.20^{+0.49}_{-0.38}$| | |$2.48^{+0.19}_{-0.26}$| | |$25.06^{+14.28}_{-16.96}$| | |$40.37^{+11.23}_{-10.31}$| | |$0.98^{+{\rm ---}}_{-0.38}$| | 53.3 | |
| IRAS 13224−3809 | |$199^{+164}_{-121}$| | |$0.69^{+0.84}_{-0.67}$| | 2.26 ± 0.14 | |$16.94^{+7.54}_{-9.44}$| | |$25.56^{12.26}_{-{\rm ---}}$| | |$0.54^{+0.34}_{-0.28}$| | 38.6 | |
| SWIFT J2127.4+5645 | |$11.9^{+9.1}_{-10.4}$| | |$2.00^{+1.30}_{-1.26}$| | |$3.40^{+1.04}_{-0.78}$| | |$4.23^{+3.21}_{-2.36}$| | |$59.81^{+{\rm ---}}_{-18.23}$| | |$0.09^{+3.25}_{-{\rm ---}}$| | 66.1 | |
| Mrk 335 | |$9.1^{+3.2}_{-2.6}$| | |$2.64^{+0.98}_{-1.06}$| | |$3.47^{+0.62}_{-0.58}$| | |$3.64^{+5.43}_{-2.21}$| | |$47.66^{+9.32}_{-8.24}$| | |$0.91^{+{\rm ---}}_{-0.27}$| | 46.0 | |
| NGC 3516 | |$2.6^{+2.4}_{-2.2}$| | |$2.37^{+2.81}_{-1.99}$| | |$2.83^{+1.28}_{-1.45}$| | |$1.52^{+3.25}_{-{\rm ---}}$| | |$23.49^{+12.56}_{-{\rm ---}}$| | |$0.86^{+{\rm ---}}_{-0.33}$| | 77.1 | |
| PG 1211+143 | |$12.5^{+6.5}_{-7.2}$| | |$1.01^{+0.41}_{-0.52}$| | |$3.18^{+0.46}_{-0.52}$| | |$1.93^{+3.45}_{-{\rm ---}}$| | |$50.91^{+{\rm ---}}_{-18.91}$| | |$0.95^{+{\rm ---}}_{-0.21}$| | 59.1 | |
| PKS 0558−504 | |$29.2^{+10.3}_{-8.4}$| | |$0.44^{+0.45}_{-{\rm ---}}$| | |$2.37^{+0.22}_{-0.17}$| | |$4.22^{+3.13}_{-2.09}$| | |$24.86^{+9.94}_{-{\rm ---}}$| | |$0.94^{+{\rm ---}}_{-0.41}$| | 20.2 | |
| . | Bending power-law model . | GR echo model . | . | |||||
|---|---|---|---|---|---|---|---|---|
| AGN name | A | νb | sh | h | θ | α | χ2 | |
| (10−3 Hz−1) | (10−4 Hz) | (rg) | |$({^\circ } )$| | |||||
| NGC 7314 | |$14.5^{+4.7}_{-3.8}$| | |$4.10^{+2.12}_{-1.98}$| | |$2.44^{+0.52}_{-0.49}$| | |$43.21^{+12.23}_{-11.02}$| | |$28.43^{13.31}_{-{\rm ---}}$| | |$0.93^{+{\rm ---}}_{-0.38}$| | 50.1 | |
| NGC 4051 | |$88.6^{+21.4}_{-19.3}$| | |$2.13^{+0.70}_{-0.73}$| | |$2.27^{+0.09}_{-0.11}$| | |$16.12^{+14.32}_{-10.31}$| | |$38.61^{+9.21}_{-8.69}$| | |$0.36^{+0.35}_{-0.22}$| | 55.3 | |
| Mrk 766 | |$12.9^{+2.3}_{-2.2}$| | |$2.69^{+0.15}_{-0.14}$| | |$2.98^{+0.16}_{-0.17}$| | |$30.22^{+20.11}_{-18.51}$| | |$24.12^{+9.43}_{-{\rm ---}}$| | |$0.67^{+0.22}_{-0.28}$| | 42.2 | |
| Ark 564 | |$17.6^{+14.6}_{-11.3}$| | |$0.78^{+1.81}_{-{\rm ---}}$| | |$1.71^{+0.18}_{-0.19}$| | |$1.92^{+2.52}_{-{\rm ---}}$| | |$53.49^{+{\rm ---}}_{-23.39}$| | |$0.49^{+0.36}_{-0.28}$| | 49.3 | |
| 1H 0707−495 | |$46.4^{+5.1}_{-7.2}$| | |$3.71^{+0.48}_{-0.38}$| | |$2.69^{+0.89}_{-0.95}$| | |$19.32^{+4.46}_{-6.45}$| | |$32.45^{+8.54}_{-9.21}$| | |$0.16^{+0.42}_{-{\rm ---}}$| | 64.5 | |
| MCG–6-30-15 | |$33.1^{+9.0}_{-7.8}$| | |$1.20^{+0.49}_{-0.38}$| | |$2.48^{+0.19}_{-0.26}$| | |$25.06^{+14.28}_{-16.96}$| | |$40.37^{+11.23}_{-10.31}$| | |$0.98^{+{\rm ---}}_{-0.38}$| | 53.3 | |
| IRAS 13224−3809 | |$199^{+164}_{-121}$| | |$0.69^{+0.84}_{-0.67}$| | 2.26 ± 0.14 | |$16.94^{+7.54}_{-9.44}$| | |$25.56^{12.26}_{-{\rm ---}}$| | |$0.54^{+0.34}_{-0.28}$| | 38.6 | |
| SWIFT J2127.4+5645 | |$11.9^{+9.1}_{-10.4}$| | |$2.00^{+1.30}_{-1.26}$| | |$3.40^{+1.04}_{-0.78}$| | |$4.23^{+3.21}_{-2.36}$| | |$59.81^{+{\rm ---}}_{-18.23}$| | |$0.09^{+3.25}_{-{\rm ---}}$| | 66.1 | |
| Mrk 335 | |$9.1^{+3.2}_{-2.6}$| | |$2.64^{+0.98}_{-1.06}$| | |$3.47^{+0.62}_{-0.58}$| | |$3.64^{+5.43}_{-2.21}$| | |$47.66^{+9.32}_{-8.24}$| | |$0.91^{+{\rm ---}}_{-0.27}$| | 46.0 | |
| NGC 3516 | |$2.6^{+2.4}_{-2.2}$| | |$2.37^{+2.81}_{-1.99}$| | |$2.83^{+1.28}_{-1.45}$| | |$1.52^{+3.25}_{-{\rm ---}}$| | |$23.49^{+12.56}_{-{\rm ---}}$| | |$0.86^{+{\rm ---}}_{-0.33}$| | 77.1 | |
| PG 1211+143 | |$12.5^{+6.5}_{-7.2}$| | |$1.01^{+0.41}_{-0.52}$| | |$3.18^{+0.46}_{-0.52}$| | |$1.93^{+3.45}_{-{\rm ---}}$| | |$50.91^{+{\rm ---}}_{-18.91}$| | |$0.95^{+{\rm ---}}_{-0.21}$| | 59.1 | |
| PKS 0558−504 | |$29.2^{+10.3}_{-8.4}$| | |$0.44^{+0.45}_{-{\rm ---}}$| | |$2.37^{+0.22}_{-0.17}$| | |$4.22^{+3.13}_{-2.09}$| | |$24.86^{+9.94}_{-{\rm ---}}$| | |$0.94^{+{\rm ---}}_{-0.41}$| | 20.2 | |
The right-hand panels in Fig. 3 show the best-fitting BPLGRE models to the soft-band PSDs of 1H 0707−495 and Mrk 766 (upper and lower panels, respectively). The residual plots of the BPL (shown in the left panels) and BPLGRE models are very similar for both sources. Perhaps a low-amplitude ‘wavy’ pattern in the BPL residuals below 10−3 Hz (more prominent in Mrk 766) is diminished in the BPLGRE residuals but, overall, we do not detect significant differences. This is consistent with the fact that the best-fitting χ2 values of both models are comparable.
In general, the best-fitting BPLGRE χ2 values are smaller than the BPL χ2 values, but this is expected because the BPLGRE model has a larger number of free parameters. In fact, the best-fitting BPLGRE null hypothesis probability in the case of the iron-line power spectra of NGC 7314 and Ark 564 is slightly smaller than the respective BPL best-fitting probabilities (1 and 0.3 per cent, respectively, compared to 1.6 and 0.6 per cent). The same result holds for the soft-band PSDs of NGC 3516 (pnull, BPLGRE = 0.1 per cent, compared to pnull,BPL = 0.3 per cent).
The quality of the BPLGRE fits does not change by fixing both the inclination angle to 45° and the spin parameter to either one or zero, in all the sources. We repeated the BPLGRE fits to the soft-band PSDs by assuming both spin values, and letting the BH mass of the objects, as well as the X-ray source height, as free parameters. In some objects the best fit was achieved in the case when α was frozen to zero, and in others when we kept α frozen to unity (not surprisingly, these were the objects where the best-fitting α value was closer to zero and to unity, respectively, as listed in Table 5). The resulting best-fitting BH masses are somewhat consistent (within a factor of a few) with the values listed in Table 1. However, the resulting best-fitting χ2 values were almost identical to the values listed in Table 5 (Δχ2 ≈ ±1 in almost all cases). We therefore present below a detailed comparison between the goodness of fit of the BPL and BPLGRE models, using the best-fitting χ2 values that are listed in Tables 2–5.
5 MODEL FIT COMPARISON
To decide which model provides the best description of the observed PSDs, the best-fitting results should be compared in a quantitative way. A commonly applied criterion is to convert the χ2 values obtained for two models into their relative probability measure is the F-test. According to Protassov et al. (2002), there are two conditions that must be satisfied for the proper use of this test: the two models that are being compared must be nested, and the null values of the additional parameters may not be on the boundary of the set of possible parameter values. In our case, the BPLGRE and BPL models are nested, since the BPL model is a sub-class of the BPLGRE model when the height is very large (strictly speaking, when h → ∞). At the same time, the ‘null’ values of h are not on the boundary of the possible parameter values (i.e. h = 0, as the height cannot be negative). We therefore use the F-test to compare the goodness of fit of the two models. The results (i.e. the value of F-statistic and the corresponding probability) are listed in the second column of Table 6. The null hypothesis in this case is that the more complicated BPLGRE model does not provide a better fit, when compared to the simpler BPL model. We found that pnull > 8 per cent for the model fits to all the iron-line and soft-band PSDs. This result supports the null hypothesis, and indicates that the BPLGRE model does not provide a better fit to the observed PSDs.
Comparison of the goodness of fit of the best-fitting models BPL and BPLGRE to the soft-band PSDs. The number in parentheses corresponds to the values for the iron-line band.
| . | . | BPL . | BPLGRE . | . | . | . |
|---|---|---|---|---|---|---|
| AGN name . | F-test . | AICc, 1 . | AICc, 2 . | Δ[AICc, 2] . | W[AICc, 2] . | ϵ2 . |
| . | ratio, prob. (per cent) . | . | . | . | . | . |
| NGC 7314 | 0.498, 68.6 | 58.324 | 64.813 | 6.489 | 0.038 | 0.039 |
| (0.255, 85.7) | (76.591) | (82.848) | (6.256) | (0.042) | (0.044) | |
| NGC 4051 | 0.822, 48.9 | 64.904 | 69.274 | 4.369 | 0.101 | 0.113 |
| (1.185, 32.6) | (56.060) | (59.733) | (3.673) | (0.137) | (0.159) | |
| Mrk 766 | 2.33, 8.7 | 55.452 | 56.186 | 0.734 | 0.409 | 0.693 |
| Ark 564 | 1.64, 19.65 | 61.317 | 63.205 | 1.888 | 0.280 | 0.389 |
| (0.378, 76.9) | (82.090) | (87.602) | (5.512) | (0.060) | (0.064) | |
| 1H 0707−495 | 0.910, 44.4 | 75.011 | 78.438 | 3.427 | 0.153 | 0.180 |
| MCG–6-30-15 | 0.248, 86.3 | 60.682 | 67.244 | 6.562 | 0.036 | 0.038 |
| (1.660, 18.9) | (59.634) | (61.676) | (2.042) | (0.265) | (0.360) | |
| IRAS 13224−3809 | 1.520, 22.3 | 49.100 | 52.588 | 3.487 | 0.149 | 0.175 |
| SWIFT J2127.4+5654 | 0.510, 67.7 | 74.958 | 80.084 | 5.125 | 0.072 | 0.077 |
| Mrk 335 | 0.701, 55.6 | 54.703 | 59.959 | 5.256 | 0.067 | 0.072 |
| NGC 3516 | 0.209, 88.9 | 84.710 | 91.009 | 6.299 | 0.041 | 0.043 |
| PG 1211+143 | 0.645, 59.0 | 68.212 | 73.094 | 4.882 | 0.080 | 0.086 |
| PKS 0558−504 | 1.162, 33.5 | 28.358 | 34.194 | 5.835 | 0.051 | 0.054 |
| . | . | BPL . | BPLGRE . | . | . | . |
|---|---|---|---|---|---|---|
| AGN name . | F-test . | AICc, 1 . | AICc, 2 . | Δ[AICc, 2] . | W[AICc, 2] . | ϵ2 . |
| . | ratio, prob. (per cent) . | . | . | . | . | . |
| NGC 7314 | 0.498, 68.6 | 58.324 | 64.813 | 6.489 | 0.038 | 0.039 |
| (0.255, 85.7) | (76.591) | (82.848) | (6.256) | (0.042) | (0.044) | |
| NGC 4051 | 0.822, 48.9 | 64.904 | 69.274 | 4.369 | 0.101 | 0.113 |
| (1.185, 32.6) | (56.060) | (59.733) | (3.673) | (0.137) | (0.159) | |
| Mrk 766 | 2.33, 8.7 | 55.452 | 56.186 | 0.734 | 0.409 | 0.693 |
| Ark 564 | 1.64, 19.65 | 61.317 | 63.205 | 1.888 | 0.280 | 0.389 |
| (0.378, 76.9) | (82.090) | (87.602) | (5.512) | (0.060) | (0.064) | |
| 1H 0707−495 | 0.910, 44.4 | 75.011 | 78.438 | 3.427 | 0.153 | 0.180 |
| MCG–6-30-15 | 0.248, 86.3 | 60.682 | 67.244 | 6.562 | 0.036 | 0.038 |
| (1.660, 18.9) | (59.634) | (61.676) | (2.042) | (0.265) | (0.360) | |
| IRAS 13224−3809 | 1.520, 22.3 | 49.100 | 52.588 | 3.487 | 0.149 | 0.175 |
| SWIFT J2127.4+5654 | 0.510, 67.7 | 74.958 | 80.084 | 5.125 | 0.072 | 0.077 |
| Mrk 335 | 0.701, 55.6 | 54.703 | 59.959 | 5.256 | 0.067 | 0.072 |
| NGC 3516 | 0.209, 88.9 | 84.710 | 91.009 | 6.299 | 0.041 | 0.043 |
| PG 1211+143 | 0.645, 59.0 | 68.212 | 73.094 | 4.882 | 0.080 | 0.086 |
| PKS 0558−504 | 1.162, 33.5 | 28.358 | 34.194 | 5.835 | 0.051 | 0.054 |
Comparison of the goodness of fit of the best-fitting models BPL and BPLGRE to the soft-band PSDs. The number in parentheses corresponds to the values for the iron-line band.
| . | . | BPL . | BPLGRE . | . | . | . |
|---|---|---|---|---|---|---|
| AGN name . | F-test . | AICc, 1 . | AICc, 2 . | Δ[AICc, 2] . | W[AICc, 2] . | ϵ2 . |
| . | ratio, prob. (per cent) . | . | . | . | . | . |
| NGC 7314 | 0.498, 68.6 | 58.324 | 64.813 | 6.489 | 0.038 | 0.039 |
| (0.255, 85.7) | (76.591) | (82.848) | (6.256) | (0.042) | (0.044) | |
| NGC 4051 | 0.822, 48.9 | 64.904 | 69.274 | 4.369 | 0.101 | 0.113 |
| (1.185, 32.6) | (56.060) | (59.733) | (3.673) | (0.137) | (0.159) | |
| Mrk 766 | 2.33, 8.7 | 55.452 | 56.186 | 0.734 | 0.409 | 0.693 |
| Ark 564 | 1.64, 19.65 | 61.317 | 63.205 | 1.888 | 0.280 | 0.389 |
| (0.378, 76.9) | (82.090) | (87.602) | (5.512) | (0.060) | (0.064) | |
| 1H 0707−495 | 0.910, 44.4 | 75.011 | 78.438 | 3.427 | 0.153 | 0.180 |
| MCG–6-30-15 | 0.248, 86.3 | 60.682 | 67.244 | 6.562 | 0.036 | 0.038 |
| (1.660, 18.9) | (59.634) | (61.676) | (2.042) | (0.265) | (0.360) | |
| IRAS 13224−3809 | 1.520, 22.3 | 49.100 | 52.588 | 3.487 | 0.149 | 0.175 |
| SWIFT J2127.4+5654 | 0.510, 67.7 | 74.958 | 80.084 | 5.125 | 0.072 | 0.077 |
| Mrk 335 | 0.701, 55.6 | 54.703 | 59.959 | 5.256 | 0.067 | 0.072 |
| NGC 3516 | 0.209, 88.9 | 84.710 | 91.009 | 6.299 | 0.041 | 0.043 |
| PG 1211+143 | 0.645, 59.0 | 68.212 | 73.094 | 4.882 | 0.080 | 0.086 |
| PKS 0558−504 | 1.162, 33.5 | 28.358 | 34.194 | 5.835 | 0.051 | 0.054 |
| . | . | BPL . | BPLGRE . | . | . | . |
|---|---|---|---|---|---|---|
| AGN name . | F-test . | AICc, 1 . | AICc, 2 . | Δ[AICc, 2] . | W[AICc, 2] . | ϵ2 . |
| . | ratio, prob. (per cent) . | . | . | . | . | . |
| NGC 7314 | 0.498, 68.6 | 58.324 | 64.813 | 6.489 | 0.038 | 0.039 |
| (0.255, 85.7) | (76.591) | (82.848) | (6.256) | (0.042) | (0.044) | |
| NGC 4051 | 0.822, 48.9 | 64.904 | 69.274 | 4.369 | 0.101 | 0.113 |
| (1.185, 32.6) | (56.060) | (59.733) | (3.673) | (0.137) | (0.159) | |
| Mrk 766 | 2.33, 8.7 | 55.452 | 56.186 | 0.734 | 0.409 | 0.693 |
| Ark 564 | 1.64, 19.65 | 61.317 | 63.205 | 1.888 | 0.280 | 0.389 |
| (0.378, 76.9) | (82.090) | (87.602) | (5.512) | (0.060) | (0.064) | |
| 1H 0707−495 | 0.910, 44.4 | 75.011 | 78.438 | 3.427 | 0.153 | 0.180 |
| MCG–6-30-15 | 0.248, 86.3 | 60.682 | 67.244 | 6.562 | 0.036 | 0.038 |
| (1.660, 18.9) | (59.634) | (61.676) | (2.042) | (0.265) | (0.360) | |
| IRAS 13224−3809 | 1.520, 22.3 | 49.100 | 52.588 | 3.487 | 0.149 | 0.175 |
| SWIFT J2127.4+5654 | 0.510, 67.7 | 74.958 | 80.084 | 5.125 | 0.072 | 0.077 |
| Mrk 335 | 0.701, 55.6 | 54.703 | 59.959 | 5.256 | 0.067 | 0.072 |
| NGC 3516 | 0.209, 88.9 | 84.710 | 91.009 | 6.299 | 0.041 | 0.043 |
| PG 1211+143 | 0.645, 59.0 | 68.212 | 73.094 | 4.882 | 0.080 | 0.086 |
| PKS 0558−504 | 1.162, 33.5 | 28.358 | 34.194 | 5.835 | 0.051 | 0.054 |
6 DISCUSSION AND CONCLUSIONS
We studied the observed PSDs of 12 X-ray bright AGN in the 0.5–1 and 5–7 keV bands, using archival XMM–Newton data. The total net exposure of the EPIC-pn light curves is larger than 350 ks in all cases (and exceeds 1 Ms in the case of 1H 0707−497). Our main aim was to search for GRE features imprinted in the observed PSDs, due to X-ray illumination of the inner disc, as suggested by P16. We fitted the 5–7 keV band PSDs of four sources, and the 0.5–1 keV band PSDs of all objects, with a BPL and with a BPL model modified by the disc transfer functions of P16. We did not find significant indications of X-ray GR reflection echo signatures in the observed power spectra of the sources in our sample.
P16 studied the PSD features in the case of X-ray reflection in the 5–7 keV band assuming a neutral disc, solar iron abundance, and the lamp-post geometry. Strictly speaking, the P16 results are applicable to the 5–7 keV band PSDs only. However, P16 argued that their predictions should be rather insensitive of the energy band, and of the assumed X-ray/disc geometry, as long as there is a significant reflection component, and the disc response function is characterized by a sharp rise, a plateau, followed by a decline at longer time-scales. In this case the corresponding transfer function, Γ(ν; h, α, θ) (and hence the observed PSD as well), should show a prominent dip and an oscillatory behaviour, with decreasing amplitude at high frequencies, similar to the disc transfer functions in the lamp-post geometry. The dip amplitude should depend mainly on the ratio of the reflected component over the total flux (i.e. continuum plus reflection) in each energy band. If this fraction is significant in the soft band, then GR echoes should be present in the observed soft-band PSDs as well.
The fact that the BPLGRE model does not improve the fit in the iron- and soft-band PSDs may argue against the P16 assumptions, i.e. the X-ray source may not be point-like but has a finite shape, or the disc is ionized, or the iron abundance is not solar. However, the non-detection of the predicted GREs may simply be due to the fact that a BPL model may fit well the observed PSDs in the frequency range where the observed PSDs are best determined (i.e. from 10−4 to 10−3 Hz), even if they have a BPLGRE shape. The expected best-fitting BPL residuals will have a small amplitude, and it may not be possible to detect them in each source, individually (see discussion in Section 3.2). We therefore estimated the average best-fitting BPL residuals of many sources. In this way we can increase the signal-to-noise ratio and detect low amplitude, but significant, residuals that cannot be detected in the residuals of the individual sources.
We calculated the best-fitting BPL residuals by dividing the iron-line and the soft-band PSDs by the corresponding best-fitting BPL model. If the BPL model was fitted well to the observed PSDs, the residuals should be consistent with unity at all frequencies. The mean iron-line residuals are plotted in Fig. 4. They are binned in frequency bins which are logarithmically spaced by a factor of λbin = 1.25 (the residuals are almost identical, irrespective of λbin). The open red squares in the same figure indicate the mean soft-band BPL best-model residuals (estimated in the same way) of the sources: NGC 4051, MCG–6-30-15, Mrk 766, Ark 564, 1H 0707−495, and IRAS 13224−3809. The BH mass estimates of these sources differ by a factor of less than 3. If there are GRE features in the AGN PSDs, the BPL best-fitting residuals should be different for sources with different BH mass. The differences are such that the residuals do not match even if we shift them by a factor equal to the ratio of the BH mass of the sources (see e.g. the differences between the expected BPL best-fitting residuals to the PSDs of a 1.73 × 106 and 1.73 × 107 M⊙ objects in the bottom plots of the left-hand panels in Fig. 2). It is for this reason that we decided to estimate the mean residuals only of these six sources only.1
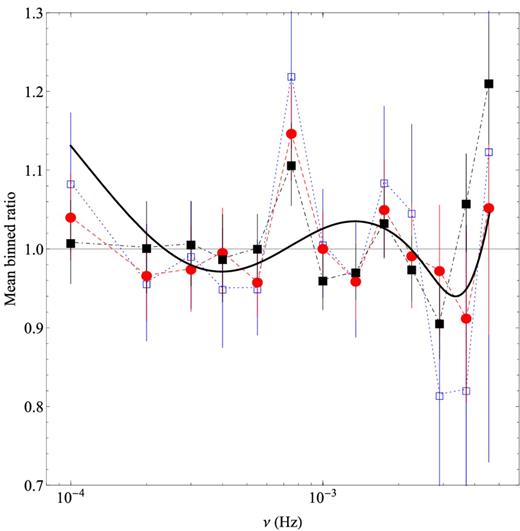
Average best-fitting BPL residuals. Open blue squares and red circles indicate the mean residuals for the iron-line band and for the soft-band PSDs of six sources, respectively. The filled black boxes indicate the mean binned residuals for the same six sources in the full band (0.3–10 keV) (see Section 6). The error bars correspond to the standard deviation of the mean in each bin. The black solid line indicates the theoretical ratio line, in the ‘highly relativistic’ case (see the bottom plot in the lower left panel in Fig. 2).
To increase even further the signal-to-noise ratio, we also considered the 0.3–10 keV band PSDs (full-band PSDs) of the same six sources that we considered in the soft-band PSDs. If the ratio of the reflection over the total flux in the full band is similar to the one in the soft and iron-line bands (which are traditionally thought to be reflection dominated), then it would be desirable to also search for the GRE features in the full-band PSDs, as in this case the Poisson noise is minimum and we can estimate more accurately the PSDs at high frequencies. We estimated the full-band PSDs as explained in Section 3; we fitted them with the BPL model, and we computed the averaged residuals. They are plotted with filled black squares in Fig. 4. Their errors reach a level of 3–4 per cent at all frequencies going up 2 × 10−3 Hz. Despite the small errors, the average residuals in all bands are consistent with unity: |$\chi ^2_{\rm iron \, line}=12.9, \chi ^{2}_{\rm soft\, band} =10.2$|, and |$\chi ^2_{\rm full \, band}$| = 19.3, for 12 degrees of freedom. This result indicates that the BPL model is fitted well to the observed PSDs and that we cannot detect any significant signature of GRE effects, or any other, deviations. The solid line in Fig. 4 indicates the expected BPL best-fitting residuals in the ‘highly relativistic’ case when MBH = 1.73 × 106 M⊙ (as plotted in the bottom plot of the lower left-hand panel in Fig. 2). The mean residuals are consistent with this line but, as we have mentioned before, this result is not significant in the sense that, statistically speaking, the residuals are also consistent with unity.
We conclude that the X-ray reflection features cannot be detected either in the soft or in the iron-line band PSDs of the individual sources. The objects in our sample are among those AGN with the longest X-ray observations with XMM–Newton. There are no features (with an amplitude larger than 3–5 per cent) that cannot be accounted for by the simple BPL model in the average best-fitting residuals of the brightest, and most variable sources in our sample, even when we consider the full-band light curves in order to increase to the maximum possible the signal-to-noise ratio.
The main reason for the non-detection of the GRE signatures in the observed PSDs may be lack of sensitivity, i.e. the observed PSDs, even when averaged, still have uncertainties that dilute the features needed to be detected in order to claim the corresponding GR effects. However, the biggest uncertainty at the moment is due to the fact that we do not know the exact shape and amplitude of the intrinsic X-ray PSDs in AGN. To demonstrate this issue, we repeat the same procedure as we did in Section 3.2. The solid line in Fig. 5 shows a BPL model with sh = 2 and νb = 8 × 10−5 Hz (this would be the bend frequency for a BH mass of 5 × 106 M⊙ if νb would scale inversely with BH mass.). The red dotted line indicates the respective ‘highly relativistic’ BPLGRE model (i.e. the same BPL model multiplied by the square of the transfer function in the ‘highly relativistic’ case, like the left-hand panels in Fig. 2). The blue dashed line, in the same figure, indicates the resulting best-fitting BPL model to the theoretical BPLGRE model. However, in this case, the high-frequency slope of the BPL model is kept frozen to the value of −2 during the fit. This would be the case if we knew a priori that this is the intrinsic PSD slope. The bottom panel in Fig. 5 shows the ratio of the BPLGRE PSD over the best-fitting BPL model. Clearly, the best-fitting residuals have a much higher amplitude in this case, being of the order of 20 per cent over almost the entire frequency range. As we mentioned above, the amplitude of the average residuals (when we consider all data together) is of the order of 3–5 per cent. Therefore, we would easily be able to spot the expected GRE features if we knew in advance the intrinsic PSD slope. More work is necessary to investigate the intrinsic PSDs, and then re-examine the agreement of the observed residuals to the expected ones.
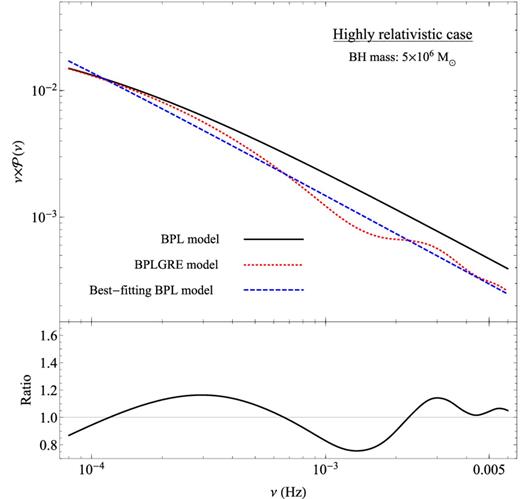
The expected GRE features for a BH mass of 5 × 106 M⊙ for the highly relativistic case. The black solid line indicates the BPL model with a high-frequency slope of −2, and a bend frequency of 8 × 10−5 Hz. The red dotted line shows the expected ‘highly relativistic’ BPLGRE model PSD (in the case of a Kerr BH and a point-like X-ray source located at a height of h = 3.6 rg). The blue dashed lines indicate the best-fitting BPL model to the BPLGRE model PSD, when the high-frequency slope is fixed to −2. The attached plot at the bottom shows the ratio of the BPLGRE model PSD over the respective best-fitting BPL model (red dotted and blue dashed lines in the upper panel, respectively).
This work was supported by the ‘AGNQUEST’ project, which is implemented under the ‘Aristeia II’ action of the ‘Education and Lifelong Learning’ operational programme of the GSRT, Greece. It was also supported in part by the grant PIRSES-GA-2012-31578 ‘EuroCal’. DE and IMM acknowledge the Science and Technology Facilities Council (STFC) for support under grant ST/G003084/1. The research leading to these results has received partial funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 312789. This research has made use of NASA's Astrophysics Data System Bibliographic Services. Finally, we are grateful to the anonymous referee for the very useful comments and suggestions that helped us in improving, significantly, the quality of the manuscript.
Based on observations obtained with XMM–Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA.
The BH estimates for the four sources with iron-band PSDs have similar BH mass estimates. We decided not to include NGC 7314 during the estimation of the mean soft-band residuals due to the poor quality of its soft-band PSD (see Emmanoulopoulos et al. 2016).
REFERENCES
APPENDIX A: IMPLICATIONS OF NON-STATIONARITY TO MODEL FIT RESULTS
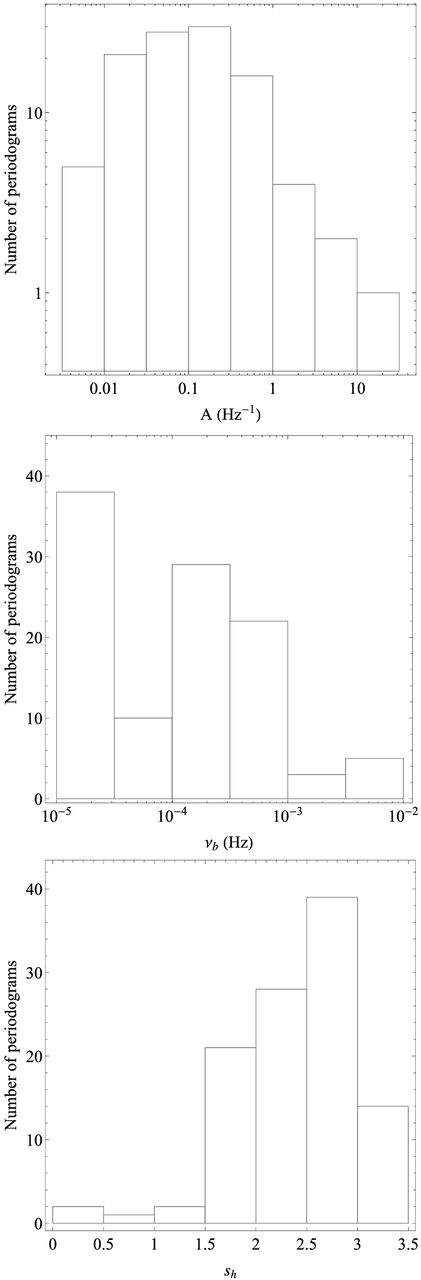
The distribution of the BPL model parameter values, from the best-fitting models to all the 121 individual, soft-band periodograms of 1H 0707−495 (with Poisson noise), using the maximum-likelihood method.
The sample mean of the A, νb, and sh distributions plotted in Fig. A1 is: 0.26 ± 0.07 Hz−1, (1.04 ± 1.01) × 10−4 Hz, and 2.43 ± 0.05, respectively (the errors correspond to the standard error of the mean). The difference between these values and the best-fitting BPL model parameter values listed in Table 3 for 1H 0707−495 is: −0.21 ± 0.11 Hz−1, (1.37 ± 1.12) × 10−4 Hz, and −0.26 ± 0.16. All three differences are less than 2.3 standard deviations away from zero.
Consequently, even if the PSD shape is variable with time, and the BPL model parameters vary as widely as the distributions plotted in Fig. A1 suggest (which is certainly not the case in reality), the best-fitting BPL results listed in Table 3 should correspond to the mean of the intrinsic distribution of the model parameter values. It is in this sense that we claim that fitting the average periodograms can yield the average PSD for a source.
APPENDIX B: NON-STATIONARITY AND PSD RESIDUALS
However, even if the best-fitting model parameter values are representative of their mean, if the PSDs are BPL-like, but variable, the average PSD may not have an exact BPL shape. This could explain the large χ2 values listed in Tables 3 and 2 for same sources.
To investigate this issue, we created 10 000 simulated light curves, following the method of Emmanoulopoulos et al. (2013). Each light curve has a duration of 100 ks, Δt = 100 s, and a mean which is randomly chosen from the ensemble of the 1H 0707−495 observed light-curve mean values. We assumed an intrinsic PSD which has a BPL shape, and we chose randomly a value from the BPL model parameter distributions shown in Fig. A1 to create each light curve. Consequently, the PSD of each light curve should be different from the others. Then, we created 1000 groups of 10 light curves, chosen randomly from the original sample. We divided them in 10 ks long segments, computed the periodogram for each one, subtracted the Poisson noise level, and calculated the average of the resulting 100 periodograms, exactly as we did for the estimation of the observed PSDs (see Section 3).
We fitted a BPL model to the average periodograms and we recorded the best-fitting χ2. In Fig. B1 we show the distribution of these χ2 values which sometimes seems to be quite large. Clearly, a χ2 value equal or larger than 68.5 is quite common (this is the best-fitting BPL χ2 value in the case of the observed, soft-band PSD of 1H 0707−495; Table 3). The vertical line in Fig. B1 indicates this value. According to the distribution of the χ2 values plotted in Fig. B1, the probability that χ2 < 58.4 is less than 0.3. However, we find that χ2 < 58.4 in around 70 per cent of the iron-line and the soft-band BPL best-fits (in eight out of the 12 sources). Clearly then, the PSDs cannot be as variable as the results plotted in Fig. A1 suggest, for most of the sources in the sample. On the other hand, non-stationary, variable PSDs may still be possible in the case of SWIFT J2127+5654, NGC 3516, and 1H 0707−495, which show the largest BPL best-fitting χ2 values among the sources (NGC 7314 and Ark 564, in the case of the iron-line band PSDs). We plan to investigate this issue further in the future.
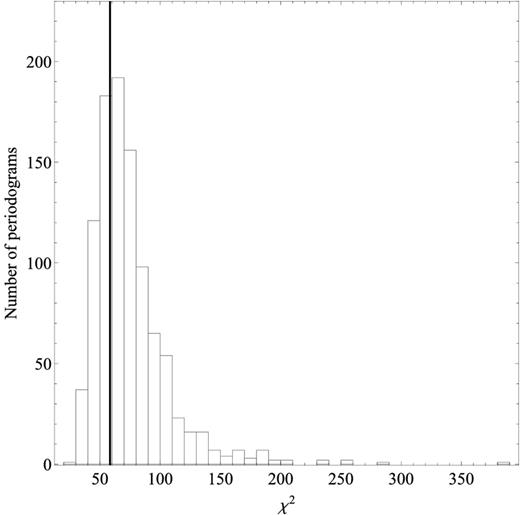
Distribution of the best-fitting χ2 values for the best-fitting BPL model to the average periodograms of the simulated light curves (see Section B). The black line corresponds to the value of χ2 equal to 58.4.



