Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

In this paper, the flight of micro (μ)-meteoroid in the day time earth environment has been discussed and the role of photoemission due to solar radiation, in addition to other relevant emission processes, viz. thermionic/charge desorption has been explored. Following Mendis et al., the meteoroid flight has been described by a consistent analytical model which manifests the continuity equations for the momentum, energy, charge and mass of micrometeoroids entering in the earth environment with a finite speed and at a finite angle. The altitude profiles of the characteristic features during flight, viz. surface heating, particle size, mass-loss, charging and its consequence on local atmospheric plasma has been examined in terms of the angle of entrance, entry speed, size, material work function/photoefficiency and incident solar flux. The numerical results show that the photoemission from micrometeoroid significantly contributes in meteoric electrons generation in its path in beginning and end phase of the flight; of course the energetics over the meteoroid in its travel is dominated by mass ablation process.

plasmas, Sun: UV radiation

1 INTRODUCTION AND MOTIVATION

The population of physical objects wandering in the interplanetary/near-earth space is largely configured by the micrometeoroids (micrometeoroids) which encounters with dense earth atmosphere in daily routine, and in this process, it produces an observable luminous phenomenon of meteor shower (Grün et al. 1985; Love & Brownlee 1993; Genge et al. 2008). The travel of meteoroid in the atmosphere essentially depends on its size, entry velocity and material composition. The study of meteor physics and consequences on its own flight and earth atmosphere, play an important role in describing the population of minor object/debris in the solar system (Love & Brownlee 1993; Genge et al. 2008) and exciting phenomena (Bronshten 1983; Ceplecha et al. 1998; Campbell-Brown & Koschny 2004; Mendis, Wong & Rosenberg 2004). An interesting feature associated with these micrometeoroids is that these can survive the interaction with the aggressive atmospheric drag and reach to the Earth surface, with a finite size/mass in form of micrometeorites (Genge et al. 2008). In its flight, micrometeoroids also give rise to the ionization trails, which is utilized for the specific radio communication, viz. meteor bursts communications (Schanker 1990). During its travel through earth atmosphere, the meteoroid undergoes numerous physical processes (Opik 1958; Love & Brownlee 1991), viz. atomic/molecular drag, deceleration, frictional heating, temperature rise (decay), mass ablation (sublimation/fusion), surface charging, meteoric electron cloud generation and excitation/ionization of atmospheric neutrals etc. Considering the complexity of the mechanisms, the studies in literature, in general, focus on any specific observation and takes account of few relevant processes to explain it further. In particular, most of the works concentrated on exploring the deceleration, heating and mass-loss (ablation) features of meteoroid and consequent atmospheric ionization (Love & Brownlee 1991; Tielens et al. 1994; Rogers, Hill & Hawkes 2005; Szasz et al. 2008); the analyses primarily refers the model developed in classic work by Opik (1958). However, in recent years, the innovative experimental campaigns, theoretical/analytical studies and numerical modelling (Love & Brownlee 1991; Mathews et al. 1997; Janches et al. 2000; Campbell-Brown & Koschny 2004; Mendis et al. 2004; Szasz et al. 2008) have strengthened our understanding of meteoroid dynamics and relevant physical processes. In particular, the role of individual mechanisms of mass-loss, viz. ablation (Love & Brownlee 1991), physical sputtering (Szasz et al. 2008), fragmentation (Campbell-Brown & Koschny 2004) and differential ablation (Tielens et al. 1994) has critically been examined.

In the process of frictional heating during flight, the meteoroid may gain sufficient temperature to initiate the process of thermionic emission which may significantly alter the particle charging state, its cooling and background plasma density. The role of thermionic emission was first recognized in few early investigations (Furman 1960, 1961; Bronshten 1991) but the problem has adequately been taken up in the work by Sorasio, Mendis & Rosenberg (2001) and Mendis, Wong & Rosenberg (2005), where a consistent theoretical model describing the flight dynamics of the micrometeoroids in the dense earth atmosphere has been proposed; the model consider the simultaneous inclusion of the equations of charge continuity, mass, momentum and temperature. However, in sake of simplicity, they have chosen dark side of the earth atmosphere (night time) for the study. In this present analysis, we are intended to extend their work and model towards the micrometeoroids flight in day time earth atmosphere. In contrast to night time, the day time earth atmospheric (ionospheric) structure is primarily determined by the incident solar radiation (Ratcliffe 1960; Gurevich 1978; Budden 1989) and of course depending on the material properties (like work function/photoelectric yield) the micrometeoroid may also lead to the photoemission flux (Mishra & Misra 2015) in addition to thermionic/charge desorption currents. The presence of large plasma density column in the ionospheric layers and the photoemission may significantly contribute in determining the charge structure of meteoroid and local atmospheric plasma density during its flight. Since the thermionic current rises exponentially with increasing temperature (∝e− 1/T), the effect of photoemission may intuitively be pronounced and may contribute significantly in beginning (and end) phase of the micrometeoroid flight where the temperature is not sufficient to trigger the excessive thermionic emission current.

We have considered the analytical model of Mendis et al. (2005) as a basis to proceed further. In writing the dynamical equations for the motion of micrometeoroids, we confine our analysis to free molecular regime (Love & Brownlee 1991) which is safely applicable for the micrometeoroids of size ≤ 1 mm and ionospheric altitude of interest i.e.h ≥ 80 km. The region of interest in the earth atmospheric altitude (80 km ≤ h ≤ 200 km) for the meteoroid flight is chosen such that the molecular interaction above entry level (∼200 km) is insignificant, while below 80 km, the speed of meteoroid is small enough and no further mass ablation occurs. The day time ionospheric model given by Gurevich (1978) has been taken into account for the analysis purpose. Photoemission due to solar radiation [particularly dominated by EUV Lyman α in the region of interest (Bauer 1973)] from the meteoroid flowing through earth atmosphere has also been taken into account along with thermionic emission/charge desorption mechanisms, in writing the equations for the charge continuity, electron production rate and the surface temperature. In fact, the meteoroid possess a finite non-zero potential as it enters in the earth atmosphere (∼200 km) due to existing plasma atmosphere and solar spectrum; this has been consistently taken into account in the present analysis and used as initial value of charge in solving the model equations. Considering the difficulty in the implementation of irregular shape effect of the meteoroid in the complex mechanisms involved in the model, the micrometeoroids are taken to be spherical in nature and assumed to retain its spherical shape during its flight through earth environment. Furthermore, in writing the equation for the temperature rise/mass ablation, the processes of physical sputtering due to meteoroid impact with energetic atmospheric atom/molecule and its fragmentation are ignored; the two effects, viz. physical sputtering and fragmentation may be accountable for the meteoroids having large size (∼500 μm)/entry speed (∼71 km s−1) (Opik 1958; Brosch et al. 2001) and weak tensile strength (Bronshten 1983), respectively. In this prospect, we confine our analysis to the fine stony particles of radius (∼10–100 μm) and entry speed (∼10–35 km s−1) where the physical sputtering and fragmentation are negligible in comparison to other terms involved in the equations of temperature/mass ablation. For our calculations, the specific parameters describing the physical properties micrometeoroids has been taken from the work of Mendis et al. (2005) where the appositeness of the data has also been justified with detailed discussion. Utilizing the analytical basis, the set of equations has been solved numerically to obtain the characteristic features of the micrometeoroids passing through day time dense earth atmosphere. The analytical formulation describing the model equations of the problem has been established in the next section (i.e. Section 2). The third section (i.e. Section 3) includes the description of the earth ionospheric structure, parameter regime for the meteoroids, relevant expressions for the physical processes incorporated in the analysis and the computational scheme. The physical interpretation and discussion of the numerical results based on analysis has been given in Section 4 on Numerical results and discussion. A summary of the outcome in Section 5 concludes the paper; the expressions and relevant parameters used for computation have been specified in Appendix section at the end.

2 ANALYTICAL FORMULATION

2.1 Kinetic equation

As the meteoroid enters into the atmospheric environment, its flight is suffered from its charging, deceleration, mass-loss and heating along its path. In this analysis, we primarily use the basic model given by Mendis et al. (2005), which is upgraded in the context of day time earth atmosphere by including the mechanisms of photoemission from and electron/ion accretion on the micrometeoroid surface in the charging and energy balance equations. Consider a homogeneous spherical meteoroid of initial radius (ro) entering in the earth atmosphere with velocity |${\upsilon _o}$| at an angle θ with horizontal; in order to reduce the computational load, we confine our analysis in the region of h ∼ (200–80 km) earth atmospheric altitude where the meteoroid interaction with local plasma environment comprising of electrons, atomic/molecular ions and neutrals is significant. Considering the small extension of the meteoroid flight with respect to earth horizontal span, the curvature of earth is ignored and simply orthogonal Cartesian coordinate is utilized in this analysis; this assumption is valid for the inclination θ ≥ 7°(Love & Brownlee 1991). Similarly, the influence of Coriolis force due to finite earth rotation is also ignored in comparison to molecular drag and gravity effects (Mendis et al. 2005). Following Mendis et al. (2005), the equation of motion for micrometeoroid flight in free molecular regime can be written as
(1)
here ρm and ρa refer to bulk density of meteoroid material and atmospheric density, respectively, while γ corresponds to free molecular drag coefficient, typically ∼0.5–1.0 (Hughes 1978).
The first term in right-hand side (rhs) in equation (1) refers to drag force acting on the meteoroid by atmospheric plasma, while the second term is acceleration due to gravity; the bold fonts in the equation refer to vector quantities. In writing this equation, we assume that the mass degradation from the micrometeoroid surface is isotropic and hence recoil force due to anisotropy is ignored for sake of simplicity in this analysis. To further analyse the problem, we refer the coordinate geometry sketched in Fig. 1 in the work by Mendis et al. (2005); in this Cartesian geometry, the origin is chosen at entry point with x-coordinate vertically downward and y-coordinate horizontally parallel to earth ground. Following this coordinate geometry, the vertical (x) and horizontal (y) component of the velocity equation (equation 1) can be written as
(1a)
(1b)
Initial surface potential (Vo) over meteoroids at entry level as a function of work function of the material for different values of parameter npo; the colour labels are marked in figure.
Figure 1.

Initial surface potential (Vo) over meteoroids at entry level as a function of work function of the material for different values of parameter npo; the colour labels are marked in figure.

Open in new tabDownload slide

One can immediately realize from equations (1a and 1b) that the horizontal component of the micrometeoroid speed ultimately (at the end of flight) becomes zero and the particle exhibits a finite vertical terminal speed proportional to the square root of the micrometeoroid terminal radius (i.e. residual radius of the particle at the end of the flight).

During flight, the meteoroids interacts with atmospheric plasma environment and frictionally heat the surface; the heating may be significant to cause the fusion of micrometeoroid material and subsequently leads to the mass sublimation/fusion. In addition, the energy is also lost through radiation to the surrounding environment and thermionic emission. The photoemission may also cause the energy loss and cooling of micrometeoroid as the electron leaving the meteoroid surface due to photoemission carries the energy equal to surface temperature; however, its contribution to the energetics over the micrometeoroid may be small in comparison to the dominant thermionic emission/mass ablation. The energy balance equation for the meteoroid traversing through atmospheric layers can be written as (Mendis et al. 2005)
(2)
where lm = (Lm/μ), κ is the free molecular heat transfer coefficient, s is the specific heat of the meteoroid material, Tm and To refer to the surface temperature of micrometeoroid and surrounding environment (radiative) temperature, ε is the thermal emissivity, σ is the Stephan–Boltzmann constant, fsub refers to the mass-loss rate due to sublimation while ffus corresponds to production rate (by mass) of liquid, Lm is the latent heat of sublimation per mole, while lf is the latent heat of fusion, μ refers to gram molecular weight of the average sublimated molecule, fth(fph) refers the rate of thermionic (photo) emission rate per unit area from the meteoroid surface, εth is the mean energy of the thermionic electrons on the meteoroid surface, εpo( ∼ kTm) is the energy carries away by photoemitted electrons and refers to surface temperature, and fec/fic are the accretion rate of electrons/ions per unit area on the meteoroid surface while εec/εic refer to the mean energy of the electrons/ions accreting on the meteoroid surface; relevant expressions are listed later in the text.
The first two terms in the rhs correspond to net power gained by micrometeoroid surface on account of drag through the earth atmosphere and electron/ion accretion over its surface. Third term refers to the energy gain from the meteoroid due to electron–ion recombination on its surface while the next two terms correspond to the energy loss due to the thermionic and photoelectric emission, respectively. It should be noticed that the energy loss per electron (and hence the cooling rate) is much larger in case of thermionic emission than that for photoemission; this is because of the fact that in case of thermionic emission, the thermal energy also helps the electron in overcoming threshold work function, while for photoemission, this threshold is overcome by solar radiation and does not contribute in cooling. Next two terms are the net power loss from the meteoroid surface due to sublimation/fusion of the meteoroid mass. The last term corresponds to the energy loss due to radiation to the surrounding environment. In writing the above equation (i.e. equation 2), we have assumed that the conductivity is large enough or the meteoroid size is small enough so that lattice temperature rises uniformly (i.e. no temperature gradient) throughout the meteoroid volume (Sorasio et al. 2001; Mendis et al. 2005). Consequently, assuming the isotropic mass-loss of the meteoroid as it traverse through earth atmosphere, the equation for change in radius (or mass) can be written as
(3)
where cf refers the fraction of fused material, lost as a spray due to atmospheric interaction.
For sake of simplification in analysis, we utilize the scheme adopted by Bronshten (1983) and Mendis et al. (2005) as ffus = 2fsub, lf = (1/4)lm and cf = 1/2. During flight, the meteoroids acquire charge on its surface due to its interaction with plasma environment. The charging primarily takes account of electron/ion accretion on and electron emission (via thermionic and photoelectric emission) from meteoroid surface and charge evaporation due to mass ablation. The equation for meteoroid charging can be written as
(4)
where fph is the photoemission rate per unit surface area while fs( = |z|/τs) refers to the rate of charge desorption in the process of mass ablation and |${\tau _{\rm{s}}}( = - r/2\dot r)$|⁠. It is necessary to mention here that fs is important only for fast moving small size micrometeoroids which continue to lose mass even as they becomes quite small and becomes comparable to time-scales associated with charging currents. The expressions for various parameters have been given in later section. The set of equations (1–4) describe full set of dynamical equations which determines the spatiotemporal dynamics of meteoroid flight in earth atmosphere. However, for the sake of simplicity in the analysis/computations, considering the fast transient phenomena of charging and heating (of the order of few microseconds) the computations has been confined only to examine the steady state dynamical evolution (viz. ∂z/∂t = 0 and |$d/dt\sim\upsilon \partial /\partial h$|⁠) of various physical features in this analysis.

2.2 Electron production rate

During flight, the meteoroid electrons generation takes place by following mechanisms: (i) collisions of atmospheric molecules/atoms with sublimated material atom/molecules, (ii) thermionic emission from the heated meteoroid surface, and (iii) photoemission from the meteoroid surface in the presence of solar radiation. If β is the number of free electrons produced per vaporized meteor atom, the production rate of electrons due to sublimation can be written as
(5)
where ms is the mass of average sublimated molecule (we use ms ∼ 40 amu (Love & Brownlee 1991)); the velocity dependence of β has been specified in Appendix section A1. The net production rate of electrons can thus be given by
(6)
where |${\dot n_{{\rm{th}}}}( = 4{\rm{\pi }}{r^2}{f_{{\rm{th}}}})$| and |${\dot n_{{\rm{ph}}}}( = 4{\rm{\pi }}{r^2}{f_{{\rm{ph}}}})$| refer to the electron generation rates through thermionic photo emission processes.

3 PHYSICAL PARAMETERS AND EXPRESSIONS

3.1 Atmospheric structure

The atmospheric plasma primarily includes electron, multispecies ions and neutral species where the partial ionization in day time is maintained by soft X-rays and far-UV solar radiation spectrum reaching to atmospheric level. The plasma composition in the ionosphere changes with change in the neutral constituents in atmosphere. For the numerical appreciation of the analytical model, the ambient atmospheric plasma parameters need to be expressed as a function of altitude. For the purpose, we utilize the atmospheric structure specified by Gurevich (1978) and confine our computations in the region of atmospheric altitude of ∼80–200 km and day time (at 12:00 noon) data. For sake of analytical convenience, we mimic the atmosphere to be configured by a neutral atom/molecule (like N2) of an average mass mn ∼ 30 amu, corresponding singly charged ions (like NO+) and electrons. Utilizing the data set given in the tables 1 and 2 of the book by Gurevich (1978), the empirical (best polynomial) fits for various plasma parameters as a function of atmospheric altitude (h, in km) has been evaluated and the algebraic functional form are given in Appendix section A2.

3.2 Meteoroid parameters

The physical and thermodynamic parameters characterizing the material properties of the micrometeoroids interacting with atmospheric plasma have been taken from recent studies (Sorasio et al. 2001; Mendis et al. 2005; Briani et al. 2013) where the choice of these parameters is also justified in the context of present study. The rate of mass-loss due to sublimation is given by Knudsen–Langmuir relation and can be expressed as (Briani et al. 2013)
(7)
where pvap is vapour pressure and may be given by log10pvap = (am − bm/Tm) (Clausius–Clapeyron equation), mo is the average mass of sublimating molecule and am/bm are the material-dependent constants. The computation takes account of following typical data for micrometeoroid primarily taken from References (Mendis et al. 2005; Briani et al. 2013):κ = 1 = γ, To = 200 K, Tmo = 100 K, Lm = 8 × 1010erg mol− 1, s = 107erg gK− 1, mo = 40 amu, μ = 40, ρm = 1g/cc, am = 10.6, bm = 13 500 K, angle of incidence at entry layer (ho = 200 km) θ = 45, meteoroid radius at entry layer ro = (10 − 100)μm, entry speed |${\upsilon _o} = (10-35){\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$| and meteoroid work function φ = (1 − 5)eV.

3.3 Charging currents over meteoroid

3.3.1 Electron–ion accretion currents

In this analysis, the meteoroid enters in the earth atmosphere with a finite speed |${\upsilon _o}$| and passes through with a finite speed (⁠|$\upsilon $|⁠), relative to the stationary atmospheric plasma through ionospheric layers. In such a situation the plasma electrons/ions are characterized by shifting Maxwellian distribution than the usual isotropic Maxwellian. This leads the case that the accretion current of electrons/ions over flowing particle increases with respect to the usual stationary plasma having Maxwellian distribution (Whipple 1981; Shukla and Mamun 2002; Mishra, Misra & Sodha 2011, 2013). Thus, in present context, the expressions for electron/ion accretion current and corresponding mean energy deposited over flowing objects has been taken from Mishra et al. (2011, 2013) and are given in Appendix section A3.

3.3.2 Thermionic emission current

During flight, the meteoroid surface gets heated due to its interaction with atmospheric plasma and the surface temperature may rise to an extent where thermionic emission may significantly contribute in its charging and energy dissipation. Corresponding expressions for emission rates and mean energy has been stated in Appendix section A4.

3.3.3 Photoemission current

The day time ionospheric layer is illuminated by solar radiation which causes photoemission from the flowing meteoroid surface. The continuous solar spectrum to the earth atmosphere is characterized by as a black body radiating at Ts ≈ 5800 K. However, for the sake of simplicity in computation and in the absence of the appropriate spectral data in desired atmospheric region, the photoemission from the meteoroid surface is assumed to be caused by dominant EUV Lyman α radiation (wavelength ∼121.57 nm) in the near-earth space (Bauer 1973). In fact, Lyman α radiation (∼121.57 nm) of EUV solar spectrum is considered as dominant source of the ionization in D-layer (∼50–90 km) of the ionosphere (Zolesi & Cander 2014) and certainly, it is available for photoemission from micrometeoroids during its flight in the atmospheric region of our interest (∼80–200 km, E-layer and above). In literature (Bauer 1973; Roble & Emery 1983), the average photon flux in near-earth space (∼200 km) associated with Lyman α radiation in solar illumination spectrum has been measured to be of the order of Λo ∼ 3 × 1011photons cm− 2s which may get enhanced up to Λo ∼ 1012photons cm− 2s during spotless solar activities (i.e. solar max). The intensity of the Lyman α radiation (i.e. photon flux), however, gets attenuated as it enters into dense lower earth atmosphere. The altitude profile of intensity in day airglow of Lyman α has been reported by Heath (1967); in this study, the measurement was taken via floating density and temperature probes launched during Aerobee-150 rocket campaign from White Sands, New Mexico. In this work, the figure (ref. Fig. 2, Heath 1967) illustrating the intensity profile of Lyman α radiation, shows that the intensity remains nearly constant in the altitude range ∼200–130 km; as it penetrates further the dense environment (i.e. h < 130 km), the intensity of the Lyman α radiation drops by a factor of ∼4 in reaching at altitude h ∼ 85 km. For the consistency of the analysis, we have utilized this intensity profile (Fig. 2, Heath 1967) to estimate the extinction factor (i.e. δ = Λ/Λo) corresponding to Lyman α radiation; the algebraic form of the empirical fit used for computations in this analysis are given in Appendix section (A5). Along with photon flux, the material dependent photoelectric yield (χ) is another key parameter referring the fraction of electrons emitted per incident photon from meteoroid surface. In general, the two effects collectively referred by parameter np( = χΛ) which essentially represents the photoelectron flux per unit normal cross-section from uncharged surface (Fowler 1955; Sodha & Guha 1971). Of course, the photoelectric yield (χ) depends on material properties and incident radiation spectrum, but in deficiency of any apposite data for meteoroid material, we have chosen a typical finite for our calculations. In order to illustrate the effect of photoemission from meteoroid during its flight, a plausible value npo = np(h ≈ 200 km) ∼ 1012cm− 2s has been used for computation in this analysis. This magnitude of npo may refer to χ = 1 and Λo = 1012photons cm− 2s; this certainly infers to the maximum possible photoelectrons available for emission during meteoroid flight. Since the parameters χ and Λo can take smaller values as well, the effect of varying npo has also further been investigated (illustrated in Figs 7 and 8) in this analysis which eventually refers the change of photoefficiency keeping photon flux constant and vice versa. The corresponding expressions for photoemission rate and mean energy from spherical objects, used in computations has been mentioned in the Appendix section (A6).

Altitude profiles of (a) meteoroid surface temperature (Tm), (b) particle size (r/ro), (c) charge (z), and (d) electrons production rate for different values of angle of incidence θ on entry layer for the parameters ro = 30 μm, ${\upsilon _o} = 25\,{\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$, npo = 1012 cm− 2s and φ = 2.5 V; the colour labels for different values of θ are marked in figure.
Figure 2.

Altitude profiles of (a) meteoroid surface temperature (Tm), (b) particle size (r/ro), (c) charge (z), and (d) electrons production rate for different values of angle of incidence θ on entry layer for the parameters ro = 30 μm, |${\upsilon _o} = 25\,{\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$|⁠, npo = 1012 cm− 2s and φ = 2.5 V; the colour labels for different values of θ are marked in figure.

Open in new tabDownload slide

3.4 Computational scheme

As stated before, we confine the analysis and computation to steady state dynamical evolution of the meteoroid flight. From preceding section, now we have the knowledge of altitude dependence of earth atmospheric structure (neutral/plasma density and temperature) in desired regime (h ∼ 80–200 km) and hence the particle and corresponding heat flux. Using ambient plasma and micrometeoroid parameters with appropriate expressions and boundary (initial) conditions (viz.|${\upsilon _x} = {\upsilon _o}Sin\theta $|⁠, |${\upsilon _y} = {\upsilon _o}Cos\theta $|⁠, r = ro, Tm = Tmo and z = zo at h = ho), equations (1–7) have been solved simultaneously with help of mathematica software to obtain the altitude evolution of micrometeoroid flight. In computations, we examine the effect of thermionic/photoemission charging (by varying work function of meteoroid and photon flux) and meteoroid parameters (like initial radius, initial velocity and angle of incidence) on the altitude profile of meteoroid flight considering day time atmospheric structure. Corresponding numerical results has been graphically presented in figures and discussed in the next section.

4 NUMERICAL RESULTS AND DISCUSSION

For the numerical appreciation of the kinetic model and understanding of the day time flight of micrometeoroids in the earth atmosphere, the computations have been performed for the typical set of meteor and plasma parameters mentioned in previous section (i.e. Section 3). The numerical results for various meteoroid/plasma parameters have graphically been presented as a function of atmospheric altitude, in figures (Figs 1-8). In the analytical model, the equation of motion of micrometeoroid in dense medium is manifested with the balance of charge and energy over the flowing object. It should be noted that, the micrometeoroid entering in the earth atmosphere (∼200 km) in the day time environment should have acquired a finite charge before entrance (>200 km); this is because of existing solar radiation and its travel through plasma environment. The charge acquired by micrometeoroid particle before entering the earth environment (i.e.ho ∼ 200 km) has been illustrated as a function of material work function (φ) in Fig. 1 which has further been used as an initial value of the charge (z) in solving the set of dynamic equations (equations 1–7) with the physical expressions/parameters given in Appendix section. The initial charge has been evaluated in terms of surface potential Vo( = zoe/ro) by balancing the photoemission and plasma electron/ion currents over the meteoroid surface corresponding to the entry layer at the altitude of ho ∼ 200km. According to uniform potential theory (Sodha, Misra & Mishra 2010; Misra & Mishra 2013), this potential is independent of particle size and hence the estimate is applicable to the meteoroid of any size; the magnitude of charge, of course, remains proportional to its radius (Sodha et al. 2010) and can be estimated immediately by using relation zo = (Voro/e). In figure, it is demonstrated for different values of the parameter npo( = χΛo) which characterize the photon flux and photoefficiency. Physically, the initial surface potential (at ∼200 km) should decrease with increasing work function (φ) and decreasing np on account of corresponding diminution in the photoelectric current; however, the effect is seen to be weakly pronounced due to small photoelectron flux in comparison to available plasma column. In this analysis, considering the solar illumination of the earth atmosphere (with dominant EUV Lyman α radiation), we have taken into account the photoemission from the micrometeoroid during its flight in dense earth environment (h ∼ 200 − 80 km), in addition to the thermionic emission current. In the very beginning phase of the flight (h ∼ 200 km), photoemission may not be significant enough to let the meteoroid acquire a positive potential but in absence of any other electron emission mechanism, it might be important in producing meteoric electrons; this is also supported by the fact that extinction factor of Lyman α radiation is nearly constant up to ∼130 km earth altitude. As the meteoroid starts off from the entry layer, the outer surface start getting heated due to significant heating mechanisms; in particular driven by air drag. As the micrometeoroid comes down further at lower atmospheric altitude (∼130 km), the surface temperature raises immensely (Tm ∼ 1000 K) due to the dominant molecular atmospheric drag and this yields the thermionic emission as a dominant charging current; an estimate of the magnitude of the emission currents can be made from the expressions given in Appendix section which predicts that thermionic current is two orders of magnitude larger than photoemission current for φ = 2.5 eV and Tm ∼ 1000 K. However, as soon as the temperature of the meteoroid reach to trigger the mass ablation process, the charge desorption also contribute significantly and may become dominant in the ablation regime (discussed later in detail). For describing the importance of electron emission processes (photoemission in particular), the dependence of the altitude profiles of meteoroid parameters has been illustrated as a function of the meteoroid work function (φ) and incident photon flux (np) in Figs (5-8); the individual contribution of photoemission current in the generation of meteoric electrons during flight has been compared with other significant emission processes. The photoemission certainly may influence the charge structure over meteoroid in lower atmosphere (close to altitude ∼80 km) where the temperature of the meteoroid is moderate (Tm ∼ 300 K) and the photoelectric emission dominates (or of same orders of magnitude) over other emission processes. Furthermore, with an intuitive physics notion, it can also be stated from the energetics written in equation (4) that the photoelectron released from meteor carries energy equivalent to its surface temperature which is significantly small (∼1/30 times) in comparison to the energy consumed in thermionic emission of each electron; thus, photoelectric effect weakly contribute in meteoroid cooling/energy dissipation in its travel to lower earth atmospheric altitude. The frictional heating dominates over the other mechanisms taken into account and further acts as dominant cooling process in mass ablation phase. It is also of interest to connect this work with the analysis by Mendis et al. (2005) where the night time flight of micrometeoroid is considered. In contrast to this, the day time ionospheric plasma considered herein is specified with higher density/temperature and solar radiation; neutral density does not get affected much. This higher plasma density/temperature influence the charge structure over meteoroid during its flight and this turns out to affect the thermionic/photoelectric electron emission flux, as it depends on instant meteoroid charge (equation 6). Physically, large plasma density column associated with day time ionosphere results in large electron flux to the meteoroid surface in its flight and as a consequence the meteoroid attains smaller positive charge; this results in larger the electron emission and hence the production rate. This fact has been shown in our calculations (Figs 6 and 8), where the electron production rate due to thermionic emission found larger during day time flight in comparison to night time estimates by Mendis et al. (2005). The photoemission is seen to contribute significantly in generating meteoric electron from meteoroid in beginning and end phase of its flight.

The effect of oblique incidence of micrometeoroids (entering at altitude ho ∼ 200 km), on their flight in the earth atmosphere and respective physical parameters has been displayed in Fig. 2. The evolution of the surface temperature of the micrometeoroids (ro ∼ 30 μm, φ = 2.5 eV) entering with an initial speed |${\upsilon _o}\sim 25\,{\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$| in the dense earth atmosphere has been illustrated in Fig. 2(a). In general, the meteoroid temperature increases as the particle starts off from the entry level and acquires a maximum value around ∼100 km due to frictional heating and then after it decreases rapidly to atmospheric radiative temperature i.e. ∼200 K due to dominant radiative losses. As the micrometeoroid starts from the entry level, the energetics lead it to a quasi-equilibrium state with local environment where its frictional heating is balanced by energy loss due to electron emission and radiative losses. This quasi-equilibrium holds at higher altitude (close to the entry level) for the particles entering at smaller angle (θ). This is because it travels larger distance (and hence spend longer time period) due to its horizontal movement and thus the quasi-equilibrium is attained at higher altitude. As micrometeoroid further comes down and penetrates the dense environment at lower altitude, their temperature increases primarily on account of frictional heating (equation 3) and attains a maximum value (Tmax) until the cumulative effect of cooling due drag induced speed deceleration and the mass ablation/radiation starts dominating. The rapid cooling of the meteoroid in the proximity of altitude (hmax, corresponding to Tmax), certainly caused by two mutually correlated factors, viz. (i) the large fraction of frictional heating is used in mass ablation, and (ii) reduced frictional heating (⁠|$ \propto {\upsilon ^3}$|⁠) as the particle comes further down and encounters with dense gas. Of course, the first aspect dominates near Tmax while the second one dominates as the temperature falls. This causes the rapid decrease in the temperature and the particle size (mass) which ultimately gets stabilize at the surface temperature equivalent to environment temperature To( ∼ 200 K) around ∼85 km. The dynamics becomes even more complex in the proximity of maximum temperature (Tmax), where all the energy exchange mechanisms, viz. atmospheric drag, mass ablation, electron emission and radiation coexists, and causes the simultaneous decay in speed and size; the evolution of the particle size and vertical/horizontal speed has been displayed in Figs 2(b)–(d), respectively. The ultimate fate of micrometeoroid flight at lower altitude is determined by quasi-static equilibrium described by equations (1–4). As depicted in Fig. 2(b), a significant decay in the particle size (and hence in mass) is noticeable from the altitude in the proximity of Tmax and there after it decreases rapidly until it attains a temperature much smaller to avoid further mass-loss due to ablation process (i.e. terminal mass). The micrometeoroid entering at small angle (viz. θ ∼ π/12) is noticed to shrink in its size by ∼30% while vertically falling particles are predicted to retain its mass by less than ∼1%. The vertical speed (⁠|${\upsilon _x}$|⁠) is noticed to drop sharply (∼96 km) in case of large incident angle (θ ∼ π/2), as it encounters large drag due to large vertical velocity component, large decay rate of particle size and presence of dense gas column in its travel. The horizontal component of velocity (⁠|${\upsilon _y}$|⁠) has been displayed in Fig. 2(d) which is primarily driven by molecular drag parallel to the earth surface and is seen to decay with earth altitude ultimately to |${\upsilon _y}\sim 0$|⁠; the drag effect is weak in case of shallow angle of micrometeoroid incidence and cover large horizontal distance in case of θ ∼ π/18. Our calculations also predict that the horizontal displacement increases with decreasing inclination (θ); more precisely the micrometeoroid entering with speed 25 km s−1 at an inclination θ∼(π/4) and ∼(π/12), traverse ∼110 km and ∼425 km horizontal distance, respectively, before its horizontal speed drop to rest due to neutral drag. Bronshten (1983) obtained that in the presence of gravity the residual of the micrometeoroid ultimately (∼80 km) acquires a finite terminal speed corresponding to |${\upsilon _y} = 0$| and |${\partial _{\rm{t}}}{\upsilon _x} = 0$|⁠; in our computations, the terminal speed is found to increase with increasing the terminal mass (or radius) i.e. with decreasing θ. This result is consistent with equation (1a) which predicts that the terminal speed (⁠|${\upsilon _{x,{\rm{t}}}}$|⁠) around ∼80 km, is proportional to the square root of terminal radius (i.e. |${\upsilon _{x,{\rm{t}}}} \propto r_{o,{\rm{t}}}^{1/2}$|⁠). The dynamical evolution of the electrical charge on the surface of micrometeoroid during its flight basically is the manifestation of the altitude variation of the surface temperature, particle size and encountering atmospheric plasma which dictates the charging currents. The charge on the particle eventually is determined by the balance of the charging currents over its surface which includes the currents due to thermionic, photoelectric, plasma electron/ion and charge desorption (mass ablation) processes; the charge profile corresponding to different angle of incidence has been displayed in Fig. 1(e). As the micrometeoroid starts off from entry layer with finite negative potential, the charge drops from its initial value and become more negative with decreasing altitude due to increase plasma density column and thermionic emission is less effective (∼180 km) in this regime. As the temperature of micrometeoroid increases due to strong frictional heating in its flight the thermionic/desorption currents become significant (∼130 km) and its magnitude tends towards positive values; this nature is consistent with the temperature profile of the micrometeoroid flight (Fig. 2a). Further increase in the temperature (as meteoroid falls down further) triggers the additional mechanism of charging (electron loss) due to mass ablation (charge desorption) and this certainly dominates in this regime ∼120–97 km (Mendis et al. 2005). The micrometeoroid is seen to acquire the maximum charge (zmax) around Tmax (∼102 km) and drops as the particle comes further down (∼98 km) because of decrease in desorption and thermionic currents; in consistency with temperature profile zmax is seen to increase with increasing θ. The particle gains terminal radius by reaching up to ∼90 km and at this point of time the surface temperature drops to To ∼ 200 K and the atmospheric plasma also gets rarefied. This result in that the charging currents due to thermionic emission/plasma particles over micrometeoroid surface become again insignificant in comparison to photoemission current and the residual particles may attain finite positive charge (∼82 km). The altitude profile of the net production rate of electrons due to cumulative effect of all the electron generation processes has been displayed in Fig. 2(f) and is noticed to be largest in case of θ ∼ π/2; this is again consistent with the altitude profile of the micrometeoroid surface temperature. In this particular case, the production of electrons due to charge desorption (mass ablation) is dominant in the range ∼97–122 km and rest of the region in altitude profile is dominated by thermionic/photoelectric electrons; this fact has further been discussed and clarified in subsequent figures.

The flight of micrometeoroids entering in the earth atmosphere (ho ∼ 200 km) with different speeds at finite acute angle (θ ∼ π/4) has been demonstrated in Fig. 3. The surface temperature altitude profile has been illustrated in Fig. 3(a) and individual profile characteristic is similar to discussed in Fig. 2(a). The micrometeoroid entering with large speed is noticed to acquire large Tmax and even at higher earth altitude. This can be understood as a consequence of larger drag associated with fast moving particles (equation 1) which may lead to quick rise in the surface temperature due to frictional heating (equation 2), sufficient enough to trigger the rapid mass ablation process. Corresponding evolution of the meteoroid size has also been estimated and shown in Fig. 3(b). The particle with smaller speed is observed to retain larger residual size, for example, a particle entering with speed ∼20 km s−1 shrinks about ∼62% of its original size (∼90 km) while in case of ∼30 km s−1, the particle shrinks about 99% of its volume (∼105 km). The vertical and horizontal components of speed are also computed (not shown in figures) and found to display a nature similar that obtained in Figs 2(c) and (d) and are consistent with the temperature evolution (Fig. 3a). The altitude profile of meteoroid charging and corresponding electron production rate has been demonstrated in Figs 3(c) and (d), respectively. It is well understood fact that in the flowing regime the accretion current of the electrons gets significantly enhanced (Whipple 1981). The large value of the negative charge in the beginning (∼180 km) can be understood in terms of enhanced electron current over its surface with increasing particle speed which effectively lead the charge towards more negative value. As the micrometeoroid comes down further, the frictional heating may lead it to positive charge and the charge desorption due mass ablation process yields it to attain maximum value around Tmax, in conformance with the altitude evolution of surface temperature (Fig. 3a). The behaviour of the electron production rate shown in Fig. 3(d) is again consistent with the altitude profile of the surface temperature (Fig. 3a) and its charge (Fig. 3c). Of course the production rate is more pronounced in case of meteoroid entering with larger velocity and occurs at higher altitude; in beginning of the flight, the production rate profile is dominated by photoelectric (∼170 km)/thermionic (∼143 km) currents which is soon taken over by mass sublimation (around ∼128 km, for |${\upsilon _o}\sim 30\,{\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$|⁠). The set of four parameters (viz. altitude evolution of the surface temperature, particle size, charge and electron production rate) representing the different size micrometeoroid flight in the earth atmosphere has been illustrated in Fig. 4. The basic features of the altitude profiles are similar as obtained in previous cases (Figs 2 and 3). Large size particle (e.g. ∼100 μm) is seen to heat up initially slower than that of smaller one (say ∼10 μm) due to their large thermal inertia. As soon as the object comes further down and air density increases the frictional heating dominates for larger particles, leading quick rise in its temperature until the mass ablation is triggered; this has been shown in Fig. 4(a). The larger meteoroid is noticed to shrink to larger extent which is consistent with the physics notion of larger the frictional heating and mass ablation. Fig. 4(b) shows that ∼10 μm particle retains up to ∼80% by volume before reaching to a terminal speed while ∼100 μm particle is noticed to lose its mass ∼98%; this is primarily due to fact that larger meteoroid acquires large temperature and remains warmer than the smaller one during rapid mass ablation. The size dependence of charging state during micrometeoroid travel has been displayed in Fig. 4(c). In the regime where mass ablation mechanism is dominant (i.e. around hmax), the charge is seen to large in case of large size particle (∼100 μm). The consequent electron production rate has been displayed in Fig. 4(d) and seen to be dominant in case of larger size micrometeoroid due to large emission and charge desorption currents.

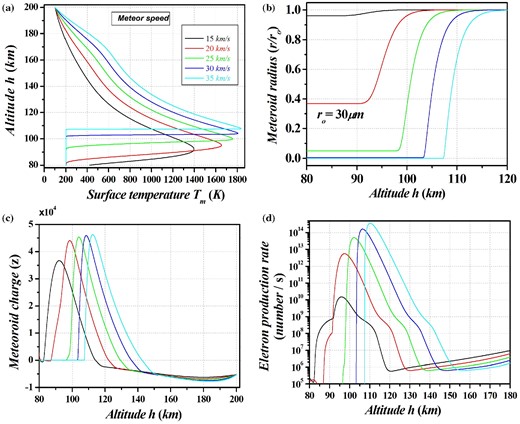
Altitude profiles of (a) meteoroid surface temperature (Tm), (b) particle size (r/ro), (c) charge (z), and (d) electrons production rate for different values of entry speed ${\upsilon _o}$ for the parameters ro = 30 μm, θ = π/4, npo = 1012 cm− 2s and φ = 2.5 V; the colour labels for different values of ${\upsilon _o}$ are marked in figure.
Figure 3.

Altitude profiles of (a) meteoroid surface temperature (Tm), (b) particle size (r/ro), (c) charge (z), and (d) electrons production rate for different values of entry speed |${\upsilon _o}$| for the parameters ro = 30 μm, θ = π/4, npo = 1012 cm− 2s and φ = 2.5 V; the colour labels for different values of |${\upsilon _o}$| are marked in figure.

Open in new tabDownload slide
Altitude profiles of (a) meteoroid surface temperature (Tm), (b) particle size (r/ro), (c) charge (z), and (d) electrons production rate for different values of meteoroid size ro for the parameters ${\upsilon _o} = 25\,{\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$, θ = π/4, npo = 1012 cm− 2s and φ = 2.5 V; the colour labels for different values of ro are marked in figure.
Figure 4.

Altitude profiles of (a) meteoroid surface temperature (Tm), (b) particle size (r/ro), (c) charge (z), and (d) electrons production rate for different values of meteoroid size ro for the parameters |${\upsilon _o} = 25\,{\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$|⁠, θ = π/4, npo = 1012 cm− 2s and φ = 2.5 V; the colour labels for different values of ro are marked in figure.

Open in new tabDownload slide

The effect of varying the work function (φ) of micrometeoroid material on its flight in atmospheric environment has been illustrated in Figs (5 and 6); this also describes the influence of the electron emission processes on various physical parameters. The decrease in the work function (φ) of meteoroid material eventually lead to an increases in the electron emission currents and may significantly alters the meteoric electron production rate and charging state of the micrometeoroid. However, this does not contribute much in energy dissipation of the meteoroid as the mass ablation remains the dominant mechanism for the surface cooling (as discussed before) and hence the altitude profile of the temperature seems unaffected (Fig. 5a). Consequently, similar trend is noticed in case of particle size evolution (Fig. 5b). The charge evolution has been shown in Fig. 5(c) where the significance of electron emission is clearly visualized. In beginning, it is dominated by thermionic plus photoemission currents, in fact, thermionic emission is dominant for low work function material; further in the mass ablation regime (∼hmax) it is assisted by charge desorption process. Corresponding net production rate of meteoric electrons in background environment has been displayed in Fig. 5(d) and demonstrate that it is dominated by the thermionic/photoelectric emission in the beginning phase of meteoroid flight. The individual altitude profiles of the currents associated with mass ablation, thermionic emission and photoemission processes has been displayed in Figs 6(a)–(c), respectively; this also refers their individual contribution in the net electron production rate (i.e. Fig. 5d). For understanding the contribution of emission currents in the generation of meteoric electrons, let us choose a particular case corresponding to φ = 2.5 V (blue curve, Fig. 6). One can see that in the altitude range (∼98–138 km), electron emission (production rate) is dominated by charge desorption (mass ablation) and thermionic emission. On the other hand, the photoemission current become significant only for the lower altitude ∼95 km or altitude larger than ∼140 km where rests of the two processes are less pronounced. In fact, our calculations estimate that the particle takes a positive potential at the very end (∼82 km) of the flight where photoelectric effect is significant emission mechanism and dominates over electron collection current; in this case, at altitude ∼80 km, the particle ends with terminal radius ∼1.5 μ and potential ∼0.35 eV. The thermionic emission is also noticed to become dominant at higher altitude over photoemission with decreasing work function. For example, in case of φ = 1.5V(pink curve), the photoemission is seen to be dominant in the beginning (>162 km) and contribute throughout the meteoroid flight (Fig. 6c), although its magnitude is smaller than the thermionic current in mid-altitude (∼120–162 km, Fig. 6b); the charge desorption in mass ablation regime is pronounced in the region of altitude ∼95–120 km. The photoemission current altitude profile is noticed to weakly depend on the particle work function in the parameter regime considered herein while φ has noticeable influence on the respective thermionic current; this is due to small number of photon flux associated with Lyman α radiation. Of course, the current associated with mass ablation is independent of material work function. In order to examine the role of incident solar radiation causing photoemission during the micrometeoroid flight, the effect of varying parameter npo has been displayed in the set of Figs 7 and 8; the parameter npo in general characterizes the photoefficiency (χ) of the meteoroid material and incident photon flux (Λo). The computations correspond to the low work function material φ ∼ 2.5 V. The altitude profiles of the surface temperature (Fig. 7a) and particle size (Fig. 7b) are noticed insensitive to the parameter npo and validate the intuitive prediction that the photoemission current does not contribute significantly in cooling. Decrease in the value of parameter npo, effectively reduces the photoemission current, and of course, it influences charging state over meteoroid during its flight, specifically in beginning phase (∼195 km), as displayed in Fig. 7(c). The reflection of decrease in photoemission flux is also noticed in the altitude profiles of the net electron production rate in Fig. 7(d) where increasing npo gives rise to large electron generation. The role of individual currents in deriving the effective density of electron cloud has been displayed in Fig. 8. The contribution of photoemission in the electron generation is noticed to decrease with decreasing npo (Fig. 8c) while the thermionic emission profile nearly independent of npo (Fig. 8b); again npo does not contribute in charge desorption in mass ablation phase (Fig. 8a). For a particular case in Fig. (8), say for npo ∼ 1011 cm− 2s(green curve), it can be seen that photoemission significantly contribute above ∼135 km in meteoric electron generation while mass ablation phase dominates h < 122 km; in between 122 km < h < 135 km thermionic emission dominates in meteoric electron generation. At the end of flight (∼80 km), depending on different npo values, the residual meteoroid particle acquires finite positive potential equivalent to ∼0.35 eV (black), ∼0.16 (red) and ∼0.02 (green), respectively.

Altitude profiles of (a) meteoroid surface temperature (Tm), (b) particle size (r/ro), (c) charge (z), and (d) electrons production rate for different values of work function of meteoroid material φ for the parameters ${\upsilon _o} = 25\,{\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$, ro = 30 μm, θ = π/4 and npo = 1012cm− 2s; the colour labels for different values of φ are marked in figure.
Figure 5.

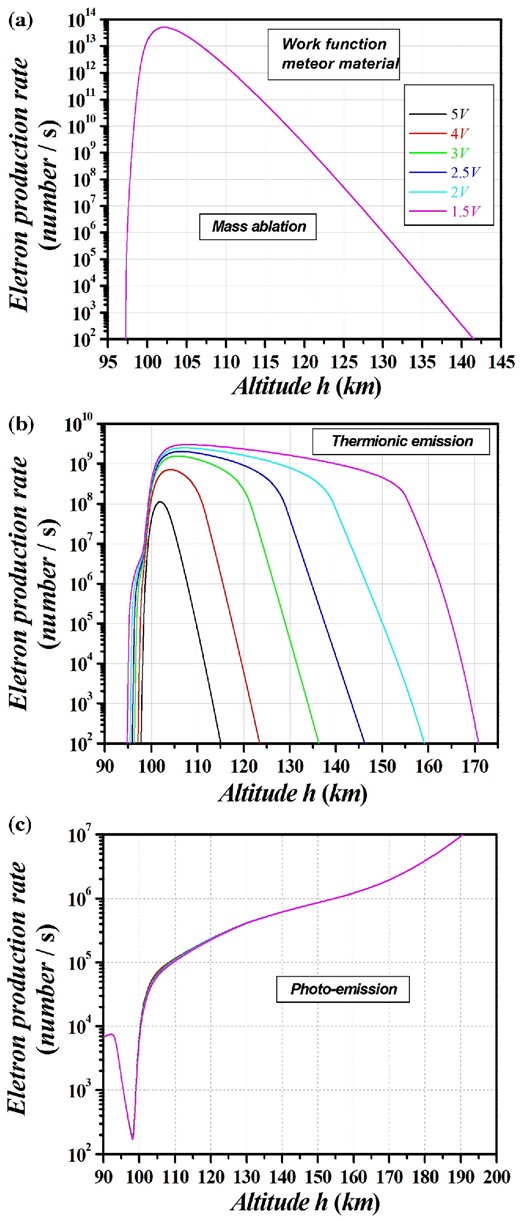
Altitude profiles of (a) meteoroid surface temperature (Tm), (b) particle size (r/ro), (c) charge (z), and (d) electrons production rate for different values of work function of meteoroid material φ for the parameters |${\upsilon _o} = 25\,{\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$|⁠, ro = 30 μm, θ = π/4 and npo = 1012cm− 2s; the colour labels for different values of φ are marked in figure.

Open in new tabDownload slide
Altitude profiles of the individual currents associated with (a) the mass ablation, (b) thermionic emission, and (c) the photoemission, respectively; the parameters and colour labels are similar to the caption of Fig. 5.
Figure 6.

Altitude profiles of the individual currents associated with (a) the mass ablation, (b) thermionic emission, and (c) the photoemission, respectively; the parameters and colour labels are similar to the caption of Fig. 5.

Open in new tabDownload slide
Altitude profiles of (a) meteoroid surface temperature (Tm), (b) particle size (r/ro), (c) charge (z), and (d) electrons production rate for different values of parameter np for the parameters ${\upsilon _o} = 25\,{\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$, ro = 30 μm, θ = π/4 and φ = 2.5 V; the colour labels for different values of npo are marked in figure.
Figure 7.

Altitude profiles of (a) meteoroid surface temperature (Tm), (b) particle size (r/ro), (c) charge (z), and (d) electrons production rate for different values of parameter np for the parameters |${\upsilon _o} = 25\,{\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$|⁠, ro = 30 μm, θ = π/4 and φ = 2.5 V; the colour labels for different values of npo are marked in figure.

Open in new tabDownload slide
Altitude profiles of the individual currents associated with (a) the mass ablation, (b) thermionic emission, and (c) the photoemission, respectively; the parameters and colour labels are similar to the caption of Fig. 7.
Figure 8.

Altitude profiles of the individual currents associated with (a) the mass ablation, (b) thermionic emission, and (c) the photoemission, respectively; the parameters and colour labels are similar to the caption of Fig. 7.

Open in new tabDownload slide

Through these numerical calculations we have shown the travel of a micrometeoroid in day time earth atmosphere where the solar radiation contributes in maintenance of earth atmospheric plasma and the photoemission from the surface of flowing micrometeoroid. The results obtained in this analysis clearly demonstrate that the meteoroid flight is sensitive to its physical and material properties. Although the photoemission does not seem to contribute much in the energetics but seen to influence the meteoric electron generation rate, specifically in the beginning (∼200–140 km, for φ ∼ 2.5 eV) and end (∼80–85 km) phase of the travel where the photoemission current may dominate over other significant charging processes; at the end of the flight (∼80 km), the photoemission may cause the residual particle to achieve finite positive potential. On the other hand, thermionic emission dominates in mid altitude (∼122–140 km) below this altitude (∼98–122 km) it is superimposed by dominant charge desorption via mass ablation. This is clearly evident from the figures (viz. Figs 6 and 8) where the altitude profile of the production rate of each individual electron emission mechanism has been illustrated. It is also noticed that the meteoroid is likely to acquire finite potential (of course negative in present case) before entering to earth atmosphere (ho ∼ 200 km) due to the presence of solar radiation/weak plasma column which certainly influence the dynamical charging state during its flight (Figs 2-8). The micrometeoroid flight affects the local plasma density significantly in its travel and the maximum effect is observed in mass ablation regime (around ∼hmax).

5 SUMMARY AND CONCLUSIONS

In this analysis, we have extended the consistent theoretical model of Mendis et al. (2005) to examine the micrometeoroid flight in the day time earth atmosphere where the atmospheric (neutral gas/plasma) structure is determined by existing solar radiation. In addition to thermionic and charge desorption processes, the solar illumination causes the photoelectron emission from the flowing meteor surface too and affects the charge structure during its flight. The flowing dynamics of the micrometeoroid in earth environment is characterized by equation of motion which takes account of the atmospheric gas molecular drag and earth gravity (equation 1). The particle heating and consequent rise in its temperature is governed by the energy balance equation which includes numerous heating (frictional/plasma accretion) and cooling (electron emission/radiation/fusion/sublimation) processes (equation 2). As the particle temperature is raised to a large value, the mass ablation (due to sublimation/fusion) causes the decay in meteoroid mass and size (equation 3). The dynamical charge over flowing meteoroid is determined by the net balance of plasma currents, electron emission (Thermionic/photoelectric) and charge desorption mechanisms over micrometeoroid surface. The analysis has been used to study the electrical charging, deceleration, heating and ablation of micrometeoroid entering the earth's atmosphere; the local electron density perturbation has also been investigated. The characteristic features of the flight are observed being sensitive to the meteoroid physical/material properties as it enters in earth environment. In the beginning phase of the flight (as the meteoroid enters in earth atmosphere), the particles achieve quasi-static equilibrium and the surface gains higher temperature at higher altitudes with increasing entering speed and decreasing angle of entrance and meteoroid size; this trend continues for the entering speed but gets inverted for the entry angle and particle size as the meteoroid approaches to mass ablation regime. The altitude profiles of temperature in each case actually dictate the other physical parameters during meteoroid flight. The particle is observed to shrink to larger extent with increasing size, entry speed and angle of entrance. Based on our analysis, the significance of the photoemission mechanism in micrometeoroid flight can be assessed by two aspects, viz. (i) production of meteoric electrons in its path, and (ii) dynamical charge over meteoroid during its flight. In the absence of any significant electron emission mechanism, the former (i) substantially dominated by photoemission current in the beginning and end phase of micrometeoroid flight; this is evident from the altitude profiles of electron generation rates Figs (6 and 8). On the other hand, primarily due to high-density plasma column and low photon flux associated with Lyman α radiation considered herein, the micrometeoroid usually takes negative potential at higher altitude however the photoemission may lead the residual micrometeoroid to a finite positive potential at the end phase of the flight (∼80 km). These facts can be specified by stating a particular case of Fig. 6 corresponding to φ = 2.5 V. For this case, the intermediate micrometeoroid flight (i.e. mid-altitude region), in particular, the frictional heating dominant regime (∼138–98 km), the charging and meteoric electron production rate is dominated by thermionic/charge desorption phenomena and the meteoroid exhibits finite positive potential. The photoemission current becomes significant only for the altitudes lower than ∼95 km or larger than ∼138 km. As meteoroid go further below 95 km, the particle tends to acquire a negative charge again as electron accretion current become dominant over available photoemission current. Photoemission current eventually dominates in charging at very end of flight (∼82 km) where the plasma column density and hence the electron collection drop significantly such that the particle acquires a small positive charge. In our calculations, for this case, the meteoroid is evaluated to end with (∼80 km) terminal radius ∼1.5 μ and potential ∼0.35 eV. Similar effects have been observed for the other cases considered herein in calculations.

This analysis is based on numerous simplifications and thus it is necessary to point out the applicability of the theoretical model; here we discuss the limitations of the present analysis and predictions. The analytical model is restricted to the free molecular regime which is consistent with our considerations of small size meteoroids (10's μm) and altitude range (80 km ≤ h ≤ 200 km). As another simplification, in order to avoid complexity in numerical calculations, the model considers the spherical shape of meteoroids and is assumed to retain its shape during ablation in its flight through the earth atmosphere. In realistic scenario, the shape is essentially irregular (non-spherical) and the mass ablation may be inhomogeneous; intuitively such particles lost longer and penetrate deeper in the earth atmosphere. In order to avoid the complexity in computations, as a simplification, we have taken dominant Lyman α radiation into account, causing photoemission from the flowing meteoroid however continuous solar spectrum may be of significance in particular for low work function materials. Further the approach and analytical model also lacks few mass-loss mechanisms, viz. physical sputtering, fragmentation which is of course negligible in the parameter regime of present study but cannot be ignored once the meteoroid of larger size (∼cm) and entry speed (∼70 km s−1) is considered. A detailed kinetics of the ionospheric structure (including the formation/annihilation of neutral/electron–ion pairs) would be an additional advancement in order to improve the analytical modelling. The uncertainty about the work function is another concern and we have already seen that it significantly influence in particular the charge structure during meteoroid flight. Another, limitation is the lack of knowledge of phase diagram of meteoroid material (even with earlier studies) in the upper atmosphere in low-pressure regime; here in this analysis, we also have followed the previous studies to define the sublimation/fusion rate given by Clausius–Claypeyron equation with arbitrary constants. These above-mentioned aspects certainly limit the applicability of the present model but of course the model gives an approximate solution for day time meteoroid flight and put forward a basis for further improvement. The overcome with these shortcoming eventually will lead us to handle the meteoroid problem in a more rigorous and systematic manner.

One of the authors (SM) is grateful to Department of Science and Technology (DST) for the financial assistance of the work.

REFERENCES

Bauer
S. J.
1973
Physics of Planetary Ionospheres
Springer-Verlag
New York

Google Scholar

OpenURL Placeholder Text

 

Briani
G.
Pace
E.
Shore
S. N.
Pupillo
G.
Passaro
A.
Aiello
S.
2013
A&A
552
A53

Crossref
Search ADS
 

Bronshten
V. A.
1983
Physics of Meteoric Phenomena
Dordrecht
Reidel

Google Scholar

OpenURL Placeholder Text

 

Bronshten
V. A.
1991
Sol. Syst. Rev.
25
93

 

Brosch
N.
Schijvarg
L. S.
Podolak
M.
Rosenkrantz
M. R.
2001
Warmbein
B.
ESA SP-495: Proceedings of the Meteoroids 2001 Conference
ESA, Noordwijk
165

Google Scholar

OpenURL Placeholder Text

 

Budden
K. G.
1989
The Propagation of Radio Waves
Cambridge Univ. Press
New York

Google Scholar

OpenURL Placeholder Text

 

Campbell-Brown
M. D.
Koschny
D.
2004
A&A
418
751

Crossref
Search ADS
 

Ceplecha
Z.
Borovicka
J.
Elford
W. G.
Revelle
D. O.
Hawkes
R. L.
Porubcan
V.
Simek
M.
1998
Space Sci. Rev.
84
327

Crossref
Search ADS
 

Furman
A. M.
1960
Sov. Astron.
4
489

 

Furman
A. M.
1961
Sov. Astron.
4
705

 

Fowler
R. H.
1955
Statistic
al Mechanics: The Theory of the Properties of Matter in Equilibrium
Cambridge Univ. Press
London

Google Scholar

OpenURL Placeholder Text

 

Genge
M.
Engrand
C.
Gounelle
M.
Taylor
S.
2008
Meteorit. Planet. Sci.
43
497

Crossref
Search ADS
 

Grün
E.
Zook
H. A.
Fechtig
H.
Giese
R. H.
1985
Icarus
62
244

Crossref
Search ADS
 

Gurevich
A. V.
1978
Nonlinear Phenomena in the Ionosphere
Springer-Verlag
New York

Google Scholar

OpenURL Placeholder Text

 

Heath
D. F.
1967
ApJ
148
L97

Crossref
Search ADS
 

Hughes
D. W.
1978
McDonnel
J. A. M.
Meteors, Cosmic Dust
Wiley
Chicherster
123

Google Scholar

OpenURL Placeholder Text

 

Janches
D.
Mathews
J. D.
Meisel
D. D.
Zhou
Q.
2000
Icarus
145
53

Crossref
Search ADS
 

Jones
W.
1997
MNRAS
288
995

Crossref
Search ADS
 

Love
S. G.
Brownlee
D. E.
1991
Icarus
89
26

Crossref
Search ADS
 

Love
S. G.
Brownlee
D. E.
1993
Science
262
550

Crossref
Search ADS
PubMed
 

Mathews
J. D.
Pl.
Hunter K.
Meisel
D. D.
Getman
V. S.
Zhou
Q.
1997
Icarus
126
157

Crossref
Search ADS
 

Mendis
D. A.
Wong
W.-H.
Rosenberg
M.
2004
Phys. Scr.
2004
141

 

Mendis
D. A.
Wong
W. H.
Rosenberg
M.
2005
J. Atmos. Sol.-Terr. Phys.
67
1178

Crossref
Search ADS
 

Mishra
S. K.
Misra
S.
Sodha
M. S.
2011
Phys. Plasmas
18
103708

Crossref
Search ADS
 

Mishra
S. K.
Misra
S.
Sodha
M. S.
2013
Phys. Plasmas
20
033705

Crossref
Search ADS
 

Mishra
S. K.
Misra
S.
2015
Phys. Plasmas
22
023706

Crossref
Search ADS
 

Misra
S.
Mishra
S. K.
2013
MNRAS
432
2985

Crossref
Search ADS
 

Opik
E. J.
1958
Physics of Meteor Flight in the Atmosphere
Interscience Pub.
New York

Google Scholar

OpenURL Placeholder Text

 

Ratcliffe
J. A.
1960
Physics of the Upper Atmosphere
Academic Press
London

Google Scholar

OpenURL Placeholder Text

 

Roble
R. G.
Emery
B. A.
1983
Planet. Space Sci.
31
597

Crossref
Search ADS
 

Rogers
L. A.
Hill
K. A.
Hawkes
R. L.
2005
Planet. Space Sci.
53
1341

Crossref
Search ADS
 

Schanker
J. Z.
1990
Meteor Burst Communications
Artech House Pub.
Boston

Google Scholar

OpenURL Placeholder Text

 

Shukla
P. K.
Mamun
A. A.
2002
Introduction to Dusty Plasma Physics
IoP
Bristol

Google Scholar

OpenURL Placeholder Text

 

Sodha
M. S.
Guha
S.
1971
Simon
A.
Thompson
W. B.
Physics of Colloidal Plasmas in Advances in Plasma Physics
Interscience Publishers
New York

Google Scholar

OpenURL Placeholder Text

 

Sodha
M. S.
Misra
S.
Mishra
S. K.
2010
Phys. Plasmas
17
113705

Crossref
Search ADS
 

Sodha
M. S.
2014
Kinetics of Complex Plasmas
Springer, New Delhi

Google Scholar

OpenURL Placeholder Text

 

Sorasio
G.
Mendis
D. A.
Rosenberg
M.
2001
Planet. Space Sci.
49
1257

Crossref
Search ADS
 

Szasz
C.
Kero
J.
Pellinen-Wannberg
A.
Meisel
D. D.
Wannberg
G.
Westman
A.
2008
Earth Moon Planets
102
373

Crossref
Search ADS
 

Tielens
A. G. G.
McKee
C. F.
Seab
C. G.
Hollenbach
D. J.
1994
ApJ
431
321

Crossref
Search ADS
 

Whipple
E. C.
1981
Rep. Prog. Phys.
44
1197

Crossref
Search ADS
 

Zolesi
B.
Cander
L. R.
2014
Ionospheric Prediction and Forecasting
Springer-Verlag
Berlin

Google Scholar

OpenURL Placeholder Text

 

APPENDIX

A1

The parameter β is sensitive to the velocity of the meteoroid and suitable empirical relations have been derived in numerous studies; the empirical fits are as follows (Mendis et al. 2005).

  • |$\beta = 3.02 \times {10^{ - 17}}{\upsilon ^{3.42}}$| (⁠|$\upsilon \ge 35\,{\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$|⁠, Bronshten (1983))

  • |$\beta = 9.4 \times {10^{ - 6}}{(\upsilon - 10)^2}{\upsilon ^{0.8}}$| (⁠|$10 \le \upsilon \le 35$|⁠, Jones (1997))

  • β = 0 (⁠|$\upsilon < 10\,{\rm{km}}\,{{\rm{s}}^{ - {\rm{1}}}}$|⁠, Jones (1997))

In these empirical fits, the velocity |$\upsilon $| is in units of km s–1.

A2

Using atmospheric data of the book by Gurevich (1978, tables 1 and 2), the algebraic form of the empirical (best polynomial) fits for various plasma parameters has been evaluated as a function of atmospheric altitude (h, in km) and are follows.
\begin{eqnarray*} {n_{\rm{n}}}({\rm{pe}}{{\rm{r}}}\,{\rm{c}}{{\rm{m}}^3}) = exp[62.327\,57 - 0.5534h + 0.002\,78{h^2}]- (4.980\,91 \times {10^{ - 6}}){h^3}] \end{eqnarray*}
\begin{eqnarray*} {n_{\rm{e}}}({\rm{pe}}{{\rm{r}}}\,{\rm{c}}{{\rm{m}}^3}) \approx {n_i}({\rm{pe}}{{\rm{r}}}\,{\rm{c}}{{\rm{m}}^3}) = {10^3}[{\rm{143}}{\rm{.014}}\,{\rm{04}} - {\rm{6}}{\rm{.983}}h + {\rm{0}}{\rm{.079}}\,{\rm{03}}{h^2} -\, ({\rm{1}}{\rm{.757}}\,{\rm{44}} \times {10^{ - 4}}){h^3}]\end{eqnarray*}
\begin{eqnarray*} {T_{\rm{n}}}({\rm{i}}{{\rm{n}}}\,{\rm{K}}) = [{\rm{1311}}{\rm{.288}}\,{\rm{97}} - {\rm{26}}{\rm{.439}}\,{\rm{72}}h + {\rm{0}}{\rm{.124}}\,{\rm{43}}{h^2} + ({\rm{6}}{\rm{.057}}\,{\rm{65}} \times {10^{ - 4}}){h^3} - ({\rm{2}}{\rm{.985}}\,{\rm{65}} \times {10^{ - 6}}){h^4}]\end{eqnarray*}
\begin{eqnarray*} {T_{\rm{e}}}({\rm{i}}{{\rm{n}}}\,{\rm{K}}) = [{\rm{ 169}}{\rm{.844}}\,{\rm{23}} + {\rm{12}}{\rm{.899}}\,{\rm{37}}h - {\rm{0}}{\rm{.371}}\,{\rm{45}}{h^2} + {\rm{0}}{\rm{.003}}\,{\rm{32}}{h^3} - ({\rm{8}}{\rm{.222}}\,{\rm{62}} \times {10^{ - 6}}){h^4}]\end{eqnarray*}
\begin{eqnarray*} {T_i}({\rm{i}}{{\rm{n}}}\,{\rm{K}}) = [{\rm{1372}}{\rm{.742}}\,{\rm{79}} - {\rm{28}}{\rm{.859}}\,{\rm{37}}h + {\rm{0}}{\rm{.159}}\,{\rm{39}}{h^2}+ ({\rm{3}}{\rm{.859}}\,{\rm{04}} \times {10^{ - 4}}){h^3} - ({\rm{2}}{\rm{.477}}\,{\rm{67}} \times {10^{ - 6}}){h^4}].\end{eqnarray*}

The atmospheric density (ρa) can be approximated by multiplying the neutral density nn with the average mass (mn ∼ 30 amu) of neutral species considered herein.

A3

Taking the recent work (Mishra et al. 2011, 2013) into account, the expressions for accretion current and corresponding mean energy over meteoroid flowing through plasma referred by shifting Maxwellian distribution can be written as follows.
\begin{eqnarray*} {\rm for}\;{v_{\rm s}} < 0:f_{\rm c} &=& n\left({v_{\rm{t}}}/8{{\rm{\pi }}^{1/2}}p\right) \left[ 2pexp( - {p^2})+ (1 + 2{p^2} - 2{v_{\rm{s}}}){\pi ^{1/2}}erf(p)\right],\nonumber\\ ({\varepsilon _{\rm{c}}}/kT) &=& [n({v_{\rm{t}}}/16{{\rm{\pi }}^{1/2}}p)/{n_{\rm{c}}}] [ p(6 + 4{v_{\rm{s}}})exp( - {p^2})+{{\pi ^{1/2}}(5 - 6{v_{\rm{s}}} + 6{p^2})erf(p)}] - {v_{\rm{s}}} \end{eqnarray*}
\begin{eqnarray*} {v_{\rm{s}}} \ge 0:{f_{\rm{c}}} &=& n({v_{\rm{t}}}/16{{\rm{\pi }}^{1/2}}p)\left[ {2\left[{p_{\rm{m}}}exp\left( - p_{\rm{n}}^2\right) - {p_{\rm{n}}}exp\left( - p_{\rm{m}}^2\right)\right]} +\, {{\pi ^{1/2}}(1 - 2{p_{\rm{m}}}{p_{\rm{n}}})[erf({p_{\rm{m}}}) - erf({p_{\rm{n}}})]} \right],\nonumber\\ ({\varepsilon _{\rm{c}}}/kT) &=& [n({v_{\rm{t}}}/32{{\rm{\pi }}^{1/2}}p)/{n_{\rm{c}}}]\left[ {6({p_{\rm{m}}}exp[ - p_{\rm{n}}^2]} -\, {{p_{\rm{n}}}exp[ - p_{\rm{m}}^2]) + 4v_{\rm{s}}^{1/2}(exp[ - p_{\rm{n}}^2] - exp[ - p_{\rm{m}}^2]),} \right. \end{eqnarray*}
where |$p = (\upsilon /{v_{\rm{t}}})$|⁠, pn = (uc − p), pm = (uc + p), |${u_{\rm{c}}} = \upsilon _{\rm{s}}^{1/2}$| and |${\upsilon _{\rm{s}}}$| is the surface potential normalized with relevant particle (electron/ion) temperature while |${\upsilon _{\rm{t}}}$| is the thermal speed of electrons/ions; the subscript ‘c’ may run over electrons (ec) and ions (ic) referring the accretion current (fc) and mean energy (εc), respectively; accretion flux fc is in units of (numbers cm− 2s). The detailed derivation of these expressions can be seen in References (Mishra et al. 2011, 2013).

A4

Following Sodha (2014), the rate of thermionic emission from spherical objects can be written as
\begin{eqnarray*} {\rm{for}}\;z \ge 0\quad \quad {f_{{\rm{th}}}}(z - 1) = \left(4{\rm{\pi }}{m_{\rm{e}}}{k^2}T_{\rm{m}}^2/{h^3}\right)(1 + z{\alpha _{\rm{m}}}) exp[ - (z{\alpha _{\rm{m}}} + {\varphi _{\rm{m}}})],\left( {\frac{{{\varepsilon _{{\rm{th}}}}(z - 1)}}{{k{T_{\rm{m}}}}}} \right) = \left( {\frac{{(2 + z{\alpha _{\rm{m}}})}}{{(1 + z{\alpha _{\rm{m}}})}} + z{\alpha _{\rm{m}}}} \right) \end{eqnarray*}
\begin{eqnarray*} {\rm{for}}\;z < 0\quad \quad {f_{{\rm{th}}}}(z - 1) = \left(4{\rm{\pi }}{m_{\rm{e}}}{k^2}T_{\rm{m}}^2/{h^3}\right)exp( - {\varphi _{\rm{m}}}),{\varepsilon _{{\rm{th}}}}(z - 1) = 2k{T_{\rm{m}}},\end{eqnarray*}
with αm = (e2/rkTm) and φm = (φ/kTm); fth has the units of (numbers cm− 2s).

A5

In order to get the altitude profile of the intensity of the Lyman α radiation (i.e. photon flux), we take the reference of fig. 2 of Heath's work (1967). The algebraic form of the empirical fit representing the attenuation factor (δ) as a function of atmospheric altitude (h, in km) can be expressed as
\begin{equation*}\delta = (\Lambda /{\Lambda _o}) = 1\quad \quad (130\,{\rm{km}} < h \le 200\,{\rm{km}})\end{equation*}
\begin{eqnarray*} \delta = (\Lambda /{\Lambda _o}) = - 3.01 + 0.053h - (1.71 \times {10^{ - 4}}){h^2} (80\,{\rm{km}} < h \le 130\,{\rm{km}}).\end{eqnarray*}

Using the above relation, the parameter np can immediately be written as np = δnpo.

A6

Following Fowler's approach (Fowler 1955) for the photoemission mechanism from the spherical objects, the rate of photoemission electrons can be written as (Sodha 2014) follows
\begin{eqnarray*} {\rm{for}}\;z \ge 0\quad \quad {f_{{\rm{ph}}}}(z - 1) = ({n_{\rm{p}}}/4)\left( {\frac{{\psi (\xi ,z{\alpha _{\rm{m}}})}}{{\Phi (\xi )}}} \right),\left( {\frac{{{\varepsilon _{{\rm{ph}}}}(z - 1)}}{{k{T_{\rm{m}}}}}} \right) = \left[ \left( {\int\limits_{z{\alpha _{\rm{m}}}}^\infty {{x^2}{{[1 + exp(x - \xi )]}^{ - 1}}dx} } \right)\Bigg/ {\psi (\xi ,z{\alpha _{\rm{m}}})}\right], \end{eqnarray*}
\begin{equation*} {\rm{for}}\;z < 0\quad \quad {f_{{\rm{ph}}}}(z - 1) = ({n_{\rm{p}}}/4). \left( {\frac{{{\varepsilon _{{\rm{ph}}}}(z - 1)}}{{k{T_{\rm{m}}}}}} \right) = \left( {\frac{1}{{\Phi (\xi )}}\int\limits_0^\infty {2xln[1 + exp(\xi - x)]\,{\rm{d}}x} } \right), \end{equation*}
with ψ(ξ, zαm) = Φ(ξ − zαm) + zαmln[1 + exp(ξ − zαm)] and |$\Phi (\mu ) = \int\limits_0^{exp\mu } {{y^{ - 1}}ln(1 + y)} \,{\rm{d}}y$|⁠; fph is in units of (numberscm− 2s).
© The Authors 2016. Published by Oxford University Press on behalf of The Royal Astronomical Society.
Issue Section:
Articles
Download all slides