-
PDF
- Split View
-
Views
-
Cite
Cite
G. Desvignes, R. N. Caballero, L. Lentati, J. P. W. Verbiest, D. J. Champion, B. W. Stappers, G. H. Janssen, P. Lazarus, S. Osłowski, S. Babak, C. G. Bassa, P. Brem, M. Burgay, I. Cognard, J. R. Gair, E. Graikou, L. Guillemot, J. W. T. Hessels, A. Jessner, C. Jordan, R. Karuppusamy, M. Kramer, A. Lassus, K. Lazaridis, K. J. Lee, K. Liu, A. G. Lyne, J. McKee, C. M. F. Mingarelli, D. Perrodin, A. Petiteau, A. Possenti, M. B. Purver, P. A. Rosado, S. Sanidas, A. Sesana, G. Shaifullah, R. Smits, S. R. Taylor, G. Theureau, C. Tiburzi, R. van Haasteren, A. Vecchio, High-precision timing of 42 millisecond pulsars with the European Pulsar Timing Array, Monthly Notices of the Royal Astronomical Society, Volume 458, Issue 3, 21 May 2016, Pages 3341–3380, https://doi.org/10.1093/mnras/stw483
Close - Share Icon Share
Abstract
We report on the high-precision timing of 42 radio millisecond pulsars (MSPs) observed by the European Pulsar Timing Array (EPTA). This EPTA Data Release 1.0 extends up to mid-2014 and baselines range from 7–18 yr. It forms the basis for the stochastic gravitational-wave background, anisotropic background, and continuous-wave limits recently presented by the EPTA elsewhere. The Bayesian timing analysis performed with temponest yields the detection of several new parameters: seven parallaxes, nine proper motions and, in the case of six binary pulsars, an apparent change of the semimajor axis. We find the NE2001 Galactic electron density model to be a better match to our parallax distances (after correction from the Lutz–Kelker bias) than the M2 and M3 models by Schnitzeler. However, we measure an average uncertainty of 80 per cent (fractional) for NE2001, three times larger than what is typically assumed in the literature. We revisit the transverse velocity distribution for a set of 19 isolated and 57 binary MSPs and find no statistical difference between these two populations. We detect Shapiro delay in the timing residuals of PSRs J1600−3053 and J1918−0642, implying pulsar and companion masses |$m_{\rm p}=1.22_{-0.35}^{+0.5}\ {\rm M}_{{\odot }}$|, |$m_{\rm c} = 0.21_{-0.04}^{+0.06}\ {\rm M}_{{\odot } }$| and |$m_{\rm p}=1.25_{-0.4}^{+0.6}\ {\rm M}_{{\odot }}$|, |$m_{\rm c} = 0.23_{-0.05}^{+0.07}\ {\rm M}_{{\odot } }$|, respectively. Finally, we use the measurement of the orbital period derivative to set a stringent constraint on the distance to PSRs J1012+5307 and J1909−3744, and set limits on the longitude of ascending node through the search of the annual-orbital parallax for PSRs J1600−3053 and J1909−3744.
1 Introduction
Three decades ago Backer et al. (1982) discovered the first millisecond pulsar (MSP), spinning at 642 Hz. Now over 300 MSPs have been found; see the Australia Telescope National Facility (ATNF) pulsar catalogue1 (Manchester et al. 2005). MSPs are thought to be neutron stars spun-up to rotation periods (generally) shorter than 30 ms via the transfer of mass and angular momentum from a binary companion (Alpar et al. 1982; Radhakrishnan & Srinivasan 1982). We know that the vast majority of the MSP population (≃80 per cent) still reside in binary systems and these objects have been shown to be incredible probes for testing physical theories. Their applications range from high-precision tests of general relativity (GR) in the quasi-stationary strong-field regime (Kramer et al. 2006; Freire et al. 2012b) to constraints on the equation of state of matter at supranuclear densities (Demorest et al. 2010; Antoniadis et al. 2013). Binary systems with an MSP and a white dwarf in wide orbits offer the most stringent tests of the strong equivalence principle (e.g. Stairs et al. 2005; Freire, Kramer & Wex 2012a; Ransom et al. 2014).
Most of these applications and associated results mentioned above arise from the use of the pulsar timing technique that relies on two properties of the radio MSPs: their extraordinary rotational and average pulse profile stability. The pulsar timing technique tracks the times of arrival (TOAs) of the pulses recorded at the observatory and compares them to the prediction of a best-fitting model. This model, which is continuously improved as more observations are made available, initially contains the pulsar's astrometric parameters, the rotational parameters and the parameters describing the binary orbit, if applicable. With the recent increase in timing precision due to e.g. improved receivers, larger available bandwidth (BW) and the use of coherent dedispersion (Hankins & Rickett 1975), parameters that have a smaller effect on the TOAs have become measurable.
The first binary pulsar found, PSR B1913+16 (Hulse & Taylor 1975), yielded the first evidence for gravitational waves (GWs) emission. Since then, several ground-based detectors have been built around the globe, e.g. Advanced LIGO (Aasi et al. 2015) and Advanced Virgo (Acernese et al. 2015), to directly detect GWs in the frequency range of 10–7000 Hz. Also a space mission, eLISA (Seoane et al. 2013), is being designed to study GWs in the millihertz regime. Pulsars, on the other hand, provide a complementary probe for GWs by opening a new window in the nHz regime (Sazhin 1978; Detweiler 1979). Previous limits on the amplitude of the stochastic GW background (GWB) have been set by studying individual MSPs (e.g. Kaspi, Taylor & Ryba 1994). However, an ensemble of pulsars spread over the sky (known as Pulsar Timing Array; PTA) is required to ascertain the presence of a GWB and discriminate between possible errors in the Solar system ephemeris or in the reference time standards (Hellings & Downs 1983; Foster & Backer 1990).
A decade ago, Jenet et al. (2005) claimed that timing a set of at least 20 MSPs with a precision of 100 ns for five years would allow a direct detection of the GWB. Such high timing precision has not yet been reached (Arzoumanian et al. 2015). None the less, Siemens et al. (2013) recently argued that when a PTA enters a new signal regime where the GWB signal starts to prevail over the low-frequency (LF) pulsar timing noise, the sensitivity of this PTA depends more strongly on the number of pulsars than the cadence of the observations or the timing precision. Hence, data sets consisting of many pulsars with long observing baselines, even with timing precision of ∼ 1 μs, constitute an important step towards the detection of the GWB. In addition to the GWB studies, such long and precise data sets allow additional timing parameters, and therefore science, to be extracted from the same data.
Parallax measurements can contribute to the construction of Galactic electron density models (Taylor & Cordes 1993; Cordes & Lazio 2002). Once built, these models can provide distance estimates for pulsars along generic lines of sight. New parallax measurements hence allow a comparison and improvement of the current free electron distribution models (Schnitzeler 2012). An accurate distance is also crucial to correct the spin-down rate of the pulsar from the bias introduced by its proper motion (Shklovskii 1970). This same correction has to be applied to the observed orbital period derivative before any test of GR can be done with this parameter (Damour & Taylor 1991).
In binary systems, once the Keplerian parameters are known, it may be possible to detect post-Keplerian (PK) parameters. These theory-independent parameters describe the relativistic deformation of a Keplerian orbit as a function of the Keplerian parameters and the a priori unknown pulsar mass (mp), companion mass (mc) and inclination angle (i). Measurement of the Shapiro delay, an extra propagation delay of the radio waves due to the gravitational potential of the companion, gives two PK parameters (range r and shape s ≡ sin i). Other relativistic effects such as the advance of periastron |$\dot{\omega }$| and the orbital decay |$\dot{P_{\rm b}}$| provide one extra PK parameter each. In GR, any PK parameter can be described by the Keplerian parameters plus the two masses of the system. Measuring three or more PK parameters therefore overconstrains the masses, allowing one to perform tests of GR (Taylor & Weisberg 1989; Kramer et al. 2006).
The robustness of the detections of these parameters can be hindered by the presence of stochastic influences like dispersion measure (DM) variations and red (LF) spin noise in the timing residuals (Coles et al. 2011; Lentati et al. 2014). Recent work by Keith et al. (2013) and Lee et al. (2014) discussed the modelling of the DM variations, while Coles et al. (2011) used Cholesky decomposition of the covariance matrix to properly estimate the parameters in the presence of red noise. Correcting for the DM variations and the effects of red noise has often been done through an iterative process. However, temponest, a Bayesian pulsar timing analysis software (Lentati et al. 2014) used in this work allows one to model these stochastic influences simultaneously while performing a non-linear timing analysis.
In this paper, we report on the timing solutions of 42 MSPs observed by the European Pulsar Timing Array (EPTA). The EPTA is a collaboration of European research institutes and radio observatories that was established in 2006 (Kramer & Champion 2013). The EPTA makes use of the five largest (at decimetric wavelengths) radio telescopes in Europe: the Effelsberg Radio Telescope in Germany (EFF), the Lovell Radio Telescope at the Jodrell Bank Observatory (JBO) in England, the Nançay Radio Telescope (NRT) in France, the Westerbork Synthesis Radio Telescope (WSRT) in the Netherlands and the Sardinia Radio Telescope (SRT) in Italy. As the SRT is currently being commissioned, no data from this telescope are included in this paper. The EPTA also operates the Large European Array for Pulsars (LEAP), where data from the EPTA telescopes are coherently combined to form a tied-array telescope with an equivalent diameter of 195 m, providing a significant improvement in the sensitivity of pulsar timing observations (Bassa et al. 2016).
This collaboration has already led to previous publications. Using multitelescope data on PSR J1012+5307, Lazaridis et al. (2009) put a limit on the gravitational dipole radiation and the variation of the gravitational constant G. Janssen et al. (2010) presented long-term timing results of four MSPs, two of which are updated in this work. More recently, van Haasteren et al. (2011) set the first EPTA upper limit on the putative GWB. Specifically for a GWB formed by circular, GW-driven supermassive black hole binaries, they measured the amplitude A of the characteristic strain level at a frequency of 1 yr−1, A < 6 × 10−15, using a subset of the EPTA data from only five pulsars.
Similar PTA efforts are ongoing around the globe with the Parkes Pulsar Timing Array (PPTA; Manchester et al. 2013) and the NANOGrav collaboration (McLaughlin 2013), also setting limits on the GWB (Demorest et al. 2013; Shannon et al. 2013a).
The EPTA data set introduced here, referred to as the EPTA Data Release 1.0, serves as the reference data set for the following studies: an analysis of the DM variations (Janssen et al., in preparation), a modelling of the red noise in each pulsar (Caballero et al. 2015), a limit on the stochastic GWB (Lentati et al. 2015b) and the anisotropic background (Taylor et al. 2015) as well as a search for continuous GWs originating from single sources (Babak et al. 2016). The organization of this paper is as follows. The instruments and methods to extract the TOAs at each observatory are described in Section 2. The combination and timing procedures are detailed in Section 3. The timing results and new parameters are presented in Section 4 and discussed in Section 5. Finally, we summarize and present some prospects about the EPTA in Section 6.
2 Observations and data processing
This paper presents the EPTA data set, up to mid-2014, that was gathered from the ‘historical’ pulsar instrumentations at EFF, JBO, NRT and WSRT with, respectively, the EBPP (Effelsberg-Berkeley Pulsar Processor), DFB (Digital FilterBank), BON (Berkeley–Orléans–Nançay) and PuMa (Pulsar Machine) backends. The data recorded with the newest generation of instrumentations, e.g. PSRIX at EFF (Lazarus et al. 2016) and PuMaII at WSRT (Karuppusamy, Stappers & van Straten 2008), will be part of a future EPTA data release.
Compared to the data set presented in van Haasteren et al. (2011), in which timing of only five pulsars was presented, this release includes 42 MSPs (listed in Table 1 with their distribution on the sky shown in Fig. 1). Among those 42 MSPs, 32 are members of binary systems. The timing solutions presented here span at least seven years, and for 16 of the MSPs the baseline extends back ∼15 yr. For the five pulsars included in van Haasteren et al. (2011), the baseline is extended by a factor of 1.7–4. When comparing our set of pulsars with the NANOGrav Nine-year Data Set (Arzoumanian et al. 2015, consisting of 37 MSPs) and the PPTA data set (Manchester et al. 2013; Reardon et al. 2016, consisting of 20 MSPs), we find an overlap of 21 and 12 pulsars, respectively. However, we note that the NANOGrav data set contains data for seven MSPs with a baseline less than two years.
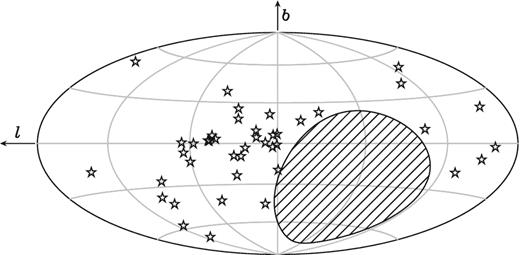
Distribution of the 42 MSPs, represented with a star, in Galactic coordinates (longitude l and latitude b). The centre of the plot is oriented towards the Galactic Center. The hatched area is the part of the sky (declination δ < −39°) that is not accessible to the EPTA.
Summary of the 42-pulsar data set. The columns present the pulsar name in the J2000 coordinate system, the observatories that contributed to the data set, the number of TOAs, the time span of the data set, the median TOA uncertainty (σTOA) taking into account the white noise parameters ‘EFAC’ and ‘EQUAD’, the rms timing residual, the spin period, the orbital period and the median flux density of the pulsar at 1400 MHz (see Section 2.3 for more details about the flux measurements). The last column gives the reference for the last published timing solution where V09, A15, R16 relate to Verbiest et al. (2009), Arzoumanian et al. (2015) and Reardon et al. (2016), respectively. The pulsars indicated by † are also named following the B1950 coordinate system, with the names B1855+09, B1937+21 and B1953+29, respectively. The quoted rms values are obtained from keeping the noise parameters, DM and red noise models at the maximum likelihood value while subtracting the DM signal from the residuals. Because of the degeneracy between the DM and red noise models, especially where no multifrequency data are available, the resulting rms quoted here can be biased towards smaller values (when the removed DM signal absorbed part of the red noise signal).
| PSR JName . | Observatories . | NTOA . | Tspan . | σTOA . | rms . | PSpin . | POrb . | S1400 . | References . |
|---|---|---|---|---|---|---|---|---|---|
| . | . | . | (yr) . | (μs) . | (μs) . | (ms) . | (d) . | (mJy) . | . |
| J0030+0451 | EFF, JBO, NRT | 907 | 15.1 | 3.79 | 4.1 | 4.9 | – | 0.8 | Abdo et al. (2009); A15 |
| J0034−0534 | NRT, WSRT | 276 | 13.5 | 8.51 | 4.0 | 1.9 | 1.59 | 0.01 | Hobbs et al. (2004b); Abdo et al. (2010) |
| J0218+4232 | EFF, JBO, NRT, WSRT | 1196 | 17.6 | 10.51 | 7.4 | 2.3 | 2.03 | 0.6 | Hobbs et al. (2004b) |
| J0610−2100 | JBO, NRT | 1034 | 6.9 | 8.14 | 4.9 | 3.9 | 0.29 | 0.4 | Burgay et al. (2006) |
| J0613−0200 | EFF, JBO, NRT, WSRT | 1369 | 16.1 | 2.57 | 1.8 | 3.1 | 1.20 | 1.7 | V09; A15; R16 |
| J0621+1002 | EFF, JBO, NRT, WSRT | 673 | 11.8 | 9.43 | 15.6 | 28.9 | 8.32 | 1.3 | Splaver et al. (2002); Nice et al. (2008) |
| J0751+1807 | EFF, JBO, NRT, WSRT | 1491 | 17.6 | 4.33 | 3.0 | 3.5 | 0.26 | 1.1 | Nice et al. (2005, 2008) |
| J0900−3144 | JBO, NRT | 875 | 6.9 | 4.27 | 3.1 | 11.1 | 18.74 | 3.2 | Burgay et al. (2006) |
| J1012+5307 | EFF, JBO, NRT, WSRT | 1459 | 16.8 | 2.73 | 1.6 | 5.3 | 0.60 | 3.0 | Lazaridis et al. (2009); A15 |
| J1022+1001 | EFF, JBO, NRT, WSRT | 908 | 17.5 | 4.02 | 2.5 | 16.5 | 7.81 | 2.9 | V09; R16 |
| J1024−0719 | EFF, JBO, NRT, WSRT | 561 | 17.3 | 3.42 | 8.3 | 5.2 | – | 1.3 | V09; Espinoza et al. (2013); A15; R16 |
| J1455−3330 | JBO, NRT | 524 | 9.2 | 7.07 | 2.7 | 8.0 | 76.17 | 0.4 | Hobbs et al. (2004b); A15 |
| J1600−3053 | JBO, NRT | 531 | 7.7 | 0.55 | 0.46 | 3.6 | 14.35 | 2.0 | V09; A15; R16 |
| J1640+2224 | EFF, JBO, NRT, WSRT | 595 | 17.3 | 4.48 | 1.8 | 3.2 | 175.46 | 0.4 | Löhmer et al. (2005); A15 |
| J1643−1224 | EFF, JBO, NRT, WSRT | 759 | 17.3 | 2.53 | 1.7 | 4.6 | 147.02 | 3.9 | V09; A15; R16 |
| J1713+0747 | EFF, JBO, NRT, WSRT | 1188 | 17.7 | 0.59 | 0.68 | 4.6 | 67.83 | 4.9 | V09; Zhu et al. (2015); A15; R16 |
| J1721−2457 | NRT, WSRT | 150 | 12.8 | 24.28 | 11.7 | 3.5 | – | 1.0 | Janssen et al. (2010) |
| J1730−2304 | EFF, JBO, NRT | 285 | 16.7 | 4.17 | 1.6 | 8.1 | – | 2.7 | V09; R16 |
| J1738+0333 | JBO, NRT | 318 | 7.3 | 5.95 | 3.0 | 5.9 | 0.35 | 0.3 | Freire et al. (2012b); A15 |
| J1744−1134 | EFF, JBO, NRT, WSRT | 536 | 17.3 | 1.21 | 0.86 | 4.1 | – | 1.6 | V09; A15; R16 |
| J1751−2857 | JBO, NRT | 144 | 8.3 | 3.52 | 3.0 | 3.9 | 110.75 | 0.4 | Stairs et al. (2005) |
| J1801−1417 | JBO, NRT | 126 | 7.1 | 3.81 | 2.6 | 3.6 | – | 1.1 | Lorimer et al. (2006) |
| J1802−2124 | JBO, NRT | 522 | 7.2 | 3.38 | 2.7 | 12.6 | 0.70 | 0.9 | Ferdman et al. (2010) |
| J1804−2717 | JBO, NRT | 116 | 8.4 | 7.23 | 3.1 | 9.3 | 11.13 | 1.0 | Hobbs et al. (2004b) |
| J1843−1113 | JBO, NRT, WSRT | 224 | 10.1 | 2.48 | 0.71 | 1.8 | – | 0.5 | Hobbs et al. (2004a) |
| J1853+1303 | JBO, NRT | 101 | 8.4 | 3.58 | 1.6 | 4.1 | 115.65 | 0.5 | Gonzalez et al. (2011); A15 |
| J1857+0943† | EFF, JBO, NRT, WSRT | 444 | 17.3 | 2.57 | 1.7 | 5.4 | 12.33 | 3.3 | V09; A15; R16 |
| J1909−3744 | NRT | 425 | 9.4 | 0.26 | 0.13 | 2.9 | 1.53 | 1.1 | V09; A15; R16 |
| J1910+1256 | JBO, NRT | 112 | 8.5 | 3.39 | 1.9 | 5.0 | 58.47 | 0.5 | Gonzalez et al. (2011); A15 |
| J1911+1347 | JBO, NRT | 140 | 7.5 | 1.78 | 1.4 | 4.6 | – | 0.6 | Lorimer et al. (2006) |
| J1911−1114 | JBO, NRT | 130 | 8.8 | 8.82 | 4.8 | 3.6 | 2.72 | 0.5 | Toscano et al. (1999a) |
| J1918−0642 | JBO, NRT, WSRT | 278 | 12.8 | 3.18 | 3.0 | 7.6 | 10.91 | 1.2 | Janssen et al. (2010); A15 |
| J1939+2134† | EFF, JBO, NRT, WSRT | 3174 | 24.1 | 0.49 | 34.5 | 1.6 | – | 8.3 | V09; A15; R16 |
| J1955+2908† | JBO, NRT | 157 | 8.1 | 14.92 | 6.5 | 6.1 | 117.35 | 0.5 | Gonzalez et al. (2011); A15 |
| J2010−1323 | JBO, NRT | 390 | 7.4 | 2.89 | 1.9 | 5.2 | – | 0.5 | Jacoby et al. (2007); A15 |
| J2019+2425 | JBO, NRT | 130 | 9.1 | 26.86 | 9.6 | 3.9 | 76.51 | 0.1 | Nice, Splaver & Stairs (2001) |
| J2033+1734 | JBO, NRT | 194 | 7.9 | 18.24 | 12.7 | 5.9 | 56.31 | 0.1 | Splaver (2004) |
| J2124−3358 | JBO, NRT | 544 | 9.4 | 5.57 | 3.2 | 4.9 | – | 2.7 | V09; R16 |
| J2145−0750 | EFF, JBO, NRT, WSRT | 800 | 17.5 | 2.64 | 1.8 | 16.1 | 6.84 | 4.0 | V09; A15; R16 |
| J2229+2643 | EFF, JBO, NRT | 316 | 8.2 | 11.18 | 4.2 | 3.0 | 93.02 | 0.1 | Wolszczan et al. (2000) |
| J2317+1439 | EFF, JBO, NRT, WSRT | 555 | 17.3 | 7.78 | 2.4 | 3.4 | 2.46 | 0.3 | Camilo et al. (1996); A15 |
| J2322+2057 | JBO, NRT | 229 | 7.9 | 12.47 | 5.9 | 4.8 | – | 0.03 | Nice & Taylor (1995) |
| PSR JName . | Observatories . | NTOA . | Tspan . | σTOA . | rms . | PSpin . | POrb . | S1400 . | References . |
|---|---|---|---|---|---|---|---|---|---|
| . | . | . | (yr) . | (μs) . | (μs) . | (ms) . | (d) . | (mJy) . | . |
| J0030+0451 | EFF, JBO, NRT | 907 | 15.1 | 3.79 | 4.1 | 4.9 | – | 0.8 | Abdo et al. (2009); A15 |
| J0034−0534 | NRT, WSRT | 276 | 13.5 | 8.51 | 4.0 | 1.9 | 1.59 | 0.01 | Hobbs et al. (2004b); Abdo et al. (2010) |
| J0218+4232 | EFF, JBO, NRT, WSRT | 1196 | 17.6 | 10.51 | 7.4 | 2.3 | 2.03 | 0.6 | Hobbs et al. (2004b) |
| J0610−2100 | JBO, NRT | 1034 | 6.9 | 8.14 | 4.9 | 3.9 | 0.29 | 0.4 | Burgay et al. (2006) |
| J0613−0200 | EFF, JBO, NRT, WSRT | 1369 | 16.1 | 2.57 | 1.8 | 3.1 | 1.20 | 1.7 | V09; A15; R16 |
| J0621+1002 | EFF, JBO, NRT, WSRT | 673 | 11.8 | 9.43 | 15.6 | 28.9 | 8.32 | 1.3 | Splaver et al. (2002); Nice et al. (2008) |
| J0751+1807 | EFF, JBO, NRT, WSRT | 1491 | 17.6 | 4.33 | 3.0 | 3.5 | 0.26 | 1.1 | Nice et al. (2005, 2008) |
| J0900−3144 | JBO, NRT | 875 | 6.9 | 4.27 | 3.1 | 11.1 | 18.74 | 3.2 | Burgay et al. (2006) |
| J1012+5307 | EFF, JBO, NRT, WSRT | 1459 | 16.8 | 2.73 | 1.6 | 5.3 | 0.60 | 3.0 | Lazaridis et al. (2009); A15 |
| J1022+1001 | EFF, JBO, NRT, WSRT | 908 | 17.5 | 4.02 | 2.5 | 16.5 | 7.81 | 2.9 | V09; R16 |
| J1024−0719 | EFF, JBO, NRT, WSRT | 561 | 17.3 | 3.42 | 8.3 | 5.2 | – | 1.3 | V09; Espinoza et al. (2013); A15; R16 |
| J1455−3330 | JBO, NRT | 524 | 9.2 | 7.07 | 2.7 | 8.0 | 76.17 | 0.4 | Hobbs et al. (2004b); A15 |
| J1600−3053 | JBO, NRT | 531 | 7.7 | 0.55 | 0.46 | 3.6 | 14.35 | 2.0 | V09; A15; R16 |
| J1640+2224 | EFF, JBO, NRT, WSRT | 595 | 17.3 | 4.48 | 1.8 | 3.2 | 175.46 | 0.4 | Löhmer et al. (2005); A15 |
| J1643−1224 | EFF, JBO, NRT, WSRT | 759 | 17.3 | 2.53 | 1.7 | 4.6 | 147.02 | 3.9 | V09; A15; R16 |
| J1713+0747 | EFF, JBO, NRT, WSRT | 1188 | 17.7 | 0.59 | 0.68 | 4.6 | 67.83 | 4.9 | V09; Zhu et al. (2015); A15; R16 |
| J1721−2457 | NRT, WSRT | 150 | 12.8 | 24.28 | 11.7 | 3.5 | – | 1.0 | Janssen et al. (2010) |
| J1730−2304 | EFF, JBO, NRT | 285 | 16.7 | 4.17 | 1.6 | 8.1 | – | 2.7 | V09; R16 |
| J1738+0333 | JBO, NRT | 318 | 7.3 | 5.95 | 3.0 | 5.9 | 0.35 | 0.3 | Freire et al. (2012b); A15 |
| J1744−1134 | EFF, JBO, NRT, WSRT | 536 | 17.3 | 1.21 | 0.86 | 4.1 | – | 1.6 | V09; A15; R16 |
| J1751−2857 | JBO, NRT | 144 | 8.3 | 3.52 | 3.0 | 3.9 | 110.75 | 0.4 | Stairs et al. (2005) |
| J1801−1417 | JBO, NRT | 126 | 7.1 | 3.81 | 2.6 | 3.6 | – | 1.1 | Lorimer et al. (2006) |
| J1802−2124 | JBO, NRT | 522 | 7.2 | 3.38 | 2.7 | 12.6 | 0.70 | 0.9 | Ferdman et al. (2010) |
| J1804−2717 | JBO, NRT | 116 | 8.4 | 7.23 | 3.1 | 9.3 | 11.13 | 1.0 | Hobbs et al. (2004b) |
| J1843−1113 | JBO, NRT, WSRT | 224 | 10.1 | 2.48 | 0.71 | 1.8 | – | 0.5 | Hobbs et al. (2004a) |
| J1853+1303 | JBO, NRT | 101 | 8.4 | 3.58 | 1.6 | 4.1 | 115.65 | 0.5 | Gonzalez et al. (2011); A15 |
| J1857+0943† | EFF, JBO, NRT, WSRT | 444 | 17.3 | 2.57 | 1.7 | 5.4 | 12.33 | 3.3 | V09; A15; R16 |
| J1909−3744 | NRT | 425 | 9.4 | 0.26 | 0.13 | 2.9 | 1.53 | 1.1 | V09; A15; R16 |
| J1910+1256 | JBO, NRT | 112 | 8.5 | 3.39 | 1.9 | 5.0 | 58.47 | 0.5 | Gonzalez et al. (2011); A15 |
| J1911+1347 | JBO, NRT | 140 | 7.5 | 1.78 | 1.4 | 4.6 | – | 0.6 | Lorimer et al. (2006) |
| J1911−1114 | JBO, NRT | 130 | 8.8 | 8.82 | 4.8 | 3.6 | 2.72 | 0.5 | Toscano et al. (1999a) |
| J1918−0642 | JBO, NRT, WSRT | 278 | 12.8 | 3.18 | 3.0 | 7.6 | 10.91 | 1.2 | Janssen et al. (2010); A15 |
| J1939+2134† | EFF, JBO, NRT, WSRT | 3174 | 24.1 | 0.49 | 34.5 | 1.6 | – | 8.3 | V09; A15; R16 |
| J1955+2908† | JBO, NRT | 157 | 8.1 | 14.92 | 6.5 | 6.1 | 117.35 | 0.5 | Gonzalez et al. (2011); A15 |
| J2010−1323 | JBO, NRT | 390 | 7.4 | 2.89 | 1.9 | 5.2 | – | 0.5 | Jacoby et al. (2007); A15 |
| J2019+2425 | JBO, NRT | 130 | 9.1 | 26.86 | 9.6 | 3.9 | 76.51 | 0.1 | Nice, Splaver & Stairs (2001) |
| J2033+1734 | JBO, NRT | 194 | 7.9 | 18.24 | 12.7 | 5.9 | 56.31 | 0.1 | Splaver (2004) |
| J2124−3358 | JBO, NRT | 544 | 9.4 | 5.57 | 3.2 | 4.9 | – | 2.7 | V09; R16 |
| J2145−0750 | EFF, JBO, NRT, WSRT | 800 | 17.5 | 2.64 | 1.8 | 16.1 | 6.84 | 4.0 | V09; A15; R16 |
| J2229+2643 | EFF, JBO, NRT | 316 | 8.2 | 11.18 | 4.2 | 3.0 | 93.02 | 0.1 | Wolszczan et al. (2000) |
| J2317+1439 | EFF, JBO, NRT, WSRT | 555 | 17.3 | 7.78 | 2.4 | 3.4 | 2.46 | 0.3 | Camilo et al. (1996); A15 |
| J2322+2057 | JBO, NRT | 229 | 7.9 | 12.47 | 5.9 | 4.8 | – | 0.03 | Nice & Taylor (1995) |
Summary of the 42-pulsar data set. The columns present the pulsar name in the J2000 coordinate system, the observatories that contributed to the data set, the number of TOAs, the time span of the data set, the median TOA uncertainty (σTOA) taking into account the white noise parameters ‘EFAC’ and ‘EQUAD’, the rms timing residual, the spin period, the orbital period and the median flux density of the pulsar at 1400 MHz (see Section 2.3 for more details about the flux measurements). The last column gives the reference for the last published timing solution where V09, A15, R16 relate to Verbiest et al. (2009), Arzoumanian et al. (2015) and Reardon et al. (2016), respectively. The pulsars indicated by † are also named following the B1950 coordinate system, with the names B1855+09, B1937+21 and B1953+29, respectively. The quoted rms values are obtained from keeping the noise parameters, DM and red noise models at the maximum likelihood value while subtracting the DM signal from the residuals. Because of the degeneracy between the DM and red noise models, especially where no multifrequency data are available, the resulting rms quoted here can be biased towards smaller values (when the removed DM signal absorbed part of the red noise signal).
| PSR JName . | Observatories . | NTOA . | Tspan . | σTOA . | rms . | PSpin . | POrb . | S1400 . | References . |
|---|---|---|---|---|---|---|---|---|---|
| . | . | . | (yr) . | (μs) . | (μs) . | (ms) . | (d) . | (mJy) . | . |
| J0030+0451 | EFF, JBO, NRT | 907 | 15.1 | 3.79 | 4.1 | 4.9 | – | 0.8 | Abdo et al. (2009); A15 |
| J0034−0534 | NRT, WSRT | 276 | 13.5 | 8.51 | 4.0 | 1.9 | 1.59 | 0.01 | Hobbs et al. (2004b); Abdo et al. (2010) |
| J0218+4232 | EFF, JBO, NRT, WSRT | 1196 | 17.6 | 10.51 | 7.4 | 2.3 | 2.03 | 0.6 | Hobbs et al. (2004b) |
| J0610−2100 | JBO, NRT | 1034 | 6.9 | 8.14 | 4.9 | 3.9 | 0.29 | 0.4 | Burgay et al. (2006) |
| J0613−0200 | EFF, JBO, NRT, WSRT | 1369 | 16.1 | 2.57 | 1.8 | 3.1 | 1.20 | 1.7 | V09; A15; R16 |
| J0621+1002 | EFF, JBO, NRT, WSRT | 673 | 11.8 | 9.43 | 15.6 | 28.9 | 8.32 | 1.3 | Splaver et al. (2002); Nice et al. (2008) |
| J0751+1807 | EFF, JBO, NRT, WSRT | 1491 | 17.6 | 4.33 | 3.0 | 3.5 | 0.26 | 1.1 | Nice et al. (2005, 2008) |
| J0900−3144 | JBO, NRT | 875 | 6.9 | 4.27 | 3.1 | 11.1 | 18.74 | 3.2 | Burgay et al. (2006) |
| J1012+5307 | EFF, JBO, NRT, WSRT | 1459 | 16.8 | 2.73 | 1.6 | 5.3 | 0.60 | 3.0 | Lazaridis et al. (2009); A15 |
| J1022+1001 | EFF, JBO, NRT, WSRT | 908 | 17.5 | 4.02 | 2.5 | 16.5 | 7.81 | 2.9 | V09; R16 |
| J1024−0719 | EFF, JBO, NRT, WSRT | 561 | 17.3 | 3.42 | 8.3 | 5.2 | – | 1.3 | V09; Espinoza et al. (2013); A15; R16 |
| J1455−3330 | JBO, NRT | 524 | 9.2 | 7.07 | 2.7 | 8.0 | 76.17 | 0.4 | Hobbs et al. (2004b); A15 |
| J1600−3053 | JBO, NRT | 531 | 7.7 | 0.55 | 0.46 | 3.6 | 14.35 | 2.0 | V09; A15; R16 |
| J1640+2224 | EFF, JBO, NRT, WSRT | 595 | 17.3 | 4.48 | 1.8 | 3.2 | 175.46 | 0.4 | Löhmer et al. (2005); A15 |
| J1643−1224 | EFF, JBO, NRT, WSRT | 759 | 17.3 | 2.53 | 1.7 | 4.6 | 147.02 | 3.9 | V09; A15; R16 |
| J1713+0747 | EFF, JBO, NRT, WSRT | 1188 | 17.7 | 0.59 | 0.68 | 4.6 | 67.83 | 4.9 | V09; Zhu et al. (2015); A15; R16 |
| J1721−2457 | NRT, WSRT | 150 | 12.8 | 24.28 | 11.7 | 3.5 | – | 1.0 | Janssen et al. (2010) |
| J1730−2304 | EFF, JBO, NRT | 285 | 16.7 | 4.17 | 1.6 | 8.1 | – | 2.7 | V09; R16 |
| J1738+0333 | JBO, NRT | 318 | 7.3 | 5.95 | 3.0 | 5.9 | 0.35 | 0.3 | Freire et al. (2012b); A15 |
| J1744−1134 | EFF, JBO, NRT, WSRT | 536 | 17.3 | 1.21 | 0.86 | 4.1 | – | 1.6 | V09; A15; R16 |
| J1751−2857 | JBO, NRT | 144 | 8.3 | 3.52 | 3.0 | 3.9 | 110.75 | 0.4 | Stairs et al. (2005) |
| J1801−1417 | JBO, NRT | 126 | 7.1 | 3.81 | 2.6 | 3.6 | – | 1.1 | Lorimer et al. (2006) |
| J1802−2124 | JBO, NRT | 522 | 7.2 | 3.38 | 2.7 | 12.6 | 0.70 | 0.9 | Ferdman et al. (2010) |
| J1804−2717 | JBO, NRT | 116 | 8.4 | 7.23 | 3.1 | 9.3 | 11.13 | 1.0 | Hobbs et al. (2004b) |
| J1843−1113 | JBO, NRT, WSRT | 224 | 10.1 | 2.48 | 0.71 | 1.8 | – | 0.5 | Hobbs et al. (2004a) |
| J1853+1303 | JBO, NRT | 101 | 8.4 | 3.58 | 1.6 | 4.1 | 115.65 | 0.5 | Gonzalez et al. (2011); A15 |
| J1857+0943† | EFF, JBO, NRT, WSRT | 444 | 17.3 | 2.57 | 1.7 | 5.4 | 12.33 | 3.3 | V09; A15; R16 |
| J1909−3744 | NRT | 425 | 9.4 | 0.26 | 0.13 | 2.9 | 1.53 | 1.1 | V09; A15; R16 |
| J1910+1256 | JBO, NRT | 112 | 8.5 | 3.39 | 1.9 | 5.0 | 58.47 | 0.5 | Gonzalez et al. (2011); A15 |
| J1911+1347 | JBO, NRT | 140 | 7.5 | 1.78 | 1.4 | 4.6 | – | 0.6 | Lorimer et al. (2006) |
| J1911−1114 | JBO, NRT | 130 | 8.8 | 8.82 | 4.8 | 3.6 | 2.72 | 0.5 | Toscano et al. (1999a) |
| J1918−0642 | JBO, NRT, WSRT | 278 | 12.8 | 3.18 | 3.0 | 7.6 | 10.91 | 1.2 | Janssen et al. (2010); A15 |
| J1939+2134† | EFF, JBO, NRT, WSRT | 3174 | 24.1 | 0.49 | 34.5 | 1.6 | – | 8.3 | V09; A15; R16 |
| J1955+2908† | JBO, NRT | 157 | 8.1 | 14.92 | 6.5 | 6.1 | 117.35 | 0.5 | Gonzalez et al. (2011); A15 |
| J2010−1323 | JBO, NRT | 390 | 7.4 | 2.89 | 1.9 | 5.2 | – | 0.5 | Jacoby et al. (2007); A15 |
| J2019+2425 | JBO, NRT | 130 | 9.1 | 26.86 | 9.6 | 3.9 | 76.51 | 0.1 | Nice, Splaver & Stairs (2001) |
| J2033+1734 | JBO, NRT | 194 | 7.9 | 18.24 | 12.7 | 5.9 | 56.31 | 0.1 | Splaver (2004) |
| J2124−3358 | JBO, NRT | 544 | 9.4 | 5.57 | 3.2 | 4.9 | – | 2.7 | V09; R16 |
| J2145−0750 | EFF, JBO, NRT, WSRT | 800 | 17.5 | 2.64 | 1.8 | 16.1 | 6.84 | 4.0 | V09; A15; R16 |
| J2229+2643 | EFF, JBO, NRT | 316 | 8.2 | 11.18 | 4.2 | 3.0 | 93.02 | 0.1 | Wolszczan et al. (2000) |
| J2317+1439 | EFF, JBO, NRT, WSRT | 555 | 17.3 | 7.78 | 2.4 | 3.4 | 2.46 | 0.3 | Camilo et al. (1996); A15 |
| J2322+2057 | JBO, NRT | 229 | 7.9 | 12.47 | 5.9 | 4.8 | – | 0.03 | Nice & Taylor (1995) |
| PSR JName . | Observatories . | NTOA . | Tspan . | σTOA . | rms . | PSpin . | POrb . | S1400 . | References . |
|---|---|---|---|---|---|---|---|---|---|
| . | . | . | (yr) . | (μs) . | (μs) . | (ms) . | (d) . | (mJy) . | . |
| J0030+0451 | EFF, JBO, NRT | 907 | 15.1 | 3.79 | 4.1 | 4.9 | – | 0.8 | Abdo et al. (2009); A15 |
| J0034−0534 | NRT, WSRT | 276 | 13.5 | 8.51 | 4.0 | 1.9 | 1.59 | 0.01 | Hobbs et al. (2004b); Abdo et al. (2010) |
| J0218+4232 | EFF, JBO, NRT, WSRT | 1196 | 17.6 | 10.51 | 7.4 | 2.3 | 2.03 | 0.6 | Hobbs et al. (2004b) |
| J0610−2100 | JBO, NRT | 1034 | 6.9 | 8.14 | 4.9 | 3.9 | 0.29 | 0.4 | Burgay et al. (2006) |
| J0613−0200 | EFF, JBO, NRT, WSRT | 1369 | 16.1 | 2.57 | 1.8 | 3.1 | 1.20 | 1.7 | V09; A15; R16 |
| J0621+1002 | EFF, JBO, NRT, WSRT | 673 | 11.8 | 9.43 | 15.6 | 28.9 | 8.32 | 1.3 | Splaver et al. (2002); Nice et al. (2008) |
| J0751+1807 | EFF, JBO, NRT, WSRT | 1491 | 17.6 | 4.33 | 3.0 | 3.5 | 0.26 | 1.1 | Nice et al. (2005, 2008) |
| J0900−3144 | JBO, NRT | 875 | 6.9 | 4.27 | 3.1 | 11.1 | 18.74 | 3.2 | Burgay et al. (2006) |
| J1012+5307 | EFF, JBO, NRT, WSRT | 1459 | 16.8 | 2.73 | 1.6 | 5.3 | 0.60 | 3.0 | Lazaridis et al. (2009); A15 |
| J1022+1001 | EFF, JBO, NRT, WSRT | 908 | 17.5 | 4.02 | 2.5 | 16.5 | 7.81 | 2.9 | V09; R16 |
| J1024−0719 | EFF, JBO, NRT, WSRT | 561 | 17.3 | 3.42 | 8.3 | 5.2 | – | 1.3 | V09; Espinoza et al. (2013); A15; R16 |
| J1455−3330 | JBO, NRT | 524 | 9.2 | 7.07 | 2.7 | 8.0 | 76.17 | 0.4 | Hobbs et al. (2004b); A15 |
| J1600−3053 | JBO, NRT | 531 | 7.7 | 0.55 | 0.46 | 3.6 | 14.35 | 2.0 | V09; A15; R16 |
| J1640+2224 | EFF, JBO, NRT, WSRT | 595 | 17.3 | 4.48 | 1.8 | 3.2 | 175.46 | 0.4 | Löhmer et al. (2005); A15 |
| J1643−1224 | EFF, JBO, NRT, WSRT | 759 | 17.3 | 2.53 | 1.7 | 4.6 | 147.02 | 3.9 | V09; A15; R16 |
| J1713+0747 | EFF, JBO, NRT, WSRT | 1188 | 17.7 | 0.59 | 0.68 | 4.6 | 67.83 | 4.9 | V09; Zhu et al. (2015); A15; R16 |
| J1721−2457 | NRT, WSRT | 150 | 12.8 | 24.28 | 11.7 | 3.5 | – | 1.0 | Janssen et al. (2010) |
| J1730−2304 | EFF, JBO, NRT | 285 | 16.7 | 4.17 | 1.6 | 8.1 | – | 2.7 | V09; R16 |
| J1738+0333 | JBO, NRT | 318 | 7.3 | 5.95 | 3.0 | 5.9 | 0.35 | 0.3 | Freire et al. (2012b); A15 |
| J1744−1134 | EFF, JBO, NRT, WSRT | 536 | 17.3 | 1.21 | 0.86 | 4.1 | – | 1.6 | V09; A15; R16 |
| J1751−2857 | JBO, NRT | 144 | 8.3 | 3.52 | 3.0 | 3.9 | 110.75 | 0.4 | Stairs et al. (2005) |
| J1801−1417 | JBO, NRT | 126 | 7.1 | 3.81 | 2.6 | 3.6 | – | 1.1 | Lorimer et al. (2006) |
| J1802−2124 | JBO, NRT | 522 | 7.2 | 3.38 | 2.7 | 12.6 | 0.70 | 0.9 | Ferdman et al. (2010) |
| J1804−2717 | JBO, NRT | 116 | 8.4 | 7.23 | 3.1 | 9.3 | 11.13 | 1.0 | Hobbs et al. (2004b) |
| J1843−1113 | JBO, NRT, WSRT | 224 | 10.1 | 2.48 | 0.71 | 1.8 | – | 0.5 | Hobbs et al. (2004a) |
| J1853+1303 | JBO, NRT | 101 | 8.4 | 3.58 | 1.6 | 4.1 | 115.65 | 0.5 | Gonzalez et al. (2011); A15 |
| J1857+0943† | EFF, JBO, NRT, WSRT | 444 | 17.3 | 2.57 | 1.7 | 5.4 | 12.33 | 3.3 | V09; A15; R16 |
| J1909−3744 | NRT | 425 | 9.4 | 0.26 | 0.13 | 2.9 | 1.53 | 1.1 | V09; A15; R16 |
| J1910+1256 | JBO, NRT | 112 | 8.5 | 3.39 | 1.9 | 5.0 | 58.47 | 0.5 | Gonzalez et al. (2011); A15 |
| J1911+1347 | JBO, NRT | 140 | 7.5 | 1.78 | 1.4 | 4.6 | – | 0.6 | Lorimer et al. (2006) |
| J1911−1114 | JBO, NRT | 130 | 8.8 | 8.82 | 4.8 | 3.6 | 2.72 | 0.5 | Toscano et al. (1999a) |
| J1918−0642 | JBO, NRT, WSRT | 278 | 12.8 | 3.18 | 3.0 | 7.6 | 10.91 | 1.2 | Janssen et al. (2010); A15 |
| J1939+2134† | EFF, JBO, NRT, WSRT | 3174 | 24.1 | 0.49 | 34.5 | 1.6 | – | 8.3 | V09; A15; R16 |
| J1955+2908† | JBO, NRT | 157 | 8.1 | 14.92 | 6.5 | 6.1 | 117.35 | 0.5 | Gonzalez et al. (2011); A15 |
| J2010−1323 | JBO, NRT | 390 | 7.4 | 2.89 | 1.9 | 5.2 | – | 0.5 | Jacoby et al. (2007); A15 |
| J2019+2425 | JBO, NRT | 130 | 9.1 | 26.86 | 9.6 | 3.9 | 76.51 | 0.1 | Nice, Splaver & Stairs (2001) |
| J2033+1734 | JBO, NRT | 194 | 7.9 | 18.24 | 12.7 | 5.9 | 56.31 | 0.1 | Splaver (2004) |
| J2124−3358 | JBO, NRT | 544 | 9.4 | 5.57 | 3.2 | 4.9 | – | 2.7 | V09; R16 |
| J2145−0750 | EFF, JBO, NRT, WSRT | 800 | 17.5 | 2.64 | 1.8 | 16.1 | 6.84 | 4.0 | V09; A15; R16 |
| J2229+2643 | EFF, JBO, NRT | 316 | 8.2 | 11.18 | 4.2 | 3.0 | 93.02 | 0.1 | Wolszczan et al. (2000) |
| J2317+1439 | EFF, JBO, NRT, WSRT | 555 | 17.3 | 7.78 | 2.4 | 3.4 | 2.46 | 0.3 | Camilo et al. (1996); A15 |
| J2322+2057 | JBO, NRT | 229 | 7.9 | 12.47 | 5.9 | 4.8 | – | 0.03 | Nice & Taylor (1995) |
In this paper, we define an observing system as a specific combination of observatory, backend and frequency band. The radio telescopes and pulsar backends used for the observations are described below.
2.1 Effelsberg Radio Telescope
The data from the 100-m Effelsberg radio telescope presented in this paper were acquired using the EBPP, an online coherent dedispersion backend described in detail by Backer et al. (1997). This instrument can process a BW up to 112 MHz depending on the DM value. The signals from the two circular polarizations are split into 32 channels each and sent to the dedisperser boards. After the dedispersion takes place, the output signals are folded (i.e. individual pulses are phase-aligned and summed) using the topocentric pulse period.
EPTA timing observations at Effelsberg were made at a central frequency of 1410 MHz until 2009 April then moved to 1360 MHz afterwards due to a change in the receiver. Additional observations at S band (2639 MHz) began in 2005 November with observations at both frequencies taken during the same two-day observing run. Typically, the observations occur on a monthly basis with an integration time per source of about 30 min. The subintegration times range from 8 to 12 min before 2009 and 2 min thereafter. For 4 pulsars, namely PSRs J0030+0451, J1024−0719, J1730−2304 and J2317+1439, there is a gap in the data from 1999 to 2005 as these sources were temporarily removed from the observing list. Data reduction was performed with the psrchive package (Hotan, van Straten & Manchester 2004). The profiles were cleaned of radio frequency interference (RFI) using the psrchivepaz tool but also examined and excised manually with the pazi tool. No standard polarization calibration using a pulsed and linearly polarized noise diode was performed. However, the EBPP automatically adjusts the power levels of both polarizations prior to each observation. The TOAs were calculated by cross-correlating the time-integrated, frequency-scrunched, total intensity profile, with an analytic and noise-free template. This template was generated using the paas tool to fit a set of von Mises functions to a profile formed from high signal-to-noise ratio (S/N) observations. In general, we used the standard ‘Fourier phase gradient’ algorithm (Taylor 1992) implemented in psrchive to estimate the TOAs and their uncertainties. We used a different template for each observing frequency, including different templates for the 1410 and 1360 MHz observations. Local time is kept by the on-site H-maser clock, which is corrected to Coordinated Universal Time (UTC) using recorded offsets between the maser and the Global Positioning System (GPS) satellites.
2.2 Lovell Radio Telescope
At Jodrell bank, the 76-m Lovell telescope is used in a regular monitoring programme to observe most of the pulsars presented in this paper. All TOAs used here were generated by using the DFB, a clone of the Parkes Digital FilterBank. Each pulsar was observed with a typical cadence of once every 10 d for 30 min with a subintegration time of 10 s. The DFB came into operation in 2009 January observing at a central frequency of 1400 MHz with a BW of 128 MHz split into 512 channels. From 2009 September, the centre frequency was changed to 1520 MHz and the BW increased to 512 MHz (split into 1024 channels) of which approximately 380 MHz was usable, depending on RFI conditions. As this is a significant change, and to account for possible profile evolution with observing frequency, both setups are considered as distinct observing systems and different templates were used. Data cleaning and TOA generation were done in a similar way to the Effelsberg data. There is no standard polarization calibration (through observations of a noise diode) applied to the DFB data. However the power levels of both polarizations are regularly and manually adjusted via a set of attenuators. Local time is kept by the on-site H-maser clock, which is corrected to UTC using recorded offsets between the maser and the GPS satellites.
2.3 Nançay Radio Telescope
The NRT is a meridian telescope with a collecting area equivalent to a 94-m dish. The moving focal carriage that allows an observing time of about one hour per source hosts the LF and high-frequency (HF) receivers covering 1.1–1.8 GHz and 1.7–3.5 GHz, respectively. A large timing programme of MSPs started in late 2004 with the commissioning of the BON instrumentation, a member of the ASP-GASP coherent dedispersion backend family (Demorest 2007). A 128 MHz BW is split into 32 channels by a CASPER2 Serendip V board and then sent to servers to be coherently dedispersed and folded to form 2-min subintegrations.
From 2004 to 2008, the BW was limited to 64 MHz and then extended to 128 MHz. At the same time, the NRT started to regularly observe a pulsed noise diode prior to each observation in order to properly correct for the difference in gain and phase between the two polarizations. In 2011 August, the L-band central frequency of the BON backend shifted from 1.4 to 1.6 GHz to accommodate the new wide-band NUPPI dedispersion backend (Liu et al. 2014). Due to known instrumental issues between 2012 November and 2013 April (i.e. loss of one of the polarization channels, mirroring of the spectrum), these data have not been included in the analysis.
The flux density values at 1.4 GHz reported in Table 1 are derived from observations recorded with the NUPPI instrument between MJD 55900 and 56700. The quasar 3C48 was chosen to be the reference source for the absolute flux calibration. These flux density values have been corrected for the declination-dependent illumination of the mirrors of the NRT. Although the NUPPI timing data are not included in this work, we used these observations to estimate the median flux densities as no other EPTA data were flux-calibrated. The NUPPI timing data will be part of a future EPTA data release along with the data from other telescopes recorded with new-generation instrumentations.
The data were reduced with the psrchive package and automatically cleaned for RFI. Except for pulsars with short orbital periods, all daily observations are fully scrunched in time and frequency to form one single profile. For PSRs J0610−2100, J0751+1807, J1738+0333, J1802−2124, the data were integrated to form 6, 12, 16 and 8 min profiles, respectively. The templates for the three observing frequencies are constructed by phase-aligning the ∼10 per cent profiles with the best S/N. The resulting integrated profiles are made noise free with the same wavelet noise removal program as in Demorest et al. (2013). As stated above, we used the standard ‘Fourier phase gradient’ from psrchive to estimate the TOAs and their uncertainties. However, we noticed that in the case of very low S/N profiles, the reported uncertainties were underestimated. Arzoumanian et al. (2015) also observed that TOAs extracted from low S/N profiles deviate from a Gaussian distribution and therefore excluded all TOAs where S/N < 8 (see appendix B of their paper for more details). Here, we made use of the Fourier domain Markov Chain Monte Carlo TOA estimator (hereafter FDM) to properly estimate the error bars in this low S/N regime. We applied the FDM method to PSRs J0034−0534, J0218+4232, J1455−3330, J2019+2425 and J2033+1734. All the BON data are time-stamped with a GPS-disciplined clock.
For PSR J1939+2134, archival data from 1990 to 1999 recorded with a swept-frequency local oscillator (hereafter referred to as DDS) at a frequency of 1410 MHz (Cognard et al. 1995) were added to the data set. These data are time-stamped with an on-site Rubidium clock, which is corrected to UTC using recorded offsets between the Rubidium clock and the Paris Observatory Universal Time.
2.4 Westerbork Synthesis Radio Telescope
The WSRT is an east–west array consisting of fourteen 25-m dishes, adding up to the equivalent size of a 94-m dish when combined as a tied-array. From 1999 to 2010, an increasing number of MSPs were observed once a month using the PuMa pulsar machine (a DFB) at WSRT (Voûte et al. 2002). In each observing session, the pulsars were observed for 25 min each at one or more frequencies centred at 350 MHz (10 MHz BW), 840 MHz (80 MHz BW) and 1380 MHz (80 MHz spread across a total of 160 MHz BW). Up to 512 channels were used to split the BW for the observations at 350 MHz. At 840 MHz and 1380 MHz, 64 channels were used per 10 MHz subband. For a more detailed description of this instrumentation, see e.g. Janssen et al. (2008). Since 2007, the 840 MHz band was no longer used for regular timing observations, however, an additional observing frequency centred at 2273 MHz using 160 MHz BW was used for a selected set of the observed pulsars. The data were dedispersed and folded offline using custom software, and then integrated over frequency and time to obtain a single profile for each observation. Gain and phase difference between the two polarizations are adjusted during the phased-array calibration of the dishes. To generate the TOAs, a high-S/N template based on the observations was used for each observing frequency separately. Local time is kept by the on-site H-maser clock, which is corrected to UTC using recorded offsets between the maser and the GPS satellites.
3 Data combination and timing
The topocentric TOAs recorded at each observatory are first converted to the Solar system barycenter (SSB) using the DE421 planetary ephemeris (Folkner, Williams & Boggs 2009) with reference to the latest terrestrial time standard from the Bureau International des Poids et Mesures (Petit 2010). The DE421 model is a major improvement on the DE200 ephemeris that was used for older published ephemerides and later found to suffer from inaccurate values of planetary masses (Splaver et al. 2005; Hotan, Bailes & Ord 2006; Verbiest et al. 2008).
We used temponest (Lentati et al. 2014), a Bayesian analysis software that uses the tempo2 pulsar timing package (Edwards, Hobbs & Manchester 2006; Hobbs, Edwards & Manchester 2006) and MULTINEST (Feroz, Hobson & Bridges 2009), a Bayesian inference tool, to evaluate and explore the parameter space of the non-linear pulsar timing model. All pulsar timing parameters are sampled in temponest with uniform priors. The timing model includes the astrometric (right ascension, α, declination, δ, proper motion in α and δ, μα and μδ) and rotational parameters (period P and period derivative |$\dot{P}$|). If the pulsar is part of a binary system, five additional parameters are incorporated to describe the Keplerian binary motion: the orbital period Pb, the projected semimajor axis x of the pulsar orbit, the longitude of periastron ω, the epoch T0 of the periastron passage and the eccentricity e. For some pulsars in our set, we require theory-independent PK parameters (Damour & Deruelle 1985, 1986) to account for deviations from a Keplerian motion, or parameters to describe changes in the viewing geometry of the systems. The parameters we used include the precession of periastron |$\dot{\omega }$|, the orbital period derivative |$\dot{P_{\rm b}}$|, the Shapiro delay (‘range’ r and ‘shape’ s; s has a uniform prior in cos i space) and the apparent derivative of the projected semimajor axis |$\dot{x}$|. These parameters are implemented in tempo2 under the ‘DD’ binary model. In the case of quasi-circular orbits, the ‘ELL1’ model is preferred and replaces ω, T0 and e with the two Laplace–Lagrange parameters κ and η and the time of ascending node Tasc (Lange et al. 2001). For the description of the Shapiro delay in PSRs J0751+1807, J1600−3053 and J1918−0642, we adopted the orthometric parametrization of the Shapiro delay introduced by Freire & Wex (2010) with the amplitude of the third harmonic of the Shapiro delay h3 and the ratio of successive harmonics ς.
Each pulsar timing model also includes two stochastic models to describe the DM variations and an additional achromatic red noise process. Both processes are modelled as stationary, stochastic signals with a power-law spectrum of the form S(f) ∝ A2f−γ, where S(f), A and γ are the power spectral density as function of frequency f, the amplitude and the spectral index, respectively. The power laws have a cutoff frequency at the lowest frequency, equal to the inverse of the data span, which is mathematically necessary for the subsequent calculation of the covariance matrix (van Haasteren et al. 2009). It has been shown that this cutoff rises naturally for the achromatic red noise power law in pulsar timing data because any LF signal's power below the cutoff frequency is absorbed by the fitting of the pulsar's rotational frequency and frequency derivative (van Haasteren et al. 2009; Lee et al. 2012). It is possible to do the same for the DM variations model, by fitting a first and a second DM derivative (parameters DM1 and DM2) in the timing model (Lee et al. 2014). Implementation of the models is made using the time–frequency method of Lentati et al. (2013). Details on this process and applications can be found in Lentati et al. (2015b) and Caballero et al. (2015). In brief, denoting matrices with boldface letters, the red noise process time-domain signal, is expressed as a Fourier series, |$\bf {t}_{\rm TN}=\bf {F}_{\rm TN}\bf {a}$|, where |$\bf {F}_{\rm TN}$| is the sum of sines and cosines with coefficients given by the matrix |$\bf {a}$|. Fourier frequencies are sampled with integer multiples of the lowest frequency, and are sampled up to 1/14 d−1. The Fourier coefficients are free parameters.
The DM variations component is modelled similarly, with the only difference being that the time-domain signal is dependent on the observing frequency. According to the dispersion law from interstellar plasma, the delay in the arrival time of the pulse depends on the inverse square of the observing frequency, see e.g. Lyne & Graham-Smith (2012). As such, the Fourier transform components are |${\bf {F}^{{\rm DM}}_{ij}={\bf {F}_{ij}}D_{i} D_{j}}$|, where the i,j indices denote the residual index number, |$D_i=1/(k\nu ^2_i)$|, and k = 2.41 × 10−16 Hz−2cm−3pc s−1, is the dispersion constant. This stochastic DM variations component is additional to the deterministic linear and quadratic components implemented as part of the tempo2 timing model. In addition, we used the standard electron density model for the solar wind included in tempo2 with a value of 4 cm−3 at 1 au. This solar wind model can be covariant with the measured astrometric parameters of the pulsar.
The power-law parametrization of the DM variations and red noise spectra means that the parameters we need to sample are the amplitudes and spectral indices of the power law. We do so by using uniform priors in the range [0, 7] for the spectral index and log-uniform priors for the amplitudes, in the log10-range [−20, −8]. For discussion on the impact of our prior-type selection, see Lentati et al. (2014) and Caballero et al. (2015). Here, we have used the least informative priors on the noise parameters. This means that the Bayesian inference will assign equal probability to these parameters if the data are insufficient to break the degeneracy between them. This approach is adequate to derive a total noise covariance matrix (addition of white noise, red noise and DM variations covariance matrices) that allows robust estimation of the timing parameters. The prior ranges are set to be wide enough to encompass any DM or red noise signal seen in the data. The lower bound on the spectral index of the red noise process is set to zero as we assume there is no blue process in the data. Together with the EFAC and EQUAD values, the DM and red noise spectral indices and amplitudes are used by the timing software to form the timing residuals.
3.1 Criterion for Shapiro delay detectability
4 Timing results
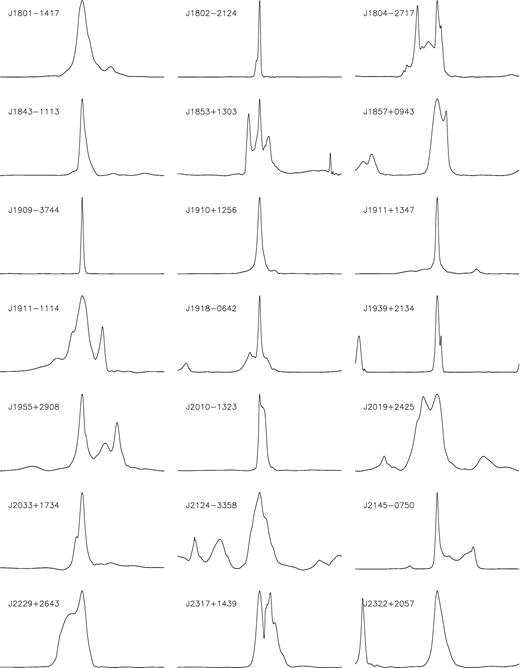
In this section, we summarize the timing results of the 42 MSPs obtained from temponest. Among these sources, six pulsars, namely PSRs J0613−0200, J1012+5307, J1600−3053, J1713+0747, J1744−1134 and J1909−3744 have been selected by Babak et al. (2016) to form the basis of the work presented by Lentati et al. (2015b), Taylor et al. (2015) and Babak et al. (2016). The quoted uncertainties represent the 68.3 per cent Bayesian credible interval of the one-dimensional marginalized posterior distribution of each parameter. The timing models are shown in Tables 2–12. These models, including the stochastic parameters, are made publicly available on the EPTA website.3 The reference profiles at L band can be found in Figs A3 and A4. Throughout the paper, we refer to rms as the weighted root mean square timing residuals. The details on the data sets used in this paper can be found in Table A1.
Timing model parameters for PSRs J0030+0451, J0034−0534, J0218+4232 and J0610−2100. Values in parentheses represent the 68.3 per cent confidence uncertainties in the last digit quoted and come from the one-dimensional marginalized posterior distribution of each parameter. The measured timing parameters are introduced in Section 3. The derived parameters show the Galactic longitude (l) and latitude (b), the parallax distance corrected from the LK bias (d), the composite proper motion (μ). The position, spin period and DM are given for the reference epoch of MJD 55000. The three kinematic contributions (|$\dot{P}_{{\rm shk}}$|, |$\dot{P}_{{\rm kz}}$| and |$\dot{P}_{{\rm dgr}}$|) to the intrinsic period derivative (|$\dot{P}_{{\rm int}}$|) are introduced in Section 5.3. For binary pulsars, the minimum companion mass, assuming a pulsar mass of 1.2 M⊙, is also indicated on the last line.
| PSR name . | J0030+0451 . | J0034−0534 . | J0218+4232 . | J0610−2100 . |
|---|---|---|---|---|
| MJD range | 51275–56779 | 51770–56705 | 50370–56786 | 54270–56791 |
| Number of TOAs | 907 | 276 | 1196 | 1034 |
| rms timing residual (μs) | 4.1 | 4.0 | 7.4 | 4.9 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 00:30:27.428 36(6) | 00:34:21.834 22(8) | 02:18:06.357 299(19) | 06:10:13.595 462(17) |
| Declination, δ | 04:51:39.707(3) | −05:34:36.722(3) | 42:32:17.3821(4) | −21:00:27.9313(4) |
| Proper motion in α (mas yr−1) | −5.9(5) | 7.9(3) | 5.31(7) | 9.0(1) |
| Proper motion in δ (mas yr−1) | −0.2(11) | −9.2(6) | −3.15(13) | 16.78(12) |
| Period, P (ms) | 4.865 453 286 352 01(19) | 1.877 181 885 831 71(10) | 2.323 090 531 512 24(8) | 3.861 324 766 195(3) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.0172(3) | 0.497 84(13) | 7.739 55(7) | 1.2298(19) |
| Parallax, π (mas) | 2.79(23) | – | – | – |
| DM (cm−3 pc) | 4.329(6) | 13.7658(19) | 61.2488(17) | 60.67(3) |
| DM1 (cm−3 pc yr−1) | 0.0007(5) | −0.0001(1) | −0.0003(2) | −0.014(8) |
| DM2 (cm−3 pc yr−2) | 0.0001(1) | −0.000 030(17) | 0.000 056(20) | 0.002(1) |
| Orbital period, Pb (d) | – | 1.589 281 825 32(14) | 2.028 846 115 61(9) | 0.286 016 0068(6) |
| Epoch of periastron, T0 (MJD) | – | 48 766.98(4) | 49 150.883(16) | 52 814.303(13) |
| Projected semimajor axis, x (lt-s) | – | 1.437 7662(5) | 1.984 4344(4) | 0.073 4891(4) |
| Longitude of periastron, ω0 (deg) | – | 313(9) | 49(3) | 67(16) |
| Orbital eccentricity, e | – | 4.3(7)× 10−6 | 6.8(4)× 10−6 | 2.9(8)× 10−5 |
| κ = e × sin ω0 | – | −3.1(7)× 10−6 | 5.1(4)× 10−6 | 2.7(8)× 10−5 |
| η = e × cos ω0 | – | 3.0(6)× 10−6 | 4.5(4)× 10−6 | 1.2(8)× 10−5 |
| Time of asc. node (MJD) | – | 48 765.599 5019(5) | 49 150.608 9170(3) | 52 814.249 581(3) |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 113.1 | 111.5 | 139.5 | 227.7 |
| Gal. latitude, b (deg) | −57.6 | −68.1 | −17.5 | −18.2 |
| LK Px Distance, d (pc) | |$354_{-27}^{+31}$| | – | – | – |
| Composite PM, μ (mas yr−1) | 5.9(5) | 12.1(5) | 6.18(9) | 19.05(11) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.015(3) | 0.036 | 0.057 | 1.2 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.078(7) | −0.056 | −0.034 | −0.082 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.0030(3) | −0.000 86 | 0.013 | 0.011 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 1.084(6) | 0.518 | 7.7 | 0.0955 |
| Characteristic age, τc (Gyr) | 7.1 | 5.7 | 0.48 | 64.0 |
| Surface magnetic field, B (× 108 G) | 2.3 | 1.0 | 4.3 | 0.6 |
| Min. companion mass (M⊙) | – | 0.13 | 0.16 | 0.02 |
| PSR name . | J0030+0451 . | J0034−0534 . | J0218+4232 . | J0610−2100 . |
|---|---|---|---|---|
| MJD range | 51275–56779 | 51770–56705 | 50370–56786 | 54270–56791 |
| Number of TOAs | 907 | 276 | 1196 | 1034 |
| rms timing residual (μs) | 4.1 | 4.0 | 7.4 | 4.9 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 00:30:27.428 36(6) | 00:34:21.834 22(8) | 02:18:06.357 299(19) | 06:10:13.595 462(17) |
| Declination, δ | 04:51:39.707(3) | −05:34:36.722(3) | 42:32:17.3821(4) | −21:00:27.9313(4) |
| Proper motion in α (mas yr−1) | −5.9(5) | 7.9(3) | 5.31(7) | 9.0(1) |
| Proper motion in δ (mas yr−1) | −0.2(11) | −9.2(6) | −3.15(13) | 16.78(12) |
| Period, P (ms) | 4.865 453 286 352 01(19) | 1.877 181 885 831 71(10) | 2.323 090 531 512 24(8) | 3.861 324 766 195(3) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.0172(3) | 0.497 84(13) | 7.739 55(7) | 1.2298(19) |
| Parallax, π (mas) | 2.79(23) | – | – | – |
| DM (cm−3 pc) | 4.329(6) | 13.7658(19) | 61.2488(17) | 60.67(3) |
| DM1 (cm−3 pc yr−1) | 0.0007(5) | −0.0001(1) | −0.0003(2) | −0.014(8) |
| DM2 (cm−3 pc yr−2) | 0.0001(1) | −0.000 030(17) | 0.000 056(20) | 0.002(1) |
| Orbital period, Pb (d) | – | 1.589 281 825 32(14) | 2.028 846 115 61(9) | 0.286 016 0068(6) |
| Epoch of periastron, T0 (MJD) | – | 48 766.98(4) | 49 150.883(16) | 52 814.303(13) |
| Projected semimajor axis, x (lt-s) | – | 1.437 7662(5) | 1.984 4344(4) | 0.073 4891(4) |
| Longitude of periastron, ω0 (deg) | – | 313(9) | 49(3) | 67(16) |
| Orbital eccentricity, e | – | 4.3(7)× 10−6 | 6.8(4)× 10−6 | 2.9(8)× 10−5 |
| κ = e × sin ω0 | – | −3.1(7)× 10−6 | 5.1(4)× 10−6 | 2.7(8)× 10−5 |
| η = e × cos ω0 | – | 3.0(6)× 10−6 | 4.5(4)× 10−6 | 1.2(8)× 10−5 |
| Time of asc. node (MJD) | – | 48 765.599 5019(5) | 49 150.608 9170(3) | 52 814.249 581(3) |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 113.1 | 111.5 | 139.5 | 227.7 |
| Gal. latitude, b (deg) | −57.6 | −68.1 | −17.5 | −18.2 |
| LK Px Distance, d (pc) | |$354_{-27}^{+31}$| | – | – | – |
| Composite PM, μ (mas yr−1) | 5.9(5) | 12.1(5) | 6.18(9) | 19.05(11) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.015(3) | 0.036 | 0.057 | 1.2 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.078(7) | −0.056 | −0.034 | −0.082 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.0030(3) | −0.000 86 | 0.013 | 0.011 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 1.084(6) | 0.518 | 7.7 | 0.0955 |
| Characteristic age, τc (Gyr) | 7.1 | 5.7 | 0.48 | 64.0 |
| Surface magnetic field, B (× 108 G) | 2.3 | 1.0 | 4.3 | 0.6 |
| Min. companion mass (M⊙) | – | 0.13 | 0.16 | 0.02 |
Timing model parameters for PSRs J0030+0451, J0034−0534, J0218+4232 and J0610−2100. Values in parentheses represent the 68.3 per cent confidence uncertainties in the last digit quoted and come from the one-dimensional marginalized posterior distribution of each parameter. The measured timing parameters are introduced in Section 3. The derived parameters show the Galactic longitude (l) and latitude (b), the parallax distance corrected from the LK bias (d), the composite proper motion (μ). The position, spin period and DM are given for the reference epoch of MJD 55000. The three kinematic contributions (|$\dot{P}_{{\rm shk}}$|, |$\dot{P}_{{\rm kz}}$| and |$\dot{P}_{{\rm dgr}}$|) to the intrinsic period derivative (|$\dot{P}_{{\rm int}}$|) are introduced in Section 5.3. For binary pulsars, the minimum companion mass, assuming a pulsar mass of 1.2 M⊙, is also indicated on the last line.
| PSR name . | J0030+0451 . | J0034−0534 . | J0218+4232 . | J0610−2100 . |
|---|---|---|---|---|
| MJD range | 51275–56779 | 51770–56705 | 50370–56786 | 54270–56791 |
| Number of TOAs | 907 | 276 | 1196 | 1034 |
| rms timing residual (μs) | 4.1 | 4.0 | 7.4 | 4.9 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 00:30:27.428 36(6) | 00:34:21.834 22(8) | 02:18:06.357 299(19) | 06:10:13.595 462(17) |
| Declination, δ | 04:51:39.707(3) | −05:34:36.722(3) | 42:32:17.3821(4) | −21:00:27.9313(4) |
| Proper motion in α (mas yr−1) | −5.9(5) | 7.9(3) | 5.31(7) | 9.0(1) |
| Proper motion in δ (mas yr−1) | −0.2(11) | −9.2(6) | −3.15(13) | 16.78(12) |
| Period, P (ms) | 4.865 453 286 352 01(19) | 1.877 181 885 831 71(10) | 2.323 090 531 512 24(8) | 3.861 324 766 195(3) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.0172(3) | 0.497 84(13) | 7.739 55(7) | 1.2298(19) |
| Parallax, π (mas) | 2.79(23) | – | – | – |
| DM (cm−3 pc) | 4.329(6) | 13.7658(19) | 61.2488(17) | 60.67(3) |
| DM1 (cm−3 pc yr−1) | 0.0007(5) | −0.0001(1) | −0.0003(2) | −0.014(8) |
| DM2 (cm−3 pc yr−2) | 0.0001(1) | −0.000 030(17) | 0.000 056(20) | 0.002(1) |
| Orbital period, Pb (d) | – | 1.589 281 825 32(14) | 2.028 846 115 61(9) | 0.286 016 0068(6) |
| Epoch of periastron, T0 (MJD) | – | 48 766.98(4) | 49 150.883(16) | 52 814.303(13) |
| Projected semimajor axis, x (lt-s) | – | 1.437 7662(5) | 1.984 4344(4) | 0.073 4891(4) |
| Longitude of periastron, ω0 (deg) | – | 313(9) | 49(3) | 67(16) |
| Orbital eccentricity, e | – | 4.3(7)× 10−6 | 6.8(4)× 10−6 | 2.9(8)× 10−5 |
| κ = e × sin ω0 | – | −3.1(7)× 10−6 | 5.1(4)× 10−6 | 2.7(8)× 10−5 |
| η = e × cos ω0 | – | 3.0(6)× 10−6 | 4.5(4)× 10−6 | 1.2(8)× 10−5 |
| Time of asc. node (MJD) | – | 48 765.599 5019(5) | 49 150.608 9170(3) | 52 814.249 581(3) |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 113.1 | 111.5 | 139.5 | 227.7 |
| Gal. latitude, b (deg) | −57.6 | −68.1 | −17.5 | −18.2 |
| LK Px Distance, d (pc) | |$354_{-27}^{+31}$| | – | – | – |
| Composite PM, μ (mas yr−1) | 5.9(5) | 12.1(5) | 6.18(9) | 19.05(11) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.015(3) | 0.036 | 0.057 | 1.2 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.078(7) | −0.056 | −0.034 | −0.082 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.0030(3) | −0.000 86 | 0.013 | 0.011 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 1.084(6) | 0.518 | 7.7 | 0.0955 |
| Characteristic age, τc (Gyr) | 7.1 | 5.7 | 0.48 | 64.0 |
| Surface magnetic field, B (× 108 G) | 2.3 | 1.0 | 4.3 | 0.6 |
| Min. companion mass (M⊙) | – | 0.13 | 0.16 | 0.02 |
| PSR name . | J0030+0451 . | J0034−0534 . | J0218+4232 . | J0610−2100 . |
|---|---|---|---|---|
| MJD range | 51275–56779 | 51770–56705 | 50370–56786 | 54270–56791 |
| Number of TOAs | 907 | 276 | 1196 | 1034 |
| rms timing residual (μs) | 4.1 | 4.0 | 7.4 | 4.9 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 00:30:27.428 36(6) | 00:34:21.834 22(8) | 02:18:06.357 299(19) | 06:10:13.595 462(17) |
| Declination, δ | 04:51:39.707(3) | −05:34:36.722(3) | 42:32:17.3821(4) | −21:00:27.9313(4) |
| Proper motion in α (mas yr−1) | −5.9(5) | 7.9(3) | 5.31(7) | 9.0(1) |
| Proper motion in δ (mas yr−1) | −0.2(11) | −9.2(6) | −3.15(13) | 16.78(12) |
| Period, P (ms) | 4.865 453 286 352 01(19) | 1.877 181 885 831 71(10) | 2.323 090 531 512 24(8) | 3.861 324 766 195(3) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.0172(3) | 0.497 84(13) | 7.739 55(7) | 1.2298(19) |
| Parallax, π (mas) | 2.79(23) | – | – | – |
| DM (cm−3 pc) | 4.329(6) | 13.7658(19) | 61.2488(17) | 60.67(3) |
| DM1 (cm−3 pc yr−1) | 0.0007(5) | −0.0001(1) | −0.0003(2) | −0.014(8) |
| DM2 (cm−3 pc yr−2) | 0.0001(1) | −0.000 030(17) | 0.000 056(20) | 0.002(1) |
| Orbital period, Pb (d) | – | 1.589 281 825 32(14) | 2.028 846 115 61(9) | 0.286 016 0068(6) |
| Epoch of periastron, T0 (MJD) | – | 48 766.98(4) | 49 150.883(16) | 52 814.303(13) |
| Projected semimajor axis, x (lt-s) | – | 1.437 7662(5) | 1.984 4344(4) | 0.073 4891(4) |
| Longitude of periastron, ω0 (deg) | – | 313(9) | 49(3) | 67(16) |
| Orbital eccentricity, e | – | 4.3(7)× 10−6 | 6.8(4)× 10−6 | 2.9(8)× 10−5 |
| κ = e × sin ω0 | – | −3.1(7)× 10−6 | 5.1(4)× 10−6 | 2.7(8)× 10−5 |
| η = e × cos ω0 | – | 3.0(6)× 10−6 | 4.5(4)× 10−6 | 1.2(8)× 10−5 |
| Time of asc. node (MJD) | – | 48 765.599 5019(5) | 49 150.608 9170(3) | 52 814.249 581(3) |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 113.1 | 111.5 | 139.5 | 227.7 |
| Gal. latitude, b (deg) | −57.6 | −68.1 | −17.5 | −18.2 |
| LK Px Distance, d (pc) | |$354_{-27}^{+31}$| | – | – | – |
| Composite PM, μ (mas yr−1) | 5.9(5) | 12.1(5) | 6.18(9) | 19.05(11) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.015(3) | 0.036 | 0.057 | 1.2 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.078(7) | −0.056 | −0.034 | −0.082 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.0030(3) | −0.000 86 | 0.013 | 0.011 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 1.084(6) | 0.518 | 7.7 | 0.0955 |
| Characteristic age, τc (Gyr) | 7.1 | 5.7 | 0.48 | 64.0 |
| Surface magnetic field, B (× 108 G) | 2.3 | 1.0 | 4.3 | 0.6 |
| Min. companion mass (M⊙) | – | 0.13 | 0.16 | 0.02 |
Timing model parameters for PSRs J0613−0200, J0621+1002, J0751+1807 and J0900−3144. See caption of Table 2 for a description of this table.
| PSR name . | J0613−0200 . | J0621+1002 . | J0751+1807 . | J0900−3144 . |
|---|---|---|---|---|
| MJD range | 50931–56795 | 52482–56780 | 50363–56793 | 54286–56793 |
| Number of TOAs | 1369 | 673 | 1491 | 875 |
| rms timing residual (μs) | 1.8 | 15.6 | 3.0 | 3.1 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 06:13:43.975 672(2) | 06:21:22.114 36(3) | 07:51:09.155 331(13) | 09:00:43.953 088(8) |
| Declination, δ | −02:00:47.225 33(7) | 10:02:38.7352(15) | 18:07:38.4864(10) | −31:44:30.895 20(13) |
| Proper motion in α (mas yr−1) | 1.822(8) | 3.23(12) | −2.73(5) | −1.01(5) |
| Proper motion in δ (mas yr−1) | −10.355(17) | −0.5(5) | −13.4(3) | 2.02(7) |
| Period, P (ms) | 3.061 844 088 094 608(15) | 28.853 861 194 0574(16) | 3.478 770 839 279 42(4) | 11.109 649 338 0938(6) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.959 013(14) | 4.730(5) | 0.778 74(5) | 4.8880(11) |
| Parallax, π (mas) | 1.25(13) | – | 0.82(17) | 0.77(44) |
| DM (cm−3pc) | 38.7746(14) | 36.47(3) | 30.246(6) | 75.707(8) |
| DM1 (cm−3pc yr−1) | 0.000 02(7) | −0.0094(3) | 0.0000(2) | 0.0009(7) |
| DM2 (cm−3pc yr−2) | −0.000 002(7) | 0.0011(2) | 0.000 04(4) | −0.0002(3) |
| Orbital period, Pb (d) | 1.198 512 575 184(13) | 8.318 6812(3) | 0.263 144 270 792(7) | 18.737 636 0594(9) |
| Epoch of periastron, T0 (MJD) | 53 113.953(4) | 49 746.866 75(19) | 51 800.283(7) | 52 682.295(5) |
| Projected semimajor axis, x (lt-s) | 1.091 444 09(6) | 12.032 0732(4) | 0.396 6158(3) | 17.248 81126(15) |
| Longitude of periastron, ω0 (deg) | 47.2(11) | 188.774(9) | 92(9) | 70.41(10) |
| Orbital eccentricity, e | 5.40(10)× 10−6 | 0.002 457 24(7) | 3.3(5)× 10−6 | 1.0490(17)× 10−5 |
| κ = e × sin ω0 | 3.96(10)× 10−6 | – | 3.3(5)× 10−6 | 9.883(17)× 10−6 |
| η = e × cos ω0 | 3.67(11)× 10−6 | – | 3.8(50)× 10−7 | 3.517(17)× 10−6 |
| Time of asc. node (MJD) | 53 113.796 354 200(16) | – | 51 800.215 868 26(4) | 52 678.630 288 19(13) |
| Orbital period derivative, |$\dot{P_{\rm b}}$| | 4.8(11)× 10−14 | – | −3.50(25)× 10−14 | – |
| First derivative of x, |$\dot{x}$| | – | – | −4.9(9)× 10−15 | – |
| Periastron advance, |$\dot{\omega }$| (deg yr−1) | – | 0.0113(6) | – | – |
| Third harmonic of Shapiro, h3 (μs) | – | – | 0.30(6) | – |
| Ratio of harmonics amplitude, ς | – | – | 0.81(17) | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 210.4 | 200.6 | 202.7 | 256.2 |
| Gal. latitude, b (deg) | −9.3 | −2.0 | 21.1 | 9.5 |
| LK Px Distance, d (pc) | |$777_{-70}^{+84}$| | – | |$999_{-146}^{+202}$| | |$815_{-211}^{+378}$| |
| Composite PM, μ (mas yr−1) | 10.514(17) | 3.27(14) | 13.7(3) | 2.26(7) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.064(7) | 0.1 | 0.16(3) | 0.011(5) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0039(4) | −0.0016 | −0.015(2) | −0.012(4) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.010(1) | 0.24 | 0.018(4) | −0.06(3) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.889(8) | 4.39 | 0.62(3) | 4.95(3) |
| Characteristic age, τc (Gyr) | 5.5 | 10.4 | 8.9 | 3.6 |
| Surface magnetic field, B (× 108 G) | 1.7 | 11.4 | 1.5 | 7.5 |
| Min. companion mass (M⊙) | 0.12 | 0.41 | 0.12 | 0.33 |
| PSR name . | J0613−0200 . | J0621+1002 . | J0751+1807 . | J0900−3144 . |
|---|---|---|---|---|
| MJD range | 50931–56795 | 52482–56780 | 50363–56793 | 54286–56793 |
| Number of TOAs | 1369 | 673 | 1491 | 875 |
| rms timing residual (μs) | 1.8 | 15.6 | 3.0 | 3.1 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 06:13:43.975 672(2) | 06:21:22.114 36(3) | 07:51:09.155 331(13) | 09:00:43.953 088(8) |
| Declination, δ | −02:00:47.225 33(7) | 10:02:38.7352(15) | 18:07:38.4864(10) | −31:44:30.895 20(13) |
| Proper motion in α (mas yr−1) | 1.822(8) | 3.23(12) | −2.73(5) | −1.01(5) |
| Proper motion in δ (mas yr−1) | −10.355(17) | −0.5(5) | −13.4(3) | 2.02(7) |
| Period, P (ms) | 3.061 844 088 094 608(15) | 28.853 861 194 0574(16) | 3.478 770 839 279 42(4) | 11.109 649 338 0938(6) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.959 013(14) | 4.730(5) | 0.778 74(5) | 4.8880(11) |
| Parallax, π (mas) | 1.25(13) | – | 0.82(17) | 0.77(44) |
| DM (cm−3pc) | 38.7746(14) | 36.47(3) | 30.246(6) | 75.707(8) |
| DM1 (cm−3pc yr−1) | 0.000 02(7) | −0.0094(3) | 0.0000(2) | 0.0009(7) |
| DM2 (cm−3pc yr−2) | −0.000 002(7) | 0.0011(2) | 0.000 04(4) | −0.0002(3) |
| Orbital period, Pb (d) | 1.198 512 575 184(13) | 8.318 6812(3) | 0.263 144 270 792(7) | 18.737 636 0594(9) |
| Epoch of periastron, T0 (MJD) | 53 113.953(4) | 49 746.866 75(19) | 51 800.283(7) | 52 682.295(5) |
| Projected semimajor axis, x (lt-s) | 1.091 444 09(6) | 12.032 0732(4) | 0.396 6158(3) | 17.248 81126(15) |
| Longitude of periastron, ω0 (deg) | 47.2(11) | 188.774(9) | 92(9) | 70.41(10) |
| Orbital eccentricity, e | 5.40(10)× 10−6 | 0.002 457 24(7) | 3.3(5)× 10−6 | 1.0490(17)× 10−5 |
| κ = e × sin ω0 | 3.96(10)× 10−6 | – | 3.3(5)× 10−6 | 9.883(17)× 10−6 |
| η = e × cos ω0 | 3.67(11)× 10−6 | – | 3.8(50)× 10−7 | 3.517(17)× 10−6 |
| Time of asc. node (MJD) | 53 113.796 354 200(16) | – | 51 800.215 868 26(4) | 52 678.630 288 19(13) |
| Orbital period derivative, |$\dot{P_{\rm b}}$| | 4.8(11)× 10−14 | – | −3.50(25)× 10−14 | – |
| First derivative of x, |$\dot{x}$| | – | – | −4.9(9)× 10−15 | – |
| Periastron advance, |$\dot{\omega }$| (deg yr−1) | – | 0.0113(6) | – | – |
| Third harmonic of Shapiro, h3 (μs) | – | – | 0.30(6) | – |
| Ratio of harmonics amplitude, ς | – | – | 0.81(17) | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 210.4 | 200.6 | 202.7 | 256.2 |
| Gal. latitude, b (deg) | −9.3 | −2.0 | 21.1 | 9.5 |
| LK Px Distance, d (pc) | |$777_{-70}^{+84}$| | – | |$999_{-146}^{+202}$| | |$815_{-211}^{+378}$| |
| Composite PM, μ (mas yr−1) | 10.514(17) | 3.27(14) | 13.7(3) | 2.26(7) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.064(7) | 0.1 | 0.16(3) | 0.011(5) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0039(4) | −0.0016 | −0.015(2) | −0.012(4) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.010(1) | 0.24 | 0.018(4) | −0.06(3) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.889(8) | 4.39 | 0.62(3) | 4.95(3) |
| Characteristic age, τc (Gyr) | 5.5 | 10.4 | 8.9 | 3.6 |
| Surface magnetic field, B (× 108 G) | 1.7 | 11.4 | 1.5 | 7.5 |
| Min. companion mass (M⊙) | 0.12 | 0.41 | 0.12 | 0.33 |
Timing model parameters for PSRs J0613−0200, J0621+1002, J0751+1807 and J0900−3144. See caption of Table 2 for a description of this table.
| PSR name . | J0613−0200 . | J0621+1002 . | J0751+1807 . | J0900−3144 . |
|---|---|---|---|---|
| MJD range | 50931–56795 | 52482–56780 | 50363–56793 | 54286–56793 |
| Number of TOAs | 1369 | 673 | 1491 | 875 |
| rms timing residual (μs) | 1.8 | 15.6 | 3.0 | 3.1 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 06:13:43.975 672(2) | 06:21:22.114 36(3) | 07:51:09.155 331(13) | 09:00:43.953 088(8) |
| Declination, δ | −02:00:47.225 33(7) | 10:02:38.7352(15) | 18:07:38.4864(10) | −31:44:30.895 20(13) |
| Proper motion in α (mas yr−1) | 1.822(8) | 3.23(12) | −2.73(5) | −1.01(5) |
| Proper motion in δ (mas yr−1) | −10.355(17) | −0.5(5) | −13.4(3) | 2.02(7) |
| Period, P (ms) | 3.061 844 088 094 608(15) | 28.853 861 194 0574(16) | 3.478 770 839 279 42(4) | 11.109 649 338 0938(6) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.959 013(14) | 4.730(5) | 0.778 74(5) | 4.8880(11) |
| Parallax, π (mas) | 1.25(13) | – | 0.82(17) | 0.77(44) |
| DM (cm−3pc) | 38.7746(14) | 36.47(3) | 30.246(6) | 75.707(8) |
| DM1 (cm−3pc yr−1) | 0.000 02(7) | −0.0094(3) | 0.0000(2) | 0.0009(7) |
| DM2 (cm−3pc yr−2) | −0.000 002(7) | 0.0011(2) | 0.000 04(4) | −0.0002(3) |
| Orbital period, Pb (d) | 1.198 512 575 184(13) | 8.318 6812(3) | 0.263 144 270 792(7) | 18.737 636 0594(9) |
| Epoch of periastron, T0 (MJD) | 53 113.953(4) | 49 746.866 75(19) | 51 800.283(7) | 52 682.295(5) |
| Projected semimajor axis, x (lt-s) | 1.091 444 09(6) | 12.032 0732(4) | 0.396 6158(3) | 17.248 81126(15) |
| Longitude of periastron, ω0 (deg) | 47.2(11) | 188.774(9) | 92(9) | 70.41(10) |
| Orbital eccentricity, e | 5.40(10)× 10−6 | 0.002 457 24(7) | 3.3(5)× 10−6 | 1.0490(17)× 10−5 |
| κ = e × sin ω0 | 3.96(10)× 10−6 | – | 3.3(5)× 10−6 | 9.883(17)× 10−6 |
| η = e × cos ω0 | 3.67(11)× 10−6 | – | 3.8(50)× 10−7 | 3.517(17)× 10−6 |
| Time of asc. node (MJD) | 53 113.796 354 200(16) | – | 51 800.215 868 26(4) | 52 678.630 288 19(13) |
| Orbital period derivative, |$\dot{P_{\rm b}}$| | 4.8(11)× 10−14 | – | −3.50(25)× 10−14 | – |
| First derivative of x, |$\dot{x}$| | – | – | −4.9(9)× 10−15 | – |
| Periastron advance, |$\dot{\omega }$| (deg yr−1) | – | 0.0113(6) | – | – |
| Third harmonic of Shapiro, h3 (μs) | – | – | 0.30(6) | – |
| Ratio of harmonics amplitude, ς | – | – | 0.81(17) | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 210.4 | 200.6 | 202.7 | 256.2 |
| Gal. latitude, b (deg) | −9.3 | −2.0 | 21.1 | 9.5 |
| LK Px Distance, d (pc) | |$777_{-70}^{+84}$| | – | |$999_{-146}^{+202}$| | |$815_{-211}^{+378}$| |
| Composite PM, μ (mas yr−1) | 10.514(17) | 3.27(14) | 13.7(3) | 2.26(7) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.064(7) | 0.1 | 0.16(3) | 0.011(5) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0039(4) | −0.0016 | −0.015(2) | −0.012(4) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.010(1) | 0.24 | 0.018(4) | −0.06(3) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.889(8) | 4.39 | 0.62(3) | 4.95(3) |
| Characteristic age, τc (Gyr) | 5.5 | 10.4 | 8.9 | 3.6 |
| Surface magnetic field, B (× 108 G) | 1.7 | 11.4 | 1.5 | 7.5 |
| Min. companion mass (M⊙) | 0.12 | 0.41 | 0.12 | 0.33 |
| PSR name . | J0613−0200 . | J0621+1002 . | J0751+1807 . | J0900−3144 . |
|---|---|---|---|---|
| MJD range | 50931–56795 | 52482–56780 | 50363–56793 | 54286–56793 |
| Number of TOAs | 1369 | 673 | 1491 | 875 |
| rms timing residual (μs) | 1.8 | 15.6 | 3.0 | 3.1 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 06:13:43.975 672(2) | 06:21:22.114 36(3) | 07:51:09.155 331(13) | 09:00:43.953 088(8) |
| Declination, δ | −02:00:47.225 33(7) | 10:02:38.7352(15) | 18:07:38.4864(10) | −31:44:30.895 20(13) |
| Proper motion in α (mas yr−1) | 1.822(8) | 3.23(12) | −2.73(5) | −1.01(5) |
| Proper motion in δ (mas yr−1) | −10.355(17) | −0.5(5) | −13.4(3) | 2.02(7) |
| Period, P (ms) | 3.061 844 088 094 608(15) | 28.853 861 194 0574(16) | 3.478 770 839 279 42(4) | 11.109 649 338 0938(6) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.959 013(14) | 4.730(5) | 0.778 74(5) | 4.8880(11) |
| Parallax, π (mas) | 1.25(13) | – | 0.82(17) | 0.77(44) |
| DM (cm−3pc) | 38.7746(14) | 36.47(3) | 30.246(6) | 75.707(8) |
| DM1 (cm−3pc yr−1) | 0.000 02(7) | −0.0094(3) | 0.0000(2) | 0.0009(7) |
| DM2 (cm−3pc yr−2) | −0.000 002(7) | 0.0011(2) | 0.000 04(4) | −0.0002(3) |
| Orbital period, Pb (d) | 1.198 512 575 184(13) | 8.318 6812(3) | 0.263 144 270 792(7) | 18.737 636 0594(9) |
| Epoch of periastron, T0 (MJD) | 53 113.953(4) | 49 746.866 75(19) | 51 800.283(7) | 52 682.295(5) |
| Projected semimajor axis, x (lt-s) | 1.091 444 09(6) | 12.032 0732(4) | 0.396 6158(3) | 17.248 81126(15) |
| Longitude of periastron, ω0 (deg) | 47.2(11) | 188.774(9) | 92(9) | 70.41(10) |
| Orbital eccentricity, e | 5.40(10)× 10−6 | 0.002 457 24(7) | 3.3(5)× 10−6 | 1.0490(17)× 10−5 |
| κ = e × sin ω0 | 3.96(10)× 10−6 | – | 3.3(5)× 10−6 | 9.883(17)× 10−6 |
| η = e × cos ω0 | 3.67(11)× 10−6 | – | 3.8(50)× 10−7 | 3.517(17)× 10−6 |
| Time of asc. node (MJD) | 53 113.796 354 200(16) | – | 51 800.215 868 26(4) | 52 678.630 288 19(13) |
| Orbital period derivative, |$\dot{P_{\rm b}}$| | 4.8(11)× 10−14 | – | −3.50(25)× 10−14 | – |
| First derivative of x, |$\dot{x}$| | – | – | −4.9(9)× 10−15 | – |
| Periastron advance, |$\dot{\omega }$| (deg yr−1) | – | 0.0113(6) | – | – |
| Third harmonic of Shapiro, h3 (μs) | – | – | 0.30(6) | – |
| Ratio of harmonics amplitude, ς | – | – | 0.81(17) | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 210.4 | 200.6 | 202.7 | 256.2 |
| Gal. latitude, b (deg) | −9.3 | −2.0 | 21.1 | 9.5 |
| LK Px Distance, d (pc) | |$777_{-70}^{+84}$| | – | |$999_{-146}^{+202}$| | |$815_{-211}^{+378}$| |
| Composite PM, μ (mas yr−1) | 10.514(17) | 3.27(14) | 13.7(3) | 2.26(7) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.064(7) | 0.1 | 0.16(3) | 0.011(5) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0039(4) | −0.0016 | −0.015(2) | −0.012(4) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.010(1) | 0.24 | 0.018(4) | −0.06(3) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.889(8) | 4.39 | 0.62(3) | 4.95(3) |
| Characteristic age, τc (Gyr) | 5.5 | 10.4 | 8.9 | 3.6 |
| Surface magnetic field, B (× 108 G) | 1.7 | 11.4 | 1.5 | 7.5 |
| Min. companion mass (M⊙) | 0.12 | 0.41 | 0.12 | 0.33 |
Timing model parameters for PSRs J1012+5307, J1022+1001, J1024−0719 and J1455−3330. See caption of Table 2 for a description of this table. † For the observer, we report here the values from the analysis in the ecliptic coordinate system, longitude λ = 153.865 866 885(16)°, latitude β = −0.063 930(14)°, proper motion in λ, μλ = −15.93(2) mas yr−1 and proper motion in β, μβ = −10(15) mas yr−1. ‡ The reason for the negative intrinsic period derivative |$\dot{P}_{{\rm int}}$| of PSR J1024−0719 is explained in Section 5.3.
| PSR name . | J1012+5307 . | J1022+1001 . | J1024−0719 . | J1455−3330 . |
|---|---|---|---|---|
| MJD range | 50647–56794 | 50361–56767 | 50460–56764 | 53375–56752 |
| Number of TOAs | 1459 | 908 | 561 | 524 |
| rms timing residual (μs) | 1.6 | 2.5 | 8.3 | 2.7 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 10:12:33.437 521(5) | 10:22:57.9992(15)† | 10:24:38.675 378(5) | 14:55:47.969 869(14) |
| Declination, δ | 53:07:02.299 99(6) | 10:01:52.78(6)† | −07:19:19.433 95(15) | −33:30:46.3801(4) |
| Proper motion in α (mas yr−1) | 2.609(8) | −18.2(64)† | −35.28(3) | 7.88(8) |
| Proper motion in δ (mas yr−1) | −25.482(11) | −3(16)† | −48.18(7) | −2.23(19) |
| Period, P (ms) | 5.255 7491 019 701 03(19) | 16.452 929 956 067 71(11) | 5.162 204 640 3157(3) | 7.987 204 929 333(3) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.712 730(17) | 4.3322(4) | 1.8553(4) | 2.428(4) |
| Parallax, π (mas) | 0.71(17) | 0.72(20) | 0.80(17) | 1.04(35) |
| DM (cm−3pc) | 9.0172(14) | 10.250(4) | 6.485(10) | 13.563(7) |
| DM1 (cm−3pc yr−1) | 0.000 16(2) | 0.0004(1) | 0.0025(8) | −0.002(4) |
| DM2 (cm−3pc yr−2) | 0.000 016(2) | 0.000 26(5) | −0.0007(2) | 0.001(1) |
| Orbital period, Pb (d) | 0.604 672 722 901(13) | 7.805 1348(11) | – | 76.174 568 631(9) |
| Epoch of periastron, T0 (MJD) | 50 700.229(13) | 50 246.7166(7) | – | 48 980.1330(10) |
| Projected semimajor axis, x (lt-s) | 0.581 817 03(12) | 16.765 4104(5) | – | 32.362 222(3) |
| Longitude of periastron, ω0 (deg) | 88(8) | 97.68(3) | – | 223.460(5) |
| Orbital eccentricity, e | 1.30(16)× 10−6 | 9.7229(14)× 10−5 | – | 1.69636(12)× 10−4 |
| κ = e × sin ω0 | 1.30(16)× 10−6 | – | – | – |
| η = e × cos ω0 | 5.1(173)× 10−8 | – | – | – |
| Time of asc. node (MJD) | 50 700.081 746 04(3) | – | – | – |
| Orbital period derivative, |$\dot{P_{\rm b}}$| | 6.1(4)× 10−14 | – | – | – |
| First derivative of x, |$\dot{x}$| | 2.0(4)× 10−15 | 1.79(12)× 10−14 | – | −1.7(4)× 10−14 |
| Periastron advance, |$\dot{\omega }$| (deg yr−1) | – | 0.0097(23) | – | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 160.3 | 242.4 | 251.7 | 330.7 |
| Gal. latitude, b (deg) | 50.9 | 43.7 | 40.5 | 22.6 |
| LK Px Distance, d (pc) | |$1148_{-175}^{+241}$| | |$1092_{-182}^{+258}$| | |$1083_{-163}^{+226}$| | |$797_{-179}^{+304}$| |
| Composite PM, μ (mas yr−1) | 25.615(11) | 19(9) | 59.72(6) | 8.19(9) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 1.0(2) | 1.6(1.4) | 4.8(10) | 0.10(4) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.077(7) | −0.24(2) | −0.057(5) | −0.035(7) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.016(3) | −0.010(2) | −0.021(4) | 0.03(1) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.8(2) | 3.0(1.4) | − 2.9(10)‡ | 2.33(4) |
| Characteristic age, τc (Gyr) | 10.3 | 8.7 | – | 5.4 |
| Surface magnetic field, B (× 108 G) | 2.1 | 7.1 | – | 4.4 |
| Min. companion mass (M⊙) | 0.10 | 0.66 | – | 0.23 |
| PSR name . | J1012+5307 . | J1022+1001 . | J1024−0719 . | J1455−3330 . |
|---|---|---|---|---|
| MJD range | 50647–56794 | 50361–56767 | 50460–56764 | 53375–56752 |
| Number of TOAs | 1459 | 908 | 561 | 524 |
| rms timing residual (μs) | 1.6 | 2.5 | 8.3 | 2.7 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 10:12:33.437 521(5) | 10:22:57.9992(15)† | 10:24:38.675 378(5) | 14:55:47.969 869(14) |
| Declination, δ | 53:07:02.299 99(6) | 10:01:52.78(6)† | −07:19:19.433 95(15) | −33:30:46.3801(4) |
| Proper motion in α (mas yr−1) | 2.609(8) | −18.2(64)† | −35.28(3) | 7.88(8) |
| Proper motion in δ (mas yr−1) | −25.482(11) | −3(16)† | −48.18(7) | −2.23(19) |
| Period, P (ms) | 5.255 7491 019 701 03(19) | 16.452 929 956 067 71(11) | 5.162 204 640 3157(3) | 7.987 204 929 333(3) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.712 730(17) | 4.3322(4) | 1.8553(4) | 2.428(4) |
| Parallax, π (mas) | 0.71(17) | 0.72(20) | 0.80(17) | 1.04(35) |
| DM (cm−3pc) | 9.0172(14) | 10.250(4) | 6.485(10) | 13.563(7) |
| DM1 (cm−3pc yr−1) | 0.000 16(2) | 0.0004(1) | 0.0025(8) | −0.002(4) |
| DM2 (cm−3pc yr−2) | 0.000 016(2) | 0.000 26(5) | −0.0007(2) | 0.001(1) |
| Orbital period, Pb (d) | 0.604 672 722 901(13) | 7.805 1348(11) | – | 76.174 568 631(9) |
| Epoch of periastron, T0 (MJD) | 50 700.229(13) | 50 246.7166(7) | – | 48 980.1330(10) |
| Projected semimajor axis, x (lt-s) | 0.581 817 03(12) | 16.765 4104(5) | – | 32.362 222(3) |
| Longitude of periastron, ω0 (deg) | 88(8) | 97.68(3) | – | 223.460(5) |
| Orbital eccentricity, e | 1.30(16)× 10−6 | 9.7229(14)× 10−5 | – | 1.69636(12)× 10−4 |
| κ = e × sin ω0 | 1.30(16)× 10−6 | – | – | – |
| η = e × cos ω0 | 5.1(173)× 10−8 | – | – | – |
| Time of asc. node (MJD) | 50 700.081 746 04(3) | – | – | – |
| Orbital period derivative, |$\dot{P_{\rm b}}$| | 6.1(4)× 10−14 | – | – | – |
| First derivative of x, |$\dot{x}$| | 2.0(4)× 10−15 | 1.79(12)× 10−14 | – | −1.7(4)× 10−14 |
| Periastron advance, |$\dot{\omega }$| (deg yr−1) | – | 0.0097(23) | – | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 160.3 | 242.4 | 251.7 | 330.7 |
| Gal. latitude, b (deg) | 50.9 | 43.7 | 40.5 | 22.6 |
| LK Px Distance, d (pc) | |$1148_{-175}^{+241}$| | |$1092_{-182}^{+258}$| | |$1083_{-163}^{+226}$| | |$797_{-179}^{+304}$| |
| Composite PM, μ (mas yr−1) | 25.615(11) | 19(9) | 59.72(6) | 8.19(9) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 1.0(2) | 1.6(1.4) | 4.8(10) | 0.10(4) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.077(7) | −0.24(2) | −0.057(5) | −0.035(7) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.016(3) | −0.010(2) | −0.021(4) | 0.03(1) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.8(2) | 3.0(1.4) | − 2.9(10)‡ | 2.33(4) |
| Characteristic age, τc (Gyr) | 10.3 | 8.7 | – | 5.4 |
| Surface magnetic field, B (× 108 G) | 2.1 | 7.1 | – | 4.4 |
| Min. companion mass (M⊙) | 0.10 | 0.66 | – | 0.23 |
Timing model parameters for PSRs J1012+5307, J1022+1001, J1024−0719 and J1455−3330. See caption of Table 2 for a description of this table. † For the observer, we report here the values from the analysis in the ecliptic coordinate system, longitude λ = 153.865 866 885(16)°, latitude β = −0.063 930(14)°, proper motion in λ, μλ = −15.93(2) mas yr−1 and proper motion in β, μβ = −10(15) mas yr−1. ‡ The reason for the negative intrinsic period derivative |$\dot{P}_{{\rm int}}$| of PSR J1024−0719 is explained in Section 5.3.
| PSR name . | J1012+5307 . | J1022+1001 . | J1024−0719 . | J1455−3330 . |
|---|---|---|---|---|
| MJD range | 50647–56794 | 50361–56767 | 50460–56764 | 53375–56752 |
| Number of TOAs | 1459 | 908 | 561 | 524 |
| rms timing residual (μs) | 1.6 | 2.5 | 8.3 | 2.7 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 10:12:33.437 521(5) | 10:22:57.9992(15)† | 10:24:38.675 378(5) | 14:55:47.969 869(14) |
| Declination, δ | 53:07:02.299 99(6) | 10:01:52.78(6)† | −07:19:19.433 95(15) | −33:30:46.3801(4) |
| Proper motion in α (mas yr−1) | 2.609(8) | −18.2(64)† | −35.28(3) | 7.88(8) |
| Proper motion in δ (mas yr−1) | −25.482(11) | −3(16)† | −48.18(7) | −2.23(19) |
| Period, P (ms) | 5.255 7491 019 701 03(19) | 16.452 929 956 067 71(11) | 5.162 204 640 3157(3) | 7.987 204 929 333(3) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.712 730(17) | 4.3322(4) | 1.8553(4) | 2.428(4) |
| Parallax, π (mas) | 0.71(17) | 0.72(20) | 0.80(17) | 1.04(35) |
| DM (cm−3pc) | 9.0172(14) | 10.250(4) | 6.485(10) | 13.563(7) |
| DM1 (cm−3pc yr−1) | 0.000 16(2) | 0.0004(1) | 0.0025(8) | −0.002(4) |
| DM2 (cm−3pc yr−2) | 0.000 016(2) | 0.000 26(5) | −0.0007(2) | 0.001(1) |
| Orbital period, Pb (d) | 0.604 672 722 901(13) | 7.805 1348(11) | – | 76.174 568 631(9) |
| Epoch of periastron, T0 (MJD) | 50 700.229(13) | 50 246.7166(7) | – | 48 980.1330(10) |
| Projected semimajor axis, x (lt-s) | 0.581 817 03(12) | 16.765 4104(5) | – | 32.362 222(3) |
| Longitude of periastron, ω0 (deg) | 88(8) | 97.68(3) | – | 223.460(5) |
| Orbital eccentricity, e | 1.30(16)× 10−6 | 9.7229(14)× 10−5 | – | 1.69636(12)× 10−4 |
| κ = e × sin ω0 | 1.30(16)× 10−6 | – | – | – |
| η = e × cos ω0 | 5.1(173)× 10−8 | – | – | – |
| Time of asc. node (MJD) | 50 700.081 746 04(3) | – | – | – |
| Orbital period derivative, |$\dot{P_{\rm b}}$| | 6.1(4)× 10−14 | – | – | – |
| First derivative of x, |$\dot{x}$| | 2.0(4)× 10−15 | 1.79(12)× 10−14 | – | −1.7(4)× 10−14 |
| Periastron advance, |$\dot{\omega }$| (deg yr−1) | – | 0.0097(23) | – | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 160.3 | 242.4 | 251.7 | 330.7 |
| Gal. latitude, b (deg) | 50.9 | 43.7 | 40.5 | 22.6 |
| LK Px Distance, d (pc) | |$1148_{-175}^{+241}$| | |$1092_{-182}^{+258}$| | |$1083_{-163}^{+226}$| | |$797_{-179}^{+304}$| |
| Composite PM, μ (mas yr−1) | 25.615(11) | 19(9) | 59.72(6) | 8.19(9) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 1.0(2) | 1.6(1.4) | 4.8(10) | 0.10(4) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.077(7) | −0.24(2) | −0.057(5) | −0.035(7) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.016(3) | −0.010(2) | −0.021(4) | 0.03(1) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.8(2) | 3.0(1.4) | − 2.9(10)‡ | 2.33(4) |
| Characteristic age, τc (Gyr) | 10.3 | 8.7 | – | 5.4 |
| Surface magnetic field, B (× 108 G) | 2.1 | 7.1 | – | 4.4 |
| Min. companion mass (M⊙) | 0.10 | 0.66 | – | 0.23 |
| PSR name . | J1012+5307 . | J1022+1001 . | J1024−0719 . | J1455−3330 . |
|---|---|---|---|---|
| MJD range | 50647–56794 | 50361–56767 | 50460–56764 | 53375–56752 |
| Number of TOAs | 1459 | 908 | 561 | 524 |
| rms timing residual (μs) | 1.6 | 2.5 | 8.3 | 2.7 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 10:12:33.437 521(5) | 10:22:57.9992(15)† | 10:24:38.675 378(5) | 14:55:47.969 869(14) |
| Declination, δ | 53:07:02.299 99(6) | 10:01:52.78(6)† | −07:19:19.433 95(15) | −33:30:46.3801(4) |
| Proper motion in α (mas yr−1) | 2.609(8) | −18.2(64)† | −35.28(3) | 7.88(8) |
| Proper motion in δ (mas yr−1) | −25.482(11) | −3(16)† | −48.18(7) | −2.23(19) |
| Period, P (ms) | 5.255 7491 019 701 03(19) | 16.452 929 956 067 71(11) | 5.162 204 640 3157(3) | 7.987 204 929 333(3) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.712 730(17) | 4.3322(4) | 1.8553(4) | 2.428(4) |
| Parallax, π (mas) | 0.71(17) | 0.72(20) | 0.80(17) | 1.04(35) |
| DM (cm−3pc) | 9.0172(14) | 10.250(4) | 6.485(10) | 13.563(7) |
| DM1 (cm−3pc yr−1) | 0.000 16(2) | 0.0004(1) | 0.0025(8) | −0.002(4) |
| DM2 (cm−3pc yr−2) | 0.000 016(2) | 0.000 26(5) | −0.0007(2) | 0.001(1) |
| Orbital period, Pb (d) | 0.604 672 722 901(13) | 7.805 1348(11) | – | 76.174 568 631(9) |
| Epoch of periastron, T0 (MJD) | 50 700.229(13) | 50 246.7166(7) | – | 48 980.1330(10) |
| Projected semimajor axis, x (lt-s) | 0.581 817 03(12) | 16.765 4104(5) | – | 32.362 222(3) |
| Longitude of periastron, ω0 (deg) | 88(8) | 97.68(3) | – | 223.460(5) |
| Orbital eccentricity, e | 1.30(16)× 10−6 | 9.7229(14)× 10−5 | – | 1.69636(12)× 10−4 |
| κ = e × sin ω0 | 1.30(16)× 10−6 | – | – | – |
| η = e × cos ω0 | 5.1(173)× 10−8 | – | – | – |
| Time of asc. node (MJD) | 50 700.081 746 04(3) | – | – | – |
| Orbital period derivative, |$\dot{P_{\rm b}}$| | 6.1(4)× 10−14 | – | – | – |
| First derivative of x, |$\dot{x}$| | 2.0(4)× 10−15 | 1.79(12)× 10−14 | – | −1.7(4)× 10−14 |
| Periastron advance, |$\dot{\omega }$| (deg yr−1) | – | 0.0097(23) | – | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 160.3 | 242.4 | 251.7 | 330.7 |
| Gal. latitude, b (deg) | 50.9 | 43.7 | 40.5 | 22.6 |
| LK Px Distance, d (pc) | |$1148_{-175}^{+241}$| | |$1092_{-182}^{+258}$| | |$1083_{-163}^{+226}$| | |$797_{-179}^{+304}$| |
| Composite PM, μ (mas yr−1) | 25.615(11) | 19(9) | 59.72(6) | 8.19(9) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 1.0(2) | 1.6(1.4) | 4.8(10) | 0.10(4) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.077(7) | −0.24(2) | −0.057(5) | −0.035(7) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.016(3) | −0.010(2) | −0.021(4) | 0.03(1) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.8(2) | 3.0(1.4) | − 2.9(10)‡ | 2.33(4) |
| Characteristic age, τc (Gyr) | 10.3 | 8.7 | – | 5.4 |
| Surface magnetic field, B (× 108 G) | 2.1 | 7.1 | – | 4.4 |
| Min. companion mass (M⊙) | 0.10 | 0.66 | – | 0.23 |
Timing model parameters for PSRs J1600−3053, J1640+2224, J1643−1224 and J1713+0747. See caption of Table 2 for a description of this table.
| PSR name . | J1600−3053 . | J1640+2224 . | J1643−1224 . | J1713+0747 . |
|---|---|---|---|---|
| MJD range | 53998–56795 | 50459–56761 | 50459–56778 | 50360–56810 |
| Number of TOAs | 531 | 595 | 759 | 1188 |
| rms timing residual (μs) | 0.46 | 1.8 | 1.7 | 0.68 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 16:00:51.903 338(4) | 16:40:16.744 834(7) | 16:43:38.161 498(8) | 17:13:49.533 1754(5) |
| Declination, δ | −30:53:49.375 42(18) | 22:24:08.841 21(13) | −12:24:58.6735(6) | 07:47:37.492 536(16) |
| Proper motion in α (mas yr−1) | −0.940(19) | 2.087(20) | 6.04(4) | 4.923(3) |
| Proper motion in δ (mas yr−1) | −6.94(7) | −11.29(4) | 4.07(15) | −3.909(5) |
| Period, P (ms) | 3.597 928 510 064 93(3) | 3.163 315 867 760 34(5) | 4.621 641 525 733 80(10) | 4.570 136 598 154 477(12) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.950 14(6) | 0.281 61(11) | 1.8461(3) | 0.852 919(13) |
| Parallax, π (mas) | 0.64(7) | – | 1.17(26) | 0.90(3) |
| DM (cm−3pc) | 52.3245(16) | 18.422(10) | 62.411(5) | 15.9930(3) |
| DM1 (cm−3pc yr−1) | −0.0003(1) | −0.0000(2) | −0.0013(3) | 0.000 06(3) |
| DM2 (cm−3pc yr−2) | 0.000 012(47) | 0.000 06(8) | 0.0000(1) | 0.000 006(5) |
| Orbital period, Pb (d) | 14.348 457 772 90(15) | 175.460 664 603(11) | 147.017 397 756(17) | 67.825 130 9745(14) |
| Epoch of periastron, T0 (MJD) | 52 506.3739(4) | 51 626.1804(3) | 49 283.9337(5) | 48 741.9737(3) |
| Projected semimajor axis, x (lt-s) | 8.801 6546(5) | 55.329 7223(5) | 25.072 6144(7) | 32.342 419 56(15) |
| Longitude of periastron, ω0 (deg) | 181.835(9) | 50.7343(5) | 321.8488(10) | 176.1989(15) |
| Orbital eccentricity, e | 1.737 23(8)× 10−4 | 7.972 99(8)× 10−4 | 5.057 46(9)× 10−4 | 7.494 21(7)× 10−5 |
| First derivative of x, |$\dot{x}$| | −2.8(5)× 10−15 | 1.07(16)× 10−14 | −4.79(15)× 10−14 | – |
| Inclination angle, i (deg) | |$68.6_{-3.8}^{+3.4}$| | – | – | 71.8(6) |
| Longitude of ascending node, Ω (deg) | – | – | – | 89.9(17) |
| Companion mass, mc (M⊙) | |$0.208_{-0.043}^{+0.059}$| | – | – | 0.290(12) |
| Third harmonic of Shapiro, h3 (μs) | 0.33(2) | – | – | – |
| Ratio of harmonics amplitude, ς | 0.68(5) | – | – | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 344.1 | 41.1 | 5.7 | 28.8 |
| Gal. latitude, b (deg) | 16.5 | 38.3 | 21.2 | 25.2 |
| LK Px Distance, d (pc) | |$1492_{-150}^{+187}$| | – | |$758_{-127}^{+185}$| | |$1108_{-33}^{+35}$| |
| Composite PM, μ (mas yr−1) | 7.00(7) | 11.49(4) | 7.28(9) | 6.286(4) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.064(8) | 0.12 | 0.05(1) | 0.049(2) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0137(9) | −0.033 | −0.018(3) | −0.0277(4) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.043(7) | 0.0013 | 0.029(8) | 0.020(2) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.86(1) | 0.196 | 1.79(2) | 0.812(2) |
| Characteristic age, τc (Gyr) | 6.7 | 25.6 | 4.1 | 8.9 |
| Surface magnetic field, B (× 108 G) | 1.8 | 0.8 | 2.9 | 1.9 |
| Min. companion mass (M⊙) | 0.19 | 0.23 | 0.11 | 0.26 |
| PSR name . | J1600−3053 . | J1640+2224 . | J1643−1224 . | J1713+0747 . |
|---|---|---|---|---|
| MJD range | 53998–56795 | 50459–56761 | 50459–56778 | 50360–56810 |
| Number of TOAs | 531 | 595 | 759 | 1188 |
| rms timing residual (μs) | 0.46 | 1.8 | 1.7 | 0.68 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 16:00:51.903 338(4) | 16:40:16.744 834(7) | 16:43:38.161 498(8) | 17:13:49.533 1754(5) |
| Declination, δ | −30:53:49.375 42(18) | 22:24:08.841 21(13) | −12:24:58.6735(6) | 07:47:37.492 536(16) |
| Proper motion in α (mas yr−1) | −0.940(19) | 2.087(20) | 6.04(4) | 4.923(3) |
| Proper motion in δ (mas yr−1) | −6.94(7) | −11.29(4) | 4.07(15) | −3.909(5) |
| Period, P (ms) | 3.597 928 510 064 93(3) | 3.163 315 867 760 34(5) | 4.621 641 525 733 80(10) | 4.570 136 598 154 477(12) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.950 14(6) | 0.281 61(11) | 1.8461(3) | 0.852 919(13) |
| Parallax, π (mas) | 0.64(7) | – | 1.17(26) | 0.90(3) |
| DM (cm−3pc) | 52.3245(16) | 18.422(10) | 62.411(5) | 15.9930(3) |
| DM1 (cm−3pc yr−1) | −0.0003(1) | −0.0000(2) | −0.0013(3) | 0.000 06(3) |
| DM2 (cm−3pc yr−2) | 0.000 012(47) | 0.000 06(8) | 0.0000(1) | 0.000 006(5) |
| Orbital period, Pb (d) | 14.348 457 772 90(15) | 175.460 664 603(11) | 147.017 397 756(17) | 67.825 130 9745(14) |
| Epoch of periastron, T0 (MJD) | 52 506.3739(4) | 51 626.1804(3) | 49 283.9337(5) | 48 741.9737(3) |
| Projected semimajor axis, x (lt-s) | 8.801 6546(5) | 55.329 7223(5) | 25.072 6144(7) | 32.342 419 56(15) |
| Longitude of periastron, ω0 (deg) | 181.835(9) | 50.7343(5) | 321.8488(10) | 176.1989(15) |
| Orbital eccentricity, e | 1.737 23(8)× 10−4 | 7.972 99(8)× 10−4 | 5.057 46(9)× 10−4 | 7.494 21(7)× 10−5 |
| First derivative of x, |$\dot{x}$| | −2.8(5)× 10−15 | 1.07(16)× 10−14 | −4.79(15)× 10−14 | – |
| Inclination angle, i (deg) | |$68.6_{-3.8}^{+3.4}$| | – | – | 71.8(6) |
| Longitude of ascending node, Ω (deg) | – | – | – | 89.9(17) |
| Companion mass, mc (M⊙) | |$0.208_{-0.043}^{+0.059}$| | – | – | 0.290(12) |
| Third harmonic of Shapiro, h3 (μs) | 0.33(2) | – | – | – |
| Ratio of harmonics amplitude, ς | 0.68(5) | – | – | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 344.1 | 41.1 | 5.7 | 28.8 |
| Gal. latitude, b (deg) | 16.5 | 38.3 | 21.2 | 25.2 |
| LK Px Distance, d (pc) | |$1492_{-150}^{+187}$| | – | |$758_{-127}^{+185}$| | |$1108_{-33}^{+35}$| |
| Composite PM, μ (mas yr−1) | 7.00(7) | 11.49(4) | 7.28(9) | 6.286(4) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.064(8) | 0.12 | 0.05(1) | 0.049(2) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0137(9) | −0.033 | −0.018(3) | −0.0277(4) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.043(7) | 0.0013 | 0.029(8) | 0.020(2) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.86(1) | 0.196 | 1.79(2) | 0.812(2) |
| Characteristic age, τc (Gyr) | 6.7 | 25.6 | 4.1 | 8.9 |
| Surface magnetic field, B (× 108 G) | 1.8 | 0.8 | 2.9 | 1.9 |
| Min. companion mass (M⊙) | 0.19 | 0.23 | 0.11 | 0.26 |
Timing model parameters for PSRs J1600−3053, J1640+2224, J1643−1224 and J1713+0747. See caption of Table 2 for a description of this table.
| PSR name . | J1600−3053 . | J1640+2224 . | J1643−1224 . | J1713+0747 . |
|---|---|---|---|---|
| MJD range | 53998–56795 | 50459–56761 | 50459–56778 | 50360–56810 |
| Number of TOAs | 531 | 595 | 759 | 1188 |
| rms timing residual (μs) | 0.46 | 1.8 | 1.7 | 0.68 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 16:00:51.903 338(4) | 16:40:16.744 834(7) | 16:43:38.161 498(8) | 17:13:49.533 1754(5) |
| Declination, δ | −30:53:49.375 42(18) | 22:24:08.841 21(13) | −12:24:58.6735(6) | 07:47:37.492 536(16) |
| Proper motion in α (mas yr−1) | −0.940(19) | 2.087(20) | 6.04(4) | 4.923(3) |
| Proper motion in δ (mas yr−1) | −6.94(7) | −11.29(4) | 4.07(15) | −3.909(5) |
| Period, P (ms) | 3.597 928 510 064 93(3) | 3.163 315 867 760 34(5) | 4.621 641 525 733 80(10) | 4.570 136 598 154 477(12) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.950 14(6) | 0.281 61(11) | 1.8461(3) | 0.852 919(13) |
| Parallax, π (mas) | 0.64(7) | – | 1.17(26) | 0.90(3) |
| DM (cm−3pc) | 52.3245(16) | 18.422(10) | 62.411(5) | 15.9930(3) |
| DM1 (cm−3pc yr−1) | −0.0003(1) | −0.0000(2) | −0.0013(3) | 0.000 06(3) |
| DM2 (cm−3pc yr−2) | 0.000 012(47) | 0.000 06(8) | 0.0000(1) | 0.000 006(5) |
| Orbital period, Pb (d) | 14.348 457 772 90(15) | 175.460 664 603(11) | 147.017 397 756(17) | 67.825 130 9745(14) |
| Epoch of periastron, T0 (MJD) | 52 506.3739(4) | 51 626.1804(3) | 49 283.9337(5) | 48 741.9737(3) |
| Projected semimajor axis, x (lt-s) | 8.801 6546(5) | 55.329 7223(5) | 25.072 6144(7) | 32.342 419 56(15) |
| Longitude of periastron, ω0 (deg) | 181.835(9) | 50.7343(5) | 321.8488(10) | 176.1989(15) |
| Orbital eccentricity, e | 1.737 23(8)× 10−4 | 7.972 99(8)× 10−4 | 5.057 46(9)× 10−4 | 7.494 21(7)× 10−5 |
| First derivative of x, |$\dot{x}$| | −2.8(5)× 10−15 | 1.07(16)× 10−14 | −4.79(15)× 10−14 | – |
| Inclination angle, i (deg) | |$68.6_{-3.8}^{+3.4}$| | – | – | 71.8(6) |
| Longitude of ascending node, Ω (deg) | – | – | – | 89.9(17) |
| Companion mass, mc (M⊙) | |$0.208_{-0.043}^{+0.059}$| | – | – | 0.290(12) |
| Third harmonic of Shapiro, h3 (μs) | 0.33(2) | – | – | – |
| Ratio of harmonics amplitude, ς | 0.68(5) | – | – | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 344.1 | 41.1 | 5.7 | 28.8 |
| Gal. latitude, b (deg) | 16.5 | 38.3 | 21.2 | 25.2 |
| LK Px Distance, d (pc) | |$1492_{-150}^{+187}$| | – | |$758_{-127}^{+185}$| | |$1108_{-33}^{+35}$| |
| Composite PM, μ (mas yr−1) | 7.00(7) | 11.49(4) | 7.28(9) | 6.286(4) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.064(8) | 0.12 | 0.05(1) | 0.049(2) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0137(9) | −0.033 | −0.018(3) | −0.0277(4) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.043(7) | 0.0013 | 0.029(8) | 0.020(2) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.86(1) | 0.196 | 1.79(2) | 0.812(2) |
| Characteristic age, τc (Gyr) | 6.7 | 25.6 | 4.1 | 8.9 |
| Surface magnetic field, B (× 108 G) | 1.8 | 0.8 | 2.9 | 1.9 |
| Min. companion mass (M⊙) | 0.19 | 0.23 | 0.11 | 0.26 |
| PSR name . | J1600−3053 . | J1640+2224 . | J1643−1224 . | J1713+0747 . |
|---|---|---|---|---|
| MJD range | 53998–56795 | 50459–56761 | 50459–56778 | 50360–56810 |
| Number of TOAs | 531 | 595 | 759 | 1188 |
| rms timing residual (μs) | 0.46 | 1.8 | 1.7 | 0.68 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 16:00:51.903 338(4) | 16:40:16.744 834(7) | 16:43:38.161 498(8) | 17:13:49.533 1754(5) |
| Declination, δ | −30:53:49.375 42(18) | 22:24:08.841 21(13) | −12:24:58.6735(6) | 07:47:37.492 536(16) |
| Proper motion in α (mas yr−1) | −0.940(19) | 2.087(20) | 6.04(4) | 4.923(3) |
| Proper motion in δ (mas yr−1) | −6.94(7) | −11.29(4) | 4.07(15) | −3.909(5) |
| Period, P (ms) | 3.597 928 510 064 93(3) | 3.163 315 867 760 34(5) | 4.621 641 525 733 80(10) | 4.570 136 598 154 477(12) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.950 14(6) | 0.281 61(11) | 1.8461(3) | 0.852 919(13) |
| Parallax, π (mas) | 0.64(7) | – | 1.17(26) | 0.90(3) |
| DM (cm−3pc) | 52.3245(16) | 18.422(10) | 62.411(5) | 15.9930(3) |
| DM1 (cm−3pc yr−1) | −0.0003(1) | −0.0000(2) | −0.0013(3) | 0.000 06(3) |
| DM2 (cm−3pc yr−2) | 0.000 012(47) | 0.000 06(8) | 0.0000(1) | 0.000 006(5) |
| Orbital period, Pb (d) | 14.348 457 772 90(15) | 175.460 664 603(11) | 147.017 397 756(17) | 67.825 130 9745(14) |
| Epoch of periastron, T0 (MJD) | 52 506.3739(4) | 51 626.1804(3) | 49 283.9337(5) | 48 741.9737(3) |
| Projected semimajor axis, x (lt-s) | 8.801 6546(5) | 55.329 7223(5) | 25.072 6144(7) | 32.342 419 56(15) |
| Longitude of periastron, ω0 (deg) | 181.835(9) | 50.7343(5) | 321.8488(10) | 176.1989(15) |
| Orbital eccentricity, e | 1.737 23(8)× 10−4 | 7.972 99(8)× 10−4 | 5.057 46(9)× 10−4 | 7.494 21(7)× 10−5 |
| First derivative of x, |$\dot{x}$| | −2.8(5)× 10−15 | 1.07(16)× 10−14 | −4.79(15)× 10−14 | – |
| Inclination angle, i (deg) | |$68.6_{-3.8}^{+3.4}$| | – | – | 71.8(6) |
| Longitude of ascending node, Ω (deg) | – | – | – | 89.9(17) |
| Companion mass, mc (M⊙) | |$0.208_{-0.043}^{+0.059}$| | – | – | 0.290(12) |
| Third harmonic of Shapiro, h3 (μs) | 0.33(2) | – | – | – |
| Ratio of harmonics amplitude, ς | 0.68(5) | – | – | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 344.1 | 41.1 | 5.7 | 28.8 |
| Gal. latitude, b (deg) | 16.5 | 38.3 | 21.2 | 25.2 |
| LK Px Distance, d (pc) | |$1492_{-150}^{+187}$| | – | |$758_{-127}^{+185}$| | |$1108_{-33}^{+35}$| |
| Composite PM, μ (mas yr−1) | 7.00(7) | 11.49(4) | 7.28(9) | 6.286(4) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.064(8) | 0.12 | 0.05(1) | 0.049(2) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0137(9) | −0.033 | −0.018(3) | −0.0277(4) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.043(7) | 0.0013 | 0.029(8) | 0.020(2) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.86(1) | 0.196 | 1.79(2) | 0.812(2) |
| Characteristic age, τc (Gyr) | 6.7 | 25.6 | 4.1 | 8.9 |
| Surface magnetic field, B (× 108 G) | 1.8 | 0.8 | 2.9 | 1.9 |
| Min. companion mass (M⊙) | 0.19 | 0.23 | 0.11 | 0.26 |
Timing model parameters for PSRs J1721−2457, J1730−2304, J1738+0333 and J1744−1134. See caption of Table 2 for a description of this table.
| PSR name . | J1721−2457 . | J1730−2304 . | J1738+0333 . | J1744−1134 . |
|---|---|---|---|---|
| MJD range | 52076–56737 | 50734–56830 | 54103–56780 | 50460–56761 |
| Number of TOAs | 150 | 268 | 318 | 536 |
| rms timing residual (μs) | 11.7 | 1.6 | 3.0 | 0.86 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 17:21:05.4979(3) | 17:30:21.668 35(13) | 17:38:53.966 375(11) | 17:44:29.407 5373(14) |
| Declination, δ | −24:57:06.17(5) | −23:04:31.16(4) | 03:33:10.8720(4) | −11:34:54.694 37(11) |
| Proper motion in α (mas yr−1) | 1.9(12) | 20.7(7) | 7.08(6) | 18.810(6) |
| Proper motion in δ (mas yr−1) | −25(16) | 9(12) | 4.97(19) | −9.36(3) |
| Period, P (ms) | 3.496 633 783 466(6) | 8.122 798 046 9486(7) | 5.850 095 860 612(5) | 4.074 545 941 825 154(15) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.556(7) | 2.0196(11) | 2.410(4) | 0.893 47(4) |
| Parallax, π (mas) | – | 0.86(32) | – | 2.38(8) |
| DM (cm−3pc) | 48.33(15) | 9.622(9) | 33.798(18) | 3.1312(17) |
| DM1 (cm−3pc yr−1) | −0.00(2) | 0.001(1) | −0.01(1) | −0.01(1) |
| DM2 (cm−3pc yr−2) | −0.002(4) | −0.0004(3) | 0.000(2) | 0.000(2) |
| Orbital period, Pb (d) | – | – | 0.354 790 739 90(3) | – |
| Epoch of periastron, T0 (MJD) | – | – | 52 500.25(3) | – |
| Projected semimajor axis, x (lt-s) | – | – | 0.343 4304(4) | – |
| Longitude of periastron, ω0 (deg) | – | – | 52(27) | – |
| Orbital eccentricity, e | – | – | 3.6(18)× 10−6 | – |
| κ = e × sin ω0 | – | – | 2.9(20)× 10−6 | – |
| η = e × cos ω0 | – | – | 2.2(16)× 10−6 | – |
| Time of asc. node (MJD) | – | – | 52 500.194 0106(3) | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 0.4 | 3.1 | 27.7 | 14.8 |
| Gal. latitude, b (deg) | 6.8 | 6.0 | 17.7 | 9.2 |
| LK Px Distance, d (pc) | – | |$904_{-216}^{+382}$| | – | |$419_{-13}^{+14}$| |
| Composite PM, μ (mas yr−1) | 26(16) | 23(5) | 8.65(12) | 21.009(15) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.7(9) | 0.9(5) | 0.15 | 0.183(6) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.002 98(5) | −0.004(1) | −0.024 | −0.002 48(6) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.047(4) | 0.07(3) | 0.039 | 0.013(1) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.0(7) | 1.0(6) | 2.24 | 0.699(7) |
| Characteristic age, τc (Gyr) | >7.9 | 12.3 | 4.1 | 9.2 |
| Surface magnetic field, B (× 108 G) | <1.6 | 2.9 | 3.7 | 1.7 |
| Min. companion mass (M⊙) | – | – | 0.08 | – |
| PSR name . | J1721−2457 . | J1730−2304 . | J1738+0333 . | J1744−1134 . |
|---|---|---|---|---|
| MJD range | 52076–56737 | 50734–56830 | 54103–56780 | 50460–56761 |
| Number of TOAs | 150 | 268 | 318 | 536 |
| rms timing residual (μs) | 11.7 | 1.6 | 3.0 | 0.86 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 17:21:05.4979(3) | 17:30:21.668 35(13) | 17:38:53.966 375(11) | 17:44:29.407 5373(14) |
| Declination, δ | −24:57:06.17(5) | −23:04:31.16(4) | 03:33:10.8720(4) | −11:34:54.694 37(11) |
| Proper motion in α (mas yr−1) | 1.9(12) | 20.7(7) | 7.08(6) | 18.810(6) |
| Proper motion in δ (mas yr−1) | −25(16) | 9(12) | 4.97(19) | −9.36(3) |
| Period, P (ms) | 3.496 633 783 466(6) | 8.122 798 046 9486(7) | 5.850 095 860 612(5) | 4.074 545 941 825 154(15) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.556(7) | 2.0196(11) | 2.410(4) | 0.893 47(4) |
| Parallax, π (mas) | – | 0.86(32) | – | 2.38(8) |
| DM (cm−3pc) | 48.33(15) | 9.622(9) | 33.798(18) | 3.1312(17) |
| DM1 (cm−3pc yr−1) | −0.00(2) | 0.001(1) | −0.01(1) | −0.01(1) |
| DM2 (cm−3pc yr−2) | −0.002(4) | −0.0004(3) | 0.000(2) | 0.000(2) |
| Orbital period, Pb (d) | – | – | 0.354 790 739 90(3) | – |
| Epoch of periastron, T0 (MJD) | – | – | 52 500.25(3) | – |
| Projected semimajor axis, x (lt-s) | – | – | 0.343 4304(4) | – |
| Longitude of periastron, ω0 (deg) | – | – | 52(27) | – |
| Orbital eccentricity, e | – | – | 3.6(18)× 10−6 | – |
| κ = e × sin ω0 | – | – | 2.9(20)× 10−6 | – |
| η = e × cos ω0 | – | – | 2.2(16)× 10−6 | – |
| Time of asc. node (MJD) | – | – | 52 500.194 0106(3) | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 0.4 | 3.1 | 27.7 | 14.8 |
| Gal. latitude, b (deg) | 6.8 | 6.0 | 17.7 | 9.2 |
| LK Px Distance, d (pc) | – | |$904_{-216}^{+382}$| | – | |$419_{-13}^{+14}$| |
| Composite PM, μ (mas yr−1) | 26(16) | 23(5) | 8.65(12) | 21.009(15) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.7(9) | 0.9(5) | 0.15 | 0.183(6) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.002 98(5) | −0.004(1) | −0.024 | −0.002 48(6) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.047(4) | 0.07(3) | 0.039 | 0.013(1) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.0(7) | 1.0(6) | 2.24 | 0.699(7) |
| Characteristic age, τc (Gyr) | >7.9 | 12.3 | 4.1 | 9.2 |
| Surface magnetic field, B (× 108 G) | <1.6 | 2.9 | 3.7 | 1.7 |
| Min. companion mass (M⊙) | – | – | 0.08 | – |
Timing model parameters for PSRs J1721−2457, J1730−2304, J1738+0333 and J1744−1134. See caption of Table 2 for a description of this table.
| PSR name . | J1721−2457 . | J1730−2304 . | J1738+0333 . | J1744−1134 . |
|---|---|---|---|---|
| MJD range | 52076–56737 | 50734–56830 | 54103–56780 | 50460–56761 |
| Number of TOAs | 150 | 268 | 318 | 536 |
| rms timing residual (μs) | 11.7 | 1.6 | 3.0 | 0.86 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 17:21:05.4979(3) | 17:30:21.668 35(13) | 17:38:53.966 375(11) | 17:44:29.407 5373(14) |
| Declination, δ | −24:57:06.17(5) | −23:04:31.16(4) | 03:33:10.8720(4) | −11:34:54.694 37(11) |
| Proper motion in α (mas yr−1) | 1.9(12) | 20.7(7) | 7.08(6) | 18.810(6) |
| Proper motion in δ (mas yr−1) | −25(16) | 9(12) | 4.97(19) | −9.36(3) |
| Period, P (ms) | 3.496 633 783 466(6) | 8.122 798 046 9486(7) | 5.850 095 860 612(5) | 4.074 545 941 825 154(15) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.556(7) | 2.0196(11) | 2.410(4) | 0.893 47(4) |
| Parallax, π (mas) | – | 0.86(32) | – | 2.38(8) |
| DM (cm−3pc) | 48.33(15) | 9.622(9) | 33.798(18) | 3.1312(17) |
| DM1 (cm−3pc yr−1) | −0.00(2) | 0.001(1) | −0.01(1) | −0.01(1) |
| DM2 (cm−3pc yr−2) | −0.002(4) | −0.0004(3) | 0.000(2) | 0.000(2) |
| Orbital period, Pb (d) | – | – | 0.354 790 739 90(3) | – |
| Epoch of periastron, T0 (MJD) | – | – | 52 500.25(3) | – |
| Projected semimajor axis, x (lt-s) | – | – | 0.343 4304(4) | – |
| Longitude of periastron, ω0 (deg) | – | – | 52(27) | – |
| Orbital eccentricity, e | – | – | 3.6(18)× 10−6 | – |
| κ = e × sin ω0 | – | – | 2.9(20)× 10−6 | – |
| η = e × cos ω0 | – | – | 2.2(16)× 10−6 | – |
| Time of asc. node (MJD) | – | – | 52 500.194 0106(3) | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 0.4 | 3.1 | 27.7 | 14.8 |
| Gal. latitude, b (deg) | 6.8 | 6.0 | 17.7 | 9.2 |
| LK Px Distance, d (pc) | – | |$904_{-216}^{+382}$| | – | |$419_{-13}^{+14}$| |
| Composite PM, μ (mas yr−1) | 26(16) | 23(5) | 8.65(12) | 21.009(15) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.7(9) | 0.9(5) | 0.15 | 0.183(6) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.002 98(5) | −0.004(1) | −0.024 | −0.002 48(6) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.047(4) | 0.07(3) | 0.039 | 0.013(1) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.0(7) | 1.0(6) | 2.24 | 0.699(7) |
| Characteristic age, τc (Gyr) | >7.9 | 12.3 | 4.1 | 9.2 |
| Surface magnetic field, B (× 108 G) | <1.6 | 2.9 | 3.7 | 1.7 |
| Min. companion mass (M⊙) | – | – | 0.08 | – |
| PSR name . | J1721−2457 . | J1730−2304 . | J1738+0333 . | J1744−1134 . |
|---|---|---|---|---|
| MJD range | 52076–56737 | 50734–56830 | 54103–56780 | 50460–56761 |
| Number of TOAs | 150 | 268 | 318 | 536 |
| rms timing residual (μs) | 11.7 | 1.6 | 3.0 | 0.86 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 17:21:05.4979(3) | 17:30:21.668 35(13) | 17:38:53.966 375(11) | 17:44:29.407 5373(14) |
| Declination, δ | −24:57:06.17(5) | −23:04:31.16(4) | 03:33:10.8720(4) | −11:34:54.694 37(11) |
| Proper motion in α (mas yr−1) | 1.9(12) | 20.7(7) | 7.08(6) | 18.810(6) |
| Proper motion in δ (mas yr−1) | −25(16) | 9(12) | 4.97(19) | −9.36(3) |
| Period, P (ms) | 3.496 633 783 466(6) | 8.122 798 046 9486(7) | 5.850 095 860 612(5) | 4.074 545 941 825 154(15) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.556(7) | 2.0196(11) | 2.410(4) | 0.893 47(4) |
| Parallax, π (mas) | – | 0.86(32) | – | 2.38(8) |
| DM (cm−3pc) | 48.33(15) | 9.622(9) | 33.798(18) | 3.1312(17) |
| DM1 (cm−3pc yr−1) | −0.00(2) | 0.001(1) | −0.01(1) | −0.01(1) |
| DM2 (cm−3pc yr−2) | −0.002(4) | −0.0004(3) | 0.000(2) | 0.000(2) |
| Orbital period, Pb (d) | – | – | 0.354 790 739 90(3) | – |
| Epoch of periastron, T0 (MJD) | – | – | 52 500.25(3) | – |
| Projected semimajor axis, x (lt-s) | – | – | 0.343 4304(4) | – |
| Longitude of periastron, ω0 (deg) | – | – | 52(27) | – |
| Orbital eccentricity, e | – | – | 3.6(18)× 10−6 | – |
| κ = e × sin ω0 | – | – | 2.9(20)× 10−6 | – |
| η = e × cos ω0 | – | – | 2.2(16)× 10−6 | – |
| Time of asc. node (MJD) | – | – | 52 500.194 0106(3) | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 0.4 | 3.1 | 27.7 | 14.8 |
| Gal. latitude, b (deg) | 6.8 | 6.0 | 17.7 | 9.2 |
| LK Px Distance, d (pc) | – | |$904_{-216}^{+382}$| | – | |$419_{-13}^{+14}$| |
| Composite PM, μ (mas yr−1) | 26(16) | 23(5) | 8.65(12) | 21.009(15) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.7(9) | 0.9(5) | 0.15 | 0.183(6) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.002 98(5) | −0.004(1) | −0.024 | −0.002 48(6) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.047(4) | 0.07(3) | 0.039 | 0.013(1) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.0(7) | 1.0(6) | 2.24 | 0.699(7) |
| Characteristic age, τc (Gyr) | >7.9 | 12.3 | 4.1 | 9.2 |
| Surface magnetic field, B (× 108 G) | <1.6 | 2.9 | 3.7 | 1.7 |
| Min. companion mass (M⊙) | – | – | 0.08 | – |
Timing model parameters for PSRs J1751−2857, J1801−1417, J1802−2124 and J1804−2717. See caption of Table 2 for a description of this table.
| PSR name . | J1751−2857 . | J1801−1417 . | J1802−2124 . | J1804−2717 . |
|---|---|---|---|---|
| MJD range | 53746–56782 | 54206–56782 | 54188–56831 | 53766–56827 |
| Number of TOAs | 144 | 126 | 522 | 116 |
| rms timing residual (μs) | 3.0 | 2.6 | 2.7 | 3.1 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 17:51:32.693 197(17) | 18:01:51.073 331(19) | 18:02:05.335 22(2) | 18:04:21.133 087(19) |
| Declination, δ | −28:57:46.520(3) | −14:17:34.526(2) | −21:24:03.653(8) | −27:17:31.335(4) |
| Proper motion in α (mas yr−1) | −7.4(1) | −10.89(12) | −1.13(12) | 2.56(15) |
| Proper motion in δ (mas yr−1) | −4.3(12) | −3.0(10) | −3(4) | −17(3) |
| Period, P (ms) | 3.914 873 259 435(3) | 3.625 096 717 1671(17) | 12.647 593 792 3794(16) | 9.343 030 844 543(4) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.121(3) | 0.530(3) | 7.291(3) | 4.085(5) |
| Parallax, π (mas) | – | – | 1.24(57) | – |
| DM (cm−3pc) | 42.84(3) | 57.26(4) | 149.614(9) | 24.74(4) |
| DM1 (cm−3pc yr−1) | −0.01(1) | 0.004(7) | −0.002(2) | −0.005(6) |
| DM2 (cm−3pc yr−2) | 0.001(2) | 0.000(2) | 0.0005(6) | 0.000(1) |
| Orbital period, Pb (d) | 110.746 460 80(4) | – | 0.698 889 254 216(9) | 11.1287 119 67(3) |
| Epoch of periastron, T0 (MJD) | 52 491.574(4) | – | 52 595.851(14) | 49 615.080(9) |
| Projected semimajor axis, x (lt-s) | 32.528 2215(20) | – | 3.718 853(3) | 7.281 4525(7) |
| Longitude of periastron, ω0 (deg) | 45.508(11) | – | 29(7) | 158.7(3) |
| Orbital eccentricity, e | 1.2795(3)× 10−4 | – | 2.9(3)× 10−6 | 3.406(16)× 10−5 |
| κ = e × sin ω0 | – | – | 1.4(4)× 10−6 | – |
| η = e × cos ω0 | – | – | 2.59(17)× 10−6 | – |
| Time of asc. node (MJD) | – | – | 52 595.795 225 02(4) | – |
| First derivative of x, |$\dot{x}$| | 4.6(8)× 10−14 | – | -3(5)× 10−15 | – |
| Sine of inclination angle, sin i | – | – | 0.971(13) | – |
| Companion mass, mc (M⊙) | – | – | 0.83(19) | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 0.6 | 14.5 | 8.4 | 3.5 |
| Gal. latitude, b (deg) | −1.1 | 4.2 | 0.6 | −2.7 |
| LK Px Distance, d (pc) | – | – | |$640_{-195}^{+436}$| | – |
| Composite PM, μ (mas yr−1) | 8.5(6) | 11.3(3) | 3(4) | 17(3) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.077 | 0.17 | 0.02(5) | 0.53 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0002 | −0.0012 | −0.000 083(4) | −0.0014 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.045 | 0.05 | 0.07(6) | 0.071 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.999 | 0.31 | 7.19(8) | 3.49 |
| Characteristic age, τc (Gyr) | 6.2 | 18.5 | 2.8 | 4.2 |
| Surface magnetic field, B (× 108 G) | 2. | 1.1 | 9.7 | 5.8 |
| Min. companion mass (M⊙) | 0.18 | – | 0.76 | 0.19 |
| PSR name . | J1751−2857 . | J1801−1417 . | J1802−2124 . | J1804−2717 . |
|---|---|---|---|---|
| MJD range | 53746–56782 | 54206–56782 | 54188–56831 | 53766–56827 |
| Number of TOAs | 144 | 126 | 522 | 116 |
| rms timing residual (μs) | 3.0 | 2.6 | 2.7 | 3.1 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 17:51:32.693 197(17) | 18:01:51.073 331(19) | 18:02:05.335 22(2) | 18:04:21.133 087(19) |
| Declination, δ | −28:57:46.520(3) | −14:17:34.526(2) | −21:24:03.653(8) | −27:17:31.335(4) |
| Proper motion in α (mas yr−1) | −7.4(1) | −10.89(12) | −1.13(12) | 2.56(15) |
| Proper motion in δ (mas yr−1) | −4.3(12) | −3.0(10) | −3(4) | −17(3) |
| Period, P (ms) | 3.914 873 259 435(3) | 3.625 096 717 1671(17) | 12.647 593 792 3794(16) | 9.343 030 844 543(4) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.121(3) | 0.530(3) | 7.291(3) | 4.085(5) |
| Parallax, π (mas) | – | – | 1.24(57) | – |
| DM (cm−3pc) | 42.84(3) | 57.26(4) | 149.614(9) | 24.74(4) |
| DM1 (cm−3pc yr−1) | −0.01(1) | 0.004(7) | −0.002(2) | −0.005(6) |
| DM2 (cm−3pc yr−2) | 0.001(2) | 0.000(2) | 0.0005(6) | 0.000(1) |
| Orbital period, Pb (d) | 110.746 460 80(4) | – | 0.698 889 254 216(9) | 11.1287 119 67(3) |
| Epoch of periastron, T0 (MJD) | 52 491.574(4) | – | 52 595.851(14) | 49 615.080(9) |
| Projected semimajor axis, x (lt-s) | 32.528 2215(20) | – | 3.718 853(3) | 7.281 4525(7) |
| Longitude of periastron, ω0 (deg) | 45.508(11) | – | 29(7) | 158.7(3) |
| Orbital eccentricity, e | 1.2795(3)× 10−4 | – | 2.9(3)× 10−6 | 3.406(16)× 10−5 |
| κ = e × sin ω0 | – | – | 1.4(4)× 10−6 | – |
| η = e × cos ω0 | – | – | 2.59(17)× 10−6 | – |
| Time of asc. node (MJD) | – | – | 52 595.795 225 02(4) | – |
| First derivative of x, |$\dot{x}$| | 4.6(8)× 10−14 | – | -3(5)× 10−15 | – |
| Sine of inclination angle, sin i | – | – | 0.971(13) | – |
| Companion mass, mc (M⊙) | – | – | 0.83(19) | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 0.6 | 14.5 | 8.4 | 3.5 |
| Gal. latitude, b (deg) | −1.1 | 4.2 | 0.6 | −2.7 |
| LK Px Distance, d (pc) | – | – | |$640_{-195}^{+436}$| | – |
| Composite PM, μ (mas yr−1) | 8.5(6) | 11.3(3) | 3(4) | 17(3) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.077 | 0.17 | 0.02(5) | 0.53 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0002 | −0.0012 | −0.000 083(4) | −0.0014 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.045 | 0.05 | 0.07(6) | 0.071 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.999 | 0.31 | 7.19(8) | 3.49 |
| Characteristic age, τc (Gyr) | 6.2 | 18.5 | 2.8 | 4.2 |
| Surface magnetic field, B (× 108 G) | 2. | 1.1 | 9.7 | 5.8 |
| Min. companion mass (M⊙) | 0.18 | – | 0.76 | 0.19 |
Timing model parameters for PSRs J1751−2857, J1801−1417, J1802−2124 and J1804−2717. See caption of Table 2 for a description of this table.
| PSR name . | J1751−2857 . | J1801−1417 . | J1802−2124 . | J1804−2717 . |
|---|---|---|---|---|
| MJD range | 53746–56782 | 54206–56782 | 54188–56831 | 53766–56827 |
| Number of TOAs | 144 | 126 | 522 | 116 |
| rms timing residual (μs) | 3.0 | 2.6 | 2.7 | 3.1 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 17:51:32.693 197(17) | 18:01:51.073 331(19) | 18:02:05.335 22(2) | 18:04:21.133 087(19) |
| Declination, δ | −28:57:46.520(3) | −14:17:34.526(2) | −21:24:03.653(8) | −27:17:31.335(4) |
| Proper motion in α (mas yr−1) | −7.4(1) | −10.89(12) | −1.13(12) | 2.56(15) |
| Proper motion in δ (mas yr−1) | −4.3(12) | −3.0(10) | −3(4) | −17(3) |
| Period, P (ms) | 3.914 873 259 435(3) | 3.625 096 717 1671(17) | 12.647 593 792 3794(16) | 9.343 030 844 543(4) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.121(3) | 0.530(3) | 7.291(3) | 4.085(5) |
| Parallax, π (mas) | – | – | 1.24(57) | – |
| DM (cm−3pc) | 42.84(3) | 57.26(4) | 149.614(9) | 24.74(4) |
| DM1 (cm−3pc yr−1) | −0.01(1) | 0.004(7) | −0.002(2) | −0.005(6) |
| DM2 (cm−3pc yr−2) | 0.001(2) | 0.000(2) | 0.0005(6) | 0.000(1) |
| Orbital period, Pb (d) | 110.746 460 80(4) | – | 0.698 889 254 216(9) | 11.1287 119 67(3) |
| Epoch of periastron, T0 (MJD) | 52 491.574(4) | – | 52 595.851(14) | 49 615.080(9) |
| Projected semimajor axis, x (lt-s) | 32.528 2215(20) | – | 3.718 853(3) | 7.281 4525(7) |
| Longitude of periastron, ω0 (deg) | 45.508(11) | – | 29(7) | 158.7(3) |
| Orbital eccentricity, e | 1.2795(3)× 10−4 | – | 2.9(3)× 10−6 | 3.406(16)× 10−5 |
| κ = e × sin ω0 | – | – | 1.4(4)× 10−6 | – |
| η = e × cos ω0 | – | – | 2.59(17)× 10−6 | – |
| Time of asc. node (MJD) | – | – | 52 595.795 225 02(4) | – |
| First derivative of x, |$\dot{x}$| | 4.6(8)× 10−14 | – | -3(5)× 10−15 | – |
| Sine of inclination angle, sin i | – | – | 0.971(13) | – |
| Companion mass, mc (M⊙) | – | – | 0.83(19) | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 0.6 | 14.5 | 8.4 | 3.5 |
| Gal. latitude, b (deg) | −1.1 | 4.2 | 0.6 | −2.7 |
| LK Px Distance, d (pc) | – | – | |$640_{-195}^{+436}$| | – |
| Composite PM, μ (mas yr−1) | 8.5(6) | 11.3(3) | 3(4) | 17(3) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.077 | 0.17 | 0.02(5) | 0.53 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0002 | −0.0012 | −0.000 083(4) | −0.0014 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.045 | 0.05 | 0.07(6) | 0.071 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.999 | 0.31 | 7.19(8) | 3.49 |
| Characteristic age, τc (Gyr) | 6.2 | 18.5 | 2.8 | 4.2 |
| Surface magnetic field, B (× 108 G) | 2. | 1.1 | 9.7 | 5.8 |
| Min. companion mass (M⊙) | 0.18 | – | 0.76 | 0.19 |
| PSR name . | J1751−2857 . | J1801−1417 . | J1802−2124 . | J1804−2717 . |
|---|---|---|---|---|
| MJD range | 53746–56782 | 54206–56782 | 54188–56831 | 53766–56827 |
| Number of TOAs | 144 | 126 | 522 | 116 |
| rms timing residual (μs) | 3.0 | 2.6 | 2.7 | 3.1 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 17:51:32.693 197(17) | 18:01:51.073 331(19) | 18:02:05.335 22(2) | 18:04:21.133 087(19) |
| Declination, δ | −28:57:46.520(3) | −14:17:34.526(2) | −21:24:03.653(8) | −27:17:31.335(4) |
| Proper motion in α (mas yr−1) | −7.4(1) | −10.89(12) | −1.13(12) | 2.56(15) |
| Proper motion in δ (mas yr−1) | −4.3(12) | −3.0(10) | −3(4) | −17(3) |
| Period, P (ms) | 3.914 873 259 435(3) | 3.625 096 717 1671(17) | 12.647 593 792 3794(16) | 9.343 030 844 543(4) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.121(3) | 0.530(3) | 7.291(3) | 4.085(5) |
| Parallax, π (mas) | – | – | 1.24(57) | – |
| DM (cm−3pc) | 42.84(3) | 57.26(4) | 149.614(9) | 24.74(4) |
| DM1 (cm−3pc yr−1) | −0.01(1) | 0.004(7) | −0.002(2) | −0.005(6) |
| DM2 (cm−3pc yr−2) | 0.001(2) | 0.000(2) | 0.0005(6) | 0.000(1) |
| Orbital period, Pb (d) | 110.746 460 80(4) | – | 0.698 889 254 216(9) | 11.1287 119 67(3) |
| Epoch of periastron, T0 (MJD) | 52 491.574(4) | – | 52 595.851(14) | 49 615.080(9) |
| Projected semimajor axis, x (lt-s) | 32.528 2215(20) | – | 3.718 853(3) | 7.281 4525(7) |
| Longitude of periastron, ω0 (deg) | 45.508(11) | – | 29(7) | 158.7(3) |
| Orbital eccentricity, e | 1.2795(3)× 10−4 | – | 2.9(3)× 10−6 | 3.406(16)× 10−5 |
| κ = e × sin ω0 | – | – | 1.4(4)× 10−6 | – |
| η = e × cos ω0 | – | – | 2.59(17)× 10−6 | – |
| Time of asc. node (MJD) | – | – | 52 595.795 225 02(4) | – |
| First derivative of x, |$\dot{x}$| | 4.6(8)× 10−14 | – | -3(5)× 10−15 | – |
| Sine of inclination angle, sin i | – | – | 0.971(13) | – |
| Companion mass, mc (M⊙) | – | – | 0.83(19) | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 0.6 | 14.5 | 8.4 | 3.5 |
| Gal. latitude, b (deg) | −1.1 | 4.2 | 0.6 | −2.7 |
| LK Px Distance, d (pc) | – | – | |$640_{-195}^{+436}$| | – |
| Composite PM, μ (mas yr−1) | 8.5(6) | 11.3(3) | 3(4) | 17(3) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.077 | 0.17 | 0.02(5) | 0.53 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0002 | −0.0012 | −0.000 083(4) | −0.0014 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.045 | 0.05 | 0.07(6) | 0.071 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.999 | 0.31 | 7.19(8) | 3.49 |
| Characteristic age, τc (Gyr) | 6.2 | 18.5 | 2.8 | 4.2 |
| Surface magnetic field, B (× 108 G) | 2. | 1.1 | 9.7 | 5.8 |
| Min. companion mass (M⊙) | 0.18 | – | 0.76 | 0.19 |
Timing model parameters for PSRs J1843−1113, J1853+1303, J1857+0943 and J1909−3744. See caption of Table 2 for a description of this table.
| PSR name . | J1843−1113 . | J1853+1303 . | J1857+0943 . | J1909−3744 . |
|---|---|---|---|---|
| MJD range | 53156–56829 | 53763–56829 | 50458–56781 | 53368–56794 |
| Number of TOAs | 224 | 101 | 444 | 425 |
| rms timing residual (μs) | 0.71 | 1.6 | 1.7 | 0.13 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 18:43:41.261 917(12) | 18:53:57.318 765(12) | 18:57:36.390 605(4) | 19:09:47.433 5737(7) |
| Declination, δ | −11:13:31.0686(7) | 13:03:44.0693(4) | 09:43:17.207 14(10) | −37:44:14.515 61(3) |
| Proper motion in α (mas yr−1) | −1.91(7) | −1.61(9) | −2.649(17) | −9.519(3) |
| Proper motion in δ (mas yr−1) | −3.2(3) | −2.79(17) | −5.41(3) | −35.775(10) |
| Period, P (ms) | 1.845 666 323 2093(6) | 4.091 797 445 6530(10) | 5.362 100 548 700 34(9) | 2.947 108 069 766 629(7) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.9554(7) | 0.8724(14) | 1.784 47(17) | 1.402 518(14) |
| Parallax, π (mas) | 0.69(33) | – | 0.70(26) | 0.87(2) |
| DM (cm−3pc) | 59.964(8) | 30.576(20) | 13.303(4) | 10.3925(4) |
| DM1 (cm−3pc yr−1) | 0.002(4) | 0.002(4) | 0.0017(2) | −0.000 32(3) |
| DM2 (cm−3pc yr−2) | 0.0005(9) | −0.0005(8) | −0.000 18(8) | 0.000 04(1) |
| Orbital period, Pb (d) | – | 115.653 788 24(3) | 12.327 171 3831(3) | 1.533 449 474 329(13) |
| Epoch of periastron, T0 (MJD) | – | 52 890.256(18) | 46 432.781(3) | 53 114.72(4) |
| Projected semimajor axis, x (lt-s) | – | 40.769 5169(14) | 9.230 7819(9) | 1.897 990 99(6) |
| Longitude of periastron, ω0 (deg) | – | 346.65(6) | 276.47(7) | 180(9) |
| Orbital eccentricity, e | – | 2.368(3)× 10−5 | 2.170(4)× 10−5 | 1.22(11)× 10−7 |
| κ = e × sin ω0 | – | – | – | −2.3(1900)× 10−10 |
| η = e × cos ω0 | – | – | – | −1.22(11)× 10−7 |
| Time of asc. node (MJD) | – | – | – | 53 113.950 741 990(10) |
| Orbital period derivative, |$\dot{P_{\rm b}}$| | – | – | – | 5.03(5)× 10−13 |
| First derivative of x, |$\dot{x}$| | – | 2.4(7)× 10−14 | −2.7(11)× 10−15 | 0.6(17) × 10−16 |
| Sine of inclination angle, sin i | – | – | 0.9987(6) | 0.997 71(13) |
| Companion mass, mc (M⊙) | – | – | 0.27(3) | 0.213(3) |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 22.1 | 44.9 | 42.3 | 359.7 |
| Gal. latitude, b (deg) | −3.4 | 5.4 | 3.1 | −19.6 |
| LK Px Distance, d (pc) | |$1092_{-318}^{666}$| | – | |$1098_{-254}^{+439}$| | |$1146_{-28}^{+30}$| |
| Composite PM, μ (mas yr−1) | 3.8(3) | 3.22(15) | 6.03(3) | 37.020(10) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.007(4) | 0.0091 | 0.05(2) | 1.12(3) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0004(3) | −0.0016 | −0.0010(3) | −0.0242(6) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.014(9) | −0.0028 | −0.0002(30) | 0.031(3) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.94(1) | 0.868 | 1.73(2) | 0.27(3) |
| Characteristic age, τc (Gyr) | 3.1 | 7.5 | 4.9 | 17.4 |
| Surface magnetic field, B (× 108 G) | 1.3 | 1.9 | 3.1 | 0.9 |
| Min. companion mass (M⊙) | – | 0.22 | 0.22 | 0.18 |
| PSR name . | J1843−1113 . | J1853+1303 . | J1857+0943 . | J1909−3744 . |
|---|---|---|---|---|
| MJD range | 53156–56829 | 53763–56829 | 50458–56781 | 53368–56794 |
| Number of TOAs | 224 | 101 | 444 | 425 |
| rms timing residual (μs) | 0.71 | 1.6 | 1.7 | 0.13 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 18:43:41.261 917(12) | 18:53:57.318 765(12) | 18:57:36.390 605(4) | 19:09:47.433 5737(7) |
| Declination, δ | −11:13:31.0686(7) | 13:03:44.0693(4) | 09:43:17.207 14(10) | −37:44:14.515 61(3) |
| Proper motion in α (mas yr−1) | −1.91(7) | −1.61(9) | −2.649(17) | −9.519(3) |
| Proper motion in δ (mas yr−1) | −3.2(3) | −2.79(17) | −5.41(3) | −35.775(10) |
| Period, P (ms) | 1.845 666 323 2093(6) | 4.091 797 445 6530(10) | 5.362 100 548 700 34(9) | 2.947 108 069 766 629(7) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.9554(7) | 0.8724(14) | 1.784 47(17) | 1.402 518(14) |
| Parallax, π (mas) | 0.69(33) | – | 0.70(26) | 0.87(2) |
| DM (cm−3pc) | 59.964(8) | 30.576(20) | 13.303(4) | 10.3925(4) |
| DM1 (cm−3pc yr−1) | 0.002(4) | 0.002(4) | 0.0017(2) | −0.000 32(3) |
| DM2 (cm−3pc yr−2) | 0.0005(9) | −0.0005(8) | −0.000 18(8) | 0.000 04(1) |
| Orbital period, Pb (d) | – | 115.653 788 24(3) | 12.327 171 3831(3) | 1.533 449 474 329(13) |
| Epoch of periastron, T0 (MJD) | – | 52 890.256(18) | 46 432.781(3) | 53 114.72(4) |
| Projected semimajor axis, x (lt-s) | – | 40.769 5169(14) | 9.230 7819(9) | 1.897 990 99(6) |
| Longitude of periastron, ω0 (deg) | – | 346.65(6) | 276.47(7) | 180(9) |
| Orbital eccentricity, e | – | 2.368(3)× 10−5 | 2.170(4)× 10−5 | 1.22(11)× 10−7 |
| κ = e × sin ω0 | – | – | – | −2.3(1900)× 10−10 |
| η = e × cos ω0 | – | – | – | −1.22(11)× 10−7 |
| Time of asc. node (MJD) | – | – | – | 53 113.950 741 990(10) |
| Orbital period derivative, |$\dot{P_{\rm b}}$| | – | – | – | 5.03(5)× 10−13 |
| First derivative of x, |$\dot{x}$| | – | 2.4(7)× 10−14 | −2.7(11)× 10−15 | 0.6(17) × 10−16 |
| Sine of inclination angle, sin i | – | – | 0.9987(6) | 0.997 71(13) |
| Companion mass, mc (M⊙) | – | – | 0.27(3) | 0.213(3) |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 22.1 | 44.9 | 42.3 | 359.7 |
| Gal. latitude, b (deg) | −3.4 | 5.4 | 3.1 | −19.6 |
| LK Px Distance, d (pc) | |$1092_{-318}^{666}$| | – | |$1098_{-254}^{+439}$| | |$1146_{-28}^{+30}$| |
| Composite PM, μ (mas yr−1) | 3.8(3) | 3.22(15) | 6.03(3) | 37.020(10) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.007(4) | 0.0091 | 0.05(2) | 1.12(3) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0004(3) | −0.0016 | −0.0010(3) | −0.0242(6) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.014(9) | −0.0028 | −0.0002(30) | 0.031(3) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.94(1) | 0.868 | 1.73(2) | 0.27(3) |
| Characteristic age, τc (Gyr) | 3.1 | 7.5 | 4.9 | 17.4 |
| Surface magnetic field, B (× 108 G) | 1.3 | 1.9 | 3.1 | 0.9 |
| Min. companion mass (M⊙) | – | 0.22 | 0.22 | 0.18 |
Timing model parameters for PSRs J1843−1113, J1853+1303, J1857+0943 and J1909−3744. See caption of Table 2 for a description of this table.
| PSR name . | J1843−1113 . | J1853+1303 . | J1857+0943 . | J1909−3744 . |
|---|---|---|---|---|
| MJD range | 53156–56829 | 53763–56829 | 50458–56781 | 53368–56794 |
| Number of TOAs | 224 | 101 | 444 | 425 |
| rms timing residual (μs) | 0.71 | 1.6 | 1.7 | 0.13 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 18:43:41.261 917(12) | 18:53:57.318 765(12) | 18:57:36.390 605(4) | 19:09:47.433 5737(7) |
| Declination, δ | −11:13:31.0686(7) | 13:03:44.0693(4) | 09:43:17.207 14(10) | −37:44:14.515 61(3) |
| Proper motion in α (mas yr−1) | −1.91(7) | −1.61(9) | −2.649(17) | −9.519(3) |
| Proper motion in δ (mas yr−1) | −3.2(3) | −2.79(17) | −5.41(3) | −35.775(10) |
| Period, P (ms) | 1.845 666 323 2093(6) | 4.091 797 445 6530(10) | 5.362 100 548 700 34(9) | 2.947 108 069 766 629(7) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.9554(7) | 0.8724(14) | 1.784 47(17) | 1.402 518(14) |
| Parallax, π (mas) | 0.69(33) | – | 0.70(26) | 0.87(2) |
| DM (cm−3pc) | 59.964(8) | 30.576(20) | 13.303(4) | 10.3925(4) |
| DM1 (cm−3pc yr−1) | 0.002(4) | 0.002(4) | 0.0017(2) | −0.000 32(3) |
| DM2 (cm−3pc yr−2) | 0.0005(9) | −0.0005(8) | −0.000 18(8) | 0.000 04(1) |
| Orbital period, Pb (d) | – | 115.653 788 24(3) | 12.327 171 3831(3) | 1.533 449 474 329(13) |
| Epoch of periastron, T0 (MJD) | – | 52 890.256(18) | 46 432.781(3) | 53 114.72(4) |
| Projected semimajor axis, x (lt-s) | – | 40.769 5169(14) | 9.230 7819(9) | 1.897 990 99(6) |
| Longitude of periastron, ω0 (deg) | – | 346.65(6) | 276.47(7) | 180(9) |
| Orbital eccentricity, e | – | 2.368(3)× 10−5 | 2.170(4)× 10−5 | 1.22(11)× 10−7 |
| κ = e × sin ω0 | – | – | – | −2.3(1900)× 10−10 |
| η = e × cos ω0 | – | – | – | −1.22(11)× 10−7 |
| Time of asc. node (MJD) | – | – | – | 53 113.950 741 990(10) |
| Orbital period derivative, |$\dot{P_{\rm b}}$| | – | – | – | 5.03(5)× 10−13 |
| First derivative of x, |$\dot{x}$| | – | 2.4(7)× 10−14 | −2.7(11)× 10−15 | 0.6(17) × 10−16 |
| Sine of inclination angle, sin i | – | – | 0.9987(6) | 0.997 71(13) |
| Companion mass, mc (M⊙) | – | – | 0.27(3) | 0.213(3) |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 22.1 | 44.9 | 42.3 | 359.7 |
| Gal. latitude, b (deg) | −3.4 | 5.4 | 3.1 | −19.6 |
| LK Px Distance, d (pc) | |$1092_{-318}^{666}$| | – | |$1098_{-254}^{+439}$| | |$1146_{-28}^{+30}$| |
| Composite PM, μ (mas yr−1) | 3.8(3) | 3.22(15) | 6.03(3) | 37.020(10) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.007(4) | 0.0091 | 0.05(2) | 1.12(3) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0004(3) | −0.0016 | −0.0010(3) | −0.0242(6) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.014(9) | −0.0028 | −0.0002(30) | 0.031(3) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.94(1) | 0.868 | 1.73(2) | 0.27(3) |
| Characteristic age, τc (Gyr) | 3.1 | 7.5 | 4.9 | 17.4 |
| Surface magnetic field, B (× 108 G) | 1.3 | 1.9 | 3.1 | 0.9 |
| Min. companion mass (M⊙) | – | 0.22 | 0.22 | 0.18 |
| PSR name . | J1843−1113 . | J1853+1303 . | J1857+0943 . | J1909−3744 . |
|---|---|---|---|---|
| MJD range | 53156–56829 | 53763–56829 | 50458–56781 | 53368–56794 |
| Number of TOAs | 224 | 101 | 444 | 425 |
| rms timing residual (μs) | 0.71 | 1.6 | 1.7 | 0.13 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 18:43:41.261 917(12) | 18:53:57.318 765(12) | 18:57:36.390 605(4) | 19:09:47.433 5737(7) |
| Declination, δ | −11:13:31.0686(7) | 13:03:44.0693(4) | 09:43:17.207 14(10) | −37:44:14.515 61(3) |
| Proper motion in α (mas yr−1) | −1.91(7) | −1.61(9) | −2.649(17) | −9.519(3) |
| Proper motion in δ (mas yr−1) | −3.2(3) | −2.79(17) | −5.41(3) | −35.775(10) |
| Period, P (ms) | 1.845 666 323 2093(6) | 4.091 797 445 6530(10) | 5.362 100 548 700 34(9) | 2.947 108 069 766 629(7) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.9554(7) | 0.8724(14) | 1.784 47(17) | 1.402 518(14) |
| Parallax, π (mas) | 0.69(33) | – | 0.70(26) | 0.87(2) |
| DM (cm−3pc) | 59.964(8) | 30.576(20) | 13.303(4) | 10.3925(4) |
| DM1 (cm−3pc yr−1) | 0.002(4) | 0.002(4) | 0.0017(2) | −0.000 32(3) |
| DM2 (cm−3pc yr−2) | 0.0005(9) | −0.0005(8) | −0.000 18(8) | 0.000 04(1) |
| Orbital period, Pb (d) | – | 115.653 788 24(3) | 12.327 171 3831(3) | 1.533 449 474 329(13) |
| Epoch of periastron, T0 (MJD) | – | 52 890.256(18) | 46 432.781(3) | 53 114.72(4) |
| Projected semimajor axis, x (lt-s) | – | 40.769 5169(14) | 9.230 7819(9) | 1.897 990 99(6) |
| Longitude of periastron, ω0 (deg) | – | 346.65(6) | 276.47(7) | 180(9) |
| Orbital eccentricity, e | – | 2.368(3)× 10−5 | 2.170(4)× 10−5 | 1.22(11)× 10−7 |
| κ = e × sin ω0 | – | – | – | −2.3(1900)× 10−10 |
| η = e × cos ω0 | – | – | – | −1.22(11)× 10−7 |
| Time of asc. node (MJD) | – | – | – | 53 113.950 741 990(10) |
| Orbital period derivative, |$\dot{P_{\rm b}}$| | – | – | – | 5.03(5)× 10−13 |
| First derivative of x, |$\dot{x}$| | – | 2.4(7)× 10−14 | −2.7(11)× 10−15 | 0.6(17) × 10−16 |
| Sine of inclination angle, sin i | – | – | 0.9987(6) | 0.997 71(13) |
| Companion mass, mc (M⊙) | – | – | 0.27(3) | 0.213(3) |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 22.1 | 44.9 | 42.3 | 359.7 |
| Gal. latitude, b (deg) | −3.4 | 5.4 | 3.1 | −19.6 |
| LK Px Distance, d (pc) | |$1092_{-318}^{666}$| | – | |$1098_{-254}^{+439}$| | |$1146_{-28}^{+30}$| |
| Composite PM, μ (mas yr−1) | 3.8(3) | 3.22(15) | 6.03(3) | 37.020(10) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.007(4) | 0.0091 | 0.05(2) | 1.12(3) |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0004(3) | −0.0016 | −0.0010(3) | −0.0242(6) |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | 0.014(9) | −0.0028 | −0.0002(30) | 0.031(3) |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.94(1) | 0.868 | 1.73(2) | 0.27(3) |
| Characteristic age, τc (Gyr) | 3.1 | 7.5 | 4.9 | 17.4 |
| Surface magnetic field, B (× 108 G) | 1.3 | 1.9 | 3.1 | 0.9 |
| Min. companion mass (M⊙) | – | 0.22 | 0.22 | 0.18 |
Timing model parameters for PSRs J1910+1256, J1911+1347, J1911−1114 and J1918−0642. See caption of Table 2 for a description of this table.
| PSR name . | J1910+1256 . | J1911+1347 . | J1911−1114 . | J1918−0642 . |
|---|---|---|---|---|
| MJD range | 53725–56828 | 54095–56827 | 53815–57027 | 52095–56769 |
| Number of TOAs | 112 | 140 | 130 | 278 |
| rms timing residual (μs) | 1.9 | 1.4 | 4.8 | 3.0 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 19:10:09.701 439(12) | 19:11:55.204 679(5) | 19:11:49.282 33(3) | 19:18:48.033 114(7) |
| Declination, δ | 12:56:25.4869(4) | 13:47:34.383 98(15) | −11:14:22.481(3) | −06:42:34.8896(4) |
| Proper motion in α (mas yr−1) | 0.28(9) | −2.90(4) | −13.75(16) | −7.16(4) |
| Proper motion in δ (mas yr−1) | −7.37(15) | −3.74(6) | −9.1(10) | −5.95(11) |
| Period, P (ms) | 4.983 584 018 674(3) | 4.625 962 539 7749(6) | 3.625 745 633 114(5) | 7.645 872 887 4589(14) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.9675(17) | 1.6927(9) | 1.395(4) | 2.5686(17) |
| Parallax, π (mas) | 1.44(74) | – | – | – |
| DM (cm−3pc) | 38.094(11) | 30.987(6) | 31.02(11) | 26.610(11) |
| DM1 (cm−3pc yr−1) | −0.003(6) | 0.000(2) | −0.02(2) | 0.003(3) |
| DM2 (cm−3pc yr−2) | 0.0000(8) | −0.0002(5) | 0.003(3) | 0.0003(5) |
| Orbital period, Pb (d) | 58.466 742 964(14) | – | 2.716 557 6619(7) | 10.913 177 7490(4) |
| Epoch of periastron, T0 (MJD) | 54 079.3152(14) | – | 50 456.5(3) | 51 575.775(7) |
| Projected semimajor axis, x (lt-s) | 21.129 1036(7) | – | 1.762 8746(9) | 8.350 4665(10) |
| Longitude of periastron, ω0 (deg) | 105.998(9) | – | 121(34) | 219.60(20) |
| Orbital eccentricity, e | 2.3023(4)× 10−4 | – | 1.6(10)× 10−6 | 2.039(8)× 10−5 |
| κ = e × sin ω0 | – | – | 1.4(11)× 10−6 | – |
| η = e × cos ω0 | – | – | −8.4(91)× 10−7 | – |
| Time of asc. node (MJD) | – | – | 50 455.611 7845(13) | – |
| First derivative of x, |$\dot{x}$| | −2.0(6)× 10−14 | – | – | 0.9(1.8) × 10−15 |
| Third harmonic of Shapiro, h3 (μs) | – | – | – | 0.86(12) |
| Ratio of harmonics amplitude, ς | – | – | – | 0.91(4) |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 46.6 | 47.5 | 25.1 | 30.0 |
| Gal. latitude, b (deg) | 1.8 | 1.8 | −9.6 | −9.1 |
| LK Px Distance, d (pc) | |$554_{-186}^{+461}$| | – | – | – |
| Composite PM, μ (mas yr−1) | 7.37(15) | 4.73(6) | 16.5(6) | 9.31(7) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.04(3) | 0.052 | 0.29 | 0.2 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0002(1) | −0.00041 | −0.0084 | −0.016 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.003(3) | −0.031 | 0.025 | 0.039 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.93(3) | 1.67 | 1.09 | 2.35 |
| Characteristic age, τc (Gyr) | 8.5 | 4.4 | 5.3 | 5.2 |
| Surface magnetic field, B (× 108 G) | 2.2 | 2.8 | 2.0 | 4.3 |
| Min. companion mass (M⊙) | 0.18 | – | 0.11 | 0.22 |
| PSR name . | J1910+1256 . | J1911+1347 . | J1911−1114 . | J1918−0642 . |
|---|---|---|---|---|
| MJD range | 53725–56828 | 54095–56827 | 53815–57027 | 52095–56769 |
| Number of TOAs | 112 | 140 | 130 | 278 |
| rms timing residual (μs) | 1.9 | 1.4 | 4.8 | 3.0 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 19:10:09.701 439(12) | 19:11:55.204 679(5) | 19:11:49.282 33(3) | 19:18:48.033 114(7) |
| Declination, δ | 12:56:25.4869(4) | 13:47:34.383 98(15) | −11:14:22.481(3) | −06:42:34.8896(4) |
| Proper motion in α (mas yr−1) | 0.28(9) | −2.90(4) | −13.75(16) | −7.16(4) |
| Proper motion in δ (mas yr−1) | −7.37(15) | −3.74(6) | −9.1(10) | −5.95(11) |
| Period, P (ms) | 4.983 584 018 674(3) | 4.625 962 539 7749(6) | 3.625 745 633 114(5) | 7.645 872 887 4589(14) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.9675(17) | 1.6927(9) | 1.395(4) | 2.5686(17) |
| Parallax, π (mas) | 1.44(74) | – | – | – |
| DM (cm−3pc) | 38.094(11) | 30.987(6) | 31.02(11) | 26.610(11) |
| DM1 (cm−3pc yr−1) | −0.003(6) | 0.000(2) | −0.02(2) | 0.003(3) |
| DM2 (cm−3pc yr−2) | 0.0000(8) | −0.0002(5) | 0.003(3) | 0.0003(5) |
| Orbital period, Pb (d) | 58.466 742 964(14) | – | 2.716 557 6619(7) | 10.913 177 7490(4) |
| Epoch of periastron, T0 (MJD) | 54 079.3152(14) | – | 50 456.5(3) | 51 575.775(7) |
| Projected semimajor axis, x (lt-s) | 21.129 1036(7) | – | 1.762 8746(9) | 8.350 4665(10) |
| Longitude of periastron, ω0 (deg) | 105.998(9) | – | 121(34) | 219.60(20) |
| Orbital eccentricity, e | 2.3023(4)× 10−4 | – | 1.6(10)× 10−6 | 2.039(8)× 10−5 |
| κ = e × sin ω0 | – | – | 1.4(11)× 10−6 | – |
| η = e × cos ω0 | – | – | −8.4(91)× 10−7 | – |
| Time of asc. node (MJD) | – | – | 50 455.611 7845(13) | – |
| First derivative of x, |$\dot{x}$| | −2.0(6)× 10−14 | – | – | 0.9(1.8) × 10−15 |
| Third harmonic of Shapiro, h3 (μs) | – | – | – | 0.86(12) |
| Ratio of harmonics amplitude, ς | – | – | – | 0.91(4) |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 46.6 | 47.5 | 25.1 | 30.0 |
| Gal. latitude, b (deg) | 1.8 | 1.8 | −9.6 | −9.1 |
| LK Px Distance, d (pc) | |$554_{-186}^{+461}$| | – | – | – |
| Composite PM, μ (mas yr−1) | 7.37(15) | 4.73(6) | 16.5(6) | 9.31(7) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.04(3) | 0.052 | 0.29 | 0.2 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0002(1) | −0.00041 | −0.0084 | −0.016 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.003(3) | −0.031 | 0.025 | 0.039 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.93(3) | 1.67 | 1.09 | 2.35 |
| Characteristic age, τc (Gyr) | 8.5 | 4.4 | 5.3 | 5.2 |
| Surface magnetic field, B (× 108 G) | 2.2 | 2.8 | 2.0 | 4.3 |
| Min. companion mass (M⊙) | 0.18 | – | 0.11 | 0.22 |
Timing model parameters for PSRs J1910+1256, J1911+1347, J1911−1114 and J1918−0642. See caption of Table 2 for a description of this table.
| PSR name . | J1910+1256 . | J1911+1347 . | J1911−1114 . | J1918−0642 . |
|---|---|---|---|---|
| MJD range | 53725–56828 | 54095–56827 | 53815–57027 | 52095–56769 |
| Number of TOAs | 112 | 140 | 130 | 278 |
| rms timing residual (μs) | 1.9 | 1.4 | 4.8 | 3.0 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 19:10:09.701 439(12) | 19:11:55.204 679(5) | 19:11:49.282 33(3) | 19:18:48.033 114(7) |
| Declination, δ | 12:56:25.4869(4) | 13:47:34.383 98(15) | −11:14:22.481(3) | −06:42:34.8896(4) |
| Proper motion in α (mas yr−1) | 0.28(9) | −2.90(4) | −13.75(16) | −7.16(4) |
| Proper motion in δ (mas yr−1) | −7.37(15) | −3.74(6) | −9.1(10) | −5.95(11) |
| Period, P (ms) | 4.983 584 018 674(3) | 4.625 962 539 7749(6) | 3.625 745 633 114(5) | 7.645 872 887 4589(14) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.9675(17) | 1.6927(9) | 1.395(4) | 2.5686(17) |
| Parallax, π (mas) | 1.44(74) | – | – | – |
| DM (cm−3pc) | 38.094(11) | 30.987(6) | 31.02(11) | 26.610(11) |
| DM1 (cm−3pc yr−1) | −0.003(6) | 0.000(2) | −0.02(2) | 0.003(3) |
| DM2 (cm−3pc yr−2) | 0.0000(8) | −0.0002(5) | 0.003(3) | 0.0003(5) |
| Orbital period, Pb (d) | 58.466 742 964(14) | – | 2.716 557 6619(7) | 10.913 177 7490(4) |
| Epoch of periastron, T0 (MJD) | 54 079.3152(14) | – | 50 456.5(3) | 51 575.775(7) |
| Projected semimajor axis, x (lt-s) | 21.129 1036(7) | – | 1.762 8746(9) | 8.350 4665(10) |
| Longitude of periastron, ω0 (deg) | 105.998(9) | – | 121(34) | 219.60(20) |
| Orbital eccentricity, e | 2.3023(4)× 10−4 | – | 1.6(10)× 10−6 | 2.039(8)× 10−5 |
| κ = e × sin ω0 | – | – | 1.4(11)× 10−6 | – |
| η = e × cos ω0 | – | – | −8.4(91)× 10−7 | – |
| Time of asc. node (MJD) | – | – | 50 455.611 7845(13) | – |
| First derivative of x, |$\dot{x}$| | −2.0(6)× 10−14 | – | – | 0.9(1.8) × 10−15 |
| Third harmonic of Shapiro, h3 (μs) | – | – | – | 0.86(12) |
| Ratio of harmonics amplitude, ς | – | – | – | 0.91(4) |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 46.6 | 47.5 | 25.1 | 30.0 |
| Gal. latitude, b (deg) | 1.8 | 1.8 | −9.6 | −9.1 |
| LK Px Distance, d (pc) | |$554_{-186}^{+461}$| | – | – | – |
| Composite PM, μ (mas yr−1) | 7.37(15) | 4.73(6) | 16.5(6) | 9.31(7) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.04(3) | 0.052 | 0.29 | 0.2 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0002(1) | −0.00041 | −0.0084 | −0.016 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.003(3) | −0.031 | 0.025 | 0.039 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.93(3) | 1.67 | 1.09 | 2.35 |
| Characteristic age, τc (Gyr) | 8.5 | 4.4 | 5.3 | 5.2 |
| Surface magnetic field, B (× 108 G) | 2.2 | 2.8 | 2.0 | 4.3 |
| Min. companion mass (M⊙) | 0.18 | – | 0.11 | 0.22 |
| PSR name . | J1910+1256 . | J1911+1347 . | J1911−1114 . | J1918−0642 . |
|---|---|---|---|---|
| MJD range | 53725–56828 | 54095–56827 | 53815–57027 | 52095–56769 |
| Number of TOAs | 112 | 140 | 130 | 278 |
| rms timing residual (μs) | 1.9 | 1.4 | 4.8 | 3.0 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 19:10:09.701 439(12) | 19:11:55.204 679(5) | 19:11:49.282 33(3) | 19:18:48.033 114(7) |
| Declination, δ | 12:56:25.4869(4) | 13:47:34.383 98(15) | −11:14:22.481(3) | −06:42:34.8896(4) |
| Proper motion in α (mas yr−1) | 0.28(9) | −2.90(4) | −13.75(16) | −7.16(4) |
| Proper motion in δ (mas yr−1) | −7.37(15) | −3.74(6) | −9.1(10) | −5.95(11) |
| Period, P (ms) | 4.983 584 018 674(3) | 4.625 962 539 7749(6) | 3.625 745 633 114(5) | 7.645 872 887 4589(14) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.9675(17) | 1.6927(9) | 1.395(4) | 2.5686(17) |
| Parallax, π (mas) | 1.44(74) | – | – | – |
| DM (cm−3pc) | 38.094(11) | 30.987(6) | 31.02(11) | 26.610(11) |
| DM1 (cm−3pc yr−1) | −0.003(6) | 0.000(2) | −0.02(2) | 0.003(3) |
| DM2 (cm−3pc yr−2) | 0.0000(8) | −0.0002(5) | 0.003(3) | 0.0003(5) |
| Orbital period, Pb (d) | 58.466 742 964(14) | – | 2.716 557 6619(7) | 10.913 177 7490(4) |
| Epoch of periastron, T0 (MJD) | 54 079.3152(14) | – | 50 456.5(3) | 51 575.775(7) |
| Projected semimajor axis, x (lt-s) | 21.129 1036(7) | – | 1.762 8746(9) | 8.350 4665(10) |
| Longitude of periastron, ω0 (deg) | 105.998(9) | – | 121(34) | 219.60(20) |
| Orbital eccentricity, e | 2.3023(4)× 10−4 | – | 1.6(10)× 10−6 | 2.039(8)× 10−5 |
| κ = e × sin ω0 | – | – | 1.4(11)× 10−6 | – |
| η = e × cos ω0 | – | – | −8.4(91)× 10−7 | – |
| Time of asc. node (MJD) | – | – | 50 455.611 7845(13) | – |
| First derivative of x, |$\dot{x}$| | −2.0(6)× 10−14 | – | – | 0.9(1.8) × 10−15 |
| Third harmonic of Shapiro, h3 (μs) | – | – | – | 0.86(12) |
| Ratio of harmonics amplitude, ς | – | – | – | 0.91(4) |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 46.6 | 47.5 | 25.1 | 30.0 |
| Gal. latitude, b (deg) | 1.8 | 1.8 | −9.6 | −9.1 |
| LK Px Distance, d (pc) | |$554_{-186}^{+461}$| | – | – | – |
| Composite PM, μ (mas yr−1) | 7.37(15) | 4.73(6) | 16.5(6) | 9.31(7) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.04(3) | 0.052 | 0.29 | 0.2 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.0002(1) | −0.00041 | −0.0084 | −0.016 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.003(3) | −0.031 | 0.025 | 0.039 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.93(3) | 1.67 | 1.09 | 2.35 |
| Characteristic age, τc (Gyr) | 8.5 | 4.4 | 5.3 | 5.2 |
| Surface magnetic field, B (× 108 G) | 2.2 | 2.8 | 2.0 | 4.3 |
| Min. companion mass (M⊙) | 0.18 | – | 0.11 | 0.22 |
Timing model parameters for PSRs J1939+2134, J1955+2908, J2010−1323 and J2019+2425. See caption of Table 2 for a description of this table.
| PSR name . | J1939+2134 . | J1955+2908 . | J2010−1323 . | J2019+2425 . |
|---|---|---|---|---|
| MJD range | 47958–56778 | 53813–56781 | 54089–56785 | 53451–56788 |
| Number of TOAs | 3174 | 157 | 390 | 130 |
| rms timing residual (μs) | 34.5 | 6.5 | 1.9 | 9.6 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 19:39:38.561 224(2) | 19:55:27.875 74(3) | 20:10:45.920 637(11) | 20:19:31.940 82(8) |
| Declination, δ | 21:34:59.125 70(4) | 29:08:43.4599(6) | −13:23:56.0668(7) | 24:25:15.0130(19) |
| Proper motion in α (mas yr−1) | 0.070(4) | −0.77(19) | 2.53(9) | −8.8(6) |
| Proper motion in δ (mas yr−1) | −0.401(5) | −4.7(3) | −5.7(4) | −19.9(7) |
| Period, P (ms) | 1.557 806 561 084 93(5) | 6.133 166 606 620(5) | 5.223 271 097 2195(3) | 3.934 524 144 385(9) |
| Period derivative, |$\dot{P}$| (× 10−20) | 10.510 65(3) | 2.979(5) | 0.4832(6) | 0.695(7) |
| Parallax, π (mas) | 0.22(8) | – | – | – |
| DM (cm−3pc) | 71.0237(13) | 104.54(6) | 22.174(11) | 17.17(12) |
| DM1 (cm−3pc yr−1) | 0.0000(4) | −0.00(1) | 0.0009(6) | −0.04(3) |
| DM2 (cm−3pc yr−2) | 0.000 03(4) | −0.002(2) | −0.0004(3) | 0.004(4) |
| Orbital period, Pb (d) | – | 117.349 099 24(8) | – | 76.511 636 05(8) |
| Epoch of periastron, T0 (MJD) | – | 46 112.470(4) | – | 50 054.652(12) |
| Projected semimajor axis, x (lt-s) | – | 31.412 661(11) | – | 38.767 653(3) |
| Longitude of periastron, ω0 (deg) | – | 29.452(10) | – | 159.07(6) |
| Orbital eccentricity, e | – | 3.3021(7) × 10−4 | – | 1.1113(11) × 10−4 |
| First derivative of x, |$\dot{x}$| | – | 4.0(14) × 10−14 | – | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 57.5 | 65.8 | 29.4 | 64.7 |
| Gal. latitude, b (deg) | −0.3 | 0.4 | −23.5 | −6.6 |
| LK Px Distance, d (pc) | |$3266_{-658}^{+1020}$| | – | – | – |
| Composite PM, μ (mas yr−1) | 0.407(5) | 4.8(3) | 6.2(4) | 21.7(7) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.000 20(6) | 0.16 | 0.051 | 0.67 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.000 0069(26) | −3e-05 | −0.056 | −0.0053 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.04(2) | −0.27 | 0.02 | −0.042 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 10.55(2) | 3.09 | 0.469 | 0.0717 |
| Characteristic age, τc (Gyr) | 0.2 | 3.1 | 17.7 | 87.0 |
| Surface magnetic field, B (× 108 G) | 4.1 | 4.4 | 1.6 | 0.5 |
| Min. companion mass (M⊙) | – | 0.17 | – | 0.29 |
| PSR name . | J1939+2134 . | J1955+2908 . | J2010−1323 . | J2019+2425 . |
|---|---|---|---|---|
| MJD range | 47958–56778 | 53813–56781 | 54089–56785 | 53451–56788 |
| Number of TOAs | 3174 | 157 | 390 | 130 |
| rms timing residual (μs) | 34.5 | 6.5 | 1.9 | 9.6 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 19:39:38.561 224(2) | 19:55:27.875 74(3) | 20:10:45.920 637(11) | 20:19:31.940 82(8) |
| Declination, δ | 21:34:59.125 70(4) | 29:08:43.4599(6) | −13:23:56.0668(7) | 24:25:15.0130(19) |
| Proper motion in α (mas yr−1) | 0.070(4) | −0.77(19) | 2.53(9) | −8.8(6) |
| Proper motion in δ (mas yr−1) | −0.401(5) | −4.7(3) | −5.7(4) | −19.9(7) |
| Period, P (ms) | 1.557 806 561 084 93(5) | 6.133 166 606 620(5) | 5.223 271 097 2195(3) | 3.934 524 144 385(9) |
| Period derivative, |$\dot{P}$| (× 10−20) | 10.510 65(3) | 2.979(5) | 0.4832(6) | 0.695(7) |
| Parallax, π (mas) | 0.22(8) | – | – | – |
| DM (cm−3pc) | 71.0237(13) | 104.54(6) | 22.174(11) | 17.17(12) |
| DM1 (cm−3pc yr−1) | 0.0000(4) | −0.00(1) | 0.0009(6) | −0.04(3) |
| DM2 (cm−3pc yr−2) | 0.000 03(4) | −0.002(2) | −0.0004(3) | 0.004(4) |
| Orbital period, Pb (d) | – | 117.349 099 24(8) | – | 76.511 636 05(8) |
| Epoch of periastron, T0 (MJD) | – | 46 112.470(4) | – | 50 054.652(12) |
| Projected semimajor axis, x (lt-s) | – | 31.412 661(11) | – | 38.767 653(3) |
| Longitude of periastron, ω0 (deg) | – | 29.452(10) | – | 159.07(6) |
| Orbital eccentricity, e | – | 3.3021(7) × 10−4 | – | 1.1113(11) × 10−4 |
| First derivative of x, |$\dot{x}$| | – | 4.0(14) × 10−14 | – | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 57.5 | 65.8 | 29.4 | 64.7 |
| Gal. latitude, b (deg) | −0.3 | 0.4 | −23.5 | −6.6 |
| LK Px Distance, d (pc) | |$3266_{-658}^{+1020}$| | – | – | – |
| Composite PM, μ (mas yr−1) | 0.407(5) | 4.8(3) | 6.2(4) | 21.7(7) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.000 20(6) | 0.16 | 0.051 | 0.67 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.000 0069(26) | −3e-05 | −0.056 | −0.0053 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.04(2) | −0.27 | 0.02 | −0.042 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 10.55(2) | 3.09 | 0.469 | 0.0717 |
| Characteristic age, τc (Gyr) | 0.2 | 3.1 | 17.7 | 87.0 |
| Surface magnetic field, B (× 108 G) | 4.1 | 4.4 | 1.6 | 0.5 |
| Min. companion mass (M⊙) | – | 0.17 | – | 0.29 |
Timing model parameters for PSRs J1939+2134, J1955+2908, J2010−1323 and J2019+2425. See caption of Table 2 for a description of this table.
| PSR name . | J1939+2134 . | J1955+2908 . | J2010−1323 . | J2019+2425 . |
|---|---|---|---|---|
| MJD range | 47958–56778 | 53813–56781 | 54089–56785 | 53451–56788 |
| Number of TOAs | 3174 | 157 | 390 | 130 |
| rms timing residual (μs) | 34.5 | 6.5 | 1.9 | 9.6 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 19:39:38.561 224(2) | 19:55:27.875 74(3) | 20:10:45.920 637(11) | 20:19:31.940 82(8) |
| Declination, δ | 21:34:59.125 70(4) | 29:08:43.4599(6) | −13:23:56.0668(7) | 24:25:15.0130(19) |
| Proper motion in α (mas yr−1) | 0.070(4) | −0.77(19) | 2.53(9) | −8.8(6) |
| Proper motion in δ (mas yr−1) | −0.401(5) | −4.7(3) | −5.7(4) | −19.9(7) |
| Period, P (ms) | 1.557 806 561 084 93(5) | 6.133 166 606 620(5) | 5.223 271 097 2195(3) | 3.934 524 144 385(9) |
| Period derivative, |$\dot{P}$| (× 10−20) | 10.510 65(3) | 2.979(5) | 0.4832(6) | 0.695(7) |
| Parallax, π (mas) | 0.22(8) | – | – | – |
| DM (cm−3pc) | 71.0237(13) | 104.54(6) | 22.174(11) | 17.17(12) |
| DM1 (cm−3pc yr−1) | 0.0000(4) | −0.00(1) | 0.0009(6) | −0.04(3) |
| DM2 (cm−3pc yr−2) | 0.000 03(4) | −0.002(2) | −0.0004(3) | 0.004(4) |
| Orbital period, Pb (d) | – | 117.349 099 24(8) | – | 76.511 636 05(8) |
| Epoch of periastron, T0 (MJD) | – | 46 112.470(4) | – | 50 054.652(12) |
| Projected semimajor axis, x (lt-s) | – | 31.412 661(11) | – | 38.767 653(3) |
| Longitude of periastron, ω0 (deg) | – | 29.452(10) | – | 159.07(6) |
| Orbital eccentricity, e | – | 3.3021(7) × 10−4 | – | 1.1113(11) × 10−4 |
| First derivative of x, |$\dot{x}$| | – | 4.0(14) × 10−14 | – | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 57.5 | 65.8 | 29.4 | 64.7 |
| Gal. latitude, b (deg) | −0.3 | 0.4 | −23.5 | −6.6 |
| LK Px Distance, d (pc) | |$3266_{-658}^{+1020}$| | – | – | – |
| Composite PM, μ (mas yr−1) | 0.407(5) | 4.8(3) | 6.2(4) | 21.7(7) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.000 20(6) | 0.16 | 0.051 | 0.67 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.000 0069(26) | −3e-05 | −0.056 | −0.0053 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.04(2) | −0.27 | 0.02 | −0.042 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 10.55(2) | 3.09 | 0.469 | 0.0717 |
| Characteristic age, τc (Gyr) | 0.2 | 3.1 | 17.7 | 87.0 |
| Surface magnetic field, B (× 108 G) | 4.1 | 4.4 | 1.6 | 0.5 |
| Min. companion mass (M⊙) | – | 0.17 | – | 0.29 |
| PSR name . | J1939+2134 . | J1955+2908 . | J2010−1323 . | J2019+2425 . |
|---|---|---|---|---|
| MJD range | 47958–56778 | 53813–56781 | 54089–56785 | 53451–56788 |
| Number of TOAs | 3174 | 157 | 390 | 130 |
| rms timing residual (μs) | 34.5 | 6.5 | 1.9 | 9.6 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 19:39:38.561 224(2) | 19:55:27.875 74(3) | 20:10:45.920 637(11) | 20:19:31.940 82(8) |
| Declination, δ | 21:34:59.125 70(4) | 29:08:43.4599(6) | −13:23:56.0668(7) | 24:25:15.0130(19) |
| Proper motion in α (mas yr−1) | 0.070(4) | −0.77(19) | 2.53(9) | −8.8(6) |
| Proper motion in δ (mas yr−1) | −0.401(5) | −4.7(3) | −5.7(4) | −19.9(7) |
| Period, P (ms) | 1.557 806 561 084 93(5) | 6.133 166 606 620(5) | 5.223 271 097 2195(3) | 3.934 524 144 385(9) |
| Period derivative, |$\dot{P}$| (× 10−20) | 10.510 65(3) | 2.979(5) | 0.4832(6) | 0.695(7) |
| Parallax, π (mas) | 0.22(8) | – | – | – |
| DM (cm−3pc) | 71.0237(13) | 104.54(6) | 22.174(11) | 17.17(12) |
| DM1 (cm−3pc yr−1) | 0.0000(4) | −0.00(1) | 0.0009(6) | −0.04(3) |
| DM2 (cm−3pc yr−2) | 0.000 03(4) | −0.002(2) | −0.0004(3) | 0.004(4) |
| Orbital period, Pb (d) | – | 117.349 099 24(8) | – | 76.511 636 05(8) |
| Epoch of periastron, T0 (MJD) | – | 46 112.470(4) | – | 50 054.652(12) |
| Projected semimajor axis, x (lt-s) | – | 31.412 661(11) | – | 38.767 653(3) |
| Longitude of periastron, ω0 (deg) | – | 29.452(10) | – | 159.07(6) |
| Orbital eccentricity, e | – | 3.3021(7) × 10−4 | – | 1.1113(11) × 10−4 |
| First derivative of x, |$\dot{x}$| | – | 4.0(14) × 10−14 | – | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 57.5 | 65.8 | 29.4 | 64.7 |
| Gal. latitude, b (deg) | −0.3 | 0.4 | −23.5 | −6.6 |
| LK Px Distance, d (pc) | |$3266_{-658}^{+1020}$| | – | – | – |
| Composite PM, μ (mas yr−1) | 0.407(5) | 4.8(3) | 6.2(4) | 21.7(7) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.000 20(6) | 0.16 | 0.051 | 0.67 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.000 0069(26) | −3e-05 | −0.056 | −0.0053 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.04(2) | −0.27 | 0.02 | −0.042 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 10.55(2) | 3.09 | 0.469 | 0.0717 |
| Characteristic age, τc (Gyr) | 0.2 | 3.1 | 17.7 | 87.0 |
| Surface magnetic field, B (× 108 G) | 4.1 | 4.4 | 1.6 | 0.5 |
| Min. companion mass (M⊙) | – | 0.17 | – | 0.29 |
Timing model parameters for PSRs J2033+1734, J2124−3358, J2145−0750 and J2229+2643. See caption of Table 2 for a description of this table.
| PSR name . | J2033+1734 . | J2124−3358 . | J2145−0750 . | J2229+2643 . |
|---|---|---|---|---|
| MJD range | 53898–56789 | 53365–56795 | 50360–56761 | 53790–56796 |
| Number of TOAs | 194 | 544 | 800 | 316 |
| rms timing residual (μs) | 12.7 | 3.2 | 1.8 | 4.2 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 20:33:27.514 18(7) | 21:24:43.847 820(11) | 21:45:50.460 593(9) | 22:29:50.885 423(18) |
| Declination, δ | 17:34:58.5249(17) | −33:58:44.9190(3) | −07:50:18.4876(4) | 26:43:57.6812(4) |
| Proper motion in α (mas yr−1) | −5.9(5) | −14.04(8) | −9.58(4) | −1.73(12) |
| Proper motion in δ (mas yr−1) | −9.1(8) | −50.14(14) | −8.86(10) | −5.82(15) |
| Period, P (ms) | 5.948 957 630 705(7) | 4.931 114 943 9851(3) | 16.052 423 919 381 30(15) | 2.977 819 341 625 67(11) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.108(9) | 2.0569(5) | 2.9788(3) | 0.1522(4) |
| Parallax, π (mas) | – | 2.50(36) | 1.53(11) | – |
| DM (cm−3pc) | 25.00(13) | 4.585(9) | 8.983(3) | 22.72(3) |
| DM1 (cm−3pc yr−1) | −0.03(2) | 0.0005(7) | 0.000 19(5) | 0.0008(5) |
| DM2 (cm−3pc yr−2) | 0.002(4) | 0.0000(3) | 0.000 006(26) | 0.0001(3) |
| Orbital period, Pb (d) | 56.307 796 17(7) | – | 6.838 902 615 32(19) | 93.015 893 90(5) |
| Epoch of periastron, T0 (MJD) | 49 878.125(11) | – | 50 313.7121(7) | 49 419.709(3) |
| Projected semimajor axis, x (lt-s) | 20.163 1167(16) | – | 10.164 1056(3) | 18.912 5228(5) |
| Longitude of periastron, ω0 (deg) | 78.09(7) | – | 200.81(4) | 14.337(11) |
| Orbital eccentricity, e | 1.2861(14)× 10−4 | – | 1.9323(12)× 10−5 | 2.5525(5)× 10−4 |
| κ = e × sin ω0 | – | – | −6.866(12)× 10−6 | – |
| η = e × cos ω0 | – | – | −1.8062(12)× 10−5 | – |
| Time of asc. node (MJD) | – | – | 50 309.897 241 07(6) | – |
| First derivative of x, |$\dot{x}$| | – | – | 8.2(7)× 10−15 | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 60.9 | 10.9 | 47.8 | 87.7 |
| Gal. latitude, b (deg) | −13.2 | −45.4 | −42.1 | −26.3 |
| LK Px Distance, d (pc) | – | |$382_{-47}^{+61}$| | |$645_{-41}^{+47}$| | – |
| Composite PM, μ (mas yr−1) | 10.8(7) | 52.07(14) | 13.05(8) | 6.07(15) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.34 | 1.2(2) | 0.43(3) | 0.038 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.041 | −0.06(1) | −0.30(2) | −0.053 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.079 | 0.008(1) | −0.007(1) | −0.03 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.891 | 0.9(2) | 2.85(1) | 0.198 |
| Characteristic age, τc (Gyr) | 10.6 | 8.9 | 8.9 | 23.9 |
| Surface magnetic field, B (× 108 G) | 2.3 | 2.1 | 6.9 | 0.8 |
| Min. companion mass (M⊙) | 0.17 | – | 0.39 | 0.11 |
| PSR name . | J2033+1734 . | J2124−3358 . | J2145−0750 . | J2229+2643 . |
|---|---|---|---|---|
| MJD range | 53898–56789 | 53365–56795 | 50360–56761 | 53790–56796 |
| Number of TOAs | 194 | 544 | 800 | 316 |
| rms timing residual (μs) | 12.7 | 3.2 | 1.8 | 4.2 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 20:33:27.514 18(7) | 21:24:43.847 820(11) | 21:45:50.460 593(9) | 22:29:50.885 423(18) |
| Declination, δ | 17:34:58.5249(17) | −33:58:44.9190(3) | −07:50:18.4876(4) | 26:43:57.6812(4) |
| Proper motion in α (mas yr−1) | −5.9(5) | −14.04(8) | −9.58(4) | −1.73(12) |
| Proper motion in δ (mas yr−1) | −9.1(8) | −50.14(14) | −8.86(10) | −5.82(15) |
| Period, P (ms) | 5.948 957 630 705(7) | 4.931 114 943 9851(3) | 16.052 423 919 381 30(15) | 2.977 819 341 625 67(11) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.108(9) | 2.0569(5) | 2.9788(3) | 0.1522(4) |
| Parallax, π (mas) | – | 2.50(36) | 1.53(11) | – |
| DM (cm−3pc) | 25.00(13) | 4.585(9) | 8.983(3) | 22.72(3) |
| DM1 (cm−3pc yr−1) | −0.03(2) | 0.0005(7) | 0.000 19(5) | 0.0008(5) |
| DM2 (cm−3pc yr−2) | 0.002(4) | 0.0000(3) | 0.000 006(26) | 0.0001(3) |
| Orbital period, Pb (d) | 56.307 796 17(7) | – | 6.838 902 615 32(19) | 93.015 893 90(5) |
| Epoch of periastron, T0 (MJD) | 49 878.125(11) | – | 50 313.7121(7) | 49 419.709(3) |
| Projected semimajor axis, x (lt-s) | 20.163 1167(16) | – | 10.164 1056(3) | 18.912 5228(5) |
| Longitude of periastron, ω0 (deg) | 78.09(7) | – | 200.81(4) | 14.337(11) |
| Orbital eccentricity, e | 1.2861(14)× 10−4 | – | 1.9323(12)× 10−5 | 2.5525(5)× 10−4 |
| κ = e × sin ω0 | – | – | −6.866(12)× 10−6 | – |
| η = e × cos ω0 | – | – | −1.8062(12)× 10−5 | – |
| Time of asc. node (MJD) | – | – | 50 309.897 241 07(6) | – |
| First derivative of x, |$\dot{x}$| | – | – | 8.2(7)× 10−15 | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 60.9 | 10.9 | 47.8 | 87.7 |
| Gal. latitude, b (deg) | −13.2 | −45.4 | −42.1 | −26.3 |
| LK Px Distance, d (pc) | – | |$382_{-47}^{+61}$| | |$645_{-41}^{+47}$| | – |
| Composite PM, μ (mas yr−1) | 10.8(7) | 52.07(14) | 13.05(8) | 6.07(15) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.34 | 1.2(2) | 0.43(3) | 0.038 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.041 | −0.06(1) | −0.30(2) | −0.053 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.079 | 0.008(1) | −0.007(1) | −0.03 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.891 | 0.9(2) | 2.85(1) | 0.198 |
| Characteristic age, τc (Gyr) | 10.6 | 8.9 | 8.9 | 23.9 |
| Surface magnetic field, B (× 108 G) | 2.3 | 2.1 | 6.9 | 0.8 |
| Min. companion mass (M⊙) | 0.17 | – | 0.39 | 0.11 |
Timing model parameters for PSRs J2033+1734, J2124−3358, J2145−0750 and J2229+2643. See caption of Table 2 for a description of this table.
| PSR name . | J2033+1734 . | J2124−3358 . | J2145−0750 . | J2229+2643 . |
|---|---|---|---|---|
| MJD range | 53898–56789 | 53365–56795 | 50360–56761 | 53790–56796 |
| Number of TOAs | 194 | 544 | 800 | 316 |
| rms timing residual (μs) | 12.7 | 3.2 | 1.8 | 4.2 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 20:33:27.514 18(7) | 21:24:43.847 820(11) | 21:45:50.460 593(9) | 22:29:50.885 423(18) |
| Declination, δ | 17:34:58.5249(17) | −33:58:44.9190(3) | −07:50:18.4876(4) | 26:43:57.6812(4) |
| Proper motion in α (mas yr−1) | −5.9(5) | −14.04(8) | −9.58(4) | −1.73(12) |
| Proper motion in δ (mas yr−1) | −9.1(8) | −50.14(14) | −8.86(10) | −5.82(15) |
| Period, P (ms) | 5.948 957 630 705(7) | 4.931 114 943 9851(3) | 16.052 423 919 381 30(15) | 2.977 819 341 625 67(11) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.108(9) | 2.0569(5) | 2.9788(3) | 0.1522(4) |
| Parallax, π (mas) | – | 2.50(36) | 1.53(11) | – |
| DM (cm−3pc) | 25.00(13) | 4.585(9) | 8.983(3) | 22.72(3) |
| DM1 (cm−3pc yr−1) | −0.03(2) | 0.0005(7) | 0.000 19(5) | 0.0008(5) |
| DM2 (cm−3pc yr−2) | 0.002(4) | 0.0000(3) | 0.000 006(26) | 0.0001(3) |
| Orbital period, Pb (d) | 56.307 796 17(7) | – | 6.838 902 615 32(19) | 93.015 893 90(5) |
| Epoch of periastron, T0 (MJD) | 49 878.125(11) | – | 50 313.7121(7) | 49 419.709(3) |
| Projected semimajor axis, x (lt-s) | 20.163 1167(16) | – | 10.164 1056(3) | 18.912 5228(5) |
| Longitude of periastron, ω0 (deg) | 78.09(7) | – | 200.81(4) | 14.337(11) |
| Orbital eccentricity, e | 1.2861(14)× 10−4 | – | 1.9323(12)× 10−5 | 2.5525(5)× 10−4 |
| κ = e × sin ω0 | – | – | −6.866(12)× 10−6 | – |
| η = e × cos ω0 | – | – | −1.8062(12)× 10−5 | – |
| Time of asc. node (MJD) | – | – | 50 309.897 241 07(6) | – |
| First derivative of x, |$\dot{x}$| | – | – | 8.2(7)× 10−15 | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 60.9 | 10.9 | 47.8 | 87.7 |
| Gal. latitude, b (deg) | −13.2 | −45.4 | −42.1 | −26.3 |
| LK Px Distance, d (pc) | – | |$382_{-47}^{+61}$| | |$645_{-41}^{+47}$| | – |
| Composite PM, μ (mas yr−1) | 10.8(7) | 52.07(14) | 13.05(8) | 6.07(15) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.34 | 1.2(2) | 0.43(3) | 0.038 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.041 | −0.06(1) | −0.30(2) | −0.053 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.079 | 0.008(1) | −0.007(1) | −0.03 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.891 | 0.9(2) | 2.85(1) | 0.198 |
| Characteristic age, τc (Gyr) | 10.6 | 8.9 | 8.9 | 23.9 |
| Surface magnetic field, B (× 108 G) | 2.3 | 2.1 | 6.9 | 0.8 |
| Min. companion mass (M⊙) | 0.17 | – | 0.39 | 0.11 |
| PSR name . | J2033+1734 . | J2124−3358 . | J2145−0750 . | J2229+2643 . |
|---|---|---|---|---|
| MJD range | 53898–56789 | 53365–56795 | 50360–56761 | 53790–56796 |
| Number of TOAs | 194 | 544 | 800 | 316 |
| rms timing residual (μs) | 12.7 | 3.2 | 1.8 | 4.2 |
| Reference epoch (MJD) | 55000 | 55000 | 55000 | 55000 |
| Measured parameters | ||||
| Right ascension, α | 20:33:27.514 18(7) | 21:24:43.847 820(11) | 21:45:50.460 593(9) | 22:29:50.885 423(18) |
| Declination, δ | 17:34:58.5249(17) | −33:58:44.9190(3) | −07:50:18.4876(4) | 26:43:57.6812(4) |
| Proper motion in α (mas yr−1) | −5.9(5) | −14.04(8) | −9.58(4) | −1.73(12) |
| Proper motion in δ (mas yr−1) | −9.1(8) | −50.14(14) | −8.86(10) | −5.82(15) |
| Period, P (ms) | 5.948 957 630 705(7) | 4.931 114 943 9851(3) | 16.052 423 919 381 30(15) | 2.977 819 341 625 67(11) |
| Period derivative, |$\dot{P}$| (× 10−20) | 1.108(9) | 2.0569(5) | 2.9788(3) | 0.1522(4) |
| Parallax, π (mas) | – | 2.50(36) | 1.53(11) | – |
| DM (cm−3pc) | 25.00(13) | 4.585(9) | 8.983(3) | 22.72(3) |
| DM1 (cm−3pc yr−1) | −0.03(2) | 0.0005(7) | 0.000 19(5) | 0.0008(5) |
| DM2 (cm−3pc yr−2) | 0.002(4) | 0.0000(3) | 0.000 006(26) | 0.0001(3) |
| Orbital period, Pb (d) | 56.307 796 17(7) | – | 6.838 902 615 32(19) | 93.015 893 90(5) |
| Epoch of periastron, T0 (MJD) | 49 878.125(11) | – | 50 313.7121(7) | 49 419.709(3) |
| Projected semimajor axis, x (lt-s) | 20.163 1167(16) | – | 10.164 1056(3) | 18.912 5228(5) |
| Longitude of periastron, ω0 (deg) | 78.09(7) | – | 200.81(4) | 14.337(11) |
| Orbital eccentricity, e | 1.2861(14)× 10−4 | – | 1.9323(12)× 10−5 | 2.5525(5)× 10−4 |
| κ = e × sin ω0 | – | – | −6.866(12)× 10−6 | – |
| η = e × cos ω0 | – | – | −1.8062(12)× 10−5 | – |
| Time of asc. node (MJD) | – | – | 50 309.897 241 07(6) | – |
| First derivative of x, |$\dot{x}$| | – | – | 8.2(7)× 10−15 | – |
| Derived parameters | ||||
| Gal. longitude, l (deg) | 60.9 | 10.9 | 47.8 | 87.7 |
| Gal. latitude, b (deg) | −13.2 | −45.4 | −42.1 | −26.3 |
| LK Px Distance, d (pc) | – | |$382_{-47}^{+61}$| | |$645_{-41}^{+47}$| | – |
| Composite PM, μ (mas yr−1) | 10.8(7) | 52.07(14) | 13.05(8) | 6.07(15) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.34 | 1.2(2) | 0.43(3) | 0.038 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.041 | −0.06(1) | −0.30(2) | −0.053 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.079 | 0.008(1) | −0.007(1) | −0.03 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.891 | 0.9(2) | 2.85(1) | 0.198 |
| Characteristic age, τc (Gyr) | 10.6 | 8.9 | 8.9 | 23.9 |
| Surface magnetic field, B (× 108 G) | 2.3 | 2.1 | 6.9 | 0.8 |
| Min. companion mass (M⊙) | 0.17 | – | 0.39 | 0.11 |
Timing model parameters for PSRs J2317+1439 and J2322+2057. See caption of Table 2 for a description of this table.
| PSR name . | J2317+1439 . | J2322+2057 . |
|---|---|---|
| MJD range | 50458–56794 | 53905–56788 |
| Number of TOAs | 555 | 229 |
| rms timing residual (μs) | 2.4 | 5.9 |
| Reference epoch (MJD) | 55000 | 55000 |
| Measured parameters | ||
| Right ascension, α | 23:17:09.236 614(11) | 23:22:22.335 16(7) |
| Declination, δ | 14:39:31.2563(4) | 20:57:02.6772(14) |
| Proper motion in α (mas yr−1) | −1.19(7) | −18.4(4) |
| Proper motion in δ (mas yr−1) | 3.33(13) | −15.4(5) |
| Period, P (ms) | 3.445 251 125 644 88(18) | 4.808 428 289 4641(17) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.2433(3) | 0.9661(20) |
| Parallax, π (mas) | 0.7(3) | – |
| DM (cm−3pc) | 21.902(6) | 13.36(4) |
| DM1 (cm−3pc yr−1) | −0.0007(8) | −0.003(5) |
| DM2 (cm−3pc yr−2) | −0.0002(2) | −0.000(1) |
| Orbital period, Pb (d) | 2.459 331 503 27(12) | – |
| Epoch of periastron, T0 (MJD) | 49 300.92(11) | – |
| Projected semimajor axis, x (lt-s) | 2.313 948 74(18) | – |
| Longitude of periastron, ω0 (deg) | 66(16) | – |
| Orbital eccentricity, e | 5.7(16)× 10−7 | – |
| κ = esin ω0 | 5.2(16)× 10−7 | – |
| η = ecos ω0 | 2.3(16)× 10−7 | – |
| Time of asc. node (MJD) | 49 300.472 4327(3) | – |
| Derived parameters | ||
| Gal. longitude, l (deg) | 91.4 | 96.5 |
| Gal. latitude, b (deg) | −42.4 | −37.3 |
| LK Px Distance, d (pc) | |$1011_{-220}^{+348}$| | – |
| Composite PM, μ (mas yr−1) | 3.53(13) | 24.0(4) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.011(4) | 0.54 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.10(3) | −0.09 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.017(6) | −0.02 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.35(4) | 0.538 |
| Characteristic age, τc (Gyr) | 15.6 | 14.2 |
| Surface magnetic field, B (× 108 G) | 1.1 | 1.6 |
| Min. companion mass (M⊙) | 0.16 | – |
| PSR name . | J2317+1439 . | J2322+2057 . |
|---|---|---|
| MJD range | 50458–56794 | 53905–56788 |
| Number of TOAs | 555 | 229 |
| rms timing residual (μs) | 2.4 | 5.9 |
| Reference epoch (MJD) | 55000 | 55000 |
| Measured parameters | ||
| Right ascension, α | 23:17:09.236 614(11) | 23:22:22.335 16(7) |
| Declination, δ | 14:39:31.2563(4) | 20:57:02.6772(14) |
| Proper motion in α (mas yr−1) | −1.19(7) | −18.4(4) |
| Proper motion in δ (mas yr−1) | 3.33(13) | −15.4(5) |
| Period, P (ms) | 3.445 251 125 644 88(18) | 4.808 428 289 4641(17) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.2433(3) | 0.9661(20) |
| Parallax, π (mas) | 0.7(3) | – |
| DM (cm−3pc) | 21.902(6) | 13.36(4) |
| DM1 (cm−3pc yr−1) | −0.0007(8) | −0.003(5) |
| DM2 (cm−3pc yr−2) | −0.0002(2) | −0.000(1) |
| Orbital period, Pb (d) | 2.459 331 503 27(12) | – |
| Epoch of periastron, T0 (MJD) | 49 300.92(11) | – |
| Projected semimajor axis, x (lt-s) | 2.313 948 74(18) | – |
| Longitude of periastron, ω0 (deg) | 66(16) | – |
| Orbital eccentricity, e | 5.7(16)× 10−7 | – |
| κ = esin ω0 | 5.2(16)× 10−7 | – |
| η = ecos ω0 | 2.3(16)× 10−7 | – |
| Time of asc. node (MJD) | 49 300.472 4327(3) | – |
| Derived parameters | ||
| Gal. longitude, l (deg) | 91.4 | 96.5 |
| Gal. latitude, b (deg) | −42.4 | −37.3 |
| LK Px Distance, d (pc) | |$1011_{-220}^{+348}$| | – |
| Composite PM, μ (mas yr−1) | 3.53(13) | 24.0(4) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.011(4) | 0.54 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.10(3) | −0.09 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.017(6) | −0.02 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.35(4) | 0.538 |
| Characteristic age, τc (Gyr) | 15.6 | 14.2 |
| Surface magnetic field, B (× 108 G) | 1.1 | 1.6 |
| Min. companion mass (M⊙) | 0.16 | – |
Timing model parameters for PSRs J2317+1439 and J2322+2057. See caption of Table 2 for a description of this table.
| PSR name . | J2317+1439 . | J2322+2057 . |
|---|---|---|
| MJD range | 50458–56794 | 53905–56788 |
| Number of TOAs | 555 | 229 |
| rms timing residual (μs) | 2.4 | 5.9 |
| Reference epoch (MJD) | 55000 | 55000 |
| Measured parameters | ||
| Right ascension, α | 23:17:09.236 614(11) | 23:22:22.335 16(7) |
| Declination, δ | 14:39:31.2563(4) | 20:57:02.6772(14) |
| Proper motion in α (mas yr−1) | −1.19(7) | −18.4(4) |
| Proper motion in δ (mas yr−1) | 3.33(13) | −15.4(5) |
| Period, P (ms) | 3.445 251 125 644 88(18) | 4.808 428 289 4641(17) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.2433(3) | 0.9661(20) |
| Parallax, π (mas) | 0.7(3) | – |
| DM (cm−3pc) | 21.902(6) | 13.36(4) |
| DM1 (cm−3pc yr−1) | −0.0007(8) | −0.003(5) |
| DM2 (cm−3pc yr−2) | −0.0002(2) | −0.000(1) |
| Orbital period, Pb (d) | 2.459 331 503 27(12) | – |
| Epoch of periastron, T0 (MJD) | 49 300.92(11) | – |
| Projected semimajor axis, x (lt-s) | 2.313 948 74(18) | – |
| Longitude of periastron, ω0 (deg) | 66(16) | – |
| Orbital eccentricity, e | 5.7(16)× 10−7 | – |
| κ = esin ω0 | 5.2(16)× 10−7 | – |
| η = ecos ω0 | 2.3(16)× 10−7 | – |
| Time of asc. node (MJD) | 49 300.472 4327(3) | – |
| Derived parameters | ||
| Gal. longitude, l (deg) | 91.4 | 96.5 |
| Gal. latitude, b (deg) | −42.4 | −37.3 |
| LK Px Distance, d (pc) | |$1011_{-220}^{+348}$| | – |
| Composite PM, μ (mas yr−1) | 3.53(13) | 24.0(4) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.011(4) | 0.54 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.10(3) | −0.09 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.017(6) | −0.02 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.35(4) | 0.538 |
| Characteristic age, τc (Gyr) | 15.6 | 14.2 |
| Surface magnetic field, B (× 108 G) | 1.1 | 1.6 |
| Min. companion mass (M⊙) | 0.16 | – |
| PSR name . | J2317+1439 . | J2322+2057 . |
|---|---|---|
| MJD range | 50458–56794 | 53905–56788 |
| Number of TOAs | 555 | 229 |
| rms timing residual (μs) | 2.4 | 5.9 |
| Reference epoch (MJD) | 55000 | 55000 |
| Measured parameters | ||
| Right ascension, α | 23:17:09.236 614(11) | 23:22:22.335 16(7) |
| Declination, δ | 14:39:31.2563(4) | 20:57:02.6772(14) |
| Proper motion in α (mas yr−1) | −1.19(7) | −18.4(4) |
| Proper motion in δ (mas yr−1) | 3.33(13) | −15.4(5) |
| Period, P (ms) | 3.445 251 125 644 88(18) | 4.808 428 289 4641(17) |
| Period derivative, |$\dot{P}$| (× 10−20) | 0.2433(3) | 0.9661(20) |
| Parallax, π (mas) | 0.7(3) | – |
| DM (cm−3pc) | 21.902(6) | 13.36(4) |
| DM1 (cm−3pc yr−1) | −0.0007(8) | −0.003(5) |
| DM2 (cm−3pc yr−2) | −0.0002(2) | −0.000(1) |
| Orbital period, Pb (d) | 2.459 331 503 27(12) | – |
| Epoch of periastron, T0 (MJD) | 49 300.92(11) | – |
| Projected semimajor axis, x (lt-s) | 2.313 948 74(18) | – |
| Longitude of periastron, ω0 (deg) | 66(16) | – |
| Orbital eccentricity, e | 5.7(16)× 10−7 | – |
| κ = esin ω0 | 5.2(16)× 10−7 | – |
| η = ecos ω0 | 2.3(16)× 10−7 | – |
| Time of asc. node (MJD) | 49 300.472 4327(3) | – |
| Derived parameters | ||
| Gal. longitude, l (deg) | 91.4 | 96.5 |
| Gal. latitude, b (deg) | −42.4 | −37.3 |
| LK Px Distance, d (pc) | |$1011_{-220}^{+348}$| | – |
| Composite PM, μ (mas yr−1) | 3.53(13) | 24.0(4) |
| |$\dot{P}_{{\rm shk}} (\times 10^{-20})$| | 0.011(4) | 0.54 |
| |$\dot{P}_{{\rm kz}} (\times 10^{-20})$| | −0.10(3) | −0.09 |
| |$\dot{P}_{{\rm dgr}} (\times 10^{-20})$| | −0.017(6) | −0.02 |
| |$\dot{P}_{{\rm int}} (\times 10^{-20})$| | 0.35(4) | 0.538 |
| Characteristic age, τc (Gyr) | 15.6 | 14.2 |
| Surface magnetic field, B (× 108 G) | 1.1 | 1.6 |
| Min. companion mass (M⊙) | 0.16 | – |
4.1 PSR J0030+0451
A timing ephemeris for this isolated pulsar has been published by Abdo et al. (2009) with a joint analysis of gamma-ray data from the FermiGamma-ray Space Telescope. Because the authors used the older DE200 version of the Solar system ephemeris model, we report here updated astrometric measurements. While our measured proper motion is consistent with the Abdo et al. (2009) value, we get a significantly lower parallax value π = 2.79 ± 0.23 mas that we attribute partly to the errors in the DE200 ephemeris. Indeed reverting back to the DE200 in our analysis yields an increased value of the parallax by 0.3 mas but still below the parallax π = 4.1 ± 0.3 mas determined by Abdo et al. (2009).
4.2 PSR J0034−0534
PSR J0034−0534 is a very faint MSP when observed at L band with a flux density S1400 = 0.01 mJy leading to profiles with very low S/N compared to most other MSPs considered here. Helped by the better timing precision at 350 MHz, we were able to improve on the previously published composite proper motion μ = 31 ± 9 mas yr−1 by Hobbs et al. (2005) to μ = 12.1 ± 0.5 mas yr−1. We also measure the eccentricity e = (4.3 ± 0.7) × 10−6 of this system for the first time. Even with our improved timing precision characterized by a timing residuals rms of 4 μs, the detection of the parallax signature (at most 2.4 μs according to Abdo et al. 2010) is still out of reach.
4.3 PSR J0218+4232
The broad shape of the pulse profile of this pulsar (with a duty cycle of about 50 per cent, see Fig. A3) and its low flux density limit our timing precision to about 7 μs and, therefore, its use for GWB detection. Du et al. (2014) recently published the pulsar composite proper motion μ = 6.53 ± 0.08 mas yr−1 from very long baseline interferometry (VLBI). With EPTA data, we find μ = 6.14 ± 0.09 mas yr−1. This value is in disagreement with the VLBI result. A possible explanation for this discrepancy is that Du et al. (2014) overfitted their model with five parameters for five observing epochs. Du et al. (2014) also reported a distance |$d=6.3_{-2.3}^{+8.0}$| kpc from VLBI parallax measurement. Verbiest & Lorimer (2014) later argued that the Du et al. (2014) parallax suffers from the Lutz–Kelker (LK) bias and corrected the distance to be |$d=3.2_{-0.6}^{+0.9}$| kpc. This distance is consistent with the 2.5–4 kpc range estimated from the properties of the white dwarf companion to PSR J0218+4232 (Bassa, van Kerkwijk & Kulkarni 2003). Even with the Verbiest & Lorimer (2014) 3σ lowest distance estimate, the parallax would induce a signature on the timing residuals of less than 800 ns (Lorimer & Kramer 2004), which is far from our current timing precision. We therefore cannot further constrain the distance with our current data set. Our measurement of the system's eccentricity e = (6.8 ± 0.4) × 10−6 is significantly lower than the previously reported value e = (22 ± 2) × 10−6 by Hobbs et al. (2004b).
4.4 PSR J0610−2100
With a very low-mass companion (0.02 M⊙ < Mc < 0.05 M⊙), PSR J0610−2100 is a member of the ‘black widow’ family, which are a group of (often) eclipsing binary MSPs believed to be ablating their companions. Here we report on a newly measured eccentricity, e = (2.9 ± 0.8) × 10−5, and an improved proper motion (μα = 9.0 ± 0.1 mas yr−1 and μδ = 16.78 ± 0.12 mas yr−1) compared to the previous values (μα = 7 ± 3 mas yr−1 and μδ = 11 ± 3 mas yr−1) from Burgay et al. (2006) derived with slightly more than two years of data. It is interesting to note that, in contrast to another well-studied black widow pulsar, PSR J2051−0827 (Lazaridis et al. 2011), no secular variations of the orbital parameters are detected in this system. There is also no evidence for eclipses of the radio signal in our data.
We checked our data for possible orbital-phase dependent DM-variation that could account for the new measurement of the eccentricity. We found no evidence for this within our DM precision. We also obtained consistent results for the eccentricity and longitude of periastron after removing TOAs for given orbital phase ranges.
4.5 PSR J0613−0200
For PSR J0613−0200, we measure a parallax π = 1.25 ± 0.13 mas that is consistent with the value published in Verbiest et al. (2009, π = 0.8 ± 0.35 mas). In addition, we report on the first detection of the orbital period derivative |$\dot{P_{\rm b}} = (4.8 \pm 1.1) \times 10^{-14}$| thanks to our 16-yr baseline. This result will be discussed further in Sec-tion 5.3. Finally, we improve on the precision of the proper motion with μα = −1.822 ± 0.008 mas yr−1 and μδ = −10.355 ± 0.017 mas yr−1.
4.6 PSR J0621+1002
Despite being the slowest rotating MSP of this data set with a period of almost 30 ms, PSR J0621+1002 has a profile with a narrow peak feature of width ∼500 μs. We are able to measure the precession of the periastron |$\dot{\omega }=0.0113\pm 0.0006$| deg yr−1 and find it to be within 1σ of the value reported by Nice, Stairs & Kasian (2008) using Arecibo data. We also find a similar value of the proper motion to Splaver et al. (2002).
4.7 PSR J0751+1807
PSR J0751+1807 is a 3.5-ms pulsar in an approximately 6-h orbit. Nice et al. (2005) originally reported a parallax π = 1.6 ± 0.8 mas and a measurement of the orbital period derivative |$\dot{P_{\rm b}}=(-6.4 \pm 0.9) \times 10^{-14}$|. Together with their detection of the Shapiro delay, they initially derived a large pulsar mass mp = 2.1 ± 0.2 M⊙. Nice et al. (2008) later corrected the orbital period derivative measurement to |$\dot{P}_{\rm b}=(-3.1\pm 0.5) \times 10^{-14}$|, giving a much lower pulsar mass mp = 1.26 ± 0.14 M⊙. Here we report on a parallax π = 0.82 ± 0.17 mas and |$\dot{P}_{{\rm b}} = (-3.5 \pm 0.25) \times 10^{-14}$| that is similar to the value in Nice et al. (2008). However, we measured a precise composite proper motion of 13.7 ± 0.3 mas yr−1, inconsistent with the result (6 ± 2 mas yr−1) from Nice et al. (2005). Nice et al. (2008) explained the issue found with the timing solution presented in Nice et al. (2005) but did not provide an update of the proper motion for comparison with our value. We are also able to measure an apparent change in the semimajor axis |$\dot{x}=(-4.9\pm 0.9) \times 10^{-15}$|. Finally, we applied the orthometric parametrization of the Shapiro delay to get h3 = (3.0 ± 0.6) × 10−7 and ς = 0.81 ± 0.17. The interpretation of these results will be discussed in Section 5.4.
4.8 PSR J0900−3144
With about seven years of timing data available for PSR J0900−3144 (discovered by Burgay et al. 2006), we detect the proper motion for the first time, revealing it to be one of the lowest composite proper motion objects among our data set with μ = 2.26 ± 0.07 mas yr−1. We also uncover a marginal signature of the parallax π = 0.77 ± 0.44 mas. However, we do not detect the signature of the Shapiro delay despite the improvement in timing precision compared to Burgay et al. (2006). Following the criterion introduced in Section 3.1, we get h3o = 0.4 μs. With δTOAs = 4.27 μs and NTOAs = 875, we find ξ = 0.14 μs. Hence, given ξ < h3o, we argue for i ≲ 60° to explain the lack of Shapiro delay detection in this system.
4.9 PSR J1012+5307
Lazaridis et al. (2009) previously presented a timing solution using a subset of these EPTA data to perform a test on gravitational dipole radiation and variation of the gravitational constant, |$\dot{G}$|. The |$\dot{x}$| and |$\dot{P_{\rm b}}$| parameters we present here are consistent with the values from Lazaridis et al. (2009) but we improve on the uncertainties of these parameters by factors of 2 and 3, respectively. None the less, we note that our value for the parallax π = 0.71 ± 0.17 mas differs by less than 2σ from the value measured by Lazaridis et al. (2009) using the DE405 ephemeris.
4.10 PSR J1022+1001
As recently pointed out by van Straten (2013), this source requires a high level of polarimetric calibration in order to reach the best timing precision. Indeed, by carefully calibrating their data, van Straten (2013) greatly improved on the timing model of Verbiest et al. (2009) and successfully unveiled the precession of the periastron |$\dot{\omega }=0.0097\pm 0.0023$| deg yr−1, the presence of Shapiro delay and the secular variation of |$\dot{x}$|. Here we find similar results with |$\dot{\omega }=0.010 \pm 0.002$| deg yr−1 and a 2σ consistent |$\dot{x}$| with a completely independent data set. None the less, we cannot confirm the measurement of Shapiro delay with our data set. For this pulsar, we get h3o = 0.62 μs. With ξ = 0.14 μs, our constraint implies that the inclination angle i ≲ 60°, in agreement with the result presented by van Straten (2013).
4.11 PSR J1024−0719
Hotan et al. (2006) were the first to announce a parallax π = 1.9 ± 0.4 mas for this nearby and isolated MSP that shows a large amount of red noise (Caballero et al. 2015). More recently, Espinoza et al. (2013) used a subset of this EPTA data set to produce an ephemeris and detected gamma-ray pulsations from this pulsar. The authors assumed the LK bias-corrected distance (Verbiest et al. 2012) from the Hotan et al. (2006) parallax value to estimate its gamma-ray efficiency. However, it should be noted that Verbiest et al. (2009) did not report on the measurement of the parallax using an extended version of the Hotan et al. (2006) data set. With this independent data set we detect a parallax π = 0.80 ± 0.17 mas, a value inconsistent with the early measurement reported by Hotan et al. (2006). A possible explanation for this discrepancy could be that Hotan et al. (2006) did not include a red noise model in their analysis.
4.12 PSR J1455−3330
The last timing solution for this pulsar was published by Hobbs et al. (2004b) and characterized by an rms of 67 μs. Thanks to our nine years of data with an rms of less than 3 μs, we successfully detect the signature of the proper motion μα = 7.88 ± 0.08 mas yr−1 and μδ = −2.23 ± 0.19 mas yr−1, the parallax π = 1.04 ± 0.35 mas and the secular variation of the semimajor axis, |$\dot{x}=(-1.7\pm 0.4)\times 10^{-14}$| for the first time.
4.13 PSR J1600−3053
This 3.6-ms pulsar can be timed at very high precision thanks to the ∼45 μs wide peak on the right edge of its profile (see Fig. A3). We present here a precise measurement of the parallax π = 0.64 ± 0.07 mas, a value marginally consistent with the π = 0.2 ± 0.15 mas from Verbiest et al. (2009). We also show a large improvement on the Shapiro delay detection through the use of the orthometric parametrization (Freire & Wex 2010) with h3 = (3.3 ± 0.2) × 10−7 and ς = 0.68 ± 0.05. The resulting mass measurement of this system is discussed in Section 5.4.
4.14 PSR J1640+2224
Löhmer et al. (2005) used early Arecibo and Effelsberg data to report on the tentative detection of Shapiro delay for this wide binary system in a 6-month orbit. From this measurement they deduced the orientation of the system to be nearly edge-on (78° < i < 88°) and a companion mass for the white dwarf |$m_{\rm p}=0.15_{-0.05}^{+0.08} {\rm \,M}_{{\odot }}$|. We cannot constrain the Shapiro delay with the current EPTA data, even though our data comprise almost twice the number of TOAs with a similar overall timing precision. The parallax signature in the residuals also remains undetected (based on Bayesian evidence4) but we find a significant |$\dot{x}=(1.07\pm 0.16)\times 10^{-14}$|, consistent with the upper limit set by Löhmer et al. (2005).
4.15 PSR J1643−1224
Using PPTA data, Verbiest et al. (2009) previously announced a parallax value π = 2.2 ± 0.4 mas that is marginally consistent with our value of π = 1.17 ± 0.26 mas. We get a similar proper motion and |$\dot{x}=(-4.79\pm 0.15) \times 10^{-14}$|, albeit measured with a greater precision.
4.16 PSR J1713+0747
PSR J1713+0747 is one of the most precisely timed pulsars over two decades (Verbiest et al. 2009; Zhu et al. 2015). Our proper motion and parallax values are consistent with the ones from Verbiest et al. (2009) and Zhu et al. (2015). None the less we cannot detect any hint of the orbital period derivative |$\dot{P_{{\rm b}}}$|. The measurement of the Shapiro delay yields the following masses of the system, |$m_{\rm p}=1.33_{-0.08}^{+0.09} {\rm \,M}_{{\odot }}$| and |$m_{\rm c}=0.289_{-0.011}^{+0.013} {\rm \,M}_{{\odot }}$|, in very good agreement with Zhu et al. (2015).
When inspecting the residuals of PSR J1713+0747, we noticed successive TOAs towards the end of 2008 that arrived significantly earlier (∼3 μs) than predicted by our ephemeris (see top panel of Fig. 2). After inspection of the original archives and comparison with other high precision data sets like those on PSRs J1744−1134 and J1909−3744, we ruled out any instrumental or clock issue as an explanation for this shift. We therefore attribute this effect to a deficiency of the electron content towards the line of sight of the pulsar. This event has also been observed by the other PTAs (Coles et al. 2015; Zhu et al. 2015) and interpreted as possibly a kinetic shell propagating through the interstellar medium (Coles et al. 2015) followed by a rarefaction of the electron content.
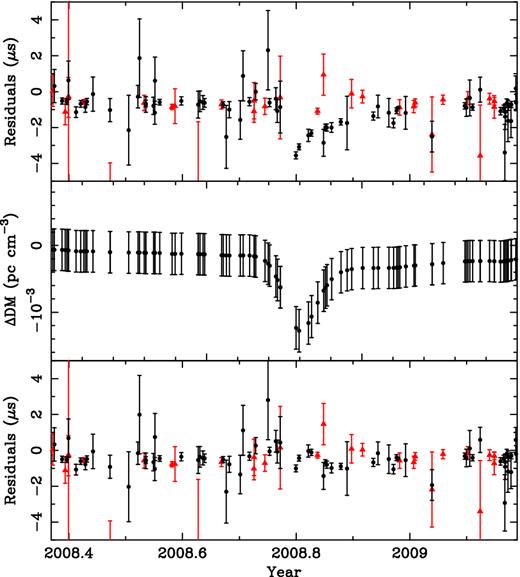
Top panel: zoom-in on the PSR J1713+0747 residuals (black dots and red triangles are L- and S-band data, respectively). Middle panel: DM signal from the maximum likelihood DM model incorporating the shapelet basis functions (see Section 4.16 for details). The bottom panel shows the residuals after subtraction of the DM signal. The uncertainties on the DM signal come directly from the 1σ uncertainties on the shapelet amplitudes used to model the event, obtained from the full Bayesian analysis.
To model this DM event we used shapelet basis functions. A thorough description of the shapelet formalism can be found in Refregier (2003), with astronomical uses being described in e.g. Refregier & Bacon (2003), Kelly & McKay (2004) and Lentati, Alexander & Hobson (2015a). Shapelets are a complete orthonormal set of basis functions that allow us to recreate the effect of non-time-stationary DM variations in a statistically robust manner, simultaneously with the rest of the analysis. We used the Bayesian evidence to determine the number of shapelet coefficients to include in the model (only one coefficient was necessary in this study, i.e. the shapelet is given by a Gaussian). Our priors on the location of the event span the entire data set, while we assume an event width of between five days and one year. The maximum likelihood results indicate an event centred around MJD 54761 with a width of 10 d. The resulting DM signal (including the shapelet functions) and the residuals corrected from it are plotted in the middle and bottom panels of Fig. 2, respectively. The DM model hence predicts a drop of (1.3 ± 0.4) × 10−3 pc cm−3.
4.17 PSR J1721−2457
Thanks to an additional five years of data compared to Janssen et al. (2010), the proper motion of this isolated MSP is now better constrained. Our current timing precision is most likely limited by the pulsar's large duty cycle (see Fig. A3) and the apparent absence of sharp features in the profile. The flux density of this pulsar is also quite low with a value of 1 mJy at 1400 MHz.
4.18 PSR J1730−2304
This low-DM and isolated MSP has a profile with multiple pulse components (see Fig. A3). As this pulsar lies very near to the ecliptic plane (β = 0| $_{.}^{\circ}$|19), we are unable to constrain its proper motion in declination, similar to the previous study (Verbiest et al. 2009). Assuming the NE2001 distance, the expected parallax timing signature would be as large as 2.3 μs. We report here on a tentative detection of the parallax, π = 0.86 ± 0.32 mas.
4.19 PSR J1738+0333
After the determination of the masses in this system from optical observations (Antoniadis et al. 2012), Freire et al. (2012b) used the precise measurements of the proper motion, parallax and |$\dot{P_{\rm b}}$| in this binary system to put constraints on scalar–tensor theories of gravity. Our measured proper motion remains consistent with their measurements. With a longer baseline and more observations recorded with the sensitive Arecibo Telescope, Freire et al. (2012b) were able to detect the parallax and the orbital period derivative of the system. However, we do not yet reach the sensitivity to detect these two parameters with our data set.
4.20 PSR J1744−1134
This isolated MSP was thought to show long-term timing noise by Hotan et al. (2006) even with a data set shorter than three years. In our data set, we detect a (red) timing noise component (see Caballero et al. 2015). The rms of the time-domain noise signal is ∼ 0.4 μs, but has a peak-to-peak variation of ∼ 2 μs. The higher latter value, however, is due to a bump which appears localized in time (MJD ∼ 54000–56000). As discussed in Caballero et al. (2015), non-stationary noise from instrumental instabilities may cause such effects, but data with better multitelescope coverage are necessary to verify such a possibility. This is further investigated in Lentati et al. (2016) using a more extended data set from the International Pulsar Timing Array (Verbiest et al. 2016).
4.21 PSR J1751−2857
Stairs et al. (2005) announced this wide (Pb = 111 d) binary MSP after timing it for four years with an rms of 28 μs without a detection of the proper motion. With six years of data at a much lower rms, we are able to constrain its proper motion (μα = −7.4 ± 0.1 mas yr−1 and μδ = −4.3 ± 1.2 mas yr−1) and detect |$\dot{x}=(4.6\pm 0.8) \times 10^{-14}$|.
4.22 PSR J1801−1417
This isolated MSP was discovered by Lorimer et al. (2006). With increased timing precision, we measure a new composite proper motion μ = 11.3 ± 0.3 mas yr−1. As our data set for this pulsar does not include multifrequency information; we cannot rule out DM variations.
4.23 PSR J1802−2124
Ferdman et al. (2010) recently reported on the mass measurement of this system by combining TOAs from the Green Bank, Parkes and Nançay radio telescopes. Therefore, our data set shows no improvement in the determination of the system parameters but gives consistent results to Ferdman et al. (2010).
4.24 PSR J1804−2717
With an rms timing residual improved by a factor of 25 compared to the last results published by Hobbs et al. (2004b), we obtain a reliable measurement of the proper motion of this system. Assuming the distance based on the NE2001 model dNE2001 = 780 pc, the parallax timing signature can amount to 1.5 μs, still below our current timing precision.
4.25 PSR J1843−1113
This isolated pulsar discovered by Hobbs et al. (2004a) is the second fastest spinning MSP in our data set. Its mean flux density (S1400 = 0.6 mJy) is among the lowest, limiting our current timing precision to ∼ 1 μs. For the first time, we report the detection of the proper motion μα = −1.91 ± 0.07 mas yr−1 and μδ = −3.2 ± 0.3 mas yr−1 and still low-precision parallax π = 0.69 ± 0.33 mas.
4.26 PSR J1853+1303
Our values of proper motion and semimajor axis change are consistent with the recent work by Gonzalez et al. (2011) using high-sensitivity Arecibo and Parkes data, though there is no evidence for the signature of the parallax in our data, most likely due to our less precise data set.
4.27 PSR J1857+0943 (B1855+09)
Our measured parallax π = 0.7 ± 0.26 mas is lower than, but still compatible with, the value reported by Verbiest et al. (2009). We also report a marginal detection of |$\dot{x} = (-2.7 \pm 1.1) \times 10^{-15}$|. Our measurement of the Shapiro delay is also similar to the previous result from Verbiest et al. (2009).
4.28 PSR J1909−3744
PSR J1909−3744 (Jacoby et al. 2003) is the most precisely timed source with an rms timing residual of about 100 ns. As these authors pointed out, this pulsar's profile has a narrow peak with a pulse duty cycle of 1.5 per cent (43 μs) at full width at half-maximum (see Fig. A4). Unfortunately its declination makes it only visible with the NRT but it will be part of the SRT timing campaign. We improved the precision of the measurement of the orbital period derivative |$\dot{P_{\rm b}}$| by a factor of 6 compared to Verbiest et al. (2009) and our constraint on |$\dot{x}$| is consistent with their tentative detection.
4.29 PSR J1910+1256
We get similar results as recently published by Gonzalez et al. (2011) with Arecibo and Parkes data. In addition, we uncover a marginal signature of the parallax π = 1.44 ± 0.74 mas, consistent with the upper limit set by Gonzalez et al. (2011).
4.30 PSR J1911+1347
With a pulse width at 50 per cent of the main peak amplitude (see Fig. A4), W50 = 89 μs (only twice the width of J1909−3744), this isolated MSP is potentially a good candidate for PTAs. Unfortunately it has so far been observed at the JBO and NRT observatories only and no multifrequency observations are available. Based on this work, this pulsar has now been included in the observing list at the other EPTA telescopes. Despite the good timing precision we did not detect the parallax but we did measure the proper motion for the first time with μα = −2.90 ± 0.04 mas yr−1 and μδ = −3.74 ± 0.06 mas yr−1.
4.31 PSR J1911−1114
The last ephemeris for this pulsar was published by Toscano et al. (1999a) 16 years ago using the DE200 planetary ephemeris. Our EPTA data set spans three times longer than the one from Toscano et al. (1999a). We hence report here on a greatly improved position, proper motion (μα = −13.75 ± 0.16 mas yr−1 and μδ = −9.1 ± 1.0 mas yr−1) and a new eccentricity e = (1.6 ± 1.0) × 10−6, lower by a factor of 10 than the previous measurement.
4.32 PSR J1918−0642
PSR J1918−0642 is another MSP studied by Janssen et al. (2010) with EPTA data. Compared to Janssen et al. (2010) we extended the baseline with an additional five years of data. We unveil the signature of Shapiro delay in this system with h3 = (8.6 ± 1.2) × 10−7 and ς = 0.91 ± 0.04. The masses of the system are discussed in Section 5.4.
4.33 PSR J1939+2134 (B1937+21)
Thanks to the addition of early Nançay DDS TOAs, our data set span over 24 years for this pulsar. This pulsar has been long known to show significant DM variations as well as a high level of timing noise (Kaspi et al. 1994); see residuals in Fig. A2. A possible interpretation of this red noise is the presence of an asteroid belt around the pulsar (Shannon et al. 2013b). Despite this red noise, the timing signature of the parallax has successfully been extracted to get π = 0.22 ± 0.08 mas, a value consistent with Kaspi et al. (1994) and Verbiest et al. (2009).
4.34 PSR J1955+2908 (B1953+29)
PSR J1955+2908 is another MSP recently analysed by Gonzalez et al. (2011). With an independent data set, we get similar results to Gonzalez et al. (2011). We report here on the tentative detection of |$\dot{x}=(4.0\pm 1.4) \times 10^{-14}$|.
4.35 PSR J2010−1323
This isolated MSP was discovered a decade ago (Jacoby et al. 2007) and no update on the pulsar's parameters has been published since then. Hence we announce here the detection of the proper motion μα = −2.53 ± 0.09 mas yr−1 and μδ = −5.7 ± 0.4 mas yr−1. Assuming the NE2001 distance of 1 kpc, the parallactic timing signature would amount to 1.17 μs but was not detected in our data.
4.36 PSR J2019+2425
Compared to the Arecibo 430-MHz data set used by Nice et al. (2001), the EPTA timing precision for this pulsar is limited due to its low flux density at 1400 MHz. Because of this, we are not able to measure the secular change of the projected semimajor axis |$\dot{x}$|.
4.37 PSR J2033+1734
In spite of a narrow peak of width ∼160 μs this MSP has a very large timing rms of 14 μs. With the absence of obvious systematics in the residuals, we attribute the poor timing precision to the extremely low flux density of this pulsar at 1400 MHz, S1400 = 0.1 mJy where all of our observations were performed. Indeed, this pulsar was discovered by Ray et al. (1996) with the Arecibo telescope at 430 MHz and later followed up by Splaver (2004) still at 430 and 820 MHz with the Green Bank 140-ft telescope. Here, we report with an independent data set at 1400 MHz a similar proper motion result to Splaver (2004).
4.38 PSR J2124−3358
For the isolated PSR J2124−3358, our measured proper motion is consistent with the already precise value published by Verbiest et al. (2009). Our parallax π = 2.50 ± 0.36 mas is also consistent with their results but with a better precision.
4.39 PSR J2145−0750
Despite its rotational period of 16 ms PSR J2145−0750 is characterized by a timing rms of 1.8 μs thanks to its narrow leading peak and large average flux density, S1400 = 7.2 mJy. The EPTA data set does not show any evidence for a variation of the orbital period of PSR J2145−0750 or a precession of periastron, even though Verbiest et al. (2009) reported a marginal detection with a slightly shorter data span characterized by a higher rms timing residual. On the other hand, we detect a significant |$\dot{x}=(8.2\pm 0.7)\times 10^{-15}$|, which is not consistent with the marginal detection, |$\dot{x}=(-3\pm 1.5)\times 10^{-15}$|, reported by Verbiest et al. (2009).
4.40 PSR J2229+2643
With eight years of data on PSR J2229+2643, we measure μα = −1.73 ± 0.12 mas yr−1 and μδ = −5.82 ± 0.15 mas yr−1. Our measured μδ is inconsistent with the last timing solution by Wolszczan et al. (2000) using the DE200 ephemeris (μα = 1 ± 4 mas yr−1 and μδ = −17 ± 4 mas yr−1). Given our much smaller timing residual rms, our use of the superior DE421 model and longer baseline, we are confident that our value is more reliable. The expected timing signature of the parallax (0.7 μs) is too small to be detected with the current data set. Note that the early Effelsberg data recorded with the EPOS backend included in Wolszczan et al. (2000) are not part of this data set.
4.41 PSR J2317+1439
Compared to Camilo, Nice & Taylor (1996) we are able to constrain the proper motion (μα = −1.19 ± 0.07 mas yr−1 and μδ = 3.33 ± 0.13 mas yr−1) and eccentricity e = (5.7 ± 1.6) × 10−7 of the system through the use of the ELL1 parametrization. We also detect a marginal signature of the parallax π = 0.7 ± 0.3 mas.
4.42 PSR J2322+2057
PSR J2322+2057 is an isolated MSP with a pulse profile consisting of two peaks separated by ≃ 200° (see Fig. A4). Nice & Taylor (1995) were the last to publish a timing solution for this last source in our data set. We measure a proper motion consistent with their results albeit with much greater precision, μ = 24.0 ± 0.4 mas yr−1.
5 Discussion
5.1 Distances
Summary of pulsar parallaxes and distance estimates. The columns give the pulsar name, the DM, the distance based on the NE2001 electron density model DNE2001 (Cordes & Lazio 2002), the distance based on the M2 and M3 models, DM2 and DM3 (Schnitzeler 2012), an upper limit on the distance |$D_{\dot{P}}$| (only indicated when this limit is <15 kpc; see text), the previously published parallax value πhist, our new measurement of the parallax π and the LK-bias-corrected parallax πcorr with the corresponding distance Dπ. For clarity, the values in bold show the updated or new parallax measurements as part of this work. The references for πhist can be found in Table 1.
| PSR JName . | DM . | DNE2001 . | DM2 . | DM3 . | |$D_{\dot{P}}$| . | πhist . | π . | πcorr . | Dπ . |
|---|---|---|---|---|---|---|---|---|---|
| . | (cm−3pc) . | (kpc) . | (kpc) . | (kpc) . | (kpc) . | (mas) . | (mas) . | (mas) . | (kpc) . |
| J0030+0451 | 4.33 | 0.32 | 0.30 | 0.37 | – | 4.1 ± 0.3 | 2.79 ± 0.23 | |$\mathbf {2.71_{-0.23}^{+0.23}}$| | |$\mathbf {0.35_{-0.03}^{+0.03}}$| |
| J0034−0534 | 13.76 | 0.54 | 1.27 | 1.23 | – | – | – | – | – |
| J0218+4232 | 61.25 | 2.67 | 5.85 | 8.67 | – | 0.16 ± 0.09 | – | |$0.22_{-0.05}^{+0.07}$| | |$3.15^{+0.85}_{-0.60}{}^a$| |
| J0610−2100 | 60.66 | 3.54 | 5.64 | 8.94 | <3.85 | – | – | – | – |
| J0613−0200 | 38.78 | 1.71 | 2.58 | 2.41 | <11.19 | 0.8 ± 0.35 | 1.25 ± 0.13 | |$\mathbf {1.21_{-0.13}^{+0.13}}$| | |$\mathbf {0.78_{-0.07}^{+0.08}}$| |
| J0621+1002 | 36.45 | 1.36 | 2.02 | 1.90 | – | – | – | – | – |
| J0751+1807 | 30.25 | 1.15 | 2.57 | 2.46 | <4.71 | 1.6 ± 0.8 | 0.82 ± 0.17 | |$\mathbf {0.74_{-0.17}^{+0.17}}$| | |$\mathbf {1.07_{-0.17}^{+0.24}}$| |
| J0900−3144 | 75.70 | 0.54 | 1.05 | 0.54 | – | – | 0.77 ± 0.44 | |$\mathbf {0.35_{-0.16}^{+0.32}}$| | |$\mathbf {0.81_{-0.21}^{+0.38}}$| |
| J1012+5307 | 9.02 | 0.41 | 0.69 | 0.76 | <2.14 | 1.22 ± 0.26 | 0.71 ± 0.17 | |$\mathbf {0.70_{-0.15}^{+0.15}}$| | |$\mathbf {1.15_{-0.17}^{+0.24}}$| |
| J1022+1001 | 10.25 | 0.45 | 0.81 | 0.87 | <3.3 | 1.8 ± 0.3 | 0.72 ± 0.20 | |$\mathbf {0.70_{-0.17}^{+0.18}}$| | |$\mathbf {1.09_{-0.18}^{+0.26}}$| |
| J1024−0719 | 6.49 | 0.39 | 0.46 | 0.50 | <0.43 | 1.9 ± 0.4 | 0.80 ± 0.17 | |$\mathbf {0.75_{-0.16}^{+0.16}}$| | |$\mathbf {1.08_{-0.16}^{+0.23}}$| |
| J1455−3330 | 13.56 | 0.53 | 0.98 | 0.74 | – | – | 1.04 ± 0.35 | |$\mathbf {0.49_{-0.24}^{+0.35}}$| | |$\mathbf {0.80_{-0.18}^{+0.30}}$| |
| J1600−3053 | 52.32 | 1.63 | 3.77 | 4.62 | – | 0.2 ± 0.15 | 0.64 ± 0.07 | |$\mathbf {0.62_{-0.07}^{+0.07}}$| | |$\mathbf {1.49_{-0.15}^{+0.19}}$| |
| J1640+2224 | 18.42 | 1.16 | 1.61 | 2.63 | <3.43 | – | – | – | – |
| J1643−1224 | 62.41 | 2.40 | 4.86 | >50 | – | 2.2 ± 0.4 | 1.17 ± 0.26 | |$\mathbf {0.99_{-0.27}^{+0.26}}$| | |$\mathbf {0.76_{-0.13}^{+0.19}}$| |
| J1713+0747 | 15.99 | 0.89 | 1.22 | 1.61 | – | 0.94 ± 0.05 | 0.90 ± 0.03 | |$\mathbf {0.90_{-0.03}^{+0.03}}$| | |$\mathbf {1.11_{-0.03}^{+0.04}}$| |
| J1721−2457 | 48.68 | 1.30 | 1.67 | 1.84 | <0.96 | – | – | – | – |
| J1730−2304 | 9.61 | 0.53 | 0.63 | 0.72 | <1.85 | – | 0.86 ± 0.32 | |$\mathbf {0.21_{-0.07}^{+0.38}}$| | |$\mathbf {0.90_{-0.22}^{+0.38}}$| |
| J1738+0333 | 33.80 | 1.43 | 2.60 | 3.16 | – | 0.68 ± 0.05 | – | |$0.67_{-0.05}^{+0.05}$| | |$1.45_{-0.10}^{+0.11}$| |
| J1744−1134 | 3.13 | 0.41 | 0.21 | 0.44 | <1.9 | 2.4 ± 0.1 | 2.38 ± 0.08 | |$\mathbf {2.37_{-0.08}^{+0.08}}$| | |$\mathbf {0.42_{-0.01}^{+0.01}}$| |
| J1751−2857 | 42.90 | 1.10 | 1.51 | 1.73 | <5.92 | – | – | – | – |
| J1801−1417 | 57.19 | 1.52 | 1.90 | 2.17 | <3.47 | – | – | – | – |
| J1802−2124 | 149.63 | 2.94 | 3.46 | 3.84 | – | – | 1.24 ± 0.57 | |$\mathbf {0.08_{-0.03}^{+0.13}}$| | |$\mathbf {0.64_{-0.19}^{+0.44}}$| |
| J1804−2717 | 24.57 | 0.78 | 1.29 | 1.13 | <4.73 | – | – | – | – |
| J1843−1113 | 59.95 | 1.70 | 2.08 | 2.45 | – | – | 0.69 ± 0.33 | |$\mathbf {0.11_{-0.04}^{+0.15}}$| | |$\mathbf {1.09_{-0.32}^{+0.67}}$| |
| J1853+1303 | 30.65 | 2.08 | 1.08 | 2.10 | – | 1.0 ± 0.3 | – | |$0.19_{-0.08}^{+0.42}$| | |$0.88_{-0.20}^{+0.34}$| |
| J1857+0943 | 13.30 | 1.17 | 0.87 | 1.17 | – | 1.1 ± 0.2 | 0.70 ± 0.26 | |$\mathbf {0.20_{-0.10}^{+0.31}}$| | |$\mathbf {1.10_{-0.25}^{+0.44}}$| |
| J1909−3744 | 10.39 | 0.46 | 0.73 | 0.72 | <1.42 | 0.79 ± 0.02 | 0.87 ± 0.02 | |$\mathbf {0.87_{-0.02}^{+0.02}}$| | |$\mathbf {1.15_{-0.03}^{+0.03}}$| |
| J1910+1256 | 38.10 | 2.33 | 2.44 | 2.33 | – | – | 1.44 ± 0.74 | |$\mathbf {0.11_{-0.04}^{+0.11}}$| | |$\mathbf {0.55_{-0.19}^{+0.46}}$| |
| J1911+1347 | 30.98 | 2.07 | 1.88 | 2.07 | – | – | – | – | |
| J1911−1114 | 30.97 | 1.23 | 2.01 | 1.86 | <6.01 | – | – | – | – |
| J1918−0642 | 26.54 | 1.24 | 1.79 | 1.75 | – | – | – | – | – |
| J1939+2134 | 71.02 | 3.56 | 4.45 | 4.81 | – | 0.13 ± 0.07 | 0.22 ± 0.08 | |$\mathbf {0.19_{-0.06}^{+0.07}}$| | |$\mathbf {3.27_{-0.66}^{+1.02}}$| |
| J1955+2908 | 104.55 | 4.64 | 6.73 | 6.75 | – | – | – | – | – |
| J2010−1323 | 22.18 | 1.02 | 1.78 | 1.95 | – | – | – | – | – |
| J2019+2425 | 17.15 | 1.50 | 1.16 | 1.50 | <1.67 | – | – | – | – |
| J2033+1734 | 25.01 | 2.00 | 1.85 | 2.17 | <10.51 | – | – | – | – |
| J2124−3358 | 4.58 | 0.27 | 0.32 | 0.37 | <0.67 | 3.1 ± 0.6 | 2.50 ± 0.36 | |$\mathbf {2.31_{-0.36}^{+0.36}}$| | |$\mathbf {0.38_{-0.05}^{+0.06}}$| |
| J2145−0750 | 8.98 | 0.57 | 0.67 | 0.79 | – | 1.6 ± 0.3 | 1.53 ± 0.11 | |$\mathbf {1.51_{-0.11}^{+0.11}}$| | |$\mathbf {0.64_{-0.04}^{+0.05}}$| |
| J2229+2643 | 22.66 | 1.43 | 1.94 | 2.23 | – | – | – | – | – |
| J2317+1439 | 21.90 | 0.83 | 2.19 | 1.39 | – | – | 0.7 ± 0.3 | |$\mathbf {0.55_{-0.18}^{+0.24}}$| | |$\mathbf {1.01_{-0.22}^{+0.35}}$| |
| J2322+2057 | 13.55 | 0.80 | 1.06 | 1.12 | <1.81 | – | – | – | – |
| PSR JName . | DM . | DNE2001 . | DM2 . | DM3 . | |$D_{\dot{P}}$| . | πhist . | π . | πcorr . | Dπ . |
|---|---|---|---|---|---|---|---|---|---|
| . | (cm−3pc) . | (kpc) . | (kpc) . | (kpc) . | (kpc) . | (mas) . | (mas) . | (mas) . | (kpc) . |
| J0030+0451 | 4.33 | 0.32 | 0.30 | 0.37 | – | 4.1 ± 0.3 | 2.79 ± 0.23 | |$\mathbf {2.71_{-0.23}^{+0.23}}$| | |$\mathbf {0.35_{-0.03}^{+0.03}}$| |
| J0034−0534 | 13.76 | 0.54 | 1.27 | 1.23 | – | – | – | – | – |
| J0218+4232 | 61.25 | 2.67 | 5.85 | 8.67 | – | 0.16 ± 0.09 | – | |$0.22_{-0.05}^{+0.07}$| | |$3.15^{+0.85}_{-0.60}{}^a$| |
| J0610−2100 | 60.66 | 3.54 | 5.64 | 8.94 | <3.85 | – | – | – | – |
| J0613−0200 | 38.78 | 1.71 | 2.58 | 2.41 | <11.19 | 0.8 ± 0.35 | 1.25 ± 0.13 | |$\mathbf {1.21_{-0.13}^{+0.13}}$| | |$\mathbf {0.78_{-0.07}^{+0.08}}$| |
| J0621+1002 | 36.45 | 1.36 | 2.02 | 1.90 | – | – | – | – | – |
| J0751+1807 | 30.25 | 1.15 | 2.57 | 2.46 | <4.71 | 1.6 ± 0.8 | 0.82 ± 0.17 | |$\mathbf {0.74_{-0.17}^{+0.17}}$| | |$\mathbf {1.07_{-0.17}^{+0.24}}$| |
| J0900−3144 | 75.70 | 0.54 | 1.05 | 0.54 | – | – | 0.77 ± 0.44 | |$\mathbf {0.35_{-0.16}^{+0.32}}$| | |$\mathbf {0.81_{-0.21}^{+0.38}}$| |
| J1012+5307 | 9.02 | 0.41 | 0.69 | 0.76 | <2.14 | 1.22 ± 0.26 | 0.71 ± 0.17 | |$\mathbf {0.70_{-0.15}^{+0.15}}$| | |$\mathbf {1.15_{-0.17}^{+0.24}}$| |
| J1022+1001 | 10.25 | 0.45 | 0.81 | 0.87 | <3.3 | 1.8 ± 0.3 | 0.72 ± 0.20 | |$\mathbf {0.70_{-0.17}^{+0.18}}$| | |$\mathbf {1.09_{-0.18}^{+0.26}}$| |
| J1024−0719 | 6.49 | 0.39 | 0.46 | 0.50 | <0.43 | 1.9 ± 0.4 | 0.80 ± 0.17 | |$\mathbf {0.75_{-0.16}^{+0.16}}$| | |$\mathbf {1.08_{-0.16}^{+0.23}}$| |
| J1455−3330 | 13.56 | 0.53 | 0.98 | 0.74 | – | – | 1.04 ± 0.35 | |$\mathbf {0.49_{-0.24}^{+0.35}}$| | |$\mathbf {0.80_{-0.18}^{+0.30}}$| |
| J1600−3053 | 52.32 | 1.63 | 3.77 | 4.62 | – | 0.2 ± 0.15 | 0.64 ± 0.07 | |$\mathbf {0.62_{-0.07}^{+0.07}}$| | |$\mathbf {1.49_{-0.15}^{+0.19}}$| |
| J1640+2224 | 18.42 | 1.16 | 1.61 | 2.63 | <3.43 | – | – | – | – |
| J1643−1224 | 62.41 | 2.40 | 4.86 | >50 | – | 2.2 ± 0.4 | 1.17 ± 0.26 | |$\mathbf {0.99_{-0.27}^{+0.26}}$| | |$\mathbf {0.76_{-0.13}^{+0.19}}$| |
| J1713+0747 | 15.99 | 0.89 | 1.22 | 1.61 | – | 0.94 ± 0.05 | 0.90 ± 0.03 | |$\mathbf {0.90_{-0.03}^{+0.03}}$| | |$\mathbf {1.11_{-0.03}^{+0.04}}$| |
| J1721−2457 | 48.68 | 1.30 | 1.67 | 1.84 | <0.96 | – | – | – | – |
| J1730−2304 | 9.61 | 0.53 | 0.63 | 0.72 | <1.85 | – | 0.86 ± 0.32 | |$\mathbf {0.21_{-0.07}^{+0.38}}$| | |$\mathbf {0.90_{-0.22}^{+0.38}}$| |
| J1738+0333 | 33.80 | 1.43 | 2.60 | 3.16 | – | 0.68 ± 0.05 | – | |$0.67_{-0.05}^{+0.05}$| | |$1.45_{-0.10}^{+0.11}$| |
| J1744−1134 | 3.13 | 0.41 | 0.21 | 0.44 | <1.9 | 2.4 ± 0.1 | 2.38 ± 0.08 | |$\mathbf {2.37_{-0.08}^{+0.08}}$| | |$\mathbf {0.42_{-0.01}^{+0.01}}$| |
| J1751−2857 | 42.90 | 1.10 | 1.51 | 1.73 | <5.92 | – | – | – | – |
| J1801−1417 | 57.19 | 1.52 | 1.90 | 2.17 | <3.47 | – | – | – | – |
| J1802−2124 | 149.63 | 2.94 | 3.46 | 3.84 | – | – | 1.24 ± 0.57 | |$\mathbf {0.08_{-0.03}^{+0.13}}$| | |$\mathbf {0.64_{-0.19}^{+0.44}}$| |
| J1804−2717 | 24.57 | 0.78 | 1.29 | 1.13 | <4.73 | – | – | – | – |
| J1843−1113 | 59.95 | 1.70 | 2.08 | 2.45 | – | – | 0.69 ± 0.33 | |$\mathbf {0.11_{-0.04}^{+0.15}}$| | |$\mathbf {1.09_{-0.32}^{+0.67}}$| |
| J1853+1303 | 30.65 | 2.08 | 1.08 | 2.10 | – | 1.0 ± 0.3 | – | |$0.19_{-0.08}^{+0.42}$| | |$0.88_{-0.20}^{+0.34}$| |
| J1857+0943 | 13.30 | 1.17 | 0.87 | 1.17 | – | 1.1 ± 0.2 | 0.70 ± 0.26 | |$\mathbf {0.20_{-0.10}^{+0.31}}$| | |$\mathbf {1.10_{-0.25}^{+0.44}}$| |
| J1909−3744 | 10.39 | 0.46 | 0.73 | 0.72 | <1.42 | 0.79 ± 0.02 | 0.87 ± 0.02 | |$\mathbf {0.87_{-0.02}^{+0.02}}$| | |$\mathbf {1.15_{-0.03}^{+0.03}}$| |
| J1910+1256 | 38.10 | 2.33 | 2.44 | 2.33 | – | – | 1.44 ± 0.74 | |$\mathbf {0.11_{-0.04}^{+0.11}}$| | |$\mathbf {0.55_{-0.19}^{+0.46}}$| |
| J1911+1347 | 30.98 | 2.07 | 1.88 | 2.07 | – | – | – | – | |
| J1911−1114 | 30.97 | 1.23 | 2.01 | 1.86 | <6.01 | – | – | – | – |
| J1918−0642 | 26.54 | 1.24 | 1.79 | 1.75 | – | – | – | – | – |
| J1939+2134 | 71.02 | 3.56 | 4.45 | 4.81 | – | 0.13 ± 0.07 | 0.22 ± 0.08 | |$\mathbf {0.19_{-0.06}^{+0.07}}$| | |$\mathbf {3.27_{-0.66}^{+1.02}}$| |
| J1955+2908 | 104.55 | 4.64 | 6.73 | 6.75 | – | – | – | – | – |
| J2010−1323 | 22.18 | 1.02 | 1.78 | 1.95 | – | – | – | – | – |
| J2019+2425 | 17.15 | 1.50 | 1.16 | 1.50 | <1.67 | – | – | – | – |
| J2033+1734 | 25.01 | 2.00 | 1.85 | 2.17 | <10.51 | – | – | – | – |
| J2124−3358 | 4.58 | 0.27 | 0.32 | 0.37 | <0.67 | 3.1 ± 0.6 | 2.50 ± 0.36 | |$\mathbf {2.31_{-0.36}^{+0.36}}$| | |$\mathbf {0.38_{-0.05}^{+0.06}}$| |
| J2145−0750 | 8.98 | 0.57 | 0.67 | 0.79 | – | 1.6 ± 0.3 | 1.53 ± 0.11 | |$\mathbf {1.51_{-0.11}^{+0.11}}$| | |$\mathbf {0.64_{-0.04}^{+0.05}}$| |
| J2229+2643 | 22.66 | 1.43 | 1.94 | 2.23 | – | – | – | – | – |
| J2317+1439 | 21.90 | 0.83 | 2.19 | 1.39 | – | – | 0.7 ± 0.3 | |$\mathbf {0.55_{-0.18}^{+0.24}}$| | |$\mathbf {1.01_{-0.22}^{+0.35}}$| |
| J2322+2057 | 13.55 | 0.80 | 1.06 | 1.12 | <1.81 | – | – | – | – |
Summary of pulsar parallaxes and distance estimates. The columns give the pulsar name, the DM, the distance based on the NE2001 electron density model DNE2001 (Cordes & Lazio 2002), the distance based on the M2 and M3 models, DM2 and DM3 (Schnitzeler 2012), an upper limit on the distance |$D_{\dot{P}}$| (only indicated when this limit is <15 kpc; see text), the previously published parallax value πhist, our new measurement of the parallax π and the LK-bias-corrected parallax πcorr with the corresponding distance Dπ. For clarity, the values in bold show the updated or new parallax measurements as part of this work. The references for πhist can be found in Table 1.
| PSR JName . | DM . | DNE2001 . | DM2 . | DM3 . | |$D_{\dot{P}}$| . | πhist . | π . | πcorr . | Dπ . |
|---|---|---|---|---|---|---|---|---|---|
| . | (cm−3pc) . | (kpc) . | (kpc) . | (kpc) . | (kpc) . | (mas) . | (mas) . | (mas) . | (kpc) . |
| J0030+0451 | 4.33 | 0.32 | 0.30 | 0.37 | – | 4.1 ± 0.3 | 2.79 ± 0.23 | |$\mathbf {2.71_{-0.23}^{+0.23}}$| | |$\mathbf {0.35_{-0.03}^{+0.03}}$| |
| J0034−0534 | 13.76 | 0.54 | 1.27 | 1.23 | – | – | – | – | – |
| J0218+4232 | 61.25 | 2.67 | 5.85 | 8.67 | – | 0.16 ± 0.09 | – | |$0.22_{-0.05}^{+0.07}$| | |$3.15^{+0.85}_{-0.60}{}^a$| |
| J0610−2100 | 60.66 | 3.54 | 5.64 | 8.94 | <3.85 | – | – | – | – |
| J0613−0200 | 38.78 | 1.71 | 2.58 | 2.41 | <11.19 | 0.8 ± 0.35 | 1.25 ± 0.13 | |$\mathbf {1.21_{-0.13}^{+0.13}}$| | |$\mathbf {0.78_{-0.07}^{+0.08}}$| |
| J0621+1002 | 36.45 | 1.36 | 2.02 | 1.90 | – | – | – | – | – |
| J0751+1807 | 30.25 | 1.15 | 2.57 | 2.46 | <4.71 | 1.6 ± 0.8 | 0.82 ± 0.17 | |$\mathbf {0.74_{-0.17}^{+0.17}}$| | |$\mathbf {1.07_{-0.17}^{+0.24}}$| |
| J0900−3144 | 75.70 | 0.54 | 1.05 | 0.54 | – | – | 0.77 ± 0.44 | |$\mathbf {0.35_{-0.16}^{+0.32}}$| | |$\mathbf {0.81_{-0.21}^{+0.38}}$| |
| J1012+5307 | 9.02 | 0.41 | 0.69 | 0.76 | <2.14 | 1.22 ± 0.26 | 0.71 ± 0.17 | |$\mathbf {0.70_{-0.15}^{+0.15}}$| | |$\mathbf {1.15_{-0.17}^{+0.24}}$| |
| J1022+1001 | 10.25 | 0.45 | 0.81 | 0.87 | <3.3 | 1.8 ± 0.3 | 0.72 ± 0.20 | |$\mathbf {0.70_{-0.17}^{+0.18}}$| | |$\mathbf {1.09_{-0.18}^{+0.26}}$| |
| J1024−0719 | 6.49 | 0.39 | 0.46 | 0.50 | <0.43 | 1.9 ± 0.4 | 0.80 ± 0.17 | |$\mathbf {0.75_{-0.16}^{+0.16}}$| | |$\mathbf {1.08_{-0.16}^{+0.23}}$| |
| J1455−3330 | 13.56 | 0.53 | 0.98 | 0.74 | – | – | 1.04 ± 0.35 | |$\mathbf {0.49_{-0.24}^{+0.35}}$| | |$\mathbf {0.80_{-0.18}^{+0.30}}$| |
| J1600−3053 | 52.32 | 1.63 | 3.77 | 4.62 | – | 0.2 ± 0.15 | 0.64 ± 0.07 | |$\mathbf {0.62_{-0.07}^{+0.07}}$| | |$\mathbf {1.49_{-0.15}^{+0.19}}$| |
| J1640+2224 | 18.42 | 1.16 | 1.61 | 2.63 | <3.43 | – | – | – | – |
| J1643−1224 | 62.41 | 2.40 | 4.86 | >50 | – | 2.2 ± 0.4 | 1.17 ± 0.26 | |$\mathbf {0.99_{-0.27}^{+0.26}}$| | |$\mathbf {0.76_{-0.13}^{+0.19}}$| |
| J1713+0747 | 15.99 | 0.89 | 1.22 | 1.61 | – | 0.94 ± 0.05 | 0.90 ± 0.03 | |$\mathbf {0.90_{-0.03}^{+0.03}}$| | |$\mathbf {1.11_{-0.03}^{+0.04}}$| |
| J1721−2457 | 48.68 | 1.30 | 1.67 | 1.84 | <0.96 | – | – | – | – |
| J1730−2304 | 9.61 | 0.53 | 0.63 | 0.72 | <1.85 | – | 0.86 ± 0.32 | |$\mathbf {0.21_{-0.07}^{+0.38}}$| | |$\mathbf {0.90_{-0.22}^{+0.38}}$| |
| J1738+0333 | 33.80 | 1.43 | 2.60 | 3.16 | – | 0.68 ± 0.05 | – | |$0.67_{-0.05}^{+0.05}$| | |$1.45_{-0.10}^{+0.11}$| |
| J1744−1134 | 3.13 | 0.41 | 0.21 | 0.44 | <1.9 | 2.4 ± 0.1 | 2.38 ± 0.08 | |$\mathbf {2.37_{-0.08}^{+0.08}}$| | |$\mathbf {0.42_{-0.01}^{+0.01}}$| |
| J1751−2857 | 42.90 | 1.10 | 1.51 | 1.73 | <5.92 | – | – | – | – |
| J1801−1417 | 57.19 | 1.52 | 1.90 | 2.17 | <3.47 | – | – | – | – |
| J1802−2124 | 149.63 | 2.94 | 3.46 | 3.84 | – | – | 1.24 ± 0.57 | |$\mathbf {0.08_{-0.03}^{+0.13}}$| | |$\mathbf {0.64_{-0.19}^{+0.44}}$| |
| J1804−2717 | 24.57 | 0.78 | 1.29 | 1.13 | <4.73 | – | – | – | – |
| J1843−1113 | 59.95 | 1.70 | 2.08 | 2.45 | – | – | 0.69 ± 0.33 | |$\mathbf {0.11_{-0.04}^{+0.15}}$| | |$\mathbf {1.09_{-0.32}^{+0.67}}$| |
| J1853+1303 | 30.65 | 2.08 | 1.08 | 2.10 | – | 1.0 ± 0.3 | – | |$0.19_{-0.08}^{+0.42}$| | |$0.88_{-0.20}^{+0.34}$| |
| J1857+0943 | 13.30 | 1.17 | 0.87 | 1.17 | – | 1.1 ± 0.2 | 0.70 ± 0.26 | |$\mathbf {0.20_{-0.10}^{+0.31}}$| | |$\mathbf {1.10_{-0.25}^{+0.44}}$| |
| J1909−3744 | 10.39 | 0.46 | 0.73 | 0.72 | <1.42 | 0.79 ± 0.02 | 0.87 ± 0.02 | |$\mathbf {0.87_{-0.02}^{+0.02}}$| | |$\mathbf {1.15_{-0.03}^{+0.03}}$| |
| J1910+1256 | 38.10 | 2.33 | 2.44 | 2.33 | – | – | 1.44 ± 0.74 | |$\mathbf {0.11_{-0.04}^{+0.11}}$| | |$\mathbf {0.55_{-0.19}^{+0.46}}$| |
| J1911+1347 | 30.98 | 2.07 | 1.88 | 2.07 | – | – | – | – | |
| J1911−1114 | 30.97 | 1.23 | 2.01 | 1.86 | <6.01 | – | – | – | – |
| J1918−0642 | 26.54 | 1.24 | 1.79 | 1.75 | – | – | – | – | – |
| J1939+2134 | 71.02 | 3.56 | 4.45 | 4.81 | – | 0.13 ± 0.07 | 0.22 ± 0.08 | |$\mathbf {0.19_{-0.06}^{+0.07}}$| | |$\mathbf {3.27_{-0.66}^{+1.02}}$| |
| J1955+2908 | 104.55 | 4.64 | 6.73 | 6.75 | – | – | – | – | – |
| J2010−1323 | 22.18 | 1.02 | 1.78 | 1.95 | – | – | – | – | – |
| J2019+2425 | 17.15 | 1.50 | 1.16 | 1.50 | <1.67 | – | – | – | – |
| J2033+1734 | 25.01 | 2.00 | 1.85 | 2.17 | <10.51 | – | – | – | – |
| J2124−3358 | 4.58 | 0.27 | 0.32 | 0.37 | <0.67 | 3.1 ± 0.6 | 2.50 ± 0.36 | |$\mathbf {2.31_{-0.36}^{+0.36}}$| | |$\mathbf {0.38_{-0.05}^{+0.06}}$| |
| J2145−0750 | 8.98 | 0.57 | 0.67 | 0.79 | – | 1.6 ± 0.3 | 1.53 ± 0.11 | |$\mathbf {1.51_{-0.11}^{+0.11}}$| | |$\mathbf {0.64_{-0.04}^{+0.05}}$| |
| J2229+2643 | 22.66 | 1.43 | 1.94 | 2.23 | – | – | – | – | – |
| J2317+1439 | 21.90 | 0.83 | 2.19 | 1.39 | – | – | 0.7 ± 0.3 | |$\mathbf {0.55_{-0.18}^{+0.24}}$| | |$\mathbf {1.01_{-0.22}^{+0.35}}$| |
| J2322+2057 | 13.55 | 0.80 | 1.06 | 1.12 | <1.81 | – | – | – | – |
| PSR JName . | DM . | DNE2001 . | DM2 . | DM3 . | |$D_{\dot{P}}$| . | πhist . | π . | πcorr . | Dπ . |
|---|---|---|---|---|---|---|---|---|---|
| . | (cm−3pc) . | (kpc) . | (kpc) . | (kpc) . | (kpc) . | (mas) . | (mas) . | (mas) . | (kpc) . |
| J0030+0451 | 4.33 | 0.32 | 0.30 | 0.37 | – | 4.1 ± 0.3 | 2.79 ± 0.23 | |$\mathbf {2.71_{-0.23}^{+0.23}}$| | |$\mathbf {0.35_{-0.03}^{+0.03}}$| |
| J0034−0534 | 13.76 | 0.54 | 1.27 | 1.23 | – | – | – | – | – |
| J0218+4232 | 61.25 | 2.67 | 5.85 | 8.67 | – | 0.16 ± 0.09 | – | |$0.22_{-0.05}^{+0.07}$| | |$3.15^{+0.85}_{-0.60}{}^a$| |
| J0610−2100 | 60.66 | 3.54 | 5.64 | 8.94 | <3.85 | – | – | – | – |
| J0613−0200 | 38.78 | 1.71 | 2.58 | 2.41 | <11.19 | 0.8 ± 0.35 | 1.25 ± 0.13 | |$\mathbf {1.21_{-0.13}^{+0.13}}$| | |$\mathbf {0.78_{-0.07}^{+0.08}}$| |
| J0621+1002 | 36.45 | 1.36 | 2.02 | 1.90 | – | – | – | – | – |
| J0751+1807 | 30.25 | 1.15 | 2.57 | 2.46 | <4.71 | 1.6 ± 0.8 | 0.82 ± 0.17 | |$\mathbf {0.74_{-0.17}^{+0.17}}$| | |$\mathbf {1.07_{-0.17}^{+0.24}}$| |
| J0900−3144 | 75.70 | 0.54 | 1.05 | 0.54 | – | – | 0.77 ± 0.44 | |$\mathbf {0.35_{-0.16}^{+0.32}}$| | |$\mathbf {0.81_{-0.21}^{+0.38}}$| |
| J1012+5307 | 9.02 | 0.41 | 0.69 | 0.76 | <2.14 | 1.22 ± 0.26 | 0.71 ± 0.17 | |$\mathbf {0.70_{-0.15}^{+0.15}}$| | |$\mathbf {1.15_{-0.17}^{+0.24}}$| |
| J1022+1001 | 10.25 | 0.45 | 0.81 | 0.87 | <3.3 | 1.8 ± 0.3 | 0.72 ± 0.20 | |$\mathbf {0.70_{-0.17}^{+0.18}}$| | |$\mathbf {1.09_{-0.18}^{+0.26}}$| |
| J1024−0719 | 6.49 | 0.39 | 0.46 | 0.50 | <0.43 | 1.9 ± 0.4 | 0.80 ± 0.17 | |$\mathbf {0.75_{-0.16}^{+0.16}}$| | |$\mathbf {1.08_{-0.16}^{+0.23}}$| |
| J1455−3330 | 13.56 | 0.53 | 0.98 | 0.74 | – | – | 1.04 ± 0.35 | |$\mathbf {0.49_{-0.24}^{+0.35}}$| | |$\mathbf {0.80_{-0.18}^{+0.30}}$| |
| J1600−3053 | 52.32 | 1.63 | 3.77 | 4.62 | – | 0.2 ± 0.15 | 0.64 ± 0.07 | |$\mathbf {0.62_{-0.07}^{+0.07}}$| | |$\mathbf {1.49_{-0.15}^{+0.19}}$| |
| J1640+2224 | 18.42 | 1.16 | 1.61 | 2.63 | <3.43 | – | – | – | – |
| J1643−1224 | 62.41 | 2.40 | 4.86 | >50 | – | 2.2 ± 0.4 | 1.17 ± 0.26 | |$\mathbf {0.99_{-0.27}^{+0.26}}$| | |$\mathbf {0.76_{-0.13}^{+0.19}}$| |
| J1713+0747 | 15.99 | 0.89 | 1.22 | 1.61 | – | 0.94 ± 0.05 | 0.90 ± 0.03 | |$\mathbf {0.90_{-0.03}^{+0.03}}$| | |$\mathbf {1.11_{-0.03}^{+0.04}}$| |
| J1721−2457 | 48.68 | 1.30 | 1.67 | 1.84 | <0.96 | – | – | – | – |
| J1730−2304 | 9.61 | 0.53 | 0.63 | 0.72 | <1.85 | – | 0.86 ± 0.32 | |$\mathbf {0.21_{-0.07}^{+0.38}}$| | |$\mathbf {0.90_{-0.22}^{+0.38}}$| |
| J1738+0333 | 33.80 | 1.43 | 2.60 | 3.16 | – | 0.68 ± 0.05 | – | |$0.67_{-0.05}^{+0.05}$| | |$1.45_{-0.10}^{+0.11}$| |
| J1744−1134 | 3.13 | 0.41 | 0.21 | 0.44 | <1.9 | 2.4 ± 0.1 | 2.38 ± 0.08 | |$\mathbf {2.37_{-0.08}^{+0.08}}$| | |$\mathbf {0.42_{-0.01}^{+0.01}}$| |
| J1751−2857 | 42.90 | 1.10 | 1.51 | 1.73 | <5.92 | – | – | – | – |
| J1801−1417 | 57.19 | 1.52 | 1.90 | 2.17 | <3.47 | – | – | – | – |
| J1802−2124 | 149.63 | 2.94 | 3.46 | 3.84 | – | – | 1.24 ± 0.57 | |$\mathbf {0.08_{-0.03}^{+0.13}}$| | |$\mathbf {0.64_{-0.19}^{+0.44}}$| |
| J1804−2717 | 24.57 | 0.78 | 1.29 | 1.13 | <4.73 | – | – | – | – |
| J1843−1113 | 59.95 | 1.70 | 2.08 | 2.45 | – | – | 0.69 ± 0.33 | |$\mathbf {0.11_{-0.04}^{+0.15}}$| | |$\mathbf {1.09_{-0.32}^{+0.67}}$| |
| J1853+1303 | 30.65 | 2.08 | 1.08 | 2.10 | – | 1.0 ± 0.3 | – | |$0.19_{-0.08}^{+0.42}$| | |$0.88_{-0.20}^{+0.34}$| |
| J1857+0943 | 13.30 | 1.17 | 0.87 | 1.17 | – | 1.1 ± 0.2 | 0.70 ± 0.26 | |$\mathbf {0.20_{-0.10}^{+0.31}}$| | |$\mathbf {1.10_{-0.25}^{+0.44}}$| |
| J1909−3744 | 10.39 | 0.46 | 0.73 | 0.72 | <1.42 | 0.79 ± 0.02 | 0.87 ± 0.02 | |$\mathbf {0.87_{-0.02}^{+0.02}}$| | |$\mathbf {1.15_{-0.03}^{+0.03}}$| |
| J1910+1256 | 38.10 | 2.33 | 2.44 | 2.33 | – | – | 1.44 ± 0.74 | |$\mathbf {0.11_{-0.04}^{+0.11}}$| | |$\mathbf {0.55_{-0.19}^{+0.46}}$| |
| J1911+1347 | 30.98 | 2.07 | 1.88 | 2.07 | – | – | – | – | |
| J1911−1114 | 30.97 | 1.23 | 2.01 | 1.86 | <6.01 | – | – | – | – |
| J1918−0642 | 26.54 | 1.24 | 1.79 | 1.75 | – | – | – | – | – |
| J1939+2134 | 71.02 | 3.56 | 4.45 | 4.81 | – | 0.13 ± 0.07 | 0.22 ± 0.08 | |$\mathbf {0.19_{-0.06}^{+0.07}}$| | |$\mathbf {3.27_{-0.66}^{+1.02}}$| |
| J1955+2908 | 104.55 | 4.64 | 6.73 | 6.75 | – | – | – | – | – |
| J2010−1323 | 22.18 | 1.02 | 1.78 | 1.95 | – | – | – | – | – |
| J2019+2425 | 17.15 | 1.50 | 1.16 | 1.50 | <1.67 | – | – | – | – |
| J2033+1734 | 25.01 | 2.00 | 1.85 | 2.17 | <10.51 | – | – | – | – |
| J2124−3358 | 4.58 | 0.27 | 0.32 | 0.37 | <0.67 | 3.1 ± 0.6 | 2.50 ± 0.36 | |$\mathbf {2.31_{-0.36}^{+0.36}}$| | |$\mathbf {0.38_{-0.05}^{+0.06}}$| |
| J2145−0750 | 8.98 | 0.57 | 0.67 | 0.79 | – | 1.6 ± 0.3 | 1.53 ± 0.11 | |$\mathbf {1.51_{-0.11}^{+0.11}}$| | |$\mathbf {0.64_{-0.04}^{+0.05}}$| |
| J2229+2643 | 22.66 | 1.43 | 1.94 | 2.23 | – | – | – | – | – |
| J2317+1439 | 21.90 | 0.83 | 2.19 | 1.39 | – | – | 0.7 ± 0.3 | |$\mathbf {0.55_{-0.18}^{+0.24}}$| | |$\mathbf {1.01_{-0.22}^{+0.35}}$| |
| J2322+2057 | 13.55 | 0.80 | 1.06 | 1.12 | <1.81 | – | – | – | – |
Because of the asymmetric error-volume, parallax measurements with significance less than ∼4σ, are unreliable as the LK bias dominates the measurement (Lutz & Kelker 1973; Verbiest, Lorimer & McLaughlin 2010). The LK-corrected parallax values as well as the derived distances5 are also given in Table 13, based on the analytical corrections proposed by Verbiest et al. (2012) and the flux density values shown in Table 1.
In total, we present 22 new parallax measurements. Seven of these new measurements are for MSPs that had no previous distance measurement, but all of these are still strongly biased since their significance is at best 3σ. For five pulsars (specifically for PSRs J0030+0451, J1012+5307, J1022+1001, J1643−1224 and J1857+0943) our parallax measurement is of comparable significance than the previously published value, but with the exception of PSR J1857+0943, our measurement precision is better than those published previously; and the lower significance is a consequence of the smaller parallax value measured (as predicted by the bias correction). Our measurement for PSR J1857+0943 is slightly less precise than the value published by Verbiest et al. (2009), but consistent within 1σ.
Finally, we present improved parallax measurements for ten pulsars: PSRs J0613−0200, J0751+1807, J1024−0719, J1600−3053, J1713+0747, J1744−1134, J1909−3744, J1939+2134, J2124−3358 and J2145−0750. For seven of these the previous measurement was already free of bias, for the remaining three (PSRs J0613−0200, J0751+1807 and J2124−3358) our update reduces the bias to below the 1σ uncertainty level (with two out of three moving in the direction predicted by the bias-correction code). For three pulsars with previously published parallax measurements we only derive upper limits, but two of these previous measurements (for PSRs J0218+4232 and J1853+1303) were of low significance and highly biased. Only PSR J1738+0333's parallax was reliably measured with GBT and Arecibo data (Freire et al. 2012b) and not confirmed by us. Four pulsars had a known parallax before the creation of the NE2001 model, namely PSRs J1713+0747 (Camilo, Foster & Wolszczan 1994), J1744−1134 (Toscano et al. 1999b), J1857+0943 and J1939+2134 (Kaspi et al. 1994). These pulsars are therefore not included in our analysis of the NE2001 distance (see below), leaving us with a total of 21 parallaxes.
5.1.1 Distance comparison with NE2001 predictions
When comparing the bias-corrected distances presented in Table 13 with those predicted by the widely used NE2001 electron-density model for the Milky Way (Cordes & Lazio 2002), we find that the model performs reasonably well overall. However, significant offsets exist, primarily at high positive latitudes and large distance (d > 2 kpc) into the Galactic plane. In Fig. 3, we plot this comparison for three ranges of Galactic latitude b (defined as low: |b| < 20°, intermediate: 20° < |b| < 40° and high: |b| > 40°) highlighting the weakness of NE2001 at high latitude. We find a mean uncertainty of 64, 55 and 117 per cent, respectively, for the NE2001 distances to be consistent with our measurement. On average, the NE2001 distances would require an uncertainty of 80 per cent. This value is significantly higher than the 25 per cent uncertainty typically assumed in the literature for this model; or than the fractional uncertainties displayed in fig. 12 of Cordes & Lazio (2002).
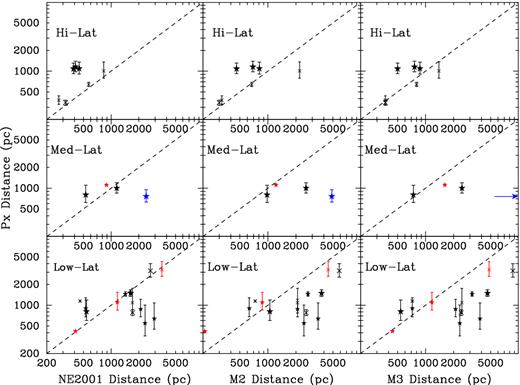
Comparison between the LK bias-corrected parallax distances (in ordinates) and the DM distances (in abscissa) for different Galactic latitudes b on logarithmic scales. The DM distances in the left-hand, middle and right-hand panels are derived from the NE2001, M2 and M3 models, respectively. Top panels: the stars show pulsars with b > 40° and the crosses pulsars with b < −40°. Middle panels: the stars show pulsars with 40° > b > 20° and the crosses pulsars with −40° < b < −20°. Bottom panels: the stars show pulsars with 20° > b > 0° and the crosses pulsars with −20° < b < 0°. The red symbols indicate pulsars with a known parallax before NE2001 was created, namely PSRs J1713+0747, J1744−1134, J1857+0943 and J1939+2134. The blue symbol indicates PSR J1643−1224 where its corresponding M3 distance is infinite and represented by an arrow.
5.1.2 Distance comparison with M2 and M3 predictions
To improve on the shortcomings of NE2001, Schnitzeler (2012, hereafter S12) recently introduced two new models of the Galactic electron density based on Taylor & Cordes (1993, hereafter TC93) and NE2001, referred to as M2 and M3 in S12. In these two models, the author selected a set of 45 lines of sight to update the original TC93 and NE2001 thick disc and fit for an exponential scaleheight of 1.59–1.31 kpc. In the selection process of these 45 lines-of-sight, S12 excluded pulsars lying in the Galactic plane, i.e. |b| < 5°; see section 4.2 of S12 for additional details.
The distance estimates given by M2 and M3 are reported in the fourth and fifth columns of Table 13. Except for seven and five pulsars, respectively, the new M2 and M3 distances are systematically higher than the NE2001 distances. In the case of PSR J1643−1224, M3 even predicts an infinite distance as it is unable to account for enough free electrons in the Galactic model towards this line of sight.
In Fig. 3, we show the comparison between the parallax distances and the NE2001, M2 and M3 distances as a function of the three Galactic latitude ranges defined in the previous section. As can be seen, the M2 and M3 predictions for high latitude pulsars are a slightly better match to the parallax distances than NE2001. However, for low latitude, the M2 and M3 distances are significantly higher than the parallax distances. To be consistent with the parallax distances, M2 requires uncertainties of 95, 200 and 53 per cent, while M3 requires 113, 202 and 41 per cent for low, intermediate and high latitude, respectively. This result is not surprising as low-latitude pulsars have been excluded in the S12 analysis. On average, M2 and M3 require an uncertainty of 96 and 102 per cent, significantly higher than our estimated uncertainty for NE2001.
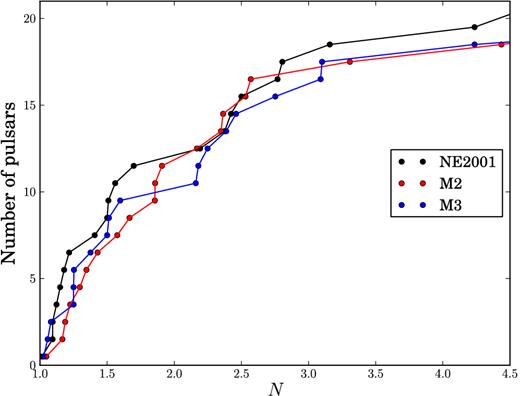
Cumulative distribution of the N factor between the DM distance and the parallax distance (see equation 5). These distributions include the 21 pulsars with measured parallaxes in Table 13. The DM distances are derived from the NE2001, M2 and M3 models and represented in black, red and blue, respectively.
5.2 Proper motions and 2D spatial velocities
Stellar evolution modelling by Tauris & Bailes (1996) and Cordes & Chernoff (1997) predicted that the recycled MSP population would have a smaller spatial velocity than the normal pulsar population. A study by Toscano et al. (1999a) found a mean transverse velocity |$\overline{V}_{\rm T}$| for MSPs of 85 ± 13 km s−1 based on a sample of 23 objects. They noted that this value is four times lower than the ordinary young pulsar velocity. The authors also observed isolated MSPs to have a velocity two-thirds smaller than the binary MSPs. With an ever increasing number of MSPs, further studies by Hobbs et al. (2005) and Gonzalez et al. (2011) found no statistical evidence for a difference in the velocity distribution of isolated and binary MSPs. Hobbs et al. (2005) reported on |$\overline{V}_{\rm T}$| = 76 ± 16 and |$\overline{V}_{\rm T}$| = 89 ± 15 km s−1 for isolated and binary MSPs, respectively, while Gonzalez et al. (2011) found |$\overline{V}_{\rm T}$| = 68 ± 16 and |$\overline{V}_{\rm T}$| = 96 ± 15 km s−1 for isolated and binary MSPs. All these results are in agreement with other work by Lommen et al. (2006).
Within our sample of 42 MSPs, we measured seven new proper motions, of which three are for isolated MSPs (PSRs J1843−1113, J1911+1347 and J2010−1323) and four are for binary MSPs (PSRs J0034−0534, J0900−3144, J1751−2857 and J1804−2717). In addition, we improved the precision of the proper-motion measurement by a factor of 10 for seven other MSPs (PSRs J0610−2100, J0613−0200, J1455−3330, J1801−1417, J1911−1114, J2229+2643 and J2317+1439).
Summary of the transverse motion of the isolated MSPs. The columns indicate the pulsar name, the composite proper motion, the distance and the corresponding transverse velocity. The last column shows the last reference with published proper motion and distance measurements. The distances refer to the best distance estimates available, either the parallax when uncertainties are given or the NE2001 distance (indicated by †) where a 80 per cent error is assumed. Values in bold face indicate the new proper-motion measurements.
| PSR JName . | μ . | Distance . | 2D velocity . | Reference . |
|---|---|---|---|---|
| . | (mas yr−1) . | (pc) . | (km s−1) . | . |
| J0030+0451 | 5.9 ± 0.5 | 350 ± 30 | 9.8 ± 1.2 | This work |
| J0645+5158 | 7.60 ± 0.20 | 700 ± 200 | 25 ± 7 | Stovall et al. (2014) |
| J0711−6830 | 21.08 ± 0.08 | 860† | 86 ± 69 | Verbiest et al. (2009) |
| J1024−0719 | 59.72 ± 0.06 | 1080 ± 230 | 306 ± 65 | This work |
| J1453+1902 | 7.5 ± 2.2 | 1150† | 41 ± 35 | Lorimer et al. (2007) |
| J1721−2457 | 25.5 ± 15.3 | 1300† | 157 ± 157 | This work |
| J1730−2304 | 22.6 ± 4.8 | 900 ± 300 | 96 ± 38 | This work |
| J1744−1134 | 21.009 ± 0.014 | 420 ± 10 | 41.8 ± 1.0 | This work |
| J1801−1417 | 11.30 ± 0.27 | 1520† | 81 ± 65 | This work |
| J1843−1113 | 3.76 ± 0.22 | 1090 ± 670 | 19 ± 12 | This work |
| J1905+0400 | 8.2 ± 0.4 | 1700† | 66 ± 53 | Gonzalez et al. (2011) |
| J1911+1347 | 4.73 ± 0.05 | 2070† | 46 ± 37 | This work |
| J1923+2515 | 24.3 ± 6.8 | 1630† | 188 ± 159 | Lynch et al. (2013) |
| J1939+2134 | 0.407 ± 0.005 | 3270 ± 1020 | 6.3 ± 2.0 | This work |
| J1944+0907 | 21.6 ± 2.5 | 1790† | 183 ± 148 | Champion et al. (2005) |
| J1955+2527 | 3.1 ± 0.7 | 7510† | 110 ± 92 | Deneva et al. (2012) |
| J2010−1323 | 6.24 ± 0.33 | 1030† | 30 ± 24 | This work |
| J2124−3358 | 52.07 ± 0.13 | 380 ± 60 | 94 ± 15 | This work |
| J2322+2057 | 24.0 ± 0.4 | 800† | 91 ± 73 | This work |
| PSR JName . | μ . | Distance . | 2D velocity . | Reference . |
|---|---|---|---|---|
| . | (mas yr−1) . | (pc) . | (km s−1) . | . |
| J0030+0451 | 5.9 ± 0.5 | 350 ± 30 | 9.8 ± 1.2 | This work |
| J0645+5158 | 7.60 ± 0.20 | 700 ± 200 | 25 ± 7 | Stovall et al. (2014) |
| J0711−6830 | 21.08 ± 0.08 | 860† | 86 ± 69 | Verbiest et al. (2009) |
| J1024−0719 | 59.72 ± 0.06 | 1080 ± 230 | 306 ± 65 | This work |
| J1453+1902 | 7.5 ± 2.2 | 1150† | 41 ± 35 | Lorimer et al. (2007) |
| J1721−2457 | 25.5 ± 15.3 | 1300† | 157 ± 157 | This work |
| J1730−2304 | 22.6 ± 4.8 | 900 ± 300 | 96 ± 38 | This work |
| J1744−1134 | 21.009 ± 0.014 | 420 ± 10 | 41.8 ± 1.0 | This work |
| J1801−1417 | 11.30 ± 0.27 | 1520† | 81 ± 65 | This work |
| J1843−1113 | 3.76 ± 0.22 | 1090 ± 670 | 19 ± 12 | This work |
| J1905+0400 | 8.2 ± 0.4 | 1700† | 66 ± 53 | Gonzalez et al. (2011) |
| J1911+1347 | 4.73 ± 0.05 | 2070† | 46 ± 37 | This work |
| J1923+2515 | 24.3 ± 6.8 | 1630† | 188 ± 159 | Lynch et al. (2013) |
| J1939+2134 | 0.407 ± 0.005 | 3270 ± 1020 | 6.3 ± 2.0 | This work |
| J1944+0907 | 21.6 ± 2.5 | 1790† | 183 ± 148 | Champion et al. (2005) |
| J1955+2527 | 3.1 ± 0.7 | 7510† | 110 ± 92 | Deneva et al. (2012) |
| J2010−1323 | 6.24 ± 0.33 | 1030† | 30 ± 24 | This work |
| J2124−3358 | 52.07 ± 0.13 | 380 ± 60 | 94 ± 15 | This work |
| J2322+2057 | 24.0 ± 0.4 | 800† | 91 ± 73 | This work |
Summary of the transverse motion of the isolated MSPs. The columns indicate the pulsar name, the composite proper motion, the distance and the corresponding transverse velocity. The last column shows the last reference with published proper motion and distance measurements. The distances refer to the best distance estimates available, either the parallax when uncertainties are given or the NE2001 distance (indicated by †) where a 80 per cent error is assumed. Values in bold face indicate the new proper-motion measurements.
| PSR JName . | μ . | Distance . | 2D velocity . | Reference . |
|---|---|---|---|---|
| . | (mas yr−1) . | (pc) . | (km s−1) . | . |
| J0030+0451 | 5.9 ± 0.5 | 350 ± 30 | 9.8 ± 1.2 | This work |
| J0645+5158 | 7.60 ± 0.20 | 700 ± 200 | 25 ± 7 | Stovall et al. (2014) |
| J0711−6830 | 21.08 ± 0.08 | 860† | 86 ± 69 | Verbiest et al. (2009) |
| J1024−0719 | 59.72 ± 0.06 | 1080 ± 230 | 306 ± 65 | This work |
| J1453+1902 | 7.5 ± 2.2 | 1150† | 41 ± 35 | Lorimer et al. (2007) |
| J1721−2457 | 25.5 ± 15.3 | 1300† | 157 ± 157 | This work |
| J1730−2304 | 22.6 ± 4.8 | 900 ± 300 | 96 ± 38 | This work |
| J1744−1134 | 21.009 ± 0.014 | 420 ± 10 | 41.8 ± 1.0 | This work |
| J1801−1417 | 11.30 ± 0.27 | 1520† | 81 ± 65 | This work |
| J1843−1113 | 3.76 ± 0.22 | 1090 ± 670 | 19 ± 12 | This work |
| J1905+0400 | 8.2 ± 0.4 | 1700† | 66 ± 53 | Gonzalez et al. (2011) |
| J1911+1347 | 4.73 ± 0.05 | 2070† | 46 ± 37 | This work |
| J1923+2515 | 24.3 ± 6.8 | 1630† | 188 ± 159 | Lynch et al. (2013) |
| J1939+2134 | 0.407 ± 0.005 | 3270 ± 1020 | 6.3 ± 2.0 | This work |
| J1944+0907 | 21.6 ± 2.5 | 1790† | 183 ± 148 | Champion et al. (2005) |
| J1955+2527 | 3.1 ± 0.7 | 7510† | 110 ± 92 | Deneva et al. (2012) |
| J2010−1323 | 6.24 ± 0.33 | 1030† | 30 ± 24 | This work |
| J2124−3358 | 52.07 ± 0.13 | 380 ± 60 | 94 ± 15 | This work |
| J2322+2057 | 24.0 ± 0.4 | 800† | 91 ± 73 | This work |
| PSR JName . | μ . | Distance . | 2D velocity . | Reference . |
|---|---|---|---|---|
| . | (mas yr−1) . | (pc) . | (km s−1) . | . |
| J0030+0451 | 5.9 ± 0.5 | 350 ± 30 | 9.8 ± 1.2 | This work |
| J0645+5158 | 7.60 ± 0.20 | 700 ± 200 | 25 ± 7 | Stovall et al. (2014) |
| J0711−6830 | 21.08 ± 0.08 | 860† | 86 ± 69 | Verbiest et al. (2009) |
| J1024−0719 | 59.72 ± 0.06 | 1080 ± 230 | 306 ± 65 | This work |
| J1453+1902 | 7.5 ± 2.2 | 1150† | 41 ± 35 | Lorimer et al. (2007) |
| J1721−2457 | 25.5 ± 15.3 | 1300† | 157 ± 157 | This work |
| J1730−2304 | 22.6 ± 4.8 | 900 ± 300 | 96 ± 38 | This work |
| J1744−1134 | 21.009 ± 0.014 | 420 ± 10 | 41.8 ± 1.0 | This work |
| J1801−1417 | 11.30 ± 0.27 | 1520† | 81 ± 65 | This work |
| J1843−1113 | 3.76 ± 0.22 | 1090 ± 670 | 19 ± 12 | This work |
| J1905+0400 | 8.2 ± 0.4 | 1700† | 66 ± 53 | Gonzalez et al. (2011) |
| J1911+1347 | 4.73 ± 0.05 | 2070† | 46 ± 37 | This work |
| J1923+2515 | 24.3 ± 6.8 | 1630† | 188 ± 159 | Lynch et al. (2013) |
| J1939+2134 | 0.407 ± 0.005 | 3270 ± 1020 | 6.3 ± 2.0 | This work |
| J1944+0907 | 21.6 ± 2.5 | 1790† | 183 ± 148 | Champion et al. (2005) |
| J1955+2527 | 3.1 ± 0.7 | 7510† | 110 ± 92 | Deneva et al. (2012) |
| J2010−1323 | 6.24 ± 0.33 | 1030† | 30 ± 24 | This work |
| J2124−3358 | 52.07 ± 0.13 | 380 ± 60 | 94 ± 15 | This work |
| J2322+2057 | 24.0 ± 0.4 | 800† | 91 ± 73 | This work |
Summary of the transverse motion of the binary MSPs. The columns indicate the pulsar name, the composite proper motion, the distance and the corresponding transverse velocity. The last column shows the last reference with published proper-motion and distance measurements. The distances refer to the best distance estimates available, either the parallax when uncertainties are given or the NE2001 distance (indicated by †) where a 80 per cent error is assumed. Values in bold face indicate the new proper-motion measurements.
| PSR JName . | μ . | Distance . | 2D velocity . | Reference . |
|---|---|---|---|---|
| . | (mas yr−1) . | (pc) . | (km s−1) . | . |
| J0034−0534 | 12.1 ± 0.5 | 540† | 31 ± 25 | This work |
| J0101−6422 | 15.6 ± 1.7 | 560† | 41 ± 33 | Kerr et al. (2012) |
| J0218+4232 | 6.18 ± 0.09 | 3150† | 92 ± 25 | Verbiest & Lorimer (2014) |
| J0437−4715 | 141.29 ± 0.06 | 156.0 ± 1.0 | 104.5 ± 0.7 | Deller et al. (2008) |
| J0610−2100 | 19.05 ± 0.11 | 3540† | 320 ± 256 | This work |
| J0613−0200 | 10.514 ± 0.016 | 780 ± 80 | 39 ± 4 | This work |
| J0636+5129 | 4.7 ± 0.9 | 490† | 11 ± 9 | Stovall et al. (2014) |
| J0751+1807 | 13.66 ± 0.23 | 1070 ± 240 | 69 ± 16 | This work |
| J0900−3144 | 2.26 ± 0.06 | 810 ± 380 | 9 ± 4 | This work |
| J1012+5307 | 25.615 ± 0.010 | 1150 ± 240 | 140 ± 29 | This work |
| J1017−7156 | 9.96 ± 0.06 | 2980† | 141 ± 113 | Ng et al. (2014) |
| J1023+0038 | 17.98 ± 0.04 | 1370 ± 40 | 116.8 ± 3.4 | Deller et al. (2012) |
| J1045−4509 | 8.01 ± 0.20 | 1960† | 74 ± 60 | Verbiest et al. (2009) |
| J1125−5825 | 10.28 ± 0.30 | 2620† | 128 ± 102 | Ng et al. (2014) |
| J1231−1411 | 104.4 ± 2.2 | 440† | 218 ± 100 | Ransom et al. (2011) |
| J1300+1240 | 96.15 ± 0.07 | 450† | 205 ± 164 | Konacki & Wolszczan (2003) |
| J1337−6423 | 9.2 ± 5.4 | 5080† | 222 ± 220 | Ng et al. (2014) |
| J1405−4656 | 48.3 ± 6.9 | 580† | 133 ± 108 | Bates et al. (2015) |
| J1431−4715 | 10.6 ± 3.6 | 1560† | 78 ± 68 | Bates et al. (2015) |
| J1446−4701 | 4.47 ± 0.22 | 1460† | 31 ± 25 | Ng et al. (2014) |
| J1455−3330 | 8.19 ± 0.09 | 800 ± 300 | 31 ± 12 | This work |
| J1543−5149 | 5.9 ± 1.7 | 2420† | 68 ± 58 | Ng et al. (2014) |
| J1600−3053 | 7.00 ± 0.07 | 1490 ± 190 | 49 ± 6 | This work |
| J1603−7202 | 7.84 ± 0.09 | 1170† | 43 ± 35 | Verbiest et al. (2009) |
| J1640+2224 | 11.485 ± 0.030 | 1160† | 63 ± 51 | This work |
| J1643−1224 | 7.28 ± 0.08 | 760 ± 190 | 26 ± 7 | This work |
| J1708−3506 | 5.7 ± 1.3 | 2790† | 75 ± 63 | Ng et al. (2014) |
| J1709+2313 | 10.2 ± 0.9 | 1410† | 68 ± 55 | Lewandowski et al. (2004) |
| J1713+0747 | 6.2865 ± 0.0032 | 1110 ± 40 | 33.1 ± 1.2 | This work |
| J1719−1438 | 11.2 ± 2.0 | 1210† | 64 ± 53 | Ng et al. (2014) |
| J1731−1847 | 6.2 ± 2.9 | 2550† | 75 ± 69 | Ng et al. (2014) |
| J1738+0333 | 8.65 ± 0.12 | 1470 ± 100 | 60 ± 4 | Freire et al. (2012b) |
| J1745−0952 | 23.9 ± 2.5 | 1830† | 207 ± 167 | Janssen et al. (2010) |
| J1745+1017 | 7.8 ± 1.0 | 1260† | 47 ± 38 | Barr et al. (2013a) |
| J1751−2857 | 8.5 ± 0.6 | 1110† | 45 ± 36 | This work |
| J1801−3210 | 13.6 ± 8.2 | 4030† | 260 ± 260 | Ng et al. (2014) |
| J1802−2124 | 3.5 ± 3.2 | 640 ± 440 | 11 ± 12 | This work |
| J1804−2717 | 17.3 ± 2.4 | 780† | 64 ± 52 | This work |
| J1816+4510 | 6.1 ± 0.9 | 2410† | 70 ± 57 | Stovall et al. (2014) |
| J1853+1303 | 3.22 ± 0.15 | 880 ± 340 | 13 ± 5 | Gonzalez et al. (2011) |
| J1857+0943 | 6.028 ± 0.022 | 1100 ± 440 | 31 ± 13 | This work |
| J1903+0327 | 5.60 ± 0.11 | 6360† | 169 ± 135 | Freire et al. (2011) |
| J1909−3744 | 37.020 ± 0.009 | 1150 ± 30 | 202 ± 5 | This work |
| J1910+1256 | 7.37 ± 0.15 | 550 ± 460 | 19 ± 16 | This work |
| J1911−1114 | 16.5 ± 0.5 | 1220† | 95 ± 76 | This work |
| J1918−0642 | 9.31 ± 0.07 | 1240† | 55 ± 44 | This work |
| J1949+3106 | 5.95 ± 0.08 | 6520† | 184 ± 147 | Deneva et al. (2012) |
| J1955+2908 | 4.75 ± 0.26 | 4640† | 104 ± 84 | This work |
| J1959+2048 | 30.4 ± 0.6 | 2490† | 359 ± 287 | Arzoumanian, Fruchter & Taylor (1994) |
| J2019+2425 | 21.7 ± 0.7 | 1490† | 153 ± 123 | This work |
| J2033+1734 | 10.8 ± 0.7 | 2000† | 102 ± 82 | This work |
| J2043+1711 | 13.0 ± 2.0 | 1760† | 108 ± 88 | Guillemot et al. (2012) |
| J2051−0827 | 5.3 ± 1.0 | 1040† | 26 ± 21 | Doroshenko et al. (2001) |
| J2129−5721 | 13.31 ± 0.10 | 420 ± 200 | 26 ± 13 | Verbiest et al. (2009) |
| J2145−0750 | 13.05 ± 0.07 | 640 ± 50 | 40 ± 3 | This work |
| J2229+2643 | 6.07 ± 0.14 | 1430† | 41 ± 33 | This work |
| J2317+1439 | 3.53 ± 0.12 | 1010 ± 350 | 17 ± 6 | This work |
| PSR JName . | μ . | Distance . | 2D velocity . | Reference . |
|---|---|---|---|---|
| . | (mas yr−1) . | (pc) . | (km s−1) . | . |
| J0034−0534 | 12.1 ± 0.5 | 540† | 31 ± 25 | This work |
| J0101−6422 | 15.6 ± 1.7 | 560† | 41 ± 33 | Kerr et al. (2012) |
| J0218+4232 | 6.18 ± 0.09 | 3150† | 92 ± 25 | Verbiest & Lorimer (2014) |
| J0437−4715 | 141.29 ± 0.06 | 156.0 ± 1.0 | 104.5 ± 0.7 | Deller et al. (2008) |
| J0610−2100 | 19.05 ± 0.11 | 3540† | 320 ± 256 | This work |
| J0613−0200 | 10.514 ± 0.016 | 780 ± 80 | 39 ± 4 | This work |
| J0636+5129 | 4.7 ± 0.9 | 490† | 11 ± 9 | Stovall et al. (2014) |
| J0751+1807 | 13.66 ± 0.23 | 1070 ± 240 | 69 ± 16 | This work |
| J0900−3144 | 2.26 ± 0.06 | 810 ± 380 | 9 ± 4 | This work |
| J1012+5307 | 25.615 ± 0.010 | 1150 ± 240 | 140 ± 29 | This work |
| J1017−7156 | 9.96 ± 0.06 | 2980† | 141 ± 113 | Ng et al. (2014) |
| J1023+0038 | 17.98 ± 0.04 | 1370 ± 40 | 116.8 ± 3.4 | Deller et al. (2012) |
| J1045−4509 | 8.01 ± 0.20 | 1960† | 74 ± 60 | Verbiest et al. (2009) |
| J1125−5825 | 10.28 ± 0.30 | 2620† | 128 ± 102 | Ng et al. (2014) |
| J1231−1411 | 104.4 ± 2.2 | 440† | 218 ± 100 | Ransom et al. (2011) |
| J1300+1240 | 96.15 ± 0.07 | 450† | 205 ± 164 | Konacki & Wolszczan (2003) |
| J1337−6423 | 9.2 ± 5.4 | 5080† | 222 ± 220 | Ng et al. (2014) |
| J1405−4656 | 48.3 ± 6.9 | 580† | 133 ± 108 | Bates et al. (2015) |
| J1431−4715 | 10.6 ± 3.6 | 1560† | 78 ± 68 | Bates et al. (2015) |
| J1446−4701 | 4.47 ± 0.22 | 1460† | 31 ± 25 | Ng et al. (2014) |
| J1455−3330 | 8.19 ± 0.09 | 800 ± 300 | 31 ± 12 | This work |
| J1543−5149 | 5.9 ± 1.7 | 2420† | 68 ± 58 | Ng et al. (2014) |
| J1600−3053 | 7.00 ± 0.07 | 1490 ± 190 | 49 ± 6 | This work |
| J1603−7202 | 7.84 ± 0.09 | 1170† | 43 ± 35 | Verbiest et al. (2009) |
| J1640+2224 | 11.485 ± 0.030 | 1160† | 63 ± 51 | This work |
| J1643−1224 | 7.28 ± 0.08 | 760 ± 190 | 26 ± 7 | This work |
| J1708−3506 | 5.7 ± 1.3 | 2790† | 75 ± 63 | Ng et al. (2014) |
| J1709+2313 | 10.2 ± 0.9 | 1410† | 68 ± 55 | Lewandowski et al. (2004) |
| J1713+0747 | 6.2865 ± 0.0032 | 1110 ± 40 | 33.1 ± 1.2 | This work |
| J1719−1438 | 11.2 ± 2.0 | 1210† | 64 ± 53 | Ng et al. (2014) |
| J1731−1847 | 6.2 ± 2.9 | 2550† | 75 ± 69 | Ng et al. (2014) |
| J1738+0333 | 8.65 ± 0.12 | 1470 ± 100 | 60 ± 4 | Freire et al. (2012b) |
| J1745−0952 | 23.9 ± 2.5 | 1830† | 207 ± 167 | Janssen et al. (2010) |
| J1745+1017 | 7.8 ± 1.0 | 1260† | 47 ± 38 | Barr et al. (2013a) |
| J1751−2857 | 8.5 ± 0.6 | 1110† | 45 ± 36 | This work |
| J1801−3210 | 13.6 ± 8.2 | 4030† | 260 ± 260 | Ng et al. (2014) |
| J1802−2124 | 3.5 ± 3.2 | 640 ± 440 | 11 ± 12 | This work |
| J1804−2717 | 17.3 ± 2.4 | 780† | 64 ± 52 | This work |
| J1816+4510 | 6.1 ± 0.9 | 2410† | 70 ± 57 | Stovall et al. (2014) |
| J1853+1303 | 3.22 ± 0.15 | 880 ± 340 | 13 ± 5 | Gonzalez et al. (2011) |
| J1857+0943 | 6.028 ± 0.022 | 1100 ± 440 | 31 ± 13 | This work |
| J1903+0327 | 5.60 ± 0.11 | 6360† | 169 ± 135 | Freire et al. (2011) |
| J1909−3744 | 37.020 ± 0.009 | 1150 ± 30 | 202 ± 5 | This work |
| J1910+1256 | 7.37 ± 0.15 | 550 ± 460 | 19 ± 16 | This work |
| J1911−1114 | 16.5 ± 0.5 | 1220† | 95 ± 76 | This work |
| J1918−0642 | 9.31 ± 0.07 | 1240† | 55 ± 44 | This work |
| J1949+3106 | 5.95 ± 0.08 | 6520† | 184 ± 147 | Deneva et al. (2012) |
| J1955+2908 | 4.75 ± 0.26 | 4640† | 104 ± 84 | This work |
| J1959+2048 | 30.4 ± 0.6 | 2490† | 359 ± 287 | Arzoumanian, Fruchter & Taylor (1994) |
| J2019+2425 | 21.7 ± 0.7 | 1490† | 153 ± 123 | This work |
| J2033+1734 | 10.8 ± 0.7 | 2000† | 102 ± 82 | This work |
| J2043+1711 | 13.0 ± 2.0 | 1760† | 108 ± 88 | Guillemot et al. (2012) |
| J2051−0827 | 5.3 ± 1.0 | 1040† | 26 ± 21 | Doroshenko et al. (2001) |
| J2129−5721 | 13.31 ± 0.10 | 420 ± 200 | 26 ± 13 | Verbiest et al. (2009) |
| J2145−0750 | 13.05 ± 0.07 | 640 ± 50 | 40 ± 3 | This work |
| J2229+2643 | 6.07 ± 0.14 | 1430† | 41 ± 33 | This work |
| J2317+1439 | 3.53 ± 0.12 | 1010 ± 350 | 17 ± 6 | This work |
Summary of the transverse motion of the binary MSPs. The columns indicate the pulsar name, the composite proper motion, the distance and the corresponding transverse velocity. The last column shows the last reference with published proper-motion and distance measurements. The distances refer to the best distance estimates available, either the parallax when uncertainties are given or the NE2001 distance (indicated by †) where a 80 per cent error is assumed. Values in bold face indicate the new proper-motion measurements.
| PSR JName . | μ . | Distance . | 2D velocity . | Reference . |
|---|---|---|---|---|
| . | (mas yr−1) . | (pc) . | (km s−1) . | . |
| J0034−0534 | 12.1 ± 0.5 | 540† | 31 ± 25 | This work |
| J0101−6422 | 15.6 ± 1.7 | 560† | 41 ± 33 | Kerr et al. (2012) |
| J0218+4232 | 6.18 ± 0.09 | 3150† | 92 ± 25 | Verbiest & Lorimer (2014) |
| J0437−4715 | 141.29 ± 0.06 | 156.0 ± 1.0 | 104.5 ± 0.7 | Deller et al. (2008) |
| J0610−2100 | 19.05 ± 0.11 | 3540† | 320 ± 256 | This work |
| J0613−0200 | 10.514 ± 0.016 | 780 ± 80 | 39 ± 4 | This work |
| J0636+5129 | 4.7 ± 0.9 | 490† | 11 ± 9 | Stovall et al. (2014) |
| J0751+1807 | 13.66 ± 0.23 | 1070 ± 240 | 69 ± 16 | This work |
| J0900−3144 | 2.26 ± 0.06 | 810 ± 380 | 9 ± 4 | This work |
| J1012+5307 | 25.615 ± 0.010 | 1150 ± 240 | 140 ± 29 | This work |
| J1017−7156 | 9.96 ± 0.06 | 2980† | 141 ± 113 | Ng et al. (2014) |
| J1023+0038 | 17.98 ± 0.04 | 1370 ± 40 | 116.8 ± 3.4 | Deller et al. (2012) |
| J1045−4509 | 8.01 ± 0.20 | 1960† | 74 ± 60 | Verbiest et al. (2009) |
| J1125−5825 | 10.28 ± 0.30 | 2620† | 128 ± 102 | Ng et al. (2014) |
| J1231−1411 | 104.4 ± 2.2 | 440† | 218 ± 100 | Ransom et al. (2011) |
| J1300+1240 | 96.15 ± 0.07 | 450† | 205 ± 164 | Konacki & Wolszczan (2003) |
| J1337−6423 | 9.2 ± 5.4 | 5080† | 222 ± 220 | Ng et al. (2014) |
| J1405−4656 | 48.3 ± 6.9 | 580† | 133 ± 108 | Bates et al. (2015) |
| J1431−4715 | 10.6 ± 3.6 | 1560† | 78 ± 68 | Bates et al. (2015) |
| J1446−4701 | 4.47 ± 0.22 | 1460† | 31 ± 25 | Ng et al. (2014) |
| J1455−3330 | 8.19 ± 0.09 | 800 ± 300 | 31 ± 12 | This work |
| J1543−5149 | 5.9 ± 1.7 | 2420† | 68 ± 58 | Ng et al. (2014) |
| J1600−3053 | 7.00 ± 0.07 | 1490 ± 190 | 49 ± 6 | This work |
| J1603−7202 | 7.84 ± 0.09 | 1170† | 43 ± 35 | Verbiest et al. (2009) |
| J1640+2224 | 11.485 ± 0.030 | 1160† | 63 ± 51 | This work |
| J1643−1224 | 7.28 ± 0.08 | 760 ± 190 | 26 ± 7 | This work |
| J1708−3506 | 5.7 ± 1.3 | 2790† | 75 ± 63 | Ng et al. (2014) |
| J1709+2313 | 10.2 ± 0.9 | 1410† | 68 ± 55 | Lewandowski et al. (2004) |
| J1713+0747 | 6.2865 ± 0.0032 | 1110 ± 40 | 33.1 ± 1.2 | This work |
| J1719−1438 | 11.2 ± 2.0 | 1210† | 64 ± 53 | Ng et al. (2014) |
| J1731−1847 | 6.2 ± 2.9 | 2550† | 75 ± 69 | Ng et al. (2014) |
| J1738+0333 | 8.65 ± 0.12 | 1470 ± 100 | 60 ± 4 | Freire et al. (2012b) |
| J1745−0952 | 23.9 ± 2.5 | 1830† | 207 ± 167 | Janssen et al. (2010) |
| J1745+1017 | 7.8 ± 1.0 | 1260† | 47 ± 38 | Barr et al. (2013a) |
| J1751−2857 | 8.5 ± 0.6 | 1110† | 45 ± 36 | This work |
| J1801−3210 | 13.6 ± 8.2 | 4030† | 260 ± 260 | Ng et al. (2014) |
| J1802−2124 | 3.5 ± 3.2 | 640 ± 440 | 11 ± 12 | This work |
| J1804−2717 | 17.3 ± 2.4 | 780† | 64 ± 52 | This work |
| J1816+4510 | 6.1 ± 0.9 | 2410† | 70 ± 57 | Stovall et al. (2014) |
| J1853+1303 | 3.22 ± 0.15 | 880 ± 340 | 13 ± 5 | Gonzalez et al. (2011) |
| J1857+0943 | 6.028 ± 0.022 | 1100 ± 440 | 31 ± 13 | This work |
| J1903+0327 | 5.60 ± 0.11 | 6360† | 169 ± 135 | Freire et al. (2011) |
| J1909−3744 | 37.020 ± 0.009 | 1150 ± 30 | 202 ± 5 | This work |
| J1910+1256 | 7.37 ± 0.15 | 550 ± 460 | 19 ± 16 | This work |
| J1911−1114 | 16.5 ± 0.5 | 1220† | 95 ± 76 | This work |
| J1918−0642 | 9.31 ± 0.07 | 1240† | 55 ± 44 | This work |
| J1949+3106 | 5.95 ± 0.08 | 6520† | 184 ± 147 | Deneva et al. (2012) |
| J1955+2908 | 4.75 ± 0.26 | 4640† | 104 ± 84 | This work |
| J1959+2048 | 30.4 ± 0.6 | 2490† | 359 ± 287 | Arzoumanian, Fruchter & Taylor (1994) |
| J2019+2425 | 21.7 ± 0.7 | 1490† | 153 ± 123 | This work |
| J2033+1734 | 10.8 ± 0.7 | 2000† | 102 ± 82 | This work |
| J2043+1711 | 13.0 ± 2.0 | 1760† | 108 ± 88 | Guillemot et al. (2012) |
| J2051−0827 | 5.3 ± 1.0 | 1040† | 26 ± 21 | Doroshenko et al. (2001) |
| J2129−5721 | 13.31 ± 0.10 | 420 ± 200 | 26 ± 13 | Verbiest et al. (2009) |
| J2145−0750 | 13.05 ± 0.07 | 640 ± 50 | 40 ± 3 | This work |
| J2229+2643 | 6.07 ± 0.14 | 1430† | 41 ± 33 | This work |
| J2317+1439 | 3.53 ± 0.12 | 1010 ± 350 | 17 ± 6 | This work |
| PSR JName . | μ . | Distance . | 2D velocity . | Reference . |
|---|---|---|---|---|
| . | (mas yr−1) . | (pc) . | (km s−1) . | . |
| J0034−0534 | 12.1 ± 0.5 | 540† | 31 ± 25 | This work |
| J0101−6422 | 15.6 ± 1.7 | 560† | 41 ± 33 | Kerr et al. (2012) |
| J0218+4232 | 6.18 ± 0.09 | 3150† | 92 ± 25 | Verbiest & Lorimer (2014) |
| J0437−4715 | 141.29 ± 0.06 | 156.0 ± 1.0 | 104.5 ± 0.7 | Deller et al. (2008) |
| J0610−2100 | 19.05 ± 0.11 | 3540† | 320 ± 256 | This work |
| J0613−0200 | 10.514 ± 0.016 | 780 ± 80 | 39 ± 4 | This work |
| J0636+5129 | 4.7 ± 0.9 | 490† | 11 ± 9 | Stovall et al. (2014) |
| J0751+1807 | 13.66 ± 0.23 | 1070 ± 240 | 69 ± 16 | This work |
| J0900−3144 | 2.26 ± 0.06 | 810 ± 380 | 9 ± 4 | This work |
| J1012+5307 | 25.615 ± 0.010 | 1150 ± 240 | 140 ± 29 | This work |
| J1017−7156 | 9.96 ± 0.06 | 2980† | 141 ± 113 | Ng et al. (2014) |
| J1023+0038 | 17.98 ± 0.04 | 1370 ± 40 | 116.8 ± 3.4 | Deller et al. (2012) |
| J1045−4509 | 8.01 ± 0.20 | 1960† | 74 ± 60 | Verbiest et al. (2009) |
| J1125−5825 | 10.28 ± 0.30 | 2620† | 128 ± 102 | Ng et al. (2014) |
| J1231−1411 | 104.4 ± 2.2 | 440† | 218 ± 100 | Ransom et al. (2011) |
| J1300+1240 | 96.15 ± 0.07 | 450† | 205 ± 164 | Konacki & Wolszczan (2003) |
| J1337−6423 | 9.2 ± 5.4 | 5080† | 222 ± 220 | Ng et al. (2014) |
| J1405−4656 | 48.3 ± 6.9 | 580† | 133 ± 108 | Bates et al. (2015) |
| J1431−4715 | 10.6 ± 3.6 | 1560† | 78 ± 68 | Bates et al. (2015) |
| J1446−4701 | 4.47 ± 0.22 | 1460† | 31 ± 25 | Ng et al. (2014) |
| J1455−3330 | 8.19 ± 0.09 | 800 ± 300 | 31 ± 12 | This work |
| J1543−5149 | 5.9 ± 1.7 | 2420† | 68 ± 58 | Ng et al. (2014) |
| J1600−3053 | 7.00 ± 0.07 | 1490 ± 190 | 49 ± 6 | This work |
| J1603−7202 | 7.84 ± 0.09 | 1170† | 43 ± 35 | Verbiest et al. (2009) |
| J1640+2224 | 11.485 ± 0.030 | 1160† | 63 ± 51 | This work |
| J1643−1224 | 7.28 ± 0.08 | 760 ± 190 | 26 ± 7 | This work |
| J1708−3506 | 5.7 ± 1.3 | 2790† | 75 ± 63 | Ng et al. (2014) |
| J1709+2313 | 10.2 ± 0.9 | 1410† | 68 ± 55 | Lewandowski et al. (2004) |
| J1713+0747 | 6.2865 ± 0.0032 | 1110 ± 40 | 33.1 ± 1.2 | This work |
| J1719−1438 | 11.2 ± 2.0 | 1210† | 64 ± 53 | Ng et al. (2014) |
| J1731−1847 | 6.2 ± 2.9 | 2550† | 75 ± 69 | Ng et al. (2014) |
| J1738+0333 | 8.65 ± 0.12 | 1470 ± 100 | 60 ± 4 | Freire et al. (2012b) |
| J1745−0952 | 23.9 ± 2.5 | 1830† | 207 ± 167 | Janssen et al. (2010) |
| J1745+1017 | 7.8 ± 1.0 | 1260† | 47 ± 38 | Barr et al. (2013a) |
| J1751−2857 | 8.5 ± 0.6 | 1110† | 45 ± 36 | This work |
| J1801−3210 | 13.6 ± 8.2 | 4030† | 260 ± 260 | Ng et al. (2014) |
| J1802−2124 | 3.5 ± 3.2 | 640 ± 440 | 11 ± 12 | This work |
| J1804−2717 | 17.3 ± 2.4 | 780† | 64 ± 52 | This work |
| J1816+4510 | 6.1 ± 0.9 | 2410† | 70 ± 57 | Stovall et al. (2014) |
| J1853+1303 | 3.22 ± 0.15 | 880 ± 340 | 13 ± 5 | Gonzalez et al. (2011) |
| J1857+0943 | 6.028 ± 0.022 | 1100 ± 440 | 31 ± 13 | This work |
| J1903+0327 | 5.60 ± 0.11 | 6360† | 169 ± 135 | Freire et al. (2011) |
| J1909−3744 | 37.020 ± 0.009 | 1150 ± 30 | 202 ± 5 | This work |
| J1910+1256 | 7.37 ± 0.15 | 550 ± 460 | 19 ± 16 | This work |
| J1911−1114 | 16.5 ± 0.5 | 1220† | 95 ± 76 | This work |
| J1918−0642 | 9.31 ± 0.07 | 1240† | 55 ± 44 | This work |
| J1949+3106 | 5.95 ± 0.08 | 6520† | 184 ± 147 | Deneva et al. (2012) |
| J1955+2908 | 4.75 ± 0.26 | 4640† | 104 ± 84 | This work |
| J1959+2048 | 30.4 ± 0.6 | 2490† | 359 ± 287 | Arzoumanian, Fruchter & Taylor (1994) |
| J2019+2425 | 21.7 ± 0.7 | 1490† | 153 ± 123 | This work |
| J2033+1734 | 10.8 ± 0.7 | 2000† | 102 ± 82 | This work |
| J2043+1711 | 13.0 ± 2.0 | 1760† | 108 ± 88 | Guillemot et al. (2012) |
| J2051−0827 | 5.3 ± 1.0 | 1040† | 26 ± 21 | Doroshenko et al. (2001) |
| J2129−5721 | 13.31 ± 0.10 | 420 ± 200 | 26 ± 13 | Verbiest et al. (2009) |
| J2145−0750 | 13.05 ± 0.07 | 640 ± 50 | 40 ± 3 | This work |
| J2229+2643 | 6.07 ± 0.14 | 1430† | 41 ± 33 | This work |
| J2317+1439 | 3.53 ± 0.12 | 1010 ± 350 | 17 ± 6 | This work |
We find an average velocity of 88 ± 17 and 93 ± 13 km s−1 for the isolated and binary MSPs, respectively. For the entire MSP data set, we get an average velocity of 92 ± 10 km s−1. Our results are consistent with the work by Hobbs et al. (2005) and Gonzalez et al. (2011).
When we keep only the pulsars with a more reliable distance estimate (i.e. pulsars with a parallax measurement), eight isolated and 20 binary MSPs are left in our sample. In this case, we find an average velocity of 75 ± 10 and 56 ± 3 km s−1 for the isolated and binary MSPs, respectively. Conversely, we get an average velocity of 98 ± 29 and 113 ± 20 km s−1 for the pulsars with a distance coming from the Galactic electron density models. The explanations for this discrepancy are twofold: the NE2001 model is overestimating the distances for low Galactic latitude as shown in Fig. 3 and our sample of 2D velocities is biased against distant low-velocity MSPs. Nearby pulsars are likely to have a parallax and a proper-motion measurement, whereas distant pulsars would most likely have a distance estimate from the NE2001 model and a proper-motion measurement for the high-velocity pulsars only.
Fig. 5 shows the histogram of the velocities for both the isolated and binary MSPs populations. A two-sample Kolgomorov–Smirnov (KS) test between the full isolated and binary MSPs velocity distributions results in a KS statistic of 0.14 and a p-value of 0.92. If we perform the same test on the pulsars with a parallax distance, we get a KS statistic of 0.25 and a p-value of 0.81. For both cases, we therefore cannot reject the null hypothesis and we argue that there is no statistical evidence for the measurements to be drawn from different distributions. This supports the scenario that both isolated and binary MSPs evolve from the same population of binary pulsars.
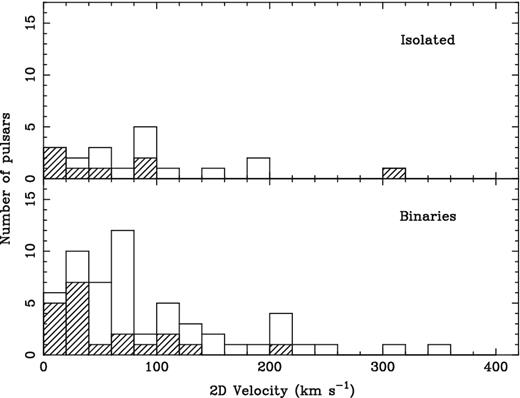
Histogram of the 2D velocity distribution for a sample of 19 isolated MSPs (top panel) and 57 binary MSPs (bottom panel). The respective average velocities are 88 ± 17 and 96 ± 12 km s−1. The hatched part of the histogram shows the pulsars with a distance estimate from the parallax measurement (eight isolated and 21 binary MSPs).
5.3 Shklovskii and Galactic acceleration contributions
To compute these contributions with full error propagation, we use the distances from Table 13 and the proper motions shown in Tables 14 and 15. These values are reported for each pulsar at the bottom of Tables 2–12. The magnitudes of all three corrective terms to |$\dot{P}$| depend on the distance d to the pulsar. Alternatively, as the pulsar braking torque causes the spin period to increase (i.e. |$\dot{P}$| to be positive) in systems where no mass transfer is taking place, we used this constraint to set an upper limit, |$D_{\dot{P}}$|, on the distance to the pulsar by assuming all the observed |$\dot{P}$| is a result of kinematic and Galactic acceleration effects. This upper limit |$D_{\dot{P}}$| is shown in column 5 of Table 13 for 19 pulsars, where this upper limit is below 15 kpc.
For all pulsars except PSRs J0610−2100, J1024−0719 and J1721−2457, the upper limits |$D_{\dot{P}}$| are consistent with both the NE2001 and M3 distances, DNE2001 and DM3, respectively. For PSR J0610−2100, DM3 = 8.94 kpc is ruled out by |$D_{\dot{P}} < 3.89$| kpc. We note that for this pulsar, DM3 is 2.5 times higher than DNE2001. For PSR J1721−2457, both DNE2001 and DM3 are ruled out by |$D_{\dot{P}} < 0.96$| kpc. The case of PSR J1024−0719 is discussed below.
The same reasoning behind the corrections of equation (7) also apply to the observed orbital period derivative |$\dot{P_{\rm b}}$|. In addition to the previous terms, we also consider the contribution due to gravitational radiation assuming GR, |$\dot{P_{\rm b}}_{\_{\rm GR}}$| but neglect the contributions from mass-loss in the binary, tidal interactions or changes in the gravitational constant G. |$\dot{P_{\rm b}}_{\_{\rm GR}}$| is therefore the only contribution independent of the distance to the pulsar system but requires an estimate of the masses of the binary.
As we measured the orbital period derivative for four pulsars (PSRs J0613−0200, J0751+1807, J1012+5307 and J1909−3744), we investigate here the possible bias in those measurements assuming the parallax distances from Table 13. Conversely, Bell & Bailes (1996, hereafter BB96) pointed out that the measurement of |$\dot{P_{\rm b}}$| would potentially lead to more accurate distance than the annual parallax. Hence, we also present a new distance estimate, |$D_{\dot{P_{\rm b}}}$|, assuming the observed |$\dot{P_{\rm b}}$| is the sum of all four contributions described above. These results are shown in Table 16.
Summary of the kinematic and relativistic contributions to the observed orbital period derivative |$\dot{P_{\rm b}}$|. The columns indicate the pulsar name, the LK-corrected parallax distance (we made the errors symmetric by always taking the highest of the two error estimates given in Table 13), the observed orbital period derivative |$\dot{P_{\rm b}}$|, the contributions to |$\dot{P_{\rm b}}$| from the Shklovskii effect, Galactic potential, differential Galactic rotation and GW radiation assuming GR. The last column shows the estimated distance assuming all |$\dot{P_{\rm b}}$| arises from these contributions. † Assuming mp = 1.4 M⊙ and i = 60°. ‡ For PSR J1012+5307, we take mc = 0.16 ± 0.02 M⊙ and i = 52 ± 4° from van Kerkwijk et al. (1996) and Callanan et al. (1998).
| PSR JName . | Dπ . | |$\dot{P_{\rm b}}$| . | |$\dot{P_{\rm b}}_{\_{\rm kin}}$| . | |$\dot{P_{\rm b}}_{\_{\rm kz}}$| . | |$\dot{P_{\rm b}}_{\_{\rm dgr}}$| . | |$\dot{P_{\rm b}}_{\_{\rm GR}}$| . | |$D_{\dot{P_{\rm b}}}$| . |
|---|---|---|---|---|---|---|---|
| . | (kpc) . | (×10−13) . | (×10−13) . | (×10−13) . | (×10−13) . | (×10−13) . | (kpc) . |
| J0613−0200 | 0.78(8) | 0.48(10) | +0.217(22) | −0.0133(14) | +0.034(4) | −0.03† | 1.68(33) |
| J0751+1807 | 1.07(24) | −0.350(25) | +0.110(25) | −0.0104(12) | +0.0125(28) | – | – |
| J1012+5307 | 1.15(24) | 0.61(4) | +0.96(20) | −0.076(7) | +0.0157(33) | −0.112(29)‡ | 0.94(3) |
| J1909−3744 | 1.15(3) | 5.03(5) | +5.07(13) | −0.1092(29) | +0.139(12) | −0.0291(7) | 1.140(11) |
| PSR JName . | Dπ . | |$\dot{P_{\rm b}}$| . | |$\dot{P_{\rm b}}_{\_{\rm kin}}$| . | |$\dot{P_{\rm b}}_{\_{\rm kz}}$| . | |$\dot{P_{\rm b}}_{\_{\rm dgr}}$| . | |$\dot{P_{\rm b}}_{\_{\rm GR}}$| . | |$D_{\dot{P_{\rm b}}}$| . |
|---|---|---|---|---|---|---|---|
| . | (kpc) . | (×10−13) . | (×10−13) . | (×10−13) . | (×10−13) . | (×10−13) . | (kpc) . |
| J0613−0200 | 0.78(8) | 0.48(10) | +0.217(22) | −0.0133(14) | +0.034(4) | −0.03† | 1.68(33) |
| J0751+1807 | 1.07(24) | −0.350(25) | +0.110(25) | −0.0104(12) | +0.0125(28) | – | – |
| J1012+5307 | 1.15(24) | 0.61(4) | +0.96(20) | −0.076(7) | +0.0157(33) | −0.112(29)‡ | 0.94(3) |
| J1909−3744 | 1.15(3) | 5.03(5) | +5.07(13) | −0.1092(29) | +0.139(12) | −0.0291(7) | 1.140(11) |
Summary of the kinematic and relativistic contributions to the observed orbital period derivative |$\dot{P_{\rm b}}$|. The columns indicate the pulsar name, the LK-corrected parallax distance (we made the errors symmetric by always taking the highest of the two error estimates given in Table 13), the observed orbital period derivative |$\dot{P_{\rm b}}$|, the contributions to |$\dot{P_{\rm b}}$| from the Shklovskii effect, Galactic potential, differential Galactic rotation and GW radiation assuming GR. The last column shows the estimated distance assuming all |$\dot{P_{\rm b}}$| arises from these contributions. † Assuming mp = 1.4 M⊙ and i = 60°. ‡ For PSR J1012+5307, we take mc = 0.16 ± 0.02 M⊙ and i = 52 ± 4° from van Kerkwijk et al. (1996) and Callanan et al. (1998).
| PSR JName . | Dπ . | |$\dot{P_{\rm b}}$| . | |$\dot{P_{\rm b}}_{\_{\rm kin}}$| . | |$\dot{P_{\rm b}}_{\_{\rm kz}}$| . | |$\dot{P_{\rm b}}_{\_{\rm dgr}}$| . | |$\dot{P_{\rm b}}_{\_{\rm GR}}$| . | |$D_{\dot{P_{\rm b}}}$| . |
|---|---|---|---|---|---|---|---|
| . | (kpc) . | (×10−13) . | (×10−13) . | (×10−13) . | (×10−13) . | (×10−13) . | (kpc) . |
| J0613−0200 | 0.78(8) | 0.48(10) | +0.217(22) | −0.0133(14) | +0.034(4) | −0.03† | 1.68(33) |
| J0751+1807 | 1.07(24) | −0.350(25) | +0.110(25) | −0.0104(12) | +0.0125(28) | – | – |
| J1012+5307 | 1.15(24) | 0.61(4) | +0.96(20) | −0.076(7) | +0.0157(33) | −0.112(29)‡ | 0.94(3) |
| J1909−3744 | 1.15(3) | 5.03(5) | +5.07(13) | −0.1092(29) | +0.139(12) | −0.0291(7) | 1.140(11) |
| PSR JName . | Dπ . | |$\dot{P_{\rm b}}$| . | |$\dot{P_{\rm b}}_{\_{\rm kin}}$| . | |$\dot{P_{\rm b}}_{\_{\rm kz}}$| . | |$\dot{P_{\rm b}}_{\_{\rm dgr}}$| . | |$\dot{P_{\rm b}}_{\_{\rm GR}}$| . | |$D_{\dot{P_{\rm b}}}$| . |
|---|---|---|---|---|---|---|---|
| . | (kpc) . | (×10−13) . | (×10−13) . | (×10−13) . | (×10−13) . | (×10−13) . | (kpc) . |
| J0613−0200 | 0.78(8) | 0.48(10) | +0.217(22) | −0.0133(14) | +0.034(4) | −0.03† | 1.68(33) |
| J0751+1807 | 1.07(24) | −0.350(25) | +0.110(25) | −0.0104(12) | +0.0125(28) | – | – |
| J1012+5307 | 1.15(24) | 0.61(4) | +0.96(20) | −0.076(7) | +0.0157(33) | −0.112(29)‡ | 0.94(3) |
| J1909−3744 | 1.15(3) | 5.03(5) | +5.07(13) | −0.1092(29) | +0.139(12) | −0.0291(7) | 1.140(11) |
To estimate the gravitational radiation contribution to |$\dot{P_{\rm b}}$| for PSR J0613−0200 without a mass measurement, we assumed mp = 1.4 M⊙ and i = 60°. The resulting distance estimate is |$D_{\dot{P_{\rm b}}} = 1.68\pm 0.33$| kpc. This result is 2.2σ consistent with the parallax distance and currently limited by the precision on the measured |$\dot{P_{\rm b}}$|. Continued timing of this pulsar will greatly improve this test as the uncertainty on |$\dot{P_{\rm b}}$| decrease as t−2.5. For PSR J0751+1807, we measure a negative orbital period derivative, |$\dot{P_{\rm b}}=(-3.50\pm 0.25) \times 10^{-14}$|, meaning the Shklovskii effect is not the dominant contribution to |$\dot{P_{\rm b}}$| in this system. We also note that our measured composite proper motion is 3.3σ higher than the value in Nice et al. (2005) resulting in a Shklovskii contribution to |$\dot{P_{\rm b}}$| that is five times larger than the one quoted in Nice et al. (2005). In the next section, we will combine the corrected orbital period derivative from acceleration bias |$\dot{P_{\rm b}}_{{\rm corr}} = \dot{P_{\rm b}} - \dot{P_{\rm b}}_{\_{\rm kin}} - \dot{P_{\rm b}}_{\_{\rm kz}} - \dot{P_{\rm b}}_{\_{\rm dgr}} = (-4.6\pm 0.4) \times 10^{-14}$| with the measurement of the Shapiro delay to constrain the masses of the two stars.
For PSR J1012+5307, we measured the orbital period derivative |$\dot{P_{\rm b}}=(6.1\pm 0.4) \times 10^{-14}$|, a value similar to the one reported by Lazaridis et al. (2009). We also find the contributions to |$\dot{P_{\rm b}}$| to be consistent with their work. After taking into account the companion mass and inclination angle from van Kerkwijk, Bergeron & Kulkarni (1996), Callanan, Garnavich & Koester (1998) to compute |$\dot{P_{\rm b}}_{\_{\rm GR}}$|, we find |$D_{\dot{P_{\rm b}}} = 940\pm 30$| pc, in very good agreement with the optical (van Kerkwijk et al. 1996; Callanan et al. 1998) and parallax distance, but more precise by a factor of 3 and 8, respectively.
The bias in the orbital period derivative measured for PSR J1909−3744 is almost solely due to the Shklovskii effect. We get |$D_{\dot{P_{\rm b}}} = 1140\pm 11$| pc. This result with a fractional uncertainty of only 1 per cent is also in very good agreement with the parallax distance.
20 years ago, BB96 predicted that after only 10 years, several of the MSPs included in this paper would have a better determination of the distance through the measurement of the Shklovskii contribution to |$\dot{P_{\rm b}}$| compared to the annual parallax. However, we achieved a better distance estimate from |$\dot{P_{\rm b}}$| than the parallax for only two pulsars so far.
We investigate here the pulsars for which we should have detected |$\dot{P_{\rm b}}$| based on the work by BB96 (i.e. PSRs J1455−3330, J2019+2425 J2145−0750 and J2317+1439). In their paper, BB96 assumed a transverse velocity of 69 km s−1 for pulsars where the proper motion was not measured and adopted the distance to the pulsar based on the TC93 Galactic electron density model.
In the case of PSR J2019+2425, our measured proper motion is similar to the value used by BB96 and the time span of our data is nine years. The peak-to-peak timing signature of the Shklovskii contribution to |$\dot{P_{\rm b}}$| (see Eq. 1 of BB96) is ΔTpm = 6 ± 5 μs, with the large uncertainty coming from the NE2001 distance assumed. For the three remaining pulsars, no proper-motion measurement was available at the time and BB96 assumed in those cases a transverse velocity of 69 km s−1. However our new results reported in Table 15 show much smaller transverse velocities for PSRs J1455−3330, J2145−0750 and J2317+1439, with 31 ± 12, 40 ± 3, 17 ± 6 km s−1 respectively, resulting in a much lower Shklovskii contribution to |$\dot{P_{\rm b}}$| than predicted by BB96, explaining the non-detection of this parameter after 10–17 yr of data with our current timing precision.
5.4 Shapiro delay and mass measurement
In Figs 6 –8, we plot, assuming GR, the joint 2D probability density function of the Shapiro delay that comes directly out of the temponest analysis for the three pulsars we achieve greatly improved mass measurements, PSRs J0751+1807, J1600−3053 and J1918−0642, respectively. For PSR J0751+1807, we use the corrected orbital period derivative, |$\dot{P_{\rm b}}_{{\rm corr}} = (-4.6\pm 0.4) \times 10^{-14}$|, derived in the previous section to further constrain the masses of the system. The projection of the parameters |$\dot{P_{\rm b}}$| and ς gives the following 68.3 per cent confidence levels: mp = 1.64 ± 0.15 M⊙ and mc = 0.16 ± 0.01 M⊙. The inclination angle is constrained with cos i < 0.64 (2σ). Our new pulsar mass measurement is 1.3σ larger from the latest mass value published in Nice et al. (2008).
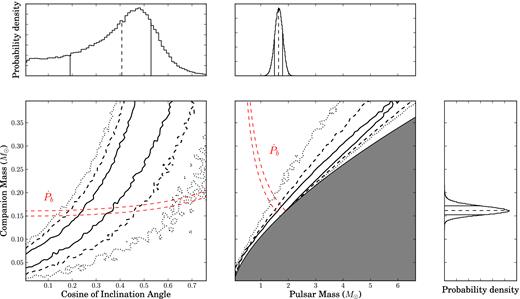
Constraints on PSR J0751+1807 parameters from the measurement of Shapiro delay and orbital period derivative |$\dot{P_{\rm b}}$|. The bottom-left plot shows the cos i − mc plane. The bottom-right plot shows the mp − mc plane. The continuous black line, the dashed line and the dotted line represent, respectively, the 68.3, 95.4 and 99.7 per cent confidence levels of the 2D probability density function. The grey area is excluded by the mass function with the condition sin i ≤ 1. The red curves indicate the 1σ constraint required by |$\dot{P_{\rm b}}$| assuming GR. The other three panels show the projected 1D distributions based on |$\dot{P_{\rm b}}$| and the inclination angle (given by ς). The dashed lines indicate the median value and the continuous lines the 1σ contours.
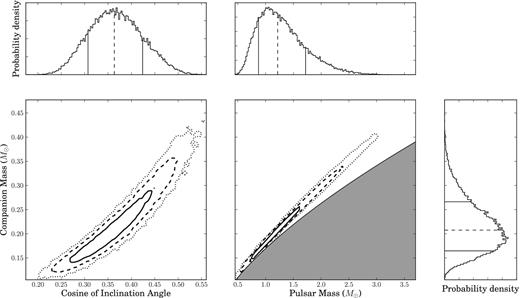
Constraints on PSR J1600−3053 parameters from the measurement of Shapiro delay. The bottom-left plot shows the cos i − mc plane. The bottom-right plot shows the mp − mc plane. The continuous black line, the dashed line and the dotted line represent, respectively, the 68.3, 95.4 and 99.7 per cent confidence levels of the 2D probability density function. The grey area is excluded by the mass function with the condition sin i ≤ 1. The other three panels show the projected 1D distributions with the dashed line indicating the median value and the continuous lines the 1σ contours.
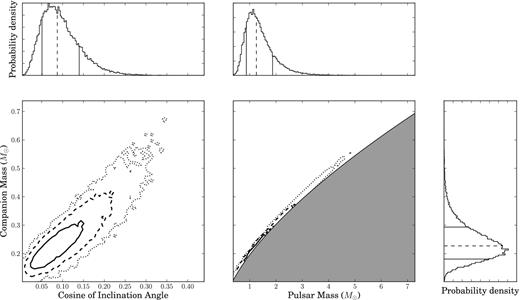
In the case of PSR J1600−3053, the posterior results from temponest give cos i = 0.36 ± 0.06, |$m_{\rm p}=1.22_{-0.35}^{+0.50}$| M⊙ and |$m_{\rm c}=0.21_{-0.04}^{0.06}$| M⊙. We now have an accurate mass of the companion compared to the marginal detection by Verbiest et al. (2009). Given the eccentricity e ∼ 1.7 × 10−4 of this system, a detection of the precession of periastron is likely to happen in the near future and would greatly improve the pulsar mass measurement.
The results for PSR J1918−0642 translate into a pulsar mass |$m_{\rm p} = 1.25_{-0.4}^{+0.6}$| M⊙ and a companion mass mc = 0.23 ± 0.07 M⊙. The cosine of the inclination angle is |$0.09_{-0.04}^{+0.05}$|. Based on the mass estimates for the companions to PSRs J1600−3053 and J1918−0642, it is expected that these are low-mass helium white dwarfs.
In Table 17, we summarize all our mass measurements and compare them to the values previously published in the literature. We find that PSRs J1713+0747, J1802−2124, J1857+0943 and J1909−3744 have a mass measurement that is in very good agreement to the values reported in the literature (Verbiest et al. 2009; Ferdman et al. 2010; Zhu et al. 2015).
Table of pulsar and companion masses. The columns indicate the pulsar name, the previously published pulsar and companion mass (Prev. mp and Prev. mc) with the corresponding publication. The last two columns show our new measurements, mp and mc. † Nice et al. (2008) did not report on the companion mass in their proceedings. ‡ The pulsar masses were not reported by Verbiest et al. (2009) so we quote the pulsar mass value based on the mass function and their companion mass.
| PSR JName . | Prev. mp . | Prev. mc . | Ref. . | mp . | mc . |
|---|---|---|---|---|---|
| . | (M⊙) . | (M⊙) . | . | (M⊙) . | (M⊙) . |
| J0751+1807 | 1.26 ± 0.14 | –† | Nice et al. (2001, 2008) | |$1.64_{-0.15}^{+0.15}$| | |$0.16_{-0.01}^{+0.01}$| |
| J1600−3053 | 0.87‡ | 0.6 ± 0.7 | Verbiest et al. (2009) | |$1.22_{-0.35}^{+0.50}$| | |$0.21_{-0.043}^{+0.06}$| |
| J1713+0747 | 1.31 ± 0.11 | 0.286 ± 0.012 | Zhu et al. (2015) | |$1.33_{-0.08}^{+0.09}$| | |$0.289_{0.011}^{+0.013}$| |
| J1802−2124 | 1.24 ± 0.11 | 0.78 ± 0.04 | Ferdman et al. (2010) | |$1.25_{-0.4}^{+0.6}$| | |$0.80_{-0.16}^{+0.21}$| |
| J1857+0943 | 1.61‡ | 0.270 ± 0.015 | Verbiest et al. (2009) | |$1.59_{-0.18}^{+0.21}$| | |$0.268_{-0.019}^{+0.022}$| |
| J1909−3744 | 1.53‡ | 0.212 ± 0.002 | Verbiest et al. (2009) | |$1.54_{-0.027}^{+0.027}$| | |$0.213_{-0.0024}^{+0.0024}$| |
| J1918−0642 | – | – | – | |$1.25_{-0.38}^{+0.61}$| | |$0.227_{-0.046}^{+0.066}$| |
| PSR JName . | Prev. mp . | Prev. mc . | Ref. . | mp . | mc . |
|---|---|---|---|---|---|
| . | (M⊙) . | (M⊙) . | . | (M⊙) . | (M⊙) . |
| J0751+1807 | 1.26 ± 0.14 | –† | Nice et al. (2001, 2008) | |$1.64_{-0.15}^{+0.15}$| | |$0.16_{-0.01}^{+0.01}$| |
| J1600−3053 | 0.87‡ | 0.6 ± 0.7 | Verbiest et al. (2009) | |$1.22_{-0.35}^{+0.50}$| | |$0.21_{-0.043}^{+0.06}$| |
| J1713+0747 | 1.31 ± 0.11 | 0.286 ± 0.012 | Zhu et al. (2015) | |$1.33_{-0.08}^{+0.09}$| | |$0.289_{0.011}^{+0.013}$| |
| J1802−2124 | 1.24 ± 0.11 | 0.78 ± 0.04 | Ferdman et al. (2010) | |$1.25_{-0.4}^{+0.6}$| | |$0.80_{-0.16}^{+0.21}$| |
| J1857+0943 | 1.61‡ | 0.270 ± 0.015 | Verbiest et al. (2009) | |$1.59_{-0.18}^{+0.21}$| | |$0.268_{-0.019}^{+0.022}$| |
| J1909−3744 | 1.53‡ | 0.212 ± 0.002 | Verbiest et al. (2009) | |$1.54_{-0.027}^{+0.027}$| | |$0.213_{-0.0024}^{+0.0024}$| |
| J1918−0642 | – | – | – | |$1.25_{-0.38}^{+0.61}$| | |$0.227_{-0.046}^{+0.066}$| |
Table of pulsar and companion masses. The columns indicate the pulsar name, the previously published pulsar and companion mass (Prev. mp and Prev. mc) with the corresponding publication. The last two columns show our new measurements, mp and mc. † Nice et al. (2008) did not report on the companion mass in their proceedings. ‡ The pulsar masses were not reported by Verbiest et al. (2009) so we quote the pulsar mass value based on the mass function and their companion mass.
| PSR JName . | Prev. mp . | Prev. mc . | Ref. . | mp . | mc . |
|---|---|---|---|---|---|
| . | (M⊙) . | (M⊙) . | . | (M⊙) . | (M⊙) . |
| J0751+1807 | 1.26 ± 0.14 | –† | Nice et al. (2001, 2008) | |$1.64_{-0.15}^{+0.15}$| | |$0.16_{-0.01}^{+0.01}$| |
| J1600−3053 | 0.87‡ | 0.6 ± 0.7 | Verbiest et al. (2009) | |$1.22_{-0.35}^{+0.50}$| | |$0.21_{-0.043}^{+0.06}$| |
| J1713+0747 | 1.31 ± 0.11 | 0.286 ± 0.012 | Zhu et al. (2015) | |$1.33_{-0.08}^{+0.09}$| | |$0.289_{0.011}^{+0.013}$| |
| J1802−2124 | 1.24 ± 0.11 | 0.78 ± 0.04 | Ferdman et al. (2010) | |$1.25_{-0.4}^{+0.6}$| | |$0.80_{-0.16}^{+0.21}$| |
| J1857+0943 | 1.61‡ | 0.270 ± 0.015 | Verbiest et al. (2009) | |$1.59_{-0.18}^{+0.21}$| | |$0.268_{-0.019}^{+0.022}$| |
| J1909−3744 | 1.53‡ | 0.212 ± 0.002 | Verbiest et al. (2009) | |$1.54_{-0.027}^{+0.027}$| | |$0.213_{-0.0024}^{+0.0024}$| |
| J1918−0642 | – | – | – | |$1.25_{-0.38}^{+0.61}$| | |$0.227_{-0.046}^{+0.066}$| |
| PSR JName . | Prev. mp . | Prev. mc . | Ref. . | mp . | mc . |
|---|---|---|---|---|---|
| . | (M⊙) . | (M⊙) . | . | (M⊙) . | (M⊙) . |
| J0751+1807 | 1.26 ± 0.14 | –† | Nice et al. (2001, 2008) | |$1.64_{-0.15}^{+0.15}$| | |$0.16_{-0.01}^{+0.01}$| |
| J1600−3053 | 0.87‡ | 0.6 ± 0.7 | Verbiest et al. (2009) | |$1.22_{-0.35}^{+0.50}$| | |$0.21_{-0.043}^{+0.06}$| |
| J1713+0747 | 1.31 ± 0.11 | 0.286 ± 0.012 | Zhu et al. (2015) | |$1.33_{-0.08}^{+0.09}$| | |$0.289_{0.011}^{+0.013}$| |
| J1802−2124 | 1.24 ± 0.11 | 0.78 ± 0.04 | Ferdman et al. (2010) | |$1.25_{-0.4}^{+0.6}$| | |$0.80_{-0.16}^{+0.21}$| |
| J1857+0943 | 1.61‡ | 0.270 ± 0.015 | Verbiest et al. (2009) | |$1.59_{-0.18}^{+0.21}$| | |$0.268_{-0.019}^{+0.022}$| |
| J1909−3744 | 1.53‡ | 0.212 ± 0.002 | Verbiest et al. (2009) | |$1.54_{-0.027}^{+0.027}$| | |$0.213_{-0.0024}^{+0.0024}$| |
| J1918−0642 | – | – | – | |$1.25_{-0.38}^{+0.61}$| | |$0.227_{-0.046}^{+0.066}$| |
Summary of the EPTA data set. The columns indicate, respectively, the pulsar name, the number of JUMPs (Nj) included in the timing solution, the maximum likelihood results for the red noise (RN) and DM models (dimensionless amplitude A and spectral index γ for each model), the observatory, frequency band (in MHz), data span in years, number of TOAs along with the maximum likelihood values for the EFAC (Ef) and EQUAD (Eq in units of seconds) parameters (EQUAD shown in log10-base).
| PSR JName . | Nj . | ARN . | γRN . | ADM . | γDM . | Observatory . | Frequency . | Year range . | NTOAs . | Ef . | Eq . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| J0030+0451 | 6 | −14.65 | 5.43 | −19.06 | 3.27 | ||||||
| EFF | 1360 | 2009.7–2013.5 | 33 | 1.17 | −9.17 | ||||||
| 1410 | 1999.3–2009.6 | 10 | 0.62 | −9.00 | |||||||
| 2639 | 2008.4–2013.4 | 34 | 1.03 | −6.80 | |||||||
| JBO | 1520 | 2012.5–2014.3 | 50 | 1.01 | −8.87 | ||||||
| NRT | 1400 | 2005.0–2011.9 | 552 | 1.18 | −6.13 | ||||||
| 1600 | 2009.0–2014.3 | 138 | 1.59 | −9.86 | |||||||
| 2000 | 2006.9–2014.0 | 90 | 1.32 | −6.07 | |||||||
| J0034−0534 | 5 | −14.93 | 1.27 | −12.43 | 2.84 | ||||||
| NRT | 1400 | 2005.9–2011.7 | 56 | 0.94 | −5.11 | ||||||
| 1600 | 2012.0–2014.1 | 10 | 2.00 | −9.50 | |||||||
| WSRT | 328 | 2000.6–2010.5 | 112 | 1.22 | −8.45 | ||||||
| 382 | 2000.6–2010.5 | 98 | 0.75 | −7.96 | |||||||
| J0218+4232 | 12 | −13.32 | 2.78 | −11.14 | 2.09 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 34 | 1.17 | −6.75 | ||||||
| 1410 | 1996.8–2009.3 | 178 | 1.21 | −8.52 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 13 | 1.50 | −6.08 | ||||||
| 1520 | 2009.6–2014.4 | 97 | 1.10 | −6.68 | |||||||
| NRT | 1400 | 2005.6–2012.2 | 406 | 1.17 | −7.45 | ||||||
| 1600 | 2009.0–2014.3 | 157 | 1.54 | −6.59 | |||||||
| 2000 | 2006.9–2013.6 | 14 | 1.46 | −5.71 | |||||||
| WSRT | 1380 | 1999.8–2010.5 | 49 | 1.55 | −6.32 | ||||||
| 328 | 2000.1–2010.5 | 125 | 1.21 | −6.51 | |||||||
| 382 | 1999.6–2010.5 | 123 | 0.98 | −8.46 | |||||||
| J0610−2100 | 2 | −12.85 | 0.23 | −13.74 | 5.46 | ||||||
| JBO | 1520 | 2010.5–2014.4 | 179 | 0.85 | −8.44 | ||||||
| NRT | 1400 | 2007.5–2011.7 | 631 | 1.62 | −9.29 | ||||||
| 1600 | 2011.2–2014.3 | 224 | 1.26 | −8.48 | |||||||
| J0613−0200 | 13 | −16.15 | 6.88 | −11.71 | 1.07 | ||||||
| EFF | 1360 | 2008.0–2013.5 | 42 | 1.01 | −6.80 | ||||||
| 1410 | 1998.3–2009.3 | 241 | 1.10 | −8.95 | |||||||
| 2639 | 2006.6–2013.5 | 64 | 1.01 | −7.79 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 24 | 1.35 | −8.44 | ||||||
| 1520 | 2009.6–2014.3 | 191 | 0.94 | −5.96 | |||||||
| NRT | 1400 | 2005.0–2011.8 | 334 | 1.02 | −6.35 | ||||||
| 1600 | 2009.0–2014.4 | 84 | 1.00 | −9.77 | |||||||
| 2000 | 2006.9–2012.8 | 51 | 1.10 | −6.41 | |||||||
| WSRT | 1380 | 1999.6–2010.5 | 171 | 1.00 | −9.59 | ||||||
| 328 | 2000.6–2010.5 | 87 | 0.75 | −6.32 | |||||||
| 382 | 2000.6–2010.5 | 80 | 0.92 | −5.69 | |||||||
| J0621+1002 | 9 | −12.04 | 2.50 | −16.98 | 3.80 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 42 | 0.83 | −9.46 | ||||||
| 1410 | 2002.6–2009.3 | 88 | 0.63 | −7.27 | |||||||
| 2639 | 2006.0–2013.4 | 47 | 0.43 | −4.39 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 18 | 1.08 | −7.86 | ||||||
| 1520 | 2009.6–2014.3 | 140 | 1.09 | −9.34 | |||||||
| NRT | 1400 | 2006.1–2011.9 | 168 | 1.23 | −6.58 | ||||||
| 1600 | 2009.0–2014.3 | 33 | 1.31 | −9.74 | |||||||
| WSRT | 1380 | 2006.0–2010.5 | 68 | 1.18 | −8.23 | ||||||
| 323 | 2007.5–2010.5 | 34 | 2.13 | −6.47 | |||||||
| 367 | 2007.5–2010.5 | 35 | 1.72 | −8.12 | |||||||
| J0751+1807 | 8 | −19.50 | 4.86 | −11.77 | 2.83 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 29 | 0.91 | −5.34 | ||||||
| 1410 | 1996.8–2004.6 | 159 | 0.98 | −5.74 | |||||||
| 2639 | 1999.2–2013.5 | 64 | 1.15 | −5.36 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 28 | 1.03 | −8.01 | ||||||
| 1520 | 2009.6–2014.3 | 179 | 1.00 | −6.09 | |||||||
| NRT | 1400 | 2005.0–2011.9 | 598 | 1.19 | −6.00 | ||||||
| 1600 | 2011.2–2014.4 | 362 | 1.07 | −7.50 | |||||||
| 2000 | 2007.5–2013.4 | 40 | 0.88 | −5.72 | |||||||
| WSRT | 1380 | 2007.4–2010.5 | 32 | 1.55 | −8.63 | ||||||
| J0900−3144 | 4 | −15.58 | 5.04 | −11.55 | 3.05 | ||||||
| JBO | 1400 | 2009.1–2009.4 | 9 | 1.09 | −9.26 | ||||||
| 1520 | 2009.7–2014.3 | 99 | 1.02 | −7.47 | |||||||
| NRT | 1400 | 2007.5–2012.1 | 321 | 1.04 | −9.21 | ||||||
| 1600 | 2009.0–2014.4 | 329 | 1.04 | −5.64 | |||||||
| 2000 | 2007.7–2014.2 | 117 | 1.28 | −8.07 | |||||||
| J1012+5307 | 14 | −13.07 | 1.52 | −17.57 | 3.46 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 37 | 0.56 | −5.47 | ||||||
| 1410 | 1997.5–2009.3 | 404 | 0.95 | −6.47 | |||||||
| 2639 | 2006.6–2013.5 | 88 | 1.02 | −7.43 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 12 | 1.13 | −7.83 | ||||||
| 1520 | 2009.8–2014.3 | 96 | 0.96 | −5.86 | |||||||
| NRT | 1400 | 2005.5–2011.7 | 239 | 1.21 | −9.32 | ||||||
| 1600 | 2009.0–2014.4 | 234 | 1.19 | −6.06 | |||||||
| 2000 | 2007.5–2014.1 | 18 | 1.18 | −9.79 | |||||||
| WSRT | 328 | 2000.9–2010.5 | 87 | 1.15 | −5.52 | ||||||
| 382 | 2000.9–2010.5 | 82 | 1.07 | −7.66 | |||||||
| 1380.1 | 1999.6–2001.2 | 26 | 1.14 | −8.21 | |||||||
| 1380.2 | 2001.2–2010.5 | 136 | 0.90 | −6.96 | |||||||
| J1022+1001 | 9 | −13.08 | 1.70 | −11.63 | 1.10 | ||||||
| EFF | 1360 | 2008.1–2013.5 | 76 | 1.02 | −5.84 | ||||||
| 1410 | 1996.8–2009.3 | 164 | 0.65 | −5.43 | |||||||
| 2639 | 2006.2–2013.5 | 88 | 2.09 | −7.32 | |||||||
| JBO | 1400 | 2009.0–2011.0 | 40 | 1.03 | −6.29 | ||||||
| 1520 | 2009.6–2014.3 | 187 | 1.30 | −5.66 | |||||||
| NRT | 1400 | 2005.0–2008.4 | 127 | 1.23 | −5.84 | ||||||
| 1600 | 2011.9–2014.3 | 44 | 1.30 | −7.12 | |||||||
| WSRT | 1380 | 2006.0–2010.5 | 58 | 0.82 | −6.01 | ||||||
| 323 | 2007.5–2010.5 | 26 | 1.67 | −4.81 | |||||||
| 367 | 2007.5–2010.0 | 17 | 0.79 | −4.96 | |||||||
| J1024−0719 | 8 | −13.69 | 3.17 | −12.96 | 6.12 | ||||||
| EFF | 1360 | 2008.1–2013.5 | 33 | 1.05 | −9.41 | ||||||
| 1410 | 1997.0–2009.3 | 27 | 0.75 | −9.76 | |||||||
| 2639 | 2006.0–2013.5 | 53 | 1.23 | −9.75 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 32 | 1.10 | −8.08 | ||||||
| 1520 | 2009.6–2014.3 | 127 | 1.19 | −8.53 | |||||||
| NRT | 1400 | 2006.0–2011.7 | 176 | 1.24 | −8.60 | ||||||
| 1600 | 2009.0–2014.3 | 77 | 0.86 | −5.88 | |||||||
| 2000 | 2006.9–2010.5 | 12 | 0.89 | −6.25 | |||||||
| WSRT | 1380 | 2007.4–2010.2 | 24 | 1.12 | −9.43 | ||||||
| J1455−3330 | 2 | −16.31 | 4.03 | −11.38 | 2.44 | ||||||
| JBO | 1520 | 2009.8–2014.3 | 25 | 1.01 | −5.80 | ||||||
| NRT | 1400 | 2005.0–2011.9 | 338 | 1.23 | −9.53 | ||||||
| 1600 | 2009.0–2014.2 | 161 | 1.04 | −8.98 | |||||||
| J1600−3053 | 3 | −16.56 | 2.71 | −11.64 | 1.41 | ||||||
| JBO | 1520 | 2011.5–2014.3 | 44 | 1.43 | −6.19 | ||||||
| NRT | 1400 | 2006.7–2011.7 | 230 | 1.15 | −7.62 | ||||||
| 1600 | 2010.8–2014.4 | 151 | 0.99 | −9.27 | |||||||
| 2000 | 2006.9–2014.2 | 106 | 1.12 | −6.58 | |||||||
| J1640+2224 | 7 | −13.11 | 0.12 | −16.87 | 0.75 | ||||||
| EFF | 1360 | 2008.1–2013.5 | 81 | 0.89 | −6.64 | ||||||
| 1410 | 1997.0–2009.7 | 122 | 0.93 | −7.96 | |||||||
| 2639 | 2006.2–2013.5 | 67 | 1.02 | −6.86 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 10 | 0.88 | −8.83 | ||||||
| 1520 | 2009.6–2014.3 | 148 | 1.32 | −8.92 | |||||||
| NRT | 1400 | 2005.0–2011.9 | 103 | 1.22 | −8.46 | ||||||
| 1600 | 2010.8–2013.8 | 24 | 1.11 | −9.45 | |||||||
| WSRT | 1380 | 2006.0–2010.2 | 40 | 1.28 | −8.82 | ||||||
| J1643−1224 | 8 | −19.04 | 3.44 | −10.99 | 1.70 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 27 | 1.08 | −8.64 | ||||||
| 1410 | 1997.0–2009.7 | 94 | 1.11 | −9.77 | |||||||
| 2639 | 2006.6–2013.5 | 43 | 0.69 | −5.37 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 11 | 0.95 | −8.85 | ||||||
| 1520 | 2009.7–2014.3 | 76 | 0.74 | −5.61 | |||||||
| NRT | 1400 | 2005.0–2011.7 | 334 | 1.24 | −7.19 | ||||||
| 1600 | 2009.0–2014.3 | 71 | 1.35 | −8.50 | |||||||
| 2000 | 2006.9–2013.6 | 49 | 1.05 | −8.45 | |||||||
| WSRT | 1380 | 2006.0–2010.5 | 54 | 1.29 | −9.87 | ||||||
| J1713+0747 | 13 | −15.29 | 5.62 | −11.98 | 1.47 | ||||||
| EFF | 1360 | 2008.1–2013.4 | 40 | 0.44 | −6.08 | ||||||
| 1410 | 1996.8–2009.7 | 164 | 0.98 | −6.42 | |||||||
| 2639 | 2006.6–2013.5 | 61 | 1.08 | −6.64 | |||||||
| JBO | 1400 | 2009.1–2011.0 | 18 | 1.27 | −6.22 | ||||||
| 1520 | 2009.6–2012.0 | 53 | 1.78 | −6.54 | |||||||
| NRT | 1400 | 2005.0–2011.6 | 354 | 1.24 | −6.81 | ||||||
| 1600 | 2009.0–2014.4 | 173 | 0.97 | −7.48 | |||||||
| 2000 | 2005.2–2013.8 | 97 | 1.23 | −7.15 | |||||||
| WSRT | 840 | 1999.5–2007.8 | 53 | 0.90 | −8.81 | ||||||
| 1380 | 1999.7–2001.1 | 22 | 0.55 | −7.98 | |||||||
| 1380 | 2001.1–2010.5 | 114 | 0.53 | −8.74 | |||||||
| 2273 | 2006.9–2010.4 | 39 | 1.05 | −7.87 | |||||||
| J1721−2457 | 3 | −16.50 | 6.68 | −10.04 | 1.22 | ||||||
| NRT | 1400 | 2006.3–2011.8 | 58 | 0.33 | −5.04 | ||||||
| 1600 | 2009.1–2014.2 | 13 | 0.77 | −5.21 | |||||||
| WSRT | 1380 | 2001.5–2010.5 | 79 | 2.38 | −5.13 | ||||||
| J1730−2304 | 7 | −16.33 | 0.11 | −11.42 | 2.37 | ||||||
| EFF | 1360 | 2010.9–2013.5 | 19 | 0.71 | −7.94 | ||||||
| 1410 | 1997.8–1999.3 | 8 | 0.72 | −8.07 | |||||||
| 2639 | 2011.0–2013.2 | 9 | 1.31 | −6.32 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 5 | 1.63 | −6.91 | ||||||
| 1520 | 2009.7–2014.5 | 83 | 1.39 | −6.90 | |||||||
| NRT | 1400 | 2005.1–2011.8 | 106 | 1.01 | −6.75 | ||||||
| 1600 | 2011.0–2014.4 | 29 | 1.07 | −8.43 | |||||||
| 2000 | 2007.4–2011.7 | 9 | 1.30 | −7.73 | |||||||
| J1738+0333 | 2 | −15.34 | 0.36 | −12.09 | 1.89 | ||||||
| JBO | 1520 | 2011.5–2014.3 | 56 | 1.06 | −5.89 | ||||||
| NRT | 1400 | 2007.0–2011.7 | 199 | 1.14 | −9.60 | ||||||
| 1600 | 2011.2–2014.3 | 63 | 1.14 | −9.24 | |||||||
| J1744−1134 | 8 | −13.85 | 2.90 | −17.65 | 4.57 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 22 | 0.58 | −6.17 | ||||||
| 1410 | 1997.0–2009.7 | 100 | 1.03 | −6.14 | |||||||
| 2639 | 2007.1–2013.4 | 42 | 0.88 | −6.14 | |||||||
| JBO | 1520 | 2009.6–2014.3 | 68 | 0.77 | −6.07 | ||||||
| NRT | 1400 | 2005.0–2011.7 | 141 | 1.43 | −6.65 | ||||||
| 1600 | 2010.9–2014.3 | 73 | 1.24 | −6.51 | |||||||
| 2000 | 2009.9–2012.7 | 27 | 1.14 | −7.42 | |||||||
| WSRT | 323 | 2007.6–2010.2 | 32 | 0.90 | −5.73 | ||||||
| 367 | 2007.6–2010.2 | 31 | 1.04 | −9.40 | |||||||
| J1751−2857 | 2 | −19.67 | 6.32 | −16.35 | 4.08 | ||||||
| JBO | 1520 | 2009.3–2014.3 | 37 | 1.56 | −7.05 | ||||||
| NRT | 1400 | 2006.0–2011.8 | 75 | 1.57 | −6.79 | ||||||
| 1600 | 2011.2–2014.3 | 32 | 1.14 | −9.56 | |||||||
| J1801−1417 | 2 | −17.96 | 6.45 | −10.84 | 2.28 | ||||||
| JBO | 1520 | 2009.7–2014.3 | 55 | 0.96 | −8.48 | ||||||
| NRT | 1400 | 2007.3–2011.8 | 49 | 1.68 | −7.12 | ||||||
| 1600 | 2009.0–2014.1 | 22 | 1.47 | −8.21 | |||||||
| J1802−2124 | 3 | −19.55 | 6.88 | −10.79 | 1.73 | ||||||
| JBO | 1520 | 2011.4–2014.5 | 26 | 1.01 | −9.85 | ||||||
| NRT | 1400 | 2007.2–2011.8 | 354 | 1.04 | −9.28 | ||||||
| 1600 | 2009.0–2014.2 | 105 | 1.07 | −6.94 | |||||||
| 2000 | 2008.3–2009.9 | 37 | 1.12 | −7.02 | |||||||
| J1804−2717 | 2 | −18.45 | 4.18 | −17.42 | 0.76 | ||||||
| JBO | 1520 | 2009.1–2014.5 | 53 | 1.14 | −6.76 | ||||||
| NRT | 1400 | 2006.1–2011.8 | 50 | 0.80 | −5.94 | ||||||
| 1600 | 2009.1–2014.2 | 13 | 1.10 | −9.67 | |||||||
| J1843−1113 | 4 | −17.38 | 5.43 | −10.94 | 1.45 | ||||||
| JBO | 1520 | 2009.6–2014.5 | 47 | 0.72 | −5.25 | ||||||
| NRT | 1400 | 2008.0–2011.8 | 63 | 0.86 | −9.34 | ||||||
| 1600 | 2010.8–2014.3 | 47 | 1.01 | −9.11 | |||||||
| WSRT | 1380 | 2004.4–2010.4 | 67 | 1.33 | −7.09 | ||||||
| J1853+1303 | 2 | −15.59 | 5.83 | −18.67 | 1.11 | ||||||
| JBO | 1520 | 2009.6–2014.5 | 34 | 1.03 | −6.18 | ||||||
| NRT | 1400 | 2006.1–2011.8 | 49 | 0.96 | −7.79 | ||||||
| 1600 | 2009.1–2014.3 | 18 | 0.79 | −5.82 | |||||||
| J1857+0943 | 8 | −13.37 | 2.53 | −17.42 | 5.06 | ||||||
| EFF | 1360 | 2008.1–2013.4 | 25 | 0.26 | −5.56 | ||||||
| 1410 | 1997.0–2009.7 | 106 | 0.80 | −8.75 | |||||||
| 2639 | 2008.2–2013.5 | 43 | 1.05 | −8.27 | |||||||
| JBO | 1400 | 2010.9–2011.0 | 7 | 1.14 | −7.37 | ||||||
| 1520 | 2009.6–2012.0 | 31 | 0.58 | −5.71 | |||||||
| NRT | 1400 | 2005.1–2011.8 | 102 | 0.77 | −6.08 | ||||||
| 1600 | 2011.0–2014.3 | 58 | 1.18 | −6.81 | |||||||
| 2000 | 2010.1–2013.5 | 13 | 1.25 | −7.40 | |||||||
| WSRT | 1380 | 2006.2–2010.5 | 59 | 1.29 | −6.09 | ||||||
| J1909−3744 | 2 | −14.18 | 2.17 | −16.84 | 6.70 | ||||||
| NRT | 1400 | 2005.0–2011.8 | 156 | 1.13 | −7.89 | ||||||
| 1600 | 2010.7–2014.4 | 219 | 0.97 | −7.17 | |||||||
| 2000 | 2005.2–2013.8 | 50 | 1.15 | −7.39 | |||||||
| J1910+1256 | 2 | −16.72 | 0.09 | −19.73 | 3.84 | ||||||
| JBO | 1520 | 2009.1–2014.5 | 46 | 0.79 | −8.57 | ||||||
| NRT | 1400 | 2006.0–2011.8 | 52 | 1.12 | −7.59 | ||||||
| 1600 | 2012.0–2014.2 | 14 | 0.66 | −7.84 | |||||||
| J1911+1347 | 2 | −14.84 | 6.85 | −12.89 | 4.27 | ||||||
| JBO | 1520 | 2009.3–2014.5 | 69 | 0.83 | −6.12 | ||||||
| NRT | 1400 | 2007.0–2011.8 | 44 | 0.86 | −6.38 | ||||||
| 1600 | 2009.1–2014.4 | 27 | 1.17 | −8.05 | |||||||
| J1911−1114 | 3 | −18.94 | 3.55 | −14.02 | 1.19 | ||||||
| JBO | 1400 | 2009.1–2009.4 | 5 | 0.90 | −7.45 | ||||||
| 1520 | 2009.6–2015.0 | 59 | 1.10 | −8.98 | |||||||
| NRT | 1400 | 2006.2–2011.8 | 52 | 1.23 | −9.21 | ||||||
| 1600 | 2012.0–2014.2 | 14 | 2.53 | −8.35 | |||||||
| J1918−0642 | 5 | −14.07 | 4.57 | −18.27 | 3.41 | ||||||
| JBO | 1400 | 2009.1–2009.6 | 12 | 1.21 | −6.44 | ||||||
| 1520 | 2009.6–2014.3 | 97 | 0.98 | −6.90 | |||||||
| NRT | 1400 | 2006.8–2011.8 | 57 | 0.92 | −5.95 | ||||||
| 1600 | 2010.9–2014.3 | 26 | 0.70 | −7.61 | |||||||
| WSRT | 1380 | 2001.5–2010.1 | 86 | 0.99 | −9.25 | ||||||
| J1939+2134 | 11 | −14.86 | 6.89 | −11.21 | 2.57 | ||||||
| EFF | 1360 | 2009.6–2011.5 | 32 | 2.05 | −6.55 | ||||||
| 1410 | 1996.8–2009.4 | 223 | 1.31 | −6.32 | |||||||
| JBO | 1520 | 2009.7–2012.0 | 54 | 0.70 | −6.63 | ||||||
| NRT | 1400 | 2005.0–2011.8 | 249 | 2.67 | −8.32 | ||||||
| 1600 | 2005.0–2014.3 | 202 | 2.13 | −8.65 | |||||||
| 2000 | 2005.0–2013.4 | 119 | 1.76 | −6.36 | |||||||
| 1400 | 1990.2–1999.8 | 2058 | 1.16 | −6.56 | |||||||
| WSRT | 1380 | 1999.6–2010.5 | 148 | 2.63 | −8.67 | ||||||
| 2273 | 2006.9–2010.5 | 37 | 1.04 | −9.79 | |||||||
| 840 | 2000.3–2007.9 | 52 | 1.44 | −8.71 | |||||||
| J1955+2908 | 3 | −17.54 | 4.95 | −16.27 | 1.38 | ||||||
| JBO | 1400 | 2009.0–2009.4 | 10 | 1.11 | −7.53 | ||||||
| 1520 | 2009.6–2014.2 | 80 | 1.01 | −8.45 | |||||||
| NRT | 1400 | 2006.2–2011.8 | 47 | 1.14 | −7.23 | ||||||
| 1600 | 2011.2–2014.3 | 20 | 1.38 | −8.80 | |||||||
| J2010−1323 | 4 | −17.75 | 2.26 | −11.66 | 3.44 | ||||||
| JBO | 1400 | 2009.1–2009.6 | 13 | 0.84 | −9.10 | ||||||
| 1520 | 2009.6–2014.3 | 87 | 1.12 | −9.17 | |||||||
| NRT | 1400 | 2007.0–2011.8 | 177 | 1.23 | −7.66 | ||||||
| 1600 | 2010.8–2014.4 | 77 | 1.11 | −7.74 | |||||||
| 2000 | 2007.3–2012.7 | 36 | 1.34 | −7.43 | |||||||
| J2019+2425 | 2 | −15.49 | 2.07 | −17.80 | 3.18 | ||||||
| JBO | 1520 | 2009.6–2014.4 | 59 | 1.41 | −9.85 | ||||||
| NRT | 1400 | 2005.2–2011.8 | 44 | 1.28 | −6.02 | ||||||
| 1600 | 2011.9–2014.3 | 27 | 1.07 | −8.00 | |||||||
| J2033+1734 | 3 | −19.52 | 0.19 | −12.39 | 2.13 | ||||||
| JBO | 1400 | 2009.1–2009.6 | 14 | 1.38 | −9.98 | ||||||
| 1520 | 2009.6–2014.4 | 86 | 0.85 | −8.78 | |||||||
| NRT | 1400 | 2006.4–2011.9 | 58 | 1.19 | −8.97 | ||||||
| 1600 | 2011.8–2014.3 | 36 | 1.32 | −7.72 | |||||||
| J2124−3358 | 4 | −16.98 | 6.07 | −14.42 | 1.20 | ||||||
| JBO | 1400 | 2009.1–2009.3 | 7 | 1.25 | −9.81 | ||||||
| 1520 | 2009.6–2014.3 | 51 | 1.14 | −9.14 | |||||||
| NRT | 1400 | 2005.0–2011.8 | 339 | 1.30 | −8.47 | ||||||
| 1600 | 2009.0–2014.4 | 97 | 1.69 | −6.15 | |||||||
| 2000 | 2006.9–2012.9 | 50 | 1.01 | −5.14 | |||||||
| J2145−0750 | 11 | −14.29 | 4.83 | −11.79 | 1.33 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 30 | 0.81 | −9.25 | ||||||
| 1410 | 1996.8–2009.6 | 117 | 0.65 | −5.92 | |||||||
| 2639 | 2006.9–2013.5 | 51 | 0.81 | −5.62 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 9 | 1.47 | −7.57 | ||||||
| 1520 | 2009.6–2014.3 | 82 | 1.05 | −6.06 | |||||||
| NRT | 1400 | 2005.0–2011.8 | 237 | 1.11 | −6.23 | ||||||
| 1600 | 2010.8–2013.9 | 125 | 1.26 | −7.60 | |||||||
| 2000 | 2007.3–2013.8 | 47 | 1.26 | −6.58 | |||||||
| WSRT | 1380 | 2006.0–2010.1 | 41 | 1.13 | −9.02 | ||||||
| 2273 | 2006.9–2007.3 | 6 | 2.82 | −8.78 | |||||||
| 323 | 2007.3–2010.2 | 30 | 1.68 | −6.10 | |||||||
| 367 | 2007.3–2010.2 | 25 | 1.34 | −5.32 | |||||||
| J2229+2643 | 5 | −15.69 | 4.55 | −17.19 | 1.80 | ||||||
| EFF | 1360 | 2010.7–2013.5 | 26 | 1.38 | −5.49 | ||||||
| 2639 | 2007.3–2013.2 | 23 | 0.54 | −5.34 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 11 | 1.91 | −5.76 | ||||||
| 1520 | 2009.6–2014.4 | 71 | 1.04 | −6.23 | |||||||
| NRT | 1400 | 2006.2–2011.8 | 150 | 1.79 | −6.67 | ||||||
| 1600 | 2010.9–2014.4 | 35 | 1.36 | −7.95 | |||||||
| J2317+1439 | 7 | −15.05 | 0.88 | −15.56 | 1.06 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 32 | 1.78 | −8.19 | ||||||
| 1410 | 1997.0–2009.6 | 15 | 1.31 | −8.40 | |||||||
| 2639 | 2007.6–2013.2 | 41 | 1.13 | −6.63 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 9 | 1.95 | −8.22 | ||||||
| 1520 | 2009.6–2014.3 | 79 | 1.03 | −8.27 | |||||||
| NRT | 1400 | 2005.0–2011.9 | 238 | 1.41 | −7.36 | ||||||
| 1600 | 2009.0–2014.4 | 93 | 1.48 | −6.84 | |||||||
| WSRT | 1380 | 2006.3–2010.5 | 48 | 1.43 | −9.11 | ||||||
| J2322+2057 | 3 | −19.91 | 6.37 | −13.89 | 3.70 | ||||||
| JBO | 1400 | 2009.1–2009.4 | 8 | 0.80 | −6.09 | ||||||
| 1520 | 2009.6–2014.4 | 113 | 1.40 | −6.01 | |||||||
| NRT | 1400 | 2006.5–2011.8 | 59 | 1.58 | −9.55 | ||||||
| 1600 | 2009.0–2014.3 | 49 | 1.21 | −7.92 |
| PSR JName . | Nj . | ARN . | γRN . | ADM . | γDM . | Observatory . | Frequency . | Year range . | NTOAs . | Ef . | Eq . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| J0030+0451 | 6 | −14.65 | 5.43 | −19.06 | 3.27 | ||||||
| EFF | 1360 | 2009.7–2013.5 | 33 | 1.17 | −9.17 | ||||||
| 1410 | 1999.3–2009.6 | 10 | 0.62 | −9.00 | |||||||
| 2639 | 2008.4–2013.4 | 34 | 1.03 | −6.80 | |||||||
| JBO | 1520 | 2012.5–2014.3 | 50 | 1.01 | −8.87 | ||||||
| NRT | 1400 | 2005.0–2011.9 | 552 | 1.18 | −6.13 | ||||||
| 1600 | 2009.0–2014.3 | 138 | 1.59 | −9.86 | |||||||
| 2000 | 2006.9–2014.0 | 90 | 1.32 | −6.07 | |||||||
| J0034−0534 | 5 | −14.93 | 1.27 | −12.43 | 2.84 | ||||||
| NRT | 1400 | 2005.9–2011.7 | 56 | 0.94 | −5.11 | ||||||
| 1600 | 2012.0–2014.1 | 10 | 2.00 | −9.50 | |||||||
| WSRT | 328 | 2000.6–2010.5 | 112 | 1.22 | −8.45 | ||||||
| 382 | 2000.6–2010.5 | 98 | 0.75 | −7.96 | |||||||
| J0218+4232 | 12 | −13.32 | 2.78 | −11.14 | 2.09 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 34 | 1.17 | −6.75 | ||||||
| 1410 | 1996.8–2009.3 | 178 | 1.21 | −8.52 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 13 | 1.50 | −6.08 | ||||||
| 1520 | 2009.6–2014.4 | 97 | 1.10 | −6.68 | |||||||
| NRT | 1400 | 2005.6–2012.2 | 406 | 1.17 | −7.45 | ||||||
| 1600 | 2009.0–2014.3 | 157 | 1.54 | −6.59 | |||||||
| 2000 | 2006.9–2013.6 | 14 | 1.46 | −5.71 | |||||||
| WSRT | 1380 | 1999.8–2010.5 | 49 | 1.55 | −6.32 | ||||||
| 328 | 2000.1–2010.5 | 125 | 1.21 | −6.51 | |||||||
| 382 | 1999.6–2010.5 | 123 | 0.98 | −8.46 | |||||||
| J0610−2100 | 2 | −12.85 | 0.23 | −13.74 | 5.46 | ||||||
| JBO | 1520 | 2010.5–2014.4 | 179 | 0.85 | −8.44 | ||||||
| NRT | 1400 | 2007.5–2011.7 | 631 | 1.62 | −9.29 | ||||||
| 1600 | 2011.2–2014.3 | 224 | 1.26 | −8.48 | |||||||
| J0613−0200 | 13 | −16.15 | 6.88 | −11.71 | 1.07 | ||||||
| EFF | 1360 | 2008.0–2013.5 | 42 | 1.01 | −6.80 | ||||||
| 1410 | 1998.3–2009.3 | 241 | 1.10 | −8.95 | |||||||
| 2639 | 2006.6–2013.5 | 64 | 1.01 | −7.79 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 24 | 1.35 | −8.44 | ||||||
| 1520 | 2009.6–2014.3 | 191 | 0.94 | −5.96 | |||||||
| NRT | 1400 | 2005.0–2011.8 | 334 | 1.02 | −6.35 | ||||||
| 1600 | 2009.0–2014.4 | 84 | 1.00 | −9.77 | |||||||
| 2000 | 2006.9–2012.8 | 51 | 1.10 | −6.41 | |||||||
| WSRT | 1380 | 1999.6–2010.5 | 171 | 1.00 | −9.59 | ||||||
| 328 | 2000.6–2010.5 | 87 | 0.75 | −6.32 | |||||||
| 382 | 2000.6–2010.5 | 80 | 0.92 | −5.69 | |||||||
| J0621+1002 | 9 | −12.04 | 2.50 | −16.98 | 3.80 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 42 | 0.83 | −9.46 | ||||||
| 1410 | 2002.6–2009.3 | 88 | 0.63 | −7.27 | |||||||
| 2639 | 2006.0–2013.4 | 47 | 0.43 | −4.39 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 18 | 1.08 | −7.86 | ||||||
| 1520 | 2009.6–2014.3 | 140 | 1.09 | −9.34 | |||||||
| NRT | 1400 | 2006.1–2011.9 | 168 | 1.23 | −6.58 | ||||||
| 1600 | 2009.0–2014.3 | 33 | 1.31 | −9.74 | |||||||
| WSRT | 1380 | 2006.0–2010.5 | 68 | 1.18 | −8.23 | ||||||
| 323 | 2007.5–2010.5 | 34 | 2.13 | −6.47 | |||||||
| 367 | 2007.5–2010.5 | 35 | 1.72 | −8.12 | |||||||
| J0751+1807 | 8 | −19.50 | 4.86 | −11.77 | 2.83 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 29 | 0.91 | −5.34 | ||||||
| 1410 | 1996.8–2004.6 | 159 | 0.98 | −5.74 | |||||||
| 2639 | 1999.2–2013.5 | 64 | 1.15 | −5.36 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 28 | 1.03 | −8.01 | ||||||
| 1520 | 2009.6–2014.3 | 179 | 1.00 | −6.09 | |||||||
| NRT | 1400 | 2005.0–2011.9 | 598 | 1.19 | −6.00 | ||||||
| 1600 | 2011.2–2014.4 | 362 | 1.07 | −7.50 | |||||||
| 2000 | 2007.5–2013.4 | 40 | 0.88 | −5.72 | |||||||
| WSRT | 1380 | 2007.4–2010.5 | 32 | 1.55 | −8.63 | ||||||
| J0900−3144 | 4 | −15.58 | 5.04 | −11.55 | 3.05 | ||||||
| JBO | 1400 | 2009.1–2009.4 | 9 | 1.09 | −9.26 | ||||||
| 1520 | 2009.7–2014.3 | 99 | 1.02 | −7.47 | |||||||
| NRT | 1400 | 2007.5–2012.1 | 321 | 1.04 | −9.21 | ||||||
| 1600 | 2009.0–2014.4 | 329 | 1.04 | −5.64 | |||||||
| 2000 | 2007.7–2014.2 | 117 | 1.28 | −8.07 | |||||||
| J1012+5307 | 14 | −13.07 | 1.52 | −17.57 | 3.46 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 37 | 0.56 | −5.47 | ||||||
| 1410 | 1997.5–2009.3 | 404 | 0.95 | −6.47 | |||||||
| 2639 | 2006.6–2013.5 | 88 | 1.02 | −7.43 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 12 | 1.13 | −7.83 | ||||||
| 1520 | 2009.8–2014.3 | 96 | 0.96 | −5.86 | |||||||
| NRT | 1400 | 2005.5–2011.7 | 239 | 1.21 | −9.32 | ||||||
| 1600 | 2009.0–2014.4 | 234 | 1.19 | −6.06 | |||||||
| 2000 | 2007.5–2014.1 | 18 | 1.18 | −9.79 | |||||||
| WSRT | 328 | 2000.9–2010.5 | 87 | 1.15 | −5.52 | ||||||
| 382 | 2000.9–2010.5 | 82 | 1.07 | −7.66 | |||||||
| 1380.1 | 1999.6–2001.2 | 26 | 1.14 | −8.21 | |||||||
| 1380.2 | 2001.2–2010.5 | 136 | 0.90 | −6.96 | |||||||
| J1022+1001 | 9 | −13.08 | 1.70 | −11.63 | 1.10 | ||||||
| EFF | 1360 | 2008.1–2013.5 | 76 | 1.02 | −5.84 | ||||||
| 1410 | 1996.8–2009.3 | 164 | 0.65 | −5.43 | |||||||
| 2639 | 2006.2–2013.5 | 88 | 2.09 | −7.32 | |||||||
| JBO | 1400 | 2009.0–2011.0 | 40 | 1.03 | −6.29 | ||||||
| 1520 | 2009.6–2014.3 | 187 | 1.30 | −5.66 | |||||||
| NRT | 1400 | 2005.0–2008.4 | 127 | 1.23 | −5.84 | ||||||
| 1600 | 2011.9–2014.3 | 44 | 1.30 | −7.12 | |||||||
| WSRT | 1380 | 2006.0–2010.5 | 58 | 0.82 | −6.01 | ||||||
| 323 | 2007.5–2010.5 | 26 | 1.67 | −4.81 | |||||||
| 367 | 2007.5–2010.0 | 17 | 0.79 | −4.96 | |||||||
| J1024−0719 | 8 | −13.69 | 3.17 | −12.96 | 6.12 | ||||||
| EFF | 1360 | 2008.1–2013.5 | 33 | 1.05 | −9.41 | ||||||
| 1410 | 1997.0–2009.3 | 27 | 0.75 | −9.76 | |||||||
| 2639 | 2006.0–2013.5 | 53 | 1.23 | −9.75 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 32 | 1.10 | −8.08 | ||||||
| 1520 | 2009.6–2014.3 | 127 | 1.19 | −8.53 | |||||||
| NRT | 1400 | 2006.0–2011.7 | 176 | 1.24 | −8.60 | ||||||
| 1600 | 2009.0–2014.3 | 77 | 0.86 | −5.88 | |||||||
| 2000 | 2006.9–2010.5 | 12 | 0.89 | −6.25 | |||||||
| WSRT | 1380 | 2007.4–2010.2 | 24 | 1.12 | −9.43 | ||||||
| J1455−3330 | 2 | −16.31 | 4.03 | −11.38 | 2.44 | ||||||
| JBO | 1520 | 2009.8–2014.3 | 25 | 1.01 | −5.80 | ||||||
| NRT | 1400 | 2005.0–2011.9 | 338 | 1.23 | −9.53 | ||||||
| 1600 | 2009.0–2014.2 | 161 | 1.04 | −8.98 | |||||||
| J1600−3053 | 3 | −16.56 | 2.71 | −11.64 | 1.41 | ||||||
| JBO | 1520 | 2011.5–2014.3 | 44 | 1.43 | −6.19 | ||||||
| NRT | 1400 | 2006.7–2011.7 | 230 | 1.15 | −7.62 | ||||||
| 1600 | 2010.8–2014.4 | 151 | 0.99 | −9.27 | |||||||
| 2000 | 2006.9–2014.2 | 106 | 1.12 | −6.58 | |||||||
| J1640+2224 | 7 | −13.11 | 0.12 | −16.87 | 0.75 | ||||||
| EFF | 1360 | 2008.1–2013.5 | 81 | 0.89 | −6.64 | ||||||
| 1410 | 1997.0–2009.7 | 122 | 0.93 | −7.96 | |||||||
| 2639 | 2006.2–2013.5 | 67 | 1.02 | −6.86 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 10 | 0.88 | −8.83 | ||||||
| 1520 | 2009.6–2014.3 | 148 | 1.32 | −8.92 | |||||||
| NRT | 1400 | 2005.0–2011.9 | 103 | 1.22 | −8.46 | ||||||
| 1600 | 2010.8–2013.8 | 24 | 1.11 | −9.45 | |||||||
| WSRT | 1380 | 2006.0–2010.2 | 40 | 1.28 | −8.82 | ||||||
| J1643−1224 | 8 | −19.04 | 3.44 | −10.99 | 1.70 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 27 | 1.08 | −8.64 | ||||||
| 1410 | 1997.0–2009.7 | 94 | 1.11 | −9.77 | |||||||
| 2639 | 2006.6–2013.5 | 43 | 0.69 | −5.37 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 11 | 0.95 | −8.85 | ||||||
| 1520 | 2009.7–2014.3 | 76 | 0.74 | −5.61 | |||||||
| NRT | 1400 | 2005.0–2011.7 | 334 | 1.24 | −7.19 | ||||||
| 1600 | 2009.0–2014.3 | 71 | 1.35 | −8.50 | |||||||
| 2000 | 2006.9–2013.6 | 49 | 1.05 | −8.45 | |||||||
| WSRT | 1380 | 2006.0–2010.5 | 54 | 1.29 | −9.87 | ||||||
| J1713+0747 | 13 | −15.29 | 5.62 | −11.98 | 1.47 | ||||||
| EFF | 1360 | 2008.1–2013.4 | 40 | 0.44 | −6.08 | ||||||
| 1410 | 1996.8–2009.7 | 164 | 0.98 | −6.42 | |||||||
| 2639 | 2006.6–2013.5 | 61 | 1.08 | −6.64 | |||||||
| JBO | 1400 | 2009.1–2011.0 | 18 | 1.27 | −6.22 | ||||||
| 1520 | 2009.6–2012.0 | 53 | 1.78 | −6.54 | |||||||
| NRT | 1400 | 2005.0–2011.6 | 354 | 1.24 | −6.81 | ||||||
| 1600 | 2009.0–2014.4 | 173 | 0.97 | −7.48 | |||||||
| 2000 | 2005.2–2013.8 | 97 | 1.23 | −7.15 | |||||||
| WSRT | 840 | 1999.5–2007.8 | 53 | 0.90 | −8.81 | ||||||
| 1380 | 1999.7–2001.1 | 22 | 0.55 | −7.98 | |||||||
| 1380 | 2001.1–2010.5 | 114 | 0.53 | −8.74 | |||||||
| 2273 | 2006.9–2010.4 | 39 | 1.05 | −7.87 | |||||||
| J1721−2457 | 3 | −16.50 | 6.68 | −10.04 | 1.22 | ||||||
| NRT | 1400 | 2006.3–2011.8 | 58 | 0.33 | −5.04 | ||||||
| 1600 | 2009.1–2014.2 | 13 | 0.77 | −5.21 | |||||||
| WSRT | 1380 | 2001.5–2010.5 | 79 | 2.38 | −5.13 | ||||||
| J1730−2304 | 7 | −16.33 | 0.11 | −11.42 | 2.37 | ||||||
| EFF | 1360 | 2010.9–2013.5 | 19 | 0.71 | −7.94 | ||||||
| 1410 | 1997.8–1999.3 | 8 | 0.72 | −8.07 | |||||||
| 2639 | 2011.0–2013.2 | 9 | 1.31 | −6.32 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 5 | 1.63 | −6.91 | ||||||
| 1520 | 2009.7–2014.5 | 83 | 1.39 | −6.90 | |||||||
| NRT | 1400 | 2005.1–2011.8 | 106 | 1.01 | −6.75 | ||||||
| 1600 | 2011.0–2014.4 | 29 | 1.07 | −8.43 | |||||||
| 2000 | 2007.4–2011.7 | 9 | 1.30 | −7.73 | |||||||
| J1738+0333 | 2 | −15.34 | 0.36 | −12.09 | 1.89 | ||||||
| JBO | 1520 | 2011.5–2014.3 | 56 | 1.06 | −5.89 | ||||||
| NRT | 1400 | 2007.0–2011.7 | 199 | 1.14 | −9.60 | ||||||
| 1600 | 2011.2–2014.3 | 63 | 1.14 | −9.24 | |||||||
| J1744−1134 | 8 | −13.85 | 2.90 | −17.65 | 4.57 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 22 | 0.58 | −6.17 | ||||||
| 1410 | 1997.0–2009.7 | 100 | 1.03 | −6.14 | |||||||
| 2639 | 2007.1–2013.4 | 42 | 0.88 | −6.14 | |||||||
| JBO | 1520 | 2009.6–2014.3 | 68 | 0.77 | −6.07 | ||||||
| NRT | 1400 | 2005.0–2011.7 | 141 | 1.43 | −6.65 | ||||||
| 1600 | 2010.9–2014.3 | 73 | 1.24 | −6.51 | |||||||
| 2000 | 2009.9–2012.7 | 27 | 1.14 | −7.42 | |||||||
| WSRT | 323 | 2007.6–2010.2 | 32 | 0.90 | −5.73 | ||||||
| 367 | 2007.6–2010.2 | 31 | 1.04 | −9.40 | |||||||
| J1751−2857 | 2 | −19.67 | 6.32 | −16.35 | 4.08 | ||||||
| JBO | 1520 | 2009.3–2014.3 | 37 | 1.56 | −7.05 | ||||||
| NRT | 1400 | 2006.0–2011.8 | 75 | 1.57 | −6.79 | ||||||
| 1600 | 2011.2–2014.3 | 32 | 1.14 | −9.56 | |||||||
| J1801−1417 | 2 | −17.96 | 6.45 | −10.84 | 2.28 | ||||||
| JBO | 1520 | 2009.7–2014.3 | 55 | 0.96 | −8.48 | ||||||
| NRT | 1400 | 2007.3–2011.8 | 49 | 1.68 | −7.12 | ||||||
| 1600 | 2009.0–2014.1 | 22 | 1.47 | −8.21 | |||||||
| J1802−2124 | 3 | −19.55 | 6.88 | −10.79 | 1.73 | ||||||
| JBO | 1520 | 2011.4–2014.5 | 26 | 1.01 | −9.85 | ||||||
| NRT | 1400 | 2007.2–2011.8 | 354 | 1.04 | −9.28 | ||||||
| 1600 | 2009.0–2014.2 | 105 | 1.07 | −6.94 | |||||||
| 2000 | 2008.3–2009.9 | 37 | 1.12 | −7.02 | |||||||
| J1804−2717 | 2 | −18.45 | 4.18 | −17.42 | 0.76 | ||||||
| JBO | 1520 | 2009.1–2014.5 | 53 | 1.14 | −6.76 | ||||||
| NRT | 1400 | 2006.1–2011.8 | 50 | 0.80 | −5.94 | ||||||
| 1600 | 2009.1–2014.2 | 13 | 1.10 | −9.67 | |||||||
| J1843−1113 | 4 | −17.38 | 5.43 | −10.94 | 1.45 | ||||||
| JBO | 1520 | 2009.6–2014.5 | 47 | 0.72 | −5.25 | ||||||
| NRT | 1400 | 2008.0–2011.8 | 63 | 0.86 | −9.34 | ||||||
| 1600 | 2010.8–2014.3 | 47 | 1.01 | −9.11 | |||||||
| WSRT | 1380 | 2004.4–2010.4 | 67 | 1.33 | −7.09 | ||||||
| J1853+1303 | 2 | −15.59 | 5.83 | −18.67 | 1.11 | ||||||
| JBO | 1520 | 2009.6–2014.5 | 34 | 1.03 | −6.18 | ||||||
| NRT | 1400 | 2006.1–2011.8 | 49 | 0.96 | −7.79 | ||||||
| 1600 | 2009.1–2014.3 | 18 | 0.79 | −5.82 | |||||||
| J1857+0943 | 8 | −13.37 | 2.53 | −17.42 | 5.06 | ||||||
| EFF | 1360 | 2008.1–2013.4 | 25 | 0.26 | −5.56 | ||||||
| 1410 | 1997.0–2009.7 | 106 | 0.80 | −8.75 | |||||||
| 2639 | 2008.2–2013.5 | 43 | 1.05 | −8.27 | |||||||
| JBO | 1400 | 2010.9–2011.0 | 7 | 1.14 | −7.37 | ||||||
| 1520 | 2009.6–2012.0 | 31 | 0.58 | −5.71 | |||||||
| NRT | 1400 | 2005.1–2011.8 | 102 | 0.77 | −6.08 | ||||||
| 1600 | 2011.0–2014.3 | 58 | 1.18 | −6.81 | |||||||
| 2000 | 2010.1–2013.5 | 13 | 1.25 | −7.40 | |||||||
| WSRT | 1380 | 2006.2–2010.5 | 59 | 1.29 | −6.09 | ||||||
| J1909−3744 | 2 | −14.18 | 2.17 | −16.84 | 6.70 | ||||||
| NRT | 1400 | 2005.0–2011.8 | 156 | 1.13 | −7.89 | ||||||
| 1600 | 2010.7–2014.4 | 219 | 0.97 | −7.17 | |||||||
| 2000 | 2005.2–2013.8 | 50 | 1.15 | −7.39 | |||||||
| J1910+1256 | 2 | −16.72 | 0.09 | −19.73 | 3.84 | ||||||
| JBO | 1520 | 2009.1–2014.5 | 46 | 0.79 | −8.57 | ||||||
| NRT | 1400 | 2006.0–2011.8 | 52 | 1.12 | −7.59 | ||||||
| 1600 | 2012.0–2014.2 | 14 | 0.66 | −7.84 | |||||||
| J1911+1347 | 2 | −14.84 | 6.85 | −12.89 | 4.27 | ||||||
| JBO | 1520 | 2009.3–2014.5 | 69 | 0.83 | −6.12 | ||||||
| NRT | 1400 | 2007.0–2011.8 | 44 | 0.86 | −6.38 | ||||||
| 1600 | 2009.1–2014.4 | 27 | 1.17 | −8.05 | |||||||
| J1911−1114 | 3 | −18.94 | 3.55 | −14.02 | 1.19 | ||||||
| JBO | 1400 | 2009.1–2009.4 | 5 | 0.90 | −7.45 | ||||||
| 1520 | 2009.6–2015.0 | 59 | 1.10 | −8.98 | |||||||
| NRT | 1400 | 2006.2–2011.8 | 52 | 1.23 | −9.21 | ||||||
| 1600 | 2012.0–2014.2 | 14 | 2.53 | −8.35 | |||||||
| J1918−0642 | 5 | −14.07 | 4.57 | −18.27 | 3.41 | ||||||
| JBO | 1400 | 2009.1–2009.6 | 12 | 1.21 | −6.44 | ||||||
| 1520 | 2009.6–2014.3 | 97 | 0.98 | −6.90 | |||||||
| NRT | 1400 | 2006.8–2011.8 | 57 | 0.92 | −5.95 | ||||||
| 1600 | 2010.9–2014.3 | 26 | 0.70 | −7.61 | |||||||
| WSRT | 1380 | 2001.5–2010.1 | 86 | 0.99 | −9.25 | ||||||
| J1939+2134 | 11 | −14.86 | 6.89 | −11.21 | 2.57 | ||||||
| EFF | 1360 | 2009.6–2011.5 | 32 | 2.05 | −6.55 | ||||||
| 1410 | 1996.8–2009.4 | 223 | 1.31 | −6.32 | |||||||
| JBO | 1520 | 2009.7–2012.0 | 54 | 0.70 | −6.63 | ||||||
| NRT | 1400 | 2005.0–2011.8 | 249 | 2.67 | −8.32 | ||||||
| 1600 | 2005.0–2014.3 | 202 | 2.13 | −8.65 | |||||||
| 2000 | 2005.0–2013.4 | 119 | 1.76 | −6.36 | |||||||
| 1400 | 1990.2–1999.8 | 2058 | 1.16 | −6.56 | |||||||
| WSRT | 1380 | 1999.6–2010.5 | 148 | 2.63 | −8.67 | ||||||
| 2273 | 2006.9–2010.5 | 37 | 1.04 | −9.79 | |||||||
| 840 | 2000.3–2007.9 | 52 | 1.44 | −8.71 | |||||||
| J1955+2908 | 3 | −17.54 | 4.95 | −16.27 | 1.38 | ||||||
| JBO | 1400 | 2009.0–2009.4 | 10 | 1.11 | −7.53 | ||||||
| 1520 | 2009.6–2014.2 | 80 | 1.01 | −8.45 | |||||||
| NRT | 1400 | 2006.2–2011.8 | 47 | 1.14 | −7.23 | ||||||
| 1600 | 2011.2–2014.3 | 20 | 1.38 | −8.80 | |||||||
| J2010−1323 | 4 | −17.75 | 2.26 | −11.66 | 3.44 | ||||||
| JBO | 1400 | 2009.1–2009.6 | 13 | 0.84 | −9.10 | ||||||
| 1520 | 2009.6–2014.3 | 87 | 1.12 | −9.17 | |||||||
| NRT | 1400 | 2007.0–2011.8 | 177 | 1.23 | −7.66 | ||||||
| 1600 | 2010.8–2014.4 | 77 | 1.11 | −7.74 | |||||||
| 2000 | 2007.3–2012.7 | 36 | 1.34 | −7.43 | |||||||
| J2019+2425 | 2 | −15.49 | 2.07 | −17.80 | 3.18 | ||||||
| JBO | 1520 | 2009.6–2014.4 | 59 | 1.41 | −9.85 | ||||||
| NRT | 1400 | 2005.2–2011.8 | 44 | 1.28 | −6.02 | ||||||
| 1600 | 2011.9–2014.3 | 27 | 1.07 | −8.00 | |||||||
| J2033+1734 | 3 | −19.52 | 0.19 | −12.39 | 2.13 | ||||||
| JBO | 1400 | 2009.1–2009.6 | 14 | 1.38 | −9.98 | ||||||
| 1520 | 2009.6–2014.4 | 86 | 0.85 | −8.78 | |||||||
| NRT | 1400 | 2006.4–2011.9 | 58 | 1.19 | −8.97 | ||||||
| 1600 | 2011.8–2014.3 | 36 | 1.32 | −7.72 | |||||||
| J2124−3358 | 4 | −16.98 | 6.07 | −14.42 | 1.20 | ||||||
| JBO | 1400 | 2009.1–2009.3 | 7 | 1.25 | −9.81 | ||||||
| 1520 | 2009.6–2014.3 | 51 | 1.14 | −9.14 | |||||||
| NRT | 1400 | 2005.0–2011.8 | 339 | 1.30 | −8.47 | ||||||
| 1600 | 2009.0–2014.4 | 97 | 1.69 | −6.15 | |||||||
| 2000 | 2006.9–2012.9 | 50 | 1.01 | −5.14 | |||||||
| J2145−0750 | 11 | −14.29 | 4.83 | −11.79 | 1.33 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 30 | 0.81 | −9.25 | ||||||
| 1410 | 1996.8–2009.6 | 117 | 0.65 | −5.92 | |||||||
| 2639 | 2006.9–2013.5 | 51 | 0.81 | −5.62 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 9 | 1.47 | −7.57 | ||||||
| 1520 | 2009.6–2014.3 | 82 | 1.05 | −6.06 | |||||||
| NRT | 1400 | 2005.0–2011.8 | 237 | 1.11 | −6.23 | ||||||
| 1600 | 2010.8–2013.9 | 125 | 1.26 | −7.60 | |||||||
| 2000 | 2007.3–2013.8 | 47 | 1.26 | −6.58 | |||||||
| WSRT | 1380 | 2006.0–2010.1 | 41 | 1.13 | −9.02 | ||||||
| 2273 | 2006.9–2007.3 | 6 | 2.82 | −8.78 | |||||||
| 323 | 2007.3–2010.2 | 30 | 1.68 | −6.10 | |||||||
| 367 | 2007.3–2010.2 | 25 | 1.34 | −5.32 | |||||||
| J2229+2643 | 5 | −15.69 | 4.55 | −17.19 | 1.80 | ||||||
| EFF | 1360 | 2010.7–2013.5 | 26 | 1.38 | −5.49 | ||||||
| 2639 | 2007.3–2013.2 | 23 | 0.54 | −5.34 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 11 | 1.91 | −5.76 | ||||||
| 1520 | 2009.6–2014.4 | 71 | 1.04 | −6.23 | |||||||
| NRT | 1400 | 2006.2–2011.8 | 150 | 1.79 | −6.67 | ||||||
| 1600 | 2010.9–2014.4 | 35 | 1.36 | −7.95 | |||||||
| J2317+1439 | 7 | −15.05 | 0.88 | −15.56 | 1.06 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 32 | 1.78 | −8.19 | ||||||
| 1410 | 1997.0–2009.6 | 15 | 1.31 | −8.40 | |||||||
| 2639 | 2007.6–2013.2 | 41 | 1.13 | −6.63 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 9 | 1.95 | −8.22 | ||||||
| 1520 | 2009.6–2014.3 | 79 | 1.03 | −8.27 | |||||||
| NRT | 1400 | 2005.0–2011.9 | 238 | 1.41 | −7.36 | ||||||
| 1600 | 2009.0–2014.4 | 93 | 1.48 | −6.84 | |||||||
| WSRT | 1380 | 2006.3–2010.5 | 48 | 1.43 | −9.11 | ||||||
| J2322+2057 | 3 | −19.91 | 6.37 | −13.89 | 3.70 | ||||||
| JBO | 1400 | 2009.1–2009.4 | 8 | 0.80 | −6.09 | ||||||
| 1520 | 2009.6–2014.4 | 113 | 1.40 | −6.01 | |||||||
| NRT | 1400 | 2006.5–2011.8 | 59 | 1.58 | −9.55 | ||||||
| 1600 | 2009.0–2014.3 | 49 | 1.21 | −7.92 |
Summary of the EPTA data set. The columns indicate, respectively, the pulsar name, the number of JUMPs (Nj) included in the timing solution, the maximum likelihood results for the red noise (RN) and DM models (dimensionless amplitude A and spectral index γ for each model), the observatory, frequency band (in MHz), data span in years, number of TOAs along with the maximum likelihood values for the EFAC (Ef) and EQUAD (Eq in units of seconds) parameters (EQUAD shown in log10-base).
| PSR JName . | Nj . | ARN . | γRN . | ADM . | γDM . | Observatory . | Frequency . | Year range . | NTOAs . | Ef . | Eq . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| J0030+0451 | 6 | −14.65 | 5.43 | −19.06 | 3.27 | ||||||
| EFF | 1360 | 2009.7–2013.5 | 33 | 1.17 | −9.17 | ||||||
| 1410 | 1999.3–2009.6 | 10 | 0.62 | −9.00 | |||||||
| 2639 | 2008.4–2013.4 | 34 | 1.03 | −6.80 | |||||||
| JBO | 1520 | 2012.5–2014.3 | 50 | 1.01 | −8.87 | ||||||
| NRT | 1400 | 2005.0–2011.9 | 552 | 1.18 | −6.13 | ||||||
| 1600 | 2009.0–2014.3 | 138 | 1.59 | −9.86 | |||||||
| 2000 | 2006.9–2014.0 | 90 | 1.32 | −6.07 | |||||||
| J0034−0534 | 5 | −14.93 | 1.27 | −12.43 | 2.84 | ||||||
| NRT | 1400 | 2005.9–2011.7 | 56 | 0.94 | −5.11 | ||||||
| 1600 | 2012.0–2014.1 | 10 | 2.00 | −9.50 | |||||||
| WSRT | 328 | 2000.6–2010.5 | 112 | 1.22 | −8.45 | ||||||
| 382 | 2000.6–2010.5 | 98 | 0.75 | −7.96 | |||||||
| J0218+4232 | 12 | −13.32 | 2.78 | −11.14 | 2.09 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 34 | 1.17 | −6.75 | ||||||
| 1410 | 1996.8–2009.3 | 178 | 1.21 | −8.52 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 13 | 1.50 | −6.08 | ||||||
| 1520 | 2009.6–2014.4 | 97 | 1.10 | −6.68 | |||||||
| NRT | 1400 | 2005.6–2012.2 | 406 | 1.17 | −7.45 | ||||||
| 1600 | 2009.0–2014.3 | 157 | 1.54 | −6.59 | |||||||
| 2000 | 2006.9–2013.6 | 14 | 1.46 | −5.71 | |||||||
| WSRT | 1380 | 1999.8–2010.5 | 49 | 1.55 | −6.32 | ||||||
| 328 | 2000.1–2010.5 | 125 | 1.21 | −6.51 | |||||||
| 382 | 1999.6–2010.5 | 123 | 0.98 | −8.46 | |||||||
| J0610−2100 | 2 | −12.85 | 0.23 | −13.74 | 5.46 | ||||||
| JBO | 1520 | 2010.5–2014.4 | 179 | 0.85 | −8.44 | ||||||
| NRT | 1400 | 2007.5–2011.7 | 631 | 1.62 | −9.29 | ||||||
| 1600 | 2011.2–2014.3 | 224 | 1.26 | −8.48 | |||||||
| J0613−0200 | 13 | −16.15 | 6.88 | −11.71 | 1.07 | ||||||
| EFF | 1360 | 2008.0–2013.5 | 42 | 1.01 | −6.80 | ||||||
| 1410 | 1998.3–2009.3 | 241 | 1.10 | −8.95 | |||||||
| 2639 | 2006.6–2013.5 | 64 | 1.01 | −7.79 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 24 | 1.35 | −8.44 | ||||||
| 1520 | 2009.6–2014.3 | 191 | 0.94 | −5.96 | |||||||
| NRT | 1400 | 2005.0–2011.8 | 334 | 1.02 | −6.35 | ||||||
| 1600 | 2009.0–2014.4 | 84 | 1.00 | −9.77 | |||||||
| 2000 | 2006.9–2012.8 | 51 | 1.10 | −6.41 | |||||||
| WSRT | 1380 | 1999.6–2010.5 | 171 | 1.00 | −9.59 | ||||||
| 328 | 2000.6–2010.5 | 87 | 0.75 | −6.32 | |||||||
| 382 | 2000.6–2010.5 | 80 | 0.92 | −5.69 | |||||||
| J0621+1002 | 9 | −12.04 | 2.50 | −16.98 | 3.80 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 42 | 0.83 | −9.46 | ||||||
| 1410 | 2002.6–2009.3 | 88 | 0.63 | −7.27 | |||||||
| 2639 | 2006.0–2013.4 | 47 | 0.43 | −4.39 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 18 | 1.08 | −7.86 | ||||||
| 1520 | 2009.6–2014.3 | 140 | 1.09 | −9.34 | |||||||
| NRT | 1400 | 2006.1–2011.9 | 168 | 1.23 | −6.58 | ||||||
| 1600 | 2009.0–2014.3 | 33 | 1.31 | −9.74 | |||||||
| WSRT | 1380 | 2006.0–2010.5 | 68 | 1.18 | −8.23 | ||||||
| 323 | 2007.5–2010.5 | 34 | 2.13 | −6.47 | |||||||
| 367 | 2007.5–2010.5 | 35 | 1.72 | −8.12 | |||||||
| J0751+1807 | 8 | −19.50 | 4.86 | −11.77 | 2.83 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 29 | 0.91 | −5.34 | ||||||
| 1410 | 1996.8–2004.6 | 159 | 0.98 | −5.74 | |||||||
| 2639 | 1999.2–2013.5 | 64 | 1.15 | −5.36 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 28 | 1.03 | −8.01 | ||||||
| 1520 | 2009.6–2014.3 | 179 | 1.00 | −6.09 | |||||||
| NRT | 1400 | 2005.0–2011.9 | 598 | 1.19 | −6.00 | ||||||
| 1600 | 2011.2–2014.4 | 362 | 1.07 | −7.50 | |||||||
| 2000 | 2007.5–2013.4 | 40 | 0.88 | −5.72 | |||||||
| WSRT | 1380 | 2007.4–2010.5 | 32 | 1.55 | −8.63 | ||||||
| J0900−3144 | 4 | −15.58 | 5.04 | −11.55 | 3.05 | ||||||
| JBO | 1400 | 2009.1–2009.4 | 9 | 1.09 | −9.26 | ||||||
| 1520 | 2009.7–2014.3 | 99 | 1.02 | −7.47 | |||||||
| NRT | 1400 | 2007.5–2012.1 | 321 | 1.04 | −9.21 | ||||||
| 1600 | 2009.0–2014.4 | 329 | 1.04 | −5.64 | |||||||
| 2000 | 2007.7–2014.2 | 117 | 1.28 | −8.07 | |||||||
| J1012+5307 | 14 | −13.07 | 1.52 | −17.57 | 3.46 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 37 | 0.56 | −5.47 | ||||||
| 1410 | 1997.5–2009.3 | 404 | 0.95 | −6.47 | |||||||
| 2639 | 2006.6–2013.5 | 88 | 1.02 | −7.43 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 12 | 1.13 | −7.83 | ||||||
| 1520 | 2009.8–2014.3 | 96 | 0.96 | −5.86 | |||||||
| NRT | 1400 | 2005.5–2011.7 | 239 | 1.21 | −9.32 | ||||||
| 1600 | 2009.0–2014.4 | 234 | 1.19 | −6.06 | |||||||
| 2000 | 2007.5–2014.1 | 18 | 1.18 | −9.79 | |||||||
| WSRT | 328 | 2000.9–2010.5 | 87 | 1.15 | −5.52 | ||||||
| 382 | 2000.9–2010.5 | 82 | 1.07 | −7.66 | |||||||
| 1380.1 | 1999.6–2001.2 | 26 | 1.14 | −8.21 | |||||||
| 1380.2 | 2001.2–2010.5 | 136 | 0.90 | −6.96 | |||||||
| J1022+1001 | 9 | −13.08 | 1.70 | −11.63 | 1.10 | ||||||
| EFF | 1360 | 2008.1–2013.5 | 76 | 1.02 | −5.84 | ||||||
| 1410 | 1996.8–2009.3 | 164 | 0.65 | −5.43 | |||||||
| 2639 | 2006.2–2013.5 | 88 | 2.09 | −7.32 | |||||||
| JBO | 1400 | 2009.0–2011.0 | 40 | 1.03 | −6.29 | ||||||
| 1520 | 2009.6–2014.3 | 187 | 1.30 | −5.66 | |||||||
| NRT | 1400 | 2005.0–2008.4 | 127 | 1.23 | −5.84 | ||||||
| 1600 | 2011.9–2014.3 | 44 | 1.30 | −7.12 | |||||||
| WSRT | 1380 | 2006.0–2010.5 | 58 | 0.82 | −6.01 | ||||||
| 323 | 2007.5–2010.5 | 26 | 1.67 | −4.81 | |||||||
| 367 | 2007.5–2010.0 | 17 | 0.79 | −4.96 | |||||||
| J1024−0719 | 8 | −13.69 | 3.17 | −12.96 | 6.12 | ||||||
| EFF | 1360 | 2008.1–2013.5 | 33 | 1.05 | −9.41 | ||||||
| 1410 | 1997.0–2009.3 | 27 | 0.75 | −9.76 | |||||||
| 2639 | 2006.0–2013.5 | 53 | 1.23 | −9.75 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 32 | 1.10 | −8.08 | ||||||
| 1520 | 2009.6–2014.3 | 127 | 1.19 | −8.53 | |||||||
| NRT | 1400 | 2006.0–2011.7 | 176 | 1.24 | −8.60 | ||||||
| 1600 | 2009.0–2014.3 | 77 | 0.86 | −5.88 | |||||||
| 2000 | 2006.9–2010.5 | 12 | 0.89 | −6.25 | |||||||
| WSRT | 1380 | 2007.4–2010.2 | 24 | 1.12 | −9.43 | ||||||
| J1455−3330 | 2 | −16.31 | 4.03 | −11.38 | 2.44 | ||||||
| JBO | 1520 | 2009.8–2014.3 | 25 | 1.01 | −5.80 | ||||||
| NRT | 1400 | 2005.0–2011.9 | 338 | 1.23 | −9.53 | ||||||
| 1600 | 2009.0–2014.2 | 161 | 1.04 | −8.98 | |||||||
| J1600−3053 | 3 | −16.56 | 2.71 | −11.64 | 1.41 | ||||||
| JBO | 1520 | 2011.5–2014.3 | 44 | 1.43 | −6.19 | ||||||
| NRT | 1400 | 2006.7–2011.7 | 230 | 1.15 | −7.62 | ||||||
| 1600 | 2010.8–2014.4 | 151 | 0.99 | −9.27 | |||||||
| 2000 | 2006.9–2014.2 | 106 | 1.12 | −6.58 | |||||||
| J1640+2224 | 7 | −13.11 | 0.12 | −16.87 | 0.75 | ||||||
| EFF | 1360 | 2008.1–2013.5 | 81 | 0.89 | −6.64 | ||||||
| 1410 | 1997.0–2009.7 | 122 | 0.93 | −7.96 | |||||||
| 2639 | 2006.2–2013.5 | 67 | 1.02 | −6.86 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 10 | 0.88 | −8.83 | ||||||
| 1520 | 2009.6–2014.3 | 148 | 1.32 | −8.92 | |||||||
| NRT | 1400 | 2005.0–2011.9 | 103 | 1.22 | −8.46 | ||||||
| 1600 | 2010.8–2013.8 | 24 | 1.11 | −9.45 | |||||||
| WSRT | 1380 | 2006.0–2010.2 | 40 | 1.28 | −8.82 | ||||||
| J1643−1224 | 8 | −19.04 | 3.44 | −10.99 | 1.70 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 27 | 1.08 | −8.64 | ||||||
| 1410 | 1997.0–2009.7 | 94 | 1.11 | −9.77 | |||||||
| 2639 | 2006.6–2013.5 | 43 | 0.69 | −5.37 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 11 | 0.95 | −8.85 | ||||||
| 1520 | 2009.7–2014.3 | 76 | 0.74 | −5.61 | |||||||
| NRT | 1400 | 2005.0–2011.7 | 334 | 1.24 | −7.19 | ||||||
| 1600 | 2009.0–2014.3 | 71 | 1.35 | −8.50 | |||||||
| 2000 | 2006.9–2013.6 | 49 | 1.05 | −8.45 | |||||||
| WSRT | 1380 | 2006.0–2010.5 | 54 | 1.29 | −9.87 | ||||||
| J1713+0747 | 13 | −15.29 | 5.62 | −11.98 | 1.47 | ||||||
| EFF | 1360 | 2008.1–2013.4 | 40 | 0.44 | −6.08 | ||||||
| 1410 | 1996.8–2009.7 | 164 | 0.98 | −6.42 | |||||||
| 2639 | 2006.6–2013.5 | 61 | 1.08 | −6.64 | |||||||
| JBO | 1400 | 2009.1–2011.0 | 18 | 1.27 | −6.22 | ||||||
| 1520 | 2009.6–2012.0 | 53 | 1.78 | −6.54 | |||||||
| NRT | 1400 | 2005.0–2011.6 | 354 | 1.24 | −6.81 | ||||||
| 1600 | 2009.0–2014.4 | 173 | 0.97 | −7.48 | |||||||
| 2000 | 2005.2–2013.8 | 97 | 1.23 | −7.15 | |||||||
| WSRT | 840 | 1999.5–2007.8 | 53 | 0.90 | −8.81 | ||||||
| 1380 | 1999.7–2001.1 | 22 | 0.55 | −7.98 | |||||||
| 1380 | 2001.1–2010.5 | 114 | 0.53 | −8.74 | |||||||
| 2273 | 2006.9–2010.4 | 39 | 1.05 | −7.87 | |||||||
| J1721−2457 | 3 | −16.50 | 6.68 | −10.04 | 1.22 | ||||||
| NRT | 1400 | 2006.3–2011.8 | 58 | 0.33 | −5.04 | ||||||
| 1600 | 2009.1–2014.2 | 13 | 0.77 | −5.21 | |||||||
| WSRT | 1380 | 2001.5–2010.5 | 79 | 2.38 | −5.13 | ||||||
| J1730−2304 | 7 | −16.33 | 0.11 | −11.42 | 2.37 | ||||||
| EFF | 1360 | 2010.9–2013.5 | 19 | 0.71 | −7.94 | ||||||
| 1410 | 1997.8–1999.3 | 8 | 0.72 | −8.07 | |||||||
| 2639 | 2011.0–2013.2 | 9 | 1.31 | −6.32 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 5 | 1.63 | −6.91 | ||||||
| 1520 | 2009.7–2014.5 | 83 | 1.39 | −6.90 | |||||||
| NRT | 1400 | 2005.1–2011.8 | 106 | 1.01 | −6.75 | ||||||
| 1600 | 2011.0–2014.4 | 29 | 1.07 | −8.43 | |||||||
| 2000 | 2007.4–2011.7 | 9 | 1.30 | −7.73 | |||||||
| J1738+0333 | 2 | −15.34 | 0.36 | −12.09 | 1.89 | ||||||
| JBO | 1520 | 2011.5–2014.3 | 56 | 1.06 | −5.89 | ||||||
| NRT | 1400 | 2007.0–2011.7 | 199 | 1.14 | −9.60 | ||||||
| 1600 | 2011.2–2014.3 | 63 | 1.14 | −9.24 | |||||||
| J1744−1134 | 8 | −13.85 | 2.90 | −17.65 | 4.57 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 22 | 0.58 | −6.17 | ||||||
| 1410 | 1997.0–2009.7 | 100 | 1.03 | −6.14 | |||||||
| 2639 | 2007.1–2013.4 | 42 | 0.88 | −6.14 | |||||||
| JBO | 1520 | 2009.6–2014.3 | 68 | 0.77 | −6.07 | ||||||
| NRT | 1400 | 2005.0–2011.7 | 141 | 1.43 | −6.65 | ||||||
| 1600 | 2010.9–2014.3 | 73 | 1.24 | −6.51 | |||||||
| 2000 | 2009.9–2012.7 | 27 | 1.14 | −7.42 | |||||||
| WSRT | 323 | 2007.6–2010.2 | 32 | 0.90 | −5.73 | ||||||
| 367 | 2007.6–2010.2 | 31 | 1.04 | −9.40 | |||||||
| J1751−2857 | 2 | −19.67 | 6.32 | −16.35 | 4.08 | ||||||
| JBO | 1520 | 2009.3–2014.3 | 37 | 1.56 | −7.05 | ||||||
| NRT | 1400 | 2006.0–2011.8 | 75 | 1.57 | −6.79 | ||||||
| 1600 | 2011.2–2014.3 | 32 | 1.14 | −9.56 | |||||||
| J1801−1417 | 2 | −17.96 | 6.45 | −10.84 | 2.28 | ||||||
| JBO | 1520 | 2009.7–2014.3 | 55 | 0.96 | −8.48 | ||||||
| NRT | 1400 | 2007.3–2011.8 | 49 | 1.68 | −7.12 | ||||||
| 1600 | 2009.0–2014.1 | 22 | 1.47 | −8.21 | |||||||
| J1802−2124 | 3 | −19.55 | 6.88 | −10.79 | 1.73 | ||||||
| JBO | 1520 | 2011.4–2014.5 | 26 | 1.01 | −9.85 | ||||||
| NRT | 1400 | 2007.2–2011.8 | 354 | 1.04 | −9.28 | ||||||
| 1600 | 2009.0–2014.2 | 105 | 1.07 | −6.94 | |||||||
| 2000 | 2008.3–2009.9 | 37 | 1.12 | −7.02 | |||||||
| J1804−2717 | 2 | −18.45 | 4.18 | −17.42 | 0.76 | ||||||
| JBO | 1520 | 2009.1–2014.5 | 53 | 1.14 | −6.76 | ||||||
| NRT | 1400 | 2006.1–2011.8 | 50 | 0.80 | −5.94 | ||||||
| 1600 | 2009.1–2014.2 | 13 | 1.10 | −9.67 | |||||||
| J1843−1113 | 4 | −17.38 | 5.43 | −10.94 | 1.45 | ||||||
| JBO | 1520 | 2009.6–2014.5 | 47 | 0.72 | −5.25 | ||||||
| NRT | 1400 | 2008.0–2011.8 | 63 | 0.86 | −9.34 | ||||||
| 1600 | 2010.8–2014.3 | 47 | 1.01 | −9.11 | |||||||
| WSRT | 1380 | 2004.4–2010.4 | 67 | 1.33 | −7.09 | ||||||
| J1853+1303 | 2 | −15.59 | 5.83 | −18.67 | 1.11 | ||||||
| JBO | 1520 | 2009.6–2014.5 | 34 | 1.03 | −6.18 | ||||||
| NRT | 1400 | 2006.1–2011.8 | 49 | 0.96 | −7.79 | ||||||
| 1600 | 2009.1–2014.3 | 18 | 0.79 | −5.82 | |||||||
| J1857+0943 | 8 | −13.37 | 2.53 | −17.42 | 5.06 | ||||||
| EFF | 1360 | 2008.1–2013.4 | 25 | 0.26 | −5.56 | ||||||
| 1410 | 1997.0–2009.7 | 106 | 0.80 | −8.75 | |||||||
| 2639 | 2008.2–2013.5 | 43 | 1.05 | −8.27 | |||||||
| JBO | 1400 | 2010.9–2011.0 | 7 | 1.14 | −7.37 | ||||||
| 1520 | 2009.6–2012.0 | 31 | 0.58 | −5.71 | |||||||
| NRT | 1400 | 2005.1–2011.8 | 102 | 0.77 | −6.08 | ||||||
| 1600 | 2011.0–2014.3 | 58 | 1.18 | −6.81 | |||||||
| 2000 | 2010.1–2013.5 | 13 | 1.25 | −7.40 | |||||||
| WSRT | 1380 | 2006.2–2010.5 | 59 | 1.29 | −6.09 | ||||||
| J1909−3744 | 2 | −14.18 | 2.17 | −16.84 | 6.70 | ||||||
| NRT | 1400 | 2005.0–2011.8 | 156 | 1.13 | −7.89 | ||||||
| 1600 | 2010.7–2014.4 | 219 | 0.97 | −7.17 | |||||||
| 2000 | 2005.2–2013.8 | 50 | 1.15 | −7.39 | |||||||
| J1910+1256 | 2 | −16.72 | 0.09 | −19.73 | 3.84 | ||||||
| JBO | 1520 | 2009.1–2014.5 | 46 | 0.79 | −8.57 | ||||||
| NRT | 1400 | 2006.0–2011.8 | 52 | 1.12 | −7.59 | ||||||
| 1600 | 2012.0–2014.2 | 14 | 0.66 | −7.84 | |||||||
| J1911+1347 | 2 | −14.84 | 6.85 | −12.89 | 4.27 | ||||||
| JBO | 1520 | 2009.3–2014.5 | 69 | 0.83 | −6.12 | ||||||
| NRT | 1400 | 2007.0–2011.8 | 44 | 0.86 | −6.38 | ||||||
| 1600 | 2009.1–2014.4 | 27 | 1.17 | −8.05 | |||||||
| J1911−1114 | 3 | −18.94 | 3.55 | −14.02 | 1.19 | ||||||
| JBO | 1400 | 2009.1–2009.4 | 5 | 0.90 | −7.45 | ||||||
| 1520 | 2009.6–2015.0 | 59 | 1.10 | −8.98 | |||||||
| NRT | 1400 | 2006.2–2011.8 | 52 | 1.23 | −9.21 | ||||||
| 1600 | 2012.0–2014.2 | 14 | 2.53 | −8.35 | |||||||
| J1918−0642 | 5 | −14.07 | 4.57 | −18.27 | 3.41 | ||||||
| JBO | 1400 | 2009.1–2009.6 | 12 | 1.21 | −6.44 | ||||||
| 1520 | 2009.6–2014.3 | 97 | 0.98 | −6.90 | |||||||
| NRT | 1400 | 2006.8–2011.8 | 57 | 0.92 | −5.95 | ||||||
| 1600 | 2010.9–2014.3 | 26 | 0.70 | −7.61 | |||||||
| WSRT | 1380 | 2001.5–2010.1 | 86 | 0.99 | −9.25 | ||||||
| J1939+2134 | 11 | −14.86 | 6.89 | −11.21 | 2.57 | ||||||
| EFF | 1360 | 2009.6–2011.5 | 32 | 2.05 | −6.55 | ||||||
| 1410 | 1996.8–2009.4 | 223 | 1.31 | −6.32 | |||||||
| JBO | 1520 | 2009.7–2012.0 | 54 | 0.70 | −6.63 | ||||||
| NRT | 1400 | 2005.0–2011.8 | 249 | 2.67 | −8.32 | ||||||
| 1600 | 2005.0–2014.3 | 202 | 2.13 | −8.65 | |||||||
| 2000 | 2005.0–2013.4 | 119 | 1.76 | −6.36 | |||||||
| 1400 | 1990.2–1999.8 | 2058 | 1.16 | −6.56 | |||||||
| WSRT | 1380 | 1999.6–2010.5 | 148 | 2.63 | −8.67 | ||||||
| 2273 | 2006.9–2010.5 | 37 | 1.04 | −9.79 | |||||||
| 840 | 2000.3–2007.9 | 52 | 1.44 | −8.71 | |||||||
| J1955+2908 | 3 | −17.54 | 4.95 | −16.27 | 1.38 | ||||||
| JBO | 1400 | 2009.0–2009.4 | 10 | 1.11 | −7.53 | ||||||
| 1520 | 2009.6–2014.2 | 80 | 1.01 | −8.45 | |||||||
| NRT | 1400 | 2006.2–2011.8 | 47 | 1.14 | −7.23 | ||||||
| 1600 | 2011.2–2014.3 | 20 | 1.38 | −8.80 | |||||||
| J2010−1323 | 4 | −17.75 | 2.26 | −11.66 | 3.44 | ||||||
| JBO | 1400 | 2009.1–2009.6 | 13 | 0.84 | −9.10 | ||||||
| 1520 | 2009.6–2014.3 | 87 | 1.12 | −9.17 | |||||||
| NRT | 1400 | 2007.0–2011.8 | 177 | 1.23 | −7.66 | ||||||
| 1600 | 2010.8–2014.4 | 77 | 1.11 | −7.74 | |||||||
| 2000 | 2007.3–2012.7 | 36 | 1.34 | −7.43 | |||||||
| J2019+2425 | 2 | −15.49 | 2.07 | −17.80 | 3.18 | ||||||
| JBO | 1520 | 2009.6–2014.4 | 59 | 1.41 | −9.85 | ||||||
| NRT | 1400 | 2005.2–2011.8 | 44 | 1.28 | −6.02 | ||||||
| 1600 | 2011.9–2014.3 | 27 | 1.07 | −8.00 | |||||||
| J2033+1734 | 3 | −19.52 | 0.19 | −12.39 | 2.13 | ||||||
| JBO | 1400 | 2009.1–2009.6 | 14 | 1.38 | −9.98 | ||||||
| 1520 | 2009.6–2014.4 | 86 | 0.85 | −8.78 | |||||||
| NRT | 1400 | 2006.4–2011.9 | 58 | 1.19 | −8.97 | ||||||
| 1600 | 2011.8–2014.3 | 36 | 1.32 | −7.72 | |||||||
| J2124−3358 | 4 | −16.98 | 6.07 | −14.42 | 1.20 | ||||||
| JBO | 1400 | 2009.1–2009.3 | 7 | 1.25 | −9.81 | ||||||
| 1520 | 2009.6–2014.3 | 51 | 1.14 | −9.14 | |||||||
| NRT | 1400 | 2005.0–2011.8 | 339 | 1.30 | −8.47 | ||||||
| 1600 | 2009.0–2014.4 | 97 | 1.69 | −6.15 | |||||||
| 2000 | 2006.9–2012.9 | 50 | 1.01 | −5.14 | |||||||
| J2145−0750 | 11 | −14.29 | 4.83 | −11.79 | 1.33 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 30 | 0.81 | −9.25 | ||||||
| 1410 | 1996.8–2009.6 | 117 | 0.65 | −5.92 | |||||||
| 2639 | 2006.9–2013.5 | 51 | 0.81 | −5.62 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 9 | 1.47 | −7.57 | ||||||
| 1520 | 2009.6–2014.3 | 82 | 1.05 | −6.06 | |||||||
| NRT | 1400 | 2005.0–2011.8 | 237 | 1.11 | −6.23 | ||||||
| 1600 | 2010.8–2013.9 | 125 | 1.26 | −7.60 | |||||||
| 2000 | 2007.3–2013.8 | 47 | 1.26 | −6.58 | |||||||
| WSRT | 1380 | 2006.0–2010.1 | 41 | 1.13 | −9.02 | ||||||
| 2273 | 2006.9–2007.3 | 6 | 2.82 | −8.78 | |||||||
| 323 | 2007.3–2010.2 | 30 | 1.68 | −6.10 | |||||||
| 367 | 2007.3–2010.2 | 25 | 1.34 | −5.32 | |||||||
| J2229+2643 | 5 | −15.69 | 4.55 | −17.19 | 1.80 | ||||||
| EFF | 1360 | 2010.7–2013.5 | 26 | 1.38 | −5.49 | ||||||
| 2639 | 2007.3–2013.2 | 23 | 0.54 | −5.34 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 11 | 1.91 | −5.76 | ||||||
| 1520 | 2009.6–2014.4 | 71 | 1.04 | −6.23 | |||||||
| NRT | 1400 | 2006.2–2011.8 | 150 | 1.79 | −6.67 | ||||||
| 1600 | 2010.9–2014.4 | 35 | 1.36 | −7.95 | |||||||
| J2317+1439 | 7 | −15.05 | 0.88 | −15.56 | 1.06 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 32 | 1.78 | −8.19 | ||||||
| 1410 | 1997.0–2009.6 | 15 | 1.31 | −8.40 | |||||||
| 2639 | 2007.6–2013.2 | 41 | 1.13 | −6.63 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 9 | 1.95 | −8.22 | ||||||
| 1520 | 2009.6–2014.3 | 79 | 1.03 | −8.27 | |||||||
| NRT | 1400 | 2005.0–2011.9 | 238 | 1.41 | −7.36 | ||||||
| 1600 | 2009.0–2014.4 | 93 | 1.48 | −6.84 | |||||||
| WSRT | 1380 | 2006.3–2010.5 | 48 | 1.43 | −9.11 | ||||||
| J2322+2057 | 3 | −19.91 | 6.37 | −13.89 | 3.70 | ||||||
| JBO | 1400 | 2009.1–2009.4 | 8 | 0.80 | −6.09 | ||||||
| 1520 | 2009.6–2014.4 | 113 | 1.40 | −6.01 | |||||||
| NRT | 1400 | 2006.5–2011.8 | 59 | 1.58 | −9.55 | ||||||
| 1600 | 2009.0–2014.3 | 49 | 1.21 | −7.92 |
| PSR JName . | Nj . | ARN . | γRN . | ADM . | γDM . | Observatory . | Frequency . | Year range . | NTOAs . | Ef . | Eq . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| J0030+0451 | 6 | −14.65 | 5.43 | −19.06 | 3.27 | ||||||
| EFF | 1360 | 2009.7–2013.5 | 33 | 1.17 | −9.17 | ||||||
| 1410 | 1999.3–2009.6 | 10 | 0.62 | −9.00 | |||||||
| 2639 | 2008.4–2013.4 | 34 | 1.03 | −6.80 | |||||||
| JBO | 1520 | 2012.5–2014.3 | 50 | 1.01 | −8.87 | ||||||
| NRT | 1400 | 2005.0–2011.9 | 552 | 1.18 | −6.13 | ||||||
| 1600 | 2009.0–2014.3 | 138 | 1.59 | −9.86 | |||||||
| 2000 | 2006.9–2014.0 | 90 | 1.32 | −6.07 | |||||||
| J0034−0534 | 5 | −14.93 | 1.27 | −12.43 | 2.84 | ||||||
| NRT | 1400 | 2005.9–2011.7 | 56 | 0.94 | −5.11 | ||||||
| 1600 | 2012.0–2014.1 | 10 | 2.00 | −9.50 | |||||||
| WSRT | 328 | 2000.6–2010.5 | 112 | 1.22 | −8.45 | ||||||
| 382 | 2000.6–2010.5 | 98 | 0.75 | −7.96 | |||||||
| J0218+4232 | 12 | −13.32 | 2.78 | −11.14 | 2.09 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 34 | 1.17 | −6.75 | ||||||
| 1410 | 1996.8–2009.3 | 178 | 1.21 | −8.52 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 13 | 1.50 | −6.08 | ||||||
| 1520 | 2009.6–2014.4 | 97 | 1.10 | −6.68 | |||||||
| NRT | 1400 | 2005.6–2012.2 | 406 | 1.17 | −7.45 | ||||||
| 1600 | 2009.0–2014.3 | 157 | 1.54 | −6.59 | |||||||
| 2000 | 2006.9–2013.6 | 14 | 1.46 | −5.71 | |||||||
| WSRT | 1380 | 1999.8–2010.5 | 49 | 1.55 | −6.32 | ||||||
| 328 | 2000.1–2010.5 | 125 | 1.21 | −6.51 | |||||||
| 382 | 1999.6–2010.5 | 123 | 0.98 | −8.46 | |||||||
| J0610−2100 | 2 | −12.85 | 0.23 | −13.74 | 5.46 | ||||||
| JBO | 1520 | 2010.5–2014.4 | 179 | 0.85 | −8.44 | ||||||
| NRT | 1400 | 2007.5–2011.7 | 631 | 1.62 | −9.29 | ||||||
| 1600 | 2011.2–2014.3 | 224 | 1.26 | −8.48 | |||||||
| J0613−0200 | 13 | −16.15 | 6.88 | −11.71 | 1.07 | ||||||
| EFF | 1360 | 2008.0–2013.5 | 42 | 1.01 | −6.80 | ||||||
| 1410 | 1998.3–2009.3 | 241 | 1.10 | −8.95 | |||||||
| 2639 | 2006.6–2013.5 | 64 | 1.01 | −7.79 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 24 | 1.35 | −8.44 | ||||||
| 1520 | 2009.6–2014.3 | 191 | 0.94 | −5.96 | |||||||
| NRT | 1400 | 2005.0–2011.8 | 334 | 1.02 | −6.35 | ||||||
| 1600 | 2009.0–2014.4 | 84 | 1.00 | −9.77 | |||||||
| 2000 | 2006.9–2012.8 | 51 | 1.10 | −6.41 | |||||||
| WSRT | 1380 | 1999.6–2010.5 | 171 | 1.00 | −9.59 | ||||||
| 328 | 2000.6–2010.5 | 87 | 0.75 | −6.32 | |||||||
| 382 | 2000.6–2010.5 | 80 | 0.92 | −5.69 | |||||||
| J0621+1002 | 9 | −12.04 | 2.50 | −16.98 | 3.80 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 42 | 0.83 | −9.46 | ||||||
| 1410 | 2002.6–2009.3 | 88 | 0.63 | −7.27 | |||||||
| 2639 | 2006.0–2013.4 | 47 | 0.43 | −4.39 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 18 | 1.08 | −7.86 | ||||||
| 1520 | 2009.6–2014.3 | 140 | 1.09 | −9.34 | |||||||
| NRT | 1400 | 2006.1–2011.9 | 168 | 1.23 | −6.58 | ||||||
| 1600 | 2009.0–2014.3 | 33 | 1.31 | −9.74 | |||||||
| WSRT | 1380 | 2006.0–2010.5 | 68 | 1.18 | −8.23 | ||||||
| 323 | 2007.5–2010.5 | 34 | 2.13 | −6.47 | |||||||
| 367 | 2007.5–2010.5 | 35 | 1.72 | −8.12 | |||||||
| J0751+1807 | 8 | −19.50 | 4.86 | −11.77 | 2.83 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 29 | 0.91 | −5.34 | ||||||
| 1410 | 1996.8–2004.6 | 159 | 0.98 | −5.74 | |||||||
| 2639 | 1999.2–2013.5 | 64 | 1.15 | −5.36 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 28 | 1.03 | −8.01 | ||||||
| 1520 | 2009.6–2014.3 | 179 | 1.00 | −6.09 | |||||||
| NRT | 1400 | 2005.0–2011.9 | 598 | 1.19 | −6.00 | ||||||
| 1600 | 2011.2–2014.4 | 362 | 1.07 | −7.50 | |||||||
| 2000 | 2007.5–2013.4 | 40 | 0.88 | −5.72 | |||||||
| WSRT | 1380 | 2007.4–2010.5 | 32 | 1.55 | −8.63 | ||||||
| J0900−3144 | 4 | −15.58 | 5.04 | −11.55 | 3.05 | ||||||
| JBO | 1400 | 2009.1–2009.4 | 9 | 1.09 | −9.26 | ||||||
| 1520 | 2009.7–2014.3 | 99 | 1.02 | −7.47 | |||||||
| NRT | 1400 | 2007.5–2012.1 | 321 | 1.04 | −9.21 | ||||||
| 1600 | 2009.0–2014.4 | 329 | 1.04 | −5.64 | |||||||
| 2000 | 2007.7–2014.2 | 117 | 1.28 | −8.07 | |||||||
| J1012+5307 | 14 | −13.07 | 1.52 | −17.57 | 3.46 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 37 | 0.56 | −5.47 | ||||||
| 1410 | 1997.5–2009.3 | 404 | 0.95 | −6.47 | |||||||
| 2639 | 2006.6–2013.5 | 88 | 1.02 | −7.43 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 12 | 1.13 | −7.83 | ||||||
| 1520 | 2009.8–2014.3 | 96 | 0.96 | −5.86 | |||||||
| NRT | 1400 | 2005.5–2011.7 | 239 | 1.21 | −9.32 | ||||||
| 1600 | 2009.0–2014.4 | 234 | 1.19 | −6.06 | |||||||
| 2000 | 2007.5–2014.1 | 18 | 1.18 | −9.79 | |||||||
| WSRT | 328 | 2000.9–2010.5 | 87 | 1.15 | −5.52 | ||||||
| 382 | 2000.9–2010.5 | 82 | 1.07 | −7.66 | |||||||
| 1380.1 | 1999.6–2001.2 | 26 | 1.14 | −8.21 | |||||||
| 1380.2 | 2001.2–2010.5 | 136 | 0.90 | −6.96 | |||||||
| J1022+1001 | 9 | −13.08 | 1.70 | −11.63 | 1.10 | ||||||
| EFF | 1360 | 2008.1–2013.5 | 76 | 1.02 | −5.84 | ||||||
| 1410 | 1996.8–2009.3 | 164 | 0.65 | −5.43 | |||||||
| 2639 | 2006.2–2013.5 | 88 | 2.09 | −7.32 | |||||||
| JBO | 1400 | 2009.0–2011.0 | 40 | 1.03 | −6.29 | ||||||
| 1520 | 2009.6–2014.3 | 187 | 1.30 | −5.66 | |||||||
| NRT | 1400 | 2005.0–2008.4 | 127 | 1.23 | −5.84 | ||||||
| 1600 | 2011.9–2014.3 | 44 | 1.30 | −7.12 | |||||||
| WSRT | 1380 | 2006.0–2010.5 | 58 | 0.82 | −6.01 | ||||||
| 323 | 2007.5–2010.5 | 26 | 1.67 | −4.81 | |||||||
| 367 | 2007.5–2010.0 | 17 | 0.79 | −4.96 | |||||||
| J1024−0719 | 8 | −13.69 | 3.17 | −12.96 | 6.12 | ||||||
| EFF | 1360 | 2008.1–2013.5 | 33 | 1.05 | −9.41 | ||||||
| 1410 | 1997.0–2009.3 | 27 | 0.75 | −9.76 | |||||||
| 2639 | 2006.0–2013.5 | 53 | 1.23 | −9.75 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 32 | 1.10 | −8.08 | ||||||
| 1520 | 2009.6–2014.3 | 127 | 1.19 | −8.53 | |||||||
| NRT | 1400 | 2006.0–2011.7 | 176 | 1.24 | −8.60 | ||||||
| 1600 | 2009.0–2014.3 | 77 | 0.86 | −5.88 | |||||||
| 2000 | 2006.9–2010.5 | 12 | 0.89 | −6.25 | |||||||
| WSRT | 1380 | 2007.4–2010.2 | 24 | 1.12 | −9.43 | ||||||
| J1455−3330 | 2 | −16.31 | 4.03 | −11.38 | 2.44 | ||||||
| JBO | 1520 | 2009.8–2014.3 | 25 | 1.01 | −5.80 | ||||||
| NRT | 1400 | 2005.0–2011.9 | 338 | 1.23 | −9.53 | ||||||
| 1600 | 2009.0–2014.2 | 161 | 1.04 | −8.98 | |||||||
| J1600−3053 | 3 | −16.56 | 2.71 | −11.64 | 1.41 | ||||||
| JBO | 1520 | 2011.5–2014.3 | 44 | 1.43 | −6.19 | ||||||
| NRT | 1400 | 2006.7–2011.7 | 230 | 1.15 | −7.62 | ||||||
| 1600 | 2010.8–2014.4 | 151 | 0.99 | −9.27 | |||||||
| 2000 | 2006.9–2014.2 | 106 | 1.12 | −6.58 | |||||||
| J1640+2224 | 7 | −13.11 | 0.12 | −16.87 | 0.75 | ||||||
| EFF | 1360 | 2008.1–2013.5 | 81 | 0.89 | −6.64 | ||||||
| 1410 | 1997.0–2009.7 | 122 | 0.93 | −7.96 | |||||||
| 2639 | 2006.2–2013.5 | 67 | 1.02 | −6.86 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 10 | 0.88 | −8.83 | ||||||
| 1520 | 2009.6–2014.3 | 148 | 1.32 | −8.92 | |||||||
| NRT | 1400 | 2005.0–2011.9 | 103 | 1.22 | −8.46 | ||||||
| 1600 | 2010.8–2013.8 | 24 | 1.11 | −9.45 | |||||||
| WSRT | 1380 | 2006.0–2010.2 | 40 | 1.28 | −8.82 | ||||||
| J1643−1224 | 8 | −19.04 | 3.44 | −10.99 | 1.70 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 27 | 1.08 | −8.64 | ||||||
| 1410 | 1997.0–2009.7 | 94 | 1.11 | −9.77 | |||||||
| 2639 | 2006.6–2013.5 | 43 | 0.69 | −5.37 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 11 | 0.95 | −8.85 | ||||||
| 1520 | 2009.7–2014.3 | 76 | 0.74 | −5.61 | |||||||
| NRT | 1400 | 2005.0–2011.7 | 334 | 1.24 | −7.19 | ||||||
| 1600 | 2009.0–2014.3 | 71 | 1.35 | −8.50 | |||||||
| 2000 | 2006.9–2013.6 | 49 | 1.05 | −8.45 | |||||||
| WSRT | 1380 | 2006.0–2010.5 | 54 | 1.29 | −9.87 | ||||||
| J1713+0747 | 13 | −15.29 | 5.62 | −11.98 | 1.47 | ||||||
| EFF | 1360 | 2008.1–2013.4 | 40 | 0.44 | −6.08 | ||||||
| 1410 | 1996.8–2009.7 | 164 | 0.98 | −6.42 | |||||||
| 2639 | 2006.6–2013.5 | 61 | 1.08 | −6.64 | |||||||
| JBO | 1400 | 2009.1–2011.0 | 18 | 1.27 | −6.22 | ||||||
| 1520 | 2009.6–2012.0 | 53 | 1.78 | −6.54 | |||||||
| NRT | 1400 | 2005.0–2011.6 | 354 | 1.24 | −6.81 | ||||||
| 1600 | 2009.0–2014.4 | 173 | 0.97 | −7.48 | |||||||
| 2000 | 2005.2–2013.8 | 97 | 1.23 | −7.15 | |||||||
| WSRT | 840 | 1999.5–2007.8 | 53 | 0.90 | −8.81 | ||||||
| 1380 | 1999.7–2001.1 | 22 | 0.55 | −7.98 | |||||||
| 1380 | 2001.1–2010.5 | 114 | 0.53 | −8.74 | |||||||
| 2273 | 2006.9–2010.4 | 39 | 1.05 | −7.87 | |||||||
| J1721−2457 | 3 | −16.50 | 6.68 | −10.04 | 1.22 | ||||||
| NRT | 1400 | 2006.3–2011.8 | 58 | 0.33 | −5.04 | ||||||
| 1600 | 2009.1–2014.2 | 13 | 0.77 | −5.21 | |||||||
| WSRT | 1380 | 2001.5–2010.5 | 79 | 2.38 | −5.13 | ||||||
| J1730−2304 | 7 | −16.33 | 0.11 | −11.42 | 2.37 | ||||||
| EFF | 1360 | 2010.9–2013.5 | 19 | 0.71 | −7.94 | ||||||
| 1410 | 1997.8–1999.3 | 8 | 0.72 | −8.07 | |||||||
| 2639 | 2011.0–2013.2 | 9 | 1.31 | −6.32 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 5 | 1.63 | −6.91 | ||||||
| 1520 | 2009.7–2014.5 | 83 | 1.39 | −6.90 | |||||||
| NRT | 1400 | 2005.1–2011.8 | 106 | 1.01 | −6.75 | ||||||
| 1600 | 2011.0–2014.4 | 29 | 1.07 | −8.43 | |||||||
| 2000 | 2007.4–2011.7 | 9 | 1.30 | −7.73 | |||||||
| J1738+0333 | 2 | −15.34 | 0.36 | −12.09 | 1.89 | ||||||
| JBO | 1520 | 2011.5–2014.3 | 56 | 1.06 | −5.89 | ||||||
| NRT | 1400 | 2007.0–2011.7 | 199 | 1.14 | −9.60 | ||||||
| 1600 | 2011.2–2014.3 | 63 | 1.14 | −9.24 | |||||||
| J1744−1134 | 8 | −13.85 | 2.90 | −17.65 | 4.57 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 22 | 0.58 | −6.17 | ||||||
| 1410 | 1997.0–2009.7 | 100 | 1.03 | −6.14 | |||||||
| 2639 | 2007.1–2013.4 | 42 | 0.88 | −6.14 | |||||||
| JBO | 1520 | 2009.6–2014.3 | 68 | 0.77 | −6.07 | ||||||
| NRT | 1400 | 2005.0–2011.7 | 141 | 1.43 | −6.65 | ||||||
| 1600 | 2010.9–2014.3 | 73 | 1.24 | −6.51 | |||||||
| 2000 | 2009.9–2012.7 | 27 | 1.14 | −7.42 | |||||||
| WSRT | 323 | 2007.6–2010.2 | 32 | 0.90 | −5.73 | ||||||
| 367 | 2007.6–2010.2 | 31 | 1.04 | −9.40 | |||||||
| J1751−2857 | 2 | −19.67 | 6.32 | −16.35 | 4.08 | ||||||
| JBO | 1520 | 2009.3–2014.3 | 37 | 1.56 | −7.05 | ||||||
| NRT | 1400 | 2006.0–2011.8 | 75 | 1.57 | −6.79 | ||||||
| 1600 | 2011.2–2014.3 | 32 | 1.14 | −9.56 | |||||||
| J1801−1417 | 2 | −17.96 | 6.45 | −10.84 | 2.28 | ||||||
| JBO | 1520 | 2009.7–2014.3 | 55 | 0.96 | −8.48 | ||||||
| NRT | 1400 | 2007.3–2011.8 | 49 | 1.68 | −7.12 | ||||||
| 1600 | 2009.0–2014.1 | 22 | 1.47 | −8.21 | |||||||
| J1802−2124 | 3 | −19.55 | 6.88 | −10.79 | 1.73 | ||||||
| JBO | 1520 | 2011.4–2014.5 | 26 | 1.01 | −9.85 | ||||||
| NRT | 1400 | 2007.2–2011.8 | 354 | 1.04 | −9.28 | ||||||
| 1600 | 2009.0–2014.2 | 105 | 1.07 | −6.94 | |||||||
| 2000 | 2008.3–2009.9 | 37 | 1.12 | −7.02 | |||||||
| J1804−2717 | 2 | −18.45 | 4.18 | −17.42 | 0.76 | ||||||
| JBO | 1520 | 2009.1–2014.5 | 53 | 1.14 | −6.76 | ||||||
| NRT | 1400 | 2006.1–2011.8 | 50 | 0.80 | −5.94 | ||||||
| 1600 | 2009.1–2014.2 | 13 | 1.10 | −9.67 | |||||||
| J1843−1113 | 4 | −17.38 | 5.43 | −10.94 | 1.45 | ||||||
| JBO | 1520 | 2009.6–2014.5 | 47 | 0.72 | −5.25 | ||||||
| NRT | 1400 | 2008.0–2011.8 | 63 | 0.86 | −9.34 | ||||||
| 1600 | 2010.8–2014.3 | 47 | 1.01 | −9.11 | |||||||
| WSRT | 1380 | 2004.4–2010.4 | 67 | 1.33 | −7.09 | ||||||
| J1853+1303 | 2 | −15.59 | 5.83 | −18.67 | 1.11 | ||||||
| JBO | 1520 | 2009.6–2014.5 | 34 | 1.03 | −6.18 | ||||||
| NRT | 1400 | 2006.1–2011.8 | 49 | 0.96 | −7.79 | ||||||
| 1600 | 2009.1–2014.3 | 18 | 0.79 | −5.82 | |||||||
| J1857+0943 | 8 | −13.37 | 2.53 | −17.42 | 5.06 | ||||||
| EFF | 1360 | 2008.1–2013.4 | 25 | 0.26 | −5.56 | ||||||
| 1410 | 1997.0–2009.7 | 106 | 0.80 | −8.75 | |||||||
| 2639 | 2008.2–2013.5 | 43 | 1.05 | −8.27 | |||||||
| JBO | 1400 | 2010.9–2011.0 | 7 | 1.14 | −7.37 | ||||||
| 1520 | 2009.6–2012.0 | 31 | 0.58 | −5.71 | |||||||
| NRT | 1400 | 2005.1–2011.8 | 102 | 0.77 | −6.08 | ||||||
| 1600 | 2011.0–2014.3 | 58 | 1.18 | −6.81 | |||||||
| 2000 | 2010.1–2013.5 | 13 | 1.25 | −7.40 | |||||||
| WSRT | 1380 | 2006.2–2010.5 | 59 | 1.29 | −6.09 | ||||||
| J1909−3744 | 2 | −14.18 | 2.17 | −16.84 | 6.70 | ||||||
| NRT | 1400 | 2005.0–2011.8 | 156 | 1.13 | −7.89 | ||||||
| 1600 | 2010.7–2014.4 | 219 | 0.97 | −7.17 | |||||||
| 2000 | 2005.2–2013.8 | 50 | 1.15 | −7.39 | |||||||
| J1910+1256 | 2 | −16.72 | 0.09 | −19.73 | 3.84 | ||||||
| JBO | 1520 | 2009.1–2014.5 | 46 | 0.79 | −8.57 | ||||||
| NRT | 1400 | 2006.0–2011.8 | 52 | 1.12 | −7.59 | ||||||
| 1600 | 2012.0–2014.2 | 14 | 0.66 | −7.84 | |||||||
| J1911+1347 | 2 | −14.84 | 6.85 | −12.89 | 4.27 | ||||||
| JBO | 1520 | 2009.3–2014.5 | 69 | 0.83 | −6.12 | ||||||
| NRT | 1400 | 2007.0–2011.8 | 44 | 0.86 | −6.38 | ||||||
| 1600 | 2009.1–2014.4 | 27 | 1.17 | −8.05 | |||||||
| J1911−1114 | 3 | −18.94 | 3.55 | −14.02 | 1.19 | ||||||
| JBO | 1400 | 2009.1–2009.4 | 5 | 0.90 | −7.45 | ||||||
| 1520 | 2009.6–2015.0 | 59 | 1.10 | −8.98 | |||||||
| NRT | 1400 | 2006.2–2011.8 | 52 | 1.23 | −9.21 | ||||||
| 1600 | 2012.0–2014.2 | 14 | 2.53 | −8.35 | |||||||
| J1918−0642 | 5 | −14.07 | 4.57 | −18.27 | 3.41 | ||||||
| JBO | 1400 | 2009.1–2009.6 | 12 | 1.21 | −6.44 | ||||||
| 1520 | 2009.6–2014.3 | 97 | 0.98 | −6.90 | |||||||
| NRT | 1400 | 2006.8–2011.8 | 57 | 0.92 | −5.95 | ||||||
| 1600 | 2010.9–2014.3 | 26 | 0.70 | −7.61 | |||||||
| WSRT | 1380 | 2001.5–2010.1 | 86 | 0.99 | −9.25 | ||||||
| J1939+2134 | 11 | −14.86 | 6.89 | −11.21 | 2.57 | ||||||
| EFF | 1360 | 2009.6–2011.5 | 32 | 2.05 | −6.55 | ||||||
| 1410 | 1996.8–2009.4 | 223 | 1.31 | −6.32 | |||||||
| JBO | 1520 | 2009.7–2012.0 | 54 | 0.70 | −6.63 | ||||||
| NRT | 1400 | 2005.0–2011.8 | 249 | 2.67 | −8.32 | ||||||
| 1600 | 2005.0–2014.3 | 202 | 2.13 | −8.65 | |||||||
| 2000 | 2005.0–2013.4 | 119 | 1.76 | −6.36 | |||||||
| 1400 | 1990.2–1999.8 | 2058 | 1.16 | −6.56 | |||||||
| WSRT | 1380 | 1999.6–2010.5 | 148 | 2.63 | −8.67 | ||||||
| 2273 | 2006.9–2010.5 | 37 | 1.04 | −9.79 | |||||||
| 840 | 2000.3–2007.9 | 52 | 1.44 | −8.71 | |||||||
| J1955+2908 | 3 | −17.54 | 4.95 | −16.27 | 1.38 | ||||||
| JBO | 1400 | 2009.0–2009.4 | 10 | 1.11 | −7.53 | ||||||
| 1520 | 2009.6–2014.2 | 80 | 1.01 | −8.45 | |||||||
| NRT | 1400 | 2006.2–2011.8 | 47 | 1.14 | −7.23 | ||||||
| 1600 | 2011.2–2014.3 | 20 | 1.38 | −8.80 | |||||||
| J2010−1323 | 4 | −17.75 | 2.26 | −11.66 | 3.44 | ||||||
| JBO | 1400 | 2009.1–2009.6 | 13 | 0.84 | −9.10 | ||||||
| 1520 | 2009.6–2014.3 | 87 | 1.12 | −9.17 | |||||||
| NRT | 1400 | 2007.0–2011.8 | 177 | 1.23 | −7.66 | ||||||
| 1600 | 2010.8–2014.4 | 77 | 1.11 | −7.74 | |||||||
| 2000 | 2007.3–2012.7 | 36 | 1.34 | −7.43 | |||||||
| J2019+2425 | 2 | −15.49 | 2.07 | −17.80 | 3.18 | ||||||
| JBO | 1520 | 2009.6–2014.4 | 59 | 1.41 | −9.85 | ||||||
| NRT | 1400 | 2005.2–2011.8 | 44 | 1.28 | −6.02 | ||||||
| 1600 | 2011.9–2014.3 | 27 | 1.07 | −8.00 | |||||||
| J2033+1734 | 3 | −19.52 | 0.19 | −12.39 | 2.13 | ||||||
| JBO | 1400 | 2009.1–2009.6 | 14 | 1.38 | −9.98 | ||||||
| 1520 | 2009.6–2014.4 | 86 | 0.85 | −8.78 | |||||||
| NRT | 1400 | 2006.4–2011.9 | 58 | 1.19 | −8.97 | ||||||
| 1600 | 2011.8–2014.3 | 36 | 1.32 | −7.72 | |||||||
| J2124−3358 | 4 | −16.98 | 6.07 | −14.42 | 1.20 | ||||||
| JBO | 1400 | 2009.1–2009.3 | 7 | 1.25 | −9.81 | ||||||
| 1520 | 2009.6–2014.3 | 51 | 1.14 | −9.14 | |||||||
| NRT | 1400 | 2005.0–2011.8 | 339 | 1.30 | −8.47 | ||||||
| 1600 | 2009.0–2014.4 | 97 | 1.69 | −6.15 | |||||||
| 2000 | 2006.9–2012.9 | 50 | 1.01 | −5.14 | |||||||
| J2145−0750 | 11 | −14.29 | 4.83 | −11.79 | 1.33 | ||||||
| EFF | 1360 | 2009.6–2013.4 | 30 | 0.81 | −9.25 | ||||||
| 1410 | 1996.8–2009.6 | 117 | 0.65 | −5.92 | |||||||
| 2639 | 2006.9–2013.5 | 51 | 0.81 | −5.62 | |||||||
| JBO | 1400 | 2009.1–2009.4 | 9 | 1.47 | −7.57 | ||||||
| 1520 | 2009.6–2014.3 | 82 | 1.05 | −6.06 | |||||||
| NRT | 1400 | 2005.0–2011.8 | 237 | 1.11 | −6.23 | ||||||
| 1600 | 2010.8–2013.9 | 125 | 1.26 | −7.60 | |||||||
| 2000 | 2007.3–2013.8 | 47 | 1.26 | −6.58 | |||||||
| WSRT | 1380 | 2006.0–2010.1 | 41 | 1.13 | −9.02 | ||||||
| 2273 | 2006.9–2007.3 | 6 | 2.82 | −8.78 | |||||||
| 323 | 2007.3–2010.2 | 30 | 1.68 | −6.10 | |||||||
| 367 | 2007.3–2010.2 | 25 | 1.34 | −5.32 | |||||||
| J2229+2643 | 5 | −15.69 | 4.55 | −17.19 | 1.80 | ||||||
| EFF | 1360 | 2010.7–2013.5 | 26 | 1.38 | −5.49 | ||||||
| 2639 | 2007.3–2013.2 | 23 | 0.54 | −5.34 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 11 | 1.91 | −5.76 | ||||||
| 1520 | 2009.6–2014.4 | 71 | 1.04 | −6.23 | |||||||
| NRT | 1400 | 2006.2–2011.8 | 150 | 1.79 | −6.67 | ||||||
| 1600 | 2010.9–2014.4 | 35 | 1.36 | −7.95 | |||||||
| J2317+1439 | 7 | −15.05 | 0.88 | −15.56 | 1.06 | ||||||
| EFF | 1360 | 2009.6–2013.5 | 32 | 1.78 | −8.19 | ||||||
| 1410 | 1997.0–2009.6 | 15 | 1.31 | −8.40 | |||||||
| 2639 | 2007.6–2013.2 | 41 | 1.13 | −6.63 | |||||||
| JBO | 1400 | 2009.0–2009.4 | 9 | 1.95 | −8.22 | ||||||
| 1520 | 2009.6–2014.3 | 79 | 1.03 | −8.27 | |||||||
| NRT | 1400 | 2005.0–2011.9 | 238 | 1.41 | −7.36 | ||||||
| 1600 | 2009.0–2014.4 | 93 | 1.48 | −6.84 | |||||||
| WSRT | 1380 | 2006.3–2010.5 | 48 | 1.43 | −9.11 | ||||||
| J2322+2057 | 3 | −19.91 | 6.37 | −13.89 | 3.70 | ||||||
| JBO | 1400 | 2009.1–2009.4 | 8 | 0.80 | −6.09 | ||||||
| 1520 | 2009.6–2014.4 | 113 | 1.40 | −6.01 | |||||||
| NRT | 1400 | 2006.5–2011.8 | 59 | 1.58 | −9.55 | ||||||
| 1600 | 2009.0–2014.3 | 49 | 1.21 | −7.92 |
5.5 Search for annual-orbital parallax
Even a null |$\dot{x}$| can, if measured precisely enough, be useful. According to equation (16), the maximum value for |$\left|\dot{x}\right|$| is |$\dot{x}_{\max } = |x \mu \cot i|$| (obtained using the inequality |sin (θμ − Ω)| ≤ 1). Thus, whenever the observed value and uncertainty represent a small fraction of the interval from |$- \dot{x}_{\max }$| to |$\dot{x}_{\max }$|, they are placing a direct constraint on sin (θμ − Ω).
In our data set, we measured the apparent variation of |$\dot{x}$| for 13 pulsars, among which six are new measurements (PSRs J0751+1807, J1455−3330, J1640+2224, J1751−2857, J1857+0943 and J1955+2908).
For the three pulsars where we measured both the Shapiro delay and the variation of the semimajor axis (i.e. PSRs J0751+1807, J1600−3053 and J1857+0943) and PSR J1909−3744 (where |$\dot{x} =0.6\pm 1.7 \times 10^{-16}$| and |$x \mu \cot i = 1.08\times 10^{-14}$|), we map the KOM-KIN space with temponest using the following procedure. First, we reduce the dimensionality of the Bayesian analysis by fixing the set of white noise parameters to their maximum likelihood values from the timing analysis. We also choose to marginalize analytically over the astrometric and spin parameters. Then we manually set the priors on KOM, KIN and M2 to encompass any physical range of solution. Finally, we perform the sampling with temponest with the constant efficiency option turned off, in order to more carefully explore the complex multi-modal parameter space. Because of the strong correlation between the companion mass and the inclination angle in the case of PSR J0751+1807, (see Fig. 6), we do not report our measurements as they were not constrained enough. The results are shown in Figs 9 –11 for the other three pulsars.
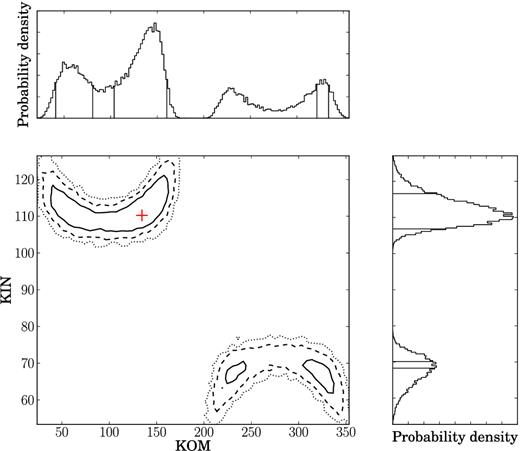
One- and two-dimensional marginalized posterior distributions of the longitude of ascending node Ω and inclination angle i for PSR J1600−3053. The continuous black line, the dashed line and the dotted line represent, respectively, the 68.3, 95.4 and 99.7 per cent confidence levels of the 2D probability density function. The red cross indicates the maximum likelihood location. The continuous lines in the panels of the projected 1D distributions of KOM and KIN show the 68.3 per cent confidence levels for each parameter.
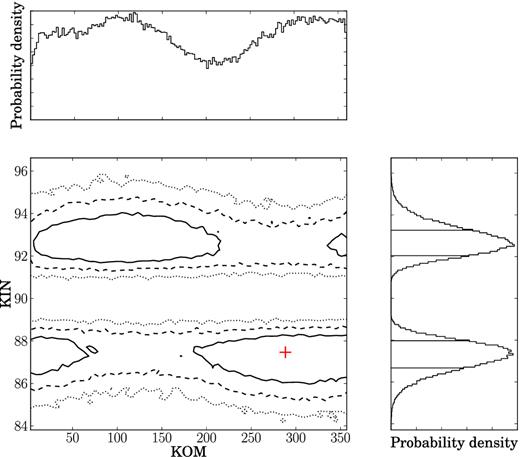
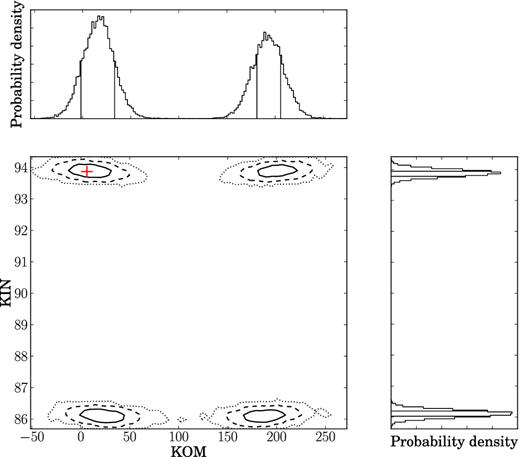
For PSR J1600−3053, the 1σ contours of the 2D posterior distribution (Fig. 9) give three solutions for (Ω, i): 219° < Ω < 244° and 63° < i < 71° or 303° < Ω < 337° and 61° < i < 72° and the preferred solution, 37° < Ω < 163° and 105° < i < 122°. The 2.5σ detection of |$\dot{x}$| in the PSR J1857+0943 binary system still limit the constraints that can be set on Ω (see Fig. 10). Even though we do not detect |$\dot{x}$| for PSR J1909−3744, we can constrain Ω (see Fig. 11) to −2° < Ω < 33° or 181° < Ω < 206°. The preferred solution is −2° < Ω < 33° and 93| $_{.}^{\circ}$|78 < i < 93| $_{.}^{\circ}$|95. However, with this EPTA data set, we still have no statistical evidence for the detection of annual-orbital parallax as we cannot distinguish between the symmetric solutions of the pulsar orbits in these three pulsars.
5.6 Comparison with the latest NANOGrav and PPTA results
While this work was under review, similar analysis by NANOGrav and the PPTA were published elsewhere (Arzoumanian et al. 2015; Reardon et al. 2016, hereafter A15 and R16, respectively). A15 presents a thorough description of their data analysis and Matthews et al. (2016, hereafter M16) report on the study of astrometric parameters. Other timing results and their interpretations (e.g. pulsar mass measurements) will be presented in a series of upcoming papers. Hence, we briefly summarize here the similarities and differences between our work and the ones by R16 and M16.
R16 used tempo2 linearized, least-squares fitting methods to present timing models for a set of 20 MSPs. White noise, DM variations and red noise are included in the timing analysis and modelled with completely independent techniques from the ones described in Section 3. For all 13 pulsars observed commonly by the EPTA and the PPTA, both PTAs achieve the detection of the parallax with consistent results (within 1.5σ). We note here that the parallax value of PSR J1909−3744 should read π = 0.81 ± 0.03 mas in R16 (Reardon, private communication). Also, the seven new proper motions values reported in this paper are for pulsars that are not observed by R16. We obtain similar results for the pulsar and companion masses to the values reported in R16, albeit with much greater precision in the case of PSRs J1600−3053. Furthermore, all our measurements of |$\dot{x}$| agree with R16. While R16 measure |$\dot{P_{\rm b}}$| in PSR J1022+1001 for the first time, the EPTA achieve the detection of |$\dot{P_{\rm b}}$| for another MSP (PSR J0613−0200), allowing us to get an independent distance estimate for these systems.
M16 report on the astrometric results for a set of 37 MSPs analysed with the linearized least-squares fitting package tempo.6 More details on the DM and red noise models included in their analysis can be found in A15. All 14 parallax measurements for the pulsars presented commonly in this work and in M16 are consistent at the 2σ level. In addition, M16 show a new parallax measurement for PSR J1918−0642 that was not detected with our data set. M16 also present updated proper motions for 35 MSPs and derived the pulsar velocities in galactocentric coordinates. The new proper-motion measurement for PSR J2010−1323 reported in our work is consistent at the 2σ level with the independent measurement from M16.
Finally, M16 discuss in detail the same discrepancy reported in Section 5.3 between their measured parallax distance for PSR J1024−0719 and its constraint from |$D_{\dot{P}}$|.
6 Conclusions
We studied an ensemble of 42 MSPs from the EPTA, combining multifrequency data sets from four different observatories, with data spanning more than 15 years for almost half of our sample. The analysis was performed with temponest allowing the simultaneous determination of the white noise parameters and modelling of the stochastic DM and red noise signals. We achieved the detection of several new parameters: seven parallaxes, nine proper motions and six apparent changes in the orbital semimajor axis. We also measured Shapiro delay in two systems, PSRs J1600−3053 and J1918−0642, with low-mass helium white dwarf companions. Further observations of PSR J1600−3053 will likely yield the detection of the advance of periastron, dramatically improving the mass measurement of this system and improving the constraints on the geometry of the system. We presented an updated mass measurement for PSR J0751+1807, roughly consistent with the previous work by Nice et al. (2008). We searched for the presence of annual-orbital parallax in three systems, PSRs J1600−3053, J1857+0943 and J1909−3744. However we could only set constraints on the longitude of ascending node in PSRs J1600−3053 and J1909−3744 with marginal evidence of annual-orbital parallax in PSR J1600−3053.
With an improved set of parallax distances, we investigated the difference between the predictions from the NE2001 Galactic electron density model and the LK-corrected parallax distances. On average we found an error of ∼80 per cent in the NE2001 distances, this error increasing further at high Galactic latitudes. Despite its flaws for high galactic latitude lines of sight, we find NE2001 to still predict more accurate distances than two recent models, M2 and M3, proposed by S12, based, respectively, on the TC93 and NE2001 models with an extended thick disc. We showed that a change in the scaleheight of the thick disc of the current electron density models also dramatically affects the pulsars that are located in the Galactic plane. Our updated set of parallaxes presented here will likely contribute to improving on any future model of the Galactic electron density model.
A comparison of the 2D velocity distribution between isolated and binary MSPs with a sample two times larger than the last published study (Gonzalez et al. 2011) still shows no statistical difference, arguing that both populations originate from the same underlying population. Through precision measurement of the orbital period derivative, we achieved better constraints on the distance to two pulsars, PSRs J1012+5307 and J1909−3744, than is possible via the detection of the annual parallax.
Based on the timing results presented in this paper and the red noise properties of the pulsars discussed in Caballero et al. (2015), we will revisit and potentially remove some MSPs from the EPTA observing list. The EPTA is also continuously adding more sources to its observing list, especially in the last five years, as more MSPs are discovered through the targeted survey of Fermi sources (Ray et al. 2012) and large-scale pulsar surveys (e.g. the PALFA, HTRU and GBNCC collaborations; Barr et al. 2013b; Ng et al. 2014; Stovall et al. 2014; Lazarus et al. 2015). Over 60 MSPs are now being regularly monitored as part of the EPTA effort.
Recent progress in digital processing, leading in some cases to an increase of the processed BW by a factor of 2–4 times, allowed new wide-band coherent dedispersion backends to be commissioned at all EPTA sites in the last few years (see e.g. Karuppusamy et al. 2008; Desvignes et al. 2011). These new instruments provide TOAs with improved precision that will be included in a future release of the EPTA data set. The long baselines of MSPs timing data presented here, especially when recorded with a single backend, are of great value, not only for the detection of the GWB but also to a wide range of astrophysics as shown in this paper.
The authors would like to thank D. Schnitzeler for providing us with the M2 and M3 distances used in this work, P. Freire, M. Bailes, T. Tauris and N. Wex for useful discussions, P. Demorest for his contribution to the pulsar instrumentation at the NRT.
Part of this work is based on observations with the 100-m telescope of the Max-Planck-Institut für Radioastronomie (MPIfR) at Effelsberg in Germany. Pulsar research at the Jodrell Bank Centre for Astrophysics and the observations using the Lovell Telescope are supported by a consolidated grant from the STFC in the UK. The Nançay radio observatory is operated by the Paris Observatory, associated with the French Centre National de la Recherche Scientifique (CNRS). We acknowledge financial support from ‘Programme National de Cosmologie et Galaxies’ (PNCG) of CNRS/INSU, France. The WSRT is operated by the Netherlands Institute for Radio Astronomy (ASTRON) with support from the Netherlands Foundation for Scientific Research (NWO).
CGB, GHJ, RK, KL, KJL, DP acknowledge the support from the ‘LEAP’ ERC Advanced Grant (337062). RNC acknowledges the support of the International Max Planck Research School Bonn/Cologne and the Bonn-Cologne Graduate School. JG and AS are supported by the Royal Society. JWTH acknowledges funding from an NWO Vidi fellowship and CGB, JWTH acknowledge the support from the ERC Starting Grant ‘DRAGNET’ (337062). KJL is supported by the National Natural Science Foundation of China (Grant No.11373011). PL acknowledges the support of the International Max Planck Research School Bonn/Cologne. CMFM was supported by a Marie Curie International Outgoing Fellowship within the 7th European Community Framework Programme. SO is supported by the Alexander von Humboldt Foundation. This research was in part supported by ST's appointment to the NASA Postdoctoral Program at the Jet Propulsion Laboratory, administered by Oak Ridge Associated Universities through a contract with NASA. RvH is supported by NASA Einstein Fellowship grant PF3-140116.
The authors acknowledge the use of the hydra and hercules computing cluster from Rechenzentrum Garching. This research has made extensive use of NASA's Astrophysics Data System, the ATNF Pulsar Catalogue and the python Uncertainties package, http://pythonhosted.org/uncertainties/.
A difference of 3 in the log evidence between two models is usually required to justify the introduction of an additional parameter (Kass & Raftery 1995).
We remind the reader that the most likely distance is not necessarily equal to the inverse of the most likely parallax, given the non-linearity of the inversion.
REFERENCES
APPENDIX A: Data description
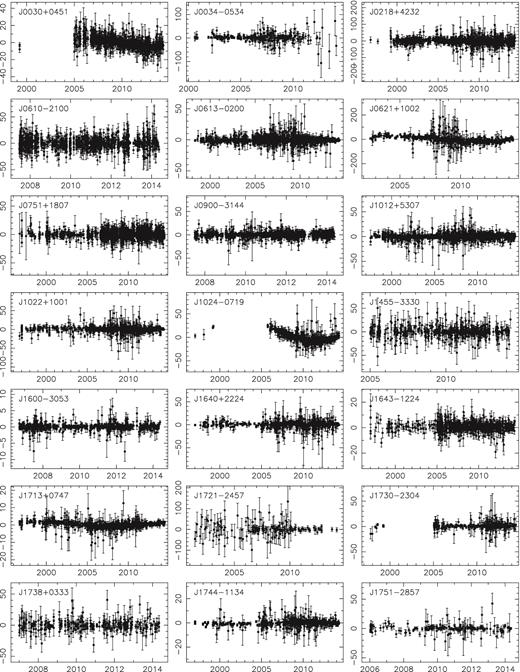
Timing residuals in microseconds (y-axis) for the first 21 pulsars as a function of time in years (x-axis). The plots show the multifrequency residuals after subtracting the contribution from the DM model. The red noise seen in the timing residuals of PSRs J0030+0451 and J1024−0719 will be discussed by Caballero et al. (2015).
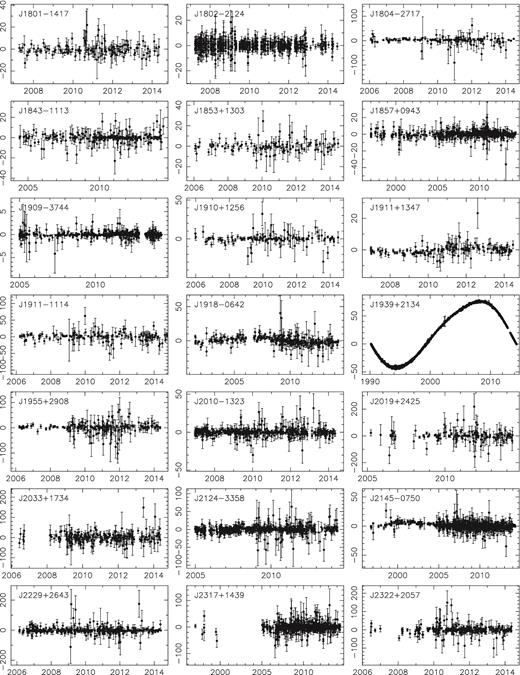
Same caption as Fig. A1 for the last 21 MSPs. The large amount of red noise seen in the timing residuals of PSR J1939+2134 will be discussed by Caballero et al. (2015).
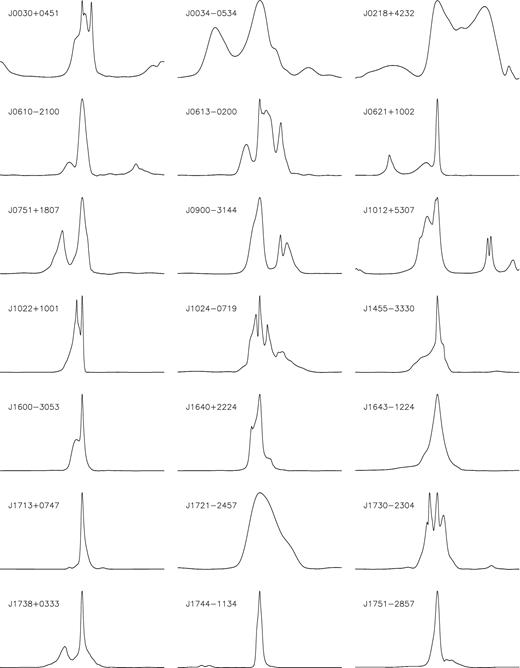
Reference profiles of total intensity I for the first 21 MSPs observed at 1400 MHz with the NRT. The profiles are centred with respect to the peak maximum. For each pulsar, the full pulse phase is shown and the intensity is in arbitrary units.