-
PDF
- Split View
-
Views
-
Cite
Cite
Hai-Lang Dai, Xi-Wei Liu, Xiang-Dong Li, Exploration of spin-down rate of neutron stars in high-mass X-ray binaries, Monthly Notices of the Royal Astronomical Society, Volume 457, Issue 4, 21 April 2016, Pages 3889–3895, https://doi.org/10.1093/mnras/stw111
Close - Share Icon Share
Abstract
We use the evolutionary population synthesis method to investigate the statistical properties of the wind-fed neutron-star (NS) compact (Porb < 10 d) high-mass X-ray binaries (HMXBs) in our Galaxy, based on different spin-down models. Model 1 assumes that the surrounding material is treated as forming a quasi-static atmosphere. Model 2 assumes that the characteristic velocity of matter and the typical Alfvén velocity of material in the magnetospheric boundary layer are comparable to the sound speed in the external medium. We find that the spin-down rate in the supersonic propeller phase in either model 1 or model 2 is too low to produce the observed number of compact HMXBs. Model 3 assumes that the infalling material is ejected with the corotation velocity at the magnetospheric radius when the magnetospheric radius is larger than the corotation radius. Model 4 uses simple integration of the magnetic torque over the magnetosphere. Both models 3 and 4 have a larger spin down rate than that given by model 1 or 2. We also find that models 3 and 4 can predict a reasonable number of observed wind-fed NS compact HMXBs. By comparing our calculated results with the observed particular distributions of wind-fed NS compact HMXBs in a Ps versus Porb diagram, we find that the subsonic propeller phase may not exist at all. However, the spin-down rates in models 3 and 4 both seem reasonable to produce the observed distribution of wind-fed NS compact HMXBs in the Ps versus Porb diagram. We cannot find which spin-down rate seems more reasonable from our calculations.
INTRODUCTION
High-mass X-ray binaries (HMXBs) are composed of a compact object that orbits a massive (>10 M⊙) donor star. The X-ray emission is due to the accretion of matter from the donor star on to the compact companion, which is a black hole or neutron star (NS). In most cases, the donor stars do not fill their Roche lobes and the compact objects accrete from the stellar wind. Canonically, HMXBs can be roughly divided into two groups: supergiant binaries and Be/X-ray binaries. In the supergiant systems, either Roche lobe or stellar wind accretion occurs, while in the Be systems commonly only the latter process takes place since the Be star is well inside its Roche lobe (Tauris & van den Heuvel 2006). Be/X-ray binaries are both transient and persistent X-ray sources. Transient systems are characterized by type II outbursts during which their flux increases by a factor of 10–104 over the quiescent level. On the other side, persistent Be/X-ray binaries show a rather flat light curve, lower luminosity, and longer spin and orbital periods (Reig 2011).
Supergiant fast X-ray transients (SFXTs) unveiled in the last few years, mainly thanks to INTEGRAL observations of the Galactic plane, are a new sub-class of supergiant HMXBs that display extreme flaring behaviour on short time-scales (approximately an hour) (Sguera et al. 2005, 2006; Negueruela et al. 2006). They host a massive OB supergiant star as identified by optical spectroscopy. The compact object is generally assumed to be a NS because of the broad-band X-ray spectral shape (0.2–100 keV), strongly resembling those of accreting X-ray pulsars in classical HMXBs (White, Nagase & Parmar 1995). A distinctive property of SFXTs is the high dynamic range, spanning three to five orders of magnitude, with sudden increases in luminosity from 1032 erg s−1 up to the flare peak luminosity (e.g. in't Zand 2005). There are currently 10 confirmed and about as many candidate SFXTs (Sidoli 2013).
The INTEGRAL observatory appears to have discovered a class of compact HMXBs, which are a new class of γ-ray sources for which a mechanism is presented by Bednarek (2009), i.e. an accreting NS inside a binary system. These newly discovered massive binaries are compact with orbital periods between a few to several days. Some contain relatively slowly rotating NSs that may allow the material to penetrate the inner NS magnetosphere.
The spin-down rate of a NS in a wind-fed NS HMXB has been investigated by many authors. The rate of loss of angular momentum of a NS, proposed by Illarionov & Sunyaev (1975), Fabian (1975) and Wickramasinghe & Whelan (1975), is obtained by assuming that the characteristic velocity of matter carrying off the required energy and the typical Alfvén velocity of material in the magnetospheric boundary layer are comparable to the sound speed in the external medium. The rate proposed by Davidson & Ostriker (1973), Kundt (1976) and van den Heuvel (1978) is obtained by simple integration of the magnetic torque over the magnetosphere and equating this to an angular momentum loss from the star by assuming that the field lines at the magnetosphere are swept back through an angle of 45°. The most rapid spin-down rate, proposed by Shakura (1975), Lipunov & Shakura (1976) and Holloway, Kundt & Wang (1978), is obtained by treating the particles striking the magnetosphere as independent particles, and by assuming that they are all accelerated to a characteristic velocity, comparable to the rotational speed of the magnetosphere, which is much larger than the sound speed in the external medium. A comprehensive picture assuming that the surrounding material is treated as forming a quasi-static atmosphere through which energy is transported was first drawn by Davies & Pringle (1981), whose model passes through four distinct phases as a NS slows down.
Mori & Ruderman (2003) suggested that two parameters can classify many proposed propeller spin-down models. Many authors have derived the spin-down rate of the propeller phase by assuming that the infalling material is ejected with the corotation velocity at the magnetospheric radius when the magnetospheric radius is larger than the corotation radius (Wang & Robertson 1985; Jiang & Li 2005; Dai, Liu & Li 2006). Besides, a large number of authors (see, e.g. Spruit & Taam 1993; Rappaport, Fregeau & Spruit 2004; D'Angelo & Spruit 2010, 2012) have investigated the spin-down rate of a NS accreting from a disc in a NS HMXB. Romanova et al. (2003) studied accretion on to a star in the propeller regime using magnetohydrodynamic simulations.
Though the propeller effect has been investigated extensively, there still remain large uncertainties about the efficiency of angular momentum loss during the propeller regime (see, e.g. Pringle & Rees 1972; Ikhsanov 2001). The investigations mentioned above were usually either theoretical or numerical. To understand the spin-down mechanism of a NS better, we should use an evolutionary population synthesis that incorporates the evolution of the NS spin. In the present paper, we describe a population synthesis study of the spin evolution of a NS in a massive binary. Obviously, it is very difficult to provide more stringent constraints on these spin-down models from theory. However, we can give additional constraints on the spin-down rate by comparing the calculated results based on the evolutionary population synthesis method by adopting different spin-down models with the observed population of compact HMXBs.
We describe the theoretical considerations in Section 2. In Section 3, we present the calculated results. Finally, we present a brief discussion and conclusions in Section 4.
MODEL
Spin evolution
We consider a binary system consisting of a 1.4 M⊙ magnetized NS and a massive donor star. The spin-down evolution of a NS in a binary system has been investigated by many authors. Generally speaking, the spin-down evolution of a NS before steady accretion occurs contains two phases: the pulsar phase and the propeller phase, as briefly presented below.
Case 1: the pulsar phase
Case 2: the propeller phase
The propeller phase begins when the pulsar phase breaks down if the magnetospheric radius |${R_{\rm m}}=[\mu ^4/(2GM\dot{M}^2)]^{1/7}$| is larger than the corotation radius |${R_{\rm c}}=(GM/\Omega _{\rm s}^2)^{1/3}$|. The angular momentum of the NS is taken away from the NS surface when the infalling plasma is ejected outward because the centrifugal barrier inhibits further accretion. Although many authors (e.g. Pringle & Rees 1972; Illarionov & Sunyaev 1975; Davies & Pringle 1981; Wang & Robertson 1985; Ikhsanov 2001; Bozzo, Falanga & Stella 2008; Shakura et al. 2012) have investigated the propeller effect extensively, the efficiency of angular momentum loss during the propeller phase is still uncertain.
Davies & Pringle (1981) suggested that the propeller phase can be divided into two subphases: a supersonic propeller phase and a subsonic propeller phase:
- The NS will enter the supersonic propeller phase when its angular velocity Ωs is large enough so that rcΩs ≫ cs(rc), where rc is the inner boundary and cs(rc) is the sound speed at the radius rc. The spin-down torque is(case c of Davies & Pringle 1981). The typical spin-down time-scale is(4)\begin{equation} N=-8\times 10^{31}\dot{M_{15}}v_{8}^2\Omega _{\rm s}^{-1}\,{\rm g\,cm^{2}\,s^{-2}} \end{equation}The spin-down of the supersonic propeller phase process ends when |${P_{\rm s}}$| reaches the equilibrium spin period:(5)\begin{equation} \tau = 1.6\times 10^7\dot{M}_{15}^{-1}v_{8}^{-2}I_{45}P_{0}^{-2}\,{\rm yr}. \end{equation}(6)\begin{equation} P_{\rm eq}= 23\mu _{30}^{2/3}\dot{M}_{15}^{-1/3}v_{8}^{-2/3}\,{\rm s}. \end{equation}
- Davies & Pringle (1981) suggested that accretion is unlikely to take place unless the material outside the magnetosphere can cool. Therefore, the NS spins at a subsonic speed and continues to lose rotational energy. The spin-down torque of the subsonic propeller phase is(case d of Davies & Pringle 1981). The typical spin-down time-scale is(7)\begin{equation} N = -1.2\times 10^{36}\mu _{30}^2(M/\mathrm{M}_{{{\odot }}})^{-1}P_{0}^{-3}\Omega _{\rm s}^{-1}\,{\rm g\,cm^{2}\,s^{-2}} \end{equation}The spin-down of the subsonic propeller phase process ends when |${P_{\rm s}}$| reaches Pbr:(8)\begin{equation} \tau \simeq 10^3\mu _{30}^{-2}(M/\mathrm{M}_{{{\odot }}})P_{0}I_{45}\,{\rm yr}. \end{equation}(9)\begin{equation} P_{\rm br}= 60\mu _{30}^{16/21}\dot{M}_{15}^{-5/7}(M/\mathrm{M}_{{{\odot }}})^{-4/21}\,{\rm s}. \end{equation}
Steady wind accretion on to the surface of the NS occurs when P > Peq. However, the present spin periods of wind-fed X-ray pulsars are not significantly different from Peq. So we stop the calculations when either Peq is reached within the main sequence lifetime or the optical star evolves off the main sequence. In the present paper, narrow HMXBs with Roche lobe overflow (RLOF) are never considered because the accreting material is most likely to come from an accretion disc. For wind-fed systems like Vela X−1, numerical calculations (e.g. Fryxell & Taam 1988; Matsuda et al. 1992; Anzer & Börner 1995; Ruffert 1999) suggested that there is no significant angular momentum transfer on to the NS when radially expanding wind matter is transferred on to it. This may lead to only small deviations from the instantaneous (equilibrium if reached) spin periods when the accretion phase starts. A random walk in their spin frequencies with alternating spin-up and spin-down (Bildsten et al. 1997) is shown by CGRO/BATSE observations.
Evolution of the mass-flow rate on to a NS
We use the evolutionary population synthesis code developed by Hurley, Pols & Tout (2000) and Hurley, Tout & Pols (2002) to explore the spin-down rate of a NS in a binary system. The evolution of single stars with binary-star interactions, such as mass accretion, mass transfer, common-envelope (CE) evolution, collisions, supernova kicks, angular momentum loss mechanisms and tidal friction, is included in this code. The parameters we adopted are mostly the same as those described by Hurley et al. (2002). The primary-mass (M1) distribution is the initial mass function of Kroupa, Tout & Gilmore (1993). A uniform distribution of the mass ratio 0 < q ≡ M2/M1 ≤ 1 is taken between 0 and 1 for the secondary star (of mass M2). For the binary separation a, we take a uniform distribution in ln a (the natural logarithm of a). We assume that one binary with M1 ≥ 8 M⊙ is born in the Galaxy per year, which gives a star formation rate S = 7.6085 yr−1. During supernova explosions, a kick velocity with a Maxwellian distribution is imparted on to a NS with a mean of 265 km s−1 (Hobbs et al. 2005).
Hurley et al. (2002) presented, in particular, a treatment of RLOF mass transfer in a primordial binary and the stability criterion for the mass transfer is described briefly here. According to whether the primary stays in thermal equilibrium when it loses mass, and the radius of the primary increases faster than the Roche lobe, mass transfer through RLOF takes place on a thermal, nuclear or dynamical time-scale. Stars with deep surface convective zones – for instance, giants or naked helium giants – will enter a CE evolution because they are generally unstable to dynamical-time-scale mass loss. The Eddington accretion rate limits the stable mass-accretion rate of the secondary star. We have not considered the situation where the secondary may be spun up and become a Be star as it accretes enough mass because the origin of Be phenomena is still unclear and it is hard to give a model of the mass-transfer processes in Be/X-ray binaries. The CE efficiency parameter α was set at α = 1 as a typical value and we varied it from 0.1 to 2 in our calculations (Dewi & Tauris 2000; Tauris & Dewi 2001). The region of the parameter space from which NS high-mass binaries form is shown in Fig. 1. We can also derive other binary parameters, such as the surface temperature, luminosities and radii of the companion stars. The mass-loss rates from the companion stars and the mass-flow rates on to the NSs can be evaluated using these parameters.
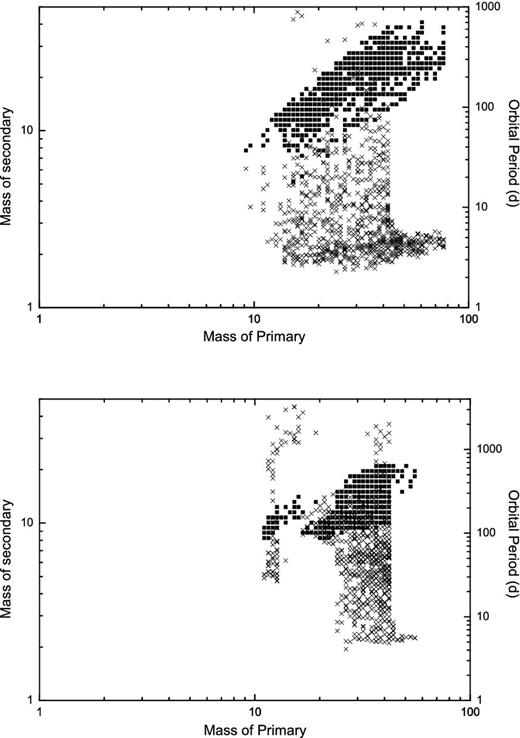
Region of parameter space in which NS high-mass binaries form. (a) Mass transfer before core-collapse of the primary star is dynamically stable. (b) Mass transfer is dynamically unstable when the progenitor binary has evolved through a CE phase. Filled squares denote the mass distribution, while crosses denote the primary mass-orbital period distribution. The CE efficiency factor adopted is a typical value of α = 1.0.
RESULTS
We calculated the evolution of the spin and the statistical properties for compact wind-fed X-ray pulsars in NS binary systems based on the theoretical models presented in Section 2. For the initial NS magnetic fields B, we assumed that log B is distributed normally with a mean of 12.5 (the typical magnetic fields of such pulsars are 3 × 1012 G) and a standard deviation of 0.3. No field decay was considered. We stopped our calculations for the spin evolution when either |${P_{\rm s}}$| reaches Peq/Pbr (depending on whether the subsonic propeller phase exists) or the companion star begins to evolve off the main sequence, for the reasons described above.
We adopt a variety of models (see Table 1), each with different assumptions for the spin-down rate and parameters that govern the evolutions in the calculations. In Table 1, DP81, WR85 and MR03 represent the spin-down models described by Davies & Pringle (1981), Wang & Robertson (1985) and Mori & Ruderman (2003), respectively. ‘No’ in Table 1 describes the situation when the subsonic propeller phase does not exist. We consider situations only when γ = −1 and γ = 0 for the spin-down model described by Mori & Ruderman (2003) because the spin-down model corresponds to WR85 and DP81 when γ = 1 and γ = 2. Fig. 2 shows the evolution of the NS spin period (with the same initial parameters of the binary) in a binary system for different models, which indicates that a longer spin period of the NS may be induced when the subsonic phase exists.
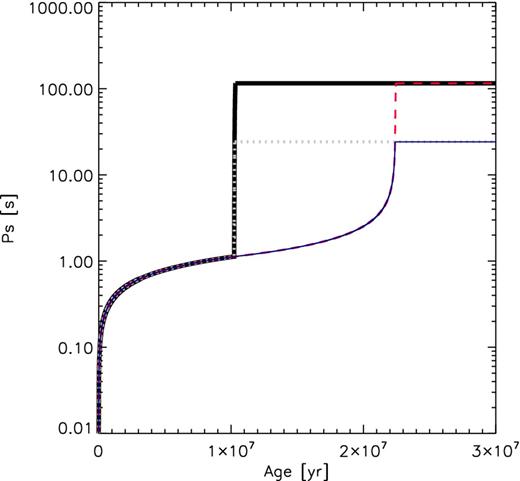
An evolutionary example of compact NS HMXBs. Evolution of NS spin period in a binary system with the same initial parameters of the binary for model A1 (red dashed line), model A2 (thin blue line), model B1 (thick black line) and model B6 (thick grey dotted line). The evolution begins after the birth of the NS.
Model parameters for binary population synthesis. The columns ‘Sup’ and ‘Sub’ denote the adopted NS spin-down models for the supersonic propeller and subsonic propeller phases, respectively. |$\dot{M}=1$| or 3 denotes the wind mass-loss rates assumed to be 1 or 3 times the standard prescription we adopted in Section 2, respectively. v8 is the wind velocity in units of 108 cm/s.
| Model . | Sup . | Sub . | α . | |$\dot{M}$| . | v8 . |
|---|---|---|---|---|---|
| A1 | DP81 | DP81 | 1 | 1 | 1 |
| A2 | DP81 | No | 1 | 1 | 1 |
| A3 | DP81 | No | 0.5 | 1 | 1 |
| A4 | DP81 | No | 1 | 3 | 1 |
| A5 | DP81 | No | 1 | 1 | 2 |
| B1 | WR85 | DP81 | 1 | 1 | 1 |
| B2 | WR85 | DP81 | 0.5 | 1 | 1 |
| B3 | WR85 | DP81 | 1 | 3 | 1 |
| B4 | WR85 | DP81 | 1 | 1 | 2 |
| B5 | WR85 | No | 0.5 | 1 | 1 |
| B6 | WR85 | No | 1 | 1 | 1 |
| B7 | WR85 | No | 0.5 | 1 | 2 |
| C1 | MR03 (γ = −1) | DP81 | 0.5 | 1 | 1 |
| C2 | MR03 (γ = 0) | DP81 | 0.5 | 1 | 1 |
| C3 | MR03 (γ = −1) | No | 0.5 | 1 | 1 |
| C4 | MR03 (γ = 0) | No | 0.5 | 1 | 1 |
| C5 | MR03 (γ = −1) | No | 1 | 0.5 | 1 |
| C6 | MR03 (γ = 0) | No | 1 | 0.5 | 1 |
| Model . | Sup . | Sub . | α . | |$\dot{M}$| . | v8 . |
|---|---|---|---|---|---|
| A1 | DP81 | DP81 | 1 | 1 | 1 |
| A2 | DP81 | No | 1 | 1 | 1 |
| A3 | DP81 | No | 0.5 | 1 | 1 |
| A4 | DP81 | No | 1 | 3 | 1 |
| A5 | DP81 | No | 1 | 1 | 2 |
| B1 | WR85 | DP81 | 1 | 1 | 1 |
| B2 | WR85 | DP81 | 0.5 | 1 | 1 |
| B3 | WR85 | DP81 | 1 | 3 | 1 |
| B4 | WR85 | DP81 | 1 | 1 | 2 |
| B5 | WR85 | No | 0.5 | 1 | 1 |
| B6 | WR85 | No | 1 | 1 | 1 |
| B7 | WR85 | No | 0.5 | 1 | 2 |
| C1 | MR03 (γ = −1) | DP81 | 0.5 | 1 | 1 |
| C2 | MR03 (γ = 0) | DP81 | 0.5 | 1 | 1 |
| C3 | MR03 (γ = −1) | No | 0.5 | 1 | 1 |
| C4 | MR03 (γ = 0) | No | 0.5 | 1 | 1 |
| C5 | MR03 (γ = −1) | No | 1 | 0.5 | 1 |
| C6 | MR03 (γ = 0) | No | 1 | 0.5 | 1 |
Model parameters for binary population synthesis. The columns ‘Sup’ and ‘Sub’ denote the adopted NS spin-down models for the supersonic propeller and subsonic propeller phases, respectively. |$\dot{M}=1$| or 3 denotes the wind mass-loss rates assumed to be 1 or 3 times the standard prescription we adopted in Section 2, respectively. v8 is the wind velocity in units of 108 cm/s.
| Model . | Sup . | Sub . | α . | |$\dot{M}$| . | v8 . |
|---|---|---|---|---|---|
| A1 | DP81 | DP81 | 1 | 1 | 1 |
| A2 | DP81 | No | 1 | 1 | 1 |
| A3 | DP81 | No | 0.5 | 1 | 1 |
| A4 | DP81 | No | 1 | 3 | 1 |
| A5 | DP81 | No | 1 | 1 | 2 |
| B1 | WR85 | DP81 | 1 | 1 | 1 |
| B2 | WR85 | DP81 | 0.5 | 1 | 1 |
| B3 | WR85 | DP81 | 1 | 3 | 1 |
| B4 | WR85 | DP81 | 1 | 1 | 2 |
| B5 | WR85 | No | 0.5 | 1 | 1 |
| B6 | WR85 | No | 1 | 1 | 1 |
| B7 | WR85 | No | 0.5 | 1 | 2 |
| C1 | MR03 (γ = −1) | DP81 | 0.5 | 1 | 1 |
| C2 | MR03 (γ = 0) | DP81 | 0.5 | 1 | 1 |
| C3 | MR03 (γ = −1) | No | 0.5 | 1 | 1 |
| C4 | MR03 (γ = 0) | No | 0.5 | 1 | 1 |
| C5 | MR03 (γ = −1) | No | 1 | 0.5 | 1 |
| C6 | MR03 (γ = 0) | No | 1 | 0.5 | 1 |
| Model . | Sup . | Sub . | α . | |$\dot{M}$| . | v8 . |
|---|---|---|---|---|---|
| A1 | DP81 | DP81 | 1 | 1 | 1 |
| A2 | DP81 | No | 1 | 1 | 1 |
| A3 | DP81 | No | 0.5 | 1 | 1 |
| A4 | DP81 | No | 1 | 3 | 1 |
| A5 | DP81 | No | 1 | 1 | 2 |
| B1 | WR85 | DP81 | 1 | 1 | 1 |
| B2 | WR85 | DP81 | 0.5 | 1 | 1 |
| B3 | WR85 | DP81 | 1 | 3 | 1 |
| B4 | WR85 | DP81 | 1 | 1 | 2 |
| B5 | WR85 | No | 0.5 | 1 | 1 |
| B6 | WR85 | No | 1 | 1 | 1 |
| B7 | WR85 | No | 0.5 | 1 | 2 |
| C1 | MR03 (γ = −1) | DP81 | 0.5 | 1 | 1 |
| C2 | MR03 (γ = 0) | DP81 | 0.5 | 1 | 1 |
| C3 | MR03 (γ = −1) | No | 0.5 | 1 | 1 |
| C4 | MR03 (γ = 0) | No | 0.5 | 1 | 1 |
| C5 | MR03 (γ = −1) | No | 1 | 0.5 | 1 |
| C6 | MR03 (γ = 0) | No | 1 | 0.5 | 1 |
Table 2 summarizes the calculated numbers of compact wind-accreting NS HMXBs (Porb < 10 d) in our Galaxy for different models (listed in Table 1). The observed compact NS HMXBs (Porb < 10 d) are listed in Table 3 (Liu, van Paradijs & van den Heuvel 2006; Reig et al. 2009; Wang 2010; Manousakis, Walter & Blondin 2012; Wang & Chang 2012, 2013; Pearlman, Corbet & Pottschmidt 2013). We find that the spin-down rate in the supersonic propeller phase given by Davies & Pringle (1981) is too low to produce the observed population of compact HMXBs, no matter whether the subsonic propeller exists or not. Our calculation shows a similar conclusion for the spin-down model described by Mori & Ruderman (2003) when γ = −1. We also find that the model suggested by Wang & Robertson (1985), Dai et al. (2006) and Jiang & Li (2005) with a larger spin-down rate than that given by Davies & Pringle (1981) can predict a reasonable number of observed wind-fed compact NS HMXBs, no matter whether the subsonic propeller phase exists or not. We also derive a similar conclusion for the spin-down model described by Mori & Ruderman (2003) when γ = 0.
Predicted present numbers in our Galaxy of compact wind-accreting NS HMXBs (Porb < 10 d).
| Model . | Number . |
|---|---|
| A1 | 9.1 × 10−3 |
| A2 | 9.2 × 10−3 |
| A3 | 1.3 × 10−2 |
| A4 | 5.3 × 10−1 |
| A5 | 0 |
| B1 | 6.4 |
| B2 | 9.9 |
| B3 | 1.9 |
| B4 | 6.5 |
| B5 | 10.3 |
| B6 | 6.7 |
| B7 | 13.6 |
| C1 | 0 |
| C2 | 4.8 |
| C3 | 0 |
| C4 | 4.9 |
| C5 | 0 |
| C6 | 4.9 |
| Model . | Number . |
|---|---|
| A1 | 9.1 × 10−3 |
| A2 | 9.2 × 10−3 |
| A3 | 1.3 × 10−2 |
| A4 | 5.3 × 10−1 |
| A5 | 0 |
| B1 | 6.4 |
| B2 | 9.9 |
| B3 | 1.9 |
| B4 | 6.5 |
| B5 | 10.3 |
| B6 | 6.7 |
| B7 | 13.6 |
| C1 | 0 |
| C2 | 4.8 |
| C3 | 0 |
| C4 | 4.9 |
| C5 | 0 |
| C6 | 4.9 |
Predicted present numbers in our Galaxy of compact wind-accreting NS HMXBs (Porb < 10 d).
| Model . | Number . |
|---|---|
| A1 | 9.1 × 10−3 |
| A2 | 9.2 × 10−3 |
| A3 | 1.3 × 10−2 |
| A4 | 5.3 × 10−1 |
| A5 | 0 |
| B1 | 6.4 |
| B2 | 9.9 |
| B3 | 1.9 |
| B4 | 6.5 |
| B5 | 10.3 |
| B6 | 6.7 |
| B7 | 13.6 |
| C1 | 0 |
| C2 | 4.8 |
| C3 | 0 |
| C4 | 4.9 |
| C5 | 0 |
| C6 | 4.9 |
| Model . | Number . |
|---|---|
| A1 | 9.1 × 10−3 |
| A2 | 9.2 × 10−3 |
| A3 | 1.3 × 10−2 |
| A4 | 5.3 × 10−1 |
| A5 | 0 |
| B1 | 6.4 |
| B2 | 9.9 |
| B3 | 1.9 |
| B4 | 6.5 |
| B5 | 10.3 |
| B6 | 6.7 |
| B7 | 13.6 |
| C1 | 0 |
| C2 | 4.8 |
| C3 | 0 |
| C4 | 4.9 |
| C5 | 0 |
| C6 | 4.9 |
| Name . | Porb (d) . | Ppulse (s) . | Name . | Porb (d) . | Ppulse (s) . |
|---|---|---|---|---|---|
| 1WGA J0648.0−4419 | 1.55 | 13.1789 | 4U 0900−40 | 8.96 | 283 |
| RX J0648.1−4419 | Vela X−1 | ||||
| 4U 1119−603 | 2.09 | 4.84 | 4U 1538−52 | 3.73 | 529 |
| Cen X−3 | |||||
| IGR J16320−4751 | 8.96 | 1309 | 4U 1700−37a | 3.41 | |
| AX J1631.9−4752 | |||||
| EXO 1722−363 | 9.74 | 413.9 | SAX J1802.7−2017 | 4.6 | 139.61 |
| IGR J17252−3616 | IGR J 18027−2016 | ||||
| XTE J 1855−026 | 6.067 | 361 | 4U 1907+09 | 8.38 | 438 |
| H 1907+097 | |||||
| 4U 1909+07 | 4.4 | 604.68 | 4U 2206+543b | 9.57c | 5560 |
| X1908+075 | 3A 2206+543 | ||||
| IGR J16493−4348 | 6.78 | 1093 | IGR J16418−4532 | 3.74 | 1240 |
| IGR J17544−2619 | 4.9 | 71 | IGR J01583+6713 | 3–12d | 469 |
| Name . | Porb (d) . | Ppulse (s) . | Name . | Porb (d) . | Ppulse (s) . |
|---|---|---|---|---|---|
| 1WGA J0648.0−4419 | 1.55 | 13.1789 | 4U 0900−40 | 8.96 | 283 |
| RX J0648.1−4419 | Vela X−1 | ||||
| 4U 1119−603 | 2.09 | 4.84 | 4U 1538−52 | 3.73 | 529 |
| Cen X−3 | |||||
| IGR J16320−4751 | 8.96 | 1309 | 4U 1700−37a | 3.41 | |
| AX J1631.9−4752 | |||||
| EXO 1722−363 | 9.74 | 413.9 | SAX J1802.7−2017 | 4.6 | 139.61 |
| IGR J17252−3616 | IGR J 18027−2016 | ||||
| XTE J 1855−026 | 6.067 | 361 | 4U 1907+09 | 8.38 | 438 |
| H 1907+097 | |||||
| 4U 1909+07 | 4.4 | 604.68 | 4U 2206+543b | 9.57c | 5560 |
| X1908+075 | 3A 2206+543 | ||||
| IGR J16493−4348 | 6.78 | 1093 | IGR J16418−4532 | 3.74 | 1240 |
| IGR J17544−2619 | 4.9 | 71 | IGR J01583+6713 | 3–12d | 469 |
| Name . | Porb (d) . | Ppulse (s) . | Name . | Porb (d) . | Ppulse (s) . |
|---|---|---|---|---|---|
| 1WGA J0648.0−4419 | 1.55 | 13.1789 | 4U 0900−40 | 8.96 | 283 |
| RX J0648.1−4419 | Vela X−1 | ||||
| 4U 1119−603 | 2.09 | 4.84 | 4U 1538−52 | 3.73 | 529 |
| Cen X−3 | |||||
| IGR J16320−4751 | 8.96 | 1309 | 4U 1700−37a | 3.41 | |
| AX J1631.9−4752 | |||||
| EXO 1722−363 | 9.74 | 413.9 | SAX J1802.7−2017 | 4.6 | 139.61 |
| IGR J17252−3616 | IGR J 18027−2016 | ||||
| XTE J 1855−026 | 6.067 | 361 | 4U 1907+09 | 8.38 | 438 |
| H 1907+097 | |||||
| 4U 1909+07 | 4.4 | 604.68 | 4U 2206+543b | 9.57c | 5560 |
| X1908+075 | 3A 2206+543 | ||||
| IGR J16493−4348 | 6.78 | 1093 | IGR J16418−4532 | 3.74 | 1240 |
| IGR J17544−2619 | 4.9 | 71 | IGR J01583+6713 | 3–12d | 469 |
| Name . | Porb (d) . | Ppulse (s) . | Name . | Porb (d) . | Ppulse (s) . |
|---|---|---|---|---|---|
| 1WGA J0648.0−4419 | 1.55 | 13.1789 | 4U 0900−40 | 8.96 | 283 |
| RX J0648.1−4419 | Vela X−1 | ||||
| 4U 1119−603 | 2.09 | 4.84 | 4U 1538−52 | 3.73 | 529 |
| Cen X−3 | |||||
| IGR J16320−4751 | 8.96 | 1309 | 4U 1700−37a | 3.41 | |
| AX J1631.9−4752 | |||||
| EXO 1722−363 | 9.74 | 413.9 | SAX J1802.7−2017 | 4.6 | 139.61 |
| IGR J17252−3616 | IGR J 18027−2016 | ||||
| XTE J 1855−026 | 6.067 | 361 | 4U 1907+09 | 8.38 | 438 |
| H 1907+097 | |||||
| 4U 1909+07 | 4.4 | 604.68 | 4U 2206+543b | 9.57c | 5560 |
| X1908+075 | 3A 2206+543 | ||||
| IGR J16493−4348 | 6.78 | 1093 | IGR J16418−4532 | 3.74 | 1240 |
| IGR J17544−2619 | 4.9 | 71 | IGR J01583+6713 | 3–12d | 469 |
To compare the calculated results with observations of compact wind-fed NS HMXBs, we show the distributions of those NS binaries with P ≳ Peq and of the observed HMXBs in a Ps versus Porb diagram (see Figs 3 and 4). The relative numbers of binary systems are indicated by the darkness of the shading. Diamonds and pluses mark the supergiant wind-fed HMXBs and supergiant fast X-ray transients, respectively, and crosses are for RLOF systems. The two joined triangles represent 4U 2206+54 for the two suggested orbital periods (Reig et al. 2009). The two joined asterisks represent IGR J01583+6713 for a possible orbital period in the range 3–12 d suggested by Wang (2010). Fig. 3 presents the calculated results for those models when the subsonic propeller phase exists. According to our calculations, we note that the spin periods are too large to compare with the observations no matter which values the parameters take when the subsonic propeller phase exists. That is, no spin-down model can produce the observed distribution of compact wind-fed NS HMXBs in a Ps versus Porb diagram when the subsonic propeller phase exists.
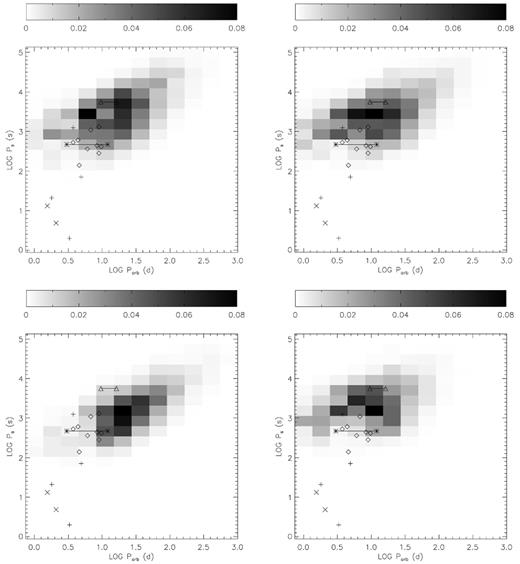
The Ps versus Porb distribution of wind-fed HMXBs. Diamonds and pluses mark the supergiant wind-fed HMXBs and supergiant fast X-ray transients, respectively, and crosses are for RLOF systems. The two joined triangles represent 4U 2206+54 for the two suggested orbital periods (Reig et al. 2009). The two joined asterisks represent IGR J01583+6713 for a possible orbital period in the range 3–12 d suggested by Wang (2010). Top, model B1 (left) and model B2 (right); bottom, model B3 (left) and model C2 (right).
Fig. 4 shows the calculated results for all the spin-down models with different values of the parameters α, v8 and |$\dot{M}$| when the subsonic propeller phase does not exist. If v8 is increased from 1 to 2, the mass-flow rates on to the NSs are lower by a factor of ∼16 in accordance with equations (15) and (16), further inducing longer equilibrium periods, which can be seen clearly in Fig. 4. The results also indicate that changes in the parameters α and |$\dot{M}$| do not significantly influence the final outcomes, which is consistent with the observed distribution of compact wind-fed NS HMXBs in our Galaxy in a Ps versus Porb diagram. So, we can conclude that the subsonic propeller phase may not exist at all from our calculated results plotted in Figs 3 and 4.
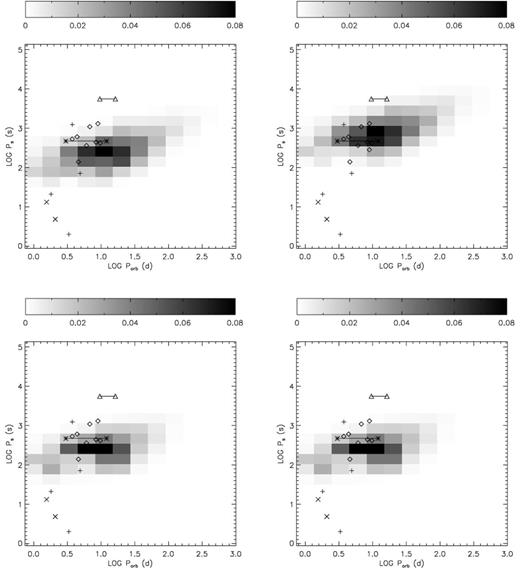
Same as Fig. 3 but top, model B5 (left) and model B7 (right); bottom, model C4 (left) and model C6 (right).
CONCLUSIONS AND DISCUSSION
We have calculated the evolution of the spin and the statistical properties for compact wind-fed X-ray pulsars in NS binary systems. The numerical results presented in Table 2 show that the spin-down rate in the supersonic propeller phase given by Davies & Pringle (1981) is too low to produce the observed number of compact HMXBs, no matter whether the subsonic propeller phase exists or not. The same conclusion can be derived for the spin-down rate in the supersonic propeller phase given by Illarionov & Sunyaev (1975) (the case of γ = −1 in Mori & Ruderman 2003). We also find that the spin-down model proposed by Wang & Robertson (1985), Dai et al. (2006) and Jiang & Li (2005) can predict a reasonable number that is consistent with the observations, no matter whether the subsonic propeller phase exists or not. The same conclusion can be inferred for the spin-down rate in the supersonic propeller phase described by Davidson & Ostriker (1973) (the case of γ = 0 in Mori & Ruderman 2003). To investigate whether the subsonic propeller phase exists or not, we compare our calculated results with the observed particular distributions of compact supergiant HMXBs in the Ps versus Porb diagram, which was described in Dai et al. (2006). From Figs 3 and 4, we can conclude that the subsonic propeller phase may not exist at all. The very long period, Ps = 5560 s, of 4U 2206+543, may be explained by an accreting magnetar model that allows it to be spun down efficiently by the propeller effect (Ikhsanov & Beskrovnaya 2010; Reig 2012; Wang & Chang 2013). However, the spin-down rate given by Davies & Pringle (1981), Dai et al. (2006) and Jiang & Li (2005), and that given by Davidson & Ostriker (1973), for the supersonic propeller phase both seem reasonable to produce the observed distributions of compact supergiant HMXBs in the Ps versus Porb diagram. We cannot conclude which spin-down rate seems more reasonable from our calculated results.
Our results are subject to some uncertainties. The different values of parameters α and |$\dot{M}$| do not have a significant influence on the final outcomes (e.g. the total number changes only by a factor of 2 or 3 even when the parameter α varies from 0.1 to 2; moreover, the different values of parameter α have little effect on the distributions in the Ps versus Porb diagram). The changes in the parameter v8 do not significantly influence the calculated number of compact NS HMXBs while it can induce a longer equilibrium period with a larger wind velocity. This further indicates that the subsonic propeller phase may not exist. Aerts & Lamers (2003) suggested that the wind velocity of supergiants increases with radius according to a β law in some special condition; however, our calculations indicate that this does not significantly affect our final results. We have also investigated the effect of the magnetic field. With a larger initial magnetic field, the models can produce a greater number of compact HMXBs (about 10 times more compact HMXBs are produced when the initial NS magnetic field becomes 10 times larger) with longer spin and orbital periods. The results also further support our conclusion that the subsonic propeller phase may not exist. However, some authors have also proposed that the magnetic field of a NS may decay during the evolution of the binary (Geppert & Rheinhardt 2001; Hollerbach & Rüdiger 2002; Zhang & Xie 2012). If we assume that the entire NS magnetic field decays, our calculations indicate that there will be fewer compact HMXBs with shorter spin and orbital periods, which has no significant effect on our conclusion. A number of authors have also suggested that some NSs receive low kick speeds of ≤50 km s−1 at birth (Pfahl et al. 2002; Podsiadlowski et al. 2004; Dewi, Podsiadlowski & Pols 2005). If all the NSs were born with such small kicks, our calculations indicate that the number of compact HMXBs produced should have been about 4–5 times higher. However, this has no significant effect on the distribution in the Ps versus Porb diagram.
We are grateful to an anonymous referee for a careful reading of the manuscript and constructive comments that significantly improved this paper. This work was supported by the National Natural Science Foundation of China under grants 11003006, 11003005, 11133001 and 11333004, and the Natural Science Foundation of Jiangsu province, China, under grant BK2010338.
REFERENCES



