The Sun as a planet-host star: proxies from SDO images for HARPS radial-velocity variations

Haywood, R. D.; Collier Cameron, A.; Unruh, Y. C.; Lovis, C.; Lanza, A.F.; Llama, J.; Deleuil, M.; Fares, R.; Gillon, M.; Moutou, C.; Pepe, F.; Pollacco, D.; Queloz, D.; Ségransan, D.

doi:10.1093/mnras/stw187

Abstract

The Sun is the only star whose surface can be directly resolved at high resolution, and therefore constitutes an excellent test case to explore the physical origin of stellar radial-velocity (RV) variability. We present HARPS observations of sunlight scattered off the bright asteroid 4/Vesta, from which we deduced the Sun's activity-driven RV variations. In parallel, the Helioseismic and Magnetic Imager instrument on board the Solar Dynamics Observatory provided us with simultaneous high spatial resolution magnetograms, Dopplergrams and continuum images of the Sun in the Fe i 6173 Å line. We determine the RV modulation arising from the suppression of granular blueshift in magnetized regions and the flux imbalance induced by dark spots and bright faculae. The rms velocity amplitudes of these contributions are 2.40 and 0.41 m s⁻¹, respectively, which confirms that the inhibition of convection is the dominant source of activity-induced RV variations at play, in accordance with previous studies. We find the Doppler imbalances of spot and plage regions to be only weakly anticorrelated. Light curves can thus only give incomplete predictions of convective blueshift suppression. We must instead seek proxies that track the plage coverage on the visible stellar hemisphere directly. The chromospheric flux index |$R^{\prime }_{HK}$| derived from the HARPS spectra performs poorly in this respect, possibly because of the differences in limb brightening/darkening in the chromosphere and photosphere. We also find that the activity-driven RV variations of the Sun are strongly correlated with its full-disc magnetic flux density, which may become a useful proxy for activity-related RV noise.

techniques: radial velocities, Sun: activity, Sun: faculae, plages, Sun: granulation, sunspots, planets and satellites: detection

INTRODUCTION

The surface of a star is constantly bustling with magnetic activity. Starspots and faculae/plage¹ inhibit convective motions taking place at the stellar surface, thus suppressing part of the blueshift naturally resulting from granulation. In addition, dark starspots (and bright faculae, to a lesser extent) coming in and out of view as the star rotates induce an imbalance between the redshifted and blueshifted halves of the star, which translates into a radial-velocity (RV) variation. Stellar activity, through the perturbation of photospheric convection, induces RV variations on much longer time-scales of the order of years, in tune with their magnetic cycles (e.g. see Santos et al. 2010; Dumusque et al. 2011; Díaz et al. 2016).

Short-term activity-induced RV variations are quasi-periodic: they are modulated by the star's rotation and change as active regions (starspots and faculae) emerge, evolve and disappear. The amplitude of these variations is 1–2 m s⁻¹ in ‘quiet’ stars (Isaacson & Fischer 2010), but they are often larger than this and can mimic or conceal the Doppler signatures of orbiting planets. This has resulted in several false detections (see Queloz et al. 2001; Bonfils et al. 2007; Huélamo et al. 2008; Boisse et al. 2009, 2011; Gregory 2011; Haywood et al. 2014; Robertson et al. 2014; Santos et al. 2014 and many others).

Understanding the RV signatures of stellar activity, especially those at the stellar rotation time-scale, is essential to develop the next generation of more sophisticated activity models and further improve our ability to detect and characterize (super-)Earths and even small Neptunes in orbits of a few days to weeks. In particular, identifying informative and reliable proxies for the activity-driven RV variations is crucial. Desort et al. (2007) found that the traditional spectroscopic indicators [the bisector span (BIS) and full width at half-maximum (FWHM) of the cross-correlation profile] and photometric variations do not give enough information for slowly rotating, Sun-like stars (low v sin i) to disentangle stellar activity signatures from the orbits of super-Earth-mass planets.

The Sun is a unique test case as it is the only star whose surface can be resolved at high resolution, therefore allowing us to investigate directly the impact of magnetic features on RV observations. Early attempts to measure the RV of the integrated solar disc did not provide quantitative results about the individual activity features responsible for RV variability. Jiménez et al. (1986) measured integrated sunlight using a resonant scattering spectrometer and found that the presence of magnetically active regions on the solar disc led to variations of up to 15 m s⁻¹. They also measured the disc-integrated magnetic flux but did not find any significant correlation with RV at the time due to insufficient precision. At about the same time, Deming et al. (1987) obtained spectra of integrated sunlight with an uncertainty level below 5 m s⁻¹, enabling them to see the RV signature of supergranulation. The trend they observed over the 2-yr period of their observations was consistent with suppression of convective blueshift from active regions on the solar surface. A few years later, Deming & Plymate (1994) confirmed the findings of both Jiménez et al. (1986) and Deming et al. (1987), only with a greater statistical significance. Not all studies were in agreement with each other; however, McMillan et al. (1993) recorded spectra of sunlight scattered off the Moon over a 5-yr period and found that any variations due to solar activity were smaller than 4 m s⁻¹.

More recently, Molaro & Centurión (2010) obtained HARPS spectra of the large and bright asteroid Ceres to construct a wavelength atlas for the Sun. They found that these spectra of scattered sunlight provided precise disc-integrated solar RVs, and proposed using asteroid spectra to calibrate high-precision spectrographs used for planet hunting, such as HIRES and HARPS (see a recent paper by Lanza et al. 2016).

In parallel, significant discoveries were made towards a precise quantitative understanding of the RV impact of solar surface features. Lagrange, Desort & Meunier (2010) and Meunier, Desort & Lagrange (2010a) used a catalogue of sunspot numbers and sizes and Michelson Doppler Imager/Solar and Heliospheric Observatory (MDI/SOHO) magnetograms to simulate integrated-Sun spectra over a full solar cycle and deduce the impact of sunspots and faculae/plage on RV variations. The work of Meunier et al. (2010a) also relied on the amplitude of convection inhibition derived by Brandt & Solanki (1990), based on spatially resolved magnetogram observations of plage and quiet regions on the Sun (i.e. independently of full-disc RV measurements).

Sunspot umbrae and penumbrae are cooler and therefore darker than the surrounding quiet photosphere, producing a flux deficit at the local rotational velocity. Faculae, which tend to be spatially associated with spot groups, are slightly brighter than the quiet photosphere, producing a spectral flux excess at the local rotational velocity. Spots have large contrasts and small area coverage, while faculae have lower contrasts but cover large areas. We thus expect their rotational Doppler signals to be of opposite signs (due to the opposite sign of their flux) and of roughly similar amplitudes. However, facular emission also occurs independently of spot activity in the more extended solar magnetic network (Chapman et al. 2001), so their contributions do not cancel out completely. Meunier et al. (2010a) found that the residual signal resulting from the rotational Doppler imbalance of both sunspots and faculae is comparable to that of the sunspots on their own. Lagrange et al. (2010) estimated the rotational perturbation due to sunspot flux deficit to be of the order of 1 m s⁻¹. In a complementary study, Meunier et al. (2010a) also investigated the effect of sunspots and faculae on the suppression of convective blueshift by magnetic regions. Sunspots occupy a much smaller area than faculae, and as they are dark, they contribute little flux, so their impact on the convective blueshift is negligible. Facular suppression of granular blueshift, however, can lead to variations in RV of up to 8–10 m s⁻¹ (Meunier et al. 2010a). Meunier, Lagrange & Desort (2010b) estimated the disc-integrated solar RV variations expected from the suppression of convective blueshift, directly from MDI/SOHO Dopplergrams and magnetograms (in the 6768 Å Ni i line). Their reconstructed RV variations, over one magnetic cycle, agree with the simulations of Meunier et al. (2010a), establishing the suppression of convective blueshift by magnetic features as the dominant source of activity-induced RV variations. Meunier et al. (2010b) also found that the regions where the convective blueshift is most strongly attenuated correspond to the most magnetically active regions, as was expected.

Following the launch of the Solar Dynamics Observatory (SDO; Pesnell, Thompson & Chamberlin 2012) in 2010, continuous observations of the solar surface brightness, velocity and magnetic fields have become available with image resolution finer than the photospheric granulation pattern. This allows us to probe the RV variations of the Sun in unprecedented detail. In the present paper, we deduce the activity-driven RV variations of the Sun based on HARPS observations of the bright asteroid Vesta (Section 2). In parallel, we use high spatial resolution continuum, Dopplergram and magnetogram images of the Fe i 6173 Å line from the Helioseismic and Magnetic Imager (HMI/SDO; Schou et al. 2012) to model the RV contributions from sunspots (and pores), faculae and granulation via inhibition of granular blueshift and flux blocking (Section 3). This allows us to create a model which we test against the HARPS observations (Section 4). Finally, we discuss the implications of our study for the effectiveness of various proxy indicators for activity-driven RV variations in stars. We show that the disc-averaged magnetic flux could become an excellent proxy for activity-driven RV variations on other stars (Section 5).

HARPS OBSERVATIONS OF SUNLIGHT SCATTERED OFF VESTA

HARPS spectra

The HARPS spectrograph, mounted on the European Southern Observatory 3.6 m telescope at La Silla, was used to observe sunlight scattered from the bright asteroid 4/Vesta (its average magnitude during the run was 7.6). Two to three measurements per night were made with simultaneous Thorium exposures for a total of 98 observations, spread over 37 nights between 2011 September 29 and December 7. The geometric configuration of the Sun and Vesta relative to the observer is illustrated in Fig. 1. At the time of the observations, the Sun was just over three years into its 11-yr magnetic cycle; the SDO data confirm that the Sun showed high levels of activity.

Figure 1.

Schematic representation of the Sun, Vesta and Earth configuration during the period of observations (not to scale).

Open in new tab Download slide

The spectra were reprocessed using the HARPS Data Reduction Software (DRS) pipeline (Baranne et al. 1996; Lovis & Pepe 2007). Instead of applying a conventional barycentric correction, the wavelength scale of the calibrated spectra was adjusted to correct for the Doppler shifts due to the relative motion of the Sun and Vesta, and the relative motion of Vesta and the observer (see Section 2.3).

The FWHM and BIS (as defined in Queloz et al. 2001) and |$\log R^{\prime }_{HK}$| index were also derived by the pipeline. The median, minimum and maximum signal-to-noise ratio of the reprocessed HARPS spectra at central wavelength 556.50 nm are 161.3, 56.3 and 257.0, respectively. Overall, HARPS achieved a precision of 75 ± 25 cm s⁻¹ (see Table A1). The reprocessed HARPS cross-correlation functions and derived RV measurements are available in the Supplementary Files that are available online.

We account for the RV modulation induced by Vesta's rotation in Section 2.4.1, and investigate sources of intra-night RV variations in Section 2.4.2. We selected the SDO images in such a way as to compensate for the different viewing points of Vesta and the SDO spacecraft: Vesta was trailing SDO, as shown in Fig. 1. This is taken into account in Section 2.5.

Solar rest frame

The data reduction pipeline for HARPS assumes that the target observed is a distant point-like star, and returns its RV relative to the Solar system barycentre. In order to place the observed RVs of Vesta in the solar rest frame, we perform the following operation:

\begin{equation} \text{RV} = \text{RV}_{\rm bary, Earth} + v_{\rm sv} + v_{\rm ve}, \end{equation}

(1)

where RV_bary,Earth is the barycentric RV of the Earth, i.e. the component of the observer's velocity relative to the Solar system barycentre, towards the apparent position of Vesta. It can be found in the fits header for each observation. The two components v_sv and v_ve, retrieved from the JPL Horizons data base,² correspond to

(1) v_sv: the velocity of Vesta relative to the Sun at the instant that light received at Vesta was emitted by the Sun;
(2) v_ve: the velocity of Vesta relative to Earth at the instant that light received by HARPS was emitted at Vesta.

This correction accounts for the RV contribution of all bodies in the Solar system and places the Sun in its rest frame. The values of RV_bary,Earth, v_sv and v_ve are given in the Supplementary Files that are available online.

Relativistic Doppler effects

The only relativistic corrections made by JPL Horizons are for gravitational bending of the light and relativistic aberration due to the motion of the observer (Giorgini, private communication). We therefore must correct for the relativistic Doppler shifts incurred. The wavelength correction factor to be applied is given by Lindegren & Dravins (2003) as

\begin{equation} \frac{\lambda _{\rm e}}{\lambda _{\rm o}} = \frac{\sqrt{1 - \frac{v^{2}}{c^{2}}} }{1+ \frac{v \cos \theta _{\rm o}}{\rm c}}, \end{equation}

(2)

where λ_e is the wavelength of the light at emission, λ_o is the wavelength that is seen when it reaches the observer, and θ_o is the angle between the direction of the emitter at emission and the observed direction of the light at reception. v is the total magnitude of the velocity vector of the observer relative to the emitter and c is the speed of light.

We apply this correction twice:

(1) The light is emitted by the Sun and received at Vesta. In this case, v is the magnitude of the velocity of Vesta with respect to the Sun (decreasing from approximately 19.9 to 19.4 km s⁻¹ over the duration of the HARPS run), and the radial component v cos θ_o is equal to v_sv (defined in Section 2.2, starting at about 1.66 km s⁻¹ and reaching 1.72 km s⁻¹ at opposition near the middle of the run).
(2) Scattered sunlight is emitted from Vesta and received at La Silla. v is the magnitude of the velocity of Vesta with respect to an observer at La Silla (increasing from 20 to 36 km s⁻¹ over the run), and v cos θ_o is v_ve (starting at 19.8 km s⁻¹ and reaching 23.3 km s⁻¹ at opposition).

The two wavelength correction factors are then multiplied together in order to compute the total relativistic correction factor to be applied to the pixel wavelengths in the HARPS spectra, from which we derive the correct RVs, shown in Fig. 2(a) (see also column 2 of Table A1). All velocities are measured at the flux-weighted mid-exposure times of observation (MJD_mid_UTC).

Figure 2.

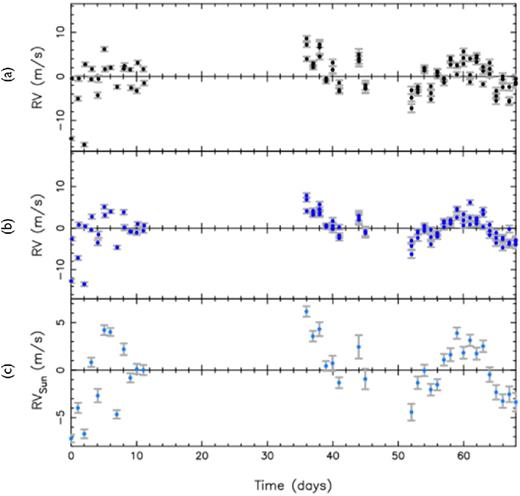
(a) HARPS RV variations in the solar rest frame, corrected for relativistic Doppler effects (but not yet corrected for Vesta's axial rotation). (b) HARPS RV variations of the Sun as a star (after removing the RV contribution of Vesta's axial rotation). (c) Nightly binned HARPS RV variations of the Sun as a star – note the change in scale on the y-axis. The values for each time series are provided in the Supplementary Files that are available online.

Open in new tab Download slide

The reader may also refer to appendix A of Lanza et al. (2016) for further details on these Doppler corrections. All quantities used to calculate these effects are listed in the Supplementary Files that are available online.

Sources of intra-night RV variations

Vesta's axial rotation

Vesta rotates every 5.34 h (Stephenson 1951), so any significant inhomogeneities in its shape or surface albedo will induce an RV modulation. Vesta's shape is close to a spheroid (Thomas et al. 1997), and Lanza & Molaro (2015) found that the RV modulation expected from shape inhomogeneities should not exceed 0.060 m s⁻¹.

Stephenson (1951) presented a photometric study of the asteroid, and suggested that its surface brightness is uneven. He reported brightness variations δm = 0.12 mag. To make a rough estimate of the amplitude of the RV modulation, we can assume that the brightness variations are due to a single dark equatorial spot on the surface of Vesta, blocking a fraction δf of the flux f. δm and δf are related as follows:

\begin{equation} \delta m = \frac{2.5\, d(\ln f)}{\log (e)} \sim 1.08\, \frac{\delta f}{f}, \end{equation}

(3)

The fractional flux deficit caused by a dark spot can thus be approximated as

\begin{equation} \frac{\delta f}{f} \sim \delta m / 1.08 \sim 0.11. \end{equation}

(4)

When the dayside of Vesta is viewed fully illuminated, this spot will give an RV modulation equal to

\begin{equation} \Delta \text{RV}_{\rm vesta} = - \frac{\delta f}{f} \, v_{\rm eq} \, \cos \theta \, \sin \theta , \end{equation}

(5)

where θ is the angle between the spot on the asteroid and our line of sight, and increases from − π/2 to + π/2 as it traverses the visible daylight hemisphere. Due to foreshortening, the RV contribution is decreased by a factor cos θ. The line-of-sight velocity varies with sin θ. The asteroid's equatorial velocity v_eq is given by

\begin{equation} v_{\rm eq} = 2\pi \, \frac{R_{\rm vesta}}{P_{\rm rot}}. \end{equation}

(6)

Using a mean radius R_vesta = 262.7 km (Russell et al. 2012) and the rotational period P_rot = 5.34 h, we obtain v_eq = 85.8 m s⁻¹. The maximum RV amplitude of Vesta's rotational modulation, expected at θ = π/4, is thus approximately 4.7 m s⁻¹. The RV modulation due to surface brightness inhomogeneity should therefore dominate strongly over shape effects.

We find that this RV contribution is well modelled as a sum of Fourier components modulated by Vesta's rotation period:

\begin{equation} \Delta \text{RV}_{\rm vesta}(t) = C \cos (2\pi - \lambda (t)) + S \sin (2\pi - \lambda (t)), \end{equation}

(7)

where λ(t) is the apparent planetographic longitude of Vesta at the flux-weighted mid-times of the HARPS observations and can be retrieved via the JPL Horizons data base (the values of λ are listed in Table A1). C and S are scaling parameters, which we determine via a global optimal scaling procedure, performed with the solar activity contributions (see Section 4.1). Since the phase-folded light curve of Vesta shows a double-humped structure (Stephenson 1951), we also tested adding further Fourier terms modulated by the first harmonic of the asteroid's rotation. The improvement to the fit was negligible, so we preferred the simpler model of equation (7).

Fig. 2(b) shows the RV observations obtained after subtracting Vesta's rotational signature, with coefficients C and S of equation (7) derived from the global fit of Section 4.1. The night-to-night scatter has been reduced, even though much of it remains in the first block of observations; this is discussed in the following section.

Additional intra-night scatter in first half of HARPS run

The RV variations in the first part of the HARPS run (nights 0 to 11 in Fig. 2) contain some significant scatter, even after accounting for Vesta's rotation. This intra-night scatter does not show in the solar FWHM, BIS or |$\log (R^{\prime }_{HK})$| variations. We investigated the cause of this phenomenon and excluded changes in colour of the asteroid or instrumental effects as a potential source of additional noise. Vesta was very bright (7.6 mag), so we deem the phase and proximity of the Moon unlikely to be responsible for the additional scatter observed.

Solar p-mode oscillations dominate the Sun's power spectrum at a time-scale of about 5 min. Most of the RV oscillations induced by p-mode acoustic waves are therefore averaged out within the 15-min HARPS exposures. Granulation motions result in RV signals of several m s⁻¹, over time-scales ranging from about 15 min to several hours. Taking multiple exposures each night and averaging them together (as plotted in panel (c) of Fig. 2) can help to significantly reduce granulation-induced RV variations.

The velocity measurements are sensitive to any displacement of the image of Vesta from the centre of the 1-arcsec fibre. Vesta had a finite angular diameter of 0.49 arcsec at the start of the run, and 0.32 arcsec at the end. Light reflected from Vesta is blueshifted by 172 m s⁻¹ at the approaching limb and redshifted by 172 m s⁻¹ at the receding limb. We simulated the effects of seeing on an ensemble of photons originating from different points on Vesta's disc, applying random angular deviations with a Gaussian seeing distribution. For a given displacement of Vesta from the centre of the fibre, we computed the mean rotational velocity displacement of those photons falling within the fibre. We found an approximately linear dependence of the mean rotational velocity on mean offset from the centre of the fibre. Our numerical simulations suggest that a mean displacement by 0.1 arcsec of the image from the centre of the fibre in the direction orthogonal to Vesta's rotation axis, averaged over the exposure, gives a velocity error that is closely approximated by the empirical expression

\begin{equation} \Delta v = 4.0\, (\frac{\theta }{0.49\,\text{arcsec}}) \,/\, \sqrt{\frac{\sigma _{\rm seeing}}{1.0\,\text{arcsec}}} \,{\rm m\,s}^{-1}, \end{equation}

(8)

where σ_seeing represents the FWHM of the Gaussian seeing distribution. This is of the same order as the excess RV scatter observed during the first part of the run, when successive observations within a night were widely separated at different airmasses. We conclude that small airmass-dependent guiding errors provide a plausible explanation. During the latter part of the run, the observations were contiguous and were thus conducted at similar airmass, leading to more consistent guiding and smaller scatter. Other factors such as asymmetric image quality, coma of the telescope varying with elevation (and sky rotation on an equatorial telescope), atmospheric dispersion, etc. may also contribute to this effect.

The remaining variations, of the order of 7–10 m s⁻¹, are modulated by the Sun's rotation and are caused by the presence of magnetic surface markers, such as sunspots and faculae. These variations are the primary focus of this paper, and we model them using SDO/HMI data in Section 3.

Time lag between Vesta and SDO observations

At the time of the observations, the asteroid Vesta was trailing the SDO spacecraft, which orbits the Earth (see Fig. 1). In order to model the solar hemisphere facing Vesta at time t, we used SDO images recorded at t + Δt, where Δt is proportional to the difference in the Carrington longitudes of the Earth/SDO and Vesta at the time of the HARPS observation. These longitudes were retrieved from the JPL Horizons data base. The shortest delay, at the start of the observations, was ∼2.8 d, while at the end of the observations it reached just over 6.5 d (see Table A1). We cannot account for the evolution of the Sun's surface features during this time, and must assume that they remain frozen in this interval. The emergence of sunspots can take place over a few days, but in general large magnetic features (sunspots and networks of faculae) evolve over time-scales of weeks rather than days. Visual inspection of animated sequences of SDO images obtained during the campaign revealed no major flux emergence events on the visible solar hemisphere.

PIXEL STATISTICS FROM SDO/HMI images

In the second part of this analysis, we aim to determine the RV contribution from granulation, sunspots and facular regions. We use high-resolution full-disc continuum intensity, line-of-sight Doppler images and line-of-sight magnetograms from the HMI instrument on board SDO.³ These were retrieved for the period spanning the HARPS observations of Vesta at times determined by the time lags detailed in Section 2.5 (the exact date and time stamps of the images are listed in the Supplementary Files that are available online). SDO/HMI images the solar disc in the Fe i 6173 Å line at a cadence of 45 s, with a spatial resolution of 1 arcsec using a CCD of 4096 × 4096 square pixels. We first converted the SDO/HMI images from pixel coordinates to heliographic coordinates, i.e. to a coordinate system centred on the Sun. This coordinate system is fixed with respect to the Sun's surface and rotates in the sidereal frame once every 25.38 d, which corresponds to a Carrington rotation period (Carrington 1859). A surface element on the Sun, whose image falls on pixel ij of the instrument detector, is at position (w_ij, n_ij, r_ij) relative to the centre of the Sun, where w is westwards, n is northwards and r is in the radial direction (see Thompson 2006 for more details on the coordinate system used). The spacecraft is at position (0, 0, r_sc). The w, n, r components of the spacecraft's position relative to each element ij can thus be written as

\begin{eqnarray} \delta w_{ij} &=& w_{ij} - 0 \nonumber\\ \delta n_{ij} &=& n_{ij} - 0 \nonumber\\ \delta r_{ij} &=& r_{ij} - r_{\rm sc}. \end{eqnarray}

(9)

The spacecraft's motion and the rotation of the Sun introduce velocity perturbations, which we determine in Sections 3.1 and 3.2, respectively. These two contributions are then subtracted from each Doppler image, thus revealing the Sun's magnetic activity velocity signatures. We compute the RV variations due to the suppression of convective blueshift and the flux blocked by sunspots on the rotating Sun in Sections 3.7.3 and 3.7.2. We show that the Sun's activity-driven RV variations are well reproduced by a scaled sum of these two contributions in Section 4. Finally, we compute the disc-averaged magnetic flux and compare it as an RV proxy against the traditional spectroscopic activity indicators in Section 5.

Spacecraft motion

The w, n, r components of the velocity incurred by the motion of the spacecraft relative to the Sun, v_sc, are given in the fits header of each SDO/HMI observation to a precision of 10⁻⁶ m s⁻¹. The magnitude of the spacecraft's velocity away from pixel ij can therefore be expressed as

\begin{equation} v_{{\rm sc}, ij} = - \frac{\delta w_{ij} \, v_{{\rm sc},w_{ij}} + \delta n_{ij} \, v_{{\rm sc},n_{ij}} + \delta r_{ij} \, v_{{\rm sc}, r_{ij}}}{d_{ij}}, \end{equation}

(10)

where

\begin{equation} d_{ij} = \sqrt{\delta w_{ij}^2 + \delta n_{ij}^2 + \delta r_{ij}^2} \end{equation}

(11)

is the distance between pixel ij and the spacecraft. We note that all relative velocities in this paper follow the natural sign convention that velocity is rate of change of distance.

Solar rotation

The solar rotation as a function of latitude was measured by Snodgrass & Ulrich (1990) in low-resolution full-disc Dopplergrams and magnetograms obtained at the Mount Wilson 150-foot tower telescope between 1967 and 1987. By cross-correlating time series of Dopplergrams and magnetograms, they were able to determine the rate of motion of surface features (primarily supergranulation cells and sunspots) and deduce the rate of rotation of the Sun's surface as a function of latitude. The solar differential rotation profile ω(ϕ) at each latitude ϕ is commonly described by a least-squares polynomial of the form

\begin{equation} \omega (\phi ) = \alpha _1 + \alpha _2 \sin ^2\phi + \alpha _3 \sin ^4\phi . \end{equation}

(12)

The best-fitting parameters found by Snodgrass & Ulrich (1990), used in this analysis, are given in Table 1. We apply this rotation profile in the heliographic frame to determine the w, n, r components induced by the solar rotation velocity along the line of sight to a given image pixel, v_rot,w, v_rot,n and v_rot,r. Normalizing again by d, we can write

\begin{equation} v_{{\rm rot}} = - \frac{\delta w \, v_{{\rm rot},w} + \delta n \, v_{{\rm rot},n} + \delta r \, v_{{\rm rot}, r}}{d}. \end{equation}

(13)

Table 1.

Open in new tab

Solar differential rotation profile parameters from Snodgrass & Ulrich (1990).

Parameter	Value (deg d⁻¹)
α₁	14.713
α₂	− 2.396
α₃	− 1.787

Table 1.

Open in new tab

Solar differential rotation profile parameters from Snodgrass & Ulrich (1990).

Parameter	Value (deg d⁻¹)
α₁	14.713
α₂	− 2.396
α₃	− 1.787

Flattened continuum intensity

We flatten the continuum intensity images using a fifth-order polynomial function L_ij with the limb-darkening constants given in Astrophysical Quantities (Allen 1973), through the idl subroutine darklimb_correct.pro.⁴ The flattened and non-flattened continuum intensities are related via the limb-darkening function L as follows:

\begin{equation} I_{{\rm flat}, ij} = \frac{I_{ij}}{L_{ij}}. \end{equation}

(14)

We also define a scaling factor |$\hat{K}$| which will be applied to L_ij later on:

\begin{equation} \hat{K} = \frac{\sum _{ij} I_{ij} \, L_{ij} \, W_{ij}}{\sum _{ij} L^{2}_{ij} \, W_{ij}}, \end{equation}

(15)

where the weighting factor W_ij is set to unity for quiet-Sun pixels, and zero elsewhere.

Unsigned magnetic field strength

The SDO/HMI instrument measures the line-of-sight magnetic field strength B_obs. The magnetic field of the Sun stands radially out of the photosphere with a strength B_r. Due to foreshortening, the observed field B_obs is less than the true (radial) field by a factor

\begin{equation} \mu _{ij} = \cos \theta _{ij}, \end{equation}

(16)

where θ_ij is the angle between the outward normal to the feature on the solar surface and the direction of the line of sight of the SDO spacecraft.

We can thus recover the full magnetic field strength by dividing by μ_ij:

\begin{equation} B_{{\rm r}, ij} = B_{{\rm obs}, ij} / \mu _{ij}. \end{equation}

(17)

The noise level in HMI magnetograms is a function of μ (Yeo, Solanki & Krivova 2013). It is lowest for pixels in the centre of the CCD, where it is close to 5 G, and increases towards the edges and reaches 8 G at the solar limb. For our analysis, we assume that the noise level is constant throughout the image with a conservative value |$\sigma _{B_{{\rm obs}, ij}}$| = 8 G, in agreement with the results of Yeo et al. (2013). We therefore set B_obs,ij and B_r,ij to 0 for all pixels with a line-of-sight magnetic field measurement (B_obs,ij) below this value.

Identifying quiet-Sun regions, faculae and sunspots

As is routinely done in solar work, we do not consider pixels that are very close to the limb (μ_ij < 0.1), as the limb-darkening model becomes unreliable on the very edge of the Sun. This affects about 1 per cent of the pixels of the solar disc.

The first three panels of Fig. 3 show an SDO/HMI flattened intensitygram, line-of-sight Dopplergram and unsigned radial magnetogram for a set of images taken on 2011 November 10, after removing the contributions from spacecraft motion and solar rotation. We identify quiet-Sun regions, faculae and sunspots by applying magnetic and intensity thresholds.

Magnetic threshold: the distribution of pixel unsigned observed magnetic field strength as a function of pixel flattened intensity is shown in Fig. 4. In the top histogram and main panel, we see that the distribution of magnetic field strength falls off sharply with increasing field strength. The vast majority of pixels are clustered close to the noise level: these pixels are part of the quiet-Sun surface. Note that the fragmented distribution of pixels with magnetic field strength less than a few gauss arises from the numerical precision in the SDO/HMI images. This is not an issue in our analysis, however, as these pixels are well below the magnetic noise threshold and we set their field value to zero. We separate active regions from quiet-Sun regions by applying a threshold in unsigned radial magnetic field strength for each pixel. Yeo et al. (2013) investigated the intensity contrast between the active and quiet photosphere using SDO/HMI data, and found an appropriate cutoff at
\begin{equation} |B_{{\rm r}, ij}| > 3\, \sigma _{B_{{\rm obs}, ij}} / \mu _{ij}, \end{equation}
(18)
where |$\sigma _{B_{{\rm obs}, ij}}$| represents the magnetic noise level in each pixel (see the last paragraph of Section 3.4). As in Yeo et al. (2013), we exclude isolated pixels that are above this threshold as they are likely to be false positives. We can thus write
\begin{equation} |B_{{\rm r, thresh}, ij}| = 24\, {\rm G} \,/\mu _{ij}. \end{equation}
(19)
The combined effects of imperfect limb-darkening correction and the μ-correction for the radial magnetic field strength at the very edge of the solar disc (μ_ij < 0.3) result in a rim of dark pixels being identified as sunspot pixels. In order to avoid this, we set all such pixels as quiet-Sun elements. In any case, sunspots become invisible near the edge of the solar disc because of the Wilson depression (Loughhead & Bray 1958), so our cut should not affect the identification of real sunspot pixels.
Intensity threshold: the distribution of line-of-sight velocity as a function of pixel flattened intensity is shown in Figs 4 and 5. The main panel allows us to further categorize active-region pixels into faculae and sunspots (umbra and penumbra). We apply the intensity threshold between faculae and spots of Yeo et al. (2013):
\begin{equation} I_{\rm thresh}\,=\,0.89\,\hat{I}_{\rm quiet}, \end{equation}
(20)
where |$\hat{I}_{\rm quiet}$| is the mean pixel flattened intensity over quiet-Sun regions. It can be calculated by summing the flattened intensity of each pixel:
\begin{equation} \hat{I}_{{\rm quiet}} = \frac{\sum _{ij} I_{{\rm flat}, ij} \, W_{ij}}{\sum _{ij} W_{ij}}, \end{equation}
(21)
where the weighting factor W_ij is set to 1 if |B_r,ij| < |B_r,thresh,ij|, 0 otherwise.

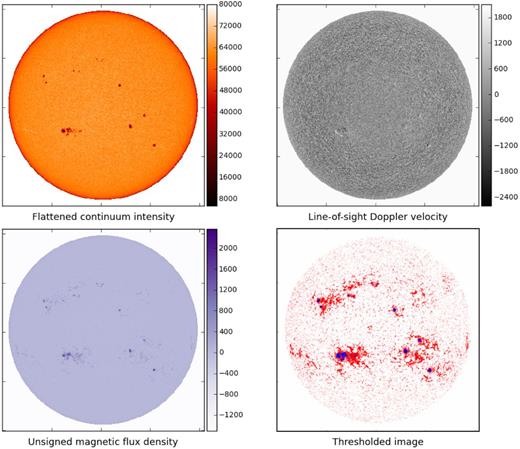
First three panels: SDO/HMI flattened intensity Iflat, line-of sight velocity v (km s−1) for the non-rotating Sun and unsigned radial magnetic flux |Br| (G) of the Sun, observed on 2011 November 10 at 00:01:30 UTC. Last panel: our thresholded image, highlighting faculae (red/lighter shade pixels) and sunspots (blue/darker shade pixels). For this set of observations (representative of the whole run), faculae account for 9 per cent of the total pixel count, while sunspots account for less than 0.4 per cent. The remaining ∼90 per cent of the pixels on the solar disc are magnetically quiet.

Figure 3.

First three panels: SDO/HMI flattened intensity I_flat, line-of sight velocity v (km s⁻¹) for the non-rotating Sun and unsigned radial magnetic flux |B_r| (G) of the Sun, observed on 2011 November 10 at 00:01:30 UTC. Last panel: our thresholded image, highlighting faculae (red/lighter shade pixels) and sunspots (blue/darker shade pixels). For this set of observations (representative of the whole run), faculae account for 9 per cent of the total pixel count, while sunspots account for less than 0.4 per cent. The remaining ∼90 per cent of the pixels on the solar disc are magnetically quiet.

Open in new tab Download slide

Figure 4.

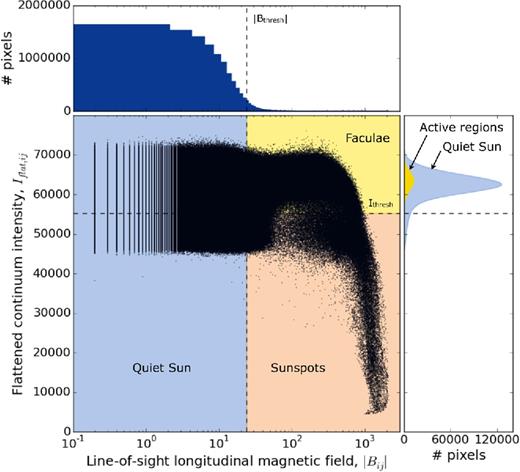
Observed pixel line-of-sight (unsigned) magnetic field strength, |B_obs,ij| (G), as a function of flattened intensity I_flat,ij, for the Sun on 2011 November 10 at 00:01:30 UTC. The top and right histograms show the distributions of |B_obs,ij| and I_flat,ij, respectively. The dashed lines represent the cutoff criteria selected to define the quiet photosphere, faculae and sunspots.

Open in new tab Download slide

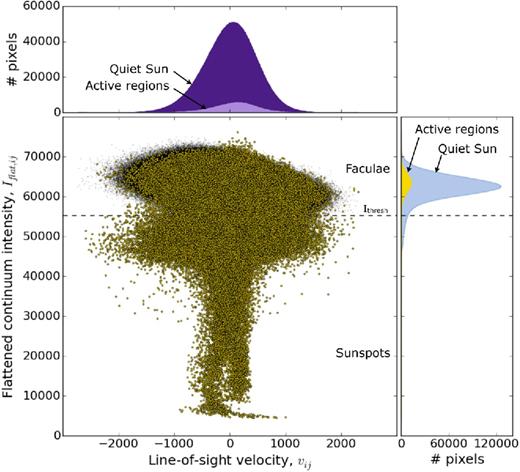
Pixel line-of-sight velocity, vij (in m s−1), as a function of flattened intensity Iflat,ij, for the Sun on 2011 November 10 at 00:01:30 UTC. The top and right histograms show the distributions of vij and Iflat,ij, respectively, in bins of 1000. In the case of active pixels (yellow dots), the line-of-sight velocity is invariant with pixel brightness. For quiet-Sun pixels (black dots), however, brighter pixels are blueshifted while fainter pixels are redshifted: this effect arises from granular motions.

Figure 5.

Pixel line-of-sight velocity, v_ij (in m s⁻¹), as a function of flattened intensity I_flat,ij, for the Sun on 2011 November 10 at 00:01:30 UTC. The top and right histograms show the distributions of v_ij and I_flat,ij, respectively, in bins of 1000. In the case of active pixels (yellow dots), the line-of-sight velocity is invariant with pixel brightness. For quiet-Sun pixels (black dots), however, brighter pixels are blueshifted while fainter pixels are redshifted: this effect arises from granular motions.

Open in new tab Download slide

In the main panel of Fig. 5, quiet-Sun pixels are plotted in black, while active-region pixels are overplotted in yellow. The last panel of Fig. 3, which shows the thresholded image according to these I_flat,ij and |B_r,ij| criteria, confirms that these thresholding criteria are effective at identifying sunspot and faculae pixels correctly.

Surface velocity flows in sunspot penumbrae and umbrae

The range of velocities in the penumbral pixels (which form the horizontal oval of yellow points just below I_thresh in Fig. 5) is large owing to the Evershed effect (Evershed 1909). The darker umbral pixels have a narrower velocity distribution, allowing the umbral flows that feed the Evershed effect to be resolved into a blueshifted and redshifted velocity component. The much broader range of velocities seen in Fig. 5 for penumbral versus umbral pixels confirms that these velocity flows accelerate with distance from the middle of the spot (Evershed 1909). This effect is highlighted in Fig. 6, which shows a zoom-in on the largest sunspot group in the images of Fig. 3. The Evershed flows are tangential to the surface. They will be most visible for sunspots located away from disc centre, where a larger proportion of them will be directed along our line of sight.

Figure 6.

Zoom-in on the largest sunspot group on the approaching hemisphere of the Sun observed on 2011 November 10 at 00:01:30 UTC. Red pixels represent faculae, while the sunspot pixels are colour-coded according to the direction of their velocity flows, thereby revealing the presence of Evershed flows: dark blue pixels are directed towards the observer (v < 0), while light cyan pixels are directed away from the observer (v > 0).

Open in new tab Download slide

The sunspot group illustrated in Fig. 6 is located near the approaching side of the Sun. The flows in its left half are directed away from the observer, while in its right half they are directed towards the observer.

Decomposing the Sun's RV into individual feature contributions

The total disc-integrated RV of the Sun is the sum of all contributions from the quiet-Sun, sunspot and faculae/plage regions. The ‘quiet’ parts of the Sun's surface are in constant motion due to granulation, while sunspots and faculae induce RV variations via two processes (cf. introduction).

Photometric effect: as the Sun rotates, the presence of dark spots or bright faculae on the solar surface breaks the Doppler balance between the approaching (blueshifted) and receding (redshifted) hemispheres. We calculated the contribution of dark spots and bright faculae separately and our findings confirm those of Meunier et al. (2010a), who found that this residual signal is approximately equal to the photometric contribution from sunspots. We note, however, that this is merely a coincidence arising from the specific geometrical configuration and ratio of sunspots to faculae/plage on the Sun. In other words, this assumption may not be valid for other stars with different spot to faculae configurations and/or filling ratios. We therefore decide to include the effect of faculae in this study (even though it is effectively negligible in the case of the Sun). Because the two contributions are correlated (see Fig. 7), we must account for them in a single term |$\Delta \hat{v}_{\rm phot}$|⁠, which we describe in Section 3.7.2.
Convective effect: sunspots and faculae are strongly magnetized features that inhibit convective motions. Sunspots, which cover a small area of the solar surface and contribute little flux, have a very small contribution. In the case of faculae, however, this contribution is large and is expected to be the dominant contribution to the total solar RV variations (Meunier et al. 2010a,b). We compute this contribution |$\Delta \hat{v}_{\rm conv}$| in Section 3.7.3.

Figure 7.

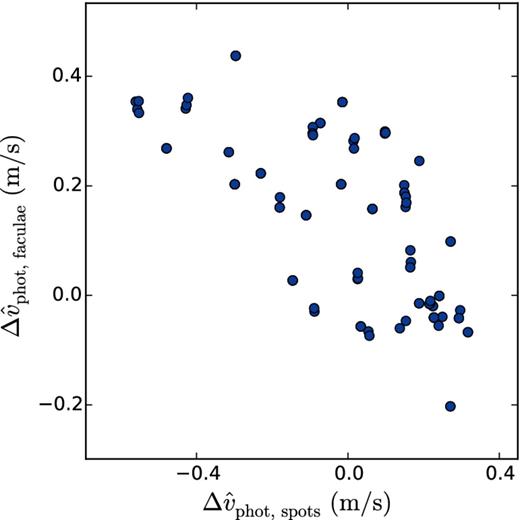
Correlation diagram showing the relationship between the rotational Doppler imbalances resulting from sunspots (horizontal axis) and faculae (vertical axis), if computed separately. The Spearman correlation coefficient is −0.69. The variations are only partially anticorrelated, reflecting both the tendency of faculae to be spatially associated with sunspot groups and the existence of faculae in bright networks not associated with sunspots. The values of these two basis functions are given in the Supplementary Files that are available online.

Open in new tab Download slide

We can thus write the total disc-integrated RV of the Sun as

\begin{equation} \hat{v} = \hat{v}_{\rm quiet} + \Delta \hat{v}_{\rm phot} + \Delta \hat{v}_{\rm conv}, \end{equation}

(22)

where |$\hat{v}_{\rm quiet}$| represents the velocity contribution of convective motions in quiet-Sun pixels, which we calculate in Section 3.7.1.

Velocity contribution of convective motions in quiet-Sun regions

We estimate the average RV of the quiet Sun by summing the intensity-weighted velocity of non-magnetized pixels, after removing the spacecraft motion and the Sun's rotation:

\begin{equation} \hat{v}_{{\rm quiet}} = \frac{\sum _{ij} (v_{ij} - \delta v_{{\rm sc}, ij} - \delta v_{{\rm rot}, ij}) \, I_{ij} \, W_{ij}}{\sum _{ij} I_{ij} \, W_{ij}}. \end{equation}

(23)

For this calculation, the weights are defined as in

\begin{eqnarray} W_{ij} &=& 1 \, \, {\rm if}\, \, |B_{{\rm r}, ij}| < |B_{{\rm r, thresh}, ij}|, \nonumber\\ W_{ij} &=& 0 \, \, {\rm if}\, \, |B_{{\rm r}, ij}| > |B_{{\rm r, thresh}, ij}|. \end{eqnarray}

(24)

This velocity field is thus averaged over the vertical motions of convection granules on the solar surface. Hot and bright granules rise up to the surface, while cooler and darker fluid sinks back towards the Sun's interior. This process is visible in the main panel of Fig. 5: quiet-Sun pixels (black dots) are clustered in a tilted ellipse. The area of the upflowing granules is larger than that enclosed in the intergranular lanes, and the granules are carrying hotter and thus brighter fluid. This results in a net blueshift, as seen in Fig. 5.

Rotational Doppler imbalance due to dark sunspots and bright faculae

This velocity perturbation can be obtained by summing the line-of-sight velocity of sunspot pixels corrected for the spacecraft's motion, and weighted by the flux deficit or excess produced by a dark spot or a bright plage, respectively:

\begin{equation} \Delta \hat{v}_{{\rm phot}} = \frac{\sum _{ij} (v_{ij} - \delta v_{{\rm sc}, ij}) \, (I_{ij} - \hat{K} \, L_{ij}) \, W_{ij}}{\sum _{ij} I_{ij}}. \end{equation}

(25)

The weights W_ij are set to 1 for pixels with |B_r,ij| > |B_r,thresh,ij| (otherwise they are set to 0).

As illustrated in Fig. 7, the photometric effects of sunspots and faculae are quite similar in amplitude and roughly anticorrelated, due to their opposite flux signs. However, because they are not strictly anticorrelated, they sum into a net signal that has an amplitude similar to the photometric effect of sunspots (Meunier et al. 2010a). The value of |$\Delta \hat{v}_{{\rm phot}}$| at each time of the HARPS observations is listed in Table A1. From the SDO images, we derive an rms amplitude of 0.17 m s⁻¹ for this signal, which is smaller than the observational uncertainties of the HARPS velocities. This value is slightly lower than that found by Meunier et al. (2010a) during the peak of the Sun's activity cycle, of 0.42 m s⁻¹, but remains broadly consistent with their results given the small amplitude of this signal.

Suppression of convective blueshift from active regions

The suppression of granular blueshift induced by magnetically active regions (|B_r,ij| > |B_r,thresh,ij|, predominantly faculae) is

\begin{equation} \Delta \hat{v}_{{\rm conv}} = \hat{v} - \hat{v}_{{\rm quiet}} - \hat{v}_{{\rm phot}}. \end{equation}

(26)

We measure the total disc-averaged velocity of the Sun |$\hat{v}$| by summing the velocity contribution of each pixel ij, weighted by their intensity I_ij, after subtracting the spacecraft motion and solar rotation:

\begin{equation} \hat{v} = \frac{\sum _{ij} (v_{ij} - \delta v_{{\rm sc}, ij} - \delta v_{{\rm rot}, ij}) \, I_{ij}}{\sum _{ij} I_{ij}}. \end{equation}

(27)

The value of |$\Delta \hat{v}_{{\rm conv}}$| at each time of the HARPS observations is listed in Table A1. The rms amplitude of this basis function (unscaled) is 1.30 m s⁻¹, which is consistent with the value of 1.39 m s⁻¹ computed by Meunier et al. (2010a) during the peak of the solar activity cycle.

REPRODUCING THE RV VARIATIONS OF THE SUN

Total RV model

We combine our model of Vesta's rotational RV signal (presented in Section 2.4.1) with the two magnetic activity basis functions determined in Sections 3.7.3 and 3.7.2, in order to reproduce the RV variations seen in the HARPS observations. The final model has the form

\begin{eqnarray} \Delta \text{RV}_{\rm model}(t) = A\,\Delta \hat{v}_{{\rm phot}}(t) + B\,\Delta \hat{v}_{{\rm conv}}(t) + \Delta \text{RV}_{\rm vesta}(t) + \text{RV}_0. \nonumber\\ \end{eqnarray}

(28)

We carry out an optimal scaling procedure in order to determine the scaling factors (A, B, C and S) of each of the contributions, as well as the constant offset RV₀ and a constant variance term s² added in quadrature to the observational errors. This variance term will account for any remaining uncorrelated noise arising from granulation motions. The SDO/HMI images were exposed for 45 s each, while the HARPS observations were exposed for 15 min and binned nightly. We expect these differences to result in a small night-to-night uncorrelated noise contribution. In addition, this variance term will absorb any residual signal of Vesta's axial rotation, which will naturally not be completely sinusoidal.

For each value of s, the basis functions are orthogonalized by subtracting their inverse-variance weighted means prior to performing the scaling. We determine the maximum likelihood via a procedure similar to the one described in Collier Cameron et al. (2006), whereby we maximize the likelihood |$\mathcal {L}$| of the solution

\begin{equation} \ln \mathcal {L} = - \frac{n}{2} \ln (2\pi ) -\frac{1}{2} \, \chi ^2 - \frac{1}{2} \, \sum _{i=1}^{i=n} \ln (\sigma ^2_i+s^2) \end{equation}

(29)

with respect to s, where χ² is the chi-squared value of the n HARPS data points, with uncertainties σ_i. This procedure is applied to the unbinned (not nightly averaged) HARPS data set, in order to determine the appropriate scaling coefficients (C and S) for Vesta's axial rotation (see equation 7). The total amplitude of the modulation induced by Vesta's rotation is equal to 2.39 m s⁻¹, which is of the same order as the amplitude we estimated in Section 2.4.1.

Agreement between HARPS observations and SDO-derived model

After all the scaling coefficients were determined, we grouped the observations in each night by computing the inverse-variance weighted average for each night. The final model is shown in Fig. 8.

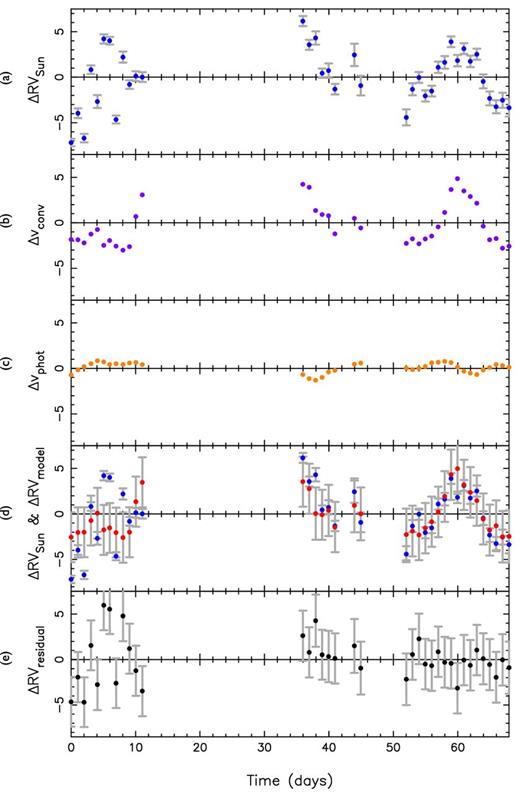
$(a) HARPS RV variations of the Sun as a star, ΔRVSun. (b) Scaled basis function for the suppression of convective blueshift, $\Delta \hat{v}_{\mathrm{conv}}$, derived from SDO/HMI images. (c) Scaled basis function for the rotational Doppler imbalance due to spots and faculae, $\Delta \hat{v}_{\mathrm{phot}}$. (d) Total RV model, ΔRVmodel (red/lighter shade, with errors including additional variance s), overlaid on top of the HARPS RV variations (blue/darker shade points). (e) Residuals obtained after subtracting the model from the observations. All RVs are in m s−1. Note that the scale of the y-axis is different from that used in Fig. 2. The values of these nightly binned time series are provided in the Supplementary Files available online.$

Figure 8.

(a) HARPS RV variations of the Sun as a star, ΔRV_Sun. (b) Scaled basis function for the suppression of convective blueshift, |$\Delta \hat{v}_{\mathrm{conv}}$|⁠, derived from SDO/HMI images. (c) Scaled basis function for the rotational Doppler imbalance due to spots and faculae, |$\Delta \hat{v}_{\mathrm{phot}}$|⁠. (d) Total RV model, ΔRV_model (red/lighter shade, with errors including additional variance s), overlaid on top of the HARPS RV variations (blue/darker shade points). (e) Residuals obtained after subtracting the model from the observations. All RVs are in m s⁻¹. Note that the scale of the y-axis is different from that used in Fig. 2. The values of these nightly binned time series are provided in the Supplementary Files available online.

Open in new tab Download slide

We list the best-fitting values of the scaling parameters for each of the basis functions in Table 2. We note that the values of A and B, which represent the difference in response of HARPS and SDO to the Doppler imbalance and the suppression of convective blueshift, differ from unity. The HMI/SDO images are based on measurements of a single spectral line, namely the Fe i 6173 Å line, which may not be representative of the several thousand lines from which the HARPS RVs are derived. The value of |$\Delta \hat{v}_{\mathrm{phot}}$| is determined by the contrast between the magnetic elements (spots, faculae) and the quiet-Sun photosphere. Most of the lines in the HARPS mask lie bluewards of Fe i 6173 Å where the contrast is greater for both types of feature. We therefore expect to have to scale the SDO-derived |$\Delta \hat{v}_{\mathrm{phot}}$| by a factor of order, but greater than, unity. We measure it to be 2.45 ± 2.02; the amplitude of |$\Delta \hat{v}_{\mathrm{phot}}$| is so small that A cannot be distinguished from unity when the additional variance s is taken into account. The strength of the convection inhibition changes with line depth (cf. Gray 2009 and Meunier et al. 2010b). We find that the HARPS response to suppression of granular blueshift is 1.85 ± 0.27 times greater than we predict from SDO.

Table 2.

Open in new tab

Best-fitting parameters and rms amplitudes resulting from the optimal scaling procedure.

Parameter	Value	Basis function	rms amplitude
			(unscaled)
A	2.45 ± 2.02	\|$\Delta \hat{v}_{{\rm phot}}$\|	0.17 m s⁻¹
B	1.85 ± 0.27	\|$\Delta \hat{v}_{{\rm conv}}$\|	1.30 m s⁻¹
C	2.19 ± 0.42	cos (2π − λ)	0.74 m s⁻¹
S	0.55 ± 0.47	sin (2π − λ)	0.66 m s⁻¹
RV₀	99.80 ± 0.28 m s⁻¹
s	2.70 m s⁻¹

Parameter	Value	Basis function	rms amplitude
			(unscaled)
A	2.45 ± 2.02	\|$\Delta \hat{v}_{{\rm phot}}$\|	0.17 m s⁻¹
B	1.85 ± 0.27	\|$\Delta \hat{v}_{{\rm conv}}$\|	1.30 m s⁻¹
C	2.19 ± 0.42	cos (2π − λ)	0.74 m s⁻¹
S	0.55 ± 0.47	sin (2π − λ)	0.66 m s⁻¹
RV₀	99.80 ± 0.28 m s⁻¹
s	2.70 m s⁻¹

Table 2.

Open in new tab

Best-fitting parameters and rms amplitudes resulting from the optimal scaling procedure.

Parameter	Value	Basis function	rms amplitude
			(unscaled)
A	2.45 ± 2.02	\|$\Delta \hat{v}_{{\rm phot}}$\|	0.17 m s⁻¹
B	1.85 ± 0.27	\|$\Delta \hat{v}_{{\rm conv}}$\|	1.30 m s⁻¹
C	2.19 ± 0.42	cos (2π − λ)	0.74 m s⁻¹
S	0.55 ± 0.47	sin (2π − λ)	0.66 m s⁻¹
RV₀	99.80 ± 0.28 m s⁻¹
s	2.70 m s⁻¹

Parameter	Value	Basis function	rms amplitude
			(unscaled)
A	2.45 ± 2.02	\|$\Delta \hat{v}_{{\rm phot}}$\|	0.17 m s⁻¹
B	1.85 ± 0.27	\|$\Delta \hat{v}_{{\rm conv}}$\|	1.30 m s⁻¹
C	2.19 ± 0.42	cos (2π − λ)	0.74 m s⁻¹
S	0.55 ± 0.47	sin (2π − λ)	0.66 m s⁻¹
RV₀	99.80 ± 0.28 m s⁻¹
s	2.70 m s⁻¹

We show a plot of the observed HARPS RVs (ΔRV_Sun) versus our SDO-modelled RVs (ΔRV_model) in Fig. 9, in a similar fashion to fig. 9 of Meunier et al. (2010b). We see good agreement between the data and the model. The Spearman correlation coefficient is 0.64 for the full data set and 0.87 when considering only the second part of the run. This is close to, although not as good as, the correlation coefficient of 0.94 found by Meunier et al. (2010b) between simulated velocities of Meunier et al. (2010a) and MDI/SOHO Dopplergrams.

Figure 9.

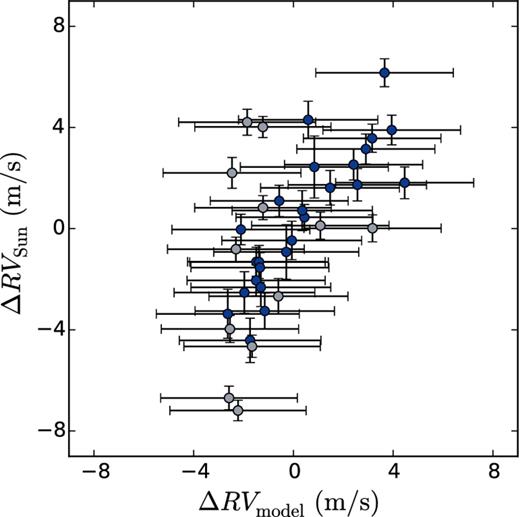
HARPS RV variations of the Sun as a star versus our model derived from SDO/HMI images. Observations from the first part of the run are highlighted in a lighter shade.

Open in new tab Download slide

Panel (e) of Fig. 8 shows the residuals remaining after subtracting the total model ΔRV_model from the HARPS observations of the Sun as a star ΔRV_Sun. We see that the residuals are within the level of the error bars, when considering an extra variance term s of 2.7 m s⁻¹. Maximum-likelihood analysis of the additional uncorrelated noise during the first part of the run (nights 0–11) yields an additional variance with rms amplitude 4.0 m s⁻¹, while the second part (nights 36–68) has an additional noise rms of 1.5 m s⁻¹. As discussed in Section 2.4.2, we attribute the excess scatter in the first block of nights to airmass-dependent guiding errors, which would have been more important in the first part of the run, where the observations within each night were taken at very different airmasses. The additional noise rms of 1.5 m s⁻¹ in the second part of the run is consistent with the rms due to solar granulation and supergranulation, ranging between 0.28 and 1.12 m s⁻¹, as recently found by Meunier et al. (2015).

Relative importance of suppression of convective blueshift and rotational velocity imbalance

We see that the activity-induced RV variations of the Sun are well reproduced by a scaled sum of the two basis functions, |$\hat{v}_{{\rm conv}}$| and |$\hat{v}_{{\rm phot}}$| (shown in panels (b) and (c) of Fig. 8, respectively). As previously predicted by Meunier et al. (2010a), we find that the suppression of convective blueshift plays a dominant role (rms of 2.40 m s⁻¹). This was also found to be the case for CoRoT-7, a main-sequence G9 star with a rotation period comparable to that of the Sun (Haywood et al. 2014). The relatively low amplitude of the modulation induced by sunspot flux blocking (rms of 0.17 m s⁻¹) is expected in slowly rotating stars with a low v sin i (Desort et al. 2007).

Zero-point of HARPS

The wavelength adjustments that were applied to the HARPS RVs were based on precise prior dynamical knowledge of the rate of change of distance between the Earth and Vesta, and between Vesta and the Sun. The offset RV₀ = 99.80 ± 0.28 m s⁻¹ thus represents the zero-point of the HARPS instrument, including the mean granulation blueshift for the Sun. A previous study of integrated sunlight reflected by the Moon, by Molaro et al. (2013), determined a value of 102.2 ± 0.86 m s⁻¹, which is significantly larger than our value. They did not account for the effect of sunspots and faculae, however, so their result could be affected by activity-induced solar variations at that time.

TOWARDS BETTER PROXIES FOR RV OBSERVATIONS

Spatial distributions of sunspots and faculae

Aigrain, Pont & Zucker (2012) have shown that it is possible to predict the rotational Doppler imbalance due to photospheric surface brightness inhomogeneities from a simultaneous high-precision optical light curve. If one further assumes that faculae/plage regions are co-spatial with spot groups, then they can also predict the form of the RV variation caused by suppression of granular blueshift. A recent analysis of the active host star CoRoT-7 by Haywood et al. (2014) modelled activity-induced RV variations via the FF′ method of Aigrain et al. (2012). The predicted Doppler imbalance was much smaller than the observed activity-driven RV variations. The associated suppression of convective blueshift was of larger amplitude than, and partially correlated with, the observed RVs. The residuals, however, had a similar amplitude and shared the covariance properties of the star's (simultaneous) light curve.

The present study provides a natural explanation of this mismatch: on the Sun, the faculae are not perfectly co-spatial with sunspot groups. Indeed, Fig. 7 shows us that the location of sunspot groups gives an incomplete prediction of the facular coverage. Since the suppression of granular blueshift is the dominant process at play in slowly rotating stars such as CoRoT-7 and the Sun, it is therefore important to develop proxies that are directly sensitive to the distribution of faculae on the stellar surface.

Correlations between RV and traditional activity indicators

Fig. 10 presents the correlations between ΔRV_Sun, |$\Delta \hat{v}_{{\rm conv}}$| and the following activity indicators: the full-disc magnetic flux |$|\hat{B}_{\rm obs}|$| and filling factor f computed from the SDO/HMI images, and the observed FWHM, BIS and |$\log (R^{\prime }_{HK})$| derived from the HARPS DRS reduction pipeline. We computed the Spearman correlation coefficient to get a measure of the degree of monotone correlation between each variable (the correlation between two variables is not necessarily linear, for example between RV and BIS). The coefficients are displayed in each panel of Fig. 10, both including and excluding the observations made in the first part of the run, which show a lot of intra-night scatter.

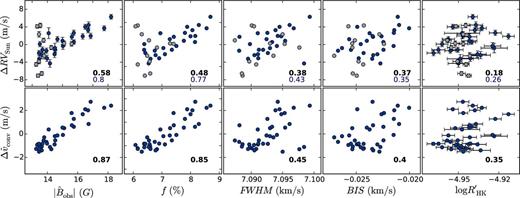
$Correlation plots of the nightly averaged HARPS RV variations of the Sun as a star ΔRVSun and suppression of convective blueshift $\Delta \hat{v}_{{\rm conv}}$ against (from left to right): the disc-averaged observed magnetic flux $|\hat{B}_{\rm obs}|$ (G), filling factor f (per cent), FWHM (km s−1), BIS (m s−1) and $\log (R^{\prime }_{HK})$. Observations from the first part of the run are highlighted in a lighter shade. Spearman correlation coefficients are displayed in the bottom-right corner of each panel: for the full observing run (in bold and black), and for the second part of the run only (in blue).$

Figure 10.

Correlation plots of the nightly averaged HARPS RV variations of the Sun as a star ΔRV_Sun and suppression of convective blueshift |$\Delta \hat{v}_{{\rm conv}}$| against (from left to right): the disc-averaged observed magnetic flux |$|\hat{B}_{\rm obs}|$| (G), filling factor f (per cent), FWHM (km s⁻¹), BIS (m s⁻¹) and |$\log (R^{\prime }_{HK})$|⁠. Observations from the first part of the run are highlighted in a lighter shade. Spearman correlation coefficients are displayed in the bottom-right corner of each panel: for the full observing run (in bold and black), and for the second part of the run only (in blue).

Open in new tab Download slide

We do not show similar correlation plots for |$\Delta \hat{v}_{{\rm phot}}$| because we do not find any significant correlations with any of the activity indicators; this is expected since |$\Delta \hat{v}_{{\rm phot}}$| is such that it crosses zero when the surface covered by spots and/or faculae is at a maximum, i.e. when they are in the middle of the stellar disc (⁠|$\Delta \hat{v}_{{\rm phot}}$| is of course still related to |$|\hat{B}_{\rm obs}|$|⁠, the FWHM, BIS and |$\log (R^{\prime }_{HK})$|⁠, but the Spearman coefficient is close to zero).

We note that the relatively weak correlation between the observed RVs and the BIS is not completely unexpected in the case of the Sun, which has a vsin i of about 2 km s⁻¹. The line profile distortions induced by solar activity, including those measured by the BIS, will therefore be smaller than the resolution of HARPS that is close to 2.5 km s⁻¹. In other words, the resolution of HARPS is not adequate to fully resolve the BIS variations in a star rotating as slowly as the Sun, which could reduce the correlation coefficients computed with the BIS.

We find a relatively weak correlation between the observed RVs and the chromospheric flux index |$\log (R^{\prime }_{HK})$|⁠, with a Spearman correlation coefficient of 0.26 for the second half of the run (0.18 for the full run).

Although naively one might expect |$\log (R^{\prime }_{HK})$| to be a good predictor of plage filling factor, and hence of the convective RV component, there are several physical factors that might reasonably be expected to degrade the correlation over short time-scales (our data set spans two to three solar rotations). Foreshortening and limb darkening affect the Ca ii H&K emission cores and the brightness-weighted line-of-sight granular velocities in different ways. Near the limb, the Ca ii emission in plages originates in higher, hotter regions of the chromosphere and remains bright. The limb darkening of facular pixels is less than that of quiet-Sun pixels, but near the limb the line-of-sight component of the radial motion of bright granule cores is reduced by foreshortening. The disc-averaged line-of-sight magnetic field strength is attenuated by both foreshortening and limb darkening in approximately the same way as the radial motion of the granular flow. This may explain why, even though the RVs and |$\log (R^{\prime }_{HK})$| values were measured simultaneously from the same spectra, the correlation between the variations in |$\log (R^{\prime }_{HK})$| and suppression of granular blueshift appears weak. In their study of long-term solar RV variations spanning over 8 years, Lanza et al. (2016) find a stronger correlation between |$\log (R^{\prime }_{HK})$| and RV variations, with a Spearman coefficient of 0.357. This positive correlation is in agreement with previous studies of quiet late-type stars (Lovis et al. 2011; Gomes da Silva et al. 2012), and shows that the |$\log (R^{\prime }_{HK})$| may be a more useful proxy for long-term RV variations induced by the stellar magnetic cycle.

We note that in Fig. 10, the variations in |$\log (R^{\prime }_{HK})$| look similar to the variations in RV, except that they are shifted by a few days (this is especially noticeable towards the end of the run). The reality and origin of this shift will be the subject of future studies, thanks to the wealth of Sun as a star RV observations that are currently being gathered by the solar telescope at HARPS-N.

Disc-averaged observed magnetic flux |$|\hat{B}_{\rm obs}|$|

We compute the full-disc line-of-sight magnetic flux of the Sun, by summing the intensity-weighted line-of-sight unsigned magnetic flux in each pixel:

\begin{equation} |\hat{B}_{\rm obs}| = \frac{\sum _{ij} |B_{{\rm obs}, ij}| \, I_{ij}}{\sum _{ij} I_{ij}}. \end{equation}

(30)

The values at the time of each HARPS observation are listed in Table A1. The variations in |$|\hat{B}_{\rm obs}|$| are shown in panel (b) of Fig. 11, together with the nightly averaged HARPS RV variations of the Sun as a star, in panel (a). We see that the variations in the disc-averaged magnetic flux are in phase with the RV variations, despite the scatter in RV in the first part of the run (discussed in Section 2.4.2). If we only consider the observations in the second part of the run, the Spearman correlation coefficient between ΔRV_Sun and |$|\hat{B}_{\rm obs}|$| is 0.80 (see Fig. 10). The correlation is stronger between |$\hat{v}_{{\rm conv}}$| and |$|\hat{B}_{\rm obs}|$|⁠, with a correlation coefficient of 0.87. This is expected since magnetized areas are known to suppress convective blueshift (see Meunier et al. 2010a,b).

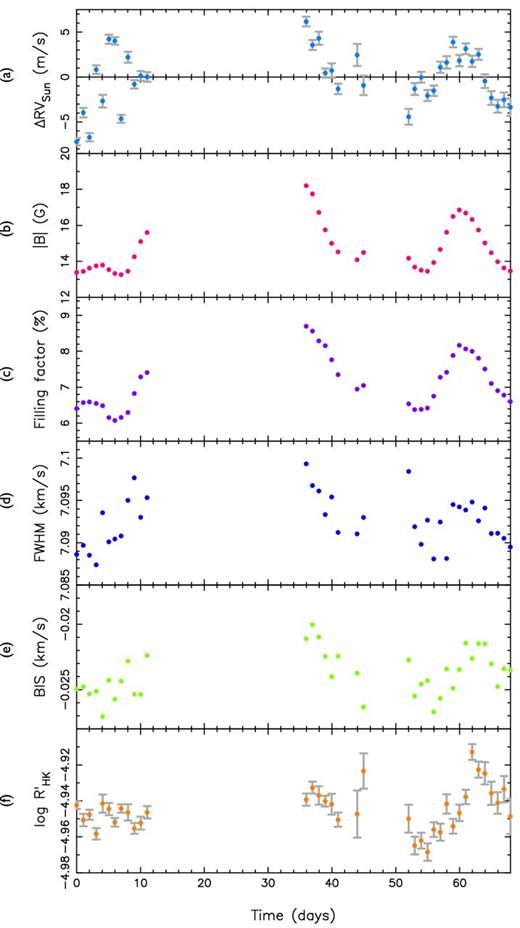
$(a) HARPS RV variations of the Sun as a star. (b and c) Time series of the disc-averaged line-of-sight magnetic flux $|\hat{B}_{\rm obs}|$ and filling factor f, respectively, determined from the SDO/HMI magnetograms. (d–f) Time series of the FWHM, BIS and $\log (R^{\prime }_{HK})$, respectively, determined from the HARPS DRS reduction pipeline. The values of these nightly binned time series are provided in the Supplementary Files available online.$

Figure 11.

(a) HARPS RV variations of the Sun as a star. (b and c) Time series of the disc-averaged line-of-sight magnetic flux |$|\hat{B}_{\rm obs}|$| and filling factor f, respectively, determined from the SDO/HMI magnetograms. (d–f) Time series of the FWHM, BIS and |$\log (R^{\prime }_{HK})$|⁠, respectively, determined from the HARPS DRS reduction pipeline. The values of these nightly binned time series are provided in the Supplementary Files available online.

Open in new tab Download slide

We note that these observations were taken close to the solar cycle maximum, during which the solar photosphere was mostly dominated by a few large sunspot groups (surrounded by facular networks). Meunier et al. (2010b) found that the convective shift attenuation is greater in larger structures, since they contain a stronger magnetic field. The relationship between convective shift attenuation and magnetic field, however, is not linear. We thus expect larger RV variations for a few large active regions than when the Sun is in a phase of lower magnetic activity, when the photosphere might be dominated by several smaller structures, even though they would still give the same total flux. In fact, Lanza et al. (2016) find a much weaker correlation between the mean total magnetic flux measured by the Synoptic Optical Long-term Investigations of the Sun (SOLIS) Vector Spectromagnetograph (VSM) instrument and RV (Spearman correlation coefficient of 0.131) over their 8-yr data set, which spans both active and less active phases of the solar cycle.

When compared against correlations with the traditional spectroscopic activity indicators (the FWHM, BIS and |$\log (R^{\prime }_{HK})$|⁠), we see that the disc-averaged magnetic flux |$|\hat{B}_{\rm obs}|$| is a much more effective predictor of activity-induced RV variations, over the time-scale of a few rotation periods. The averaged magnetic flux may therefore be a useful proxy for activity-driven RV variations as it should map on to areas of strong magnetic fields, which suppress the Sun's convective blueshift. The line-of-sight magnetic flux density and filling factor on the visible hemisphere of a star can be measured from the Zeeman broadening of magnetically sensitive lines (Robinson 1980; Reiners et al. 2013). Their product gives the disc-averaged flux density that we are deriving from the solar images. We note that such measurements are still very difficult to make for other stars than the Sun, because the Zeeman splitting of magnetically sensitive lines is so small that the technique can only be applied to bright, slowly rotating stars. Fortunately, such stars are also the best targets for planet searches.

Magnetic filling factor f

In addition to the disc-averaged observed magnetic flux, we also computed the filling factor of magnetic regions on the solar disc. It is weighted by the foreshortening at the location of each pixel, and counted as a fraction of the total pixel count:

\begin{equation} f = \frac{1}{N_{\rm pix}} \, \sum _{ij} W_{ij}, \end{equation}

(31)

where N_pix is the total number of pixels in the solar disc and the weight W_ij is set to 1 in magnetically active regions, and 0 in the quiet Sun. The variations of the filling factor are shown in panel (c) of Fig. 11. As expected, they follow the disc-averaged magnetic flux closely. The correlation with the predicted ΔRV_conv and the observed ΔRV_Sun is none the less weaker than that found for the brightness-weighted line-of-sight magnetic field |$|\hat{B}_{\rm obs}|$|⁠, since no correction is made for limb darkening.

CONCLUSION

In the present analysis, we decomposed activity-induced RV variations into identifiable contributions from sunspots, faculae and granulation, based on Sun as a star RV variations deduced from HARPS spectra of the bright asteroid Vesta and high spatial resolution images in the Fe i 6173 Å line taken with the HMI instrument aboard the SDO. We find that the RV variations induced by solar activity are mainly caused by the suppression of convective blueshift from magnetically active regions, while the flux deficit incurred by the presence of sunspots on the rotating solar disc only plays a minor role. We further compute the disc-averaged line-of-sight magnetic flux and show that although we cannot yet measure it with precision on other stars at present, it is a very good proxy for activity-driven RV variations, much more so than the FWHM and BIS of the cross-correlation profile, and the Ca ii H&K activity index. These findings are in agreement with the previous works of Meunier et al. (2010a,b).

In addition to the existing 2011 HARPS observations of sunlight scattered off Vesta, there will soon be a wealth of direct solar RV measurements taken with HARPS-N, which will be regularly fed sunlight through a small 2-inch telescope developed specifically for this purpose. A prototype for this is currently being commissioned at HARPS-N (see Dumusque et al. 2015; Glenday et al., in preparation). Gaining a deeper understanding of the physics at the heart of activity-driven RV variability will ultimately enable us to better model and remove this contribution from RV observations, thus revealing the planetary signals.

We wish to thank the referee for their thoughtful comments, which have greatly helped improve the analysis presented in this paper. RDH gratefully acknowledges STFC studentship grant number ST/J500744/1, and a grant from the John Templeton Foundation. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the John Templeton Foundation. ACC and RF acknowledge support from STFC consolidated grants numbers ST/J001651/1 and ST/M001296/1. JL acknowledges support from NASA Origins of the Solar System grant No. NNX13AH79G and from STFC grant ST/M001296/1. The Solar Dynamics Observatory was launched by NASA on 2011 February 11, as part of the Living With A Star programme. This research has made use of NASA's Astrophysics Data System Bibliographic Services. We also used data from Haywood et al. (2016).

1

Plages are formed in the upper photosphere, chromosphere and upper layers of the stellar atmosphere (Lean 1997; Murdin 2002). They are not part of the lower photosphere, where the continuum absorption lines originate, from which the RV of a star is measured; however, plage regions do map closely to faculae and sunspots (Schrijver 2002; Hall 2008).

2

Solar System Dynamics Group, Horizons On-Line Ephemeris System, 4800 Oak Grove Drive, Jet Propulsion Laboratory, Pasadena, CA 91109 USA – Information: http://ssd.jpl.nasa.gov/, [email protected]

3

HMI data products can be downloaded online via the Joint Science Operations Center website: http://jsoc.stanford.edu.

4

Source code available at http://hesperia.gsfc.nasa.gov/ssw/gen/idl/solar/

REFERENCES

Aigrain

S.

Pont

F.

Zucker

S.

2012

MNRAS

419

3147

Julian date	RV	σ_RV	FWHM	BIS	\|$\log (R^{\prime }_{HK}$\|⁠)	\|$\sigma _{\log (R^{\prime }_{HK})}$\|	Δt	λ	\|$\hat{v}_{{\rm phot}}$\|	\|$\hat{v}_{{\rm conv}}$\|	\|$\|\hat{B}_{\rm obs}\|$\|	f
(MJD_mid_UTC)	(km s⁻¹)	(km s⁻¹)	(km s⁻¹)	(km s⁻¹)			(d)	(deg)	(m s⁻¹)	(m s⁻¹)	(G)	(per cent)
2455834.48296192	0.085 70	0.000 43	7.089 02	− 0.024 17	− 4.9411	0.0024	2.8365	143.99	− 0.122 949	6.612 382	13.390 075	6.442 092
2455834.61321887	0.099 36	0.000 39	7.0883	− 0.025 59	− 4.9435	0.0019	2.8451	351.75	− 0.122 949	6.612 382	13.390 075	6.442 092
2455835.53355275	0.094 77	0.000 49	7.089 03	− 0.024 78	− 4.9513	0.0028	2.8901	39.73	− 0.372 071	6.728 378	13.461 877	6.553 660
2455835.66225392	0.099 36	0.000 60	7.090 69	− 0.024 77	− 4.9498	0.0044	2.9002	247.49	− 0.369 973	6.800 018	13.456 769	6.559 029
2455836.50488464	0.084 31	0.000 46	7.089 78	− 0.024 77	− 4.9450	0.0027	2.9396	171.93	− 0.148 130	6.458 323	13.693 823	6.750 327
2455836.63463460	0.102 54	0.000 47	7.087 21	− 0.025 89	− 4.9506	0.0029	2.9487	19.69	− 0.149 324	6.451 065	13.612 058	6.682 767
2455837.58225198	0.099 16	0.000 43	7.086 32	− 0.024 37	− 4.9575	0.0026	2.9941	112.57	− 0.062 027	7.066 728	13.760 690	6.785 311
2455837.66801992	0.101 48	0.000 54	7.089 11	− 0.026 32	− 4.9597	0.0041	3.0056	252.95	− 0.062 027	7.066 728	13.760 690	6.785 311
2455838.56557661	0.095 52	0.000 65	7.093 28	− 0.026 98	− 4.9373	0.0043	3.0525	261.60	− 0.104 478	7.448 517	13.797 603	6.798 914
2455838.67384272	0.099 25	0.000 77	7.0939	− 0.027 17	− 4.9475	0.0061	3.0623	81.28	− 0.104 478	7.448 517	13.797 603	6.798 914
2455839.56369186	0.106 00	0.000 49	7.090 53	− 0.023 31	− 4.9480	0.0031	3.1099	78.70	0.282 247	6.290 580	13.538 572	6.711 449
2455839.66500316	0.101 44	0.000 54	7.089 58	− 0.025 47	− 4.9404	0.0038	3.1058	241.53	0.282 247	6.290 580	13.538 572	6.711 449
2455840.54096382	0.101 81	0.000 42	7.090 45	− 0.025 73	− 4.9519	0.0024	3.1535	216.48	0.492 760	6.355 797	13.337 171	6.545 630
2455841.51821591	0.097 43	0.000 44	7.0908	− 0.024 34	− 4.9443	0.0023	3.2110	359.87	0.548 444	6.054 414	13.267 717	6.419 010
2455842.54067654	0.101 56	0.000 58	7.093 98	− 0.023 31	− 4.9419	0.0041	3.2579	210.63	0.285 453	5.964 030	13.453 311	6.502 014
2455842.64940682	0.102 21	0.000 65	7.096 29	− 0.022 21	− 4.9521	0.0051	3.2673	30.31	0.285 453	5.964 030	13.453 311	6.502 014
2455843.53446953	0.101 35	0.000 42	7.097 55	− 0.024 79	− 4.9529	0.0023	3.3128	16.47	0.289 295	6.042 467	14.255 929	7.096 244
2455843.66473254	0.097 22	0.000 57	7.097 89	− 0.0264	− 4.9598	0.0043	3.3214	229.83	0.289 295	6.042 467	14.255 929	7.096 244
2455844.53056656	0.096 56	0.000 58	7.090 06	− 0.024 79	− 4.9538	0.0039	3.3722	187.91	0.338 963	7.427 578	15.036 871	7.600 587
2455844.66179197	0.102 92	0.000 50	7.095 19	− 0.0258	− 4.9513	0.0033	3.3799	41.27	0.412 640	7.942 586	15.167 705	7.742 510
2455845.54569082	0.101 43	0.000 53	7.093 54	− 0.0214	− 4.9472	0.0032	3.4265	33.04	0.214 037	9.072 355	15.656 077	8.091 010
2455845.65206487	0.098 30	0.000 54	7.097 19	− 0.023 43	− 4.9456	0.0036	3.4313	201.48	0.147 598	9.104 808	15.530 288	7.938 438
2455870.51420322	0.108 43	0.000 59	7.098 49	− 0.019 02	− 4.9355	0.0032	4.7844	86.70	− 0.230 017	9.870 595	18.187 723	9.696 133
2455870.52215421	0.107 01	0.000 53	7.101 07	− 0.021 57	− 4.9399	0.0035	4.7834	97.93	− 0.230 017	9.870 595	18.187 723	9.696 133
2455870.53060607	0.103 79	0.000 53	7.098 26	− 0.022 32	− 4.9419	0.0036	4.7819	109.16	− 0.230 017	9.870 595	18.187 723	9.696 133
2455871.50280525	0.102 50	0.000 61	7.093 61	− 0.018 83	− 4.9341	0.0033	4.8375	241.14	− 0.247 643	9.628 828	17.731 211	9.520 507
2455871.51026399	0.101 90	0.000 53	7.097 64	− 0.020 95	− 4.9334	0.0033	4.8370	252.37	− 0.247 643	9.628 828	17.731 211	9.520 507
2455871.51752074	0.102 79	0.000 53	7.098 29	− 0.020 04	− 4.9307	0.0033	4.8366	269.21	− 0.247 643	9.628 828	17.731 211	9.520 507
2455872.49503353	0.106 38	0.001 77	7.103 66	− 0.023 63	− 4.8856	0.0193	4.8869	46.81	− 0.217 090	8.539 591	16.708 896	8.931 849
2455872.50361680	0.107 06	0.000 63	7.098 57	− 0.0206	− 4.9459	0.0044	4.8853	63.65	− 0.212 479	8.339 659	16.718 279	8.928 224
2455872.51065080	0.104 33	0.000 66	7.093 74	− 0.021 82	− 4.9417	0.0046	4.8852	74.88	− 0.232 778	8.259 415	16.704 289	8.916 693
2455872.51832551	0.104 31	0.000 66	7.094 74	− 0.020 18	− 4.9297	0.0044	4.8914	86.10	− 0.218 351	8.044 784	16.715 321	8.926 018
2455873.50406872	0.098 70	0.000 50	7.091 24	− 0.022 93	− 4.9400	0.0030	4.9404	240.54	− 0.159 657	7.999 471	15.740 116	8.388 542
2455873.51131777	0.099 37	0.000 50	7.092 52	− 0.021 97	− 4.9425	0.0031	4.9401	251.76	− 0.149 055	8.115 433	15.749 984	8.389 838
2455873.51863681	0.099 33	0.000 51	7.096 35	− 0.022 45	− 4.9380	0.0030	4.9397	262.99	− 0.137 447	8.065 520	15.735 783	8.370 678
2455874.50355099	0.101 33	0.000 77	7.096 52	− 0.023 86	− 4.9467	0.0051	4.9964	57.42	− 0.289 008	8.449 905	15.011 817	7.870 854
2455874.51074342	0.102 94	0.000 74	7.092 61	− 0.023 14	− 4.9402	0.0057	4.9962	68.65	− 0.305 588	8.072 379	14.993 994	7.858 010
2455874.51805876	0.101 32	0.000 89	7.097 96	− 0.025 44	− 4.9379	0.0069	4.9958	79.87	− 0.305 588	8.072 379	14.993 994	7.858 010
2455875.50408302	0.098 39	0.000 58	7.089 79	− 0.024 18	− 4.9544	0.0040	5.0515	234.30	− 0.160 578	7.051 506	14.539 260	7.545 515
2455875.51155021	0.096 71	0.000 57	7.091 51	− 0.023 84	− 4.9472	0.0039	5.0509	245.52	− 0.160 578	7.051 506	14.539 260	7.545 515
2455875.51886866	0.096 45	0.000 58	7.092 36	− 0.019 25	− 4.9500	0.0040	5.0506	256.75	− 0.160 578	7.051 506	14.539 260	7.545 515
2455878.50606288	0.104 81	0.001 23	7.093 06	− 0.023 84	− 4.9368	0.0129	5.2162	44.91	0.239 367	7.862 843	14.083 289	7.241 949
2455878.51386630	0.103 96	0.001 25	7.087 15	− 0.020 17	− 4.9521	0.0137	5.2153	56.14	0.219 175	7.727 767	14.087 698	7.262 066
2455878.52076438	0.103 24	0.001 20	7.092 72	− 0.026 94	− 4.9529	0.0128	5.2153	67.36	0.215 755	7.792 477	14.102 572	7.257 334
2455879.50702795	0.097 25	0.001 12	7.094 57	− 0.025 22	− 4.9197	0.0103	5.2777	227.38	0.232 115	7.128 572	14.466 632	7.447 019
2455879.51427708	0.097 05	0.001 07	7.089 51	− 0.028 34	− 4.9360	0.0100	5.2774	238.61	0.230 304	6.983 342	14.483 479	7.457 781
2455879.52152229	0.097 81	0.001 05	7.094 96	− 0.025 36	− 4.9146	0.0093	5.2771	249.84	0.232 562	7.438 171	14.526 323	7.492 319
2455886.55971131	0.096 68	0.000 85	7.099 98	− 0.021 19	− 4.9537	0.0073	5.6625	109.52	0.232 784	6.416 208	14.173 657	6.983 742
2455886.56696080	0.094 96	0.000 86	7.094 83	− 0.023 48	− 4.9481	0.0075	5.6622	120.75	0.232 784	6.416 208	14.173 657	6.983 742
2455886.57392844	0.092 57	0.000 93	7.100 74	− 0.0237	− 4.9477	0.0086	5.6622	131.98	0.232 784	6.416 208	14.173 657	6.983 742
2455887.52342644	0.096 87	0.000 60	7.090 76	− 0.023 92	− 4.9636	0.0042	5.7196	224.60	0.254 368	6.578 471	13.681 434	6.611 017
2455887.53095415	0.097 45	0.000 67	7.091 91	− 0.026 85	− 4.9726	0.0052	5.7190	235.83	0.254 368	6.578 471	13.681 434	6.611 017
2455887.53806579	0.096 16	0.000 72	7.093 53	− 0.026 17	− 4.9578	0.0056	5.7189	247.06	0.254 368	6.578 471	13.681 434	6.611 017
2455888.52593242	0.101 10	0.000 60	7.090 39	− 0.026 13	− 4.9661	0.0043	5.7727	47.04	0.157 666	6.316 140	13.525 647	6.498 637
2455888.53317611	0.101 58	0.000 59	7.088 31	− 0.022 24	− 4.9623	0.0043	5.7724	58.27	0.157 666	6.316 140	13.525 647	6.498 637
2455888.54049630	0.101 75	0.000 62	7.090 83	− 0.025 48	− 4.9577	0.0047	5.7720	69.50	0.157 666	6.316 140	13.525 647	6.498 637
2455889.52578074	0.097 55	0.000 60	7.091 31	− 0.026 11	− 4.9642	0.0045	5.8284	223.87	0.183 892	6.607 664	13.455 927	6.430 930
2455889.53310116	0.096 01	0.000 60	7.093 05	− 0.024 11	− 4.9633	0.0046	5.8280	235.10	0.183 892	6.607 664	13.455 927	6.430 930
2455889.54034195	0.094 61	0.000 65	7.093 77	− 0.022 42	− 4.9796	0.0054	5.8277	246.32	0.183 892	6.607 664	13.455 927	6.430 930
2455890.50917526	0.100 97	0.000 59	7.088 86	− 0.028 67	− 4.9505	0.0040	5.8867	12.62	0.079 914	6.820 067	13.946 109	6.891 653
2455890.51649149	0.100 74	0.000 58	7.087 63	− 0.026 59	− 4.9564	0.0040	5.8863	23.85	0.079 914	6.820 067	13.946 109	6.891 653
2455890.52382222	0.099 96	0.000 59	7.087 79	− 0.024 85	− 4.9611	0.0042	5.8859	35.08	0.079 914	6.820 067	13.946 109	6.891 653
2455891.52246765	0.099 41	0.000 60	7.091 51	− 0.025 35	− 4.9591	0.0044	5.9428	211.90	0.079 914	6.820 067	13.946 109	6.891 653
2455891.52978471	0.099 21	0.000 63	7.0924	− 0.025 49	− 4.9649	0.0049	5.9424	223.12	− 0.128 128	7.724 229	15.031 973	7.761 893
2455891.53703495	0.098 40	0.000 63	7.093 53	− 0.026 16	− 4.9482	0.0049	5.9421	234.35	− 0.128 128	7.724 229	15.031 973	7.761 893
2455892.52735539	0.103 98	0.000 61	7.086 42	− 0.022 54	− 4.9442	0.0045	5.9935	34.33	0.250 746	8.037 871	15.638 486	7.970 436
2455892.53453612	0.103 58	0.000 79	7.091 45	− 0.024 41	− 4.9370	0.0068	5.9932	45.55	0.239 745	8.154 407	15.602 640	7.956 911
2455892.54214391	0.102 47	0.000 69	7.0878	− 0.023 79	− 4.9422	0.0054	5.9995	62.40	0.239 745	8.154 407	15.602 640	7.956 911
2455893.51437423	0.100 22	0.000 59	7.095 16	− 0.024 93	− 4.9440	0.0040	6.0551	194.30	0.178 788	9.501 673	16.492 246	8.578 127
2455893.52626540	0.102 39	0.000 57	7.091 83	− 0.025 14	− 4.9578	0.0040	6.0501	211.14	0.178 788	9.501 673	16.492 246	8.578 127
2455893.53359078	0.102 28	0.000 60	7.096 83	− 0.024 59	− 4.9607	0.0044	6.0497	222.37	0.178 788	9.501 673	16.492 246	8.578 127
2455894.50541095	0.102 65	0.000 59	7.094 96	− 0.023 71	− 4.9499	0.0041	6.0988	354.27	− 0.143 119	10.188 700	16.843 670	8.978 122
2455894.51266019	0.104 00	0.000 62	7.093 07	− 0.023 55	− 4.9416	0.0044	6.1054	5.49	− 0.143 119	10.188 700	16.843 670	8.978 122
2455894.52011844	0.105 48	0.000 68	7.094 66	− 0.023 04	− 4.9486	0.0052	6.1049	16.72	− 0.143 119	10.188 700	16.843 670	8.978 122
2455895.51190055	0.098 55	0.000 58	7.0944	− 0.0217	− 4.9341	0.0038	6.1617	182.30	− 0.219 694	9.459 038	16.678 771	8.985 445
2455895.51928533	0.100 14	0.000 61	7.093 07	− 0.022 48	− 4.9339	0.0041	6.1613	193.53	− 0.219 694	9.459 038	16.678 771	8.985 445
2455895.52668202	0.103 85	0.000 60	7.094 09	− 0.020 13	− 4.9456	0.0041	6.1608	204.76	− 0.219 694	9.459 038	16.678 771	8.985 445
2455896.51221054	0.103 11	0.000 62	7.095 55	− 0.0246	− 4.9082	0.0042	6.2170	359.11	− 0.118 240	9.149 870	16.324 338	8.893 371
2455896.51945075	0.104 02	0.000 64	7.0943	− 0.021 61	− 4.9219	0.0044	6.2167	10.34	− 0.118 240	9.149 870	16.324 338	8.893 371
2455896.52676887	0.104 50	0.000 65	7.0945	− 0.0215	− 4.9086	0.0045	6.2163	21.56	− 0.118 240	9.149 870	16.324 338	8.893 371
2455897.51313557	0.098 05	0.000 57	7.0929	− 0.021 41	− 4.9279	0.0041	6.2716	175.91	0.310 313	8.521 387	15.731 010	8.518 003
2455897.52017185	0.101 99	0.000 61	7.090 74	− 0.020 29	− 4.9207	0.0045	6.2715	187.14	0.310 313	8.521 387	15.731 010	8.518 003
2455897.52797234	0.101 03	0.000 66	7.094 31	− 0.022 93	− 4.9178	0.0049	6.2776	203.98	0.310 313	8.521 387	15.731 010	8.518 003
2455898.51251923	0.100 34	0.000 76	7.094 42	− 0.025 29	− 4.9139	0.0059	6.3278	352.71	0.208 771	7.346 064	15.023 078	7.994 100
2455898.51955262	0.102 92	0.000 74	7.095 72	− 0.020 88	− 4.9290	0.0060	6.3277	3.94	0.193 525	7.375 161	15.016 566	7.987 264
2455898.52692661	0.101 53	0.000 78	7.091 94	− 0.018 18	− 4.9312	0.0067	6.3272	15.17	0.193 006	7.321 089	15.020 403	7.988 140
2455899.51280365	0.094 28	0.000 77	7.092 21	− 0.021 72	− 4.9295	0.0065	6.3830	169.51	0.355 292	6.343 507	14.470 741	7.472 408
2455899.51984723	0.095 35	0.000 75	7.088 03	− 0.025 29	− 4.9478	0.0066	6.3829	180.74	0.360 379	6.548 910	14.477 587	7.468 980
2455899.52750987	0.096 53	0.000 76	7.093 12	− 0.021 94	− 4.9296	0.0063	6.3822	191.96	0.340 881	6.579 109	14.478 097	7.470 433
2455900.51316244	0.099 20	0.000 71	7.089 69	− 0.024 18	− 4.9457	0.0060	6.4382	346.30	0.270 016	6.616 161	13.979 841	7.170 614
2455900.52048381	0.097 37	0.000 71	7.091 26	− 0.026 17	− 4.9389	0.0059	6.4378	357.53	0.290 577	6.656 814	13.981 226	7.170 553
2455900.52779857	0.099 82	0.000 73	7.0925	− 0.023 89	− 4.9388	0.0062	6.4444	14.37	0.287 024	6.723 330	13.985 253	7.170 031
2455901.51376528	0.094 12	0.000 84	7.087 55	− 0.026 95	− 4.9244	0.0074	6.4932	163.10	0.527 470	5.870 234	13.607 637	6.908 622
2455901.52080259	0.094 32	0.000 79	7.094 11	− 0.023 79	− 4.9370	0.0068	6.4931	174.32	0.526 638	5.968 377	13.626 008	6.919 914
2455901.52818692	0.097 43	0.000 84	7.089 43	− 0.019 41	− 4.9387	0.0078	6.4996	191.16	0.528 856	5.908 731	13.682 738	6.957 918
2455902.51342158	0.098 49	0.001 00	7.095 81	− 0.022 93	− 4.9453	0.0099	6.5491	339.89	0.080 486	5.991 561	13.461 406	6.723 588
2455902.52087765	0.098 11	0.000 94	7.087 12	− 0.023 49	− 4.9608	0.0097	6.5555	356.73	0.072 490	6.135 274	13.455 276	6.727 012
2455902.52825791	0.099 28	0.000 96	7.086 18	− 0.024 03	− 4.9391	0.0096	6.5551	7.96	0.084 431	6.272 675	13.472 634	6.750 239

Month:	Total Views:
December 2016	1
January 2017	4
February 2017	12
March 2017	12
April 2017	7
May 2017	13
June 2017	22
July 2017	9
August 2017	5
September 2017	5
October 2017	3
November 2017	9
December 2017	4
January 2018	4
February 2018	2
March 2018	1
April 2018	7
May 2018	12
June 2018	11
July 2018	6
August 2018	8
September 2018	5
October 2018	12
November 2018	18
December 2018	7
January 2019	7
February 2019	7
March 2019	13
April 2019	18
May 2019	20
June 2019	12
July 2019	30
August 2019	13
September 2019	29
October 2019	34
November 2019	18
December 2019	10
January 2020	64
February 2020	17
March 2020	15

Article Contents

The Sun as a planet-host star: proxies from SDO images for HARPS radial-velocity variations Free

Abstract

INTRODUCTION

HARPS OBSERVATIONS OF SUNLIGHT SCATTERED OFF VESTA

HARPS spectra

Solar rest frame

Relativistic Doppler effects

Sources of intra-night RV variations

Vesta's axial rotation

Additional intra-night scatter in first half of HARPS run

Time lag between Vesta and SDO observations

PIXEL STATISTICS FROM SDO/HMI images

Spacecraft motion

Solar rotation

Flattened continuum intensity

Unsigned magnetic field strength

Identifying quiet-Sun regions, faculae and sunspots

Surface velocity flows in sunspot penumbrae and umbrae

Decomposing the Sun's RV into individual feature contributions

Velocity contribution of convective motions in quiet-Sun regions

Rotational Doppler imbalance due to dark sunspots and bright faculae

Suppression of convective blueshift from active regions

REPRODUCING THE RV VARIATIONS OF THE SUN

Total RV model

Agreement between HARPS observations and SDO-derived model

Relative importance of suppression of convective blueshift and rotational velocity imbalance

Zero-point of HARPS

TOWARDS BETTER PROXIES FOR RV OBSERVATIONS

Spatial distributions of sunspots and faculae

Correlations between RV and traditional activity indicators

Disc-averaged observed magnetic flux |$|\hat{B}_{\rm obs}|$|

Magnetic filling factor f

CONCLUSION

REFERENCES

SUPPORTING INFORMATION

APPENDIX A:

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

The Sun as a planet-host star: proxies from SDO images for HARPS radial-velocity variations