-
PDF
- Split View
-
Views
-
Cite
Cite
E. M. Schneiter, A. Esquivel, C. S. Villarreal D'Angelo, P. F. Velázquez, A. C. Raga, A. Costa, Photoionization of planetary winds: case study HD 209458b, Monthly Notices of the Royal Astronomical Society, Volume 457, Issue 2, 01 April 2016, Pages 1666–1674, https://doi.org/10.1093/mnras/stw076
Close - Share Icon Share
Abstract
Close-in hot Jupiters are exposed to a tremendous photon flux that ionizes the neutral escaping material from the planet leaving an observable imprint that makes them an interesting laboratory for testing theoretical models. In this work, we present 3D hydrodynamic simulations with radiation transfer calculations of a close-in exoplanet in a blow-off state. We calculate the Ly α absorption and compare it with observations of HD 209458b and previous simplified model results. Our results show that the hydrodynamic interaction together with a proper calculation of the photoionization process are able to reproduce the main features of the observed Ly α absorption, in particular at the blue-shifted wings of the line. We found that the ionizing stellar flux produce an almost linear effect on the amount of absorption in the wake. Varying the planetary mass-loss rate and the radiation flux, we were able to reproduce the 10 per cent absorption observed at −100 km s−1.
1 INTRODUCTION
The discovery of the first hot Jupiter transiting its host star HD 209458 took place more than a decade ago (see Charbonneau et al. 2000; Henry et al. 2000). The analysis of data samples of the extrasolar planet transit HD 209458b obtained with the Space Telescope Imaging Spectrograph (STIS) on board of the Hubble Space Telescope (HST) made by Vidal-Madjar et al. (2003) revealed the existence of an extended upper atmosphere, and opened a discussion on whether the atmosphere is being lost (see Ben-Jaffel 2007, 2008). Vidal-Madjar et al. (2008) revisited the observations and the theoretical works based on the picture of an escaping atmosphere (e.g. Lammer et al. 2003; Lecavelier des Etangs et al. 2004; Yelle 2004, 2006; Baraffe et al. 2005; Tian et al. 2005; García Muñoz 2007; Schneiter et al. 2007) and confirmed it. Since then numerous theoretical works have been carried out shifting the discussion to the escaping mechanism, putting the focus on trying to explain the absorption produced at high velocities (see Holmström et al. 2008; Ekenbäck et al. 2010; Bourrier & Lecavelier des Etangs 2013; Tremblin & Chiang 2013; Villarreal D'Angelo et al. 2014). Vidal-Madjar et al. (2008) evaluated the absorption seen during transit within the ‘blue’ and the ‘red’ sides (of the wavelength domain defined in Ben-Jaffel 2007) finding a 9.8 ± 1.8 and 5.2 ± 1.0 per cent absorption, respectively.
Vidal-Madjar et al. (2003) first interpreted the absorption as hydrogen atoms in the exosphere undergoing hydrodynamic escape, accelerated by the stellar radiation pressure. Later, Schneiter et al. (2007) developed a 3D hydrodynamic model of the interaction between the stellar wind and the gas escaping from the planet (HD 209458b). By comparing the calculated Ly α absorption with the observations they were able to estimate an upper limit for the planetary mass-loss rate (|$\dot{M}_\mathrm{p}$|). In Villarreal D'Angelo et al. (2014), the stellar wind conditions were improved by comprehensively studying the stellar wind parameters. This was done by using a polytropic model to estimate the initial conditions for the stellar wind at the radial distance (from the centre of the star) at which it was imposed. Several stellar wind velocities where tested together with the coupled stellar wind temperature (T*), finding a suitable range for |$\dot{M}_\mathrm{p}$| ([3–5] × 1010 g s−1). Schneiter et al. (2007) and Villarreal D'Angelo et al. (2014), distinguished the planetary wind from the stellar wind with the aid of a passive scalar, and calculated the Ly α absorption assuming that all neutral material with temperatures above 105 K was ionized. These works were able to reproduce the velocity range of neutral planetary atoms responsible for the observed absorption in the Ly α line.
The work done in Holmström et al. (2008) and its follow up Ekenbäck et al. (2010) reproduce the absorption observed at Doppler shift −100 km s−1. They simulated the production of energetic neutral hydrogen through charge exchange between stellar wind protons and exospheric hydrogen, assuming stellar wind conditions similar to those at an equivalent distance in our Sun. Tremblin & Chiang (2013) further explored the charge-exchange scenario by means of a 2D hydrodynamic model, making emphasis on the mixing layer between both winds.
Bourrier & Lecavelier des Etangs (2013) presented a 3D Monte Carlo numerical particle model developed to simulate the escaping gas of an exoplanet. In their model the focus was set on the radiation pressure, taking into account the ionization, the self-shielding, and the stellar wind interaction. The charge-exchange process was included as an impulse given by the incoming stellar wind proton, aiming, this way, to explain the blue-shifted absorption.
Even though most of these models employ different acceleration mechanism for the neutral particles, they all have been capable of reproducing the global structure of the upper atmosphere of exoplanets undergoing mass-loss due to Roche lobe overflow, predicting planetary mass-loss rates in the range 109–1011 g s−1, leaving the question of which particle acceleration mechanism is responsible for the absorption at high Doppler shift, still open.
Recent progress has been made to model the planetary mass-loss rate including the effect of magnetic fields in both the star and the planet. It has been shown for instance that space weather events (such as coronal mass ejection) or the parameters of the planetary system itself, can have an influence on the mass-loss from the planet (see for example Adams 2011; Cohen et al. 2011a,b; Owen & Adams 2014; Trammell, Li & Arras 2014; Matsakos, Uribe & Königl 2015). Owen & Adams (2014) find, through a number of numerical simulations that include the stellar ultraviolet (UV) flux, that the presence of magnetic fields, can reduce the amount of planetary mass-loss rate by approximately an order of magnitude if the planet can sustain moderate magnetic fields values (Bp > 1 G). Finally, as mentioned in Cohen et al. (2011a,b) and in Owen & Adams (2014), the interaction of the planetary magnetosphere with the magnetized stellar wind is expected to be highly dynamic and change with time according to the parameters of the planetary system.
Here, we present a 3D numerical model of the hydrodynamic interaction between the winds that includes in a self-consistent manner the calculation of the photoionization, and we focus in the effects of varying the ionizing flux, the stellar wind parameters and the mass-loss rate of the planet. Similar simulations have recently been presented by Tripathi et al. (2015), where the evaporation of the exoplanet atmosphere is modelled with radiation hydrodynamics. In such work, an asymmetric planetary wind is produced by a plane–parallel radiative field and stellar wind. However, their focus is in the mass-loss from the planet, and not on the extended wake.
The model, some details of the code, and the parameters employed are presented in Section 2. The results are presented in Section 3 and discussed in Section 4. The concluding remarks are given in Section 5.
2 THE MODEL
We used the radiation-hydrodynamics code guacho (Esquivel et al. 2009; Esquivel & Raga 2013) to produce synthetic Ly α absorption maps of a hot Jupiter around a solar-type star (i.e. the HD 209458 system).
2.1 The hydrodynamics core
The hydrodynamics equations (left-hand side of equations 1–3), are advanced with a second-order Godunov method with an approximate Riemann solver (Harten-Lax-van Leer-Contact; Toro 1999), and a linear reconstruction of the primitive variables using the minmod slope limiter to ensure stability.
2.2 Source terms
At every time-step, the hydrodynamic variables are updated, with the updated values the source terms (right-hand side of equations 1–3) are computed and added to the solution in a semi-implicit scheme.
2.2.1 Gravity
For the gravitational force, we add to each cell on the grid the acceleration due to two point masses, the mass of the planet (whose position changes as it orbits around the star), and the mass of star. The mass of the star is reduced to 1/3 of the actual value for the computation of the gravitational acceleration, to emulate the effect of the radiation pressure force that acts in opposition to gravity (see for example Vidal-Madjar et al. 2003).
A more detailed calculation of the radiation pressure is possible. For instance, Bourrier & Lecavelier des Etangs (2013) and Bourrier, Ehrenreich & Lecavelier des Etangs (2015), calculated the ratio of the radiation pressure to gravitational forces (the β parameter in their models, which is proportional to the Ly α flux) to model the evaporation of the atmospheres of HD 209458b and HD 189733b. Such calculation involves the knowledge of the Ly α emission as seen by each cell, which is beyond the scope of the present paper. We plan to pursue this refinement in a future study.
2.2.2 Heating, cooling, and radiative transfer
2.3 Parameters of the simulations
The star/planet system is modelled as the interaction of two isotropic wind sources in orbit. There are many physical processes that could lead to an anisotropic planetary wind. For instance, a tidally locked planet would lead to the same hemisphere facing the host star, and, unless there are atmospheric flows that transport heat efficiently (see Showman et al. 2008; Batygin & Stanley 2014, for a discussion on internal flows) that are capable of thermalizing the whole atmosphere, the winds will be asymmetric. This effect has been studied before in Villarreal D'Angelo et al. (2014) by means of a few toy models. In that work, in spite of the simplicity of the models, only a minor effect in the wake structure that produced most of the Ly α absorption was found. Recently, a more detailed calculation of the photo-evaporation of the planet atmosphere was presented in Tripathi et al. (2015). They used 3D radiation hydrodynamics and arrive to the same value of |$\dot{M}_\mathrm{p}$| that we adopt (2 × 1010 g s−1). For simplicity, and left to a future work, we assume isotropic planetary and stellar winds.
We place the source that corresponds to the star at the centre of the computational domain, which coincides with the origin of a Cartesian grid. The planet orbits the star in the xz-plane in an anticlockwise direction. Both winds are reimposed at every time-step with the planet position updated according to its orbital period (τorb = 3.52 d). The orbit is assumed circular with a radius of |$0.047\,\mathrm{{\rm au}}$|. The initial position of the planet is 25° ‘behind’ the x-axis to ensure that the wake is formed by the time it reaches the z-axis, which we have taken to be the line of sight (LOS), unless otherwise stated.
We ran a total of 19 models, varying the stellar wind temperature and velocity, the photoionizing rate and the mass-loss rate of the planet. For clarity, we present the parameters used in the simulations in two tables. In Table 1, we show the star and planet parameters, and the symbols we use for them. In this table, we show the ranges of the parameters that we vary as well as some common quantities in the simulations. In Table 2, we show the details of each of the models.
| Stellar parameters . | Symbol . | Value . |
|---|---|---|
| Radius | R* | 1.146 R⊙ |
| Mass | M* | 1.148 M⊙ |
| Wind velocity | v★ | 130–372 km s−1 |
| Wind launch radius | Rw, ★ | 3.5–6.9 R* |
| Wind temperature | T★ | 1–3 MK |
| Mass-loss rate | |$\dot{M_{\ast }}$| | 2.0 M⊙ yr−1 |
| Ionizing photon rate | S0 | 2.4 × 1038 s−1 |
| Planetary parameters | Symbol | Value |
| Radius | Rp | 1.38 RJup |
| Mass | Mp | 0.67 MJup |
| Wind velocity | vp | 10 km s−1 |
| Wind launch radius | Rw, p | 3 Rp |
| Wind temperature | Tp | 1 × 104 K |
| Mass-loss rate | |$\dot{M}_\mathrm{p}$| | (1–2) × 1010 g s−1 |
| Stellar parameters . | Symbol . | Value . |
|---|---|---|
| Radius | R* | 1.146 R⊙ |
| Mass | M* | 1.148 M⊙ |
| Wind velocity | v★ | 130–372 km s−1 |
| Wind launch radius | Rw, ★ | 3.5–6.9 R* |
| Wind temperature | T★ | 1–3 MK |
| Mass-loss rate | |$\dot{M_{\ast }}$| | 2.0 M⊙ yr−1 |
| Ionizing photon rate | S0 | 2.4 × 1038 s−1 |
| Planetary parameters | Symbol | Value |
| Radius | Rp | 1.38 RJup |
| Mass | Mp | 0.67 MJup |
| Wind velocity | vp | 10 km s−1 |
| Wind launch radius | Rw, p | 3 Rp |
| Wind temperature | Tp | 1 × 104 K |
| Mass-loss rate | |$\dot{M}_\mathrm{p}$| | (1–2) × 1010 g s−1 |
| Stellar parameters . | Symbol . | Value . |
|---|---|---|
| Radius | R* | 1.146 R⊙ |
| Mass | M* | 1.148 M⊙ |
| Wind velocity | v★ | 130–372 km s−1 |
| Wind launch radius | Rw, ★ | 3.5–6.9 R* |
| Wind temperature | T★ | 1–3 MK |
| Mass-loss rate | |$\dot{M_{\ast }}$| | 2.0 M⊙ yr−1 |
| Ionizing photon rate | S0 | 2.4 × 1038 s−1 |
| Planetary parameters | Symbol | Value |
| Radius | Rp | 1.38 RJup |
| Mass | Mp | 0.67 MJup |
| Wind velocity | vp | 10 km s−1 |
| Wind launch radius | Rw, p | 3 Rp |
| Wind temperature | Tp | 1 × 104 K |
| Mass-loss rate | |$\dot{M}_\mathrm{p}$| | (1–2) × 1010 g s−1 |
| Stellar parameters . | Symbol . | Value . |
|---|---|---|
| Radius | R* | 1.146 R⊙ |
| Mass | M* | 1.148 M⊙ |
| Wind velocity | v★ | 130–372 km s−1 |
| Wind launch radius | Rw, ★ | 3.5–6.9 R* |
| Wind temperature | T★ | 1–3 MK |
| Mass-loss rate | |$\dot{M_{\ast }}$| | 2.0 M⊙ yr−1 |
| Ionizing photon rate | S0 | 2.4 × 1038 s−1 |
| Planetary parameters | Symbol | Value |
| Radius | Rp | 1.38 RJup |
| Mass | Mp | 0.67 MJup |
| Wind velocity | vp | 10 km s−1 |
| Wind launch radius | Rw, p | 3 Rp |
| Wind temperature | Tp | 1 × 104 K |
| Mass-loss rate | |$\dot{M}_\mathrm{p}$| | (1–2) × 1010 g s−1 |
| Runs . | |$\dot{M}_\mathrm{p}$| . | v* . | Grida . | T . | Photon Rate . |
|---|---|---|---|---|---|
| . | ( × 1010 g s−1) . | (km s−1) . | (au) . | ( × 106 K) . | (s−1) . |
| A1a | 1 | 130 | 0.2 × 0.05 × 0.2 | 1 | 0.2 × S0 |
| A1b | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | 0.2 × S0 |
| A2a | 1 | 130 | 0.2 × 0.05 × 0.2 | 1 | S0 |
| A2b | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | S0 |
| ANRb | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | No rad |
| A3a | 1 | 130 | 0.2 × 0.05 × 0.2 | 1 | 5 × S0 |
| A3b | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | 5 × S0 |
| B1a | 1 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 0.2 × S0 |
| B1b | 2 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 0.2 × S0 |
| B2a | 1 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | S0 |
| B2b | 2 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | S0 |
| B3a | 1 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 5 × S0 |
| B3b | 2 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 5 × S0 |
| C1a | 1 | 372 | 0.3 × 0.075 × 0.3 | 3 | 0.2 × S0 |
| C1b | 2 | 372 | 0.3 × 0.075 × 0.3 | 3 | 0.2 × S0 |
| C2a | 1 | 372 | 0.3 × 0.075 × 0.3 | 3 | S0 |
| C2b | 2 | 372 | 0.3 × 0.075 × 0.3 | 3 | S0 |
| C3a | 1 | 372 | 0.3 × 0.075 × 0.3 | 3 | 5 × S0 |
| C3b | 2 | 372 | 0.3 × 0.075 × 0.3 | 3 | 5 × S0 |
| Runs . | |$\dot{M}_\mathrm{p}$| . | v* . | Grida . | T . | Photon Rate . |
|---|---|---|---|---|---|
| . | ( × 1010 g s−1) . | (km s−1) . | (au) . | ( × 106 K) . | (s−1) . |
| A1a | 1 | 130 | 0.2 × 0.05 × 0.2 | 1 | 0.2 × S0 |
| A1b | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | 0.2 × S0 |
| A2a | 1 | 130 | 0.2 × 0.05 × 0.2 | 1 | S0 |
| A2b | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | S0 |
| ANRb | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | No rad |
| A3a | 1 | 130 | 0.2 × 0.05 × 0.2 | 1 | 5 × S0 |
| A3b | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | 5 × S0 |
| B1a | 1 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 0.2 × S0 |
| B1b | 2 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 0.2 × S0 |
| B2a | 1 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | S0 |
| B2b | 2 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | S0 |
| B3a | 1 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 5 × S0 |
| B3b | 2 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 5 × S0 |
| C1a | 1 | 372 | 0.3 × 0.075 × 0.3 | 3 | 0.2 × S0 |
| C1b | 2 | 372 | 0.3 × 0.075 × 0.3 | 3 | 0.2 × S0 |
| C2a | 1 | 372 | 0.3 × 0.075 × 0.3 | 3 | S0 |
| C2b | 2 | 372 | 0.3 × 0.075 × 0.3 | 3 | S0 |
| C3a | 1 | 372 | 0.3 × 0.075 × 0.3 | 3 | 5 × S0 |
| C3b | 2 | 372 | 0.3 × 0.075 × 0.3 | 3 | 5 × S0 |
aAll simulations have the same resolution, but to avoid neutral material from the tail leaving the domain we had to increase the grid size in some of the runs.
| Runs . | |$\dot{M}_\mathrm{p}$| . | v* . | Grida . | T . | Photon Rate . |
|---|---|---|---|---|---|
| . | ( × 1010 g s−1) . | (km s−1) . | (au) . | ( × 106 K) . | (s−1) . |
| A1a | 1 | 130 | 0.2 × 0.05 × 0.2 | 1 | 0.2 × S0 |
| A1b | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | 0.2 × S0 |
| A2a | 1 | 130 | 0.2 × 0.05 × 0.2 | 1 | S0 |
| A2b | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | S0 |
| ANRb | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | No rad |
| A3a | 1 | 130 | 0.2 × 0.05 × 0.2 | 1 | 5 × S0 |
| A3b | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | 5 × S0 |
| B1a | 1 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 0.2 × S0 |
| B1b | 2 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 0.2 × S0 |
| B2a | 1 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | S0 |
| B2b | 2 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | S0 |
| B3a | 1 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 5 × S0 |
| B3b | 2 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 5 × S0 |
| C1a | 1 | 372 | 0.3 × 0.075 × 0.3 | 3 | 0.2 × S0 |
| C1b | 2 | 372 | 0.3 × 0.075 × 0.3 | 3 | 0.2 × S0 |
| C2a | 1 | 372 | 0.3 × 0.075 × 0.3 | 3 | S0 |
| C2b | 2 | 372 | 0.3 × 0.075 × 0.3 | 3 | S0 |
| C3a | 1 | 372 | 0.3 × 0.075 × 0.3 | 3 | 5 × S0 |
| C3b | 2 | 372 | 0.3 × 0.075 × 0.3 | 3 | 5 × S0 |
| Runs . | |$\dot{M}_\mathrm{p}$| . | v* . | Grida . | T . | Photon Rate . |
|---|---|---|---|---|---|
| . | ( × 1010 g s−1) . | (km s−1) . | (au) . | ( × 106 K) . | (s−1) . |
| A1a | 1 | 130 | 0.2 × 0.05 × 0.2 | 1 | 0.2 × S0 |
| A1b | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | 0.2 × S0 |
| A2a | 1 | 130 | 0.2 × 0.05 × 0.2 | 1 | S0 |
| A2b | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | S0 |
| ANRb | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | No rad |
| A3a | 1 | 130 | 0.2 × 0.05 × 0.2 | 1 | 5 × S0 |
| A3b | 2 | 130 | 0.2 × 0.05 × 0.2 | 1 | 5 × S0 |
| B1a | 1 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 0.2 × S0 |
| B1b | 2 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 0.2 × S0 |
| B2a | 1 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | S0 |
| B2b | 2 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | S0 |
| B3a | 1 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 5 × S0 |
| B3b | 2 | 205 | 0.2 × 0.05 × 0.2 | 1.3 | 5 × S0 |
| C1a | 1 | 372 | 0.3 × 0.075 × 0.3 | 3 | 0.2 × S0 |
| C1b | 2 | 372 | 0.3 × 0.075 × 0.3 | 3 | 0.2 × S0 |
| C2a | 1 | 372 | 0.3 × 0.075 × 0.3 | 3 | S0 |
| C2b | 2 | 372 | 0.3 × 0.075 × 0.3 | 3 | S0 |
| C3a | 1 | 372 | 0.3 × 0.075 × 0.3 | 3 | 5 × S0 |
| C3b | 2 | 372 | 0.3 × 0.075 × 0.3 | 3 | 5 × S0 |
aAll simulations have the same resolution, but to avoid neutral material from the tail leaving the domain we had to increase the grid size in some of the runs.
The stellar wind is imposed fully ionized near the sonic point with the corresponding temperature and velocity, the density follows an ∝ r−2 profile, scaled to give the corresponding mass-loss rate. The temperature and velocity of the winds were extrapolated from the surface of the star to the launch position with the aid of a polytropic model with index close 1.01 (see Villarreal D'Angelo et al. 2014).
The planetary wind is imposed with an ionization fraction of 0.8, at 3Rp (roughly the Hill radius). This choice is based on the results obtained in Murray-Clay, Chiang & Murray (2009), where a 1D model for photo-evaporative mass-loss from a hot Jupiter is constructed. They focus on the escape of hydrogen originated on the substellar point of the planet, and assume that mass-loss occurs in the form of a steady, hydrodynamic, transonic wind. Their results predict that 20 per cent of the material remains neutral at 3Rp. This value, however, depends strongly on the model assumptions. For instance, Koskinen et al. (2013) predicts a transition H i/H ii at an altitude of 3.1 Rp, implying that 50 per cent of the escaping material remains neutral at this altitude. The mass-loss rate adopted is also consistent with that obtained in Tripathi et al. (2015), who presented 3D simulations of the photo-evaporation near the planet atmosphere.
In our models, the temperature and terminal velocity are set constant at the base of the planetary wind, while the density profile is scaled to give the desired mass-loss rate.
Based on luminosity estimated for HD 209458 in Sanz-Forcada et al. (2011, they find log LEUV < 27.74 erg s−1), we have chosen a S0 = 2.46 × 1038 s−1 for the stellar photon rate, which corresponds to a flux of F0 = 884 erg cm−2 s−1 at the orbital distance of HD 209458b. Other works, where focus is set on the escape process which utilize the EUV and X-ray as energy input consider a range in luminosities/fluxes. For instance, Tian et al. (2005) use the current solar luminosity value, yielding a flux of F = 0.15 erg cm−2 s−1 at 1 au (roughly a tenth of ours); while Owen & Jackson (2012) adopt a larger photon rate (S* = 1040 s− 1). Murray-Clay et al. (2009) use the solar EUV flux of 450 erg s−1 at |$0.05\,\mathrm{{\rm au}}$|, which corresponds to an S* = 1.4 × 1037 s− 1. Similar values have been adopted in the works of Owen & Adams (2014) and Matsakos et al. (2015). To evaluate the effect of the ionizing photon rate on the escaping planetary material and somehow cover the range of values discussed in the literature we use three different values for the photon flux in our simulations (0.2, 1 , 5) × S0.
Fig. 1 shows the computational domain with a rendering of the density. The system has reached a fully quasi-stationary state with a long curved wake behind the planet. The initial conditions are evolved for an integration time of 3.8 d, in which the planet completes an orbit around the star.
3 RESULTS
As explored in previous works, the interaction between the stellar and planetary winds forms a wake structure similar to what is shown in Fig. 1. The parameters we used for the wind sources result in similar morphology in all cases, where the morphological differences lie in the details. For instance, a rapid wind from the star results in a less curved and more radial wake than a slow wind, or a higher mass-loss rate of the planet produces a larger bow-shock. Fig. 2 shows the density stratification, temperature and ionizing heating rate for a cut in the orbital plane after an evolution time of t = 2.9 d.

3D rendering of the density of one of the models (C1b, see Table 2), after an integration time of 3.8 d.
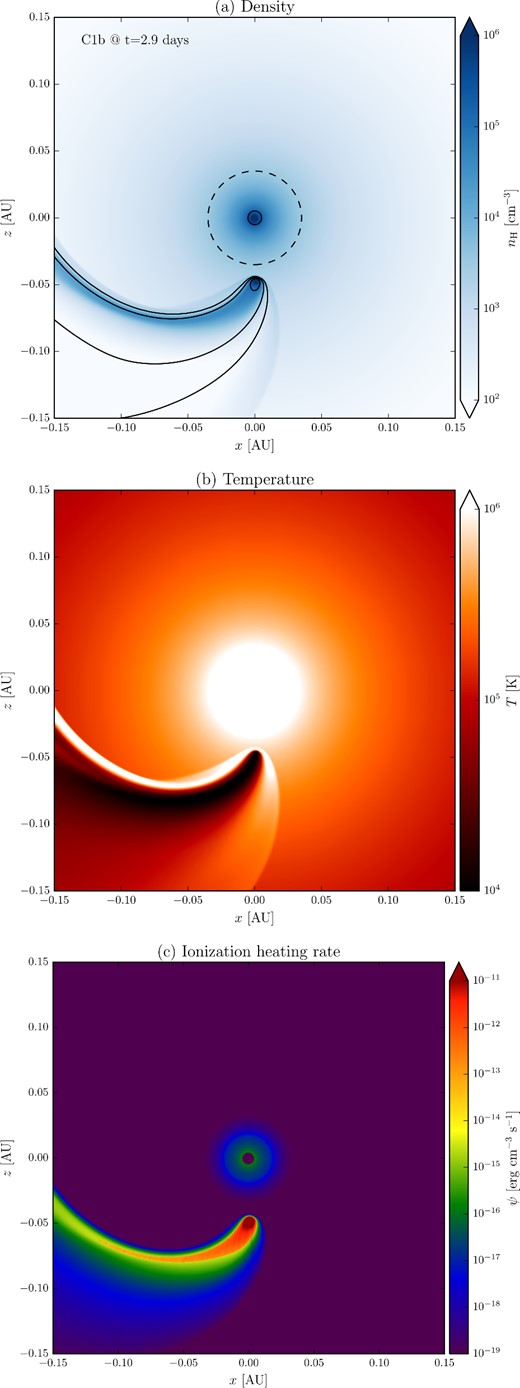
2D cuts in the orbital plane (y = 0) of (a) density, (b) temperature, and (c) ionization heating rate, at t = 2.9 d for model C1b. In the top panel, we show the size of the central star (solid line circle) and the size of the region at which the wind is imposed (dashed line circle). In the same panel, we also show ionization fraction isocontours at values of 0.9 (the most interior to the planet), 0.99, and 0.999 (the most exterior).
In the top panel, we indicate by a solid circle the extent of HD 209458 (the photon packages are launched from this radius), and with a dashed circle the size of the region in which the stellar wind is imposed. In addition, the top panel of this figure includes the ionization fraction isocontours at 0.9 (close to the planet), 0.99, and 0.999 levels. The ionization structure of the tail is significantly different from our previous models, where the photoionization was not considered, and a fully neutral planetary wind was imposed. In Schneiter et al. (2007) and Villarreal D'Angelo et al. (2014), we assumed that material arising from the planetary wind with a temperature T < 105 K was neutral (and it was considered to estimate the Ly α absorption). In the models with photoionization, we now assume an ionization fraction of 0.8, which increases rapidly, implying that there is less material available to absorb.
From the other two panels, temperature and ionization heating rate stratification (b and c) it is clear how the impinging photons heat up the trailing planetary material and how the planet and the high density interaction region shield the outer part of escaping neutral atoms in the wake.
3.1 Ly α absorption
The total absorption can be calculated by integrating |$\tau _\mathrm{v_{los}}$| in velocity. The Ly α emission from the star would be absorbed by a factor (1 − e−τ), where τ is the optical depth integrated over all velocities. Fig. 3 shows an example (same model shown in Figs 1 and 2) of the total absorption fraction calculated from the models during a transit, as it would be seen by an observer in the −z direction (with the inclination of HD 209458b).
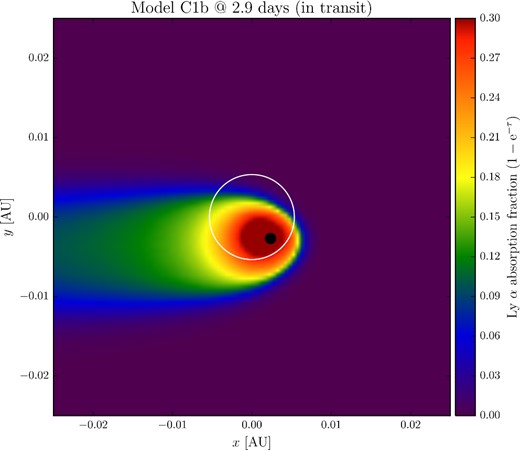
Map of Ly α optical depth (integrated over all velocities) for model C1b in transit as observed from the −z-axis (integration time of 2.9 d). The map showed is zoom-in of the entire domain. Both the star and the planet are shown in scale by the white circle and black disc, respectively.
After computing the Ly α absorption as a function of time, we found that the wake reaches a quasi-stationary state in only a fraction of the orbital period. This is somewhat different from our previous models, where at least half a period was required to reach such a stationary state. The main reason is that the photoionization results in a smaller neutral tail.
Fig. 4 shows the absorption of the stellar emission as a function of time, first from the +z direction (t < 2.2 d) and the subsequent transit as would be measured from the −z direction (see Fig. 2) for all the models.

Velocity averaged total absorption as a function of time calculated from an observer situated in the +z (first transit t < 2.2 d) and −z directions (second transit, t > 2.2 d). The models are grouped into panels according to the stellar wind velocity, as indicated in the title. The colour coding represents the ionizing flux: 0.2 S0 (orange), S0 (green), and 5 S0 (purple). The dots joined by dotted lines correspond to |$\dot{M}_\mathrm{p} =2\times 10^{10}\,\mathrm{g\,s^{-1}}$|, and the solid lines to |$\dot{M}_\mathrm{p} =1\times 10^{10}\,\mathrm{g\,s^{-1}}$|. The green vertical stripe represents the times when a portion of the planetary disc blocks the star (i.e. the planet is in transit).
We have separated the models according to the stellar wind velocity. Panel (a) shows all the models with v* = 130 km s− 1, including the reference model ANRb that has the same parameters as A2b (see Table 2 for details) but does not include the photoionization process. In this model, the absorption was computed as in Schneiter et al. (2007), that is, assuming that only material originally from the planet with temperatures below 105 K absorb the Ly α emission. Panels (b) and (c) show the absorption for the models with 205 and 372 km s−1, respectively. Notice that there are only minor differences in the first and second transits, showing that the quasi-stationary wake structure forms rapidly. The absorption in Fig. 4 was calculated excluding the velocity range between −40 and 40 km s−1, which for Earth-based observations is contaminated by the geocoronal emission.
From the plots, we can see that the maximum absorption changes when doubling |$\dot{M}_{{\rm p}}$|. This is in accordance with the results obtained in Schneiter et al. (2007) and Villarreal D'Angelo et al. (2014). At the same time the total absorption is greatly affected by the change in FEUV, producing appreciable changes both in the maximum absorption as well as in the tail of the wake (absorption after the transit of the planet), a denser and more extended structure is formed for low ionizing fluxes.
From the detection made with the STIS on board of the HST in 2001 (see Vidal-Madjar et al. 2003), it is clear that the deepest absorption signatures are found in the blue wing of the Ly α line, in the velocity range between −130 and −40 km s−1. Whereas the red side of the Doppler-Shifted absorption, defined within the velocity range between 32 and 100 km s−1 is less significant. To study these features, we show in Fig. 5 the stellar emission as a function of velocity, for all the models, at the time of maximum absorption during the second transit (t = 2.9 d).

Normalized stellar emission at t = 2.9 d as a function of LOS velocity. The models are grouped in the same manner as in Fig. 4. Panel (a) includes the line profile for a simulations without radiation transfer (black line), calculated with the passive scalar and the ionization temperature as in Schneiter et al. (2007) and Villarreal D'Angelo et al. (2014). The yellow stripe represents the part of the line that is contaminated with the geocoronal glow and was omitted form the total absorption calculation.
From Fig. 5, we notice that the absorption depends strongly on the ionizing flux, especially on the blue side of the spectrum, contrary to what it is observed on the red side, where all models show similar behaviour.
It is expected that higher ionizing fluxes result in a lower absorption, as photoionized material becomes transparent to Ly α. In addition, neutral material in the wake of the planetary wind accelerates due to its hydrodynamical interaction with the stellar wind, as well as due to radiation pressure (modelled here as a deficit in the gravitational pull of the star). The neutral wake therefore accelerates towards the observer (see Fig. 2), and interacts with the Ly α emission from the star producing the prominent blue-shifted absorption, whose maximum value shifts towards more negative velocities when the ionizing flux diminish.
To compare our results with the observations, we took the original off-transit data (reproduced from Vidal-Madjar et al. 2003), and multiplied them by the velocity dependent absorption factor in our models. The resulting Ly α profiles can be compared with the in-transit observations in Fig. 6 (also reproduced from Vidal-Madjar et al. 2003).

Ly α observations (reproduced from Vidal-Madjar et al. 2003), and the corresponding synthetic absorption calculated with our models. The colour and line coding is the same as in previous figures, and it is indicated in the label.
The observations show absorption in both the blue part of the spectrum (in the velocity range from −130 to −40 km s−1), as well as in the red part of the spectrum (velocity range from 32 to 100 km s−1) with an attenuation of ∼10 and ∼5 per cent, respectively.
Most of the models reproduce the level of absorption in the blue wing (except models with low stellar flux that overestimate the absorption for all velocities), considering the large uncertainties in the observations. The red wing absorption is generally underestimated, and only a couple of models show very little absorption around 90 km s−1.
In Figs 5 and 6, the region shaded in yellow corresponds to the part of the spectrum contaminated by geocoronal emission in observations, thus it should not be considered when comparing our models with observations.
4 DISCUSSION
The models presented here are closer to a self-consistent study of the stellar-planetary wind interaction than the two previous works (Schneiter et al. 2007; Villarreal D'Angelo et al. 2014), where a proper photoionizating photon flux was not included.
Focusing on the outer part of the planetary atmosphere (r ≳ 3Rp), and adjusting the hydrodynamic parameters according the results in Schneiter et al. (2007) and Villarreal D'Angelo et al. (2014), we have done a study of the influence of the high energy photon flux on the escaping part of the atmosphere. The maximum absorption is shown in Fig. 4 (the portion shaded in green which corresponds to the planet transit), where a strong almost linear dependence on the high ionizing flux is found. The importance of the planetary mass-loss rate becomes less obvious (almost negligible) within the accepted range estimated in previous works (Schneiter et al. 2007; Villarreal D'Angelo et al. 2014). At the same time, |$\dot{M}_\mathrm{p}$| does affect the absorption in the tail (after the planetary transit). This result is not surprising, since most of the neutral material is swept, by the stellar wind, to produce the tail which, due to the orbital motion, and gravitational pull, it becomes curved getting exposed to the photoionizing flux incoming from the star (see Figs 1 and 2).
In our simulations, we fix the mass-loss rate of the planet and the stellar flux for each model. This implies, according to the equation (9), to assume a certain value for the heating efficiency at the position where the planetary wind is launched. Hence, in our models, the heating efficiency varies from 2 to 100 per cent. At the present, it is unclear what is the best value for η, but with our models we will be covering almost all possible values. In the literature, several authors tried to constrain this factor: Tian et al. (2005) adopted an η = 0.6 for a pure atomic H atmosphere, Ehrenreich & Désert (2011) obtained an η > 1 based on the values of mass-loss rate from Vidal-Madjar et al. (2003) and Linsky et al. (2010) and the luminosity value from Kashyap, Drake & Saar (2008) and Lammer et al. (2009) suggest η ∼ [10–25] per cent.
As a first approximation, from Fig. 6, we can say that the lowest value of F0 cannot reproduce the observed absorption, hence this models are not expected to be representative of the planetary system parameters. So, the highest values of η (∼[50–100] per cent) are not expected to define the planetary atmosphere of HD 209458b.
It would be important to have some observational constraint to the value of η, as mentioned by Ehrenreich & Désert (2011). This could shed some light into the atmospheric composition of exoplanets.
When comparing our models with the observations, in particular focusing on the Doppler blue-shifted part of the curve (Fig. 6), we see that the v* = 130 km s− 1 peak is better fitted with the S0 photon rate, whereas a lower absolute velocity part of the spectrum (between −40 and −75 km s−1) is better fitted with a larger photon rate (5 × S0) flux. The same trend is observed for larger wind velocity. Certainly with a more fine parameter coverage, one could reproduce the absorption in more detail, however this is beyond the scope of this paper.
In a recent work, Tremblin & Chiang (2013) study the effect of charge exchange in the mixing region of the two winds. With their choice of parameters they are able to reproduce an asymmetric absorption (also favouring the blue wing), in particular the ∼10 per cent absorption at −100 km s−1. Their parameters are similar to our model A1b, but with the inclusion of a treatment for charge exchange between the stellar and planetary winds.
In contrast to the studies of Tremblin & Chiang (2013) and Holmström et al. (2008), our simulations did not include charge exchange but where still able to produce absorption at high blue Doppler-shift velocities, but due to the pure hydrodynamic interaction, along with the global radiation pressure.2 It is clear that both effects are expected to be present, and charge exchange in models as ours would enhance the absorption in the blue. An assessment of their relative (or collective) contribution is left for a follow up study.
The inclusion of the radiation transfer calculation also shows that the previous estimates of the planetary mass-loss rates where a bit low. It is clear from Fig. 4 that the same hydrodynamical parameters result in a overestimation of the absorption respect to the models that do include the photoionization of the tail. Therefore, to reach a similar absorption with the photoionization included requires a larger mass-loss rate. However the mass-loss rates used in this work are compatible to previous estimates.
5 CONCLUSIONS
We used the 3D numerical hydrodynamic code guacho, to simulate the interaction of the wind escaping a hot Jupiter (with parameters resembling HD 209458b) and a photoionized wind coming from a solar-type star (HD 209458).
The ionizing flux was found to have a great influence on the neutral hydrogen escaping from the planet, producing an almost linear effect on the absorption of the wake. With planetary mass-loss rates within the range proposed in Schneiter et al. (2007) and Villarreal D'Angelo et al. (2014), it is possible to find EUV fluxes that reproduce the observed absorption measured in Vidal-Madjar et al. (2003) down to velocities less than −100 km s−1. Performing 3D simulations that include the orbital motion of the planet is a natural way of obtaining a non-symmetric hydrogen envelop that is subject to the incoming stellar photons and wind.
Our models show that the hydrodynamic interaction between the planetary and stellar wind is able to reproduce the asymmetric absorption towards high blue-shifted velocities, as observed in Vidal-Madjar et al. (2003). Such asymmetric absorption has been also attributed to charge-exchange between the fast stellar wind and the slow planetary wind (Tremblin & Chiang 2013).
In a subsequent paper, we plan to include the effects of the stellar magnetic fields together with the charge-exchange interaction. This will allow us to further constraint the photon flux and its influence on the acceleration of the neutral escaping material.
MS acknowledges the financial support from the PICT project 2566/OC-AR and the fellowship grant ‘BECA EXTERNA AGOSTO 2013’ given by CONICET. AE, ACR, and PFV acknowledge support from DGAPA-PAPIIT (UNAM) grants IN109715, IG100214, and CONACYT grant 167611. Authors also thank for financial support from CONACYT-CONICET joint grant CAR 190489.
We have made a convergence test to ensure that this number of photon packets is sufficient. We repeated the same calculation for a model (B2b) with 105, 106, 107, and 5 × 107 photon packets. We then computed the Ly α absorption profile. With 107 rays the results were almost indistinguishable from those with a larger number.
REFERENCES



