Testing the gas mass density profile of galaxy clusters with distance duality relation

Cao, Shuo; Biesiada, Marek; Zheng, Xiaogang; Zhu, Zong-Hong

doi:10.1093/mnras/stv2999

Abstract

In this paper, assuming the validity of distance duality relation, η = D_L(z)(1 + z)⁻²/D_A(z) = 1, where D_A(z) and D_L(z) are the angular and the luminosity distance, respectively, we explore two kinds of gas mass density profiles of clusters: the isothermal β model and the non-isothermal double-β model. In our analysis, performed on 38 massive galaxy clusters observed by Chandra (within the redshift range of 0.14 < z < 0.89), we use two types of cluster gas mass fraction data corresponding to different mass density profiles fitted to the X-ray data. Using two general parameterizations of η(z) (phenomenologically allowing for distance duality violation), we find that the non-isothermal double-β model agrees better with the distance duality relation, while the isothermal β model tends to be marginally incompatible with the Etherington theorem at 68.3 per cent confidence level (CL). However, current accuracy of the data does not allow to distinguish between the two models for the gas-density distribution at a significant level.

cosmology: miscellaneous, distance scale, X-rays: galaxies: clusters

1 INTRODUCTION

The distance duality relation (DDR thereafter): D_L/D_A(1 + z)⁻² = 1, which relates the luminosity distance D_L(z) to the angular diameter distance D_A(z) at a given redshift z, is known to hold in any metric theory of gravity. Hence, it has extensively been applied in modern observational cosmology (Schneider, Ehlers & Falco 1992; Bassett & Kunz 2004; Cunha, Marassi & Santos 2007; Zhu et al. 2008; Cao & Liang 2011; Holanda, Lima & Ribeiro 2011; Mantz et al. 2014). Until now, different astronomical observations have been used to check the validity of this reciprocity relation using the following expression

\begin{equation} \frac{D_{\scriptstyle L}}{D_{\scriptstyle A}}{(1+z)}^{-2}= \eta (z), \end{equation}

(1)

where η(z) could be a function of the redshift z (of course DDR corresponds to η(z) = const. = 1). For instance, Uzan, Aghanim & Mellier (2004) used the D_A estimated from Sunyaev–Zeldovich effect (SZE) and X-ray surface brightness of 18 galaxy clusters (Reese et al. 2002), and found DDR consistent with the observations at 1σ confidence level (CL). The validity of the DDR was further confirmed by De Bernardis, Giusarma & Melchiorri (2006), with a larger sample of angular diameter distances from 38 galaxy clusters (Bonamente et al. 2006). More recently, instead of testing the reciprocity relation itself, Holanda et al. (2011) discussed the possibility of using DDR (i.e. assuming that it is true) to test the geometrical shape of galaxy clusters. They used two angular diameter distance D_A measurements based on two different cluster geometries: ellipsoidal β model underlying De Filippis et al. (2005) data and spherical β model assumed by (Bonamente et al. 2006). They found that ellipsoidal geometry was more consistent with the DDR, and concluded that it was a better model to describe galaxy clusters.

In this paper, we propose a new method to derive observed η_obs(z) parameter from the cluster gas mass fraction f_gas = M_gas/M_tot inferred from X-ray data, and we use the assumption that DDR should be valid (i.e. η(z) = 1) to discuss appropriateness of two cluster gas mass density profiles assumed. More specifically, we use two data sets of cluster gas mass fraction derived from Chandra X-ray data (LaRoque et al. 2006) under two different assumptions about the gas mass density profiles: isothermal β model and non-isothermal double-β model.

In our analysis we consider two particular parameterizations of phenomenological η(z) dependence:(i) η = η₀ + η_P1z; (ii) η(z) = η₀ + η_P2z/(1 + z). The first expression is a linear parametrization equivalent to the first order Taylor expansion in redshift. The second one is inspired by the commonly used Chevalier-Polarski-Linder (CPL) parametrization for dark energy equation of state (Chevallier & Polarski 2001; Linder 2003) and is equivalent to the first order expansion in the scale factor a(t) which is the only gravitational degree of freedom in Freedman–Robertson–Walker cosmology. These two parametrizations have been extensively used to investigate the properties of dark energy in the literature (Cao et al. 2012; Cao & Zhu 2014; Cao et al. 2015). Assuming that the Etherington theorem is valid (which is quite reasonable assumption), the best-fitting value obtained with a given data set should be η₀ = 1 and η_P = 0. Our results indicate that the non-isothermal double-β model tends to be more compatible with the reciprocity relation than the isothermal β model. This kind of result is an interesting example of how general principles (like DDR) could be used to assess the validity of assumptions concerning local physical conditions.

This paper is organized as follows. In Section 2, we introduce two samples of gas mass fraction data from 38 X-ray luminous galaxy clusters and their corresponding mass density profiles. Statistical method and constraint results on η(z) parameters are presented in Section 3. Finally, we summarize our main conclusions and make a discussion in Section 4.

2 GALAXY CLUSTER SAMPLES

The cluster gas mass fraction is defined as a ratio of the X-ray emitting gas mass to the total mass of a cluster, i.e. f_gas = M_gas/M_tot. Gas mass M_gas is derived from the X-ray surface brightness while the total mass M_tot can be obtained by assuming that the gas is in hydrostatic equilibrium with the cluster Navarro-Frenk-White (NFW) potential. In order to perform appropriate calculations, one needs the gas mass density profile. Therefore, in our analysis aimed at constraining free parameters (η₀, η_P) in general expression for η(z), we will use the gas mass fractions obtained with different gas mass density profiles.

In order to calculate η_obs from the data (according to equation (6) shown below) we use two sets of gas mass fraction f_gas both derived from a sample of 38 luminous X-ray clusters with temperatures T_gas > 5 keV, observed by Chandra X-ray Observatory (LaRoque et al. 2006) located at redshifts from z = 0.14 to z = 0.89. In fact, LaRoque et al. (2006) presented results of their analysis using exclusively X-ray data (for isothermal β-model) and a combination of Chandra X-ray data and BIMA/OVRO interferometric radio SZE data for the double-β model. However, according to Holanda, Gonçalves & Alcaniz (2012), the gas mass fraction measurement via SZE depends only on the angular diameter distance, so it is insensitive to the validity of the DDR. Therefore, only the high resolution Chandra X-ray data are considered in our analysis. The above mentioned two sets of f_gas were obtained within the most commonly used isothermal β model and under assumption of the non-isothermal double-β model, respectively.

Fig. 1 displays these data and their observational statistical uncertainties. We will also consider possible systematic uncertainties influencing the derived gas mass fraction following the discussion in (Bonamente et al. 2006) concerning their method of calculating the angular diameter distances of galaxy clusters. The effect of these systematical uncertainties on the gas mass fractions is summarized in table 3 of LaRoque et al. (2006). Note that the systematic difference between f_gas derived from the isothermal β model and the double-β model still exists. From a purely statistical point of view, non-parametric Wilcoxon signed rank test reveals that difference between these two data sets is significant at the level of p = 0.0001. More specifically, the assumption of isothermality can potentially affect the gas mass fraction measurements by about (−5 per cent) through its effects on both gas mass and total mass. Therefore, an appropriate systematic uncertainty will be assigned to the gas mass fractions derived from the isothermal β model. In order to show the major sources of uncertainty in the present analysis, we display the ratio between systematic and statistical uncertainties for these data in Fig. 2.

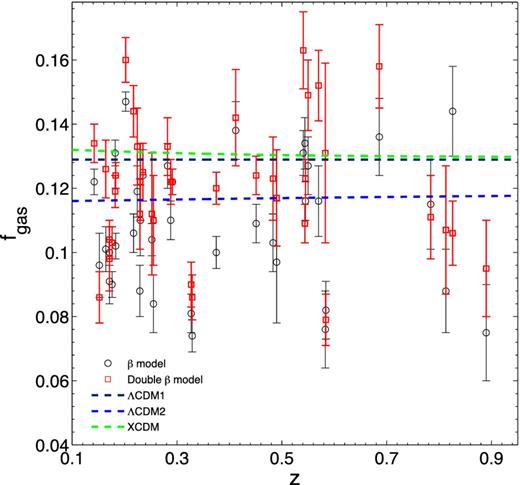
$The cluster gas mass fraction data derived from a sample of 38 luminous X-ray clusters observed by Chandra X-ray Observatory (LaRoque et al. 2006). Black circles and red squares with the error bars correspond to the results obtained under the assumption of isothermal β model and non-isothermal double-β model, respectively. The predictions of fgas(z) under the assumption of DDR are also overplotted, for the three reference cosmologies (see Table 1) considered in this paper.$

Figure 1.

The cluster gas mass fraction data derived from a sample of 38 luminous X-ray clusters observed by Chandra X-ray Observatory (LaRoque et al. 2006). Black circles and red squares with the error bars correspond to the results obtained under the assumption of isothermal β model and non-isothermal double-β model, respectively. The predictions of f_gas(z) under the assumption of DDR are also overplotted, for the three reference cosmologies (see Table 1) considered in this paper.

Open in new tab Download slide

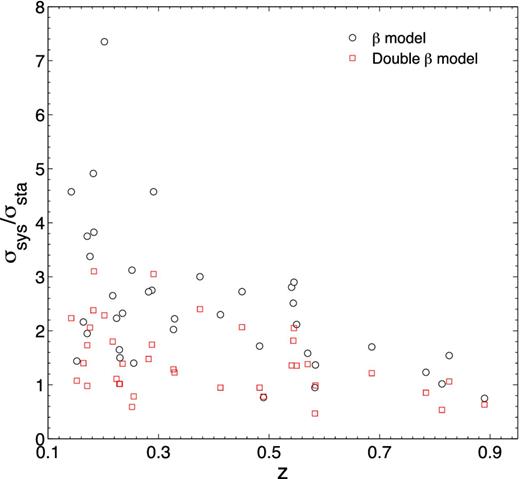
$The ratio between systematic and statistical uncertainties for the cluster gas mass fraction data. Black circles and red squares with the error bars correspond to the results obtained under the assumption of isothermal β model and non-isothermal double-β model, respectively.$

Figure 2.

The ratio between systematic and statistical uncertainties for the cluster gas mass fraction data. Black circles and red squares with the error bars correspond to the results obtained under the assumption of isothermal β model and non-isothermal double-β model, respectively.

Open in new tab Download slide

In the frequently used isothermal β model, the 3-dimensional electron number density n_e can be written as (Cavaliere & Fusco-Femiano 1976, 1978; Grego et al. 2001; Reese et al. 2002; Ettori et al. 2004)

\begin{equation} n_{\rm e}(r) = n_{{\rm e}0} \left(1 + \frac{r^2}{r_c^2} \right)^{-3\beta /2}, \end{equation}

(2)

where n_e0 is the central electron number density, r is the radius from the centre of the cluster, r_c is the core radius of the intracluster medium (ICM), and β is a power-law index. Although it has been widely used as a useful assumption in galaxy cluster studies, the isothermal β model still encounters some problems with describing the central emission excess seen in some clusters (Mohr, Mathiesen & Evrard 1999; LaRoque et al. 2006) and the X-ray surface brightness at r > (1–1.5) r₂₅₀₀, where r₂₅₀₀ is the radius at which the mean enclosed mass density is equal to 2500ρ_crit. Such features, non-compatible with the isothermal β model have been observed in archival ROSAT data and numerical simulations (Mohr et al. 1999; Borgani et al. 2004).

Therefore, in order to overcome the limitations of the simplest isothermal β model we have also considered a more sophisticated cluster plasma model, the non-isothermal double-β model. More specifically, its density profile is assumed to be of the following form:

\begin{eqnarray} n_{\rm e}(r) = n_{{\rm e}0} \left[ f \left(1 + \frac{r^2}{\,r_{c_1}^2}\right) ^{-3\beta /2} + (1-f)\left(1 + \frac{r^2}{\,r_{c_2}^2}\right)^{-3\beta /2}\right],\nonumber\\ \end{eqnarray}

(3)

where |$r_{{\rm c}_1}$| is the core radius representing the narrow, peaked central density component contributing to the central density n_e0 by a factor 0 ≤ f ≤ 1, and |$r_{{\rm c}_2}$| is the other core radius describing the broad, shallow outer density profile.

Let us now describe how we extracted the observed DDR parameter η_obs from the cluster gas mass fraction data. Massive galaxy cluster are the largest known bound systems in the Universe and are expected to provide a unique information of the matter content of the Universe. The baryonic-to-total mass ratio of clusters should closely match the ratio of Ω_b/Ω_m, where Ω_b and Ω_m are the present dimensionless density parameter of the baryonic matter and dust matter, respectively. Since the reconstructed f_gas depends on the angular diameter distances at different redshifts, |$f_{{\rm gas}} \propto D_{A}^{1.5}(z)$|⁠, a number of studies have used it to probe the acceleration of the Universe and thus the properties of dark energy (Allen et al. 2004, 2008; Ettori et al. 2009; Cao & Zhu 2014).

Our starting point is the following general expression for the gas mass fraction (see e.g. Allen et al. 2008; Holanda et al. 2011):

\begin{eqnarray} f_{\rm gas}(z)&=& KA\Upsilon \left(\frac{\Omega _{\rm b}}{\Omega _{\rm m}}\right) \left(\frac{D_L^{\rm ref}(z)}{D_L(z)}\right) \left(\frac{D_A^{\rm ref}(z)}{D_A(z)}\right)^{1/2} \nonumber \\ &=& KA\Upsilon \left(\frac{\Omega _{\rm b}}{\Omega _{\rm m}}\right) \eta _{{\rm obs}}^{-3/2} \left(\frac{D_A^{\rm ref}(z)}{D_A(z)}\right)^{3/2} \end{eqnarray}

(4)

Here, η_obs is the value of the DDR parameter implied by observations. K is a calibration constant characterizing the systematic uncertainty on the overall normalization (Mantz et al. 2014). We use K = 0.94 ± 0.09 based on recent results from weak lensing mass measurements (Allen et al. 2013; Applegate et al. 2014). A is an angular correction factor quantifying the shift of the angular scale |$\theta ^{\rm }_{2500}$| of the r₂₅₀₀ radius from |$\theta ^{\rm ref}_{2500}$| obtained in the reference cosmology assumed to be ΛCDM (Mantz et al. 2014). So, the A factor reads

\begin{equation} A = \left(\frac{\theta ^{\rm ref}_{2500}}{\theta ^{\rm }_{2500}}\right)^{\varepsilon } \sim \left(\frac{H(z) D_{\rm A}(z)}{H^{\rm ref}(z) D_{\rm A}^{\rm ref}(z)}\right)^{\varepsilon }\,, \end{equation}

(5)

where the exponent ε assessed for the 0.8–1.2 θ₂₅₀₀ shell (Allen et al. 2013; Mantz et al. 2014) is ε = 0.442 ± 0.035. ϒ is the gas depletion parameter related to thermodynamic history of X-ray emitting gas in the course of cluster formation. More specifically, this factor is modelled as ϒ₂₅₀₀ = ϒ₀(1 + α_ϒz). We adopt uniform priors, ϒ₀ = 0.845 ± 0.042 and α_ϒ = 0.00 ± 0.05 in our paper. This is motivated by the recent hydrodynamic simulations of the hottest clusters within 0.8–1.2 r₂₅₀₀ shells (Battaglia et al. 2012; Planelles et al. 2013). Ω_b is fixed at the best-fitting value Ω_bh² = 0.02205 ± 0.00028 suggested by Planck observations (Planck Collaboration XVI 2014). D_A(z) denotes the true angular diameter distance and |$D_{\rm A}^{\rm ref}(z)$| is the angular diameter distance calculated in the reference cosmological model, which is a flat ΛCDM model with Ω_m = 0.30, h = 0.70 (standard concordance model).

By combing equations (4) and (5), we can obtain the observed value of η_obs as

\begin{equation} \eta _{{\rm obs}}^{3/2}= K\Upsilon _{\rm 0}(1+\alpha _{\rm \Upsilon }z)\frac{\Omega _{\rm b}}{\Omega _{\rm m}}f_{\rm gas}^{-1} \left(\frac{H(z)}{H^{\rm ref}(z)}\right)^{\varepsilon } \left( \frac{D_A^{\rm ref}(z)}{D_A(z)}\right)^{3/2-\varepsilon }.\!\!\! \end{equation}

(6)

It is apparent that in our analysis, η(z) function includes two effects: possible DDR violation and our uncertainty with respect to the true cosmological model. Since our main goal is to test cluster gas mass density profiles based on the validity of DDR, D_A(z) will be calculated in three ways. First, by assuming the standard model with Ω_m = 0.30 and H₀ = 70.0 km s⁻¹ Mpc⁻¹, which is equivalent to the reference cosmology in cluster studies and very similar to the WMAP9 constraints (Komatsu et al. 2011). Secondly, by taking the best-fitting matter density parameter and Hubble constant given by Planck Collaboration: Ω_m = 0.315 and H₀ = 67.3 km s⁻¹ Mpc⁻¹ (Planck Collaboration XVI 2014), in the framework of ΛCDM model. And thirdly, by considering the XCDM model, i.e. the one in which the equation of state p = wρ for dark energy has constant w parameter. More precisely, we take the best-fitting parameters from Planck+WMAP9 data: Ω_m = 0.294, w = −1.05, and H₀ = 70.4 km s⁻¹ Mpc⁻¹ (Cai, Guo & Tang 2014). Summary of three cosmologies adopted here can be found in Table 1. For comparison, the predictions of f_gas(z) within these three cosmologies under the assumption of DDR and using the central values of four nuisance parameters are also shown in Fig. 1.

Table 1.

Open in new tab

Parameters of three cosmologies considered: standard concordance ΛCDM model (ΛCDM1), ΛCDM best fitted to Planck data (ΛCDM1), XCDM model best fitted to Planck+WMAP9 data.

Cosmology	Cosmological parameters
ΛCDM1	Ω_m = 0.30, H₀ = 70.0 km s⁻¹ Mpc⁻¹
ΛCDM2	Ω_m = 0.315, H₀ = 67.3 km s⁻¹ Mpc⁻¹
XCDM	Ω_m = 0.294, w = −1.05, H₀ = 70.4 km s⁻¹ Mpc⁻¹

Cosmology	Cosmological parameters
ΛCDM1	Ω_m = 0.30, H₀ = 70.0 km s⁻¹ Mpc⁻¹
ΛCDM2	Ω_m = 0.315, H₀ = 67.3 km s⁻¹ Mpc⁻¹
XCDM	Ω_m = 0.294, w = −1.05, H₀ = 70.4 km s⁻¹ Mpc⁻¹

Table 1.

Open in new tab

Parameters of three cosmologies considered: standard concordance ΛCDM model (ΛCDM1), ΛCDM best fitted to Planck data (ΛCDM1), XCDM model best fitted to Planck+WMAP9 data.

Cosmology	Cosmological parameters
ΛCDM1	Ω_m = 0.30, H₀ = 70.0 km s⁻¹ Mpc⁻¹
ΛCDM2	Ω_m = 0.315, H₀ = 67.3 km s⁻¹ Mpc⁻¹
XCDM	Ω_m = 0.294, w = −1.05, H₀ = 70.4 km s⁻¹ Mpc⁻¹

Cosmology	Cosmological parameters
ΛCDM1	Ω_m = 0.30, H₀ = 70.0 km s⁻¹ Mpc⁻¹
ΛCDM2	Ω_m = 0.315, H₀ = 67.3 km s⁻¹ Mpc⁻¹
XCDM	Ω_m = 0.294, w = −1.05, H₀ = 70.4 km s⁻¹ Mpc⁻¹

3 ANALYSIS AND RESULTS

As we already mentioned, η(z) function captures phenomenologically our uncertainty not only about the DDR but also about true cosmological model and possibly other systematics. Therefore it is reasonable to treat it as a function of redshift and start with two quite natural parameterizations:

\begin{eqnarray} \eta (z)& =& \eta _0+\eta _{P1}z, \nonumber\\ \eta (z)& =& \eta _0+\eta _{P2}z/(1+z), \end{eqnarray}

(7)

where η₀ and η_P parameters quantify the shift from the expected standard result (η₀ = 1, η_P = 0).

Using routines available within cosmomc package (Lewis & Bridle 2002), we preformed Monte Carlo simulations of the posterior likelihood |${\cal L} \sim \exp {(- \chi ^2 / 2)}$|⁠, where

\begin{equation} \chi ^{2} = \sum \frac{{\left[\eta (z)- \eta _{{\rm obs}}(z) \right] }^{2}}{\sigma ^2_{\eta _{{\rm obs}}} }, \end{equation}

(8)

η_obs(z) was calculated from the f_gas data via equation (6) and |$\sigma _{\eta _{{\rm obs}}}$| was calculated according to the standard law of uncertainty propagation. Besides the statistical errors of X-ray observations, we have also considered systematic errors concerning instrument calibration ±6 per cent, X-ray background +2 per cent, hydrostatic equilibrium −10 per cent, and isothermal assumption −5 per cent (LaRoque et al. 2006). Combined in quadrature, they result in a typical relative error of 10 per cent for the f_gas measurements with isothermal β model and 15 per cent for the f_gas measurements with the non-isothermal double-β model. We would like to stress, however, that according to recent numerical simulations and comparisons between X-ray and lensing masses (Lau, Kravtsov & Nagai 2009; Landry et al. 2013; Giles et al. 2015), the mass obtained under hydrostatic equilibrium assumption underestimates the true mass especially at large radii. This results in overestimating the gas mass fraction and the systematic uncertainties due to hydrostatic equilibrium assumption can eventually be larger than 10 per cent. This effect still needs to be investigated with more available data. In our analysis, based on the results of (Lau et al. 2009; Landry et al. 2013), a systematic uncertainty of +10 per cent on the total mass M_tot is applied for all clusters, which corresponds to a systematic error of −10 per cent on f_gas.

We performed an Markov Chain Monte Carlo analysis and marginalized over the nuisance parameters (K, ϒ₀, α_ϒ, ε) by multiplying the probability distribution functions and then integrating (Ganga et al. 1997). When D_A(z) is calculated within the fiducial model (Ω_m = 1 − Ω_Λ, H₀) = (0.30, 70 km s⁻¹ Mpc⁻¹) consistent with WMAP9 observations, we obtain the results shown in Table 2. Obviously both statistical and systematic uncertainties should be included in the analysis. Therefore they have been displayed explicitly in Table 2. In the case of the first parametrization η(z) = η₀ + η_P1z, the best-fitting η parameters are η₀ = 1.068 ± 0.133, η_P1 = −0.084 ± 0.187 (stat+sys) for the isothermal β model and η₀ = 0.991 ± 0.117, η_P1 = −0.037 ± 0.147 (stat+sys) for the non-isothermal double-β model. One can see that gas mass fractions obtained from the non-isothermal double beta model, are in better agreement with the reciprocity relation (η₀ = 1, η_P1 = 0). However, from the statistical point of view this preference is marginal.

Table 2.

Open in new tab

Summary of the results for η(z) = η₀ + η_P1z and η(z) = η₀ + η_P2z/(1 + z), respectively, at 1σ confidence level for the β model and double-β model. The statistical and systematic uncertainties in η are shown separately. Two samples including the n = 38 full sample and the n = 29 sub-sample are used (see text for definitions). Source of cosmological priors are also given in brackets.

β model: parameterizations (sample/cosmology)	η₀	η_P1
η(z) = η₀ + η_P1z (Full sample/ΛCDM1)	η₀ = 1.068 ± 0.099(stat) ± 0.034(sys)	η_P1 = −0.084 ± 0.058(stat) ± 0.129(sys)
η(z) = η₀ + η_P2z/(1 + z) (Full sample/ΛCDM1)	η₀ = 1.080 ± 0.104(stat) ± 0.051(sys)	η_P2 = −0.148 ± 0.117(stat) ± 0.276(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM1)	η₀ = 1.108 ± 0.115(stat) ± 0.033(sys)	η_P1 = −0.144 ± 0.075(stat) ± 0.312(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM2)	η₀ = 1.028 ± 0.104(stat) ± 0.037(sys)	η_P1 = −0.127 ± 0.072(stat) ± 0.127(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/ΛCDM2)	η₀ = 1.060 ± 0.112(stat) ± 0.047(sys)	η_P2 = −0.276 ± 0.134(stat) ± 0.282(sys)
η(z) = η₀ + η_P1z (Sub-sample/XCDM)	η₀ = 1.242 ± 0.127(stat) ± 0.041(sys)	η_P1 = −0.265 ± 0.087(stat) ± 0.148(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/XCDM)	η₀ = 1.285 ± 0.135(stat) ± 0.052(sys)	η_P2 = −0.529 ± 0.166(stat) ± 0.305(sys)
Double-β model: parameterizations (sample/cosmology)	η₀	η_P2
η(z) = η₀ + η_P1z (Full sample/ΛCDM1)	η₀ = 0.991 ± 0.102(stat) ± 0.015(sys)	η_P1 = −0.037 ± 0.060(stat) ± 0.087(sys)
η(z) = η₀ + η_P2z/(1 + z) (Full sample/ΛCDM1)	η₀ = 1.002 ± 0.104(stat) ± 0.027(sys)	η_P2 = −0.092 ± 0.114(stat) ± 0.178(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM1)	η₀ = 0.981 ± 0.104(stat) ± 0.017(sys)	η_P1 = −0.023 ± 0.069(stat) ± 0.089(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/ΛCDM1)	η₀ = 0.996 ± 0.108(stat) ± 0.030(sys)	η_P2 = −0.078 ± 0.132(stat) ± 0.184(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM2)	η₀ = 0.915 ± 0.095(stat) ± 0.018)(sys)	η_P1 = −0.015 ± 0.064(stat) ± 0.082(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/ΛCDM2)	η₀ = 0.924 ± 0.102(stat) ± 0.024(sys)	η_P2 = −0.049 ± 0.121(stat) ± 0.182(sys)
η(z) = η₀ + η_P1z (Sub-sample/XCDM)	η₀ = 1.101 ± 0.117(stat) ± 0.024(sys)	η_P1 = −0.139 ± 0.078(stat) ± 0.08(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/XCDM)	η₀ = 1.123 ± 0.121(stat) ± 0.027(sys)	η_P2 = −0.257 ± 0.143(stat) ± 0.196(sys)

β model: parameterizations (sample/cosmology)	η₀	η_P1
η(z) = η₀ + η_P1z (Full sample/ΛCDM1)	η₀ = 1.068 ± 0.099(stat) ± 0.034(sys)	η_P1 = −0.084 ± 0.058(stat) ± 0.129(sys)
η(z) = η₀ + η_P2z/(1 + z) (Full sample/ΛCDM1)	η₀ = 1.080 ± 0.104(stat) ± 0.051(sys)	η_P2 = −0.148 ± 0.117(stat) ± 0.276(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM1)	η₀ = 1.108 ± 0.115(stat) ± 0.033(sys)	η_P1 = −0.144 ± 0.075(stat) ± 0.312(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM2)	η₀ = 1.028 ± 0.104(stat) ± 0.037(sys)	η_P1 = −0.127 ± 0.072(stat) ± 0.127(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/ΛCDM2)	η₀ = 1.060 ± 0.112(stat) ± 0.047(sys)	η_P2 = −0.276 ± 0.134(stat) ± 0.282(sys)
η(z) = η₀ + η_P1z (Sub-sample/XCDM)	η₀ = 1.242 ± 0.127(stat) ± 0.041(sys)	η_P1 = −0.265 ± 0.087(stat) ± 0.148(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/XCDM)	η₀ = 1.285 ± 0.135(stat) ± 0.052(sys)	η_P2 = −0.529 ± 0.166(stat) ± 0.305(sys)
Double-β model: parameterizations (sample/cosmology)	η₀	η_P2
η(z) = η₀ + η_P1z (Full sample/ΛCDM1)	η₀ = 0.991 ± 0.102(stat) ± 0.015(sys)	η_P1 = −0.037 ± 0.060(stat) ± 0.087(sys)
η(z) = η₀ + η_P2z/(1 + z) (Full sample/ΛCDM1)	η₀ = 1.002 ± 0.104(stat) ± 0.027(sys)	η_P2 = −0.092 ± 0.114(stat) ± 0.178(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM1)	η₀ = 0.981 ± 0.104(stat) ± 0.017(sys)	η_P1 = −0.023 ± 0.069(stat) ± 0.089(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/ΛCDM1)	η₀ = 0.996 ± 0.108(stat) ± 0.030(sys)	η_P2 = −0.078 ± 0.132(stat) ± 0.184(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM2)	η₀ = 0.915 ± 0.095(stat) ± 0.018)(sys)	η_P1 = −0.015 ± 0.064(stat) ± 0.082(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/ΛCDM2)	η₀ = 0.924 ± 0.102(stat) ± 0.024(sys)	η_P2 = −0.049 ± 0.121(stat) ± 0.182(sys)
η(z) = η₀ + η_P1z (Sub-sample/XCDM)	η₀ = 1.101 ± 0.117(stat) ± 0.024(sys)	η_P1 = −0.139 ± 0.078(stat) ± 0.08(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/XCDM)	η₀ = 1.123 ± 0.121(stat) ± 0.027(sys)	η_P2 = −0.257 ± 0.143(stat) ± 0.196(sys)

Table 2.

Open in new tab

Summary of the results for η(z) = η₀ + η_P1z and η(z) = η₀ + η_P2z/(1 + z), respectively, at 1σ confidence level for the β model and double-β model. The statistical and systematic uncertainties in η are shown separately. Two samples including the n = 38 full sample and the n = 29 sub-sample are used (see text for definitions). Source of cosmological priors are also given in brackets.

β model: parameterizations (sample/cosmology)	η₀	η_P1
η(z) = η₀ + η_P1z (Full sample/ΛCDM1)	η₀ = 1.068 ± 0.099(stat) ± 0.034(sys)	η_P1 = −0.084 ± 0.058(stat) ± 0.129(sys)
η(z) = η₀ + η_P2z/(1 + z) (Full sample/ΛCDM1)	η₀ = 1.080 ± 0.104(stat) ± 0.051(sys)	η_P2 = −0.148 ± 0.117(stat) ± 0.276(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM1)	η₀ = 1.108 ± 0.115(stat) ± 0.033(sys)	η_P1 = −0.144 ± 0.075(stat) ± 0.312(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM2)	η₀ = 1.028 ± 0.104(stat) ± 0.037(sys)	η_P1 = −0.127 ± 0.072(stat) ± 0.127(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/ΛCDM2)	η₀ = 1.060 ± 0.112(stat) ± 0.047(sys)	η_P2 = −0.276 ± 0.134(stat) ± 0.282(sys)
η(z) = η₀ + η_P1z (Sub-sample/XCDM)	η₀ = 1.242 ± 0.127(stat) ± 0.041(sys)	η_P1 = −0.265 ± 0.087(stat) ± 0.148(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/XCDM)	η₀ = 1.285 ± 0.135(stat) ± 0.052(sys)	η_P2 = −0.529 ± 0.166(stat) ± 0.305(sys)
Double-β model: parameterizations (sample/cosmology)	η₀	η_P2
η(z) = η₀ + η_P1z (Full sample/ΛCDM1)	η₀ = 0.991 ± 0.102(stat) ± 0.015(sys)	η_P1 = −0.037 ± 0.060(stat) ± 0.087(sys)
η(z) = η₀ + η_P2z/(1 + z) (Full sample/ΛCDM1)	η₀ = 1.002 ± 0.104(stat) ± 0.027(sys)	η_P2 = −0.092 ± 0.114(stat) ± 0.178(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM1)	η₀ = 0.981 ± 0.104(stat) ± 0.017(sys)	η_P1 = −0.023 ± 0.069(stat) ± 0.089(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/ΛCDM1)	η₀ = 0.996 ± 0.108(stat) ± 0.030(sys)	η_P2 = −0.078 ± 0.132(stat) ± 0.184(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM2)	η₀ = 0.915 ± 0.095(stat) ± 0.018)(sys)	η_P1 = −0.015 ± 0.064(stat) ± 0.082(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/ΛCDM2)	η₀ = 0.924 ± 0.102(stat) ± 0.024(sys)	η_P2 = −0.049 ± 0.121(stat) ± 0.182(sys)
η(z) = η₀ + η_P1z (Sub-sample/XCDM)	η₀ = 1.101 ± 0.117(stat) ± 0.024(sys)	η_P1 = −0.139 ± 0.078(stat) ± 0.08(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/XCDM)	η₀ = 1.123 ± 0.121(stat) ± 0.027(sys)	η_P2 = −0.257 ± 0.143(stat) ± 0.196(sys)

β model: parameterizations (sample/cosmology)	η₀	η_P1
η(z) = η₀ + η_P1z (Full sample/ΛCDM1)	η₀ = 1.068 ± 0.099(stat) ± 0.034(sys)	η_P1 = −0.084 ± 0.058(stat) ± 0.129(sys)
η(z) = η₀ + η_P2z/(1 + z) (Full sample/ΛCDM1)	η₀ = 1.080 ± 0.104(stat) ± 0.051(sys)	η_P2 = −0.148 ± 0.117(stat) ± 0.276(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM1)	η₀ = 1.108 ± 0.115(stat) ± 0.033(sys)	η_P1 = −0.144 ± 0.075(stat) ± 0.312(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM2)	η₀ = 1.028 ± 0.104(stat) ± 0.037(sys)	η_P1 = −0.127 ± 0.072(stat) ± 0.127(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/ΛCDM2)	η₀ = 1.060 ± 0.112(stat) ± 0.047(sys)	η_P2 = −0.276 ± 0.134(stat) ± 0.282(sys)
η(z) = η₀ + η_P1z (Sub-sample/XCDM)	η₀ = 1.242 ± 0.127(stat) ± 0.041(sys)	η_P1 = −0.265 ± 0.087(stat) ± 0.148(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/XCDM)	η₀ = 1.285 ± 0.135(stat) ± 0.052(sys)	η_P2 = −0.529 ± 0.166(stat) ± 0.305(sys)
Double-β model: parameterizations (sample/cosmology)	η₀	η_P2
η(z) = η₀ + η_P1z (Full sample/ΛCDM1)	η₀ = 0.991 ± 0.102(stat) ± 0.015(sys)	η_P1 = −0.037 ± 0.060(stat) ± 0.087(sys)
η(z) = η₀ + η_P2z/(1 + z) (Full sample/ΛCDM1)	η₀ = 1.002 ± 0.104(stat) ± 0.027(sys)	η_P2 = −0.092 ± 0.114(stat) ± 0.178(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM1)	η₀ = 0.981 ± 0.104(stat) ± 0.017(sys)	η_P1 = −0.023 ± 0.069(stat) ± 0.089(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/ΛCDM1)	η₀ = 0.996 ± 0.108(stat) ± 0.030(sys)	η_P2 = −0.078 ± 0.132(stat) ± 0.184(sys)
η(z) = η₀ + η_P1z (Sub-sample/ΛCDM2)	η₀ = 0.915 ± 0.095(stat) ± 0.018)(sys)	η_P1 = −0.015 ± 0.064(stat) ± 0.082(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/ΛCDM2)	η₀ = 0.924 ± 0.102(stat) ± 0.024(sys)	η_P2 = −0.049 ± 0.121(stat) ± 0.182(sys)
η(z) = η₀ + η_P1z (Sub-sample/XCDM)	η₀ = 1.101 ± 0.117(stat) ± 0.024(sys)	η_P1 = −0.139 ± 0.078(stat) ± 0.08(sys)
η(z) = η₀ + η_P2z/(1 + z) (Sub-sample/XCDM)	η₀ = 1.123 ± 0.121(stat) ± 0.027(sys)	η_P2 = −0.257 ± 0.143(stat) ± 0.196(sys)

According to the findings of LaRoque et al. (2006), some objects: Abell 665, ZW 3146, RX J1347.5−1145, MS 1358.4 + 6245, Abell 1835, MACS J1423+2404, Abell 1914, Abell 2163, Abell 2204 have questionable reduced χ². By excluding these objects from the full sample we obtained a sub-sample of 29 galaxy clusters, on which we performed a similar analysis. The results are displayed in Fig. 3. As compared with the previous case, one can see that the non-isothermal double-β model is in even much better agreement with the DDR (η₀ = 0.981 ± 0.121, η_P1 = −0.023 ± 0.158; ± corresponds to 68.3 per cent CL) than the isothermal β model (η₀ = 1.108 ± 0.148, η_P1 = −0.144 ± 0.387). When compared with the previous analysis, the incompatibility of the isothermal β-model with the validity of DDR is clearly more evident at 1σ, although the significance of this conclusion is not high enough from the statistical point of view.

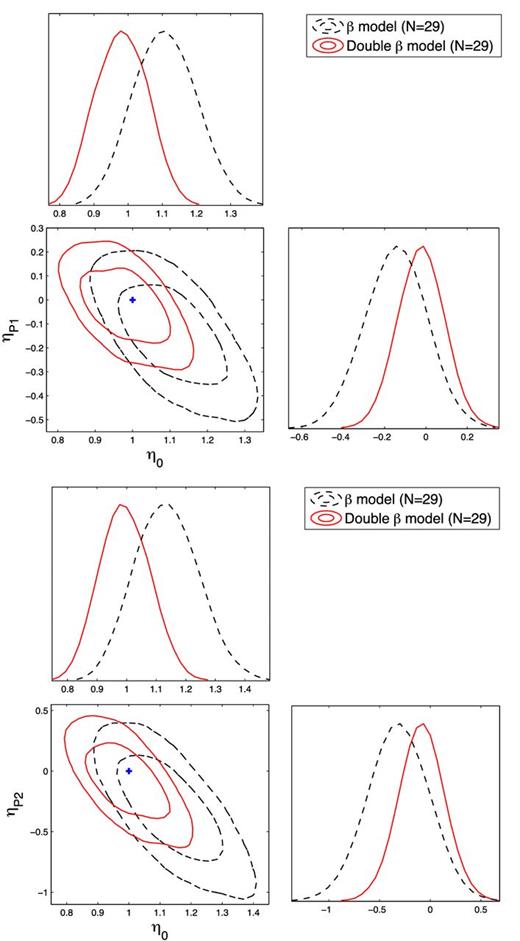
Confidence contours and marginalized likelihood distribution functions for the parameters in η(z) = η0 + ηP1z and η(z) = η0 + ηP2z/(1 + z) relation. Black dashed lines and red lines correspond to the fits obtained on the full n = 29 sub-sample under the assumption of isothermal β model and non-isothermal double-β model, respectively. The blue cross represents the expected case when the DDR holds exactly (η0 = 1, ηP1,2 = 0).

Figure 3.

Confidence contours and marginalized likelihood distribution functions for the parameters in η(z) = η₀ + η_P1z and η(z) = η₀ + η_P2z/(1 + z) relation. Black dashed lines and red lines correspond to the fits obtained on the full n = 29 sub-sample under the assumption of isothermal β model and non-isothermal double-β model, respectively. The blue cross represents the expected case when the DDR holds exactly (η₀ = 1, η_P1,2 = 0).

Open in new tab Download slide

In the case of second parametrization η(z) = η₀ + η_P2z/(1 + z), results for the n = 38 full sample and n = 29 sub-sample, are shown in Table 2. Respective confidence regions on the η₀ − η_P2 plane and marginalized likelihood distributions for the parameters are shown in Fig. 3. As one can see the double-β model again seems to be favoured over the isothermal β-model.

As we already mentioned, one can contemplate other types of best-fitting ‘true’ cosmology instead of the standard concordance ΛCDM model. Therefore, we also considered the ΛCDM model but with parameters bets fitted to the Planck data. In this case, we only analysed the n = 29 sub-sample and the results are presented on Table 2 and Fig. 4. Moreover, since ΛCDM while useful has its own conceptual problems and might not be the ultimate model of the Universe, we have also considered quintessential XCDM model. In particular, we have taken its parameters (w, Ω_m = 1 − Ω_Λ, H₀) = (−1.05, 0.294, 70.4 km s⁻¹ Mpc⁻¹) according to Cai et al. (2014) best fit to Planck+WMAP9 data. The results obtained with n = 29 sub-sample are presented in Table 2 and Fig. 5.

Figure 4.

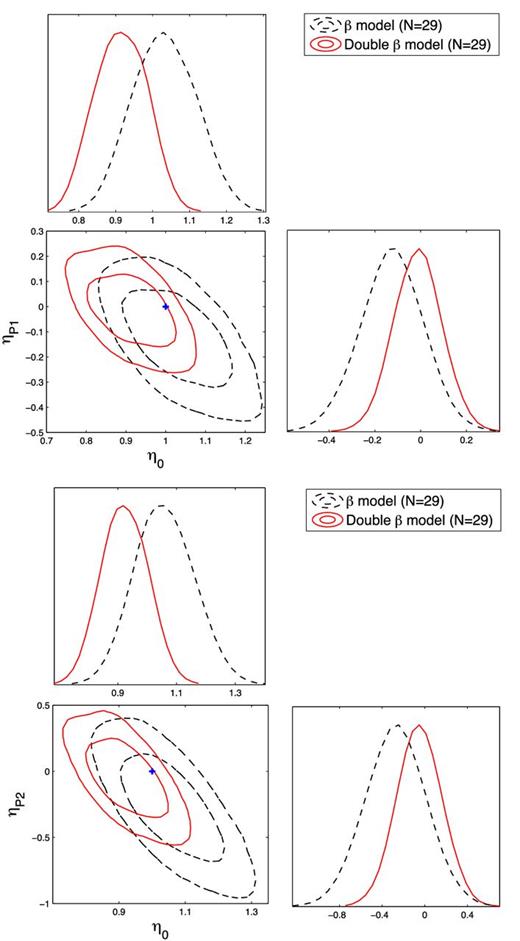
Confidence contours and marginalized likelihood distribution functions for the η parameters for the case when Planck best-fitting ΛCDM parameters were taken to represent a ‘true’ cosmology. Black dashed lines and red lines correspond to the fits obtained on the n = 29 sub-sample under the assumption of isothermal β model and non-isothermal double-β model. The blue cross represents the expected case when the DDR holds exactly.

Open in new tab Download slide

Figure 5.

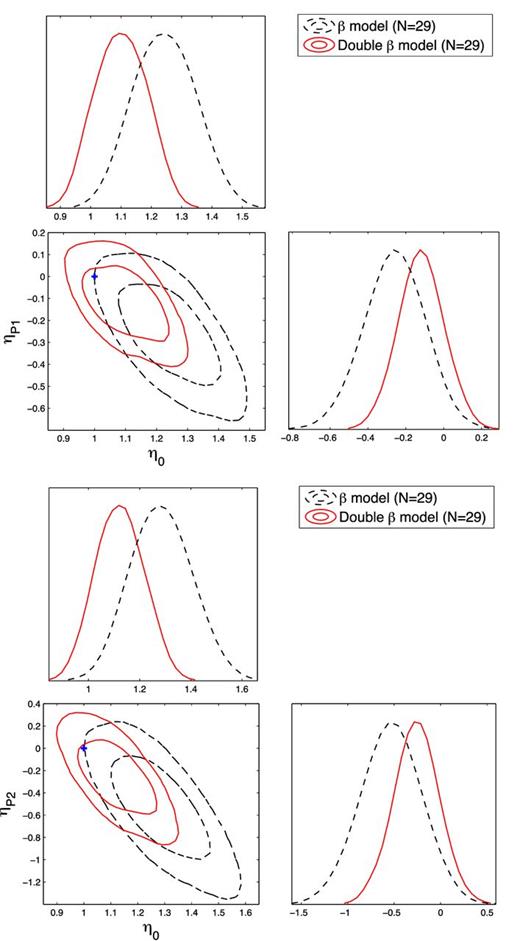
The same as Fig. 4, but for the case when XCDM model was taken to represent a ‘true’ cosmology.

Open in new tab Download slide

Even though, considering both statistical and systematic uncertainties, we find (at the level of best-fitting values) that isothermal β-model is incompatible with the validity of DDR at 1σ, it is difficult to distinguish these two density models by using f_gas measurements. As discussed in (LaRoque et al. 2006), the results of f_gas derived from models including the single-β model and double-β model fit to the X-ray data agree well enough to claim that the cluster core can be accounted for by either excluding it from the fit or modelling the gas with the double β-model.

We have also checked whether one can get tighter constraints on η (and hence gain more discriminative power concerning alternative density profiles) by fixing η_P = 0. The results are shown in Fig. 6. One can see that the two model density profiles are statistically compatible but again the double-β model looks better with the mode of the likelihood coinciding with the DDR expectation η = 1.

Figure 6.

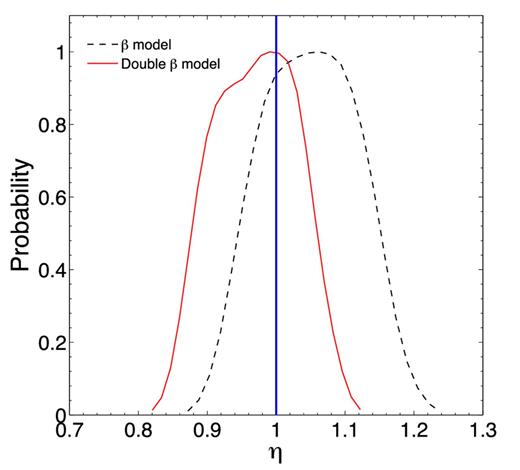
Likelihood functions for η parameter corresponding to the isothermal β model (black dashed line) and non-isothermal double-β model (red continuous line). Results are obtained with the n = 29 sub-sample of clusters. WMAP9 best-fitting ΛCDM parameters were taken to represent a ‘true’ cosmology. The blue vertical line represents the expected case when the DDR holds exactly.

Open in new tab Download slide

4 CONCLUSIONS

Clusters of galaxies are the largest virialized objects in the Universe. Therefore, they can serve as excellent probes of cosmology: their number density can be predicted and tested against observations. More than that, combined X-ray and Sunyaev–Zeldovich observations can in principle be used to measure absolute distances to the clusters and to test cosmology (the Hubble constant, dark energy etc.). However, for cosmological applications we need to have at least a reliable ‘proxy’ for the gas mass distribution in clusters and this is otherwise known to be complicated (e.g. from strong and weak lensing studies). So we need to compromise by making assumptions like isothermal β model or its ‘offspring’ – the non-isothermal double-β model. In this paper, we addressed the question of which of these two proxies is more supported by the data.

Our judgement was based on the assumed validity of the DDR — the DDR (for which there are good reasons to believe that it's true). To be specific, we have studied two samples of cluster gas mass fraction data obtained from 38 X-ray luminous galaxy clusters observed by Chandra in the redshift range 0.14 ∼ 0.89 (LaRoque et al. 2006) the full sample and its n = 29 sub-sample produced by excluding some ‘suspect’ clusters.

Bearing in mind, that in practice some systematic effects might disturb the DDR relation, we parametrized it in two ways: η(z) = η₀ + η_P1z and η(z) = η₀ + η_P2z/(1 + z). Then we checked which of the two ‘proxy’ models for gas mass distribution (isothermal β-model and non-isothermal double β-model) performs better. Our result is that within standard concordance cosmology (ΛCDM1) double-β model is marginally better respecting the DDR (at 1 σ level). If one takes instead ΛCDM parameters best fitted to Planck data, both models are compatible. However, within the quintessential XCDM cosmology double-β model is preferred at 2σ level. The preference of the double-β model over isothermal β model can be best seen on marginalized distributions of η₀, η_P parameters where it shows up irrespectively of the cosmology assumed.

We conclude by saying that as the cluster sample size increases with upcoming X-ray cluster surveys, we hope the method proposed in this paper may prove useful to improve the constraints on cluster gas mass density profiles.

The authors are grateful to the referee for very useful comments that allowed us to improve the paper. This work was supported by the Ministry of Science and Technology National Basic Science Program (Project 973) under Grant Nos. 2012CB821804 and 2014CB845806, the Strategic Priority Research Program ‘The Emergence of Cosmological Structure’ of the Chinese Academy of Sciences (No. XDB09000000), the National Natural Science Foundation of China under Grant Nos. 11503001, 11373014 and 11073005, the Fundamental Research Funds for the Central Universities and Scientific Research Foundation of Beijing Normal University, and China Postdoctoral Science Foundation under grant no. 2015T80052 and the Opening Project of Key Lab of Computational Astrophysics of Chinese Academy of Science. This research was also partly supported by the Poland-China Scientific & Technological Cooperation Committee Project No. 35-4. MB obtained approval of foreign talent introducing project in China and gained special fund support of foreign knowledge introducing project.

REFERENCES

Allen

S. W.

Schmidt

R. W.

Ebeling

H.

Fabian

A. C.

van Speybroeck

L.

MNRAS

2004

353

457

Crossref

Search ADS

Allen

S. W.

Rapetti

D. A.

Schmidt

R. W.

Ebeling

H.

Morris

R. G.

Fabian

A. C.

MNRAS

2008

383

879

Crossref

Search ADS

Allen

S. W.

Mantz

A. B.

Morris

R. G.

Applegate

D. E.

Kelly

P. L.

von der Linden

A.

Rapetti

D. A.

Schmidt

R. W.

2013

preprint (arXiv:1307.8152v1)

Applegate

D. E.

et al.

MNRAS

2014

439

48

Crossref

Search ADS

Bassett

B. A.

Kunz

M.

Phys. Rev. D

2004

69

101305

Crossref

Search ADS

Battaglia

N.

Bond

J. R.

Pfrommer

C.

Sievers

J. L.

ApJ

2012

758

75

Crossref

Search ADS

Bonamente

M.

Joy

M. K.

LaRoque

S. J.

Carlstrom

J. E.

Reese

E. D.

Dawson

K. S.

ApJ

2006

647

25

Crossref

Search ADS

Borgani

S.

et al.

MNRAS

2004

348

1078

Crossref

Search ADS

Cai

R.-G.

Guo

Z.-K.

Tang

B.

Int. J. Mod. Phys. D

2014

24

1550071

Crossref

Search ADS

Cao

S.

Liang

N.

Res. Astron. Astrophys.

2011

11

1199

Crossref

Search ADS

Cao

S.

Zhu

Z.-H.

Phys. Rev. D

2014

90

083006

Crossref

Search ADS

Cao

S.

Pan

Y.

Biesiada

M.

Godlowski

W.

Zhu

Z.-H.

J. Cosmol. Astropart. Phys.

2012

03

016

Crossref

Search ADS

Cao

S.

Biesiada

M.

Gavazzi

R.

Pirkowska

A.

Zhu

Z-H.

ApJ

2015

806

185

Crossref

Search ADS

Cavaliere

A.

Fusco-Femiano

R.

A&A

1976

49

137

Cavaliere

A.

Fusco-Femiano

R.

A&A

1978

70

677

Chevallier

M.

Polarski

D.

Int. J. Mod. Phys. D

2001

10

213

Crossref

Search ADS

Cunha

J. V.

Marassi

L.

Santos

R. C.

Int. J. Mod. Phys. D

2007

16

403

Crossref

Search ADS

De Bernardis

F.

Giusarma

E.

Melchiorri

A.

Int. J. Mod. Phys. D

2006

15

759

Crossref

Search ADS

De Filippis

E.

Sereno

M.

Bautz

M. W.

Longo

G.

ApJ

2005

625

108

Crossref

Search ADS

Ettori

S.

Tozzi

P.

Borgani

S.

Rosati

P.

A&A

2004

417

13

Crossref

Search ADS

Ettori

S.

Morandi

A.

Tozzi

P.

Balestra

I.

Borgani

S.

Rosati

P.

Lovisari

L.

Terenziani

F.

A&A

2009

501

61

Crossref

Search ADS

Ganga

K.

Ratra

B.

Gunderson

J. O.

Sugiyama

N.

ApJ

1997

484

7

Crossref

Search ADS

Giles

P. A.

Maughan

B. J.

Hamana

T.

Miyazaki

S.

Birkinshaw

M.

Ellis

R. S.

Massey

R.

MNRAS

2015

447

3044

Crossref

Search ADS

Grego

L.

Carlstrom

J. E.

Reese

E D.

Holder

G. P.

Holzapfel

W. L.

Joy

M. K.

Mohr

J. J.

Patel

S.

ApJ

2001

552

2

Crossref

Search ADS

Holanda

R. F. L.

Lima

J. A. S.

Ribeiro

M. B.

A&A

2011

528

L14

Crossref

Search ADS

Holanda

R. F. L.

Gonçalves

R. S.

Alcaniz

J. S.

J. Cosmol. Astropart. Phys.

2012

1206

022

Crossref

Search ADS

Landry

D.

Bonamente

M.

Giles

P.

Maughan

B.

Joy

M.

Murray

S.

MNRAS

2013

433

2790

Crossref

Search ADS

LaRoque

S. J.

Bonamente

M.

Carlstrom

J. E.

Joy

M. K.

Nagai

D.

Reese

E. D.

Dawson

K. S.

ApJ

2006

652

917

Crossref

Search ADS

Lau

E. T.

Kravtsov

A. V.

Nagai

D.

ApJ

2009

705

1129

Crossref

Search ADS

Lewis

A.

Bridle

S.

Phys. Rev. D

2002

66

103

Linder

E. V.

Phys. Rev. Lett.

2003

90

091301

Crossref

Search ADS

PubMed

Mantz

A.

Allen

S. W.

Morris

R. G.

Rapetti

D. A.

Applegate

D. E.

Kelly

P. L.

von der Linden

A.

Schmidt

R. W.

MNRAS

2014

440

2077

Crossref

Search ADS

Mohr

J. J.

Mathiesen

B.

Evrard

A. E.

ApJ

1999

517

627

Crossref

Search ADS

Planck Collaboration XVI

A&A

2014

571

A16

Crossref

Search ADS

Planelles

S.

Borgani

S.

Dolag

K.

Ettori

S.

Fabjan

D.

Murante

G.

Tornatore

L.

MNRAS

2013

431

1487

Crossref

Search ADS

Reese

E. D.

Carlstrom

J. E.

Joy

M.

Mohr

J. J.

Grego

L.

Holzapfel

W. L.

ApJ

2002

581

53

Crossref

Search ADS

Schneider

P.

Ehlers

J.

Falco

E. E.

Gravitational Lenses

1992

Berlin

Springer-Verlag

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Uzan

J. P.

Aghanim

N.

Mellier

Y.

Phys. Rev. D

2004

70

083533

Crossref

Search ADS

WMAP Collaboration:

Komatsu

E.

et al.

ApJS

2011

192

18

Crossref

Search ADS

Zhu

Z.-H.

Hu

M.

Alcaniz

J. S.

Liu

Y.-X.

A&A

2008

483

15

Crossref

Search ADS

Download all slides

Month:	Total Views:
January 2017	2
February 2017	5
March 2017	1
April 2017	4
May 2017	1
June 2017	7
July 2017	3
September 2017	1
November 2017	1
December 2017	2
January 2018	1
March 2018	3
April 2018	1
June 2018	4
July 2018	1
August 2018	1
December 2018	1
January 2019	4
March 2019	1
April 2019	9
May 2019	3
June 2019	2
July 2019	7
August 2019	3
September 2019	6
October 2019	4
November 2019	16
December 2019	4
January 2020	5
February 2020	7
March 2020	4
April 2020	6
May 2020	1
June 2020	6
July 2020	5
August 2020	2
September 2020	12
October 2020	4
November 2020	1
December 2020	5
January 2021	1
February 2021	4
March 2021	11
April 2021	3
May 2021	3
June 2021	6
July 2021	3
August 2021	9
September 2021	5
October 2021	6
November 2021	3
January 2022	6
February 2022	9
March 2022	7
April 2022	7
May 2022	7
June 2022	15
July 2022	13
August 2022	9
September 2022	21
October 2022	11
November 2022	9
December 2022	9
January 2023	18
February 2023	11
March 2023	6
April 2023	13
May 2023	2
June 2023	3
July 2023	5
August 2023	4
September 2023	6
October 2023	1
November 2023	9
December 2023	13
January 2024	14
February 2024	4
March 2024	8
April 2024	14
May 2024	14
June 2024	5
July 2024	13
August 2024	3
September 2024	4
October 2024	6
November 2024	7
December 2024	9
January 2025	3
February 2025	7
March 2025	13
April 2025	7
May 2025	8

Article Contents

Testing the gas mass density profile of galaxy clusters with distance duality relation

Abstract

1 INTRODUCTION

2 GALAXY CLUSTER SAMPLES

3 ANALYSIS AND RESULTS

4 CONCLUSIONS

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Testing the gas mass density profile of galaxy clusters with distance duality relation Free

Abstract

1 INTRODUCTION

2 GALAXY CLUSTER SAMPLES

3 ANALYSIS AND RESULTS

4 CONCLUSIONS

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Testing the gas mass density profile of galaxy clusters with distance duality relation