Did the Solar system form in a sequential triggered star formation event?

Abstract

1 INTRODUCTION

One of the outstanding challenges in star and planet formation is to understand and characterize the birth environment of our Solar system (e.g. Adams 2010; Pfalzner et al. 2015). One potential constraint is the presence of the daughter isotopes of short-lived radioisotopes (SLRs) found in meteorites thought to originate from the epoch of planet formation around the Sun (Lee, Papanastassiou & Wasserburg 1976). Their abundances and short half-lives suggest a rapid inclusion in meteorites during the early stages of Solar system formation.

Several radioisotopes with half-lives ranging from tens of days to several Myr are present in meteorites, but two – ²⁶Al and ⁶⁰Fe – were most probably produced by nucleosynthesis in the cores of massive (>20 M_⊙) stars (Goswami 2004). It is possible to produce ²⁶Al by cosmic ray spallation (Lee et al. 1998; Shu et al. 2001) and both ²⁶Al and ⁶⁰Fe from pollution from asymptotic giant branch (AGB) stars (Busso, Gallino & Wasserburg 1999). However, AGB stars are rare in young star-forming regions (Kastner & Myers 1994) and spallation alone cannot be responsible for the enrichment due to the absence of ⁶⁰Fe. For this reason, the supernovae of massive stars are thought to be the most likely origin of these isotopes. The exact details of the delivery mechanism(s) for these isotopes are still debated, and there are two main hypotheses.

In the first, referred to as ‘disc pollution’, ²⁶Al and ⁶⁰Fe are delivered directly to the Sun's protoplanetary disc from the supernova of one or more massive stars. Chevalier (2000) and Ouellette, Desch & Hester (2007) estimate that, in order to receive the required amounts of enrichment, the Sun must have been between ∼0.1 and 0.3 pc from the supernova so as to strike a balance between capturing enough of the ejecta without destroying too much of the disc (e.g. Armitage 2000; Scally & Clarke 2001; Adams et al. 2004).

At first glance, the disc pollution scenario appears rather improbable. Parker et al. (2014a) use N-body simulations of star-forming regions to determine the fraction of Sun-like stars that are enriched by a supernova explosion at distances ∼0.1–0.3 pc from massive stars when they explode, f_enrich. They then considered whether each enriched Sun-like star had always been a ‘singleton’ (Malmberg et al. 2007) – i.e. never in a binary star system, f_enrich,sing., and finally, whether these enriched singletons had suffered perturbing encounters with other stars in this dense stellar environment, f_{enrich,sing.,unp.}.

The fraction of enriched, single, unperturbed stars is of the order of f_{enrich,sing.,unp.} ∼ 1 per cent (Parker et al. 2014a) – see also Adams, Fatuzzo & Holden (2014) – and is calculated by summing together 20 similar simulations (to improve statistics) and assuming that the star-forming regions all disperse into the Galactic field. If one determines this fraction on a region-by-region basis, then some simulations eject the supernova progenitor before enrichment (due to multiple interactions with other massive stars, e.g. Allison & Goodwin 2011; Oh, Kroupa & Pflamm-Altenburg 2015) and so f_{enrich,sing.,unp.} can often be zero (see also Gounelle & Meibom 2008; Adams et al. 2014).

Alternatively, several authors have proposed that the delivery of ²⁶Al and ⁶⁰Fe comes from the giant molecular cloud (GMC) from which the Sun formed. This second scenario, which we will refer to as ‘sequential triggering’ (Gaidos et al. 2009; Gounelle et al. 2009; Gounelle & Meynet 2012; Gritschneder et al. 2012; Gounelle 2015), postulates that ²⁶Al and ⁶⁰Fe were delivered to the GMC in a series of star-forming events, and the supernova that delivered ⁶⁰Fe triggered the formation of the Sun.

Gounelle & Meynet (2012) provide a detailed picture of this scenario. A first star formation event of several thousand stars contains several massive stars whose supernovae enrich the nearby GMC and trigger a second star formation event, 10 Myr after the first (in order to allow some of the ⁶⁰Fe to decay). This second star formation event also contains ∼1000 stars to increase the probability of that event containing a Wolf–Rayet (WR) star. WR winds are rich in ²⁶Al, and in the Gounelle & Meynet (2012) model, the wind of this WR star causes a third generation of stars to form. It is in this third generation that the Sun – with the correct levels of ²⁶Al and ⁶⁰Fe – forms.

The sequential triggering scenario has been suggested as a way of enriching the Solar system meteorites without the need for the improbable astrophysical conditions required by the disc pollution scenario (close but non-destructive encounter with supernova, no previous or subsequent interactions with the ∼2000-4000 other stars in the region, efficient coupling of hot supernova ejecta to the cold disc material).

In principle, ²⁶Al and ⁶⁰Fe could also be delivered to the Solar system if stars form spontaneously (as opposed to triggering) in a GMC that has already been polluted. We briefly comment on this scenario in Sections 3 and 4.

In this paper, we investigate whether the sequential triggering scenario is more likely than the disc pollution scenario. We start by discussing the dynamical implications of multiple star formation events through triggering in Section 2. We then discuss the efficiency and nature of triggered star formation in hydrodynamical simulations in Section 3. We conclude in Section 4.

2 DYNAMICAL EVOLUTION OF SEQUENTIAL EVENTS

The triggered sequential star formation scenario suggested by Gounelle & Meynet (2012) requires three discrete star formation events, each forming ∼1000 stars, with the first two separated in time by roughly 10 Myr and a third occurring ∼15 Myr after the first.

If several star-forming events did sequentially lead to the formation of the Solar system, then these events must remain largely discrete, due to the absence of observed age spreads of more than several Myr in nearby star-forming regions (Jeffries et al. 2011; Reggiani et al. 2011). The triggered scenario for the formation of the Sco Cen OB association discussed in Preibisch & Zinnecker (2007) suggests that the sequential events must be spatially discrete due to a lack of age spreads within the subgroups.

Star-forming regions do not remain static, however. Multiple simulations (e.g. Klessen & Kroupa 2001; Moeckel & Bate 2010; Gieles, Moeckel & Clarke 2012; Parker & Meyer 2012; Parker & Dale 2013) show that two-body interactions cause a region to relax by expanding, so that the median stellar density may decrease by several orders of magnitude within 10 Myr. This implies a large amount of expansion, which means that if supernovae and other feedback mechanisms are triggering further star formation events, they must remain spatially discrete even after dynamical evolution.

In addition to two-body relaxation, the expulsion of residual gas has been shown to cause the expansion of star-forming regions due to a rapid decrease in the total potential (e.g. Tutukov 1978; Hills 1980; Lada, Margulis & Dearborn 1984; Goodwin & Bastian 2006; Baumgardt & Kroupa 2007; Pfalzner et al. 2014, and many more), if the gas is treated as a background potential. Simulations which include a more realistic treatment of the gas (Offner, Hansen & Krumholz 2009; Dale, Ercolano & Bonnell 2012; Kruijssen et al. 2012) suggest that when the local star formation efficiency is high, removing this remnant gas does not lead to significant expansion of the regions. The principal reason is that the local star formation efficiency within the subclusters is high, and so the potential there is dominated by the stars. Removing any leftover gas therefore has a negligible effect on the potential inside the subclusters, or on their subsequent dynamical evolution in these simulations. The contribution (if any) of gas expulsion to the expansion of star-forming regions is, however, still hotly debated in the literature.

Regardless of the agent of expansion, if sequential triggered star formation did form the Solar system, a minimum distance between events must be required to prevent significant, or even bi-modal age spreads of 10–15 Myr which would presumably be observable in similar star-forming regions today (Preibisch & Zinnecker 2007). In order to determine this minimum distance, we take a simulation of star-formation from the suite by Dale et al. (2014) – ‘Run J’, which forms 564 sink particles, of which more than 10 are O-type stars with mass >20 M_⊙ and will contribute ⁶⁰Fe to the GMC from their supernovae. We then take the sink particle distribution (masses, positions and velocities) in this simulation and evolve it with the kira integrator in the Starlab environment (Portegies Zwart et al. 1999, 2001).

Full details of the dynamical evolution of this simulation are described in Parker, Dale & Ercolano (2015). In Fig. 1(a), we show the spatial distribution of the simulation after the smoothed particle hydrodynamics (SPH) calculation described in Dale et al. (2014), but before any subsequent N-body evolution. Fig. 1(b) shows the simulation following 10 Myr of evolution, after the star formation event has dynamically relaxed and expanded (the median stellar density in this simulation decreases from 51 stars pc⁻² to 2.5 stars pc⁻² in 10 Myr; Parker et al. 2015).

Figure 1.

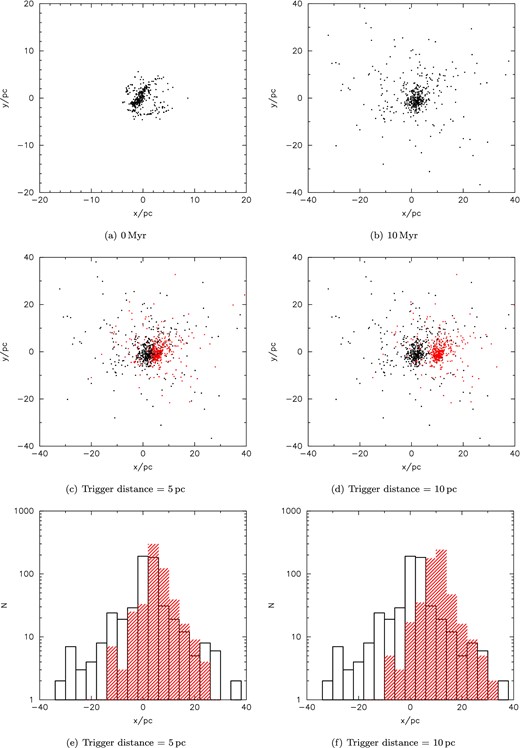
Dynamical evolution of simulation Run J with dual feedback from Parker et al. (2015) at (a) 0 Myr and (b) 10 Myr. Panels (c) and (d) show the simulation at 10 Myr but also include the same simulation superimposed at an age of 5 Myr (red points), assuming it represents a second star formation event triggered at a distance of (c) 5 pc and (d) 10 pc. Panels (e) and (f) show the numbers of stars along the x-axis for the two superimposed star formation events; the older event is shown by the black open histogram, and the younger event is shown by the red hashed histogram, assuming it was triggered at a distance of (c) 5 pc and (d) 10 pc.

Open in new tabDownload slide

In order to mimic the triggering of a second star formation event, and its subsequent dynamical evolution, we superimpose a second version of the same simulation, but with an age of 5 Myr, in the same field of view (the red points).¹ We assume that this second event was triggered at a distance of either 5 pc (Fig. 1c) or 10 pc (Fig. 1d). Clearly, at either distance a significant fraction of younger stars appear in the line of sight of older stars. In order to quantify this somewhat, we bin the two populations along the x-axis and the resultant histograms are shown in Fig. 1(e) and (f). If the second event is triggered at a distance of 5 pc, then 50 per cent of stars along the line of sight would be observed to have an age 5 Myr younger than the older population.

So far, we have only considered one simulation, which is rather low density initially and contains only 564 stars. Whilst the low density reduces the number of interactions that cause the region to expand, the low number of stars more readily leads to the dissoloution of the region (Gieles et al. 2012; Moeckel et al. 2012; Parker & Meyer 2012; Parker & Dale 2013). If we consider the very dense simulations (initial surface densities of Σ = 10⁴stars pc⁻²) presented in Parker et al. (2014b) of regions containing N = 1500 stars undergoing cool collapse, we obtain a very similar histogram. The reason is that more stars are ejected due to the high initial density and subsequent violent relaxation, leading to a wide spatial distribution.

We also consider a more benign environment, in which we simulate N = 1500 stars in a Plummer sphere (Plummer 1911) with initial half-mass radius 0.8 pc (corresponding to a median surface density of Σ = 100 stars pc⁻²). A Plummer sphere is already a relaxed system and as such is an unrealistic model for the spatial and kinematic outcome of star formation. However, because of its modest dynamical evolution, it does not expand at the same rate as the simulations discussed above (see Fig. 2a). When using Plummer spheres to approximate the star formation events, we see that an observed age bi-modality at a distance of 10 pc would still be present, but at a much lower level than in the more realistic models of the evolution of star formation environments (Fig. 2b).

Figure 2.

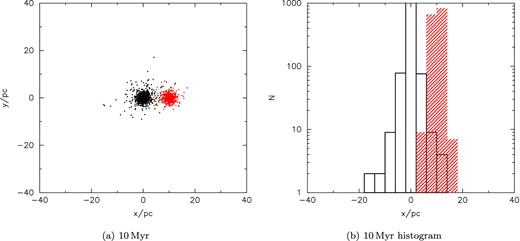
Dynamical evolution of a simulation of a Plummer sphere after 10 Myr (black points) and a second triggered event after 5 Myr (red points), assuming a triggering distance of 10 pc. In panel (b), we show the numbers of stars along the x-axis for the two superimposed star formation events; the older event is shown by the black open histogram, and the younger event is shown by the red hashed histogram, assuming it was triggered at a distance of 10 pc.

Open in new tabDownload slide

Based on these simple dynamical models, we suggest that the triggered sequence of star formation events that formed the Solar system would need to be separated by at least 10 pc. Assuming that star formation environments are initially unrelaxed systems, as observed (Peretto, André & Belloche 2006; André et al. 2010) and corroborated by simulations (Bate 2012; Dale et al. 2012, 2014; Parker et al. 2014b), then in order to avoid age spreads/bi-modality, which are not observed, a distance of at least 40 pc between events may be required to provide spatially and temporally discrete events.

This is quite a stringent requirement. Heyer et al. (2009) analysed a sample of 158 Milky Way molecular clouds, determining their masses and radii. Of these, 139 (88 per cent) have radii less than 40 pc, making it unlikely that a star formation event could trigger a second in the same cloud at a separation in excess of 40 pc, and 87 (55 per cent) have radii less than 20 pc, making this outright impossible. Such a large required separation likely demands that the triggered population and the triggering agent are formed in different molecular clouds.

Furthermore, the UV radiation flux from a star-forming region containing ∼1000 stars with radius 1 pc is likely to be of order F_UV = 3 erg s⁻¹ cm⁻² (Fatuzzo & Adams 2008). At a distance of 40 pc from the region, this value will decrease to F_UV = 1.8 × 10⁻³ erg s⁻¹ cm⁻², which is only marginally higher than the ambient value for the interstellar medium (F_UV = 1.6 × 10⁻³ erg s⁻¹ cm⁻²; Habing 1968). We will discuss the efficiency of triggering at such distances in the following section.

Finally, we note that 40 pc is likely to be the minimum projected distance that two star formation events could be separated by. In our plots showing two clusters of different ages, the second (triggered) cluster has been superimposed in the field perpendicular to the line of sight. In reality, the triggered cluster could appear in the fore- or background of the first cluster, thereby increasing the amount of temporal mixing in the field of view.

3 CONSTRAINTS FROM HYDRODYNAMIC SIMULATIONS

The effects of feedback from massive stars on the star formation process within turbulent molecular clouds, and in particular the ability of photoionizing feedback to trigger star formation, has recently been investigated by Dale, Ercolano & Bonnell (2013). In general, it was found that triggering by expanding H ii regions over a time-scale of 1–3 Myr was of rather minor importance, with the principal outcome of photoionizing feedback being that smaller quantities of stellar mass (and sometimes, fewer stars) were produced in clouds suffering the effects of feedback. In some simulations, significant numbers of stars were caused to form by feedback, but the effect on the total stellar mass and number of stars was offset by disruption of accretion flows on to clusters, and destruction of dense star-forming gas, preventing the formation of stars that would have been born in the absence of feedback.

By taking advantage of the Lagrangian nature of SPH, Dale et al. (2013) identified which stars in their simulations were triggered, based on the criterion of whether or not the gas from which a given object formed was involved in star formation or not in a companion calculation where ionization was absent. In simulations where sink particles could be treated as individual stars, they found that the number fractions of triggered objects ranged from 10–40 per cent, and that the mass fractions of triggered objects were similar at 8–37 per cent. It is therefore possible in principle for a stellar population to trigger the formation of another one of comparable mass, as is required by the model of Gounelle & Meynet (2012).

However, the main result of the Dale et al. (2013) studies was that the triggered stars were spatially, temporally and dynamically mixed with their spontaneously formed counterparts. In particular, there was no bi-modality observed either in the spatial distribution of the stars (triggered or otherwise) with respect to the ionizing stars, or in the ages of objects, whether measured from their time of formation or the point where they acquired their final masses. In some simulations, the fraction of triggered stars increases with three-dimensional distance from the O-type stars, but the increase is not monotonic or sudden, and fails to exceed ≈60 per cent even at the largest distances from the ionizing stars, as shown in Fig. 3 for simulations I and J from Dale et al. (2013). (Run I forms a total of 168 stars from a GMC with initial mass 10⁴ M_⊙ and radius 10 pc whereas Run J forms a total of 685 stars from a GMC with initial mass 10⁴ M_⊙ and radius 5 pc.)

Figure 3.

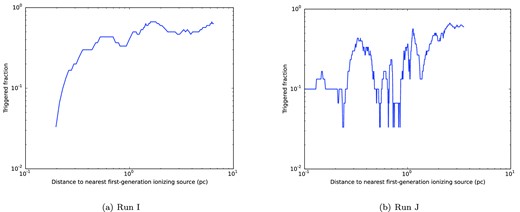
Fraction of stars which are triggered as a function of three-dimensional distance from the nearest ionizing source in Runs I (left-hand panel) and J (right-hand panel) from Dale et al. (2013).

Open in new tabDownload slide

The general increase in the fraction of triggered stars with distance from the ionizing sources is a result of the redistribution of star formation discussed in Dale et al. (2013). The ionizing sources inhabit centrally condensed clusters comprising stars which formed along with them, are therefore not triggered, and whose space–density generally declines with distance from the ionizing sources. The action of feedback is to deflect potentially star-forming gas out of the clusters and sweep it into the walls of bubbles, which also gather gas from further out in the clouds that was not forming stars. Most of the star formation in the later stages of the simulation therefore occurs in this admixture of gas near the bubble walls. Most of the triggered objects are thus to be found in the bubble walls, moving away from the ionizing sources, but they are mixed with a population of non-triggered objects formed from material prevented from accreting on the clusters. The triggered and spontaneously formed stellar populations are thus well mixed even on few-Myr time-scales, and there is no appreciable gap in time between the formation of the ionizing stars and the formation of the triggered population.

The non-monotonic nature of the increase in the triggered fraction with radius owes to the clustered nature of star formation, and to the highly irregular shapes of the bubbles. This in turn is caused by the very inhomogeneous structures of the clouds and the accretion flows directed inwards towards the clusters, which results in the bubbles expanding at very different rates in different directions.

An alternative scenario considered by Dale, Clark & Bonnell (2007), Dale & Bonnell (2012), Gritschneder et al. (2009), Bisbas et al. (2011) and Ngoumou et al. (2015) was to consider a cloud or clump which did not possess any massive stars itself being externally illuminated by a source of ionizing photons. The models of Gritschneder et al. (2009), Bisbas et al. (2011) and Ngoumou et al. (2015) consider the external ionization of a stable Bonnor– Ebert sphere, and produce an effective triggered fraction of 100 per cent, since the initial conditions are stable in the absence of feedback. This avoids the issue of triggered and spontaneously formed populations in the target cloud being spatially mixed. While the simulations of Dale et al. (2013) fail to generate triggered stars separated from the ionizing sources by more than 10 pc, Bisbas et al. (2011) find that lower ionizing fluxes (either from fainter sources, or greater separations between the sources and the clouds) result in the formation of more stars. Since the Bonnor–Ebert spheres are stable, the time interval between formation of the first stellar population and the collapse of the irradiated cloud could be arbitrarily long, but once the ionizing source begins operating, evolution of the irradiated cloud is rapid. However, the stellar population which would be associated with the ionizing sources in these calculations is not considered, and would in reality expand dynamically, as in the N-body calculations discussed above. Additionally, the clumps considered in these simulations have masses of only a few tens of solar masses and thus cannot form large clusters. Finding a smooth, stable Bonnor–Ebert sphere able to form a ∼10³ M_⊙ cluster in reality is unlikely.

Dale et al. (2007) and Dale & Bonnell (2012) instead illuminated massive turbulent (and therefore intrinsically unstable) clouds, which would form stars spontaneously in the absence of external feedback. They found that the increase in the numbers or masses of stars formed due to feedback was modest, particularly if the irradiated cloud was gravitationally bound. They consequently observed that the triggered populations were contaminated by the presence of spontaneously formed stars. In these calculations, the instability of the clouds precludes long time intervals before the initiation of star formation inside them. The separations between the photon sources and the clouds considered were only a few to 10 pc. Increasing this distance is likely to reduce further the influence of photoionization on the star formation process in these clouds since the perturbing effect on the gravitational collapse already in progress will be lessened. We note that increasing the separation between the ionizing source and the target cloud to 40 pc, as would be required to prevent dynamical mixing, entails a decrease in the ionizing flux felt by the cloud by factors of the order of 10 compared to the models of Dale et al. (2007) and Dale & Bonnell (2012). It is therefore difficult to imagine that the target cloud be placed far enough from the ionizing source that the stellar population associated with the massive star does not become dynamically mixed with the stars formed by the cloud, yet still be close enough for the ionizing flux to trigger significant additional star formation.

In principle, the spontaneous formation of stars in a GMC that has already been polluted by supernovae ejecta can deliver ²⁶Al and ⁶⁰Fe to the Solar system. However, one would expect low-mass stars from the first epoch of star formation to be present, and therefore some degree of observable age spread to also occur. This places a constraint on the number fraction of second or third generation stars that can form spontaneously in the parent cloud of the first star formation event, in that the number of second/third generation stars must be so small as to go unnoticed.

Supernovae are the most powerful form of stellar feedback at large scales, and the interaction of single supernovae with molecular clouds has recently been modelled by Iffrig & Hennebelle (2015). Supernovae were detonated inside, on the edge of, and outside a 10⁴ M_⊙ turbulent cloud. Neither of the latter two simulations had any significant effect on the quantity of dense star-forming material in the clouds on 5 Myr time-scales. The supernovae failed to trigger any additional star formation for similar reasons to those preventing photoionization triggering star formation in the simulations of Dale & Bonnell (2012), namely that external feedback was unable to penetrate the dense inner regions of the clouds.

4 CONCLUSIONS

We have analysed N-body and SPH simulations of star formation to investigate the probability that the Solar system could have formed in a sequentially triggered series of star formation events in order to explain the levels of ²⁶Al and ⁶⁰Fe in the protosolar nebula. This mechanism has recently been suggested as a more astrophysically likely alternative to the direct pollution of a protoplanetary disc from supernova ejecta. Our main results can be summarized as follows.

(i) If a series of star formation events are triggered by supernovae and other feedback mechanisms, the dynamical evolution driven by two-body relaxation in the first event(s) would likely result in a significant age spread, or even age bi-modality in the star formation region. Determining the ages of pre-main-sequence stars is notoriously difficult, and the postulated presence (or not) of age spreads of a few Myr is currently a contentious issue in the literature (Soderblom et al. 2014). We suggest that if sequential triggering were a common outcome in star formation, then age spreads (or even bi-modality) of more than 10 Myr would be common in the local Universe. Since such age spreads are not observed in clusters, our results could be construed as part of a more general argument that sequential triggering of star formation is rare, since it is difficult to prevent the distinct stellar populations from mixing dynamically. (The lack of observed age spreads also constrains the fraction of stars that can form spontaneously at later epochs.) We will develop this idea further in later papers.

(ii) Whilst triggering can result in significant new populations of stars (in terms of number of stars and their fraction of the total mass) in SPH simulations, these triggered stars are distributed in the same temporal and spatial phase space as the first generation of stars, hence ruling out the formation of discrete populations by triggering, as required in some models for Solar system formation. We also note that the simulations in question did not include magnetic fields. Krumholz, Stone & Gardiner (2007) showed that the presence of a magnetic field softens the shock around an expanding H ii region, and is therefore likely to suppress the triggering of star formation below the levels observed by Dale et al. (2013).

(iii) In theory, it is possible to trigger the formation of stars in a stable Bonnor–Ebert sphere, which could account for temporally separated star formation events. However, these events are likely to be low mass and therefore not contain the WR star(s) required for ²⁶Al pollution. Furthermore, the problem of containing the stars in spatially discrete areas of the star-forming region would still be an issue.

Our results suggest that the astrophysical conditions required for sequential triggering of two or three spatially and temporally discrete star formation events are at best highly unlikely, and that the delivery of ²⁶Al and ⁶⁰Fe to the early Solar system from this scenario is no less improbable than in the disc pollution scenario. However, we caution that outstanding issues also exist for the disc pollution scenario (Gounelle & Meibom 2008; Parker et al. 2014a), and we will investigate these further in a future paper.

We thank the referee, Fred Adams, for his prompt and helpful review. RJP acknowledges support from the Royal Astronomical Society in the form of a research fellowship. This research was also supported by the DFG cluster of excellence ‘Origin and Structure of the Universe’ (JED).

REFERENCES