-
PDF
- Split View
-
Views
-
Cite
Cite
D. R. Madison, X.-J. Zhu, G. Hobbs, W. Coles, R. M. Shannon, J. B. Wang, C. Tiburzi, R. N. Manchester, M. Bailes, N. D. R. Bhat, S. Burke-Spolaor, S. Dai, J. Dempsey, M. Keith, M. Kerr, P. Lasky, Y. Levin, S. Osłowski, V. Ravi, D. Reardon, P. Rosado, R. Spiewak, W. van Straten, L. Toomey, L. Wen, X. You, Versatile directional searches for gravitational waves with Pulsar Timing Arrays, Monthly Notices of the Royal Astronomical Society, Volume 455, Issue 4, 01 February 2016, Pages 3662–3673, https://doi.org/10.1093/mnras/stv2534
Close - Share Icon Share
Abstract
By regularly monitoring the most stable millisecond pulsars over many years, pulsar timing arrays (PTAs) are positioned to detect and study correlations in the timing behaviour of those pulsars. Gravitational waves (GWs) from supermassive black hole binaries (SMBHBs) are an exciting potentially detectable source of such correlations. We describe a straightforward technique by which a PTA can be ‘phased-up’ to form time series of the two polarization modes of GWs coming from a particular direction of the sky. Our technique requires no assumptions regarding the time-domain behaviour of a GW signal. This method has already been used to place stringent bounds on GWs from individual SMBHBs in circular orbits. Here, we describe the methodology and demonstrate the versatility of the technique in searches for a wide variety of GW signals including bursts with unmodelled waveforms. Using the first six years of data from the Parkes Pulsar Timing Array, we conduct an all-sky search for a detectable excess of GW power from any direction. For the lines of sight to several nearby massive galaxy clusters, we carry out a more detailed search for GW bursts with memory, which are distinct signatures of SMBHB mergers. In all cases, we find that the data are consistent with noise.
1 INTRODUCTION
Pulsar timing arrays (PTAs) provide a unique means for detecting gravitational waves (GWs) with frequencies between approximately 10−9 and 10−6 Hz. Sensitivity at such frequencies makes PTAs key for searching for and eventually studying GWs from supermassive black hole binaries (SMBHBs) with masses greater than 107 M⊙ (Sesana & Vecchio 2010). PTAs are therefore indispensable for understanding galaxy evolution over cosmological time-scales, for investigating the mechanisms by which the final parsec problem (Milosavljević & Merritt 2003) may be solved, and for probing strong gravitational fields.
The PTA concept was initially conceived decades ago (Detweiler 1979; Hellings & Downs 1983; Foster & Backer 1990), and is now being realized by several international collaborations. The European Pulsar Timing Array (EPTA; Kramer & Champion 2013), the North American Nanohertz Observatory for Gravitational Waves (NANOGrav; McLaughlin 2013), and the Parkes Pulsar Timing Array (PPTA; Manchester et al. 2013) collaborations use sensitive radio telescopes to observe the most rotationally stable millisecond pulsars (MSPs) known and measure the highest-precision pulse times of arrival (ToAs) possible on a regular basis. Measured ToAs are compared to predictions of timing models that aim to account for all of the known physical effects that modulate the regularity with which pulses arrive at Earth-based observatories (Edwards, Hobbs & Manchester 2006). After sufficiently long periods of time, the differences between measured ToAs and model predictions, the timing residuals, may begin to show structure indicative of errors in terrestrial time standards (Hobbs et al. 2012), incorrect Solar system ephemerides (Champion et al. 2010), or the influence of GWs on the pulsar-Earth system. To analyse such effects, the various PTAs are also combining their data and expertise in the International Pulsar Timing Array (IPTA; Hobbs et al. 2010; Manchester 2013) which is poised to become the most sensitive tool for such investigations.
The GW signals potentially detectable by PTAs fall into two classes. First, individually resolvable sources such as SMBHBs in circular (Arzoumanian et al. 2014; Zhu et al. 2014; Babak et al. 2015) or eccentric orbits (Ravi et al. 2014; Huerta et al. 2015), and burst sources, especially so-called ‘bursts with memory’ (BWMs) from the final merger of SMBHBs (van Haasteren & Levin 2010; Cordes & Jenet 2012; Wang et al. 2015; Arzoumanian et al. 2015a) or potentially from exotic sources like phase transitions in the early Universe (Cutler et al. 2014). Secondly, an isotropic stochastic background (SB) of GWs created by the incoherent superposition of many unresolved SMBHBs scattered throughout the Universe (van Haasteren et al. 2011; Demorest et al. 2013; Shannon et al. 2013, 2015; Arzoumanian et al. 2015b; Lentati et al. 2015). An isotropic SB is an idealization and recent work has begun to place limits on anisotropic features of the background (Taylor et al. 2015). In this paper, we are concerned primarily with individually resolvable sources or small groups of bright sources clustered in a particular direction, though our techniques may also prove useful in studies of a SB.
When GWs from a single direction interact with the Earth, regardless of their detailed waveforms, they produce a distinctly quadrupolar correlation pattern in the timing residuals of the pulsars in a PTA. By exploiting this fact, pulsar timing data sets from many different pulsars can be coherently combined, or ‘phased-up’, so as to enhance a PTA's sensitivity to GWs from particular directions. Here, we develop a formalism that enables this procedure. The strengths of this technique include the following.
GW signals are included as part of the pulsar timing model. This means that all the issues relating to actual data sets (uneven observing cadence, different pulsars having different data spans and noise properties, the necessity to fit for pulsar parameters, etc.) are modelled simultaneously with the GW search using standard pulsar timing techniques.
As part of the timing model, the covariances between the GW signal and the other timing model parameters are easily obtained.
The algorithms underlying our technique are fast, so they do not require large computing resources. The GW signal is condensed out of the raw observations into a much smaller data volume.
The technique makes no assumption about the actual form of the GW and so is useful for detecting unexpected GW signals as well as anticipated signals like BWMs or continuous waves (CWs) from SMBHBs in circular orbits. Inspection of the GW signal stream produced with our technique can help to determine what type of optimized signal detection schemes to implement.
In Section 2, we discuss how GWs manifest themselves in pulsar timing measurements and introduce our so-called |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| technique. In Section 3, we describe how |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| can be used in matched-filter searches for specific gravitational waveforms. In Section 4, we describe the PPTA Data Release 1 (DR1) and the simulated data sets we analyse for the remainder of the paper and indicate where these publicly available data can be accessed. In Section 5, using |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$|, we conduct an all-sky search for detectable GW power from any direction with any time-domain behaviour. In Section 6, we study in greater detail the lines-of-sight to the Virgo, Fornax, Norma, Perseus, and Coma galaxy clusters, nearby massive clusters that are likely origins for the first detection by PTAs of an isolated GW source; for each of these special directions, we conduct a search for BWMs, clear indicators of the final merger of an SMBHB. In Section 7, we demonstrate that the correlations induced in PTA residuals from clock errors, inaccuracies in Solar system ephemerides, and GWs can be measured simultaneously without confusion. Finally, in Section 8, we summarize and conclude our work with some final remarks.
2 PLANAR GRAVITATIONAL WAVES AND PULSAR TIMING
2.1 Timing model development and noise
As equation (4) indicates, A⋆ is an integral of the difference in two terms: an ‘Earth term’ common to all pulsar timing data sets and a ‘pulsar term’ that differs between data sets owing to the different positions and distances of the pulsars. For burst GWs with durations much shorter than the light travel times between Earth and the pulsars in a PTA (thousands of years, typically), when the Earth term is active the various pulsar terms are all quiescent and the pulsar terms are negligible. However, the GWs from a SMBHB will be in the band of frequencies potentially detectable by PTAs for the order of millions of years. If we treat a SMBHB as a monochromatic source of sinusoidal GWs (i.e. ignore the secular frequency evolution of the source over thousand-year time-scales), then each pulsar term will be a sinusoid of the same frequency as the Earth term, a nearly identical amplitude, and an essentially random and uniformly distributed phase. The pulsar term can perfectly add to the Earth term, perfectly cancel it, or anything in-between. The pulsar terms are uncorrelated in different pulsar timing data sets. If NP pulsars with approximately equal timing precision are analysed and their residuals coherently combined, the self-noise from these pulsar terms is suppressed by |$N_{\rm P}^{1/2}$| (Hellings & Downs 1983). For discussion of frequency evolution anticipated from SMBHBs and prospects for including pulsar terms in the signal model rather than treating them as sources of noise, see e.g. Arzoumanian et al. (2014) and Wang, Mohanty & Jenet (2014).
2.2 Building GWs into timing models
We model A+(t) and A×(t) as linearly interpolated functions on a grid of Nτ times τμ. In principle, different grids could be used for the + and × polarizations, but for simplicity, we will use an identical grid for each of them. The grid does not need to be evenly spaced; for some pulsar timing data sets where the ToA sampling is sparse in decades-old data but relatively uniform and dense in more modern data, variable spacing in the interpolation grid may be appropriate. An advantage to modelling A+(t) and A×(t) as linear interpolants rather than a higher-order polynomial or Fourier series is that individual bad ToAs or small time-spans of bad ToAs, either with large uncertainties or apparent biases, mainly influence the estimates of A+(t) and A×(t) locally rather than over larger spans of data or the whole data set.
These models for A+ and A×, which we refer to as |${\cal A}_+$| and |${\cal A}_\times$|, are incorporated into a global fit to the full set of ToAs that is carried out simultaneously with all the timing models for all the pulsars in the array. The |${\cal A}_+(t)$| and |${\cal A}_\times (t)$| time series must be constrained so that they are not covariant with the astrometric or spin parameters of the individual pulsar timing models. The products of this fitting procedure are |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$|, the maximum-likelihood estimators of |${\cal A}_+$| and |${\cal A}_{\times}$|, and a matrix, |${\boldsymbol C}_{+\times}$|, describing covariances in |$\hat{\cal A}_+$| and |$\hat{\cal A}_{\times}$|.
The |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series are a complete representation of the GWs coming from a particular direction in that they carry all the information with respect to such GWs that is contained in the ToAs. One cannot obtain a better signal estimator using the ToAs than can be done with the auxiliary time series alone. Full details of the implementation of the global fit and the constraints that need to be applied to |${\cal A}_+(t)$| and |${\cal A}_\times (t)$| during the fitting procedure are given in Appendix A. These algorithms have been implemented in the tempo2 software package (Edwards et al. 2006, see appendix B for usage details).
3 Searching |$\skew{6.4}\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| for Anticipated GW Waveforms
Although one of the great strengths of the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series is that it can be used to study GWs without an underlying signal model, we demonstrate here how searches for specific waveforms can be implemented directly in the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series after they have been computed. Zhu et al. (2014) developed a procedure for conducting a matched-filter search for a specific waveform in |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| and applied it to DR1 from the PPTA in a search for CWs. The upper limit on the amplitude of CWs derived in that paper is among the most stringent achieved to date (for competitive limits, see Arzoumanian et al. 2014; Babak et al. 2015). Here, we will review the essential elements needed to carry out a matched-filter search in |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| and elaborate on certain points, but will focus on a different, simpler signal model: a BWM. We will apply these methods in a small targeted search for BWMs from nearby massive galaxy clusters using DR1 later in this paper. Wang et al. (2015) searched DR1 for BWMs but did not utilize |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series. Our search is different and complementary to the work described in that paper; |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| techniques produce consistent results with Wang et al. (2015) and are ultimately more computationally efficient.
In conducting the global fit that generates |$\hat{{\cal A}}_+$| and |$\hat{{\cal A}}_\times$|, we must compute a global parameter covariance matrix (see Appendix A for a detailed discussion). A 2Nτ × 2Nτ sub-block of this matrix describes the correlated uncertainties in |$\hat{{\cal A}}_+$| and |$\hat{{\cal A}}_\times$|; we call this sub-block |${\boldsymbol C}_{+\times }$|. As discussed in Zhu et al. (2014), |${\boldsymbol C}_{+\times }$| is not a full-rank matrix because of the constraints applied to |$\hat{{\cal A}}_+$| and |$\hat{{\cal A}}_\times$| and is thus non-invertible. We define |$\tilde{{\boldsymbol C}}_{+\times }={\boldsymbol EFE}^T$| where |${\boldsymbol E}$| is a matrix containing the eigenvectors of |${\boldsymbol C}_{+\times }$| associated with non-null eigenvalues and |${\boldsymbol F}$| is a square diagonal matrix containing those non-null eigenvalues. This generalized covariance matrix is the covariance matrix on the subspace orthogonal to the constraints and is manifestly invertible: |${\tilde{\boldsymbol C}}_{+\times }^{-1}={\boldsymbol EF}^{-1}{\boldsymbol E}^T$|. Also, we define the projection operator |${\boldsymbol P}={\boldsymbol EE}^T$|.
This signal parameter estimator, |$\hat{\alpha }$|, is biased. The bias is a consequence of the constraints applied to |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$|. As an extreme example, if a GW signal was purely quadratic, that signal would be entirely filtered out of |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| by the constraints and the GW signal could never be reconstructed. Blandford, Narayan & Romani (1984) and Madison, Chatterjee & Cordes (2013) describe the procedure of fitting certain functional forms out of timing residuals as equivalent to applying a frequency-domain filter to the residual fluctuation spectrum. Analogously, the constraints applied to |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| destructively filter out some features of the GW signal. However, the spectral shape of constraint-induced filters depends upon the time-span of the data set. As more data are gathered, the constraints and the GW signal become less covariant, less of the GW signal is filtered out, and the bias in estimation of the signal parameters is reduced. Furthermore, through simulations, the bias can be quantified, allowing for robust and trustworthy parameter estimation.
4 REAL AND SIMULATED DATA SETS
For much of the remainder of this paper, we work with both simulated and real data sets. Our simulated data sets were produced using a newly developed software package called ptaSimulate.1 The simulated data sets we analyse are as follows.2
Sim1: 20 synthetic pulsars are generated with random sky positions (statistically uniform on the sphere). We assume weekly ToA measurements with 50 ns timing precision. The timing models for each pulsar only include fits for three spin parameters (rotational phase, frequency, and frequency derivative). The timing residuals for each pulsar are consistent with 50 ns rms white Gaussian noise.
Sim2: as in Sim1, but a bright GW burst has been injected into both GW polarization channels of the simulation from a source at right ascension 0 h and declination 0°. The pulsar locations differ from those in Sim1, but are again drawn from a distribution that is uniform on the sphere. The white Gaussian noise added to each ToA again has an rms of 50 ns, but we use a different realization of noise from that in Sim1.
Sim3: we have generated 20 simulated pulsars with the same positions as the 20 pulsars comprising the PPTA DR1. We have assumed these pulsars are observed every two weeks and have ToA uncertainties consistent with 100 ns rms Gaussian white noise. In each pulsar timing model, we fit only for rotational phase, frequency, and frequency derivative. We have simulated a clock error by generating the simulated data with TAI and reprocessing them with BIPM2013, two different realizations of terrestrial time. We have simulated an ephemeris error by using Jet Propulsion Laboratory ephemeris DE414 (Standish 2006) to generate the simulated data and DE421 (Folkner, Williams & Boggs 2008) to reprocess it.
Sim4: as in Sim3, but a GW burst has also been injected into the simulated timing data. The realization of 100 ns rms Gaussian white noise in Sim4 differs from that in Sim3.
We analyse a version of the PPTA DR1 (Manchester et al. 2013) that has been updated to include detailed noise models developed and used by Wang et al. (2015) and Zhu et al. (2014). The noise models account for additional white noise in the data beyond that anticipated from radiometer noise alone (jitter is a likely contribution to this) and, using the techniques developed in Coles et al. (2011), correlated red timing noise.
5 ALL-SKY SEARCHES FOR EXCESS GW POWER
In Fig. 1, we display the results of this search procedure when applied to Sim1, Sim2, and DR1 (listed in order from top to bottom). We have sampled |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| at 74 evenly spaced epochs, corresponding to a cadence of 30 d. The left panels indicate the value of D at each sky position. The black dot in these left panels indicates the position on the sky that yielded the greatest value of D. The right panels depict the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series associated with the direction on the sky that yielded this greatest value of the detection statistic. For the analysis of Sim1, our null example, |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| appears by eye to be consistent with zero signal and, indeed, the maximum value of D that is realized is 174.8, consistent with approximately 18.7 per cent of realizations of noise.
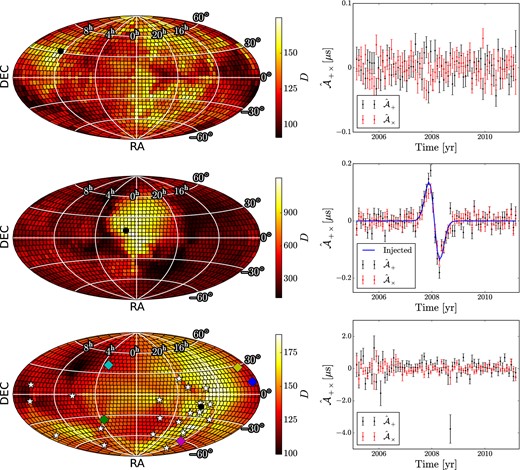
Left: the total power detection statistic, D, as it varies over the sky. The black circle indicates the position on the sky that yielded the greatest value of D. Right: the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series for the direction of the sky that yielded the greatest value of D. Top: analysis of Sim1. The detection statistic never exceeds values that are inconsistent with noise. Middle: analysis of Sim2. The detection statistic clearly indicates that the data are inconsistent with the noise, we are able to localize the location of the injected GW source, and we can reconstruct the waveform of the injected burst. Bottom: analysis of the six-year DR1 from the PPTA. The stars indicate the positions of the 20 pulsars included in DR1. The coloured diamonds indicate the positions of five nearby massive galaxy clusters: Virgo (blue), Fornax (green), Norma (magenta), Perseus (cyan), and Coma (yellow). There is no significant evidence for GW power in DR1.
The bottom row of plots in Fig. 1 depicts the results of our search for directional GWs in the PPTA's DR1. The search is carried out in the same way as for the simulated data sets, but we have used a generalized least-squares fitting routine (as described in Coles et al. 2011) in order to account for the different red noise present in different pulsars.3 The white stars in the bottom left panel indicate the positions of the 20 pulsars comprising DR1. The distribution of pulsars on the sky does not approach statistical uniformity and the noise properties of the pulsars are not all equal as in Sim1 and Sim2. With Nτ = 74, Nc = 7 (as discussed in Appendix A), and Ns = 20, D would have to exceed approximately 194 to claim an excess of GW power with 99 per cent confidence or 184 for 95 per cent confidence. The maximum value of D we find in our analysis of DR1 is 188.5, which is between the 95 per cent and 99 per cent confidence thresholds.
Even though this value of D is consistent with a null detection, it is close to values of interest. However, there is a reason to be sceptical of this marginally high value of D. The |$\hat{\cal A}_+$| time series associated with this maximal value of D from DR1 has a 4.2σ outlier at an epoch near September of 2008. This epoch is contemporaneous with the commissioning of a new pulsar timing backend at Parkes. Many ToAs from this brief era have been excluded from DR1 for displaying obvious systematic issues, but it is likely that systematic artefacts may still be present in the data. If this one outlier in the |$\hat{\cal A}_+$| time series is artificially forced towards zero until its 1σ error bar is consistent with zero, the value of D from this pointing is reduced to approximately 171, consistent with approximately 30 per cent of noise realizations.
This result with DR1 underscores the importance of the IPTA project in two ways. First, if the marginally significant result we have discussed is indeed just a systematic artefact in PPTA data, comparison with measurements from the EPTA and NANOGrav from around September of 2008 of a subset of pulsars that overlaps with the PPTA sample should be able to resolve the issue. Secondly, if the outlier in the PPTA data set is a very short duration, very bright GW burst, it will be present in the data sets of all three PTAs comprising the IPTA and a joint analysis of the combined data sets will bolster the significance of the result.
6 TARGETED INVESTIGATIONS OF NEARBY MASSIVE GALAXY CLUSTERS
Simon et al. (2014) recently conducted a detailed analysis of surveys of local galaxies in order to identify potential directions on the sky from which an initial detection of resolvable GWs by PTAs is likely to originate, so-called ‘GW hotspots’. They singled out, in order of increasing distance from Earth, several massive galaxy clusters: Virgo, Fornax, Norma, Perseus, and Coma. The directions to these clusters are indicated in the bottom left panel of Fig. 1 with coloured diamonds. These clusters are all within 100 Mpc of Earth and all but Fornax, the smallest of the five, contain upwards of 500 galaxies. In Fig. 2, we plot the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series produced when DR1 is phased up to the directions of each of these galaxy clusters. All are consistent with noise.
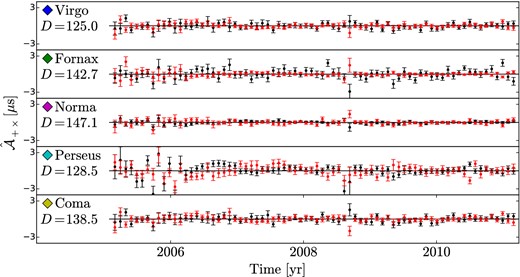
The |$\hat{\cal A}_+$| (black) and |$\hat{\cal A}_\times$| (red) time series produced when DR1 is phased up to the locations of the massive Virgo, Fornax, Norma, Perseus, and Coma galaxy clusters. All pointings are consistent with noise only (as indicated by the D value quoted in each panel). The diamonds in each panel are colour coded with the diamonds in the bottom left panel of Fig. 1 indicating the directions to these clusters.
There are several notable features in Fig. 2. First, all five pointings have some marginal outliers near the 2008 September commissioning of the new pulsar timing backend at Parkes that was discussed earlier. We demonstrated in our analysis of Sim2 (depicted in Fig. 2) that a GW burst can be localized on the sky and the five clusters we consider here are from widely separated directions; this gives further weight to the argument that there are systematic issues with DR1 near September of 2008 and it is very unlikely that the excess power in |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| is from a spatially localized GW source. Secondly, the scatter in all pointings is larger earlier in the time-span; this is due largely to an increase in the observing cadence over time and thus a greater number of ToAs contributing to each |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| sample later in the data set. The change in the observing cadence has not led to any issues in our analysis of DR1, but this illustrates the possible need for unequal spacing in the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| sample grid in other data sets. Finally, the scatter in the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series is biggest in our pointing towards the Perseus cluster and smallest in our pointing towards the Norma cluster. The Perseus cluster is in the opposite direction of the sky from the peak concentration of PPTA pulsars while the Norma cluster is very nearly in the same direction as many of the PPTA pulsars. This is a reflection of the point we discussed in Section 2 that pulsar timing measurements are more sensitive to GWs coming from directions of the sky near the direction of the pulsar. It is well known that an anisotropic distribution of well-timed pulsars leads to anisotropic sensitivity to GWs; this again highlights the importance of the IPTA and close collaboration and data sharing between pulsar astronomers in the Northern and Southern Hemispheres.
6.1 A BWM Search in |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$|
Although we find no evidence for excess GW power in the directions of any of these five clusters, to search for a specific waveform, a matched-filter search of |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| is more sensitive than a total power search. Building on our discussion from Section 3, as a test case, we here conduct a search for BWMs in these five pointings.
We define a different detection statistic for this search: |$D_B=\hat{\alpha }^T{\boldsymbol \Sigma }^{-1}\hat{\alpha }$|. This is nearly identical to the detection statistic used in the BWM search conducted by Wang et al. (2015), but here we do our search directly in |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$|. In the absence of signal, DB will follow χ2 statistics with 2 degrees of freedom. We will search epochs within the innermost 80 per cent of each of the five |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| pointings in Fig. 2 for evidence of a BWM occurring. We restrict ourselves to this window because detecting a BWM requires the ability to accurately assess the pulsar timing behaviour both pre- and post-burst. Arzoumanian et al. (2015a) recently showed that in a BWM search over many trial burst epochs, there are approximately five statistically independent trials; this fact must be accounted for in assessing the false alarm probability in our search. In order for the data to be inconsistent with 95 per cent of realizations of noise, with Ns = 5, DB must exceed approximately 9.2.
In the top panel of Fig. 3, we show the values of DB derived from our search; we find nothing inconsistent with noise. Knowing |${\boldsymbol \Sigma }$|, however, allows us to compute the minimum value of |α| needed to exceed the 95 per cent confidence threshold in DB. We display this quantity, which we call hB, min, in the middle panel of Fig. 3. The strain amplitude of a BWM is hB ≈ 1.5 × 10−13(μ/109M⊙)(d/10Mpc)−1 where μ is the reduced mass of the binary and d is the luminosity distance between the binary and Earth; we have assumed the binary has a typical inclination angle of π/3 (Madison et al. 2014). Taking the luminosity distances to Virgo, Fornax, Norma, Perseus, and Coma, as 17 Mpc, 19 Mpc, 68 Mpc, 74 Mpc, and 99 Mpc, respectively (see Simon et al. 2014, and references therein), we have generated the bottom panel of Fig. 3 displaying the minimal reduced mass, μmin, of a merging SMBHB that would have produced a BWM bright enough to exceed our 95 per cent confidence threshold on DB. The likelihood of such a massive merger occurring in one of these galaxy clusters during our observing span is exceedingly small, but as the span of our data set grows, our sensitivity to BWMs will improve and we will become sensitive to less massive mergers.
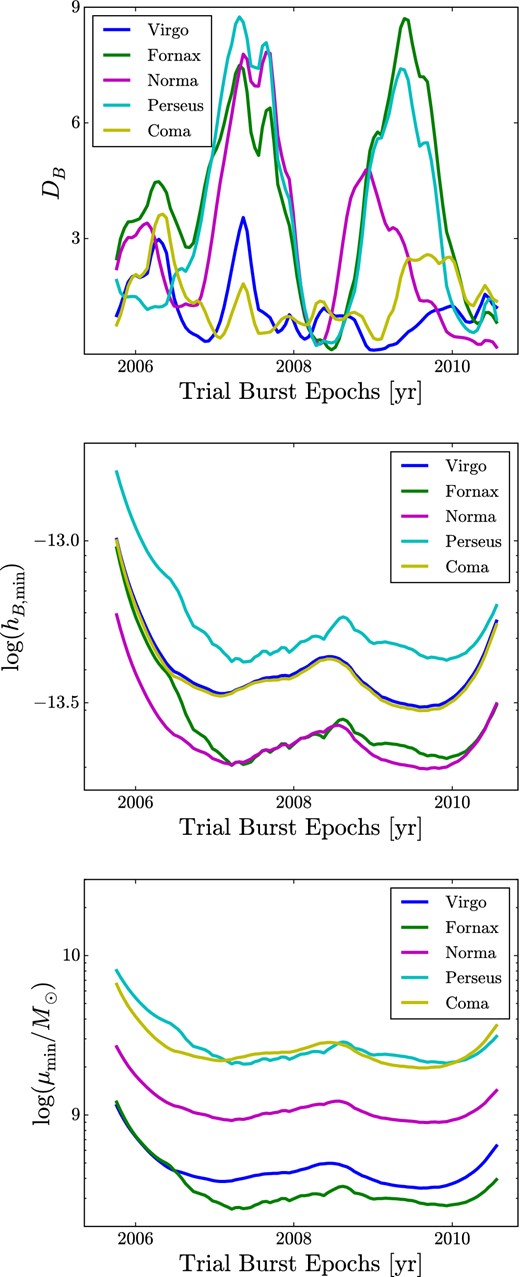
Top: the detection statistic, DB, derived from a search for BWMs in the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series associated with the directions to five nearby massive galaxy clusters. DB needs to exceed approximately 9.2 in order to be inconsistent with more than 95 per cent of noise realizations. Middle: the minimum amplitude of a BWM that would have yielded a value of DB exceeding 9.2. Bottom: assuming a statistically average inclination angle for a merging SMBHB, based on the luminosity distance to each of the five galaxy clusters we investigate, the minimum reduced mass of a merging SMBHB that would have produced a detectable BWM.
The |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series associated with the directions towards these five galaxy clusters can be accessed along with DR1 and our simulated data sets following the link mentioned above. Instructions by which results for any other pointing can be quickly produced with tempo2 can be found in the usage details of Appendix B. Following the BWM example detailed here and the analysis of Zhu et al. (2014), analogous searches for any type of parametrized waveform can be easily carried out.
7 MULTIPOLE MENAGERIE: CLOCK ERRORS, INACCURATE EPHEMERIDES, AND GRAVITATIONAL WAVES
As we mentioned in Section 1, GWs are not the sole means by which timing residuals from all the pulsars in a PTA can become correlated. Faults in terrestrial time standards can induce monopolar correlations between pulsar timing data sets (Hobbs et al. 2012). Errors in our estimated position for the SSB from, for example, inaccuracies in the measured mass of Saturn can lead to dipolar correlations between pulsar timing residuals (Champion et al. 2010). In order for |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series to be useful in studies of GW-induced inter-pulsar timing correlations, they must be able to reliably differentiate the distinctly quadrupolar signature of a GW from the monopolar or dipolar signatures of these other effects; in Fig. 4, we demonstrate that our techniques can effectively do this.
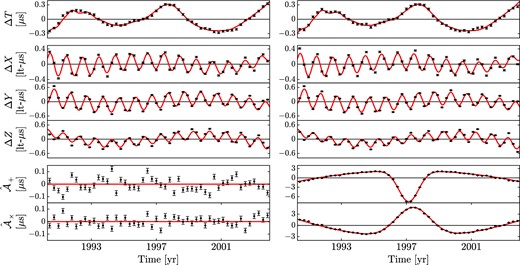
Simultaneous extraction from a 20-pulsar simulated PTA of the monopolar signature of clock errors (top panel), the dipolar signature of an inaccurate Solar system ephemeris (the second, third, and fourth panels from the top), and the two polarization modes of a GW (the bottom two panels). The left panels, depicting an analysis of Sim3, contain no GW signal, while the right panels, depicting an analysis of Sim4, contain the bright GW burst described in equation (16).
The left panels of Fig. 4 depict our analysis of Sim3 in which clock errors and ephemeris errors have been simulated but there is no GW signal present. We simultaneously fit for the timing models of all the pulsars in our simulated array along with linear-interpolant models for clock errors (as in Hobbs et al. 2012), vectorial offsets between the true SSB and its assumed location (as in Champion et al. 2010), and the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series for the direction on the sky from which we eventually inject a GW burst in Sim4. From top to bottom, we display the clock signal (we call this ΔT), the three Cartesian components of the simulated vector displacement in the assumed SSB (called ΔX, ΔY, and ΔZ), and the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series. The red lines indicate the injected signal with the best-fitting (in a least-squares sense) quadratic removed; the quadratic removal is necessary because of the quadratic fit carried out for each pulsar. The black dots indicate the recovered signal. We are able to accurately recover the clock and ephemeris-error signals present in the data and the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| are consistent with a null result. Significant monopolar and dipolar correlations present in the data have not produced spurious signal in the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| channels.
The examples depicted in Fig. 4 illustrate the ability to successfully differentiate the correlations induced in pulsar timing data sets from clock errors, ephemeris errors, and GWs and to recover the relevant signals without substantial bias. However, suppose someone was only interested in searching for a GW signal. If a clock or ephemeris error were leading to correlations across multiple pulsar timing data sets and only |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| were fitted, the unaccounted-for correlations from the clock or ephemeris error would bias the GW signal-recovery and potentially lead to spurious claims of GW detection (for related discussion, see Tiburzi et al. 2015). We emphasize the importance of accounting for potential clock- or ephemeris-error correlations in any PTA effort to detect GWs.
8 CONCLUSIONS
In this paper, we have described a technique that allows the signal of a planar GW from a particular direction of the sky to be distilled from PTA data. This plane wave could be from a single distant source, such as an individual SMBHB, or from a collection of distant sources that are sufficiently close together on the sky like a massive galaxy cluster; how close together sources need to be depends on the angular resolution of the PTA which depends on the spatial distribution of well-timed pulsars. The angular resolution of PTAs will improve over time as timing techniques are improved and as new pulsars are discovered and incorporated into PTAs.
We have assumed that GWs behave according to the predictions of linearized general relativity. Some alternative theories of gravity allow for additional polarization modes of GWs such as longitudinal or breathing modes (Lee 2013); our formalism cannot currently address these alternative theories of gravity, but could with modification. With these caveats regarding the polarization of GWs in mind, since our methods require no assumptions about the time-domain behaviour of GWs, they provide a general and flexible tool that will help maximize the discovery potential of PTAs, potentially facilitating the discovery of wholly unanticipated sources.
Most modern efforts to detect GWs with PTAs utilize sophisticated Bayesian inference codes (van Haasteren et al. 2011; Vigeland & Vallisneri 2014; Arzoumanian et al. 2014; Lentati et al. 2015). Our total-power all-sky GW search in Section 5 and our targeted search for BWMs in Section 6 are frequentist in nature, but as |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| are built into the PTA timing model, they can be straightforwardly incorporated into Bayesian analyses. We feel that the |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| method will complement Bayesian GW searches by providing important diagnostic time series that will allow by-eye examination of GW signals. Furthermore, |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series facilitate a significant condensation of the data volume necessary for GW investigations, and as such, can potentially reduce the computational resources required for even very advanced Bayesian search codes.
Finally, we point out that modern PTA data sets are constantly growing and evolving. As technology advances and allows for upgrades in radio instrumentation and as more nations and observatories become major contributors to PTA endeavours, the data come in a wider variety of forms and from more varied sources. PTA data are becoming more and more heterogeneous and unwieldy to work with. For the purposes of GW investigations, |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series will aid in the creation of a compressed and homogenized auxiliary data set that isolates all of the important GW information.
For this work, we have used data from the Parkes radio telescope. The Parkes radio telescope is part of the Australia Telescope, which is funded by the Commonwealth of Australia for operation as a National Facility managed by the Commonwealth Scientific and Industrial Research Organization (CSIRO). DRM is a Jansky Fellow of the National Radio Astronomy Observatory (NRAO). NRAO is a facility of the National Science Foundation (NSF) operated under cooperative agreement by Associated Universities, Inc. DRM also acknowledges support from a sub-award to Cornell University from West Virginia University through NSF/PIRE grant 0968296, the NANOGrav Physics Frontiers Center NSF award PHY-1430284, and the New York NASA Space Grant Consortium. X-JZ and LW acknowledge funding support from the Australian Research Council. GH is supported by Australian Research Council grant FT120100595. JW is supported by NSFC project No. 11403086 and the West Light Foundation CAS XBBS201322. SO is supported by the Alexander von Humboldt Foundation.
ptaSimulate and documentation for it can be accessed at (https://bitbucket.org/psrsoft/ptasimulate).
All the data sets (real and simulated) used in this paper are available from http://dx.doi.org/10.4225/08/560A00E2036F6
In contrast to searches for a GW background, the signals of interest here have significantly different spectral characteristics than the intrinsic red noise often observed in pulsar data sets.
REFERENCES
APPENDIX A: Approximate Representation of A+ and A×
The matrices |${{\boldsymbol C}_g}$| and |${{\boldsymbol M}_g}$| can be used along with a vector of all of the timing residuals, |${\boldsymbol \delta t}^T = [{{\boldsymbol \delta t}_1}^T\ldots {\boldsymbol \delta t_{N_{\rm P}}}^T]$|, in equations (6) and (7) to carry out a global fit simultaneously for the timing models of all the pulsars in the array and the model for a quadrupolar GW signal coming from direction |${\hat{\boldsymbol n}}$|. However, without some additional conditioning, the fit will be ill-behaved because certain components of signals in A+ and A× will induce structure in each pulsar's timing residuals that will be indistinguishable from structure caused by incorrect estimates of that pulsar's timing model parameters, resulting in a singular parameter covariance matrix.
In addition to the spin parameters of a pulsar, for the purposes of precision pulsar timing, the celestial coordinates of the pulsar are always fit for, and if the precision with which the pulsar can be timed warrants it, two proper motion terms and a parallax are also fit for. The influence of these astrometric parameters on timing models principally concerns the calculation of the Roemer delay – the difference in light-travel-time for pulses arriving at Earth-based observatories and the SSB. Small estimation errors in the position parameters of a pulsar lead to annual sinusoidal fluctuations in the timing residuals of that pulsar. The sinusoid can be of any phase. Similarly, incorrect estimates for proper motion lead to annual sinusoidal fluctuations of any phase in a pulsar's residuals, but the amplitude of the sinusoid grows linearly in time as the expected pulsar position deviates more and more from the true pulsar position.
In the context of fitting linear interpolants to individual pulsar timing data sets to model time-variable dispersion measure, Keith et al. (2013) were the first to discuss and implement the constraints discussed above. Because pulsar timing models often fit for parallax, errors in which induce sinusoidal oscillations with a half-year period in timing residuals, Keith et al. (2013) also constrained their linear interpolants to not contain such biannual sinusoids. But, a parallax constraint is unnecessary for the global, multi-pulsar fits we are discussing. Fitting for parallax in all the pulsars in an array does not generate problems when globally fitting for |${\cal A}_+$| and |${\cal A}_\times$| in the same way as fitting for the pulsars’ rotational parameters, positions, or proper motions. Estimation errors in the parallax induce sinusoidal structure in the timing residuals of a pulsar with a specific phase that depends only on the equatorial longitude of that pulsar. If a GW were to induce biannual sinusoidal structure in a pulsar's residuals, it would have to have a very specific phase to potentially be confused as an error in the parallax estimate for that pulsar, but then, the residuals of other pulsars in the PTA would also show evidence of biannual sinusoidal fluctuations with the same phase in their timing residuals and with amplitudes that vary in accordance with the quadrupolar nature of a GW. If they do, these biannual sinusoidal fluctuations can be reliably ascribed to the activity of a GW in the vicinity of Earth. If they do not, the fluctuations can instead be ascribed to an estimation error in the parallax of one pulsar. For these reasons, no additional constraints regarding parallax must be enforced on |${\cal A}_+$| and |${\cal A}_\times$|.
APPENDIX B: TEMPO2 USAGE
Here we provide details for how to make use of the routines described in this paper. In almost all cases the |${\cal A}_+(t)$| and |${\cal A}_\times (t)$| time series will be included as part of a global fit. The following parameters should therefore be provided in a global parameter file (which we assume is called ‘apac.par’):
# The following line sets (S) the
#quadrupolar (Q) interpolation function
#(IFUNC) for the plus (p) polarization.
#The 1 indicates the type of interpolation
#(linear) and the 2 indicates that this
#will be fitted globally to all pulsars
SQIFUNC_p 1 2
# The next line is the same for the
#cross polarization
SQIFUNC_c 1 2
# We now need to define the direction
#(in radians) of the quadrupole for the
#plus and cross functions
#(usually they are the same)
QIFUNC_POS_P <ra> <dec>
QIFUNC_POS_c <ra> <dec>
# We now define the actual grid points
#for the plus polarization
QIFUNC_p1 <mjd> <val> <err>
QIFUNC_p2 <mjd> <val> <err>
# and also for the cross polarization
QIFUNC_c1 <mjd> <val> <err>
QIFUNC_c2 <mjd> <val> <err>
# We then ensure that the constraints
#are correctly applied
CONSTRAIN QIFUNC_p
CONSTRAIN QIFUNC_c
Assuming that four pulsars have been observed, their parameters are in individual files (psr1.par, psr2.par, psr3.par and psr4.par) and their ToAs are in psr1.tim, psr2.tim etc., then the tempo2 fit can be carried out using:
tempo2 -f psr1.par psr1.tim -f psr2.par
psr2.tim -f psr3.par psr3.tim -f psr4.par
psr4.tim -global apac.par
To include red noise models (defined in model.dat), use:
tempo2 -f psr1.par psr1.tim -f psr2.par
psr2.tim -f psr3.par psr3.tim -f psr4.par
psr4.tim -global apac.par -dcf model.dat
The |$\hat{\cal A}_+$| and |$\hat{\cal A}_\times$| time series are written to files called ‘aplus_t2.dat’ and ‘across_t2.dat’. The covariance matrix |${\boldsymbol C}_{+\times }$| is written to a file called ‘aplus_across.cvm’.



