-
PDF
- Split View
-
Views
-
Cite
Cite
A. B. Pushkarev, Y. Y. Kovalev, Milky Way scattering properties and intrinsic sizes of active galactic nuclei cores probed by very long baseline interferometry surveys of compact extragalactic radio sources, Monthly Notices of the Royal Astronomical Society, Volume 452, Issue 4, 01 October 2015, Pages 4274–4282, https://doi.org/10.1093/mnras/stv1539
Close - Share Icon Share
Abstract
We have measured the angular sizes of radio cores of active galactic nuclei (AGNs) and analysed their sky distributions and frequency dependences to study synchrotron opacity in AGN jets and the strength of angular broadening in the interstellar medium. We have used archival very long baseline interferometry (VLBI) data of more than 3000 compact extragalactic radio sources observed at frequencies, ν, from 2 to 43 GHz to measure the observed angular size of VLBI cores. We have found a significant increase in the angular sizes of the extragalactic sources seen through the Galactic plane (|b| ≲ 10°) at 2, 5 and 8 GHz, about one-third of which show significant scattering. These sources are mainly detected in directions to the Galactic bar, the Cygnus region and a region with galactic longitudes 220° ≲ l ≲ 260° (the Fitzgerald window). The strength of interstellar scattering of the AGNs is found to correlate with the Galactic Hα intensity, free-electron density and Galactic rotation measure. The dependence of scattering strengths on source redshift is insignificant, suggesting that the dominant scattering screens are located in our Galaxy. The observed angular size of Sgr A* is found to be the largest among thousands of AGNs observed over the sky; we discuss possible reasons for this strange result. Excluding extragalactic radio sources with significant scattering, we find that the angular size of opaque cores in AGNs scales typically as ν−1, confirming predictions of a conical synchrotron jet model with equipartition.
INTRODUCTION
Radio waves emitted by a compact background radio source are influenced by propagation effects whenever passing through an ionized medium containing free-electron density fluctuations Δne/ne. Diffraction phenomena associated with scattering result in the angular broadening of a compact bright source, the scattered size of which scales as ν−k, where k ∼ 2 depending on the form of the spatial power spectrum of electron density turbulence (e.g. Goodman & Narayan 1985; Cordes, Pidwerbetsky & Lovelace 1986). If no scattering is present, the observed angular size of opaque cores (i.e. apparent jet base) in active galactic nuclei (AGNs) is expected to scale approximately as ν−1 (Blandford & Königl 1979; Königl 1981, see Section 4.2 for model assumptions;). Departures from this dependence are also possible and can be caused by pressure and density gradients in the jet or by external absorption from the surrounding medium (see Lobanov 1998; Kovalev et al. 2008a; Sokolovsky et al. 2011; Pushkarev et al. 2012, and references therein). This theoretical expectation has never been confirmed statistically by observations of large samples of AGN radio cores.
Based on theoretical models, intergalactic scattering is negligible and can be barely detected with either space very long baseline interferometry (VLBI) or a low-frequency interferometer. In the most optimistic scenario, when a background radio source intersects a galaxy halo with overdensity ∼1000 relative to the mean baryon density of the Universe and the outer scale of turbulence ∼1 kpc, the scatter broadening contribution by the intergalactic medium would be about 0.1 mas at 2 GHz (Koay & Macquart 2015). Therefore, the angular broadening is expected to be strongly dominated by interstellar scattering in the Galaxy.
About two decades since the commissioning of the Very Long Baseline Array (VLBA) in 1994 (Napier et al. 1994), thousands of active galactic nuclei have now been observed with the VLBA and global VLBI arrays at many frequency bands (for details, see Section 2), thereby making it possible to investigate the scattering properties within and outside the Galactic plane. Particularly useful are massive dual-band truly simultaneous 2.3- and 8.4-GHz VLBI observations, originally driven by astrometric and geophysical applications. We use these results (i) to investigate the scattering properties of the Milky Way, and (ii) to measure the scatter-free frequency dependence of core sizes in AGN jets and to compare it with theoretical predictions.
MULTIFREQUENCY DATA AND MEASUREMENTS OF AGN CORE SIZES
For the purposes of our analysis, we made use of data from the Radio Fundamental Catalogue (RFC1), which comprise all sources observed with VLBI under absolute astrometry and geodesy programmes from 1980 to 2014, as well as other major VLBI surveys, described below. As the observed AGNs are highly variable objects, we need data taken simultaneously at different frequencies to analyse the effect of angular broadening. Therefore, we used the truly simultaneous, the most complete and deep survey data at S and X bands centred at 2.3 and 8.4 GHz, respectively. The frequencies are rounded to integer values later in the text for simplicity. These data were mostly obtained within the VLBA Calibrator Survey (VCS; Beasley et al. 2002; Fomalont et al. 2003; Petrov et al. 2005, 2006, 2008; Kovalev et al. 2007) and Research and Development – VLBA (RDV; Petrov et al. 2009) observing sessions (e.g. Pushkarev & Kovalev 2012; Piner et al. 2012). A total of 11 607 epochs of observations were used to observe the 3778 sources with declinations above ≈−45° at 2 GHz, while a total of 12 142 epochs were used to observe 4096 sources distributed over the entire sky at 8 GHz. Additionally, we made some use of data at 5 GHz mainly coming from the VLBI Imaging and Polarimetry Survey (VIPS; Helmboldt et al. 2007; Petrov & Taylor 2011), and the VLBA Calibrator Survey (VCS-7, VCS-8; Petrov, in preparation); at 8 GHz from the VLBA+GBT observing programme for Fermi–AGN associations (Kovalev & Petrov 2011); at 15 GHz from the VLBA 2-cm Survey (Kellermann et al. 1998, 2004), the monitoring of jets in active galactic nuclei with VLBA experiments (MOJAVE; Lister et al. 2009; Lister et al. 2013); at 24 GHz from the VLBI Exploration of Radio Astrometry (VERA) and VLBA K-band (Petrov et al. 2007; Petrov, Honma & Shibata 2012a) and the International Celestial Reference Frame (ICRF) at higher frequencies (Charlot et al. 2010); at 43 GHz from the QCAL-1 43-GHz Calibrator Survey (Petrov et al. 2012b) and the VLBA-BU Blazar Monitoring Programme.2
The parsec-scale morphology of AGNs probed by VLBI observations is typically represented by a one-sided core–jet structure, with a compact core that dominates the total flux density, and a weaker outflow that quickly dims downstream. Therefore, a model of two circular Gaussian components has been fitted to the self-calibrated visibility data for all sources, with the most compact component assigned as the VLBI core following the approach by Kovalev et al. (2005).
The structure modelling has been performed with the procedure modelfit in the difmap package (Shepherd 1997) using an automated approach. Cores were found to be unresolved in a fraction of epochs for a fraction of sources (i.e. their fitted angular sizes were smaller than a corresponding resolution limit calculated following Kovalev et al. 2005). In rare cases, the core components had a low (<10) signal-to-noise ratio. We excluded data for such epochs to remove any bias they might introduce. In cases where multi-epoch data can be used for the core size estimates, a single median value was used for each source in the analysis. The resulting samples contain 2888 and 3019 sources at 2 and 8 GHz (Table 1), respectively, with measured sizes of the cores, of which 2327 sources have simultaneous observations at 2 and 8 GHz (Fig. 1).
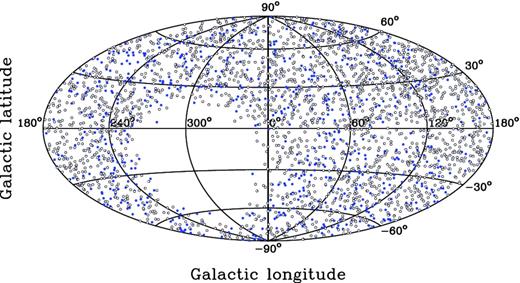
Sky distribution of 3019 RFC sources shown in Aitoff equal-area projection of the celestial sphere in galactic coordinates and used in the analysis after applying the selection criteria. Open dots represent 2327 sources observed simultaneously at 2 and 8 GHz. Blue solid dots denote the other 692 objects observed at 8 GHz only. The sources shown here exclude those with low-core signal-to-noise ratio or unresolved cores.
Kendall's τ-test correlation statistics for the measured size of cores observed over the entire sky at different frequencies versus the absolute galactic latitude shown in Fig. 2. Errors are given at 95 per cent level of significance. N is the number of sources and p is the probability that the correlation occurred by chance.
| ν, GHz . | τ . | N . | p . |
|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . |
| 2.3 | −0.136 ± 0.012 | 2888 | 5 × 10−28 |
| 5.0 | −0.135 ± 0.013 | 2108 | 2 × 10−20 |
| 8.4 | −0.051 ± 0.011 | 3019 | 3 × 10−5 |
| 15.4 | −0.015 ± 0.030 | 513 | 0.61 |
| 24.4 | −0.026 ± 0.033 | 402 | 0.43 |
| 43.1 | −0.063 ± 0.060 | 119 | 0.31 |
| ν, GHz . | τ . | N . | p . |
|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . |
| 2.3 | −0.136 ± 0.012 | 2888 | 5 × 10−28 |
| 5.0 | −0.135 ± 0.013 | 2108 | 2 × 10−20 |
| 8.4 | −0.051 ± 0.011 | 3019 | 3 × 10−5 |
| 15.4 | −0.015 ± 0.030 | 513 | 0.61 |
| 24.4 | −0.026 ± 0.033 | 402 | 0.43 |
| 43.1 | −0.063 ± 0.060 | 119 | 0.31 |
Kendall's τ-test correlation statistics for the measured size of cores observed over the entire sky at different frequencies versus the absolute galactic latitude shown in Fig. 2. Errors are given at 95 per cent level of significance. N is the number of sources and p is the probability that the correlation occurred by chance.
| ν, GHz . | τ . | N . | p . |
|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . |
| 2.3 | −0.136 ± 0.012 | 2888 | 5 × 10−28 |
| 5.0 | −0.135 ± 0.013 | 2108 | 2 × 10−20 |
| 8.4 | −0.051 ± 0.011 | 3019 | 3 × 10−5 |
| 15.4 | −0.015 ± 0.030 | 513 | 0.61 |
| 24.4 | −0.026 ± 0.033 | 402 | 0.43 |
| 43.1 | −0.063 ± 0.060 | 119 | 0.31 |
| ν, GHz . | τ . | N . | p . |
|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . |
| 2.3 | −0.136 ± 0.012 | 2888 | 5 × 10−28 |
| 5.0 | −0.135 ± 0.013 | 2108 | 2 × 10−20 |
| 8.4 | −0.051 ± 0.011 | 3019 | 3 × 10−5 |
| 15.4 | −0.015 ± 0.030 | 513 | 0.61 |
| 24.4 | −0.026 ± 0.033 | 402 | 0.43 |
| 43.1 | −0.063 ± 0.060 | 119 | 0.31 |
APPARENT CORE SIZE INSIDE AND OUTSIDE THE GALACTIC PLANE
In Fig. 2, we plot the angular size θ of the cores as a function of the absolute value of galactic latitude |b|, as scattering effects are most essential for compact components. The general behaviour shows that sources in the Galactic plane (|b| ≲ 10°), comprising about 14 per cent of the samples at 2 and 8 GHz, have on average larger apparent angular sizes relative to sources at higher galactic latitudes. In particular, at 8 GHz, the spline values gradually decrease by a factor of ∼1.7 between |b| ≈ 1° and |b| ≈ 10° and then remain nearly constant at larger latitudes. At lower frequency, the 2-GHz spline shows similar behaviour but with the size decrease present along the entire range of |b|. At both frequencies, the non-parametric Kendall's τ-test confirms a highly significant (p8 GHz = 2 × 10−6, p2 GHz = 10−9) negative correlation between θ and |b| within the Galactic plane. At 5 GHz, the correlation is also highly significant, while at higher frequencies, 15, 24 and 43 GHz, scattering is much weaker with no significant correlation observed. The all-sky correlation statistics for the measured observed size of the VLBI core at different frequencies against the absolute value of the galactic latitude is summarized in Table 1, where we list observing frequency in column (1), ranked correlation coefficient in column (2), the number of sources in column (3) and the probability of correlation by chance in column (4). We estimated the uncertainties of the non-parametric Kendall's τ correlation coefficients listed in Tables 1 and 4 at a significance level of 95 per cent, using a randomization technique based on (i) randomly selecting 80 per cent of a sample, (ii) calculating the τ and (iii) repeating steps (i) and (ii) 2000 times, and then constructing the confidence intervals. The VLBI core sizes measured at different frequencies in a range from 2 to 43 GHz for 4963 sources used in our analysis and presented in Fig. 2 are listed in Table 2. We note that for sources with rich parsec-scale morphology the estimated core sizes might depend strongly on the model chosen to represent the structure.
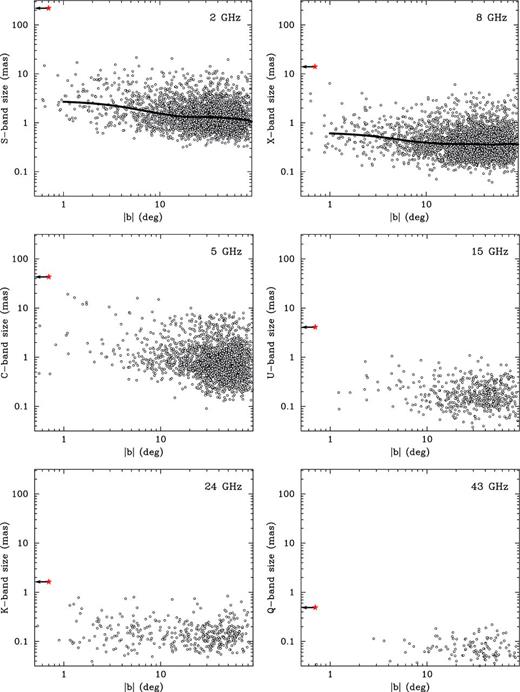
Observed full width at half-maximum (FWHM) angular size of the VLBI core component of AGNs at 2, 5, 8, 15, 24 and 43 GHz versus the absolute value of galactic latitude. Each point represents a single source; a median is used for sources with size measurements at more than one epoch. Thick lines represent the cubic spline interpolation and are shown for the 2- and 8-GHz data only, characterized by the best completeness properties, the most uniform sky distribution and the largest number of sources. Sgr A* is shown by a star symbol. Correlation statistics are presented in Table 1.
Apparent angular sizes of the VLBI cores of 4963 AGNs determined by modelfit. Columns are as follows: (1) source name in J2000.0 notation; (2) Galactic latitude; (3) Galactic longitude; (4) redshift from the continuously updated Optical Characteristics of Astrometric Radio Sources (OCARS) data base at http://www.gao.spb.ru/english/as/ac_vlbi/ocars.txt (reference to original redshift data can be found in this compiled data base, a description of which is given in Malkin & Titov 2008); (5)–(10) FWHM of the fitted circular Gaussian at 2, 5, 8, 15, 24 and 43 GHz, respectively. If a source was observed over multiple epochs, the median of the observed angular size is given. This table is available in its entirety in a machine-readable form in the online journal. A portion is shown here for guidance regarding its form and content.
| . | b . | l . | z . | θ2 . | θ5 . | θ8 . | θ15 . | θ24 . | θ43 . |
|---|---|---|---|---|---|---|---|---|---|
| Name . | (deg) . | (deg) . | . | (mas) . | (mas) . | (mas) . | (mas) . | (mas) . | (mas) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . |
| J0000−3221 | −77.752 | 357.466 | 1.275 | 0.98 | – | 0.45 | – | – | – |
| J0000+4054 | −20.968 | 112.163 | – | 3.65 | – | 2.90 | – | – | – |
| J0001+1456 | −46.228 | 104.539 | 0.399 | – | 1.16 | – | – | – | – |
| J0001+1914 | −42.054 | 105.998 | 3.100 | 0.94 | – | 0.19 | – | – | – |
| J0001+4440 | −17.292 | 113.181 | – | – | 0.46 | – | – | – | – |
| J0001+6051 | −1.419 | 116.869 | – | 4.30 | – | 1.02 | – | – | – |
| J0002−2153 | −77.642 | 52.802 | – | – | – | 0.24 | – | – | – |
| J0003−1547 | −74.105 | 75.364 | 0.508 | – | – | 0.54 | – | – | – |
| J0003−1927 | −76.560 | 63.669 | 2.000 | 1.52 | – | 0.94 | – | – | – |
| J0003+2129 | −40.002 | 107.437 | 0.450 | – | – | 0.34 | 0.17 | – | – |
| . | b . | l . | z . | θ2 . | θ5 . | θ8 . | θ15 . | θ24 . | θ43 . |
|---|---|---|---|---|---|---|---|---|---|
| Name . | (deg) . | (deg) . | . | (mas) . | (mas) . | (mas) . | (mas) . | (mas) . | (mas) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . |
| J0000−3221 | −77.752 | 357.466 | 1.275 | 0.98 | – | 0.45 | – | – | – |
| J0000+4054 | −20.968 | 112.163 | – | 3.65 | – | 2.90 | – | – | – |
| J0001+1456 | −46.228 | 104.539 | 0.399 | – | 1.16 | – | – | – | – |
| J0001+1914 | −42.054 | 105.998 | 3.100 | 0.94 | – | 0.19 | – | – | – |
| J0001+4440 | −17.292 | 113.181 | – | – | 0.46 | – | – | – | – |
| J0001+6051 | −1.419 | 116.869 | – | 4.30 | – | 1.02 | – | – | – |
| J0002−2153 | −77.642 | 52.802 | – | – | – | 0.24 | – | – | – |
| J0003−1547 | −74.105 | 75.364 | 0.508 | – | – | 0.54 | – | – | – |
| J0003−1927 | −76.560 | 63.669 | 2.000 | 1.52 | – | 0.94 | – | – | – |
| J0003+2129 | −40.002 | 107.437 | 0.450 | – | – | 0.34 | 0.17 | – | – |
Apparent angular sizes of the VLBI cores of 4963 AGNs determined by modelfit. Columns are as follows: (1) source name in J2000.0 notation; (2) Galactic latitude; (3) Galactic longitude; (4) redshift from the continuously updated Optical Characteristics of Astrometric Radio Sources (OCARS) data base at http://www.gao.spb.ru/english/as/ac_vlbi/ocars.txt (reference to original redshift data can be found in this compiled data base, a description of which is given in Malkin & Titov 2008); (5)–(10) FWHM of the fitted circular Gaussian at 2, 5, 8, 15, 24 and 43 GHz, respectively. If a source was observed over multiple epochs, the median of the observed angular size is given. This table is available in its entirety in a machine-readable form in the online journal. A portion is shown here for guidance regarding its form and content.
| . | b . | l . | z . | θ2 . | θ5 . | θ8 . | θ15 . | θ24 . | θ43 . |
|---|---|---|---|---|---|---|---|---|---|
| Name . | (deg) . | (deg) . | . | (mas) . | (mas) . | (mas) . | (mas) . | (mas) . | (mas) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . |
| J0000−3221 | −77.752 | 357.466 | 1.275 | 0.98 | – | 0.45 | – | – | – |
| J0000+4054 | −20.968 | 112.163 | – | 3.65 | – | 2.90 | – | – | – |
| J0001+1456 | −46.228 | 104.539 | 0.399 | – | 1.16 | – | – | – | – |
| J0001+1914 | −42.054 | 105.998 | 3.100 | 0.94 | – | 0.19 | – | – | – |
| J0001+4440 | −17.292 | 113.181 | – | – | 0.46 | – | – | – | – |
| J0001+6051 | −1.419 | 116.869 | – | 4.30 | – | 1.02 | – | – | – |
| J0002−2153 | −77.642 | 52.802 | – | – | – | 0.24 | – | – | – |
| J0003−1547 | −74.105 | 75.364 | 0.508 | – | – | 0.54 | – | – | – |
| J0003−1927 | −76.560 | 63.669 | 2.000 | 1.52 | – | 0.94 | – | – | – |
| J0003+2129 | −40.002 | 107.437 | 0.450 | – | – | 0.34 | 0.17 | – | – |
| . | b . | l . | z . | θ2 . | θ5 . | θ8 . | θ15 . | θ24 . | θ43 . |
|---|---|---|---|---|---|---|---|---|---|
| Name . | (deg) . | (deg) . | . | (mas) . | (mas) . | (mas) . | (mas) . | (mas) . | (mas) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . |
| J0000−3221 | −77.752 | 357.466 | 1.275 | 0.98 | – | 0.45 | – | – | – |
| J0000+4054 | −20.968 | 112.163 | – | 3.65 | – | 2.90 | – | – | – |
| J0001+1456 | −46.228 | 104.539 | 0.399 | – | 1.16 | – | – | – | – |
| J0001+1914 | −42.054 | 105.998 | 3.100 | 0.94 | – | 0.19 | – | – | – |
| J0001+4440 | −17.292 | 113.181 | – | – | 0.46 | – | – | – | – |
| J0001+6051 | −1.419 | 116.869 | – | 4.30 | – | 1.02 | – | – | – |
| J0002−2153 | −77.642 | 52.802 | – | – | – | 0.24 | – | – | – |
| J0003−1547 | −74.105 | 75.364 | 0.508 | – | – | 0.54 | – | – | – |
| J0003−1927 | −76.560 | 63.669 | 2.000 | 1.52 | – | 0.94 | – | – | – |
| J0003+2129 | −40.002 | 107.437 | 0.450 | – | – | 0.34 | 0.17 | – | – |
The sources with large angular sizes (>1 mas at 8 GHz and >5 mas at 2 GHz) within the Galactic plane are non-uniformly distributed with the galactic longitude l (Fig. 3). The distribution peaks represent the direction to the Galactic Centre (GC) and bar in the region 340° ≲ l ≲ 20°, towards the Cygnus region in the region 65° ≲ l ≲ 90° and towards the star-forming regions in the Perseus and Local (Orion) arms (Vázquez et al. 2008) and the Vela supernova remnant in the region 220° ≲ l ≲ 260°. Screens with significant scattering strength are expected in these regions. We will analyse and present the patchy distributions of scatter-broadened compact extragalactic sources elsewhere. We also note the lack of the broadened sources along the direction to the Galactic anticentre (l ∼ 180°), where less interstellar scattering is expected within the Galactic plane. The gap of sources around l ∼ 300° is due to the absence of the southernmost AGNs in available VLBI surveys, especially at 2 GHz, as can be seen from the sky distribution in Fig. 1.
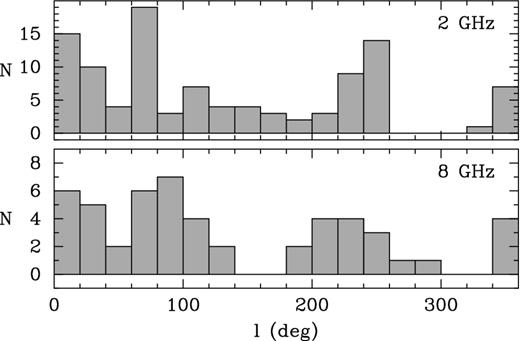
Histograms of the galactic longitude for the large-sized Galactic plane sources from Fig. 2 with angular size exceeding 5 mas at 2 GHz (top) and 1 mas at 8 GHz (bottom).
Because the Sun is about 26 ± 3 pc away from the Galactic plane as inferred from classical Cepheids (Majaess, Turner & Lane 2009), we tested for possible asymmetry in the angular size distributions for the sources with negative and positive galactic latitude within the Galactic plane. The latter population shows an ∼8 per cent excess in quantity (Fig. 1) but no significant difference in the angular size at 2 and 8 GHz is found by a Kolmogorov–Smirnov (K–S) test. Mean values also agree within the errors, with 3.0 ± 0.3 mas (0° < b < 10°) and 2.6 ± 0.3 (−10° < b < 0°) at 2 GHz and 0.60 ± 0.06 mas (0° < b < 10°) and 0.63 ± 0.08 (−10° < b < 0°) at 8 GHz. Additionally, no significant difference between k-index distributions for these groups of sources is found by a K–S test (see more details in Section 4).
SEPARATING INTRINSIC AND EXTERNAL EFFECTS: FREQUENCY DEPENDENCE OF AGN CORE SIZE
We compiled a sample of 2327 sources that have been observed at 2 and 8 GHz simultaneously and for which the k-index was successfully estimated for the size–frequency dependence θ ∝ ν−k for each object using the corresponding measured VLBI core sizes. If a source had more than one epoch of observations, then the median value of k was derived. We show the resulting distribution of the k-index with two histograms: for 335 sources within the Galactic plane (Fig. 4, left, |b| < 10°) and 1992 sources at |b| > 10° (Fig. 4, right). The k-index distribution for the sources at low galactic latitudes was fitted with two Gaussians, the best-fitting peaks of which are 0.91 and 1.76. The lower and higher peaked Gaussians represent two groups of sources, non-scattered and scattered by intervening screens, respectively. The k-index distribution for the sources out of the Galactic plane (Fig. 4, right) shows that most of them are not affected significantly by angular broadening. The distribution is fitted by a single Gaussian with the best-fitting peak at 0.90, which is consistent with the left Gaussian for the Galactic plane AGN. Because the first peak is observed for both distributions (Table 3) while the second peak is visible for the Galactic plane only, this confirms that the latter has an origin that is extrinsic to the AGN.
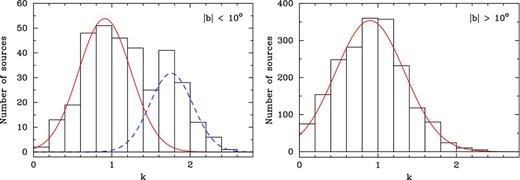
Histograms of the k-index in a size–frequency dependence θ ∝ ν−k for the sources within the Galactic plane (left) and away from it (right). For sources with multi-epoch observations, median values of k are used. Two Gaussians are fitted to the left-panel distribution representing non-scattered (μ = 0.91) and scatter-broadened (μ = 1.76) sources. The right-panel distribution is fitted with a single Gaussian. Details on the fits are shown in Table 3. Bins with negative k values are not shown, comprising about 0.3 and 2.4 per cent of the sources with k down to −0.01 and −0.47 at low and high Galactic latitudes, respectively.
Parameters of the Gaussians fitted to the k-index distributions in Fig. 4. The presented parameters are found from the following Gaussian fit: |$\lambda \exp [(k-\mu )^2/(2\sigma ^2)]/(\sigma \sqrt{2\pi })$|.
| |b| . | λ . | μ . | σ . |
|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . |
| <10° | 0.67 | 0.91 | 0.33 |
| 0.33 | 1.76 | 0.28 | |
| >10° | 1.00 | 0.90 | 0.44 |
| |b| . | λ . | μ . | σ . |
|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . |
| <10° | 0.67 | 0.91 | 0.33 |
| 0.33 | 1.76 | 0.28 | |
| >10° | 1.00 | 0.90 | 0.44 |
Parameters of the Gaussians fitted to the k-index distributions in Fig. 4. The presented parameters are found from the following Gaussian fit: |$\lambda \exp [(k-\mu )^2/(2\sigma ^2)]/(\sigma \sqrt{2\pi })$|.
| |b| . | λ . | μ . | σ . |
|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . |
| <10° | 0.67 | 0.91 | 0.33 |
| 0.33 | 1.76 | 0.28 | |
| >10° | 1.00 | 0.90 | 0.44 |
| |b| . | λ . | μ . | σ . |
|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . |
| <10° | 0.67 | 0.91 | 0.33 |
| 0.33 | 1.76 | 0.28 | |
| >10° | 1.00 | 0.90 | 0.44 |
We note that only about one-third of the sources within |b| < 10° shows angular scatter-broadening external to the source. As the typical value of k for the scattered sources is less than the expected k ≈ 2, this could indicate that the angular sizes of some turbulent eddies are comparable to those of the VLBI cores, and refractive effects might also play a role in scattering (e.g. Cordes et al. 1986; Pushkarev et al. 2013). Alternatively, it can be partly caused by variability of scattering properties of intervening screen on the line of sight to a source (e.g. Koay et al. 2011; Pushkarev et al. 2013; de Bruyn & Macquart 2015). If a scatter-broadened source has more than one epoch of observations and a scattering screen either changes its characteristics or moves away, the median k would decrease. In total, about 30 per cent of the analysed sources with |b| < 10° had two or more epochs of observations, making scattering variability potentially responsible for the lower k. To test this scenario, we repeated the analysis constructing a k-index distribution using (i) the first epoch only for each source and (ii) the last epoch only. In all three cases, the obtained distributions and fitted Gaussians are similar, indicating that the slightly lower value of k cannot be explained by a net movement of screens away from the line of sight. To confirm that significant variability of scattering is a rare phenomenon on a time-scale of a few years, we analysed the distribution of (k2 − k1) for each of the 108 sources within the Galactic plane that had more than one epoch, where k2 is the value of k in the last epoch and k1 is the value of k in the first epoch. Indeed, we obtained a narrow distribution peaking at 0, with a median value 0.01 and a standard deviation 0.55.
Another possible reason why we observe the lower values of k in scatter-broadened sources is that the scattering effects do not dominate. Because the observed angular size |$\theta _\mathrm{obs} = (\theta ^2_\mathrm{int} + \theta ^2_\mathrm{scat})^{1/2}$|, where θint is the intrinsic source size and θscat is the scatter broadening, the observed angular size will scale with ν−2 only if θscat ≫ θint and θscat completely dominates. If θscat is only slightly larger than θint, then 1 < k < 2.
In order to test that the different resolutions of 2- and 8-GHz VLBI data do not affect the robustness of the derived k ∼ 1 value (Table 3) and to make sure that this result is not due to degradation of angular resolution towards lower frequencies, we performed the same analysis for the Galactic plane sources using matching resolution at both frequencies. The maximum (u, v) radius |$r_{uv}^\mathrm{max}$| at 8 GHz was limited to that derived from the corresponding 2-GHz data sets. The resulting typical value of |$r_{uv}^\mathrm{max}$| in the data was about 65 Mλ. We took steps to avoid blending effects that lead to the innermost portions of the jet component being fitted as part of the core component in the 8-GHz data, thereby falsely increasing the fitted sizes of the VLBI core component. To implement this, we fit the core component at both frequency bands as an elliptical Gaussian, the major axis of which typically aligns with the innermost jet direction (Kovalev et al. 2005), while a minor axis θmin sets the transverse width of the outflow in the radio core. The values of k-index were derived using the VLBI core widths θmin transverse to the jet direction. The obtained distribution for |b| < 10° was fitted with two Gaussians with the best-fitting peaks at 0.98 and 1.70, very close to the peaks derived from the full resolution data sets (Table 3).
In Fig. 5, we present the expected dependence between the core size at 2 GHz and k-index. It confirms that large observed sizes are indeed found from strongly scattered sources with high k instead of being intrinsic to the jets. The distribution of galactic longitude for sources with k > 1.4 was confirmed to be similar to that in Fig. 3 (top).
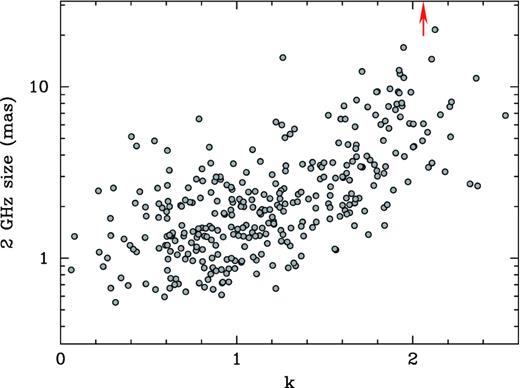
Observed angular core size at 2 GHz as a function of a two-frequency k-index for 335 sources within the Galactic plane |b| < 10°. Sgr A* (θ2 GHz ≈ 220 mas) is beyond the plot limit and indicated by the arrow.
Of the 2327 analysed sources, 1594 (68 per cent) have measured redshifts distributed in the range of 0 ≲ z ≲ 4.7. We tested a relationship between the k-index and redshift and found no significant dependence, confirming that the screens that dominate in scattering are located in our Galaxy. This is consistent with other studies that did not find significant redshift dependence of scatter broadening using VLBI but for a much smaller sample of 58 sources (Lazio et al. 2008), and using interstellar scintillation of 128 sources (Koay et al. 2012).
Testing connection with rotation measure, free-electron density and H|$\boldsymbol {\alpha }$| Galactic distributions
The positions of the scatter-broadened sources are expected to match with the sky regions where an excess of electron density is measured. To test this idea, we searched for correlations between k-index values and the following: (i) angular broadening at 1 GHz, θscat, 1GHz, derived from the NE2001 Galactic free electron density model, which in turn is based on pulsar observations and also includes scattering properties of extragalactic and other Galactic radio sources (Cordes & Lazio 2002); (ii) absolute value of rotation measures (Taylor, Stil & Sunstrum 2009); (iii) Hα emission used as a tracer of ionized gas (Finkbeiner 2003). In all cases, highly significant correlation was established using the non-parametric Kendall's τ-test (Table 4). The strongest correlation shown in Fig. 6 is detected between the k-index derived from our analysis and Hα intensity. This is most probably because of the highest resolution of Hα data among the three data sets used. It has an angular resolution reaching 2.5-arcmin pixel2 at b = 0° from the full-sky composite Hα map (Finkbeiner 2003). The observed correlations confirm the extrinsic origin of the k ≈ 2 frequency dependence of the AGN core sizes in the Galactic plane.
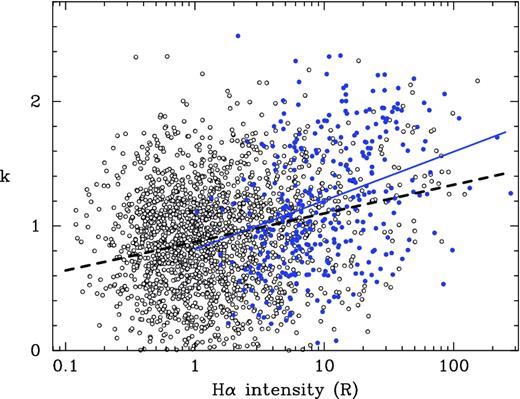
Correlation between the k-index for 2327 extragalactic radio sources and Hα intensity in Rayleighs (1R = 106 photons cm−2 s−1 sr−1) measured along the corresponding position of the sky. Filled dots represent the Galactic plane sources. Solid and dashed lines are the least-squares fit to the Galactic plane and all-sky samples, respectively. The fits differ significantly.
Kendall's τ-test correlation statistics for k-index values and rotation measures RM, angular broadening θscat, 1 GHz from the NE2001 model (Cordes & Lazio 2002), and Hα intensity. Errors are given at 95 per cent level of significance. N is the number of sources and p is the probability that the correlation occurred by chance.
| Correlation . | |b| < 10° . | . | |b| > 10° . | . | |b| > 0° . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | τ . | N . | p . | . | τ . | N . | p . | . | τ . | N . | p . |
| (1) . | (2) . | (3) . | (4) . | . | (5) . | (6) . | (7) . | . | (8) . | (9) . | (10) . |
| k vs RM | 0.122 ± 0.034 | 335 | 5 × 10−3 | 0.058 ± 0.015 | 1992 | 1 × 10−4 | 0.095 ± 0.014 | 2327 | 7 × 10−14 | ||
| k vs θscat, 1 GHz | 0.188 ± 0.033 | 335 | 3 × 10−7 | 0.078 ± 0.014 | 1992 | 2 × 10−7 | 0.137 ± 0.013 | 2327 | 5 × 10−23 | ||
| k vs Hα | 0.249 ± 0.030 | 335 | 1 × 10−11 | 0.083 ± 0.015 | 1992 | 4 × 10−8 | 0.146 ± 0.012 | 2327 | 9 × 10−26 | ||
| Correlation . | |b| < 10° . | . | |b| > 10° . | . | |b| > 0° . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | τ . | N . | p . | . | τ . | N . | p . | . | τ . | N . | p . |
| (1) . | (2) . | (3) . | (4) . | . | (5) . | (6) . | (7) . | . | (8) . | (9) . | (10) . |
| k vs RM | 0.122 ± 0.034 | 335 | 5 × 10−3 | 0.058 ± 0.015 | 1992 | 1 × 10−4 | 0.095 ± 0.014 | 2327 | 7 × 10−14 | ||
| k vs θscat, 1 GHz | 0.188 ± 0.033 | 335 | 3 × 10−7 | 0.078 ± 0.014 | 1992 | 2 × 10−7 | 0.137 ± 0.013 | 2327 | 5 × 10−23 | ||
| k vs Hα | 0.249 ± 0.030 | 335 | 1 × 10−11 | 0.083 ± 0.015 | 1992 | 4 × 10−8 | 0.146 ± 0.012 | 2327 | 9 × 10−26 | ||
Kendall's τ-test correlation statistics for k-index values and rotation measures RM, angular broadening θscat, 1 GHz from the NE2001 model (Cordes & Lazio 2002), and Hα intensity. Errors are given at 95 per cent level of significance. N is the number of sources and p is the probability that the correlation occurred by chance.
| Correlation . | |b| < 10° . | . | |b| > 10° . | . | |b| > 0° . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | τ . | N . | p . | . | τ . | N . | p . | . | τ . | N . | p . |
| (1) . | (2) . | (3) . | (4) . | . | (5) . | (6) . | (7) . | . | (8) . | (9) . | (10) . |
| k vs RM | 0.122 ± 0.034 | 335 | 5 × 10−3 | 0.058 ± 0.015 | 1992 | 1 × 10−4 | 0.095 ± 0.014 | 2327 | 7 × 10−14 | ||
| k vs θscat, 1 GHz | 0.188 ± 0.033 | 335 | 3 × 10−7 | 0.078 ± 0.014 | 1992 | 2 × 10−7 | 0.137 ± 0.013 | 2327 | 5 × 10−23 | ||
| k vs Hα | 0.249 ± 0.030 | 335 | 1 × 10−11 | 0.083 ± 0.015 | 1992 | 4 × 10−8 | 0.146 ± 0.012 | 2327 | 9 × 10−26 | ||
| Correlation . | |b| < 10° . | . | |b| > 10° . | . | |b| > 0° . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | τ . | N . | p . | . | τ . | N . | p . | . | τ . | N . | p . |
| (1) . | (2) . | (3) . | (4) . | . | (5) . | (6) . | (7) . | . | (8) . | (9) . | (10) . |
| k vs RM | 0.122 ± 0.034 | 335 | 5 × 10−3 | 0.058 ± 0.015 | 1992 | 1 × 10−4 | 0.095 ± 0.014 | 2327 | 7 × 10−14 | ||
| k vs θscat, 1 GHz | 0.188 ± 0.033 | 335 | 3 × 10−7 | 0.078 ± 0.014 | 1992 | 2 × 10−7 | 0.137 ± 0.013 | 2327 | 5 × 10−23 | ||
| k vs Hα | 0.249 ± 0.030 | 335 | 1 × 10−11 | 0.083 ± 0.015 | 1992 | 4 × 10−8 | 0.146 ± 0.012 | 2327 | 9 × 10−26 | ||
Intrinsic AGN core size: theory predictions and experimental results
Theoretically, the rcore ∝ ν−1 dependence, where rcore is the distance of the apparent jet base (radio core) at a given frequency from the true jet origin, was predicted by Blandford & Königl (1979) in their idealized model of a steady radio jet assuming the following: (i) the jet is conical with a small half-opening angle φ; (ii) the jet is supersonic and free (i.e. |$\varphi >\mathcal {M}$|, where |$\mathcal {M}$| is the Mach number); (iii) the jet has constant velocity; (iv) a power-law energy distribution N(E) ∝ E−2 along the jet; (v) there is an approximate equipartition between jet particle and magnetic field energy densities. The assumption of a conical geometry (see observational evidence by Asada & Nakamura 2012; Pushkarev et al. 2014) leads to θcore ∝ rcore ∝ ν−1 dependence.
This is consistent with what we have derived for the majority of the non-scattered sources (Fig. 4, Table 3), and also with the opacity-driven core shift effect results (e.g. Lobanov 1998; Kovalev, Lobanov & Pushkarev 2008b; O'Sullivan & Gabuzda 2009; Sokolovsky et al. 2011; Kutkin et al. 2014). Despite the fact that the k-index distribution is centred close to 1, its wide distribution indicates that departures from the model assumptions are possible in many cases. This can be caused by, for example, pressure and density gradients in the outflow (Lobanov 1998) or non-conical jet geometry. Errors of the derived k-index values additionally widen the distribution. We have analysed a subsample of 344 sources out of the Galactic plane that have rich multifrequency data of the angular size measurements covering four, five or six frequencies. From these multifrequency data, we found that in 25 per cent of the 344 sources, the k-index values do significantly deviate from the value of 1. Nevertheless, based on the large number statistics, it is likely that the k-index distribution does indeed peak at a value close to 1.
SCATTERING PROPERTIES OF SGR A*
In Fig. 2 (star symbol), we also show Sgr A*, a compact radio source in the centre of the Galaxy. The angular size of the object was calculated using a size-wavelength fit 1.0324 λ2.0598 derived by Zensus, Krichbaum & Britzen (2007), giving about 14 mas at 8 GHz and 220 mas at 2 GHz, which are larger by a factor of about 2 and 10, respectively, than the maximum apparent size of an AGN core in our sample. Angular size statistics are given in Table 5, where the errors of the median sizes were estimated using the randomization technique described in Section 3. The size of Sgr A* at 8 and 15 GHz calculated from the fit derived by Zensus et al. (2007) is consistent with later measurements from other studies (e.g. Bower et al. 2014).
Angular size statistics. The columns present the following: (1) central observing frequency; (2) median angular size for AGN cores outside the Galactic plane and its error at 95 per cent level of significance; (3) number of sources used to estimate (2); (4) median angular size for AGN cores inside the Galactic plane and its error at 95 per cent level of significance; (5) number of sources used to estimate (4); (6) all-sky maximum of measured core angular size; (7) angular size of Sgr A* for comparison.
| Frequency . | θmed (|b| > 10°) . | N . | θmed (|b| < 10°) . | N . | θmax . | θ (Sgr A*) . |
|---|---|---|---|---|---|---|
| (GHz) . | (mas) . | . | (mas) . | . | (mas) . | (mas) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| 2.3 | 1.29 ± 0.03 | 2502 | 1.97 ± 0.15 | 386 | 21.55 | 220 |
| 5.0 | 0.74 ± 0.03 | 1988 | 1.12 ± 0.21 | 120 | 19.16 | 43 |
| 8.4 | 0.37 ± 0.01 | 2606 | 0.44 ± 0.04 | 413 | 6.37 | 14 |
| 15.4 | 0.16 ± 0.01 | 464 | 0.23 ± 0.05 | 48 | 1.04 | 4 |
| 24.4 | 0.13 ± 0.01 | 289 | 0.15 ± 0.03 | 113 | 0.81 | 1.6 |
| 43.1 | 0.07 ± 0.01 | 109 | 0.07 ± 0.03 | 10 | 0.22 | 0.5 |
| Frequency . | θmed (|b| > 10°) . | N . | θmed (|b| < 10°) . | N . | θmax . | θ (Sgr A*) . |
|---|---|---|---|---|---|---|
| (GHz) . | (mas) . | . | (mas) . | . | (mas) . | (mas) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| 2.3 | 1.29 ± 0.03 | 2502 | 1.97 ± 0.15 | 386 | 21.55 | 220 |
| 5.0 | 0.74 ± 0.03 | 1988 | 1.12 ± 0.21 | 120 | 19.16 | 43 |
| 8.4 | 0.37 ± 0.01 | 2606 | 0.44 ± 0.04 | 413 | 6.37 | 14 |
| 15.4 | 0.16 ± 0.01 | 464 | 0.23 ± 0.05 | 48 | 1.04 | 4 |
| 24.4 | 0.13 ± 0.01 | 289 | 0.15 ± 0.03 | 113 | 0.81 | 1.6 |
| 43.1 | 0.07 ± 0.01 | 109 | 0.07 ± 0.03 | 10 | 0.22 | 0.5 |
Angular size statistics. The columns present the following: (1) central observing frequency; (2) median angular size for AGN cores outside the Galactic plane and its error at 95 per cent level of significance; (3) number of sources used to estimate (2); (4) median angular size for AGN cores inside the Galactic plane and its error at 95 per cent level of significance; (5) number of sources used to estimate (4); (6) all-sky maximum of measured core angular size; (7) angular size of Sgr A* for comparison.
| Frequency . | θmed (|b| > 10°) . | N . | θmed (|b| < 10°) . | N . | θmax . | θ (Sgr A*) . |
|---|---|---|---|---|---|---|
| (GHz) . | (mas) . | . | (mas) . | . | (mas) . | (mas) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| 2.3 | 1.29 ± 0.03 | 2502 | 1.97 ± 0.15 | 386 | 21.55 | 220 |
| 5.0 | 0.74 ± 0.03 | 1988 | 1.12 ± 0.21 | 120 | 19.16 | 43 |
| 8.4 | 0.37 ± 0.01 | 2606 | 0.44 ± 0.04 | 413 | 6.37 | 14 |
| 15.4 | 0.16 ± 0.01 | 464 | 0.23 ± 0.05 | 48 | 1.04 | 4 |
| 24.4 | 0.13 ± 0.01 | 289 | 0.15 ± 0.03 | 113 | 0.81 | 1.6 |
| 43.1 | 0.07 ± 0.01 | 109 | 0.07 ± 0.03 | 10 | 0.22 | 0.5 |
| Frequency . | θmed (|b| > 10°) . | N . | θmed (|b| < 10°) . | N . | θmax . | θ (Sgr A*) . |
|---|---|---|---|---|---|---|
| (GHz) . | (mas) . | . | (mas) . | . | (mas) . | (mas) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| 2.3 | 1.29 ± 0.03 | 2502 | 1.97 ± 0.15 | 386 | 21.55 | 220 |
| 5.0 | 0.74 ± 0.03 | 1988 | 1.12 ± 0.21 | 120 | 19.16 | 43 |
| 8.4 | 0.37 ± 0.01 | 2606 | 0.44 ± 0.04 | 413 | 6.37 | 14 |
| 15.4 | 0.16 ± 0.01 | 464 | 0.23 ± 0.05 | 48 | 1.04 | 4 |
| 24.4 | 0.13 ± 0.01 | 289 | 0.15 ± 0.03 | 113 | 0.81 | 1.6 |
| 43.1 | 0.07 ± 0.01 | 109 | 0.07 ± 0.03 | 10 | 0.22 | 0.5 |
Why is the angular size of Sgr A* so unusual? We discuss two possibilities here. First, the peculiarity of Sgr A* might be an observing bias if we miss sources with comparably large angular sizes as a result of lack of data for the imaging technique that requires at least four stations to closure amplitudes. Indeed, the correlated flux density of a heavily resolved source quickly drops with increasing baseline projection (e.g. fig. 2 in Gwinn et al. 2014) and attains the typical VCS detection limit of about 50 mJy (Kovalev et al. 2007). To test this scenario, we estimated the minimum total flux density level |$S_\mathrm{min}^\mathrm{tot}$|, below which we can potentially miss large-sized sources. Considering a circular Gaussian source model with a size of Sgr A* at 8 GHz, 14.4 mas, we found that the shortest VLBA baseline projections formed by four inner stations reach the VCS detection limit of ≈50 mJy if |$S_\mathrm{min}^\mathrm{tot}= 100$|–150 mJy, depending on the uv-plane coverage. Remember that Stot > 1 Jy for Sgr A* at 8 GHz. Note that in the RDV sessions, in addition to the VLBA stations, a number of other antennas participated (normally six to eight additional radio telescopes) forming an array with shorter baseline projections. This implies that the level of |$S_\mathrm{min}^\mathrm{tot}$| in the RDV data sets is even lower than that derived from the VCS data. We conclude that it is unlikely that our sample, which is flux density complete down to about 200 mJy at 8.6 GHz above declination −30° (Kovalev et al. 2007), misses sources with large observed angular sizes similar to that of Sgr A* at the corresponding observing frequency.
We miss sources that are either a few times larger in size than Sgr A*, such as the extragalactic radio source NGC 6334B, which is the most strongly scattered object known, with an angular size of 3 arcsec at 20-cm wavelength (Trotter, Moran & Rodríguez 1998; Moran et al. 1990), or considerably weaker sources. In principle, an obvious reason for the seeming uniqueness of Sgr A* could be an insufficient source density of sky coverage (see the GC region in Fig. 7) and deepness of the all-sky sample being analysed.
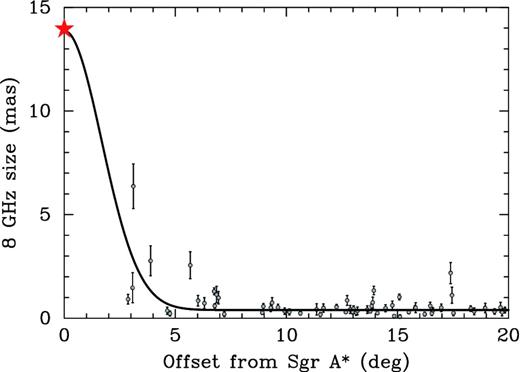
Observed angular size of AGN cores at 8 GHz as a function of angular separation from Sgr A* shown by a star symbol, with a clear negative dependence fitted by a Gaussian with the FWHM ∼4°and background level ∼0.4 mas, suggesting the hyperstrong scattering screen in the immediate vicinity of Sgr A*.
The second possibility is that the scattering strength of the screen towards Sgr A* could be extremely strong, making it the most heavily scatter-broadened source at centimetre wavelengths. This suggests that a turbulent scattering screen with substantially enhanced free-electron density is located in the immediate vicinity of Sgr A*. Scattering strength peaking at the GC decreases with the angular distance from it, and is fitted by a Gaussian with FWHM of about 4°(Fig. 7), providing an estimate of a size for the intermediate-strength scattering region. Observing radio sources in the GC region, Roy (2013) found that scattering sizes decrease linearly with increasing angular distance from the GC up to about 1°. The sources in our sample are not very close to the GC. One of the nearest object, J1744−3116, observed at 8 GHz, is 3°away from Sgr A* and has a scatter-broadened source size that is smaller by a factor of ∼2. The only source in the GC region with an angular size comparable to Sgr A*, measured at 8.7 and 15.4 GHz by Bower et al. (2014), is the recently discovered magnetar gravitationally bound to Sgr A* about 3 arcsec away, or at a linear separation of ≈0.07–2 pc (Rea et al. 2013). Assuming a single thin-screen model, Bower et al. (2014) used the combination of temporal smearing (Spitler et al. 2014) and angular broadening of the magnetar emission as a powerful tool for assessing the distance, and concluded that the screen is located roughly 6 kpc from Sgr A* towards the Sun. However, it seems very unlikely that the line of sight to the cloud of the ionized medium with the extremely strong scattering strength in the Galaxy passes by chance exactly through the GC.
We can place some constraints on the scattering screen media using the relations of a thin-screen model. First, as shown by Vandenberg (1976) and Lazio et al. (2008), the scattered size θscat ∝ neDLS, where DLS is the distance from a source to the scattering screen. Therefore, a close (0.1–1 pc from Sgr A*) screen must be a factor of 103–104 more dense than the one located roughly halfway (Bower et al. 2014) to broaden a source to the same angular size. Secondly, |$\theta _\mathrm{scat}\propto \Delta n_{\rm e}/\sqrt{a}$| (Lyne & Graham-Smith 2012), where Δne is the fluctuation in electron density on a linear scale a. Therefore, an alternative scenario for the close screen is that it is more turbulent, with a smaller inner length-scale of turbulence (Armstrong, Rickett & Spangler 1995) estimated to be about 300 km in size (Gwinn et al. 2014). It is also possible that both the increased density and smaller inner scale work jointly, resulting in the very strong scattering. However, it should be noted that a close (to Sgr A*) screen scenario is strongly inconsistent with the reported detailed properties of the magnetar (e.g. Bower et al. 2014; Spitler et al. 2014).
SUMMARY
We have found a highly significant negative correlation between the angular size of about 3000 compact extragalactic radio sources observed with VLBI at 2, 5 and 8 GHz and the absolute value of galactic latitude. At the higher frequency, 15 GHz, the correlation is significant only for sources within the Galactic plane. At both 24 and 43 GHz, where scattering becomes considerably weaker, no significant correlation is present.
The k-index (with larger values, ∼2, being associated with scattering) is found to correlate with rotation measure, free electron density and Hα emission distributions over the Galaxy. The strongest correlation is established between the k-index and Hα intensity that directly traces ionized gas with high resolution. No significant connection is established between the k-index and redshift, strongly suggesting that the screens that dominate in scattering are situated in the Galaxy.
Only about one-third of AGNs viewed through the Galactic plane (|b| < 10°) by VLBI show significant angular broadening caused by interstellar scattering. The positional distribution of these objects forms three major regions on the sky where scattering is essential, marking the GC, the Cygnus region and active star-forming regions in the Perseus and Local arms at galactic longitudes l ≈ 220°–260°, known as the Fitzgerald window (Vázquez et al. 2008). At higher galactic latitudes (|b| > 10°) we have found no positional clustering of scattered sources. The fraction of sources with k > 1.8 decreases to 4 per cent for sources at |b| > 10°. This suggests that significant angular broadening should not be expected outside the Galactic plane within the RadioAstron (Kardashev et al. 2013) space VLBI survey of AGNs. However, the extreme angular resolution of RadioAstron at 18, 6 and 1.3 cm could allow observers to detect lower magnitudes of scatter broadening.
The angular size for the majority of non-scattered AGN cores scales approximately as ν−1 following the model prediction of a conical jet with synchrotron self-absorption and equipartition between the particles and magnetic field energy density (Blandford & Königl 1979; Königl 1981). We note that the distribution around k = 1 is wide, which hints at many cases with departures from this typical picture.
The angular size of Sgr A* is the largest compared to that of thousands of AGNs all over the sky observed from 2 to 43 GHz, more than a factor of 10 larger than the maximum AGN core size found at 2 GHz. This suggests that Sgr A* is scattered by a compact hyper-turbulent screen encompassing the source itself. However, this conclusion is in contrast to the convincing results of Bower et al. (2014), Spitler et al. (2014) and Wucknitz (2014) for the magnetar near Sgr A*. This points to the scattering properties towards the GC being more complex than that described in current models.
The next significant step in studying scattering is expected from an analysis of AGNs and pulsars at extreme angular resolutions being performed by the Space VLB interferometer RadioAstron and comparison with predictions of a scattering substructure (Johnson & Gwinn 2015; Popov et al. 2015).
We thank C. Gwinn, M. Johnson, G. Bower, A. Deller, D. Jauncey, O. Wucknitz, I. Pashchenko, E. Kravchenko, L. Petrov, M. Popov and K. Sokolovsky for discussions and comments. We thank the anonymous referee for useful comments that helped to improve the manuscript. We are very grateful to the teams referred to in Section 2 for making their fully calibrated VLBI fits data publicly available and to Leonid Petrov for maintaining, at the Astrogeo Center,3 the data base of brightness distributions, correlated flux densities and images of compact radio sources produced with VLBI. This research has made use of data from the MOJAVE data base, which is maintained by the MOJAVE team (Lister et al. 2009). This study makes use of 43-GHz VLBA data from the VLBA-BU Blazar Monitoring Programme, funded by the National Aeronautics and Space Administration (NASA) through the Fermi Guest Investigator Programme. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated by Associated Universities, Inc. This study was supported in part by the Russian Foundation for Basic Research grant 13-02-12103. This research has made use of NASA's Astrophysics Data System.
REFERENCES
SUPPORTING INFORMATION
Additional Supporting Information may be found in the online version of this article:
Table 2. Apparent angular sizes of the VLBI cores of 4963 AGNs determined by modelfit. (Supplementary Data).
Please note: Oxford University Press are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.



