Compensated-current instability of kinetic Alfvén waves

Malovichko, P.; Voitenko, Y.; De Keyser, J.

doi:10.1093/mnras/stv1533

Abstract

We study a non-resonant instability of kinetic Alfvén waves (KAWs) driven by compensated currents. Such currents set up in response to energetic ion beams occurring in many space and astrophysical plasmas, like foreshock regions in the solar wind and around supernova remnants. Kinetic effects of the background ion gyroradius make the KAW instability stronger than its magnetohydrodynamic (MHD) counterpart and shift its maximum to shorter wavelengths. The KAW growth time can be very short, approaching the proton gyroperiod in the terrestrial foreshock ahead of the quasi-perpendicular bow shock region. The oblique Alfvén instability driven by the cosmic rays in the interstellar and intergalactic plasmas develops mostly in the MHD regime and can extend in the KAW regime only at large fluxes of cosmic rays. Short cross-field wavelengths of growing Alfvén modes facilitate stochastic cross-field acceleration of cosmic rays.

instabilities, plasmas, waves, solar wind, ISM: supernova remnants

INTRODUCTION

Compensated-current systems are often created in space and astrophysical plasmas by energetic ion beams. In particular, high-energy ion beams accelerated by shocks set up compensating (return) currents upstream of the terrestrial bow shock (Paschmann et al. 1981, and references therein), around supernova remnants (Bell 2005, and references therein), and in many other astrophysical environments (Zweibel & Everett 2010, and references therein). Helium ions streaming with respect to the protons in the solar wind (Marsch 2006, and references therein) also set up a kind of compensated-current system.

Several plasma eigenmodes can be driven unstable in such systems, directly by the ion beams (Sentman, Edmiston & Frank 1981; Winske & Leroy 1984; Gary 1985), and also by the neutralizing return currents set up in response to the beam currents (Winske & Leroy 1984; Bell 2004; Buchner & Elkina 2006; Chen & Wu 2012, and references therein). The wave generation involves both the resonant (Duijveman, Hoyng & Ionson 1981; Gary 1985; Buchner & Elkina 2006) and non-resonant (Winske & Leroy 1984; Bell 2004; Achterberg 2013) wave–particle interactions. Kinetic resonant instabilities of Alfvén, fast and slow modes, driven by the ion beams, have been studied extensively. Among them, the parallel-propagating Alfvén and fast modes (Gary 1985) appeared to be most unstable at beam velocities larger than several Alfvén velocities. At lower, slightly super-Alfvénic beam velocities, oblique Alfvén instabilities become stronger (Voitenko 1998; Daughton, Gary & Winske 1999; Gary et al. 2000; Voitenko & Goossens 2003). The ion-acoustic mode can be destabilized as well (Gary 1985) but is of minor importance.

In the context of high-energy streaming cosmic rays (CRs), the Bell instability (Bell 2004), its modifications and alternatives attracted recently a lot of interest (see e.g. Amato & Blasi 2009; Bret 2009; Zweibel & Everett 2010; Schure et al. 2012; Achterberg 2013, and references therein). Starting from Bell (2004), the primary focus of this research was on the magnetic field-aligned modes and on destabilizing effects produced by the parallel wave dispersion. These limitations were discussed and relaxed in our previous paper (Malovichko, Voitenko & De Keyser 2014, Paper I hereafter) where we found a new Alfvénic instability at oblique propagation driven by compensated currents. It is essential for this instability that its wavelength perpendicular to the background magnetic field |$\boldsymbol {B}_{0}$| is comparable to the beam gyroradius, which makes the beam kinetic effects important.

On the other hand, kinetic effects of the finite background ion gyroradius were neglected in Paper I, which may be justified only if the perpendicular wavelengths of unstable fluctuations are much longer than the background ion gyroradius. Consequently, the unstable fluctuations studied in Paper I were in fact oblique magnetohydrodynamic Alfvén waves (MHD AWs) modified only by the beam-driven compensated currents. However, the background plasma is in many cases not so cold (or the unstable wavelengths are not so large), in which cases kinetic effects of finite background ion gyroradius must be taken into account in oblique Alfvén waves. This is done in this paper, where we relax the limitation of the cold background and study a compensated-current instability of kinetic Alfvén waves (KAWs) – oblique Alfvén mode modified by kinetic effects of the thermal ion gyroradius.

KAWs have been extensively studied in view of their ability to interact with particles kinetically via Cherenkov (Voitenko 1995, 1998) and ion–cyclotron (Winske & Leroy 1984; Daughton et al. 1999; Voitenko & Goossens 2003; Verscharen & Chandran 2013) resonances. These resonant interactions provide generation and dissipation mechanisms for KAWs and make them important mediators for energy transport and release in many laboratory and space plasmas. Non-resonant aperiodic KAW instability can be driven by (non-compensated) electric currents flowing across |$\boldsymbol {B}_{0} $| (Siversky, Voitenko & Goossens 2006) and along |$\boldsymbol {B}_{0}$| (Malovichko & Iukhimuk 1992; Malovichko 2007), and by neutral plasma flows along |$\boldsymbol {B}_{0}$| with velocity shears (Siversky, Voitenko & Goossens 2005). Our present study shows that the KAW branch can be made unstable non-resonantly in the compensated-current systems.

MODEL

We consider a low-density ion beam propagating along |$\boldsymbol {B}_{0}$|⁠. The background consists of the steady ions and counter-streaming electrons that provide a neutralizing return current

\begin{equation} \sum _{e}n_{\rm e}u_{z\rm e}=n_{\rm b}u_{\rm b}. \end{equation}

(1)

All the plasma component are modelled by the u_α-shifted Maxwellian velocity distributions

\begin{equation} f_{0\alpha }=\frac{n_{\alpha }}{(2\pi T_{\alpha }/m_{\alpha })^{3/2}}\exp \left( -\frac{m_{\alpha }v_{\bot }^{2}}{2T_{\alpha }}-\frac{m_{\alpha }(v_{z}-u_{\alpha })^{2}}{2T_{\alpha }}\right), \end{equation}

(2)

where n_α, T_α and u_α are the mean number density, temperature and parallel bulk velocity, respectively, m_α is the particle mass and |$\boldsymbol {v}=\left( v_{x},v_{y,}v_{z}\right)$| velocity-space coordinates. The species α can be background ions (i), background electrons (e) and beam ions (b). The beam electrons (be) can be included if they exist. The subscripts z and ⊥ indicate directions parallel and perpendicular to |$\boldsymbol {B}_{0}$|⁠. The total charge of the plasma is zero.

The nontrivial solutions to the Maxwell–Vlasov set of equations exist if the wave frequency ω and the wave vector |$\boldsymbol {k}=(k_{x},0,k_{z})$| satisfy the following dispersion equation (e.g. Alexandrov, Bogdankevič & Rukhadze 1984):

\begin{equation} \left|k^{2}\delta _{ij}-k_{i}k_{j}-\frac{\omega ^{2}}{c^{2}}\varepsilon _{ij}\right|=0, \end{equation}

(3)

where ε_ij is the dielectric tensor, and δ_ij is the Kronecker delta-symbol. In the low-frequency approximation, when (ω′/ω_Bi)² ≪ 1 and (k_zV_Tα/ω_Bα)² ≪ 1, the expressions for ε_ij given by Alexandrov et al. (1984) can be reduced as follows:

\begin{eqnarray} \varepsilon _{xx} &\simeq &1+\sum _{\alpha }\left( \frac{\omega _{P\alpha }}{ \omega _{B\alpha }}\right) ^{2}\left( \frac{\omega _{\alpha }^{\prime }}{ \omega }\right) ^{2}\frac{\left( 1-A_{0}\left( \mu _{\alpha }^{2}\right) \right) }{\mu _{\alpha }^{2}}; \nonumber \\ \varepsilon _{xy} &=&-\varepsilon _{yx}\simeq -i\sum _{\alpha }\frac{\omega _{P\alpha }^{2}}{\omega _{B\alpha }\omega }\frac{\omega _{\alpha }^{^{\prime }}}{\omega }A_{0}^{\prime }\left( \mu _{\alpha }^{2}\right) ; \nonumber \\ \varepsilon _{xz} &=&\varepsilon _{zx}\simeq \sum _{\alpha }\left( \frac{ \omega _{P\alpha }}{\omega _{B\alpha }}\right) ^{2}\frac{\omega _{\alpha }^{^{\prime }}}{\omega }\frac{k_{x}u_{\alpha }}{\omega }\frac{\left( 1-A_{0}\left( \mu _{\alpha }^{2}\right) \right) }{\mu _{\alpha }^{2}}; \nonumber \\ \varepsilon _{yy} &\simeq &\varepsilon _{xx}-2\sum _{\alpha }\left( \frac{ \omega _{P\alpha }}{\omega _{B\alpha }}\right) ^{2}\left( \frac{\omega _{\alpha }^{\prime }}{\omega }\right) ^{2}\mu _{\alpha }^{2} \nonumber \\ &&\times \left[ \sum _{n\ne 0}\frac{A_{n}^{\prime }\left( \mu _{\alpha }^{2}\right) }{n^{2}}-\left( \frac{\omega _{B\alpha }}{\omega _{\alpha }^{\prime }}\right) ^{2}A_{0}^{\prime }\left( \mu _{\alpha }^{2}\right) J_{+}\left( \xi _{\alpha }\right) \right] ; \nonumber \\ \varepsilon _{yz} &=&-\varepsilon _{zy}\simeq -i\frac{k_{x}}{k_{z}} \sum _{\alpha }\frac{\omega _{P\alpha }^{2}}{\omega _{B\alpha }\omega } A_{0}^{\prime }(\mu _{\alpha }^{2})\left[ \frac{\omega _{\alpha }^{\prime }}{ \omega }-J_{+}\left( \xi _{\alpha }\right) \right] ; \nonumber \\ \varepsilon _{zz} &\simeq &1+\sum _{\alpha }\left( \frac{\omega _{P\alpha }}{ k_{z}V_{T\alpha }}\right) ^{2}A_{0}\left( \mu _{\alpha }^{2}\right) \left[ 1-J_{+}\left( \xi _{\alpha }\right) \right] \nonumber \\ &&+\sum _{\alpha }\left( \frac{\omega _{P\alpha }}{\omega _{B\alpha }}\right) ^{2}\left( \frac{k_{x}u_{\alpha }}{\omega }\right) ^{2}\frac{\left( 1-A_{0}\left( \mu _{\alpha }^{2}\right) \right) }{\mu _{\alpha }^{2}}, \end{eqnarray}

(4)

where |$\omega _{\alpha }^{\prime }=\omega -k_{z}u_{\alpha }$|⁠, |$A_{0}\left( \mu _{\alpha }^{2}\right) =I_{0}\left( \mu _{\alpha }^{2}\right) \exp \left( -\mu _{\alpha }^{2}\right),$||$I_{0}\left( \mu _{\alpha }^{2}\right)$| is the zero-order modified Bessel function, μ_α = k_xV_Tα/ω_Bα is the normalized perpendicular wavenumber, |$A_{0}^{\prime }(x)={\rm d}A_{0}(x)/{\rm d}x$|⁠, ω_Pα (ω_Bα) is the plasma (cyclotron) frequency, |$V_{T\alpha }=\sqrt{T_{\alpha }/m_{\alpha }}$| is the thermal velocity and |$\xi _{\alpha }=\omega _{\alpha }^{^{\prime }}/(k_{z}V_{T\alpha })$|⁠. Function

\begin{equation} J_{+}\left( \xi _{\alpha }\right) =\xi _{\alpha }\exp \left( -\frac{\xi _{\alpha }^{2}}{2}\right) \int _{i\infty }^{\xi _{\alpha }}{\rm d}t\exp \left( \frac{t^{2}}{2}\right), \end{equation}

(5)

introduced by Alexandrov et al. (1984), can be expressed via the well-known plasma W-function as |$J_{+}\left( x\right) =-i\sqrt{\pi /2}xW\left( x/ \sqrt{2}\right)$|⁠. The small and large argument expansions of J₊(x) are, respectively,

\begin{equation} J_{+}\left( x\right) =x^{2}+O\left( x^{4}\right) - {i}\sqrt{\frac{\pi }{2}} x\exp \left( -\frac{x^{2}}{2}\right),\hphantom{|x|}\qquad \qquad \left|x\right|\ll 1; \end{equation}

(6)

and

\begin{equation} J_{+}\left( x\right) =1+\frac{1}{x^{2}}+O\left( \frac{1}{x^{4}}\right) - {i}\eta \sqrt{\frac{\pi }{2}}x\exp \left( -\frac{x^{2}}{2}\right),\qquad \left|x\right|\gg 1, \end{equation}

(7)

where η = 0 for Imx > 0, η = 1 for Imx = 0 and η = 2 for Imx < 0.

SOLUTION FOR KINETIC ALFVéN MODE

In our previous paper (Malovichko et al. 2014), we found a solution of equation (3) that describes MHD Alfvén and fast modes coupled by kinetic effects in the hot ion beam. Kinetic effects in the background ions were ignored, which can be justified in the cases of background temperatures much lower than the beam temperatures, and the unstable perpendicular wavelength not much shorter than the beam ion gyroradius. Here we study situations where kinetic effects of the background ion gyroradius cannot be neglected if they are important for the beam ions. By expanding elements of the dielectric tensor ε_ij in low-β plasmas, where ξ_e ≪ 1 ≪ ξ_i, the dispersion equation (3) reduces to

\begin{equation} \left( \omega ^{2}-\omega _{\rm A}^{2}\right) \left( \omega ^{2}-\omega _{\rm F}^{2}\right) \simeq \omega _{Bi}^{2}\omega _{\rm A}^{2}K_{\rm F}^{2}\left( 1+A_{0}^{\prime }(\mu _{\rm b}^{2})\right) ^{2}\bar{j}_{\rm b}^{2}, \end{equation}

(8)

where |$\bar{j}_{\rm b}=n_{\rm b}V_{\rm b}/n_{\rm i}V_{\rm A}$| is the ion beam current j_b = en_bV_b normalized by the Alfvén current j_A = en_iV_A, |$V_{\rm A}=B_{0}/\sqrt{4\pi n_{\rm i}m_{\rm i}}$| is the background Alfvén velocity, n_i is the background ion number density and V_b is the bulk beam velocity (e is the proton charge and we assumed that the ions are protons). The frequencies of kinetically modified eigenmodes are given by ω_A = k_zV_AK_A and ω_F = kV_AK_F, where subscripts A and F stand for the Alfvén and fast modes, respectively. The dispersion functions

\begin{equation} K_{\rm A}=K_{\rm A}\left( \mu _{\rm i}^{2}\right) =\sqrt{\frac{\mu _{\rm i}^{2}}{ 1-A_{0}\left( \mu _{\rm i}^{2}\right) }+\frac{T_{\rm e}}{T_{\rm i}}\mu _{\rm i}^{2}} \end{equation}

(9)

and

\begin{equation} K_{\rm F}=K_{\rm F}\left( \mu _{\rm i}^{2}\right) =\left( \frac{1-A_{0}\left( \mu _{\rm i}^{2}\right) }{\mu _{\rm i}^{2}}-2\mu _{\rm i}^{2}\sum _{n\ne 0}\frac{ A_{n}^{\prime }\left( \mu _{\rm i}^{2}\right) }{n^{2}}\right) ^{-1/2} \end{equation}

(10)

describe deviations from MHD Alfvén and fast wave dispersions introduced by the kinetic effects of finite ion gyroradius in the background plasma. Both these functions reduce to unity in the MHD limit for the background ions, K_F = K_A = 1 at |$\mu _{\rm i}^{2}=0$|⁠.

Equation (8) contains KAW mode (first parentheses in the left-hand side) and fast mode (second parentheses), coupled by the kinetic effects in the beam (right-hand side). If there is no beam, |$\bar{j}_{\rm b}=0$|⁠, or the beam gyroradius is negligible, |$\mu _{\rm b}^{2}=0$|⁠, then the coupling term in equation (8) vanishes and we recover the decoupled KAW, ω = ω_A, and fast mode, ω = ω_F. In the MHD limit for the background ions (⁠|$\mu _{\rm i}^{2}\rightarrow 0$|⁠), but with still kinetic beam ions (⁠|$\mu _{\rm b}^{2}\ne 0$|⁠), we have K_F = K_A = 1 and equation (8) reduces to the dispersion equation derived by Malovichko et al. (2014).

Our present goal is to account simultaneously for the background and beam kinetic effects of finite ion gyroradius, |$\mu _{\rm i}^{2}\ne 0$| and |$\mu _{\rm b}^{2}\ne 0$|⁠. In this case the unstable solution of (8) emerges on the KAW branch and can be cast in the form

\begin{eqnarray} \omega ^{2}&=&\omega _{\rm A}^{2}+\left( \frac{\omega _{\rm F}^{2}-\omega _{\rm A}^{2}}{2 }\right) -\sqrt{\left( \frac{\omega _{\rm F}^{2}-\omega _{\rm A}^{2}}{2}\right) ^{2}+\omega _{Bi}^{2}\omega _{\rm A}^{2}K_{\rm F}^{2}\left( 1+A_{0}^{\prime }(\mu _{\rm b}^{2})\right) ^{2}\bar{j}_{\rm b}^{2}}. \end{eqnarray}

(11)

Our consequent analysis is based on this basic dispersion relation for Alfvénic perturbations modified by ion beams and kinetic effects. The destabilizing term, containing |$\bar{j}_{\rm b}$| and kinetic factors of finite |$\mu _{\rm b}^{2}$| and |$\mu _{\rm i}^{2}$|⁠, can make the KAW branch aperiodically unstable. Another solution is stable and we will not consider it here.

INSTABILITY ANALYSIS

Threshold

From (11) one can see that the destabilizing term, proportional to |$\bar{j}_{\rm b}$|⁠, shifts down the KAW frequency squared and can make it purely imaginary, ω² < 0, which makes the KAW branch aperiodically unstable. This happens at the wavenumbers satisfying the following condition:

\begin{equation} \bar{j}_{\rm b}>\frac{\mu _{\rm b}}{1+A_{0}^{\prime }\left( \mu _{\rm b}^{2}\right) } \left( \frac{k}{k_{x}}\right) \left( \frac{V_{\rm A}}{V_{Tb}}\right). \end{equation}

(12)

The instability threshold current can be found by minimizing the right-hand side of the above condition,

\begin{equation} \bar{j}_{\rm b}>\bar{j}_{\mathrm{thr}}\simeq 1.33\frac{V_{\rm A}}{V_{Tb}}. \end{equation}

(13)

The self-consistency conditions of our analysis require also that |$\bar{j}_{ \mathrm{thr}}\ge 1.33\sqrt{T_{\rm i}/T_{\rm b}}$|⁠. The above threshold conditions are exactly the same as were found and analysed by Malovichko et al. (2014) for relatively cold background plasma, neglecting related kinetic effects. Consequently, the unstable wavenumber range do not expand in response to the effects of finite μ_i. In terms of μ_i, the unstable wavenumber range is μ_i1 ≤ μ_i ≤ μ_i2, where the upper and lower boundaries are

\begin{equation*} \mu _{\rm i2}\simeq \frac{V_{Ti}}{V_{\rm A}}\bar{j}_{\rm b};\quad \mu _{\rm i1}\simeq \frac{2 }{3}\frac{T_{\rm i}}{T_{\rm b}}\mu _{\rm i2}^{-1}. \end{equation*}

At the same time, as we will see later, the effects of finite μ_i modify significantly the instability growth rate and the position of its maximum in the unstable range.

Wavenumber dependence of the instability growth rate

First, we investigate the instability growth rate γ =Im(ω) as function of the normalized perpendicular and parallel wavenumbers μ_i = k_⊥ρ_i and ν_i = k_zδ_i. The normalization parameters are the background ion gyroradius ρ_i = V_Ti/ω_Bi and the background ion inertial length δ_i = V_A/ω_Bi. Furthermore, we present the instability growth rate that follows from equation (11) in the dimensionless form:

\begin{eqnarray} \frac{\gamma }{\omega _{Bi}}&=&\left\lbrace -0.5\left( \frac{V_{\rm A}^{2}}{V_{Ti}^{2} }\mu _{\rm i}^{2}K_{\rm F}^{2}+\nu _{\rm i}^{2}\left( K_{\rm F}^{2}+K_{\rm A}^{2}\right) \right) \right. \nonumber \\ &&+\left. \sqrt{0.25\left( \frac{V_{\rm A}^{2}}{V_{Ti}^{2}}\mu _{\rm i}^{2}K_{\rm F}^{2}+\nu _{\rm i}^{2}\left( K_{\rm F}^{2}-K_{\rm A}^{2}\right) \right) ^{2}+\nu _{\rm i}^{2}K_{\rm A}^{2}K_{\rm F}^{2}\left( 1+A_{0}^{\prime }(\frac{T_{\rm b}}{ T_{\rm i}}\mu _{\rm i}^{2})\right) ^{2}\bar{j}_{\rm b}^{2}}\right\rbrace ^{1/2}. \end{eqnarray}

(14)

In the MHD limit for the background ions, μ_i → 0, the wave dispersion functions |$K_{\rm F}^{2}=K_{\rm A}^{2}$| =1 and the growth rate (14) reduces to the expression obtained by Malovichko et al. (2014):

\begin{eqnarray} \frac{\gamma _{\rm MHD}}{\omega _{Bi}}&=&\left\lbrace -\left( 0.5\frac{V_{\rm A}^{2}}{ V_{Ti}^{2}}\mu _{\rm i}^{2}K_{\rm F}^{2}+\nu _{\rm i}^{2}\right) \right. +\left. \sqrt{0.25\left( \frac{V_{\rm A}^{2}}{V_{Ti}^{2}}\mu _{\rm i}^{2}\right) ^{2}+\nu _{\rm i}^{2}\left( 1+A_{0}^{\prime }(\frac{T_{\rm b}}{T_{\rm i}}\mu _{\rm i}^{2})\right) ^{2}\bar{j}_{\rm b}^{2}}\right\rbrace ^{1/2}, \end{eqnarray}

(15)

where we use the normalized wavenumber μ_i instead of μ_b used by Malovichko et al. (2014) and denote the corresponding growth rate γ_MHD.

The growth rate (14) dependent on the parallel and perpendicular wavenumbers is shown in Fig. 1, where the beam and plasma parameters are chosen to be compatible with those in the quasi-perpendicular foreshock region: T_b/T_i ≃ 25, |$V_{\rm A}^{2}/V_{Ti}^{2}\simeq 1$|⁠, |$\bar{j} _{\rm b}\simeq 1.5$|⁠. To allow the comparison with the previous results, we also plot the growth rate (15) for MHD Alfvén waves. The solid contours with shadowing show the growth rate (14) accounting for the finite background ion gyroradius, whereas the dashed contours are used to show equation (15) describing MHD AWs.

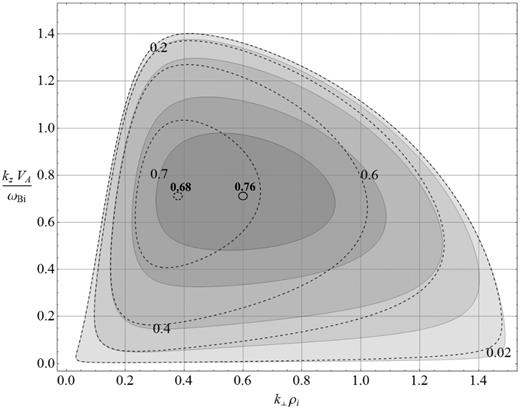
$Contour plot of the KAW growth rate in the (kz, k⊥) plane (solid lines and shading). The parallel (kz) and perpendicular (k⊥) wavenumbers are normalized by the ion inertial length and the beam ion gyroradius: $\mu _{\rm i}=k_{\perp } \rho _{\rm i}$ and $ \nu _{\rm i}=k_{z} \delta _{\rm i}$. The normalized beam current $\bar{j}_{\rm b}=1.5$ and the beam temperature Tb = 25Ti. The growth rate of the MHD AW instability is shown for comparison by dashed lines. The corresponding maximal growth rates are indicated by small circles (solid line for KAWs and dash line for MHD AWs).$

Figure 1.

Contour plot of the KAW growth rate in the (k_z, k_⊥) plane (solid lines and shading). The parallel (k_z) and perpendicular (k_⊥) wavenumbers are normalized by the ion inertial length and the beam ion gyroradius: |$\mu _{\rm i}=k_{\perp } \rho _{\rm i}$| and |$ \nu _{\rm i}=k_{z} \delta _{\rm i}$|⁠. The normalized beam current |$\bar{j}_{\rm b}=1.5$| and the beam temperature T_b = 25T_i. The growth rate of the MHD AW instability is shown for comparison by dashed lines. The corresponding maximal growth rates are indicated by small circles (solid line for KAWs and dash line for MHD AWs).

Open in new tab Download slide

Surprisingly, corrections introduced by the effects of finite background ion gyroradius become significant at still very low background ion temperature as compared to the beam ion temperature, T_i/T_b ∼ 0.04, which implies a relatively small dispersive parameter |$\mu _{\rm i}^{2}\approx 0.04\mu _{\rm b}^{2}$| that describes the finite-μ_i effects. It appears that, in general, the impact of the finite background ion gyroradius is twofold: (i) to increase the growth rate at all wavenumbers (this follows from the fact that all solid contours in Fig. 1 encircle corresponding dash contours), and (ii) to shift the growth rate towards higher perpendicular wavenumbers μ_i (solid contours are shifted to higher μ_i). Note that the solid contour γ/ω_Bi = 0.7 does not have its dashed counterpart, which means that γ is significantly larger than γ_MHD. With the mentioned above values of the plasma parameters the finite-μ_i effects roughly double the wavenumber at maximum and make the corresponding growth rate about 10 per cent larger. The KAW growth rate has a maximum γ_m ≃ 0.76 attained at μ_im ≃ 0.6 and ν_im ≃ 0.7, indicated in the figure by the small circle. For comparison, the ‘MHD approximation’ μ_i = 0 for the background ions would give a lower maximum γ_m^(MHD) ≃ 0.68 at the smaller perpendicular wavenumber μ_im^(MHD) ≃ 0.37 and about the same parallel wavenumber ν_im^(MHD) ≃ 0.7 (see the small dashed circle in Fig. 1). On the other hand, as we already mentioned in the previous section, the range of unstable wavenumbers does not change.

In Fig. 1 (and in several other figures below), the instability growth rate near maximum is not much smaller than the ion gyrofrequency. Such large growth rates result from the large values chosen for the beam current to emphasize that the increment can be large, approaching to the gyrofrequency. The next-order terms |$\sim \gamma ^{4}/\omega _{Bi}^{4}$| may come into play and reduce γ², but not as much as to remove the instability. That the instability does not vanish is insured by the extended unstable wavenumber range surrounding the maximum, in which the condition |$\gamma ^{2}/\omega _{Bi}^{2}\ll 1$| is satisfied (see e.g. outer contours in Fig. 1).

As in Paper I, we can find the maximum of equation (14) with respect to the parallel wavenumber |$\gamma _{\mu }\left( \mu _{\rm b}\right) =\max _{\nu _{\rm i}}$| γ(μ_b, ν_i). This procedure is straightforward but in the case of finite μ_i the resulting analytical expression becomes quite cumbersome and will not be written down explicitly. For the reference, the graphical representation of this maximum as function of μ_i is shown in Fig. 2 together with the same maximum but neglecting kinetic background effects of finite μ_i. The beam temperature and current are the same as in Fig. 1, T_b/T_i = 25 and |$\bar{j}_{\rm b}=1.5$|⁠. This plot provides a straightforward comparison and evidence for the strong influence of the background kinetic effects on the growth rate: the growth rate increases and the maximum shifts to higher μ_i. At low values of μ_i, in the region of increasing growth rate in Fig. 2, the growth rates with and without effects of background ion gyroradius are almost the same, γ ≈ γ_MHD. But when approaching the growth rate maximum the difference becomes significant and increases further at larger μ_i, up to about factor 2. Again, the KAW growth rate is about two times larger than the MHD one at μ_i > 1.2, where condition |$\gamma ^{2}/\omega _{Bi}^{2}\ll 1$| is well satisfied.

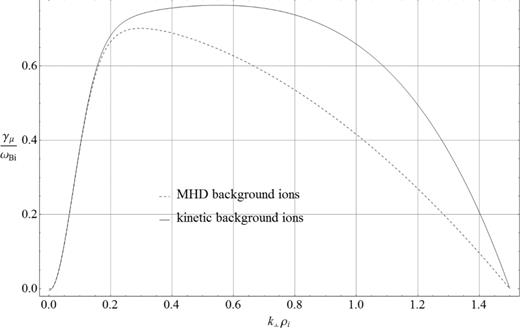
$The growth rate $ \gamma _{ \mu }/ \omega _{Bi}$ for KAWs (solid line) and for MHD AWs (dashed line) as function of the normalized perpendicular wavenumber $ \mu _{\rm i}=k_{\perp } \rho _{\rm i}$ for the beam/background temperature ratio Tb/Ti = 50 and the beam current $\bar{j}_{\rm b}=1.5$.$

Figure 2.

The growth rate |$ \gamma _{ \mu }/ \omega _{Bi}$| for KAWs (solid line) and for MHD AWs (dashed line) as function of the normalized perpendicular wavenumber |$ \mu _{\rm i}=k_{\perp } \rho _{\rm i}$| for the beam/background temperature ratio T_b/T_i = 50 and the beam current |$\bar{j}_{\rm b}=1.5$|⁠.

Open in new tab Download slide

Properties of the compensated-current KAW instability

Let us turn to the instability growth rate, which can be found as the absolute maximum of the wavenumber-dependent growth rate, |$\gamma _{\mathrm{m }}=\max _{\mu _{\rm b}}\gamma _{\mu }\left( \mu _{\rm b}\right)$|⁠. This maximum of γ_μ(μ_b) is attained at certain perpendicular wavenumber μ_b = μ_bm (the corresponding parallel wavenumber ν_i = ν_im is already fixed in γ_μ(μ_b)). For the plasma parameters used in Figs 1 and 2, this maximum γ_m ≃ 0.76 is attained at μ_im ≃ 0.6 (ν_im ≃ 0.7.

Now we can vary plasma parameters and investigate how the growth rate γ_m varies in response. The contour plot Fig. 3 shows how the instability growth rate γ_m depends on the most critical beam parameters, the normalized beam current |$\bar{j}_{\rm b}$| and the beam/ion temperature ratio T_b/T_i. In general, similarly to the instability of MHD AWs (Malovichko et al. 2014), the KAW growth rate increases with increasing |$\bar{j}_{\rm b}$| and T_b. However, the finite-μ_i effects make this increase faster, and larger values of the instability growth rate γ_m are attained at every particular |$\bar{j}_{\rm b}$| and T_b/T_i. It is seen that the difference between γ_m and γ_m^(MHD) is small near the threshold values of |$\bar{j}_{\rm b}$| and V_Tb/V_A defined by equation (13), but becomes significant when |$\bar{j}_{\rm b}$| and/or V_Tb/V_A depart from the threshold. Consequently, the finite-μ_i effects become much stronger for the well over-threshold beam currents.

$Contour plot of the maximum KAW growth rate $ \gamma _{ \mathrm{m}}/ \omega _{Bi}$ (solid lines and shading) as function of the normalized beam current $\bar{j}_{\rm b}$ and the beam/background temperature ratio Tb/Ti. The maximum growth rate $ \gamma _{ \mathrm{m}}^{\left( {\rm MHD}\right) }$, based on the non-kinetic treatment of the background ions, is shown for comparison by dash lines.$

Figure 3.

Contour plot of the maximum KAW growth rate |$ \gamma _{ \mathrm{m}}/ \omega _{Bi}$| (solid lines and shading) as function of the normalized beam current |$\bar{j}_{\rm b}$| and the beam/background temperature ratio T_b/T_i. The maximum growth rate |$ \gamma _{ \mathrm{m}}^{\left( {\rm MHD}\right) }$|⁠, based on the non-kinetic treatment of the background ions, is shown for comparison by dash lines.

Open in new tab Download slide

Geometrical properties of generated fluctuations can be represented by the wavevector tilt angle with respect to the background magnetic field,

\begin{equation*} \phi _{\mathrm{m}}=\arctan \frac{k_{\perp \mathrm{m}}}{k_{z\mathrm{m}}} =\arctan \left( \frac{V_{\rm A}}{V_{Ti}}\frac{\mu _{i\mathrm{m}}}{\nu _{i\mathrm{ m}}}\right). \end{equation*}

This angle is shown in Fig. 4 as function of the beam current |$\bar{j}_{\rm b}$| for different beam temperatures, T_b/T_i = 50, 250 and 750 for the solid lines from the top to bottom. The dashed lines show the same angle but neglecting effects of the finite gyroradius for the background ions. At small near-threshold currents the generated perturbations are quite oblique but not much different from the MHD AWs found by Malovichko et al. (2014). For all beam temperatures the tilt angle decreases with the beam current |$\bar{j}_{\rm b}$| increasing above |$\bar{j}_{\mathrm{thr}}$|⁠. However, contrary to the MHD AW, at |$\bar{j}_{\rm b}\gtrsim 1$| the KAW tilt angle stops decreasing and reaches a minimum, after which it grows to an asymptotic value ϕ_m ≃ 53° at large |$\bar{j}_{\rm b}$|⁠.

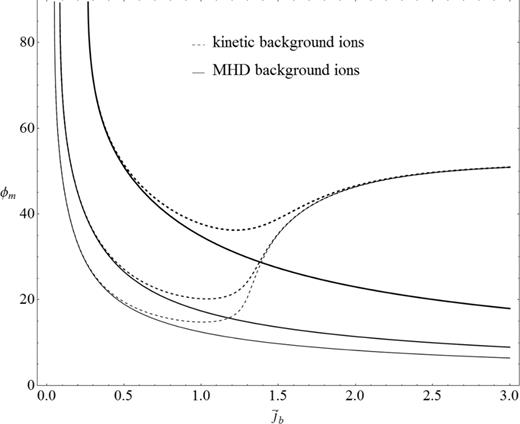
$The wavevector tilt angle $ \phi _{\mathrm{m}}$ (values are in degrees) as function of the normalized current $\bar{j}_{\rm b}$ for the beam/background temperature ratios Tb/Ti = 50, 250 and 750 (solid and dashed lines from top to bottom). More oblique waves are generated in the hotter backgrounds and/or cooler beams.$

Figure 4.

The wavevector tilt angle |$ \phi _{\mathrm{m}}$| (values are in degrees) as function of the normalized current |$\bar{j}_{\rm b}$| for the beam/background temperature ratios T_b/T_i = 50, 250 and 750 (solid and dashed lines from top to bottom). More oblique waves are generated in the hotter backgrounds and/or cooler beams.

Open in new tab Download slide

The effects introduced by the finite gyroradius of the background ions make the anisotropy more pronounced (solid lines) than it would be in the case of MHD AWs (dashed lines). Together with the fact that the finite-μ_i effects shift the maximum towards larger perpendicular wavenumbers, this confirms that the unstable Alfvénic mode is in fact the KAW mode in a wide range of beam and plasma parameters.

The ratio |$\mu _{\rm i}^{2}/\mu _{\rm b}^{2}$| can be used to estimate the relative importance of the finite-μ_i effects. In the cases where the beam and background ions are of the same type (in this paper protons), |$\mu _{\rm i}^{2}/\mu _{\rm b}^{2}=T_{\rm i}/T_{\rm b}$|⁠. Say, for T_i/T_b = 0.3, the tilt angle ϕ_m ≃ 52° in the case |$\bar{j}_{\rm b}=0.3$| and V_Tb/V_A = 20, which is significantly larger than the corresponding tilt angle of MHD AW instability, ϕ_m ≃ 32°. From Fig. 4 we see that, in general, more oblique fluctuations are generated by the KAW instability. In the near-threshold regime, where the generated perturbations are very oblique in both the MHD and kinetic AW cases, 45° < ϕ_m < 90°, the tilt angle is not much affected by the μ_i effects. On the contrary, with growing |$\bar{j} _{\rm b}$| and/or T_b/T_i in the well over-threshold regime, where the MHD AW tilt angle becomes very small, the KAW tilt angle remains relatively large, ϕ_m ≳ 50°.

In the strongly dispersive well over-threshold limit, |$\bar{j}_{\rm b}>1$|⁠, the maximum growth rate can be approximated as

\begin{equation*} \gamma _{\mathrm{m}}\approx 0.19\omega _{Bi}\frac{1+T_{\rm i}/T_{\rm e}}{ 0.5+T_{\rm i}/T_{\rm e}}\bar{j}_{\rm b}^{2}. \end{equation*}

This scaling has however a rather limited applicability because already at |$\bar{j}_{\rm b}\gtrsim 2$| the growth rate γ_m becomes as large as the ion–cyclotron frequency ω_Bi, which is the upper boundary of the low-frequency approximation.

OBLIQUE ALFVéN INSTABILITY IN COMPENSATED-CURRENT SYSTEMS

Terrestrial foreshock regions

There are three types of proton beams in the terrestrial foreshock regions (Paschmann et al. 1981; Tsurutani & Rodriguez 1981): (i) beams created by ‘reflected’ protons associated with the quasi-perpendicular shocks; (ii) beams created by ‘diffusive’ protons associated with the quasi-parallel shocks; (iii) ‘intermediate’ beams associated with the oblique shocks. For the fast ‘reflected’ beams we will use the characteristic temperature T_b/T_i = 50 and velocity V_b/V_A = 20, for the diffusive beams T_b/T_i = 750 and V_b/V_A = 5, and for the intermediate beams T_b/T_i = 250 and V_b/V_A = 10. The beam number densities are similar in all three cases and vary in the range n_b/n₀ = 0.01–0.1. To make the comparison straightforward, we assume n_b/n₀ = 0.04 in all three cases. Recent observations of the foreshock waves (Narita et al. 2006; Hobara et al. 2007) and their possible relations with the compensated-current instability of MHD AWs were discussed in the previous paper (Paper I). Here we focus on the new effects introduced in the Alfvénic instability by the effects of finite gyroradius for the background ions, which make the instability essentially the KAW instability.

The KAW growth rate in the quasi-perpendicular, intermediate and quasi-parallel foreshock regions is shown in Fig. 5 as function of the normalized perpendicular wavenumber μ_i. The instability tends to be strongest in the quasi-perpendicular foreshock region, where kinetic effects of background ion gyroradius are most pronounced. The largest perpendicular wavenumbers μ_i are generated in this region, which emphasizes the importance of the background kinetic effects and hence KAWs there. Intermediate and diffusive beams generate Alfvén waves with significantly smaller perpendicular wavenumbers, which can be well described by the MHD approximation for the background ions, μ_i = 0.

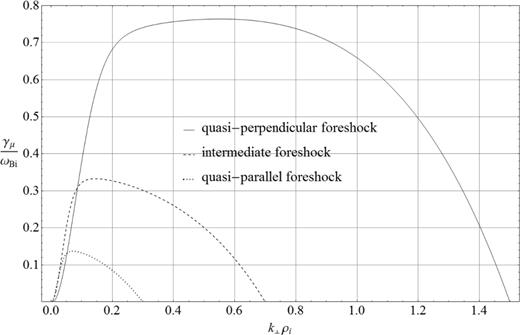
$The instability growth rate as function of the perpendicular wavenumber in the plasma conditions typical for the quasi-perpendicular foreshock (beam currents $\bar{j}_{\rm b}=1.5$ and beam temperature Tb = 50Ti, solid line), intermediate foreshock ($\bar{j}_{\rm b}=0.7$ and Tb = 250Ti, dashed line) and quasi-parallel foreshock ($\bar{j} _{\rm b}=0.3$ and Tb = 750Ti). The finite-$ \mu _{\rm i}$ effects are most pronounced in the quasi-perpendicular foreshocks.$

Figure 5.

The instability growth rate as function of the perpendicular wavenumber in the plasma conditions typical for the quasi-perpendicular foreshock (beam currents |$\bar{j}_{\rm b}=1.5$| and beam temperature T_b = 50T_i, solid line), intermediate foreshock (⁠|$\bar{j}_{\rm b}=0.7$| and T_b = 250T_i, dashed line) and quasi-parallel foreshock (⁠|$\bar{j} _{\rm b}=0.3$| and T_b = 750T_i). The finite-|$ \mu _{\rm i}$| effects are most pronounced in the quasi-perpendicular foreshocks.

Open in new tab Download slide

In comparison to our previous results on the MHD AW instability (Paper I), we see that the effects of background μ_i make the ion beams more unstable in the quasi-perpendicular foreshocks. This fact supports the ‘evolutionary model’ of the foreshock ion beams, in which the quasi-perpendicular foreshock beams are relaxed by some instability and then convected by the solar wind and contribute to the beams in intermediate and quasi-parallel foreshocks. The waves generated in the quasi-perpendicular foreshocks follow the same evolution: they are also convected by the solar wind and contribute to the oblique wave spectra observed in the intermediate and quasi-parallel foreshocks.

The bimodal wavenumber distribution has been reported for the waves observed upstream of the bow shock (see fig. 9 by Narita et al. 2006). In terms of the thermal ion gyroradius scale, the waves observed in the quasi-perpendicular foreshock are grouped around two peaks at μ_i1 ≃ 0.06 and μ_i2 ≃ 0.4. As is seen from Fig. 5, the dominant group of the waves around μ_i2 ≃ 0.4 can be easily generated by the compensated-current KAW instability studied here. On the other hand, the sub-dominant group around μ_i1 ≃ 0.06 do not require the kinetic treatment for background ions and can be generated by the MHD AW instability (Paper I). Then the reason for this bimodal wave distribution can be bimodal distributions of the beam currents and/or ion temperatures because of the different conditions in the slow versus fast solar winds. The quasi-perpendicular foreshock waves are relatively more oblique than the waves in the quasi-parallel foreshock, which can be explained by the KAW nature of the instability in the quasi-perpendicular foreshocks (see Fig. 4).

Cosmic rays

Since cosmic rays (CRs) are much more energetic than the terrestrial foreshock ions, the ratio of their gyroradius ρ_CR ∼ c/γ_rω_Bi to the thermal ion gyroradius ρ_i is much higher in most astrophysical environments. We consider here three examples: (i) CRs in the relatively cool interstellar medium around supernova remnants (background ion temperature T_i ∼ 10⁴ K, magnetic field B₀ ∼ 10⁻⁵ G and number density n_i ∼ 1 cm⁻³), (ii) in the hotter superbubbles (T_i ∼ 10⁶ K, B₀ ∼ 5 × 10⁻⁶ G and n_i ∼ 10⁻² cm⁻³); and (iii) in the hot background plasma of the galaxy clusters (T_i ∼ 10⁷ K, B₀ ∼ 10⁻⁶ G and n_i ∼ 10⁻³ cm⁻³) (see e.g. Zweibel & Everett 2010, and references therein). The CR/background ion gyroradius ratios are ρ_CR/ρ_i ≃ 3 × 10⁴, 3 × 10³, and 10³ for three above cases, respectively.

In Fig. 6, we present the k_⊥-dependence of the growth rate of the instability driven by the well over-threshold CR current |$\bar{j}_{\rm b}=1.7$| around supernova remnants, in superbubbles, and in the intercluster medium. It appears that the instability with shortest perpendicular wavelengths λ_⊥ = 2πρ_CR/2.2 × 10^{− 4} ≃ 1.7 × 10⁸ cm is generated around the supernova remnants and with longest, λ_⊥ = 2πρ_CR/2.2 × 10^{− 4} ≃ in the intercluster plasma. On the other hand, the normalized growth rate at maximum is the same in all three cases, γ_m/ω_Bi ≃ 0.9, and this maximum is achieved at the same perpendicular wavenumber normalized by the background ion gyroradius, k_⊥ρ_i ≃ 0.75. These properties indicate that the most unstable perturbations have the characteristic length-scales close to ρ_i and are therefore controlled by effects of the thermal ion gyroradius rather than the CR gyroradius. Consequently, the KAW mode is generated by such strong CR currents.

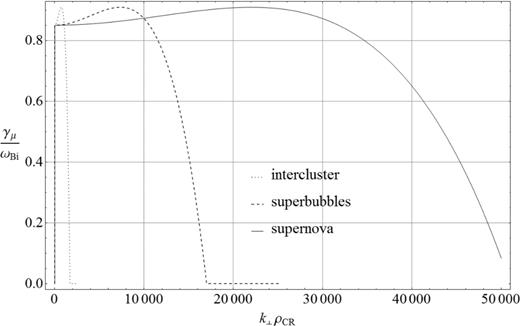
$The growth rate of the KAW instability driven by the strong flux of CRs $\bar{j}_{\rm b}=1.7$ around supernova remnants, in superbubbles and in intercluster medium. The background plasma conditions are: Ti ∼ 104 K, B0 ∼ 10−5 G and ni ∼ 1 cm−3 around supernova remnants; Ti ∼ 106 K, B0 ∼ 5 × 10−6 G and ni ∼ 10−2 cm−3 in superbubbles; and Ti ∼ 107 K, B0 ∼ 10−6 G and ni ∼ 10−3 cm−3 in intercluster medium.$

Figure 6.

The growth rate of the KAW instability driven by the strong flux of CRs |$\bar{j}_{\rm b}=1.7$| around supernova remnants, in superbubbles and in intercluster medium. The background plasma conditions are: T_i ∼ 10⁴ K, B₀ ∼ 10⁻⁵ G and n_i ∼ 1 cm⁻³ around supernova remnants; T_i ∼ 10⁶ K, B₀ ∼ 5 × 10⁻⁶ G and n_i ∼ 10⁻² cm⁻³ in superbubbles; and T_i ∼ 10⁷ K, B₀ ∼ 10⁻⁶ G and n_i ∼ 10⁻³ cm⁻³ in intercluster medium.

Open in new tab Download slide

On the contrary, the more realistic weaker CR currents |$\bar{j}_{\rm b}<1$| drive the instability with much longer perpendicular wavelengths controlled by the CR gyroradius rather than the thermal ion gyroradius. The MHD Alfvén instability is driven in such cases, for which the perpendicular wavenumbers are already essential to make kinetic effects of finite CR gyroradius possible, but the background response still remains MHD-like. Indeed, assuming the background magnetic field B₀ ∼ 3 × 10⁻⁶ G and the CR flux n_CRV_b ∼ 10⁴ cm⁻² s⁻¹ (Zweibel & Everett 2010), we estimate |$\bar{j}_{\rm b}=1.53\times 10^{-2}$| around supernova remnants, which gives rise to the oblique MHD Alfvén instability with the maximum growth rate γ_m/ω_Bi ≃ 0.007 65 attained at k_⊥ρ_CR ≃ 8. Taking into account ω_Bi ≃ 0.03 s⁻¹ and ρ_CR ≃ 3 × 10¹² cm, we get γ_m ≃ 2.2 × 10⁻⁴ s⁻¹ in absolute numbers.

Since |$\bar{j}_{\rm b}\gg \bar{j}_{\mathrm{thr}}\simeq 3\times 10^{-5}$|⁠, we are in the asymptotic well over-threshold regime, where oblique and field-aligned (Bell) instabilities have the same growth rate γ_m ≃ 2.2 × 10⁻⁴ s⁻¹ (compare with maximum in fig. 3 by Zweibel & Everett 2010). It means there are two unstable ranges in the wavenumber space, one at k_⊥ρ_CR ≃ 8 (oblique instability) and another at k_⊥ρ_CR ≃ 0 (Bell instability). In addition, the Bell instability requires that the background plasma and CRs are uniform in across |$\boldsymbol {B}_{0}$| (the non-uniformity scale |$L_{\perp }k_{\rm Bell}=0.5\delta _{\rm i}^{-1}\bar{j}_{\rm b}$|⁠).

DISCUSSION

In the present study, we focused on the analytical investigation of the KAW instability. Several well-known instabilities, including Bell and Weibel, do not appear in our analysis because we used specific approximations designed to capture the oblique Alfvén instability. Detailed comparative study of the KAW instability with other instabilities in parameter space is subject for future studies. Here we shortly discuss the oblique Alfvén instability in comparison to extensively studied Bell instability, and some observational consequences of the former.

Oblique Alfvén instability versus Bell instability

Oblique AW instability is closest by nature to the extensively studied Bell instability. Both instabilities are made possible by demagnetization of one or several plasma components streaming along B₀ (it is the ion beam in our case). Demagnetization here means that the response of some plasma component to the sufficiently small-scale fluctuations is reduced (and vice versa). The principal difference between two is in the physical mechanism thereby the beam/CR ions (or any other species streaming along B₀) are demagnetized. In the oblique AW instability the beam ions are demagnetized not by the small parallel wavelength of perturbations 1/k_∥ < V_Tb∥/ω_Bi (or 1/k_∥ < V_b0∥/ω_Bi if the beam is cold) as in the Bell instability (Bell 2004; Achterberg 2013), but by the small perpendicular wavelengths 1/k_⊥ < V_Tb⊥/ω_Bi (cf. Malovichko et al. 2014). That is why our instability is essentially oblique and maximizes at large perpendicular wavenumbers, whereas the Bell instability attains maximum at parallel propagation at large parallel wavenumbers. Consequently, the beam-ion gyroradius effects destabilize the essentially oblique (kinetic) Alfvén mode, whereas the quasi-parallel Alfvén mode is driven by the Bell mechanism.

Essentially the same effect, preferential ion demagnetization at short perpendicular wavelengths, makes Alfvén waves unstable in the neutral plasma flows with velocity shears (Siversky et al. 2005). As the demagnetization effects arise due to finite ion gyroradius (finite k_⊥ρ_i), the velocity-shear-generated Alfvén waves are not MHD but kinetic (i.e. KAWs).

It is often stated that effects of large beam-ion gyroradius (as compared to the parallel wavelength) make the Bell instability possible, which is strictly speaking incorrect. The reference scale for the parallel wavelength is the parallel transit scale V_Tb∥/ω_Bi (or V_b0∥/ω_Bi if the beam is cold) rather than the (perpendicular) ion gyroradius V_Tb⊥/ω_Bi . Achterberg did took into account the ion gyroradius terms ∼k_⊥V_⊥/ω_Bi (up to the first order) but only for the background ions, not for the beam. In the Achterberg approximation the KAW mode exists but its compensated-current instability cannot be captured.

To illustrate further principal differences between two instabilities, let us consider a plasma model used by Bret (2009). This model comprises two electron components counter-streaming |$\parallel \boldsymbol {B}_{0}$| on the steady ion background. It is easy to see that our instability does not exist in this setting whereas the Bell instability exists. The reason is that both electron components remain equally magnetized at any cross-B₀ scale of trial perturbations (hence our instability is absent), but the differential streaming of the electrons ∥B₀ can lead to their different demagnetizations, and hence the Bell instability is possible.

Our growth rate in the supernova remnant (γ_m ≃ 2.2 × 10⁻⁴ s⁻¹) is obtained for |$\bar{j}_{\mathrm{CR}}=1.53\times 10^{-2}$|⁠, which is more than two orders larger than the instability threshold |$\bar{j}_{\mathrm{thr}}\approx 3\times 10^{-5}$|⁠. In this well over-threshold regime our growth rate is the same as the Bell growth rate and both instabilities should develop. However, they develop in different wavenumber domains, which in certain circumstances (thermal anisotropies, plasma inhomogeneity, etc.) may affect their growth rates in different ways. For example, the background thermal effects at high temperatures reduce the Bell growth rate (e.g. Achterberg 2013, and references therein) but increase ours (the KAW effect).

Polarization of the kinetic Alfvén mode is variable and can be right- or left-handed elliptic depending on the wavenumber, propagation angle (with respect to |$\boldsymbol {B}_{0}$|⁠), and plasma beta (Zhao et al. 2014). Adding also the beam and plasma currents makes this dependence even more complicated and requires further analysis in the parameter space, which will be subject for a separate study.

Some observational consequences

Observational consequences and effects produced by the oblique AW instability are quite different from those of the (parallel) Bell instability. The most straightforward is the different orientation of generated magnetic filaments. Namely, magnetic filaments oriented across the initial background magnetic field |$\boldsymbol {B}_{0}$| would indicate the Bell instability, whereas magnetic filaments elongated along |$\boldsymbol {B} _{0}$| are typical for the oblique Alfvén instability.

Cross-|$\boldsymbol {B}_{0}$| stochastic acceleration of CRs is another important effect that can be introduced by the oblique AW instability. This acceleration is made possible by small cross-|$\boldsymbol {B} _{0}$| scales of generated oblique AWs, comparable to (or sometimes even much smaller than) the CR gyroradius. Actually, oblique instability is naturally designed for stochastic CR acceleration because its perpendicular scale is linked to the CR gyroradius. The required (threshold) magnetic AW amplitudes and their consistency with the free energy available in the system will be analysed in future.

Electric field component |$\boldsymbol {E}_{z}\parallel \boldsymbol {B}_{0}$| arises in AWs at oblique propagation. Due to |$\boldsymbol {E}_{z}$|⁠, oblique AWs undergo kinetic wave–particle interactions at Cherenkov resonances, which should lead to the plasma pre-heating in astrophysical foreshocks.

An admixture of the jitter-like radiation (due to the presence of small-scale AWs), in addition to the synchrotron (due to the presence of large-scale |$\boldsymbol {B}_{0}$|⁠), can be produced in our setting and, if observed, used for diagnostic purposes. We are not aware of such observations.

CONCLUSIONS

Accounting for the perpendicular dispersive effects introduced by the finite ion gyroradii in the beam and in the background plasma, we investigated a non-resonant instability of kinetic-scale Alfvén waves (KAWs) in compensated-current systems. The instability emerges on the KAW dispersion branch due to the coupling with the fast mode via the current term proportional to |$\bar{j}_{\rm b}$|⁠. Thus we extended the applicability limits of Paper I, where only for MHD Alfvén waves have been taken into account. The kinetic Alfvénic dispersion branch is made aperiodically unstable by the mismatch between the wave responses to the demagnetized ion beam current and the magnetized background electron current. We found that the effects of finite background ion gyroradius play a destabilizing role.

The main properties of the compensated-current KAW instability are summarized as follows.

The KAW instability is driven by the same effects as the MHD AW instability – perpendicular dispersive effects of finite beam gyroradius (terms ∼k_⊥ρ_b). Effects of the finite background gyroradius (terms ∼k_⊥ρ_i) enforce the instability (the KAW effect).
The threshold beam current is the same as for the oblique MHD AW instability, |$\bar{j}_{\mathrm{thr}}\simeq 1.33V_{\rm A}/V_{Tb}$|⁠. The increasing beam current and temperature play a destabilizing role.
At well above-threshold currents the KAW effect increases the instability growth rate significantly, about two times in the vicinity of the upper boundary of the instability μ_i ≲ μ_i2. The most unstable perpendicular wavenumbers in this case tend to be controlled by ρ_i rather than ρ_b.
The KAW instability is more oblique than the MHD AW instability.
Short cross-field wavelengths of generated KAWs make them available for stochastic cross-field acceleration of the beam ions.

Fluctuations with varying obliquity, regularly observed in the terrestrial foreshock, can be explained in terms of the MHD AW instability in the case of less oblique propagation with small μ_i ≪ 1, and by the KAW instability in the cases of more oblique propagation with μ_i ∼ 1. The obliquity is difficult to explain by competing instabilities, left-/right-hand resonant (Gary 1985), fire-hose (Sentman et al. 1981), ‘antiparallel non-resonant’ (Winske & Leroy 1984), and ‘parallel non-resonant’ (Bell 2004, 2005), all of which are magnetic field-aligned. To this end we note that the oblique dispersion equation derived by Bell (2005) and discussed by Schure et al. (2012) is dominated by the parallel dispersive effects rather than the perpendicular ones and is maximized at parallel propagation. As we already discussed in Paper I, the previous studies did not take into account the perpendicular dispersion effects of the finite ion gyroradius proper.

CRs in typical astrophysical environments drive the oblique Alfvén instability in the MHD regime. For the well over-threshold CR currents |$\bar{j}_{\rm b}\gg \bar{j}_{\mathrm{thr}}$|⁠, the asymptotic scaling of the oblique AW growth rate is |$\gamma _{\mathrm{m}}\sim 0.5\bar{j}_{\rm b}\omega _{Bi}$|⁠, which is the same scaling as for the Bell instability. Moderate CR fluxes n_CRV_b ∼ 10⁴ cm⁻² s⁻¹ (Zweibel & Everett 2010) are already well over-threshold and hence should drive both the oblique AW and Bell instabilities with the same growth rate γ_m ≃ 2.2 × 10⁻⁴ s⁻¹. In this case we expect two distinct components of magnetic fluctuations in different wavenumber domains, generated by oblique (at large k_⊥) and parallel (at large k_z) Alfvén instabilities. The large-k_⊥ component can accelerate CRs stochastically, converting energy of parallel flows into cross-|$\boldsymbol {B}_{0}$| energy of CRs. The growth rates of two instabilities become different in the near-threshold regime and/or in a hot background, which will be subject of future comparative studies.

This research was supported by the Belgian Science Policy Office (through Prodex/Cluster PEA 90316 and IAP Programme project P7/08 CHARM), and by the European Commission (through FP7 Program project 313038 STORM).

REFERENCES

Achterberg

A.

MNRAS

2013

436

705

Month:	Total Views:
November 2016	1
December 2016	1
January 2017	1
February 2017	2
August 2017	1
November 2017	3
February 2018	2
March 2018	1
May 2018	1
August 2018	1
October 2018	1
November 2018	4
December 2018	7
January 2019	6
February 2019	5
March 2019	7
April 2019	7
May 2019	7
June 2019	4
July 2019	3
August 2019	6
September 2019	5
October 2019	8
November 2019	5
December 2019	3
January 2020	7
February 2020	8
March 2020	12
April 2020	4
May 2020	2
June 2020	5
July 2020	2
August 2020	3
September 2020	8
October 2020	4
November 2020	2
January 2021	2
February 2021	3
March 2021	9
April 2021	3

Article Contents

Compensated-current instability of kinetic Alfvén waves Free

Abstract

INTRODUCTION

MODEL

SOLUTION FOR KINETIC ALFVéN MODE

INSTABILITY ANALYSIS

Threshold

Wavenumber dependence of the instability growth rate

Properties of the compensated-current KAW instability

OBLIQUE ALFVéN INSTABILITY IN COMPENSATED-CURRENT SYSTEMS

Terrestrial foreshock regions

Cosmic rays

DISCUSSION

Oblique Alfvén instability versus Bell instability

Some observational consequences

CONCLUSIONS

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Compensated-current instability of kinetic Alfvén waves