-
PDF
- Split View
-
Views
-
Cite
Cite
Otoniel Denis-Alpizar, Thierry Stoecklin, Rovibrational rate coefficients of NO+ in collision with He, Monthly Notices of the Royal Astronomical Society, Volume 451, Issue 3, 11 August 2015, Pages 2986–2990, https://doi.org/10.1093/mnras/stv1137
Close - Share Icon Share
Abstract
The nitrosylium ion was observed very recently for the first time in the interstellar medium. We compute the rotationally inelastic cross-sections and rate coefficients for the two lowest vibrational levels of NO+ colliding with He. The most favoured transitions are found to correspond to even Δj. We also compare the rank order of the magnitudes of the rotational transition rate coefficients for each of the two lowest vibrational levels of NO+ and find that they can differ slightly for a few temperatures.
1 INTRODUCTION
The nitrosylium ion (NO+) was found in the Earth's upper atmosphere more than three decades ago (Nicholls 1977) while its first detection in the interstellar medium was reported very recently (Cernicharo et al. 2014). This first detection of NO+ in the cold dense core of Barnard 1-b is an important step in understanding the interstellar chemistry of molecules containing N and O atoms, in particular for studying the formation of N-bearing organic species, which play a crucial role in the chemistry relevant to life. The possible existence of NO+ in the interstellar medium was considered long ago by Herbst & Klemperer (1973), Pickles & Williams (1977) and Singh & Maciel (1980). These authors discussed the most probable mechanism of formation of this cation in molecular clouds and concluded that charge transfer reactions between NO and various cations (C+, H+ and CH|$_{3}^{+}$|), proton elimination of interstellar protonated nitrogen by an oxygen atom and exothermic reactions between N+ and oxygen-containing species were all possible while dissociative recombination with electrons is its main destruction mechanism. Because of its detection in Earth's upper atmosphere, there have been several theoretical studies of collisions involving NO+. Its collisions with e− (Faure & Tennyson 2001) are, for example, well documented while its vibrational quenching by He (Hawley & Smith 1991; Zenevich et al. 1995) and H2 (Federer et al. 1985; Viggiano et al. 1989) were also studied experimentally long ago. In 2001, Soldán, Lee & Wright (2002) developed a rigid-rotor two-dimensional (2D) potential energy surface (PES) for the He–NO+ system and used it to calculate the He–NO+ bound states. More recently, a 3D PES including the vibration of NO+ was developed by our group (Stoecklin & Voronin 2011) to study the vibrational relaxation of NO+ by collision with He. We also calculated the bound states of the He–NO+ complex and found very good agreement with the 2D results of Soldán. In the same study, we compared and discussed the calculated vibrational quenching rate coefficients with the available experimental data. These two comparisons assessed the validity of the PES, which is used in the present study to calculate the rotational excitation rates of NO+ for its two lowest vibrational levels. These data, which are required in models of non-local thermodynamic equilibrium cold interstellar clouds, should allow the NO+ molecular abundance to be estimated. The rotational excitation calculations are performed for the two different vibrational levels to test the usual hypothesis that the results will be the same. We then discuss the validity of this hypothesis, which is commonly used by experimentalists (Islam, Smith & Wiebrecht 1995). They indeed usually measure rotationally inelastic rate coefficients for a vibrationally excited level and identify them with those inside the fundamental vibrational state.
The paper is organized as follows. In Section 2 we give a brief account of the main characteristics of the PES used and give the parameters of the close-coupling calculations. The results are presented and discussed in Section 3 and the conclusion in Section 4.
2 METHOD
2.1 Potential energy surface
We use the surface developed in our previous work, where it was described in detail (Stoecklin & Voronin 2011). Also, we will only recap here its main features. It is based on a grid of approximately 900 ab initio points computed at the coupled cluster level [BCCD(T)] with Brueckner orbitals in the supermolecule approach and using an augmented correlation consisting of a quadruple-zeta basis set (aug-cc-pVQZ) supplemented by a set of bond functions. The superposition error of the basis set was corrected using the counterpoise procedure (Boys & Bernardi 1970).
The analytical model of the 3D PES was obtained using a fitting procedure based on the reproducing kernel Hilbert space approach. The well depth of the complex is De = 195.42 cm−1 (24.23 meV) in the bent configuration with r = 2.0092a0, R = 5.26a0 and θ = 80.42°, where r is the NO+ interatomic distance, R is the distance of He to the centre of mass of NO+, and θ is the Jacobi He–N centre of mass angle.
2.2 Scattering calculations
We computed the inelastic cross-sections of NO+ in collision with He at the close-coupling level. The close-coupled equations in the space fixed frame were solved using the log-derivative propagator implemented in our atom–diatomic molecule code Newmat (Stoecklin, Voronin & Rayez 2002). At each point of the propagation grid, the matrix elements of the potential were found by expanding the potential using Legendre polynomials retaining terms up to l = 7 on a grid of 14 points, which were used to calculate the Gauss–Hermite quadrature of the vibrational part of the integral. A discrete variable representation along the Gauss–Hermite grid of the diatomic rovibrational wave functions was calculated by solving the exact diatomic equations using the potential and a finite basis representation of imaginary exponential wave functions as described, for example, by Colbert & Miller (1992).
The convergence of the quenching cross-section as a function of the maximum intermolecular distance and total angular momentum was checked for each collisional energy. The minimum propagation distance used was 50a0. As mentioned in the introduction, we did two sets of calculations. In the first one, we took into account only the ground vibrational level and calculated the rotational transitions for this level while in the second set we use two vibrational levels and calculated the rotational transitions for the first excited vibrational level. In the first case, we found that 20 rotational levels were sufficient to converge the inelastic cross-sections for energies lower than 700 cm−1 while at higher energies, the basis set was extended to include always at least one closed rotational channel. In the second set of calculations, the inclusion of 20 rotational states for each of the two vibrational levels was sufficient to converge the cross-sections in the [10−5, 2000] cm−1 collision energy interval of our calculations (1 eV ≈ 8066 cm−1).
3 RESULTS AND DISCUSSION
We computed the cross-sections of the system for collisional energies varying from 10−5 to 2000 cm−1. From these cross-sections, we also calculated the rate coefficients using equation (1).
Fig. 1 represents the dependence of the rotational rate coefficients as a function of temperature for transitions from the j = 5 rotational level for the ground vibrational state of NO+. The same representation is presented in Fig. 2 for transitions from the j = 6 rotational level for the first excited vibrational state of NO+. These two figures show clearly that the most favoured transitions correspond to Δj = 2.
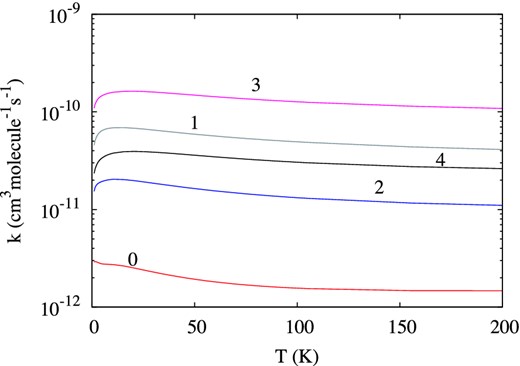
Rotational de-excitation rate coefficients of NO+ (ν = 0, j = 5 → ν = 0, j′) in collision with He as a function of temperature. The final level is indicated by an integer designating the final rotational quantum number.
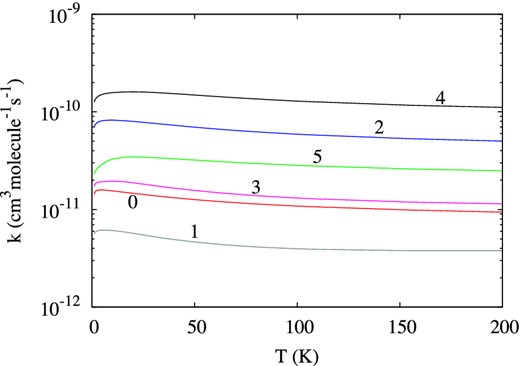
Rotational de-excitation rate coefficients of NO+ (ν = 1, j = 6 → ν = 1, j′) in collision with He as a function of temperature. The final level is indicated by an integer designating the final rotational quantum number.
We will not comment here on the vibrational quenching of NO+ as this was discussed in detail in our first paper (Stoecklin & Voronin 2011), which was dedicated to this system, but simply note that vibrational quenching is 4 orders of magnitude smaller than rotational quenching for this system as illustrated in Fig. 3. We will instead focus here on a comparison between the rotational transitions for each of the two lowest vibrational states of NO+ represented in Fig. 3. In this figure, we compare the rotational quenching rate coefficients of NO+(ν = 0, j = 2) and NO+(ν = 1, j = 2). This figure shows that the hypothesis that the rotational transition rate coefficients for the fundamental vibrational level are identical to those inside any vibrationally excited state is correct in the [1, 100] K interval, which is typical for astrochemical conditions. However, for temperatures lower than 1 K or higher than 100 K we can see differences between both sets of rate coefficients, which we believe have not been mentioned before. It is necessary to investigate how these differences appear in the state-to-state rate coefficients.

Comparison of the rotational quenching rate coefficients of NO+(j = 2) in collision with He for the fundamental ν = 0 (red) and the first excited ν = 1 (blue) vibrational states as a function of temperature. The vibrational quenching is represented in black.
In Fig. 4, we compare the rate coefficients associated with the rotational transitions from the j = 3, 4, 5, 6 and 7 initial rotational levels for the ν = 0 (left-hand panels) and ν = 1 (right-hand panels) vibrational levels of NO+ at selected temperatures. We see again that transitions with even Δj are more favourable. A similar propensity rule was found, for example, for the collision of HCN with He (Denis-Alpizar et al. 2013). This behaviour was analysed previously by several authors, like Sarrasin et al. (2010). It simply shows that coefficients associated with even values of l dominate the expansion of the intermolecular potential in the Legendre polynomial or in other words that NO+ behaves like a homonuclear molecule. On the other hand, the differences in magnitude between the rotational rate coefficients calculated for different vibrational levels are very small. For a given vibrational state, the rank orders of the rotational transition rate coefficients for the three temperatures analysed (1, 10 and 100 K) depend on the initial rotational quantum number ji and on Δj. Even though the differences are small, it is also important to notice that the rank order of the rotational transition rate coefficients is a function of temperature and there are differences for the ν = 0 and ν = 1 vibrational states.

Comparison of the rotational de-excitation rate coefficients of NO+(ji) in collision with He for the vibrational levels ν = 0 and 1 at 1, 10 and 100 K.
Rovibrational rate coefficients (cm3 molecule−1 s−1) of NO+ in collision with He at selected temperatures. The proportionality factor P10 is also reported.
| . | T = 1 K . | T = 10 K . | T = 100 K . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ji . | jf . | |$k_{j_{i},1\rightarrow j_{f},0}$| . | |$k_{j_{i},0\rightarrow j_{f},0}$| . | P10 . | |$k_{j_{i},1\rightarrow j_{f},0}$| . | |$k_{j_{i},0 \rightarrow j_{f},0}$| . | P10 . | |$k_{j_{i},1\rightarrow j_{f},0}$| . | |$k_{j_{i},0 \rightarrow j_{f},0}$| . | P10 . |
| Odd Δj transitions | ||||||||||
| 1 | 0 | 1.3 × 10−15 | 3.3 × 10−11 | 4 × 10−5 | 6.3 × 10−16 | 5.1 × 10−11 | 1 × 10−5 | 2.4 × 10−16 | 6.1 × 10−11 | 4 × 10−6 |
| 2 | 1 | 7.3 × 10−16 | 4.9 × 10−11 | 1 × 10−5 | 8.5 × 10−16 | 6.4 × 10−11 | 1 × 10−5 | 4.6 × 10−16 | 5.1 × 10−11 | 9 × 10−6 |
| 3 | 0 | 7.0 × 10−17 | 1.2 × 10−11 | 6 × 10−6 | 1.6 × 10−16 | 1.2 × 10−11 | 1 × 10−5 | 1.0 × 10−16 | 4.7 × 10−12 | 2 × 10−5 |
| 3 | 2 | 4.6 × 10−16 | 4.4 × 10−11 | 1 × 10−5 | 6.8 × 10−16 | 4.8 × 10−11 | 1 × 10−5 | 5.5 × 10−16 | 4.0 × 10−11 | 1 × 10−5 |
| 4 | 1 | 1.4 × 10−16 | 1.4 × 10−11 | 1 × 10−5 | 2.5 × 10−16 | 1.8 × 10−11 | 1 × 10−5 | 2.3 × 10−16 | 9.8 × 10−12 | 2 × 10−5 |
| 4 | 3 | 4.1 × 10−16 | 2.6 × 10−11 | 2 × 10−5 | 6.1 × 10−16 | 4.0 × 10−11 | 2 × 10−5 | 5.6 × 10−16 | 3.2 × 10−11 | 2 × 10−5 |
| 5 | 0 | 9.5 × 10−17 | 2.9 × 10−12 | 3 × 10−5 | 7.3 × 10−17 | 2.7 × 10−12 | 3 × 10−5 | 6.9 × 10−17 | 1.6 × 10−12 | 4 × 10−5 |
| 5 | 2 | 1.9 × 10−16 | 1.6 × 10−11 | 1 × 10−5 | 2.9 × 10−16 | 2.0 × 10−11 | 1 × 10−5 | 2.6 × 10−16 | 1.3 × 10−11 | 2 × 10−5 |
| 5 | 4 | 4.8 × 10−16 | 2.4 × 10−11 | 2 × 10−5 | 6.0 × 10−16 | 3.8 × 10−11 | 2 × 10−5 | 5.4 × 10−16 | 3.0 × 10−11 | 2 × 10−5 |
| 6 | 1 | 1.7 × 10−16 | 4.6 × 10−12 | 4 × 10−5 | 1.5 × 10−16 | 6.6 × 10−12 | 2 × 10−5 | 1.3 × 10−16 | 4.2 × 10−12 | 3 × 10−5 |
| 6 | 3 | 2.6 × 10−16 | 1.5 × 10−11 | 2 × 10−5 | 3.3 × 10−16 | 2.3 × 10−11 | 1 × 10−5 | 2.7 × 10−16 | 1.5 × 10−11 | 2 × 10−5 |
| 6 | 5 | 4.0 × 10−16 | 1.9 × 10−11 | 2 × 10−5 | 5.3 × 10−16 | 3.5 × 10−11 | 2 × 10−5 | 5.1 × 10−16 | 2.9 × 10−11 | 2 × 10−5 |
| 7 | 0 | 1.0 × 10−17 | 1.0 × 10−12 | 1 × 10−5 | 1.8 × 10−17 | 1.5 × 10−12 | 1 × 10−5 | 2.0 × 10−17 | 1.0 × 10−12 | 2 × 10−5 |
| 7 | 2 | 1.2 × 10−16 | 8.2 × 10−12 | 1 × 10−5 | 1.4 × 10−16 | 1.1 × 10−11 | 1 × 10−5 | 1.5 × 10−16 | 6.6 × 10−12 | 2 × 10−5 |
| 7 | 4 | 2.3 × 10−16 | 2.2 × 10−11 | 1 × 10−5 | 3.0 × 10−16 | 2.7 × 10−11 | 1 × 10−5 | 2.9 × 10−16 | 1.6 × 10−11 | 2 × 10−5 |
| 7 | 6 | 4.2 × 10−16 | 2.3 × 10−11 | 2 × 10−5 | 5.3 × 10−16 | 3.4 × 10−11 | 2 × 10−5 | 5.3 × 10−16 | 2.8 × 10−11 | 2 × 10−5 |
| Averaged P01 | 1.8 × 10−5 | 1.5 × 10−5 | 2.0 × 10−5 | |||||||
| Even Δj transitions | ||||||||||
| 2 | 0 | 3.0 × 10−16 | 5.3 × 10−11 | 6 × 10−6 | 2.8 × 10−16 | 8.2 × 10−11 | 3 × 10−6 | 1.8 × 10−16 | 5.1 × 10−11 | 3 × 10−6 |
| 3 | 1 | 4.4 × 10−16 | 1.5 × 10−10 | 3 × 10−6 | 5.2 × 10−16 | 1.7 × 10−10 | 3 × 10−6 | 4.6 × 10−16 | 1.1 × 10−10 | 4 × 10−6 |
| 4 | 0 | 1.3 × 10−16 | 3.8 × 10−11 | 3 × 10−6 | 1.2 × 10−16 | 4.2 × 10−11 | 3 × 10−6 | 1.5 × 10−16 | 2.4 × 10−11 | 6 × 10−6 |
| 4 | 2 | 5.4 × 10−16 | 1.4 × 10−10 | 4 × 10−6 | 6.0 × 10−16 | 1.8 × 10−10 | 3 × 10−6 | 5.2 × 10−16 | 1.2 × 10−10 | 4 × 10−6 |
| 5 | 1 | 4.5 × 10−16 | 4.6 × 10−11 | 1 × 10−5 | 3.5 × 10−16 | 6.9 × 10−11 | 5 × 10−6 | 3.0 × 10−16 | 4.9 × 10−11 | 6 × 10−6 |
| 5 | 3 | 7.4 × 10−16 | 1.1 × 10−10 | 7 × 10−6 | 7.6 × 10−16 | 1.6 × 10−10 | 5 × 10−6 | 6.0 × 10−16 | 1.3 × 10−10 | 5 × 10−6 |
| 6 | 0 | 7.4 × 10−17 | 1.1 × 10−11 | 6 × 10−6 | 7.5 × 10−17 | 1.6 × 10−11 | 5 × 10−6 | 5.4 × 10−17 | 1.1 × 10−11 | 5 × 10−6 |
| 6 | 2 | 5.9 × 10−16 | 5.3 × 10−11 | 1 × 10−5 | 5.4 × 10−16 | 7.8 × 10−11 | 7 × 10−6 | 4.1 × 10−16 | 5.8 × 10−11 | 7 × 10−6 |
| 6 | 4 | 7.3 × 10−16 | 1.0 × 10−10 | 7 × 10−6 | 7.6 × 10−16 | 1.5 × 10−10 | 5 × 10−6 | 6.0 × 10−16 | 1.3 × 10−10 | 5 × 10−6 |
| 7 | 1 | 2.2 × 10−16 | 2.7 × 10−11 | 8 × 10−6 | 2.1 × 10−16 | 3.1 × 10−11 | 7 × 10−6 | 1.4 × 10−16 | 2.2 × 10−11 | 6 × 10−6 |
| 7 | 3 | 5.8 × 10−16 | 6.8 × 10−11 | 9 × 10−6 | 5.5 × 10−16 | 8.6 × 10−11 | 6 × 10−6 | 4.6 × 10−16 | 6.2 × 10−11 | 7 × 10−6 |
| 7 | 5 | 5.8 × 10−16 | 1.1 × 10−10 | 5 × 10−6 | 6.2 × 10−16 | 1.5 × 10−10 | 4 × 10−6 | 5.8 × 10−16 | 1.3 × 10−10 | 4 × 10−6 |
| Averaged P01 | 6.6 × 10−6 | 4.7 × 10−6 | 5.3 × 10−6 | |||||||
| . | T = 1 K . | T = 10 K . | T = 100 K . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ji . | jf . | |$k_{j_{i},1\rightarrow j_{f},0}$| . | |$k_{j_{i},0\rightarrow j_{f},0}$| . | P10 . | |$k_{j_{i},1\rightarrow j_{f},0}$| . | |$k_{j_{i},0 \rightarrow j_{f},0}$| . | P10 . | |$k_{j_{i},1\rightarrow j_{f},0}$| . | |$k_{j_{i},0 \rightarrow j_{f},0}$| . | P10 . |
| Odd Δj transitions | ||||||||||
| 1 | 0 | 1.3 × 10−15 | 3.3 × 10−11 | 4 × 10−5 | 6.3 × 10−16 | 5.1 × 10−11 | 1 × 10−5 | 2.4 × 10−16 | 6.1 × 10−11 | 4 × 10−6 |
| 2 | 1 | 7.3 × 10−16 | 4.9 × 10−11 | 1 × 10−5 | 8.5 × 10−16 | 6.4 × 10−11 | 1 × 10−5 | 4.6 × 10−16 | 5.1 × 10−11 | 9 × 10−6 |
| 3 | 0 | 7.0 × 10−17 | 1.2 × 10−11 | 6 × 10−6 | 1.6 × 10−16 | 1.2 × 10−11 | 1 × 10−5 | 1.0 × 10−16 | 4.7 × 10−12 | 2 × 10−5 |
| 3 | 2 | 4.6 × 10−16 | 4.4 × 10−11 | 1 × 10−5 | 6.8 × 10−16 | 4.8 × 10−11 | 1 × 10−5 | 5.5 × 10−16 | 4.0 × 10−11 | 1 × 10−5 |
| 4 | 1 | 1.4 × 10−16 | 1.4 × 10−11 | 1 × 10−5 | 2.5 × 10−16 | 1.8 × 10−11 | 1 × 10−5 | 2.3 × 10−16 | 9.8 × 10−12 | 2 × 10−5 |
| 4 | 3 | 4.1 × 10−16 | 2.6 × 10−11 | 2 × 10−5 | 6.1 × 10−16 | 4.0 × 10−11 | 2 × 10−5 | 5.6 × 10−16 | 3.2 × 10−11 | 2 × 10−5 |
| 5 | 0 | 9.5 × 10−17 | 2.9 × 10−12 | 3 × 10−5 | 7.3 × 10−17 | 2.7 × 10−12 | 3 × 10−5 | 6.9 × 10−17 | 1.6 × 10−12 | 4 × 10−5 |
| 5 | 2 | 1.9 × 10−16 | 1.6 × 10−11 | 1 × 10−5 | 2.9 × 10−16 | 2.0 × 10−11 | 1 × 10−5 | 2.6 × 10−16 | 1.3 × 10−11 | 2 × 10−5 |
| 5 | 4 | 4.8 × 10−16 | 2.4 × 10−11 | 2 × 10−5 | 6.0 × 10−16 | 3.8 × 10−11 | 2 × 10−5 | 5.4 × 10−16 | 3.0 × 10−11 | 2 × 10−5 |
| 6 | 1 | 1.7 × 10−16 | 4.6 × 10−12 | 4 × 10−5 | 1.5 × 10−16 | 6.6 × 10−12 | 2 × 10−5 | 1.3 × 10−16 | 4.2 × 10−12 | 3 × 10−5 |
| 6 | 3 | 2.6 × 10−16 | 1.5 × 10−11 | 2 × 10−5 | 3.3 × 10−16 | 2.3 × 10−11 | 1 × 10−5 | 2.7 × 10−16 | 1.5 × 10−11 | 2 × 10−5 |
| 6 | 5 | 4.0 × 10−16 | 1.9 × 10−11 | 2 × 10−5 | 5.3 × 10−16 | 3.5 × 10−11 | 2 × 10−5 | 5.1 × 10−16 | 2.9 × 10−11 | 2 × 10−5 |
| 7 | 0 | 1.0 × 10−17 | 1.0 × 10−12 | 1 × 10−5 | 1.8 × 10−17 | 1.5 × 10−12 | 1 × 10−5 | 2.0 × 10−17 | 1.0 × 10−12 | 2 × 10−5 |
| 7 | 2 | 1.2 × 10−16 | 8.2 × 10−12 | 1 × 10−5 | 1.4 × 10−16 | 1.1 × 10−11 | 1 × 10−5 | 1.5 × 10−16 | 6.6 × 10−12 | 2 × 10−5 |
| 7 | 4 | 2.3 × 10−16 | 2.2 × 10−11 | 1 × 10−5 | 3.0 × 10−16 | 2.7 × 10−11 | 1 × 10−5 | 2.9 × 10−16 | 1.6 × 10−11 | 2 × 10−5 |
| 7 | 6 | 4.2 × 10−16 | 2.3 × 10−11 | 2 × 10−5 | 5.3 × 10−16 | 3.4 × 10−11 | 2 × 10−5 | 5.3 × 10−16 | 2.8 × 10−11 | 2 × 10−5 |
| Averaged P01 | 1.8 × 10−5 | 1.5 × 10−5 | 2.0 × 10−5 | |||||||
| Even Δj transitions | ||||||||||
| 2 | 0 | 3.0 × 10−16 | 5.3 × 10−11 | 6 × 10−6 | 2.8 × 10−16 | 8.2 × 10−11 | 3 × 10−6 | 1.8 × 10−16 | 5.1 × 10−11 | 3 × 10−6 |
| 3 | 1 | 4.4 × 10−16 | 1.5 × 10−10 | 3 × 10−6 | 5.2 × 10−16 | 1.7 × 10−10 | 3 × 10−6 | 4.6 × 10−16 | 1.1 × 10−10 | 4 × 10−6 |
| 4 | 0 | 1.3 × 10−16 | 3.8 × 10−11 | 3 × 10−6 | 1.2 × 10−16 | 4.2 × 10−11 | 3 × 10−6 | 1.5 × 10−16 | 2.4 × 10−11 | 6 × 10−6 |
| 4 | 2 | 5.4 × 10−16 | 1.4 × 10−10 | 4 × 10−6 | 6.0 × 10−16 | 1.8 × 10−10 | 3 × 10−6 | 5.2 × 10−16 | 1.2 × 10−10 | 4 × 10−6 |
| 5 | 1 | 4.5 × 10−16 | 4.6 × 10−11 | 1 × 10−5 | 3.5 × 10−16 | 6.9 × 10−11 | 5 × 10−6 | 3.0 × 10−16 | 4.9 × 10−11 | 6 × 10−6 |
| 5 | 3 | 7.4 × 10−16 | 1.1 × 10−10 | 7 × 10−6 | 7.6 × 10−16 | 1.6 × 10−10 | 5 × 10−6 | 6.0 × 10−16 | 1.3 × 10−10 | 5 × 10−6 |
| 6 | 0 | 7.4 × 10−17 | 1.1 × 10−11 | 6 × 10−6 | 7.5 × 10−17 | 1.6 × 10−11 | 5 × 10−6 | 5.4 × 10−17 | 1.1 × 10−11 | 5 × 10−6 |
| 6 | 2 | 5.9 × 10−16 | 5.3 × 10−11 | 1 × 10−5 | 5.4 × 10−16 | 7.8 × 10−11 | 7 × 10−6 | 4.1 × 10−16 | 5.8 × 10−11 | 7 × 10−6 |
| 6 | 4 | 7.3 × 10−16 | 1.0 × 10−10 | 7 × 10−6 | 7.6 × 10−16 | 1.5 × 10−10 | 5 × 10−6 | 6.0 × 10−16 | 1.3 × 10−10 | 5 × 10−6 |
| 7 | 1 | 2.2 × 10−16 | 2.7 × 10−11 | 8 × 10−6 | 2.1 × 10−16 | 3.1 × 10−11 | 7 × 10−6 | 1.4 × 10−16 | 2.2 × 10−11 | 6 × 10−6 |
| 7 | 3 | 5.8 × 10−16 | 6.8 × 10−11 | 9 × 10−6 | 5.5 × 10−16 | 8.6 × 10−11 | 6 × 10−6 | 4.6 × 10−16 | 6.2 × 10−11 | 7 × 10−6 |
| 7 | 5 | 5.8 × 10−16 | 1.1 × 10−10 | 5 × 10−6 | 6.2 × 10−16 | 1.5 × 10−10 | 4 × 10−6 | 5.8 × 10−16 | 1.3 × 10−10 | 4 × 10−6 |
| Averaged P01 | 6.6 × 10−6 | 4.7 × 10−6 | 5.3 × 10−6 | |||||||
Rovibrational rate coefficients (cm3 molecule−1 s−1) of NO+ in collision with He at selected temperatures. The proportionality factor P10 is also reported.
| . | T = 1 K . | T = 10 K . | T = 100 K . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ji . | jf . | |$k_{j_{i},1\rightarrow j_{f},0}$| . | |$k_{j_{i},0\rightarrow j_{f},0}$| . | P10 . | |$k_{j_{i},1\rightarrow j_{f},0}$| . | |$k_{j_{i},0 \rightarrow j_{f},0}$| . | P10 . | |$k_{j_{i},1\rightarrow j_{f},0}$| . | |$k_{j_{i},0 \rightarrow j_{f},0}$| . | P10 . |
| Odd Δj transitions | ||||||||||
| 1 | 0 | 1.3 × 10−15 | 3.3 × 10−11 | 4 × 10−5 | 6.3 × 10−16 | 5.1 × 10−11 | 1 × 10−5 | 2.4 × 10−16 | 6.1 × 10−11 | 4 × 10−6 |
| 2 | 1 | 7.3 × 10−16 | 4.9 × 10−11 | 1 × 10−5 | 8.5 × 10−16 | 6.4 × 10−11 | 1 × 10−5 | 4.6 × 10−16 | 5.1 × 10−11 | 9 × 10−6 |
| 3 | 0 | 7.0 × 10−17 | 1.2 × 10−11 | 6 × 10−6 | 1.6 × 10−16 | 1.2 × 10−11 | 1 × 10−5 | 1.0 × 10−16 | 4.7 × 10−12 | 2 × 10−5 |
| 3 | 2 | 4.6 × 10−16 | 4.4 × 10−11 | 1 × 10−5 | 6.8 × 10−16 | 4.8 × 10−11 | 1 × 10−5 | 5.5 × 10−16 | 4.0 × 10−11 | 1 × 10−5 |
| 4 | 1 | 1.4 × 10−16 | 1.4 × 10−11 | 1 × 10−5 | 2.5 × 10−16 | 1.8 × 10−11 | 1 × 10−5 | 2.3 × 10−16 | 9.8 × 10−12 | 2 × 10−5 |
| 4 | 3 | 4.1 × 10−16 | 2.6 × 10−11 | 2 × 10−5 | 6.1 × 10−16 | 4.0 × 10−11 | 2 × 10−5 | 5.6 × 10−16 | 3.2 × 10−11 | 2 × 10−5 |
| 5 | 0 | 9.5 × 10−17 | 2.9 × 10−12 | 3 × 10−5 | 7.3 × 10−17 | 2.7 × 10−12 | 3 × 10−5 | 6.9 × 10−17 | 1.6 × 10−12 | 4 × 10−5 |
| 5 | 2 | 1.9 × 10−16 | 1.6 × 10−11 | 1 × 10−5 | 2.9 × 10−16 | 2.0 × 10−11 | 1 × 10−5 | 2.6 × 10−16 | 1.3 × 10−11 | 2 × 10−5 |
| 5 | 4 | 4.8 × 10−16 | 2.4 × 10−11 | 2 × 10−5 | 6.0 × 10−16 | 3.8 × 10−11 | 2 × 10−5 | 5.4 × 10−16 | 3.0 × 10−11 | 2 × 10−5 |
| 6 | 1 | 1.7 × 10−16 | 4.6 × 10−12 | 4 × 10−5 | 1.5 × 10−16 | 6.6 × 10−12 | 2 × 10−5 | 1.3 × 10−16 | 4.2 × 10−12 | 3 × 10−5 |
| 6 | 3 | 2.6 × 10−16 | 1.5 × 10−11 | 2 × 10−5 | 3.3 × 10−16 | 2.3 × 10−11 | 1 × 10−5 | 2.7 × 10−16 | 1.5 × 10−11 | 2 × 10−5 |
| 6 | 5 | 4.0 × 10−16 | 1.9 × 10−11 | 2 × 10−5 | 5.3 × 10−16 | 3.5 × 10−11 | 2 × 10−5 | 5.1 × 10−16 | 2.9 × 10−11 | 2 × 10−5 |
| 7 | 0 | 1.0 × 10−17 | 1.0 × 10−12 | 1 × 10−5 | 1.8 × 10−17 | 1.5 × 10−12 | 1 × 10−5 | 2.0 × 10−17 | 1.0 × 10−12 | 2 × 10−5 |
| 7 | 2 | 1.2 × 10−16 | 8.2 × 10−12 | 1 × 10−5 | 1.4 × 10−16 | 1.1 × 10−11 | 1 × 10−5 | 1.5 × 10−16 | 6.6 × 10−12 | 2 × 10−5 |
| 7 | 4 | 2.3 × 10−16 | 2.2 × 10−11 | 1 × 10−5 | 3.0 × 10−16 | 2.7 × 10−11 | 1 × 10−5 | 2.9 × 10−16 | 1.6 × 10−11 | 2 × 10−5 |
| 7 | 6 | 4.2 × 10−16 | 2.3 × 10−11 | 2 × 10−5 | 5.3 × 10−16 | 3.4 × 10−11 | 2 × 10−5 | 5.3 × 10−16 | 2.8 × 10−11 | 2 × 10−5 |
| Averaged P01 | 1.8 × 10−5 | 1.5 × 10−5 | 2.0 × 10−5 | |||||||
| Even Δj transitions | ||||||||||
| 2 | 0 | 3.0 × 10−16 | 5.3 × 10−11 | 6 × 10−6 | 2.8 × 10−16 | 8.2 × 10−11 | 3 × 10−6 | 1.8 × 10−16 | 5.1 × 10−11 | 3 × 10−6 |
| 3 | 1 | 4.4 × 10−16 | 1.5 × 10−10 | 3 × 10−6 | 5.2 × 10−16 | 1.7 × 10−10 | 3 × 10−6 | 4.6 × 10−16 | 1.1 × 10−10 | 4 × 10−6 |
| 4 | 0 | 1.3 × 10−16 | 3.8 × 10−11 | 3 × 10−6 | 1.2 × 10−16 | 4.2 × 10−11 | 3 × 10−6 | 1.5 × 10−16 | 2.4 × 10−11 | 6 × 10−6 |
| 4 | 2 | 5.4 × 10−16 | 1.4 × 10−10 | 4 × 10−6 | 6.0 × 10−16 | 1.8 × 10−10 | 3 × 10−6 | 5.2 × 10−16 | 1.2 × 10−10 | 4 × 10−6 |
| 5 | 1 | 4.5 × 10−16 | 4.6 × 10−11 | 1 × 10−5 | 3.5 × 10−16 | 6.9 × 10−11 | 5 × 10−6 | 3.0 × 10−16 | 4.9 × 10−11 | 6 × 10−6 |
| 5 | 3 | 7.4 × 10−16 | 1.1 × 10−10 | 7 × 10−6 | 7.6 × 10−16 | 1.6 × 10−10 | 5 × 10−6 | 6.0 × 10−16 | 1.3 × 10−10 | 5 × 10−6 |
| 6 | 0 | 7.4 × 10−17 | 1.1 × 10−11 | 6 × 10−6 | 7.5 × 10−17 | 1.6 × 10−11 | 5 × 10−6 | 5.4 × 10−17 | 1.1 × 10−11 | 5 × 10−6 |
| 6 | 2 | 5.9 × 10−16 | 5.3 × 10−11 | 1 × 10−5 | 5.4 × 10−16 | 7.8 × 10−11 | 7 × 10−6 | 4.1 × 10−16 | 5.8 × 10−11 | 7 × 10−6 |
| 6 | 4 | 7.3 × 10−16 | 1.0 × 10−10 | 7 × 10−6 | 7.6 × 10−16 | 1.5 × 10−10 | 5 × 10−6 | 6.0 × 10−16 | 1.3 × 10−10 | 5 × 10−6 |
| 7 | 1 | 2.2 × 10−16 | 2.7 × 10−11 | 8 × 10−6 | 2.1 × 10−16 | 3.1 × 10−11 | 7 × 10−6 | 1.4 × 10−16 | 2.2 × 10−11 | 6 × 10−6 |
| 7 | 3 | 5.8 × 10−16 | 6.8 × 10−11 | 9 × 10−6 | 5.5 × 10−16 | 8.6 × 10−11 | 6 × 10−6 | 4.6 × 10−16 | 6.2 × 10−11 | 7 × 10−6 |
| 7 | 5 | 5.8 × 10−16 | 1.1 × 10−10 | 5 × 10−6 | 6.2 × 10−16 | 1.5 × 10−10 | 4 × 10−6 | 5.8 × 10−16 | 1.3 × 10−10 | 4 × 10−6 |
| Averaged P01 | 6.6 × 10−6 | 4.7 × 10−6 | 5.3 × 10−6 | |||||||
| . | T = 1 K . | T = 10 K . | T = 100 K . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ji . | jf . | |$k_{j_{i},1\rightarrow j_{f},0}$| . | |$k_{j_{i},0\rightarrow j_{f},0}$| . | P10 . | |$k_{j_{i},1\rightarrow j_{f},0}$| . | |$k_{j_{i},0 \rightarrow j_{f},0}$| . | P10 . | |$k_{j_{i},1\rightarrow j_{f},0}$| . | |$k_{j_{i},0 \rightarrow j_{f},0}$| . | P10 . |
| Odd Δj transitions | ||||||||||
| 1 | 0 | 1.3 × 10−15 | 3.3 × 10−11 | 4 × 10−5 | 6.3 × 10−16 | 5.1 × 10−11 | 1 × 10−5 | 2.4 × 10−16 | 6.1 × 10−11 | 4 × 10−6 |
| 2 | 1 | 7.3 × 10−16 | 4.9 × 10−11 | 1 × 10−5 | 8.5 × 10−16 | 6.4 × 10−11 | 1 × 10−5 | 4.6 × 10−16 | 5.1 × 10−11 | 9 × 10−6 |
| 3 | 0 | 7.0 × 10−17 | 1.2 × 10−11 | 6 × 10−6 | 1.6 × 10−16 | 1.2 × 10−11 | 1 × 10−5 | 1.0 × 10−16 | 4.7 × 10−12 | 2 × 10−5 |
| 3 | 2 | 4.6 × 10−16 | 4.4 × 10−11 | 1 × 10−5 | 6.8 × 10−16 | 4.8 × 10−11 | 1 × 10−5 | 5.5 × 10−16 | 4.0 × 10−11 | 1 × 10−5 |
| 4 | 1 | 1.4 × 10−16 | 1.4 × 10−11 | 1 × 10−5 | 2.5 × 10−16 | 1.8 × 10−11 | 1 × 10−5 | 2.3 × 10−16 | 9.8 × 10−12 | 2 × 10−5 |
| 4 | 3 | 4.1 × 10−16 | 2.6 × 10−11 | 2 × 10−5 | 6.1 × 10−16 | 4.0 × 10−11 | 2 × 10−5 | 5.6 × 10−16 | 3.2 × 10−11 | 2 × 10−5 |
| 5 | 0 | 9.5 × 10−17 | 2.9 × 10−12 | 3 × 10−5 | 7.3 × 10−17 | 2.7 × 10−12 | 3 × 10−5 | 6.9 × 10−17 | 1.6 × 10−12 | 4 × 10−5 |
| 5 | 2 | 1.9 × 10−16 | 1.6 × 10−11 | 1 × 10−5 | 2.9 × 10−16 | 2.0 × 10−11 | 1 × 10−5 | 2.6 × 10−16 | 1.3 × 10−11 | 2 × 10−5 |
| 5 | 4 | 4.8 × 10−16 | 2.4 × 10−11 | 2 × 10−5 | 6.0 × 10−16 | 3.8 × 10−11 | 2 × 10−5 | 5.4 × 10−16 | 3.0 × 10−11 | 2 × 10−5 |
| 6 | 1 | 1.7 × 10−16 | 4.6 × 10−12 | 4 × 10−5 | 1.5 × 10−16 | 6.6 × 10−12 | 2 × 10−5 | 1.3 × 10−16 | 4.2 × 10−12 | 3 × 10−5 |
| 6 | 3 | 2.6 × 10−16 | 1.5 × 10−11 | 2 × 10−5 | 3.3 × 10−16 | 2.3 × 10−11 | 1 × 10−5 | 2.7 × 10−16 | 1.5 × 10−11 | 2 × 10−5 |
| 6 | 5 | 4.0 × 10−16 | 1.9 × 10−11 | 2 × 10−5 | 5.3 × 10−16 | 3.5 × 10−11 | 2 × 10−5 | 5.1 × 10−16 | 2.9 × 10−11 | 2 × 10−5 |
| 7 | 0 | 1.0 × 10−17 | 1.0 × 10−12 | 1 × 10−5 | 1.8 × 10−17 | 1.5 × 10−12 | 1 × 10−5 | 2.0 × 10−17 | 1.0 × 10−12 | 2 × 10−5 |
| 7 | 2 | 1.2 × 10−16 | 8.2 × 10−12 | 1 × 10−5 | 1.4 × 10−16 | 1.1 × 10−11 | 1 × 10−5 | 1.5 × 10−16 | 6.6 × 10−12 | 2 × 10−5 |
| 7 | 4 | 2.3 × 10−16 | 2.2 × 10−11 | 1 × 10−5 | 3.0 × 10−16 | 2.7 × 10−11 | 1 × 10−5 | 2.9 × 10−16 | 1.6 × 10−11 | 2 × 10−5 |
| 7 | 6 | 4.2 × 10−16 | 2.3 × 10−11 | 2 × 10−5 | 5.3 × 10−16 | 3.4 × 10−11 | 2 × 10−5 | 5.3 × 10−16 | 2.8 × 10−11 | 2 × 10−5 |
| Averaged P01 | 1.8 × 10−5 | 1.5 × 10−5 | 2.0 × 10−5 | |||||||
| Even Δj transitions | ||||||||||
| 2 | 0 | 3.0 × 10−16 | 5.3 × 10−11 | 6 × 10−6 | 2.8 × 10−16 | 8.2 × 10−11 | 3 × 10−6 | 1.8 × 10−16 | 5.1 × 10−11 | 3 × 10−6 |
| 3 | 1 | 4.4 × 10−16 | 1.5 × 10−10 | 3 × 10−6 | 5.2 × 10−16 | 1.7 × 10−10 | 3 × 10−6 | 4.6 × 10−16 | 1.1 × 10−10 | 4 × 10−6 |
| 4 | 0 | 1.3 × 10−16 | 3.8 × 10−11 | 3 × 10−6 | 1.2 × 10−16 | 4.2 × 10−11 | 3 × 10−6 | 1.5 × 10−16 | 2.4 × 10−11 | 6 × 10−6 |
| 4 | 2 | 5.4 × 10−16 | 1.4 × 10−10 | 4 × 10−6 | 6.0 × 10−16 | 1.8 × 10−10 | 3 × 10−6 | 5.2 × 10−16 | 1.2 × 10−10 | 4 × 10−6 |
| 5 | 1 | 4.5 × 10−16 | 4.6 × 10−11 | 1 × 10−5 | 3.5 × 10−16 | 6.9 × 10−11 | 5 × 10−6 | 3.0 × 10−16 | 4.9 × 10−11 | 6 × 10−6 |
| 5 | 3 | 7.4 × 10−16 | 1.1 × 10−10 | 7 × 10−6 | 7.6 × 10−16 | 1.6 × 10−10 | 5 × 10−6 | 6.0 × 10−16 | 1.3 × 10−10 | 5 × 10−6 |
| 6 | 0 | 7.4 × 10−17 | 1.1 × 10−11 | 6 × 10−6 | 7.5 × 10−17 | 1.6 × 10−11 | 5 × 10−6 | 5.4 × 10−17 | 1.1 × 10−11 | 5 × 10−6 |
| 6 | 2 | 5.9 × 10−16 | 5.3 × 10−11 | 1 × 10−5 | 5.4 × 10−16 | 7.8 × 10−11 | 7 × 10−6 | 4.1 × 10−16 | 5.8 × 10−11 | 7 × 10−6 |
| 6 | 4 | 7.3 × 10−16 | 1.0 × 10−10 | 7 × 10−6 | 7.6 × 10−16 | 1.5 × 10−10 | 5 × 10−6 | 6.0 × 10−16 | 1.3 × 10−10 | 5 × 10−6 |
| 7 | 1 | 2.2 × 10−16 | 2.7 × 10−11 | 8 × 10−6 | 2.1 × 10−16 | 3.1 × 10−11 | 7 × 10−6 | 1.4 × 10−16 | 2.2 × 10−11 | 6 × 10−6 |
| 7 | 3 | 5.8 × 10−16 | 6.8 × 10−11 | 9 × 10−6 | 5.5 × 10−16 | 8.6 × 10−11 | 6 × 10−6 | 4.6 × 10−16 | 6.2 × 10−11 | 7 × 10−6 |
| 7 | 5 | 5.8 × 10−16 | 1.1 × 10−10 | 5 × 10−6 | 6.2 × 10−16 | 1.5 × 10−10 | 4 × 10−6 | 5.8 × 10−16 | 1.3 × 10−10 | 4 × 10−6 |
| Averaged P01 | 6.6 × 10−6 | 4.7 × 10−6 | 5.3 × 10−6 | |||||||
4 CONCLUSIONS
In this work, we report the first rotationally inelastic rate coefficients for NO+ in its ground and first excited vibrational levels colliding with He. We found that even rotational transitions are favoured and that the largest rate coefficients are associated with Δj = 2 transitions. Vibrational quenching is found to be 4 orders of magnitude smaller than rotational quenching and is then negligible for this system. We checked that the rotational quenching rate coefficients for the ν = 0 and ν = 1 vibrational states are identical in the [1, 100] K temperature interval but found that they can exhibit small differences outside these limits. We furthermore found that the rank order of the rotational transition rate coefficients is a function of temperature and may differ for the ν = 0 and ν = 1 vibrational states. We also verified that the rotational transition rate coefficients involving two different vibrational states can be assumed to be proportional to the same rotational transition rate coefficient for the ground vibrational state. We, however, demonstrated that this proportionality factor may differ by 1 order of magnitude for even and odd Δj transitions. These results should be kept in mind when comparing experimental and theoretical results.
This work was supported by the Agence Nationale de la Recherche (ANR-Hydrides), contract ANR-12-BS05-0011-01. Computer time for this study was provided by the Mésocentre de Calcul Intensif Aquitaine computing facilities of Université de Bordeaux and Université de Pau et des Pays de l'Adour.
REFERENCES



