-
PDF
- Split View
-
Views
-
Cite
Cite
H. Tagawa, M. Umemura, N. Gouda, T. Yano, Y. Yamai, Early cosmic merger of multiple black holes, Monthly Notices of the Royal Astronomical Society, Volume 451, Issue 2, 01 August 2015, Pages 2174–2184, https://doi.org/10.1093/mnras/stv1099
Close - Share Icon Share
Abstract
We perform numerical simulations on the merger of multiple black holes (BHs) in primordial gas at early cosmic epochs. We consider two cases of BH mass: MBH = 30 and 104 M⊙. Attention is concentrated on the effect of the dynamical friction by gas in a host object. The simulations incorporate such general relativistic effects as the pericentre shift and gravitational wave emission. As a result, we find that multiple BHs are able to merge into one BH within 100 Myr in a wide range of BH density. The merger mechanism is revealed to be categorized into three types: gas-drag-driven merger (type A), interplay-driven merger (type B), and three-body-driven merger (type C). We find the relation between the merger mechanism and the ratio of the gas mass within the initial BH orbit (Mgas) to the total BH mass (∑MBH). Type A merger occurs if Mgas ≳ 105∑MBH, type B if Mgas ≲ 105∑MBH, and type C if Mgas ≪ 105∑MBH. Supposing the gas and BH density based on the recent numerical simulations on first stars, all the BH remnants from first stars are likely to merge into one BH in ∼ 107 yr through the type B or C mechanism. Also, we find that multiple massive BHs (MBH = 104 M⊙) distributed over several parsec can merge into one BH through the type B mechanism, if the gas density is higher than 5 × 106 cm−3. The present results imply that the BH merger may contribute significantly to the formation of supermassive BHs at high-redshift epochs.
1 INTRODUCTION
In the last two decades, it has been demonstrated that massive galaxies harbour supermassive black holes (SMBHs) in the centres of their bulge components (Kormendy & Ho 2013, and references therein). Also, at redshifts higher than 6, quasars are found that possess SMBHs with the mass higher than 109 M⊙ (Fan et al. 2001; Kurk et al. 2007). The formation history of these SMBHs is among the most significant unsolved issues in astrophysics (Volonteri & Bellovary 2012; Haiman 2013). Two recently discovered high-redshift quasars, ULAS J112010+641 with the mass of MBH = 2 × 109 M⊙ at redshift z = 7.085 (Mortlock et al. 2011) and SDSS J01001+2802 with MBH = 1.2 × 1010 M⊙ at z = 6.30 (Wu et al. 2015) have raised a serious problem for the formation of SMBHs. Possible building blocks for such high-redshift SMBHs are the remnants of first stars. The initial mass function of first stars is thought to be more or less top-heavy (Abel, Bryan & Norman 2000; Nakamura & Umemura 2001; Bromm, Coppi & Larson 2002; Yoshida et al. 2006; Greif et al. 2011; Hirano et al. 2014; Susa, Hasegawa & Tominaga 2014). First stars of several tens M⊙ undergo supernovae, leaving black holes (BHs) of few tens M⊙ (Heger & Woosley 2002). For SMBHs to grow from such first star remnants through mass accretion at z ≳ 6, a super-Eddington accretion rate is requisite. If SMBHs grow continuously by mass accretion from BH remnants of ∼20 M⊙, the Eddington ratio (λ) is required to be λ = 1.4 for ULAS J112010+641, or λ = 1.3 for SDSS J01001+2802. However, the continuous accretion is unlikely to be sustained due to feedbacks, and thus the average mass accretion rates should be lower than the Eddington rate (Alvarez, Wise & Abel 2009; Milosavljevic, Couch & Bromm 2009). On the other hand, seed BHs may stem from supermassive stars of 104–6 M⊙ as a result of the direct collapse of primordial density fluctuations (Umemura, Loeb & Turner 1993; Bromm & Loeb 2003; Inayoshi & Omukai 2012). These BHs are thought to be incorporated into a primordial galaxy of ∼108–109 M⊙ (Greene 2012). If an SMBH grows via gas accretion from such a massive BH (MBH), the constraint on the accretion rate can be alleviated.
Another possible pathway of SMBH formation is the merger of BHs. If the merger of multiple BHs precedes the growth via gas accretion, the merged BH can be a seed of a SMBH. So far, the merger of SMBHs in a galaxy has been argued extensively. As for a binary of SMBHs, Begelman, Blandford & Rees (1980) pointed out that the orbit of a binary SMBH cannot shrink below 1 pc due to the loss cone depletion (the depletion of stars on orbits that intersect the binary SMBH), which is often called the final parsec problem (e.g. Merritt & Poon 2004). It is argued that if the host galaxy provides an aspherical potential, a binary SMBH may overcome the final parsec problem (Khan, Just & Merritt 2011; Khan et al. 2012, 2013). However, this solution of the problem is still under debate (Vasiliev, Antonini & Merritt 2014). If there are more than two SMBHs in a galaxy, the dynamical relaxation of SMBHs is significantly controlled by the gravity of SMBHs themselves, especially by three-body interaction. When a third MBH intrudes into a binary SMBH, one SMBH carries away angular momentum from the remaining two SMBHs, reducing the binary separation and eventually inducing the merger of the binary (Iwasawa, Funato & Makino 2006). In the case of many SMBHs, the stellar dynamical friction allows a binary MBH to interact frequently with other SMBHs, and then the decay of the binary orbits leads to the merger (Tanikawa & Umemura 2011, 2014).
In a first-generation object formed at an early cosmic epoch, the dynamical friction by stars is unlikely to work effectively, since the initial mass function is top-heavy and most stars undergo supernovae. However, the dynamical friction by gas could work. Recent radiation hydrodynamic simulations on the formation of first stars show that several or more stars form in a primordial gas cloud with the density of around 107 cm−3 and the extension of 1000 au, where the gas fraction is 99 per cent (Greif et al. 2011; Umemura et al. 2012; Susa 2013; Susa et al. 2014). In this circumstance, BH remnants of first stars are most likely subject to the dynamical friction by abundant gas. The gas dynamical friction has been considered as a mechanism that prompts the BH merger (Ostriker 1999; Tanaka & Haiman 2009). Hitherto, the merger processes by the gas dynamical friction have been investigated in the case of two MBHs (e.g. Escala et al. 2004, 2005). In this paper, we explore the merger of multiple BHs, supposing a first-generation object of ∼105–106 M⊙ or a gas-rich primordial galaxy of ∼108–109 M⊙.
The paper is organized as follows. In Section 2, we describe the numerical method. In Section 3, we show the numerical results. In Section 4, we discuss the merger criterion through the gas friction. In Section 5, we summarize the paper.
2 METHOD OF NUMERICAL SIMULATIONS
Here, we present the framework of numerical simulations.
2.1 Equation of motion
2.2 Key parameters
2.3 Gas drag and potential
2.4 Gas temperature
We find that, in both cases of BH mass, the heating rate is lower than the cooling rate over the range of parameters in which the simulations are performed. Therefore, the gas temperature is expected to settle at T ≈ 103 K. In this paper, we assume the gas temperature to be 1000 K. Then, the sound speed is given as Cs = 3.709 (km s)−1.
2.5 Relativistic effects
2.6 Merger condition
2.7 Numerical scheme
To avoid cancellation of significant digits when such tiny scales as 100 rsch are resolved, we calculate the BHs evolution in the coordinate where the origin is always set to the centre of mass for the closest pair of BHs. This prescription is based on the simulations on the merger of multiple BHs (Tanikawa & Umemura 2011), and allows us to pursue accurately the orbit of the BHs until the merger condition is satisfied.
2.8 Set-up of simulations
We set up 10 BHs as a fiducial case, and besides investigate the cases of two or three BHs to scrutinize the key physics of merger. The initial positions of BHs are given randomly in the x–y plane within rtyp. Also, we give the velocity to each BH as the sum of a circular component and a random component. The circular velocity is given to balance against the gravity in the x–y plane. The random velocity is given according to a Gaussian distribution with the same dispersion as the circular velocity. The random velocity is given in the xyz space. In the case of two BHs, we give only circular velocity without initial eccentricity. This condition is desired to discriminate the BH merger purely by the gas friction.
We calculate each run until 100 Myr, since the background environments of the host objects are likely to change in 100 Myr. Also, we terminate the simulation, if all BHs merge into one BH.
3 NUMERICAL RESULTS
3.1 Dependence on gas density and BH density
The results of 10 BH systems are summarized in Tables 1 and 2. Table 1 is those for the case of MBH = 30 M⊙ and Table 2 is for MBH = 104 M⊙. The column is the initial extension of the BH distribution (rtyp) and the corresponding BH density (ρBH), while the row is the assumed gas density (ngas) in the system. Nm is the number of the merged BHs (nine means all BHs merged into one). The ‘type’ shows the merger mechanism, which is classified in the next section. Also, the termination time of simulations, tfin, is shown.
| rtyp (pc) . | 1.0 . | 0.464 . | 0.215 . | 0.1 . | 0.0464 . | 0.0215 . | 0.01 . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρBH (M⊙ pc−3) . | 7.2 × 101 . | 7.2 × 102 . | 7.2 × 103 . | 7.2 × 104 . | 7.2 × 105 . | 7.2 × 106 . | 7.2 × 107 . | |||||||
| . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . |
| ngas (cm−3) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | |||||||
| 0 | – | 5 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1012 | 1.0 × 108 | 1.0 × 108 | 3.6 × 107 | 4.4 × 106 | 1.7 × 106 | 7.0 × 105 | 4.3 × 105 | |||||||
| 2 | A | 8 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1011 | 1.0 × 108 | 1.0 × 108 | 1.3 × 107 | 1.8 × 105 | 1.8 × 105 | 2.3 × 104 | 2.8 × 104 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | 9 | B | |
| 1010 | 1.0 × 108 | 4.5 × 107 | 5.1 × 106 | 5.9 × 105 | 7.4 × 104 | 6.3 × 104 | 1.7 × 105 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | |
| 5 × 109 | 1.0 × 108 | 2.9 × 107 | 3.1 × 106 | 4.5 × 105 | 1.6 × 105 | 3.4 × 105 | 7.7 × 104 | |||||||
| 8 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | |
| 109 | 1.0 × 108 | 2.4 × 107 | 3.5 × 106 | 2.6 × 105 | 4.3 × 105 | 3.5 × 105 | 3.0 × 105 | |||||||
| 8 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 108 | 1.0 × 108 | 1.2 × 107 | 1.3 × 106 | 6.5 × 105 | 4.3 × 105 | 5.5 × 105 | 5.1 × 105 | |||||||
| 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 108 | 3.0 × 107 | 5.1 × 106 | 4.0 × 106 | 5.5 × 106 | 3.6 × 106 | 4.2 × 106 | 1.2 × 107 | |||||||
| 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 107 | 4.5 × 107 | 3.7 × 106 | 2.2 × 107 | 3.2 × 107 | 1.3 × 107 | 4.7 × 106 | 3.6 × 106 | |||||||
| 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 107 | 3.8 × 107 | 2.3 × 107 | 1.7 × 107 | 3.3 × 107 | 1.8 × 107 | 2.9 × 107 | 1.7 × 107 | |||||||
| 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 106 | 4.2 × 107 | 3.9 × 107 | 4.2 × 107 | 4.7 × 107 | 6.3 × 107 | 3.5 × 107 | 3.1 × 107 | |||||||
| 6 | B | 6 | B | 8 | B | 6 | C | 8 | C | 6 | C | 6 | C | |
| 106 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 2 | C | 6 | C | 6 | C | 4 | C | 5 | C | 3 | C | 4 | C | |
| 5 × 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 1 | C | 0 | – | 1 | C | 2 | C | 0 | – | |
| 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 0 | – | 1 | C | 0 | – | 0 | – | 0 | – | |
| 104 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| rtyp (pc) . | 1.0 . | 0.464 . | 0.215 . | 0.1 . | 0.0464 . | 0.0215 . | 0.01 . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρBH (M⊙ pc−3) . | 7.2 × 101 . | 7.2 × 102 . | 7.2 × 103 . | 7.2 × 104 . | 7.2 × 105 . | 7.2 × 106 . | 7.2 × 107 . | |||||||
| . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . |
| ngas (cm−3) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | |||||||
| 0 | – | 5 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1012 | 1.0 × 108 | 1.0 × 108 | 3.6 × 107 | 4.4 × 106 | 1.7 × 106 | 7.0 × 105 | 4.3 × 105 | |||||||
| 2 | A | 8 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1011 | 1.0 × 108 | 1.0 × 108 | 1.3 × 107 | 1.8 × 105 | 1.8 × 105 | 2.3 × 104 | 2.8 × 104 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | 9 | B | |
| 1010 | 1.0 × 108 | 4.5 × 107 | 5.1 × 106 | 5.9 × 105 | 7.4 × 104 | 6.3 × 104 | 1.7 × 105 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | |
| 5 × 109 | 1.0 × 108 | 2.9 × 107 | 3.1 × 106 | 4.5 × 105 | 1.6 × 105 | 3.4 × 105 | 7.7 × 104 | |||||||
| 8 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | |
| 109 | 1.0 × 108 | 2.4 × 107 | 3.5 × 106 | 2.6 × 105 | 4.3 × 105 | 3.5 × 105 | 3.0 × 105 | |||||||
| 8 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 108 | 1.0 × 108 | 1.2 × 107 | 1.3 × 106 | 6.5 × 105 | 4.3 × 105 | 5.5 × 105 | 5.1 × 105 | |||||||
| 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 108 | 3.0 × 107 | 5.1 × 106 | 4.0 × 106 | 5.5 × 106 | 3.6 × 106 | 4.2 × 106 | 1.2 × 107 | |||||||
| 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 107 | 4.5 × 107 | 3.7 × 106 | 2.2 × 107 | 3.2 × 107 | 1.3 × 107 | 4.7 × 106 | 3.6 × 106 | |||||||
| 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 107 | 3.8 × 107 | 2.3 × 107 | 1.7 × 107 | 3.3 × 107 | 1.8 × 107 | 2.9 × 107 | 1.7 × 107 | |||||||
| 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 106 | 4.2 × 107 | 3.9 × 107 | 4.2 × 107 | 4.7 × 107 | 6.3 × 107 | 3.5 × 107 | 3.1 × 107 | |||||||
| 6 | B | 6 | B | 8 | B | 6 | C | 8 | C | 6 | C | 6 | C | |
| 106 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 2 | C | 6 | C | 6 | C | 4 | C | 5 | C | 3 | C | 4 | C | |
| 5 × 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 1 | C | 0 | – | 1 | C | 2 | C | 0 | – | |
| 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 0 | – | 1 | C | 0 | – | 0 | – | 0 | – | |
| 104 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| rtyp (pc) . | 1.0 . | 0.464 . | 0.215 . | 0.1 . | 0.0464 . | 0.0215 . | 0.01 . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρBH (M⊙ pc−3) . | 7.2 × 101 . | 7.2 × 102 . | 7.2 × 103 . | 7.2 × 104 . | 7.2 × 105 . | 7.2 × 106 . | 7.2 × 107 . | |||||||
| . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . |
| ngas (cm−3) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | |||||||
| 0 | – | 5 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1012 | 1.0 × 108 | 1.0 × 108 | 3.6 × 107 | 4.4 × 106 | 1.7 × 106 | 7.0 × 105 | 4.3 × 105 | |||||||
| 2 | A | 8 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1011 | 1.0 × 108 | 1.0 × 108 | 1.3 × 107 | 1.8 × 105 | 1.8 × 105 | 2.3 × 104 | 2.8 × 104 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | 9 | B | |
| 1010 | 1.0 × 108 | 4.5 × 107 | 5.1 × 106 | 5.9 × 105 | 7.4 × 104 | 6.3 × 104 | 1.7 × 105 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | |
| 5 × 109 | 1.0 × 108 | 2.9 × 107 | 3.1 × 106 | 4.5 × 105 | 1.6 × 105 | 3.4 × 105 | 7.7 × 104 | |||||||
| 8 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | |
| 109 | 1.0 × 108 | 2.4 × 107 | 3.5 × 106 | 2.6 × 105 | 4.3 × 105 | 3.5 × 105 | 3.0 × 105 | |||||||
| 8 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 108 | 1.0 × 108 | 1.2 × 107 | 1.3 × 106 | 6.5 × 105 | 4.3 × 105 | 5.5 × 105 | 5.1 × 105 | |||||||
| 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 108 | 3.0 × 107 | 5.1 × 106 | 4.0 × 106 | 5.5 × 106 | 3.6 × 106 | 4.2 × 106 | 1.2 × 107 | |||||||
| 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 107 | 4.5 × 107 | 3.7 × 106 | 2.2 × 107 | 3.2 × 107 | 1.3 × 107 | 4.7 × 106 | 3.6 × 106 | |||||||
| 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 107 | 3.8 × 107 | 2.3 × 107 | 1.7 × 107 | 3.3 × 107 | 1.8 × 107 | 2.9 × 107 | 1.7 × 107 | |||||||
| 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 106 | 4.2 × 107 | 3.9 × 107 | 4.2 × 107 | 4.7 × 107 | 6.3 × 107 | 3.5 × 107 | 3.1 × 107 | |||||||
| 6 | B | 6 | B | 8 | B | 6 | C | 8 | C | 6 | C | 6 | C | |
| 106 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 2 | C | 6 | C | 6 | C | 4 | C | 5 | C | 3 | C | 4 | C | |
| 5 × 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 1 | C | 0 | – | 1 | C | 2 | C | 0 | – | |
| 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 0 | – | 1 | C | 0 | – | 0 | – | 0 | – | |
| 104 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| rtyp (pc) . | 1.0 . | 0.464 . | 0.215 . | 0.1 . | 0.0464 . | 0.0215 . | 0.01 . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρBH (M⊙ pc−3) . | 7.2 × 101 . | 7.2 × 102 . | 7.2 × 103 . | 7.2 × 104 . | 7.2 × 105 . | 7.2 × 106 . | 7.2 × 107 . | |||||||
| . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . |
| ngas (cm−3) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | |||||||
| 0 | – | 5 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1012 | 1.0 × 108 | 1.0 × 108 | 3.6 × 107 | 4.4 × 106 | 1.7 × 106 | 7.0 × 105 | 4.3 × 105 | |||||||
| 2 | A | 8 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1011 | 1.0 × 108 | 1.0 × 108 | 1.3 × 107 | 1.8 × 105 | 1.8 × 105 | 2.3 × 104 | 2.8 × 104 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | 9 | B | |
| 1010 | 1.0 × 108 | 4.5 × 107 | 5.1 × 106 | 5.9 × 105 | 7.4 × 104 | 6.3 × 104 | 1.7 × 105 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | |
| 5 × 109 | 1.0 × 108 | 2.9 × 107 | 3.1 × 106 | 4.5 × 105 | 1.6 × 105 | 3.4 × 105 | 7.7 × 104 | |||||||
| 8 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | |
| 109 | 1.0 × 108 | 2.4 × 107 | 3.5 × 106 | 2.6 × 105 | 4.3 × 105 | 3.5 × 105 | 3.0 × 105 | |||||||
| 8 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 108 | 1.0 × 108 | 1.2 × 107 | 1.3 × 106 | 6.5 × 105 | 4.3 × 105 | 5.5 × 105 | 5.1 × 105 | |||||||
| 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 108 | 3.0 × 107 | 5.1 × 106 | 4.0 × 106 | 5.5 × 106 | 3.6 × 106 | 4.2 × 106 | 1.2 × 107 | |||||||
| 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 107 | 4.5 × 107 | 3.7 × 106 | 2.2 × 107 | 3.2 × 107 | 1.3 × 107 | 4.7 × 106 | 3.6 × 106 | |||||||
| 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 107 | 3.8 × 107 | 2.3 × 107 | 1.7 × 107 | 3.3 × 107 | 1.8 × 107 | 2.9 × 107 | 1.7 × 107 | |||||||
| 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 106 | 4.2 × 107 | 3.9 × 107 | 4.2 × 107 | 4.7 × 107 | 6.3 × 107 | 3.5 × 107 | 3.1 × 107 | |||||||
| 6 | B | 6 | B | 8 | B | 6 | C | 8 | C | 6 | C | 6 | C | |
| 106 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 2 | C | 6 | C | 6 | C | 4 | C | 5 | C | 3 | C | 4 | C | |
| 5 × 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 1 | C | 0 | – | 1 | C | 2 | C | 0 | – | |
| 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 0 | – | 1 | C | 0 | – | 0 | – | 0 | – | |
| 104 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| rtyp (pc) . | 10.0 . | 4.64 . | 2.15 . | 1.0 . | 0.464 . | 0.215 . | 0.1 . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρBH (M⊙ pc−3) . | 2.4 × 101 . | 2.4 × 102 . | 2.4 × 103 . | 2.4 × 104 . | 2.4 × 105 . | 2.4 × 106 . | 2.4 × 107 . | |||||||
| . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . |
| ngas (cm−3) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | |||||||
| 0 | – | 4 | A | 7 | A | 9 | A | 9 | A | 9 | A | 9 | A | |
| 1012 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.3 × 107 | 1.5 × 106 | 1.7 × 105 | 2.2 × 104 | |||||||
| 0 | – | 5 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1011 | 1.0 × 108 | 1.0 × 108 | 4.6 × 107 | 5.0 × 106 | 5.8 × 105 | 7.2 × 104 | 1.6 × 104 | |||||||
| 4 | A | 8 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1010 | 1.0 × 108 | 1.0 × 108 | 1.7 × 107 | 2.0 × 106 | 2.5 × 105 | 9.3 × 104 | 4.1 × 104 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | |
| 109 | 1.0 × 108 | 5.8 × 107 | 7.0 × 106 | 9.6 × 105 | 7.6 × 105 | 9.0 × 105 | 2.4 × 106 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 108 | 1.0 × 108 | 5.0 × 107 | 1.0 × 107 | 1.5 × 106 | 9.5 × 105 | 7.6 × 105 | 6.7 × 105 | |||||||
| 7 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 108 | 1.0 × 108 | 2.5 × 107 | 3.7 × 106 | 8.3 × 106 | 4.9 × 106 | 5.6 × 106 | 7.9 × 106 | |||||||
| 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 107 | 7.3 × 107 | 2.0 × 107 | 1.3 × 107 | 7.1 × 106 | 1.2 × 107 | 3.5 × 106 | 9.4 × 106 | |||||||
| 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 107 | 7.7 × 107 | 3.5 × 107 | 9.3 × 107 | 6.0 × 107 | 3.3 × 107 | 3.6 × 107 | 4.1 × 107 | |||||||
| 8 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 106 | 1.0 × 108 | 8.3 × 107 | 3.9 × 107 | 8.5 × 107 | 4.6 × 107 | 4.8 × 107 | 7.9 × 107 | |||||||
| 5 | B | 7 | B | 4 | B | 9 | B | 5 | C | 5 | C | 6 | C | |
| 106 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 6.5 × 107 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 3 | B | 3 | C | 3 | C | 3 | C | 6 | C | 4 | C | 4 | C | |
| 5 × 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 0 | – | 0 | – | 0 | – | 1 | C | 0 | – | |
| 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 1 | C | 0 | – | 1 | C | 1 | C | 1 | C | |
| 5 × 104 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 0 | – | 0 | – | 0 | – | 0 | – | 1 | C | |
| 104 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| rtyp (pc) . | 10.0 . | 4.64 . | 2.15 . | 1.0 . | 0.464 . | 0.215 . | 0.1 . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρBH (M⊙ pc−3) . | 2.4 × 101 . | 2.4 × 102 . | 2.4 × 103 . | 2.4 × 104 . | 2.4 × 105 . | 2.4 × 106 . | 2.4 × 107 . | |||||||
| . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . |
| ngas (cm−3) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | |||||||
| 0 | – | 4 | A | 7 | A | 9 | A | 9 | A | 9 | A | 9 | A | |
| 1012 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.3 × 107 | 1.5 × 106 | 1.7 × 105 | 2.2 × 104 | |||||||
| 0 | – | 5 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1011 | 1.0 × 108 | 1.0 × 108 | 4.6 × 107 | 5.0 × 106 | 5.8 × 105 | 7.2 × 104 | 1.6 × 104 | |||||||
| 4 | A | 8 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1010 | 1.0 × 108 | 1.0 × 108 | 1.7 × 107 | 2.0 × 106 | 2.5 × 105 | 9.3 × 104 | 4.1 × 104 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | |
| 109 | 1.0 × 108 | 5.8 × 107 | 7.0 × 106 | 9.6 × 105 | 7.6 × 105 | 9.0 × 105 | 2.4 × 106 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 108 | 1.0 × 108 | 5.0 × 107 | 1.0 × 107 | 1.5 × 106 | 9.5 × 105 | 7.6 × 105 | 6.7 × 105 | |||||||
| 7 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 108 | 1.0 × 108 | 2.5 × 107 | 3.7 × 106 | 8.3 × 106 | 4.9 × 106 | 5.6 × 106 | 7.9 × 106 | |||||||
| 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 107 | 7.3 × 107 | 2.0 × 107 | 1.3 × 107 | 7.1 × 106 | 1.2 × 107 | 3.5 × 106 | 9.4 × 106 | |||||||
| 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 107 | 7.7 × 107 | 3.5 × 107 | 9.3 × 107 | 6.0 × 107 | 3.3 × 107 | 3.6 × 107 | 4.1 × 107 | |||||||
| 8 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 106 | 1.0 × 108 | 8.3 × 107 | 3.9 × 107 | 8.5 × 107 | 4.6 × 107 | 4.8 × 107 | 7.9 × 107 | |||||||
| 5 | B | 7 | B | 4 | B | 9 | B | 5 | C | 5 | C | 6 | C | |
| 106 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 6.5 × 107 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 3 | B | 3 | C | 3 | C | 3 | C | 6 | C | 4 | C | 4 | C | |
| 5 × 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 0 | – | 0 | – | 0 | – | 1 | C | 0 | – | |
| 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 1 | C | 0 | – | 1 | C | 1 | C | 1 | C | |
| 5 × 104 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 0 | – | 0 | – | 0 | – | 0 | – | 1 | C | |
| 104 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| rtyp (pc) . | 10.0 . | 4.64 . | 2.15 . | 1.0 . | 0.464 . | 0.215 . | 0.1 . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρBH (M⊙ pc−3) . | 2.4 × 101 . | 2.4 × 102 . | 2.4 × 103 . | 2.4 × 104 . | 2.4 × 105 . | 2.4 × 106 . | 2.4 × 107 . | |||||||
| . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . |
| ngas (cm−3) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | |||||||
| 0 | – | 4 | A | 7 | A | 9 | A | 9 | A | 9 | A | 9 | A | |
| 1012 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.3 × 107 | 1.5 × 106 | 1.7 × 105 | 2.2 × 104 | |||||||
| 0 | – | 5 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1011 | 1.0 × 108 | 1.0 × 108 | 4.6 × 107 | 5.0 × 106 | 5.8 × 105 | 7.2 × 104 | 1.6 × 104 | |||||||
| 4 | A | 8 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1010 | 1.0 × 108 | 1.0 × 108 | 1.7 × 107 | 2.0 × 106 | 2.5 × 105 | 9.3 × 104 | 4.1 × 104 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | |
| 109 | 1.0 × 108 | 5.8 × 107 | 7.0 × 106 | 9.6 × 105 | 7.6 × 105 | 9.0 × 105 | 2.4 × 106 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 108 | 1.0 × 108 | 5.0 × 107 | 1.0 × 107 | 1.5 × 106 | 9.5 × 105 | 7.6 × 105 | 6.7 × 105 | |||||||
| 7 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 108 | 1.0 × 108 | 2.5 × 107 | 3.7 × 106 | 8.3 × 106 | 4.9 × 106 | 5.6 × 106 | 7.9 × 106 | |||||||
| 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 107 | 7.3 × 107 | 2.0 × 107 | 1.3 × 107 | 7.1 × 106 | 1.2 × 107 | 3.5 × 106 | 9.4 × 106 | |||||||
| 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 107 | 7.7 × 107 | 3.5 × 107 | 9.3 × 107 | 6.0 × 107 | 3.3 × 107 | 3.6 × 107 | 4.1 × 107 | |||||||
| 8 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 106 | 1.0 × 108 | 8.3 × 107 | 3.9 × 107 | 8.5 × 107 | 4.6 × 107 | 4.8 × 107 | 7.9 × 107 | |||||||
| 5 | B | 7 | B | 4 | B | 9 | B | 5 | C | 5 | C | 6 | C | |
| 106 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 6.5 × 107 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 3 | B | 3 | C | 3 | C | 3 | C | 6 | C | 4 | C | 4 | C | |
| 5 × 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 0 | – | 0 | – | 0 | – | 1 | C | 0 | – | |
| 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 1 | C | 0 | – | 1 | C | 1 | C | 1 | C | |
| 5 × 104 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 0 | – | 0 | – | 0 | – | 0 | – | 1 | C | |
| 104 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| rtyp (pc) . | 10.0 . | 4.64 . | 2.15 . | 1.0 . | 0.464 . | 0.215 . | 0.1 . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρBH (M⊙ pc−3) . | 2.4 × 101 . | 2.4 × 102 . | 2.4 × 103 . | 2.4 × 104 . | 2.4 × 105 . | 2.4 × 106 . | 2.4 × 107 . | |||||||
| . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . | Nm . | Type . |
| ngas (cm−3) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | tfin (yr) . | |||||||
| 0 | – | 4 | A | 7 | A | 9 | A | 9 | A | 9 | A | 9 | A | |
| 1012 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.3 × 107 | 1.5 × 106 | 1.7 × 105 | 2.2 × 104 | |||||||
| 0 | – | 5 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1011 | 1.0 × 108 | 1.0 × 108 | 4.6 × 107 | 5.0 × 106 | 5.8 × 105 | 7.2 × 104 | 1.6 × 104 | |||||||
| 4 | A | 8 | A | 9 | A | 9 | A | 9 | A | 9 | A | 9 | B | |
| 1010 | 1.0 × 108 | 1.0 × 108 | 1.7 × 107 | 2.0 × 106 | 2.5 × 105 | 9.3 × 104 | 4.1 × 104 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | |
| 109 | 1.0 × 108 | 5.8 × 107 | 7.0 × 106 | 9.6 × 105 | 7.6 × 105 | 9.0 × 105 | 2.4 × 106 | |||||||
| 5 | A | 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 108 | 1.0 × 108 | 5.0 × 107 | 1.0 × 107 | 1.5 × 106 | 9.5 × 105 | 7.6 × 105 | 6.7 × 105 | |||||||
| 7 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 108 | 1.0 × 108 | 2.5 × 107 | 3.7 × 106 | 8.3 × 106 | 4.9 × 106 | 5.6 × 106 | 7.9 × 106 | |||||||
| 9 | A | 9 | A | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 107 | 7.3 × 107 | 2.0 × 107 | 1.3 × 107 | 7.1 × 106 | 1.2 × 107 | 3.5 × 106 | 9.4 × 106 | |||||||
| 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 107 | 7.7 × 107 | 3.5 × 107 | 9.3 × 107 | 6.0 × 107 | 3.3 × 107 | 3.6 × 107 | 4.1 × 107 | |||||||
| 8 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | 9 | B | |
| 5 × 106 | 1.0 × 108 | 8.3 × 107 | 3.9 × 107 | 8.5 × 107 | 4.6 × 107 | 4.8 × 107 | 7.9 × 107 | |||||||
| 5 | B | 7 | B | 4 | B | 9 | B | 5 | C | 5 | C | 6 | C | |
| 106 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 6.5 × 107 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 3 | B | 3 | C | 3 | C | 3 | C | 6 | C | 4 | C | 4 | C | |
| 5 × 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 0 | – | 0 | – | 0 | – | 1 | C | 0 | – | |
| 105 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 1 | C | 0 | – | 1 | C | 1 | C | 1 | C | |
| 5 × 104 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
| 0 | – | 0 | – | 0 | – | 0 | – | 0 | – | 0 | – | 1 | C | |
| 104 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | 1.0 × 108 | |||||||
In the case of MBH = 30 M⊙ (Table 1), we find that if ngas is in the range from 5 × 106 to 108 cm−3, then all the BHs merge into one MBH over six orders of BH density (ρBH = 72–7.2 × 107 M⊙ pc−3). Also, if the gas density is higher than ngas = 5 × 105 cm−3, the BH merger occurs once at least in 100 Myr. In the recent numerical simulations on first stars (Greif et al. 2011; Susa 2013; Susa et al. 2014), the density of BH remnants is expected to be ρBH ≈ 107 M⊙ pc−3 and the gas density is to be in the range of ngas ≈ 107–108 cm−3. Hence, the present numerical results imply that all the BH remnants from first stars are likely to merge into one BH.
In the case of MBH = 104 M⊙ (Table 2), we find that if ngas is in the range from 5 × 106 to 109 cm−3, then all the BHs merge into one MBH over five orders of BH density (ρBH = 2.4 × 102–2.4 × 107 M⊙ pc−3). Interestingly, in the gas denser than 5 × 106 cm−3, multiple BHs can merge into one, even if the typical separation is greater than several pc. This result implies that the BH merger is able to contribute significantly to the formation of SMBHs at high redshifts. Similar to the case of MBH = 30 M⊙, if the gas density is higher than ngas = 5 × 105 cm−3, the BH merger occurs once at least.
In both cases of BH mass, if the gas density is very high and simultaneously the BH density is very low (upper left in Tables 1 and 2), no merger occurs. This is due to the fact that the deep gravitational potential by gas enhances the circular velocities of BHs and therefore a self-gravitating system of BHs is hardly able to form.
As shown in terms of the types of merger in Tables 1 and 2, the merger mechanism changes systematically with the gas density (ngas) and the BH density (ρBH). Details of the merger mechanism are described in the following.
3.2 Types of merger mechanism
Here, we scrutinize the merger mechanism and classify the mechanism. When a BH binary merges due to the dynamical friction by gas, the separation of the same pair of BHs monotonically shrinks, while the three-body interaction between a close BH binary and an intruding BH often replaces one BH in the binary by the intruder and therefore the separation of the closest pair changes violently. In Figs 1– 5, we show the separation of the closest pair within all BHs as a function of time, where the colours of lines change at every event of the BH merger.
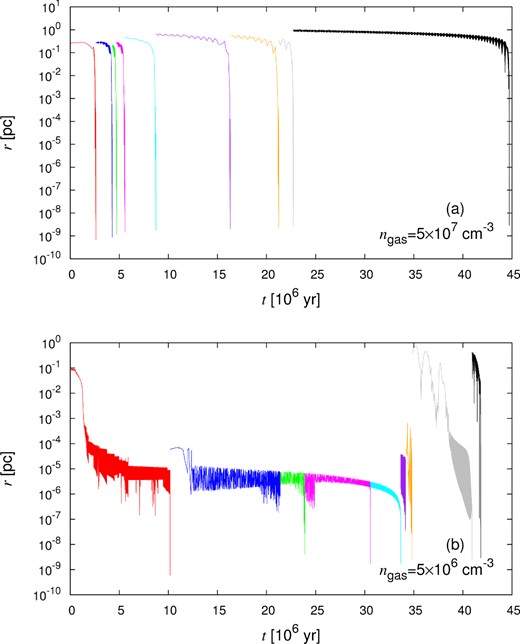
The separation of the closest pair within all BHs as a function of time. The initial BH mass is MBH = 30 M⊙, the initial typical extension of the BH distribution is rtyp = 1.0 pc, and the gas density is ngas = 5 × 107 (top) or 5 × 106 cm−3 (bottom).
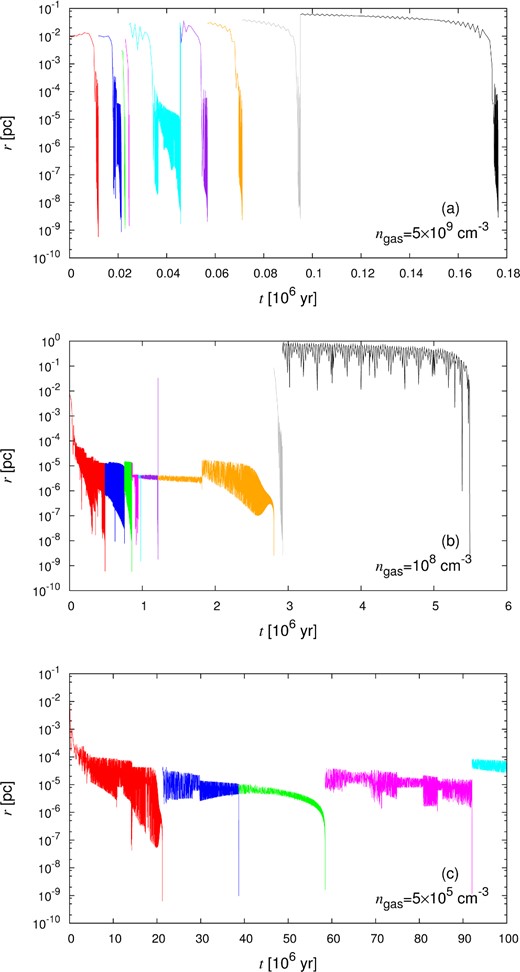
Same as Fig. 1, but for rtyp = 0.1 pc, and ngas = 5 × 109 (top), 108 (middle), or 5 × 105 cm−3 (bottom).

Same as Fig. 1, but for MBH = 104 M⊙, rtyp = 10.0 pc, and ngas = 5 × 107 cm−3.
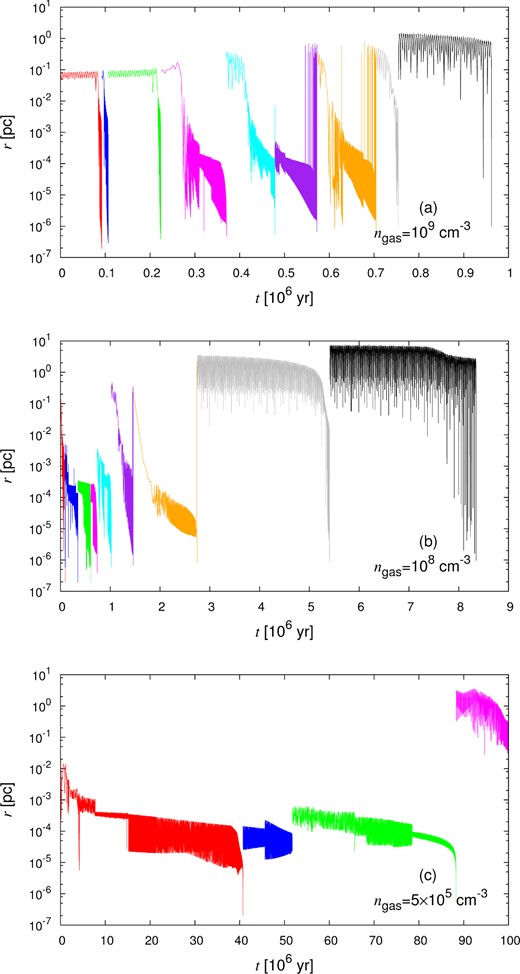
Same as Fig. 1, but for MBH = 104 M⊙, rtyp = 1.0 pc, and ngas = 109 (top), 108 (middle), or 5 × 105 cm−3 (bottom).
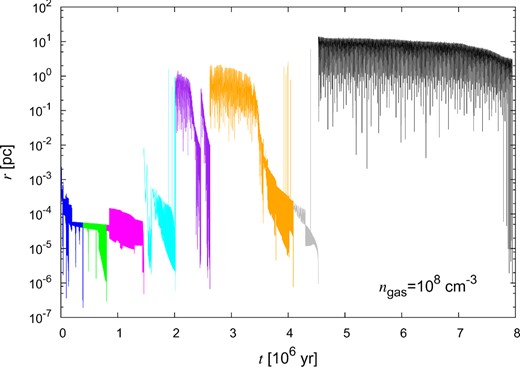
Same as Fig. 1, but for MBH = 104 M⊙, rtyp = 0.1 pc, and ngas = 108 cm−3.
Fig. 1 shows the case of low-mass BHs (MBH = 30 M⊙). The initial extension of the BH distribution is rtyp = 1.0 pc. The upper panel corresponds to higher gas density, and the lower panel to lower gas density. As seen in the upper panel, the apocentre and pericentre distances of the closest pair decay smoothly, eventually resulting in the merger. Such smooth decay indicates that the gas dynamical friction drives the merger. On the hand, in the lower panel of Fig. 1, the orbit is highly eccentric, since the apocentre and pericentre distances are largely different. The distances sometimes oscillate violently. Such strong variance is thought to be caused by the three-body interaction, since the simultaneous interaction with a fourth or fifth BH seems quite rare from a viewpoint of probability. Actually, we have confirmed that the contribution of a fourth or fifth BH is little. Thus, we call such interaction the three-body interaction. After the apocentre decays to less than ∼10−8 pc, the pair separation lessens rapidly due to the effect of the GW emission, and eventually the BH binary merges.
We classify the merger mechanism according to the manner of decay just before the GW promotes the merger. Here, the merger mechanism is categorized into three types: gas-drag-driven merger (type A), three-body-driven merger (type C), and interplay-driven merger (type B). In type A, the dynamical friction by gas effectively decays the orbit and then the GW drives the merger. The type A is seen in the cases with higher gas density and lower BH density, as expected. The examples of type A are shown in the top panels of Figs 1–4. In both types B and C, the strong disturbance of the orbit is induced by the three-body interaction during the first merger. But in type B, after the first few mergers by three-body interaction, the orbit decays slowly for long time through the gas dynamical friction. The examples of type B are seen in the middle panels of Figs 2, 4, and 5. In these results, after the mergers driven by three-body interaction, the orbit evolution starts from a larger separation than initial typical separation (rtyp). Such increase of separation is due to the slingshot mechanism when an intruder interacts with the binary. This causes a negative effect on the merger time-scale. In other words, the three-body interaction may play a positive and negative role for the merger.1 In type C, the strong disturbance of the orbit continues until the final merger. The three-body interaction of BHs solely transfers the angular momentum, eventually allowing the merger via the GW radiation. Type C is seen in the cases of high BH density. The examples of type C are shown in the bottom panels of Figs 2 and 4.
As shown in Tables 1 and 2, in the cases of lower BH density (higher rtyp), type A is seen in a broad range of gas density. In the cases of higher BH density, type B is dominant in higher gas density environments. On the other hand, type C is common in lower gas density. However, if the gas density is very low, no merger occurs even in the same density of BHs. This implies that the gas dynamical friction plays a non-negligible role even for type C.
3.3 BH number dependence
To clarify the physics of BH merger, we perform reference simulations with the different number of BHs. In Fig. 6, we compare the resultant merger time in 10 BH systems (tN = 10) to that in three BH (tN = 3) or two BH systems (tN = 2). Each panel corresponds to a different set of parameters. Red, pink, and blue open symbols, respectively, represent the types A, B, and C mergers in 10 BH systems. Brown- and green-filled symbols show the averaged merger time in the runs of three BH and two BH systems, respectively. Note that the averaged merger time (tfin) has the variance of about a factor of 2 that comes from the initial set-up of random number.
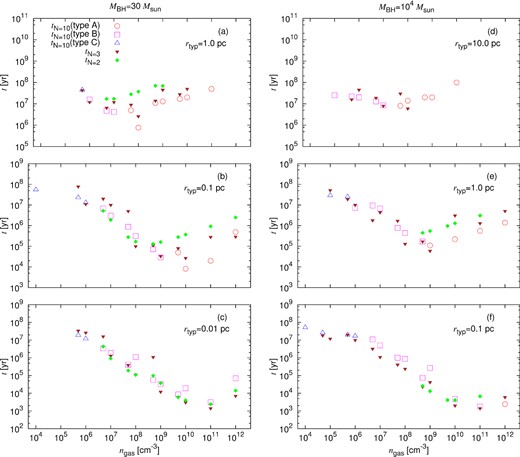
Merger time in 10 BH systems (tN = 10) as a function of gas number density ngas. The left-hand panels are the cases with low-mass BHs (MBH = 30 M⊙), and right-hand panels are those with high-mass BHs (MBH = 104 M⊙). The top, middle, and bottom panels show the results for lower, intermediate, and higher BH density, respectively. Red, pink, and blue open symbols represent the results of the types A, B, and C mergers, respectively. Green- and brown-filled symbols are the results of two BH (tN = 2) and three BH (tN = 3) systems, respectively.
In the cases of two BHs, we give only circular velocity initially. Since there is no three-body interaction, the merger of two BH systems is always driven by the gas dynamical friction. On the other hand, in the systems of three BHs, three-body interaction as well as the gas dynamical friction can work to induce the merger. We can see that the merger time-scales in type C accord with those in three BH systems. In other words, no merger occurs in two BH systems in the parameters of type C. Thus, the classification of type C in which the merger is driven by the three-body interaction is justified.
On the other hand, in type A and type B, both two BH and three BH systems can merge. In the parameters of type A, the merger time-scales in 10 BH systems are systematically shorter than those in three BH systems. In the 10 BH systems, more BHs suffer from the gas dynamical friction and the angular momenta of BHs are extracted simultaneously. Therefore, the 10 BH systems can merge in shorter time on average. As shown in top left- and top right-hand panels, two BH or three BH systems cannot merge in higher gas density environments, whereas 10 BH systems can merge. These results imply that the dynamical friction on 10 BHs enhances the three-body interaction, eventually allowing the merger. In the bottom right-hand panel, the averaged merger time in 10 BH systems is slightly longer than that in three BH systems, in the cases with lower gas density (ngas < 108 cm−3). This is expected by the negative feedback as discussed in Section 3.2.
3.4 Effect of recoil
In the above, we have not considered the effects of GW recoil. The recoil velocity ranges from several tens to several thousands km s−1 (Kesden, Sperhake & Berti 2010). Tanikawa & Umemura (2014) have shown that if the recoil velocity is lower than the virial velocity in the system, multiple BHs can eventually merge. In the present simulations, the virial velocity is higher than a few hundreds km s−1 for ngas ≥ 108 cm−3 and Mgas ≥ 106 M⊙ in the case of MBH = 30 M⊙, and for ngas ≥ 106 cm−3 and Mgas ≥ 107 M⊙ in the case of MBH = 104 M⊙. Actually, we have imposed random velocities on BHs at a level of the virial velocity, and revealed the conditions under which all BHs can merge. Hence, the merger condition is expected not to change, if the recoil velocity is lower than the virial velocity. To confirm this, we have simulated the several cases in which the recoil velocity is incorporated. As a result, we have found that if the recoil velocity is lower than the virial (escape) velocity, then the averaged merger time and the number of merged BHs are not changed. If the recoil velocity is higher than the escape velocity, then the merged BH escapes from the system. The actual magnitude of recoil velocity is determined by the alignment of spins of two MBHs (Schnittman & Buonanno 2007; Kesden et al. 2010). The spins tend to be aligned through the gas accretion on to BHs. Assuming the level of the recoil velocity for BHs with aligned spins, we have performed further simulations and found that if the escape velocity of the system is higher than ∼140 km s−1, then the BH merger proceeds in a similar way to the simulations without the recoil.
4 CRITERION FOR GAS DRAG
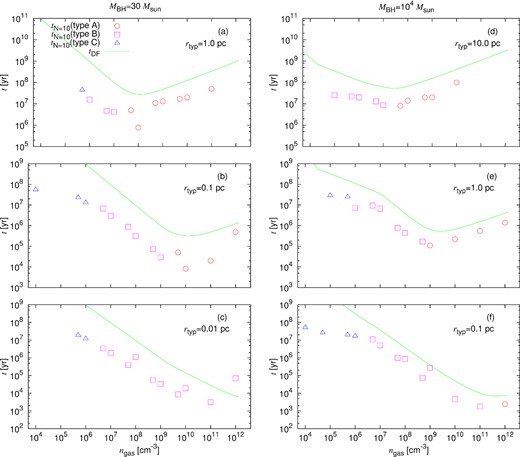
Same as Fig. 6, but the analytic estimates of gas dynamical friction time-scale, tDF, are plotted by green lines instead of the results of two BH and three BH systems.
In Fig. 7, we see the dependence of the merger time-scale on the BH density (or rtyp). With the increasing BH density (decreasing rtyp), the right-hand side of the power-law shifts lower. This shift stems from the decrease in the gravitational potential of gas within rtyp. This tendency is also seen in the numerical results of 10 BH systems. Thus, the rough tendency of the merger time in the type A region is explained by the analytic time-scale. Therefore, we regard tDF as an appropriate estimate for the merger solely by the gas dynamical friction.
As described above, type A is always seen in higher gas density than the turning point of the double power law of tDF. These results imply that the turning point provides the critical gas density, above which the merger is driven by the gas dynamical friction. The turning point is determined by the ratio of the gas mass within rtyp, Mgas, to the total BH mass, ∑MBH. In the analytic estimate, the turning point appears around Mgas ≃ 1.4 × 105∑MBH as the average of the each panel in Fig. 7. As for the numerical results, we can assess the turning points in the top and middle panels, since the turning points are not clear in the bottom panels. In the cases of 30 M⊙ BHs, the gas density at the turning points is 107 cm−3 in upper left-hand panel or 1010 cm−3 in middle left-hand panels. Then, the ratio of Mgas to ∑MBH at the turning points is 1.4 × 105 in both cases. In the cases of 104 M⊙ BHs, it is 107 cm−3 in upper right-hand panel, or 109 cm−3 in middle right-hand panels. Hence, the Mgas-to-∑MBH ratio is 4.2 × 105 or 4.2 × 104, respectively. These results show that the critical gas density above which type A is dominant is given by the condition of Mgas/∑MBH ≈ 105. Based on the simulations on the formation of first objects (Greif et al. 2011; Susa et al. 2014), Mgas is likely to be lower than 105∑MBH. Thus, type B and type C are expected to be more common mechanism of BH merger.
5 CONCLUSIONS
In this paper, we have investigated the merger of multiple BH systems in an early cosmic epoch, incorporating the dynamical friction by gas. For the purpose, we have performed highly accurate numerical simulations taking into account such general relativistic effects as the pericentre shift and GW emission. Consequently, we have found the following.
Multiple BHs are able to merge into one BH within 100 Myr in a wide range of parameters. In the case of MBH = 30 M⊙, if ngas is in the range from 5 × 106 to 108 cm−3, then all the BHs can merge for the BH density of ρBH = 72–7.2 × 107 M⊙ pc−3. In the case of MBH = 104 M⊙, if ngas is in the range from 5 × 106 to 109 cm−3, then all the BHs can merge for the BH density of ρBH = 2.4 × 102–2.4 × 107 M⊙ pc−3. Commonly, if the gas density is higher than ngas = 5 × 105 cm−3, the BH merger occurs once at least in 100 Myr.
The merger mechanism is classified into three types: gas-drag-driven merger (type A), three-body-driven merger (type C), and interplay-driven merger (type B). A criterion between type B and type C is almost concordant with the results of two BH or three BH systems.
Based on the argument of merger time-scales, type A merger has turned out to occur, if the gas mass within the initial BH orbit (Mgas) is higher than 105∑MBH, where ∑MBH is the total mass of BHs.
Supposing the gas and BH density based on the recent numerical simulations on first stars (Greif et al. 2011; Umemura et al. 2012, Susa 2013; Susa et al. 2014), all the BH remnants from first stars are likely to merge into one BH in ∼ 107 yr through the type B or C mechanism.
As for a primordial galaxy possessing MBHs with MBH = 104 M⊙, it is suggested that in environments of gas density higher than 5 × 106 cm−3, multiple BHs can merge into one through the type B mechanism, even if the typical separation is greater than several pc. This result implies that the BH merger is able to contribute significantly to the formation of SMBHs at high redshifts.
A point we have not considered in this paper is the effect of mass accretion on to BHs. During the motion of BHs in gas, some gas can fall on to BHs through the Bondi–Hoyle–Littleton accretion. This effect may significantly affect the merger processes of BHs. This issue will be studied in a forthcoming paper. Besides, in a primordial galaxy, the stellar dynamical friction may work cooperatively with the gas friction to extract the angular momenta. Such synergism is also an issue to be explored in the future.
Numerical computations and analyses were carried out on Cray XC30 and computers at Center for Computational Astrophysics, National Astronomical Observatory of Japan, respectively. This work was supported in part by Grant-in-Aid for Scientific Research (B) by JSPS (15H03638).
In the present study, we assume the uniform gas. However, in a real galaxy, the gas distribution is likely to become diffuse in outer regions. If the velocity of the kicked BH is high enough, the BH cannot fall back but may escape.



