-
PDF
- Split View
-
Views
-
Cite
Cite
Ana L. Chies-Santos, Bruno Rodríguez del Pino, Alfonso Aragón-Salamanca, Steven P. Bamford, Meghan E. Gray, Christian Wolf, Asmus Böhm, David T. Maltby, Irene Pintos-Castro, Miguel Sanchéz-Portal, Tim Weinzirl, OMEGA – OSIRIS Mapping of Emission-line Galaxies in A901/2 – I. Survey description, data analysis, and star formation and AGN activity in the highest density regions, Monthly Notices of the Royal Astronomical Society, Volume 450, Issue 4, 11 July 2015, Pages 4458–4474, https://doi.org/10.1093/mnras/stv779
Close - Share Icon Share
Abstract
We present an overview of and first results from the OMEGA (OSIRIS Mapping of Emission-line Galaxies in the multicluster system A901/2) survey. The ultimate goal of this project is to study star formation and active galactic nucleus (AGN) activity across a broad range of environments at a single redshift. Using the tuneable-filter mode of the Optical System for Imaging and low-Intermediate-Resolution Integrated Spectroscopy (OSIRIS) instrument on Gran Telescopio Canarias, we target H α and |$[\mathrm{N}\,\small {II}]$| emission lines over an ∼0.5 × 0.5 deg2 region containing the z ∼ 0.167 multicluster system A901/2. In this paper, we describe the design of the survey, the observations and the data analysis techniques developed. We then present early results from two OSIRIS pointings centred on the cores of the A901a and A902 clusters. AGN and star-forming (SF) objects are identified using the |$[\mathrm{N}\,\small {II}]\,/\,\mathrm{H}\,\alpha$| versus WH α diagnostic diagram. The AGN hosts are brighter, more massive, and possess earlier type morphologies than SF galaxies. Both populations tend to be located towards the outskirts of the high-density regions we study. The typical H α luminosity of these sources is significantly lower than that of field galaxies at similar redshifts, but greater than that found for A1689, a rich cluster at z ∼ 0.2. The H α luminosities of our objects translate into star formation rates (SFRs) between ∼0.02 and 6 M⊙ yr−1. Comparing the relationship between stellar mass and H α-derived SFR with that found in the field indicates a suppression of star formation in the cores of the clusters. These findings agree with previous investigations of this multicluster structure, based on other star formation indicators, and demonstrate the power of tuneable filters for this kind of study.
1 INTRODUCTION
Galaxies are not randomly distributed in the Universe: while most are part of groups and clusters, they are also found in isolation or in the field. The observed properties of galaxies are strongly dependent on the environment in which they reside (Dressler 1980). In the local universe, galaxies in low-density environments are more likely to have spiral morphologies, blue colours and be forming stars, whereas those living in high-density regions are largely bulge-dominated, red and passive (Balogh et al. 2004; Bamford et al. 2009). These two populations may be connected by one or more evolutionary processes by which galaxies falling into denser environments have their star formation quenched and their internal velocity dispersions increased.
Both internal and external processes can drive this transformation. External processes such as ram-pressure stripping (Gunn & Gott 1972; Abadi, Moore & Bower 1999; Bekki, Couch & Shioya 2002), tidal interactions (Larson, Tinsley & Caldwell 1980; Bekki 1999) galaxy harassment (Moore et al. 1996) or mergers (Barnes 1992; Bekki 1999) can produce such morphological changes and cause the removal and/or consumption of gas, leading to the halt of star formation. On the other hand, processes related to internal galaxy properties, such as mass (Haines et al. 2006) and mass-dependent feedback mechanisms (Bundy et al. 2006) can also be responsible for the quenching of star formation, as can feedback from supernovae and active galactic nuclei (AGNs; Booth & Schaye 2009; Newton & Kay 2013). In fact, environment also seems to be connected with the probability of a galaxy to host an AGN: while low-luminosity AGNs do not show particular preference for any kind of environment (Martini et al. 2002, 2006; Miller et al. 2003), luminous AGNs are preferentially found in the field (Kauffmann et al. 2004) and groups (Popesso & Baviano 2006) rather than in clusters. Peng et al. (2010) and Thomas et al. (2010) showed that both stellar-mass and environmentally driven quenching of star formation are important in governing the evolution of a galaxy and that their effects can be separated from each other.
Vogt et al. (2004) and Jaffé et al. (2011) have shown that galaxies falling into clusters experience a removal of their gas, which in principle should lead to a gradual decline of the star formation activity. However, the average star formation rate (SFR) in star-forming (SF) galaxies remains roughly constant with environment, and it is only the fraction of SF galaxies that changes (Balogh et al. 2004; Bamford et al. 2008; Poggianti et al. 2008; Verdugo, Ziegler & Gerken 2008). The extent of ongoing star formation within a galaxy has also been shown to correlate with environment (Moss & Whittle 2000; Koopmann & Kenney 2004; Bamford, Milvang-Jensen & Aragón-Salamanca 2007), implying a truncation of the star formation taking place first in the outer parts of the infalling galaxies. In fact, the last episode of star formation in cluster disc galaxies is seen to be concentrated towards the central regions (Johnston, Aragón-Salamanca & Merrifield 2014; Rodríguez Del Pino et al. 2014).
In order to understand the full degree of transformation and the relative role played by external and internal processes, we selected the field of the A901/2 multicluster system at z ∼ 0.167. This large structure has been the subject of study of the STAGES project (Gray et al. 2009), where a wealth of data exists: an 80-orbit F606WHubble Space Telescope (HST)/ACS mosaic covering the full ∼0.5 × 0.5 deg2 (∼5 × 5 Mpc2) span of the system, complemented by extensive multiwavelength observations with XMM–Newton, GALEX, Spitzer, 2dF, GMRT, Magellan, and the 17-band COMBO-17 photometric redshift survey (Wolf et al. 2003, 2004). The broad range of galaxy environments and luminosities sampled by these observations provide the perfect laboratory to study both obscured and unobscured star formation, stellar masses, AGN activity and galaxy morphologies.
Previous work in the A901/2 field has included studies of both star formation (Gray et al. 2004) and AGN activity and how they relate to galaxy environment. Wolf, Gray & Meisenheimer (2005) discovered red spirals in the system which suggested reduced current SFRs in a large fraction of the galaxies. Gallazzi et al. (2009) found an overall suppression in the fraction of SF galaxies with density by combining the UV/optical SEDs from COMBO-17 and Spitzer 24 μm photometry. The surviving star formation was shown to be obscured and hosted by a relatively large fraction of red spirals located primarily in the cluster infall regions (Wolf et al. 2009). In a more recent work, Bösch et al. (2013) find that this suppression of star formation is partially driven by ram-pressure stripping, which could lead to the production of red spirals and, ultimately, S0s. Although the integrated star formation properties have yielded important results, the actual spatial scale of the SF regions and how it is affected by the environment remain unknown. Likewise, initial attempts at quantifying the AGN activity in the field of A901/2 were made by Gilmour et al. (2007) and Gallazzi et al. (2009) using XMM–Newton X-ray and Spitzer 24 μm data, respectively. However, the lack of emission-line diagnostics means that the AGN census remains incomplete.
In order to obtain spatially resolved emission-line diagnostics, we have used the Gran Telescopio Canarias (GTC) Optical System for Imaging and low-Intermediate-Resolution Integrated Spectroscopy (OSIRIS) in tuneable-filter mode to obtain very deep spatially resolved emission-line images of the complete A901/2 STAGES field. We have targeted the H α (λ0 = 6563 Å) and |$[\mathrm{N}\,\small {II}]$| (λ0 = 6583 Å) lines. The former is the best optical tracer of SFR (Kennicutt 1998), whereas the combination of the two lines provides one of the most reliable optical AGN diagnostics available (Cid Fernandes et al. 2010).
In this paper, we present the design of the OSIRIS Mapping of Emission-line Galaxies in A901/2 (OMEGA) survey, the data reduction procedures adopted and a first analysis of two of the 20 pointings, demonstrating some of the science that the survey can achieve. OMEGA has been designed to address star formation and AGN activity as a function of galaxy properties and environment in A901/2. In the present work, we show a tentative census of AGN and SF galaxies in the highest density cluster regions. A full environmental analysis of both integrated and spatially resolved galaxy properties will be presented in subsequent papers.
We adopt an H0 = 70 km s−1 Mpc−1, Ωm = 0.3 and ΩΛ = 0.7 cosmology throughout.
2 DESCRIPTION OF THE PROGRAMME AND DESIGN OF THE OBSERVATIONS
The OMEGA survey was designed to obtain very deep spatially resolved emission-line images for the A901/2 multicluster system and, in turn, recover low-resolution spectra in a wavelength range that covers H α and |$[\mathrm{N}\,\small {II}]$| for the galaxies of the system. Moreover, OMEGA is intended to sample the 16.0 ≤ mR ≤ 23 magnitude range. This roughly corresponds to stellar masses of 9.0 ≤ log (M⋆/M⊙) ≤ 11.5 at the cluster redshift, reaching lower SFRs than possible at high-z. The survey is based on a 90 h ESO/GTC Large Programme allocation (PI: A. Aragón-Salamanca).
In order to meet the objectives of OMEGA, we make use of the tuneable-filter capabilities of the OSIRIS instrument (Cepa 2013; Cepa et al. 2013), located at the Nasmyth-B focus of the 10.4 m GTC, at the Roque de los Muchachos Observatory on La Palma.
Tuneable-filter imaging is a method that lies between classical narrow-band imaging and spectroscopy, in terms of observing time costs and the quality of the information obtained. Although the spectral resolution is relatively low, the wavelength sampling is quite sufficient for reliable star formation and AGN activity estimates for most of the cluster members. Mapping the spectral region around H α, |$[\mathrm{N}\,\small {II}]\,\lambda 6548$| and |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| for all the galaxies in the A901/2 system would be much more expensive with traditional spectroscopy. A further advantage of tuneable-filter imaging, with respect to slit spectroscopy, is the spatial information it provides. While long-slit spectroscopy normally only provides information along one of the axes of the galaxies (usually chosen to be the major axis), tuneable-filter imaging provides 2D maps. The tuneable-filter technique has not been much employed previously in this field. A heroic attempt includes the CADIS survey of emission-line galaxies (ELGs) measuring SFRs between z = 0.25 and z = 1.2 (Hippelein et al. 2003).
Our increased spectral resolution over standard narrow-band H α imaging surveys (see e.g. Kennicutt 1992; Gallego et al. 1997) has the advantages of avoiding contamination from the |$[\mathrm{N}\,\small {II}]$| line in the star formation estimates and enabling AGN to be identified (Cid Fernandes et al. 2010). Finally, while integral field spectrograph (IFS) surveys, such as CALIFA and MaNGA, also provide spatial information, their fields of view (FOV) are much smaller than that of OSIRIS. Even large IFSs – such as MUSE, recently installed on the VLT – have an FOV that is ∼50 times smaller than that of OSIRIS. The full unvignetted FOV of OSIRIS is 7.8 × 7.8 arcmin2, imaged using two 2048 × 4096 Marconi CCDs with a 9.4 arcsec gap between them. The plate scale, using 2 × 2 pixel binning, is 0.25 arcsec pixel−1. We can therefore obtain spectral and spatial information for a much larger number of galaxies, and thus gain a much more complete picture, than is possible with current IFSs.
The OSIRIS tuneable-filter system consists of two reflecting plates (a Fabry–Pérot etalon) working in a collimated beam. The resulting interference allows only specific narrow wavelength ranges to be transmitted. One can tune the properties of the filter by modifying the separation between the optical plates of the device. Standard narrow-band order-sorting filters (OSFs) are used to isolate specific interference orders. Reliable observations are limited to a circular FOV of radius 4 arcmin, within which they are assured to be free from contamination by other orders. OSIRIS has two different tuneable filters, one for the blue and the other for the red wavelength range. We use the latter, which is capable of tuning filters to wavelengths in the 6510–9350 Å range with a spectral resolution of 14 Å full width at half-maximum (FWHM).
In Fig. 1, we show the OSIRIS observed fields as circles 8 arcmin in diameter, overlaid on top of the footprint of the 80-tile STAGES HST/ACS mosaic (Gray et al. 2009) and ground-based COMBO-17 R-band image (Wolf et al. 2004). Cluster galaxies with mR < 23.5 are also plotted. Given the available observing time, the initial plan was to tile the FOV uniformly in a 4 × 5 grid. However, the north-east and north-west tiles contain bright stars that would have produced reflection ghosts, seriously compromising the quality of the data for these tiles. For this reason, we decided to re-locate these two pointings to cover the regions with the highest galaxy densities, which correspond to Fields 21 (A901a) and 22 (A902). These fields are referred to as F21 and F22, respectively.
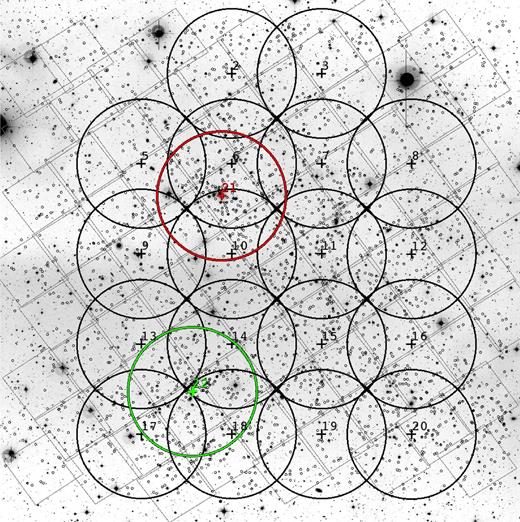
The OSIRIS observed fields (labelled 2–3, 5–22), represented as circles of radius 4 arcmin, overlaid on top of the footprint of the 80-tile STAGES HST/ACS mosaic and a COMBO-17 R-band image. The very small black circles mark the positions of cluster galaxies with mR < 23, where cluster membership is defined as in Gray et al. (2009) using the COMBO-17 photometric redshifts.
Fig. 2 shows the spectroscopically determined redshift distribution of galaxies within 1.2 Mpc diameter apertures centred upon the three main cluster cores. The redshifts were drawn from a spectroscopic survey of the 300 brightest cluster galaxies in the region obtained with the AAT 2dF spectrograph (Gray et al., in preparation). The dashed lines indicate the redshift range probed by our observations. Within these redshift ranges, we target both the H α and |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| emission lines. The z ranges are slightly narrower for the two pointed observations of the A901a and A902 regions (F21 and F22).
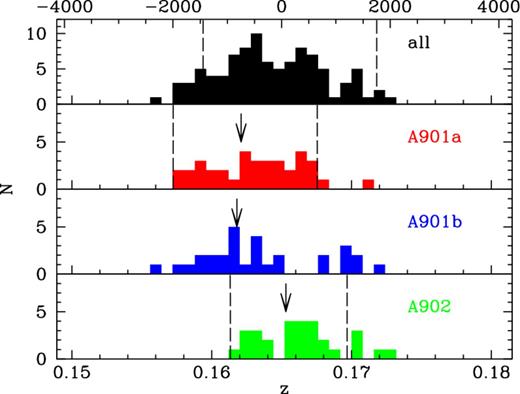
Spectroscopically determined redshift distribution of galaxies within 1.2-Mpc diameter apertures around the three main cluster cores, from a limited spectroscopic survey of the ∼300 brightest galaxies in the region, taken with the AAT 2dF instrument. Arrows mark the positions of the brightest cluster galaxies. Dashed lines indicate the velocity range probed by OMEGA: the top histogram indicates the limits of the survey proper (Fields 2, 3 and 5–20), while the ranges for the two pointed observations of the A901a and A902 cluster cores presented in this paper (Fields 21 and 22, respectively) are specially tuned (cf. Table 1).
For an optimal deblending of H α and |$[\mathrm{N}\,\small {II}]$|, the tuneable-filter FWHM bandwidth is set to 14 Å, and the spacing between successive wavelengths to 7 Å. Therefore, in order to cover the desired wavelength range in F21 and F22 we require 14 and 12 wavelength settings, respectively, whereas for the rest of the fields we need 16 wavelength settings (see Figs 2 and 3, and Table 1). Moreover, for each wavelength setting, three dithered images are taken typically with an ∼40 pixel (10 arcsec) separation. This increases our number of images (and individual wavelengths sampled) by a factor of 3 and ensures that the inter-CCD gap is imaged. A total of 42 and 36 images have been obtained for Fields 21 and 22, respectively, and 48 for the remaining 18 fields. Note however, that the wavelength varies across the field, according to equation (1). In Fig. 4, we show an illustration of this dependence.
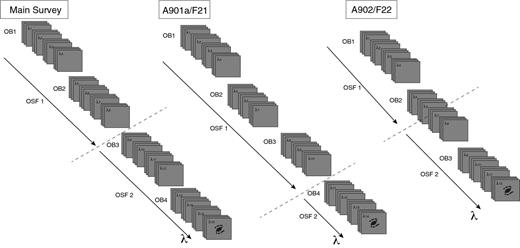
A cartoon illustrating the design of the observations for the main survey and the two cluster core fields (F21 and F22). Note that this illustration is valid in the case of a single galaxy, for which the wavelength is almost constant (for a given image there is wavelength variation across the field of view, see equation 1 and Fig. 4). A given galaxy is observed using a series of wavelength setups λi and a three-position dithered pattern. In each dithered position, the wavelength changes slightly because the distance to the centre of the field changes. The order-sorting filter (OSF) separates the different tuned wavelengths. The observations are executed in ‘observing blocks’ (OBs). See http://www.nottingham.ac.uk/astronomy/omega/videos/ for videos with successive frames of a given galaxy.
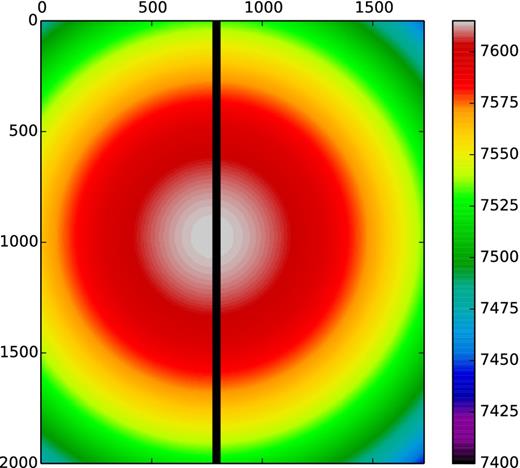
A mock reduced image with λc = 7615 Å, illustrating the radial wavelength dependence according to the colour bar (labelled by wavelength in Å). The vertical line in the middle represents the 9.4 arcsec gap between CCD1 and CCD2 and the axis are in pixels.
| OBs (main survey) . | OBs (A901a/F21) . | OBs (A902/F22) . | λc (Å) . | λave (Å) . | Order-sorting filter . | Exp. time (s) . |
|---|---|---|---|---|---|---|
| 1 | 7615 | 7595 | f 754/50 | 3 × 200 | ||
| 1 | 7622 | 7602 | f 754/50 | 3 × 200 | ||
| 1 | 1 | 7629 | 7609 | f 754/50 | 3 × 200 | |
| 1 | 1 | 7636 | 7616 | f 754/50 | 3 × 200 | |
| 1 | 2 | 1 | 7643 | 7623 | f 754/50 | 3 × 200 |
| 1 | 2 | 1 | 7650 | 7630 | f 754/50 | 3 × 200 |
| 2 | 2 | 1 | 7657 | 7637 | f 754/50 | 3 × 200 |
| 2 | 3 | 1 | 7664 | 7644 | f 754/50 | 3 × 200 |
| 2 | 3 | 2 | 7671 | 7651 | f 754/50 | 3 × 200 |
| 2 | 3 | 2 | 7678 | 7658 | f 754/50 | 3 × 200 |
| 3 | 4 | 2 | 7685 | 7665 | f 770/50 | 3 × 200 |
| 3 | 4 | 2 | 7692 | 7672 | f 770/50 | 3 × 200 |
| 3 | 4 | 3 | 7699 | 7679 | f 770/50 | 3 × 200 |
| 3 | 4 | 3 | 7706 | 7686 | f 770/50 | 3 × 200 |
| 4 | 3 | 7713 | 7693 | f 770/50 | 3 × 200 | |
| 4 | 3 | 7720 | 7700 | f 770/50 | 3 × 200 | |
| 4 | 7727 | 7707 | f 770/50 | 3 × 200 | ||
| 4 | 7734 | 7714 | f 770/50 | 3 × 200 |
| OBs (main survey) . | OBs (A901a/F21) . | OBs (A902/F22) . | λc (Å) . | λave (Å) . | Order-sorting filter . | Exp. time (s) . |
|---|---|---|---|---|---|---|
| 1 | 7615 | 7595 | f 754/50 | 3 × 200 | ||
| 1 | 7622 | 7602 | f 754/50 | 3 × 200 | ||
| 1 | 1 | 7629 | 7609 | f 754/50 | 3 × 200 | |
| 1 | 1 | 7636 | 7616 | f 754/50 | 3 × 200 | |
| 1 | 2 | 1 | 7643 | 7623 | f 754/50 | 3 × 200 |
| 1 | 2 | 1 | 7650 | 7630 | f 754/50 | 3 × 200 |
| 2 | 2 | 1 | 7657 | 7637 | f 754/50 | 3 × 200 |
| 2 | 3 | 1 | 7664 | 7644 | f 754/50 | 3 × 200 |
| 2 | 3 | 2 | 7671 | 7651 | f 754/50 | 3 × 200 |
| 2 | 3 | 2 | 7678 | 7658 | f 754/50 | 3 × 200 |
| 3 | 4 | 2 | 7685 | 7665 | f 770/50 | 3 × 200 |
| 3 | 4 | 2 | 7692 | 7672 | f 770/50 | 3 × 200 |
| 3 | 4 | 3 | 7699 | 7679 | f 770/50 | 3 × 200 |
| 3 | 4 | 3 | 7706 | 7686 | f 770/50 | 3 × 200 |
| 4 | 3 | 7713 | 7693 | f 770/50 | 3 × 200 | |
| 4 | 3 | 7720 | 7700 | f 770/50 | 3 × 200 | |
| 4 | 7727 | 7707 | f 770/50 | 3 × 200 | ||
| 4 | 7734 | 7714 | f 770/50 | 3 × 200 |
| OBs (main survey) . | OBs (A901a/F21) . | OBs (A902/F22) . | λc (Å) . | λave (Å) . | Order-sorting filter . | Exp. time (s) . |
|---|---|---|---|---|---|---|
| 1 | 7615 | 7595 | f 754/50 | 3 × 200 | ||
| 1 | 7622 | 7602 | f 754/50 | 3 × 200 | ||
| 1 | 1 | 7629 | 7609 | f 754/50 | 3 × 200 | |
| 1 | 1 | 7636 | 7616 | f 754/50 | 3 × 200 | |
| 1 | 2 | 1 | 7643 | 7623 | f 754/50 | 3 × 200 |
| 1 | 2 | 1 | 7650 | 7630 | f 754/50 | 3 × 200 |
| 2 | 2 | 1 | 7657 | 7637 | f 754/50 | 3 × 200 |
| 2 | 3 | 1 | 7664 | 7644 | f 754/50 | 3 × 200 |
| 2 | 3 | 2 | 7671 | 7651 | f 754/50 | 3 × 200 |
| 2 | 3 | 2 | 7678 | 7658 | f 754/50 | 3 × 200 |
| 3 | 4 | 2 | 7685 | 7665 | f 770/50 | 3 × 200 |
| 3 | 4 | 2 | 7692 | 7672 | f 770/50 | 3 × 200 |
| 3 | 4 | 3 | 7699 | 7679 | f 770/50 | 3 × 200 |
| 3 | 4 | 3 | 7706 | 7686 | f 770/50 | 3 × 200 |
| 4 | 3 | 7713 | 7693 | f 770/50 | 3 × 200 | |
| 4 | 3 | 7720 | 7700 | f 770/50 | 3 × 200 | |
| 4 | 7727 | 7707 | f 770/50 | 3 × 200 | ||
| 4 | 7734 | 7714 | f 770/50 | 3 × 200 |
| OBs (main survey) . | OBs (A901a/F21) . | OBs (A902/F22) . | λc (Å) . | λave (Å) . | Order-sorting filter . | Exp. time (s) . |
|---|---|---|---|---|---|---|
| 1 | 7615 | 7595 | f 754/50 | 3 × 200 | ||
| 1 | 7622 | 7602 | f 754/50 | 3 × 200 | ||
| 1 | 1 | 7629 | 7609 | f 754/50 | 3 × 200 | |
| 1 | 1 | 7636 | 7616 | f 754/50 | 3 × 200 | |
| 1 | 2 | 1 | 7643 | 7623 | f 754/50 | 3 × 200 |
| 1 | 2 | 1 | 7650 | 7630 | f 754/50 | 3 × 200 |
| 2 | 2 | 1 | 7657 | 7637 | f 754/50 | 3 × 200 |
| 2 | 3 | 1 | 7664 | 7644 | f 754/50 | 3 × 200 |
| 2 | 3 | 2 | 7671 | 7651 | f 754/50 | 3 × 200 |
| 2 | 3 | 2 | 7678 | 7658 | f 754/50 | 3 × 200 |
| 3 | 4 | 2 | 7685 | 7665 | f 770/50 | 3 × 200 |
| 3 | 4 | 2 | 7692 | 7672 | f 770/50 | 3 × 200 |
| 3 | 4 | 3 | 7699 | 7679 | f 770/50 | 3 × 200 |
| 3 | 4 | 3 | 7706 | 7686 | f 770/50 | 3 × 200 |
| 4 | 3 | 7713 | 7693 | f 770/50 | 3 × 200 | |
| 4 | 3 | 7720 | 7700 | f 770/50 | 3 × 200 | |
| 4 | 7727 | 7707 | f 770/50 | 3 × 200 | ||
| 4 | 7734 | 7714 | f 770/50 | 3 × 200 |
Since the wavelength varies across the FOV, the central wavelength λc of each wavelength setting needs to be optimized in such a way that the desired wavelength range is covered for as many galaxies as possible. The average wavelength λave of each setting was calculated as the mean λ within the central 5.6-arcmin diameter circle of each pointing (the approximate area uniquely covered by one tile). For Fields F2–F20, 7609 ≤ λave(Å) ≤ 7714, ensuring that both H α and |$[\mathrm{N}\,\small {II}]$| are observed in the 0.1594 ≤ z ≤ 0.1718 redshift ranges. This corresponds to rest-frame velocities in the range −1447 ≤ v(km s−1) ≤ 1751, where v = 0 corresponds to z = 0.167, the average redshift of the structure. For Field F21, 7595 ≤ λave (Å) ≤ 7686, and for F22, 7623 ≤ λave (Å) ≤ 7700, thus covering a slightly narrower redshift/velocity range for these two fields (see Fig. 2 and Table 1 for details). Note that these are average values: the exact wavelength range covered for each galaxy depends on its position with respect to the centre of the pointing. Moreover, given the significant tile overlap, a sizeable fraction of the galaxies will be observed in more than one pointing, increasing the available wavelength range and the number of independent wavelength samples obtained.
A summary of the observational setup is given in Table 1. The observations were executed in ‘observing blocks’ (OBs), as shown in Table 1 and illustrated in Fig. 3. They were carried out during the first halves of 2012 and 2013, and completed in 2014 February.
3 DATA REDUCTION
In this section, we describe the data reduction methods we have developed for the OMEGA data.
3.1 Imaging data reduction
The data reduction was carried out with the Osiris Offline Pipeline software (OOPs; Ederoclite 2012). The OOPs reduction consists of two steps. In the first step, we prepare the calibration files ‘masterbias’ and ‘masterflat’ combining the individual bias and flat-field frames taken at the telescope. Flat-fields were obtained using dome flats with the filter tuned to the same wavelength as the science observations. Usually three to five flat frames were taken each night at each wavelength. In the second step, we reduce the science frames: we remove the overscan and subtract the bias from the science frames and divide these frames by the masterflat. The vignetted regions of the images are also trimmed at this stage.
The final step carried out within OOPs is the sky subtraction. Due to the wavelength variation across the FOV, sky OH emission lines appear as rings (see top panel of Fig. 5). To correct for these features, each science exposure is artificially dithered on a 3 × 3 grid. The dither step size (a few arcseconds) is larger than the vast majority of the sources, but small compared to the ring features. Therefore, median-combining the dithered images leaves only the sky rings. These can then be subtracted from the original image. Fig. 5 presents the first image of Field 21, with λc = 7615 Å. The upper panel shows the raw image while the bottom panel displays the final output from OOPs.

Example of the first image of F21 with λc = 7615 Å. Top panel: raw image. Bottom panel: after OOPs processing. The red circle has a radius of 4 arcmin, within which the observations are free from contamination by other interference orders.
As mentioned in Section 2, we obtain three dithered exposures for each λc (see Fig. 3). This dithering introduces small shifts in the wavelength corresponding to each pixel. As we wish to retain this information, to improve our spectral sampling, we do not co-add the dithered images. To correct for cosmic rays, we therefore employ a similar routine to qzap in iraf applying a 3σ clipping with a flux ratio of 0.1 (comparison value between the flux in the surrounding pixels and the flux in the candidate one to check whether the pixel has been hit by a cosmic ray).
Bad pixels are corrected using the iraf task FIXPIX. Astrometry solutions are found using CCMAP and CCSETWCS with the COMBO-17 R-band image as reference. In order to avoid unnecessary distortions, we work with the two separate CCDs of OSIRIS throughout the analysis, obtaining astrometric solutions with rms accuracies ≤0.1 arcsec.
3.2 Wavelength calibration
The nature of the observations mean that the wavelength of a given object will depend on the central wavelength of each image as well as its distance to the optical centre. Both parameters change from exposure to exposure. The variation of wavelength across the FOV for a given central wavelength is shown in Fig. 4.
The wavelength calibration of the OSIRIS tuneable filter has been a question of debate (Méndez-Abreu et al. 2011) because its accuracy is crucial for studies of extended sources, as well as for estimating redshifts of both point-like and extended sources. Fortunately, the sizes of our objects are small (the largest objects in F21 and F22 have a radius of ∼7 arcsec), and hence the wavelength changes are negligible across individual objects in the OMEGA sample (at most ∼2 Å, i.e. much smaller than the spectral resolution, 14 Å FWHM). The general form of the λ calibration follows from equation (1). The optical centre is located on pixel X0 = 1051 and Y0 = 976 (CCD1) and X0 = −10 and Y0 = 976 (CCD2) of the raw images, according to the OSIRIS website.1 This corresponds to X0 = 772, Y0 = 976 (CCD1) and X0 = −35 and Y0 = 976 (CCD2) on the images output from OOPs. Although there are other optical centres listed in the literature (Méndez-Abreu et al. 2011 and the OSIRIS manual), the change they introduce is smaller than 0.2 per cent in wavelength. Using either of these values makes no difference for the purposes of the current paper. Here, we are interested primarily in the measurement of the H α and |$[\mathrm{N}\,\small {II}]$| line fluxes, and not in the determination of accurate redshifts. However, in future papers, the combination of the images for all 20 OMEGA fields will allow us to evaluate the accuracy of the wavelength calibration using a very large number of galaxies in the overlap regions (see Fig. 1) that are observed two or even three times. Furthermore, the available AAT 2dF spectroscopic redshifts will provide an external cross-check.
3.3 Flux calibration and zero-point estimation
Different image sets (OBs) for a single field are not necessarily observed on the same night or with the same observing conditions. In order to perform consistent photometry, we therefore need to correct for differences in the seeing conditions, transparency and airmass.
To match the seeing conditions our procedure is as follows: we measure the PSF in all the images using unsaturated stars with mR, COMBO-17 < 19 (from the STAGES catalogue of Gray et al. 2009). We then convolve each image with a Gaussian function of the required width to produce images with the same PSF. From now on, we use images matched to the worst seeing, which is 1.2 arcsec. These operations were performed using the iraf tasks PSFMEASURE and GAUSSIAN.
To calibrate our fluxes we use the Vega magnitudes of the same stars in the closest COMBO-17 filter, W753f, as standard magnitudes. This filter samples the range 7440–7620 Å. Vega magnitudes were calculated from the photon fluxes tabulated in the COMBO-17 catalogue. Our zero-point functions are shown in Fig. 6. Because there is a strong absorption feature caused by a double telluric sky line at λ = 7633 Å, the zero-point function has a strong wavelength dependence.
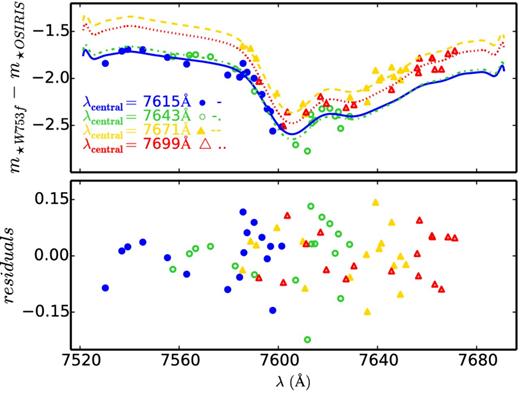
Top panel: the wavelength-dependent zero point, |$\mathit {{\rm zp}}(\lambda )=m_{\star \,\mathrm{OSIRIS}}-m_{\star \,\mathrm{W753f}}$|, for 4 different dithered images in Field 21. Each set of ∼25 stars is shown with a different colour and symbol. We only show 4 of the total 42 images for clarity. In order to model the effect of the telluric line, we fit a polynomial. The best solution for each image set is shown by the lines. Bottom panel: the residuals with respect to the polynomial fits.
In order to correct for the effect of the atmospheric telluric absorption, we fit this feature with a series of Chebyshev polynomials. The shape of the absorption feature is constant, except for a scaling factor and offset that vary with the observing conditions. We therefore fit all the zero-point functions simultaneously, to obtain a general set of polynomial coefficients, together with an offset and scaling factor for each set of dithered images (14 in the case of Field 21, and 12 for Field 22). We use a similar fitting technique to that described later, in Section 4.1. In Fig. 6, we show the zero points, as well as our fits and their residuals, as a function of wavelength. For clarity, we only show these for 4 images from the set of 14 dithered images.
The scatter in the zero point introduces additional wavelength-dependent errors that must be incorporated in our photometric uncertainties. We estimate these by taking a 3σ-clipped standard deviation of the residuals in bins of 10 Å. These zero-point errors are found to be always ≲ 0.1 mag.
3.4 Galaxy photometry
We perform aperture photometry on the galaxies with phot. We measure each galaxy using two apertures: a PSF-matched aperture of radius 1.2 arcsec (5 pixels, from now on referred to as RPSF) and a total aperture (essentially the Kron radius; Bertin & Arnouts 1996), with |$R_{\rm tot} = 2.5 \times \mathit {{\rm SMA}}$|. Here |$\mathit {{\rm SMA}}$| is the second central moment of the light distribution, derived from ACS images with SExtractor and contained within the STAGES catalogue (Gray et al. 2009). We use these two different aperture radii as appropriate throughout the paper. RPSF provides information about the nucleus of a given galaxy, while Rtot averages over its full extent. Fig. 7 shows the spectra constructed for one of the galaxies in F21 using both RPSF or Rtot apertures.
![Left-hand panel: the flux-calibrated spectra for the central (filled red circles) and total (open green circles) apertures of the bright (mR ∼ 18.7) galaxy with STAGES ID 42713. The locations of H α (λ0 = 6562.8 Å) and the two $[\mathrm{N}\,\small {II}]$ lines (λ0 = 6548.1 Å and 6583.5 Å) are indicated. Right-hand panel: image of galaxy 42713 at λ = 7646 Å, with the total and PSF apertures overlaid as solid green and dashed red lines, respectively. This image has not been convolved to the standard PSF although the fluxes are actually measured on the convolved images. The image is 40 pixels on a side, which corresponds to 10 arcsec or 28 kpc at z = 0.167. The colour bar indicates the flux in counts.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/450/4/10.1093/mnras/stv779/2/m_stv779fig7.jpeg?Expires=1750285007&Signature=qGBoO0pyHQrXIMRjB464FZBpuQEEmk1sqFq54rMgbtS5hNZ1RH0tUgsN2JvHc1pprlvMTzOCrGZCLtEumKmhRH64l7zbIctICtjgJ6lsUiTEVvpxDGTCrBlVt~K5ncmRgTOjjTXc4OPazUuUO5GxsX61XdnkN~fFs5fjXFHW~6qpDMD4NSnqp3PnZfHUJHk-6imge~IVw0HnRC5MYwpeVXc4ANZOYPrRQYgXpS68BM-MBGHz-IEclRhGGe-TBmBRS9GPmPrbbRHootI1QWIQpjh2h7XyZ3bgsGkUWPh84AG8uqjI0zLwcus~iOLNg86bDiLiFE8S5lHZWsRK0-T7Rg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Left-hand panel: the flux-calibrated spectra for the central (filled red circles) and total (open green circles) apertures of the bright (mR ∼ 18.7) galaxy with STAGES ID 42713. The locations of H α (λ0 = 6562.8 Å) and the two |$[\mathrm{N}\,\small {II}]$| lines (λ0 = 6548.1 Å and 6583.5 Å) are indicated. Right-hand panel: image of galaxy 42713 at λ = 7646 Å, with the total and PSF apertures overlaid as solid green and dashed red lines, respectively. This image has not been convolved to the standard PSF although the fluxes are actually measured on the convolved images. The image is 40 pixels on a side, which corresponds to 10 arcsec or 28 kpc at z = 0.167. The colour bar indicates the flux in counts.
3.5 Building the spectra
After the flux and wavelength calibrations are performed, we are able to construct a spectrum for each of the galaxies in the observed fields. An example of such a spectrum can be found in the left-hand panel of Fig. 7, where we indicate the location of H α and the two |$[\mathrm{N}\,\small {II}]$| lines with their respective rest-frame wavelengths. By design, the wavelength range of the spectra for cluster members should cover both H α and |$[\mathrm{N}\,\small {II}]\,\lambda 6583$|, which will appear as emission lines in galaxies hosting star formation and/or AGN activity. In addition to finding spectra of galaxies with clear emission lines, we also expect to obtain spectra of galaxies with weak or absent emission (or absorption in H α) lines.
4 ANALYSIS
4.1 Spectral fitting
Our goal is to measure fluxes for H α as well as the brightest |$[\mathrm{N}\,\small {II}]$| line at 6583 Å. We also wish to obtain reliable constraints for the continuum, in order to measure the equivalent widths (WH α and |${W}_{[\mathrm{N}\,\small {II}]}$|) of these lines. Due to the limited wavelength coverage and the moderate spectral resolution and sampling of our spectra, this exercise becomes very challenging for weak ELGs.
To account for all the features present in our spectra, we fit them with a composite of three Gaussian functions and a linear continuum. Since the ratio of the fluxes of the two nitrogen lines (|$[\mathrm{N}\,\small {II}]\,\lambda 6583 / [\mathrm{N}\,\small {II}]\,\lambda 6548$|) is fixed by atomic physics to a value of 3.06 (determined by the ratio between the transition probabilities of each line; Osterbrock & Ferland 1989), we only need one parameter to fit both their fluxes. We therefore fit, at most, six parameters: continuum intercept, continuum slope, redshift, flux of H α, width of H α and flux of |$[\mathrm{N}\,\small {II}]\,\lambda 6583$|.
In order to exploit all the information contained in our data, the fitting procedure must evaluate all possible combinations of the parameters in a thorough yet efficient way. Conventional fitting techniques, such as Levenberg–Marquardt optimization, can be sensitive to the initial values, and can become trapped in local maxima in the parameter likelihood space. These problems can be ameliorated by using Markov Chain Monte Carlo (MCMC) techniques. In particular, we use the software emcee (Foreman-Mackey et al. 2013), which implements the Affine Invariant MCMC Ensemble sampler of Goodman & Weare (2010).
MCMC methods aim to draw samples from the posterior probability density distribution, which describes how likely each possible set of model parameters is given the data. From Bayes Theorem, the posterior is given by the product of the prior distribution (which can be thought of as pre-existing constraints on the parameter values) and the likelihood function (which describes how closely the data correspond to the model, for a given set of parameters). MCMC algorithms explore the parameter space along a chain. At each step, new values for the parameters are proposed. These are accepted or rejected, depending on the probability of the proposed values relative to that of the current parameter set. If the probability is higher, then the proposed parameters will be adopted. However, if the probability is lower, there remains some chance of the new values being accepted. In this way, the parameter space is thoroughly explored, and ultimately sampled in proportion to the posterior probability density.
The Affine Invariant MCMC Ensemble sampler uses multiple ‘walkers’ to produce a set of chains. These are started at different points of the parameter space. Each walker explores following a proposal distribution that depends on the current position of the rest of the walkers. In this way, the parameter space can be mapped more efficiently than with the original Metropolis–Hastings algorithm. We also make use of parallel tempering, in which additional sets of walkers take significantly larger steps than the standard set. This eases communication between different maxima in the case of multimodal posterior distributions and generally speeds up convergence.
The performance of the MCMC depends on two issues: the ‘initialization bias’ and the ‘autocorrelation in equilibrium’ (Sokal 1996). The first one refers to the need of reaching the equilibrium distribution and therefore ‘erasing’ any dependence on the initial conditions. This can be achieved by estimating the autocorrelation time in the burn-in phase, and producing chains long enough for them to move away from the initial conditions. The burn-in phase will then be discarded and not included in the posterior distributions. The second one implies that once the chains have reached equilibrium, we need to take enough samples to obtain a statistically significant estimate of the errors. Therefore, the performance of MCMC will strongly depend on the length of the chains and the number of walkers, but also on the election of the priors. To ensure a good performance for our analysis, we use 300 walkers, a burn-in phase of 500 iterations (∼10 times the autocorrelation time) which are discarded and 500 iterations after the burn-in phase to sample the posterior distributions.
An example of the performance of this algorithm using a four-parameter model (described below) for the spectrum of one of our galaxies is shown in Fig. 8. Unless otherwise specified, we summarize our fit results using the median value of the (marginalized) posterior distribution of each parameter, and estimate uncertainties from the 16th and 84th percentiles.
![Parameter–parameter likelihood distributions with 1σ (solid), 2σ (dashed) and 3σ (dash–dotted) contours obtained for the four-parameter model of the Rtot aperture spectrum of galaxy 42 713 (the same galaxy shown in Fig. 7). On the top right, we show the observed spectrum (blue points) together with the model fits (red lines). We plot only 1/100 of all the individual MCMC fits for clarity, but they are all very similar. The median values of the parameters’ probability distribution are plotted as a white cross on the two-dimensional distributions. The parameters shown are the continuum flux density, the redshift and the integrated fluxes of the H α and $[\mathrm{N}\,\small {II}]\,\lambda 6583$ emission lines. Fluxes are given in c.g.s units.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/450/4/10.1093/mnras/stv779/2/m_stv779fig8.jpeg?Expires=1750285007&Signature=CDd9lhGCL8AiV3JOkzN44HfD~yTTHoK3si9IozbNu9kpCgvX0Q1vLj7fUMlKAfnFBG94Zy8Bs26i6zaM89ejv5TzEUOcJL22m1AZk6mBl6HL~Wa7WRkMBNjXyqEJDoQ2yoVgLh26HAIMGlOsHFtapXBNNMnmh7YYF~z2qIV-tdzc8kRPqoaqrzdDAgIGBMkSsPgUWpjc0vIZEOi5kO-xRHuh~-t31lXyT5FqGtdSQUnu9-j93iP893LrWYgWdVaALMMjchV1LNbyWFFh0cJ3rj03mJGb1iVynJWiK93ufQ6SYt5cAhN28kZI4VgkS~MQ89vjEp1vTH0mrg3-Fa3eDg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Parameter–parameter likelihood distributions with 1σ (solid), 2σ (dashed) and 3σ (dash–dotted) contours obtained for the four-parameter model of the Rtot aperture spectrum of galaxy 42 713 (the same galaxy shown in Fig. 7). On the top right, we show the observed spectrum (blue points) together with the model fits (red lines). We plot only 1/100 of all the individual MCMC fits for clarity, but they are all very similar. The median values of the parameters’ probability distribution are plotted as a white cross on the two-dimensional distributions. The parameters shown are the continuum flux density, the redshift and the integrated fluxes of the H α and |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| emission lines. Fluxes are given in c.g.s units.
A crucial element of this process is to set the priors that appropriately constrain the regions of parameter space to be explored. From what we already know of our model and data, we set the following priors:
|$F_{[\mathrm{N}\,\small {II}]\,\lambda 6583} > 0$|;
redshift consistent with the H α line being within the wavelength range probed by our spectrum, with an additional 20 Å window on each side and
|$F_{[\mathrm{N}\,\small {II}]\,\lambda 6583} < 3\,(F_{\mathrm{H}\alpha } + \rm continuum)$|.
The first of these forces the flux of |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| (which, physically, can never be negative) to be positive; the second assumes that the H α line lies within the spectral range and the third sets an upper limit for the |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| flux such that it cannot be larger than three times the flux of H α (which is the maximum value of |$[\mathrm{N}\,\small {II}]\,/\,\mathrm{H}\,\alpha$| observed in the |$[\mathrm{N}\,\small {II}]\,/\,\mathrm{H}\,\alpha$| versus WH α (WHAN) diagram; Cid Fernandes et al. 2010), including the possibility of up to 3 Å equivalent width of absorption in H α.
As mentioned above, we define our model using six different parameters. This number can be reduced if we assume some properties of our spectra. First, one can assume that the slope of the continuum is roughly the same for all the galaxies, which is reasonable considering the short wavelength range covered by the OMEGA spectra (≤200 Å). Secondly, the width of the emission lines will be limited by the instrumental resolution and only substantially broadened in cases of strong AGN (1000–25 000 km s−1). Due to the low spectral resolution and the faintness of some of the objects, adding these constraints will improve the reliability of our estimates.
In order to find a fixed value for the slope of the continuum and for the instrumental width of the lines, we first performed six-parameter MCMC runs considering only those galaxies that show clear emission lines. We then select galaxies with less than 15 per cent uncertainty in the estimation of the flux and width of the H α line, and the median value of the redshift consistent with H α and |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| being within the wavelength range. In total, we find 28 galaxies that fulfil these requirements. For these galaxies, Fig. 9 shows the distribution of the line-width and the slope of the continuum. The continuum slope is consistent with zero, while the distribution of the width of the lines shows a clear peak at 7.5 Å. These findings allow us to confidently fix these two parameters and use only four-parameter models to fit the spectra.
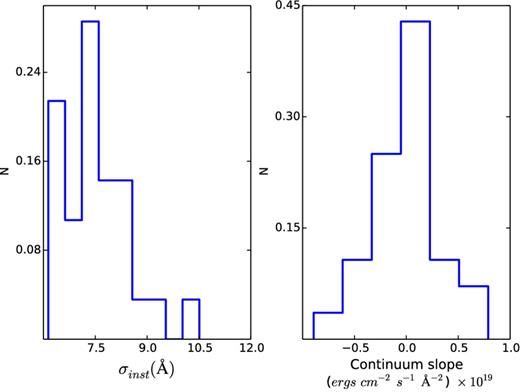
Distribution of the width (σ) of the spectral lines and the continuum slope for a sample of 28 galaxies with very clear emission lines. As a reference, the continuum level of a mR = 20 galaxy is ∼5 × 10−18 erg cm−2 Å−1.
4.2 Defining the OMEGA sample of ELGs
After fitting the H α and |$[\mathrm{N}\,\small {II}]$| lines as described above, in this section we describe the different criteria we use to define the sample of ELGs we will use in the remainder of the paper. We start with all objects in the STAGES catalogue with 16 ≤ mR ≤ 23.0 that are detected in both COMBO-17 (combo_flag > 1) and in HST (stages_flag > 1). At this stage, we do not require them to also be flagged as cluster members according to the definition of Gray et al. (2009).2
We use measurements made within the total aperture, Rtot, as defined in the previous section. Our final sample of ELGs in F21 and F22 contains 124 objects fulfilling the following selection criteria:
|$\mathrm{relative\,\,error}\, (\it W _{\mathrm{H}\alpha }) < {\mathrm{0.15}}$|;
probability of detecting the H α line in emission, P(FHα > 0) > 99.7 and
the H α line falls within the wavelength range probed by our observations.
Out of these 124 objects, 103 have been morphologically classified by the STAGES collaboration (see e.g. Wolf et al. 2009; Maltby et al. 2010). The galaxies without morphological classification have zphot > 0.4, the STAGES cut-off for visual classification. Of the 124 ELGs, 72 are classified as clusters members in the STAGES catalogue based on their COMBO-17 photometry (combo_flag > 3).
For the parts of our analysis that make use of both H α and |$[\mathrm{N}\,\small {II}]$| measurements (e.g. Section 5.1), we define a subsample requiring both H α and |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| to be within our wavelength range. This subsample contains 82 ELGs with both Rtot and RPSF aperture measurements.
4.3 Detection efficiency and limits
Our ability to detect H α emission depends on a complex interplay between the brightness of a galaxy, its size, and its H α flux and equivalent width. For instance, for a given H α flux, galaxies with stronger continuum will be harder to detect. Figs 10 and 11 show the distribution of the H α fluxes and equivalent widths (WH α) for the 124 ELGs in our sample. We are able to detect galaxies with H α fluxes as low as ∼1.3 × 10−17 erg cm−2 s−1. Given the relatively small sample presented in here (only galaxies in F21 and F22), we leave for a later paper a detailed discussion of the H α flux and equivalent-width distributions and their dependence on the intrinsic properties of the galaxies and the environment. Reassuringly, the WH α distribution we obtain is broadly compatible with the one found by Balogh et al. (2004). For equivalent widths larger than ∼20–30 Å the distribution declines steeply, following roughly a power law. At lower equivalent widths, the distribution flattens out until incompleteness probably kicks in below ∼5 Å. When interpreting our data it is important to bear in mind that the sensitivity of our survey declines for lower equivalent widths.
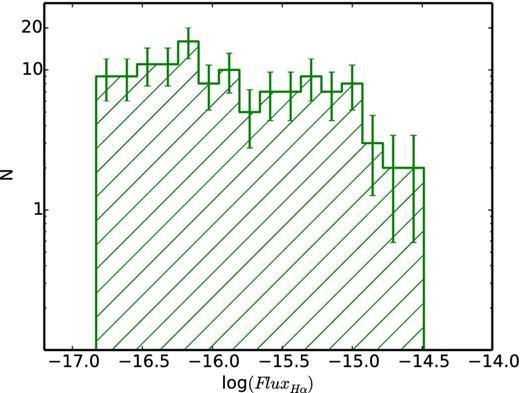
The distribution of the H α flux for the 124 ELGs in our sample, where the error bars are |$1/\sqrt{N}$|.
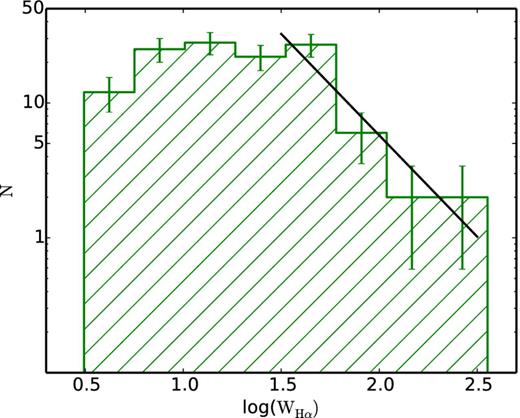
The distribution of WH α for the 124 ELGs in our sample, where the error bars are |$1/\sqrt{N}$|. For equivalent widths larger than ∼20–30 Å the distribution declines steeply with incompleteness kicking in below ∼5 Å. We have fitted a line with slope −1.5 and an intercept of 3.8.
Due to the complex nature of the H α detection process, it would be very difficult to model accurately the detection limits and the completeness of our sample from first principles. Instead, we follow an empirical approach that takes advantage of the wealth of data available from the STAGES data base. H α emission is expected to be present in blue, SF galaxies. Moreover, many red spirals have been shown to have a certain degree of star formation (Wolf et al. 2005). Here, we compare our H α detections with the numbers of blue-cloud and red spiral galaxies (SF candidates) in the STAGES catalogue in order to evaluate how efficient the OMEGA survey is at detecting SF galaxies and to assess the sample completeness.
In the top panel of Fig. 12, we show the mR distribution for the galaxies in our sample where H α has been detected (green). For comparison, we overplot in yellow the distributions for all COMBO-17 cluster galaxies in the same FOV and in blue those identified as SF. SF galaxies are either blue-cloud or red-spiral galaxies (Gray et al. 2009). The dashed histograms show the same COMBO-17 samples corrected for completeness and contamination (see below). One caveat here is that we do not separate the so-called retired galaxies (Cid Fernandes et al. 2011; Yan & Blanton 2012), which also have H α emission, from the SF ones. More details are given in Section 5.1, when we discuss AGN activity.
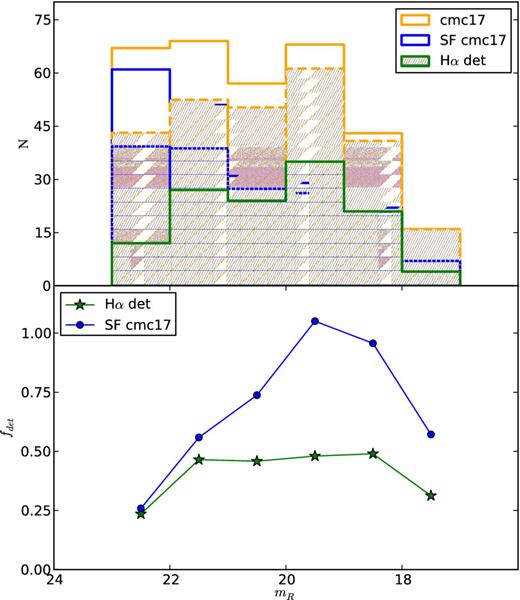
Top panel: the mR distribution of galaxies determined to be cluster members using the COMBO-17 photometric redshifts (sample denoted cmc17, in yellow), and the subset of these that are expected to be SF (galaxies classified as blue cloud or red spiral, in blue). The dashed histograms indicate the same cmc17 and SF cmc17 samples, but corrected for completeness and contamination as discussed in the text. The green square-filled histogram is the distribution of galaxies for which H α has been detected in our OSIRIS spectra. Bottom panel: the H α detection rate, expressed as a fraction of the full sample of cluster members (fHα det; green stars) and as the fraction of SF cluster members (fSFHα det; blue circles), plotted as a function of mR. See text and equations (8) and (9) for details.
The parent sample of COMBO-17 galaxies in F21 and F22 contains ∼1400 objects, with 326 galaxies expected to be cluster members (listed in the STAGES catalogue as having 16.0 ≤ mR ≤ 23 and combo_flag >3) with stellar masses 9.0 ≤ log (M⋆/M⊙) ≤ 11.5. Of these, 203 are either red spirals (sed_flag_cl = 2) or belong to the blue cloud (sed_flag_cl = 3), both thus considered to be SF galaxies, based on their COMBO-17 SEDs. We securely detect H α in 124 objects. From this, we estimate that we are able to detect H α in ∼40 per cent of the cluster members and in ∼60 per cent of the cluster SF galaxies more massive than 109.0 M⊙.
We effectively detect H α for all SF cluster members brighter than mR ∼ 20. Fainter than this, the completeness drops off, as expected – only galaxies that are bright in H α are detected. Note that the apparent drop for galaxies brighter than mR ∼ 19 is due to low number statistics in the brightest bins. As a fraction of all cluster members, the completeness does not depend strongly on mR since at lower masses a greater fraction of cluster galaxies are SF. Note that fdet > 1 means that we are detecting H α in more galaxies than are expected to be SF (based on the sed_flag_cl flag). This reflects both the uncertainty in the COMBO-17 SED classification and the high sensitivity of our survey.
5 RESULTS
As a preview of the kind of scientific issues that we will be able to address using OMEGA data, in this section we identify SF galaxies and AGN from our ELG sample, and investigate their properties, including mass and morphology. This is done by cross-matching our OMEGA observations with the STAGES catalogue (Gray et al. 2009). In addition, we present the H α luminosity function (LF) in the densest regions in order to understand how comparable our H α SFRs are to literature values of other sources. We finally compare our H α-derived SFRs to UV and IR ones from Gray et al. (2009). In subsequent papers, we will present a full analysis for the complete data set.
5.1 AGN and star-forming galaxies
In Fig. 13 we show the WHAN (Cid Fernandes et al. 2010, 2011) diagram for our ELGs. Here, we use the RPSF aperture, as this provides the cleanest measurement of the nuclear emission of the galaxy. The WHAN diagram is an alternative economical form of the widely used BPT diagnostic diagram (Baldwin, Phillips & Terlevich 1981). Cid Fernandes et al. (2010, 2011) have convincingly shown that the ratio of |$[\mathrm{N}\,\small {II}]$| to H α is truly powerful in separating AGN from SF galaxies, especially when the equivalent width of H α is also considered.
![A diagnostic plot of $[\mathrm{N}\,\small {II}]\,/\,\mathrm{H}\,\alpha$ versus WH α, the so-called WHAN diagram (Cid Fernandes et al. 2010). The vertical and horizontal lines separate regions with different sources of ionization (Cid Fernandes et al. 2010, 2011). We only show detections using RPSF aperture measurements where both H α and $[\mathrm{N}\,\small {II}]$ fall in the OMEGA probed wavelength range: a total of 82 ELGs. From these, we find 10 secure (≥3σ confidence) AGN hosts (Seyferts; red circles) and 16 star-forming (SF) galaxies (blue stars). The green points represent galaxies for which the classification is uncertain and/or contain mixed sources of ionization.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/450/4/10.1093/mnras/stv779/2/m_stv779fig13.jpeg?Expires=1750285007&Signature=1w9KVV8oA2CLFCZ3p3snPJrifbD7yU2kdHrLI3bizVloUBrPLYdbuYGiqL7lfUDE5vR~nKoPVYBue6gDlQoIqihFANJ6a3EkGEtSulneKAk8272bXX8UHvEe-Ptx26fXu4-R6ChlasV2bZtzAT8uvHs0NlI7Vc4AntDN4ScR5oZXnV96R-BKJVPbakkoqKJbq8h4SzJF02~85F04bPdCh7kPj4zuKfoj838HvakL8VT-PD8zV9SxUSp0nTqEl6UteMkjrgfKLjNTVV6jjY7IL9tgLqJruQsXvXYD9pZYqs-BkH9yF4EvfNBB~tQVip4PFJdJBxGnJmpex7RV6BL9yA__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
A diagnostic plot of |$[\mathrm{N}\,\small {II}]\,/\,\mathrm{H}\,\alpha$| versus WH α, the so-called WHAN diagram (Cid Fernandes et al. 2010). The vertical and horizontal lines separate regions with different sources of ionization (Cid Fernandes et al. 2010, 2011). We only show detections using RPSF aperture measurements where both H α and |$[\mathrm{N}\,\small {II}]$| fall in the OMEGA probed wavelength range: a total of 82 ELGs. From these, we find 10 secure (≥3σ confidence) AGN hosts (Seyferts; red circles) and 16 star-forming (SF) galaxies (blue stars). The green points represent galaxies for which the classification is uncertain and/or contain mixed sources of ionization.
Using the probability density distributions obtained for the continuum level and fluxes in H α and |$[\mathrm{N}\,\small {II}]$|, we can obtain the probability density distributions of the WH α and the |$[\mathrm{N}\,\small {II}]\,/\,\mathrm{H}\,\alpha$| flux ratio. Assuming standard values to differentiate sources of ionization in the WHAN diagram (cf. Fig. 13), we can therefore calculate the probability for each galaxy in our sample being dominated by star formation or AGN activity. Following this, 10 objects have a greater than 99.7 per cent probability (≥3σ confidence) of hosting a dominant AGN (Seyfert; red circles), while 16 have a similar probability of being SF-dominated (blue stars). The remaining 56 galaxies (green points) have less certain classifications due to the observational uncertainties on |$[\mathrm{N}\,\small {II}]\,/\,\mathrm{H}\,\alpha$|. Obviously, it is possible to classify galaxies into SF and AGN with less certainty by lowering the probability threshold. This would increase the size of the SF and AGN samples, but the confidence for each individual object would be reduced. Nevertheless, since we have robust probability distributions for the line ratios, the statistical properties of such samples can still be analysed rigorously. It is important to bear in mind, however, that in reality there is no hard division between SF- and AGN-dominated systems. Better observational errors would place the galaxies more accurately on the WHAN diagram, but since the boundaries are somewhat fuzzy (and depend on other physical parameters such as metallicity and interstellar medium density), the classifications would, in many cases, remain uncertain: a significant fraction of the green points may well contain mixed sources of ionization.
One interesting population revealed by the WHAN diagram is the so-called retired galaxy population (Cid Fernandes et al. 2011; Yan & Blanton 2012; Stasińska et al. 2015). They are located in the bottom-right part of such diagram, which is also occupied by LINER-type AGN. These retired galaxies have stopped forming stars, their gas is believed to be ionized by hot low-mass evolved stars, and they do not have a detectable contribution from an AGN. Furthermore, their H α emission is often extended (Belfiore et al. 2015). This population will be addressed in detail in a subsequent paper, when we analyse the resolved emission-line images.
In the following, we explore how the properties of the SF galaxies and AGN hosts that we have identified compare to one another and to the overall population of ELGs. We consider here their total mR, morphologies and stellar masses.
In Figs 14 and 15, we present histograms of mR and stellar masses for the ELGs with both H α and |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| secure detections. The distributions of the secure AGN (Seyferts) and SF objects are also shown. Galaxies hosting AGN are brighter in the R band and more massive than SF galaxies. Moreover, the overall behaviour of the H α-detected galaxies appears to mimic the mass and mR distribution of SF galaxies, suggesting that the majority of the galaxies with uncertain classifications are SF-dominated.
![The distribution of the R-band magnitudes from COMBO-17 for ELGs with detected $[\mathrm{N}\,\small {II}]\,\lambda 6583$ and H α (green line), as well as for the subsamples of high-confidence AGN (Seyferts; red histogram) and SF objects (in blue). See text for details.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/450/4/10.1093/mnras/stv779/2/m_stv779fig14.jpeg?Expires=1750285007&Signature=eErA0YVwPaw72OLRB~XmlR9qSEDy6Kd5x0ZUXj3GcWO6NWGgLN5gzo8EhzdH6h24TgMP6PG8qtG1sq0z7qEBt333VY3j1Cyt9EtIyDAHx5OnRkf3rLfuFuvn0JJ~h92mzQy3eZYgUNMUL3FZczRrW3Tsj-CTcnN6zQxDlbbMP6hRwkQ6lLuMPO3T1e09-8Hlu5Py2Xf-ZBE9hXualuv-UyUqCKMxd~7vp14ueGQ9eglnVPn~65vmSZ7HRVzfmE2YSbzg-QBGNuOg1hbudEIanOOlzL0aL3iZRYFn2qAQe~HDFSEsBb1rYd5rAZI5IXb4kKIZxr9g4rHrT-9r5E4TIg__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The distribution of the R-band magnitudes from COMBO-17 for ELGs with detected |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| and H α (green line), as well as for the subsamples of high-confidence AGN (Seyferts; red histogram) and SF objects (in blue). See text for details.
![Stellar mass distribution for ELGs with detected $[\mathrm{N}\,\small {II}]\,\lambda 6583$ and H α, together with the AGN and SF subsamples. Object selection and lines as in Fig. 14.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/450/4/10.1093/mnras/stv779/2/m_stv779fig15.jpeg?Expires=1750285007&Signature=LEYNBEhiKEdgj89TEVH8pwjxDDmUe8XKrYzbF06240fvSj3XjJTHaRZ78hGB~lniXMoLM3VpcLKDtG5XIp888d9qp42iptEp164aQJ~6rMEhjXRrGDuBRaLHZrPNS9LkGA3G--vikuLQ6LMjuptETJfxd1mLKuNW8HPdL1nvGioNlJYbpkXrmWYu~WqvkcnzJUymRoA3uDMDAxZ2kHFztJ~nHh7McVkVhKrSNaYvwYHjz6soslePhU2oHzzUzCK22SgZrXetcFlC-Xd28gVJv-8t3B-9viITER6a7x2A02E8z-ZAOQ5NNRDdAlwCrPJGYYGZKzbv5Zg0IcDrR4WCrw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Stellar mass distribution for ELGs with detected |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| and H α, together with the AGN and SF subsamples. Object selection and lines as in Fig. 14.
In Fig. 16, we show the distribution of morphologies. Galaxies determined to be hosting AGN with ≥3σ confidence are typically of earlier type than those for which the dominant source of ionization is SF or uncertain.
![The distribution of morphologies for ELGs with detected $[\mathrm{N}\,\small {II}]\,\lambda 6583$ and H α as well as the subsamples of the high-confidence (≥3σ) AGN and SF objects.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/450/4/10.1093/mnras/stv779/2/m_stv779fig16.jpeg?Expires=1750285007&Signature=VixELIxnX9UWrXSF3i3c~60UmhQIFrx7k7NeIlUqMyBaI6XIyNxKktOqYnzguOCLtltBOvd269ZBfgP-MdEPUzBr1~Ys2NZFLSmyIIbOjgrU7U5vfQhc952k4gmzDumy8Tl7Fy4mCUDO14F8cORdNpIjB~Nol2QhS6BzzVyWVL67m15OKnMUEITsb9sJAn157ecWP5g~4ycO3TVPEWdBuEVrJ1j6bPgebN9GOhKYIPBB0y4Y4-x2eYgUh3oFqDdg3NlP9EBV5W-AatoDNsLZAUIR8njeFaC7BNu6bJcEX0P5bswbPoxHoAQLnA9moW9Bmt44P9spoa3KvUCpi2yE6g__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The distribution of morphologies for ELGs with detected |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| and H α as well as the subsamples of the high-confidence (≥3σ) AGN and SF objects.
In Fig. 17, we show the distribution on the sky of the galaxies in the F21 and F22 regions down to mR < 23 that are classified as cluster members in the STAGES catalogue. Galaxies with more than 3σ confidence of being AGN- or SF-dominated (see Fig. 13) are denoted by red and blue filled circles, respectively, whereas other H α secure detections are indicated by filled green circles. The centres of A901a and A902 are marked with black crosses and are defined as the location of the brightest cluster galaxies. We note that secure SF and AGN galaxies are located towards the outer parts of the clusters and are completely absent in the central regions, especially when looking at F22.
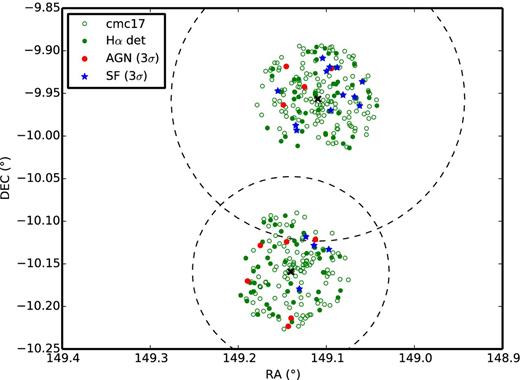
The distribution on the sky of the cluster galaxies (as determined by COMBO-17; denoted cmc17 in the legend) in the F21 and F22 regions down to mR < 23. ELGs (where H α has been securely detected) are represented by green filled circles. Galaxies classified as AGN or star forming with ≥3σ confidence are shown as solid red circles and blue stars, respectively. The centres of A901a and A902 (determined from the brightest cluster galaxies) are marked with black crosses. The large dashed circles show the r200 radii of A901 and A902 derived from the weak lensing analysis of Heymans et al. (2008).
Gilmour et al. (2007) presented a catalogue of XMM-detected point sources in the A901/902 field (see their table 12). From the 12 X-ray sources that they identify as likely AGN within the cluster, 4 objects fall in the FOV of F21 and F22. Only one of them is part of our ELG sample with securely detected H α (ID11827). However, this galaxy is not classed as an AGN because the |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| line used in the classification process falls outside the wavelength range probed by the F22 observations. Reassuringly, the |$[\mathrm{N}\,\small {II}]\,\lambda 6548$| line is detected and, based on its intensity, this object has a 93.5 per cent probability of being an AGN. Moreover, preliminary analysis of an overlapping field (which samples a slightly different wavelength range) indicates that |$[\mathrm{N}\,\small {II}]\,\lambda 6583$| is clearly detected for this object, indicating that it is probably an AGN. For a second X-ray AGN (ID41435) neither H α nor |$[\mathrm{N}\,\small {II}]$| fall in the wavelength range probed by our observations. For the remaining two X-ray AGNs (ID12953 and ID44351), our observations sample both H α and |$[\mathrm{N}\,\small {II}]$| but their H α lines are below our detection probability threshold (P(FHα > 0) < 99.7; see Section 4.2) and therefore do not make it into our ELG sample. In summary, one out of the four X-ray AGNs that we could have detected is also highly likely to be an optical AGN. The others have either too faint emission lines or do not have H α or |$[\mathrm{N}\,\small {II}]$| in our probed wavelength range. It is possible that these objects may be heavily obscured Compton-thick AGN and therefore would not be expected to show optical signs of nuclear activity. On the other hand, the fact that none of the 10 highly likely optical AGN found in the OMEGA survey are associated with a Gilmour et al. (2007) X-ray source clearly shows that OMEGA is able to detect a large number of optical AGN with relatively weak or no X-ray emission.
5.2 The H α luminosity function
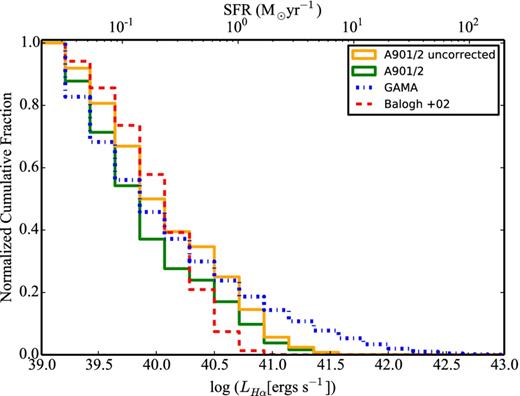
The cumulative H α luminosity function for the highest density regions of A901/2 corrected (solid green line) and uncorrected (solid yellow line) for contamination and completeness. For comparison, we show the H α LF from the cluster A1689 at z = 0.18 (blue dash–dotted line; Balogh et al. 2002) and the field from the GAMA survey at z = 0.1–0.2 (red dashed line; Gunawardhana et al. 2013). The densest regions studied by OMEGA have SFRs that fall in between those of the cluster A1689 and the field.
For comparison, we show the A1689 LF (at z = 0.18) from Balogh et al. (2002) as well as the field H α LF from GAMA (Gunawardhana et al. 2013). For the field H α LF we use the best-fitting parameters of the Saunders function (Saunders et al. 1990) that Gunawardhana et al. (2013) obtain for the redshift bin z = 0.1–0.2 (log L* = 34.55, log C = −2.67, α = −1.35, σ = 0.47) to reconstruct the corresponding normalized cumulative fraction. For A1689, we use the Schechter function parameters: α = −0.1 and L* = 1040 erg s−1 given by Balogh et al. (2002), to reconstruct the cumulative H α LF. Compared to the field sample from Gunawardhana et al. (2013), the densest parts of A901/2 contain galaxies with lower, on average, SFRs. Conversely, A901/2 hosts brighter H α emitters than A1689. This is not a surprise, as A1689 is a more evolved and denser cluster than the densest regions of A901/2 (Lemze et al. 2009; Alamo-Martínez et al. 2013). We conclude that in the densest regions of the A901/2 system star formation has been significantly suppressed compared to the field, but not as much as in denser, more evolved, cluster environments.
5.3 Star formation rates
The SFR–stellar mass relation is a useful diagnostic for the star formation properties and history of a galaxy population. In this parameter space, there is a reasonably well-defined main sequence whose properties have been characterized at different redshifts (see e.g. Whitaker et al. 2012). Several tracers across the electromagnetic spectrum may be used to estimate the SFR of a given galaxy. The STAGES catalogue of Gray et al. (2009) provides UV and IR SFRs for the A901/2 region. Rest-frame UV light originates mainly from massive stars and thus directly traces young stellar populations (with main-sequence lifetimes ≲ 108 yr); however, it is strongly attenuated by dust. The SFR from the UV continuum is often dubbed ‘current SFR’. The interstellar medium associated with an SF region can be quite dusty, so a significant fraction of the UV luminosity produced by massive young stars can be absorbed. This radiation heats the dust and is re-emitted in the far-infrared. Moreover, the interstellar medium around young massive stars is ionized by the Lyman-continuum photons they emit. The recombination of this ionized gas produces H α emission lines. The SFR from the H α nebular emission is often dubbed ‘instantaneous SFR’, tracing stars with main-sequence lifetimes of ≲ 2 × 107 yr (Mo, van den Bosch & White 2010). In the following figures, we adopt an H α SFR with 1 mag of extinction (see equation 11). At this point, we do not attempt to subtract the AGN contribution to the SFR from the H α fluxes. Resolved star formation properties will be studied in a subsequent manuscript.
We compare our H α SFR against those from other available tracers in Fig. 19. The UV SFRs are based on the UV luminosity estimated using the 2800 Å rest-frame luminosity from COMBO-17, which has a complete coverage around the A901/2 multicluster system. The UV SFRs have been corrected for extinction as part of the SED-fitting procedure. Details can be found in Gallazzi et al. (2009) and Wolf et al. (2009). The IR SFRs are determined from Spitzer/MIPS 24 μm data. In the cases where there was no detection in the IR, upper limits to the SFRs were estimated (Wolf et al. 2009). The green data points (denoted ‘UV+IR’ in the figure legend) represent the composite SFR measurements. Note that these points, which account for the obscured and unobscured star formation, are, on average, ∼0.3 dex above the one-to-one line. This difference may be due to the H α SFR estimates missing heavily obscured SF, but it could also be indicative of a declining SFR, given the different time-scales of the indicators. In the case of the SFRs from the UV alone, the correlation with the H α SFR is stronger, which is not surprising as the UV and H α are sensitive to comparable SF time-scales, with the UV tracing slightly longer ones than H α. However, there is also a clear ∼0.3 dex offset since the effect of extinction is significantly stronger in the UV than in the red.
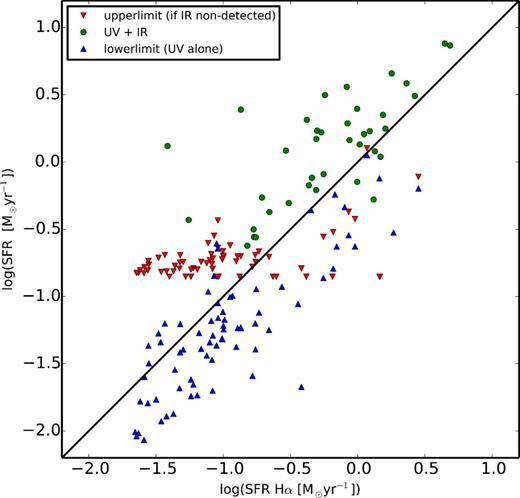
The log SFRHα determined from Rtot aperture measurements compared with other estimates of log SFR. See legend and text for details on the meaning of the different data points.

Stellar mass versus SFR(H α) determined from Rtot aperture measurements. The galaxies with a 3σ confidence of being AGN- or SF-dominated, with selection based on the PSF aperture (see Fig. 13) are denoted by red circles and blue stars, respectively. The dashed-line is an SFR–mass relation for field star-forming galaxies at z = 0.167 (Whitaker et al. 2012). Comparing our secure H α detections to the dashed-line representing the field galaxies indicates a suppression of star formation in these high-density regions.
The stellar masses used by Whitaker et al. (2012) are derived from medium-band photometry using Bruzual & Charlot (2003) models that assume a Chabrier (2003) initial mass function (IMF), solar metallicity and the Calzetti et al. (2000) extinction law. The stellar masses that we use were estimated by Borch et al. (2006) using the COMBO-17 photometry in conjunction with a template library derived using the PEGASE stellar population models (Fioc & Rocca-Volmerange 1997) with solar metallicity and a Kroupa (2001) IMF. The different IMFs used by Whitaker et al. (2012) and Borch et al. (2006) would only change the stellar masses by ∼10 per cent. Moreover, the stellar masses derived in these works are quantitatively consistent with those derived using a simple colour-based stellar mass-to-light ratio (Bell et al. 2003). We are therefore confident that the stellar masses used here can be directly compared, and that any systematic differences will not affect our conclusions. The SFRs estimated by Whitaker et al. (2012) are based on UV+IR indicators, and are therefore expected to be on average ∼0.3 dex higher, than the H α-based ones. This has to be taken into account when comparing our data with that of Whitaker et al. (2012). Nevertheless, even if we consider such offset and any likely systematic uncertainties, it is clear that most of our H α-detected galaxies would still fall clearly below the field SFR–mass relation, consistent with the differences found between our H α LF and the field one (Fig. 18). This confirms that many of the SF galaxies located in the centres of the A901/2 clusters appear to have their SFR significantly suppressed relative to the field. This suppression seems to occur at all stellar masses.
At first sight, this seems to contradict previous results which suggest that the average SFR in SF galaxies remains roughly constant with environment, and it is only the fraction of SF galaxies that changes (Balogh et al. 2004; Bamford et al. 2008; Poggianti et al. 2008; Verdugo et al. 2008). However, this contradiction is only apparent. The relative fraction of SF and non-SF galaxies depends on the depth of the survey. Because we are able to detect very low H α fluxes (and thus very low levels of star formation), our sample contains H α-emitting galaxies that would have been missed by most other surveys. Therefore, strongly suppressed galaxies still appear as H α emitters in our sample. Cluster galaxies with strong star formation (exemplified by the blue stars in Fig. 20) have levels of SF comparable with those found in the field. If only galaxies with strong star formation are detected in a survey, it would appear that their SF has not been suppressed. Since galaxies with very low levels of star formation would not have been detected in H α in most other surveys, they would have been (erroneously) classified as non-SF and one would conclude that only the relative fraction of SF and non-SF galaxies has been affected by the environment.
Wolf et al. (2009) reached the same conclusion based on rest-frame UV and 24 μm data of Abell 901/2. They found a large population of lower SFR galaxies, mostly red spiral galaxies seemingly in transition from normally SF galaxies to quiescent ones. This population had higher FIR luminosities than expected from their broad-band optical colour alone, suggesting that the specific SFR (SSFR) of the average red spiral at a given stellar mass was only three times lower than the SSFR of the average blue spiral at similar mass. An earlier study by Wolf et al. (2005) had already revealed this population from optical photometry alone, using medium-band imaging to discriminate between red colours due to high age in the absence of dust and those due to moderate age in the presence of moderate amounts of dust, thus differentiating between what they called ‘old red’ galaxies and ‘dusty red’ galaxies. The average SSFR estimated from |$[\mathrm{O}\,\small {II}]$| emission in their ‘dusty red’ population was four times lower than that in blue galaxies. While this paper investigates only a small part of the same cluster, we find a similar transition population in SFRs estimated from H α now. We are thus suggesting that this cluster contains a rich population of moderately SF galaxies filling the previously considered gap between non-SF and SF galaxies. This view is now supported by evidence from a range of tracers, from UV and 24 μm, from |$[\mathrm{O}\,\small {II}]$| and Hα emission, and from a detailed analysis of the optical SED. A detailed study of the environmental dependence of the SF for the full galaxy sample will be presented in a subsequent paper.
6 SUMMARY AND CONCLUSIONS
In this paper, we have introduced the OMEGA survey. The ultimate goal of this project is to study star formation and AGN activity across a broad range of environments at a single redshift. Using the tuneable-filter mode of the OSIRIS instrument on the 10.4 m GTC we have targeted H α and |$[\mathrm{N}\,\small {II}]$| emission lines over an ∼0.5 × 0.5 deg2 region covering the z ∼ 0.167 multicluster system containing Abell 901 and 902.
Based on observations of 2 out of the 20 fields covered by this survey, this paper outlines the data reduction procedures followed and describes the analysis we have developed in order to reliably measure the fluxes and equivalent widths of the H α and |$[\mathrm{N}\,\small {II}]$| lines. We present the quantitative criteria used to define a robust sample of ELGs and analyse its properties in terms of detection efficiency, detection limits and completeness. This paper also presents some examples of the kind of science that can be done with the survey. The scientific results we discuss are based on only 10 per cent of the surveyed area, corresponding to the highest density regions of the A901/2 structure. An analysis of the full survey is left for future papers, but interesting results are already emerging.
In these two fields, we detect 124 ELGs down to H α fluxes ∼1.3 × 10−17 erg cm−2 s−1, corresponding to H α luminosities ∼1039 erg s−1 at the distance of the A901/2 system. This allows us to probe integrated SFRs as low as ∼0.02 M⊙ yr−1. We estimate that we are able to detect H α emission in ∼40 per cent of the cluster members with stellar masses above ∼109 M⊙, and ∼60 per cent of the galaxies expected to be forming stars according to their SEDs in the same mass range.
Using the WHAN diagram (Cid Fernandes et al. 2010, 2011), which plots WH α versus the |$[\mathrm{N}\,\small {II}]$|/H α ratio, we are able to identify 10 bona-fide AGN in the Abell 901 and 902 clusters. The AGN hosts tend to be brighter and more massive than the SF galaxies. Moreover, the AGN host galaxies usually have earlier morphologies than the general SF galaxy population.
The ELGs we detect, both SF and AGN, tend to avoid the central highest density regions of the clusters.
The H α LF of the galaxies in the densest regions of Abell 901/2 contains brighter H α emitters than that of more massive and richer clusters at comparable redshifts (e.g. Abell 1689 at z = 0.18). However, our sample contains a lower proportion of very luminous H α emitters than the field galaxy population at similar redshifts. This indicates a progressive suppression of the star formation activity in galaxies when we move from the field to clusters of increasing richness/mass.
The SFR–stellar mass relation we observe in the densest regions of A901/2 falls well below the relation for field galaxies found by Whitaker et al. (2012) at similar redshifts. In other words, the average specific SFR (or SFR per unit stellar mass) is significantly lower in these clusters that in the field, confirming the star formation suppressing effect of the clusters.
The SFRs determined from the H α luminosities correlate very well with the SFRs estimated from the rest-frame UV photometry, but are typically a factor of ∼2 higher. The strong correlation indicates that the UV light and H α trace roughly comparable star formation time-scales but the effect of extinction is significantly stronger in the UV than in the red. H α-determined SFRs also correlate well with those determined combining the UV and IR emission, but the offset is now reversed: the H α SFR estimates would miss heavily obscured star formation and are thus a factor ∼2 smaller. Some of the difference could also be due to a declining SFR, since H α and the IR probe different star formation time-scales.
We have found that the OSIRIS tuneable filter is a highly effective instrument for mapping the emission lines of galaxies at z ∼ 0.2. In this paper, we have presented several good examples of its scientific capabilities and potential. These results have been obtained using only a small fraction of the complete OMEGA data set and therefore provide only a partial view of the star formation and AGN properties of the galaxies in the Abell 901/902 structure, biased towards the highest density regions. A more complete picture, covering a much broader range of environments, will emerge once the full sample is analysed in future papers. Moreover, here we have only considered the integrated emission-line properties of the galaxies. OMEGA also provides spatially resolved emission-line maps which will be used to study how the spatial distribution of the star formation is affected by internal and environmental factors. In future papers we will also explore the information on the chemical composition of the ionized gas encoded in the H α/|$[\mathrm{N}\,\small {II}]$| emission-line ratio.
Based on observations made with the Gran Telescopio Canarias (acquired through an ESO Large Programme), installed in the Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias, in the island of La Palma. Antonio Cabrera Lavers is thanked for invaluable support during the observations and Alessandro Ederoclite for advice with the use of OOPs. This work has made use of The University of Nottingham HPC facility, ‘Minerva’. ACS acknowledges funding from a CNPq, BJT-A fellowship (400857/2014-6). SPB and MEG gratefully acknowledge the receipt of an STFC Advanced Fellowship. AB is funded by the Austrian Science Foundation FWF (grant P23946-N16).
The first two authors have contributed equally to this paper.
Membership of the A901/2 cluster structure is determined taking into account the COMBO-17 photometric redshifts and their uncertainties. Given the high accuracy of these redshifts, the procedure maximizes completeness without introducing unacceptable contamination. Details are given in Section 3.3 of Gray et al. (2009). See, in particular, their fig. 13 and equation 8.



