Calcium-rich gap transients: tidal detonations of white dwarfs? Free

Abstract

1 INTRODUCTION

The field of time domain astronomy has recently exploded with the detection of many new classes of transient sources. Considerable progress has so far been made at optical wavelengths with the advent of a host of new programs designed to search for sources at a variety of cadences. They are also more sensitive to finding sources at different luminosities in the gap between that of novae and traditional supernovae (Kasliwal 2011). Some of the best-known current transient surveys are at optical wavelengths: the Palomar Transient Factory (PTF; Rau et al. 2009), the Panoramic Survey Telescope and Rapid Response System (Hodapp et al. 2004) and the Public European Southern Observatory Spectroscopic Survey for Transient Objects (Smartt et al. 2014). New observatories (e.g. the Large Synoptic Survey Telescope), including some at other wavelengths (e.g. the Square Kilometre Array, eRosita), are being planned as well. These observatories enable us to better map out the parameter space of known transients as well as discover new classes of transients.

One of the recently discovered classes is ‘calcium-rich gap transients’ – so called because their spectra contain strong forbidden and permitted calcium lines, and they have peak absolute magnitudes in the gap between classical novae and supernovae. These transients have a set of observational characteristics which distinguish them from other classes of optical transients. These properties are summarized well by Kasliwal et al. (2012, hereafter K12):

• similar to type I supernovae, showing no hydrogen lines in their spectra;

• absolute magnitudes in the range from −15.5 to −16.5 (a factor of about 10–30 fainter than the type Ia supernovae, which have M_R of about −19.3);

• characteristic velocities of approximately 6000–11 000 km s⁻¹;

• very large calcium abundances, as inferred from their nebular spectra;

• faster evolution than average type Ia supernovae with a rise time ≤15 d, whereas type Ia have rise times ∼18 d (though it is within the full range of type Ia rise times found; e.g. Hayden et al. 2010);

• current, small sample favours the outskirts of known galaxies.

As such, many of the properties of these objects are intermediate between those of classical novae and type Ia supernovae.

Previous studies of calcium-rich gap transients have used the common relations for type Ia supernovae to estimate some basic parameters of the explosion. K12 estimate the masses of the ejecta by setting the ejecta mass proportional to |$v t_r^2$| (v = photospheric velocity, t_r = rise time), as first suggested by Arnett (1982), and scaling to type Ia supernovae. This yields typical total masses of ∼0.3–0.7 M_⊙, where the fraction of ⁵⁶Ni produced is very small (e.g. 0.016 M_⊙ for PTF 10iuv). However, Arnett's modelling explicitly requires that there be substantial ⁵⁶Ni in the supernova ejecta, and modelling of the nebular spectrum of SN 2005E in K12 gives a mass about half as large as the Arnett formula does. Type Ia supernovae are predominantly powered by radioactive decay of iron-peak elements, where the amount of nickel produced would be large and the amount of calcium produced would be small (e.g. Woosley, Taam & Weaver 1986; Bildsten et al. 2007). Therefore, the modelling falls short in properly describing the explosion.

Various models exist to explain the unusual characteristics of these transients, many of which are summarized in K12. Many of them have at least one serious flaw that makes them unable to explain these transients. To explain the calcium-rich gap transient, SN 2005E, Perets et al. (2010) concluded that they were witnessing helium detonation in an interacting double white dwarf (WD) system with a helium WD mass donor (Shen & Bildsten 2009; Waldman et al. 2011), but the light curve is not well matched. Various channels for the detonation of sub-Chandrasekhar-mass WDs exist (Woosley & Weaver 1994; Woosley & Kasen 2011), but such models do not provide a good match to the observed light curves. Accretion-induced collapse of a rapidly rotating WD into a neutron star (Metzger et al. 2009) is also ruled out based on the predicted shape of the light curves, as well as the large velocities and abundances of intermediate elements predicted. Recently, Metzger (2012) presented a one-dimensional nuclear-dominated thick accretion flow model resulting from the unstable mass transfer following Roche lobe overflow, but it does not produce the right amount of helium and calcium to match many of these transients. Some of the difficulty in finding a ‘best-fit’ model may arise in the heterogeneous nature of the current sample: there may be selection bias in finding these transients far from their host galaxies, a range of velocity widths in the lines in the nebular spectra, different light-curve evolutions, for examples.

In Metzger (2012), another scenario is mentioned: the tidal disruption of a WD by a neutron star or black hole (BH) leading to a nuclear runaway (detonation). Holcomb et al. (2013) also briefly discuss the conditions for successful helium detonation in low-mass WDs and it in the context of an anomalous supernova (one of the calcium-rich gap transients; Perets et al. 2010). However, an extensive discussion clearly pointing out many lines of evidence supporting the theory that the class of calcium-rich gap transients to tidally-induced detonations of low-mass WDs does not exist in the literature. Some other work has considered the tidal disruption of a WD in other contexts but without connection to calcium-rich gap transients. Clausen & Eracleous (2011) considered the emission spectrum after the disruption but not detonation of a WD by a BH; the spectrum is incomplete because they did not consider the fusion of heavy elements in the tidal debris (considered only mass fractions of 67 per cent oxygen, 32 per cent carbon, and 1 per cent helium). While investigating the vertical compression of tidally disrupted debris, Stone, Sari & Loeb (2013) noted the possible importance of WD tidal disruptions to gravitational wave signals. Finally, Shcherbakov et al. (2013) proposed that a highly unusual combination of a gamma-ray burst and a supernova explosion could be explained by a WD tidal disruption.

In this work we consider the tidal disruption leading to nuclear runaway (detonation) of WDs in more detail to explain the calcium-rich gap transients. The goal of the paper is mainly to discuss the plausibility of this scenario in connection to calcium-rich gap transients, something that has not yet been done in the literature. Future more detailed analyses of this scenario in the context of Ca-rich gap transients will need to be undertaken when better multiwavelength (especially high-energy) observations become available. These are needed to solve some of the large uncertainties and degeneracies in various model parameters discussed throughout the text.

In Section 2, we describe the model and how it can explain various observational characteristics: masses, abundances, light curves, and the positions of these sources. Then in Section 3, we discuss some possible scenarios that could produce the tidal detonation and calculate expected rates of these transients to verify if the proposed origin is plausible. In Section 4, we then analyse a Chandra observation of one of these transients, which enables us to place upper limits on the masses of the WD and BH in the progenitor system. Finally in Section 5, we summarize our results and suggest observational tests of our model.

2 MATCHING THEORY WITH OBSERVATION

We propose that the model developed by Rosswog, Ramirez-Ruiz & Hix (2009, hereafter R09) naturally explains the set of calcium-rich gap transients. R09 use a three-dimensional smoothed particle hydrodynamic method to simulate the close interaction between a WD and a more compact object (a BH) that completely disrupts the WD. When a WD passes too close to a BH (within the Roche or tidal disruption radius), the differential gravitational force from the BH will overcome the gravitational force of the WD. This tidal force can elongate the WD in the orbital direction and compress the WD in the direction perpendicular to the orbit to a high-enough density and pressure to initiate runaway nuclear burning. If the nuclear energy is greater than the binding energy of the star, an explosive nuclear detonation occurs, producing a luminous transient event.

The tidal disruption leading to the possible detonation of a WD will only occur when M_BH ≲ 2 × 10⁵ M_⊙ or stellar- or intermediate-mass BHs,¹ (IMBHs; see R09 for a more detailed discussion). R09 consider 100 M_⊙ < M_BH < 10 000 M_⊙, but BHs at a larger range of masses (up to M_BH ≈ 10⁵ M_⊙ or M_BH < 100 M_⊙) or even neutron stars may be viable detonators as well. Next, we discuss how each of a set of testable theoretical predictions of this model can be explained by current observations of this group of transients.

2.1 The mass of the detonated white dwarf and abundances of leftover material

There already exist a set of strong theoretical and observational ways to constrain the mass of the detonated WD in this scenario. We first explore the upper limit to the mass of the WD, which is most strongly motivated by the abundance patterns in the nebular spectra.

As implied by the name, these calcium-rich gap transients produce a relatively large amount of calcium. However, they do not produce a large amount of iron-peak elements (see the spectra in K12). This is only well matched to the tidal detonation scenario if M_WD ≲ 0.6 M_⊙ (R09). As R09 present the most realistic description of a tidal detonation of a WD to date, this is currently the best estimate of reaction rates in this scenario. However, there are some important limitations to this work. The upper limit to the WD mass is not very precise because the WD mass grids presented in R09 are very coarse and might be a function of other parameters (e.g. tidal radius relative to pericentre, BH mass). In addition, the exact boundary of the upper limit is also not well-determined because the nucleosynthesis calculations presented in R09 are based on a simplified nuclear reaction network.

This latter point is particularly important because this implies one cannot make specific abundance predictions from this model. For instance, silicon is taken to represent all the elements within the quasi-equilibrium group near silicon in this network. Therefore, given that calcium lies within this group, as does scandium, it should not be a surprise that large amounts of calcium are not specifically predicted. The tentative detection of strontium in one calcium-rich transient (Sullivan et al. 2011) would potentially present a problem, as strontium cannot be produced in this scenario, but it should be noted that this detection is of marginal significance and only has been seen in one object. A clear prediction of this picture is that, as a sample of events with well-measured abundances emerges, progressively higher ratios of the iron-peak elements to the elements near silicon in atomic number will be seen as the peak luminosities rise. However, since we expect a range of impact parameters for the tidal detonation model, future work may require a very large sample size to discern these trends.

In addition to the abundance analysis, which requires that M_WD < 0.6 M_⊙, the density-dependent Roche limit may favour the tidal disruption of lower mass WDs. Lower mass WDs have lower densities (ρ) because they are larger. Because the minimum distance at which an object is disrupted by tidal forces scales as ρ^−1/3, this may imply that lower mass WDs are more susceptible to stretching and compression, possibly making them easier to detonate. However, based on the limited number of grids in R09, it is not clear whether this susceptibility outweighs other effects (e.g. needing to reach a critical density to detonate, which would require more compression); more work on this topic is clearly needed.

If this is true, then this would imply that the lowest mass WDs are be preferred in this scenario. This is a problem for single-star evolution, as it only produces WDs with M ≳ 0.45 M_⊙ for the lowest mass evolved stars in the Universe (e.g. Marsh, Dhillon & Duck 1995; Kepler et al. 2007). However, binary processes can produce lower mass systems (common envelope evolution and Roche lobe overflow; e.g. Nelemans et al. 2001) and account for the low-mass WDs found in the last couple decades (e.g. Bergeron, Saffer & Liebert 1992; Bragaglia, Renzini & Bergeron 1995). The lowest mass WDs yet found are commonly referred to as extremely low mass WDs ∼0.2 M_⊙ and are helium dominated (e.g. Liebert et al. 2004; Kilic et al. 2007; Vennes et al. 2011; Hermes et al. 2013). Putting these constraints together, we conclude that 0.2 M_⊙ ≲ M_WD ≲ 0.6 M_⊙.

2.2 The continuing power source and light curve

Absorption lines in type Ia SNe tend to become narrower with time, as the outer layers become more diluted by the expansion of the ejecta and the line-forming region recedes to lower velocities (e.g. Filippenko 1997; Foley, Sanders & Kirshner 2011). However, Valenti et al. (2014) observe the opposite trend in one of the calcium-rich gap transients, SN 2012hn: constant photospheric velocity (as inferred from the blueshift of absorption lines) and increasing linewidths, which are better explained by a continuing energy source.

In supernovae, the radiative decay of nickel serves as a continuing source of energy after the original ejection of material in the explosion. However, as discussed in the previous section, iron-peak elements are not appreciably seen for calcium-rich gap transients nor would we expect them in this scenario. R09 find that, in the low-mass WDs (∼0.2 M_⊙), only about 0.03 M_⊙ of iron-peak elements are likely to be produced in the explosion, and the detonated 0.6 M_⊙ model produces an abundance of iron-peak elements ∼4 × less than the detonated 1.2 M_⊙ models.

Instead, the power source can be naturally explained by fall-back accretion of a fraction of the WD material on to the BH. The very hot inflow of gas (a few tens to hundreds of million K) not only produces an optical flare but also produces copious X-ray emission. The highly blueshifted and broadened lines (up to thousands of km s⁻¹) can be explained by motions of material associated with the accretion flow, as seen for both stellar and supermassive BHs (e.g. disc winds; Murray et al. 1995; Miller et al. 2008; King et al. 2012; Tombesi et al. 2015).

For instance, R09 show that for the detonation of a 0.2 M_⊙ WD by a 1000 M_⊙ BH, the accretion rate on to the central BH will initially be very large (∼10^−5.4 M_⊙ s⁻¹) for the first approximately 10 min and then decay as t^−5/3 (Rees 1988; Phinney 1989). Detailed modelling of the optical light curve using type Ia templates has been challenging for all previous work and is beyond the scope of this paper. Nevertheless, a comparison of the slope of late-time R-band light curve (∼10–100 d after the peak) of a few of the calcium-rich gap transients with well-sampled light curves (e.g. SN 2005E, PTF 10iuv) indicates that the tidal detonation scenario (⁠|$\dot{M} \propto t^{-5/3}$|⁠) seems to provide a better match than the exponential radioactive decay of ⁵⁶Ni as done in K12, even when taking into account more of the decay chain (⁵⁶Co and the kinetic energy loss from its β + decay; e.g. Dado & Dar 2013). Another more complicated possibility is that the optical light curves could be explained by the decay of lower mass elements (⁴⁸Cr → ⁴⁸V → ⁴⁸Ti and ⁴⁴Ti → ⁴⁴Sc → ⁴⁴Ca), producing late-time emission (Valenti et al. 2014).

Later on, when the accretion rate falls below the Eddington rate on to this BH, L_Edd ≈ 10⁴¹(M_BH/10³ M_⊙) erg s⁻¹ or |$\dot{M}_{{\rm Edd}} = 2.2 \times 10^{-5} (M_{{\rm BH}} / 10^3$| M_⊙) M_⊙ yr⁻¹ (standard radiative efficiency 0.1 assumed; e.g. Novikov & Thorne 1973), which occurs approximately 7 months after the detonation of a 0.2 M_⊙ WD around a 1000 M_⊙ BH in R09, the X-ray luminosity should begin to decay. However, the exact brightness and evolution of the X-ray bright phase depends a number of poorly constrained parameters: the WD's initial mass and trajectory, the mass of the BH and the structure of the initially super-Eddington accretion flow (e.g. Lodato & Rossi 2011; Jiang, Stone & Davis 2014), for example.

As an illustration of the importance of the assumed structure of the accretion flow, the viscous accretion time-scale is proportional to the ratio of the disc scaleheight to tidal disruption radius squared (Li, Narayan & Menou 2002; Metzger 2012). Accretion discs can radically vary in scaleheight depending on the accretion mode, which is tied to the efficiency of radiative cooling (Hayasaki, Stone & Loeb 2015). These uncertainties make the viscous dissipation time-scale uncertain by many orders of magnitude. This strongly affects our ability to apply upper limits to physically meaningful parameters (M_WD, M_BH) in our X-ray observations of one of the calcium-rich gap transients in Section 4.

2.3 Positional information

To date, the calcium-rich gap transients have been located predominantly on the outskirts of their host galaxies (if this is not a selection bias, which is not clear at the present time). Yuan et al. (2013) find that the transients are usually well beyond the extent of the nearby host galaxies (∼5 × the K-band half-light radius on average). They conclude that these transients do not trace the stellar-mass profile but could be matched to globular clusters or dwarf galaxies.

Initial non-detection limits for many of the sources (M_R ≳ −10–12 mag) required that host stellar clusters have L ≲ 10⁷ L_⊙ (Kasliwal et al. 2012). However, recent, much deeper observations searching for hosts for a couple of the transients have ruled out all but the faintest dwarf galaxies and globular clusters (M_R ≳ −5.3 mag for SN 2005E, M_R ≳ −5.6 mag for SN 2012hn and M_R ≳ −7.3 mag for SN 2003H; Lyman et al. 2014).²

For these systems, these observations make the scenario of the tidal detonation of a WD caused by a random, flyby encounter with an IMBH very unlikely because the encounter rate would be too small without the presence of a dense stellar system. In these cases, interactions producing high-velocity runaway systems must be considered (Foley 2015), where the detonations occur in isolated three-body systems. We provide a detailed discussion of random encounter rates and possible three-body interaction scenarios that can satisfy these requirements in Section 3.

2.3.1 Can these stellar systems survive?

3 SPECIFIC ORBITAL SCENARIOS AND RATES DISCUSSED

As discussed in the previous section, likely host systems for these transients are faint dwarf galaxies or globular clusters given our scenario. Precise rate predictions for this scenario cannot be calculated at the present time due to considerable uncertainties in multiple key parameters: the fraction of globular clusters and faint dwarf galaxies which contain intermediate- or stellar-mass BHs, the masses of those BHs, the masses of the WDs that might be detonated, the structural parameters (and hence central stellar densities) of the clusters and/or faint dwarf galaxies which contain those BHs, etc. We only consider rough estimates to test if this model is plausible or not. A thorough analysis is well beyond the scope of this paper and is very challenging because it would have to be quite complex, taking into account (not an exhaustive list): the binary fraction around the primary BH, general relativistic corrections, stellar densities, the replenishment rate of the loss cone of the BH, the spin of the BH, the mass ratio of the BH in the case of a binary, etc., while having good observational constraints for the relevant parameters.

We consider two basic plausible scenarios in which a WD could get close enough to a BH with M_BH ≲ 10⁵ M_⊙ to be tidally disrupted: (1) the chance flyby of a single WD to an IMBH and (2) the perturbation of a three-body system, which is especially needed for the stellar-mass BHs with lower interaction cross-sections (⁠|$\propto R_{{\rm BH}}^2 \propto M_{{\rm BH}}^2$|⁠). Then we consider how these ideas fit with the locations of these events.

3.1 Chance white dwarf flyby of an intermediate-mass black hole

Given the larger interaction cross-section of an IMBH, chance flybys in dense stellar systems could occur often enough to be observable calcium-rich gap transients. Rate estimates testing for plausibility are easier to make for globular clusters, so we consider them first, despite the fact that the positions of the transients far from the centres of bright nearby galaxies may favour faint dwarf galaxies as the sites of the explosions.

3.1.1 Rates in globular clusters

Baumgardt, Makino & Ebisuzaki (2004) estimate a rate of ∼10⁻⁹ WD tidal disruptions per globular cluster per year, assuming typical clusters have a 1000 M_⊙ BH and a central stellar density of 10⁵ stars parsec⁻³. Given ∼400 globular clusters per typical Milky Way-like galaxy (taking a number larger than that for the Milky Way, since its specific frequency of globular clusters is relatively low; Galleti et al. 2007), and a density of galaxies of about 1 Mpc⁻³, then within 200 Mpc, there should be ∼10¹⁰ globular clusters within the distance range out to which the calcium-rich gap transients have been seen. If ∼10 per cent contain IMBHs, then it would be reasonable to expect ∼1 tidal detonation per year. Given that the tidal disruption rate goes as the square of the BH mass (Baumgardt et al. 2004), the rate would be expected to increase in the event that there is a broad distribution of BH masses. The crude rate calculation can be taken as evidence of plausibility, under the assumption that some non-negligible fraction of globular clusters contain IMBHs.

At the present time, the evidence that globular clusters contain IMBHs is weak. Some claims have been made on the basis of stellar dynamical evidence for an increase in the characteristic velocities of stars in the centres of a few clusters (e.g. Newell, Da Costa & Norris 1976; Gerssen et al. 2002; Gebhardt, Rich & Ho 2002; Noyola, Gebhardt & Bergmann 2008). On the other hand, in most cases, the data can be equally well explained by mass segregation of neutron stars and WDs down to the central regions of the cluster, causing an increase in the mass-to-light ratio without an IMBH (e.g. Illingworth & King 1977; Baumgardt et al. 2003). Alternatives to radial velocity searches, such as proper motion searches for dynamical evidence (McLaughlin et al. 2006; Anderson & van der Marel 2010) and searches for radio emission (Maccarone 2004; Maccarone, Fender & Tzioumis 2005; de Rijcke, Buyle & Dejonghe 2006; Bash et al. 2008; Maccarone & Servillat 2008; Cseh et al. 2010; Lu & Kong 2011; Strader et al. 2012) have failed to find any IMBHs in Galactic globular clusters. The M31 cluster G1 does show both dynamical evidence for a BH and radio emission (Ulvestad, Greene & Ho 2007), although more recent radio follow-ups have failed to detect a source at that position, indicating either that the detection was spurious or the source is strongly variable (Miller-Jones et al. 2012).

Despite the lack of evidence thus far for IMBHs in globular clusters, IMBHs may have been more easily formed through the formation of more massive stars in lower metallicity environments (e.g. Belczynski et al. 2010). This may also be helpful because it does not require the merger of stellar-mass BHs (e.g. Miller & Hamilton 2002), where the gravitational radiation rocket effect (Redmount & Rees 1989) can eject the IMBH from the cluster (Holley-Bockelmann et al. 2008). Indeed, deep observations of globular clusters around the Galaxy and other galaxies over the last few decades have discovered globular clusters at large galactocentric radii and shown that they have low metallicities (e.g. Searle & Zinn 1978; Rhode & Zepf 2004). However, whether or not the globular cluster radial composition gradient (Zinn 1985) extends farther out into the halo is not clear (Van Den Bergh 2003).

As discussed Section 2.1, the tidally disrupted object must be a low-mass WD and is likely a helium WD. Unfortunately, the number density of helium WDs in globular clusters is not well known. Helium WDs cannot form at the present epoch through normal single-star evolution; they can only form through binary evolutionary processes (see e.g. Hansen, Kalogera & Rasio 2003). In globular clusters, this can happen through a direct collision between a red giant and a compact star. This mechanism has been proposed for producing the ultra-compact X-ray binaries in globular clusters (Verbunt 1987) and is probably at work in NGC 6397 (Grindlay et al. 2001; Taylor et al. 2001; Hansen et al. 2003; Strickler et al. 2009).

Placing observational constraints on the density of helium WDs in nearby globular clusters is extremely difficult because they are so faint and may not be possible because they should escape from the centres due to mass segregation (e.g. Fregeau et al. 2002). Only in the presence of an IMBH, which appears to be absent in these systems, is mass segregation quenched because the interactions with the IMBH dominate over the interactions with other stars (Gill et al. 2008).

3.1.2 Rates in dwarf galaxies

Observations clearly show a dearth of dwarf galaxies within a few tens of kpc and those found in this region are highly disturbed (e.g. Saggitarius Dwarf, M32, Willman 1, Ursa Major II; Johnston, Spergel & Hernquist 1995; Bekki et al. 2001; Willman et al. 2005; Muñoz, Geha & Willman 2010). The ‘classical’ dwarf spheroidal galaxies orbiting the Milky Way are all located at least 25 kpc from the Galactic centre (e.g. Gallagher & Wyse 1994), as are the new ultra-faint dwarf galaxies (e.g. Belokurov et al. 2010). Streams of past disruption events of dwarf galaxies by the Milky Way clearly suggest this is still occurring locally (e.g. Johnston, Hernquist & Bolte 1996). The preferential locations of faint dwarf galaxies are in contrast to the distribution of globular clusters, which includes many objects within a few kpc of the Galactic centre. Therefore, the finding that the few calcium-rich gap transients so far are located at large galactocentric radii provides early suggestive evidence in favour of faint dwarf galaxies rather than globular clusters as the host sites (barring a selection bias).

Thus far, the best case for an IMBH in a small dwarf galaxy is that of HLX-1 near ESO 243-49 (Farrell et al. 2009). This system shows X-ray emission that peaks about 10⁴² erg s⁻¹, shows state transitions like stellar-mass BHs (Godet et al. 2009), is spectroscopically confirmed to be a member of the cluster of galaxies against which it is projected (Wiersema et al. 2010), and recently has been found to be in a cluster or faint dwarf galaxy which likely has a young population (Farrell et al. 2012). It has been suggested that the companion star to the possible IMBH may have been tidally captured, given its rather long orbital period (Lasota et al. 2011).

Next, we proceed to test this scenario for plausibility as we did for globular clusters, although the rate estimate for tidal detonations is quite crude because the input parameters are so poorly constrained. We use the tidal disruption rate relation from Baumgardt et al. (2004), where the key, variable parameters are the IMBH mass (M_IMBH), the central stellar density (n_c), and the central velocity dispersion (v_c). Given an upper limit on the mass of the host galaxies of many of these events of ∼10⁷ M_⊙ (K12) and the BH–bulge mass relation (e.g. McConnell & Ma 2013), dwarf galaxies would have M_IMBH ∼ afew × 10⁴ M_⊙, roughly consistent with the upper limit derived in Section 4. A tidal detonation would occur in dwarf galaxies with dense central stellar clusters like M60-UCD1 (Strader et al. 2013) but at least a factor of a few fainter. Considering that the central surface density of M60-UCD1 is close to but slightly less than that of the densest globular clusters, we adopt n_c ∼ 10⁴ stars pc⁻³. We adopt v_c = 40 km s⁻¹ as in Section 2.3, assuming that σ is not considerably different from v_c.

Assuming the tidal disruption rate roughly scales as |$M_{{\rm IMBH}}^2 n_{\rm c}^{7/5} v_{\rm c}^{-21/5}$| (Baumgardt et al. 2004), we find that the dwarf galaxies with IMBHs have a tidal disruption rate per object about 20 times higher than globular clusters. Then, assuming 1/10 globular clusters have IMBHs, we would need only 1/200 as many dense dwarf galaxies as globular clusters to produce the observed rate of calcium-rich gap transients. Surveys of these galaxies are far from complete but Phillipps et al. (2001), for example, estimate that there are ∼100 dwarf galaxies in the central region of the Fornax cluster in the magnitude range where they would be plausible hosts for IMBHs, and this region contains considerably less than 20 000 globular clusters (e.g. Ostrov, Forte & Geisler 1998). Thus, faint, dense dwarf galaxies appear to be a viable candidate site for tidal detonations of helium WDs by IMBHs for at least some of the calcium-rich gap transients.

3.2 Three-body interactions

There are a variety of ways in which three-body interactions could perturb a WD to send it into a close encounter with a BH. Such interactions are frequently intrinsically chaotic (e.g. Portegies Zwart & Boekholt 2014), even resulting in orbital flips, for instance (Li et al. 2014). Given the very large body of literature regarding three-body interactions (see Valtonen & Karttunen 2006; Musielak & Quarles 2014, for summaries), we only briefly describe and discuss a few possible scenarios that would induce the tidal disruption of a WD. Again, this summary is meant only as a demonstration of plausibility for three-body interactions as a possible channel for the WD tidal detonations, not an exhaustive discussion or a detailed analysis of any particular model.

While the study of the three-body problem goes back hundreds of years to as early as the days of Sir Isaac Newton, considerable development on the problem has occurred in approximately the last half century (e.g. Eggleton & Kiseleva 1995). Much work has been focused on the well-known Kozai–Lidov mechanism, where perturbations in the three-body system transfer angular momentum between orbital modes with different eccentricity and inclination (Kozai 1962; Lidov 1962). Since then, numerous simulations (e.g. Anosova 1990) have been carried out to explore the large family of solutions that exist, from larger N-body encounters (Leigh & Geller 2012) to higher order expansions (octupole; Naoz et al. 2013). The importance of three-body interactions has also been explored for a variety of astrophysical contexts outside of the Solar system (e.g. ultra-luminous X-ray sources, Blecha et al. 2006; blue straggler stars in dense globular clusters, Chatterjee et al. 2013; gravitational waves, Antonini, Murray & Mikkola 2014; the final parsec problem involving the merger of supermassive BHs, Khan et al. 2013; the motions of stars around BHs in galaxy centres, Sesana, Haardt & Madau 2006, 2007, 2008; extrasolar planets, Mardling 2013; WD mergers, Hamers et al. 2013). We now consider its importance for the tidal disruption of WDs when they are paired with a BH and another member (another star or remnant) in a triple system. We consider paths to exchange angular momentum which do and do not involve mass transfer.

First, we consider a few examples of three-body interactions that will exchange angular momentum without mass transfer. The first two options require the Kozai–Lidov mechanism and are enhanced in higher mass ratio systems. Rapid eccentricity oscillations (Ivanov, Polnarev & Saha 2005) can make the magnitude of angular momentum in the inner binary comparable to the total angular momentum of the system. When numerically evolving the triple system, Antognini et al. (2014) find that, because the general relativistic terms are sensitive to the orbital eccentricity, the inner binary can merge well within a few Gyr, or even faster if the mass ratio is large because it is proportional to the amplitude of the eccentricity oscillations; this would be the case for a WD and BH inner binary. Secondly, a BH binary system in a stellar cusp strongly enhances the rate of tidal disruption over two-body relaxation for a single BH (Chen et al. 2009, 2011). This was originally demonstrated for a supermassive BH and another BH in a binary in the centre of a stellar cusp of a galaxy, but also applies to a stellar-mass BH and IMBH pair in the centre of a globular cluster or dwarf galaxy, which are relevant for calcium-rich gap transients. The tidal disruption rate in this case is at least approximately an order of magnitude larger than a single IMBH fed by two-body relaxation (Wang & Merritt 2004) but it also quickly depletes the loss cone in ≲ 10⁶ yr.

Yet another way a triple system can cause a WD in the inner binary to migrate towards a BH is through the tidal excitation of high-frequency p-modes. These can redistribute angular momentum in a triple system (Fuller et al. 2013), causing the inner binary to inspiral. Finally, the redistribution of angular momentum does not have to occur within a triple star system to significantly perturb a close binary. A close flyby of another star/remnant or binary can induce a high-enough eccentricity in a WD–BH binary that forces the WD to pass within the tidal disruption radius (see Heggie & Rasio 1996; Maccarone 2005, for detailed discussions).

Finally, we consider two examples which involve mass transfer. In the first of these cases, Stahler (2010) show that the mass transfer/accretion of gas from a dense interstellar medium (star-forming region) can act as a way to transfer angular momentum. When moving through and accreting the dense gas, the orbit can be shrunk by dissipating angular momentum through acoustic waves. This would require the site of the transient to be near a dense molecular cloud; however, these transients are not generally associated with star formation (Lyman et al. 2013). Another possibility is that mass is transferred from star to star within the binary or lost as the stars evolve off of the main sequence (Michaely & Perets 2014). This can happen in a much older stellar population and induce a chaotic orbital behaviour.

As has just been made clear, there are a multitude of various ways three-body interactions can lead to the tidal disruption of a WD, many of which do not require extremely dense stellar systems (e.g. the importance of three-body interactions in lower density stellar groups; Leigh & Geller 2013). This makes it very difficult if not impossible to rule out the tidal disruption origin on interaction cross-section arguments alone.

4 THE PARTICULAR CASE OF SN 2012hn

To test the proposed origin of the calcium-rich gap transients as tidal disruptions of WDs, we observed one of these sources, SN 2012hn (Valenti et al. 2014) to look for accretion emission during the decay phase. SN 2012hn has all of the typical characteristics of calcium-rich gap transients as outlined in Section 1. It is also fairly nearby, at a distance of only 27 Mpc, in the outskirts of the galaxy NGC 2272.

Since accretion is observed most unambiguously in the X-rays, we used the Chandra X-ray Observatory. We observed SN 2012hn with Chandra for a continuous 30 ks on 2013 August 17 (OBS_ID = 15668), 533 d after the explosion, which occurred on 2012 March 12. Data were taken in timed exposure mode and telemetered in very faint mode. Data reduction and analysis were completed using ciao version 4.6 (Fruscione et al. 2006) and sherpa version 2 (Freeman, Doe & Siemiginowska 2001). We reprocessed the level=1 event file using the chandra_repro script to apply the most recent calibration updates available (caldb version 4.6.1.1).

The source was not detected in the observation. To calculate upper limits to the source flux, we extracted source and background spectra using specextract at the location of the transient in a 6 arcsec radius circle and a 25 arcsec radius annulus excluding the source region, respectively. We jointly fit the unbinned source and background spectra at 0.5–8.0 keV using the C-statistic, which is similar to the Cash (1979) statistic but with an approximate goodness-of-fit measure. Since we constrain L_X ≲ 0.02L_Edd for any BH mass we consider, the accretion disc is in the canonical low/hard state (e.g. Maccarone 2003), in which the spectrum is usually well described by a power-law model. For the source spectral model (xsphabs × xspowerlaw), we set the photon index of the power law, Γ = 1.6. This value is typical for accretion in average X-ray binary populations (e.g. Sell et al. 2011). The column density, N_H was frozen at the galactic foreground value (Dickey & Lockman 1990). The background spectrum was fitted with a Γ = 1.4 power law, consistent with the hard X-ray background (e.g. Tozzi et al. 2006). We find a 3σ upper limit to the unabsorbed flux, F_0.5–8keV < 5.1 × 10⁻¹⁵ erg cm² s⁻¹. At a distance of 27 Mpc, this corresponds to L_0.5–8keV < 4.4 × 10³⁸ erg s⁻¹.

To put this upper limit in context, we adopt the analytical relations from Li et al. (2002) for the similar case of the tidal disruption of a star by a supermassive BH to calculate joint upper limits on the mass of the WD and BH assumed to be involved in the disruption (given the X-ray luminosity upper limit above at the time of the observation). While more complex numerical models exist (e.g. Piran, Sadowski & Tchekhovskoy 2015), we opt to use the simpler analytical formulation to derive parameter limits, especially since the source is not X-ray detected.

First, we combine equations 10 and 11 from Li et al. (2002) to calculate the fall-back accretion rate, |$\dot{M}$|⁠, as a function of time, t, fall-back fraction, f and mass of the BH, M_BH. We then calculate the accretion efficiency, ϵ, using equation 12 from Li et al. (2002). In addition, we make a few more assumptions that simplify or improve our model:

• We use the mass–radius relation for WDs, assuming the mean molecular weight per free electron, μ_e = 2 (e.g. Hansen, Kawaler & Trimble 2004, their equation 7.103).

• We assume that f = 0.35, as suggested by R09.

• We take into account the accretion disc state transition of accreting BH binaries so that |$L \propto \dot{m}$| for L/L_Edd ≥ 0.02 and |$L \propto \dot{m}^2$| for L/L_Edd < 0.02 (e.g. Esin, McClintock & Narayan 1997; Maccarone 2003).

• To account for the fraction of light falling in the Chandra bandpass, we assume a bolometric correction, δ, of 0.85 in the high, soft state and 0.1 in the low, hard state (e.g. Portegies Zwart, Dewi & Maccarone 2004).

Figure 1.

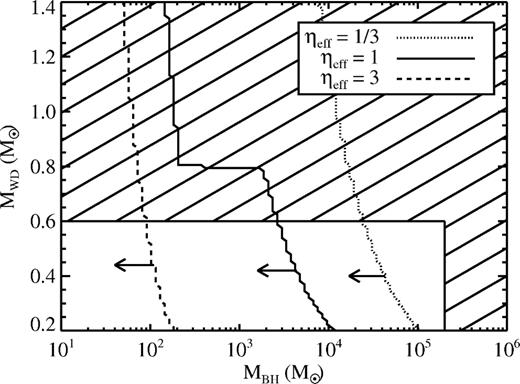
Joint upper limits for the mass of the WD and BH involved in the tidal detonation of SN 2012hn. Our X-ray observation upper limit excludes parameter space to the upper right of the curves. A description of η_eff and how these limits are calculated is provided in Section 4. The horizontal jump that appears on the plot for η_eff = 1 is the hard-/soft-state transition (the state transition is not crossed on the other plotted curves). The excluded parameter space, where the WD is swallowed whole or the WD produces too many heavy elements, is discussed in Section 4 (note: the boundaries are approximate).

Open in new tabDownload slide

From this analysis, we have placed weak constraints on the BH mass. It is clear that these observations are not deep enough or taken close enough to the time of the transient to place strongly constraining upper limits on the host system under this model.

5 SUMMARY AND TESTS OF THE MODEL

In this work, we have proposed that tidal detonations of low-mass WDs are the source of at least some of the calcium-rich gap transients. We have shown that the predictions of this model are at least qualitatively consistent with observations of the systems discovered thus far. Throughout this work, we have assessed this model using rough comparisons to test for plausibility; however, because of the large range of ways in which the tidal detonation can arise and the large uncertainties in key parameters in these systems, detailed quantitative comparisons are not possible at the present time and currently may not be computationally feasible.

A few clear, testable predictions can be made if this scenario is correct:

• If these transients are random flyby encounters of low-mass WDs with IMBHs, most of the calcium-rich gap transients should be associated with low-luminosity, preferably dense stellar groups. However, if three-body interactions drive a WD already orbiting a BH into it, then these systems could be anywhere and could include ejected systems (e.g. Foley 2015).

• If very faint dwarf spheriodals or ultra-faint dwarfs are the hosts of the calcium-rich gap transients and are distributed like the brighter dwarf ellipticals, then these explosions might occur preferentially in clusters or dense groups of galaxies (Vader & Sandage 1991; Sabatini et al. 2003). Of the three most recent transients presented by K12, two were located in clusters of galaxies, as was one of the two archival events.

• X-ray emission should be seen from the gap transients, and should follow a t^−5/3 decay law.

Using this latter prediction, we sought to catch one of these calcium-rich gap transients, SN 2012hn, in the decay phase of the light curve. Unfortunately, we did not detect the source in our follow-up X-ray observations. However, assuming our hypothesis is correct that this transient was a tidal detonation event of a WD, M_BH ≲ 10⁵ M_⊙ and M_WD ≲ 0.6 M_⊙ in this scenario. The upper limits are not very constraining because the effective efficiency that includes the accretion efficiency, fall-back efficiency and the bolometric correction is highly uncertain. If this scenario is correct, a future X-ray observation of one of these sources as close as possible to the time of the transient might detect it and provide much stronger constraints on the masses and the nature of the event.

Finally, concerning the first two points above, some initial work has been completed to search for the hosts of a few of these transients without success (Lyman et al. 2014). These recent observations rule out for a few sources, including SN 2012hn, that the transient was caused by the tidal detonation induced by a random flyby of an IMBH because the upper limits to the masses of host stellar associations are too low. However, the current sample of calcium-rich gap transients might be heterogeneous, and Lyman et al. only placed stringent upper limits for a few sources. In addition, the stringent upper limits rule out most but not all globular clusters and dwarf galaxies. Finally, there are numerous ways three-body interactions could perturb the orbits of a stellar system to force a WD too close to a stellar-mass BH or neutron star. Future detailed, multiwavelength observations are clearly needed to constrain this and other various models for these transients.

We are grateful to Giuseppe Lodato, Cole Miller, Hagai Perets and Denija Crnojevic for useful discussions. This work has been funded through Chandra grant GO4-15061X.

REFERENCES