-
PDF
- Split View
-
Views
-
Cite
Cite
L. Fernández-Menchero, G. Del Zanna, N. R. Badnell, Validity of the ICFT R-matrix method: Be-like Al 9+ a case study, Monthly Notices of the Royal Astronomical Society, Volume 450, Issue 4, 11 July 2015, Pages 4174–4183, https://doi.org/10.1093/mnras/stv887
Close - Share Icon Share
Abstract
We have carried out 98-level configuration-interaction/close-coupling (CI/CC) intermediate coupling frame transformation (ICFT) and Breit–Pauli R-matrix calculations for the electron-impact excitation of Be-like Al 9+. The close agreement that we find between the two sets of effective collision strengths demonstrates the continued robustness of the ICFT method. On the other hand, a comparison of this data with previous 238-level CI/CC ICFT effective collision strengths shows that the results for excitation up to n = 4 levels are systematically and increasingly underestimated over a wide range of temperatures by R-matrix calculations whose CC expansion extends only to n = 4 (98-levels). Thus, we find to be false a recent conjecture that the ICFT approach may not be completely robust. The conjecture was based upon a comparison of 98-level CI/CC Dirac R-matrix effective collision strengths for Al 9+ with those from the 238-level CI/CC ICFT R-matrix calculations. The disagreement found recently is due to a lack of convergence of the CC expansion in the 98-level CI/CC Dirac work. The earlier 238-level CI/CC ICFT work has a superior target to the 98-level CI/CC Dirac one and provides more accurate atomic data. Similar considerations need to be made for other Be-like ions and for other sequences.
1 INTRODUCTION
Electron-impact excitation is the dominant process for populating the radiating states of ions whose emission lines form the basis for the spectroscopic diagnostic modelling of non-equilibrium astrophysical and laboratory plasmas. As such, a great deal of effort over many years has gone in to calculating a large amount of collision data, which is incorporated into data bases and modelling suites such as CHIANTI1 and OPEN-ADAS.2 The pre-eminent methodology used is the R-matrix one. However, there are many variations on this theme.
The intermediate coupling frame transformation (ICFT) R-matrix method is an approximation to the Breit–Pauli R-matrix method (BPRM) which neglects the spin–orbit interaction between the colliding electron and the ion. Thus, it is physically well motivated. There is a good deal of literature which verifies the accuracy of the ICFT approach; the original comparisons of the results of ICFT and Breit–Pauli (BP) R-matrix calculations by Griffin, Badnell & Pindzola (1998) and Griffin et al. (1999) on Mg-like ions and Badnell & Griffin (1999) on Ni4+; more recent ones by Liang & Badnell (2010) comparing ICFT R-matrix and Dirac Atomic R-matrix Code (DARC) calculations for Ne-like Fe16+ and Kr26+, Liang, Whiteford & Badnell (2009) on ICFT with BP and DARC for Na-like Fe15+; and most recently Badnell & Ballance (2014) compared the results of ICFT, BPRM and DARC calculations for Fe2+. The differences observed between ICFT and other R-matrix results are all well within the uncertainties to be expected due to the use of different configuration interaction (CI) and close-coupling (CC) expansions and resonance resolution. Indeed, the Badnell & Ballance (2014) work on Fe2+ used identical atomic structures and CC expansions for the ICFT and BP R-matrix calculations and found excellent agreement, better than 5 per cent. Their DARC calculations out of necessity used a somewhat different atomic structure, and the low-level structure of Fe2+ is challenging, but still gave agreement to within ∼20 per cent at 104 K.
Extensive calculations have been carried out applying the ICFT R-matrix method to whole isoelectronic sequences (for elements, typically, up to Zn), the most recent ones being Mg-like (Fernández-Menchero, Del Zanna & Badnell 2014b), Be-like (Fernández-Menchero, Del Zanna & Badnell 2014a) and B-like (Liang, Badnell & Zhao 2012) – this last paper contains references to earlier sequences.
Thus, it is both surprising and of great concern to find a work which counters this trend; Aggarwal & Keenan (2015a) made a comparison of the results of a 98-level DARC calculation on Be-like Al 9+ (Aggarwal & Keenan 2014b) with a 238-level ICFT R-matrix one (Fernández-Menchero et al. 2014a). Aggarwal & Keenan (2015a) found that the effective collision strengths obtained from the 238-level ICFT R-matrix calculation were significantly larger than the DARC ones in many instances and they suggested that the results of Fernández-Menchero et al. (2014a) were less reliable, querying the ICFT method, resonance resolution and its high energy/temperature behaviour.
In addition, Aggarwal & Keenan (2015a) alighted on the recent paper by Storey, Sochi & Badnell (2014) which reported a problem in the outer-region ICFT calculation of O2+, when compared to a full BP calculation, and suggested that this could be the main cause of the discrepancies for Al 9+. However, Storey et al. (2014) noted that such an issue only arises when resonance effective quantum numbers become small. The problem is peculiar to low-charge ions such as O2+ and unusually small R-matrix box sizes. Storey et al. (2014) focused on providing a solution to their problem at hand. We note that the problem does not arise in the first place if the R-matrix box size is increased (beyond its default in their case) to encompass a spectroscopic n = 3 orbital, say. This is why the issue had not arisen before; all previous calculations (including Fernández-Menchero et al. 2014a) used larger, often much larger, box sizes. The problem noted by Storey et al. (2014) is not relevant in general. Aggarwal & Keenan (2015a) noted a similar trend for other ions of the Be-like sequence Cl13+, K15+, Ge28+ (Aggarwal & Keenan 2014a) and Ti18+ (Aggarwal & Keenan 2012).
Where does that leave us with regard to the discrepancies noted by Aggarwal & Keenan (2015a)? The concern of Aggarwal & Keenan (2015a) was the disagreement between R-matrix calculations of (apparent) comparable complexity. However, the works of Aggarwal & Keenan (2014b) and Fernández-Menchero et al. (2014a) are not of comparable complexity. We show here that the much larger CC expansion used by Fernández-Menchero et al. (2014a, 238 versus 98 levels) gives rise to a systematic enhancement of effective collision strengths over a wide range of temperatures, which increases as one excites higher-and-higher levels.
In addition, we analyse the uncertainty in the effective collision strengths due to the incompleteness of the CI expansion, the validity of the ICFT versus BP method, viz. the neglect of the spin–orbit interaction of the colliding electron, and the effect of resonance resolution and position on low-temperature effective collision strengths.
The paper is organized as follows. In Section 2, we describe the methodology we used for the different calculations we have performed. In Section 3, we discuss the atomic structure of Al 9+ and present results for energies, line strengths and infinite energy plane wave Born collision strengths. In Section 4, we compare and contrast effective collision strengths. In Section 5, we present our main conclusions. Atomic units are used unless otherwise specified.
2 METHODOLOGY
In the following sections, we compare the results of the 238-level configuration-interaction/close-coupling (CI/CC) ICFT R-matrix calculation by Fernández-Menchero et al. (2014a) for Al 9+ with the results of new ICFT and BP 98-level CI/CC R-matrix calculations – the latter being the same sized CI & CC expansions that were used by Aggarwal & Keenan (2012, 2014a,b). Where possible (meaningful), our new 98-level CC calculations follow the same prescription as Fernández-Menchero et al. (2014a) e.g. with respect to angular momentum and energy specification.
The target description uses the autostructure program (Badnell 2011). Fernández-Menchero et al. (2014a) included all of the configurations 1s2 {2s2, 2s2p, 2p2} and 1s2 {2s, 2p} nl with n = 3–7 and l = s, p, d, f, g for n = 3 − 5 and l = s, p, d for n = 6, 7, which makes a total of 238 levels. In this work, we restrict ourselves to n = 4 (with l = s, p, d, f) which gives a total of 98 levels. The Thomas–Fermi potential scaling parameters, λnl, for the atomic structure calculation with the CI basis set of 98 levels are given in Table 1, those for the CI calculation with 238 levels are given in Fernández-Menchero et al. (2014a). The λnl parameters for the 98-level CI calculation were obtained in the same way as the ones for the 238-level calculation (Fernández-Menchero et al. 2014a); by minimizing the equally weighted sum of all LS-coupling term energies.
| Orbital . | λnl . |
|---|---|
| 1s | 1.571 75 |
| 2s | 1.296 75 |
| 2p | 1.170 81 |
| 3s | 1.290 04 |
| 3p | 1.159 58 |
| 3d | 1.297 91 |
| 4s | 1.297 97 |
| 4p | 1.154 13 |
| 4d | 1.302 12 |
| 4f | 1.509 16 |
| Orbital . | λnl . |
|---|---|
| 1s | 1.571 75 |
| 2s | 1.296 75 |
| 2p | 1.170 81 |
| 3s | 1.290 04 |
| 3p | 1.159 58 |
| 3d | 1.297 91 |
| 4s | 1.297 97 |
| 4p | 1.154 13 |
| 4d | 1.302 12 |
| 4f | 1.509 16 |
| Orbital . | λnl . |
|---|---|
| 1s | 1.571 75 |
| 2s | 1.296 75 |
| 2p | 1.170 81 |
| 3s | 1.290 04 |
| 3p | 1.159 58 |
| 3d | 1.297 91 |
| 4s | 1.297 97 |
| 4p | 1.154 13 |
| 4d | 1.302 12 |
| 4f | 1.509 16 |
| Orbital . | λnl . |
|---|---|
| 1s | 1.571 75 |
| 2s | 1.296 75 |
| 2p | 1.170 81 |
| 3s | 1.290 04 |
| 3p | 1.159 58 |
| 3d | 1.297 91 |
| 4s | 1.297 97 |
| 4p | 1.154 13 |
| 4d | 1.302 12 |
| 4f | 1.509 16 |
For the collision calculations, we use the inner-region R-matrix programs of Hummer et al. (1993), Berrington, Eissner & Norrington (1995) and the outer-region stgf program of Berrington et al. (1987); Badnell (1999) plus the ICFT one of Griffin et al. (1998). We will compare the results of ICFT and BPRM to treat relativistic effects in the scattering problem. Both can use the exact same BP atomic structure. This is important as it enables us to isolate differences due solely to the differing treatment of relativistic effects in the scattering. We note that Berrington et al. (2005) have shown that the BPRM gives essentially the same results as the Dirac one for Z ≲ 30.
The ICFT R-matrix method first carries-out an LS-coupling CC calculation for the CI target described above and it includes the mass–velocity and Darwin one-body relativistic operators. The LS-coupling reactance K-matrices are first recoupled to jK-coupling and then transformed to intermediate coupling using the term coupling coefficients (Hummer et al. 1993) for the BP target. This imposes the exact same atomic structure on the ICFT K-matrices as a BP one which uses the same CI expansion and radial orbitals. In particular, the fine-structure levels within a term are non-degenerate in the final scattering calculation. This method is the one which was used by Fernández-Menchero et al. (2014a).
The second method which we use is the BP one. In this method, the CC expansion is made in intermediate coupling as well, in addition to the target CI, i.e. the one-body effective (nuclear plus Blume & Watson) spin–orbit operator is included in the (N + 1)-electron Hamiltonian. The BP formalism increases considerably the size of the Hamiltonian matrix, which makes it impractical to use this method for 238 CC levels.
The essential physical difference between the ICFT and BPRM is the neglect by the former of the effective spin–orbit interaction between the colliding electron and the ion. The practical benefit of the ICFT method over the BP one is the diagonalization of much smaller (N + 1)-electron Hamiltonian matrices and a much smaller set of coupled scattering equations to be solved in the outer-region by stgf.
3 STRUCTURE
Table 2 compares our energies for the first 98 levels of Al 9+ calculated with the 98- and 238-level CI targets. These energies are compared also with the observed ones tabulated in the NIST3 data base, which were taken from work of Martin & Zalubas (1979). There are 10 levels in Table 2 which do not follow the same order in both structure calculations: from level index 82–84 and from 88–94. We use the order of the 98-level CI calculation to index levels for comparison purposes. Energies calculated with both CI expansions have differences smaller than 0.5 per cent with the observed ones for most of the levels, and differences of around 2 per cent for the low lying singlet states. In general, the differences are similar to those found by Aggarwal & Keenan (2014b). In the original paper from Martin & Zalubas (1979), there are several gaps in the level energies, and some of them are labelled as ‘inaccurate’, so we refer the reader to the original work to avoid hasty conclusions.
Al9+ target levels. Key: i: level index; Conf.: configuration; Level: level IC designation (largest weight); ENIST: observed energy from the NIST data base (Martin & Zalubas 1979); E98: calculated energy with 98-level CI expansion; E238: calculated energy with 238-level CI expansion (see the text); per cent: percentage difference between theoretical and NIST data. All energies are in cm−1.
| i . | Conf. . | level . | ENIST . | E98 . | (%) . | E238 . | (%) . | i . | Conf. . | level . | ENIST . | E98 . | (%) . | E238 . | (%) . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2s2 | 1S0 | 0. | 0. | (0) | 0. | (0) | 50 | 2s 4p | |$\mathrm{^3P_{1 }^{o}}$| | – | 2504724. | (−) | 2500556. | (−) |
| 2 | 2s 2p | |$\mathrm{^3P_{0 }^{o}}$| | 155148. | 155722. | (0.4) | 155539. | (0.3) | 51 | 2s 4p | |$\mathrm{^3P_{2 }^{o}}$| | – | 2505125. | (−) | 2500975. | (−) |
| 3 | 2s 2p | |$\mathrm{^3P_{1 }^{o}}$| | 156798. | 157487. | (0.4) | 157404. | (0.4) | 52 | 2s 4p | |$\mathrm{^1P_{1 }^{o}}$| | – | 2508073. | (–) | 2503514. | (–) |
| 4 | 2s 2p | |$\mathrm{^3P_{2 }^{o}}$| | 160429. | 161146. | (0.4) | 161278. | (0.5) | 53 | 2s 4d | 3D1 | – | 2520502. | (–) | 2516248. | (–) |
| 5 | 2s 2p | |$\mathrm{^1P_{1 }^{o}}$| | 300490. | 309273. | (2.9) | 307209. | (2.2) | 54 | 2s 4d | 3D2 | – | 2520573. | (–) | 2516321. | (–) |
| 6 | 2p2 | 3P0 | 404574. | 408026. | (0.9) | 407826. | (0.8) | 55 | 2s 4d | 3D3 | – | 2520682. | (–) | 2516434. | (–) |
| 7 | 2p2 | 3P1 | 406517. | 409969. | (0.8) | 409888. | (0.8) | 56 | 2s 4d | 1D2 | 2527560. | 2530218. | (0.1) | 2525880. | (−0.1) |
| 8 | 2p2 | 3P2 | 409690. | 413420. | (0.9) | 413526. | (0.9) | 57 | 2s 4f | |$\mathrm{^3F_{2 }^{o}}$| | 2528570. | 2530774. | (0.1) | 2526258. | (−0.1) |
| 9 | 2p2 | 1D2 | 449732. | 458157. | (1.9) | 457831. | (1.8) | 58 | 2s 4f | |$\mathrm{^3F_{3 }^{o}}$| | 2528570. | 2530815. | (0.1) | 2526299. | (−0.1) |
| 10 | 2p2 | 1S0 | 553783. | 567794. | (2.5) | 567267. | (2.4) | 59 | 2s 4f | |$\mathrm{^3F_{4 }^{o}}$| | 2528570. | 2530871. | (0.1) | 2526355. | (−0.1) |
| 11 | 2s 3s | 3S1 | 1855760. | 1856089. | (0.0) | 1852844. | (−0.2) | 60 | 2s 4f | |$\mathrm{^1F_{3 }^{o}}$| | – | 2533730. | (–) | 2528991. | (–) |
| 12 | 2s 3s | 1S0 | 1884420. | 1886214. | (0.1) | 1882216. | (−0.1) | 61 | 2p 4s | |$\mathrm{^3P_{0 }^{o}}$| | – | 2661563. | (–) | 2655681. | (–) |
| 13 | 2s 3p | |$\mathrm{^1P_{1 }^{o}}$| | 1923850. | 1925826. | (0.1) | 1922358. | (−0.1) | 62 | 2p 4s | |$\mathrm{^3P_{1 }^{o}}$| | – | 2662724. | (–) | 2656820. | (–) |
| 14 | 2s 3p | |$\mathrm{^3P_{0 }^{o}}$| | – | 1928630. | (–) | 1925009. | (–) | 63 | 2p 4s | |$\mathrm{^3P_{2 }^{o}}$| | – | 2666840. | (–) | 2661460. | (–) |
| 15 | 2s 3p | |$\mathrm{^3P_{1 }^{o}}$| | – | 1929220. | (–) | 1925611. | (–) | 64 | 2p 4s | |$\mathrm{^1P_{1 }^{o}}$| | – | 2673641. | (–) | 2666939. | (–) |
| 16 | 2s 3p | |$\mathrm{^3P_{2 }^{o}}$| | – | 1930059. | (–) | 1926462. | (–) | 65 | 2p 4p | 1P1 | – | 2681281. | (–) | 2675347. | (–) |
| 17 | 2s 3d | 3D1 | 1965860. | 1967770. | (0.1) | 1964163. | (−0.1) | 66 | 2p 4p | 3D1 | – | 2684513. | (–) | 2678722. | (–) |
| 18 | 2s 3d | 3D2 | 1966080. | 1967980. | (0.1) | 1964378. | (−0.1) | 67 | 2p 4p | 3D2 | – | 2684938. | (–) | 2679129. | (–) |
| 19 | 2s 3d | 3D3 | 1966300. | 1968296. | (0.1) | 1964701. | (−0.1) | 68 | 2p 4p | 3D3 | – | 2688348. | (–) | 2682876. | (–) |
| 20 | 2s 3d | 1D2 | 1992340. | 1997586. | (0.3) | 1993399. | (0.1) | 69 | 2p 4p | 3S1 | – | 2691166. | (–) | 2684805. | (–) |
| 21 | 2p 3s | |$\mathrm{^3P_{0 }^{o}}$| | 2057140. | 2055664. | (−0.1) | 2050249. | (−0.3) | 70 | 2p 4p | 3P0 | – | 2691420. | (–) | 2685788. | (–) |
| 22 | 2p 3s | |$\mathrm{^3P_{1 }^{o}}$| | 2057140. | 2057249. | (0.0) | 2051958. | (−0.3) | 71 | 2p 4p | 3P1 | – | 2694295. | (–) | 2688609. | (–) |
| 23 | 2p 3s | |$\mathrm{^3P_{2 }^{o}}$| | 2057140. | 2060910. | (0.2) | 2055983. | (−0.1) | 72 | 2p 4p | 3P2 | – | 2694733. | (–) | 2689496. | (–) |
| 24 | 2p 3s | |$\mathrm{^1P_{1 }^{o}}$| | 2091870. | 2090063. | (−0.1) | 2084057. | (−0.4) | 73 | 2p 4d | |$\mathrm{^3F_{2 }^{o}}$| | – | 2697404. | (–) | 2691501. | (–) |
| 25 | 2p 3p | 1P1 | 2094820. | 2097317. | (0.1) | 2093229. | (−0.1) | 74 | 2p 4d | |$\mathrm{^3F_{3 }^{o}}$| | – | 2699888. | (–) | 2694096. | (–) |
| 26 | 2p 3p | 3D1 | 2102330. | 2105510. | (0.2) | 2101249. | (−0.1) | 75 | 2p 4d | |$\mathrm{^1D_{2 }^{o}}$| | – | 2700756. | (–) | 2695172. | (–) |
| 27 | 2p 3p | 3D2 | 2103900. | 2107151. | (0.2) | 2102917. | (−0.0) | 76 | 2p 4p | 1D2 | 2696850. | 2702087. | (0.2) | 2696558. | (−0.0) |
| 28 | 2p 3p | 3D3 | 2107390. | 2110622. | (0.2) | 2106614. | (−0.0) | 77 | 2p 4d | |$\mathrm{^3F_{4 }^{o}}$| | – | 2702915. | (–) | 2697461. | (–) |
| 29 | 2p 3p | 3S1 | 2119690. | 2123472. | (0.2) | 2118706. | (−0.0) | 78 | 2p 4d | |$\mathrm{^3D_{1 }^{o}}$| | – | 2705726. | (–) | 2700008. | (–) |
| 30 | 2p 3p | 3P0 | – | 2132252. | (–) | 2126478. | (–) | 79 | 2p 4d | |$\mathrm{^3D_{2 }^{o}}$| | – | 2706671. | (–) | 2701074. | (–) |
| 31 | 2p 3p | 3P1 | 2128680. | 2133785. | (0.2) | 2128247. | (−0.0) | 80 | 2p 4f | 1F3 | – | 2707963. | (–) | 2701789. | (–) |
| 32 | 2p 3p | 3P2 | 2130410. | 2135720. | (0.2) | 2130292. | (−0.0) | 81 | 2p 4f | 3F3 | – | 2708388. | (–) | 2702400. | (–) |
| 33 | 2p 3d | |$\mathrm{^3F_{2 }^{o}}$| | – | 2139901. | (–) | 2135677. | (–) | 82 | 2p 4d | |$\mathrm{^3D_{3 }^{o}}$| | – | 2708430. | (–) | 2703108. | (–) |
| 34 | 2p 3d | |$\mathrm{^3F_{3 }^{o}}$| | – | 2142598. | (–) | 2138636. | (–) | 83 | 2p 4f | 3F2 | – | 2708468. | (–) | 2702641. | (–) |
| 35 | 2p 3d | |$\mathrm{^1D_{2 }^{o}}$| | 2141580. | 2144437. | (0.1) | 2140459. | (−0.1) | 84 | 2p 4f | 3F4 | – | 2708819. | (–) | 2702505. | (–) |
| 36 | 2p 3d | |$\mathrm{^3F_{4 }^{o}}$| | – | 2145366. | (–) | 2141681. | (–) | 85 | 2p 4d | |$\mathrm{^3P_{2 }^{o}}$| | – | 2710818. | (–) | 2705109. | (–) |
| 37 | 2p 3p | 1D2 | 2148410. | 2157057. | (0.4) | 2150745. | (0.1) | 86 | 2p 4d | |$\mathrm{^3P_{1 }^{o}}$| | – | 2711544. | (–) | 2705747. | (–) |
| 38 | 2p 3d | |$\mathrm{^3D_{1 }^{o}}$| | 2160650. | 2165232. | (0.2) | 2159945. | (−0.0) | 87 | 2p 4d | |$\mathrm{^3P_{0 }^{o}}$| | – | 2711943. | (–) | 2706094. | (–) |
| 39 | 2p 3d | |$\mathrm{^3D_{2 }^{o}}$| | 2161960. | 2165961. | (0.2) | 2160762. | (−0.1) | 88 | 2p 4f | 3P3 | – | 2712961. | (–) | 2706897. | (–) |
| 40 | 2p 3d | |$\mathrm{^3D_{3 }^{o}}$| | 2163340. | 2167469. | (0.2) | 2162400. | (−0.0) | 89 | 2p 4f | 3P4 | – | 2713531. | (–) | 2707350. | (–) |
| 41 | 2p 3d | |$\mathrm{^3P_{2 }^{o}}$| | 2170190. | 2174402. | (0.2) | 2169739. | (−0.0) | 90 | 2p 4f | 3P5 | – | 2715225. | (–) | 2708632. | (–) |
| 42 | 2p 3d | |$\mathrm{^3P_{1 }^{o}}$| | 2171680. | 2175473. | (0.2) | 2170906. | (−0.0) | 91 | 2p 4f | 3D3 | – | 2716473. | (–) | 2710743. | (–) |
| 43 | 2p 3d | |$\mathrm{^3P_{0 }^{o}}$| | – | 2176019. | (–) | 2171512. | (–) | 92 | 2p 4f | 1D4 | – | 2717105. | (–) | 2710218. | (–) |
| 44 | 2p 3p | 1S0 | – | 2193603. | (–) | 2186094. | (–) | 93 | 2p 4f | 3D2 | – | 2717141. | (–) | 2711361. | (–) |
| 45 | 2p 3d | |$\mathrm{^1F_{3 }^{o}}$| | 2192860. | 2203326. | (0.5) | 2195894. | (0.1) | 94 | 2p 4p | 1S0 | – | 2717922. | (–) | 2706869. | (–) |
| 46 | 2p 3d | |$\mathrm{^1P_{1 }^{o}}$| | – | 2208387. | (–) | 2201414. | (–) | 95 | 2p 4f | 3D1 | – | 2718397. | (–) | 2712736. | (–) |
| 47 | 2s 4s | 3S1 | – | 2477026. | (–) | 2472580. | (–) | 96 | 2p 4f | 1D2 | – | 2719895. | (–) | 2713991. | (–) |
| 48 | 2s 4s | 1S0 | – | 2488107. | (–) | 2483578. | (–) | 97 | 2p 4d | |$\mathrm{^1F_{3 }^{o}}$| | – | 2722212. | (–) | 2715080. | (–) |
| 49 | 2s 4p | |$\mathrm{^3P_{0 }^{o}}$| | – | 2504555. | (–) | 2500383. | (–) | 98 | 2p 4d | |$\mathrm{^1P_{1 }^{o}}$| | – | 2723448. | (–) | 2716711. | (–) |
| i . | Conf. . | level . | ENIST . | E98 . | (%) . | E238 . | (%) . | i . | Conf. . | level . | ENIST . | E98 . | (%) . | E238 . | (%) . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2s2 | 1S0 | 0. | 0. | (0) | 0. | (0) | 50 | 2s 4p | |$\mathrm{^3P_{1 }^{o}}$| | – | 2504724. | (−) | 2500556. | (−) |
| 2 | 2s 2p | |$\mathrm{^3P_{0 }^{o}}$| | 155148. | 155722. | (0.4) | 155539. | (0.3) | 51 | 2s 4p | |$\mathrm{^3P_{2 }^{o}}$| | – | 2505125. | (−) | 2500975. | (−) |
| 3 | 2s 2p | |$\mathrm{^3P_{1 }^{o}}$| | 156798. | 157487. | (0.4) | 157404. | (0.4) | 52 | 2s 4p | |$\mathrm{^1P_{1 }^{o}}$| | – | 2508073. | (–) | 2503514. | (–) |
| 4 | 2s 2p | |$\mathrm{^3P_{2 }^{o}}$| | 160429. | 161146. | (0.4) | 161278. | (0.5) | 53 | 2s 4d | 3D1 | – | 2520502. | (–) | 2516248. | (–) |
| 5 | 2s 2p | |$\mathrm{^1P_{1 }^{o}}$| | 300490. | 309273. | (2.9) | 307209. | (2.2) | 54 | 2s 4d | 3D2 | – | 2520573. | (–) | 2516321. | (–) |
| 6 | 2p2 | 3P0 | 404574. | 408026. | (0.9) | 407826. | (0.8) | 55 | 2s 4d | 3D3 | – | 2520682. | (–) | 2516434. | (–) |
| 7 | 2p2 | 3P1 | 406517. | 409969. | (0.8) | 409888. | (0.8) | 56 | 2s 4d | 1D2 | 2527560. | 2530218. | (0.1) | 2525880. | (−0.1) |
| 8 | 2p2 | 3P2 | 409690. | 413420. | (0.9) | 413526. | (0.9) | 57 | 2s 4f | |$\mathrm{^3F_{2 }^{o}}$| | 2528570. | 2530774. | (0.1) | 2526258. | (−0.1) |
| 9 | 2p2 | 1D2 | 449732. | 458157. | (1.9) | 457831. | (1.8) | 58 | 2s 4f | |$\mathrm{^3F_{3 }^{o}}$| | 2528570. | 2530815. | (0.1) | 2526299. | (−0.1) |
| 10 | 2p2 | 1S0 | 553783. | 567794. | (2.5) | 567267. | (2.4) | 59 | 2s 4f | |$\mathrm{^3F_{4 }^{o}}$| | 2528570. | 2530871. | (0.1) | 2526355. | (−0.1) |
| 11 | 2s 3s | 3S1 | 1855760. | 1856089. | (0.0) | 1852844. | (−0.2) | 60 | 2s 4f | |$\mathrm{^1F_{3 }^{o}}$| | – | 2533730. | (–) | 2528991. | (–) |
| 12 | 2s 3s | 1S0 | 1884420. | 1886214. | (0.1) | 1882216. | (−0.1) | 61 | 2p 4s | |$\mathrm{^3P_{0 }^{o}}$| | – | 2661563. | (–) | 2655681. | (–) |
| 13 | 2s 3p | |$\mathrm{^1P_{1 }^{o}}$| | 1923850. | 1925826. | (0.1) | 1922358. | (−0.1) | 62 | 2p 4s | |$\mathrm{^3P_{1 }^{o}}$| | – | 2662724. | (–) | 2656820. | (–) |
| 14 | 2s 3p | |$\mathrm{^3P_{0 }^{o}}$| | – | 1928630. | (–) | 1925009. | (–) | 63 | 2p 4s | |$\mathrm{^3P_{2 }^{o}}$| | – | 2666840. | (–) | 2661460. | (–) |
| 15 | 2s 3p | |$\mathrm{^3P_{1 }^{o}}$| | – | 1929220. | (–) | 1925611. | (–) | 64 | 2p 4s | |$\mathrm{^1P_{1 }^{o}}$| | – | 2673641. | (–) | 2666939. | (–) |
| 16 | 2s 3p | |$\mathrm{^3P_{2 }^{o}}$| | – | 1930059. | (–) | 1926462. | (–) | 65 | 2p 4p | 1P1 | – | 2681281. | (–) | 2675347. | (–) |
| 17 | 2s 3d | 3D1 | 1965860. | 1967770. | (0.1) | 1964163. | (−0.1) | 66 | 2p 4p | 3D1 | – | 2684513. | (–) | 2678722. | (–) |
| 18 | 2s 3d | 3D2 | 1966080. | 1967980. | (0.1) | 1964378. | (−0.1) | 67 | 2p 4p | 3D2 | – | 2684938. | (–) | 2679129. | (–) |
| 19 | 2s 3d | 3D3 | 1966300. | 1968296. | (0.1) | 1964701. | (−0.1) | 68 | 2p 4p | 3D3 | – | 2688348. | (–) | 2682876. | (–) |
| 20 | 2s 3d | 1D2 | 1992340. | 1997586. | (0.3) | 1993399. | (0.1) | 69 | 2p 4p | 3S1 | – | 2691166. | (–) | 2684805. | (–) |
| 21 | 2p 3s | |$\mathrm{^3P_{0 }^{o}}$| | 2057140. | 2055664. | (−0.1) | 2050249. | (−0.3) | 70 | 2p 4p | 3P0 | – | 2691420. | (–) | 2685788. | (–) |
| 22 | 2p 3s | |$\mathrm{^3P_{1 }^{o}}$| | 2057140. | 2057249. | (0.0) | 2051958. | (−0.3) | 71 | 2p 4p | 3P1 | – | 2694295. | (–) | 2688609. | (–) |
| 23 | 2p 3s | |$\mathrm{^3P_{2 }^{o}}$| | 2057140. | 2060910. | (0.2) | 2055983. | (−0.1) | 72 | 2p 4p | 3P2 | – | 2694733. | (–) | 2689496. | (–) |
| 24 | 2p 3s | |$\mathrm{^1P_{1 }^{o}}$| | 2091870. | 2090063. | (−0.1) | 2084057. | (−0.4) | 73 | 2p 4d | |$\mathrm{^3F_{2 }^{o}}$| | – | 2697404. | (–) | 2691501. | (–) |
| 25 | 2p 3p | 1P1 | 2094820. | 2097317. | (0.1) | 2093229. | (−0.1) | 74 | 2p 4d | |$\mathrm{^3F_{3 }^{o}}$| | – | 2699888. | (–) | 2694096. | (–) |
| 26 | 2p 3p | 3D1 | 2102330. | 2105510. | (0.2) | 2101249. | (−0.1) | 75 | 2p 4d | |$\mathrm{^1D_{2 }^{o}}$| | – | 2700756. | (–) | 2695172. | (–) |
| 27 | 2p 3p | 3D2 | 2103900. | 2107151. | (0.2) | 2102917. | (−0.0) | 76 | 2p 4p | 1D2 | 2696850. | 2702087. | (0.2) | 2696558. | (−0.0) |
| 28 | 2p 3p | 3D3 | 2107390. | 2110622. | (0.2) | 2106614. | (−0.0) | 77 | 2p 4d | |$\mathrm{^3F_{4 }^{o}}$| | – | 2702915. | (–) | 2697461. | (–) |
| 29 | 2p 3p | 3S1 | 2119690. | 2123472. | (0.2) | 2118706. | (−0.0) | 78 | 2p 4d | |$\mathrm{^3D_{1 }^{o}}$| | – | 2705726. | (–) | 2700008. | (–) |
| 30 | 2p 3p | 3P0 | – | 2132252. | (–) | 2126478. | (–) | 79 | 2p 4d | |$\mathrm{^3D_{2 }^{o}}$| | – | 2706671. | (–) | 2701074. | (–) |
| 31 | 2p 3p | 3P1 | 2128680. | 2133785. | (0.2) | 2128247. | (−0.0) | 80 | 2p 4f | 1F3 | – | 2707963. | (–) | 2701789. | (–) |
| 32 | 2p 3p | 3P2 | 2130410. | 2135720. | (0.2) | 2130292. | (−0.0) | 81 | 2p 4f | 3F3 | – | 2708388. | (–) | 2702400. | (–) |
| 33 | 2p 3d | |$\mathrm{^3F_{2 }^{o}}$| | – | 2139901. | (–) | 2135677. | (–) | 82 | 2p 4d | |$\mathrm{^3D_{3 }^{o}}$| | – | 2708430. | (–) | 2703108. | (–) |
| 34 | 2p 3d | |$\mathrm{^3F_{3 }^{o}}$| | – | 2142598. | (–) | 2138636. | (–) | 83 | 2p 4f | 3F2 | – | 2708468. | (–) | 2702641. | (–) |
| 35 | 2p 3d | |$\mathrm{^1D_{2 }^{o}}$| | 2141580. | 2144437. | (0.1) | 2140459. | (−0.1) | 84 | 2p 4f | 3F4 | – | 2708819. | (–) | 2702505. | (–) |
| 36 | 2p 3d | |$\mathrm{^3F_{4 }^{o}}$| | – | 2145366. | (–) | 2141681. | (–) | 85 | 2p 4d | |$\mathrm{^3P_{2 }^{o}}$| | – | 2710818. | (–) | 2705109. | (–) |
| 37 | 2p 3p | 1D2 | 2148410. | 2157057. | (0.4) | 2150745. | (0.1) | 86 | 2p 4d | |$\mathrm{^3P_{1 }^{o}}$| | – | 2711544. | (–) | 2705747. | (–) |
| 38 | 2p 3d | |$\mathrm{^3D_{1 }^{o}}$| | 2160650. | 2165232. | (0.2) | 2159945. | (−0.0) | 87 | 2p 4d | |$\mathrm{^3P_{0 }^{o}}$| | – | 2711943. | (–) | 2706094. | (–) |
| 39 | 2p 3d | |$\mathrm{^3D_{2 }^{o}}$| | 2161960. | 2165961. | (0.2) | 2160762. | (−0.1) | 88 | 2p 4f | 3P3 | – | 2712961. | (–) | 2706897. | (–) |
| 40 | 2p 3d | |$\mathrm{^3D_{3 }^{o}}$| | 2163340. | 2167469. | (0.2) | 2162400. | (−0.0) | 89 | 2p 4f | 3P4 | – | 2713531. | (–) | 2707350. | (–) |
| 41 | 2p 3d | |$\mathrm{^3P_{2 }^{o}}$| | 2170190. | 2174402. | (0.2) | 2169739. | (−0.0) | 90 | 2p 4f | 3P5 | – | 2715225. | (–) | 2708632. | (–) |
| 42 | 2p 3d | |$\mathrm{^3P_{1 }^{o}}$| | 2171680. | 2175473. | (0.2) | 2170906. | (−0.0) | 91 | 2p 4f | 3D3 | – | 2716473. | (–) | 2710743. | (–) |
| 43 | 2p 3d | |$\mathrm{^3P_{0 }^{o}}$| | – | 2176019. | (–) | 2171512. | (–) | 92 | 2p 4f | 1D4 | – | 2717105. | (–) | 2710218. | (–) |
| 44 | 2p 3p | 1S0 | – | 2193603. | (–) | 2186094. | (–) | 93 | 2p 4f | 3D2 | – | 2717141. | (–) | 2711361. | (–) |
| 45 | 2p 3d | |$\mathrm{^1F_{3 }^{o}}$| | 2192860. | 2203326. | (0.5) | 2195894. | (0.1) | 94 | 2p 4p | 1S0 | – | 2717922. | (–) | 2706869. | (–) |
| 46 | 2p 3d | |$\mathrm{^1P_{1 }^{o}}$| | – | 2208387. | (–) | 2201414. | (–) | 95 | 2p 4f | 3D1 | – | 2718397. | (–) | 2712736. | (–) |
| 47 | 2s 4s | 3S1 | – | 2477026. | (–) | 2472580. | (–) | 96 | 2p 4f | 1D2 | – | 2719895. | (–) | 2713991. | (–) |
| 48 | 2s 4s | 1S0 | – | 2488107. | (–) | 2483578. | (–) | 97 | 2p 4d | |$\mathrm{^1F_{3 }^{o}}$| | – | 2722212. | (–) | 2715080. | (–) |
| 49 | 2s 4p | |$\mathrm{^3P_{0 }^{o}}$| | – | 2504555. | (–) | 2500383. | (–) | 98 | 2p 4d | |$\mathrm{^1P_{1 }^{o}}$| | – | 2723448. | (–) | 2716711. | (–) |
Al9+ target levels. Key: i: level index; Conf.: configuration; Level: level IC designation (largest weight); ENIST: observed energy from the NIST data base (Martin & Zalubas 1979); E98: calculated energy with 98-level CI expansion; E238: calculated energy with 238-level CI expansion (see the text); per cent: percentage difference between theoretical and NIST data. All energies are in cm−1.
| i . | Conf. . | level . | ENIST . | E98 . | (%) . | E238 . | (%) . | i . | Conf. . | level . | ENIST . | E98 . | (%) . | E238 . | (%) . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2s2 | 1S0 | 0. | 0. | (0) | 0. | (0) | 50 | 2s 4p | |$\mathrm{^3P_{1 }^{o}}$| | – | 2504724. | (−) | 2500556. | (−) |
| 2 | 2s 2p | |$\mathrm{^3P_{0 }^{o}}$| | 155148. | 155722. | (0.4) | 155539. | (0.3) | 51 | 2s 4p | |$\mathrm{^3P_{2 }^{o}}$| | – | 2505125. | (−) | 2500975. | (−) |
| 3 | 2s 2p | |$\mathrm{^3P_{1 }^{o}}$| | 156798. | 157487. | (0.4) | 157404. | (0.4) | 52 | 2s 4p | |$\mathrm{^1P_{1 }^{o}}$| | – | 2508073. | (–) | 2503514. | (–) |
| 4 | 2s 2p | |$\mathrm{^3P_{2 }^{o}}$| | 160429. | 161146. | (0.4) | 161278. | (0.5) | 53 | 2s 4d | 3D1 | – | 2520502. | (–) | 2516248. | (–) |
| 5 | 2s 2p | |$\mathrm{^1P_{1 }^{o}}$| | 300490. | 309273. | (2.9) | 307209. | (2.2) | 54 | 2s 4d | 3D2 | – | 2520573. | (–) | 2516321. | (–) |
| 6 | 2p2 | 3P0 | 404574. | 408026. | (0.9) | 407826. | (0.8) | 55 | 2s 4d | 3D3 | – | 2520682. | (–) | 2516434. | (–) |
| 7 | 2p2 | 3P1 | 406517. | 409969. | (0.8) | 409888. | (0.8) | 56 | 2s 4d | 1D2 | 2527560. | 2530218. | (0.1) | 2525880. | (−0.1) |
| 8 | 2p2 | 3P2 | 409690. | 413420. | (0.9) | 413526. | (0.9) | 57 | 2s 4f | |$\mathrm{^3F_{2 }^{o}}$| | 2528570. | 2530774. | (0.1) | 2526258. | (−0.1) |
| 9 | 2p2 | 1D2 | 449732. | 458157. | (1.9) | 457831. | (1.8) | 58 | 2s 4f | |$\mathrm{^3F_{3 }^{o}}$| | 2528570. | 2530815. | (0.1) | 2526299. | (−0.1) |
| 10 | 2p2 | 1S0 | 553783. | 567794. | (2.5) | 567267. | (2.4) | 59 | 2s 4f | |$\mathrm{^3F_{4 }^{o}}$| | 2528570. | 2530871. | (0.1) | 2526355. | (−0.1) |
| 11 | 2s 3s | 3S1 | 1855760. | 1856089. | (0.0) | 1852844. | (−0.2) | 60 | 2s 4f | |$\mathrm{^1F_{3 }^{o}}$| | – | 2533730. | (–) | 2528991. | (–) |
| 12 | 2s 3s | 1S0 | 1884420. | 1886214. | (0.1) | 1882216. | (−0.1) | 61 | 2p 4s | |$\mathrm{^3P_{0 }^{o}}$| | – | 2661563. | (–) | 2655681. | (–) |
| 13 | 2s 3p | |$\mathrm{^1P_{1 }^{o}}$| | 1923850. | 1925826. | (0.1) | 1922358. | (−0.1) | 62 | 2p 4s | |$\mathrm{^3P_{1 }^{o}}$| | – | 2662724. | (–) | 2656820. | (–) |
| 14 | 2s 3p | |$\mathrm{^3P_{0 }^{o}}$| | – | 1928630. | (–) | 1925009. | (–) | 63 | 2p 4s | |$\mathrm{^3P_{2 }^{o}}$| | – | 2666840. | (–) | 2661460. | (–) |
| 15 | 2s 3p | |$\mathrm{^3P_{1 }^{o}}$| | – | 1929220. | (–) | 1925611. | (–) | 64 | 2p 4s | |$\mathrm{^1P_{1 }^{o}}$| | – | 2673641. | (–) | 2666939. | (–) |
| 16 | 2s 3p | |$\mathrm{^3P_{2 }^{o}}$| | – | 1930059. | (–) | 1926462. | (–) | 65 | 2p 4p | 1P1 | – | 2681281. | (–) | 2675347. | (–) |
| 17 | 2s 3d | 3D1 | 1965860. | 1967770. | (0.1) | 1964163. | (−0.1) | 66 | 2p 4p | 3D1 | – | 2684513. | (–) | 2678722. | (–) |
| 18 | 2s 3d | 3D2 | 1966080. | 1967980. | (0.1) | 1964378. | (−0.1) | 67 | 2p 4p | 3D2 | – | 2684938. | (–) | 2679129. | (–) |
| 19 | 2s 3d | 3D3 | 1966300. | 1968296. | (0.1) | 1964701. | (−0.1) | 68 | 2p 4p | 3D3 | – | 2688348. | (–) | 2682876. | (–) |
| 20 | 2s 3d | 1D2 | 1992340. | 1997586. | (0.3) | 1993399. | (0.1) | 69 | 2p 4p | 3S1 | – | 2691166. | (–) | 2684805. | (–) |
| 21 | 2p 3s | |$\mathrm{^3P_{0 }^{o}}$| | 2057140. | 2055664. | (−0.1) | 2050249. | (−0.3) | 70 | 2p 4p | 3P0 | – | 2691420. | (–) | 2685788. | (–) |
| 22 | 2p 3s | |$\mathrm{^3P_{1 }^{o}}$| | 2057140. | 2057249. | (0.0) | 2051958. | (−0.3) | 71 | 2p 4p | 3P1 | – | 2694295. | (–) | 2688609. | (–) |
| 23 | 2p 3s | |$\mathrm{^3P_{2 }^{o}}$| | 2057140. | 2060910. | (0.2) | 2055983. | (−0.1) | 72 | 2p 4p | 3P2 | – | 2694733. | (–) | 2689496. | (–) |
| 24 | 2p 3s | |$\mathrm{^1P_{1 }^{o}}$| | 2091870. | 2090063. | (−0.1) | 2084057. | (−0.4) | 73 | 2p 4d | |$\mathrm{^3F_{2 }^{o}}$| | – | 2697404. | (–) | 2691501. | (–) |
| 25 | 2p 3p | 1P1 | 2094820. | 2097317. | (0.1) | 2093229. | (−0.1) | 74 | 2p 4d | |$\mathrm{^3F_{3 }^{o}}$| | – | 2699888. | (–) | 2694096. | (–) |
| 26 | 2p 3p | 3D1 | 2102330. | 2105510. | (0.2) | 2101249. | (−0.1) | 75 | 2p 4d | |$\mathrm{^1D_{2 }^{o}}$| | – | 2700756. | (–) | 2695172. | (–) |
| 27 | 2p 3p | 3D2 | 2103900. | 2107151. | (0.2) | 2102917. | (−0.0) | 76 | 2p 4p | 1D2 | 2696850. | 2702087. | (0.2) | 2696558. | (−0.0) |
| 28 | 2p 3p | 3D3 | 2107390. | 2110622. | (0.2) | 2106614. | (−0.0) | 77 | 2p 4d | |$\mathrm{^3F_{4 }^{o}}$| | – | 2702915. | (–) | 2697461. | (–) |
| 29 | 2p 3p | 3S1 | 2119690. | 2123472. | (0.2) | 2118706. | (−0.0) | 78 | 2p 4d | |$\mathrm{^3D_{1 }^{o}}$| | – | 2705726. | (–) | 2700008. | (–) |
| 30 | 2p 3p | 3P0 | – | 2132252. | (–) | 2126478. | (–) | 79 | 2p 4d | |$\mathrm{^3D_{2 }^{o}}$| | – | 2706671. | (–) | 2701074. | (–) |
| 31 | 2p 3p | 3P1 | 2128680. | 2133785. | (0.2) | 2128247. | (−0.0) | 80 | 2p 4f | 1F3 | – | 2707963. | (–) | 2701789. | (–) |
| 32 | 2p 3p | 3P2 | 2130410. | 2135720. | (0.2) | 2130292. | (−0.0) | 81 | 2p 4f | 3F3 | – | 2708388. | (–) | 2702400. | (–) |
| 33 | 2p 3d | |$\mathrm{^3F_{2 }^{o}}$| | – | 2139901. | (–) | 2135677. | (–) | 82 | 2p 4d | |$\mathrm{^3D_{3 }^{o}}$| | – | 2708430. | (–) | 2703108. | (–) |
| 34 | 2p 3d | |$\mathrm{^3F_{3 }^{o}}$| | – | 2142598. | (–) | 2138636. | (–) | 83 | 2p 4f | 3F2 | – | 2708468. | (–) | 2702641. | (–) |
| 35 | 2p 3d | |$\mathrm{^1D_{2 }^{o}}$| | 2141580. | 2144437. | (0.1) | 2140459. | (−0.1) | 84 | 2p 4f | 3F4 | – | 2708819. | (–) | 2702505. | (–) |
| 36 | 2p 3d | |$\mathrm{^3F_{4 }^{o}}$| | – | 2145366. | (–) | 2141681. | (–) | 85 | 2p 4d | |$\mathrm{^3P_{2 }^{o}}$| | – | 2710818. | (–) | 2705109. | (–) |
| 37 | 2p 3p | 1D2 | 2148410. | 2157057. | (0.4) | 2150745. | (0.1) | 86 | 2p 4d | |$\mathrm{^3P_{1 }^{o}}$| | – | 2711544. | (–) | 2705747. | (–) |
| 38 | 2p 3d | |$\mathrm{^3D_{1 }^{o}}$| | 2160650. | 2165232. | (0.2) | 2159945. | (−0.0) | 87 | 2p 4d | |$\mathrm{^3P_{0 }^{o}}$| | – | 2711943. | (–) | 2706094. | (–) |
| 39 | 2p 3d | |$\mathrm{^3D_{2 }^{o}}$| | 2161960. | 2165961. | (0.2) | 2160762. | (−0.1) | 88 | 2p 4f | 3P3 | – | 2712961. | (–) | 2706897. | (–) |
| 40 | 2p 3d | |$\mathrm{^3D_{3 }^{o}}$| | 2163340. | 2167469. | (0.2) | 2162400. | (−0.0) | 89 | 2p 4f | 3P4 | – | 2713531. | (–) | 2707350. | (–) |
| 41 | 2p 3d | |$\mathrm{^3P_{2 }^{o}}$| | 2170190. | 2174402. | (0.2) | 2169739. | (−0.0) | 90 | 2p 4f | 3P5 | – | 2715225. | (–) | 2708632. | (–) |
| 42 | 2p 3d | |$\mathrm{^3P_{1 }^{o}}$| | 2171680. | 2175473. | (0.2) | 2170906. | (−0.0) | 91 | 2p 4f | 3D3 | – | 2716473. | (–) | 2710743. | (–) |
| 43 | 2p 3d | |$\mathrm{^3P_{0 }^{o}}$| | – | 2176019. | (–) | 2171512. | (–) | 92 | 2p 4f | 1D4 | – | 2717105. | (–) | 2710218. | (–) |
| 44 | 2p 3p | 1S0 | – | 2193603. | (–) | 2186094. | (–) | 93 | 2p 4f | 3D2 | – | 2717141. | (–) | 2711361. | (–) |
| 45 | 2p 3d | |$\mathrm{^1F_{3 }^{o}}$| | 2192860. | 2203326. | (0.5) | 2195894. | (0.1) | 94 | 2p 4p | 1S0 | – | 2717922. | (–) | 2706869. | (–) |
| 46 | 2p 3d | |$\mathrm{^1P_{1 }^{o}}$| | – | 2208387. | (–) | 2201414. | (–) | 95 | 2p 4f | 3D1 | – | 2718397. | (–) | 2712736. | (–) |
| 47 | 2s 4s | 3S1 | – | 2477026. | (–) | 2472580. | (–) | 96 | 2p 4f | 1D2 | – | 2719895. | (–) | 2713991. | (–) |
| 48 | 2s 4s | 1S0 | – | 2488107. | (–) | 2483578. | (–) | 97 | 2p 4d | |$\mathrm{^1F_{3 }^{o}}$| | – | 2722212. | (–) | 2715080. | (–) |
| 49 | 2s 4p | |$\mathrm{^3P_{0 }^{o}}$| | – | 2504555. | (–) | 2500383. | (–) | 98 | 2p 4d | |$\mathrm{^1P_{1 }^{o}}$| | – | 2723448. | (–) | 2716711. | (–) |
| i . | Conf. . | level . | ENIST . | E98 . | (%) . | E238 . | (%) . | i . | Conf. . | level . | ENIST . | E98 . | (%) . | E238 . | (%) . |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2s2 | 1S0 | 0. | 0. | (0) | 0. | (0) | 50 | 2s 4p | |$\mathrm{^3P_{1 }^{o}}$| | – | 2504724. | (−) | 2500556. | (−) |
| 2 | 2s 2p | |$\mathrm{^3P_{0 }^{o}}$| | 155148. | 155722. | (0.4) | 155539. | (0.3) | 51 | 2s 4p | |$\mathrm{^3P_{2 }^{o}}$| | – | 2505125. | (−) | 2500975. | (−) |
| 3 | 2s 2p | |$\mathrm{^3P_{1 }^{o}}$| | 156798. | 157487. | (0.4) | 157404. | (0.4) | 52 | 2s 4p | |$\mathrm{^1P_{1 }^{o}}$| | – | 2508073. | (–) | 2503514. | (–) |
| 4 | 2s 2p | |$\mathrm{^3P_{2 }^{o}}$| | 160429. | 161146. | (0.4) | 161278. | (0.5) | 53 | 2s 4d | 3D1 | – | 2520502. | (–) | 2516248. | (–) |
| 5 | 2s 2p | |$\mathrm{^1P_{1 }^{o}}$| | 300490. | 309273. | (2.9) | 307209. | (2.2) | 54 | 2s 4d | 3D2 | – | 2520573. | (–) | 2516321. | (–) |
| 6 | 2p2 | 3P0 | 404574. | 408026. | (0.9) | 407826. | (0.8) | 55 | 2s 4d | 3D3 | – | 2520682. | (–) | 2516434. | (–) |
| 7 | 2p2 | 3P1 | 406517. | 409969. | (0.8) | 409888. | (0.8) | 56 | 2s 4d | 1D2 | 2527560. | 2530218. | (0.1) | 2525880. | (−0.1) |
| 8 | 2p2 | 3P2 | 409690. | 413420. | (0.9) | 413526. | (0.9) | 57 | 2s 4f | |$\mathrm{^3F_{2 }^{o}}$| | 2528570. | 2530774. | (0.1) | 2526258. | (−0.1) |
| 9 | 2p2 | 1D2 | 449732. | 458157. | (1.9) | 457831. | (1.8) | 58 | 2s 4f | |$\mathrm{^3F_{3 }^{o}}$| | 2528570. | 2530815. | (0.1) | 2526299. | (−0.1) |
| 10 | 2p2 | 1S0 | 553783. | 567794. | (2.5) | 567267. | (2.4) | 59 | 2s 4f | |$\mathrm{^3F_{4 }^{o}}$| | 2528570. | 2530871. | (0.1) | 2526355. | (−0.1) |
| 11 | 2s 3s | 3S1 | 1855760. | 1856089. | (0.0) | 1852844. | (−0.2) | 60 | 2s 4f | |$\mathrm{^1F_{3 }^{o}}$| | – | 2533730. | (–) | 2528991. | (–) |
| 12 | 2s 3s | 1S0 | 1884420. | 1886214. | (0.1) | 1882216. | (−0.1) | 61 | 2p 4s | |$\mathrm{^3P_{0 }^{o}}$| | – | 2661563. | (–) | 2655681. | (–) |
| 13 | 2s 3p | |$\mathrm{^1P_{1 }^{o}}$| | 1923850. | 1925826. | (0.1) | 1922358. | (−0.1) | 62 | 2p 4s | |$\mathrm{^3P_{1 }^{o}}$| | – | 2662724. | (–) | 2656820. | (–) |
| 14 | 2s 3p | |$\mathrm{^3P_{0 }^{o}}$| | – | 1928630. | (–) | 1925009. | (–) | 63 | 2p 4s | |$\mathrm{^3P_{2 }^{o}}$| | – | 2666840. | (–) | 2661460. | (–) |
| 15 | 2s 3p | |$\mathrm{^3P_{1 }^{o}}$| | – | 1929220. | (–) | 1925611. | (–) | 64 | 2p 4s | |$\mathrm{^1P_{1 }^{o}}$| | – | 2673641. | (–) | 2666939. | (–) |
| 16 | 2s 3p | |$\mathrm{^3P_{2 }^{o}}$| | – | 1930059. | (–) | 1926462. | (–) | 65 | 2p 4p | 1P1 | – | 2681281. | (–) | 2675347. | (–) |
| 17 | 2s 3d | 3D1 | 1965860. | 1967770. | (0.1) | 1964163. | (−0.1) | 66 | 2p 4p | 3D1 | – | 2684513. | (–) | 2678722. | (–) |
| 18 | 2s 3d | 3D2 | 1966080. | 1967980. | (0.1) | 1964378. | (−0.1) | 67 | 2p 4p | 3D2 | – | 2684938. | (–) | 2679129. | (–) |
| 19 | 2s 3d | 3D3 | 1966300. | 1968296. | (0.1) | 1964701. | (−0.1) | 68 | 2p 4p | 3D3 | – | 2688348. | (–) | 2682876. | (–) |
| 20 | 2s 3d | 1D2 | 1992340. | 1997586. | (0.3) | 1993399. | (0.1) | 69 | 2p 4p | 3S1 | – | 2691166. | (–) | 2684805. | (–) |
| 21 | 2p 3s | |$\mathrm{^3P_{0 }^{o}}$| | 2057140. | 2055664. | (−0.1) | 2050249. | (−0.3) | 70 | 2p 4p | 3P0 | – | 2691420. | (–) | 2685788. | (–) |
| 22 | 2p 3s | |$\mathrm{^3P_{1 }^{o}}$| | 2057140. | 2057249. | (0.0) | 2051958. | (−0.3) | 71 | 2p 4p | 3P1 | – | 2694295. | (–) | 2688609. | (–) |
| 23 | 2p 3s | |$\mathrm{^3P_{2 }^{o}}$| | 2057140. | 2060910. | (0.2) | 2055983. | (−0.1) | 72 | 2p 4p | 3P2 | – | 2694733. | (–) | 2689496. | (–) |
| 24 | 2p 3s | |$\mathrm{^1P_{1 }^{o}}$| | 2091870. | 2090063. | (−0.1) | 2084057. | (−0.4) | 73 | 2p 4d | |$\mathrm{^3F_{2 }^{o}}$| | – | 2697404. | (–) | 2691501. | (–) |
| 25 | 2p 3p | 1P1 | 2094820. | 2097317. | (0.1) | 2093229. | (−0.1) | 74 | 2p 4d | |$\mathrm{^3F_{3 }^{o}}$| | – | 2699888. | (–) | 2694096. | (–) |
| 26 | 2p 3p | 3D1 | 2102330. | 2105510. | (0.2) | 2101249. | (−0.1) | 75 | 2p 4d | |$\mathrm{^1D_{2 }^{o}}$| | – | 2700756. | (–) | 2695172. | (–) |
| 27 | 2p 3p | 3D2 | 2103900. | 2107151. | (0.2) | 2102917. | (−0.0) | 76 | 2p 4p | 1D2 | 2696850. | 2702087. | (0.2) | 2696558. | (−0.0) |
| 28 | 2p 3p | 3D3 | 2107390. | 2110622. | (0.2) | 2106614. | (−0.0) | 77 | 2p 4d | |$\mathrm{^3F_{4 }^{o}}$| | – | 2702915. | (–) | 2697461. | (–) |
| 29 | 2p 3p | 3S1 | 2119690. | 2123472. | (0.2) | 2118706. | (−0.0) | 78 | 2p 4d | |$\mathrm{^3D_{1 }^{o}}$| | – | 2705726. | (–) | 2700008. | (–) |
| 30 | 2p 3p | 3P0 | – | 2132252. | (–) | 2126478. | (–) | 79 | 2p 4d | |$\mathrm{^3D_{2 }^{o}}$| | – | 2706671. | (–) | 2701074. | (–) |
| 31 | 2p 3p | 3P1 | 2128680. | 2133785. | (0.2) | 2128247. | (−0.0) | 80 | 2p 4f | 1F3 | – | 2707963. | (–) | 2701789. | (–) |
| 32 | 2p 3p | 3P2 | 2130410. | 2135720. | (0.2) | 2130292. | (−0.0) | 81 | 2p 4f | 3F3 | – | 2708388. | (–) | 2702400. | (–) |
| 33 | 2p 3d | |$\mathrm{^3F_{2 }^{o}}$| | – | 2139901. | (–) | 2135677. | (–) | 82 | 2p 4d | |$\mathrm{^3D_{3 }^{o}}$| | – | 2708430. | (–) | 2703108. | (–) |
| 34 | 2p 3d | |$\mathrm{^3F_{3 }^{o}}$| | – | 2142598. | (–) | 2138636. | (–) | 83 | 2p 4f | 3F2 | – | 2708468. | (–) | 2702641. | (–) |
| 35 | 2p 3d | |$\mathrm{^1D_{2 }^{o}}$| | 2141580. | 2144437. | (0.1) | 2140459. | (−0.1) | 84 | 2p 4f | 3F4 | – | 2708819. | (–) | 2702505. | (–) |
| 36 | 2p 3d | |$\mathrm{^3F_{4 }^{o}}$| | – | 2145366. | (–) | 2141681. | (–) | 85 | 2p 4d | |$\mathrm{^3P_{2 }^{o}}$| | – | 2710818. | (–) | 2705109. | (–) |
| 37 | 2p 3p | 1D2 | 2148410. | 2157057. | (0.4) | 2150745. | (0.1) | 86 | 2p 4d | |$\mathrm{^3P_{1 }^{o}}$| | – | 2711544. | (–) | 2705747. | (–) |
| 38 | 2p 3d | |$\mathrm{^3D_{1 }^{o}}$| | 2160650. | 2165232. | (0.2) | 2159945. | (−0.0) | 87 | 2p 4d | |$\mathrm{^3P_{0 }^{o}}$| | – | 2711943. | (–) | 2706094. | (–) |
| 39 | 2p 3d | |$\mathrm{^3D_{2 }^{o}}$| | 2161960. | 2165961. | (0.2) | 2160762. | (−0.1) | 88 | 2p 4f | 3P3 | – | 2712961. | (–) | 2706897. | (–) |
| 40 | 2p 3d | |$\mathrm{^3D_{3 }^{o}}$| | 2163340. | 2167469. | (0.2) | 2162400. | (−0.0) | 89 | 2p 4f | 3P4 | – | 2713531. | (–) | 2707350. | (–) |
| 41 | 2p 3d | |$\mathrm{^3P_{2 }^{o}}$| | 2170190. | 2174402. | (0.2) | 2169739. | (−0.0) | 90 | 2p 4f | 3P5 | – | 2715225. | (–) | 2708632. | (–) |
| 42 | 2p 3d | |$\mathrm{^3P_{1 }^{o}}$| | 2171680. | 2175473. | (0.2) | 2170906. | (−0.0) | 91 | 2p 4f | 3D3 | – | 2716473. | (–) | 2710743. | (–) |
| 43 | 2p 3d | |$\mathrm{^3P_{0 }^{o}}$| | – | 2176019. | (–) | 2171512. | (–) | 92 | 2p 4f | 1D4 | – | 2717105. | (–) | 2710218. | (–) |
| 44 | 2p 3p | 1S0 | – | 2193603. | (–) | 2186094. | (–) | 93 | 2p 4f | 3D2 | – | 2717141. | (–) | 2711361. | (–) |
| 45 | 2p 3d | |$\mathrm{^1F_{3 }^{o}}$| | 2192860. | 2203326. | (0.5) | 2195894. | (0.1) | 94 | 2p 4p | 1S0 | – | 2717922. | (–) | 2706869. | (–) |
| 46 | 2p 3d | |$\mathrm{^1P_{1 }^{o}}$| | – | 2208387. | (–) | 2201414. | (–) | 95 | 2p 4f | 3D1 | – | 2718397. | (–) | 2712736. | (–) |
| 47 | 2s 4s | 3S1 | – | 2477026. | (–) | 2472580. | (–) | 96 | 2p 4f | 1D2 | – | 2719895. | (–) | 2713991. | (–) |
| 48 | 2s 4s | 1S0 | – | 2488107. | (–) | 2483578. | (–) | 97 | 2p 4d | |$\mathrm{^1F_{3 }^{o}}$| | – | 2722212. | (–) | 2715080. | (–) |
| 49 | 2s 4p | |$\mathrm{^3P_{0 }^{o}}$| | – | 2504555. | (–) | 2500383. | (–) | 98 | 2p 4d | |$\mathrm{^1P_{1 }^{o}}$| | – | 2723448. | (–) | 2716711. | (–) |
In practice, we find that changes in the line strength, S, or |$\Omega ^{\rm PWB}_{\infty }$| between two different atomic structures change not only the infinite energy values but also the (background) ordinary collision strength correspondingly over a wide range of collision energies, and hence the effective collision strength over a wide range of temperatures, unless dominated by resonances. A 20 per cent change, say, in S or |$\Omega ^{\rm PWB}_{\infty }$| provides a very realistic measure of the resulting change in effective collision strengths. Thus, care must be taken when attempting to deduce anything about scattering methods from differences in the collision data without reference to differences in the underlying atomic structure.
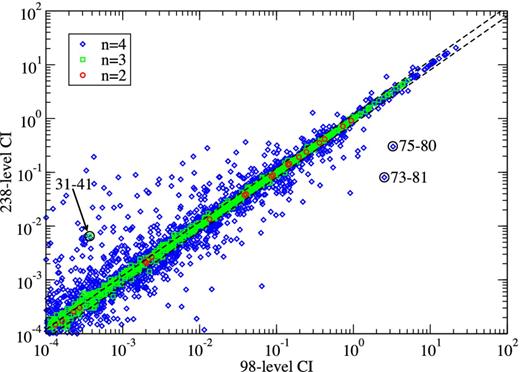
A comparison of y∞ (see equation 4) for the 98- versus 238-level CI atomic structures for transitions amongst the 98 lowest common levels of Al 9+. ○: transitions with upper level with n = 2; □: transitions with upper level with n = 3; ⋄: transitions with upper level with n = 4; dashed lines: 20 per cent fractional difference.
We circle several transitions for comment. The transition 31–41: |$\mathrm{2p3p\,^3P_1{\rm -}2p3d\,^3P_2^{o}}$| is a dipole one, its line strength changes by a factor of 18 between the 98- and 238-level structures. Note also the transitions 75–80: |$\mathrm{2p4d\,^1D_2^{o}{\rm -}2p4f\,^1F_3}$| and 73–81: |$\mathrm{2p4d\,^3F_2^{o}{\rm -}2p4f\,^3F_3}$|. Both transitions are dipole allowed and quite strong and yet differ by about a factor of 20 and 30 between the two structures. These levels lie towards the upper end of the 98-level CI expansion. These differences highlight the need for as accurate an atomic description as possible to obtain the best target for accurate collision data and the need to exercise extreme caution when making comparisons of collision data based on different atomic structures.
4 COLLISIONS
In this section, we carry-out a series of comparisons of effective collision strengths for Al 9+ at the temperature of peak abundance for an electron collisional plasma (Bryans et al. 2006). We then look at issues relating in particular to low-temperature (e.g. photoionized) plasmas and much higher temperature plasmas (e.g. solar flares).
4.1 Peak abundance temperature
In Fig. 2, we compare our 98-level CC ICFT and BP R-matrix Maxwellian effective collision strengths, ϒ, for all inelastic transitions in Al 9+ at the temperature of peak abundance, 106 K, in an electron collisional plasma. We recall that both calculations use the exact same (98-level CI) structure. We note excellent agreement between the two scattering methods, as illustrated by the points lying on the diagonal, only 82 points out of 4753 have a difference larger than 10 per cent. This is to be contrasted with the spread of points shown in Fig. 1 which results from our two different atomic structures.
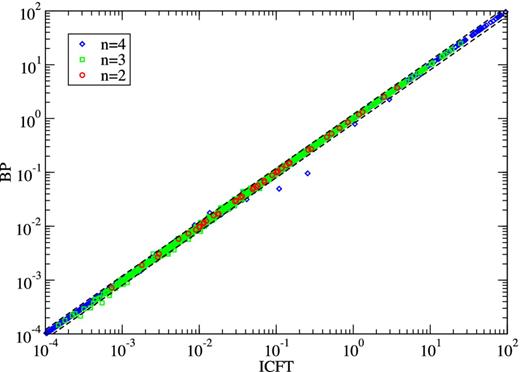
A comparison of effective collision strengths from 98-level CI/CC ICFT versus BP R-matrix calculations for all inelastic transitions amongst the 98 levels of Al 9+ at Te = 106 K. ○: transitions with upper level n = 2; □: transitions with upper level n = 3; ⋄: transitions with upper level n = 4; dashed lines: 20 per cent fractional difference.
Only two points differ from the diagonal more than 50 per cent, at around ϒ = 10−1, they correspond to the transitions 67–75: |$\mathrm{2p4p\,^3D_2{\rm -}2p4d\,^1D_2^{o}}$| and 83–98: |$\mathrm{2p4f\,^3F_2{\rm -}2p4d\,^1P_1^{o}}$|. Both are dipole allowed through spin–orbit mixing only. It is likely that including the spin–orbit interaction in the collision calculation causes the difference, providing additional mixing via the (N + 1)-electron Hamiltonian diagonalization.
Next, in Fig. 3 we compare our 98- versus 238-level CI/CC ICFT effective collision strengths as a whole. In contrast to Fig. 2, we see a much wider spread of points, i.e. the agreement between different scattering methods is much (much) better than that obtained using different CI basis sets. Like the comparison of line strengths and |$\Omega ^{\rm PWB}_{\infty }$| shown in Fig. 1, we note the excellent and very good agreement between the two sets of results for transitions up to n = 2 and 3, respectively, while there is a much wider spread in the comparison for transitions up to n = 4. However, unlike the atomic structure comparison, there is a systematic shift above the diagonal. The 238-level CC results are systematically larger than the 98-level ones. Thus, we conclude that this is not due to the differences in atomic structure, which were evenly distributed above and below the diagonal, rather that this is a measure of the lack of convergence of the CC expansion in the 98-level CC calculation for the transitions involving n = 4 levels. This mirrors the lack of convergence of the 98-level CI expansion for n = 4 levels. We note that there are still more than one hundred levels which lie above the n = 4 levels in the 238-level CI/CC case.
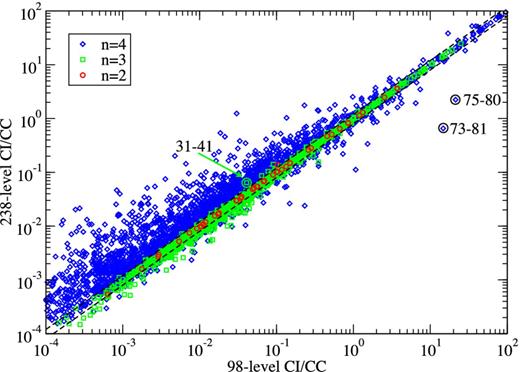
A comparison of effective collision strengths from 98- versus 238-level CI/CC ICFT R-matrix calculations for all inelastic transitions amongst the 98 lowest common levels of Al 9+ at Te = 106 K. ○: transitions with upper level n = 2; □: transitions with upper level n = 3; ⋄: transitions with upper level n = 4; dashed lines: 20 per cent fractional difference.
Specifically, one half of the transitions in Fig. 3 differ by more than 30 per cent. The number of transitions differing by more than 20 per cent (lines indicated in the plot) correspond to 1 for n = 2 (out of 45), 256 for n = 3 (out of 990) and 2331 for n = 4 (out of 3718). Note also that the three transitions which were circled in Fig. 1 are again circled in Fig. 3. The strong transitions 75–80 and 73–81 do illustrate how outliers in the atomic structure comparison (factor 20 and 30 difference) show-up as outliers in the collision comparison (factor 10 and 20 difference). For the weaker transition 31–41, the resonances in the collision calculation ‘dampen’ the difference in atomic structure, it being ‘just’ a factor of 1.6 now. In Table 3, we give the exact number of transitions which have a difference δ = |ϒ98 − ϒ238|/ϒ238 larger than a given percentage for the y∞ for the 98- versus 238-level CI atomic structures as well as the ϒ at T = 106 K for the 98-level CC ICFT versus BP and the 98- versus 238-level CC ICFT comparisons.
Number of transitions in Figs 1–3 which differ by more than a certain relative error δ = |ϒ98 − ϒ238|/ϒ238 (or ϒ → y∞), as a percentage.
| Rel. error . | Fig. 1: y∞ . | Fig. 2: 98 CI/CC ϒ . | Fig. 3: ICFT ϒ . |
|---|---|---|---|
| (per cent) . | 98 versus 238 CI . | BP versus ICFT . | 98 versus 238 CI/CC . |
| 1 | 3778 | 1336 | 4579 |
| 2 | 3600 | 803 | 4400 |
| 3 | 3416 | 500 | 4243 |
| 4 | 3266 | 350 | 4077 |
| 5 | 3141 | 260 | 3928 |
| 6 | 3022 | 206 | 3798 |
| 7 | 2914 | 158 | 3676 |
| 8 | 2804 | 127 | 3569 |
| 9 | 2722 | 106 | 3460 |
| 10 | 2644 | 82 | 3357 |
| 20 | 2068 | 22 | 2582 |
| 30 | 1643 | 9 | 2090 |
| 40 | 1356 | 4 | 1725 |
| 50 | 1163 | 2 | 1449 |
| 75 | 846 | 2 | 1113 |
| 100 | 707 | 2 | 901 |
| 150 | 538 | 1 | 647 |
| 200 | 443 | 0 | 505 |
| 300 | 336 | 0 | 320 |
| 1000 | 187 | 0 | 88 |
| Total | 4035 | 4753 | 4753 |
| Rel. error . | Fig. 1: y∞ . | Fig. 2: 98 CI/CC ϒ . | Fig. 3: ICFT ϒ . |
|---|---|---|---|
| (per cent) . | 98 versus 238 CI . | BP versus ICFT . | 98 versus 238 CI/CC . |
| 1 | 3778 | 1336 | 4579 |
| 2 | 3600 | 803 | 4400 |
| 3 | 3416 | 500 | 4243 |
| 4 | 3266 | 350 | 4077 |
| 5 | 3141 | 260 | 3928 |
| 6 | 3022 | 206 | 3798 |
| 7 | 2914 | 158 | 3676 |
| 8 | 2804 | 127 | 3569 |
| 9 | 2722 | 106 | 3460 |
| 10 | 2644 | 82 | 3357 |
| 20 | 2068 | 22 | 2582 |
| 30 | 1643 | 9 | 2090 |
| 40 | 1356 | 4 | 1725 |
| 50 | 1163 | 2 | 1449 |
| 75 | 846 | 2 | 1113 |
| 100 | 707 | 2 | 901 |
| 150 | 538 | 1 | 647 |
| 200 | 443 | 0 | 505 |
| 300 | 336 | 0 | 320 |
| 1000 | 187 | 0 | 88 |
| Total | 4035 | 4753 | 4753 |
Number of transitions in Figs 1–3 which differ by more than a certain relative error δ = |ϒ98 − ϒ238|/ϒ238 (or ϒ → y∞), as a percentage.
| Rel. error . | Fig. 1: y∞ . | Fig. 2: 98 CI/CC ϒ . | Fig. 3: ICFT ϒ . |
|---|---|---|---|
| (per cent) . | 98 versus 238 CI . | BP versus ICFT . | 98 versus 238 CI/CC . |
| 1 | 3778 | 1336 | 4579 |
| 2 | 3600 | 803 | 4400 |
| 3 | 3416 | 500 | 4243 |
| 4 | 3266 | 350 | 4077 |
| 5 | 3141 | 260 | 3928 |
| 6 | 3022 | 206 | 3798 |
| 7 | 2914 | 158 | 3676 |
| 8 | 2804 | 127 | 3569 |
| 9 | 2722 | 106 | 3460 |
| 10 | 2644 | 82 | 3357 |
| 20 | 2068 | 22 | 2582 |
| 30 | 1643 | 9 | 2090 |
| 40 | 1356 | 4 | 1725 |
| 50 | 1163 | 2 | 1449 |
| 75 | 846 | 2 | 1113 |
| 100 | 707 | 2 | 901 |
| 150 | 538 | 1 | 647 |
| 200 | 443 | 0 | 505 |
| 300 | 336 | 0 | 320 |
| 1000 | 187 | 0 | 88 |
| Total | 4035 | 4753 | 4753 |
| Rel. error . | Fig. 1: y∞ . | Fig. 2: 98 CI/CC ϒ . | Fig. 3: ICFT ϒ . |
|---|---|---|---|
| (per cent) . | 98 versus 238 CI . | BP versus ICFT . | 98 versus 238 CI/CC . |
| 1 | 3778 | 1336 | 4579 |
| 2 | 3600 | 803 | 4400 |
| 3 | 3416 | 500 | 4243 |
| 4 | 3266 | 350 | 4077 |
| 5 | 3141 | 260 | 3928 |
| 6 | 3022 | 206 | 3798 |
| 7 | 2914 | 158 | 3676 |
| 8 | 2804 | 127 | 3569 |
| 9 | 2722 | 106 | 3460 |
| 10 | 2644 | 82 | 3357 |
| 20 | 2068 | 22 | 2582 |
| 30 | 1643 | 9 | 2090 |
| 40 | 1356 | 4 | 1725 |
| 50 | 1163 | 2 | 1449 |
| 75 | 846 | 2 | 1113 |
| 100 | 707 | 2 | 901 |
| 150 | 538 | 1 | 647 |
| 200 | 443 | 0 | 505 |
| 300 | 336 | 0 | 320 |
| 1000 | 187 | 0 | 88 |
| Total | 4035 | 4753 | 4753 |
We can confirm further that the systematic increase of the effective collision strengths to n = 4 in the 238-level CC calculation over those of the 98-level CC calculation is due to the lack of convergence of the CC expansion in the latter. Like the convergence of the CI expansion, the convergence of the CC expansion is essentially independent of the coupling scheme, i.e. the specific R-matrix method used, be it LS, ICFT, BP or DARC. We illustrate this in Fig. 4 where we make a similar comparison of 54- versus 130-term CC LS-coupling R-matrix effective collision strengths. We see the same systematic increase for transitions to n = 4 as in the comparison of ICFT R-matrix effective collision strengths.

A comparison of effective collision strengths from 54- versus 130-term CI/CC LS-coupling R-matrix calculations for all inelastic transitions amongst the 54 lowest common terms of Al 9+ at Te = 106 K. ○: transitions with upper term n = 2; □: transitions with upper term n = 3; ⋄: transitions with upper term n = 4; dashed lines: 20 per cent fractional difference.
The plots we have shown so far are useful in the respect that they allow us to make comparisons as a function of the strength of a transition – larger differences are acceptable for weaker transitions. On the other hand, because of the wide range of strengths, it is necessary for such plots to be logarithmic. If we plot the ratio of results from two different calculations, we can make a linear comparison. We do this in Fig. 5 for the same comparison as we made in Fig. 3, and with respect to the lower level of the transition (Fig. 5a) or the upper one (Fig. 5b). Fig. 5(a) shows that the transitions with the largest scatter are those from 2s 3l (lower level index 11–20) and 2s 4l (lower level index 47–60) up to n = 4, and where we have highlighted by symbol/colour all upper levels with the same n-value. It bears a very strong resemblance to the same comparison (Fig. 2) made by Aggarwal & Keenan (2015a) to compare the 98-level CI/CC DARC effective collision strengths with the 238-level CI/CC ICFT ones, except that they did not differentiate (highlight) the different n-values of the upper levels. In contrast, Fig. (5b) clarifies that the differences in the effective collision strengths become increasingly larger as the upper levels excited move closer to the last one included in the 98-level CC calculation. This in turn means that the effective collision strengths to the uppermost levels of the 238-level CC calculation of Fernández-Menchero et al. (2014a) are increasingly unconverged with respect to the CC expansion. However, based on the present convergence study to n = 2 and 3, we can expect that their results for transitions up to n = 4 to be well converged, but those to n = 5 less so since only a partial set of n = 6, 7 levels (to l = 2) were included in their CC expansion.
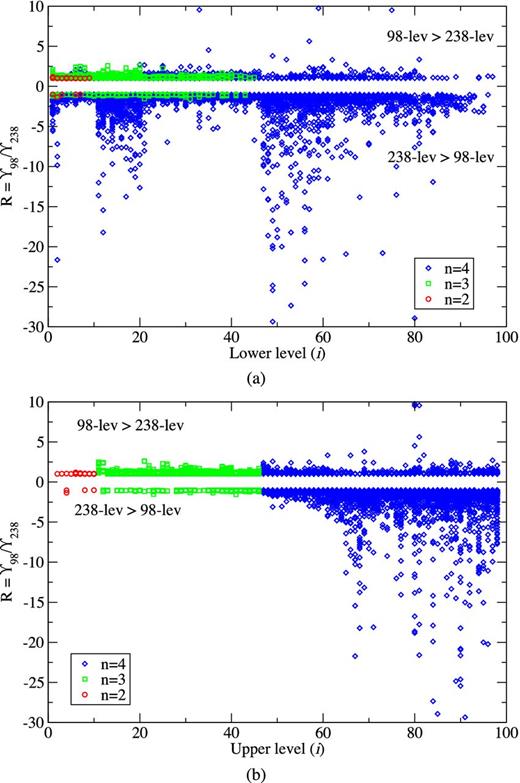
The ratio of effective collision strengths from 98- versus 238-level CI/CC ICFT R-matrix calculations versus (a) lower level and (b) upper level index, for all inelastic transitions amongst the 98 lowest common levels of Al 9+ at Te = 106 K. Positive values indicate ϒ98 > ϒ238 and negative values ϒ238 > ϒ98. ○: transitions with upper level n = 2; □: transitions with upper level n = 3; ⋄: transitions with upper level n = 4.
While all of the plots shown so far are visually appealing, especially Fig. 5, none of them give any indication of the number of transitions whose quantities differ by any given amount – we cannot tell the density of points close to the diagonal (Figs 1–4) or sitting at unity (Fig. 5). We must be wary of such plots misleading us as to the level of agreement, as opposed to disagreement. Only a table like Table 3 gives such an answer.
Thus, these comparisons demonstrate that the observation by Aggarwal & Keenan (2015a), that the 238-level CC effective collisions strengths of Fernández-Menchero et al. (2014a) are systematically and increasingly larger with higher excitations than the 98-level CC results of Aggarwal & Keenan (2014b) over a wide range of temperatures is correct, but it is due to the lack of convergence of the CC expansion of the 98-level CC results of Aggarwal & Keenan (2014b), particularly with respect to the n = 4 levels.
Finally, there is in fact a good accord between comparable calculations, viz. 98-level CI/CC, we make such a comparison of ICFT versus DARC in Fig. 6. The increasing difference seen as one progresses to higher levels is a reflection of the increasing lack of convergence in the atomic structure. While both use the same CI expansion, there is no reason for both to give the same unconverged result. It is interesting to note that the weakest transitions, mostly forbidden ones, show better agreement than some of the stronger allowed ones. Aggarwal & Keenan (2015a) have already made a detailed comparison of 98-level CI/CC DARC and 238-CI/CC ICFT effective collisions strengths for transitions from the ground state. They highlighted several transitions to n = 4 which were discrepant, particularly at high temperatures. We consider them in detail in Section 4.3.
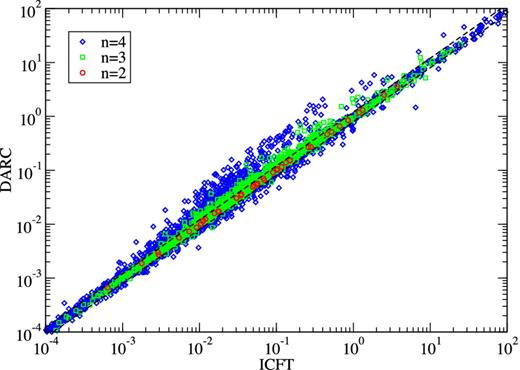
A comparison of effective collision strengths from 98-level CI/CC ICFT versus Dirac R-matrix (Aggarwal & Keenan 2014b) calculations for all inelastic transitions amongst the 98 levels of Al 9+ at Te = 106 K. ○: transitions with upper level n = 2; □: transitions with upper level n = 3; ⋄: transitions with upper level n = 4; dashed lines: 20 per cent fractional difference.
4.2 Low temperature
The effective collision strengths that we have presented so far have been relevant to the temperature of peak abundance (of Al 9+) in an electron collisional plasma, such as found in the solar atmosphere and magnetic fusion devices. In photoionized plasmas, the same charge state exists at much lower temperatures. The role of resonances becomes more important at low temperatures both with respect to their magnitude, resolution and, in particular, their position. Fernández-Menchero et al. (2014a) carried out an exhaustive analysis of the convergence of the effective collision strengths with respect to the energy step used to map-out the resonances. They calculated the effective collision strengths ϒ by convolution of the ordinary collision strengths Ω with a Maxwellian electron energy distribution. Then they reduced the energy step by a factor one-half and re-calculated ϒ. After repeatedly reducing the energy step down to a factor one-eighth from the original one, the worst case transition from the ground state, the 1–78, only changed by 10 per cent relative to the previous value of ϒ, at the lowest temperature calculated of 2 × 104 K, and by 1 per cent at 106 K.
We note that Aggarwal & Keenan (2015a) incorrectly reported the energy step used in the resonance region by Fernández-Menchero et al. (2014a). As they stated, Fernández-Menchero et al. (2014a) used an energy step in the resonance region that scales as ∼z in the ion charge, not z2, along the sequence. In particular, the step length used was 6.94 × 10−6z2 Ry for Al 9+, 4.89 × 10−6z2 Ry for Cl13+, 4.09 × 10−6z2 Ry for K15+, 3.30 × 10−6z2 Ry for Ti18+, and 2.02 × 10−6z2 Ry for Ge28+. These steps are comparable to the ones used by Aggarwal & Keenan (2012, 2014a,b), being slightly finer for Al 9+, and slightly coarser for Ge28+. Fernández-Menchero et al. (2014a) used this fine mesh only over 2J = 1–23, which corresponds to their exchange calculation. They used their coarse energy mesh across the resonance region as well for 2J = 25–89. Such J-values can only give rise to high-n resonances, which by definition are narrow. A simple calculation with autostructure reveals that the strongest resonances have widths <10−5 Ryd. Thus, the results provided by Fernández-Menchero et al. (2014a) are converged with respect to the collision energy step and all significant resonances are well resolved. Differences in low temperature effective collision strengths between Aggarwal & Keenan (2014b) and Fernández-Menchero et al. (2014a) cannot be ascribed to the resolution of the resonances.
The largest source of error in the low-temperature effective collision strengths arises from the inaccuracy in the positioning of resonances which lie just above threshold when the temperature (in energy units) starts to become comparable in magnitude with the uncertainty in position of these resonances. To a first approximation, this uncertainty in position is given by the difference between the calculated and observed values for the energy level to which the resonance is attached. In general, the specific level is not known, without detailed resonance analysis. Energy level accuracy can be improved theoretically via the use of pseudo-states or purely ‘experimentally’ through the use of observed energies or by a combination of theory and observation using term energy corrections. Each has its limitations: the use of pseudo-states can lead to pseudo-resonances at higher energies while not all levels may be known observationally. Storey et al. (2014) discuss the various considerations that need to be made in order to calculate accurate data at very low temperatures for planetary nebulae, for example.
Fig. 7 shows a comparison of 98- and 238-level CC ICFT effective collision strengths for transitions between the lowest common 98 levels of Al 9+ at a photoionized plasma temperature of 2 × 104 K (Kallman & Bautista 2001). The same energy grid was used in both cases in the resonance region. Differences are much larger than the ones seen at the temperature of peak abundance in an electron collisional plasma, even for transitions between the low-lying levels (n = 2). The increased differences in the effective collision strengths is likely due to the position of the resonances, especially where the 238-level CC effective collision strengths are smaller than the 98-level ones. In addition, the systematic enhancement of the effective collision strengths to n = 4 levels due to resonances attached to n > 4 is increased due to the greater relative contribution from resonances; i.e. the lack of convergence of the CC expansion for these levels in the 98-level calculation becomes even more significant. However, at low temperatures, most modelling applications involve transitions from the ground state, and perhaps a metastable. The factor exp (−ΔE/kT) arising in the excitation rate coefficient means that only the lowest few excited levels are of interest, i.e. transitions within n = 2.
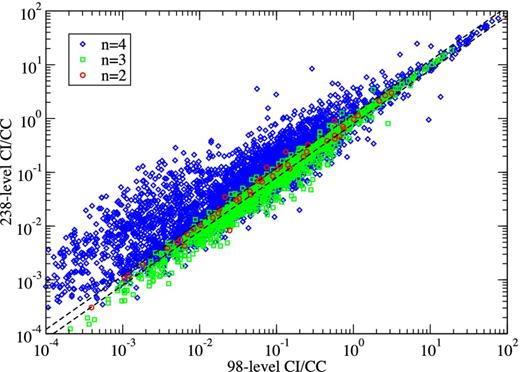
A comparison of effective collision strengths from 98- versus 238-level CI/CC ICFT R-matrix calculations for all inelastic transitions amongst the 98 lowest common levels of Al 9+ at Te = 2 × 104 K. ○: transitions with upper level n = 2; □: transitions with upper level n = 3; ⋄: transitions with upper level n = 4; dashed lines: 20 per cent fractional difference.
The inaccuracy in the position of the resonances makes effective collision strengths from both Fernández-Menchero et al. (2014a) and Aggarwal & Keenan (2012, 2014a,b) increasingly unreliable at low temperatures. For example, if we shift all resonances down in energy by 0.002 Ryd (comparable with the accuracy of some energy levels) then the effective collision strength for the |$1{\rm -}4: \mathrm{2s^2\,^1S_0{\rm -}2s2p\,^3P_2^o}$| transition changes by a factor of 2 at 2 × 104 K, although this is reduced to a 20 per cent effect by 2 × 105 K. Nevertheless, such results can be used for estimation purposes.
4.3 High temperature
We calculate effective collision strengths over a wide range of temperatures, as defined by the OPEN-ADAS adf04 file format viz. 2 × 102–2 × 106 (z + 1)2 K, to cover all possible applications to electron-collisional plasmas. Higher temperature effective collision strengths require ordinary collision strengths to higher energies, which in turn require the contribution from higher partial waves, and this needs to be handled efficiently and accurately by R-matrix calculations.
Aggarwal & Keenan (2015a) highlighted several transitions (1–64, 1–70 and 1–80) for which they observed large differences between the 238-level CI/CC ICFT results of Fernández-Menchero et al. (2014a) and the 98-level CI/CC DARC ones of Aggarwal & Keenan (2014b), particularly at high temperatures. They suggested that the use of the Burgess & Tully (1992) formulae at high energy was perhaps a major source of error, i.e. that the ICFT calculations did not go high enough in energy for the collision strengths to have reached their asymptotic form. Aggarwal & Keenan (2015a) also commented-on the neglect of electron exchange by Fernández-Menchero et al. (2014a) at high J.
The ‘top-up’ procedure used for angular momentum is described in Fernández-Menchero et al. (2014a). In addition, Fernández-Menchero et al. (2014a) included electron exchange for angular momenta up to 2J = 23, and then used a non-exchange calculation for the rest of the angular momenta calculated: 2J = 25–89. (Aggarwal & Keenan 2014b included exchange for all of the angular momenta calculated, up to 2J = 91.) The method used by Fernández-Menchero et al. (2014a) is not a source of significant inaccuracy. By 2J = 25 the smallest exchange multipole is larger than 10. Neglect of higher exchange multipoles causes a small underestimate at the highest temperatures for a few very weak highly forbidden transitions, i.e. ones that not only have no target mixing with allowed transitions (i.e. zero limit points) but also are not strongly enhanced by coupling. By extending the inclusion of exchange to 2J = 51, we find no transition differing by more than 5 per cent up to 2 × 107 K, rising to 10 per cent at 2 × 108 K, for Al 9+.
With regards to energy, Fernández-Menchero et al. (2014a) extended the outer region R-matrix calculation up to three times the ionization potential, 88 Ry in the case of Al 9+. They then carried out a linear interpolation of the reduced collision strength, y, as a function of the reduced scattering energy, x ∈ [0, 1], for dipole and Born allowed transitions (while forbidden transitions were extrapolated) as follows.
- Dipole transitions(6)\begin{eqnarray} x & = & 1\ -\ \frac{\ln C}{\ln \left( \varepsilon \,+\,C \right)} \nonumber \\ y & = & \frac{\Omega }{\ln \left( \varepsilon \,+\,\mathrm{e}\right)} \end{eqnarray}
- Born transitions(7)\begin{eqnarray} x & = & \frac{\varepsilon }{\varepsilon \,+\,C} \nonumber \\ y & = & \Omega \end{eqnarray}
- Forbidden transitions(8)\begin{eqnarray} x & = & \frac{\varepsilon }{\varepsilon \,+\,C} \nonumber \\ y & = & \left( \varepsilon \,+\,1 \right)^{\alpha }\,\Omega , \end{eqnarray}
Fig. 8 shows the reduced collision strength in a Burgess–Tully (x, y) plot from the 238-level CI/CC ICFT calculation for Al 9+ by Fernández-Menchero et al. (2014a). Fig. 8(a) is for a strong dipole transition |$1{\rm -}52:\mathrm{2s^2\,^1S_0{\rm -}2s4p\,^1P_1^o}$|, Fig. 8(b) the dipole transition |$1{\rm -}64: \mathrm{2s^2\,^1S_0{\rm -}2p4s\,^1P_1^o}$| which takes place through configuration mixing, Fig. 8(c) the Born-allowed transition 1-70: 2s2 1S0-2p4p 3P0 which also takes place only through configuration mixing, and Fig. 8(d) is for the forbidden transition 1-80: 2s2 1S0-2p4f 1F3 which is a very weak two-electron jump. An automatically determined value of α = 1 for this transition was used to extrapolate the reduced collision strength as a function of reduced energy – see equation (8). Fig. 8 shows that all of the transitions have reached the assumed asymptotic form. What then is the source of the differences in high-temperature effective collision strengths noted by Aggarwal & Keenan (2015a)? The answer lies in the atomic structure.
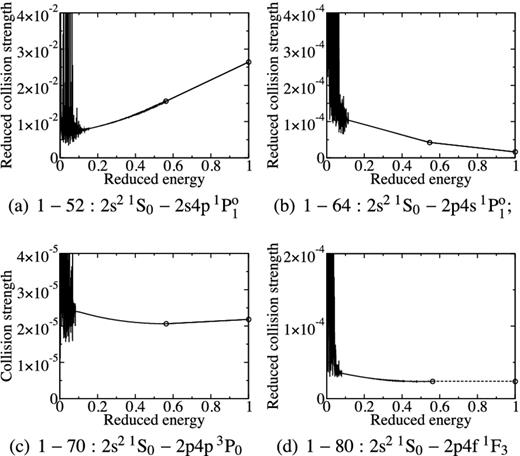
Reduced collision strengths versus energy from 238-level CI/CC ICFT R-matrix calculations for selected transitions of Al 9+. ○: denotes the last finite calculated and infinite energy points; dashed line: indicates extrapolation for a forbidden transition (C = 2).
In Table 4, we compare effective collision strengths from the 98- and 238-level CI/CC ICFT calculations with the 98-level CI/CC DARC ones (Aggarwal & Keenan 2014b). We note first that results for the strong dipole transition 1–21 are independent of atomic structure (98- versus 238-level CI y∞ = 4S/3) and CC expansion (98- versus 238-level CC ϒ). However, if we consider the weak dipole transition 1–64 we see that the limit value (y∞) is a factor 6.2 larger for the 98- versus 238-level CI (BP) case and this leads to a factor of 2.08 in the corresponding ICFT effective collision strengths at 2 × 107 K. Indeed, the difference in effective collision strengths would likely be larger were it not for the fact that the 238-level CI/CC is (much) larger at (much) lower temperatures due to additional resonances and coupling. The DARC structure limit point reported by Aggarwal & Keenan (2015a) is similar to the 98-level CI BP one. Correspondingly, the 98-level CI/CC DARC and ICFT effective collision strengths agree to within ∼20 per cent over the entire temperature range shown in Table 4.
Comparison of effective collision strengths, ϒ, at selected finite temperatures, and the reduced quantity y∞ at infinite temperature. See Table 2 for the transition indices i, j.
| . | DARC . | . | ICFT . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i − j . | 98-level CI/CC . | . | 98-level CI/CC . | . | 238-level CI/CC . | ||||||||
| T(K) . | 2 × 104 . | 106 . | 2 × 107 . | . | 2 × 104 . | 106 . | 2 × 107 . | ∞ . | . | 2 × 104 . | 106 . | 2 × 107 . | ∞ . |
| 1–52 | 1.09 (−2) | 1.01 (−2) | 3.01 (−2) | 1.14 (−2) | 1.02 (−2) | 3.20 (−2) | 2.40 (−2) | 1.53 (−2) | 9.68 (−3) | 3.22 (−2) | 2.64 (−2) | ||
| 1–64 | 5.49 (−4) | 1.78 (−4) | 1.70 (−4) | 5.80 (−4) | 1.80 (−4) | 1.96 (−4) | 1.01 (−4) | 3.12 (−3) | 2.94 (−4) | 9.40 (−5) | 1.63 (−5) | ||
| 1–70 | 2.68 (−5) | 1.26 (−5) | 5.29 (−6) | 3.48 (−5) | 1.11 (−5) | 4.24 (−6) | 2.68 (−6) | 6.99 (−5) | 3.10 (−5) | 2.18 (−5) | 2.18 (−5) | ||
| 1–80 | 4.52 (−5) | 2.51 (−5) | 8.45 (−6) | 4.63 (−5) | 2.47 (−5) | 7.05 (−6) | – | 7.04 (−4) | 8.66 (−5) | 1.09 (−5) | – | ||
| . | DARC . | . | ICFT . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i − j . | 98-level CI/CC . | . | 98-level CI/CC . | . | 238-level CI/CC . | ||||||||
| T(K) . | 2 × 104 . | 106 . | 2 × 107 . | . | 2 × 104 . | 106 . | 2 × 107 . | ∞ . | . | 2 × 104 . | 106 . | 2 × 107 . | ∞ . |
| 1–52 | 1.09 (−2) | 1.01 (−2) | 3.01 (−2) | 1.14 (−2) | 1.02 (−2) | 3.20 (−2) | 2.40 (−2) | 1.53 (−2) | 9.68 (−3) | 3.22 (−2) | 2.64 (−2) | ||
| 1–64 | 5.49 (−4) | 1.78 (−4) | 1.70 (−4) | 5.80 (−4) | 1.80 (−4) | 1.96 (−4) | 1.01 (−4) | 3.12 (−3) | 2.94 (−4) | 9.40 (−5) | 1.63 (−5) | ||
| 1–70 | 2.68 (−5) | 1.26 (−5) | 5.29 (−6) | 3.48 (−5) | 1.11 (−5) | 4.24 (−6) | 2.68 (−6) | 6.99 (−5) | 3.10 (−5) | 2.18 (−5) | 2.18 (−5) | ||
| 1–80 | 4.52 (−5) | 2.51 (−5) | 8.45 (−6) | 4.63 (−5) | 2.47 (−5) | 7.05 (−6) | – | 7.04 (−4) | 8.66 (−5) | 1.09 (−5) | – | ||
Comparison of effective collision strengths, ϒ, at selected finite temperatures, and the reduced quantity y∞ at infinite temperature. See Table 2 for the transition indices i, j.
| . | DARC . | . | ICFT . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i − j . | 98-level CI/CC . | . | 98-level CI/CC . | . | 238-level CI/CC . | ||||||||
| T(K) . | 2 × 104 . | 106 . | 2 × 107 . | . | 2 × 104 . | 106 . | 2 × 107 . | ∞ . | . | 2 × 104 . | 106 . | 2 × 107 . | ∞ . |
| 1–52 | 1.09 (−2) | 1.01 (−2) | 3.01 (−2) | 1.14 (−2) | 1.02 (−2) | 3.20 (−2) | 2.40 (−2) | 1.53 (−2) | 9.68 (−3) | 3.22 (−2) | 2.64 (−2) | ||
| 1–64 | 5.49 (−4) | 1.78 (−4) | 1.70 (−4) | 5.80 (−4) | 1.80 (−4) | 1.96 (−4) | 1.01 (−4) | 3.12 (−3) | 2.94 (−4) | 9.40 (−5) | 1.63 (−5) | ||
| 1–70 | 2.68 (−5) | 1.26 (−5) | 5.29 (−6) | 3.48 (−5) | 1.11 (−5) | 4.24 (−6) | 2.68 (−6) | 6.99 (−5) | 3.10 (−5) | 2.18 (−5) | 2.18 (−5) | ||
| 1–80 | 4.52 (−5) | 2.51 (−5) | 8.45 (−6) | 4.63 (−5) | 2.47 (−5) | 7.05 (−6) | – | 7.04 (−4) | 8.66 (−5) | 1.09 (−5) | – | ||
| . | DARC . | . | ICFT . | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i − j . | 98-level CI/CC . | . | 98-level CI/CC . | . | 238-level CI/CC . | ||||||||
| T(K) . | 2 × 104 . | 106 . | 2 × 107 . | . | 2 × 104 . | 106 . | 2 × 107 . | ∞ . | . | 2 × 104 . | 106 . | 2 × 107 . | ∞ . |
| 1–52 | 1.09 (−2) | 1.01 (−2) | 3.01 (−2) | 1.14 (−2) | 1.02 (−2) | 3.20 (−2) | 2.40 (−2) | 1.53 (−2) | 9.68 (−3) | 3.22 (−2) | 2.64 (−2) | ||
| 1–64 | 5.49 (−4) | 1.78 (−4) | 1.70 (−4) | 5.80 (−4) | 1.80 (−4) | 1.96 (−4) | 1.01 (−4) | 3.12 (−3) | 2.94 (−4) | 9.40 (−5) | 1.63 (−5) | ||
| 1–70 | 2.68 (−5) | 1.26 (−5) | 5.29 (−6) | 3.48 (−5) | 1.11 (−5) | 4.24 (−6) | 2.68 (−6) | 6.99 (−5) | 3.10 (−5) | 2.18 (−5) | 2.18 (−5) | ||
| 1–80 | 4.52 (−5) | 2.51 (−5) | 8.45 (−6) | 4.63 (−5) | 2.47 (−5) | 7.05 (−6) | – | 7.04 (−4) | 8.66 (−5) | 1.09 (−5) | – | ||
For the case of the (weak) Born-allowed transition 1–70, we see a similar trend in the comparisons, viz. differences in structure (y∞) leading to corresponding differences in high-temperature effective collision strengths, strong resonance enhancement at lower temperature for the 238- versus 98-level CI/CC results and agreement to within 30 per cent between the DARC and ICFT 98-level CI/CC results. (Aggarwal & Keenan 2015a do not report Born limits for this transition, but clearly the sensitivity to atomic structure we see reflected in the two BP Born limits accounts for the remaining difference.) Finally, for the weak forbidden 1–80 transition, we note a very similar set of comparisons as for the 1–70 transition, indeed, the DARC and ICFT 98-level CI/CC results agree more closely (20 per cent). The 238-level CI/CC ICFT result is increasingly enhanced by resonances over the 98-level CI/CC one at low temperatures, by a factor 15 at 2 × 104 K. We note that including higher-J exchange multipoles does not change the effective collision strength to 3 significant figures even at the highest temperature considered. There are several equally forbidden transitions (1–61, 68, 69, not shown) for which the pattern of dis/agreement is very similar to that for the 1–80, in all cases.
In summary, the results of the 98-level CI/CC DARC calculation of Aggarwal & Keenan (2014b) are in much closer agreement (indeed, no significant differences) with the present 98-level CI/CC ICFT results than the 238-level CI/CC ones across a wide range of temperatures for all of the transitions highlighted by Aggarwal & Keenan (2015a). However, the results of the calculations obtained using the 238-level CI target have a better converged atomic structure and, correspondingly, give more accurate effective collision strengths, especially at high temperatures, while the much better convergence of the 238-level CC expansion provides more accurate results across a wide range of temperatures.
5 CONCLUSIONS
Reliable and accurate electron-impact excitation data are key to the successful spectroscopic diagnostic modelling of non-LTE plasmas. We have compared and contrasted differences in such data for the benchmark Be-like Al 9+ ion which we have calculated using the R-matrix method. Such differences arise through: (1) differing approximations of relativistic effects, (2) uncertainties in atomic structure and (3) errors due to the lack of convergence of the CC expansion. Error (3) is quantifiable and can be reduced systematically and reliably – we illustrated this by comparing new 98-level and previous 238-level CC ICFT R-matrix calculations. We find that effective collision strengths to n = 4 levels are significantly enhanced over a wide range of temperatures by coupling to n > 4 levels. Uncertainty (2) is quantifiable but is more difficult to reduce and constrain as an error – we compared 98-level and 238-level CI expansion calculations of line strengths and infinite energy plane-wave Born collision strengths to illustrate this point. Again, transitions to n = 4 levels are most susceptible to lack of convergence but now of the CI expansion. Differences (1) between ICFT and BP R-matrix treatments of relativistic effects are small, and negligible relative to (2) and (3), as is to be expected for an element which lies below Zn. We illustrated this by a comparison of new 98-level CI/CC ICFT and BP R-matrix effective collision strengths which use the exact same atomic structure. We also find good accord between our 98-level CI/CC results and previous ones from a 98-level CI/CC Dirac–Coulomb R-matrix calculation, particularly for transitions from the ground-level.
However, based upon the study of effects (1), (2) and (3), we conclude that the original 238-level CI/CC ICFT R-matrix results are the most complete to-date with respect to convergence of both the CI and CC expansions and a reliable treatment of relativistic effects. Or to put it more simply, the earlier 238-level CI/CC ICFT work (Fernández-Menchero et al. 2014a) has a superior target to the 98-level CI/CC DARC one (Aggarwal & Keenan 2014b) and provides more accurate atomic data.
Thus, we find to be false the recent conjecture by Aggarwal & Keenan (2015a) that the ICFT approach may not be completely robust. Their conjecture was based upon a comparison of 98-level CI/CC Dirac R-matrix effective collision strengths (Aggarwal & Keenan 2014b) with those from 238-level CI/CC ICFT R-matrix calculations (Fernández-Menchero et al. 2014a). Rather, Aggarwal & Keenan (2015a) have failed to appreciate the size of the effect which the lack of convergence, in both the CC and CI expansions, has on transitions to the higher lying states (n = 4 in the case of a 98-level CI/CC expansion for Al 9+). This can only be quantified by extending the expansions.
There is nothing special about Al 9+ with regards to the convergence of the CC expansion. Except perhaps at the lowest charge states, as they discussed, the effective collision strengths for all ions in the Be-like sequence, from B+ to Kr32+ calculated by Fernández-Menchero et al. (2014a)4 using the 238 level CI/CC expansion are the most complete and reliable to-date. The use of a 98-level CI/CC expansion for Al 9+ (Aggarwal & Keenan 2014b), Cl13+, K15+, Ge28+ (Aggarwal & Keenan 2014a) and Ti18+ (Aggarwal & Keenan 2012) means that these effective collision strengths for transitions up to n = 4 are increasingly an underestimate over a wide range of temperatures, including the temperature of peak abundance.
There is nothing special about Be-like ions. The 136-level CC DARC calculations of Aggarwal & Keenan (2014c) for Fe13+ are shown to be a systematic underestimate compared to the 197-level CC ICFT calculations of Liang et al. (2010, in addition, Liang et al. used a much larger CI expansion 2985 versus 136 levels) – see Del Zanna et al. (in preparation) for another detailed analysis similar to that presented in this paper. The convergence of the CC expansion increasingly affects the accuracy of collision data to the highest lying states in all R-matrix calculations. Likewise, the accuracy of the atomic structure becomes more uncertain for the most highly excited states of the CI expansion.
In general, care must be exercised when comparing collision data calculated using different atomic structures and/or CC expansions lest one draws false conclusions. Finally, given Figs 1 and 3 and Table 3, we suggest that it is fanciful to assign a single accuracy rating of 20 per cent, say, to an entire collision data set.
This work was funded by STFC (UK) through the University of Strathclyde UK APAP network grant ST/J000892/1 and the University of Cambridge DAMTP astrophysics grant.
Fig. 5 of the paper of Fernández-Menchero et al. (2014a) compared their effective collision strengths for the transition 2s2 1S0-2s2p 3P1 of P11+ with the corresponding interpolated results from Keenan (1988). The fitting coefficients of Keenan (1988) were taken in numerical form from CHIANTI v7.1 rather than being transcribed from the original paper (Landi et al., 2013). However, one of the coefficients was missing a sign, as pointed out by Aggarwal & Keenan (2015a). This will be corrected in the next release of CHIANTI. The calculated results of Fernández-Menchero et al. (2014a) for this transition are now only 50 per cent larger than the interpolated ones (Keenan 1988) at the temperature of peak abundance (1.8 × 106 K), for example.
REFERENCES
APPENDIX A: C2+
Just recently, another paper by Aggarwal & Keenan (2015b) has appeared, this time on Be-like C2+, making much the same claims that have just been refuted, quite generally, above. Aggarwal & Keenan (2015b) have extended their CI/CC expansion up to n = 5 this time, but this 166-level expansion still falls short of the 238-level expansion up to nl = 7d of Fernández-Menchero et al. (2014a). This may reduce the systematic differences (underestimates) of their results up to n = 4 somewhat compared to those of Fernández-Menchero et al. (2014a) but the low-charge state means that the errors and uncertainties due to the difference between the two atomic structures will be much larger than for Al9+. Arguably, a BP R-matrix with pseudo-states calculation is required for C2+ to give a definitive representation of the CI/CC expansion for all level-resolved transitions.



