-
PDF
- Split View
-
Views
-
Cite
Cite
Nicholas J. Wright, Janet E. Drew, Michael Mohr-Smith, The massive star population of Cygnus OB2, Monthly Notices of the Royal Astronomical Society, Volume 449, Issue 1, 1 May 2015, Pages 741–760, https://doi.org/10.1093/mnras/stv323
Close - Share Icon Share
Abstract
We have compiled a significantly updated and comprehensive census of massive stars in the nearby Cygnus OB2 association by gathering and homogenizing data from across the literature. The census contains 169 primary OB stars, including 52 O-type stars and 3 Wolf–Rayet stars. Spectral types and photometry are used to place the stars in a Hertzsprung–Russell diagram, which is compared to both non-rotating and rotating stellar evolution models, from which stellar masses and ages are calculated. The star formation history and mass function of the association are assessed, and both are found to be heavily influenced by the evolution of the most massive stars to their end states. We find that the mass function of the most massive stars is consistent with a ‘universal’ power-law slope of Γ = 1.3. The age distribution inferred from stellar evolutionary models with rotation and the mass function suggest the majority of star formation occurred more or less continuously between 1 and 7 Myr ago, in agreement with studies of low- and intermediate-mass stars in the association. We identify a nearby young pulsar and runaway O-type star that may have originated in Cyg OB2 and suggest that the association has already seen its first supernova. Finally we use the census and mass function to calculate the total mass of the association of |$16\,500^{+3800}_{-2800}$| M⊙, at the low end, but consistent with, previous estimates of the total mass of Cyg OB2. Despite this Cyg OB2 is still one of the most massive groups of young stars known in our Galaxy making it a prime target for studies of star formation on the largest scales.
1 INTRODUCTION
Cygnus OB2 is the nearest region to the Sun that can lay claim to being amongst the most massive clusters or associations in our galaxy (e.g. Knödlseder 2000; Hanson 2003; Wright & Drake 2009). The region is known to harbour many tens of O-type stars and hundreds of OB stars (e.g. Massey & Thompson 1991; Comerón et al. 2002; Kiminki et al. 2007), though estimates of the total mass of the association from both high- and low-mass stars range over an order of magnitude from (2–10) × 104 M⊙ (Knödlseder 2000; Hanson 2003; Drew et al. 2008; Wright et al. 2010b). The association is itself the most obvious example of recent star formation in the massive Cygnus X complex, a region of ongoing star formation (Reipurth & Schneider 2008) that spans ∼200 pc at a distance of 1.4 ± 0.08 kpc (Rygl et al. 2012). The size and proximity of Cyg OB2 therefore make it a template for studies of distant, massive star clusters and OB associations in the Milky Way and in nearby galaxies.
The high-mass stellar content of Cyg OB2 has been well studied over the past half century since the association was first identified by Münch & Morgan (1953) and a number of mid- to late-O stars within it were classified by Johnson & Morgan (1954). Further members were identified and classified by Morgan, Johnson & Roman (1954) and Schulte (1956, 1958). While many of these classifications were revised over the following decades (e.g. Walborn 1973), it was not until the work of Massey & Thompson (1991) that a more extensive spectral survey of the region was conducted, resulting in the identification of 42 O-type stars and 26 B-type stars. A decade later the number of known OB stars increased again with the works of Comerón et al. (2002) and Hanson (2003) following the photometric study of Knödlseder (2000). Since then the number of very massive O-type stars has not increased significantly, with the more recent and deeper surveys uncovering predominantly B-type stars (e.g. Kiminki et al. 2007; Comerón & Pasquali 2012; Kobulnicky et al. 2012). This apparent dearth of new O-type stars discovered in Cyg OB2, despite deeper observations, particularly in the near-infrared (near-IR), and through spectroscopic observing campaigns, may suggest that our census of massive O-type stars is nearing completion.
The age of Cyg OB2 has proved to be a complex subject, due in no small part to the large spatial size of the association and the lack of any clearly recognizable limit to its extent. Hanson (2003) compiled a sample of 85 OB stars in Cyg OB2, from which the presence of a number of mid O-type dwarf stars and high-luminosity blue supergiants led her to conclude that the age of Cyg OB2 could not be much older than a few million years, and settled on an age of 2 Myr, with a spread of 1 Myr. The evolved giant and supergiant stars present were argued by Hanson (2003) to be contaminating non-members, brought into the association as the search for cluster members was extended over a larger area (e.g. Comerón et al. 2002). However, studies of A-type stars in Cyg OB2 have revealed a population of 5–7 Myr old stars towards and to the south of the association (Drew et al. 2008), while X-ray studies of low-mass stars in the association suggest an age of 3–5 Myr (Wright et al. 2010b). If the OB stars in Cyg OB2 are younger than the low-mass stars it could suggest that the massive stars formed after the low-mass stars, a feature observed in some other young clusters (e.g. Povich & Whitney 2010) that has interesting implications for theories of massive star formation and feedback.
The initial mass function (IMF) of high-mass stars provides a powerful diagnostic of the star formation process and is also therefore an area of considerable interest, particularly as to whether the IMF varies between OB associations and star clusters (e.g. Bastian, Covey & Meyer 2010), particularly given recent suggestions that Cyg OB2 has always been a low-density association and did not evolve from a star cluster. Massey & Thompson (1991) found the high-mass IMF in Cyg OB2 to be considerably flatter than found for other regions in the galaxy, though Kiminki et al. (2007) found it to be much steeper than the canonical Salpeter IMF (Salpeter 1955) from an expanded sample, while Wright et al. (2010b) found the lower mass IMF to be in agreement with the Salpeter value.
Work over the past decade has assembled the data needed to form a much fuller view of the OB population in Cyg OB2, thanks to a combination of new spectroscopic surveys of both primary OB stars and their binary companions (e.g. Kiminki et al. 2007; Kobulnicky et al. 2012), improvements in the stellar effective temperature scale that consider line-blanketing and non-LTE (local thermodynamic equilibrium) effects (Martins, Schaerer & Hillier 2005), and the availability of revised stellar evolution models for massive stars that take into account the important effects of stellar mass-loss and rotation (Ekström et al. 2012). Weidner & Vink (2010) found that masses derived from rotating stellar evolutionary models were in much better agreement with dynamical masses for stars in binary systems than were masses derived from non-rotating stellar models, which may go some way towards addressing previous reports of a non-standard IMF in Cyg OB2. Finally, recent high-spatial resolution optical and near-IR Galactic plane surveys (Drew et al. 2005; Lucas et al. 2008; Groot et al. 2009) provide the necessary photometry to resolve close and blended stars in the commonly used catalogues of Massey & Thompson (1991) and the 2 Micron All Sky Survey (2MASS; Skrutskie et al. 2006) – both of which suffer from some degree of blending that is occasionally ignored by users of the data.
Our objective for this work is to bring together all available information on the massive star population in Cyg OB2, gathering spectroscopy from across the literature and selecting the best available photometry for these sources. Our hope is that this will allow a quantitative analysis of the star formation history, IMF, and total mass of Cyg OB2. In Section 2 we outline the compilation of spectroscopic and photometric data from the literature for our census of 169 OB stars, almost doubling the sample of 85 OB stars studied by Hanson (2003). In Section 3 we use this data to calibrate the extinction towards Cyg OB2 and verify the extinction law for this sightline that is then used to derive individual extinctions towards the massive stars. In Section 4 we compile a Hertzsprung–Russell (HR) diagram for the population of massive stars, from which individual stellar masses and ages are derived. In Section 5 we study the age distribution of these stars to infer the star formation history of the association and in Section 6 we study their mass function. In Section 7, we use these results to estimate the total stellar mass of the association, and finally in Section 8 we summarize our conclusions.
2 COMPILATION OF THE SAMPLE
In this section we compile the available photometry and spectroscopy from the literature. Fig. 1 shows the distribution of known OB stars in Cyg OB2 and the wider Cygnus X region centred on the densest part of the association. One of the difficulties with compiling a census of Cyg OB2 is that as an association and not a centrally condensed cluster it is not immediately obvious where to set the limits of such a study. We focus on a 1-deg2 circular area centred on Cyg OB2 #8 – the trapezium of O stars at RA 20h33m16s, Dec. +41°18′45′′ long regarded as being at the heart of the association (e.g. Hanson 2003; Vink et al. 2008). This is equivalent to a radius of ∼14 pc at the distance of Cyg OB2. This choice has a number of advantages, most notably that it includes the clear overdensity that constitutes Cyg OB2, but does not extend too far into the ‘field’ population of OB stars that exists across Cygnus X (e.g. Comerón et al. 2008).

Mid-IR 12 μm image of the Cygnus X giant molecular cloud compiled from Wide-Field Infrared Survey (Wright et al. 2010a) data and spanning 4 × 3 deg2 (100 × 75 pc2 at the distance of Cyg OB2). Known O, B, and Wolf–Rayet stars are shown as red, green, and yellow dots, respectively (compiled from the literature as outlined in Section 2.1). The white circle shows the 1 deg2 region studied in this work, which is centred on the ‘trapezium’ of O stars known as Cyg OB2 #8, itself marked with a white diamond, and as broadly cospatial with the Cygnus OB2 Chandra Legacy Survey (Wright et al. 2014a).
2.1 Spectroscopic data
The census was compiled by searching the literature for all spectroscopically classified stars of spectral type B5 or earlier, a range of spectral types that can provide a solid diagnosis of the age, mass function, and spatial extent of the association. This resulted in 167 stars (22 with known binary companions) from 18 different publications. To limit any potential discrepancies arising from using stars classified by different authors wherever possible, we use classifications made by comparison with the stellar atlas of Walborn & Fitzpatrick (1990). Fortunately, this includes the majority of known OB stars in Cyg OB2. When a star is classified in this way in multiple papers, the practice here is to adopt the classification made at the highest spectral resolution.
The majority of stars come from the studies of Massey & Thompson (1991, 50 stars, or 26 per cent of both primary and secondary stars) and Kiminki et al. (2007, 78 stars or 41 per cent), which show excellent agreement with each other when their classifications overlap. A further 27 stars (14 per cent) were taken from a series of papers by the latter team of authors (Kiminki, McSwain & Kobulnicky 2008; Kiminki et al. 2009, 2012; Kobulnicky et al. 2012). The remaining 37 spectral classifications (19 per cent) used in this work come from 12 different studies with between one and seven classifications each, including many studies devoted to a single particularly interesting star. Classifications from these focused studies were favoured where possible as they often uncovered previously unknown binary companions that changed the classification of the primary star.
Spectral classifications are presented in Table B1 with references, known binary companions, and source numbers under the systems initiated by Johnson & Morgan (1954, the Schulte system, e.g. Cyg OB2 #5), Massey & Thompson (1991, e.g. MT426), and Comerón et al. (2002, e.g. A26). We note that the star listed as ‘A11’ by Comerón et al. (2002) is actually MT267 from Massey & Thompson (1991), and is listed as the latter in this work. By comparing spectral classifications of the same star performed by different authors, we estimate the uncertainty in the spectral types presented here to be approximately half a subtype for O and early B-type (B0–B1) stars and one subtype for later B-type stars. The standard deviation in luminosity class is approximately half a luminosity class for O-type stars, one luminosity class for early B-type stars (B0–B2), and may be higher for later B-type stars, but there is insufficient data for a meaningful comparison. These uncertainties are used in all following calculations to derive uncertainties on other parameters.
2.2 Model atmosphere fits
In this work physical parameters for stars will mainly be based on spectral types from the literature, using the effective temperature scales of Martins et al. (2005), Trundle et al. (2007), and Humphreys & McElroy (1984). However, effective temperatures derived from model atmosphere fits should be more reliable, both because they are not quantized in spectral subtypes (or half subtypes), but also because they take into account other parameters such as stellar mass-loss and chemical abundances.
We searched the literature and identified 11 stars with suitable model atmosphere fits from the works of Herrero, Puls & Najarro (2002) and Negueruela et al. (2008). We did not include the model atmosphere fits from Herrero et al. (1999) since these used mass-loss rates and line blanketing analyses that have since been superseded (Herrero, private communication). We have also excluded stars that have since been found to be binaries with similar luminosities, as these will have blended spectra that will affect the model atmosphere fits.
The 11 stars with model atmosphere fits are listed in Table 1 with the fitted effective temperatures and gravities. Compared to the effective temperatures and gravities determined from the spectral types (also listed in Table 1) there is good agreement within the uncertainties. Given that both methods employ the same effective temperature scale, this is perhaps not surprising.
Model atmosphere fits used in this work. The 11 stars with model atmosphere fits used in this work, with effective temperatures and gravities taken from the fits and calculated from the spectral types listed. Effective temperatures and gravities calculated as a function of spectral type using the data from Martins et al. (2005) and Trundle et al. (2007), where possible. Uncertainties on the spectral type parameters are estimated from the spectral type and luminosity class uncertainties estimated in Section 2.1 and are approximately ±1000 K (approximately ±3000 K for the early B-type stars) and ±0.1 dex. Model atmosphere fits taken from Herrero et al. (2002, H02) and Negueruela et al. (2008, N08), and spectral types from Massey & Thompson (1991, MT91), Kiminki et al. (2007, K07), and Kobulnicky et al. (2012, K12a).
| Name . | Spectral types . | . | Model atmosphere fit . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| . | Type . | Ref . | Teff(K) . | log g . | . | Teff (K) . | |$\sigma _{T_{\rm eff}}$| (K) . | log g . | σlog g . | Ref . |
| #2 | B1 I | MT91 | 24 300 | – | 28 000 | 1000 | 3.21 | 0.1 | H02 | |
| #4 | O7 III | K07 | 36 077 | 3.61 | 35 500 | 1000 | 3.52 | 0.1 | H02 | |
| #8C | O5 III | K07 | 40 307 | 3.69 | 41 000 | 1500 | 3.81 | 0.1 | H02 | |
| #10 | O9 I | K07 | 31 368 | 3.23 | 29 000 | 1000 | 3.11 | 0.1 | H02 | |
| #11 | O5 If + B0 V | K12a | 38 612 | 3.57 | 37 000 | 1500 | 3.61 | |$^{+0.15}_{-0.10}$| | H02 | |
| MT267 (A11) | O7.5 III | K12a | 35 019 | 3.59 | 36 000 | 1500 | 3.6 | 0.2 | N08 | |
| A15 | O7 I | N08 | 34 990 | 3.40 | 35 000 | 1000 | 3.2 | 0.2 | N08 | |
| A24 | O6.5 III | N08 | 37 134 | 3.63 | 37 500 | 1500 | 3.6 | 0.2 | N08 | |
| A26 | O9.5 V | N08 | 31 884 | 3.92 | 35 000 | 1000 | 3.9 | 0.2 | N08 | |
| A33 | B0.2 V | N08 | 29 390 | – | 31 000 | 1500 | 4.0 | 0.2 | N08 | |
| A38 | O8 V | N08 | 34 877 | 3.92 | 36 000 | 1500 | 4.0 | 0.2 | N08 | |
| Name . | Spectral types . | . | Model atmosphere fit . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| . | Type . | Ref . | Teff(K) . | log g . | . | Teff (K) . | |$\sigma _{T_{\rm eff}}$| (K) . | log g . | σlog g . | Ref . |
| #2 | B1 I | MT91 | 24 300 | – | 28 000 | 1000 | 3.21 | 0.1 | H02 | |
| #4 | O7 III | K07 | 36 077 | 3.61 | 35 500 | 1000 | 3.52 | 0.1 | H02 | |
| #8C | O5 III | K07 | 40 307 | 3.69 | 41 000 | 1500 | 3.81 | 0.1 | H02 | |
| #10 | O9 I | K07 | 31 368 | 3.23 | 29 000 | 1000 | 3.11 | 0.1 | H02 | |
| #11 | O5 If + B0 V | K12a | 38 612 | 3.57 | 37 000 | 1500 | 3.61 | |$^{+0.15}_{-0.10}$| | H02 | |
| MT267 (A11) | O7.5 III | K12a | 35 019 | 3.59 | 36 000 | 1500 | 3.6 | 0.2 | N08 | |
| A15 | O7 I | N08 | 34 990 | 3.40 | 35 000 | 1000 | 3.2 | 0.2 | N08 | |
| A24 | O6.5 III | N08 | 37 134 | 3.63 | 37 500 | 1500 | 3.6 | 0.2 | N08 | |
| A26 | O9.5 V | N08 | 31 884 | 3.92 | 35 000 | 1000 | 3.9 | 0.2 | N08 | |
| A33 | B0.2 V | N08 | 29 390 | – | 31 000 | 1500 | 4.0 | 0.2 | N08 | |
| A38 | O8 V | N08 | 34 877 | 3.92 | 36 000 | 1500 | 4.0 | 0.2 | N08 | |
Model atmosphere fits used in this work. The 11 stars with model atmosphere fits used in this work, with effective temperatures and gravities taken from the fits and calculated from the spectral types listed. Effective temperatures and gravities calculated as a function of spectral type using the data from Martins et al. (2005) and Trundle et al. (2007), where possible. Uncertainties on the spectral type parameters are estimated from the spectral type and luminosity class uncertainties estimated in Section 2.1 and are approximately ±1000 K (approximately ±3000 K for the early B-type stars) and ±0.1 dex. Model atmosphere fits taken from Herrero et al. (2002, H02) and Negueruela et al. (2008, N08), and spectral types from Massey & Thompson (1991, MT91), Kiminki et al. (2007, K07), and Kobulnicky et al. (2012, K12a).
| Name . | Spectral types . | . | Model atmosphere fit . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| . | Type . | Ref . | Teff(K) . | log g . | . | Teff (K) . | |$\sigma _{T_{\rm eff}}$| (K) . | log g . | σlog g . | Ref . |
| #2 | B1 I | MT91 | 24 300 | – | 28 000 | 1000 | 3.21 | 0.1 | H02 | |
| #4 | O7 III | K07 | 36 077 | 3.61 | 35 500 | 1000 | 3.52 | 0.1 | H02 | |
| #8C | O5 III | K07 | 40 307 | 3.69 | 41 000 | 1500 | 3.81 | 0.1 | H02 | |
| #10 | O9 I | K07 | 31 368 | 3.23 | 29 000 | 1000 | 3.11 | 0.1 | H02 | |
| #11 | O5 If + B0 V | K12a | 38 612 | 3.57 | 37 000 | 1500 | 3.61 | |$^{+0.15}_{-0.10}$| | H02 | |
| MT267 (A11) | O7.5 III | K12a | 35 019 | 3.59 | 36 000 | 1500 | 3.6 | 0.2 | N08 | |
| A15 | O7 I | N08 | 34 990 | 3.40 | 35 000 | 1000 | 3.2 | 0.2 | N08 | |
| A24 | O6.5 III | N08 | 37 134 | 3.63 | 37 500 | 1500 | 3.6 | 0.2 | N08 | |
| A26 | O9.5 V | N08 | 31 884 | 3.92 | 35 000 | 1000 | 3.9 | 0.2 | N08 | |
| A33 | B0.2 V | N08 | 29 390 | – | 31 000 | 1500 | 4.0 | 0.2 | N08 | |
| A38 | O8 V | N08 | 34 877 | 3.92 | 36 000 | 1500 | 4.0 | 0.2 | N08 | |
| Name . | Spectral types . | . | Model atmosphere fit . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| . | Type . | Ref . | Teff(K) . | log g . | . | Teff (K) . | |$\sigma _{T_{\rm eff}}$| (K) . | log g . | σlog g . | Ref . |
| #2 | B1 I | MT91 | 24 300 | – | 28 000 | 1000 | 3.21 | 0.1 | H02 | |
| #4 | O7 III | K07 | 36 077 | 3.61 | 35 500 | 1000 | 3.52 | 0.1 | H02 | |
| #8C | O5 III | K07 | 40 307 | 3.69 | 41 000 | 1500 | 3.81 | 0.1 | H02 | |
| #10 | O9 I | K07 | 31 368 | 3.23 | 29 000 | 1000 | 3.11 | 0.1 | H02 | |
| #11 | O5 If + B0 V | K12a | 38 612 | 3.57 | 37 000 | 1500 | 3.61 | |$^{+0.15}_{-0.10}$| | H02 | |
| MT267 (A11) | O7.5 III | K12a | 35 019 | 3.59 | 36 000 | 1500 | 3.6 | 0.2 | N08 | |
| A15 | O7 I | N08 | 34 990 | 3.40 | 35 000 | 1000 | 3.2 | 0.2 | N08 | |
| A24 | O6.5 III | N08 | 37 134 | 3.63 | 37 500 | 1500 | 3.6 | 0.2 | N08 | |
| A26 | O9.5 V | N08 | 31 884 | 3.92 | 35 000 | 1000 | 3.9 | 0.2 | N08 | |
| A33 | B0.2 V | N08 | 29 390 | – | 31 000 | 1500 | 4.0 | 0.2 | N08 | |
| A38 | O8 V | N08 | 34 877 | 3.92 | 36 000 | 1500 | 4.0 | 0.2 | N08 | |
For the remainder of this work, for the 11 stars listed in Table 1, we used the effective temperatures derived from the model atmosphere fits and then calculated intrinsic colours and bolometric corrections (BC) for these stars as a function of effective temperature (instead of spectral type), as described below.
2.3 Photometric data
Photometric data in the optical and near-IR was gathered from the literature to complement the spectroscopy. In the optical the primary source of photometry was the UBV data from Massey & Thompson (1991), which is commonly used for studies of Cyg OB2. However, some of these photometric measurements are tagged by Massey & Thompson (1991) as ‘blended’, including 11 stars in our sample. We therefore supplemented the UBV data with Ug′r′ photometry from the Ultra-violet Excess Survey (UVEX, Groot et al. 2009) and converted this on to the UBV system (see Appendix A). For the 11 ‘blended’ sources, 7 had sufficient photometry to calculate full UBV photometry while 4 had only U and g′ UVEX photometry (r′ was saturated) and so only UB photometry was calculated. In addition, 12 sources in our sample were not from the original Massey & Thompson (1991) sample (predominantly from the near-IR sample gathered by Comerón et al. 2002), and we therefore sought UVEX photometry to homogenize our sample. Of these 12 sources, 9 had sufficient photometry to derive U and B photometry, while the remaining 3 were either saturated in the UVEX images or the sources were not observed. For all these sources the photometric uncertainties used were propagated from the UVEX photometric uncertainties and the dispersions on the transformations used.
Near-IR photometry was taken from 2MASS for the majority of stars. In view of the low spatial resolution of the 2MASS observations that could lead to blending in some cases, we sought replacement photometry from the UKIDSS-GPS (United Kingdom Infrared Deep Sky Survey Galactic Plane Survey; Lucas et al. 2008), but were only able to obtain unsaturated photometry for three sources. For these sources, we replaced their 2MASS photometry by UKIDSS photometry using the transformations in Lucas et al. (2008).
The final photometric data used in this study is presented in Table B1 on the UBV and 2MASS JHKs photometric systems. The vast majority (93 per cent or 155 out of 167) of the primary stars have optical photometry in at least two of the UBV bands, and all of the targets have near-IR photometry in J, H, and Ks.
2.4 Binary stars and their influence on stellar parameters
Unresolved binary systems can lead to the miscalculation of the properties of the primary star. The contribution of light from a binary companion, which in involved systems is cooler than the primary, will make the primary appear cooler and more luminous, which could potentially lead to the star being diagnosed as more evolved and higher mass. The binary population of massive stars in Cyg OB2 has recently been well studied (e.g. Kiminki et al. 2007, 2009, 2012; Caballero-Nieves et al. 2014) and 22 of our 167 primary stars have secondaries with known spectral types, although it is likely that there still remain a number of undiscovered binary companions in this sample.
For objects with known companions, it is possible to correct for the light of the secondary when using the observed photometry as long as the spectral type of both stars is known. This is relatively simple when the luminosity ratio of the binary system is known in all the relevant bands, or if the bolometric luminosity ratio is known and the stars are of similar spectral type (e.g. Cyg OB2 #5 is an O7 I + O6 I binary with a bolometric luminosity ratio of 3.1; Linder et al. 2009). For other binary systems this is trickier and we must make an assumption about the relative in-band fluxes of the two stars, for which the simplest approach and that adopted here is to assume that the ratio of fluxes is equal to the ratio of intrinsic fluxes according to spectral type from Martins et al. (2005) for O-type stars and Conti, Crowther & Leitherer (2008) for B-type stars.
Doing this for our sample, we find that the typical (rms) adjustment to the colour of the primary star is very small, 0.006 mag, having a negligible effect on the extinctions. This is because the strongest effect occurs when two stars have significantly different intrinsic colours, but in such systems the stars usually have very different luminosities and therefore the influence of the secondary is small. The rms increase in the observed magnitude is more significant at 0.5 mag, equivalent to a 37 per cent reduction in the bolometric luminosity. This luminosity reduction (magnitude increase) varies from 8 per cent (0.09) for Cyg OB2 #11 (O5 If + B0 V) to 50 per cent (0.75) for very similar pairs of stars such as Cyg OB2 #73 (O8 III + O8 III) and B17, an O7 I + O9 I binary.
Cyg OB2 does contain one known triple system, MT429, which Kiminki et al. (2012) find to be a B0 V + B3 V + B6 V system. For simplicity we consider only the two brightest components of the system because the B6V star is too faint to affect the colour or luminosity of the primary star. We also note that while Cyg OB2 #22, an O3 If + O6 V binary (Walborn 2002), has been resolved in high angular resolution images with a separation of ∼1.5 arcsec between the two components (Mason et al. 2009; Maíz Apellániz 2010), these observations do not provide sufficient photometry to place both components on the HR diagram separately, therefore we only consider the primary star in this work (after applying the corrections for the secondary noted above).
2.5 Completeness
It is difficult to estimate the completeness of a sample that is compiled from so many different sources of spectroscopy, each of which is based on a different method of photometric selection, area of study, and spectroscopic completeness. However, one possible indicator of the level of completeness of our sample is the fact that the most recent spectroscopic studies (e.g. Kiminki et al. 2007; Kobulnicky et al. 2012) have discovered only B-type stars and not new O-type stars, possibly suggesting that the majority of O-type stars in Cyg OB2 have already been detected. The fact that the most recent studies have found stars with similar extinctions to previous studies (Comerón & Pasquali 2012) also suggests that a previously undiscovered population of highly obscured (AV > 10 mag) O-type stars does not exist. Based upon this, we will make the assumption that our census of massive stars is complete for O-type stars in Cyg OB2, which is broadly equivalent to being complete down to 15 M⊙ for zero-age main-sequence (MS) stars, or 20 M⊙ if one takes into account some further evolution. In a future paper, we will attempt to test this assumption about our completeness using new spectroscopic observations of Cyg OB2.
3 THE EXTINCTION TOWARDS CYGNUS OB2
In this section, the spectral types and photometry are used to rederive the form of the extinction law towards Cyg OB2 and then calculate individual extinctions for all the stars in our sample. To achieve this, we use the unreddened colours from Martins & Plez (2006) for O-type stars (the ‘observational’ Teff scale) and from Fitzgerald (1970) and Koornneef (1983) for B-type stars, adjusted for B0–B1 stars to provide a smooth transition with the O star colours.
3.1 The extinction law towards Cygnus OB2
To determine the form of the extinction law towards Cyg OB2, we selected a high-confidence subset of 18 stars from within our sample to which we perform spectral energy distribution (SED) fitting. We selected only single O-type MS stars classified by Massey & Thompson (1991) and with no evidence of having a similar-luminosity binary companion. By using only O-type stars, we reduce the uncertainty due to the effective temperature and the binarity of the stars, both of which increase towards later spectral types. In addition we required all stars to have been detected in, and have low errors (<0.05 in UBV and <0.02 in JHKs) in, all six photometric bands. These criteria resulted in the sample of 18 stars in Table 2.
Stellar sample used to determine the extinction law towards Cyg OB2. All stars classified by Massey & Thompson (1991) with source numbers from that work, except those noted with #, which are labelled on the Schulte system. Note that while MT005 and MT611 have been observed to have binary companions (Caballero-Nieves et al. 2014), the companions are significantly fainter than the primary stars (δV = 2.8 and δK = 4.9, respectively) and are therefore unlikely to affect the SEDs of the primary stars.
| Spectral type . | Number . | RV . | AV . |
|---|---|---|---|
| O6 V | 005 | 2.95 ± 0.04 | 6.00 ± 0.04 |
| O9 V | #14 | 2.88 ± 0.04 | 4.49 ± 0.03 |
| O8 V | #6 | 2.89 ± 0.04 | 4.48 ± 0.03 |
| O8.5 V | #17 | 2.93 ± 0.04 | 4.88 ± 0.03 |
| O8 V | 376 | 2.89 ± 0.04 | 4.85 ± 0.03 |
| O8 V | 390 | 2.83 ± 0.04 | 6.49 ± 0.04 |
| O8 V | 455 | 2.85 ± 0.04 | 6.01 ± 0.04 |
| O9.5 V | #23 | 2.90 ± 0.04 | 5.06 ± 0.04 |
| O8.5 V | #8D | 2.86 ± 0.04 | 5.07 ± 0.04 |
| O7.5 V | #24 | 2.94 ± 0.04 | 5.59 ± 0.03 |
| O8 V | 485 | 2.87 ± 0.04 | 5.25 ± 0.03 |
| O8.5 V | 507 | 2.89 ± 0.04 | 5.34 ± 0.04 |
| O7.5 V | 534 | 2.88 ± 0.04 | 6.26 ± 0.04 |
| O8 V | #74 | 2.89 ± 0.03 | 6.36 ± 0.04 |
| O7 V | 611 | 2.97 ± 0.04 | 5.51 ± 0.04 |
| O9 V | #41 | 2.84 ± 0.04 | 6.04 ± 0.04 |
| O9 V | #75 | 3.08 ± 0.04 | 5.48 ± 0.04 |
| O7 V | #29 | 3.02 ± 0.04 | 5.35 ± 0.03 |
| Spectral type . | Number . | RV . | AV . |
|---|---|---|---|
| O6 V | 005 | 2.95 ± 0.04 | 6.00 ± 0.04 |
| O9 V | #14 | 2.88 ± 0.04 | 4.49 ± 0.03 |
| O8 V | #6 | 2.89 ± 0.04 | 4.48 ± 0.03 |
| O8.5 V | #17 | 2.93 ± 0.04 | 4.88 ± 0.03 |
| O8 V | 376 | 2.89 ± 0.04 | 4.85 ± 0.03 |
| O8 V | 390 | 2.83 ± 0.04 | 6.49 ± 0.04 |
| O8 V | 455 | 2.85 ± 0.04 | 6.01 ± 0.04 |
| O9.5 V | #23 | 2.90 ± 0.04 | 5.06 ± 0.04 |
| O8.5 V | #8D | 2.86 ± 0.04 | 5.07 ± 0.04 |
| O7.5 V | #24 | 2.94 ± 0.04 | 5.59 ± 0.03 |
| O8 V | 485 | 2.87 ± 0.04 | 5.25 ± 0.03 |
| O8.5 V | 507 | 2.89 ± 0.04 | 5.34 ± 0.04 |
| O7.5 V | 534 | 2.88 ± 0.04 | 6.26 ± 0.04 |
| O8 V | #74 | 2.89 ± 0.03 | 6.36 ± 0.04 |
| O7 V | 611 | 2.97 ± 0.04 | 5.51 ± 0.04 |
| O9 V | #41 | 2.84 ± 0.04 | 6.04 ± 0.04 |
| O9 V | #75 | 3.08 ± 0.04 | 5.48 ± 0.04 |
| O7 V | #29 | 3.02 ± 0.04 | 5.35 ± 0.03 |
Stellar sample used to determine the extinction law towards Cyg OB2. All stars classified by Massey & Thompson (1991) with source numbers from that work, except those noted with #, which are labelled on the Schulte system. Note that while MT005 and MT611 have been observed to have binary companions (Caballero-Nieves et al. 2014), the companions are significantly fainter than the primary stars (δV = 2.8 and δK = 4.9, respectively) and are therefore unlikely to affect the SEDs of the primary stars.
| Spectral type . | Number . | RV . | AV . |
|---|---|---|---|
| O6 V | 005 | 2.95 ± 0.04 | 6.00 ± 0.04 |
| O9 V | #14 | 2.88 ± 0.04 | 4.49 ± 0.03 |
| O8 V | #6 | 2.89 ± 0.04 | 4.48 ± 0.03 |
| O8.5 V | #17 | 2.93 ± 0.04 | 4.88 ± 0.03 |
| O8 V | 376 | 2.89 ± 0.04 | 4.85 ± 0.03 |
| O8 V | 390 | 2.83 ± 0.04 | 6.49 ± 0.04 |
| O8 V | 455 | 2.85 ± 0.04 | 6.01 ± 0.04 |
| O9.5 V | #23 | 2.90 ± 0.04 | 5.06 ± 0.04 |
| O8.5 V | #8D | 2.86 ± 0.04 | 5.07 ± 0.04 |
| O7.5 V | #24 | 2.94 ± 0.04 | 5.59 ± 0.03 |
| O8 V | 485 | 2.87 ± 0.04 | 5.25 ± 0.03 |
| O8.5 V | 507 | 2.89 ± 0.04 | 5.34 ± 0.04 |
| O7.5 V | 534 | 2.88 ± 0.04 | 6.26 ± 0.04 |
| O8 V | #74 | 2.89 ± 0.03 | 6.36 ± 0.04 |
| O7 V | 611 | 2.97 ± 0.04 | 5.51 ± 0.04 |
| O9 V | #41 | 2.84 ± 0.04 | 6.04 ± 0.04 |
| O9 V | #75 | 3.08 ± 0.04 | 5.48 ± 0.04 |
| O7 V | #29 | 3.02 ± 0.04 | 5.35 ± 0.03 |
| Spectral type . | Number . | RV . | AV . |
|---|---|---|---|
| O6 V | 005 | 2.95 ± 0.04 | 6.00 ± 0.04 |
| O9 V | #14 | 2.88 ± 0.04 | 4.49 ± 0.03 |
| O8 V | #6 | 2.89 ± 0.04 | 4.48 ± 0.03 |
| O8.5 V | #17 | 2.93 ± 0.04 | 4.88 ± 0.03 |
| O8 V | 376 | 2.89 ± 0.04 | 4.85 ± 0.03 |
| O8 V | 390 | 2.83 ± 0.04 | 6.49 ± 0.04 |
| O8 V | 455 | 2.85 ± 0.04 | 6.01 ± 0.04 |
| O9.5 V | #23 | 2.90 ± 0.04 | 5.06 ± 0.04 |
| O8.5 V | #8D | 2.86 ± 0.04 | 5.07 ± 0.04 |
| O7.5 V | #24 | 2.94 ± 0.04 | 5.59 ± 0.03 |
| O8 V | 485 | 2.87 ± 0.04 | 5.25 ± 0.03 |
| O8.5 V | 507 | 2.89 ± 0.04 | 5.34 ± 0.04 |
| O7.5 V | 534 | 2.88 ± 0.04 | 6.26 ± 0.04 |
| O8 V | #74 | 2.89 ± 0.03 | 6.36 ± 0.04 |
| O7 V | 611 | 2.97 ± 0.04 | 5.51 ± 0.04 |
| O9 V | #41 | 2.84 ± 0.04 | 6.04 ± 0.04 |
| O9 V | #75 | 3.08 ± 0.04 | 5.48 ± 0.04 |
| O7 V | #29 | 3.02 ± 0.04 | 5.35 ± 0.03 |
Reddened stellar spectra were calculated using CMFGEN non-LTE model spectra (Hillier & Miller 1998), as used by Martins et al. (2005), reddened using the extinction curves presented by Fitzpatrick & Massa (2007) as a function of RV and AV. Reddening coefficients were determined using Kitt Peak UBV filter profiles (appropriate for the observations of Massey & Thompson 1991) and 2MASS JHKs filter profiles (Skrutskie et al. 2006). Combining these with the intrinsic colours for O-type dwarf stars presented by Martins & Plez (2006) results in reddened photometry as a function of spectral type, RV, and AV.
χ2 fits were performed between the observed photometry and the reddened model photometry allowing RV to vary in steps of 0.01 in the range 2.5–3.5 and with AV varying between 4.0–7.0 mag in steps of 0.01 mag. The distance modulus was left as a free parameter to account for variations in the intrinsic distance and luminosity of stars. The best fits are shown in Fig. 2 and listed in Table 2.
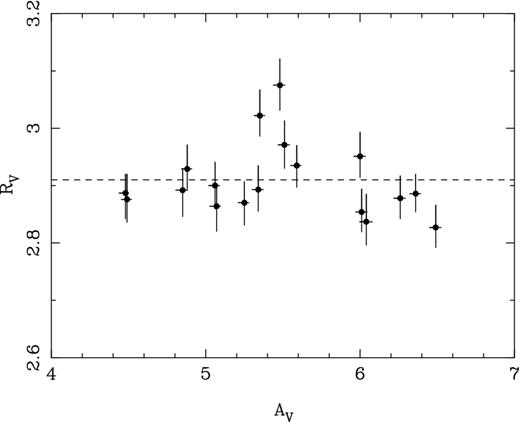
RV versus AV for our high-confidence sample of 18 single O-type dwarfs derived using χ2 fits between the observed photometry and reddened model spectra using the Fitzpatrick & Massa (2007) reddening curves. 1σ error bars are shown derived from the χ2 fits. The weighted mean RV = 2.91 ± 0.06 is shown as a dashed line.
The weighted mean extinction law from our χ2 fits is RV = 2.91 ± 0.06 (taken as such for the remainder of this work), in good agreement with previous studies based on optical colours (e.g. Hanson 2003, measured RV = 3.0). However, this value is in disagreement with the findings of Comerón & Pasquali (2012) who use a combination of optical and near-IR photometry to derive RV = 4.0 using a Cardelli, Clayton & Mathis (1989) extinction law for OB stars over a wider area across the Cygnus X molecular cloud. This disagreement is likely explained by there being two different extinction laws at work along different sight lines: a ‘standard’ RV ∼ 3 extinction law towards Cyg OB2 (due to obscuration from the Cygnus Rift, which lies predominantly in the foreground; Guarcello et al. 2012), and an ‘anomalous’ RV ∼ 4 extinction law away from Cyg OB2, possible due to a change in the grain size distribution favouring larger dust grains within the Cygnus X molecular cloud (which has already been dispersed from the vicinity of Cyg OB2; see Fig. 1). A similar picture of two extinction laws has been observed by Povich et al. (2011) towards the Carina molecular cloud.
For reference, this new extinction law is presented in Table 3 for extinctions between AV = 4.0–7.0 (the typical range observed in Cyg OB2; see Section 3.2) and compared to that found previously by Hanson (2003) from comparison of UBVJHKs colour excesses compared to the Lejeune & Schaerer (2001) intrinsic colours. The extinction law is relatively unchanged in the optical, but has changed significantly in the near-IR, due mostly to shifts in the near-IR intrinsic colours of O-type stars between the works of Lejeune & Schaerer (2001) and Martins & Plez (2006).
| Band (λ) . | Aλ/AV . | |||
|---|---|---|---|---|
| . | This work . | Hanson . | ||
| . | AV = 4.0 . | AV = 5.5 . | AV = 7.0 . | . |
| U (3372 Å) | 1.593 | 1.599 | 1.605 | 1.600 |
| B (4404 Å) | 1.321 | 1.318 | 1.316 | 1.333 |
| V (5428 Å) | 1.000 | 1.000 | 1.000 | 1.000 |
| J (1.27 μm) | 0.233 | 0.234 | 0.235 | 0.282 |
| H (1.67 μm) | 0.138 | 0.139 | 0.140 | 0.175 |
| Ks (2.16 μm) | 0.0840 | 0.0845 | 0.0850 | 0.125 |
| Band (λ) . | Aλ/AV . | |||
|---|---|---|---|---|
| . | This work . | Hanson . | ||
| . | AV = 4.0 . | AV = 5.5 . | AV = 7.0 . | . |
| U (3372 Å) | 1.593 | 1.599 | 1.605 | 1.600 |
| B (4404 Å) | 1.321 | 1.318 | 1.316 | 1.333 |
| V (5428 Å) | 1.000 | 1.000 | 1.000 | 1.000 |
| J (1.27 μm) | 0.233 | 0.234 | 0.235 | 0.282 |
| H (1.67 μm) | 0.138 | 0.139 | 0.140 | 0.175 |
| Ks (2.16 μm) | 0.0840 | 0.0845 | 0.0850 | 0.125 |
| Band (λ) . | Aλ/AV . | |||
|---|---|---|---|---|
| . | This work . | Hanson . | ||
| . | AV = 4.0 . | AV = 5.5 . | AV = 7.0 . | . |
| U (3372 Å) | 1.593 | 1.599 | 1.605 | 1.600 |
| B (4404 Å) | 1.321 | 1.318 | 1.316 | 1.333 |
| V (5428 Å) | 1.000 | 1.000 | 1.000 | 1.000 |
| J (1.27 μm) | 0.233 | 0.234 | 0.235 | 0.282 |
| H (1.67 μm) | 0.138 | 0.139 | 0.140 | 0.175 |
| Ks (2.16 μm) | 0.0840 | 0.0845 | 0.0850 | 0.125 |
| Band (λ) . | Aλ/AV . | |||
|---|---|---|---|---|
| . | This work . | Hanson . | ||
| . | AV = 4.0 . | AV = 5.5 . | AV = 7.0 . | . |
| U (3372 Å) | 1.593 | 1.599 | 1.605 | 1.600 |
| B (4404 Å) | 1.321 | 1.318 | 1.316 | 1.333 |
| V (5428 Å) | 1.000 | 1.000 | 1.000 | 1.000 |
| J (1.27 μm) | 0.233 | 0.234 | 0.235 | 0.282 |
| H (1.67 μm) | 0.138 | 0.139 | 0.140 | 0.175 |
| Ks (2.16 μm) | 0.0840 | 0.0845 | 0.0850 | 0.125 |
3.2 The extinction of Cygnus OB2 members
Using the Fitzpatrick & Massa (2007) RV = 2.91 extinction law derived above, we calculated individual extinctions for the 164 primary O- and B-type stars in our sample (not including the WR stars) from the comparison between observed and intrinsic colours. We favoured the B − Ks colour for this due to its long baseline and the availability of the relevant photometry for the vast majority (160 or 98 per cent) of our sources. For one star B-band photometry was unavailable, so we used the V − Ks colour, and for three stars only near-IR photometry was available, so we used the J − Ks colour. Uncertainties in the derived extinction were calculated using a Monte Carlo (MC) simulation taking into account the uncertainties in the photometry, spectral classification, the intrinsic colours (assumed to be half the difference between the colours of neighbouring subtypes), and the reddening law of RV = 2.91 ± 0.06. The typical uncertainty in the extinction is ∼0.3 mag in the V band. Extinctions and uncertainties are presented in Table B1.
Fig. 3 shows the extinction distribution, which varies from AV = 2.2 mag for MT140 (an O9.5 I star on the western side of the association) to AV = 10.2 mag for the central blue hypergiant Cyg OB2 #12 (a B3.5 Ie star, and one of the most luminous known stars in the Milky Way; Morgan et al. 1954; Clark et al. 2012), though the majority lie in the range AV = 4–7 mag with a median of AV = 5.4 mag and 25 per cent and 75 per cent quartiles of 4.7 and 6.5 mag. Error bars on the extinction distribution histogram were derived from the individual uncertainties using an MC simulation. The large spread in extinction compared to the typical uncertainty in AV suggests that the spread is real and is either due to foreground extinction from the Cygnus Rift or intra-association extinction within Cyg OB2.
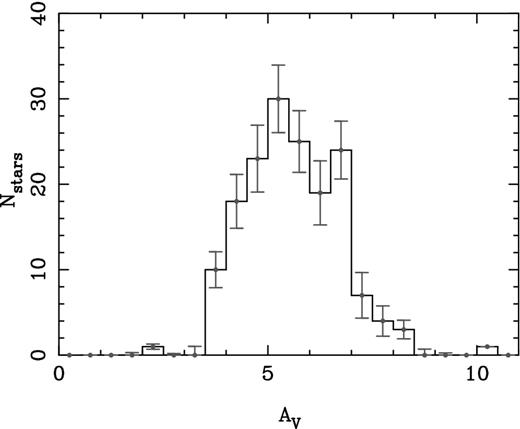
Histogram of the extinctions calculated for all 164 massive OB stars in this work with 1σ error bars derived from MC simulations.
Fig. 4 shows a spatial map of the extinction across Cyg OB2 in the form of a Voronoi tessellation. The extinction distribution varies smoothly across the association, from AV ∼ 4–5 mag in the north-west (where a known ‘reddening hole’ exists; Reddish, Lawrence & Pratt 1967) to AV ∼ 6–7 to the south of the association and on the outskirts.
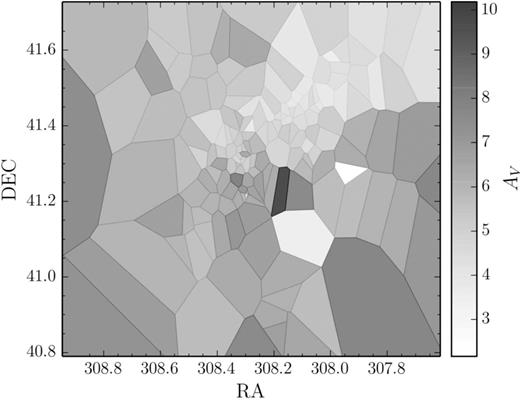
Voronoi tessellated extinction map (one star per Voronoi cell) for all 164 massive stars in Cyg OB2 with the extinction indicated by the grey-scale colour. The circular border of our study is approximately at the border of this image.
These results are in good agreement with previous studies of both the high- (Hanson 2003) and low-mass populations (Wright et al. 2010b), albeit with a smaller spread than the latter, likely due to the higher precision afforded by having known spectral types and a calibrated extinction law. The extinction is larger than that derived by Guarcello et al. (2012) from their riz study by ∼1 mag (they derive a median extinction of AV = 4.3 mag), though we observe the same spatial variation in extinction that they do. The anomalously low extinction derived by Guarcello et al. (2012), particularly compared to many other studies, may be due to the difficulties deriving extinction from isochrone fits in the riz filter system that requires a complex transformation from BVI colours.
The high extinction for Cyg OB2 #12, >2 mag larger than any of the stars surrounding it, is particularly apparent. Some of this extinction may be due to circumstellar material, given the advanced evolutionary stage of this object and that material is known to surround other very massive stars (e.g. Wright et al. 2014b); however, Clark et al. (2012) could find no evidence for a near- to mid-IR excess in the SED of this object, arguing against a significant amount of warm circumstellar dust. It is also possible that the SED we have assumed is wrong, given the unusual character of the star.
4 HR DIAGRAM FOR Cyg OB2
In this section, we place the stars on the HR diagram and compare their positions with both rotating and non-rotating stellar evolutionary tracks to derive stellar masses and ages. Cyg OB2 also includes four evolved massive stars (such as Wolf–Rayet stars) whose positions on the HR diagram and resulting stellar properties cannot be derived in the same way as the less-evolved OB stars. We have gathered the properties of these stars from the literature, adjusting for a distance of 1.45 kpc if necessary, and derive additional physical properties (such as upper or lower limits on stellar ages of masses) by comparison with the evolutionary models used in this work or from our current, but far from complete, understanding of the evolution of massive stars. These stars and their properties are included in Table B1 and included in all later analysis where possible.
4.1 Calculation of Lbol and Teff
Bolometric luminosities were calculated using the observed Ks band magnitudes because of the high extinction towards Cyg OB2 and the typical uncertainty of 0.3 mag in AV resulting from this. The considerably lower uncertainty in AK compared to AV is preferable despite the higher uncertainty in BCK over BCV (due to the strong sensitivity of the SED to wind parameters at longer wavelengths; Martins & Plez 2006). BC were taken from Martins & Plez (2006) for O-type stars, Crowther, Lennon & Walborn (2006) for B-type supergiants, and Humphreys & McElroy (1984) for less luminous B-type stars, although there is very little variation with luminosity class. Effective temperatures were determined as a function of spectral type using the tabulations of Martins et al. (2005, ‘observed’ scale) for O-type stars, Trundle et al. (2007) for early (B0–B3) B-type stars and Humphreys & McElroy (1984) for later B-type stars, all of which show a good agreement between each other.
The accepted distance to Cyg OB2 has been reduced over the last few decades due to improved observations and calibration data. Reddish, Lawrence & Pratt (1966) originally placed the association at a distance of 2.1 kpc, while Massey & Thompson (1991) estimated a nearer distance of ∼1.75 kpc [distance modulus (DM) = 11.20] following their spectroscopic study of massive stars in the association. The recent recalibration of OB star absolute magnitudes led Hanson (2003) to determine an average distance of 1.2 kpc (DM = 10.44) but concluded based on inconsistencies with current stellar wind theory that this was too low and suggested a value of 1.45 kpc (DM = 10.80). This is the value we use in this work, which is in agreement with the parallax distance of 1.40 ± 0.08 kpc for the Cygnus X complex (Rygl et al. 2012).
The uncertainties in our values of Teff and Lbol were derived from MC simulations. For the former we use the quoted uncertainties in Teff from Martins et al. (2005), Trundle et al. (2007), and Humphreys & McElroy (1984), while for the latter we take into account the uncertainties in the observed photometry, derived extinctions, BC (σ = 0.1 mag for O-type stars in the K band, Martins & Plez 2006, and assumed to be σ = 0.2 mag for B-type stars), and spectral classification. For the distance to Cyg OB2, we assume that the distance of 1.45 kpc is correct (small variations in this value up to a few hundred parsecs do not significantly affect the results of this paper, though larger values do).
4.2 The HR diagram
The new HR diagram for Cyg OB2 showing 167 stars is shown in Fig. 5 compared to the isochrones and evolutionary tracks from the non-rotating models of Lejeune & Schaerer (2001) and in Fig. 6 compared to the rotating models of Ekström et al. (2012). The non-rotating models at a metallicity of Z = 0.02 are shown partly for comparison with previous studies (e.g. Hanson 2003; Comerón & Pasquali 2012), and also to contrast with the more recent, rotating models at the revised solar metallicity of Z = 0.014. An indication of the uncertainties on Lbol and Teff are shown in Figs 5 and 6 for each spectral subclass (where possible) and in Fig. 6 for individual stars to illustrate the spread they induce in the HR diagram. For O-type stars the uncertainties are typically small, ∼0.02 dex in log Teff and ∼0.1 dex in log L/L⊙, though for the B-type stars the errors rise significantly to ∼0.07 dex in log Teff and ∼0.2 dex in log L/L⊙ due to classification uncertainties and the larger difference in log Teff between spectral subtypes.
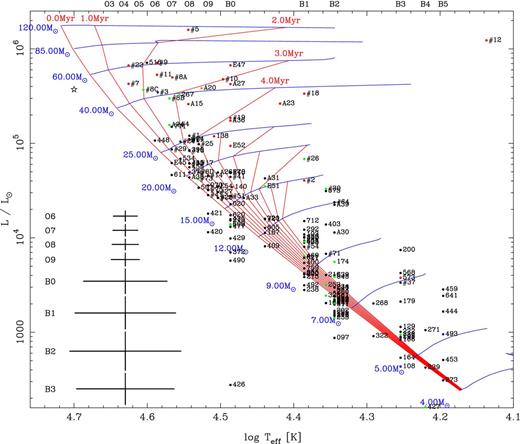
HR diagram for Cyg OB2 showing all the stars compiled in this work colour-coded by their luminosity class (dwarfs are black, subgiants are blue, giants are green, bright giants are orange, and supergiants are red, while WR stars are shown with a star symbol) and with source numbers noted according to the scheme adopted in this paper. The figure shows isochrones and evolutionary tracks from Lejeune & Schaerer (2001) with ages and masses labelled. The effective temperature scales used for MS O- and B-type stars are shown along the top of the diagram and mean 1σ errors bars for each subtype are shown to the bottom left.
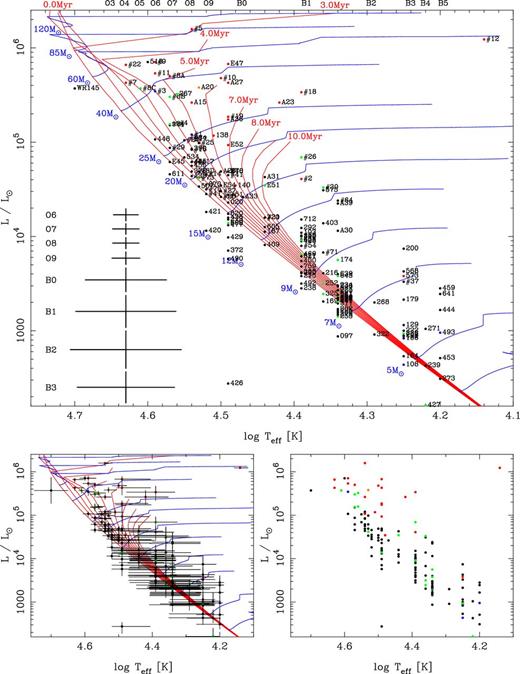
HR diagram for Cyg OB2 showing all the stars compiled in this work as per Fig. 5, with the difference that the main panel shows isochrones and evolutionary tracks for rotating (vini/vcrit = 0.4) models from Ekström et al. (2012, smoothed for clarity) with the ages and masses labelled. The bottom-left figure shows the error bars for each source and the isochrones and evolutionary tracks. The bottom-right figure shows the distribution of all stars without labels and evolutionary tracks.
As noted by previous authors (e.g. Massey & Thompson 1991; Hanson 2003), there is a well-populated MS extending up to O5.5V,1 for which there is now the data to extend it down to mid-B spectral types.
4.3 A large luminosity spread amongst the B stars
Many evolved massive stars are evident, both at masses M > 25 M⊙ where such evolution can occur within 2–10 Myr, and at lower masses where evolved B-type stars occupy positions in the HR diagram suggesting ages >10 Myr. Hanson (2003) noted in her sample a large luminosity spread in the B1–B2 dwarfs and this is also apparent here, although it is now more concentrated towards the MS (most likely because the massive stars discovered recently have been fainter as the depth of spectroscopic observations has increased). Hanson (2003) and Negueruela et al. (2008) have suggested that their position in the HR diagram may be due to them being foreground contaminants from a separate population. However, we note that for their luminosities to be consistent with foreground, MS B-type stars would require some of the most overluminous stars to lie at distances as low as ∼500 pc, which would be inconsistent with their high extinctions (the five most overluminous B-type stars all have AV > 5.5 mag) and the estimated distance to the extinguishing Cygnus rift of 800–1400 pc (Guarcello et al. 2012; Sale et al. 2014).
Alternatively, the apparently large luminosity spread amongst the B-type stars could be due to the large uncertainties in Lbol and Teff at these spectral types that are smearing out the MS in this range. Observational uncertainties in spectral type combined with the steep relationship between Teff and spectral subtype in this range creates large uncertainties in Teff amongst the early B-type stars. Comparing the observed spread in the HR diagram with our estimated uncertainties suggests there is no significant evidence favouring a foreground population of B-type stars or a cospatial population of mature (>10 Myr) stars to explain the observed spread. This argument is supported by the fact that the seemingly high-luminosity B-type stars have a similar spatial distribution to the low-luminosity B-type stars, suggesting they are unlikely to be a separate population.
4.4 Possible foreground and background contaminants
A small number of stars fall significantly below the MS in the HR diagram such as MT170 (B5 V, log L/L⊙ = 1.74), MT426 (B0 V, log L/L⊙ = 2.51), and MT427 (B4 III, log L/L⊙ = 2.19). MT170 and MT427 appear to be background sources, most likely at distances of ∼ 2.19–3.5 kpc if they are on the MS (a number of Hii regions and massive young stellar objects have been identified at similar distances by Xu et al. 2013). Their moderate extinctions (AV = 3.6 and 3.8 mag, respectively) are acceptable given that they are projected against the ‘reddening hole’ in the north-west of the association (see also Drew et al. 2008, who find evidence of a population for A-type stars at such distances in this direction).
The low luminosity of MT426 is harder to explain as it would imply that the star is ∼10 kpc distant yet has an extinction of only AV ∼ 4 whilst being projected against the centre of the association where the extinction is typically AV = 6–7 mag (Fig. 4). MT426 is listed by Massey & Thompson (1991) as having ‘blended’ photometry (see Appendix A) with V = 14.05 mag and B − V = 1.95 mag. These values have led previous authors to derive reasonable extinctions and luminosities for this star, yet such values would imply a Ks-band magnitude of ∼8.4, yet the source is not detected by 2MASS. Inspection of the UVEX and UKIDSS images reveals a second point source that is highly blended in the lower spatial resolution Massey & Thompson (1991) and 2MASS images with its neighbour MT425. The UVEX and UKIDSS photometry, which we have used, does not appear discrepant and we believe it to be sound. It is possible that the spectral type of B0 V is erroneous, given the blending reported by Massey & Thompson (1991) and the fact that those authors report an identical spectral type for its neighbour (though Kiminki et al. 2007, report the same spectral type, although it may also have suffered blending).
Due to the unresolved nature of MT426 and the fact that MT170 and MT427 appear to be background sources, we argue that all three are non-members of Cyg OB2 and exclude them from further analysis of the association. They are noted in Table B1 as ‘Unresolved’ or ‘Background’ sources, and physical properties are not derived for them.
Finally, we note that the membership status of Cyg OB2 #12 has been questioned in the past because of its advanced evolutionary state compared to the early O-type stars in the association and its high luminosity (Walborn 1973), with the suggestion that the star might be a foreground, though it could also be an luminous blue variable (Clark et al. 2012) or a similar-luminosity binary (Caballero-Nieves et al. 2014 recently identified a companion to the star, but note that it is too faint to affect the calculated properties of the star).
4.5 Physical quantities derived from the HR Diagram
Stellar ages and initial masses were calculated based on the position of each star in the HR diagram relative to the non-rotating Z = 0.02 models of Lejeune & Schaerer (2001, commonly used for previous studies of Cyg OB2) and the rotating Z = 0.014 (the revised solar metallicity value; Asplund, Grevesse & Sauval 2005) models of Ekström et al. (2012), both from the Geneva group. The rotating models have an initial rotation rate of vini/vcrit = 0.4, which corresponds to typical MS velocities of 110–220 km s−1 for massive stars (Ekström et al. 2012), in agreement with observations (e.g. Dufton et al. 2006). However, it is not currently clear whether stars are born with a narrow or broad range of initial rotation velocities.
Stellar mass-loss is an important ingredient in stellar models, highly influenced by the metallicity (Meynet et al. 1994), rotation rate (Maeder & Meynet 2000), and the exact mass-loss prescription used (e.g. Vink, de Koter & Lamers 2001). The non-rotating evolutionary models of Lejeune & Schaerer (2001) used the radiative mass-loss rates from de Jager, Nieuwenhuijzen & van der Hucht (1988) for stars in the blue part of the HR diagram, while Ekström et al. (2012) update this with the prescription from Vink et al. (2001) where possible, and also take into account supra-Eddington and mechanical mass-loss processes in their models. Different mass-loss rates can play a significant role in the evolution of massive stars, their positions in the HR diagram, and therefore the physical parameters derived in such a way. These differences are most pronounced for red supergiants and the most massive stars (40–120 M⊙; Ekström et al. 2012), with the latter having considerably increased MS lifetimes when mass-loss rates are increased (Meynet et al. 1994). For moderately massive stars (20–40 M⊙), the effects of mass-loss can be less notable (e.g. Meynet et al. 1994 note that the MS lifetime of 25 M⊙ stars increased by only 5 per cent when the mass-loss rate was doubled).
The ages and masses derived from these models are listed in Table B1 with uncertainties. For the vast majority of objects this is a simple process and we do this on the assumption that all the stars are on their first journey across the HR diagram from hotter to cooler temperatures (generally a valid assumption since stars move back to hotter temperatures much faster and therefore it is rarer to observe stars during this transition). For stars that fall to the left of the zero-age MS in the HR diagram, we assume that their positions are due to uncertainties in their luminosity or effective temperature and that these are zero-age MS objects.
To derive uncertainties on the age and initial mass of stars, we run an MC simulation that takes into account both the observational uncertainties on Lbol and Teff as well as uncertainties due to unresolved binary companions and an intrinsic spread in both luminosity and temperature for a star of a given initial mass and age. The latter simulates the spread in the HR diagram at a given initial mass and age caused by variations in fundamental parameters such as rotation and metallicity, and was estimated to be 0.12 dex in log L/L⊙ and 0.02 dex in log Teff from inspection of the spread in the upper MS in rotating stellar models, and an extrapolation of the spread measured by Houk et al. (1997) in Hipparcos data. The effects of unresolved secondaries were modelled in our MC simulation using the binary characteristics found by Kiminki & Kobulnicky (2012) for Cyg OB2: a binary fraction of 90 per cent for O-type stars (we assume a slightly lower binary fraction of 80 per cent for the B-type stars) and a flat mass ratio distribution over the range q = 0.005–1.0. The added luminosity uncertainty due to unresolved binary companions is generally small, typically adding an uncertainty of 0.1 dex, and therefore we do not consider more complex multiple systems. The uncertainties shown in Figs 5 and 6 (for both individual stars and representative values for each spectral subtype) are the uncertainties on the calculated values of Lbol and Teff only and do not take into account these additional uncertainties used when calculating the stellar mass and age. The median fractional uncertainty on the stellar mass is found to be σM/M ∼ 0.14 and for stellar age is στ/τ ∼ 0.3 (for stars in the range 0–10 Myr).
5 THE AGE OF Cyg OB2
Using the stellar ages derived from the HR diagram, we can assess the age distribution of stars in Cyg OB2 and hence the star formation history of the region. This is shown in Fig. 7 using both the non-rotating and rotating evolutionary models to highlight the different age distribution that they each imply. We only show the 47 stars more massive than 20 M⊙ (down to a MS spectral type of ∼B0.5 V) based on our estimated completeness level and because the positions of stars less massive than this in the HR diagram do not provide an accurate indication of their ages (due to the closeness of the isochrones and the large uncertainty on Teff for these stars). This excludes all the apparently overluminous B-type stars discussed earlier. The uncertainties shown in Fig. 7 were calculated from an MC simulation of the data analysis and binning process.

Histograms showing the distribution of derived ages for stars with reliably determined ages from the non-rotating (left) and rotating (right) models. The ages of all stars with M ≥ 20 M⊙ are shown with a black line. In the left-hand panel, we also show in red the age distribution of stars with 20 ≤ M/M⊙ ≤ 40, which should be complete and unbiased in the age range of 0–4.5 Myr. In the right-hand panel, we show in red the age distribution of stars with 20 ≤ M/M⊙ ≤ 35 that are unbiased in the age range of 0–6 Myr. 1σ uncertainties are shown for all histograms derived from an MC simulation of the data analysis and binning process.
5.1 Comparison of age distributions from rotating and non-rotating models
The age distribution of massive stars derived from the non-rotating models shows a strong peak at 2–3 Myr with the majority of stars in the age range of 0–5 Myr, in good agreement with previous studies of the massive star population of Cyg OB2 (e.g. Hanson 2003; Comerón & Pasquali 2012). However, since a 20 M⊙ star has a lifetime of only ∼8 Myr (in the Lejeune & Schaerer 2001 models) then our sample of massive stars with masses >20 M⊙ is only sensitive to stars <8 Myr old. We therefore cannot reliably infer the star formation history greater than 8 Myr ago when using these models. Furthermore this distribution is biased by the fact that the most massive stars have total lifetimes <4 Myr. For example a 60 M⊙ star is estimated to have a total lifespan of ∼3.5 Myr, and therefore any such stars born more than 4 Myr ago will not be seen now. To rectify this well-known bias, we also show in Fig. 7 the distribution of ages of stars in the mass range 20 ≤ M/M⊙ ≤ 40, which should be unbiased in the age range of 0–4.5 Myr. This presents a slightly different picture with a smaller peak suggesting that this peak age is an observational bias caused by the short lifetimes of the most massive members of the association.
The rotating stellar models of Ekström et al. (2012, Fig. 7) show a different picture with a prominent but wide peak at an age of 4–5 Myr. The increase in the typical age of massive stars in Cyg OB2 when using the rotating stellar models can be attributed to the changes in evolutionary time-scales induced by rotation, which increases the MS lifetime by ∼25 per cent (Ekström et al. 2012). The marked influence of this on stellar ages is evident in the two HR diagrams (Figs 5 and 6). For example, the group of O4–7 supergiants with L/L⊙ ∼ 5 × 105 L⊙ have ages of 1–3 Myr according to the non-rotating models, but have ages of 3–5 Myr from the rotating models. The older ages are in better agreement with those derived from lower mass stars in Cyg OB2, e.g. Drew et al. (2008) estimate an age of 5–7 Myr from A-type stars, while Wright et al. (2010b) derive an age of 3.5–5.25 Myr from an X-ray selected sample of approximately solar-mass stars.
The increased stellar lifetimes of rotating stellar models means that the mass range over which our sample is unbiased has also changed relative to the non-rotating models. Fig. 7 shows the age distribution of stars in the mass range 20 ≤ M/M⊙ ≤ 35, which should be complete in the age range 0–6 Myr. This distribution is remarkably flat over the unbiased age range, suggesting a relatively constant level of star formation over the last 6 Myr. The peak stellar age previously observed at 4–5 Myr is mostly due to stars in the HR diagram (Fig. 6) at masses of 40–60 M⊙ (the O4–7 supergiants noted earlier) that have maximum stellar ages of <5 Myr. The large number of slightly lower mass (25–50 M⊙) stars with ages of 5–6 Myr (the O7–9 supergiants observed in the HR diagram) could suggest that many of the more massive members have already evolved to their end states and their loss biases the observed age distribution.
The comparisons with both sets of evolutionary models indicate a number of stars in Cyg OB2 with very young ages, ≤1 Myr. The existence of such young stars is not impossible but appears unlikely given that long wavelength images (e.g. Fig. 1, and Schneider et al. 2006) show that the majority of dust and molecular gas been evacuated from the cavity in which Cyg OB2 resides. Furthermore both Wright et al. (2010b) and Guarcello et al. (2013) found a paucity of Class I or heavily embedded low-mass stars within the association, suggesting the low-mass stellar population is not so young (though this could also be due to the high levels of feedback in the vicinity of the association; Wright et al. 2012; Guarcello et al. 2014). The typical uncertainties in the HR diagram shown in Figs 5 and 6 suggests that the positions of these stars are not incompatible with them being slightly older (>1–2 Myr) and the lack of very massive stars (>30 M⊙) with ages <1 Myr (where the large separation of isochrones allows young ages to be estimated more accurately) supports this idea.
To conclude, our unbiased age distribution derived from rotating stellar models suggests a relatively constant level of star formation over the past ∼6 Myr (Fig. 7) with some evidence for a peak in the star formation intensity between 4–5 Myr ago. We cannot be certain from this sample when star formation in the region began, but there is some evidence that it started at least ∼6–8 Myr ago. Addressing the question of when star formation ceased is harder, but our best estimate is that it ended ∼1 Myr ago. As will be discussed in Section 6.1, these results are in approximate agreement with our star formation history fits to the mass function of stars in Cyg OB2. The use of different mass-loss prescriptions is not expected to significantly affect the evolution of stars in our ‘unbiased’ mass range of 20–35 M⊙ (Meynet et al. 1994), and therefore this is unlikely to explain the age spread observed. It is possible that the large spread in the HR diagram could instead be due to a single-aged population with an extremely large range of rotation velocities, which has been shown to lead to large spreads in the HR diagram (Brott et al. 2011) and could reproduce the entire spread seen in our HR diagram. However, for this to be the case the stars nearest the zero-aged MS in the HR diagram would have to be rotating very rapidly with speeds of 400–450 km s−1, including Cyg OB2 #20 and #29, for which Herrero et al. (1999) measured V sin i = 25 and 180 km s−1, respectively. This would therefore require Cyg OB2 #20 to have been observed virtually pole-on, which makes this scenario unlikely, though further high-resolution spectroscopy of other stars in Cyg OB2 would be useful to test this hypothesis in more detail. It is also worth noting though that this scenario is not supported by measurements of rotation rates in other clusters (e.g. Dufton et al. 2006).
The uncertainties in the stellar ages we have calculated could explain some of this spread, but do not appear to be sufficiently large enough to explain the entire ∼5 Myr spread. Furthermore, the age distribution of our ‘unbiased’ sample shown in Fig. 7 does not resemble a single-aged population broadened by observational uncertainties (which should have a more centrally-concentrated peak) and does appear to represent a spread of ages amongst the OB star population.
5.2 Implications for large age spreads in OB associations
Large age spreads have been reported in many star clusters and associations, typically diagnosed from luminosity spreads in colour–magnitude diagrams for low-mass pre-MS stars. Some authors have suggested that such spreads in luminosity do not equate to age spreads and may instead be due to intrinsic luminosity spreads amongst a coeval population (e.g. Hillenbrand, Bauermeister & White 2008; Jeffries et al. 2011) potentially caused by different accretion histories (e.g. Baraffe, Chabrier & Gallardo 2009). Age spreads diagnosed from post-MS massive stars are not believed to suffer from such issues since the intrinsic spread and measurement uncertainties in Lbol and Teff are typically smaller than the separation of isochrones (see also Massey 2003). Therefore if the HR diagram is sufficiently well sampled to overcome statistical and observational uncertainties (as it is here), age spreads derived from high-mass post-MS stellar evolution models can provide more accurate age diagnostics than low- and intermediate-mass pre-MS stellar evolution models.
The reported age spreads for low-mass stars are often argued as representing a continuous period of star formation within a single cluster or association and in a small area of space (e.g. Palla & Stahler 2000). Cyg OB2 however occupies a much larger region than typical young compact star clusters such as the Orion Nebula Cluster, with the stars spread over >10 pc. It has recently been argued that Cyg OB2 has always been a large and low-density OB association and was never a dense and compact star cluster (Wright et al. 2014c, see also Parker et al. 2014)). It is therefore possible that the observed age spread is due to either an age gradient or a series of discrete star-forming events that have since mixed. This would imply that Cyg OB2 was not born as a single star cluster but as a ‘distribution’ of smaller groups or clusters of stars with a range of stellar ages. We searched for evidence of a spatial variation in the stellar age distribution to support this theory, but could not find any such evidence. If the association is composed of multiple populations of different ages then they are well mixed.
6 THE UPPER END OF THE IMF IN Cyg OB2
In this section we analyse the IMF of the massive stars in Cyg OB2, as derived using rotating stellar models (because Weidner & Vink 2010 find that such masses are in much better agreement with dynamical masses than those derived from non-rotating stellar models). Fig. 8 shows a histogram of the masses of all 167 stars in our sample, showing a rapid increase as one goes from high to low masses, with the data flattening off for stars less massive than our estimated completeness limit of ∼20 M⊙. To calculate the power-law slope of the mass function, we fitted these data using an ordinary least-squares regression of Y on X (OLS (Y|X); Isobe et al. 1990) of the form dN/d log m ∝ m−Γ, and for the mass bins >20 M⊙. Because the uncertainty on this fit is just a fitting uncertainty, we also performed an MC simulation to determine the true uncertainty, varying the masses of the individual stars according to their uncertainties and adjusting the number of stars in each bin as appropriate. The 1σ spread in the best-fitting slope that results is then combined with the fitting error to produce the true uncertainty on the mass function slope. The best-fitting mass function slope for all stars in our sample is Γ = 2.06 ± 0.06, significantly steeper than the canonical Salpeter slope of Γ ∼ 1.35 (Salpeter 1955), although it agrees with that determined by other authors for the massive stars in Cyg OB2 (e.g. Kiminki et al. 2007; Comerón & Pasquali 2012). Note however that this uncertainty is still falsely low because it does not take into account the random sampling of the IMF.
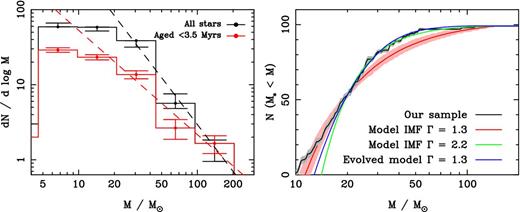
Mass functions for massive stars in Cyg OB2 derived using the rotating stellar models of Ekström et al. (2012). Left: histograms showing the distribution of derived masses for all 167 stars in our sample (black histogram, with 1σ error bars determined from MC simulations) and for an age-unbiased sample of 82 stars aged <3.5 Myr (red histogram, with 1σ error bars). Both histograms have been fitted using an ordinary least-squares regression of Y on X (OLS (Y|X), Isobe et al. 1990) for the mass bins >20 M⊙, giving slopes of Γ = 2.06 ± 0.06 and 1.39 ± 0.19 for the complete and age-unbiased samples, respectively (note that these uncertainties do not take into account random sampling of the IMF). Right: a cumulative mass function showing N (M⋆ < M) as a function of M for all 98 stars in our sample more massive than 10 M⊙ (black line) with the 1σ uncertainty (calculated from MC simulations) shown in grey. Also shown are the results of simulated IMFs for Γ = 1.3 (red line, with 1σ random sampling uncertainty shown in pink) and Γ = 2.2 (green line) calculated using the equations of Maschberger (2013, see full explanation in the text). The blue line shows a simulated and evolved IMF for Γ = 1.3 for stars aged 3–7 Myr (i.e. a constant star formation rate from 3 to 7 Myr ago, and no star formation since then). The uncertainties for three simulated IMFs are similar and so only one is shown for clarity.
The mass distribution of stars in our sample is likely to be altered by the loss of the most massive stars that have already evolved to their end states (Section 5), steepening the observed mass function. To counter this, we have attempted to identify an unbiased sample of stars from which to study the IMF in Cyg OB2, selecting all stars with ages <3.5 Myr, which we estimate from the rotating stellar models (Fig. 6) as the age at which the most massive stars in Cyg OB2 will have evolved to their end states. The mass function of this unbiased sample of 82 stars is shown in Fig. 8, which shows a slightly shallower slope to that of the full sample. An OLS (Y|X) fit gives a slope of Γ ∼ 1.39 ± 0.19, in good agreement with the concept of a universal IMF at high masses with a slope of Γ = 1.3 (Kroupa, Aarseth & Hurley 2001; Bastian et al. 2010). This value also agrees with the mass function measured at lower masses (Γ = 1.09 ± 0.13; Wright et al. 2010b), and the mass function of massive stars found by Massey & Thompson (1991) of Γ = 1.0 ± 0.3, although their sample was considerably smaller than the current sample and may therefore have been incomplete.
6.1 The cumulative mass function
To avoid the well-known and negative effects of binning our data, and to overcome any uncertainties arising from the narrow age range used for the unbiased mass sample, we have also considered the mass function of stars in Cyg OB2 represented as a cumulative function (CF). This is shown in Fig. 8 with 1σ uncertainties calculated from an MC simulation using the full uncertainties on all stellar masses (the 1σ uncertainties shown are very small due to the cumulative nature of the function and the lack of binning).
The CF shows a steady increase up to ∼30 M⊙, and then flattens off, reaching a total of 98 stars with masses >10 M⊙. We compare our CF with simulated IMFs generated using the equations described in Maschberger (2013), varying α (=Γ + 1), but fixing β = 1.4 (the low-mass exponent has no effect on the high-mass IMF, but is required for the calculations) and drawing individual stellar masses from the mass range 0.01–150 M⊙. We continue to do this until the number of stars with M > 20 M⊙ reaches the observed number of 98 and use this to produce a CF scaled to the observed number of stars with M < 20 M⊙. The simulated IMF is generated 10 000 times and the median CF shown in Fig. 8 with ±1σ range illustrated.
We initially simulated an unevolved (i.e. counting all stars) ‘universal’ IMF (Kroupa et al. 2001) with Γ = 1.3, but found that this overpredicted the number of very massive stars (>50 M⊙) relative to the moderately massive stars (20–50 M⊙) and we can reject a standard, unevolved mass function of this type with a confidence of ∼3σ. Varying Γ we found a best fit with an unevolved IMF for |$\Gamma = 2.2^{+0.6}_{-0.3}$|, in approximate agreement with that found fitting a binned IMF for our entire sample (but with larger uncertainties that also take into account the random sampling of the IMF).
We then simulated a number of evolved mass functions using the ‘universal’ Γ = 1.3 IMF and different star formation histories. For a star of a given mass and age, we compute its position in the HR diagram according to the models of Ekström et al. (2012) and remove those stars that have evolved beyond their reddest position in the HR diagram. This excludes WR stars from the simulated mass functions, matching our observed CF that also leaves them out (because of the difficulty of determining their initial masses).
We found that a number of different star formation histories provided satisfactory fits (within 1σ) to the observed mass function, preventing us from accurately determining it in this way, though we were able to place some partial constraints on it. We find fits using a ‘universal’ Γ = 1.3 IMF requires the star formation rate over the last ∼3 Myr to be very low, <20 per cent of the total star formation in Cyg OB2, with the fit improving slightly as the fraction of star formation in this time period decreases. Exploring models with this feature, we find acceptable fits when the duration of star formation is at least 2 Myr (i.e. a constant level of star formation from 3 to 5 Myr ago), with the best fit obtained for a model with a constant star formation rate over the time period of 3–7 Myr ago, in reasonable agreement with that found from the distribution of stellar ages studied earlier. Significant star formation prior to ∼7 Myr ago degrades the fit to the cumulative mass function. These results are in good agreement with the stellar age distribution discussed in in Section 5.
To conclude, the current mass function of massive stars in Cyg OB2 is relatively steep, with a slope of Γ ∼ 2.1, but the stellar age distribution suggests that it has been steepened by the most massive stars evolving to their end states. From both an unbiased sample of stars and modelling an evolved cumulative mass function, we find that the mass function is consistent with the canonical Γ = 1.3 ‘universal’ IMF (Salpeter 1955; Kroupa et al. 2001).
6.2 Have there been any supernovae in Cyg OB2?
There is considerable evidence, both in the age distribution of stars and in the steepened IMF, to suggest that some of the most massive stars in Cyg OB2 have already evolved to their end states and therefore that there has already been a supernova within the region.
Despite this there are not any known supernova remnants (SNRs) within Cyg OB2, although Green (2009) does list a number of SNRs in the wider Cygnus X region (including γ-Cygni, G78.2+2.1) but these are predominantly to the west in the Cyg OB1 and OB9 associations. Butt et al. (2003) identified an expanding shell of molecular and dusty material from CO J = 1–0 and IRAS observations that they suggested could be due to an SNR, but this cavity could equally arise from the combined effects of ionizing radiation and stellar winds from the massive stars in Cyg OB2. The lack of observed SNRs in Cyg OB2 does not however rule out any previous supernovae in the association, since SNRs typically remain visible for only ∼10 000 yr (e.g. Levenson et al. 1998) and may not leave any detectable signature when expanding into hot, low-density media such as the cleared-out cavities in OB associations (Chu 1997).
There have been a number of very-high-energy sources identified towards Cyg OB2 that have been considered as possible compact stellar remnants (e.g. Bednarek 2003; Butt et al. 2006), but confirming their nature or identifying counterparts at other wavelengths has proved difficult. Abdo et al. (2009) discovered an ∼115 800 yr old γ-ray pulsar (J2032+4127) with a frequency of 6.98 Hz towards Cyg OB2, which has since been detected in the radio with the same frequency (Camilo et al. 2009) and is also believed to be associated with the previously unidentified TeV source J2032+4130 (Aharonian et al. 2002) as its pulsar wind nebula. Camilo et al. (2009) argue that the pulsar is likely to be located within the Cyg OB2 association, and combined with our newly derived age of ∼1–7 Myrs this is consistent with the pulsar originating within Cyg OB2 supporting the theory that the association has already seen it's first supernova.
Another indication of past supernovae is the presence of high-velocity ‘runaway’ OB stars that are ejected when their binary companion explodes as a supernova (Blaauw 1961). Comerón & Pasquali (2007) identified an O4 If runaway star with a proper motion of ∼40 km s−1 moving away from Cyg OB2 and argued that the star was likely ejected from the association ∼1.7 Myr ago. The authors estimate a mass of 70 ± 15 M⊙ and an age of ∼1.6 Myr (by comparisons with non-rotating stellar isochrones) suggesting the star was ejected from Cyg OB2 shortly after it was born, and therefore not from a supernova explosion. The other mechanism for stellar ejection is via dynamical encounters in dense stellar systems (Poveda, Ruiz & Allen 1967), yet this process requires much higher stellar densities than are believed to have existed in Cyg OB2 (Wright et al. 2014c) making it unlikely. Using the rotating stellar models of Ekström et al. (2012), and with updated photometry we recalculated the properties of this star. We find B − Ks = 5.27 mag (using Tycho-2 and 2MASS photometry; Høg et al. 2000; Cutri et al. 2003), which for a star of type O4 If with (B − Ks)0 = −1.15 mag (Martins & Plez 2006) gives AV = 5.22 mag (using the reddening law determined above) and therefore log Lbol = 5.85 L⊙ and Teff = 40 422 K. This implies an initial mass of ∼55 M⊙ and an age of 4–5 Myr. This would suggest the star was ejected from Cyg OB2 when it was about ∼3 Myr old, the age at which the most massive star in a population might explode as a supernova. This is therefore consistent with a scenario whereby the star's very massive (>100 M⊙) companion exploded as a supernova and ejected its companion from the association. The remnant of the massive star was presumably ejected from Cyg OB2 in the opposite direction and could be searched for to verify this scenario.
7 THE TOTAL MASS OF Cyg OB2
Using a sample of massive stars that is believed to be complete within a given mass range, and the assumption that the IMF has a ‘universal’ form in all star clusters and OB associations, it is possible to estimate the total mass of a group of stars beyond that which have been detected. To do this for Cyg OB2, we have selected a mass range of 20–40 M⊙ for which we believe our sample is complete (at least for stars aged <6 Myr). Above 40 M⊙ our sample will be incomplete for stars aged <6 Myr and below 20 M⊙ we have argued that our sample is likely to be observationally incomplete. Based on the stellar masses determined above the number of stars in this mass range is |$36^{+1}_{-4}$| (uncertainties calculated from MC simulations).
To estimate the total mass of Cyg OB2, we ran an MC simulation by sampling stellar masses from a ‘universal’ IMF with α = 2.30 (Γ = 1.3) and β = 1.40 (Kroupa et al. 2001; Maschberger 2013) across the entire mass range. We proceeded to count the total mass of stars produced and the number of stars in the mass range of 20–40 M⊙, until the latter number reached the observed number of stars in that mass range. We performed this simulation 10 000 times, recording the total stellar mass that was necessary in each iteration to produce the observed number of stars. Furthermore, we varied the observed number of stars, |$36^{+1}_{-4}$|, in each iteration according to the uncertainties on that number. This MC simulation therefore takes into account both the uncertainty in the total number of stars observed, and the variation in the number of stars in a cluster of a given mass due to the random sampling of the mass function.
We find that the observed number of massive stars in Cyg OB2 in the mass range of 20–40 M⊙ can be reproduced if the association has a total stellar mass of |$16500^{+3800}_{-2800}$| M⊙. This is based on three assumptions. First that we are complete in the chosen mass range, as argued above. Secondly, that the vast majority of star formation in Cyg OB2 occurred in the last 6 Myr (broadly supported by the age distribution and the mass function simulations, though it is difficult to test this assumption without extending the completeness of the sample to lower masses). The final assumption is that the IMF in Cyg OB2 is well represented by the ‘universal’ IMF of Kroupa et al. (2001). This is supported by our IMF simulations at high stellar masses and that found at lower masses (Wright et al. 2010b); however, a small variation can lead to large differences in the total stellar mass. For example increasing (decreasing) the high-mass exponent α by 0.1 increases (decreases) the total stellar mass by 5600 (3900) M⊙. However, for comparison with other young clusters and associations that have also adopted such an IMF, we believe this is the most appropriate choice.
Our mass estimate is smaller than some previous mass estimates of Cyg OB2, notably that of Knödlseder (2000) who estimated a mass of (4–10) × 104 M⊙ for the association. Knödlseder (2000) based their estimate on the number of stars brighter than a given magnitude (equivalent to an F3 V star) from a background-subtracted 2MASS star counts study. The choice of a background region in this crowded and complex area of the Galactic plane is fraught with difficulties and could lead to large uncertainties in any resulting star counts or mass estimates. Knödlseder (2000) also estimate the total number of O stars in Cyg OB2 to be 120 ± 20, an estimate almost double the size of our census and one which other studies have not supported (e.g. Hanson 2003). Our mass estimate is more consistent with recent estimates based on studies of lower mass stars, e.g. Wright et al. (2010b) estimated (2–4) × 104 M⊙ from an X-ray study and Drew et al. (2008) estimated (1–4) × 104 M⊙ from a photometric study of A-type stars in the association.
8 CONCLUSIONS
We have compiled a census of all known massive stars in the nearby OB association Cygnus OB2. We have gathered data from across the literature to achieve a census containing 169 primary OB stars, including 52 O-type stars and 3 WR stars.
We have used the sample to measure the extinction law towards Cyg OB2, fitting the available photometry to a Fitzpatrick & Massa (2007) RV = 2.91 ± 0.06 extinction law. This is in good agreement with that determined by Hanson (2003) in the optical and differing only in the near-IR due to shifts in the intrinsic near-IR colours of O-type stars in recent years. We use this new law to derive individual extinctions for all the stars in our sample, the majority of which have extinctions AV = 4–7 mag, with a typical uncertainty of ∼0.3 mag.
An HR diagram was compiled and compared to both non-rotating and rotating stellar evolution tracks, from which stellar masses and ages are calculated. Uncertainties are derived for all quantities using an MC simulation that takes into account all available uncertainties including quantified classification uncertainties, photometric uncertainties, extinction law uncertainties, estimated spreads in fundamental parameters, and unresolved binaries.
The distribution of stellar masses is assessed using both a binned mass function and a cumulative mass function, both of which are affected by the loss of the most massive stars to stellar evolution. The current mass function is relatively steep with a slope of Γ = 2.2 (in agreement with that found by Kiminki et al. 2007), though when considering either an unbiased sample of stellar masses or by modelling the effects of stellar evolution on the mass function we find it to be consistent with a Salpeter-like ‘universal’ slope of Γ = 1.3.
The non-rotating stellar evolution models suggest a peak stellar age of 2–3 Myr, as derived by previous authors, while the rotating stellar models suggest a slightly older peak age of 4–5 Myr. The results from the rotating stellar models are favoured, both for physical reasons, and because the age distribution that they imply is in better agreement with that found from studies of low- and intermediate-mass stars. When considering only stars in a mass range unaltered by evolutionary effects the age distribution is not inconsistent with a relatively constant level star formation over at least the past ∼6 Myr. Our star formation history fits to the mass function of stars in Cyg OB2 suggest star formation most likely began ∼7 Myr ago. The lack of molecular material or dust in the immediate vicinity of the associations suggests star formation likely ceased at least ∼1 Myr ago, and this is also supported by our mass function models. Our best estimate is that the majority of star formation occurred during the period of 1–7 Myr ago, with a possible peak in the star formation intensity between 4–5 Myr ago.
Given the evidence from both the age distribution and the mass function that some of the most massive stars have already evolved to their end states, we searched the literature for evidence of this and found both a young pulsar and a runaway O star that may have originated in Cyg OB2, consistent with the view that Cyg OB2 has already seen its first supernova.
Finally, we use an MC simulation to estimate the total mass of the association, taking into account the loss of the most massive stars, and estimate a total stellar mass of |$16\,500^{+3800}_{-2800}$| M⊙ (assuming a Kroupa et al. 2001 IMF) that has formed over the past 6 Myr. This is at the lower end of many previous estimates, based on the number of low- and intermediate-mass stars, but consistent given the uncertainties involved in extrapolating the IMF.
In conclusion, our new census of massive stars in Cyg OB2 provides an updated view of the high-mass stellar population in one of the largest groups of young stars in our Galaxy and for the first time these results show a good agreement with those determined for low- and intermediate-mass stars, thereby providing a coherent picture for this massive OB association. In a future paper, we will use new photometry and spectroscopy to search for previously undiscovered massive stars, extending this census to both lower luminosity B-type stars in Cyg OB2, and O- and B-type stars over a wider area and further along the sightline.
We would like to thank Facundo Albacete Colombo, Nate Bastian, Mario Guarcello, Artemio Herrero, Ian Howarth, Raman Prinja, and Nolan Walborn for useful discussions and comments on this paper. We would like to thank the referee, Matthew Povich, for a helpful and insightful report that improved the content of this paper. NJW was supported by a Royal Astronomical Society research fellowship. This research has made use of NASA's Astrophysics Data System and Simbad and VizieR data bases, operated at CDS, Strasbourg, France.
The O5 V star A37 falls outside of our survey area and therefore is not included in this study, and may not actually be a member of Cyg OB2, as suggested by Hanson (2003).
Cambridge Astronomical Surveys Unit – Colours and Transformations for the Isaac Newton Telescope Wide Field Survey: http://www.ast.cam.ac.uk/∼wfcsur/technical/photom/colours/.
REFERENCES
APPENDIX A: UVEX PHOTOMETRY AND TRANSFORMATIONS TO THE UBV SYSTEM
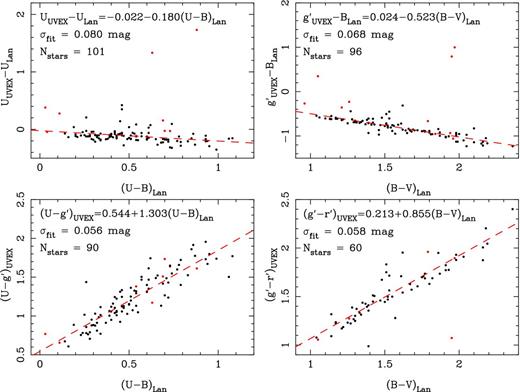
Calibration of transformations between the Massey & Thompson (1991) UBV photometry and the UVEX Ug′r′ photometry. All stars are shown as black dots, with the stars listed by Massey & Thompson (1991) as ‘blended’ shown with red dots. The best-fitting transformation obtained using a least-squares fit that excludes the ‘blended’ stars are shown with red dashed lines and are listed in each panel with the number of stars used for the fit and the dispersion on the best fit.
APPENDIX B: THE FINAL CATALOGUE
The full census of known OB stars in Cyg OB2 is presented in Table B1 in order of increasing primary spectral subtype and with derived observational (AV), physical (Teff, Lbol), and stellar (M, age) quantities (the latter calculated using the Ekström et al. 2012 rotating evolutionary models). Stars that fall to the left of the zero-aged MS in the HR diagram are listed as having ages of 0 Myr, while those whose positions in the HR diagram suggest ages >10 Myr are listed as such (see Section 4.5 for discussion of these issues). References for spectral classifications are noted at the end of the table. The full table, which also contains UBV and JHKs photometry, stellar quantities derived using the Lejeune & Schaerer (2001) non-rotating models, along with 1σ uncertainties on all derived properties, is available from Vizier.
| RA . | Dec. . | Spectral . | Spectral . | Source number . | AV . | log L . | Teff . | M . | Age . | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (J2000.0) . | (J2000.0) . | type . | reference . | S58 . | MT91 . | C02 . | (mag) . | (L⊙) . | (K) . | (M⊙) . | (Myr) . |
| 20:32:03.10 | 41:15:19.9 | WC4 | vH88 | – | – | WR144 | – | 4.99 | 5.05 | >20 | 2–8 |
| 20:32:06.28 | 40:48:29.7 | WN7o/CE + O7 V((f)) | S96,M09 | – | – | WR145 | – | 5.57 | 4.70 | >25 | 2–7 |
| 20:35:47.09 | 41:22:44.7 | WC6 + O8 III | D00,D00 | – | – | WR146 | 7.83 | 5.06 | 4.90 | >25 | 2–4 |
| 20:33:08.78 | 41:13:18.1 | O3 If + O6 V | W02,W02 | 22 | 417 | – | 6.92 | 5.82 | 4.63 | 49.9 | 4.12 |
| 20:33:14.16 | 41:20:21.5 | O3 If | MT91 | 7 | 457 | – | 5.30 | 5.63 | 4.63 | 46.7 | 2.67 |
| 20:33:18.02 | 41:18:31.0 | O5 III | K07 | 8C | 483 | – | 4.85 | 5.57 | 4.61 | 41.6 | 3.34 |
| 20:33:10.74 | 41:15:08.0 | O5 I + O3.5 III | NZ12,NZ12 | 9 | 431 | – | 6.76 | 5.85 | 4.59 | 51.6 | 4.26 |
| 20:34:08.54 | 41:36:59.3 | O5 If + B0 V | K12a,K12a | 11 | 734 | – | 5.40 | 5.73 | 4.59 | 43.7 | 4.56 |
| 20:33:23.46 | 41:09:12.9 | O5.5 V | MT91 | – | 516 | – | 7.43 | 5.85 | 4.60 | 51.6 | 4.21 |
| 20:33:13.25 | 41:13:28.6 | O6 V | MT91 | – | 448 | – | 7.22 | 5.03 | 4.59 | 28.6 | 0.76 |
| 20:31:37.50 | 41:13:21.1 | O6 IV + O9 III | K08,K08 | 3 | – | – | 5.84 | 5.54 | 4.59 | 38.0 | 4.18 |
| 20:33:15.18 | 41:18:50.1 | O6 I + O5.5 III | dB04,dB04 | 8A | 465 | – | 4.84 | 5.70 | 4.57 | 41.1 | 5.00 |
| 20:33:14.84 | 41:18:41.4 | O6.5 III | MT91 | 8B | 462 | – | 5.12 | 5.48 | 4.57 | 35.2 | 4.56 |
| 20:34:44.10 | 40:51:58.0 | O6.5 III | N08 | – | – | A24 | 7.29 | 5.19 | 4.57 | 29.6 | 3.41 |
| 20:33:40.88 | 41:30:18.5 | O7 V | MT91 | – | 611 | – | 5.54 | 4.66 | 4.57 | 22.3 | 0 |
| 20:34:13.50 | 41:35:02.6 | O7 V | MT91 | 29 | 745 | – | 5.36 | 4.94 | 4.57 | 25.4 | 1.78 |
| 20:34:29.52 | 41:31:45.5 | O7 V + O9 V | K08,K08 | – | 771 | – | 6.93 | 5.18 | 4.57 | 29.0 | 3.50 |
| 20:31:59.61 | 41:14:50.4 | O7 V | C12 | – | – | E45 | 5.89 | 4.79 | 4.57 | 23.3 | 0.17 |
| 20:32:13.77 | 41:27:12.7 | O7 III | K07 | 4 | 217 | – | 4.39 | 5.20 | 4.56 | 28.6 | 4.14 |
| 20:32:22.43 | 41:18:19.0 | O7 I + O6 I + O9 V | B76,B76,D13 | 5 | – | – | 6.02 | 6.20 | 4.54 | 93.1 | 2.95 |
| 20:31:36.91 | 40:59:09.1 | O7 I | N08 | – | – | A15 | 8.26 | 5.42 | 4.54 | 31.8 | 5.25 |
| 20:30:27.30 | 41:13:25.0 | O7 I + O9 I | S10,S10 | – | – | B17 | 8.08 | 5.03 | 4.54 | 24.8 | 4.17 |
| 20:33:17.49 | 41:17:09.2 | O7.5 V | MT91 | 24 | 480 | – | 5.63 | 5.02 | 4.55 | 25.4 | 3.40 |
| 20:33:26.77 | 41:10:59.5 | O7.5 V | MT91 | – | 534 | – | 6.36 | 4.84 | 4.55 | 23.4 | 1.77 |
| 20:32:31.50 | 41:14:08.0 | O7.5 III | K12a | – | 267 | – | 8.03 | 5.51 | 4.56 | 34.7 | 5.17 |
| 20:31:10.57 | 41:31:53.0 | O8 V | K08 | 1 | 059 | – | 5.18 | 5.08 | 4.54 | 25.5 | 4.46 |
| 20:32:27.67 | 41:26:21.7 | O8 V | MT91 | 15 | 258 | – | 4.36 | 4.79 | 4.54 | 21.9 | 2.45 |
| 20:32:38.58 | 41:25:13.6 | O8 V | H03 | 16 | 299 | – | 4.40 | 4.92 | 4.54 | 23.4 | 3.65 |
| 20:32:45.45 | 41:25:37.3 | O8 V | MT91 | 6 | 317 | – | 4.54 | 5.04 | 4.54 | 24.8 | 4.28 |
| 20:32:59.17 | 41:24:25.7 | O8 V | MT91 | – | 376 | – | 4.90 | 4.69 | 4.54 | 20.9 | 1.04 |
| 20:33:02.94 | 41:17:43.3 | O8 V | MT91 | – | 390 | – | 6.63 | 4.93 | 4.54 | 23.5 | 3.70 |
| 20:33:13.67 | 41:13:05.7 | O8 V | MT91 | – | 455 | – | 6.13 | 4.75 | 4.54 | 21.4 | 1.89 |
| 20:33:18.08 | 41:21:36.6 | O8 V | MT91 | – | 485 | – | 5.32 | 4.79 | 4.54 | 21.8 | 2.40 |
| 20:33:30.43 | 41:35:57.5 | O8 V | MT91 | 74 | 555 | – | 6.45 | 5.04 | 4.54 | 24.9 | 4.31 |
| 20:32:34.80 | 40:56:17.0 | O8 V | N08 | – | – | A38 | 6.31 | 4.64 | 4.54 | 20.3 | 0.41 |
| 20:34:21.95 | 41:17:01.6 | O8 III + O8 III | K09,K09 | 73 | – | – | 6.27 | 4.62 | 4.53 | 19.6 | 1.36 |
| 20:33:02.90 | 40:47:25.0 | O8 II | H03 | – | – | A20 | 8.13 | 5.58 | 4.53 | 35.0 | 5.72 |
| 20:32:50.03 | 41:23:44.6 | O8.5 V | MT91 | 17 | 339 | – | 4.92 | 4.79 | 4.53 | 21.2 | 3.67 |
| 20:33:16.36 | 41:19:01.9 | O8.5 V | MT91 | 8D | 473 | – | 5.13 | 4.69 | 4.53 | 20.2 | 2.59 |
| 20:33:21.04 | 41:17:40.1 | O8.5 V | MT91 | – | 507 | – | 5.41 | 4.53 | 4.53 | 18.7 | 0.13 |
| 20:33:25.67 | 41:33:26.6 | O8.5 V | MT91 | 25 | 531 | – | 5.46 | 4.99 | 4.53 | 23.5 | 4.88 |
| 20:31:45.39 | 41:18:26.8 | O8.5 I | MT91 | – | 138 | – | 6.57 | 5.07 | 4.51 | 23.6 | 6.11 |
| 20:31:18.31 | 41:21:21.7 | O9 V + B6 V | K12a,K12a | – | 070 | – | 6.86 | 4.55 | 4.52 | 18.4 | 1.97 |
| 20:32:16.53 | 41:25:36.4 | O9 V | MT91 | 14 | 227 | – | 4.55 | 4.66 | 4.52 | 19.1 | 3.61 |
| 20:33:09.58 | 41:13:00.6 | O9 V + B9 V | K09,K09 | – | 421 | – | 6.77 | 4.26 | 4.52 | 16.3 | 0 |
| 20:34:04.95 | 41:05:13.2 | O9 V | MT91 | 41 | 716 | – | 6.12 | 4.45 | 4.52 | 17.5 | 0.26 |
| 20:34:09.52 | 41:34:13.4 | O9 V | MT91 | 75 | 736 | – | 5.43 | 4.50 | 4.52 | 18.0 | 1.07 |
| 20:33:09.41 | 41:12:58.2 | O9 V | K07 | – | 420 | – | 6.54 | 4.06 | 4.52 | 15.2 | 0 |
| 20:31:49.65 | 41:28:26.8 | O9 III | K09 | 20 | 145 | – | 4.12 | 4.42 | 4.50 | 16.8 | 1.46 |
| 20:33:46.15 | 41:33:00.5 | O9 I | K07 | 10 | 632 | – | 5.66 | 5.68 | 4.50 | 37.4 | 5.54 |
| 20:33:15.74 | 41:20:17.2 | O9.5 V | MT91 | 23 | 470 | – | 5.13 | 4.42 | 4.50 | 16.8 | 1.35 |
| 20:33:59.57 | 41:17:36.1 | O9.5 V + B0 V | MT91,K12 | 27 | 696 | – | 5.81 | 4.48 | 4.50 | 17.2 | 2.58 |
| 20:30:57.70 | 41:09:57.0 | O9.5 V | N08 | – | – | A26 | 6.69 | 4.69 | 4.50 | 18.7 | 5.31 |
| 20:34:16.05 | 41:02:19.6 | O9.5 V | C12 | – | – | E54 | 6.23 | 4.54 | 4.50 | 17.6 | 3.62 |
| 20:31:46.00 | 41:17:27.4 | O9.5 I | MT91 | – | 140 | – | 2.17 | 4.54 | 4.48 | 16.6 | 5.97 |
| 20:32:13.07 | 41:27:24.9 | B0 V | MT91 | – | 213 | – | 4.30 | 4.18 | 4.49 | 14.5 | 0 |
| 20:32:59.61 | 41:15:14.6 | B0 V | MT91 | 41 | 378 | – | 6.93 | 4.65 | 4.49 | 17.5 | 6.55 |
| 20:33:10.10 | 41:13:10.1 | B0 V | MT91 | 51 | 425 | – | 6.55 | 4.44 | 4.49 | 16.0 | 4.32 |
| 20:33:10.34 | 41:13:06.4 | B0 V | MT91 | – | 426 | – | Unresolved | ||||
| 20:33:10.50 | 41:22:22.8 | B0 V + B3 V | MT91,K12 | – | 429 | – | 5.45 | 3.99 | 4.49 | 13.5 | 0 |
| 20:33:37.02 | 41:16:11.4 | B0 V | MT91 | 70 | 588 | – | 5.85 | 4.69 | 4.49 | 17.9 | 6.80 |
| 20:33:59.32 | 41:05:38.4 | B0 V | MT91 | – | 692 | – | 5.74 | 4.14 | 4.49 | 14.2 | 0 |
| 20:30:51.12 | 41:20:21.6 | B0 V | K07 | – | 020 | – | 7.20 | 4.36 | 4.49 | 15.5 | 2.65 |
| 20:32:58.79 | 41:04:29.9 | B0 V + B2 V | K07,K09 | – | 372 | – | 6.98 | 3.85 | 4.49 | 12.9 | 0 |
| 20:33:11.02 | 41:10:31.9 | B0 V | K07 | – | 435 | – | 7.13 | 4.20 | 4.49 | 14.6 | 0 |
| 20:33:17.40 | 41:12:38.7 | B0 V | K07 | – | 477 | – | 6.49 | 4.12 | 4.49 | 14.1 | 0 |
| 20:33:18.56 | 41:24:49.3 | B0 V | K07 | – | 490 | – | 5.77 | 3.76 | 4.49 | 12.5 | 0 |
| 20:33:42.38 | 41:11:45.8 | B0 V | K07 | – | 620 | – | 6.24 | 4.24 | 4.49 | 14.7 | 0.19 |
| 20:32:39.51 | 40:52:47.5 | B0 V | C12 | – | – | E48 | 6.60 | 4.69 | 4.49 | 17.9 | 6.78 |
| 20:32:34.90 | 40:52:39.0 | B0.2 V | N08 | – | – | A33 | 6.80 | 4.42 | 4.47 | 15.1 | 6.62 |
| 20:33:21.14 | 41:35:52.0 | B0 III | K07 | – | 509 | – | 6.66 | 4.14 | 4.49 | 14.2 | 0 |
| 20:33:39.14 | 41:19:26.1 | B0 Iab | MT91 | 19 | 601 | – | 5.72 | 5.27 | 4.49 | 26.0 | 6.74 |
| 20:34:44.70 | 40:51:46.0 | B0 Ia | H03 | – | – | A27 | 7.58 | 5.63 | 4.49 | 35.2 | 5.94 |
| 20:34:58.70 | 41:36:17.0 | B0 Ib + B0 III | H03,K09 | – | – | A36 | 6.05 | 5.24 | 4.49 | 25.5 | 6.78 |
| 20:32:39.06 | 41:00:07.8 | B0 Ia | C12 | – | – | E47 | 6.53 | 5.83 | 4.49 | 42.3 | 4.79 |
| 20:33:38.22 | 40:53:41.2 | B0 Ib | C12 | – | – | E52 | 5.91 | 4.97 | 4.49 | 21.2 | 7.06 |
| 20:32:03.74 | 41:25:10.9 | B0.5 V | MT91 | – | 187 | – | 5.31 | 4.05 | 4.44 | 12.3 | 3.74 |
| 20:32:27.76 | 41:28:51.9 | B0.5 V | MT91 | 21 | 259 | – | 3.80 | 4.20 | 4.44 | 12.9 | 7.63 |
| 20:33:39.84 | 41:22:52.4 | B0.5 V + B2.5 V | K12,K12 | – | 605 | – | 4.66 | 4.10 | 4.44 | 12.5 | 5.39 |
| 20:34:06.10 | 41:08:09.6 | B0.5 V + B1.5 V | K12,K12 | – | 720 | – | 6.95 | 4.20 | 4.44 | 12.9 | 7.73 |
| 20:32:39.50 | 40:52:47.0 | B0.5 V | N08 | – | – | A31 | 7.20 | 4.63 | 4.44 | 15.7 | >10 |
| 20:33:06.62 | 41:21:13.3 | B0.5 V | K07 | – | 409 | – | 5.96 | 3.91 | 4.44 | 11.6 | 0 |
| 20:33:18.70 | 40:59:37.9 | B0.5 III | C12 | – | – | E51 | 6.63 | 4.54 | 4.44 | 14.9 | >10 |
| 20:32:13.53 | 41:27:30.0 | B1 V | MT91 | – | 215 | – | 4.05 | 3.58 | 4.39 | 9.2 | 0 |
| 20:32:37.03 | 41:23:05.1 | B1 V | MT91 | – | 292 | – | 5.31 | 4.09 | 4.39 | 10.9 | >10 |
| 20:32:38.87 | 41:25:20.8 | B1 V | K07 | – | 300 | – | 4.34 | 3.62 | 4.39 | 9.2 | 0.90 |
| 20:33:04.42 | 41:17:08.9 | B1 V | K07 | 54 | 395 | – | 5.96 | 3.90 | 4.39 | 10.2 | >10 |
| 20:33:05.22 | 41:17:51.6 | B1 V | K07 | – | 400 | – | 5.54 | 3.74 | 4.39 | 9.6 | 6.58 |
| 20:33:15.37 | 41:29:56.6 | B1 V | MT91 | – | 467 | – | 5.41 | 3.97 | 4.39 | 10.4 | >10 |
| 20:33:23.24 | 41:13:41.9 | B1 V | MT91 | 66 | 515 | – | 6.77 | 4.01 | 4.39 | 10.6 | >10 |
| 20:31:33.38 | 41:22:49.0 | B1 V + B2 V | K07,K12a | – | 103 | – | 6.37 | 4.04 | 4.39 | 10.7 | >10 |
| 20:32:14.56 | 41:22:33.7 | B1 V | K07 | – | 220 | – | 5.38 | 3.61 | 4.39 | 9.1 | 0.61 |
| 20:32:21.35 | 41:18:35.5 | B1 V | K07 | – | 238 | – | 5.71 | 3.45 | 4.39 | 8.7 | 0 |
| 20:32:50.69 | 41:15:02.2 | B1 V | K07 | – | 343 | – | 6.55 | 4.00 | 4.39 | 10.6 | >10 |
| 20:32:56.66 | 41:23:41.0 | B1 V | K07 | – | 365 | – | 4.81 | 3.62 | 4.39 | 9.2 | 1.14 |
| 20:33:10.46 | 41:20:57.6 | B1 V | K07 | – | 428 | – | 6.00 | 3.95 | 4.39 | 10.4 | >10 |
| 20:33:19.16 | 41:17:44.9 | B1 V | K07 | – | 492 | – | 5.67 | 3.50 | 4.39 | 8.9 | 0 |
| 20:33:23.37 | 41:20:17.2 | B1 V | K07 | – | 517 | – | 5.24 | 3.79 | 4.39 | 9.8 | 9.10 |
| 20:33:42.57 | 41:14:56.9 | B1 V | K07 | – | 621 | – | 6.46 | 3.79 | 4.39 | 9.8 | 9.02 |
| 20:34:04.43 | 41:08:08.4 | B1 V | K07 | – | 712 | – | 6.15 | 4.18 | 4.39 | 11.4 | >10 |
| 20:34:24.56 | 41:26:24.7 | B1 V | K07 | – | 759 | – | 5.85 | 3.68 | 4.39 | 9.4 | 3.52 |
| 20:30:39.70 | 41:08:48.0 | B0.7 Ib | H03 | – | – | A23 | 7.38 | 5.42 | 4.42 | 26.3 | 7.04 |
| 20:33:47.88 | 41:20:41.7 | B1 III | MT91 | 26 | 642 | – | 5.77 | 4.84 | 4.39 | 15.9 | >10 |
| 20:33:15.51 | 41:27:32.9 | B1 III | K07 | – | 469 | – | 5.13 | 3.81 | 4.39 | 9.8 | 9.88 |
| 20:33:46.85 | 41:08:01.9 | B1 III | K07 | – | 635 | – | 5.78 | 3.96 | 4.39 | 10.4 | >10 |
| 20:31:22.03 | 41:31:28.0 | B1 I | MT91 | 2 | 083 | – | 3.98 | 4.61 | 4.39 | 14.3 | >10 |
| 20:33:30.81 | 41:15:22.7 | B1 Ib | MT91 | 18 | 556 | – | 6.47 | 5.53 | 4.39 | 28.9 | 6.68 |
| 20:31:56.27 | 41:33:05.3 | B1.5 V | MT91 | – | 169 | – | 4.41 | 3.31 | 4.36 | 7.8 | 0 |
| 20:33:05.55 | 41:43:40.1 | B1.5 V | MT91 | – | 403 | – | 5.48 | 4.14 | 4.36 | 10.7 | >10 |
| 20:33:34.36 | 41:18:11.6 | B1.5 V | MT91 | – | 575 | – | 6.73 | 4.49 | 4.36 | 12.6 | >10 |
| 20:33:48.88 | 41:19:40.9 | B1.5 V | MT91 | 71 | 646 | – | 5.11 | 3.83 | 4.36 | 9.3 | >10 |
| 20:32:13.75 | 41:27:42.0 | B1.5 V | K07 | – | 216 | – | 4.28 | 3.61 | 4.36 | 8.7 | >10 |
| 20:34:43.51 | 41:29:04.8 | B1.5 III | MT91 | 30 | 793 | – | 5.73 | 4.52 | 4.36 | 12.7 | >10 |
| 20:32:26.50 | 41:19:13.7 | B1.5 III + B1 V | K07,K08 | – | 252 | – | 5.40 | 3.50 | 4.36 | 8.3 | 4.65 |
| 20:32:46.74 | 41:26:15.9 | B1.5 III | K07 | – | 325 | – | 4.98 | 3.39 | 4.36 | 8.0 | 0 |
| 20:33:18.55 | 41:15:35.4 | B2 Ve | K07 | 64 | 488 | – | 8.27 | 4.38 | 4.34 | 11.6 | >10 |
| 20:31:22.10 | 41:12:03.0 | B2 V | N08 | – | – | A30 | 6.27 | 4.06 | 4.34 | 10.0 | >10 |
| 20:32:27.30 | 40:55:18.0 | B2 V | H03 | – | – | A39 | 6.05 | 4.35 | 4.34 | 11.5 | >10 |
| 20:30:59.43 | 41:35:59.6 | B2 V | K07 | – | 042 | – | 4.58 | 3.35 | 4.34 | 7.7 | 0 |
| 20:31:30.49 | 41:37:15.6 | B2 V | K07 | – | 097 | – | 4.40 | 2.94 | 4.34 | 6.8 | 0 |
| 20:32:03.01 | 41:32:30.7 | B2 Ve | K07 | – | 186 | – | 4.53 | 3.19 | 4.34 | 7.3 | 0 |
| 20:32:07.95 | 41:22:00.3 | B2 V | K07 | – | 202 | – | 4.92 | 3.23 | 4.34 | 7.4 | 0 |
| 20:32:14.63 | 41:27:40.3 | B2 V | K07 | – | 221 | – | 4.67 | 3.43 | 4.34 | 8.0 | 5.15 |
| 20:32:19.66 | 41:20:39.7 | B2 V | K07 | – | 234 | – | 4.47 | 3.48 | 4.34 | 8.1 | 8.63 |
| 20:32:22.15 | 41:27:41.7 | B2 V | K07 | – | 241 | – | 4.18 | 3.32 | 4.34 | 7.7 | 0 |
| 20:32:25.50 | 41:24:51.8 | B2 V | K07 | – | 248 | – | 4.57 | 3.47 | 4.34 | 8.1 | 8.27 |
| 20:32:32.68 | 41:27:04.4 | B2 V | K07 | – | 275 | – | 3.92 | 3.17 | 4.34 | 7.3 | 0 |
| 20:32:37.78 | 41:26:15.3 | B2 V | K07 | – | 295 | – | 4.25 | 3.21 | 4.34 | 7.4 | 0 |
| 20:32:42.90 | 41:20:16.4 | B2 V + B3 V | K07,K12 | – | 311 | – | 4.95 | 3.29 | 4.34 | 7.6 | 0 |
| 20:33:22.49 | 41:22:16.9 | B2 V | K07 | – | 513 | – | 5.07 | 3.33 | 4.34 | 7.7 | 0 |
| 20:33:24.78 | 41:22:04.5 | B2 Ve | K07 | – | 522 | – | 4.90 | 3.34 | 4.34 | 7.7 | 0 |
| 20:33:31.68 | 41:21:46.1 | B2 V | K07 | – | 561 | – | 4.67 | 3.38 | 4.34 | 7.8 | 2.13 |
| 20:33:47.63 | 41:09:06.5 | B2 V | K07 | – | 639 | – | 5.94 | 3.60 | 4.34 | 8.4 | >10 |
| 20:33:48.83 | 41:37:39.7 | B2 Ve | K07 | – | 650 | – | 5.70 | 3.35 | 4.34 | 7.7 | 0 |
| 20:31:56.90 | 41:31:48.0 | B2 III | K12a | – | 174 | – | 4.39 | 3.75 | 4.34 | 8.8 | >10 |
| 20:32:26.10 | 41:29:39.0 | B2 III | K07 | – | 250 | – | 3.91 | 3.42 | 4.34 | 8.0 | 4.66 |
| 20:32:27.26 | 41:21:56.2 | B2 III | K07 | – | 255 | – | 5.06 | 3.15 | 4.34 | 7.2 | 0 |
| 20:32:30.72 | 41:07:04.1 | B2 III | K07 | – | 264 | – | 3.56 | 3.37 | 4.34 | 7.7 | 1.25 |
| 20:33:11.39 | 41:17:58.9 | B2 III | K07 | – | 441 | – | 5.18 | 3.31 | 4.34 | 7.6 | 0 |
| 20:33:48.40 | 41:13:14.1 | B2 III | K07 | – | 645 | – | 6.19 | 3.58 | 4.34 | 8.4 | >10 |
| 20:30:50.75 | 41:35:06.0 | B2 II | MT91 | – | 021 | – | 4.42 | 3.32 | 4.34 | 7.7 | 0 |
| 20:32:46.45 | 41:24:22.4 | B2.5 V | K07 | – | 322 | – | 4.85 | 2.96 | 4.29 | 6.1 | 0 |
| 20:32:31.42 | 41:30:51.4 | B2.5 V | K07 | – | 268 | – | 5.19 | 3.30 | 4.29 | 6.8 | >10 |
| 20:32:54.35 | 41:15:22.1 | B3 V | K07 | 37 | 358 | – | 6.55 | 3.52 | 4.25 | 7.0 | >10 |
| 20:31:33.59 | 41:36:04.3 | B3 V | K07 | – | 106 | – | 4.58 | 2.92 | 4.25 | 5.6 | >10 |
| 20:31:41.60 | 41:28:20.9 | B3 V | K07 | – | 129 | – | 4.72 | 3.06 | 4.25 | 5.9 | >10 |
| 20:31:55.28 | 41:35:27.8 | B3 V | K07 | – | 164 | – | 4.54 | 2.73 | 4.25 | 5.3 | 0 |
| 20:31:59.82 | 41:37:14.3 | B3 V | K07 | – | 179 | – | 5.02 | 3.33 | 4.25 | 6.4 | >10 |
| 20:32:06.85 | 41:17:56.8 | B3 V | K07 | – | 200 | – | 6.41 | 3.87 | 4.25 | 8.0 | >10 |
| 20:32:15.03 | 41:19:30.8 | B3 V | K07 | – | 222 | – | 5.02 | 3.00 | 4.25 | 5.8 | >10 |
| 20:32:38.34 | 41:28:56.6 | B3 V | K07 | – | 298 | – | 4.47 | 2.95 | 4.25 | 5.7 | >10 |
| 20:33:33.38 | 41:08:36.3 | B3 V | K07 | – | 568 | – | 6.71 | 3.63 | 4.25 | 7.3 | >10 |
| 20:31:34.12 | 41:31:08.0 | B3 IV | K07 | – | 108 | – | 4.53 | 2.64 | 4.25 | 5.1 | 0 |
| 20:32:04.74 | 41:28:44.5 | B3 IV | K07 | – | 191 | – | 3.83 | 2.94 | 4.25 | 5.6 | >10 |
| 20:32:49.67 | 41:25:36.4 | B3 III | K07 | – | 336 | – | 4.23 | 2.97 | 4.25 | 5.7 | >10 |
| 20:33:33.97 | 41:19:38.4 | B3 I | K07 | – | 573 | – | 5.25 | 3.58 | 4.25 | 7.1 | >10 |
| 20:32:40.88 | 41:14:29.3 | B3.5 Ia+ | MT91 | 12 | 304 | – | 10.18 | 6.09 | 4.14 | 110 | 3.0 |
| 20:32:21.76 | 41:34:24.6 | B4 V | K07 | – | 239 | – | 3.92 | 2.63 | 4.22 | 4.7 | 2.66 |
| 20:32:32.34 | 41:22:57.6 | B4 V | K07 | – | 271 | – | 5.14 | 3.02 | 4.22 | 5.4 | >10 |
| 20:33:10.27 | 41:23:44.9 | B4 III | K07 | – | 427 | – | Background | ||||
| 20:31:56.23 | 41:35:12.3 | B5 V | K07 | – | 170 | – | Background | ||||
| 20:32:32.54 | 41:26:46.7 | B5 V | K07 | – | 273 | – | 4.53 | 2.49 | 4.20 | 4.3 | 3.92 |
| 20:33:11.81 | 41:24:05.8 | B5 V | K07 | – | 444 | – | 5.25 | 3.22 | 4.20 | 5.7 | >10 |
| 20:33:13.37 | 41:26:39.7 | B5 V | K07 | – | 453 | – | 4.27 | 2.71 | 4.20 | 4.7 | >10 |
| 20:33:14.34 | 41:19:33.0 | B5 V | K07 | – | 459 | – | 6.65 | 3.45 | 4.20 | 6.2 | >10 |
| 20:33:47.58 | 41:29:57.7 | B5 V | K07 | – | 641 | – | 5.71 | 3.39 | 4.20 | 6.1 | >10 |
| 20:33:19.26 | 41:24:44.8 | B5 IV | K07 | – | 493 | – | 5.56 | 2.98 | 4.20 | 5.2 | >10 |
| RA . | Dec. . | Spectral . | Spectral . | Source number . | AV . | log L . | Teff . | M . | Age . | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (J2000.0) . | (J2000.0) . | type . | reference . | S58 . | MT91 . | C02 . | (mag) . | (L⊙) . | (K) . | (M⊙) . | (Myr) . |
| 20:32:03.10 | 41:15:19.9 | WC4 | vH88 | – | – | WR144 | – | 4.99 | 5.05 | >20 | 2–8 |
| 20:32:06.28 | 40:48:29.7 | WN7o/CE + O7 V((f)) | S96,M09 | – | – | WR145 | – | 5.57 | 4.70 | >25 | 2–7 |
| 20:35:47.09 | 41:22:44.7 | WC6 + O8 III | D00,D00 | – | – | WR146 | 7.83 | 5.06 | 4.90 | >25 | 2–4 |
| 20:33:08.78 | 41:13:18.1 | O3 If + O6 V | W02,W02 | 22 | 417 | – | 6.92 | 5.82 | 4.63 | 49.9 | 4.12 |
| 20:33:14.16 | 41:20:21.5 | O3 If | MT91 | 7 | 457 | – | 5.30 | 5.63 | 4.63 | 46.7 | 2.67 |
| 20:33:18.02 | 41:18:31.0 | O5 III | K07 | 8C | 483 | – | 4.85 | 5.57 | 4.61 | 41.6 | 3.34 |
| 20:33:10.74 | 41:15:08.0 | O5 I + O3.5 III | NZ12,NZ12 | 9 | 431 | – | 6.76 | 5.85 | 4.59 | 51.6 | 4.26 |
| 20:34:08.54 | 41:36:59.3 | O5 If + B0 V | K12a,K12a | 11 | 734 | – | 5.40 | 5.73 | 4.59 | 43.7 | 4.56 |
| 20:33:23.46 | 41:09:12.9 | O5.5 V | MT91 | – | 516 | – | 7.43 | 5.85 | 4.60 | 51.6 | 4.21 |
| 20:33:13.25 | 41:13:28.6 | O6 V | MT91 | – | 448 | – | 7.22 | 5.03 | 4.59 | 28.6 | 0.76 |
| 20:31:37.50 | 41:13:21.1 | O6 IV + O9 III | K08,K08 | 3 | – | – | 5.84 | 5.54 | 4.59 | 38.0 | 4.18 |
| 20:33:15.18 | 41:18:50.1 | O6 I + O5.5 III | dB04,dB04 | 8A | 465 | – | 4.84 | 5.70 | 4.57 | 41.1 | 5.00 |
| 20:33:14.84 | 41:18:41.4 | O6.5 III | MT91 | 8B | 462 | – | 5.12 | 5.48 | 4.57 | 35.2 | 4.56 |
| 20:34:44.10 | 40:51:58.0 | O6.5 III | N08 | – | – | A24 | 7.29 | 5.19 | 4.57 | 29.6 | 3.41 |
| 20:33:40.88 | 41:30:18.5 | O7 V | MT91 | – | 611 | – | 5.54 | 4.66 | 4.57 | 22.3 | 0 |
| 20:34:13.50 | 41:35:02.6 | O7 V | MT91 | 29 | 745 | – | 5.36 | 4.94 | 4.57 | 25.4 | 1.78 |
| 20:34:29.52 | 41:31:45.5 | O7 V + O9 V | K08,K08 | – | 771 | – | 6.93 | 5.18 | 4.57 | 29.0 | 3.50 |
| 20:31:59.61 | 41:14:50.4 | O7 V | C12 | – | – | E45 | 5.89 | 4.79 | 4.57 | 23.3 | 0.17 |
| 20:32:13.77 | 41:27:12.7 | O7 III | K07 | 4 | 217 | – | 4.39 | 5.20 | 4.56 | 28.6 | 4.14 |
| 20:32:22.43 | 41:18:19.0 | O7 I + O6 I + O9 V | B76,B76,D13 | 5 | – | – | 6.02 | 6.20 | 4.54 | 93.1 | 2.95 |
| 20:31:36.91 | 40:59:09.1 | O7 I | N08 | – | – | A15 | 8.26 | 5.42 | 4.54 | 31.8 | 5.25 |
| 20:30:27.30 | 41:13:25.0 | O7 I + O9 I | S10,S10 | – | – | B17 | 8.08 | 5.03 | 4.54 | 24.8 | 4.17 |
| 20:33:17.49 | 41:17:09.2 | O7.5 V | MT91 | 24 | 480 | – | 5.63 | 5.02 | 4.55 | 25.4 | 3.40 |
| 20:33:26.77 | 41:10:59.5 | O7.5 V | MT91 | – | 534 | – | 6.36 | 4.84 | 4.55 | 23.4 | 1.77 |
| 20:32:31.50 | 41:14:08.0 | O7.5 III | K12a | – | 267 | – | 8.03 | 5.51 | 4.56 | 34.7 | 5.17 |
| 20:31:10.57 | 41:31:53.0 | O8 V | K08 | 1 | 059 | – | 5.18 | 5.08 | 4.54 | 25.5 | 4.46 |
| 20:32:27.67 | 41:26:21.7 | O8 V | MT91 | 15 | 258 | – | 4.36 | 4.79 | 4.54 | 21.9 | 2.45 |
| 20:32:38.58 | 41:25:13.6 | O8 V | H03 | 16 | 299 | – | 4.40 | 4.92 | 4.54 | 23.4 | 3.65 |
| 20:32:45.45 | 41:25:37.3 | O8 V | MT91 | 6 | 317 | – | 4.54 | 5.04 | 4.54 | 24.8 | 4.28 |
| 20:32:59.17 | 41:24:25.7 | O8 V | MT91 | – | 376 | – | 4.90 | 4.69 | 4.54 | 20.9 | 1.04 |
| 20:33:02.94 | 41:17:43.3 | O8 V | MT91 | – | 390 | – | 6.63 | 4.93 | 4.54 | 23.5 | 3.70 |
| 20:33:13.67 | 41:13:05.7 | O8 V | MT91 | – | 455 | – | 6.13 | 4.75 | 4.54 | 21.4 | 1.89 |
| 20:33:18.08 | 41:21:36.6 | O8 V | MT91 | – | 485 | – | 5.32 | 4.79 | 4.54 | 21.8 | 2.40 |
| 20:33:30.43 | 41:35:57.5 | O8 V | MT91 | 74 | 555 | – | 6.45 | 5.04 | 4.54 | 24.9 | 4.31 |
| 20:32:34.80 | 40:56:17.0 | O8 V | N08 | – | – | A38 | 6.31 | 4.64 | 4.54 | 20.3 | 0.41 |
| 20:34:21.95 | 41:17:01.6 | O8 III + O8 III | K09,K09 | 73 | – | – | 6.27 | 4.62 | 4.53 | 19.6 | 1.36 |
| 20:33:02.90 | 40:47:25.0 | O8 II | H03 | – | – | A20 | 8.13 | 5.58 | 4.53 | 35.0 | 5.72 |
| 20:32:50.03 | 41:23:44.6 | O8.5 V | MT91 | 17 | 339 | – | 4.92 | 4.79 | 4.53 | 21.2 | 3.67 |
| 20:33:16.36 | 41:19:01.9 | O8.5 V | MT91 | 8D | 473 | – | 5.13 | 4.69 | 4.53 | 20.2 | 2.59 |
| 20:33:21.04 | 41:17:40.1 | O8.5 V | MT91 | – | 507 | – | 5.41 | 4.53 | 4.53 | 18.7 | 0.13 |
| 20:33:25.67 | 41:33:26.6 | O8.5 V | MT91 | 25 | 531 | – | 5.46 | 4.99 | 4.53 | 23.5 | 4.88 |
| 20:31:45.39 | 41:18:26.8 | O8.5 I | MT91 | – | 138 | – | 6.57 | 5.07 | 4.51 | 23.6 | 6.11 |
| 20:31:18.31 | 41:21:21.7 | O9 V + B6 V | K12a,K12a | – | 070 | – | 6.86 | 4.55 | 4.52 | 18.4 | 1.97 |
| 20:32:16.53 | 41:25:36.4 | O9 V | MT91 | 14 | 227 | – | 4.55 | 4.66 | 4.52 | 19.1 | 3.61 |
| 20:33:09.58 | 41:13:00.6 | O9 V + B9 V | K09,K09 | – | 421 | – | 6.77 | 4.26 | 4.52 | 16.3 | 0 |
| 20:34:04.95 | 41:05:13.2 | O9 V | MT91 | 41 | 716 | – | 6.12 | 4.45 | 4.52 | 17.5 | 0.26 |
| 20:34:09.52 | 41:34:13.4 | O9 V | MT91 | 75 | 736 | – | 5.43 | 4.50 | 4.52 | 18.0 | 1.07 |
| 20:33:09.41 | 41:12:58.2 | O9 V | K07 | – | 420 | – | 6.54 | 4.06 | 4.52 | 15.2 | 0 |
| 20:31:49.65 | 41:28:26.8 | O9 III | K09 | 20 | 145 | – | 4.12 | 4.42 | 4.50 | 16.8 | 1.46 |
| 20:33:46.15 | 41:33:00.5 | O9 I | K07 | 10 | 632 | – | 5.66 | 5.68 | 4.50 | 37.4 | 5.54 |
| 20:33:15.74 | 41:20:17.2 | O9.5 V | MT91 | 23 | 470 | – | 5.13 | 4.42 | 4.50 | 16.8 | 1.35 |
| 20:33:59.57 | 41:17:36.1 | O9.5 V + B0 V | MT91,K12 | 27 | 696 | – | 5.81 | 4.48 | 4.50 | 17.2 | 2.58 |
| 20:30:57.70 | 41:09:57.0 | O9.5 V | N08 | – | – | A26 | 6.69 | 4.69 | 4.50 | 18.7 | 5.31 |
| 20:34:16.05 | 41:02:19.6 | O9.5 V | C12 | – | – | E54 | 6.23 | 4.54 | 4.50 | 17.6 | 3.62 |
| 20:31:46.00 | 41:17:27.4 | O9.5 I | MT91 | – | 140 | – | 2.17 | 4.54 | 4.48 | 16.6 | 5.97 |
| 20:32:13.07 | 41:27:24.9 | B0 V | MT91 | – | 213 | – | 4.30 | 4.18 | 4.49 | 14.5 | 0 |
| 20:32:59.61 | 41:15:14.6 | B0 V | MT91 | 41 | 378 | – | 6.93 | 4.65 | 4.49 | 17.5 | 6.55 |
| 20:33:10.10 | 41:13:10.1 | B0 V | MT91 | 51 | 425 | – | 6.55 | 4.44 | 4.49 | 16.0 | 4.32 |
| 20:33:10.34 | 41:13:06.4 | B0 V | MT91 | – | 426 | – | Unresolved | ||||
| 20:33:10.50 | 41:22:22.8 | B0 V + B3 V | MT91,K12 | – | 429 | – | 5.45 | 3.99 | 4.49 | 13.5 | 0 |
| 20:33:37.02 | 41:16:11.4 | B0 V | MT91 | 70 | 588 | – | 5.85 | 4.69 | 4.49 | 17.9 | 6.80 |
| 20:33:59.32 | 41:05:38.4 | B0 V | MT91 | – | 692 | – | 5.74 | 4.14 | 4.49 | 14.2 | 0 |
| 20:30:51.12 | 41:20:21.6 | B0 V | K07 | – | 020 | – | 7.20 | 4.36 | 4.49 | 15.5 | 2.65 |
| 20:32:58.79 | 41:04:29.9 | B0 V + B2 V | K07,K09 | – | 372 | – | 6.98 | 3.85 | 4.49 | 12.9 | 0 |
| 20:33:11.02 | 41:10:31.9 | B0 V | K07 | – | 435 | – | 7.13 | 4.20 | 4.49 | 14.6 | 0 |
| 20:33:17.40 | 41:12:38.7 | B0 V | K07 | – | 477 | – | 6.49 | 4.12 | 4.49 | 14.1 | 0 |
| 20:33:18.56 | 41:24:49.3 | B0 V | K07 | – | 490 | – | 5.77 | 3.76 | 4.49 | 12.5 | 0 |
| 20:33:42.38 | 41:11:45.8 | B0 V | K07 | – | 620 | – | 6.24 | 4.24 | 4.49 | 14.7 | 0.19 |
| 20:32:39.51 | 40:52:47.5 | B0 V | C12 | – | – | E48 | 6.60 | 4.69 | 4.49 | 17.9 | 6.78 |
| 20:32:34.90 | 40:52:39.0 | B0.2 V | N08 | – | – | A33 | 6.80 | 4.42 | 4.47 | 15.1 | 6.62 |
| 20:33:21.14 | 41:35:52.0 | B0 III | K07 | – | 509 | – | 6.66 | 4.14 | 4.49 | 14.2 | 0 |
| 20:33:39.14 | 41:19:26.1 | B0 Iab | MT91 | 19 | 601 | – | 5.72 | 5.27 | 4.49 | 26.0 | 6.74 |
| 20:34:44.70 | 40:51:46.0 | B0 Ia | H03 | – | – | A27 | 7.58 | 5.63 | 4.49 | 35.2 | 5.94 |
| 20:34:58.70 | 41:36:17.0 | B0 Ib + B0 III | H03,K09 | – | – | A36 | 6.05 | 5.24 | 4.49 | 25.5 | 6.78 |
| 20:32:39.06 | 41:00:07.8 | B0 Ia | C12 | – | – | E47 | 6.53 | 5.83 | 4.49 | 42.3 | 4.79 |
| 20:33:38.22 | 40:53:41.2 | B0 Ib | C12 | – | – | E52 | 5.91 | 4.97 | 4.49 | 21.2 | 7.06 |
| 20:32:03.74 | 41:25:10.9 | B0.5 V | MT91 | – | 187 | – | 5.31 | 4.05 | 4.44 | 12.3 | 3.74 |
| 20:32:27.76 | 41:28:51.9 | B0.5 V | MT91 | 21 | 259 | – | 3.80 | 4.20 | 4.44 | 12.9 | 7.63 |
| 20:33:39.84 | 41:22:52.4 | B0.5 V + B2.5 V | K12,K12 | – | 605 | – | 4.66 | 4.10 | 4.44 | 12.5 | 5.39 |
| 20:34:06.10 | 41:08:09.6 | B0.5 V + B1.5 V | K12,K12 | – | 720 | – | 6.95 | 4.20 | 4.44 | 12.9 | 7.73 |
| 20:32:39.50 | 40:52:47.0 | B0.5 V | N08 | – | – | A31 | 7.20 | 4.63 | 4.44 | 15.7 | >10 |
| 20:33:06.62 | 41:21:13.3 | B0.5 V | K07 | – | 409 | – | 5.96 | 3.91 | 4.44 | 11.6 | 0 |
| 20:33:18.70 | 40:59:37.9 | B0.5 III | C12 | – | – | E51 | 6.63 | 4.54 | 4.44 | 14.9 | >10 |
| 20:32:13.53 | 41:27:30.0 | B1 V | MT91 | – | 215 | – | 4.05 | 3.58 | 4.39 | 9.2 | 0 |
| 20:32:37.03 | 41:23:05.1 | B1 V | MT91 | – | 292 | – | 5.31 | 4.09 | 4.39 | 10.9 | >10 |
| 20:32:38.87 | 41:25:20.8 | B1 V | K07 | – | 300 | – | 4.34 | 3.62 | 4.39 | 9.2 | 0.90 |
| 20:33:04.42 | 41:17:08.9 | B1 V | K07 | 54 | 395 | – | 5.96 | 3.90 | 4.39 | 10.2 | >10 |
| 20:33:05.22 | 41:17:51.6 | B1 V | K07 | – | 400 | – | 5.54 | 3.74 | 4.39 | 9.6 | 6.58 |
| 20:33:15.37 | 41:29:56.6 | B1 V | MT91 | – | 467 | – | 5.41 | 3.97 | 4.39 | 10.4 | >10 |
| 20:33:23.24 | 41:13:41.9 | B1 V | MT91 | 66 | 515 | – | 6.77 | 4.01 | 4.39 | 10.6 | >10 |
| 20:31:33.38 | 41:22:49.0 | B1 V + B2 V | K07,K12a | – | 103 | – | 6.37 | 4.04 | 4.39 | 10.7 | >10 |
| 20:32:14.56 | 41:22:33.7 | B1 V | K07 | – | 220 | – | 5.38 | 3.61 | 4.39 | 9.1 | 0.61 |
| 20:32:21.35 | 41:18:35.5 | B1 V | K07 | – | 238 | – | 5.71 | 3.45 | 4.39 | 8.7 | 0 |
| 20:32:50.69 | 41:15:02.2 | B1 V | K07 | – | 343 | – | 6.55 | 4.00 | 4.39 | 10.6 | >10 |
| 20:32:56.66 | 41:23:41.0 | B1 V | K07 | – | 365 | – | 4.81 | 3.62 | 4.39 | 9.2 | 1.14 |
| 20:33:10.46 | 41:20:57.6 | B1 V | K07 | – | 428 | – | 6.00 | 3.95 | 4.39 | 10.4 | >10 |
| 20:33:19.16 | 41:17:44.9 | B1 V | K07 | – | 492 | – | 5.67 | 3.50 | 4.39 | 8.9 | 0 |
| 20:33:23.37 | 41:20:17.2 | B1 V | K07 | – | 517 | – | 5.24 | 3.79 | 4.39 | 9.8 | 9.10 |
| 20:33:42.57 | 41:14:56.9 | B1 V | K07 | – | 621 | – | 6.46 | 3.79 | 4.39 | 9.8 | 9.02 |
| 20:34:04.43 | 41:08:08.4 | B1 V | K07 | – | 712 | – | 6.15 | 4.18 | 4.39 | 11.4 | >10 |
| 20:34:24.56 | 41:26:24.7 | B1 V | K07 | – | 759 | – | 5.85 | 3.68 | 4.39 | 9.4 | 3.52 |
| 20:30:39.70 | 41:08:48.0 | B0.7 Ib | H03 | – | – | A23 | 7.38 | 5.42 | 4.42 | 26.3 | 7.04 |
| 20:33:47.88 | 41:20:41.7 | B1 III | MT91 | 26 | 642 | – | 5.77 | 4.84 | 4.39 | 15.9 | >10 |
| 20:33:15.51 | 41:27:32.9 | B1 III | K07 | – | 469 | – | 5.13 | 3.81 | 4.39 | 9.8 | 9.88 |
| 20:33:46.85 | 41:08:01.9 | B1 III | K07 | – | 635 | – | 5.78 | 3.96 | 4.39 | 10.4 | >10 |
| 20:31:22.03 | 41:31:28.0 | B1 I | MT91 | 2 | 083 | – | 3.98 | 4.61 | 4.39 | 14.3 | >10 |
| 20:33:30.81 | 41:15:22.7 | B1 Ib | MT91 | 18 | 556 | – | 6.47 | 5.53 | 4.39 | 28.9 | 6.68 |
| 20:31:56.27 | 41:33:05.3 | B1.5 V | MT91 | – | 169 | – | 4.41 | 3.31 | 4.36 | 7.8 | 0 |
| 20:33:05.55 | 41:43:40.1 | B1.5 V | MT91 | – | 403 | – | 5.48 | 4.14 | 4.36 | 10.7 | >10 |
| 20:33:34.36 | 41:18:11.6 | B1.5 V | MT91 | – | 575 | – | 6.73 | 4.49 | 4.36 | 12.6 | >10 |
| 20:33:48.88 | 41:19:40.9 | B1.5 V | MT91 | 71 | 646 | – | 5.11 | 3.83 | 4.36 | 9.3 | >10 |
| 20:32:13.75 | 41:27:42.0 | B1.5 V | K07 | – | 216 | – | 4.28 | 3.61 | 4.36 | 8.7 | >10 |
| 20:34:43.51 | 41:29:04.8 | B1.5 III | MT91 | 30 | 793 | – | 5.73 | 4.52 | 4.36 | 12.7 | >10 |
| 20:32:26.50 | 41:19:13.7 | B1.5 III + B1 V | K07,K08 | – | 252 | – | 5.40 | 3.50 | 4.36 | 8.3 | 4.65 |
| 20:32:46.74 | 41:26:15.9 | B1.5 III | K07 | – | 325 | – | 4.98 | 3.39 | 4.36 | 8.0 | 0 |
| 20:33:18.55 | 41:15:35.4 | B2 Ve | K07 | 64 | 488 | – | 8.27 | 4.38 | 4.34 | 11.6 | >10 |
| 20:31:22.10 | 41:12:03.0 | B2 V | N08 | – | – | A30 | 6.27 | 4.06 | 4.34 | 10.0 | >10 |
| 20:32:27.30 | 40:55:18.0 | B2 V | H03 | – | – | A39 | 6.05 | 4.35 | 4.34 | 11.5 | >10 |
| 20:30:59.43 | 41:35:59.6 | B2 V | K07 | – | 042 | – | 4.58 | 3.35 | 4.34 | 7.7 | 0 |
| 20:31:30.49 | 41:37:15.6 | B2 V | K07 | – | 097 | – | 4.40 | 2.94 | 4.34 | 6.8 | 0 |
| 20:32:03.01 | 41:32:30.7 | B2 Ve | K07 | – | 186 | – | 4.53 | 3.19 | 4.34 | 7.3 | 0 |
| 20:32:07.95 | 41:22:00.3 | B2 V | K07 | – | 202 | – | 4.92 | 3.23 | 4.34 | 7.4 | 0 |
| 20:32:14.63 | 41:27:40.3 | B2 V | K07 | – | 221 | – | 4.67 | 3.43 | 4.34 | 8.0 | 5.15 |
| 20:32:19.66 | 41:20:39.7 | B2 V | K07 | – | 234 | – | 4.47 | 3.48 | 4.34 | 8.1 | 8.63 |
| 20:32:22.15 | 41:27:41.7 | B2 V | K07 | – | 241 | – | 4.18 | 3.32 | 4.34 | 7.7 | 0 |
| 20:32:25.50 | 41:24:51.8 | B2 V | K07 | – | 248 | – | 4.57 | 3.47 | 4.34 | 8.1 | 8.27 |
| 20:32:32.68 | 41:27:04.4 | B2 V | K07 | – | 275 | – | 3.92 | 3.17 | 4.34 | 7.3 | 0 |
| 20:32:37.78 | 41:26:15.3 | B2 V | K07 | – | 295 | – | 4.25 | 3.21 | 4.34 | 7.4 | 0 |
| 20:32:42.90 | 41:20:16.4 | B2 V + B3 V | K07,K12 | – | 311 | – | 4.95 | 3.29 | 4.34 | 7.6 | 0 |
| 20:33:22.49 | 41:22:16.9 | B2 V | K07 | – | 513 | – | 5.07 | 3.33 | 4.34 | 7.7 | 0 |
| 20:33:24.78 | 41:22:04.5 | B2 Ve | K07 | – | 522 | – | 4.90 | 3.34 | 4.34 | 7.7 | 0 |
| 20:33:31.68 | 41:21:46.1 | B2 V | K07 | – | 561 | – | 4.67 | 3.38 | 4.34 | 7.8 | 2.13 |
| 20:33:47.63 | 41:09:06.5 | B2 V | K07 | – | 639 | – | 5.94 | 3.60 | 4.34 | 8.4 | >10 |
| 20:33:48.83 | 41:37:39.7 | B2 Ve | K07 | – | 650 | – | 5.70 | 3.35 | 4.34 | 7.7 | 0 |
| 20:31:56.90 | 41:31:48.0 | B2 III | K12a | – | 174 | – | 4.39 | 3.75 | 4.34 | 8.8 | >10 |
| 20:32:26.10 | 41:29:39.0 | B2 III | K07 | – | 250 | – | 3.91 | 3.42 | 4.34 | 8.0 | 4.66 |
| 20:32:27.26 | 41:21:56.2 | B2 III | K07 | – | 255 | – | 5.06 | 3.15 | 4.34 | 7.2 | 0 |
| 20:32:30.72 | 41:07:04.1 | B2 III | K07 | – | 264 | – | 3.56 | 3.37 | 4.34 | 7.7 | 1.25 |
| 20:33:11.39 | 41:17:58.9 | B2 III | K07 | – | 441 | – | 5.18 | 3.31 | 4.34 | 7.6 | 0 |
| 20:33:48.40 | 41:13:14.1 | B2 III | K07 | – | 645 | – | 6.19 | 3.58 | 4.34 | 8.4 | >10 |
| 20:30:50.75 | 41:35:06.0 | B2 II | MT91 | – | 021 | – | 4.42 | 3.32 | 4.34 | 7.7 | 0 |
| 20:32:46.45 | 41:24:22.4 | B2.5 V | K07 | – | 322 | – | 4.85 | 2.96 | 4.29 | 6.1 | 0 |
| 20:32:31.42 | 41:30:51.4 | B2.5 V | K07 | – | 268 | – | 5.19 | 3.30 | 4.29 | 6.8 | >10 |
| 20:32:54.35 | 41:15:22.1 | B3 V | K07 | 37 | 358 | – | 6.55 | 3.52 | 4.25 | 7.0 | >10 |
| 20:31:33.59 | 41:36:04.3 | B3 V | K07 | – | 106 | – | 4.58 | 2.92 | 4.25 | 5.6 | >10 |
| 20:31:41.60 | 41:28:20.9 | B3 V | K07 | – | 129 | – | 4.72 | 3.06 | 4.25 | 5.9 | >10 |
| 20:31:55.28 | 41:35:27.8 | B3 V | K07 | – | 164 | – | 4.54 | 2.73 | 4.25 | 5.3 | 0 |
| 20:31:59.82 | 41:37:14.3 | B3 V | K07 | – | 179 | – | 5.02 | 3.33 | 4.25 | 6.4 | >10 |
| 20:32:06.85 | 41:17:56.8 | B3 V | K07 | – | 200 | – | 6.41 | 3.87 | 4.25 | 8.0 | >10 |
| 20:32:15.03 | 41:19:30.8 | B3 V | K07 | – | 222 | – | 5.02 | 3.00 | 4.25 | 5.8 | >10 |
| 20:32:38.34 | 41:28:56.6 | B3 V | K07 | – | 298 | – | 4.47 | 2.95 | 4.25 | 5.7 | >10 |
| 20:33:33.38 | 41:08:36.3 | B3 V | K07 | – | 568 | – | 6.71 | 3.63 | 4.25 | 7.3 | >10 |
| 20:31:34.12 | 41:31:08.0 | B3 IV | K07 | – | 108 | – | 4.53 | 2.64 | 4.25 | 5.1 | 0 |
| 20:32:04.74 | 41:28:44.5 | B3 IV | K07 | – | 191 | – | 3.83 | 2.94 | 4.25 | 5.6 | >10 |
| 20:32:49.67 | 41:25:36.4 | B3 III | K07 | – | 336 | – | 4.23 | 2.97 | 4.25 | 5.7 | >10 |
| 20:33:33.97 | 41:19:38.4 | B3 I | K07 | – | 573 | – | 5.25 | 3.58 | 4.25 | 7.1 | >10 |
| 20:32:40.88 | 41:14:29.3 | B3.5 Ia+ | MT91 | 12 | 304 | – | 10.18 | 6.09 | 4.14 | 110 | 3.0 |
| 20:32:21.76 | 41:34:24.6 | B4 V | K07 | – | 239 | – | 3.92 | 2.63 | 4.22 | 4.7 | 2.66 |
| 20:32:32.34 | 41:22:57.6 | B4 V | K07 | – | 271 | – | 5.14 | 3.02 | 4.22 | 5.4 | >10 |
| 20:33:10.27 | 41:23:44.9 | B4 III | K07 | – | 427 | – | Background | ||||
| 20:31:56.23 | 41:35:12.3 | B5 V | K07 | – | 170 | – | Background | ||||
| 20:32:32.54 | 41:26:46.7 | B5 V | K07 | – | 273 | – | 4.53 | 2.49 | 4.20 | 4.3 | 3.92 |
| 20:33:11.81 | 41:24:05.8 | B5 V | K07 | – | 444 | – | 5.25 | 3.22 | 4.20 | 5.7 | >10 |
| 20:33:13.37 | 41:26:39.7 | B5 V | K07 | – | 453 | – | 4.27 | 2.71 | 4.20 | 4.7 | >10 |
| 20:33:14.34 | 41:19:33.0 | B5 V | K07 | – | 459 | – | 6.65 | 3.45 | 4.20 | 6.2 | >10 |
| 20:33:47.58 | 41:29:57.7 | B5 V | K07 | – | 641 | – | 5.71 | 3.39 | 4.20 | 6.1 | >10 |
| 20:33:19.26 | 41:24:44.8 | B5 IV | K07 | – | 493 | – | 5.56 | 2.98 | 4.20 | 5.2 | >10 |
References: D13 – Dzib et al. (2013); C12 – Comerón & Pasquali (2012); D00 – Dougherty, Williams & Pollacco (2000); dB04 – De Becker, Rauw & Manfroid (2004); H03 – Hanson (2003); K07 – Kiminki et al. (2007); K08 – Kiminki et al. (2008); K09 – Kiminki et al. (2009); K12 – Kiminki et al. (2012); K12a – Kobulnicky et al. (2012); MT91 – Massey & Thompson (1991); N08 – Negueruela et al. (2008); NZ12 – Nazé et al. (2012); S96 – Smith, Shara & Moffat (1996); S10 – Stroud et al. (2010); vH88 – van der Veen & Habing (1988); W02 – Walborn (2002); B76 – Bohannan & Conti (1976); M09 – Muntean et al. (2009).
| RA . | Dec. . | Spectral . | Spectral . | Source number . | AV . | log L . | Teff . | M . | Age . | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (J2000.0) . | (J2000.0) . | type . | reference . | S58 . | MT91 . | C02 . | (mag) . | (L⊙) . | (K) . | (M⊙) . | (Myr) . |
| 20:32:03.10 | 41:15:19.9 | WC4 | vH88 | – | – | WR144 | – | 4.99 | 5.05 | >20 | 2–8 |
| 20:32:06.28 | 40:48:29.7 | WN7o/CE + O7 V((f)) | S96,M09 | – | – | WR145 | – | 5.57 | 4.70 | >25 | 2–7 |
| 20:35:47.09 | 41:22:44.7 | WC6 + O8 III | D00,D00 | – | – | WR146 | 7.83 | 5.06 | 4.90 | >25 | 2–4 |
| 20:33:08.78 | 41:13:18.1 | O3 If + O6 V | W02,W02 | 22 | 417 | – | 6.92 | 5.82 | 4.63 | 49.9 | 4.12 |
| 20:33:14.16 | 41:20:21.5 | O3 If | MT91 | 7 | 457 | – | 5.30 | 5.63 | 4.63 | 46.7 | 2.67 |
| 20:33:18.02 | 41:18:31.0 | O5 III | K07 | 8C | 483 | – | 4.85 | 5.57 | 4.61 | 41.6 | 3.34 |
| 20:33:10.74 | 41:15:08.0 | O5 I + O3.5 III | NZ12,NZ12 | 9 | 431 | – | 6.76 | 5.85 | 4.59 | 51.6 | 4.26 |
| 20:34:08.54 | 41:36:59.3 | O5 If + B0 V | K12a,K12a | 11 | 734 | – | 5.40 | 5.73 | 4.59 | 43.7 | 4.56 |
| 20:33:23.46 | 41:09:12.9 | O5.5 V | MT91 | – | 516 | – | 7.43 | 5.85 | 4.60 | 51.6 | 4.21 |
| 20:33:13.25 | 41:13:28.6 | O6 V | MT91 | – | 448 | – | 7.22 | 5.03 | 4.59 | 28.6 | 0.76 |
| 20:31:37.50 | 41:13:21.1 | O6 IV + O9 III | K08,K08 | 3 | – | – | 5.84 | 5.54 | 4.59 | 38.0 | 4.18 |
| 20:33:15.18 | 41:18:50.1 | O6 I + O5.5 III | dB04,dB04 | 8A | 465 | – | 4.84 | 5.70 | 4.57 | 41.1 | 5.00 |
| 20:33:14.84 | 41:18:41.4 | O6.5 III | MT91 | 8B | 462 | – | 5.12 | 5.48 | 4.57 | 35.2 | 4.56 |
| 20:34:44.10 | 40:51:58.0 | O6.5 III | N08 | – | – | A24 | 7.29 | 5.19 | 4.57 | 29.6 | 3.41 |
| 20:33:40.88 | 41:30:18.5 | O7 V | MT91 | – | 611 | – | 5.54 | 4.66 | 4.57 | 22.3 | 0 |
| 20:34:13.50 | 41:35:02.6 | O7 V | MT91 | 29 | 745 | – | 5.36 | 4.94 | 4.57 | 25.4 | 1.78 |
| 20:34:29.52 | 41:31:45.5 | O7 V + O9 V | K08,K08 | – | 771 | – | 6.93 | 5.18 | 4.57 | 29.0 | 3.50 |
| 20:31:59.61 | 41:14:50.4 | O7 V | C12 | – | – | E45 | 5.89 | 4.79 | 4.57 | 23.3 | 0.17 |
| 20:32:13.77 | 41:27:12.7 | O7 III | K07 | 4 | 217 | – | 4.39 | 5.20 | 4.56 | 28.6 | 4.14 |
| 20:32:22.43 | 41:18:19.0 | O7 I + O6 I + O9 V | B76,B76,D13 | 5 | – | – | 6.02 | 6.20 | 4.54 | 93.1 | 2.95 |
| 20:31:36.91 | 40:59:09.1 | O7 I | N08 | – | – | A15 | 8.26 | 5.42 | 4.54 | 31.8 | 5.25 |
| 20:30:27.30 | 41:13:25.0 | O7 I + O9 I | S10,S10 | – | – | B17 | 8.08 | 5.03 | 4.54 | 24.8 | 4.17 |
| 20:33:17.49 | 41:17:09.2 | O7.5 V | MT91 | 24 | 480 | – | 5.63 | 5.02 | 4.55 | 25.4 | 3.40 |
| 20:33:26.77 | 41:10:59.5 | O7.5 V | MT91 | – | 534 | – | 6.36 | 4.84 | 4.55 | 23.4 | 1.77 |
| 20:32:31.50 | 41:14:08.0 | O7.5 III | K12a | – | 267 | – | 8.03 | 5.51 | 4.56 | 34.7 | 5.17 |
| 20:31:10.57 | 41:31:53.0 | O8 V | K08 | 1 | 059 | – | 5.18 | 5.08 | 4.54 | 25.5 | 4.46 |
| 20:32:27.67 | 41:26:21.7 | O8 V | MT91 | 15 | 258 | – | 4.36 | 4.79 | 4.54 | 21.9 | 2.45 |
| 20:32:38.58 | 41:25:13.6 | O8 V | H03 | 16 | 299 | – | 4.40 | 4.92 | 4.54 | 23.4 | 3.65 |
| 20:32:45.45 | 41:25:37.3 | O8 V | MT91 | 6 | 317 | – | 4.54 | 5.04 | 4.54 | 24.8 | 4.28 |
| 20:32:59.17 | 41:24:25.7 | O8 V | MT91 | – | 376 | – | 4.90 | 4.69 | 4.54 | 20.9 | 1.04 |
| 20:33:02.94 | 41:17:43.3 | O8 V | MT91 | – | 390 | – | 6.63 | 4.93 | 4.54 | 23.5 | 3.70 |
| 20:33:13.67 | 41:13:05.7 | O8 V | MT91 | – | 455 | – | 6.13 | 4.75 | 4.54 | 21.4 | 1.89 |
| 20:33:18.08 | 41:21:36.6 | O8 V | MT91 | – | 485 | – | 5.32 | 4.79 | 4.54 | 21.8 | 2.40 |
| 20:33:30.43 | 41:35:57.5 | O8 V | MT91 | 74 | 555 | – | 6.45 | 5.04 | 4.54 | 24.9 | 4.31 |
| 20:32:34.80 | 40:56:17.0 | O8 V | N08 | – | – | A38 | 6.31 | 4.64 | 4.54 | 20.3 | 0.41 |
| 20:34:21.95 | 41:17:01.6 | O8 III + O8 III | K09,K09 | 73 | – | – | 6.27 | 4.62 | 4.53 | 19.6 | 1.36 |
| 20:33:02.90 | 40:47:25.0 | O8 II | H03 | – | – | A20 | 8.13 | 5.58 | 4.53 | 35.0 | 5.72 |
| 20:32:50.03 | 41:23:44.6 | O8.5 V | MT91 | 17 | 339 | – | 4.92 | 4.79 | 4.53 | 21.2 | 3.67 |
| 20:33:16.36 | 41:19:01.9 | O8.5 V | MT91 | 8D | 473 | – | 5.13 | 4.69 | 4.53 | 20.2 | 2.59 |
| 20:33:21.04 | 41:17:40.1 | O8.5 V | MT91 | – | 507 | – | 5.41 | 4.53 | 4.53 | 18.7 | 0.13 |
| 20:33:25.67 | 41:33:26.6 | O8.5 V | MT91 | 25 | 531 | – | 5.46 | 4.99 | 4.53 | 23.5 | 4.88 |
| 20:31:45.39 | 41:18:26.8 | O8.5 I | MT91 | – | 138 | – | 6.57 | 5.07 | 4.51 | 23.6 | 6.11 |
| 20:31:18.31 | 41:21:21.7 | O9 V + B6 V | K12a,K12a | – | 070 | – | 6.86 | 4.55 | 4.52 | 18.4 | 1.97 |
| 20:32:16.53 | 41:25:36.4 | O9 V | MT91 | 14 | 227 | – | 4.55 | 4.66 | 4.52 | 19.1 | 3.61 |
| 20:33:09.58 | 41:13:00.6 | O9 V + B9 V | K09,K09 | – | 421 | – | 6.77 | 4.26 | 4.52 | 16.3 | 0 |
| 20:34:04.95 | 41:05:13.2 | O9 V | MT91 | 41 | 716 | – | 6.12 | 4.45 | 4.52 | 17.5 | 0.26 |
| 20:34:09.52 | 41:34:13.4 | O9 V | MT91 | 75 | 736 | – | 5.43 | 4.50 | 4.52 | 18.0 | 1.07 |
| 20:33:09.41 | 41:12:58.2 | O9 V | K07 | – | 420 | – | 6.54 | 4.06 | 4.52 | 15.2 | 0 |
| 20:31:49.65 | 41:28:26.8 | O9 III | K09 | 20 | 145 | – | 4.12 | 4.42 | 4.50 | 16.8 | 1.46 |
| 20:33:46.15 | 41:33:00.5 | O9 I | K07 | 10 | 632 | – | 5.66 | 5.68 | 4.50 | 37.4 | 5.54 |
| 20:33:15.74 | 41:20:17.2 | O9.5 V | MT91 | 23 | 470 | – | 5.13 | 4.42 | 4.50 | 16.8 | 1.35 |
| 20:33:59.57 | 41:17:36.1 | O9.5 V + B0 V | MT91,K12 | 27 | 696 | – | 5.81 | 4.48 | 4.50 | 17.2 | 2.58 |
| 20:30:57.70 | 41:09:57.0 | O9.5 V | N08 | – | – | A26 | 6.69 | 4.69 | 4.50 | 18.7 | 5.31 |
| 20:34:16.05 | 41:02:19.6 | O9.5 V | C12 | – | – | E54 | 6.23 | 4.54 | 4.50 | 17.6 | 3.62 |
| 20:31:46.00 | 41:17:27.4 | O9.5 I | MT91 | – | 140 | – | 2.17 | 4.54 | 4.48 | 16.6 | 5.97 |
| 20:32:13.07 | 41:27:24.9 | B0 V | MT91 | – | 213 | – | 4.30 | 4.18 | 4.49 | 14.5 | 0 |
| 20:32:59.61 | 41:15:14.6 | B0 V | MT91 | 41 | 378 | – | 6.93 | 4.65 | 4.49 | 17.5 | 6.55 |
| 20:33:10.10 | 41:13:10.1 | B0 V | MT91 | 51 | 425 | – | 6.55 | 4.44 | 4.49 | 16.0 | 4.32 |
| 20:33:10.34 | 41:13:06.4 | B0 V | MT91 | – | 426 | – | Unresolved | ||||
| 20:33:10.50 | 41:22:22.8 | B0 V + B3 V | MT91,K12 | – | 429 | – | 5.45 | 3.99 | 4.49 | 13.5 | 0 |
| 20:33:37.02 | 41:16:11.4 | B0 V | MT91 | 70 | 588 | – | 5.85 | 4.69 | 4.49 | 17.9 | 6.80 |
| 20:33:59.32 | 41:05:38.4 | B0 V | MT91 | – | 692 | – | 5.74 | 4.14 | 4.49 | 14.2 | 0 |
| 20:30:51.12 | 41:20:21.6 | B0 V | K07 | – | 020 | – | 7.20 | 4.36 | 4.49 | 15.5 | 2.65 |
| 20:32:58.79 | 41:04:29.9 | B0 V + B2 V | K07,K09 | – | 372 | – | 6.98 | 3.85 | 4.49 | 12.9 | 0 |
| 20:33:11.02 | 41:10:31.9 | B0 V | K07 | – | 435 | – | 7.13 | 4.20 | 4.49 | 14.6 | 0 |
| 20:33:17.40 | 41:12:38.7 | B0 V | K07 | – | 477 | – | 6.49 | 4.12 | 4.49 | 14.1 | 0 |
| 20:33:18.56 | 41:24:49.3 | B0 V | K07 | – | 490 | – | 5.77 | 3.76 | 4.49 | 12.5 | 0 |
| 20:33:42.38 | 41:11:45.8 | B0 V | K07 | – | 620 | – | 6.24 | 4.24 | 4.49 | 14.7 | 0.19 |
| 20:32:39.51 | 40:52:47.5 | B0 V | C12 | – | – | E48 | 6.60 | 4.69 | 4.49 | 17.9 | 6.78 |
| 20:32:34.90 | 40:52:39.0 | B0.2 V | N08 | – | – | A33 | 6.80 | 4.42 | 4.47 | 15.1 | 6.62 |
| 20:33:21.14 | 41:35:52.0 | B0 III | K07 | – | 509 | – | 6.66 | 4.14 | 4.49 | 14.2 | 0 |
| 20:33:39.14 | 41:19:26.1 | B0 Iab | MT91 | 19 | 601 | – | 5.72 | 5.27 | 4.49 | 26.0 | 6.74 |
| 20:34:44.70 | 40:51:46.0 | B0 Ia | H03 | – | – | A27 | 7.58 | 5.63 | 4.49 | 35.2 | 5.94 |
| 20:34:58.70 | 41:36:17.0 | B0 Ib + B0 III | H03,K09 | – | – | A36 | 6.05 | 5.24 | 4.49 | 25.5 | 6.78 |
| 20:32:39.06 | 41:00:07.8 | B0 Ia | C12 | – | – | E47 | 6.53 | 5.83 | 4.49 | 42.3 | 4.79 |
| 20:33:38.22 | 40:53:41.2 | B0 Ib | C12 | – | – | E52 | 5.91 | 4.97 | 4.49 | 21.2 | 7.06 |
| 20:32:03.74 | 41:25:10.9 | B0.5 V | MT91 | – | 187 | – | 5.31 | 4.05 | 4.44 | 12.3 | 3.74 |
| 20:32:27.76 | 41:28:51.9 | B0.5 V | MT91 | 21 | 259 | – | 3.80 | 4.20 | 4.44 | 12.9 | 7.63 |
| 20:33:39.84 | 41:22:52.4 | B0.5 V + B2.5 V | K12,K12 | – | 605 | – | 4.66 | 4.10 | 4.44 | 12.5 | 5.39 |
| 20:34:06.10 | 41:08:09.6 | B0.5 V + B1.5 V | K12,K12 | – | 720 | – | 6.95 | 4.20 | 4.44 | 12.9 | 7.73 |
| 20:32:39.50 | 40:52:47.0 | B0.5 V | N08 | – | – | A31 | 7.20 | 4.63 | 4.44 | 15.7 | >10 |
| 20:33:06.62 | 41:21:13.3 | B0.5 V | K07 | – | 409 | – | 5.96 | 3.91 | 4.44 | 11.6 | 0 |
| 20:33:18.70 | 40:59:37.9 | B0.5 III | C12 | – | – | E51 | 6.63 | 4.54 | 4.44 | 14.9 | >10 |
| 20:32:13.53 | 41:27:30.0 | B1 V | MT91 | – | 215 | – | 4.05 | 3.58 | 4.39 | 9.2 | 0 |
| 20:32:37.03 | 41:23:05.1 | B1 V | MT91 | – | 292 | – | 5.31 | 4.09 | 4.39 | 10.9 | >10 |
| 20:32:38.87 | 41:25:20.8 | B1 V | K07 | – | 300 | – | 4.34 | 3.62 | 4.39 | 9.2 | 0.90 |
| 20:33:04.42 | 41:17:08.9 | B1 V | K07 | 54 | 395 | – | 5.96 | 3.90 | 4.39 | 10.2 | >10 |
| 20:33:05.22 | 41:17:51.6 | B1 V | K07 | – | 400 | – | 5.54 | 3.74 | 4.39 | 9.6 | 6.58 |
| 20:33:15.37 | 41:29:56.6 | B1 V | MT91 | – | 467 | – | 5.41 | 3.97 | 4.39 | 10.4 | >10 |
| 20:33:23.24 | 41:13:41.9 | B1 V | MT91 | 66 | 515 | – | 6.77 | 4.01 | 4.39 | 10.6 | >10 |
| 20:31:33.38 | 41:22:49.0 | B1 V + B2 V | K07,K12a | – | 103 | – | 6.37 | 4.04 | 4.39 | 10.7 | >10 |
| 20:32:14.56 | 41:22:33.7 | B1 V | K07 | – | 220 | – | 5.38 | 3.61 | 4.39 | 9.1 | 0.61 |
| 20:32:21.35 | 41:18:35.5 | B1 V | K07 | – | 238 | – | 5.71 | 3.45 | 4.39 | 8.7 | 0 |
| 20:32:50.69 | 41:15:02.2 | B1 V | K07 | – | 343 | – | 6.55 | 4.00 | 4.39 | 10.6 | >10 |
| 20:32:56.66 | 41:23:41.0 | B1 V | K07 | – | 365 | – | 4.81 | 3.62 | 4.39 | 9.2 | 1.14 |
| 20:33:10.46 | 41:20:57.6 | B1 V | K07 | – | 428 | – | 6.00 | 3.95 | 4.39 | 10.4 | >10 |
| 20:33:19.16 | 41:17:44.9 | B1 V | K07 | – | 492 | – | 5.67 | 3.50 | 4.39 | 8.9 | 0 |
| 20:33:23.37 | 41:20:17.2 | B1 V | K07 | – | 517 | – | 5.24 | 3.79 | 4.39 | 9.8 | 9.10 |
| 20:33:42.57 | 41:14:56.9 | B1 V | K07 | – | 621 | – | 6.46 | 3.79 | 4.39 | 9.8 | 9.02 |
| 20:34:04.43 | 41:08:08.4 | B1 V | K07 | – | 712 | – | 6.15 | 4.18 | 4.39 | 11.4 | >10 |
| 20:34:24.56 | 41:26:24.7 | B1 V | K07 | – | 759 | – | 5.85 | 3.68 | 4.39 | 9.4 | 3.52 |
| 20:30:39.70 | 41:08:48.0 | B0.7 Ib | H03 | – | – | A23 | 7.38 | 5.42 | 4.42 | 26.3 | 7.04 |
| 20:33:47.88 | 41:20:41.7 | B1 III | MT91 | 26 | 642 | – | 5.77 | 4.84 | 4.39 | 15.9 | >10 |
| 20:33:15.51 | 41:27:32.9 | B1 III | K07 | – | 469 | – | 5.13 | 3.81 | 4.39 | 9.8 | 9.88 |
| 20:33:46.85 | 41:08:01.9 | B1 III | K07 | – | 635 | – | 5.78 | 3.96 | 4.39 | 10.4 | >10 |
| 20:31:22.03 | 41:31:28.0 | B1 I | MT91 | 2 | 083 | – | 3.98 | 4.61 | 4.39 | 14.3 | >10 |
| 20:33:30.81 | 41:15:22.7 | B1 Ib | MT91 | 18 | 556 | – | 6.47 | 5.53 | 4.39 | 28.9 | 6.68 |
| 20:31:56.27 | 41:33:05.3 | B1.5 V | MT91 | – | 169 | – | 4.41 | 3.31 | 4.36 | 7.8 | 0 |
| 20:33:05.55 | 41:43:40.1 | B1.5 V | MT91 | – | 403 | – | 5.48 | 4.14 | 4.36 | 10.7 | >10 |
| 20:33:34.36 | 41:18:11.6 | B1.5 V | MT91 | – | 575 | – | 6.73 | 4.49 | 4.36 | 12.6 | >10 |
| 20:33:48.88 | 41:19:40.9 | B1.5 V | MT91 | 71 | 646 | – | 5.11 | 3.83 | 4.36 | 9.3 | >10 |
| 20:32:13.75 | 41:27:42.0 | B1.5 V | K07 | – | 216 | – | 4.28 | 3.61 | 4.36 | 8.7 | >10 |
| 20:34:43.51 | 41:29:04.8 | B1.5 III | MT91 | 30 | 793 | – | 5.73 | 4.52 | 4.36 | 12.7 | >10 |
| 20:32:26.50 | 41:19:13.7 | B1.5 III + B1 V | K07,K08 | – | 252 | – | 5.40 | 3.50 | 4.36 | 8.3 | 4.65 |
| 20:32:46.74 | 41:26:15.9 | B1.5 III | K07 | – | 325 | – | 4.98 | 3.39 | 4.36 | 8.0 | 0 |
| 20:33:18.55 | 41:15:35.4 | B2 Ve | K07 | 64 | 488 | – | 8.27 | 4.38 | 4.34 | 11.6 | >10 |
| 20:31:22.10 | 41:12:03.0 | B2 V | N08 | – | – | A30 | 6.27 | 4.06 | 4.34 | 10.0 | >10 |
| 20:32:27.30 | 40:55:18.0 | B2 V | H03 | – | – | A39 | 6.05 | 4.35 | 4.34 | 11.5 | >10 |
| 20:30:59.43 | 41:35:59.6 | B2 V | K07 | – | 042 | – | 4.58 | 3.35 | 4.34 | 7.7 | 0 |
| 20:31:30.49 | 41:37:15.6 | B2 V | K07 | – | 097 | – | 4.40 | 2.94 | 4.34 | 6.8 | 0 |
| 20:32:03.01 | 41:32:30.7 | B2 Ve | K07 | – | 186 | – | 4.53 | 3.19 | 4.34 | 7.3 | 0 |
| 20:32:07.95 | 41:22:00.3 | B2 V | K07 | – | 202 | – | 4.92 | 3.23 | 4.34 | 7.4 | 0 |
| 20:32:14.63 | 41:27:40.3 | B2 V | K07 | – | 221 | – | 4.67 | 3.43 | 4.34 | 8.0 | 5.15 |
| 20:32:19.66 | 41:20:39.7 | B2 V | K07 | – | 234 | – | 4.47 | 3.48 | 4.34 | 8.1 | 8.63 |
| 20:32:22.15 | 41:27:41.7 | B2 V | K07 | – | 241 | – | 4.18 | 3.32 | 4.34 | 7.7 | 0 |
| 20:32:25.50 | 41:24:51.8 | B2 V | K07 | – | 248 | – | 4.57 | 3.47 | 4.34 | 8.1 | 8.27 |
| 20:32:32.68 | 41:27:04.4 | B2 V | K07 | – | 275 | – | 3.92 | 3.17 | 4.34 | 7.3 | 0 |
| 20:32:37.78 | 41:26:15.3 | B2 V | K07 | – | 295 | – | 4.25 | 3.21 | 4.34 | 7.4 | 0 |
| 20:32:42.90 | 41:20:16.4 | B2 V + B3 V | K07,K12 | – | 311 | – | 4.95 | 3.29 | 4.34 | 7.6 | 0 |
| 20:33:22.49 | 41:22:16.9 | B2 V | K07 | – | 513 | – | 5.07 | 3.33 | 4.34 | 7.7 | 0 |
| 20:33:24.78 | 41:22:04.5 | B2 Ve | K07 | – | 522 | – | 4.90 | 3.34 | 4.34 | 7.7 | 0 |
| 20:33:31.68 | 41:21:46.1 | B2 V | K07 | – | 561 | – | 4.67 | 3.38 | 4.34 | 7.8 | 2.13 |
| 20:33:47.63 | 41:09:06.5 | B2 V | K07 | – | 639 | – | 5.94 | 3.60 | 4.34 | 8.4 | >10 |
| 20:33:48.83 | 41:37:39.7 | B2 Ve | K07 | – | 650 | – | 5.70 | 3.35 | 4.34 | 7.7 | 0 |
| 20:31:56.90 | 41:31:48.0 | B2 III | K12a | – | 174 | – | 4.39 | 3.75 | 4.34 | 8.8 | >10 |
| 20:32:26.10 | 41:29:39.0 | B2 III | K07 | – | 250 | – | 3.91 | 3.42 | 4.34 | 8.0 | 4.66 |
| 20:32:27.26 | 41:21:56.2 | B2 III | K07 | – | 255 | – | 5.06 | 3.15 | 4.34 | 7.2 | 0 |
| 20:32:30.72 | 41:07:04.1 | B2 III | K07 | – | 264 | – | 3.56 | 3.37 | 4.34 | 7.7 | 1.25 |
| 20:33:11.39 | 41:17:58.9 | B2 III | K07 | – | 441 | – | 5.18 | 3.31 | 4.34 | 7.6 | 0 |
| 20:33:48.40 | 41:13:14.1 | B2 III | K07 | – | 645 | – | 6.19 | 3.58 | 4.34 | 8.4 | >10 |
| 20:30:50.75 | 41:35:06.0 | B2 II | MT91 | – | 021 | – | 4.42 | 3.32 | 4.34 | 7.7 | 0 |
| 20:32:46.45 | 41:24:22.4 | B2.5 V | K07 | – | 322 | – | 4.85 | 2.96 | 4.29 | 6.1 | 0 |
| 20:32:31.42 | 41:30:51.4 | B2.5 V | K07 | – | 268 | – | 5.19 | 3.30 | 4.29 | 6.8 | >10 |
| 20:32:54.35 | 41:15:22.1 | B3 V | K07 | 37 | 358 | – | 6.55 | 3.52 | 4.25 | 7.0 | >10 |
| 20:31:33.59 | 41:36:04.3 | B3 V | K07 | – | 106 | – | 4.58 | 2.92 | 4.25 | 5.6 | >10 |
| 20:31:41.60 | 41:28:20.9 | B3 V | K07 | – | 129 | – | 4.72 | 3.06 | 4.25 | 5.9 | >10 |
| 20:31:55.28 | 41:35:27.8 | B3 V | K07 | – | 164 | – | 4.54 | 2.73 | 4.25 | 5.3 | 0 |
| 20:31:59.82 | 41:37:14.3 | B3 V | K07 | – | 179 | – | 5.02 | 3.33 | 4.25 | 6.4 | >10 |
| 20:32:06.85 | 41:17:56.8 | B3 V | K07 | – | 200 | – | 6.41 | 3.87 | 4.25 | 8.0 | >10 |
| 20:32:15.03 | 41:19:30.8 | B3 V | K07 | – | 222 | – | 5.02 | 3.00 | 4.25 | 5.8 | >10 |
| 20:32:38.34 | 41:28:56.6 | B3 V | K07 | – | 298 | – | 4.47 | 2.95 | 4.25 | 5.7 | >10 |
| 20:33:33.38 | 41:08:36.3 | B3 V | K07 | – | 568 | – | 6.71 | 3.63 | 4.25 | 7.3 | >10 |
| 20:31:34.12 | 41:31:08.0 | B3 IV | K07 | – | 108 | – | 4.53 | 2.64 | 4.25 | 5.1 | 0 |
| 20:32:04.74 | 41:28:44.5 | B3 IV | K07 | – | 191 | – | 3.83 | 2.94 | 4.25 | 5.6 | >10 |
| 20:32:49.67 | 41:25:36.4 | B3 III | K07 | – | 336 | – | 4.23 | 2.97 | 4.25 | 5.7 | >10 |
| 20:33:33.97 | 41:19:38.4 | B3 I | K07 | – | 573 | – | 5.25 | 3.58 | 4.25 | 7.1 | >10 |
| 20:32:40.88 | 41:14:29.3 | B3.5 Ia+ | MT91 | 12 | 304 | – | 10.18 | 6.09 | 4.14 | 110 | 3.0 |
| 20:32:21.76 | 41:34:24.6 | B4 V | K07 | – | 239 | – | 3.92 | 2.63 | 4.22 | 4.7 | 2.66 |
| 20:32:32.34 | 41:22:57.6 | B4 V | K07 | – | 271 | – | 5.14 | 3.02 | 4.22 | 5.4 | >10 |
| 20:33:10.27 | 41:23:44.9 | B4 III | K07 | – | 427 | – | Background | ||||
| 20:31:56.23 | 41:35:12.3 | B5 V | K07 | – | 170 | – | Background | ||||
| 20:32:32.54 | 41:26:46.7 | B5 V | K07 | – | 273 | – | 4.53 | 2.49 | 4.20 | 4.3 | 3.92 |
| 20:33:11.81 | 41:24:05.8 | B5 V | K07 | – | 444 | – | 5.25 | 3.22 | 4.20 | 5.7 | >10 |
| 20:33:13.37 | 41:26:39.7 | B5 V | K07 | – | 453 | – | 4.27 | 2.71 | 4.20 | 4.7 | >10 |
| 20:33:14.34 | 41:19:33.0 | B5 V | K07 | – | 459 | – | 6.65 | 3.45 | 4.20 | 6.2 | >10 |
| 20:33:47.58 | 41:29:57.7 | B5 V | K07 | – | 641 | – | 5.71 | 3.39 | 4.20 | 6.1 | >10 |
| 20:33:19.26 | 41:24:44.8 | B5 IV | K07 | – | 493 | – | 5.56 | 2.98 | 4.20 | 5.2 | >10 |
| RA . | Dec. . | Spectral . | Spectral . | Source number . | AV . | log L . | Teff . | M . | Age . | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (J2000.0) . | (J2000.0) . | type . | reference . | S58 . | MT91 . | C02 . | (mag) . | (L⊙) . | (K) . | (M⊙) . | (Myr) . |
| 20:32:03.10 | 41:15:19.9 | WC4 | vH88 | – | – | WR144 | – | 4.99 | 5.05 | >20 | 2–8 |
| 20:32:06.28 | 40:48:29.7 | WN7o/CE + O7 V((f)) | S96,M09 | – | – | WR145 | – | 5.57 | 4.70 | >25 | 2–7 |
| 20:35:47.09 | 41:22:44.7 | WC6 + O8 III | D00,D00 | – | – | WR146 | 7.83 | 5.06 | 4.90 | >25 | 2–4 |
| 20:33:08.78 | 41:13:18.1 | O3 If + O6 V | W02,W02 | 22 | 417 | – | 6.92 | 5.82 | 4.63 | 49.9 | 4.12 |
| 20:33:14.16 | 41:20:21.5 | O3 If | MT91 | 7 | 457 | – | 5.30 | 5.63 | 4.63 | 46.7 | 2.67 |
| 20:33:18.02 | 41:18:31.0 | O5 III | K07 | 8C | 483 | – | 4.85 | 5.57 | 4.61 | 41.6 | 3.34 |
| 20:33:10.74 | 41:15:08.0 | O5 I + O3.5 III | NZ12,NZ12 | 9 | 431 | – | 6.76 | 5.85 | 4.59 | 51.6 | 4.26 |
| 20:34:08.54 | 41:36:59.3 | O5 If + B0 V | K12a,K12a | 11 | 734 | – | 5.40 | 5.73 | 4.59 | 43.7 | 4.56 |
| 20:33:23.46 | 41:09:12.9 | O5.5 V | MT91 | – | 516 | – | 7.43 | 5.85 | 4.60 | 51.6 | 4.21 |
| 20:33:13.25 | 41:13:28.6 | O6 V | MT91 | – | 448 | – | 7.22 | 5.03 | 4.59 | 28.6 | 0.76 |
| 20:31:37.50 | 41:13:21.1 | O6 IV + O9 III | K08,K08 | 3 | – | – | 5.84 | 5.54 | 4.59 | 38.0 | 4.18 |
| 20:33:15.18 | 41:18:50.1 | O6 I + O5.5 III | dB04,dB04 | 8A | 465 | – | 4.84 | 5.70 | 4.57 | 41.1 | 5.00 |
| 20:33:14.84 | 41:18:41.4 | O6.5 III | MT91 | 8B | 462 | – | 5.12 | 5.48 | 4.57 | 35.2 | 4.56 |
| 20:34:44.10 | 40:51:58.0 | O6.5 III | N08 | – | – | A24 | 7.29 | 5.19 | 4.57 | 29.6 | 3.41 |
| 20:33:40.88 | 41:30:18.5 | O7 V | MT91 | – | 611 | – | 5.54 | 4.66 | 4.57 | 22.3 | 0 |
| 20:34:13.50 | 41:35:02.6 | O7 V | MT91 | 29 | 745 | – | 5.36 | 4.94 | 4.57 | 25.4 | 1.78 |
| 20:34:29.52 | 41:31:45.5 | O7 V + O9 V | K08,K08 | – | 771 | – | 6.93 | 5.18 | 4.57 | 29.0 | 3.50 |
| 20:31:59.61 | 41:14:50.4 | O7 V | C12 | – | – | E45 | 5.89 | 4.79 | 4.57 | 23.3 | 0.17 |
| 20:32:13.77 | 41:27:12.7 | O7 III | K07 | 4 | 217 | – | 4.39 | 5.20 | 4.56 | 28.6 | 4.14 |
| 20:32:22.43 | 41:18:19.0 | O7 I + O6 I + O9 V | B76,B76,D13 | 5 | – | – | 6.02 | 6.20 | 4.54 | 93.1 | 2.95 |
| 20:31:36.91 | 40:59:09.1 | O7 I | N08 | – | – | A15 | 8.26 | 5.42 | 4.54 | 31.8 | 5.25 |
| 20:30:27.30 | 41:13:25.0 | O7 I + O9 I | S10,S10 | – | – | B17 | 8.08 | 5.03 | 4.54 | 24.8 | 4.17 |
| 20:33:17.49 | 41:17:09.2 | O7.5 V | MT91 | 24 | 480 | – | 5.63 | 5.02 | 4.55 | 25.4 | 3.40 |
| 20:33:26.77 | 41:10:59.5 | O7.5 V | MT91 | – | 534 | – | 6.36 | 4.84 | 4.55 | 23.4 | 1.77 |
| 20:32:31.50 | 41:14:08.0 | O7.5 III | K12a | – | 267 | – | 8.03 | 5.51 | 4.56 | 34.7 | 5.17 |
| 20:31:10.57 | 41:31:53.0 | O8 V | K08 | 1 | 059 | – | 5.18 | 5.08 | 4.54 | 25.5 | 4.46 |
| 20:32:27.67 | 41:26:21.7 | O8 V | MT91 | 15 | 258 | – | 4.36 | 4.79 | 4.54 | 21.9 | 2.45 |
| 20:32:38.58 | 41:25:13.6 | O8 V | H03 | 16 | 299 | – | 4.40 | 4.92 | 4.54 | 23.4 | 3.65 |
| 20:32:45.45 | 41:25:37.3 | O8 V | MT91 | 6 | 317 | – | 4.54 | 5.04 | 4.54 | 24.8 | 4.28 |
| 20:32:59.17 | 41:24:25.7 | O8 V | MT91 | – | 376 | – | 4.90 | 4.69 | 4.54 | 20.9 | 1.04 |
| 20:33:02.94 | 41:17:43.3 | O8 V | MT91 | – | 390 | – | 6.63 | 4.93 | 4.54 | 23.5 | 3.70 |
| 20:33:13.67 | 41:13:05.7 | O8 V | MT91 | – | 455 | – | 6.13 | 4.75 | 4.54 | 21.4 | 1.89 |
| 20:33:18.08 | 41:21:36.6 | O8 V | MT91 | – | 485 | – | 5.32 | 4.79 | 4.54 | 21.8 | 2.40 |
| 20:33:30.43 | 41:35:57.5 | O8 V | MT91 | 74 | 555 | – | 6.45 | 5.04 | 4.54 | 24.9 | 4.31 |
| 20:32:34.80 | 40:56:17.0 | O8 V | N08 | – | – | A38 | 6.31 | 4.64 | 4.54 | 20.3 | 0.41 |
| 20:34:21.95 | 41:17:01.6 | O8 III + O8 III | K09,K09 | 73 | – | – | 6.27 | 4.62 | 4.53 | 19.6 | 1.36 |
| 20:33:02.90 | 40:47:25.0 | O8 II | H03 | – | – | A20 | 8.13 | 5.58 | 4.53 | 35.0 | 5.72 |
| 20:32:50.03 | 41:23:44.6 | O8.5 V | MT91 | 17 | 339 | – | 4.92 | 4.79 | 4.53 | 21.2 | 3.67 |
| 20:33:16.36 | 41:19:01.9 | O8.5 V | MT91 | 8D | 473 | – | 5.13 | 4.69 | 4.53 | 20.2 | 2.59 |
| 20:33:21.04 | 41:17:40.1 | O8.5 V | MT91 | – | 507 | – | 5.41 | 4.53 | 4.53 | 18.7 | 0.13 |
| 20:33:25.67 | 41:33:26.6 | O8.5 V | MT91 | 25 | 531 | – | 5.46 | 4.99 | 4.53 | 23.5 | 4.88 |
| 20:31:45.39 | 41:18:26.8 | O8.5 I | MT91 | – | 138 | – | 6.57 | 5.07 | 4.51 | 23.6 | 6.11 |
| 20:31:18.31 | 41:21:21.7 | O9 V + B6 V | K12a,K12a | – | 070 | – | 6.86 | 4.55 | 4.52 | 18.4 | 1.97 |
| 20:32:16.53 | 41:25:36.4 | O9 V | MT91 | 14 | 227 | – | 4.55 | 4.66 | 4.52 | 19.1 | 3.61 |
| 20:33:09.58 | 41:13:00.6 | O9 V + B9 V | K09,K09 | – | 421 | – | 6.77 | 4.26 | 4.52 | 16.3 | 0 |
| 20:34:04.95 | 41:05:13.2 | O9 V | MT91 | 41 | 716 | – | 6.12 | 4.45 | 4.52 | 17.5 | 0.26 |
| 20:34:09.52 | 41:34:13.4 | O9 V | MT91 | 75 | 736 | – | 5.43 | 4.50 | 4.52 | 18.0 | 1.07 |
| 20:33:09.41 | 41:12:58.2 | O9 V | K07 | – | 420 | – | 6.54 | 4.06 | 4.52 | 15.2 | 0 |
| 20:31:49.65 | 41:28:26.8 | O9 III | K09 | 20 | 145 | – | 4.12 | 4.42 | 4.50 | 16.8 | 1.46 |
| 20:33:46.15 | 41:33:00.5 | O9 I | K07 | 10 | 632 | – | 5.66 | 5.68 | 4.50 | 37.4 | 5.54 |
| 20:33:15.74 | 41:20:17.2 | O9.5 V | MT91 | 23 | 470 | – | 5.13 | 4.42 | 4.50 | 16.8 | 1.35 |
| 20:33:59.57 | 41:17:36.1 | O9.5 V + B0 V | MT91,K12 | 27 | 696 | – | 5.81 | 4.48 | 4.50 | 17.2 | 2.58 |
| 20:30:57.70 | 41:09:57.0 | O9.5 V | N08 | – | – | A26 | 6.69 | 4.69 | 4.50 | 18.7 | 5.31 |
| 20:34:16.05 | 41:02:19.6 | O9.5 V | C12 | – | – | E54 | 6.23 | 4.54 | 4.50 | 17.6 | 3.62 |
| 20:31:46.00 | 41:17:27.4 | O9.5 I | MT91 | – | 140 | – | 2.17 | 4.54 | 4.48 | 16.6 | 5.97 |
| 20:32:13.07 | 41:27:24.9 | B0 V | MT91 | – | 213 | – | 4.30 | 4.18 | 4.49 | 14.5 | 0 |
| 20:32:59.61 | 41:15:14.6 | B0 V | MT91 | 41 | 378 | – | 6.93 | 4.65 | 4.49 | 17.5 | 6.55 |
| 20:33:10.10 | 41:13:10.1 | B0 V | MT91 | 51 | 425 | – | 6.55 | 4.44 | 4.49 | 16.0 | 4.32 |
| 20:33:10.34 | 41:13:06.4 | B0 V | MT91 | – | 426 | – | Unresolved | ||||
| 20:33:10.50 | 41:22:22.8 | B0 V + B3 V | MT91,K12 | – | 429 | – | 5.45 | 3.99 | 4.49 | 13.5 | 0 |
| 20:33:37.02 | 41:16:11.4 | B0 V | MT91 | 70 | 588 | – | 5.85 | 4.69 | 4.49 | 17.9 | 6.80 |
| 20:33:59.32 | 41:05:38.4 | B0 V | MT91 | – | 692 | – | 5.74 | 4.14 | 4.49 | 14.2 | 0 |
| 20:30:51.12 | 41:20:21.6 | B0 V | K07 | – | 020 | – | 7.20 | 4.36 | 4.49 | 15.5 | 2.65 |
| 20:32:58.79 | 41:04:29.9 | B0 V + B2 V | K07,K09 | – | 372 | – | 6.98 | 3.85 | 4.49 | 12.9 | 0 |
| 20:33:11.02 | 41:10:31.9 | B0 V | K07 | – | 435 | – | 7.13 | 4.20 | 4.49 | 14.6 | 0 |
| 20:33:17.40 | 41:12:38.7 | B0 V | K07 | – | 477 | – | 6.49 | 4.12 | 4.49 | 14.1 | 0 |
| 20:33:18.56 | 41:24:49.3 | B0 V | K07 | – | 490 | – | 5.77 | 3.76 | 4.49 | 12.5 | 0 |
| 20:33:42.38 | 41:11:45.8 | B0 V | K07 | – | 620 | – | 6.24 | 4.24 | 4.49 | 14.7 | 0.19 |
| 20:32:39.51 | 40:52:47.5 | B0 V | C12 | – | – | E48 | 6.60 | 4.69 | 4.49 | 17.9 | 6.78 |
| 20:32:34.90 | 40:52:39.0 | B0.2 V | N08 | – | – | A33 | 6.80 | 4.42 | 4.47 | 15.1 | 6.62 |
| 20:33:21.14 | 41:35:52.0 | B0 III | K07 | – | 509 | – | 6.66 | 4.14 | 4.49 | 14.2 | 0 |
| 20:33:39.14 | 41:19:26.1 | B0 Iab | MT91 | 19 | 601 | – | 5.72 | 5.27 | 4.49 | 26.0 | 6.74 |
| 20:34:44.70 | 40:51:46.0 | B0 Ia | H03 | – | – | A27 | 7.58 | 5.63 | 4.49 | 35.2 | 5.94 |
| 20:34:58.70 | 41:36:17.0 | B0 Ib + B0 III | H03,K09 | – | – | A36 | 6.05 | 5.24 | 4.49 | 25.5 | 6.78 |
| 20:32:39.06 | 41:00:07.8 | B0 Ia | C12 | – | – | E47 | 6.53 | 5.83 | 4.49 | 42.3 | 4.79 |
| 20:33:38.22 | 40:53:41.2 | B0 Ib | C12 | – | – | E52 | 5.91 | 4.97 | 4.49 | 21.2 | 7.06 |
| 20:32:03.74 | 41:25:10.9 | B0.5 V | MT91 | – | 187 | – | 5.31 | 4.05 | 4.44 | 12.3 | 3.74 |
| 20:32:27.76 | 41:28:51.9 | B0.5 V | MT91 | 21 | 259 | – | 3.80 | 4.20 | 4.44 | 12.9 | 7.63 |
| 20:33:39.84 | 41:22:52.4 | B0.5 V + B2.5 V | K12,K12 | – | 605 | – | 4.66 | 4.10 | 4.44 | 12.5 | 5.39 |
| 20:34:06.10 | 41:08:09.6 | B0.5 V + B1.5 V | K12,K12 | – | 720 | – | 6.95 | 4.20 | 4.44 | 12.9 | 7.73 |
| 20:32:39.50 | 40:52:47.0 | B0.5 V | N08 | – | – | A31 | 7.20 | 4.63 | 4.44 | 15.7 | >10 |
| 20:33:06.62 | 41:21:13.3 | B0.5 V | K07 | – | 409 | – | 5.96 | 3.91 | 4.44 | 11.6 | 0 |
| 20:33:18.70 | 40:59:37.9 | B0.5 III | C12 | – | – | E51 | 6.63 | 4.54 | 4.44 | 14.9 | >10 |
| 20:32:13.53 | 41:27:30.0 | B1 V | MT91 | – | 215 | – | 4.05 | 3.58 | 4.39 | 9.2 | 0 |
| 20:32:37.03 | 41:23:05.1 | B1 V | MT91 | – | 292 | – | 5.31 | 4.09 | 4.39 | 10.9 | >10 |
| 20:32:38.87 | 41:25:20.8 | B1 V | K07 | – | 300 | – | 4.34 | 3.62 | 4.39 | 9.2 | 0.90 |
| 20:33:04.42 | 41:17:08.9 | B1 V | K07 | 54 | 395 | – | 5.96 | 3.90 | 4.39 | 10.2 | >10 |
| 20:33:05.22 | 41:17:51.6 | B1 V | K07 | – | 400 | – | 5.54 | 3.74 | 4.39 | 9.6 | 6.58 |
| 20:33:15.37 | 41:29:56.6 | B1 V | MT91 | – | 467 | – | 5.41 | 3.97 | 4.39 | 10.4 | >10 |
| 20:33:23.24 | 41:13:41.9 | B1 V | MT91 | 66 | 515 | – | 6.77 | 4.01 | 4.39 | 10.6 | >10 |
| 20:31:33.38 | 41:22:49.0 | B1 V + B2 V | K07,K12a | – | 103 | – | 6.37 | 4.04 | 4.39 | 10.7 | >10 |
| 20:32:14.56 | 41:22:33.7 | B1 V | K07 | – | 220 | – | 5.38 | 3.61 | 4.39 | 9.1 | 0.61 |
| 20:32:21.35 | 41:18:35.5 | B1 V | K07 | – | 238 | – | 5.71 | 3.45 | 4.39 | 8.7 | 0 |
| 20:32:50.69 | 41:15:02.2 | B1 V | K07 | – | 343 | – | 6.55 | 4.00 | 4.39 | 10.6 | >10 |
| 20:32:56.66 | 41:23:41.0 | B1 V | K07 | – | 365 | – | 4.81 | 3.62 | 4.39 | 9.2 | 1.14 |
| 20:33:10.46 | 41:20:57.6 | B1 V | K07 | – | 428 | – | 6.00 | 3.95 | 4.39 | 10.4 | >10 |
| 20:33:19.16 | 41:17:44.9 | B1 V | K07 | – | 492 | – | 5.67 | 3.50 | 4.39 | 8.9 | 0 |
| 20:33:23.37 | 41:20:17.2 | B1 V | K07 | – | 517 | – | 5.24 | 3.79 | 4.39 | 9.8 | 9.10 |
| 20:33:42.57 | 41:14:56.9 | B1 V | K07 | – | 621 | – | 6.46 | 3.79 | 4.39 | 9.8 | 9.02 |
| 20:34:04.43 | 41:08:08.4 | B1 V | K07 | – | 712 | – | 6.15 | 4.18 | 4.39 | 11.4 | >10 |
| 20:34:24.56 | 41:26:24.7 | B1 V | K07 | – | 759 | – | 5.85 | 3.68 | 4.39 | 9.4 | 3.52 |
| 20:30:39.70 | 41:08:48.0 | B0.7 Ib | H03 | – | – | A23 | 7.38 | 5.42 | 4.42 | 26.3 | 7.04 |
| 20:33:47.88 | 41:20:41.7 | B1 III | MT91 | 26 | 642 | – | 5.77 | 4.84 | 4.39 | 15.9 | >10 |
| 20:33:15.51 | 41:27:32.9 | B1 III | K07 | – | 469 | – | 5.13 | 3.81 | 4.39 | 9.8 | 9.88 |
| 20:33:46.85 | 41:08:01.9 | B1 III | K07 | – | 635 | – | 5.78 | 3.96 | 4.39 | 10.4 | >10 |
| 20:31:22.03 | 41:31:28.0 | B1 I | MT91 | 2 | 083 | – | 3.98 | 4.61 | 4.39 | 14.3 | >10 |
| 20:33:30.81 | 41:15:22.7 | B1 Ib | MT91 | 18 | 556 | – | 6.47 | 5.53 | 4.39 | 28.9 | 6.68 |
| 20:31:56.27 | 41:33:05.3 | B1.5 V | MT91 | – | 169 | – | 4.41 | 3.31 | 4.36 | 7.8 | 0 |
| 20:33:05.55 | 41:43:40.1 | B1.5 V | MT91 | – | 403 | – | 5.48 | 4.14 | 4.36 | 10.7 | >10 |
| 20:33:34.36 | 41:18:11.6 | B1.5 V | MT91 | – | 575 | – | 6.73 | 4.49 | 4.36 | 12.6 | >10 |
| 20:33:48.88 | 41:19:40.9 | B1.5 V | MT91 | 71 | 646 | – | 5.11 | 3.83 | 4.36 | 9.3 | >10 |
| 20:32:13.75 | 41:27:42.0 | B1.5 V | K07 | – | 216 | – | 4.28 | 3.61 | 4.36 | 8.7 | >10 |
| 20:34:43.51 | 41:29:04.8 | B1.5 III | MT91 | 30 | 793 | – | 5.73 | 4.52 | 4.36 | 12.7 | >10 |
| 20:32:26.50 | 41:19:13.7 | B1.5 III + B1 V | K07,K08 | – | 252 | – | 5.40 | 3.50 | 4.36 | 8.3 | 4.65 |
| 20:32:46.74 | 41:26:15.9 | B1.5 III | K07 | – | 325 | – | 4.98 | 3.39 | 4.36 | 8.0 | 0 |
| 20:33:18.55 | 41:15:35.4 | B2 Ve | K07 | 64 | 488 | – | 8.27 | 4.38 | 4.34 | 11.6 | >10 |
| 20:31:22.10 | 41:12:03.0 | B2 V | N08 | – | – | A30 | 6.27 | 4.06 | 4.34 | 10.0 | >10 |
| 20:32:27.30 | 40:55:18.0 | B2 V | H03 | – | – | A39 | 6.05 | 4.35 | 4.34 | 11.5 | >10 |
| 20:30:59.43 | 41:35:59.6 | B2 V | K07 | – | 042 | – | 4.58 | 3.35 | 4.34 | 7.7 | 0 |
| 20:31:30.49 | 41:37:15.6 | B2 V | K07 | – | 097 | – | 4.40 | 2.94 | 4.34 | 6.8 | 0 |
| 20:32:03.01 | 41:32:30.7 | B2 Ve | K07 | – | 186 | – | 4.53 | 3.19 | 4.34 | 7.3 | 0 |
| 20:32:07.95 | 41:22:00.3 | B2 V | K07 | – | 202 | – | 4.92 | 3.23 | 4.34 | 7.4 | 0 |
| 20:32:14.63 | 41:27:40.3 | B2 V | K07 | – | 221 | – | 4.67 | 3.43 | 4.34 | 8.0 | 5.15 |
| 20:32:19.66 | 41:20:39.7 | B2 V | K07 | – | 234 | – | 4.47 | 3.48 | 4.34 | 8.1 | 8.63 |
| 20:32:22.15 | 41:27:41.7 | B2 V | K07 | – | 241 | – | 4.18 | 3.32 | 4.34 | 7.7 | 0 |
| 20:32:25.50 | 41:24:51.8 | B2 V | K07 | – | 248 | – | 4.57 | 3.47 | 4.34 | 8.1 | 8.27 |
| 20:32:32.68 | 41:27:04.4 | B2 V | K07 | – | 275 | – | 3.92 | 3.17 | 4.34 | 7.3 | 0 |
| 20:32:37.78 | 41:26:15.3 | B2 V | K07 | – | 295 | – | 4.25 | 3.21 | 4.34 | 7.4 | 0 |
| 20:32:42.90 | 41:20:16.4 | B2 V + B3 V | K07,K12 | – | 311 | – | 4.95 | 3.29 | 4.34 | 7.6 | 0 |
| 20:33:22.49 | 41:22:16.9 | B2 V | K07 | – | 513 | – | 5.07 | 3.33 | 4.34 | 7.7 | 0 |
| 20:33:24.78 | 41:22:04.5 | B2 Ve | K07 | – | 522 | – | 4.90 | 3.34 | 4.34 | 7.7 | 0 |
| 20:33:31.68 | 41:21:46.1 | B2 V | K07 | – | 561 | – | 4.67 | 3.38 | 4.34 | 7.8 | 2.13 |
| 20:33:47.63 | 41:09:06.5 | B2 V | K07 | – | 639 | – | 5.94 | 3.60 | 4.34 | 8.4 | >10 |
| 20:33:48.83 | 41:37:39.7 | B2 Ve | K07 | – | 650 | – | 5.70 | 3.35 | 4.34 | 7.7 | 0 |
| 20:31:56.90 | 41:31:48.0 | B2 III | K12a | – | 174 | – | 4.39 | 3.75 | 4.34 | 8.8 | >10 |
| 20:32:26.10 | 41:29:39.0 | B2 III | K07 | – | 250 | – | 3.91 | 3.42 | 4.34 | 8.0 | 4.66 |
| 20:32:27.26 | 41:21:56.2 | B2 III | K07 | – | 255 | – | 5.06 | 3.15 | 4.34 | 7.2 | 0 |
| 20:32:30.72 | 41:07:04.1 | B2 III | K07 | – | 264 | – | 3.56 | 3.37 | 4.34 | 7.7 | 1.25 |
| 20:33:11.39 | 41:17:58.9 | B2 III | K07 | – | 441 | – | 5.18 | 3.31 | 4.34 | 7.6 | 0 |
| 20:33:48.40 | 41:13:14.1 | B2 III | K07 | – | 645 | – | 6.19 | 3.58 | 4.34 | 8.4 | >10 |
| 20:30:50.75 | 41:35:06.0 | B2 II | MT91 | – | 021 | – | 4.42 | 3.32 | 4.34 | 7.7 | 0 |
| 20:32:46.45 | 41:24:22.4 | B2.5 V | K07 | – | 322 | – | 4.85 | 2.96 | 4.29 | 6.1 | 0 |
| 20:32:31.42 | 41:30:51.4 | B2.5 V | K07 | – | 268 | – | 5.19 | 3.30 | 4.29 | 6.8 | >10 |
| 20:32:54.35 | 41:15:22.1 | B3 V | K07 | 37 | 358 | – | 6.55 | 3.52 | 4.25 | 7.0 | >10 |
| 20:31:33.59 | 41:36:04.3 | B3 V | K07 | – | 106 | – | 4.58 | 2.92 | 4.25 | 5.6 | >10 |
| 20:31:41.60 | 41:28:20.9 | B3 V | K07 | – | 129 | – | 4.72 | 3.06 | 4.25 | 5.9 | >10 |
| 20:31:55.28 | 41:35:27.8 | B3 V | K07 | – | 164 | – | 4.54 | 2.73 | 4.25 | 5.3 | 0 |
| 20:31:59.82 | 41:37:14.3 | B3 V | K07 | – | 179 | – | 5.02 | 3.33 | 4.25 | 6.4 | >10 |
| 20:32:06.85 | 41:17:56.8 | B3 V | K07 | – | 200 | – | 6.41 | 3.87 | 4.25 | 8.0 | >10 |
| 20:32:15.03 | 41:19:30.8 | B3 V | K07 | – | 222 | – | 5.02 | 3.00 | 4.25 | 5.8 | >10 |
| 20:32:38.34 | 41:28:56.6 | B3 V | K07 | – | 298 | – | 4.47 | 2.95 | 4.25 | 5.7 | >10 |
| 20:33:33.38 | 41:08:36.3 | B3 V | K07 | – | 568 | – | 6.71 | 3.63 | 4.25 | 7.3 | >10 |
| 20:31:34.12 | 41:31:08.0 | B3 IV | K07 | – | 108 | – | 4.53 | 2.64 | 4.25 | 5.1 | 0 |
| 20:32:04.74 | 41:28:44.5 | B3 IV | K07 | – | 191 | – | 3.83 | 2.94 | 4.25 | 5.6 | >10 |
| 20:32:49.67 | 41:25:36.4 | B3 III | K07 | – | 336 | – | 4.23 | 2.97 | 4.25 | 5.7 | >10 |
| 20:33:33.97 | 41:19:38.4 | B3 I | K07 | – | 573 | – | 5.25 | 3.58 | 4.25 | 7.1 | >10 |
| 20:32:40.88 | 41:14:29.3 | B3.5 Ia+ | MT91 | 12 | 304 | – | 10.18 | 6.09 | 4.14 | 110 | 3.0 |
| 20:32:21.76 | 41:34:24.6 | B4 V | K07 | – | 239 | – | 3.92 | 2.63 | 4.22 | 4.7 | 2.66 |
| 20:32:32.34 | 41:22:57.6 | B4 V | K07 | – | 271 | – | 5.14 | 3.02 | 4.22 | 5.4 | >10 |
| 20:33:10.27 | 41:23:44.9 | B4 III | K07 | – | 427 | – | Background | ||||
| 20:31:56.23 | 41:35:12.3 | B5 V | K07 | – | 170 | – | Background | ||||
| 20:32:32.54 | 41:26:46.7 | B5 V | K07 | – | 273 | – | 4.53 | 2.49 | 4.20 | 4.3 | 3.92 |
| 20:33:11.81 | 41:24:05.8 | B5 V | K07 | – | 444 | – | 5.25 | 3.22 | 4.20 | 5.7 | >10 |
| 20:33:13.37 | 41:26:39.7 | B5 V | K07 | – | 453 | – | 4.27 | 2.71 | 4.20 | 4.7 | >10 |
| 20:33:14.34 | 41:19:33.0 | B5 V | K07 | – | 459 | – | 6.65 | 3.45 | 4.20 | 6.2 | >10 |
| 20:33:47.58 | 41:29:57.7 | B5 V | K07 | – | 641 | – | 5.71 | 3.39 | 4.20 | 6.1 | >10 |
| 20:33:19.26 | 41:24:44.8 | B5 IV | K07 | – | 493 | – | 5.56 | 2.98 | 4.20 | 5.2 | >10 |
References: D13 – Dzib et al. (2013); C12 – Comerón & Pasquali (2012); D00 – Dougherty, Williams & Pollacco (2000); dB04 – De Becker, Rauw & Manfroid (2004); H03 – Hanson (2003); K07 – Kiminki et al. (2007); K08 – Kiminki et al. (2008); K09 – Kiminki et al. (2009); K12 – Kiminki et al. (2012); K12a – Kobulnicky et al. (2012); MT91 – Massey & Thompson (1991); N08 – Negueruela et al. (2008); NZ12 – Nazé et al. (2012); S96 – Smith, Shara & Moffat (1996); S10 – Stroud et al. (2010); vH88 – van der Veen & Habing (1988); W02 – Walborn (2002); B76 – Bohannan & Conti (1976); M09 – Muntean et al. (2009).



