-
PDF
- Split View
-
Views
-
Cite
Cite
Yu. A. Fadeyev, Evolutionary status of Polaris, Monthly Notices of the Royal Astronomical Society, Volume 449, Issue 1, 1 May 2015, Pages 1011–1017, https://doi.org/10.1093/mnras/stv412
Close - Share Icon Share
Abstract
Hydrodynamic models of short-period Cepheids were computed to determine the pulsation period as a function of evolutionary time during the first and third crossings of the instability strip. The equations of radiation hydrodynamics and turbulent convection for radial stellar pulsations were solved with the initial conditions obtained from the evolutionary models of Population I stars (X = 0.7, Z = 0.02) with masses from 5.2 to 6.5 M⊙ and the convective core overshooting parameter 0.1 ≤ αov ≤ 0.3. In Cepheids with period of 4 d the rate of pulsation period change during the first crossing of the instability strip is over 50 times larger than that during the third crossing. Polaris is shown to cross the instability strip for the first time and to be the fundamental mode pulsator. The best agreement between the predicted and observed rates of period change was obtained for the model with mass of 5.4 M⊙ and the overshooting parameter αov = 0.25. The bolometric luminosity and radius are L = 1.26 × 103 L⊙ and R = 37.5 R⊙, respectively. In the HR diagram, Polaris is located at the red edge of the instability strip.
1 INTRODUCTION
Polaris (α UMi) is a short-period (Π ≈ 3.969 d) small-amplitude Cepheid with steadily increasing pulsation period (Fernie 1966; Arellano Ferro 1983; Dinshaw et al. 1989). The rate of period change is estimated from |$\dot{\Pi }= 4.5\ \mathrm{s\ yr}^{-1}$| (Turner et al. 2005) to |$\dot{\Pi }= 4.9\ \mathrm{s\ yr}^{-1}$| (Spreckley & Stevens 2008). These values are over an order of magnitude larger than the rates of period change in most of the Cepheids with a period of Π ≈ 4 d. This lead Berdnikov et al. (1997) to the conclusion that Polaris is undergoing the first crossing of the instability strip after the main-sequence phase. Neilson et al. (2012) and Neilson (2014) however casted doubts on this assumption and argued that Polaris is evolving along the blue loop. They also showed that the observed rate of period change is more consistent with predictions from stellar evolution models provided that Polaris is currently loosing mass at a rate of |$\dot{M} \sim 10^{-6} \,\mathrm{M}_{\odot }\,\mathrm{yr}^{-1}$|.
Since about the middle twentieth century, Polaris showed decrease in photometric and radial velocity amplitudes (Arellano Ferro 1983; Fernie, Kamper & Seager 1993). Dinshaw et al. (1989) supposed that Polaris is approaching the red edge of the instability strip but in 1994–1997 the decrease in amplitude had stopped (Kamper & Fernie 1998). Recent photometric and radial velocity measurements reveal slow increase of the pulsation amplitude (Bruntt et al. 2008; Lee et al. 2008; Spreckley & Stevens 2008). The cause of the amplitude growth remains unknown. Fernie et al. (1993), Evans, Sasselov & Short (2002), and Turner et al. (2005) reported that Polaris lies well inside the instability strip.
Polaris is the nearest Cepheid and determination of its pulsation mode is of great importance in establishing the Cepheid period–luminosity relation. Feast & Catchpole (1997) showed that the Hipparcos trigonometrical parallax data are consistent with first overtone pulsation in Polaris. This conclusion was later confirmed by non-linear stellar pulsation models by Bono et al. (2001). However, recent measurements of photometric and spectroscopic parallaxes seem to be more consistent with fundamental mode pulsation (Turner et al. 2013).
The Hipparcos parallax of 7.54 ± 0.11 mas (van Leeuwen 2007) implies a distance to Polaris of d = 133 ± 2 pc but the spectroscopic and photometric parallaxes give the distance from d = 99 ± 2 pc (Turner et al. 2013) to d = 110 pc (Usenko & Klochkova 2008). Therefore the mean angular diameter of 3.28 mas measured with the Navy Prototype Optical Interferometer (Nordgren et al. 2000) corresponds to the linear radius of R = 47 R⊙ for the distance d = 133 pc and R = 35 R⊙ for d = 99 pc.
Polaris is the primary component of a close binary system with an orbital period of 29.6 yr. Evans et al. (2008) directly detected the secondary component using UV images (λ ∼ 2255 Å) obtained with the Hubble Space Telescope and found that Polaris has a mass in the range M = 3.1–6.7 M⊙. This is the first direct estimate of the Cepheid dynamical mass.
In this work, we aim to clarify some contradictions mentioned above. We calculate the rates of period change in Cepheids with periods near 4 d and determine the evolutionary status of Polaris by comparing the observed rate with theoretical predictions. To this end, we compute the non-linear stellar pulsation models as solution of the equations of radiation hydrodynamics and turbulent convection with initial conditions obtained from the evolutionary computations. Such an approach the author used earlier to obtain theoretical rates of pulsation period change in Large Magellanic Cloud and Galactic Cepheids (Fadeyev 2013, 2014). In comparison with previous works, both evolutionary and hydrodynamical computations of this study were carried out with improved input physics. As shown below, determination of the evolutionary status provides constraints on the pulsation mode and the fundamental parameters of Polaris.
2 METHODS OF COMPUTATION
2.1 Stellar evolution
This work is aimed at determining the pulsation period Π as a function of evolutionary time tev during the first and third crossings of the Cepheid instability strip. We computed the evolutionary tracks for non-rotating Population I stars with initial masses 5.2 M⊙ ≤ MZAMS ≤ 6.5 M⊙ evolving from the zero-age main sequence (ZAMS) until the end of core helium burning. Initial mass fractional abundances of hydrogen and heavy elements are X = 0.7 and Z = 0.02, respectively. The initial relative abundances of the elements heavier than helium normalized by Z were determined according to Asplund et al. (2009). Evolutionary computations were done with a code implementing the Henyey method (Fadeyev 2007, 2010). Below we comment some improvements used in this work.
Thermodynamic quantities are obtained by interpolation in the tables calculated with the library of programs FreeEOS (Irwin 2012). Rosseland opacities are computed from OPAL data (Iglesias & Rogers 1996) complemented at low temperatures by the opacities from Ferguson et al. (2005). The nuclear reaction rates are from the NACRE data base (Angulo et al. 1999) with updates for reactions 14N(p, γ)15O, 4He(αα, γ)12C, and 12C(α, γ)16O that were taken from the REACLIB data base (Rauscher et al. 2010).
In the evolutionary computations, convection is treated according to the mixing-length theory (Böhm-Vitense 1958) using a mixing-length parameter |$\alpha _\Lambda =1.6$|. Boundaries of convective zones are determined with the Schwarzschild criterion but the convective core is extended in radius by αovHP, where HP is the pressure scale height and αov is the dimensionless overshooting parameter ranging from 0.1 to 0.3.
To assure the gradual growth of the convective core during the core helium burning phase the evolutionary models were computed with ∼104 mass zones. The mass-loss rate |$\dot{M}$| during the main-sequence phase is from formulae by Vink, de Koter & Lamers (1999, 2000, 2001) and outside their domain |$\dot{M}$| is evaluated according to Nieuwenhuijzen & de Jager (1990). It should be noted that in our problem the role of mass-loss is insignificant. For example, the mass of the Cepheid MZAMS = 5.9 M⊙ during the first and third crossings of the instability strip is M = 5.89 and 5.84 M⊙, respectively.
Bearing in mind the importance of initial conditions for correct determination of the predicted rates of pulsation period change, we carried out additional evolutionary computations for stars with initial composition X = 0.72, Z = 0.014 and the overshooting parameter αov = 0.1. Results of these computations were compared with evolutionary models of non-rotating stars with initial masses 5 and 7 M⊙ (Ekström et al. 2012). The difference in luminosity and time-scales was found to be less than 5 per cent.
2.2 Non-linear stellar pulsation
In our study we consider the self-excited radial oscillations. The initial hydrodynamic model is computed by interpolating the zonal quantities of the evolutionary model and interpolation errors play the role of small initial perturbations. To diminish the amplitude of initial perturbations, we used fine zoning in mass in the outer layers of the evolutionary model so that as many as 3 × 103 outer mass zones had the relative radius r > 0.1R, where R is the radius of the star. All hydrodynamic models were computed for N = 500 mass zones. The mass intervals increase geometrically inwards with the ratio of q ≈ 1.03. The radius r1 and luminosity L1 at the innermost zone are assumed to be time-independent. The radius of the inner boundary satisfies the condition r1 ≤ 0.1R.
3 RATES OF PULSATION PERIOD CHANGE
Fig. 1 shows the pulsation growth rate η as a function of effective temperature Teff during the first and third crossings of the instability strip for hydrodynamic models of the evolutionary sequence MZAMS = 5.9 M⊙, αov = 0.1. The evolutionary time tev, stellar luminosity L, and stellar radius R at the edges of the instability strip are determined for η = 0 by linear interpolation between two adjacent hydrodynamic models with growth rates of opposite signs. The time spent in the instability strip is Δtev, 1 = 1.60 × 104 yr during the first crossing and Δtev, 3 = 4.26 × 105 yr during the third crossing. The ratio Δtev3/Δtev1 increases with mass and ranges from 25 to 30 for 5.6 M⊙ ≤ MZAMS ≤ 6.1 M⊙.
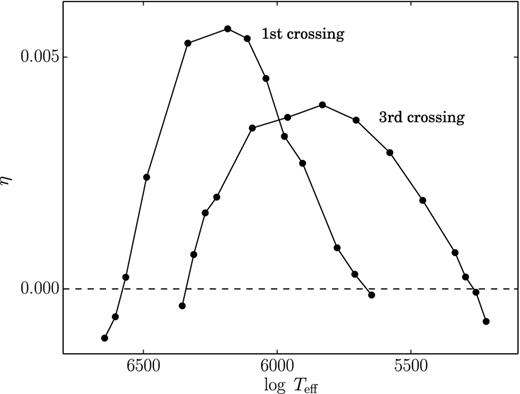
The pulsation growth rate η as a function of effective temperature Teff during the first and third crossings of the instability strip for the evolutionary sequence MZAMS = 5.9 M⊙, αov = 0.1. Hydrodynamic models are shown by filled circles.
Evolutionary tracks for stars with initial masses 5.6 and 5.9 M⊙ (αov = 0.1) are displayed in Fig. 2. The sections of the evolutionary tracks corresponding to pulsations with increasing period (the first and third crossings of the instability strip) are shown by dotted lines. Cepheids with decreasing periods are beyond the scope of the present study and therefore the second crossing of the instability strip is not indicated in the plots.
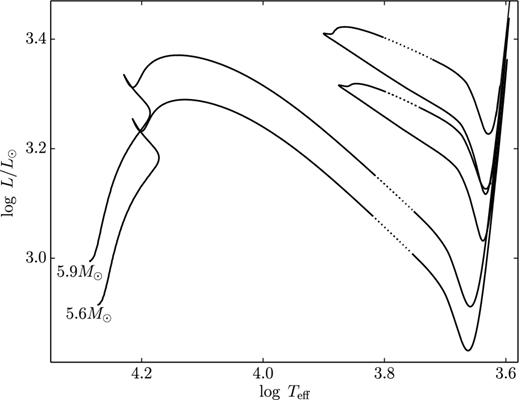
Evolutionary tracks of stars MZAMS = 5.6 and 5.9 M⊙ (αov = 0.1). The sections of tracks corresponding to the first and third crossings of the instability strip are indicated by dotted lines.
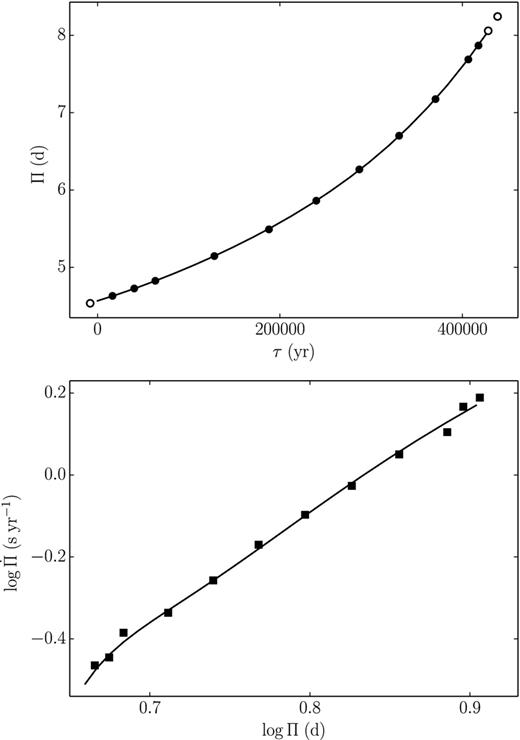
The upper panel of Fig. 3 shows the temporal dependence of the pulsation period Π during the first crossing of the instability strip for the evolutionary sequence MZAMS = 5.9 M⊙, αov = 0.1. For the sake of convenience we use τ = tev − tev, b as an independent variable, where tev, b is the evolutionary time at the blue edge of the instability strip. Periods of pulsationally stable and pulsationally unstable models are shown by open circles and filled circles, respectively.

The pulsation period Π as a function of evolutionary time τ (upper panel) and the rate of period change |$\dot{\Pi }$| as a function of period Π (lower panel) during the first crossing of the instability strip for the evolutionary sequence MZAMS = 5.9 M⊙, αov = 0.1. In the upper panel solid lines show the second-order polynomial fits, open circles and filled circles show the periods of pulsationally stable and pulsationally unstable models, respectively. Open triangles show the periods of the secondary mode near the mode switching. In the lower panel, solid lines show time derivatives of analytical fits. Solid squares represent the time derivatives obtained by numerical differentiation.
During the first crossing of the instability strip, the star begins to pulsate in the first overtone but as the star approaches the red edge it becomes the fundamental-mode pulsator. For hydrodynamic models near the pulsational mode switching, we evaluated the periods of the first overtone (1h) and fundamental mode (f) using the additional discrete Fourier transform of EK. The sampling interval was limited by the amplitude growth stage when the power spectrum reveals the presence of secondary modes with decaying amplitudes. Periods of such modes are shown in the upper panel of Fig. 3 by open triangles. The boundary between the first overtone and fundamental mode pulsators is defined as a middle point between two adjacent hydrodynamic models with different orders of the primary mode. For the first crossing of the instability strip, the second-order algebraic polynomials approximate the temporal dependence Π(τ) with an rms error less than 0.1 per cent. In the upper panel of Fig. 3, the analytical fits are shown by solid lines.
Time derivatives of analytical fits to Π(τ) are shown in the lower panel of Fig. 3 as a function of pulsation period Π. For the sake of convenience, the rate of pulsation period change |$\dot{\Pi }$| is expressed in units of seconds per year. Solid squares show estimates of |$\dot{\Pi }$| obtained by numerical differentiation. The small deviation of numerical derivatives from the analytical fits to |$\dot{\Pi }(\tau )$| is due to the limited accuracy of evolutionary calculations.
Fig. 4 displays the temporal dependence of Π (upper panel) and the plot of |$\dot{\Pi }$| as a function of Π (lower panel) for models of the evolutionary sequence MZAMS = 5.9 M⊙, αov = 0.1 during the third crossing of the instability strip. All hydrodynamic models were found to pulsate in the fundamental mode. The temporal dependence Π(τ) is fitted with the relative rms error less than 0.1 per cent by the fourth-order algebraic polynomial.
Same as Fig. 3, but for the third crossing of the instability strip. All hydrodynamic models show pulsations in the fundamental mode. The solid lines represent the fourth-order polynomial fitting (upper panel) and its time derivative (lower panel).
The results of polynomial fitting for hydrodynamic models with pulsation periods 2 d ≤ Π ≤ 8 d are displayed in Fig. 5 where the rates of period change |$\dot{\Pi }$| are plotted as a function of period Π for evolutionary sequences with initial masses 5.4 M⊙ ≤ MZAMS ≤ 5.9 M⊙ and the overshooting parameter αov = 0.1. Each curve in this diagram describes the evolution of values Π, |$\dot{\Pi }$| as the star crosses the instability strip. The solid and dashed lines represent the fundamental mode and first overtone, respectively. The plots located in the upper part of Fig. 5 represent the first crossing of the instability strip and the plots located in the lower part of the diagram correspond to the third crossing. As is clearly seen, for Cepheids with a period of Π ≈ 4 d the rate of period change during the first crossing of the instability strip |$\dot{\Pi }_1$| is over 50 times larger than the rate of period change during the third crossing |$\dot{\Pi }_3$|. It should be noted that large values of the ratio |$\dot{\Pi }_1/\dot{\Pi }_3$| are also typical for long-period Cepheids (Fadeyev 2014).
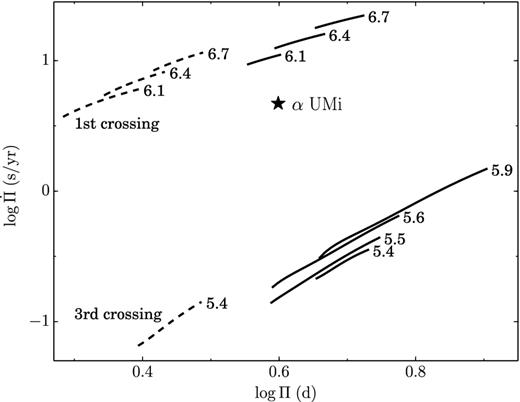
The rate of period change |$\dot{\Pi }$| as a function of pulsation period Π for evolutionary sequences with αov = 0.1 during the first and third crossings of the instability strip. The numbers at the curves indicate the initial stellar mass MZAMS in solar units. Solid and dashed lines correspond to the fundamental mode and first overtone, respectively.
The position of Polaris is marked in Fig. 5 for the period Π⋆ = 3.969 d and the rate of period change |$\dot{\Pi }_\star =4.7\,\mathrm{s\,yr}^{-1}$| which is the mean value of the observational estimates by Turner et al. (2005) and Spreckley & Stevens (2008). Even a cursory glance at Fig. 5 leads us to the following conclusions: (1) Polaris crosses the instability strip for the first time; (2) Polaris is the fundamental mode pulsator. Below we discuss in more detail both these conclusions.
The diagram in Fig. 5 was obtained for the evolutionary sequences computed with the overshooting parameter αov = 0.1 and the ratio of the predicted to observed rates of period change is |$\dot{\Pi }/\dot{\Pi }_\star \approx 2$|. However, the rate of period change during the first crossing of the instability strip depends on the assumed overshooting during the main-sequence evolutionary phase, so that agreement between theory and observations can be substantially improved. This is illustrated by Fig. 6 where the ratio |$\dot{\Pi }/\dot{\Pi }_\star$| is plotted as a function of initial mass MZAMS for several values of the overshooting parameter αov. The upper and lower error bars correspond to the observational estimates by Turner et al. (2005) and Spreckley & Stevens (2008), respectively. As seen from Fig. 6, the best agreement between the predicted and observed rates of period change (|$\dot{\Pi }/\dot{\Pi }_\star \approx 1.25$|) is obtained for the overshooting parameter αov = 0.25 and the initial stellar mass 5.4 M⊙ ≤ MZAMS ≤ 5.45 M⊙.
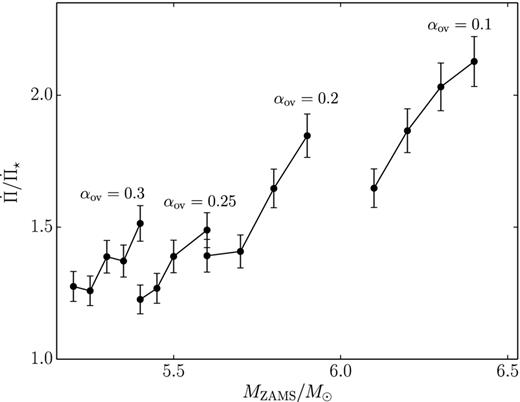
The ratio of the predicted to observed rates of period change |$\dot{\Pi }/\dot{\Pi }_\star$| as a function of initial stellar mass MZAMS for the overshooting parameters αov = 0.1, 0.2, 0.25, and 0.3.
4 FUNDAMENTAL PARAMETERS OF POLARIS
To determine the pulsation mode of first-crossing Cepheids with period of Π = 3.969 d, we considered the grid of evolutionary and hydrodynamic models with initial stellar masses 5.2 M⊙ ≤ MZAMS ≤ 6.5 M⊙ and the overshooting parameter ranging from 0.1 to 0.3. Typical results obtained for the overshooting parameter αov = 0.2 are shown in Fig. 7.
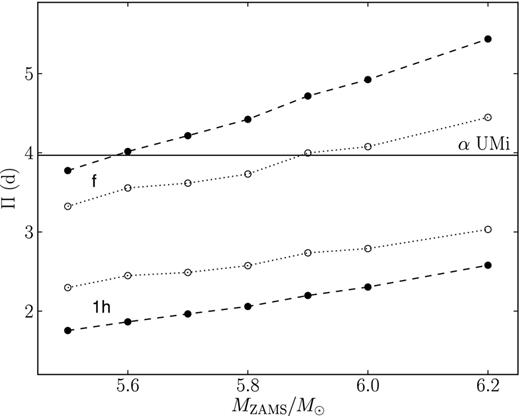
The pulsation period at the blue edge (lower dashed line) and red edge (upper dashed line) of the instability strip for models of first-crossing Cepheids computed with the overshooting parameter αov = 0.2. Lower and upper dotted lines show the periods of the first overtone and fundamental mode at the mode switch boundary. Filled and open circles represent the interpolated values of the period.
The filled circles connected by dashed lines in Fig. 7 show the pulsation period at the blue and red edges of the instability strip, whereas the open circles connected by dotted lines show the pulsation period at the mode switch. Thus, for a fixed value of MZAMS, the plots in Fig. 7 show the range of periods for pulsations in the first overtone and in the fundamental mode. The similar diagrams were obtained for other values of the overshooting parameter αov and no models pulsating in the first overtone with period of Π = 3.969 d were found. Therefore, Polaris is undoubtedly a fundamental-mode pulsator.
Intersection of the dashed and dotted lines with the solid horizontal line Π = 3.969 d in Fig. 7 gives the lower and upper values for the initial stellar mass MZAMS, respectively. The upper and lower values of the mass M, radius R, and luminosity L are evaluated by interpolation between the evolutionary tracks.
Fig. 8 shows the evolutionary tracks in the HR diagram for stars with initial masses 5.5 and 6.2 M⊙ (αov = 0.2). The dashed lines show the blue and red edges of the instability strip. The mode switch boundary shown by the dotted line is not the straight line due to difficulties in determining the exact location of the point of mode switch. Models with pulsation period Π⋆ = 3.969 d are shown by the star symbol.
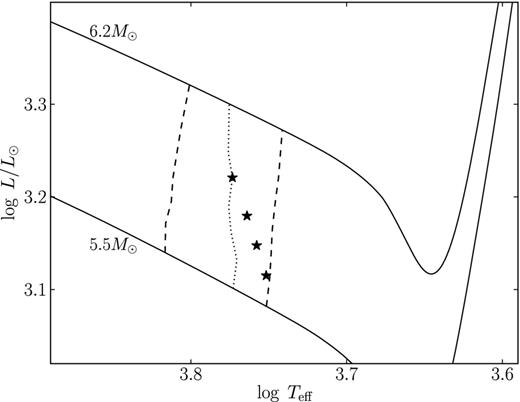
Evolutionary tracks of stars with initial masses 5.5 and 6.2 M⊙ (αov = 0.2) near the first crossing of the instability strip. Dashed lines show the blue and red edges of the instability strip. The dotted line shows the mode switch boundary. The star symbols show the location of models with the pulsation period Π⋆ = 3.969 d.
The lower and upper values of fundamental parameters for Polaris are given in Table 1. The last column gives the distance to Polaris d evaluated from the observed angular diameter θL = 3.28 mas (Nordgren et al. 2000).
| αov . | M/M⊙ . | L/L⊙ . | R/R⊙ . | Teff . | d . |
|---|---|---|---|---|---|
| . | . | . | . | (K) . | (pc) . |
| 0.1 | 6.38 | 1770 | 39.9 | 5930 | 113 |
| 6.08 | 1390 | 39.3 | 5630 | 111 | |
| 0.2 | 5.88 | 1660 | 38.7 | 5930 | 110 |
| 5.59 | 1300 | 37.8 | 5640 | 107 | |
| 0.25 | 5.59 | 1510 | 37.9 | 5850 | 107 |
| 5.39 | 1260 | 37.4 | 5640 | 106 | |
| 0.3 | 5.39 | 1450 | 37.5 | 5820 | 106 |
| 5.19 | 1220 | 36.7 | 5630 | 104 |
| αov . | M/M⊙ . | L/L⊙ . | R/R⊙ . | Teff . | d . |
|---|---|---|---|---|---|
| . | . | . | . | (K) . | (pc) . |
| 0.1 | 6.38 | 1770 | 39.9 | 5930 | 113 |
| 6.08 | 1390 | 39.3 | 5630 | 111 | |
| 0.2 | 5.88 | 1660 | 38.7 | 5930 | 110 |
| 5.59 | 1300 | 37.8 | 5640 | 107 | |
| 0.25 | 5.59 | 1510 | 37.9 | 5850 | 107 |
| 5.39 | 1260 | 37.4 | 5640 | 106 | |
| 0.3 | 5.39 | 1450 | 37.5 | 5820 | 106 |
| 5.19 | 1220 | 36.7 | 5630 | 104 |
| αov . | M/M⊙ . | L/L⊙ . | R/R⊙ . | Teff . | d . |
|---|---|---|---|---|---|
| . | . | . | . | (K) . | (pc) . |
| 0.1 | 6.38 | 1770 | 39.9 | 5930 | 113 |
| 6.08 | 1390 | 39.3 | 5630 | 111 | |
| 0.2 | 5.88 | 1660 | 38.7 | 5930 | 110 |
| 5.59 | 1300 | 37.8 | 5640 | 107 | |
| 0.25 | 5.59 | 1510 | 37.9 | 5850 | 107 |
| 5.39 | 1260 | 37.4 | 5640 | 106 | |
| 0.3 | 5.39 | 1450 | 37.5 | 5820 | 106 |
| 5.19 | 1220 | 36.7 | 5630 | 104 |
| αov . | M/M⊙ . | L/L⊙ . | R/R⊙ . | Teff . | d . |
|---|---|---|---|---|---|
| . | . | . | . | (K) . | (pc) . |
| 0.1 | 6.38 | 1770 | 39.9 | 5930 | 113 |
| 6.08 | 1390 | 39.3 | 5630 | 111 | |
| 0.2 | 5.88 | 1660 | 38.7 | 5930 | 110 |
| 5.59 | 1300 | 37.8 | 5640 | 107 | |
| 0.25 | 5.59 | 1510 | 37.9 | 5850 | 107 |
| 5.39 | 1260 | 37.4 | 5640 | 106 | |
| 0.3 | 5.39 | 1450 | 37.5 | 5820 | 106 |
| 5.19 | 1220 | 36.7 | 5630 | 104 |
5 CONCLUSIONS
The evolutionary and pulsational models together with the observed period Π⋆ allow us to obtain the lower and upper estimates of the initial mass of Polaris. As seen in Fig. 6, a major cause of uncertainty in the determination of mass is the overshooting parameter αov which is the unknown a priori quantity. The comparison of theoretical predictions with the observed rate of period increase leads to the narrower mass range 5.2 M⊙ ≤ MZAMS ≤ 5.7 M⊙ and to the constraint on the overshooting parameter αov ≥ 0.2. The best agreement with observations (|$\dot{\Pi }/\dot{\Pi }_\star \approx 1.25$|) was found for the model MZAMS = 5.4 M⊙, αov = 0.25 which locates near the red edge of the instability strip. The mass, M = 5.39 M⊙, is within the range 3.1 M⊙ ≤ M ≤ 6.7 M⊙ of the measured dynamical mass (Evans et al. 2008).
The mean linear radius R = 37.5 R⊙ for the overshooting parameter αov = 0.25 (see Table 1) and the observed angular diameter θL = 3.28 mas (Nordgren et al. 2000) lead to the distance of d = 106 pc. This value is consistent with photometric and spectroscopic parallaxes implying a distance from 99 pc (Turner et al. 2013) to 110 pc (Usenko & Klochkova 2008). To further improve theoretical predictions one has to take into account effects of initial chemical composition. For example, preliminary computations showed that the increase of the fractional mass abundance of hydrogen from X = 0.7 to 0.73 leads to decrease in |$\dot{\Pi }$| by ≈12 per cent.
The fact that Polaris is evolving on a Kelvin–Helmholtz time-scale after the main-sequence phase and is crossing the instability strip for the first time allows us to conclude that effects of mass-loss do not play a significant role in evolutionary changes of the pulsation period.
Decrease of the ratio |$\dot{\Pi }/\dot{\Pi }_\star$| with decreasing initial mass MZAMS at the fixed value of the overshooting parameter favours the closer location of Polaris to the red edge of the instability strip. This assumption does not necessarily contradict the growth of the pulsation amplitude observed for two last decades. Indeed, the balance between the κ-mechanism exciting pulsational instability and convection which suppresses oscillations can cyclically change due to variations of magnetic field on time-scale longer than the pulsation period. Therefore, the currently observed increase of the pulsation amplitude might be due to the growth of a magnetic field which tends to weaken convection (Stothers 2009). Longitudinal magnetic fields from 10 to 30 G were detected in Polaris by Borra, Fletcher & Poeckert (1981), whereas Usenko et al. (2010) reported on detection of variable magnetic field from −109 to 162 G.
This study is based on the convection model by Kuhfuß (1986) which contains several parameters of order unity. The most uncertain of them are γrad and αm in expressions for the radiative cooling time (equation 11) and kinetic turbulent viscosity (equation 14), respectively. The values of these parameters affect the damping of oscillations and are inferred from observational constraints (for example, the width of the instability strip). At the same time, the uncertainty in the values of γrad and αm does not play an important role in determining the pulsation period. This is due to the fact that the depth of the convective zone in Cepheids is only a few per cent of the stellar radius, whereas the length of the fundamental mode period is of the order of two sound travel times between the centre and the surface of the star.
The study was supported by the Basic Research Program P-21 of the Russian Academy of Sciences ‘Nonstationary phenomena in the Universe’.



