Boosting the accuracy of SPH techniques: Newtonian and special-relativistic tests

Rosswog, S.

doi:10.1093/mnras/stv225

Abstract

We study the impact of different discretization choices on the accuracy of smoothed particle hydrodynamics (SPH) and we explore them in a large number of Newtonian and special-relativistic benchmark tests. As a first improvement, we explore a gradient prescription that requires the (analytical) inversion of a small matrix. For a regular particle distribution, this improves gradient accuracies by approximately 10 orders of magnitude and the SPH formulations with this gradient outperform the standard approach in all benchmark tests. Secondly, we demonstrate that a simple change of the kernel function can substantially increase the accuracy of an SPH scheme. While the ‘standard’ cubic spline kernel generally performs poorly, the best overall performance is found for a high-order Wendland kernel which allows for only very little velocity noise and enforces a very regular particle distribution, even in highly dynamical tests. Thirdly, we explore new SPH volume elements that enhance the treatment of fluid instabilities and, last, but not least, we design new dissipation triggers. They switch on near shocks and in regions where the flow – without dissipation – starts to become noisy. The resulting new SPH formulation yields excellent results even in challenging tests where standard techniques fail completely.

hydrodynamics, instabilities, relativistic processes, shock waves, methods: numerical

1 INTRODUCTION

Smoothed particle hydrodynamics (SPH) is a completely mesh-free, fully conservative hydrodynamics method originally suggested by Lucy (1977) and Gingold & Monaghan (1977) in an astrophysical context. By now, SPH has spread far beyond its original scope and it has also found a multitude of applications in engineering. For detailed overviews over the various aspects of the method and its applications, the interested reader is referred to recent SPH reviews (Monaghan 2005; Rosswog 2009; Springel 2010a; Monaghan 2012; Price 2012; Rosswog 2014).

SPH has long been appreciated for a number of properties that are highly desirable in an astrophysical simulation. One of them is SPH's natural adaptivity that comes without the burden of additional infrastructure such as an adaptive mesh. SPH is not constrained by any prescribed geometry (as is usually the case in Eulerian approaches), the SPH particles simply follow the gas flow. SPH naturally has tendency to ‘refine on density’ and therefore vacuum is modelled with ease: it is simply devoid of SPH particles and no computational resources are wasted for modelling it. In Eulerian approaches, vacuum usually needs to be modelled as a low-density fluid and the interaction of the ‘real’ fluid with the background medium can introduce substantial artefacts such as spurious friction or shocks which need to be disentangled from the physical results.

The probably most salient advantage of SPH, however, is that the conservation of mass, energy, momentum and angular momentum can be ‘hardwired’ into discrete SPH formulations so that conservation is guaranteed independent of the numerical resolution. In practice, this conservation is only limited by, say, time integration accuracy or the accuracy with which gravitational forces are calculated. These issues, however, are fully controllable and can be adjusted to the desired accuracy. The exact conservation is usually enforced via symmetries in the SPH particle labels together with gradients that are antisymmetric with respect to the exchange of two particles. In SPH, this is usually ensured by the use of radial kernels, |$W(\boldsymbol {r})= W(|\boldsymbol {r}|)$|⁠, and the application of direct kernel gradients with the property |$\nabla _a W(|\boldsymbol {r}_a - \boldsymbol {r}_b|) = - \nabla _b W(|\boldsymbol {r}_a - \boldsymbol {r}_b|)$|⁠. See, for example, section 2.4 in Rosswog (2009) for detailed discussion of conservation in SPH. Below, we will also discuss an alternative gradient estimate that shares the same antisymmetry properties.

Another, highly desirable property is Galilean invariance. For an Eulerian approach, it is crucial to perform a simulation in the best possible reference frame. For example, a binary system modelled in a space-fixed frame may completely spuriously spiral in and merge while the same simulation performed in the frame of the binary system would have delivered the correct, stable orbital revolution (New & Tohline 1997). For further examples related with Galilean invariance, see Springel (2010b). Closely related is SPH's perfect advection property: a property assigned to an SPH particle, say a nuclear composition, is simply (and exactly) carried along as the particle moves. This is highly desirable in a number of contexts, for example, when fluid trajectories need to be post-processed with nuclear reaction networks.

But as every numerical method, SPH has also properties where improvements would be welcome and this is the topic of this paper. Most SPH codes use artificial viscosity to ensure the Rankine–Hugoniot relations in shocks. Often, artificial viscosity is considered a drawback, but a well-designed artificial dissipation scheme should perform similar to an approximate Riemann solver. The major challenge in this respect is to design switches that apply dissipation only where needed and not elsewhere. We discuss such switches in detail in Section 6.3. Another drawback of standard SPH approaches that has received much attention in recent years is that, depending on the numerical setup, at contact discontinuities spurious surface tension forces can emerge that can suppress subtle fluid instabilities (Agertz et al. 2007; Read, Hayfield & Agertz 2010; Springel 2010a). The reason for these surface tension forces is a mismatch in the smoothness of the internal energy and the density. This observation also provides strategies to cure the problem, either by smoothing the internal energies via artificial conductivity (Price 2008) or by reformulating SPH in terms of volume elements that differ from the usual choice m/ρ (Saitoh & Makino 2013; Hopkins 2013). Such approaches are discussed in detail and generalized to the special-relativistic case in Section 5.

SPH as derived from a Lagrangian has a built-in ‘re-meshing’ mechanism: while the particles follow the fluid flow, they try to arrange themselves into optimal relative positions that maximize the sum of the particle volumes. In other words, the SPH force is a sum of a regularization term and the approximation to the hydrodynamic force. For optimally distributed particles, the first term vanishes and the second one becomes identical to the Euler momentum equation. If the particles are, however, arranged in a non-optimal way, they start to move to improve the local distribution and this will appear as noise. Such motion is unavoidable, for example, in a multidimensional shock where the particles have to transition from the pre- to the post-shock lattice. While this re-meshing mechanism is highly desirable, the related motions should be very subtle. This can be achieved by using very smooth kernels and some dissipation in regions where such re-meshing occurs. Two improvements for this ‘noise issue’ are discussed below. One is related to the choice of the smoothing kernel, see Section 4, and the other one to a ‘noise trigger’ for artificial dissipation, see Section 6.3.

Last but not least, there is a drawback that is related to one of SPH's strengths, its refinement on density. If low-density regions are geometrically close to high-density regions and they are the major interest of the investigation, SPH is seriously challenged: even when huge particle numbers are invested, the low-density region will always be poorly resolved. For such problems, SPH may not be the right method and one may possibly obtain good results with substantially less effort by resorting to adaptive mesh refinement methods.

In this paper, we want to explore a number of technical improvements of SPH methods. Our main focus is multidimensional, special-relativistic hydrodynamics, but all discussed improvements can straight forwardly be applied also in purely Newtonian simulations. To demonstrate that the improvements also work in the Newtonian regime, we show a number of tests in this limit. Thereby, we address in particular tests where ‘standard’ SPH approaches yield very poor results. As we will demonstrate below, the suggested new SPH formulations yield excellent results also in these challenging tests. All the tests that are shown here – whether Newtonian or special-relativistic – have been performed with a new, special-relativistic SPH code called sphincs_sr.

The paper is organized as follows. In Section 3, we discuss a number of kernel interpolation techniques as a basis for the following sections. In Section 4, we discuss different kernel functions and assess their accuracy in estimating a constant density and the gradient of a linear function for the case that particles are arranged as a perfect lattice. We subsequently generalize the family of SPH volume elements that has recently been suggested by Hopkins (2013) and an integral-based gradient estimate (Garcia-Senz, Cabezon & Escartin 2012) to the special-relativistic case. These ingredients are combined into a number of different SPH formulations in Section 6 which are systematically explored in Section 7. By comparing the performance of the different SPH formulations, one can gauge how important a particular measure is for the considered benchmark test. Our large set of benchmark tests shows that the accuracy of SPH can be drastically improved with respect to commonly made choices (high, constant dissipation; standard volume element; kernel gradients and the M₄ kernel). Our results are finally summarized in Section 8.

2 TRANSLATION BETWEEN NEWTONIAN AND SPECIAL-RELATIVISTIC APPROACHES

The focus of this work is the improvement of SPH techniques, and we demonstrate them at Newtonian and – with future applications in mind – special-relativistic hydrodynamic examples. In the following, we mainly stay in the special-relativistic picture, but the notation can be straight forwardly translated to the Newtonian case.

Mass
We use here the (fixed) baryon number per SPH particle ν, this corresponds to (fixed) SPH particle mass m.
Density
In the relativistic treatment, we need to distinguish between densities measured in our computing frame (CF) (N) and those measured in the local fluid rest frame (n; they differ by a Lorentz factor, see equation 46). In the Newtonian limit (γ = 1), of course, both densities coincide. The prescription how to calculate N, equation (40), corresponds to the usual Newtonian density summation for ρ.
Velocity
The derivation from a relativistic Lagrangian suggests to use the canonical momentum per baryon, |$\boldsymbol {S}$|⁠, as momentum variable. This is beneficial, since the form of the equations becomes very similar to the Newtonian case and since it avoids numerical complications (such as time derivatives of Lorentz factors) which would otherwise appear (Laguna, Miller & Zurek 1993). Inspection of equation (54) (γ → 1, ν → m, inserting speed of light) shows that the corresponding Newtonian quantity is the velocity.
Energy
Again, the Lagrangian derivation suggests to use the canonical energy per baryon. The resulting energy equation looks very similar to the Newtonian equation for the thermokinetic energy, u + v²/2, see, for example, section 2.3.2 in Rosswog (2009). But the simplicity of the evolution, equations comes at the price of recovering the primitive variables by an iteration at every time step. This topic is discussed in Section 6.4.
Suggested improvements
The suggestions such as the gradient estimate, see Section 3, kernel choice, see Section 4, volume element, see Section 5, and dissipation triggers, see Section 6.3, then carry over straight forwardly. We have not performed extensive tests, though, to double check whether our parameters can be blindly applied in Newtonian formulations.

3 INTERPOLATION AND GRADIENTS

As a basis for the later SPH discretizations in Section 6, we briefly discuss here some basic properties of discrete kernel interpolations. For now, we keep the SPH volume element, V_b, unspecified, we discuss particular choices in Section 5. Nothing in this section is specific to the special-relativistic case. In the following, we use the convention that upper indices refer to spatial directions while lower indices refer to SPH particle identities. Usually, we will use ‘a’ for the particle of interest and ‘b’ for a neighbour particle. We will follow the convention of summing from 1 to the number of spatial dimensions D over spatial indices that appear twice. In some cases, though, we explicitly write out the summation for clarity.

3.1 SPH kernel interpolation

At the heart of SPH is the smooth representation of a quantity f known at discrete (‘particle’) positions |$\boldsymbol {r}_b$| by

\begin{equation} \langle f \rangle (\boldsymbol {r})= \sum _b V_b f_b W(|\boldsymbol {r}-\boldsymbol {r}_b|,h), \end{equation}

(1)

where W is a smoothing kernel whose width is set by the smoothing length h. Particular choices of the smoothing kernel are discussed in Section 4. To assess the accuracy of the approximation (1), one can Taylor-expand f_b around |$\boldsymbol {r}$|

\begin{equation} f_b\approx f(\boldsymbol {r})+ (\boldsymbol {r}_b - \boldsymbol {r}) \cdot \nabla f(\boldsymbol {r}) +\cdots \end{equation}

(2)

and insert it into equation (1)

\begin{eqnarray} \langle f \rangle (\boldsymbol {r}) &\simeq & f(\boldsymbol {r}) \sum _b V_b W(|\boldsymbol {r}-\boldsymbol {r}_b|,h)\nonumber\\ && +\; \nabla f \cdot \sum _b V_b (\boldsymbol {r}_b - \boldsymbol {r})W(|\boldsymbol {r}-\boldsymbol {r}_b|,h). \end{eqnarray}

(3)

Requiring that |$\langle f \rangle (\boldsymbol {r})$| be a close approximation to |$f(\boldsymbol {r})$| then provides us with the ‘quality indicators’ for the discrete kernel interpolation:

\begin{equation} \mathcal {Q}_{1}: \quad \sum _b V_b \; W(|\boldsymbol {r}-\boldsymbol {r}_b|,h) \simeq 1 \end{equation}

(4)

\begin{equation} \mathcal {Q}_{2}: \quad \sum _b V_b \; (\boldsymbol {r}_b - \boldsymbol {r}) \; W(|\boldsymbol {r}-\boldsymbol {r}_b|,h) \simeq 0, \end{equation}

(5)

which – for a good particle distribution – should be fulfilled to high accuracy. |$\mathcal {Q}_{1}$| simply states that the particles should provide a good partition of unity.

3.2 Standard SPH gradient

A standard SPH procedure is to take directly the gradient of the interpolant equation (1)

\begin{equation} \left(\nabla f \right)_{{\rm SPH}} (\boldsymbol {r})= \sum _b V_b f_b \nabla W(|\boldsymbol {r}-\boldsymbol {r}_b|,h). \end{equation}

(6)

Although this estimate is known to be of moderate accuracy only, it is advantageous because the involved kernel gradient has the desired antisymmetry property, |$\nabla _r W(|\boldsymbol {r}-\boldsymbol {r}_b|,h)= - \nabla _{r_b} W(|\boldsymbol {r}-\boldsymbol {r}_b|,h)$|⁠, which makes it easy to obtain a fully conservative set of SPH equations, see e.g. section 2.4 in Rosswog (2009) for an explicit discussion of numerical conservation in SPH. One can again proceed as above and insert a Taylor expansion into equation (6) to obtain

\begin{eqnarray} \langle \nabla f \rangle (\boldsymbol {r}) &=& \sum _b V_b \left\lbrace f(\boldsymbol {r}) + (\boldsymbol {r}_b - \boldsymbol {r}) \cdot \nabla f +\cdots \ \right\rbrace\nonumber\\ &&{\times}\;\nabla W(|\boldsymbol {r}-\boldsymbol {r}_b|,h). \end{eqnarray}

(7)

Requiring |$\langle \nabla f \rangle (\boldsymbol {r})$| be a close approximation to |$\nabla f (\boldsymbol {r})$| then delivers the quality indicators of this gradient estimate:

\begin{equation} \mathcal {Q}_{3}: \quad \sum _b V_b \nabla W(|\boldsymbol {r}-\boldsymbol {r}_b|,h)\simeq 0, \end{equation}

(8)

\begin{equation} \mathcal {Q}_{4}: \quad \sum _b V_b (\boldsymbol {r}_b - \boldsymbol {r})^i \nabla ^j W(|\boldsymbol {r}-\boldsymbol {r}_b|,h)\simeq \delta ^{ij}. \end{equation}

(9)

|$\mathcal {Q}_{3}$| is simply the gradient of |$\mathcal {Q}_{1}$| and therefore again an expression of the partition of unity requirement.

3.3 Constant-exact gradient

It is obvious that the gradient estimate equation (6) does not necessarily vanish for constant function values f_b = f₀, which is sometimes referred to as lack of zeroth-order consistency. The gradient only vanishes in the case when |$\mathcal {Q}_{3}$| is fulfilled exactly. This property, however, can be enforced by simply subtracting the leading error term, see equation (7),

\begin{equation} \left(\nabla f \right)_{{\rm CE}} (\boldsymbol {r})= \sum _b V_b (f_b - f(\boldsymbol {r})) \nabla W(|\boldsymbol {r}-\boldsymbol {r}_b|,h), \end{equation}

(10)

so that now a constant function is reproduced exactly. For a non-regular particle distribution, this substantially improves the gradient estimate, see Section 3.6, but it comes at the price that it does not have the desired antisymmetry and therefore makes it much harder to obtain exact conservation.

3.4 Linear-exact gradient

A linear-exact (LE) gradient estimate can be constructed (Price 2004) starting from equations (6) and (7) specified to particle position a

\begin{eqnarray} \sum _b V_b f_b \nabla _a W_{ab}= \sum _b V_b \left\lbrace f_a + (\boldsymbol {r}_b - \boldsymbol {r}_a) \cdot \nabla _a f +\cdots \ \right\rbrace \nabla _a W_{ab},\nonumber\\ \end{eqnarray}

(11)

which can be rearranged into

\begin{equation} \sum _b V_b (f_b-f_a) \nabla _a^k W_{ab}= \nabla _a^i f \sum _b V_b (\boldsymbol {r}_b - \boldsymbol {r}_a)^i \nabla _a^k W_{ab}. \end{equation}

(12)

By matrix inversion, one obtains a linearly exact gradient estimate

\begin{equation} \left(\nabla _a f\right)^i_{\rm LE}= M^{ik} J_f^k, \end{equation}

(13)

where

\begin{equation} M^{ik}= \left(\sum _b V_b (\boldsymbol {r}_b - \boldsymbol {r}_a)^i \nabla _a^k W_{ab}\right)^{-1} \end{equation}

(14)

and

\begin{equation} J_f^k= \sum _b V_b (f_b-f_a) \nabla _a^k W_{ab}. \end{equation}

(15)

M^ik contains information about the local particle distribution while |$J_f^k$| contains the function values at the neighbouring particles. Obviously, the calculation of M^ik requires the inversion of a D × D-matrix, but this can be done analytically and does not represent a major computational burden.

3.5 Integral-based gradient

More than five decades ago, it was realized that derivatives can also be estimated by actually performing an integration (Lanczos 1956). The resulting generalized derivative has a number of interesting properties. Among them is its existence even where conventional derivatives are not defined and the property that its value is the average of the left- and right-hand side limit of the derivative. As an example, the Lanczos derivative of |x| at x = 0 is D_L(|x|) = 0. From a numerical perspective, this derivative has the desirable property that it is rather insensitive to noise in the data from which the derivative is to be estimated.

In an SPH context, integral-based estimates for second derivatives have been applied frequently, mainly because they are substantially less noise-prone than those resulting from directly taking second derivatives of kernel approximations (Brookshaw 1985; Monaghan 2005). For first-order derivatives, however, such integral approximations (IAs) have only been explored very recently (Cabezon, Garcia-Senz & Escartin 2012, Garcia-Senz et al. 2012; Jiang, Lu & Lu 2014). We will assess the accuracy of the integral-based gradient estimates under idealized conditions in Section 3.6, and, in more practical, dynamical tests in Section 7.

The function |$f(\boldsymbol {r}^{\prime })$| in the expression

\begin{equation} \tilde{\boldsymbol {I}}_f (\boldsymbol {r}) \equiv \int [f(\boldsymbol {r}^{\prime }) - f(\boldsymbol {r})] \; (\boldsymbol {r}^{\prime } - \boldsymbol {r}) \; W(|\boldsymbol {r} - \boldsymbol {r}^{\prime }|, h) \; \mathrm{d}V^{\prime } \end{equation}

(16)

can be Taylor-expanded around |$\boldsymbol {r}$|⁠, so that one finds

\begin{eqnarray} \tilde{I}^i_f (\boldsymbol {r}) \!=\!\! \int \left[ (\nabla f)^k _{\vert _{\boldsymbol {r}}} (\boldsymbol {r}^{\prime } \!-\! \boldsymbol {r})^k\right] \; (\boldsymbol {r}^{\prime } \!-\! \boldsymbol {r})^i \; W(|\boldsymbol {r} \!-\! \boldsymbol {r}^{\prime }|, h) \; \mathrm{d}V^{\prime } \!+\! O(f^{\prime \prime }).\nonumber\\ \end{eqnarray}

(17)

Therefore, the gradient component representation, which is exact for linear functions, is given by

\begin{equation} (\nabla f)^k (\boldsymbol {r})= \tilde{C}^{ki}(\boldsymbol {r}) \; \tilde{I}^i_f (\boldsymbol {r}), \end{equation}

(18)

where the matrix |$\tilde{C}$| is the inverse of the symmetric matrix |$\tilde{\tau }$| whose components read

\begin{equation} \tilde{\tau }^{ki}(\boldsymbol {r}) = \int (\boldsymbol {r}^{\prime } - \boldsymbol {r})^k \; (\boldsymbol {r}^{\prime } - \boldsymbol {r})^i \; W(|\boldsymbol {r} - \boldsymbol {r}^{\prime }|, h) \; \mathrm{d}V^{\prime }. \end{equation}

(19)

|$\tilde{\tau }^{ki}$| contains only position information while |$\boldsymbol {I}$| also contains the function to be differentiated. In the following, we will approximate the integrals in equations (16) and (19) by conventional SPH summations over particles (the resulting summation approximations have no tilde), which yields

\begin{equation} \tau ^{ki}(\boldsymbol {r})= \sum _b V_b (\boldsymbol {r}_b - \boldsymbol {r})^k \; (\boldsymbol {r}_b - \boldsymbol {r})^i \; W(|\boldsymbol {r} - \boldsymbol {r}_b|, h) \end{equation}

(20)

and

\begin{equation} (\boldsymbol {I}_f (\boldsymbol {r}))_{\rm fIA} = \sum _b V_b [f_b - f(\boldsymbol {r})] \; (\boldsymbol {r}_b - \boldsymbol {r}) \; W(|\boldsymbol {r} - \boldsymbol {r}_b|, h). \end{equation}

(21)

Whenever we use this expression in a gradient estimate, we refer to it as the ‘full integral approximation’, or fIA for short.

It is worth mentioning that for a radial kernel, the gradient can be written as

\begin{equation} \nabla _a W_{ab}(h_a)= - \frac{\mathrm{\partial} W}{\mathrm{\partial} u} \frac{\boldsymbol {r}_b - \boldsymbol {r}_a}{h_a |\boldsymbol {r}_a - \boldsymbol {r}_b|}= (\boldsymbol {r}_b - \boldsymbol {r}_a) Y_{ab}(h_a), \end{equation}

(22)

where |$u= |\boldsymbol {r}_a - \boldsymbol {r}_b|/h_a$| and Y is also a valid, positively definite and compactly supported kernel function. Therefore, if equation (22) is inserted in equations (14) and (15), one recovers the fIA-gradient formula, i.e. the LE- and fIA-gradient approach are actually equivalent.

If we now assume that the quality indicator |$\mathcal {Q}_{2}$|⁠, equation (5), is fulfilled to good accuracy, we can drop the term containing |$f(\boldsymbol {r})$| to obtain

\begin{equation} (\boldsymbol {I}_f (\boldsymbol {r}))_{\rm IA}= \sum _b V_b f_b \; (\boldsymbol {r}_b - \boldsymbol {r}) \; W(|\boldsymbol {r} - \boldsymbol {r}_b|, h). \end{equation}

(23)

We refer to equation (18) with |$(\boldsymbol {I}_f (\boldsymbol {r}))_{\rm IA}$| as ‘integral approximation’ or IA for short. How good this approximation is in practice depends on the regularity of the particle distribution, see also Section 3.6. As pointed out by Garcia-Senz et al. (2012), this last approximation breaks the exactness of the gradient of linear functions, but, on the other hand, it rewards us with a gradient estimate that is antisymmetric with respect to the exchange of |$\boldsymbol {r}_b$| and |$\boldsymbol {r}$|⁠. This is crucial to ensure that the strongest property of SPH, the exact conservation, remains preserved. From equation (23), it is obvious that the gradient only vanishes exactly in the case of constant f_b if |$\mathcal {Q}_{2}$|⁠, equation (5), is fulfilled exactly. So rather than having to fulfil several quality criteria for the function interpolant and its gradient, equations (4) to (9), we only need to ensure the interpolation quality in the form of equation (5) in order to also have accurate gradient estimates.

So our gradient estimate in IA reads explicitly

\begin{eqnarray} (\nabla f)_{\rm IA}^k (\boldsymbol {r})&=& C^{kd}(\boldsymbol {r}) \; \left(I^d_f (\boldsymbol {r})\right)_{\rm IA}\nonumber \\ &=& \sum _b V_b f_b \sum _{d=1}^{D} C^{kd}(\boldsymbol {r},h) (\boldsymbol {r}_b - \boldsymbol {r})^d W(|\boldsymbol {r}-\boldsymbol {r}_b|,h). \end{eqnarray}

(24)

From the comparison with equation (6), it is obvious that the second sum takes over the role that is usually played by the kernel gradient:

\begin{eqnarray} \nabla ^k W(|\boldsymbol {r} - \boldsymbol {r}_b|,h) \rightarrow \sum _{d=1}^{D} C^{kd}(\boldsymbol {r},h) (\boldsymbol {r}_b - \boldsymbol {r})^d W(|\boldsymbol {r}-\boldsymbol {r}_b|,h). \end{eqnarray}

(25)

We will make use of this replacement in Section 6.2 to obtain an alternative SPH formulation with integral-based derivative estimates.

3.6 Assessment of the gradient accuracy

We briefly want to assess the accuracy of the different gradient estimates equations (6), (10), (13), (21) and (24) (with the standard cubic spline kernel) in a numerical experiment. Our experiment is similar to the one in Rosswog (2010): we set up particles on a 2D hexagonal lattice in [−1, 1] × [−1, 1], corresponding to a close-packed (CP) distribution of spheres with radius r_s. The particles are assigned the same baryon number/masses and pressures that rise linearly with the x-coordinate so that the slope is ∂_xP = 1. The numerical gradient estimate, (∂_xP)_num, is calculated via equation (6) ‘SPH-gradient’, equation (13) the ‘LE-gradient’, equation (21) full integral approximation, ‘fIA-gradient’ and equation (23) ‘IA-gradient’. In Fig. 1, we display the error ϵ = |(∂_xP)_num − ∂_xP|/|∂_xP| as a function of the parameter η by which we set the smoothing length

\begin{equation} h_a= \eta V_a^{1/D} \end{equation}

(26)

based on the particle volume V_b. For this perfectly regular particle distribution, the quality indicators, equation (4) and (5), are fulfilled to high accuracy and therefore the constant exact (CE) gradient is practically identical to the standard SPH estimate and therefore it is not shown in the left-hand panel of Fig. 1. For the same reason, the IA-approximation, equation (23), is very accurate and yields a gradient estimate (red) that is roughly 10 orders of magnitude better than the standard SPH gradient estimate (black). The fIA and the LE prescription reproduce the exact result to within machine precision, but, as noted above, they lack the desirable antisymmetry property that facilitates exact numerical conservation.

$Sensitivity of different gradient prescriptions to the regularity of the particle distribution. The left-hand panel shows results for a perfect 2D hexagonal lattice corresponding to the closest packing of spheres of radius rs. The right-hand panel shows results for a slightly perturbed hexagonal lattice that was obtained by displacing each particle in a hexagonal lattice in a random direction by a distance Δra that has been randomly chosen from [0, 10−3rs]. The parameter η determines the smoothing length via $h_a= \eta V_a^{1/D}$, where Va is the particle volume. ‘Std. SPH gradient’ refers to the direct gradient of the SPH interpolant equation (6), ‘CE gradient’ stands for ‘constant exact gradient’ and is calculated according to equation (10), ‘IA gradient’ is calculated from equation (24), the ‘fIA gradient’ from equation (21) and the ‘LE gradient’ from equation (13). For a regular particle distribution, the gradient estimate can be improved by about 10 orders of magnitude by using the IA-prescription (left; the CE gradient coincides with the standard SPH estimate and is therefore not shown). But even a small perturbation of the lattice degrades, the gradient quality to an accuracy similar to the standard SPH estimate (right-hand panel). The LE- and the fIA gradient are hardly affected and therefore not shown in the right-hand panel. See text for more details.$

Figure 1.

Sensitivity of different gradient prescriptions to the regularity of the particle distribution. The left-hand panel shows results for a perfect 2D hexagonal lattice corresponding to the closest packing of spheres of radius r_s. The right-hand panel shows results for a slightly perturbed hexagonal lattice that was obtained by displacing each particle in a hexagonal lattice in a random direction by a distance Δr_a that has been randomly chosen from [0, 10⁻³r_s]. The parameter η determines the smoothing length via |$h_a= \eta V_a^{1/D}$|⁠, where V_a is the particle volume. ‘Std. SPH gradient’ refers to the direct gradient of the SPH interpolant equation (6), ‘CE gradient’ stands for ‘constant exact gradient’ and is calculated according to equation (10), ‘IA gradient’ is calculated from equation (24), the ‘fIA gradient’ from equation (21) and the ‘LE gradient’ from equation (13). For a regular particle distribution, the gradient estimate can be improved by about 10 orders of magnitude by using the IA-prescription (left; the CE gradient coincides with the standard SPH estimate and is therefore not shown). But even a small perturbation of the lattice degrades, the gradient quality to an accuracy similar to the standard SPH estimate (right-hand panel). The LE- and the fIA gradient are hardly affected and therefore not shown in the right-hand panel. See text for more details.

Open in new tab Download slide

As expected from the term that was neglected to obtain equation (24), the quality of antisymmetric gradient estimate is sensitive to the particle distribution. To illustrate this, we perform a variant of the previous experiment in which we slightly perturb the perfect hexagonal lattice. To each particle position |$\boldsymbol {r}_a$|⁠, we add a randomly oriented vector |$\Delta \boldsymbol {r}_a$| whose modulus is chosen randomly from the interval [0, 10⁻³r_s]. Even this very subtle perturbation substantially degrades the accuracy of those gradients that do not account for the actual particle distribution, i.e. for the standard SPH- and the IA-gradient prescriptions. The CE-, LE- and fIA-gradient estimates make use of the information on the local particle distribution and are therefore hardly deteriorated. For the perturbed distribution, the IA-gradient has no more obvious advantage with respect to the standard SPH gradient, both now show comparable errors. Therefore, further, dynamical, tests are required to see whether a regular enough particle distribution can be maintained during dynamical simulation and to judge whether the IA-gradient prescription really improves the accuracy in practice. As will be shown below, however, and consistent with the findings of Garcia-Senz et al. (2012), the integral-based, antisymmetric IA-approach by far outperforms the traditional direct kernel gradients in all dynamical tests.

4 KERNEL CHOICE

4.1 Kernels

In Section 3, we have briefly collected some kernel interpolation basics. Traditionally, ‘bell-shaped’ kernels with vanishing derivatives at the origin have been preferred as SPH kernels because they are rather insensitive to the exact positions of nearby particles and therefore they are good density estimators (Monaghan 1992). For most bell-shaped kernels, however, a ‘pairing instability’ sets in once the smoothing length exceeds a critical value. When it sets in, particles start to form pairs and, in the worst case, two particles are effectively replaced by one. This has no dramatic effect other than halving the effective particle number, though, still at the original computational expense. Recently, there have been several studies that (re-)proposed peaked kernels (Read et al. 2010; Valcke et al. 2010) as a possible cure for the pairing instability. Such kernels have the benefit of producing very regular particle distributions, but as the experiments below show, they require the summation over many neighbouring particles for an acceptable density estimate. It has recently been pointed out by Dehnen & Aly (2012), however, that, contrary to what was previously thought, the pairing instability is not caused by the vanishing central derivative, but instead a necessary condition for stability against pairing is a non-negative Fourier transform of the kernels. For example, the Wendland kernel family (out of which we explore one member below), has a vanishing central derivative, but does not fall prey to the pairing instability. This is, of course, advantageous for convergence studies since the kernel support size is not restricted.

In the following, we collect a number of kernels whose properties are explored below. We give the kernels in the form in which they are usually presented in the literature, but to ensure a fair comparison in tests, we scale them to a support of 2h, as the most commonly used SPH kernel, M₄, see below. So if a kernel has a normalization σ_lh for a support of lh, it has, in D spatial dimensions, normalization σ_kh = (l/k)^Dσ_lh when it is stretched to a support of kh.

4.1.1 Kernels with vanishing central derivatives

B-spline functions: M₄ and M₆ kernels. The most commonly used SPH kernels are the so-called B-spline functions (Schoenberg 1946), M_n, which are generated as Fourier transforms:

\begin{equation} M_n(x,h)= \frac{1}{2 \pi } \int _{-\infty }^\infty \left[ \frac{\sin (kh/2)}{kh/2}\right]^n \cos (kx) \mathrm{d}k. \end{equation}

(27)

The smoothness of the M_n functions increases with n and they are continuous up to the (n − 2)th derivative. Since SPH requires at the very least the continuity in the first and second derivative, the cubic spline kernel M₄

\begin{equation} w_4(q)= \left\lbrace \begin{array}{ll}\frac{1}{4}(2-q)^3 - (1-q)^3 &\quad 0 \le q < 1\\ \frac{1}{4}(2-q)^3 &\quad 1 \le q < 2\\ 0 &\quad {\rm else} \end{array}\right. \end{equation}

(28)

is the lowest order member of this kernel family that is a viable option. It is often considered the ‘standard choice’ in SPH. The normalized SPH kernel then has the form

\begin{equation} W(|\boldsymbol {r}-\boldsymbol {r}^{\prime }|,h)= \frac{\sigma _n}{h^D} w_n(q), \end{equation}

(29)

where¹|$q= |\boldsymbol {r}-\boldsymbol {r}^{\prime }|/h$|⁠. The normalizations are obtained from

\begin{equation} \sigma ^{-1}= \left\lbrace \begin{array}{ll}2 \int _0^{Q} w(q) \mathrm{d}q &\quad {\rm in \; 1D} \\ \int _0^{Q} w(q) \; 2 \pi \; q\; \mathrm{d}q &\quad {\rm in \; 2D} \\ \int _0^{Q} w(q) \; 4 \pi \; q^2 \; \mathrm{d}q &\quad {\rm in \; 3D}, \end{array}\right. \end{equation}

(30)

where Q is the kernel support which is equal to 2 for M₄. This yields values of [2/3, 10/(7π), 1/π] in one, two and three dimensions.

The M₆ kernel (truncated at support Q = 3) is given as

\begin{eqnarray} w_6(q)= \left\lbrace \begin{array}{ll}(3-q)^5 - 6(2-q)^5 + 15(1-q)^5 &\quad 0 \le q < 1\\ (3-q)^5 - 6(2-q)^5 &\quad 1 \le q < 2\\ (3-q)^5 &\quad 2 \le q < 3\\ 0 &\quad {\rm else} \end{array}\right.\nonumber\\ \end{eqnarray}

(31)

with normalizations of [1/120, 7/(478π), 1/(120π)] in one, two and three dimensions. Note that for a fair comparison in all plots, the M₆ kernel is rescaled to a support on 2h.

A parametrized family of Kernels. More recently, a one-parameter family of kernels has been suggested (Cabezon, Garcia-Senz & Relano 2008)

\begin{equation} W_{{\rm H},n}= \frac{\sigma _{{{\rm H},n}}}{h^D} \left\lbrace \begin{array}{ll}1 &\quad q = 0\\ \left( \frac{\sin [\frac{\pi }{2} q]}{\frac{\pi }{2} q}\right)^n &\quad 0 < q \le 2\\ 0 &\quad {\rm else,} \end{array}\right. \end{equation}

(32)

where n determines the smoothness and the shape of the kernel, see Fig. 2. The normalization of this kernel family can be expressed as a fifth-order polynomial whose coefficients can be found in table 2 of Cabezon et al. (2008). In this form, n is allowed to vary continuously between 2 and 7. We use here exactly the form described in their paper, in particular all kernels have a support of R_k = 2. The W_H,3 kernel is a very close approximation to the M₄, see Fig. 2, while W_H,5 is very similar to M₆, provided they are stretched to have the same support. For practical calculations, we use the W_H,n kernels for n-values from 3 to 9, the corresponding normalizations are given in Table 1.

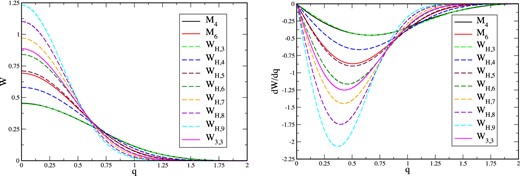
Comparison of the standard spline kernels M4 and M6 with the kernel family WH,n (kernels left, their derivatives right). Note that for ease of comparison the M6 kernel has been stretched to a support of Rk = 2. WH,3 is a close approximation of M4 and, if scaled to the same support, WH,5 is similar to M6. Also shown is the Wendland kernel W3,3.

Figure 2.

Comparison of the standard spline kernels M₄ and M₆ with the kernel family W_H,n (kernels left, their derivatives right). Note that for ease of comparison the M₆ kernel has been stretched to a support of R_k = 2. W_H,3 is a close approximation of M₄ and, if scaled to the same support, W_H,5 is similar to M₆. Also shown is the Wendland kernel W_3,3.

Open in new tab Download slide

Table 1.

Open in new tab

Normalization constant σ_H,n of the W_H,n kernels in one, two and three dimensions.

Normalization σ_H,n of the W_H,n kernels
	n= 3	n= 4	n= 5	n= 6	n= 7	n= 8	n= 9
1D	0.660 203 38	0.752 215 01	0.834 353 71	0.909 204 80	0.978 402 21	1.043 052 35	1.103 944 01
2D	0.450 733 24	0.580 312 18	0.710 379 46	0.840 709 99	0.971 197 17	1.101 784 66	1.232 440 06
3D	0.317 878 09	0.458 917 52	0.617 012 65	0.790 449 59	0.977 949 35	1.178 510 74	1.391 322 15

Normalization σ_H,n of the W_H,n kernels
	n= 3	n= 4	n= 5	n= 6	n= 7	n= 8	n= 9
1D	0.660 203 38	0.752 215 01	0.834 353 71	0.909 204 80	0.978 402 21	1.043 052 35	1.103 944 01
2D	0.450 733 24	0.580 312 18	0.710 379 46	0.840 709 99	0.971 197 17	1.101 784 66	1.232 440 06
3D	0.317 878 09	0.458 917 52	0.617 012 65	0.790 449 59	0.977 949 35	1.178 510 74	1.391 322 15

Table 1.

Open in new tab

Normalization constant σ_H,n of the W_H,n kernels in one, two and three dimensions.

Normalization σ_H,n of the W_H,n kernels
	n= 3	n= 4	n= 5	n= 6	n= 7	n= 8	n= 9
1D	0.660 203 38	0.752 215 01	0.834 353 71	0.909 204 80	0.978 402 21	1.043 052 35	1.103 944 01
2D	0.450 733 24	0.580 312 18	0.710 379 46	0.840 709 99	0.971 197 17	1.101 784 66	1.232 440 06
3D	0.317 878 09	0.458 917 52	0.617 012 65	0.790 449 59	0.977 949 35	1.178 510 74	1.391 322 15

Normalization σ_H,n of the W_H,n kernels
	n= 3	n= 4	n= 5	n= 6	n= 7	n= 8	n= 9
1D	0.660 203 38	0.752 215 01	0.834 353 71	0.909 204 80	0.978 402 21	1.043 052 35	1.103 944 01
2D	0.450 733 24	0.580 312 18	0.710 379 46	0.840 709 99	0.971 197 17	1.101 784 66	1.232 440 06
3D	0.317 878 09	0.458 917 52	0.617 012 65	0.790 449 59	0.977 949 35	1.178 510 74	1.391 322 15

Wendland kernels. An interesting class of kernels with compact support and positive Fourier transforms are the so-called Wendland functions (Wendland 1995). In various areas of applied mathematics, they have long been appreciated for their good interpolation properties, but they have not received much attention as SPH kernels. Recently, they have been discussed in some detail in Dehnen & Aly (2012), where it was in particular found that these kernels are not prone to the pairing instability, despite having a vanishing central derivative. We only experiment here with one particular example, the C⁶ smooth

\begin{equation} W_{3,3}= \frac{\sigma _W}{h^3} \left(1 - q \right)_{+}^8 ( 32 q^3 + 25 q^2 + 8 q + 1 ) , \end{equation}

(33)

see e.g. Schaback & Wendland (2006), where the symbol (.)₊ denotes the cutoff function max(., 0). The normalization σ_W is 78/(7π) and 1365/(64π) in two and three dimensions. As we will demonstrate in the below benchmark tests, this kernel has some very interesting properties, in particular it maintains a highly ordered particle distribution in dynamical simulations and it does not fall prey to the pairing instability.

4.1.2 Kernels with non-vanishing central derivatives

Here, we briefly discuss two kernel functions with non-vanishing central derivatives. The first example is the ‘linear quartic’ (LIQ) kernel that has been suggested (Valcke et al. 2010) to achieve a regular particle distribution and to improve SPH's performance in Kelvin–Helmholtz (KH) tests. The second example is shown mainly for pedagogical reasons: it illustrates how a very subtle change to the core of the well-appreciated M₆ kernel seriously compromises its accuracy.

Linear quartic kernel, LIQ. The centrally peaked LIQ kernel (Valcke et al. 2010) reads

\begin{eqnarray} &&\!\!\!\!&&{W_{\rm LIQ}(q)}\nonumber\\ &&\!\!= \frac{\sigma _{\rm LIQ}}{h^D} \left\lbrace \begin{array}{ l l l}F - u &\quad {\rm for \; } u \le x_s\\ A u^4 + B u^3 + C u^2 + D u + E &\quad {\rm for \; } x_s < u \le 1\\ 0 &\quad {\rm else } \end{array} \right. \end{eqnarray}

(34)

with x_s = 0.3, A = −1.458, B = 3.790, C = −2.624, D = −0.2915, E = 0.5831 and F = 0.6500 and u = q/2. The normalization constant σ_LIQ is 2.962 in 2D and 3.947 in 3D.

Quartic core M₆ kernel, QCM₆. We briefly explore a modification of the M₆ kernel so that it remains very smooth, but has a non-vanishing derivative in the centre. This quartic core M₆ kernel (QCM₆) is constructed by replacing the second derivative of the M₆ kernel for q < q_c by a parabola whose parameters have been chosen so that it fits smoothly and differentially the M₆ kernel at the transition radius q_c = 0.759 298 which is defined by the condition d²w₆/dq²(q_c) = 0. The QCM₆-kernel then reads:

\begin{eqnarray} &&\!\!\!\!&&{W_{{\rm QCM}_6}(q)}\nonumber\\ &&= \frac{\sigma _{{\rm QCM}_6}}{h^D} \left\lbrace \begin{array}{ll}A q^4 + B q^2 + C q + D&\quad 0 \le q < q_c\nonumber\\ (3-q)^5 - 6(2-q)^5 + 15(1-q)^5&\quad q_c \le q < 1\nonumber\\ (3-q)^5 - 6(2-q)^5 &\quad 1 \le q < 2\nonumber\\ (3-q)^5 &\quad 2 \le q < 3\nonumber\\ 0 &\quad {\rm else.} \end{array}\right.\nonumber\\ \end{eqnarray}

(35)

The coefficients A, B, C and D are determined from the conditions |$w_{\rm QCM_6}(q_c)= w_6(q_c)$|⁠, |$w^{\prime }_{\rm QCM_6}(q_c)= w^{\prime }_6(q_c)$|⁠, |$w^{\prime \prime }_{\rm QCM_6}(q_c)= w^{\prime \prime }_6(q_c)$| and |$w^{\prime \prime \prime }_{\rm QCM_6}(q_c)= w^{\prime \prime \prime }_6(q_c)$|⁠, where the primes indicate the derivatives with respect to q. The resulting numerical values are given in Table 2. Note that QCM₆ is continuous everywhere up to the third derivative. The peaked kernels LIQ and QCM₆ are compared in Fig. 3.

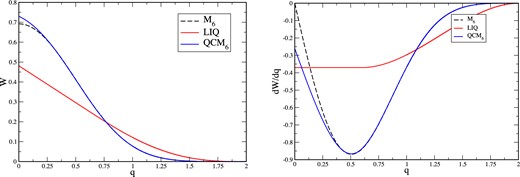
The peaked kernels LIQ and QCM6: kernel W on the left and its derivative dW/dq on the right. The QCM6 kernel has been constructed so that it hardly deviates from M6, but has a non-vanishing central derivative. For comparison also the M6 kernel plotted (dashed lines).

Figure 3.

The peaked kernels LIQ and QCM₆: kernel W on the left and its derivative dW/dq on the right. The QCM₆ kernel has been constructed so that it hardly deviates from M₆, but has a non-vanishing central derivative. For comparison also the M₆ kernel plotted (dashed lines).

Open in new tab Download slide

Table 2.

Open in new tab

Parameters of the QCM₆.

Parameter	Numerical value
A	11.017 537
B	−38.111 922
C	−16.619 585
D	69.785 768
σ_1D	8.245 880 E-3
σ_2D	4.649 647 E-3
σ_3D	2.650 839 E-3

Table 2.

Open in new tab

Parameters of the QCM₆.

Parameter	Numerical value
A	11.017 537
B	−38.111 922
C	−16.619 585
D	69.785 768
σ_1D	8.245 880 E-3
σ_2D	4.649 647 E-3
σ_3D	2.650 839 E-3

4.2 Accuracy assessment

4.2.1 Kernel support size

We give in Table 3 the values η that are used in the numerical experiments. They are chosen to be very large, but small enough to avoid pairing. Also given is the value q_c, where |dW/dq| has its maximum, η_c = 1/q_c and the corresponding neighbour number for a hexagonal lattice, N_c.

Table 3.

Open in new tab

Values q_c where the kernel derivative |dW(q)/dq| has the maximum, η_c = 1/q_c. N_c is the neighbour number for a hexagonal lattice that corresponds to q_c and η is the value used in our experiments. The latter has been chosen so that it is as large as possible without becoming pairing unstable, or, in cases where no pairing occurs, as large as computational sources allowed.

Kernel	q_c	η_c	N_c	η
M₄	0.667	1.500	28	1.2
M₆	0.506	1.976	49	1.6
W_H,3	0.661	1.512	28	1.2
W_H,4	0.567	1.765	39	1.5
W_H,5	0.504	1.984	49	1.6
W_H,6	0.458	2.183	59	1.7
W_H,7	0.423	2.364	70	1.8
W_H,8	0.395	2.531	80	1.9
W_H,9	0.372	2.690	90	2.2
W_3,3	0.430	2.323	n.a.	2.2
LIQ	n.a.	n.a.	n.a.	2.2
QCM₆	0.506	1.976	49	2.2

Kernel	q_c	η_c	N_c	η
M₄	0.667	1.500	28	1.2
M₆	0.506	1.976	49	1.6
W_H,3	0.661	1.512	28	1.2
W_H,4	0.567	1.765	39	1.5
W_H,5	0.504	1.984	49	1.6
W_H,6	0.458	2.183	59	1.7
W_H,7	0.423	2.364	70	1.8
W_H,8	0.395	2.531	80	1.9
W_H,9	0.372	2.690	90	2.2
W_3,3	0.430	2.323	n.a.	2.2
LIQ	n.a.	n.a.	n.a.	2.2
QCM₆	0.506	1.976	49	2.2

Table 3.

Open in new tab

Values q_c where the kernel derivative |dW(q)/dq| has the maximum, η_c = 1/q_c. N_c is the neighbour number for a hexagonal lattice that corresponds to q_c and η is the value used in our experiments. The latter has been chosen so that it is as large as possible without becoming pairing unstable, or, in cases where no pairing occurs, as large as computational sources allowed.

Kernel	q_c	η_c	N_c	η
M₄	0.667	1.500	28	1.2
M₆	0.506	1.976	49	1.6
W_H,3	0.661	1.512	28	1.2
W_H,4	0.567	1.765	39	1.5
W_H,5	0.504	1.984	49	1.6
W_H,6	0.458	2.183	59	1.7
W_H,7	0.423	2.364	70	1.8
W_H,8	0.395	2.531	80	1.9
W_H,9	0.372	2.690	90	2.2
W_3,3	0.430	2.323	n.a.	2.2
LIQ	n.a.	n.a.	n.a.	2.2
QCM₆	0.506	1.976	49	2.2

Kernel	q_c	η_c	N_c	η
M₄	0.667	1.500	28	1.2
M₆	0.506	1.976	49	1.6
W_H,3	0.661	1.512	28	1.2
W_H,4	0.567	1.765	39	1.5
W_H,5	0.504	1.984	49	1.6
W_H,6	0.458	2.183	59	1.7
W_H,7	0.423	2.364	70	1.8
W_H,8	0.395	2.531	80	1.9
W_H,9	0.372	2.690	90	2.2
W_3,3	0.430	2.323	n.a.	2.2
LIQ	n.a.	n.a.	n.a.	2.2
QCM₆	0.506	1.976	49	2.2

4.2.2 Density estimates

To assess the density estimation accuracy, we perform a simple experiment: we place the SPH particles on a hexagonal lattice and assign all of them a constant value for the baryon number², ν₀. Since the effective area belonging to each particle with radius r_s in a CP configuration is |$A_{\rm eff}= 2 \sqrt{3} r_{\rm s}^2$|⁠, the theoretical density value is N₀ = ν₀/A_eff. We now measure the average relative deviation between the estimated and the theoretical density value, |$\epsilon _{N}= \sum _{a=1}^{N_{\rm part}} |N_a - N_0|/(N_0 \; N_{\rm part})$|⁠, the results are shown in the left-hand panel of Fig. 4 as a function of the smoothing length parameter η, see equation (26). For clarity, we only show the odd members of the W_H,n family. Note that we show the results up to large values of η where, in a dynamical simulation, some of the kernels would already have become pairing unstable. The ‘dips’ in the left-hand panel occur where the density error changes sign. The right-hand panel of Fig. 4 illustrates this for the case of the M₄ kernel.

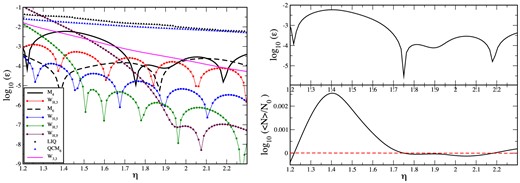
$Accuracy of density estimates for different kernels. Particles are placed on a hexagonal lattice so that the density is uniform and the SPH density estimate is compared with the theoretical value to calculate the relative density error, see the left-hand panel. The parameter η determines the smoothing length, $h_a= \eta V_a^{1/D}$; LIQ: linear-quartic, QCM6: quartic core M6. To clarify the nature of the ‘dips’ in the left-hand panel, we plot in the right-hand panel the logarithm of the relative density error (upper right) and log (〈N〉/N0) for the case of the cubic spline kernel M4. The dips occur when the density error changes sign (exact value is indicated by the dashed red line).$

Figure 4.

Accuracy of density estimates for different kernels. Particles are placed on a hexagonal lattice so that the density is uniform and the SPH density estimate is compared with the theoretical value to calculate the relative density error, see the left-hand panel. The parameter η determines the smoothing length, |$h_a= \eta V_a^{1/D}$|⁠; LIQ: linear-quartic, QCM₆: quartic core M₆. To clarify the nature of the ‘dips’ in the left-hand panel, we plot in the right-hand panel the logarithm of the relative density error (upper right) and log (〈N〉/N₀) for the case of the cubic spline kernel M₄. The dips occur when the density error changes sign (exact value is indicated by the dashed red line).

Open in new tab Download slide

The ‘standard’, cubic spline kernel M₄ does not perform particularly well and simply replacing it by, say, the M₆ kernel increases the density estimate already by roughly two orders of magnitude. If larger smoothing length can be afforded, however, the density estimate can be further substantially improved. For example, the W_H,9 kernel for η > 2 achieves in this test approximately four orders of magnitude lower errors than what the M₄ can achieve for η = 1.2 (for larger values it becomes pairing unstable). The Wendland kernel achieves a continuous improvement in the density estimate with increasing η and, as Dehnen & Aly (2012) argue, this protects the kernel against becoming pairing unstable. Although the W_3,3 results in this test are less accurate than those of the higher order W_H,n kernels, we gave preference to the Wendland kernel as our standard choice, since W_3,3 allows only for very little noise, see below.

Both peaked kernels perform very poorly in this test, even for a very large support. It is particularly interesting to observe how the subtle change of the core of the M₆ kernel (compare dashed black and the blue curve in Fig. 3) seriously compromises the density estimation ability (compare the dashed black curve with the blue triangles in Fig. 4).

4.2.3 Gradient estimates

We repeat the experiment described in Section 3.6 with the ‘standard’ SPH gradient, equation (6), for a number of different kernels. We set up particles on a 2D hexagonal lattice in [−1, 1] × [−1, 1], corresponding to a CP distribution of spheres with radius r_s. All particles possess the same baryon numbers ν_b and are assigned pressures that rise linearly with the x-coordinate so that the slope is (∂_xP) = 1. In Fig. 5, we show the impact of the kernel choice on the gradient accuracy (again, the M₆ is stretched to a support of 2h). The M₆ kernel (dashed black) yields, roughly speaking, a two orders of magnitude improvement over the standard SPH kernel M₄ (solid black). Provided one is willing to apply larger neighbour numbers, the accuracy can be further improved by using smoother kernels. Once more, the high-order members of the W_H,n kernel family perform very well for large η values. And, again, the Wendland kernel continuously improves the gradient estimate with increasing η. None of peaked kernels reaches an accuracy substantially below 10⁻², not even for very large η-values.

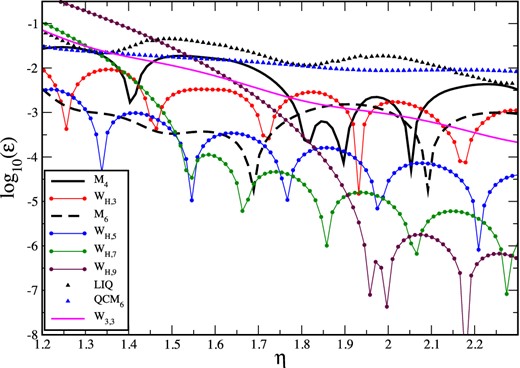
$Accuracy of gradient estimates (calculated via equation 6) for different kernels. Particles are placed on a hexagonal lattice so that the density is uniform and the pressure linearly increasing. The parameter η determines the smoothing length, $h_a= \eta V_a^{1/D}$; LIQ: linear-quartic, QCM6: quartic core M6.$

Figure 5.

Accuracy of gradient estimates (calculated via equation 6) for different kernels. Particles are placed on a hexagonal lattice so that the density is uniform and the pressure linearly increasing. The parameter η determines the smoothing length, |$h_a= \eta V_a^{1/D}$|⁠; LIQ: linear-quartic, QCM₆: quartic core M₆.

Open in new tab Download slide

5 GENERALIZED VOLUME ELEMENTS

Here, we discuss the volume elements that are needed for the kernel techniques described in Section 3. In the following discussion, we use the baryon number ν and the CF baryon number density N, but every relation straight forwardly translates into Newtonian SPH by simply replacing ν with the particle mass m and N with the mass density ρ.

At contact discontinuities, the pressure is continuous, but density and internal energy suffer a discontinuity. For a polytropic equation of state (EOS), P = (Γ − 1)un, where n is the baryon number density in the local rest frame,³ the product of density and internal energy must be the same on both sides of the discontinuity to ensure a single value of P at the discontinuity, i.e. n₁u₁ = n₂u₂. Here, the subscripts label the two sides of the discontinuity. If this constraint is violated on a numerical level, say, because density and internal energy have a different smoothness across the discontinuity, spurious forces occur that act like a surface tension. This can occur in ‘standard’ SPH formulations since the density is estimated by a kernel-weighted sum over neighbouring particles and therefore is smooth, while the internal energy is a property assigned to each particle that enters ‘as is’ (i.e. un-smoothed) in the SPH evolution equations. Such spurious surface tension forces can compromise the ability to accurately handle subtle fluid instabilities, see for example Agertz et al. (2007), Springel (2010a) and Read et al. (2010). One may, however, question whether an unresolvably sharp transition in u is a viable initial condition in the first place. Note that Godunov-type SPH formulations (Inutsuka 2002; Cha & Whitworth 2003; Cha, Inutsuka & Nayakshin 2010; Murante et al. 2011; Puri & Ramachandran 2014) do not seem to suffer from such surface tension problems.

The problem can be alleviated if also the internal energy is smoothed, for example by applying some artificial thermal conductivity. This approach has been shown to work well in the case of KH instabilities (Price 2008; Valdarnini 2012). But it is actually a non-trivial problem to design appropriate triggers that supply conductivity in the right amounts exclusively where needed, but not elsewhere. Artificial conductivity applied where it is undesired can have catastrophic consequences, say by spuriously removing pressure gradients that are needed to maintain a hydrostatic equilibrium.

An alternative and probably more robust cure comes from using different volume elements in the SPH discretization process. Saitoh & Makino (2013) pointed out that SPH formulations that do not include density explicitly in the equations of motion avoid the pressure becoming multivalued at contact discontinuities. Since the density usually enters the equation of motion via the choice of the volume element ν_a/N_a (or m_a/ρ_a, respectively, in the Newtonian case), a different choice can possibly avoid the problem altogether. This observation is consistent with the findings of Heß & Springel (2010) who used a Voronoi tessellation to calculate particle volumes. In their approach, no spurious surface tension effects have been observed. Closer to the original SPH spirit is the class of kernel-based particle volume estimates that have recently been suggested by Hopkins (2013) as a generalization of the Saitoh & Makino (2013) approach. In the following, we will make use of these ideas for our relativistic SPH formulations.

We explore different ways to calculate kernel-based particle volume estimates V_a from which the densities follow as

\begin{equation} N_a= \frac{\nu _a}{V_a} . \end{equation}

(36)

An obvious possibility for a volume element is the inverse of the local SPH-particle number density (calculated in the CF), estimated by a kernel sum

\begin{equation} V^{(1)}_a= \left(\sum _b W_{ab}(h_a)\right)^{-1}. \end{equation}

(37)

While this is a natural choice, one is in principle free to generalize this estimate by weighting each kernel with an additional quantity X

\begin{equation} V^{(X)}_a= \frac{X_a}{\sum _b X_b W_{ab}(h_a)} \equiv \frac{X_a}{\kappa _{X, a}}. \end{equation}

(38)

There is a lot of freedom in the choice of X and we will here only explore a small set of (Lorentz invariant) weights and assess their suitability in numerical experiments. If the weight X = 1 is chosen, one obviously recovers the volume element of equation (37) and the baryon number density is simply given by the number density estimate weighted with the particle's own baryon number

\begin{equation} N^{(1)}_a= \nu _a \sum _b W_{ab}(h_a). \end{equation}

(39)

Since only the baryon number of the particle itself enters, this form in principle allows for sharp density transitions (say, via a uniform particle distribution with discontinuous ν-behaviour). As confirmed by the experiments in Section 7.3, this removes spurious surface tension effects.

If instead X = ν is chosen, one recovers the standard SPH density estimate

\begin{equation} N^{(\nu )}_a= \sum _b \nu _b W_{ab}(h_a). \end{equation}

(40)

Another choice is X = P^k, which yields

\begin{equation} N^{(P^k)}_a= \nu _a\sum _b \left(\frac{P_b}{P_a} \right)^k W_{ab}(h_a). \end{equation}

(41)

One may wonder whether the pressure P_a in the denominator may not give an inappropriately large weight in case of substantial pressure differences between neighbouring particles, say in a shock. Indeed, for the relativistic Sod-type shock, Section 7.6.1, with a pressure ratio of the order of 10⁷, and the choice k = 1 we have observed a small density ‘precursor’ spike within approximately one smoothing length of the shock. To avoid such artefacts, we choose a small value, k = 0.05, for which no anomalies have been observed. Obviously, for k = 0 one recovers the previous case of X = 1. If the pressure is used as a weight in the volume/density estimate, an iteration is required for self-consistent values of N and P. This is explained in detail in Section 6.1.3.

To illustrate the impact that the choice of the volume element has on the resulting pressure across a contact discontinuity, we perform the following experiment. We place particles on a uniform hexagonal lattice, assign baryon numbers so that the densities for x < 0 have value N₁ = 1 and N₂ = 2 for x > 0 and internal energies as to reproduce a constant pressure P₀ = 1 on both sides, u_i = P₀/((Γ − 1)n_i). Here, i labels the side and Γ = 5/3 is the polytropic exponent. Once set up, we measure the densities according to equation (36) and since here n = N, we calculate the pressure distribution across the discontinuity, once for each choice of X. The standard SPH volume element corresponding to weight factor X = ν produces a smooth density transition, see upper panel of Fig. 6 that together with the sharp change in u causes the ‘pressure blip’ (orange oval) that is also frequently seen in SPH shock tests and that is the reason behind the spurious surface tension forces discussed above. The same experiment, if repeated using X = P^k, does not show any noticeable deviation from the desired value of unity. The phenomenon of spurious surface tension is further explored by numerical experiments in Section 7.3.

Figure 6.

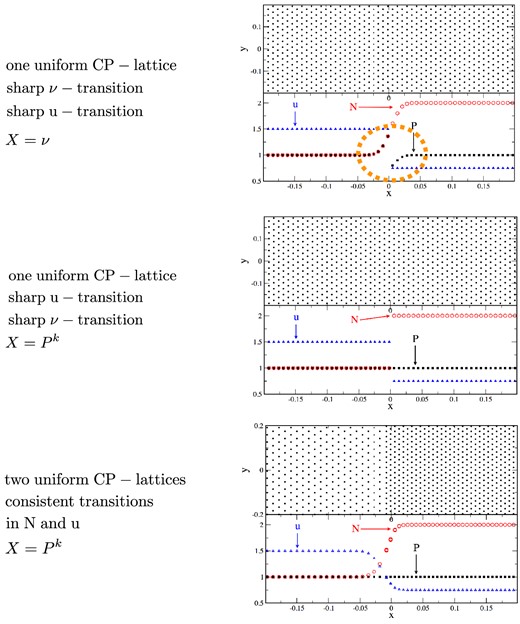
Different ways to set up a contact discontinuity. In the upper panel, particles are placed on a uniform hexagonal lattice (‘close packed’, CP) and masses/baryon numbers and internal energies are assigned as to reproduce the constant states, with a sharp transition at x = 0. Since the subsequent density calculation (with X = ν) produces a smooth density transition, the mismatch between a sharp internal energy u and a smooth density N leads to a ‘pressure blip’ (orange oval) that leads to spurious surface tension forces at the interface. If for the same setup X = P^k is used, both N and u have a sharp transition and the pressure blip disappears, see middle panel. The lower panel shows an alternative setup with equal masses/baryon numbers where the density structure is encoded in the particle distribution (here two uniform hexagonal lattices). The corresponding density calculation (with X = P^k) also produces a smooth density transition, but the internal energy is consistently (and therefore smoothly) assigned from the calculated density and the condition of uniform pressure.

Open in new tab Download slide

As an alternative numerical model for a contact discontinuity, we show in the last panel of Fig. 6 a setup for the case of constant particle masses/baryon numbers. In this case, the information about the density is encoded in the particle distribution, for which we use here two uniform hexagonal lattices. Also here (X = P^k) the density transition is smooth, but the internal energy is calculated (via an iteration) from the condition of constant pressure, so that the smoothness of N and u are consistent with each other.

6 SPECIAL-RELATIVISTIC SPH

We will now apply the techniques discussed in Sections 3–5 to the case of ideal, special-relativistic fluid dynamics. Excellent descriptions of various aspects of the topic (mostly geared towards Eulerian methods) can be found in a number of recent textbooks (Alcubierre 2008; Baumgarte & Shapiro 2010; Goedbloed, Keppens & Poedts 2010; Rezzolla & Zanotti 2013). In a first step, see Section 6.1, we generalize the derivation from the Lagrangian of an ideal relativistic fluid to the case of the generalized volume elements as introduced in equation (38). This leads to a generalization of the kernel-gradient-based equations given in Rosswog (2010). In a second formulation, see Section 6.2, we use integral-based gradient estimates, see equation (25), again for the case of a general volume element.

6.1 Special-relativistic SPH with kernel derivatives

We assume a flat space–time metric, η_μν, with signature (−,+,+,+) and use units in which the speed of light is equal to unity, c = 1. We reserve Greek letters for space–time indices from 0…3 with 0 being the temporal component, i and j refer to spatial components and SPH particles are labelled by a, b and k.

Written in Einstein sum convention, the Lagrangian of a special-relativistic perfect fluid can be written as (Fock 1964)

\begin{equation} L= - \int T^{\mu \nu } U_\mu U_\nu \mathrm{d}V, \end{equation}

(42)

where the energy–momentum tensor reads

\begin{equation} T^{\mu \nu }= (e + P) U^{\mu } U^{\nu } + P \eta ^{\mu \nu }. \end{equation}

(43)

We can write the energy density as a sum of a rest mass and an internal energy contribution

\begin{equation} e= \rho _{\rm rest} c^2 + u \rho _{\rm rest}= n m_0 c^2 (1 + u/c^2), \end{equation}

(44)

where, for now, the speed of light is shown explicitly. The baryon number density n is measured in the local fluid rest frame and the average baryon mass is denoted by m₀. With the conventions that all energies are written in units of m₀c² and c = 1, we can use the normalization of the four-velocity, U_μU^μ = −1, to simplify the Lagrangian to

\begin{equation} L= - \int n(1+u) \mathrm{d}V. \end{equation}

(45)

The number density as measured in the CF, see equation (36), is – due to length contraction – increased by a Lorentz factor with respect to the local fluid rest frame

\begin{equation} N= \gamma n . \end{equation}

(46)

Therefore, the Lagrangian can be written as

\begin{equation} L= - \int \mathrm{d}V N \left(\frac{1+u}{\gamma }\right) \end{equation}

(47)

or

\begin{equation} L\simeq - \sum _b V_b N_b \frac{1+u_b}{\gamma _b}= \sum _b \nu _b \frac{1+u_b}{\gamma _b}, \end{equation}

(48)

where the (fixed) baryon number carried by particle b, ν_b, has been introduced. To obtain the equations of motion from the Euler–Lagrange equations, we need ∇_aN_b and dN_b/dt for which we use (see equation 38)

\begin{eqnarray} \nabla _a \kappa _{X,b}&=& \frac{1}{\tilde{\Omega }_b} \sum _k X_k \nabla _a W_{bk}(h_b) \quad {\rm and} \end{eqnarray}

(49)

\begin{eqnarray} \frac{\mathrm{d} \kappa _{X,b}}{\mathrm{d}t}&=& \frac{1}{\tilde{\Omega }_b} \sum _k X_k \boldsymbol {v}_{bk} \cdot \nabla _b W_{bk}(h_b) , \end{eqnarray}

(50)

with the ‘grad-h’ terms

\begin{equation} \tilde{\Omega }_b= 1 - \frac{\nu _b}{X_b} \frac{\mathrm{\partial} h_b}{\mathrm{\partial} N_b} \sum _k X_k \frac{\mathrm{\partial} W_{kb}(h_b)}{\mathrm{\partial} h_b}. \end{equation}

(51)

The derivatives of the CF number densities then become

\begin{equation} \nabla _a N_b= \frac{\nu _b}{X_b \tilde{\Omega }_b} \sum _k X_k \nabla _a W_{bk}(h_b) \end{equation}

(52)

and

\begin{equation} \frac{\mathrm{d} N_a}{\mathrm{d}t} = \frac{\nu _a}{X_a \tilde{\Omega }_a} \sum _b X_b \boldsymbol {v}_{ab} \cdot \nabla _a W_{ab}(h_a). \end{equation}

(53)

6.1.1 The general momentum equation

From straightforward differentiation of equation (48) using equation (46), the first law of thermodynamics, |$\mathrm{\partial} u_b/\mathrm{\partial} n_b= P_b/n_b^2$|⁠, and |$\mathrm{\partial} (\gamma _b^{-1})/ \mathrm{\partial} \boldsymbol {v}_a= \gamma _b \boldsymbol {v}_b \delta _{ab}$|⁠, one finds the canonical momentum (for the explicit steps, see Rosswog 2009)

\begin{equation} \boldsymbol {p}_a \equiv \frac{\mathrm{\partial} L}{\mathrm{\partial} \boldsymbol {v}_a}= \nu _a \boldsymbol {S}_a= \nu _a \gamma _a \boldsymbol {v}_a \left(1+u_a + \frac{P_a}{n_a}\right) \end{equation}

(54)

and the evolution equation for the canonical momentum per baryon, |$\boldsymbol {S}_a$|⁠, follows directly from the Euler–Lagrange equations (equation 155 in Rosswog 2009)

\begin{eqnarray} \frac{\mathrm{d} \boldsymbol {S}_a}{\mathrm{d}t} = \!-\! \frac{1}{\nu _a} \sum _{b} \left\lbrace \frac{P_a V_a^2}{\tilde{\Omega }_a} \frac{X_b}{X_a} \nabla _a W_{ab}(h_a) \!\!+\!\! \frac{P_b V_b^2}{\tilde{\Omega }_b} \frac{X_a}{X_b} \nabla _a W_{ab}(h_b) \right\rbrace .\nonumber\\ \end{eqnarray}

(55)

For the choice V_k = ν_k/N_k, this reduces to the momentum equation given in Rosswog (2010).

6.1.2 The general energy equation

The energy derived from the Lagrangian is

\begin{equation} E\equiv \sum _a \frac{\mathrm{\partial} L}{\mathrm{\partial} \boldsymbol {v}_a} \cdot \boldsymbol {v}_a - L = \sum _a \nu _a \epsilon _a, \end{equation}

(56)

where the canonical energy per baryon is

\begin{equation} \epsilon _a = \boldsymbol {v}_a \cdot \boldsymbol {S}_a + \frac{1+u_a}{\gamma _a} = \gamma \left(1 + u_a + \frac{P_a}{n_a} \right) - \frac{P_a}{N_a}, \end{equation}

(57)

or,

\begin{equation} \epsilon _a = \gamma \mathcal {E}- \frac{P}{N}, \end{equation}

(58)

where we have used the specific, relativistic enthalpy

\begin{equation} \mathcal {E}= 1 + u + \frac{P}{n}. \end{equation}

(59)

The subsequent derivation is identical to the one in Rosswog (2009) up to their equation (165),

\begin{equation} \frac{\mathrm{d} \epsilon _a}{\mathrm{d}t}= \boldsymbol {v}_a \cdot \frac{\mathrm{d} \boldsymbol {S}_a}{\mathrm{d}t} + \frac{P_a}{N_a^2} \frac{\mathrm{d} N_a}{\mathrm{d}t}, \end{equation}

(60)

which, upon using equations (53) and (55), yields the special-relativistic energy equation

\begin{eqnarray} \frac{\mathrm{d} \epsilon _a}{\mathrm{d}t}= - \frac{1}{\nu _a} \sum _b \bigg\lbrace \frac{P_a V_a^2}{\tilde{\Omega }_a} \frac{X_b}{X_a} \boldsymbol {v}_b \cdot \nabla _a W_{ab}(h_a)\nonumber\\ + \frac{P_b V_b^2}{\tilde{\Omega }_b} \frac{X_a}{X_b} \boldsymbol {v}_a \cdot \nabla _a W_{ab}(h_b)\bigg\rbrace . \end{eqnarray}

(61)

Again, for V_k = ν_k/N_k, this reduces to the energy equation given in Rosswog (2010).

The set of equations needs to be closed by an EOS. In all of the tests presented below, we use a polytropic EOS

\begin{equation} P= (\Gamma -1)n u, \end{equation}

(62)

where Γ is the polytropic exponent (keep in mind our convention of measuring energies in units of m₀c²). The corresponding sound speed is

\begin{equation} c_{\rm s}= \sqrt{\frac{(\Gamma -1) (\mathcal {E}-1)}{\mathcal {E}}}. \end{equation}

(63)

The choices of the variables N, |$\boldsymbol {S}$| and ϵ are suggested by the Lagrangian derivation and they avoid problems that have plagued earlier relativistic SPH formulations. For a comparison with Eulerian approaches, we refer to the literature, e.g. to Marti & Müller (2003) or Keppens et al. (2012).

6.1.3 Consistent values for smoothing lengths, densities and weights

The smoothing lengths, the CF density and possibly the weight X depend on each other. If the weight depends on the density, say for the case X = P^k, we first perform a few steps to find accurate values of the new pressure: (a) calculate new volumes according to equation (38) using the smoothing lengths and weights from the previous time step, (b) from the resulting new value of the density we update the pressure according to equation (62), (c) update the smoothing length according to equation (26) (d) once more update the volume and (e) again the pressure. This pressure value is finally used to perform an iteration between volume, equation (38), and the smoothing length, equation (26). Due to the previous steps, the guess values at this stage are already very accurate, so that on average only one iteration is needed to meet our convergence criterion |N⁽ⁿ⁺¹⁾ − N⁽ⁿ⁾|/N⁽ⁿ⁺¹⁾ < 10⁻⁴.

While this procedure requires a number of iterations, we find that it is worth the effort, since a careless update of the smoothing length can produce a fair amount of noise that can compromise the quality of a simulation. An inaccurate update of the smoothing lengths may be a largely overlooked source of noise in many SPH codes.

6.2 Special-relativistic SPH based on IAs to derivatives

As an alternative, we suggest a relativistic SPH formulation that is based on the IA of gradients given in equation (24). This generalizes the Newtonian formulation of Garcia-Senz et al. (2012). If we use the formal replacement, equation (25), we can write alternative, integral-based relativistic SPH equations as

\begin{equation} \frac{\mathrm{d}\boldsymbol {S}_a}{\mathrm{d}t}= - \frac{1}{\nu _a} \sum _b \left\lbrace P_a V_a^2 \frac{X_b}{X_a} \boldsymbol {G}_{a} + P_b V_b^2 \frac{X_a}{X_b} \boldsymbol {G}_{b} \right\rbrace \end{equation}

(64)

and

\begin{equation} \frac{\mathrm{d} \epsilon _a}{\mathrm{d}t} = - \frac{1}{\nu _a} \sum _b \left\lbrace P_a V_a^2 \frac{X_b}{X_a} \boldsymbol {v}_b\cdot \boldsymbol {G}_{a} + P_b V_b^2 \frac{X_a}{X_b} \boldsymbol {v}_a\cdot \boldsymbol {G}_{b} \right\rbrace , \end{equation}

(65)

where

\begin{equation} \left(\boldsymbol {G}_{a}\right)^k= \sum _{d=1}^D C^{kd}(\boldsymbol {r}_a,h_a) (\boldsymbol {r}_b - \boldsymbol {r}_a)^d W_{ab}(h_a) \end{equation}

(66)

and

\begin{equation} \left(\boldsymbol {G}_{b}\right)^k= \sum _{d=1}^D C^{kd}(\boldsymbol {r}_b,h_b) (\boldsymbol {r}_b - \boldsymbol {r}_a)^d W_{ab}(h_b). \end{equation}

(67)

The density calculation remains unchanged from equation (36). Note that contrary to Garcia-Senz et al. (2012), we do not apply ‘grad-h’ terms here since they result from derivatives of the kernel function. Since the functions |$\boldsymbol {G}_k$| share the same symmetries as the usual kernel derivatives (i.e. they change their sign if a and b are interchanged), this alternative relativistic SPH formulation also enforces the numerical conservation of physically conserved quantities by construction.

In this scheme, the smoothing lengths are updated exactly as described above for the kernel-gradient based method, see Section 6.1.3.

6.3 Dissipative terms

In order to handle shocks properly, additional measures need to be taken to ensure that appropriate amounts of entropy are generated in shocks. This can be done by implementing a Riemann solver or by adding explicit, artificial dissipation terms which is the approach that we follow here. We use the form of the dissipative terms suggested by Chow & Monaghan (1997)

\begin{equation} \left(\frac{\mathrm{d}\boldsymbol {S}_a}{\mathrm{d}t}\right)_{\rm diss}= - \sum _b \nu _b \Pi _{ab} \overline{\nabla _a W_{ab}} \end{equation}

(68)

\begin{equation} \left(\frac{\mathrm{d}\epsilon _a}{\mathrm{d}t}\right)_{\rm diss}= - \sum _b \nu _b \boldsymbol {\Omega }_{ab} \cdot \overline{\nabla _a W_{ab}}, \end{equation}

(69)

where

\begin{eqnarray} \Pi _{ab}&=& - \frac{K_{ab} v_{{\rm sig},ab}}{\bar{N}_{ab}} \left(\boldsymbol {S}_a^\ast -\boldsymbol {S}_b^\ast \right) \cdot \hat{e}_{ab} \end{eqnarray}

(70)

\begin{eqnarray} \boldsymbol {\Omega }_{ab}&=& - \frac{K_{ab} v_{{\rm sig},ab}}{\bar{N}_{ab}} \left(\epsilon _a^\ast -\epsilon _b^\ast \right)\hat{e}_{ab}, \end{eqnarray}

(71)

for approaching particles and Π_ab = 0 and |$\boldsymbol {\Omega }_{ab}=0$| otherwise. The parameter K_ab is the arithmetic average of the dissipation parameters of the particles a and b whose steering is explained in detail in Section 6.3.1. We use the symmetrized kernel gradient

\begin{equation} \overline{\nabla _a W_{ab}} = \frac{1}{2}\left[\nabla _a W_{ab}(h_a) + \nabla _a W_{ab}(h_b) \right], \end{equation}

(72)

together with

\begin{equation} \gamma _k^\ast = \frac{1}{\sqrt{1-(\boldsymbol {v}_k\cdot \hat{e}_{ab})^2}}, \end{equation}

(73)

\begin{equation} \boldsymbol {S}_k^\ast = \gamma ^\ast _k \left(1+u_k+\frac{P_k}{n_k}\right) \boldsymbol {v}_k \end{equation}

(74)

and

\begin{equation} \vec{\epsilon }_k^\ast = \gamma ^\ast _k \left(1+u_k+\frac{P_k}{n_k}\right) - \frac{P_k}{N_k}. \end{equation}

(75)

For the formulation based on the IA of gradients, |$\overline{\nabla _a W_{ab}}$| needs to be replaced by

\begin{equation} \overline{\boldsymbol {G}}_{ab}= \frac{1}{2}\left[\boldsymbol {G}_a + \boldsymbol {G}_b \right]. \end{equation}

(76)

We found that it is actually important to consistently apply either kernel or IA-gradients in both the non-dissipative and dissipative terms. For example, in geometrically complicated tests such as the blast–bubble interactions shown in Sections 7.8.1 and 7.8.2 we found that slight mismatches in the gradient estimates can lead to instabilities that are serious enough to crash a simulation. With consistent gradients in both types of terms, no such instabilities ever were observed.

For the signal speed, we use (Rosswog 2010)

\begin{equation} v_{{\rm sig},ab}= {\rm max}(\alpha _a,\alpha _b), \end{equation}

(77)

where

\begin{equation} \alpha _k^{\pm }= {\rm max}\left(0,\pm \lambda ^\pm _k\right) \end{equation}

(78)

with |$\lambda ^\pm _k$| being the extreme local eigenvalues of the Euler equations, see e.g. Marti & Müller (2003),

\begin{equation} \lambda ^\pm _k= \frac{v_\parallel \left(1-c_{{\rm s},k}^2\right) \pm c_{{\rm s},k} \sqrt{(1-v^2)\left(1-v_\parallel ^2 - v_\perp ^2 c_{{\rm s},k}^2\right)}}{1-v^2 c_{{\rm s},k}^2} \end{equation}

(79)

and c_s,k being the relativistic sound velocity of particle k, see equation (63). In 1D, this simply reduces to the usual velocity addition law, |$\lambda ^\pm _k= (v_k\pm c_{{\rm s},k})/(1\pm v_k c_{{\rm s},k})$|⁠.

6.3.1 Controlling the amount of dissipation: triggers on shocks and velocity noise

Artificial dissipation is really only needed under specific circumstances such as to produce entropy in shocks where it mimics nature's behaviour, though on a larger, resolvable scale. Nevertheless, in older SPH implementations artificial dissipation was (and still often is) applied everywhere, regardless of whether it is actually needed or not and, as a consequence, one is modelling some kind of a viscous fluid rather than the intended inviscid Euler equations.

Morris & Monaghan (1997) suggested as a cure to provide each particle with its own dissipation parameter K_a and to evolve this dissipation parameter according to an additional ordinary differential equation (ODE)⁴

\begin{equation} \frac{\mathrm{d}K_a}{\mathrm{d}t}= \mathcal {K}^+_{\;a} - \mathcal {K}_{\;a}^-. \end{equation}

(80)

They suggested for the source term

\begin{equation} \mathcal {K}_a^+= {\rm max}\left(-(\nabla \cdot \boldsymbol {v})_a,0\right) \end{equation}

(81)

and

\begin{equation} \mathcal {K}_a^- = \frac{K_a(t) - K_{\rm min}}{\tau _a} \end{equation}

(82)

for the decay term, where K_min represents a minimum, ‘floor’ value for the viscosity parameter and τ_a is the individual decay time-scale. This approach (or slight modifications of it) has been shown to substantially reduce unwanted effects in practical simulations (Rosswog et al. 2000; Dolag et al. 2005; Wetzstein et al. 2009).

Recently, Cullen & Dehnen (2010) suggested further improvements to the Morris & Monaghan (1997) approach. They argued that a floor value for the viscosity parameter is unnecessary and that the original scheme may, in some situations, be too slow to reach the required values of the dissipation parameter. They suggest to immediately raise the viscosity parameter to the desired value rather than obtaining it by integrating the above ODE. Moreover, and as already noted in the original paper of Morris & Monaghan (1997), a scheme with the originally suggested source term, equation (81), would also spuriously trigger on a constant slow compression with |$\nabla \cdot \boldsymbol {v}$|= const. Therefore, Cullen & Dehnen (2010) suggested to trigger on the time derivative of |$\nabla \cdot \boldsymbol {v}$|⁠. They further pointed out that |$\nabla \cdot \boldsymbol {v}$| as calculated by standard SPH gradients can have substantial errors which trigger unnecessary dissipation in shear flows even if standard shear-limiters (Balsara 1995) are used.

Strategy. Before we come to the detailed expressions used here, we want to briefly summarize our strategy when to apply dissipation. The challenge is to assign at each time step to each particle an appropriate dissipation parameter K_a. We trigger dissipation by (a) shocks and (b) (to a lesser extent) by velocity noise. The presence of a noise trigger allows us to let the dissipation parameter decay extremely quickly: if noise should appear, the noise trigger will take care of it. Like in Cullen & Dehnen (2010), the current viscosity value is compared to a ‘desired’ value and, if indicated, it is raised immediately. In our case, the desired parameter value is the maximum of a shock and noise value

\begin{equation} K_{a,\rm des}= {\rm max}(K_{a,\rm shock},K_{a,\rm noise}), \end{equation}

(83)

and if K_{a, des} > K_a(t), we instantaneously set K_a = K_{a, des}, otherwise K_a(t) smoothly decays according to

\begin{equation} \frac{\mathrm{d}K_a}{\mathrm{d}t}= - \mathcal {K}_{\;a}^-= - \frac{K_a(t)}{\tau _a}. \end{equation}

(84)

Note that all the velocity gradients that enter our dissipation scheme are calculated via the accurate gradient prescriptions of the fIA, see equation (21). This is similar to recent approaches by Cullen & Dehnen (2010) and Read & Hayfield (2012) that also used more accurate, non-standard gradient estimates.

Shock trigger. We use the temporal change of the compression as a shock indicator (Cullen & Dehnen 2010)

\begin{equation} A_{a,\rm shock}= {\rm max} \left( - \frac{\mathrm{d} (\nabla \cdot \boldsymbol {v})_a}{\mathrm{d}t},0 \right). \end{equation}

(85)

We have also performed a number of experiments combining both spatial (Read & Hayfield 2012) and temporal changes (Cullen & Dehnen 2010) of the compression, but did not find any obvious advantage with respect to equation (85). Since the latter is simple to calculate (as a numerical derivative) and does not involve second derivatives, we use it in the subsequent tests. From this shock indicator, we calculate the desired shock dissipation parameter

\begin{equation} K_{a,\rm shock}= K_{\rm max} \frac{A_{a,\rm shock}}{A_{a,\rm shock} + (c_{{\rm s},a}/h_a)^2}. \end{equation}

(86)

Noise trigger. We also wish to have the possibility to apply dissipation in regions of ‘velocity noise’. This is less crucial than the shock trigger and not really required, but it improves the convergence (as shown at the example of the Gresho–Chan vortex). Noisy regions are characterized by fluctuations in the sign of |$\nabla \cdot \boldsymbol {v}$|⁠, i.e. some particles feel an expansion while their neighbours get compressed. Therefore, the ratio

\begin{equation} \frac{S_{1,a}}{S_{2,a}}\equiv \frac{\sum _b (\nabla \cdot \boldsymbol {v})_{b,\rm fIA}}{\sum _b |\nabla \cdot \boldsymbol {v}|_{b,\rm fIA}} \end{equation}

(87)

can deviate from ±1 in a noisy region since contributions of different sign are added up in S_1,a and therefore such deviations can be used as a ‘noise indicator 1’:

\begin{equation} \mathcal {N}_a^{(1)}= \left| \frac{\tilde{S}_{1,a}}{S_{2,a}} - 1\right|, \end{equation}

(88)

where the quantity

\begin{equation} \tilde{S}_{1,a}= \left\lbrace \begin{array}{ll}-S_{1,a} & {\rm if} \; (\nabla \cdot \boldsymbol {v})_{a} < 0 \\ \quad S_{1,a} & {\rm else}\end{array}\right.. \end{equation}

(89)

If all particles in the neighbourhood are either compressed or expanding, |$\mathcal {N}_a^{(1)}$| vanishes.

The noise trigger of equation (88) actually only triggers on the signs of |$\nabla \cdot \boldsymbol {v}$| and does not take into account how substantial the compressions/expansions are compared to the ‘natural scale’ c_s/h. The above noise trigger therefore switches on even if the fluctuation is not very substantial, but only causes a very small level of the dissipation parameter (∼0.02 for our typical parameters, see below). One might therefore, alternatively, consider to simply apply a constant ‘dissipation floor’ K_min. We chose, however, the trigger-version, both for the aesthetic reason that we do not want untriggered dissipation and since the triggered version shows a slightly higher convergence rate in the Gresho–Chan test. The differences, however, are not very significant.

We also want to add a noise trigger that takes the significance of the noise in comparison to the natural scale c_s/h into account. This turns out to have beneficial effects to get rid of ‘post-shock wiggles’ that can still be present when the shock-triggered dissipation has already decayed. To this end, we calculate average |$\nabla \cdot \boldsymbol {v}$| values separately for each sign:

\begin{eqnarray} \mathcal {S}^+_a &=& \frac{1}{ N^+} \; \sum _{b, \nabla \cdot \boldsymbol {v}_b>0}^{N^+} \gamma _b \nabla \cdot \boldsymbol {v}_b \end{eqnarray}

(90)

\begin{eqnarray} \mathcal {S}^-_a &=& - \frac{1}{N^-} \; \sum _{b, \nabla \cdot \boldsymbol {v}_b<0}^{N^-} \gamma _b \nabla \cdot \boldsymbol {v}_b, \end{eqnarray}

(91)

where N⁺/N⁻ is number of neighbour particles with positive/negative |$\nabla \cdot \boldsymbol {v}$| and γ_b is the Lorentz factor. The quantity that we trigger on is the product of both quantities. If there are sign fluctuations, but they are small compared to c_s/h, the product is very small, if we have a uniform expansion or compression one of the factors will be zero. So only for sign changes and significantly large compressions/expansions will the product have a substantial value. Therefore, our ‘noise indicator 2’ reads

\begin{equation} \mathcal {N}_a^{(2)}= \sqrt{\mathcal {S}^+_a \mathcal {S}^-_a}. \end{equation}

(92)

The final noise parameter is then

\begin{equation} K_{a,{\rm noise}}= K_{\rm max} \; {\rm max}\left(\kappa ^{(1)}_{a},\kappa ^{(2)}_{a}\right), \end{equation}

(93)

where

\begin{equation} \kappa ^{(1)}_{a}= \frac{\mathcal {N}^{(1)}_a}{ \mathcal {N}^{(1)}_a+ \mathcal {N}_{\rm \; \; noise}} \end{equation}

(94)

and

\begin{equation} \kappa ^{(2)}_{a}= \frac{\mathcal {N}^{(2)}_a}{\mathcal {N}^{(2)}_a + 0.2 (c_{{\rm s},a}/h_a)}. \end{equation}

(95)

The reference value |$\mathcal {N}_{\rm \; \; noise}$| is determined via the Gresho–Chan vortex test, see Section 7.4. The desired dissipation parameter is then chosen as in equation (83) from equations (86) and (93).

Parameters. We determine the dimensionless parameters in the above scheme by a large number of numerical experiments. If not triggered, the dissipation parameter K_a decays on a time-scale

\begin{equation} \tau _a= \chi \frac{h_a}{c_{{\rm s},a}}, \end{equation}

(96)

where we use χ = 2 to ensure a very rapid decay. In the Gresho–Chan test, we find good results for |$\mathcal {N}_{\rm \; \; noise}= 50$|⁠, for the maximally possible dissipation parameter we use K_max = 1.5. We found this set of parameters represents a reasonable compromise for all tests.

The functioning of our dissipation triggers is illustrated in Fig. 32.

6.4 Recovery of the primitive variables

Similar to many grid-based approaches, we have to pay a price for the simplicity of the evolution equations (55)/(61) or (64)/(65) with the need to recover the physical variables from the numerical ones (Chow & Monaghan 1997; Rosswog 2010). The strategy is to express all variables in equation (62) in terms of the updated variables |$\boldsymbol {S}, \epsilon , N$| and the pressure P, then solve for the new pressure, and finally substitute backwards until all physical variables are available.

First, solve the momentum equation, equation (54), for the velocity, which together with equation (57) provides us with

\begin{eqnarray} \boldsymbol {v}= \frac{\boldsymbol {S}}{\epsilon + P/N} \;\; {\rm and} \;\; \gamma (P)= \frac{1}{\sqrt{1 - S^2/(\epsilon + P/N)^2}} \;\; {\rm and}\nonumber\\ \;\; n(P)= \frac{N}{\gamma (P)}. \end{eqnarray}

(97)

We now still need to find u(P) so that we can substitute everything in equation (62). This can be obtained by solving equation (59) for u and by using equation (46)

\begin{equation} u(P)= \frac{\epsilon }{\gamma } + \frac{P}{\gamma N} (1-\gamma ^2) -1. \end{equation}

(98)

The new value of P is then obtained by a root-finding algorithm for

\begin{equation} f(P) \equiv P - (\Gamma -1) \; n(P) \; u(P) = 0. \end{equation}

(99)

Once the new, consistent value of P is found, one successively recovers (a) the Lorentz factor and velocity from equation (97) (b) the rest-frame density from equation (46) (c) the internal energy from equation (98) and (d) the enthalpy from equation (59).

6.5 Time integration

We use the optimal third-order TVD algorithm (Gottlieb & Shu 1998) with global time step to integrate the system of equations. The time step is simply chosen according to

\begin{equation} \Delta t= C \; {\rm min} \left(\Delta t_{\rm C}, \Delta t_{\rm F} \right), \end{equation}

(100)

where Δt_C = h_min/v_sig,max, |$\Delta t_{\rm F}= \sqrt{h_{\rm min}/|{\rm d}\boldsymbol {S}/{\rm d}t|_{\rm max}}$|⁠, h_min is the minimum smoothing length and |$|{\rm d}\boldsymbol {S}/{\rm d}t|_{\rm max}$| is the maximum momentum derivative of all particles. For the pre-factor, we conservatively use C = 0.5.

7 MULTIDIMENSIONAL BENCHMARK TESTS

All of the following tests, whether in the Newtonian or special-relativistic regime, are performed with a new 2D SPH code, called sphincs_sr. At the current stage, it is by no means optimized, its entire purpose is to explore different (special-relativistic) SPH formulations.

In the following, we scrutinize the effects of the different new elements in number of benchmark tests by using four different SPH formulations:

Formulation 1 (⁠|$\mathcal {F}_1$|⁠):
- Density: equations (36) and (38) with weight X = P^k, k = 0.05
- Momentum equation: equation (64)
- Energy equation: equation (65)
- Dissipative terms: see Section 6.3, use equation (76)
- Kernel: Wendland kernel W_3,3 with η = 2.2, see equation (26)
We expect results of similar quality for the W_H,9 kernel, but since the Wendland kernel W_3,3 produced less noise in the ‘noise box’ and the Gresho–Chan vortex test we chose it as our default kernel.
Formulation 2 (⁠|$\mathcal {F}_2$|⁠):
- Density: equations (36) and (38) with weight X = P^k, k = 0.05
- Momentum equation: equation (55)
- Energy equation: equation (61)
- Dissipative terms: see Section 6.3, use equation (72)
- Kernel: Wendland kernel W_3,3 with η = 2.2, see equation (26)
The difference between |$\mathcal {F}_1$| and |$\mathcal {F}_2$| measures the impact of the different gradient prescriptions.
Formulation 3 (⁠|$\mathcal {F}_3$|⁠):
- Density: equations (36) and (38) with weight X = ν
- Momentum equation: equation (64)
- Energy equation: equation (65)
- Dissipative terms: see Section 6.3, use equation (76)
- Kernel: Wendland kernel W_3,3 with η = 2.2, see equation (26)
Same as |$\mathcal {F}_1$|⁠, but with the more ‘standard’ choice X = ν to explore the impact of volume element.
Formulation 4 (⁠|$\mathcal {F}_4$|⁠):
- Density: equations (36) and (38) with weight X = ν
- Momentum equation: equation (55)
- Energy equation: equation (61)
- Dissipative terms: see Section 6.3, use equation (76), constant dissipation parameter K = 1
- Kernel: M₄ kernel with η = 1.2, see equation (26)
These are choices close to what is used in many SPH codes. As will become clear below, these are rather poor choices, i.e. in many cases the accuracy of a code could be substantially increased by a number of relatively simple measures with respect to ‘standard recipes’.

Usually, we will focus on the results of the |$\mathcal {F}_1$| formulation, but when larger deviations for other formulations occur, we also show a brief comparison.

All of the following tests are performed with the special-relativistic code sphincs_sr. But since the discussed improvements are not specific to special relativity but instead concern SPH techniques in general, we discuss both Newtonian and special-relativistic tests. Each of the tests is marked accordingly: ‘N’ for Newtonian and ‘SR’ for special relativity.

7.1 Initial particle distribution (N/SR)

The initial conditions and in particular the initial particle distribution are crucial for the accuracy of an SPH simulation. Of course, the quality indicators |$\mathcal {Q}_{1}$|–|$\mathcal {Q}_{4}$|⁠, equations (4) to (9), should be fulfilled to good accuracy and this suggests to use some type of lattice. Unfortunately, this is not enough and the particle distribution should have at least two more properties: (a) it should be stable for the used SPH formulation–lattice combination, i.e. particles in pressure equilibrium should remain in their configuration and (b) there should not be preferred directions in the particle distribution. Condition (a) means that the particles should be in a minimum energy configuration and how this relates to the kernel choice and the form of the SPH equations is from a theoretical point of view poorly understood to date. Simply placing particles on some type of lattice is usually not good enough: the particles will in most cases begin moving off the lattice and introduce noise. We will explore this explicitly in Section 7.2. Condition (b) is necessary since preferred directions can lead to artefacts, for example, a shock travelling along a preferred direction of a lattice will collect preferentially particles in this direction and this can lead to unwanted ‘ringing’ effects. An example of this effect is shown in Fig. 17.

In the following tests, we will, as a default, place the SPH particles on a hexagonal lattice, see Fig. 7, upper-left panel, but if artefacts can occur we will use a ‘glass-like’ particle distribution instead (upper-rightmost panel). To produce the glass, our strategy is to start from a hexagonal lattice, perturb it heavily and subsequently drive that particles into positions so that they represent a good partition of unity, see equation (4). We proceed according to the following steps.

Place the desired number of particles on a hexagonal lattice (upper-left panel) corresponding to the closest packing of spheres with radii r_s, where each particle has an effective volume of |$2 \sqrt{3} r_{\rm s}^2$| (Fig. 7, first panel, upper row).
Apart from ‘frozen’ boundary particles, perturb the particles heavily by displacing them by a distance r₀ = 0.9r_s in a random direction (Fig. 7, second panel, upper row).
The perturbed particle distribution is then driven to a good partition of unity by applying pseudo-forces proportional to the negative gradient of the quality indicator |$\mathcal {Q}_1$|⁠, see equation (4). Since in the end we want a uniform particle distribution so that all volumes V_b should finally be the same, V₀, we take the volumes out of the sum, use a uniform smoothing length |$h_0= 2.2 \sqrt{V_0}$| and as pseudo-force simply
\begin{equation} \boldsymbol {f}_a= - \sum _b \nabla _a W_{ab}(h_a) \end{equation}
(101)
together with the Wendland kernel. The maximum value of all particles at the initial, heavily perturbed distribution is denoted |$\boldsymbol {f}_{\rm max}^0$|⁠. Obviously, equation (101) just corresponds to a force opposite to the gradient of the SPH particle number density as measured via a kernel summation, so driving the particles to a uniform number density.
As a next step, an iteration is performed. Rather than really using an acceleration and a time step, we apply a displacement so that the particle with the maximum force |$\boldsymbol {f}_{\rm max}^0$| is allowed to be displaced in the first iteration by a distance r₀ = 0.5r_s and in all subsequent iterations by
\begin{equation} \delta \boldsymbol {r}_a = \frac{r_0}{f_{\rm max}^0} \boldsymbol {f}_a. \end{equation}
(102)
This iteration is performed until max|$_a (|\delta \boldsymbol {r}_a|)/r_{\rm s} < 10^{-3}$|⁠. Since the algorithm is designed to take small steps, it takes a large number of steps to meet the convergence criterion (several hundreds for the above parameters); however, the iterations are computationally inexpensive, since they can all be performed with a once (generously large) created neighbour list, so that neighbours only need to be searched once.

Figure 7.

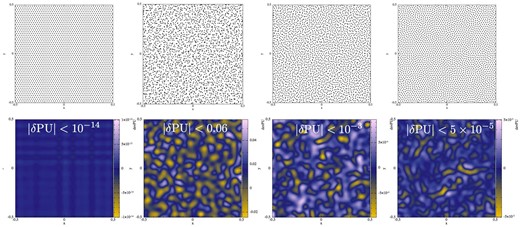
Particle distributions (first row): initial hexagonal lattice (left-hand column), heavily perturbed hexagonal lattice (second column), after 10 iterations (third column) and final distribution (fourth column). The second row shows the deviation from a partition of unity, δPU. Note that the colour bar shows vastly different scales.

Open in new tab Download slide

An example for 10 K particles is shown in Fig. 7: after the initial, heavy perturbation, the maximum of the deviation from the partition of unity is

\begin{equation} \delta {\rm PU}_a \equiv | 1 - \sum _b V_b W_{ab}(h_a)| \end{equation}

(103)

up to 6 per cent, but after only 10 iterations it is below 10⁻³ and once the criterion is met it is below 5 × 10⁻⁵ everywhere. The final particle distribution does not have globally preferred directions, but, of course, this comes at the price of a not perfect (but good!) partition of unity.

7.2 Static I: ‘Noise box’ (N)

To date, there is still only poor theoretical understanding which particle configurations represent stable minimum energy configurations and how this depends on the chosen kernel. As a heuristic approach, one can apply a ‘relaxation method’ where artificial damping is used to drive the particles into a near-optimal configuration. However, this can be very time consuming, it is not necessarily clear when the equilibrium has been reached and the approach can become very challenging in practice for complicated initial conditions.

Often, the particles are simply placed on a lattice which ensures accurate interpolation properties, see Sections 3.1 and 3.2, but this does not guarantee that the particles are in a stable equilibrium position. In practice, for most kernel–lattice combinations the particles will start ‘moving off the lattice’ and keep moving unless they are explicitly damped. It has been observed (Springel 2010a) that this moving-off-the-lattice can hamper proper convergence in KH instabilities and, as we will see below, it also plays a major role in the convergence of the Gresho–Chan vortex problem.

We perform here a simple experiment where we place 10K particles in the domain [0,1] × [0,1] so that their density is N = 1 and their pressure is P = 100 everywhere (Γ = 5/3). We add margins of three smoothing lengths with of ‘frozen boundary particles’ at each side. We perform the experiment twice, once with a hexagonal or ‘CP’ (‘CP-lattice’; left-hand panel in Fig. 8) and once with a quadratic lattice (‘Q-lattice’; right-hand panel in Fig. 8). Ideally, these configurations should be perfectly preserved. Subsequently, we let the inner particles evolve freely (in practice we set our noise parameter to |$\mathcal {N}_{\rm \; \; noise}= 10^6$|⁠, see equation 94, so that the noise trigger does not switch on and no dissipation is applied) and thereby monitor the average particle velocity (in units of the sound speed, 〈v〉/c_s) as a function of time (in units of the sound crossing time, τ_s).

Figure 8.

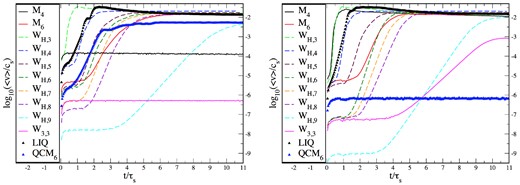
Results of the ‘noise box test’ for an initial hexagonal (left) and Q-lattice (right). Shown is the logarithm of the average particle velocity (in units of the sound speed) as a function of time (in units of the sound crossing time through the computational domain). For both initial lattice configurations and nearly all kernel choices, the particles start eventually moving off the lattice and move with average velocities of 1–2 per cent of the speed of sound. For the hexagonal lattice, only the cubic spline kernel (solid black, right-hand panel; ‘M₄’) and the Wendland kernel (W_3,3) are stable. For the Q-lattice only, the modified quintic spline kernel (blue triangles; ‘QCM₆’) retains the particles in their original configuration on the time-scale of the experiment.

Open in new tab Download slide

There are a number of interesting conclusions from this experiment. First, for almost all kernel choices, the particles eventually move off the initial lattice and move with average velocities of 1–2 per cent of the sound speed. Interesting exceptions are the cubic spline kernel for which the hexagonal lattice seems to be a stable minimum energy configuration (〈v〉/c_s ≈ 10⁻⁴). The Wendland kernel W_3,3 remains to an even higher accuracy (〈v〉/c_s ≈ 5 × 10⁻⁷) on the CP lattice. The W_H,9-kernel remains for around three sound crossing times perfectly on the CP lattice, but then the particles begin to move and settle to a noise level comparable to the lower order kernels (〈v〉/c_s ≈ 10⁻²). It is also interesting that kernels that are naively expected to be close approximations to each other show a very different behaviour in this test. The W_H,3-kernel, which closely approximates M₄, see Fig. 2, shows a very different noise behaviour: at the chosen η (=1.2, like M₄), it already starts forming pairs while M₄ stays nearly perfectly on the CP lattice. Also, the W_H,5-kernel is substantially more noisy than the original M₆-kernel. The modified quintic spline kernel, QCM₆, although not very accurate in previous tests, see Figs 4 and 5, shows actually only little noise. It does not stay on the CP lattice, but nevertheless only produces little noise (〈v〉/c_s ≈ 5 × 10⁻³), and it is the only kernel that remains exactly on the Q-lattice (〈v〉/c_s < 10⁻⁶). Both the W_H,9- and the W_3,3-kernels move off the Q-lattice after about three sound crossing times, but W_3,3 shows a much lower noise level (〈v〉/c_s < 10⁻³ versus ≈10⁻²).

The behaviour in this ‘noisebox test’ is consistent with the results in the Gresho–Chan vortex, see Section 7.4, where noise is one of the accuracy-limiting factors. Also in this latter test, the W_3,3 shows the least noise, followed by the QCM₆-kernel, which performs even better than W_H,9. Interestingly, there seems to be no clear relation between the degree of noise and the kernel order, at least not for the explored initial configurations. The stability properties of particle distributions deserve more theoretical work in the future.

7.3 Static II: surface tension test (N)

As discussed in Section 5, depending on the initial setup, the standard choice for the SPH volume element V_b = ν_b/N_b (or V_b = m_b/ρ_b in the Newtonian case) can lead to spurious surface tension forces across contact discontinuities which can prevent subtle instabilities from growing.

To test for the presence of such a spurious surface tension for the different choices of the volume element, we set up the following experiment. We distribute 20K particles homogeneously on a hexagonal lattice within an outer box of [−1, 1] × [−1, 1]. For the triangular central region with edge points (⁠|$-0.5,-\sqrt{3}/4$|⁠), (⁠|$0.5,-\sqrt{3}/4$|⁠) and (⁠|$0,\sqrt{3}/4$|⁠), we assign the density N_i = 1.0, the outer region has density N_o = 2.0, the pressure is P = P₀ = 2.5 everywhere and the polytropic exponent is chosen as Γ = 5/3. Ideally, the system should stay in exactly this state if it is allowed to evolve. Possibly, present spurious surface tension forces would have the tendency to deform the inner triangle into a circle. We perform this test with formulation |$\mathcal {F}_1$| and |$\mathcal {F}_3$|⁠, but the only difference that matters here is the volume element. In fact, after only t = 5 or about 2.6 sound crossing times, the standard X = ν-discretization has already suffered a substantial deformation, see Fig. 9, while |$\mathcal {F}_1$| does not show any sign of surface tension and is indistinguishable from the original configuration (left-hand panel). The choice X = 1, by the way, yields identical results to X = P^k.

Figure 9.

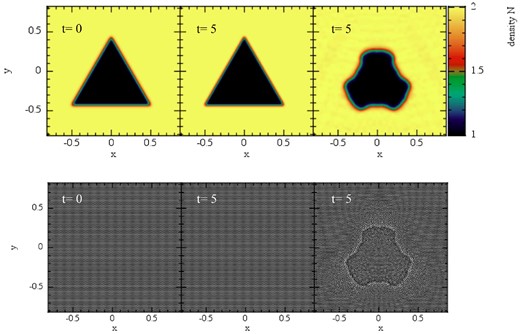
Surface tension test: evolution of a triangular region in pressure equilibrium with its surroundings. The first row shows the density N, the second the corresponding particle distribution. The first column shows the initial condition, the second column the result for weighting factor X = P^k (visually identical to the results obtained with X = 1) and the last column shows the result for the standard SPH volume choice (X = ν corresponding to V_b = ν_b/N_b, or, V_b = m_b/ρ_b in Newtonian language). The standard SPH volume choice shows at t = 5 already strong deformations that are the result of spurious surface tension forces. The alternative choices X = P^k and X = 1 (not shown) perfectly preserve the original shape.

Open in new tab Download slide

7.4 Gresho–Chan-like vortex (N)

The Gresho–Chan vortex (Gresho & Chan 1990) is considered a particularly difficult test in general and in particular for SPH. As shown in Springel (2010a), standard SPH shows very poor convergence in this test. The test deals with a stationary vortex that should be in stable equilibrium. Since centrifugal forces and pressure gradients balance exactly, any deviation from the initial configuration that develops over time is spurious and of purely numerical origin. The azimuthal component of the velocity in this test rises linearly up to a maximum value of v₀ which is reached at r = R₁ and subsequently decreases linearly back to zero at 2R₁

\begin{equation} {v_\varphi (r)}= v_0 \left\lbrace \begin{array}{ll}u \quad\quad\quad\ {\rm for}\quad u \le 1 \\ 2 - u \quad {\rm for \quad } 1 < u \le 2 \\ 0 \quad\quad\quad {\rm for \quad } u > 2, \\ \end{array} \right. \end{equation}

(104)

where u = r/R₁. If we require that centrifugal and pressure accelerations balance, the pressure becomes

\begin{eqnarray} P(r)= P_0 + \left\lbrace \begin{array}{ l l l}\frac{1}{2} v_0^2 u^2 \quad\quad\quad\quad\;\;\;\; {\rm for \quad } u \le 1 \\ 4 v_0^2 \left(\frac{u^2}{8} - u + \ln {u} + 1 \right) \quad\quad{\rm for \quad } 1 < u \le 2 \\ 4 v_0^2 \left(\ln 2 - \frac{1}{2}\right) \;\; \quad\quad{\rm for \quad } u > 2. \end{array} \right.\nonumber \end{eqnarray}

(105)

In the literature on non-relativistic hydrodynamics (Liska & Wendroff 2003; Springel 2010a; Dehnen & Aly 2012; Read & Hayfield 2012), usually v₀ = 1 is chosen together with R₁ = 0.2, a uniform density ρ = 1 and a polytropic exponent of 5/3. Since we want to run this Newtonian test with our special-relativistic code, we choose R₁ = 2 × 10⁻⁴, P₀ = 5 × 10⁻⁷ and v₀ = 10⁻³ to be safely in the non-relativistic limit. For this test, the particles are placed on a hexagonal lattice in the domain [0, 10⁻³] × [0, 10⁻³].

The differential rotation displaces the particles from their original hexagonal lattice positions and therefore introduces some amount of noise. The noise trigger |$\mathcal {N}_{\rm \; \;1}$|⁠, see equation (88), triggers local values of K_a of up to 0.04, |$\mathcal {N}_{\rm \; \;2}$| does not switch on, just as it should. Also, the shock trigger works very well and does practically not switch on at all: in an initial transient phase, it suggests (still negligible) values for the dissipation parameter K_a of ∼10⁻³ and then decays quickly to <10⁻⁶. We have used this test to gauge our noise triggers. We find good results for a noise reference value of |$\mathcal {N}_{\rm \; \; noise} = 50$|⁠, this will be explored further below.

As a first test, we compare the performance of the different formulations |$\mathcal {F}_1$| to |$\mathcal {F}_4$| for 50K particles, see Fig. 10 .

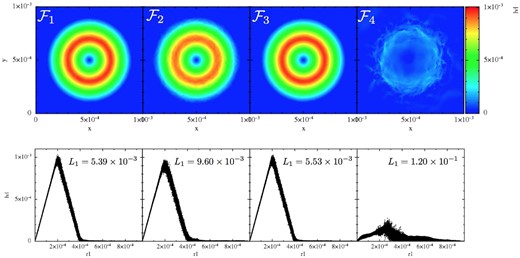
$Performance of the different SPH formulations in the Gresho–Chan vortex test (from left to right column: $\mathcal {F}_1$ to $\mathcal {F}_4$; snapshots are shown at t = 1, all 50K particles are displayed). The upper row shows $|\boldsymbol {v}|$ colour-coded in the x–y-plane, the lower row shows the velocity as a function of the distance to the vortex centre. In the lower row also the L1-error is indicated. The constant high dissipation in $\mathcal {F}_4$ seriously deteriorates the result compared to $\mathcal {F}_1$ to $\mathcal {F}_4$. The impact of the integral-based versus kernel-derivative gradients can be judged by comparing $\mathcal {F}_1$ (integral-based; first column) to $\mathcal {F}_2$ (kernel gradient based; otherwise identical; second column). The choice of the volume element hardly makes a difference in this test (see $\mathcal {F}_1$ versus $\mathcal {F}_3$).$

Figure 10.

Performance of the different SPH formulations in the Gresho–Chan vortex test (from left to right column: |$\mathcal {F}_1$| to |$\mathcal {F}_4$|⁠; snapshots are shown at t = 1, all 50K particles are displayed). The upper row shows |$|\boldsymbol {v}|$| colour-coded in the x–y-plane, the lower row shows the velocity as a function of the distance to the vortex centre. In the lower row also the L₁-error is indicated. The constant high dissipation in |$\mathcal {F}_4$| seriously deteriorates the result compared to |$\mathcal {F}_1$| to |$\mathcal {F}_4$|⁠. The impact of the integral-based versus kernel-derivative gradients can be judged by comparing |$\mathcal {F}_1$| (integral-based; first column) to |$\mathcal {F}_2$| (kernel gradient based; otherwise identical; second column). The choice of the volume element hardly makes a difference in this test (see |$\mathcal {F}_1$| versus |$\mathcal {F}_3$|⁠).

Open in new tab Download slide

Both |$\mathcal {F}_1$| and |$\mathcal {F}_3$| perform nearly identically well in this test, indicating that (as expected) the choice of the volume element has essentially no influence on the result. The integral-based gradients (⁠|$\mathcal {F}_1$| and |$\mathcal {F}_3$|⁠) are substantially less noisy than the kernel-gradient-based ones (⁠|$\mathcal {F}_2$|⁠). Consistent with the findings of Springel (2010a), the |$\mathcal {F}_4$| formulation performs very poorly, mainly due to the unnecessarily high dissipation, but also due to the cubic spline kernel, see below. In the lower row of the figure, we display |$|\boldsymbol {v}|$| as a function of the distance from the vortex centre r1 and also measure the L₁-error norms for the velocity,

\begin{equation} L_1= \frac{1}{N v_0} \sum _{a=1}^{N} |\boldsymbol {v}_a - \boldsymbol {v}(\boldsymbol {r}_a)|, \end{equation}

(106)

with |$\boldsymbol {v}(\boldsymbol {r}_a)$| being the exact stationary solution at position of particle a. The error values for the different formulations are indicated in the lower row of the figure.

To better understand the role of the chosen kernel function, we perform an additional experiment, where we use the best SPH formulation, |$\mathcal {F}_1$|⁠, but vary the kernel (with the smoothing lengths as indicated in Table 3). As already noticed in the ‘noise-box’ test, different kernels exhibit different levels of noise which is crucial for the accuracy in this test. In Fig. 11, we show the results for 25K particles for the CS, M₆, W_H,9 and the W_3,3 kernel. The upper row shows the velocity, colour-coded as function of the position, the lower row displays the velocity as function of the distance to the vortex centre. For our chosen noise reference value |$\mathcal {N}_{\rm \; \; noise}$|⁠, only very little dissipation is released in response to particle noise. Therefore, at the shown time t = 1, the triangular velocity shape is still reasonably well captured in all cases, though with substantial noise overlaid in all cases but W_H,9 and W_3,3. A large fraction of the error is due to the particles moving off their original hexagonal lattice. These results are consistent with the findings from the ‘noise box’ test, see above, and show once more that the W_3,3 kernel only produces a very small amount of noise in comparison to the other explored kernels. We have run this test for the peaked kernels, each time with the same support as the W_3,3 kernel (η = 2.2), not shown. While the LIQ kernel performs poorly and produces very noisy results with a large error (L₁ = 6.06 × 10⁻²), the QCM₆ kernel performs again astonishingly well, though not as good as W_3,3. It produces symmetric, relatively noise-free results with an error of only L₁ = 1.06 × 10⁻², actually even slightly better than the W_H,9 kernel (L₁ = 1.58 × 10⁻²).

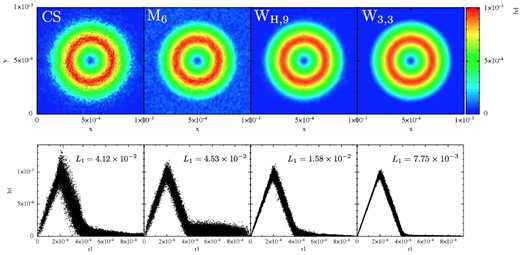
$Performance of different kernels in the Gresho–Chan vortex test. All tests used 25K particles and the SPH formulation $\mathcal {F}_1$ (apart from the kernel choice, of course), results are shown at t = 1. Upper row: $|\boldsymbol {v}|$ in x–y-plane, lower row: $|\boldsymbol {v}|$ as a function of the distance from the vortex centre. From left to right: cubic spline, quintic spline, WH,9 and Wendland kernel. In the lower row also the L1 error norm of the velocity is given. Clearly, the Wendland kernel produces the most accurate result.$

Figure 11.

Performance of different kernels in the Gresho–Chan vortex test. All tests used 25K particles and the SPH formulation |$\mathcal {F}_1$| (apart from the kernel choice, of course), results are shown at t = 1. Upper row: |$|\boldsymbol {v}|$| in x–y-plane, lower row: |$|\boldsymbol {v}|$| as a function of the distance from the vortex centre. From left to right: cubic spline, quintic spline, W_H,9 and Wendland kernel. In the lower row also the L₁ error norm of the velocity is given. Clearly, the Wendland kernel produces the most accurate result.

Open in new tab Download slide

We also explore the convergence with the effective, one-dimensional particle number N_1D of the different formulations in Fig. 12. Clearly, the ‘standard SPH recipe’ formulation |$\mathcal {F}_4$| (blue triangles) performs very poorly, consistent with the findings of Springel (2010a) who concludes that (standard) SPH does not converge to the correct solution. Both our formulations |$\mathcal {F}_1$| (black circles) and |$\mathcal {F}_3$| (green diamonds) converge roughly linearly (long-dashed line). The kernel-gradient version |$\mathcal {F}_2$| converges roughly |$\propto \!N_{\rm 1D}^{-0.6}$|⁠, consistent with the findings of Dehnen & Aly (2012). Recently, also Hu et al. (2014) have implemented a number of worthwhile modifications into the gadget code (Springel 2005) that substantially improve the convergence in the Gresho–Chan vortex. They measured a convergence rate close to 0.8. Read & Hayfield (2012) report a convergence rate close to 0.9.

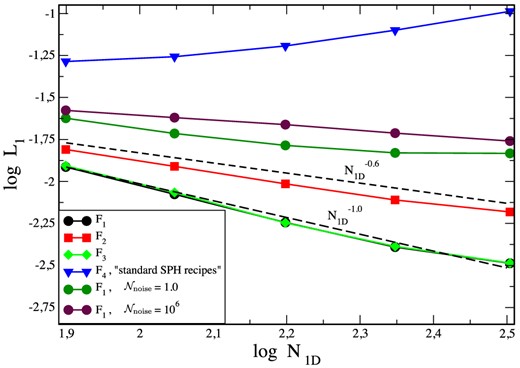
$Convergence in Gresho–Chan vortex test. Our best SPH formulation $\mathcal {F}_1$ converges close to linearly with the effective, one-dimensional particle number N1D (long-dashed line), $\mathcal {F}_3$ performs very similar. Our version with kernel derivatives, $\mathcal {F}_2$, converges somewhat slower, roughly $\propto\! N_{\rm 1D}^{0.6}$ (short-dashed line), consistent with the findings of Dehnen and Aly (2012). The noise trigger clearly improves the convergence, both too little ($\mathcal {N}_{\rm \; \; noise}= 10^6$) and too high sensitivity ($\mathcal {N}_{\rm \; \; noise}= 1.0$) to noise deteriorate the convergence rate. The ‘standard SPH recipe’ formulation, $\mathcal {F}_4$, fails this test rather catastrophically.$

Figure 12.

Convergence in Gresho–Chan vortex test. Our best SPH formulation |$\mathcal {F}_1$| converges close to linearly with the effective, one-dimensional particle number N_1D (long-dashed line), |$\mathcal {F}_3$| performs very similar. Our version with kernel derivatives, |$\mathcal {F}_2$|⁠, converges somewhat slower, roughly |$\propto\! N_{\rm 1D}^{0.6}$| (short-dashed line), consistent with the findings of Dehnen and Aly (2012). The noise trigger clearly improves the convergence, both too little (⁠|$\mathcal {N}_{\rm \; \; noise}= 10^6$|⁠) and too high sensitivity (⁠|$\mathcal {N}_{\rm \; \; noise}= 1.0$|⁠) to noise deteriorate the convergence rate. The ‘standard SPH recipe’ formulation, |$\mathcal {F}_4$|⁠, fails this test rather catastrophically.

Open in new tab Download slide

We also perform experiments to explore the impact of the noise trigger on the convergence: once we run the test without dissipation (in practice |$\mathcal {N}_{\rm \; \; noise}= 10^6$|⁠) and once we deliberately apply too much dissipation (⁠|$\mathcal {N}_{\rm \; \; noise}= 1.0$|⁠). In the first case, there is steady (though slower, approximately |$\propto\! N_{\rm 1D}^{-0.6}$|⁠) convergence, whereas the excessive dissipation in the second case seems to hamper convergence. The moderately triggered dissipation by noise therefore increases the convergence rate. This is our main motivation for using the noise trigger |$\mathcal {N}^{(1)}$|⁠, see equation (88). For many tests, however, we would expect to obtain very similar results even if this (small) source of dissipation was ignored.

7.5 Advection tests (SR)

For our Lagrangian schemes, advection tests do not represent any particular challenge since the code actually has not much to do apart from accurately recovering the primitive variables and advancing the particle positions. Therefore, advection is essentially perfect. We briefly demonstrate the excellent advection properties in the two following tests.

7.5.1 Advection I

In this first test, we start from the configuration of the surface tension test, see Section 7.3, with 7K particles placed inside the domain [−1, 1] × [−1, 1]. We now give each fluid element a velocity in x-direction of v_x = 0.9999 corresponding to a Lorentz factor of γ ≈ 70.7 and apply periodic boundary conditions. In Fig. 13, we show the results for the |$\mathcal {F}_1$| equation set. After 10 times crossing the computational domain,⁵ the shape of the triangle has not changed in any noticeable way. The |$\mathcal {F}_2$| results are visually identical, |$\mathcal {F}_3$| and |$\mathcal {F}_4$| (not shown) deform the triangle like in the previous surface tension test.

Figure 13.

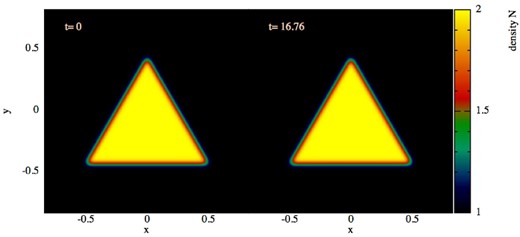
Advection test 1: the initial density pattern shown on the left, constant pressure everywhere, is advected with v_x = 0.9999 (c = 1) corresponding to a Lorentz factor γ = 70.7 through the computational domain with periodic boundary conditions. Right-hand panel: shape after 10 times crossing the computational domain.

Open in new tab Download slide

7.5.2 Advection II

In this second test, we distribute 40K particles in [−1, 1] × [−1, 1]. We place our periodic boundary conditions four smoothing length inside of this domain and denote their coordinates by x₁/x₂ and y₁/y₂. The particles inside are the ‘core’ particles, the particles outside are appropriate copies that enforce the periodic boundary conditions. We set up a density pattern

\begin{eqnarray} N(x,y)= 1 + 0.5 \sin [x \; 2\pi /(x_2-x_1)] \cos [y \; 2\pi /(y_2-y_1)],\nonumber\\ \end{eqnarray}

(107)

use Γ = 5/3 and adjust the internal energy so that the pressure is equal to unity everywhere. All particles receive a constant boost velocity of 0.9c in positive x-direction, corresponding to a Lorentz factor of γ = 2.29. The initial density is shown in the left-hand panel of Fig. 14, the density after crossing the box five times is shown in the right-hand panel, both patterns are virtually identical.

Figure 14.

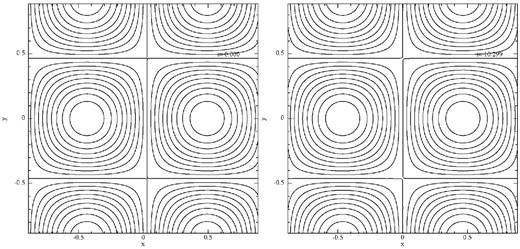
Advection test 2: a density pattern is advected with a velocity of 0.9 c (γ = 2.29) through a box with periodic boundaries. The initial condition (t = 0.000) is shown in the left-hand panel, the result after crossing the box five times (t = 10.299) is shown on the right.

Open in new tab Download slide

7.6 Riemann problems (SR)

Since we have tested a large variety shock benchmark tests in previous work (Rosswog 2010, 2011) and the results of the new formulations do not differ substantially in shocks, we restrict ourselves here to a few standard shock tests and focus on multidimensional tests where either the differences due to the new numerical elements are more pronounced or where SPH has been criticized to not perform well.

7.6.1 Riemann problem I: Sod-type shock

This mildly relativistic shock tube (γ_max ≈ 1.4) has become a widespread benchmark for relativistic hydrodynamics codes (Marti & Müller 1996; Chow & Monaghan 1997; Siegler 2000; Del Zanna & Bucciantini 2002; Marti & Müller 2003). It uses a polytropic exponent of Γ = 5/3, vanishing initial velocities everywhere, the left state has a pressure P_L = 40/3 and a density N_L = 10, while the right state is prepared with P_R = 10⁻⁶ and N_R = 1.

We place 50K particles initially on a hexagonal lattice in [−0.4, 0.4] × [−0.02, 0.02], with particles in the low-density region being rotated by 30°, see below, and use our standard parameter set. The SPH result of the |$\mathcal {F}_1$| formulation (squares, at t= 0.3) agrees very well with the exact solution (solid line), see Fig. 15. Only directly after the shock front some ‘re-meshing noise’ is visible. This is unavoidable since the particles have to move from their initial configuration into a new one which also involves small velocity components in y-direction. This re-meshing noise could be further reduced by applying more dissipation, though at the price of reducing the height of the density plateau near x = 0.25. Note, that with the presented dissipation scheme the theoretical density peak is reached with only 50K particles while in earlier work (Rosswog 2010) it was hardly reached even with 140K particles. This is mainly due to the new shock trigger where the dissipation parameter peaks ∼2 smoothing lengths ahead of the shock and starts decaying immediately after, similar to the case of the Cullen & Dehnen (2010) shock trigger.

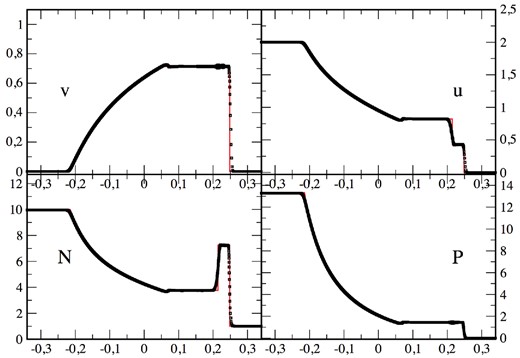
$2D relativistic Sod-type shock tube at t = 0.3. The SPH result ($\mathcal {F}_1$ formulation, 50K particles; note that every particle is shown, i.e. no averaging has been applied) is shown as black squares, the red line is the exact solution.$

Figure 15.

2D relativistic Sod-type shock tube at t = 0.3. The SPH result (⁠|$\mathcal {F}_1$| formulation, 50K particles; note that every particle is shown, i.e. no averaging has been applied) is shown as black squares, the red line is the exact solution.

Open in new tab Download slide

A comparison between the different formulations for only 20K particles (at t = 0.3) is shown Fig. 16. We focus on the post-shock plateau of N since here dissipation effects are particularly visible. The |$\mathcal {F}_1$| formulation delivers the cleanest and ‘edgiest’ result. Note that the choice of X = ν (⁠|$\mathcal {F}_3$|⁠) introduces additional density oscillations. This ‘lattice-ringing’ phenomenon at low dissipation using the standard volume element (i.e. for |$\mathcal {F}_3$|⁠) has been observed in a number of the following tests (KH instabilities, Section 7.7.1), the blast–bubble interactions and the ‘blast-in-a-box’ problem, see Section 7.8). The clearly worst, excessively dissipative result is obtained with formulation |$\mathcal {F}_4$|⁠.

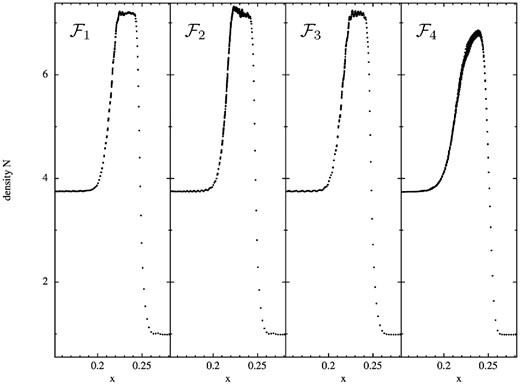
$Low-resolution (20K particles) 2D Sod shock tube test. Shown is the post-shock density plateau at t = 0.3 for the SPH formulations $\mathcal {F}_1$ to $\mathcal {F}_4$ (left to right). The plateau is best captured by the formulations that use the integral-based kernel ($\mathcal {F}_1$ and $\mathcal {F}_3$), among them the version with volume weight X = Pk ($\mathcal {F}_1$) shows fewer oscillations. The version with weight X = Pk but direct kernel gradients ($\mathcal {F}_2$) still works reasonably well, but the ‘standard SPH recipe’ formulation ($\mathcal {F}_4$) is excessively dissipative. Note that the small oscillations in the plateau could be further reduced, though at the expense of more dissipation.$

Figure 16.

Low-resolution (20K particles) 2D Sod shock tube test. Shown is the post-shock density plateau at t = 0.3 for the SPH formulations |$\mathcal {F}_1$| to |$\mathcal {F}_4$| (left to right). The plateau is best captured by the formulations that use the integral-based kernel (⁠|$\mathcal {F}_1$| and |$\mathcal {F}_3$|⁠), among them the version with volume weight X = P^k (⁠|$\mathcal {F}_1$|⁠) shows fewer oscillations. The version with weight X = P^k but direct kernel gradients (⁠|$\mathcal {F}_2$|⁠) still works reasonably well, but the ‘standard SPH recipe’ formulation (⁠|$\mathcal {F}_4$|⁠) is excessively dissipative. Note that the small oscillations in the plateau could be further reduced, though at the expense of more dissipation.

Open in new tab Download slide

In the previous cases, we had rotated the particle distribution on the RHS by 30° to avoid continuously collecting particles along the direction of motion. We illustrate the impact of this measure in the experiment shown in Fig. 17, left-hand panel: we set up a low-resolution (5K particles) version of the above test, once we use the same lattice orientation on both sides (left-hand column, left-hand panel) and once we rotate the distribution by 30° (right-hand column, left-hand panel). While both cases capture the overall solution well, the case without rotation shows a substantial ‘re-meshing noise’ behind the shock while in the rotated case the particles remain well ordered without much velocity noise. Such noise could be removed by adding more dissipation, but rotating the particle distribution is certainly the better option. In the right-hand panel of Fig. 17, we show the results of another experiment (30K particles) where we demonstrate the working of our dissipation triggers. The dissipation parameter K is shown together with the desired values from the noise trigger. We also show the values for the entropy function A, as reconstructed from pressure and density via A = P/n^Γ.

Figure 17.

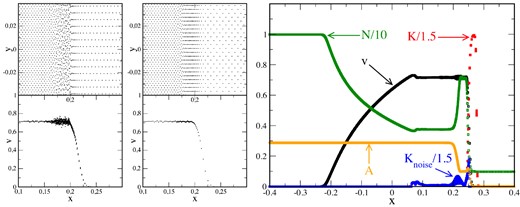
Left: the importance of the initial particle lattice is illustrated by zooming into the shock front of a low-resolution, 2D, relativistic Sod simulation (5K particles). The left-hand column shows the result (particle distribution, above, and velocity, below) for the case where on both sides of the shock a hexagonal lattice with a symmetry axis along the shock motion direction was used. The only difference in the right-hand column is that the initial lattice on the right-hand side was rotated by 30°. This substantially reduces the ‘re-meshing noise’ in the velocity (near x ≈ 0.2) behind the shock. Right: 2D shock tube test (30K particles) where also the dissipation parameter K is shown (red). The blue circles show the parameter values suggested by the noise trigger, the orange symbols show the values of the entropy function A = P/n^Γ.

Open in new tab Download slide

7.6.2 Riemann problem II: relativistic Planar Shock Reflection

As a second problem, we show the result of another standard relativistic shock benchmark test where two gas streams collide, see e.g. Hawley et al. (1984), Eulderink & Mellema (1995), Falle & Komissarov (1996) and Aloy et al. (1999). We use a polytropic exponent of Γ = 5/3 and the left and right state are given by [n, v_x, v_y, u]_L = [1.0, 0.9, 0.0, 2.29 × 10⁻⁵] and [n, v_x, v_y, u]_R = [1.0, −0.9, 0.0, 2.29 × 10⁻⁵], where the incoming velocities correspond to Lorentz factors of γ = 2.29. The result from a simulation with 160K particles initially placed on a hexagonal lattice between [−2.0, 2.0] × [−0.05, 0.05] at t = 0.875 is shown in Fig. 18. Overall, there is excellent agreement with the exact solution (red line), only at the centre an ‘overheating’ or ‘wall heating’ phenomenon occurs in the density and internal energy. This is a well-known phenomenon (Norman & Winkler 1986; Noh 1987; Eulderink & Mellema 1995; Mignone & Bodo 2005) that plagues a large number (if not all) shock-capturing schemes (including, e.g. the Roe, HLLE and HLLC Riemann solvers).

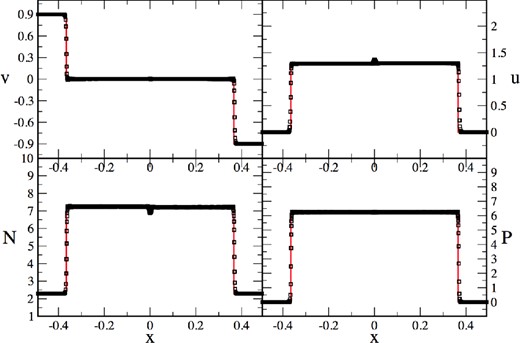
$2D, relativistic planar shock reflection test where two gas streams collide with vx = ±0.9c. The exact solution is shown by the solid, red line the SPH solution ($\mathcal {F}_1$ formulation, t = 0.875) is shown as black squares.$

Figure 18.

2D, relativistic planar shock reflection test where two gas streams collide with v_x = ±0.9c. The exact solution is shown by the solid, red line the SPH solution (⁠|$\mathcal {F}_1$| formulation, t = 0.875) is shown as black squares.

Open in new tab Download slide

As a more extreme version of this test, we use initial velocities of 0.9995c, i.e. [n, v_x, v_y, u]_L = [1.0, 0.9995, 0.0, 2.29 × 10⁻⁵] and [n, v_x, v_y, u]_R = [1.0, −0.9995, 0.0, 2.29 × 10⁻⁵]. Here, the incoming velocities correspond to Lorentz factors of γ = 31.6. We use the same setup as above, but only 80K particles in the same computational domain. Also in this extreme test, the solution is robustly and accurately captured, see Fig. 19. The solution with the |$\mathcal {F}_1$| formulation and our standard parameter set is shown (at t = 0.5) as blue circles and agrees very well with the exact solution (red line). Only at the origin, a wall-heating phenomenon occurs in the internal energy and the density. As an experiment, we repeat the same test with exactly the same setup and parameters, but now we use a dissipation floor K_min = 1, see equation (82). The continued dissipation reduces the amount of wall heating. This is consistent with earlier studies, e.g. Noh (1987) and Rosswog & Price (2007), that find that wall heating is reduced by applying artificial conductivity. The other formulations perform similar well, with differences consistent with those seen in Riemann problem I (see Fig. 16): |$\mathcal {F}_2$| and |$\mathcal {F}_3$| show slightly larger oscillations in the shocked region, |$\mathcal {F}_4$| leads to rounder edges, but also, like the black square solution in Fig. 19, to a slightly quieter shocked region and reduced wall heating due to the larger dissipation.

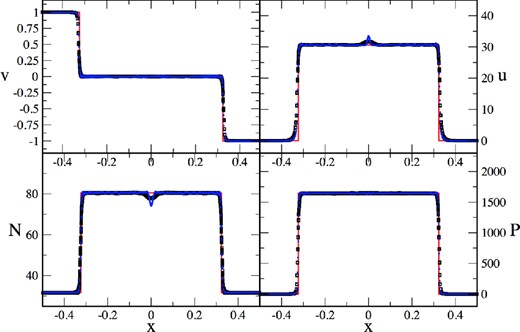
$Two-dimensional, relativistic planar shock reflection test where two gas streams collide with vx = ±0.9995c. The exact solution is shown by the solid, red line the SPH solution ($\mathcal {F}_1$ formulation, t = 0.5) is shown as blue circles for our standard parameter set and as black squares for the same parameters but a dissipation floor Kmin = 1, see equation (82).$

Figure 19.

Two-dimensional, relativistic planar shock reflection test where two gas streams collide with v_x = ±0.9995c. The exact solution is shown by the solid, red line the SPH solution (⁠|$\mathcal {F}_1$| formulation, t = 0.5) is shown as blue circles for our standard parameter set and as black squares for the same parameters but a dissipation floor K_min = 1, see equation (82).

Open in new tab Download slide

7.6.3 Riemann problem III: Einfeldt-type rarefaction test

Here, we explore the ability to properly capture rarefaction waves by means of an Einfeldt-type (Einfeldt et al. 1991) test. The initial conditions⁶ are given by [n, v_x, v_y, P]_L = [0.1, −0.5, 0.0, 0.05] and [n, v_x, v_y, P]_R = [0.1, 0.5, 0.0, 0.05], so that two rarefaction waves (γ ≈ 1.15) are launched in opposite directions. This test had originally been designed to point out a failure mode of Riemann solvers that can return negative densities or pressures in strong rarefaction waves. We setup this test with only 5K particles, placed on a hexagonal lattice between [−0.45, 0.45] × [−0.05, 0.05]. Note that despite the very low particle number, the results of the numerical simulation (⁠|$\mathcal {F}_1$|-formulation; squares; t = 0.3) agree very well with the exact solution (red, solid line), see Fig. 20.

Figure 20.

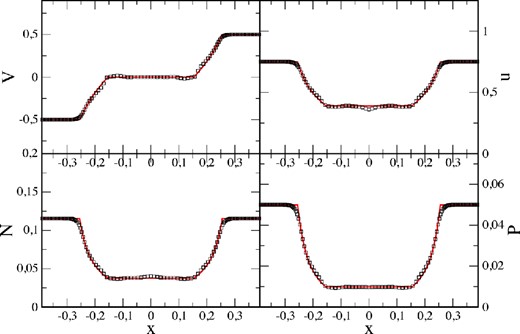
Result of a 2D, Einfeldt-type rarefaction test. The SPH solution (at t = 0.3) is shown as black squares, the exact result as solid, red line. Note that only 5000 particles have been used for this two-dimensional test.

Open in new tab Download slide

7.7 Fluid instabilities (N)

7.7.1 KH instabilities

To scrutinize the ability of the different formulations to capture KH instabilities, we set up an experiment similar to, for example, Robertson et al. (2010) and Garcia-Senz et al. (2012). We place 50K equal mass particles in the domain [0, 1] × [0, 1] so that the horizontal stripe between |$y^{\rm h}_1= 0.25$| and |$y^{\rm h}_2= 0.75$| has density N = 2, while the upper and lower stripes have a density N = 1. Periodic boundary conditions are applied everywhere, the polytropic exponent is Γ = 5/3 and the pressure is P = P₀ = 2.5. The middle, high-density stripe moves with v_x = 0.5 to the right, while the other stripes with v_x = −0.5 to the left. Since we favour equal-mass particles, we setup a ‘quasi-CP’ particle distribution where the effective sphere radius varies with the y-coordinate. Similar to earlier work (Rosswog 2010), we make use of Fermi-functions to create a resolvable transitions. For the ‘double-step’ of this test where a function A changes at |$y^{\rm h}_1$| smoothly from a value A₁ to a value A₂ and at |$y^{\rm h}_2$| from a value A₂ to a value A₃, we use

\begin{eqnarray} A(y)= F\left(A_1,A_2,y^{\rm h}_1,\Delta y,y\right) + F\left(A_2,A_3,y^{\rm h}_2,\Delta y,y\right) - A_2,\nonumber\\ \end{eqnarray}

(108)

where

\begin{equation} F(A,B,y_{t},\Delta y,y)= \frac{A - B}{\exp ((y-y_t)/\Delta y) + 1} + B. \end{equation}

(109)

For the characteristic transition width Δy, we choose the sum of the sphere radii |$r_{\rm s}^{\rm h}$|/|$r_{\rm s}^{\rm l}$| in the high-/low-density region, which we consider a natural choice. In this setup, equal-mass particles reproduce the desired density pattern via their spatial distribution. An example of such a particle distribution (with 8K particles) is shown in Fig. 21, left-hand panel.

Figure 21.

Left-hand panel: example of a ‘quasi-CP’ particle distribution (8K particles) for a KH experiment that produces for equal-mass particles a double-step density distribution. Right-hand panel: growth of the rms y-velocity component as a function of time in the different experiments. The solid lines with circles refer to the strongly triggered cases (v_{y, 0} = 0.1; up to t = 3), dashed lines with squares to the weakly triggered experiments (v_{y, 0} = 0.01; up to t = 5) and dotted lines with triangles to the numerically triggered experiments (up to t = 8).

Open in new tab Download slide

Like in Garcia-Senz et al. (2012), we perturb the interface with a velocity component in y-direction

\begin{equation} v_y(x)= v_{y,0} \sin (2 \pi x), \end{equation}

(110)

for v_x(y) a double-step transition according to equation (108) is used. Note that the particles in the transition region are not necessarily in an equilibrium configuration and subsequent particle re-configurations may trigger additional KH modes apart from the desired one (at least for the high-accuracy formulation |$\mathcal {F}_1$|⁠). Therefore, we perform a ‘relaxation on the fly’, i.e. for t < 0.5 we keep the dissipation parameter K_a on a value of unity and only subsequently we let it evolve freely. This procedure works very well and only triggers the desired mode. Following Garcia-Senz et al. (2012), we perform this test in two flavours: once with a substantial initial perturbation of v_y,0 = 0.1 and the second time we only use v_y,0 = 0.01.

The results for v_y,0 = 0.1 for the different formulations |$\mathcal {F}_1$| (top row) to |$\mathcal {F}_4$| (bottom row) are shown in Fig. 22, each time at t = 0.5, 1.0, 2.0 and 3.0. Overall, there is good agreement between the different SPH formulations, all show a healthy KH growth. Only |$\mathcal {F}_4$| is, as expected, excessively diffusive. In the v_y,0 = 0.01 case, the instability grows slower; therefore, we show in Fig. 23 snapshots at t = 1.0, 3.0, 4.0 and 5.0. Once more, all formulations, even the worst and most diffusive |$\mathcal {F}_4$|⁠, are able to capture the instability. This is different from the findings of Garcia-Senz et al. (2012), their standard SPH formulation does not show a healthy growth, despite their slightly larger particle number (62.5K compared to our 50K). The difference may come from subtleties, for example, they use particles of different masses while we use equal-mass particles. Their particles are placed on a Q-lattice (which is not an equilibrium configuration, see Section 7.2) while ours are on a hexagonal lattice. Moreover, since we apply the dissipation to the numerical variables, see Section 6.3, which contain also the specific energy, this introduces a small amount of conductivity, which might help the instability to grow (Price 2008). Last but not least, we have found that the exact algorithm for the smoothing length update can introduce a fair amount of noise. In our algorithm, we have taken particular care to avoid noise and to have consistent values to a very high accuracy, see Section 6.1.3.

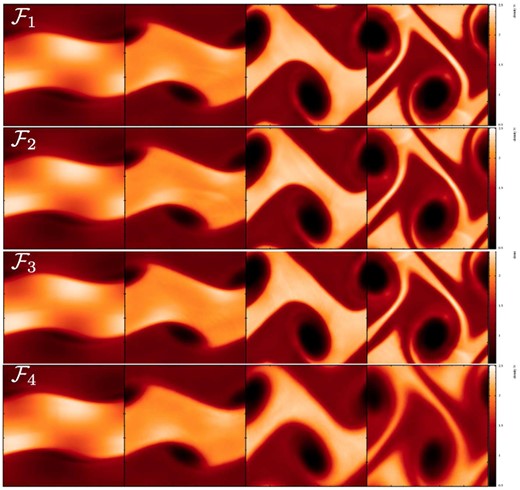
$Comparison of the performance of the different formulation (with 50K particles; colour-coded is the density N) in a KH test triggered by a moderate initial velocity perturbation of vy,0 = 0.1. Each row corresponds to the result of one formulation (top to down: $\mathcal {F}_1$ to $\mathcal {F}_4$), each of the panels in one row refers to t= 0.5, 1.0, 2.0 and 3.0. The $\mathcal {F}_1$ formulation performs best, but the differences between the different formulations are overall only moderate.$

Figure 22.

Comparison of the performance of the different formulation (with 50K particles; colour-coded is the density N) in a KH test triggered by a moderate initial velocity perturbation of v_y,0 = 0.1. Each row corresponds to the result of one formulation (top to down: |$\mathcal {F}_1$| to |$\mathcal {F}_4$|⁠), each of the panels in one row refers to t= 0.5, 1.0, 2.0 and 3.0. The |$\mathcal {F}_1$| formulation performs best, but the differences between the different formulations are overall only moderate.

Open in new tab Download slide

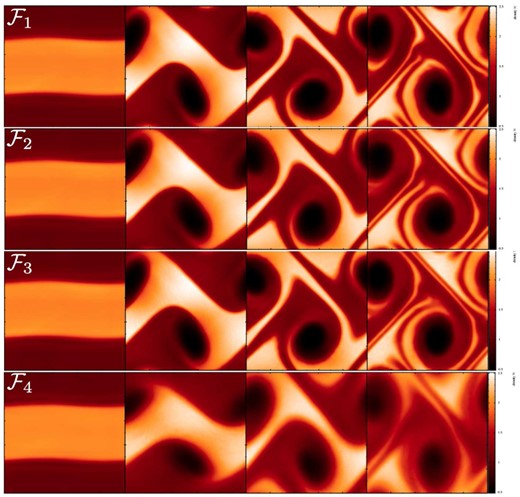
$Comparison of the performance of the different formulation (with 50K particles; colour-coded is the density N) in a KH test triggered by a small initial velocity perturbation amplitude of only vy,0 = 0.01. Each row corresponds to the result of one formulation (top to down: $\mathcal {F}_1$ to $\mathcal {F}_4$), each of the panels in one row refers to t = 1.0, 3.0, 4.0 and 5.0. All cases show a healthy growth of the instability despite the only very small perturbation.$

Figure 23.

Comparison of the performance of the different formulation (with 50K particles; colour-coded is the density N) in a KH test triggered by a small initial velocity perturbation amplitude of only v_y,0 = 0.01. Each row corresponds to the result of one formulation (top to down: |$\mathcal {F}_1$| to |$\mathcal {F}_4$|⁠), each of the panels in one row refers to t = 1.0, 3.0, 4.0 and 5.0. All cases show a healthy growth of the instability despite the only very small perturbation.

Open in new tab Download slide

In a further KH test, no particular mode is excited and the instability is seeded numerically. To this end, we place 200K particles in three stripes of cubic lattices in the computational domain [−1, 1] × [−1, 1], with high-density strip of N = 2 moving with v = 0.2 to the right, while the low-density strips with N = 1 move with v = −0.2 to the left, the pressure is P = 10 and the polytropic exponent Γ = 5/3. The results are shown in Fig. 24 at times t = 4.0, 6.0 and 8.0. In all cases apart from |$\mathcal {F}_4$|⁠, a KH instability with the characteristic billows develops. In the very diffusive |$\mathcal {F}_4$| case, perturbations still grow at the end of the simulation, but at an extremely slow pace. Note that in the case of the ‘standard’ SPH volume element, |$\mathcal {F}_3$|⁠, small vibrations in the particle distributions emerge which appear in the plot as an overlaid ‘grid-like’ pattern (this is not an artefact of the visualization). Such vibrations have also been observed in other tests with |$\mathcal {F}_3$|⁠, see for example Fig. 16. Comparing |$\mathcal {F}_1$| and |$\mathcal {F}_2$| one sees that the more accurate integral-based gradients resolve sharper features in comparison to the kernel-based variant.

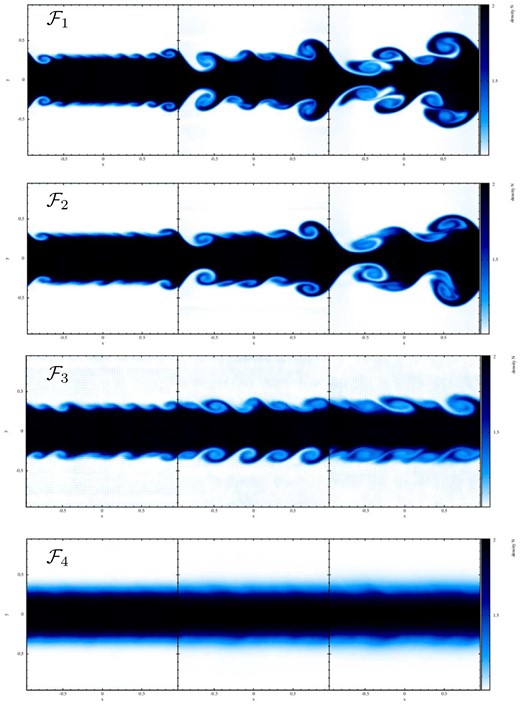
$Numerically triggered KH instability (200K particles; colour-coded is the density N). The high-density band (N = 2) initially moves at −0.2c to the left, while the low-density bands (N = 1) move at 0.2c to the right. No particular mode is excited, the instability grows from small numerical perturbations as the particles at the interface pass along each other. Snapshots are shown at t = 4.0, 6.0 and 8.0 (left to right) for the SPH formulations $\mathcal {F}_1$ (top) to $\mathcal {F}_4$(bottom). Note that the grid-like structure for the $\mathcal {F}_3$ result is not an artefact of the visualization, here the particles vibrate around their lattice positions.$

Figure 24.

Numerically triggered KH instability (200K particles; colour-coded is the density N). The high-density band (N = 2) initially moves at −0.2c to the left, while the low-density bands (N = 1) move at 0.2c to the right. No particular mode is excited, the instability grows from small numerical perturbations as the particles at the interface pass along each other. Snapshots are shown at t = 4.0, 6.0 and 8.0 (left to right) for the SPH formulations |$\mathcal {F}_1$| (top) to |$\mathcal {F}_4$|(bottom). Note that the grid-like structure for the |$\mathcal {F}_3$| result is not an artefact of the visualization, here the particles vibrate around their lattice positions.

Open in new tab Download slide

We measure the instability growth via the rms y-velocity component

\begin{equation} v_{y, {\rm rms}}= \sqrt{\frac{1}{N} \sum _b^N v_{y,b}^2} \end{equation}

(111)

as a function of time, see Fig. 21, right-hand panel, for all three sets of experiments (v_y,0 = 0.1 with solid lines with circles; v_y,0 = 0.01 with dashed lines with squares; numerically triggered with dots and triangle symbols). Generally, the |$\mathcal {F}_1$|-formulation grows fastest, although in the triggered experiments the differences to the |$\mathcal {F}_3$| is small. The |$\mathcal {F}_2$| formulation always grows slower than |$\mathcal {F}_1$|⁠. Although the choice of the volume element makes a difference (comparison |$\mathcal {F}_1$| and |$\mathcal {F}_3$|⁠), the major effect seems to come from the more accurate, integral-based gradients, at least for our setup of the test problem. This might be different for alternative setups. In the numerically triggered experiments, |$\mathcal {F}_3$| very early develops a moderate value for the y-velocity component, which is related to the short-wavelength noise mentioned above, visible in the third row of Fig. 24 as a grid-like pattern underlying the overall density distribution. Such particle noise could possibly hamper the growth of weakly triggered instabilities Springel (2010a). Clearly, the formulation with standard methods, |$\mathcal {F}_4$|⁠, generally shows the slowest growth or – if not triggered explicitly – hardly grows at all.

As a last example, we follow the evolution of 1000K particles with the |$\mathcal {F}_1$| formulation, again without explicitly triggering a particular mode, we simply wait until small numerical perturbations grow into healthy KH billows, see Fig. 25.

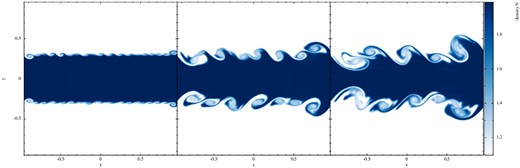
$Growth of a KH instability ($\mathcal {F}_1$-formulation) that has not been triggered explicitly (1000K particles). The density N is shown at t = 2.0, 4.0 and 5.25.$

Figure 25.

Growth of a KH instability (⁠|$\mathcal {F}_1$|-formulation) that has not been triggered explicitly (1000K particles). The density N is shown at t = 2.0, 4.0 and 5.25.

Open in new tab Download slide

7.7.2 Rayleigh–Taylor instabilities

The Rayleigh–Taylor (RT) instability is another classical test case. In its simplest form, it occurs when a denser fluid rests on top of a lighter one in a gravitational field. When perturbed, the denser fluid begins to sink down and the release of gravitational energy triggers a characteristic, ‘mushroom-like’ flow pattern, both for the lighter fluid rising up and the heavier one sinking down. Generally, SPH is thought to be seriously challenged in dealing with RT instabilities, but as we will show below, the suggested measures provide a major improvement also in this case.

We consider two fluid layers with density N₁ and N₂ (N₂ > N₁), separated by a transition located at y_t in an external gravitational field |$\boldsymbol {g}= g \hat{e}_y$|⁠. Since the equilibrium configuration is at rest and the initial velocity perturbation is tiny, we do not distinguish in this setup between local rest-frame and CF densities. We model the external gravitational field as an additional, constant acceleration term in the momentum equation (either equation 55 or 64). To have a well-defined problem, we model the interface by a narrow, but resolvable transition with a width that tends to zero as the resolution increases. Explicitly, we use a Fermi function

\begin{equation} N(y)= N_2 - \frac{\Delta N}{1 + \exp {\left(\frac{y - y_t}{\Delta y}\right)}}, \end{equation}

(112)

where ΔN = N₂ − N₁ and Δy characterizes the transition width of the density step, similar to the KH case, see Section 7.7.1. The hydrostatic equilibrium condition then yields the pressure distribution as a function of height as

\begin{eqnarray} P(y)= g \; \Delta y \; \Delta N \; \ln \left[\frac{1 + \exp \left(-\frac{y-y_t}{\Delta y}\right)}{1 + \exp \left(\frac{y_t}{\Delta y}\right)}\right] + g N_2 y + P(0).\nonumber\\ \end{eqnarray}

(113)

To set up a particle distribution with equal baryon numbers (‘masses’) for each SPH particle, we set up a CP lattice in which the sphere radius r_s varies with y, similar to the KH test above. Again, the transition between the two regions is mediated by varying r_s according to a Fermi function with transition width |$\Delta y= r_{\rm s}^{(1)} + r_{\rm s}^{(2)}$|⁠. We choose the following numbers: the particles are placed in the domain [−0.5, 0.5] × [−1, 1], densities are N₁ = 1, N₂ = 2, the polytropic exponent Γ = 5/3, the pressure P₀= 1 and the external acceleration g = −0.5. These numbers are oriented at the RT test in Garcia-Senz et al. (2012), but our setup differs from theirs with respect to (a) our transition region is smooth, (b) becomes infinitely sharp with particle number going to infinity and (c) in our case, the density information is encoded in the particle distribution (due to our equal baryon number particles) rather than in the particle baryon numbers as in the work of Garcia-Senz et al. (2012). Finally, to trigger the instability, we perturb the interface region slightly (like in Abel 2011 and Garcia-Senz et al. 2012) by

\begin{eqnarray} \delta v_y= &&\left\lbrace \begin{array}{ll}\frac{v_0}{4} \left[1 + \cos \left\lbrace 8 \pi \left(x + \frac{1}{4}\right) \right\rbrace \right] \left[ 1 + \cos \left\lbrace 5 \pi \left(y - \frac{1}{2}\right)\right\rbrace \right] \\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad |y| < 0.25 \\ 0 \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\;\,\, {\rm else}\end{array}\right.,\nonumber\\ \end{eqnarray}

(114)

with a very low perturbation amplitude of v₀ = 0.01. Periodic boundary conditions are applied at x = ±0.5, in the y-direction all derivatives are enforced to vanish for |y| > 0.8.

The hydrodynamic evolution for |$\mathcal {F}_1$| to |$\mathcal {F}_4$| is shown (each time at t = 2.5, 5.0 and 8.25) in Fig. 26. Consistent with the findings of other tests, |$\mathcal {F}_1$| develops the finest density structures and the instability grows fastest. The results for |$\mathcal {F}_2$| and |$\mathcal {F}_3$| are not very different, though, they also show a healthy growth of RT mushrooms. Like in the untriggered KH case, the ‘standard method approach’ |$\mathcal {F}_4$| fails completely and does not allow the weakly triggered instability to grow.

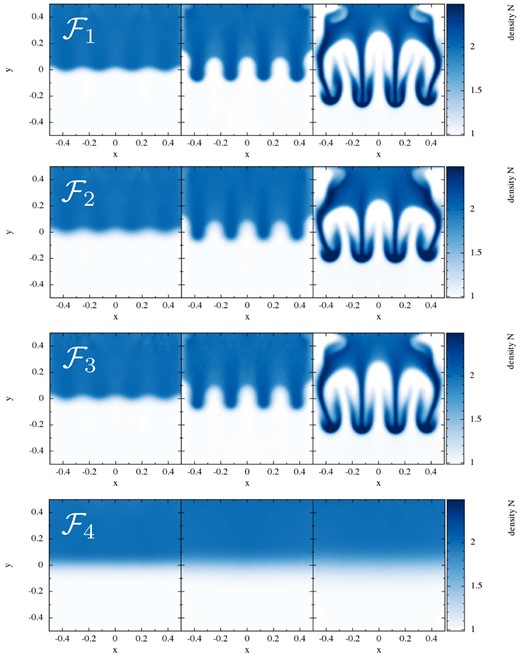
$Growth of a weakly triggered RT instability (50K particles) for the SPH formulations $\mathcal {F}_1$ to $\mathcal {F}_4$. For each formulation, the snapshots are taken at t = 2.5, 5.0 and 8.25.$

Figure 26.

Growth of a weakly triggered RT instability (50K particles) for the SPH formulations |$\mathcal {F}_1$| to |$\mathcal {F}_4$|⁠. For each formulation, the snapshots are taken at t = 2.5, 5.0 and 8.25.

Open in new tab Download slide

In modern adaptive mesh refinement simulations, e.g. Keppens et al. (2012), secondary KH events occur on the falling spikes/pillars. The resolution in our tests is not large enough to resolve them. This is mainly due to the large smoothing length required for the Wendland kernel and due to the use of equal-mass/baryon number particles which lead to particularly low resolution in the low-density regions.

7.8 Combined tests

We also perform a number of more complex tests for which no exact solutions are available and the results need to be compared to other methods documented in the literature. These tests illustrate the robustness and flexibility of the new approaches and demonstrate that a complex interplay between shocks, rarefaction and fluid instabilities can be handled with ease.

7.8.1 Relativistic blast–bubble interaction I (SR)

The interaction of a relativistic blast wave with a spherical bubble that is in pressure equilibrium with its surroundings is a challenging test that probes the ability of capturing shocks, allowing for instabilities and to adapt geometrically. Here, we set up the initial conditions exactly as in He & Tang (2012), their example 6.8, who performed this test with their 2D, special-relativistic adaptive mesh refinement code. This setup results in mildly relativistic velocities (v ≈ 0.35, γ ≈ 1.07). To this end, we place 10⁵ particles on a hexagonal lattice in the domain [0, 325] × [−45, 45] with reflective boundaries at y = ±45 and the states at the left and right end of the domain are frozen. The left-moving shock is initially located at x = 265 and the left/right state are given by

\begin{eqnarray} (N,P,v_x,v_y)= \left\lbrace \begin{array}{ l l}(1, 0.05, 0, 0)&\quad\!\!\! {\rm for \, } x \le 265\\ (1.865\,225, 0.15, \!-\!0.196\,781, 0)&\quad\!\!\! {\rm for \, } x > 265.\\ \end{array} \right.\nonumber\\ \end{eqnarray}

(115)

A polytropic EOS is used with an adiabatic exponent Γ = 5/3. In front of the shock wave, we place a spherically symmetric bubble with radius R_B = 25, centred around (215, 0). The low-density bubble is in pressure equilibrium with its surroundings and in the state given by [N, P, v_x, v_y]_B = [0.1358, 0.05, 0, 0].

In Fig. 27, we show the density at t = 90, 180, 270, 360, 450, as in the original paper, for the |$\mathcal {F}_1$| formulation. The results agree excellently with those found in the relativistic adaptive mesh refinement approach of He & Tang (2012), see their figs 13 and 14, including the shape and location of the various travelling waves.

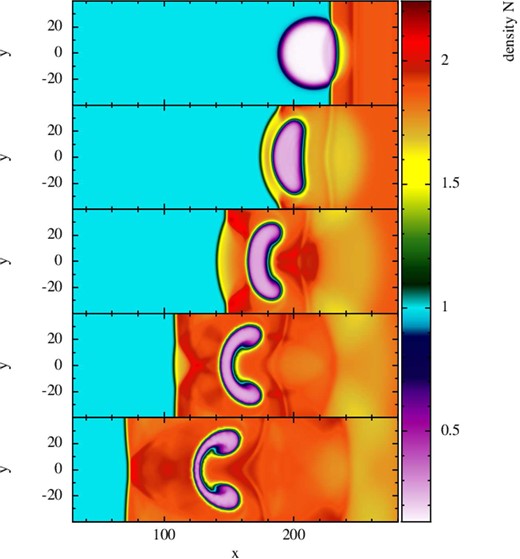
$Blast–bubble interaction I: a blast wave is impacting from the right on to a low-density bubble in pressure equilibrium. This test has been performed with the $\mathcal {F}_1$ formulation and 100K particles. Snapshots are shown at t = 90, 180, 270, 360 and 450.$

Figure 27.

Blast–bubble interaction I: a blast wave is impacting from the right on to a low-density bubble in pressure equilibrium. This test has been performed with the |$\mathcal {F}_1$| formulation and 100K particles. Snapshots are shown at t = 90, 180, 270, 360 and 450.

Open in new tab Download slide

To explore the impact of the various new ingredients, we repeated this test for formulations |$\mathcal {F}_1$| to |$\mathcal {F}_4$| with only 50K particles. A comparison of the results at t = 500 is displayed in Fig. 28. |$\mathcal {F}_1$| clearly performs best, |$\mathcal {F}_4$| does not capture any of the ‘curling in’ of the upper and lower lobe. Here, the gradient accuracy seems crucial (compare |$\mathcal {F}_1$| and |$\mathcal {F}_3$| with |$\mathcal {F}_2$| and |$\mathcal {F}_4$|⁠).

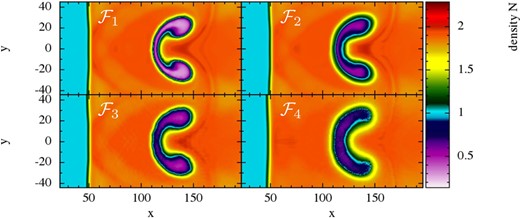
$Comparison of different approaches for blast–bubble interaction I for low resolution (50K particles; at t = 500). Once more, the $\mathcal {F}_1$ formulation clearly performs best, both gradient accuracy (compare $\mathcal {F}_1$ and $\mathcal {F}_2$) and the volume element (upper row versus lower row) impact on the result.$

Figure 28.

Comparison of different approaches for blast–bubble interaction I for low resolution (50K particles; at t = 500). Once more, the |$\mathcal {F}_1$| formulation clearly performs best, both gradient accuracy (compare |$\mathcal {F}_1$| and |$\mathcal {F}_2$|⁠) and the volume element (upper row versus lower row) impact on the result.

Open in new tab Download slide

7.8.2 Relativistic blast–bubble interaction II (SR)

This test is similar to the previous one, but now the bubble has a larger density of N = 3.1538, as in He & Tang (2012), their example 6.9. The higher density results in a different flow pattern, just as in non-relativistic hydrodynamics. This setup results in mildly relativistic velocities (v ≈ 0.35, γ ≈ 1.07). Fig. 29 shows snapshots (200K particles) at t = 100, 200, 300, 400 and 500, just as in the original paper. Again, we find excellent agreement with their results. We again explore the sensitivity to our new ingredients by re-running this test with formulations |$\mathcal {F}_1$| to |$\mathcal {F}_4$| with only 50K particles. The results at t = 500 are displayed in Fig. 30. The tendencies are similar to the previous test. While |$\mathcal {F}_1$| to |$\mathcal {F}_3$| show reasonable agreement, |$\mathcal {F}_1$| shows the cleanest, oscillation-free bubble surface. |$\mathcal {F}_1$| and |$\mathcal {F}_3$| at least show a vague reminiscence of the ‘hole’ near x = 160, y = 0 that is found in high-resolution case. For such small-scale features, the gradient accuracy seems crucial. Again, some oscillations appear for |$\mathcal {F}_3$| near x = 180). Not much structure is visible in the case of |$\mathcal {F}_4$| due to the very large dissipation and surface tension effects.

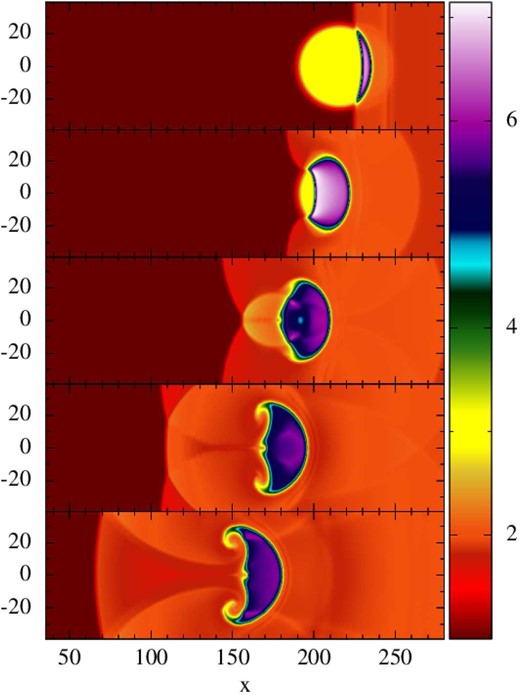
$Blast–bubble interaction II: a blast wave is impacting from the right on to a high-density bubble in pressure equilibrium. This test has been performed with the $\mathcal {F}_1$ formulation and 200K particles. Snapshots are shown at t = 100, 200, 300, 400 and 500. Colour-coded is the CF baryon density N.$

Figure 29.

Blast–bubble interaction II: a blast wave is impacting from the right on to a high-density bubble in pressure equilibrium. This test has been performed with the |$\mathcal {F}_1$| formulation and 200K particles. Snapshots are shown at t = 100, 200, 300, 400 and 500. Colour-coded is the CF baryon density N.

Open in new tab Download slide

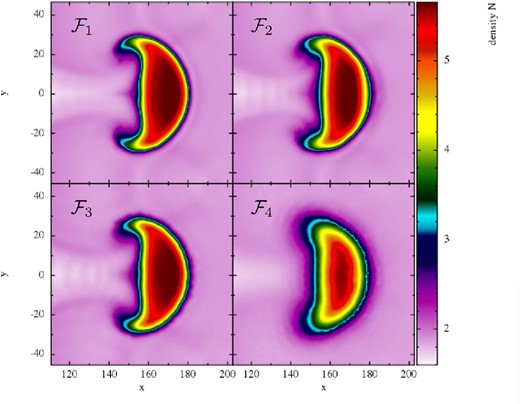
$Comparison of different approaches $\mathcal {F}_1$ to $\mathcal {F}_4$ for a low-resolution comparison of blast–bubble interaction II test (50K particles; t = 500).$

Figure 30.

Comparison of different approaches |$\mathcal {F}_1$| to |$\mathcal {F}_4$| for a low-resolution comparison of blast–bubble interaction II test (50K particles; t = 500).

Open in new tab Download slide

7.8.3 ‘Blast in a box’ (SR)

This test simulates an overpressured central region that expands in a perfectly, spherically symmetric manner. Once the blast is reflected by the boundaries, a complicated interaction between shock–shock and shock–contact discontinuities sets in. In the Newtonian setup of, e.g. Stone et al. (2008), these interactions create the Richtmyer–Meshkov instabilities in the central low-density region. The Richtmyer–Meshkov instabilities in this test are a serious challenge for SPH simulations since they occur in the lowest density regions which are very poorly resolved. Therefore, we run this test at a relatively large resolution (600K particles), but also compare low-resolution simulations (200K) of the different formulations.

In this test, we have experimented somewhat with the initial particle setup, since lattices may lead to a ‘pile up’ of particles in certain directions. We have experimented with a particle setup as described in Section 7.1, but since the combination of Wendland kernel and IA-gradient produces also very symmetrical results for a hexagonal lattice we use for simplicity such a setup in the following tests.

As the actual test problem, we set up 600K particles in the domain [−0.5, 0.5] × [−0.75, 0.75] with periodic boundary conditions everywhere. We use a polytropic EOS with Γ = 5/3. The initial state is characterized by

\begin{eqnarray} (N, P, v_x, v_y)= \left\lbrace \begin{array}{ l l}(1, 10, 0, 0) {\rm for \; } \sqrt{x^2+y^2} \le 0.1 (1, 0.1, 0, 0) {\rm for \; } \sqrt{x^2+y^2} > 0.1. \end{array} \right.\nonumber \end{eqnarray}

(116)

This setup results in maximum Lorentz factors of γ ≈ 3.6. The results (density) for the |$\mathcal {F}_1$| formulation at t = 0.2, 0.7, 1.0, 2.0, 3.0 and 4.0 are shown in Fig. 31. Note the perfectly spherically symmetric expansion of the overpressured bubble despite the lack of exact particle symmetry with respect to the explosion centre. Despite the use of an exact hexagonal lattice with its sixfold symmetry for the initial particle configuration, no ‘particle pile up’ is observed along those directions. This is one of the appreciated qualities of the Wendland kernel, some of the other kernels are explored below. The shocks are reflected back and forth from the boundaries and produce a number of Richtmyer–Meshkov ‘mushrooms’ (high density moving into the central, low-density region; also near x = 0 at the upper and lower boundary), see the last panel of Fig. 31. Note that they are hard to resolve since – on the one hand – the density there is lowest here and we are using a very large kernel support (η = 2.2) so that the resolution length in this region is rather large. Since our initial particle distribution is not symmetric with respect to the reflecting boundaries, the central Richtmyer–Meshkov instabilities are not expected to show a symmetry with respect to the coordinate axis. This is different from simulations by fixed-mesh codes where the grid is usually aligned with the reflecting boundaries and the symmetry in the instabilities can be considered as a quality measure of the simulation.

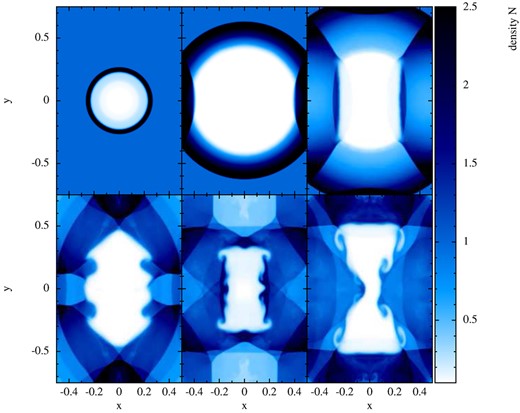
$Blast in a box: shown are snapshots at t = 0.2, 0.7, 1.0, 2.0, 3.0, 4.0 (left to right, top to bottom, $\mathcal {F}_1$) of the CF baryon number density. Note the mushroom-like structures appearing in the central and upper/lower parts of panels 5 and 6.$

Figure 31.

Blast in a box: shown are snapshots at t = 0.2, 0.7, 1.0, 2.0, 3.0, 4.0 (left to right, top to bottom, |$\mathcal {F}_1$|⁠) of the CF baryon number density. Note the mushroom-like structures appearing in the central and upper/lower parts of panels 5 and 6.

Open in new tab Download slide

To illustrate the working of the dissipation switches in such a geometrically complicated situation, we show in Fig. 32 snapshots at t = 0.5 of the simulation shown in Fig. 31. As can be seen from the lower left panel, the shock trigger really only switches on at the shock location, where it produces a razor-sharp circle of high K-values. The noise trigger produces dissipation where particles are arranging themselves after the shock as passed.

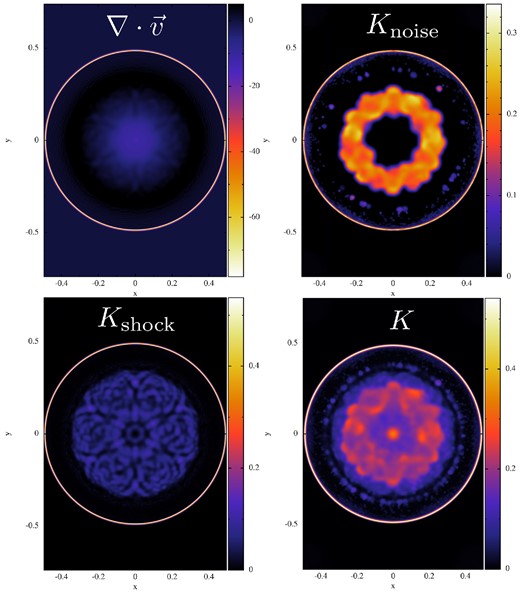
$Illustration of the dissipation switches at the ‘blast in a box’ problem (at t = 0.5). Shown are snapshots of $\nabla \cdot \boldsymbol {v}$, upper left, the instantaneous value of Knoise, added to calm down particles when they are noisy, see equation (93), upper right, the instantaneous value of Kshock, see equation (86), lower left, and the currently used value of K.$

Figure 32.

Illustration of the dissipation switches at the ‘blast in a box’ problem (at t = 0.5). Shown are snapshots of |$\nabla \cdot \boldsymbol {v}$|⁠, upper left, the instantaneous value of K_noise, added to calm down particles when they are noisy, see equation (93), upper right, the instantaneous value of K_shock, see equation (86), lower left, and the currently used value of K.

Open in new tab Download slide

We also briefly compare the four SPH formulations for the case where only 200K particles are used, see Fig. 33. in the low-density central region. Vague anticipations of the Richtmyer–Meshkov instabilities appear in |$\mathcal {F}_1$| to |$\mathcal {F}_3$|⁠, but not in |$\mathcal {F}_4$|⁠. The Richtmyer–Meshkov instabilities for |$\mathcal {F}_2$| seem actually slightly more pronounced than those of |$\mathcal {F}_1$|⁠. We attribute this to the larger noise level for the case of kernel-gradient formulations that helps triggering the instabilities. The mushroom-like structure near x = 0 at the upper and lower boundaries are most developed for |$\mathcal {F}_1$|⁠. As outlined above, however, the major deficiency here is simply the lack of resolution.

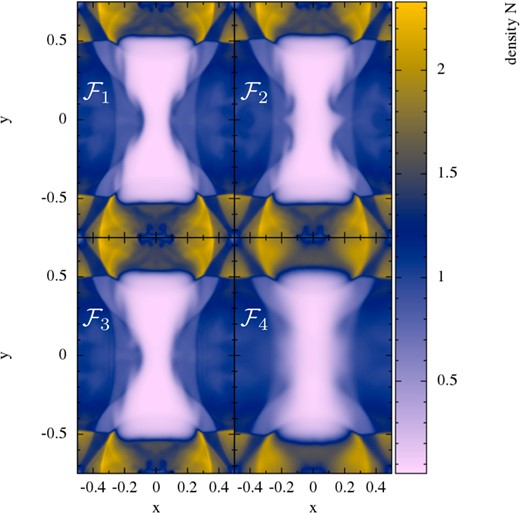
$Comparison of the different formulations ($\mathcal {F}_1$, upper left, to $\mathcal {F}_4$, lower right) for a low-resolution version (200K) of the ‘blast-in-box’ test.$

Figure 33.

Comparison of the different formulations (⁠|$\mathcal {F}_1$|⁠, upper left, to |$\mathcal {F}_4$|⁠, lower right) for a low-resolution version (200K) of the ‘blast-in-box’ test.

Open in new tab Download slide

We use this to compare the new gradient prescription with the standard, kernel-gradient approach. We use 200K particles and compare |$\mathcal {F}_1$| and |$\mathcal {F}_2$|⁠. In Fig. 34, we show density snapshots at t= 0.3. At this stage, the pattern should be perfectly spherically symmetric; however, in the |$\mathcal {F}_2$| case the sixfold symmetry of the underlying hexagonal lattice becomes visible while |$\mathcal {F}_1$| shows practically perfect symmetry. Note, however, that a special colour scheme was chosen to make the noticeable but still moderate differences visible.

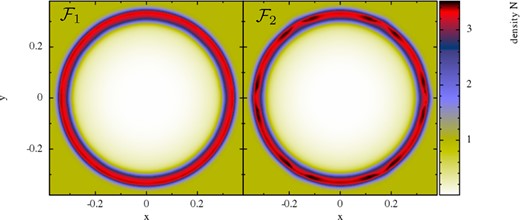
$Comparison between the IA-gradient ($\mathcal {F}_1$, left) and the standard kernel gradient ($\mathcal {F}_2$, right) for a low-resolution version (200K) of the ‘blast-in-box’ test. The IA-gradient shows essentially perfect symmetry while the kernel-gradient shows signs of sixfold symmetry of the underlying hexagonal particle lattice. Note, however, that the differences are small and a particular colour scheme has been chosen to them well visible.$

Figure 34.

Comparison between the IA-gradient (⁠|$\mathcal {F}_1$|⁠, left) and the standard kernel gradient (⁠|$\mathcal {F}_2$|⁠, right) for a low-resolution version (200K) of the ‘blast-in-box’ test. The IA-gradient shows essentially perfect symmetry while the kernel-gradient shows signs of sixfold symmetry of the underlying hexagonal particle lattice. Note, however, that the differences are small and a particular colour scheme has been chosen to them well visible.

Open in new tab Download slide

We perform another test to compare the performance of different kernels under challenging conditions. In particular, we are interested in the level of noise and the question whether the grid symmetries are reflected in aggregated quantities such as the density. To this end, we performed this test with the |$\mathcal {F}_1$| formulation, but once we use the CS kernel (η = 1.2), once the M₆ kernel (η = 1.6), once W_H,9 (η = 2.2) and once the Wendland kernel W_3,3 (η = 2.2). For this test, 79K particles were used. The results at t = 0.45, just before the shock hits the first set of walls, is shown in Fig. 35. The first row shows the density N and the second and third one show |$\nabla \cdot \boldsymbol {v}$| which is a sensitive indicator for the presence of noise. The kernel functions are noted in the panels. Clearly, after the passage of the shock the particles have to re-arrange themselves into a new configuration, so some particle motion and therefore a non-zero value of |$\nabla \cdot \boldsymbol {v}$| is expected. The cubic spline kernel produces the noisiest results, followed by M₆ and the higher order kernels. The Wendland kernel performs slightly better than W_H,9, especially close to the explosion centre where it produces the most symmetric results of all kernels. It is also the only kernel that does not show any sign of the sixfold symmetry of the original hexagonal lattice configuration. Consistent with our previous tests, the Wendland kernel produces the cleanest and least noisy results.

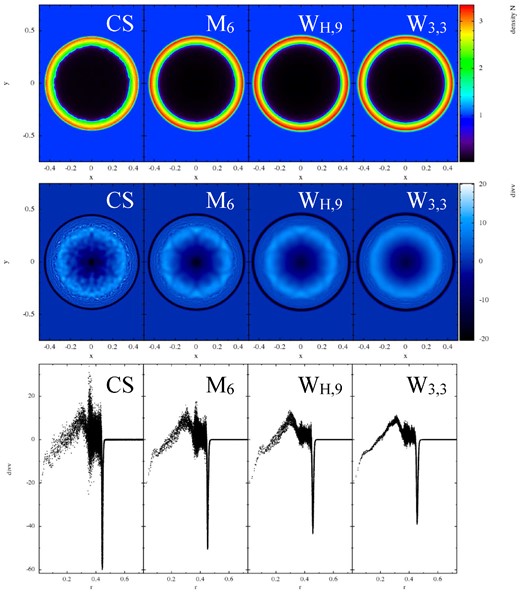
$Importance of the kernel choice in the ‘blast-in-a-box’ test. All tests are performed with the $\mathcal {F}_1$ formulation, apart from the kernel choice. The upper row shows the CF baryon number density and the other rows show $\nabla \cdot \boldsymbol {v}$ as an indicator for the presence of noise, one colour-coded in the XY-plane (middle) and once as function of the distance from the explosion centre (bottom). The first column shows the result for the cubic spline kernel (η = 1.2), the second the M6 kernel (η = 1.6) and column three and four show the results for WH,9 and the Wendland kernel (both with η = 2.2).$

Figure 35.

Importance of the kernel choice in the ‘blast-in-a-box’ test. All tests are performed with the |$\mathcal {F}_1$| formulation, apart from the kernel choice. The upper row shows the CF baryon number density and the other rows show |$\nabla \cdot \boldsymbol {v}$| as an indicator for the presence of noise, one colour-coded in the XY-plane (middle) and once as function of the distance from the explosion centre (bottom). The first column shows the result for the cubic spline kernel (η = 1.2), the second the M₆ kernel (η = 1.6) and column three and four show the results for W_H,9 and the Wendland kernel (both with η = 2.2).

Open in new tab Download slide

8 SUMMARY

In this paper, we have explored the impact of various SPH discretization choices. Motivated by future relativistic applications, we have developed a 2D special-relativistic SPH code, called sphincs_sr, that allows us to explore a large number of different choices. All the tests of this paper – whether in the Newtonian or special-relativistic limit – have been performed with this new code. Part of the motivation of this paper was to show that modern SPH formulations perform very well even in challenging tests where more traditional SPH approaches fail badly.

The effects of the improvements are the following.

Gradients
The first measure concerns the calculations of gradients. We have explored here in particular a prescription that starts from an integral-based function representation and requires the (analytical) inversion of a small matrix. By neglecting appropriate terms, one can recover the same desirable antisymmetry property in particle indices as the standard SPH kernel gradient (for radial kernel functions). Thus, numerical conservation can be ensured in a similar manner as in standard SPH. Such gradient prescriptions had been explored earlier in an astrophysical context by Garcia-Senz et al. (2012) and Cabezon et al. (2012) and, in an engineering context, by Jiang et al. (2014). As we show in Section 3.6, the gradient accuracy can be dramatically increased (∼ 10 orders of magnitude!) if the particle distribution is regular, see Fig. 1. The new prescription also yields much more accurate results under less idealized circumstances. The SPH formulations with the new gradient prescriptions are able to resolve smaller details and they result in less velocity noise (compare |$\mathcal {F}_1$| and |$\mathcal {F}_3$|⁠), see, for example, Figs 10 and 16. Moreover, the gradient prescription turns out to be very beneficial in resolving fluid instabilities, see Section 7.7.
Kernel choice
Apart from the commonly used, ‘standard’ SPH kernel M₄ and the M₆ kernel, we have explored examples of peaked kernels and in particular some high-order members of a recently suggested kernel family (Cabezon et al. 2008) and a high-order Wendland kernel (Wendland 1995). We found that the most commonly used SPH kernel M₄ actually performs rather poorly, see for example Figs 4, 5, 11 and 35. The M₆ kernel is better, but the results still can be substantially improved by employing higher order kernels. The overall best performance was found for the Wendland kernel. It allows for only very little velocity noise, even in highly dynamical situations, see Figs 8, 11 and 35. The explored peaked kernels performed very poorly in practically every respect, even for very large kernel supports.
Volume elements
Motivated by recent suggestions of Saitoh & Makino (2013) and Hopkins (2013), we have generalized our previous relativistic SPH formulation to a class of more general volume elements, see equation (38), that differ from the traditional choice m/ρ in the Newtonian and ν/N in the special-relativistic case. We have in particular explored the case where the weighting quantity is a power of the pressure, |$X_b= P_b^k$|⁠, k = 0.05. This formulation removes spurious surface tension effects, see Fig. 9, and it performs in all of the tests at least as good, but sometimes substantially better than the standard choice X_b = ν_b (corresponding to the usual SPH density sum). In fact, for the standard SPH choice X_b = ν_b together with low dissipation, we have seen in a number of tests ‘lattice ringing effects’, see for example, Figs 24, 30, 28 and 33. Other choices for the weight X are certainly possible and should be explored in future studies.
Dissipation triggers
We have also designed new triggers to decide where dissipation should be applied. Our general strategy is ‘react immediately, decay fast’: if the triggers indicate a desired value that is higher than the currently used value, the dissipation parameter is raised immediately to the indicated value (Cullen & Dehnen 2010) and subsequently it decays exponentially on a very short time-scale. We trigger on both shocks and velocity noise. Our shock trigger is based on the temporal change of the velocity divergence, very similar to the approach of Cullen & Dehnen (2010). We also trigger on the occurrence of velocity noise, see equations (88) and (92). The first of these noise triggers only releases very little dissipation, based on fluctuations in the sign of |$\nabla \cdot \boldsymbol {v}$|⁠. This small amount of extra dissipation substantially improves the convergence rate in the Gresho–Chan test, see Fig. 12, but for a number of tests probably very good results would be obtained even if this trigger was ignored. The second trigger hardly ever switches on, but when it does so, it efficiently damps possibly remaining post-shock oscillations/noise. The addition of such noise triggers allows us to safely choose a very short decay time for the dissipation parameter, since possibly appearing noise is efficiently taken care of. An illustration of the functioning of our dissipation triggers is shown in Figs 17 and 32. In summary, our treatment takes at each time step for each particle a decision on the required dissipation value. This leads to a very local dissipation and essentially removes unwanted effects while providing accurate and robust solutions, even in strong shocks, see Section 7.6.

To disentangle the different effects in benchmark tests, we use four different SPH formulations, in the paper referred to as |$\mathcal {F}_1$| to |$\mathcal {F}_4$|⁠, which are explained in detail at the beginning of Section 7. The first one, |$\mathcal {F}_1$|⁠, contains all suggested improvements, while |$\mathcal {F}_4$| uses every time the worst choices (CS-kernel, direct kernel derivatives, standard SPH volume element and constant, large dissipation parameters), choices that are actually not too far from what is implemented in a number of frequently used SPH codes. The |$\mathcal {F}_1$| formulation delivers excellent results, even in those tests where the ‘standard choices’ fail completely. For example, |$\mathcal {F}_4$| does not converge to the correct solution in the Gresho–Chan vortex, consistent with earlier findings of Springel (2010a), while |$\mathcal {F}_1$| converges in this test close to linearly. Another example are the weakly triggered or untriggered fluid instabilities, see Sections 7.7.1 and 7.7.2, where |$\mathcal {F}_4$| hardly shows any evolution at all while all other formulations show a healthy growth of the instabilities.

We have found |$\mathcal {F}_1$| to be a major improvement over commonly made choices, whether in Newtonian or relativistic tests. So far, no efforts have been undertaken to optimize any of the SPH formulations in terms of computational speed and in this form |$\mathcal {F}_1$| takes approximately twice as much time as |$\mathcal {F}_4$|⁠, mainly due to the required matrix inversion and the substantially larger neighbour number (η = 2.2 rather than 1.2; see equation 26). While we think that the results more than justify the additional computational effort even in the purely hydrodynamic case, the inclusion of other physics ingredients such as self-gravity may actually make the extra effort practically negligible.

In recent years, a number of projects have been carried out to compare numerical hydrodynamics methods that are commonly used in astrophysics (Price & Federrath 2010; Creasey et al. 2011; Bauer & Springel 2012; Scannapieco et al. 2012; Sijacki et al. 2012; Torrey et al. 2012; Bird et al. 2013; Hayward et al. 2014; Hubber, Falle & Goodwin 2013; Nelson et al. 2013). At least to some extent, these investigations were triggered by Lagrangian Voronoi-tesselation codes having become available both for Newtonian (Springel 2010b) and special-relativistic hydrodynamics (Duffell & MacFadyen 2011). Where shortcomings of SPH were identified, they were attributed to excessive dissipation, velocity noise and gradient accuracy. As demonstrated in this study, all these issues can be substantially improved by the suggested measures. Comparisons of the suggested |$\mathcal {F}_1$| SPH formulation (or its Newtonian equivalents) with other methods are left to future studies.

It is a pleasure to acknowledge inspiring discussions with Daniel Price and Joe Monaghan during a sabbatical stay at Monash University. Also the hospitality of the University of Queensland in Brisbane and Monash University, Clayton, Vic 3800, Australia is gratefully acknowledged. The stay in Australia was supported by the DFG by a grant to initiate and intensify bilateral collaboration. This work has further been supported by the Deutsche Forschungsgemeinschaft (DFG) under grant number RO-3399/5-1, by the Swedish Research Council (VR) under grant 621-2012-4870 and by the CompStar network, COST Action MP1304. This work has profited from visits to Oxford which were supported by a DAAD grant ‘Projektbezogener Personenaustausch mit Großbritannien’ under grant number 313-ARC-XXIII-Ik and from visits to La Scuola Internazionale Superiore di Studi Avanzati (SISSA), Trieste, Italy. It is a pleasure to acknowledge in particular the hospitality of John Miller (Oxford, Trieste). SR also gratefully acknowledges the hospitality of Andrew MacFadyen (New York University) and of Enrico Ramirez-Ruiz (UC Santa Cruz) and their home institutions where part of this work was carried out. The stay in Santa Cruz was generously supported by the David and Lucile Packard Foundation. Many of the figures of this article were produced with the visualization software splash (Price & Monaghan 2007). The author also thanks Marius Dan and Franco Vazza for their careful reading of the manuscript. It is a pleasure to acknowledge detailed conversations with Walter Dehnen and to thank him for his insightful comments and a number of useful suggestions.

1

We use the convention that W refers to the full normalized kernel while w is the un-normalized shape of the kernel.

2

This is equivalent to assigning a constant particle mass for the Newtonian case.

3

As will be described in more detail below, we measure energies here in units of the baryon rest mass energy m₀c². The Newtonian correspondence of the expression is, of course, P = (Γ − 1)uρ.

4

We express here everything in terms of our notation where the dissipation parameter is called K. In the literature on non-relativistic SPH, the dissipation parameters are usually called α and β. To translate our approach to non-relativistic SPH, one may replace K by α and choose β as a multiple (usually = 2) of α.

5

The numerical value, t = 16.76, comes from our periodic boundaries being four smoothing length inside the nominal box boundaries.

6

Note that we are specifying here local rest-frame densities rather than CF densities. This is simply for a straightforward comparison with the analytical result obtained by the code ‘riemann-vt.f’ from Marti & Müller (2003).

REFERENCES

Abel

T.

,

MNRAS

,

2011

, vol.

413

pg.

271

Crossref

Search ADS

Agertz

O.

et al. ,

MNRAS

,

2007

, vol.

380

pg.

963

Crossref

Search ADS

Alcubierre

M.

,

Introduction to 3+1 Numerical Relativity

,

2008

Oxford

Oxford Univ. Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Aloy

M. A.

Ibanez

J. M.

Marti

J. M.

Müller

E.

,

ApJS

,

1999

, vol.

122

pg.

151

Crossref

Search ADS

Balsara

D.

,

J. Comput. Phys.

,

1995

, vol.

121

pg.

357

Crossref

Search ADS

Bauer

A.

Springel

V.

,

MNRAS

,

2012

, vol.

423

pg.

2558

Crossref

Search ADS

Baumgarte

T. W.

Shapiro

S. L.

,

Numerical Relativity: Solving Einstein's Equations on the Computer

,

2010

Cambridge

Cambridge Univ. Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Bird

S.

Vogelsberger

M.

Sijacki

D.

Zaldarriaga

M.

Springel

V.

Hernquist

L.

,

MNRAS

,

2013

, vol.

429

pg.

3341

Crossref

Search ADS

Brookshaw

L.

,

PASA

,

1985

, vol.

6

pg.

207

Crossref

Search ADS

Cabezon

R. M.

Garcia-Senz

D.

Relano

A.

,

J. Comput. Phys.

,

2008

, vol.

227

pg.

8523

Crossref

Search ADS

Cabezon

R. M.

Garcia-Senz

D.

Escartin

J. A.

,

A&A

,

2012

, vol.

545

pg.

A112

Crossref

Search ADS

Cha

S.-H.

Whitworth

A. P.

,

MNRAS

,

2003

, vol.

340

pg.

73

Crossref

Search ADS

Cha

S.-H.

Inutsuka

S.-I.

Nayakshin

S.

,

MNRAS

,

2010

, vol.

403

pg.

1165

Crossref

Search ADS

Chow

J. E.

Monaghan

J.

,

J. Comput. Phys.

,

1997

, vol.

134

pg.

296

Crossref

Search ADS

Creasey

P.

Theuns

T.

Bower

R. G.

Lacey

C. G.

,

MNRAS

,

2011

, vol.

415

pg.

3706

Crossref

Search ADS

Cullen

L.

Dehnen

W.

,

MNRAS

,

2010

, vol.

408

pg.

669

Crossref

Search ADS

Dehnen

W.

Aly

H.

,

MNRAS

,

2012

, vol.

425

pg.

1068

Crossref

Search ADS

Del Zanna

L.

Bucciantini

N.

,

A&A

,

2002

, vol.

390

pg.

1177

Crossref

Search ADS

Dolag

K.

Vazza

F.

Brunetti

G.

Tormen

G.

,

MNRAS

,

2005

, vol.

364

pg.

753

Crossref

Search ADS

Duffell

P. C.

MacFadyen

A. I.

,

ApJS

,

2011

, vol.

197

pg.

15

Crossref

Search ADS

Einfeldt

B.

Roe

P. L.

Munz

C. D.

Sjogreen

B.

,

J. Comput. Phys.

,

1991

, vol.

92

pg.

273

Crossref

Search ADS

Eulderink

F.

Mellema

G.

,

A&AS

,

1995

, vol.

110

pg.

587

Falle

S. A. E. G.

Komissarov

S. S.

,

MNRAS

,

1996

, vol.

278

pg.

586

Crossref

Search ADS

Fock

V.

,

Theory of Space, Time and Gravitation

,

1964

Oxford

Pergamon

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Garcia-Senz

D.

Cabezon

R.

Escartin

J.

,

A&A

,

2012

, vol.

538

pg.

A9

Crossref

Search ADS

Gingold

R. A.

Monaghan

J. J.

,

MNRAS

,

1977

, vol.

181

pg.

375

Crossref

Search ADS

Goedbloed

J. P.

Keppens

R.

Poedts

S.

,

Advanced Magnetohydrodynamics

,

2010

Cambridge

Cambridge Univ. Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Gottlieb

S.

Shu

C. W.

,

Math. Comput.

,

1998

, vol.

67

pg.

73

Crossref

Search ADS

Gresho

P. M.

Chan

S. T.

,

Int. J. Numer. Methods Fluids

,

1990

, vol.

11

pg.

621

Crossref

Search ADS

Hawley

J. F.

Smarr

L. L.

Wilson

J. R.

,

ApJ

,

1984

, vol.

277

pg.

296

Crossref

Search ADS

Hayward

C. C.

Torrey

P.

Springel

V.

Hernquist

L.

Vogelsberger

M.

,

MNRAS

,

2014

, vol.

442

pg.

1992

Crossref

Search ADS

He

P.

Tang

H.

,

Commun. Comput. Phys.

,

2012

, vol.

11

pg.

114

Crossref

Search ADS

Heß

S.

Springel

V.

,

MNRAS

,

2010

, vol.

406

pg.

2289

Crossref

Search ADS

Hopkins

P. F.

,

MNRAS

,

2013

, vol.

428

pg.

2840

Crossref

Search ADS

Hubber

D. A.

Falle

S. A. E. G.

Goodwin

S. P.

,

MNRAS

,

2013

, vol.

432

pg.

711

Crossref

Search ADS

Hu

C.-Y.

Naab

T.

Walch

S.

Moster

B. P.

Oser

L.

,

MNRAS

,

2014

, vol.

443

pg.

1173

Crossref

Search ADS

Inutsuka

S.-I.

,

J. Comput. Phys.

,

2002

, vol.

179

pg.

238

Crossref

Search ADS

Jiang

T.

Lu

L.-G.

Lu

W.-G.

,

Comput. Mech.

,

2014

, vol.

53

pg.

977

Crossref

Search ADS

Keppens

R.

Meliani

Z.

van Marle

A. J.

Delmont

P.

Vlasis

A.

van der Holst

B.

,

J. Comput. Phys.

,

2012

, vol.

231

pg.

718

Crossref

Search ADS

Laguna

P.

Miller

W. A.

Zurek

W. H.

,

ApJ

,

1993

, vol.

404

pg.

678

Crossref

Search ADS

Lanczos

C.

,

Applied Analysis

,

1956

Englewood Cliffs, NJ

Prentice-Hall

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Liska

R.

Wendroff

B.

,

SIAM J. Sci. Comput.

,

2003

, vol.

25

pg.

995

Crossref

Search ADS

Lucy

L.

,

AJ

,

1977

, vol.

82

pg.

1013

Crossref

Search ADS

Marti

J.

Müller

E.

,

J. Comput. Phys.

,

1996

, vol.

123

pg.

1

Crossref

Search ADS

Marti

J. M.

Müller

E.

,

Living Rev. Relativ.

,

2003

, vol.

6

pg.

7

Crossref

Search ADS

Mignone

A.

Bodo

G.

,

MNRAS

,

2005

, vol.

364

pg.

126

Crossref

Search ADS

Monaghan

J. J.

,

ARA&A

,

1992

, vol.

30

pg.

543

Crossref

Search ADS

Monaghan

J. J.

,

Rep. Prog. Phys.

,

2005

, vol.

68

pg.

1703

Crossref

Search ADS

Monaghan

J. J.

,

Ann. Rev. Fluid Mech.

,

2012

, vol.

44

pg.

323

Crossref

Search ADS

Morris

J.

Monaghan

J.

,

J. Comput. Phys.

,

1997

, vol.

136

pg.

41

Crossref

Search ADS

Murante

G.

Borgani

S.

Brunino

R.

Cha

S.-H.

,

MNRAS

,

2011

, vol.

417

pg.

136

Crossref

Search ADS

Nelson

D.

Vogelsberger

M.

Genel

S.

Sijacki

D.

Keres

D.

Springel

V.

Hernquist

L.

,

MNRAS

,

2013

, vol.

429

pg.

3353

Crossref

Search ADS

New

K. C. B.

Tohline

J. E.

,

ApJ

,

1997

, vol.

490

pg.

311

Crossref

Search ADS

Noh

W. F.

,

J. Comput. Phys.

,

1987

, vol.

72

pg.

78

Crossref

Search ADS

Norman

M. L.

Winkler

K.-H.

Winkler

K.-H.

Norman

M. L.

,

Astrophysical Radiation Hydrodynamics

,

1986

Dordrecht

Reidel

pg.

449

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Price

D.

,

PhD thesis

,

2004

Univ. Cambridge

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Price

D. J.

,

J. Comput. Phys.

,

2008

, vol.

227

pg.

10040

Crossref

Search ADS

Price

D. J.

,

J. Comput. Phys.

,

2012

, vol.

231

pg.

759

Crossref

Search ADS

Price

D. J.

Federrath

C.

,

MNRAS

,

2010

, vol.

406

pg.

1659

Price

D.

Monaghan

J.

,

MNRAS

,

2007

, vol.

374

pg.

1347

Crossref

Search ADS

Puri

K.

Ramachandran

P.

,

J. Comput. Phys.

,

2014

, vol.

270

pg.

432

Crossref

Search ADS

Read

J. I.

Hayfield

T.

,

MNRAS

,

2012

, vol.

422

pg.

3037

Crossref

Search ADS

Read

J. I.

Hayfield

T.

Agertz

O.

,

MNRAS

,

2010

, vol.

405

pg.

1513

Rezzolla

L.

Zanotti

O.

,

Relativistic Hydrodynamics

,

2013

Oxford

Oxford Univ. Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Robertson

B. E.

Kravtsov

A. V.

Gnedin

N. Y.

Abel

T.

Rudd

D. H.

,

MNRAS

,

2010

, vol.

401

pg.

2463

Crossref

Search ADS

Rosswog

S.

,

New Astron. Rev.

,

2009

, vol.

53

pg.

78

Crossref

Search ADS

Rosswog

S.

,

J. Comput. Phys.

,

2010

, vol.

229

pg.

8591

Crossref

Search ADS

Rosswog

S.

Griebel

M.

Schweitzer

M. A.

,

Lecture Notes in Computational Science and Engineering, Meshfree Methods for Partial Differential Equations V

,

2011

Heidelberg

Springer

pg.

89

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Rosswog

S.

,

2014

preprint (arXiv:1406.4224)

Rosswog

S.

Price

D.

,

MNRAS

,

2007

, vol.

379

pg.

915

Crossref

Search ADS

Rosswog

S.

Davies

M. B.

Thielemann

F.-K.

Piran

T.

,

A&A

,

2000

, vol.

360

pg.

171

Saitoh

T. R.

Makino

J.

,

ApJ

,

2013

, vol.

768

pg.

44

Crossref

Search ADS

Scannapieco

C.

et al. ,

MNRAS

,

2012

, vol.

423

pg.

1726

Crossref

Search ADS

Schaback

R.

Wendland

H.

,

Acta Numer.

,

2006

, vol.

15

pg.

543

Crossref

Search ADS

Schoenberg

I.

,

Q. Appl. Math.

,

1946

, vol.

4

pg.

45

Siegler

S.

,

PhD thesis

,

2000

Eberhard-Karls-Universität Tübingen

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Sijacki

D.

Vogelsberger

M.

Kereš

D.

Springel

V.

Hernquist

L.

,

MNRAS

,

2012

, vol.

424

pg.

2999

Crossref

Search ADS

Springel

V.

,

MNRAS

,

2005

, vol.

364

pg.

1105

Crossref

Search ADS

Springel

V.

,

ARA&A

,

2010a

, vol.

48

pg.

391

Crossref

Search ADS

Springel

V.

,

MNRAS

,

2010b

, vol.

401

pg.

791

Crossref

Search ADS

Stone

J. M.

Gardiner

T. A.

Teuben

P.

Hawley

J. F.

Simon

J. B.

,

ApJS

,

2008

, vol.

178

pg.

137

Crossref

Search ADS

Torrey

P.

Vogelsberger

M.

Sijacki

D.

Springel

V.

Hernquist

L.

,

MNRAS

,

2012

, vol.

427

pg.

2224

Crossref

Search ADS

Valcke

S.

de Rijcke

S.

Rödiger

E.

Dejonghe

H.

,

MNRAS

,

2010

, vol.

408

pg.

71

Crossref

Search ADS

Valdarnini

R.

,

A&A

,

2012

, vol.

546

pg.

A45

Crossref

Search ADS

Wendland

H.

,

Adv. Comput. Math.

,

1995

, vol.

4

pg.

389

Crossref

Search ADS

Wetzstein

M.

Nelson

A. F.

Naab

T.

Burkert

A.

,

ApJS

,

2009

, vol.

184

pg.

298

Crossref

Search ADS

Download all slides

Month:	Total Views:
February 2017	1
March 2017	2
April 2017	4
May 2017	9
June 2017	13
July 2017	3
August 2017	5
September 2017	8
November 2017	2
December 2017	4
January 2018	5
March 2018	5
April 2018	5
May 2018	4
June 2018	15
July 2018	16
August 2018	13
September 2018	12
October 2018	5
November 2018	11
December 2018	6
January 2019	12
February 2019	11
March 2019	18
April 2019	25
May 2019	24
June 2019	14
July 2019	13
August 2019	15
September 2019	5
October 2019	9
November 2019	14
December 2019	15
January 2020	39
February 2020	15
March 2020	11
April 2020	17
May 2020	7
June 2020	10
July 2020	13
August 2020	28
September 2020	31
October 2020	10
November 2020	6
December 2020	11
January 2021	23
February 2021	17
March 2021	26
April 2021	15
May 2021	9
June 2021	21
July 2021	30
August 2021	21
September 2021	17
October 2021	28
November 2021	23
December 2021	16
January 2022	21
February 2022	18
March 2022	34
April 2022	34
May 2022	19
June 2022	19
July 2022	30
August 2022	34
September 2022	21
October 2022	40
November 2022	14
December 2022	10
January 2023	20
February 2023	16
March 2023	13
April 2023	16
May 2023	12
June 2023	19
July 2023	29
August 2023	15
September 2023	21
October 2023	30
November 2023	19
December 2023	31
January 2024	33
February 2024	32
March 2024	44
April 2024	15
May 2024	31
June 2024	21
July 2024	45
August 2024	17
September 2024	13
October 2024	23
November 2024	21
December 2024	13
January 2025	23
February 2025	18
March 2025	47
April 2025	9
May 2025	7

Article Contents

Boosting the accuracy of SPH techniques: Newtonian and special-relativistic tests

Abstract

1 INTRODUCTION

2 TRANSLATION BETWEEN NEWTONIAN AND SPECIAL-RELATIVISTIC APPROACHES

3 INTERPOLATION AND GRADIENTS

3.1 SPH kernel interpolation

3.2 Standard SPH gradient

3.3 Constant-exact gradient

3.4 Linear-exact gradient

3.5 Integral-based gradient

3.6 Assessment of the gradient accuracy

4 KERNEL CHOICE

4.1 Kernels

4.1.1 Kernels with vanishing central derivatives

4.1.2 Kernels with non-vanishing central derivatives

4.2 Accuracy assessment

4.2.1 Kernel support size

4.2.2 Density estimates

4.2.3 Gradient estimates

5 GENERALIZED VOLUME ELEMENTS

6 SPECIAL-RELATIVISTIC SPH

6.1 Special-relativistic SPH with kernel derivatives

6.1.1 The general momentum equation

6.1.2 The general energy equation

6.1.3 Consistent values for smoothing lengths, densities and weights

6.2 Special-relativistic SPH based on IAs to derivatives

6.3 Dissipative terms

6.3.1 Controlling the amount of dissipation: triggers on shocks and velocity noise

6.4 Recovery of the primitive variables

6.5 Time integration

7 MULTIDIMENSIONAL BENCHMARK TESTS

7.1 Initial particle distribution (N/SR)

7.2 Static I: ‘Noise box’ (N)

7.3 Static II: surface tension test (N)

7.4 Gresho–Chan-like vortex (N)

7.5 Advection tests (SR)

7.5.1 Advection I

7.5.2 Advection II

7.6 Riemann problems (SR)

7.6.1 Riemann problem I: Sod-type shock

7.6.2 Riemann problem II: relativistic Planar Shock Reflection

7.6.3 Riemann problem III: Einfeldt-type rarefaction test

7.7 Fluid instabilities (N)

7.7.1 KH instabilities

7.7.2 Rayleigh–Taylor instabilities

7.8 Combined tests

7.8.1 Relativistic blast–bubble interaction I (SR)

7.8.2 Relativistic blast–bubble interaction II (SR)

7.8.3 ‘Blast in a box’ (SR)

8 SUMMARY

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only