-
PDF
- Split View
-
Views
-
Cite
Cite
Antonio J. Cuesta, Licia Verde, Adam Riess, Raul Jimenez, Calibrating the cosmic distance scale ladder: the role of the sound-horizon scale and the local expansion rate as distance anchors, Monthly Notices of the Royal Astronomical Society, Volume 448, Issue 4, 21 April 2015, Pages 3463–3471, https://doi.org/10.1093/mnras/stv261
Close - Share Icon Share
Abstract
We exploit cosmological model-independent measurements of the expansion history of the Universe to provide a cosmic distance ladder. These are supernovae Type Ia used as standard candles (at redshift between 0.01 and 1.3) and baryon acoustic oscillations (at redshifts between 0.1 and 0.8) as standard rulers. We calibrate (anchor) the ladder in two ways: first using the local H0 value as an anchor at z = 0 (effectively calibrating the standard candles) and secondly using the cosmic microwave background-inferred sound-horizon scale as an anchor (giving the standard ruler length) as an inverse distance ladder. Both methods are consistent, but the uncertainty in the expansion history H(z) is smaller if the sound-horizon scale is used. We present inferred values for the sound horizon at radiation drag rd which do not rely on assumptions about the early expansion history nor on cosmic microwave background measurements but on the cosmic distance ladder and baryon acoustic oscillations measurements. We also present derived values of H0 from the inverse distance ladder and we show that they are in very good agreement with the extrapolated value in a Λ cold dark matter model from Planck cosmic microwave background data.
1 INTRODUCTION
Accurate distance determinations at cosmological distances have been one of the observational evidences on which the standard cosmological model is built. It is the distance redshift relation that gives us the Universe's expansion history and from there we gather information about the Universe's content (dark matter and most importantly dark energy) e.g. Riess et al. (1998) and Perlmutter et al. (1999).
Since no one technique could, until recently, measure distances of extragalactic or cosmologically distant objects,1 a succession of methods was used. In this approach – the cosmic distance ladder – each rung of the ladder provides the information necessary to determine the distance of the next rung, see e.g. Rowan-Robinson (1985) for an historical introduction. Traditionally, the cosmic distance ladder relies on standard candles and in particular Type 1a supernovae (SN1a), to extend the ladder well into the Hubble flow, i.e. at distances beyond roughly 100 Mpc. SN1a are still today one of the key data sets to map the expansion history of the Universe at z ≲ 1 (e.g. Riess et al. 2007; Hicken et al. 2009; Conley et al. 2011; Suzuki et al. 2012; Betoule et al. 2014; Sako et al. 2014). On their own however they only provide an ‘uncalibrated’ distance scale as the absolute magnitude of the standard candle cannot be accurately modelled or derived from theory. In other words, the (relative) distance scale they provide must be calibrated, and this is traditionally done with a distance ladder.
Since 2005 another technique to measure extragalactic distances has become possible (Cole et al. 2005; Eisenstein et al. 2005) and it is called baryon acoustic oscillations (BAO). In the past 10 yr, BAO measurements have undergone a spectacular development having now been measured from several independent surveys with few per cent precision over the redshift range from z = 0.1 to z > 1 (see e.g. Beutler et al. 2011; Anderson et al. 2014; Font-Ribera et al. 2014; Kazin et al. 2014; Ross et al. 2014; Tojeiro et al. 2014; Delubac et al. 2015). This is a standard ruler technique: the length of sound horizon at recombination is imprinted in the clustering of dark matter and its tracers like galaxies, provided one can accurately model the possible evolution of the observational signature due to gravitational instability. The distance scale given by the BAO feature as measured from large-scale structure must also be calibrated by knowing the size of the standard ruler. This is provided by cosmic microwave background (CMB) observations. The sound-horizon determination from CMB data is somewhat cosmological model-dependent, as it is sensitive to the early expansion history and the composition of the early Universe. Nevertheless, it is exquisitely well measured – its error bar being below 1 per cent – for models with standard early expansion history (e.g. standard number of effective neutrino species etc.), and extremely robust to systematic and instrumental errors (see e.g. Planck Collaboration XVI 2014b). However, a recent model-independent determination of the standard ruler size is given by Heavens, Jimenez & Verde (2014).
If standard candles, calibrated from the local measurement of H0 provide a ‘direct’ cosmic distance ladder (from nearby out towards cosmological distances), the BAO provides an ‘inverse’ cosmic distance ladder, calibrated at recombination z ∼ 1100 and extended in, towards lower redshifts.
The spectacular progress in surveying the Universe of the past decade means that SN1a and BAO measurements now overlap in redshift and the statistical errors in both distance measures as function of redshifts are reaching percent level.
This implies that now the direct and inverse cosmic distance ladders overlap and can be calibrated off one another, see Fig. 1.
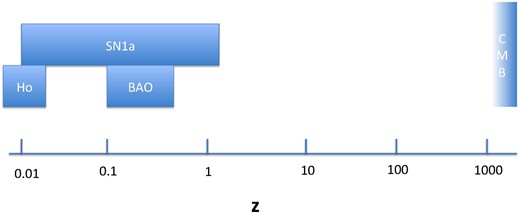
Schematic diagram of the redshift ranges covered by each of the data sets used in this paper. From low to high redshift, we show the local measurement of the expansion rate H0, the luminosity distances of SN1a, the distance determinations from the BAO in galaxy clustering, and the sound-horizon scale in the CMB.
Here, we consider the SN1a distance ladder and the BAO one first separately then jointly. This paper shows a similar approach to that shown in Aubourg et al. (2014) and Heavens et al. (2014), in the sense that they also combine BAO and SN1a to build a distance ladder. However, there are differences. In Aubourg et al. (2014), only the inverse cosmic distance ladder is considered to derive the value of the Hubble constant, so there is no attempt to infer the value of the sound-horizon scale, which we do here. The approach in Heavens et al. (2014) is different in aims and underlying assumptions. While we work in the framework of the Λ cold dark matter (ΛCDM) model and its extension, their analysis only relies on the assumptions of homogeneity and isotropy, a metric theory of gravity, a smooth expansion history, and the existence of standard candles (SN1a) and a standard BAO ruler (i.e. no dark energy modelling or general relativity is assumed, only a Friedmann–Robertson–Walker metric). With only these assumptions, and using standard clocks as an additional data set, they measure both the Hubble constant and the size of the standard ruler. They also explore the role that a prior on the Hubble constant (similar to the one we use here in the direct distance ladder) plays on the results.
We begin by reviewing the basic equations and the state of the art in Section 2. Then in Section 3, we present the data sets we use. In Section 4, we proceed to first calibrate the cosmic distance ladder represented by the SN1a to the sound-horizon measurement provided by the CMB via the BAO measurements. This provides an inverse distance ladder and a derived determination of the Hubble constant. Then we calibrate the SN1a +BAO distance ladder with the local H0 measurement and infer values for the sound horizon at radiation drag which are independent on early Universe physics. Finally, we report constraints on the expansion history both absolute H(z) and relative E(z) = H(z)/H0. We draw our conclusions in Section 5.
2 STATE OF THE ART AND BACKGROUND
From the above discussion it should be clear how important an absolute distance scale is and how this is directly related to the H0 determination. In the era of precision cosmology, discrepancies of about 10 per cent, in supposedly well-known cosmological parameters such as the Hubble constant, have generated contradictory claims about being an indication for new physics that might explain the difference (e.g. Marra et al. 2013; Verde, Protopapas & Jimenez 2013, 2014; Bennett et al. 2014; Wyman et al. 2014). Such is the case of the difference between direct measurements of the local expansion rate from Riess et al. (2011) even after the recalibration of the distance to NGC 4258 2 from Humphreys et al. (2013), 73.0 ± 2.4 km s−1 Mpc−1, and the value of H0 extrapolated assuming a ΛCDM model from the epoch of recombination to redshift z = 0 from CMB measurements by the Planck satellite (Planck Collaboration XVI 2014b), 67.3 ± 1.2 km s−1 Mpc−1. It is important to stress that the CMB estimates of H0 are extrapolations, and therefore are cosmological model-dependent.
The state of the art in CMB data is provided by the temperature anisotropy measurements by the Planck satellite (Planck Collaboration I 2014a; Planck Collaboration XVI 2014b) which is almost always combined with the polarization data at low multipoles from the Wilkinson Microwave Anisotropy Probe (WMAP) satellite (Bennett et al. 2013) referred to as WP. The Planck data are often further complemented by higher multipoles measurements by the ACT and SPT experiments (Reichardt et al. 2012; Das et al. 2014) referred to as highL.
We can quantify how model-dependent is the CMB-based H0 determination using the publicly released Monte Carlo markov chains (MCMC) ran by the Planck collaboration to explore the cosmological parameter space and find parameter estimates. We find that the Planck+WP data set constraints H0 to be within 64.2 < H0 < 70.4 km s−1 Mpc−1 (at 99 per cent confidence level) for the flat ΛCDM model, whereas this becomes 43.3 < H0 < 71.4 km s−1 Mpc−1 for the non-flat ΛCDM (OΛCDM) model (43.2 < H0 < 69.3 km s−1 Mpc−1 when using Planck+WP+highL), and 58.7 < H0 < 100 km s−1 Mpc−1 (with the upper boundary being set by the prior) for a model where the dark energy is not a cosmological constant but its equation-of-state parameter does not change in time (the wCDM model). Therefore, a ‘concordance’ value of 70 km s−1 Mpc−1 (Bennett et al. 2014) or the central measured value by Riess et al. (2011) and Humphreys et al. (2013) 73.0 km s−1 Mpc−1 can be considered ruled out or perfectly acceptable depending on the context of the cosmological model (as already discussed in the literature see e.g. Verde et al. 2014). This is summarized in the left-hand panel of Fig. 2 where 68 per cent confidence regions are shown.
![Left-hand panel: comparison between local measurements [using Riess et al. 2011 and Humphreys et al. 2013 (dark blue, upper bar) and its reinterpretation by Efstathiou 2014 (light blue, lower bar)] and CMB-derived measurements of the Hubble constant from Planck+WP data (labelled as Planck) for several assumed cosmologies. The error bars correspond to 68 per cent confidence. The tension between the local and the CMB determinations is evident for some models (ΛCDM and OΛCDM) but not for others (wCDM or NeffΛCDM). The two measurements labelled ‘Planck ΛCDM’ refer to the Planck collaboration measurement (dark red, lower bar; Planck Collaboration XVI 2014b) and the re-analysis of Spergel, Flauger & Hlozek (2015, light red, upper bar). The bars in faded out colours represent reinterpretations of the original data sets represented in solid colours. Right-hand panel: the sound-horizon scale: its determination is virtually cosmology independent for cosmologies that differ on late-time history of the Universe, but the determination is extremely sensitive to uncertainties in the early (pre-recombination) history.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/448/4/10.1093/mnras/stv261/2/m_stv261fig2.jpeg?Expires=1749951944&Signature=PwIyEnF52a5p-7fOzKVby9YQbF29H8qJHEdxuoGxm5TW1KdK9idjQaufGuYXQOw9aDUx2X~en6xsvQoubm0YyY4Av21H4HFmJmrzvSl2U66--8fC7rTYjgOqjUi6ByO~n4JFwohBzsjPZ8l-Zhxz4j0UnP0UEX~4pg7gboE8JkL7cRZ6eQF5H9dXPsy06gnXTxVNGL9jf84C28CSb~lubxFxbloOnZwHnHF1ZXD4OfXJIK-PXeQe7-V504m4V3Ag0l9uBvs1XPHA7jR0TzKcYu-z-4mSHu-mmQF3DpKwyY~CE3nS4Iv-3BsM6v8bclKw39YrsNzoXVBeY83y4YoUnw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Left-hand panel: comparison between local measurements [using Riess et al. 2011 and Humphreys et al. 2013 (dark blue, upper bar) and its reinterpretation by Efstathiou 2014 (light blue, lower bar)] and CMB-derived measurements of the Hubble constant from Planck+WP data (labelled as Planck) for several assumed cosmologies. The error bars correspond to 68 per cent confidence. The tension between the local and the CMB determinations is evident for some models (ΛCDM and OΛCDM) but not for others (wCDM or NeffΛCDM). The two measurements labelled ‘Planck ΛCDM’ refer to the Planck collaboration measurement (dark red, lower bar; Planck Collaboration XVI 2014b) and the re-analysis of Spergel, Flauger & Hlozek (2015, light red, upper bar). The bars in faded out colours represent reinterpretations of the original data sets represented in solid colours. Right-hand panel: the sound-horizon scale: its determination is virtually cosmology independent for cosmologies that differ on late-time history of the Universe, but the determination is extremely sensitive to uncertainties in the early (pre-recombination) history.
Re-analysis by Spergel et al. (2015) dropping the 217GHz data of the Planck data set and re-analysis of the direct distance ladder by Efstathiou (2014) report a modest shift (less than 0.5σ) in their Hubble constant determinations. This can be appreciated in Fig. 2 left-hand panel.
The CMB on the other hand, offers directly the absolute distance calibrator for the BAO, the sound horizon at radiation drag,3rd. This quantity is exquisitely well measured, yet it shows some small cosmological dependence. For example, while it is measured with a 0.4 per cent uncertainty in the ΛCDM model for the Planck+WP data set (rd = 147.49 ± 0.59 Mpc; Planck Collaboration XVI 2014b), its central value is about 2.7 per cent, or 4 Mpc, lower in a model where the effective number of neutrino species, Neff, is not fixed to the standard value corresponding to three neutrino families, but is allowed to vary,4NeffΛCDM, rd = 143.5 ± 3.3 Mpc (Planck Collaboration XVI 2014b). This is illustrated in the right-hand panel of Fig. 2, where the error bars correspond to 68 per cent confidence.
In summary, there is a residual cosmological dependence in rd, which is however very mild when the late-time expansion history or the geometry is concerned. In these cases, the standard ruler is measured with better than per cent precision. However, as expected, when the early expansion history is affected (as in the case with a possible dark-radiation component, illustrated by the Neff case), the rd determination is degraded to a 2.3 per cent measurement (68 per cent confidence). It is important to bear in mind that a 3 per cent knowledge of the rd calibrator at z ∼ 1100 is comparable to that of the H0 one at z = 0. In other words, the inverse distance ladder calibration is significantly better than the direct one only if the early expansion history is virtually fixed.
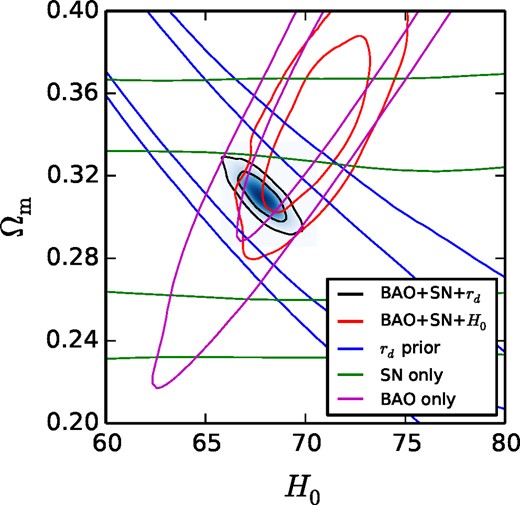
Constraints in the Ωm–H0 plane from BAO only, SN1a only, and the combinations BAO+SN1a+H0 and BAO+SN1a+rd. A ΛCDM model is assumed. Here, rd is considered a derived parameter which depends on the densities of matter, baryons, and radiation, but we will drop that assumption in our analysis. The contours represent the 1σ and 2σ regions.
From these equations, it is clear that uncalibrated standard candles and rulers can only yield relative expansion history information i.e. H(z)/H0. Moreover, to infer constraints on the expansion history H(z)/H0 from dL(z) and dV(z) an underlying cosmological model must be assumed (for example, the curvature). Because of the integral nature of D(z), while for a given E(z) only an assumption about curvature is needed to relate E(z) to D(z), to invert the relation going from D(z) to E(z) requires assuming a functional form for E(z). Rather than working with a model-independent form for E(z) (like a polynomial, or some function specified by its values at certain redshift values), here we use a suite of cosmological models: ΛCDM, OΛCDM, wCDM and NeffΛCDM. In this case, the parameters describing the expansion history are the standard cosmological background parameters relative to that model.
In what follows, sometimes we will have to assume a fiducial cosmology, we take the Planck best-fitting ΛCDM model, where Ωm = 0.315, ΩΛ = 0.685, H0 = 67.3 km s−1 Mpc−1, and rd = 147.49 Mpc.
3 DATA SETS
In this section, we describe the cosmological data sets we use in this analysis. These are the recent BAO measurements from the SDSS-III BOSS survey (Dawson et al. 2013) data release 11 and a recent compilation of Supernovae data which we describe in details below. A compilation of the state-of-the-art galaxy BAO measurements is shown in the left-hand panel of Fig. 4 and the SN1a measurements we use here are shown in the right-hand panel of Fig. 4. Clearly most of the statistical power for the BAO (when used in conjunction with SN1a) comes from the two BOSS measurements, which we use here.
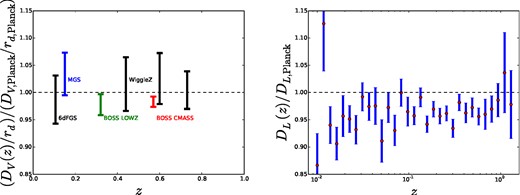
Left: the distance–redshift relation as probed by current BAO measurements. The quantity plotted is DV(z)/rd = ((1 + z)2DA(z)2cz/H(z))1/3/rd normalized by the values for our fiducial cosmology given by the best-fitting parameters from the Planck analysis for a ΛCDM model BAO measurements shown in black are not used here, but are included in this plot for completeness. Right: the luminosity distance–redshift relation from SN1a measurements normalized by the fiducial cosmology values. Here, the JLA sample has been binned using 31 nodes equally separated in log(1+z). We remind the reader that these bins are correlated, therefore their full covariance matrix is included in our analysis and required to establish concordance with Planck.
Both data sets are complementary in the sense that the distance measurements determined using BAO have high precision, but they sparsely cover the redshift range. In particular, at low redshifts, due to the limited volume that can be observed, the error bars are large. On the other hand, the SN1a compilation by Betoule et al. (2014) samples the redshift range 0.01 < z < 1.0 really well. This gives a relative distance measurement (this is shown in Fig. 8), with the normalization being unknown. Supernovae are usually normalized at z = 0 using H0 and BAO at z = 1100 using rd. But since the two ‘ladders’ overlap, they can be calibrated off each other.
3.1 BAO data
The galaxy BAO measurements shown in Fig. 4 are the 6dF measurement at low redshift (Beutler et al. 2011), rd/DV(0.106) = 0.336 ± 0.015, the Main Galaxy Sample (MGS) BAO from SDSS-II (Ross et al. 2014), DV(0.15)/rd = 4.47 ± 0.16 the two measurements from galaxy BAO from the baryon oscillation spectroscopic survey (SDSS-III BOSS; Anderson et al. 2014; Tojeiro et al. 2014), DV(0.32)/rd = 8.465 ± 0.175 and DV(0.57)/rd = 13.77 ± 0.13 and the reconstructed WiggleZ measurements of Kazin et al. (2014) |$D_V(0.44)(r^{\rm fid}_{\rm d}/r_{\rm d})=1716\pm 83$| Mpc, |$D_V(0.60)(r^{\rm fid}_{\rm d}/r_{\rm d})=2221\pm 101$| Mpc, and |$D_V(0.73)(r^{\rm fid}_{\rm d}/r_{\rm d})=2516\pm 86$| Mpc.
The BOSS measurement at z = 0.57 used here is the anisotropic measurement presented in Anderson et al. (2014), which measures DA(z) and H(z) rather than DV(z). For simplicity, we only include those measurements with smaller uncertainties at a given redshift. Those are the MGS BAO and the two galaxy BAO measurements shown in the left-hand panel of Fig. 4 in blue, green, and red, respectively. We have also tested the effect of adding the anisotropic BAO results from the Lyman-α forest of BOSS by Font-Ribera et al. (2014) and Delubac et al. (2015). Since they do not change our results significantly, we will not include them here.
We have tested the consistency between the above compilation of BAO measurements and a ΛCDM model as described by the Planck best-fitting cosmological parameters. To do so, we adopt the approach proposed in Verde et al. (2013, 2014) of measuring the multidimensional Tension (T) and interpret it in terms of odds using the Jeffreys’ scale. In Table 1, we report ln T and the odds that a set of BAO distance measurements (starting from low to high redshift) are consistent with Planck ΛCDM cosmology. In the Jeffreys’ scale odds less that 1:3 or ln T < 1 indicate that there is no indication of inconsistency. Strong or highly significant tension would need odds <1: 12 and <1: 150.
Odds (Cumulative in redshift up to zmax) that BAO measurements are consistent with Planck ΛCDM cosmology.
| zmax . | ln T . | Odds . |
|---|---|---|
| 0.20 | 0.231 496 | 1:1.2 |
| 0.35 | 0.294 514 | 1:1.3 |
| 0.44 | 0.327 827 | 1:1.4 |
| 0.57 | 0.531 189 | 1:1.7 |
| 0.60 | 0.790 740 | 1:2.2 |
| 0.73 | 0.805 645 | 1:2.2 |
| zmax . | ln T . | Odds . |
|---|---|---|
| 0.20 | 0.231 496 | 1:1.2 |
| 0.35 | 0.294 514 | 1:1.3 |
| 0.44 | 0.327 827 | 1:1.4 |
| 0.57 | 0.531 189 | 1:1.7 |
| 0.60 | 0.790 740 | 1:2.2 |
| 0.73 | 0.805 645 | 1:2.2 |
Odds (Cumulative in redshift up to zmax) that BAO measurements are consistent with Planck ΛCDM cosmology.
| zmax . | ln T . | Odds . |
|---|---|---|
| 0.20 | 0.231 496 | 1:1.2 |
| 0.35 | 0.294 514 | 1:1.3 |
| 0.44 | 0.327 827 | 1:1.4 |
| 0.57 | 0.531 189 | 1:1.7 |
| 0.60 | 0.790 740 | 1:2.2 |
| 0.73 | 0.805 645 | 1:2.2 |
| zmax . | ln T . | Odds . |
|---|---|---|
| 0.20 | 0.231 496 | 1:1.2 |
| 0.35 | 0.294 514 | 1:1.3 |
| 0.44 | 0.327 827 | 1:1.4 |
| 0.57 | 0.531 189 | 1:1.7 |
| 0.60 | 0.790 740 | 1:2.2 |
| 0.73 | 0.805 645 | 1:2.2 |
For (isotropic) BAO, the distance measurements is encoded in terms of the angle-averaged distance DV(z). Being a combination of DA(z) and H(z) converting this type of measurement to a pure constraint on H(z) or a pure constraint on DA(z) or a direct comparison with the supernova measurements of DL(z) (but see Lampeitl et al. 2010), requires the assumption of a particular cosmological model, i.e. a shape of the expansion history. H(z) is particularly sensitive to changes in curvature and dark energy, at the redshifts probed by BAO from galaxy clustering and SN1a samples.
3.2 SNe data
The compilation of 740 SN1a by Betoule et al. (2014) comprises 239 supernovae by the SuperNovae Legacy Survey (SNLS) and 374 from the Sloan Digital Sky Survey (SDSS) as well as 118 supernovae from low-redshift surveys and a few (9) of them beyond z > 1 observed using the Hubble Space Telescope. These are binned in 31 bins equally spaced in log (1 + z) as in the appendix of Betoule et al. (2014).
The distance information from supernovae data is encoded in terms of the distance modulus μ(z), (see equation 6) implying that there is a one-to-one relation between μ(z) and the luminosity distance DL(z) = (1 + z)2DA(z) for a given value of M.
This relation has been calibrated in (Betoule et al. 2014, see appendix E and tables F1 and F2) from apparent magnitude of their SN1a compilation together with the colour terms, shape of the light-curve terms, and nuisance parameters, in an unbiased manner. We marginalize over M as in the SN1a JLA module provided by Betoule et al. (2014).
4 CALIBRATING THE COSMIC LADDER
wWe consider the following models for the expansion history ΛCDM, OΛCDM, wCDM and NeffΛCDM. Thus E(z) is described by 1 (for ΛCDM) or 2 (other models) parameters and H(z) depends on one extra parameter H0. We use the publicly available code CosmoMC (Lewis & Bridle 2002) to run MCMC and explore the posterior distributions and cosmological constraints for the SN1a and BAO data sets described in Section 3. We include BAO from LOWZ and CMASS as implemented in the current version of the code and also the SN1a JLA module provided by Betoule et al. (2014) at the website http://supernovae.in2p3.fr/sdss_snls_jla/ReadMe.html. We explore a complete set of cosmology runs (see Table 5), in which we combine BAO+SN1a, BAO+rd (BAO+ a CMB derived rd prior) and BAO+SN1a+rd. In the case of ΛCDM, we also explore the cosmological constraints from BAO and SN1a on their own (see Table 3).
4.1 The Hubble constant and the inverse distance ladder
To calibrate the BAO on the sound-horizon scale for each of the models considered we use the corresponding Planck prior on rd (shown in the right-hand panel of Fig. 2 and in the Planck+WP column of Table 4). Results are reported in Table 2. These results are also shown in the right-hand panel of Fig. 6. Note that the determination in the ΛCDM model rules out a Hubble constant of 74km s−1 Mpc−1, and is therefore somewhat in tension with the local determination of Riess et al. (2011) and Humphreys et al. (2013), as already pointed out before in the literature. Late-time changes to the expansion history (wCDM, OΛCDM) do not change this conclusion but early changes (see the Neff case) do. This is at the core of the recent proposals for a new concordance model with sterile neutrinos (e.g. Hamann & Hasenkamp 2013; Battye & Moss 2014; Dvorkin et al. 2014; Wyman et al. 2014).
Comparison between Hubble constant values for different data sets and cosmological models. Units are km s−1 Mpc−1. The * denotes the case where rd is a derived parameter depending on the densities of matter, baryon and radiation. In this case, we fix the baryon and radiation densities to their best-fitting Planck values.
| H0(km s−1 Mpc−1) . | BAO+SN* . | BAO+rd . | BAO+SN+rd . | Planck+WP . |
|---|---|---|---|---|
| ΛCDM | 68.6 ± 2.2 | 64.7 ± 2.2 | 67.7 ± 1.1 | 67.3 ± 1.2 |
| OΛCDM | 64.5 ± 7.4 | 64.8 ± 2.2 | 67.6 ± 1.1 | 56.3 ± 5.4 |
| wCDM | 72.5 ± 11.1 | 66.1 ± 2.3 | 67.7 ± 1.1 | 83.1 ± 10.7 |
| NeffΛCDM | 75.7 ± 4.5 | 66.8 ± 2.7 | 69.7 ± 1.9 | 70.7 ± 3.2 |
| H0(km s−1 Mpc−1) . | BAO+SN* . | BAO+rd . | BAO+SN+rd . | Planck+WP . |
|---|---|---|---|---|
| ΛCDM | 68.6 ± 2.2 | 64.7 ± 2.2 | 67.7 ± 1.1 | 67.3 ± 1.2 |
| OΛCDM | 64.5 ± 7.4 | 64.8 ± 2.2 | 67.6 ± 1.1 | 56.3 ± 5.4 |
| wCDM | 72.5 ± 11.1 | 66.1 ± 2.3 | 67.7 ± 1.1 | 83.1 ± 10.7 |
| NeffΛCDM | 75.7 ± 4.5 | 66.8 ± 2.7 | 69.7 ± 1.9 | 70.7 ± 3.2 |
Comparison between Hubble constant values for different data sets and cosmological models. Units are km s−1 Mpc−1. The * denotes the case where rd is a derived parameter depending on the densities of matter, baryon and radiation. In this case, we fix the baryon and radiation densities to their best-fitting Planck values.
| H0(km s−1 Mpc−1) . | BAO+SN* . | BAO+rd . | BAO+SN+rd . | Planck+WP . |
|---|---|---|---|---|
| ΛCDM | 68.6 ± 2.2 | 64.7 ± 2.2 | 67.7 ± 1.1 | 67.3 ± 1.2 |
| OΛCDM | 64.5 ± 7.4 | 64.8 ± 2.2 | 67.6 ± 1.1 | 56.3 ± 5.4 |
| wCDM | 72.5 ± 11.1 | 66.1 ± 2.3 | 67.7 ± 1.1 | 83.1 ± 10.7 |
| NeffΛCDM | 75.7 ± 4.5 | 66.8 ± 2.7 | 69.7 ± 1.9 | 70.7 ± 3.2 |
| H0(km s−1 Mpc−1) . | BAO+SN* . | BAO+rd . | BAO+SN+rd . | Planck+WP . |
|---|---|---|---|---|
| ΛCDM | 68.6 ± 2.2 | 64.7 ± 2.2 | 67.7 ± 1.1 | 67.3 ± 1.2 |
| OΛCDM | 64.5 ± 7.4 | 64.8 ± 2.2 | 67.6 ± 1.1 | 56.3 ± 5.4 |
| wCDM | 72.5 ± 11.1 | 66.1 ± 2.3 | 67.7 ± 1.1 | 83.1 ± 10.7 |
| NeffΛCDM | 75.7 ± 4.5 | 66.8 ± 2.7 | 69.7 ± 1.9 | 70.7 ± 3.2 |
Comparison assuming the ΛCDM cosmological model of the CMB measurement of the sound horizon rd and the direct measurement of the Hubble constant H0 with extrapolations from BAO and SN data. The * denotes the case where rd is a derived parameter depending on the densities of matter, baryon and radiation. In this case, we fix the baryon and radiation densities to their best-fitting Planck values.
| Data set . | rd (Mpc) . | H0 (km s−1 Mpc−1) . |
|---|---|---|
| Planck+WP | 147.49 ± 0.59 | – |
| Riess | – | 73.0 ± 2.4 |
| BAO+SN+H0 | 137.0 ± 5.0 | 72.9 ± 2.4 |
| BAO+SN+rd | 147.5 ± 0.6 | 67.7 ± 1.1 |
| BAO+SN* | 145.5 ± 5.9 | 68.6 ± 2.2 |
| BAO+H0 | 132.1 ± 5.7 | 72.6 ± 2.4 |
| BAO+rd | 147.5 ± 0.6 | 64.7 ± 2.2 |
| SN+H0 | 149 ± 17 | 73.0 ± 2.4 |
| SN+rd | 147.5 ± 0.6 | 69.9 ± 0.8 |
| BAO* | 124 ± 14 | 77.0 ± 6.6 |
| SN* | 162 ± 27 | Unconstrained |
| Data set . | rd (Mpc) . | H0 (km s−1 Mpc−1) . |
|---|---|---|
| Planck+WP | 147.49 ± 0.59 | – |
| Riess | – | 73.0 ± 2.4 |
| BAO+SN+H0 | 137.0 ± 5.0 | 72.9 ± 2.4 |
| BAO+SN+rd | 147.5 ± 0.6 | 67.7 ± 1.1 |
| BAO+SN* | 145.5 ± 5.9 | 68.6 ± 2.2 |
| BAO+H0 | 132.1 ± 5.7 | 72.6 ± 2.4 |
| BAO+rd | 147.5 ± 0.6 | 64.7 ± 2.2 |
| SN+H0 | 149 ± 17 | 73.0 ± 2.4 |
| SN+rd | 147.5 ± 0.6 | 69.9 ± 0.8 |
| BAO* | 124 ± 14 | 77.0 ± 6.6 |
| SN* | 162 ± 27 | Unconstrained |
Comparison assuming the ΛCDM cosmological model of the CMB measurement of the sound horizon rd and the direct measurement of the Hubble constant H0 with extrapolations from BAO and SN data. The * denotes the case where rd is a derived parameter depending on the densities of matter, baryon and radiation. In this case, we fix the baryon and radiation densities to their best-fitting Planck values.
| Data set . | rd (Mpc) . | H0 (km s−1 Mpc−1) . |
|---|---|---|
| Planck+WP | 147.49 ± 0.59 | – |
| Riess | – | 73.0 ± 2.4 |
| BAO+SN+H0 | 137.0 ± 5.0 | 72.9 ± 2.4 |
| BAO+SN+rd | 147.5 ± 0.6 | 67.7 ± 1.1 |
| BAO+SN* | 145.5 ± 5.9 | 68.6 ± 2.2 |
| BAO+H0 | 132.1 ± 5.7 | 72.6 ± 2.4 |
| BAO+rd | 147.5 ± 0.6 | 64.7 ± 2.2 |
| SN+H0 | 149 ± 17 | 73.0 ± 2.4 |
| SN+rd | 147.5 ± 0.6 | 69.9 ± 0.8 |
| BAO* | 124 ± 14 | 77.0 ± 6.6 |
| SN* | 162 ± 27 | Unconstrained |
| Data set . | rd (Mpc) . | H0 (km s−1 Mpc−1) . |
|---|---|---|
| Planck+WP | 147.49 ± 0.59 | – |
| Riess | – | 73.0 ± 2.4 |
| BAO+SN+H0 | 137.0 ± 5.0 | 72.9 ± 2.4 |
| BAO+SN+rd | 147.5 ± 0.6 | 67.7 ± 1.1 |
| BAO+SN* | 145.5 ± 5.9 | 68.6 ± 2.2 |
| BAO+H0 | 132.1 ± 5.7 | 72.6 ± 2.4 |
| BAO+rd | 147.5 ± 0.6 | 64.7 ± 2.2 |
| SN+H0 | 149 ± 17 | 73.0 ± 2.4 |
| SN+rd | 147.5 ± 0.6 | 69.9 ± 0.8 |
| BAO* | 124 ± 14 | 77.0 ± 6.6 |
| SN* | 162 ± 27 | Unconstrained |
A more general analysis is found in Section 4 in Aubourg et al. (2014) by the BOSS collaboration in which they present H0 constraints for more general cosmological models. We refer the reader to that paper for more details.
4.2 The sound horizon from the distance ladder and H0
In this section rather than using a prior from the sound horizon rd we use the measurements from the local expansion rate H0 to calibrate the standard ruler from the BAO on the (relative) distance versus redshift relation from supernovae data.
As shown in Fig. 5, once we include a prior on the Hubble constant, the inferred distribution of the sound-horizon scale is almost independent of the assumed cosmological model.
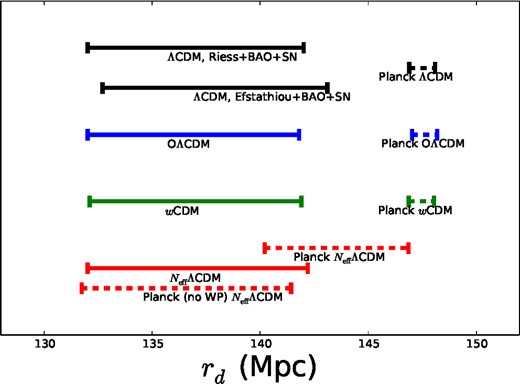
Constraints on the sound horizon rd derived from SN1a+BAO+H0 chains. Dashed lines show the constraints from CMB only, whereas solid lines show our results.
We find values consistent with Planck and WMAP9 measurements (see Table 4). In this table, we also show the values, assuming a ΛCDM model, of the sound-horizon scale when the Hubble constant prior is dropped (i.e. BAO+SN1a), but where we fix the radiation and baryon densities at their best-fitting values. Note that the error on the rd value inferred from the distance ladder (and therefore insensitive to the early expansion history) is comparable to that obtained from CMB measurements in the case of the NeffΛCDM from Planck +WP data and smaller than that obtained from Planck data alone.
4.3 Expansion history between 0 < z ≲ 1
The expansion history of the Universe as derived by these intermediate redshifts cosmological probes is however much more dependent on the assumed cosmological model. In Fig. 6, we show the derived expansion history for the ΛCDM cosmology. The quantity shown in the plot is the expansion rate |$\dot{a}=H(z)/(1+z)$| as a function of redshift z. Note how the uncertainty in the expansion history H(z) depends on the error bar on the distance calibrator rd (right-hand panel) or H0 (left-hand panel).
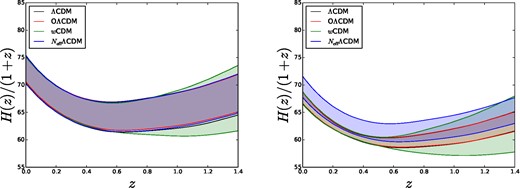
Expansion history from BAO+SN1a+H0 (left-hand panel) and BAO+SN1a+rd (right-hand panel). Contours enclose the 68 per cent region of possible values of H(z) at that z.
On the other hand, the shape of the expansion history i.e. E(z) is much more robust to the underlying cosmology as shown in Fig. 7. While with only two BAO measurements E(z) is not well constrained even in the ΛCDM model (Fig. 8), the fine redshift sampling offered by SN1a yields a good determination of E(z) over the full redshift range for the full set of models considered here. In particular, the quantity E(z)/(1 + z) reported in Fig. 7, is useful to show the transition from a decelerating uiverse when matter dominates to an accelerated phase at late times dominated by dark energy. The significance of this transition is robust to the choice of the underlying model.
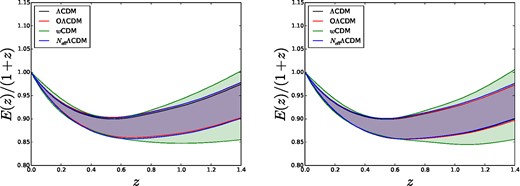
Expansion history (normalized to H0) from BAO+SN1a using the ΛCDM, NeffΛCDM, OΛCDM and the wCDM cosmological models. Contours enclose the 68 per cent region of possible values of H(z)/H0 at that z.
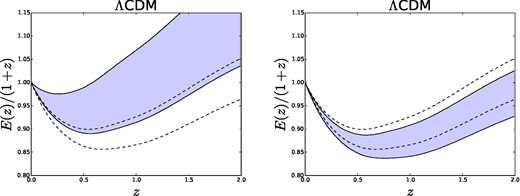
Expansion history (normalized to H0) from BAO only (left) and SN1a only (right) assuming a ΛCDM cosmological model. Contours enclose the 68 per cent region of possible values of H(z)/H0 at that z. In both panels, the dotted lines correspond to the BAO+SN1a+rd combination.
5 CONCLUSIONS
We have shown how distance measurements from BAO combined with distance moduli from SN1a can be used as a cosmic distance ladder. This ladder can be calibrated at z ∼ 0 using local determinations of the Hubble constant or at high redshift using the CMB determination of the sound horizon at radiation drag. The first approach is the classic (direct) cosmic distance ladder calibration while we refer to the second as an inverse cosmic distance ladder. While the direct calibration is affected by a host of astrophysical processes it is cosmological model-independent. The inverse ladder has much smaller calibration errors if the early (z > 1000) expansion history is standard, but it is model-dependent.
In particular, we find that BAO and SN1a are quite complementary. SN1a luminosity distance data constrain very well the shape of the expansion history and they finely probe the redshift range 0 < z < 1.3 so that the shape of the expansion history, E(z), is very well constrained but the overall normalization must be set externally for example by a direct determination of H0. BAO on the other hand cover sparsely the redshift range but can be used to tie in the low-redshift Universe to the high-redshift one as the standard ruler is set at radiation drag (z of |${\cal O} (1000)$|).
The comparison between the two approaches is useful for two purposes. (i) explore the origin of possible discrepancies between the cosmological constraints from the CMB and the ones derived from local measurements of the expansion rate. This approach is useful to disentangle information coming from the early Universe and from the late one which are governed by different physical processes. Comparing early-time versus late time constraints has been and will continue to be an insightful way to probe new physics beyond the adopted cosmological model. (ii) to map directly the expansion history of the Universe.
We have presented the reconstructed expansion histories derived by this combination of data sets for different cosmologies, and we find them to be very stable (both in shape and uncertainties), even when the curvature of the Universe or when the equation of state of dark energy are left as free parameters.
By calibrating the BAO+SN1a cosmic distance ladder on the sound horizon at radiation drag, rd, we obtain a robust determination of H0 of 67.7 ± 1.1 km s−1 Mpc−1. A similar result is presented in Aubourg et al. (2014) by the BOSS collaboration, in which they study cosmological models with more degrees of freedom than here, i.e. in a general polynomial form of H(z)2 that depends on (1 + z)α, with α=0,1,2,3. The results are completely consistent with those presented here. This is also true when comparing to Heavens et al. (2014), whose assumptions are completely generic. Using slightly different BAO data they find rd=142.3 ± 6.1 Mpc which is within 1σ of our result for the OΛCDM case. Overall, there is a broad agreement between the different analyses, implying that there seems to be no indication for deviations from ΛCDM, despite the different approaches and family of deviations considered.
On the other hand, we can calibrate the same ladder on local measurements of H0 obtaining a constraint on rd which is independent on assumptions about early time physics and early expansion history. We find 137.0 ± 5.0 Mpc for ΛCDM, and similar results for OΛCDM, wCDM, and NeffΛCDM, as shown in Table 4. This measurement is only weakly dependent on the assumed model for the late-time expansion history and on the assumed geometry. The determination of rd is consistent with the value measured by Planck of 147.5 ± 0.6 Mpc for a standard cosmology with three neutrinos. Conversely, this measurement of rd places a limit on the number of relativistic species Neff of 4.62 ± 0.88. While with current CMB data there is still a degeneracy between Neff and other cosmological parameters which propagates into a large uncertainty in rd for this model, this could be resolved by better measurements of the CMB damping tail and better peak localization in the (E-mode) polarization (e.g. Hou et al. 2013).
Comparison between sound-horizon values for different data sets and cosmological models. Units are Mpc. The * denotes the case where rd is a derived parameter depending on the densities of matter, baryon and radiation. In this case, we fix the baryon and radiation densities to their best-fitting Planck values.
| rd (Mpc) . | BAO+SN* . | BAO+H0 . | BAO+SN+H0 . | Planck+WP . | Planck . |
|---|---|---|---|---|---|
| ΛCDM | 145.5 ± 5.9 | 132.1 ± 5.7 | 137.0 ± 5.0 | 147.5 ± 0.6 | 147.5 ± 0.6 |
| OΛCDM | 155.9 ± 16.2 | 132.0 ± 5.8 | 136.9 ± 4.9 | 147.6 ± 0.6 | 147.6 ± 0.6 |
| wCDM | 140.9 ± 22.0 | 132.5 ± 6.3 | 137.0 ± 4.9 | 147.5 ± 0.6 | 147.5 ± 0.6 |
| NeffΛCDM | 132.0 ± 8.7 | 132.1 ± 5.7 | 137.1 ± 5.1 | 143.5 ± 3.3 | 136.6 ± 4.9 |
| rd (Mpc) . | BAO+SN* . | BAO+H0 . | BAO+SN+H0 . | Planck+WP . | Planck . |
|---|---|---|---|---|---|
| ΛCDM | 145.5 ± 5.9 | 132.1 ± 5.7 | 137.0 ± 5.0 | 147.5 ± 0.6 | 147.5 ± 0.6 |
| OΛCDM | 155.9 ± 16.2 | 132.0 ± 5.8 | 136.9 ± 4.9 | 147.6 ± 0.6 | 147.6 ± 0.6 |
| wCDM | 140.9 ± 22.0 | 132.5 ± 6.3 | 137.0 ± 4.9 | 147.5 ± 0.6 | 147.5 ± 0.6 |
| NeffΛCDM | 132.0 ± 8.7 | 132.1 ± 5.7 | 137.1 ± 5.1 | 143.5 ± 3.3 | 136.6 ± 4.9 |
Comparison between sound-horizon values for different data sets and cosmological models. Units are Mpc. The * denotes the case where rd is a derived parameter depending on the densities of matter, baryon and radiation. In this case, we fix the baryon and radiation densities to their best-fitting Planck values.
| rd (Mpc) . | BAO+SN* . | BAO+H0 . | BAO+SN+H0 . | Planck+WP . | Planck . |
|---|---|---|---|---|---|
| ΛCDM | 145.5 ± 5.9 | 132.1 ± 5.7 | 137.0 ± 5.0 | 147.5 ± 0.6 | 147.5 ± 0.6 |
| OΛCDM | 155.9 ± 16.2 | 132.0 ± 5.8 | 136.9 ± 4.9 | 147.6 ± 0.6 | 147.6 ± 0.6 |
| wCDM | 140.9 ± 22.0 | 132.5 ± 6.3 | 137.0 ± 4.9 | 147.5 ± 0.6 | 147.5 ± 0.6 |
| NeffΛCDM | 132.0 ± 8.7 | 132.1 ± 5.7 | 137.1 ± 5.1 | 143.5 ± 3.3 | 136.6 ± 4.9 |
| rd (Mpc) . | BAO+SN* . | BAO+H0 . | BAO+SN+H0 . | Planck+WP . | Planck . |
|---|---|---|---|---|---|
| ΛCDM | 145.5 ± 5.9 | 132.1 ± 5.7 | 137.0 ± 5.0 | 147.5 ± 0.6 | 147.5 ± 0.6 |
| OΛCDM | 155.9 ± 16.2 | 132.0 ± 5.8 | 136.9 ± 4.9 | 147.6 ± 0.6 | 147.6 ± 0.6 |
| wCDM | 140.9 ± 22.0 | 132.5 ± 6.3 | 137.0 ± 4.9 | 147.5 ± 0.6 | 147.5 ± 0.6 |
| NeffΛCDM | 132.0 ± 8.7 | 132.1 ± 5.7 | 137.1 ± 5.1 | 143.5 ± 3.3 | 136.6 ± 4.9 |
| . | BAO only . | SN only . | BAO+SN . | BAO+H0 . | BAO+rd . | BAO+SN+H0 . | BAO+SN+rd . |
|---|---|---|---|---|---|---|---|
| ΛCDM | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| OΛCDM | No | No | Yes | Yes | Yes | Yes | Yes |
| wCDM | No | No | Yes | Yes | Yes | Yes | Yes |
| NeffΛCDM | No | No | Yes | Yes | Yes | Yes | Yes |
| . | BAO only . | SN only . | BAO+SN . | BAO+H0 . | BAO+rd . | BAO+SN+H0 . | BAO+SN+rd . |
|---|---|---|---|---|---|---|---|
| ΛCDM | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| OΛCDM | No | No | Yes | Yes | Yes | Yes | Yes |
| wCDM | No | No | Yes | Yes | Yes | Yes | Yes |
| NeffΛCDM | No | No | Yes | Yes | Yes | Yes | Yes |
| . | BAO only . | SN only . | BAO+SN . | BAO+H0 . | BAO+rd . | BAO+SN+H0 . | BAO+SN+rd . |
|---|---|---|---|---|---|---|---|
| ΛCDM | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| OΛCDM | No | No | Yes | Yes | Yes | Yes | Yes |
| wCDM | No | No | Yes | Yes | Yes | Yes | Yes |
| NeffΛCDM | No | No | Yes | Yes | Yes | Yes | Yes |
| . | BAO only . | SN only . | BAO+SN . | BAO+H0 . | BAO+rd . | BAO+SN+H0 . | BAO+SN+rd . |
|---|---|---|---|---|---|---|---|
| ΛCDM | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| OΛCDM | No | No | Yes | Yes | Yes | Yes | Yes |
| wCDM | No | No | Yes | Yes | Yes | Yes | Yes |
| NeffΛCDM | No | No | Yes | Yes | Yes | Yes | Yes |
With all of the above, we find currently no compelling evidence to invoke non-standard cosmological models to explain the expansion history between redshifts 0 < z < 1.3. The modest difference (∼2σ) between the value of the Hubble constant measured directly and that inferred from the BAO+SN1a+rd ladder (in the context of ΛCDM, wCDM or OΛCDM) and likewise the difference (∼2σ) in the sound horizon measured by Planck and inferred from the BAO+SN1a+H0 ladder may easily result from chance. Indeed, substitution of WMAP data for Planck reduces this discrepancy further (Bennett et al. 2014). However, if the significance of this difference in future experiments rose above chance and beyond the reach of their systematic errors the approach illustrated here of comparing direct and inverse distance ladders could provide evidence for new physics.
AJC and LV are supported by supported by the European Research Council under the European Community's Seventh Framework Programme FP7-IDEAS-Phys.LSS 240117. LV and RJ acknowledge Mineco grant FPA2011-29678-C02-02. Based on observations obtained with Planck (http://www.esa.int/Planck), an ESA science mission with instruments and contributions directly funded by ESA Member States, NASA, and Canada. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/.
Hereafter, we refer to this recalibrated value simply as ‘Riess’.
This is slightly different from the sound horizon at recombination but the two quantities are tied to one another.
Recall that Neff parameterises non-standard early expansion history.



