-
PDF
- Split View
-
Views
-
Cite
Cite
Chuyuan Yang, Li Zhang, Jiancheng Wang, On the escape and propagation of high-energy protons near young supernova remnants, Monthly Notices of the Royal Astronomical Society, Volume 448, Issue 4, 21 April 2015, Pages 3423–3428, https://doi.org/10.1093/mnras/stv255
Close - Share Icon Share
Abstract
The escape and propagation of high-energy protons near young supernova remnants (SNRs) are investigated in the frame of non-linear diffusive shock acceleration (NLDSA) model by using two methods. In the first method, the particle diffusion is assumed to be different inside and outside the absorbing boundary of the particles accelerated in the SNR shock, and the proton spectra at a given distance of the outer region and corresponding π0 decay γ-ray spectra can be calculated if a molecular cloud is assumed to be at the distance. In the second method, the total spectrum of high-energy protons escaping from an absorbing boundary during the SNR evolution time is treated as injection rate of the protons and the proton spectrum is calculated in the accumulative diffusion model. Our results show that (1) the spectrum of high-energy protons escaping from a young SNR does not have a power-law form and the protons concentrate on high-energy region and (2) the escaping proton spectra and corresponding π0 decay γ-ray spectra predicted in both methods are different, indicating that the second method overestimates the propagation effect. We may conclude that the first method is a more realistic description of the escape and propagation of high-energy protons near SNRs.
1 INTRODUCTION
It is generally believed that the galactic cosmic-rays (CRs) with energies below the knee energy ∼1015 eV would be accelerated at the shock of supernova remnants (SNRs) via diffusive shock acceleration (DSA). Observationally, some circumstantial pieces of evidence indicate that the bulk of CRs are indeed accelerated in SNRs although it is not clear whether SNRs can accelerate CRs up to the knee energy (see for example, the review of Blasi 2013). One of the evidence is based on the fact that π0 decay γ-rays in proton–proton collision have been detected from several SNRs close to molecular clouds (MCs; Tavani et al. 2010; Ackermann et al. 2013), indicating that the protons accelerated in an SNR can escape from the SNR and interact with the MCs. Theoretically, as pointed out by Dermer (2012), accurate modelling of γ ray spectra is needed in determining whether or not new physics is being observed, and hence accurate modelling of escaping CR spectra is required. Here we will focus on the escape and propagation of high-energy protons accelerated in the SNRs interacting with MCs and π0 decay γ-ray production.
To study the escape of high-energy protons accelerated in the SNRs, we need the acceleration mechanism at an SNR shock. At present, non-linear diffusive shock acceleration (NLDSA) with the reaction of accelerated particles on to the shock structure has been proposed and treated with different approaches: a two-fluid (e.g. Malkov & Drury 2001, for a review), a numerical kinetic (e.g. Ellison, Baring & Jones 1996; Berezhko & Völk 1997; Kang & Jones 2006; Zirakashvili & Aharonian 2010) and a semi-analytical kinetic approach (e.g. Blasi 2002; Amato & Blasi 2005, 2006; Caprioli et al. 2008). These models provide us with the processes of accelerating particles in shock front and the methods to deal with the escape of high-energy particles at an absorbing boundary.
However, at present, there are two methods in treating the propagation of the escaping particles outside the SNR. In the first method, the escaping particle distribution with a power-law form and the point-like source of the escaping particles are assumed, then the analytic models for the particle propagation around the SNR can be given (Atoyan, Aharonian & Völk 1995; Aharonian & Atoyan 1996) and are extended to include finite-size sources and finite-size target MCs (Li & Chen 2010, 2012; Ohira, Murase & Yamazaki 2011; Thoudam & Hörandel 2012). In the second method, on the other hand, based on the model given by Telezhinsky, Dwarkadas & Phol (2012a), where cosmic ray acceleration in young Type Ia SNRs is investigated by test-particle DSA theory and one-dimensional hydrodynamical simulations of their evolution, Telezhinsky, Dwarkadas & Phol (2012b) have investigated the spectra of escaped particles based on time-dependent acceleration history by dividing deferent diffusion regions. What is the main difference of the escaping particle spectra predicted between these methods? In other words, what is the limitation of the analytic models?
In this paper, we will focus on the question mentioned above. On the one hand, following the method given by Telezhinsky et al. (2012b), we assume that the particle diffusion is different inside and outside the escape boundary of the particles accelerated in the SNR shock, and then calculate the escaping particle spectrum in the NLDSA model given by Zirakashvili & Ptuskin (2012). On the other hand, we calculate the escaping particle spectrum in the accumulative diffusion model which includes finite-size sources given by Li & Chen (2010). We will compare the escaping proton spectra and π0 decay γ-rays when the protons collide with the MCs predicted by these models.
2 THE MODELS
Zirakashvili & Ptuskin (2012) proposed a new numerical model of NLDSA. In the model, time-dependent hydrodynamical equations for the gas density ρ(r, t), gas velocity u(r, t), gas pressure Pg(r, t) and the equation for the quasi-isotropic CR momentum distribution N(r, t, p) are numerically solved in the spherically symmetrical case based on a finite-difference method, where particle accelerations by both forward and reverse SNR shocks are included. It has been shown that the parameters describing the reverse shock can be significantly different from those describing the forward shock, resulting in significantly different properties of radiation components from the reverse and forward shocks (Zirakashvili & Ptuskin 2012; Zirakashvili et al. 2014). Therefore, for a given SNR, the spectra of accelerated particles at any time t and the spectra of particles produced during the whole evolution of the SNR.
In the NLDSA given by Zirakashvili & Ptuskin (2012), the diffusion is Bohm-like type in the vicinity of the forward shock with a radius Rf (see their equation 7). It has been known that the diffusion far from the forward shock is Galactic diffusion, but the transition from Bohm-like diffusion close to the forward shock to the Galactic diffusion is not clearly understood. Following Telezhinsky et al. (2012b, also see Telezhinsky et al. 2012a), here we assume that the transition in diffusion coefficient occurs at 2Rf and the accelerated particles are injected into the interstellar medium at Resc = 2Rf. Physically, one possible explanation for Resc ≈ 2Rf is as follows. Since the accelerated protons with a maximum energy Emax can be trapped by the shock when their gyroradius, rg = Emax/eB, is the same as the shock radius itself, the maximum extent of the accelerated protons precursor would be one shock radius ahead of the shock, or two shock radii from the origin. Therefore, the particles will diffuse in two different regions (hereafter called as inner and outer regions of the SNR), where the diffusion is Bohm-like type in the region of r ≤ 2Rf but the Galactic diffusion at the region of r > 2Rf. Here we focus on the acceleration of protons in an SNR and proton's propagation at the region of r > 2Rf.
In our calculations, it is assumed that the shock of the SNR with an energy of explosion ESN = 1.0 × 1051 erg and an ejecta mass Mej = 1.4 M⊙ propagates in the medium with a hydrogen number density nH = 0.01 cm−3, a magnetic field strength B0 = 5 μG, a temperature T = 104 K, and the index of ejecta velocity distribution k = 7. Other model parameters include the fraction xHe = nHe/nH = 0.1 of helium nuclei, the parameter of ejecta velocity distribution, and the initial forward shock velocity is V0f = 2.9 × 104 km s−1. As an example, in Fig. 1 we show the evolutions of both velocity and radius for forward shock (top panel) and the spatial integrated spectrum of accelerated proton at t = 2000 yr and the spectrum of the total escaped or runaway particles which have already left the remnant through an absorbing boundary (Resc = 2Rf) during 2000 yr (bottom panel).
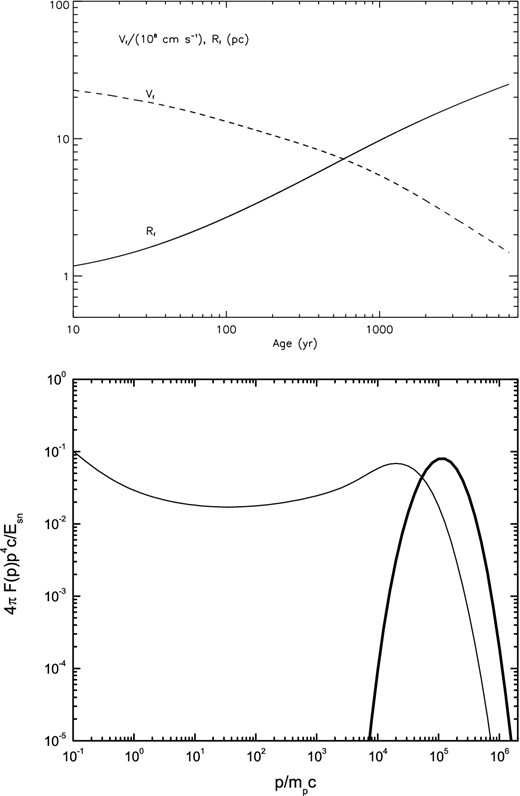
Top panel: the evolutions of forward shock velocity and forward shock radius. Bottom panel: spatial integrated spectrum (thin solid line) of accelerated protons at the SNR evolution time of 2000 yr and the total spectrum (thick solid line) of escaping protons which have already left the remnant through an absorbing boundary (Resc = 2Rf) during 2000 yr.
Therefore, there are two kinds of high-energy protons near a given SNR: runaway protons and diffusion Galactic protons. If an MC is near the SNR, the protons will collide the dense MC and γ-rays will be produced through π0 decay in the proton–proton interaction process. In this paper, we assume that an MC with a mass of Mc = 2.5 × 105 M⊙ and a number density of nc = 100 cm−3 is located at the distance Rd. We will use the analytic approximation given by Kelner, Aharonian & Bugayov (2006) to calculate the photon emissivity dNγ/dEγ.
3 CALCULATED RESULTS
We now calculate the escaping proton spectra and π0 decay γ-ray spectra using Model A and Model B, respectively. At first, we compare the escaping proton spectra at different distances predicted in Model A and Model B for an SNR with an age tage = 1000 yr. Note that at tage = 1000 yr, the NLDSA simulation gives Vf = 5405.8 (km s− 1), Rf = 9.7 pc (and then Resc = 2Rf = 19.4 pc) and δ = 0.5 for the parameter used here. Although the simulated results could be same as SN 1006 with Vf = 5000 (km s− 1), Rf = 10 pc at age of 1000 yr because of low-density environment. On the contrary, another source of Tycho evolved in high-density environment, its shock velocity can reduce to 5000 (km s− 1) at the age of 440 yr. Therefore, the evolution of an SNR strongly depends on the surroundings. In this paper, we only investigate the reasonable protons distribution in vicinity of SNR in models A and B, but not apply to any specific source of SNRs. In Fig. 2, we show the escaping proton spectra at the distances of Rd = 20, 50 and 100 pc predicted in Model A and Model B for a given time tage = 1000 yr. In both models, the predicted proton spectra at Rd = 20 pc, which is close to the absorbing boundary with a radius Resc = 19.4 pc, are almost same. However, as the increase of the distance, the difference between the predicted results of the models appears. At Rd = 100 pc, for example, the spectrum in Model A is different from that in Model B, particular in the lower energy part of the spectra. According to Model B, the lower energy part of escaping spectrum at Resc is exponentially suppressed due to the propagation effect. Therefore, compared to Model A, Model B overestimates the propagation effect. On the other hand, the maximum flux and corresponding energy in both models are also different. For example, at Rd = 100 pc, the maximum flux in Model B is lower than that in Model A, but the corresponding energy in Model B is slightly larger than that in Model A, indicating that the energies for which the maximum flux is not yet reached in both models are different. It can be predicted that a larger difference between the escaping proton spectra predicted in Model A and Model B will appear as further increase of the distance.
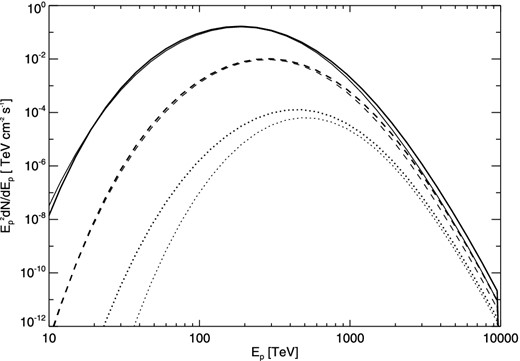
Escaping proton spectra at different distances Rd = 20 pc (solid line), 50 pc (dashed line) and 100 pc (dotted line) at evolution time tage = 1000 yr predicted in Model A (thick lines) and Model B (thin lines). The value of parameter δ in equation (1) is taken to be 0.5.
As shown in equation (1), the Galactic diffusion coefficient is proportional to (Ep/10 GeV)− δ (δ ≈ 0.3–0.7), so different values of δ would reflect different diffusion outside the absorbing boundary Resc (or in the interstellar space). In Fig. 3, we show the escaping proton spectra at time tage = 1000 yr and Rd = 100 pc in Model A and Model B for different values of δ. It can be seen from the figure: (1) the results predicted in both models indicate that amplitude of the maximum flux increases but the energy position of the maximum flux shifts to lower energy as the increase of δ, and (2) that in this case of Rd = 100 pc the difference between the predicted results of both models is significant for smaller values of δ (e.g. δ = 0.4 and 0.5), but the difference mainly appears on higher energy range as the increase of δ (see the case of δ = 0.7).
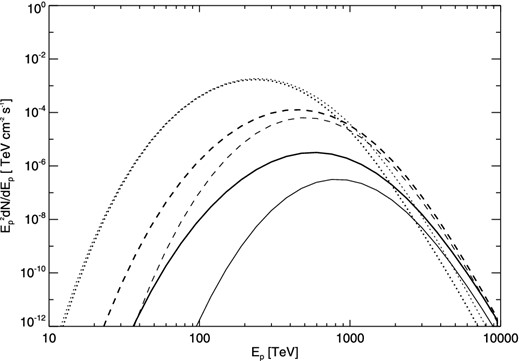
Escaping proton spectra for different values of δ = 0.4 (solid line), 0.5 (dashed line) and 0.7 (dotted line) at evolution time tage = 1000 yr and Rd = 100 pc predicted in Model A (thick lines) and Model B (thin lines).
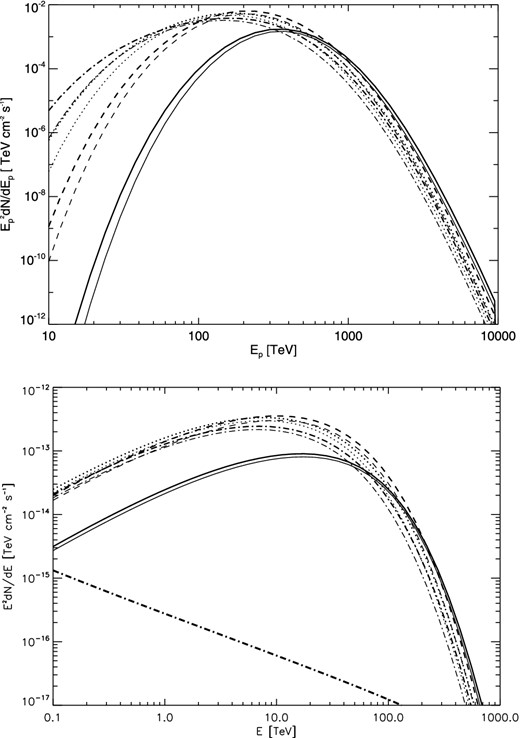
We now consider the case of the escaping proton spectra at a given distance and corresponding π0 decay γ-ray spectra for different SNR evolution times. We show the calculating results at Rd = 100 pc for tage = 1000, 3000, 5000 and 7000 yr by using Model A and Model B in Fig. 4, where an MC with Mc = 2.5 × 105 M⊙ and nc = 100 cm−3 is assumed to locate at Rd. The NLDSA simulation gives Vf = 2682.6 (km s− 1) and Rf = 17.1 pc at tage = 3000 yr and Vf = 1875.7 (km s− 1), Rf = 21.6 pc at tage = 5000 yr and Vf = 1478.6 (km s− 1), Rf = 24.9 pc at tage = 7000 yr for the parameter used here. Note that the relative distances between Rd and Resc are different for different SNR evolution times, i.e. the relative distance Rd − Resc is smaller for a larger evolution time. Therefore, the predicted results in both models have larger differences for larger relative distances, and tend to have smaller difference as the decrease of Rd − Resc.
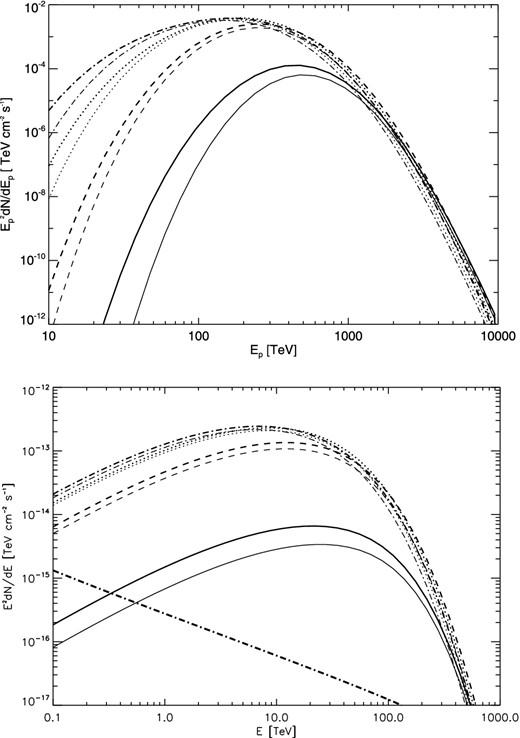
Top panel: escaping proton spectra at Rd = 100 pc for different SNR evolution time tage = 1000 yr (solid lines), 3000 yr (dashed lines), 5000 yr (dotted lines) and 7000 yr (dash-dotted line) predicted in Model A (thick line) and Model B (thin line). Bottom panel: corresponding π0 decay γ-ray spectra, where an MC with Mc = 2.5 × 105 M⊙ and nc = 100 cm−3 at Rd = 100 pc is assumed. The thick dash-dotted line represents the contribution of diffusion Galactic protons. The value of parameter δ in equation (1) is taken to be 0.5.
Finally, we consider the case of the predicted results at a given relative distance for different SNR evolution times in Model A and Model B. We show calculated results at Rd − Resc = 50 pc for different SNR evolution time tage = 1000, 3000, 5000 and 7000 yr in Fig. 5. The results show that the proton spectra for different SNR evolution times are different at a fixed relative distance Rd − Resc, where an MC is located (top panel of Fig. 5), resulting in different π0 decay γ-ray spectra (bottom panel of Fig. 5). Moreover, the energy position of the maximum flux shifts to lower energy as the increase of SNR evolution times and the lower part of the proton spectrum becomes gradually steep. In other words, the increase of SNR evolution times results in the increase of low-energy protons. On the other hand, comparing the top panel of Fig. 5 with that of Fig. 4, the propagation effect is obvious, in particular for young SNR (say tage = 1000 yr), and then the results (both proton spectra and π0 decay γ-ray spectra) predicted in Model A and Model B have larger differences.
4 DISCUSSION AND CONCLUSIONS
In this paper, we have studied the escape and propagation of high-energy protons near young SNRs in the frame of NLDSA model given by Zirakashvili & Ptuskin (2012) by using two methods. In the first method (Model A), assuming the particle diffusion is different inside and outside the absorbing boundary of the particles accelerated in the SNR shock (i.e. the diffusion coefficients in two regions are different and the diffusion in the outer region corresponds to the Galactic diffusion), we have calculated the proton spectra at a given distance of the outer region and corresponding π0 decay γ-ray spectra if an MC is assumed to be at the distance. In the second method (Model B), we have treated the total spectrum of escaping protons, which have already left the remnant through an absorbing boundary during the SNR evolution time, as injection rate of the protons which propagate in the outer region, and then calculated the proton spectrum in the accumulative diffusion model given by Li & Chen (2010). Our results show that the spectrum of high-energy protons escaping from a young SNR does not have a power-law form and the protons concentrate on high-energy region. But, as the increase of the SNR evolution time, the protons in low-energy region will significantly increase, so we may conclude that the power-law approximation of the proton injection rate is valid for old SNRs.
On the other hand, we have calculated the escaping proton spectra and corresponding π0 decay γ-ray spectra in both models. Both models predict almost same proton spectra close to the absorbed boundary (2Rf), but different ones at a larger diffusive distance, in particular for the lower energy part of the proton spectrum (for example, see Fig. 2). Since Model A naturally extends the numerical model of the NLDSA given by Zirakashvili & Ptuskin (2012) from the Bohm-like diffusion region to the Galactic diffusion region, but Model B bases on the assumption of impulsive injection at 2Rf which is valid only for the SNR ages of >104–105 yr (Aharonian & Atoyan 1996), Model A is a more realistic description of the escape and propagation of high-energy protons near SNRs. In other words, Model B overestimates the propagation effect. From our results, when the distance of the source to the molecular cloud is larger, the γ-ray spectra predicted by two models are different for same model parameters (see the bottom panel of Fig. 4), especially for the lower energy part of the spectrum. In fact, recent observations of HESS show that some TeV sources are positionally coincident with SNRs (Abramowski et al. 2014, 2015). As mentioned by Aharonian & Atoyan (1996), an improvement of Model B is to use continuous injection approximation instead of impulsive injection approximation for the case of young SNRs.
Finally, it should be noted that Telezhinsky et al. (2012b) simply assumed a sudden transition from Bohm to Galactic diffusion at ∼2Rf, Malkov et al. (2013) studied a link between the CR acceleration with a very strong self-generated wave-particle scattering and their subsequent propagation with a very weak interstellar turbulence for galactic CR generation and pointed out that ion–neutral collisions in the SNR vicinity steepen proton spectrum by one power relative to test particle approximation of the DSA because of an evanescence of Alfv́en waves that allows proton's escape in a certain momentum range. Afterwards, Telezhinsky, Dwarkadas & Phol (2013) introduced an exponential transition from Bohm to Galactic diffusion at ∼2Rf. However, the transition from Bohm-like diffusion in the vicinity of SNR to Galactic diffusion further away is not clearly understood at present and need to be investigated further.
We would like to thank the anonymous referee for his/her very instructive comments. This work is partially supported by the National Science Foundation of China (11433004, 11173020, 11133006, 11163006, 11173054, 11303012) and the Strategic Priority Research Program ‘The Emergence of Cosmological Structures’ of the Chinese Academy of Sciences, Grant No. XDB09000000.



