-
PDF
- Split View
-
Views
-
Cite
Cite
C. O. Heinke, A. Bahramian, N. Degenaar, R. Wijnands, The nature of very faint X-ray binaries: hints from light curves, Monthly Notices of the Royal Astronomical Society, Volume 447, Issue 4, 11 March 2015, Pages 3034–3043, https://doi.org/10.1093/mnras/stu2652
Close - Share Icon Share
Abstract
Very faint X-ray binaries (VFXBs), defined as having peak luminosities LX of 1034–1036 erg s−1, have been uncovered in significant numbers, but remain poorly understood. We analyse three published outburst light curves of two transient VFXBs using the exponential and linear decay formalism of King & Ritter. The decay time-scales and brink luminosities suggest orbital periods of order 1 h. We review various estimates of VFXB properties, and compare these with suggested explanations of the nature of VFXBs. We suggest that: (1) VFXB outbursts showing linear decays might be explained as partial drainings of the disc of ‘normal’ X-ray transients, and many VFXB outbursts may belong to this category; (2) VFXB outbursts showing exponential decays are best explained by old, short-period systems involving mass transfer from a low-mass white dwarf or brown dwarf; (3) persistent (or quasi-persistent) VFXBs, which maintain an LX of 1034–1035 erg s−1 for years, may be explained by magnetospheric choking of the accretion flow in a propeller effect, permitting a small portion of the flow to accrete on to the neutron star's surface. We thus predict that (quasi-) persistent VFXBs may also be transitional millisecond pulsars, turning on as millisecond radio pulsars when their LX drops below 1032 erg s−1.
1 INTRODUCTION
Low-mass X-ray binaries (LMXBs) transfer matter from a low-mass star on to a neutron star (NS) or black hole (BH), via an accretion disc. Generally, those with the highest mass-transfer rates are persistent systems, while others are transients, spending most of their time in a quiescent state with little or no accretion, interrupted by occasional outbursts. In persistent systems, relatively high mass-transfer rates, and heating of the accretion disc through friction and X-ray irradiation, maintain the disc in an ionized state with high viscosity, permitting the mass to continue accreting at the rate it enters the disc (Osaki 1974; White, Kaluzienski & Swank 1984; Lasota 2001; Coriat, Fender & Dubus 2012). The outbursts of transient LMXBs often follow a fast-rise, exponential-decay shape (e.g. Chen, Shrader & Livio 1997), which can be understood in a disc instability model, in which continued accumulation of matter in the disc eventually ionizes the disc and raises its viscosity, leading to rapid dumping of the disc material (Cannizzo, Ghosh & Wheeler 1982; Faulkner, Lin & Papaloizou 1983; Meyer & Meyer-Hofmeister 1984; Huang & Wheeler 1989).
Transient LMXBs in our Galaxy with relatively high peak X-ray luminosity LX (≳4 × 1036 erg s−1) are easy to find with a variety of all-sky monitors (e.g. the RXTE All-Sky Monitor), if their X-rays are not too heavily absorbed by interstellar gas and dust. A number of fainter transients, with peak LX of a few ×1036 erg s−1, were detected by the Wide Field Cameras on BeppoSAX, in many cases showing thermonuclear bursts that prove the accretor is a NS (Heise et al. 1999). These systems showing fainter outbursts also tend to have shorter outbursts, with exponential folding times often <10 d (in't Zand et al. 2001; Cornelisse et al. 2002a). It has been suggested that the majority of these systems contain partly degenerate (brown dwarf) donors, which have evolved past the orbital period minimum for hydrogen-rich donor stars (King 2000).
A fainter class of transients, with peak LX below 1036 erg s−1, came into clear view through observations with Chandra, XMM–Newton, and Swift (Hands et al. 2004; Muno et al. 2005; Porquet et al. 2005; Sakano et al. 2005; Wijnands et al. 2006; Degenaar & Wijnands 2009). These very-faint X-ray binaries (VFXBs) are mostly transients with quiescent luminosities below 1033 erg s−1, though some (apparently) persistent or quasi-persistent sources are known (e.g. in't Zand et al. 2005; Del Santo et al. 2007; Degenaar et al. 2010; Armas Padilla, Degenaar & Wijnands 2013). The VFXBs are likely connected to the ‘burst-only’ sources identified through bursts with BeppoSAX without detectable (>1036 erg s−1) non-burst emission (Cocchi et al. 2001; Cornelisse et al. 2002a,b; Campana 2009).
VFXBs are hard to understand, as they do not follow the standard patterns of behaviour in other X-ray binaries (as we show below), although X-ray binaries that usually show VFXB behaviour seem to be as numerous as X-ray binaries that typically show brighter outbursts (Muno et al. 2005). We note three ways1 in which VFXBs show unusual behaviours:
When time-averaged accretion rates are measured (if multiple outbursts seen), they are often very low (Degenaar & Wijnands 2009, 2010). These low time-averaged accretion luminosities have been suggested to be very hard to explain in standard binary evolution models, which have difficulty reaching mass-transfer rates below 10−13 M⊙ yr−1 within the age of the Universe, as discussed in detail by King & Wijnands (2006); but see Section 3.1.
They invariably have low peak X-ray luminosities, and low integrated luminosities over a single outburst. This indicates that the amount of material accreting from the disc at one time is small (see Sections 2.3 and 3.2).
Persistent and quasi-persistent VFXBs maintain persistent mass transfer over long (years) periods of time, at rates far too low to maintain an irradiated disc. This conclusion depends upon the orbital period; but see Section 3.3.
Several suggestions to explain the origin of VFXB behaviours have been proposed – mostly concentrating on explaining behaviour (i). In this paper, we analyse the light curves of some VFXB outbursts using the predictions for accretion disc behaviour from King & Ritter (1998 hereafter KR). We then discuss the suggested explanations, and utilize the known information about these objects to improve our understanding of them.
2 ANALYSIS OF VFXB LIGHT CURVES
2.1 Formalism
KR derive analytical expressions for the outburst light curve of a typical transient LMXB, predicting whether (for a given peak LX and outer disc radius) the light curve will follow an exponential or linear shape, the time-scale of the exponential decay τe, the peak mass accretion rate (allowing calculation, for a given efficiency, of LX), and the time when the exponential decay terminates, replaced with a linear decay that drops to (nearly) zero within another τe. The details of these calculations were worked out in KR, made more rigorous by King (1998), extended to include evaporation by Dubus, Hameury & Lasota (2001), applied to observations by Shahbaz, Charles & King (1998) and Powell, Haswell & Falanga (2007), and supported by smoothed-particle-hydrodynamics accretion simulations in Truss et al. (2002). Alternative calculations have been worked out by, among others, Lipunova & Shakura (2000) and Ertan & Alpar (2002), using different methods; we do not attempt to compare these here. We summarize the key points here.
KR suggest 1015 cm2 s−1 for ν. This falls in the middle of the range of values derived by Shahbaz et al. (1998) for ν from fitting observed LMXB light curves, which are typically lower for exponential decays, and higher for linear decays. Powell et al. (2007) select a value of ν = 4 × 1014 cm2 s−1, which places the inferred value of R0 between the circularization radius Rcirc and the distance from the compact object to the inner Lagrange point, b1, for the well-observed outbursts of SAX J1808.4−3658 and XTE J0929−314. This produces rough agreement between the circularization radius and inferred radius of the disc for all four of the relatively faint NS LMXB outbursts analysed by Powell et al. (2007), though the bright NS and BH outbursts seem to require ν to be a factor of ∼2 larger. An increasing ν for larger-radius discs is reasonable, as ν is predicted to increase with R (see e.g. KR).
A small secondary maximum is sometimes observed in LMXB outbursts, and in this model may be attributed to a portion of the outer disc which is initially shielded from irradiation by, e.g., disc warps (KR, Truss et al. 2002). This secondary maximum is expected to occur roughly τe after the peak; this can contaminate the fitting of the declines if the observing cadence is insufficient to resolve this (as is likely the case in some data we consider here).
Shahbaz et al. (1998) studied outburst X-ray light curves of a number of transient LMXBs, and characterized them as showing exponential and/or linear decays. Fitting them with the formalism mentioned above, Shahbaz et al. estimated physical parameters of the LMXB accretion discs, including the viscosity ν and the size and mass of the accreting discs. These analyses were extended by Powell et al. (2007), specifically focusing on comparing the disc circularization radii (calculated from the known orbital parameters) and the inferred disc radii (using either the luminosity or exponential decay criterion). Similar analyses have been done for Aquila X-1 (Šimon 2002; Campana, Coti Zelati & D'Avanzo 2013), 4U 1608−52 (Šimon 2004), transients in M31 (e.g. Williams et al. 2004, 2006), the high-mass X-ray binaries V0332+53 (Mowlavi et al. 2006) and CI Cam (Šimon et al. 2006), and the accreting millisecond pulsars IGR J00291+5934 (Torres et al. 2008) and IGR J17511−3057 (Falanga et al. 2011). These studies have tended to find general agreement, though the values of the viscosity ν and luminosity normalization ϕ appear to differ systematically for shorter- versus longer-period systems. Nevertheless, the majority of transient LMXB outbursts have not been followed with the sensitivity and cadence required to resolve the predicted transition.
The interpretation of observed ‘brinks’ as a transition from when the entire disc is ionized, to when it is not, is not the only potential explanation. Powell et al. (2007) identified a feature in SAX J1808.4−3658's light curve as this transition, while Shahbaz et al. (1998) interpreted the same feature as a secondary maximum. Zhang, Yu & Zhang (1998) and Campana et al. (1998) interpreted a brink in the light curve of Aquila X-1 as the transition from direct accretion on to the NS surface, to a ‘propeller’ regime where the inner accretion disc is cut off at the magnetospheric radius (see also, e.g., Hartman, Galloway & Chakrabarty 2011; Asai et al. 2013; Campana et al. 2014). This interpretation allows the inference of the NS magnetic field, which in each case seems reasonable, so this interpretation cannot be ruled out. If the propeller interpretation of the brink is correct for any source, it means that the disc radius inferred from the brink should be considered as an upper limit for that source (since the brink when the outer edge stops being ionized would presumably happen at a lower luminosity). We note, however, that brinks in the light curves of several BH LMXBs (4U 1543−475, XTE J1550−564, GRO J1655−40, GX 339−4) have been suggested (Powell et al. 2007), and brinks may also be visible in the light curves of, e.g., XTE J1908+094 (Jonker et al. 2004) and XTE J1752−223 (Russell et al. 2012). However, such brinks are not obvious in all X-ray transient light curves (and a variety of features could be produced by varying obscuration of the accretion disc, e.g. Narayan & McClintock 2005), so this paradigm cannot be considered completely secure.
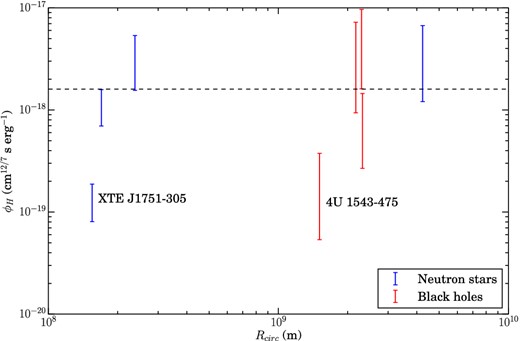
Required values of ϕH to satisfy |$R_{\rm disc}^{12/7} = \phi _H L_{\rm t}$|, for eight transients with orbital information in Powell et al. (2007). The ranges for each system reflect the ϕH value if Rdisc is either Rcirc (the lower ϕH) or the primary Roche lobe radius b. Other errors, such as the distance, are not included. The dashed horizontal line indicates our suggested value of ϕH.
2.2 Specific light curves
The data for VFXB outbursts are significantly less complete than for brighter LMXB outbursts, due to the inability of typical all-sky monitors to detect VFXB outbursts, requiring pointed observations. The available data is mostly from Swift/XRT monitoring observations of the Galactic Centre (Degenaar & Wijnands 2009, 2010), as Swift/XRT provides high sensitivity and the capacity to undertake monitoring observations frequently. We show here limited data on three outbursts by two VFXBs.
The highest quality VFXB light curve is that of the 2013 outburst of CXO J174540.0−290005, reaching LX (2–10 keV) 4 × 1035 erg s−1. The data were presented in Koch et al. (2014), including near-daily Swift/XRT observations along with multiple Chandra and NuSTAR observations (see Fig. 2). We fit the 2013 outburst decline with an exponential, converting to a linear decline. We exclude two Swift data points around MJD = 56457 from our fit; these appear to be a reflare. The exponential drop is relatively well measured, and the linear decay time-scale, though not well constrained, is consistent. For this outburst, we have enough data to simultaneously fit the exponential decay time-scale τe, the brink luminosity Lt and its time tt, and the time-scale of the linear decay τl (see Table 1). The inferred radii are 1.4 ± 0.2 × 1010 cm (from the decay time-scale) and |$0.7^{+0.2}_{-0.1}\times 10^{10}$| cm (from the brink luminosity), where the errors are propagated only from the fit. Considering our lack of knowledge of ν and ϕ, these are reasonably consistent.

Light curve of CXO J174540.0−290005's 2013 outburst (data from Koch et al. 2014). The model fit includes an exponential decay (red solid line) and a linear decay (blue dashed line); see text for details. Residuals of the fit are plotted in the lower panel for the data used.
Parameters of our fits to the light curves of three VFXT outbursts. LP: peak luminosity (2–10 keV) of outburst. Lt: brink luminosity (change from exponential to linear decline). τe: time-scale of exponential decline. τl: time-scale of linear decay. R0(τe): accretion disc radius inferred from exponential decay time-scale (see text), in cm. R0(Lt): accretion disc radius inferred from brink luminosity (see text), in cm. Errors are 90 per cent uncertainties. P are periods, in hours, estimated using the methods listed; Lpeak,1 is the linear relation from Wu et al. (2010), while Lpeak,2 is the linear relation with saturated peak luminosity for Porb above 10 h, also from Wu et al. (2010). *represents hard limits (limits reached by model constraints and not actual 90 per cent uncertainty). |$^@$|indicates the brink was not observed in this case.
| Source . | CXO J174540.0−290005 . | XMM J174457−2850.3 . | |
|---|---|---|---|
| outburst . | (2013) . | (2006) . | (2008) . |
| Lt (1034 erg s−1) | 4.6|$^{+2.4*}_{-0.2*}$| | (5)|$^@$| | 11|$^{+3*}_{-6*}$| |
| LP (1034 erg s−1) | 39±4 | 21±3 | 76±7 |
| tt (MJD) | |$56447^{+4}_{-5}$| | |$54037^{+12}_{-1}$| | |$54650^{+2*}_{-1*}$| |
| τe (d) | |$1.8^{+0.7}_{-0.4}$| | |$1.1^{+1.8}_{-0.5}$| | |$2.4^{+0.1}_{-0.7*}$| |
| τl (d) | |$8^{+8}_{-6*}$| | – | |$4.7^{+0.4}_{-2.2*}$| |
| R0(τe) | 1.4 ± 0.2 × 1010 | |$1.1^{+0.7}_{-0.3}\times 10^{10}$| | |$1.6^{+0.1}_{-0.2}\times 10^{10}$| |
| R0(Lt) | |$0.7^{+0.2}_{-0.1}\times 10^{10}$| | – | |$1.1^{+0.2}_{-0.4}\times 10^{10}$| |
| P(τe) | |$1.4^{+0.3}_{-0.3}$| | |$1.0^{+1.0}_{-0.4}$| | |$1.7^{+0.2}_{-0.3}$| |
| P(Lt) | |$0.5^{+0.2}_{-0.1}$| | – | |$1.0^{+0.2}_{-0.5}$| |
| P(Lpeak,1) | |$0.2^{+0.1}_{-0.1}$| | – | |$0.6^{+0.3}_{-0.2}$| |
| P(Lpeak,2) | 0.8 | – | 1.4 |
| Source . | CXO J174540.0−290005 . | XMM J174457−2850.3 . | |
|---|---|---|---|
| outburst . | (2013) . | (2006) . | (2008) . |
| Lt (1034 erg s−1) | 4.6|$^{+2.4*}_{-0.2*}$| | (5)|$^@$| | 11|$^{+3*}_{-6*}$| |
| LP (1034 erg s−1) | 39±4 | 21±3 | 76±7 |
| tt (MJD) | |$56447^{+4}_{-5}$| | |$54037^{+12}_{-1}$| | |$54650^{+2*}_{-1*}$| |
| τe (d) | |$1.8^{+0.7}_{-0.4}$| | |$1.1^{+1.8}_{-0.5}$| | |$2.4^{+0.1}_{-0.7*}$| |
| τl (d) | |$8^{+8}_{-6*}$| | – | |$4.7^{+0.4}_{-2.2*}$| |
| R0(τe) | 1.4 ± 0.2 × 1010 | |$1.1^{+0.7}_{-0.3}\times 10^{10}$| | |$1.6^{+0.1}_{-0.2}\times 10^{10}$| |
| R0(Lt) | |$0.7^{+0.2}_{-0.1}\times 10^{10}$| | – | |$1.1^{+0.2}_{-0.4}\times 10^{10}$| |
| P(τe) | |$1.4^{+0.3}_{-0.3}$| | |$1.0^{+1.0}_{-0.4}$| | |$1.7^{+0.2}_{-0.3}$| |
| P(Lt) | |$0.5^{+0.2}_{-0.1}$| | – | |$1.0^{+0.2}_{-0.5}$| |
| P(Lpeak,1) | |$0.2^{+0.1}_{-0.1}$| | – | |$0.6^{+0.3}_{-0.2}$| |
| P(Lpeak,2) | 0.8 | – | 1.4 |
Parameters of our fits to the light curves of three VFXT outbursts. LP: peak luminosity (2–10 keV) of outburst. Lt: brink luminosity (change from exponential to linear decline). τe: time-scale of exponential decline. τl: time-scale of linear decay. R0(τe): accretion disc radius inferred from exponential decay time-scale (see text), in cm. R0(Lt): accretion disc radius inferred from brink luminosity (see text), in cm. Errors are 90 per cent uncertainties. P are periods, in hours, estimated using the methods listed; Lpeak,1 is the linear relation from Wu et al. (2010), while Lpeak,2 is the linear relation with saturated peak luminosity for Porb above 10 h, also from Wu et al. (2010). *represents hard limits (limits reached by model constraints and not actual 90 per cent uncertainty). |$^@$|indicates the brink was not observed in this case.
| Source . | CXO J174540.0−290005 . | XMM J174457−2850.3 . | |
|---|---|---|---|
| outburst . | (2013) . | (2006) . | (2008) . |
| Lt (1034 erg s−1) | 4.6|$^{+2.4*}_{-0.2*}$| | (5)|$^@$| | 11|$^{+3*}_{-6*}$| |
| LP (1034 erg s−1) | 39±4 | 21±3 | 76±7 |
| tt (MJD) | |$56447^{+4}_{-5}$| | |$54037^{+12}_{-1}$| | |$54650^{+2*}_{-1*}$| |
| τe (d) | |$1.8^{+0.7}_{-0.4}$| | |$1.1^{+1.8}_{-0.5}$| | |$2.4^{+0.1}_{-0.7*}$| |
| τl (d) | |$8^{+8}_{-6*}$| | – | |$4.7^{+0.4}_{-2.2*}$| |
| R0(τe) | 1.4 ± 0.2 × 1010 | |$1.1^{+0.7}_{-0.3}\times 10^{10}$| | |$1.6^{+0.1}_{-0.2}\times 10^{10}$| |
| R0(Lt) | |$0.7^{+0.2}_{-0.1}\times 10^{10}$| | – | |$1.1^{+0.2}_{-0.4}\times 10^{10}$| |
| P(τe) | |$1.4^{+0.3}_{-0.3}$| | |$1.0^{+1.0}_{-0.4}$| | |$1.7^{+0.2}_{-0.3}$| |
| P(Lt) | |$0.5^{+0.2}_{-0.1}$| | – | |$1.0^{+0.2}_{-0.5}$| |
| P(Lpeak,1) | |$0.2^{+0.1}_{-0.1}$| | – | |$0.6^{+0.3}_{-0.2}$| |
| P(Lpeak,2) | 0.8 | – | 1.4 |
| Source . | CXO J174540.0−290005 . | XMM J174457−2850.3 . | |
|---|---|---|---|
| outburst . | (2013) . | (2006) . | (2008) . |
| Lt (1034 erg s−1) | 4.6|$^{+2.4*}_{-0.2*}$| | (5)|$^@$| | 11|$^{+3*}_{-6*}$| |
| LP (1034 erg s−1) | 39±4 | 21±3 | 76±7 |
| tt (MJD) | |$56447^{+4}_{-5}$| | |$54037^{+12}_{-1}$| | |$54650^{+2*}_{-1*}$| |
| τe (d) | |$1.8^{+0.7}_{-0.4}$| | |$1.1^{+1.8}_{-0.5}$| | |$2.4^{+0.1}_{-0.7*}$| |
| τl (d) | |$8^{+8}_{-6*}$| | – | |$4.7^{+0.4}_{-2.2*}$| |
| R0(τe) | 1.4 ± 0.2 × 1010 | |$1.1^{+0.7}_{-0.3}\times 10^{10}$| | |$1.6^{+0.1}_{-0.2}\times 10^{10}$| |
| R0(Lt) | |$0.7^{+0.2}_{-0.1}\times 10^{10}$| | – | |$1.1^{+0.2}_{-0.4}\times 10^{10}$| |
| P(τe) | |$1.4^{+0.3}_{-0.3}$| | |$1.0^{+1.0}_{-0.4}$| | |$1.7^{+0.2}_{-0.3}$| |
| P(Lt) | |$0.5^{+0.2}_{-0.1}$| | – | |$1.0^{+0.2}_{-0.5}$| |
| P(Lpeak,1) | |$0.2^{+0.1}_{-0.1}$| | – | |$0.6^{+0.3}_{-0.2}$| |
| P(Lpeak,2) | 0.8 | – | 1.4 |
The 2006 outburst of CXO J174540.0−290005 (Degenaar & Wijnands 2009) was less frequently sampled (Fig. 3), with only three points defining the decay. The outburst appears to have a flat top with LX ∼ 2 × 1035 erg s−1 lasting ∼3 d (versus ∼7 d for the brighter 2013 outburst), decaying to ∼5 × 1034 erg s−1. Since this LX range corresponds to the exponential part of the 2013 decay, we fit this decay with an exponential. We are only able to effectively constrain the exponential decay time-scale. We fix the limiting luminosity of the exponential decay to 4.8 × 1034 erg s−1 (assuming the same ratio of Lt/Le as in the 2013 outburst); changing this does not have a large impact. We find similar (possibly slightly smaller) values for the inferred radii as in the 2013 outburst, with larger uncertainties (see Table 1); below we use 1.1 × 1010 cm as our best estimate for CXO J174540.0−290005.
The 2008 outburst of XMM J174457−2850.3 (Degenaar & Wijnands 2010) is the second most useful data set, with a decay defined by six observations (Fig. 4). We cannot be certain that we have observed the peak of the outburst, since the beginning of the outburst was not identified. We can fit all the same quantities as in the 2013 outburst of CXO J174540.0−290005, though the transition from exponential to linear decay is not clearly resolved (Table 1). The inferred radii are |$1.6^{+0.1}_{-0.2}\times 10^{10}$| cm (from the decay time-scale), and |$1.1^{+0.2}_{-0.4}\times 10^{10}$| cm (from the brink luminosity); combining these, we estimate ∼1.4 × 1010 cm. This transient is known to contain a NS, from the detection of a thermonuclear burst (Degenaar et al. 2014).
2.3 Implications of outburst fluences, peak luminosities
The low peak luminosities and integrated outburst luminosities can be used to infer quantitative conclusions. We first address the integrated outburst luminosities of VFXBs, in general and for the transients studied above, using the formalism of King (2000). King (2000) showed that the faint (peak LX < 1037 erg s−1) transients discovered by BeppoSAX in the Galactic Centre (e.g. SAX J1808.4−3658) were consistent with LMXBs that had evolved beyond their period minimum, agreeing with evolutionary modelling of specific sources (e.g. Bildsten & Chakrabarty 2001). We have not seen this calculation illustrated before for VFXBs.
3 NATURE OF VFXBs
VFXBs may be an inhomogeneous group of objects. Thus, the unusual behaviours mentioned above may have different (sometimes overlapping) explanations. We address these in turn below.
3.1 Behaviour (i): low time-averaged mass-transfer rate
King & Wijnands (2006) specifically considered whether standard binary evolution – either ultracompact binaries (mass-losing white dwarfs), or cataclysmic variable-like late evolution (mass-losing main-sequence stars) – could produce low time-averaged mass-transfer rates, and concluded that with standard assumptions, rates of <10−13 M⊙ yr−1 could not be reached within a Hubble time.
First, we check whether King & Wijnands (2006) used the correct mass-transfer rate for comparison. Assuming a NS accretor (as verified for a number of VFXBs, see below), the inferred mass-transfer rates from Degenaar & Wijnands 2010 (their table 2) of the eight transients in the Swift Galactic Centre monitoring region (all of which produced at least one VFXB outburst during the monitoring, i.e. Lpeak < 1036 erg s−1) are: (3–8) × 10−11, (7–14) × 10−13, (2–6) × 10−11, (1–10) × 10−12, (5–20) × 10−13, 5 × 10−13, ≲1 × 10−12, and ≲4 × 10−13 M⊙ yr−1. Of these, only two appear to be clearly below 10−12 M⊙ yr−1, and none are required to be below 10−13 M⊙ yr−1. For CXO J174540.0−290005, Degenaar & Wijnands (2010) estimated (3–15) × 10−13 M⊙ yr−1. Koch et al. (2014) used the presence of a second outburst, and a longer history, to better constrain its average mass-transfer rate, quoting 7 × 10−14 M⊙ yr−1; we correct an error in their work to estimate 5 × 10−13 M⊙ yr−1.
Accretion rates near 10−12 M⊙ yr−1 can be reached by standard binary evolution within a Hubble time. One path is via ultracompact binary evolution, which reaches 10−12 M⊙ yr−1 in a couple of Gyr at orbital periods near 1 h (Iben & Tutukov 1985; Deloye & Bildsten 2003), and can reach 10−13 M⊙ yr−1 in a Hubble time. The other path is cataclysmic variable-like post-period-minimum evolution, which produces roughly ∼10−12 M⊙ yr−1 in 10 Gyr at orbital periods near 2 h (Rappaport, Joss & Webbink 1982; Howell, Nelson & Rappaport 2001).6 Since the orbital evolution in each case slows down with time, the majority of old X-ray binaries are expected to have mass-transfer rates below 10−11 M⊙ yr−1 (e.g. Stehle, Kolb & Ritter 1997); this is consistent with the distribution of observed mass-transfer rates above.
For completeness, we consider the possibilities King & Wijnands (2006) suggested to explain the low time-averaged mass-transfer rates of VFXBs: (a) hydrogen-poor companions in old LMXBs containing BHs, (b) low initial companion masses (e.g. brown dwarf companions when mass transfer starts), or (c) intermediate-mass (M ∼ 1000 M⊙) BH accretors. For many VFXBs, NS accretors have been verified through X-ray bursts (SAX J1828.5−1037, Cornelisse et al. 2002a; 1RXS J171824.2−402934, Kaptein et al. 2000; XMMU J174716.1−281048, Del Santo et al. 2007; AX J1754.2−2754, Sakano et al. 2002; Chelovekov & Grebenev 2007; 1RXH J173523.7−354013, Degenaar et al. 2010; IGR J17062−6143, Degenaar et al. 2013; and XMM J174457−2850.3, Degenaar et al. 2014), ruling out that these objects are BHs, and thus that most VFXBs are BH systems accreting from hydrogen-poor companions. The presence of VFXBs outside the centres of globular clusters (M15 X-3, Heinke, Cohn & Lugger 2009; IGR 17361−4441, Bozzo et al. 2011), while intermediate-mass BHs should rapidly sink to the cluster centres, also rules out intermediate-mass BHs for the known globular cluster VFXBs.
Maccarone & Patruno (2013) suggested that most VFXBs may be ‘period-gap’ systems, in which the secondary has detached from its Roche lobe while evolving from a period of ∼3 down to ∼2 h, and that mass transfer is due to a wind. Accretion from the wind of main-sequence stars has previously been suggested for low-luminosity X-ray sources (Bleach 2002; Pfahl, Rappaport & Podsiadlowski 2002; Willems & Kolb 2003). However, the wind-loss rates (10−14–10−16 M⊙ yr−1) considered for M dwarfs (which compare reasonably to Proxima Cen's measured mass-loss rate of 4 × 10−15 M⊙ yr−1, Wood et al. 2001) are too low to explain the measured time-averaged mass-transfer rates of the majority of known VFXBs, even before accounting for a wind accretion efficiency that is likely to be well below the Bondi–Hoyle–Littleton rate (see Bleach 2002).
Declining radiative efficiency of advective flows at low luminosities, and thus in short-period BH X-ray binaries, has been suggested repeatedly (e.g. Wu et al. 2010; Maccarone & Patruno 2013; Knevitt et al. 2014), and could help to explain the behaviour of some VFXBs suspected of containing BHs (e.g. Swift J1357.2−093313, Corral-Santana et al. 2013). In Section 3.3 below, we discuss how reduced radiative efficiency (in the form of outflows, rather than advective flows) may also be a factor in some NS VFXBs.
3.2 Behaviour (ii): outburst fluences, peak luminosities
The peak luminosities of VFXB transients suggest very small accretion discs, or that only part of the accretion discs are drained. For some VFXB outbursts (e.g. the fainter outbursts of GRS 1741−2853 and AX J1745.6−2901), it is very likely that only part of the disc participated in the outburst, as discussed by Degenaar & Wijnands 2010 (cf. Maitra & Bailyn 2008). Indeed, AX J1745.6−2901 has a known 8.4-h eclipse period (Maeda et al. 1996; Porquet et al. 2007), proving the presence of a much larger disc.7 Armas Padilla et al. (2013) show that the optical/X-ray correlation from the likely BH VFXB Swift J1357.2−0933 indicates that the disc is not strongly irradiated (but cf. Shahbaz et al. 2013, who find evidence for an irradiated disc), suggesting that not all of the disc is heated, and thus supporting the suggestion that not all of the disc accretes in many VFXB outbursts. However, the exponential decays studied in Section 2 above indicate that, within the framework of the KR model, we can infer the disc sizes for some VFXB outbursts.
The calculations above based on peak luminosities suggest predicted orbital periods of 1–100 min. The integrated outburst luminosity calculations give similar predictions, of order 12 min for the particular systems studied here. The empirical relations between peak luminosity and orbital period (Wu et al. 2010) predict between 12 and 84 min. However, the low range of these predictions (<30 min) gives an orbital period so small that the mass-transfer rate driven by (inescapable) gravitational radiation would be above ∼10−10 M⊙ yr−1. For periods <20 min, the system could not even be transient in the disc instability model (see Deloye & Bildsten 2003; Lasota, Dubus & Kruk 2008; Heinke et al. 2013).
Our calculations of the exponential decay time-scales and brink luminosities provide period estimates around 1 h. These are in excellent agreement with the evolutionary predictions of ultracompact evolution (discussed above), which give mass-transfer rates in the right range for this period range. There is even a perfect example of a borderline VFXB, the accreting millisecond pulsar NGC 6440 X-2, with a peak LX typically 1–2 × 1036 erg s−1, an orbital period of 57 min (Altamirano et al. 2010), and a time-averaged mass-transfer rate of ∼10−12 M⊙ yr−1 (Heinke et al. 2010).
Alternatively, standard cataclysmic variable-like evolution gives periods not much longer (∼2h) with mass-transfer rates of 10−12 M⊙ yr−1. The poster child for such an evolution would be IGR J00291+5934, another accreting millisecond pulsar with peak LX values ranging from 2 × 1036 down to 9 × 1035 erg s−1 (Hartman et al. 2011), an orbital period of 2.47 h, a low-mass (partly degenerate) companion, and a time-averaged mass-transfer rate of ∼3 × 10−12 M⊙ yr−1 (Galloway et al. 2005). We do not feel that the various indirect estimates of the orbital period discussed in this work are accurate enough to distinguish between a 1 h orbit versus a 2 h orbit. Spectroscopic (likely infrared) observations would be of great interest to search for the presence, or lack, of hydrogen lines, during outbursts from these systems.
3.3 Behaviour (iii): persistent mass transfer at low rates
in't Zand et al. (2009) suggested that the persistent VFXB 1RXS J171824.2−402934 must be an ultracompact binary with orbital period <7 min, in order to maintain its disc in an ionized state at its average LX of 8 × 1034 erg s−1. This would be consistent with the short orbital periods suggested by the low peak luminosities and integrated outburst luminosities of VFXB transients. However, such short-period systems will have high mass-transfer rates due to gravitational radiation, and thus remain persistent, bright sources (Deloye & Bildsten 2003; Lasota et al. 2008), leading to a clear contradiction. Furthermore, some persistent VFXBs show evidence of longer orbital periods; 1RXH J173523.7−354013 (persistent at 2 × 1035 erg s−1) shows strong Hα emission in its optical spectrum (Degenaar et al. 2010); and M15 X-3 has an optical companion with a spectral energy distribution matching a 0.44 M⊙ star (Heinke et al. 2009, Arnason et al., in preparation). Somehow, the persistent VFXBs are continuing to accrete at very low rates.
Heinke et al. (2009) suggested that the propeller effect (the inhibition of accretion when the NS magnetosphere is rotating more quickly than the Keplerian orbital speed at the disc/magnetosphere boundary; Illarionov & Sunyaev 1975) may be responsible for the inhibition of regular accretion in VFXBs. Some current numerical work indicates that the propeller effect can build up a waiting (‘trapped’) disc, rather than throwing material efficiently from the system (D'Angelo & Spruit 2010, 2012). Other numerical work indicates that the propeller effect may eject most of the infalling material from the binary (Romanova et al. 2003; Ustyugova et al. 2006). In either case, a fraction (for instance, 10 per cent in some simulations of Romanova et al. 2004) of the infalling material can still accrete continuously on to the star. Such a situation may explain the existence of persistent, or quasi-persistent, VFXBs.
Observational evidence in favour of such a situation is the ‘active’ quiescent state (with LX between 1033 and 1034 erg s−1) of three ‘transitional pulsars’, which have been seen as millisecond radio pulsars as well as in accreting states (Archibald et al. 2009; Papitto et al. 2013; Bassa et al. 2014; Bogdanov et al. 2014; Patruno et al. 2014). The rapid switches between this ‘active’ quiescent state and a much lower-LX ‘passive’ state (Linares et al. 2014) suggest that the X-ray luminosity in the ‘active’ state is driven by a tongue of accretion down on to the NS, from a ‘trapped’ disc. Archibald et al. (2014) recently identified pulsations during the ‘active’ (3 × 1033 erg s−1) state from the transitional pulsar PSR J1023+0038, which proves that accretion is continuing on to the NS surface. Degenaar et al. (2014) suggested that the VFXB XMM J174457−2850.3 (which we studied in Section 2 above) may also be a transitional pulsar, spending significant time in a similar ‘active’ state around 1033–1034 erg s−1, in between periods of quiescence (at LX ∼ 5 × 1032 erg s−1) and outburst (1035–1036 erg s−1).
Here we suggest, for the first time, that many, or all, of the persistent and quasi-persistent VFXBs may be transitional pulsars in ‘active’ states. The transitional pulsar idea provides a reasonable explanation for how several quasi-persistent VFXBs could remain at ∼1034 erg s−1 for years, turn ‘off’ for one or more years, then resume their low luminosity. For instance, AX J1754.2−2754 appeared to be a persistent VFXB, but disappeared for up to a year before turning back on (Bassa et al. 2008; Jonker & Keek 2008); it has also been suggested (on the basis of its low outburst optical magnitude) that this object should be ultracompact (Bassa et al. 2008). M15 X-3 was detected (retrospectively) by ROSAT in the mid-1990s at 1034 erg s−1, then was faint (∼3 × 1031 erg s−1 in 2001–2002, then returned to 1034 erg s−1 in seven observations between 2005 and 2013 (Heinke et al. 2009, Arnason et al. in preparation). A possible problem with this interpretation is the lack of detection of pulsations in the persistent VFXB 1RXS J171824.2−402934 (Patruno 2010).
Some of the (quasi-)persistent VFXBs have time-averaged mass-transfer rates that appear too low for the system parameters. As an example, M15 X-3 has an estimated time-averaged mass-transfer rate of 2 × 10−13 M⊙ yr−1 (Heinke et al. 2009), but the companion star is estimated to have a mass of ∼0.4 M⊙, allowing an inference of a roughly 4-h orbital period (Arnason et al. in preparation). An active propeller could eject the majority of the inflowing material. Alternatively, irradiation-driven mass-transfer cycles, acting over periods of ∼108 yr (see e.g. Hameury, King & Lasota 1989; Büning & Ritter 2004; Benvenuto, De Vito & Horvath 2014), could alter the evolution of systems like M15 X-3. These cycles are also a natural explanation for the substantially higher mass-transfer rates in many persistent X-ray binaries, compared to those predicted by evolutionary models (Podsiadlowski, Rappaport & Pfahl 2002). Ritter (2008) pointed out that irradiation-driven mass-transfer instabilities only work if the system is persistent. That is, when the system returns to its high accretion rate after a low state, it must be persistent, so as to sustain the irradiation over a thermal time-scale; this does not exclude X-ray binaries from being transient during the low phase of their mass-transfer cycles.
4 CONCLUSIONS
The nature of the objects producing VFXB outbursts (peaking between ∼1034 and 1036 erg s−1) is one of the key open questions in X-ray binary research, especially since these outbursts significantly outnumber ‘normal’ (>1036 erg s−1) outbursts, and a majority of LMXBs in the Galactic Centre area have only been seen to exhibit VFXB outbursts. We applied the accretion disc light-curve formalism of KR to the light curves of three VFXB outbursts, from two VFXBs in the Galactic Centre. Particularly for the 2013 outburst of CXO J174540.0−290005, we found evidence for an exponential decay followed by a linear decay, in accord with the predictions of KR for a completely ionized disc. The time-scale of the exponential decay, the luminosity of the ‘brink’ where the linear decay begins, and the time-scale of the linear decay, allow a rough inference of the accretion disc radius, and thus suggest an orbital period of order one hour for these two systems. Most of the VFXB outburst light curves have too few points for reliable constraints, indicating the usefulness of daily Swift/XRT monitoring of the Galactic Centre, and daily monitoring of other VFXB outbursts after detection.
This inference depends on using values for the viscosity, and luminosity scaling, parameters like those which Powell et al. (2007) found accurately described the outbursts from several other short-period NS transients. Estimates of the accretion disc size and orbital period from peak luminosities and total accreted mass give similar values, predicting orbital periods between 12 and 84 min. Orbital periods below 30 min are inconsistent with the predicted high mass-transfer rate of such short-period systems, within the disc instability outburst model.
Comparing the time-averaged mass-transfer rates of well-studied VFXB transients with the predictions of evolutionary theory, we find that ultracompact binary evolution can easily reach the observed rates for orbital periods of 60–90 min, while CV-like evolution of hydrogen-rich companions evolving to larger periods after the ∼90-min period minimum can also reach most of this range. Thus, we suggest that the most likely companions in transient VFXB systems are very low mass white dwarfs, with orbital periods near 1 h. We also cannot rule out very low mass brown dwarfs, with orbital periods near 2 h, and recommend optical/infrared spectroscopy to search for H and He lines in VFXBs during outbursts.
A portion of VFXB outbursts are known to arise from LMXBs that also produce brighter outbursts. These are likely to involve only part of the accretion disc (Degenaar & Wijnands 2010). A clear prediction of KR (illustrated by Shahbaz et al. 1998) is that such outbursts will show exclusively linear, not exponential, declines; it should be possible to distinguish linear versus exponential decays in faint Galactic Centre transients with frequent (daily) monitoring.
The existence of persistent, and quasi-persistent, VFXBs is another challenge. Keeping a disc ionized via persistent accretion at such low luminosities would require orbital periods of only a few minutes; but such short orbital periods would necessarily produce mass-transfer rates orders of magnitude greater than observed, and two quasi-persistent VFXBs show definite evidence for hydrogen-rich donor stars. We propose that a rapidly rotating NS magnetosphere chokes the accretion flow (producing a propeller, or a dead disc, situation), permitting only limited accretion. This suggests that the quasi-persistent VFXBs may also be identified with transitional millisecond pulsars, turning on as radio pulsars when accretion is fully stopped and their X-ray luminosity drops below 1033 erg s−1. X-ray monitoring of these intriguing systems is thus suggested, to enable target-of-opportunity radio pulsation detections during low states.
We thank the Swift team for their assistance in obtaining the observations that have made this work possible. COH is supported by an NSERC Discovery Grant, an Alberta Ingenuity New Faculty Award, and an Alexander von Humboldt Fellowship. ND is supported by NASA through Hubble Postdoctoral Fellowship grant number HST-HF-51287.01-A from STScI. We acknowledge extensive use of the ADS and arXiv.
Alexander von Humboldt Fellow, at Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, D-53121 Bonn, Germany.
Hubble Fellow.
The behaviours of thermonuclear bursts at low accretion rates are also theoretically challenging (e.g. Peng, Brown & Truran 2007), but we do not address that issue here.
The accretor is certainly a NS for XMM J174457−2850.3 (Degenaar et al. 2014); as many VFXBs are known to be NSs, this is a reasonable guess for CXO J174540.0−290005 as well.
We note that Maccarone & Patruno (2013) claim that KR state LP = 2.3 × 1036R11 erg s−1; this equation appears to be a misprint of |$L_{\rm P} = 2.3\times 10^{36} R_{11}^2$|, calculated in Wu et al. (2010) to estimate the peak L of systems which experience only a linear decay, based on equations 31 and 32 of KR.
Note that Wu et al. (2010) used 3–200 keV X-ray luminosities.
No errors were provided for this relation, which was not found to be as good a description of the data as the linear fit.
This implies a high inclination, which might suggest that AX J1745.6−2901 was actually much brighter, and not really a VFXB. However, the detection of X-ray bursts reaching nearly the Eddington luminosity for a NS at the Galactic Centre (Degenaar & Wijnands 2009; Degenaar et al. 2012) indicates that we see most of its LX, and thus that it does indeed show VFXB outbursts (its 2006 outburst, during which two X-ray bursts were detected, peaked at 9 × 1035 erg s−1). In any case, statistical arguments rule out that the majority of VFXBs are faint purely due to inclination effects (Wijnands et al. 2006).





