Intrinsic physical conditions and structure of relativistic jets in active galactic nuclei

Nokhrina, E. E.; Beskin, V. S.; Kovalev, Y. Y.; Zheltoukhov, A. A.

doi:10.1093/mnras/stu2587

Abstract

The analysis of the frequency dependence of the observed shift of the cores of relativistic jets in active galactic nuclei (AGNs) allows us to evaluate the number density of the outflowing plasma n_e and, hence, the multiplicity parameter λ = n_e/n_GJ, where n_GJ is the Goldreich–Julian number density. We have obtained the median value for λ_med = 3 × 10¹³ and the median value for the Michel magnetization parameter σ_{M, med} = 8 from an analysis of 97 sources. Since the magnetization parameter can be interpreted as the maximum possible Lorentz factor Γ of the bulk motion which can be obtained for relativistic magnetohydrodynamic (MHD) flow, this estimate is in agreement with the observed superluminal motion of bright features in AGN jets. Moreover, knowing these key parameters, one can determine the transverse structure of the flow. We show that the poloidal magnetic field and particle number density are much larger in the centre of the jet than near the jet boundary. The MHD model can also explain the typical observed level of jet acceleration. Finally, casual connectivity of strongly collimated jets is discussed.

radiation mechanisms: non-thermal, galaxies: active, galaxies: jets, quasars: general, radio continuum: galaxies

1 INTRODUCTION

Strongly collimated jets represent one of the most visible signs of the activity of compact astrophysical sources. They are observed both in relativistic objects such as active galactic nuclei (AGNs) and microquasars, and in young stars where the motion of matter is definitely non-relativistic. This implies that we are dealing with some universal and extremely efficient mechanism of energy release.

At present the magnetohydrodynamic (MHD) model of activity of compact objects is accepted by most astrophysicists (Mestel 1999; Krolik 1999). At the heart of the MHD approach lies the model of the unipolar inductor, i.e. a rotating source of direct current. It is believed that the electromagnetic energy flux – the Poynting flux – plays the main role in the energy transfer from the ‘central engine’ to active regions. The conditions for the existence of such a ‘central engine’ are satisfied in all the compact sources mentioned above. Indeed, all compact sources are assumed to harbour a rapidly spinning central body (black hole, neutron star or young star) and some regular magnetic field, which leads to the emergence of strong induction electric fields. The electric fields, in turn, lead to the appearance of longitudinal electric currents resulting in effective energy losses and particle acceleration.

The first studies of the electromagnetic model of compact sources (namely radio pulsars) were carried out as early as the end of the 1960s (Goldreich & Julian 1969; Michel 1969). It was evidenced that there are objects in the Universe in which electrodynamical processes can play the decisive role in the energy release. Then, Blandford (1976) and Lovelace (1976) independently suggested that the same mechanism can also operate in AGNs, and for nearly 40 years this model has remained the leading one.

Remember that within the MHD approach the total energy losses P_jet can be easily evaluated as P_jet ∼ IU, where I is the total electric current flowing along the jet, and U ∼ ER₀ is the electro-motive force exerted on the black hole on the scale R₀. If the central engine (black hole for AGNs) rotates with the angular velocity Ω in the external magnetic field B₀, one can evaluate the electric field as E ∼ (ΩR₀/c)B₀. On the other hand, assuming that for AGNs the current density j is fully determined by the relativistic outflow of the Goldreich–Julian (GJ) charge density ρ_GJ = ΩB₀/(2πc) (i.e. the minimum charge density required for the screening of the longitudinal electric field in the magnetosphere), one can write down j ≈ cρ_GJ. It gives

\begin{equation} I \sim \Omega B_{0}R_{0}^2. \end{equation}

(1)

As for AGNs, one can set R₀ ≈ r_g = 2GM/c² to obtain the well-known evaluation (Blandford & Znajek 1977)

\begin{equation} P_{\rm jet} \sim \left(\frac{\Omega r_{\rm g}}{c}\right)^{2} B_{0}^{2} r_{\rm g}^{2} c. \end{equation}

(2)

In particular, comparing expressions (1) and (2), one can straightforwardly obtain

\begin{equation} I \approx c^{1/2}P_{\rm jet}^{1/2}. \end{equation}

(3)

For AGNs it corresponds to 10¹⁹–10²¹ A. Certainly, the question as to whether it is possible to consider a black hole immersed in an external magnetic field as a unipolar inductor turned out to be also rather nontrivial (Punsly 2001; Beskin 2009; Okamoto 2009).

As a result, the MHD model was successfully used to describe a lot of processes in active nuclei including the problem of the stability of jets (Benford 1981; Hardee & Norman 1988; Appl & Camenzind 1992; Istomin & Pariev 1994; Bisnovatyi-Kogan 2007; Lyubarsky 2009) and their synchrotron radiation (Blandford & Königl 1979; Pariev, Istomin & Beresnyak 2003; Lyutikov, Pariev & Gabuzda 2005). In particular, it was shown both analytically (Bogovalov 1995; Heyvaerts & Norman 2003; Beskin & Nokhrina 2009) and numerically (Komissarov et al. 2006; Tchekhovskoy, McKinney & Narayan 2009; Porth et al. 2011; McKinney, Tchekhovskoy & Blanford 2012) that for sufficiently small ambient pressure the dense core can be formed. This is related both to advances in the theory which have at last formulated sufficiently simple analytical relations (Blandford & Znajek 1977; Beskin 2010), and to the breakthrough in numerical simulations (Komissarov et al. 2006; Tchekhovskoy et al. 2009; Porth et al. 2011; McKinney et al. 2012) which confirmed theoretical predictions.

Moreover, recently Kronberg et al. (2011) demonstrated that in QSO 3C 303 the jet does possess large enough toroidal magnetic field, the appropriate longitudinal electric current along the jet I ≈ 1.7 × 10¹⁹ A being as large as the electric current I_GJ (equation 1) which is necessary to support the Poynting energy flux. Besides, the lack of γ-ray radiation as probed by the Fermi Observatory for AGN jets observed at small enough viewing angles ϑ < 5° (Savolainen et al. 2010) can be easily explained as well. Indeed, as was found (see e.g. Beskin 2010), within well-collimated magnetically dominated MHD jets the Lorentz factors of the particle bulk motion can be evaluated as

\begin{equation} \Gamma \approx r_{\perp }/R_{\rm L}, \end{equation}

(4)

where r_⊥ is the distance from the jet axis, and R_L = c/Ω is the light cylinder radius. Thus, the energy of particles radiating in small enough angles ϑ with respect to the jet axis is to be much smaller than that corresponding to peripheral parts of a jet.

The most important MHD parameters describing relativistic flows (which was originally introduced for radio pulsars) are the Michel magnetization parameter σ_M and the multiplicity parameter λ. The first one determines the maximum possible bulk Lorentz factor Γ of the flow when all the energy transported by the Poynting flux is transmitted to particles. The second one is the dimensionless multiplicity parameter λ = n_e/n_GJ, which is defined as the ratio of the number density n_e to the GJ number density n_GJ = ΩB/2πce. It is important that these two parameters are connected by the simple relation (Beskin 2010)

\begin{equation} \sigma _{\rm M} \approx \frac{1}{\lambda }\left(\frac{P_{\rm jet}}{P_{\rm A}}\right)^{1/2}. \end{equation}

(5)

Here, P_A = m²c⁵/e² ≈ 10¹⁷ erg s⁻¹ is the minimum energy losses of the central engine which can accelerate particles to relativistic energies, and P_jet is the total energy losses of the compact object.

Unfortunately, up to now neither the magnetization nor the multiplicity parameters were actually known as the observations could not give us the direct information about the number density and bulk energy of particles. The core-shift method has been applied to obtain the concentration n_e, magnetic field B (Lobanov 1998; O'Sullivan & Gabuzda 2009; Pushkarev et al. 2012; Zdziarski et al. 2014) and the jet composition (Hirotani 2005) in AGN jets. However, evaluation of multiplicity and Michel magnetization parameters, which needs to estimate the total jet power, has not been done. From a theoretical point of view if the inner parts of the accretion disc are hot enough, then electron–positron pairs can be produced by two-photon collisions, where photons with sufficient energy originate from the inner parts of the accretion disc (Blandford & Znajek 1977; Moscibrodzka et al. 2011). In this case λ ∼ 10¹⁰–10¹³, and the Michel magnetization parameter σ_M ∼ 10–10³. The second model takes into account the appearance of the region where the GJ plasma density is equal to zero due to general relativity effects that corresponds to the outer gap in the pulsar magnetosphere (Beskin, Istomin & Pariev 1992; Hirotani & Okamoto 1998). This model gives λ ∼ 10²–10³, and σ_M ∼ 10¹⁰–10¹³.

This large difference in the estimates for the magnetization parameter σ_M leads to two completely different pictures of the flow structure in jets. In particular, it determines whether the flow is magnetically or particle dominated. The point is that for ordinary jets r_⊥/R_L ∼ 10⁴–10⁵. As a result, using the universal asymptotic solution Γ ≈ r_⊥/R_L (4), one can obtain that the values σ_M ∼ 10–10³ correspond to the saturation regime when almost all the Poynting flux P_em is transmitted to the particle kinetic energy flux P_part. On the other hand, for σ_M ∼ 10¹² the jet remains magnetically dominated (P_part ≪ P_em). Thus, the determination of the Michel magnetization parameter σ_M is the key point in the analysis of the internal structure of relativistic jets.

The paper is organized as follows. In Section 2, it is shown that VLBI (very long baseline interferometry) observations of synchrotron self-absorption in AGN jets allow us to evaluate the number density of the outflowing plasma n_e and, hence, the multiplicity parameter λ. We discuss the source sample and present the result for multiplicity and Michel magnetization parameters in Section 3. The values λ ∼ 10¹³ obtained from the analysis of 97 sources shows that for most jets the magnetization parameter σ_M ≲ 30. Since the magnetization parameter is the maximum possible value of the Lorentz factor of the relativistic bulk flow, this estimate is consistent with observed superluminal motion. In Section 4, it is shown that for physical parameters determined above, the poloidal magnetic field and particle number density are much larger in the centre of the jet than near its boundary. Finally, in Section 5 the casual connectivity of strongly collimated supersonic jets is discussed. Throughout the paper, we use the Λ cold dark matter cosmological model with H₀ = 71 km s⁻¹ Mpc⁻¹, Ω_m = 0.27 and |$\Omega _\Lambda =0.73$| (Komatsu et al. 2009).

2 THE METHOD

2.1 General relations

To determine the multiplicity parameter λ and the Michel magnetization parameter σ_M one can use the dependence on the visible position of the core of the jet from the observation frequency (Blandford & Königl 1979; Gould 1979; Marscher 1983; Lobanov 1998; Hirotani 2005; Kovalev et al. 2008; O'Sullivan & Gabuzda 2009; Sokolovsky et al. 2011; Pushkarev et al. 2012). This effect is associated with the absorption of the synchrotron photon gas by relativistic electrons (positrons) in a jet.

Typically, the parsec-scale radio morphology of a bright AGN manifests a one-sided jet structure due to Doppler boosting that enhances the emission of the approaching jet. The apparent base of the jet is commonly called the ‘core’, and it is often the brightest and most compact feature in VLBI images of AGN. The VLBI core is thought to represent the jet region where the optical depth is equal to unity.

We will employ the following model to connect the physical parameters at the jet launching region with the observable core-shift. There is a MHD relativistic outflow of non-emitting plasma moving with bulk Lorentz factor Γ and number density n_e in the observer rest frame. On the latter we superimpose the flow of emitting particles with distribution |${\rm d}n_{{\rm syn}*} = k_{{\rm e}*}\gamma _{*}^{-1+2\alpha }{\rm d}\gamma _{*}$|⁠, γ_* ∈ [γ_min*; γ_max*]. Here, n_syn* is number density of emitting plasma, k_e* is number density amplitude and γ_* is the emitting particles’ Lorentz factor. All the parameters with subscript ‘*’ are taken in the non-emitting plasma rest frame, i.e. in the frame which locally moves with the bulk Lorentz factor Γ.

We suppose that the emitting particles radiate synchrotron photons in the jet's magnetic field, and these photons scatter off the same electrons, which lead to the photon absorption (Gould 1979; Lobanov 1998; Hirotani 2005). The corresponding turn-over frequency ν_m*, the frequency at which the flux density S_ν has a maximum, can be evaluated using expressions from Gould (1979) as

\begin{equation} \nu _\mathrm{m*}^{(5-2\alpha )}=\frac{c_{\alpha }^{2}(1-2\alpha )}{5(5-2\alpha )}\frac{e^{4}}{m^{2}c^{2}}\left(\frac{e}{2\pi mc}\right)^{3-2\alpha }R_{*}^{2}B_*^{3-2\alpha }k_{\rm e*}^{2}. \end{equation}

(6)

The function c_α ( · ) is a composition of gamma-functions defined by Gould (1979), and for α = −1/2 we have c_α (2) = 1.396. Constants e, m and c are the electron charge, electron mass and the speed of light correspondingly. Finally, B_* is the magnitude of disordered magnetic field in an emitting region with a characteristic size R_* along the line of sight.

Although we assume that the toroidal magnetic field dominates in the jet, an assumption of disordered magnetic field in our opinion can be retained, because, for an optically thin jet, the photon meets both directions of field. Thus, the mean magnetic field along the photon path is almost zero, which mimics the behaviour of a disordered field. As a result, the parameters in the observer rest frame and plasma rest frame are connected by the following equations:

\begin{equation} \frac{\nu _{\rm m*}}{\nu _{\rm m}}=\frac{1+z}{\delta }, \end{equation}

(7)

\begin{equation} R_{*}=\frac{2\,r_*\chi _*}{\sin {\varphi _*}}=\frac{2\,r\chi }{\delta \sin {\varphi }}, \end{equation}

(8)

\begin{equation} B_{*}=\sqrt{B^2-E^2}\approx \frac{B_{\varphi }}{\Gamma }\approx \frac{B}{\Gamma }, \end{equation}

(9)

\begin{equation} k_{\rm e*}=\frac{k_{\rm e}}{\Gamma }, \end{equation}

(10)

where z is the redshift,

\begin{equation} \delta =\frac{1}{\Gamma \left(1-\beta \cos \varphi \right)} \end{equation}

(11)

is the Doppler factor, χ is the jet half-opening angle and φ is a viewing angle.

Further, the number density of emitting electrons n_syn is connected with the amplitude k_e as

\begin{equation} k_{\rm e}=n_{\rm syn}\frac{2\alpha }{\gamma _{\rm max}^{2\alpha }-\gamma _{\rm min}^{2\alpha }}, \end{equation}

(12)

where γ = γ_*Γ. For α = −1/2, we get

\begin{equation} k_{\rm e}\approx n_{\rm syn}\gamma _{\rm min}. \end{equation}

(13)

We also put n_syn = ξn_e. Here ξ is a ratio of the number density of emitting particles to the MHD flow number density. The portion of particles effectively accelerated by the internal shocks was found by Sironi, Spitkovsky & Arons (2013) to be about 1 per cent, so we take ξ ≈ 0.01.

Finally, we assume (Lobanov 1998; Hirotani 2005) the following power-law behaviour for the magnetic field and particle density dependence on distance:

\begin{equation} B(r)=B_{1}\left(\frac{r}{r_{1}}\right)^{-1}, \end{equation}

(14)

\begin{equation} n_{\rm e}(r)=n_1\left(\frac{r}{r_1}\right)^{-2}, \end{equation}

(15)

where B₁ is the magnetic field and n₁ is the number density at r₁ = 1 pc, respectively. For these scalings of particle density and magnetic field with the distance the turn-over frequency ν_m as a function of r does not depend on α and can be written as

\begin{equation} \nu _{\rm m}\propto r^{-1}. \end{equation}

(16)

This scaling has been confirmed by Sokolovsky et al. (2011) in measurements of core shifts for 20 AGNs made for nine frequencies each. Using these dependences of magnetic field and particle number density of distance r, we obtain in the observer rest frame

\begin{eqnarray} \left(\nu _{\rm m}\frac{1+z}{\delta }\frac{r}{r_1}\right)^{5-2\alpha } &=& C\left(\frac{2e^2}{mc}\right)^2 \left(\frac{e}{2\pi mc}\right)^{3-2\alpha } \nonumber\\ && \times \left(\frac{r_1\chi }{\delta \sin \varphi }\,\xi \gamma _{\rm min}\right)^2 \Gamma ^{-5+2\alpha } B_1^{3-2\alpha }n_1^2, \end{eqnarray}

(17)

where |$C=c_{\alpha }^2(1-2\alpha )/5(5-2\alpha )$|⁠.

On the other hand, the values B₁ and n₁ can be related through introducing the flow magnetization parameter σ – the ratio of Poynting vector to particle kinetic energy flux at a given distance along the flow (see Appendix A). Let us define the magnetization σ_ξ as a ratio of Poynting vector to the total kinetic energy flux of emitting and non-emitting particles:

\begin{equation} \sigma _{\xi }=\frac{\left|\boldsymbol {S}\right|}{\left|\boldsymbol {K}+\boldsymbol {K}_{\rm syn}\right|}. \end{equation}

(18)

Here, the kinetic energy flux of emitting electrons is

\begin{equation} \left|\boldsymbol {K}_{\rm syn}\right|=\int _{\gamma _{\rm min}}^{\gamma _{\rm max}} (\gamma m c^2)(|\boldsymbol {v}_{\rm p}|){\rm d}n_{\rm syn}= k_{\rm e}mc^3F(\gamma _{\rm min},\gamma _{\rm max}), \end{equation}

(19)

and function F ( · ) for α = −1/2 is defined by the following expression:

\begin{eqnarray} &&{ F(\gamma _{\rm min},\gamma _{\rm max})=\left({\rm ch}^{-1}\gamma _{\rm max}-{\rm ch}^{-1}\gamma _{\rm min}\right)}\nonumber\\ &&{\qquad \quad -\left(\frac{\sqrt{\gamma ^2_{\rm max}-1}}{\gamma _{\rm max}}-\frac{\sqrt{\gamma ^2_{\rm min}-1}}{\gamma _{\rm min}}\right)\approx \ln \left(2\gamma _{\rm max}\right)-1.} \end{eqnarray}

(20)

Estimating now the Poynting vector as

\begin{equation} \left|\boldsymbol {S}\right|\approx \frac{cB^2_{\varphi }}{4\pi }, \end{equation}

(21)

and particle kinetic energy fluxes as

\begin{equation} \left|\boldsymbol {K}+\boldsymbol {K}_{\rm syn}\right|\approx mc^3n_{\rm e}\left(\Gamma +\xi F\gamma _{\rm min}\right), \end{equation}

(22)

we obtain the following relationship between magnetic field and particle number density:

\begin{equation} B^2=\sigma _{\xi } 4\pi mc^2 n_{\rm e} \Gamma . \end{equation}

(23)

In what follows, we neglect the term ξFγ_min in comparison with Γ. Further on we omit the index ξ. Using equation (23), we get

\begin{equation} \begin{array}{l}\displaystyle \left(\nu _{\rm m}\frac{1+z}{\delta }\frac{r}{r_1}\right)^{5-2\alpha } =C\left(\frac{2e^2}{mc}\right)^2\left(\frac{e}{2\pi mc}\right)^{3-2\alpha } \\ \ \\ \displaystyle \times \left(4\pi mc^2\right)^{1.5-\alpha }\left(\frac{r_1\chi }{\delta \sin \varphi } \,\xi \gamma _{\rm min}\right)^2\Gamma ^{-5+2\alpha } \\ \ \\ \displaystyle \times \left(\sigma _1\Gamma _1\right)^{1.5-\alpha } n_1^{3.5-\alpha }. \end{array} \end{equation}

(24)

As to the number density n₁, it can be defined through the multiplicity parameter λ and total jet energy losses P_jet as (see Appendix B for more detail)

\begin{equation} n_1=\frac{\lambda }{2\pi \left(r_1\chi \right)^2}\frac{mc^2}{e^2}\sqrt{\frac{P_{\rm jet}}{P_{\rm A}}}. \end{equation}

(25)

2.2 The saturation regime

To determine the intrinsic parameters of relativistic jets, let us consider two cases for the different magnetization at 1 pc. In what follows, we assume that the flow at its base is highly, or at least mildly, magnetized, i.e. σ_M > 1.

First, we assume that up to the distance r = 1 pc the plasma has been effectively accelerated so that the Poynting flux is smaller in comparison with the particle kinetic energy flux, i.e. σ₁ ≲ 1. In other words, the acceleration reached the saturation regime (Beskin 2010). Combining now equations (4) and (A8), it is easy to obtain that this case corresponds to σ_M < 10⁵. Accordingly, the bulk Lorentz factor at r = 1 pc can be evaluated as

\begin{equation} \Gamma _1 \approx \sigma _{\rm M}. \end{equation}

(26)

In this case equation (24) can be rewritten as

\begin{equation} \left(\nu _{\rm m}\frac{1+z}{\delta }\frac{r\chi }{c}\right)^{5-2\alpha } =C \left(\frac{2^{-1.5+\alpha }}{\pi ^{5-2\alpha }}\right) \left(\frac{\xi \gamma _{\rm min}}{\delta \sin \varphi }\right)^2\lambda ^{7-2\alpha }. \end{equation}

(27)

Using now the relationship between the angular distance θ_d and the distance from the jet base r

\begin{equation} r\sin \varphi =\theta _{\rm d}\frac{D_{\rm L}}{(1+z)^2}, \end{equation}

(28)

where D_L is the luminosity distance, we obtain

\begin{equation} \begin{array}{l}\displaystyle \left(\frac{\theta _{\rm d}}{\rm mas}\right) =3.4\times 10^{-19}\left(\frac{D_{\rm L}}{\rm Gpc}\right)^{-1} \left(\frac{\nu _{\rm m}}{\rm GHz}\right)^{-1} {\delta (1+z)}\\ \ \\ \displaystyle \times \frac{\sin \varphi }{\chi } \left(\frac{\xi \gamma _{\rm min}}{\delta \sin \varphi }\right)^{2/(5-2\alpha )}\lambda ^{(7-2\alpha )/(5-2\alpha )}. \end{array} \end{equation}

(29)

This expression can be rewritten as a following relationship between the core position and the observation frequency:

\begin{equation} \left(\frac{\theta _{\rm d}}{\rm mas}\right)=\left(\frac{\eta }{\rm mas\, GHz}\right) \left(\frac{\nu _{\rm m}}{\rm GHz}\right)^{-1}. \end{equation}

(30)

Having the measured core-shift Δr_mas in milliarcseconds for two frequencies ν_{m, 1} and ν_{m, 2}, we obtain for α = −1/2:

\begin{equation} \begin{array}{l}\displaystyle \lambda =7.3\times 10^{13}\left(\frac{\eta }{\rm mas\, GHz}\right)^{3/4} \left(\frac{D_{\rm L}}{\rm Gpc}\right)^{3/4}\\ \ \\ \displaystyle \times \left(\frac{\chi }{1+z}\right)^{3/4}\frac{1}{(\delta \sin \varphi )^{1/2}} \frac{1}{(\xi \gamma _{\rm min})^{1/4}} \\ \ \\ \displaystyle =2.3\times 10^{14}\left(\frac{\eta }{\rm pc\, GHz}\right)^{3/4} \left(\frac{D_{\rm L}}{\rm Gpc}\right)^{3/4}\\ \ \\ \displaystyle \times \left(\frac{\chi }{1+z}\right)^{3/4}\frac{1}{(\delta \sin \varphi )^{1/2}} \frac{1}{(\xi \gamma _{\rm min})^{1/4}}. \end{array} \end{equation}

(31)

Accordingly, using equation (5), we obtain

\begin{equation} \begin{array}{l}\displaystyle \sigma _{\rm M}=1.4\left[\left(\frac{\eta }{\rm mas\, GHz}\right) \left(\frac{D_{\rm L}}{\rm Gpc}\right)\frac{\chi }{1+z}\right]^{-3/4} \\ \ \\ \displaystyle \times \sqrt{\delta \sin \varphi } \left(\xi \gamma _{\rm min}\right)^{1/4}\sqrt{\frac{P_{\rm jet}}{10^{45}{\,\rm erg\, s^{-1}}}}= \\ \ \\ \displaystyle =0.44\left[\left(\frac{\eta }{\rm pc\, GHz}\right) \left(\frac{D_{\rm L}}{\rm Gpc}\right)\frac{\chi }{1+z}\right]^{-3/4} \\ \ \\ \displaystyle \times \sqrt{\delta \sin \varphi } \left(\xi \gamma _{\rm min}\right)^{1/4}\sqrt{\frac{P_{\rm jet}}{10^{45}{\,\rm erg\, s^{-1}}}}. \end{array} \end{equation}

(32)

As we see, this value is in agreement with our assumption σ_M < 10⁵.

2.3 Highly magnetized outflow

Let us now assume that the flow is still highly magnetized at a distance of the observable core. This implies that the Michel magnetization parameter σ_M > 10⁵. Using now relation (A8), one can obtain

\begin{equation} \sigma _1\Gamma _1\approx \sigma _{\rm M}. \end{equation}

(33)

On the other hand, equation (24) can be rewritten as

\begin{equation} \begin{array}{l}\displaystyle \lambda =2.5\times 10^{11}\left[\left(\frac{\eta }{\rm mas\, GHz}\right) \left(\frac{D_{\rm L}}{\rm Gpc}\right)\left(\frac{\chi }{1+z}\right)\right]^3 \\ \ \\ \displaystyle \times \Gamma ^{3/2}\frac{1}{(\delta \sin \varphi )^2}\frac{1}{\xi \gamma _{\rm min}} \left(\frac{P_{\rm jet}}{10^{45} \,\rm erg\, s^{-1}}\right)^{-3/2}. \end{array} \end{equation}

(34)

This gives the following expression for the Michel magnetization parameter

\begin{equation} \begin{array}{l}\displaystyle \sigma _{\rm M}=4\times 10^{2} \left[\left(\frac{\eta }{\rm mas\, GHz}\right) \left(\frac{D_{\rm L}}{\rm Gpc}\right)\left(\frac{\chi }{1+z}\right)\right]^{-3} \\ \ \\ \displaystyle \times \Gamma ^{-3/2}(\delta \sin \varphi )^2\xi \gamma _{\rm min} \left(\frac{P_{\rm jet}}{10^{45} \,\rm erg\, s^{-1}}\right)^{2}. \end{array} \end{equation}

(35)

As we see, these values are in contradiction with our assumption σ_M > 10⁵. Thus, one can conclude that it is the saturation limit that corresponds to parsec-scale relativistic jets under consideration.

3 THE STATISTICS FOR MULTIPLICITY PARAMETER

Several methods can be applied to measure the apparent shift of the core position as discussed by Kovalev et al. (2008). As a result, a magnitude of the shift, designated by η, can be measured and presented in units [mas GHz] or [pc GHz]. Knowing this quantity, one can use the expressions (31)–(35) to estimate the multiplicity and magnetization parameters.

3.1 The sample of objects

In our analysis, we use the results of two surveys of the apparent core shift in AGN jets: Sokolovsky et al. (2011) show results for 20 objects obtained from nine frequencies between 1.4 and 15.3 GHz (S-sample) and Pushkarev et al. (2012) have results for 163 AGN from four frequencies covering 8.1–15.3 GHz (P-sample). Of these we use only those sources for which the apparent opening angle is known from Pushkarev et al. (2009). As a result, 97 sources are left from the P-sample and 5 from the S-sample. Although all of S-sample sources are in P-sample, we have included them as an independent measurement of core shift. Moreover, for objects 0215+015 and 1219+285, the two measurements of core shift have been made for two different epochs, and we included them too. This leaves us with 97 sources and 104 measurements of core shift.

The distance to the objects is determined from the redshift and accepted cosmology model. For a Doppler factor we use the estimate δ ≈ β_app, where measured apparent velocity β_app is a ratio of apparent speed of a bright feature in a jet to the speed of light. We believe this to be a good estimate because Cohen et al. (2007) have showed using Monte Carlo simulations that the probability density p(δ| β_app) to observe a Doppler factor for a given apparent velocity is peaked around unity. This is done under an assumption that the measured β_app does represent the underlying jet flow. The redshifts z and the apparent velocities β_app are taken from Lister et al. (2013).

The value of observation angle φ we obtain from the set of equations for Doppler factor δ and apparent velocity

\begin{equation} \beta _{\rm app}=\frac{\beta \sin \varphi }{1-\beta \cos \varphi }. \end{equation}

(36)

Taking δ = β_app, we obtain from equations (11) and (36) for the observation angle the relation

\begin{equation} \varphi ={\rm atan}\left(\frac{2\beta _{\rm app}}{2\beta _{\rm app}^2-1}\right). \end{equation}

(37)

The half-opening angle related to the observed opening angle χ_app as

\begin{equation} \chi =\chi _{\rm app}\sin \varphi /2. \end{equation}

(38)

We use the values for χ_app derived by Pushkarev et al. (2009) with typical errors of 1| $_{.}^{\circ}$|5. We also have chosen parameter γ_min = 1.

We evaluate the total jet power P_jet through the relationship (Cavagnolo et al. 2010) between the luminosities of jets in radio band and mechanical jet power, needed to form the cavities in surrounding gas. The power law, found by Cavagnolo et al. (2010) for a range of frequencies 200–400 MHz is

\begin{equation} \left(\frac{P_{\rm jet}}{10^{43}\,\rm erg\, s^{-1}}\right)=3.5 \left(\frac{P_{200-400}}{10^{40}\,\rm erg\, s^{-1}}\right)^{0.64}. \end{equation}

(39)

In order to find flux density measurements at the 92 cm band for each source we use the CATS data base (Verkhodanov et al. 1997) which accumulates measurements at different epochs and from the different catalogues. The data which we use in this paper were originally reported by De Breuck et al. (2002), Douglas et al. (1996), Ghosh, Gopal-Krishna & Rao (1994), Kühr et al. (1979), Kühr et al. (1981), Gregory & Condon (1991), Mitchell et al. (1994) and Rengelink et al. (1997) with a typical flux density accuracy of about 10 per cent.

The typical error for core-shift measurements in Pushkarev et al. (2012) and Sokolovsky et al. (2011) is 0.05 mas. There are 23 objects in our sample that have the core-shift values less than 0.05 mas. For them we have replaced the core-shift values by 0.05 mas for our calculations for convenience of the λ and σ_M analysis.

3.2 Results and discussion

Using the formula (31), we obtain the following result for the equipartition regime. The obtained values for the multiplication parameter λ and magnetization parameter σ_M are presented in Table 1. Their distributions are shown in Fig. 1 and Fig. 2, respectively. In cases when more than one estimate is determined per source (e.g. for 0215+015), an average value is used in the histograms. The resultant median value for the multiplicity parameter λ_med = 3 × 10¹³, and median value for magnetization parameter σ_M, med = 8. The multiplicity parameter for our sample lies in the interval (3 × 10¹²; 4 × 10¹⁴), and the Michel magnetization parameter σ_M lies correspondingly in the (0.4; 61) interval.

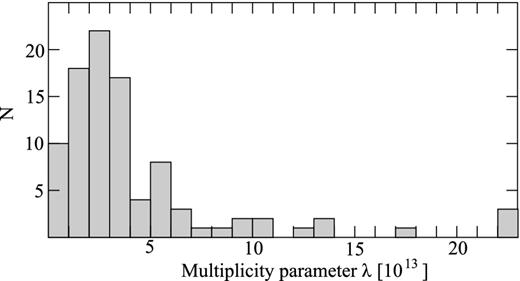
Distributions of the multiplicity parameter λ for the sample of 97 sources. Two objects with λ = 2.8 × 1014 and 3.6 × 1014 lie out of the shown range of values.

Figure 1.

Distributions of the multiplicity parameter λ for the sample of 97 sources. Two objects with λ = 2.8 × 10¹⁴ and 3.6 × 10¹⁴ lie out of the shown range of values.

Open in new tab Download slide

Figure 2.

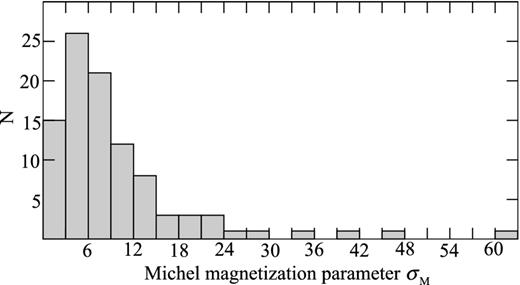
Distributions of the Michel magnetization parameter σ_M for the sample of 97 sources.

Open in new tab Download slide

Table 1.

Open in new tab

Jet parameters and derived multiplication and magnetization parameters.

Source	z	β_app	χ_app	S_0.3	P_jet	Reference	Δr_core	Epoch	λ	σ
		(c)	(°)	(Jy)	(10⁴⁵ erg s⁻¹)	for S_0.3	(mas)	for Δr_core	(10¹³)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)
0003−066	0.347	8.40	16.3	2.17	1.07	2	0.035	2006-07-07	1.21	9.69
0106+013	2.099	24.37	23.6	2.85	10.50	6	0.005	2006-07-07	2.02	23.67
0119+115	0.570	18.57	15.6	2.24	1.86	6	0.347	2006-06-15	3.84	4.27
0133+476	0.859	15.36	21.7	1.63	2.54	8	0.131	2006-08-09	3.52	5.80
0202+149	0.405	15.89	16.4	6.25	2.39	3	0.122	2006-09-06	1.63	10.90
0202+319	1.466	10.15	13.4	0.76	2.99	8	0.013	2006-08-09	2.17	11.13
0212+735	2.367	6.55	16.4	1.54	5.17	8	0.149	2006-07-07	9.82	4.41
0215+015	1.715	25.06	36.7	0.88	3.90	5	0.088	2006-04-28	3.75	7.54
							0.241	2006-12-01	7.97	3.54
0234+285	1.206	21.99	19.8	1.45	3.52	5	0.275	2006-09-06	5.29	4.79
0333+321	1.259	13.07	8.0	3.68	6.72	7	0.279	2006-07-07	4.10	8.62
0336−019	0.852	24.45	26.8	2.49	3.26	6	0.117	2006-08-09	2.66	8.68
0403−132	0.571	20.80	16.4	7.62	4.45	2	0.346	2006-05-24	3.66	6.95
0420−014	0.916	5.74	22.7	0.87	1.84	3	0.267	2006-10-06	13.49	1.30
0458−020	2.286	13.57	23.1	3.54	11.20	3	0.006	2006-11-10	3.20	17.26
0528+134	2.070	17.34	16.1	1.02	5.85	2	0.167	2006-10-06	4.81	7.40
0529+075	1.254	18.03	56.4	1.75	4.54	2	0.110	2006-08-09	3.83	7.58
0605−085	0.870	19.19	14.0	1.43	2.39	3	0.096	2006-11-10	1.66	11.95
0607−157	0.323	1.918	35.1	2.31	0.96	3	0.240	2006-09-06	28.46	0.38
0642+449	3.396	8.53	23.4	0.70	7.68	8	0.110	2006-10-06	5.27	8.29
0730+504	0.720	14.07	14.8	0.71	1.20	8	0.262	2006-05-24	4.27	3.21
0735+178	0.450	5.04	21.0	1.81	1.23	8	0.039	2006-04-28	2.56	5.07
0736+017	0.189	13.79	17.9	1.79	0.42	3	0.079	2006-06-15	0.82	8.38
0738+313	0.631	10.72	10.5	1.26	1.48	3	0.183	2006-09-06	2.85	5.23
0748+126	0.889	14.58	16.2	1.45	2.65	2	0.098	2006-08-09	2.41	8.69
0754+100	0.266	14.40	13.7	0.74	0.39	2	0.266	2006-04-28	2.06	3.32
0804+499	1.436	1.15	35.3	0.60	2.49	8	0.094	2006-10-06	35.88	0.61
0805−077	1.837	41.76	18.8	2.60	9.26	2	0.207	2006-05-24	3.12	14.09
0823+033	0.505	12.88	13.4	0.63	0.71	5	0.141	2006-06-15	2.12	4.71
0827+243	0.942	19.81	14.6	0.71	1.80	2	0.150	2006-05-24	2.52	6.92
0829+046	0.174	10.13	18.7	0.67	0.21	2	0.109	2006-07-07	1.28	3.82
0836+710	2.218	21.08	12.4	5.06	17.75	2	0.186	2006-09-06	3.81	16.43
0851+202	0.306	15.14	28.5	1.11	0.56	3	0.028	2006-04-28	1.08	7.69
0906+015	1.026	22.08	17.5	1.54	3.05	3	0.168	2006-10-06	3.04	7.56
0917+624	1.453	12.07	15.9	1.27	4.07	8	0.112	2006-08-09	3.95	7.14
0923+392	0.695	2.76	10.8	3.28	3.03	5	0.042	2006-07-07	3.23	6.69
0945+408	1.249	20.20	14.0	2.94	6.30	2	0.083	2006-06-15	1.80	18.92
1036+054	0.473	5.72	6.5	0.75	0.80	2	0.195	2006-05-24	2.77	3.80
1038+064	1.265	10.69	6.7	1.59	4.32	2	0.106	2006-10-06	2.02	14.01
1045−188	0.595	10.51	8.0	2.79	2.46	2	0.156	2006-09-06	2.01	9.45
1127−145	1.184	14.89	16.1	5.63	8.94	6	0.096	2006-08-09	2.73	14.77
1150+812	1.250	10.11	15.0	1.39	3.81	8	0.087	2006-06-15	3.31	8.03
1156+295	0.725	24.59	16.7	4.33	3.89	8	0.162	2006-09-06	2.15	11.40
1219+044	0.966	0.82	13.0	1.14	2.52	4	0.133	2006-05-24	22.11	0.94
1219+285	0.103	9.12	13.9	1.77	0.19	3	0.182	2006-02-12	1.11	4.04
							0.142	2007-04-30	0.93	4.87
							0.199	2006-11-10	1.19	3.78
1222+216	0.434	26.60	10.8	3.98	1.90	5	0.180	2006-04-28	1.14	14.13
1226+023	0.158	14.86	10	63.72	3.25	3	0.020	2006-03-09	0.31	60.77
1253−055	0.536	20.58	14.4	16.56	6.31	3	0.048	2006-04-05	0.75	39.84
1308+326	0.997	27.48	18.5	1.42	2.79	8	0.143	2006-07-07	2.35	9.33
1334−127	0.539	16.33	12.6	1.91	1.71	2	0.237	2006-10-06	2.61	5.98
1413+135	0.247	1.78	8.8	2.74	0.81	2	0.230	2006-08-09	6.02	1.64
1458+718	0.904	6.61	4.5	19.64	13.30	8	0.081	2006-09-06	1.46	32.22
							0.136	2007-03-01	2.16	21.84
1502+106	1.839	17.53	37.9	1.08	4.92	3	0.052	2006-07-07	3.59	8.92
1504−166	0.876	3.94	18.4	1.80	2.79	3	0.148	2006-12-01	9.56	2.05
1510−089	0.360	28.00	15.2	2.75	1.22	3	0.122	2006-04-28	0.93	13.47
1514−241	0.049	6.39	7.8	2.06	0.08	3	0.188	2006-04-28	0.56	5.15
1538+149	0.606	8.74	16.1	2.82	2.36	3	0.032	2006-06-15	1.68	11.09
1546+027	0.414	12.08	12.9	0.70	0.61	3	0.010	2006-08-09	0.87	10.32
1606+106	1.232	19.09	24.0	2.67	5.30	7	0.057	2006-07-07	2.11	14.84
1611+343	1.400	29.15	26.9	4.20	8.44	3	0.057	2006-06-15	1.79	22.54
1633+382	1.813	29.22	22.6	2.51	8.28	8	0.119	2006-09-06	3.07	13.50
1637+574	0.751	13.59	10.7	1.32	1.88	8	0.117	2006-05-24	1.92	8.94
1638+398	1.666	15.85	53.8	0.64	3.11	8	0.007	2006-08-09	4.68	5.36
1641+399	0.593	19.27	12.9	9.93	5.13	8	0.211	2006-06-15	2.29	11.99
1655+077	0.621	14.77	5.5	2.36	2.33	6	0.080	2006-11-10	0.73	25.39
							0.086	2007-06-01	0.77	24.05
1726+455	0.717	2.30	16.5	0.49	0.95	8	0.009	2006-09-06	5.18	2.34
1730−130	0.902	27.35	10.4	6.46	6.54	3	0.174	2006-07-07	1.67	19.72
1749+096	0.322	7.90	16.8	1.20	0.61	6	0.061	2006-06-15	1.43	6.15
1751+288	1.118	3.87	12.1	0.40	1.55	2	0.007	2006-10-06	3.60	4.62
1758+388	2.092	2.21	17.9	0.18	1.82	8	0.079	2006-11-10	13.98	1.42
1803+784	0.680	10.79	18.4	1.92	2.23	8	0.029	2006-09-06	1.71	10.80
							0.061	2007-05-03	1.98	9.31
1823+568	0.664	26.17	6.8	2.63	2.52	8	0.052	2006-07-07	0.42	46.21
1828+487	0.692	13.07	7.1	47.78	15.60	3	0.117	2006-08-09	1.39	35.35
1849+670	0.657	23.08	16.6	0.86	1.22	8	0.024	2006-05-24	0.88	15.50
1908−201	1.119	4.39	23.9	2.70	5.21	2	0.246	2006-03-09	18.03	1.69
1928+738	0.302	8.17	9.8	4.81	1.40	8	0.147	2006-04-28	1.72	7.66
1936−155	1.657	5.34	35.2	0.67	3.45	2	0.215	2006-07-07	22.92	1.15
2008−159	1.180	4.85	9.7	0.73	2.41	2	0.008	2006-11-10	2.65	7.89
2022−077	1.388	23.23	19.6	2.63	6.67	2	0.006	2006-04-05	1.51	23.67
2121+053	1.941	11.66	34.0	0.63	3.99	2	0.152	2006-06-15	10.29	2.83
2128−123	0.501	5.99	5.0	1.47	1.23	3	0.223	2006-10-06	2.52	5.20
2131−021	1.284	19.96	18.4	2.66	6.11	6	0.089	2006-08-09	2.39	14.14
2134+004	1.932	5.04	15.2	0.99	4.85	6	0.188	2006-07-07	12.35	2.60
2136+141	2.427	4.15	32.5	0.94	6.16	6	0.008	2006-09-06	10.28	3.64
2145+067	0.999	2.83	23.2	3.76	5.18	3	0.008	2006-10-06	6.97	4.31
2155−152	0.672	18.12	17.6	2.41	2.43	3	0.405	2006-12-01	5.34	3.60
2200+420	0.069	9.95	26.2	1.82	0.12	8	0.032	2006-04-05	0.47	7.30
2201+171	1.076	17.66	13.6	1.00	2.63	2	0.380	2006-05-24	5.64	3.82
2201+315	0.295	8.27	12.8	1.82	0.88	3	0.347	2006-10-06	3.90	2.67
							0.192	2007-04-30	2.50	3.80
2209+236	1.125	2.29	14.2	0.39	1.51	2	0.038	2006-12-01	6.03	2.73
2216−038	0.901	6.73	15.6	2.25	3.57	6	0.011	2006-08-09	2.55	9.57
2223−052	1.404	20.34	11.7	13.59	18.00	3	0.199	2006-10-06	3.21	18.33
2227−088	1.560	2.00	15.8	1.41	5.14	2	0.186	2006-07-07	22.85	1.40
2230+114	1.037	8.62	13.3	8.51	9.25	3	0.278	2006-02-12	7.36	5.45
2243−123	0.632	5.24	14.8	1.45	1.71	1	0.161	2006-09-06	5.73	2.79
2251+158	0.859	13.77	40.9	12.47	9.39	3	0.124	2006-06-15	8.31	4.72
2345−167	0.576	11.47	15.8	2.81	2.21	3	0.167	2006-11-10	3.24	5.54
2351+456	1.986	21.56	20.1	2.23	8.54	8	0.196	2006-05-24	5.35	7.99

Source	z	β_app	χ_app	S_0.3	P_jet	Reference	Δr_core	Epoch	λ	σ
		(c)	(°)	(Jy)	(10⁴⁵ erg s⁻¹)	for S_0.3	(mas)	for Δr_core	(10¹³)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)
0003−066	0.347	8.40	16.3	2.17	1.07	2	0.035	2006-07-07	1.21	9.69
0106+013	2.099	24.37	23.6	2.85	10.50	6	0.005	2006-07-07	2.02	23.67
0119+115	0.570	18.57	15.6	2.24	1.86	6	0.347	2006-06-15	3.84	4.27
0133+476	0.859	15.36	21.7	1.63	2.54	8	0.131	2006-08-09	3.52	5.80
0202+149	0.405	15.89	16.4	6.25	2.39	3	0.122	2006-09-06	1.63	10.90
0202+319	1.466	10.15	13.4	0.76	2.99	8	0.013	2006-08-09	2.17	11.13
0212+735	2.367	6.55	16.4	1.54	5.17	8	0.149	2006-07-07	9.82	4.41
0215+015	1.715	25.06	36.7	0.88	3.90	5	0.088	2006-04-28	3.75	7.54
							0.241	2006-12-01	7.97	3.54
0234+285	1.206	21.99	19.8	1.45	3.52	5	0.275	2006-09-06	5.29	4.79
0333+321	1.259	13.07	8.0	3.68	6.72	7	0.279	2006-07-07	4.10	8.62
0336−019	0.852	24.45	26.8	2.49	3.26	6	0.117	2006-08-09	2.66	8.68
0403−132	0.571	20.80	16.4	7.62	4.45	2	0.346	2006-05-24	3.66	6.95
0420−014	0.916	5.74	22.7	0.87	1.84	3	0.267	2006-10-06	13.49	1.30
0458−020	2.286	13.57	23.1	3.54	11.20	3	0.006	2006-11-10	3.20	17.26
0528+134	2.070	17.34	16.1	1.02	5.85	2	0.167	2006-10-06	4.81	7.40
0529+075	1.254	18.03	56.4	1.75	4.54	2	0.110	2006-08-09	3.83	7.58
0605−085	0.870	19.19	14.0	1.43	2.39	3	0.096	2006-11-10	1.66	11.95
0607−157	0.323	1.918	35.1	2.31	0.96	3	0.240	2006-09-06	28.46	0.38
0642+449	3.396	8.53	23.4	0.70	7.68	8	0.110	2006-10-06	5.27	8.29
0730+504	0.720	14.07	14.8	0.71	1.20	8	0.262	2006-05-24	4.27	3.21
0735+178	0.450	5.04	21.0	1.81	1.23	8	0.039	2006-04-28	2.56	5.07
0736+017	0.189	13.79	17.9	1.79	0.42	3	0.079	2006-06-15	0.82	8.38
0738+313	0.631	10.72	10.5	1.26	1.48	3	0.183	2006-09-06	2.85	5.23
0748+126	0.889	14.58	16.2	1.45	2.65	2	0.098	2006-08-09	2.41	8.69
0754+100	0.266	14.40	13.7	0.74	0.39	2	0.266	2006-04-28	2.06	3.32
0804+499	1.436	1.15	35.3	0.60	2.49	8	0.094	2006-10-06	35.88	0.61
0805−077	1.837	41.76	18.8	2.60	9.26	2	0.207	2006-05-24	3.12	14.09
0823+033	0.505	12.88	13.4	0.63	0.71	5	0.141	2006-06-15	2.12	4.71
0827+243	0.942	19.81	14.6	0.71	1.80	2	0.150	2006-05-24	2.52	6.92
0829+046	0.174	10.13	18.7	0.67	0.21	2	0.109	2006-07-07	1.28	3.82
0836+710	2.218	21.08	12.4	5.06	17.75	2	0.186	2006-09-06	3.81	16.43
0851+202	0.306	15.14	28.5	1.11	0.56	3	0.028	2006-04-28	1.08	7.69
0906+015	1.026	22.08	17.5	1.54	3.05	3	0.168	2006-10-06	3.04	7.56
0917+624	1.453	12.07	15.9	1.27	4.07	8	0.112	2006-08-09	3.95	7.14
0923+392	0.695	2.76	10.8	3.28	3.03	5	0.042	2006-07-07	3.23	6.69
0945+408	1.249	20.20	14.0	2.94	6.30	2	0.083	2006-06-15	1.80	18.92
1036+054	0.473	5.72	6.5	0.75	0.80	2	0.195	2006-05-24	2.77	3.80
1038+064	1.265	10.69	6.7	1.59	4.32	2	0.106	2006-10-06	2.02	14.01
1045−188	0.595	10.51	8.0	2.79	2.46	2	0.156	2006-09-06	2.01	9.45
1127−145	1.184	14.89	16.1	5.63	8.94	6	0.096	2006-08-09	2.73	14.77
1150+812	1.250	10.11	15.0	1.39	3.81	8	0.087	2006-06-15	3.31	8.03
1156+295	0.725	24.59	16.7	4.33	3.89	8	0.162	2006-09-06	2.15	11.40
1219+044	0.966	0.82	13.0	1.14	2.52	4	0.133	2006-05-24	22.11	0.94
1219+285	0.103	9.12	13.9	1.77	0.19	3	0.182	2006-02-12	1.11	4.04
							0.142	2007-04-30	0.93	4.87
							0.199	2006-11-10	1.19	3.78
1222+216	0.434	26.60	10.8	3.98	1.90	5	0.180	2006-04-28	1.14	14.13
1226+023	0.158	14.86	10	63.72	3.25	3	0.020	2006-03-09	0.31	60.77
1253−055	0.536	20.58	14.4	16.56	6.31	3	0.048	2006-04-05	0.75	39.84
1308+326	0.997	27.48	18.5	1.42	2.79	8	0.143	2006-07-07	2.35	9.33
1334−127	0.539	16.33	12.6	1.91	1.71	2	0.237	2006-10-06	2.61	5.98
1413+135	0.247	1.78	8.8	2.74	0.81	2	0.230	2006-08-09	6.02	1.64
1458+718	0.904	6.61	4.5	19.64	13.30	8	0.081	2006-09-06	1.46	32.22
							0.136	2007-03-01	2.16	21.84
1502+106	1.839	17.53	37.9	1.08	4.92	3	0.052	2006-07-07	3.59	8.92
1504−166	0.876	3.94	18.4	1.80	2.79	3	0.148	2006-12-01	9.56	2.05
1510−089	0.360	28.00	15.2	2.75	1.22	3	0.122	2006-04-28	0.93	13.47
1514−241	0.049	6.39	7.8	2.06	0.08	3	0.188	2006-04-28	0.56	5.15
1538+149	0.606	8.74	16.1	2.82	2.36	3	0.032	2006-06-15	1.68	11.09
1546+027	0.414	12.08	12.9	0.70	0.61	3	0.010	2006-08-09	0.87	10.32
1606+106	1.232	19.09	24.0	2.67	5.30	7	0.057	2006-07-07	2.11	14.84
1611+343	1.400	29.15	26.9	4.20	8.44	3	0.057	2006-06-15	1.79	22.54
1633+382	1.813	29.22	22.6	2.51	8.28	8	0.119	2006-09-06	3.07	13.50
1637+574	0.751	13.59	10.7	1.32	1.88	8	0.117	2006-05-24	1.92	8.94
1638+398	1.666	15.85	53.8	0.64	3.11	8	0.007	2006-08-09	4.68	5.36
1641+399	0.593	19.27	12.9	9.93	5.13	8	0.211	2006-06-15	2.29	11.99
1655+077	0.621	14.77	5.5	2.36	2.33	6	0.080	2006-11-10	0.73	25.39
							0.086	2007-06-01	0.77	24.05
1726+455	0.717	2.30	16.5	0.49	0.95	8	0.009	2006-09-06	5.18	2.34
1730−130	0.902	27.35	10.4	6.46	6.54	3	0.174	2006-07-07	1.67	19.72
1749+096	0.322	7.90	16.8	1.20	0.61	6	0.061	2006-06-15	1.43	6.15
1751+288	1.118	3.87	12.1	0.40	1.55	2	0.007	2006-10-06	3.60	4.62
1758+388	2.092	2.21	17.9	0.18	1.82	8	0.079	2006-11-10	13.98	1.42
1803+784	0.680	10.79	18.4	1.92	2.23	8	0.029	2006-09-06	1.71	10.80
							0.061	2007-05-03	1.98	9.31
1823+568	0.664	26.17	6.8	2.63	2.52	8	0.052	2006-07-07	0.42	46.21
1828+487	0.692	13.07	7.1	47.78	15.60	3	0.117	2006-08-09	1.39	35.35
1849+670	0.657	23.08	16.6	0.86	1.22	8	0.024	2006-05-24	0.88	15.50
1908−201	1.119	4.39	23.9	2.70	5.21	2	0.246	2006-03-09	18.03	1.69
1928+738	0.302	8.17	9.8	4.81	1.40	8	0.147	2006-04-28	1.72	7.66
1936−155	1.657	5.34	35.2	0.67	3.45	2	0.215	2006-07-07	22.92	1.15
2008−159	1.180	4.85	9.7	0.73	2.41	2	0.008	2006-11-10	2.65	7.89
2022−077	1.388	23.23	19.6	2.63	6.67	2	0.006	2006-04-05	1.51	23.67
2121+053	1.941	11.66	34.0	0.63	3.99	2	0.152	2006-06-15	10.29	2.83
2128−123	0.501	5.99	5.0	1.47	1.23	3	0.223	2006-10-06	2.52	5.20
2131−021	1.284	19.96	18.4	2.66	6.11	6	0.089	2006-08-09	2.39	14.14
2134+004	1.932	5.04	15.2	0.99	4.85	6	0.188	2006-07-07	12.35	2.60
2136+141	2.427	4.15	32.5	0.94	6.16	6	0.008	2006-09-06	10.28	3.64
2145+067	0.999	2.83	23.2	3.76	5.18	3	0.008	2006-10-06	6.97	4.31
2155−152	0.672	18.12	17.6	2.41	2.43	3	0.405	2006-12-01	5.34	3.60
2200+420	0.069	9.95	26.2	1.82	0.12	8	0.032	2006-04-05	0.47	7.30
2201+171	1.076	17.66	13.6	1.00	2.63	2	0.380	2006-05-24	5.64	3.82
2201+315	0.295	8.27	12.8	1.82	0.88	3	0.347	2006-10-06	3.90	2.67
							0.192	2007-04-30	2.50	3.80
2209+236	1.125	2.29	14.2	0.39	1.51	2	0.038	2006-12-01	6.03	2.73
2216−038	0.901	6.73	15.6	2.25	3.57	6	0.011	2006-08-09	2.55	9.57
2223−052	1.404	20.34	11.7	13.59	18.00	3	0.199	2006-10-06	3.21	18.33
2227−088	1.560	2.00	15.8	1.41	5.14	2	0.186	2006-07-07	22.85	1.40
2230+114	1.037	8.62	13.3	8.51	9.25	3	0.278	2006-02-12	7.36	5.45
2243−123	0.632	5.24	14.8	1.45	1.71	1	0.161	2006-09-06	5.73	2.79
2251+158	0.859	13.77	40.9	12.47	9.39	3	0.124	2006-06-15	8.31	4.72
2345−167	0.576	11.47	15.8	2.81	2.21	3	0.167	2006-11-10	3.24	5.54
2351+456	1.986	21.56	20.1	2.23	8.54	8	0.196	2006-05-24	5.35	7.99

Notes. Columns are as follows: (1) source name (B1950); (2) redshift z as collected by (Lister et al. 2013); (3) apparent velocity measured by (Lister et al. 2013); (4) apparent opening angle measured by Pushkarev et al. (2009); (5) flux density at the 92 cm band; (6) derived total jet power; (7) 92 cm flux density reference: 1 – De Breuck et al. (2002), 2 – Douglas et al. (1996), 3 – Ghosh et al. (1994), 4 – Gregory & Condon (1991), 5 – Kühr et al. (1979), 6 – Kühr et al. (1981), 7 – Mitchell et al. (1994), 8 – Rengelink et al. (1997); (8) core shift for frequencies 8.1 − 15.3 GHz, measured in mas (Sokolovsky et al. 2011; Pushkarev et al. 2012); (9) an epoch of the core-shift measurements by Pushkarev et al. (2012) for the year 2006 and by Sokolovsky et al. (2011) for the year 2007; (10) derived multiplicity parameter; (11) derived the Michel magnetization parameter.

Table 1.

Open in new tab

Jet parameters and derived multiplication and magnetization parameters.

Source	z	β_app	χ_app	S_0.3	P_jet	Reference	Δr_core	Epoch	λ	σ
		(c)	(°)	(Jy)	(10⁴⁵ erg s⁻¹)	for S_0.3	(mas)	for Δr_core	(10¹³)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)
0003−066	0.347	8.40	16.3	2.17	1.07	2	0.035	2006-07-07	1.21	9.69
0106+013	2.099	24.37	23.6	2.85	10.50	6	0.005	2006-07-07	2.02	23.67
0119+115	0.570	18.57	15.6	2.24	1.86	6	0.347	2006-06-15	3.84	4.27
0133+476	0.859	15.36	21.7	1.63	2.54	8	0.131	2006-08-09	3.52	5.80
0202+149	0.405	15.89	16.4	6.25	2.39	3	0.122	2006-09-06	1.63	10.90
0202+319	1.466	10.15	13.4	0.76	2.99	8	0.013	2006-08-09	2.17	11.13
0212+735	2.367	6.55	16.4	1.54	5.17	8	0.149	2006-07-07	9.82	4.41
0215+015	1.715	25.06	36.7	0.88	3.90	5	0.088	2006-04-28	3.75	7.54
							0.241	2006-12-01	7.97	3.54
0234+285	1.206	21.99	19.8	1.45	3.52	5	0.275	2006-09-06	5.29	4.79
0333+321	1.259	13.07	8.0	3.68	6.72	7	0.279	2006-07-07	4.10	8.62
0336−019	0.852	24.45	26.8	2.49	3.26	6	0.117	2006-08-09	2.66	8.68
0403−132	0.571	20.80	16.4	7.62	4.45	2	0.346	2006-05-24	3.66	6.95
0420−014	0.916	5.74	22.7	0.87	1.84	3	0.267	2006-10-06	13.49	1.30
0458−020	2.286	13.57	23.1	3.54	11.20	3	0.006	2006-11-10	3.20	17.26
0528+134	2.070	17.34	16.1	1.02	5.85	2	0.167	2006-10-06	4.81	7.40
0529+075	1.254	18.03	56.4	1.75	4.54	2	0.110	2006-08-09	3.83	7.58
0605−085	0.870	19.19	14.0	1.43	2.39	3	0.096	2006-11-10	1.66	11.95
0607−157	0.323	1.918	35.1	2.31	0.96	3	0.240	2006-09-06	28.46	0.38
0642+449	3.396	8.53	23.4	0.70	7.68	8	0.110	2006-10-06	5.27	8.29
0730+504	0.720	14.07	14.8	0.71	1.20	8	0.262	2006-05-24	4.27	3.21
0735+178	0.450	5.04	21.0	1.81	1.23	8	0.039	2006-04-28	2.56	5.07
0736+017	0.189	13.79	17.9	1.79	0.42	3	0.079	2006-06-15	0.82	8.38
0738+313	0.631	10.72	10.5	1.26	1.48	3	0.183	2006-09-06	2.85	5.23
0748+126	0.889	14.58	16.2	1.45	2.65	2	0.098	2006-08-09	2.41	8.69
0754+100	0.266	14.40	13.7	0.74	0.39	2	0.266	2006-04-28	2.06	3.32
0804+499	1.436	1.15	35.3	0.60	2.49	8	0.094	2006-10-06	35.88	0.61
0805−077	1.837	41.76	18.8	2.60	9.26	2	0.207	2006-05-24	3.12	14.09
0823+033	0.505	12.88	13.4	0.63	0.71	5	0.141	2006-06-15	2.12	4.71
0827+243	0.942	19.81	14.6	0.71	1.80	2	0.150	2006-05-24	2.52	6.92
0829+046	0.174	10.13	18.7	0.67	0.21	2	0.109	2006-07-07	1.28	3.82
0836+710	2.218	21.08	12.4	5.06	17.75	2	0.186	2006-09-06	3.81	16.43
0851+202	0.306	15.14	28.5	1.11	0.56	3	0.028	2006-04-28	1.08	7.69
0906+015	1.026	22.08	17.5	1.54	3.05	3	0.168	2006-10-06	3.04	7.56
0917+624	1.453	12.07	15.9	1.27	4.07	8	0.112	2006-08-09	3.95	7.14
0923+392	0.695	2.76	10.8	3.28	3.03	5	0.042	2006-07-07	3.23	6.69
0945+408	1.249	20.20	14.0	2.94	6.30	2	0.083	2006-06-15	1.80	18.92
1036+054	0.473	5.72	6.5	0.75	0.80	2	0.195	2006-05-24	2.77	3.80
1038+064	1.265	10.69	6.7	1.59	4.32	2	0.106	2006-10-06	2.02	14.01
1045−188	0.595	10.51	8.0	2.79	2.46	2	0.156	2006-09-06	2.01	9.45
1127−145	1.184	14.89	16.1	5.63	8.94	6	0.096	2006-08-09	2.73	14.77
1150+812	1.250	10.11	15.0	1.39	3.81	8	0.087	2006-06-15	3.31	8.03
1156+295	0.725	24.59	16.7	4.33	3.89	8	0.162	2006-09-06	2.15	11.40
1219+044	0.966	0.82	13.0	1.14	2.52	4	0.133	2006-05-24	22.11	0.94
1219+285	0.103	9.12	13.9	1.77	0.19	3	0.182	2006-02-12	1.11	4.04
							0.142	2007-04-30	0.93	4.87
							0.199	2006-11-10	1.19	3.78
1222+216	0.434	26.60	10.8	3.98	1.90	5	0.180	2006-04-28	1.14	14.13
1226+023	0.158	14.86	10	63.72	3.25	3	0.020	2006-03-09	0.31	60.77
1253−055	0.536	20.58	14.4	16.56	6.31	3	0.048	2006-04-05	0.75	39.84
1308+326	0.997	27.48	18.5	1.42	2.79	8	0.143	2006-07-07	2.35	9.33
1334−127	0.539	16.33	12.6	1.91	1.71	2	0.237	2006-10-06	2.61	5.98
1413+135	0.247	1.78	8.8	2.74	0.81	2	0.230	2006-08-09	6.02	1.64
1458+718	0.904	6.61	4.5	19.64	13.30	8	0.081	2006-09-06	1.46	32.22
							0.136	2007-03-01	2.16	21.84
1502+106	1.839	17.53	37.9	1.08	4.92	3	0.052	2006-07-07	3.59	8.92
1504−166	0.876	3.94	18.4	1.80	2.79	3	0.148	2006-12-01	9.56	2.05
1510−089	0.360	28.00	15.2	2.75	1.22	3	0.122	2006-04-28	0.93	13.47
1514−241	0.049	6.39	7.8	2.06	0.08	3	0.188	2006-04-28	0.56	5.15
1538+149	0.606	8.74	16.1	2.82	2.36	3	0.032	2006-06-15	1.68	11.09
1546+027	0.414	12.08	12.9	0.70	0.61	3	0.010	2006-08-09	0.87	10.32
1606+106	1.232	19.09	24.0	2.67	5.30	7	0.057	2006-07-07	2.11	14.84
1611+343	1.400	29.15	26.9	4.20	8.44	3	0.057	2006-06-15	1.79	22.54
1633+382	1.813	29.22	22.6	2.51	8.28	8	0.119	2006-09-06	3.07	13.50
1637+574	0.751	13.59	10.7	1.32	1.88	8	0.117	2006-05-24	1.92	8.94
1638+398	1.666	15.85	53.8	0.64	3.11	8	0.007	2006-08-09	4.68	5.36
1641+399	0.593	19.27	12.9	9.93	5.13	8	0.211	2006-06-15	2.29	11.99
1655+077	0.621	14.77	5.5	2.36	2.33	6	0.080	2006-11-10	0.73	25.39
							0.086	2007-06-01	0.77	24.05
1726+455	0.717	2.30	16.5	0.49	0.95	8	0.009	2006-09-06	5.18	2.34
1730−130	0.902	27.35	10.4	6.46	6.54	3	0.174	2006-07-07	1.67	19.72
1749+096	0.322	7.90	16.8	1.20	0.61	6	0.061	2006-06-15	1.43	6.15
1751+288	1.118	3.87	12.1	0.40	1.55	2	0.007	2006-10-06	3.60	4.62
1758+388	2.092	2.21	17.9	0.18	1.82	8	0.079	2006-11-10	13.98	1.42
1803+784	0.680	10.79	18.4	1.92	2.23	8	0.029	2006-09-06	1.71	10.80
							0.061	2007-05-03	1.98	9.31
1823+568	0.664	26.17	6.8	2.63	2.52	8	0.052	2006-07-07	0.42	46.21
1828+487	0.692	13.07	7.1	47.78	15.60	3	0.117	2006-08-09	1.39	35.35
1849+670	0.657	23.08	16.6	0.86	1.22	8	0.024	2006-05-24	0.88	15.50
1908−201	1.119	4.39	23.9	2.70	5.21	2	0.246	2006-03-09	18.03	1.69
1928+738	0.302	8.17	9.8	4.81	1.40	8	0.147	2006-04-28	1.72	7.66
1936−155	1.657	5.34	35.2	0.67	3.45	2	0.215	2006-07-07	22.92	1.15
2008−159	1.180	4.85	9.7	0.73	2.41	2	0.008	2006-11-10	2.65	7.89
2022−077	1.388	23.23	19.6	2.63	6.67	2	0.006	2006-04-05	1.51	23.67
2121+053	1.941	11.66	34.0	0.63	3.99	2	0.152	2006-06-15	10.29	2.83
2128−123	0.501	5.99	5.0	1.47	1.23	3	0.223	2006-10-06	2.52	5.20
2131−021	1.284	19.96	18.4	2.66	6.11	6	0.089	2006-08-09	2.39	14.14
2134+004	1.932	5.04	15.2	0.99	4.85	6	0.188	2006-07-07	12.35	2.60
2136+141	2.427	4.15	32.5	0.94	6.16	6	0.008	2006-09-06	10.28	3.64
2145+067	0.999	2.83	23.2	3.76	5.18	3	0.008	2006-10-06	6.97	4.31
2155−152	0.672	18.12	17.6	2.41	2.43	3	0.405	2006-12-01	5.34	3.60
2200+420	0.069	9.95	26.2	1.82	0.12	8	0.032	2006-04-05	0.47	7.30
2201+171	1.076	17.66	13.6	1.00	2.63	2	0.380	2006-05-24	5.64	3.82
2201+315	0.295	8.27	12.8	1.82	0.88	3	0.347	2006-10-06	3.90	2.67
							0.192	2007-04-30	2.50	3.80
2209+236	1.125	2.29	14.2	0.39	1.51	2	0.038	2006-12-01	6.03	2.73
2216−038	0.901	6.73	15.6	2.25	3.57	6	0.011	2006-08-09	2.55	9.57
2223−052	1.404	20.34	11.7	13.59	18.00	3	0.199	2006-10-06	3.21	18.33
2227−088	1.560	2.00	15.8	1.41	5.14	2	0.186	2006-07-07	22.85	1.40
2230+114	1.037	8.62	13.3	8.51	9.25	3	0.278	2006-02-12	7.36	5.45
2243−123	0.632	5.24	14.8	1.45	1.71	1	0.161	2006-09-06	5.73	2.79
2251+158	0.859	13.77	40.9	12.47	9.39	3	0.124	2006-06-15	8.31	4.72
2345−167	0.576	11.47	15.8	2.81	2.21	3	0.167	2006-11-10	3.24	5.54
2351+456	1.986	21.56	20.1	2.23	8.54	8	0.196	2006-05-24	5.35	7.99

Source	z	β_app	χ_app	S_0.3	P_jet	Reference	Δr_core	Epoch	λ	σ
		(c)	(°)	(Jy)	(10⁴⁵ erg s⁻¹)	for S_0.3	(mas)	for Δr_core	(10¹³)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)
0003−066	0.347	8.40	16.3	2.17	1.07	2	0.035	2006-07-07	1.21	9.69
0106+013	2.099	24.37	23.6	2.85	10.50	6	0.005	2006-07-07	2.02	23.67
0119+115	0.570	18.57	15.6	2.24	1.86	6	0.347	2006-06-15	3.84	4.27
0133+476	0.859	15.36	21.7	1.63	2.54	8	0.131	2006-08-09	3.52	5.80
0202+149	0.405	15.89	16.4	6.25	2.39	3	0.122	2006-09-06	1.63	10.90
0202+319	1.466	10.15	13.4	0.76	2.99	8	0.013	2006-08-09	2.17	11.13
0212+735	2.367	6.55	16.4	1.54	5.17	8	0.149	2006-07-07	9.82	4.41
0215+015	1.715	25.06	36.7	0.88	3.90	5	0.088	2006-04-28	3.75	7.54
							0.241	2006-12-01	7.97	3.54
0234+285	1.206	21.99	19.8	1.45	3.52	5	0.275	2006-09-06	5.29	4.79
0333+321	1.259	13.07	8.0	3.68	6.72	7	0.279	2006-07-07	4.10	8.62
0336−019	0.852	24.45	26.8	2.49	3.26	6	0.117	2006-08-09	2.66	8.68
0403−132	0.571	20.80	16.4	7.62	4.45	2	0.346	2006-05-24	3.66	6.95
0420−014	0.916	5.74	22.7	0.87	1.84	3	0.267	2006-10-06	13.49	1.30
0458−020	2.286	13.57	23.1	3.54	11.20	3	0.006	2006-11-10	3.20	17.26
0528+134	2.070	17.34	16.1	1.02	5.85	2	0.167	2006-10-06	4.81	7.40
0529+075	1.254	18.03	56.4	1.75	4.54	2	0.110	2006-08-09	3.83	7.58
0605−085	0.870	19.19	14.0	1.43	2.39	3	0.096	2006-11-10	1.66	11.95
0607−157	0.323	1.918	35.1	2.31	0.96	3	0.240	2006-09-06	28.46	0.38
0642+449	3.396	8.53	23.4	0.70	7.68	8	0.110	2006-10-06	5.27	8.29
0730+504	0.720	14.07	14.8	0.71	1.20	8	0.262	2006-05-24	4.27	3.21
0735+178	0.450	5.04	21.0	1.81	1.23	8	0.039	2006-04-28	2.56	5.07
0736+017	0.189	13.79	17.9	1.79	0.42	3	0.079	2006-06-15	0.82	8.38
0738+313	0.631	10.72	10.5	1.26	1.48	3	0.183	2006-09-06	2.85	5.23
0748+126	0.889	14.58	16.2	1.45	2.65	2	0.098	2006-08-09	2.41	8.69
0754+100	0.266	14.40	13.7	0.74	0.39	2	0.266	2006-04-28	2.06	3.32
0804+499	1.436	1.15	35.3	0.60	2.49	8	0.094	2006-10-06	35.88	0.61
0805−077	1.837	41.76	18.8	2.60	9.26	2	0.207	2006-05-24	3.12	14.09
0823+033	0.505	12.88	13.4	0.63	0.71	5	0.141	2006-06-15	2.12	4.71
0827+243	0.942	19.81	14.6	0.71	1.80	2	0.150	2006-05-24	2.52	6.92
0829+046	0.174	10.13	18.7	0.67	0.21	2	0.109	2006-07-07	1.28	3.82
0836+710	2.218	21.08	12.4	5.06	17.75	2	0.186	2006-09-06	3.81	16.43
0851+202	0.306	15.14	28.5	1.11	0.56	3	0.028	2006-04-28	1.08	7.69
0906+015	1.026	22.08	17.5	1.54	3.05	3	0.168	2006-10-06	3.04	7.56
0917+624	1.453	12.07	15.9	1.27	4.07	8	0.112	2006-08-09	3.95	7.14
0923+392	0.695	2.76	10.8	3.28	3.03	5	0.042	2006-07-07	3.23	6.69
0945+408	1.249	20.20	14.0	2.94	6.30	2	0.083	2006-06-15	1.80	18.92
1036+054	0.473	5.72	6.5	0.75	0.80	2	0.195	2006-05-24	2.77	3.80
1038+064	1.265	10.69	6.7	1.59	4.32	2	0.106	2006-10-06	2.02	14.01
1045−188	0.595	10.51	8.0	2.79	2.46	2	0.156	2006-09-06	2.01	9.45
1127−145	1.184	14.89	16.1	5.63	8.94	6	0.096	2006-08-09	2.73	14.77
1150+812	1.250	10.11	15.0	1.39	3.81	8	0.087	2006-06-15	3.31	8.03
1156+295	0.725	24.59	16.7	4.33	3.89	8	0.162	2006-09-06	2.15	11.40
1219+044	0.966	0.82	13.0	1.14	2.52	4	0.133	2006-05-24	22.11	0.94
1219+285	0.103	9.12	13.9	1.77	0.19	3	0.182	2006-02-12	1.11	4.04
							0.142	2007-04-30	0.93	4.87
							0.199	2006-11-10	1.19	3.78
1222+216	0.434	26.60	10.8	3.98	1.90	5	0.180	2006-04-28	1.14	14.13
1226+023	0.158	14.86	10	63.72	3.25	3	0.020	2006-03-09	0.31	60.77
1253−055	0.536	20.58	14.4	16.56	6.31	3	0.048	2006-04-05	0.75	39.84
1308+326	0.997	27.48	18.5	1.42	2.79	8	0.143	2006-07-07	2.35	9.33
1334−127	0.539	16.33	12.6	1.91	1.71	2	0.237	2006-10-06	2.61	5.98
1413+135	0.247	1.78	8.8	2.74	0.81	2	0.230	2006-08-09	6.02	1.64
1458+718	0.904	6.61	4.5	19.64	13.30	8	0.081	2006-09-06	1.46	32.22
							0.136	2007-03-01	2.16	21.84
1502+106	1.839	17.53	37.9	1.08	4.92	3	0.052	2006-07-07	3.59	8.92
1504−166	0.876	3.94	18.4	1.80	2.79	3	0.148	2006-12-01	9.56	2.05
1510−089	0.360	28.00	15.2	2.75	1.22	3	0.122	2006-04-28	0.93	13.47
1514−241	0.049	6.39	7.8	2.06	0.08	3	0.188	2006-04-28	0.56	5.15
1538+149	0.606	8.74	16.1	2.82	2.36	3	0.032	2006-06-15	1.68	11.09
1546+027	0.414	12.08	12.9	0.70	0.61	3	0.010	2006-08-09	0.87	10.32
1606+106	1.232	19.09	24.0	2.67	5.30	7	0.057	2006-07-07	2.11	14.84
1611+343	1.400	29.15	26.9	4.20	8.44	3	0.057	2006-06-15	1.79	22.54
1633+382	1.813	29.22	22.6	2.51	8.28	8	0.119	2006-09-06	3.07	13.50
1637+574	0.751	13.59	10.7	1.32	1.88	8	0.117	2006-05-24	1.92	8.94
1638+398	1.666	15.85	53.8	0.64	3.11	8	0.007	2006-08-09	4.68	5.36
1641+399	0.593	19.27	12.9	9.93	5.13	8	0.211	2006-06-15	2.29	11.99
1655+077	0.621	14.77	5.5	2.36	2.33	6	0.080	2006-11-10	0.73	25.39
							0.086	2007-06-01	0.77	24.05
1726+455	0.717	2.30	16.5	0.49	0.95	8	0.009	2006-09-06	5.18	2.34
1730−130	0.902	27.35	10.4	6.46	6.54	3	0.174	2006-07-07	1.67	19.72
1749+096	0.322	7.90	16.8	1.20	0.61	6	0.061	2006-06-15	1.43	6.15
1751+288	1.118	3.87	12.1	0.40	1.55	2	0.007	2006-10-06	3.60	4.62
1758+388	2.092	2.21	17.9	0.18	1.82	8	0.079	2006-11-10	13.98	1.42
1803+784	0.680	10.79	18.4	1.92	2.23	8	0.029	2006-09-06	1.71	10.80
							0.061	2007-05-03	1.98	9.31
1823+568	0.664	26.17	6.8	2.63	2.52	8	0.052	2006-07-07	0.42	46.21
1828+487	0.692	13.07	7.1	47.78	15.60	3	0.117	2006-08-09	1.39	35.35
1849+670	0.657	23.08	16.6	0.86	1.22	8	0.024	2006-05-24	0.88	15.50
1908−201	1.119	4.39	23.9	2.70	5.21	2	0.246	2006-03-09	18.03	1.69
1928+738	0.302	8.17	9.8	4.81	1.40	8	0.147	2006-04-28	1.72	7.66
1936−155	1.657	5.34	35.2	0.67	3.45	2	0.215	2006-07-07	22.92	1.15
2008−159	1.180	4.85	9.7	0.73	2.41	2	0.008	2006-11-10	2.65	7.89
2022−077	1.388	23.23	19.6	2.63	6.67	2	0.006	2006-04-05	1.51	23.67
2121+053	1.941	11.66	34.0	0.63	3.99	2	0.152	2006-06-15	10.29	2.83
2128−123	0.501	5.99	5.0	1.47	1.23	3	0.223	2006-10-06	2.52	5.20
2131−021	1.284	19.96	18.4	2.66	6.11	6	0.089	2006-08-09	2.39	14.14
2134+004	1.932	5.04	15.2	0.99	4.85	6	0.188	2006-07-07	12.35	2.60
2136+141	2.427	4.15	32.5	0.94	6.16	6	0.008	2006-09-06	10.28	3.64
2145+067	0.999	2.83	23.2	3.76	5.18	3	0.008	2006-10-06	6.97	4.31
2155−152	0.672	18.12	17.6	2.41	2.43	3	0.405	2006-12-01	5.34	3.60
2200+420	0.069	9.95	26.2	1.82	0.12	8	0.032	2006-04-05	0.47	7.30
2201+171	1.076	17.66	13.6	1.00	2.63	2	0.380	2006-05-24	5.64	3.82
2201+315	0.295	8.27	12.8	1.82	0.88	3	0.347	2006-10-06	3.90	2.67
							0.192	2007-04-30	2.50	3.80
2209+236	1.125	2.29	14.2	0.39	1.51	2	0.038	2006-12-01	6.03	2.73
2216−038	0.901	6.73	15.6	2.25	3.57	6	0.011	2006-08-09	2.55	9.57
2223−052	1.404	20.34	11.7	13.59	18.00	3	0.199	2006-10-06	3.21	18.33
2227−088	1.560	2.00	15.8	1.41	5.14	2	0.186	2006-07-07	22.85	1.40
2230+114	1.037	8.62	13.3	8.51	9.25	3	0.278	2006-02-12	7.36	5.45
2243−123	0.632	5.24	14.8	1.45	1.71	1	0.161	2006-09-06	5.73	2.79
2251+158	0.859	13.77	40.9	12.47	9.39	3	0.124	2006-06-15	8.31	4.72
2345−167	0.576	11.47	15.8	2.81	2.21	3	0.167	2006-11-10	3.24	5.54
2351+456	1.986	21.56	20.1	2.23	8.54	8	0.196	2006-05-24	5.35	7.99

Notes. Columns are as follows: (1) source name (B1950); (2) redshift z as collected by (Lister et al. 2013); (3) apparent velocity measured by (Lister et al. 2013); (4) apparent opening angle measured by Pushkarev et al. (2009); (5) flux density at the 92 cm band; (6) derived total jet power; (7) 92 cm flux density reference: 1 – De Breuck et al. (2002), 2 – Douglas et al. (1996), 3 – Ghosh et al. (1994), 4 – Gregory & Condon (1991), 5 – Kühr et al. (1979), 6 – Kühr et al. (1981), 7 – Mitchell et al. (1994), 8 – Rengelink et al. (1997); (8) core shift for frequencies 8.1 − 15.3 GHz, measured in mas (Sokolovsky et al. 2011; Pushkarev et al. 2012); (9) an epoch of the core-shift measurements by Pushkarev et al. (2012) for the year 2006 and by Sokolovsky et al. (2011) for the year 2007; (10) derived multiplicity parameter; (11) derived the Michel magnetization parameter.

The Doppler factor of a flow can be also obtained through the variability method by measuring the amplitude and duration of a flare (Hovatta et al. 2009). Making an assumption that the latter corresponds to the time needed for light to cross the emitting region, and assuming that the intrinsic brightness temperature is known (from the equipartition argument), one can derive the beaming Doppler factor. We have used the variability Doppler factors obtained by Hovatta et al. (2009) for 50 objects with measured core-shifts (Pushkarev et al. 2012) instead of our original assumption for Doppler factor δ = β_app and have found that our estimates for λ and σ_M stay the same within a factor of 2.

We estimate the total typical accuracy of λ and σ_M values in Table 1 to be of a factor of a few. It is mostly due to the assumptions and simplifications introduced and, to a less of an extent, due to accuracy of observational parameters of the jets. We note that while an estimate for every source is not highly accurate, the distributions in Figs 1 and 2 should represent the sample properties well.

There are three objects in our sample that have the Michel magnetization parameter σ_M < 1, which means that the flow is not magnetically dominated at its base. And we have overall nine sources with σ_M < 2, which is in contradiction with our assumption of at least a mildly magnetized flow. This is a small fraction (9 per cent) of all 97 sources, so we feel that for the majority sources there is no contradiction of our assumptions and the resultant value for the Michel magnetization parameter.

For the highly magnetized regime, we come to a contradiction. Indeed, taking, for example, a source 0215+015, which has the Michel magnetization parameter σ_0215 + 015 = σ_M, med, we obtain from equation (35) for a highly magnetized regime the following value:

\begin{equation} \sigma _{\rm M,\,mag}=\frac{3.6\times 10^{5}}{\Gamma ^{3/2}}. \end{equation}

(40)

In a highly magnetized regime, the scaling (4) holds, and for Γ = r_⊥/R_L ≈ 10⁴–10⁵ we come to σ_M, mag ≈ 10⁻²–10⁻¹. This is in contradiction with our assumption for a magnetized regime with initial magnetization σ_M > 10⁵.

We see that the magnetization parameter λ obtained from the observed core-shift has the order of magnitude 10¹²–10¹⁴ which agrees with the two-photon conversion model of plasma production in a black hole magnetosphere (Blandford & Znajek 1977; Moscibrodzka et al. 2011). Thus, we obtain the key physical parameters of the jets being σ_M ∼ 10 and λ ∼ 10¹³. As a result, knowing these parameters and using a rather simple one-dimensional MHD approach, we can determine the internal structure of jets.

4 ON THE INTERNAL STRUCTURE OF JETS

As was shown by Beskin & Malyshkin (2000), Beskin & Nokhrina (2009) and Lyubarsky (2009), for well-collimated jets the one-dimensional cylindrical MHD approximation (when the problem is reduced to the system of two ordinary differential equations, see above mentioned papers for more detail) allows us to reproduce main results obtained later by two-dimensional numerical simulation (Komissarov et al. 2006; Tchekhovskoy et al. 2009; Porth et al. 2011; McKinney et al. 2012). In particular, both analytical and numerical consideration predict the existence of a dense core in the centre of a jet for low enough ambient pressure p_ext. Thus, knowing main parameters obtained above we can determine the transverse structure of jets using rather simple 1D analytical approximation. The only parameters we need are the Michel magnetization σ_M and the transverse dimension of a jet R_jet (or, the ambient pressure p_ext). In particular, transversal profiles of the Lorentz factor Γ, number density n_e and magnetic field B can be well reproduced. In this section, we apply this approach to clarify the real structure of relativistic jets.

In Fig. 3, we present logarithmic plots of Lorentz factor and number density across the jet for λ = 10¹³, jet radius R_jet = 1 pc and σ = 5, 15 and 30. Fig. 4 shows logarithmic plots of poloidal and toroidal components of magnetic field across the jet with the same parameters as in Fig. 3. As we see, these results point to the existence of more dense central core in the centre of a jet. Indeed, for our parameters the number density in the centre of a jet is greater by a factor of a thousand than at the edge. However the Lorentz factor in the central core is small (see Fig. 3b). Thus, these results are in qualitative agreement with previous studies.

Figure 3.

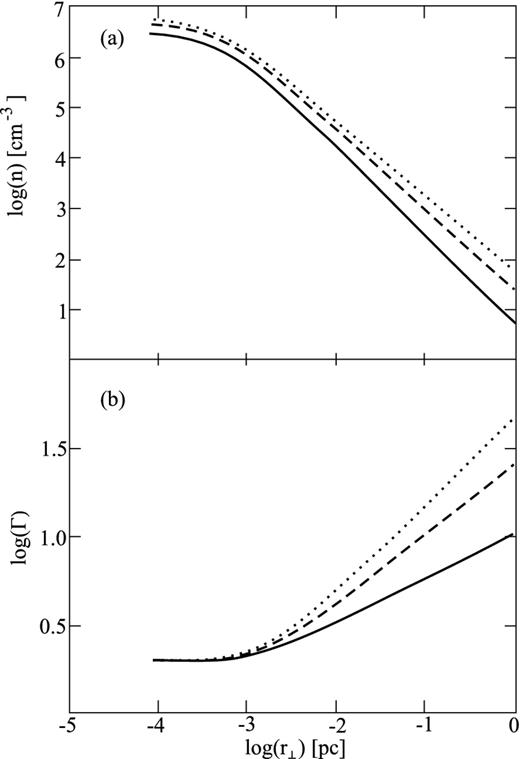
Transversal profile of the number density n_e (a) and Lorentz factor Γ (b) in logarithmical scale for λ = 10¹³, jet radius R_jet = 1 pc and three different values of σ: 5 (solid line), 15 (dashed line) and 30 (dotted line).

Open in new tab Download slide

Figure 4.

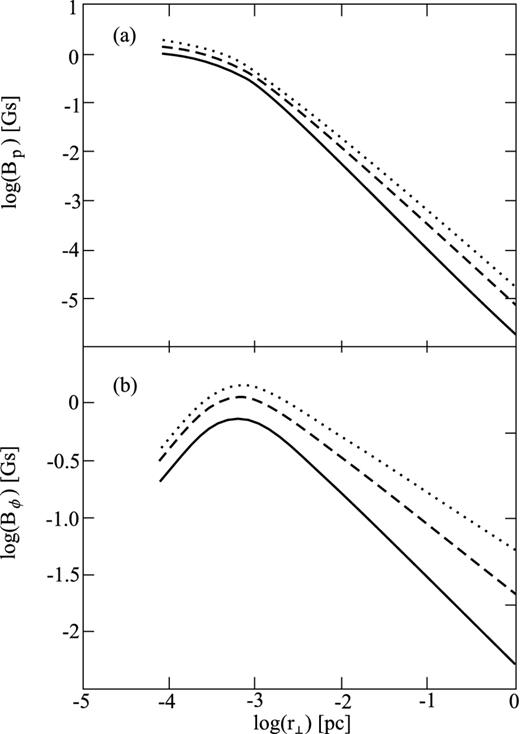
Transversal profile of poloidal (a) and toroidal (b) components of magnetic field in logarithmical scale for the same parameters and line types as in Fig. 3.

Open in new tab Download slide

Knowing how the Lorentz factor on the edge of jet depends on its radius and making a simple assumption about the form of the jet, we can calculate the dependence of the Lorentz factor on the coordinate along the jet. The result is presented in Fig. 5 for the cases of parabolic |$\zeta \propto r_{\perp }^2$| and |$\zeta \propto r_{\perp }^3$| form of the jet. Here, ζ is the distance along the axis. We also assume that the jet has a radius of about 10 pc at the distance 100 pc in both cases, which corresponds to a half-opening angle of the jet θ_jet ≈ 0.1. According to Fig. 5, particle acceleration in the frame of the AGN host galaxy on the scales 60–100 pc has values about |$\dot{\Gamma }/\Gamma =10^{-3}$| yr⁻¹ with very little dependence of this value on the particular form of a jet boundary. This agrees nicely with results of the VLBI acceleration study in AGN jets by Homan et al. (2009, 2014).

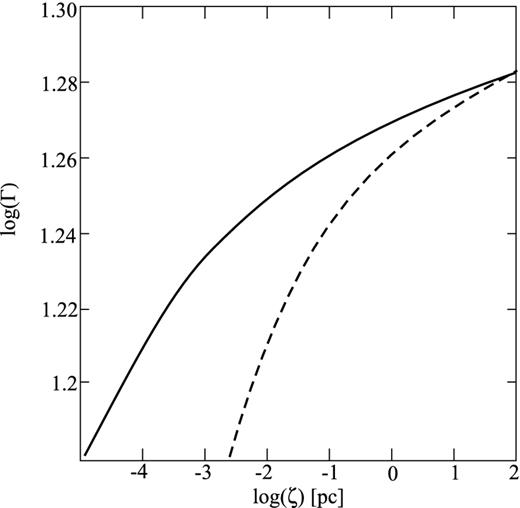
$Dependence of Lorentz factor on coordinate along the jet in assumption of $\zeta \propto r_{\perp }^3$ (solid line) and $\zeta \propto r_{\perp }^2$ (dashed line) form of the jet.$

Figure 5.

Dependence of Lorentz factor on coordinate along the jet in assumption of |$\zeta \propto r_{\perp }^3$| (solid line) and |$\zeta \propto r_{\perp }^2$| (dashed line) form of the jet.

Open in new tab Download slide

5 STUDYING THE CAUSAL CONNECTIVITY OF THE CYLINDRICAL JET MODEL

The calculated multiplication parameter λ with the Michel magnetization parameter σ_M as well as the observed half-opening angle of a jet χ allow us to test causal connectivity across a jet for the cylindrical model. Every spacial point of a supermagnetosonic outflow has its own ‘Mach cone’ of causal influence. In case of a uniform flow the cone originating at the given point with its surface formed by the characteristics of a flow is a domain, where any signal from the point is known. For a non-uniform flow the cone becomes some vortex-like shape, depending on the flow property, but sustaining the property of a causal domain for a given point.

In a jet, if the characteristic inlet from any point of a set of boundary points reaches the jet axis, we say that the axis is causally connected with the boundary. On the contrary, if there is a characteristic that does not reach the axis, we have a causally disconnected flow. In the latter case, a question arises about the self-consistency of an MHD solution of the flow, since the inner parts of such a flow do not have any information about the properties of the confining medium. The examples of importance of causal connectivity in a flow and its connection with the effective plasma acceleration has been pointed out by Komissarov et al. (2009) and Tchekhovskoy et al. (2009).

In the case of the cylindrical jet model, the question of causality is even more severe. For a cylindrical model we take into account the force balance across a jet only, so the trans-field equation governing the flow becomes one-dimensional. For every initial condition at the axis its solution gives the flow profile and the position of a boundary, defined so as to contain the whole magnetic flux. Any physical value at the boundary such as, for example, the pressure, may be calculated from this solution. Or, we in fact reverse the problem, and for a given outer pressure at the boundary we find the initial conditions at the jet axis. Thus, we use the dependence of the jet properties at the axis from the conditions at the boundary. In this case, the boundary and the axis must be causally connected. In other words, for a strictly cylindrical flow the conditions at the boundary at the distance ζ₀ from the jet origin must be ‘known’ to the point at the axis at the same ζ₀.

In the cylindrical model, the dynamics of a flow along the jet is achieved by ‘piling up’ the described above cross cuts so as to either make the needed boundary form, or to model the variable outer pressure. In this case, the jet boundaries should be constrained by the ‘Mach cone’ following causal connection for the model to be self-consistent. Thus, we come to the following criteria: we may assert that we can neglect the jet-long derivatives in a trans-field equation if any characteristic, outlet from a boundary at ζ₀, not only reaches the axis, but does it at ζ: |ζ − ζ₀| ≪ ζ₀.

For an axisymmetric flow, the condition of a causal connectivity across the flow may be written (Tchekhovskoy et al. 2009) in the simplest case as

\begin{equation} \theta _{\rm F}>\theta _{\rm j}, \end{equation}

(41)

where θ_F is a half-opening angle of a fast Mach cone at the boundary. This condition means that the characteristic from the jet boundary, locally having its half-opening angle θ_F with regard to the local poloidal flow velocity, reaches the axis. For an ultrarelativistic flow, θ_F may be defined as (Tchekhovskoy et al. 2009)

\begin{equation} \sin ^2\theta _{\rm F} = \frac{1}{M^2_{\rm F}}=\frac{\Gamma _{\rm max}-\Gamma }{\Gamma ^{3}}. \end{equation}

(42)

In the cylindrical approach, we can check the causal connection across the jet both by applying condition (41), and by tracking the net of characteristics, outlet from the boundary. This can be done for a different jet boundary shapes. Let us introduce the causality function

\begin{equation} f=\frac{\Gamma _{\rm max}-\Gamma }{\Gamma ^{3}}\times \frac{1}{\sin ^{2}\theta _{\rm j}}. \end{equation}

(43)

It follows from (41) and (42) that for f > 1 causal connectivity holds, and for f < 1 it does not. If a jet boundary form is given by a function ζ = ζ(r_⊥), where r_⊥ is an axial radius, the half-opening jet angle is defined by

\begin{equation} \sin \theta _{\rm j} = \frac{\mathrm{\partial} r_{\perp }}{\mathrm{\partial} \zeta } \left[1+\left(\frac{\mathrm{\partial} r_{\perp }}{\mathrm{\partial} \zeta }\right)^{2}\right]^{-1/2}. \end{equation}

(44)

Fig. 6 shows the causality function for a paraboloidal flow (see Beskin & Nokhrina 2009) |$\zeta \propto r_{\perp }^{2}$|⁠, for a jet with a boundary shaped as |$\zeta \propto r_{\perp }^{3}$|⁠, and |$\zeta \propto r_{\perp }^{3/2}$|⁠. For the latter flow shape f < 1 for every distance. Thus, the first two outflows are causally connected, and the last one may be causally disconnected.

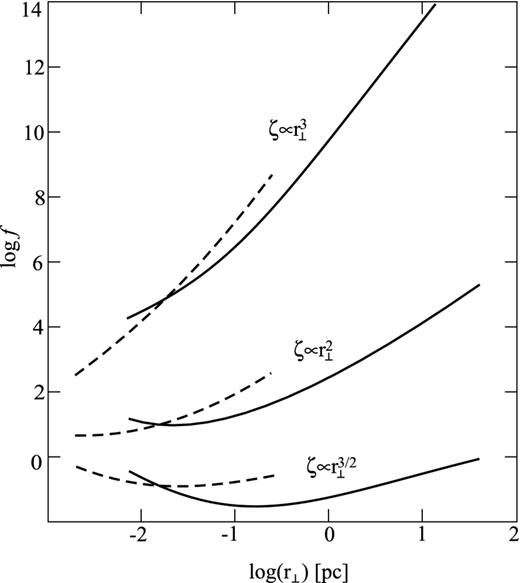
$The causality function f for different magnetic surface shapes for Γ > Γmax/2, i.e. further the equipartition. Solid lines are shown for σM = 100 while dotted lines for σM = 10. The upper curves correspond to $\zeta \propto r_{\perp }^{3}$, the curves in the middle – to $\zeta \propto r_{\perp }^{2}$, and the lower curves – to $\zeta \propto r_{\perp }^{3/2}$.$

Figure 6.

The causality function f for different magnetic surface shapes for Γ > Γ_max/2, i.e. further the equipartition. Solid lines are shown for σ_M = 100 while dotted lines for σ_M = 10. The upper curves correspond to |$\zeta \propto r_{\perp }^{3}$|⁠, the curves in the middle – to |$\zeta \propto r_{\perp }^{2}$|⁠, and the lower curves – to |$\zeta \propto r_{\perp }^{3/2}$|⁠.

Open in new tab Download slide

The cylindrical approach allows us to investigate the set of characteristics to check the causality of a flow. Let us discuss the paraboloidal flow first. We can calculate the Mach half-opening angle at each point, starting from the boundary and so tracking the exact characteristics. This half-opening angle is defined with regard to the flow velocity direction. Although in the cylindrical approach all the velocities have only the ζ-component, we may introduce the r_⊥-component by taking into account the given form of each magnetic surface. The latter is defined by the function

\begin{equation} X=\sqrt{r_{\perp }^{2}+\zeta ^{2}}-\zeta ={\rm const}, \end{equation}

(45)

and for inner parts of a flow Ψ = Ψ₀X. Thus, we define the angle θ_ℓ of a field-line tangent to a vertical direction as |${\rm tg}\theta _{\ell } = \left|B_{r_{\perp }}\right|/\left|B_{\zeta }\right| = \mathrm{\partial} r_{\perp }/\mathrm{\partial} \zeta$|⁠, and at the given point of a flow we outlet the fast characteristic with regard to thus defined flow direction. We present in Fig. 7 (centre panel) the net of characteristics for a paraboloidal flow depicted as described above. The characteristics are calculated starting from the jet boundary towards the axis. They are parametrized by the square of fast magnetosonic Mach number M_F² at the axis at the same ζ, where the characteristic starts. This is done uniformly regarding the Mach number, thus the characteristics are plotted at different distances from each other. It can be seen that all the characteristics for parabolic jet boundary reach the axis at ζ not much greater than ζ₀. The same result holds for a flow |$\zeta \propto r_{\perp }^{3}$| either (see Fig. 7, left-hand panel). On the contrary, each characteristic, depicted in Fig. 7 (right-hand panel) for a flow |$\zeta \propto r_{\perp }^{3/2}$|⁠, reaches the axis at a distance along a flow much greater than the ζ-coordinate of its origin. This suggests that the cylindrical approach is definitely not valid in this case.

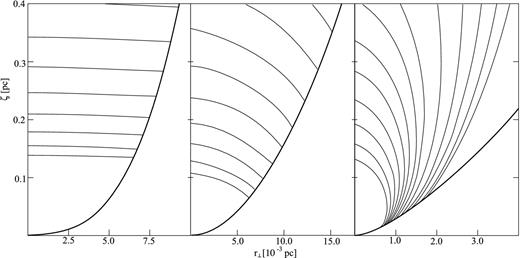
$The net of inbound characteristics for a power-law form of a jet boundary $\zeta \propto r_{\perp }^{3}$ (left-hand panel), $\zeta \propto r_{\perp }^{2}$ (centre panel), $\zeta \propto r_{\perp }^{3/2}$ (right-hand panel).$

Figure 7.

The net of inbound characteristics for a power-law form of a jet boundary |$\zeta \propto r_{\perp }^{3}$| (left-hand panel), |$\zeta \propto r_{\perp }^{2}$| (centre panel), |$\zeta \propto r_{\perp }^{3/2}$| (right-hand panel).

Open in new tab Download slide

6 DISCUSSION

We show that the multiplicity parameter λ, which is the ratio of number density n_e of outflowing plasma to GJ number density n_GJ, can be obtained from the direct observations of core shift, apparent opening angle and radio power of a jet. The formula (31) uses the following assumptions, taken from the theoretical model: (i) the acceleration process of plasma effectively stops (saturates) when there is an equipartition regime, i.e. the Poynting flux is equal to the plasma kinetic energy flux; (ii) we assume the certain power-law scalings for magnetic field B(r) and number density n_e(r) as a functions of distance r (Lobanov 1998). These scalings are confirmed by Sokolovsky et al. (2011). We also see that these power laws are a good approximation from modelling the internal jet structure in Section 4.

In contrast with Lobanov (1998) and Hirotani (2005) we do not assume the equipartition regime of radiating particles with magnetic field, but the relation between the particles (radiating and non-radiating) kinetic energy and Poynting flux. We assume that only the small fraction of particles ∼1 per cent radiates (Sironi et al. 2013) and introduce the correlation between particle number density and magnetic field through the flow magnetization σ. Although for σ ∼ 1 both approaches give effectively the same relation between particle number density and magnetic field, for highly magnetized regime σ ≫ 1 our approach yields the different result. Probing both the equipartition regime σ ∼ 1 and highly magnetized regime σ ≫ 1 at parsec scales we conclude that the latter does not hold.

Using the obtained Michel magnetization parameter σ_M, one can easily explain the observationally derived values 2Γχ ≈ 0.1 (Clausen-Brown et al. 2013; Zamaninasab et al. 2014), where Γ is Lorentz factor of bulk plasma motion and χ is a jet half-opening angle. Indeed, as was found by Tchekhovskoy, McKinney & Narayan (2008), Beskin (2010), 2Γχ ≈ 1 in the whole domain where Γ ≪ σ, independent of the collimation geometry. This implies that 2Γχ ≈ 1 up to the distance from the origin whence the transverse dimension of a jet R_jet/R_L = σ_M. At larger distances Γ remains practically constant, but for a parabolic geometry the opening angle decreases with the distance ζ as ζ^−1/2 ≈ r^−1/2. As a result, one can write down

\begin{equation} 2\Gamma \chi \sim \sqrt{\frac{\sigma _{\rm M} R_\mathrm{L}}{R_\mathrm{jet}}}\sim 0.1. \end{equation}

(46)

This result is in agreement with the criteria of casual connectivity across a jet. Indeed, for an outflow with an equipartition between the Poynting and particle energy flux, we can write down

\begin{equation} 2\Gamma \chi =\frac{1}{\sqrt{f}}<1 \end{equation}

(47)

for a boundary causally connected with an axis. In Section 5, we have shown that for flows collimated better than a parabola, casuality connectivity across the jet holds further, i.e. for Γ > Γ_max/2.

7 SUMMARY

The analysis of the frequency dependence of the observed shift of the core of relativistic AGN jets allows us to determine physical parameters of the jets such as the plasma number density and the magnetic field inside the flow. We have estimated the multiplicity parameter λ to be of the order of 10¹²–10¹⁵. It is consistent with the Blandford–Znajek model (Blandford & Znajek 1977) of the electron–positron generation in the magnetosphere of the black hole (see Moscibrodzka et al. 2011, as well). These values are in agreement with the particle number density n_e which was found independently by Lobanov (1998).

As the transverse jet structure depends strongly on the flow regime, whether it is in equipartition or magnetically dominated, it is important to know the relation between the observed and maximum Lorentz factor. The Michel magnetization parameter σ_M is equal to the maximum Lorentz factor of plasma bulk motion. Typical derived values of σ_M ≲ 30, in agreement with the Lorentz factor estimated from VLBI jet kinematics (e.g. Cohen et al. 2007; Lister et al. 2009b, 2013) and radio variability (Jorstad et al. 2005; Hovatta et al. 2009; Savolainen et al. 2010). This implies that a flow is in the saturation regime. Since for strongly collimated flow the condition of causal connection is fulfilled (see e.g. Komissarov et al. 2009; Tchekhovskoy et al. 2009), the internal structure of an outflow can be modelled within the cylindrical approach (Beskin & Malyshkin 2000; Beskin & Nokhrina 2009). It has been shown that the results of the modelling, such as Lorentz factor dependence on the jet distance, are in good agreement with the observations. In particular, the relative growth of Lorentz factor |$\dot{\Gamma }/\Gamma$| with the distance along the axis is slow for the jets in saturation regime, having the magnitude ∼10⁻³ yr⁻¹. This result may account for the recent measurements of acceleration in AGN jets (Homan et al. 2014).

We plan to address the following points in a separate paper: (i) the role of the inhomogeneity of the magnetic field and particle number density in a core, (ii) the action of the radiation drag force (Li, Begelman & Chiueh 1992; Beskin, Zakamska & Sol 2004; Russo & Thompson 2013), (iii) the possible influence of mass loading (Komissarov 1994; Derishev et al. 2003; Stern & Poutanen 2006) on the jet magnetization and dynamics.

We would like to acknowledge E. Clausen-Brown, D. Gabuzda, M. Sikora, A. Lobanov, T. Savolainen, M. Barkov and the anonymous referee for useful comments. We thank the anonymous referee for suggestions which helped to improve the paper. This work was supported in part by the Russian Foundation for Basic Research grant 13-02-12103. YYK was also supported in part by the Dynasty Foundation. This research has made use of data from the MOJAVE data base that is maintained by the MOJAVE team (Lister et al. 2009a), and data accumulated by the CATS data base (Verkhodanov et al. 1997). This research has made use of NASA's Astrophysics Data System.

REFERENCES

Appl

S.

Camenzind

M.

,

A&A

,

1992

, vol.

256

pg.

354

Benford

G.

,

ApJ

,

1981

, vol.

247

pg.

792

Crossref

Search ADS

Beskin

V. S.

,

MHD Flows in Compact Astrophysical Objects

,

2009

Berlin

Springer-Verlag

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Beskin

V. S.

,

Phys.-Usp.

,

2010

, vol.

53

pg.

1199

Crossref

Search ADS

Beskin

V. S.

Malyshkin

L. M.

,

Astron. Lett.

,

2000

, vol.

26

pg.

4

Crossref

Search ADS

Beskin

V. S.

Nokhrina

E. E.

,

MNRAS

,

2009

, vol.

397

pg.

1486

Crossref

Search ADS

Beskin

V. S.

Istomin

Ya. N.

Pariev

V. I.

,

SvA

,

1992

, vol.

36

pg.

642

Beskin

V. S.

Zakamska

N. L.

Sol

H.

,

MNRAS

,

2004

, vol.

347

pg.

587

Crossref

Search ADS

Bisnovatyi-Kogan

G. S.

,

Ap&SS

,

2007

, vol.

311

pg.

287

Crossref

Search ADS

Blandford

R. D.

,

MNRAS

,

1976

, vol.

176

pg.

465

Crossref

Search ADS

Blandford

R. D.

Königl

A.

,

ApJ

,

1979

, vol.

232

pg.

34

Crossref

Search ADS

Blandford

R. D.

Znajek

R. L.

,

MNRAS

,

1977

, vol.

179

pg.

433

Crossref

Search ADS

Bogovalov

S. V.

,

Astron. Lett.

,

1995

, vol.

21

pg.

565

Cavagnolo

K. W.

McNamara

B. R.

Nulsen

P. E. J.

Carilli

C. L.

Jones

C.

Bîrzan

L.

,

ApJ

,

2010

, vol.

720

pg.

1066

Crossref

Search ADS

Clausen-Brown

E.

Savolainen

T.

Pushkarev

A. B.

Kovalev

Y. Y.

Zensus

J. A.

,

A&A

,

2013

, vol.

558

pg.

A144

Crossref

Search ADS

Cohen

M. H.

Lister

M. L.

Homan

D. C.

Kadler

M.

Kellermann

K. I.

Kovalev

Y. Y.

Vermeulen

R. C.

,

ApJ

,

2007

, vol.

658

pg.

232

Crossref

Search ADS

De Breuck

C.

Tang

Y.

de Bruyn

A. G.

Röttgering

H.

van Breugel

W.

,

A&A

,

2002

, vol.

394

pg.

59

Crossref

Search ADS

Derishev

E. V.

Aharonian

F. A.

Kocharovsky

V. V.

Kocharovsky

Vl. V.

,

Phys. Rev. D

,

2003

, vol.

68

pg.

043003

Crossref

Search ADS

Douglas

J. N.

Bash

F. N.

Bozyan

F. A.

Torrence

G. W.

Wolfe

C.

,

AJ

,

1996

, vol.

111

pg.

1945

Crossref

Search ADS

Ghosh

T.

Gopal-Krishna Rao

A. P.

,

A&AS

,

1994

, vol.

106

pg.

29

Goldreich

P.

Julian

W. H.

,

ApJ

,

1969

, vol.

157

pg.

869

Crossref

Search ADS

Gould

R. J.

,

A&A

,

1979

, vol.

76

pg.

306

Gregory

P. C.

Condon

J. J.

,

ApJS

,

1991

, vol.

75

pg.

1011

Crossref

Search ADS

Hardee

P. E.

Norman

M. L.

,

ApJ

,

1988

, vol.

334

pg.

70

Crossref

Search ADS

Heyvaerts

J.

Norman

C.

,

ApJ

,

2003

, vol.

596

pg.

1240

Crossref

Search ADS

Hirotani

K.

,

ApJ

,

2005

, vol.

619

pg.

73

Crossref

Search ADS

Hirotani

K.

Okamoto

I.

,

ApJ

,

1998

, vol.

497

pg.

563

Crossref

Search ADS

Homan

D. C.

Kadler

M.

Kellermann

K. I.

Kovalev

Y. Y.

Lister

M. L.

Ros

E.

Savolainen

T.

Zensus

J. A.

,

ApJ

,

2009

, vol.

706

pg.

1253

Crossref

Search ADS

Homan

D. C.

Lister

M. L.

Kovalev

Y. Y.

Pushkarev

A. B.

Savolainen

T.

Kellermann

K. I.

Richards

J. L.

Ros

E.

,

ApJ

,

2014

preprint (arXiv:1410.8502)

Hovatta

T.

Valtaoja

E.

Tornikoski

M.

Lähteenmäki

A.

,

A&A

,

2009

, vol.

498

pg.

723

Crossref

Search ADS

Istomin

Ya. N.

Pariev

V. I.

,

MNRAS

,

1994

, vol.

267

pg.

629

Crossref

Search ADS

Jorstad

S. G.

et al. ,

AJ

,

2005

, vol.

130

pg.

1418

Crossref

Search ADS

Komatsu

E.

et al. ,

ApJS

,

2009

, vol.

180

pg.

330

Crossref

Search ADS

Komissarov

S.

,

MNRAS

,

1994

, vol.

269

pg.

394

Crossref

Search ADS

Komissarov

S.

Barkov

M.

Vlahakis

N.

Königl

A.

,

MNRAS

,

2006

, vol.

380

pg.

51

Crossref

Search ADS

Komissarov

S. S.

Vlahakis

N.

Königl

A.

Barkov

M. V.

,

MNRAS

,

2009

, vol.

394

pg.

1182

Crossref

Search ADS

Kovalev

Y. Y.

Lobanov

A. P.

Pushkarev

A. B.

Zensus

J. A.

,

A&A

,

2008

, vol.

483

pg.

759

Crossref

Search ADS

Krolik

J.

,

Active Galactic Nuclei: From the Central Black Hole to the Galactic Environment

,

1999

Princeton, NJ

Princeton Univ. Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Kronberg

P. P.

Lovelace

R. V. E.

Lapenta

G.

Colgate

S. A.

,

ApJ

,

2011

, vol.

741

pg.

L15

Crossref

Search ADS

Kühr

H.

Nauber

U.

Pauliny-Toth

I. I. K.

Witzel

A.

,

MPIfR Preprint no. 55, A Catalogue of Radio Sources

,

1979

Bonn

Max-Planck Institut für Radioastronomie

pg.

1

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Kühr

H.

Witzel

A.

Pauliny-Toth

I. I. K.

Nauber

U.

,

A&AS

,

1981

, vol.

45

pg.

367

Li

Z.-Y.

Begelman

M.

Chiueh

T.

,

ApJ

,

1992

, vol.

384

pg.

567

Crossref

Search ADS

Lister

M. L.

et al. ,

AJ

,

2009a

, vol.

137

pg.

3718

Crossref

Search ADS

Lister

M. L.

et al. ,

AJ

,

2009b

, vol.

138

pg.

1874

Crossref

Search ADS

Lister

M. L.

et al. ,

AJ

,

2013

, vol.

146

pg.

120

Crossref

Search ADS

Lobanov

A. P.

,

A&A

,

1998

, vol.

330

pg.

79

Lovelace

R. W. E.

,

Nature

,

1976

, vol.

262

pg.

649

Crossref

Search ADS

Lyubarsky

Yu. E.

,

ApJ

,

2009

, vol.

308

pg.

1006

Lyutikov

M.

Pariev

V. I.

Gabuzda

D. C.

,

MNRAS

,

2005

, vol.

360

pg.

869

Crossref

Search ADS

McKinney

J. C.

Tchekhovskoy

A.

Blanford

R. D.

,

MNRAS

,

2012

, vol.

423

pg.

2083

Crossref

Search ADS

Marscher

A. P.

,

ApJ

,

1983

, vol.

264

pg.

296

Crossref

Search ADS

Mestel

L.

,

Stellar Magnetism

,

1999

Oxford

Clarendon Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Michel

F. C.

,

ApJ

,

1969

, vol.

158

pg.

727

Crossref

Search ADS

Mitchell

K. J.

et al. ,

ApJS

,

1994

, vol.

93

pg.

441

Crossref

Search ADS

Moscibrodzka

M.

Gammie

C. F.

Dolence

J. C.

Shiokawa

H.

,

ApJ

,

2011

, vol.

735

pg.

9

Crossref

Search ADS

O'Sullivan

S. P.

Gabuzda

D. C.

,

MNRAS

,

2009

, vol.

400

pg.

26

Crossref

Search ADS

Okamoto

I.

,

PASJ

,

2009

, vol.

61

pg.

971

Pariev

V. I.

Istomin

Ya. N.

Beresnyak

A. R.

,

A&A

,

2003

, vol.

403

pg.

805

Crossref

Search ADS

Porth

O.

Fendt

Ch.

Meliani

Z.

Vaidya

B.

,

ApJ

,

2011

, vol.

737

pg.

42

Crossref

Search ADS

Punsly

B.

,

Black Hole Gravitohydromagnetics

,

2001

Berlin

Springer-Verlag

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Pushkarev

A. B.

Kovalev

Y. Y.

Lister

M. L.

Savolainen

T.

,

A&A

,

2009

, vol.

507

pg.

L33

Crossref

Search ADS

Pushkarev

A. B.

Hovatta

T.

Kovalev

Y. Y.

Lister

M. L.

Lobanov

A. P.

Savolainen

T.

Zensus

J. A.

,

A&A

,

2012

, vol.

545

pg.

A113

Crossref

Search ADS

Rengelink

R. B.

Tang

Y.

de Bruyn

A. G.

Miley

G. K.

Bremer

M. N.

Roettgering

H. J. A.

Bremer

M. A. R.

,

A&AS

,

1997

, vol.

124

pg.

259

Crossref

Search ADS

Russo

M.

Thompson

Ch.

,

ApJ

,

2013

, vol.

767

pg.

142

Crossref

Search ADS

Savolainen

T.

Homan

D. C.

Hovatta

T.

Kadler

M.

Kovalev

Y. Y.

Lister

M. L.

Ros

E.

Zensus

J. A.

,

A&A

,

2010

, vol.

512

pg.

A24

Crossref

Search ADS

Sironi

L.

Spitkovsky

A.

Arons

J.

,

ApJ

,

2013

, vol.

771

pg.

54

Crossref

Search ADS

Sokolovsky

K. V.

Kovalev

Y. Y.

Pushkarev

A. B.

Lobanov

A. P.

,

A&A

,

2011

, vol.

532

pg.

A38

Crossref

Search ADS

Stern

B. E.

Poutanen

J.

,

MNRAS

,

2006

, vol.

372

pg.

1217

Crossref

Search ADS

Tchekhovskoy

A.

McKinney

J.

Narayan

R.

,

MNRAS

,

2008

, vol.

388

pg.

551

Crossref

Search ADS

Tchekhovskoy

A.

McKinney

J.

Narayan

R.

,

ApJ

,

2009

, vol.

699

pg.

1789

Crossref

Search ADS

Verkhodanov

O. V.

Trushkin

S. A.

Andernach

H.

Cherenkov

V. N.

Hunt

G.

Payne

H.

,

ASP Conf. Ser. Vol. 125, Astronomical Data Analysis Software and Systems VI

,

1997

San Fransisco

Astron. Soc. Pac.

pg.

322

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Zamaninasab

M.

Clausen-Brown

E.

Savolainen

T.

Tchekhovskoy

A.

,

Nature

,

2014

, vol.

510

pg.

126

Crossref

Search ADS

PubMed

Zdziarski

A. A.

Sikora

M.

Pjanka

P.

Tchekhovskoy

A.

,

MNRAS

,

2014

preprint (arXiv:1410.7310)

APPENDIX A: MAGNETIZATION PARAMETER

The standard Grad–Shafranov approach for MHD flows uses the following energy integral E, conserved at the magnetic flux surface Ψ:

\begin{equation} E(\Psi )=\frac{c\Omega _{\rm F}(\Psi )I}{2\pi }+m\eta (\Psi )c^2\Gamma . \end{equation}

(A1)

Here magnetic field in spherical coordinates {r; θ; φ} is defined by

\begin{equation} \boldsymbol {B}=\frac{{\nabla }\Psi \times \boldsymbol {e}_{\varphi }}{2\pi r\sin \theta }-\frac{2I}{cr\sin \theta }\boldsymbol {e}_{\varphi }, \end{equation}

(A2)

electric field

\begin{equation} \boldsymbol {E}=-\frac{\Omega _{\rm F}}{2\pi c}{\nabla }\Psi , \end{equation}

(A3)

Ω_F is a rotational velocity and a function of magnetic flux Ψ, I is a current and

\begin{equation} \eta (\Psi )=\frac{n_{\rm e,*}|\boldsymbol {u}_{\rm p}|}{|\boldsymbol {B}_{\rm p}|}=\frac{n_{\rm e}|\boldsymbol {v}_{\rm p}|}{|\boldsymbol {B}_{\rm p}|}. \end{equation}

(A4)

Here we assume the flow to be cold, so the particle enthalpy is simply its rest mass. The Poynting vector

\begin{equation} \boldsymbol {S}=\frac{c}{4\pi }\boldsymbol {E}\times \boldsymbol {B}=\frac{c}{2\pi }\Omega _{\rm F}I\boldsymbol {B}_{\rm p}. \end{equation}

(A5)

The particle kinetic energy flux

\begin{equation} \boldsymbol {K}=\left(\Gamma mc^2\right)\left(n_{\rm e}\boldsymbol {v}_p\right)=\Gamma mc^2\eta (\Psi )\boldsymbol {B}_{\rm p}. \end{equation}

(A6)

Thus, we can introduce the magnetization parameter, variable along the flow, as

\begin{equation} \sigma =\frac{|\boldsymbol {S}|}{|\boldsymbol {K}|}=\frac{1}{\Gamma }\frac{1}{2\pi c}\frac{\Omega _{\rm F}I}{m\eta }. \end{equation}

(A7)

On the other hand, there is Michel's magnetization parameter σ_M, which has a meaning of magnetization at the base of an outflow, is constant, and is defined by

\begin{equation} \sigma _{\rm M}=\frac{E}{mc^2\eta }=\frac{c\Omega _{\rm F}I}{2\pi m\eta c^2}+\Gamma =\Gamma \left(\sigma +1\right). \end{equation}

(A8)

APPENDIX B: MULTIPLICITY PARAMETER

The continuity of relativistic plasma number density flux through two cuts, perpendicular to bulk flow, can be written as

\begin{equation} \lambda n_{\rm GJ} R_{\rm in}^2c=n_1\left(r_1\chi \right)^2c. \end{equation}

(B1)

Here we assume the flow velocity equal to c. Using the expression for the GJ concentration

\begin{equation} n_{\rm GJ}=\frac{\Omega B}{2\pi ce} \end{equation}

(B2)

and expression for the full losses due to currents flowing in a magnetosphere

\begin{equation} P_{\rm jet}=\frac{\left(\Omega B\right)^2 R_{\rm in}^4}{c}, \end{equation}

(B3)

we get

\begin{equation} n_1=\frac{\lambda }{2\pi \left(r_1\chi \right)^2}\frac{mc^2}{e^2}\sqrt{\frac{P_{\rm jet}}{P_{\rm A}}}. \end{equation}

(B4)

Download all slides

Month:	Total Views:
November 2016	1
February 2017	5
March 2017	1
April 2017	5
May 2017	5
June 2017	3
July 2017	3
August 2017	6
October 2017	2
November 2017	2
December 2017	2
January 2018	5
February 2018	2
March 2018	25
April 2018	8
May 2018	16
June 2018	10
July 2018	19
August 2018	15
September 2018	12
October 2018	7
November 2018	11
December 2018	5
January 2019	5
February 2019	9
March 2019	9
April 2019	18
May 2019	13
June 2019	4
July 2019	9
August 2019	21
September 2019	11
October 2019	3
November 2019	15
December 2019	6
January 2020	4
February 2020	5
March 2020	7
April 2020	7
May 2020	49
June 2020	28
July 2020	2
August 2020	5
September 2020	4
October 2020	1
November 2020	6
December 2020	8
January 2021	1
February 2021	4
March 2021	11
April 2021	6
May 2021	3
June 2021	5
July 2021	9
August 2021	1
September 2021	4
October 2021	7
November 2021	10
December 2021	2
January 2022	4
February 2022	4
March 2022	10
April 2022	17
May 2022	2
June 2022	6
July 2022	25
August 2022	11
September 2022	10
October 2022	16
November 2022	5
December 2022	3
January 2023	15
February 2023	6
March 2023	6
April 2023	9
May 2023	10
June 2023	8
July 2023	3
August 2023	11
September 2023	17
October 2023	20
November 2023	6
December 2023	20
January 2024	10
February 2024	12
March 2024	9
April 2024	7
May 2024	14
June 2024	6
July 2024	15
August 2024	8
September 2024	7
October 2024	8
November 2024	9
December 2024	4
January 2025	7
February 2025	13
March 2025	10
April 2025	6
May 2025	10

Article Contents

Intrinsic physical conditions and structure of relativistic jets in active galactic nuclei

Abstract

1 INTRODUCTION

2 THE METHOD

2.1 General relations

2.2 The saturation regime

2.3 Highly magnetized outflow

3 THE STATISTICS FOR MULTIPLICITY PARAMETER

3.1 The sample of objects

3.2 Results and discussion

4 ON THE INTERNAL STRUCTURE OF JETS

5 STUDYING THE CAUSAL CONNECTIVITY OF THE CYLINDRICAL JET MODEL

6 DISCUSSION

7 SUMMARY

REFERENCES

APPENDIX A: MAGNETIZATION PARAMETER

APPENDIX B: MULTIPLICITY PARAMETER

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Intrinsic physical conditions and structure of relativistic jets in active galactic nuclei

Abstract

1 INTRODUCTION

2 THE METHOD

2.1 General relations

2.2 The saturation regime

2.3 Highly magnetized outflow

3 THE STATISTICS FOR MULTIPLICITY PARAMETER

3.1 The sample of objects

3.2 Results and discussion

4 ON THE INTERNAL STRUCTURE OF JETS

5 STUDYING THE CAUSAL CONNECTIVITY OF THE CYLINDRICAL JET MODEL

6 DISCUSSION

7 SUMMARY

REFERENCES

APPENDIX A: MAGNETIZATION PARAMETER

APPENDIX B: MULTIPLICITY PARAMETER

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only