-
PDF
- Split View
-
Views
-
Cite
Cite
Edmond Cheung, Jonathan R. Trump, E. Athanassoula, Steven P. Bamford, Eric F. Bell, A. Bosma, Carolin N. Cardamone, Kevin R. V. Casteels, S. M. Faber, Jerome J. Fang, Lucy F. Fortson, Dale D. Kocevski, David C. Koo, Seppo Laine, Chris Lintott, Karen L. Masters, Thomas Melvin, Robert C. Nichol, Kevin Schawinski, Brooke Simmons, Rebecca Smethurst, Kyle W. Willett, Galaxy Zoo: Are bars responsible for the feeding of active galactic nuclei at 0.2 < z < 1.0?, Monthly Notices of the Royal Astronomical Society, Volume 447, Issue 1, 11 February 2015, Pages 506–516, https://doi.org/10.1093/mnras/stu2462
Close - Share Icon Share
Abstract
We present a new study investigating whether active galactic nuclei (AGN) beyond the local universe are preferentially fed via large-scale bars. Our investigation combines data from Chandra and Galaxy Zoo: Hubble (GZH) in the AEGIS (All-wavelength Extended Groth strip International Survey), COSMOS (Cosmological Evolution Survey), and (Great Observatories Origins Deep Survey-South) GOODS-S surveys to create samples of face-on, disc galaxies at 0.2 < z < 1.0. We use a novel method to robustly compare a sample of 120 AGN host galaxies, defined to have 1042 erg s−1 < LX < 1044 erg s−1, with inactive control galaxies matched in stellar mass, rest-frame colour, size, Sérsic index, and redshift. Using the GZH bar classifications of each sample, we demonstrate that AGN hosts show no statistically significant enhancement in bar fraction or average bar likelihood compared to closely-matched inactive galaxies. In detail, we find that the AGN bar fraction cannot be enhanced above the control bar fraction by more than a factor of 2, at 99.7 per cent confidence. We similarly find no significant difference in the AGN fraction among barred and non-barred galaxies. Thus we find no compelling evidence that large-scale bars directly fuel AGN at 0.2 < z < 1.0. This result, coupled with previous results at z = 0, implies that moderate-luminosity AGN have not been preferentially fed by large-scale bars since z = 1. Furthermore, given the low bar fractions at z > 1, our findings suggest that large-scale bars have likely never directly been a dominant fuelling mechanism for supermassive black hole growth.
1 INTRODUCTION
Most simulations of galaxy evolution require some kind of feedback that correlates with bulge mass (and is often assumed to be active galactic nucleus – AGN – feedback) to reproduce key observations, such as the colour bimodality of galaxies (e.g. Springel, Di Matteo & Hernquist 2005; Croton et al. 2006; Cimatti et al. 2013). Yet, the mechanism that funnels gas towards the central supermassive black hole that powers the AGN is still unknown (e.g. Hopkins & Hernquist 2006; Hopkins & Quataert 2011; Hopkins, Kocevski & Bundy 2014; see Fabian 2012; Kormendy & Ho 2013; Heckman & Best 2014 for recent reviews).
Major mergers are often cited as a key trigger for AGN activity (Sanders et al. 1988; Barnes & Hernquist 1991; Mihos & Hernquist 1996; Di Matteo, Springel & Hernquist 2005; Hopkins et al. 2005a,b). Although major mergers seem to drive the most luminous and rapidly accreting AGN (Sanders et al. 1988; Kartaltepe et al. 2010; Koss et al. 2010; Treister et al. 2012; Trump 2013; Hopkins et al. 2014), low- to moderate-luminosity AGN, which make up the majority of AGN by number, seem to be fuelled by processes that do not visibly disturb the discy structure of galaxies (Schawinski et al. 2010, 2011, 2012; Cisternas et al. 2011; Kocevski et al. 2012; Simmons et al. 2012, 2013).
An obvious process that satisfies this constraint is secular evolution (Kormendy 1979; Martinet 1995; Kormendy & Kennicutt 2004; Athanassoula 2013; Sellwood 2014). A major driver of secular evolution in disc galaxies is large-scale bars,1 and they are predicted to affect galaxies in a variety of ways, including the fuelling of AGN (Simkin, Su & Schwarz 1980; Noguchi 1988; Shlosman, Frank & Begelman 1989; Shlosman, Begelman & Frank 1990; Wada & Habe 1992). The non-axisymmetric potential of a bar is predicted to funnel interstellar gas into the central kpc (Athanassoula 1992) – which has been confirmed by multiple observational works (Regan, Vogel & Teuben 1995; Regan, Sheth & Vogel 1999; Sakamoto et al. 1999; Sheth et al. 2000, 2002, 2005; Zurita et al. 2004) – where a possible nested, secondary bar may further funnel gas to the inner ∼10 pc. From this distance, cloud–cloud collisions may lead to inflows on to the AGN accretion disc. Collectively, this scenario is known as ‘bars within bars’ (Shlosman et al. 1989, 1990; Hopkins & Quataert 2010, 2011). Observations at low redshift, however, find no excess of primary bars in active galaxies (Ho, Filippenko & Sargent 1997; Mulchaey & Regan 1997; Malkan, Gorjian & Tam 1998; Hunt & Malkan 1999; Martini & Pogge 1999; Regan & Mulchaey 1999; Erwin & Sparke 2002; Martini et al. 2003; Lee et al. 2012b; Cisternas et al. 2013, but see Knapen, Shlosman & Peletier 2000; Laine et al. 2002; Laurikainen, Salo & Buta 2004; Oh, Oh & Yi 2012; Alonso, Coldwell & Lambas 2013; Galloway et al., in preparation). There is also no direct correlation between primary bars and secondary bars, with ∼30 per cent of all disc galaxies having a secondary bar (Mulchaey & Regan 1997; Martini & Pogge 1999; Regan & Mulchaey 1999; Erwin & Sparke 2002; Laine et al. 2002). These results indicate that bars – both primary and secondary bars – may not fuel AGN.
Almost all previous observational work on the bar–AGN connection has been limited to the local universe, where the number density of AGN is low. Thus a compelling link between bars and AGN might still be found at earlier epochs, when the number density of AGN is higher (Ueda et al. 2003; Silverman et al. 2008b; Aird et al. 2010). In this work we focus on galaxies at 0.2 < z < 1.0. The upper limit of z = 1 is based on Melvin et al. (2014), who show that bars are detectable out to z = 1 with the Hubble Space Telescope Advanced Camera for Surveys (HST/ACS).
We describe the data in Section 2. Our sample selection, and in particular, our selection of control samples of inactive galaxies is detailed in Section 3. Section 4 presents our main result that there is no statistically significant excess of bars in AGN hosts. We discuss the implications of our results in Section 5. Conclusions follow in Section 6. Throughout this paper, we assume a flat cosmological model with H0 = 70 km s−1 Mpc−1, Ωm = 0.30, and ΩΛ = 0.70, and all magnitudes are given in the AB magnitude system.
2 DATA
In this section, we briefly describe the three surveys and their respective data products that are used in this paper. We also describe Galaxy Zoo: Hubble (GZH), which uses high-resolution HST/ACS imaging to accurately visually classify galaxies. Thus this paper will only focus on the area of these surveys that have HST/ACS imaging. A summary of the three surveys is presented in Table 1.
| . | AEGIS . | COSMOS . | GOODS-S . |
|---|---|---|---|
| Area (deg2) | 0.197 | 1.8 | 0.07 |
| HST/ACS exp. time (s)a | 2180 | 2028 | 2223 |
| Pixel scale (arcsec pixel−1) | 0.03 | 0.05 | 0.03 |
| PSF FWHM (arcsec) | 0.120 | 0.090 | 0.125 |
| . | AEGIS . | COSMOS . | GOODS-S . |
|---|---|---|---|
| Area (deg2) | 0.197 | 1.8 | 0.07 |
| HST/ACS exp. time (s)a | 2180 | 2028 | 2223 |
| Pixel scale (arcsec pixel−1) | 0.03 | 0.05 | 0.03 |
| PSF FWHM (arcsec) | 0.120 | 0.090 | 0.125 |
| . | AEGIS . | COSMOS . | GOODS-S . |
|---|---|---|---|
| Area (deg2) | 0.197 | 1.8 | 0.07 |
| HST/ACS exp. time (s)a | 2180 | 2028 | 2223 |
| Pixel scale (arcsec pixel−1) | 0.03 | 0.05 | 0.03 |
| PSF FWHM (arcsec) | 0.120 | 0.090 | 0.125 |
| . | AEGIS . | COSMOS . | GOODS-S . |
|---|---|---|---|
| Area (deg2) | 0.197 | 1.8 | 0.07 |
| HST/ACS exp. time (s)a | 2180 | 2028 | 2223 |
| Pixel scale (arcsec pixel−1) | 0.03 | 0.05 | 0.03 |
| PSF FWHM (arcsec) | 0.120 | 0.090 | 0.125 |
2.1 AEGIS
The All-wavelength Extended Groth strip International Survey (AEGIS; Davis et al. 2007) is an international collaboration that produced one of the most comprehensive multiwavelength data sets currently available. This data set includes HST/ACS imaging, which is centred on the Extended Groth Strip (EGS) region and is composed of 63 pointings in both the F606W (V) and the F814W (I) filters. The final images have a pixel scale of 0.03 arcsec pixel− 1 and a point-spread function (PSF) of 0.12 arcsec full width at half-maximum (FWHM). The HST/ACS images cover a total area of ∼ 710 arcmin2.
The multiwavelength coverage of AEGIS also includes Chandra ACIS-I (Garmire et al. 2003) X-ray observations that have a nominal exposure of 800 ks (Nandra et al. 2005; Georgakakis et al. 2006; Laird et al. 2009).
The spectroscopic redshifts (z) of AEGIS are from the DEEP2 and DEEP3 redshift surveys (Davis et al. 2003; Cooper et al. 2011, 2012; Newman et al. 2013), which used the DEIMOS spectrograph (Faber et al. 2003) on the Keck II telescope. Spectroscopic redshifts with quality code of 3 or 4 are considered secure; we only consider these spectroscopic redshifts throughout this paper.
Measurements of AEGIS galaxy properties are from Cheung et al. (2012), who compiled several galaxy measurements from several different sources. Stellar masses, M*, are from Huang et al. (2013), and are estimated by fitting the multiwavelength AEGIS photometry to a grid of synthetic SEDs from Bruzual & Charlot (2003), assuming a Salpeter (1955) initial mass function (IMF) and solar metallicity. These synthetic SEDs span a range of ages, dust content, and exponentially declining star formation histories (SFHs).
Rest-frame U − B colours are obtained through the kcorrect v4.2 code (Blanton & Roweis 2007) with CFHT BRI photometry and spectroscopic redshifts as inputs.
Structural parameters such as the global Sérsic index (n), effective radius (re), and axis ratio (b/a) are measured with GIM2D through a single Sérsic fit on the HST/ACS V and I images (Simard et al. 2002).
2.2 COSMOS
The Cosmological Evolution Survey (COSMOS; Koekemoer et al. 2007; Scoville et al. 2007) is the largest contiguous HST/ACS imaging survey to date, covering ∼ 1.8 deg2 in the F814W (I) band and consists of 590 pointings. The final images have a pixel scale of 0.05 arcsec pixel− 1 and a PSF of 0.09 arcsec FWHM.
In addition to the HST/ACS coverage, COSMOS also includes Chandra ACIS-I observations that cover the central part of the COSMOS field with four pointings, each totalling to a nominal exposure of 200 ks (Elvis et al. 2009). We use the Chandra COSMOS catalogue as described in Civano et al. (2012).
The spectroscopic zs of COSMOS are mainly from zCOSMOS (Lilly et al. 2009). Supplemental spectroscopic zs are from the Chandra COSMOS survey (e.g. from Trump et al. 2009). We only consider spectroscopic zs that are deemed secure by these surveys, e.g. for zCOSMOS, we only consider zs with confidence class of 3.x, 4.x, 1.5, 2.4, 2.5, 9.3, 9.5, 13.x, 14.x, 23.x, and 24.x.
Measurements of COSMOS galaxy properties are from a variety of sources. Stellar masses and rest-frame U − V colours are from the UltraVISTA survey (Muzzin et al. 2013). The M*s are estimated using fast (Kriek et al. 2009) to fit the galaxy SEDs to Bruzual & Charlot (2003) models, assuming solar metallicity, a Chabrier (2003) IMF, a Calzetti et al. (2000) dust extinction law, and exponentially declining SFHs.
The rest-frame U − V colours are estimated by using eazy (Brammer, van Dokkum & Coppi 2008) to determine the colours by integrating the best-fitting SED through the redshifted filter curves over the appropriate wavelength range.
The structural parameters of COSMOS galaxies, i.e. n, re, and b/a, are provided by the ACS-GC catalogue (Griffith et al. 2012); they used galfit (Peng et al. 2002) to fit a single Sérsic profile on the HST/ACS I images.
2.3 GOODS-S
The Great Observatories Origins Deep Survey (GOODS; Dickinson et al. 2003; Giavalisco et al. 2004; Rix et al. 2004) is a deep multiwavelength survey that includes the deepest HST images to date. The GOODS survey targeted two separate fields, the Hubble Deep-Field North (HDF-N; now referred to as GOODS-N) and the Chandra Deep-Field South (CDF-S; now referred to as GOODS-S). We will only use the GOODS-S for this paper.
The HST/ACS imaging of GOODS-S was carried out in several bands, of which we are only interested in two – F606W (V) and F850LP (z). The imaging comprises of 15 pointings, with a final pixel scale of the images of 0.03 arcsec pixel− 1 and a PSF of 0.125 arcsec FWHM. The HST/ACS imaging area of GOODS-S covers a total area of ∼ 160 arcmin2.
In addition to containing the deepest Hubble images to date, GOODS-S also contains the deepest Chandra observations to date. The 4 Ms CDF-S Survey (Luo et al. 2008; Xue et al. 2011) made 54 Chandra ACIS-I observations over a period of three Chandra observing cycles in 2000, 2007, and 2010. We use the catalogue presented by Xue et al. (2011).
The spectroscopic zs of GOODS-S come from a variety of sources, many of which are listed in table 2 of Griffith et al. (2012). We only consider redshifts of the highest quality (≥3).
Stellar masses and rest-frame U − B colours of GOODS-S galaxies are from the CANDELS survey (Barro et al. 2011; Grogin et al. 2011; Koekemoer et al. 2011; Guo et al. 2013; Williams et al. 2014). The M*s are estimated with the fast code by fitting galaxy SEDs based on optical to infrared photometry to models of Bruzual & Charlot (2003), assuming a Chabrier (2003) IMF. They also assumed a Calzetti et al. (2000) extinction law, solar metallicity, and exponentially declining SFHs.
Rest-frame U − B colours are estimated with the eazy code by fitting galaxy SEDs to the templates from Muzzin et al. (2013).
The structural parameters of GOODS-S galaxies, i.e. n, re, and b/a, are provided by the ACS-GC catalogue (Griffith et al. 2012); they used galfit (Peng et al. 2002) to fit a single Sérsic profile on the HST/ACS V and z images.
2.4 Calculating LX
To identify AGN, we use full-band (0.5–10 keV for AEGIS and COSMOS, 0.5–8 keV for GOODS-S) X-ray fluxes from Chandra observations described by Laird et al. (2009), Civano et al. (2012), and Xue et al. (2011) for AEGIS, COSMOS, and GOODS-S, respectively. We calculate X-ray luminosities using the equation |$L_{\rm X} = 4\pi d^2_{\rm L}f_{x}(1+z)^{\Gamma -2}$|, where dL is the luminosity distance, z is the redshift, fx is the flux, and Γ is the power-law photon index. We set Γ = 1.8, which is a typical power-law photon index for intrinsic AGN spectra. In Section 3.2, we select AGN using these X-ray luminosities.
2.5 Galaxy Zoo: Hubble
Our work relies on bar identifications from the GZH citizen science project (Melvin et al. 2014). Volunteers were asked to visually classify the morphologies of galaxies at z ∼ 1 based on HST/ACS optical imaging from the surveys listed above. Like the previous Galaxy Zoo project, Galaxy Zoo 2 (Willett et al. 2013), GZH used a decision tree with multiple branches and nested, dependent questions.2 These questions include, ‘Is there a sign of a bar feature through the centre of the galaxy?’, which can only be reached if a volunteer identifies some type of a feature (e.g. clumps, spiral arms, rings, bars) or a disc within a galaxy. Thus a galaxy must have a feature or a disc in order to be classified as barred.
Each galaxy is classified by at least 33 volunteers, with the median number of volunteers per galaxy being 47. These classifications produce vote percentages that we refer to throughout as ‘likelihoods’; e.g. if 25 out of 50 volunteers classified a galaxy as having a bar, then the bar likelihood is pbar = 0.5, moduli small corrections to downweight consistently unreliable classifiers (following the procedure explained in Willett et al. 2013).
GZH only classifies galaxies brighter than the following magnitudes: for AEGIS and COSMOS, HST/ACS F814W <23.5 (AB) mag, and for GOODS-S, HST/ACS F850LP<23.5 (AB) mag.
2.5.1 Selecting barred galaxies
We consider galaxies to be barred if they have bar likelihoods greater than 0.5 (pbar ≥ 0.5) and no obvious dust lanes3 (pdust lane < 0.5). The bar threshold of pbar = 0.5 is based on previous Galaxy Zoo works that have shown it to be a reliable indicator of strong bar features (Masters et al. 2011, 2012; Willett et al. 2013; Melvin et al. 2014).
To calculate the bar fraction, fbar, one can divide the total number of barred galaxies by the total number of disc galaxies in the sample. Varying the bar likelihood threshold between 0.3 ≤ pbar ≤ 0.6 does not change our qualitative conclusions.
In our analysis, we also use the average bar likelihood, |$\overline{p}_{\rm bar}$|, defined as the average of all the bar likelihoods of a sample of galaxies. This parameter is another measure of bar presence and has been used by other studies (e.g. Skibba et al. 2012; Casteels et al. 2013; Cheung et al. 2013).
3 SAMPLE SELECTION
Since our study seeks to determine if AGN activity is linked with bars, we first construct a parent sample of face-on, disc-dominated objects whose bars can be robustly identified (Section 3.1). We then select AGN-hosting galaxies from this parent sample based on their X-ray luminosity (Section 3.2). Finally, we construct samples of inactive control galaxies that are matched to the AGN galaxies (Section 3.3). The number counts of these samples are listed in Table 2.
Sample statistics. The first row represents the total number of galaxies at 0.2 < z < 1.0 with secure spectroscopic zs and HST/ACS imaging in our sample, and the second row represents the number of face-on disc galaxies that are in the previous row. The rest of the table shows the median counts from the 100 AGN control samples (see Section 3.3), and the resulting bar fraction, fbar, and average bar likelihood, |$\overline{p}_{\rm bar}$|.
| . | AEGIS . | COSMOS . | GOODS-S . |
|---|---|---|---|
| 0.2 < z < 1.0 | 3958 | 6673 | 1023 |
| Face-on disc | 1227 | 2244 | 260 |
| AGN | 25 | 86 | 9 |
| Control | 75 | 258 | 27 |
| Barred AGN | 2 | 12 | 0 |
| Barred control | 6 | 28 | 2 |
| fbar,AGN | |$0.08_{-0.03}^{+0.09}$| | |$0.14_{-0.03}^{+0.05}$| | |$0.07_{-0.05}^{+0.10a}$| |
| fbar, Control | |$0.08_{-0.02}^{+0.04}$| | |$0.11_{-0.02}^{+0.02}$| | |$0.07_{-0.03}^{+0.08}$| |
| |$\overline{p}_{\rm bar,\ AGN}$| | 0.23 ± 0.04 | 0.23 ± 0.03 | 0.12 ± 0.03 |
| |$\overline{p}_{\rm bar,\ Control}$| | 0.20 ± 0.02 | 0.20 ± 0.01 | 0.18 ± 0.04 |
| . | AEGIS . | COSMOS . | GOODS-S . |
|---|---|---|---|
| 0.2 < z < 1.0 | 3958 | 6673 | 1023 |
| Face-on disc | 1227 | 2244 | 260 |
| AGN | 25 | 86 | 9 |
| Control | 75 | 258 | 27 |
| Barred AGN | 2 | 12 | 0 |
| Barred control | 6 | 28 | 2 |
| fbar,AGN | |$0.08_{-0.03}^{+0.09}$| | |$0.14_{-0.03}^{+0.05}$| | |$0.07_{-0.05}^{+0.10a}$| |
| fbar, Control | |$0.08_{-0.02}^{+0.04}$| | |$0.11_{-0.02}^{+0.02}$| | |$0.07_{-0.03}^{+0.08}$| |
| |$\overline{p}_{\rm bar,\ AGN}$| | 0.23 ± 0.04 | 0.23 ± 0.03 | 0.12 ± 0.03 |
| |$\overline{p}_{\rm bar,\ Control}$| | 0.20 ± 0.02 | 0.20 ± 0.01 | 0.18 ± 0.04 |
aAccording to Cameron (2011), when fbar = 0, one can adopt the median of the beta distribution likelihood function as one's best guess for the true fbar.
Sample statistics. The first row represents the total number of galaxies at 0.2 < z < 1.0 with secure spectroscopic zs and HST/ACS imaging in our sample, and the second row represents the number of face-on disc galaxies that are in the previous row. The rest of the table shows the median counts from the 100 AGN control samples (see Section 3.3), and the resulting bar fraction, fbar, and average bar likelihood, |$\overline{p}_{\rm bar}$|.
| . | AEGIS . | COSMOS . | GOODS-S . |
|---|---|---|---|
| 0.2 < z < 1.0 | 3958 | 6673 | 1023 |
| Face-on disc | 1227 | 2244 | 260 |
| AGN | 25 | 86 | 9 |
| Control | 75 | 258 | 27 |
| Barred AGN | 2 | 12 | 0 |
| Barred control | 6 | 28 | 2 |
| fbar,AGN | |$0.08_{-0.03}^{+0.09}$| | |$0.14_{-0.03}^{+0.05}$| | |$0.07_{-0.05}^{+0.10a}$| |
| fbar, Control | |$0.08_{-0.02}^{+0.04}$| | |$0.11_{-0.02}^{+0.02}$| | |$0.07_{-0.03}^{+0.08}$| |
| |$\overline{p}_{\rm bar,\ AGN}$| | 0.23 ± 0.04 | 0.23 ± 0.03 | 0.12 ± 0.03 |
| |$\overline{p}_{\rm bar,\ Control}$| | 0.20 ± 0.02 | 0.20 ± 0.01 | 0.18 ± 0.04 |
| . | AEGIS . | COSMOS . | GOODS-S . |
|---|---|---|---|
| 0.2 < z < 1.0 | 3958 | 6673 | 1023 |
| Face-on disc | 1227 | 2244 | 260 |
| AGN | 25 | 86 | 9 |
| Control | 75 | 258 | 27 |
| Barred AGN | 2 | 12 | 0 |
| Barred control | 6 | 28 | 2 |
| fbar,AGN | |$0.08_{-0.03}^{+0.09}$| | |$0.14_{-0.03}^{+0.05}$| | |$0.07_{-0.05}^{+0.10a}$| |
| fbar, Control | |$0.08_{-0.02}^{+0.04}$| | |$0.11_{-0.02}^{+0.02}$| | |$0.07_{-0.03}^{+0.08}$| |
| |$\overline{p}_{\rm bar,\ AGN}$| | 0.23 ± 0.04 | 0.23 ± 0.03 | 0.12 ± 0.03 |
| |$\overline{p}_{\rm bar,\ Control}$| | 0.20 ± 0.02 | 0.20 ± 0.01 | 0.18 ± 0.04 |
aAccording to Cameron (2011), when fbar = 0, one can adopt the median of the beta distribution likelihood function as one's best guess for the true fbar.
3.1 Face-on disc selection
The face-on disc samples for each field are defined by the following criteria:
0.2 < z < 1.0 – to obtain the most accurate X-ray luminosities and to identify broad-line AGN (which may contaminate their host galaxy measurements), we choose only galaxies with secure spectroscopic redshifts. Although the ability to identify a bar is not uniform over this redshift range, our robust matching of AGN and inactive control galaxies ensures that the two samples have the same distributions of completeness for bar detection: see Section 3.4.
b/a > 0.5 – since bars in highly inclined galaxies are difficult to identify, we exclude edge-on galaxies with global axis ratios less than or equal to 0.5.
re > 8 pixels – selecting galaxies with re larger than 8 pixels, which corresponds to about twice the FWHM of the HST/ACS PSF, ensures that any bars with semimajor axes ≳ 3 kpc will be identified. Since the typical bar lengths in the local universe are 2–7 kpc (Erwin 2005; Gadotti 2011; Hoyle et al. 2011), we should be able to detect most large-scale barred galaxies, assuming bars at z > 0 are similar to bars at z ∼ 0.
NBar question/NTotal ≥ 0.15 – in order to answer the bar question, the GZH decision tree requires a volunteer to classify a galaxy as displaying some kind of feature or disc. Thus demanding that at least 15 per cent of a galaxy's classifiers answer the bar question results in an effective selection for disc galaxies. Although the number of AGN is sensitive to the exact NBar question/NTotal threshold, our qualitative conclusions are not, e.g. requiring NBar question/NTotal ≥ 0.75 does not change our ultimate conclusion. Moreover, the majority of our NBar question/NTotal ≥ 0.15 sample has more than 10 bar classifications, which is more than most visual bar classifications (e.g. Nair & Abraham 2010b; Lee et al. 2012a).
pmerge < 0.65 – in order to separate out the effects of mergers from our analysis, we choose non-interacting galaxies by requiring a merging likelihood (pmerge) less than 0.65. This criterion mirrors that of Melvin et al. (2014) and eliminates a small fraction of our sample. Discarding this criterion does not affect our conclusion.
3.2 AGN selection
Out of these face-on disc samples (one from each survey), we select AGN hosts with X-ray luminosities 1042 erg s− 1 < LX < 1044 erg s− 1. The lower limit removes starburst galaxies with weak X-ray emission (Bauer et al. 2002), and the upper limit excludes qua-sars that may have optical point sources which would contaminate the measurements of their host galaxies (Silverman et al. 2008a).
We also discard luminous unobscured AGN which might also contaminate the visible appearance of their host galaxy measurements. In AEGIS and COSMOS, we use broad emission lines to identify such AGN since they dominate the optical spectra of their host galaxies. There are zero broad-line AGN in AEGIS and five broad-line AGN in COSMOS, which we reject from our sample. GOODS-S lacks a public catalogue of broad-line AGN, and so we instead use low X-ray hardness (HR < −0.3; Mainieri et al. 2007) as a proxy for unobscured AGN: this results in the rejection of one AGN. The rejection or inclusion of these six potential-contaminant AGN does not affect our qualitative conclusions.
Table 2 lists the final AGN count for each survey.
3.3 Control selection
For each AGN host galaxy, we select three unique, non-AGN control galaxies from the same survey (AEGIS, COSMOS, or GOODS-S) that are matched in M*, U − B,4n, re, and z. These parameters have been shown to correlate with both AGN presence and bar presence (e.g. Kauffmann et al. 2003; Nandra et al. 2007; Schawinski et al. 2009; Masters et al. 2011; Cheung et al. 2013) and thus must be controlled for in order to uncover any underlying bar–AGN connection.
For a given AGN host galaxy, we first select a pool of control galaxies satisfying the following conditions:
|log M*, AGN/M*| < 0.35
|(U − B)AGN − (U − B)| < 0.4
|log re, AGN/r| < 0.48
|nAGN − n| < 2.0
|zAGN − z| < 0.4.
These limits are tuned in order to find enough control galaxies for each AGN. Our conclusions are not sensitive to the exact limits, e.g. reducing these limits by 50 per cent does not change the conclusions.
With this initial pool of control galaxies, we perform a five-stage matching process that iteratively reduces the pool until it reaches a final set of three unique and matched control galaxies. The first stage cuts the initial pool of control galaxies to the 15 closest matched galaxies in one of the matching parameters, i.e. M*, AGN, U − BAGN, (see footnote 4) nAGN, re, AGN, or zAGN. Each successive stage matches the remaining control galaxies to one of the unused matching parameters and eliminates the three worst matched galaxies. Thus the second stage reduces the pool to 12, the third stage reduces the pool to 9, the fourth reduces the pool to 6, and finally, the fifth stage reduces the pool to 3. Ultimately, for each survey we have a control sample that contains no duplicates and is three times larger than the AGN sample (see Table 2).
This five-stage matching process was performed for each AGN host in our sample. However, there were four AGN – one from AEGIS, one from COSMOS, and two from GOODS-S – that were discarded due to a lack of control galaxies for the AGN host. These host galaxies have abnormally high n for their rest-frame colours and/or M* compared to the pool of control galaxies.
The AGN and control samples that this matching technique produces are affected by the order in which we match the AGN hosts to the control galaxies and the order in which the matching parameters are used. In order to adequately sample the parameter space, we repeat this five-stage matching technique 100 times for each survey, with each iteration randomly shuffling the order of the AGN hosts, the order of the control galaxies, and the order of the matching parameters. Ultimately, we generate 100 AGN samples and 100 control samples for each survey. For brevity and clarity, we define an ‘AGN-control sample’ to be all AGN hosts and their corresponding control galaxies for a given survey and for a given matching iteration. We use the median counts and the resulting fbar and |$\overline{p}_{\rm bar}$| of the 100 AGN control samples in presenting our results (see Table 2).
To demonstrate the quality of our matching procedure, Fig. 1 presents stacked histograms of the distribution of parameter differences between the AGN hosts and their matched control galaxies. Each panel stacks 100 translucent histograms, with each histogram representing one AGN control sample. To elaborate, each histogram represents the difference in a parameter between each AGN and its three control galaxies for a given realization. The highly shaded regions represent the most populated parameter space, which are generally centred around 0 with small spreads, as supported by the mean and standard deviation at the upper left of each panel, indicating that our matching technique works well. Moreover, we also calculated the two-sample Kolmogorov–Smirnov (KS) null probability for each pair of AGN control parameter distributions, where small values indicate that the two distributions in question are probably not from the same underlying distribution. We display the median KS null probability, PKS, of all 100 pairs of AGN control distributions in each panel, most of which show high values, indicating that the AGN and control samples are consistent.

Normalized histograms of differences in matching parameters of the AGN and control samples. From top to bottom, the parameters are: stellar mass (M*), rest-frame colour (U − B or U − V), effective radius (re), global Sérsic index (n), and spectroscopic redshift (z). Each panel overlays 100 histograms, one for each AGN control sample realization; the mean (μ), standard deviation (σ), and the KS null probability (PKS) is displayed in the upper left of each panel. The shading reveals the amount of overlap. Most of the histograms peak around zero, implying that the AGN and control galaxies are generally well matched. The histograms of GOODS-S are slightly broader and more skewed than those of AEGIS and COSMOS, which is due to the relatively small sample size of GOODS-S.
However, it is clear that the histograms of GOODS-S are slightly broader and more skewed than those of AEGIS and COSMOS, especially in Sérsic index and redshift, as supported by PKS. The relatively small sample size of GOODS-S (see Table 2) makes it difficult to identify well-matched control galaxies for the GOODS-S AGN hosts. However, Section 4 shows that the results from the GOODS-S sample are consistent with those of AEGIS and COSMOS, indicating that the skewness of the GOODS-S AGN control samples does not bias our analysis.
To further illustrate the quality of our matching technique, we show images of two matched sets of AGN control galaxies from each survey in Fig. 2. Each set of AGN control galaxies is reassuringly similar in appearance, confirming that our matching technique is reasonable.

HST/ACS images of two matched sets of AGN control galaxies for AEGIS (left), COSMOS (middle), and GOODS-S (right). Each AGN (upper-left image of each block) has three matched, non-AGN control galaxies. Galaxies with pbar > 0.5 are considered barred. Galaxies within each AGN control set are similar in appearance, demonstrating the quality of our matching technique. Images are from Griffith et al. (2012).
The X-ray luminosity–redshift distribution of all X-ray sources in our chosen redshift range, i.e. from the first row of Table 2 labelled ‘0.2 < z < 1.0’, is shown in Fig. 3. The dashed horizontal lines define our AGN selection. The black points encircled in green represent the AGN that satisfy our face-on disc criteria, and hence are eligible to undergo our matching process. The red points encircled in green represent the face-on disc AGN that have enough control galaxies, and thus are in our AGN samples. Fig. 3 shows that our AGN samples span most of LX–z space. It also shows that the number of moderate-luminosity AGN increases with z, a well-known behaviour that has been shown by previous works (e.g. Ueda et al. 2003; Silverman et al. 2008b; Aird et al. 2010).
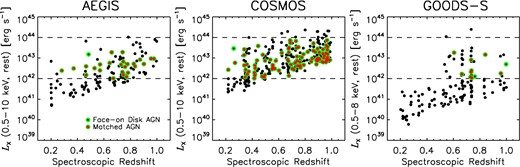
X-ray luminosity versus spectroscopic redshift for all sources detected in the AEGIS (left), COSMOS (middle), and GOODS-S (right) surveys in our chosen redshift range. The dashed horizontal lines represent the lower and upper limits of our AGN selection. Our AGN samples, i.e. the red points encircled in green, span most of LX–z space.
3.4 Redshift effects on bar detection
Although redshift effects (e.g. cosmological surface brightness dimming, angular size change, band shifting) hinder bar detection, our experiment is a relative comparison between two matched samples that controls for redshift and several of the most correlated parameters of bar presence (e.g. stellar mass, colour, and Sérsic index; Nair & Abraham 2010b; Masters et al. 2011; Lee et al. 2012a; Cheung et al. 2013), so our study naturally takes this bias into account. Assuming that there are no AGN-dependent selection effects, our experiment should be robust against any known bar detection biases.
As an additional check, we tested for differential redshift effects by splitting our sample into two redshift intervals, 0.20 < z < 0.84 and 0.84 < z < 1.00, and repeating our analysis. We chose these z intervals because Sheth et al. (2008) argued that the ability to detect bars at z > 0.84 is hampered by the overlap of the HST/ACS I band with the rest-frame near-UV, where clumpy star formation can hide smooth bar structures. However, as pointed out by Melvin et al. (2014), the majority of the light gathered in the HST/ACS I band at 0.84 < z < 1.00 is from the rest-frame optical, and it is only beyond z ∼ 1 that this filter becomes dominated by rest-frame UV where bar detection may be hindered. Therefore we do not expect a reduction in our ability to detect bars above z = 0.84. Repeating our analysis for these two z intervals corroborates our expectations: there is no statistically significant (<3σ) difference in the AGN sample's bar fraction and the control sample's bar fraction at either 0.20 < z < 0.84 or at 0.84 < z < 1.00. Therefore we find no redshift dependence on our results, indicating that our results are not affected by redshift biases.
4 RESULTS
4.1 Do AGN hosts contain an excess of large-scale bars?
The main result of this paper is shown in Fig. 4, which plots the bar fraction, fbar, and the average bar likelihood, |$\overline{p}_{\rm bar}$|, of the AGN and non-AGN control samples for the AEGIS, COSMOS, and GOODS-S surveys. The uncertainties shown for fbar are 68.3 per cent binomial confidence limits, calculated using quantiles of the beta distribution given the bar counts, total sample counts, and desired confidence level5 (Cameron 2011). The uncertainties shown for |$\overline{p}_{\rm bar}$| are calculated as |$\sigma /\sqrt{N}$|, where σ is the standard deviation of pbar, and N is the total number of galaxies.
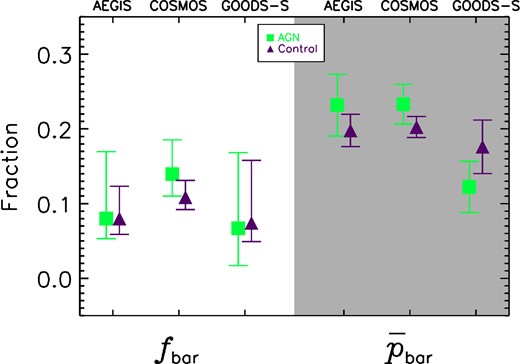
Left: the bar fraction, fbar, of the AGN (green squares) and non-AGN control samples (purple triangles) for the AEGIS, COSMOS, and GOODS-S surveys. Right: the average bar likelihood, |$\overline{p}_{\rm bar}$|, of the AGN and non-AGN control samples for the three surveys. The error bars on fbar and |$\overline{p}_{\rm bar}$| are the 68.3 per cent binomial confidence limits and standard error, respectively. There is no statistically significant difference in fbar or |$\overline{p}_{\rm bar}$| between the AGN and non-AGN control samples across all three surveys, indicating that there is no large excess of bars in AGN hosts.
We find no statistically significant enhancement in fbar or |$\overline{p}_{\rm bar}$| in AGN hosts compared to the non-AGN control galaxies. The probabilities that each survey's fbar, AGN and fbar, Control are different, given the binomial errors, are insignificant (≲1σ). Conducting a two-sample KS test on the pbar distributions of each survey's AGN and control samples reveals that the AGN and control samples are consistent with being drawn from the same parent sample to the 99.9 per cent level.
With our results, we can quantify the level of bar excess in AGN hosts that we can eliminate by combining all three surveys together. Using the combined counts of AGN, controls, barred AGN, and barred controls, we find that the bar fraction of the combined AGN sample cannot be greater than twice the bar fraction of the combined control sample at 99.7 per cent confidence. Therefore, we conclude that there is no large excess of bars in AGN hosts.
4.2 Are large-scale bars efficient fuellers of AGN?
A slightly different, but related question is, ‘Are bars efficient fuellers of AGN?’ We answer this question by studying the AGN fraction of barred and non-barred galaxies, as presented in Fig. 5. From our face-on disc sample (see Section 3.1), we select barred galaxies with the criteria described in Section 2.5.1. We then create a control sample of non-barred galaxies by demanding that pbar < 0.05 and by using our five-stage matching technique that we described in Section 3.3. That is, for each barred galaxy, we find three non-barred galaxies matched in stellar mass, rest-frame colour, size, Sérsic index, and redshift. Using the AGN criteria defined in Section 3.2, Fig. 5 shows that there is no statistically significant excess of AGN among barred galaxies.
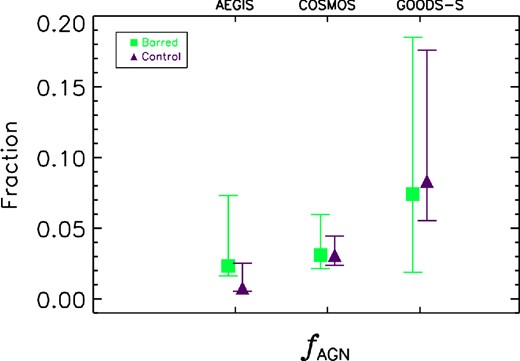
The AGN fraction, fAGN, of the barred (green squares) and non-barred control samples (purple triangles) for the AEGIS, COSMOS, and GOODS-S surveys. The error bars on fAGN are the 68.3 per cent binomial confidence limits. There is no statistically significant difference in fAGN between the barred and non-barred control samples across all three surveys, indicating that there is no statistically significant excess of AGN in barred galaxies.
5 DISCUSSION
At z ∼ 0, several works have previously found no link between bars and AGN (Ho et al. 1997; Mulchaey & Regan 1997; Malkan et al. 1998; Hunt & Malkan 1999; Martini & Pogge 1999; Regan & Mulchaey 1999; Erwin & Sparke 2002; Martini et al. 2003; Lee et al. 2012b; Cisternas et al. 2013, but see Knapen et al. 2000; Laine et al. 2002; Laurikainen et al. 2004; Oh et al. 2012; Alonso et al. 2013; Galloway et al., in preparation), and our results suggest that this absence of direct bar-driven AGN activity persists out to z = 1. Our chosen redshift range corresponds to an epoch where approximately half of the local supermassive black hole mass density was formed (Aird et al. 2010), indicating that bars are not directly responsible for the buildup of at least half of the local supermassive black hole mass density. Moreover, the paucity of bars at z > 1 (Kraljic, Bournaud & Martig 2012; Simmons et al. 2014) indicates that bars were probably not closely associated with AGN at z > 1 either. Therefore, large-scale bars are likely not the primary fuelling mechanism for supermassive black hole growth over cosmic time.
Recently, Cisternas et al. (2014) also searched for a bar–AGN connection using a slightly smaller sample of 95 AGN in COSMOS, with both photometric and spectroscopic redshifts at 0.15 < z < 0.84. Their results are broadly consistent with ours, with neither a significant bar excess among AGN nor an AGN excess among barred galaxies at z > 0.4. However, Cisternas et al. (2014) do suggest a marginal excess of bars among AGN (compared to non-AGN) at z ∼ 0.3, which we do not detect in our results. This difference is likely due to slight differences in bar identification,6 or due to the differences in our matching of AGN and inactive galaxies: our samples are matched in five parameters, while Cisternas et al. (2014) matched AGN and inactive galaxies in stellar mass and redshift only. However, these are only small differences, and the results of Cisternas et al. (2014) are consistent with our conclusion that bars do not dominate AGN fuelling at z ≲ 1.
However, before ruling out bars as the primary fuelling mechanism for supermassive black hole growth, one must ask if the bar–AGN connection can be concealed if a bar dissolves while a black hole is still accreting the bar-funnelled gas. In the present analysis, we are assuming that the bar instantaneously funnels gas to the central black hole upon its formation, and moreover, that there is no delay in AGN activity.
The typical lifetimes of AGN and bars are uncertain. For AGN, the current estimates range from 106 to 108 yr (Haehnelt & Rees 1993; Martini 2004, see Hanny's Voorwerp in Keel et al. 2012 for an example of an AGN with a short lifetime). For bars, early simulations of isolated disc galaxies by Bournaud & Combes (2002) indicate that they are short-lived, with a lifetime of 1–2× 109 yr. The latest simulations of isolated disc galaxies by Athanassoula, Machado & Rodionov (2013), however, indicate that bars are long-lived, with a lifetime as long as 1010 yr. This latter result is supported by recent zoom-in cosmological simulations by Kraljic et al. (2012), who show that bars formed at z ≈ 1 generally persist down to z = 0. Despite the uncertainty in both AGN and bar lifetimes, even the shortest bar lifetime is an order of magnitude larger than the longest AGN lifetime, meaning that the bar–AGN connection is not likely to be concealed by short bar lifetimes.
Small-scale, nuclear bars may also fuel supermassive black hole growth. Unfortunately, we are unable to resolve such small structures in our images. However, work in the local universe shows that nuclear bars are not more frequent in AGN hosts compared to non-AGN hosts (Mulchaey & Regan 1997; Martini & Pogge 1999; Regan & Mulchaey 1999; Erwin & Sparke 2002; Laine et al. 2002). This result mirrors that of large-scale bars, suggesting that nuclear bars do not fuel supermassive black hole growth at z ∼ 0 either. Whether nuclear bars can fuel AGN at z > 0 will be left for future work.
Interestingly, studies of the relative angle between AGN accretion discs and host galaxy discs are consistent with our interpretation that bars do not fuel AGN. If AGN accretion discs are fuelled by bar-funnelled gas, then one would expect this gas to have an angular momentum vector that is parallel to the bulk of the gaseous disc of the galaxy. However, it appears that the accretion discs are randomly orientated with respect to their host galaxies (Ulvestad & Wilson 1984; Kinney et al. 2000; Schmitt et al. 2002, 2003; Greenhill et al. 2009), which fits with our interpretation that bars do not directly fuel AGN.
This misalignment could be interpreted even more generally – there simply may not be a galactic-scale black hole fuelling mechanism. Instead, a collection of processes, including minor mergers (e.g. Kaviraj 2014a,b), cooling flows (e.g. Best et al. 2007), and multibody interactions with star clusters or clouds (e.g. Genzel, Hollenbach & Townes 1994), may work to transport gas into the vicinity of the black hole. This process, known as ‘stochastic fuelling’ (Sanders 1984), has been implemented in models that successfully reproduce observations of low- to intermediate-luminosity AGN (Hopkins & Hernquist 2006; Hopkins et al. 2014).
6 CONCLUSIONS
In this paper, we present a new study on the bar–AGN connection beyond the local universe. We combine Chandra and GZH data in the AEGIS, COSMOS, and GOODS-S surveys to determine whether AGN are preferentially fed by large-scale bars at 0.2 < z < 1.0.
Using GZH classifications and galaxy structural measurements, we select non-merging, face-on disc galaxies that have sizes large enough to accurately identify large-scale bars. From this face-on disc sample, we identify AGN with X-ray luminosities 1042 erg s− 1 < LX < 1044 erg s− 1. We then use a novel multiparameter technique to construct control samples of non-AGN galaxies robustly matched to the AGN hosts in stellar mass, rest-frame colour, Sérsic index, effective radius, and redshift. With these samples, we find no statistically significant excess of barred galaxies in AGN hosts (and no excess of AGN in barred galaxies). Specifically, we find that the bar fraction of the AGN sample cannot be greater than twice the bar fraction of the control sample at 99.7 per cent confidence. The simplest interpretation is that AGN are not preferentially nor directly fed via large-scale bars at 0.2 < z < 1.0.
Authors from UC Santa Cruz acknowledge financial support from the NSF Grant AST 08-08133. KS gratefully acknowledges support from Swiss National Science Foundation Grant PP00P2_138979/1. JRT acknowledges support by NASA through Hubble Fellowship grant HST-HF-51330.01 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS 5-26555. EA and AB acknowledge financial support to the DAGAL network from the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme FP7/2007-2013/ under REA grant agreement number PITN-GA-2011-289313. They also acknowledge financial support from the CNES (Centre National d'Etudes Spatiales – France). RCN acknowledges STFC Rolling Grant ST/I001204/1 ‘Survey Cosmology and Astrophysics’. BS gratefully acknowledges support from the Oxford Martin School and from the Henry Skynner Junior Research Fellowship at Balliol College, Oxford. LFF and KWW acknowledge support from the UMN GIA programme.
EC thanks Ramin A. Skibba, Michael Williams, Sugata Kaviraj, Yicheng Guo, Hassen Yesuf, and Guillermo Barro for useful discussions. The JavaScript Cosmology Calculator (Wright 2006) and topcat (Taylor 2005) were used in the preparation of this paper. We also thank the anonymous referee for a helpful report.
This publication has been made possible by the participation of more than 85,000 volunteers in the Galaxy Zoo project. Their contributions are individually acknowledged at http://authors.galaxyzoo.org/
Unless otherwise stated, we use ‘bars’ to refer to large-scale structures in isolated systems, i.e. we do not consider bars created through interactions. These large-scale bars are commonly referred to as primary bars while small-scale (less than, or of the order of 1 kpc) bars are commonly referred to as secondary bars.
The complete decision tree is available at http://data.galaxyzoo.org
The exclusion of this criterion does not significantly affect the measured bar fractions, nor does it change our conclusions.
U − V for COSMOS
For small samples, one can refer to the reference tables in Cameron (2011).
The discrepancy in GZH bar fractions and those used by Cisternas et al. (2014, which are similar to those of Sheth et al. 2008), has been explored in Melvin et al. (2014); the most likely reason for this difference is that our pbar threshold of 0.5 tends to identify strong bars, meaning that our work concerns mainly strong bars. The bar fractions used by Cisternas et al. (2014) are consistent with the total bar fractions of Sheth et al. (2008), meaning that their work concerns both strong and weak bars.



