Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

We propose a new fast method for estimation of the impact probability of near-Earth objects (NEOs), based on the assumption that the errors in coordinates and velocities have a normal distribution at all times. In this method, a unique coordinate system associated with the nominal orbit of an asteroid is used. One of the coordinates of this system is the mean anomaly in the osculating orbit of an asteroid. This system allows one to take into account the distribution of virtual asteroids mainly along the nominal asteroid orbit. The probability is calculated as a six-dimensional integral of the probability density functions of coordinates and velocity errors. This method has a limitation on usage due to this assumption. Close approaches to massive bodies can break the normal distribution of virtual asteroids and disturb the impact probability value. The impact probabilities for eight asteroids have been calculated by the proposed method. A comparison of these values with probabilities obtained by the Monte Carlo method shows good agreement for seven of them. For 2007 VK184, which has three close approaches to major planets, the impact probability obtained by the new method differs by about five times, but the proposed method takes several orders of magnitude fewer computation time than the Monte Carlo one. Also, we have demonstrated the advantage of using a curvilinear coordinate system in comparison with a Cartesian one.

methods: numerical, celestial mechanics, minor planets, asteroids: general

1 INTRODUCTION

The problem of estimating the impact probability of an asteroid with the Earth at time t and times in its vicinity can be separated into two subproblems. The first one consists of determining the nominal orbit, which is described by six orbital parameters, and finding the distribution function of their errors. The area of parameter errors can be described by a ‘cloud’ of virtual asteroids (VAs). This cloud surrounds the position of an asteroid in the nominal orbit and the cloud size and density are determined by a function of the distribution of parameter errors. The second problem is to determine the positions of VAs at time t and to estimate their impact possibilities with the Earth.

The easiest and most theoretically based method to estimate the probability is the Monte Carlo method. In this method, a great number of numerical experiments are carried out and the probability of an event is determined as the ratio of the number of simulations in which the event happened to the number of all samples. In our case, we choose objects from the cloud of VAs at a particular epoch and propagate their orbits until a time a little greater than t, i.e. till the time at which all chosen VAs cross the nearest point in their trajectory to the Earth. This easy and theoretically based method has an essential drawback: the number of VAs chosen must be large enough to produce sufficient accuracy in the probability estimation, which leads to a time-consuming method. The estimation of the number of VAs, m, the orbits of which it is necessary to propagate, is determined as
\begin{equation*} m = \frac{P_{\rm MC}(1-P_{\rm MC})}{\sigma _{\rm MC}^2}, \end{equation*}
where σMC is the error in probability PMC. Thus, in order to calculate an impact probability 10−6 with 50 per cent accuracy, it is necessary to propagate 4 × 106 VA orbits. Also, we should emphasize that the addition of even one new observation changes the nominal orbit and the distribution function of VAs and we have to start the estimation of probability from the beginning. Thus, the Monte Carlo method can be impractical for low impact probabilities.

A more efficient method is the method called line-of-variation sampling (Milani et al. 2002). In this method, instead of a six-dimensional cloud of VAs, we consider a one-dimensional region that is hopefully representative of the entire six-dimensional one. For this purpose, we can use the line of variations (LOV), which is the line of weakness of the orbit determination solution. This line is defined by the eigendirection associated with the largest eigenvalue of the correlation matrix. In order to find this eigendirection, the singular decomposition of the correlation matrix can be used. Choosing VAs along the LOV, we determine a region of VAs that will collide with the Earth. Even though interpolation along the LOV is generally more efficient than the Monte Carlo method, we cannot be confident that the LOV approach will detect all potential collisions (Milani et al. 2002). Also, it requires one to perform simulations too, but not as many as in the Monte Carlo method. In Milani et al. (2005a), one can see the theory for generating the LOV and Milani et al. (2005b) include techniques for nonlinear impact hazard assessment.

Nowadays, a great number of near-Earth objects (NEOs) are discovered and the amount of asteroids discovered per month increases. We need to be able to estimate their impact probabilities quickly.

In this work, we propose a new high-speed method based on the assumption that the parameter errors of an asteroid's orbit have a normal distribution at all times. Methods based on this assumption are generally called linear methods of impact probability estimation. This assumption leads to limitations in using these methods. Gravitational perturbations from massive bodies, which significantly change the orbit of an object, can break the normal distribution of parameter errors of an asteroid's orbit and hence distort the impact probability value. Also, since the distribution of VAs is mainly along the nominal orbit (if the possible collision time is far from the last observation), the normal distribution law of VAs in Cartesian coordinates does not imply a real one. Consequently, linear methods, which use a Cartesian coordinate system (e.g. the target-plane method: Milani et al. 2002), have an added limitation in their usage. In this work, we try to eliminate the last limitation. In order to do this, we introduce a special curvilinear coordinate system that allows us to take into account the distribution of VAs mainly along the nominal orbit at time t, even if t is far from the last observation. Also, a comparison between using Cartesian and introduced coordinate systems is given in this work.

2 THE GENERAL IDEA

Let us consider a set of observations that allows us to determine six parameters of the orbit of an asteroid. We assume that the parameter errors have a normal distribution at all times. Hence the impact probability at time t equals the six-dimensional integral
(1)
where |$\boldsymbol {{x}}=(x_1,\ldots ,x_6)$| is a six-dimensional vector of deviations of the orbital parameters from the nominal values, |${\bf N}$| is a normal matrix (inverse of the covariance matrix), calculated at time t, |$\det {{\bf N}}$| is the determinant of the matrix |${\bf N}$|⁠, T denotes the matrix transpose operation and Θ is a six-dimensional volume of the Earth in these orbital parameters.

It is convenient to use coordinates and velocities as orbital parameters to define Θ. In this case, in the space of velocities, Θ is (−∞, +∞) × (−∞, +∞) × (−∞, +∞). Consequently, the six-dimensional integral can be integrated analytically over the velocity components. Let (x4, x5, x6) denote the velocity components. Consider integrating (1) over the component x6.

Let nij be an element of matrix |${\bf N}$| in the ith row and jth column, m6 = n16x1 + n26x2 + ⋅⋅⋅ + n56x5. Then the integral over component x6 is
\begin{equation*} S_6= \int \nolimits _{-\infty }^{+\infty } {\rm e}^{-({1}/{2}) n_{66} x_6^2-m_6 x_6 } \,{\rm d}x_6. \end{equation*}
Introduce a new variable |$y_6=\sqrt{n_{66}} x_6$|⁠. Then
\begin{eqnarray*} S_6&=& \frac{1}{\sqrt{n_{66}}} {\rm e}^{{m_6^2}/({2n_{66}})} \int \nolimits _{-\infty }^{+\infty } {\rm e}^{-\left(\frac{y_6}{\sqrt{2}} + \frac{m_6}{\sqrt{2n_{66}}}\right)^2 } \,{\rm d}y_6 \\ &=& \frac{\sqrt{2\pi }}{\sqrt{n_{66}}} {\rm e}^{{m_6^2}/({2n_{66}})}. \end{eqnarray*}
Consequently, after integrating over x6, the normal distribution remains and the components of the matrix are changed according to the rule
\begin{equation*} n_{jk} \rightarrow n_{jk} - \frac{n_{j6} n_{k6}}{n_{66}}. \end{equation*}
Also, the constant factor is multiplied by |$({\sqrt{2\pi }})/({\sqrt{n_{66}}})$|⁠. The integrals over x5 and x4 are calculated similarly. After these operations, we have a three-dimensional integral that can be calculated numerically. It is supposed that the Earth has a sphere form in Cartesian coordinates. To take into account the gravitational attraction of the Earth, the radius of the Earth is increased by |$\sqrt{1 + {v_{\rm s}^2}/{v_{\infty }^2} }$|⁠, where vs is the escape velocity and v∞ is a small body's velocity at infinity in the Earth–asteroid two-body problem.

3 NEW COORDINATE SYSTEM

If the time at which it is necessary to estimate the probability of collision differs by some revolution periods of a small body around the Sun from the time of the last observation, the area of possible positions of VAs is noticeably stretched along the nominal orbit, due to distinctions in the mean motions of VAs. Eventually the difference in the travelled path of VAs can reach an entire revolution, although variations of their positions in the plane perpendicular to the orbit can remain small. It is difficult to take this fact into account using a normal distribution in Cartesian coordinates.

We propose using a curvilinear frame (ξ, η, M) related to the nominal orbit. To construct this system, we do the following. First of all, we fix the osculating ellipse of a small body at time t (i.e. the five parameters of the osculating ellipse). The mean anomaly M in the osculating orbit is one of the coordinates of this system. The origin of the linear coordinates ξ, η is the point on the ellipse corresponding to M.

The ξ-axis is perpendicular to the plane of the fixed ellipse:
\begin{equation*} \boldsymbol {e_{\xi }} = (\sin i \cdot \sin \Omega , -\sin i \cdot \cos \Omega , \cos i), \end{equation*}
where i is the orbit inclination and Ω the longitude of the ascending node.

The axis η lies in the plane of the fixed ellipse. Let A be a point, the ξ, η, M coordinates of which are determined, and B be the projection of point A on to the plane of the fixed ellipse. The η-axis contains point B. This system is required to be orthogonal (i.e. the vectors |$\boldsymbol {e_{\xi }}, \boldsymbol {e_{\eta }}, \boldsymbol {e_M}$| must be mutually orthogonal vectors). This system is schematically illustrated in Fig. 1.

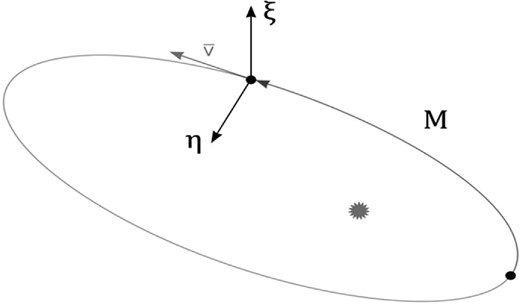
The (ξ, η, M) coordinate system.
Figure 1.

The (ξ, η, M) coordinate system.

Open in new tabDownload slide
Let us consider in detail how to find the coordinates ξ, η, M of any point in space if we know its Cartesian coordinates. First of all, we project this point on to the plane of the fixed ellipse. Coordinate ξ is the distance between the point and its projection on to this plane. Consider the condition |$\boldsymbol {e_{\eta }} \bot \boldsymbol {e_M}$| in Cartesian coordinates in the plane of the fixed ellipse, with the origin in the centre of the ellipse. Let (x0, y0) be the coordinates of the point projection, (x1, y1) be the coordinates of the point on the ellipse corresponding to M, E be an eccentric anomaly and a be a semi-major axis of the ellipse. Then
\begin{equation*} \begin{array}{l}\left\lbrace \begin{array}{l}x_1= a \cos E, \\ y_1= a \sqrt{1-{\rm e}^2} \sin E, \\ \end{array} \right. \\ \boldsymbol {e_M} = (-\sin M, \cos M). \end{array} \end{equation*}
Consequently, the condition |$\boldsymbol {e_{\eta }} \bot \boldsymbol {e_M}$| is
(2)

Note that at M = 0 and M = π the left-hand side of the above equation has different signs, hence in both regions [0, π) and [π, 2π) there is at least one root. We choose the root (M) that corresponds to the closest point to (x0, y0).

4 CALCULATING AN IMPACT PROBABILITY

In order to calculate the integral (1) using |$(\xi , \eta , M, \dot{\xi },\dot{\eta },\dot{M})$| as orbital parameters, we have to define the normal matrix |${\bf N}$|ξη M in these coordinates. The six-dimensional vector of Cartesian coordinates and velocities of the asteroid |$\boldsymbol {X_0}$| and the normal matrix |${{\bf N}_{xyz}^0}$| are calculated at epoch t0 using the positional observations. From t0 to t, we integrate the equations of asteroid motion numerically, taking perturbations into account, and obtain the matrix of isochronal derivatives |$ {\boldsymbol\Phi }(t_0,t)$| of Cartesian coordinates and velocities:
\begin{equation*} {\boldsymbol\Phi }(t_0,t) = \left( \begin{array}{ccc}\frac{{\mathrm{\partial} } x }{{\mathrm{\partial} } x_0} &\quad \cdots &\quad \frac{{\mathrm{\partial} } x }{{\mathrm{\partial} } \dot{z}_0} \\ \vdots &\quad \ddots &\quad \vdots \\ \frac{{\mathrm{\partial} } \dot{z} }{{\mathrm{\partial} } x_0} &\quad \cdots &\quad \frac{{\mathrm{\partial} } \dot{z} }{{\mathrm{\partial} } \dot{z}_0} \\ \end{array} \right). \end{equation*}

The normal matrix in Cartesian coordinates and velocities at time t is defined as |${{\bf N}_{xyz}} = (\mathbf {\boldsymbol\Phi }^{\rm T})^{-1} \cdot {{\bf N}_{xyz}^0} \cdot \mathbf {\boldsymbol\Phi }^{-1}$|⁠. The osculating ellipse is fixed. The asteroid's coordinates and velocities in the introduced coordinate system |$\xi , \eta , M, \dot{\xi },\dot{\eta },\dot{M}$| are computed (⁠|$\xi =\eta =\dot{\xi }=\dot{\eta }=0$|⁠, since the asteroid is in the osculating ellipse).

At time t the transfer matrix is determined as follows:
\begin{equation*} {\bf Q} = \left( \begin{array}{ccc}\frac{{\mathrm{\partial} } \xi }{{\mathrm{\partial} } x} \quad \cdots \quad \frac{{\mathrm{\partial} } \xi }{{\mathrm{\partial} } \dot{z}}\\ \vdots \quad \ddots \quad \vdots \\ \frac{{\mathrm{\partial} } \dot{M} }{{\mathrm{\partial} } x} \quad \cdots \quad \frac{{\mathrm{\partial} } \dot{M} }{{\mathrm{\partial} } \dot{z}} \\ \end{array} \right). \end{equation*}
We computed these derivatives numerically using the general formula
\begin{equation*} \frac{{\rm d}f}{{\rm d}x} = \frac{f(x+\Delta x) - f(x-\Delta x)}{2\Delta x}. \end{equation*}
The normal matrix |${\bf N}$|ξηM is defined as follows:
\begin{equation*} {{\bf N}_{\xi \eta M}} = {\bf Q}^{\rm T} \cdot {{\bf N}_{xyz}} \cdot {\bf Q}. \end{equation*}
Then the integral (1) is integrated analytically over the velocity components |$\dot{\xi },\dot{\eta },\dot{M}$| from −∞ to +∞ (see Section 2). After that, we have a three-dimensional integral, the matrix |${\bf N}$|ξηM becomes a 3 × 3 matrix |${{\bf N}_{\xi \eta M}^{\prime }}$| and the six-dimensional region Θ becomes a three-dimensional one.

Now we have to define the region Θ in the introduced coordinate system. In order to do this, we modify the introduced system so that Θ has a sphere-like shape. Let the coordinates of the Earth's centre in this system be (ξt, ηt, Mt). Then the projection of Θ on to the coordinate M is the interval |$[-\frac{R_\oplus}{V}\dot{M}+M_t,\, \frac{R_\oplus }{V}\dot{M}+M_t]$|⁠, where R⊕ is the Earth's radius and V is the magnitude of the heliocentric velocity of the asteroid at time t.

Consider the coordinate system (ξ, η, M/d), where |$d = {\dot{M}}/{V}$|⁠. In this frame, the projection Θ on to the (ξ, η) plane is a circle with radius R⊕ and the projection Θ on to the coordinate M/d is an interval with semi-length also R⊕. Since the Earth's radius R⊕ ≪ 1au, Θ can be considered as a full sphere in coordinates (ξ, η, M/d). This is a good approximation to estimate an impact probability. In order to find the normal matrix |${\bf N}$|ξη(M/d) in the coordinates (ξ, η, M/d), we need to multiply the elements of the matrix |${{\bf N}_{\xi \eta M}^{\prime }}$| in the third column and the elements in the third row by d (in this case the element in the third column and third row is multiplied by d2).

To decrease the time of numerical calculation of the integral, we use a singular decomposition of the matrix |${{\bf N}_{\xi \eta ({M}/{d})}} = {{\bf U} \cdot {\bf N}^* \cdot {\bf U}^{-1}}$|⁠, where |${\bf N}^{\ast}$| a diagonal 3 × 3 matrix and |${\bf U}$| is an orthogonal matrix. Consider the coordinate system (ξ*, η*, M/d*), which is a product of the orthogonal matrix |${\bf U}$| and (ξ, η, M/d). Since this is an orthogonal transformation, the region Θ remains a full sphere with the same radius in the frame (ξ*, η*, M/d*). This transformation yields the fact that there are no linear correlations between ξ*, η* and M/d*, since |${\bf N}^{\ast}$| is a diagonal matrix. Then Θ is replaced with a cube with semi-side R⊕ (and the same centre). Since there are no correlations and the region Θ is a cube, the three-dimensional integral in coordinates (ξ*, η*, M/d*) becomes a multiplication of three one-dimensional Laplace integrals:
\begin{equation*} \int \nolimits _{-R_\oplus}^{+R_\oplus} {\rm e}^{- ({1}/{2}) ({y^2}/{\sigma ^2})} \,\mathrm{d}y. \end{equation*}

Using singular decomposition allows us to decrease the computation time of the integral by several orders of magnitude.

5 RESULTS

To verify this method, we considered impact probabilities for eight asteroids. We chose these asteroids randomly from the website of the Jet Propulsion Laboratory, NASA,1 but ensuring impact probabilities more than 10−7. Their orbits were calculated by a method based on an exhaustive search for orbital planes (Bondarenko, Vavilov & Medvedev 2014). The normal matrix at the initial epoch was computed by a differential method. In Table 1, the characteristics of asteroid orbits are represented. The selected asteroids have different values of orbital inclinations 0.9 < i < 25.1 and a wide range of eccentricities 0.16 < e < 0.74.

Table 1.
Open in new tab

Characteristics of asteroid orbits.

Objecta (au)ei (°)σ (′′)ΔT (d)k
2006 QV891.200.231.10.4410.8368
2007 VK1841.730.571.20.3960.01102
2008 CK701.110.466.00.444.6677
2009 JF11.870.746.00.551.2325
2008 JL32.160.540.90.404.1031
2005 BS11.970.572.60.573.1325
2005 QK761.400.5222.90.651.6814
2007 KO41.100.1625.10.493.0014
Objecta (au)ei (°)σ (′′)ΔT (d)k
2006 QV891.200.231.10.4410.8368
2007 VK1841.730.571.20.3960.01102
2008 CK701.110.466.00.444.6677
2009 JF11.870.746.00.551.2325
2008 JL32.160.540.90.404.1031
2005 BS11.970.572.60.573.1325
2005 QK761.400.5222.90.651.6814
2007 KO41.100.1625.10.493.0014

Notes: ‘Object’ is the asteroid designation, a the semi-major axis, e eccentricity, i orbital inclination, σ the root-mean-square error of observations, k the number of observations and ΔT the arc of observations.

Table 1.
Open in new tab

Characteristics of asteroid orbits.

Objecta (au)ei (°)σ (′′)ΔT (d)k
2006 QV891.200.231.10.4410.8368
2007 VK1841.730.571.20.3960.01102
2008 CK701.110.466.00.444.6677
2009 JF11.870.746.00.551.2325
2008 JL32.160.540.90.404.1031
2005 BS11.970.572.60.573.1325
2005 QK761.400.5222.90.651.6814
2007 KO41.100.1625.10.493.0014
Objecta (au)ei (°)σ (′′)ΔT (d)k
2006 QV891.200.231.10.4410.8368
2007 VK1841.730.571.20.3960.01102
2008 CK701.110.466.00.444.6677
2009 JF11.870.746.00.551.2325
2008 JL32.160.540.90.404.1031
2005 BS11.970.572.60.573.1325
2005 QK761.400.5222.90.651.6814
2007 KO41.100.1625.10.493.0014

Notes: ‘Object’ is the asteroid designation, a the semi-major axis, e eccentricity, i orbital inclination, σ the root-mean-square error of observations, k the number of observations and ΔT the arc of observations.

The impact probabilities for these eight asteroids were calculated by the proposed method in the introduced coordinate system (ξ, η, M). Also, we calculated them using the scheme described above in a Cartesian coordinate system. To check the values obtained, the probabilities were also computed by the Monte Carlo method. The absolute error of probability calculated by the Monte Carlo method is estimated according to |$\sigma _{\rm MC} = ({\sqrt{P_{\rm MC}(1-P_{\rm MC})}})/{\sqrt{m}}$|⁠, where m is the number of realizations, PMC the probability and relative error δMC = σMC/PMC. Results of calculations are given in Table 2, where ‘object’ is the asteroid designation, PξηM and Pxyz are the probabilities calculated by the proposed method in the coordinate system (ξ, η, M) and in a Cartesian coordinate system, respectively, and t is the time at which the impact probability calculated by this method reaches its maximum value. To find t, we calculated impact probabilities at different times in the vicinity of some initial approximation of t. As initial approximation, we took the time when the distance between the Earth and the nominal asteroid orbit is minimum. We calculate this time using the program of Baluyev for determining Minimum Orbital Intersection Distance (Kholshevnikov & Vasiliev 1999; Baluyev & Kholshevnikov 2005).

Table 2.
Open in new tab

Comparison of different methods of estimation of impact probabilities.

Objectt (d)PxyzPξηMPMC3δMC (per cent)ΔPxyz (per cent)ΔPξηM (per cent)COP
2006 QV892019 Sep 09.382.5 × 10−32.2 × 10−31.8 × 10−3639234.7 × 10−3
2007 VK1842048 Jun 03.092.9 × 10−53.0 × 10−56.2 × 10−6323643872.8 × 10−3
2008 CK702030 Feb 14.676.7 × 10−46.4 × 10−46.4 × 10−415406.7 × 10−4
2009 JF12022 May 06.346.7 × 10−46.6 × 10−47.4 × 10−416−10−126.6 × 10−4
2008 JL32027 May 01.414.7 × 10−44.7 × 10−43.0 × 10−41559584.7 × 10−4
2005 BS12016 Jan 14.4401.5 × 10−41.4 × 10−416−10021.6 × 10−4
2005 QK762030 Feb 26.3203.8 × 10−54.3 × 10−520−100−124.1 × 10−5
2007 KO42015 Nov 23.2004.0 × 10−77.3 × 10−754−100−462.5 × 10−6
Objectt (d)PxyzPξηMPMC3δMC (per cent)ΔPxyz (per cent)ΔPξηM (per cent)COP
2006 QV892019 Sep 09.382.5 × 10−32.2 × 10−31.8 × 10−3639234.7 × 10−3
2007 VK1842048 Jun 03.092.9 × 10−53.0 × 10−56.2 × 10−6323643872.8 × 10−3
2008 CK702030 Feb 14.676.7 × 10−46.4 × 10−46.4 × 10−415406.7 × 10−4
2009 JF12022 May 06.346.7 × 10−46.6 × 10−47.4 × 10−416−10−126.6 × 10−4
2008 JL32027 May 01.414.7 × 10−44.7 × 10−43.0 × 10−41559584.7 × 10−4
2005 BS12016 Jan 14.4401.5 × 10−41.4 × 10−416−10021.6 × 10−4
2005 QK762030 Feb 26.3203.8 × 10−54.3 × 10−520−100−124.1 × 10−5
2007 KO42015 Nov 23.2004.0 × 10−77.3 × 10−754−100−462.5 × 10−6
Table 2.
Open in new tab

Comparison of different methods of estimation of impact probabilities.

Objectt (d)PxyzPξηMPMC3δMC (per cent)ΔPxyz (per cent)ΔPξηM (per cent)COP
2006 QV892019 Sep 09.382.5 × 10−32.2 × 10−31.8 × 10−3639234.7 × 10−3
2007 VK1842048 Jun 03.092.9 × 10−53.0 × 10−56.2 × 10−6323643872.8 × 10−3
2008 CK702030 Feb 14.676.7 × 10−46.4 × 10−46.4 × 10−415406.7 × 10−4
2009 JF12022 May 06.346.7 × 10−46.6 × 10−47.4 × 10−416−10−126.6 × 10−4
2008 JL32027 May 01.414.7 × 10−44.7 × 10−43.0 × 10−41559584.7 × 10−4
2005 BS12016 Jan 14.4401.5 × 10−41.4 × 10−416−10021.6 × 10−4
2005 QK762030 Feb 26.3203.8 × 10−54.3 × 10−520−100−124.1 × 10−5
2007 KO42015 Nov 23.2004.0 × 10−77.3 × 10−754−100−462.5 × 10−6
Objectt (d)PxyzPξηMPMC3δMC (per cent)ΔPxyz (per cent)ΔPξηM (per cent)COP
2006 QV892019 Sep 09.382.5 × 10−32.2 × 10−31.8 × 10−3639234.7 × 10−3
2007 VK1842048 Jun 03.092.9 × 10−53.0 × 10−56.2 × 10−6323643872.8 × 10−3
2008 CK702030 Feb 14.676.7 × 10−46.4 × 10−46.4 × 10−415406.7 × 10−4
2009 JF12022 May 06.346.7 × 10−46.6 × 10−47.4 × 10−416−10−126.6 × 10−4
2008 JL32027 May 01.414.7 × 10−44.7 × 10−43.0 × 10−41559584.7 × 10−4
2005 BS12016 Jan 14.4401.5 × 10−41.4 × 10−416−10021.6 × 10−4
2005 QK762030 Feb 26.3203.8 × 10−54.3 × 10−520−100−124.1 × 10−5
2007 KO42015 Nov 23.2004.0 × 10−77.3 × 10−754−100−462.5 × 10−6

For illustration of the accuracy of the methods, in Table 2 we present ΔPxyz and ΔPξηM. These values are the relative distinction of Pxyz and PξηM from PMC, respectively, and are given by ΔP = (P − PMC)/PMC. If value ΔP > 0, then the impact probability obtained by the proposed method is ΔP per cent higher than the one calculated by the Monte Carlo method; otherwise, if ΔP < 0, the impact probability obtained by the proposed method is lower.

We also presented in Table 2 a maximum impact probability, which was introduced by Chesley (2006). We propose to call it the Collisional Orbit Probability (COP). This is the impact probability at time t that the asteroid would have if it passed through the centre of the Earth at time t (and has the same distribution of VAs). This value indicates the size of the dispersion ellipsoid. The larger this value, the smaller the size of the dispersion ellipsoid of VAs at time t. The value of COP depends on the method used to calculate it and has the same limitations. If this value is calculated using this method, the coordinates of the Earth's centre are taken to be zero (ξt = ηt = Mt = 0).

The table shows that the probabilities PξηM are close to those obtained by the Monte Carlo method, but the proposed method requires much less time for calculation (e.g. four million times less for 2007 KO4: it takes about 2 s using an Intel Core i7-2600 3.40-GHz processor). Also, the relative errors of the Monte Carlo method (3δMC) are small, i.e. the values PMC are accurate enough. The exception is asteroid 2007 VK184. The PξηM value for this object is 384 per cent higher than PMC (about five times). This is likely due to close approaches to the Earth (in 2014, distance r = 0.177 au), Venus (in 2030, r = 0.064 au) and Mars (in 2036, r = 0.066 au). However, the COP value for this asteroid obtained by the Monte Carlo method equals (2.76 ± 0.13) × 10−3, which coincides with the one obtained by the proposed method (2.77 × 10−3). Therefore the value of COP seems to be more stable.

The impact probabilities of the three asteroids obtained in Cartesian coordinates equal zero (ΔPxyz = −100 per cent). Note that for these asteroids the values of COP are the smallest, i.e. the dispersion ellipsoids of VAs are the largest. Since the extension of the area of VA distribution is mainly along the nominal orbit of an asteroid, then the greater this area the more the VA distribution in Cartesian coordinates differs from the real distribution of VAs. For five asteroids, the value PξηM is close to COP, indicating that the nominal orbit of the asteroid does not differ strongly from one that leads to collision.

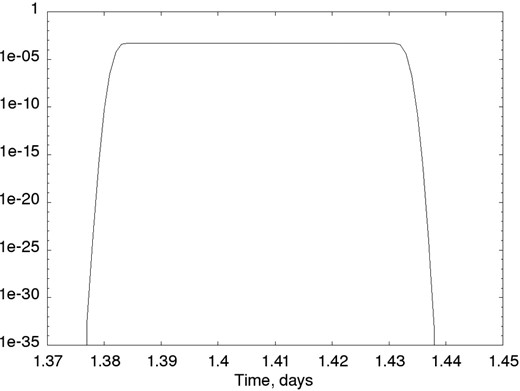
In Fig. 2, the impact probability of the asteroid 2008 JL3 as a function of time (in the vicinity of May 1) is represented. The probability grows immediately from 10−35 to the maximum value 4.7 × 10−4. The region where the probability reaches its maximum value is about 0.06 d (≈90 min). The small size of this time region is a consequence of small errors of ξ and η and a large error of the mean anomaly. Due to this, the maximum value of probability is close to the cumulative one. The behaviour of the impact probability is similar for all asteroids considered.

Impact probability of 2008 JL3 on 2027 May 1.
Figure 2.

Impact probability of 2008 JL3 on 2027 May 1.

Open in new tabDownload slide

6 CONCLUSION

A high-speed method for estimation of the impact probability of asteroids with the Earth has been developed. This method is based on the assumption that errors in the coordinates and velocities of an asteroid have a normal distribution at all times. The important advantage of this method is using the unique coordinate system related to the nominal orbit of an asteroid. This system allows one to take into account the distribution of VAs mainly along the nominal orbit. The mean anomaly M in the osculating orbit of the asteroid is one of the coordinates of the system introduced; the other two coordinates ξ, η are linear ones and their origin lies in the osculating orbit. The probability is calculated as a six-dimensional integral of VA distribution function. Also, we proposed a technique that allows us to decrease by several orders of magnitude the time of this integral's computation in the introduced coordinate system.

This method can give inaccurate values of the impact probability in cases when there are close approaches to massive bodies before the potential collision, which can break the normal distribution of asteroid parameter errors. However, it works well enough and quickly if close approaches either are absent or do not have a noticeable effect on the result. It should be emphasized that newly discovered objects generally have a short observation arc and few observations; hence generally they have large errors in their orbit parameters. In this case, at the time of close approach we can estimate the impact probability using the proposed method, yet after this close approach the orbit parameter errors become much larger and therefore the impact probability becomes much smaller, so it can make no sense to calculate it after close approach.

The impact probabilities for eight asteroids have been calculated by the proposed method. Comparison of these values with values obtained by the Monte Carlo method for seven of them shows good agreement. The impact probability for asteroid 2007 VK184 obtained by the proposed method is about five times higher than the one obtained by the Monte Carlo method. This is likely due to close approaches with the Earth, Mars and Venus before the time of potential collision. Also in this work, we illustrated the advantage of using the new system instead of a Cartesian one. To estimate the size of the dispersion ellipsoid of VAs we used an indicator COP (Collisional Orbit Probability), which equals the impact probability at time t that the asteroid would have if it passed through the centre of the Earth at time t. The value of COP depends on the method used to calculate it and has the same limitations. Nevertheless, the value of COP seems to be more stable than the impact probability value. We found a dependence between this indicator COP and those asteroids for which the values of impact probabilities obtained in a Cartesian coordinate system are unsatisfactory.

We are very grateful to S. R. Chelsey for useful advices and helpful comments. This work is supported by the Institute of Applied Astronomy of Russian Academy of Science.

1

http://neo.jpl.nasa.gov/risk/

REFERENCES

Baluyev
R. V.
Kholshevnikov
K. V.
, 
Cel. Mech. Dyn. Astron.
,
2005
, vol.
91
pg.
287
Crossref
Search ADS
 
Bondarenko Yu
. S.
Vavilov
D. E.
Medvedev Yu
. D.
, 
Solar System Research
,
2014
, vol.
48
pg.
212
Crossref
Search ADS
 
Chesley
S.
Daniela
L.
Sylvio Ferraz
M.
Angel
F. Julio
, 
Proc. IAU Symp. 229, Asteroids, Comets, Meteors
,
2006
Cambridge
Cambridge University Press
pg.
215

Google Scholar

OpenURL Placeholder Text

 
Milani
A.
Chesley
S. R.
Chodas
P. W.
Valsecchi
G. B.
Bottke
W. F.
Cellino
A.
Jr
Paolicchi
P.
Binzel
R. P.
, 
Asteroid III, Space Science Series
,
2002
Tucson
Univ. Arizona Press
pg.
55

Google Scholar

OpenURL Placeholder Text

 
Milani
A.
Sansaturio
M. E.
Tommei
G.
Arratia
O.
Chesley
S. R.
, 
A&A
,
2005a
, vol.
431
pg.
729
Crossref
Search ADS
 
Milani
A.
Chesley
S. R.
Sansaturio
M. E.
Tommei
G.
Valsecchi
G. B.
, 
Icarus
,
2005b
, vol.
173
pg.
362
Crossref
Search ADS
 
Kholshevnikov
K. V.
Vasiliev
N. N.
, 
Cel. Mech. Dyn. Astron.
,
1999
, vol.
75
pg.
75
Crossref
Search ADS
 
© 2014 The Authors Published by Oxford University Press on behalf of the Royal Astronomical Society
Issue Section:
Article
Download all slides