Radiation drag in the field of a non-spherical source

Bini, D.; Geralico, A.; Passamonti, A.

doi:10.1093/mnras/stu2082

Abstract

The motion of a test particle in the gravitational field of a non-spherical source endowed with both mass and mass quadrupole moment is investigated when a test radiation field is also present. The background is described by the Erez–Rosen solution, which is a static space–time belonging to the Weyl class of solutions to the vacuum Einstein's field equations, and reduces to the familiar Schwarzschild solution when the quadrupole parameter vanishes. The radiation flux has a fixed but arbitrary (non-zero) angular momentum. The interaction with the radiation field is assumed to be Thomson-like, i.e. the particles absorb and re-emit radiation, thus suffering for a friction-like drag force. Such an additional force is responsible for the Poynting–Robertson effect, which is well established in the framework of Newtonian gravity and has been recently extended to the general theory of relativity. The balance between gravitational attraction, centrifugal force and radiation drag leads to the occurrence of equilibrium circular orbits which are attractors for the surrounding matter for every fixed value of the interaction strength. The presence of the quadrupolar structure of the source introduces a further degree of freedom: there exists a whole family of equilibrium orbits parametrized by the quadrupole parameter, generalizing previous works. This scenario is expected to play a role in the context of accretion matter around compact objects.

acceleration of particles, accretion, accretion discs, gravitation, radiation: dynamics, relativistic processes

1 INTRODUCTION

Most of the compact objects currently investigated and modelled in astrophysics are ‘observable’ because of the presence of some matter or radiation around them (we will often term them as ‘central objects’ below). At the lowest order of approximation, the associated gravitational field can be described by the spherically symmetric Schwarzschild solution, when shape deformation and rotation effects of the source can be neglected, and matter can be considered as a collection of test particles moving along geodesics. However, this is only an idealized situation which is likely not to represent any real astrophysical system. The dynamics of a body orbiting a compact object is indeed strongly influenced by the combined effect of the overall gravitational field, the surrounding matter and in turn the radiation distribution associated with high-energy processes arising thereby. A typical example is represented by a luminous compact object surrounded by orbiting matter, such as accretion discs around a neutron star or a black hole. The most luminous and persistent sources of electromagnetic radiation in the Universe are the active galactic nuclei (AGNs), which are believed to be powered by mass accretion on to black holes. Their emitting range is from 10⁴⁰ erg s⁻¹ (e.g. the nuclei of some nearby galaxies) to more than 10⁴⁷ erg s⁻¹ (distant quasars), which is far beyond the Eddington luminosity (about 10⁴⁴ erg s⁻¹). Therefore, the X-ray variability in AGNs and the disc emission lines might contain imprints of the radiation drag effects.

In a series of papers, we have studied the dynamics of test particles in a given gravitational background while subject to a Thomson-type interaction with a superimposed test radiation field, namely the so called Poynting–Robertson (PR) effect (Poynting 1903; Robertson 1937). We modelled the radiation flux as made of photons emitted all along a common direction from a point-like source, leading to an effective drag force to be added to the gravitational force. More realistic descriptions would take into account the finite size of the radiating source and allow for photons to be emitted in any direction. However, the computation of the radiation force in this case usually requires complicated numerical ray-tracing calculations for null geodesics in the background space–time. The general relativistic stress–energy tensor associated with such a more general scenario was constructed for the first time in the pioneering work of Abramowicz, Ellis & Lanza (1990), who considered the special case of test bodies radially moving in the space–time of a spherically symmetric non-rotating radiation source with finite radius to model jets and solar winds. They studied the radial equilibrium solutions in which the test particle remains at rest under the combined inward gravitational attraction and the outward photon pressure (the ‘Eddington sphere’). The stability of this equilibrium configuration has been recently investigated by Stahl et al. (2012), who have also discussed its implications for Hoyle–Lyttleton accretion on to a luminous star (see also Oh, Park & Kim 2013). Wielgus et al. (2012), Stahl et al. (2013) and Mishra & Kluźniak (2014) have then analysed the effects of a luminosity variation on the Eddington sphere, especially in view of the possible occurrence of coronal ejection from the system. Within this framework, leaving the spherical symmetry makes the problem very difficult to be addressed. The generalization of the Abramowicz et al. approach to the case of an arbitrary particle motion in the equatorial plane of a rotating source is due to Miller & Lamb (1996), but in the limit of slow rotation only. Their model was then used by Oh, Kim & Lee (2010) to study the existence of equilibrium solutions.

Following the original Robertson approach, we have considered so far different space–time solutions of astrophysical interest endowed with reflection symmetry with respect to the equatorial plane, like black hole solutions (Schwarzschild and Kerr; Bini, Jantzen & Stella 2009; Bini et al. 2011a, 2012) or radiating space–times (Vaidya; Bini et al. 2011b). We have also discussed the effect of coupling with additional properties of test particles (like intrinsic spin; Bini & Geralico 2010). The main result of our previous analysis is that particles moving on the symmetry plane (which do not escape) are definitely attracted to a certain critical radius where they orbit the central source maintaining equilibrium. In general, the critical radius is not unique for sufficiently large values of the impact parameter of the photons as well as of the strength of the radiation field.

Here we explore the case of a central source having a quadrupolar structure as described by the Erez–Rosen solution. This is an exact solutions to the vacuum Einstein's field equations which generalizes the Schwarzschild space–time to the case of a gravitational source endowed with an arbitrary mass quadrupole moment, and hence it is specified by two parameters, the mass M and the quadrupole parameter q. This situation has a strong astrophysical motivation and represents a natural generalization of previous results, even if rotational effects are neglected. In fact, also the Kerr solution possesses a non-vanishing quadrupole moment, but the latter is induced by the space–time rotation. Here, the quadrupole parameter q describes a genuine mass quadrupole moment directly related to the shape deformation of the source. For instance, the supermassive objects hosted in galaxy centres are generally expected to be also endowed with a non-negligible mass quadrupole moment, which may affect the dynamics of stars moving in the region very close to the central object (Merritt et al. 2010). Besides rotation, torques from the source's quadrupole moment cause in general precession of the stellar orbital planes, which can be measured by high-precision astrometry. This is the case of the compact cluster of stars orbiting the centre of the Milky Way galaxy at milliparsec distances, monitored since many years (Gillessen et al. 2009).

Taking into account quadrupolar deformations is also important when considering the space–time region around neutron stars, which can assume a pronounced oblate configuration. Neutron stars can be part of low-mass X-ray binaries (LMXBs), where they are spun up by matter that accretes from a companion, which is typically either a low-mass star or a white dwarf. For a dynamically negligible magnetic field, the accretion disc of LMXBs can extend down to the star's surface, where curvature effects dominate. Therefore, the observed flux emitted in the inner part of the disc may contain the signatures of a more complicated structure of the source, which can be inferred from available X-ray data. However, significant quadrupolar deformations are mainly due to rotation, as in the case of Kerr black holes or rapidly rotating neutron stars. Hence, an accurate description of the above systems would need also the inclusion of rotation, which is but beyond the scope of the present analysis, mostly motivated to better understand the role of the quadrupole.

The main outcome of this work is the analysis of the effects induced on the equilibrium solutions by the quadrupolar deformation of the source. This is a typical feature of particles undergoing PR effect already discussed in previous works, as already mentioned. We will show that the presence of the quadrupolar structure of the source of the gravitational field may affect the conditions for equilibrium in a significant way, introducing an additional degree of freedom with respect to spherically symmetric sources represented by the quadrupole parameter. This feature can in principle give rise to observable effects.

We use geometrical units (c = G = 1) and follow notations and conventions of Misner, Thorne & Wheeler (1973). The metric signature is +2. Latin indices run from 1 to 3, greek indices from 0 to 3.

2 TEST PARTICLES UNDERGOING PR EFFECT IN THE EREZ–ROSEN SPACE–TIME

The gravitational field of a non-rotating mass with a quadrupole moment can be described by the Erez–Rosen solution (Erez & Rosen 1959; Doroshkevich, Zel'dovich & Novikov 1965; Young & Coulter 1969). It belongs to the static Weyl class of solutions with the line element written in prolate spheroidal coordinates (t, x, y, ϕ), with x ≥ 1 and −1 ≤ y ≤ 1, as follows (Stephani et al. 2003):

\begin{eqnarray} {\rm d} s^2 &=& -f{\rm d} t^2+\frac{\sigma^2}{f}\bigg\{e^{2\gamma}\left(x^2-y^2\right)\left(\frac{{\rm d} x^2}{x^2-1}+\frac{{\rm d} y^2}{1-y^2}\right)\nonumber\\ && +\;(x^2-1)(1-y^2){\rm d}\phi^2\bigg\}\,, \end{eqnarray}

(1)

where σ is a constant and the quantities f and γ are functions of x and y only. The metric functions are given by

\begin{eqnarray} f&=&\frac{x-1}{x+1}{\rm e}^{-2qP_2Q_2}, \nonumber \\ \gamma &=&\frac{1}{2}(1+q)^2 \ln \frac{x^2-1}{x^2-y^2} \nonumber\\ &&+\, 2q(1-P_2)Q_1 + q^2(1-P_2) \bigg [ (1+P_2)(Q_1^2-Q_2^2)\nonumber \\ &&+\,\frac{1}{2}(x^2-1)(2Q_2^2 - 3xQ_1Q_2 + 3 Q_0Q_2 - Q_2^{\prime })\bigg ] , \end{eqnarray}

(2)

where P_l(y) and Q_l(x) are Legendre polynomials of the first and second kind, respectively (see Appendix ), and q is the dimensionless quadrupole parameter. Positive values of q correspond to prolate configurations, i.e. the mass is mostly concentrated along the axes y = ±1, whereas negative values to oblate ones. When q = 0, the metric (1) reduces to the Schwarzschild solution provided that σ be identified with the mass of the source, namely σ = M. Transition of this metric form to the more familiar one associated with standard Schwarzschild-like coordinates is accomplished by the following coordinate transformation x = r/M − 1 and y = cos θ. Furthermore, the above solution reduces to the well-known Hartle–Thorne space–time (Hartle & Thorne 1967, 1968) with vanishing rotation parameter when linearized with respect to the quadrupole parameter.

A suitable family of fiducial observers is that of the so called static observers, with unit timelike 4-velocity |$n\equiv e_{\hat{t}}= (1/\sqrt{f})\mathrm{\partial} _t\,$| aligned with the timelike Killing vector ∂_t. They are accelerated with acceleration a(n) = ∇_nn. An orthonormal frame adapted to the static observers is thus given by

\begin{eqnarray} e_{\hat{t}}=n, \,\quad e_{\hat{x}}=\frac{1}{\sqrt{g_{xx}}}\mathrm{\partial} _x\,,\qquad e_{\hat{y}}=\frac{1}{\sqrt{g_{yy}}}\mathrm{\partial} _y\,,\quad e_{\hat{\phi }}=\frac{1}{\sqrt{g_{\phi \phi }}}\mathrm{\partial} _\phi .\!\!\!\!\!\!\!\nonumber\\ \end{eqnarray}

(3)

The four acceleration as well as the curvature vectors k(xⁱ, n), where xⁱ = x, y, ϕ, associated with the diagonal metric coefficients (Jantzen, Carini & Bini 1992; Bini, Carini & Jantzen 1997a,b; Bini, de Felice & Jantzen 1999) only have non-zero components in the x–y two-plane of the tangent space, i.e.

\begin{eqnarray} a(n) & = & a(n)^{\hat x} e_{\hat x} + a(n)^{\hat y} e_{\hat y} \nonumber\\ & = &\partial_{\hat x}(\ln\sqrt{f}) e_{\hat x} + \partial_{\hat y}(\ln\sqrt{f}) e_{\hat y} \,, \nonumber\\ k(x^i,n)& = & k(x^i,n)^{\hat x} e_{\hat x} + k(x^i,n)^{\hat y} e_{\hat y} \nonumber\\ & = & -\partial_{\hat x}(\ln \sqrt{g_{ii}}) e_{\hat x} - \partial_{\hat y}(\ln \sqrt{g_{ii}})e_{\hat y} \,. \end{eqnarray}

(4)

We limit our analysis to the symmetry plane y = 0. Therefore, both the acceleration and the curvature vectors are directed along the x-axis, which hereafter will be referred to as the ‘radial’ direction.

2.1 Photon field

Let a pure electromagnetic radiation field be superposed as a test field on the gravitational background described by the metric (1) and (2), with the energy–momentum tensor

\begin{equation} T^{\alpha \beta }=\Phi ^2 k^\alpha k^\beta , \qquad k^\alpha k_\alpha =0, \end{equation}

(5)

where k is assumed to be tangent to an affinely parametrized (ingoing/outgoing) null geodesic in the symmetry plane, i.e. k^α∇_αk^β = 0 with k^y = 0. We then have

\begin{equation} k=E(n)[n+\hat{\nu }(k,n)]\,, \qquad \hat{\nu }(k,n)=\sin \beta \, e_{\hat{x}}+\cos \beta \, e_{\hat{\phi }}, \end{equation}

(6)

where

\begin{equation} E(n)= - k \cdot n =\frac{E}{\sqrt{f}} \end{equation}

(7)

is the relative energy of the photons and

\begin{equation} \cos \beta =\frac{bf}{\sigma \sqrt{x^2-1}}. \end{equation}

(8)

The constant b = L/E denotes the photon impact parameter defined in terms of the conserved energy E = −k_t > 0 and angular momentum L = k_ϕ associated with the timelike and azimuthal Killing vectors, respectively. The case sin β > 0 corresponds to outgoing photons (increasing radial distance from the central source) and sin β < 0 to incoming photons (decreasing x).

Since k is completely determined, the coordinate dependence of the quantity Φ then follows from the conservation equations T^αβ_{; β} = 0, and will only depend on x in the symmetry plane. From equation (5) using the geodesic condition for k, these can be written as

\begin{equation} 0=\nabla _\beta (\Phi ^2 k^\beta ) =\frac{1}{\sqrt{-g}}\mathrm{\partial} _\beta (\sqrt{-g}\,\Phi ^2 k^\beta ) , \end{equation}

(9)

implying that |$0=\mathrm{\partial} _x(\sqrt{-g}\,\Phi ^2 k^x)$|⁠. Therefore, we find |$\sqrt{-g}\,\Phi ^2 k^x = {\rm const} = E \Phi _0^2$|⁠, leading to

\begin{equation} \Phi ^2=\sigma \Phi _0^2\frac{{\rm e}^{-\gamma }}{x\,|b \tan \beta |} =\sigma \Phi _0^2\frac{{\rm e}^{-\gamma }f}{x\sqrt{\sigma ^2(x^2-1)-b^2f^2}} . \end{equation}

(10)

In the limit b → 0 corresponding to photons in radial motion the flux simplifies as

\begin{equation} \Phi ^2=\Phi _0^2\frac{{\rm e}^{-\gamma }f}{x\sqrt{x^2-1}} . \end{equation}

(11)

The photon motion in the symmetry plane has been investigated by Bini et al. (2013) through the analysis of the associated effective potential. A number of interesting features has been discussed there, including the occurrence of multiple ‘photon spheres’ corresponding to spatially circular null orbits due to the presence of a non-vanishing mass quadrupole moment. Fig. 1 shows the behaviour of the relative velocity lines of the radiation field (with respect to the observers n) as well as that of the radiation flux as a function of the radial distance in the case of a Erez–Rosen space–time with a selected value of the quadrupole parameter in comparison with the spherically symmetric Schwarzschild solution. In the latter case, the flux is peaked at x = 2 (i.e. r = 3M) and approaches a finite value at the horizon, for the chosen (high) value of the photon impact parameter. In the case of a non-spherical source, instead, the behaviour of the flux strongly depends on q. Fig. 1 shows a typical situation corresponding to a prolate configuration (q = 5). As it is evident, there exists a forbidden region to photons extending from x = 1 up to a certain value of x, where the flux diverges, hence manifesting a completely different behaviour in comparison with the Schwarzschild case. For oblate configurations the situation is instead similar to the spherically symmetric case.

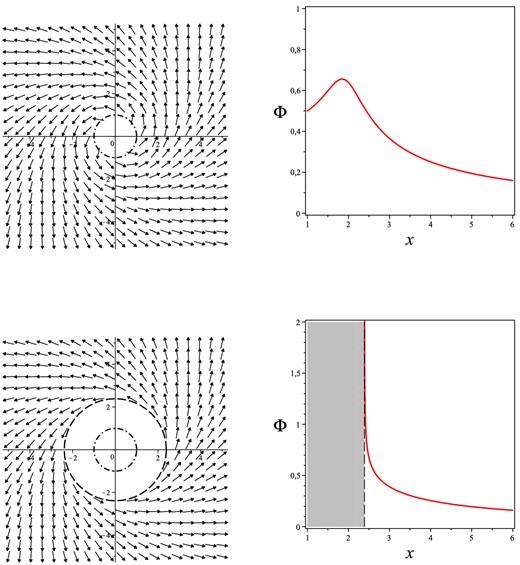
$First row: the unit velocity direction field of photons $\hat{\nu }(k,n)$ given by equation (6) is shown in the left-hand panel for b/σ = 5 and q = 0. The right-hand panel shows instead the behaviour of the photon flux (in units of Φ0) for the same choice of parameters. Second row: same value of the photon impact parameter as above, but with non-zero quadrupole parameter q = 5. The region inside the dashed circle at x ≈ 2.39 is forbidden to photons due to the restriction cos β ≤ 1 as from equation (8).$

Figure 1.

First row: the unit velocity direction field of photons |$\hat{\nu }(k,n)$| given by equation (6) is shown in the left-hand panel for b/σ = 5 and q = 0. The right-hand panel shows instead the behaviour of the photon flux (in units of Φ₀) for the same choice of parameters. Second row: same value of the photon impact parameter as above, but with non-zero quadrupole parameter q = 5. The region inside the dashed circle at x ≈ 2.39 is forbidden to photons due to the restriction cos β ≤ 1 as from equation (8).

Open in new tab Download slide

2.2 Particle dynamics

Consider now a test particle moving in the symmetry plane y = 0 accelerated by the radiation field, i.e. with 4-velocity

\begin{equation} U=\gamma (U,n) [n+ \nu (U,n)]\,,\quad \nu (U,n)\equiv \nu ^{\hat{x}}e_{\hat{x}}+\nu ^{\hat{\phi }}e_{\hat{\phi }} , \end{equation}

(12)

where |$\gamma (U,n)=1/\sqrt{1-||\nu (U,n)||^2}\equiv \gamma$| is the Lorentz factor (not to be confused with the metric function) and the abbreviated notation |$\nu ^{\hat{a}}\equiv \nu (U,n)^{\hat{a}}$| has been used. A straightforward calculation gives the coordinate components of U

\begin{eqnarray} U^t\equiv \frac{{\rm d}t}{{\rm d}\tau }=\frac{\gamma }{\sqrt{f}}\,, \!\!\!\!\!\qquad U^x\equiv \frac{{\rm d}x}{{\rm d}\tau }=\frac{\gamma \nu ^{\hat{x}}}{\sqrt{g_{xx}}}\,, \!\!\!\!\!\qquad U^\phi \equiv \frac{{\rm d}\phi }{{\rm d}\tau }=\frac{\gamma \nu ^{\hat{\phi }}}{\sqrt{g_{\phi \phi }}}, \!\!\!\!\!\nonumber\\ \end{eqnarray}

(13)

where τ is the proper time parameter along the particle's world line, and U^y ≡ dy/dτ = 0.

The scattering of radiation as well as the (constant) momentum-transfer cross-section |$\tilde{\sigma }$| of the particle are assumed to be independent of the direction and frequency of the radiation so that the associated force is given by (Poynting 1903; Robertson 1937)

\begin{equation} {\mathcal {F}}_{\rm (rad)}(U)^\alpha = -\tilde{\sigma }P(U)^\alpha {}_\beta \, T^{\beta }{}_\mu \, U^\mu , \end{equation}

(14)

where |$P(U)^\alpha {}_\beta =\delta ^\alpha _\beta +U^\alpha U_\beta$| projects orthogonally to U. Explicitly

\begin{eqnarray} {\mathcal {F}}_{\rm (rad)}(U)^\alpha =-\tilde{\sigma }\Phi ^2 [P(U)^\alpha {}_\beta k^\beta ]\, (k_\mu U^\mu ) =\tilde{\sigma }\, [\Phi E(U)]^2\, \hat{\mathcal {V}}(k,U)^\alpha , \!\!\!\!\!\nonumber\\ \end{eqnarray}

(15)

where

\begin{equation} E(U)=-U\cdot k = \gamma E(n)[1-\sin \beta \nu ^{\hat{x}}-\cos \beta \nu ^{\hat{\phi }}], \end{equation}

(16)

is the photon energy as measured by U and

\begin{equation} \hat{\mathcal {V}}\equiv \hat{\mathcal {V}}(k,U) =\frac{k}{E(U)}-U, \end{equation}

(17)

is the photon relative velocity in the test particle local rest space with the property |$\hat{\mathcal {V}}\cdot U=0$|⁠. The decomposition of the radiation force with respect to n is thus given by

\begin{equation} {\mathcal {F}}_{\rm (rad)}(U)={\mathcal {F}}_{\rm (rad)}(U)^{\hat{t}}n +{\mathcal {F}}_{\rm (rad)}(U)^{\hat{x}}e_{\hat{x}} +{\mathcal {F}}_{\rm (rad)}(U)^{\hat{\phi }}e_{\hat{\phi }}, \end{equation}

(18)

with components |${\mathcal {F}}_{\rm (rad)}(U)^{\hat{t}}={\mathcal {F}}_{\rm (rad)}(U)^{\hat{x}} \nu ^{\hat{x}} + {\mathcal {F}}_{\rm (rad)}(U)^{\hat{\phi }} \nu ^{\hat{\phi }}$| and

\begin{eqnarray} {\mathcal {F}}_{\rm (rad)}(U)^{\hat{x}} & = &\tilde{\sigma }\, [\Phi E(U)]^2\, \hat{\mathcal {V}}^{\hat{x}}, \nonumber \\ {\mathcal {F}}_{\rm (rad)}(U)^{\hat{\phi }} & = &\tilde{\sigma }\, [\Phi E(U)]^2\, \hat{\mathcal {V}}^{\hat{\phi }} , \end{eqnarray}

(19)

with

\begin{eqnarray} \hat{\mathcal {V}}{}^{\hat{x}}&=&\sin \beta \frac{E(n)}{E(U)} -\gamma \nu ^{\hat{x}},\nonumber \\ \hat{\mathcal {V}}{}^{\hat{\phi }}&=&\cos \beta \frac{E(n)}{E(U)} -\gamma \nu ^{\hat{\phi }}. \end{eqnarray}

(20)

Test particle motion is then described by the equation

\begin{equation} m a(U)^\mu \equiv m \frac{\rm {D} U^\mu }{{\rm d}\tau }={\mathcal {F}}_{\rm (rad)}(U)^\mu . \end{equation}

(21)

The frame components of the particle 4-acceleration a(U) in the symmetry plane are given by

\begin{eqnarray} a(U)^{\hat{t}} &=&a(U)^{\hat{x}} \nu ^{\hat{x}} +a(U)^{\hat{\phi }} \nu ^{\hat{\phi }},\nonumber \\ \gamma ^{-2}a(U)^{\hat{x}} &=& a(n)^{\hat{x}}+k(\phi ,n)^{\hat{x}}\,\nu ^{\hat{\phi }}{}^2 \nonumber\\ &&+\,\gamma \left[\nu ^{\hat{x}}\nu ^{\hat{\phi }}\frac{{\rm d}\nu ^{\hat{\phi }}}{{\rm d}\tau } +(1-\nu ^{\hat{\phi }}{}^2)\frac{{\rm d}\nu ^{\hat{x}}}{{\rm d}\tau }\right], \nonumber \\ a(U)^{\hat{y}} &=& 0, \nonumber \\ \gamma ^{-2}a(U)^{\hat{\phi }} &=& -\nu ^{\hat{x}}\nu ^{\hat{\phi }}\, k(\phi ,n)^{\hat{x}} +\gamma \left[\nu ^{\hat{x}}\nu ^{\hat{\phi }}\frac{{\rm d}\nu ^{\hat{x}}}{{\rm d}\tau } +(1-\nu ^{\hat{x}}{}^2)\frac{{\rm d}\nu ^{\hat{\phi }}}{{\rm d}\tau }\right]. \!\!\!\!\nonumber\\ \end{eqnarray}

(22)

From equation (21), the evolution equations for the frame components of the linear velocity then read as

\begin{eqnarray} \frac{{\rm d}\nu ^{\hat{x}}}{{\rm d}\tau } &=&-\gamma (1-\nu ^{\hat{x}}{}^2)\left[a(n)^{\hat{x}}-\frac{{\mathcal {F}}_{\rm (rad)}(U)^{\hat{x}}}{m\gamma ^2}\right] \nonumber\\ &&-\,\gamma \nu ^{\hat{\phi }}\left[\nu ^{\hat{\phi }}k(\phi ,n)^{\hat{x}}+\nu ^{\hat{x}}\frac{{\mathcal {F}}_{\rm (rad)}(U)^{\hat{\phi }}}{m\gamma ^2}\right], \nonumber \\ \frac{{\rm d}\nu ^{\hat{\phi }}}{{\rm d}\tau } &=&(1-\nu ^{\hat{\phi }}{}^2)\frac{{\mathcal {F}}_{\rm (rad)}(U)^{\hat{\phi }}}{m\gamma } \nonumber\\ &&+\,\gamma \nu ^{\hat{x}}\nu ^{\hat{\phi }}\left[a(n)^{\hat{x}}+k(\phi ,n)^{\hat{x}} -\frac{{\mathcal {F}}_{\rm (rad)}(U)^{\hat{x}}}{m\gamma ^2}\right], \end{eqnarray}

(23)

which should be considered together with equation (13). The explicit expressions for the radial components of the acceleration as well as curvature vectors are listed in Appendix.

Examples of numerical integration of the orbits are shown in Fig. 2 for a fixed value of the radiation field strength and different values of the quadrupole parameter. The case of a spherically symmetric source (q = 0) is also shown for comparison. Initial conditions are chosen so that the particle trajectory is initially tangent to a circular orbit with a value of the azimuthal velocity which is either less than (first row) or equal to (second row) the geodesic one. As a general feature, unless the particle has a sufficiently high initial speed that it can escape to infinity, it is forced to end up in a circular orbit which is an equilibrium solution, representing the balance between gravitational attraction, centrifugal force and radiation drag, as discussed in the next section. Fig. 2 shows that particles feel a gravitational field with different strength if the source is oblate (q < 0) or prolate (q > 0). In the former case, the incoming particle feels a stronger gravitational field as it approaches the gravity source. For prolate configurations, instead, the gravitational mass is mainly concentrated along the y-axis, so that a particle moving sufficiently close to the source will feel a decreasing gravitational field. As a result, the balance between inward gravitational force and outward radiation force will occur at larger radii.

$First row: particle orbits on the symmetry plane for b = 3, A = 0.3 (in units of σ) and different values of the quadrupole parameter: q = 0 (left), q = 5 (middle) and q = −5 (right). Initial conditions have been chosen as x(0) = 5, ϕ(0) = 0, $\nu ^{\hat{r}}(0)=0$ and $\nu ^{\hat{\phi }}(0)=0.2$. Cartesian-like coordinates [xcos ϕ, xsin ϕ] have been used. The equilibrium circular orbits are at x ≈ 1.134, x ≈ 2.238 and x ≈ 1.139, respectively. Second row: same parameter choice as above, but with different $\nu ^{\hat{\phi }}(0)=\nu _{\rm g}\approx [0.5,0.487,0.513]$, respectively. The equilibrium circular orbits are at x ≈ 1.134, x ≈ 4.962 and x ≈ 1.139, respectively.$

Figure 2.

First row: particle orbits on the symmetry plane for b = 3, A = 0.3 (in units of σ) and different values of the quadrupole parameter: q = 0 (left), q = 5 (middle) and q = −5 (right). Initial conditions have been chosen as x(0) = 5, ϕ(0) = 0, |$\nu ^{\hat{r}}(0)=0$| and |$\nu ^{\hat{\phi }}(0)=0.2$|⁠. Cartesian-like coordinates [xcos ϕ, xsin ϕ] have been used. The equilibrium circular orbits are at x ≈ 1.134, x ≈ 2.238 and x ≈ 1.139, respectively. Second row: same parameter choice as above, but with different |$\nu ^{\hat{\phi }}(0)=\nu _{\rm g}\approx [0.5,0.487,0.513]$|⁠, respectively. The equilibrium circular orbits are at x ≈ 1.134, x ≈ 4.962 and x ≈ 1.139, respectively.

Open in new tab Download slide

3 EQUILIBRIUM SOLUTIONS

The set of equations (23) and (13) admits an equilibrium solution which corresponds to a circular orbit with constant speed at a given distance x = x₀ from the central source. In fact, setting |$\nu ^{\hat{x}}=0$| and |$\nu ^{\hat{\phi }}=\nu ^{\hat{\phi }}_0=$| const. in the above equations we get the conditions

\begin{eqnarray} 0&=& a(n)^{\hat{x}}+\nu ^{\hat{\phi }}_0{}^2k(\phi ,n)^{\hat{x}}-\frac{A}{\sigma ^2}\frac{\Phi ^2}{\Phi _0^2}\frac{\sin \beta _0}{f\gamma _0}(1-\cos \beta _0\nu ^{\hat{\phi }}_0) ,\nonumber \\ 0&=&A\frac{\Phi ^2}{\Phi _0^2}\frac{\gamma _0^3}{f}(\cos \beta _0 -\nu ^{\hat{\phi }}_0)(1 -\nu ^{\hat{\phi }}_0\cos \beta _0) , \end{eqnarray}

(24)

where it is understood that all functions of x are evaluated at x = x₀ and we have used the notation |$\tilde{\sigma }\Phi _0^2 E^2=mA$|⁠, as in Bini et al. (2011a). The second equation (24) yields the critical circular velocity

\begin{equation} \nu ^{\hat{\phi }}_0 = \cos \beta _0 = \frac{bf}{\sigma \sqrt{x^2-1}} \qquad \rightarrow \qquad \gamma _0= \frac{1}{|\sin \beta _0|} , \end{equation}

(25)

which turns out to be equal to the photon azimuthal velocity (see equation 8). Substituting then into the first equation gives an implicit relation determining the critical ‘radius’ x₀ itself as a function of b, which can be also written as

\begin{equation} a(n)^{\hat{x}}\left(1-\frac{\nu ^{\hat{\phi }}_0{}^2}{\nu _{\rm g}^2}\right)=\frac{A}{\sigma ^2}\frac{\Phi ^2}{\Phi _0^2}\frac{{\rm sgn}(\sin \beta _0)}{f\gamma _0^4} , \end{equation}

(26)

where the circular geodesic (A = 0) azimuthal velocities |$\nu ^{\hat{\phi }}=\pm \nu _{\rm g}$|⁠, with

\begin{equation} \nu _{\rm g}=\left[\frac{f_x(x^2-1)}{2xf-f_x(x^2-1)}\right]^{1/2}\,, \qquad \gamma _{\rm g}=\frac{1}{\sqrt{1-\nu _{\rm g}^2}}, \end{equation}

(27)

have been introduced, satisfying the relation |$a(n)^{\hat{x}}+\nu _{\rm g}^2k(\phi ,n)^{\hat{x}}=0$|⁠. Partial derivatives of the metric functions with respect to x and y are indicated by a subscript. Solving equation (26) for A finally gives

\begin{equation} \frac{A}{\sigma }={\rm sgn}(\sin \beta _0)\gamma _0^3\left(1-\frac{\nu ^{\hat{\phi }}_0{}^2}{\nu _{\rm g}^2}\right)\frac{f_x}{2\sqrt{f}}(x^2-1) . \end{equation}

(28)

Fig. 3 shows the behaviour of the critical azimuthal velocity (first row) as well as critical photon impact parameter (second row) as a function of the radial distance for selected values of the friction parameter A (in units of σ) and different values of the quadrupole parameter. The critical speed is less/greater than the geodesic speed in the case of outgoing/ingoing photons (sin β₀ > 0 / sin β₀ < 0). The features of equilibrium are different depending on whether prolate or oblate sources are considered. In the former case, for increasing values of A the curves lie in the region above the geodesic velocity for ingoing photons, with the asymptotic limit |$\nu ^{\hat{\phi }}_0\rightarrow 1$| for A → ∞. For outgoing photons, instead, the curves are below the geodesic one, continuing to move out far from the source for increasing values of A without limit. In the case of oblate sources, instead, the situation is very similar to the Schwarzschild one (Bini et al. 2011a). Consider first the case of outgoing photons. The curves of constant A start at the value A = 0 at the hypersurface x = 1 (vertical axis) and on the geodesic velocity curves, and increase in value towards the saddle point on the separatrix curve at a certain value of A. For A further increasing past that value, the curves fill the inner sector above that point (near the hypersurface x = 1). At the same time, in the region below the meeting point they move farther out to larger radii, moving out to infinity in the limit A → 1, corresponding to the fact that for A > 1, test particles are pushed out to infinity in this region. In the case of ingoing photons, instead, all the curves of constant A are confined in the region above the geodesic velocity.

$First row: critical azimuthal velocity versus critical radius for equally spaced values of A from 0 to 1 at intervals of 0.1 and thereafter values of [1, 2, 3, 4, 5, 10] (in units of σ) in both cases of outgoing flux (sin β0 > 0, red curves) and ingoing flux (sin β0 < 0, blue curves) and different values of the quadrupole parameter: q = 0 (left), q = 10 (middle) and q = −10 (right). The thick solid curves indicate the geodesic velocities corresponding to A = 0, whereas the thick dashed curves correspond to A = 1. The separatrix is for A ≈ 0.647 in the case q = 0 and A ≈ 0.850 in the case q = −10. The thick loop curves enclose the region of unstable intermediate radius orbits for those values of $\nu ^{\hat{\phi }}_0$ (or, equivalently, b) for which three critical radii exist. Second row: critical photon impact parameter versus critical radius.$

Figure 3.

First row: critical azimuthal velocity versus critical radius for equally spaced values of A from 0 to 1 at intervals of 0.1 and thereafter values of [1, 2, 3, 4, 5, 10] (in units of σ) in both cases of outgoing flux (sin β₀ > 0, red curves) and ingoing flux (sin β₀ < 0, blue curves) and different values of the quadrupole parameter: q = 0 (left), q = 10 (middle) and q = −10 (right). The thick solid curves indicate the geodesic velocities corresponding to A = 0, whereas the thick dashed curves correspond to A = 1. The separatrix is for A ≈ 0.647 in the case q = 0 and A ≈ 0.850 in the case q = −10. The thick loop curves enclose the region of unstable intermediate radius orbits for those values of |$\nu ^{\hat{\phi }}_0$| (or, equivalently, b) for which three critical radii exist. Second row: critical photon impact parameter versus critical radius.

Open in new tab Download slide

The equilibrium condition (28) can also be written in terms of the photon impact parameter in place of the critical speed, by using equation (25). The resulting equation determines the critical radius in terms of the photon impact parameter. For fixed values of b and A, one or more values of x₀ may satisfy it, which may correspond to stable orbits or not. The stability analysis of critical orbits is done in the next section. For each curve in the plots shown in the second row of Fig. 3 corresponding to fixed values of A, the number of its intersections with the horizontal line at each value of b indicates the number of critical radii which exist for that case. Those horizontal curves which pass through the interior of the closed shaded regions correspond to the case in which three critical radii exist, with the unstable orbit of the three lying in the interior, while those passing outside these loops correspond to the single stable critical radius case.

Finally, Fig. 4 shows the behaviour of the critical radius as a function of the quadrupole parameter for selected values of the friction parameter A and different values of the the photon impact parameter b (in units of σ). For small values of b there exists in general a single equilibrium radius for every value of the quadrupole parameter, which is closer to the source as the configuration is more oblate. For larger values of the photon impact parameter multiple solutions appear for q ≲ 4. Increasing the strength of the radiation field then causes the latter behaviour to occur for even smaller values of b.

Figure 4.

Critical radius versus quadrupole parameter for selected values of the strength of the radiation field A = 0 (left), A = 0.3 (middle) and A = 0.7 (right) and different values of the photon impact parameter b = [0, 1.5, 2.5, 3, 3.5, 3.75, 4].

Open in new tab Download slide

In the limit of vanishing photon impact parameter b = 0 equation (25) implies |$\nu ^{\hat{\phi }}_0=0$|⁠, which corresponds to ‘suspension orbits,’ i.e. particle trajectories end up at a certain point in the symmetry plane. The equilibrium condition (26) reduces to

\begin{equation} a(n)^{\hat{x}}=\frac{A}{\sigma ^2}\frac{\Phi ^2}{\Phi _0^2}\frac{1}{f} =\frac{A}{\sigma ^2}\frac{{\rm e}^{-\gamma }}{x\sqrt{x^2-1}} , \end{equation}

(29)

and implicitly gives the suspension radius as a function of A for fixed values of the quadrupole parameter.

3.1 Stability of the critical orbits

Let us study the stability properties of the critical circular orbits under small first-order linear perturbations of the equilibrium solution, whose parametric equation is given by

\begin{equation} x=x_0\,, \quad \phi =\phi _0(\tau )\,, \quad \nu ^{\hat{x}}=0\,, \quad \nu ^{\hat{\phi }}=\nu ^{\hat{\phi }}_0, \end{equation}

(30)

or symbolically |$X^\alpha =X_0^\alpha$| (⁠|$\alpha =x,\phi ,\nu ^{\hat{x}},\nu ^{\hat{\phi }}$|⁠). Note that this analysis will not check for stability against perturbations away from the equatorial plane.

Consider the linear perturbations of this solution |$X^\alpha =X_0^\alpha +X_1^\alpha$|⁠, namely

\begin{eqnarray} x &=& x_0+x_1(\tau)\,, \quad\phi=\phi_0(\tau)+\phi_1(\tau)\,, \nonumber\\ \nu^{\hat x} &=& \nu^{\hat x}_1(\tau)\,, \quad \nu^{\hat \phi}=\nu^{\hat \phi}_0+\nu^{\hat \phi}_1(\tau)\,, \end{eqnarray}

(31)

which leads to the following linear system of constant coefficient homogeneous linear differential equations

\begin{equation} \frac{{\rm d}X_1^\alpha }{{\rm d}\tau }=C^\alpha {}_\beta X_1^\beta , \end{equation}

(32)

which can easily be solved in terms of the eigenvalues and eigenvectors of the coefficient matrix. The real parts of all eigenvalues must be non-negative for stability. The explicit expressions for the non-zero coefficients are

\begin{eqnarray} C^1{}_{3}&=&\frac{\gamma _0}{\sqrt{g_{xx}}}\,,\!\!\!\!\!\!\!\qquad C^2{}_{1} = \gamma _0\nu ^{\hat{\phi }}_0k(\phi ,n)^{\hat{x}}\frac{\sqrt{g_{xx}}}{\sqrt{g_{\phi \phi }}}\,,\!\!\!\!\!\!\!\qquad C^2{}_{4} = \frac{\gamma _0^3}{\sqrt{g_{\phi \phi }}} ,\nonumber \\ C^3{}_{1}&=& \!-\gamma _0\sqrt{g_{xx}}\left\lbrace \left(E(n)_{\hat{x}\hat{x}}-a(n)^{\hat{x}}{}^2\right)-\nu ^{\hat{\phi }}_0{}^2\left(E(n)_{\hat{y}\hat{y}}-k(\phi ,n)^{\hat{x}}{}^2\right)\right.\nonumber \\ & &+\,C^4{}_{4}\left[-(2-\nu ^{\hat{\phi }}_0{}^2)a(n)^{\hat{x}}+(1-2\nu ^{\hat{\phi }}_0{}^2)k(\phi ,n)^{\hat{x}}\right.\nonumber\\ &&+\left.\left.(1-\nu ^{\hat{\phi }}_0{}^2)k(y,n)^{\hat{x}}\right] \right\rbrace ,\nonumber \\ C^3{}_{3} &=& -2C^4{}_{4}\,,\qquad C^3{}_{4}=-2\gamma _0^3\nu ^{\hat{\phi }}_0(a(n)^{\hat{x}}+k(\phi ,n)^{\hat{x}}) , \nonumber \\ C^4{}_{1}&=&\frac{\sqrt{g_{xx}}}{2\gamma _0^3}C^3{}_{4}C^4{}_{4}\,,\qquad C^4{}_{3}=\frac{\nu ^{\hat{\phi }}_0}{\gamma _0}(k(\phi ,n)^{\hat{x}}-C^4{}_{4}),\nonumber\\ C^4{}_{4} &=& \frac{A\sigma ^2}{\gamma _0f\sqrt{g_{yy}}\sqrt{g_{\phi \phi }}},\!\! \!\! \end{eqnarray}

(33)

with A given by equation (28). The quantities |$E(n)_{\hat{a}\hat{b}}$| in the above equations are the frame components with respect to n of the electric part of the Riemann tensor defined by E(n)_αβ = R_αμβνn^μn^ν.

The associated eigenvalue equation is

\begin{equation} \lambda [\lambda ^3+c_2\lambda ^2+c_1\lambda +c_0]=0, \end{equation}

(34)

where

\begin{eqnarray} &&{\frac{c_0}{c_2}+c_1+2c_2^2 = 2\frac{\gamma_0^2}{\gamma_{\rm g}^2}\frac{\nu^{\hat \phi}_0{}^2}{\nu_{\rm g}^2}a(n)^{\hat x}\left[ c_2-\gamma_0^2(\nu^{\hat \phi}_0{}^2-\nu_{\rm g}^2)\frac{a(n)^{\hat x}}{\nu_{\rm g}^2} \right] \,,}\nonumber\\ &&{c_1 \!+\! 2c_2^2 = \frac{\gamma_0^2}{\gamma_{\rm g}^2}\Omega_{\rm (ep)}^2\!+\!\gamma_0^2(\nu^{\hat \phi}_0{}^2-\nu_{\rm g}^2)\left[-E(n)_{\hat y\hat y}+\frac{a(n)^{\hat x}{}^2}{\nu_{\rm g}^4}(3-2\nu_{\rm g}^2) \right]}\nonumber\\ &&{\qquad\qquad\,\;-\;c_2\left[k(y,n)^{\hat x}-\gamma_0^2a(n)^{\hat x}\left(2-3\nu^{\hat \phi}_0{}^2+\frac1{\nu_{\rm g}^2}\right)\right] \,,} \nonumber\\ &&{c_2 = C^4{}_{4} \,,} \end{eqnarray}

(35)

and

\begin{equation} \Omega _{\rm (ep)}^2=3\frac{a(n)^{\hat{x}}{}^2}{\nu _{\rm g}^2}+\gamma _{\rm g}^2(E(n)_{\hat{x}\hat{x}}-\nu _{\rm g}^2E(n)_{\hat{y}\hat{y}}), \end{equation}

(36)

is the corresponding proper time normalized version of the time coordinate epicyclic frequency governing the radial perturbations of circular geodesics. In the Schwarzschild case, it reduces to

\begin{equation} \Omega _{\rm (ep)}^2=\frac{x_0-5}{\sigma ^2(x_0-2)(x_0+1)^3} =\frac{M}{r_0^3}\frac{r_0-6M}{r_0-3M}. \end{equation}

(37)

The explicit expressions for the eigenvalues can be obtained straightforwardly. In the case of geodesic motion (i.e. A = 0 and |$\nu ^{\hat{\phi }}_0=\pm \nu _{\rm g}$|⁠), the eigenvalue equation (34) reduces to

\begin{equation} \lambda ^2(\lambda ^2+\Omega _{\rm (ep)}^2)=0, \end{equation}

(38)

since c₀ = 0 = c₂ and |$c_1=\Omega _{\rm (ep)}^2$|⁠.

The behaviour of the eigenvalues as functions of the radial distance from the central source shows that for a given value of the quadrupole parameter there exist in general two disconnected regions where circular orbits are stable (see Fig. 3): one very close to the singularity, and another for larger radii, which is relevant for observational effects. Therefore, we refer to the left boundary of that region as the radius corresponding to the innermost stable circular orbit (ISCO). The behaviour of the ISCO radius as a function of the quadrupole parameter is shown in Fig. 5 for both fixed values of b (left-hand panel) and fixed values of A (right-hand panel). We find that the orbits are always stable for prolate configurations with q ≳ 6.

Figure 5.

The behaviour of the ISCO radius as a function of the quadrupole parameter is shown for outgoing photon flux for fixed values of b = [1.5, 3, 3.75] in the left-hand panel and for fixed values of A = [0, 0.5, 0.75] in the right-hand panel (in units of σ). Each point in the curves corresponds to a given value of A in the former case, and to a given value of b in the latter case. A selection of points identified by a dot with the value of either A or b indicated below is also shown.

Open in new tab Download slide

4 CONCLUDING REMARKS

In any attempt to construct a realistic model of test particle motion around compact objects to be constrained by observations one should take into account both the structure of these objects and the effects of the presence of electromagnetic or radiation fields surrounding them. Black holes are commonly expected to be hosted at the centre of galaxies as well as in X-ray binary systems (see e.g. Narayan & McClintock 2013 and references therein). According to the Einstein theory of gravity, an uncharged black hole is completely specified by its total mass and angular momentum, which determine all the higher order mass and current moments of the gravitational field. In particular, the mass quadrupole moment of a spinning black hole is proportional to the angular momentum squared. However, general relativity allows for exact solutions which represent compact objects with additional structure, i.e. with the multipole moments of the associated gravitational field expressed in terms of an arbitrary set of parameters (Stephani et al. 2003). For instance, the Erez–Rosen solution, which we adopt in the present paper, generalizes the Schwarzschild space–time to the case of a gravitational source endowed with an arbitrary mass quadrupole moment, and hence it is specified by two parameters, the mass M and the quadrupole parameter q. As expected, the presence of the quadrupole affects the motion of test particles and photons in a significant way (Armenti 1972; de Felice 1990; Quevedo 1990; Bini et al. 2013).

There is a growing interest in the current literature in constraining the geometry around compact objects with observations in both the electromagnetic and gravitational wave spectra. In fact, both space- and ground-based advanced gravitational wave detectors (like LISA¹ and advanced LIGO²/Virgo³) are expected to detect, e.g. the gravitational waves emitted during the inspiral of binary systems. Any deviation from either the Schwarzschild or Kerr black hole geometry will then lead to a phase difference in the gravitational waveforms as well as to the ‘ringdown radiation’ in the form of the so-called quasinormal modes of the end state of the merger (Ryan 1995, 1997; Barack & Cutler 2007; Rodriguez, Mandel & Gair 2012; Berti, Cardoso & Starinets 2009).

It is also a general feature that compact objects are surrounded by an accretion disc, which forms due to the diffuse material orbiting them coming from either the companion in the case of stellar-mass objects in X-ray binary systems, or from the interstellar medium in the case of supermassive objects in galactic nuclei. For these systems, the effect of a non-vanishing quadrupolar structure can also be inferred from available X-ray data, by studying for instance relativistic broadening of iron lines (Psaltis & Johannsen 2013), disc's thermal spectrum (Bambi & Barausse 2011), quasi-periodic oscillations (Johannsen & Psaltis 2011), X-ray polarization (Krawczynski 2012) and mean radiative efficiency of AGN (Bambi 2011). In many of the existing models, accretion flows are represented by thin discs lying in the equatorial plane of the compact object, and the particles in the disc typically move on circular orbits. Since the space–time curvature experienced by the disc is largest at the inner edge, where most of the observed flux is emitted, its location is of special importance. It is usually taken to coincide with the ISCO, which depends on the mass and angular momentum in the case of a Kerr black hole, but may depends on other space–time parameters, if more general solutions are considered.

In this paper, we have studied the motion of test particles undergoing PR effect (i.e. scattered by a superposed test radiation field) in the field of a static non-spherical source described by the Erez–Rosen solution. The radiation field is modelled by photons which move on the equatorial plane and have an arbitrary, but constant angular momentum. The particle–photon interaction produces non-geodesic orbits around the central body whose features depend both on the radiation field strength and the photon impact parameter, but also on the value of the mass quadrupole parameter of the source. In fact, particles as well as photons are expected to feel a gravitational field with different strength in the region close to the source with respect to the spherically symmetric case (q = 0) depending on whether the central object is oblate (q < 0) or prolate (q > 0). In the former case, the incoming particle feels a stronger gravitational field as it approaches the gravity source. For prolate configurations, instead, the gravitational mass is mainly concentrated along the y-axis, i.e. orthogonally to the symmetry plane where the motion takes place, so that a particle moving sufficiently close to the gravity source will feel a decreasing gravitational field, since most of the gravitational action is being neutralized there.

The main outcome of our analysis is that there exists a whole family of equilibrium solutions (circular orbits) representing the balance between gravitational attraction, centrifugal force and radiation drag. In fact, if the strength of the radiation field is fixed, the quadrupole parameter of the source can be used to parametrize this family, so leading to a scenario which is more rich with respect to that of a spherically symmetric source. The associated stability analysis has allowed us to determine the ISCO radius as a function of the parameters characterizing the radiation field as well as of the quadrupole parameter of the source. We have found that for a given value of the quadrupole parameter there exist in general two disconnected regions where circular orbits are stable: one very close to the central object, and another for larger radii, which is relevant for observational effects. This analysis can be straightforwardly extended to more general situations, e.g. by accounting for quadrupolar sources also endowed with non-vanishing rotation.

DB and AG acknowledge ICRANet for partial support. All the authors thank Professor L. Stella for useful discussions at the beginning of the present project. AP acknowledges support from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 267251 ‘Astronomy Fellowships in Italy (AstroFIt)’.

1

Laser Interferometer Space Antenna project homepage, NASA. URL: http://lisa.nasa.gov/.

2

LIGO Scientific Collaboration project homepage, LIGO Laboratory. URL: http://ligo.org/.

3

VIRGO Project Home Page project homepage, VIRGO Project. URL: https://wwwcascina.virgo.infn.it/.

REFERENCES

Abramowicz

M. A.

Ellis

G. F. R.

Lanza

A.

,

A&A

,

1990

, vol.

361

pg.

470

Armenti

A.

,

Celest. Mech.

,

1972

, vol.

6

pg.

383

Crossref

Search ADS

Bambi

C.

,

Phys. Rev. D

,

2011

, vol.

83

pg.

103003

Crossref

Search ADS

Bambi

C.

Barausse

E.

,

ApJ

,

2011

, vol.

731

pg.

121

Crossref

Search ADS

Barack

L.

Cutler

C.

,

Phys. Rev. D

,

2007

, vol.

75

pg.

042003

Crossref

Search ADS

Berti

E.

Cardoso

V.

Starinets

A. O.

,

Class. Quantum Gravity

,

2009

, vol.

26

pg.

163001

Crossref

Search ADS

Bini

D.

Geralico

A.

,

Class. Quantum Gravity

,

2010

, vol.

27

pg.

185014

Crossref

Search ADS

Bini

D.

Carini

P.

Jantzen

R. T.

,

Int. J. Mod. Phys. D

,

1997a

, vol.

6

pg.

1

Crossref

Search ADS

Bini

D.

Carini

P.

Jantzen

R. T.

,

Int. J. Mod. Phys. D

,

1997b

, vol.

6

pg.

143

Crossref

Search ADS

Bini

D.

de Felice

F.

Jantzen

R. T.

,

Class. Quantum Gravity

,

1999

, vol.

16

pg.

2105

Crossref

Search ADS

Bini

D.

Jantzen

R. T.

Stella

L.

,

Class. Quantum Gravity

,

2009

, vol.

26

pg.

055009

Crossref

Search ADS

Bini

D.

Geralico

A.

Jantzen

R. T.

Semerák

O.

Stella

L.

,

Class. Quantum Gravity

,

2011a

, vol.

28

pg.

035008

Crossref

Search ADS

Bini

D.

Geralico

A.

Jantzen

R. T.

Semerák

O.

,

Class. Quantum Gravity

,

2011b

, vol.

28

pg.

245019

Crossref

Search ADS

Bini

D.

Falanga

M.

Geralico

A.

Stella

L.

,

Class. Quantum Gravity

,

2012

, vol.

29

pg.

055014

Crossref

Search ADS

Bini

D.

Crosta

M.

de Felice

F.

Geralico

A.

Vecchiato

A.

,

Class. Quantum Gravity

,

2013

, vol.

30

pg.

045009

Crossref

Search ADS

de Felice

F.

,

Rend. Mat.

,

1990

, vol.

10

pg.

59

Doroshkevich

A.

Zel'dovich Ya

. B.

Novikov

I. D.

,

Sov. Phys.–JETP

,

1965

, vol.

22

pg.

122

Erez

G.

Rosen

N.

,

Bull. Res. Counc. Israel

,

1959

, vol.

8F

pg.

47

Geroch

R.

,

J. Math. Phys.

,

1970

, vol.

11

pg.

2580

Crossref

Search ADS

Gillessen

S.

Eisenhauer

F.

Trippe

S.

Alexander

T.

Genzel

R.

Martins

F.

Ott

T.

,

ApJ

,

2009

, vol.

692

pg.

1075

Crossref

Search ADS

Hansen

R. O.

,

J. Math. Phys.

,

1974

, vol.

15

pg.

46

Crossref

Search ADS

Hartle

J. B.

Thorne

K. S.

,

ApJ

,

1967

, vol.

150

pg.

1005

Crossref

Search ADS

Hartle

J. B.

Thorne

K. S.

,

ApJ

,

1968

, vol.

153

pg.

807

Crossref

Search ADS

Jantzen

R. T.

Carini

P.

Bini

D.

,

Ann. Phys.

,

1992

, vol.

215

pg.

1

Crossref

Search ADS

Johannsen

T.

Psaltis

D.

,

ApJ

,

2011

, vol.

726

pg.

11

Crossref

Search ADS

Krawczynski

H.

,

ApJ

,

2012

, vol.

754

pg.

133

Crossref

Search ADS

Mashhoon

B.

Quevedo

H.

,

Nuovo Cimento B

,

1995

, vol.

110

pg.

291

Crossref

Search ADS

Merritt

D.

Alexander

T.

Mikkola

S.

Will

C. M.

,

Phys. Rev. D

,

2010

, vol.

81

pg.

062002

Crossref

Search ADS

Miller

M. C.

Lamb

F. K.

,

ApJ

,

1996

, vol.

470

pg.

1033

Crossref

Search ADS

Mishra

B.

Kluźniak

W.

,

A&A

,

2014

, vol.

566

pg.

A62

Crossref

Search ADS

Misner

C. W.

Thorne

K. S.

Wheeler

J. A.

,

Gravitation

,

1973

San Francisco

Freeman & Co.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Narayan

R.

McClintock

J. E.

,

2013

preprint (arXiv:1312.6698)

Oh

J. S.

Kim

H.

Lee

H. M.

,

Phys. Rev. D

,

2010

, vol.

81

pg.

084005

Crossref

Search ADS

Oh

J. S.

Park

C.

Kim

H.

,

Gen. Relativ. Gravit.

,

2013

, vol.

45

pg.

41

Crossref

Search ADS

Poynting

J. H.

,

Phil. Trans. R. Soc.

,

1903

, vol.

203

pg.

525

Psaltis

D.

Johannsen

T.

,

ApJ

,

2012

, vol.

745

pg.

1

Crossref

Search ADS

Quevedo

H.

,

Fortschr. Phys.

,

1990

, vol.

38

pg.

733

Crossref

Search ADS

Robertson

H. P.

,

MNRAS

,

1937

, vol.

97

pg.

423

Crossref

Search ADS

Rodriguez

C. L.

Mandel

I.

Gair

J. R.

,

Phys. Rev. D

,

2012

, vol.

85

pg.

062002

Crossref

Search ADS

Ryan

F. D.

,

Phys. Rev. D

,

1995

, vol.

52

pg.

5707

Crossref

Search ADS

Ryan

F. D.

,

Phys. Rev. D

,

1997

, vol.

56

pg.

1845

Crossref

Search ADS

Stahl

A.

Wielgus

M.

Abramowicz

M.

Kluźniak

W.

Yu

W.

,

A&A

,

2012

, vol.

546

pg.

A54

Crossref

Search ADS

Stahl

A.

Kluźniak

W.

Wielgus

M.

Abramowicz

M.

,

A& A

,

2013

, vol.

555

pg.

A114

Crossref

Search ADS

Stephani

H.

Kramer

D.

MacCallum

M. A. H.

Hoenselaers

C.

Herlt

E.

,

Exact Solutions of Einstein's Field Equations

,

2003

2nd edn

Cambridge

Cambridge Univ. Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Wielgus

M.

Stahl

A.

Abramowicz

M.

Kluźniak

W.

,

A&A

,

2012

, vol.

545

pg.

A123

Crossref

Search ADS

Young

J. H.

Coulter

C. A.

,

Phys. Rev.

,

1969

, vol.

184

pg.

1313

Crossref

Search ADS

APPENDIX A: GEOMETRICAL PROPERTIES OF THE EREZ–ROSEN SOLUTION

The Legendre polynomials entering the definition of the metric functions (2) are listed below:

\begin{eqnarray} P_0(z)&=&1\,,\qquad P_1(z)=z\,,\qquad P_2(z)=-\frac{1}{2}(1-3z^2),\nonumber \\ Q_0(z)&=&\frac{1}{2}\ln \left(\frac{z+1}{z-1}\right)\,,\qquad Q_1(z)=zQ_0(z)-1,\nonumber\\ Q_2(z)&=&-\frac{1}{2}\left[Q_0(z)-3zQ_1(z)\right.]. \end{eqnarray}

(A1)

According to the Geroch–Hansen (Geroch 1970; Hansen 1974) definition of relativistic multipole moments |${\mathcal {M}}_n$|⁠, the mass monopole moment associated with this solution is |${\mathcal {M}}_0=M$| and the quadrupole moment is given by |${\mathcal {M}}_2=(2/15)qM^3$|⁠. Higher multipole moments of the order n = 2k, k = 2, 3, 4, …, are determined by q and M in such a way that they all vanish when q = 0.

The presence of the quadrupole parameter q changes significantly the structure of the space–time as compared with the Schwarzschild solution. In particular, the hypersurface x = 1, which is null in the Schwarzschild case, becomes directionally singular. Furthermore, its character depends both on the value of q. For instance, in the symmetry plane y = 0 this hypersurface is null for |$1-\sqrt{5}<q<1+\sqrt{5}$| and timelike otherwise (see e.g. Quevedo 1990; Mashhoon & Quevedo 1995).

The explicit expressions for the radial components of the acceleration as well as curvature vectors in the symmetry plane y = 0 are listed below:

\begin{eqnarray} a(n)^{\hat{x}} &=&\frac{1}{2}\frac{\sqrt{x^2-1}}{\sigma x}{\rm e}^{-\gamma }\frac{f_x}{\sqrt{f}}, \nonumber \\ k(x,n)^{\hat{x}} &=&k(\phi ,n)^{\hat{x}}-{\rm e}^{-\gamma }\frac{\sqrt{f}}{\sigma x^2\sqrt{x^2-1}}[(x^2-1)(x\gamma _x-1)-2], \nonumber \\ k(y,n)^{\hat{x}} &=&k(\phi ,n)^{\hat{x}}-{\rm e}^{-\gamma }\frac{\sqrt{f}}{\sigma x^2\sqrt{x^2-1}}[(x^2-1)x\gamma _x-1], \nonumber \\ k(\phi ,n)^{\hat{x}} &=&a(n)^{\hat{x}}-{\rm e}^{-\gamma }\frac{\sqrt{f}}{\sigma \sqrt{x^2-1}}, \end{eqnarray}

(A2)

with

\begin{eqnarray} f&=&\frac{x-1}{x+1}{\rm e}^{qQ_2}\,,\!\!\!\!\quad \frac{f_x}{f}=\frac{2}{x^2-1}+qQ_2^{\prime }\,,\!\!\!\!\quad \gamma _x=\frac{(x^2-1)f_x^2}{4xf^2}, \nonumber \\ \frac{f_{xx}}{f}&=&-\frac{4}{(x^2-1)(x+1)}+q\left(Q_2^{\prime \prime }+\frac{4}{x^2-1}Q_2^{\prime }\right)+q^2Q_2^{\prime }{}^2, \nonumber\\ \frac{f_{yy}}{f}&=&-6qQ_2, \end{eqnarray}

(A3)

and Q₂ satisfies the following second-order differential equation

\begin{equation} Q_2^{\prime \prime }+\frac{2x}{x^2-1}Q_2^{\prime }-\frac{6}{x^2-1}Q_2=0. \end{equation}

(A4)

Finally, the relevant frame components of the electric part of the Riemann tensor are given by

\begin{eqnarray} E(n)_{\hat{x}\hat{x}} &=&\frac{1}{2}\frac{{\rm e}^{-2\gamma }}{\sigma ^2x^2}\left[(x^2-1)(f_{xx}-\gamma _xf_x)+\frac{f_x}{f}\right], \nonumber \\ E(n)_{\hat{y}\hat{y}} &=&-E(n)_{\hat{x}\hat{x}}+\frac{1}{4}\frac{{\rm e}^{-2\gamma }}{\sigma ^2x^2}\frac{f_x}{f}\left[(x^2-1)f_x-2xf\right]. \end{eqnarray}

(A5)

Download all slides

Month:	Total Views:
April 2017	1
August 2017	2
October 2017	2
January 2018	12
February 2018	3
March 2018	10
April 2018	2
May 2018	2
June 2018	9
July 2018	10
August 2018	5
September 2018	7
October 2018	4
November 2018	1
December 2018	2
January 2019	5
February 2019	2
March 2019	6
April 2019	11
May 2019	8
June 2019	2
July 2019	5
August 2019	4
September 2019	5
October 2019	3
November 2019	7
December 2019	6
January 2020	4
February 2020	3
April 2020	3
May 2020	1
June 2020	1
July 2020	6
August 2020	2
September 2020	1
October 2020	4
November 2020	1
December 2020	4
February 2021	1
March 2021	5
April 2021	6
May 2021	1
July 2021	3
September 2021	5
October 2021	2
November 2021	3
December 2021	1
January 2022	2
February 2022	3
March 2022	6
April 2022	4
May 2022	5
June 2022	8
July 2022	10
August 2022	15
September 2022	11
October 2022	3
November 2022	1
December 2022	2
January 2023	1
February 2023	2
April 2023	6
May 2023	1
June 2023	4
August 2023	8
September 2023	1
October 2023	2
November 2023	2
December 2023	5
January 2024	4
February 2024	3
March 2024	3
April 2024	7
May 2024	7
June 2024	2
July 2024	7
August 2024	2
September 2024	3
October 2024	7
November 2024	2
January 2025	1
February 2025	1
March 2025	11
April 2025	1
May 2025	8

Article Contents

Radiation drag in the field of a non-spherical source

Abstract

1 INTRODUCTION

2 TEST PARTICLES UNDERGOING PR EFFECT IN THE EREZ–ROSEN SPACE–TIME

2.1 Photon field

2.2 Particle dynamics

3 EQUILIBRIUM SOLUTIONS

3.1 Stability of the critical orbits

4 CONCLUDING REMARKS

REFERENCES

APPENDIX A: GEOMETRICAL PROPERTIES OF THE EREZ–ROSEN SOLUTION

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Radiation drag in the field of a non-spherical source Free

Abstract

1 INTRODUCTION

2 TEST PARTICLES UNDERGOING PR EFFECT IN THE EREZ–ROSEN SPACE–TIME

2.1 Photon field

2.2 Particle dynamics

3 EQUILIBRIUM SOLUTIONS

3.1 Stability of the critical orbits

4 CONCLUDING REMARKS

REFERENCES

APPENDIX A: GEOMETRICAL PROPERTIES OF THE EREZ–ROSEN SOLUTION

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Radiation drag in the field of a non-spherical source