Kelvin–Helmholtz instability of counter-rotating discs

Quach, Dan; Dyda, Sergei; Lovelace, Richard V. E.

doi:10.1093/mnras/stu2130

Abstract

Observations of galaxies and models of accreting systems point to the occurrence of counter-rotating discs where the inner part of the disc (r < r₀) is corotating and the outer part is counter-rotating. This work analyses the linear stability of radially separated co- and counter-rotating thin discs. The strong instability found is the supersonic Kelvin–Helmholtz instability. The growth rates are of the order of or larger than the angular rotation rate at the interface. The instability is absent if there is no vertical dependence of the perturbation. That is, the instability is essentially three dimensional. The non-linear evolution of the instability is predicted to lead to a mixing of the two components, strong heating of the mixed gas, and vertical expansion of the gas, and annihilation of the angular momenta of the two components. As a result, the heated gas will free-fall towards the disc's centre over the surface of the inner disc.

accretion, accretion discs, instabilities, galaxies: evolution, galaxies: formation

1 INTRODUCTION

Commonly considered models of accretion discs have gas rotating in one direction with a turbulent viscosity acting to transport angular momentum outwards and matter inwards. However, observations indicate that there are more complicated, possibly transient, disc structures on a galactic scale. Observations of normal galaxies have revealed co/counter-rotating gas/gas, gas/stars, and stars/stars discs in many galaxies of all morphological types – ellipticals, spirals, and irregulars (Rubin 1994a,b; Galetta 1996; recent review by Corsini 2014). There is limited evidence of counter-rotating gas components in discs around stars (Remijan & Hollis 2006; Tang et al. 2012). Theory and simulations of co/counter-rotating gas/gas discs around stars and black holes predict enormously enhanced accretion rates resulting from the presence of the two components which can give rise to outbursts from these discs (Lovelace & Chou 1996; Kuznetsov et al. 1999; Nixon, King & Price 2012; Dyda et al. 2014).

Counter-rotation in disc galaxies appears in a variety of configurations including cases where (1) two cospatial populations of stars rotate in opposite directions, (2) the stars rotate in one direction and the gas rotates in the opposite direction, and (3) two spatially separated gas discs rotate in opposite directions (Corsini 2014). Of particular interest here is the example of case (3), the ‘Evil Eye’ galaxy NGC 4826 in which the direction of rotation of the gas reverses going from the inner (180 km s⁻¹) to the outer disc (−200 km s⁻¹) with an inward radial accretion speed of more than 100 km s⁻¹ in the transition zone, whereas the stars at all radii rotate in the same direction as the gas in the inner disc, which has a radius of ∼1200 pc (Braun et al. 1994; Rubin 1994b).

On a stellar mass scale, Remijan & Hollis (2006) and Tang et al. (2012) found evidence of accretion of counter-rotating gas in star-forming systems. Accreted counter-rotating matter may encounter an existing corotating disc as in low-mass X-ray binary sources where the accreting, magnetized rotating neutron stars are observed to jump between states where they spin-up and those where they spin-down. Nelson et al. (1997) and Chakrabarty et al. (1997) have proposed that the change from spin-up to spin-down results from a reversal of the angular momentum of the wind-supplied accreting matter. The interface between the oppositely rotating components would be subject to the Kelvin–Helmholtz instability.

In the formation of massive black holes in the nuclei of active galaxies, King & Pringle (2006, 2007) argue that in order for the rapid growth of the massive black holes (observed at high red-shifts) to be compatible with the Eddington limit on their emission, the gas accretion is from a sequence of clouds with randomly oriented angular momenta. This process would lead to the formation of a disc with the rotation direction alternating as a function of radius.

Section 2 develops the theory for the stability analysis and obtains explicit growth rates for the supersonic Kelvin–Helmholtz instability between radially separated co- and counter-rotating thin disc components. Section 3 discusses possible non-linear consequences of the instability. Section 4 gives the main conclusions.

2 THEORY

2.1 Disc equilibrium

We consider the stability of a thin counter-rotating disc around a star or black hole. Fig. 1 shows the rotation curve we consider. We use an inertial cylindrical (r, ϕ, z) coordinate system. The equilibrium has (∂/∂t = 0) and (∂/∂ϕ = 0), with the flow velocity |$\boldsymbol {u} = u_\phi (r) = r\Omega$|⁠. That is, the accretion velocity u_r and the vertical velocity u_z are assumed negligible compared with u_ϕ. The equilibrium flow satisfies −ρrΩ² = −dp/dr + ρg_r, where ρ is the density, p the pressure, g_r = −∂Φ/∂r, and Φ the gravitational potential. We consider thin discs with half-thickness h ≈ (c_s/u_ϕ)r ≪ r, where c_s is the sound speed. In this limit, |$\Omega =(g_r/r)^{1/2}[1+{\cal O}(h^2/r^2)]$|⁠. We consider Keplerian discs where g_r = GM/r² (with M the mass of the central object) as well as more general discs, for example, flat rotation curve discs relevant to galaxies where g_r ∝ r⁻¹. We neglect the vertical structure of the equilibrium disc assuming ∂/∂z = 0 for the equilibrium quantities (e.g., ρ, p, and u_ϕ). Our treatment parallels that of Lovelace, Turner & Romanova (2009; hereafter LTR09), but it generalizes that work to include the z-dependence of the perturbations.

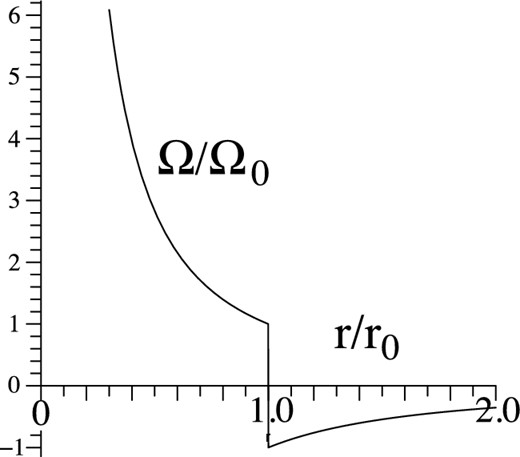
Angular velocity of the counter-rotating Keplerian disc where gr = GM/r2 with M the mass of the central object.

Figure 1.

Angular velocity of the counter-rotating Keplerian disc where g_r = GM/r² with M the mass of the central object.

Open in new tab Download slide

2.2 Perturbation equations

The perturbed quantities are: the density, |$\tilde{\rho } = \rho + \delta \rho (r,\phi ,z,t)$|⁠; the pressure is |$\tilde{p} = p+\delta p(r,\phi ,z,t)$|⁠; and the flow velocity is |$\tilde{\boldsymbol u} = {\boldsymbol u} +\delta {\boldsymbol u}(r,\phi ,z,t)$| with |${\boldsymbol {\delta u}} = (\delta u_r,\delta u_\phi , \delta u_z)$|⁠. We neglect the self-gravity of the disc as commented on at the end of this section. The equations for the perturbed flow are

\begin{equation} {D \tilde{\rho }\over Dt} + \tilde{\rho }\ {\bf \nabla }\cdot \tilde{\boldsymbol u} = 0, \end{equation}

(1)

\begin{equation} {D \tilde{\boldsymbol u}\over Dt} = -{1\over \tilde{\rho }} {\bf \nabla } \tilde{p} - {\bf \nabla }\Phi , \end{equation}

(2)

\begin{equation} {D S\over Dt} = 0, \end{equation}

(3)

where |$D/Dt \equiv \mathrm{\partial} /\mathrm{\partial} t + \tilde{\boldsymbol u}\cdot {\bf \nabla }$|⁠, and where |$S \equiv {\tilde{p}}/(\tilde{\rho })^\gamma$| is the entropy of the disc matter.

We consider perturbations δp, δρ... of the form

\begin{equation} f(r)\exp (im\phi +ik_z - i\omega t), \end{equation}

(4)

where m = 0, 1, 2, … is the azimuthal mode number, ω the angular frequency, and k_z the wavenumber in the z-direction. From equation (1), we find

\begin{equation} i\Delta \omega \ \delta \rho = {\bf \nabla } \cdot (\rho \ \delta {\boldsymbol u}), \end{equation}

(5)

where Δω(r) ≡ ω − mΩ(r) and Ω = u_ϕ/r. From equation (2)

\begin{equation} i\Delta \omega \delta u_r + 2 \Omega \delta u_\phi = {1\over \rho }{\mathrm{\partial} \delta p\over \mathrm{\partial} r} -{\delta \rho \over \rho ^2} {\mathrm{d} p \over \mathrm{d}r}, \end{equation}

(6)

\begin{equation} i\Delta \omega \delta u_\phi - {\kappa ^2 \over 2 \Omega } \delta u_r = ik_\phi {\delta p \over \rho }, \end{equation}

(7)

\begin{equation} i\Delta \omega \delta u_z = ik_z {\delta p\over \rho }. \end{equation}

(8)

Here,

\begin{equation*} \kappa \equiv \left[{1\over r^3} {\mathrm{d}(r^4 \Omega ^2)\over \mathrm{d}r}\right]^{1/ 2} \nonumber \end{equation*}

is the radial epicyclic frequency and k_ϕ ≡ m/r is the azimuthal wavenumber. From equation (3), we have

\begin{equation} \delta p = c_{\rm s}^2 -{i\rho c_{\rm s}^2 \over \Delta \omega L_S}\delta u_r, \end{equation}

(9)

where

\begin{equation} {1\over L_S} \equiv {1\over \gamma }{\mathrm{d} \ln (S) \over \mathrm{d}r},\quad \quad c_{\rm s}\equiv \left({\gamma p\over \rho }\right)^{1/2} , \end{equation}

(10)

with L_S the length-scale of the disc's entropy variation, and c_s the sound speed.

Introducing Ψ ≡ δp/ρ, equations (6)– (8) can be rewritten as

\begin{equation} \rho \delta u_r =i{\cal F} \left[{\Delta \omega \over \Omega } \left({\mathrm{\partial} \Psi \over \mathrm{\partial} r} -{\Psi \over L_*}\right)-2 k_\phi \Psi \right], \end{equation}

(11)

\begin{eqnarray} \rho \delta u_\phi &=& \mathcal {F} \Bigg \lbrace \frac{\kappa ^2}{2 \Omega ^2} \left( \frac{\mathrm{\partial} \Psi }{\mathrm{\partial} r} -\frac{\Psi }{L_S}\right) \nonumber\\ && -\,k_\phi \left( \frac{\Delta \omega }{\Omega } +\frac{{\rm d} p/{\rm d} r}{\rho \Omega \Delta \omega L_S} \right)\Psi \Bigg \rbrace , \end{eqnarray}

(12)

\begin{equation} \rho \delta u_z = \rho \frac{k_z}{\Delta \omega } \Psi , \end{equation}

(13)

where

\begin{equation} {\cal F} \equiv {\rho \Omega \over {\cal D}}, \end{equation}

(14)

and

\begin{equation} {\cal D}=\kappa ^2- (\Delta \omega )^2 -{\mathrm{d}p/\mathrm{d}r \over \rho L_S}. \end{equation}

(15)

Equations (9) and (11) can be combined to give

\begin{equation} \delta \rho = {\rho \Psi \over c_{\rm s}^2} -{{\cal F} \over \Delta \omega L_S} \left[{\Delta \omega \over \Omega } \left({\mathrm{\partial} \Psi \over \mathrm{\partial} r}-{\Psi \over L_S}\right)-2k_\phi \Psi \right]. \end{equation}

(16)

Equations (11)– (13) and (16) can now be substituted into equation (5) to give a single differential equation for Ψ(r),

\begin{eqnarray} &&\!\!\!\!\frac{1}{r}\frac{\mathrm{\partial} }{\mathrm{\partial} r} \left(\frac{r \mathcal {F}}{\Omega } \frac{\mathrm{\partial} \Psi }{\mathrm{\partial} r}\right) = \bigg [{\rho \over c_{\rm s}^2}+ {k_\phi ^2{\cal F} \over \Omega } +{1\over r}{\mathrm{\partial} \over \mathrm{\partial} r} \left({r{\cal F} \over \Omega L_S}\right) +{{\cal F} \over \Omega L_S ^2} \bigg ]\Psi \nonumber\\ &&+\ \left[2k_\phi {\cal F}{\mathrm{d} \ln ( g{\cal F}) \over \mathrm{d}r}\right]{\Psi \over \Delta \omega } + \bigg [{k_\phi ^2(\mathrm{d}p/\mathrm{d}r){\cal F} \over \rho \Omega L_S} - \rho k_z^2 \bigg ]{\Psi \over (\Delta \omega )^2}, \end{eqnarray}

(17)

where g ≡ exp (2∫dr/L_S). This equation generalizes equation (13) of LTR09 by including the z-dependence of the perturbations which contributes the last term in this equation.

The condition neglecting the self-gravity is that the Toomre parameter Q = κc_s/(πGΣ) be larger than about r/h, where h is the disc's half-thickness and Σ = 2hρ is its surface mass density (Lovelace & Hohlfeld 2013).

2.3 Specific model

In order to simplify the analysis, we consider barotropic disc matter where |$L_S^{-1} \rightarrow 0$| so that g = 1. Further, we consider the counter-rotation curve shown in Fig. 1, namely,

\begin{equation} \Omega = \left\lbrace \begin{array}{lr}(g_r/r)^{1/2} & r < r_0, \\ -(g_r/r)^{1/2} & r > r_0. \end{array} \right. \end{equation}

(18)

We can then solve equation (17) for Ψ₋ for r < r₀ and Ψ₊ for r > r₀ and then match the solutions to the jump-condition across r = r₀ which follows from the equation.

We consider solutions of the form

\begin{equation} \begin{array}{lr}\Psi _- \propto \exp \big [+k_{r-}(r-r_0) \big ], & r<r_0 \\ \Psi _+ \propto \exp \big [-k_{r+}(r-r_0)\big ], & r>r_0. \end{array} \end{equation}

(19)

We assume |k_{r ±}|r₀ ≫ 1 so that radial variations of the equilibrium quantities can be neglected. In order that the perturbations decay going away from r₀, we must have ℜ(k_{r ±}) > 0, which can be checked a posteriori.

For r≷r₀, equation (17) gives the dispersion relations

\begin{equation} c_{\rm s}^2(-k_{r\pm }^2 + k_\phi ^2)=[\kappa ^2 - (\Delta \omega _\pm )^2]\left[\frac{k_z^2 c_{\rm s}^2}{(\Delta \omega _\pm )^2} - 1 \right], \end{equation}

(20)

where Δω_± ≡ ω − mΩ_±. For k_z = 0, the dispersion relations take the more familiar form |$(\Delta \omega _\pm )^2 = \kappa ^2 +c_{\rm s}^2 (-k_{r\pm }^2 +k_\phi ^2)$|⁠.

It is useful to introduce the following dimensionless variables

\begin{equation} \overline{k}_z = k_z h, \ \ \overline{k}_\phi = k_\phi h, \ \ \overline{\Omega } = \frac{\Omega }{\Omega _0},\ \ \overline{\kappa } = \frac{\kappa }{\Omega _0},\ \ \overline{\Delta \omega } = \frac{\Delta \omega }{\Omega _0}, \end{equation}

(21)

where h = c_s/Ω₀ and |$\Omega _0 = \sqrt{g_r(r_0)/r_0}$|⁠. Dropping the overbars gives k_{r ±}(ω),

\begin{equation} k_{r\pm }^2(\omega ) = k_\phi ^2 - [\kappa ^2 - (\Delta \omega _\pm )^2]\left[\frac{k_z^2}{(\Delta \omega _\pm )^2} - 1 \right]. \end{equation}

(22)

Multiplying equation (17) by r, integrating over r from r₀ − ϵ to r₀ + ϵ, letting ϵ → 0, and taking into account that Ψ(r) is continuous across r₀ gives

\begin{equation} \frac{k_{r+}}{\mathcal {D}_+} + \frac{k_{r-}}{\mathcal {D}_-} = \mathcal {R}(\omega ), \end{equation}

(23)

where

\begin{equation} \mathcal {R}(\omega ) = k_\phi \left(\frac{1}{\mathcal {D}_+} + \frac{1}{\mathcal {D}_-}\right)\left(\frac{1}{\Delta \omega _+} + \frac{1}{\Delta \omega _-}\right). \end{equation}

(24)

The left-hand side of equation (23) is from the left-hand side of equation (17). The right-hand side, |${\cal R}$|⁠, is from the right-hand term of equation (17) involving |${\rm d}{\cal F}/{\rm d}r$| which is |${\rm d}{\cal F}/{\rm d}r = ({\cal F}_+ -{\cal F}_-)\delta (r-r_0)$|⁠.

For the assumed thin discs, |$\overline{\Omega } = 1+{\cal O}(h^2/r_0^2)$| for Keplerian discs and other rotation curves. On the other hand,

\begin{equation} \mathcal {D}_\pm =\left\lbrace \begin{array}{lr}1 -(\Delta \omega _\pm )^2 \ \ \ \ {\rm Keplerian,}\\ {\kappa }^2 -(\Delta \omega _\pm )^2 \ \ {\rm other \ rotation \ curves,} \end{array} \right. \end{equation}

(25)

and Δω_± = ω ± m with ω measured in units of Ω₀.

Equation (23) can be squared twice to obtain

\begin{equation} G(\omega ) =\left(\frac{k_{r+}^2}{\mathcal {D}_+^2} - \frac{k_{r-}^2}{\mathcal {D}_-^2} - \mathcal {R}^2\right)^2 - \frac{4 k_{r-}^2 \mathcal {R}^2}{\mathcal {D}_-^2} = 0. \end{equation}

(26)

The possibility of spurious roots of this equation not satisfying equation (23) has to be checked a posteriori. Equation (26) can be expanded out as a 16th-order polynomial in ω.

Important properties of G(ω) are readily verified: first, for m = 0 the perturbation is stable, |${\cal R}=0$|⁠, and therefore k_{r +} = k_{r −} = 0 so that either ω = ±κ (radial epicyclic motion) or ω = ±k_z (vertically propagating sound wave). For this reason, we consider m ≥ 1 in the following. Secondly, G(ω) = G( − ω). Thirdly, [G(ω)]★ = G(ω★). It follows that the solutions for ω of G(ω) = 0 = [G(ω)]★ are either purely real or purely imaginary.

The roots of G(ω) can be located by making a contour plot of

\begin{equation} F(\omega )=\big \lbrace \Re [G(\omega )]\big \rbrace ^2 + \big \lbrace \Im [G(\omega )]\big \rbrace ^2, \end{equation}

(27)

in the ω = ω_R + iω_I plane with Maple or Mathematica. Fig. 2 shows the unstable roots for low m values for a Keplerian disc with h/r₀ = 0.1. There is stability (ω = real) for k_z < k_zc(m). For this range of k_z, the ω roots are real. We have verified that for k_z > k_zc, the roots satisfy equation (23) as well as the conditions ℜ(k_{r ±}) > 0 needed for the modes to be localized around r₀. Fig. 3 shows the real and imaginary parts of k_{r ±} as a function of k_z for m = 1 also for a Keplerian disc with h/r₀ = 0.1.

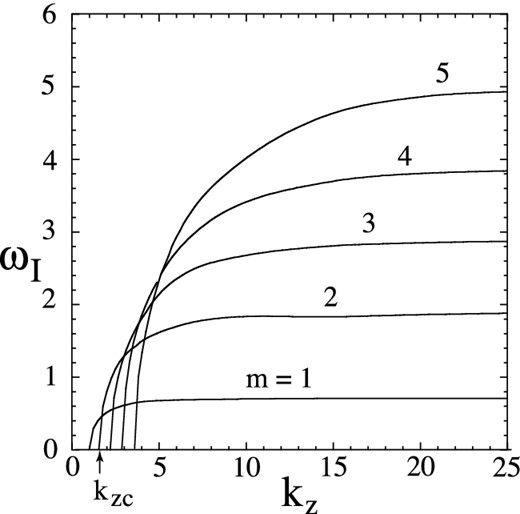
Wavenumber dependence of the growth rate of the instability, ℑ(ω) = ωI, for different values of m for a Keplerian disc with h/r0 = 0.1. Note that ωI is in units of Ω0 and kz is in units of h−1.

Figure 2.

Wavenumber dependence of the growth rate of the instability, ℑ(ω) = ω_I, for different values of m for a Keplerian disc with h/r₀ = 0.1. Note that ω_I is in units of Ω₀ and k_z is in units of h⁻¹.

Open in new tab Download slide

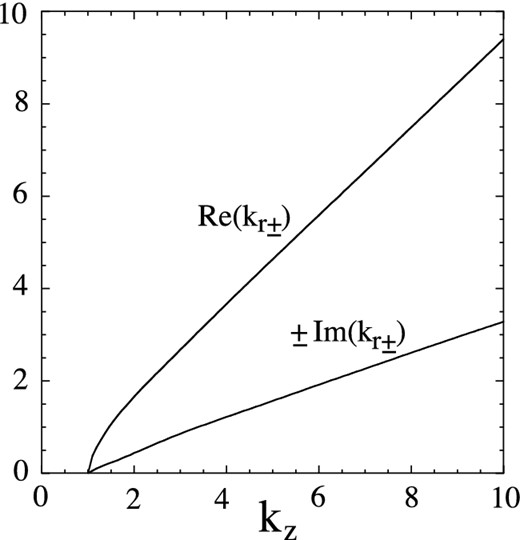
Radial wavenumber, ℜ(kr ±) and ℑ(kr ±), as a function of kz for m = 1 for a Keplerian disc with h/r0 = 0.1. The wavenumbers are in units of h−1.

Figure 3.

Radial wavenumber, ℜ(k_{r ±}) and ℑ(k_{r ±}), as a function of k_z for m = 1 for a Keplerian disc with h/r₀ = 0.1. The wavenumbers are in units of h⁻¹.

Open in new tab Download slide

A significant simplification of the dispersion relation (26) is possible in the limit where k_z ≫ k_ϕ = m(h/r₀). In this limit,

\begin{equation} k_{r\pm } = - {\cal D}_\pm \left(\frac{k_z^2}{\Delta \omega _\pm ^2} - 1 \right), \end{equation}

(28)

and

\begin{equation} \frac{k_{r+}^2}{\mathcal {D}_+^2} = \frac{k_{r-}^2}{\mathcal {D}_-^2}. \end{equation}

(29)

By combining equations (28) and (29), we obtain a function with roots that can be determined analytically. By rewriting this function as an ordinary polynomial, we obtain a ninth-order polynomial. Factoring out the ω = 0 root gives the eighth-order polynomial

\begin{eqnarray} &&\omega ^8 - (2{\kappa }^2 + 2 k_z^2 + 4 m^2)\omega ^6 + ({\kappa }^4 + 5 k_z^2 {\kappa }^2 \nonumber\\ &&+ 2 m^2 {\kappa }^2 + 2 k_z^2 m^2 + 6 m^4)\omega ^4 + (-4 k_z^2 {\kappa }^4- 2 m^2 {\kappa }^4+ 6 k_z^2 m^2 {\kappa }^2 \nonumber\\ &&+ 2 m^4 {\kappa }^2 + 2 k_z^2 m^4 - 4 m^6)\omega ^2 + (k_z^2 {\kappa }^6 - 4 k_z^2 m^2 {\kappa }^4+ m^4 {\kappa }^4 \nonumber\\ &&+ 5 k_z^2 m^4 {\kappa }^2- 2 m^6 {\kappa }^2 - 2 k_z^2 m^6 + m^8) = 0. \end{eqnarray}

(30)

Rewriting the equation in this form removes the duplicate solutions from the original polynomial. There are four real roots, ω_R = ±(m ± κ) which are the normal modes of a unidirectional disc, and the four roots

\begin{equation} \begin{array}{lr}\omega = \pm \left[k_z^2 + m^2 + \sqrt{k_z^2 (-{\kappa }^2 + k_z^2 + 4 m^2)}\right]^{1/2} ,\\ \omega = \pm \left[k_z^2 + m^2 - \sqrt{k_z^2 (-{\kappa }^2 + k_z^2 + 4 m^2)}\right]^{1/2} .\\ \end{array} \end{equation}

(31)

The first set of roots give stable oscillations. The second set gives purely imaginary ω values. The unstable root is

\begin{equation} \omega _I = \left[{\sqrt{k_z^2(k_z^2+4m^2-{\kappa }^2)}-m^2-k_z^2}\right]^{1/2} . \end{equation}

(32)

For k_z large compared with unity, ω_I → m.

Solving for ω_I = 0 gives the threshold value

\begin{equation} k_{zc} = \Big [\frac{m^4}{2m^2 - {\kappa }^2}\Big ]^{1/2} . \end{equation}

(33)

This expression agrees accurately with the solutions obtained from the full dispersion relation (equation 23). Note that for a Keplerian disc, κ = 1, so that all of the modes m = 1, 2, … are unstable. For flat rotation curves relevant to disc galaxies, u_ϕ =const, so that |$\kappa =\sqrt{2}$| and consequently the mode m = 1 is stable. This mode is also stable for a rigid rotation curve disc where κ = 2. Note that the dependence of the growth rate on κ shows the dependence of the instability on the curvature of the disc.

The growth rates found here are in approximate agreement with the predictions for a planar vortex sheet |$\omega ^2 =(k_\Vert c_{\rm s})^2[1+{\cal M}_p^2/4 -(1+{\cal M}_p^2)^{1/2}]$|⁠, where |${\cal M}_p \equiv (k_\phi /k_\Vert ){\cal M}_T \le {\cal M}_T$| with |$k_\Vert = \sqrt{k_\phi ^2+k_z^2}$| the wavenumber parallel to the interface, and |${\cal M}_T =2 r_0\Omega _0/c_{\rm s}$| the Mach number of the total velocity jump (see, e.g. Choudhury & Lovelace 1984). In this case, instability ω² < 0 occurs for |${\cal M}_p < 2^{3/2}$| which corresponds to |$k_z h > m(1/2 -h^2/r_0^2)^{1/2} \approx m/\sqrt{2}$|⁠. This agrees with equation (33) for κ = 0. The correspondence of the instability found here and the vortex sheet instability establishes that the instability found here is the supersonic Kelvin–Helmholtz instability. Landau's (1944) study of the stability of a supersonic vortex sheet assumed k_z = 0 and found linear stability for |${\cal M}_T > 2^{3/2}$|⁠. However, under this condition linear instability occurs for k_z ≠ 0 when |$\left[k_\phi (k_\phi ^2+k_z^2)^{-1/2}\right]{\cal M}_T < 2^{3/2}$|⁠.

3 NON-LINEAR EVOLUTION

Although the growth rate increases with increasing wavenumber k_z, the large k_z modes are not expected to be important because their growth will saturate at a small amplitude |$\delta r \sim k_z^{-1}$| and involve mixing only small amounts of co- and counter-rotating matter. For this reason, we consider the long wavelength modes, k_z ∼ h⁻¹ and |$k_\phi \ge r_0^{-1}$|⁠. The perturbations have the form

\begin{eqnarray} \Psi _\pm \propto \exp \big [\mp \Re (k_{r\pm })(r-r_0)\big ] \exp \big [i(m\phi \mp \Im (k_{r\pm })(r-r_0)\big ]. \nonumber\\ \end{eqnarray}

(34)

The maximum of the perturbation is a tightly wrapped leading spiral r = r₀ ± mϕ/ℑ(k_{r ±}) with m arms. Fig. 4 shows the nature of the spiral for m = 1.

Figure 4.

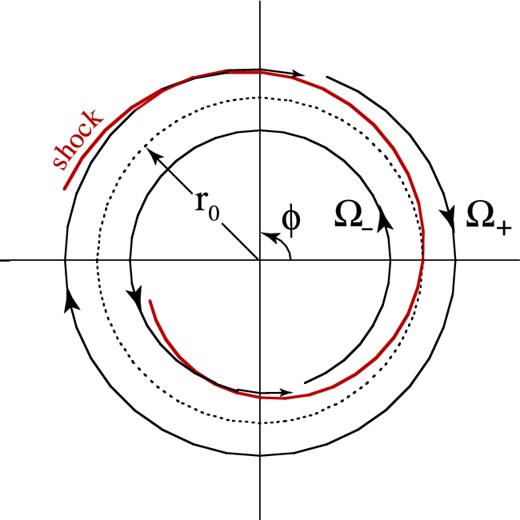
Polar plot of a one armed (m = 1) perturbation which has steepened to form an oblique shock. The gas crossing the shock is deflected towards the interface of the two components.

Open in new tab Download slide

The spiral wave can lead to the formation of an oblique shock under some conditions. Upstream of the wave, the magnitude of the normal component of the gas velocity relative to the wave is u_n = θr₀Ω₀, where θ = m|ℑ(k_{r ±})r₀|⁻¹ ≪ 1. If the upstream normal Mach number |${\cal M}_n = u_n/c_{\rm s} >1,$| there is an oblique shock. On the downstream side, the normal Mach number is less than unity. For r > r₀, the gas is deflected inwards and acquires a radial velocity u_r = −βr₀Ω₀, where |$\beta =[2/(1+\gamma )](1-{\cal M}_n^{-2})\theta$|⁠. For r < r₀, the oblique shock gives outward radial velocity u_r = βr₀Ω₀.

The co- and counter-rotating disc components have a natural repulsion for each other for the following reason. The mixing of the two components will involve strong shocks. A possible geometry for m = 1 is sketched in Fig. 5 where there are two strong standing shocks, each with Mach number |${\cal M} = u_\phi /c_{\rm s} \gg 1$|⁠. In the region between the shocks, the angular momenta of the two components are annihilated and the gas is strongly heated. The ratio of the gas temperatures downstream to upstream of the normal shock is |$T_2/T_1 \approx 1+2(\gamma -1)\gamma {\cal M}^2/(\gamma +1)^2$|⁠. This ratio is ∼20 for |${\cal M} =10$| and γ = 7/5. The heated gas will expand vertically increasing its scaleheight by a factor |$\sqrt{T_2/T_1}\gg 1$|⁠. With no centrifugal force, the gas will free-fall over the surfaces of the inner disc towards the disc's centre.

Figure 5.

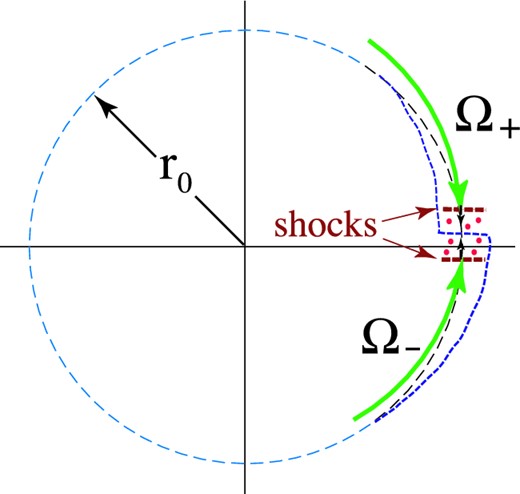
Polar plot suggesting the formation of strong normal shocks leading the annihilation of the angular momenta of the co- and counter-rotating components and the heating of this gas.

Open in new tab Download slide

The mass-loss rate from this process is |$\dot{M}_{\rm ann} = 4 m h r_0 \Delta r \rho \Omega _0$|⁠, where Δr is the radial amplitude of the interface perturbation. This loss rate is larger than the Shakura & Sunyaev (1973) accretion rate by a factor of the order of |$(m/\pi )(\Delta r/h)({\cal M}/\alpha )$|⁠, where α is the dimensionless viscosity coefficient for a disc rotating in one direction. It is commonly estimated to be in the range 10⁻³–0.1. The Kelvin–Helmholtz instability evidently gives a spatially localized effective viscosity coefficient |$\alpha _{\rm eff} \sim (m/\pi ) {\cal M}$| assuming Δr ∼ h. Thus, the region between the co- and counter-rotating components will be rapidly emptied of gas and a gap will form. Subsequently, the outer disc will spread inwards and the inner disc outwards due to the turbulent viscosity. Consequently, the gap will close after a definite period and the mentioned heating and annihilation of angular momentum will repeat.

4 CONCLUSIONS

Observations of galaxies and models of accreting systems point to the occurrence of counter-rotating discs where the inner part of the disc (r < r₀) is corotating and the outer part is counter-rotating. This work analyses the linear stability of radially separated co- and counter-rotating thin discs. The strong instability is the supersonic Kelvin–Helmholtz instability. The growth rates are of the order of or larger than the angular rotation rate at the interface Ω(r₀). The instability is absent if there is no vertical dependence of the perturbation, that is, if k_z = 0. That is, the instability is essentially a three-dimensional instability. Thus, this instability is not captured by the analysis of Li & Narayan (2004) where k_z = 0 and where the gas is treated as incompressible. Counter-rotating Keplerian discs are unstable for azimuthal mode numbers m = 1, 2, …, whereas for a flat rotation curve relevant to disc galaxies, the unstable mode numbers are m = 2, 3, …. We note that when there is a density change across the interface, there is necessarily a corresponding change in the entropy. This changes the jump condition across the interface and leads in general to propagating unstable modes where ω = ω_R + iω_I with ω_R ≠ 0 and ω_I > 0. The important new term in the jump condition comes from the term |$({\cal F}/\Omega L_S^2)\Psi$| on the right-hand side of equation (17).

The non-linear phase of the instability will involve the mixing of co- and counter-rotating gas which will involve strong shocks, strong heating of the gas, and annihilation of the angular momenta of the two gas components. The heated gas will expand vertically and since it has zero angular momentum it will free-fall to the disc's centre over the surface of the inner disc. Thus, the region between the co- and counter-rotating components will be rapidly emptied of gas and a gap will form. In effect, the two components have a repulsive interaction. This is suggestive of the Leidenfrost effect (Leidenfrost 1966) where a liquid droplet is levitated above a hot surface by the vapour pressure between the droplet and the surface. Subsequent to the gap formation, the outer disc will spread inwards and the inner disc outwards due to the turbulent viscosity. Consequently, the gap will close after a definite period and the heating and annihilation of angular momentum will repeat.

Three-dimensional hydrodynamic simulations are of course required to fully understand the non-linear evolution of the counter-rotating discs. Although axisymmetric disc simulations do not allow for the Kelvin–Helmholtz instability, the inclusion of viscosity can model the effect of the turbulent viscosity due to the instability. In an early study by Kuznetsov et al. (1999), the effective viscosity was the numerical viscosity due to the finite grid. In a recent study by Dyda et al. (2014), a high-resolution grid was used with all components of the viscous stress tensor included to model an isotropic Shakura–Sunyaev α-viscosity. Both studies clearly show the development of a gap between the co- and counter-rotating components and enhanced accretion. The study by Dyda et al. (2014) shows the quasi-periodic closing and opening of the gap.

We thank M.M. Romanova for valuable discussions and an anonymous referee for valuable comments. This work was supported in part by NASA grants NNX11AF33G and NSF grant AST-1211318.

REFERENCES

Braun

R.

Walterbos

R. A. M.

Kennicutt

R. C.

Tacconi

L. J.

,

ApJ

,

1994

, vol.

420

pg.

558

Crossref

Search ADS

Chakrabarty

D.

et al. ,

ApJ

,

1997

, vol.

481

pg.

L101

Crossref

Search ADS

Choudhury

S. R.

Lovelace

R. V. E.

,

ApJ

,

1984

, vol.

283

pg.

331

Crossref

Search ADS

Corsini

E. M.

Iodice

E.

Corsini

E. M.

,

ASP Conf. Ser. Vol. 486, Multi-Spin Galaxies

,

2014

San Francisco

Astron. Soc. Pac.

pg.

51

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Dyda

S.

Lovelace

R. V. E.

Ustyugova

G. V.

Romanova

M. M.

Koldoba

A. V.

,

MNRAS

,

2014

in press

10.1093/mnras/stu2131

Crossref

Galetta

G.

Buta

R.

Crocker

D.

Elmegreen

B.

,

ASP Conf. Ser. Vol. 91, IAU Colloq. 157: Barred Galaxies

,

1996

San Francisco

Astron. Soc. Pac.

pg.

11

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

King

A. R.

Pringle

J. E.

,

MNRAS

,

2006

, vol.

373

pg.

L90

Crossref

Search ADS

King

A. R.

Pringle

J. E.

,

MNRAS

,

2007

, vol.

377

pg.

L25

Crossref

Search ADS

Kuznetsov

O. A.

Lovelace

R. V. E.

Romanova

M. M.

Chechetkin

V. M.

,

ApJ

,

1999

, vol.

514

pg.

691

Crossref

Search ADS

Landau

L.

,

Dokl. Akad. Nauk SSSR, V

,

1944

, vol.

44

pg.

339

Leidenfrost

J. G.

,

Int. J. Heat Mass Transfer

,

1966

, vol.

9

pg.

1153

Crossref

Search ADS

Li

L.

Narayan

R.

,

ApJ

,

2004

, vol.

601

pg.

414

Crossref

Search ADS

Lovelace

R. V. E.

Chou

T.

,

ApJ

,

1996

, vol.

468

pg.

L25

Crossref

Search ADS

Lovelace

R. V. E.

Hohlfeld

R. G.

,

MNRAS

,

2013

, vol.

429

pg.

529

Crossref

Search ADS

Lovelace

R. V. E.

Turner

L.

Romanova

M. M.

,

ApJ

,

2009

, vol.

701

pg.

225

(LTR09)

Crossref

Search ADS

Nelson

R. W.

et al. ,

ApJ

,

1997

, vol.

488

pg.

L117

Crossref

Search ADS

Nixon

C. J.

King

A. R.

Price

D. J.

,

MNRAS

,

2012

, vol.

422

pg.

2547

Crossref

Search ADS

Remijan

A. J.

Hollis

J. M.

,

ApJ

,

2006

, vol.

640

pg.

842

Crossref

Search ADS

Rubin

V. C.

,

AJ

,

1994a

, vol.

107

pg.

173

Crossref

Search ADS

Rubin

V. C.

,

AJ

,

1994b

, vol.

108

pg.

456

Crossref

Search ADS

Shakura

N. I.

Sunyaev

R. A.

,

A&A

,

1973

, vol.

24

pg.

337

Tang

Y. W.

Guilloteau

S.

Piétu

V.

Dutrey

A.

Ohashi

N.

Ho

P. T. P.

,

A&A

,

2012

, vol.

547

pg.

A84

Crossref

Search ADS

Download all slides

Month:	Total Views:
February 2017	1
March 2017	1
June 2017	2
August 2017	3
October 2017	1
January 2018	9
February 2018	5
March 2018	8
April 2018	4
May 2018	5
June 2018	7
July 2018	10
August 2018	7
September 2018	9
October 2018	7
November 2018	4
December 2018	1
January 2019	8
February 2019	10
March 2019	8
April 2019	10
May 2019	19
June 2019	10
July 2019	7
August 2019	8
September 2019	9
October 2019	8
November 2019	11
December 2019	11
January 2020	12
February 2020	11
March 2020	10
April 2020	10
May 2020	5
June 2020	7
July 2020	6
August 2020	10
September 2020	9
October 2020	6
November 2020	3
December 2020	6
January 2021	2
February 2021	8
March 2021	12
April 2021	8
May 2021	7
June 2021	10
July 2021	6
August 2021	3
September 2021	10
October 2021	8
November 2021	6
December 2021	2
January 2022	9
February 2022	5
March 2022	12
April 2022	3
May 2022	6
June 2022	2
July 2022	7
August 2022	8
September 2022	14
October 2022	21
November 2022	10
December 2022	7
January 2023	6
February 2023	7
March 2023	6
April 2023	4
May 2023	9
June 2023	4
July 2023	1
August 2023	6
September 2023	2
October 2023	2
November 2023	2
December 2023	6
January 2024	3
February 2024	7
March 2024	5
April 2024	16
May 2024	9
June 2024	2
July 2024	11
August 2024	5
September 2024	8
October 2024	14
November 2024	10
December 2024	4
January 2025	4
February 2025	5
March 2025	11
May 2025	16

Article Contents

Kelvin–Helmholtz instability of counter-rotating discs

Abstract

1 INTRODUCTION

2 THEORY

2.1 Disc equilibrium

2.2 Perturbation equations

2.3 Specific model

3 NON-LINEAR EVOLUTION

4 CONCLUSIONS

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Kelvin–Helmholtz instability of counter-rotating discs Free

Abstract

1 INTRODUCTION

2 THEORY

2.1 Disc equilibrium

2.2 Perturbation equations

2.3 Specific model

3 NON-LINEAR EVOLUTION

4 CONCLUSIONS

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Kelvin–Helmholtz instability of counter-rotating discs